• 强化学习发展史
  • 引言
  • (1) 行为心理学: 被动反射
    • 巴甫洛夫的狗
    • Hebbian 法则
    • 分析
  • (2) 主动行为与试错探索：主动探索
    • 桑代克的猫
    • 斯金纳的老鼠
    • 分析
  • (3) 探索行为与内在表征的萌芽: 建模预演
    • 托尔曼的迷宫老鼠
    • 从“Trial & Error”到“Latent Learning”
    • 分析
  • (4) 基于策略的RL: 试错->期望提升
  • (5) 时序差分
    • TD
    • TD(0)
    • n-step TD
    • Monte Carlo
    • 生物学意义
  • (6) Value-Based 评估->决策
    • 贝尔曼方程
    • 贝尔曼最优方程
    • 值函数
    • 值迭代 VI
    • 策略迭代 PI
    • 截断式策略迭代 TPI
    • on-policy vs. off-policy 分野
    • SARSA
    • `Q-Learning
    • DQN
  • todo
  • (7) AC 架构: 双轮驱动
    • REINFORCE 问题
    • AC
    • AC vs GAN
    • A2C -> A3C
    • AC 问题
    • PPO
    • GRPO
  • (8) 动机觉醒 —— 内部奖励与自主探索
    • 好奇心
    • 状态熵
    • 进展感/掌控感
  • (9) 社会智能 —— 多智能体与博弈
    • MARL
  • (10) 语言即世界– LLMs × RL 的闭环共舞
    • LLM4RL
• 结束

强化学习发展史

往期站内RL主题

• 强化学习笔记
• 强化学习工具包

引言

资料

• 强化学习的10层境界：从巴甫洛夫的狗到贝叶斯大脑：（上）, 中, （下）

今天的人工智能早已不是当年只能执行规则的自动机。它拥有了“感知”、“计划”、“探索”、“协作”甚至“推理”的能力

这些能力背后，都指向同一个核心问题：

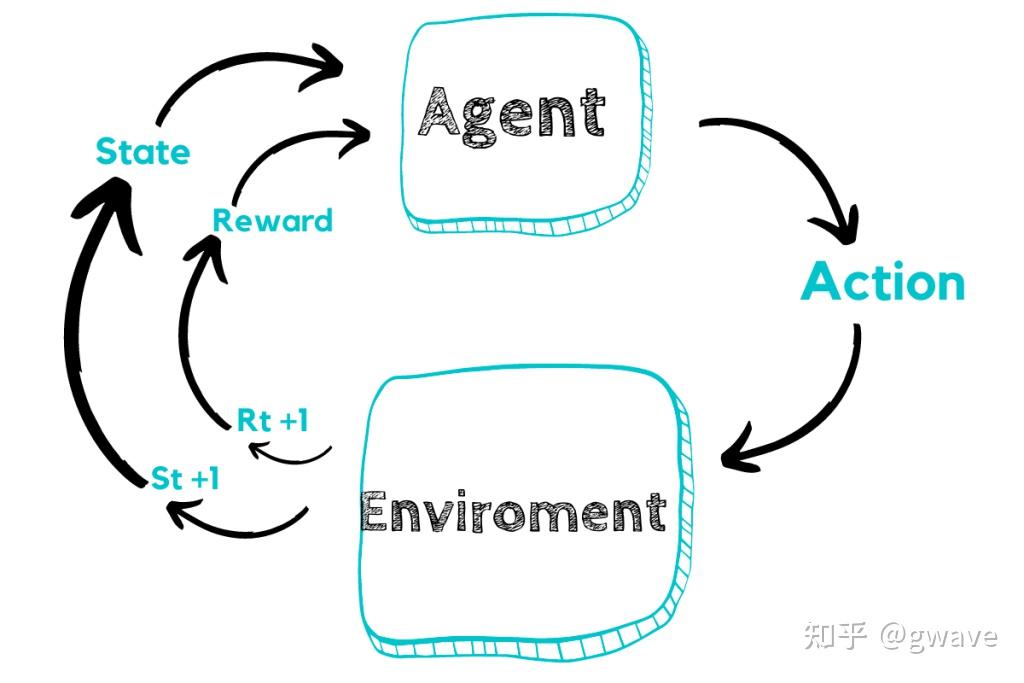
智能体（Agent）如何通过与环境的交互，不断学习并优化自己的行为策略？

这正是强化学习（Reinforcement Learning, RL）所关注的核心命题。

但 RL 并非凭空诞生，思想根基深植于行为心理学、神经科学与控制论的沃土之中：

• 从巴甫洛夫的狗与 Hebb 突触可塑性法则，到桑代克的猫、斯金纳箱中的老鼠等行为主义实验
• 再到当代的多智能体系统（Multi-Agent RL, MARL）与大语言模型（LLMs）。

强化学习，是这条从生物智能延伸至人工智能的进化主线上的算法结晶。

RL 从早期的单体智能体决策模型，拓展到多智能体交互与博弈，并正迈向以语言驱动策略生成、认知对齐的新范式。

• 一方面试图摆脱对大规模监督数据的依赖，转向经验驱动的学习（Sutton）
• 另一方面结合世界模型的构建（LeCun），朝向更具因果性与抽象性的智能体发展。

强化学习，正逐步成为连接神经科学原理与现代 AI 决策系统的桥梁。

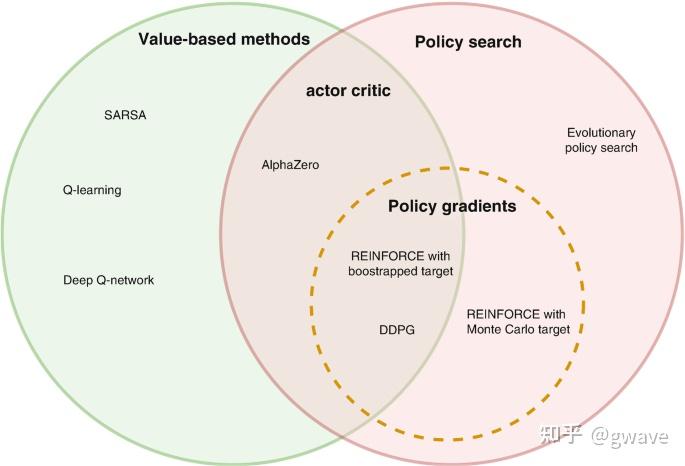
强化学习方法分两大“门派”：

• 基于价值的方法（Value-based）与基于策略的方法（Policy-based）。

经典教材通常从值函数、贝尔曼方程等数学推导起步，这虽然严谨且按历史轨迹，但离当下的前沿实践仍有距离，复杂的数学公式也容易劝退不少读者。

2019年3月, 机器学习先驱阿尔伯塔大学教授 Richard S. Sutton(强化学习) 著名的文章《苦涩的教训》的开篇的一段话，其中一句是

70 年的人工智能研究史告诉我们，利用计算能力的一般方法最终是最有效的方法。

【2025-3-5】美国计算机协会 （ACM） 今天授予 Andrew Barto 和 Richard Sutton 2024 年 ACM A.M. 图灵奖，表彰他们为强化学习奠定了概念和算法基础。

• 公众号文章 强化学习之父获ACM图灵奖

(1) 行为心理学: 被动反射

巴甫洛夫的狗 + Hebb 学习法则 —— 环境信号与神经连接（爬行脑）

两种早期认知机制启示：

• 巴甫洛夫的狗: 环境中的状态可以预测未来奖励；
• Hebbian 学习: 大脑或网络可通过“经验”改变内部参数以适应这种预测。

RL 框架中：

• 状态（如铃声）被编码为输入；
• 奖励（如食物）是目标信号；
• 模型会通过某种形式的权重更新（Hebb 或反向传播）来调整状态与奖励之间的映射。

即便是在现代深度强化学习中，这一思想依然保留。

例如，在深度强化学习DQN 中，神经网络通过梯度下降来更新参数，本质上也是 Hebbian 学习的计算机实现。

巴甫洛夫的狗

从铃声到流口水：条件反射

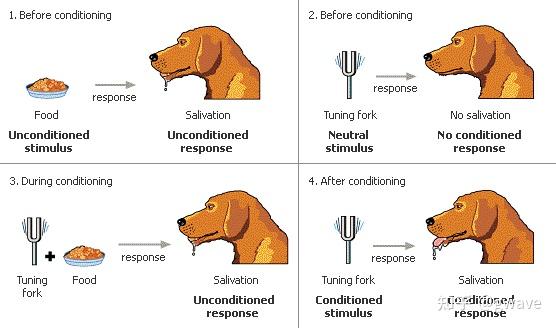
人类对“学习”行为的最早科学理解，伊万·巴甫洛夫（Ivan Pavlov)的狗是起点。

• 

19世纪末到20世纪初，巴甫洛夫的实验揭示了惊人现象：

• 狗在听到铃声后，即使没有看到食物，也会开始分泌唾液。
• 起初，狗只会对食物产生唾液反应（天然的无条件反射），但当铃声与食物反复配对后，铃声本身就成为了触发唾液分泌的“信号”。
• 这种新形成的刺激—反应关联，被称为条件反射（Conditioned Reflex）。

示意图

• 

智能体的学习表现为对环境中某些信号的响应习得，是一种典型的被动学习机制。

Hebbian 法则

Hebbian 法则：神经元之间的“联络加强”

1949年，加拿大心理学家 Donald Hebb 在其著作《行为的组织》中提出了生理学假设：

“Neurons that fire together, wire together.”—— 同时激活的神经元，其连接将被加强。

Hebbian 学习法则理论描述了基于时间关联的突触可塑性。

如果在一段时间里神经元A经常激活神经元B，那么它们之间的突触连接会变得更强，从而在未来更容易一起激活。

Hebb 理论的核心在于：“学习=连接权重的变化”。

这不仅为巴甫洛夫的行为实验提供了神经层面的解释，也成为后来的神经网络、感知机（Perceptron）和突触权重更新机制的生物启发源泉。

深度学习的起源。

分析

这时的智能体能力非常有限：

• 感知输入：能识别环境中的简单信号
• 奖励关联：状态与奖励之间的被动关联学习，建立状态与奖励的静态联系

智能体不需要决策，仅仅通过环境信号塑造行为反应，神经元连接强度会改变（权重更新）

这是后续策略学习中价值函数构建的神经基础，但智能体没有主动选择的能力，也尚未形成主动行为策略。

(2) 主动行为与试错探索：主动探索

桑代克的猫与斯金纳的老鼠 —— 主动行为与试错探索（哺乳脑）

桑代克的猫

桑代克的猫：尝试—错误机制（Trial and Error）

20世纪初，美国心理学家爱德华·桑代克（Edward Thorndike）提出了“效果律（Law of Effect）”，通过一系列著名的“猫逃出迷箱（Puzzle Box）”实验发现：

• 猫在被关进一个装置中时，会不断地抓挠、乱动，直到偶然触碰开关而成功逃脱。
• 多次重复之后，猫逃脱所需的时间明显缩短，并越来越快速地做出“正确动作”。

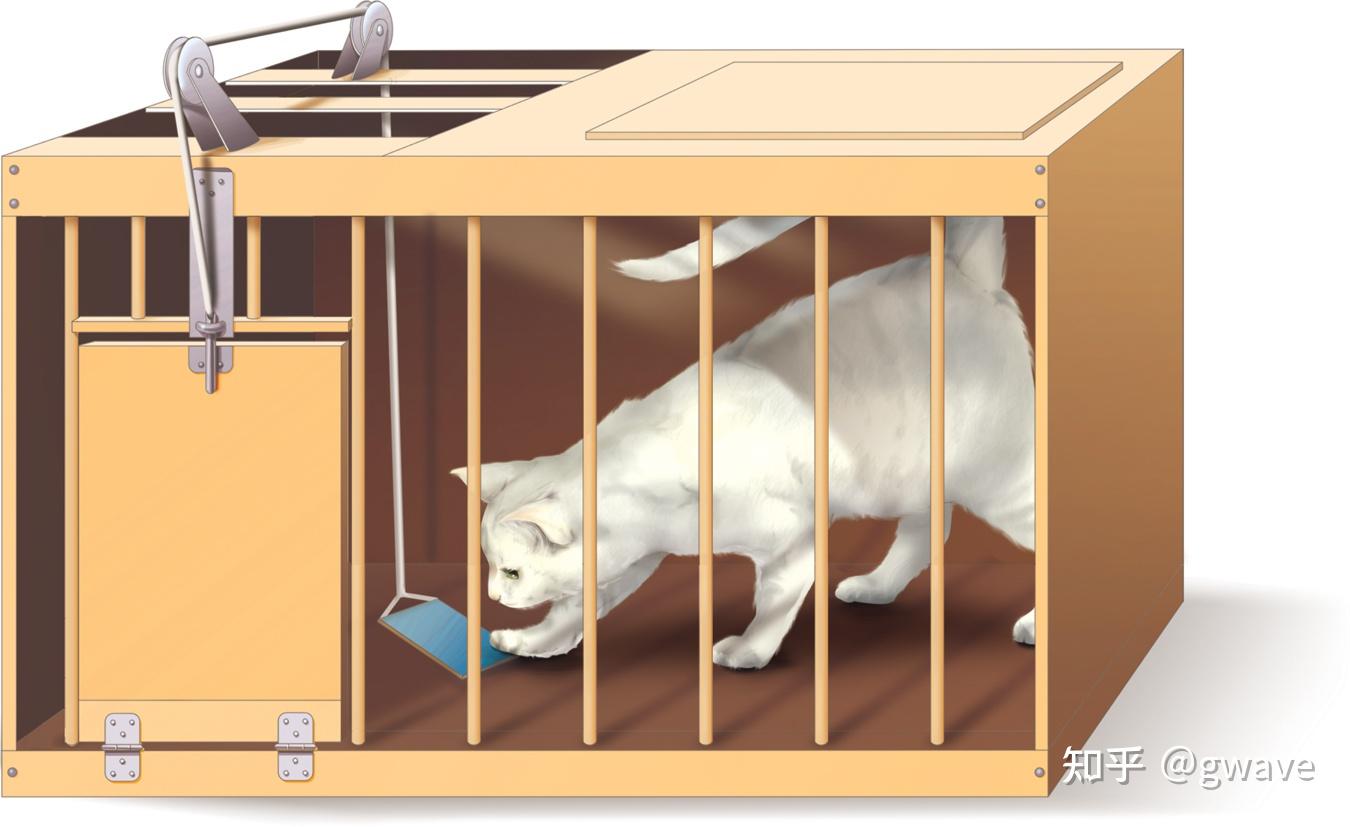
这表明：

• 行为不是一次性学会的，而是在反复尝试错误的过程中，通过正向结果“筛选”出来的。

这种“Trial and Error（尝试-错误）”学习机制，强调行为与后果之间的因果联系，是强化学习中最早出现的主动行为调整模式。智能体不再只是被动响应，而是开始基于结果优化自己的行为。

斯金纳的老鼠

斯金纳的老鼠：行为塑造与强化机制

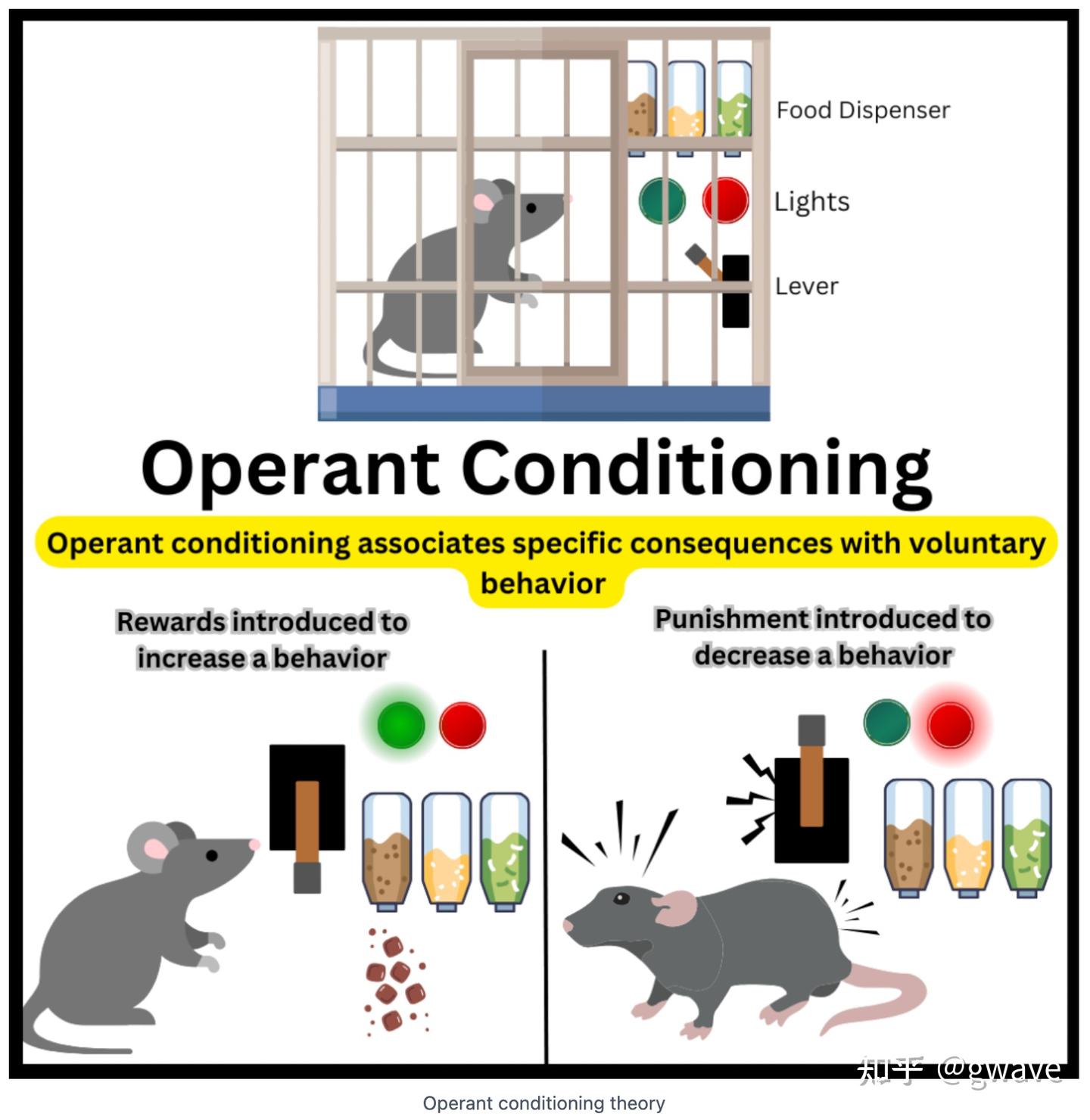
20世纪中叶，B.F. 斯金纳（B.F. Skinner） 在“操作性条件作用（Operant Conditioning）”理论中进一步发展了行为主义。

他设计了著名的“斯金纳箱（Skinner Box）”：

• 一个封闭的实验装置，老鼠被放置其中，环境中设置了一个可按压的杠杆，按下后会触发食物投放器。
• 

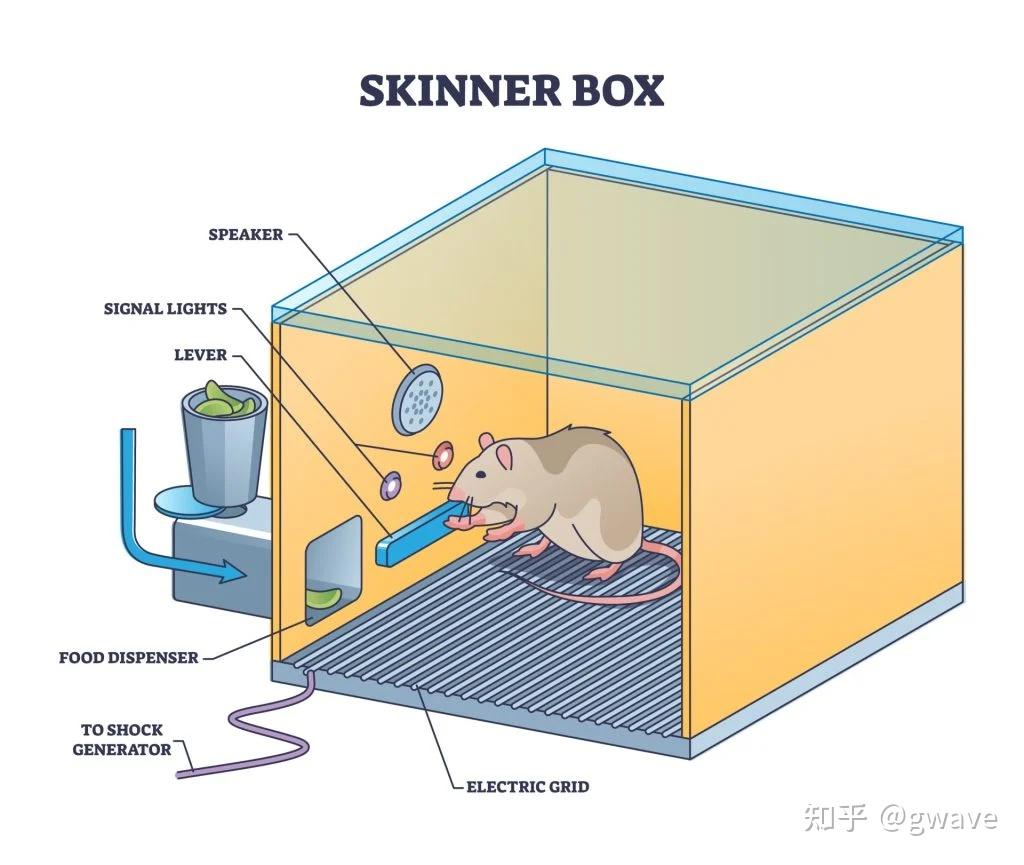
最初，老鼠在箱中四处探索，偶然碰到杠杆得到食物奖励。

经过多次试验后，它便会主动、有目的地按压杠杆以获取奖励，这揭示了“行为的后果会影响未来的行为概率”这一核心规律，也就是强化学习中“行动—奖励”的基本逻辑单元。

行为塑造（Shaping）：让目标行为“逐步浮现”

真正体现斯金纳理论深度的是“行为塑造（Shaping）”策略。

• 复杂行为不应期待一次性学会，而应通过阶段性地强化逐步接近目标的行为，让智能体沿着正确轨迹“攀升”。

这一过程通常如下：

• 第一阶段：老鼠只要靠近杠杆，就给予食物奖励；
• 第二阶段：老鼠必须抬起前肢靠近杠杆，才能得到奖励；
• 第三阶段：只有当老鼠真正按下杠杆，才给予奖励。

通过逐步强化更接近目标行为的动作，让智能体朝目标逐渐靠近。

• 
• Operant Conditioning theory

这种逐步引导式策略与今天深度强化学习中的稀疏奖励（Sparse Reward）设计和探索—利用权衡（Exploration vs Exploitation）思想不谋而合。

这种分层奖励机制使得智能体在稀疏或难以探索的任务中也能逐渐学习复杂行为。

这一思想后来被广泛应用于Reward Shaping、Curriculum Learning（课程式学习），以及分层强化学习（Hierarchical RL）等现代方法中。

负强化（Negative Reward）：抑制不期望的行为

斯金纳箱另一个常见设置：双按钮机制。

• 一个按钮带来奖励
• 另一个按钮触发电击、蜂鸣等不良刺激。

老鼠逐渐学会避开负面刺激源，这种基于“惩罚”信号的学习过程被称为负强化（Negative Reinforcement），或更广义上的惩罚学习（Punishment Learning）。

它不仅用于强化正确行为，也用于抑制错误策略，体现了“奖励最大化 + 惩罚最小化”的联合目标。

分析

这一层级的智能体学习方式，已从被动响应转向主动试错。其在强化学习中的映射：

• 试错 Trial & Error：Agent（老鼠/鸽子 ） 会探索环境，尝试不同动作（Action），并根据回报调整行为策略；
• 操作性条件作用 （Operant Conditioning）：对应现代 RL 中的“策略学习“（Policy Learning）思想，即通过试探行为与奖励之间的关系，优化行为概率分布；
• Shaping：通过设计阶段性奖励或分层任务，逐步引导学习过程，避免陷入稀疏奖励困境。

经典的 REINFORCE 算法就源自于这一思想：智能体尝试多种行为，根据行为带来的回报大小，提升带来好回报的动作概率。

从被动反应者变成主动行为者，从“刺激—反应”走向“行为—结果“，已具有探索行为与行为后果评估的能力, 使智能体首次具备了“主动探索—结果反馈—行为更新”的基本闭环，为强化学习提供了“试错+反馈”这一最基本学习机制。

在巴普洛夫的狗的环境感知、奖励关联的基础上，开始输出行为，并会根据奖励结果强化某些行为（行为概率调整），实现的策略优化，具有初步的决策能力，但尚不具备精确策略建模能力。

本层代表了智能体从“被动反射”迈向“主动行为”的关键一步，标志着从神经反应走向决策策略的过渡。

(3) 探索行为与内在表征的萌芽: 建模预演

托尔曼的迷宫老鼠与认知地图 —— 探索行为与内在表征的萌芽（大脑皮层）

前两个境界中，智能体仍是典型的“反应者”——行为完全依赖于当下的刺激和奖励，没有对未来的预期，也没有对世界结构的理解。

托尔曼的迷宫老鼠

然而，到了第三境界，一位名叫爱德华·托尔曼（Edward Tolman 1886-1959）的美国心理学家，让世界第一次见识到了“智能体可以为将来而学习”。

托尔曼迷宫老鼠

• 

背离行为主义的“异类实验”

在20世纪40年代，当斯金纳的“操作性条件作用”理论大行其道之时，托尔曼却提出了极具颠覆性的观点：

• 动物不是被动地对刺激作出反应，而是会主动形成对环境的“认知地图”。

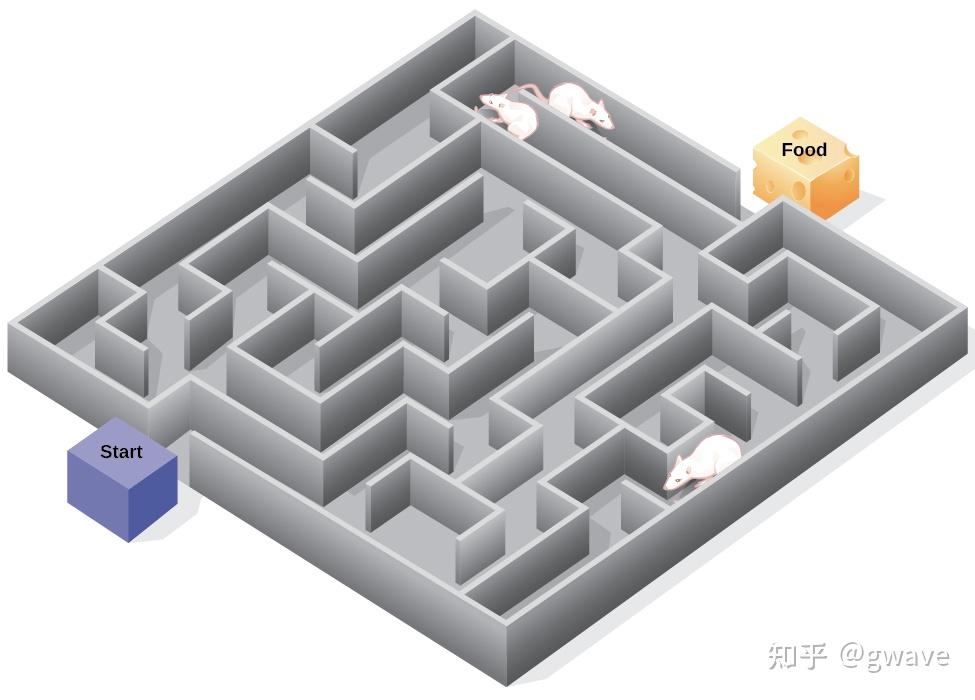
托尔曼的经典实验，让三组老鼠分别在迷宫中进行任务：

• 第一组：每次走到终点就获得食物奖励；
• 第二组：从不提供奖励；
• 第三组：最初没有奖励，但在第11天开始提供奖励。

实验结果显示：

• 第三组老鼠在第11天开始获得奖励后，几乎瞬间就达到了第一组的表现水平，甚至更快。

这表明：老鼠在前10天虽然没有外部奖励，但它们并非“什么也没学到”——而是在无奖励条件下主动探索并构建了环境的内部表示，一旦有了动机（奖励），便迅速发挥出来。

从“Trial & Error”到“Latent Learning”

这项实验挑战了传统行为主义的两个核心假设：

• 1）学习必须有奖励驱动；
• 2）学习是通过“尝试—错误”逐步积累的。

托尔曼的研究表明：

• 动物在没有奖励的情况下进行“潜在学习”（Latent Learning），并在之后的适当时机中将其释放。

这种能力的存在，预示着智能体不再只是条件反射的集合，而是具备更复杂的内在建模机制。

后人所称的认知地图（Cognitive Map）——对空间结构和环境状态之间关系的内部建模。

• 模型建构（Model-Based RL）：智能体不再只依赖“值函数”或“策略网络”来决定行动，而是显式学习环境状态转移和奖励模型，即“如果我这么做，会发生什么”，用数学公式表达就是两个概率分布：
  • 1）状态转移模型： p(s'|s,a) 表示在当前状态 s 下采取动作 a 后转移到下一个状态 s' 的概率；
  • 2）奖励模型： p(r|s,a) 表示在状态 s 下采取动作 a 后获得奖励 r 的概率。
• 探索行为（Intrinsic Motivation）：鼓励智能体在没有外部奖励的情况下主动探索，比如通过奖励“信息增益”、“预测误差”或“访问新颖状态”等内部激励机制产生探索行为。最近一年RL领域出现了不少这个方向的文章。
• 表征学习（Representation Learning）：通过神经网络自动提取状态的低维嵌入表示，被视为深度强化学习中的“认知地图压缩版本”。
• Zero-Shot / Few-Shot 迁移学习：一旦构建了认知地图，智能体就可以在新的任务或目标位置变化时迅速适应（类似迷宫终点变动后的重新路径选择）。

分析

从“反应者”到“建模者”的飞跃

前两个境界中，智能体仍然是一个典型的“反应者”——行为完全依赖于当下的刺激和奖励，没有对未来的预期，也没有对世界结构的理解。

然而，托尔曼的迷宫老鼠揭示了一个惊人的转折：

• 智能体可以在没有奖励的情况下，自主探索环境，构建内在的“认知地图”，并在未来使用这些地图做出更高效的决策。
• 

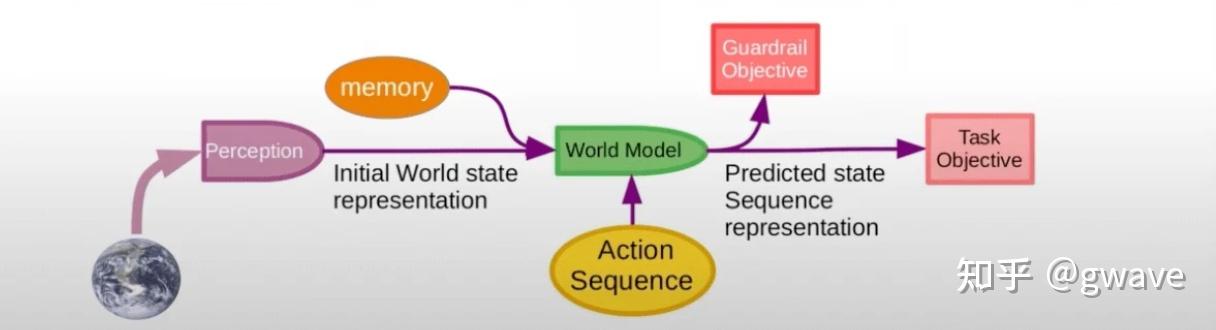
这种能力标志着智能体从“刺激—反应”的生存机制，跃迁到了“建模—规划”的认知机制。

智能不再是被动地回应过去经验，而是主动地预演未来可能的情境。

托尔曼的实验，为今天的“世界模型”（World Model）思想提供了最早的生物学雏形。

这一思想如今被 Yann LeCun 等人视为迈向通用人工智能（AGI）的核心路径之一，也日益成为神经网络与强化学习研究的关键方向，可能也是通往AGI之路上的一块重要基石。

从认知地图到控制论：反馈与目标导向行为

托尔曼提出“认知地图”理念打破了行为主义将动物视为“刺激-反应”机器的传统，指出它们具备建立内部世界模型的能力。

这一观念也为后来的强化学习打下了基础——智能体不再仅靠外部奖惩塑造行为，而是可以预判环境变化、规划未来路径。

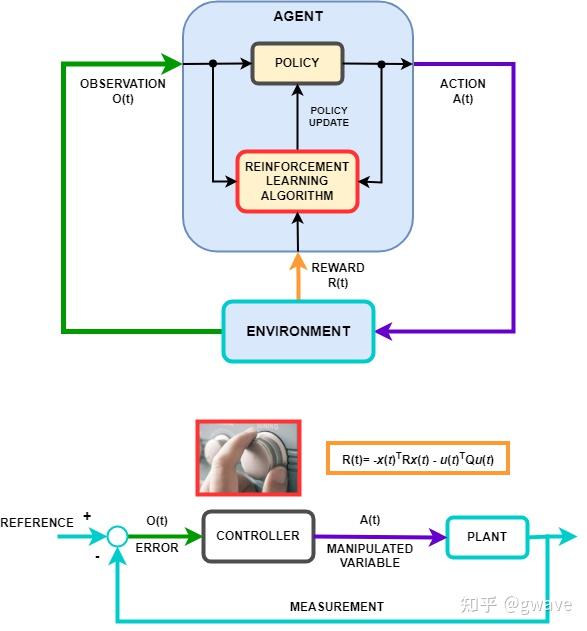
这与20世纪40年代兴起的控制论（Cybernetics）思想不谋而合。控制论由诺伯特·维纳（Norbert Wiener）提出，强调通过反馈机制实现系统的自我调节与目标控制。

在一个典型的控制系统中（如恒温器、导弹制导），系统会感知自身状态与目标之间的偏差，通过调整行为不断接近目标，从而实现稳定控制。

reinforcement-learning-for-control-systems-applications

• 

这一理念正好映射到强化学习智能体中：

• 当前状态 S 对应系统观测；
• 策略 π 对应控制器的调节机制；
• 价值函数或奖励 R 是衡量偏差的目标信号；
• 行为 A 的改变 是反馈控制的动作输出。

这个意义上，把现代强化学习看作是控制论在人工智能领域的延伸：

• 从动物行为的实验室走向具备目标导向、自我调整能力的智能体系统，而认知地图、世界模型、Model-Based RL 正是这条路径上的里程碑。

“控制的本质是对未来的预测。” —— 诺伯特·维纳

强化学习与控制论，虽然诞生于不同学科，但殊途同归，都在试图回答同一个问题：如何让系统自主地行动，以实现长期目标。

P.S. 控制论是AI诞生的重要来源之一。

至此，行为心理学的探索暂告一段落。从巴甫洛夫的狗，到斯金纳的老鼠，再到托尔曼的迷宫，逐步见证了“学习”从被动反应到主动探索、再到建模预演的认知跃迁。

它们不仅为强化学习打下了深刻的生物与心理学基础，也揭示了智能体从低级刺激反应到高级规划推理的进化轨迹。

(4) 基于策略的RL: 试错->期望提升

前三个境界中，智能体的行为逐步进化：从条件反射式的被动响应（巴甫洛夫），到行为被奖励塑造（斯金纳），再到主动探索环境、形成认知地图（托尔曼）。但这一切，仍然是经验驱动下的“试错学习”。

智能体或许知道“什么行为有效”，却并不理解如何系统地优化自己的行为策略。

真正的强化学习算法首次登场 —— 一次意义深远的范式飞跃就此发生。

为智能体引入了可微分的目标函数（Objective Function）， 像指南针指引行为的优化方向。策略不再依赖盲目的试错，而是通过梯度上升，沿着最大化长期期望奖励的方向不断前进。

这一机制，正是基于策略的方法（Policy-based Methods）的核心思想：从“凭经验尝试”走向“按目标优化”，从心理学启发走入数学可导的算法世界。

reinforcement-learning-for-business-real-life-examples

• 

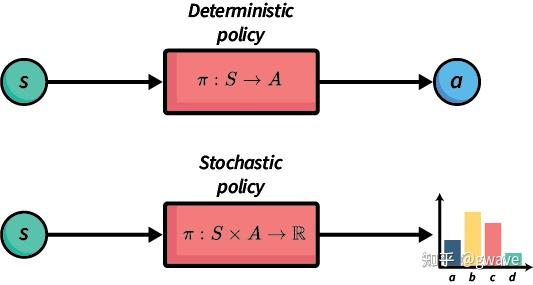
策略 Policy 可以是确定性策略（Deterministic Policy），也可以是随机策略（Stochastic Policy），如 softmax 分布带温度控制的策略。

• 
• MDPs

策略可以被视为一个函数，它接收状态 S作为输入，输出动作 A 或对应的动作分布。

智能体的目标不是被动地建模环境或评估状态价值，而是直接学习如何行动 —— 即通过优化策略函数，使其在与环境的交互中获得更高的长期奖励。

相比早期的“盲目试错”，这里的学习过程更像是“通过反复交互，试图让未来更好”

智能体不再只通过“看看哪里有奖励”来调整行为，而是系统性地优化这个函数，使得策略参数逐渐趋向让行为更优。这就是从“经验主义试错”进化到“梯度驱动优化”的跃迁。

引入策略函数：智能体首次拥有了“行为蓝图”

在前两个境界，智能体主要通过试错（Trial and Error）来学习——行为成功就加强连接或重复尝试，失败就避免。这虽然朴素有效，但缺乏一种明确的、可以系统优化的“行为表达形式”。

策略梯度（Policy Gradient）：策略优化的利剑

• 通过采样状态-动作轨迹，并利用回报信号来估计目标函数对策略参数的梯度，以此推动策略朝着期望回报更高的方向改进。

policy-g

• 

简单公式背后蕴含着划时代的思想：

• 通过“梯度上升”来主动改进智能体的行为倾向，使其更倾向于做出带来高回报的决策。

这种方法的最大优势：无需显式建模环境。

即便面对一个不可微分、不可逆，甚至完全未知的环境，依然可以基于交互数据来改进策略。

这种“黑箱优化”能力，让策略梯度方法具备极强的适应性和泛化能力。

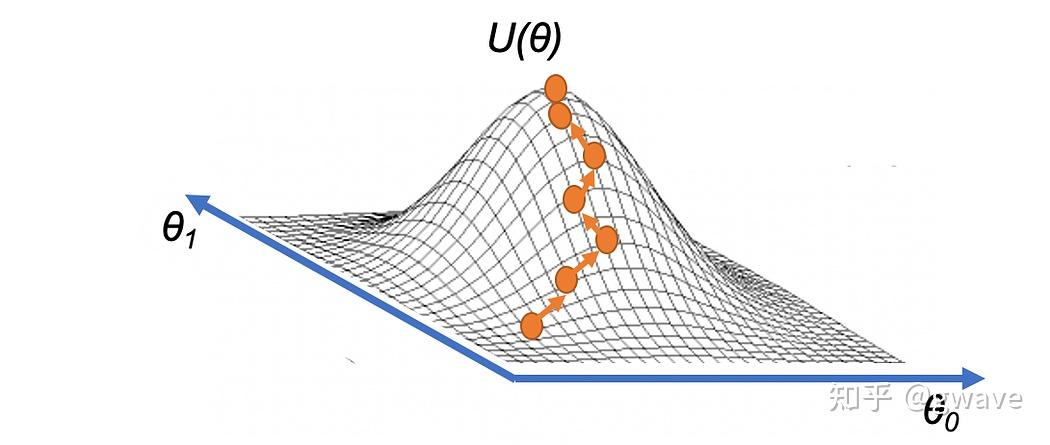
此外，它也不需要显式计算每个状态或动作的价值，就像即使没有地图，也能凭借“上坡方向”不断爬山 —— 这就是策略梯度方法的直觉之美。

REINFORCE：策略梯度开山之作

1992 年，美国东北大学教授 Ronald J. Williams (1945-2024) 提出了著名的 REINFORCE 算法，标志着策略优化的正式诞生，也是反向传播的共同作者。

这是第一种实现“策略梯度”（Policy Gradient）思想的强化学习方法，其核心思想非常直白却极具启发性

• 如果某个行为最终带来了高累积回报, 那么就应该增加采取该行为的概率

REINFORCE 正是将这种“经验塑造”的思想转化为了可微分的目标函数，使得智能体可以直接对策略进行梯度更新，开启了强化学习的“可优化时代”。

REINFORCE 支持两种策略表示方式：

• 表格形式（Tabular）：适用于状态和动作离散可枚举的简单环境；
• 参数化形式（Parametric）：如通过神经网络建模策略，输入状态，输出动作概率分布，从而适配更复杂、连续的决策任务。

从基于结果调整行为的“经验反馈”，跃迁到通过策略函数事前预期的“行为倾向建模”。

不同于以往依赖环境回报反复修正行为的方式，基于策略的 Agent 可以在没有显式状态值评估机制的前提下，直接学习“哪种行为在长期更可能带来奖励”。

终于可以摆脱那些“繁琐又间接”的基于价值的方法，不再死守 Bellman 方程，不必反复估计状态值或动作值，“单刀直入”，直奔核心目标：优化行为策略本身。

智能体的关键任务，不是先画好一张地图，而是尽快学会在复杂地形中活下来。

把 Agent 想象成一位被空投到敌后、手上只有一把武器的特种兵——在没有现成地图的情况下，他仍然必须迅速判断方向，占领高地，达成目标。这时再回头绘制环境模型，“远水救不了近火”。

Beyond-DQN

• 

从心理学视角：

• 这一阶段的智能体已经具备了“习得性、目标导向行为”的能力，不再只是应激反应，而是有内在行为偏好的决策者；

从机器学习角度：

• 这是强化学习首次引入了梯度驱动的优化机制，也是向现代深度学习体系靠拢的起点。

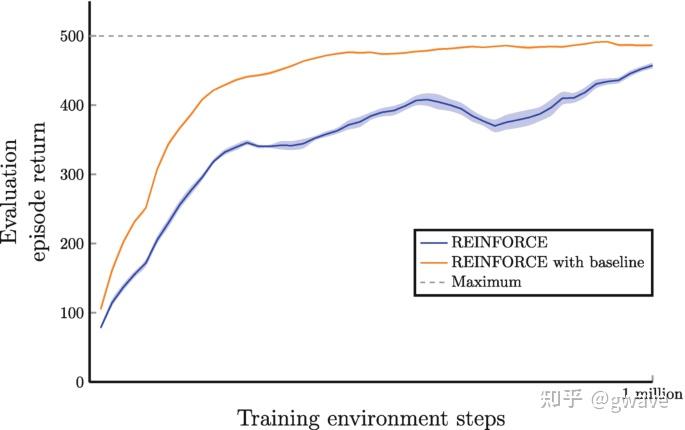
尽管 REINFORCE 提供简单直接的策略优化路径，但存在严重问题：方差太大，学习不稳定。

• REINFORCE 中，轨迹的总回报 R 被用于“奖励”或“惩罚”某个行为的 log-probability。
• 但回报 R 本身波动极大，可能受到随机事件的剧烈影响，从而导致策略更新方向剧烈摆动。
• 想象：同样的行为，有时因为运气好得分高、有时因为环境变化得分低，这种“情绪化”的反馈显然不利于稳定学习。

为此，Baseline 技术应运而生。

核心思想: 减去一个“基线”值，使得更新方向只取决于“当前行为是否优于平均水平”

减少方差的智慧：Baseline 技术的引入

• 

好处：

• 减小方差：将策略更新集中在“真正优于平均水平”的行为上，提升学习稳定性。
• 保持无偏性：虽然减去了 baseline，但不会引入系统性偏差（因为 baseline 与行为无关，不影响期望）。

Proximal-Policy-Optimization-PPO

• 

正是这个小trick，使策略梯度方法从“概念验证PoC”走向了“可实用系统”的关键一步。

如今，几乎所有主流策略梯度算法（包括 A2C、PPO、TRPO 等）都引入了 baseline

(5) 时序差分

TD 学习与 Bootstrapping —— 时间差分的悄然革命

策略梯度方法如 REINFORCE 确实开启了用梯度优化策略的新时代，但显著缺点：必须等到整条轨迹结束之后，才能计算累积回报，进而更新策略。

然而，现实世界中的回报往往是延迟的，智能体希望能在回合（episode）尚未结束时就尽早修正自己的行为倾向。

甚至更理想：每一步都能更新一次策略（或者值函数）。

TD

这种“边走边学”的愿望，正是时间差分学习（Temporal Difference Learning, TD）诞生的背景。

类比：

• REINFORCE 策略更新，像 Batch Gradient Descent：只有在经历完整轨迹后，才更新一次。不同点是：因为未来回报的不确定性叠加，导致方差大，梯度估计波动性强，收敛效率较低。
• 而 TD Learning（特别是 TD(0)）则更像是 Stochastic Gradient Descent (SGD)：每走一步就更新一步，误差信号快速传播，效率更高。
• 更进一步，n-step TD 和 TD(λ) 则可以视作 Mini-batch Gradient Descent —— 在完整轨迹（Batch）与单步更新（SGD）之间，提供可调节的折中方案，兼顾稳定性与响应速度。

正是由于 TD 学习能在不中断任务的前提下，逐步修正估计，它成为现代强化学习中最具工程实用性的基础技术之一，而且比策略梯度法更早被成功用于游戏智能体与机器人控制中。

于是，“及时学习”的需求催生了时间差分学习（Temporal Difference Learning, 简称 TD ——这是一场更贴近生命体认知节奏的革命。

Temporal-difference learning

• 

REINFORCE 只能在轨迹终点总结“整场行动的得失”，再反向影响整条路径，缺乏沿途的“早期信号”。

• 士兵必须打完整场仗，回营后才能总结得失；

而时间差分学习（TD Learning），则可以边打边学，每走一步都获得“即时反馈” —— 不再非得靠终点打分，而是让每一步都蕴含对未来的预期。

TD 学习带来的思想转变是：

• “我不需要知道全部未来，我只需知道：下一步的大致方向。”

Agent 不再依赖轨迹终点给出评价，而是在走的每一步中，就“感知下一步的未来”。

• 如果说 REINFORCE 是一种“经验反馈”（retrospective）—— 只能在整条轨迹结束后，回顾性地调整策略；
• 那么 时间差分学习（TD Learning）则代表“预期引导”（prospective） —— 它利用对未来的估计，在当前就开始修正行为。

这种方法 摆脱了对完整轨迹回报的依赖，转而使用未来价值的预测（Bootstrapping）来引导当前更新。

由此带来两大优势：

• 更快的收敛速度，尤其是在训练初期；
• 更稳定的更新过程，显著减少方差；

这是一种真正意义上的“范式变革”：智能体从后验总结经验，进化为前瞻性地预估未来并调整行为，强化学习向更接近生命体认知节奏的方向迈进。

TD(0)

TD(0)是最简单的时间差分估计（TD Learning)

误差项（TD Error）反映“当前估计”和“从未来看回来”的差距；

因为用的是自己的估计值，所以这类方法被称为 Bootstrapping 自举

• 因为用自己的估计值来修正自身——就像“左脚踩右脚往上跳”，虽然听起来有点悖论，但在数学上却是完全可行的。
• 不依赖真实的完整回报，而是拿未来某个状态的估值当作当前目标的一部分，以此逐步逼近真实的长期回报。

Temporal-Difference-Learning

• 

分析

• TD(0) ≈ SGD：每走一步更新一步，噪声大但更新快；
• REINFORCE ≈ Batch GD：全轨迹才更新一次，更新稳定但效率低；

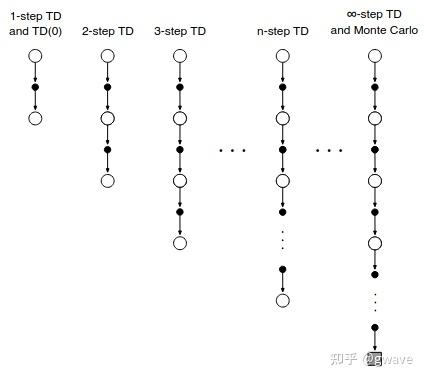
n-step TD

那有没有折衷如 mini-batch GD 的TD呢？n-step TD

• 等 n 步之后再更新估值，用这 n 步内的真实奖励，加上第 n 步的预测，作为当前的目标

introducing-n-step-temporal-difference-methods

• 

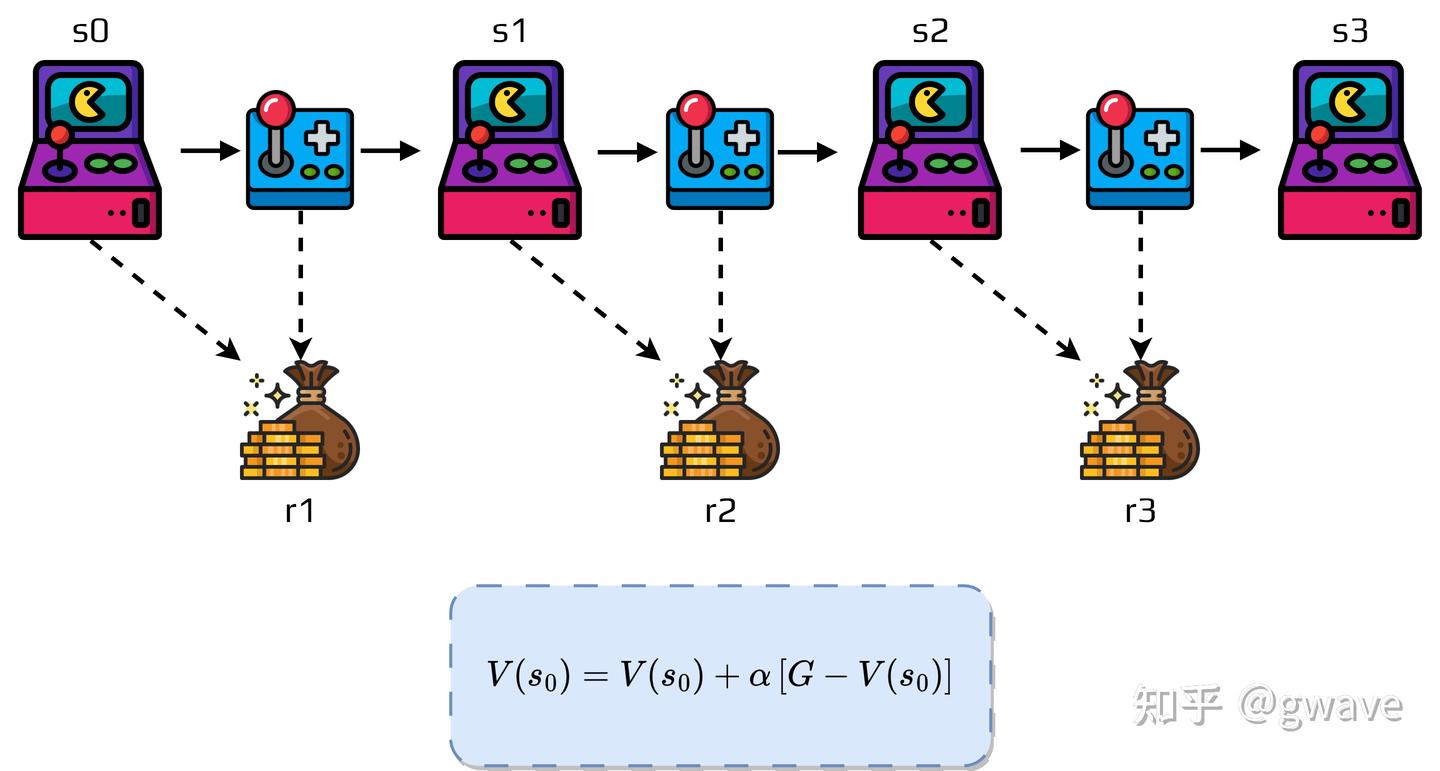
Monte Carlo

Monte Carlo 方法（MC） 核心思想：

• “不预判未来，只在全部经历之后回顾总结。”

具体步骤：

• 智能体必须完整执行一条轨迹，直到 整个episode 结束；
• 然后基于实际经历，直接计算每个状态或动作的真实回报：
• 再用这些“最终成绩单”来更新策略或价值估计，不依赖任何对未来的预测。

这种方式就像一个士兵打完整场仗后回营复盘：只有在战争尘埃落定后，才能回顾每一步的得失，反思哪些决策值得保留、哪些需要修正。

简单直观，却也带来了明显的缺点：必须等待整个 episode 结束才能得到反馈，学习节奏较慢，数据利用效率较低。

“Monte Carlo”一词源于摩纳哥的著名赌城，因其与随机试验和概率密切相关，在机器学习中常用来泛指一类通过随机采样进行估计的方法。

REINFORCE 方法其实正是一种基于 Monte Carlo 的策略梯度算法。使用 episode 中采样得到的总回报来指导策略更新，不使用 bootstrapping，因此理论上无偏，但也面临高方差和训练不稳定的问题。

生物学意义

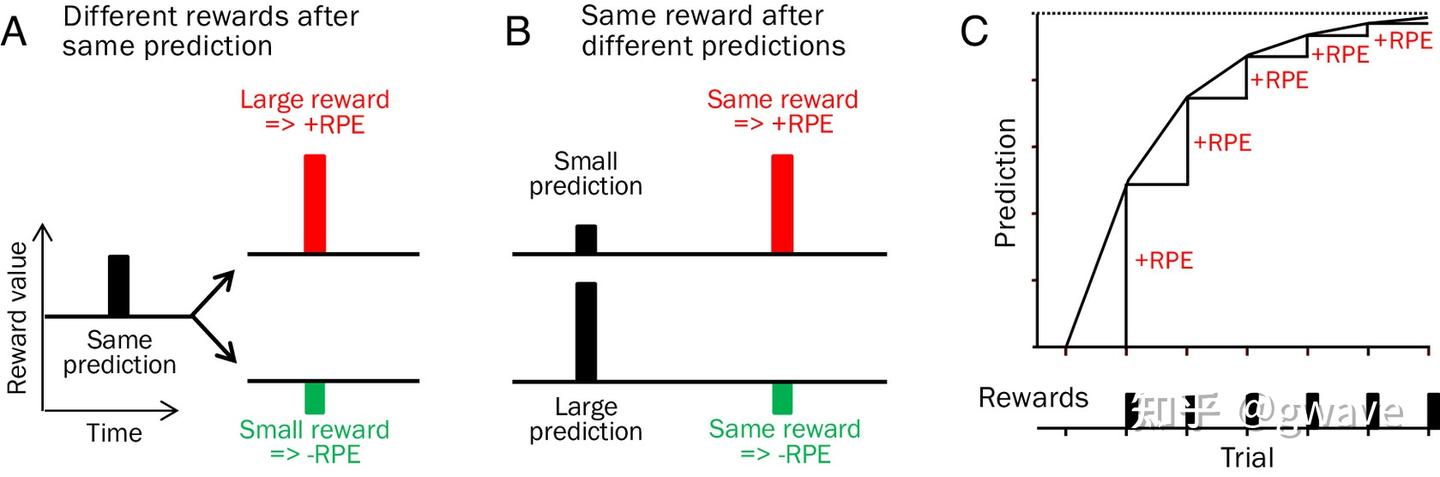
1997 年，剑桥大学神经科学教授 Wolfram Schultz 等人的实验发现：

• 灵长类动物中中脑多巴胺神经元的放电模式，与 TD 学习中的 prediction error 高度一致。

具体表现为：

• 意外获得奖励时（比预期更好） → 多巴胺释放增加（正向 TD 误差）；
• 奖励如预期而至 → 多巴胺神经元没有额外反应（TD 误差接近 0）；
• 期待奖励却未获得 → 多巴胺释放减少（负向 TD 误差）；

知足常乐，其实是一种对多巴胺系统的精准优化。你的快乐（多巴胺）并不来源于绝对的奖励值，而是源于实际得到的奖励与预期之间的差值。

从强化学习的视角看，这正是所谓的“时间差分误差”（TD error）

多巴胺的释放，正是对这个差值的响应(RPE)。如果你对未来的期望很低，即使获得平凡的结果，也能带来正向的惊喜，释放更多多巴胺，让你感到愉悦。反之，期望太高，即使结果不差，也可能因“低于预期”而失落。

所以真正的幸福，不在于你得到了什么，而在于你得到了“超过预期的什么”。这正是“知足常乐”的神经科学与计算认知基础。

pnas

• 

(6) Value-Based 评估->决策

智能体从条件反射的初级反应，进化为具备策略函数、能够通过梯度优化实现“自我提升”的智能体。

然而，这些策略优化方法虽然高效，却更像是“摸着石头过河” —— 缺乏对环境结构的深入建模，也未构建出系统化的世界观。

贝尔曼方程（Bellman Equation） —— 一个可递归、具备“预见未来”能力的结构化公式。

与策略直接优化不同，贝尔曼方程的核心思想：当前行为的好坏取决于其对未来长期回报的影响。

• 智能体不再只是“在当下做出合理选择”，而是开始尝试“在脑海中绘制未来的地图”，以评估和规划最优行为。

基于价值函数的方法，正是通过不断逼近贝尔曼方程的解，来学习状态或动作的长期价值（Value），进而引导策略更新。

• 通过这种方式，智能体不仅“知道当下该做什么”，更“知道做了之后会发生什么” —— 决策的基础从即时反馈，跃升为预测驱动的价值评估。

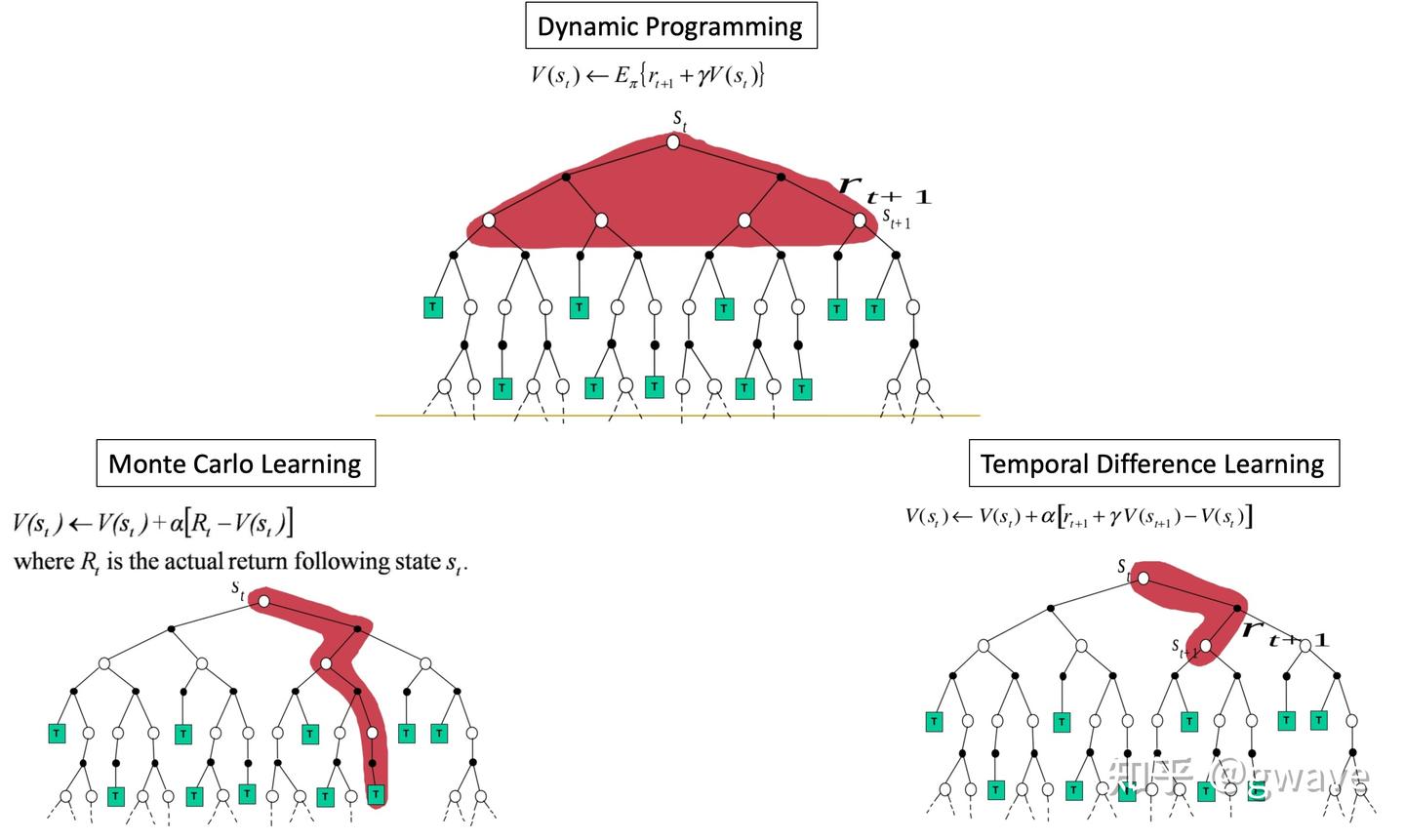
基于价值的方法源于上世纪 1950 年代的动态规划(Dynamic Planning, DP)理论，在马尔可夫决策过程（MDP）等问题中取得了大量成功，因此在多数强化学习教材中（如 Sutton 等人的经典著作）被安排在第二章位置。

然而，放眼当下，随着深度强化学习与基于策略的无模型方法（Model-Free Policy Optimization）迅速发展，Value-based 方法的相对“性价比”有所下降。其在高维、复杂任务中的局限性逐渐显现

summary

• 

基于价值（Value-based）的方法，核心思路不再是直接优化策略本身，而是先学会“评估”每个状态或动作的价值。这种评估是通过期望累计回报来衡量

贝尔曼方程

“贝尔曼方程”（Bellman Equation），又称“动态规划方程”（Dynamic Programming Equation），由动态规划之父理查德·贝尔曼（Richard Bellman）（1920-1984）于20世纪50年代提出，最初用于研究导弹控制中的最优决策问题。

Richard Bellman 1920-1984)

• 

从历史上看，贝尔曼方程的提出时间甚至早于1956年达特茅斯会议（人工智能的公认起点），它是动态规划（Dynamic Programming）这一数学优化方法能够实现最优解的必要条件。

核心思想：

• 将某一时刻的决策问题的“最优值”，表示为当前选择所带来的即时收益，加上该选择引导出的子问题的最优值。
• 

将一个动态优化问题拆解为一系列更小、更易求解的子问题。这种分而治之的结构，被贝尔曼称为“最优性原理”（Principle of Optimality），即：“一个最优策略的任一子策略，亦必然是该子问题的最优策略”。

贝尔曼方程最初广泛应用于控制理论和应用数学等工程领域，随后在经济学中也发挥了深远影响，成为动态最优化分析中的基础工具。

几乎所有能够借助最优控制理论（Optimal Control Theory）求解的问题，也都可以通过构造并分析相应的贝尔曼方程来解决。

注意

• “贝尔曼方程”通常特指离散时间（discrete-time）优化问题中的动态规划方程。
• 而在处理连续时间（continuous-time）最优化问题时，其对应形式则是一类偏微分方程，称为汉密尔顿-雅可比-贝尔曼方程（Hamilton–Jacobi–Bellman Equation，简称 HJB 方程）。
• HJB 方程是连续时间最优控制理论的核心工具，是贝尔曼原理在连续系统中的自然延伸。

在强化学习中，贝尔曼方程是连接环境、策略与价值函数的桥梁，构成了值迭代（Value Iteration）、策略迭代（Policy Iteration）等一系列核心算法的理论基础，也为后续如 Q-learning、DQN 等方法的发展奠定了根基。

“维度诅咒”（Curse of Dimensionality）也是Richard Bellman最早提出(coined)的。他还是普林斯顿史上最快获得博士学位的人（3个月完成学位，在服役之后）（二战期间，他在Los Alamos的理论物理组工作）

贝尔曼最优方程

强化学习最终目标通常不是评估某个既定策略，而是找到最优策略，使得智能体在任何状态下都能获得尽可能高的长期收益。

• 拿地图导航来举例，地图不仅要能计算出通过不同路线到达目的地的时间（贝尔曼方程），还要给出最短/最快路径。

这时，贝尔曼最优方程（Bellman Optimality Equation，BOE）登场, 不再是条件性的“根据某个策略”，而是直接刻画了在所有策略中表现最优的那个策略的递推关系，同样分为状态和动作两个方程

强化学习中最关键的跃迁：从“评估某种行为的价值”，进化为“选择最优行为”。

• Q表示行动的质量(Quality)，Q-Learning和DQN的Q都是这里来的。

贝尔曼最优方程也提出“自洽性”的悖论问题：如何知道某个策略是最优的？

答案：

• 我们并不知道，但可以构造出满足自洽方程的最优值函数，然后从中导出最优策略。
• 换句话说，“先有价值，后有策略”，最优行为源于对未来价值的理解，而非经验或模仿。

贝尔曼最优方程不仅是强化学习中的核心公式，更是一种哲学宣言：

“真正的智能，不应只是对当前情况的应激反应，而是基于对未来的预测来做出当下的最优选择。”

它为后续一系列最优策略学习方法（如值迭代、策略迭代、Q-learning 等）提供了统一的数学基础，也为通往 AGI 的道路，搭建了“理性决策”的桥梁。

值函数

强化学习的价值哲学中，值函数（Value Function）是通向最优策略的核心中介。贝尔曼方程提供将“未来期望回报”进行递归建模的方式，使得智能体可以在不显式建模环境的情况下，评估每个状态-动作的长远收益。

而基于值函数的最优性算法，正是试图在不直接学习策略函数的前提下，通过逼近最优值函数来反推出最优策略。

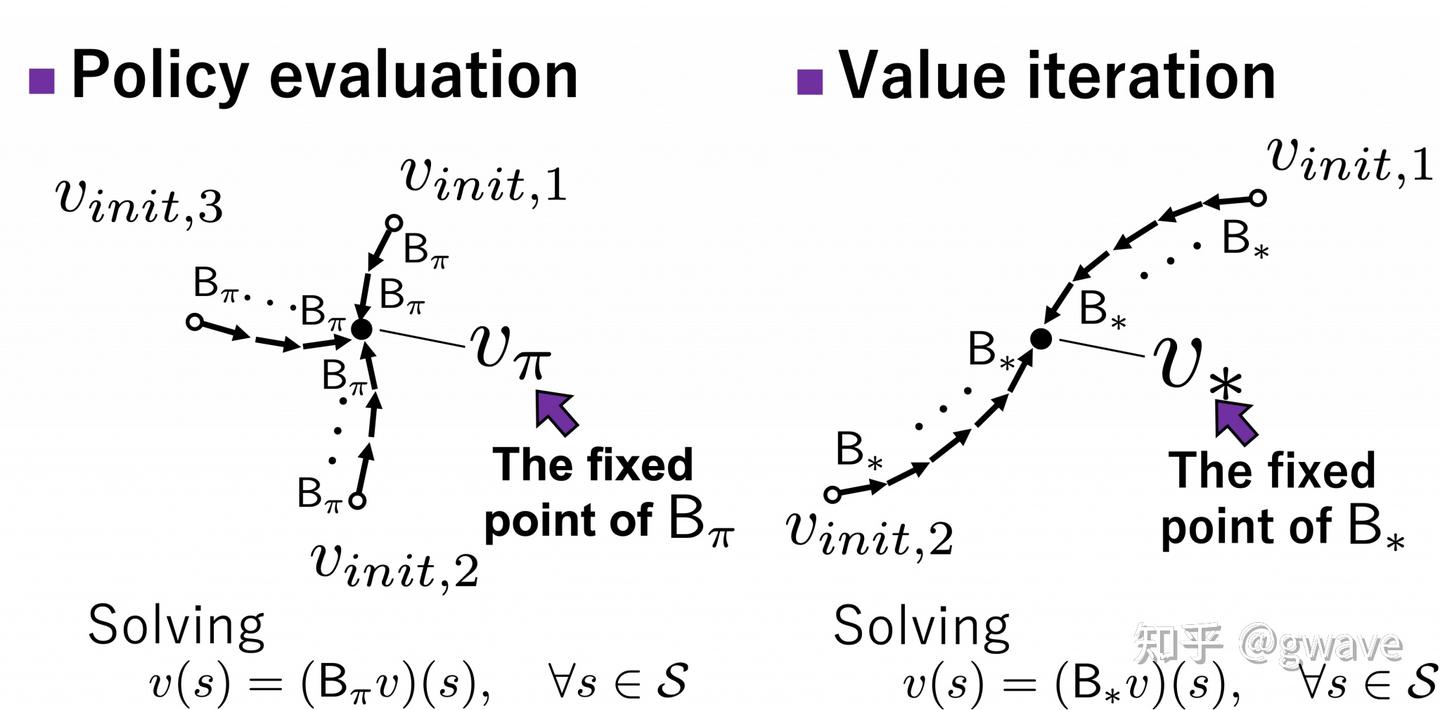
基于贝尔曼思想的核心算法：值迭代（Value Iteration）、策略迭代（Policy Iteration），以及二者之间折中方案——截断式策略迭代（Truncated Policy Iteration）。

• bellman-equation
• 

值迭代 VI

值迭代（Value Iteration， VI） 是最早被提出的动态规划算法之一(Bellman 1957)，也被称为 backward induction（反向归纳）。

核心思想：不显式维护策略，而是将策略优化过程融合进值函数更新。

策略梯度方法可能因梯度信息局部而陷入次优解，价值迭代（Value Iteration, VI）具备全局性的更新特性。

每一轮迭代中，同时对所有状态的价值函数进行更新，使得整个策略空间在全局层面上趋向最优解。这种“同时扫过全部状态空间”的更新机制，使其更容易跳出局部最优。

但问题

• 这种全局更新也带来了更高的计算成本，尤其在状态空间较大时，收敛速度较慢。
• VI 中并不显式存储和更新策略，而是通过值函数间接推导，使得策略的演化过程难以追踪。
• VI 将策略评估与策略改进融合在一步“贪婪最大化”中，缺乏可调的中间过程，不利于学习动态的控制与分析。

策略迭代 PI

为了克服这些限制，一种更具可解释性和调节性的迭代方法应运而生 —— 策略迭代（Policy Iteration, PI）。

策略迭代（Policy Iteration, PI）是一种“双循环”结构的求解方法，由斯坦福大学 Ronald Howard (1934-2024) 于 1960 年提出。

• 

核心思想非常直观：先评估当前策略的表现，再基于评估结果改进策略，循环往复直到收敛。

策略评估与策略改进两个阶段交替执行，直到策略不再改变，即达到了策略收敛

• 策略迭代在有限状态空间下总是收敛到最优策略

截断式策略迭代 TPI

在策略迭代（Policy Iteration）和值迭代（Value Iteration）之间，还种折衷方案：截断式策略迭代（Truncated Policy Iteration）

截断式策略迭代（Truncated Policy Iteration, TPI） 是一种在策略迭代（Policy Iteration, PI）与价值迭代（Value Iteration, VI）之间折中权衡的中间路径，在实际强化学习任务中被广泛应用。

PI 与 VI 都可以被视为 TPI 的特例：当评估步数趋于无穷时，TPI 退化为标准的 PI；当评估步数为 1 时，则等价于 VI：

• k=1 时，TPI 就变成了 值迭代 VI
• k→∞ 时，TPI 就退化为 策略迭代 PI

实际任务中，适度的 k 值（如 3~10） 通常能显著提升效率而几乎不影响策略质量

这种结构上的连续性，使三者关系类似于梯度下降中的 Batch Gradient Descent、Stochastic Gradient Descent 与 Mini-batch Gradient Descent；类似的还有上一层讨论过的MC, n-step TD和TD(0)。

TPI 核心思想: 每轮策略改进之前，仅进行有限步数的策略评估，从而在计算效率与策略收敛性之间取得良好平衡。

• 它既继承了 VI 的高效性，又保留了 PI 中对策略收敛的更强控制，是强化学习中一种兼具实用性与理论价值的方法。

TPI 不仅在理论上构建了 PI 与 VI 的连续谱，也启发了现代 RL 中一系列有限更新 + 策略改进的近似方法，如：

• Generalized Policy Iteration（GPI）：一种理论框架或“范式”，描述了强化学习中策略评估与策略改进交替进行的基本过程，无论评估精度如何（精确或近似），只要两者交替进行，策略总会不断改进并趋于最优，PI、VI、TPI、Q-learning、SARSA 等都属于 GPI 范畴。
• 深度强化学习中的 DQN（Q-learning） 与 A3C 等 Actor-Critic 方法；
• TRPO / PPO 中以 trust region 或近端更新限制策略变动，也是一种“截断改进”的思想延续。

TPI 兼具稳定性与效率的中间路径，不仅在理论上贯通了策略迭代PI与值迭代VI，也在现代RL的深度版本中广泛出现，体现出从离线到在线、从近似到精确的连续性思想。

离线学习是在固定数据上训练策略，在线学习则是在与环境实时交互中边试边学。打个比方：离线 = 看录像学打拳；在线 = 上台边打边学。

on-policy vs. off-policy 分野

值函数RL方法下，如果对环境的模型不了解，就需要考虑使用SARSA 和 Q-Learning 最为经典的 无模型（model-free） 算法，它们都通过更新状态-动作值函数 来逐步逼近最优策略。

然而，更新路径却体现出两种核心思想的对立：on-policy 与 off-policy。这不仅是更新机制的技术区别，更是智能体“如何面对不确定未来”的哲学分野。

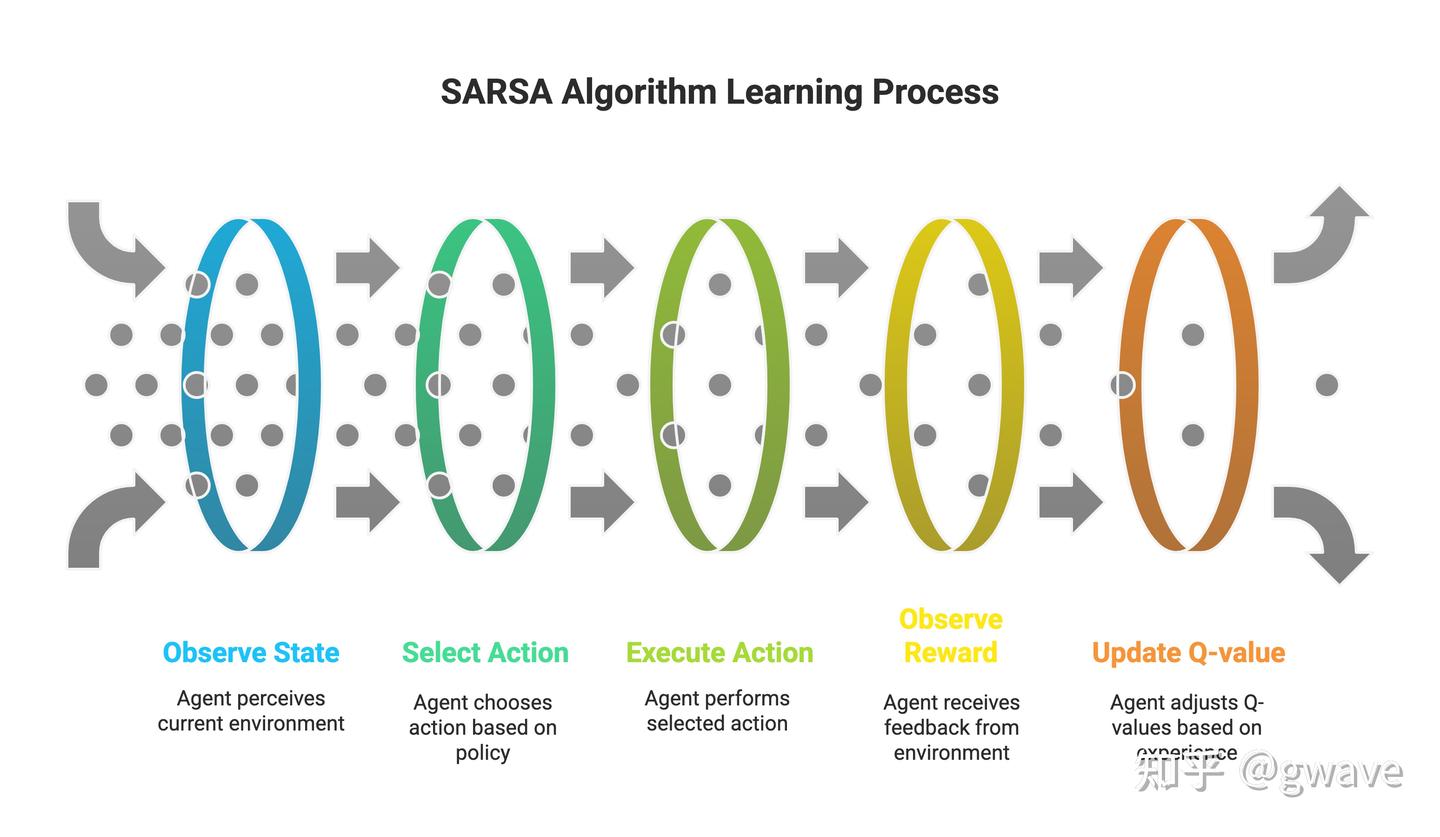
SARSA

SARSA：基于当前策略的价值更新（on-policy）

sarsa-in-machine-learning

• 

SARSA 的名字来自于它更新所依赖的五个变量: S, A, R, S’, A’, 是 TD 学习在动作值上的 on-policy 版本，最后那一项可以理解为TD-Target。

SARSA 是 TD 学习在 动作值层面的 on-policy 实现，它既继承了 TD 的增量更新风格，也具备某种“伪梯度上升”的结构。

SARSA 是一种 on-policy 学习方法, 虽然增强了学习的稳定性和安全性，尤其适用于需要规避风险的环境（如机器人控制），但也带来了两个明显的缺点：

• 学习过于保守：它评估“我实际会怎么走”的结果，哪怕这不是最优路径，也会围绕它进行微调。
• 收敛慢、易陷入局部最优：在策略初期，探索行为较多时，SARSA 也会“学习探索行为的后果”，从而影响最优策略的学习速度。

`Q-Learning

为了解决 SARSA 的这类问题，Q-Learning 被提出作为一种 off-policy 的强化学习方法。

它跳出了当前策略的限制，每一步都朝着最优策略的方向更新：不管当前行为是否最优，它始终用下一个状态中“看起来最好的动作”来指导更新。

这种“大胆假设、激进优化”的思路，使得 Q-Learning 更有机会快速学到理论上最优的策略，尤其适合在模型明确、训练目标清晰的环境中使用（如围棋、博弈 AI、游戏等）。

• SARSA 是“跟着自己脚步走”
• 而 Q-Learning 是“向着山顶努力走”，哪怕此刻脚下偏离了方向。

注意

• on-policy：learn和act是一个策略；
• off-policy：learn和act的策略是两个不同的策略。

Q-Learning 虽然同样以五元组为基础进行更新，但它与 SARSA 的核心区别在于目标值的计算方式

更新公式分析

• Sarsa（On-policy）：更新当前这一步的 Q 值，是基于我实际上走了哪一步后的回报进行估计的。
  • 行为策略 = 目标策略（on-policy），强调对当前实际行为后果的总结，更新更保守。
• Q-Learning（Off-policy）：虽然实际走了某一步，但在更新时假设自己下次一定选最优动作，来估算未来收益。
  • 行为策略 ≠ 目标策略（off-policy），强调对理想最优行为的推演，更新更激进。

设计实际任务

• 想要保守一点、减少因为过度乐观导致的风险：用 SARSA；
• 想要快点学出最优策略，能承受一定的不稳定性：用 Q-Learning。

Q-Learning 和 SARSA，分别是理想主义者（总假设下一步是是最优的完美行为）和现实主义者（承认自己会犯错）的代名词。

Q-Learning 虽然在小规模离散状态空间中非常有效，但在面对大规模或连续空间问题时暴露出一些关键缺陷

• Q值通过查表方式保存，在连续和高维情况下，表变得很大，容易导致 “维度灾难”；
• 表格型方法不能对未见过的状态进行推理；
• 学习过程的不稳定与过估计现象。

DQN

为了解决这些问题，DeepMind 在 2015 年提出了 Deep Q-Network（DQN），开启了深度强化学习的新时代。

Q-Learning 是由 Christopher J.C.H. Watkins 于 1989 年在其博士论文中首次提出的，为后续的 深度 Q 网络（DQN） 奠定了基础，是强化学习史上的一个重要里程。

2015 年，DeepMind 发布的里程碑工作 —— Deep Q-Network（DQN）, 一段令人震撼的视频出现在 NeurIPS 的舞台上：智能体盯着一块像素屏幕，不断挥动“球拍”击打上方砖块，逐渐学会打出人类玩家都难以企及的“穿墙打法”。而它的“眼睛”只有像素，“大脑”只是一个深度神经网络。

DQN 首次将深度神经网络成功地应用于强化学习任务中，使得代理人不依赖任何手工特征，仅通过图像像素与奖励信号，就能在 Atari 2600 多款游戏中超越人类水平。这一成就标志着深度强化学习（Deep Reinforcement Learning）的正式崛起。

核心思想：

• 在传统 Q-Learning 中，我们维护一个 Q 表，记录每个状态-动作对的估计价值
• 本质上是一个 有限状态空间下的离散查表操作

DQN 突破点：

• 用神经网络来逼近 Q 函数，取代查表，从而拓展到高维状态空间。

为了解决强化学习中特有的不稳定性和收敛困难，DQN 引入了三项重要机制：

• 1）目标网络（Target Network），设置一个冻结参数的网络 Q(s, a; \theta^-) 来生成目标值 y_t，并每隔若干步将主网络参数复制过去，缓解训练震荡。
• 2）经验回放（Experience Replay），将Agent经历的状态转移 (s, a, r, s’) 存入回放缓存，从中随机采样小批量进行训练，打破样本之间的时间相关性，提升样本利用效率。
• 3）Mini-batch SGD（小批量梯度下降）在每一步中，从经验池中采样一小批数据，用标准的梯度下降优化损失函数，提升训练稳定性。

DQN 不仅在 Atari 游戏中展现惊人实力，还为后续的深度强化学习方法（如 Double DQN、Dueling DQN、Rainbow 等）奠定了基础。

• 为 AlphaGo 提供了关键模块，在 AlphaGo 的自我博弈训练中，动作选择策略网络 和 价值评估网络 都是从 DQN 演化而来的结构；
• AlphaGo Zero 更进一步，采用纯自我对弈训练，完全不依赖人类数据，展示了 RL 的真正潜力。也人们首次看到了AGI的一点点微光。

todo

通往AGI之路：

• 第七境界：双轮驱动 —— Actor-Critic 与 PPO
  • 协同进化，价值与策略共同驱动智能体成长
• 第八境界：动机觉醒 —— 内部奖励与自主探索
  • 从被动响应环境，到主动追寻目标
• 第九境界：社会智能 —— 多智能体与博弈
  • 在合作与竞争中涌现规则、身份与语言
• 第十境界：语言即激励 —— LLM 引导的策略生成
  • 语言不只是观察，更是策略、目标、动机的统一表达

(7) AC 架构: 双轮驱动

REINFORCE 问题

REINFORCE 用一条公式揭示了“好行为应被强化”的朴素逻辑。

然而，这把利剑虽锋利，却也颇为难驾驭。问题出在高方差。

REINFORCE 每次都要等一整个轨迹跑完，用回报来估计梯度，这种全局评估带来了巨大的不确定性。

• 一次好运或厄运，可能让策略更新方向偏离应有的轨迹。
• 就像一个学生考试只看总分，不管过程细节，很难知道哪道题做对了，哪里需要改进。

需要一种更细腻、更稳定的评估方式：能不能在每一步都告诉策略“这个动作值不值”？”

答案: 引入 Critic（评论家），为每个状态—动作组合打分。

这样，策略（Actor）不再孤军奋战，而是在价值函数的引导下，沿着更合理的方向前进。

这就是 Actor-Critic方法诞生的契机。融合了策略优化与价值评估的优点，开启了强化学习“双轮驱动”的新时代。

AC

Actor-Critic：双轮协作的智慧进化

策略梯度方法（如 REINFORCE）虽然直观易懂，能够直接从回报中学习策略，但其训练过程常常面临高方差问题。

原因: 采用 Monte Carlo 方式估计回报，即整条轨迹跑完后，用总回报 来更新策略。

这种“轨迹级”的更新方法对每一步动作的反馈过于粗糙（因为，在这个动作之后，还有很多未来随机因素影响最终总回报），训练效率低下，稳定性也较差。

• 

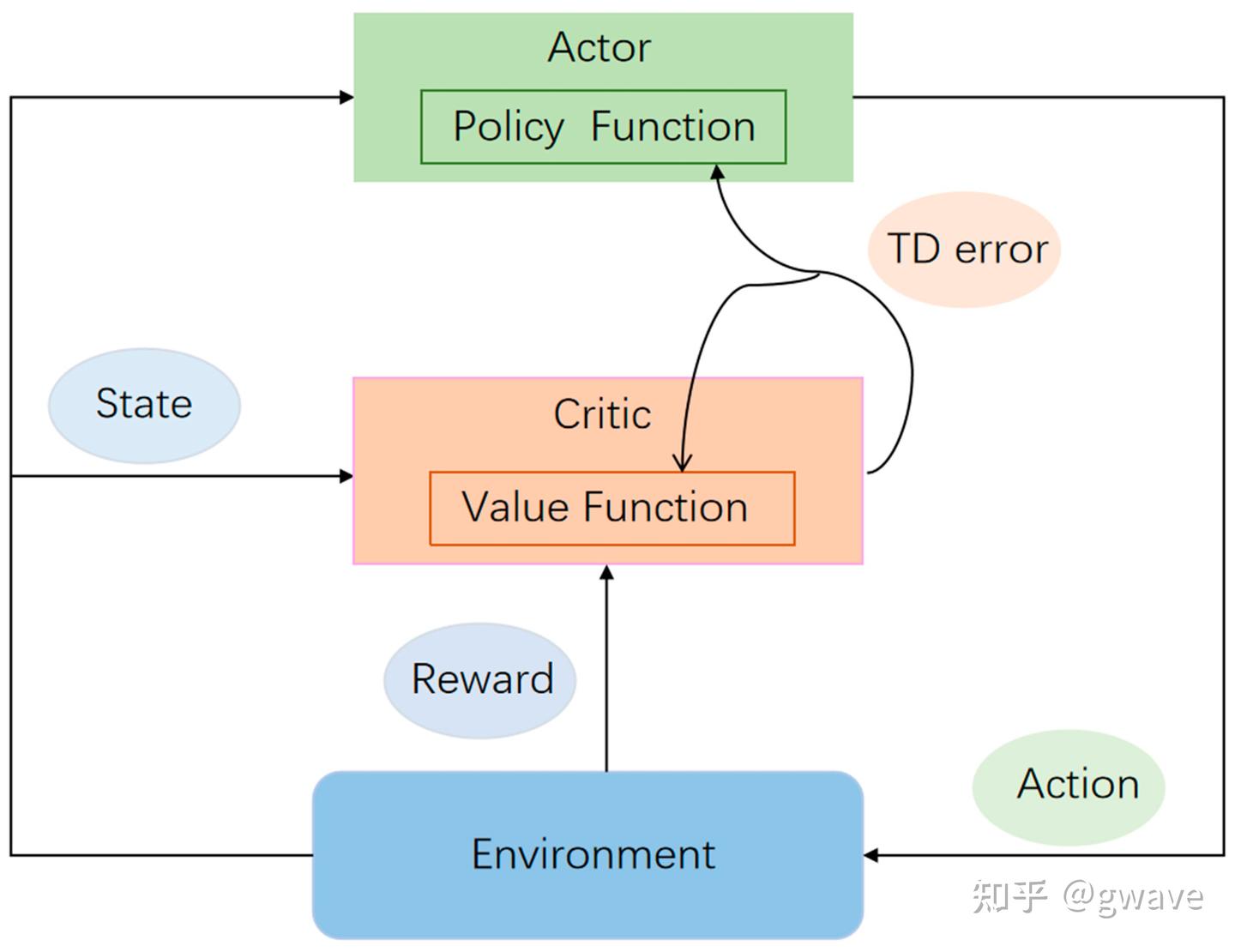
因此，引入新的“评审”——Critic，与策略网络 Actor 形成了协同工作的一对网络：

• Actor 决定采取什么动作，而 Critic 则评估这个动作的价值，并指导 Actor 如何调整策略。

Critic 学习的是值函数（如 V(s) 或 Q(s,a) ），而 Actor 则根据策略梯度公式更新策略，整体思路如下：

“Actor 基于策略梯度学习策略，Critic 通过估计值函数来评估 Actor 的行为好坏。”

这种结构称为 Actor-Critic，实质上是将 REINFORCE 的全轨迹回报替换为使用 TD 学习（Temporal Difference）的 bootstrapping 值，降低了方差（critic使用的值估计平滑了随机性），提高了训练效率（无需等到Episode结束）

• deep-rl-a2c
• 

AC vs GAN

Actor-Critic 架构在结构上与生成对抗网络（GAN）相似。虽然分别诞生于强化学习和生成建模两个领域，但都体现出“两个网络协同博弈、彼此驱动学习”的核心思想。

• Actor-Critic 中，Actor 是策略网络，负责生成动作；Critic 是评估器，判断当前动作是否“值得鼓励”。
  • Actor 根据 Critic 的反馈调整自己的参数，以便未来能做出更优的决策。
• 而在 GAN 中，Generator 生成伪造样本，Discriminator 判别样本真伪。
  • Generator 目标是不断改进生成策略，欺骗Discriminator；
  • 而Discriminator则努力分辨真伪，从而促使Generator学习出更“真实”的分布。
• 换句话说，Actor 相当于 Generator，都负责“动手”；Critic 类似于 Discriminator，负责“动嘴“–打分与反馈。
• 不同:
  • GAN 中的两个智能体相互对抗，是零和博弈（Zero-sum Game)；
  • 而 Actor-Critic 中，二者目标一致，共同最大化整体回报，本质上是一种 合作性博弈（Cooperative Game）。

这种结构与 GAN（生成对抗网络）颇有几分相似：Actor 像生成器，Critic 像判别器。然而不同于 GAN 中的零和博弈，Actor-Critic 中双方目标一致，彼此协作，共同提升策略性能。

二者都属于“双网络博弈”结构，却一个对抗, 一个共生，呈现出不同的学习动态：

• GAN 追求两者博弈下的纳什均衡
• 而 Actor-Critic 并不追求收敛于均衡，而是由 Critic 引导 Actor 攀登策略性能的“回报山峰”。

Actor 与 Critic 是一个合作性博弈系统中的两个子智能体，互为师徒、彼此成就。

• Actor 借 Critic 的眼，看清未来回报的方向；
• Critic 借 Actor 的脚，踏遍环境状态的山河。

从博弈论的角度来看，Actor-Critic 结构可形式化为一种协作型的 Stackelberg 博弈（Stackelberg Game）。在这种博弈中，参与方分为“领导者（Leader）”与“跟随者（Follower）”，两者在策略制定上存在先后顺序，而目标并非相互对抗，而是共同最大化某个全局效用函数。

A2C -> A3C

Actor-Critic 中，Critic 并不直接估计整条轨迹的回报，而是估算 Advantage（优势函数），表示“这个动作相较于平均水平好多少”。

因此，Actor-Critic 方法中其实有两个 “A”：一个是 Actor，一个是 Advantage，这也让它得名 A2C（Advantage Actor-Critic）。

再加上一点工程技巧——并行多个智能体进行异步更新，那么就演化为著名的 A3C（Asynchronous Advantage Actor-Critic），进一步提升了训练效率和稳定性

AC 问题

Actor-Critic 虽然解决了高方差问题，却也引入了新的挑战：

• 价值评估的不稳定可能反过来误导策略更新，尤其是在使用深度神经网络时。

策略梯度和价值估计“双轮驱动”的威力：策略在价值函数的引导下，学习得更快更稳。

然而，A2C 存在一个关键问题是：策略更新可能太激进。

• 由于策略是直接优化的，如果每一步更新幅度太大，模型可能会“遗忘”旧策略，陷入策略崩塌（policy collapse）或训练不稳定的境地。
• 这就像一个演员在评论家的指点下改进表演，但每次改动都太剧烈，反而失去了原本的风格。

仅仅有“轮子”还不够，还要有减震器。

PPO

PPO（Proximal Policy Optimization） 出场, 带“安全带”的策略梯度法，对每一次策略更新都加以限制，防止跳得太远、走得太快。

Proximal Policy Optimization（PPO）在 A2C 基础上，引入“克制更新”的思想，确保每次策略更新都“不过火”，稳步推进。

这种“靠近优化”（Proximal Optimization）策略，主要通过两种方式实现：

• 截断重要性采样比值（Clipped Objective）：约束新旧策略的差异在一个范围内（比如 1.0±0.2），避免过大跳跃；
• 提前终止更新（Early Stopping）：一旦策略偏离旧策略太远，就提前中止梯度更新。

PPO 采用了一种“剪切（Clip）目标函数”的策略优化方式，确保更新过程保持在一个合理范围内，就像在悬崖边为学生装上了护栏，既能大胆尝试，又不至于跌落深渊。

• 
• PPO

PPO 就是“给 Actor 上了安全带”，在 Critic 的指导下小步快跑，成为当前强化学习中最稳定、最实用的策略优化算法之一

相比 REINFORCE 高方差、Actor-Critic 不稳定等问题，PPO 实现了策略优化的“三性统一”：稳定性、效率、收敛性

因此成为深度强化学习中最主流的算法之一，广泛用于游戏智能体、机器人控制和语言模型微调等任务。

其关键改进主要有三点：

• 1）概率比值 (probability ratio)作为策略梯度的调整因子；
• 2）Clip 机制防止策略的激进更新；
• 3）优势函数（Advantage）引导。

PPO 的成功，不仅在于它优化效果好、泛化能力强，更重要的是它让强化学习真正走进了工业界。

今天，无论是游戏、机器人控制，还是大模型对齐训练，PPO 都是主流中的主流。它与 Actor-Critic 的融合，为策略优化奠定了坚实而优雅的基石。

GRPO

传统的 PPO 依赖 Critic 网络估算 V(s)，但对于参数量巨大的 LLMs，这带来了高昂的显存开销和训练复杂度。

DeepSeek 提出 GRPO，其突破在于：

• 弃用价值函数，只用当前模型生成多个候选输出（group sampling），并通过组内平均得分作为 baseline

优势估计（Advantage Estimation）不再依赖 Critic 网络。相反，它通过 组内输出的相对表现 来构建优势函数，从而彻底省去了价值函数的学习。这一设计不仅减少了模型参数和训练成本，还规避了 Critic 带来的高方差估计问题。

与PPO相比，GRPO 优点在于：

• 完全去除 Critic 模块：无需估计状态值或动作值，模型更轻量。
• Variance 更低：组内排序、归一化等方式天然降低了梯度估计的方差。
• 训练收敛更快：适用于大语言模型的自然语言生成任务，尤其在 RLHF 场景中表现良好。

但也存在一定局限性：

• 优势估计精度有限：群体优势只能基于当前 prompt 的 group 表现，缺乏对未来回报的建模，估计可能偏离最优。如果某组（通常容量为 6–8 个回答）的整体质量较差，也就是所有候选答案的奖励都处于一个较低水平，那么 GRPO 的“群体优势”计算就会失真，策略会向着“局部最优”（其实也比较差）的结果收敛，强化劣质输出，只看眼前，看不见长远，不利于多步决策，个人认为这是GRPO的核心短板。
• 对奖励模型高度依赖：如果 Reward Model 本身质量不高或打分不稳定，容易导致策略学习偏移。
• 抗噪性弱：PPO 中 Critic 提供了对 noisy reward 的平滑能力，GRPO 则直接受奖励影响，鲁棒性下降。
• 缺乏 Bootstrapping 能力：无法通过值函数将长期收益回传，难以建模长期依赖任务。
• 策略更新缺乏理论保障：虽然GRPO保留了类似 PPO 的 clipping 结构，其核心仍基于 group 内部排序，缺乏严格理论边界约束，可能出现训练不稳定或过拟合 batch 的问题（特别在Group分布不平衡时）。

(8) 动机觉醒 —— 内部奖励与自主探索

策略优化的核心: “如何更好地学习外部奖励信号”，不管是通过值函数（Actor-Critic）、策略比值（PPO），还是通过相对排序（GRPO），其本质都属于外部驱动（extrinsic motivation） —— 代理被动地追随环境给予的奖励信号。

然而，人类的学习远不止如此。

并非总是依赖外部反馈，有时，会因为好奇、兴趣、挑战自我、保持秩序感，甚至是“完成一件事的快感”而持续学习。

这类无需外部奖励的驱动，称“内在动机”（intrinsic motivation）。

强化学习中，动机觉醒的到来，是对智能体“自主性”的一次觉醒：

• “智能体不仅在寻找最大回报的策略，更在寻找探索世界的理由。”

将内在动机视为一种自我构造的奖励信号，并注入到策略学习过程中

内部奖励有几种常见形式：

• 好奇心（Curiosity）：激励智能体探索模型尚不熟悉的状态（例如基于 prediction error 的 Novelty bonus）。
  • 常见方法如 ICM（Intrinsic Curiosity Module）、RND（Random Network Distillation）等。
• 状态熵（State Entropy）：激励智能体进入高度不确定的状态，鼓励广泛探索，而非陷入局部策略。
  • 代表方法如 MaxEnt RL（最大熵强化学习）。
• 进展/掌控感（Competence / Empowerment）：让智能体学习如何更有效地影响环境、达到目标，而非仅获取即时奖励。

好奇心

人类并不会只因外部奖励而行动。常常因为“想知道接下来会发生什么”而主动去尝试、去探索

这种源自未知与不确定性的内在冲动，被称为好奇心（Curiosity）。

强化学习中，好奇心驱动的探索是一类典型的内在动机机制，其核心思想：

“如果模型当前无法很好预测某个状态的后续变化，那么这个状态就值得探索。”

这种机制为强化学习智能体引入了一种自我监督的方式：

• 即便外部环境没有明确给出奖励，智能体也可以根据自身的预测误差生成“伪奖励”，从而主动进入那些尚未掌握的状态空间。

原理：基于预测误差的内部奖励

• 前向预测器
• 误差函数

代表方法

• Pathak et al. (2017)提出ICM（Intrinsic Curiosity Module），其核心思想：
  • 使用编码器将原始图像状态压缩为特征向量，基于特征空间中的预测误差计算内部奖励，优点是在像素级状态下仍能稳定工作，适用于视觉任务；
• Burda et al. (2018) 提出的RND（Random Network Distillation）随机初始化一个 target 网络，然后训练一个 predictor 网络去逼近它。预测误差越大，表示状态越“新颖”
  • 与 ICM 不同点：RND 不需要前向模型，只基于状态本身的难以预测性，稳定性更强，训练更简单；
• DeepMind 提出的结合 episodic memory + lifelong novelty 的方法NGU（Never Give Up），兼顾短期新颖和长期好奇探索，适合复杂游戏环境（如 Atari、DM Lab）。

近两年，好奇心驱动（curiosity-driven）探索机制的工作仍在持续演进，并展现出更高的稳定性与环境适应性。

2025年，一项系统性研究(The impact of intrinsic rewards on exploration in Reinforcement Learning)对包括 ICM、RND、状态计数等主流好奇心算法进行了统一实验比较，结果表明：

• 这些方法在不同状态空间维度（如图像空间 vs. 低维特征空间）下的性能差异显著，其中基于特征空间预测误差的机制（如 ICM）在高维视觉任务中更具优势，而基于状态新颖度的估计方法（如 RND）在训练稳定性方面表现更优。

好奇心算法预测误差来源

• 2024 年的新方法引入重建误差与未来预测误差的对比分析机制，以区分“暂时不可预测状态”与“结构性新颖状态”，有效避免了传统好奇心方法陷入环境噪声或混乱状态的误导。
• 此外，还有工作将好奇心信号用于指导注意力机制，引导智能体更聚焦于“结构性信息缺失区域”，提高策略更新的样本效率。
• 还有研究尝试将好奇心动态调节为时间折扣因子的函数，提出时间调度式内在动机（Temporal-Scaled Curiosity），使探索行为更加阶段性、任务感知。

好奇心相关研究重点已从“是否探索”向“何时探索、探索何处”过渡，重心从粗糙的预测误差信号，逐步迁移到更稳健、可解释的好奇心建模机制。

这些进展不仅提升了训练效率与策略泛化能力，也让好奇心在更复杂的实际任务（如多阶段视觉导航、策略泛化、多模态输入）中展现出更广泛的适用性。

虽然好奇心机制增强了探索性，但也存在一些典型问题：

• 无意义探索（Noisy TV problem）：预测误差并不总能代表“有价值”的状态，例如电视随机播放的画面预测误差高，但不一定对任务有帮助
• 陷入局部误差陷阱：模型可能会一直尝试在某些“难预测但无意义”的区域刷分
• 与真实奖励冲突：有时好奇心驱动的探索可能干扰主任务的收敛（特别是在 reward 很稀疏的环境下）

应用场景与意义

好奇心驱动的探索尤其适用于以下场景：

• 外部奖励极其稀疏（Sparse Reward）的任务
• 无监督预训练（如世界模型、自监督强化学习）
• Open-ended exploration，例如游戏、机器人导航

更进一步，好奇心机制也被视为迈向“自主智能体”的关键一步 —— 它赋予了智能体一种“自我生成任务”的能力，从而不再完全依赖外部信号。

状态熵

状态熵与最大熵强化学习：从最优行为到信息量最大的行为

如果说好奇心方法旨在发现“新奇”状态，那么最大熵强化学习（Maximum Entropy Reinforcement Learning, MaxEnt RL）在策略层面鼓励“保持不确定性”——即让智能体在执行策略时，不仅追求回报最大化，还希望保有足够的行为多样性与探索性。

算法

• Soft Actor-Critic (SAC)：结合 actor-critic 结构与最大熵目标，在离线/连续控制任务中表现优异；
• REDQ (Randomized Ensemble Double Q-learning)：强化 Q 函数的估计鲁棒性，在最大熵目标下展现更高样本效率；
• AWAC (Advantage Weighted Actor-Critic)：将离线数据用于加权策略改进，引入最大熵目标以提升探索多样性。

此外，最大熵思想也被用于联合奖励与好奇心信号的融合场景，例如将外部奖励与内部奖励共同建模为最大熵下的目标分布。

最大熵方法从策略空间角度出发，不再关注某一个“最优行为”，而是学习一组“高信息量”的行为分布，让智能体具备更多选择的自由度。

这种自由度恰恰是智能“自主性”的体现：当任务不确定、奖励稀疏时，熵项鼓励智能体大胆尝试不同行为；当策略逐渐收敛时，智能体则能自然减少探索，向目标聚焦。

总之，最大熵强化学习为智能体赋予了更强的“行动开放性”，在动机觉醒的过程中，不再只是为了奖励而行，而是为了学习和保留更丰富的行为策略。

进展感/掌控感

进展 / 掌控感（Competence / Empowerment）

如果说“好奇心”驱动智能体探索未知的世界，那么进展感（Competence）与掌控感（Empowerment），则体现了智能体在环境中逐步建立主观能动性的过程。

标志着智能体不再只是“被动感知”，而是在主动尝试“影响世界”。

与传统内在动机机制（如新颖性、预测误差）不同，Empowerment 和 Competence 不再仅关注“不确定”与“意外”，而是转向一种更深层的思考：我能对世界产生多大的影响？我能实现什么样的成长？

• 掌控感（Empowerment）：信息论视角下的“影响力渴望”
  • Empowerment 起源于信息论，其核心思想是：智能体倾向于选择那些能带来更多未来可能性的状态，也即最大化“自身的潜在影响力”。
  • 越是“掌控未来”的状态，越值得前往
• 进展感（Competence Progress）：目标导向的“能力递增”
  • 相比之下，Competence 更强调“目标导向性学习”：智能体是否能完成一个个逐步升级的任务，是否在这个过程中感受到自己的成长。
  • 代表 Curriculum Learning（课程式学习）

Curriculum Learning（课程式学习）中：

• 智能体先完成简单任务；
• 然后被引导去挑战更高难度；
• 每一次完成，都会强化其“我能做到”的信念；

很多 Competence 机制会将目标可达性（goal achievability）纳入奖励函数——智能体不是被鼓励去“尝试”，而是被鼓励去“做到”。

(9) 社会智能 —— 多智能体与博弈

传统强化学习聚焦于单智能体与环境之间的交互。

然而，真实世界往往是由多个智能体组成的复杂系统，无论是蚂蚁群体觅食，还是人类社会协作决策。

这促使多智能体强化学习（Multi-Agent Reinforcement Learning, MARL）应运而生。

MARL

MARL 框架下，环境不再静态，其他智能体的行为也构成环境的一部分。

这一转变不仅带来了非平稳性（Non-stationarity）问题，也为智能体提供了更丰富的交互可能性。合作、竞争与协同策略成为智能体学习的核心课题。

分类

1. 合作型（Cooperative）: 共享目标，并最大化全体的总奖励
   • 多机器人系统、协同导航、无人机编队等场景。
2. 对抗型（Competitive）: 博弈或敌对环境中，智能体之间存在明确的竞争关系，彼此试图最大化自身收益的同时最小化对手的得分，常见于零和博弈（Zero-Sum Game）设置中。
   • 典型案例包括棋类游戏（如围棋、国际象棋）或其他敌对性的策略博弈场景。
3. 混合型（Mixed-Interest）: 既有合作又有冲突的动态关系，其中智能体之间的目标部分一致、部分对立。在这类环境中，智能体可能需要在“结盟”与“对抗”之间权衡。
   • 常见于诸如金融交易（Trading）、城市交通调度（Traffic Systems）、以及多玩家电子游戏等复杂交互场景。

多智能体强化学习（MARL）的三种典型学习范式：

• (a) 集中训练、集中执行（Centralized Training and Centralized Execution, CTCE）：在该范式中，所有智能体共享统一的策略网络，该策略适用于所有个体的行为决策。可以将 n 个智能体整体视作一个“虚拟的大智能体”进行建模与训练。尽管实现简单，但其适用性有限，通常仅适用于完全可观测、同质智能体的静态环境中。
• (b) 集中训练、分散执行（Centralized Training with Decentralized Execution, CTDE）
  • 当前最常见且最流行的学习范式。在训练阶段，智能体可以访问全局信息，如其他智能体的观察、动作或隐藏状态，从而提升训练稳定性和策略优化效率；而在执行阶段，系统回归到分布式结构，每个智能体只能基于自身的局部观察独立做出决策，无法访问他人信息。CTDE 在保证可扩展性和泛化能力的同时，兼顾训练效率与执行灵活性，广泛应用于协作、多机器人控制、竞技博弈等场景中。
• (c) 分散训练、分散执行（Decentralized Training and Decentralized Execution, DTDE）
  • 完全分散式学习（Fully Decentralized Learning）中，每个智能体在训练和执行过程中都无法获取任何其他智能体的信息，完全独立地更新自身策略。其训练目标仍是最大化全局团队奖励，因此需在缺乏协作信号的情况下学习出可协调的策略。该范式适用于高可扩展性要求的复杂环境，尤其是包含合作-竞争混合动机（mixed-interest）或智能体数量极大的场景（如 Swarm 系统）。
  • 然而，DTDE 也带来了显著挑战，尤其是环境非平稳性问题：由于其他智能体在不断学习和更新策略，对于任意一个个体而言，环境动态是不断变化的，这使得学习过程更加不稳定、收敛更困难。

算法

• 价值分解网络（VDN）
  • 价值分解网络（Value Decomposition Networks） 是一种应用于多智能体场景的算法，适用于集中训练、分散执行（CTDE）的范式
• QMIX: VDN（Value Decomposition Networks） 提出的价值函数分解方法基础上发展而来的。两者在基本思想上保持一致：均采用联合动作价值函数（Joint Action-Value Function）因式分解策略，将全局 Q 值拆解为多个智能体的个体 Q 值，从而支持去中心化执行（Decentralized Execution）。这种设计使得每个智能体在执行阶段仅需依赖自身的局部观测和个体价值函数即可独立决策，无需访问其他智能体的信息或全局状态。
• Swarm RL: 高度去中心化的组织形式，其中每个智能体仅依赖自身的局部观测，并与邻近的智能体进行信息交互，无需全局控制器或集中式通信机制而进行自组织。

与单智能体相比，MARL面临以下挑战：

• 非平稳性（Non-Stationarity）
  • 在多智能体场景中，由于其他智能体的存在，每个智能体所处的环境变得动态化。随着智能体不断更新其策略，从任意智能体的视角来看，环境的动态特性也随之发生变化。
  • 这违反了马尔可夫性质（Markov Property），因为状态转移概率和奖励函数不再是固定不变的。每个智能体的最优策略会随着他人行为的调整而改变，导致学习过程出现不稳定性。
• 部分可观测性（Partial Observability）
  • 大多数多智能体环境中，智能体无法获得对环境状态或其他智能体动作的完整观察。每个智能体只能观测到环境的一部分，从而在决策过程中引入了不确定性。
  • 此时问题变为一个部分可观测马尔可夫决策过程（POMDP），智能体需要在信息不完整的情况下进行推理和决策。
  • 这增加了策略学习的难度，因为智能体不仅要应对环境的不确定性，还需要预测其他智能体的行为。
• 可扩展性与联合动作空间（Scalability and Joint Action Space）
  • 随着智能体数量的增加，联合动作空间呈指数级增长。对于 n 个智能体，其动作集合分别为 A1,A2,…,An，那么联合动作空间为 (A1xA2x…xAn)
  • 这一状态-动作空间的扩展显著增加了计算复杂度，使得传统强化学习方法效率大大降低。当智能体数量增加时，寻找最优策略将变得不可计算，从而需要更具可扩展性的学习算法。
• 归因分配问题（Credit Assignment）
  • 多智能体场景中，归因分配问题指的是如何确定每个智能体的动作对整个团队目标的贡献程度。
  • 该问题在合作场景中尤为复杂，因为多个智能体必须共同努力来最大化一个共享的全局奖励。
  • 传统方法往往难以准确评估个体贡献，通常只是将全局奖励粗略地分解为个体效用，而未考虑每个智能体的行为是否从全局角度来看是最优的。

(10) 语言即世界– LLMs × RL 的闭环共舞

语言的边界，就是我们所能思考与理解的世界的边界。

• – 维特根斯坦《逻辑哲学论》（Tractatus Logico-Philosophicus）

解决语言的问题，也许正意味着解决智能的问题。

但若转向诺奖得主丹尼尔卡尼曼的“双系统理论”，今天的 LLMs 更像是系统1——直觉、快速、擅长模式识别，却缺乏系统2所代表的缓慢、推理、逻辑演绎与计划。智能的另一半——深度认知与目标导向行为——仍有待补全。

• 
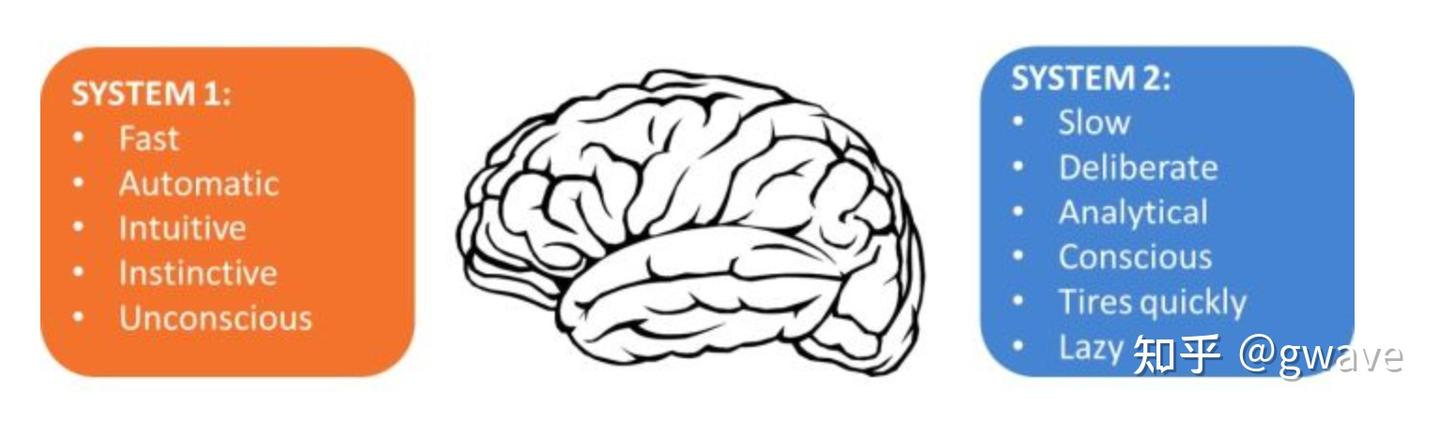
• 当语言不再仅传递意义，而开始驱动选择、塑造偏好、生成奖励时，语言本身便成为了智能的核心能量——语言即激励，语言即行动。

LLM4RL

“世界是事实的总和，而非事物的总和。”

维特根斯坦在《逻辑哲学论》中这句话，开启了语言哲学的一个高峰：

• 语言不仅是沟通工具，更是我们构建世界的方式。

在过去的 AI 发展历程中，语言始终被当作“输入”或“输出”处理——我们用语言提问，机器给出回答，仿佛语言只是一种接口。

而现在，这种认知正在被颠覆。大语言模型（LLMs）不仅能够理解语言，还能生成复杂的思维路径、指令结构、推理链条，甚至激发人类行动。当我们开始用语言让 AI 设计奖励函数、调整偏好结构、规划未来行为，语言就不再是“内容”，而是“动因”。

语言从世界的描述者，变成了世界的塑造者。这正是“语言即激励”的第一重意义：语言不再是智能系统的终点，而是它的起点。

认知注入的智能体范式

LLM-enhanced Reinforcement Learning 指的是将预训练大语言模型（LLMs）所具备的多模态理解、推理生成、高阶认知能力，引入强化学习（RL）框架中，作为智能体认知能力的增强模块。这一方法与传统的基于模型的强化学习（Model-based RL）最大的区别在于，它引入了知识密集型的通用模型作为认知先验。这一范式带来三大核心优势：

1. 起点即高点：认知能力预注入: 得益于 LLM 的预训练能力，RL 智能体在“出生”时便具备了高阶认知，比如推理、规划、总结与抽象等，而不是从零开始在环境中试错学习。
2. 强泛化：跨域迁移的能力: 传统 RL 模型大多是“数据驱动”，而 LLM 是“知识驱动”。它们经过大规模多领域语料训练，具有良好的迁移能力，能够帮助智能体在新任务、新环境中迅速适应，而无需从头训练。
3. 交互补强：克服语言模型的“静态性”: 预训练语言模型的最大限制在于：它们无法主动与环境互动，无法持续学习、校正知识偏差。而 RL 框架恰好弥补了这一点——智能体通过与环境交互生成任务相关的数据，在上下文中“喂给” LLM，从而实现“in-context grounding”；LLM 在任务环境中被动态塑造和微调，从静态生成器转化为自我优化的认知体。

LLM 功能

• 充当信息处理器
• 奖励设计器
• 决策制定
• 生成建模

还有尚未被强化学习社区广泛接纳的重要思想

• “贝叶斯大脑”（Bayesian Brain）
• “自由能原理”（Free Energy Principle）。

它试图将智能的本质建构为一种最小化预测误差的主动推理机制，在哲学、神经科学和机器学习之间搭起了一座桥梁。

但由于其尚不成熟（如马尔可夫毯遭挑战）、工程路径不清晰，目前仍处于理论研究的前沿。

结束