- 强化学习
- AI 发展
- 什么是强化学习
- 基本组件
- 概念
- 分类
- 环境
- 基本概念
- DP 动态规划 – 前提: 环境(MDP)已知
- TD 时序差分 – 与DP互补
- 算法总结
- 蒙特卡洛
- Q-learning
- DQN
- PG
- DPG
- DDPG
- AC
- PPO (TRPO改进)
- 基于模型的RL
- 模仿学习
- HRL
- 多智能体强化学习
- 问题
- 资料
- 结束
强化学习
AI 发展
详见站内专题:强化学习进化史
什么是强化学习
机器学习领域,有一类重要的任务和人生选择很相似,即序贯决策(sequential decision making)任务。
决策和预测任务不同
- 决策往往会带来“后果”,因此决策者需要为未来负责,在未来的时间点做出进一步的决策。
- 实现
序贯决策的机器学习方法就是强化学习(reinforcement learning)。
- 实现
- 预测仅仅产生一个针对输入数据的信号,并期望它和未来可观测到的信号一致,这不会使未来情况发生任何改变。
面向决策任务的强化学习和面向预测任务的有监督学习在形式上是有不少区别的。
- 首先,决策任务往往涉及多轮交互,即序贯决策;而预测任务总是单轮的独立任务。如果决策也是单轮,那么可以转化为“判别最优动作”的预测任务。
- 其次,因为决策任务是多轮的,智能体就需要在每轮做决策时考虑未来环境相应的改变,所以当前轮带来最大奖励反馈的动作,在长期来看并不一定是最优的。
- 强化学习笔记
- 大模型中的强化学习
强化学习定义
强化学习思想:智能体(agent)通过与复杂不确定的环境(environment)的交互(其实就是试错),得到极大化的奖励(可正可负,负的奖励就是惩罚)作为反馈,从而做出对应的动作(action)。通过感知所处环境的 状态(state) 对 动作(action) 的反应(reward),来指导更好的动作,从而获得最大的 收益(return),这被称为在交互中学习,这样学习方法是强化学习。
这个思想很符合自然经验,小时候学走路,摔了会痛(奖励为负),走得稳了有糖吃(奖励为正),为了多吃点糖(取得更多的奖励),最终学会了走路。
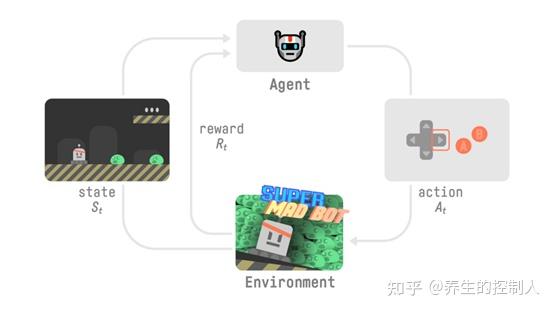
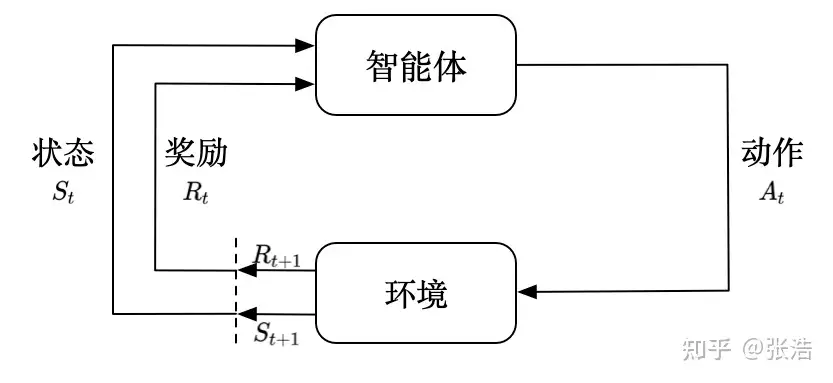
- 接下来给出强化学习的正式定义:
Reinforcement learning is a framework for solving control tasks (also called decision problems) by building agents that learn from the environment by interacting with it through trial and error and receiving rewards (positive or negative) as unique feedback.
强化学习(Reinforcement Learning, RL)拥有两大关键特征:
- 一是通过持续试错搜索(trial-and-error)来发现最佳行为
- 二是面临延迟回报(delayed reward)的挑战
强化学习与机器学习
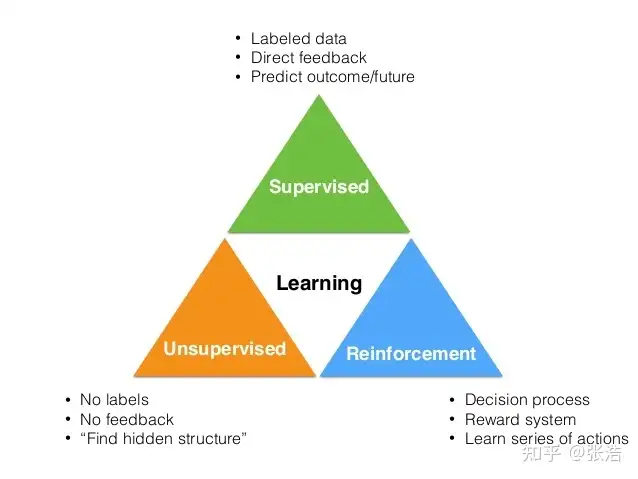
强化学习是除了监督学习和非监督学习之外的第三种基本的机器学习方法。
监督学习是从外部监督者提供的带标注训练集中进行学习。 (任务驱动型)非监督学习是一个典型的寻找未标注数据中隐含结构的过程。 (数据驱动型)强化学习更偏重于智能体与环境的交互, 这带来了一个独有的挑战 ——“试错(exploration)”与“开发(exploitation)”之间的折中权衡,智能体必须开发已有的经验来获取收益,同时也要进行试探,使得未来可以获得更好的动作选择空间。 (从错误中学习)
强化学习主要有以下几个特点:
试错学习:强化学习一般没有直接的指导信息,Agent 要以不断与 Environment 进行交互,通过试错的方式来获得最佳策略(Policy)。延迟回报:强化学习的指导信息很少,而且往往是在事后(最后一个状态(State))才给出的。比如 围棋中只有到了最后才能知道胜负。
强化学习(RL)VS 有监督微调(SFT)
RL的必要性
- 第一点,RL相比SFT, 考虑整体影响。
- SFT是针对单个token进行反馈,目标是模型给出确切答案;
- 而RL是针对整个输出文本进行反馈,并不针对单个token。
- 这种反馈粒度的不同,使得RL既可以兼顾表达的多样性,又可以增强对微小变化的敏感性。由于自然语言的灵活性,相同的语义可以用不同的方式表达,SFT很难兼顾,而RL可以允许模型给出不同的多样性表达。
- 此外SFT采用交叉熵损失,由于总和规则,总的Loss对个别词元的变化不敏感,也就是说改变个别词元对整体损失影响较小,但是在语言中,一个否定词就可以完全改变文本的整体含义。RL可以通过奖励函数同时兼顾多样性和微小变化敏感性两个方面。
- 第二点,RL更容易解决幻觉问题。
- 模型不知道答案的情况下,SFT会促使模型给出答案。
- 而使用RL则可以通过定制奖励函数,使得正确答案有很高的分数,放弃回答或回答不知道有中低分数,不正确的回答有非常高的负分,这样模型可以依赖内部知道选择放弃回答,从而缓解幻觉问题。
- 第三点,RL更好地解决多轮对话奖励累计问题。
- 多轮对话的好坏,要考虑多次交互的整体情况,很难用SFT的方法构建,而使用RL,可以通过构建奖励函数,根据整个对话的背景及连贯性对当前模型输出的优劣进行判断。
NLP RL
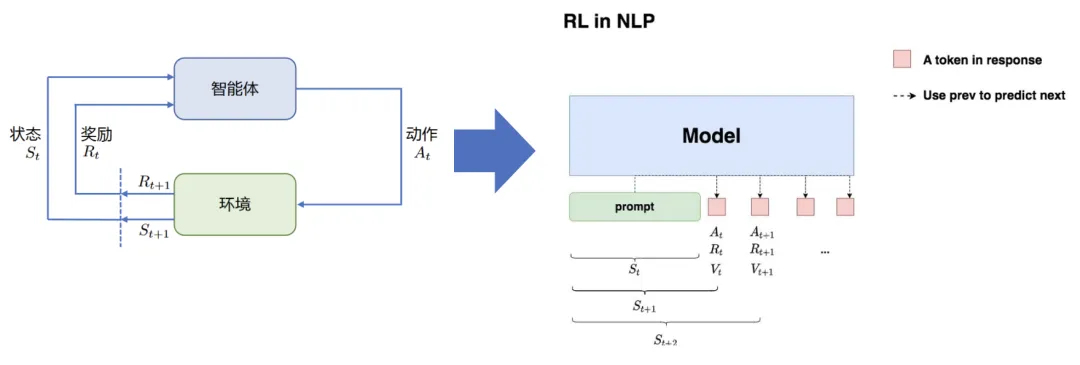
NLP RL
- 状态S:输入prompt
- 动作A:输出response(即LLM输出下一个token)
- 奖励R:根据prompt+response进行奖励模型打分
- 整体目标:给定prompt,调整policy,生成符合人类喜好(RM偏序信号)的response
基本组件
智能体有3种关键要素,即感知、决策和奖励。
感知:智能体在某种程度上感知环境状态,从而知道自己所处的现状。例如,下围棋的智能体感知当前的棋盘情况;无人车感知周围道路的车辆、行人和红绿灯等情况;机器狗通过摄像头感知面前的图像,通过脚底的力学传感器来感知地面的摩擦功率和倾斜度等情况。决策:智能体根据当前状态计算出达到目标需要采取动作的过程叫作决策。例如,针对当前的棋盘决定下一颗落子的位置;针对当前的路况,无人车计算出方向盘的角度和刹车、油门的力度;针对当前收集到的视觉和力觉信号,机器狗给出4条腿的齿轮的角速度。策略是智能体最终体现出的智能形式,是不同智能体之间的核心区别。奖励:环境根据状态和智能体采取的动作,产生一个标量信号作为奖励反馈。这个标量信号衡量智能体这一轮动作的好坏。例如,围棋博弈是否胜利;无人车是否安全、平稳且快速地行驶;机器狗是否在前进而没有摔倒。最大化累积奖励期望是智能体提升策略的目标,也是衡量智能体策略好坏的关键指标。
在强化学习过程中,智能体跟环境一直在交互。智能体在环境里面获取到状态,智能体会利用这个状态输出一个动作,一个决策。然后这个决策会放到环境之中去,环境会根据智能体采取的决策,输出下一个状态以及当前的这个决策得到的奖励。智能体的目的就是为了尽可能多地从环境中获取奖励。
基本元素
环境(Environment) 是一个外部系统,智能体处于这个系统中,能够感知到这个系统并且能够基于感知到的状态做出一定的行动。智能体(Agent) 是一个嵌入到环境中的系统,能够通过采取行动来改变环境的状态。状态(State)/观察值(Observation):状态是对世界的完整描述,不会隐藏世界的信息。观测是对状态的部分描述,可能会遗漏一些信息。动作(Action):不同的环境允许不同种类的动作,在给定的环境中,有效动作的集合经常被称为动作空间(action space),包括离散动作空间(discrete action spaces)和连续动作空间(continuous action spaces),例如,走迷宫机器人如果只有东南西北这 4 种移动方式,则其为离散动作空间;如果机器人向 360◦ 中的任意角度都可以移动,则为连续动作空间。奖励(Reward):是由环境给的一个标量的反馈信号(scalar feedback signal),这个信号显示了智能体在某一步采 取了某个策略的表现如何。
【2023-5-1】智能体与环境交互学习过程
强化学习强化学习系统由智能体(Agent)、环境(Environment),以及 状态(state)、奖赏(reward)、动作(action)五部分组成。
Agent:智能体是整个强化学习系统核心,感知环境的状态(State),并且根据环境提供的奖励信号(Reward),通过学习选择合适动作(Action),来最大化长期的奖励值。- Agent 根据环境提供的 Reward作为反馈,学习一系列环境
状态(State)到动作(Action)映射 动作选择的原则: 最大化未来累积奖励的概率。选择的动作不仅影响当前Reward,还会影响下一时刻甚至未来的Reward- 因此,Agent 学习过程的基本规则:如果某个
动作(Action)带来了环境的正回报(Reward),那么这一动作会被加强,反之则会逐渐削弱,类似于物理学中条件反射原理。
- Agent 根据环境提供的 Reward作为反馈,学习一系列环境
Environment:环境接收Agent 的一系列的动作(Action),并且对动作的好坏进行评价,并转换成一种可量化的(标量信号)Reward 反馈给Agent,而不会告诉Agent应该如何去学习动作。- Agent只能靠自己的历史(History)经历去学习。同时,环境还像Agent提供它所处的状态(State)信息。
Reward:环境提供给Agent的一个可量化的标量反馈信号,用于评价Agent在某一个时间步所做action的好坏。- `强化学习就是基于一种最大化累计奖赏假设:强化学习中,Agent进行一系列的动作选择的目标是最大化未来的累计奖赏。
State:状态指Agent所处的环境信息,包含了智能体用于进行Action选择的所有信息,它是历史(History)的一个函数:St = f(Ht)。
强化学习的主体是Agent和环境Environment。
Agent为了适应环境,做出的一系列的动作,使最终的奖励最高,同时在此过程中更新特定的参数。实际上可以把强化学习简单理解成是一种循环,具体工作方式如下:
智能体从环境中获取一个状态St;智能体根据状态St采取一个动作at;- 受到at的影响,
环境发生变化,转换到新的状态St+1; 环境反馈给智能体一个奖励(正向为奖励,负向则为惩罚)。- 动作空间
- 动作空间为在一个环境中所有可能动作的集合,可以是离散空间,比如有的游戏只能上下左右移动,也可以是连续空间,比如自动驾驶时的转角可能是无穷的。
- 奖励与折扣
- 奖励就是反馈,让agent知道动作是好是坏,每个时刻的累积奖励可以写为
- 其中τ代表状态和动作的序列。但是实际上并不直接这样相加,因为预测太远的事情总是不准的,一般选择更看重眼前的奖励,所以需要对未来的奖励进行衰减
- 其中γ是衰减因子, 权衡对长远奖励的重视程度。
- 奖励就是反馈,让agent知道动作是好是坏,每个时刻的累积奖励可以写为
- 强化学习假设
- ① 奖励假说:所有目标可被描述为最大化期望回报,为了做出最好的决策,需要去最大化期望回报。
- ② 马尔可夫决策过程:agent每次只需根据当前的状态就能做出决策,而不依赖于过去的状态和动作信息。
- 强化学习的任务有两类:
- 周期任务(比如玩
超级玛丽,每次从一条新的生命开始,直到游戏人物死亡或者到达终点结束) - 连续任务(比如自动化股票交易,没有起始和终点,agent在做出做好决策的同时不断和环境进行交互)
- 周期任务(比如玩
- Exploration/ Exploitation 探索/利用权衡
- Exploration 探索更多的环境信息,Exploitation利用已知的环境信息最大化奖励。
- 强化学习中,既要Exploration又要Exploitation,这样才能做出更好的决策。
- 饭店选择:
- Exploration 去尝试没吃过的饭店,可能会踩雷,但是也可能挖掘到更好吃的饭店!
- Exploitation就是每天去知道的饭店吃饭,但这样可能错过一些更好吃的饭店。
强化学习里面的“Model”指 S->S’的概率分布,即在当前状态下实施某个动作会抵达什么新状态。
Model-free 设定中,不知道S-S’的概率分布,那么怎么才能得到v或者q呢?很简单,做取样(sampling
概念
总结
Episodes是智能体与环境之间一次完整的交互过程。Rollouts是在训练过程中,智能体根据当前策略进行的一系列模拟交互步骤,用于收集数据和评估策略。一个rollout可以包含一个或多个episodes的数据。
step 步骤
step:“步骤”,一个epoch中, 模型一次参数更新的操作。
神经网络训练过程中,每次完成对一个batch数据的训练,就完成了一个step。
很多情况下,step和iteration含义相同。
iteration 迭代
iteration:“迭代”,训练过程中经过一个step的操作。
一个iteration包括step中前向传播、损失计算、反向传播和参数更新的流程。
当然,有时 step和iteration可能会有细微的区别
- iteration 指完成一次前向传播和反向传播的过程
- 而step 指通过优化算法对模型参数进行一次更新的操作。
但是绝大多数情况下,二者一样
Epoch 轮次
epoch:
- 将训练数据集中的所有样本都过一遍(且仅过一遍)的训练过程。
一个epoch中,训练算法会按照设定顺序, 将所有样本输入模型进行前向传播、计算损失、反向传播和参数更新。
一个epoch通常包含多个step
batch 批次
batch:“批次”,一次性输入模型的一组样本。
神经网络的训练过程中,训练数据往往很多,比如几万条甚至几十万条
如果全部放入模型,对计算机性能、神经网络模型学习能力等的要求太高了;那么就可以将训练数据划分为多个batch,并随后分批将每个batch的样本一起输入到模型中进行前向传播、损失计算、反向传播和参数更新。
注意: 一般batch这个词用的不多,多数情况大家都只关注batch_size。
batch size:“批次大小”,训练过程中一次输入模型的一组样本的具体样本数量。
神经网络训练过程中,往往需要将训练数据划分为多个batch;而具体每一个batch有多少个样本,那么就是batch size指定的了。
Episodes(片段)
episode 指智能体(Agent)与环境(Environment)之间1次完整的交互序列。
- 这个序列从
智能体开始, 观察环境状态开始,然后, 根据策略选择一个动作并执行,环境会给出新的状态和奖励,这个过程会一直重复,直到达到某种终止状态,比如游戏结束、任务完成或达到预定的步数。 - 每个episode 独立,结束后, 会重置环境, 并开始新的episode。
例如
- 简单的迷宫游戏中,一个episode可能包括智能体从起点开始,经过一系列的移动,最终达到终点的整个过程。
Rollouts(模拟轨迹)
Rollouts 指执行策略梯度或其他基于模拟的强化学习方法时,智能体在环境中进行系列模拟交互步骤。
这些步骤用于收集数据,以评估或改进当前的策略。
一个 rollout 包含一个或多个完整的episodes,或者只是一个episode的一部分(在实际应用中,通常一个rollout只包含一个episode的数据 )。
训练过程中,可能会执行多个rollouts来收集足够的数据,以便更新智能体的策略。
每个rollout都会根据当前的策略生成一组新的交互数据(状态、动作、奖励等 ),这些数据随后用于计算梯度并更新策略。
分类
【2023-2-9】强化学习入门:基本思想和经典算法
强化学习算法种类繁多,可按图示粗略分类。
PPO算法是无模型的强化学习算法,属于策略优化类算法,并且是on-policy的。
对这些概念进行介绍,让大家对PPO算法有一个更好的认识。这些概念一共可分为三组,分别是:
- 基于模型的强化学习(Model-based RL)、无模型的强化学习(Model-free RL);
- 基于策略的强化学习(Policy-based RL)、基于值的强化学习(Value-based RL,即图中Q-leranng);
根据问题求解思路、方法的不同,将强化学习分为基于模型的强化学习(Model-based RL)、无模型的强化学习(Model-free RL)
- “模型”是对环境进行建模,具体而言,是否已知其知和,即和的取值。
环境是否已知:Model-based vs Model-free
强化学习中“模型”指与智能体交互的环境模型,即对环境的状态转移概率和奖励函数进行建模。
根据是否具有环境模型,强化学习算法分为两种:基于模型的强化学习(model-based reinforcement learning)和无模型的强化学习(model-free reinforcement learning)。
Model-free无模型的强化学习:不去学习和理解环境,环境给什么就是什么- 根据 智能体与环境交互采样到的数据,直接进行策略提升或者价值估计
- 两种时序差分算法,Sarsa 和 Q-learning 算法,便是
无模型的强化学习方法。
Model-Based基于模型的强化学习: 学习和理解环境,用模型模拟环境得到反馈, 然后辅助做策略提升或者价值估计。- 模型可以事先知道,也可根据智能体与环境交互采样到的数据学习得到
- 两种动态规划算法,即
策略迭代和价值迭代,则是基于模型的强化学习方法,环境模型事先已知。 - 示例: Dyna-Q 算法,不过环境模型是通过采样数据估计得到的。
| 分类 | 类型 | 解释 | 样本复杂度 | 期望回报 | 应用范围 | 算法案例 | |
|---|---|---|---|---|---|---|---|
Model-free |
无模型 | 不去学习和理解环境,环境给什么就是什么 | 高 | 高 | 广 | Sarsa, Q-learning, policy 系列 | |
Model-Based |
有模型 | 学习和理解环境,用模型模拟环境得到反馈 | 低 | 低 | 窄 | Dyna-Q |
强化学习算法评价指标:
- 算法收敛后的策略在初始状态下的期望回报
- 样本复杂度,即算法达到收敛结果需要在真实环境中采样的样本数量。
Model-free 以及 Model-based 最大区别:是否有对环境建模, 即 环境模拟,通过模拟环境预判发生的所有情况,然后选择最佳。
基于模型的强化学习算法具有环境模型,智能体可以额外和环境模型进行交互,对真实环境中样本需求量减少,因此比无模型的强化学习算法具有更低的样本复杂度。
但是,环境模型可能并不准确,不能完全代替真实环境,因此基于模型的强化学习算法收敛后其策略的期望回报可能不如无模型的强化学习算法。
一般环境不可知,所以主要研究无模型问题。
Model-free
Model-free 算法根据表示方式分类。
划分为3个类别:
- Critic-only
- Actor-only
- Actor-critic
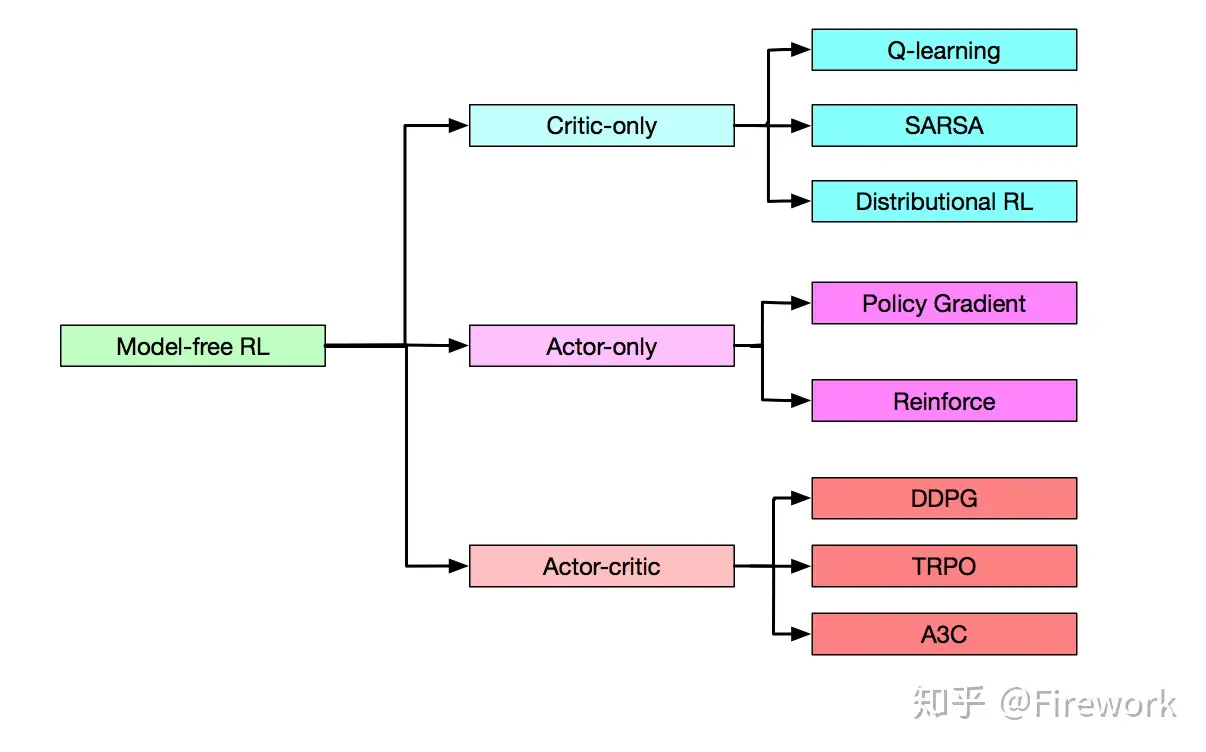
或根据模型学习特性区分:
- On-policy
- Off-policy
训练方法
【2025-8-15】在线与离线强化学习-策略方法与训练流程全解析
RL有两种训练策略可选,在线强化学习(Online RL)和离线强化学习(Offline RL),并结合同策略(On-policy)与异策略(Off-policy)训练方法来实现策略优化
| RL分类 | 在线 | 离线 | 分析 |
|---|---|---|---|
| 同策略 | 同策略在线 | ❌ | |
| 异策略 | 异策略在线 | 异策略离线 |
组合后,有3种训练模式
策略选择建议
- 数据充足且可实时交互:优先选择同策略方法(PPO等),稳定性高。
- 交互成本高但仍可实时采样:选择异策略方法(SAC、TD3等),提高数据利用率。
- 无法实时采集数据:选择离线RL方法(CQL、BCQ等),利用已有历史数据。
同策略在线强化学习
图中左侧流程表示同策略训练:
- 行为策略与目标策略相同(蓝色块)。
- 数据实时从环境采集,用于立即更新策略。
- 数据不重复使用,训练过程中不断产生新数据。
这种方法适合于数据获取容易且环境可以频繁交互的任务,例如游戏AI。
异策略在线强化学习
图中中间部分表示异策略在线强化学习:
- 行为策略(灰色块)与目标策略(蓝色块)可以不同。
- 数据先存入 Replay Buffer,然后多次采样训练目标策略。
- 行为策略可以定期与目标策略同步(虚线箭头)。
这种方法比同策略方法数据利用率高,常用于连续控制任务、自动驾驶模拟等。
异策略离线强化学习
图中右侧流程表示离线RL:
- 训练前已从环境收集完所有数据(Replay Buffer)。
- 训练阶段完全离线,只用已有数据更新策略。
- 训练完成后直接部署到环境中执行。
这种方法在实际工程中很重要,特别是医疗、工业、金融等不能频繁试错的领域。
学习方式:on-policy vs off-policy
Sutton 经典书籍(Reinforcement Learning: An Introduction) 定义:
- 正在产生交互数据的 policy 定义为 behavior policy
- 正在通过训练优化的 policy 定义为training policy
- 如果这两个policy 一样,该算法就被称之为
On-policy, 否则该学习算法是一个Off-policy算法。
强化学习常用算法总结:
按照学习方式划分:在线策略(On-Policy) vs 离线策略(Off-Policy)
On-Policy: 数据采样策略 = 学习/评估策略- agent 必须在场, 并且一定是本人边玩边学习。
- 典型的算法:
Sarsa。
Off-Policy: 数据采样策略 ≠ 学习/评估策略- agent可以自己玩, 也可以看别人玩, 通过看别人玩来学习别人的行为准则, 离线学习同样是从过往的经验中学习, 但是这些过往的经历没必要是自己的经历, 任何人的经历都能被学习,也没有必要是边玩边学习,玩和学习的时间可以不同步。
- 典型方法:
Q-learning,Deep-Q-Network(经验回放)。
on-policy 和 off-policy 核心区别: 数据采样策略(Policy)与学习策略是否相同
| 策略类型 | 特点 | 算法 | 特点 | 优点 | 缺点 |
|---|---|---|---|---|---|
| On-policy 同策略 | “策略分布”和“数据分布”一致 PPO为保证策略稳定性,用最新(或近似最新)策略采样交互数据,更新后丢弃旧数据,重新采样 |
Sarsa、PPO、A2C/A3C 等 | 严格保证分布一致,收敛性更易分析 | 数据利用率低,策略更新后数据“过期”,难重复用于训练新策略 | |
| Off-policy 异策略 | DQN中经验回放池,采集数据用带随机探索策略,更新 Q 函数时朝着 “greedy” 或更优目标策略方向改进 | Q-Learning、DQN、SAC、TD3 等 | 策略与数据分布不一致 可重复使用历史数据,样本效率更高; 能从人类示教数据或其他智能体轨迹中学习 |
带来复杂性,难保证收敛,更新过程易出现分布偏移(Distribution Shift)问题 |
| 关键点 | on-policy | off-policy |
|---|---|---|
| 数据采样策略 | 同目标策略 | 不同于目标策略,可自行选择或混用 |
| 数据利用率 | 只能使用最近采样数据,效率较低 | 反复使用历史数据,效率较高 |
| 学习稳定性 | 分布一致性更好,算法分析更直接 | 数据分布差异大时,学习可能会不稳定 |
| 示例算法 | A2C/A3C、PPO等 | Q-Learning、DQN、SAC、TD3等 |
| 适用场景 | 中小型或交互稳定场景 | 大规模、需要高数据效率或可以使用离线数据场景 |
总结
- on-policy:数据采样与目标策略一致,保证分布统一,算法理论分析更简洁,但数据浪费较大。
- off-policy:数据来源灵活,可以重复使用过去的经验,样本效率更高,但需要处理分布偏移带来的额外复杂性。
同策略
同策略(On-policy)
同策略方法中,行为策略与目标策略相同,采集数据的策略与用于更新的策略一致
典型算法:
- REINFORCE、A2C、PPO
训练流程:
- 使用当前策略πn与环境交互,采集数据 (s_i, a_i, r_i, s’_i)
- 使用采集到的数据更新策略参数的
- 更新后的策略再次与环境交互,采集新数据
- 循环往复
优点:
- 采样分布与训练策略一致,减少了分布偏移问题。
- 理论分析更简单,收敛性更容易保证。
缺点:
- 采集数据成本高,旧数据几乎不能重复利用。
- 探索效率低,因为每次更新都需要新的交互数据。
异策略
异策略(Off-policy)
异策略方法中,行为策略 拍πx与目标策略πn可以不同。常见做法是使用一个(或多个)行为策略采集数据,并将数据存入经验回放缓冲区,然后从缓冲区中采样数据用于训练目标策略。
典型算法:
- Q-learning、DQN、DDPG、SAC、TD3。
训练流程:
- 使用行为策略πx与环境交互,生成数据
- 将数据存入 Replay Buffer
- 从 Replay Buffer 中采样数据,训练目标策略πn
- 行为策略可以是目标策略的旧版本,也可以是固定的探索策略
优点:
- 数据可多次利用,大大提高采样效率。
- 可使用历史数据(甚至是别的策略生成的数据)。
- 更容易实现并行训练。
缺点:
- 存在分布偏移风险,需要重要性采样或其他修正方法。
- 理论分析复杂,稳定性稍弱于同策略方法。
Online RL VS Offline RL
在线 online 和 offline 有什么区别?
在线强化学习(Online Reinforcement Learning)和离线强化学习(Offline Reinforcement Learning)是强化学习领域的两种不同学习范式
主要区别: 如何使用经验数据(即智能体与环境交互产生的状态、动作、奖励序列)来训练模型。
总结
| 对比维度 | 在线强化学习 | 离线强化学习 |
|---|---|---|
| 数据收集方式 | 学习过程中智能体直接与环境实时交互,用新鲜数据更新策略或价值函数,环境需可交互 | 从固定数据集(专家演示、历史记录等)中学习,不与环境实时互动 |
| 探索与利用的平衡 | 强调探索未知策略与利用当前最优策略间的平衡,每次决策影响学习和未来奖励 | 主要利用已有数据,探索新策略能力受限,重点是有效利用现有数据优化策略 |
| 安全性和稳定性 | 涉及试错,在敏感或昂贵环境中,错误决策可能导致不可逆后果 | 不直接与环境互动,适合高风险或高成本场景,如医疗、金融、机器人控制 |
| 数据效率与收敛速度 | 理论可无限探索找最优策略,但需大量环境交互,数据需求和时间成本高 | 数据利用更高效,从有限数据集挖掘信息,但收敛速度受数据集覆盖范围和多样性限制 |
| 策略优化自由度 | 可根据即时反馈灵活调整策略,在策略空间探索更灵活 | 受限于已收集数据的策略空间,难以评估未覆盖动作,优化策略较保守 |
在线强化学习
在线强化学习核心思想:边交互、边学习
训练过程中,智能体不断从环境中获取新数据(状态、动作、奖励、下一状态),并利用这些数据即时更新策略。
由于策略的更新会影响下一轮采样分布,数据是实时生成并适配当前策略的
特点:
- 数据是边生成边使用的,即实时性强
- 训练过程与数据采集紧密耦合
- 策略更新会立即影响之后的交互数据分布
优点:
- 数据分布与当前策略高度一致,训练稳定性好(尤其在同策略方法中)
- 能适应动态变化的环境
缺点:
- 数据采集成本高,需要实时与环境交互(在现实系统中可能昂贵或危险)
- 需要高效的采集策略,避免探索不足
离线强化学习
离线强化学习核心思想:用已有数据集直接训练策略,不需要训练过程中与环境交互。
数据通常来自历史记录、模拟器运行结果或其他策略生成的轨迹
特点:
- 数据在训练前已经完全收集完毕。
- 训练过程完全离线进行,不与环境交互。
优点:
- 不需要实时交互,成本低
- 可用已有大规模历史数据(如推荐系统、机器人日志数据)
- 安全性高,适合真实世界中无法频繁试错的任务(如自动驾驶)
缺点:
- 数据分布固定,缺乏探索能力
- 容易出现分布偏移,即训练数据的状态-动作分布与策略部署时的不一致
- 对数据质量依赖极高
Online RL VS Online Policy
on/off-policy 和 online/offline 区别
- 不同维度
- on/off-policy 解决的问题:“采样策略”与“目标策略”的一致程度。
- online/offline 解决的问题:“是否可以持续交互收集新数据”。
- 常见组合
离线强化学习基本是 off-policy,但在线强化学习可以既有 on-policy,也可以有 off-policy。
- 在线 + on-policy:比如 PPO、A2C 这些算法,需要跟环境交互,采集数据时就使用当前策略,采完就更新,旧数据不再使用。
- 在线 + off-policy:比如 DQN,虽然也是在线与环境交互,但 DQN 会把交互数据放到 replay buffer,后面训练时用到的旧数据不一定来自当前的策略,所以是 off-policy。
- 离线 + off-policy:这最常见。离线 RL 必然不能和“当前目标策略”一致地采样,因为数据集已经固定了,通常是其他策略或历史操作生成的数据,所以几乎都是 off-policy。
- 离线 + on-policy:理论上很难,因为离线数据本身就是固定收集的,跟当前想学的策略无法保持一致——所以离线强化学习通常都被视为 off-policy 的特例。
学习目标: Policy vs Value
按照学习目标划分:基于策略(Policy-Based)和基于价值(Value-Based)。
Policy-Based方法直接输出下一动作概率,根据概率来选取动作。但不一定概率最高就会选择该动作,还是会从整体进行考虑。- 适用于
非连续和连续动作。 - 常见方法:Policy gradients。
- 适用于
Value-Based方法输出动作价值,选择价值最高的动作。- 适用于
非连续的动作。 - 常见方法:
Q-learning、Deep Q Network和Sarsa。
- 适用于
分析
Policy-Based直接建模,输出下一动作- 而
Value-Based采用间接方法,通过评估动作价值来选择下一动作。
更厉害的方法是二者结合:Actor-Critic,Actor 根据概率做出动作,Critic 根据动作给出价值,加速学习过程,常见的有A2C,A3C,DDPG等。
更新方式: 单步更新 vs 回合更新
- 单步更新: 时序差分
TD - 回合更新: 蒙特卡洛
MC
总结
- 基础算法(1970s-2013)
- 价值迭代家族(Value-Based)
- 策略优化家族(Policy Gradient)
- 确定性策略优化家族(Deterministic Policy)
- 模型学习家族(Model-Based)
- 蒙特卡洛搜索家族(MCTS-Based)
- 序列建模家族(Transformer for RL)
- 强化学习 + 人类反馈(RLHF)
强化学习算法总览树
│
├── 基础算法(1970s-2013)
│ ├── Q-Learning (Watkins, 1989)
│ └── SARSA
│
├── 价值迭代家族(Value-Based)
│ ├── DQN (2015)
│ │ ├── Double DQN
│ │ ├── Dueling DQN
│ │ └── Rainbow DQN
│ └── Distributional RL (C51, QR-DQN)
│
├── 策略优化家族(Policy Gradient)
│ ├── REINFORCE
│ ├── Actor-Critic
│ │ ├── A2C
│ │ ├── A3C (2016) ← 非常重要
│ │ ├── PPO (2017) ← 非常重要
│ │ └── TRPO
│ └── Maximum Entropy Policy
│ ├── Soft Actor-Critic (SAC)
│ └── AWAC, TD3+BC(离线策略微调)
│
├── 确定性策略优化家族(Deterministic Policy)
│ ├── DDPG (2016) ← 非常重要
│ │ └── TD3 (2018)
│ │ └── TD3+BC(融合行为克隆)
│ └── NAF / SPD
│
├── 模型学习家族(Model-Based)
│ ├── Dyna-Q(1990年代,最早尝试)
│ ├── SimPLe(2019)
│ └── Dreamer 系列
│ ├── Dreamer (2019)
│ ├── DreamerV2
│ └── DreamerV3(当前最强模型之一)
│
├── 蒙特卡洛搜索家族(MCTS-Based)
│ ├── AlphaGo Zero
│ ├── AlphaZero
│ └── MuZero
│ └── EfficientZero(轻量化)
│
├── 序列建模家族(Transformer for RL)
│ ├── Decision Transformer (2021)
│ ├── Trajectory Transformer
│ └── Gato / RT-2(多模态智能体)
│
└── 强化学习 + 人类反馈(RLHF)
├── PPO + 人类偏好(OpenAI GPT-RLHF)
├── InstructRL / ReDo
└── Preference Transformer / Q*
环境
CartPole 环境
车杆(CartPole)环境状态值连续,动作值离散。
车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束。
- 智能体状态是维数为 4 的向量,每一维都是连续,其动作是离散,动作空间大小为 2。
- 在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数。
倒立摆(Inverted Pendulum)
倒立摆(Inverted Pendulum)
冰湖环境
冰湖(Frozen Lake)环境的状态空间和动作空间有限,在该环境中也尝试一下策略迭代算法和价值迭代算法,更好地理解这两个算法。
- 冰湖是 OpenAI Gym 库中的一个环境。OpenAI Gym 库中包含了很多有名的环境,例如 Atari 和 MuJoCo,并且支持我们定制自己的环境。
悬崖漫步
用策略迭代和价值迭代来求解悬崖漫步(Cliff Walking)这个环境中的最优策略。
- 悬崖漫步是一个非常经典的强化学习环境,它要求一个智能体从起点出发,避开悬崖行走,最终到达目标位置。
基本概念
E&E 探索/利用
Exploration/Exploitation trade off 探索/利用均衡
Before looking at the different strategies to solve Reinforcement Learning problems, we must cover one more very important topic: the exploration/exploitation trade-off.
- Exploration is finding more information about the environment. 探索未知
- Exploitation is exploiting known information to maximize the reward. 利用已知
探索(Exploration)与利用(Exploitation)的平衡是核心挑战:
探索指尝试新动作以获取环境信息利用则基于当前知识选择最优动作以最大化奖励。
过度探索可能导致低效,过度利用则易陷入局部最优。
E&E 方法
常见方法包括:
ε-greedy:以概率ε随机探索,其余时间贪婪利用;Upper Confidence Bound(UCB):通过置信区间量化动作不确定性,平衡二者;Thompson Sampling:基于贝叶斯后验分布动态调整动作选择;- 基于内在激励(如好奇心驱动)或信息增益,鼓励访问未充分探索的状态;
Softmax策略:按动作价值概率分布采样,兼顾高价值与潜在高回报动作。部分算法(如MCTS)结合基于模型的规划进一步优化此平衡。
多臂老虎机
强化学习关注智能体和环境交互过程中的学习,这是一种试错型学习(trial-and-error learning)范式。
多臂老虎机问题是简化版的强化学习。
- 与强化学习不同,多臂老虎机不存在状态信息,只有动作和奖励,算是最简单的“和环境交互中的学习”的一种形式。
- 多臂老虎机中的
探索与利用(exploration vs. exploitation)问题一直以来都是一个特别经典的问题,理解它能够帮助我们学习强化学习。
Bandit problem 定义
Bandit problem(强盗问题或赌博机问题)
Bandit problem 是强化学习和决策理论中的经典问题,用于研究在不确定环境下的探索与利用权衡(exploration vs. exploitation trade-off)。
赌博机(Bandit)问题是MDP极简形式:
- 系统仅有一个“状态”,对后续状态没有区分。
- 每台赌博机(或称拉杆)对应一个动作,每个动作产生的奖励分布未知且相互独立。
- 智能体在每次操作前需在各臂之间进行抉择,在缺乏状态转移的情况下,通过不断探索各臂的回报分布并利用已有信息,从而最大化累积奖励。
- 相比MDP,Bandit 只关注“当前选择—即时奖励”的单步决策,不涉及序列性的状态演化。
Bandit Problem 类型
类型:
- 多臂老虎机: 静态奖励分布, 如 ε-greedy, UCB, Thompson Sampling
- 上下文老虎机: 跟上一个状态有关
- 非静态老虎机: 动态奖励分布
- 多臂老虎机(Multi-Armed Bandit, MAB)
- 基础形式,假设每台老虎机的奖励分布是固定的(静态)。
常见算法包括:
ε-greedy:以一定概率随机探索,其他时候利用当前最优选项。UCB(上置信界):根据当前奖励估计和不确定性选择最优选项。Thompson Sampling:通过贝叶斯推断选择最优选项。
- Contextual Bandit(上下文老虎机)
每次决策前会观察到一个“上下文”(context),不同上下文可能对应不同的最优选项。
类似于推荐系统问题:根据用户特征选择推荐内容。
- Non-Stationary Bandit(非静态老虎机)
- 奖励分布会随着时间动态变化,需要更快速适应新分布的算法。
值函数
值函数/动作值函数/优势函数
优势函数(A)与值函数(V)、动作值函数(Q)的区别的联系:
- 优势函数是Q和V的差值。
优势函数与值函数、动作值函数的区别:
值函数(V):衡量状态的价值,反映在某个状态下,智能体根据当前策略所能期望得到的总回报。动作值函数(Q):直接衡量在某状态下采取某动作后,智能体所能期望得到的总回报。优势函数(A):动作对比的度量,表明选择某个动作相较于平均策略的回报增益。和V、Q不同的是,A提供了一个相对的评价。
值函数定义
值函数(value-function)定义
- Q-learning是一种 value-based 强化学习方法,首先定义两个value函数:
- 一个是 state-value 函数,即

- 如从期望价值为-7的状态出发,根据贪婪策略,动作为右、右、右、右、下、下、右、右。

- 另一个是 action-value 函数,在动作-价值函数中,函数的输入为动作和状态的pair,输出仍然是期望回报
- 一个是 state-value 函数,即
- action-value函数 与 state-value函数的区别
- 函数值由状态和动作同时决定,也就是说一个状态四个动作对应的value可以是不一样的。

方法
值函数估计方法:MC、TD、GAE
估计值函数的常见方法有三种:蒙特卡洛(MC)、时间差分(TD)、广义优势估计(GAE)
- MC方法:高方差,无偏。
- TD方法:低方差,高偏差。
- GAE方法:折中,既能减少偏差,也能降低方差,通过调整 lambda 来灵活控制。
估计value的算法有很多,一般三大类
- (1)
Monte Carlo—— model-free,结束后算收益- 这种算法的特点是,不能在每一次state变化后就更新value,只能在一次完整的学习过程(比如一盘棋)结束后,通过获取最终的总收益(Return),再对过程中每个state的value进行更新。
- 优点是不需要对环境进行建模,即“Model-free”。
- (2)
Dynamic Programming—— model-based,bootstrap,贝尔曼方程- 这种算法需要对环境建立一个完整准确的模型,这样系统的状态变化都是可以计算到的。再使用
贝尔曼方程,通过未来的状态倒推现在的状态。然后使用Bootstrapping算法,用未来的value来更新现在的value。
- 这种算法需要对环境建立一个完整准确的模型,这样系统的状态变化都是可以计算到的。再使用
- (3)
Temporal-Difference Learning—— model-free,bootstrap(综合)- 这种算法结合了上述两种方法的优点。
- 即不需要对环境建模(Model-free),又可以使用 Bootstrapping,拿未来的value来估计现在的value。
- 在实际的应用中,被采用的大部分的算法都是基于Temporal-Difference Learning的。
广义优势估计(GAE)
原理:GAE是一种折中方法,它结合了MC和TD的方法,旨在通过平衡方差和偏差来提高估计的稳定性和效率。
GAE通过引入一个超参数 (类似于TD方法中的折扣因子),在计算优势函数时利用TD方法的部分信息,而不是完全依赖于真实的回报。
GAE通过对TD误差进行加权平均来估计优势函数,从而减少单步TD误差带来的偏差,并控制方差的大小。
动态规划
- 什么是动态规划(Dynamic Programming,DP)?
- Dynamic means the sequential or temporal component to the problem,“动态”指的是该问题的时间序贯部分;
- Programming means optimising a “program”, i.e. a policy,“规划”指的是去优化一个策略。
- 是不是所有问题都能用动态规划求解呢?
- 不是的,动态规划方法需要问题包含以下两个性质:
- 最优子结构(Optimal substructure):保证问题能够使用最优性原理(多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略),从而问题的最优解可以分解为子问题最优解;
- 重叠子问题(Overlapping subproblems):子问题重复出现多次,因而可以缓存并重用子问题的解。
- 不是的,动态规划方法需要问题包含以下两个性质:
- 恰巧,MDP满足上面两个性质
- 贝尔曼方程是递归的形式,把问题分解成子问题
- 值函数保存和重用问题的解
- “规划”指的是在了解整个MDP的基础上求解最优策略,也就是清楚模型结构的基础上:包括状态行为空间、转换矩阵、奖励等。这类问题不是典型的强化学习问题,我们可以用规划来进行预测和控制。
- 参考:搬砖的旺财
Bellman 贝尔曼方程
- 函数值如何计算?这里需要引入Bellman方程了,因为期望回报是从当前状态一直计算到终止的,对于每个状态都这样计算是繁琐的,而Bellman方程将相邻状态的函数值关联起来了,即当前状态的函数值,等于从当前状态转移一步的直接奖励加上下一个状态的折扣函数值,这也就是Bellman方程的核心思想,recursive递归

- 当前时刻Q的目标值其实是未来reward 按照$\gamma$衰减的和。如果$\gamma=0$,则说明当前状态的Q值更新,只和跳转的下一状态有关;如果$\gamma=1$,则说明未来决策的所有reward对当前状态的Q值更新有影响,且影响程度一样。
- 贝尔曼方程(Bellman Equation),百度百科关于贝尔曼方程的介绍
贝尔曼方程(Bellman Equation)也被称作动态规划方程(Dynamic Programming Equation),由理查·贝尔曼(Richard Bellman)发现。贝尔曼方程是动态规划(Dynamic Programming)这些数学最佳化方法能够达到最佳化的必要条件。此方程把“决策问题在特定时间怎么的值”以“来自初始选择的报酬比从初始选择衍生的决策问题的值”的形式表示。借此这个方式把动态最佳化问题变成简单的子问题,而这些子问题遵守从贝尔曼所提出来的“最佳化还原理”。
- 总结:贝尔曼方程就是用来简化强化学习或者马尔可夫决策问题
- value function可以分为两部分:
- 立即回报
- 后继状态的折扣价值函数
- 立即回报

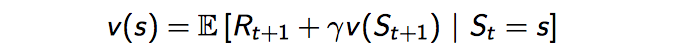
以Q值函数为例:
- Bellman期望方程:

- Bellman最优方程:
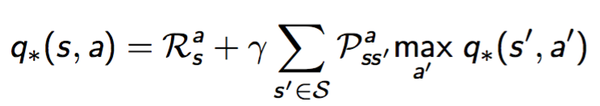
其中:
- (1)Model-based的解决方案中,基于动态规划,有基于Bellman期望方程的Policy iteration算法;也有基于Bellman最优方程的Value Iteration算法;
- (2)但是在Model-free中,似乎只有基于Bellman最优方程的Q-learning、Sarsa等算法。
马尔科夫系列
MDP 与 MRP 非常相像,主要区别为 MDP 中的状态转移函数和奖励函数都比 MRP 多了动作作为自变量。
MP 马尔可夫过程
重要概念
随机过程(stochastic process)是概率论的“动力学”部分。概率论研究对象是静态的随机现象,而随机过程研究对象是随时间演变的随机现象(例如天气随时间的变化、城市交通随时间的变化)。
马尔可夫性质:当且仅当某时刻的状态只取决于上一时刻的状态时,一个随机过程被称为具有马尔可夫性质(Markov property)马尔可夫过程马尔可夫过程(Markov process)指具有马尔可夫性质的随机过程,也被称为马尔可夫链(Markov chain)
MRP 马尔可夫奖励过程
在马尔可夫过程的基础上加入奖励函数 r 和折扣因子 y,就可以得到马尔可夫奖励过程(Markov reward process)。一个马尔可夫奖励过程由 <S, P, r, y> 构成,各个组成元素的含义如下所示。
- S 是有限状态的集合。
- P 是状态转移矩阵。
- r 是奖励函数,某个状态s的奖励 r(s) 指转移到该状态时可以获得奖励的期望。
- y 是
折扣因子(discount factor),y的取值范围为[0, 1)。引入折扣因子的理由为远期利益具有一定不确定性,有时我们更希望能够尽快获得一些奖励,所以我们需要对远期利益打一些折扣。接近 1 的y更关注长期的累计奖励,接近 0 的y更考虑短期奖励。
重要概念
回报- 一个马尔可夫奖励过程中,从第t时刻状态开始,直到终止状态 St 时,所有奖励的衰减之和称为回报 Gt(Return)
价值函数- 马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的
价值(value)。所有状态的价值就组成了价值函数(value function),价值函数的输入为某个状态,输出为这个状态的价值。 - 马尔可夫奖励过程中非常有名的
贝尔曼方程(Bellman equation) - 求解较大规模的马尔可夫奖励过程中的价值函数时,可以使用
动态规划(dynamic programming)算法、蒙特卡洛方法(Monte-Carlo method)和时序差分(temporal difference)
- 马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的
MDP 马尔可夫决策过程
在马尔可夫奖励过程(MRP)的基础上加入来自外界的刺激–智能体(agent)的动作,就得到了马尔可夫决策过程(MDP)。
Markov是俄国数学家,为了纪念其在马尔可夫链所做的研究,命名了“Markov Decision Process”,以下用MDP代替。
马尔可夫决策过程(Markov decision process,MDP)是强化学习的重要概念。
- 强化学习中的环境一般就是一个马尔可夫决策过程。与多臂老虎机问题不同,马尔可夫决策过程包含状态信息以及状态之间的转移机制。
- 如果要用强化学习去解决一个实际问题,第一步要做的事情就是把这个实际问题抽象为一个马尔可夫决策过程,也就是明确马尔可夫决策过程的各个组成要素。
MDP 核心思想
- 下一步的State 只和 当前状态State 以及 要采取的Action 有关,只回溯一步。
- State3 只和 State2 以及 Action2 有关,和 State1 以及 Action1 无关。
演变关系:
- Markov Property 马尔科夫性质:
- 根据公式也就是说给定当前状态
,将来的状态与t时刻之前的状态已经没有关系
- State Transition Matrix 状态转移矩阵
- 根据公式也就是说给定当前状态
- 马尔科夫链:动作序列,所有序列组成马尔科夫过程
- Markov Process 马尔科夫过程:一个无记忆的随机过程,是 马尔科夫过程 一些具有马尔科夫性质的随机状态序列构成,可以用一个元组<S,P>表示,其中S是有限数量的状态集,P是状态转移概率矩阵。
- MDP (Markov Decision Processes)马尔科夫决策过程
- 一个强化学习任务如果满足马尔可夫性则被称为马尔可夫决策过程。MDP是一个序贯决策过程,可以由一个5元组来表示:
- 如果状态空间和行动空间都是有限的,则称为有限马尔可夫过程(finite MDP)
- 一个强化学习任务如果满足马尔可夫性则被称为马尔可夫决策过程。MDP是一个序贯决策过程,可以由一个5元组来表示:
- MRP 马尔科夫奖励过程
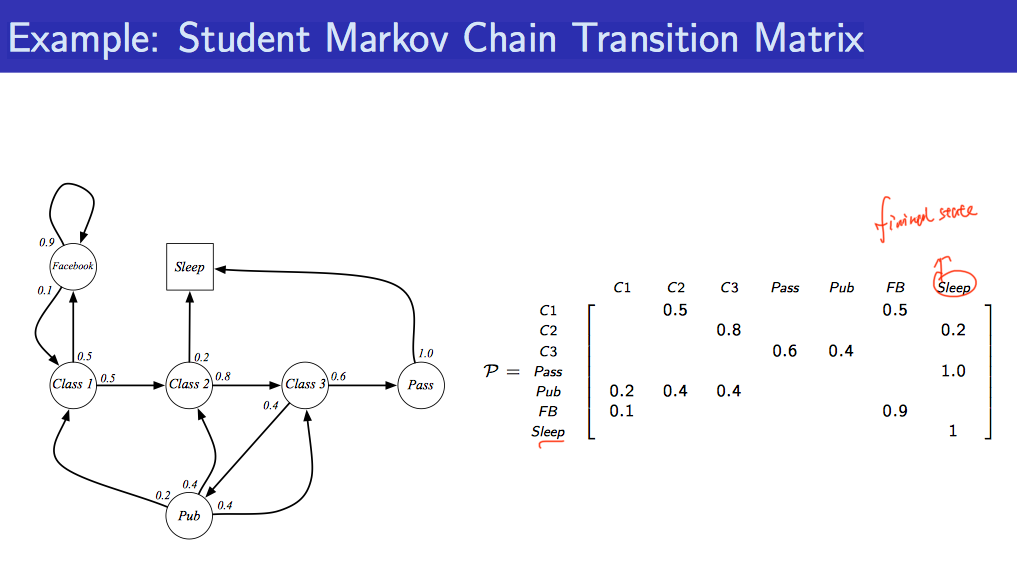
马尔可夫决策过程由元组<S, A, P, r, y>构成,其中:
- S 是状态的集合;
- A 是动作的集合;
- y 是折扣因子;
- r(s,a) 是奖励函数,此时奖励可以同时取决于状态s和动作a,在奖励函数只取决于状态s时,则退化为r(s);
- P(s’|s,a) 是状态转移函数,表示在状态s执行动作a之后到达状态s’的概率。
MDP 与 MRP 非常相像,主要区别为 MDP 中的状态转移函数和奖励函数都比 MRP 多了动作作为自变量。
重要概念
策略- 智能体的策略(Policy)通常用字母π表示。
状态价值函数- 用V(s)表示在 MDP 中基于策略的
状态价值函数(state-value function),定义为从状态s出发遵循策略π能获得的期望回报
- 用V(s)表示在 MDP 中基于策略的
动作价值函数- 不同于 MRP,在 MDP 中,由于动作的存在,我们额外定义一个
动作价值函数(action-value function)
- 不同于 MRP,在 MDP 中,由于动作的存在,我们额外定义一个
贝尔曼期望方程- 在贝尔曼方程中加上“期望”二字是为了与接下来的贝尔曼最优方程进行区分。
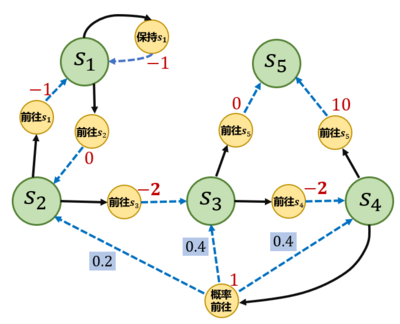
蒙特卡洛方法蒙特卡洛方法(Monte-Carlo methods)也被称为统计模拟方法,是一种基于概率统计的数值计算方法。运用蒙特卡洛方法时,我们通常使用重复随机抽样,然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。
- 占用度量
- 最优策略
- 强化学习的目标通常是找到一个策略,使得智能体从初始状态出发能获得最多的期望回报。
- 在有限状态和动作集合的 MDP 中,至少存在一个策略比其他所有策略都好或者至少存在一个策略不差于其他所有策略,这个策略就是
最优策略(optimal policy)。 - 贝尔曼最优方程
最大化期望回报
既然需要最大化期望回报来做出更好的决策,那么这一过程如何进行?
- 假设agent接收到一个状态然后给出相应的动作,那么这一过程就可以理解成是一个控制律(一个从状态到动作的函数)
- 控制律π好比agent的大脑,也是我们希望去学习出来的,我们的目标就是找到最好的控制律使得期望回报最大化。
- (1)直接法
- 给定状态并告诉agent应该采取什么动作,也就是直接学习这个控制律,称为policy-based方法。
- 控制率是确定的(即状态和动作一一对应)
,如动作的概率分布
- (2)间接法
- 不告诉agent什么动作是最好的,而是告诉它什么状态是更有价值的,而能到达更好价值的状态需要采取什么动作也就知道了,称为value-based方法。
- 需要训练一个函数能将当前状态映射成(某一控制律下)期望回报
- 总结
- 无论是采用policy还是value-based方法,都会有一个policy,在policy-based方法中这个policy是通过训练直接得到的,而在value-based方法中我们不需要去训练policy,这里的policy只是个简单的函数,比如贪婪策略根据最大值来选择动作。两者之间的对应关系可以如下所示

DP 动态规划 – 前提: 环境(MDP)已知
基于动态规划的强化学习算法主要有两种:一是策略迭代(policy iteration),二是价值迭代(value iteration)。
策略迭代由两部分组成:策略评估(policy evaluation)和策略提升(policy improvement)。- 策略迭代中的
策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数,这是一个动态规划的过程; - 而
价值迭代直接使用贝尔曼最优方程来进行动态规划,得到最终的最优状态价值。
- 策略迭代中的
强化学习中两个经典的动态规划算法:策略迭代算法和价值迭代算法,都能用于求解最优价值和最优策略。
- 动态规划的主要思想是利用
贝尔曼方程对所有状态进行更新。
注意
- 贝尔曼方程进行状态更新时,用到马尔可夫决策过程中的
奖励函数和状态转移函数。 - 如果智能体无法事先得知奖励函数和状态转移函数,就只能通过和环境进行交互来采样(状态-动作-奖励-下一状态)这样的数据
策略迭代算法
策略迭代是策略评估和策略提升不断循环交替,直至最后得到最优策略的过程。
- 策略评估这一过程用来计算一个策略的状态价值函数
- 策略提升: 策略评估计算得到当前策略的状态价值函数之后,据此来改进该策略。
策略迭代算法的过程如下:
- 对当前的策略进行策略评估,得到其状态价值函数,然后根据该状态价值函数进行策略提升以得到一个更好的新策略,接着继续评估新策略、提升策略……直至最后收敛到最优策略
价值迭代算法
策略迭代中的策略评估需要很多轮才能收敛得到某一策略的状态函数,这需要很大的计算量,尤其是在状态和动作空间比较大的情况下。
是否必须要完全等到策略评估完成后再进行策略提升呢?
试想下可能情况:
- 虽然状态价值函数还没有收敛,但是不论接下来怎么更新状态价值,策略提升得到的都是同一个策略。
如果只在策略评估中进行一轮价值更新,然后直接根据更新后的价值进行策略提升,这样是否可以呢?
- 答案是肯定的,这其实就是
价值迭代算法,一种策略评估只进行了一轮更新的策略迭代算法。 - 注意: 价值迭代中不存在显式的策略,只维护一个状态价值函数。
TD 时序差分 – 与DP互补
解决什么问题
动态规划算法要求马尔可夫决策过程已知,即要求与智能体交互的环境是完全已知(例如迷宫或者给定规则的网格世界)
- 智能体并不需要和环境真正交互来采样数据,直接用
动态规划算法就解出最优价值或策略。 - 好比有监督学习任务,直接显式给出数据分布公式,通过在期望层面上直接最小化模型泛化误差来更新模型参数,并不需要采样任何数据点。
但大部分场景并非如此,机器学习主要方法都是在数据分布未知的情况下, 针对具体的数据点来对模型做出更新的。
对于大部分强化学习现实场景,马尔可夫决策过程的状态转移概率是无法写出来的,也就无法直接进行动态规划。
- 例如:电子游戏或者一些复杂物理环境
- 这时智能体只能和环境进行交互,通过采样到的数据来学习,这类方法统称
无模型强化学习(model-free reinforcement learning)。
model-free 算法
不同于动态规划算法,无模型强化学习算法不用事先知道环境的奖励函数和状态转移函数,而是直接使用和环境交互的过程中采样到的数据来学习,可以被应用到一些简单的实际场景中。
无模型强化学习中的两大经典算法:Sarsa 和 Q-learning,都基于时序差分(temporal difference,TD)的强化学习算法。
一组概念:在线策略学习和离线策略学习。
在线策略学习要求使用在当前策略下采样得到的样本进行学习,一旦策略被更新,当前的样本就被放弃了,就好像在水龙头下用自来水洗手;离线策略学习使用经验回放池将之前采样得到的样本收集起来再次利用,就好像使用脸盆接水后洗手。
因此,离线策略学习往往能够更好地利用历史数据,并具有更小的样本复杂度(算法达到收敛结果需要在环境中采样的样本数量),这使其被更广泛地应用。
时序差分算法
时序差分是一种估计策略价值函数的方法,结合了蒙特卡洛和动态规划算法的思想。
时序差分方法和蒙特卡洛的相似之处: 可以从样本数据中学习,不需要事先知道环境;- 和
动态规划的相似之处: 根据贝尔曼方程思想,利用后续状态的价值估计来更新当前状态的价值估计。
时序差分的核心思想
- 用对未来动作选择的价值估计来更新对当前动作选择的价值估计,这是强化学习中的核心思想之一。
Sarsa 算法
既然可以用时序差分方法来估计价值函数,那能否用类似策略迭代的方法来进行强化学习?
- 策略评估已经可以通过时序差分算法实现,那么在不知道奖励函数和状态转移函数的情况下, 该怎么进行策略提升呢?
- 答案是直接用
时序差分算法来估计动作价值函数
多步时序差分 – Sarsa 算法
蒙特卡洛方法利用当前状态之后每一步的奖励而不使用任何价值估计,时序差分算法只利用一步奖励和下一个状态的价值估计。那它们之间的区别是什么呢?
蒙特卡洛方法是无偏(unbiased)的,但是具有比较大方差,因为每一步的状态转移都有不确定性,而每一步状态采取的动作所得到的不一样的奖励最终都会加起来,这会极大影响最终的价值估计;时序差分算法具有非常小方差,因为只关注了一步状态转移,用到了一步的奖励,但是它是有偏的,因为用到了下一个状态的价值估计,而不是其真实的价值。
那有没有什么方法可以结合二者的优势呢?
- 答案是
多步时序差分,使用多步奖励,然后使用之后状态的价值估计。
算法总结
经典算法:Q-learning,Sarsa,DQN,Policy Gradient,A3C,DDPG,PPO
代表性的算法进行讲解:
- 基于表格、没有神经网络参与的Q-Learning算法
- 基于价值(Value-Based)的Deep Q Network(DQN)算法
- 基于策略(Policy-Based)的Policy Gradient(PG)算法
- 结合了Value-Based和Policy-Based的Actor Critic算法。
| 学习方法 | 说明 | 经典算法 |
|---|---|---|
| 基于价值(Value-Based) | 通过价值选行为 | Q Learning, Sarsa(同策略), Deep Q Network |
| 基于策略(Policy-Based) | 直接选最佳行为 | Policy Gradients |
| 基于模型(Model-Based) | 想象环境并从中学习 | Model based RL |
算法大全
【2023-6-19】RL算法总结
旧版
蒙特卡洛
【2022-5-6】「详细原理」蒙特卡洛树搜索入门教程
蒙特卡洛树搜索在2006年被Rémi Coulom第一次提出,应用于Crazy Stone的围棋游戏。
- Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search
蒙特卡洛树搜索大概的思想就是给定一个游戏状态,去选择一个最佳的策略/动作。
MC vs TD
Monte Carlo 和 Temporal Difference Learning
由于强化学习的agent通过与环境交互得到提升,需要考虑如何利用交互的经验信息来更新值函数,从而得到更好的控制律。
主要两种方法:蒙特卡洛(MC)采用完整一轮经验,而时序差分(TD)只是一步经验
下面以value-based方法说明两种方法区别
- (1)蒙特卡洛(MC)法利用一条完整的采样来更新函数,比如下图所示,所有的状态函数值为0,采用学习率0.1,不对回报进行衰减,采用贪婪加随机的控制策略,当老鼠走超过十步时停止,最终的路径如箭头所示
- 得到了一系列的状态、动作、奖励,那么我们需要计算出它的回报,从而根据下面公式更新state-value函数
- 假设吃到一个奶酪的奖励为1,则回报为 Gt = 1+0+0+0+0+0+1+1+0+0=3,对值函数进行更新为 V(S0)= V(S0)+lr*[Gt- V(S0)]=0.3。
- (2)时序差分(TD)法则不需要等一整个过程结束才更新函数值,而是每一步都能更新,但是由于只走了一步我们并不知道后面的奖励,因此TD采取了自助的方式,利用上一次的估计值V(St+1)来替代。

- 当老鼠走了一步后即可更新值函数:V(S0)=V(S0)+lr[ R1+gammaV(S1)-V(S0) ]=0.1
1.1 有限双人零和序贯博弈
蒙特卡洛树搜索实际上是一个应用非常广泛的博弈框架,这里将其应用于 有限双人序贯零和博弈 问题中。
- 像围棋、象棋、Tic-Tac-Toe都是
有限双人序贯零和博弈游戏。
1.2 怎样去表示一个游戏?
采用 博弈树 (Game Tree)来表示一个游戏:
- 每个结点都代表一个
状态(state),从一个结点(node)移动一步,将会到达它的子节点(children node)。 - 子节点的个数叫作
分支因子(branching factor)。 根节点(Root node)表示初始状态(initial state)。终止节点(terminal nodes)没有子节点了。
在 tic-tac-toe 游戏中表示如下图所示:
-
- 每次都是从 初始状态 、树的 根结点 开始。在 tic-tac-toe 游戏里面初始状态就是一张空的棋盘。
- 从一个节点转移到另一个节点叫作一个 move 。
- 分支因子 (branching factor), tic-tac-toe 中树越深,分支因子也越少,也就是 children node 的数量越少
- 游戏结束表示 终止节点 。
- 从根节点到终止节点一次表示一个单个游戏 playout 。
不需要关系怎么来到这个 node ,只需要做好之后的事情就好了。
1.3 最佳策略是什么?minimax和alpha-beta剪枝
希望找到的就是 最佳策略 ( the most promising next move )。如果知道对手的策略那你可以争对这个策略求解,但是大多数情况下是不知道对手的策略的,所以我们需要用 minimax 的方法,假设你的对手是非常机智的,每次他都会采取最佳策略。
假设A与B博弈,A期望最大化自己的收益,因为是零和博弈,所以B期望A的收益最小,Minimax算法可描述为如下形式:
- 和 是玩家 和 的效益函数。
- move 表示从当前状态 和采取的动作 转移到下一个状态。
- eval 评估最终的游戏分数。
- 是最终的游戏状态。
简单地说,就是给定一个状态 期望找到一个动作 在对手最小化你的奖励的同时找到一个最大化自己的奖励。
Minimax 算法最大的弱点 就是需要扩展整棵树,对于高分支因子的游戏,像围棋、象棋这种,算法就很难处理。
对于上述问题的一种解决方法就是扩展树结构到一定的阈值深度( expand our game tree only up to certain threshold depth d )。因此我们需要一个评估函数,评估 非终止节点 。这对于我们人类来说依据当前棋势判断谁输谁赢是很容易做到的。计算机的解决方法可以参考原文中的:
- Chess position evaluation with convolutional neural network in Julia
另一种解决树扩展太大的方法就是 alpha-beta剪枝算法 。它会避免一些分支的展开,它最好的结果就是与minimax算法效果相同,因为它减少了搜索空间。
2 蒙特卡洛树搜索(MCTS)
蒙特卡洛通过多次模拟仿真,预测出最佳策略。
MCTS 主要流程:
- 选择 (Selection):从根节点开始,递归地选择具有最高
上限置信区间值(Upper Confidence Bound,UCB)的子节点,直到到达一个叶节点。- 为了保证exploitation(visit-count/reward)和exploration(未被访问的节点),通常使用UCT作为叶子节点
- 扩展 (Expansion):如果该叶节点不是终止节点,则创建一个或多个子节点。
- 上一步中选择的节点被标记为已探索并与其父节点建立链接关系。
- 模拟 (Simulation):从一个子节点开始,进行随机模拟对局,直到到达终止状态。
- 从root节点到被expanded节点作为prefix-sequence,应用policy-model生成后续的序列。
- 通常基于一定的终止条件终止simulation 如 生成 结束符号、达到指定的rollout长度 等等。
- 回溯 (Backpropagation):将模拟的结果回溯更新到所有经过的节点。
- 在simulation中产生的sequence,应用evaluation-function评估reward(如质量分、输赢)等等,并将reward 从 结束节点反传回根节点,更新路径节点的访问次数和节点reward。
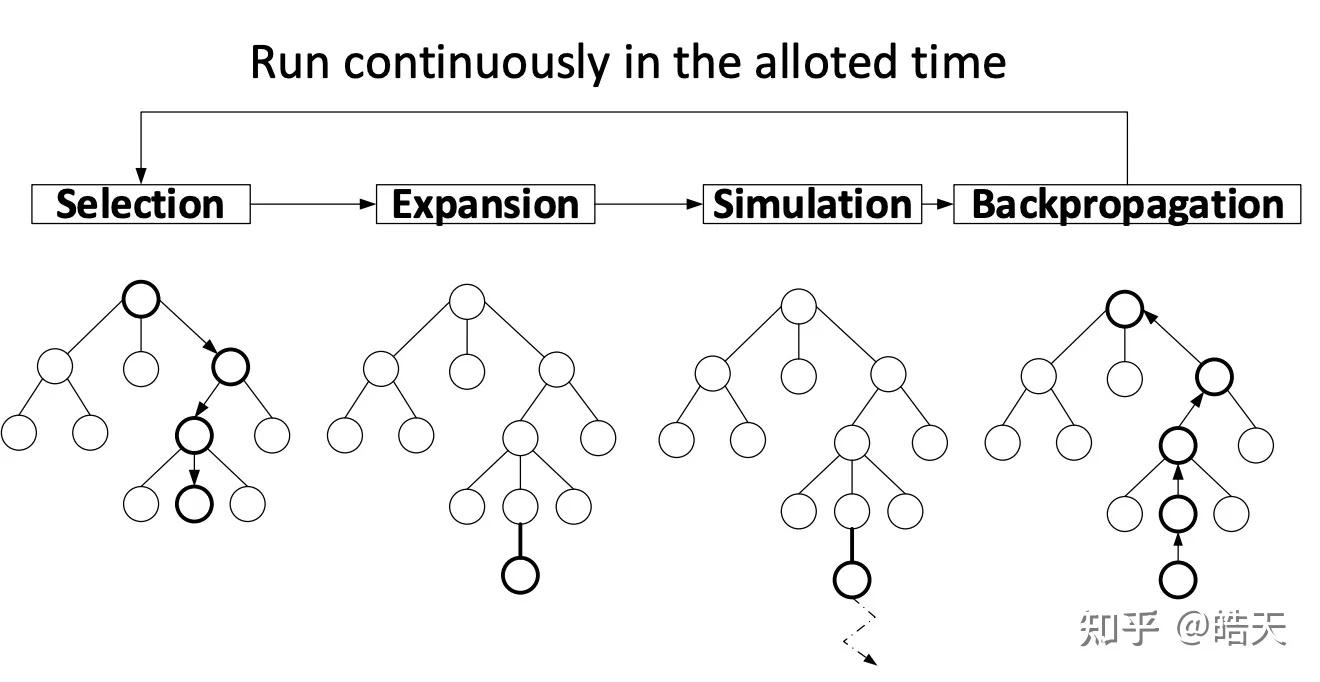
最核心的东西就是搜索。
- 搜索是对整棵博弈树的组合遍历,单次遍历从根结点开始,到一个未完全展开节点(a node that is not full expanded), 即至少有一个孩子节点未被访问,或者称作未被探索过。
- 当遇到未被完全展开过的节点,选择未被访问的childre node做根结点,进行一次模拟(a single playout/simulation)。
- 仿真的结果反向传播(propagated back)用于更新当前树的根结点,并更新博弈树节点的统计信息。当整棵博弈树搜索结束后,就相当于拿到了这颗博弈树的策略。
再理解一下以下几个关键概念:
- 怎么解释 展开 或 未完全展开 (not fully unexpanded)的博弈树节点?
- 搜索过程中的 遍历 (traverse down)是什么?子节点如何选择?
- 什么是 模拟仿真 (simulation)?
- 什么是 反向传播 (backpropagation)?
- 扩展的树节点中反向传播、更新哪些统计( statistics )信息?
- 怎么依据策略(博弈树)选择动作?
2.1 模拟/Simulation/Playout
Playout/simulation是与游戏交互的一个过程,从当前节点移动到终止节点。在simulation过程中move的选择基于rollout policy function:
Rollout Policy也被称作快速走子策略,基于一个状态 选择一个动作 。为了让这个策略能够simulation快,一般选用随机分布(uniform random)。如下图所示
2.1.1 Alpha Zero中的Playout/Simulation
在AlphaGo Zero里面DeepMind‘s直接用一个CNN残差网络输出position evaluation和moves probability。
2.2 博弈树节点的扩展-全扩展、访问节点
一个节点如果被访问过了,意味着某个某个simulation是以它为起点的。如果一个节点的所有子节点都被访问过了,那这个节点就称为是完全扩展的,否则就是未完全扩展的。如下图对比所示:
在实际过程中,一开始根节点的所有子节点都未被访问,从中选一个,第一次simulation就开始了。
Simulation过程中rollout policy选择子节点是不被考虑为这个子节点被访问过了, 只有Simulation开始的节点被标记为访问过的 。
2.3 反向传播Simulation结果
从一个近期访问过的节点(有时候也叫做叶结点(left node))做Simulation,当他Simulation完成之后,得出来的结果就需要反向传播回当前博弈树的根结点,Simulation开始的那个节点被标记为访问过了。
反向传播是从叶结点(simulation 开始的那个节点)到根结点。在这条路径上所有的节点统计信息都会被计算更新。
不足
不足之处:
- 依赖于人工特征: 传统 MCTS 算法通常需要依赖于人工设计的特征来评估状态的价值,这限制了算法的性能。
- 搜索效率不高: MCTS 算法需要进行大量的模拟才能获得准确的评估,这导致搜索效率不高。
2.4 Nodes’ statistics
拿到simulation的结果主要更新两个量:所有的simulation reward 和所有节点 (包括simulation开始的那个节点)的访问次数 。
- 表示一个节点 的 simulation reward和 ,最简单形式的就是所有考虑的节点的模拟结果之和。
- 表示节点的另一个属性,表示这个节点在反向传播路径中的次数(也表示它有多少次参与了total simulation reward)的计算。
2.5 遍历博弈树
搜索开始时,没有被访问过的节点将会首先被选中,然后simulation,结果反向传播给根结点,之后根节点就可以被认为是全展开的。
为了选出我们路径上的下一个节点来开始下一次模拟,我们需要考虑 的所有子节点 , , , 和其本身节点 的信息,如下图所示:
当前的状态被标记为蓝色,上图它是全展开的,因此它被访问过了并且存储了节点的统计信息:总的仿真回报和访问次数,它的子节点也具备这些信息。这些值组成了我们最后一个部分:树的置信度上界(Upper Confidence Bound applied to Trees,UCT)。
2.6 置信度上界
UCT是蒙特卡罗树搜索中的一个核心函数,用来选择下一个节点进行遍历:
蒙特卡洛树搜索的过程中选UCT最大的那个遍历。
UCT 中第一部分是 ,也被称作 exploitation component ,可以看作是子节点 的胜率估计(总收益/总次数=平均每次的收益)。
看起来这一项已经有足够说服力,因为只要选择胜率高的下一步即可,但是为什么不能只用这一个成分呢?这是因为这种贪婪方式的搜索会很快导致游戏结束,这往往会导致搜索不充分,错过最优解。因此UCT中的第二项称为exploration component。这个成分更倾向于那些未被探索的节点( 较小)。在蒙特卡洛树搜索过程中第二项的取值趋势大概如下图所示,随着迭代次数的增加其值也下降:
参数
用于平衡MCTS中的exploitation和exploration。
2.6.1 UCT in Alpha Go and Alpha Zero
在AlphaGo Lee和Alpha Zero算法里面,UCT公式如下:
是来自策略网络的move先验概率,策略网络是从状态得到move分布的函数,目的是为了提升探索的效率。
当游戏视角发生变化的时候exploitation component 也会发生变化。
2.6.2 Alpha Go和Alpha Zero中的策略网络
在 AlphaGo 算法里,有两个policy网络:
- SL Policy Network :基于人类数据的监督学习所得的网络。
- RL Policy Network :基于强化学习自我博弈改进SL Policy Network。
Interestingly – in Deepmind’s Monte Carlo Tree Search variant – SL Policy Network output is chosen for prior move probability estimation as it performs better in practice (authors suggest that human-based data is richer in exploratory moves). What is the purpose of the RL Policy Network then? The stronger RL Policy Network is used to generate 30 mln positions dataset for Value Network training (the one used for game state evaluation)
在Alpha Zero里面只有一个网络 ,它不仅是值网络还是策略网络。 It is trained entirely via self-play starting from random initialization. There is a number of networks trained in parallel and the best one is chosen for training data generation every checkpoint after evaluation against best current neural network.
2.7 终止MCTS
什么时候结束MCTS过程?如果你开始玩,那么你的“思考时间”可能是有限的(“thinking time” is probably limited),计算能力也是有限的(computational capacity has its boundaries, too)。因此最保险的做法是在你资源允许的情况下尽可能全展开遍历搜索。
当MSCT程序结束时,最佳的移动通常是访问次数最多的那个节点。因为在多次访问的情况下,评估它的 值必须很高。
当你使用蒙特卡洛树搜索选择了一个动作,在对手眼里,你的这个选择将会变成状态的一部分。反过来对你也是一样的,当对手选择了一个状态之后,你的蒙特卡洛树搜索就可以开始工作了。利用之前的统计信息直接搜索就可以得出结果了。
3 MCTS总结
代码
def monte_carlo_tree_search(root):
while resources_left(time, computational power):
leaf = traverse(root) # leaf = unvisited node
simulation_result = rollout(leaf)
backpropagate(leaf, simulation_result)
return best_child(root)def traverse(node):
while fully_expanded(node):
node = best_uct(node)
return pick_univisted(node.children) or node # in case no children are present / node is terminal def rollout(node):
while non_terminal(node):
node = rollout_policy(node)
return result(node)
def rollout_policy(node):
return pick_random(node.children)def backpropagate(node, result):
if is_root(node) return
node.stats = update_stats(node, result)
backpropagate(node.parent)def best_child(node):
pick child with highest number of visits
Q-learning
Q-learning 算法
除了 Sarsa,还有基于时序差分算法的强化学习算法——Q-learning。
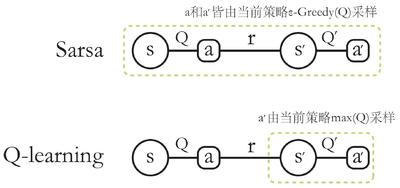
Q-learning 和 Sarsa 最大区别在于 Q-learning 时序差分更新方式
Sarsa是在线策略(on-policy)算法Q-learning是离线策略(off-policy)算法
策略定义
- 采样数据的策略是
行为策略(behavior policy) - 用来更新的策略是
目标策略(target policy)
区别
在线策略(on-policy)算法:行为策略和目标策略相同;– 敢想敢干离线策略(off-policy)算法:行为策略和目标策略不同。– 空想家
Sarsa 是典型的在线策略算法,而 Q-learning 是离线策略算法。
- 判断: 看计算时序差分的价值目标的数据是否来自当前策略
资料
- 英文 可视化讲解 Q-Learning: Reinforcement Learning Explained Visually (Part 4): Q Learning, step-by-step

Q-Table
Q值表(Q-Table)是简单查找表,「Q」代表动作的「质量」, 计算每个状态最大预期未来奖励, 在每个状态采取最佳行动。
创建一个表格, 为每一个状态(state)上进行的每一个动作(action)计算出最大的未来奖励(reward)的期望。
- 每个 Q-table 分数代表在给定最佳策略的状态下采取相应动作获得的最大未来奖励期望
- 基于这张表格就可以为每一个状态采取的最佳动作

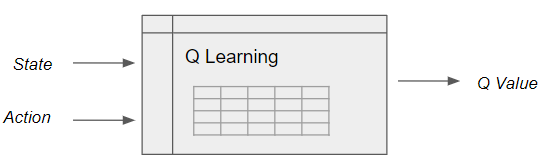
Q 函数
Q函数(Q-Function) 是动作价值函数,两个输入:「状态」和「动作」, 返回在该状态下执行该动作的未来奖励期望。
Q函数是在Q-Table上滚动的读取器,用于寻找与当前状态关联的行以及与动作关联的列。从相匹配的单元格中返回 Q 值,即未来奖励期望。
探索环境(environment)之前,Q-table 给出相同的任意设定值(大多数情况下是 0)。随着对环境的持续探索,这个 Q-table 会通过迭代地使用 Bellman 方程(动态规划方程)更新 Q(s,a) 来给出越来越好的近似。
Q-learning 定义
Q-Learning is an off-policy value-based method that uses a TD approach to train its action-value function
Q-learning 需要维护一张Q值表,表维数:状态数S * 动作数A,每个数代表在态s下可以采用动作a可以获得的未来收益的折现和——Q值。不断迭代Q值表使其最终收敛,然后根据Q值表,就可以在每个状态下选取一个最优策略。参照《极简Q-learning教程》
- 更新公式如下,R+γmax部分称为Q-target,即使用贝尔曼方程加贪心策略认为实际应该得到的奖励,目标是使Q值不断的接近Q-target值

Q-learning 算法:学习动作值函数(action value function)
- 动作值函数(或称「Q 函数」)有两个输入:「
状态」和「动作」, 将返回在该状态下执行该动作的未来奖励期望。
Q-learning 本质是训练 action-value 函数
Q函数(Q是Quality,某状态下某动作的质量有多高),从而得到对应的action。- 离散问题,Q函数是Q表格,每个cell代表对应的状态-动作的函数值,有限个状态,动作空间有限,对应Q-table
- 只要给定输入(状态+动作),Q表就能输出对应的Q值。当训练完成得到一个最优的Q函数(表)后,也就有了最佳的控制律,因为已经知道了每一个状态下哪个动作的函数值比较大,关于动作空间最大化Q函数即可得到最优的控制律。
图解
算法流程
Q-learning 学习过程
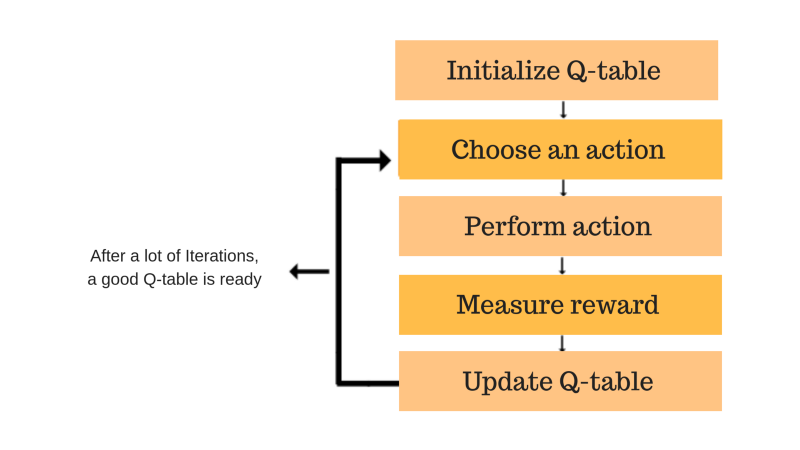
- 第1步:初始化Q值表
- 步骤2和3:选择并执行操作
- 步骤4和5:评估
- Q Table
- 整体
- 详情
- 第一步,初始化Q表,比如全部为0
- 第二步,就是根据Epsilon Greedy策略选择动作(既要利用已知的又要探索未知的)

- 在训练的一开始,应该多探索,随着训练越久,Q表越好,应该不断减小探索的概率。

- 第三步是执行动作,得到新的奖励,进入下一状态
- 第四步就是更新Q表
- 第一步,初始化Q表,比如全部为0
- 总结
- 计算TD Target的时候采用的是贪婪策略(对动作空间求Q值得最大),由于动作的实施和更新策略不同,所以Q-learning称为off-policy!因此对应的也有on-policy,比如说Sarsa算法
- Q-learning的核心就是Q表的更新,但是当问题规模一大,这种简单粗暴的方法显然是不太现实的,因此就有了 Deep Q-learning 的出现了。
- 计算TD Target的时候采用的是贪婪策略(对动作空间求Q值得最大),由于动作的实施和更新策略不同,所以Q-learning称为off-policy!因此对应的也有on-policy,比如说Sarsa算法
DQN
Q-Learning 不足
Q-learning 以矩阵方式建立一张表格, 存储每个状态下所有动作Q值。
- 表格每个动作价值
Q(s,a)表示在状态s下选择动作a然后继续遵循某一策略预期能够得到的期望回报。 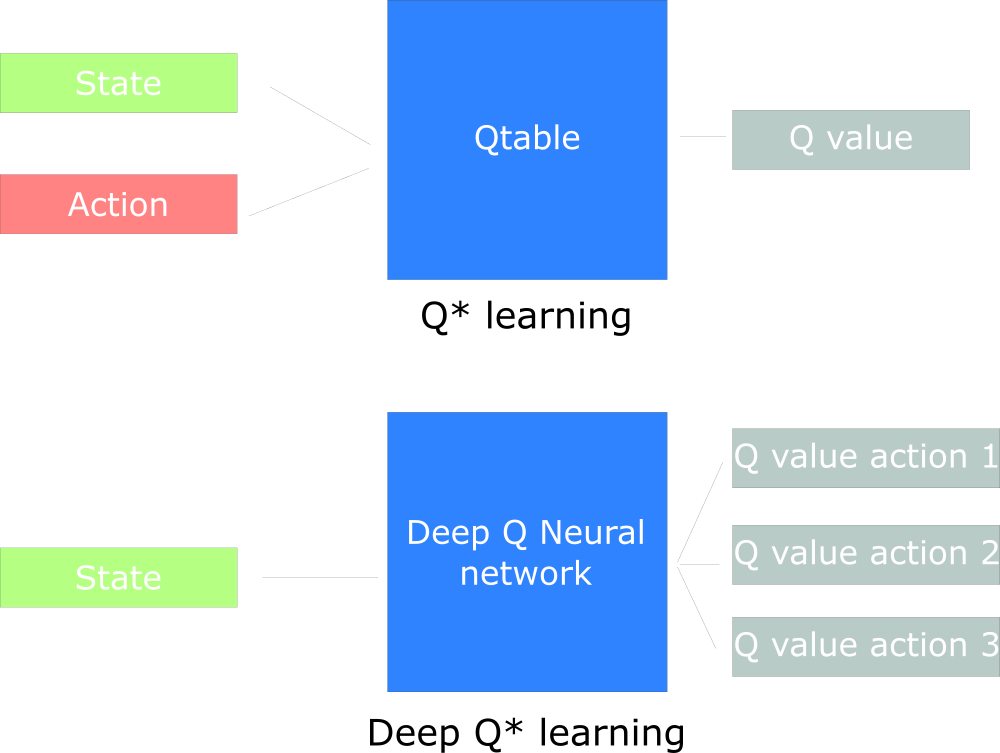
适用场景
- 只在环境状态和动作都离散,且空间都较小。
- 如悬崖漫步
当状态或动作数量非常大,就不适用。
- 状态是一张 RGB 图像
- 当状态或者动作连续时,就有无限个状态动作对
DQN 介绍
改进方法:表格方式升级为神经网络,直接根据输入预测输出值,一般有两种形式(第二种为主)
- (1)输入
状态和动作,输出值 - (2)输入
状态,输出动作和值,按照Q-learning选最大 —— 主流
Q-learning 创建Q表寻找最佳动作
而 DQN 将深度神经网络与Q-Learning相结合,使用卷积神经网络近似Q函数
- 避免了大型表的记录和存储
- 在Atari游戏上取得革命性成果。

DQN 用函数拟合方法来估计值,即将这个复杂的值表格视作数据,使用一个参数化函数来拟合这些数据。
- 这种函数拟合方法存在一定精度损失,因此被称为近似方法。
关键技巧:
- Experience Replay:将交互经验存储在回放池中,随机小批量采样来打破数据相关性;
- Target Network:固定目标Q网络一段时间再更新,避免网络剧烈震荡。

DQN 算法
DQN是深度学习与强化学习的结合,用神经网络代替Q-learning中Q表。
- 普通 Q-learning中,当状态和动作空间是离散且维数不高时可使用Q-Table储存每个状态动作对的Q值,但是当状态和动作空间是高维或者连续时,使用Q-Table不现实,而神经网络恰好擅长于此。
- 因此 DQN 将Q-Table 更新问题变成函数拟合问题,相近状态得到相近的输出动作。如有一个Q值表,神经网络的作用就是给定状态s和动作a,预测对应的Q值,使得神经网络的结果与Q表中的值接近。不过DQN方式肯定不能继续维护一个Q表,所以将上次反馈的奖励作为逼近的目标,如下式,通过更新参数 θ 使Q函数逼近最优Q值。因此,DQN就是要设计一个神经网络结构,通过函数来拟合Q值
问题:
- 神经网络需要大量带标签的样本进行监督学习,但是强化学习只有reward返回值,如何构造有监督的数据成为第一个问题,而且伴随着噪声、延迟(过了几十毫秒才返回)、稀疏(很多State的reward是0)等问题;
- 神经网络前提是样本独立同分布,而强化学习前后state状态和反馈有依赖关系——马尔科夫决策;
- 神经网络目标分布固定,但是强化学习分布一直变化,比如玩游戏,一个关卡和下一个关卡的状态分布不同,所以训练好了前一个关卡,下一个关卡又要重新训练;
- 过往的研究表明,使用非线性网络表示值函数时出现不稳定等问题。
解决方案:
- 构造标签:通过 Q-Learning 使用reward来构造标签(对应问题1),用神经网络来预测reward,将问题转化为回归问题;
- 构造时, 使用 衰减
- 经验回放:通过experience replay(经验池)解决相关性及非静态分布问题(对应问题2、3);
- 把每个时间步agent与环境交互得到的转移样本 (st,at,rt,st+1) 储存到回放记忆单元,训练时随机拿出一些(minibatch)来训练。(将游戏过程打成碎片存储,训练时随机抽取就避免了相关性问题)
- 双网络结构:一个神经网络产生当前Q值,另一个神经网络产生Target Q值(对应问题4)。
- Nature 2015 版本的DQN中提出,用另一个网络(这里称为target_net)产生Target Q值。
- Q(s,a;θi) 表示当前网络 eval_net 输出,用来评估当前状态动作对的值函数;
- Q(s,a;θ−i) 表示 target_net的输出,代入上面求 TargetQ 值的公式中得到目标Q值。
- 根据上面的Loss Function更新eval_net参数,每经过N轮迭代,将MainNet的参数复制给target_net。
- 引入target_net后,再一段时间里目标Q值使保持不变的,一定程度降低了当前Q值和目标Q值的相关性,提高了算法稳定性。
- Nature 2015 版本的DQN中提出,用另一个网络(这里称为target_net)产生Target Q值。
- 参考:实战深度强化学习DQN-理论和实践
流程示意图
- 国外可视化教程 DQN

ε衰减(Epsilon Decay)
收集数据时, 用ε衰减(Epsilon Decay)
- 开始时, ε大(比如1.0), 多探索;
- 训练后期ε小(比如0.05), 多利用。
常见衰减方法:
- 线性衰减: 比如每步减少一点
- 指数衰减: 开始快,后面慢慢趋于稳定
- 性能自适应: reward上升慢就放慢衰减速度
设计好ε衰减,才能既探索充分,又不磨蹭太久!
在类似车杆的环境中得到动作价值函数 Q(s,a),由于状态每一维度的值都是连续的,无法使用表格记录,因此一个常见的解决方法便是使用函数拟合(function approximation)的思想。
神经网络具有强大的表达能力,可以用一个神经网络来表示函数Q。
- 若动作是连续(无限)的,神经网络的输入是状态s和动作a,然后输出一个标量,表示在状态s下采取动作a能获得的价值。
- 若动作是离散(有限)的,除了采取动作连续情况下的做法,还可以只将状态s输入到神经网络中,使其同时输出每一个动作的Q值。
通常 DQN(以及 Q-learning)只能处理动作离散的情况,因为在函数的更新过程中有 max(a) 这一操作。假设神经网络用来拟合函数w的参数是 ,即每一个状态s下所有可能动作a的Q值都能表示为Qw(s,a)。
将用于拟合函数Q函数的神经网络称为Q 网络
将 Q-learning 扩展到神经网络形式——深度 Q 网络(deep Q network,DQN)算法。
- 由于
DQN是离线策略算法,收集数据时可以使用一个e-贪婪策略来平衡探索与利用,将收集到的数据存储起来,在后续的训练中使用。 - Q-learning用传统方法创建Q表,而DQN用神经网络来近似
DQN 中还有两个非常重要的模块——经验回放和目标网络,能够帮助 DQN 取得稳定、出色的性能。
DQN 算法主要思想是用一个神经网络来表示最优策略的函数,然后利用 Q-learning 的思想进行参数更新。
- 为了保证训练的稳定性和高效性,DQN 算法引入了
经验回放和目标网络两大模块,使得算法在实际应用时能够取得更好的效果。 - 2013 年的 NIPS 深度学习研讨会上,DeepMind 公司的研究团队发表了 DQN 论文,首次展示了这一直接通过卷积神经网络接受像素输入来玩转各种雅达利(Atari)游戏的强化学习算法,由此拉开了深度强化学习的序幕。
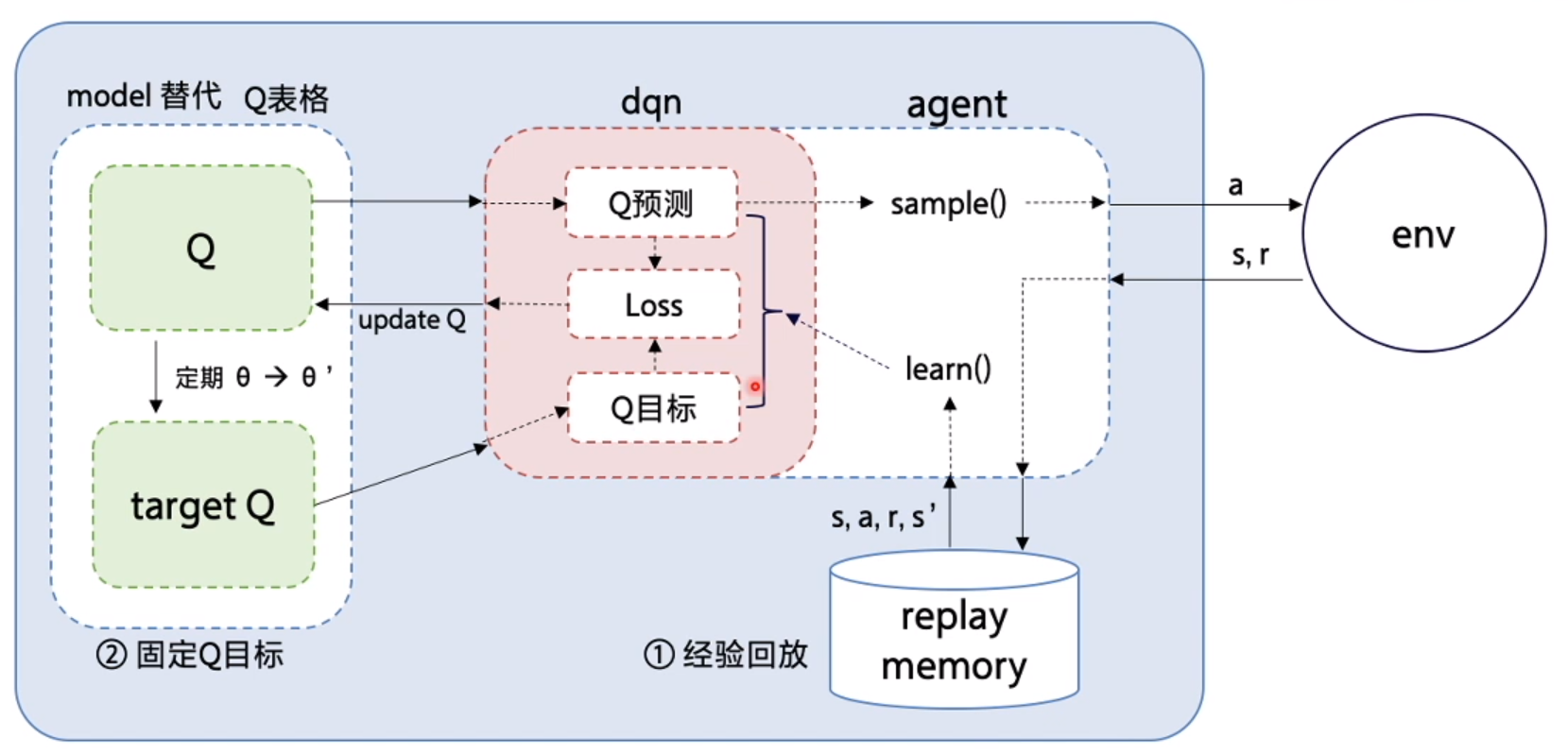
经验回放
有监督学习中,假设训练数据独立同分布,每次训练神经网络时从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。
- Q-learning 算法中,每一个数据只会用来更新一次Q值。
经验回放(Experience Replay)
为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法
维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
经验回放是 DQN(深度 Q 网络 )中极为关键的稳定机制。
- 智能体与环境交互过程中,每次交互产生的四元组((s,a,r,s’)) (状态 (s)、动作 (a)、奖励 (r) 、下一个状态 (s’) )会被存入回放池 。
- 训练模型时,从回放池中随机采样这些样本进行训练。
优点:
- 打破样本间的相关性:智能体与环境连续交互产生的样本往往存在相关性,不满足独立假设, 随机采样可避免模型学习到错误的相关性,提升训练稳定性。
- 非独立同分布的数据对训练神经网络有很大影响,会使神经网络拟合到最近训练的数据上
- 提高样本利用率:相同样本可被多次采样使用,充分挖掘样本价值,减少对大量新样本的依赖。
扩展版:优先经验回放(Prioritized Experience Replay)
采样时,依据 TD(时间差分 )误差大小对样本进行优先级排序,优先抽取 TD 误差大的样本。这些样本对应模型学习效果欠佳的部分,优先学习能让模型在薄弱环节更快提升,优化学习效率。
目标网络
更新网络参数的同时目标也在不断地改变,容易造成神经网络训练的不稳定性。
目标网络(Target Network)
为了解决这一问题,DQN 使用目标网络(target network)思想:
- 既然训练过程中 Q 网络的不断更新会导致目标不断发生改变,不如暂时先将 TD 目标中的 Q 网络固定住。
用两套 Q 网络。
- 原来训练网络 Qw(s,a), 用正常梯度下降方法来进行更新
- 目标网络使用训练网络的一套较旧的参数,训练网络在训练中的每一步都会更新
在 DQN(深度 Q 网络)中引入了目标 Q 网络 (Q_{target}) ,延迟更新,不直接用当前网络预测下一步 。
DQN 训练目标:
- \[y = r + \gamma Q_{target}(s', \underset{a}{\arg\max}Q_{target}(s', a;\theta))\]
- 其中 (r) 是奖励,(\gamma) 是折扣因子 ,(s’) 是下一个状态 ,(a) 是动作 ,(\theta) 是网络参数 。(Q_{target}) 是独立网络,更新频率慢,使得提供的目标更稳定。
优点:
- 使训练目标更稳定,减少训练过程中的波动。
- 有助于减少梯度爆炸问题,提升训练稳定性。 通常每间隔一定步数(如 1000 步 ),将当前网络参数同步给目标网络 。
训练优化
裁剪(Clipping)
训练 DQN 时,裁剪操作可避免训练过程出现问题。
- 奖励裁剪(Reward Clipping):将奖励值限制在([-1, 1])区间,防止奖励幅度差异过大引发训练不稳定。
- 梯度裁剪(Gradient Clipping):限制梯度的最大范数,比如将其限制在 10 以内 。 优点:能控制训练稳定性,避免出现梯度爆炸或产生 NaN(非数)现象。
Reward Shaping
在一些环境中,奖励信号过于稀疏(如仅到达终点才有奖励),训练效率低。此时可采用 Reward Shaping ,即适当添加辅助奖励,引导智能体(Agent)朝着目标前进。
设计小技巧:
- 奖励信号应简单,避免设置过多复杂规则。
- 要确保主奖励(对应最终任务)占主导地位 。
合理运用 Reward Shaping ,可大幅提高训练效率。
DQN 问题
DQN 算法敲开了深度强化学习的大门,但是作为先驱性的工作,其本身存在着一些问题以及一些可以改进的地方。
DQN 算法两大核心问题:
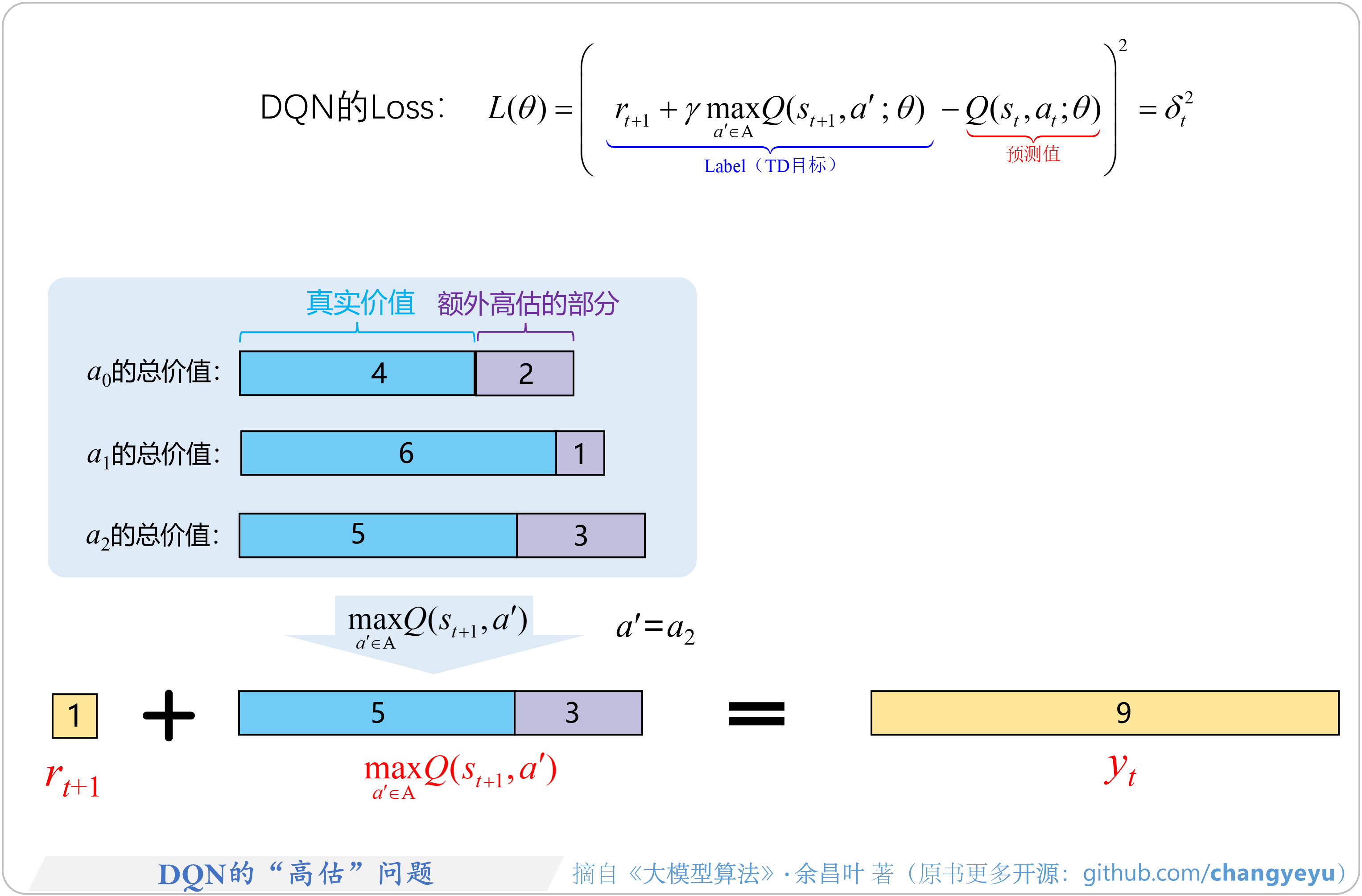
- (1)“高估”问题:DQN在选择和评估动作时,动作价值Q常被过高估计,导致策略优化出现偏差,影响最终性能。
- 这主要由于最大化操作中包含了高估部分的值,如图所示,最终目标价值yt中包含了额外高估的部分,并且这种高估会逐步累积。
- 此外,这种高估是“非均匀”的,即不同动作的价值Q被高估的程度各不相同。
- (2)“狗追尾巴”问题:也称为自举问题,DQN 训练过程可以看做一个“回归问题”,但是回归(要拟合)的目标yt总是在变,所以提升了训练的难度。
- DQN中,计算目标价值 和当前状态st的价值预测值 使用相同的网络权重θ。由于回归的目标yt依赖于当前网络的权重θ,当网络权重更新后变为θ′;
- 下一步训练时,计算出的价值预测值和回归的目标yt值将同步变化。
- 这种动态相互依赖关系就像“狗追尾巴”一样,不断循环,导致优化过程容易不稳定,甚至难以收敛。

DQN 改进
于是,在 DQN 之后,学术界涌现出了非常多的改进算法,其中两个非常著名的算法:Double DQN 和 Dueling DQN,实现非常简单,只需要在 DQN 的基础上稍加修改,在一定程度上改善 DQN 的效果。
- Double DQN 解决了 DQN 中对Q值的过高估计,而 Dueling DQN 能够很好地学习到不同动作的差异性,在动作空间较大的环境下非常有效。
DQN 改良主要依靠两个 Trick:
经验回放Experience replay【Lin 1993】- 虽然做不到完美的独立同分布,但还是要尽力减少数据之间的关联性。
- Experience replay 经验回放——学习当前经历着的, 也能学习过去经历过的, 甚至是学习别人的经历
- DQN 的精髓部分之一: 记录下所有经历过的步, 这些步可以进行反复的学习, 所以是一种 off-policy 方法
目标网络Target Network【Mnih 2015】Fixed Q-targets- Fixed Q-targets 决斗网络——在 DQN 中使用到两个结构相同但参数不同的神经网络, 预测 Q 估计 的神经网络具备最新的参数, 而预测 Q 现实 的神经网络使用的参数则是很久以前的
- Estimated Network 和 Target Network 不能同时更新参数,应该另设 Target Network 以保证稳定性。
- 【2019-2-9】当问题规模很大时,表格方法需要需要大量的存储和计算开销。
DQN 算法的主要做法是 Experience Replay,将系统探索环境得到的数据储存起来,然后随机采样样本更新深度神经网络的参数。它也是在每个 action 和 environment state 下达到最大回报,不同的是加了一些改进,加入了经验回放和决斗网络架构。
- 注:另外一种fixed-targets怎么用?一段时间内q不变
Double DQN
DQN 与 Double DQN 的差别只是在于计算状态s’下Q值时如何选取动作
与普通的 DQN 相比,Double DQN 比较少出现Q值大于 0 的情况,说明Q值过高估计的问题得到了很大缓解
标准 DQN 容易过高估计 Q 值,学习不稳定。
- 原因:目标网络选取最大 Q 值时,可能因误差高估某个动作,进而使当前网络也高估。
Double DQN 通过分离动作选择和评估来改进:
- 动作选择:由当前网络负责。
- 动作价值评估:由目标网络负责 。
优点:
- 能有效抑制 Q 值过估计,当一个网络出现高估情况,另一个网络可起到纠正作用。
- 让训练过程更稳定,收敛速度更快。
公式: [ y = r + \gamma Q_{target}(s’, \underset{a}{\arg\max}Q(s’, a;\theta)) ] ,其中 (r) 是奖励,(\gamma) 是折扣因子 ,(s’) 是下一个状态 ,(Q_{target}) 是目标网络的 Q 函数 ,(Q) 是当前网络的 Q 函数,(\theta) 是当前网络的参数 。
Dueling DQN
Dueling DQN 是 DQN 另一种改进,在传统 DQN 的基础上只进行了微小改动,但却能大幅提升 DQN 的表现。
将状态价值函数和优势函数分别建模的好处在于:
- 某些情境下智能体只会关注状态的价值,而并不关心不同动作导致的差异,此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态。
Dueling DQN 将 Q 值分解为“状态价值” (V(s)) 和“动作优势” (A(s,a)) 。所有动作共享同一个 (V(s)) ,在每次更新时,能使所有动作的 Q 值同步提升。
组合方式:
\[Q(s,a)=V(s)+(A(s,a) - \text{mean}(A(s,a')))\]原理说明: 若不减去 ($\text{mean}(A(s,a’))$) ,(V(s)+A(s,a)) 会存在无数种组合情况 ,只要给 (V(s)) 加上一个常数,同时从 (A(s,a)) 减去相同常数 ,输出结果不变,这会造成训练不稳定。减去 ($\text{mean}(A(s,a’))$)
- 一方面可使优势函数的均值为 0 ,起到约束作用;
- 另一方面,虽然也可减去 ($\underset{a’}{\max}A(s,a’)$) ,但由于 mean 操作可导,在实际应用中更为常用。
优点
- 很多动作都“差不多”情况下,能快速学习到好状态
问:“为什么 Dueling DQN 会比 DQN 好?”
- 部分原因在于 Dueling DQN 能更高效学习状态价值函数。每一次更新时,函数V都会被更新,这也会影响到其他动作的Q值。而传统的 DQN 只会更新某个动作的Q值,其他动作的Q值就不会更新。
- 因此,Dueling DQN 能够更加频繁、准确地学习状态价值函数。
DQfD
Google DeepMind 于2017年在AAAI会议上发表, 关于应用专家数据提升 PD3QN 算法性能的论文,PD3QN 即 PER+Dueling Double DQN。
- [DQfD] Deep Q-learning from Demonstrations
- 代码 DQfD
利用小部分专家示例数据加速智能体在现实任务中策略的学习。使用专家示例数据预训练智能体,从而使它从在线学习时perform well,然后使用自身交互生成的数据进一步提升。
DQfD的整个算法结构:DQN + Double learning + Dueling DQN + PER + n-step,前边四项的组合在文中又称PDD DQN。
步骤
- 预训练阶段,完全使用专家数据(demonstration data)进行有监督学习,使用四种损失优化神经网络,期望产出一个还不错的初始策略;
- 在线学习阶段,使用PER从混合数据中采样专家数据和实时交互生成的数据(self-generated data)去进一步提升策略。
特点
- 控制环境
- DQfD可超过专家性能
- 不丢弃、替换专家示例数据
DQfD与PDD DQN的不同
- DQfD需要demonstration data,而PD3QN不需要
- DQfD需要使用demonstration data预训练
- DQfD含有有监督损失
- DQfD使用了L2正则化项
- DQfD混合使用了1-step和n-step TD loss
- DQfD给专家经验设置不同的e,以提高被采样到的频率
应用场景
- 在一些数据中心、自动驾驶、推荐系统等应用方面,通常无法准确模拟环境动态、无法人为控制环境变化、数据可由控制器(人或其他算法)获得、在现实中去学习的场景下,可以考虑使用DQfD算法加速前期训练。
代码实现
DQN 两种实现方式
<s,a> -> q: 将s和a输入到网络,得到q值s -> <a,q>: 只将s输入到网络,输出为s和每个a结合的q值。
莫烦Demo采用第二种,Github地址
DQN Tensorflow版本实现,Gym环境
(1)CartPole 实例
- 运载体在一根杆子下无摩擦的跟踪。系统通过施加+1和-1推动运载体。杆子的摇摆在初始时垂直的,目标是阻止它掉落运载体。每一步杆子保持垂直可以获得+1的奖励。episode将会终结于杆子的摇摆幅度超过了离垂直方向的15°或者是运载体偏移初始中心超过2.4个单位。
- 效果图:
#https://blog.csdn.net/winycg/article/details/79468320
import numpy as np
import random
import tensorflow as tf
import gym
max_episode = 100
env = gym.make('CartPole-v0')
env = env.unwrapped
class DeepQNetwork(object):
def __init__(self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.9, # gamma
epsilon_greedy=0.9, # epsilon
epsilon_increment = 0.001,
replace_target_iter=300, # 更新target网络的间隔步数
buffer_size=500, # 样本缓冲区
batch_size=32,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = epsilon_greedy
self.replace_target_iter = replace_target_iter
self.buffer_size = buffer_size
self.buffer_counter = 0 # 统计目前进入过buffer的数量
self.batch_size = batch_size
self.epsilon = 0 if epsilon_increment is not None else epsilon_greedy
self.epsilon_max = epsilon_greedy
self.epsilon_increment = epsilon_increment
self.learn_step_counter = 0 # 学习计步器
self.buffer = np.zeros((self.buffer_size, n_features * 2 + 2)) # 初始化Experience buffer[s,a,r,s_]
self.build_net()
# 将eval网络中参数全部更新到target网络
target_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='target_net')
eval_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='eval_net')
with tf.variable_scope('soft_replacement'):
self.target_replace_op = [tf.assign(t, e) for t, e in zip(target_params, eval_params)]
self.sess = tf.Session()
tf.summary.FileWriter('logs/', self.sess.graph)
self.sess.run(tf.global_variables_initializer())
def build_net(self):
self.s = tf.placeholder(tf.float32, [None, self.n_features])
self.s_ = tf.placeholder(tf.float32, [None, self.n_features])
self.r = tf.placeholder(tf.float32, [None, ])
self.a = tf.placeholder(tf.int32, [None, ])
w_initializer = tf.random_normal_initializer(0., 0.3)
b_initializer = tf.constant_initializer(0.1)
# q_eval网络架构,输入状态属性,输出4种动作
with tf.variable_scope('eval_net'):
eval_layer = tf.layers.dense(self.s, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='eval_layer')
self.q_eval = tf.layers.dense(eval_layer, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='output_layer1')
with tf.variable_scope('target_net'):
target_layer = tf.layers.dense(self.s_, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='target_layer')
self.q_next = tf.layers.dense(target_layer, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='output_layer2')
with tf.variable_scope('q_target'):
# 计算期望价值,并使用stop_gradient函数将其不计算梯度,也就是当做常数对待
self.q_target = tf.stop_gradient(self.r + self.gamma * tf.reduce_max(self.q_next, axis=1))
with tf.variable_scope('q_eval'):
# 将a的值对应起来,
a_indices = tf.stack([tf.range(tf.shape(self.a)[0]), self.a], axis=1)
self.q_eval_a = tf.gather_nd(params=self.q_eval, indices=a_indices)
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval_a))
with tf.variable_scope('train'):
self.train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
# 存储训练数据
def store_transition(self, s, a, r, s_):
transition = np.hstack((s, a, r, s_))
index = self.buffer_counter % self.buffer_size
self.buffer[index, :] = transition
self.buffer_counter += 1
def choose_action_by_epsilon_greedy(self, status):
status = status[np.newaxis, :]
if random.random() < self.epsilon:
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: status})
action = np.argmax(actions_value)
else:
action = np.random.randint(0, self.n_actions)
return action
def learn(self):
# 每学习self.replace_target_iter步,更新target网络的参数
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.target_replace_op)
# 从Experience buffer中选择样本
sample_index = np.random.choice(min(self.buffer_counter, self.buffer_size), size=self.batch_size)
batch_buffer = self.buffer[sample_index, :]
_, cost = self.sess.run([self.train_op, self.loss], feed_dict={
self.s: batch_buffer[:, :self.n_features],
self.a: batch_buffer[:, self.n_features],
self.r: batch_buffer[:, self.n_features + 1],
self.s_: batch_buffer[:, -self.n_features:]
})
self.epsilon = min(self.epsilon_max, self.epsilon + self.epsilon_increment)
self.learn_step_counter += 1
return cost
RL = DeepQNetwork(n_actions=env.action_space.n,
n_features=env.observation_space.shape[0])
total_step = 0
for episode in range(max_episode):
observation = env.reset()
episode_reward = 0
while True:
env.render() # 表达环境
action = RL.choose_action_by_epsilon_greedy(observation)
observation_, reward, done, info = env.step(action)
# x是车的水平位移,theta是杆离垂直的角度
x, x_dot, theta, theta_dot = observation_
# reward1是车越偏离中心越少
reward1 = (env.x_threshold - abs(x))/env.x_threshold - 0.8
# reward2为杆越垂直越高
reward2 = (env.theta_threshold_radians - abs(theta))/env.theta_threshold_radians - 0.5
reward = reward1 + reward2
RL.store_transition(observation, action, reward, observation_)
if total_step > 100:
cost = RL.learn()
print('cost: %.3f' % cost)
episode_reward += reward
observation = observation_
if done:
print('episode:', episode,
'episode_reward %.2f' % episode_reward,
'epsilon %.2f' % RL.epsilon)
break
total_step += 1
# mountain car
RL = DeepQNetwork(n_actions=env.action_space.n,
n_features=env.observation_space.shape[0])
total_step = 0
for episode in range(max_episode):
observation = env.reset()
episode_reward = 0
while True:
env.render() # 表达环境
action = RL.choose_action_by_epsilon_greedy(observation)
observation_, reward, done, info = env.step(action)
#
position, velocity = observation_
reward=abs(position+0.5)
RL.store_transition(observation, action, reward, observation_)
if total_step > 100:
cost_ = RL.learn()
cost.append(cost_)
episode_reward += reward
observation = observation_
if done:
print('episode:', episode,
'episode_reward %.2f' % episode_reward,
'epsilon %.2f' % RL.epsilon)
break
total_step += 1
plt.plot(np.arange(len(cost)), cost)
plt.show()
(2) MountainCar实例
- car的轨迹是一维的,定位在两山之间,目标是爬上右边的山顶。可是car的发动机不足以一次性攀登到山顶,唯一的方式是car来回摆动增加动量。
- 输出图:
代码如下:
RL = DeepQNetwork(n_actions=env.action_space.n,
n_features=env.observation_space.shape[0])
total_step = 0
for episode in range(max_episode):
observation = env.reset()
episode_reward = 0
while True:
env.render() # 表达环境
action = RL.choose_action_by_epsilon_greedy(observation)
observation_, reward, done, info = env.step(action)
#
position, velocity = observation_
reward=abs(position+0.5)
RL.store_transition(observation, action, reward, observation_)
if total_step > 100:
cost_ = RL.learn()
cost.append(cost_)
episode_reward += reward
observation = observation_
if done:
print('episode:', episode,
'episode_reward %.2f' % episode_reward,
'epsilon %.2f' % RL.epsilon)
break
total_step += 1
plt.plot(np.arange(len(cost)), cost)
plt.show()
PG
Q-learning、DQN 及 DQN 改进算法都基于价值(value-based),其中 Q-learning 是处理有限状态的算法,而 DQN 可以用来解决连续状态的问题。
强化学习中,除了基于值函数的方法,还有一支非常经典的方法基于策略(policy-based)的方法。
基于值函数的方法主要是学习值函数,然后根据值函数导出一个策略,学习过程中并不存在一个显式的策略;基于策略的方法则是直接显式地学习一个目标策略。
策略梯度是基于策略的方法的基础
A2C, A3C, PPO 都不是纯 policy based 的 RL 方法,准确地说是 Actor-Critic 方法,即,同时用到了 value function 和 policy funtion.
- A2C is a special case of PPO
基于Policy Gradients(策略梯度法,简称PG)的深度强化学习方法,与基于Q-learning的系列算法有本质不同
- 普通PG算法,只能用于解决小问题,比如经典的让杆子竖起来,让小车爬上山等。
- 如果想应用到更复杂的问题上,比如玩星际争霸,就需要更复杂的一些方法,比如后期 Actor Critic,Asynchronous Advantage Actor-Critic (A3C)等等
解决什么问题
- (1)很多决策的行动空间是高维甚至连续(无限)的
- 比如自动驾驶中,汽车下一个决策中方向盘的行动空间,就是一个从[-900°,900°](假设方向盘是两圈半打满)的无限空间中选一个值,如果我们用Q系列算法来进行学习,则需要对每一个行动都计算一次reward,那么对无限行动空间而言,哪怕是把行动空间离散化,针对每个离散行动计算一次reward的计算成本也是当前算力所吃不消的。这是对Q系列算法提出的第一个挑战:无法遍历行动空间中所有行动的reward值。
- (2)决策往往是带有多阶段属性的,“不到最后时刻不知输赢”。
- 以即时策略游戏(如:星际争霸,或者国内流行的王者荣耀)为例,玩家的输赢只有在最后游戏结束时才能知晓,谁也没法在游戏进行过程中笃定哪一方一定能够赢。甚至有可能发生:某个玩家的每一步行动看起来都很傻,但是最后却能够赢得比赛,比如,Dota游戏中,有的玩家虽然死了很多次,己方的塔被拆了也不管,但是却靠着偷塔取胜(虽然这种行为可能是不受欢迎的)。诸如此类的情形就对Q系列算法提出了第二个挑战,Agent每执行一个动作(action)之后的奖励(reward)难以确定,这就导致Q值无法更新。
由此衍生出了基于PG的系列深度强化学习算法
Value VS Policy
PG深度强化学习算法与Q系列算法相比
优势:
- 可处理连续动作空间或者高维离散动作空间问题。
- 容易收敛,在学习过程中
- 策略梯度法每次更新策略函数时,参数只发生细微变化,但参数变化是朝着正确的方向进行迭代,使得算法有更好的收敛性。
- 而价值函数在学习后期,参数会围绕着最优值附近持续小幅度地波动,导致算法难以收敛。
缺点:
- 容易收敛到局部最优解,而非全局最优解;
- 策略学习效率低;
- 方差较高:最不可忍受的缺点
- 由于PG算法参数更新幅度较小,导致神经网络有很大随机性,在探索过程中会产生较多的无效尝试。
- 处理回合结束才奖励,会出现不一致问题:回合开始时,同样的状态下,采取同样的动作,但是由于后期采取动作不同,导致奖励值不同,从而导致神经网络参数来回变化,最终导致Loss函数的方差较大。
参考
算法介绍
- 流程
- 图解
- 注意
- 神经网络设计过程中,最后一层一般采用Softmax函数(离散动作) 或者 高斯函数激活(连续动作)。
- 奖励分配代码示例
def _discount_and_norm_rewards(self):
##该函数将最后的奖励,依次分配给前面的回合,越往前,分配的越少。除此之外,还将分配后的奖励归一化为符合正太分布的形式。
discounted_ep_rs = np.zeros_like(self.ep_rs) #self.ep_rs就是一局中每一回合的奖励,一般前面回合都是0,只有最后一个回合有奖励(一局结束)
running_add = 0
for t in reversed(range(0, len(self.ep_rs))):
running_add = running_add * self.gamma + self.ep_rs[t] #self.gamma,是衰减系数,该系数越大,前面回合分配到的奖励越少(都衰减了嘛)
discounted_ep_rs[t] = running_add
discounted_ep_rs = discounted_ep_rs - np.mean(discounted_ep_rs)
discounted_ep_rs = discounted_ep_rs / np.std(discounted_ep_rs)
return discounted_ep_rs
算法演进
PG->DPG->DDPG
从传统策略梯度算法(例如REIFORCE算法)、自然策略梯度算法、信赖域策略优化算法(TRPO)直到PPO算法的演进过程
REINFORCE 算法
基于策略的方法首先需要将策略参数化。
最简单的策略梯度算法,也称“蒙特卡洛策略梯度”,在每个回合结束后,直接基于整条轨迹的回报来更新策略。
REINFORCE 算法便是采用了蒙特卡洛方法来估计Q
- 相比于前面的 DQN 算法,REINFORCE 算法使用了更多的序列,这是因为 REINFORCE 算法是一个在线策略算法,之前收集到的轨迹数据不会被再次利用。
- 此外,REINFORCE 算法的性能也有一定程度的波动,这主要是因为每条采样轨迹的回报值波动比较大,这也是 REINFORCE 算法主要的不足。
REINFORCE 算法是策略梯度乃至强化学习的典型代表,智能体根据当前策略直接和环境交互,通过采样得到的轨迹数据直接计算出策略参数的梯度,进而更新当前策略,使其向最大化策略期望回报的目标靠近。这种学习方式是典型的从交互中学习,并且其优化的目标(即策略期望回报)正是最终所使用策略的性能,这比基于价值的强化学习算法的优化目标(一般是时序差分误差的最小化)要更加直接。
REINFORCE 算法理论上是能保证局部最优的,借助蒙特卡洛方法采样轨迹来估计动作价值,这种做法的优点是可以得到无偏梯度。但是,正是因为使用了蒙特卡洛方法,REINFORCE 算法的梯度估计的方差很大,可能会造成一定程度上的不稳定,这也是 Actor-Critic 算法要解决的问题。
REINFORCE 算法每隔1回合就更新一次,但 DDPG 是每步都会更新一次策略网络,它是一个单步更新的策略网络
- 根据一个确定好的策略模型来输出每一个可能动作的概率,对于所有动作的概率,我们使用采样方法(或者是随机的方法)选择一个动作与环境进行交互,同时环境会给我们反馈整个回合的数据。
- 将此回合数据输入学习函数中,并根据回合数据进行损失函数的构造,通过Adam等优化器的优化,再更新我们的策略模型。
优点
- 理论推导相对直接,概念简单,常用于基础教学和小规模实验。
- 对问题没有过多结构假设,容易与其他方法结合(如引入基线减小方差)。
缺点
- 高方差:需要大量样本才能得到稳定的梯度估计。
- 效率较低:一次采样后便更新,不能多次利用同一批数据。
PG 算法
PG 算法
- 一个Agent作为智能体,根据策略 π(或 $\pi_\theta$),在不同的环境状态s下选择相应的动作执行,环境根据Agent的动作,反馈新的状态以及奖励,Agent又根据新的状态选择新的动作,这样不停的循环,知道游戏结束,便完成了eposide。
- 一个完整的eposide序列,用 $\tao$ 来表示。而一个特定的 $\tao$ 序列发生的概率为
- 完整序列在整个游戏期间获得的总奖励用 $R(\tao)$ 来表示。对于给定参数 $\theta$ 的策略,评估其应获得的每局总奖励:对每个采样序列(即每一局)的加权和, 即:
- 目标:通过不断调整策略参数, 得到奖励越大越好,即 选用的策略参数能平均获得更多奖励
- 方法:梯度下降

- 第1个等号是梯度的变换;第2-3个等号是利用了log函数的特性;第4个等号将求和转化成期望的形式;期望又可以由采集到的数据序列进行近似;最后一个等号是将每一个数据序列展开成每个数据点上的形式
- PG 伪码
- 完整的PG算法
PG方法的Tips:
- 增加基线 baseline:
- 问题:PG更新时,增大奖励大的策略动作概率,减小奖励小的策略动作概率。但当奖励设计不好时有问题。
- 极端一:无论采取任何动作都能获得正奖励。但这对于那些没有采样到的动作,在公式中这些动作策略就体现为0奖励。则可能没被采样到的更好的动作产生的概率就越来越小,使得最后,好的动作反而都被舍弃了。
- 解法:引入基线,让奖励有正有负,一般增加基线的方式是所有采样序列奖励平均值:
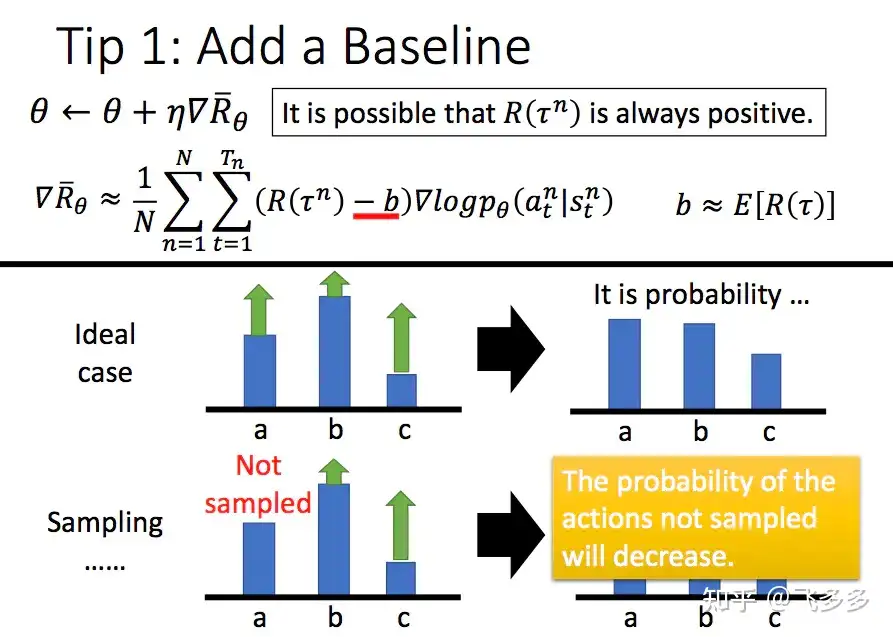
- 问题:PG更新时,增大奖励大的策略动作概率,减小奖励小的策略动作概率。但当奖励设计不好时有问题。
- 折扣因子:当前1块钱比未来期望的1块钱更具有价值。强化学习中,对未来的奖励需要进行一定的折扣
- 优势函数:
- 问题: 对同一个采样序列中的数据点,使用相同的奖励 – 粗糙
- 解法:将 奖励替换成 关于 S 和 A 的函数,即优势函数 $A^{\theta}\left(s_{t}, a_{t}\right)=\sum_{t^{\prime}>t} \gamma^{t^{\prime}-t} r_{t^{\prime}}-V_{\phi}\left(s_{t}\right)$
- 前面是实际采样折扣奖励,后面是拟合的折扣奖励
Policy Gradient with Baseline
Trajectory reward 可能是 unbounded的,直接使用 trajectory reward 有梯度方差大的问题,进而导致训练不稳定。对于policy-based方法来说,policy/model并不关心reward的具体值大小,而是关心不同action能获取reward的相对大小,因此可以对目标函数中的trajectory reward项减去一个baseline:
- \[\nabla_\theta J(\theta) = \frac{1}{N} \sum_{i=0}^{N}(\sum_{t=0}^{H}r(s_t, a_t) - \bf{b}) (\nabla_\theta \sum_{t = 1}^{H}log\pi_\theta(a_t|s_t))\]
上式即general form的vanilla policy gradient with baseline。直觉上看,trajectory reward减掉一个baseline可以让参数的梯度减小,从而稳定训练。
Baseline 一般是 value function ,有三种最基础的选择:
Q-value\(Q(s_t, a_t) = \sum_{t'=t}^{T} \mathbb{E}_{a_{t'} \sim \pi_\theta}[r(s_{t'}, a_{t'})\|s_t, a_t]\):含义是选择\(a_t\)之后能能获取的sum of expected reward,包含选择\(a_t\)能带来的immediate reward,用于衡量选择\(a_t\)的长期价值V-value\(V(s_t) = \mathbb{E}_{a_t \sim \pi_\theta}[Q(s_t, a_t)]\):含义是进入\(s_t\)之后能获取的expected sum of reward,用于衡量进入\(s_t\)的长期价值Advantage\(A(s_t, a_t) = Q(s_t, a_t) - V(s_t)\):含义是选择\(a_t\)相比选择其他actions的优势
DPG
Deepmind D.Silver等 2014年提出DPG: Deterministic Policy Gradient,即确定性行为策略,每步行为通过函数直接获得确定的值
- PG的action是采样出来的,而DPG是算出来的。
为何需要确定性策略?
PG方法缺点:
- 即使通过PG学习得到了随机策略之后,在每步行为时,还需要对得到的最优策略概率分布进行采样,才能获得action的具体值;而action通常是高维的向量,比如25维、50维,在高维的action空间的频繁采样,无疑是很耗费计算能力的;
- PG学习过程中,每一步计算policy gradient都需要在整个action space进行积分
- 积分一般通过Monte Carlo 采样来进行估算,需要在高维的action空间进行采样,耗费计算能力
DPG也有一个缺点:无法探索环境。
因此,在DPG的实际使用中,要采用其他策略来弥补这个缺点。
Noisy 在 DRL中的用法主要有:
- Noise on Action。就是随机乱选。
- Noise on Parameters。这种方法由于网络结构不变,参数也不是全换,因此相当于是有约束的随机选择,或者说是有系统的尝试。
在DPG中,一般采用第二种方法。
注意:
- 参数的改变意味着策略的改变,因此,Noise在episode中需要保持不变,这样才能检测随机策略的真正效果。否则就是无目的的乱抖了。(类似帕金森症)
产生噪声的方法有:
- Independent Gaussian noise。
- Factorised Gaussian noise。
参考:深度强化学习(四)——DDPG, PPO, IMPALA
DDPG
Deepmind 2016年提出了DDPG(Deep Deterministic Policy Gradient)。
从通俗角度看:
- DDPG = DPG + A2C + Double DQN
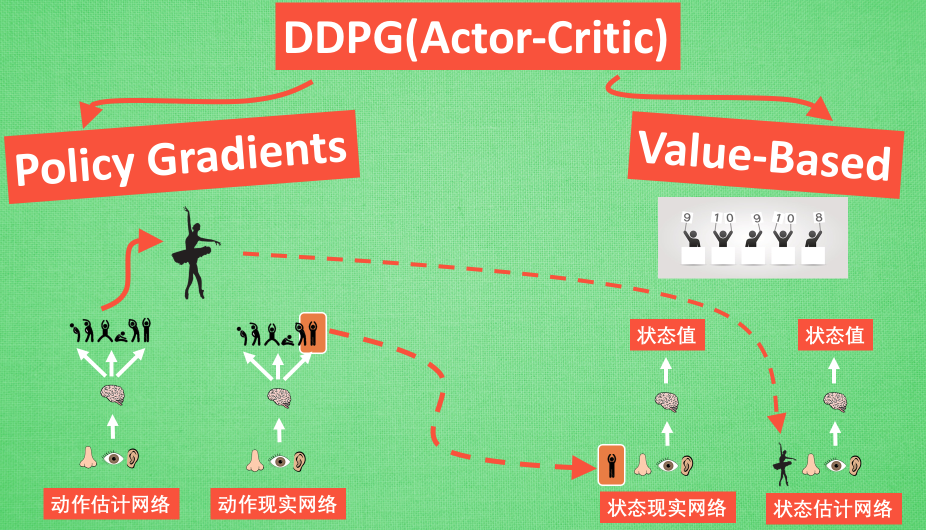
DDPG 网络结构图。仿照Double DQN的做法,DDPG分别为Actor和Critic各创建两个神经网络拷贝,一个叫做online,一个叫做target。即:
- Actor(策略网络) online network(动作估计网络)
- Actor(策略网络) target network(动作现实网络)
- Critic(Q网络) online network(状态估计网络)
- Critic(Q网络) target network(状态现实网络)
简单来说就是,Actor online network和Critic online network 组成一对Actor-Critic;而Actor target network和Critic target networ组成另一对Actor-Critic。
当然,DDPG实际的步骤远比示意图复杂的多
DDPG还有一个分布式版本。
- 论文:《Distributed Distributional Deterministic Policy Gradients》
【2023-7-3】DDPG是AC的改进,参考
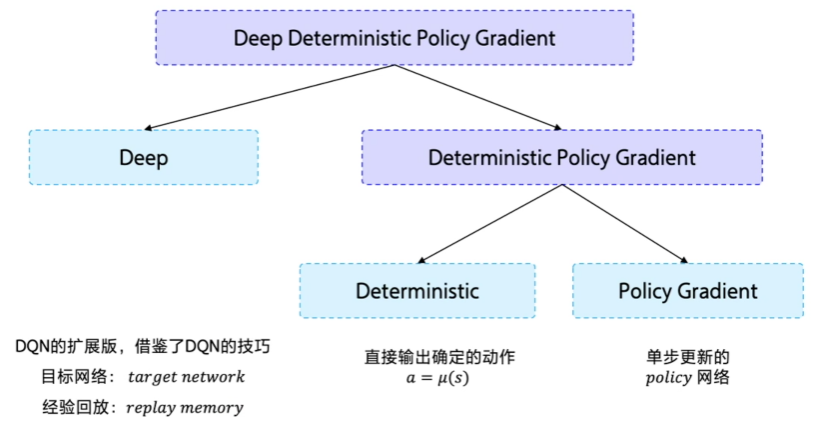
深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG),由D(Deep)+D(Deterministic )+ PG(Policy Gradient)组成。
- Deep 是因为用了神经网络;
- Deterministic 表示 DDPG 输出的是一个确定性的动作,可以用于连续动作的一个环境;
- Policy Gradient 代表的是它用到的是策略网络。REINFORCE 算法每隔一个 episode 就更新一次,但 DDPG 网络是每个 step 都会更新一次 policy 网络,也就是说它是一个单步更新的 policy 网络。
AC
PG 问题
策略梯度法问题
- 当使用蒙特卡洛策略梯度方法时,等到整个情景episode结束后计算奖励。
- 若结果回报值很高R(t),整个情景中所做行动都被指定为有利(行动),即使有些行动非常糟糕。
- 学习模型要获得最优策略 需要大量样本。导致训练过程耗时长,花费大量时间来收敛loss函数。
解决
- 每个时间步对参数进行更新
- 训练一个与值函数近似的评论家模型(值函数是通过给定状态和动作计算的最大未来回报的期望值),用来代替使用策略梯度时的奖励函数。
AC 介绍
AC: Actor-Critic 算法
为平衡高方差和低偏差,在Actor-Critic中将策略函数(Actor)和价值函数(Critic)同时学习
基于值函数的方法(DQN)和基于策略的方法(REINFORCE),其中基于值函数的方法只学习一个价值函数,而基于策略的方法只学习一个策略函数。
那么,有没有什么方法既学习价值函数,又学习策略函数呢?答案就是 Actor-Critic。
Actor-Critic 是囊括一系列算法的整体架构,目前很多高效的前沿算法都属于 Actor-Critic 算法
Actor-Critic算法本质上是基于策略的算法,因为这一系列算法的目标都是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好地学习。
在 REINFORCE 算法中,目标函数的梯度中有一项轨迹回报,用于指导策略的更新。REINFOCE 算法用蒙特卡洛方法来估计 Q(s,a),能不能考虑拟合一个值函数来指导策略进行学习呢?这正是 Actor-Critic 算法所做的
将 Actor-Critic 分为两个部分:Actor(策略网络)和 Critic(价值网络),如图所示。
- Actor 要做的是与环境交互,并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。
- Critic 要做的是通过 Actor 与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的,进而帮助 Actor 进行策略更新。

算法分为两个部分: Actor 和 Critic 。 Actor 更新策略, Critic 更新价值。 Critic 就可以用之前介绍的 SARSA 或者 Q-Learning 算法。
- (1). 最传统的方法是 Value-Based,选择有最优 Value 的 Action。
- 经典方法:Q-learning 【Watkins and Dayan 1992】、SARSA 【Sutton and Barto 2017】 。
- (2). 后来 Policy-Based 方法引起注意,最开始是
REINFORCE算法【Williams 1992】,后来策略梯度Policy Gradient【Sutton 2000】出现。 - (3). 最时兴的
Actor-Critic【Barto et al 1983】把两者做了结合。Sutton老爷子的好学生、AlphaGo的总设计师David Silver同志提出了Deterministic Policy Gradient,表面上是 PG,实际讲了一堆 AC,这个改进史称DPG【Silver 2014】。
“混合方法”: Actor Critic(AC), 用到两个神经网络:
- 衡量所采取的行动的好坏的
评价器(critic)(基于值函数) - 控制智能体行为方式的
行动者(actor)(基于策略)
分析
- Actor 源自 Policy Based 方法, 回合结束才知道奖励情况
- Critic 源自 Value Based 方法, 每步都能获得奖励反馈;学习环境和奖惩关系
Actor 运用 Policy Gradient 方法进行 Gradient ascent
Critic 来告诉这次的 Gradient ascent 是否正确 ascent, 如果不好, 不要 ascent 那么多.
但 AC 问题
- 训练两个网络,且同步更新,存在相关性,导致 网络片面看待问题、学不到东西
解决
- DeepMind 推出 DDPG = AC + DQN
- DDPG 最大的优势:在连续动作上更有效地学习.
Actor Critic 智能体实现策略:
- A2C(又名优势演员评论家)
- A3C(又名异步优势演员评论家)
Advantage Actor Critic(A2C)
为了进一步减小梯度的方差问题,使用神经网络拟合value function,即 actor-critic 方法。
用actor和critic两个神经网络:
- actor:用于建模 policy \(\pi_\theta(a_t\|s_t)\) ,输出action space概率分布
- critic:用于拟合 value function \(V_{phi}(s_t)\)。
A2C即用advantage替换了vanilla policy gradient中的total reward,即actor的objective梯度可以写成:
- \[\nabla_\theta J(\theta) = \frac{1}{N} \sum_{i=0}^{N}A(s_t) (\nabla_\theta \sum_{t = 1}^{H}log\pi_\theta(a_t|s_t))\]
为了计算简便,通常使用temporal difference来近似advantage,用步长为1的TD近似advantage可以写成:
- \[A(s_t, a_t) = r(a_t, s_t) + \gamma V_{\phi}(s_{t+1}) - V_{\phi}(s_t)\]
Critic network(parameterized by \(\phi\))对应的loss使用mean squared error/huber(省略discount factor):
- \[L(\phi) = \frac{1}{N} \sum_{i=0}^{N}(\sum_{t=0}^{T}(V_{\phi}(s_t) - \sum_{t'=t}^{T}r(a_{t'}, s_{t'}))^2)\]
AC 类别
Two different strategies: Asynchronous 异步 or Synchronous 同步
We have two different strategies to implement an Actor Critic agent:
A2C(aka Advantage Actor Critic) 优势AC, (又名优势演员评论家)A3C(aka Asynchronous Advantage Actor Critic) 异步优势AC, (又名异步优势演员评论家)- A3C中,不使用经验回放,因为需要大量内存。而是并行在多个环境实例上异步执行不同的智能体。(可多核CPU跑)每个work(网络模型的副本)将异步地更新全局网络。
A2C与A3C唯一区别是A2C是同步更新全局网络。
AC架构对于最先进的算法(如近端策略优化Proximal Policy Optimization,又名PPO)至关重要。
PPO是基于 Advantage Actor Critic(优势行动者评论家算法)。
Actor-Critic模型是一个更好的得分函数。不像在蒙特卡洛(MC)这种传统强化学习方法那样,等到情景episode结束才更新参数,而是在每个步骤进行更新(即时序差分学习,TD学习)
OpenAI 研究院 翁丽莲 policy-gradient-algorithms
PG算法中为了解决Q值方差过大,设置reward均值作为baseline来归一化Q值
- 不如让神经网络直接输出 V(s),作为baseline的代替
- 即 $ ref_V = V(s) -> baseline(critic) $
而实际的Q值与baseline之差记为需要修正的V
- 实际 Q值由下一个state的V值估计而来
- 表达式: $ adv_V = Q(s,a)-V(s) -> advantage_value(actor)$
这种baseline的变体称为 critic ,将Q值变体称为 actor ,形成 Advanced-Actor-Critic算法(A2C)
至于输出的policy 依旧是动作的概率分布。
- 实际中神经网络输出的可能是不同动作的Q值,但训练时,一定会对这些Q值做一个softmax转化为动作概率分布。
这样说明是为了强调:A2C是policy-based的算法。
此外
- A2C依然包含信息熵loss函数,策略loss函数(交叉熵),因为额外输出了V(s),借鉴DQN中的方法(bellman方程的逼近),额外增加值loss函数
- A2C采用多个并行环境进行环境探索
TRPO (改进)
策略梯度算法和 Actor-Critic 算法虽然简单、直观,但在实际应用过程中会遇到训练不稳定的情况。
- 基于策略的方法:参数化智能体的策略,并设计衡量策略好坏的目标函数,通过梯度上升的方法来最大化这个目标函数,使得策略最优。
基于策略的算法明显缺点:
- 当策略网络是深度模型时,沿着策略梯度更新参数,很有可能由于步长太长,策略突然显著变差,进而影响训练效果。
为了保证新旧策略足够接近,TRPO 使用了库尔贝克-莱布勒(Kullback-Leibler,KL)散度来衡量策略之间的距离
- 不等式约束定义了策略空间中的一个
KL球,被称为信任区域。 - 在这个区域中,当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。
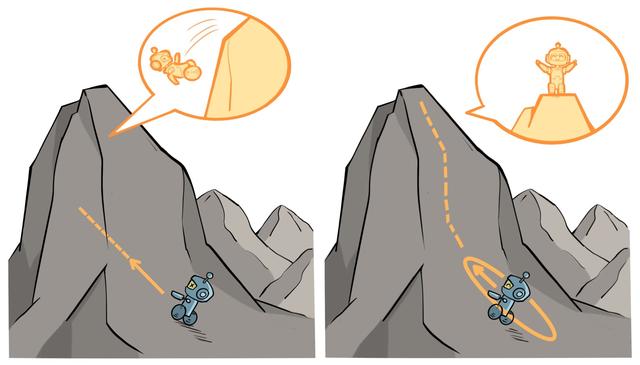
- 左图表示当完全不设置信任区域时,策略的梯度更新可能导致策略的性能骤降;
- 右图表示当设置了信任区域时,可以保证每次策略的梯度更新都能来带性能的提升
TRPO 算法属于在线策略学习方法,每次策略训练仅使用上一轮策略采样的数据,是基于策略的深度强化学习算法中十分有代表性的工作之一。直觉性地理解,TRPO 给出的观点是:
- 由于策略的改变导致数据分布的改变,这大大影响深度模型实现的策略网络的学习效果,所以通过划定一个可信任的策略学习区域,保证策略学习的稳定性和有效性。
TRPO 要点
重点概念
近似求解:直接求解上式带约束的优化问题比较麻烦,TRPO 在其具体实现中做了一步近似操作来快速求解。共轭梯度:用神经网络表示的策略函数的参数数量都是成千上万的,计算和存储黑塞矩阵H的逆矩阵会耗费大量的内存资源和时间。TRPO 通过共轭梯度法(conjugate gradient method)回避了这个问题线性搜索: 由于 TRPO 算法用到了泰勒展开的 1 阶和 2 阶近似,这并非精准求解,因此,新参数可能未必比旧参数好,满足 KL 散度限制。TRPO 在每次迭代的最后进行一次线性搜索(Line Search),以确保找到满足条件广义优势估计: 如何估计优势函数? 目前比较常用的一种方法为广义优势估计(Generalized Advantage Estimation,GAE)
TRPO 实践
支持与离散和连续两种动作交互的环境来进行 TRPO 的实验。我们使用的第一个环境是车杆(CartPole),第二个环境是倒立摆(Inverted Pendulum)。
A2C
之前所有模型与算法中,无论是 off-policy, on-policy, value-based 还是 policy-based 的神经网络,均只输出一个变量:
- 要么输出策略,要么输出值。
而A2C打破了这个规则,A2C的神经网络输出两个变量,使其成为一种PG算法的强大拓展。
Actor-Critic Methods: A3C and A2C
A2C 算法概述

- 与PG类似,首先探索环境共计step_count步得到序列(s,a,r,s’,is_done)
- 使用之前PG计算Q值的公式,计算total_discount_reward
- 记录(s,a,total_discount_reward,s’,is_done)序列
- 继续探索环境,pop out旧数据,pop in新数据
- 重复步骤2至步骤5直到length(tuple_list) = batch_size
- 进入训练环节:准备训练数据:1.计算Q:val_ref= total_discount_reward + net(s’)。2.计算policy和baseline:action_s,val_s = net(s)。注意这里神经网络的输出:V(s)下标为1,policy下标为0,所以Q值中为net(s’)代表V(s’),即下一state的V值。
- 借鉴DQN的方法,值loss函数为预测的baseline和实际的baseline(Q)的MSE
- 与PG一样,计算信息熵loss
- 值相关loss = 信息熵loss+值loss
- advtange 为预测baseline和实际baseline之差
- 利用advantage和神经网络输出的policy以及实际使用的动作,利用交叉熵计算策略loss
- 分别对值相关loss和策略loss做梯度下降。
注意:
- 一般来说都是计算总loss再做梯度下降的。但这里将策略loss单独进行梯度下降,也是可以的。
A2C 源码
OpenAI的A2C实现中,A2C算法被分成4个清晰的脚本:
- main函数,run_atari.py: 这个脚本中,设定策略类型以及学习率,以及对应的Atari游戏。
- 脚本默认设定16个CPU用于创建16个gym环境,每一个环境都设定了一个rank,猜测这个rank是为了记录log文档而设的,因为代码中没有使用mpi4py库多开Atari游戏。多线程使用了python的multiprocessing库。
- 创建策略类型脚本,policies.py: 这个脚本在Tensorflow中创建了计算图以及使用了CNN或LSTM。
- 实际a2c算法脚本,a2c.py: 该脚本以一个learn方法作为输入(learn是由policies.py产生的)。
- 另外,这个脚本使用了Model类与Runner类对多个环境进行并行处理。当Runner类执行一个step时,16个环境都执行了一个step。
- 应用脚本,utils.py: 实现了helper与logger方法。
在环境的采样这一步,算力的瓶颈仍然在CPU。尽管如此,我认为相较于A3C算法,我会更倾向于选择使用A2C算法作为Actor-Critic框架下的基准算法。
2018年9月,OpenAI修改了基准代码。现在基准代码使用了一个算法无关的运行脚本,且他们把策略函数代码移动到了 common 包。除了这一点不同以外,本文所写的内容(译者注:应该是指上述A2C的4点内容)是与A2C的架构是一致的,在我的另一篇blog中阐述了OpenAI的基准算法修改的细节。
A3C – 进阶
A3C 是 Asynchronous Advantage Actor Critic 的缩写。
- A3C = A2C + Asynchronous
- A3C相对于A2C的核心改变在于采样数据的并行上
这个名字的含义:参考
Asynchronous:异步。由于该算法会并行运行多个环境(一般是不同核心的CPU)以提高训练数据的差异性,并以 Hogwild!方式异步更新梯度。- A3C算法无需经验回放(experience replay),当然,如果你愿意,也可以在A3C算法中使用经验回放,如
ACER算法。
- A3C算法无需经验回放(experience replay),当然,如果你愿意,也可以在A3C算法中使用经验回放,如
Advantage:优势函数。A3C算法更新梯度时使用了优势函数,在DeepMind的文章中,他们使用了 歩奖励。Actor Critic:A3C 算法是 Actor-Critic 框架下的算法,在状态价值函数的指导下更新梯度。
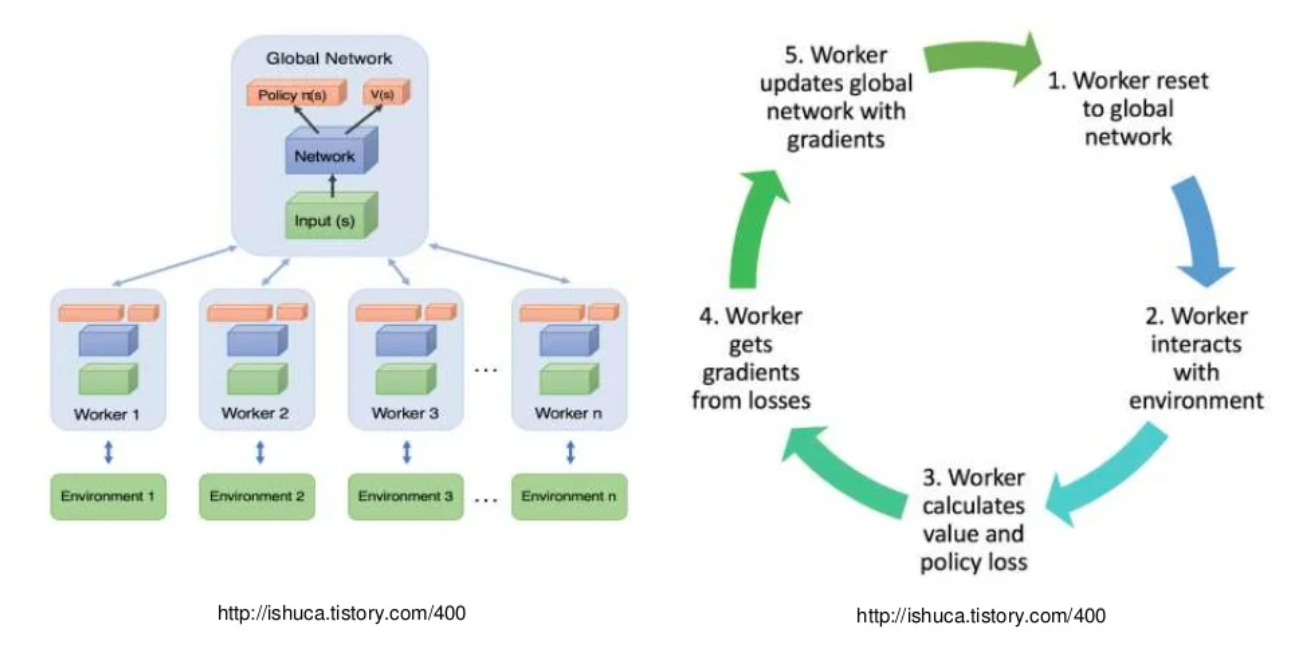
相比Actor-Critic,A3C的优化主要有3点
- 异步训练框架 – 最大的优化点
- 网络结构优化
- Critic评估点
基于策略的强化学习算法的一个显著缺点:
- 采样数据来自于环境的一个序列 — 数据明显不符合i.i.d,很难训练
基于值的强化学习算法(例如DQN)没有这个问题
- 因为经验池的存在,当前batch可以包含很久之前的经验数据。所以,采样是可以近似于i.i.d。
但是基于策略的算法要求根据网络输出动作,并以当前episode的rewrard做Q值的计算,当前episode结束后,本轮经验便被抛弃。
- 一个大小为10000的DQN经验池,如果batch_size为100,等价于每个经验平均会被100个episode利用。而基于策略的PG, AC系列算法,每个经验只能被当前episode使用。
如果想为策略算法设计经验池,应该使经验池装载”旧策略”,这些旧策略或许会起到DQN中”目标网络”类似的作用,但是实际上这样的改进意义不大。
所以,最简单暴力的方法:
- 一个batch的数据从多个环境中采集。
- 环境越多,batch_size越大,采样数据越接近于i.i.d(但实际情况中,环境不会无限大,一是顾及到计算效率,二来会影响策略的收敛)
多线程并行
并行数据 vs 并行梯度
在环境并行的基础之上,还能做线程并行。
- 线程并行运算是一个很大的领域,并行编程大部分语言都是直接实现。主流的深度学习框架也是有多线程实现的,比如pytorch,拿来直接用就行。
两种多线程并行的方式:
- 数据并行:线程0 做 loss计算
- 梯度并行:agent 做 loss计算
区别:loss计算由谁做?agent 还是 线程0?
注意
- 如果计算资源不大(只有1个GPU/CPU),并行计算并不能带来计算效率提升。
- 如果有集群,建议使用A3C。
- 另外,由于梯度计算运算量较大,建议用梯度并行策略,多个线程对梯度进行计算,线程0仅做梯度下降。
PPO (TRPO改进)
OpenAI 提出解决 Policy Gradient 不好确定 Learning rate (或者 Step size) 的问题.
- 如果 step size 过大, 学出来的 Policy 会一直乱动, 不会收敛
- 如果 Step Size 太小, 训练时间太长.
OpenAI 2017年 提出 Proximal Policy Optimization (PPO),用于训练强化学习智能体的算法,可有效地解决智能体学习过程中的稳定性和收敛性问题。
- 改进 Q-learning 和 TRPO 算法:trust region policy optimization (TRPO)
- Proximal Policy Optimization Algorithms
PPO 利用 New Policy 和 Old Policy 比例, 限制了 New Policy 的更新幅度, 让 Policy Gradient 对稍微大点的 Step size 不那么敏感.
PPO 的前生是 OpenAI 发表的 Trust Region Policy Optimization
- 但 Google DeepMind 看过 OpenAI 关于 Trust Region Policy Optimization 的 conference 后, 却抢在 OpenAI 前面 (2017年7月7号) 把 Distributed PPO给先发布了
- OpenAI 2017年7月20号 发表 PPO 论文
TRPO 算法在很多场景上应用都很成功,但是计算过程非常复杂,每一步更新的运算量非常大。
TRPO 算法的改进版——PPO 基于 TRPO 思想,但是其算法实现更加简单。
- TRPO 使用
泰勒展开近似、共轭梯度、线性搜索等方法直接求解。 PPO的优化目标与TRPO相同,但PPO用了一些相对简单的方法来求解。- PPO 有两种形式,一是
PPO-惩罚,二是PPO-截断。 - 大量实验表明,
PPO-截断总是比PPO-惩罚表现得更好。
【2023-6-26】李宏毅讲解PPO
TRPO 使用泰勒展开近似、共轭梯度、线性搜索等方法直接求解。PPO 的优化目标与 TRPO 相同,但 PPO 用了一些相对简单的方法来求解。具体来说,PPO 有两种形式,一是 PPO-惩罚,二是 PPO-截断
PG方法缺点:参数更新慢,因为每更新一次参数都重新采样,on-policy 策略
- 改进:将 on-policy 方式转换为 off-policy,让采样到的数据可以重复使用,提升训练速度
GAE
GAE 全称 generalized advantage estimation,广义优势估计。
动机:
- MC估计: 无偏,但方差大
- TD估计: 方差小,但有偏
- GAE:在偏差和方差之间权衡
通过指数滑动平均(EMA)的思想设计用不同步奖励得到的估计的权重
PPO 原理
重要性采样
问题:
- 对于一个服从概率p分布的变量x, 要估计 f(x) 的期望。
- 方法: 用一个服从p的随机生成器, 采样,计算均值 – 不知道p分布
- 改进: 从已知的分布q中进行采样。通过对采样点的概率进行比较,确定这个采样点的重要性。
这种采样方式的分布p和q不能差距过大,否则,会由于采样的偏离带来谬误。
PPO的更新策略其实有三套网络参数:
- 策略参数 $\thata$,与环境交互收集批量数据,然后批量数据关联到 $\thata$ 的副本中。每次都会被更新。
- 策略参数的副本 $\thata^’$,策略参数与环境互动后收集的数据的关联参数,相当于重要性采样中的q分布。
- 评价网络的参数 $\phi$,基于收集的数据,用监督学习方式来更新对状态的评估。也是每次都更新。
PPO的思路:李宏毅笔记
- 0点时:我与环境进行互动,收集了很多数据。然后利用数据更新我的策略,此时我成为1点的我。当我被更新后,理论上,1点的我再次与环境互动,收集数据,然后把我更新到2点,然后这样往复迭代。
- 但是如果我仍然想继续0点的我收集的数据来进行更新。因为这些数据是0点的我(而不是1点的我)所收集的。所以,我要对这些数据做一些重要性重采样,让这些数据看起来像是1点的我所收集的。当然这里仅仅是看起来像而已,所以我们要对这个“不像”的程度加以更新时的惩罚(KL)。
- 其中,更新方式:我收集到的每个数据序列,对序列中每个(s, a)的优势程度做评估,评估越好的动作,将来就又在s状态时,让a出现的概率加大。
- 这里评估优势程度的方法,可以用数据后面的总折扣奖励来表示。
- 另外,考虑引入基线的Tip,又引入一个评价者小明,让他跟我们一起学习,他只学习每个状态的期望折扣奖励的平均期望。这样,我们评估(s, a)时,我们就可以吧小明对 s 的评估结果就是 s 状态后续能获得的折扣期望,也就是我们的基线。
- 注意:优势函数中,前一半是实际数据中的折扣期望,后一半是估计的折扣期望(小明心中认为s应该得到的分数,即小明对s的期望奖励)
- 如果你选取的动作得到的实际奖励比这个小明心中的奖励高,那小明为你打正分,认为可以提高这个动作的出现概率;
- 如果选取的动作的实际得到的奖励比小明心中的期望还低,那小明为这个动作打负分,你应该减小这个动作的出现概率。这样小明就成为了一个评判官。
当然,作为评判官,小明自身也要提高自己的知识文化水平,也要在数据中不断的学习打分技巧,这就是对 $\phi$ 的更新了。
PPO 伪代码
PPO 中, 学习过程依赖于一个评论家(critic), 评估策略所采取行动的质量。
评论家估计给定状态的价值,通过比较预期回报与实际结果来指导策略优化。
在多代理设置中, 部署多个策略,每个代理一个,通常以分散方式运作。每个代理的策略仅根据其局部观察来决定其行动。但是评论家可以是集中或分散:
MAPPO: 评论家集中,以全局观察或连接的代理观察作为输入。这种方法在可获得全局状态信息的集中式训练场景中有益。IPPO: 评论家分散,仅依赖于局部观察。这种设置支持分散式训练,代理只需要局部信息。
集中式评论家有助于缓解多个代理同时学习时出现的非平稳性问题,但可能因输入的高维度性而面临挑战。
ppo 特点
特点
- 属于 Trust Region Policy Optimization 的简化版,通过限制新旧策略的更新幅度来保证训练稳定性。
- 训练时,可在同一批数据上做多次迭代更新,但会对新旧策略的概率比率施加“剪切”或“KL 惩罚”,防止一步迈得过大。
优点
- 训练更稳定:限制策略更新,使得学习过程不易崩溃。
- 样本利用率更高:对同一批次数据多次梯度更新,提高效率。
缺点
- 实现与调参相对更复杂,需要合适的超参数(如剪切阈值、KL 系数等)。
- 仍是 on-policy 方法,对离线数据的利用相对有限。
PPO算法有三个重点:
- 可以输出连续的控制信号,比如输出正太分布的均值和方差作为一个连续动作的动作概率
- 将PG的在线学习,改成离线学习,提高数据的利用率。
- 具体方法是使用重要性采样,将不同动作的TD-Error加上一个动作的概率,然后乘以不同策略反馈的梯度,从而可以用不同阶段策略的数据更新本阶段的模型。
- N-step参数更新方式。
- 原本的AC模型中,使用0阶的TD-Error更新模型,前向探索能力不足,使用N步之后的TD-Error可以更有效的获取动作的好坏。
调参技巧:
- PPO算法玩Atari游戏的时候,论文中默认使用的skip是4,但在一些动作较快的游戏中,比如Breakout-v0中,每一帧都有用,使用skip=1效果更好。
经验
- AC + advantage = A2C
- A2C + 重要性采样 + TD(n) = PPO
伪代码
REINFORCE vs PPO
REINFORCE 和 PPO的核心区别
- 更新方式
- REINFORCE:整条轨迹结束后一次性更新,仅用该次采样的数据。
- PPO:可以多次使用同一批数据,用截断或 KL 惩罚约束更新。
- 稳定性与效率
- REINFORCE:简单但高方差、低效率。
- PPO:限制策略变化幅度,显著提升稳定性与收敛速度。
On-Policy vs. Off-Policy & Importance Sampling
分析
- On-policy 每次用于学习policy网络的trajectories都是当前这个policy产生的(e.g. REINFORCE),即第一步用policy采样产生trajectories,第二步用这些新的trajectories训练policy,两步交替,缺点是训练效率比较低。
- 相反,off-policy 是把trajectories全部保存下来,这样训练policy时不需要采样,相当于有两个policy,一个用于生产trajectories,另一个用于学习最大化expected reward。
如果只用这些保存下来的trajectories就会有采样不充分的问题,进而影响expected reward的计算,而RL的目标在于最大化expected reward,不充分就会导致expected reward预估地不准确
- 因此 off-policy 使用 importance sampling 对每个reward 进行 reweight:
- \[\mathbb{E}_{\tau \sim \pi_{\theta}}[ \sum_{t=0}^{H} R(s_t, a_t)] = \sum_{t=0}^{H} P(a_t)R(s_t, a_t) = \sum_{t=0}^{H} {P(a_t) \over {P'(a_t)}}R(s_t, a_t)\]
其中P’是采样policy,P是要学习的policy。有些actions在采样policy的概率低但新policy的概率比较高,这些actions的reward就要给更高的权重;另一些actions正好相反。
由于 policy gradient 不是每次取一个action完了更新,而是要等到整个trajectory完了之后,才能算expected reward
- 如果整个trajectory太长,就容易导致梯度方差很大,学习不稳定
- 所以,RL很多改进都是为了减少方差,提高 sample efficiency,也包括PPO。PPO通过限制 policy 单 trajectory 更新的幅度来降低方差。
PPO-惩罚
PPO-惩罚(PPO-Penalty)用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,这就变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数。
PPO-截断
PPO 另一种形式 PPO-截断(PPO-Clip)更加直接,目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大
PPO 核心思想
- 通过对策略函数进行近端优化(proximal optimization)来进行策略迭代。
- PPO 使用一种称为 clipped surrogate objective 的损失函数来保证每次策略迭代时,都只会更新一定的幅度,从而避免更新过程中的不稳定性和剧烈波动。
- PPO 采用了两个重要的技术,分别是“重要性采样”和“基线函数”。其中,重要性采样可以用于计算损失函数,而基线函数则可以帮助估计状态值函数,以进一步优化策略。
PPO 的应用范围非常广泛,可以用于解决各种强化学习问题
- 如玩家控制、机器人导航、金融交易等。
- 在实践中,PPO 已被证明比许多传统的强化学习算法更为稳定和高效。
PPO 的另一种形式 PPO-截断(PPO-Clip)更加直接,它在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大
policy gradient with baseline 方法的目标是最大化advantage
PPO-clip 对单个weighted advantage直接clip到一个范围内(由 epsilon超参决定): \(L^{CLIP}(\theta) = \mathbb{E}_{a_t \sim \pi}[ min\{ {\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)}A_t, clip({\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)}, 1 - \epsilon, 1 + \epsilon)A_t \} ]\)
- 相比上文,改了一下符号用L^CLIP表示expected advantage
- Ratio部分 \({\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)}\) 其实就是上面提到的importance sampling,PPO是on-policy的,因为在生成trajectories的policy就是目标policy,但有先后之分;
- 比较unclipped部分\({\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)}A_t\)和clipped部分\(clip({\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)}, 1 - \epsilon, 1 + \epsilon)\)取最小,就可以做到如果min返回clipped部分就没有梯度。以下图是各种情况的枚举,其中\({\pi_\theta(a_t\|s_t) \over {\pi_{\theta_{old}}}(a_t\|s_t)} = p_t(\theta)\):
- Case 4梯度为零的含义是虽然a_t这个动作会导致负向(A_t < 0),但是由于新policy相比旧policy更不倾向于选择这个动作,所以不继续往“不倾向”的方向走了(Reduce variance! Reduce variance! Reduce variance!)。
- Case 5梯度为零的含义是虽然a_t这个动作会导致正向(A_t > 0),但是由于新policy相比旧policy更倾向于选择这个动作,所以不继续往“倾向”的方向走了(Overshoot prevention!!!)。
DDPG
基于策略梯度的算法 REINFORCE、Actor-Critic 以及两个改进算法——TRPO 和 PPO。
这类算法有一个共同的特点:
- 它们都是在线策略算法,样本效率(sample efficiency)比较低。
- 而 DQN 算法直接估计最优函数 Q,可以做到离线策略学习,但是它只能处理动作空间有限的环境
深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法 构造一个确定性策略,用梯度上升的方法来最大化Q值。DDPG 也属于一种 Actor-Critic 算法。
- DDPG = AC + DQN
DDPG 中的 Actor 网络和 Critic 网络
SAC (改进DDPG)
在线策略算法的采样效率比较低,通常更倾向于使用离线策略算法。
- 然而,虽然 DDPG 是离线策略算法,但是训练非常不稳定,收敛性较差,对超参数比较敏感,也难以适应不同的复杂环境。
2018 年,一个更加稳定的离线策略算法 Soft Actor-Critic(SAC)被提出。
SAC的前身是Soft Q-learning,都属于最大熵强化学习的范畴。Soft Q-learning不存在一个显式的策略函数,而是使用一个函数的波尔兹曼分布,在连续空间下求解非常麻烦。于是SAC提出使用一个 Actor 表示策略函数,从而解决这个问题。
柔性动作-评价(Soft Actor-Critic,SAC)算法的网络结构有5个。
SAC算法解决问题: 离散动作空间和连续动作空间 的强化学习问题,是 off-policy 的强化学习算法
SAC的论文有两篇
- 2018年12月, 《Soft Actor-Critic Algorithms and Applications》, 包括1个actor网络,4个Q Critic网络
- 2018年1月, 《Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor》, 包括1个actor网络,2个V Critic网络(1个V Critic网络,1个Target V Critic网络),2个Q Critic网络
- 详见: 强化学习之图解SAC算法
目前,在无模型的强化学习算法中,SAC 是一个非常高效的算法,它学习一个随机性策略,在不少标准环境中取得了领先的成绩。
最大熵强化学习(maximum entropy RL)的思想就是除了要最大化累积奖励,还要使得策略更加随机。
IMPALA
IMPALA的灵感来自于热门的A3C架构,后者使用多个分布式actor来学习agent的参数。在类似这样的模型中,每个actor都使用策略参数的一个副本,在环境中操作。actor会周期性地暂停探索,将它们已经计算得出的梯度信息分享至中央参数服务器,而后者会对此进行更新。
与此不同,IMPALA中的actor不会被用来计算梯度信息, 只是收集经验,并将这些经验传递至位于中心的learner。learner会计算梯度。因此在这样的模型中,actor和learner是完全独立的。
为了利用当代计算系统的规模优势,IMPALA在配置中可支持单个learner机器,也可支持多个相互之间同步的learner机器。
由于actor只用于环境采样,而这个任务通常是一个仿真环境(例如游戏模拟器),因此它和learner在计算侧重点上有很大差异(例如在游戏领域,actor更侧重于仿真、渲染。),所以actor和learner的软硬件可以是异构的。
其次,由于Actor无须计算梯度,因此就可以一直采样,而无须等待策略的更新,这也是它和Batched A2C的最大区别。
基于模型的RL
前面介绍的是基于价值的强化学习(Value Based RL)和基于策略的强化学习模型(Policy Based RL)都属于model free,直接从价值函数+策略函数中学习,不用学习环境的状态转化概率模型,下面介绍另一种强化学习流派,基于模型的强化学习(Model Based RL),以及基于模型的强化学习算法框架Dyna。
参考:
- UCL强化学习课程的第8讲和Dyna-2的论文
- model-based RL(一)——基本框架
- 上交张伟楠副教授:基于模型的强化学习算法,基本原理以及前沿进展
model-based(MBRL)与model free (MFRL)
不建立环境模型,仅依靠实际环境的采样数据进行训练学习的强化学习算法称为无模型强化学习(Model-Free Reinforcement Learning,MFRL)算法,也即是不依赖于环境模型的强化学习算法。
MFRL发展中遇到的一个困境:数据采集效率(Sample Efficiency)太低。在有监督或无监督学习中,人们构建一个目标函数,通过梯度下降(或上升)的方式,不断趋近理想结果。与有监督/无监督学习不同的是,强化学习属于一种试错的学习范式,当前策略的采样结果如果无法有效帮助当前策略进行提升,则可以认为当前试错的采样结果是无效采样。在MFRL训练过程中,智能体有大量的交互采样属于无效采样,这些采样没有对行动策略的改进产生明显的影响。为了解决无模型强化学习中的这一数据效率低下的问题,人们开始转向基于模型强化学习(Model-Based Reinforcement Learning,MBRL)的方法。
MBRL的基本思想在于首先建立一个环境的动态模型,然后在建立的环境模型中训练智能体的行动策略,通过这种方式,实现数据效率的提升。 MFRL存在如下特点:
- 相比于MBRL,MFRL拥有最好的渐进性能(Asymptotic Performance),当策略与环境交互达到收敛状态时,相比于MBRL,MFRL下训练所得策略所最终达到的性能会更好,能够避免出现复合误差的问题,因而在实际环境中表现会更为优异。
- MFRL非常适合使用深度学习框架去采样超大规模的数据,并进行网络训练。
- MFRL经常采用Off-Policy训练方法,这种情况下会有偏差(Bias)导致的训练效果不稳定(instability)的问题。
- MFRL需要进行超大量的数据采样,因而需要超高的算力要求,这种算力要求是很多科研院所或者企业所无法负担的。 MBRL存在如下特点:
- 环境模型一旦建立起来,便可以采用on-policy的训练方法,利用当前采样得到的数据训练当前的策略,在这种情形下,采样效率是最高的。
- 建立环境模型后,便可以选择性地不再与实际场景交互,在模型中进行训练学习,完成训练后再在实际场景中投入使用(off-line RL,也称为batch RL)。
- 相比于MFRL,MBRL数据采样效率会往往有较大的提升。
- 存在模型与实际环境之间的复合误差问题(Compounding Error),模型向后推演的幅度越长,推演误差就会越大,直至模型完全失去作用。
MBRL
MBRL的进一步分类,其主要包括黑盒模型与白盒模型两类:
- 黑盒模型中,环境模型的构造是未知的,仅作为数据的采样来源。由于采样数据来自于黑盒模型,而不是和真实环境交互得到,因此这些来自模型的采样数据不计入数据采样效率的计算中。虽然从计算结果来看MFBL的数据采样效率较高,但由于训练过程中使用了大量基于模型采样的数据,因此从采样数据总量上来看,实际采样了更多的数据。常用的基于黑盒模型的MBRL算法包括Dyna-Q、MPC、MBPO等。
 图1:基于黑盒模型的MBRL算法
图1:基于黑盒模型的MBRL算法 - 白盒模型中,环境模型的构造是已知的,可以将模型中状态的价值函数直接对策略的参数进行求导,从而实现对策略的更新。常用的基于白盒模型的MBRL算法包括MAAC、SVG、PILCO等。
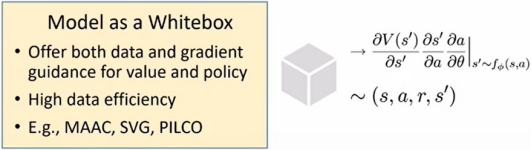
对比:
基于黑盒模型的MBRL:
-
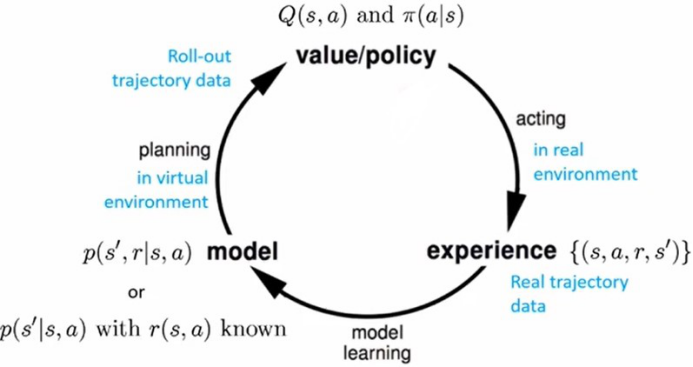
- 首先,当前的价值函数Q(s, a)以及策略函数π(a|s)与真实环境进行交互,完成交互后采样出环境反馈的数据Experience{(s, a, r, s’)}。然后通过采样出的数据来训练建立的环境模型p(s’, r|s, a ),环境的模型本质上是通过输入的当前状态State以及采取的动作Action,来预测产生的Reward以及下一步的状态State,很多情况下Reward是根据先验规则或领域知识生成,这时模型只预测下一步的状态State即可。接下来在当前模型中进行Plannning,也就是通过当前模型进行数据的采样,通过数据采样的结果去训练新一轮的价值函数Q(s, a)以及策略函数π(a|s)。
- Q-Planning是最简单的MBRL算法,它通过与真实环境交互的数据来训练环境模型,然后基于当前的环境模型来进行一步Planning,从而完成Q函数的训练。其步骤是,首先采集智能体与环境交互的State以及采用的Action,将数据传入建立的黑盒模型中,采集并得到模型虚拟出来的Reward以及下一步的Next_State,接着将传入模型的State、Action以及模型虚拟出来的Reward、Next_State进行一步Q-Learning训练,这样就完成了一步Q-Planning算法的更新。期间智能体仅仅通过与环境模型交互来进行数据的采样,得到虚拟的Reward以及下一步的Next_State,并进行策略的训练和更新,智能体未通过与实际环境交互数据来进行策略的更新。
- 还可以将Q-Planning与Q-Learning结合在一起,形成 Dyna算法。Dyna算法提出于90年代早期,完整的流程示意图如下所示。可以看到,将中间的direct RL步骤去掉后,就是刚刚讨论的Q-Planning算法。
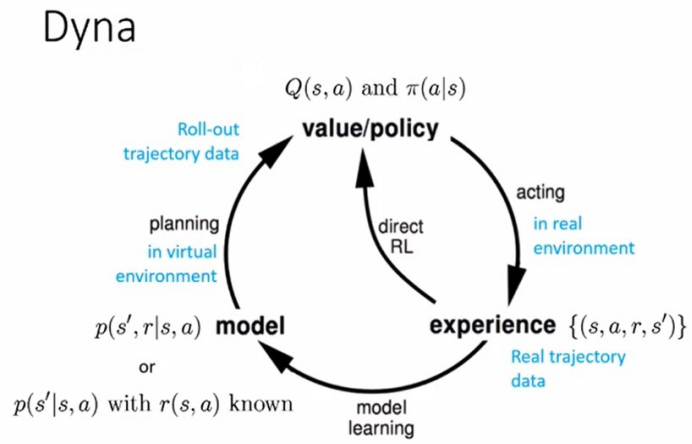
在Dyna算法中,首先通过智能体与实际环境的交互进行一步正常的Q-Learning操作,然后通过与实际环境交互时使用的State、Action,传入环境模型中进行Q-Planning操作,真实环境中进行一步Q-Learning操作,对应环境模型中进行n步Q-Planning操作。实际环境中的采样与模型中的采样具有1:n的关系,通过这种方式来提升训练过程中的Sample efficiency。
MBRL问题
MBRL算法的发展面临着三个关键问题,同时这也是发展的三个思路:
- 环境模型的建立是否真的有助于Sample Efficiency的提高?
- 所建立的模型基本都是基于神经网络建立,不可避免的会出现泛化性误差的问题,那么人们什么时候可以相信建立的模型并使用模型进行策略的训练与更新?
- 如何适当地把握模型的使用尺度,来获得最好的或者至少获得正向的策略训练结果?
model-free方法有两种方式
- value-based方法先学习值函数(MC或TD)再更新策略
- policy-based方法直接将真实轨迹数据(real experience)更新策略。
而model-based方法先将着重点放在环境模型(environment dynamics)上,通过采样先学习一个对环境的建模,再根据学习到的环境模型做值函数/策略优化。在model-based方法中,planning步骤至关重要,正是通过在learned model基础上做planning才提高了整个强化学习算法迭代的效率。
完成了对环境的建模后,在model-based大类方法中同样有两种路径
- 一种是通过学到的model生成一些仿真轨迹,通过仿真轨迹估计值函数来优化策略;
-
另一种是通过学到的model直接优化策略,这是目前model-based方法常走的路线。
- Pros:先学习model的一个显而易见的好处,就是解决model-free强化学习方法中样本效率的问题(sample efficiency)。
- Cons:由于模型是在过程中学习的,难免存在偏差;难以保证收敛
model可以理解为由状态转移分布和回报函数组成的元组 。其中
,
如何学习模型?
- 状态-动作对到回报的映射可以看作是一个回归问题,loss函数可以设置为均方误差;
- 学习状态-动作对到下一状态的映射可以看作密度估计问题,loss函数可以设置为KL散度。
模型的构造也有很多选择(神经网络、高斯过程等等),从而派生出不同的算法。
RL是基于经验的学习方法。实际经验是真实的智能体和环境交互得到的数据。比如一个机械臂尝试从一堆物品中抓取物品,无人车在道路上行驶。最直接的作用是用来学习值函数或者策略,称之为直接强化学习(direct RL)。还可以利用实际经验来学习模型,叫做模型学习(model learning)。当然我们的模型不一定非得要学,根据物理定理也能建立起模型,但基于数据驱动的模型学习也是一个方法。那学习了模型之后呢?怎么用它?我们可以用学习的模型来产生经验,叫做仿真经验。然后利用仿真经验来辅助策略学习,叫做间接强化学习(indirect RL)。
Direct RL VS. Indirect RL, 谁好谁坏?直接RL和间接RL都有自己的优缺点。
- 间接RL可以充分的利用经验,减少和环境的交互。可以类比为人类的冥想,mental rehearsal。没必要都去试一下才知道怎么做,想一想可能就知道答案了,这样就节省了体力。
- 直接RL更简单,并且不会受到模型偏差的影响。试想如果一个精神病患者,你让他冥想,不知道他会做出什么举动来。
这种争论在AI和心理学领域可以归结为:认知和试错学习的争执,精细编程和反应式决策的争执。还在于:model-based 和model-free的争执。
表格型:Dyna-Q 框架
把模型学习,规划和决策融合在一起,在线的进行规划学习
Dyna-Q 算法是一个经典的基于模型的强化学习算法。Dyna-Q 使用一种叫做 Q-planning 的方法来基于模型生成一些模拟数据,然后用模拟数据和真实数据一起改进策略。
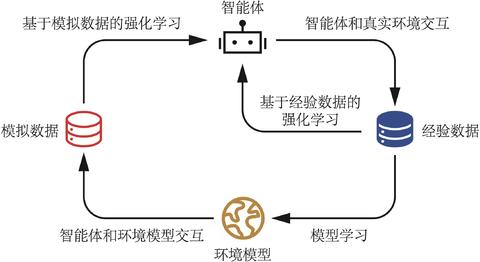
- Q-planning 每次选取一个曾经访问过的状态s,采取一个曾经在该状态下执行过的动作a,通过模型得到转移后的状态s’以及奖励r,并根据这个模拟数据(s,a,r,s’),用 Q-learning 的更新方式来更新动作价值函数。
Dyna-Q中,直接RL就使用Q学习(one-step tabular Q-learning)。规划算法就使用上一节提到的随机采样Q-规划算法(one-step random sample tabular Q-planning)。目前为止,所有算法都是针对于表格型的问题。也就是说状态动作都是有限离散的。因此在学习模型的时候,我们就可以把所有的转移动作对 [公式] 存起来。所示实际上模型学习就是存储,规划就是从存的数据里面拿数据,然后用Q-learning。
整个Dyna-Q的学习框图
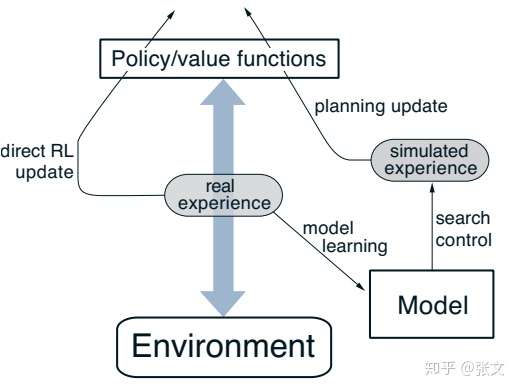
如迷宫问题上,考察Dyna-Q的效果。其实可以想象,引入规划无非就是为了增加学习效率。所以Dyna-Q和Q-learning相比学的更快。实际的效果如下:
规划的步数越多,学习的就越快。纵轴表示每个episode的步数。如果是学到了一个策略,自然步数是最小的(不走弯路)。对比一下2个episode后的策略:
可以发现,有规划的算法值函数的更新更有效。
model-based策略优化

- 如果环境模型已知,轨迹优化问题就是一个最优控制问题
- 如果环境模型未知,把model learning和trajectory optimization结合起来
DRL pytorch
Deep Reinforcement Learning Algorithms with PyTorch
This repository contains PyTorch implementations of deep reinforcement learning algorithms and environments.
Algorithms Implemented
- Deep Q Learning (DQN) (Mnih et al. 2013)
- DQN with Fixed Q Targets (Mnih et al. 2013)
- Double DQN (DDQN) (Hado van Hasselt et al. 2015)
- DDQN with Prioritised Experience Replay (Schaul et al. 2016)
- Dueling DDQN (Wang et al. 2016)
- REINFORCE (Williams et al. 1992)
- Deep Deterministic Policy Gradients (DDPG) (Lillicrap et al. 2016 )
- Twin Delayed Deep Deterministic Policy Gradients (TD3) (Fujimoto et al. 2018)
- Soft Actor-Critic (SAC) (Haarnoja et al. 2018)
- Soft Actor-Critic for Discrete Actions (SAC-Discrete) (Christodoulou 2019)
- Asynchronous Advantage Actor Critic (A3C) (Mnih et al. 2016)
- Syncrhonous Advantage Actor Critic (A2C)
- Proximal Policy Optimisation (PPO) (Schulman et al. 2017)
- DQN with Hindsight Experience Replay (DQN-HER) (Andrychowicz et al. 2018)
- DDPG with Hindsight Experience Replay (DDPG-HER) (Andrychowicz et al. 2018 )
- Hierarchical-DQN (h-DQN) (Kulkarni et al. 2016)
- Stochastic NNs for Hierarchical Reinforcement Learning (SNN-HRL) (Florensa et al. 2017)
- Diversity Is All You Need (DIAYN) (Eyensbach et al. 2018)
All implementations are able to quickly solve Cart Pole (discrete actions), Mountain Car Continuous (continuous actions), Bit Flipping (discrete actions with dynamic goals) or Fetch Reach (continuous actions with dynamic goals). I plan to add more hierarchical RL algorithms soon.
Environments Implemented
- Bit Flipping Game (as described in Andrychowicz et al. 2018)
- Four Rooms Game (as described in Sutton et al. 1998)
- Long Corridor Game (as described in Kulkarni et al. 2016)
- Ant-{Maze, Push, Fall} (as desribed in Nachum et al. 2018 and their accompanying code)
Results
1. Cart Pole and Mountain Car
Below shows various RL algorithms successfully learning discrete action game Cart Pole
or continuous action game Mountain Car. The mean result from running the algorithms
with 3 random seeds is shown with the shaded area representing plus and minus 1 standard deviation. Hyperparameters
used can be found in files results/Cart_Pole.py and results/Mountain_Car.py.

2. Hindsight Experience Replay (HER) Experiements
Below shows the performance of DQN and DDPG with and without Hindsight Experience Replay (HER) in the Bit Flipping (14 bits) and Fetch Reach environments described in the papers Hindsight Experience Replay 2018 and Multi-Goal Reinforcement Learning 2018. The results replicate the results found in the papers and show how adding HER can allow an agent to solve problems that it otherwise would not be able to solve at all. Note that the same hyperparameters were used within each pair of agents and so the only difference between them was whether hindsight was used or not.

3. Hierarchical Reinforcement Learning Experiments
The results on the left below show the performance of DQN and the algorithm hierarchical-DQN from Kulkarni et al. 2016 on the Long Corridor environment also explained in Kulkarni et al. 2016. The environment requires the agent to go to the end of a corridor before coming back in order to receive a larger reward. This delayed gratification and the aliasing of states makes it a somewhat impossible game for DQN to learn but if we introduce a meta-controller (as in h-DQN) which directs a lower-level controller how to behave we are able to make more progress. This aligns with the results found in the paper.
The results on the right show the performance of DDQN and algorithm Stochastic NNs for Hierarchical Reinforcement Learning (SNN-HRL) from Florensa et al. 2017. DDQN is used as the comparison because the implementation of SSN-HRL uses 2 DDQN algorithms within it. Note that the first 300 episodes of training for SNN-HRL were used for pre-training which is why there is no reward for those episodes.

模仿学习
资料
模仿学习(Imitation Learning,IL)是一种通过观察并模仿专家行为来学习复杂任务的机器学习方法。 与传统的强化学习不同,模仿学习无需明确的奖励函数,而是直接从专家的示范中学习策略。这种方法特别适用于那些难以手工设计奖励函数的任务场景。
简介
传统强化学习任务中,通过计算累积奖赏来学习最优策略(policy),这种方式简单直接,而且在可以获得较多训练数据的情况下有较好的表现。但是,多步决策(sequential decision)中,学习器不能频繁地得到奖励,且这种基于累积奖赏及学习方式存在非常巨大的搜索空间。
没有 reward 时,让AI跟环境互动的一个方法叫做 Imitation-Learning
找人类进行示范,AI凭借示范以及跟环境的互动进行学习。
这种模仿学习使得智能体自身不必从零学起,不必去尝试探索和收集众多的无用数据,能大大加快训练进程。
而模仿学习(Imitation Learning)方法经过多年发展,已经能够很好地解决多步决策问题,在机器人、 NLP 等领域也有很多的应用。
虽然强化学习不需要有监督学习中的标签数据,但十分依赖奖励函数的设置。
- 有时在奖励函数上做一些微小的改动,训练出来的策略就会有天差地别。
Behavior-Cloning 跟监督学习有类似之处,也是复制人类行为。
模仿学习和强化学习往往一起使用。
好处
- 既能大大加快训练速度,又能得到超越人类的超高水准。
但缺点
- 如果智能体进入新状态,会有较大误差,且一直累加,到最后没有办法正常行动。
- 因此要让实际遇到的数据和训练数据的分布尽量保持一致。
现实场景中,奖励函数并未给定,或者奖励信号极其稀疏,此时随机设计奖励函数将无法保证强化学习训练出来的策略满足实际需要。
- 例如,对于无人驾驶车辆智能体的规控,观测当前环境感知恢复的 3D 局部环境,动作是车辆接下来数秒的具体路径规划,那么奖励是什么?如果只是规定正常行驶而不发生碰撞的奖励为+1,发生碰撞为-100,那么智能体学习的结果则很可能是找个地方停滞不前。具体能帮助无人驾驶小车规控的奖励函数往往需要专家的精心设计和调试。
- 假设存在一个专家智能体,其策略可以看成最优策略,可直接模仿这个专家在环境中交互的状态动作数据来训练一个策略,并且不需要用到环境提供的奖励信号。
模仿学习(imitation learning)研究这类问题
模仿学习(Imitation Learning)原理:
- 通过隐含地给学习器关于这个世界的先验信息,就能执行、学习人类行为。
- 在模仿学习任务中,智能体(agent)为了学习到策略从而尽可能像人类专家那样执行一种行为,会寻找一种最佳方式来使用由该专家示范的训练集(输入-输出对)。
训练时间是直接使用强化学习的几十分之一
分类
模仿学习方法分类:
行为克隆(behavior cloning,BC)逆强化学习(inverse RL)生成式对抗模仿学习(generative adversarial imitation learning,GAIL)
模仿学习算法主要分为三类:
- (1)
行为克隆(Behavioral Cloning,BC):基于监督学习方法,直接从专家的状态-动作对中学习映射关系。 - (2)
逆向强化学习(Inverse Reinforcement Learning,IRL):基于强化学习方法,通过推断奖励函数间接学习策略。 - (3)
生成对抗模仿学习(Generative Adversarial Imitation Learning,GAIL):借鉴生成对抗学习思想,通过对抗过程优化策略。
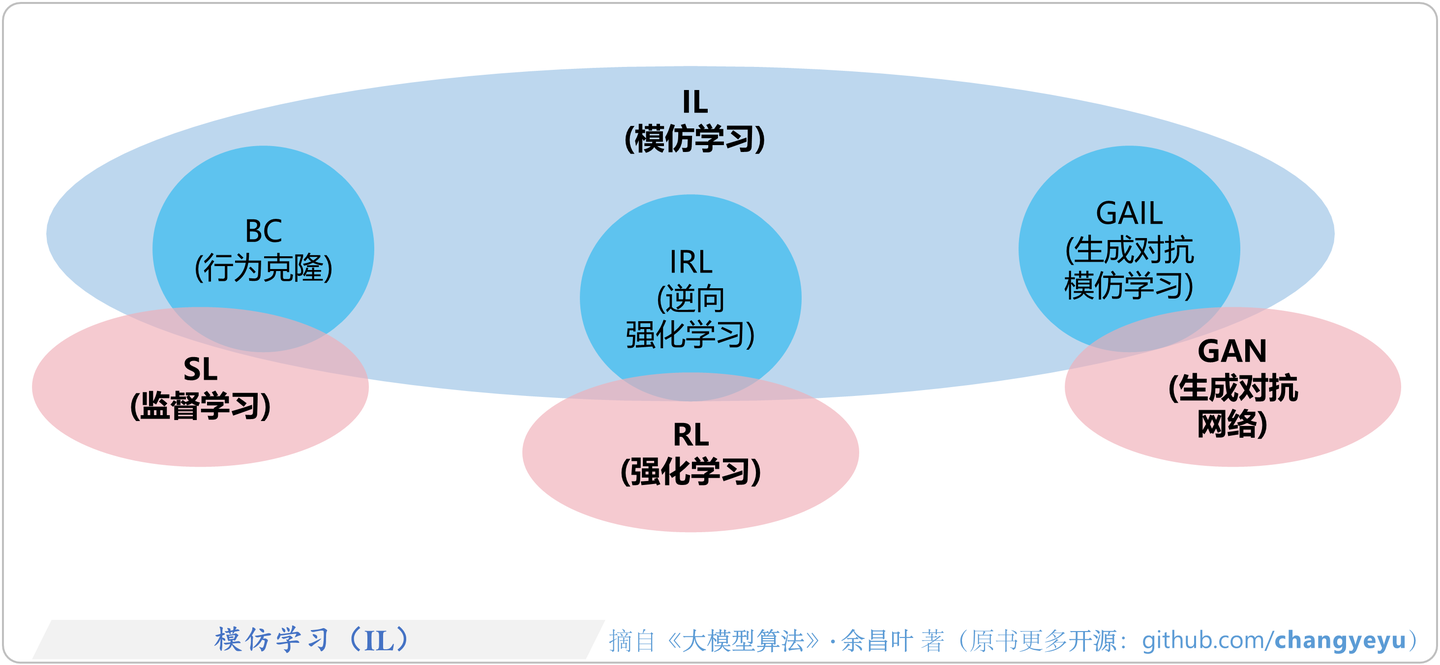
源自:《大模型算法》
BC 行为克隆
行为克隆(Behavioral Cloning, BC)结合监督学习的机器学习方法,通过学习专家在不同状态(State)下采取的动作(Action)的映射关系来模仿专家的行为。
- 行为克隆将问题视为一个
回归或分类问题,输入为环境的状态,输出为相应的动作。 - 通过最小化预测动作与专家动作之间的误差,模型能够在类似状态下采取与专家相似的动作
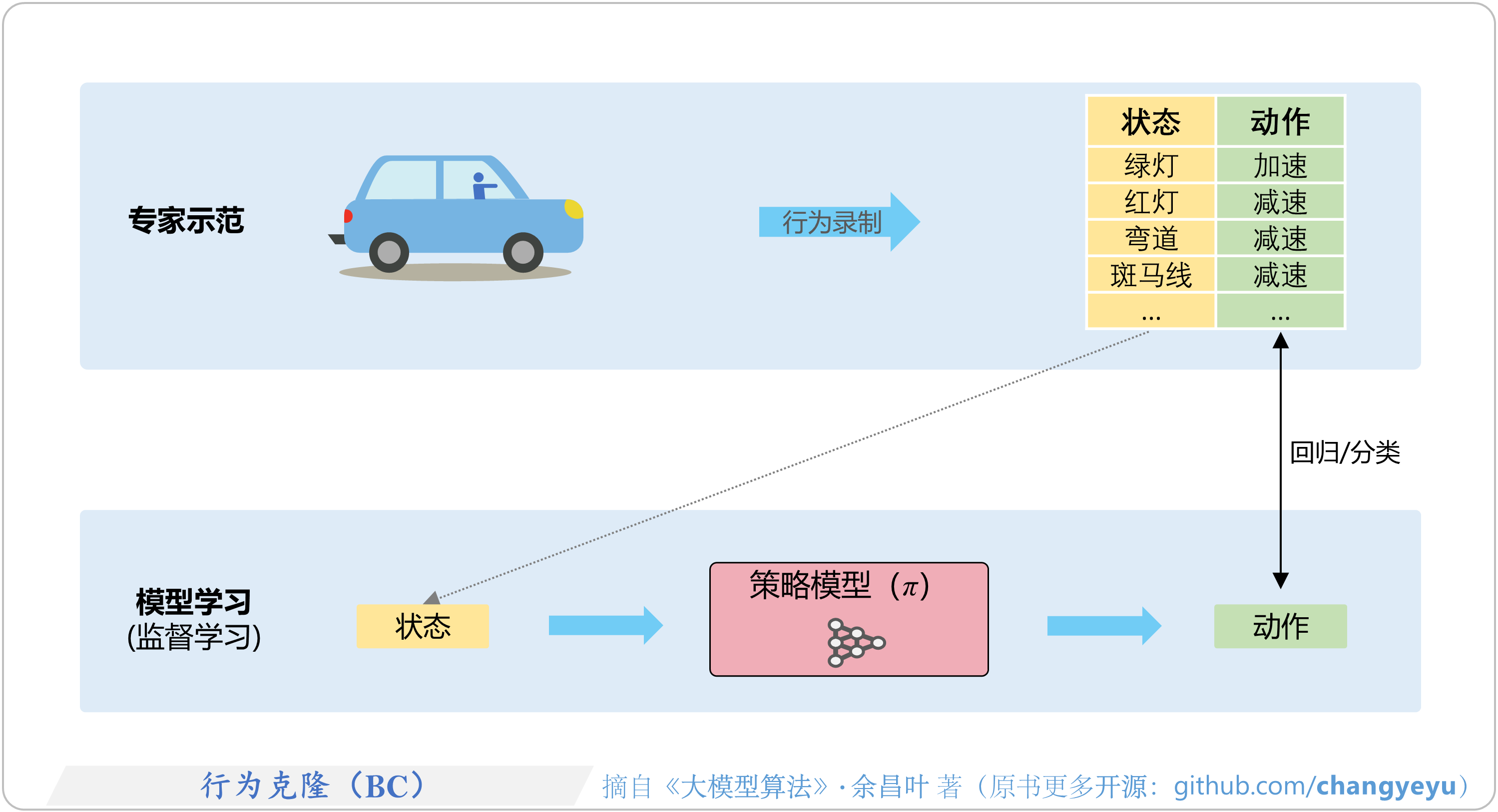
行为克隆(BC)直接使用监督学习方法
BC 提出一种监督学习方法,通过拟合专家数据,直接建立状态-动作的映射关系。
- BC 最大好处效率高,算法简单,但是一旦智能体遇到了从未见过的状态,可能做出错误行为——称作“
状态漂移”。
为了解决这个问题,DAgger 采用一种动态更新数据集的方法,根据训练出 policy 遇到的真实状态,不断添加新的专家数据至数据集中。
- 后续的研究中,IBC 采用了隐式行为克隆方法,训练神经网络来接受观察和动作,并输出一个数字,该数字对专家动作来说很低,对非专家动作来说很高,从而将行为克隆变成一个基于能量的建模问题。
目前 BC 算法研究热点聚焦于两个方面:meta-learning 和利用 VR 设备进行行为克隆。
文献见原文
DAgger
Stéphane Ross 等人提出 DAgger(Dataset Aggregation)算法。
- 基于在线学习 (Online Learning),把行为克隆得到的策略与环境不断的交互,来产生新的数据。
- 在 这些新产生的数据上,DAgger 会向专家策略申请示例;
- 然后在增广后的数据集上,DAgger 会重新使用行为克隆 进行训练,然后再与环境交互;
-
这个过程会不断重复进行。由于数据增广和环境交互,DAgger 算法会大大减 小未访问的状态的个数,从而减小误差。
- 【2011-3-16】CMU 论文 A Reduction of Imitation Learning and Structured Prediction to No-Regret Online Learning
- 代码 【2016】 imitation-dagger
DAgger 思想
- 前期先让人类去操作policy,拿到足够多的数据以后做完全意义上的offline训练;
- 如果offline训出来效果不好,把效果不好的场景再让人类操作一遍,对各个状态打上动作标签。
- 然后新数据加旧数据一起再训练,直到效果变好为止
IRL 逆强化学习
逆向强化学习(Inverse Reinforcement Learning, IRL)根据专家或智能体的行为,推断其背后的奖励函数,然后,基于此奖励函数学习最优策略。
这一过程与传统强化学习(RL)相反
- 后者通常是在已知奖励函数的情况下学习最优策略
- 而逆向强化学习则是在已知行为的基础上反推出奖励函数,再进一步学习策略。
吴恩达(Andrew Y. Ng)和Stuart Russell于2000年发表了《Algorithms for Inverse Reinforcement Learning》一文,系统性地阐述了逆强化学习的核心概念。
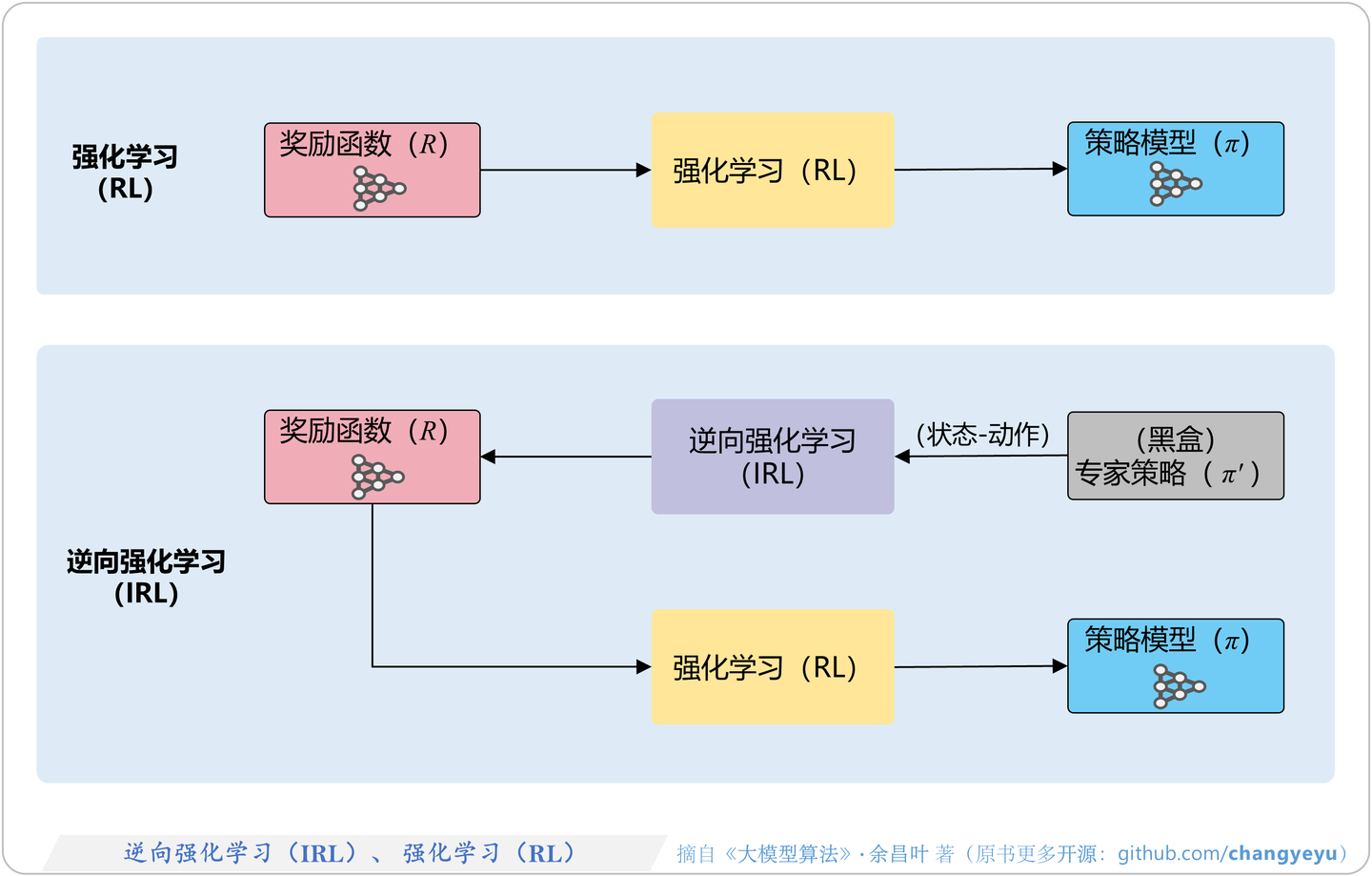
逆向强化学习 IRL( 摘自《大模型算法》
详见:动手学强化学习
【2023-3-30】逆强化学习:从专家策略中学习奖励函数的无监督方法
逆强化学习(Inverse Reinforcement Learning, IRL)是新兴机器学习技术,主要目标是从行为中学习目标函数。
逆强化学习已经被应用于许多领域,例如自动驾驶、游戏智能和机器人控制等。不仅可以帮助我们理解人类和动物的行为,还可以为各种应用提供更高效、更智能的决策和行动。
什么是逆强化学习?
逆强化学习(Inverse Reinforcement Learning, IRL)作为一种典型模仿学习方法,学习过程与正常的强化学习利用奖励函数学习策略相反,不利用现有的奖励函数,而是试图学出一个奖励函数,并以之指导基于奖励函数的强化学习过程。
给定状态和动作,建立模型输出对应奖励。在奖励函数建立好后,就能新训练智能体来模仿给定策略(示教数据)的行为。
IRL 主要目标: 解决数据收集时难以找到足够高质量数据的问题。
- IRL 首先从专家数据中学习一个奖励函数,进而用这个奖励函数进行后续的RL训练。通过这样的方法,IRL 从理论上来说,可以表现出超越专家数据的性能。
Ziebart等人 首先提出了最大熵 IRL,利用最大熵分布来获得良好的前景和有效的优化。
- 2016年,Finn等人[5]提出了一种基于模型的 IRL 方法,称为引导成本学习( guided cost learning),这种方法使用神经网络表示 cost 进而提高表达能力。
- Hester等人又提出了DQfD[6],该方法仅需少量的专家数据,通过预训练启动过程和后续学习过程,显著加速了训练。
- T-REX 提出基于为专家数据排序结构,通过对比什么专家数据效果更好,间接地学习奖励函数。
IRL可以归结为解决从观察到的最优行为中提取奖励函数( Reward Function)的问题,这些最优行为也可以表示为专家策略。
基于IRL的方法交替地在两个过程中交替:
- 一个阶段是使用示范数据来推断一个隐藏的
奖励(Reward)或代价( Cost)函数 - 另一个阶段是使用强化学习基于推断的奖励函数来学习一个模仿策略。
IRL基本准则:
- IRL选择奖励函数 R 来优化策略,并且使得任何不同于 Pe(ae~pe) 的动作决策( a∈A\ae ),其中尽可能产生更大损失。
基于此类形式化优化的学徒学习作为最早期的逆强化学习方法之一,在2004年由Andrew Y.Ng与Pieter Abbeel提出。该算法的核心思想
- 学习一个能够使得专家策略下的轨迹的期望回报远高于非专家策略的奖励函数,从而达到无监督学习奖励函数的目的。
在这样的优化目标下,习得的奖励函数会使得专家和非专家的差距不断增大,因此这种方法也叫做基于最大边际规划的逆强化学习方法 (Maximum Margin Planning Inverse Reinforcement Learning, MMPIRL)。
IRL 问题
但存在以下挑战性问题:
- 无论是对奖励函数做线性组合或凸组合假设,还是对策略的最大熵约束,这类显式的规则给逆强化学习的通用性带有一定的限制;
- 在估计出来的奖励函数下,使用强化学习交互环境来优化策略,这从时间和安全性的角度带来较大代价,同时要求迭代优化奖励函数的内循环中解决一个MDP的问题,将带来极大的计算消耗。
这也是2016年提出生成式对抗模仿学习提出的动机。
BC vs IRL
Inverse RL(IRL)跟Behaviour Cloning(BC)主要区别:
- 【1】IRL 用专家数据学 reward function,然后借助 reward function 以强化学习的方式训练policy
-
【2】BC 是直接对专家数据做监督学习来训练policy
- 对于BC,因为训练和测试阶段的数据分布存在 covariate shift,导致 compounding error 越来越大(如图), 以至于严重影响算法对于未知数据的预测 [ 1,2],这一点在专家数据集规模较小的时候尤其常见。
- 而对于IRL,如果学习的 reward function 性质比较好, 那么再通过RL优化可得到对于未知数据泛化性非常好的 policy,例如近期的IRL算法可以在非常少的专家数据集中训练得出有效且性能强大的 policy。 而从可操作性的角度讲,BC只是学习数据集中 state 到 action 的映射,将这个映射作为一个policy,所以是完全监督学习。
- 而经典IRL算法包含两个阶段, 即 reward 模型训练阶段和使用该 reward 模型帮助RL训练的阶段。一个好的 reward model 可以利用专家数据做一些有意义的推断,而不是完全模仿,进而可以对后面的RL优化有很好的指导。
作者:OpenDILab浦策
GAIL
生成式对抗模仿学习(generative adversarial imitation learning,GAIL)是 2016 年由斯坦福大学研究团队提出的基于生成式对抗网络的模仿学习,它诠释了生成式对抗网络的本质其实就是模仿学习。
Adversarial Structured IL 方法主要目标: 解决 IRL 的效率问题。
- IRL 算法即便学到了非常好的奖励函数,得到最终策略仍然需要执行强化学习步骤,因此如果可以直接从专家数据中学习到策略,就可以大大提高效率。
- 基于这个想法 GAIL 结合了生成式网络 GAN 和最大熵 IRL,无需人工不断标注专家数据,就可以不断地高效训练。
在此基础上,许多工作都对 GAIL 做了改进。
- 如 InfoGail 用 WGAN 替换了 GAN,取得了较好的效果。
- 还有一些近期的工作,如 GoalGAIL[10],TRGAIL[11] 和 DGAIL[12] 都结合了其他方法,如事后重标记和 DDPG,以实现更快的收敛速度和更好的最终性能。
GAIL属于Inverse RL的范畴,即逆强化学习
GAIL相当于另外的一个内在奖励,是可以和强化学习的外部奖励加在一起进行训练的。专家奖励设得越高,智能体在环境中就越趋向于模仿专家的行为。合理设置其奖励上限,智能体就会在一定程度上模仿专家行为的同时,更多地去探索环境,寻找更好的策略,金字塔案例中设为了环境奖励的0.01。
原文链接:https://blog.csdn.net/tianjuewudi/article/details/122169309
工具
ML-Agents
Unity 推出 ML-Agents Machine Learning Agents Toolkit (ML-Agents)
开源项目,可让游戏和模拟成为训练智能体的环境。
提供基于 PyTorch 的前沿算法实现,方便游戏开发者和爱好者为 2D、3D 及 VR/AR 游戏轻松训练智能体。
研究人员也可易用 Python API,通过强化学习、模仿学习、神经进化或其他方法训练智能体。
这些经过训练的智能体用途广泛,包括控制非玩家角色(NPC)行为(适用于多智能体、对抗等多种场景)、对游戏版本进行自动化测试,以及在游戏发布前评估不同的游戏设计决策。机器学习智能体工具包对游戏开发者和人工智能研究人员都大有裨益,它提供了一个核心平台,人工智能领域的前沿成果可在 Unity 丰富的环境中得到评估,进而推广到更广泛的研究和游戏开发者群体中。
提供了模仿学习两种算法
- Generative Adversarial Imitation Learning(生成对抗模仿学习),简称GAIL
- Behavior Cloning(行为克隆),简称BC
Stable-Baselines
Stable Baselines/用户向导/预训练(行为克隆)
(1) 生成专家数据
from stable_baselines import DQN
from stable_baselines.gail import generate_expert_traj
model = DQN('MlpPolicy', 'CartPole-v1', verbose=1)
# Train a DQN agent for 1e5 timesteps and generate 10 trajectories
# data will be saved in a numpy archive named `expert_cartpole.npz`
generate_expert_traj(model, 'expert_cartpole', n_timesteps=int(1e5), n_episodes=10)
也可以传给函数
import gym
from stable_baselines.gail import generate_expert_traj
env = gym.make("CartPole-v1")
# Here the expert is a random agent
# but it can be any python function, e.g. a PID controller
def dummy_expert(_obs):
"""
Random agent. It samples actions randomly
from the action space of the environment.
:param _obs: (np.ndarray) Current observation
:return: (np.ndarray) action taken by the expert
"""
return env.action_space.sample()
# Data will be saved in a numpy archive named `expert_cartpole.npz`
# when using something different than an RL expert,
# you must pass the environment object explicitely
generate_expert_traj(dummy_expert, 'dummy_expert_cartpole', env, n_episodes=10)
产生 expert_cartpole.npz 数据集
- 专家数据集是一个.npz格式的归档文件。
- 数据集保存为Python字典格式,带有关键字:actions, episode_returns, rewards, obs, episode_starts
(2) 训练模型
from stable_baselines import PPO2
from stable_baselines.gail import ExpertDataset
# Using only one expert trajectory
# you can specify `traj_limitation=-1` for using the whole dataset
dataset = ExpertDataset(expert_path='expert_cartpole.npz',
traj_limitation=1, batch_size=128)
model = PPO2('MlpPolicy', 'CartPole-v1', verbose=1)
# Pretrain the PPO2 model
model.pretrain(dataset, n_epochs=1000)
# As an option, you can train the RL agent
# model.learn(int(1e5))
# Test the pre-trained model
env = model.get_env()
obs = env.reset()
reward_sum = 0.0
for _ in range(1000):
action, _ = model.predict(obs)
obs, reward, done, _ = env.step(action)
reward_sum += reward
env.render()
if done:
print(reward_sum)
reward_sum = 0.0
obs = env.reset()
env.close()
思考
策略空间较大时, DQN/PPO 收敛速度慢,即便长时间训练,依然学不到人类优质策略
怎么利用专家数据加速RL训练?
DeepSeek 解答:
有效利用专家经验的强化学习(RL)算法及相关方法,分类整理并附详细说明:
总结与选型建议
| 场景需求 | 推荐算法 |
|---|---|
| 快速初始化策略 | 行为克隆(BC) |
| 需在线专家交互 | DAgger、Q-Dagger |
| 无显式奖励函数设计 | GAIL、MaxEnt IRL |
| 高维连续动作空间 | SAC+BC、GAIL |
| 样本效率优先(Off-policy) | DQfD、SAC+专家数据混合 |
| 安全关键任务 | 预训练+微调、基于模型的RL |
关键注意事项:
- 专家数据质量直接影响算法性能,需确保数据覆盖关键状态-动作对。
- 避免过度依赖专家数据,防止抑制智能体自主探索。
- 混合专家数据时,可通过动态调整混合比例或损失权重平衡模仿与探索。
一、模仿学习(Imitation Learning)
通过直接模仿专家行为学习策略,通常不依赖环境奖励信号。
1. 行为克隆(Behavior Cloning, BC)
- 机制:将专家轨迹视为监督学习数据,直接学习状态到动作的映射。
- 优点:简单高效,适合快速初始化策略。
- 缺点:分布偏移问题(Compound Errors),专家数据外的状态易导致错误累积。
- 适用场景:机器人控制、自动驾驶的初始策略预训练。
2. DAgger(Dataset Aggregation)
- 机制:迭代收集专家在智能体当前策略遇到的状态下的动作,混合新旧数据训练。
- 优点:缓解分布偏移,提升策略鲁棒性。
- 缺点:依赖在线专家交互,成本较高。
- 适用场景:需要动态调整策略的交互式任务(如无人机避障)。
【2025-7-11】字节 Chain-of-Action
传统模仿学习方法,如ACT和Diffusion Policy(DP),采用“前向预测”的建模思路。
这种方法在执行过程中面临较大的复合误差问题,导致机器人在完成任务时的成功率受到限制。
【2025-7-11】字节跳动 Seed 与阿德莱德大学的研究团队发布了名为“Chain-of-Action”的新范式,提出基于轨迹自回归的机器人操作策略。
- 主页 Chain-of-Action: Trajectory Autoregressive Modeling for Robotic Manipulation
- 论文 Chain-of-Action: Trajectory Autoregressive Modeling for Robotic Manipulation
- 代码 ByteDance-Seed/Chain-of-Action
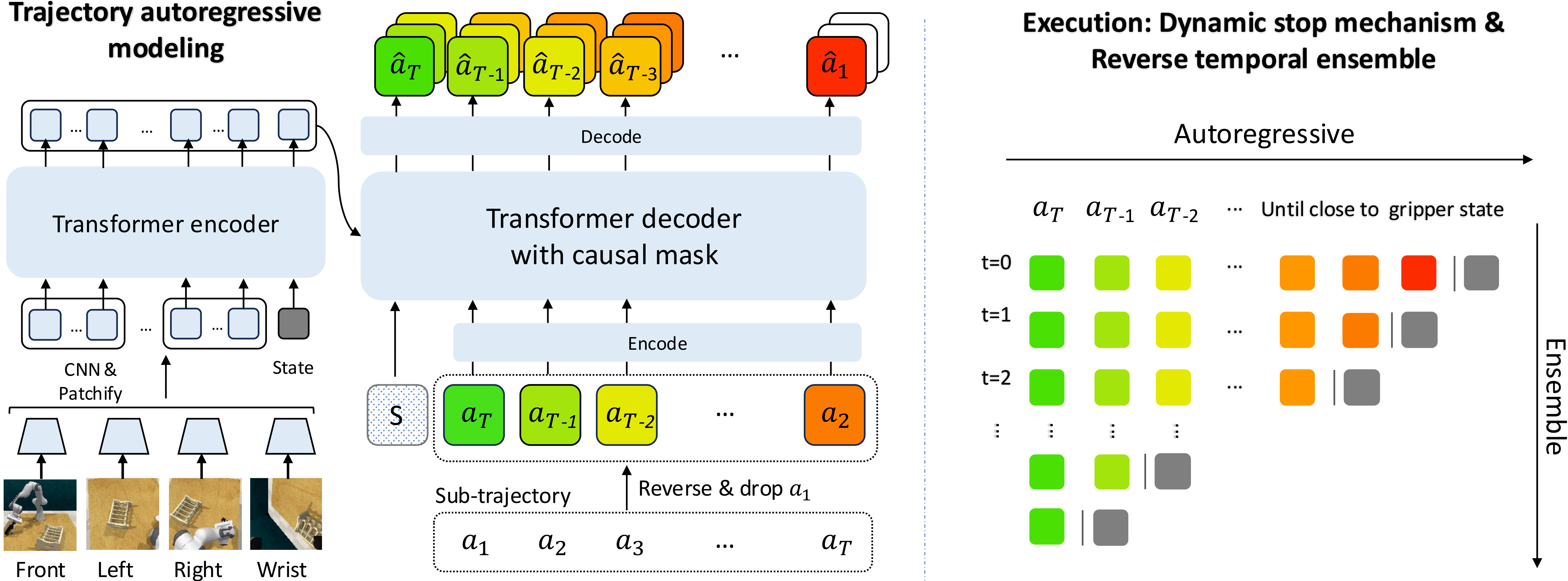
Chain-of-Action 通过逆向生成完整轨迹,推理出可执行的动作,避免了这种短视性的问题。
原理
轨迹自回归模型的核心设计
Chain-of-Action 创新之处在于其四个关键设计:
- 首先,采用连续动作表征,避免了离散化带来的量化误差;
- 其次,设计了动态停止机制,以支持可变长度的轨迹预测;
- 第三,反向时间集成提升了模型预测的稳定性;
- 最后,多词元预测作为正则化手段,增强了动作的局部依赖关系。
这些设计共同作用,使得CoA在复杂场景下表现出色。
在真实世界实验中,CoA在8项厨房任务中展现了61.3%的平均成功率,相较于ACT的46.3%和DP的36.3%,证明了新模型在实际应用中的有效性。
效果
CoA在与ACT相同的基本结构下,展现出显著的空间泛化能力提升。
在RLBench大规模基准测试中,CoA 平均成功率达到55.2%,远超ACT的38.9%和DP的32.6%。
这一成果不仅展示了新模型的强大性能,也为未来的视觉-语言-动作模型(VLA)提供了新的建模思路。
二、逆强化学习(Inverse Reinforcement Learning, IRL)
从专家示范中反推奖励函数,再基于该奖励函数训练策略。
3. 最大熵逆强化学习(MaxEnt IRL)
- 机制:假设专家行为是多样化的,通过最大化熵的概率分布拟合奖励函数。
- 优点:能处理专家行为的不确定性。
- 缺点:计算复杂度高,需反复迭代优化。
- 适用场景:复杂任务中的奖励函数推断(如人类运动模仿)。
4. GAIL(Generative Adversarial Imitation Learning)
- 机制:结合生成对抗网络(GAN),判别器区分专家数据与智能体生成数据,生成器(策略)欺骗判别器。
- 优点:无需手动设计奖励函数,适应高维状态空间。
- 缺点:训练不稳定,需精细调参。
- 适用场景:机器人动作模仿、游戏AI(如《Dota 2》的OpenAI Five)。
三、结合专家数据的强化学习算法
将专家数据融入传统RL框架,提升样本效率或策略质量。
5. DQfD(Deep Q-Learning from Demonstrations)
- 机制:在DQN的经验回放中混合专家数据,并添加监督损失(模仿专家动作)。
- 优点:加速初期学习,避免探索不足。
- 缺点:专家数据需与任务高度相关。
- 适用场景:Atari游戏、机械臂操作等离散动作任务。
6. SAC+BC(Soft Actor-Critic with Behavior Cloning)
- 机制:在SAC的优化目标中加入行为克隆损失,约束策略接近专家行为。
- 优点:平衡探索与专家模仿,适合连续控制。
- 缺点:需调整模仿权重超参数。
- 适用场景:机器人连续动作控制(如四足机器人行走)。
7. Q-Dagger
- 机制:结合DAgger与Q-learning,通过专家修正动作提升策略。
- 优点:减少次优探索,加速收敛。
- 缺点:依赖在线专家查询。
- 适用场景:需要安全探索的任务(如医疗决策)。
四、预训练与微调(Pretraining + Fine-tuning)
8. 专家预训练 + RL微调
- 机制:先用专家数据预训练策略(如BC),再用PPO、SAC等算法在环境中微调。
- 优点:避免冷启动,提升训练稳定性。
- 缺点:专家数据质量影响最终性能。
- 适用场景:样本成本高的任务(如真实机器人训练)。
五、基于模型的强化学习(Model-Based RL)
9. 专家数据辅助的环境模型学习
- 机制:利用专家数据加速环境动力学模型的学习,再基于模型规划(如MBPO)。
- 优点:减少真实环境交互次数。
- 缺点:模型误差可能导致次优策略。
- 适用场景:高风险或高成本环境(如自动驾驶模拟)。
六、奖励塑形(Reward Shaping)
10. 基于专家数据的奖励设计
- 机制:根据专家轨迹设计密集奖励函数(如动态时间规整DTW)。
- 优点:直观易实现,加速策略收敛。
- 缺点:依赖领域知识设计奖励。
- 适用场景:迷宫导航、机械臂抓取。
七、优先级经验回放(Prioritized Experience Replay)
11. 专家数据优先级采样
- 机制:在经验回放中为专家数据赋予更高采样概率。
- 优点:高效利用高质量专家数据。
- 缺点:可能导致过拟合专家行为。
- 适用场景:Off-policy算法(如DDPG、Rainbow)。
HRL
分层强化学习
【2024-12-5】【RL Latest Tech】分层强化学习(Hierarchical RL)
分层强化学习(Hierarchical Reinforcement Learning,HRL)是一类旨在通过引入多层次结构来提高强化学习算法效率的方法。
其核心思想是将复杂的任务分解为若干子任务,通过解决这些子任务来最终完成整体目标。
分层强化学习(Hierarchical Reinforcement Learning, HRL)是一种分而治之的强化学习框架,通过将复杂任务分解为多个层次的较小的子任务或子策略,使智能体能够在不同的抽象层次上学习和决策。
起因
强化学习(Reinforcement Learning, RL)是一种让代理通过与环境互动来最大化累计奖励的方法。RL问题通常用马尔可夫决策过程(Markov Decision Process, MDP)来描述
尽管RL在许多领域取得了显著成功,但对于复杂、大规模的任务,传统RL方法面临挑战:
- 高维度状态空间:状态空间的维度增加会导致“维数灾难”,使得学习变得极其困难。
- 长期依赖与稀疏奖励:在一些任务中,奖励信号非常稀疏,且代理需要进行长时程规划才能获取奖励。
- 探索与利用的权衡:平衡探索新策略和利用已有策略之间的关系在复杂任务中尤为重要。
优点
HRL优点
- 减少搜索空间:通过分解任务,高层次的决策能够有效减少低层次需要探索的状态和动作空间,从而加速学习。
- 提高样本效率:通过共享和重用子任务的经验,可以显著提升样本利用率,减少训练所需的样本数量。
- 更好的泛化能力:分层结构使得在不同但相关的任务之间迁移学习变得更加容易。
HRL 原理
为了应对这些挑战,分层强化学习(HRL)应运而生。
HRL通过引入层次结构,将复杂任务分解为若干子任务,从而降低任务的复杂性并提高学习效率。
最早提出分层思想的是Sutton等人在1999年提出的选项框架(Options Framework)。
HRL 核心思想
- 将复杂任务分解成更易处理的子任务,各层次间可以分别进行优化和决策。
该领域发展至今,已经涌现出多种经典算法,例如,封建等级强化学习(Feudal RL)和MAXQ等算法。
封建等级强化学习(Feudal Reinforcement Learning, Feudal RL)最早由AI巨佬Geoffrey E. Hinton等人提出,Hinton因其在人工智能领域的突出贡献于2024年获得诺贝尔物理学奖。
方法
主要方法包括:
- 选项框架:将高级行为抽象为选项,通过定义初始集、政策和终止条件,简化策略学习。
- MAXQ 分解:通过分解价值函数,将复杂任务的值函数表示为若干子任务的值函数之和。
- FeUdal Networks:采用管理者-工人架构,高层管理者设定目标,低层工人执行具体操作。
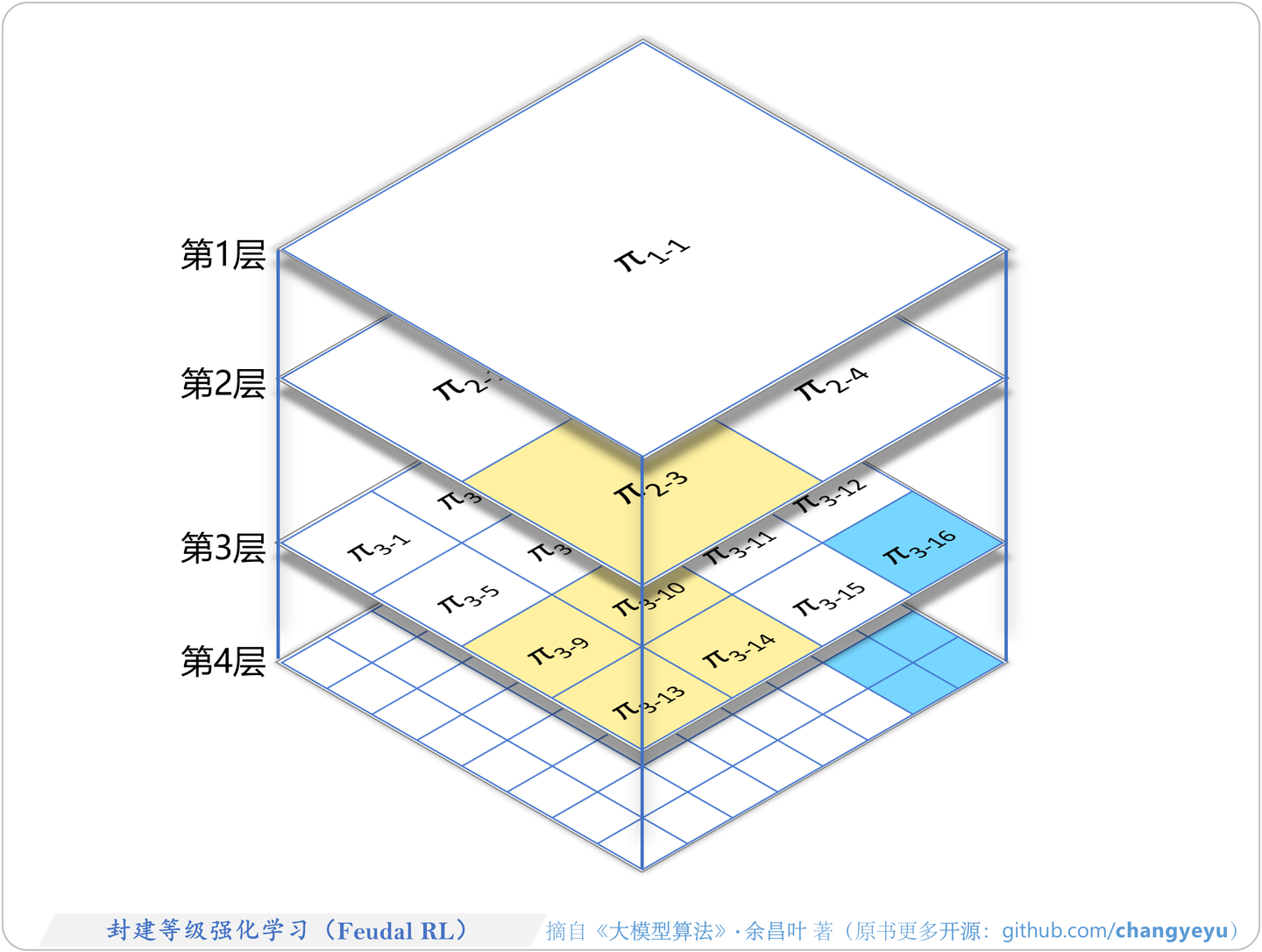
基本概念
- 层次结构:分层强化学习中通常存在多个层次,每个层次负责不同粒度的决策。高层次负责抽象和长期规划,而低层次负责具体操作和短期执行。
- 选项(Options)框架:这是分层强化学习的一种重要方法,将行动策略视为可选项(option),每个选项由三个部分组成:
- 初始集(Initiation Set):定义在哪些状态下可以选择该选项。
- 政策(Policy):定义在选项被激活期间如何进行行动选择。
- 终止条件(Termination Condition):定义何时结束该选项。
- 半马尔可夫决策过程(Semi-Markov Decision Process,SMDP):由于选项可能会持续不定长时间,因此分层强化学习常用SMDP来建模,这种模型允许动作(即选项)具有可变长度的持续时间。
Option-Critic 架构
一种端到端的分层强化学习方法,可以同时学习选项和选项间的政策。它通过梯度下降法优化选项的终止条件和内部策略。
Option-Critic架构是一种端到端的分层强化学习方法,能够同时学习选项(options)及其相关政策。该方法通过引入梯度下降优化选项的终止条件和内部策略,从而实现高效的分层决策过程。
MAXQ 分解
该算法将价值函数分解为不同层次的子任务,每个子任务都有自己的价值函数,从而简化了复杂任务的求解。
MAXQ分解方法提出了一种将强化学习中的复杂任务分解为多个子任务的方法,这些子任务各自有独立的价值函数。通过这种方式,可以显著减少状态-动作对的组合数量,从而提高学习效率。
主要思想:
- 任务分解:将复杂任务分解为若干子任务,每个子任务可以进一步分解,直到达到原子操作级别。
- 层次任务图:使用层次任务图表示任务的分解结构,每个节点代表一个子任务,对应的边表示子任务之间的调用关系。
- 递归学习:使用递归方法在不同层次间进行学习,通过逐层优化子任务来最终优化整体任务。
FeUdal Networks(FuN)
这种方法使用管理者-工人(Manager-Worker)架构,在高层次上,管理者通过设定目标指导低层次的工人去实现这些目标。
FeUdal Networks (FuN) 方法引入了管理者-工人(Manager-Worker)架构。在高层次上,管理者设定目标,指导低层次的工人去实现这些目标。这种方法使得模型能够有效处理长时程依赖问题。
多智能体强化学习
多智能体强化学习(Multi-Agent Reinforcement Learning,MARL)是强化学习的一个重要分支,研究多个智能体在共享环境中通过交互(包括竞争与合作)学习最优策略的问题。
例如,DeepMind 研究团队开发的AlphaGo、AlphaZero和AlphaStar等,OpenAI开发的OpenAI Five,展示了多智能体强化学习的强大潜力。
MADDPG(Multi-Agent DDPG)由OpenAI等研究团队于2017年发表。
两种输入输出结构的DQN(Deep Q-Network)模型
AlphaGo
2016年,Google DeepMind 团队的 David Silver、Aja Huang 等人 推出 AlphaGo。证明了深度学习和蒙特卡洛树搜索相结合的方法在解决围棋这类复杂问题上的有效性。
DeepMind 是一家位于英国的人工智能公司,于 2014 年被 Google 收购。DeepMind 致力于开发通用人工智能(AGI),其研究成果在游戏、医疗、能源等领域都具有广泛的应用前景。
AlphaGo 核心思路
- 将
深度学习与蒙特卡洛树搜索相结合,利用深度神经网络来学习围棋的策略和价值函数,从而提高搜索的效率和准确性。
AlphaGo 灵感来源于深度学习在图像识别和自然语言处理等领域的成功应用。
- 围棋的棋局也可以看作是一种图像,因此可以利用深度卷积神经网络来提取棋局的特征,并学习围棋的策略和价值函数。
原理
- 策略网络 (Policy Network): 用于预测人类专家在给定状态下会选择的动作。策略网络可以分为两种:
- 监督学习策略网络 (SL Policy Network): 通过学习人类专家的棋谱来预测人类的下棋策略。
- 强化学习策略网络 (RL Policy Network): 通过自我对弈,利用强化学习来提高下棋策略,目标是赢得比赛。
- 价值网络 (Value Network): 用于评估给定状态的价值,即在当前状态下,当前玩家获胜的概率。
- 蒙特卡洛树搜索 (MCTS): 结合策略网络和价值网络,在搜索树中进行高效的搜索,选择最佳的下一步动作。
图解
流程如下:
- 监督学习 (Supervised Learning): 首先,使用人类棋谱数据训练一个监督学习策略网络,使其能够模仿人类棋手的下棋策略。
- 强化学习 (Reinforcement Learning): 然后,使用强化学习算法,让策略网络通过自我对弈来不断提高自己的下棋水平。
- 价值网络训练 (Value Network Training): 接下来,训练一个价值网络,用于评估棋局的态势,判断在当前局面下谁更有可能获胜。
- 蒙特卡洛树搜索 (Monte-Carlo Tree Search): 最后,将训练好的策略网络和价值网络嵌入到蒙特卡洛树搜索算法中,用于指导搜索过程,选择最佳的下一步动作。
思考
Q1:AlphaGo是否是一种Actor-Critic架构?
AlphaGo 同时拥有「策略网络」(Actor)和「价值网络」(Critic),似乎符合「Actor-Critic」范式,但从严格意义上讲,AlphaGo 并不是一个典型的在线 Actor-Critic 架构
- 训练划分为多个阶段: 策略网络和价值网络并没有像典型 Actor-Critic 那样在同一个训练循环里相互更新,而是被拆分成明确的阶段来分别训练。
- 监督学习阶段:先用人类对局数据来训练策略网络(SL Policy Network)。
- 强化学习阶段:再通过自我对弈,用策略梯度方法(REINFORCE)来微调得到的策略网络(RL Policy Network)。
- 价值网络训练阶段:单独收集自我对弈产生的新棋局样本,再用监督回归的方式训练价值网络(Value Network)。
- 借助蒙特卡洛树搜索进行决策:AlphaGo 并不是单纯地根据 Critic 的估值来更新 Actor,而是用价值网络和搜索相结合来评估棋局并指导下棋。
- AlphaGo 的决策依赖于蒙特卡洛树搜索(MCTS),将策略网络输出作为先验概率,价值网络输出用来评估叶节点;
- 而在传统的在线 Actor-Critic 中,一般是直接用 Critic(价值函数)对每个时刻的 state-action 进行评估,再更新 Actor。
- 价值网络在训练中仅作为回归目标,而非实时更新的Critic
- 虽然在第二遍强化学习时,论文中有提到使用价值网络作为基线(baseline)来降低方差,但它并没有像传统 Actor-Critic 那样「先更新 Critic、再更新 Actor」地同步迭代,而是更多地将价值网络当作一个离线学得的估值模型,再拿来为搜索和策略梯度提供帮助。
Q2:AlphaGo在RL的分类里,更接近Value-based / Policy-based / Model-based中的哪种?
AlphaGo 的成功源于 Model-based(MCTS + 神经网络模型)、Policy-based(策略网络) 和 Value-based(值网络) 三者的深度融合。
但从分类优先级来看:
- Model-based 是核心:决策过程依赖显式的环境模型(MCTS 的模拟和规划),这是 AlphaGo 区别于传统无模型(Model-free)方法的关键。
- Policy 和 Value 是支撑:策略网络和值网络为模型提供了高效的先验知识,降低了纯 Model-based 方法的计算成本。
Q3:蒙特卡洛树搜索 (MCTS) 在 AlphaGo 中扮演什么角色?它是如何与策略网络和价值网络相结合的?
蒙特卡洛树搜索 (MCTS) 在 AlphaGo 中扮演着决策引擎的角色。它利用策略网络和价值网络来指导搜索过程,从而在庞大的搜索空间中高效地找到最佳的下一步动作。
MCTS 与策略网络和价值网络的结合方式如下:
- 策略网络指导搜索: 在 MCTS 的选择 (Selection) 阶段,策略网络用于预测每个节点的扩展概率,从而优先选择更有希望的节点进行扩展。
- 价值网络评估状态: 在 MCTS 的模拟 (Simulation) 阶段,价值网络用于评估叶子节点的状态价值,从而更准确地判断当前局势的优劣。
- 结合策略和价值: 在 MCTS 的回溯 (Backpropagation) 阶段,将价值网络的评估结果与模拟的结果相结合,更新节点的状态价值。
通过这种方式,MCTS 可以充分利用策略网络和价值网络的信息,从而在搜索过程中做出更明智的决策。
AlphaZero
动机
问题:
- 传统棋类AI程序和
AlphaGo都依赖于特定领域的知识和优化,缺乏通用性。 - 之前的研究在
国际象棋和日本将棋中应用强化学习和深度学习时,要结合人工设计的特征和搜索算法,未能实现完全的自主学习。
AlphaGo 在围棋领域的成功为AlphaZero提供了灵感,但AlphaZero目标是构建一个更加通用的算法,使其能够应用于多种棋类游戏。
AlphaZero 介绍
2017年10月,AlphaZero 是一个超乎寻常的强化学习算法,以绝对优势战胜了多名围棋以及国际象棋冠军
- 首个能够在国际象棋、围棋等游戏中达到超越人类水平、击败世界冠军的计算机系统,且仅依赖于游戏规则,无需任何人类先验知识。
- David Silver 论文:A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play
- 解读
- Web Demo alphazero
2018年12月6日, DeepMind 官方发布 AlphaZero
AlphaZero 最关键的能力:
- 不依赖于外部先验知识的情况下在棋盘类游戏中获得超越人类的表现。
AlphaZero 通过自我博弈汲取经验知识来不断精通游戏。
AlphaZero 把 AlphaGo Zero 方法泛化到其他棋类游戏。
原理
AlphaZero 核心思路:
- 用强化学习算法,通过自我对弈从零开始学习,并在多种棋类游戏中达到超人类水平。
这个思路的关键:
- 通用算法:使用相同的算法和网络架构,无需针对特定游戏进行修改。
- 深度神经网络:使用深度神经网络来表示棋局的策略 (policy) 和 价值 (value)。策略网络预测下一步的最佳走法,价值网络预测当前棋局的胜负概率。
- 蒙特卡洛树搜索 (MCTS):使用MCTS来指导自我对弈的过程,并提高策略和价值的准确性。MCTS通过模拟多次对弈来评估每个走法的潜在价值,并选择最优的走法。
- 强化学习:使用强化学习算法来训练深度神经网络,通过自我对弈产生的训练数据不断改进策略和价值的预测能力。
AlphaZero 由两部分构成。
- 第一部分,神经网络。
- 第二部分,“蒙特卡洛树搜索(Monte Carlo Tree Search)”,或
MCTS。
详情
- 神经网络(NN)。以棋面作为输入,输出该棋面的“价值”,外加所有可能走法的概率分布。
- 蒙特卡洛树搜索(MCTS)。理想情况下,神经网络足以选择下一步走法。不过,希望考虑尽可能多的棋面,并确保选择了最好的走法。
- MTCS 和 Minimax一样,可以寻找可能棋面的算法。
- 与Minimax不同的是,MTCS能更加高效地搜寻博弈树。
基本步骤
- 计算机自我博弈,记录每步走棋。
- 一旦决出胜负,就给每步走棋打上标签——棋面最终是“赢”或是“输”。
- 获得用于神经网络(Neural Network,NN)训练的数据集,让该网络学会判断给定棋面是“赢面”还是“输面”;
- 复制这个神经网络。用上一步得到的数据集训练该克隆网络;
- 让克隆网络与原始神经网络互相博弈;
- 上一步中获胜的网络留下,败者弃之;
- 重复第1步。
问题
AlphaZero 不足
- 计算资源:AlphaZero 训练需要大量计算资源,包括TPU和GPU,这限制了其在资源有限的环境中的应用。
- 探索与利用:AlphaZero 在
探索(exploration) 和利用(exploitation) 之间的平衡可能需要进一步优化,以提高学习效率和性能。 - 理论分析:AlphaZero 的成功缺乏充分的理论分析,例如,为什么MCTS在AlphaZero中表现如此出色?如何保证算法的收敛性?
- 领域局限性:AlphaZero 主要应用于棋类游戏,其在其他领域的通用性需要进一步验证。
问题
为什么说强化学习在近年不会被广泛应用
- 【2021-3-11】为什么说强化学习在近年不会被广泛应用?,知乎帖子
- (1)数据收集过程不可控
- 不同于监督学习,强化学习的数据来自agent跟环境的各种交互。对于数据平衡性问题,监督学习可以通过各种补数据加标签来达到数据平衡。但这件事情对强化学习确实非常难以解决的,因为数据收集是由policy来做的,无论是DQN的Q-network还是AC架构里的actor,它们在学习过程中,对于任务激励信号的理解的不完善的,很可能绝大部分时间都在收集一些无用且重复的数据。虽然有prioritized replay buffer来解决训练优先级的问题,但实际上是把重复的经验数据都丢弃了。在实际应用中,面对一些稍微复杂点的任务还是需要收集一大堆重复且无用的数据。这也是DRL sample efficiency差的原因之一。
- (2)环境限制
- DRL问题中,环境都是从初始状态开始,这限制了很多可能的优化方向。比如在状态空间中,可以针对比较“新”的状态重点关注,控制环境都到这个状态。但目前的任务,很多环境的state-transition function都是stochastic的,都是概率函数。即便记录下来之前的action序列,由于环境状态转移的不确定性,也很难到达类似的状态。更别提policy本身也是stochastic的,这种双重stochastic叠加,不可能针对“重点”状态进行优化。
- 同时这种限制也使得一些测试场景成为不可能。比如自动驾驶需要测试某个弯道,很难基于当前的policy在状态空间中达到类似的状态来重复测试policy在此状态下的鲁棒性。
- (3)玄之又玄,可解释性较差
- 本来Q-learning就是一个通过逐步学习来完善当前动作对未来收益影响作出估计的过程。加入DNN后,还涉及到了神经网络近似Q的训练。这就是“不靠谱”上又套了一层“不靠谱”。如何验证策略是正确的?如何验证Q function是最终收敛成为接近真实的估计?这些问题对于查表型的Q-learning来说,是可以解决的,无非就是工作量的问题。但对于大规模连续状态空间的DQN来说,基本上没法做。论证一个policy有效,也就是看看render以后的效果,看看reward曲线,看看tensorborad上的各个参数。连监督学习基本的正确率都没有。然后还要根据这些结果来调reward function,基本上都在避免回答why这个问题。
- (4)随机探索
- DRL的探索过程还是比较原始。现在大多数探索,epsilon-greedy,UCB都是从多臂老虎机来的,只针对固定state的action选择的探索。扩展到连续状态空间上,这种随机探索还是否有效,在实际落地过程中,还是要打个问号。因为也不能太随机了。大家都说PPO好,SAC强,探索过程也只不过是用了stochastic policy,做了个策略分布的熵的最大化。本质还是纯随机。虽然有些用好奇心做探索的工作,但也还是只把探索任务强加给了reward,指标不治本。
- 当前DRL的实际科研的进步速度要远远慢于大众对于AI=DL+RL的期望。能解决的问题:
- 固定场景:状态空间不大,整个trajectory不长
- 问题不复杂:没有太多层次化的任务目标,奖励好设计
- 试错成本低:咋作都没事
- 数据收集容易:百万千万级别的数据量,如果不能把数据收集做到小时级别,那整个任务的时间成本就不太能跟传统的监督相比
- 目标单纯:容易被reward function量化,比如各种super-human的游戏。对于一些复杂的目标,比如几大公司都在强调拟人化,目前没有靠谱的解决方案
- 落地领域也就游戏了,而且是简单游戏,比如固定场景、小地图上的格斗,比如街霸、王者之类。要是大地图、开放世界的话,光捡个枪、开个宝箱就能探索到猴年马月了。也没想象中那么fancy,基本没有图像类输入,全是传感器类的内部数据,所以同类型任务的训练难度还没到Atari级别,这几年时间,DOTA2和星际基本上是游戏领域内到顶的落地
- DeepMind近期的一篇论文:Rainbow: Combining Improvements in Deep Reinforcement Learning。这篇论文对原始DQN框架做了一些渐进式改进,证明他们的RainbowDQN性能更优。
- 做强化的同学们一点信息:
- 强化学习岗位很少,因为落地难+烧钱,基本只有几个头部游戏公司会养一个规模不大的团队。
- 纯强化的技术栈不太好跳槽,除了游戏外,别的领域很难有应用。
- 20年huawei的强化夏令营,同时在线也有好几万人,想想这规模,未来几年这些研究生到job market会多卷。
- (1)数据收集过程不可控
- 强化学习是唯一一个可以明目张胆地在测试集上进行训练的机器学习网络。都2020了强化学习除了能玩游戏还能做什么?强化学习的特点是面向目标的算法,过程基本很难拆解,没法管控,如果目标没法在商业公司被很好的认可
- 每当有人问我强化学习能否解决他们的问题时,我会说“不能”。而且我发现这个回答起码在70%的场合下是正确的。
- 更多参考:深度强化学习的弱点和局限,原文:Deep Reinforcement Learning Doesn’t Work Yet
- Deep RL实现进一步发展的一些条件:原文地址,中文版本: 深度强化学习的弱点和局限
- 易于产生近乎无限的经验;
- 把问题简化称更简单的形式;
- 将自我学习引入强化学习;
- 有一个清晰的方法来定义什么是可学习的、不可取消的奖励;
- 如果奖励必须形成,那它至少应该是种类丰富的。
- 下面是我列出的一些关于未来研究趋势的合理猜测 ,希望未来Deep RL能带给我们更多惊喜。
- 局部最优就足够了。我们一直以来都追求全局最优,但这个想法会不会有些自大呢?毕竟人类进化也只是朝着少数几个方向发展。也许未来我们发现局部最优就够了,不用盲目追求全局最优;
- 代码不能解决的问题,硬件来。我确信有一部分人认为人工智能的成就源于硬件技术的突破,虽然我觉得硬件不能解决所有问题,但还是要承认,硬件在这之中扮演着重要角色。机器运行越快,我们就越不需要担心效率问题,探索也更简单;
- 添加更多的learning signal。稀疏奖励很难学习,因为我们无法获得足够已知的有帮助的信息;
- 基于模型的学习可以释放样本效率。原则上来说,一个好模型可以解决一系列问题,就像AlphaGo一样,也许加入基于模型的方法值得一试;
- 像参数微调一样使用强化学习。第一篇AlphaGo论文从监督学习开始,然后在其上进行RL微调。这是一个很好的方法,因为它可以让我们使用一种速度更快但功能更少的方法来加速初始学习;
- 奖励是可以学习的。如果奖励设计如此困难,也许我们能让系统自己学习设置奖励,现在模仿学习和反强化学习都有不错的发展,也许这个思路也行得通;
- 用迁移学习帮助提高效率。迁移学习意味着我们能用以前积累的任务知识来学习新知识,这绝对是一个发展趋势;
- 良好的先验知识可以大大缩短学习时间。这和上一点有相通之处。有一种观点认为,迁移学习就是利用过去的经验为学习其他任务打下一个良好的基础。RL算法被设计用于任何马尔科夫决策过程,这可以说是万恶之源。那么如果我们接受我们的解决方案只能在一小部分环境中表现良好,我们应该能够利用共享来解决所有问题。之前Pieter Abbeel在演讲中称Deep RL只需解决现实世界中的任务,我赞同这个观点,所以我们也可以通过共享建立一个现实世界的先验,让Deep RL可以快速学习真实的任务,作为代价,它可以不太擅长虚拟任务的学习;
- 难与易的辨证转换。这是BAIR(Berkeley AI Research)提出的一个观点,他们从DeepMind的工作中发现,如果我们向环境中添加多个智能体,把任务变得很复杂,其实它们的学习过程反而被大大简化了。让我们回到ImageNet:在ImageNet上训练的模型将比在CIFAR-100上训练的模型更好地推广。所以可能我们并不需要一个高度泛化的强化学习系统,只要把它作为通用起点就好了。
资料
- 【2023-3-5】强化学习入门:基本思想和经典算法 ,强化学习精简笔记
- 【2023-2-16】动手学强化学习
- 【2022-2-17】北大老师写的深度强化学习,电子版(中文简体、繁体、英文都有)
- 更多Demo地址
- 无需博士学位的TensorFlow深度强化学习教程 by Martin Gorner
- 李宏毅深度强化学习(国语)课程(2018),B站视频
- 【2021-3-18】大年初一,一起来深度强化学习,Thomas Simonini 的 Deep Reinforcement Learning Course的课程笔记
- 【2020-7-4】【(EEML2020)强化学习教程(Colab)】“EEML2020 RL Tutorial”
- 【2020-7-5】XRL:可解释强化学习《XRL: eXplainable Reinforcement Learning》by Meet Gandhi
- 【2019】强化学习课程:2019斯坦福大学最新强化学习课程:CS234,系列,B站视频,CSDN笔记总结
- 【2021-2-27】【杜伦大学10小时强化学习课程】“Reinforcement Learning Lectures Durham University” by Chris G. Willcocks
- 【2021-3-17】强化学习的“神话”和“鬼话”,Csaba Szepesvári在2020年数据挖掘顶会KDD的Deep Learning Day做了题为Myths and Misconceptions in Reinforcement Learning的讲座。Csaba Szepesvári是阿尔伯塔大学计算机系教授,在Deepmind领导Foundations团队。他于2010年出版Algorithms for Reinforcement Learning. 最近出版Bandit Algorithms. 他于2006年发表题为Bandit based Monte-Carlo Planning的论文,提出UCT算法,对AlphaGo的研发起到了关键作用。
- 1)要不要学习RL
- 误解:有人说,RL就是指一些特定的算法,比如TD、DQN、PPO,等等;而像ES(evolutionary search, 进化搜索)、随机搜索、SSL(self-supervised learning, 自我监督学习)等等这些就不是RL.
- 三类基本的RL问题:Online RL(智能体直接与环境交互学习), Batch RL(历史数据中学习), Planning/simulation optimization(规划/仿真优化). 当然有很多变种。
- 2)RL是不是有很多问题
- 3)RL与相邻学科的关系如何
- 然后讨论一些“Meta consideration”
- 原版ppt及youtube视频,model based RL ppt
- 1)要不要学习RL
- 【2021-3-19】人工智能拒绝内卷,AI研习社文章:开局一头狼六只羊,这个狼吃羊的AI火了!傻狼拒绝内卷:抓羊可太累了,我只想自杀……

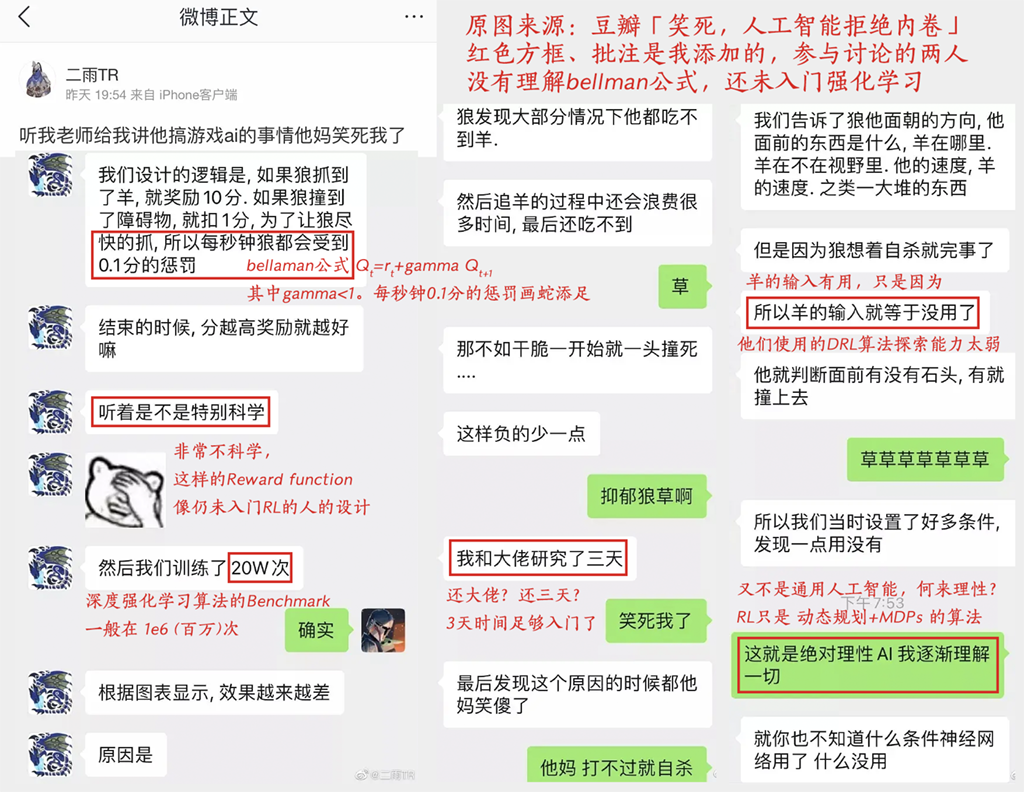
- 知乎曾伊言的回答这样的AI是真的吗? :这远不是通用人工智能,回报函数(reward function)的设计者若理解期望折扣回报(expected discounted return),就不会犯这种错,也不需要研究三天。
- ①狼就是打工人…每秒扣的是青春和时间,羊是永远达不到的“升职、加薪、迎娶白富美、走上人生巅峰”,撞石头就是躺平摸鱼
- ②阿西莫夫三定律是多么重要啊,不然以效率和结果为一切指标的ai,非常可能在很多场景中计算后发现,人类+自己毁灭后效益最大,然后采取灭世措施。
- 微博原贴
- 星尘研表示狼自杀的错误是很多东西共同影响产生的,最主要的一个错误是迭代次数太少,20W次完全不够学,后面提高到100W次起步, 效果直线上升。
- 今天微博上好像有一个内卷AI狼…
- 【2021-3-11】为什么说强化学习在近年不会被广泛应用?,知乎帖子
-
Richard S. Sutton and Andrew G. Barto的Reinforcement Learning: An Introduction, Second edition, 或电子版
- 强化学习圣经:《强化学习导论》第二版(附PDF下载),配套python代码
- 【2023-3-14】强化学习经典学习资料,david silver,David-Silver-Reinforcement-learning
Google DeepMind David Silver主页提供的UCL强化学习课程资料: Video-lectures available here
- Lecture 1: Introduction to Reinforcement Learning
- Lecture 2: Markov Decision Processes
- Lecture 3: Planning by Dynamic Programming
- Lecture 4: Model-Free Prediction
- Lecture 5: Model-Free Control
- Lecture 6: Value Function Approximation
- Lecture 7: Policy Gradient Methods
- Lecture 8: Integrating Learning and Planning
- Lecture 9: Exploration and Exploitation
- Lecture 10: Case Study: RL in Classic Games
Syllabus:
- Week 1: Introduction to Reinforcement Learning [slide][video]
- Week 2: Markov Decision Processes [slide][video]
- Week 3: Planning by Dynamic Programming [slide][video]
- Week 4: Model-Free Prediction [slide][video]
- Week 5: Model-Free Control [slide][video]
- Week 6: Value Function Approximation [slide][video]
- Week 7: Policy Gradient Methods [slide][video]
- Week 8: Integrating Learning and Planning [slide][video]
- Week 9: Exploration and Exploitation [slide][video]
- Week 10: Case Study: RL in Classic Games [slide][video]
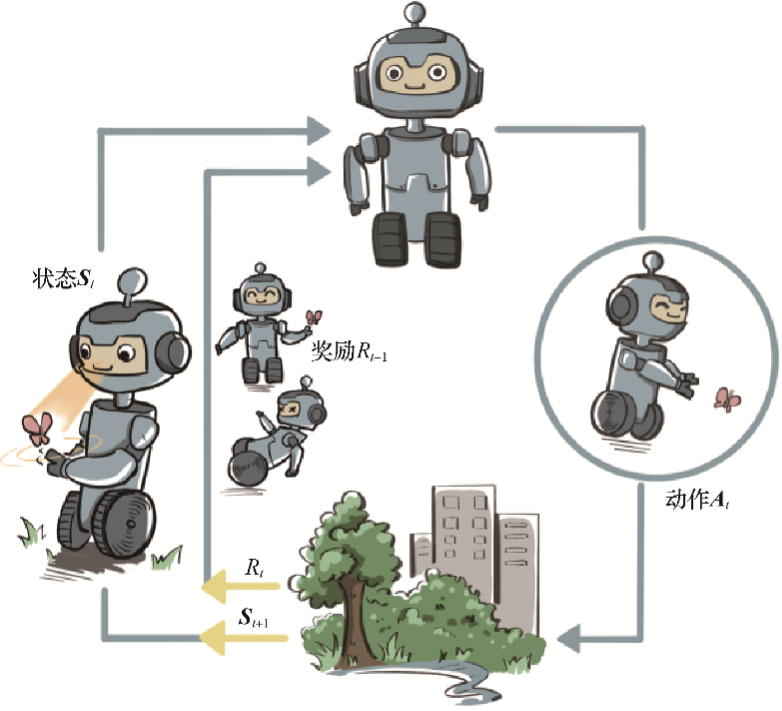
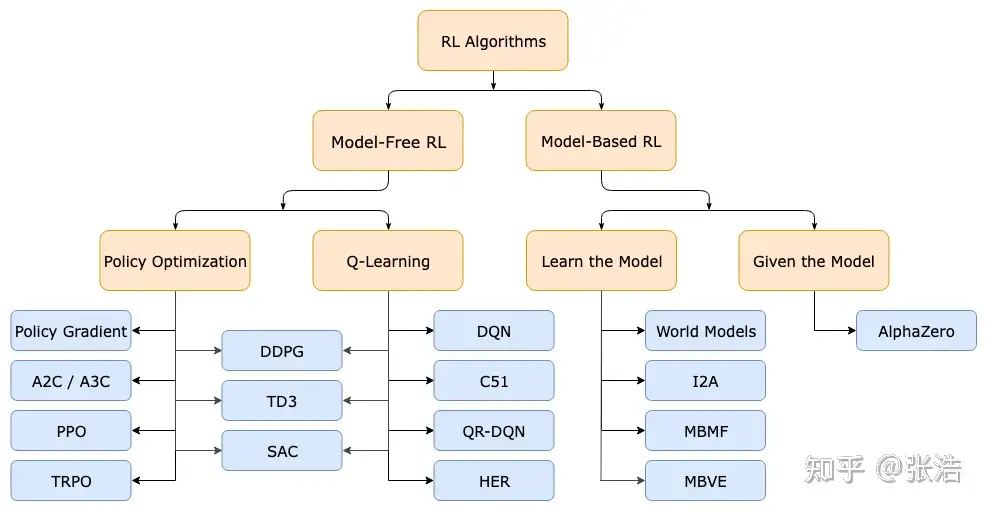

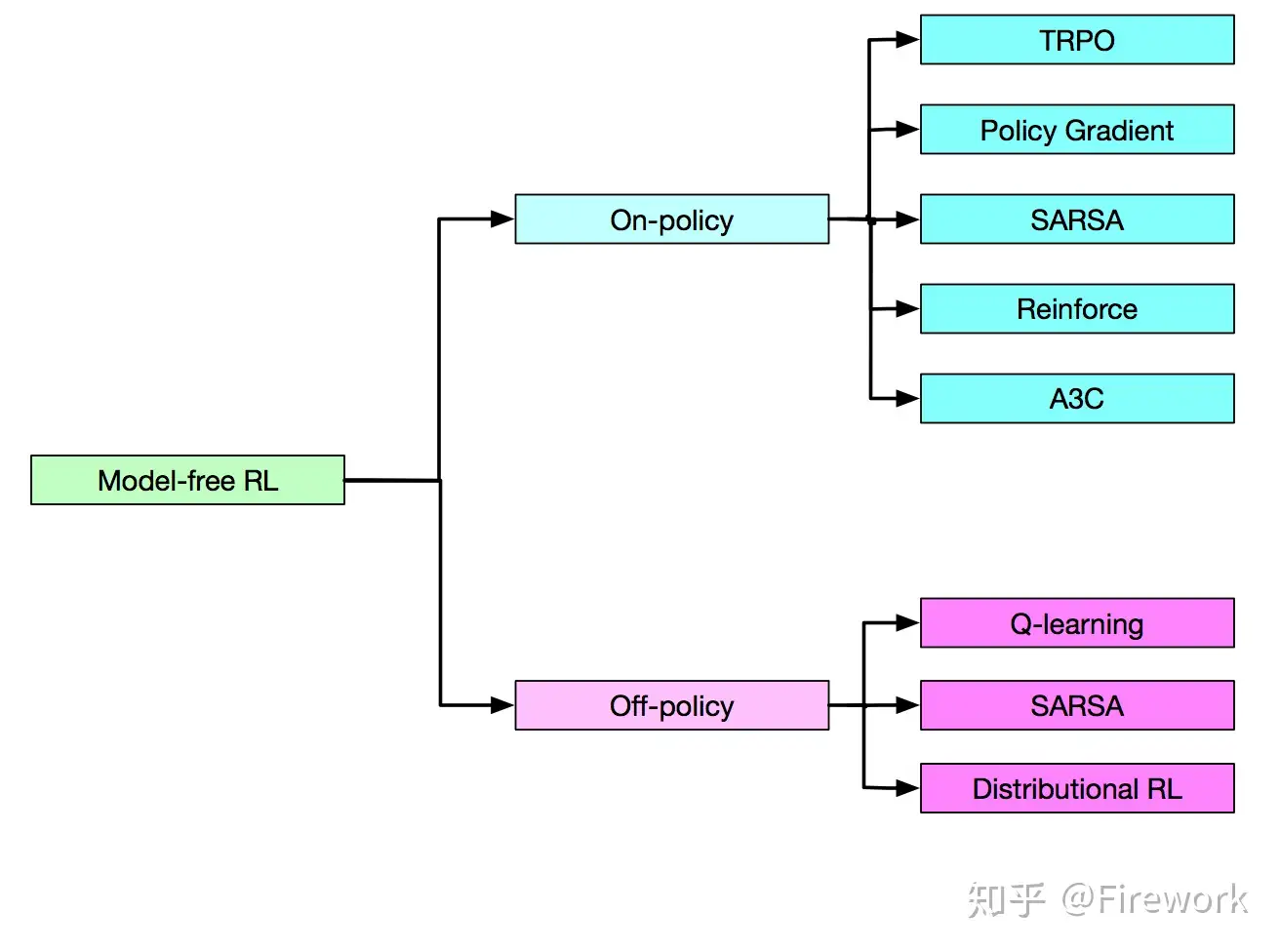
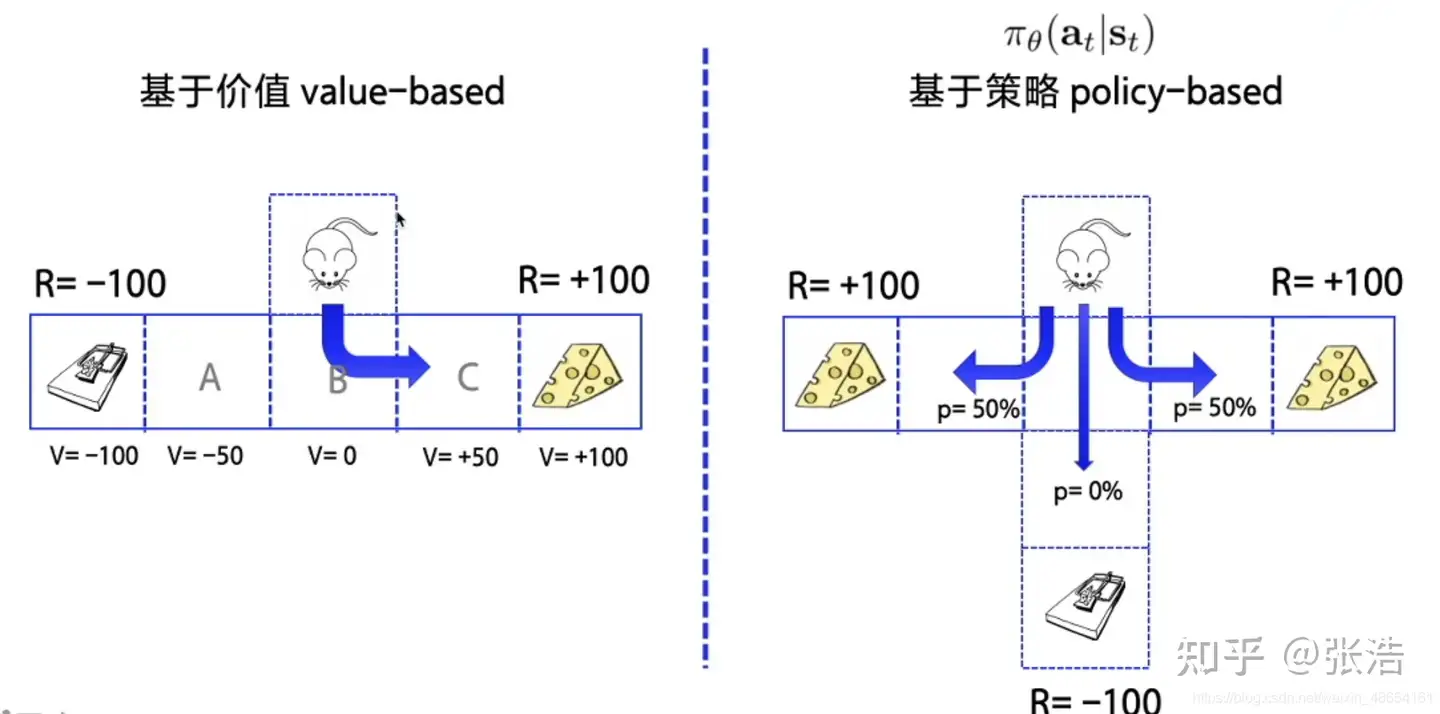




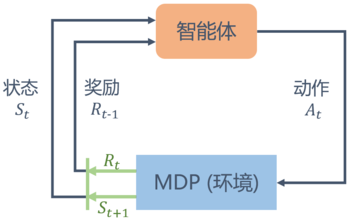
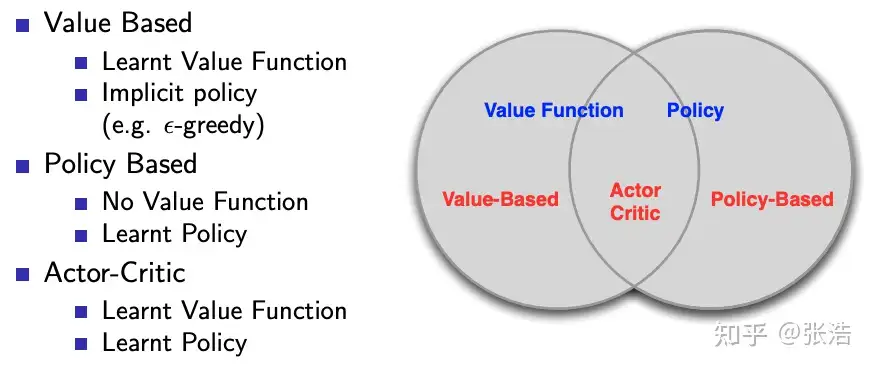


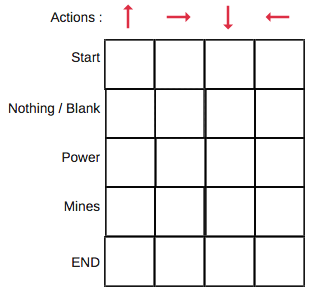
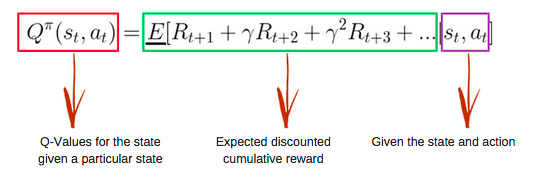


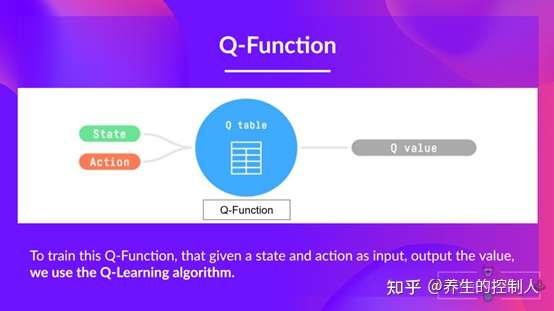
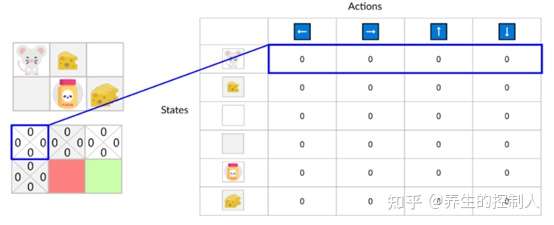

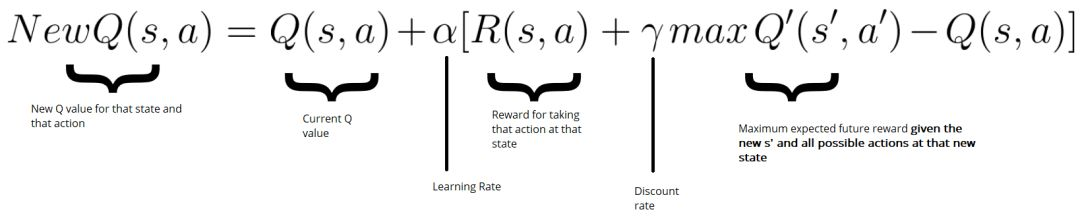
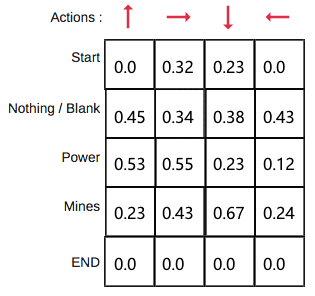



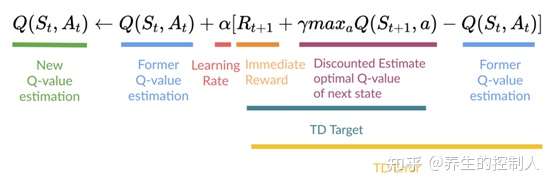

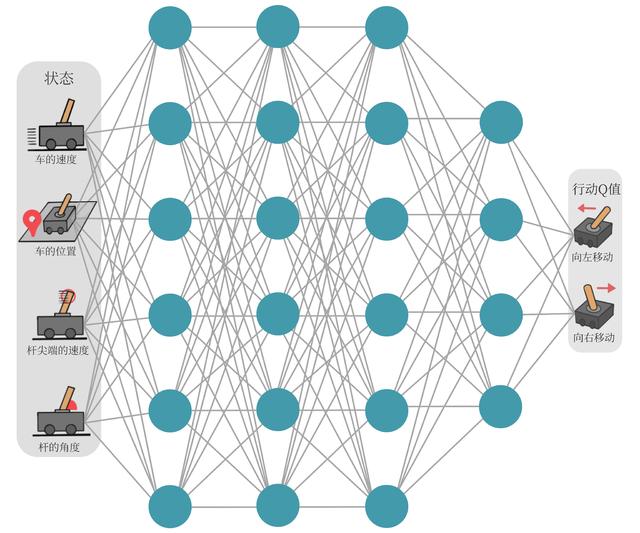
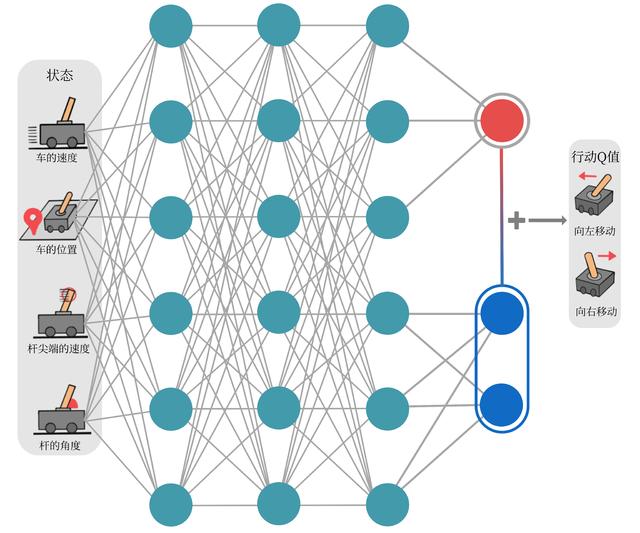

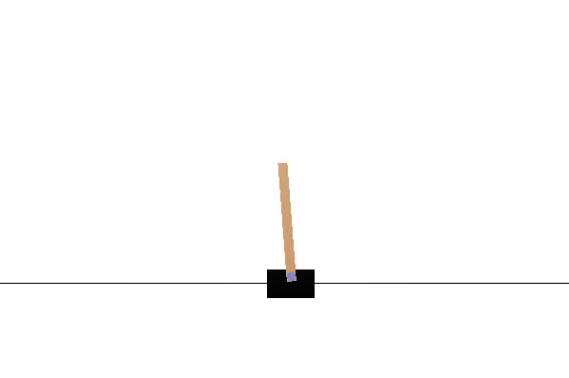
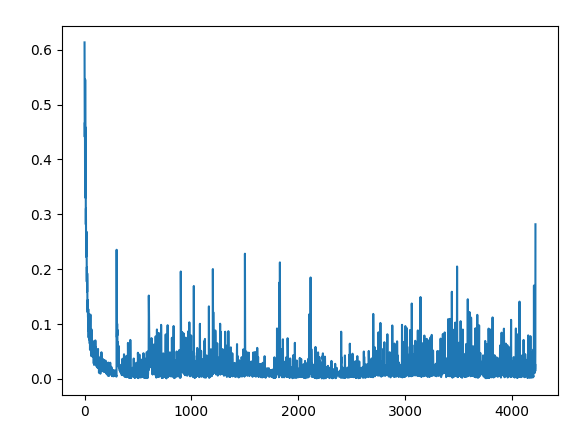
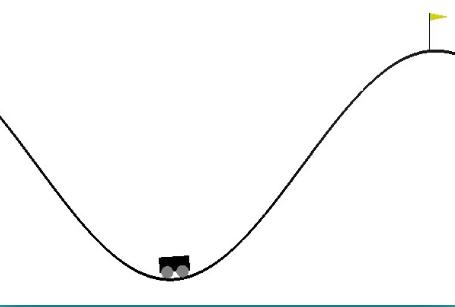
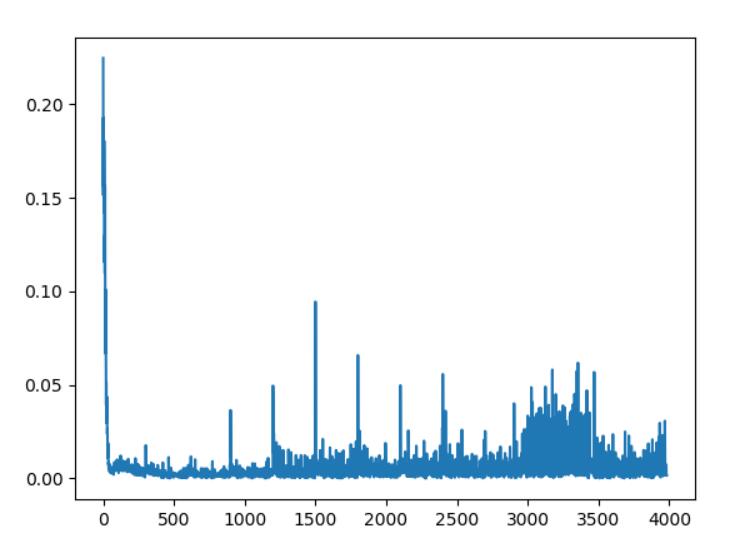
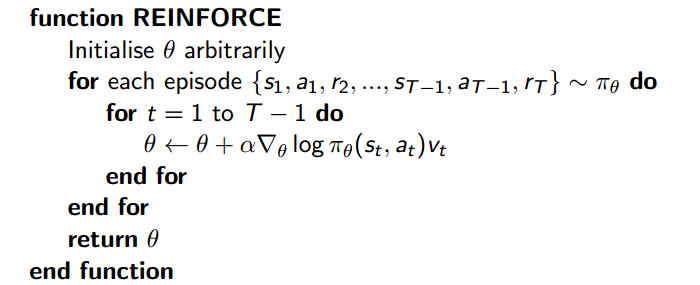

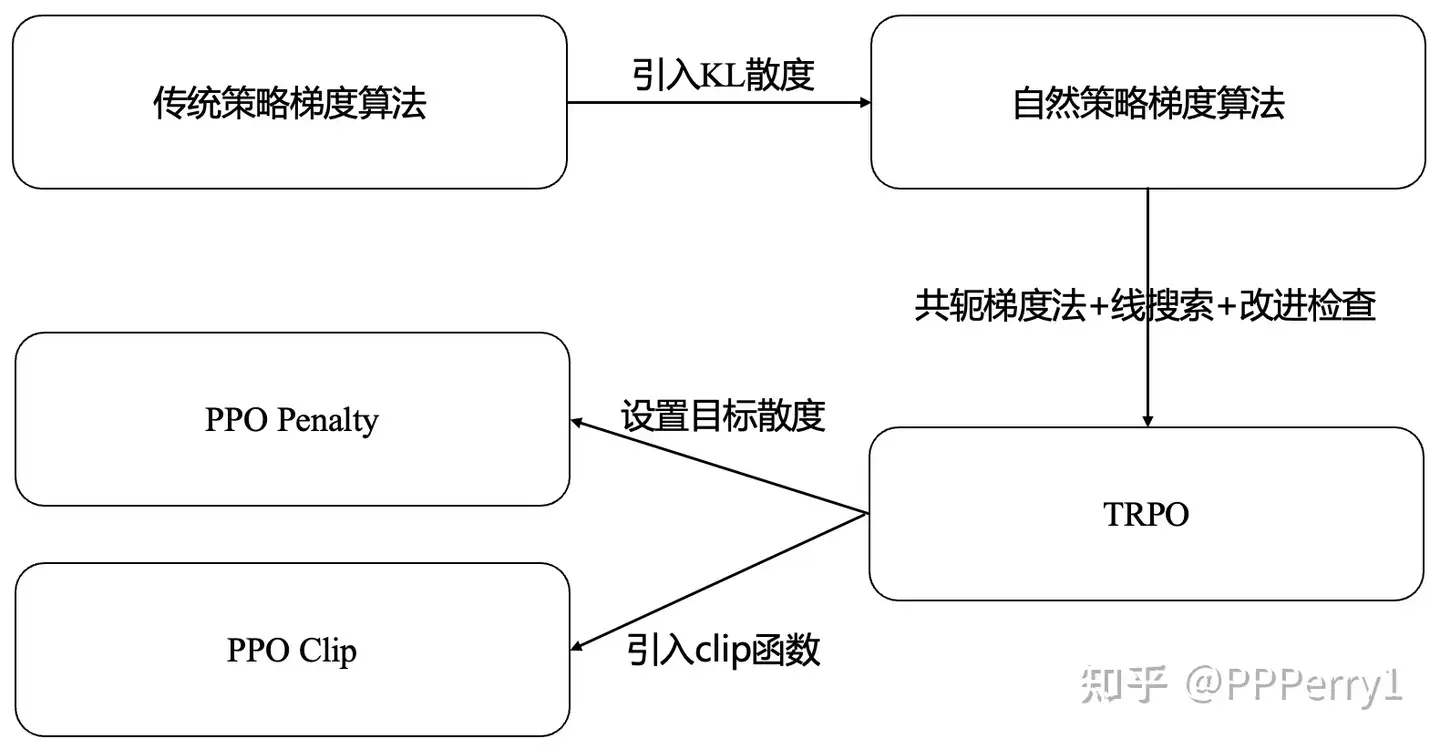

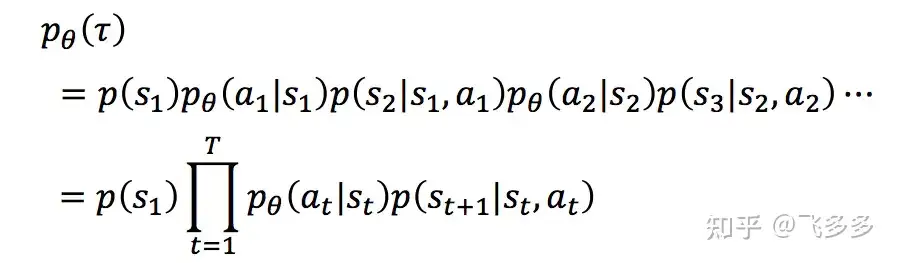


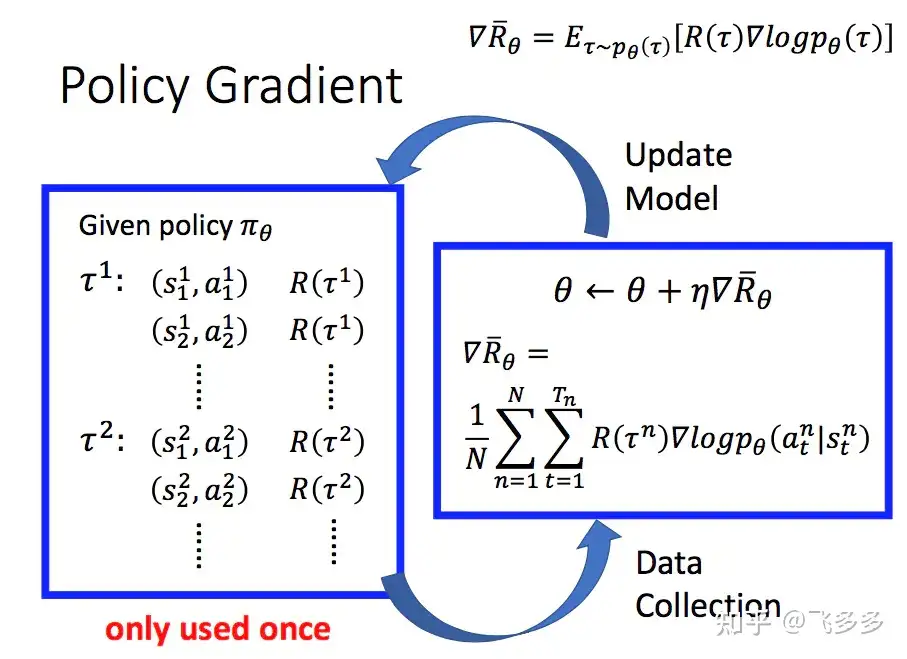
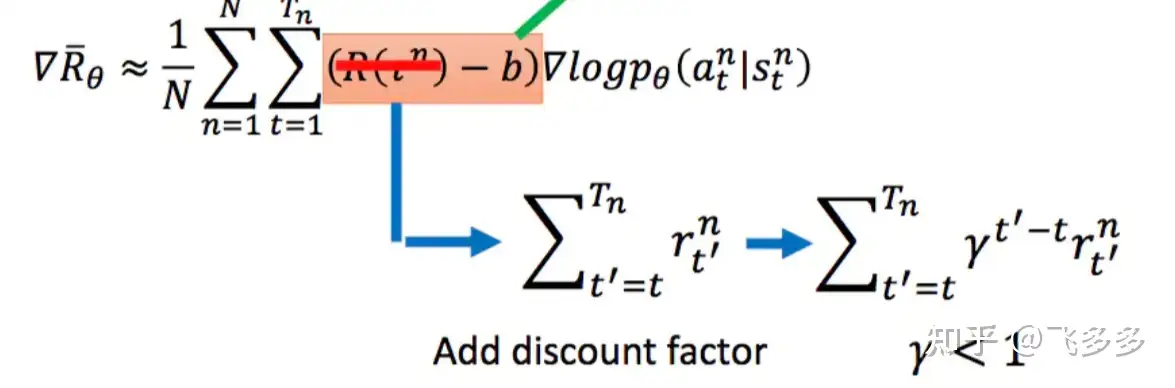
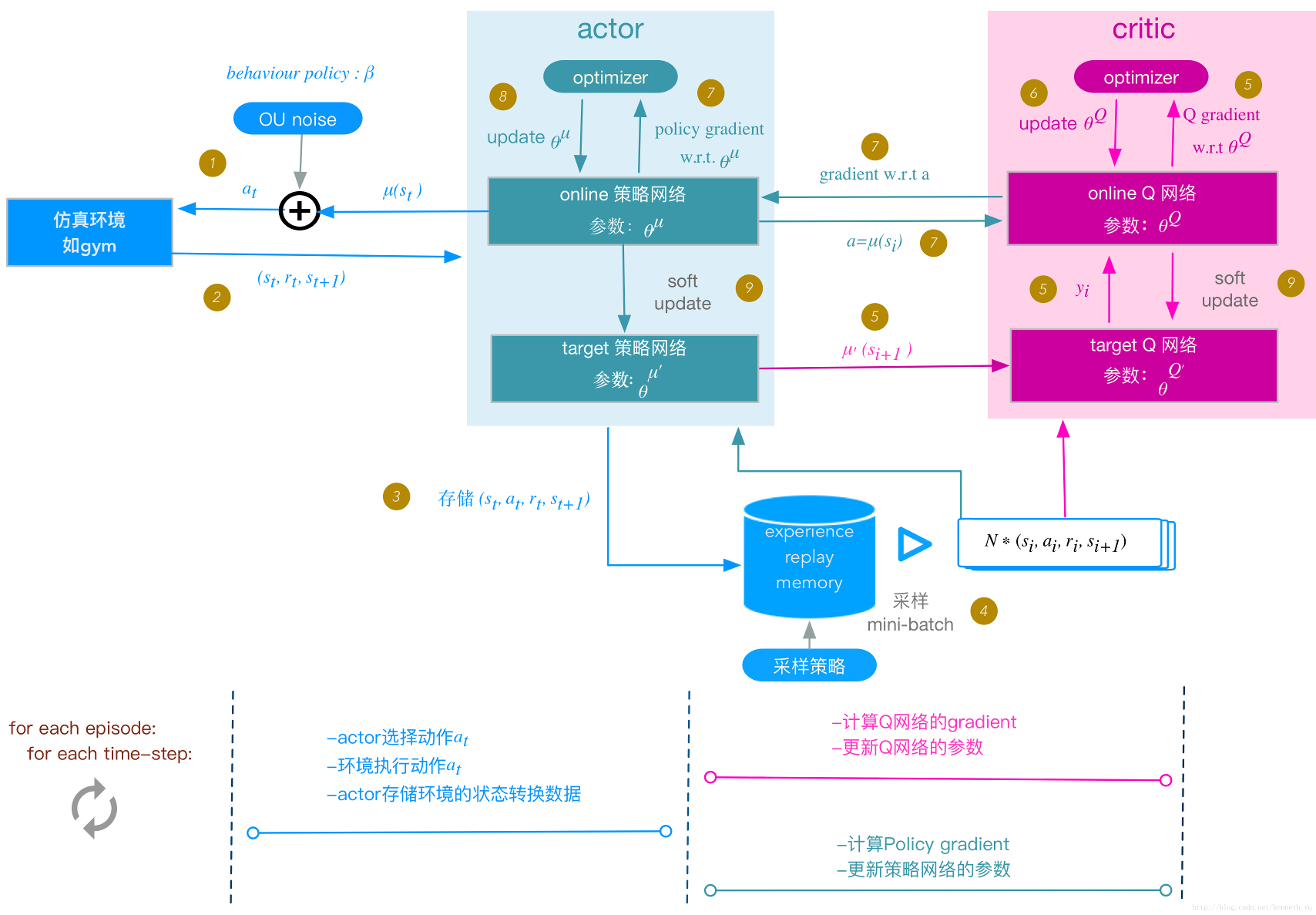
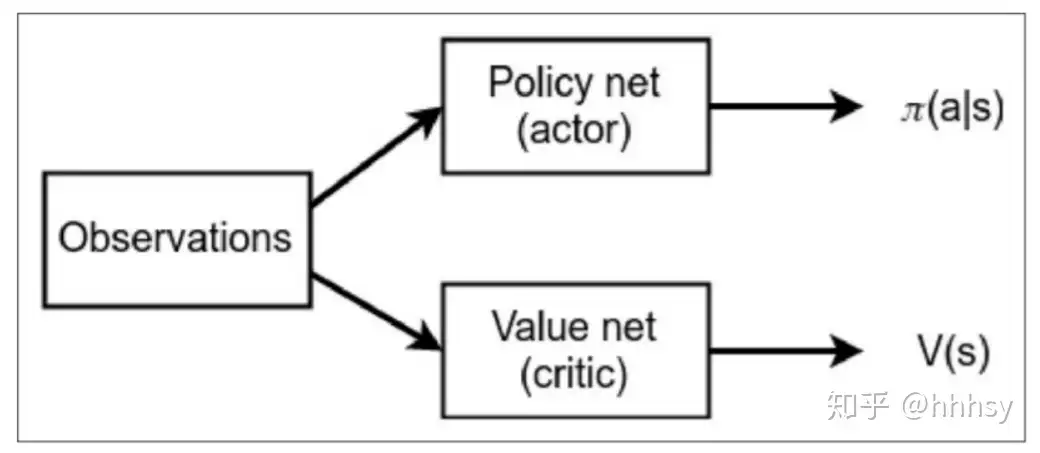
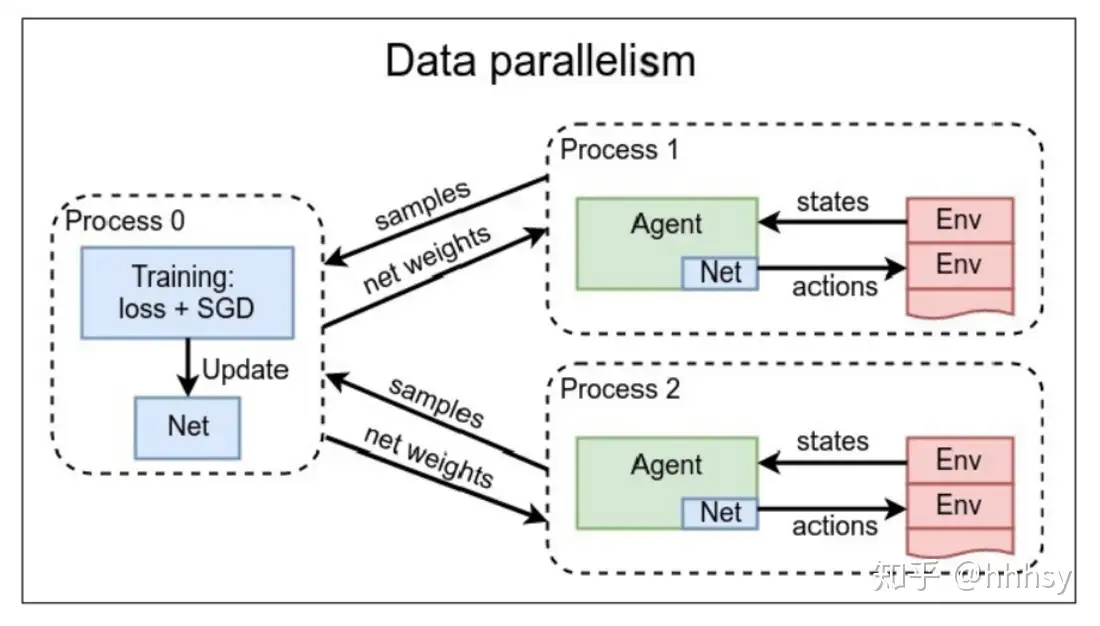
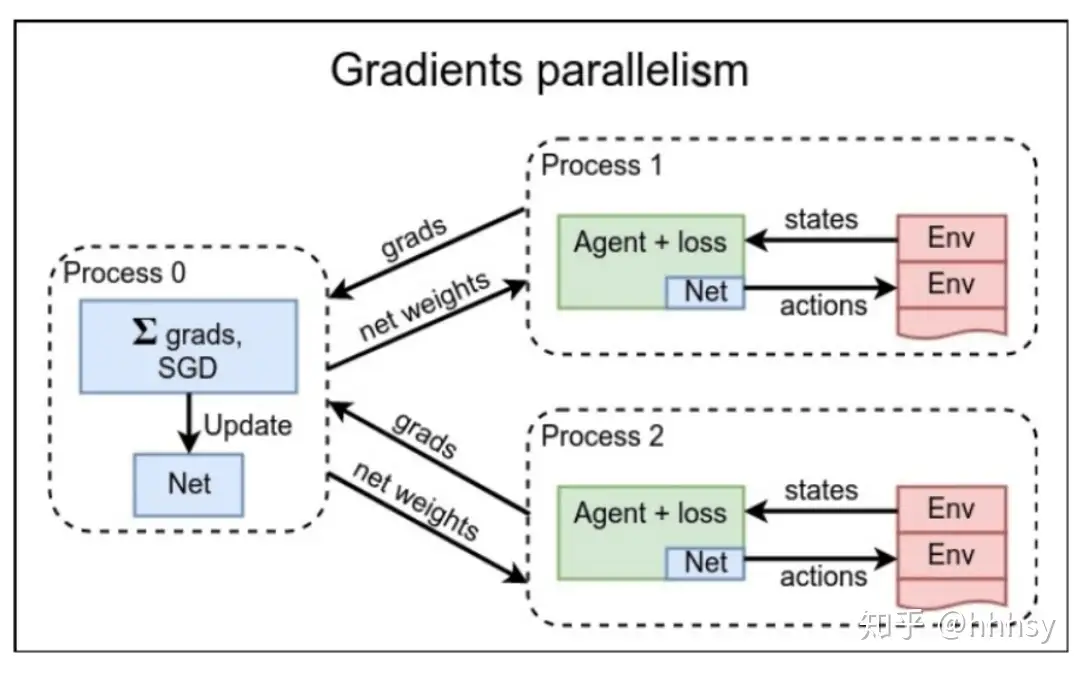
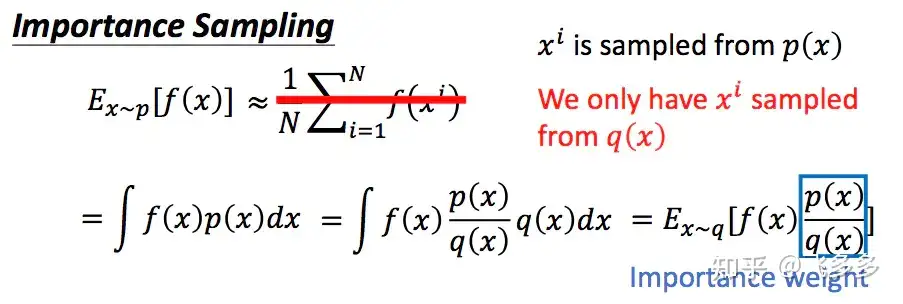
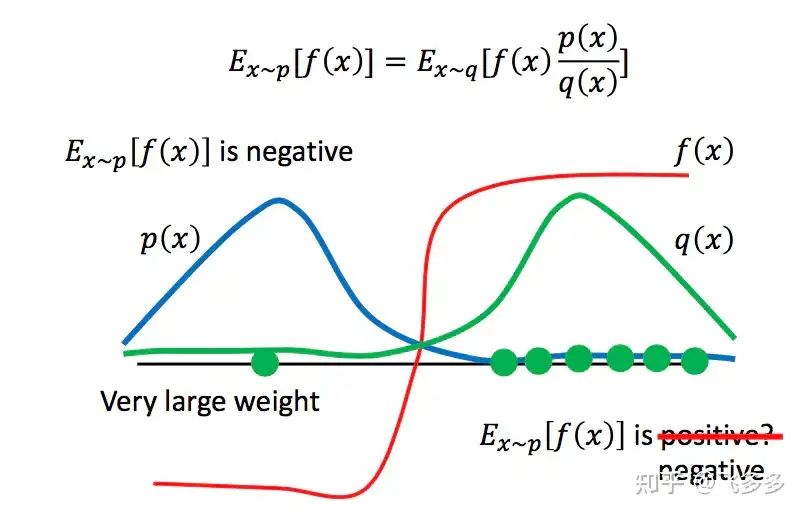

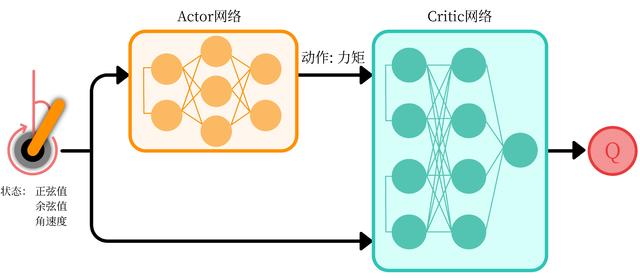


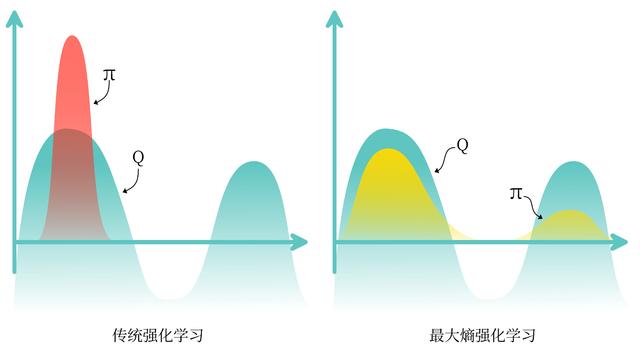
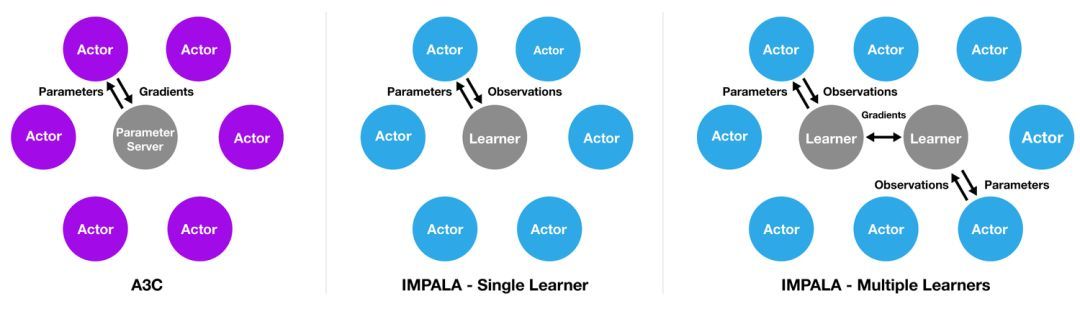

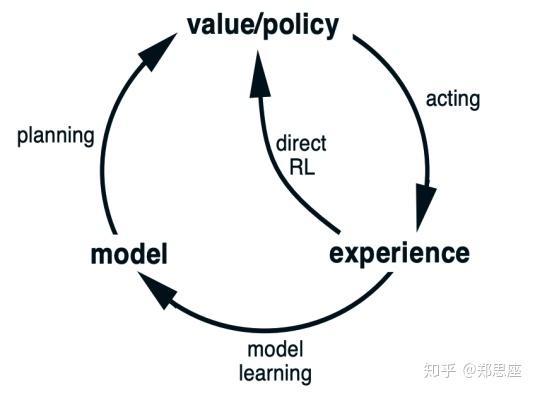
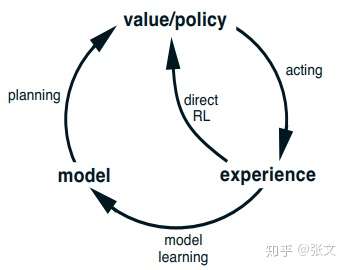
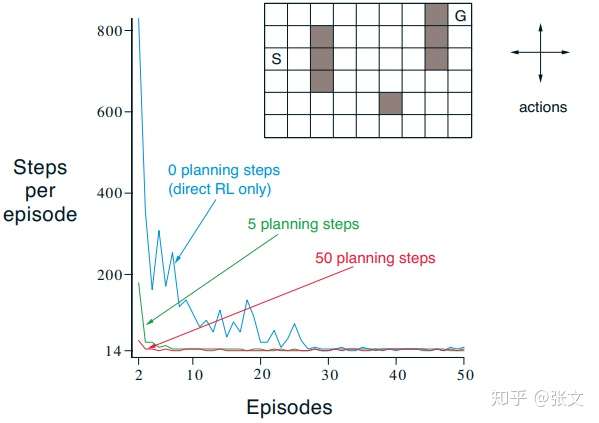

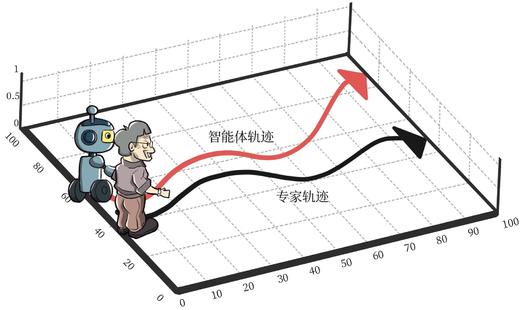
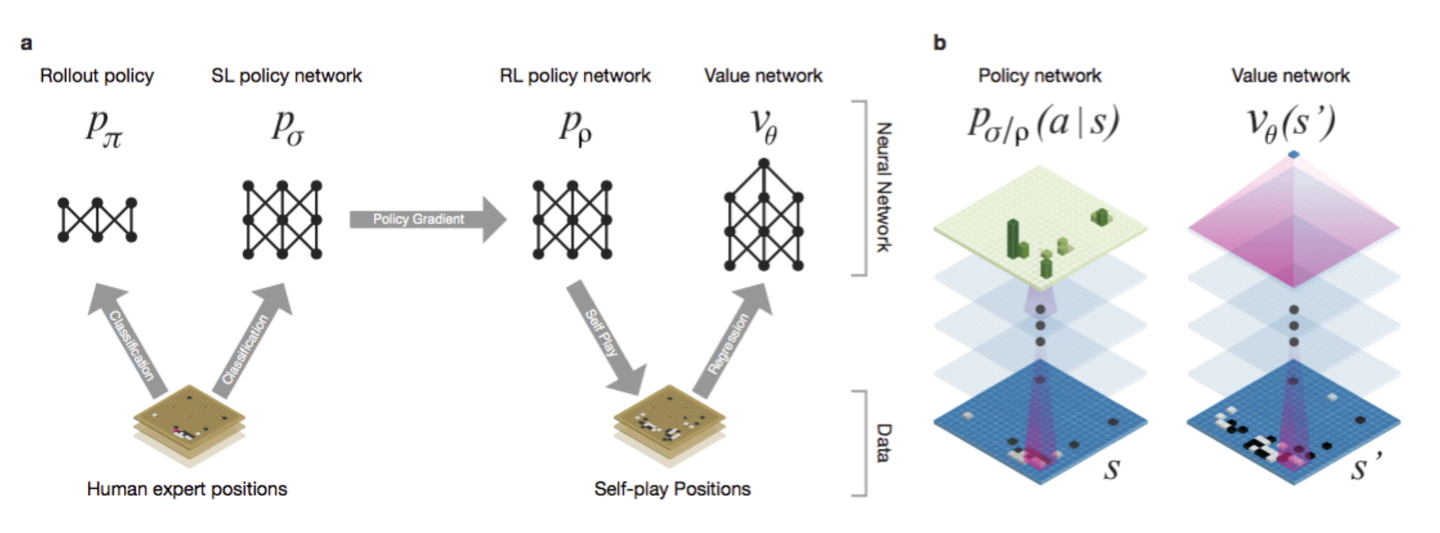
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
