- 机器学习总结
- 机器学习课程
- 机器学习基础
- 深度学习
- 强化学习
- 周志华《机器学习》笔记
- (4)线性模型
- 结束
机器学习总结
【2023-1-28】机器学习思想 img
- 没有免费的午餐定理(No Free Lunch Theorem/NFL定理 )。NFL定理对于“盲目的算法崇拜”有毁灭性的打击。在某个领域、特定假设下表现卓越的算法不一定在另一个领域也能是“最强者”。正因如此,才需要研究和发明更多的机器学习算法来处理不同的假设和数据。
- 奥卡姆剃刀定理(Occam’s Razor - Ockham定理) 如果两个模型A和B对数据的解释能力完全相同,那么选择较为简单的那个模型
- 集成学习(Ensemble Learning) 思想 个体学习的准确性和多样性本身就存在冲突,一般的,准确性很高后,要增加多样性就需牺牲准确性。
- 频率学派(Frequentism)和贝叶斯学派(Bayesian) - 不可知论
- 数据是王道,garbage in,garbage out
- 分治学习思想
- 终身学习思想
演化历史
华盛顿大学教授 Pedro Domingos:机器学习领域五大流派
- ① 符号主义:使用符号、规则和逻辑来表征知识和进行逻辑推理,最喜欢的算法是:规则和决策树
- ② 贝叶斯派:获取发生的可能性来进行概率推理,最喜欢的算法是:朴素贝叶斯或马尔可夫
- ③ 联结主义:使用概率矩阵和加权神经元来动态地识别和归纳模式,最喜欢的算法是:神经网络
- ④ 进化主义:生成变化,然后为特定目标获取其中最优的,最喜欢的算法是:遗传算法
- ⑤ Analogizer:根据约束条件来优化函数(尽可能走到更高,但同时不要离开道路),最喜欢的算法是:支持向量机

| 流派 | 时间 | icon | 起源 | 核心思想 | 问题 | 代表算法 | 代表应用 | 代表人物 | 备注 |
|---|---|---|---|---|---|---|---|---|---|
符号主义(Symbolists) |
1980年代 |  |
逻辑学、哲学 | 认知即计算,通过对符号的演绎和逆演绎进行结果预测 | 知识结构 | 逆演绎算法(Inverse deduction) | 知识图谱 | Tom Mitchell、Steve Muggleton、Ross Quinlan |  |
贝叶斯派(Bayesians) |
1990-2000年 |  |
统计学 | 主观概率估计,发生概率修正,最优决策 | 不确定性 | 概率推理(Probabilistic inference) | 反垃圾邮件、概率预测 | David Heckerman、Judea Pearl、Michael Jordan |  |
联结主义(Connectionist) |
2010年 |  |
神经科学 | 对大脑进行仿真 | 信度分配 | 反向传播算法(Backpropagation)、深度学习(Deep learning) | 机器视觉、语音识别 | Yann LeCun、Geoff Hinton、Yoshua Bengio |  |
进化主义(Evolutionaries) |
- |  |
进化生物学 | 对进化进行模拟,使用遗传算法和遗传编程 | 结构发现 | 基因编程(Genetic programming) | 海星机器人 | John Koda、John Holland、Hod Lipson |  |
行为类比主义(Analogizer) |
- |  |
心理学 | 新旧知识间的相似性 | 相似性 | 核机器(Kernel machines)、近邻算法(Nearest Neightor) | Netflix推荐系统 | Peter Hart、Vladimir Vapnik、Douglas Hofstadter |  |
- 从20世纪80年代开始,机器学习五大流派不断演化,各个阶段都有相应的主导流派:
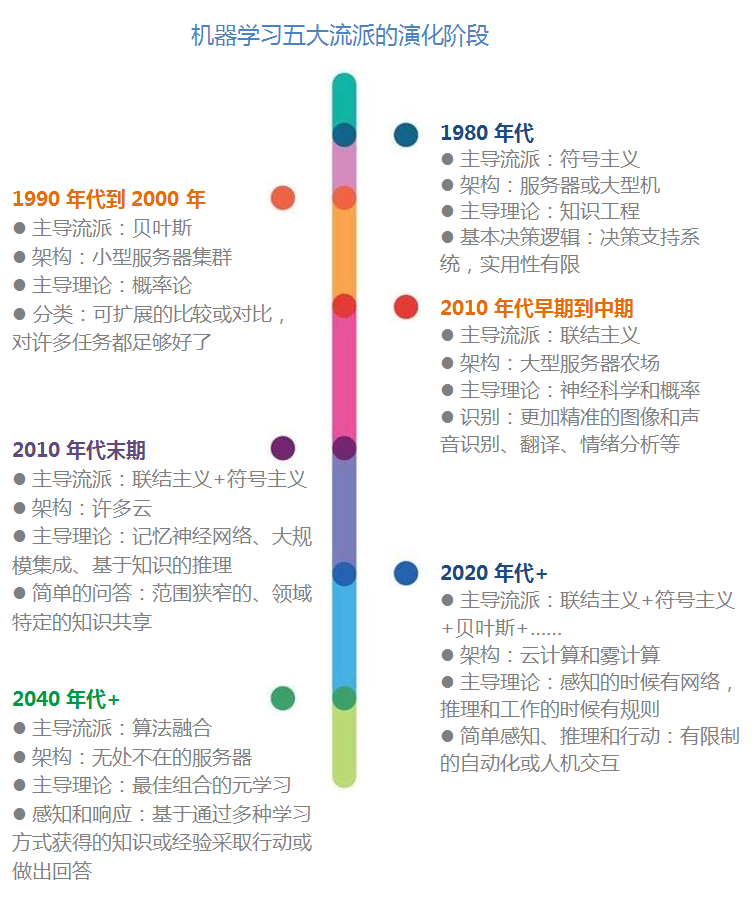
- 华盛顿大学教授 Pedro Domingos 曾详细地对机器学习领域的五大流派进行了详细的盘点,写了34页的PPT,各个流派的核心思想和演化过程进行了详细的介绍
这些流派逐渐融合
-

- 【2020-12-31】图解机器学习
- 按照现阶段主流分类来看,机器学习主要分为四类:
- 经典机器学习;
- 强化学习;
- 神经网络和深度学习;
- 集成方法;
- 【2021-1-2】机器学习的12张思维导图
多模态
【2022-7-25】聊聊多模态学习
多模态机器学习,英文全称 MultiModal Machine Learning (MMML),旨在通过机器学习的方法实现处理和理解多源模态信息的能力。
每一种信息的来源或者形式,都可以称为一种模态。例如
- 人有触觉,听觉,视觉,嗅觉;信息有语音、视频、文字等媒介;
- 多种多样的传感器,如雷达、红外、加速度计等。
以上的每一种都可以称为一种模态。
模态也可以有非常广泛的定义,比如我们可以把两种不同的语言当做是两种模态,甚至在两种不同情况下采集到的数据集,亦可认为是两种模态。
当下,多模态技术有着相当广泛的应用场景,如淘宝搜图、AI字幕、AI虚拟数字人、仿人交互、智能助手、商品推荐和信息流广告、视频帧人脸帧的图向量检索、语音交互等等。
机器学习算法
【2021-5-24】为什么机器学习算法难以优化?一文详解算法优化内部机制
典型分类
机器学习经过几十年的发展,衍生出了很多种分类方法
监督 vs 无监督
按学习模式的不同,可分为监督学习、半监督学习、无监督学习和强化学习。
机器学习分成:
监督学习:- 分类
- 回归
无监督学习- 聚类
- 降维
半监督学习: 混合学习( Hybrid Learning)强化学习
【2023-12-25】监督学习、无监督学习、半监督学习、强化学习、自监督学习
| 类型 | 原理 | 特征 | 标签 | 数据 | 方法 | 图解 |
|---|---|---|---|---|---|---|
| 监督学习 | 学习特征与标签的映射关系 | 有 | 有 | 样本独立同分布 | 分类、回归 | 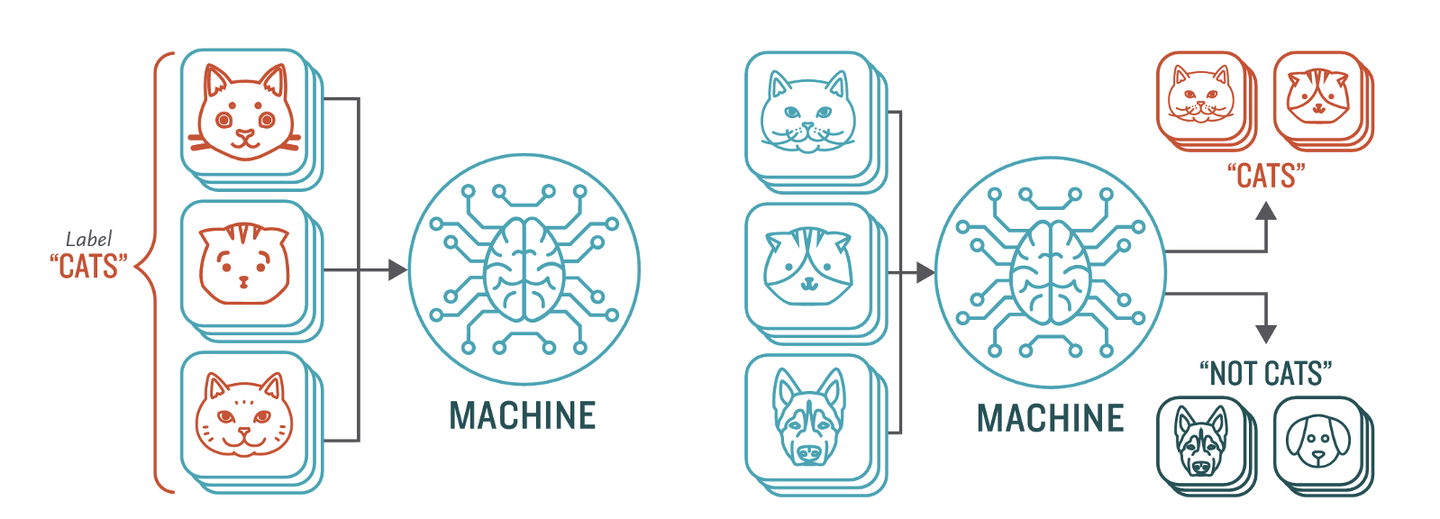 |
| 半监督学习 | 学习特征与标签的映射关系,混合学习( Hybrid Learning) | 有 | 部分 | 半监督分类、回归、聚类、异常检测、GAN | 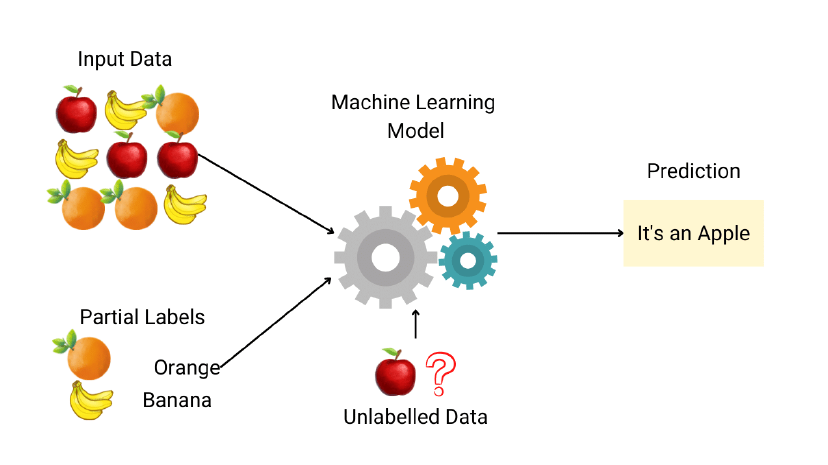 |
|
| 无监督学习 | 自动发现数据中的潜在模式,本质是统计 | 有 | 无 | 聚类、降维、关联规则、异常检测 | 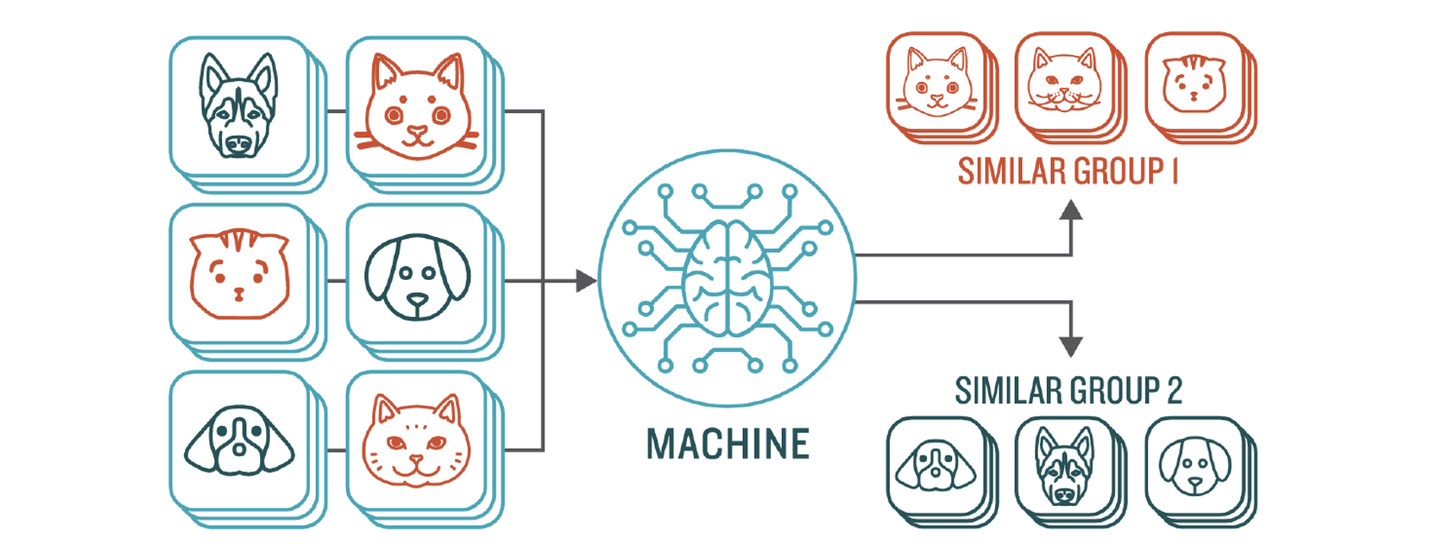 |
|
| 强化学习 | 智能体在环境中不断试错来学习,根据奖励信号来调整行为策略,最大化累积奖励 | 样本时序依赖 | DQN | 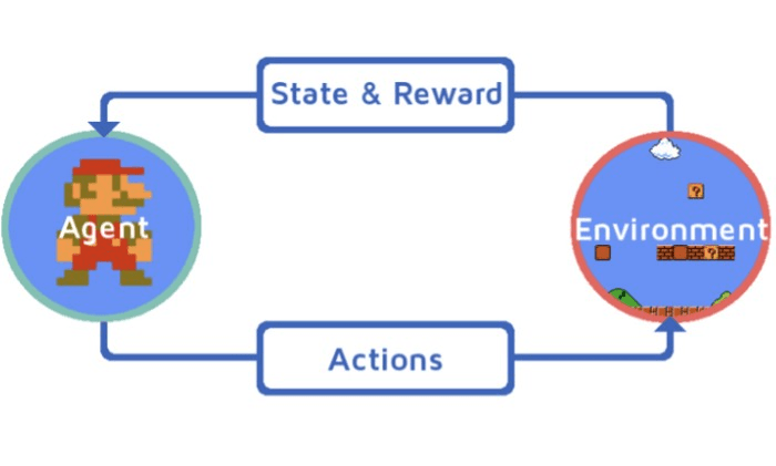 |
自监督学习(self-supervised learning,简写SSL)不需要人工标注训练数据,模型主要训练从大规模无监督数据中挖掘能够应用于自身的监督信息,从而从输入的一部分数据中去学习另一部分。
自监督学习容易误解为无监督学习中的聚类
- 因为都把不同的未标记事物进行分类
- 但其实自监督学习最大化同类样本在 Embedding 空间中表征的相似性,同时最小化异类样本之间表征的相似性。
分类图解
机器学习可以分为四大块:
分类(Classification): 监督学习,给定了非连续(离散)的属性值,通过一定的逻辑将样本进行归类回归(Regression): 监督学习,产生连续连续的结果,通常是一条回归曲线,和分类问题相似聚类(Clustering): 无监督学习,没有给定属性值,通过一定的标准将样本划分为不同的集合,同一集合内样本像似,不同集合样本相异-
降维(Dimensionality Reduction): 用维数更低的子空间来表示原来高维的特征空间 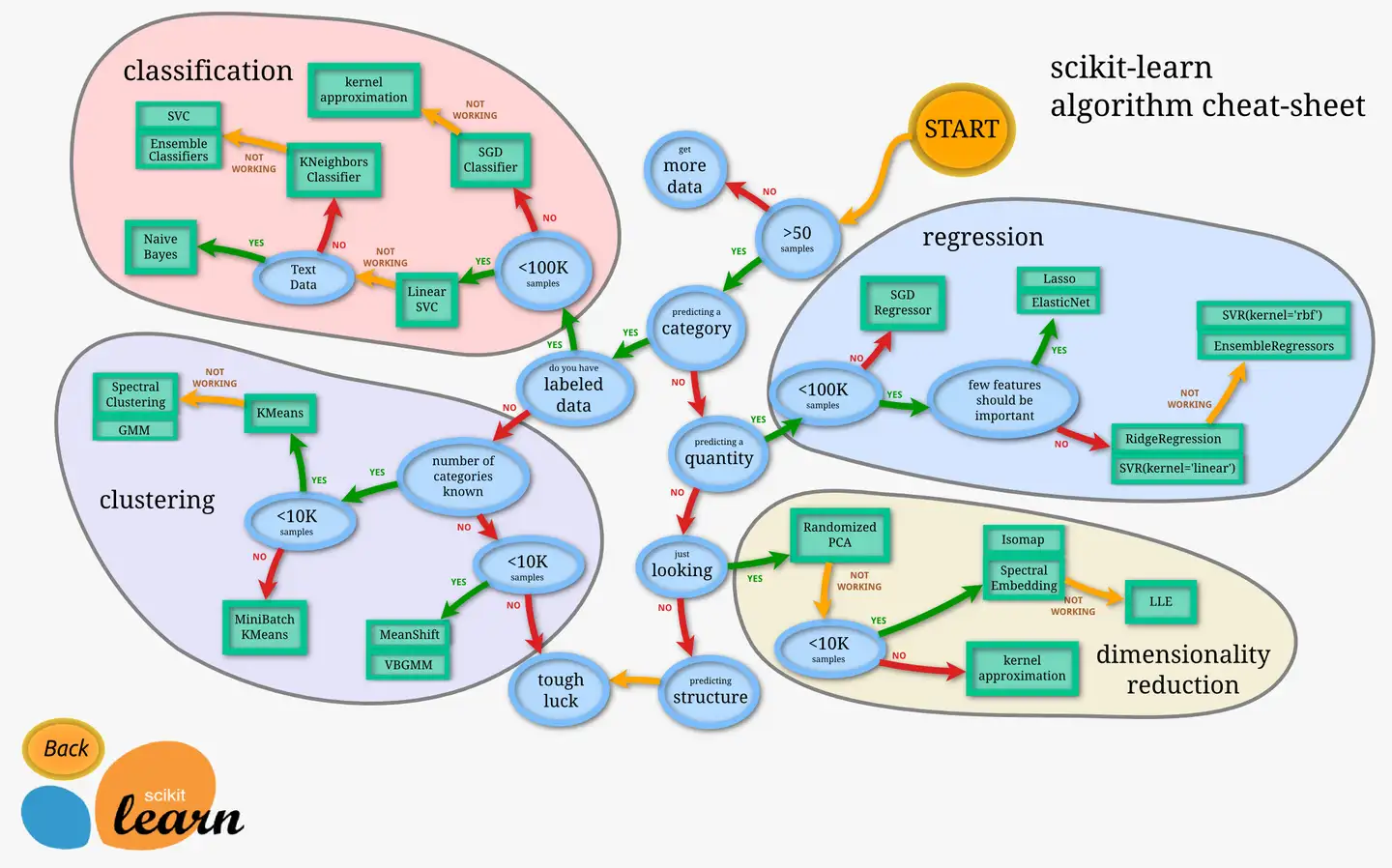
生成模型 & 判别模型
定义
定义
作者:politer
机器学习任务是从属性X预测标记Y,即求概率 $ P(Y|X)$;
判别式模型: 求得 $ P(Y|X) $ ,对未见示例 X,根据 $ P(Y|X) $ 可以求得标记Y,即直接判别出来,如图左所示, 直接得到了判别边界,- 所以传统的机器学习算法( 线性回归模型、支持向量机SVM等 )都是
判别式模型, 特点都是输入属性X可以直接得到Y - 对于二分类任务来说,实际得到一个score,当score大于threshold时则为正类,否则为反类
- 根本原因: 对于某示例$X_1$,对正例和反例的标记的
条件概率之和等于1,即 $ P(Y_1|X_1)+P(Y_2|X_1)=1)$
- 所以传统的机器学习算法( 线性回归模型、支持向量机SVM等 )都是
生成式模型: 求得 $ P(Y,X) $ ,对于未见示例X,要求出X与不同标记之间的联合概率分布,然后大的获胜,如图右所示,并没有什么边界存在,对于未见示例(红三角),求两个联合概率分布(有两个类),比较一下,取那个大的。- “生成”$(X,Y)$样本的概率分布(或称为依据)
- 机器学习中
朴素贝叶斯模型、隐马尔可夫模型HMM等 都是生成式模型 - Naive Bayes,对于输入X,要求出好几个
联合概率,然后较大的那个就是预测结果~ - 根本原因: 对于某示例$X_1$,对正例和反例标记的联合概率不等于1,即 $ P(Y_1,X_1)+P(Y_2,X_1)<1$ ,要遍历所有的X和Y的联合概率求和,即$ sum(P(X,Y))=1$
- 具体可参见楼上woodyhui提到的维基百科Generative model里的例子
举例:确定一个羊是山羊还是绵羊
判别式模型:从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是山羊/绵羊的概率。生成式模型:根据山羊的特征学习出一个山羊模型,然后根据绵羊特征学习出一个绵羊模型,然后从这只羊中提取特征,放到山羊模型中, 看概率是多少,在放到绵羊模型中看概率是多少,哪个大就是哪个。- 判别式模型是根据一只羊的特征可以直接给出这只羊的概率(比如logistic regression,这概率大于0.5时则为正例,否则为反例),而生成式模型是都要试一试,最大的概率的那个就是最后结果~
作者:Microstrong
判别式模型特点:
- 判别式模型直接学习决策函数 $ Y=f(X)$ 或者
条件概率$P(Y|X)$ ,不能反映训练数据本身的特性,但它寻找不同类别之间的最优分裂面,反映的是异类数据之间的差异,直接面对预测往往学习准确度更高。 - 具体来说有以下特点:
- 对
条件概率建模,学习不同类别之间的最优边界。 - 捕捉不同类别特征的差异信息,不学习本身分布信息,无法反应数据本身特性。
- 学习成本较低,需要的计算资源较少。
- 需要的样本数可以较少,少样本也能很好学习。
- 预测时拥有较好性能。
- 无法转换成生成式。
- 对
生成式模型的特点:
- 生成式模型学习的是
联合概率密度分布 $P(X,Y)$ ,可以从统计角度表示分布的情况,能够反映同类数据本身的相似度,它不关心到底划分不同类的边界在哪里。 - 生成式模型的学习收敛速度更快,当样本容量增加时,学习到的模型可以更快的收敛到真实模型,当存在隐变量时,依旧可以用生成式模型,此时判别式方法就不行了。
- 具体来说,有以下特点:
- 对
联合概率建模,学习所有分类数据的分布。 - 学习到的数据本身信息更多,能反应数据本身特性。
- 学习成本较高,需要更多的计算资源。
- 需要的样本数更多,样本较少时学习效果较差。
- 推断时性能较差。
- 一定条件下能转换成判别式。
- 对
总之,判别式模型和生成式模型都是使后验概率最大化,判别式是直接对后验概率建模,而生成式模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率。
算法归类
对比
生成模型与判别模型对比
| 问题 | 生成模型 | 判别模型 |
|---|---|---|
| 模型拟合 | 更容易 | 要解决凸优化问题 |
| 添加新类别 | 只需改动一点 | 要重训练 |
| 数据丢失 | 可以处理 | 无法处理 |
| 处理无标签数据 | 处理半监督问题 | 无法处理 |
| 输入和输出的对称 | 可以逆着从输出推断输入 | 无法处理 |
| 特征预处理 | 无法处理 | 可以推广到 GLM |
| 概率矫正 | 概率易走极端 | 概率较正确 |
监督学习 (supervised learning) 划分为两大类方法:生成模型 (generative model) 与判别模型 (discriminative model),贝叶斯方法正是生成模型的代表 (还有隐马尔科夫模型)。
算法总结
- 微软-ML算法指南:pdf版下载地址

- 详细讲解How to choose algorithms for Microsoft Azure Machine Learning
- 【2020-7-15】新版
- scikit-learn官方总结,Scikit-learn Cookbook:英文本,中文译本,MarkDown格式。【2018-6-12】scikit-learn中文翻译版,主页,scikit-learn网页版,Github版,wiki版,视频版。sklearn库中文版完全手册下载
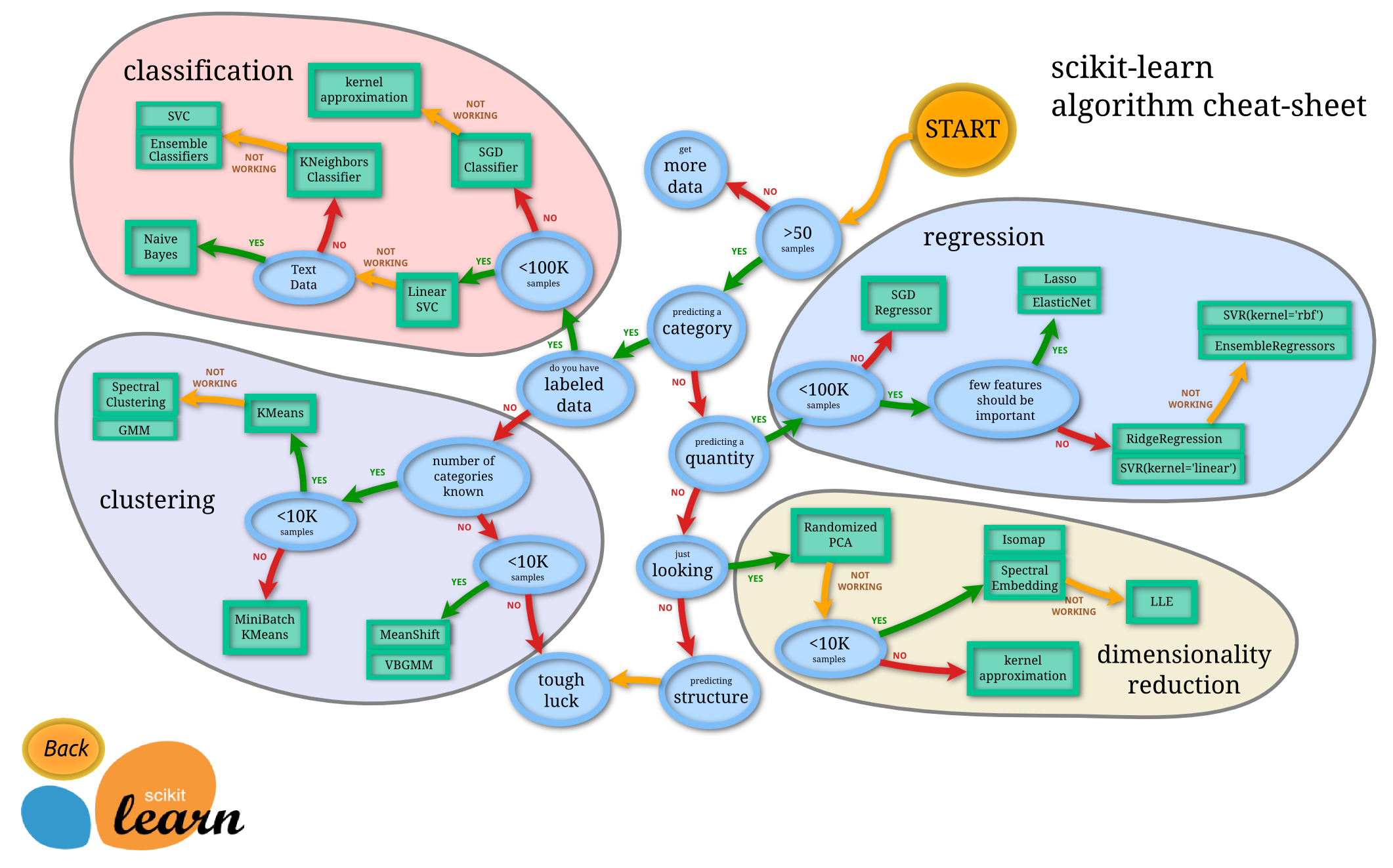
- 【2017-12-20】Dlib机器学习指南,方法选择:
,中文版,dlib中文指南-图
类型及应用

【2022-7-3】机器学习通识篇
- 主动学习(active learning)
- 大多数情况下,有类标的数据比较稀少而没有类标的数据是相当丰富的,但是对数据进行人工标注又非常昂贵,此时学习算法可以主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注,因此需要一个外在的专业人员能够对其进行标注的实体,即主动学习是交互进行的。这个筛选过程是主动学习主要研究点。
- 归纳式学习(inductive learning)
- Induction is reasoning from observed training cases to general rules, which are then applied to the test cases.
- 简而言之,归纳式学习是从训练样本中学习规则然后应用在测试样本中。监督学习就是一种归纳学习。
- 监督学习(supervised learning)
- 半监督学习(semi-supervised learning)
- 无监督学习(unsupervised learning)
- 直推式学习(transductive learning)
- Transduction is reasoning from observed, specific training cases to specific test cases.
- 直推式学习是同时使用训练样本和测试样本来训练模型,然后再次使用测试样本来测试模型效果。
监督学习
监督学习(Supervised Learning)是从有标签的训练数据中学习模型,然后对某个给定的新数据利用模型预测它的标签。如果分类标签精确度越高,则学习模型准确度越高,预测结果越精确。
- 样本和样本标签成对出现
- 监督学习是机器学习中最成熟的学习方法
监督学习主要用于回归和分类。
- 常见的回归算法有线性回归、回归树、K邻近、Adaboost、神经网络等。
- 常见的分类算法有朴素贝叶斯、决策树、SVM、逻辑回归、K邻近、Adaboost、神经网络等。
半监督学习
半监督学习(Semi-Supervised Learning)是利用少量标注数据和大量无标注数据进行学习的模式。半监督学习侧重于在有监督的分类算法中加入无标记样本来实现半监督分类。
半监督学习的研究的历史可以追溯到20世纪70年代,这一时期,出现了自训练(Self-Training)、直推学习(Transductive Learning)、生成式模型(Generative Model)等学习方法。
解决的问题
在许多实际问题中,有标签样本和无标签样本往往同时存在,且无标签样本较多,而有标签样本则相对较少。
- 标记数据可能很耗时。假设有1000000张狗图像,将它们输入到分类算法中,目的是预测每个图像是否包含波士顿狗。如果我们想将所有这些图像用于监督分类任务,我们需要一个人查看每个图像并确定是否存在波士顿狗。
- 标记数据可能很昂贵。原因一:要想让人费尽心思去搜100万张狗狗照片,我们可能得掏钱。
- 虽然充足的有标签样本能够有效提升学习性能,但是获取样本标签往往是非常困难的,因为标记样本可能需要专家知识、特殊的设备以及大量的时间。
- 相比于有标签样本,大量的无标签样本广泛存在且非常容易收集。但是,监督学习算法无法利用无标签样本,在有标签样本较少时,难以取得较强的泛化性能。
- 虽然无监督学习算法能够使用无标签样本,但准确性较差。
- 在有标签样本较少时,如何利用无标签样本提升学习性能己成为机器学习及其应用中的重要研究问题。
针对以上问题,学者们想:能否在训练过程中同时使用有标签样本和无标签样本,由此提出了
半监督学习。
半监督学习的基本假设
由于有标签样本较少,为了有效利用大量的无标签样本,半监督学习需要采用合适的半监督假设将学习模型和无标签样本的数据分布联系起来。
- 研究也表明:半监督学习方法的性能依赖于所用的半监督假设!
目前的机器学习技术大多基于独立同分布假设,即数据样本独立地采样于同一分布。
除了独立同分布假设,为了学习到泛化的结果,监督学习技术大多基于平滑(smoothness)假设,即相似或相邻的样本点的标记也应当相似。而在半监督学习中这种平滑假设则体现为两个较为常见的假设:聚类(cluster)假设与流型(manifold)假设。
半监督算法仅在数据的结构保持不变的假设下起作用,没有这样的假设,不可能从有限的训练集推广到无限的不可见的集合。具体地假设有:平滑假设(smoothness assumption)、聚类假设(cluster assumption)、流型假设(maniford assumption)
- 聚类假设(cluster assumption)与流型假设(maniford assumption)这两种假设一般是一致的,属于监督学习中平滑假设的在半监督学习中的推广。
- 流型假设比聚类假设更为一般,因为流型假设是相似的样本点具有相似的性质而不是聚类假设所认为的相同的标记,对于聚类假设无法成立的回归问题上流型假设却可以成立。
1、平滑假设(smoothness assumption)
如果两个样本 x1 ,x2 相似,则相应输出 y1 , y2 也应如此。这意味着如果两个输入相同类,并且属于同一簇,则它们相应的输出需要相近,反之亦成立。 即相似或相邻的样本点的标记也应当相似。
2、聚类假设(cluster assumption)
聚类假设是指同一聚类中的样本点很可能具有同样的类别标记。
- 这个假设可以通过另一种等价的方式进行表达,那就是决策边界所穿过的区域应当是数据点较为稀疏的区域,因为如果决策边界穿过数据点较为密集的区域那就很有可能将一个聚类中的样本点分为不同的类别这与聚类假设矛盾。
- 聚类假设关注样本空间的整体特征,它利用大量无标签样本探测样本分布稠密和稀疏的区域,从而更好地约束决策边界。
- 基于聚类假设的半监督算法通常要求决策边界穿过样本分布稀疏的区域,并能最大化不同聚类簇间的类间间隔。
- 通过利用无标签样本约束目标函数,基于聚类假设的算法能够同时优化有标签样本和无标签样本的类间间隔。
3、流型假设(maniford assumption)
流型假设是指高维中的数据存在着低维的特性。
- 另一种类似的表述为:“处于一个很小的局部邻域内的示例具有相似的性质”。
- 高维数据中的数据的低维的特性是通过局部邻域相似性体现的,比如一个在三维空间卷曲的二维纸带,高维的数据全局的距离度量由于维度过高而显得没有区分度,但是如果只考虑局部范围的距离度量,那就会有一定意义。
- 流形假设主要关注样本空间的局部特征,它利用大量的无标签样增加样本空间的密度,从而更准确地获取样本的局部近邻关系。
- 基于流形假设的半监督算法要求决策边界在数据嵌入到的低维流形上平稳地变化。
半监督学习分类
根据不同的学习场景,现有的半监督学习算法可分为四类:
- 半监督分类
- 半监督回归
- 半监督聚类
- 半监督降维 其中,半监督分类是半监督学习中研宄最多的问题。
半监督学习的主要目标是利用隐藏在大量无标签样本中的数据分布信息来提升仅使用少量有标签样本时的学习性能。
常见的半监督学习算法有 Pseudo-Label、Π-Model、Temporal Ensembling、Mean Teacher、VAT、UDA、MixMatch、ReMixMatch、FixMatch等。
更多:半监督学习(Semi-supervised Learning)算法
无监督学习
无监督学习(Unsupervised Learning)是从未标注数据中寻找隐含结构的过程。
- 只能利用训练样本的数据分布或样本间的关系将样本划分到不同的聚类簇或给出样本对应的低维结构。
- 无监督特征方法利用训练样本的数据分布信息(如训练样本的方差以及局部结构等)去评估特征的关联性,大部分是利用到统计信息。
- 由于缺少样本标签的引导,无监督特征选择方法可能无法选择出有效的特征,也就是会缺乏先验知识,无法自主决策判断真假,显得比较“笨拙”。
无监督学习主要用于关联分析、聚类和降维。
常见的无监督学习算法有稀疏自编码(Sparse Auto-Encoder)、主成分分析(Principal Component Analysis, PCA)、K-Means算法(K均值算法)、DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise)、最大期望算法(Expectation-Maximization algorithm, EM)等。
强化学习
强化学习(Reinforcement Learning)类似于监督学习,但未使用样本数据进行训练,是是通过不断试错进行学习的模式。
在强化学习中,有两个可以进行交互的对象:智能体(Agnet)和环境(Environment),还有四个核心要素:策略(Policy)、回报函数(收益信号,Reward Function)、价值函数(Value Function)和环境模型(Environment Model),其中环境模型是可选的。
强化学习常用于机器人避障、棋牌类游戏、广告和推荐等应用场景中。
机器学习工具
Google ml-kit 本地
Google ml-kit 工具包提供多种识别能力:OCR、人脸检测、图片加标签、目标检测跟踪、姿势检测以及图片分类
NLP类API功能: 语种识别、翻译、智能回复、实体提取
| 特性 | 设备 | 云端 |
|---|---|---|
| 文本识别 | √ | √ |
| 人脸识别 | √ | × |
| 条形码识别 | √ | × |
| 图像标记 | √ | √ |
| 地标识别 | × | √ |
| 自定义模型装载 | √ | × |
机器学习课程
Introduction to machine learning
【2022-10-25】Introduction to machine learning, 蒙特利尔大学,机器学习ppt总结资料,源自:Deep Learning Summer School, Montreal 2015, 演讲资料
统计学习方法
《统计学习方法》总结:
- 【2019-1-23】Python代码,【2020-6-26】北大研究生的代码实现,第二版课件下载,【2019-11-11】清华教授配套的课件-百度云
统计学习导论
- An-Introduction-to-Statistical-Learning
- Introduction in Statistical Learning with application in R (ISLR),是ESL的入门简单版,作者好像是一样的。
- 官方中文版,英文版
- 【2020-11-10】《统计学习导论》这本书配套视频,英文字幕加中文机翻字幕,配套的R语言教程附在每章的结尾处,github有人用python实现
- 统计学习(机器学习)入门(统计学习导论配套视频)中英字幕
机器学习白板推导
李宏毅课程学习笔记
- 在线笔记
- 李宏毅,机器学习,机器学习-李宏毅(2019) Machine Learning
- 李宏毅, 官网ppt, B站-深度学习19(完整版),一共94节
- 【2021-1-24】李宏毅机器学习知识点脑图
Google机器学习速成课
视频
- 【2020-12-04】对偶机器学习,Duality in machine learning
PRML: 模式识别和机器学习
- 经典书籍:模式识别与机器学习
- 目录
- PRML是模式识别和机器学习领域的经典著作,出版于2007年。该书作者 Christpher M. Bishop 是模式识别和机器学习领域的专家,其1995年所著的“Nerual Networks for Pattern Recognition”也是模式识别、人工神经网络领域的经典著作。
- 将 Bishop 大神的 PRML 称为机器学习圣经一点也不为过,该书系统地介绍了模式识别和机器学习领域内详细的概念与基础。书中有对概率论基础知识的介绍,也有高阶的线性代数和多元微积分的内容,适合高校的研究生以及人工智能相关的从业人员学习。
目录
PRML主要内容:配套代码,Github地址
- 第一章是引子,用曲线拟合让读者对机器学习有个大概理解。
- 第二章主要是介绍了一下基础的统计知识,包括期望方差的计算、高斯分布的参数估计与理解、高斯分布的性质等。
- 第三章和第四章主要在讲最基础的线性模型,并且展示了如何将其应用在分类和回归的场景下,贝叶斯方法是整本书的核心。
- 第五章介绍了神经网络,在线性模型的基础上引入了多层感知机模型,即常说的 BP 网络。
- 第六章讲的是核方法,核是两个样本的内积,也可以理解为某个
希尔伯特空间中由内积定义的“距离”。主要讲了线性模型转成核表达的方式、核的构建以及高斯过程。 - 第七章是向量机,向量机讲的是贝叶斯模型如何通过先验找到一个稀疏的模型。
- 第八章是讲的图模型,对变量的独立性、隐变量和参数的区别(这个会在变分贝叶斯中体现)做了很好的阐释。
- 第九章讲了混合模型和 EM算法,涉及了隐变量的概念和 EM 算法等。
- 第十章讲的是变分推断,解决了基于现在的模型的分布假设,推断参数难的问题。
- 第十一章讲采样方法,介绍了不同采样方法的优缺点,并重点讲了MCMC采样。
- 第十二章讲主成分分析,是考察多个变量间相关性一种多元统计方法,研究如何通过少数几个主成分来揭示多个变量间的内部结构。
- 第十三章讲的是序列数据,序列数据的特点及马尔可夫假设等。
- 第十四章讲的是 Ensemble,包括适应性的 boosting 最著名的 AdaBoost,以及一些其他的集成方法。
MLAPP:《机器学习:概率视角》——《Machine Learning: a Probabilistic Perspective》
- 作者是谷歌研究员Kevin Patrick Murphy,自2012年出版以来就一直被列为机器学习经典著作之一。本书可以作为PRML的姊妹篇,基于概率论和概率模型的角度来理解机器学习模型
- 电子版: Machine Learning: a Probabilistic Perspective
- 中文翻译
【2022-3-28】新版
- 【2012】Machine Learning: a Probabilistic Perspective
- 【2022-02-08】Probabilistic Machine Learning: An Introduction
- 【2022-3-14】Probabilistic Machine Learning: Advanced Topics
目录
全书包括28个章节,可以算是鸿篇巨制。MLaPP 读书笔记
- Chapter 1: 引言 Introduction,笔记
- 由于现在处于信息爆炸的时代,机器学习的意义在于,发现数据中的模式,并用于新数据的预测之中
- 机器学习三种类型:
- 有监督学习:给定训练集,求从输入到输出的映射;每个输入的维度都是一个特征;predictive or supervised method
- 包含:分类、回归
- 无监督学习:从一推的数据集中找到某些模式,但是不会有显示的标注数据和目标函数,即知识发现(knowledge discovery);descriptive and unsupervised learning;包含:聚类、降维、稀疏图模型、矩阵完成(matric completion,如图像修复/协同过滤/购物篮分析)
- 强化学习:一般都会有一个 agent,通过环境给予的 reward or punishment 来学习正确的做出决策,执行 action,decision theory 是强化学习的基础;reinforcement learning
- 有监督学习:给定训练集,求从输入到输出的映射;每个输入的维度都是一个特征;predictive or supervised method
- 另一种分类:分类标准:参数的数量是固定还是随训练数据的增多而增多
- 参数模型(parametric),如分类、回归
- 非参数模型(non-parametric),如 k-NN
- 对抗维度灾难的主要方法是对数据分布的性质做一些假设,归纳偏置(inductive bias)
- Chapter 2: 概率 Probability,笔记
- 两种概率流派
- 频率学派:frequentist interpretation,参数固定,概率可以看作是多次事件实验的发生的频率的逼近,很多次抛硬币实验,会发现最终硬币会出现正面的概率为0.5
- 贝叶斯学派:Bayesian interpretation,参数变化(服从一定分布),把概率当做是量化事件不确定型的工具,好处是可以估算那些无法进行多次重复实验的事件,如2020年之前北极冰川融化的概率
- 概率基础知识:Discrete random variables 离散随机变量、Joint probabilities 联合概率、Conditional probability 条件概率、Bayes rule 贝叶斯规则、Independence and conditional independence 独立和条件独立、Continuous random variables 连续随机变量、Quantiles 分位数、Mean and variance 均值和方差
- Some common discrete distributions 常见离散分布:The binomial and Bernoulli distributions 二项分布和伯努利分布、The multinomial and numtinoulli distributions 多项式分布和多努利分布
- Some commom continuous distributions 常见连续分布:Gaussian (normal) distribution 高斯分布、Degenerate pdf 退化的概率密度函数、The Laplace distribution 拉普拉斯分布、The gamma distribution 伽马分布、The Beta distribution 贝塔分布、Pareto distribution 柏拉图分布
- Joint probability distributions 联合概率分布:Covariance and correlation 协方差和相关性、The multivariate Gaussian 多元高斯、Multivariate Student t distribution 多元 t 分布、Dirichlet distribution 狄利克雷分布
- Tranformations of random variables 随机变量的变换:Linear transformations 线性变换、General transformations 一般变换、Central limit theorem 中心极限定理
- Monte Carlo approximation 蒙特卡洛近似
- Information theory 信息理论:Entropy 熵、cross-entropy 交叉熵、KL divergence 离散度、Mutual information 互信息
- 两种概率流派
- Chapter 3: 面向离散数据的生成式模型 Generative models for discrete data,笔记
- 生成模型(generative model)按照贝叶斯公式构造分类器
- Bayesian concept learning 贝叶斯概念学习
- 概念学习(Concept learning)其实是一个二分类问题,学习的是一个指示函数(Indicator function),但是和二分类问题不同,我们可以仅仅只从正例中学习
- Likelihood 似然、Prior 先验、Posterior 后验、Posterior predictive distribution 后验预测分布:似然、先验、后验、后验预测
- The Dirichlet-multinomial model:似然、先验、后验、后验预测
- The beta-binomial model 贝塔-二项式模型:似然、先验、后验、后验预测
- Naive Bayes classification 朴素贝叶斯分类器:MLE
- Chapter 4: 高斯模型 Gaussian models,笔记
- 基础:MLE for an MVN 多元高斯模型的极大似然估计、Maximum entropy derivation of the Gaussian * 从最大熵中推导出高斯模型
- Gaussian discriminant analysis 高斯判别分析:Quadratic discriminant analysis (QDA) 二次判别分析、Linear discriminant analysis (LDA) 线性判别分析、Two-class LDA 二分类 LDA、MLE for discriminant analysis、Strategies for preventing overfitting、Regularized LDA * 正则化 LDA、Diagonal LDA 对角化 LDA、Nearest shrunken centroids classifier
- Inference in jointly Gaussian distributions 联合高斯分布的推断:Marginals and conditionals 边缘概率和条件概率、Information form(距参量moment parameters)
- Linear Gaussian systems 线性高斯系统
- Digression: The Wishart distribution * 题外话:Wishart 分布
- Inferring the parameters of an MVN 推断 MVN 的参数
- Chapter 5: 贝叶斯统计 Bayesian statistics,笔记
- 贝叶斯统计的核心内容:用后验分布(posterior distributino)来总结一切
- Summarizing posterior distributions 总结后验分布:MAP estimation 最大后验估计、Credible intervals 置信区间、Inference for a difference in proportions
- Bayesian model selection 贝叶斯模型选择:Bayesian Occam’s razor 贝叶斯奥卡姆剃刀效应、Computing the marginal likelihood (evidence)、Bayes factors 贝叶斯因子
- Priors 先验:Uninformative priors 无信息先验、Jeffreys priors、Robust priors 鲁棒先验、Mixtures of conjugate priors 共轭先验的混合
- Hierarchical Bayes 层次贝叶斯:
- Empirical Bayes 经验贝叶斯
- Bayesian decision theory 贝叶斯决策理论
- Chapter 6: 频率统计 Frequentist statistics,笔记
- 频率学派统计学(frequentist statistics),经典统计学(classical statistics),或者叫正统统计学(orthodox statistics),设计了一些不把参数当做随机变量的统计推断方法,从而避免了使用贝叶斯法则和先验。频率学派依赖于抽样分布(sampling distribution),而贝叶斯学派则依赖后验分布(posterior distribution)
- Sampling distribution of an estimator 估计量的抽样分布:Bootstrap(蒙特卡洛方法来估计抽样分布,分有参数和无参数两种)
- Frequentist decision theory 频率学派决策理论:Bayes risk 贝叶斯风险、Minimax risk 最小化最大风险
- Desirable properties of estimators 想要的估计量性质:Consistent estimators 一致估计量、Unbiased estimators 无偏估计量、Minimum variance estimators 最小化方差估计量、The bias-variance tradeoff 偏置-方差之间的权衡
- Empirical risk minimization 经验风险最小化:Regularized risk minimization 正则化风险最小化、Structural risk minimization 结构风险最小化、Estimating the risk using cross validation 用交叉验证估计风险、Upper bounding the risk using statistical learning theory * 用统计学习理论来估计风险上界、Surrogate loss function 代理损失函数
- Pathologies of frequentist statistics * 频率统计的病态
- Chapter 7: 线性回归 Linear regression,笔记
- 线性回归(Linear Regression)是统计学和机器学习中的主力军(work horse),当用核函数等做基函数扩充(basis function expansion)时,又可以模拟非线性关系。除了回归问题,如果用伯努利或者多努利分布代替高斯分布,那么就可以用来做分类问题(classification)
- Model specification 模型确定:残差服从高斯分布,最大化似然函数就等价于最小化残差平方和,无法处理异常点(outlier)
- MLE (or least squares) 最大似然估计(最小二乘法)
- Derivation of the MLE 最大似然估计推导:Geometric interpretation 几何解释、Convexity 凸性、Robust linear regression 鲁棒线性回归(解决异常点问题)、Ridge regression 岭回归(解决过拟合问题)、Connection with PCA(OLS 和 ridge regression 都是属于 shrinkage method。主成分回归(PCR Principle Components Regression)指的是先用主成分分析降维,然后再用岭回归做回归)
- Bayesian linear regression 贝叶斯线性回归
- Chapter 8: 逻辑回归 Logistic regression,笔记
- LR 是一个非常重要的模型,几乎所有的机器学习职位面试都会问到
- Model specification:把线性回归的高斯分布,换成伯努利分布,就成了逻辑斯特回归,变成了分类模型
- Model fitting 模型拟合:MLE、Steepest descent 梯度下降、Newton’s method 牛顿法、Iteratively reweighted least squares (IRIS)、Quasi-Newton (variable metric) methods 拟牛顿法、ℓ2 regularization L2正则化、Multi-class logistic regression 多分类LR
- Bayesian logistic regression
- Online learning and stochastic optimazation
- Generative vs discriminative classifiers 生成分类器 VS 判别分类器:两种模式的详细对比
- Chapter 9: 广义线性模型和指数族 Generalized linear models and the exponential family,笔记
- 很多概率分布其实都是属于指数家族簇,比如高斯,伯努利,泊松,狄利克雷分布等。当然,均匀分布和学生 t 分布除外。可以用指数家族分布来表示 class-conditional density,由此建立广义线性模型(GLM, Generalized Linear Model)这个生成分类器。
- The exponential family 指数家族
- Generalized linear models (GLMs) 广义线性模型:Linear or Logistic Regression 都算是广义线性模型的特例
- Probit regression 概率回归
- Multi-task learning 多任务学习
- Generalized linear mixed models
- Learning to rank 学习排序:pointwise、pairwise、listwise、Loss function for ranking 排序损失函数
- Chapter 10: 有向图模型(贝叶斯网络) Directed graphical models (Bayes nets)
- Chapter 11: 混合模型与EM算法 Mixture models and the EM algorithm,笔记
- 图模型尝试在不同的观察变量之间建立条件独立关系,另一种思路则是用隐变量模型,即 LVMs, Latent variable models,这种模型假设观察变量都是从一个共同的“隐变量”中得到的。
- 隐变量的意思就是无法观测到,没有数据,可以人为定义个数和表示的含义。因此聚类算法中的簇就可以看做是隐变量,而有监督学习中如果给了簇的标定数据,就变成观察数据了,叫做标签。
- Mixture models 混合模型:Mixtures of Gaussians 高斯混合模型、Mixture of multinoullis 多努利混合模型、Using mixture models for clustering 使用混合模型做聚类、Mixtures of experts 混合专家
- Parameter estimation for mixture models 混合模型的参数估计:Unidentifiability 不可确定性、Computing a MAP estimate is non-convex
- The EM algorithm:EM for GMMs
- Model slection for latent varibale models
- Fitting models with missing data
- Chapter 12: 隐式线性模型 Latent linear models
- Chapter 13: 稀疏线性模型 Sparse linear models
- Chapter 14: 核方法 Kernels
- Chapter 15: 高斯过程 Gaussian processes
- Chapter 16: 自适应基函数模型 Adaptive basis function model
- Chapter 17: 马尔可夫模型和隐马尔可夫模型 Markov and hidden Markov Models
- Chapter 18: 状态空间模型 State space models
- Chapter 19: 无向图模型(马尔可夫随机域) Undirected graphical models (Markov random fields)
- Chapter 20: 图模型精准推断 Exact inference algorithms for graphical models
- Chapter 21: 变分推断 Variational inference
- Chapter 22: 更进变分推断 More variational inference
- Chapter 23: 蒙特卡洛推断 Monte Carlo inference algorithms
- Chapter 24: 马尔科夫链蒙特卡洛推断 MCMC inference algorithms
- Chapter 25: 聚类 Clustering
- Chapter 26: 图模型结构学习 Graphical model structure learning
- Chapter 27: 因变量 Latent variable models for discrete data
- Chapter 28: 深度学习 Deep learning
GitHub上同步开源随书代码,Python代码实现
ESL:统计学习基础
ESL 指的是 The Elements of Statistical Learning。
- 序言
- 第二版序言
- 第一版序言
- 1 简介
- 1.1 导言
- 2 监督学习概要
- 2.1 导言
- 2.2 变量类型和术语
- 2.3 两种预测的简单方法
- 2.4 统计判别理论
- 2.5 高维问题的局部方法
- 2.6 统计模型,监督学习和函数逼近
- 2.7 结构化的回归模型
- 2.8 限制性估计的种类
- 2.9 模型选择和偏差-方差的权衡
- 文献笔记
- 3 回归的线性方法
- 3.1 导言
- 3.2 线性回归模型和最小二乘法
- 3.3 子集的选择
- 3.4 收缩的方法
- 3.5 运用派生输入方向的方法
- 3.6 选择和收缩方法的比较
- 3.7 多重输出的收缩和选择
- 3.8 Lasso 和相关路径算法的补充
- 3.9 计算上的考虑
- 文献笔记
- 4 分类的线性方法
- 4.1 导言
- 4.2 指示矩阵的线性回归
- 4.3 线性判别分析
- 4.4 逻辑斯蒂回归
- 4.5 分离超平面
- 文献笔记
- 5 基展开和正规化
- 5.1 导言
- 5.2 分段多项式和样条
- 5.3 滤波和特征提取
- 5.4 光滑样条
- 5.5 光滑参数的自动选择
- 5.6 非参逻辑斯蒂回归
- 5.7 多维样条
- 5.8 正则化和再生核希尔伯特空间理论
- 5.9 小波光滑
- 文献笔记
- 附录-B 样条的计算
- 6 核光滑方法
- 6.0 导言
- 6.1 一维核光滑器
- 6.2 选择核的宽度
- 6.3IRpIRp中的局部回归
- 6.4IRpIRp中的结构化局部回归模型
- 6.5 局部似然和其他模型
- 6.6 核密度估计和分类
- 6.7 径向基函数和核
- 6.8 混合模型的密度估计和分类
- 6.9 计算上的考虑
- 文献笔记
- 7 模型评估及选择
- 7.1 导言
- 7.2 偏差,方差和模型复杂度
- 7.3 偏差-方差分解
- 7.4 测试误差率的 optimism
- 7.5 样本内预测误差的估计
- 7.6 参数的有效个数
- 7.7 贝叶斯方法和 BIC
- 7.8 最小描述长度
- 7.9 VC 维
- 7.10 交叉验证
- 7.11 自助法
- 7.12 条件测试误差或期望测试误差
- 文献笔记
- 8 模型推断和平均
- 8.1 导言
- 8.2 自助法和最大似然法
- 8.3 贝叶斯方法
- 8.4 自助法和贝叶斯推断之间的关系
- 8.5 EM 算法
- 8.6 从后验分布采样的 MCMC
- 8.7 袋装法
- 8.8 模型平均和堆栈
- 8.9 随机搜索
- 文献笔记
- 9 增广模型,树,以及相关方法
- 9.0 导言
- 9.1 广义可加模型
- 9.2 基于树的方法
- 9.3 PRIM
- 9.4 多变量自适应回归样条
- 9.5 专家的分层混合
- 9.6 缺失数据
- 9.7 计算上的考虑
- 文献笔记
- 10 增强和可加树
- 10.1 boosting 方法
- 10.2 boosting 拟合可加模型
- 10.3 向前逐步加性建模
- 10.4 指数损失和 AdaBoost
- 10.5 为什么是指数损失
- 10.6 损失函数和鲁棒性
- 10.7 数据挖掘的现货方法
- 10.8 垃圾邮件的例子
- 10.9 boosting 树
- 10.10 Gradient Boosting 的数值优化
- 10.11 大小合适的 boosting 树
- 10.12 正则化
- 文献笔记
- 11 神经网络
- 11.1 导言
- 11.2 投影寻踪回归
- 11.3 神经网络
- 11.4 拟合神经网络
- 11.5 训练神经网络的一些问题
- 11.6 模拟数据的例子
- 11.7 邮编数字的例子
- 文献笔记
- 12 支持向量机和灵活的判别方法
- 12.1 导言
- 12.2 支持向量分类器
- 12.3 支持向量机和核
- 12.4 广义线性判别分析
- 12.5 FDA
- 12.6 PDA
- 12.7 混合判别分析
- 计算上的考虑
- 文献笔记
- 13 原型方法和最近邻
- 13.1 导言
- 13.2 原型方法
- 13.3 k 最近邻分类器
- 13.4 自适应的最近邻方法
- 13.5 计算上的考虑
- 文献笔记
- 14 非监督学习
- 14.1 导言
- 14.2 关联规则
- 14.3 聚类分析
- 14.4 自组织图
- 14.5 主成分,主曲线以及主曲面
- 14.6 非负矩阵分解
- 14.7 独立成分分析和探索投影寻踪
- 14.8 多维缩放
- 14.9 非线性降维和局部多维缩放
- 14.10 谷歌的 PageRank 算法
- 文献笔记
- 15 随机森林
- 15.1 导言
- 15.2 随机森林的定义
- 15.3 随机森林的细节
- 15.4 随机森林的分析
- 文献笔记
- 16 集成学习
- 16.1 导言
- 16.2 增强和正则路径
- 16.3 学习集成
- 文献笔记
- 17 无向图模型
- 17.1 导言
- 17.2 马尔科夫图及其性质
- 17.3 连续变量的无向图模型
- 17.4 离散变量的无向图模型
- 文献笔记
- 18 高维问题
- 18.1 当 p 大于 N
- 18.2 对角线性判别分析和最近收缩重心
- 18.3 二次正则的线性分类器
- 18.4 一次正则的线性分类器
- 18.5 当特征不可用时的分类
- 18.6 有监督的主成分
- 18.7 特征评估和多重检验问题
- 文献笔记
机器学习基础
入门教程
【2022-9-25】参考 school-of-ai
深度学习入门:
- 布朗学院新鲜出炉,交互式图解人工智能
- Google PlayGround神经网络训练在线演示,汉化版,手写数字识别3D交互体验
- 神经网络讲解【3Blue1Brown优质讲解】,该系列一共4个视频,第一个如下:
- 神经网络Web Demo,可在线体验神经网络训练过程
- 神经网络3D仿真特效(多种网络结构对比)
- 手写数字识别在线体验
【2024-9-16】Amazon 出品的 MLU-Explain, 网页动态显示机器学习概念
基本流程
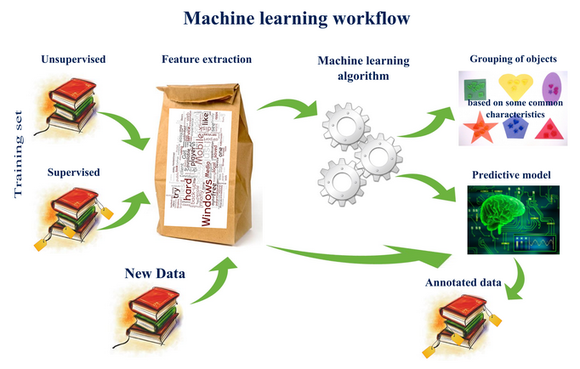
机器学习的工作方式
- ①选择数据:将你的数据分成三组:训练数据、验证数据和测试数据
- ②模型数据:使用训练数据来构建使用相关特征的模型
- ③验证模型:使用你的验证数据接入你的模型
- ④测试模型:使用你的测试数据检查被验证的模型的表现
- ⑤使用模型:使用完全训练好的模型在新数据上做预测
- ⑥调优模型:使用更多数据、不同的特征或调整过的参数来提升算法的性能表现
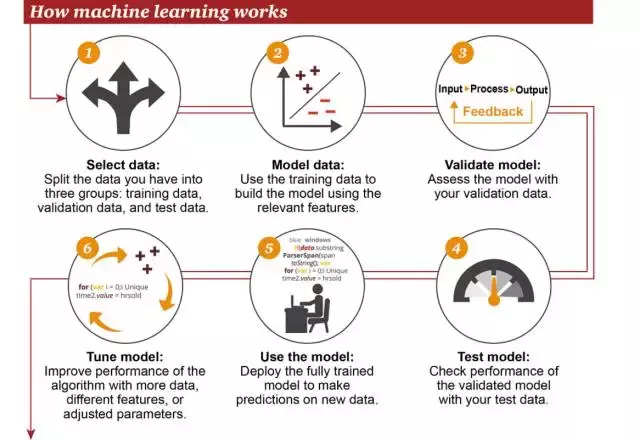
机器学习建模的大致流程:
- (1) 首先对原数据作清洗,筛选,特征标记等处理工作。
- (2) 然后使用处理后的数据来训练指定模型,并根据诊断情况来不断迭代训练模型。
- (3) 最后将训练调整好的模型应用到真实的场景中。
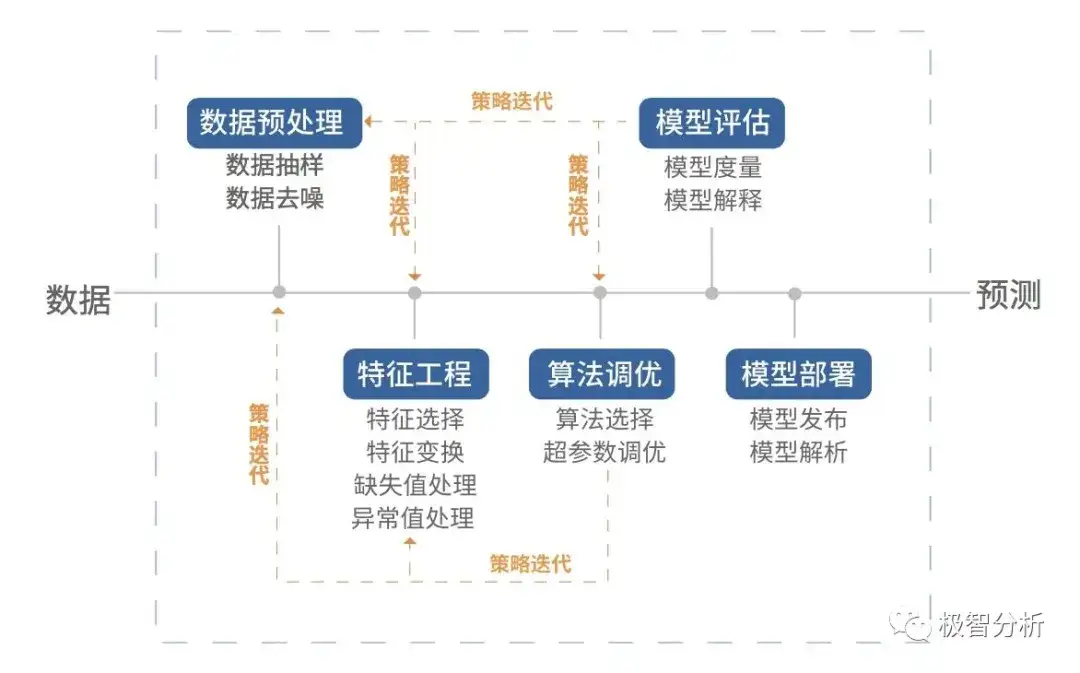
三个步骤:
- 数据准备与预处理
- 模型选择与训练
- 模型验证与参数调优
工程部署
按照机器学习的基本流程划分文件及目录,常见的结构如下:
- data:数据目录,包含:
- train.txt
- test.txt
- validation.txt(可选)
- bin:核心代码,主要包含:
- model.py:模型定义
- feature.py:特征工程部分,离线训练和在线评估都有
- train.py:模型训练代码
- predict.py:在线预测(inference,推断)
- model:模型存放
- log:日志目录
- 训练日志,如tensorboard日志
- conf:配置文件
- common:公共库、组件
- eva.py:效果评估
云端环境
- Google colab,与github直接打通,免费GPU(Tesla T4)
- 如果无法访问,建议使用Kaggle,fastai接入指南,从0到1走进kaggle
- 【2019-05-12】kaggle注册时可能收不到验证码,原因是伟大的墙,解决方法:①找个v-p-n②kaggle注册无法激活怎么办
- fastai官方代码库
基础概念
数据集划分
- 【2017-12-25】知乎:机器学习中的测试机和训练集如何划分?,与时间强相关的问题需要按照时间划分,否则(大部分ML问题)应该随机抽样,与时间无关(应用了未来函数)。随机划分保证了训练集和测试集的历史场景是类似的,就类似于这些数据都是同一台机器同一时期产生的两类数据集。这样计算出的准确率能最真实的反映模型对这段数据学习的效果
把所有数据都用来训练模型的话,建立的模型自然是最契合这些数据的,测试表现也好。但换了其它数据集测试这个模型效果可能就没那么好了。为了防止过拟合,就需要将数据集分成训练集、验证集、测试集。
作用分别是:
训练集(train set):用来训练模型验证集(validation set):评估模型预测的好坏及调整对应的参数测试集(test set:测试已经训练好的模型的推广能力
数据集划分
训练集和测试集大多数人都较容易区分,但关于验证集和测试集的关系却往往会搞混
| 维度 | 验证集 | 测试集 |
|---|---|---|
| 是否参与训练 | 否 | 否 |
| 作用 | 超参调优,防止模型过拟合 | 评估模型最终的泛化能力 |
| 使用次数 | 多次使用 | 仅一次 |
| 缺陷 | 多次训练调参后逼近的验证集可能只代表一部分非训练集,导致模型泛化能力不够 | 测试集由于量大,一般只取训练集中的一部分 |
训练集/测试集分布不一致?
【2022-10-16】训练/测试集分布不一致解法总结
- 训练集高分,测试集预测提交后发现分数很低,为什么?
- 有可能是训练集和测试集分布不一致,导致模型过拟合训练集
(1)发生原因
训练集和测试集分布不一致也被称作数据集偏移(Dataset Shift) 。
西班牙格拉纳达大学Francisco Herrera教授在他PPT里提到数据集偏移有三种类型:
协变量偏移(Covariate Shift): 独立变量的偏移,指训练集和测试集的输入服从不同分布,但背后是服从同一个函数关系,如图1所示。先验概率偏移(Prior Probability Shift): 目标变量的偏移。概念偏移(Concept Shift): 独立变量和目标变量之间关系的偏移。
资料
- Dataset Shift in Classification: Approaches and Problems - Francisco Herrera, PPT
最常见的有两种原因:
样本选择偏差(Sample Selection Bias): 训练集是通过有偏方法得到的,例如: 非均匀选择(Non-uniform Selection),导致训练集无法很好表征的真实样本空间。环境不平稳(Non-stationary Environments): 当训练集数据的采集环境跟测试集不一致时会出现该问题,一般是由于时间或空间的改变引起的。
在分类任务上,有时候官方随机划分数据集,没有考虑类别平衡问题
- 目标变量不均衡:训练集类别A数据量远多于类别B,而测试集相反,这类样本选择偏差问题会导致训练好的模型在测试集上鲁棒性很差,因为训练集没有很好覆盖整个样本空间。
- 输入特征不均衡:输入特征也可能出现样本选择偏差问题,比如要预测泰坦尼克号乘客存活率,而训练集输入特征里“性别”下更多是男性,而测试集里“性别”更多是女性,这样也会导致模型在测试集上表现差。
样本选择偏差也有些特殊的例子
- 阿里天池2021“AI Earth”人工智能创新挑战赛,官方提供两类数据集作为训练集,分别是CMIP模拟数据和SODA真实数据,然后测试集又是SODA真实数据,CMIP模拟数据是通过系列气象模型仿真模拟得到的,即有偏方法,但选手都会选择将模拟数据加入训练,因为训练集真实数据太少了,可模拟数据的加入也无可避免的引入了样本选择偏差。
环境不平稳带来的数据偏移,最常见是在时序比赛里,用历史时序数据预测未来时序,未来突发事件很可能带来时序的不稳定表现,这便带来了分布差异。环境因素不仅限于时间和空间,还有数据采集设备、标注人员等。
(2)如何识别
有三种判断方法
- KDE (核密度估计)分布图
- 如何对比训练集和测试集的分布?画概率密度函数
直方图,但直方图看分布有两点缺陷: 受bin宽度影响大和不平滑 - 因此多数人会偏向于使用
核密度估计图(Kernel Density Estimation, KDE),KDE是非参数检验,用于估计分布未知的密度函数,相比于直方图,它受bin影响更小,绘图呈现更平滑,易于对比数据分布。 - KDE 工具包:seaborn.kdeplot()
- 如何对比训练集和测试集的分布?画概率密度函数
- KS检验
- KDE是
PDF来对比,而KS检验是基于CDF(累计分布函数Cumulative Distribution Function) 来检验两个数据分布是否一致,它也是非参数检验方法(即不知道数据分布情况)。 - 若KS统计值小且p值大,则我们可以接受KS检验的原假设H0,即两个数据分布一致。
- 工具包:调用scipy.stats.ks_2samp()可轻松得到KS的统计值(最大垂直差)和假设检验下的p值
- 注意: p值<0.01,强烈建议拒绝原假设H0,p值越大,越倾向于原假设H0成立。
- KDE是
- 对抗验证
- 思路:构建一个分类器去分类训练集和测试集,如果模型能清楚分类,说明训练集和测试集存在明显区别(即分布不一致),否则反之。
- 具体步骤如下:
- 训练集和测试集合并,同时新增标签‘Is_Test’去标记训练集样本为0,测试集样本为1。
- 构建分类器(例如LGB, XGB等)去训练混合后的数据集(可采用交叉验证的方式),拟合目标标签‘Is_Test’。
- 输出交叉验证中最优的AUC分数。AUC越大(越接近1),越说明训练集和测试集分布不一致。
-
- 相关代码可参考Qiuyan918在Kaggle的Microsoft Malware Prediction比赛中使用实例代码
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 创建样例特征
train_mean, train_cov = [0, 2], [(1, .5), (.5, 1)]
test_mean, test_cov = [0, .5], [(1, 1), (.6, 1)]
train_feat, _ = np.random.multivariate_normal(train_mean, train_cov, size=50).T
test_feat, _ = np.random.multivariate_normal(test_mean, test_cov, size=50).T
# 绘KDE对比分布
sns.kdeplot(train_feat, shade = True, color='r', label = 'train')
sns.kdeplot(test_feat, shade = True, color='b', label = 'test')
plt.xlabel('Feature')
plt.legend()
plt.show()
# ---------- KS ---------
from scipy import stats
stats.ks_2samp(train_feat, test_feat)
# 输出:KstestResult(statistic=0.2, pvalue=0.2719135601522248)
# 统计值较低,p值大于10%但不是很高,因此反映分布略微不一致。
(3)解决方法
解决方法
- 构造合适的验证集
- 构建跟测试集分布近似相同的验证集,保证线下验证跟线上测试分数不会抖动,这样我们就能得到稳定的benchmark
- Qiuyan918在基于对抗验证的基础上,提出了三种构造合适的验证集的办法:
- 人工划分验证集
- TimeSeriesSplit:Sklearn提供的TimeSeriesSplit。
- 固定窗口滑动划分法:固定时间窗口,不断在数据集上滑动,获得训练集和验证集。(个人推荐这种)
- 选择和测试集最相似的样本作为验证集
- 对训练集的预测概率进行降序排列,选择概率最大的前20%样本划分作为验证集,这样就能从原始数据集中得到分布跟测试集接近的一个验证集
- 评估划分好的验证集跟测试集的分布状况,评估方法:将验证集和测试集做对抗验证,若AUC越小,说明划分出的验证集和测试集分布越接近(即分类器越分不清验证集和测试集)。
- 有权重的交叉验证
- 方法:测试集中样本区别对待,分布一致的权重大,不一致的权重小,这样有助于线下得到不易抖动的评估分数。
- 工具包:在lightgbm库的Dataset初始化参数中,便提供了样本加权的参数weight,详见文档,人工划分验证集的图中,对抗验证的分类器预测训练集的Is_Test概率作为权重即可。
- 删除分布不一致特征
- 直接删去这种特征。该方法在各大比赛中十分常见。例如: 在2018年蚂蚁金服风险大脑-支付风险识别比赛中,亚军团队根据特征在训练集和测试集上的表现,去除分布差异较大的特征
- 修正分布不一致的特征输入
- 蚂蚁金服比赛里,亚军团队发现”用户交易请求”特征在训练集中包含0、1和-1,而测试集只有1和0样本,因此他们对训练集删去了特征值为-1的样本,减少该特征在训练集和测试集的差异
- 修正分布不一致的预测输出
- 在“AI Earth”人工智能创新挑战赛里,我们有提到官方提供两类数据集作为训练集,分别是CMIP模拟数据和SODA真实数据,然后测试集又是SODA真实数据,其中前排参赛者YueTan就将CMIP和SODA的目标特征分布画在一起,然后发现SODA的值更集中,且整体分布偏右一些,所以对用CMIP训练得到的预测值加了一个小的常数,修正CMIP下模型的预测输出,使得它分布更偏向于SODA分布
- 伪标签
- 伪标签是半监督方法,利用未标注数据加入训练,我们先看看伪标签的思路,再讨论为什么它可能在一定程度上对分布不一致的数据集有帮助。伪标签最常见的方法是:
- 使用有标注的训练集训练模型M;
- 然后用模型M预测未标注的测试集;
- 选取测试集中预测置信度高的样本加入训练集中;
- 使用标注样本和高置信度的预测样本训练模型M’;
- 预测测试集,输出预测结果。
- TripleLift知乎主提供的入门版伪标签思路图
-
- 其它
数据不均衡
由于数据分布不平衡造成的。解决方法如下:
- 1)采样,对小样本加噪声采样,对大样本进行下采样
- 2)进行特殊的加权,如在Adaboost中或者SVM中
- 3)采用对不平衡数据集不敏感的算法
- 4)改变评价标准:用AUC/ROC来进行评价
- 5)采用Bagging/Boosting/Ensemble等方法
- 6)考虑数据的先验分布
机器学习模型分类
监督/非监督
监督学习算法有哪些?
- 感知机、SVM、人工神经网络、决策树、逻辑回归
判别 vs 生成
区别
- 生成式模型是根据概率乘出结果,联合概率
- 由数据直接学习决策函数 Y = f(X),或者由条件分布概率
P(Y|X)作为预测模型,即判别模型。 - 常见的判别模型有:K近邻、SVM、决策树、感知机、线性判别分析(LDA)、线性回归、传统的神经网络、逻辑斯蒂回归、boosting、条件随机场
- 由数据直接学习决策函数 Y = f(X),或者由条件分布概率
- 判别式模型是给出输入计算出结果,条件概率
- 由数据学习联合概率密度分布函数 P(X,Y),然后求出条件概率分布
P(Y|X)作为预测的模型,即生成模型。 - 常见的生成模型有:朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机
- 由数据学习联合概率密度分布函数 P(X,Y),然后求出条件概率分布
由生成模型可得到判别模型,但由判别模型得不到生成模型。
判别式模型有:
- Logistic Regression(Logistical 回归)
- Linear discriminant analysis(线性判别分析)
- Supportvector machines(支持向量机)
- Boosting(集成学习)
- Conditional random fields(条件随机场)
- Linear regression(线性回归)
- Neural networks(神经网络)
常见的生成式模型有:
- Gaussian mixture model and othertypes of mixture model(高斯混合及其他类型混合模型)
- Hidden Markov model(隐马尔可夫)
- NaiveBayes(朴素贝叶斯)
- AODE(平均单依赖估计)
- Latent Dirichlet allocation(LDA主题模型)
- Restricted Boltzmann Machine(限制波兹曼机)
线性/非线性模型
如果模型是参数的线性函数,并且存在线性分类面,那么就是线性分类器,否则不是。
- 线性分类器:LR,贝叶斯分类,单层感知机、线性回归。
- 非线性分类器:决策树、RF、GBDT、多层感知机。
SVM两种都有(看线性核还是高斯核)。
- 线性分类器速度快、编程方便,但是可能拟合效果不会很好。
- 非线性分类器编程复杂,但是效果拟合能力强。
线性分类器有三大类:感知器准则函数、SVM、Fisher准则,而贝叶斯分类器不是线性分类器。
- 感知准则函数 :准则函数以使错分类样本到分界面距离之和最小为原则。其优点是通过错分类样本提供的信息对分类器函数进行修正,这种准则是人工神经元网络多层感知器的基础。
- 支持向量机 :基本思想是在两类线性可分条件下,所设计的分类器界面使两类之间的间隔为最大,它的基本出发点是使期望泛化风险尽可能小。(使用核函数可解决非线性问题)
- Fisher 准则 :更广泛的称呼是线性判别分析(LDA),将所有样本投影到一条远点出发的直线,使得同类样本距离尽可能小,不同类样本距离尽可能大,具体为最大化“广义瑞利商”。
根据两类样本一般类内密集,类间分离的特点,寻找线性分类器最佳的法线向量方向,使两类样本在该方向上的投影满足类内尽可能密集,类间尽可能分开。这种度量通过类内离散矩阵SwSw和类间离散矩阵SbSb实现。
分类/回归
分类算法有哪些?
- SVM、神经网络、随机森林、逻辑回归、KNN、贝叶斯
归一化
哪些机器学习算法不需要做归一化处理?
- 概率模型不需要归一化,因为不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、RF。
- 而像Adaboost、GBDT、XGBoost、SVM、LR、KNN、KMeans之类的最优化问题就需要归一化。
标准化 vs 归一化
标准化依照特征矩阵的列处理数据,其通过求z-score方法,将样本的特征值转换到同一量纲下。归一化依照特征矩阵的行处理数据,其目的在于样本向量在点乘运算或其他核函数计算相似性时,拥有统一的标准,都转化为“单位向量”。
特征向量的缺失值处理:
- 缺失值较多.直接将该特征舍弃掉,否则可能反倒会带入较大的noise,对结果造成不良影响。
- 缺失值较少,其余的特征缺失值都在10%以内,我们可以采取很多的方式来处理:
- 1) 把NaN直接作为一个特征,假设用0表示;
- 2) 用均值填充;
- 3) 用随机森林等算法预测填充
特征工程
随机森林如何评估特征重要性。
衡量变量重要性的方法有两种,Decrease GINI 和 Decrease Accuracy:
- 1) Decrease GINI:对于回归问题,直接使用argmax(VarVarLeftVarRight)作为评判标准,即当前节点训练集的方差Var减去左节点的方差VarLeft和右节点的方差VarRight。
- 2) Decrease Accuracy:对于一棵树Tb(x),我们用OOB样本可以得到测试误差1;然后随机改变OOB样本的第j列:保持其他列不变,对第j列进行随机的上下置换,得到误差2。至此,我们可以用误差1-误差2来刻画变量j的重要性。基本思想就是,如果一个变量j足够重要,那么改变它会极大的增加测试误差;反之,如果改变它测试误差没有增大,则说明该变量不是那么的重要。
特征选择
特征选择是一个重要的数据预处理过程,主要有两个原因:
- 一是减少特征数量、降维,使模型泛化能力更强,减少过拟合;
- 二是增强对特征和特征值之间的理解。
特征选择方式:
- 去除方差较小的特征。
- 正则化。1正则化能够生成稀疏的模型。L2正则化的表现更加稳定,由于有用的特征往往对应系数非零。
- 随机森林,对于分类问题,通常采用基尼不纯度或者信息增益,对于回归问题,通常采用的是方差或者最小二乘拟合。一般不需要feature engineering、调参等繁琐的步骤。它的两个主要问题,1是重要的特征有可能得分很低(关联特征问题),2是这种方法对特征变量类别多的特征越有利(偏向问题)。
- 稳定性选择。是一种基于二次抽样和选择算法相结合较新的方法,选择算法可以是回归、SVM或其他类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法,不断的重复,最终汇总特征选择结果,比如可以统计某个特征被认为是重要特征的频率(被选为重要特征的次数除以它所在的子集被测试的次数)。理想情况下,重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数,而最无用的特征得分将会接近于0。
特征工程方法
参数与超参数
- 模型参数:参数属于模型内部的配置变量,它们通常在建模过程自动学习得出。如:线性回归或逻辑回归中的系数、支持向量机中的支持向量、神经网络中的权重。
- 模型超参数:超参数属于模型外部的配置变量,他们通常由研究员根据自身建模经验手动设定。如学习速率,迭代次数,层数、K近邻中的K值。
激活函数
常用的非线性激活函数有sigmoid、tanh、relu等等
- 前两者 sigmoid/tanh 常见于全连接层,后者relu常见于卷积层。
为什么引入非线性激励函数?
- 如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了。
Sigmoid、Tanh、ReLu 激活函数
Sigmoid的函数表达式
- $f(z)=\frac{1}{1+\exp{-z}}$
Sigmoid函数的功能
- 把一个实数压缩至0到1之间。
- 当z是非常大的正数时,g(z)会趋近于1
- 而z是非常小的负数时,则g(z)会趋近于0
压缩至0到1有何用处呢?
- 把激活函数看作一种“分类的概率”,比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。
问题
- 为什么ReLu要好过于Tanh和Sigmoid function?
- 为什么LSTM模型中既存在Sigmoid又存在Tanh两种激活函数?
- 二者目的不一样:
- sigmoid 用在了各种gate上,产生0~1之间的值,这个一般只有sigmoid最直接了。
- tanh 用在了状态和输出上,是对数据的处理,这个用其他激活函数或许也可以。
- 二者目的不一样:
误差分解
误差分解:偏差方差
【2022-1-16】广义的偏差(bias)描述的是预测值和真实值之间的差异,方差(variance)描述距的是预测值作为随机变量的离散程度。
- 《Understanding the Bias-Variance Tradeoff》当中有一副图形象地向我们展示了偏差和方差的关系:
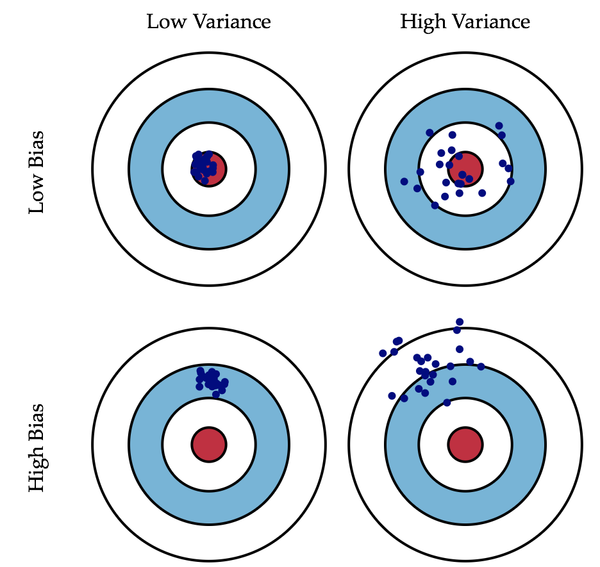
-
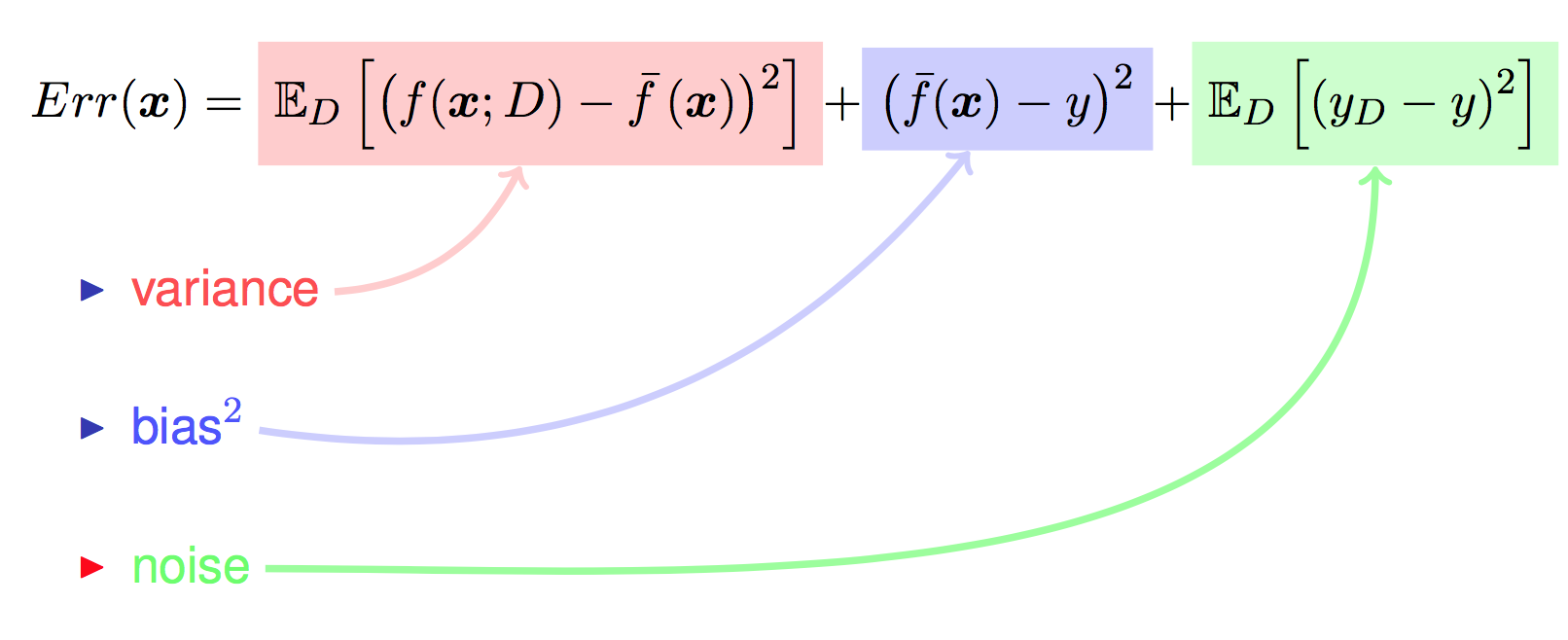
- 【2021-3-14】偏差、方差关系,偏差Bias和方差Variance——机器学习中的模型选择
- 误差的期望值可以分解为三个部分:
泛化误差可以分解为偏差(Biase)、方差(Variance)和噪声(Noise) - 误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方

- 泛化误差 = 错误率(error) => $ error(x) = {bias}^2(x) + var(x) + \varepsilon^2$
- 解释
- Bias是 f* 的期望到目标模型之间的偏差,Variance是 f* 到 f* 的期望之间的偏差

- 左边是高偏差低方差的情况,右边是低偏差高方差的情况
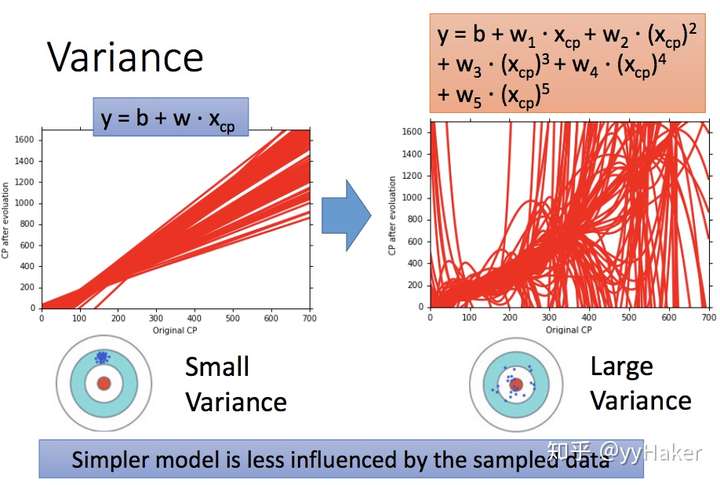
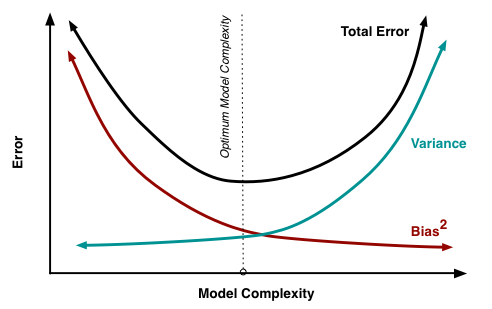
- 越是越是简单的模型,Variance越小;越是复杂的模型,Variance越大,而且简单的模型更不容易被某些噪声数据所干扰。同样,我们发现越是简单的模型Bias越大,越是复杂的模型Bias越小。

- 越是越是简单的模型,Bias越大Variance越小;越是复杂的模型,Bias越小Variance越大,都会导致泛化误差高。所以,机器学习模型的泛化误差是由Bias和Variance相互影响的
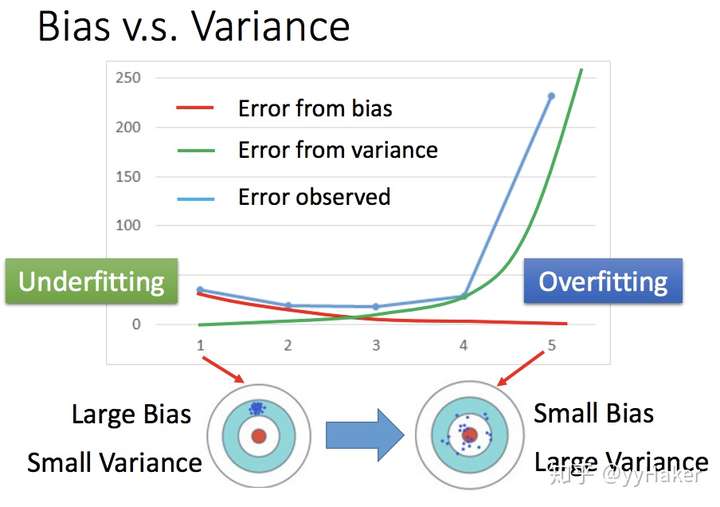
- 误差的期望值可以分解为三个部分:
- 偏差(准)、方差(稳)的选择
- 不同复杂度模型的对比
- 选择相对较好的模型的顺序: 稳 > 准
- 方差小,偏差小(既稳又准) > 方差小,偏差大(稳但不准) > 方差大,偏差小(准但不稳) > 方差大,偏差大(既不准又不稳)。
- 稳定性>精准度:方差小,偏差大 之所以排位靠前,是因为比较稳定。
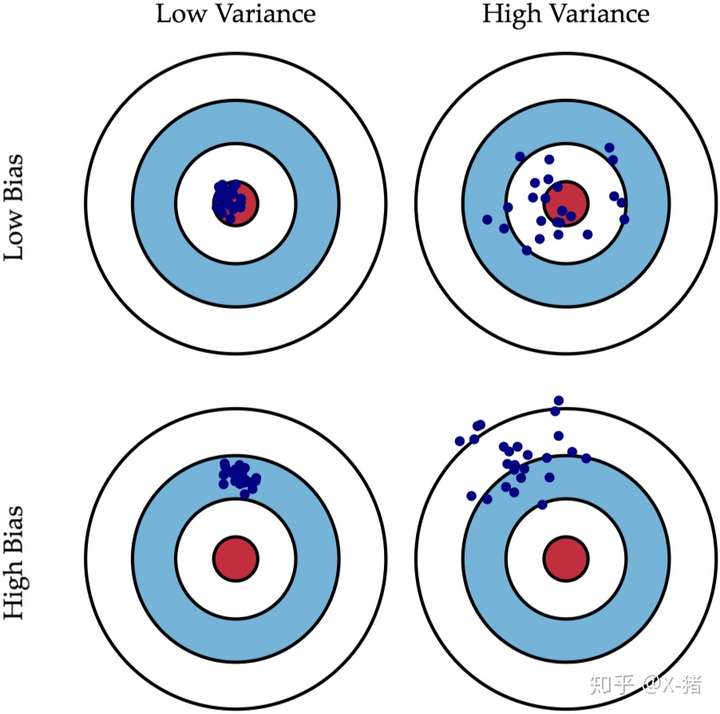
- 不同复杂度模型的对比
交叉验证
知乎:Xiaotian ZUO
K-fold和Cross validation的区别。
- K-fold的全称就是K-fold cross validation。 Cross validation一般有两种,一种是holdout,一种是k-fold。
- holdout把数据集分成training,validation和test。很多AI项目都会这样来划分。
- k-fold cross validation。介绍算法的时候,一般会称为cross validation,因为字面含义比较清晰;调试的时候,喜欢用k-fold,因为动了k。
交叉验证方法:
- Hold out 留一法: 在训练前,把数据集根据一定比例分成training和test,模型通过training来训练,test来评估。训练的时候常常继续把training分成training和validation,使用validation的反馈来帮助调整参数。严格来说,并不完全可以算作cross validation。
- k-fold cross validation(k折交叉验证): 数据量不够大时,或者想追求更精确的训练结果时,可以将数据集均匀分成k份,每次用其中的一份数据集作为test,其它的k-1份作为training,学习k次,最后得到k个模型,用k个模型预测的平均值作为结果。
- leave-p-out cross validation(留p交叉验证): 遍历数据集中所有可能的p个数据的组合,分别做测试集,每次使用剩下的数据作为训练集。不是特别常用,因为复杂度太高,得到的模型个数是阶乘级别。 另外有一些延伸的奇技淫巧,包括但不限于:
- leave-one-out cross validation(留1交叉验证): 每次只使用一份数据,而不是一份数据集来作为测试集。等于p为1的留p验证,也等于k为数据集大小的k折验证。
- Iterated K-fold validation with shuffling: 每次都进行数据随机排列,然后进行完整的k-fold。适用于数据量小的情况。
- 嵌套k-fold,不怎么常见,但是可以了解一下。在工业级别的项目上,目前我还没使用过这个。
【2022-9-25】交叉验证主要有三种说法:一文彻底理解:训练集,验证集,测试集,交叉验证
- 李航老师的《统计学习方法》中模型选择方法分为两类,一个是正则化,一个是交差验证,交叉验证又分为简单交叉验证、s折交叉验证、留一交叉验证。
- 周志华老师的《机器学习》中,模型评估有三种方式,留出法、交叉验证(分为 k 折交叉验证和留一法)、自助法。
- sklearn 官方文档中,train_test_split 作为留出法的实现方式,而交叉验证进行数据集划分(迭代器)又分为K折(KFold)、p 次 k 折交(RepeatedKFold)、留一(LeaveOneOut )、留 p(LeavePOut)、随机(ShuffleSplit)等等
泛化
常规机器学习流程:
- 训练集上训练模型,验证集调参,最终测试集上的表现作为模型的泛化能力
什么是泛化能力
什么是泛化能力?
- 机器学习算法对新鲜样本的适应能力 —— 模型对未知数据的预测能力
- 学习的目的是学到隐含在数据背后的规律,对具有同一规律的学习集以外的数据,经过训练的网络也能给出合适的输出,该能力称为泛化能力。
奥卡姆剃刀定律在机器学习方面的运用如下:
- 机器学习模型越简单,良好的实证结果就越有可能不仅仅基于样本的特性。
- 现今将奥卡姆剃刀定律正式应用于统计学习理论和计算学习理论领域。这些领域已经形成了泛化边界,即统计化描述模型根据以下因素泛化到新数据的能力:
- 模型的复杂程度
- 模型在处理训练数据方面的表现 虽然理论分析在理想化假设下可提供正式保证,但在实践中却很难应用。机器学习速成课程则侧重于实证评估,以评判模型泛化到新数据的能力。
机器学习模型旨在根据以前未见过的新数据做出良好预测。但是,如果要根据数据集构建模型,如何获得以前未见过的数据呢?一种方法是将您的数据集分成两个子集:
- 训练集:用于训练模型的子集。
- 测试集:用于测试模型的子集。
在测试集上表现是否良好是衡量能否在新数据上表现良好的有用指标,前提是:
- 测试集足够大。
- 不会反复使用相同的测试集来作假。
各种误差:
- 模型对训练集数据的误差称为经验误差,对测试集数据的误差称为泛化误差。模型对训练集以外样本的预测能力就称为模型的泛化能力,追求这种泛化能力始终是机器学习的目标
过拟合(overfitting)和欠拟合(underfitting)是导致模型泛化能力不高的两种常见原因,都是模型学习能力与数据复杂度之间失配的结果。“欠拟合”常常在模型学习能力较弱,而数据复杂度较高的情况出现,此时模型由于学习能力不足,无法学习到数据集中的“一般规律”,因而导致泛化能力弱。与之相反,“过拟合”常常在模型学习能力过强的情况中出现,此时的模型学习能力太强,以至于将训练集单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,同样这种情况也会导致模型泛化能力下降。过拟合与欠拟合的区别在于,欠拟合在训练集和测试集上的性能都较差,而过拟合往往能较好地学习训练集数据的性质,而在测试集上的性能较差。在神经网络训练的过程中,欠拟合主要表现为输出结果的高偏差,而过拟合主要表现为输出结果的高方差
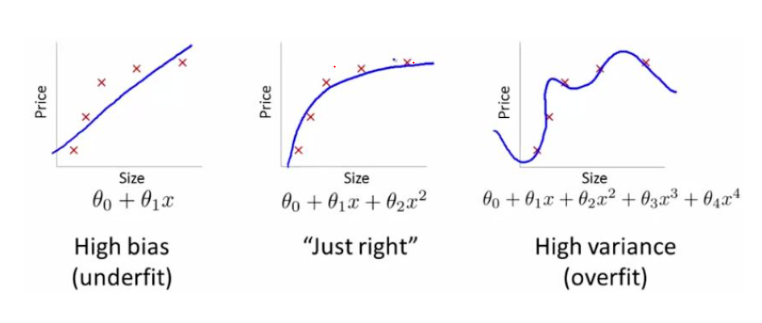
欠拟合
欠拟合出现原因
- 模型复杂度过低
- 特征量过少
- 欠拟合的情况比较容易克服,常见解决方法有
- 增加新特征,可以考虑加入进特征组合、高次特征,来增大假设空间
- 添加多项式特征,这个在机器学习算法里面用的很普遍,例如将线性模型通过添加二次项或者三次项使模型泛化能力更强
- 减少正则化参数,正则化的目的是用来防止过拟合的,但是模型出现了欠拟合,则需要减少正则化参数
- 使用非线性模型,比如核SVM 、决策树、深度学习等模型
- 调整模型的容量(capacity),通俗地,模型的容量是指其拟合各种函数的能力
- 容量低的模型可能很难拟合训练集;使用集成学习方法,如Bagging ,将多个弱学习器Bagging
过拟合
什么是过拟合?
- 虽然绿色的分类面可以完美地将两组数据分开,但是这个分类面对训练集非常敏感,在测试机上的效果很有可能不如黑色的分类面。
- 网上有人找到一张将过拟合非常有意思的图,过拟合可以将任何东西都看成模型想看成的东西,也许古代对星座的划分也算得上是一种过拟合吧!
过拟合出现原因
- 建模样本选取有误,如样本数量太少,选样方法错误,样本标签错误等,导致选取的样本数据不足以代表预定的分类规则
- 样本噪音干扰过大,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
- 假设的模型无法合理存在,或者说是假设成立的条件实际并不成立
- 参数太多,模型复杂度过高
- 对于决策树模型,如果我们对于其生长没有合理的限制,其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event),使其虽然可以完美匹配(拟合)训练数据,但是无法适应其他数据集
- 对于神经网络模型:
- a)对样本数据可能存在分类决策面不唯一,随着学习的进行,,BP算法使权值可能收敛过于复杂的决策面;
- b)权值学习迭代次数足够多(Overtraining),拟合了训练数据中的噪声和训练样例中没有代表性的特征
过拟合的根本原因: 用有限的观测样本去估计整体
- 对于参数化模型 P(Y|X;θ),通过极大似然估计来估计参数θ。
- 如果观测样本十分有限,而模型的拟合能力又很强,那么最后一个等式的误差会非常大
- 对于非参数模型,通常需要利用观测样本的一个子集来估计期望值等总体的统计量。
- 例如决策树模型,在每个叶子节点上,只用到满足该叶子节点对应规则的样本来估计期望值——正例的概率或者目标的期望值。 如果样本有限而决策树的叶子节点又特别多(模型复杂度高),那么落到一个叶子节点的样本数就非常有限,导致估计的误差很大!
过拟合的解决方案
- 正则化(Regularization)(L1和L2)
- 数据扩增,即增加训练数据样本
- Dropout
- Early stopping
泛化危机
【2022-10-21】神经网络的泛化跟内插外推无关,因为高维学习几乎总是对应着外推
- Learning in High Dimension Always Amounts to Extrapolation, Yann LeCun领导的FAIR团队关于澄清深度学习泛化能力的研究结论。
- 数学上,深度学习可以看作是函数逼近,自然而然地,一些研究把函数逼近里的数据
内插、外推概念应用到深度学习的解释上。 - 概念上,在一维数据,
内插对应样本在数据集的区间内,外插对应样本在数据集的区间外; - 拓展到高维,内插和外插分别对应样本在数据集的
凸包(convex hull)边界之内和之外。 - 据此,产生了对深度学习泛化能力如此之好的一种几何逻辑上非常直观合理的直觉解释:
- 测试样本是训练数据集的
内插,也就是测试样本在训练数据集的凸包之内,因为模型训练时training loss几乎为零,即完全拟合训练数据集,所以,测试样本的泛化性能非常棒。不同任务之间的迁移学习或者预训练也可以类似解释。Almost perfect theory!
- 测试样本是训练数据集的
- FAIR的论文利用综合数据集和实际数据集从理论和实验两方面说明
- 在高维(>100)空间里内插发生的概率几乎为零,无论数据集的
本质维数(intrinsic dimension)是多大。也就是说,从内插外推的维度来理解深度学习泛化的努力可以放弃了,基于数据集内插假设的研究成果都是误解。
- 在高维(>100)空间里内插发生的概率几乎为零,无论数据集的
【2021-11-28】泛化性的危机!LeCun发文质疑:测试集和训练集永远没关系
杨立昆(Yann LeCun)
- (1)机器学习固有观念都错了
- ① 算法之所以起作用,是因为能正确的内插训练数据
- ② 测试集上表现好的模型,泛化性能就好
- ③ 泛化性能取决于插值方式:内插、外推
- ④ 机器学习任务+数据集中,只有内插,没有外推(ood呢?)
- (2)泛化危机
- ① 无论数据流形(data manifold)的基本本征维数(intrinstic dimension)如何,内插都不会出现在高维空间(>100)中。
- ② 由于实际使用的数据量(受限于计算能力),新样本极不可能位于该数据集的convex hull里(即内插),当前任务基本都是外推
- ③ 外推并不能体现模型的泛化能力,也不该用内插、外推作为泛化性能指标。
- ④ 数据集大小应该相对于数据维度呈指数增长
- 高维空间下,测试集和训练集没有关系,模型做的一直只有外推没有内插,那么刷榜竞赛还有意义吗?
- (3)那怎么办?
- 构建合适的内插、外推几何定义,与泛化能力保持一致
观点:
在测试集上表现更好的模型,泛化性一定更好。
不一定!
内插(interpolation)和外推(extrapolation)是机器学习、函数近似(function approximation)中两个重要的概念。
- 机器学习中,当一个测试样本的输入处于训练集输入范围时,模型预测过程称为「内插」,而落在范围外时,称为「外推」。
- 数学角度,外推其实是与内插并列的一个概念。多项式插值、样条插值等插值方法中,通过已知的、离散的数据点,在范围内推求新数据点,即称为内插(Interpolation)。而如果在已知数据在范围外推求新数据点,则是外推(Extrapolate)。
一直以来深度学习的研究都依赖于两个概念:
- 最先进的算法之所以工作得这么好,是因为它们能够正确地内插训练数据;
- 在任务和数据集中只有内插,而没有外推。 图灵奖得主Yann LeCun团队在arxiv挂了一篇论文公开质疑这两个概念是错误的
从理论上和经验上来说,无论是合成数据还是真实数据,几乎可以肯定的是无论数据流形(data manifold)的基本本征维数(intrinstic dimension)如何,内插都不会出现在高维空间(>100)中。
- 本征维度即在降维或者压缩数据过程中,为了让你的数据特征最大程度的保持,你最低限度需要保留哪些features,它同时也告诉了可以把数据压缩到什么样的程度,所以你需要了解哪些 feature 对数据集影响是最大的。
考虑到当前计算能力可以承载的实际数据量,新观察到的样本极不可能位于该数据集的convex hull中。因此,他们得出了两个结论:
- 目前使用和研究的模型基本都是外推的了;
- 鉴于这些模型所实现的超越人类的性能,外推机制也不一定非要避免,但这也不是泛化性能的指标。 可能有人认为像图像这样的数据可能位于低维流形上,因此从直觉和经验上认为无论高维环境空间如何,内插都会发生。但这种直觉会产生误导,事实上,即使在具有一维流形的极端情况下,底层流形维度也不会变化。
内插和外推提供了一种关于给定数据集的新样本位置的直观几何特征,这些术语通常被用作几何代理来预测模型在看不见的样本上的性能。从以往的经验来看似乎已经下了定论,即模型的泛化性能取决于模型的插值方式。这篇文章通过实验证明了这个错误观念。并且研究人员特别反对使用内插和外推作为泛化性能的指标,从现有的理论结果和彻底的实验中证明,为了保持新样本的插值,数据集大小应该相对于数据维度呈指数增长。简而言之,模型在训练集内的行为几乎不会影响该模型的泛化性能,因为新样本几乎肯定位于该凸包(convex)之外。
正则化: L1 & L2
正则化解决过拟合问题
- 求解模型最优解一般优化最小经验风险
- 在经验风险上加入模型复杂度这一项(正则化项是模型参数向量的范数),并使用一个rate比率来权衡模型复杂度与以往经验风险权重,如果模型复杂度越高,结构化的经验风险会越大,现在的目标就变为了结构经验风险的最优化,可以防止模型训练过度复杂,有效的降低过拟合的风险。
奥卡姆剃刀原理,能解释已知数据且简单才是最好的模型。
L1范数(L1 norm,Losso回归)指向量中各个元素绝对值之和,也叫“稀疏规则算子”(Lasso regularization,岭回归)。
- 比如 向量
A=[1,-1,3], 那么A的L1范数为|1|+|-1|+|3|.
简单总结一下就是:
L1范数: 为x向量各个元素绝对值之和。L2范数: 为x向量各个元素平方和的1/2次方,L2范数又称 Euclidean范数 或 Frobenius范数Lp范数: 为x向量各个元素绝对值p次方和的1/p次方。
支持向量机学习过程中,L1范数实际是一种对于成本函数求解最优的过程,因此,L1范数正则化通过向成本函数中添加L1范数,使得学习得到的结果满足稀疏化,从而方便人类提取特征。
- L1范数可以使权值稀疏,方便特征提取。
- L2范数可以防止过拟合,提升模型的泛化能力。
L1和L2正则先验分别服从什么分布
- L1是
拉普拉斯分布 - L2是
高斯分布
梯度下降
梯度下降最快吗
梯度下降法并不是下降最快的方向,它只是目标函数在当前的点的切平面(当然高维问题不能叫平面)上下降最快的方向。
- 牛顿方向(考虑海森矩阵)一般被认为是下降最快的方向,可以达到Superlinear的收敛速度。
- 梯度下降类的算法的收敛速度一般是Linear甚至Sublinear的(在某些带复杂约束的问题)。
牛顿法和梯度下降法有什么不同?拟牛顿法(Quasi-Newton Methods),共轭梯度法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
梯度消失/爆炸
如何解决梯度消失和梯度膨胀?
- 链式法则:每一层神经元对上一层输出的偏导乘上权重
- 反向传播中链式法则带来的连乘,如果有数很小趋于0,结果就会特别小(梯度消失);如果数都比较大,可能结果会很大(梯度爆炸)。
(1)梯度消失:
- 如果都小于1,那么即使是0.99,经过足够多层传播之后,误差对输入层的偏导会趋于0。
- 解法:采用ReLU激活函数有效解决梯度消失。
(2)梯度膨胀:
- 如果都大于1,经过足够多层传播之后,误差对输入层的偏导会趋于无穷大
- 解法:通过激活函数来解决。或 提取截断
评估方法
TP、FN(真的判成假的)、FP(假的判成真)、TN四种(可以画一个表格)
常用的指标:
- 精度precision = TP/(TP+FP) = TP/~P (~p为预测为真的数量)
- 召回率 recall = TP/(TP+FN) = TP/ P
- F1值:2/F1 = 1/recall + 1/precision
- ROC曲线:ROC空间是一个以伪阳性率(FPR,false positive rate)为X轴,真阳性率(TPR, true positive rate)为Y轴的二维坐标系所代表的平面。其中真阳率TPR = TP P = recall, 伪阳率FPR = FP N
算法分析
贝叶斯
概念
-
条件概率(又称后验概率):事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A B),读作“在B条件下A的概率”。 - 联合概率:两个事件共同发生的概率。A与B的联合概率表示为P(A∩B)或者P(A,B)。
- 边缘概率(又称先验概率):某个事件发生的概率。
- 边缘概率获取方式:联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
为什么朴素贝叶斯如此“朴素”?
- 假定所有特征在数据集中同样重要且独立。
- 实际上,这个假设在现实世界中不真实,因此,说朴素贝叶斯真的很“朴素”。
CRF/HMM
CRF,HMM(隐马模型),MEMM(最大熵隐马模型)都常用来做序列标注建模。
- 隐马模型最大的缺点: 由于其输出独立性假设,导致其不能考虑上下文的特征,限制了特征的选择。
- 最大熵隐马模型解决了隐马的问题,可以任意选择特征,但由于其在每一节点都要进行归一化,所以只能找到局部最优值,同时也带来了标记偏见的问题,即凡是训练语料中未出现的情况全都忽略掉。
- 条件随机场很好的解决了这一问题,不在每个节点归一化,而是所有特征进行全局归一化,因此可以求得全局最优值。
总结:进化过程
CRF->HMM->MEMM
对比
- EM算法:只有观测序列,无状态序列时来学习模型参数,即Baum-Welch算法
- 维特比算法:用动态规划解决HMM的预测问题,不是参数估计
- 前向后向算法:用来算概率
- 极大似然估计:即观测序列和相应的状态序列都存在时的监督学习算法,用来估计参数
SVD/PCA
SVD和PCA
- PCA的理念是使得数据投影后的方差最大,找到这样一个投影向量,满足方差最大的条件即可。
- 而经过了去除均值的操作之后,就可以用SVD分解来求解这样一个投影向量,选择特征值最大的方向。
K-Means
Kmeans的复杂度?
- 时间复杂度:O(tKmn),其中,t为迭代次数,K为簇的数目,m为记录数,n为维数
- 空间复杂度:O((m+K)n),其中,K为簇的数目,m为记录数,n为维数。
优化
- 用Kd树 或 Ball Tree 将所有观测实例构建成一颗 kd树,之前每个聚类中心都是需要和每个观测点做依次距离计算,现在这些聚类中心根据kd树只需要计算附近的一个局部区域即可。
- K-means++算法:选择初始seeds的基本思想,初始的聚类中心之间的相互距离要尽可能的远。
SVM
SVM,全称是support vector machine,中文名叫支持向量机。SVM是一个面向数据的分类算法,它的目标是为确定一个分类超平面,从而将不同的数据分隔开。
支持向量机学习方法包括构建由简至繁的模型:线性可分支持向量机、线性支持向量机及非线性支持向量机。
- 当训练数据线性可分时,通过硬间隔最大化,学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
- 当训练数据近似线性可分时,通过软间隔最大化,也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
- 当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
优化问题从两个角度进行考察,一个是 primal 问题,一个是 dual 问题,对偶问题
- 一般情况下对偶问题给出主问题最优值的下界,在强对偶性成立的情况下由对偶问题可以得到主问题的最优下界,对偶问题是凸优化问题,可以进行较好的求解
- SVM中就是将Primal问题转换为dual问题进行求解,从而进一步引入核函数的思想。
GBDT
GBDT(Gradient Boosting Decision Tree)算法
相比 ID3 和 C4.5 只能进行分类任务,CART 还可以进行回归任务,是目前最主流的决策树算法
XGBoost
XGBoost 类似于 GBDT 的优化版,不论是精度还是效率上都有了提升。
与GBDT相比,具体优点有:
- 损失函数是用泰勒展式二项逼近,而不是像GBDT里的就是一阶导数;
- 对树的结构进行了正则化约束,防止模型过度复杂,降低了过拟合的可能性;
- 节点分裂的方式不同,GBDT是用的基尼系数,XGBoost是经过优化推导后的。
XGBoost 的一些特点
- 速度快:计算效率很高,尤其适合大数据。
- XGBoost的并行是在特征粒度上
- 准确性高:
- XGBoost 在比赛和实际应用中常常表现优异,因为它在训练过程中逐步减少误差。
- 可以防止过拟合:
- XGBoost 有一些机制可以防止模型过度拟合,比如设置最大深度、学习率等参数。
XGBoost 像很多「小树」组成的团队,这些小树各自负责一部分任务,彼此互相纠正错误,最终得出一个更加准确的预测。对于大部分表格数据问题,比如预测价格、用户行为等,XGBoost 都是一个表现很好的选择。
为什么XGBoost要用泰勒展开,优势在哪里?
- XGBoost用一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得二阶倒数形式, 可以在不选定损失函数具体形式的情况下用于算法优化分析. 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性。
XGBoost 如何寻找最优特征?是又放回还是无放回的呢?
- XGBoost 在训练的过程中给出各个特征的评分,从而表明每个特征对模型训练的重要性.
- XGBoost 利用梯度优化模型算法, 样本是不放回的(想象一个样本连续重复抽出,梯度来回踏步会不会高兴)。但XGBoost支持子采样, 也就是每轮计算可以不使用全部样本。
XGBoost 特别擅长解决结构化数据问题,比如表格数据。
- 全称「eXtreme Gradient Boosting」,意思是「极限梯度提升」
XGBoost 是梯度提升的升级版,很多细节上做了优化,训练更快、效果更好。
比如
- 用「并行计算」技术,让计算机同时进行多个计算,大大加速了训练速度。
- 一些优化的数学技巧,可以不损失准确性的前提下更快地找到答案。
原理
xgboost 算法流程
针对训练集
- xgboost 先用 CART树 训练得到一个模型,每个样本都会产生一个偏差值;
- 然后将样本偏差值作为新的训练集,继续使用CART树训练得到一个新模型;
- 以此重复,直至达到某个退出条件为止。
算法流程图
回归、分类任务的区别在于损失函数
- 分类:损失函数用 logloss 等
- 回归: 损失函数用 rmse 等
分类树、回归树 算法思想一致,都是在XGBOOST框架下,不停的去拟合上一轮的残差(都是0.5分开始)
两者的损失函数不同,造成两者生长的策略有所不同,导致 XGBOOST 参数像是 minchildweight 设置的值域也不同.
实现
XGBoost 进行分类任务的基本示例
Python实现
- xgboost 库
- sklearn 库
xgboost 库
xgboost 是大规模并行 boosted tree 的工具
- 陈天奇 Tianqi Chen and Carlos Guestrin.
- 论文 XGBoost: A Scalable Tree Boosting System
- 目前最快最好的开源boosted tree工具包,比常见的工具包快10倍以上
- kaggle比赛的夺冠方案
XGBoost的优点
- 正则化
- XGBoost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
- 并行处理
- XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行的?注意XGBoost的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。XGBoost的并行是在特征粒度上的。
- 决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
- 灵活性
- XGBoost支持用户自定义目标函数和评估函数,只要目标函数二阶可导就行。
- 缺失值处理
- 对于特征的值有缺失的样本,xgboost可以自动学习出它的分裂方向
- 剪枝
- XGBoost 先从顶到底建立所有可以建立的子树,再从底到顶反向进行剪枝。比起GBM,这样不容易陷入局部最优解。
- 内置交叉验证
- XGBoost允许在每一轮boosting迭代中使用交叉验证。因此,可以方便地获得最优boosting迭代次数。而GBM使用网格搜索,只能检测有限个值。
多种数据格式:
- libsvm 格式的文本数据;
- Numpy 二维数组;
- XGBoost 二进制的缓存文件。
加载的数据存储在对象 DMatrix 中
data = np.random.rand(5,10) # 5 entities, each contains 10 features
label = np.random.randint(2, size=5) # binary target
dtrain = xgb.DMatrix( data, label=label) # numpy 格式
dtrain1 = xgb.DMatrix('train.svm.txt') # libsvm 格式
XGBoost 使用 key-value字典的方式存储参数
params = {
'booster': 'gbtree',
'objective': 'multi:softmax', # 多分类的问题
'num_class': 10, # 类别数,与 multisoftmax 并用
'gamma': 0.1, # 用于控制是否后剪枝的参数,越大越保守,一般0.1、0.2这样子。
'max_depth': 12, # 构建树的深度,越大越容易过拟合
'lambda': 2, # 控制模型复杂度的权重值的L2正则化项参数,参数越大,模型越不容易过拟合。
'subsample': 0.7, # 随机采样训练样本
'colsample_bytree': 0.7, # 生成树时进行的列采样
'min_child_weight': 3,
'silent': 1, # 设置成1则没有运行信息输出,最好是设置为0.
'eta': 0.007, # 如同学习率
'seed': 1000,
'nthread': 4, # cpu 线程数
}
更多: xgboost用法
回归
用 XGBoost 进行销售预测
import xgboost as xgb
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 加载数据集
data = pd.read_csv("sales_data.csv")
# 划分特征和标签
X = data.drop(columns=["Sales"])
y = data["Sales"]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义XGBoost回归器
model = xgb.XGBRegressor()
# 训练模型
model.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = model.predict(X_test)
# 计算均方根误差(RMSE)
rmse = mean_squared_error(y_test, y_pred, squared=False)
print("Root Mean Squared Error:", rmse)
分类:
- 用 XGBoost 构建风险评分模型
import xgboost as xgb
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义参数
params = {'objective': 'multi:softmax', 'num_class': 3, 'eta': 0.1, 'max_depth': 3}
# 转换数据集格式
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)
# 训练模型
model = xgb.train(params, dtrain, num_boost_round=100)
# 预测
y_pred = model.predict(dtest)
# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
sklearn 库
用XGBoost对医疗数据进行分类
import xgboost as xgb
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# 加载数据集
data = load_iris()
X, y = data.data, data.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义XGBoost分类器
model = xgb.XGBClassifier()
# 训练模型
model.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = model.predict(X_test)
# 打印分类报告
print("Classification Report:")
print(classification_report(y_test, y_pred))
Python 实现
参考: csdn
代码
### XGBoost定义
class XGBoost:
def __init__(self, n_estimators=300, learning_rate=0.001,
min_samples_split=2,
min_gini_impurity=999,
max_depth=2):
# 树的棵数
self.n_estimators = n_estimators
# 学习率
self.learning_rate = learning_rate
# 结点分裂最小样本数
self.min_samples_split = min_samples_split
# 结点最小基尼不纯度
self.min_gini_impurity = min_gini_impurity
# 树最大深度
self.max_depth = max_depth
# 用于分类的对数损失
# 回归任务可定义平方损失
# self.loss = SquaresLoss()
self.loss = LogisticLoss()
# 初始化分类树列表
self.trees = []
# 遍历构造每一棵决策树
for _ in range(n_estimators):
tree = XGBoost_Single_Tree(
min_samples_split=self.min_samples_split,
min_gini_impurity=self.min_gini_impurity,
max_depth=self.max_depth,
loss=self.loss)
self.trees.append(tree)
# xgboost拟合方法
def fit(self, X, y):
y = cat_label_convert(y)
y_pred = np.zeros(np.shape(y))
# 拟合每一棵树后进行结果累加
for i in range(self.n_estimators):
tree = self.trees[i]
y_true_pred = np.concatenate((y, y_pred), axis=1)
tree.fit(X, y_true_pred)
iter_pred = tree.predict(X)
y_pred -= np.multiply(self.learning_rate, iter_pred)
# xgboost预测方法
def predict(self, X):
y_pred = None
# 遍历预测
for tree in self.trees:
iter_pred = tree.predict(X)
if y_pred is None:
y_pred = np.zeros_like(iter_pred)
y_pred -= np.multiply(self.learning_rate, iter_pred)
y_pred = np.exp(y_pred) / np.sum(np.exp(y_pred), axis=1, keepdims=True)
# 将概率预测转换为标签
y_pred = np.argmax(y_pred, axis=1)
return y_pred
集成学习
Bagging与Boosting的区别:
- 取样方式不同。
- Bagging采用均匀取样,而Boosting根据错误率取样。
- Bagging的各个预测函数没有权重,而Boosting是有权重的。
- Bagging的各个预测函数可以并行生成,而Boosing的各个预测函数只能顺序生成。
LR
Logistic回归目的
- 从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。
- 因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
LR vs 线性回归
LR与线性回归的区别与联系?
- 逻辑回归和线性回归都是广义线性回归
- 经典线性模型的优化目标函数是最小二乘,而逻辑回归则是似然函数
- 另外线性回归在整个实数域范围内进行预测,敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1] 间的一种回归模型,因而对于这类问题来说,逻辑回归的鲁棒性比线性回归的要好。
逻辑回归模型本质上是一个线性回归模型,逻辑回归都是以线性回归为理论支持的。
- 但线性回归模型无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
LR VS SVM
- Logit回归目标函数是最小化后验概率,Logit回归可以用于预测事件发生概率的大小
- SVM目标是结构风险最小化,SVM可以有效避免模型过拟合。
LR和SVM的联系与区别?
联系
- 1、LR和SVM都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题)
- 2、两个方法都可以增加不同的正则化项,如L1、L2等等。所以在很多实验中,两种算法的结果是很接近的。
区别:
- 1、LR是参数模型,SVM是非参数模型。
- 2、从目标函数来看,区别在于逻辑回归采用的是Logistical Loss,SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
- 3、SVM的处理方法是只考虑Support Vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
- 4、逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
- 5、Logic 能做的 SVM能做,但可能在准确率上有问题,SVM能做的Logic有的做不了。
神经网络
神经网络的发展
- MP模型+sgn -> 单层感知机(只能线性)+sgn— Minsky 低谷 —> 多层感知机+BP+Sigmoid— (低谷) —> 深度学习+Pretraining+ReLU/Sigmoid
RNN/LSTM
LSTM结构推导,为什么比RNN好?
- 推导forget gate,input gate,cell state, hidden information等的变化;
- LSTM有进有出, 且当前cell informaton是通过input gate控制之后叠加的,RNN是叠乘,因此LSTM可以防止梯度消失或者爆炸。
CNN
对图像(不同的数据窗口数据)和滤波矩阵(一组固定的权重:因为每个神经元的多个权重固定,所以又可以看做一个恒定的滤波器filter)做内积(逐个元素相乘再求和)的操作就是所谓的『卷积』操作,也是卷积神经网络。
池化
- 取区域平均或最大
深度学习
斯坦佛-吴恩达
- 【2020-1-2】吴恩达机器学习课程资料,含ppt、word、markdown版笔记,黄海广总结
- 【2021-5-17】machine-learning-yearning, 机器学习秘笈中文版
强化学习
李宏毅
伯克利
斯坦福
周志华《机器学习》笔记
- 摘自:github
(1) 绪论
机器学习是目前信息技术中最激动人心的方向之一,其应用已经深入到生活的各个层面且与普通人的日常生活密切相关。本文为清华大学最新出版的《机器学习》教材的Learning Notes,书作者是南京大学周志华教授,多个大陆首位彰显其学术奢华。本篇主要介绍了该教材前两个章节的知识点以及自己一点浅陋的理解。
1 绪论
傍晚小街路面上沁出微雨后的湿润,和熙的细风吹来,抬头看看天边的晚霞,嗯,明天又是一个好天气。走到水果摊旁,挑了个根蒂蜷缩、敲起来声音浊响的青绿西瓜,一边满心期待着皮薄肉厚瓢甜的爽落感,一边愉快地想着,这学期狠下了工夫,基础概念弄得清清楚楚,算法作业也是信手拈来,这门课成绩一定差不了!哈哈,也希望自己这学期的machine learning课程取得一个好成绩!
1.1 机器学习的定义
正如我们根据过去的经验来判断明天的天气,吃货们希望从购买经验中挑选一个好瓜,那能不能让计算机帮助人类来实现这个呢?机器学习正是这样的一门学科,人的“经验”对应计算机中的“数据”,让计算机来学习这些经验数据,生成一个算法模型,在面对新的情况中,计算机便能作出有效的判断,这便是机器学习。
另一本经典教材的作者Mitchell给出了一个形式化的定义,假设:
- P:计算机程序在某任务类T上的
性能。 - T:计算机程序希望实现的
任务类。 - E:表示
经验,即历史的数据集。
若该计算机程序通过利用经验E在任务T上获得了性能P的改善,则称该程序对E进行了学习。
1.2 机器学习的一些基本术语
假设我们收集了一批西瓜的数据,例如:
- (色泽=青绿;根蒂=蜷缩;敲声=浊响)
- (色泽=乌黑;根蒂=稍蜷;敲声=沉闷)
- (色泽=浅自;根蒂=硬挺;敲声=清脆)……
每对括号内是一个西瓜的记录,定义:
- 所有记录的集合为:
数据集。 - 每一条记录为:一个
实例(instance)或样本(sample)。- 例如:色泽或敲声,单个的特点为
特征(feature)或属性(attribute)。
- 例如:色泽或敲声,单个的特点为
- 对于一条记录,如果在坐标轴上表示,每个西瓜都可以用坐标轴中的一个点表示,一个点也是一个向量
- 例如(青绿,蜷缩,浊响),即每个西瓜为:一个特征向量(feature vector)。
- 一个样本的特征数为:
维数(dimensionality),该西瓜的例子维数为3,当维数非常大时,也就是现在说的“维数灾难”。
计算机程序学习经验数据生成算法模型的过程中,每一条记录称为一个“训练样本”,同时在训练好模型后,我们希望使用新的样本来测试模型的效果,则每一个新的样本称为一个“测试样本”。定义:
- 所有训练样本的集合为:
训练集(trainning set),[特殊]。 - 所有测试样本的集合为:
测试集(test set),[一般]。 -
机器学习出来的模型适用于新样本的能力为:
泛化能力(generalization),即从特殊到一般。西瓜的例子中,我们是想计算机通过学习西瓜的特征数据,训练出一个决策模型,来判断一个新的西瓜是否是好瓜。可以得知我们预测的是:西瓜是好是坏,即好瓜与差瓜两种,是离散值。同样地,也有通过历年的人口数据,来预测未来的人口数量,人口数量则是连续值。定义:
- 预测值为离散值的问题为:
分类(classification)。 -
预测值为连续值的问题为:
回归(regression)。我们预测西瓜是否是好瓜的过程中,很明显对于训练集中的西瓜,我们事先已经知道了该瓜是否是好瓜,学习器通过学习这些好瓜或差瓜的特征,从而总结出规律,即训练集中的西瓜我们都做了标记,称为标记信息。但也有没有标记信息的情形,例如:我们想将一堆西瓜根据特征分成两个小堆,使得某一堆的西瓜尽可能相似,即都是好瓜或差瓜,对于这种问题,我们事先并不知道西瓜的好坏,样本没有标记信息。定义:
- 训练数据有标记信息的学习任务为:
监督学习(supervised learning),容易知道上面所描述的分类和回归都是监督学习的范畴。 - 训练数据没有标记信息的学习任务为:
无监督学习(unsupervised learning),常见的有聚类和关联规则。
2 模型的评估与选择
2.1 误差与过拟合
我们将学习器对样本的实际预测结果与样本的真实值之间的差异成为:误差(error)。定义:
- 在训练集上的误差称为
训练误差(training error)或经验误差(empirical error)。 - 在测试集上的误差称为
测试误差(test error)。 - 学习器在所有新样本上的误差称为
泛化误差(generalization error)。
显然,我们希望得到的是在新样本上表现得很好的学习器,即泛化误差小的学习器。因此,我们应该让学习器尽可能地从训练集中学出普适性的“一般特征”,这样在遇到新样本时才能做出正确的判别。然而,当学习器把训练集学得“太好”的时候,即把一些训练样本的自身特点当做了普遍特征;同时也有学习能力不足的情况,即训练集的基本特征都没有学习出来。我们定义:
- 学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了,称为:
过拟合(overfitting)。 - 学习能太差,训练样本的一般性质尚未学好,称为:
欠拟合(underfitting)。
可以得知:在过拟合问题中,训练误差十分小,但测试误差教大;在欠拟合问题中,训练误差和测试误差都比较大。目前,欠拟合问题比较容易克服,例如增加迭代次数等,但过拟合问题还没有十分好的解决方案,过拟合是机器学习面临的关键障碍。
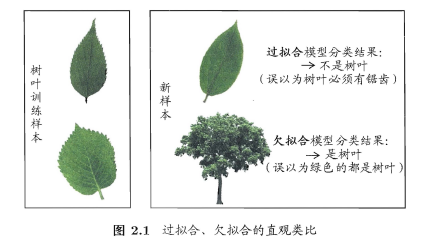
2.2 评估方法
在现实任务中,我们往往有多种算法可供选择,那么我们应该选择哪一个算法才是最适合的呢?如上所述,我们希望得到的是泛化误差小的学习器,理想的解决方案是对模型的泛化误差进行评估,然后选择泛化误差最小的那个学习器。但是,泛化误差指的是模型在所有新样本上的适用能力,我们无法直接获得泛化误差。
因此,通常我们采用一个“测试集”来测试学习器对新样本的判别能力,然后以“测试集”上的“测试误差”作为“泛化误差”的近似。显然:我们选取的测试集应尽可能与训练集互斥,下面用一个小故事来解释why:
假设老师出了10 道习题供同学们练习,考试时老师又用同样的这10道题作为试题,可能有的童鞋只会做这10 道题却能得高分,很明显:这个考试成绩并不能有效地反映出真实水平。 回到我们的问题上来,我们希望得到泛化性能好的模型,好比希望同学们课程学得好并获得了对所学知识”举一反三”的能力; 训练样本相当于给同学们练习的习题,测试过程则相当于考试。显然,若测试样本被用作训练了,则得到的将是过于”乐观”的估计结果。
2.3 训练集与测试集的划分方法
如上所述:我们希望用一个“测试集”的“测试误差”来作为“泛化误差”的近似,因此我们需要对初始数据集进行有效划分,划分出互斥的“训练集”和“测试集”。
下面介绍几种常用的划分方法:
2.3.1 留出法
将数据集D划分为两个互斥的集合,一个作为训练集S,一个作为测试集T,满足D=S∪T且S∩T=∅,常见的划分为:大约2/3-4/5的样本用作训练,剩下的用作测试。
需要注意的是:训练/测试集的划分要尽可能保持数据分布的一致性,以避免由于分布的差异引入额外的偏差,常见的做法是采取分层抽样。同时,由于划分的随机性,单次的留出法结果往往不够稳定,一般要采用若干次随机划分,重复实验取平均值的做法。
2.3.2 交叉验证法
将数据集D划分为k个大小相同的互斥子集,满足D=D1∪D2∪…∪Dk,Di∩Dj=∅(i≠j),同样地尽可能保持数据分布的一致性,即采用分层抽样的方法获得这些子集。
交叉验证法的思想是:每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就有K种训练集/测试集划分的情况,从而可进行k次训练和测试,最终返回k次测试结果的均值。交叉验证法也称“k折交叉验证”,k最常用的取值是10,下图给出了10折交叉验证的示意图。
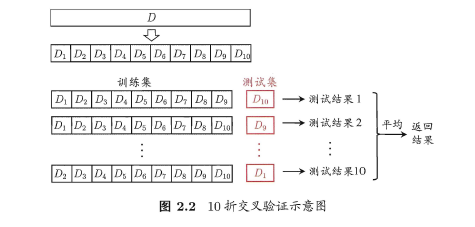
与留出法类似,将数据集D划分为K个子集的过程具有随机性,因此K折交叉验证通常也要重复p次,称为p次k折交叉验证,常见的是10次10折交叉验证,即进行了100次训练/测试。特殊地当划分的k个子集的每个子集中只有一个样本时,称为“留一法”,显然,留一法的评估结果比较准确,但对计算机的消耗也是巨大的。
2.3.3 自助法
我们希望评估的是用整个D训练出的模型。但在留出法和交叉验证法中,由于保留了一部分样本用于测试,因此实际评估的模型所使用的训练集比D小,这必然会引入一些因训练样本规模不同而导致的估计偏差。留一法受训练样本规模变化的影响较小,但计算复杂度又太高了。“自助法”正是解决了这样的问题。
自助法的基本思想是:给定包含m个样本的数据集D,每次随机从D中挑选一个样本,将其拷贝放入D’,然后再将该样本放回初始数据集D 中,使得该样本在下次采样时仍有可能被采到。重复执行m 次,就可以得到了包含m个样本的数据集D’。可以得知在m次采样中,样本始终不被采到的概率取极限为:
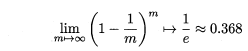
这样,通过自助采样,初始样本集D中大约有36.8%的样本没有出现在D’中,于是可以将D’作为训练集,D-D’作为测试集。自助法在数据集较小,难以有效划分训练集/测试集时很有用,但由于自助法产生的数据集(随机抽样)改变了初始数据集的分布,因此引入了估计偏差。在初始数据集足够时,留出法和交叉验证法更加常用。
2.4 调参
大多数学习算法都有些参数(parameter) 需要设定,参数配置不同,学得模型的性能往往有显著差别,这就是通常所说的”参数调节”或简称”调参” (parameter tuning)。
学习算法的很多参数是在实数范围内取值,因此,对每种参数取值都训练出模型来是不可行的。常用的做法是:对每个参数选定一个范围和步长λ,这样使得学习的过程变得可行。例如:假定算法有3 个参数,每个参数仅考虑5 个候选值,这样对每一组训练/测试集就有555= 125 个模型需考察,由此可见:拿下一个参数(即经验值)对于算法人员来说是有多么的happy。
最后需要注意的是:当选定好模型和调参完成后,我们需要使用初始的数据集D重新训练模型,即让最初划分出来用于评估的测试集也被模型学习,增强模型的学习效果。用上面考试的例子来比喻:就像高中时大家每次考试完,要将考卷的题目消化掉(大多数题目都还是之前没有见过的吧?),这样即使考差了也能开心的玩耍了~。
(2) 性能度量
本篇主要是对第二章剩余知识的理解,包括:性能度量、比较检验和偏差与方差。
在上一篇中,我们解决了评估学习器泛化性能的方法,即用测试集的“测试误差”作为“泛化误差”的近似,当我们划分好训练/测试集后,那如何计算“测试误差”呢?这就是性能度量,例如:均方差,错误率等,即“测试误差”的一个评价标准。有了评估方法和性能度量,就可以计算出学习器的“测试误差”,但由于“测试误差”受到很多因素的影响,例如:算法随机性或测试集本身的选择,那如何对两个或多个学习器的性能度量结果做比较呢?这就是比较检验。最后偏差与方差是解释学习器泛化性能的一种重要工具。写到后面发现冗长之后读起来十分没有快感,故本篇主要知识点为性能度量。
2.5 性能度量
性能度量(performance measure)是衡量模型泛化能力的评价标准,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评判结果。本节除2.5.1外,其它主要介绍分类模型的性能度量。
2.5.1 最常见的性能度量
在回归任务中,即预测连续值的问题,最常用的性能度量是“均方误差”(mean squared error),很多的经典算法都是采用了MSE作为评价函数,想必大家都十分熟悉。

在分类任务中,即预测离散值的问题,最常用的是错误率和精度,错误率是分类错误的样本数占样本总数的比例,精度则是分类正确的样本数占样本总数的比例,易知:错误率+精度=1。
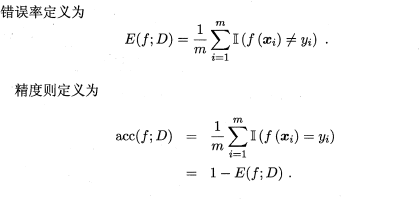

2.5.2 查准率/查全率/F1
错误率和精度虽然常用,但不能满足所有的需求,例如:在推荐系统中,我们只关心推送给用户的内容用户是否感兴趣(即查准率),或者说所有用户感兴趣的内容我们推送出来了多少(即查全率)。因此,使用查准/查全率更适合描述这类问题。对于二分类问题,分类结果混淆矩阵与查准/查全率定义如下:

初次接触时,FN与FP很难正确的理解,按照惯性思维容易把FN理解成:False->Negtive,即将错的预测为错的,这样FN和TN就反了,后来找到一张图,描述得很详细,为方便理解,把这张图也贴在了下边:
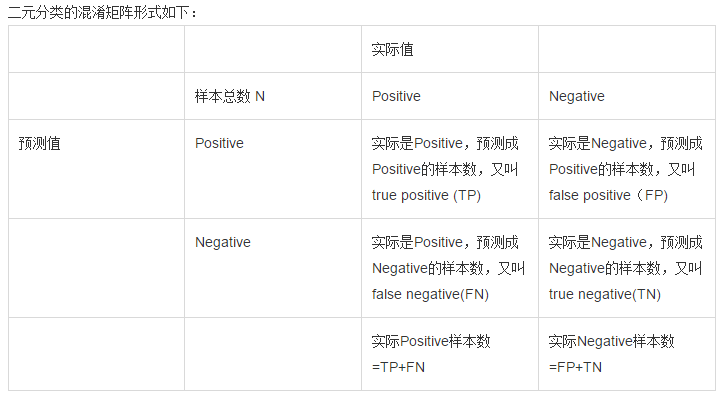
正如天下没有免费的午餐,查准率和查全率是一对矛盾的度量。例如我们想让推送的内容尽可能用户全都感兴趣,那只能推送我们把握高的内容,这样就漏掉了一些用户感兴趣的内容,查全率就低了;如果想让用户感兴趣的内容都被推送,那只有将所有内容都推送上,宁可错杀一千,不可放过一个,这样查准率就很低了。
“P-R曲线”正是描述查准/查全率变化的曲线,P-R曲线定义如下:根据学习器的预测结果(一般为一个实值或概率)对测试样本进行排序,将最可能是“正例”的样本排在前面,最不可能是“正例”的排在后面,按此顺序逐个把样本作为“正例”进行预测,每次计算出当前的P值和R值,如下图所示:
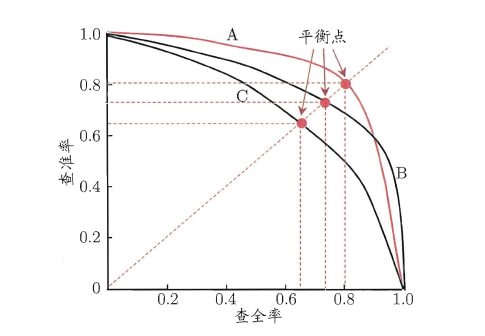
P-R曲线如何评估呢?
- 若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全包住,则称:B的性能优于A。
- 若A和B的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。
- 但一般来说,曲线下的面积是很难进行估算的,所以衍生出了“
平衡点”(Break-Event Point,简称BEP),即当P=R时的取值,平衡点的取值越高,性能更优。
P和R指标有时会出现矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure,又称F-Score。F-Measure是P和R的加权调和平均,即:
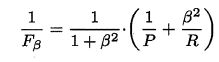
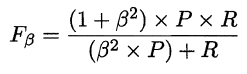
特别地,当β=1时,也就是常见的F1度量,是P和R的调和平均,当F1较高时,模型的性能越好。
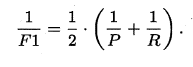

有时候我们会有多个二分类混淆矩阵,例如:多次训练或者在多个数据集上训练,那么估算全局性能的方法有两种,分为宏观和微观。
简单理解,宏观就是先算出每个混淆矩阵的P值和R值,然后取得平均P值macro-P和平均R值macro-R,在算出Fβ或F1,而微观则是计算出混淆矩阵的平均TP、FP、TN、FN,接着进行计算P、R,进而求出Fβ或F1。
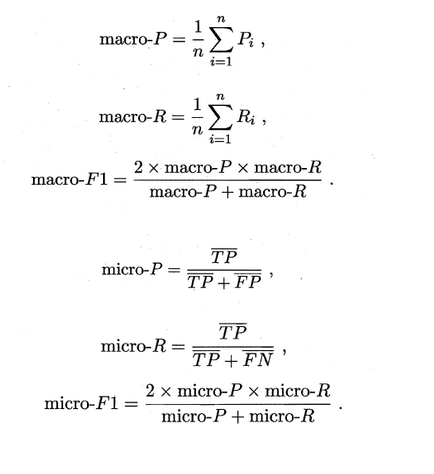
2.5.3 ROC与AUC
如上所述:学习器对测试样本的评估结果一般为一个实值或概率,设定一个阈值,大于阈值为正例,小于阈值为负例,因此这个实值的好坏直接决定了学习器的泛化性能,若将这些实值排序,则排序的好坏决定了学习器的性能高低。ROC曲线正是从这个角度出发来研究学习器的泛化性能,ROC曲线与P-R曲线十分类似,都是按照排序的顺序逐一按照正例预测,不同的是ROC曲线以“真正例率”(True Positive Rate,简称TPR)为横轴,纵轴为“假正例率”(False Positive Rate,简称FPR),ROC偏重研究基于测试样本评估值的排序好坏。

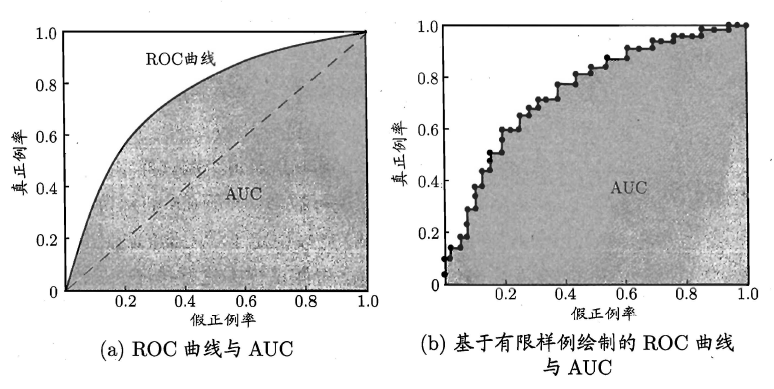
简单分析图像,可以得知:当FN=0时,TN也必须0,反之也成立,我们可以画一个队列,试着使用不同的截断点(即阈值)去分割队列,来分析曲线的形状,(0,0)表示将所有的样本预测为负例,(1,1)则表示将所有的样本预测为正例,(0,1)表示正例全部出现在负例之前的理想情况,(1,0)则表示负例全部出现在正例之前的最差情况。限于篇幅,这里不再论述。
现实中的任务通常都是有限个测试样本,因此只能绘制出近似ROC曲线。绘制方法:首先根据测试样本的评估值对测试样本排序,接着按照以下规则进行绘制。

同样地,进行模型的性能比较时
- 若一个学习器A的ROC曲线被另一个学习器B的ROC曲线完全包住,则称B的性能优于A。
- 若A和B的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。
ROC曲线下的面积定义为AUC(Area Uder ROC Curve),不同于P-R的是,这里的AUC是可估算的,即AOC曲线下每一个小矩形的面积之和。
易知:AUC越大,证明排序的质量越好
- AUC为1时,证明所有正例排在了负例的前面
- AUC为0时,所有的负例排在了正例的前面。
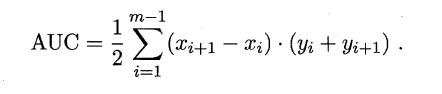
2.5.4 代价敏感错误率与代价曲线
上面的方法中,将学习器的犯错同等对待,但在现实生活中,将正例预测成假例与将假例预测成正例的代价常常是不一样的,例如:将无疾病–>有疾病只是增多了检查,但有疾病–>无疾病却是增加了生命危险。以二分类为例,由此引入了“代价矩阵”(cost matrix)。
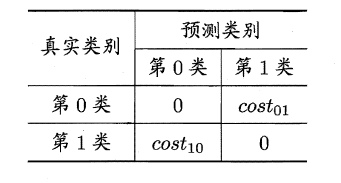
在非均等错误代价下,我们希望的是最小化“总体代价”,这样“代价敏感”的错误率(2.5.1节介绍)为:
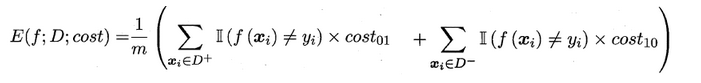
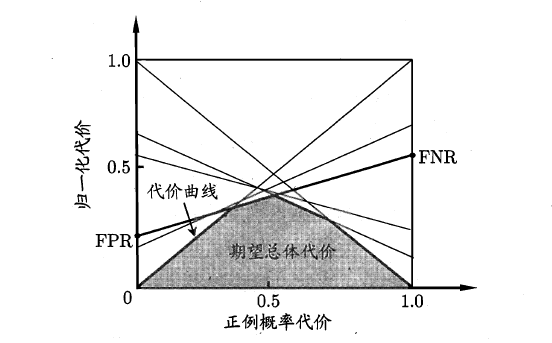
同样对于ROC曲线,在非均等错误代价下,演变成了“代价曲线”,代价曲线横轴是取值在[0,1]之间的正例概率代价,式中p表示正例的概率,纵轴是取值为[0,1]的归一化代价。
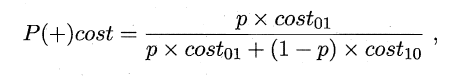
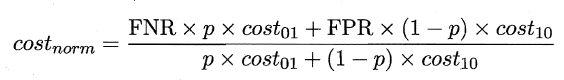
代价曲线的绘制很简单:设ROC曲线上一点的坐标为(TPR,FPR) ,则可相应计算出FNR,然后在代价平面上绘制一条从(0,FPR) 到(1,FNR) 的线段,线段下的面积即表示了该条件下的期望总体代价;如此将ROC 曲线土的每个点转化为代价平面上的一条线段,然后取所有线段的下界,围成的面积即为在所有条件下学习器的期望总体代价,如图所示:
在此模型的性能度量方法就介绍完了,以前一直以为均方误差和精准度就可以了,现在才发现天空如此广阔~
(3)假设检验&方差偏差
在上两篇中,我们介绍了多种常见的评估方法和性能度量标准,这样我们就可以根据数据集以及模型任务的特征,选择出最合适的评估和性能度量方法来计算出学习器的“测试误差“。但由于“测试误差”受到很多因素的影响,例如:算法随机性(例如常见的K-Means)或测试集本身的选择,使得同一模型每次得到的结果不尽相同,同时测试误差是作为泛化误差的近似,并不能代表学习器真实的泛化性能,那如何对单个或多个学习器在不同或相同测试集上的性能度量结果做比较呢?这就是比较检验。最后偏差与方差是解释学习器泛化性能的一种重要工具。本篇延续上一篇的内容,主要讨论了比较检验、方差与偏差。
2.6 比较检验
在比较学习器泛化性能的过程中,统计假设检验(hypothesis test)为学习器性能比较提供了重要依据,即若A在某测试集上的性能优于B,那A学习器比B好的把握有多大。 为方便论述,本篇中都是以“错误率”作为性能度量的标准。
2.6.1 假设检验
“假设”指的是对样本总体的分布或已知分布中某个参数值的一种猜想,例如:假设总体服从泊松分布,或假设正态总体的期望u=u0。回到本篇中,我们可以通过测试获得测试错误率,但直观上测试错误率和泛化错误率相差不会太远,因此可以通过测试错误率来推测泛化错误率的分布,这就是一种假设检验。

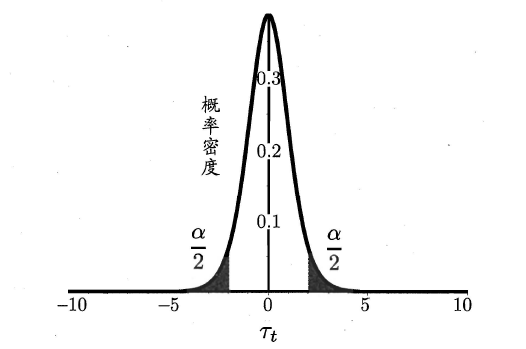
2.6.2 交叉验证t检验

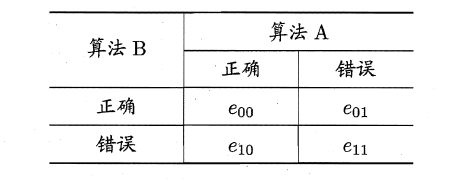
2.6.3 McNemar检验
MaNemar主要用于二分类问题,与成对t检验一样也是用于比较两个学习器的性能大小。
主要思想是:
若两学习器的性能相同,则A预测正确B预测错误数应等于B预测错误A预测正确数,即e01=e10,且|e01-e10|服从N(1,e01+e10)分布。
因此,如下所示的变量服从自由度为1的卡方分布,即服从标准正态分布N(0,1)的随机变量的平方和,下式只有一个变量,故自由度为1,检验的方法同上:
做出假设–>求出满足显著度的临界点–>给出拒绝域–>验证假设。
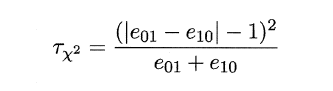
2.6.4 Friedman检验与Nemenyi后续检验
上述的三种检验都只能在一组数据集上,F检验则可以在多组数据集进行多个学习器性能的比较,基本思想是在同一组数据集上,根据测试结果(例:测试错误率)对学习器的性能进行排序,赋予序值1,2,3…,相同则平分序值,如下图所示:

若学习器的性能相同,则它们的平均序值应该相同,且第i个算法的平均序值ri服从正态分布N((k+1)/2,(k+1)(k-1)/12),则有:

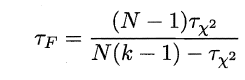
服从自由度为k-1和(k-1)(N-1)的F分布。下面是F检验常用的临界值:
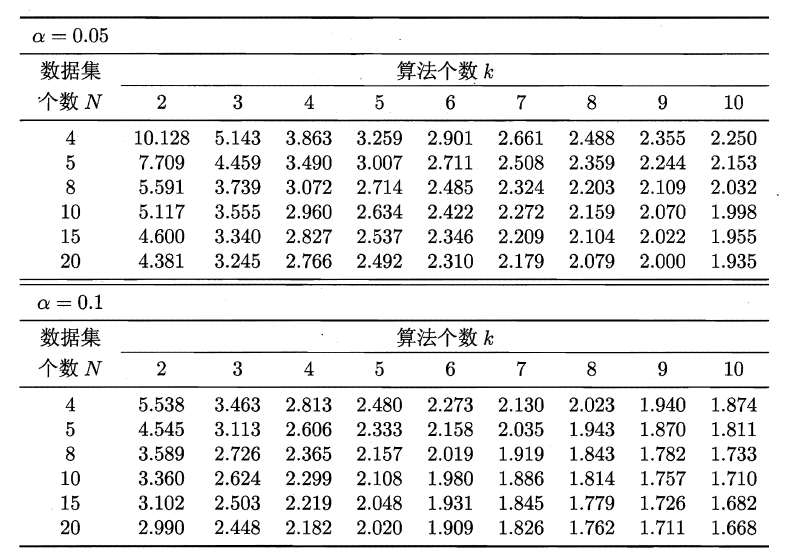
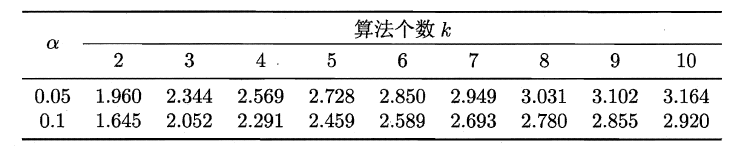
若“H0:所有算法的性能相同”这个假设被拒绝,则需要进行后续检验,来得到具体的算法之间的差异。常用的就是Nemenyi后续检验。Nemenyi检验计算出平均序值差别的临界值域,下表是常用的qa值,若两个算法的平均序值差超出了临界值域CD,则相应的置信度1-α拒绝“两个算法性能相同”的假设。
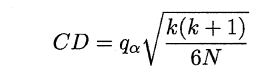
2.7 偏差与方差
偏差-方差分解是解释学习器泛化性能的重要工具。在学习算法中,偏差指的是预测的期望值与真实值的偏差,方差则是每一次预测值与预测值得期望之间的差均方。实际上,偏差体现了学习器预测的准确度,而方差体现了学习器预测的稳定性。通过对泛化误差的进行分解,可以得到:
- 期望泛化误差=方差+偏差
- 偏差刻画学习器的拟合能力
- 方差体现学习器的稳定性
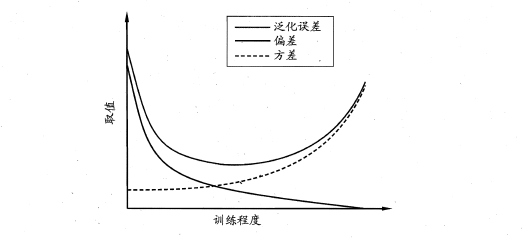
易知:方差和偏差具有矛盾性,这就是常说的偏差-方差窘境(bias-variance dilamma),随着训练程度的提升,期望预测值与真实值之间的差异越来越小,即偏差越来越小,但是另一方面,随着训练程度加大,学习算法对数据集的波动越来越敏感,方差值越来越大。换句话说:
在欠拟合时,偏差主导泛化误差,而训练到一定程度后,偏差越来越小,方差主导了泛化误差。因此训练也不要贪杯,适度辄止。
(4)线性模型
笔记的前一部分主要是对机器学习预备知识的概括,包括机器学习的定义/术语、学习器性能的评估/度量以及比较,本篇之后将主要对具体的学习算法进行理解总结,本篇则主要是第3章的内容–线性模型。
3、线性模型
谈及线性模型,其实我们很早就已经与它打过交道,还记得高中数学必修3课本中那个顽皮的“最小二乘法”吗?这就是线性模型的经典算法之一:根据给定的(x,y)点对,求出一条与这些点拟合效果最好的直线y=ax+b,之前我们利用下面的公式便可以计算出拟合直线的系数a,b(3.1中给出了具体的计算过程),从而对于一个新的x,可以预测它所对应的y值。前面我们提到:在机器学习的术语中,当预测值为连续值时,称为“回归问题”,离散值时为“分类问题”。本篇先从线性回归任务开始,接着讨论分类和多分类问题。
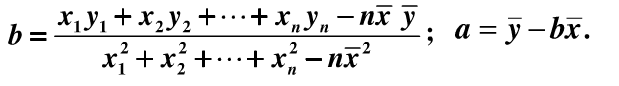
3.1 线性回归
线性回归问题就是试图学到一个线性模型尽可能准确地预测新样本的输出值,例如:通过历年的人口数据预测2017年人口数量。在这类问题中,往往我们会先得到一系列的有标记数据,例如:2000–>13亿…2016–>15亿,这时输入的属性只有一个,即年份;也有输入多属性的情形,假设我们预测一个人的收入,这时输入的属性值就不止一个了,例如:(学历,年龄,性别,颜值,身高,体重)–>15k。
有时这些输入的属性值并不能直接被我们的学习模型所用,需要进行相应的处理,对于连续值的属性,一般都可以被学习器所用,有时会根据具体的情形作相应的预处理,例如:归一化等;对于离散值的属性,可作下面的处理:
- 若属性值之间存在“序关系”,则可以将其转化为连续值,例如:身高属性分为“高”“中等”“矮”,可转化为数值:{1, 0.5, 0}。
- 若属性值之间不存在“序关系”,则通常将其转化为向量的形式,例如:性别属性分为“男”“女”,可转化为二维向量:{(1,0),(0,1)}。
(1)当输入属性只有一个的时候,就是最简单的情形,也就是我们高中时最熟悉的“最小二乘法”(Euclidean distance),首先计算出每个样本预测值与真实值之间的误差并求和,通过最小化均方误差MSE,使用求偏导等于零的方法计算出拟合直线y=wx+b的两个参数w和b,计算过程如下图所示:

(2)当输入属性有多个的时候,例如对于一个样本有d个属性{(x1,x2…xd),y},则y=wx+b需要写成:
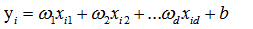
通常对于多元问题,常常使用矩阵的形式来表示数据。在本问题中,将具有m个样本的数据集表示成矩阵X,将系数w与b合并成一个列向量,这样每个样本的预测值以及所有样本的均方误差最小化就可以写成下面的形式:

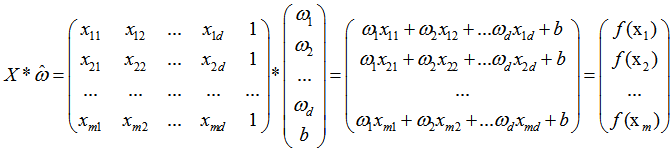
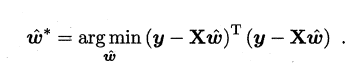
同样地,我们使用最小二乘法对w和b进行估计,令均方误差的求导等于0,需要注意的是,当一个矩阵的行列式不等于0时,我们才可能对其求逆,因此对于下式,我们需要考虑矩阵(X的转置*X)的行列式是否为0,若不为0,则可以求出其解,若为0,则需要使用其它的方法进行计算,书中提到了引入正则化,此处不进行深入。

另一方面,有时像上面这种原始的线性回归可能并不能满足需求,例如:y值并不是线性变化,而是在指数尺度上变化。这时我们可以采用线性模型来逼近y的衍生物,例如lny,这时衍生的线性模型如下所示,实际上就是相当于将指数曲线投影在一条直线上,如下图所示:
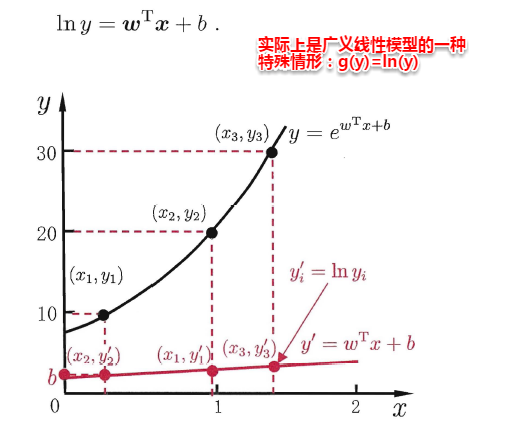
更一般地,考虑所有y的衍生物的情形,就得到了“广义的线性模型”(generalized linear model),其中,g(*)称为联系函数(link function)。
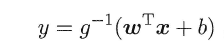
3.2 线性几率回归
回归就是通过输入的属性值得到一个预测值,利用上述广义线性模型的特征,是否可以通过一个联系函数,将预测值转化为离散值从而进行分类呢?线性几率回归正是研究这样的问题。对数几率引入了一个对数几率函数(logistic function),将预测值投影到0-1之间,从而将线性回归问题转化为二分类问题。
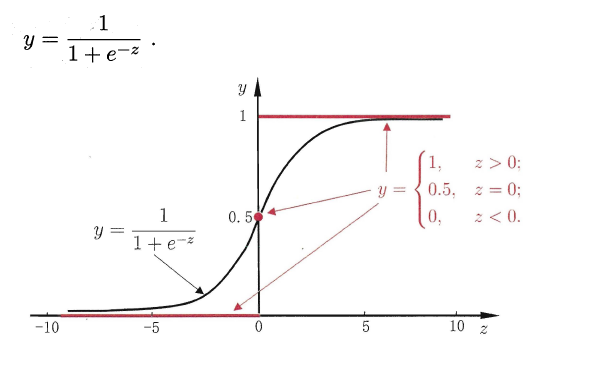

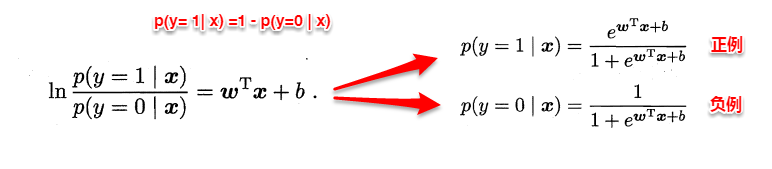
若将y看做样本为正例的概率,(1-y)看做样本为反例的概率,则上式实际上使用线性回归模型的预测结果器逼近真实标记的对数几率。因此这个模型称为“对数几率回归”(logistic regression),也有一些书籍称之为“逻辑回归”。下面使用最大似然估计的方法来计算出w和b两个参数的取值,下面只列出求解的思路,不列出具体的计算过程。

3.3 线性判别分析
线性判别分析(Linear Discriminant Analysis,简称LDA),其基本思想是:
将训练样本投影到一条直线上,使得同类的样例尽可能近,不同类的样例尽可能远。
如图所示:
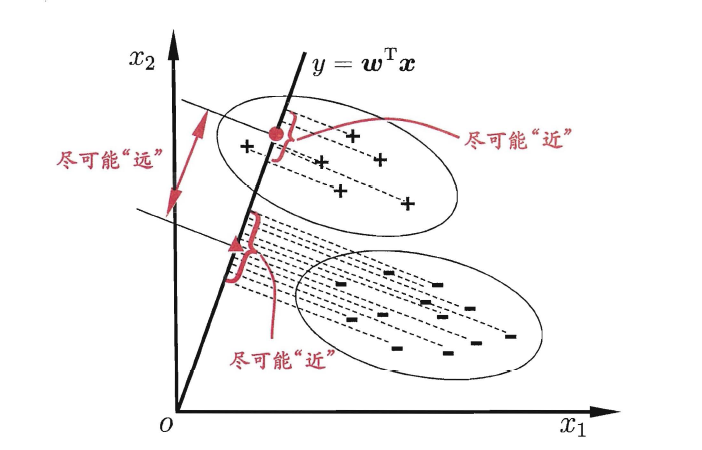

想让同类样本点的投影点尽可能接近,不同类样本点投影之间尽可能远,即:让各类的协方差之和尽可能小,不用类之间中心的距离尽可能大。基于这样的考虑,LDA定义了两个散度矩阵。
- 类内散度矩阵(within-class scatter matrix)
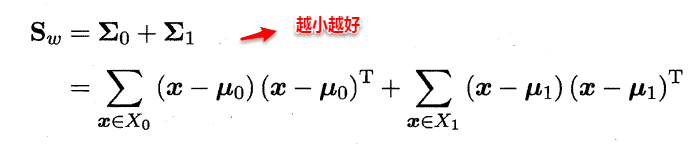
- 类间散度矩阵(between-class scaltter matrix)
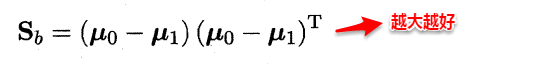
因此得到了LDA的最大化目标:“广义瑞利商”(generalized Rayleigh quotient)。
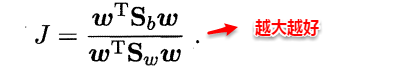
从而分类问题转化为最优化求解w的问题,当求解出w后,对新的样本进行分类时,只需将该样本点投影到这条直线上,根据与各个类别的中心值进行比较,从而判定出新样本与哪个类别距离最近。求解w的方法如下所示,使用的方法为λ乘子。

若将w看做一个投影矩阵,类似PCA的思想,则LDA可将样本投影到N-1维空间(N为类簇数),投影的过程使用了类别信息(标记信息),因此LDA也常被视为一种经典的监督降维技术。
3.4 多分类学习
现实中我们经常遇到不只两个类别的分类问题,即多分类问题,在这种情形下,我们常常运用“拆分”的策略,通过多个二分类学习器来解决多分类问题,即将多分类问题拆解为多个二分类问题,训练出多个二分类学习器,最后将多个分类结果进行集成得出结论。
最为经典的拆分策略有三种:
- “一对一”(OvO)
- “一对其余”(OvR)
- “多对多”(MvM)
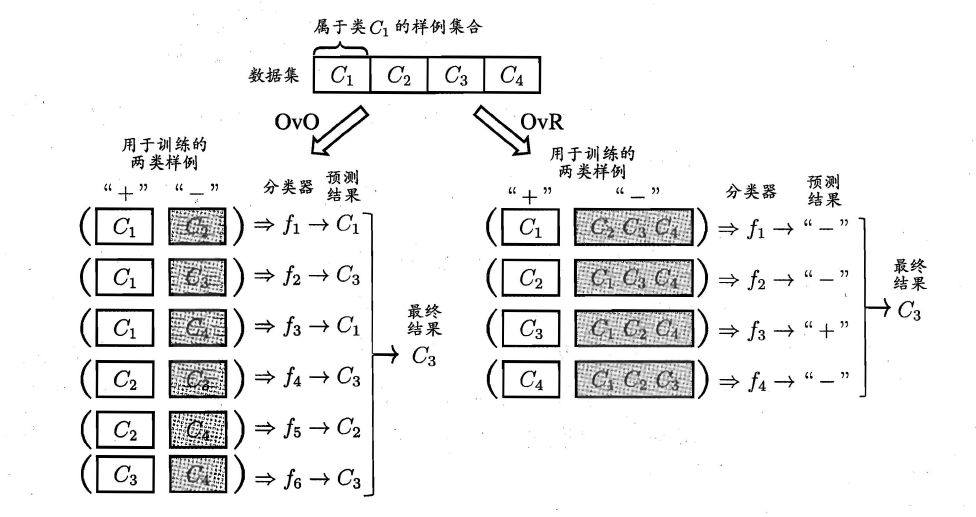
核心思想与示意图如下所示。
-
OvO:给定数据集D,假定其中有N个真实类别,将这N个类别进行两两配对(一个正类/一个反类),从而产生N(N-1)/2个二分类学习器,在测试阶段,将新样本放入所有的二分类学习器中测试,得出N(N-1)个结果,最终通过投票产生最终的分类结果。
-
OvM:给定数据集D,假定其中有N个真实类别,每次取出一个类作为正类,剩余的所有类别作为一个新的反类,从而产生N个二分类学习器,在测试阶段,得出N个结果,若仅有一个学习器预测为正类,则对应的类标作为最终分类结果。
-
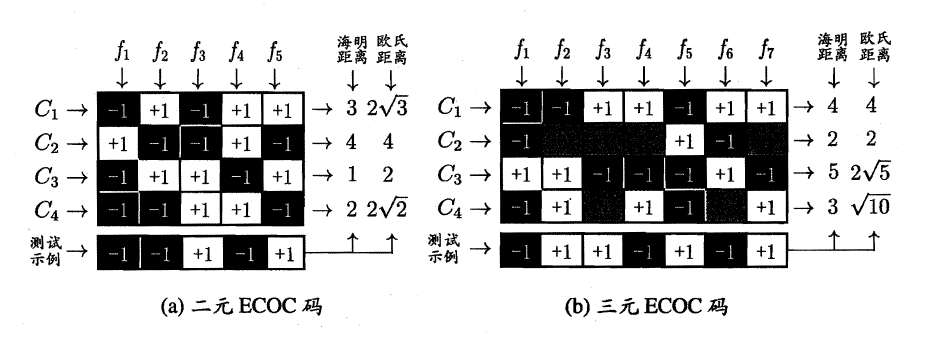
MvM:给定数据集D,假定其中有N个真实类别,每次取若干个类作为正类,若干个类作为反类(通过ECOC码给出,编码),若进行了M次划分,则生成了M个二分类学习器,在测试阶段(解码),得出M个结果组成一个新的码,最终通过计算海明/欧式距离选择距离最小的类别作为最终分类结果。
3.5 类别不平衡问题
类别不平衡(class-imbanlance)就是指分类问题中不同类别的训练样本相差悬殊的情况,例如正例有900个,而反例只有100个,这个时候我们就需要进行相应的处理来平衡这个问题。常见的做法有三种:
- 在训练样本较多的类别中进行“
欠采样”(undersampling),比如从正例中采出100个,常见的算法有:EasyEnsemble。 - 在训练样本较少的类别中进行“
过采样”(oversampling),例如通过对反例中的数据进行插值,来产生额外的反例,常见的算法有SMOTE。 - 直接基于原数据集进行学习,对预测值进行“再缩放”处理。其中再缩放也是
代价敏感学习的基础。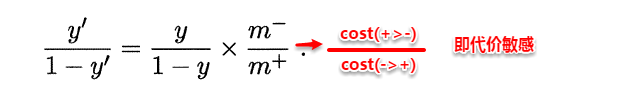
(5)决策树
上篇主要介绍和讨论了线性模型。首先从最简单的最小二乘法开始,讨论输入属性有一个和多个的情形,接着通过广义线性模型延伸开来,将预测连续值的回归问题转化为分类问题,从而引入了对数几率回归,最后线性判别分析LDA将样本点进行投影,多分类问题实质上通过划分的方法转化为多个二分类问题进行求解。本篇将讨论另一种被广泛使用的分类算法–决策树(Decision Tree)。
【2023-1-31】决策树可视化,dtreeviz工具, XGBoost Examples
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import dtreeviz
iris = load_iris()
X = iris.data
y = iris.target
clf = DecisionTreeClassifier(max_depth=4)
clf.fit(X, y)
viz_model = dtreeviz.model(clf,
X_train=X, y_train=y,
feature_names=iris.feature_names,
target_name='iris',
class_names=iris.target_names)
v = viz_model.view() # render as SVG into internal object
v.show() # pop up window
v.save("/tmp/iris.svg") # optionally save as svg
4、决策树
4.1 决策树基本概念
顾名思义,决策树是基于树结构来进行决策的,在网上看到一个例子十分有趣,放在这里正好合适。现想象一位捉急的母亲想要给自己的女娃介绍一个男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。 *****
这个女孩的挑剔过程就是一个典型的决策树,即相当于通过年龄、长相、收入和是否公务员将男童鞋分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么使用下图就能很好地表示女孩的决策逻辑(即一颗决策树)。
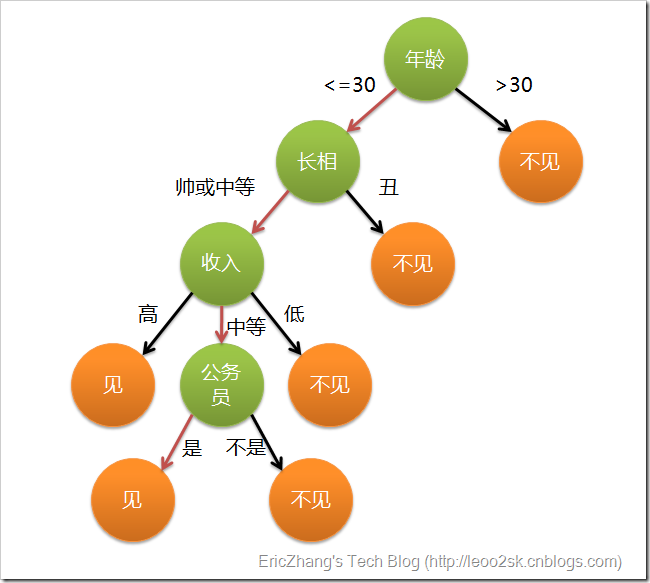
在上图的决策树中,决策过程的每一次判定都是对某一属性的“测试”,决策最终结论则对应最终的判定结果。一般一颗决策树包含:一个根节点、若干个内部节点和若干个叶子节点,易知:
* 每个非叶节点表示一个特征属性测试。
* 每个分支代表这个特征属性在某个值域上的输出。
* 每个叶子节点存放一个类别。
* 每个节点包含的样本集合通过属性测试被划分到子节点中,根节点包含样本全集。
4.2 决策树的构造
决策树的构造是一个递归的过程,有三种情形会导致递归返回:
- (1) 当前结点包含的样本全属于同一类别,这时直接将该节点标记为叶节点,并设为相应的类别;
- (2) 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分,这时将该节点标记为叶节点,并将其类别设为该节点所含样本最多的类别;
- (3) 当前结点包含的样本集合为空,不能划分,这时也将该节点标记为叶节点,并将其类别设为父节点中所含样本最多的类别。
算法的基本流程如下图所示:

可以看出:决策树学习的关键在于如何选择划分属性,不同的划分属性得出不同的分支结构,从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”,即属于同一类别。因此下面便是介绍量化纯度的具体方法,决策树最常用的算法有三种:ID3,C4.5和CART。
4.2.1 ID3算法
ID3算法使用信息增益为准则来选择划分属性,“信息熵”(information entropy)是度量样本结合纯度的常用指标,假定当前样本集合D中第k类样本所占比例为pk,则样本集合D的信息熵定义为:

假定通过属性划分样本集D,产生了V个分支节点,v表示其中第v个分支节点,易知:分支节点包含的样本数越多,表示该分支节点的影响力越大。故可以计算出划分后相比原始数据集D获得的“信息增益”(information gain)。
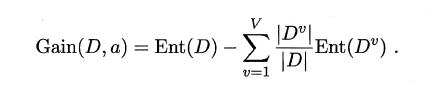
信息增益越大,表示使用该属性划分样本集D的效果越好,因此ID3算法在递归过程中,每次选择最大信息增益的属性作为当前的划分属性。
4.2.2 C4.5算法
ID3算法存在一个问题,就是偏向于取值数目较多的属性,例如:如果存在一个唯一标识,这样样本集D将会被划分为|D|个分支,每个分支只有一个样本,这样划分后的信息熵为零,十分纯净,但是对分类毫无用处。因此C4.5算法使用了“增益率”(gain ratio)来选择划分属性,来避免这个问题带来的困扰。首先使用ID3算法计算出信息增益高于平均水平的候选属性,接着C4.5计算这些候选属性的增益率,增益率定义为:
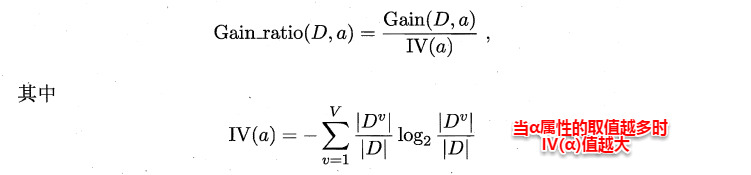
4.2.3 CART算法
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼指数反映的是从样本集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小越好,基尼指数定义如下:
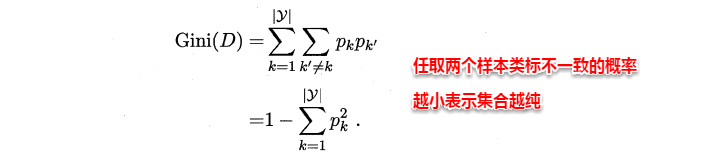
进而,使用属性α划分后的基尼指数为:
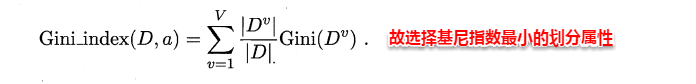
4.3 剪枝处理
从决策树的构造流程中我们可以直观地看出:不管怎么样的训练集,决策树总是能很好地将各个类别分离开来,这时就会遇到之前提到过的问题:过拟合(overfitting),即太依赖于训练样本。剪枝(pruning)则是决策树算法对付过拟合的主要手段,剪枝的策略有两种如下:
* `预剪枝`(prepruning):在构造的过程中先评估,再考虑是否分支。
* `后剪枝`(post-pruning):在构造好一颗完整的决策树后,自底向上,评估分支的必要性。
评估指的是性能度量,即决策树的泛化性能。之前提到:可以使用测试集作为学习器泛化性能的近似,因此可以将数据集划分为训练集和测试集。
- 预剪枝表示在构造数的过程中,对一个节点考虑是否分支时,首先计算决策树不分支时在测试集上的性能,再计算分支之后的性能,若分支对性能没有提升,则选择不分支(即剪枝)。
- 后剪枝则表示在构造好一颗完整的决策树后,从最下面的节点开始,考虑该节点分支对模型的性能是否有提升,若无则剪枝,即将该节点标记为叶子节点,类别标记为其包含样本最多的类别。
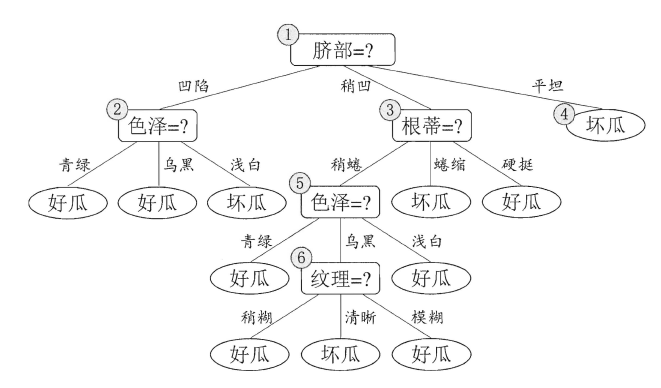
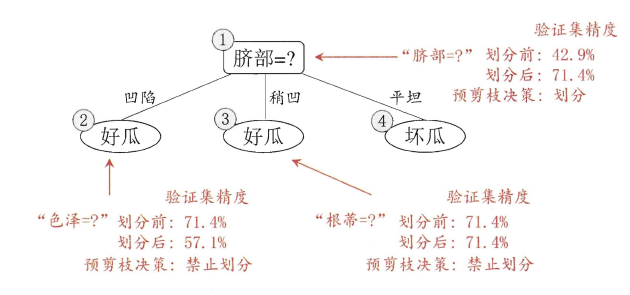
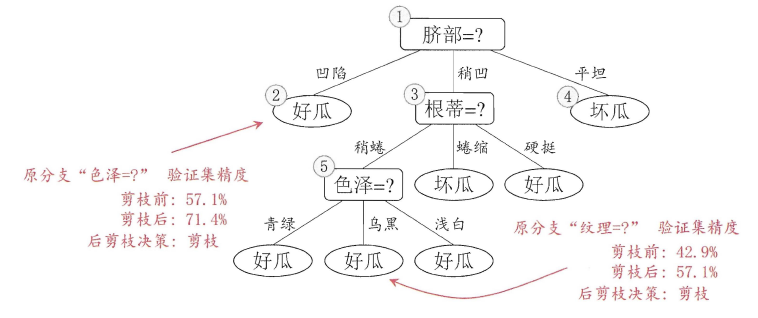
上图分别表示不剪枝处理的决策树、预剪枝决策树和后剪枝决策树。预剪枝处理使得决策树的很多分支被剪掉,因此大大降低了训练时间开销,同时降低了过拟合的风险,但另一方面由于剪枝同时剪掉了当前节点后续子节点的分支,因此预剪枝“贪心”的本质阻止了分支的展开,在一定程度上带来了欠拟合的风险。而后剪枝则通常保留了更多的分支,因此采用后剪枝策略的决策树性能往往优于预剪枝,但其自底向上遍历了所有节点,并计算性能,训练时间开销相比预剪枝大大提升。
##4.4 连续值与缺失值处理
对于连续值的属性,若每个取值作为一个分支则显得不可行,因此需要进行离散化处理,常用的方法为二分法,基本思想为:
给定样本集D与连续属性α,二分法试图找到一个划分点t将样本集D在属性α上分为≤t与>t。
* 首先将α的所有取值按升序排列,所有相邻属性的均值作为候选划分点(n-1个,n为α所有的取值数目)。
* 计算每一个划分点划分集合D(即划分为两个分支)后的信息增益。
* 选择最大信息增益的划分点作为最优划分点。 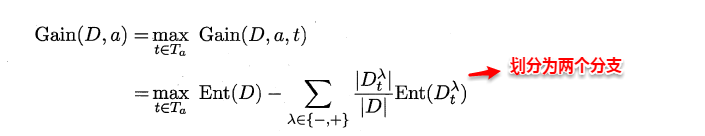
现实中常会遇到不完整的样本,即某些属性值缺失。有时若简单采取剔除,则会造成大量的信息浪费,因此在属性值缺失的情况下需要解决两个问题:
- (1)如何选择划分属性。
- (2)给定划分属性,若某样本在该属性上缺失值,如何划分到具体的分支上。
假定为样本集中的每一个样本都赋予一个权重,根节点中的权重初始化为1,则定义:

对于(1):通过在样本集D中选取在属性α上没有缺失值的样本子集,计算在该样本子集上的信息增益,最终的信息增益等于该样本子集划分后信息增益乘以样本子集占样本集的比重。即:

对于(2):若该样本子集在属性α上的值缺失,则将该样本以不同的权重(即每个分支所含样本比例)划入到所有分支节点中。该样本在分支节点中的权重变为:

(6)神经网络
上篇主要讨论了决策树算法。首先从决策树的基本概念出发,引出决策树基于树形结构进行决策,进一步介绍了构造决策树的递归流程以及其递归终止条件,在递归的过程中,划分属性的选择起到了关键作用,因此紧接着讨论了三种评估属性划分效果的经典算法,介绍了剪枝策略来解决原生决策树容易产生的过拟合问题,最后简述了属性连续值/缺失值的处理方法。本篇将讨论现阶段十分热门的另一个经典监督学习算法–神经网络(neural network)。
5、神经网络
在机器学习中,神经网络一般指的是“神经网络学习”,是机器学习与神经网络两个学科的交叉部分。所谓神经网络,目前用得最广泛的一个定义是“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”。
5.1 神经元模型
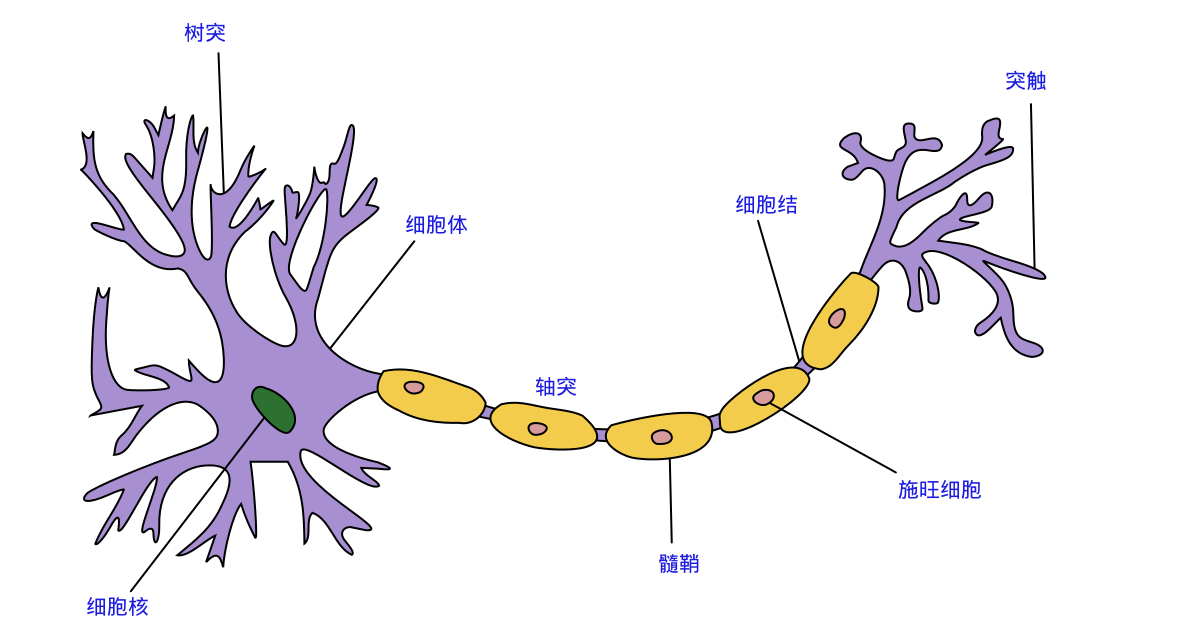
神经网络中最基本的单元是神经元模型(neuron)。在生物神经网络的原始机制中,每个神经元通常都有多个树突(dendrite),一个轴突(axon)和一个细胞体(cell body),树突短而多分支,轴突长而只有一个;在功能上,树突用于传入其它神经元传递的神经冲动,而轴突用于将神经冲动传出到其它神经元,当树突或细胞体传入的神经冲动使得神经元兴奋时,该神经元就会通过轴突向其它神经元传递兴奋。神经元的生物学结构如下图所示,不得不说高中的生化知识大学忘得可是真干净…
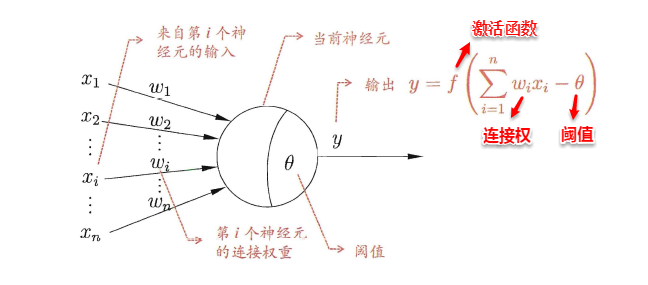
一直沿用至今的“M-P神经元模型”正是对这一结构进行了抽象,也称“阈值逻辑单元“,其中树突对应于输入部分,每个神经元收到n个其他神经元传递过来的输入信号,这些信号通过带权重的连接传递给细胞体,这些权重又称为连接权(connection weight)。细胞体分为两部分,前一部分计算总输入值(即输入信号的加权和,或者说累积电平),后一部分先计算总输入值与该神经元阈值的差值,然后通过激活函数(activation function)的处理,产生输出从轴突传送给其它神经元。M-P神经元模型如下图所示:
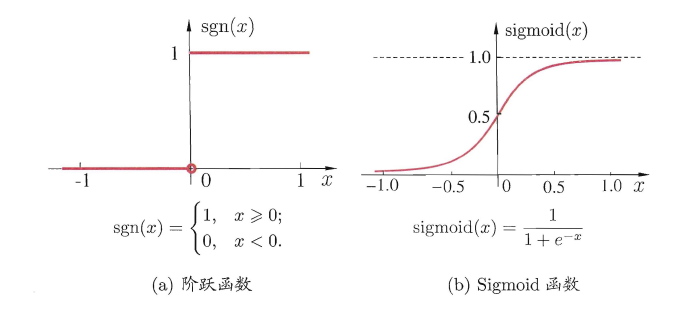
与线性分类十分相似,神经元模型最理想的激活函数也是阶跃函数,即将神经元输入值与阈值的差值映射为输出值1或0,若差值大于零输出1,对应兴奋;若差值小于零则输出0,对应抑制。但阶跃函数不连续,不光滑,故在M-P神经元模型中,也采用Sigmoid函数来近似, Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内,所以也称为挤压函数(squashing function)。
将多个神经元按一定的层次结构连接起来,就得到了神经网络。它是一种包含多个参数的模型,比方说10个神经元两两连接,则有100个参数需要学习(每个神经元有9个连接权以及1个阈值),若将每个神经元都看作一个函数,则整个神经网络就是由这些函数相互嵌套而成。
5.2 感知机与多层网络
感知机(Perceptron)是由两层神经元组成的一个简单模型,但只有输出层是M-P神经元,即只有输出层神经元进行激活函数处理,也称为功能神经元(functional neuron);输入层只是接受外界信号(样本属性)并传递给输出层(输入层的神经元个数等于样本的属性数目),而没有激活函数。这样一来,感知机与之前线性模型中的对数几率回归的思想基本是一样的,都是通过对属性加权与另一个常数求和,再使用sigmoid函数将这个输出值压缩到0-1之间,从而解决分类问题。不同的是感知机的输出层应该可以有多个神经元,从而可以实现多分类问题,同时两个模型所用的参数估计方法十分不同。
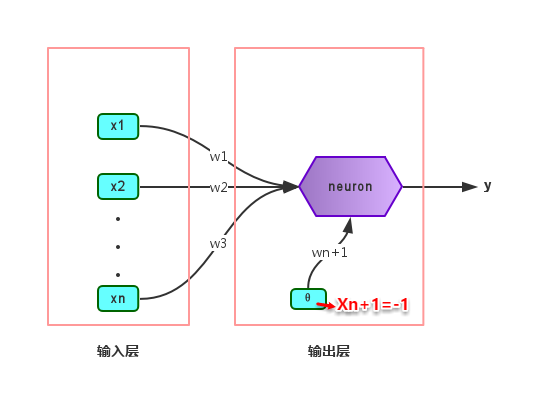
给定训练集,则感知机的n+1个参数(n个权重+1个阈值)都可以通过学习得到。阈值Θ可以看作一个输入值固定为-1的哑结点的权重ωn+1,即假设有一个固定输入xn+1=-1的输入层神经元,其对应的权重为ωn+1,这样就把权重和阈值统一为权重的学习了。简单感知机的结构如下图所示:
感知机权重的学习规则如下:对于训练样本(x,y),当该样本进入感知机学习后,会产生一个输出值,若该输出值与样本的真实标记不一致,则感知机会对权重进行调整,若激活函数为阶跃函数,则调整的方法为(基于梯度下降法):

其中 η∈(0,1)称为学习率,可以看出感知机是通过逐个样本输入来更新权重,首先设定好初始权重(一般为随机),逐个地输入样本数据,若输出值与真实标记相同则继续输入下一个样本,若不一致则更新权重,然后再重新逐个检验,直到每个样本数据的输出值都与真实标记相同。容易看出:感知机模型总是能将训练数据的每一个样本都预测正确,和决策树模型总是能将所有训练数据都分开一样,感知机模型很容易产生过拟合问题。
由于感知机模型只有一层功能神经元,因此其功能十分有限,只能处理线性可分的问题,对于这类问题,感知机的学习过程一定会收敛(converge),因此总是可以求出适当的权值。但是对于像书上提到的异或问题,只通过一层功能神经元往往不能解决,因此要解决非线性可分问题,需要考虑使用多层功能神经元,即神经网络。多层神经网络的拓扑结构如下图所示:
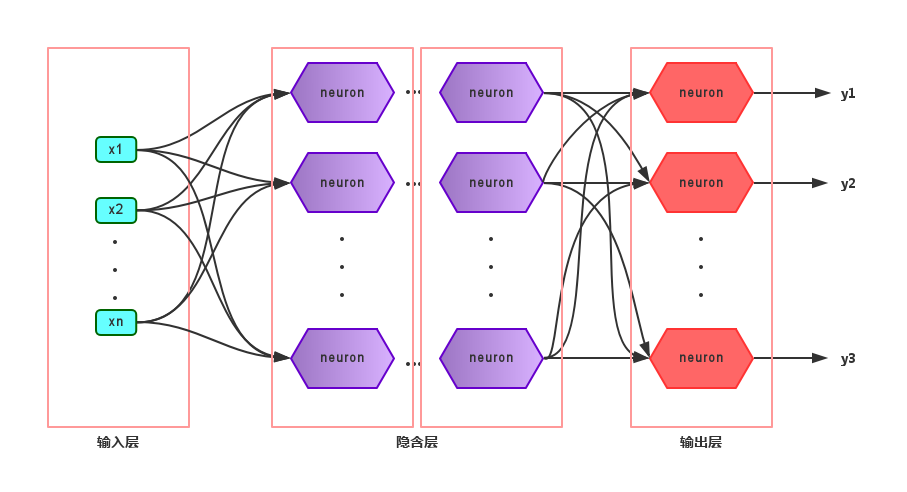
在神经网络中,输入层与输出层之间的层称为隐含层或隐层(hidden layer),隐层和输出层的神经元都是具有激活函数的功能神经元。只需包含一个隐层便可以称为多层神经网络,常用的神经网络称为“多层前馈神经网络”(multi-layer feedforward neural network),该结构满足以下几个特点:
* 每层神经元与下一层神经元之间完全互连
* 神经元之间不存在同层连接
* 神经元之间不存在跨层连接
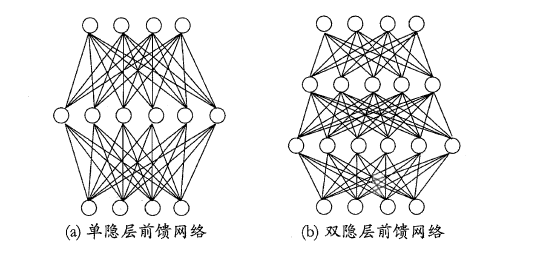
根据上面的特点可以得知:这里的“前馈”指的是网络拓扑结构中不存在环或回路,而不是指该网络只能向前传播而不能向后传播(下节中的BP神经网络正是基于前馈神经网络而增加了反馈调节机制)。神经网络的学习过程就是根据训练数据来调整神经元之间的“连接权”以及每个神经元的阈值,换句话说:神经网络所学习到的东西都蕴含在网络的连接权与阈值中。
5.3 BP神经网络算法
由上面可以得知:神经网络的学习主要蕴含在权重和阈值中,多层网络使用上面简单感知机的权重调整规则显然不够用了,BP神经网络算法即误差逆传播算法(error BackPropagation)正是为学习多层前馈神经网络而设计,BP神经网络算法是迄今为止最成功的的神经网络学习算法。
一般而言,只需包含一个足够多神经元的隐层,就能以任意精度逼近任意复杂度的连续函数[Hornik et al.,1989],故下面以训练单隐层的前馈神经网络为例,介绍BP神经网络的算法思想。
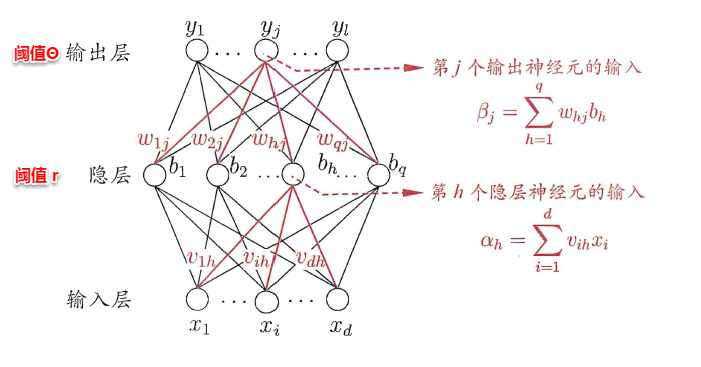
上图为一个单隐层前馈神经网络的拓扑结构,BP神经网络算法也使用梯度下降法(gradient descent),以单个样本的均方误差的负梯度方向对权重进行调节。可以看出:BP算法首先将误差反向传播给隐层神经元,调节隐层到输出层的连接权重与输出层神经元的阈值;接着根据隐含层神经元的均方误差,来调节输入层到隐含层的连接权值与隐含层神经元的阈值。BP算法基本的推导过程与感知机的推导过程原理是相同的,下面给出调整隐含层到输出层的权重调整规则的推导过程:

学习率η∈(0,1)控制着沿反梯度方向下降的步长,若步长太大则下降太快容易产生震荡,若步长太小则收敛速度太慢,一般地常把η设置为0.1,有时更新权重时会将输出层与隐含层设置为不同的学习率。BP算法的基本流程如下所示:

BP算法的更新规则是基于每个样本的预测值与真实类标的均方误差来进行权值调节,即BP算法每次更新只针对于单个样例。需要注意的是:BP算法的最终目标是要最小化整个训练集D上的累积误差,即:
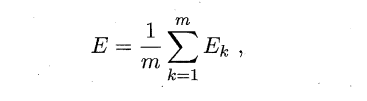
如果基于累积误差最小化的更新规则,则得到了累积误差逆传播算法(accumulated error backpropagation),即每次读取全部的数据集一遍,进行一轮学习,从而基于当前的累积误差进行权值调整,因此参数更新的频率相比标准BP算法低了很多,但在很多任务中,尤其是在数据量很大的时候,往往标准BP算法会获得较好的结果。另外对于如何设置隐层神经元个数的问题,至今仍然没有好的解决方案,常使用“试错法”进行调整。
前面提到,BP神经网络强大的学习能力常常容易造成过拟合问题,有以下两种策略来缓解BP网络的过拟合问题:
早停:将数据分为训练集与测试集,训练集用于学习,测试集用于评估性能,若在训练过程中,训练集的累积误差降低,而测试集的累积误差升高,则停止训练。- 引入
正则化(regularization):基本思想是在累积误差函数中增加一个用于描述网络复杂度的部分,例如所有权值与阈值的平方和,其中λ∈(0,1)用于对累积经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计。
5.4 全局最小与局部最小
模型学习的过程实质上就是一个寻找最优参数的过程,例如BP算法试图通过最速下降来寻找使得累积经验误差最小的权值与阈值,在谈到最优时,一般会提到局部极小(local minimum)和全局最小(global minimum)。
* 局部极小解:参数空间中的某个点,其邻域点的误差函数值均不小于该点的误差函数值。
* 全局最小解:参数空间中的某个点,所有其他点的误差函数值均不小于该点的误差函数值。
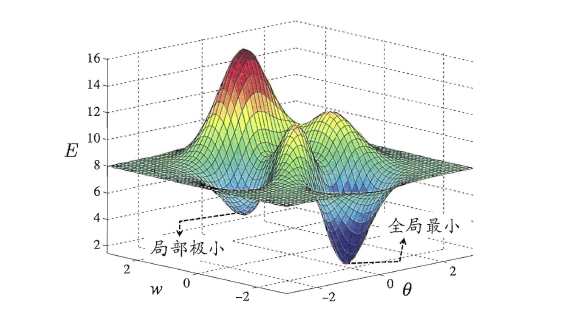
要成为局部极小点,只要满足该点在参数空间中的梯度为零。局部极小可以有多个,而全局最小只有一个。全局最小一定是局部极小,但局部最小却不一定是全局最小。显然在很多机器学习算法中,都试图找到目标函数的全局最小。梯度下降法的主要思想就是沿着负梯度方向去搜索最优解,负梯度方向是函数值下降最快的方向,若迭代到某处的梯度为0,则表示达到一个局部最小,参数更新停止。因此在现实任务中,通常使用以下策略尽可能地去接近全局最小。
* 以多组不同参数值初始化多个神经网络,按标准方法训练,迭代停止后,取其中误差最小的解作为最终参数。
* 使用“模拟退火”技术,这里不做具体介绍。
* 使用随机梯度下降,即在计算梯度时加入了随机因素,使得在局部最小时,计算的梯度仍可能不为0,从而迭代可以继续进行。
5.5 深度学习
理论上,参数越多,模型复杂度就越高,容量(capability)就越大,从而能完成更复杂的学习任务。深度学习(deep learning)正是一种极其复杂而强大的模型。
怎么增大模型复杂度呢?两个办法,一是增加隐层的数目,二是增加隐层神经元的数目。前者更有效一些,因为它不仅增加了功能神经元的数量,还增加了激活函数嵌套的层数。但是对于多隐层神经网络,经典算法如标准BP算法往往会在误差逆传播时发散(diverge),无法收敛达到稳定状态。
那要怎么有效地训练多隐层神经网络呢?一般来说有以下两种方法:
-
无监督逐层训练(unsupervised layer-wise training):每次训练一层隐节点,把上一层隐节点的输出当作输入来训练,本层隐结点训练好后,输出再作为下一层的输入来训练,这称为预训练(pre-training)。全部预训练完成后,再对整个网络进行微调(fine-tuning)训练。一个典型例子就是深度信念网络(deep belief network,简称DBN)。这种做法其实可以视为把大量的参数进行分组,先找出每组较好的设置,再基于这些局部最优的结果来训练全局最优。 -
权共享(weight sharing):令同一层神经元使用完全相同的连接权,典型的例子是卷积神经网络(Convolutional Neural Network,简称CNN)。这样做可以大大减少需要训练的参数数目。
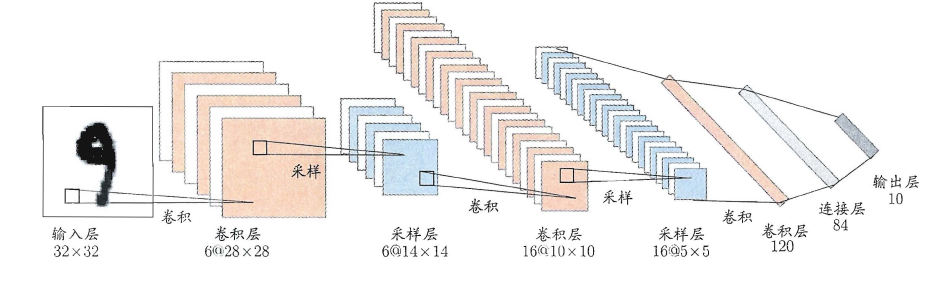
深度学习可以理解为一种特征学习(feature learning)或者表示学习(representation learning),无论是DBN还是CNN,都是通过多个隐层来把与输出目标联系不大的初始输入转化为与输出目标更加密切的表示,使原来只通过单层映射难以完成的任务变为可能。即通过多层处理,逐渐将初始的“低层”特征表示转化为“高层”特征表示,从而使得最后可以用简单的模型来完成复杂的学习任务。
传统任务中,样本的特征需要人类专家来设计,这称为特征工程(feature engineering)。特征好坏对泛化性能有至关重要的影响。而深度学习为全自动数据分析带来了可能,可以自动产生更好的特征。
(7)支持向量机
上篇主要介绍了神经网络。首先从生物学神经元出发,引出了它的数学抽象模型–MP神经元以及由两层神经元组成的感知机模型,并基于梯度下降的方法描述了感知机模型的权值调整规则。由于简单的感知机不能处理线性不可分的情形,因此接着引入了含隐层的前馈型神经网络,BP神经网络则是其中最为成功的一种学习方法,它使用误差逆传播的方法来逐层调节连接权。最后简单介绍了局部/全局最小以及目前十分火热的深度学习的概念。本篇围绕的核心则是曾经一度取代过神经网络的另一种监督学习算法–支持向量机(Support Vector Machine),简称SVM。
SVM 历史
SVM历史 参考
- 1963年,Vapnik在解决模式识别问题时提出了支持向量方法。起决定性作用的样本为支持向量
- 1971年,Kimeldorf构造基于支持向量构建核空间的方法
- 1995年,Vapnik等人正式提出统计学习理论。
理论改进:
- 模糊支持向量机
- 最小二乘支持向量机
- 加权支持向量机
- 主动学习的支持向量机
- 粗糙集与支持向量机的结合
- 基于决策树的支持向量机
- 分级聚类的支持向量机
SVM 类型
SVM 的基本形式是一个有监督的线性二分类模型,间隔最大化的分类器。主要包括以下几种形式:
- 当训练数据线性可分时,支持向量机通过硬间隔最大化学习分类器,称为
硬间隔支持向量机; 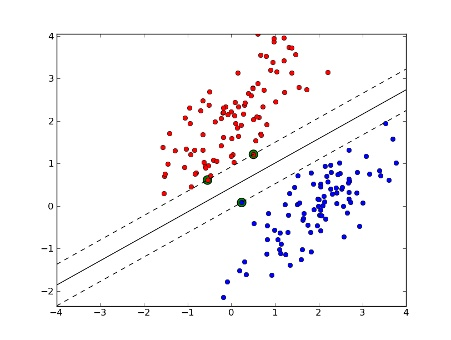
- 当训练数据近似线性可分时,支持向量机通过软间隔最大化学习分类器,称为
软间隔支持向量机; 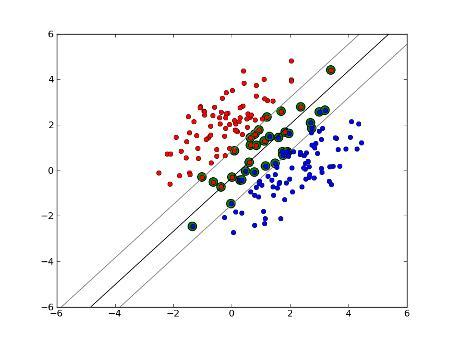
- 当训练数据线性不可分时,支持向量机通过核技巧和软间隔最大化学习分类器,称为
非线性支持向量机; 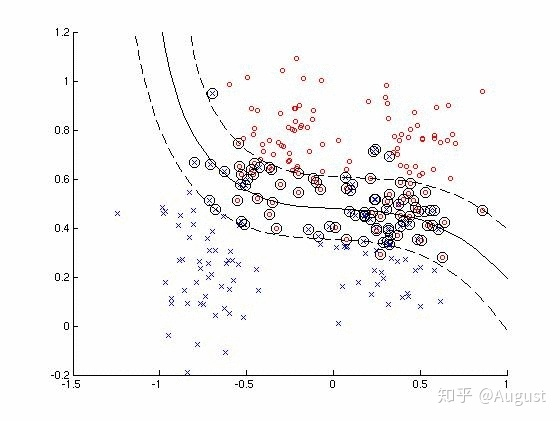
此外,SVM 既支持二元分类也支持多元分类,既支持分类问题也支持回归问题。
6、支持向量机
支持向量机是一种经典的二分类模型,基本模型定义为特征空间中最大间隔的线性分类器,其学习的优化目标便是间隔最大化,因此支持向量机本身可以转化为一个凸二次规划求解的问题。
6.1 函数间隔与几何间隔
对于二分类学习,假设现在的数据是线性可分的,这时分类学习最基本的想法就是找到一个合适的超平面,该超平面能够将不同类别的样本分开,类似二维平面使用ax+by+c=0来表示,超平面实际上表示的就是高维的平面,如下图所示:
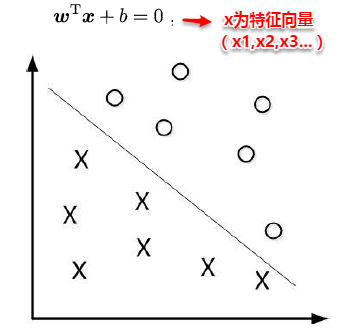
对数据点进行划分时,易知:当超平面距离与它最近的数据点的间隔越大,分类的鲁棒性越好,即当新的数据点加入时,超平面对这些点的适应性最强,出错的可能性最小。因此需要让所选择的超平面能够最大化这个间隔Gap(如下图所示), 常用的间隔定义有两种,一种称之为函数间隔,一种为几何间隔,下面将分别介绍这两种间隔,并对SVM为什么会选用几何间隔做了一些阐述。
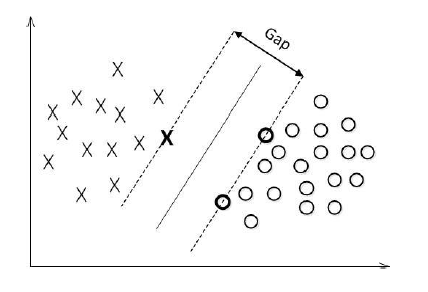
6.1.1 函数间隔
在超平面w’x+b=0确定的情况下,|w’x+b|能够代表点x距离超平面的远近,易知:当w’x+b>0时,表示x在超平面的一侧(正类,类标为1),而当w’x+b<0时,则表示x在超平面的另外一侧(负类,类别为-1),因此(w’x+b)y 的正负性恰能表示数据点x*是否被分类正确。于是便引出了函数间隔的定义(functional margin):
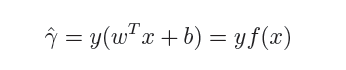
而超平面(w,b)关于所有样本点(Xi,Yi)的函数间隔最小值则为超平面在训练数据集T上的函数间隔:
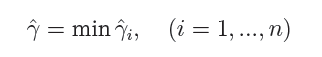
可以看出:这样定义的函数间隔在处理SVM上会有问题,当超平面的两个参数w和b同比例改变时,函数间隔也会跟着改变,但是实际上超平面还是原来的超平面,并没有变化。例如:w1x1+w2x2+w3x3+b=0其实等价于2w1x1+2w2x2+2w3x3+2b=0,但计算的函数间隔却翻了一倍。从而引出了能真正度量点到超平面距离的概念–几何间隔(geometrical margin)。
6.1.2 几何间隔
几何间隔代表的则是数据点到超平面的真实距离,对于超平面w’x+b=0,w代表的是该超平面的法向量,设x为超平面外一点x在法向量w方向上的投影点,x与超平面的距离为r,则有x=x-r(w/||w||),又x在超平面上,即w’x+b=0,代入即可得:
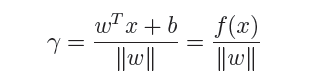
为了得到r的绝对值,令r呈上其对应的类别y,即可得到几何间隔的定义:
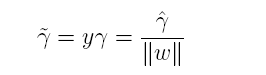
从上述函数间隔与几何间隔的定义可以看出:实质上函数间隔就是|w’x+b|,而几何间隔就是点到超平面的距离。
6.2 最大间隔与支持向量
通过前面的分析可知:函数间隔不适合用来最大化间隔,因此这里我们要找的最大间隔指的是几何间隔,于是最大间隔分类器的目标函数定义为:
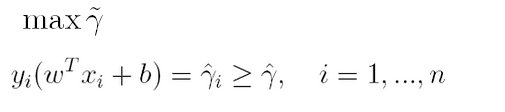
一般地,我们令r^为1(这样做的目的是为了方便推导和目标函数的优化),从而上述目标函数转化为:
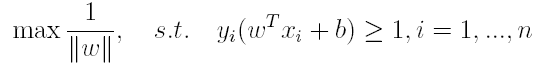
对于y(w’x+b)=1的数据点,即下图中位于w’x+b=1或w’x+b=-1上的数据点,我们称之为支持向量(support vector),易知:对于所有的支持向量,它们恰好满足y(w’x+b)=1,而所有不是支持向量的点,有y(w’x+b)>1。
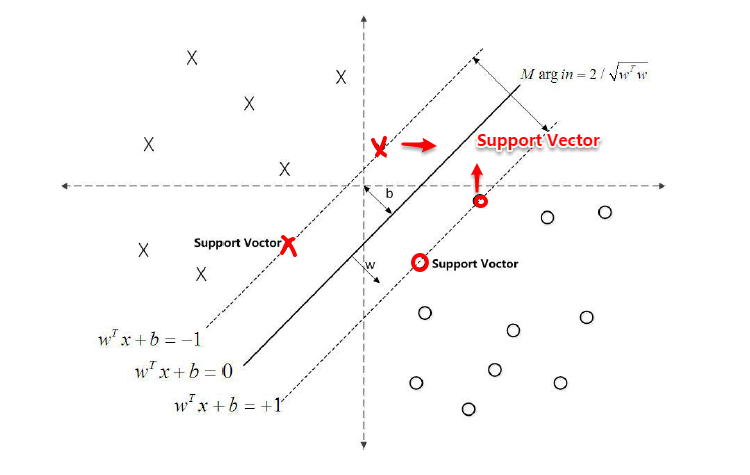
6.3 从原始优化问题到对偶问题
对于上述得到的目标函数,求1/||w||的最大值相当于求||w||^2的最小值,因此很容易将原来的目标函数转化为:
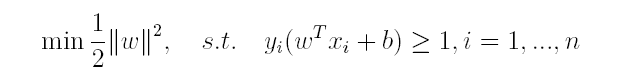
即变为了一个带约束的凸二次规划问题,按书上所说可以使用现成的优化计算包(QP优化包)求解,但由于SVM的特殊性,一般我们将原问题变换为它的对偶问题,接着再对其对偶问题进行求解。为什么通过对偶问题进行求解,有下面两个原因:
* 一是因为使用对偶问题更容易求解;
* 二是因为通过对偶问题求解出现了向量内积的形式,从而能更加自然地引出核函数。
对偶问题,顾名思义,可以理解成优化等价的问题,更一般地,是将一个原始目标函数的最小化转化为它的对偶函数最大化的问题。对于当前的优化问题,首先我们写出它的朗格朗日函数:
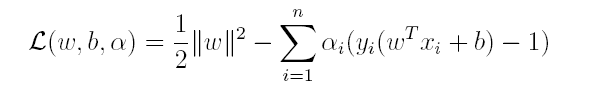
上式很容易验证:
- 当其中有一个约束条件不满足时,L的最大值为 ∞(只需令其对应的α为 ∞即可);
- 当所有约束条件都满足时,L的最大值为1/2||w||^2(此时令所有的α为0)
因此实际上原问题等价于:
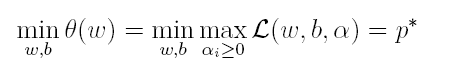
由于这个的求解问题不好做,因此一般我们将最小和最大的位置交换一下(需满足KKT条件) ,变成原问题的对偶问题:
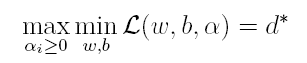
这样就将原问题的求最小变成了对偶问题求最大(用对偶这个词还是很形象),接下来便可以先求L对w和b的极小,再求L对α的极大。
(1)首先求L对w和b的极小,分别求L关于w和b的偏导,可以得出:
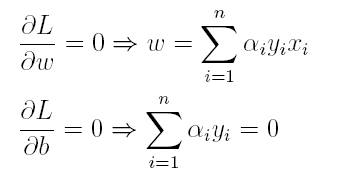
将上述结果代入L得到:
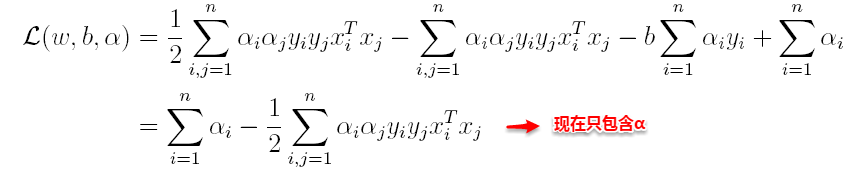
(2)接着L关于α极大求解α(通过SMO算法求解,此处不做深入)。
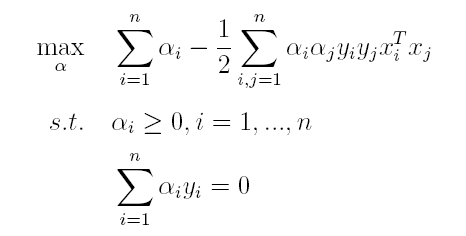
(3)最后便可以根据求解出的α,计算出w和b,从而得到分类超平面函数。
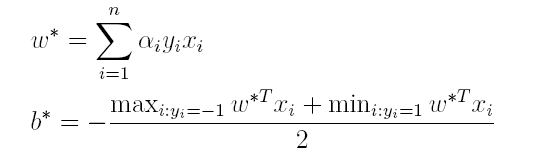
在对新的点进行预测时,实际上就是将数据点x*代入分类函数f(x)=w’x+b中,若f(x)>0,则为正类,f(x)<0,则为负类,根据前面推导得出的w与b,分类函数如下所示,此时便出现了上面所提到的内积形式。
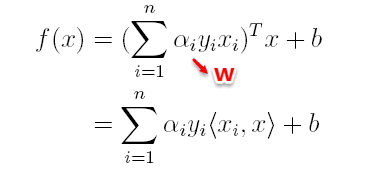
这里实际上只需计算新样本与支持向量的内积,因为对于非支持向量的数据点,其对应的拉格朗日乘子一定为0,根据最优化理论(K-T条件),对于不等式约束y(w’x+b)-1≥0,满足:
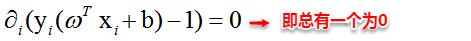
6.4 核函数
由于上述的超平面只能解决线性可分的问题,对于线性不可分的问题,例如:异或问题,我们需要使用核函数将其进行推广。一般地,解决线性不可分问题时,常常采用映射的方式,将低维原始空间映射到高维特征空间,使得数据集在高维空间中变得线性可分,从而再使用线性学习器分类。如果原始空间为有限维,即属性数有限,那么总是存在一个高维特征空间使得样本线性可分。若∅代表一个映射,则在特征空间中的划分函数变为:
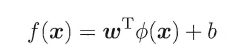
按照同样的方法,先写出新目标函数的拉格朗日函数,接着写出其对偶问题,求L关于w和b的极大,最后运用SOM求解α。可以得出:
(1)原对偶问题变为:
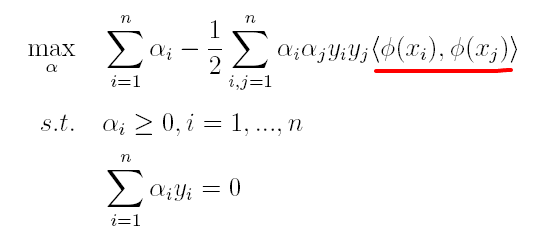
(2)原分类函数变为:
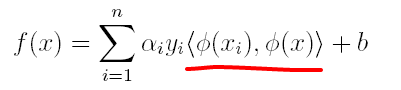
求解的过程中,只涉及到了高维特征空间中的内积运算,由于特征空间的维数可能会非常大,例如:若原始空间为二维,映射后的特征空间为5维,若原始空间为三维,映射后的特征空间将是19维,之后甚至可能出现无穷维,根本无法进行内积运算了,此时便引出了核函数(Kernel)的概念。

因此,核函数可以直接计算隐式映射到高维特征空间后的向量内积,而不需要显式地写出映射后的结果,它虽然完成了将特征从低维到高维的转换,但最终却是在低维空间中完成向量内积计算,与高维特征空间中的计算等效(低维计算,高维表现),从而避免了直接在高维空间无法计算的问题。引入核函数后,原来的对偶问题与分类函数则变为:
(1)对偶问题:
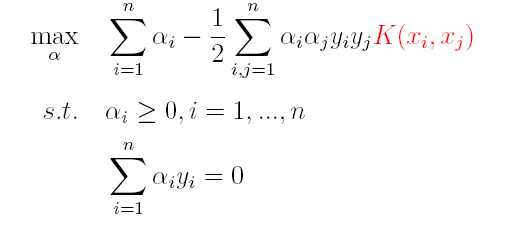
(2)分类函数:
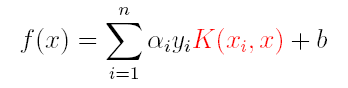
因此,在线性不可分问题中,核函数的选择成了支持向量机的最大变数,若选择了不合适的核函数,则意味着将样本映射到了一个不合适的特征空间,则极可能导致性能不佳。同时,核函数需要满足以下这个必要条件:

由于核函数的构造十分困难,通常我们都是从一些常用的核函数中选择,下面列出了几种常用的核函数:

6.5 软间隔支持向量机
前面的讨论中,我们主要解决了两个问题:
- 当数据线性可分时,直接使用最大间隔的超平面划分;
- 当数据线性不可分时,则通过核函数将数据映射到高维特征空间,使之线性可分。
然而在现实问题中,对于某些情形还是很难处理,例如数据中有噪声的情形,噪声数据(outlier)本身就偏离了正常位置,但是在前面的SVM模型中,我们要求所有的样本数据都必须满足约束,如果不要这些噪声数据还好,当加入这些outlier后导致划分超平面被挤歪了,如下图所示,对支持向量机的泛化性能造成很大的影响。
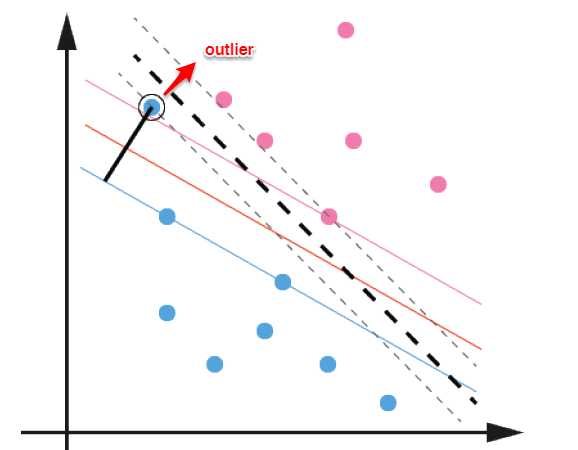
为了解决这一问题,我们需要允许某一些数据点不满足约束,即可以在一定程度上偏移超平面,同时使得不满足约束的数据点尽可能少,这便引出了“软间隔”支持向量机的概念
* 允许某些数据点不满足约束y(w'x+b)≥1;
* 同时又使得不满足约束的样本尽可能少。
这样优化目标变为:
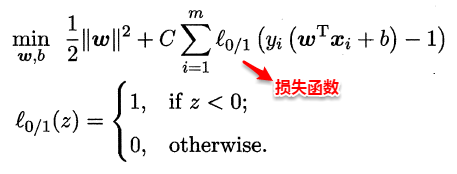
如同阶跃函数,0/1损失函数虽然表示效果最好,但是数学性质不佳。因此常用其它函数作为“替代损失函数”。
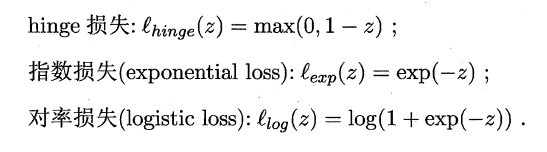
支持向量机中的损失函数为hinge损失,引入“松弛变量”,目标函数与约束条件可以写为:
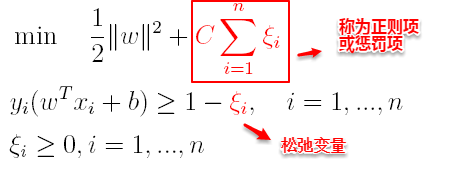
其中C为一个参数,控制着目标函数与新引入正则项之间的权重,这样显然每个样本数据都有一个对应的松弛变量,用以表示该样本不满足约束的程度,将新的目标函数转化为拉格朗日函数得到:
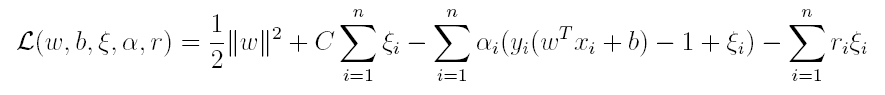
按照与之前相同的方法,先让L求关于w,b以及松弛变量的极小,再使用SMO求出α,有:
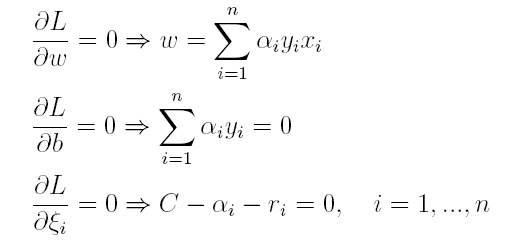
将w代入L化简,便得到其对偶问题:

将“软间隔”下产生的对偶问题与原对偶问题对比可以发现:新的对偶问题只是约束条件中的α多出了一个上限C,其它的完全相同,因此在引入核函数处理线性不可分问题时,便能使用与“硬间隔”支持向量机完全相同的方法。
—-在此SVM就介绍完毕。
(8)贝叶斯
上篇主要介绍和讨论了支持向量机。从最初的分类函数,通过最大化分类间隔,max(1/||w||),min(1/2||w||^2),凸二次规划,朗格朗日函数,对偶问题,一直到最后的SMO算法求解,都为寻找一个最优解。接着引入核函数将低维空间映射到高维特征空间,解决了非线性可分的情形。最后介绍了软间隔支持向量机,解决了outlier挤歪超平面的问题。本篇将讨论一个经典的统计学习算法–贝叶斯分类器。
7、贝叶斯分类器
贝叶斯分类器是一种概率框架下的统计学习分类器,对分类任务而言,假设在相关概率都已知的情况下,贝叶斯分类器考虑如何基于这些概率为样本判定最优的类标。在开始介绍贝叶斯决策论之前,我们首先来回顾下概率论委员会常委–贝叶斯公式。

7.1 贝叶斯决策论
若将上述定义中样本空间的划分Bi看做为类标,A看做为一个新的样本,则很容易将条件概率理解为样本A是类别Bi的概率。在机器学习训练模型的过程中,往往我们都试图去优化一个风险函数,因此在概率框架下我们也可以为贝叶斯定义“条件风险”(conditional risk)。
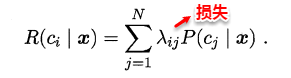
我们的任务就是寻找一个判定准则最小化所有样本的条件风险总和,因此就有了贝叶斯判定准则(Bayes decision rule):为最小化总体风险,只需在每个样本上选择那个使得条件风险最小的类标。
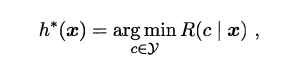
若损失函数λ取0-1损失,则有:
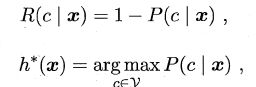
即对于每个样本x,选择其后验概率P(c\|x)最大所对应的类标,能使得总体风险函数最小,从而将原问题转化为估计后验概率P(c\|x)。一般这里有两种策略来对后验概率进行估计:
- 判别式模型:直接对 P(c\|x)进行建模求解。例我们前面所介绍的决策树、神经网络、SVM都是属于判别式模型。
- 生成式模型:通过先对联合分布P(x,c)建模,从而进一步求解 P(c\|x)。
贝叶斯分类器就属于生成式模型,基于贝叶斯公式对后验概率P(c\|x) 进行一项神奇的变换,巴拉拉能量…. P(c\|x)变身:
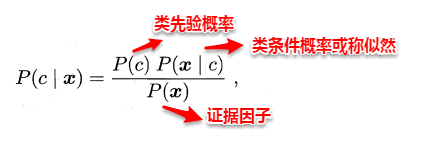
对于给定的样本x,P(x)与类标无关,P(c)称为类先验概率,p(c\|x)称为类条件概率。这时估计后验概率P(c\|x)就变成为估计类先验概率和类条件概率的问题。对于先验概率和后验概率,在看这章之前也是模糊了我好久,这里普及一下它们的基本概念。
- 先验概率: 根据以往经验和分析得到的概率。
- 后验概率:后验概率是基于新的信息,修正原来的先验概率后所获得的更接近实际情况的概率估计。
实际上先验概率就是在没有任何结果出来的情况下估计的概率,而后验概率则是在有一定依据后的重新估计,直观意义上后验概率就是条件概率。下面直接上Wiki上的一个例子,简单粗暴快速完事…

回归正题,对于类先验概率P(c),p(c)就是样本空间中各类样本所占的比例,根据大数定理(当样本足够多时,频率趋于稳定等于其概率),这样当训练样本充足时,p(c)可以使用各类出现的频率来代替。因此只剩下类条件概率p(c\|x),它表达的意思是在类别c中出现x的概率,它涉及到属性的联合概率问题,若只有一个离散属性还好,当属性多时采用频率估计起来就十分困难,因此这里一般采用极大似然法进行估计。
7.2 极大似然法
极大似然估计(Maximum Likelihood Estimation,简称MLE),是一种根据数据采样来估计概率分布的经典方法。常用的策略是先假定总体具有某种确定的概率分布,再基于训练样本对概率分布的参数进行估计。运用到类条件概率p(c\|x )中,假设p(c\|x)服从一个参数为θ的分布,问题就变为根据已知的训练样本来估计θ。
极大似然法的核心思想就是:
估计出的参数使得已知样本出现的概率最大,即使得训练数据的似然最大。

所以,贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程,一般分为以下四个步骤:
- 1.写出似然函数;
- 2.对似然函数取对数,并整理;
- 3.求导数,令偏导数为0,得到似然方程组;
- 4.解似然方程组,得到所有参数即为所求。
例如:假设样本属性都是连续值,p(c\|x)服从一个多维高斯分布,则通过MLE计算出的参数刚好分别为:
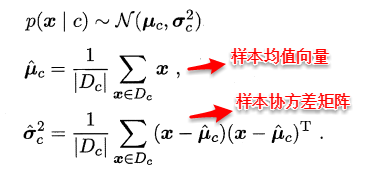
上述结果看起来十分合乎实际,但是采用最大似然法估计参数的效果很大程度上依赖于作出的假设是否合理,是否符合潜在的真实数据分布。这就需要大量的经验知识,搞统计越来越值钱也是这个道理,大牛们掐指一算比我们搬砖几天更有效果。
7.3 朴素贝叶斯分类器
不难看出:原始的贝叶斯分类器最大的问题在于联合概率密度函数的估计,首先需要根据经验来假设联合概率分布,其次当属性很多时,训练样本往往覆盖不够,参数的估计会出现很大的偏差。为了避免这个问题,朴素贝叶斯分类器(naive Bayes classifier)采用了“属性条件独立性假设”,即样本数据的所有属性之间相互独立。这样类条件概率p(c\|x)可以改写为:
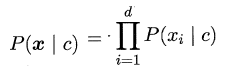
这样,为每个样本估计类条件概率变成为每个样本的每个属性估计类条件概率。

相比原始贝叶斯分类器,朴素贝叶斯分类器基于单个的属性计算类条件概率更加容易操作,需要注意的是:若某个属性值在训练集中和某个类别没有一起出现过,这样会抹掉其它的属性信息,因为该样本的类条件概率被计算为0。因此在估计概率值时,常常用进行平滑(smoothing)处理,拉普拉斯修正(Laplacian correction)就是其中的一种经典方法,具体计算方法如下:

当训练集越大时,拉普拉斯修正引入的影响越来越小。对于贝叶斯分类器,模型的训练就是参数估计,因此可以事先将所有的概率储存好,当有新样本需要判定时,直接查表计算即可。
针对朴素贝叶斯,人们觉得它too sample,sometimes too naive!因此又提出了半朴素的贝叶斯分类器,具体有SPODE、TAN、贝叶斯网络等来刻画属性之间的依赖关系,此处不进行深入,等哪天和贝叶斯邂逅了再回来讨论。在此鼎鼎大名的贝叶斯介绍完毕,下一篇将介绍这一章剩下的内容–EM算法,朴素贝叶斯和EM算法同为数据挖掘的十大经典算法,想着还是单独介绍吧~
(9)EM
上篇主要介绍了贝叶斯分类器,从贝叶斯公式到贝叶斯决策论,再到通过极大似然法估计类条件概率,贝叶斯分类器的训练就是参数估计的过程。朴素贝叶斯则是“属性条件独立性假设”下的特例,它避免了假设属性联合分布过于经验性和训练集不足引起参数估计较大偏差两个大问题,最后介绍的拉普拉斯修正将概率值进行平滑处理。本篇将介绍另一个当选为数据挖掘十大算法之一的EM算法。
8、EM算法
EM(Expectation-Maximization)算法是一种常用的估计参数隐变量的利器,也称为“期望最大算法”,是数据挖掘的十大经典算法之一。EM算法主要应用于训练集样本不完整即存在隐变量时的情形(例如某个属性值未知),通过其独特的“两步走”策略能较好地估计出隐变量的值。
8.1 EM算法思想
EM是一种迭代式的方法,它的基本思想就是:
若样本服从的分布参数θ已知,则可以根据已观测到的训练样本推断出隐变量Z的期望值(E步),若Z的值已知则运用最大似然法估计出新的θ值(M步)。重复这个过程直到Z和θ值不再发生变化。
简单来讲:假设我们想估计A和B这两个参数,在开始状态下二者都是未知的,但如果知道了A的信息就可以得到B的信息,反过来知道了B也就得到了A。可以考虑首先赋予A某种初值,以此得到B的估计值,然后从B的当前值出发,重新估计A的取值,这个过程一直持续到收敛为止。

现在再来回想聚类的代表算法K-Means:
【首先随机选择类中心=>将样本点划分到类簇中=>重新计算类中心=>不断迭代直至收敛】
不难发现这个过程和EM迭代的方法极其相似,事实上,若将样本的类别看做为“隐变量”(latent variable)Z,类中心看作样本的分布参数θ,K-Means就是通过EM算法来进行迭代的,与我们这里不同的是,K-Means的目标是最小化样本点到其对应类中心的距离和,上述为极大化似然函数。
8.2 EM算法数学推导
在上篇极大似然法中,当样本属性值都已知时,我们很容易通过极大化对数似然,接着对每个参数求偏导计算出参数的值。但当存在隐变量时,就无法直接求解,此时我们通常最大化已观察数据的对数“边际似然”(marginal likelihood)。
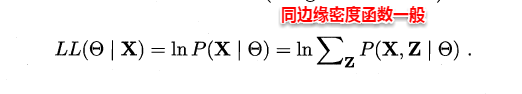
这时候,通过边缘似然将隐变量Z引入进来,对于参数估计,现在与最大似然不同的只是似然函数式中多了一个未知的变量Z,也就是说我们的目标是找到适合的θ和Z让L(θ)最大,这样我们也可以分别对未知的θ和Z求偏导,再令其等于0。
然而观察上式可以发现,和的对数(ln(x1+x2+x3))求导十分复杂,那能否通过变换上式得到一种求导简单的新表达式呢?这时候 Jensen不等式就派上用场了,先回顾一下高等数学凸函数的内容:
Jensen’s inequality:过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方。理解起来也十分简单,对于凸函数f(x)’‘>0,即曲线的变化率是越来越大单调递增的,所以函数越到后面增长越厉害,这样在一个区间下,函数的均值就会大一些了。
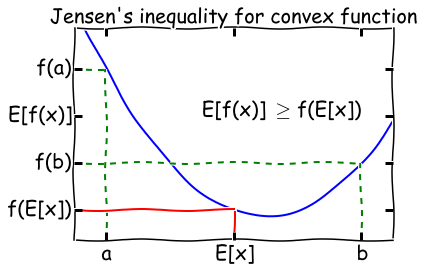
因为ln(*)函数为凹函数,故可以将上式“和的对数”变为“对数的和”,这样就很容易求导了。
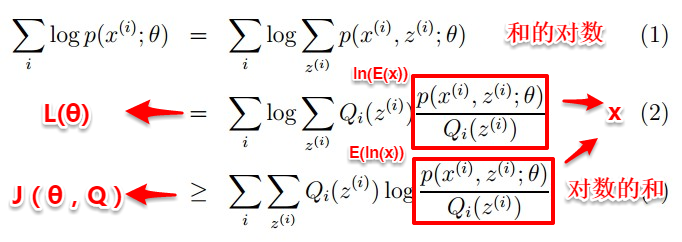
接着求解Qi和θ:首先固定θ(初始值),通过求解Qi使得J(θ,Q)在θ处与L(θ)相等,即求出L(θ)的下界;然后再固定Qi,调整θ,最大化下界J(θ,Q)。不断重复两个步骤直到稳定。通过jensen不等式的性质,Qi的计算公式实际上就是后验概率:
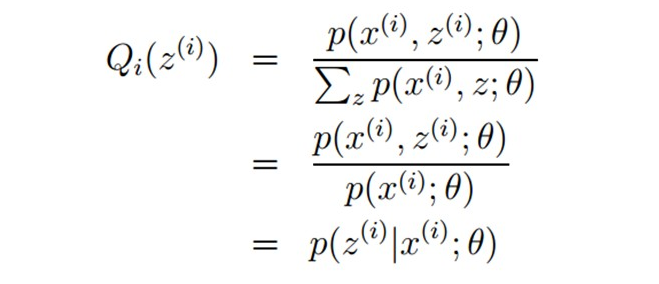
通过数学公式的推导,简单来理解这一过程:
- 固定θ计算Q的过程就是在建立L(θ)的下界,即通过jenson不等式得到的下界(E步);
- 固定Q计算θ则是使得下界极大化(M步),从而不断推高边缘似然L(θ)。
- 从而循序渐进地计算出L(θ)取得极大值时隐变量Z的估计值。
EM算法也可以看作一种“坐标下降法”,首先固定一个值,对另外一个值求极值,不断重复直到收敛。这时候也许大家就有疑问,问什么不直接这两个家伙求偏导用梯度下降呢?这时候就是坐标下降的优势,有些特殊的函数,例如曲线函数z=y^2+x^2+x^2y+xy+…,无法直接求导,这时如果先固定其中的一个变量,再对另一个变量求极值,则变得可行。
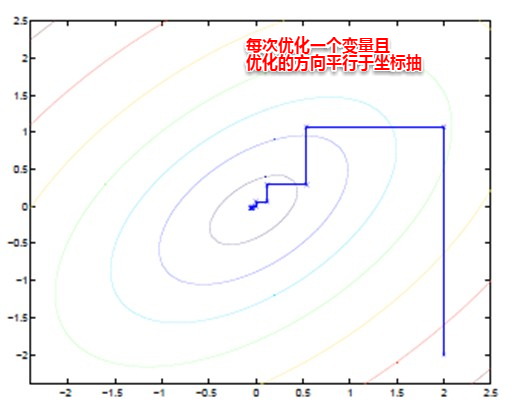
8.3 EM算法流程
看完数学推导,算法的流程也就十分简单了,这里有两个版本,版本一来自西瓜书,周天使的介绍十分简洁;版本二来自于大牛的博客。结合着数学推导,自认为版本二更具有逻辑性,两者唯一的区别就在于版本二多出了红框的部分,这里我也没得到答案,欢迎骚扰讨论~
版本一:

版本二:

(10) 集成学习
- kaggle中关于集成学习的介绍
- 使用sklearn进行集成学习——理论
上篇主要介绍了鼎鼎大名的EM算法,从算法思想到数学公式推导(边际似然引入隐变量,Jensen不等式简化求导),EM算法实际上可以理解为一种坐标下降法,首先固定一个变量,接着求另外变量的最优解,通过其优美的“两步走”策略能较好地估计隐变量的值。本篇将继续讨论下一类经典算法–集成学习。
9、集成学习介绍
顾名思义,集成学习(ensemble learning)指的是将多个学习器进行有效地结合,组建一个“学习器委员会”,其中每个学习器担任委员会成员并行使投票表决权,使得委员会最后的决定更能够四方造福普度众生,即其泛化性能要能优于其中任何一个学习器。
【2021-10-29】比啃西瓜书更好的机器学习视频教程
集成学习先产生一组“个体学习器”(individual learner),再用某种策略将它们结合起来。通常来说,很多现有的学习算法都足以从训练数据中产生一个个体学习器。一般来说,我们会将这种由个体学习器集成的算法分为两类
- 同质(homogeneous)的,即集成中仅包含同种类型的一个体学习器,像“决策树集成”中就仅包含决策树,“神经网络集成”中就全是神经网络。同质集成中的个体学习器又称为基学习器(base learner),相应的学习算法也被称为基学习算法(base learning algorithm)。
- 异质(heterogenous)的,相对同质,异质集成中的个体学习其就是由不同的学习算法生成的,这是,个体学习器就被称为组件学习器(component learner) 其中用的比较多的是同质学习器。同质学习器按照个体学习器之间是否存在依赖关系可以分为两类:
- 第一个是个体学习器之间存在强依赖关系,一系列个体学习器基本都需要串行生成,代表算法是boosting系列算法;
- 第二个是个体学习器之间不存在强依赖关系,一系列个体学习器可以并行生成,代表算法是bagging和随机森林(Random Forest)系列算法。
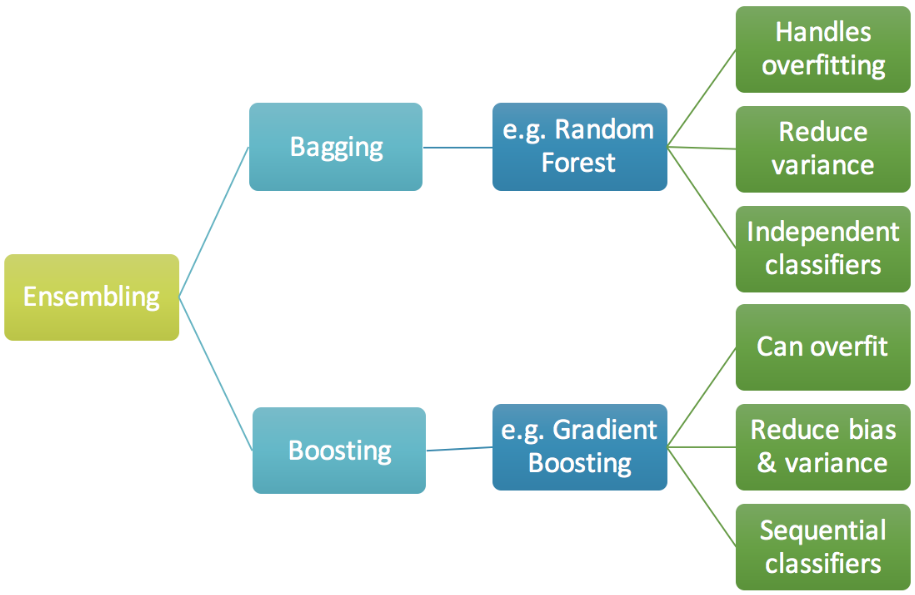
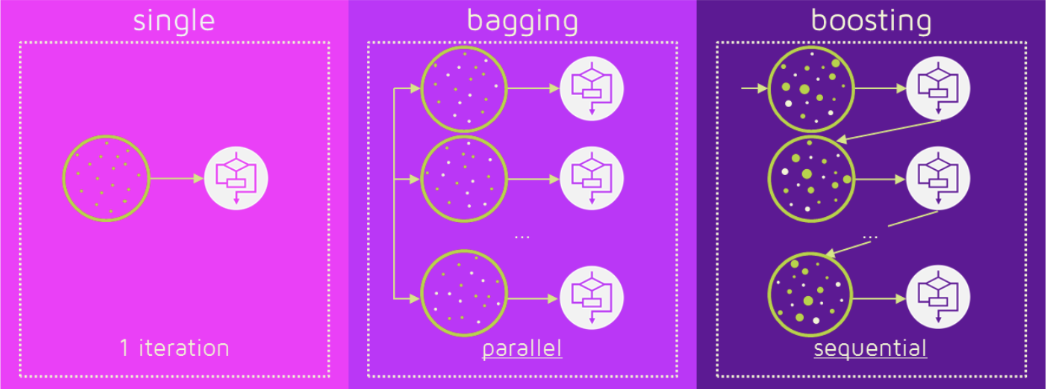
周志华西瓜书中通过Hoeffding不等式证明了,随着集成中个体分类器数目的增大,集成的错误率将指数级下降,最终趋于零。
【2022-5-14】经典机器学习系列之【集成学习】
集成学习先产生一组“个体学习器”(individual learner),再通过某种策略将其结合起来。依据每个个体学习器所采用的学习算法是否相同,可以分为同质集成和异质集成。
- 同质集成中,个体学习器由相同的学习算法生成,个体学习器称为基学习器。
- 异质集成中,个体学习器由不同的学习算法生成,个体学习器称为组件学习器。
集成学习器性能要好于单个个体学习器需要满足好而不同的两点要求:
- 个体学习器效果好,至少好于随机猜测。
- 个体学习器相互独立。 第一个条件相对来说比较容易实现,在当前问题下训练一个模型,结果比瞎猜的结果好就行了。第二个条件是集成学习研究的核心问题。每个个体学习器学习的都是同一个问题,所以个体学习器不可能做到完全相互独立。想想小时候,老师让你发表不同的观点,想想写论文的时候找创新点,人都很难做到这样一件事情,何况它只是一个小小的学习算法。
(1)简易集成方法
- ① 最大投票数 (Max voting):在分类中,每个模型的预测都是一次投票。最终预测来自得票最多的预测即为最大投票数。
- ② 平均 (Averaging):在求平均值时,最终输出是所有预测的平均值。这适用于回归问题。例如,在随机森林回归中,最终结果是来自各个决策树的预测的平均值。
- ③ 加权平均 (Weighted average):在加权平均中,具有更高预测能力的基础模型更为重要。在价格预测示例中,将为每个回归量分配一个权重。权重之和等于一。
(2)高级集成方法
- ① 装袋(Bagging)
- Bagging 随机抽取数据样本,构建学习算法,并使用均值来寻找 Bagging 概率。它也称为 bootstrap 聚合。Bagging 聚合了来自多个模型的结果,以获得一个概括的结果。
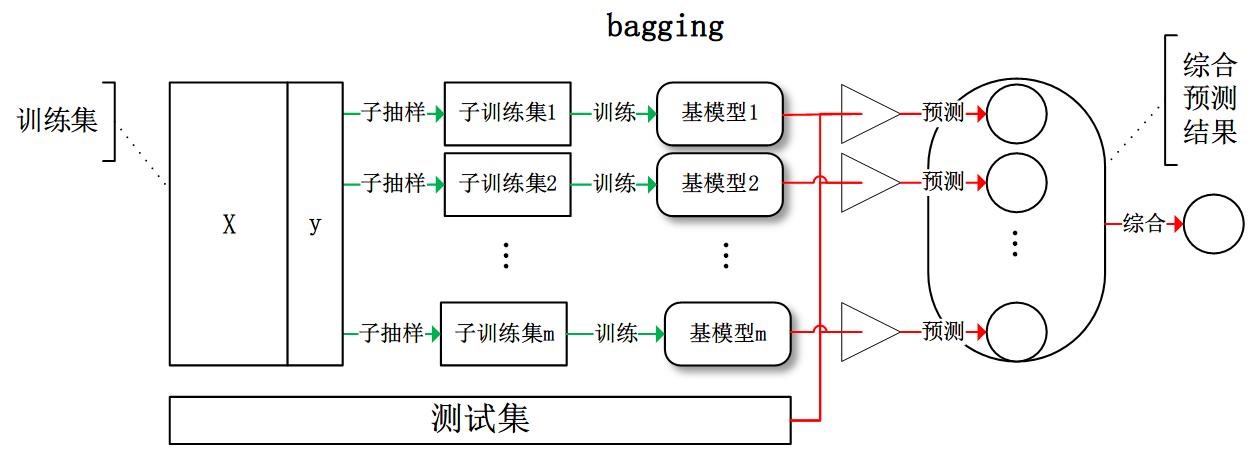
- ② 增强(Boosting)
- Boosting是一种机器学习集成技术,通过将弱学习器转换为强学习器来减少偏差和方差。弱学习器以顺序方式应用于数据集。第一步是构建初始模型并将其拟合到训练集中。然后拟合试图修复第一个模型产生的错误的第二个模型
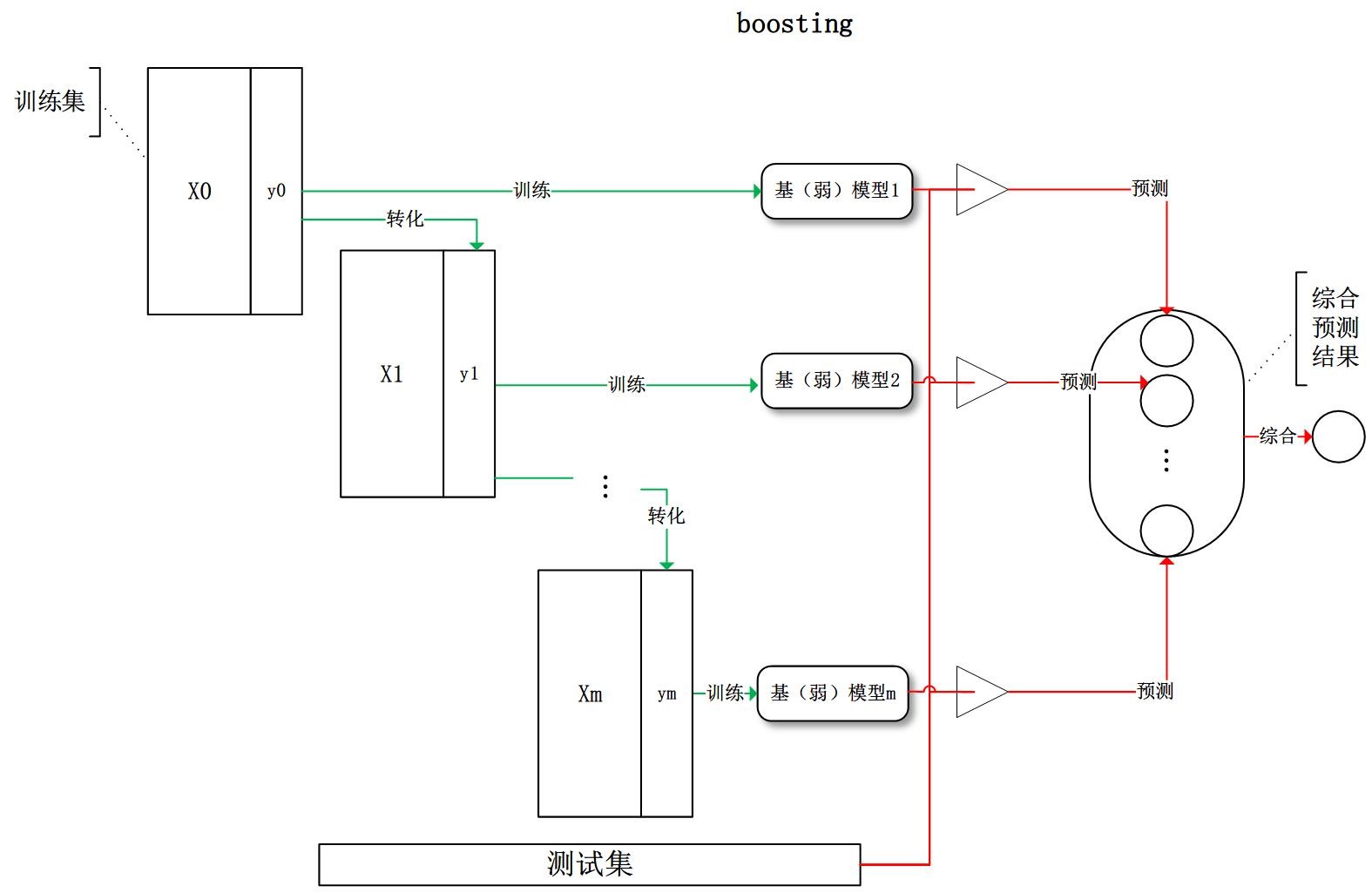
- ③ 堆叠(Stacking):堆叠是组合各种估计量以减少它们的偏差的过程。来自每个估计器的预测堆叠在一起,并用作计算最终预测的最终估计器(通常称为元模型)的输入。最终估计器的训练通过交叉验证进行。堆叠可以用于回归和分类问题。
- ④ 混合(Blending):混合类似于堆叠,但使用训练集中的一个保持集来进行预测。因此,仅在保留集上进行预测。预测和保持集用于构建对测试集进行预测的最终模型。你可以将混合视为一种堆叠,其中元模型根据基本模型在保留验证集上所做的预测进行训练。
- 混合的概念在Kaggle奖竞赛中流行起来,根据Kaggle集成指南:“混合是 Netflix 获奖者引入的一个词。它非常接近于堆叠泛化,但更简单一点,信息泄漏的风险也更小。一些研究人员交替使用“堆叠集成”和“混合”。通过混合,你不是为训练集创建折叠预测,而是创建一个小的保持集,比如训练集的 10%。然后 stacker 模型只在这个保持集上训练。”
- ⑤ 混合与堆叠(Blending vs stacking)
- 混合比堆叠更简单,可以防止模型中的信息泄漏。泛化器和堆栈器使用不同的数据集。但是,混合使用较少的数据并可能导致过度拟合。交叉验证在堆叠上比混合更可靠。与在混合中使用小的保留数据集相比,它计算了更多的折叠。
训练样本扰动:
- 从原始训练样本中产生不同的样本子集,然后利用不同样本子集训练不同的个体学习器。如Bagging中使用的自助采样,Boosting中使用的序列采样。
集成学习工程实现
集成学习常用库广义可以分为有两类:Bagging算法和Boosting算法。
常见的集成学习有以下几种:
- Boosting
- Bagging
- Stacking 其中boosting和bagging应用最多。比如目前流行的xgboost就是(gradient)boosting的一种,而random forest则是bagging的一种。
集成学习模式主要分为两种:
- 采用同一基模型,在样本的不同子集上进行训练,从而得到对应的多个不同的具体模型。这类学习方法的代表就是 boosting, bagging。
- 采用多种基模型,在同一样本上进行训练,将多个模型组合起来得到具体模型。voting 和 stacking都是采用这类方式。
sklearn中对应的方法和模型类型:
| 方法名称 | 基模型 |
|---|---|
| Adaboost | 单个模型 |
| Bagging | 单个模型 |
| Gradient boost | 决策树 |
| Voting | 多个模型 |
| Staking | 多个模型 |
在sklearn中实现这样的集成学习是非常简单的,只需要一句代码即可。训练和预测和直接使用机器学习模型是完全一样的语法。
(1)单一模型集成:单一模型集成 - - 以Adaboost为例
以iris数据集作为样本,将100个Logistic Regression模型用Adaboost集成起来
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
# boost集成方法
from sklearn.ensemble import AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
X, y = load_iris(return_X_y=True)
# 100个同质模型集成
clf = AdaBoostClassifier(LogisticRegression(), n_estimators=100)
# 训练
clf.fit(X,y)
# 预测
clf.predict(X)
# 结果
# array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
# 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
# 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2,
# 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 1, 1, 2, 2, 2, 2,
# 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2])
(2)多模型集成 - - 以Voting例
Voting是一种多模型集成的常用方法,它先将多个模型进行投票,再按照投票结果对模型进行组合。这里我们以iris数据集为基础,将Logistic Regression, 高斯朴素贝叶斯和随机森林进行集成。
from sklearn import datasets
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
# 基模型
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
clf3 = GaussianNB()
# 异质模型组装,投票机制
eclf = VotingClassifier(
# 异质基模型组装
estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
voting='hard')
# 效果评估
for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
scores = cross_val_score(clf, X, y, scoring='accuracy', cv=5)
print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
# 结果
# Accuracy: 0.95 (+/- 0.04) [Logistic Regression]
# Accuracy: 0.94 (+/- 0.04) [Random Forest]
# Accuracy: 0.91 (+/- 0.04) [naive Bayes]
# Accuracy: 0.95 (+/- 0.04) [Ensemble]
9.1 个体与集成
集成学习的基本结构为:先产生一组个体学习器,再使用某种策略将它们结合在一起。集成模型如下图所示:
在上图的集成模型中
- 若个体学习器都属于同一类别,例如都是决策树或神经网络,则称该集成为
同质的(homogeneous); - 若个体学习器包含多种类型,例如既有决策树又有神经网络,则称该集成为
异质的(heterogenous)。
同质集成:个体学习器称为“
基学习器”(base learner),对应的学习算法为“基学习算法”(base learning algorithm)。 异质集成:个体学习器称为“组件学习器”(component learner)或直称为“个体学习器”。
要让集成起来的泛化性能比单个学习器都要好,虽说团结力量大但也有木桶短板理论调皮捣蛋,那如何做到呢?这就引出了集成学习的两个重要概念:准确性和多样性(diversity)。
- 准确性指的是个体学习器不能太差,要有一定的准确度;
- 多样性则是个体学习器之间的输出要具有差异性。
通过下面的这三个例子可以很容易看出这一点,准确度较高,差异度也较高,可以较好地提升集成性能。
现在考虑二分类的简单情形,假设基分类器之间相互独立(能提供较高的差异度),且错误率相等为 ε,则可以将集成器的预测看做一个伯努利实验,易知当所有基分类器中不足一半预测正确的情况下,集成器预测错误,所以集成器的错误率可以计算为:
此时,集成器错误率随着基分类器的个数的增加呈指数下降,但前提是基分类器之间相互独立,在实际情形中显然是不可能的,假设训练有A和B两个分类器,对于某个测试样本,显然满足:P(A=1 | B=1)> P(A=1),因为A和B为了解决相同的问题而训练,因此在预测新样本时存在着很大的联系。因此,个体学习器的“准确性”和“差异性”本身就是一对矛盾的变量,准确性高意味着牺牲多样性,所以产生“好而不同”的个体学习器正是集成学习研究的核心。
现阶段有三种主流的集成学习方法:Boosting、Bagging以及随机森林(Random Forest),接下来将进行逐一介绍。
模型融合就是通过融合多个不同的模型提升性能。
- 最容易理解的模型融合有针对分类问题的Voting和回归问题的Average。
- 在其基础上有改进或稍微复杂的有Bagging,Boosting,Stacking等。
融合策略
Voting:用多个模型对样本进行分类,以“投票”的形式,投票最多者为最终的分类。Average:对不同模型得出的结果取平均或加权平均。
集成方法
Bagging:先利用多次有放回抽样生成不同的训练集, 训练出不同的模型,将这些模型的输出结果通过上述两种方法综合得到最终的结果。随机森林就是基于Bagging算法的一个典型例子。Boosting:一种迭代的方法,每一次训练的时候都更加关心分类错误的样例,增加更大的权重,下次迭代目标就是能够更容易辨别出上一轮分类错误的样例。最终将这些弱分类器进行加权相加。Stacking:本质上是分层结构。第一层是k折交叉的训练集,针对于每一折,由除自己以外的其他的训练数据训练出模型,并以此模型对这一折进行预测。按照此流程进行k次之后,得到用不同模型预测训练集标签的结果,按顺序罗列之后作为第二层的训练集。再用k次训练的模型预测测试集标签,将得到的结果除以k取平均,作为第二层的测试集。随后,我们再用另一个模型去训练第二层的训练集并预测第二层的测试集,获取对原始的测试集的预测结果进行评估。
9.2 Boosting(1990)
Boosting是一种串行的工作机制,即个体学习器的训练存在依赖关系,必须一步一步序列化进行。其基本思想是:
增加前一个基学习器在训练训练过程中预测错误样本的权重,使得后续基学习器更加关注这些打标错误的训练样本,尽可能纠正这些错误,一直向下串行直至产生需要的T个基学习器,Boosting最终对这T个学习器进行加权结合,产生学习器委员会。
1990年,Robert E Schapire提出 Boosting 方法。大体思想是对容易分类错误的训练实例加强学习,与人类重复背英语单词类似。
Boosting族算法最著名、使用最为广泛的就是AdaBoost,因此下面主要是对AdaBoost算法进行介绍。
AdaBoost使用的是指数损失函数,因此AdaBoost的权值与样本分布的更新都是围绕着最小化指数损失函数进行的。看到这里回想一下之前的机器学习算法,不难发现机器学习的大部分带参模型只是改变了最优化目标中的损失函数:
- 如果是Square loss,那就是最小二乘了;
- 如果是Hinge Loss,那就是著名的SVM了;
- 如果是log-Loss,那就是Logistic Regression了。
定义基学习器的集成为加权结合,则有:
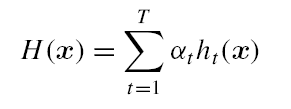 AdaBoost算法的指数损失函数定义为:
AdaBoost算法的指数损失函数定义为: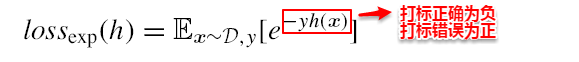
具体说来,整个Adaboost 迭代算法分为3步:
- 初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权值:1/N。
- 训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权值就被降低;相反,如果某个样本点没有被准确地分类,那么它的权值就得到提高。然后,权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
整个AdaBoost的算法流程如下所示:
可以看出:AdaBoost的核心步骤就是计算基学习器权重和样本权重分布,那为何是上述的计算公式呢?这就涉及到了我们之前为什么说大部分带参机器学习算法只是改变了损失函数,就是因为大部分模型的参数都是通过最优化损失函数(可能还加个规则项)而计算(梯度下降,坐标下降等)得到,这里正是通过最优化指数损失函数从而得到这两个参数的计算公式,具体的推导过程此处不进行展开。
Boosting算法要求基学习器能对特定分布的数据进行学习,即每次都更新样本分布权重,这里书上提到了两种方法:“重赋权法”(re-weighting)和“重采样法”(re-sampling),书上的解释有些晦涩,这里进行展开一下:
重赋权法 : 对每个样本附加一个权重,这时涉及到样本属性与标签的计算,都需要乘上一个权值。 重采样法 : 对于一些无法接受带权样本的及学习算法,适合用“重采样法”进行处理。方法大致过程是,根据各个样本的权重,对训练数据进行重采样,初始时样本权重一样,每个样本被采样到的概率一致,每次从N个原始的训练样本中按照权重有放回采样N个样本作为训练集,然后计算训练集错误率,然后调整权重,重复采样,集成多个基学习器。
从偏差-方差分解来看:Boosting算法主要关注于降低偏差,每轮的迭代都关注于训练过程中预测错误的样本,将弱学习提升为强学习器。从AdaBoost的算法流程来看,标准的AdaBoost只适用于二分类问题。在此,当选为数据挖掘十大算法之一的AdaBoost介绍到这里,能够当选正是说明这个算法十分婀娜多姿,背后的数学证明和推导充分证明了这一点,限于篇幅不再继续展开。
- 【2020-12-31】
- Boosting 方法通常考虑的也是同质弱学习器,只不过它的思想是「分而治之」。它以一种高度自适应的方法顺序地学习这些弱学习器,且后续弱模型重点学习上一个弱模型误分类的数据。
- 这就相当于不同的弱分类器,专注于部分数据,达到「分而治之」的效果。如下所示,Boosting 就是以串行组合不同模型的范式。大名鼎鼎的 XGBoost、LightGBM 这些库或算法,都采用的 Boosting 方法。
Sklearn库中,用Gradient Tree Boosting或GBDT(Gradient Boosting Descision Tree)。它是一个关于任意可微损失函数的一个泛化,可以用来解决分类和回归问题。
- n_estimators :控制弱学习器的数量
- learning_rate:控制最后组合中弱学习器的权重,,需要在learning_rate和n_estimators间有个权衡
- max_depth:单个回归估计的最大深度。最大深度限制了树的结点数量。调整该参数的最佳性能:最好的值取决于输入的变量
from sklearn.ensemble import GradientBoostingClassifier # For Classification
from sklearn.ensemble import GradientBoostingRegressor # For Regression
clf = GradientBoostingClassfier(n_estimators=100, learning_rate=1.0, max_depth=1)
clf.fit(X_train, y_train)
9.3 Bagging(1996)
相比之下,Bagging与随机森林算法就简洁了许多,上面已经提到产生“好而不同”的个体学习器是集成学习研究的核心,即在保证基学习器准确性的同时增加基学习器之间的多样性。而这两种算法的基本思想都是通过“自助采样”的方法来增加多样性。
Bagging:
- 1996年,伯克利大学 Leo Breiman 提出 Bagging (Bootstrap AGGregatING)方法。其思想是对训练集有放回抽取训练样例,从而为每一个基本分类器都构造出一个跟训练集同样大小但各不相同的的训练集,从而训练出不同的基本分类器。
Bagging是一种并行式的集成学习方法,即基学习器的训练之间没有前后顺序可以同时进行,Bagging使用“有放回”采样的方式选取训练集,对于包含m个样本的训练集,进行m次有放回的随机采样操作,从而得到m个样本的采样集,这样训练集中有接近36.8%的样本没有被采到。按照相同的方式重复进行,我们就可以采集到T个包含m个样本的数据集,从而训练出T个基学习器,最终对这T个基学习器的输出进行结合。
Bagging算法的流程如下所示:
可以看出Bagging主要通过样本的扰动来增加基学习器之间的多样性,因此Bagging的基学习器应为那些对训练集十分敏感的不稳定学习算法,例如:神经网络与决策树等。从偏差-方差分解来看,Bagging算法主要关注于降低方差,即通过多次重复训练提高稳定性。不同于AdaBoost的是,Bagging可以十分简单地移植到多分类、回归等问题。总的说起来则是:AdaBoost关注于降低偏差,而Bagging关注于降低方差。
- 【2020-12-31】Bagging 方法通常考虑的是同质弱学习器,相互独立地并行学习这些弱学习器,并按照某种确定性的平均过程将它们组合起来。假设所有弱学习器都是决策树模型,那么这样做出来的 Bagging 就是随机森林。
9.3 Random Forest 随机森林(2001) —— Bagging的扩展
输入属性扰动通常是从初始属性集中抽取出若干个属性子集,然后利用不同的属性子集训练出不同的个体学习器。比如:
- 1998年,Tin Kam Ho所提出的随机子空间方法,英文 Random subspace method(RSM),又叫 attribute bagging 或者 feature bagging。随机子空间(RSM)通过使用随机的部分特征,而不是所有特征来训练每个分类器,来降低每个分类器之间的相关性。
- RSM的方法常用于特征数比较多的场景中,如核磁共振、基因组序列、CSI(信道状态信息)。
- 在训练完成之后,依据预测结果再做进一步的处理,如投票或结合先验概率。

- 2001年,Leo Breiman所提出的随机森林(Random Forests)算法。是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。
随机森林(Random Forest)是Bagging的一个拓展体,它的基学习器固定为决策树,多棵树也就组成了森林,而“随机”则在于选择划分属性的随机,随机森林在训练基学习器时,也采用有放回采样的方式添加样本扰动,同时它还引入了一种属性扰动,即在基决策树的训练过程中,在选择划分属性时,RF先从候选属性集中随机挑选出一个包含K个属性的子集,再从这个子集中选择最优划分属性,一般推荐: K=log2(d)
这样随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,从而进一步提升了基学习器之间的差异度。
优缺点
- 相比决策树的Bagging集成,随机森林的起始性能较差(由于属性扰动,基决策树的准确度有所下降),但随着基学习器数目的增多,随机森林往往会收敛到更低的泛化误差。
- 同时不同于Bagging中决策树从所有属性集中选择最优划分属性,随机森林只在属性集的一个子集中选择划分属性,因此训练效率更高。
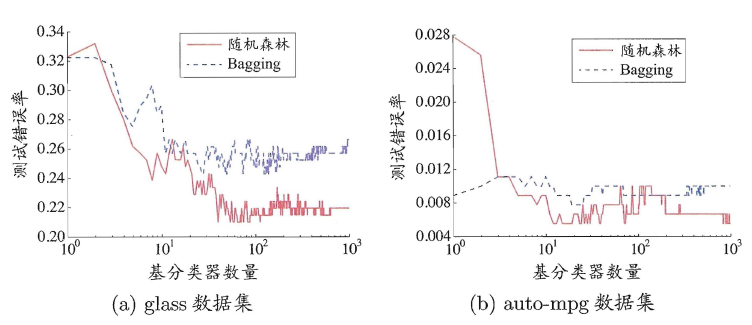
Stacking
Stacking利用交叉验证进行了模型融合,但是双层的训练结构其实也会一定程度上会造成错误的累加。虽然初衷是降低泛化的误差,但是略显复杂的模型结构也容易造成过拟合。
def get_stacking(clf,X_train,y_train,X_test,n_folds):
"""
x_train, y_train, x_test 的值应该为numpy里面的数组类型 numpy.ndarray .
"""
#初始化
train_num, test_num = X_train.shape[0], X_test.shape[0]
second_level_train_set = np.zeros((train_num,))
second_level_test_set = np.zeros((test_num,))
test_nfolds_sets = np.zeros((test_num, n_folds))
#创建k折数据
skf = StratifiedKFold(n_splits=n_folds)
for i,(train_index, test_index) in enumerate(skf.split(X_train,y_train)):
X_tra, y_tra = X_train[train_index], y_train[train_index]
X_tst, y_tst = X_train[test_index], y_train[test_index]
clf.fit(X_tra, y_tra)
#获得第二层训练集
second_level_train_set[test_index] = clf.predict(X_tst)
test_nfolds_sets[:,i] = clf.predict(X_test)
#获得第二层测试集,取平均
second_level_test_set[:] = test_nfolds_sets.mean(axis=1)
return second_level_train_set, second_level_test_set
get_stacking()是针对一个模型进行k折交叉验证。和Voting方法相同,同样导入所需要的的模型。
import joblib
rfmodel = joblib.load("download_w2v_rf.m")
svm1model = joblib.load("download_w2v_svm.m")
svm2model = joblib.load("download_w2v_10epochs_svm.m")
nn1model = joblib.load("download_w2v_nn.m")
nn2model = joblib.load("download_w2v_10epochs_nn.m")
train_sets = []
test_sets = []
for clf in [rfmodel, svm1model, svm2model, nn1model, nn2model]:
train_set, test_set = get_stacking(clf, X_train, y_train, X_test,n_folds=5)
train_sets.append(train_set)
test_sets.append(test_set)
meta_train = np.concatenate([result_set.reshape(-1,1) for result_set in train_sets], axis=1)
meta_test = np.concatenate([y_test_set.reshape(-1,1) for y_test_set in test_sets], axis=1)
这时已经获取了第二层的训练集和测试集,接下来我们再用一个新的模型去进行训练和预测。
from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import f1_score
#Find the svm(rbf) model with highest f1 score
clfsecond = svm.SVC()
grid_values = {'gamma': [0.001, 0.01, 0.05, 0.1, 1, 10],
'C':[0.01, 0.1, 1, 10, 100]}
grid_clf = GridSearchCV(clfsecond, param_grid = grid_values,scoring = 'f1_macro')
grid_clf.fit(meta_train, y_train)
y_grid_pred = grid_clf.predict(meta_test)
print('Test set F1: ', f1_score(y_test,y_grid_pred,average='macro'))
print('Grid best parameter (max. f1): ', grid_clf.best_params_)
print('Grid best score (accuracy): ', grid_clf.best_score_)
最终合适的参数为{‘C’: 10, ‘gamma’: 0.01}。在这组参数下,我们获得的结果为85.83%的准确率和82.65%的macro f1,果然效果不是很好。当然,在这次实践中效果一般,不能否定其价值,也许是我在某些细节上还没有做到位,也欢迎大家给予更多意见和建议。
9.4 结合策略
结合策略指的是在训练好基学习器后,如何将这些基学习器的输出结合起来产生集成模型的最终输出,下面将介绍一些常用的结合策略:
- 简单平均法:简单地将输出结果平均一下
- 加权平均法:乘以权值系数将其加起来。
- 绝对多数投票法(majority voting):即若某标记得票过半数,则分类为该标记,否则拒绝分类。
- 相对多数投票法(plurality voting):分类为得票最多的标记,若同时有多个标记获最高票,则从中随机选取一个。
- 加权投票法(weighted voting):给每个个体学习器预测的类标记赋一个权值,分类为权值最大的标记。这里的权值通常为该个体学习器的分类置信度(类成员概率)。
9.4.1 Average 平均法(回归问题)
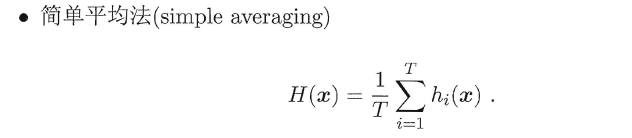
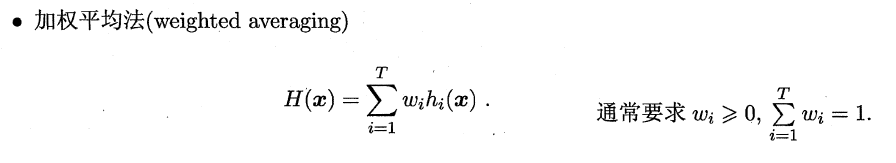
易知简单平均法是加权平均法的一种特例,加权平均法可以认为是集成学习研究的基本出发点。由于各个基学习器的权值在训练中得出,一般而言,在个体学习器性能相差较大时宜使用加权平均法,在个体学习器性能相差较小时宜使用简单平均法。
9.4.2 Voting 投票法(分类问题)

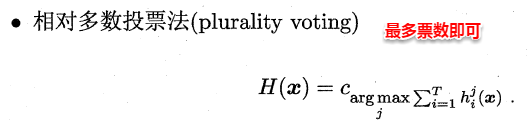
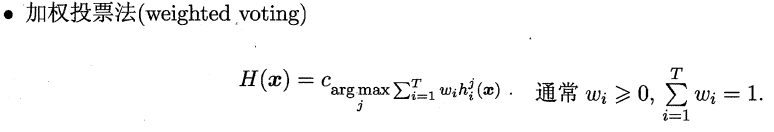
绝对多数投票法(majority voting)提供了拒绝选项,这在可靠性要求很高的学习任务中是一个很好的机制。同时,对于分类任务,各个基学习器的输出值有两种类型,分别为类标记和类概率。

一些在产生类别标记的同时也生成置信度的学习器,置信度可转化为类概率使用,一般基于类概率进行结合往往比基于类标记进行结合的效果更好,需要注意的是对于异质集成,其类概率不能直接进行比较,此时需要将类概率转化为类标记输出,然后再投票。
案例:
- 首先有几个预先存好的模型。最好是奇数个,这样不会出现特别多的平票的情况。
- 用5个模型进行voting,分别是TextCNN,以及5个和10个epochs分别训练出来的Word2Vec模型下,各自的SVM和神经网络分类器。
- 该融合模型可以达到了90.77%的准确率和88.57%的macro f1,这在我目前的所有模型中达到最好的效果,也比上一节只是用SVM分类器多个指标提高了1%以上。
#模型融合
import joblib
import h5py
from tensorflow.keras.models import load_model
#导入五个提前保存好的模型
cnnmodel = load_model('textcnn.h5')
svm1model = joblib.load("download_w2v_svm.m")
svm2model = joblib.load("download_w2v_10epochs_svm.m")
nn1model = joblib.load("download_w2v_nn.m")
nn2model = joblib.load("download_w2v_10epochs_nn.m")
#由于CNN模型和其他分类器模型所产生的标签格式是不一致的
#因此需要应用不同的测试集特征格式,并将预测结果进行统一
y_cnnpred = cnnmodel.predict(X_testcnn, batch_size=64,
verbose=0, steps=None,
callbacks=None, max_queue_size=10,
workers=1, use_multiprocessing=False)
y_svm1pred = svm1model.predict_proba(X_testclf)
y_svm2pred = svm2model.predict_proba(X_testclf)
y_nn1pred = nn1model.predict_proba(X_testclf)
y_nn2pred = nn2model.predict_proba(X_testclf)
#获取one-hot标签形式
y_cnnpred = np.rint(y_cnnpred)
y_nn1pred = np.rint(y_nn1pred)
y_nn2pred = np.rint(y_nn2pred)
y_svm1pred = np.rint(y_svm1pred)
y_svm2pred = np.rint(y_svm2pred)
#加和投票
y_ensemble = y_cnnpred + y_svm1pred + y_svm2pred + y_nn1pred + y_nn2pred
y_pred_ensemble = y_ensemble.argmax(axis=1)
#Confusion Matrix and report
print(confusion_matrix(y_test, y_pred_ensemble))
print(classification_report(y_test, y_pred_ensemble, digits=4))
9.4.3 学习法
学习法是一种更高级的结合策略,即学习出一种“投票”的学习器,Stacking是学习法的典型代表。Stacking的基本思想是:
首先训练出T个基学习器,对于一个样本它们会产生T个输出,将这T个基学习器的输出与该样本的真实标记作为新的样本,m个样本就会产生一个m*T的样本集,来训练一个新的“投票”学习器。
投票学习器的输入属性与学习算法对Stacking集成的泛化性能有很大的影响,书中已经提到:投票学习器采用类概率作为输入属性,选用多响应线性回归(MLR)一般会产生较好的效果。

9.5 多样性(diversity)
在集成学习中,基学习器之间的多样性是影响集成器泛化性能的重要因素。因此增加多样性对于集成学习研究十分重要,一般的思路是在学习过程中引入随机性,常见的做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。
数据样本扰动,即利用具有差异的数据集来训练不同的基学习器。例如:有放回自助采样法,但此类做法只对那些不稳定学习算法十分有效,例如:决策树和神经网络等,训练集的稍微改变能导致学习器的显著变动。 输入属性扰动,即随机选取原空间的一个子空间来训练基学习器。例如:随机森林,从初始属性集中抽取子集,再基于每个子集来训练基学习器。但若训练集只包含少量属性,则不宜使用属性扰动。 输出表示扰动,此类做法可对训练样本的类标稍作变动,或对基学习器的输出进行转化。 算法参数扰动,通过随机设置不同的参数,例如:神经网络中,随机初始化权重与随机设置隐含层节点数。
在此,集成学习就介绍完毕,看到这里,大家也会发现集成学习实质上是一种通用框架,可以使用任何一种基学习器,从而改进单个学习器的泛化性能。据说数据挖掘竞赛KDDCup历年的冠军几乎都使用了集成学习,看来的确是个好东西~
GBDT 并行化
【2023-6-18】 GBDT 并行化训练
常用分布式训练是参数服务器。
- worker把sample的统计结果推送到单台参数服务器机器上,参数服务器汇总后,再推送到worker端。类似于单reducer的方式。
相比于参数服务器的中心化方案,这里提到的都是去中心化方案。
- LightGBM 与 XGBoost的其中一个区别,是实现了真正的分布式,原因是 LightGBM不依托 hive,TaskManager之间可以暴露端口进行通信,而Hivemall依托Hive,只能实现无通信的分布式。
分布式目前一共是4种方案
- Bagging
- 完全非中心化的架构,通过Data Parallel的方式将数据打散为多份,分布式训练,最后训练多颗子树,在最终阶段进行Bagging输出。其实严格来说,这个不是GBDT分布式了,而是一个随机森林了
- Feature Parallel,特征并行流程; 数据量是瓶颈,时间复杂度O(#data)
- 数据按列切分成不同的worker,
- 每个结点保留全部的数据,但分裂时只使用特定的特征,每个worker使用自己的feature进行分裂,输出候选的分裂集splits
- worker之间通信,选取gain提升最多的split,然后统一执行相同的split
- Data Parallel, 通信成本的时间复杂度是O(2 * #feature * #bin)
- 数据并行是类似于Bagging的方式,按照行分裂,区别是在于分裂点的计算上。
- 数据并行下,每个worker统计自己的分裂点的数据
- 汇总操作采用All-reduce的方式(将每台机器的子样本结果,发送给所有机器,然后在每台机器上都reduce全部的子样本;常规的reduce是把子样本结果发送给一台机器,在那台机器上汇总)
- Voting
- 近似算法,认为大样本情况下,局部最优分裂和整体最优分类是近似的
其中
- Bagging方式是不带通信机制的;
- 另外三种则通过通信做到了针对GBDT的分布式训练
LightGBM文档建议按下面方式选择并行方式
- 数据量小 → 特征并行
- 数据和特征都大 → 投票并行
- 否则 → 数据并行
| 维度 | #data is small | #data is large |
|---|---|---|
| #feature is small | Feature Parallel | Data Parallel |
| #feature is large | Feature Parallel | Voting Parallel |
作者:迪吉老农 链接:https://www.jianshu.com/p/529282e5aee8
(11)聚类
上篇主要介绍了一种机器学习的通用框架–集成学习方法,首先从准确性和差异性两个重要概念引出集成学习“好而不同”的四字真言,接着介绍了现阶段主流的三种集成学习方法:
AdaBoost,AdaBoost采用最小化指数损失函数迭代式更新样本分布权重和计算基学习器权重Bagging,Bagging通过自助采样引入样本扰动增加了基学习器之间的差异性Random Forest,随机森林则进一步引入了属性扰动- 最后简单概述了集成模型中的三类结合策略:
平均法、投票法及学习法,其中Stacking是学习法的典型代表。本篇将讨论无监督学习中应用最为广泛的学习算法–聚类。
10、聚类算法
聚类是一种经典的无监督学习方法,无监督学习的目标是通过对无标记训练样本的学习,发掘和揭示数据集本身潜在的结构与规律,即不依赖于训练数据集的类标记信息。聚类则是试图将数据集的样本划分为若干个互不相交的类簇,从而每个簇对应一个潜在的类别。
聚类直观上来说是将相似的样本聚在一起,从而形成一个类簇(cluster)。那首先的问题是如何来度量相似性(similarity measure)呢?这便是距离度量,在生活中我们说差别小则相似,对应到多维样本,每个样本可以对应于高维空间中的一个数据点,若它们的距离相近,我们便可以称它们相似。那接着如何来评价聚类结果的好坏呢?这便是性能度量,性能度量为评价聚类结果的好坏提供了一系列有效性指标。
10.1 距离度量
谈及距离度量,最熟悉的莫过于欧式距离了,从年头一直用到年尾的距离计算公式:即对应属性之间相减的平方和再开根号。度量距离还有其它的很多经典方法,通常它们需要满足一些基本性质:

最常用的距离度量方法是“闵可夫斯基距离”(Minkowski distance):
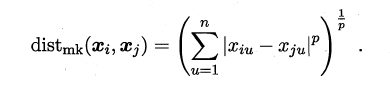
当p=1时,闵可夫斯基距离即曼哈顿距离(Manhattan distance):
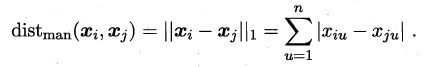
当p=2时,闵可夫斯基距离即欧氏距离(Euclidean distance):
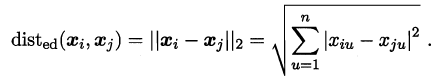
我们知道属性分为两种:连续属性和离散属性(有限个取值)。对于连续值的属性,一般都可以被学习器所用,有时会根据具体的情形作相应的预处理,例如:归一化等;而对于离散值的属性,需要作下面进一步的处理:
若属性值之间存在序关系,则可以将其转化为连续值,例如:身高属性“高”“中等”“矮”,可转化为{1, 0.5, 0}。 若属性值之间不存在序关系,则通常将其转化为向量的形式,例如:性别属性“男”“女”,可转化为{(1,0),(0,1)}。
在进行距离度量时,易知连续属性和存在序关系的离散属性都可以直接参与计算,因为它们都可以反映一种程度,我们称其为“有序属性”;而对于不存在序关系的离散属性,我们称其为:“无序属性”,显然无序属性再使用闵可夫斯基距离就行不通了。
对于无序属性,我们一般采用VDM进行距离的计算,例如:对于离散属性的两个取值a和b,定义:
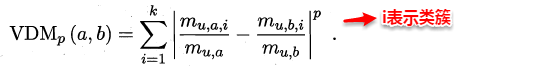
于是,在计算两个样本之间的距离时,我们可以将闵可夫斯基距离和VDM混合在一起进行计算:

若我们定义的距离计算方法是用来度量相似性,例如下面将要讨论的聚类问题,即距离越小,相似性越大,反之距离越大,相似性越小。这时距离的度量方法并不一定需要满足前面所说的四个基本性质,这样的方法称为:非度量距离(non-metric distance)。
10.2 性能度量
由于聚类算法不依赖于样本的真实类标,就不能像监督学习的分类那般,通过计算分对分错(即精确度或错误率)来评价学习器的好坏或作为学习过程中的优化目标。一般聚类有两类性能度量指标:外部指标和内部指标。
10.2.1 外部指标
即将聚类结果与某个参考模型的结果进行比较,以参考模型的输出作为标准,来评价聚类好坏。假设聚类给出的结果为λ,参考模型给出的结果是λ*,则我们将样本进行两两配对,定义:

显然a和b代表着聚类结果好坏的正能量,b和c则表示参考结果和聚类结果相矛盾,基于这四个值可以导出以下常用的外部评价指标:

10.2.2 内部指标
内部指标即不依赖任何外部模型,直接对聚类的结果进行评估,聚类的目的是想将那些相似的样本尽可能聚在一起,不相似的样本尽可能分开,直观来说:簇内高内聚紧紧抱团,簇间低耦合老死不相往来。定义:

基于上面的四个距离,可以导出下面这些常用的内部评价指标:

10.3 原型聚类
原型聚类即“基于原型的聚类”(prototype-based clustering),原型表示模板的意思,就是通过参考一个模板向量或模板分布的方式来完成聚类的过程,常见的K-Means便是基于簇中心来实现聚类,混合高斯聚类则是基于簇分布来实现聚类。
10.3.1 K-Means
K-Means的思想十分简单,首先随机指定类中心,根据样本与类中心的远近划分类簇,接着重新计算类中心,迭代直至收敛。但是其中迭代的过程并不是主观地想象得出,事实上,若将样本的类别看做为“隐变量”(latent variable),类中心看作样本的分布参数,这一过程正是通过EM算法的两步走策略而计算出,其根本的目的是为了最小化平方误差函数E:
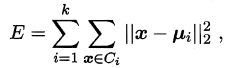
K-Means的算法流程如下所示:

10.3.2 学习向量量化(LVQ)
LVQ也是基于原型的聚类算法,与K-Means不同的是,LVQ使用样本真实类标记辅助聚类,首先LVQ根据样本的类标记,从各类中分别随机选出一个样本作为该类簇的原型,从而组成了一个原型特征向量组,接着从样本集中随机挑选一个样本,计算其与原型向量组中每个向量的距离,并选取距离最小的原型向量所在的类簇作为它的划分结果,再与真实类标比较。
若划分结果正确,则对应原型向量向这个样本靠近一些 若划分结果不正确,则对应原型向量向这个样本远离一些
LVQ算法的流程如下所示:

10.3.3 高斯混合聚类
现在可以看出K-Means与LVQ都试图以类中心作为原型指导聚类,高斯混合聚类则采用高斯分布来描述原型。现假设每个类簇中的样本都服从一个多维高斯分布,那么空间中的样本可以看作由k个多维高斯分布混合而成。
对于多维高斯分布,其概率密度函数如下所示:
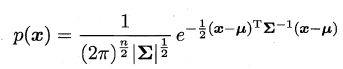
其中u表示均值向量,∑表示协方差矩阵,可以看出一个多维高斯分布完全由这两个参数所确定。接着定义高斯混合分布为:
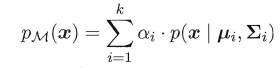
α称为混合系数,这样空间中样本的采集过程则可以抽象为:(1)先选择一个类簇(高斯分布),(2)再根据对应高斯分布的密度函数进行采样,这时候贝叶斯公式又能大展身手了:

此时只需要选择PM最大时的类簇并将该样本划分到其中,看到这里很容易发现:这和那个传说中的贝叶斯分类不是神似吗,都是通过贝叶斯公式展开,然后计算类先验概率和类条件概率。但遗憾的是:这里没有真实类标信息,对于类条件概率,并不能像贝叶斯分类那样通过最大似然法美好地计算出来,因为这里的样本可能属于所有的类簇,这里的似然函数变为:
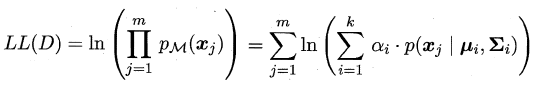
可以看出:简单的最大似然法根本无法求出所有的参数,这样PM也就没法计算。这里就要召唤出之前的EM大法,首先对高斯分布的参数及混合系数进行随机初始化,计算出各个PM(即γji,第i个样本属于j类),再最大化似然函数(即LL(D)分别对α、u和∑求偏导 ),对参数进行迭代更新。
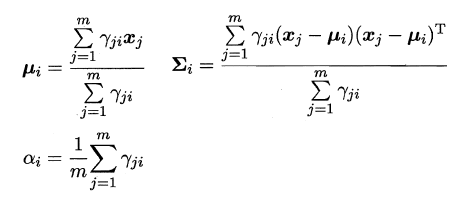
高斯混合聚类的算法流程如下图所示:

10.4 密度聚类
密度聚类则是基于密度的聚类,它从样本分布的角度来考察样本之间的可连接性,并基于可连接性(密度可达)不断拓展疆域(类簇)。其中最著名的便是DBSCAN算法,首先定义以下概念:

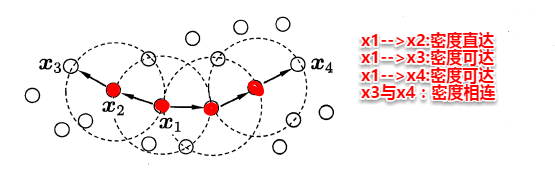
简单来理解DBSCAN便是:找出一个核心对象所有密度可达的样本集合形成簇。首先从数据集中任选一个核心对象A,找出所有A密度可达的样本集合,将这些样本形成一个密度相连的类簇,直到所有的核心对象都遍历完。DBSCAN算法的流程如下图所示:

10.5 层次聚类
层次聚类是一种基于树形结构的聚类方法,常用的是自底向上的结合策略(AGNES算法)。假设有N个待聚类的样本,其基本步骤是:
1.初始化–>把每个样本归为一类,计算每两个类之间的距离,也就是样本与样本之间的相似度; 2.寻找各个类之间最近的两个类,把他们归为一类(这样类的总数就少了一个); 3.重新计算新生成的这个类与各个旧类之间的相似度; 4.重复2和3直到所有样本点都归为一类,结束。
可以看出其中最关键的一步就是计算两个类簇的相似度,这里有多种度量方法:
* 单链接(single-linkage):取类间最小距离。 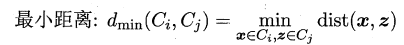
* 全链接(complete-linkage):取类间最大距离 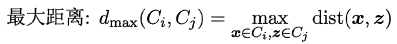
* 均链接(average-linkage):取类间两两的平均距离 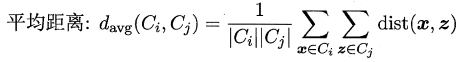
很容易看出:单链接的包容性极强,稍微有点暧昧就当做是自己人了,全链接则是坚持到底,只要存在缺点就坚决不合并,均连接则是从全局出发顾全大局。层次聚类法的算法流程如下所示:

在此聚类算法就介绍完毕,分类/聚类都是机器学习中最常见的任务,我实验室的大Boss也是靠着聚类起家,从此走上人生事业钱途…之巅峰,在书最后的阅读材料还看见Boss的名字,所以这章也是必读不可了…
如何选择聚类数目?
- 【2020-10-26】比elbow方法更好的聚类评估指标
- (1)对于k-means聚类方法,最常用的方法是elbow 方法(又称
肘部法则)。它需要在一个循环中多次运行算法,聚类的数量不断增加,然后绘制聚类得分作为聚类数量的函数。- 得分是k-means目标函数上输入数据的度量,即某种形式的簇内距离相对于簇间距离
- elbow方法的默认k-means得分会产生相对不明确的结果。
- (2)Silhouette Coefficient
- Silhouette Coefficient是用每个样本的平均簇内距离a)和平均最近簇间距离(b)计算出来的。样本的轮廓系数为(b - a) / max(a, b)。
- 平均silhouette系数在k=5时增大,然后k值越大,平均silhouette系数急剧减小,即在k=5处有一个明显的峰值,这就是原始数据集生成的簇数。
- silhouette系数与elbow法的平缓弯曲相比,表现出峰值特性。这更容易可视化和归因。
- (3)BIC评分采用高斯混合模型
- Bayesian Information Criterion (BIC) ,适用于k-means以外的聚类方法—— Gaussian Mixture Model (GMM)。
- GMM将一个数据簇看作是具有独立均值和方差的多个高斯数据集的叠加。然后应用Expectation-Maximization (EM)算法来近似地确定这些平均值和方差。
- jupyter代码实战
(12)降维与度量学习
上篇主要介绍了几种常用的聚类算法,首先从距离度量与性能评估出发,列举了常见的距离计算公式与聚类评价指标,接着分别讨论了K-Means、LVQ、高斯混合聚类、密度聚类以及层次聚类算法。K-Means与LVQ都试图以类簇中心作为原型指导聚类,其中K-Means通过EM算法不断迭代直至收敛,LVQ使用真实类标辅助聚类;高斯混合聚类采用高斯分布来描述类簇原型;密度聚类则是将一个核心对象所有密度可达的样本形成类簇,直到所有核心对象都遍历完;最后层次聚类是一种自底向上的树形聚类方法,不断合并最相近的两个小类簇。本篇将讨论机器学习常用的方法–降维与度量学习。
11、降维与度量学习
样本的特征数称为维数(dimensionality),当维数非常大时,也就是现在所说的“维数灾难”,具体表现在:在高维情形下,数据样本将变得十分稀疏,因为此时要满足训练样本为“密采样”的总体样本数目是一个触不可及的天文数字,谓可远观而不可亵玩焉…训练样本的稀疏使得其代表总体分布的能力大大减弱,从而消减了学习器的泛化能力;同时当维数很高时,计算距离也变得十分复杂,甚至连计算内积都不再容易,这也是为什么支持向量机(SVM)使用核函数“低维计算,高维表现”的原因。
缓解维数灾难的一个重要途径就是降维,即通过某种数学变换将原始高维空间转变到一个低维的子空间。在这个子空间中,样本的密度将大幅提高,同时距离计算也变得容易。这时也许会有疑问,这样降维之后不是会丢失原始数据的一部分信息吗?这是因为在很多实际的问题中,虽然训练数据是高维的,但是与学习任务相关也许仅仅是其中的一个低维子空间,也称为一个低维嵌入,例如:数据属性中存在噪声属性、相似属性或冗余属性等,对高维数据进行降维能在一定程度上达到提炼低维优质属性或降噪的效果。
11.1 K近邻学习
k近邻算法简称kNN(k-Nearest Neighbor),是一种经典的监督学习方法,同时也实力担当入选数据挖掘十大算法。其工作机制十分简单粗暴:给定某个测试样本,kNN基于某种距离度量在训练集中找出与其距离最近的k个带有真实标记的训练样本,然后给基于这k个邻居的真实标记来进行预测,类似于前面集成学习中所讲到的基学习器结合策略:分类任务采用投票法,回归任务则采用平均法。接下来本篇主要就kNN分类进行讨论。
从上图【来自Wiki】中我们可以看到,图中有两种类型的样本,一类是蓝色正方形,另一类是红色三角形。而那个绿色圆形是我们待分类的样本。基于kNN算法的思路,我们很容易得到以下结论:
如果K=3,那么离绿色点最近的有2个红色三角形和1个蓝色的正方形,这3个点投票,于是绿色的这个待分类点属于红色的三角形。 如果K=5,那么离绿色点最近的有2个红色三角形和3个蓝色的正方形,这5个点投票,于是绿色的这个待分类点属于蓝色的正方形。
可以发现:kNN虽然是一种监督学习方法,但是它却没有显式的训练过程,而是当有新样本需要预测时,才来计算出最近的k个邻居,因此kNN是一种典型的懒惰学习方法,再来回想一下朴素贝叶斯的流程,训练的过程就是参数估计,因此朴素贝叶斯也可以懒惰式学习,此类技术在训练阶段开销为零,待收到测试样本后再进行计算。相应地我们称那些一有训练数据立马开工的算法为“急切学习”,可见前面我们学习的大部分算法都归属于急切学习。
很容易看出:kNN算法的核心在于k值的选取以及距离的度量。k值选取太小,模型很容易受到噪声数据的干扰,例如:极端地取k=1,若待分类样本正好与一个噪声数据距离最近,就导致了分类错误;若k值太大, 则在更大的邻域内进行投票,此时模型的预测能力大大减弱,例如:极端取k=训练样本数,就相当于模型根本没有学习,所有测试样本的预测结果都是一样的。一般地我们都通过交叉验证法来选取一个适当的k值。
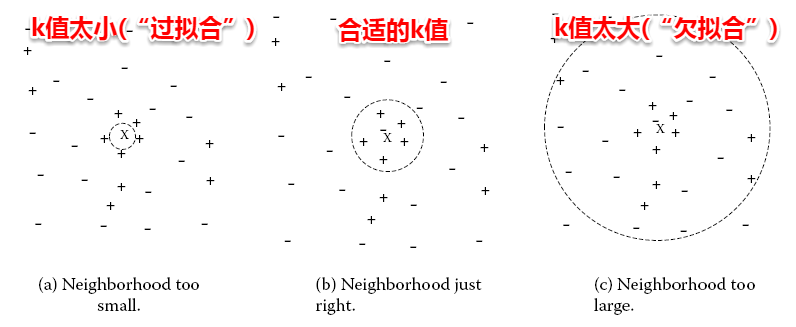
对于距离度量,不同的度量方法得到的k个近邻不尽相同,从而对最终的投票结果产生了影响,因此选择一个合适的距离度量方法也十分重要。在上一篇聚类算法中,在度量样本相似性时介绍了常用的几种距离计算方法,包括闵可夫斯基距离,曼哈顿距离,VDM等。在实际应用中,kNN的距离度量函数一般根据样本的特性来选择合适的距离度量,同时应对数据进行去量纲/归一化处理来消除大量纲属性的强权政治影响。
11.2 MDS算法
不管是使用核函数升维还是对数据降维,我们都希望原始空间样本点之间的距离在新空间中基本保持不变,这样才不会使得原始空间样本之间的关系及总体分布发生较大的改变。“多维缩放”(MDS)正是基于这样的思想,MDS要求原始空间样本之间的距离在降维后的低维空间中得以保持。
假定m个样本在原始空间中任意两两样本之间的距离矩阵为D∈R(mm),我们的目标便是获得样本在低维空间中的表示Z∈R(d’m , d’< d),且任意两个样本在低维空间中的欧式距离等于原始空间中的距离,即||zi-zj||=Dist(ij)。因此接下来我们要做的就是根据已有的距离矩阵D来求解出降维后的坐标矩阵Z。

令降维后的样本坐标矩阵Z被中心化,中心化是指将每个样本向量减去整个样本集的均值向量,故所有样本向量求和得到一个零向量。这样易知:矩阵B的每一列以及每一列求和均为0,因为提取公因子后都有一项为所有样本向量的和向量。
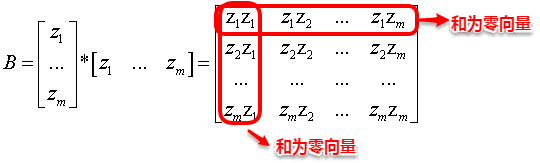
根据上面矩阵B的特征,我们很容易得到等式(2)、(3)以及(4):

这时根据(1)–(4)式我们便可以计算出bij,即*bij=(1)-(2)(1/m)-(3)(1/m)+(4)(1/(m^2))*,再逐一地计算每个b(ij),就得到了降维后低维空间中的内积矩阵B(B=Z’Z),只需对B进行特征值分解便可以得到Z。MDS的算法流程如下图所示:

11.3 主成分分析(PCA)
不同于MDS采用距离保持的方法,主成分分析(PCA)直接通过一个线性变换,将原始空间中的样本投影到新的低维空间中。简单来理解这一过程便是:PCA采用一组新的基来表示样本点,其中每一个基向量都是原来基向量的线性组合,通过使用尽可能少的新基向量来表出样本,从而达到降维的目的。
假设使用d’个新基向量来表示原来样本,实质上是将样本投影到一个由d’个基向量确定的一个超平面上(即舍弃了一些维度),要用一个超平面对空间中所有高维样本进行恰当的表达,最理想的情形是:若这些样本点都能在超平面上表出且这些表出在超平面上都能够很好地分散开来。但是一般使用较原空间低一些维度的超平面来做到这两点十分不容易,因此我们退一步海阔天空,要求这个超平面应具有如下两个性质:
最近重构性:样本点到超平面的距离足够近,即尽可能在超平面附近; 最大可分性:样本点在超平面上的投影尽可能地分散开来,即投影后的坐标具有区分性。
这里十分神奇的是:最近重构性与最大可分性虽然从不同的出发点来定义优化问题中的目标函数,但最终这两种特性得到了完全相同的优化问题:
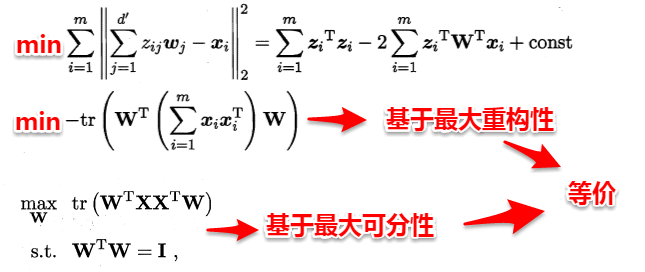
接着使用拉格朗日乘子法求解上面的优化问题,得到:

因此只需对协方差矩阵进行特征值分解即可求解出W,PCA算法的整个流程如下图所示:

另一篇博客给出更通俗更详细的理解:主成分分析解析(基于最大方差理论)
11.4 核化线性降维
说起机器学习你中有我/我中有你/水乳相融…在这里能够得到很好的体现。正如SVM在处理非线性可分时,通过引入核函数将样本投影到高维特征空间,接着在高维空间再对样本点使用超平面划分。这里也是相同的问题:若我们的样本数据点本身就不是线性分布,那还如何使用一个超平面去近似表出呢?因此也就引入了核函数,即先将样本映射到高维空间,再在高维空间中使用线性降维的方法。下面主要介绍核化主成分分析(KPCA)的思想。
若核函数的形式已知,即我们知道如何将低维的坐标变换为高维坐标,这时我们只需先将数据映射到高维特征空间,再在高维空间中运用PCA即可。但是一般情况下,我们并不知道核函数具体的映射规则,例如:Sigmoid、高斯核等,我们只知道如何计算高维空间中的样本内积,这时就引出了KPCA的一个重要创新之处:即空间中的任一向量,都可以由该空间中的所有样本线性表示。证明过程也十分简单:

这样我们便可以将高维特征空间中的投影向量wi使用所有高维样本点线性表出,接着代入PCA的求解问题,得到:

化简到最后一步,发现结果十分的美妙,只需对核矩阵K进行特征分解,便可以得出投影向量wi对应的系数向量α,因此选取特征值前d’大对应的特征向量便是d’个系数向量。这时对于需要降维的样本点,只需按照以下步骤便可以求出其降维后的坐标。可以看出:KPCA在计算降维后的坐标表示时,需要与所有样本点计算核函数值并求和,因此该算法的计算开销十分大。

11.5 流形学习
流形学习(manifold learning)是一种借助拓扑流形概念的降维方法,流形是指在局部与欧式空间同胚的空间,即在局部与欧式空间具有相同的性质,能用欧氏距离计算样本之间的距离。这样即使高维空间的分布十分复杂,但是在局部上依然满足欧式空间的性质,基于流形学习的降维正是这种“邻域保持”的思想。其中等度量映射(Isomap)试图在降维前后保持邻域内样本之间的距离,而局部线性嵌入(LLE)则是保持邻域内样本之间的线性关系,下面将分别对这两种著名的流行学习方法进行介绍。
11.5.1 等度量映射(Isomap)
等度量映射的基本出发点是:高维空间中的直线距离具有误导性,因为有时高维空间中的直线距离在低维空间中是不可达的。因此利用流形在局部上与欧式空间同胚的性质,可以使用近邻距离来逼近测地线距离,即对于一个样本点,它与近邻内的样本点之间是可达的,且距离使用欧式距离计算,这样整个样本空间就形成了一张近邻图,高维空间中两个样本之间的距离就转为最短路径问题。可采用著名的Dijkstra算法或Floyd算法计算最短距离,得到高维空间中任意两点之间的距离后便可以使用MDS算法来其计算低维空间中的坐标。
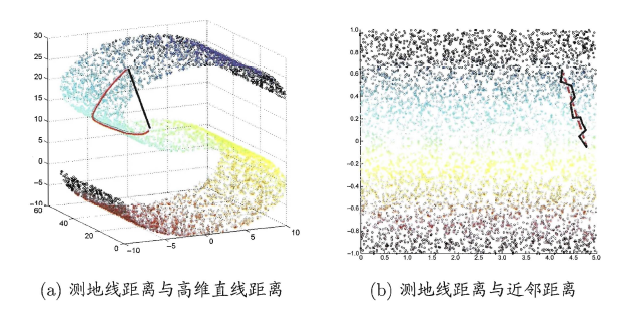
从MDS算法的描述中我们可以知道:MDS先求出了低维空间的内积矩阵B,接着使用特征值分解计算出了样本在低维空间中的坐标,但是并没有给出通用的投影向量w,因此对于需要降维的新样本无从下手,书中给出的权宜之计是利用已知高/低维坐标的样本作为训练集学习出一个“投影器”,便可以用高维坐标预测出低维坐标。Isomap算法流程如下图:

对于近邻图的构建,常用的有两种方法:一种是指定近邻点个数,像kNN一样选取k个最近的邻居;另一种是指定邻域半径,距离小于该阈值的被认为是它的近邻点。但两种方法均会出现下面的问题:
若邻域范围指定过大,则会造成“短路问题”,即本身距离很远却成了近邻,将距离近的那些样本扼杀在摇篮。 若邻域范围指定过小,则会造成“断路问题”,即有些样本点无法可达了,整个世界村被划分为互不可达的小部落。
11.5.2 局部线性嵌入(LLE)
不同于Isomap算法去保持邻域距离,LLE算法试图去保持邻域内的线性关系,假定样本xi的坐标可以通过它的邻域样本线性表出:
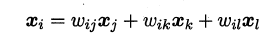
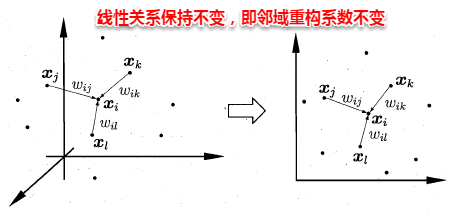
LLE算法分为两步走,首先第一步根据近邻关系计算出所有样本的邻域重构系数w:
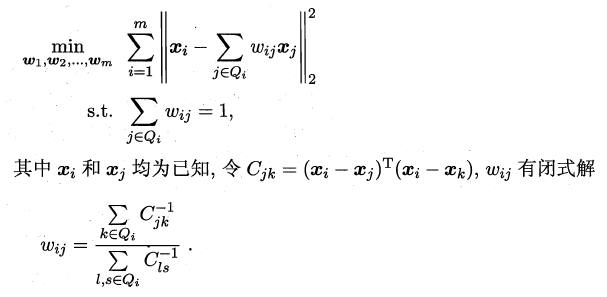
接着根据邻域重构系数不变,去求解低维坐标:
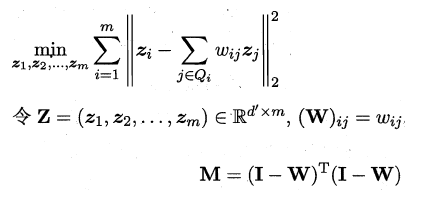
这样利用矩阵M,优化问题可以重写为:

M特征值分解后最小的d’个特征值对应的特征向量组成Z,LLE算法的具体流程如下图所示:

11.6 度量学习
本篇一开始就提到维数灾难,即在高维空间进行机器学习任务遇到样本稀疏、距离难计算等诸多的问题,因此前面讨论的降维方法都试图将原空间投影到一个合适的低维空间中,接着在低维空间进行学习任务从而产生较好的性能。事实上,不管高维空间还是低维空间都潜在对应着一个距离度量,那可不可以直接学习出一个距离度量来等效降维呢?例如:咋们就按照降维后的方式来进行距离的计算,这便是度量学习的初衷。
首先要学习出距离度量必须先定义一个合适的距离度量形式。对两个样本xi与xj,它们之间的平方欧式距离为:
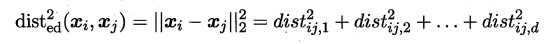
若各个属性重要程度不一样即都有一个权重,则得到加权的平方欧式距离:
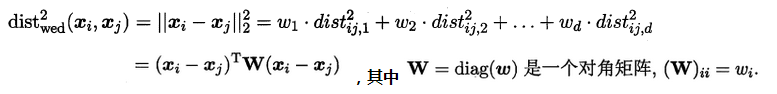
此时各个属性之间都是相互独立无关的,但现实中往往会存在属性之间有关联的情形,例如:身高和体重,一般人越高,体重也会重一些,他们之间存在较大的相关性。这样计算距离就不能分属性单独计算,于是就引入经典的马氏距离(Mahalanobis distance):
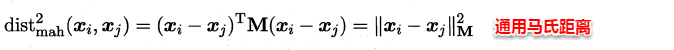
标准的马氏距离中M是协方差矩阵的逆,马氏距离是一种考虑属性之间相关性且尺度无关(即无须去量纲)的距离度量。
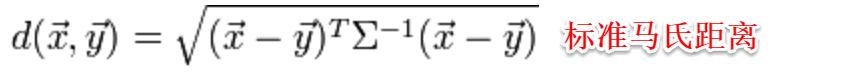
矩阵M也称为“度量矩阵”,为保证距离度量的非负性与对称性,M必须为(半)正定对称矩阵,这样就为度量学习定义好了距离度量的形式,换句话说:度量学习便是对度量矩阵进行学习。现在来回想一下前面我们接触的机器学习不难发现:机器学习算法几乎都是在优化目标函数,从而求解目标函数中的参数。同样对于度量学习,也需要设置一个优化目标,书中简要介绍了错误率和相似性两种优化目标,此处限于篇幅不进行展开。
在此,降维和度量学习就介绍完毕。降维是将原高维空间嵌入到一个合适的低维子空间中,接着在低维空间中进行学习任务;度量学习则是试图去学习出一个距离度量来等效降维的效果,两者都是为了解决维数灾难带来的诸多问题。也许大家最后心存疑惑,那kNN呢,为什么一开头就说了kNN算法,但是好像和后面没有半毛钱关系?正是因为在降维算法中,低维子空间的维数d’通常都由人为指定,因此我们需要使用一些低开销的学习器来选取合适的d’,kNN这家伙懒到家了根本无心学习,在训练阶段开销为零,测试阶段也只是遍历计算了距离,因此拿kNN来进行交叉验证就十分有优势了~同时降维后样本密度增大同时距离计算变易,更为kNN来展示它独特的十八般手艺提供了用武之地。
(13)特征选择与稀疏学习
上篇主要介绍了经典的降维方法与度量学习,首先从“维数灾难”导致的样本稀疏以及距离难计算两大难题出发,引出了降维的概念,即通过某种数学变换将原始高维空间转变到一个低维的子空间,接着分别介绍了kNN、MDS、PCA、KPCA以及两种经典的流形学习方法,k近邻算法的核心在于k值的选取以及距离的度量,MDS要求原始空间样本之间的距离在降维后的低维空间中得以保持,主成分分析试图找到一个低维超平面来表出原空间样本点,核化主成分分析先将样本点映射到高维空间,再在高维空间中使用线性降维的方法,从而解决了原空间样本非线性分布的情形,基于流形学习的降维则是一种“邻域保持”的思想,最后度量学习试图去学习出一个距离度量来等效降维的效果。本篇将讨论另一种常用方法–特征选择与稀疏学习。
12、特征选择与稀疏学习
最近在看论文的过程中,发现对于数据集行和列的叫法颇有不同,故在介绍本篇之前,决定先将最常用的术语罗列一二,以后再见到了不管它脚扑朔还是眼迷离就能一眼识破真身了~对于数据集中的一个对象及组成对象的零件元素:
统计学家常称它们为观测(observation)和变量(variable); 数据库分析师则称其为记录(record)和字段(field); 数据挖掘/机器学习学科的研究者则习惯把它们叫做样本/示例(example/instance)和属性/特征(attribute/feature)。
回归正题,在机器学习中特征选择是一个重要的“数据预处理”(data preprocessing)过程,即试图从数据集的所有特征中挑选出与当前学习任务相关的特征子集,接着再利用数据子集来训练学习器;稀疏学习则是围绕着稀疏矩阵的优良性质,来完成相应的学习任务。
12.1 子集搜索与评价
一般地,我们可以用很多属性/特征来描述一个示例,例如对于一个人可以用性别、身高、体重、年龄、学历、专业、是否吃货等属性来描述,那现在想要训练出一个学习器来预测人的收入。根据生活经验易知:并不是所有的特征都与学习任务相关,例如年龄/学历/专业可能很大程度上影响了收入,身高/体重这些外貌属性也有较小的可能性影响收入,但像是否是一个地地道道的吃货这种属性就八杆子打不着了。因此我们只需要那些与学习任务紧密相关的特征,特征选择便是从给定的特征集合中选出相关特征子集的过程。
与上篇中降维技术有着异曲同工之处的是,特征选择也可以有效地解决维数灾难的难题。具体而言:降维从一定程度起到了提炼优质低维属性和降噪的效果,特征选择则是直接剔除那些与学习任务无关的属性而选择出最佳特征子集。若直接遍历所有特征子集,显然当维数过多时遭遇指数爆炸就行不通了;若采取从候选特征子集中不断迭代生成更优候选子集的方法,则时间复杂度大大减小。这时就涉及到了两个关键环节:1.如何生成候选子集;2.如何评价候选子集的好坏,这便是早期特征选择的常用方法。书本上介绍了贪心算法,分为三种策略:
前向搜索:初始将每个特征当做一个候选特征子集,然后从当前所有的候选子集中选择出最佳的特征子集;接着在上一轮选出的特征子集中添加一个新的特征,同样地选出最佳特征子集;最后直至选不出比上一轮更好的特征子集。 后向搜索:初始将所有特征作为一个候选特征子集;接着尝试去掉上一轮特征子集中的一个特征并选出当前最优的特征子集;最后直到选不出比上一轮更好的特征子集。 双向搜索:将前向搜索与后向搜索结合起来,即在每一轮中既有添加操作也有剔除操作。
对于特征子集的评价,书中给出了一些想法及基于信息熵的方法。假设数据集的属性皆为离散属性,这样给定一个特征子集,便可以通过这个特征子集的取值将数据集合划分为V个子集。例如:A1={男,女},A2={本科,硕士}就可以将原数据集划分为2*2=4个子集,其中每个子集的取值完全相同。这时我们就可以像决策树选择划分属性那样,通过计算信息增益来评价该属性子集的好坏。

此时,信息增益越大表示该属性子集包含有助于分类的特征越多,使用上述这种子集搜索与子集评价相结合的机制,便可以得到特征选择方法。值得一提的是若将前向搜索策略与信息增益结合在一起,与前面我们讲到的ID3决策树十分地相似。事实上,决策树也可以用于特征选择,树节点划分属性组成的集合便是选择出的特征子集。
12.2 过滤式选择(Relief)
过滤式方法是一种将特征选择与学习器训练相分离的特征选择技术,即首先将相关特征挑选出来,再使用选择出的数据子集来训练学习器。Relief是其中著名的代表性算法,它使用一个“相关统计量”来度量特征的重要性,该统计量是一个向量,其中每个分量代表着相应特征的重要性,因此我们最终可以根据这个统计量各个分量的大小来选择出合适的特征子集。
易知Relief算法的核心在于如何计算出该相关统计量。对于数据集中的每个样例xi,Relief首先找出与xi同类别的最近邻与不同类别的最近邻,分别称为猜中近邻(near-hit)与猜错近邻(near-miss),接着便可以分别计算出相关统计量中的每个分量。对于j分量:
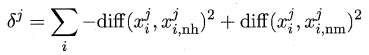
直观上理解:对于猜中近邻,两者j属性的距离越小越好,对于猜错近邻,j属性距离越大越好。更一般地,若xi为离散属性,diff取海明距离,即相同取0,不同取1;若xi为连续属性,则diff为曼哈顿距离,即取差的绝对值。分别计算每个分量,最终取平均便得到了整个相关统计量。
标准的Relief算法只用于二分类问题,后续产生的拓展变体Relief-F则解决了多分类问题。对于j分量,新的计算公式如下:
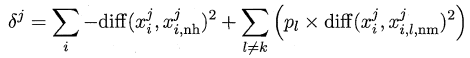
其中pl表示第l类样本在数据集中所占的比例,易知两者的不同之处在于:标准Relief 只有一个猜错近邻,而Relief-F有多个猜错近邻。
12.3 包裹式选择(LVW)
与过滤式选择不同的是,包裹式选择将后续的学习器也考虑进来作为特征选择的评价准则。因此包裹式选择可以看作是为某种学习器量身定做的特征选择方法,由于在每一轮迭代中,包裹式选择都需要训练学习器,因此在获得较好性能的同时也产生了较大的开销。下面主要介绍一种经典的包裹式特征选择方法 –LVW(Las Vegas Wrapper),它在拉斯维加斯框架下使用随机策略来进行特征子集的搜索。拉斯维加斯?怎么听起来那么耳熟,不是那个声名显赫的赌场吗?歪果仁真会玩。怀着好奇科普一下,结果又顺带了一个赌场:
蒙特卡罗算法:采样越多,越近似最优解,一定会给出解,但给出的解不一定是正确解; 拉斯维加斯算法:采样越多,越有机会找到最优解,不一定会给出解,且给出的解一定是正确解。
举个例子,假如筐里有100个苹果,让我每次闭眼拿1个,挑出最大的。于是我随机拿1个,再随机拿1个跟它比,留下大的,再随机拿1个……我每拿一次,留下的苹果都至少不比上次的小。拿的次数越多,挑出的苹果就越大,但我除非拿100次,否则无法肯定挑出了最大的。这个挑苹果的算法,就属于蒙特卡罗算法——尽量找较好的,但不保证是最好的。
而拉斯维加斯算法,则是另一种情况。假如有一把锁,给我100把钥匙,只有1把是对的。于是我每次随机拿1把钥匙去试,打不开就再换1把。我试的次数越多,打开(正确解)的机会就越大,但在打开之前,那些错的钥匙都是没有用的。这个试钥匙的算法,就是拉斯维加斯的——尽量找最好的,但不保证能找到。
LVW算法的具体流程如下所示,其中比较特别的是停止条件参数T的设置,即在每一轮寻找最优特征子集的过程中,若随机T次仍没找到,算法就会停止,从而保证了算法运行时间的可行性。

12.4 嵌入式选择与正则化
前面提到了的两种特征选择方法:过滤式中特征选择与后续学习器完全分离,包裹式则是使用学习器作为特征选择的评价准则;嵌入式是一种将特征选择与学习器训练完全融合的特征选择方法,即将特征选择融入学习器的优化过程中。在之前《经验风险与结构风险》中已经提到:经验风险指的是模型与训练数据的契合度,结构风险则是模型的复杂程度,机器学习的核心任务就是:在模型简单的基础上保证模型的契合度。例如:岭回归就是加上了L2范数的最小二乘法,有效地解决了奇异矩阵、过拟合等诸多问题,下面的嵌入式特征选择则是在损失函数后加上了L1范数。
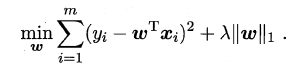
L1范数美名又约Lasso Regularization,指的是向量中每个元素的绝对值之和,这样在优化目标函数的过程中,就会使得w尽可能地小,在一定程度上起到了防止过拟合的作用,同时与L2范数(Ridge Regularization )不同的是,L1范数会使得部分w变为0, 从而达到了特征选择的效果。
总的来说:L1范数会趋向产生少量的特征,其他特征的权值都是0;L2会选择更多的特征,这些特征的权值都会接近于0。这样L1范数在特征选择上就十分有用,而L2范数则具备较强的控制过拟合能力。可以从下面两个方面来理解:
(1)下降速度:L1范数按照绝对值函数来下降,L2范数按照二次函数来下降。因此在0附近,L1范数的下降速度大于L2范数,故L1范数能很快地下降到0,而L2范数在0附近的下降速度非常慢,因此较大可能收敛在0的附近。
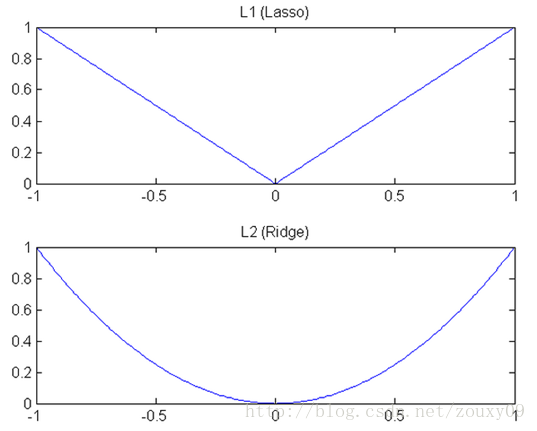
(2)空间限制:L1范数与L2范数都试图在最小化损失函数的同时,让权值W也尽可能地小。我们可以将原优化问题看做为下面的问题,即让后面的规则则都小于某个阈值。这样从图中可以看出:L1范数相比L2范数更容易得到稀疏解。
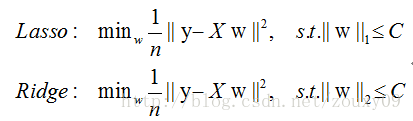
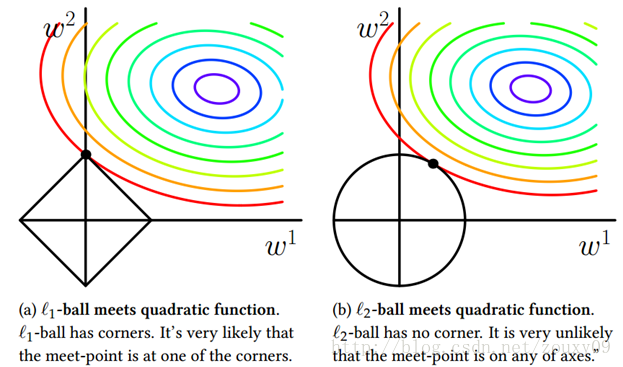
12.5 稀疏表示与字典学习
当样本数据是一个稀疏矩阵时,对学习任务来说会有不少的好处,例如很多问题变得线性可分,储存更为高效等。这便是稀疏表示与字典学习的基本出发点。稀疏矩阵即矩阵的每一行/列中都包含了大量的零元素,且这些零元素没有出现在同一行/列,对于一个给定的稠密矩阵,若我们能通过某种方法找到其合适的稀疏表示,则可以使得学习任务更加简单高效,我们称之为稀疏编码(sparse coding)或字典学习(dictionary learning)。
给定一个数据集,字典学习/稀疏编码指的便是通过一个字典将原数据转化为稀疏表示,因此最终的目标就是求得字典矩阵B及稀疏表示α,书中使用变量交替优化的策略能较好地求得解,深感陷进去短时间无法自拔,故先不进行深入…

12.6 压缩感知
压缩感知在前些年也是风风火火,与特征选择、稀疏表示不同的是:它关注的是通过欠采样信息来恢复全部信息。在实际问题中,为了方便传输和存储,我们一般将数字信息进行压缩,这样就有可能损失部分信息,如何根据已有的信息来重构出全部信号,这便是压缩感知的来历,压缩感知的前提是已知的信息具有稀疏表示。下面是关于压缩感知的一些背景:

在此,特征选择与稀疏学习就介绍完毕。在很多实际情形中,选了好的特征比选了好的模型更为重要,这也是为什么厉害的大牛能够很快地得出一些结论的原因,谓:吾昨晚夜观天象,星象云是否吃货乃无用也~
(14)计算学习理论
上篇主要介绍了常用的特征选择方法及稀疏学习。首先从相关/无关特征出发引出了特征选择的基本概念,接着分别介绍了子集搜索与评价、过滤式、包裹式以及嵌入式四种类型的特征选择方法。子集搜索与评价使用的是一种优中生优的贪婪算法,即每次从候选特征子集中选出最优子集;过滤式方法计算一个相关统计量来评判特征的重要程度;包裹式方法将学习器作为特征选择的评价准则;嵌入式方法则是通过L1正则项将特征选择融入到学习器参数优化的过程中。最后介绍了稀疏表示与压缩感知的核心思想:稀疏表示利用稀疏矩阵的优良性质,试图通过某种方法找到原始稠密矩阵的合适稀疏表示;压缩感知则试图利用可稀疏表示的欠采样信息来恢复全部信息。本篇将讨论一种为机器学习提供理论保证的学习方法–计算学习理论。
13、计算学习理论
计算学习理论(computational learning theory)是通过“计算”来研究机器学习的理论,简而言之,其目的是分析学习任务的本质,例如:在什么条件下可进行有效的学习,需要多少训练样本能获得较好的精度等,从而为机器学习算法提供理论保证。
首先我们回归初心,再来谈谈经验误差和泛化误差。假设给定训练集D,其中所有的训练样本都服从一个未知的分布T,且它们都是在总体分布T中独立采样得到,即独立同分布(independent and identically distributed,i.i.d.),在《贝叶斯分类器》中我们已经提到:独立同分布是很多统计学习算法的基础假设,例如最大似然法,贝叶斯分类器,高斯混合聚类等,简单来理解独立同分布:每个样本都是从总体分布中独立采样得到,而没有拖泥带水。例如现在要进行问卷调查,要从总体人群中随机采样,看到一个美女你高兴地走过去,结果她男票突然冒了出来,说道:you jump,i jump,于是你本来只想调查一个人结果被强行撒了一把狗粮得到两份问卷,这样这两份问卷就不能称为独立同分布了,因为它们的出现具有强相关性。
回归正题,泛化误差指的是学习器在总体上的预测误差,经验误差则是学习器在某个特定数据集D上的预测误差。在实际问题中,往往我们并不能得到总体且数据集D是通过独立同分布采样得到的,因此我们常常使用经验误差作为泛化误差的近似。
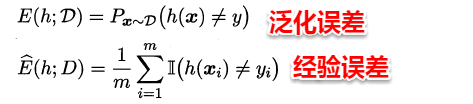
13.1 PAC学习
在高中课本中,我们将函数定义为:从自变量到因变量的一种映射;对于机器学习算法,学习器也正是为了寻找合适的映射规则,即如何从条件属性得到目标属性。从样本空间到标记空间存在着很多的映射,我们将每个映射称之为概念(concept),定义:
若概念c对任何样本x满足c(x)=y,则称c为目标概念,即最理想的映射,所有的目标概念构成的集合称为“概念类”; 给定学习算法,它所有可能映射/概念的集合称为“假设空间”,其中单个的概念称为“假设”(hypothesis); 若一个算法的假设空间包含目标概念,则称该数据集对该算法是可分(separable)的,亦称一致(consistent)的; 若一个算法的假设空间不包含目标概念,则称该数据集对该算法是不可分(non-separable)的,或称不一致(non-consistent)的。
举个简单的例子:对于非线性分布的数据集,若使用一个线性分类器,则该线性分类器对应的假设空间就是空间中所有可能的超平面,显然假设空间不包含该数据集的目标概念,所以称数据集对该学习器是不可分的。给定一个数据集D,我们希望模型学得的假设h尽可能地与目标概念一致,这便是概率近似正确 (Probably Approximately Correct,简称PAC)的来源,即以较大的概率学得模型满足误差的预设上限。




上述关于PAC的几个定义层层相扣:定义12.1表达的是对于某种学习算法,如果能以一个置信度学得假设满足泛化误差的预设上限,则称该算法能PAC辨识概念类,即该算法的输出假设已经十分地逼近目标概念。定义12.2则将样本数量考虑进来,当样本超过一定数量时,学习算法总是能PAC辨识概念类,则称概念类为PAC可学习的。定义12.3将学习器运行时间也考虑进来,若运行时间为多项式时间,则称PAC学习算法。
显然,PAC学习中的一个关键因素就是假设空间的复杂度,对于某个学习算法,若假设空间越大,则其中包含目标概念的可能性也越大,但同时找到某个具体概念的难度也越大,一般假设空间分为有限假设空间与无限假设空间。
13.2 有限假设空间
13.2.1 可分情形
可分或一致的情形指的是:目标概念包含在算法的假设空间中。对于目标概念,在训练集D中的经验误差一定为0,因此首先我们可以想到的是:不断地剔除那些出现预测错误的假设,直到找到经验误差为0的假设即为目标概念。但由于样本集有限,可能会出现多个假设在D上的经验误差都为0,因此问题转化为:需要多大规模的数据集D才能让学习算法以置信度的概率从这些经验误差都为0的假设中找到目标概念的有效近似。

通过上式可以得知:对于可分情形的有限假设空间,目标概念都是PAC可学习的,即当样本数量满足上述条件之后,在与训练集一致的假设中总是可以在1-σ概率下找到目标概念的有效近似。
13.2.2 不可分情形
不可分或不一致的情形指的是:目标概念不存在于假设空间中,这时我们就不能像可分情形时那样从假设空间中寻找目标概念的近似。但当假设空间给定时,必然存一个假设的泛化误差最小,若能找出此假设的有效近似也不失为一个好的目标,这便是不可知学习(agnostic learning)的来源。

这时候便要用到Hoeffding不等式:
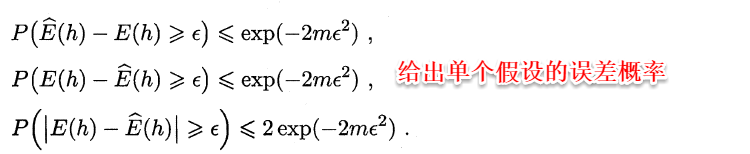
对于假设空间中的所有假设,出现泛化误差与经验误差之差大于e的概率和为:
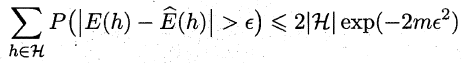
因此,可令不等式的右边小于(等于)σ,便可以求出满足泛化误差与经验误差相差小于e所需的最少样本数,同时也可以求出泛化误差界。
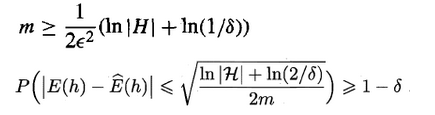
13.3 VC维
现实中的学习任务通常都是无限假设空间,例如d维实数域空间中所有的超平面等,因此要对此种情形进行可学习研究,需要度量假设空间的复杂度。这便是VC维(Vapnik-Chervonenkis dimension)的来源。在介绍VC维之前,需要引入两个概念:
增长函数:对于给定数据集D,假设空间中的每个假设都能对数据集的样本赋予标记,因此一个假设对应着一种打标结果,不同假设对D的打标结果可能是相同的,也可能是不同的。随着样本数量m的增大,假设空间对样本集D的打标结果也会增多,增长函数则表示假设空间对m个样本的数据集D打标的最大可能结果数,因此增长函数描述了假设空间的表示能力与复杂度。
打散:例如对二分类问题来说,m个样本最多有2^m个可能结果,每种可能结果称为一种“对分”,若假设空间能实现数据集D的所有对分,则称数据集能被该假设空间打散。
因此尽管假设空间是无限的,但它对特定数据集打标的不同结果数是有限的,假设空间的VC维正是它能打散的最大数据集大小。通常这样来计算假设空间的VC维:若存在大小为d的数据集能被假设空间打散,但不存在任何大小为d+1的数据集能被假设空间打散,则其VC维为d。
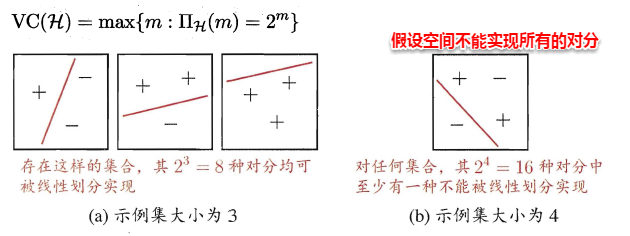
同时书中给出了假设空间VC维与增长函数的两个关系:
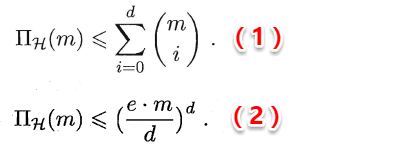
直观来理解(1)式也十分容易: 首先假设空间的VC维是d,说明当m<=d时,增长函数与2^m相等,例如:当m=d时,右边的组合数求和刚好等于2^d;而当m=d+1时,右边等于2^(d+1)-1,十分符合VC维的定义,同时也可以使用数学归纳法证明;(2)式则是由(1)式直接推导得出。
在有限假设空间中,根据Hoeffding不等式便可以推导得出学习算法的泛化误差界;但在无限假设空间中,由于假设空间的大小无法计算,只能通过增长函数来描述其复杂度,因此无限假设空间中的泛化误差界需要引入增长函数。


上式给出了基于VC维的泛化误差界,同时也可以计算出满足条件需要的样本数(样本复杂度)。若学习算法满足经验风险最小化原则(ERM),即学习算法的输出假设h在数据集D上的经验误差最小,可证明:任何VC维有限的假设空间都是(不可知)PAC可学习的,换而言之:若假设空间的最小泛化误差为0即目标概念包含在假设空间中,则是PAC可学习,若最小泛化误差不为0,则称为不可知PAC可学习。
13.4 稳定性
稳定性考察的是当算法的输入发生变化时,输出是否会随之发生较大的变化,输入的数据集D有以下两种变化:

若对数据集中的任何样本z,满足:
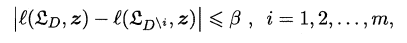
即原学习器和剔除一个样本后生成的学习器对z的损失之差保持β稳定,称学习器关于损失函数满足β-均匀稳定性。同时若损失函数有上界,即原学习器对任何样本的损失函数不超过M,则有如下定理:
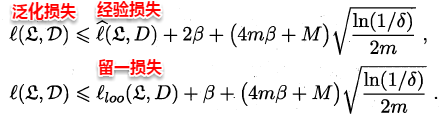
事实上,若学习算法符合经验风险最小化原则(ERM)且满足β-均匀稳定性,则假设空间是可学习的。稳定性通过损失函数与假设空间的可学习联系在了一起,区别在于:假设空间关注的是经验误差与泛化误差,需要考虑到所有可能的假设;而稳定性只关注当前的输出假设。
在此,计算学习理论就介绍完毕,一看这个名字就知道这一章比较偏底层理论了,最终还是咬着牙看完了它,这里引用一段小文字来梳理一下现在的心情:“孤岂欲卿治经为博士邪?但当涉猎,见往事耳”,就当扩充知识体系吧~
(15)半监督学习
上篇主要介绍了机器学习的理论基础,首先从独立同分布引入泛化误差与经验误差,接着介绍了PAC可学习的基本概念,即以较大的概率学习出与目标概念近似的假设(泛化误差满足预设上限),对于有限假设空间:
- (1)可分情形时,假设空间都是PAC可学习的,即当样本满足一定的数量之后,总是可以在与训练集一致的假设中找出目标概念的近似;
- (2)不可分情形时,假设空间都是不可知PAC可学习的,即以较大概率学习出与当前假设空间中泛化误差最小的假设的有效近似(Hoeffding不等式)。
- 对于无限假设空间,通过增长函数与VC维来描述其复杂度,若学习算法满足经验风险最小化原则,则任何VC维有限的假设空间都是(不可知)PAC可学习的,同时也给出了泛化误差界与样本复杂度。稳定性则考察的是输入发生变化时输出的波动,稳定性通过损失函数与假设空间的可学习理论联系在了一起。
本篇将讨论一种介于监督与非监督学习之间的学习算法–半监督学习。
14、半监督学习
前面我们一直围绕的都是监督学习与无监督学习
- 监督学习指的是训练样本包含标记信息的学习任务,例如:常见的分类与回归算法;
- 无监督学习则是训练样本不包含标记信息的学习任务,例如:聚类算法。
在实际生活中,常常会出现一部分样本有标记和较多样本无标记的情形,例如:做网页推荐时需要让用户标记出感兴趣的网页,但是少有用户愿意花时间来提供标记。若直接丢弃掉无标记样本集,使用传统的监督学习方法,常常会由于训练样本的不充足,使得其刻画总体分布的能力减弱,从而影响了学习器泛化性能。那如何利用未标记的样本数据呢?
一种简单的做法是通过专家知识对这些未标记的样本进行打标,但随之而来的就是巨大的人力耗费。若我们先使用有标记的样本数据集训练出一个学习器,再基于该学习器对未标记的样本进行预测,从中挑选出不确定性高或分类置信度低的样本来咨询专家并进行打标,最后使用扩充后的训练集重新训练学习器,这样便能大幅度降低标记成本,这便是主动学习(active learning),其目标是使用尽量少的/有价值的咨询来获得更好的性能。
显然,主动学习需要与外界进行交互/查询/打标,其本质上仍然属于一种监督学习。事实上,无标记样本虽未包含标记信息,但它们与有标记样本一样都是从总体中独立同分布采样得到,因此它们所包含的数据分布信息对学习器的训练大有裨益。如何让学习过程不依赖外界的咨询交互,自动利用未标记样本所包含的分布信息的方法便是半监督学习(semi-supervised learning),即训练集同时包含有标记样本数据和未标记样本数据。
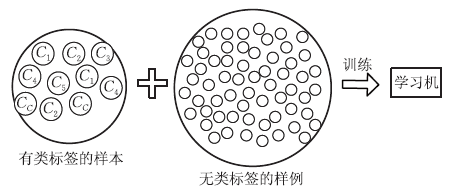
此外,半监督学习还可以进一步划分为纯半监督学习和直推学习,两者的区别在于:前者假定训练数据集中的未标记数据并非待预测数据,而后者假定学习过程中的未标记数据就是待预测数据。主动学习、纯半监督学习以及直推学习三者的概念如下图所示:
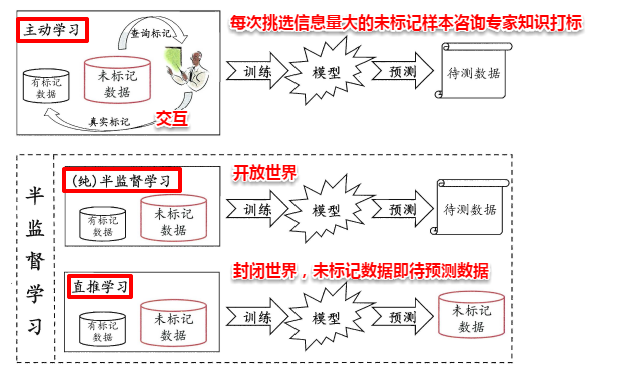
14.1 生成式方法
生成式方法(generative methods)是基于生成式模型的方法,即先对联合分布P(x,c)建模,从而进一步求解 P(c | x),此类方法假定样本数据服从一个潜在的分布,因此需要充分可靠的先验知识。例如:前面已经接触到的贝叶斯分类器与高斯混合聚类,都属于生成式模型。现假定总体是一个高斯混合分布,即由多个高斯分布组合形成,从而一个子高斯分布就代表一个类簇(类别)。高斯混合分布的概率密度函数如下所示:

不失一般性,假设类簇与真实的类别按照顺序一一对应,即第i个类簇对应第i个高斯混合成分。与高斯混合聚类类似地,这里的主要任务也是估计出各个高斯混合成分的参数以及混合系数,不同的是:对于有标记样本,不再是可能属于每一个类簇,而是只能属于真实类标对应的特定类簇。

直观上来看,基于半监督的高斯混合模型有机地整合了贝叶斯分类器与高斯混合聚类的核心思想,有效地利用了未标记样本数据隐含的分布信息,从而使得参数的估计更加准确。同样地,这里也要召唤出之前的EM大法进行求解,首先对各个高斯混合成分的参数及混合系数进行随机初始化,计算出各个PM(即γji,第i个样本属于j类,有标记样本则直接属于特定类),再最大化似然函数(即LL(D)分别对α、u和∑求偏导 ),对参数进行迭代更新。
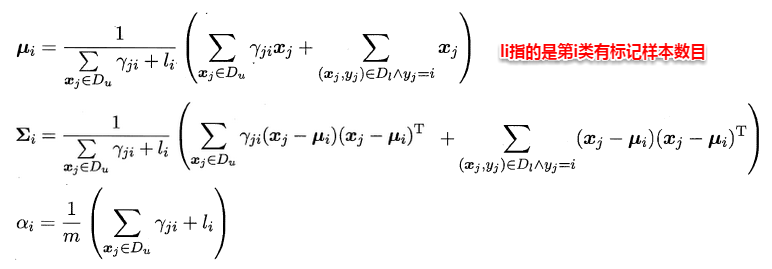
当参数迭代更新收敛后,对于待预测样本x,便可以像贝叶斯分类器那样计算出样本属于每个类簇的后验概率,接着找出概率最大的即可:
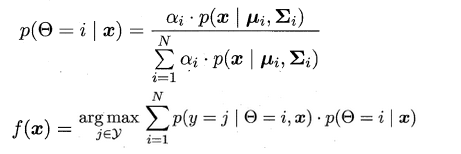
可以看出:基于生成式模型的方法十分依赖于对潜在数据分布的假设,即假设的分布要能和真实分布相吻合,否则利用未标记的样本数据反倒会在错误的道路上渐行渐远,从而降低学习器的泛化性能。因此,此类方法要求极强的领域知识和掐指观天的本领。
14.2 半监督SVM
监督学习中的SVM试图找到一个划分超平面,使得两侧支持向量之间的间隔最大,即“最大划分间隔”思想。对于半监督学习,S3VM则考虑超平面需穿过数据低密度的区域。TSVM是半监督支持向量机中的最著名代表,其核心思想是:尝试为未标记样本找到合适的标记指派,使得超平面划分后的间隔最大化。TSVM采用局部搜索的策略来进行迭代求解,即首先使用有标记样本集训练出一个初始SVM,接着使用该学习器对未标记样本进行打标,这样所有样本都有了标记,并基于这些有标记的样本重新训练SVM,之后再寻找易出错样本不断调整。整个算法流程如下所示:
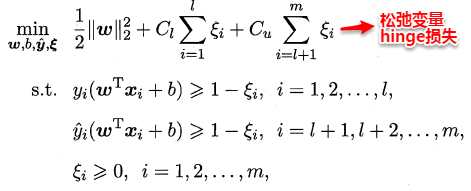

14.3 基于分歧的方法
基于分歧的方法通过多个学习器之间的分歧(disagreement)/多样性(diversity)来利用未标记样本数据,协同训练就是其中的一种经典方法。协同训练最初是针对于多视图(multi-view)数据而设计的,多视图数据指的是样本对象具有多个属性集,每个属性集则对应一个试图。例如:电影数据中就包含画面类属性和声音类属性,这样画面类属性的集合就对应着一个视图。首先引入两个关于视图的重要性质:
相容性:即使用单个视图数据训练出的学习器的输出空间是一致的。例如都是{好,坏}、{+1,-1}等。 互补性:即不同视图所提供的信息是互补/相辅相成的,实质上这里体现的就是集成学习的思想。
协同训练正是很好地利用了多视图数据的“相容互补性”,其基本的思想是:首先基于有标记样本数据在每个视图上都训练一个初始分类器,然后让每个分类器去挑选分类置信度最高的样本并赋予标记,并将带有伪标记的样本数据传给另一个分类器去学习,从而你依我侬/共同进步。
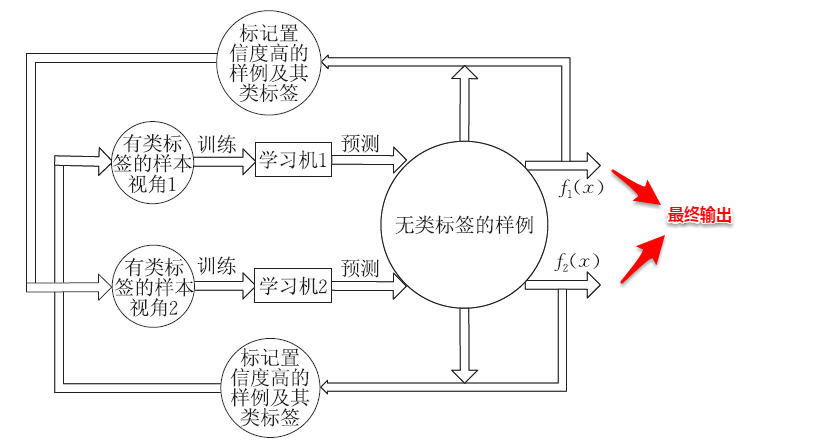

14.4 半监督聚类
前面提到的几种方法都是借助无标记样本数据来辅助监督学习的训练过程,从而使得学习更加充分/泛化性能得到提升;半监督聚类则是借助已有的监督信息来辅助聚类的过程。一般而言,监督信息大致有两种类型:
必连与勿连约束:必连指的是两个样本必须在同一个类簇,勿连则是必不在同一个类簇。 标记信息:少量的样本带有真实的标记。
下面主要介绍两种基于半监督的K-Means聚类算法:第一种是数据集包含一些必连与勿连关系,另外一种则是包含少量带有标记的样本。两种算法的基本思想都十分的简单:对于带有约束关系的k-均值算法,在迭代过程中对每个样本划分类簇时,需要检测当前划分是否满足约束关系,若不满足则会将该样本划分到距离次小对应的类簇中,再继续检测是否满足约束关系,直到完成所有样本的划分。算法流程如下图所示:

对于带有少量标记样本的k-均值算法,则可以利用这些有标记样本进行类中心的指定,同时在对样本进行划分时,不需要改变这些有标记样本的簇隶属关系,直接将其划分到对应类簇即可。算法流程如下所示:

在此,半监督学习就介绍完毕。十分有趣的是:半监督学习将前面许多知识模块联系在了一起,足以体现了作者编排的用心。结合本篇的新知识再来回想之前自己做过的一些研究,发现还是蹚了一些浑水,也许越是觉得过去的自己傻,越就是好的兆头吧~
(16) 概率图模型
上篇主要介绍了半监督学习,首先从如何利用未标记样本所蕴含的分布信息出发,引入了半监督学习的基本概念,即训练数据同时包含有标记样本和未标记样本的学习方法;接着分别介绍了几种常见的半监督学习方法:生成式方法基于对数据分布的假设,利用未标记样本隐含的分布信息,使得对模型参数的估计更加准确;TSVM给未标记样本赋予伪标记,并通过不断调整易出错样本的标记得到最终输出;基于分歧的方法结合了集成学习的思想,通过多个学习器在不同视图上的协作,有效利用了未标记样本数据 ;最后半监督聚类则是借助已有的监督信息来辅助聚类的过程,带约束k-均值算法需检测当前样本划分是否满足约束关系,带标记k-均值算法则利用有标记样本指定初始类中心。本篇将讨论一种基于图的学习算法–概率图模型。
15、概率图模型
现在再来谈谈机器学习的核心价值观,可以更通俗地理解为:根据一些已观察到的证据来推断未知,更具哲学性地可以阐述为:未来的发展总是遵循着历史的规律。其中基于概率的模型将学习任务归结为计算变量的概率分布,正如之前已经提到的:生成式模型先对联合分布进行建模,从而再来求解后验概率,例如:贝叶斯分类器先对联合分布进行最大似然估计,从而便可以计算类条件概率;判别式模型则是直接对条件分布进行建模。
概率图模型(probabilistic graphical model)是一类用图结构来表达各属性之间相关关系的概率模型,一般而言:图中的一个结点表示一个或一组随机变量,结点之间的边则表示变量间的相关关系,从而形成了一张“变量关系图”。若使用有向的边来表达变量之间的依赖关系,这样的有向关系图称为贝叶斯网(Bayesian nerwork)或有向图模型;若使用无向边,则称为马尔可夫网(Markov network)或无向图模型。
15.1 隐马尔可夫模型(HMM)
隐马尔可夫模型(Hidden Markov Model,简称HMM)是结构最简单的一种贝叶斯网,在语音识别与自然语言处理领域上有着广泛的应用。HMM中的变量分为两组:状态变量与观测变量,其中状态变量一般是未知的,因此又称为“隐变量”,观测变量则是已知的输出值。在隐马尔可夫模型中,变量之间的依赖关系遵循如下两个规则:
1. 观测变量的取值仅依赖于状态变量; 2. 下一个状态的取值仅依赖于当前状态,通俗来讲:现在决定未来,未来与过去无关,这就是著名的马尔可夫性。
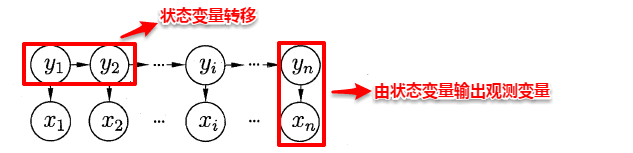
基于上述变量之间的依赖关系,我们很容易写出隐马尔可夫模型中所有变量的联合概率分布:
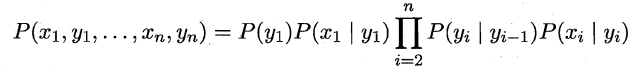
易知:欲确定一个HMM模型需要以下三组参数:

当确定了一个HMM模型的三个参数后,便按照下面的规则来生成观测值序列:

在实际应用中,HMM模型的发力点主要体现在下述三个问题上:

15.1.1 HMM评估问题
HMM评估问题指的是:给定了模型的三个参数与观测值序列,求该观测值序列出现的概率。例如:对于赌场问题,便可以依据骰子掷出的结果序列来计算该结果序列出现的可能性,若小概率的事件发生了则可认为赌场的骰子有作弊的可能。解决该问题使用的是前向算法,即步步为营,自底向上的方式逐步增加序列的长度,直到获得目标概率值。在前向算法中,定义了一个前向变量,即给定观察值序列且t时刻的状态为Si的概率:
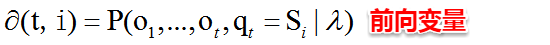
基于前向变量,很容易得到该问题的递推关系及终止条件:

因此可使用动态规划法,从最小的子问题开始,通过填表格的形式一步一步计算出目标结果。
15.1.2 HMM解码问题
HMM解码问题指的是:给定了模型的三个参数与观测值序列,求可能性最大的状态序列。例如:在语音识别问题中,人说话形成的数字信号对应着观测值序列,对应的具体文字则是状态序列,从数字信号转化为文字正是对应着根据观测值序列推断最有可能的状态值序列。解决该问题使用的是Viterbi算法,与前向算法十分类似地,Viterbi算法定义了一个Viterbi变量,也是采用动态规划的方法,自底向上逐步求解。
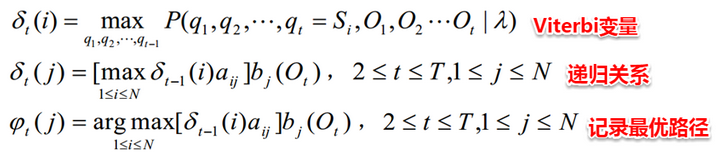
15.1.3 HMM学习问题
HMM学习问题指的是:给定观测值序列,如何调整模型的参数使得该序列出现的概率最大。这便转化成了机器学习问题,即从给定的观测值序列中学习出一个HMM模型,该问题正是EM算法的经典案例之一。其思想也十分简单:对于给定的观测值序列,如果我们能够按照该序列潜在的规律来调整模型的三个参数,则可以使得该序列出现的可能性最大。假设状态值序列也已知,则很容易计算出与该序列最契合的模型参数:

但一般状态值序列都是不可观测的,且即使给定观测值序列与模型参数,状态序列仍然遭遇组合爆炸。因此上面这种简单的统计方法就行不通了,若将状态值序列看作为隐变量,这时便可以考虑使用EM算法来对该问题进行求解:
- 【1】首先对HMM模型的三个参数进行随机初始化;
- 【2】根据模型的参数与观测值序列,计算t时刻状态为i且t+1时刻状态为j的概率以及t时刻状态为i的概率。

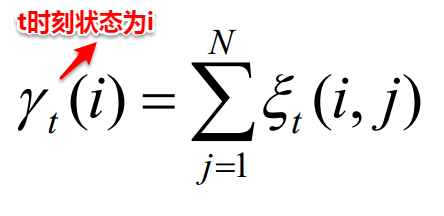
- 【3】接着便可以对模型的三个参数进行重新估计:

- 【4】重复步骤2-3,直至三个参数值收敛,便得到了最终的HMM模型。
15.2 马尔可夫随机场(MRF)
马尔可夫随机场(Markov Random Field)是一种典型的马尔可夫网,即使用无向边来表达变量间的依赖关系。在马尔可夫随机场中,对于关系图中的一个子集,若任意两结点间都有边连接,则称该子集为一个团;若再加一个结点便不能形成团,则称该子集为极大团。MRF使用势函数来定义多个变量的概率分布函数,其中每个(极大)团对应一个势函数,一般团中的变量关系也体现在它所对应的极大团中,因此常常基于极大团来定义变量的联合概率分布函数。具体而言,若所有变量构成的极大团的集合为C,则MRF的联合概率函数可以定义为:

对于条件独立性,马尔可夫随机场通过分离集来实现条件独立,若A结点集必须经过C结点集才能到达B结点集,则称C为分离集。书上给出了一个简单情形下的条件独立证明过程,十分贴切易懂,此处不再展开。基于分离集的概念,得到了MRF的三个性质:
全局马尔可夫性:给定两个变量子集的分离集,则这两个变量子集条件独立。 局部马尔可夫性:给定某变量的邻接变量,则该变量与其它变量条件独立。 成对马尔可夫性:给定所有其他变量,两个非邻接变量条件独立。
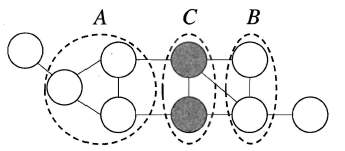
对于MRF中的势函数,势函数主要用于描述团中变量之间的相关关系,且要求为非负函数,直观来看:势函数需要在偏好的变量取值上函数值较大,例如:若x1与x2成正相关,则需要将这种关系反映在势函数的函数值中。一般我们常使用指数函数来定义势函数:

15.3 条件随机场(CRF)
前面所讲到的隐马尔可夫模型和马尔可夫随机场都属于生成式模型,即对联合概率进行建模,条件随机场则是对条件分布进行建模。CRF试图在给定观测值序列后,对状态序列的概率分布进行建模,即P(y | x)。直观上看:CRF与HMM的解码问题十分类似,都是在给定观测值序列后,研究状态序列可能的取值。CRF可以有多种结构,只需保证状态序列满足马尔可夫性即可,一般我们常使用的是链式条件随机场:
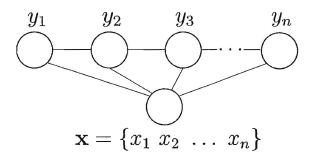
与马尔可夫随机场定义联合概率类似地,CRF也通过团以及势函数的概念来定义条件概率P(y | x)。在给定观测值序列的条件下,链式条件随机场主要包含两种团结构:单个状态团及相邻状态团,通过引入两类特征函数便可以定义出目标条件概率:
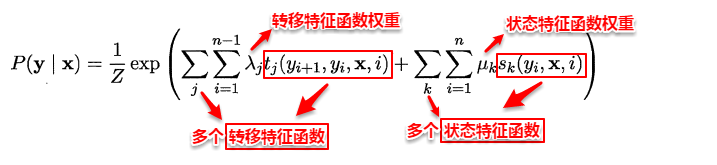
以词性标注为例,如何判断给出的一个标注序列靠谱不靠谱呢?转移特征函数主要判定两个相邻的标注是否合理,例如:动词+动词显然语法不通;状态特征函数则判定观测值与对应的标注是否合理,例如: ly结尾的词–>副词较合理。因此我们可以定义一个特征函数集合,用这个特征函数集合来为一个标注序列打分,并据此选出最靠谱的标注序列。也就是说,每一个特征函数(对应一种规则)都可以用来为一个标注序列评分,把集合中所有特征函数对同一个标注序列的评分综合起来,就是这个标注序列最终的评分值。可以看出:特征函数是一些经验的特性。
15.4 学习与推断
对于生成式模型,通常我们都是先对变量的联合概率分布进行建模,接着再求出目标变量的边际分布(marginal distribution),那如何从联合概率得到边际分布呢?这便是学习与推断。下面主要介绍两种精确推断的方法:变量消去与信念传播。
15.4.1 变量消去
变量消去利用条件独立性来消减计算目标概率值所需的计算量,它通过运用乘法与加法的分配率,将对变量的积的求和问题转化为对部分变量交替进行求积与求和的问题,从而将每次的运算控制在局部,达到简化运算的目的。
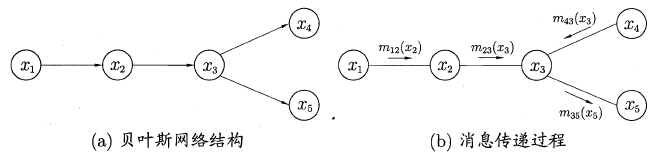
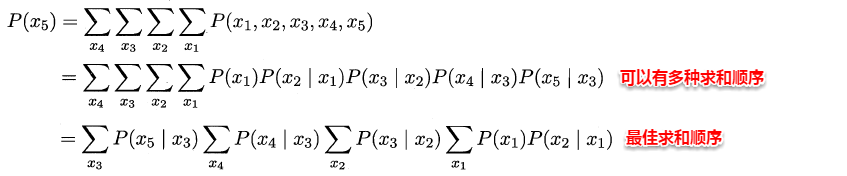
15.4.2 信念传播
若将变量求和操作看作是一种消息的传递过程,信念传播可以理解成:一个节点在接收到所有其它节点的消息后才向另一个节点发送消息,同时当前节点的边际概率正比于他所接收的消息的乘积:
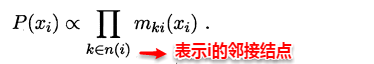
因此只需要经过下面两个步骤,便可以完成所有的消息传递过程。利用动态规划法的思想记录传递过程中的所有消息,当计算某个结点的边际概率分布时,只需直接取出传到该结点的消息即可,从而避免了计算多个边际分布时的冗余计算问题。
1.指定一个根节点,从所有的叶节点开始向根节点传递消息,直到根节点收到所有邻接结点的消息(从叶到根); 2.从根节点开始向叶节点传递消息,直到所有叶节点均收到消息(从根到叶)。
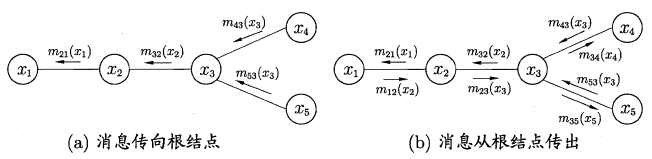
15.5 LDA话题模型
话题模型主要用于处理文本类数据,其中隐狄利克雷分配模型(Latent Dirichlet Allocation,简称LDA)是话题模型的杰出代表。在话题模型中,有以下几个基本概念:词(word)、文档(document)、话题(topic)。
词:最基本的离散单元; 文档:由一组词组成,词在文档中不计顺序; 话题:由一组特定的词组成,这组词具有较强的相关关系。
在现实任务中,一般我们可以得出一个文档的词频分布,但不知道该文档对应着哪些话题,LDA话题模型正是为了解决这个问题。具体来说:LDA认为每篇文档包含多个话题,且其中每一个词都对应着一个话题。因此可以假设文档是通过如下方式生成:

这样一个文档中的所有词都可以认为是通过话题模型来生成的,当已知一个文档的词频分布后(即一个N维向量,N为词库大小),则可以认为:每一个词频元素都对应着一个话题,而话题对应的词频分布则影响着该词频元素的大小。因此很容易写出LDA模型对应的联合概率函数:
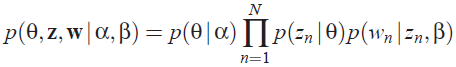
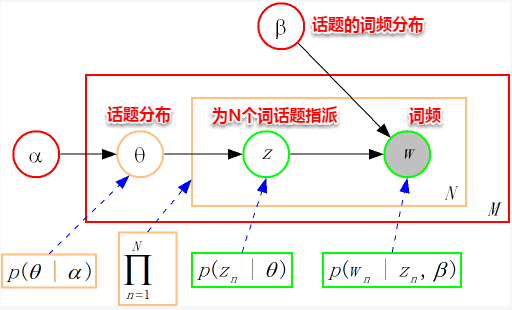
从上图可以看出,LDA的三个表示层被三种颜色表示出来:
corpus-level(红色): α和β表示语料级别的参数,也就是每个文档都一样,因此生成过程只采样一次。 document-level(橙色): θ是文档级别的变量,每个文档对应一个θ。 word-level(绿色): z和w都是单词级别变量,z由θ生成,w由z和β共同生成,一个单词w对应一个主题z。
通过上面对LDA生成模型的讨论,可以知道LDA模型主要是想从给定的输入语料中学习训练出两个控制参数α和β,当学习出了这两个控制参数就确定了模型,便可以用来生成文档。其中α和β分别对应以下各个信息:
α:分布p(θ)需要一个向量参数,即Dirichlet分布的参数,用于生成一个主题θ向量; β:各个主题对应的单词概率分布矩阵p(w|z)。
把w当做观察变量,θ和z当做隐藏变量,就可以通过EM算法学习出α和β,求解过程中遇到后验概率p(θ,z|w)无法直接求解,需要找一个似然函数下界来近似求解,原作者使用基于分解(factorization)假设的变分法(varialtional inference)进行计算,用到了EM算法。每次E-step输入α和β,计算似然函数,M-step最大化这个似然函数,算出α和β,不断迭代直到收敛。
在此,概率图模型就介绍完毕。上周受到协同训练的启发,让实验的小伙伴做了一个HMM的slides,结果扩充了好多知识,所以完成这篇笔记还是花费了不少功夫,还刚好赶上实验室没空调回到解放前的日子,可谓汗流之作…
(17)强化学习
上篇主要介绍了概率图模型,首先从生成式模型与判别式模型的定义出发,引出了概率图模型的基本概念,即利用图结构来表达变量之间的依赖关系;接着分别介绍了隐马尔可夫模型、马尔可夫随机场、条件随机场、精确推断方法以及LDA话题模型:HMM主要围绕着评估/解码/学习这三个实际问题展开论述;MRF基于团和势函数的概念来定义联合概率分布;CRF引入两种特征函数对状态序列进行评价打分;变量消去与信念传播在给定联合概率分布后计算特定变量的边际分布;LDA话题模型则试图去推断给定文档所蕴含的话题分布。本篇将介绍最后一种学习算法–强化学习。
16、强化学习
强化学习(Reinforcement Learning,简称RL)是机器学习的一个重要分支,前段时间人机大战的主角AlphaGo正是以强化学习为核心技术。在强化学习中,包含两种基本的元素:状态与动作,在某个状态下执行某种动作,这便是一种策略,学习器要做的就是通过不断地探索学习,从而获得一个好的策略。例如:在围棋中,一种落棋的局面就是一种状态,若能知道每种局面下的最优落子动作,那就攻无不克/百战不殆了~
若将状态看作为属性,动作看作为标记,易知:监督学习和强化学习都是在试图寻找一个映射,从已知属性/状态推断出标记/动作,这样强化学习中的策略相当于监督学习中的分类/回归器。但在实际问题中,强化学习并没有监督学习那样的标记信息,通常都是在尝试动作后才能获得结果,因此强化学习是通过反馈的结果信息不断调整之前的策略,从而算法能够学习到:在什么样的状态下选择什么样的动作可以获得最好的结果。
16.1 基本要素
强化学习任务通常使用马尔可夫决策过程(Markov Decision Process,简称MDP)来描述,具体而言:机器处在一个环境中,每个状态为机器对当前环境的感知;机器只能通过动作来影响环境,当机器执行一个动作后,会使得环境按某种概率转移到另一个状态;同时,环境会根据潜在的奖赏函数反馈给机器一个奖赏。综合而言,强化学习主要包含四个要素:状态、动作、转移概率以及奖赏函数。
状态(X):机器对环境的感知,所有可能的状态称为状态空间; 动作(A):机器所采取的动作,所有能采取的动作构成动作空间; 转移概率(P):当执行某个动作后,当前状态会以某种概率转移到另一个状态; 奖赏函数(R):在状态转移的同时,环境给反馈给机器一个奖赏。
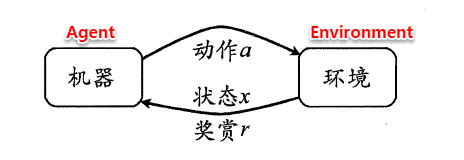
因此,强化学习的主要任务就是通过在环境中不断地尝试,根据尝试获得的反馈信息调整策略,最终生成一个较好的策略π,机器根据这个策略便能知道在什么状态下应该执行什么动作。常见的策略表示方法有以下两种:
确定性策略:π(x)=a,即在状态x下执行a动作; 随机性策略:P=π(x,a),即在状态x下执行a动作的概率。
一个策略的优劣取决于长期执行这一策略后的累积奖赏,换句话说:可以使用累积奖赏来评估策略的好坏,最优策略则表示在初始状态下一直执行该策略后,最后的累积奖赏值最高。长期累积奖赏通常使用下述两种计算方法:

16.2 K摇摆赌博机
首先我们考虑强化学习最简单的情形:仅考虑一步操作,即在状态x下只需执行一次动作a便能观察到奖赏结果。易知:欲最大化单步奖赏,我们需要知道每个动作带来的期望奖赏值,这样便能选择奖赏值最大的动作来执行。若每个动作的奖赏值为确定值,则只需要将每个动作尝试一遍即可,但大多数情形下,一个动作的奖赏值来源于一个概率分布,因此需要进行多次的尝试。
单步强化学习实质上是K-摇臂赌博机(K-armed bandit)的原型,一般我们尝试动作的次数是有限的,那如何利用有限的次数进行有效地探索呢?这里有两种基本的想法:
仅探索法:将尝试的机会平均分给每一个动作,即轮流执行,最终将每个动作的平均奖赏作为期望奖赏的近似值。 仅利用法:将尝试的机会分给当前平均奖赏值最大的动作,隐含着让一部分人先富起来的思想。
可以看出:上述两种方法是相互矛盾的,仅探索法能较好地估算每个动作的期望奖赏,但是没能根据当前的反馈结果调整尝试策略;仅利用法在每次尝试之后都更新尝试策略,符合强化学习的思(tao)维(lu),但容易找不到最优动作。因此需要在这两者之间进行折中。
16.2.1 ε-贪心
ε-贪心法基于一个概率来对探索和利用进行折中,具体而言:在每次尝试时,以ε的概率进行探索,即以均匀概率随机选择一个动作;以1-ε的概率进行利用,即选择当前最优的动作。ε-贪心法只需记录每个动作的当前平均奖赏值与被选中的次数,便可以增量式更新。

16.2.2 Softmax
Softmax算法则基于当前每个动作的平均奖赏值来对探索和利用进行折中,Softmax函数将一组值转化为一组概率,值越大对应的概率也越高,因此当前平均奖赏值越高的动作被选中的几率也越大。Softmax函数如下所示:


16.3 有模型学习
若学习任务中的四个要素都已知,即状态空间、动作空间、转移概率以及奖赏函数都已经给出,这样的情形称为“有模型学习”。假设状态空间和动作空间均为有限,即均为离散值,这样我们不用通过尝试便可以对某个策略进行评估。
16.3.1 策略评估
前面提到:在模型已知的前提下,我们可以对任意策略的进行评估(后续会给出演算过程)。一般常使用以下两种值函数来评估某个策略的优劣:
状态值函数(V):V(x),即从状态x出发,使用π策略所带来的累积奖赏; 状态-动作值函数(Q):Q(x,a),即从状态x出发,执行动作a后再使用π策略所带来的累积奖赏。
根据累积奖赏的定义,我们可以引入T步累积奖赏与r折扣累积奖赏:
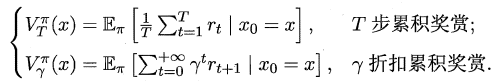
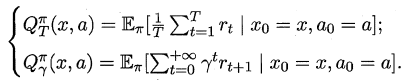
由于MDP具有马尔可夫性,即现在决定未来,将来和过去无关,我们很容易找到值函数的递归关系:

类似地,对于r折扣累积奖赏可以得到:
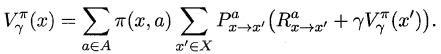
易知:当模型已知时,策略的评估问题转化为一种动态规划问题,即以填表格的形式自底向上,先求解每个状态的单步累积奖赏,再求解每个状态的两步累积奖赏,一直迭代逐步求解出每个状态的T步累积奖赏。算法流程如下所示:

对于状态-动作值函数,只需通过简单的转化便可得到:
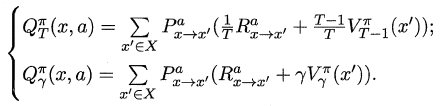
16.3.2 策略改进
理想的策略应能使得每个状态的累积奖赏之和最大,简单来理解就是:不管处于什么状态,只要通过该策略执行动作,总能得到较好的结果。因此对于给定的某个策略,我们需要对其进行改进,从而得到最优的值函数。
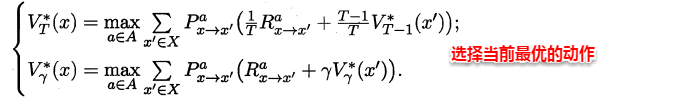
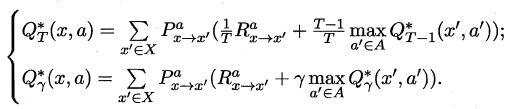
最优Bellman等式改进策略的方式为:将策略选择的动作改为当前最优的动作,而不是像之前那样对每种可能的动作进行求和。易知:选择当前最优动作相当于将所有的概率都赋给累积奖赏值最大的动作,因此每次改进都会使得值函数单调递增。
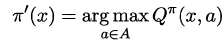
将策略评估与策略改进结合起来,我们便得到了生成最优策略的方法:先给定一个随机策略,现对该策略进行评估,然后再改进,接着再评估/改进一直到策略收敛、不再发生改变。这便是策略迭代算法,算法流程如下所示:

可以看出:策略迭代法在每次改进策略后都要对策略进行重新评估,因此比较耗时。若从最优化值函数的角度出发,即先迭代得到最优的值函数,再来计算如何改变策略,这便是值迭代算法,算法流程如下所示:

16.4 蒙特卡罗强化学习
在现实的强化学习任务中,环境的转移函数与奖赏函数往往很难得知,因此我们需要考虑在不依赖于环境参数的条件下建立强化学习模型,这便是免模型学习。蒙特卡罗强化学习便是其中的一种经典方法。
由于模型参数未知,状态值函数不能像之前那样进行全概率展开,从而运用动态规划法求解。一种直接的方法便是通过采样来对策略进行评估/估算其值函数,蒙特卡罗强化学习正是基于采样来估计状态-动作值函数:对采样轨迹中的每一对状态-动作,记录其后的奖赏值之和,作为该状态-动作的一次累积奖赏,通过多次采样后,使用累积奖赏的平均作为状态-动作值的估计,并引入ε-贪心策略保证采样的多样性。

在上面的算法流程中,被评估和被改进的都是同一个策略,因此称为同策略蒙特卡罗强化学习算法。引入ε-贪心仅是为了便于采样评估,而在使用策略时并不需要ε-贪心,那能否仅在评估时使用ε-贪心策略,而在改进时使用原始策略呢?这便是异策略蒙特卡罗强化学习算法。

16.5 AlphaGo原理浅析
本篇一开始便提到强化学习是AlphaGo的核心技术之一,刚好借着这个东风将AlphaGo的工作原理了解一番。正如人类下棋那般“手下一步棋,心想三步棋”,Alphago也正是这个思想,当处于一个状态时,机器会暗地里进行多次的尝试/采样,并基于反馈回来的结果信息改进估值函数,从而最终通过增强版的估值函数来选择最优的落子动作。
其中便涉及到了三个主要的问题:(1)如何确定估值函数(2)如何进行采样(3)如何基于反馈信息改进估值函数,这正对应着AlphaGo的三大核心模块:深度学习、蒙特卡罗搜索树、强化学习。
1.深度学习(拟合估值函数)
由于围棋的状态空间巨大,像蒙特卡罗强化学习那样通过采样来确定值函数就行不通了。在围棋中,状态值函数可以看作为一种局面函数,状态-动作值函数可以看作一种策略函数,若我们能获得这两个估值函数,便可以根据这两个函数来完成:(1)衡量当前局面的价值;(2)选择当前最优的动作。那如何精确地估计这两个估值函数呢?这就用到了深度学习,通过大量的对弈数据自动学习出特征,从而拟合出估值函数。
2.蒙特卡罗搜索树(采样)
蒙特卡罗树是一种经典的搜索框架,它通过反复地采样模拟对局来探索状态空间。具体表现在:从当前状态开始,利用策略函数尽可能选择当前最优的动作,同时也引入随机性来减小估值错误带来的负面影响,从而模拟棋局运行,使得棋盘达到终局或一定步数后停止。
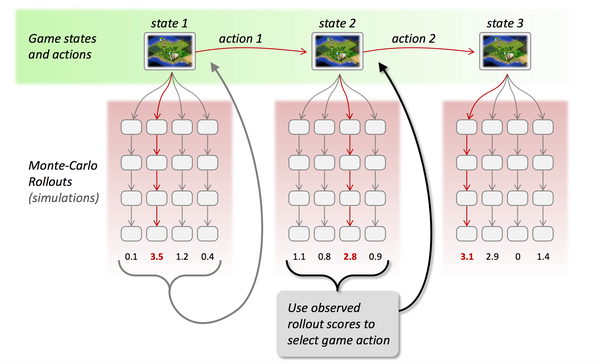
3.强化学习(调整估值函数)
在使用蒙特卡罗搜索树进行多次采样后,每次采样都会反馈后续的局面信息(利用局面函数进行评价),根据反馈回来的结果信息自动调整两个估值函数的参数,这便是强化学习的核心思想,最后基于改进后的策略函数选择出当前最优的落子动作。
在此,强化学习就介绍完毕。同时也意味着大口小口地啃完了这个西瓜,十分记得去年双11之后立下这个Flag,现在回想起来,大半年的时间里在嚼瓜上还是花费了不少功夫。有人说:当你阐述的能让别人看懂才算是真的理解,有人说:在写的过程中能发现那些只看书发现不了的东西,自己最初的想法十分简单:当健忘症发作的时候,如果能看到之前按照自己思路写下的文字,回忆便会汹涌澎湃一些~
最后,感谢自己这大半年以来的坚持~Get busy living, or get busy dying!
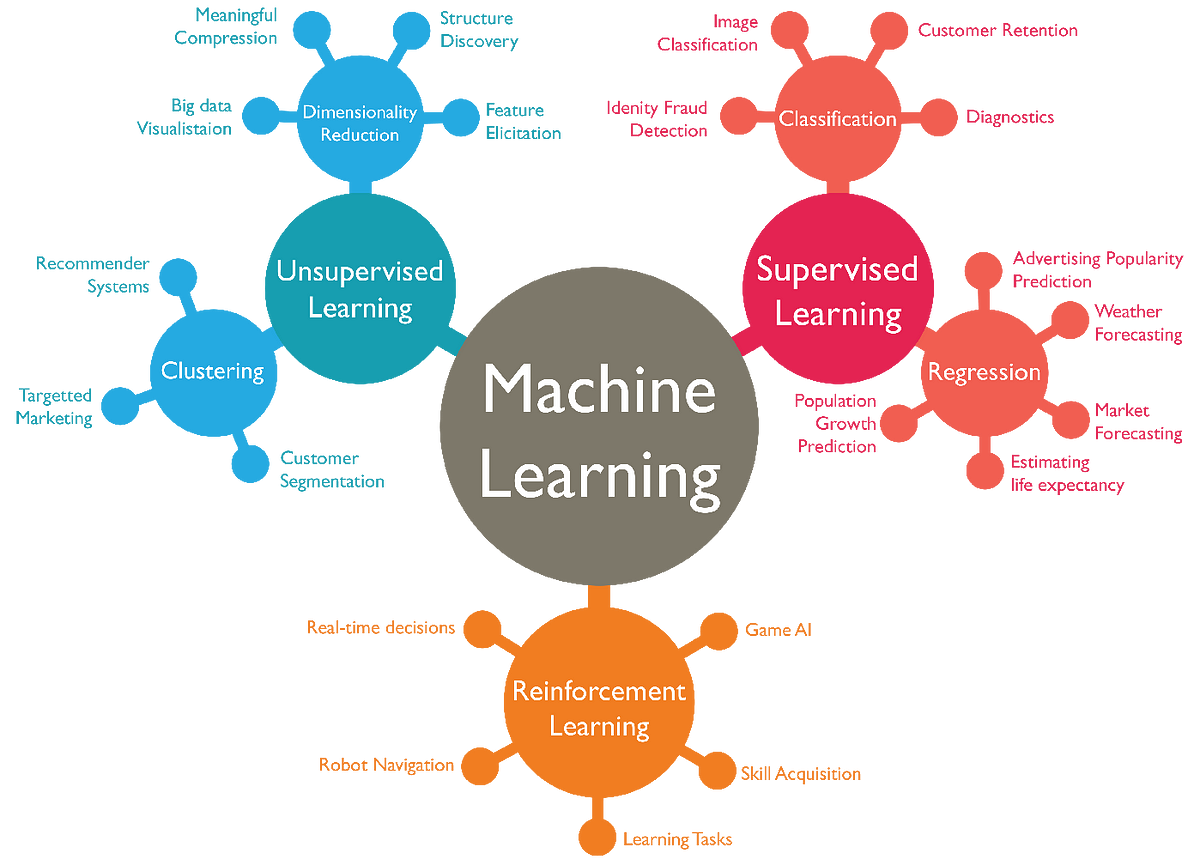

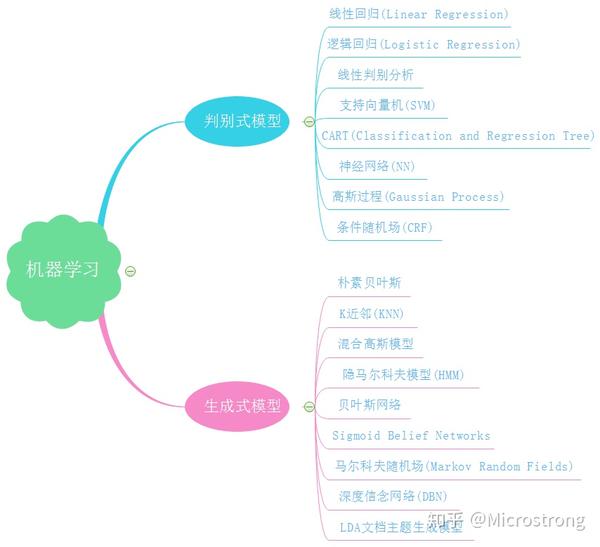




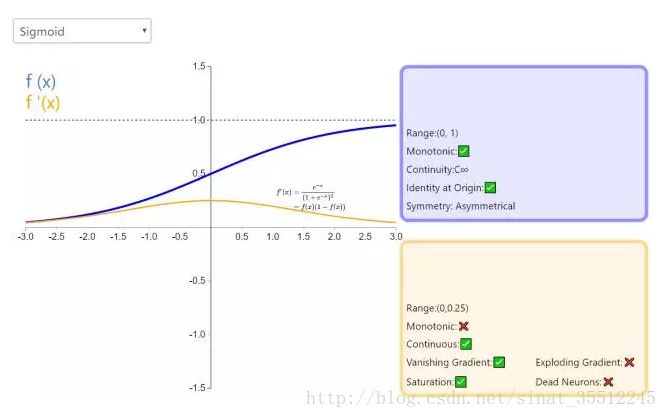
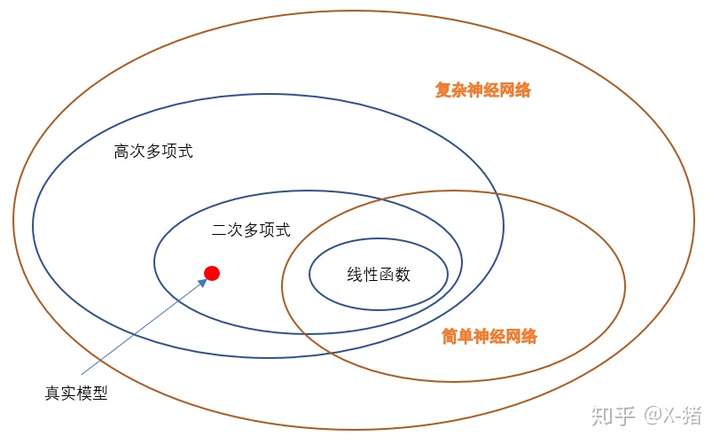

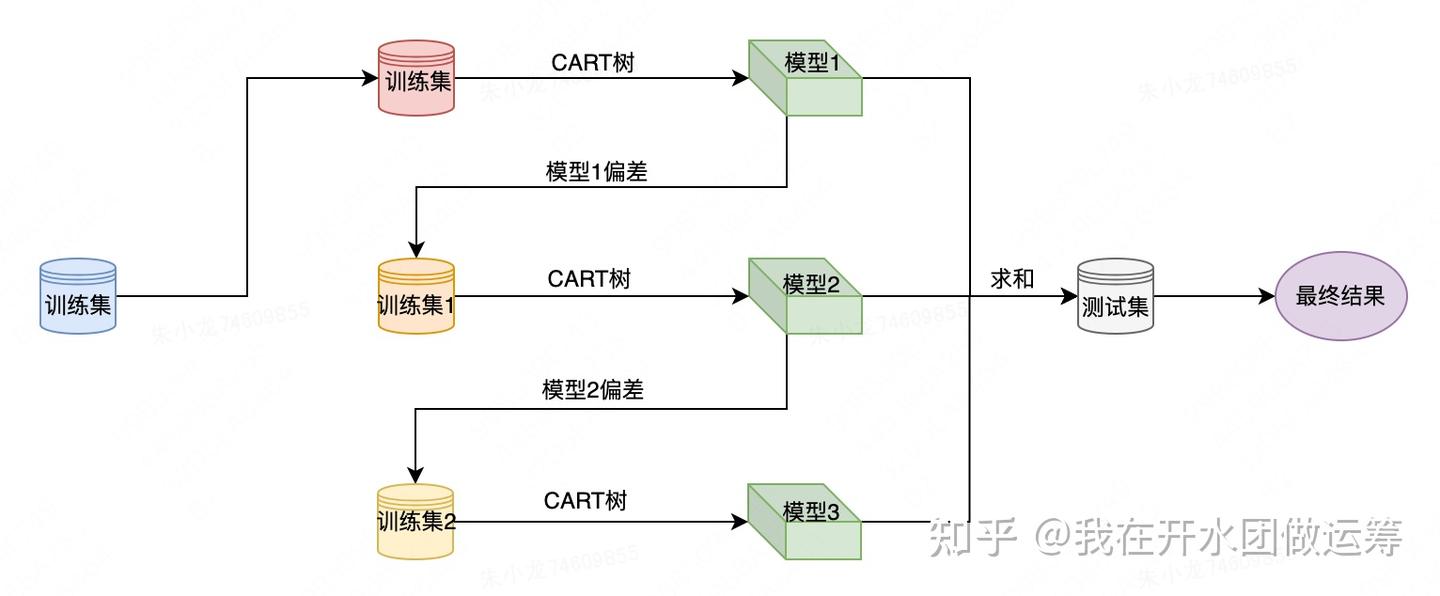

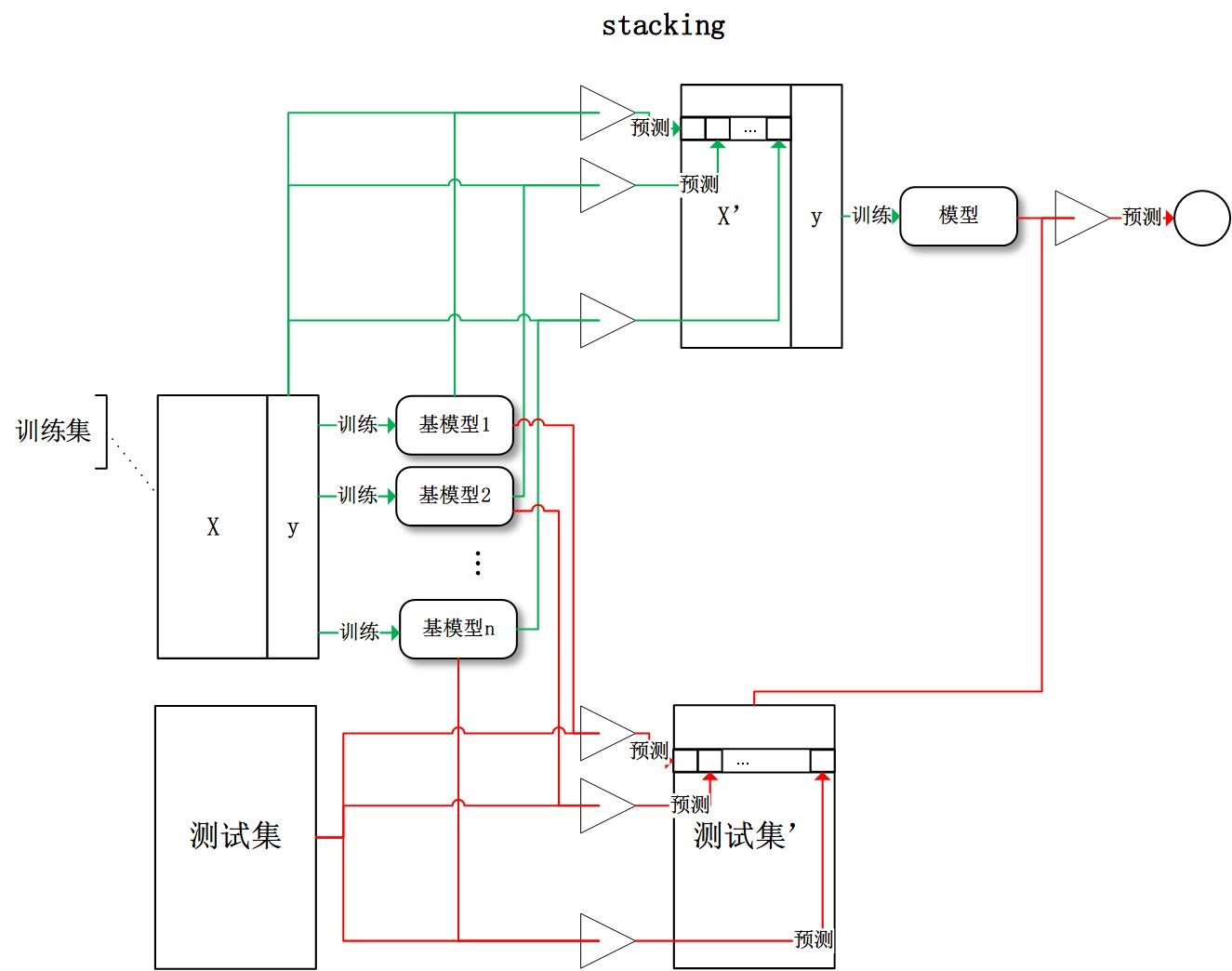


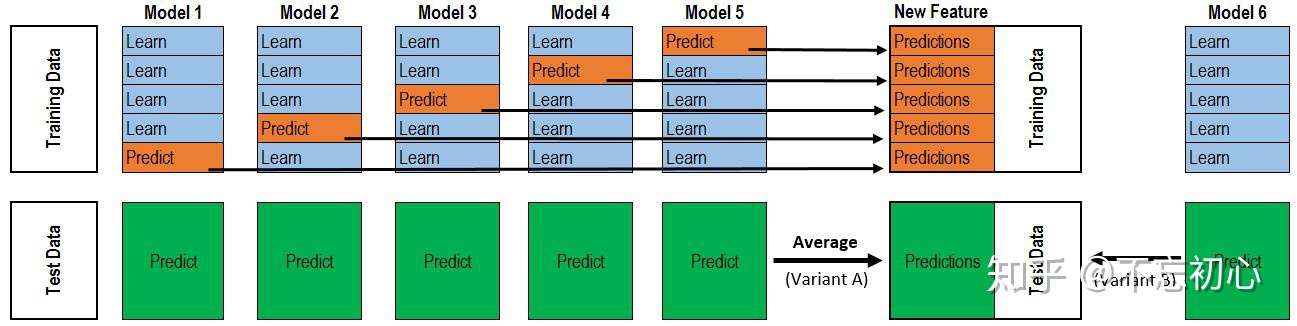

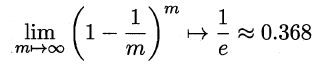
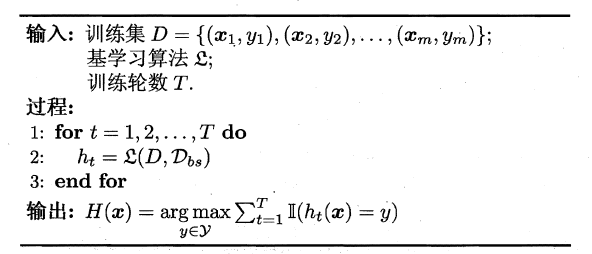

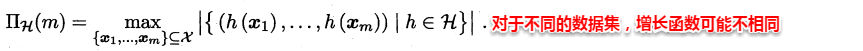
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
