数学简史
- 数学历史
  - 数学危机
- 数学体系
数学大师
- 哈密尔顿
  - 四元数
为什么要学数学
- 同构映射
- 分析还原
数学教学
丘成桐：数理与人文
资料
- 数学工具
  - Mathematica
  - Matlab
  - Maple
  - GeoGebra
  - Mathigon
  - Penrose
- 数列
- 动图演示数学之美
- 影视资源

【2021-3-9】130张炫酷动图, 让你秒懂高中理科所有原理——物理篇
【2022-9-28】数学与机器学习，牛津大学Elizaveta Semenova ppt总结, 基本数学工具包括线性代数、解析几何、矩阵分解、向量微积分、优化、概率和统计。本报告包括线性代数、微积分、概率和统计学。

【2024-6-2】魔方原理，动图讲解

数学简史

数学的深渊

数学简史——帮你快速梳理数学知识的脉络，B站地址

【2020-9-5】2020年8月4日下午五点（北京时间）,丘成桐讲数学简史，ppt截图

陶哲轩-地上最强数学家访谈

【2020-12-11】数学的酷炫你不懂
【2021-2-28】拉马努金和哈代：两位数学巨匠的惺惺相惜

数学历史

数学危机

数学史上贯穿了矛盾，同时也贯穿着人们对于矛盾的讨论。当一个矛盾激化到可以影响整个数学基础的时候，就会产生数学危机。而对于这种危机的化解，往往就是数学史上的新发展，可以将原本是数学拓展到更加深层次的领域上去。

历史上三次数学危机，给人们带来了很大麻烦，也有人因此惨死。危机的产生是因为理论本身有缺陷，但是就是通过解决这种缺陷，人类对于自然的认识才会上升到一个新的高度。每一次数学危机即是数学发展的产物，也是数学发展的思想源泉。

要了解第三次数学基础危机，需要先了解康托尔、罗素、希尔伯特和哥德尔。

无理数──第一次数学危机

现代意义下的数学，也就是作为演绎系统的纯粹数学，来源于古希腊毕达哥拉斯学派。它是一个唯心主义学派，兴旺的时期为公元前500年左右。他们认为，“万物皆数”(指整数)，数学的知识是可靠的、准确的，而且可以应用于现实的世界，数学的知识由于纯粹的思维而获得，不需要观察、直觉和日常经验。

毕达哥拉斯，是人类历史上一位著名的数学家。他建立的必氏学派始终信奉着数是万物的本源，正所谓“万物皆数”。

世间万物都是由数字按照一定比例和结构所构成的，并提出了一切数均可以表示为整数或者整数之比的概念。
毕教主最为辉煌的成就就是证明了勾股定理，但是辉煌的背后也有着他自己的心酸。因为他在研究三角形的时候发现了三角形的三边比不能表示成整数或者整数之比。但是毕教主毕竟是一派之主，自己否定自己的理论未免有些太过于打脸，所以他选择隐瞒，假装什么都不知道。
当然，这件事是瞒不住的。一个叫希帕索斯的人就在当时提出一个问题：“边长为1的正方形，其对角线的长度是多少？” 正是因为这个问题触动了毕氏学派的理论根基，所以希帕索斯被处以抛入大海的刑罚。
在之后便没有人敢于质疑毕教主的理论。两百年后，欧多克索斯在毕教主理论基础上建立了一套比较完善的比例理论，巧妙的避开了无理数的逻辑，并且在相当大程度上保留了毕氏学派的理论，算是缓解了这次数学危机。
但是他仅仅是通过几何的方式避免直接接触无理数，这样只是巧妙避开了人们的质疑，但是并没有真正解决这个危机。
直到19世纪下半叶，实数理论建立后，无理数才被彻底的搞清楚，这样一来无理数的合法地位才在数学大厦中真正建立，这持续了几千年第一次数学危机宣告彻底解决。

第一次数学危机：毕达哥拉斯学派认为“数及万物”，并且宇宙一切数都为有理数，也就是说数轴上全是有理数，而有理数全部都可以被表示成两个整数相除。其学生希帕索斯提出质疑：一个直角三角形，两直角边边长为1，根据勾股定理（顺便说一句，勾股定理也叫毕达哥拉斯定理），第三边边长为根号2，然而根号2不能被表示成任何两个整数相除，所以根号2就不是有理数。这个事实在我们今天的人类看来是非常简单的东西，但在当年，这个简单的事实却动摇了毕达哥拉斯学派的根基。当时毕达哥拉斯学派就是数学界的霸王，可想而知这影响有多么可怕。结局：毕达哥拉斯学派无法解决这个问题，于是将提出问题的人解决——把希帕索斯淹死。

大约公元前５世纪，不可通约量的发现导致了毕达哥拉斯悖论。当时的毕达哥拉斯学派重视自然及社会中不变因素的研究，把几何、算术、天文、音乐称为”四艺”，在其中追求宇宙的和谐规律性。他们认为：宇宙间一切事物都可归结为整数或整数之比，毕达哥拉斯学派的一项重大贡献是证明了勾股定理，但由此也发现了一些直角三角形的斜边不能表示成整数或整数之比（不可通约）的情形，如直角边长均为１的直角三角形就是如此。这一悖论直接触犯了毕氏学派的根本信条，导致了当时认识上的”危机”，从而产生了第一次数学危机。

公元前370年，这个矛盾被毕氏学派的欧多克斯通过给比例下新定义的方法解决了。他的处理不可通约量的方法，出现在欧几里得《原本》第５卷中。欧多克斯和狄德金于1872年给出的无理数的解释与现代解释基本一致。今天中学几何课本中对相似三角形的处理，仍然反映出由不可通约量而带来的某些困难和微妙之处。第一次数学危机对古希腊的数学观点有极大冲击。这表明，几何学的某些真理与算术无关，几何量不能完全由整数及其比来表示，反之却可以由几何量来表示出来，整数的权威地位开始动摇，而几何学的身份升高了。
危机也表明，直觉和经验不一定靠得住，推理证明才是可靠的，从此希腊人开始重视演译推理，并由此建立了几何公理体系，这不能不说是数学思想上的一次巨大革命！

微积分的幽灵-无穷小——第二次危机

这次危机的萌芽出现在大约公元前450年，芝诺注意到由于对无限性的理解问题而产生的矛盾，提出了关于时空的有限与无限的四个悖论：

“两分法”：向着一个目的地运动的物体，首先必须经过路程的中点，然而要经过这点，又必须先经过路程的1/4点……，如此类推以至无穷。—— 结论是：无穷是不可穷尽的过程，运动是不可能的。
“阿基里斯追不上乌龟”：阿基里斯(《荷马史诗》中的善跑的英雄)总是首先必须到达乌龟的出发点，因而乌龟必定总是跑在前头。这个论点同两分法悖论一样，所不同的是不必把所需通过的路程一再平分。
“飞矢不动”：意思是箭在运动过程中的任一瞬时间必在一确定位置上，因而是静止的，所以箭就不能处于运动状态。
“操场或游行队伍”：A、B两件物体以等速向相反方向运动。从静止的c来看，比如说A、B都在1小时内移动了2公里，可是从A看来，则B在1小时内就移动了4公里。运动是矛盾的，所以运动是不可能的。芝诺揭示的矛盾是深刻而复杂的。前两个悖论诘难了关于时间和空间无限可分，因而运动是连续的观点，后两个悖论诘难了时间和空间不能无限可分，因而运动是间断的观点。芝诺悖论的提出可能有更深刻的背景，不一定是专门针对数学的，但是它们在数学王国中却掀起了一场轩然大被。它们说明了希腊人已经看到“无穷小”与“很小很小”的矛盾，但他们无法解决这些矛盾。其后果是，希腊几何证明中从此就排除了无穷小。

经过许多人多年的努力，终于在17世纪晚期，形成了无穷小演算——微积分这门学科。牛顿和莱布尼兹被公认为微积分的奠基者，他们的功绩主要在于：

把各种有关问题的解法统一成微分法和积分法；
有明确的计算步骤；
微分法和积分法互为逆运算。由于运算的完整性和应用的广泛性，微积分成为当时解决问题的重要工具。同时，关于微积分基础的问题也越来越严重。关键问题就是无穷小量究竞是不是零？无穷小及其分析是否合理？由此而引起了数学界甚至哲学界长达一个半世纪的争论，造成了第二次数学危机。

无穷小量究竟是不是零？两种答案都会导致矛盾。牛顿对它曾作过三种不同解释：

1669年说它是一种常量；
1671年又说它是一个趋于零的变量；
1676年它被“两个正在消逝的量的最终比”所代替。但是，他始终无法解决上述矛盾。莱布尼兹曾试图用和无穷小量成比例的有限量的差分来代替无穷小量，但是他也没有找到从有限量过渡到无穷小量的桥梁。

英国大主教贝克莱于1734年写文章，攻击流数(导数)“是消失了的量的鬼魂……能消化得了二阶、三阶流数的人，是不会因吞食了神学论点就呕吐的。”他说，用忽略高阶无穷小而消除了原有的错误，“是依靠双重的错误得到了虽然不科学却是正确的结果”。贝克莱虽然也抓住了当时微积分、无穷小方法中一些不清楚不合逻辑的问题，不过他是出自对科学的厌恶和对宗教的维护，而不是出自对科学的追求和探索。

当时一些数学家和其他学者，也批判过微积分的一些问题，指出其缺乏必要的逻辑基础。例如，罗尔曾说：“微积分是巧妙的谬论的汇集。”在那个勇于创造时代的初期，科学中逻辑上存在这样那样的问题，并不是个别现象。

18世纪的数学思想的确是不严密的、直观的，强调形式的计算而不管基础的可靠。其中特别是：没有清楚的无穷小概念，从而导数、微分、积分等概念不清楚；无穷大概念不清楚；发散级数求和的任意性等等；符号的不严格使用；不考虑连续性就进行微分，不考虑导数及积分的存在性以及函数可否展成幂级数等等。

直到19世纪20年代，一些数学家才比较关注于微积分的严格基础。从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始，到威尔斯特拉斯、狄德金和康托的工作结束，中间经历了半个多世纪，基本上解决了矛盾，为数学分析奠定了一个严格的基础。

波尔查诺给出了连续性的正确定义；阿贝尔指出要严格限制滥用级数展开及求和；柯西在1821年的《代数分析教程》中从定义变量出发，认识到函数不一定要有解析表达式；他抓住极限的概念，指出无穷小量和无穷大量都不是固定的量而是变量，无穷小量是以零为极限的变量；并且定义了导数和积分；狄里赫利给出了函数的现代定义。在这些工作的基础上，威尔斯特拉斯消除了其中不确切的地方，给出现在通用的极限的定义，连续的定义，并把导数、积分严格地建立在极限的基础上。

19世纪70年代初，威尔斯特拉斯、狄德金、康托等人独立地建立了实数理论，而且在实数理论的基础上，建立起极限论的基本定理，从而使数学分析建立在实数理论的严格基础之上。

17世纪时牛顿与莱布尼茨各种独立创立了以无穷小分析为基础的微积分理论。当时的微积分又叫做无穷小分析。虽然微积分的发明极大推动了数学研究的发展，但是毕竟初期建立的体系总有不完善的地方。而这次的不完善却是致命的。

当时一个叫贝克莱的人提出一个悖论—— 无穷小量到底是不是0
因为在当时的体系中无穷小量即是0，又不是0，那么它到底是什么？
这让微积分的建立者们很是恼火。贝克莱也嘲笑无穷小量为“已死量的幽灵”。
直到19世纪70年代，魏尔斯特拉斯、柯西等人建立实数理论，并在实数理论上建立起极限的基本定理，才缓解了这无穷小的幽灵所引发的危机。
但是故事总是曲折的，魏尔斯特拉斯举出了一个处处不可微但是却连续的函数例子，说明了直观思维和几何作图的不可靠，必须诉诸严格的概念和推理。
这导致了数学家们更加深入的讨论实数论，并导致了集合论的诞生。关于无穷小量，阿拉丁认为它至今都是一个幽灵，因为关于实无限和潜无限在如今的数学体系中相辅相成，平分秋色。

第二次数学危机：关于跑得最快的阿基里斯永远追不上起点领先的乌龟的悖论。为了追上乌龟，阿基里斯总是要先跑到乌龟之前所在的点，而在这个时间段之内乌龟也前进了一段距离，而阿基里斯仍然需要追到乌龟此刻所在的点，然而在这个过程中乌龟又前进了。在数学上这是一个涉及到级数和（为了追上乌龟，阿基里斯需要跑多远的距离）以及步骤无穷多（时间空间无限分割）、时间无穷小（时间和距离被分割到无穷小）的问题。我当年在数学专业学习的时候，第一次在理科图书馆看到这个逻辑时也被忽悠了一瞬间。就算学习了收敛级数，知道距离和以及时间和都是有限的，也还是脑子里一直有个小问题：按照芝诺思考这个问题的步骤，经过无限个步骤后，每一小段阿基里斯需要追上乌龟的时间即使趋于无穷小，也还都仍然是个正数，那么看起来阿基里斯还是永远追不上乌龟。后来结合物理上时空的一些理论，得知悖论产生的实质是，这个悖论是建立在将时间和空间进行了无限分割的基础上的，而事实上，时间和空间却并非连续可进行无限分割的。

此外，牛顿、莱布尼兹的微积分也受到了质疑，质疑点是：无穷小到底**是不是0。这质疑使得堂堂的微积分感到了恐慌。当然现在微积分已经稳了，危机解除。

自相矛盾的理发师—第三次数学危机

数学基础的第三次危机是由1897年的突然冲击而出现的，从整体上看到现在还没有解决到令人满意的程度。这次危机是由于在康托的一般集合理论的边缘发现悖论造成的。由于集合概念已经渗透到众多的数学分支，并且实际上集合论已经成了数学的基础，因此集合论中悖论的发现自然地引起了对数学的整个基本结构的有效性的怀疑。

1897年，福尔蒂揭示了集合论的第一个悖论；
两年后，康托发现了很相似的悖论，它们涉及到集合论中的结果。
1902年，罗素发现了一个悖论，它除了涉及集合概念本身外不涉及别的概念。

罗素，英国人，哲学家、逻辑学家、数学家。1902年著述《数学原理》，继而与怀德海合著《数学原理》(1910年～1913年)，把数学归纳为一个公理体系，是划时代的著作之一。他在很多领域都有大量著作，并于1950年获得诺贝尔文学奖。他关心社会现象，参加和平运动，开办学校。1968～1969年出版了他的自传。

罗素悖论曾被以多种形式通俗化，其中最著名的是罗索于1919年给出的，它讲的是某村理发师的困境。理发师宣布了这样一条原则：

他只给不自己刮胡子的人刮胡子。当人们试图答复下列疑问时，就认识到了这种情况的悖论性质：“理发师是否可以给自己刮胡子？”如果他给自己刮胡子，那么他就不符合他的原则；如果他不给自己刮胡子，那么他按原则就该为自己刮胡子。罗素悖论使整个数学大厦动摇了，无怪乎弗雷格在收到罗素的信之后，在他刚要出版的《算术的基本法则》第2卷本末尾写道：“一位科学家不会碰到比这更难堪的事情了，即在工作完成之时，它的基础垮掉了。当本书等待付印的时候，罗素先生的一封信把我就置于这种境地”。狄德金原来打算把《连续性及无理数》第3版付印，这时也把稿件抽了回来。发现拓扑学中“不动点原理”的布劳恩也认为自己过去做的工作都是“废话”，声称要放弃不动点原理。

自从在康托的集合论和发现上述矛盾之后，还产生了许多附加的悖论。集合论的现代悖论与逻辑的几个古代悖论有关系。例如公元前四世纪的欧伯利得悖论：“我现在正在做的这个陈述是假的”。如果这个陈述是真的，则它是假的；然而，如果这个陈述是假的，则它又是真的了。于是，这个陈述既不能是真的，又不能是假的，怎么也逃避不了矛盾。更早的还有埃皮门尼德(公元前6世纪，克利特人)悖论：“克利特人总是说谎的人”。只要简单分析一下，就能看出这句话也是自相矛盾的。

集合论中悖论的存在，明确地表示某些地方出了毛病。自从发现它们之后，人们发表了大量关于这个课题的文章，并且为解决它们作过大量的尝试。就数学而论，看来有一条容易的出路：人们只要把集合论建立在公理化的基础上，加以充分限制以排除所知道的矛盾。

第一次这样的尝试是策梅罗于1908年做出的，以后还有多人进行了加工。但是，此程序曾受到批评，因为它只是避开了某些悖论，而未能说明这些悖论；此外，它不能保证将来不出现别种悖论。

另一种程序既能解释又能排除已知悖论。如果仔细地检查就会发现：上面的每一个悖论都涉及一个集合S和S的一个成员M(既M是靠S定义的)。这样的一个定义被称作是“非断言的”，而非断言的定义在某种意义上是循环的。例如，考虑罗素的理发师悖论：用M标志理发师，用S标示所有成员的集合，则M被非断言地定义为“S的给并且只给不自己刮胡子人中刮胡子的那个成员”。此定义的循环的性质是显然的——理发师的定义涉及所有的成员，并且理发师本身就是这里的成员。因此，不允许有非断言的定义便可能是一种解决集合论的己知悖论的办法。然而，对这种解决办法，有一个严重的责难，即包括非断言定义的那几部分数学是数学家很不愿丢弃的，例如定理“每一个具有上界的实数非空集合有最小上界(上确界)”。

解决集合论的悖论的其它尝试，是从逻辑上去找问题的症结，这带来了逻辑基础的全面研究。

从1900年到1930年左右，数学的危机使许多数学家卷入一场大辩论当中。他们看到这次危机涉及到数学的根本，因此必须对数学的哲学基础加以严密的考察。在这场大辩论中，原来不明显的意见分歧扩展成为学派的争论。以罗素为代表的逻缉主义、以布劳威为代表的直觉主义、以希尔伯特为代表的形式主义三大数学哲学学派应运而生。它们都是唯心主义学派，它们都提出了各自的处理一般集合论中的悖论的办法。他们在争论中尽管言语尖刻，好象势不两立，其实各自的观点都吸收了对方的看法而又有很多变化。

1931年，哥德尔不完全性定理的证明暴露了各派的弱点，哲学的争论黯淡了下来。此后，各派力量沿着自己的道路发展演化。尽管争论的问题远未解决，但大部分数学家并不大关心哲学问题。直到近年，数学哲学问题才又激起人们的兴趣。

承认无穷集合、承认无穷基数，就好象一切灾难都出来了，这就是第三次数学危机的实质。尽管悖论可以消除，矛盾可以解决，然而数学的确定性却在一步一步地丧失。现代公理集合论中一大堆公理，简直难说孰真孰假，可是又不能把它们都消除掉，它们跟整个数学是血肉相连的。所以，第三次数学危机表面上解决了，实质上更深刻地以其它形式延续着。

数学中的矛盾既然是固有的，它的激烈冲突——危机就不可避免。危机的解决给数学带来了许多新认识、新内容，有时也带来了革命性的变化。把20世纪的数学同以前全部数学相比，内容要丰富得多，认识要深入得多。在集合论的基础上，诞生了抽象代数学、拓扑学、泛函分析与测度论，数理逻辑也兴旺发达成为数学有机体的一部分。古代的代数几何、微分几何、复分析现在已经推广到高维。代数数论的面貌也多次改变，变得越来越优美、完整。一系列经典问题完满地得到解决，同时又产生更多的新问题。特别是二次大战之后，新成果层出不穷，从来间断。数学呈现无比兴旺发达的景象，而这正是人们同数学中的矛盾、危机斗争的产物。

集合论的产生可谓是打了很多数学家的脸。因为当康托尔最初创立集合论体系时就遭到了很多数学家的抨击。

但是久而久之，这些数学家们发现从集合论出发可以建立原有的整个数学大厦，这些“厚颜无耻”的数学家们又表示“一切数学成果都可以建立在集合论上。”
但是不久，一个叫罗素的人提出一个悖论，这个悖论可以通过一个故事描述：
- 在某个城市中有一位理发师，他的广告词是这样写的：“本人的理发技艺十分高超，誉满全城。我将为本城所有不给自己刮脸的人刮脸，我也只给这些人刮脸。我对各位表示热诚欢迎！”来找他刮脸的人络绎不绝，自然都是那些不给自己刮脸的人。
- 可是，有一天，这位理发师从镜子里看见自己的胡子长了，他本能地抓起了剃刀，你们看他能不能给他自己刮脸呢？如果他不给自己刮脸，他就属于“不给自己刮脸的人”，他就要给自己刮脸，而如果他给自己刮脸呢？他又属于“给自己刮脸的人”，他就不该给自己刮脸。
- 如果把每个人看成一个集合，这个集合的元素被定义成这个人刮脸的对象。那么，理发师宣称，他的元素，都是城里不属于自身的那些集合，并且城里所有不属于自身的集合都属于他。
那么他是否属于他自己？这个逻辑上的说法无懈可击，瞬间击垮了人们对于集合论的赞同，德国数学家弗雷格对于这个问题表示：一位科学家不会碰到比这更难堪的事情了，在他工作即将结束时，他的基础体系崩溃了！
直到1931年库尔特.哥德尔证明：
- 任何一个数学系统，只要他是从有限的公理和基本的概念推导出来的，并且从中可以推导出自然数系统，就可以在其中找到一个命题，对于这个命题，我们既没有办法证明，也没有办法推翻。
- 这就是哥德尔不完全定理。他的证明结束了关于数学基础的讨论，宣告了把数学彻底形式化的愿望是不可能实现的。

第三次数学危机：罗素为了质疑康托尔的集合论（集合三个特点：确定性、互异性、无序性），而提出了“理发师悖论”。假设有一个理发师，他在门口挂上牌子：我给且只给不为自己刮胡子的人刮胡子。那么，这个理发师是否可以给自己刮胡子？该悖论运用到集合上，则为：假设有一个集合，它是所有不属于自己的集合的集合。那么这个集合是什么东西？（如果集合A属于A,则根据定义，A应该不属于A；如果集合A不属于A，则根据定义，A应该属于A）。然而它是符合康托尔关于集合的定义的。

这个问题直至现在还没有得到很完美的解决。而我们的数学家康托尔当年则被这个问题逼疯了。可怜的康托尔，当年写出集合论时是何等荣耀。然而高帽子真不是好戴的，一被戴上就恐惧被摘。偏偏天才多是偏执狂。

数学史上的第三次危机，是由1897年的突然冲击而出现的。到现在，从整体来看，还没有解决到令人满意的程度。这次危机是由于在康托的一般集合理论的边缘发现悖论造成的。由于集合概念已经渗透到众多的数学分支，并且实际上集合论成了数学的基础，因此集合论中悖论的发现自然地引起了对数学的整个基本结构的有效性的怀疑。

1897年，福尔蒂揭示了集合论中的第一个悖论。
两年后，康托发现了很相似的悖论。
1902年，罗素又发现了一个悖论，它除了涉及集合概念本身外不涉及别的概念。罗素悖论曾被以多种形式通俗化。其中最著名的是罗素于1919年给出的，它涉及到某村理发师的困境。理发师宣布了这样一条原则：他给所有不给自己刮脸的人刮脸，并且，只给村里这样的人刮脸。当人们试图回答下列疑问时，就认识到了这种情况的悖论性质：”理发师是否自己给自己刮脸？”如果他不给自己刮脸，那么他按原则就该为自己刮脸；如果他给自己刮脸，那么他就不符合他的原则。

数学有三次革命，第一次是微积分，第二次是不完备性，第三次是阿列夫一运算法则。当然第三次还没到来，现在数学的上限是可数无穷集，如果哪天有人找到不可数无穷集的运算法则，那就是科学之巅。

【2022-5-21】掀翻数学的第三次危机为什么让所有数学家都疯了？

罗素悖论就是个谬论，第一，所有不属于集合A的元素组成的集合当然不再是集合A了，强行让它等于集合A那就是自相矛盾。第二，集合定义为满足某种性质的元素组成的总体，把集合自身放进自己的元素里，是不符合定义的。

数学体系

知识体系 img

【2024-2-21】古代数学计量单位，参考

一、十、百、千、万、亿、兆、京、垓、秭、穰、沟、涧、正、载、极、恒河沙、阿僧祇、那由他、不可思议、无量，大数，全仕祥，古戈尔，频波罗，京杰罗，不可说不可说转，超限数，绝对无限，绝对无量，绝对小数，绝对大数，绝对超限数，绝对恒河沙，绝对那由他，绝对不可思议，绝对古戈尔，绝对频波罗，绝对京杰罗，绝对有量，绝对有限，绝对界限，绝对有解，绝对无解，绝对有量大海，绝对无量大海，绝对无限小数，绝对无限大数。

1.数学基础

数学基础研究的是逻辑或集合论中的问题，它们是数学的语言。逻辑与集合论领域思考的是数学本身的执行框架。在某种程度上，它研究的是证明与数学现实的本质，与哲学接近。

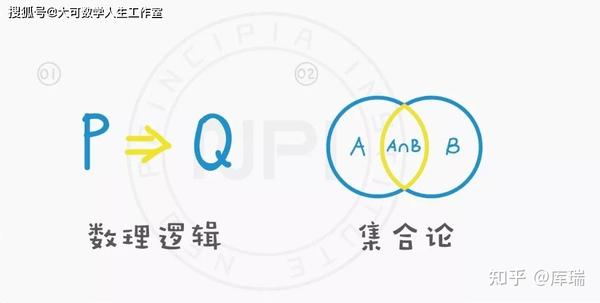
数理逻辑和基础（Mathematical logic and foundations）

数理逻辑是这一部分的核心，但是对逻辑法则的良好理解产生于它们第一次被使用之后。除了在计算机科学、哲学和数学中正式地使用了基础的命题逻辑之外，这一领域还涵盖了普通逻辑和证明论，最终形成了模型论。在此，一些著名的结果包括哥德尔不完全性定理以及与递归论相关的丘奇论题。

2.代数学

代数是对计数、算术、代数运算和对称性的一些关键的概念进行提炼而发展的。通常来说，这些领域仅通过几个公理就可定义它们的研究对象，然后再考虑这些对象的示例、结构和应用。其他非常偏代数的领域包括代数拓扑、信息与通信，以及数值分析。

数论（Number theory）

数论是纯数学中最古老、也是最庞大的分支之一。显然，它关心的是与数字有关的问题，这通常是整数或有理数（分数）。除了涉及到全等性、可除性、素数等基本主题之外，数论现在还包括对环与数域的非常偏代数的研究；还有用于渐近估计和特殊函数的分析方法和几何主题；除此之外，它与密码学、数学逻辑甚至是实验科学之间都存在着重要的联系。

群论（Group theory）

群论研究的是那些定义了可逆结合的“乘积”运算的集合。这包括了其他数学对象的对称集合，使群论在所有其他数学中占有一席之地。有限群也许是最容易被理解的，但矩阵群和几何图形的对称性同样也是群的中心示例。

李群（Lie Group）

李群是群论中的一个重要的特殊分支。它们具有代数结构，但同时也是空间的子集，并且还包含几何学；此外，它们的某些部分看起来就像欧几里德空间，这使得我们可以对它们进行解析（例如求解微分方程）。因此李群和其他拓扑群位于纯数学的不同领域的收敛处。

交换环和交换代数（Commutative rings and algebra）

交换环是与整数集类似的集合，它允许加法和乘法。尤其有趣的是数论、域论和相关领域中的环。

结合环和结合代数（Associative rings and algebra）

结合环论可被看作是交换环的非交换类比。它包括对矩阵环、可除环（如四元数），以及在群论中重要的环的研究。数学家开发了各种工具，以便能够研究一般化的环。

非结合环和非结合代数（Nonassociative rings and algebras）

非结合环论进一步地拓宽了研究范围。这里的通用理论较弱，但这种环的特殊情况是至关重要的：尤其是李代数，以及约当代数和其他类型。

域论与多项式（Field theory and polynomials）

域论研究的是集合（如实数直线），所有一般的算术性质都包含在实直线上，包括除法性质。研究多场对多项式方程具有重要意义，因而它在数论和群论中也都具有应用意义。

一般代数系统（General algebraic system）

一般代数系统包括那些具有非常简单的公理构成，以及那些不容易被包含在群、环、域或其他代数系统中的结构。

代数几何（Algebraic geometry）

代数几何将代数与几何相结合，使二者彼此互利。例如，于1995年被证明的“费马大定理”，表面上看是关于数论的陈述，但其实是通过几何工具才得以证明。反过来，由方程定义的集合的几何性质，是用复杂的代数机制来研究的。这是一个魅力非常的领域，许多重要的课题都非常深奥，椭圆曲线就数其中之一。

线性代数（Linear algebra）

线性代数，有时会被“乔装”成矩阵论，它考虑的是能维持线性结构的集合与函数。它涵盖的数学范围非常广，包括公理处理、计算问题、代数结构，甚至几何的一些部分；此外，它还为分析微分方程、统计过程甚至许多物理现象提供了重要的工具。

范畴论（Category theory）

范畴论是一个相对较新的数学领域，它为讨论代数与几何的各个领域提供了一个通用的框架。

K理论（K theory）

K理论是代数与几何的有趣结合。最初是为了拓扑空间（向量丛）定义，现在也为环（模）定义，它为这些物体提供了额外的代数信息。

组合数学（Combinatorics）

组合数学（或称为离散数学）则着眼于集合的结构，其中某些子集是可区分的。例如，一副图是许多点的集合，其中一些边（两个点的集合）是给定的。其他的组合问题要求对具有给定属性的集合的子集进行计数。这是一个很庞大的领域，计算机科学家和其他数学以外的人对此都非常感兴趣。

序集合（Ordered sets）

序集合（格）可以为例如一个域的子域集合，给出一个统一的结构。各种特殊类型的格都具有异常完好的结构，并且应用在群论和代数拓扑等多个领域中。

3.几何学

几何学是数学中最古老的领域之一，几个世纪以来，它经历了数次重生。从一个极端来看，几何学包括对首次在欧几里得的《几何原本》中出现的刚性结构的精确研究；从另一个极端来看，一般拓扑学关注的是形状之间最基本的亲缘关系。代数几何中也隐含着一个非常微妙的“几何”概念，但如上文所注，它其实更偏向于代数。其他的一些也能算得上是几何的领域有K理论、李群、多复变函数、变分算、整体分析与流行上的分析。

几何学（Geometry）

几何学是一门从多方面研究的学科。这一大块区域包括经典的欧几里德几何和非欧几何、解析几何、重合几何（包括射影平面）、度规性质（长度与角度），还有组合几何学——如从有限群论中出现的几何。

流形（Manifolds）

流形是像球体一样的空间，从局部来看它像是欧几里德空间。在这些空间里，我们可以讨论（局部的）线性映射，还能讨论函数的光滑性。它们还包括许多常见的表面。多面复形是由许多块的欧几里德空间的部分组成的空间。这些空间类型认可关于映射与嵌入问题的精确答案，它们尤其适用于代数拓扑中的计算，能细致的区分等价的各种不同概念。

凸几何与离散几何（Convex and discrete geometry）

凸几何与离散几何包括对在欧几里得空间中的凸子集的研究。它们包括对多边形和多面体的研究，并经常与离散数学和群论重合；分段线性流形让它们与拓扑学交叉。除此之外，这一领域也包括欧几里得空间中的镶嵌与堆积问题。

微分几何（Differential geometry）

微分几何是现代物理学的语言，也是数学领域的一片乐土。通常，我们考虑的集合是流形（也就是说，局部类似于欧几里德空间），并且配备了距离度量。它包括对曲线和曲面的曲率研究。局域型问题既适用又有助于微分方程的研究；整体型问题会经常调用代数拓扑。

一般拓扑学（General topology）

一般拓扑学研究的是只含有不精确定义的“闭合”（足以决定哪些函数是连续的）的空间。通常会研究一些带有附加结构的空间（比如度量空间，或者紧致豪斯多夫空间），并观察一些属性（如紧致）是如何与子空间、积空间等共享的。拓扑学广泛应用于几何学与分析学，也使得出现一些奇异的例子和集论难题。

代数拓扑（Algebraic topology）

代数拓扑是研究附属于拓扑空间的代数对象，代数不变量说明了空间的某些刚度。这包括各种（上）同调论、同伦群，以及一些更偏几何的工具，例如纤维丛。其代数机制（主要来自同调代数）非常强大，使人生畏。

4.分析学

应用数学的研究领域有哪些？ - 让教育更容易的回答

分析学研究的是从微积分和相关领域中获得的结果。我们可以将它进一步划分为5个小部分：

微积分与实分析
复变量
微分方程与积分方程
泛函分析
数值分析与最优化

【微积分与实分析】

实函数（Real functions）

实函数是微积分课堂会介绍的内容，其中的重点在于它们的导数和积分，以及一般的不等式。这一领域包括常见的函数，如有理函数，是最适合讨论与初等微积分学的相关问题的领域。

测度与积分（Measure and integration）

测度论与积分研究的是一般空间的长度、表面积和体积，是积分理论全面发展的一个关键特征，并且，它还为概率论提供了基本框架。

特殊函数（Special functions）

特殊函数就是超出常见的三角函数或指数函数的特定函数。被研究的那些领域（例如超几何函数、正交多项式等等）会很自然的出现于分析、数论、李群和组合数学领域。

差分方程与函数方程（Difference and functional equations）

差分方程和函数方程都像微分方程一样涉及到函数的推导，但它们的前提却不尽相同：差分方程的定义关系不是微分方程，而是函数值的差。函数方程（通常）在几个点上有函数值之间的代数关系作为前提。

序列与级数（Sequences and series）

序列与级数实际上只是极限法中最常见的例子；收敛性判别准则和收敛速度与找到“答案”同样重要。（对于函数序列来说，找到“问题”也同样重要。）一些特殊的级数（如已知函数的泰勒级数）以及用于快速求和的一般方法可引来很大的兴趣。积分可被用来求级数，分析可用来求级数的稳定性。级数的运算（如乘法或逆运算）也同样是重要的课题。

【复变量】

复变函数（Functions of a complex variable）

复变函数研究的是假设在复数上定义函数的可微性的影响。有趣的是，这种效应与实函数有明显不同，它们受到的约束要严格得多，特别是我们可以对它们的整体行为、收敛性等作出非常明确的评论。这一领域包括黎曼曲面，它们在局部看起来像复平面，但却并不是同一个空间。复变量技术在多个领域（例如电磁学）都具有很大的应用。

位势论（Potential theory）

位势论研究的是调和函数。从数学的角度上看，它们都是拉普拉斯方程Del(u)=0的解；从物理学的角度上看，它们是给整个空间提供（由质量或电荷所产生的）势能的函数。

多复变函数与解析空间（Several complex variable and analytic spaces）

多复变函数研究的是一个以上的复变量的函数。由复可微性所赋予的严格约束意味着，至少在局部上，这些函数的行为与多项式几乎一样。对于相关空间的研究也趋向于与代数几何类似，除了在代数结构之外还使用了分析工具。在这些空间上的微分方程和它们的自同构（automorphism）为其提供了与其他领域的有用连接。

【微分方程与积分方程】

常微分方程（Ordinary differential equation）

常微分方程（ODE）是求解的未知数是一个函数、而非一个数值的方程，其中的已知信息会将这个未知函数与其导数联系起来。这类方程很少有明确的答案，但会有大量的信息来定性地描述它们的解。微分方程有许多重要的类别，它们在工程与科学领域的应用非常广泛。

偏微分方程（Partial differential equations ）

偏微分方程（PDE）的形式与常微分方程大体相同，只是偏微分方程试图求解的函数含有的变量不止一个。在求解过程中，我们也同样需要能定性描述它的解的信息。例如在许多情况下，只有当某些参数属于特定的集合（比如整数集）时，解才存在。它们与自然科学，尤其是物理、热力学和量子力学有着非常密切的关系。

动力系统与遍历论（Dynamical systems and ergodic theory）

动力系统研究的是函数从空间到自身的迭代。理论上来说这一领域与流形上的微分方程密切相关，但在实践中，它的重点在于基础的集合（例如不变集或极限集）以及极限系统的混沌行为。

积分方程（Integral equations）

积分方程自然是要寻找满足其积分关系的函数。例如，每一次的函数值都可能与之前所有时间的平均值有关。这一领域中包括混合了积分与微分的方程。微分方程的许多方面会反复出现，比如定性问题、近似法，以及有助于简化问题的变换与算子等。

变分法与最优化（Calculus of variations and optimization）

变分法与最优化寻找的是可以优化目标函数的函数或几何对象。当然，这还包括对寻找最优结果所需d技术的探讨，例如逐次逼近法或是线性规划。除此之外，还存在大量用来建立与描述最优解的研究。在许多情况下，最优函数或最优曲线可以表示为微分方程的解。常见的应用包括寻找在某种意义上的最短曲线和最小曲面。该领域也适用于经济学或控制理论中的优化问题。

整体分析（Global analysis）

整体分析（或流形分析）研究的是流形的微分方程的整体性质。除了常微分方程理论中的一些适用于局部的工具之外，整体技术还包括使用映射的拓扑空间。这一领域还与流形理论、无限维流形和奇点流形有关，因此也与突变理论相关。除此之外，它还涉及到优化问题，从而与变分法重叠。

【泛函分析】

泛函分析（Functional analysis）

泛函分析研究的是微分方程的全局，例如它会将一个微分算子看作为一组函数的线性映射。因此，这个领域就变成了对（无限维的）向量空间的研究，这种向量空间具有某种度规或其他结构，包括环结构（例如巴拿赫代数和C*-代数）。度量、导数和对偶性的适当一般化也属于这一领域。

傅里叶分析（Fourier analysis）

傅里叶分析利用三角多项式研究函数的近似与分解。这一领域在许多分析应用中都具有不可估量的价值，它拥有许多具体而又强大的结果，包括收敛性判别准则、估计和不等式以及存在唯一性结果。它的扩展包括对奇异积分理论、傅里叶变换和适当的函数空间的研究。这一领域还包括其他的正交函数族的近似，包括正交多项式和小波。

抽象调和分析（Abstract harmonic analysis）

抽象调和分析：如果说傅里叶级数研究的是周期性的实函数，即在整数变换群下能维持不变的实函数，那么抽象调和分析研究的就是在一个子群下维持不变的一般群上的函数。它包括的主题涉及到特异性的不同等级，这又涉及到对李群或局部紧致阿贝尔群的分析。这一领域也与拓扑群的表示论有重合之处。

积分变换（Integral transforms）

积分变换包括傅里叶变换以及拉普拉斯变换、Radon变换等其他变换。除此之外它还包括卷积运算与算子演算。

算子理论（Operator theory）

算子理论研究泛函分析中的向量空间之间的变换，例如微分算子或自伴算子。分析可以研究单个算子的谱，也可以研究多个算子的半群结构。

【数值分析与最优化】

数值分析（Numerical analysis）

数值分析涉及到数值数据的计算方法的研究。这在许多问题中意味着要制造一系列的近似；因此，这些问题涉及到收敛的速度、答案的准确性（甚至是有效性）以及回应的完整性（有很多问题，我们很难从程序的终端中判断它是否还存在其他解决方案）。数学上的许多问题都可以归结为线性代数问题——一个需要用数值方法来研究的领域；与之相关的重大问题是处理初始数据所需的时间。微分方程的数值解需要确定的不仅是几个数值，而是整个函数；尤其是收敛性必须由某种整体准则来加以判断。这一领域中还包括数值模拟、最优化、图形分析，以及开发文件的工作代码等课题。

逼近与展开（Approximations and expansions）

逼近与展开主要考虑的是用特殊类型的函数来逼近实函数。这包括使用线性函数、多项式（不仅仅是泰勒多项式）、有理函数的逼近；其中三角多项式的近似被划分在傅里叶分析中。这一领域包括拟合优度的判别标准、误差范围、逼近族的变化的稳定性、以及在近似情况下保留的函数特性（如可微性）。有效的技术对于特定种类的逼近也是很有价值的。这一领域也同样覆盖了插值与样条。

运筹学/数学规划（Operations research, mathematical programming）

运筹学被喻为是研究最佳资源分配的领域。根据设置中的选项和约束，它可以涉及到线性规划、二次规划、凸规划、整数规划或布尔规划。这一类别中也包括博弈论，博弈论实际上并不是关于博弈的课题，而是关于最优化，它研究的是哪一种策略组合能产出最佳结果。这一领域还包括数学经济学。

5.应用数学

现在我们来谈谈许多人最关心的数学部分——发展能将数学运用到数学领域之外的数学工具。

概率与统计领域考虑的是用数字信息来量化对事件的观察，显然，它们所使用的工具与发展是数学性的，是一个与分析学高度重叠的领域。但另一方面，在这一领域发展的思想，主要被用于非数学领域。

概率论与随机过程（Probability theory and stochastic processes）

概率论应用于有限集合时就是简单的计数组合分析，因此其技术与结果都与离散数学类似。当考虑无穷的可能结果集时，这个理论就得以体现它的价值。它涉及到大量的测度论以及对结果详细严谨的解释。更多的分析是随着对分布函数的研究而进入到这一领域的，极限定理则暗示着集中趋势。应用于重复的转移或随时间的转移会导致马尔科夫过程和随机过程。在考虑随机结构时，概率的概念会应用到数学中，尤其是在某些情况下，它可以产生甚至对纯数学都非常好的算法。

统计学（Statistics）

统计学是一门从数据中获取、合成、预测并作出推论的科学。对平均值与标准偏差的基本计算足以概括一个大的、有限的、正态分布的数据集；之所以有统计领域的存在，是因为数据通常并不会被很好地呈现。如果我们不知道数据集中的所有元素，我们就必须讨论采样和实验设计；如果数据有不正常之处，就需要我们用其他参数或者采用非参数方法对它们进行汇总；当涉及到多个数据时，我们需研究不同变量之间的交互的度量。其他的研究课题包括对时间相关数据的研究，以及避免歧义或悖论的必要基础。它的计算方法（例如曲线拟合）对科学、工程以及金融和精算等领域的工作都具有特别重要的应用意义。

计算机科学（Computer science）

计算机科学，如今它更是一门独立的学科，它研究很多数学方面的问题。在这一领域中，除了从离散数学里的许多问题中所产生的可计算性问题，以及与递归论相关的逻辑问题之外，它还考虑调度问题、随机模型等等。

信息与通信（Information and communication）

信息与通信包括一些代数学家特别感兴趣的问题，尤其是编码理论（与线性代数和有限群有关）和加密（与数论和组合数学有关）。许多适合这个领域的主题都可以用图论的术语来表达，例如网络流和电路设计。数据压缩和可视化都与统计有重叠部分。

质点力学和系统力学（Mechanics of particles and systems）

质点力学和系统力学研究的是粒子或固体的动力学，它包括旋转与振动的物体。会用到变分原理（能量最小化）和微分方程。

固体力学（Mechanics of solids）

固体力学考虑的是弹性与塑性、波传播、工程，以及土壤和晶体等特定固体的问题。

流体力学（Fluid mechanics）

流体力学研究的是空气、水和其他流体的运动问题：压缩、湍流、扩散、波传播等等。从数学的角度来看，这包括对微分方程解的研究，这就涉及到大规模的数值计算方法（例如有限元法）。

光学/电磁理论（Optics, electromagnetic theory）

光学、电磁理论是研究电磁波的传播与演化的理论，它包括的主题有干涉和衍射。除了分析的一些普通分支，这一领域还涉及到一些与几何相关的主题，比如光线的传播路径。

经典热力学/热传导（Classical thermodynamics, heat transfer ）

经典热力学和热传导研究的是热量在物质中的流动，这包括相变和燃烧。从历史的角度来看，它是傅里叶级数的起源。

量子理论（Quantum Theory）

量子理论研究的是薛定谔（微分）方程的解，与此同时它还包括大量的李群理论和量子群论、分布理论，以及与泛函分析、杨-米尔斯问题、费曼图等有关的问题。

统计力学/物质结构（Statistical mechanics, structure of matter）

统计力学和物质结构研究的是粒子的大尺度系统，它包括随机系统和运动或进化系统。研究的具体物质类型包括液体、晶体、金属和其他固体。

相对论与引力理论（Relativity and gravitational theory）

相对论与引力理论将微分几何、分析和群论应用于一些大尺度或极端情况下的物理学（例如黑洞和宇宙学）。

天文学和天体物理学（Astronomy and astrophysics）

天文学和天体物理学：由于天体力学在数学上是质点力学的一部分，因此这一领域的主要应用大多与恒星和星系的结构、演化以及相互作用有关。

地球物理（Geophysics）

地球物理学的应用通常涉及到力学和流体力学，但它是在大尺度上研究问题。

系统论/控制论（Systems theory; control）

系统论以及控制论研究的是复杂系统（如工程系统）随着时间发生的演化。特别是，人们可能会试图对系统进行识别（即确定主导系统发展的方程或参数），或对系统进行控制（即通过选择某些参数以达到期望的状态）。特别令人感兴趣的是稳定性问题，以及随机变化和噪声对系统的影响。虽然这通常属于“控制论”或“机器人学”领域，但在实践中，这是微分（或差分）方程、泛函分析、数值分析和整体分析（或微分几何）的应用领域。

生物学与其他科学（Biology and other sciences）

数学还与许多学科（包括化学、生物学、遗传学、医学、心理学、社会学和其他社会科学）具有明确的联系。在化学和生物化学中，图论、微分几何和微分方程的作用是显而易见的。医学技术必须用到信息传递和可视化的技术。生物学（包括分类学和考古生物学）会使用统计推断和其他工具。经济学和金融学也大量使用到统计学工具，尤其是时间序列分析；有一些主题更具有组合性，例如投票理论。（出于某些原因，数学经济学被归在运筹学的范畴内。）更多的行为科学（包括语言学）都会用到大量的统计技术，其中会涉及到实验设计和其他偏组合类的主题。

以上罗列的便是数学家所从事的研究，但绝对不是唯一的分类标准，而且我们也没能完整地罗列出所有的领域，比如数学家还研究量子代数（quantum algebra）、分形学（Fractal）、数学史以及数学教育等等。

数学大师

一张图让你读懂：为何他会成为数学系所有学生的噩梦

在漫漫的人类历史长河中

各个伟大的数学家

犹如布满“数学星空”中的星群

他们追求最高的精确

最合理的逻辑

用生命燃烧真理

然而在这一群数学天才中

却只有“上帝之子”欧拉

曾“偷取”上帝之语

在人类文明中

迸发出惊人的智慧光辉

欧拉定理

欧拉常数

欧拉定理

欧拉角

定义符号

欧拉公式

欧拉是我们所有人的导师。

不仅仅是因为，每一个进入学校接受教育的人，都要学习，他所创造的数学知识。

更是因为，他用苦难而光辉的一生，教导人们如何做人，如何做学问，如何生存。

在极少天赋异禀的天才之中，我们很难再有机会见到，像欧拉这般，一生勤勉，为学术失明，却不曾因此，而停止前进的步伐。

甚至用尽最后一刻，去照亮人类数学文明的每一个角落。

而这个犹如上帝语言的e^iπ+1=0，是一个代表“潜心修炼，理性思索”的数学符号，将持续引领一批批优秀的数学科研工作者，继续前行。

哈密尔顿

四元数

四元数基本概念

【2022-1-16】1843年一个叫做哈密尔顿的数学家发明了一种叫四元数算法，就是利用复数的特性来计算三维空间中的旋转。然而当时已经有两种计算三维旋转的方法了。

第一种是欧拉算法，最直观，就是围绕着XYZ轴分别旋转几度。但欧拉算法有一个万向锁问题。太复杂不想解释，就是在一种特定的旋转模式下一个轴会锁死，再怎么转都没用。
- 欧拉角的几种表示法，例如常见的偏航角（yaw）俯仰角（pitch）翻滚角（roll），比较直观
- 但有很多缺点，文中说的万向死锁是一个，同一旋转的欧拉角不唯一也是一个问题，另外欧拉角的反运算也非常不直观。
第二种则是矩阵算法。矩阵表示法虽然好计算，但信息冗余，欧拉早就研究清楚了三维旋转就是3个自由变量，但矩阵要用9个量（3×3），互相之间有大量非自由约束，例如行列归一，三向正交等。
四元数算法可以避免万向锁问题。而且四元数算法计算速度还比矩阵算法快。四元数也是表示旋转最干净的方法（归一化的四元数只有3个自由量）。

四元数是简单的超复数。复数是由实数加上虚数单位 i 组成，其中i²= -1。相似地，四元数都是由实数加上三个虚数单位 i、j和k 组成，而且它们有如下的关系：

i² = j² = k² = -1， iº = jº = kº = 1
每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为a + bi+ cj + dk，其中a、b、c 、d是实数。对于i、j和k本身的几何意义可以理解为一种旋转，其中i旋转代表Z轴与Y轴相交平面中Z轴正向向Y轴正向的旋转，j旋转代表X轴与Z轴相交平面中X轴正向向Z轴正向的旋转，k旋转代表Y轴与X轴相交平面中Y轴正向向X轴正向的旋转，-i、-j、-k分别代表i、j、k旋转的反向旋转。

四元数相比其他形式的优点：

解决万向节死锁（Gimbal Lock）问题
仅需存储4个浮点数，相比矩阵更加轻量
四元数无论是求逆、串联等操作，相比矩阵更加高效

哈密尔顿研究出这个算法后，就积极的推广。但当时的数学界根本不接受。

首要的原因就是这个算法太抽象了，难以理解。欧拉算法很直观，在脑子里就可以想象得出来。虽然有万向锁问题，但遇到的概率很小，真的遇到了，大不了就用矩阵算法呗。而四元数算法虽然比矩阵算法快，但也就快那么一丢丢，没必要为了节省这一丢丢时间特意去用一种更抽象的算法。
其次是四元数算法连基本的乘法交换律都满足不了。这对崇尚简洁优雅的数学家们而言，太邪恶了。所以哈密尔顿到死都没看到自己的研究成果被数学界认可。后来四元数是怎么突破历史的封印的呢？是由于三维动画的兴起。在三维动画中一个普通的模型上面的点线面的数量都可能达到几万，如果是好莱坞大片的话，甚至会达到亿。这就意味着当视线转动一个角度时，场景中所有模型上的点线面都得重新绘制，光影也要重新渲染。这其中的计算量可想而知。对于影视剧还算幸运，它们是先渲染完再放给观众看的。而3d游戏则需要实时渲染，游戏每运行一秒，背后都要进行海量的运算。所以从三维动画诞生之日起，计算机图形学家们就一直在寻找提升计算速度的办法，然后他们就发现了四元数这个香馍馍了。别看它一次计算只比矩阵算法快了一点点，几亿次运算下来，就真的是快了亿点点。所以我很反感“是金子总会发亮这句话”，一个数学公式想要发亮都那么难，何况人乎？也许是终有一天是会发亮，只不过那时候人已经不知道在哪了

现代GPU在处理旋转（通常是在vertex shading阶段）并不是用四元数的，而是矩阵。刚体旋转需要3×3矩阵，不过GPU通常用4×4，同时处理三向伸缩和平移。因为3D引擎的基本模块就是向量乘加器，天生适合矩阵运算而不是四元数。但3D编程确实喜欢用4元数表示旋转，是因为其独特的数学特性。3D编程通常用四元数表示旋转，执行时再把四元数转换成矩阵交给GPU去运算。

为什么要学数学

数学职业家：学习数学是为了学习思维方式

数学会培养人两种思维方式：同构映射和分析还原。

同构映射

同构映射是指面对一个复杂问题或复杂系统，先把其本质结构抽象出来，映射到一个同构或同态的我们了解的结构上去，通过这个我们了解结构的性质和变化规律，反过来了解复杂问题或结构的性质和变化规律。

这个思维方式是抽象代数，微分几何和拓扑典型的方式，最早是伽罗华在研究一元N次方程代数解的过程中发现的，通过讨论解结构同构的交换群的对称性质，得到了5次以上方程不可能代数解这种超出常识和直觉的结论。

其实现在这种思维方法已经非常普及，我们在处理政治，军事，经济问题时，经常采用同构映射方法，把问题化繁为简，把复杂问题变成一个我们了解的结构上的问题。这个以前举过很多例子，不再重复。

分析还原

分析还原是数学分析的典型方法，简单说就是分而治之，把一个复杂系统或复杂问题分解成一堆模块，而这些被分解的模块，往往是已经了解或者利用现有知识和技术容易搞清楚的，然后搞清楚这些模块，再组合还原到原始系统或原始问题，根据研究模块得到的判断，来对整体问题或系统进行判断。

例如魏尔斯特拉斯定理：任意一个连续函数可以用多项式级数逼近, 就是这种思想，把连续函数展开成多项式（泰勒级数和傅利叶级数是其具体表达形式之一），通过研究容易得多的多项式性质（例如微分，积分，连续），然后通过收敛性判断还原到原来函数性质。

分而治之在国家管理、巨型项目管理和巨型企业管理中是常用方法，那就是任务分解，当然这个管理方法的核心是分解后的还原和分解后模块处理过程的控制协调。

所以，数学提供的思维方式

简单说就是映射 + 极限（所以搞清楚这两个名词的含义十分有价值）
稍微复杂一点说就是化繁为简 + 分而治之
最准确说就是同构映射 + 分析还原。

这套思维方法，能够让我们准确，迅速，简单明了抓住问题重点，了解核心问题，听懂别人云山雾罩后面的想法和本质（我曾经为某著名大人物的发言做过笔记，后来给他看，他惊叹：我原来讲的东西这么深刻，这么高屋建瓴。其实他在讲的时候，估计自己都不知道自己在讲什么，就是漫山遍野的乱砍）。

有人会问，我为什么要用数学来做介绍的载体？我想有两个原因

第一个原因是数学可能是唯一一个老师一开课，就会说：本课程的基本目的就是为了培养你们什么什么思维方式的（如果是北大数学系和科大数学系毕业的老师，一定都会这么说，因为这是他们的传统。其他学校不了解）学科，其他学科估计都没有这么威武霸气；
第二个原因是数学有若干人类耀眼的天才留下的巨大思维财富，人类到目前为止，可能主要天才的大多数不是物理就是数学，数学的天才我们大多耳熟能详
- 举例来讲，牛顿，莱布尼茨，高斯，欧拉，黎曼，拉格朗日，拉普拉斯，柯西，伽罗华，阿贝尔，康托，魏尔斯特拉斯，狄利赫里，庞加莱，希尔伯特，哥德尔，诺特，巴纳赫，柯尔莫哥洛夫，冯诺依曼等等。

当然物理学的天才也是熠熠生辉的，例如牛顿，爱因斯坦，麦克斯韦，伽里略，海森堡，薛定鄂，狄拉克，普朗克，玻尔，洛仑兹，法拉第，杨振宁，费曼等等。

这里稍微要说几句杨振宁。杨振宁创立的规范场论，在现代物理学中地位非常重要，与量子力学和相对论可以相提并论，1994 年，美国富兰克林学会颁发鲍尔奖给杨振宁时，对他的评价是极高的：

“他提出了一个广义的场论，这个理论综合了有关自然界的物理规律，为我们对宇宙中基本的力提供了一种理解。作为20世纪观念上的杰作，它解释了原子内部粒子的相互作用，他的理论很大程度上重构了近40年来的物理学和现代几何学”。

不管怎么说，杨振宁的规范场论，已经排列在牛顿、麦克斯韦和爱因斯坦这一类伟大的工作之列。他是目前唯一还活着的人类最伟大的物理学家，没有之一。有的人因为人家娶一个年轻老婆而唧唧歪歪，莫名其妙，这羡慕嫉妒恨也太夸张了。

当然，判断一个学科是否伟大，不仅仅是看其诞生了多少天才，更需要看其发现或证明了多少超出直觉和常识的伟大定理，例如数学中，就有

哥德尔不完全性定理（公理系统存在不可证伪，也不可证真的命题）；
Brouwer不动点定理（连续映射存在不动点x0=f(x0))；
诺特定理（系统每一个对称性对应一个物理守恒定律）；
康托连续统的不可数性定理；
科恩对ZF公理系统连续统假设的不可判定性定理；
伽罗华定理（5次以上方程无根式解）；
魏尔斯特拉斯连续函数逼近定理（包括泰勒定理和傅里叶级数收敛定理）；
牛顿--莱布尼兹分微积分基本定理（积分是微分的逆运算）；
中心极限定理（多因素干扰下的随机系统收敛于正态分布）等等伟大定理。

当然不仅仅是数学有伟大定理，在经济学中，也有一些超出人类直觉和常识的伟大定理，例如

科斯定理（交易成本为零时，产权与效率无关）；
阿罗均衡存在定理（供需一定有平衡点）；
阿罗不可能定理（不存在绝对公平）；
萨缪尔森大道定理（经济增长一定存在最优路径）；
资源优化存在定理（凸约束下，非劣解一定存在）；
网络分工优化存在定理（分工网络存在最优解）等等。

不过人类发现的超出常识和直觉最伟大的定理还是物理学的，例如

牛顿力学方程，开启了蒸汽机时代，引导了工业革命；
麦克斯韦方程，开启了电气化时代，目前一切与电有关的行业，电子，电气，电工，电力，电机等等都是他的结果；
薛定谔方程，开启了信息化时代，没量子力学，就没有现在的微电子，计算机；
爱因斯坦方程，开启了原子能时代等等。

当然，不仅仅数学在训练人的思维方式，其他学科也在，只是不这么理直气壮而已。例如

经济学就强调实证（为类比提供对象）和归纳（类比）的思维方式
管理学强调仿真建模（本质是搭建信息流，物流和资金流的逻辑结构和反馈通道，构建计划、组织、指挥、控制和协调平台）和流程（本质是建立一直算法，对数学来讲，任何步骤，次序，流程都是算法）。

但是从思维培训的效率来讲，远远不如数学，一般情况下，一个具有成熟经济学思维方式的人，至少需要20年时间才能形成，管理学也需要十年，而数学培养出熟悉化繁为简+分而治之的思维方式，一般情况5年就能成功。

思维方式是人类知识的结构，没有结构的知识，就是一堆散件，也就相当于散装水泥，乱堆的砖头，一团乱麻的钢材和满地的玻璃碎片。有结构的知识，可以成为一幢摩天大厦。

所以：知识不是力量，思维方式才是力量。成功不靠知识多少，而是靠运用知识的能力—-你的思维方式是否强大。知识不能改变命运，改变命运靠你的知识组成的大厦的高度。

最后再强调一点，保持自己的好奇心和好学，是保证自己思维面对复杂问题或复杂系统时，还能象小刀切黄油一样简单明了的唯一方法。

从前有一匹马叫“代码”

数学教学

【2020-3-8】Teaching kids real math with computers

丘成桐：数理与人文

摘自：丘成桐：数理与人文-原创完整版

作者简介：

丘成桐，当代数学大师，现任哈佛大学讲座教授，学术影响遍及理论物理和几乎所有核心数学分支。年仅33岁就获得代表数学界最高荣誉的菲尔兹奖(1982)，此后获得MacArthur天才奖(1985)、瑞典皇家科学院Crafoord奖(1994)、美国国家科学奖(1997)、沃尔夫奖(2010)等众多大奖。现为美国科学院院士、中国科学院和俄罗斯科学院的外籍院士。

编者按

鉴于网上流传的各种根据现场演讲整理的文本，本社特刊发经丘成桐先生亲自修订的最终版本供读者参考。简体中文版载于高等教育出版社“数学与人文”丛书第17辑《数学的艺术》，网络转载请注明出处，其他商业机构转载请联系本社。http://academic.hep.com.cn/mh

1. 引言

从古到今，无论是科技，数学，或人文科学，内容愈来愈丰富，分枝也愈来愈多。考其原因：

一方面是由于工具愈来愈多，能够发现不同现象的能力也比以前大得多
一方面全世界的人口大量增长，不同种族，不同宗教，不同习俗的人，在互相交流后，不同观点的学问得到融会贯通，迸出火花，从而产生新的学问。

从前孔子讨论自己的学问时说：吾道一以贯之。现在的学科这么多，这么复杂，今天有人能做得到孔子所说的一以贯之吗？我现在来探讨这个问题。

学者在构造一门新的学问，或是引导某一门学问走向新的方向时，我们会问：

他们的原创力从何而来？
为什么有些人看得特别远，找得到前人没有发现的观点？
这是不是一个理性的选择？还是因为读万卷书而得到的结果？

上述这些当然都是极其重要的原因，但是我认为最重要的创造力，有了踏实的基础后，却源于丰富的感情。

2. 文以载道，气象万千

在中国文学史上，我们看到：

屈原作楚辞
李陵作河梁送别诗
太史公作史记
诸葛亮写出师表
曹植作赠白马王彪诗
庚信作哀江南赋
王粲作登楼赋
陶渊明作归去来辞

他们的作品都可以说是千古绝唱。

然后，我们又看到李白，杜甫，白居易，李商隐，李煜，柳永，晏殊，苏轼，秦观，宋徽宗，辛弃疾，一直到清朝的纳兰容若，曹雪芹，他们的文章诗词，热情澎湃，回肠荡气，感情从笔尖下滔滔不绝的倾泻出来，成为我们今天见到的瑰丽的作品。看来，这些作者，并未刻意为文，却是情不能自禁。绝妙好文，冲笔而出。

何以故？孟子説：吾善养吾浩然之气也。太史公说：意有所鬱结也。能够影响古今传世文章的气必需要至柔至远，至大至刚！

南北朝时，刘勰著文心雕龙，他评论五经，认为从文学的角度来看，经文都是上品，以其载道也，载道的文章必定富有文气。道不一定是道德，也可以是自然之道。至于数理方面，也讲究相似的文气。

自希腊的科学家到现代的大科学家，文笔泰半优美雅洁。正如上述；他们并没有刻意为文，然而文既载道，自然可观。数理之与人文，实有错综交流的共通点，互为学习。

3. 科学的基础：公理和哲学

古代希腊人和中国战国时的名家，雅好辩论，寻根究底。在西方，因此而产生了公理的研究，影响了整个自然科学的发展。从欧几里得的几何公理到牛顿的三大定律，到爱因斯坦的统一场论，莫不与公理的思维有关。

无论在西方或是在中国，科学的突变或革命都以深刻的哲学思想为背景。希腊哲学崇尚自然，为近代的自然科学和数学发展打好了基础。中国人偏重人文，在科学主要的贡献在应用科学。但有趣的是中国人提出五行学说，希腊人也企图用五种基本元素来解释自然现象，柏拉图甚至用当时发现的五个最对称的正则多面体来跟这些元素一一对应。中国人提出阴阳的观点，西方人也讲究对偶，事实上，希腊数学家研究的射影几何就已经有pole（极点）和polar（极线）的观念。文艺复兴时的画家则研究 perspective geometry（投影几何），对偶的观念，从那些时候，已经开始了。

值得一提的是：对偶的观念虽然肇源于哲学和文艺思想，但对近代数学和理论物理的影响，至大且巨。在现代数学和粒子物理中，由对偶理论推广到对称群的观点，得到的结果，更是具体入微。七十年前，物理学家已经发现负电子的对偶是正电子，而几何学家则发现光滑的紧致空间存在着庞加莱对偶性质，到了七零年代，高能物理学最成功的标准型理论的主要骨干就是几个重要的对称群的表示，这种表示理论在近代几何和数论也有着奠基性的重要。近三十多年来，物理学家发现他们在七十年代引入的超对称观念，可以提供粒子物理和几何丰富的思想，它预测所有粒子都有超对称的对偶粒子，同时极小的空间和极大的空间可以有相同的物理现象，假如实验能够证明超对称的想法是正确的话，阴阳对隅就可以在基本物理中具体的表现出来了，说不定现代物理的概念可以修正和改进中国人对阴阳的看法。

文艺复兴的科学家理文并重，他们也将科学应用到绘画和音乐上去。从笛卡儿，伽利略到牛顿和莱布尼茨这些大科学家们在研究科学时，都讲究哲学思想，通过这种思想来探索大自然的基本原理。以后伟大的数学家高斯，黎曼，希尔伯特，外尔(Hermann Weyl)等都寻求数学和物理的哲学思想。黎曼创造黎曼几何，就从哲学和物理的观点来探讨空间的基本结构。至于爱因斯坦在创造广义相对论时，除了用到黎曼几何外的观念，更大量的采用到哲学家恩斯特·马赫(Ernst Mach)的想法。

4.地域文化对科学人文的影响

每个国家，每个地方，甚至每个大学，它们发展出来的科学，技术，虽然都由同样的科学基础推导而来，结果却往往迥异。这是什么原因呢？除了制度和经费投入不一样以外，更重要的是它们有不同的文化背景，不同地方的科学家对自然界有不同的感受。他们写出来的科学文章，和科技成果往往受到家庭社会背景和宗教习俗的影响。他们学习的诗词歌赋，文学历史也都与他们的科技成就有密切的关系。

举个例子，在中国成长的数学家，就受到地域和导师的影响很大，不少的中国数学家喜欢读几何，大概是受到陈省身先生的影响，其次是读解析数论，则是受到华罗庚先生的影响。而这些数学家里，又以江浙人占大多数，大概是这些地方比较富庶，又得西方风气之先。印度的学者，则受 Srinivasa Ramanujan 和 Harish Chandra 的影响，喜欢数论和群表示论。日本近代数学的几位奠基者，包括高木贞治(Takagi Teiji)在内，家里都是精通兰学的学者，对荷兰文有很好的认识，因此他们比较容易接受西方的数学观念。

我遇见过很多大科学家，尤其是有原创性的科学家，对文艺都有涉猎。他们的文笔流畅，甚至可以媲美文学家的作品。其实文艺除了能够陶冶性情以外，文艺创作与科学创作的方法实有共通的地方。

5. 中国人的感情和理想

出色的理文创作，必须有浓厚的感情和理想，在这一点上，中国人并不比西方人逊色。中国古代学者都有浓厚的感情，它们充分的表现在诗词歌赋上。

其实中国文化在文艺以外的活动，表现出来的感情也是极为丰满的。在中国古代，不少人为了理想而不惜性命。当年张骞出使西域，间（闯？）关万里。西域的文化、农产和牲畜，因此源源不绝地输入中原。而卫青和霍去病奔驰大漠，窦宪勒石燕然，出生入死，才去除匈奴数百年来在北方做成的祸患。霍去病曾说：匈奴未灭，何以家为？有了这些勇气，这种志愿。他们才能够建立这些名垂千古的事迹。

东晋时，外族入侵，中原板荡，祖狄谋复中原之地，带兵渡江时，祖狄击楫而誓，说“祖狄不能清中原而复济者，有如此江！”这是何等的志气！何等的应许！

在魏晋南北朝和唐朝，僧人为求佛法，不惜舍命于沙漠和大海，终于带回大量的经卷。其中一个典型的例子是东晋时的法显，他为求佛法，在五十九岁的高龄，行走河西走廊，过玉门关，横越沙河，翻过葱岭，直达印度。其间历尽艰险，苦学梵文和抄写经典后，又在海上多次遇难，才回到中原。全程十三年四个月，他自已在佛国记里面说：“顾寻所经，不觉心动汗流。所以乘危履险，不惜此形者，盖是志有所存。专其愚直，故投命于不必全之地，以达万一之冀。”这种毅力，真是值得我们钦佩。

宋朝文天祥被蒙古人囚禁时，作正气歌。他认为天地间有一种正气，这个气是文学家和科学家共同享有的，也就是孟子说的浩然之气。我们在创作的时候，这种气会表现出来。现代的杰出科学工作者，肉体上未必经得起上述诸贤的艰苦经验，但他们做研究时坚持的意志却可以跟上述诸贤媲美。初学者需要欣赏和学习这种意志。

6. 科学和人文的共同点

诗人墨客，诗词歌赋，最能表达这种高尚的情怀。所以科学家与文学家有很多能够产生共鸣的地方。事实上，科学家和文学家除了有共同的感情以外，在研究的方法上，也有很多类似的地方。

在我从前写了一篇文章，我用不同的例子指出数学家可以用和古代中国文学家赋比兴类似的手法，做出第一流的创作。

现在再举另一个例子：

苏东坡是北宋的大文豪，一代词宗。他作了一首洞仙歌：

冰肌玉骨，自清凉无汗。水殿风来暗香满。绣帘开，一点明月窥人，人未寝，倚枕钗横鬓乱。起来擕素手，庭户无声，时见疏星渡河汉。试问夜如何，夜已三更，金波淡，玉绳低转。但屈指，西风几时来，又不道，流年暗中偷换。

这词的背景是：苏轼在七岁时，见过眉山地方的一个老尼，姓朱，年约九十，自已说曾经去过蜀主孟昶的宫廷中。有一日，天气炎热，蜀主和他的妃子花蕊夫人深夜纳凉于摩诃池上。孟昶作了一首词，这个尼姑还能记得这首词，并告诉了苏轼。四十年后，苏轼只能够记得词中头两句。苏轼有天得暇，寻找词曲，猜测这词应该为洞仙歌令。苏轼因此循着这两句的做意和猜测蜀主的想法，将这首词续完。

苏轼续词对中国文学是一个贡献。但我们想想，不同的文人对着残缺的词句，一定会有不同的反应。

假如是清代的乾嘉学者，就可能花很多时间对这件事做考据，得出一个结论：就是这词不可考！因此不会去续这首词。
有一些文人，可能没有能力去猜测到这词的词牌名，当然也不会做任何事。
另外有一些文人，可能像苏轼一样，猜到了词牌名，却没有兴趣去将它续起来。
还有一些文人，虽然找到词牌名，但文艺功力太差，续出来的可能是没有趣味的词。
但是苏轼却兴致勃勃地花了时间去推敲，去猜测，写了一篇传世的杰作！

我为什么要举这个例子呢？因为科研的创作，有类似的情形。上述四个不同的描述正好反映了清初到近代，中国科学发展的几个阶段！

但有一点值得注意的是: 苏轼深爱文学，才会在四十年后还记得七岁学过的词的前两句，但是纵然这是绝妙好句，有多少人过了一两年后还记得别人写的词？从这里也可以看到学者的感情所在。坦白说，我本人五十年前读这首词，到现在也还记得词中这两句。但是我教我的小孩念词，过了两三年后他们就全部忘记了。

现在来看看科学的发展，在一九零五年时，物理学家知道两个重要的理论，就是牛顿的引力场论和狭义相对论。他们都与引力有关，同时都基本正确，却互相矛盾。爱因斯坦对这个问题有无比的兴趣，他知道这两个理论是一个更完美的引力理论的一部分，他在数学家闵科夫斯基，高斯，黎曼和希尔伯特的幇忙下，完成了旷世大作，就是我们钦佩的广义相对论。

爱因斯坦的创意和能力当然远胜于苏轼补洞仙词，但却有点相似。我来做一个不大合适的比拟，苏轼记得蜀主的两句词，一句可比拟为牛顿力学，另一句可比拟为狭义相对论里面的洛伦兹转换。爱氏花了十年功夫来研究引力场，就是从这两件事情做出发点，用他深入的物理洞察力和数学家提出的数学结构，才完成他留名千古的引力理论！这一点有点像苏轼在续词时，对四川有深入的了解，又能体会到孟昶和花蕊夫人在摩诃池水晶殿里的情形，心有所感，才能以他高明的手法续完这首词。

但这里有一个重要的分别，假如爱丁顿(Arthur Stanley Eddington)在一九一九年时没有用望远镜观察证明广义相对论的话，则无论爱因斯坦的理论多漂亮，仍然不是一个重要的工作。物理学需要实验，数学需要证明，文学却不需要这么严格，但是离现象界太远的文学，终究不是上乘的文学。

一首词续得好，需要有文学修养，也需要有意境，才能够天衣无缝，但和大型歌剧或小说比较，它的创作，还是来得容易些。

7. 文学和科学中的大型创作

现在来看看文学和科学的领域里，大型的结构是如何被创作出来的。中国最有名的经典著作要数红楼梦，它的作者曹雪芹并没有将这部巨著全部完成，这可是千古憾事，我们如何将它续完呢? 除了需要有出色的文学技巧外，还需要了解该书的内容和背景，由于这部书的内容错综复杂，从现代的观点来看，可能需要用统计和数学的方法来帮忙。

当年曹雪芹写红楼梦，借用了自身的经历来描述封建社会大家族所遇到的无可避免的腐败和堕落，也描述了当年家族的荣华富贵。他与评书人脂砚斋，一路著书，一路触目愁肠断。整本书可以说是以血书成，作者自己也说：十年辛苦非寻常。书中表现出来的笔墨，充满了他澎湃的感情，但却是有条有理的创造和叙述。在这本书差不多完成时，作者却因伤感而去逝了，“芹为泪尽而逝”。但至今还没有任何作者能够将这部巨著完满地续成，对曹雪芹当年的想法如何处理，还是争论不已的大问题。

曹雪芹和他的家族的经历当然是多姿多釆，但是他不可能将真事尽数写下来。毕竟事情有先后轻重之分，又为了将真事隐去，他不可能不创造一些情节，一些诗词，一些交谈内容来完成一个完整的图画，他用了种种不同的手法，将旧社会与大家庭的腐败以及个人的经历用他富有感情的文笔表现出来。曹雪芹以后，很多学者想学他的写法，效果却相差甚远，除了文艺水平不如曹雪芹外，他们写书时感情的浓郁和曹雪芹的内心世界是无可比拟的。

红楼梦的创作过程有如一个大型的数学创作，或者一个大型的科学创作。数学家和科学家，也是企图构造一个架构，来描述见到的数学真理，或是大自然的现象。在这个大型结构里，有很多已知的现象或者定理。在这些表面上没有明显联系的现象里，我们要企图找到它们的关系。当然我们还需要证明这些关系的真实性，也需要知道这些关系引起的效果。

但如何找到这些联系的方法，因作家而异。在小说的创作里，小说家的能力和经历，会表现在这些地方。一个好的科学家，都会创造自己的观点，或者自己的哲学观点，来观察我们研究的大结构，例如韦伊(André Weil)要用代数几何的方法来研究数论的问题，而朗兰兹(Robert Langlands)要用自守型表示理论来研究数论。他们在建立现代数论的大结构时，就用了不同的手法来联系数论中不同的重要部分，得到数论中很多重要的结论，值得惊讶的是：他们得到的结论往往一样，殊途同归。当年我和一群朋友建立几何分析这门学问时，就采取一个观点，就是大量的几何现象需要用非线性微分方程来解释，方程的解往往可以决定空间的几何性质。几何学家想研究的现象包括了子流形和不同的几何结构，我在一九七六年完成的卡拉比猜想就是要构造复流形上的几何结构，方法是解非线性微分方程。

以后大家开始重视这种方法，非线性方程因此横跨各个领域。除了复几何外，我当时想做三维空间的几何结构问题。但是我的同学瑟斯顿(William Thurston)也认识到这个问题的重要性，他用徧向于拓朴学和黎曼面的方法，将这个问题的重要部分率先解决了。可见做学问的方法不拘一格。但是三维空间的结构问题，最后还得用几何分析的方法来完成。

8. 科学的美和科学家的主观的感情

能够左右科学发展大流的科学必须有如下的性质：它能够对大自然对数学的现象有普遍和深入的了解，在物理学，我们对一些现象进行抽象，进行解释，从而构造一些理论，在得到这些理论后，我们去推导，去找寻新的现象，于是重新观察，重新做实验，来验证这些构造出来的理论。当这些理论被验证后，假如应用范围很广泛，我们就称它为定律。受到欧几里得公理化的影响，牛顿力学的基础在三大定律，三大定律的叙述极为简单，而描述的现象却极度深刻，它的真实不受时空的限制！这是一千多年来，无数物理学家智慧的结晶。

从历史中，我们看到将无数有意义的现象抽象和总结而成为定律时，中间的过程总是富有情感的！在解决大问题关键的时候，科学家的主观的感情起着极为重要的一面，这个感情是科学发现的原动力！面对着震撼我们心弦的真理时，好的科学家会不顾一切，不惜冒生命的危险去发掘真理，去挑战传统的理论，甚至于得罪权贵，伽利略对教会的着名挑战就是这个感情表现的一面。

为什么?

当一个科学家发现他们推导出来的定律或定埋是如此的简洁，如此的普遍，如此的有力地解释各种现象时，他们不能不赞叹自然结构的美妙，也为这个定律或这个定理的完成而满意。这个过程值得一个科学家投入毕生的精力！苟真理之可知，虽九死其犹未悔！

文学艺术也一样，红楼梦，莎士比亚，诗经，楚辞表现出来的感情，跨越时空，普罗大众都能够感受到，好的艺术必须能够表现出作者的感情，即使写景，也可以融合感情在内！曹雪芹写红楼梦，笔尖带着他毕生的感情，所以以后学红楼梦的作者不知多少，但是都缺乏这个深入的感情，所以都没有学好。

由于艺术家的经验是在他们存身的社会吸取得来的，也是在观察普罗大众得到的，他们的著作反映的感情也往往代表着当时社会大众的感情，这一点和科学观察有类似的地方。

用一个主要的思想来建造大型科学结构跟文艺创作也很相似，曹雪芹创作红楼梦时的一个重要观点就是以情悟道，以四大家族的衰败来拱托这个感情。罗贯中写三国演义，就是要弘扬以刘氏为正统，贬低曹魏氏的思想。

二十世纪代数几何和算术几何的发展就是一个宏伟的结构，比红楼梦的写作，更瑰丽，更结实，但它是由数十名大数学家共同完成的。在整个数学洪流中，我们见到大数学家各展所能，发展不同的技巧，解决了很多悬而未决的问题，但是要左右整个大流方向的数学家，实在不多，我们上面提到过的Weil和Langlands就是很好的例子。

我们需要培养一些能望尽天涯路，又能衣带渐宽终不悔的学者，这是需要浓郁的文化和感情的背景才能产生出来。正如宋徽宗词中的叙述：天遥地远，万水千山，知他故宫何处，怎不思量，除梦里有时曾去！

从这里，也许可以看到中西数学的不同。直到如今，除了少数两三个大师外，中国数学家走的研究道路基本上还是萧规曹随，在创新的路上，提不起勇气，不敢走前人没有走过的路！我想这一点与中国近几十年来，文艺教育不充足，对数理感情的培养不够有关。

9. 科学和人文学家要求的完美图画

我们现在来看另外一个例子来解释数理与人文共通的地方：文学家和科学家都想构造一个完美的图画，但每个作者有不同的手法。

在汉朝，中国数学家已经开始研究如何去解方程式，包括计算立方根，到宋朝时，己经可以解多次方程，比西方早几百年，但解决的方法是数字解，对方程的结构没有深入的了解。

一个最简单的问题就是解二次方程： X² + 1 = 0

这个方程没有实数解，事实上，无论 X 是任何实数，方程的左边总是大于零，所以这个方程式没有实数的解，因此中国古代数学家不去讨论这个方程式。

大约在四百多年前，西方数学家开始注意这个方程，文艺复兴后的意大利数学家发现它跟解三次和四次方程有关。他们知道上述二次方程没有实数解，就假设它还是有解，将这个想像中的解叫做虚数。

虚数的发现，可了不起得很！它可以媲美轮子的发现。有了虚数后，西方学者发现所有多项式都有解，而且解的数目刚好是多项式的次数。所以有了虚数后，多项式的理论才成为完美的理论。完美的数学理论很快就得到无穷的应用。事实上，其后物理学家和工程学家发现虚数是用来解释所有波动现象最佳的方法，这包括音乐，流体，和量子力学里面波动力学的种种现象。数论研究物件的重要部分是整数，但为了研究整数，我们不能避免地要大量的用到复数的理论来帮忙。在十九世纪初叶，柯西和黎曼开始了复变函数的研究，将我们的眼界由一维推广到二维，改变了现代数学的发展。黎曼又引入了 Zeta 函数，发现了复函数的解析性质可以给出整数中的质数(prime number)的基本性质。另一方面，他也因此而开发了高维拓朴这个学科。

由于复数的成功，数学家企图将它推广，制造新的数域，很快就发现除非放弃一些条件，那是不可能的。但是哈密尔顿(William Rowan Hamilton)和凯利(Arthur Cayley)先生却在放弃复数域中某些性质后，引进四元数(quarterion)和八元数(Cayley numbers)这两个新的数域。这些新的数域影响了狄拉克(Paul Dirac)在量子力学的构想，创造了Dirac方程式。从这里可以看到数学家和物理学家为了追求完美化而得到重要的结果。

其实物理学上很多伟大的发现，是伟大的科学家通过一些思考的实验和他们深入的洞察力得到的。爱因斯坦创造广义相对论时，人类观察到的宇宙空间实在不大，他却得到数学家的大力帮助。在爱因斯坦完成广义相对论后，外尔和很多科学家开始融合引力场理论和电磁场理论，外尔率先提出规范场的理论，经过十年的挣扎，才将麦克斯韦的电磁理论看作和广义相对论类似的规范场论，在物理学上，这是一个伟大的突破。廿多年以后，泡利(Wolfgang Pauli)，杨振宁和米尔斯(Robert L. Mills)将规范群推广到非交换群后，完成了一般的规范场理论，成为近代物理学标准模型的基础。

有趣的是，外尔说：假如理论和见到的现象界有冲突时，而这个理论漂亮而简洁的时候，我宁愿相信理论。这个看法对规范场理论的发展，有很大的帮助！在这里，我们看到文学家和科学家类似的地方。Dirac在完成他的方程后，他说我的方程式比我自己更有深度，因为它优美地描述了基本粒子的性质，并在实验室中得到证明，有些性质是Dirac在创造这个方程前没有办法想像的。这是科学创新中产生的一个奇妙的现象，我们用以了解真理的工具往往会带领我们向前，不断的向前摸索！

将一个问题或现象完美化，然后，将完美化后的结果应用到新的数学理论，来解释新的现象，这是数学家的惯用手法，这与文学家有很多相似的地方，只不过文学家用这种手法来表达他们的感情罢了。

举例来说，在中国古代很多传说，很多是凭想像，将得到的一些知识，循当时作者或当政者的需要而完成一些著作，所以我们看到东汉刘向父子作伪经，也看到山海经的写作，夸大地描述很多无法证明的事件。

中国诗词也有不少的例子。例如，李商隐和李白就创作了“锦瑟无端五十弦”和“白发三千丈”这两句夸大的诗句。

在明清的传奇小说里，这种写法更加流行，西游记里面描述的很多事情只有很少部分是事实，三国演义里孔明借东风的事是作者为了夸大诸葛亮的能力而写出来的。

文学家为了欣赏现象或者舒解情怀而夸大而完美化，但数学家却为了了解现象而构建完美的背景

。我们在现象界可能看不到数学家虚拟结构的背景，但正如数学家创造虚数的过程一样，这些虚拟的背景却有能力来解释自然界的奇妙现象，在数学家的眼中，这些虚拟背景，往往在现象界中呼之欲出，对很多数学家来说，虚数和圆球的观念都可以看做自然界的一部份。现在粒子物理学里面有一个成功的理论叫做夸克理论，它和虚数理论有异曲同工之妙，人们从来没有看见过夸克，但是我们感觉到它的存在。

有些时候，数学家花了几千页纸的理论来将一些模煳不清的具体现象用极度抽象的方法去统一，去描述，去解释。这是数学家追求完美化的极致，值得惊奇的是，这些抽象的方法居然可以解决一些极为重要的具体问题，最出名的例子就是格罗滕迪克(Alexandre Grothendieck)在Weil猜想上的伟大工作。物理学家在七十年代引进的超对称也是将对称的观念极度推广，我们虽然在实验室还没有见到超对称的现象，但它已经引起了很多重要的物理和数学上的思维。

10. 优良的科学家需要人文的训练

近代数学家在数学不同的分枝取得巨大的成果，与文学家的手段极为类似。所以我说好的数学家最好有人文的训练，从变化多姿的人生和大自然界得到的灵感来将我们的科学和数学完美化，而不是禁锢自己的脚步和眼光，只跟着前人的著作，作小量的改进，就以为自己是一个大学者。

中国数学家，太注重应用，不在乎数学严格的推导，更不在乎数学的完美化

，到了明清，中国数学家实在无法跟文艺复兴的数学家比拟。

有清一代，数学更是不行，没有原创性！可能是受到乾嘉考证的影响，大多好的数学家跑去考证九章算术，和唐宋的数学著作，不做原创性的工作。和同一个时代，文艺复兴以后的意大利，英国，德法的学者不断的尝试的态度迥异。找寻原创性的数学思想，影响了牛顿力学。因此而产生了多次的工业革命。

到今天，中国的理论科学家在原创性还是比不上世界最先进的水准，我想一个重要的原因是我们的科学家在人文的修养还是不够，对自然界的真和美感情不够丰富！这种感情对科学对文学家说，其实是共通的。我们中华民族是一个富有感情和富有深度的民族。上述的文学家诗人小说家的作品，比诸全世界，都不遑多让！

但是我们的科学家对人文的修养却不大注意，我们管理教育的官员们却有很奇怪的教育政策，他们大概认为语文和历史的教育并不重要，用了一些浅显而没有深度的通识教育来代替这些重要的学问，大概他们以为国外注重通识教育的缘故吧。但这是舍本逐末的事情。坦白说，我还没有看到过一个有水准的国家和城市不反反复复地去教导国民们本国或本地的历史的。我两个孩子在美国一个小镇读书。他们在小学，在中学，将美国三百年的事情念得滚瓜烂熟！因为这是美国文化的基础。

我敢说：

不懂或是不熟习历史的国民，他们的感觉必定是认为自己是无根的一代，一般来说，他们的文化的根基比较肤浅，容易受人愚弄和误导。

这是因为他们看不清楚现在发生事情的前因后果。史为明镜，它不单指出古代伟人成功和失败的原因，它也将千年来我们祖先留下来的感情传给我们，我们为秦皇汉武，唐宗宋祖创下的丰功伟绩，感到骄傲，为他们的子孙走错的路而感叹！中国五千年丰富的文化使我们充满自信心！我们为什么不好好地利用我们祖先留给我们的遗产？

或许有人说，我不想做大科学家，所以不用走我所说的道路。其实这事并没有矛盾。当一个年轻人对自己要学习的学问有浓厚的感情后，学习任何学问都会轻而易举！至于数学和语文并重，则是先进国家如美国等一向认为是理所当然的。美国比较好的大学收生时都看SAT的成绩，最重要部分，考的就是语文和数学。

除了考试以外，美国好的中学也鼓励孩子多元化，尽量涉猎包括人文和数理的科目。美国有很多高质量的科普杂志，销量往往都在百万本以上。而中国好的科普不多，销量也少得可怜，从这点就可以看到中西文化的异同，希望我们会渐渐的改进！

11. 博雅教育

最后要指出，数理人文和所谓博雅教育(liberal education)有莫大关系。哈佛大学文理学院院长在2006年的周年通讯中说：让我重申博雅教育的重要性。

博雅教育的目标广阔，既着眼于基础知识，鉴古知今，推理分析，又能培养学生在艺术上的创造性，兼且对科学的概念和实验的精准性有所了解，同时也强调因材施教 (Bildung)，反对重覆不断的操练(Übung)，顶住了过早学科化(specialization)和专业化(professionalization)的潮流。以培养专业人才为目标是好些名校的优良传统，但这绝非哈佛大学的使命。哈佛学子在专注于某门学问的同时，我们希望他们成为一个事事关心、善于分析和独立思考的人，毕业后矢志贡献于社会，并终生学习不已。

台湾实业家、台积电董事长张忠谋先生对上述看法甚为赞同。他说：

博雅教育启发我的兴趣，充实我的人生，影响非常大。我曾说过，如果没有红楼梦，莎士比亚，贝多芬等等，我的生命会缺少一块。对于我的工作而言，博雅教育增进我的独立判断的思考能力，让我从工程师，工程经理，总经理，执行长到董事长一路走来，无论担任何种职务都受益良多。

张董事长在企业上极为成功，可以见到数理和人文关系的重要性。

美国名校的教育使得不少的学者跨越不同的领域而得到极大的成就！有些学生在本科时读英文系，毕业后却可以成功地创立高科技公司。当代数学物理有极为杰出贡献的威腾(Edward Witten)教授在本科时念历史。这些例子在美国名校不胜枚举，但在华人社会却不多见。这应当是归功于美国博雅教育的结果，也就是数理人文并重的结果。

中国的教育始终离不开科举的阴影，以考试取士，系统化的出题目，学生们对学问的兴趣，集中在解题上，科研的精神仍是学徒制，很难看到寻找真理的乐趣。

西方博雅教育的精神确实能增广我们的视野，激励我们的感情，更能够培养大学问的成长。举例来说，哈佛大学的 Freshman seminar，可以说是于学无所不窥! 连我前年写的一本叫做《大宇之形》的科普书，物理系有些教授也用来做为通识课本。多读多看课本以外的书，对我们做学问，做人处世都会有大帮助！

好的文学诗词，发自作者内心，生生不息。将人与人的关系，人对自然界的感受表现出来。激情处，可以动天地，泣鬼神。而至于万古长存，不朽不灭！伟大的科学家不也是同样的要找到自然界的真实，和它永恒的美丽吗?

12. 后记

我在中国博物馆看到罗丹的遗嘱，在这遗嘱里我们看到雕塑家和科学家有着相同的目标。节录如下：

生在你们以前的大师，你们要虔诚地爱他们。

可是要小心，不要模仿你的前辈。

尊重传统，把传统所包含永远富有生命力的东西区别出来

对“自然”的爱好和真挚，这才是天才作家的两种强烈的渴望。他们都崇拜自然，从没有说过谎。所以传统把钥匙交给你们，依靠这把钥匙，你们能避开守旧的桎梏。也正是传统，告诫你们要不断地探求真实，并阻止你们盲从任何一位大师。

但愿“自然”成为你们惟一的女神。

对于自然，你们要绝对信仰。你们要确信，“自然”是永远不会丑恶的，要一心一意忠于自然。

在艺术家眼中，一切都是美的，因为他锐利的目光能够穿透任何人或物，发现其“性格”，换句话说，能够发现其外形下透露出的内在真理；而这个真理就是美的本身。虔诚地钻研吧，你们一定能找到美，因为你们将会发现真实。奋发地工作吧!

要有耐心！不要指望灵感。灵感是不存在的。艺术家的优良品质，无非是智慧、专心、真挚、意志。像一个诚实的工人一样完成你们的工作吧。

在我看来，罗丹教导我们的，何止是艺术，他每一句话都可用在科研的创新上，我们用我们真摰纯朴的感情去找寻大自然的美丽，大自然的真实。我们都感谢以前的大师，我们在他们的肩膀上向前摸索，但我们也知道他们的道路不是唯一的，让我们勇往直前，建立我们自己了解大自然的道路！

资料

数学工具

【2024-2-1】三大数学软件（Matlab、Mathematica、Maple）后两个已经名不副实，长期吃老本不思进取，性能低下bug太多只会吹牛，近年来被开源免费的GeoGebra吊打，GeoGebra的发展势头很猛，超越Matlab也是迟早的事

matlab 是工程软件，不是数学软件。想干掉他的人多了，如scilab、octave、Julia……，但其至今仍活的有声有色。

Mathematica

【2023-4-3】wolfram language 是图灵完备的编程语言, 计算机代数系统

mathematica软件擅长数学，科学计算；
MATLAB 是竞争对手.但是 MATLAB 不是图灵完备的, 编程能力比较差；

近期还有用mathematica实现chatgpt

Matlab

Maple

GeoGebra

在线几何作图GeoGebra（源自马同学高等数学）
【2019-07-15】马同学高等数学：如何通俗讲解牛顿法
切线方程：

\[f \left( x _ { n + 1 } \right) - f \left( x _ { n } \right) = f ^ { \prime } \left( x _ { n } \right) \left( x _ { n + 1 } - x _ { n } \right)\]

【2019-07-15】神经网络分类面到底什么样？可交互

Mathigon

【2019-04-09】可交互数学课本Mathigon,github地址

Penrose

【2024-9-27】CMU Penrose

Demo
示例 examples

用 Penrose 创建图像，要在三个特定的文件中编写代码

三个文件分别对应于：

.domain 文件，定义特定领域的语言。
.substance 文件，创建数学内容的物质。
.style 文件，指定视觉表示的样式。

数列

【2023-1-28】数列推理问题常见解法

数字推理，顾名思义即为探索数列排列规律，并正确填补空缺数字的一类题目，形成规律至少需要三个数字，我们要做的则是从这三个或者更多数字中找出连接他们的“线”，或者明目张胆、或者遮遮掩掩，不变的是总能牵一发而动全身，而这样的“线”你有把握找到几条呢？

解法

1、数字间涉及和、差
- （1）等差关系：数列中各个数字成等差数列；二级等差：数列中相邻两个数相减后的差值成等差数列。
- （2）移动求和或差。从第三项起，每一项都是前两项之和或差
- 找规律：2，15，41，80，？
2、数字间涉及乘除
- （1）等比关系：数列中相邻两个数的比值相等；二级等比：数列中相邻两个数相减后的差值成等比数列
- （2）移动求积或商关系。从第三项起，每一项都是前两项之积或商。
- Tip：观察数列数字间的变化幅度的大小
  - 如果前几项较小，末项却突然增大数倍，可以考虑等比数列；
  - 如果数列的起伏不大，变化幅度小且逐渐递增或递减，则可考虑等差数列。
- 找规律填空：7，9，-1，5，（）
3、平方关系、立方关系、乘方关系
- 平方、立方是数字推理中的常客，而这就需要对常见数字的平方（和）、立方（和）都有所了解，解题时注意各项数字是否为整数的平方或立方，或是与左右相邻或相近的数字，如果是，就可以考虑平方数列或立方数列。
- 找规律：1=3，2=14，3=39；4=？
4、翻转数列
- 有些数字推理中并不存在计算，而是需要另辟蹊径，比如换个“角度”看。
- 找规律填空：0、1、8、11、69、88、96、101、( )
5、非整数数列
- 通常会对整数间的关系比较敏感，但数字推理中也不乏特立独行的存在，比如分数数列，比如带根号的数列。
- 分数数项有时需要我们先做通分处理，且通常需要把分子和分母看作两个不同的数列来计算；遇到带根号的数项则可尝试开根号或转换成根号内乘方的形式。如果数列内有多项分数或根式，一般都需要将其余项均化为分数或者根式。这类数列并不比整数数列棘手，运算规则都是相通的，熟能生巧。
6、质数数列
- 质数又称素数，条件是在大于1的自然数中，除了1和它本身以外不再有其他因数。质数数列都是围绕质数做文章，这就需要我们对常见的质数、排列都有所了解才行。
- 问号处应填入什么数？1，3，6，11，18，29，42，？
7、特定的数列规律、转换方式
- 比如圆周率、进制转换、斐波那契数列、发音规律、笔划顺序、字母对应、钟表数字与角度对应等等，不知道这个数列的可能永远解不出来，但知道了这个规律就会变得非常简单。
8、双重数列
- （1）每两项为一组，以组合为单位呈现运算规律，例如每两项之比/差相同、又或者每组以某种方式计算后得到的新数项间存在联系等等。
- 2、5、6、10、11、16、？
- （2）两个数列相隔，可能其中一个数列无任何规律，也可能两个数列的规律不同、需要分别看待。通常如果一个数列的项数比较长，或有两项是括号项，我们就可以往奇、偶项数列和两两分组数列去考虑了。当数字的个数超过7个时，为双重数列的可能性相当大。1，12，4，10，7，（），10，6
9、组合数列
- 最有挑战的终于来了！如果你在33IQ的数字推理题库里逛过，会发现以前面那8种数列单独出的题几乎是不存在的，即使出现了也难度不高，更多的是8种数列关系两两组合、甚至三种组合，环环相套、题中有题。最常见的当属和差关系+乘除关系、和差关系+平方立方关系，不常见的就得诸位看官自行摸索了。
- 9126, 11218, 13346, 12516, 14734, ？