- 优化算法
- 结束
优化算法
总结
【2022-5-19】关于神经网络,一个学术界搞错了很多年的问题
- 比较各种优化算法的性质,包括传统的 SGD,Momentum SGD,AdaGrad,RMSProp 和 Adam 等;可视化分析
- SGD optimization on loss surface contours
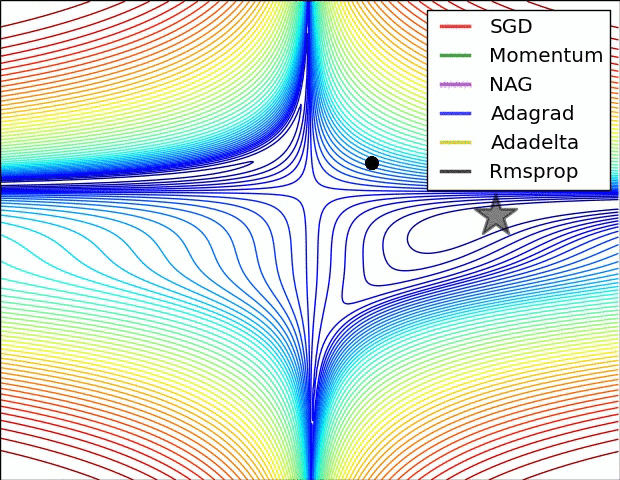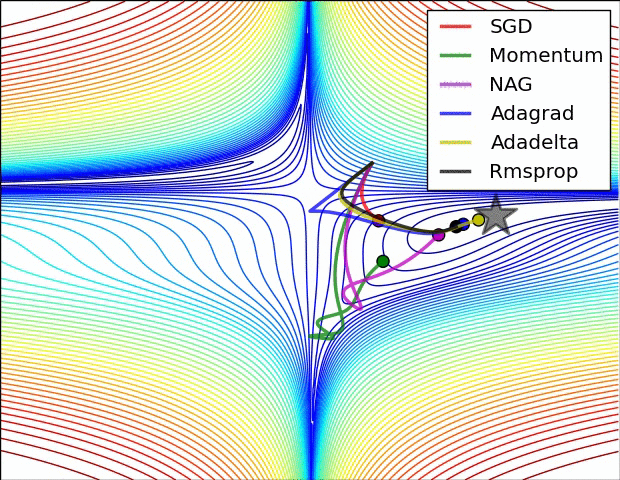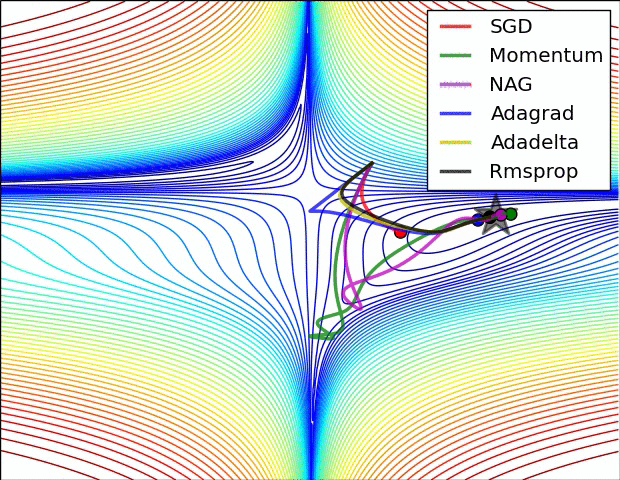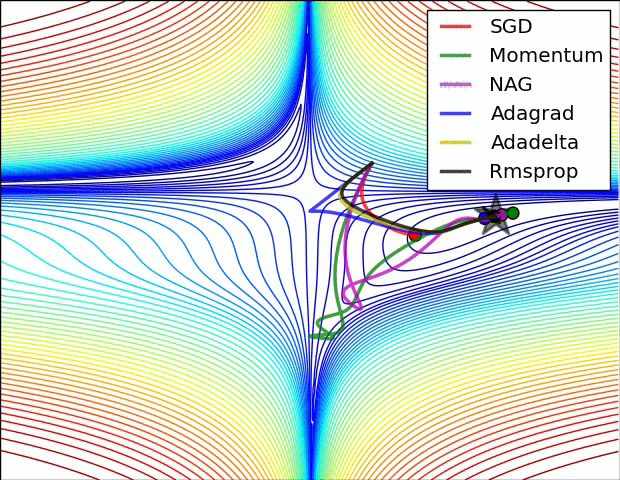
- 不同算法在损失面等高线图中的学习过程,它们均同同一点出发,但沿着不同路径达到最小值点。其中 Adagrad、Adadelta、RMSprop 从最开始就找到了正确的方向并快速收敛;SGD 找到了正确方向但收敛速度很慢;SGD-M 和 NAG 最初都偏离了航道,但也能最终纠正到正确方向,SGD-M 偏离的惯性比 NAG 更大。
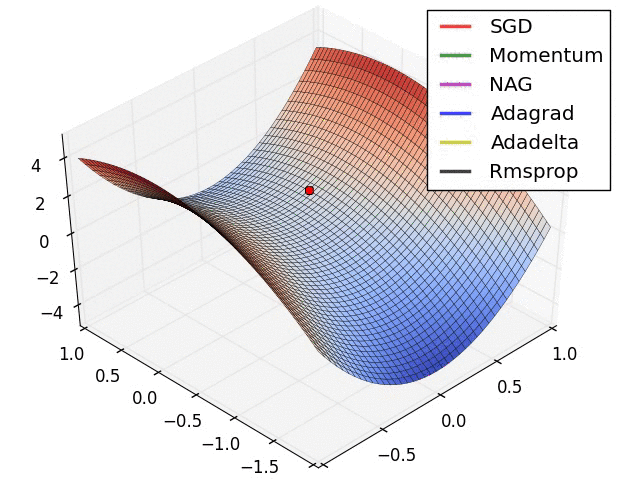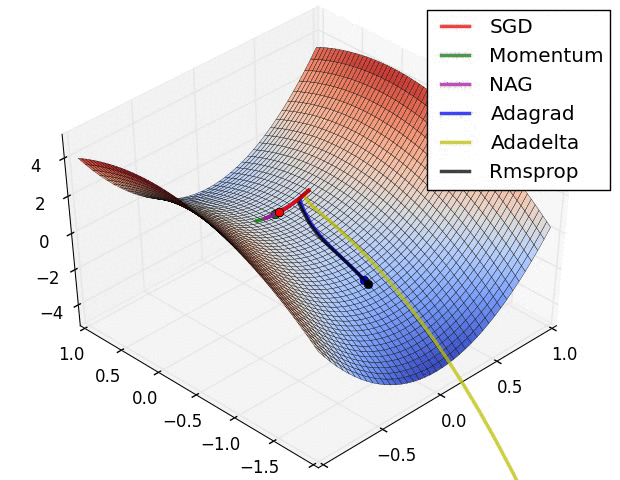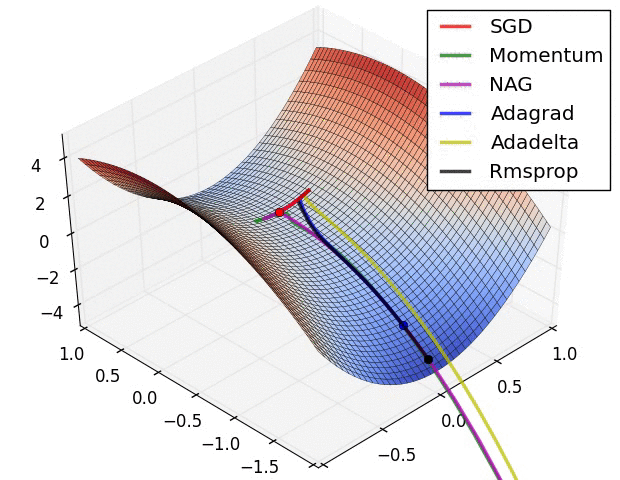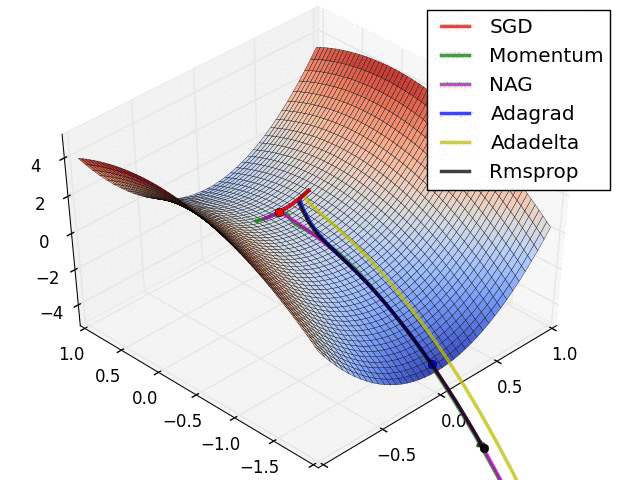
- SGD optimization on saddle point

- 不同算法在鞍点处的表现。这里,SGD、SGD-M、NAG 都受到了鞍点的严重影响,尽管后两者最终还是逃离了鞍点;而 Adagrad、RMSprop、Adadelta 都很快找到了正确的方向。
- 【2020-8-20】【斯坦福凸优化短课程资料(Python)】’cvx_short_course - Materials for a short course on convex optimization.’ by Stanford University Convex Optimization Group
- 【2020-11-2】源自贪心学院的机器学习高阶培训目录
- 凸集的判断
- First-Order Convexity
- Second-order Convexity
- Operations Preserve Convexity
-
二次规划问题(QP)
- 【2021-5-24】为什么机器学习算法难以优化?一文详解算法优化内部机制,英文原文,损失的线性组合无处不在,如正则化函数、权重衰减和 Lasso 算法。。虽然有些陷阱,但仍然被广泛用作标准方法。这些线性组合常常让算法难以调整。本文作者提出了以下论点:
- 机器学习中的许多问题应该被视为多目标问题,但目前并非如此;正则化函数、权重衰减和 Lasso 算法。正则化已经创建了多目标损失,用λ参数在这二者之间调整平衡。第一个目标是最大程度地覆盖数据,第二个目标是保持与先前的分布接近。在这种情况下,偶尔会使用 KL 退火来引入一个可调参数β,以帮助处理这种损失的多目标性。强化学习中的策略损失也通常是损失的线性组合,如PPO、SAC 和 MPO 的策略损失及其可调整参数α的熵正则化方法。一些组合损失的方法听起来很有吸引力,但实际上是不稳定且危险的。平衡行为通常更像是在「走钢丝」。
- 以上问题导致这些机器学习算法的超参数难以调整;
- 检测这些问题何时发生几乎是不可能的,因此很难解决这些问题。
- 理想情况下,多目标损失线性组合后的优化路径,当调整 α 时,可以选择两个损失之间的折衷,并选择最适合自身应用的点。图
- 而实际往往是,无论怎样调整参数α,都不能很好地权衡两种损失。图
- 一般采取早停法(early stopping),以使得论文中的数据是有效的。但为什么这种方法有时有效,有时却无法提供可调参数?模型参数θ对模型输出的影响是不同的。可视化下不可见的东西,即两个优化的帕累托前沿。这是模型可以实现且是不受其他任何解决方案支配的解决方案的集合。通过调整损失的超参数,你通常希望仅在同一个前沿找到一个不同的点。凹,凸


- 两个帕累托前沿之间的差异会使得第一种情况的调优效果很好,但是在更改模型后却严重失败了。事实证明,当帕累托前沿为凸形时,我们可以通过调整α参数来实现所有可能的权衡效果。但是,当帕累托前沿为凹形时,该方法似乎不再有效。
- 为什么凹帕累托前沿面的梯度下降优化会失败?凸, 凹

- 调整α,此空间将保持一个平面。毕竟更改α只会更改该平面的倾斜度。在凸的情况下,可以通过调整α来实现帕累托曲线上的任何解。α大一点会将星星拉到左侧,α小一点会将星星拉到右侧。优化过程的每个起点都将在相同的解上收敛,这对于α的所有值都是正确的。

- 当我们调整α时,该平面以与凸情况下完全相同的方式倾斜,但由于帕累托前沿面的形状,将永远只能到达该前沿面上的两个点,即凹曲线末端的两个点。使用基于梯度下降方法无法找到曲线上的 × 点(实际上想要达到的点)。为什么?因为这是一个鞍点(saddle point)。
- 线性损失组合方法的问题:
- 第一,即使没有引入超参数来权衡损失,说梯度下降试图在反作用力之间保持平衡也是不正确的。根据模型可实现的解,可以完全忽略其中一种损失,而将注意力放在另一种损失上,反之亦然,这取决于初始化模型的位置;
- 第二,即使引入了超参数,也将在尝试后的基础上调整此超参数。研究中往往是运行一个完整的优化过程,然后确定是否满意,再对超参数进行微调。重复此优化循环,直到对性能满意为止。这是一种费时费力的方法,通常涉及多次运行梯度下降的迭代;
- 第三,超参数不能针对所有的最优情况进行调整。无论进行多少调整和微调,你都不会找到可能感兴趣的中间方案。这不是因为它们不存在,它们一定存在,只是因为选择了一种糟糕的组合损失方法;
- 第四,必须强调的是,对于实际应用,帕累托前沿面是否为凸面以及因此这些损失权重是否可调始终是未知的。它们是否是好的超参数,取决于模型的参数化方式及其影响帕累托曲线的方式。但是,对于任何实际应用,都无法可视化或分析帕累托曲线。可视化比原始的优化问题要困难得多。因此出现问题并不会引起注意;
- 最后,如果你真的想使用这些线性权重来进行权衡,则需要明确证明整个帕累托曲线对于正在使用的特定模型是凸的。因此,使用相对于模型输出而言凸的损失不足以避免问题。如果参数化空间很大(如果优化涉及神经网络内部的权重,则情况总是如此),你可能会忘记尝试这种证明。需要强调的是,基于某些中间潜势(intermediate latent),显示这些损失的帕累托曲线的凸度不足以表明你具有可调参数。凸度实际上需要取决于参数空间以及可实现解决方案的帕累托前沿面。
- 请注意:在大多数应用中,帕累托前沿面既不是凸的也不是凹的,而是二者的混合体,这扩大了问题。以一个帕累托前沿面为例,凸块之间有凹块。每个凹块不仅可以确保无法通过梯度下降找到解,还可以将参数初始化的空间分成两部分,一部分可以在一侧的凸块上找到解,而另一部分智能在另一侧上找到解。如下动图所示,在帕累托前沿面上有多个凹块会使问题更加复杂。多凹点
最优化
简介
运筹学是研究优化理论的学科(包括凸优化),而人工智能模型最后几乎都能化简成求解一个能量/损失函数的优化问题。
因此,运筹学可以称为人工智能、大数据的“引擎”。
- 摘自:最优化算法的前世今生
-
人生不如意之事十之八九,想达到我们想要达到的目标时,通常都有各种各样的限制。那么所谓最优化问题,就是指用最优的方式去平衡理想与现实之间的关系。
- 最古老的优化问题:邮差送信
距离度量
【2021-7-15】NLP 语义相似度计算 整理总结
在很多NLP任务中,都涉及到语义相似度的计算,例如:
- 在搜索场景下(对话系统、问答系统、推理等),query和Doc的语义相似度;
- feeds场景下Doc和Doc的语义相似度;
- 在各种分类任务,翻译场景下,都会涉及到语义相似度语义相似度的计算
基本概念
TF:Term frequency即关键词词频,是指一篇文章中关键词出现的频率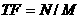
IDF:Inverse document frequency指逆向文本频率,是用于衡量关键词权重的指数
向量空间模型
向量空间模型简称VSM,是 Vector Space Model 的缩写。在此模型中,文本被看作是由一系列相互独立的词语组成的,若文档 D 中包含词语 t1,t2,…,tN,则文档表示为D(t1,t2,…,tN)。由于文档中词语对文档的重要程度不同,并且词语的重要程度对文本相似度的计算有很大的影响,因而可对文档中的每个词语赋以一个权值 w,以表示该词的权重,其表示如下:D(t1,w1;t2,w2;…,tN,wN),可简记为 D(w1,w2,…,wN),此时的 wk 即为词语 tk的权重,1≤k≤N。关于权重的设置,我们可以考虑的方面:词语在文本中的出现频率(tf),词语的文档频率(df,即含有该词的文档数量,log N/n。很多相似性计算方法都是基于向量空间模型的。
总结
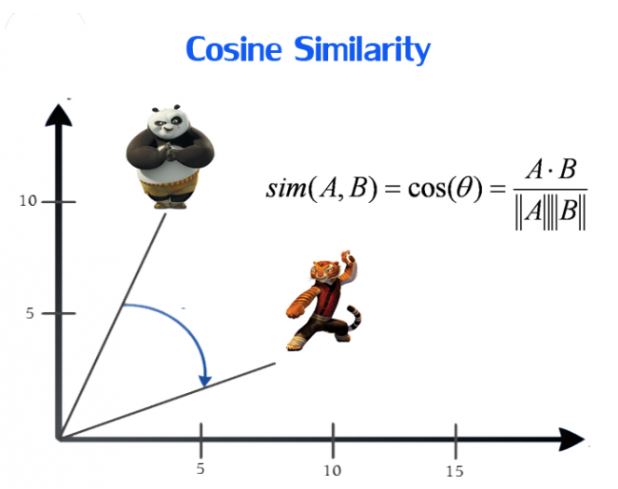
余弦相似度(Cosine)
余弦相似性通过测量两个向量的夹角余弦值来度量相似性。
问题:
- 表示方向上的差异,但对距离不敏感。
- 关心距离上的差异时,会对计算出的每个(相似度)值都减去一个均值,称为调整余弦相似度。
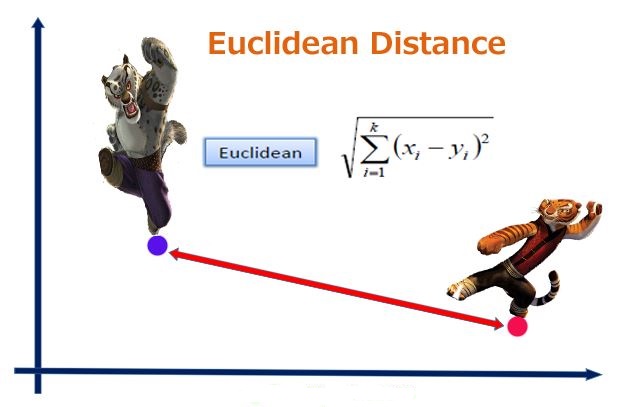
欧式距离
考虑的是点的空间距离,各对应元素做差取平方求和后开方。能体现数值的绝对差异。
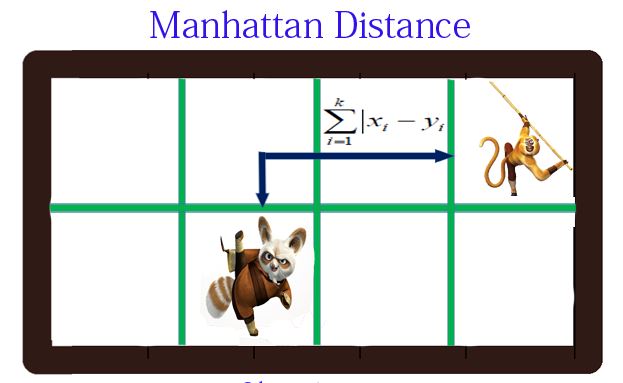
曼哈顿距离(Manhattan Distance)
向量各坐标的绝对值做查后求和。
d(i,j)=|X1-X2|+|Y1-Y2|d(i,j)=|X1-X2| +|Y1-Y2|- img
明可夫斯基距离(Minkowski distance)
明氏距离是曼哈顿距离、欧氏距离的推广,是对多个距离度量公式的概括性的表述。
分析
- 当 p=1, “明可夫斯基距离”变成“曼哈顿距离”
- 当 p=2, “明可夫斯基距离”变成“欧几里得距离”
- 当 p=∞, “明可夫斯基距离”变成“切比雪夫距离”
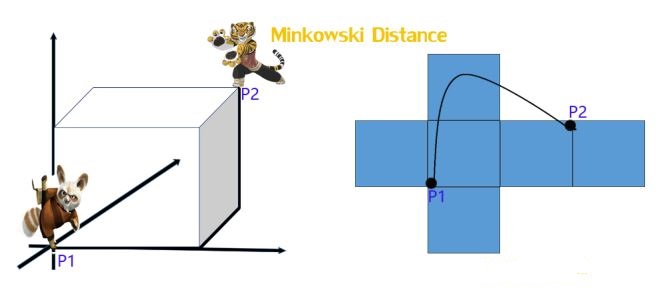
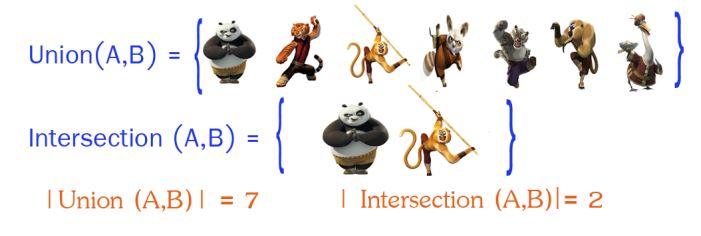
Jaccard 相似系数(Jaccard Coefficient)
Jaccard系数主要用于计算符号度量或布尔值度量的向量的相似性。即,无需比较差异大小,只关注是否相同。Jaccard系数只关心特征是否一致(共有特征的比例)。
然后利用公式进行计算:
皮尔森相关系数(Pearson Correlation Coefficient)
皮尔森相关系数又称为相关相似性。
或表示为:
这就是1中所提到的调整余弦相似度,向量内各对应元素减去均值求积后求和,记为结果1;各对应元素减去均值平方求和再求积,记为结果2;结果1比结果2。
针对线性相关情况,可用于比较因变量和自变量间相关性如何。
SimHash + 汉明距离(Hamming Distance)
Simhash:谷歌发明,根据文本转为64位的字节,计算汉明距离判断相似性。汉明距离:在信息论中,两个等长字符串的汉明距离是两者间对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如:- “10110110”和“10011111”的汉明距离为3;
- “abcde”和“adcaf”的汉明距离为3.
斯皮尔曼(等级)相关系数(SRC :Spearman Rank Correlation)
和上述类似,不同的是将对于样本中的原始数据Xi,Yi转换成等级数据xi,yi,即xi等级和yi等级。并非考虑原始数据值,而是按照一定方式(通常按照大小)对数据进行排名,取数据的不同排名结果代入公式。
实际上,可通过简单的方式进行计算,n表示样本容量,di表示两向量X和Y内对应元素的等级的差值,等级di = xi - yi,则:
BM25算法
原理
- BM25算法,通常用来作搜索相关性平分:对Query进行语素解析,生成语素qi;然后,对于每个搜索结果D,计算每个语素qi与D的相关性得分,最后,将qi相对于D的相关性得分进行加权求和,从而得到Query与D的相关性得分。
- BM25算法的一般性公式如下:
- img

- 其中,Q表示Query,qi表示Q解析之后的一个语素(对中文而言,我们可以把对Query的分词作为语素分析,每个词看成语素qi。);d表示一个搜索结果文档;Wi表示语素qi的权重;R(qi,d)表示语素qi与文档d的相关性得分。
- img
- BM25算法的相关性得分公式可总结为:
- 代码实现,完整版
import math
import jieba
from utils import utils
# 测试文本
text = '''
自然语言处理是计算机科学领域与人工智能领域中的一个重要方向。
它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。
自然语言处理是一门融语言学、计算机科学、数学于一体的科学。
因此,这一领域的研究将涉及自然语言,即人们日常使用的语言,
所以它与语言学的研究有着密切的联系,但又有重要的区别。
自然语言处理并不是一般地研究自然语言,
而在于研制能有效地实现自然语言通信的计算机系统,
特别是其中的软件系统。因而它是计算机科学的一部分。
'''
class BM25(object):
def __init__(self, docs):
self.D = len(docs)
self.avgdl = sum([len(doc)+0.0 for doc in docs]) / self.D
self.docs = docs
self.f = [] # 列表的每一个元素是一个dict,dict存储着一个文档中每个词的出现次数
self.df = {} # 存储每个词及出现了该词的文档数量
self.idf = {} # 存储每个词的idf值
self.k1 = 1.5
self.b = 0.75
self.init()
def init(self):
for doc in self.docs:
tmp = {}
for word in doc:
tmp[word] = tmp.get(word, 0) + 1 # 存储每个文档中每个词的出现次数
self.f.append(tmp)
for k in tmp.keys():
self.df[k] = self.df.get(k, 0) + 1
for k, v in self.df.items():
self.idf[k] = math.log(self.D-v+0.5)-math.log(v+0.5)
def sim(self, doc, index):
score = 0
for word in doc:
if word not in self.f[index]:
continue
d = len(self.docs[index])
score += (self.idf[word]*self.f[index][word]*(self.k1+1)
/ (self.f[index][word]+self.k1*(1-self.b+self.b*d
/ self.avgdl)))
return score
def simall(self, doc):
scores = []
for index in range(self.D):
score = self.sim(doc, index)
scores.append(score)
return scores
if __name__ == '__main__':
sents = utils.get_sentences(text)
doc = []
for sent in sents:
words = list(jieba.cut(sent))
words = utils.filter_stop(words)
doc.append(words)
print(doc)
s = BM25(doc)
print(s.f)
print(s.idf)
print(s.simall(['自然语言', '计算机科学', '领域', '人工智能', '领域']))
Dice 系数法(DiceCoefficient)
- todo
编辑距离
字符串的相似性比较应用场合很多,像拼写纠错、文本去重、上下文相似性等。
评价字符串相似度最常见的办法就是:把一个字符串通过插入、删除或替换这样的编辑操作,变成另外一个字符串,所需要的最少编辑次数,这种就是编辑距离(edit distance)度量方法,也称为Levenshtein距离。海明距离是编辑距离的一种特殊情况,只计算等长情况下替换操作的编辑次数,只能应用于两个等长字符串间的距离度量。
其他常用的度量方法还有:Jaccard distance、J-W距离(Jaro–Winkler distance)、余弦相似性(cosine similarity)、欧氏距离(Euclidean distance)等。
【2021-11-8】Python Levenshtein 计算文本之间的距离
- pip install difflib
- pip install python-Levenshtein
import difflib
query_str = '市公安局'
s1 = '广州市邮政局'
s2 = '广州市公安局'
s3 = '广州市检查院'
seq = difflib.SequenceMatcher(None, s1, s2)
ratio = seq.ratio()
print 'difflib similarity1: ', ratio
# difflib 去掉列表中不需要比较的字符
seq = difflib.SequenceMatcher(lambda x: x in ' 我的雪', str1,str2)
ratio = seq.ratio()
print 'difflib similarity2: ', ratio
print(difflib.SequenceMatcher(None, query_str, s1).quick_ratio())
print(difflib.SequenceMatcher(None, query_str, s2).quick_ratio())
print(difflib.SequenceMatcher(None, query_str, s3).quick_ratio())
# 0.4
# 0.8 --> 某一种相似度评判标准下的最相似的文本……
# 0.08695652173913043
import Levenshtein
# (1) 汉明距离,str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数
Levenshtein.hamming('hello', 'world') # 4
Levenshtein.hamming('abc', 'abd') # 1
# (2) 编辑距离(也成Levenshtein距离)。是描述由一个字串转化成另一个字串最少的操作次数,在其中的操作包括插入、删除、替换
Levenshtein.distance('hello', 'world') # 4
Levenshtein.distance('abc', 'abd') # 1
Levenshtein.distance('abc', 'aecfaf') # 4
# (3) 莱文斯坦比。计算公式 r = (sum - ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和,ldist是类编辑距离
# 注意:这里的类编辑距离不是2中所说的编辑距离,2中三种操作中每个操作+1,而在此处,删除、插入依然+1,但是替换+2
# 这样设计的目的:ratio('a', 'c'),sum=2,按2中计算为(2-1)/2 = 0.5,’a’,'c’没有重合,显然不合算,但是替换操作+2,就可以解决这个问题。
Levenshtein.ratio('hello', 'world') # 0.2
Levenshtein.ratio('abc', 'abd') # 0.6666666666666666
Levenshtein.ratio('abc', 'aecfaf') # 0.4444444444444444
# (4) jaro距离
Levenshtein.jaro('hello', 'world') # 0.43333333333333335
Levenshtein.jaro('abc', 'abd') # 0.7777777777777777
Levenshtein.jaro('abc', 'aecfaf') # 0.6666666666666666
# (5) Jaro–Winkler距离
Levenshtein.jaro_winkler('hello', 'world') # 0.43333333333333335
Levenshtein.jaro_winkler('abc', 'abd') # 0.8222222222222222
Levenshtein.jaro_winkler('abc', 'aecfaf') # 0.7
分类
目标函数分为两大类
- 第一类是
最大化,包括最大化盈利,最大化效率。 - 另一类是
最小化,包括最小化费用、时间和错误率。在金融行业,我们可以最大化预测股价的正确率,也可以最小化费用、最小化时间和错误率。
当然,可以同时最大化盈利,最小化费用和时间。所以这两种任务可以组合起来出现在同一个问题框架下,这就是对于目标函数的定义。
最优化问题分类:
- 无约束优化问题:直接求导、最速下降法、共轭梯度法、牛顿法等;
- 等式约束优化问题:
拉格朗日(Lagrange)乘数法; - 不等式约束优化问题:
KKT条件。
凸优化
现实生活中,几乎所有问题的本质都是非凸的
基础概念
凸优化入门最重要的4个概念: 仿射集、凸集、凸函数、凸优化
仿射集(Affine Set)- 仿射集是对仿射组合affine combination封闭的集合;与某方程 Ax=b 的解空间等价;是一个平移后的线性空间;也是一个超平面
凸集(Convex Set)- 凸集是对 凸组合convex combination封闭的集合;等价于对随机向量的期望运算封闭
- 凸集的性质:
- 凸集的有限交还是凸集(易证);
- 仿射变换保凸;
- 仿射集是凸集;
凸函数(Convex Function)- 凸函数的等价定义就是琴生不等式!(首先是定义在凸集上的,其次期望的函数值小于等于函数值的期望)
- 凸函数的性质:凸函数的sublevel set都是凸的。即 {x|f(x)<=alpha} 都是凸的。
凸优化(Convex Optimization)- 凸优化本质是:可行域是凸集,且目标函数是凸函数的优化问题。
总结
- 仿射集:是一个平移后的线性空间;
- 凸集:对随机向量的期望运算封闭;
- 凸函数:首先是定义在凸集上的,其次期望的函数值小于等于函数值的期望;
- 凸优化:可行域是凸集,且目标函数是凸函数
凸函数、凸集、凸锥(简称“三凸”)的定义
凸函数
【2021-5-31】理解凸性:为什么梯度下降适用于线性回归
首先,通过凸集和凸函数定义凸度。
凸集的定义如下:
在二维中,我们可以将凸集视为一个形状,无论您用什么线连接集中的两个点,都不会在集外。
- (左)凸集,(中)非凸集,(右)凸集
凸集的定义正好体现在凸函数的定义中,如下所示:
可以直观地把凸函数想象成这样的函数:
- 如果你画一条从 $(x,f(x))$ 到 $(y,f(y))$ 的直线,那么凸函数的图像就会在这条直线的下方。
下面是三个例子,应用这个直觉来确定函数是否是凸的。
- (左)具有唯一优化器的凸函数,(中)非凸函数,(右)具有多个优化器的凸函数
可以看到中间的图不是凸的,因为当我们绘制连接图上两个点的线段时,有一些点(x,f(x))大于f(x)上对应的点。
左边和右边的图形都是凸的。不管在这些图上画什么线段,这个线段总是在函数图的上面或者等于函数图。
梯度下降以最简单的形式没有找到全局最小化器。
注:直线 $y=wx+b$ 既是凸函数,又是凹函数
LR是凸函数
【2020-9-2】logistic 回归 当约束所有的参数为非负的时候还是有全局最优的吗?
- LR是凸函数,已被证明(逻辑回归目标函数为凸函数证明);损失函数的
海塞矩阵是正定的- 如何判定凸函数? 若函数二阶导数为正,则该函数为凸函数, 同理,对于多元函数,则是其Hessian矩阵为正定矩阵,则该函数为凸函数;
- 凸函数的局部最优解即是全局最优解
- 凸优化:目标函数是
凸函数而且优化变量的可行域是凸集,是因为缺其中任何一个条件都不能保证局部最优解是全局最优解
- kkt 是个必要条件, 不敢完全判断带约束的也是有全局最优的解;
- 带约束的优化, 可行域如果不是凹区域, 凸函数在这个可行域上也是有全局最优解;如果可行域是凸集,则凸函数在这个可行域上也是有全局最优解的,参考:理解凸优化,熊军的笔记
代码
# coding=utf8
"""
本代码主要实现两种带约束的lr的算法步骤:
数据集: iris 数据集
"""
import torch
from torch.nn.functional import cross_entropy
from torch.optim import SGD
from sklearn.datasets import load_iris
from torch.utils.data import dataset
from torch.utils.data import dataloader
import seaborn as sns
import matplotlib.pyplot as plt
class Ds(dataset.Dataset):
"""
构建一个dataset类, 继承torch官方的Dataset
"""
def __init__(self):
super(dataset.Dataset, self).__init__()
iris_data = load_iris()
self.data = iris_data['data']
self.labels = iris_data['target']
def __len__(self):
return len(self.labels)
def __getitem__(self, item):
x = self.data[item]
y = self.labels[item]
x = torch.Tensor(x)
y = torch.LongTensor([y])
return x, y
class Trainer(object):
def __init__(self):
"""
训练集合的特征个数是4, 类别是3
"""
self.model = torch.nn.Linear(4, 3)
self.zeros = torch.zeros(3, 4)
self.modify_weight()
# 打印初始的模型参数, 确保所有的参数大于等于0
print(self.model.weight)
def train(self, epochs=1000, batch_size=16, lr=0.01):
dl = self.get_data_loader(batch_size)
loss_func = cross_entropy # 定义损失函数为logistic的损失函数
optimizer = SGD(self.model.parameters(), lr=lr)
loss_arr = []
for epoch in range(epochs):
cur_loss = self.train_epoch(epoch, dl, loss_func, optimizer)
loss_arr.append(cur_loss)
print("*" * 100)
print("following is the parameters of the model")
for name, parameters in self.model.named_parameters():
print(name)
print(parameters.data)
print(loss_arr)
do_plot(list(range(epochs)), loss_arr)
def train_epoch(self, epoch, dl, loss_func, optimizer):
self.model.train()
loss_arr = []
for batch in dl:
self.model.zero_grad() # 将所有的gradient 重置为0
x, y = batch
y = torch.squeeze(y, 1) # 将里面的二维数组变成一维数组
pred = self.model(x)
loss = loss_func(pred, y) # 计算logloss
loss.backward()
optimizer.step()
self.modify_weight()
print(f"epoch is: {epoch}, training loss is: {loss.item()}")
loss_arr.append(loss.item())
return sum(loss_arr) / len(loss_arr)
def get_data_loader(self, batch_size):
# 初始化iris 的dataset
ds = Ds()
dl = dataloader.DataLoader(ds, batch_size)
return dl
def modify_weight(self):
"""
用来修改模型,让模型参数在可行区域
"""
new_para = torch.max(self.zeros, self.model.weight.data)
self.model.weight.data.copy_(new_para)
def do_plot(epoch_arr, loss_arr):
"""
用来画不同epoch 对应的loss
"""
sns.lineplot(x="epoch", y="loss", data={"epoch": epoch_arr, "loss": loss_arr})
plt.show()
if __name__ == "__main__":
trainer = Trainer()
trainer.train()
什么是凸优化
什么是凸优化?抛开凸优化中的种种理论和算法不谈,纯粹的看优化模型,凸优化就是:
- 1、在最小化(最大化)的要求下
- 2、目标函数是一个凸函数(凹函数)
- 3、同时约束条件所形成的可行域集合是一个凸集。
以上三个条件都必须满足。而世间万物千变万化,随便抽一个函数或集合它都可能不是凸的。
为什么凸优化重要
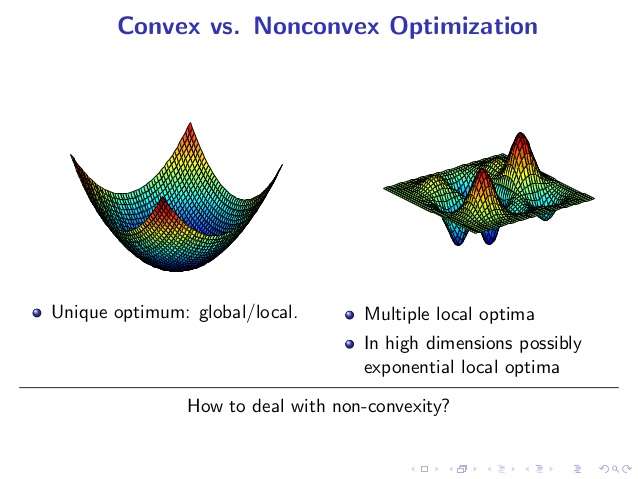
Convex VS Non-Convex
对比
凸优化-相对简单
- (1)凸优化有个非常重要的定理,任何局部最优解即为全局最优解。
- 因此,只要设计一个较为简单的局部算法,例如贪婪算法(Greedy Algorithm)或梯度下降法(Gradient Decent),收敛求得的局部最优解即为全局最优。因此求解凸优化问题相对来说是比较高效的。
- (2)可微分的凸优化问题满足KKT条件,因此容易求解:
这也是为什么机器学习中凸优化的模型非常多,毕竟机器学习处理海量的数据,需要非常高效的算法。
非凸优化-非常困难
- 非凸优化问题被认为是非常难求解的,因为可行域集合可能存在无数个局部最优点,通常求解全局最优的算法复杂度是指数级的(NP难)
- 最经典的算法要算蒙特卡罗投点法了,大概思想: 随便投个点,然后在附近区域(可以假设convex)用两种方法的进行搜索,得到局部最优值。然后随机再投个点,再找到局部最优点–如此反复,直到满足终止条件。
- 假设有1w个局部最优点,你至少要投点1w次吧?并且还要假设每次投点都投到了不同的区域,不然只会搜索到以前搜索过的局部最优点。
这个世上的绝大部分优化问题非凸。既然如此,为什么凸优化这么重要,以及凸优化有什么用呢?
- 另外,凸优化并不能看成是某一种优化方法)
无非三点:参考 凸优化为什么重要
- 1、相当一部分问题是或等价于凸优化问题。
- 有许多问题都可以直接建立成凸优化模型
- 比如:线性规划LP(Linear Programming)、某些特殊的二次规划QP(Quadratic Programming)、锥规划CP(Conic Programming)其中包括:要求约束中变量落在一个二阶锥里的二阶锥规划SOCP(Second Order Cone Programming)、要求约束中变量是半正定矩阵的半定规划SDP(Semi-Definite Programming)等)。
- 以上这些类型,总之就是要符合凸优化上述的要求。需要说明的就是,许多可行域都可以看作是
凸锥(Convex Cone)的交集,所以将以上一些类型的约束混合起来,依然是凸优化问题。
- 还有些问题可以等价的转化为凸优化问题。
- 例如 Linear-Fractional Programming (LFP),目标函数是两个仿射函数(Affine Function)的比,约束是一个多面体。这种目标函数具有既是拟凸又是拟凹的性质,通过一个叫做 Charnes-Cooper transformation 的转化,可以变成一个线性规划。同时,如果我们要最大化 LFP 的目标函数,且其约束仅是一个0-1整数约束(这显然不是一个凸集),我们可以将其直接松弛(Relax)成0到1的约束,并且和原问题等价。因为最大化拟凸函数,最优值一定可以落在可行域的极点上。这个结论可以用来帮助解决 Multi Nomial Logit(MNL)选择模型下的商品搭配问题( Assortment Optimization)。
- 又例如,与组合优化相关的整数规划模型里,当最小化一个线性函数 ,变量 只能取整数,约束条件为 时,如果 为整数向量且 是完全幺模(Totally Unimodular)的矩阵,我们可以将原问题松弛,即将整数约束去掉,变成线性规划。此时的最优解必然仍为整数,且即是原问题的最优解。这一结论经常用于调度(Scheduling)问题和指派(Appointment)问题。以上两类问题即是与凸优化直接等价的问题,还有一些优化问题本身就是NP-Hard,怎么处理我们后面再说。
- 有许多问题都可以直接建立成凸优化模型
- 2、大部分凸优化问题解起来比较快,也即多项式时间可解问题(P)。
- 如果问题能直接或间接(但必须是等价的)转化成上面我提到的那些类型,那恭喜你,后面的事儿基本就可以交给solver啦,当然大规模问题还需要考虑诸如列生成(Column Generation)之类的方法,提高运算效率。
- 那为什么大部分凸优化解起来比较快呢?这涉及到凸函数的局部最优即全局最优的性质以及
凸集分离定理(Seperation Theorem)。 - 根据凸函数(或凹函数)的定义,可以想象成站在函数的曲线上去搜索最优解,所要做的无非就是向下到底(或向上到顶),需要考虑的是用什么样的角度迈出第一步以及每的步子要迈多大才更快的到达最优值。同时,作为凸集的可行域,更容易在有限范围内迅速锁定最优解,而不用四处打探。
- 以线性规划为例(目标函数既凸且凹,所以最大化最小化皆可),想象你在目标函数那个超平面上一路狂奔,因为是最小化(或最大化),你得往觉得最轻松(或费劲)的下坡(上坡)方向跑,跑着跑着,你就碰到可行域这个多面体的墙壁了。没关系,你感觉贴着壁的某个方向还是可以轻松(或费劲)地继续跑,跑着跑着到了一个拐角,即所谓的极点。你觉得再走下去就费劲(或省力)了,这样就找到了一个最优的极小值(极大值),否则,你可以沿着墙壁继续走下去。如果,这个时候的可行域不是凸集,而是被人胡乱咬了一口,形成了凹凸不平的缺口。如上方法搜索,你可能已经到达这个缺口的某一个角落,前方已经没有任何能改善你可行解的道路了,你可以就此停止吗?不能!因为想象有另一个你,也如上所述,跑到了这个缺口的另一个无处可走的角落,他也认为自己可以停止了,那你们就还需要比较两个各自所在的位置的解,哪一个会更优。当然,可能还有第三个你,第四个你。。。但不要忘了,每一个你的搜索都需要时间,最终的比较也需要时间(除非你们之间没有缺口,可能都会继续跑下去,到达了一个共同的最优值)。所以非凸的可行域要比一个凸集的可行域麻烦的多。(注:以上形象化的描述的未必就是多项式时间的算法。现实中如单纯形法就不是多项式时间的算法,但实际运用中仍然很高效。)
- 当然,也有例外,即虽然是凸优化但不是多项式时间可解的。比如在约束中,要求变量是一个Copositive 矩阵或者 Completely Positive 矩阵,这两种矩阵所在的锥恰为
对偶锥。此类问题很难解的原因在于,要去检查一个矩阵是不是落在这样的锥里,就已经不是多项式时间可以解决的了,更不用说整个优化问题。
- 3、很多非凸优化或NP-Hard的问题可以转化(并非是等价的)为P的凸优化问题。并给出问题的界或近似。这对如何设计合理的算法,或衡量算法结果的优劣起到很大的帮助。非凸优化的问题基本上都是NP-Hard的,所以要找到其最优解,理论上是不确定有一个多项式时间的算法的,所以这时候会考虑设计一些近似算法,或者启发式算法,就要依靠凸优化。要把一个优化问题转化为凸优化的方法和例子有很多。
- 对偶(Duality)是每个学习运筹学或者凸优化的人都必须熟练掌握的方法,对偶有很多种,本科运筹就教会大家写一个线性规划的对偶形式,高等数学里面也会提到用到拉格朗日乘子之类的约束优化问题,也即解拉格朗日对偶或者KKT条件。一般的,对于许多非凸优化的问题,我们仍然可以写出它的拉格朗日对偶。如原问题如下 ,拉格朗日对偶为 ,其中 。可以看到 是关于 的线性函数,因此 一定是一个关于 的凹函数。因此,由我们之前给的定义来看,拉格朗日对偶永远都是一个关于对偶变量的凸优化问题,并且根据弱对偶定理,可以给出原问题的下界。
- 松弛(Relaxation)也是常用的方法之一,在第一点里,我们举了一些例子可以通过松弛,去掉整数约束,使其等价为凸优化。通常情况下,我们松弛原问题,只能得到一个可行域更大的问题,如果原问题是求最小,则松弛后的问题的最优值一定小于等于原问题的最优值,这也是一种给出下界的方法。松弛不仅仅用于整数约束,只要利于将可行域非凸变为凸集皆可。例如,某问题有一约束为 ,就不构成一个凸集,但等价于 和 ,前一个不等式即构成凸集,因此我们可以将后一个不等式从约束中去除,就得到原问题的一个凸优化松弛问题。
- 还可以举一个同时用到对偶加松弛的例子,在第二点的最后,我们聊到Copositive(CoP) 矩阵与 Completely Positive(CP)矩阵,他们的锥与半正定(PSD)矩阵锥的关系是 。组合优化中很多问题都可以松弛成一个Completely Positive规划(去掉一个矩阵为Rank 1 的条件),由于Copositive和Completely Positive互为对偶锥,所以我们可以先写出对偶,写成 Copositive 规划,然后在某些假设之下,能证明 Copositive 规划与原问题等价。当然,如果没有那些假设,还可以尝试将Completely Positive约束,松弛成半正定矩阵的约束,因为Completely Positive必然是半正定,同时还加上Completely Positive的性质,如矩阵的所有元素都大于等于0。这样我们就得到了原问题的一个凸优化且易解的对偶松弛问题,一个SDP Relaxation。
- 当然,相应的处理方法还有很多,面临一些随机优化(Stochastic Optimization)、机会约束规划(Chance Constrained Programming)、鲁棒优化(Robust Optimization)、离散凸优化(Discrete Convex Optimization)问题,还有更多其他的处理方法,就不在此一一道来。更多内容,可以看各位答案里推荐的书籍,都是经典教材。
运筹学
线性规划是运筹学最基础的课程,其可行域(可行解的集合)是多面体(polyhedron),具有着比普通的凸集更好的性质。因此是比较容易求解的(多项式时间可解)
运筹学中(混合)整数规划与非凸优化的关系
- (混合)
整数规划被称为极度非凸问题(highly nonconvex problem),如下图: 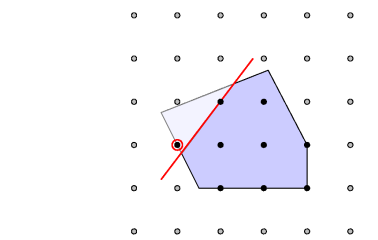
- 实心黑点组成的集合,是一个离散集,按照1中判断一个集合是否为凸集的技巧,我们很容易验证这个离散集是非凸的。
- 因此整数规划问题也是一个非凸优化问题,并且它也是NP难的。
- 整数规划的求解思路,被分解为求解一个个的线性规划(凸优化)问题。
(混合)整数规划为何重要?
- 虽然时间是连续的,但是社会时间却是离散的。
- 例如时刻表,通常都是几时几分,即使精确到几秒,它还是离散的(整数)。没见过小数计数的时刻表吧?
- 对现实社会各行各业问题数学建模的时候,整数变量有时是不可避免的。例如:x辆车,y个人。x,y这里便是整数变量,小数是没有意义的。
滴滴派单算法
【2023-4-14】浅谈滴滴派单算法, 从出租车扬召到司机在滴滴平台抢单最后到平台派单,大家今天的出行体验已经发生了翻天覆地的变化,面对着每天数千万的呼叫,滴滴的派单算法一直在持续努力让更多人打到车
- 派单算法视频介绍
- 滴滴KDD 2019 论文详解:基于深度价值网络的多司机智能派单模型, 提出了一种新的基于深度强化学习与半马尔科夫决策过程的智能派单应用,在同时考虑时间与空间的长期优化目标的基础上利用深度神经网络进行更准确有效的价值估计。
从国内外的网约车公司,包括友商Uber、Lyft都基于派单的产品形态进行司机和乘客之间的交易撮合,Uber上市的时候把派单引擎也作为核心技术能力放在了招股书中;再看我们的国内的外卖平台,核心派单系统的优劣也决定了整个平台的交易效率(单均配送成本)和用户体验(配送时长);最后,整个大物流行业近年来也不断在进行线上化的改造,如何撮合货物和司机,以及更好的拼单能力也是整个交易环节的关键和商业模式是否成立的前提。从运人到运物,派单引擎目前越来越多的被应用在现实的商业和生活中。
订单分配
- 在派单系统中将 乘客发出的订单 分配给 在线司机 的过程
派单策略主要原则:
- 站在全局视角,尽量去满足尽可能多的出行需求,保证乘客的每一个叫车需求都可以更快更确定的被满足,并同时尽力去提升每一个司机的接单效率,让总的接驾距离和时间最短。
如何理解这个原则呢?
- 策略会站在全局角度去达成全局最优,这样对于每一个独立的需求来看,派单可能就不是“局部最优 ”,不过就算在这个策略下仍然有70%~80%的需求也是符合当前距离最近的贪心派单结果的。
(1) 批量匹配(全局最优)
- 派单策略中最为基础的部分,就是为了解决上一节所提到的时序问题。这个算法几乎是所有类似派单系统为了解决这个问题的最基础模型,在Uber叫做Batching Matching,我们内部也叫做“全局最优” 或者 “延迟集中分单”
- 这个Idea其实也非常直观,由于用户订单的产生和司机的出现往往并不在同一时间点,在时间维度上贪婪的分单方式(即每个订单出现时即选择附近最近的司机派单)并不能获得全局最优的效果。一个自然的想法就是先让乘客和司机稍等一会,待收集了一段时间的订单和司机信息后,再集中分配。这样,有了相对较多、较密集的订单、司机后,派单策略即可找到更近更合理的派单方式了。
- 找寻司机和订单分配的全局最优是一个
二分图匹配问题(bipartite graph matching) ,一边是乘客、一边是司机,可用运筹优化中各种解决Matching问题的方法进行求解。
(2) 基于供需预测的分单
- “如果有先知告诉我们未来每一个订单的生成时间&地点,每一个司机的上线时间&地点,派单就会变成非常轻松的一件事”
刚才所说的批量匹配的方法,理论上能够保证那一个批次的匹配是最优的。但是这样就够了吗?
- 很遗憾,以上所述的延迟集中分单的策略只能解决部分的问题,仍不是一个完全的方案。其最大的问题,在于用户对系统派单的 响应时间 容忍度有限,很多情况下短短的几秒钟即会使用户对平台丧失信心,从而取消订单。故实际线上我们只累积了几秒钟的订单和司机信息进行集中分单,而这在大局上来说仍可近似看做时间维度上的贪婪策略。
- 若想即时的获得最优派单结果,唯一的方法是利用对未来的预测,即进行基于供需预测的分单。这种想法说来玄妙,其实核心内容也很简单:如果我们预测出未来一个区域更有可能有更多的订单/司机,那么匹配的时候就让这个区域的司机/订单更多去等待匹配这同一个区域的订单/司机。
(3) 连环派单
- 基于供需预测的分单有很大意义,但由于预测的不确定性,其实际效果很难得到保证。为此,我们使用了一种更有确定性的预测方式来进行派单,即 连环派单。
- “连环派单,即将订单指派给 即将结束服务 的司机,条件为如果司机的终点与订单位置很相近”
- 与预测订单的分布相反,连环派单预测的是下一时刻空闲司机的所在位置。由于高峰期空闲司机多为司机完成订单后转换而来,预测司机的位置就变成了一个相对确定性的问题,即监测司机到目的地的距离和时间。当服务中的司机距终点很近,且终点离乘客新产生的订单也很近时,便会命中连环派单逻辑。司机在结束上一单服务后,会立刻进入新订单的接单过程中,有效地压缩了订单的应答时间、以及司机的接单距离。
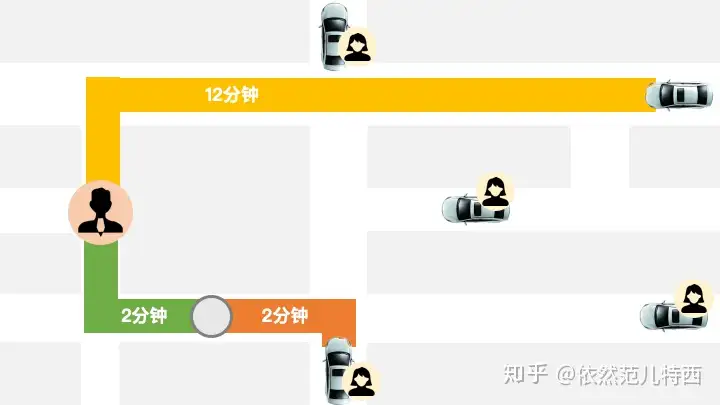
整个派单算法核心克服的是未来供需的不确定性,动态的时空结构的建模,以及用户行为的不确定性,对于这些不确定性我们现在更多采用深度学习方法对我们的时空数据&用户行为进行建模预测。
把 订单 分配给 最近的司机 ?
- 滴滴的派单算法最大的原则就是 “就近分配” (70%~80%的订单就是分配给了最近的司机),据我所知,目前世界上其他的竞品公司(包括Uber),也均是基于这个原则分单的。
当距离完全一样的情况下,当前系统主要考虑司机服务分优劣,服务分较高的司机会获取到这个订单(注:服务分对分单的影响,简单的理解可以换算为多少分可以换成多少米距离的优势,这块不是今天的重点就不展开介绍),再说明一下,系统用到的是地图的导航距离,而非人直观看到的直线距离,有时候差一个路口就会因为需要掉头导致距离差异很大;并且如果司机的定位出现问题,也会出现分单过远的情况。
然而,只按照就近分配,先到先得的贪心策略,并不能满足平台所有乘客和司机的诉求。只基于当前时刻和当前局部的订单来进行决策,忽视了未来新的订单&司机的变化,还忽视了和你相邻的其他区域甚至整个城市的需求(注:在时序上来看,新的司机&订单的出现会导致,贪心策略反而违背了就近分配的目标)。
为什么有时候附近有辆空车却不能指派给你呢?
- 一方面,司机正好网络出现故障,或者正在和客服沟通等等导致司机无法听单
- 另一方面,并不是所有的车都能够符合服务订单的要求,最基本的策略其实是人工设定的规则过滤。
- 规则A:快车司机不能接专车订单
- 规则B:保证司机接单后不会通过限行限号区域
- 规则C:为设定实时目的地的司机过滤不顺路区域
- 规则D:为只听预约单司机过滤实时订单
- 规则E:同一个订单只会发给一个司机一次
- 规则并不会造成分单时不公平的效果,而完全是为了业务能正常运行而设立的,这些策略承担着保证业务正确性的重要职责。
(1) 如果有N个乘客、M个司机
考虑最复杂的多对多情况,这也是线上系统每天高峰期都需要面对的挑战,一般把这种情况会形式化为一个二部图匹配问题,在运筹领域也叫做matching的问题
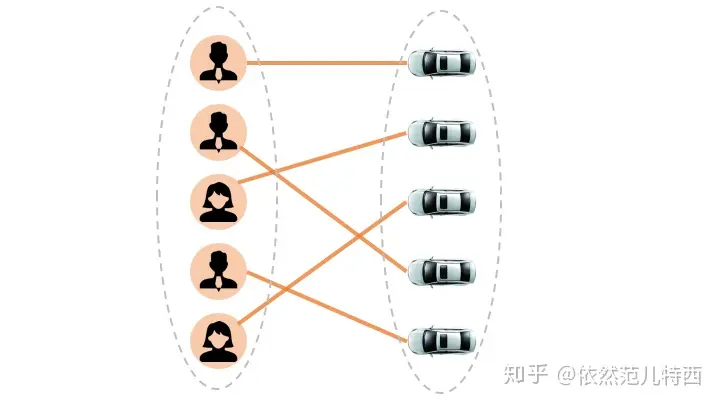
- 有20个乘客,20个司机,乘客都可以被这20个司机中的一个接驾,系统需要把这20个乘客都分配出去,并且让大家的总体接驾时长最短。听上去是不是有点复杂?组合数学的知识,这其中可能的解法存在20的阶乘那么多,20的阶乘是什么概念呢?201918…1= 2432902008176640000,这个数巨大无比,想要完全的暴力搜索是绝对不可能的。
(2) 如果有N个乘客、M个司机,一会再来几个乘客和司机?
这就是派单问题最大的挑战,不仅要当前这个时刻的最优,还要考虑未来一段时间整体最优,新来的司机和乘客会在整个分配的网络中实时插入新的节点,如何更好的进行分配也就发生了新的变化,所以如何考虑时序对非常重要,这个问题在业内也被称为 Dynamic VRP问题,这个Dynamic也就是随时间时序变化的意思,这也就是为什么滴滴的派单问题远复杂于物流行业的相对静态的货物和路线的规划问题。假设知道了未来供需的完全真实的变化,仿真告诉我们,系统有可能可以利用同样的运力完成1.2~1.5倍的需求量,这也是派单算法的同学持续为之努力的方向。
- 文嵩曾说派单问题比alpha go还要难,其实这两个问题还确实有点相似,都是在超大的搜索空间中找到一个近似最优的解,而alpha go则会在一个更加明确的游戏规则和环境中进行求解,它的难点在于博弈,而派单问题难点在于未来供需不确定性&用户行为的不确定性。
神经网络损失函数
神经网络损失函数是凸函数吗?不是
- 深度学习里的损失函数,是一个高度复合的函数。
- 什么叫复合函数?例如h(x)=f(g(x))就是一个f和g复合函数。
- 当f,g都是线性的时候,h是线性的。
- 但在深度学习里用到的函数,Logistic, ReLU等等,都是非线性,并且非常多。把他们复合起来形成的函数h,便是非凸的。
- 求解这个非凸函数的最优解,类似于求凸优化中某点的gradient,然后按照梯度最陡的方向搜索。不同的是,复合函数无法求gradient,于是这里使用Back Propagation求解一个类似梯度的东西,反馈能量,然后更新。
深度学习的优化问题在运筹学看来是“小儿科”
- 深度学习中的优化问题,虽然目标函数非常复杂,但是它没有约束,是一个无约束优化问题!
- 运筹学由目标函数和约束条件组成,而约束条件是使得运筹学的优化问题难以求解的重要因素(需要搜寻可行解)。
要点
- 全局最优不一定是好的解,局部最优不一定是差的解
- NN中设计得激活函数是为了引入非线性变换,凸不凸都可以;
- NN不凸,是多个隐藏层导致的,即使每一层激活函数都是凸的,目标函数依旧是非凸问题。
- 激活函数设计为凸就可以得到凸的优化目标,然而NN不凸,是多个隐藏层导致的,即使每一层激活函数都是凸的,目标函数依旧是非凸问题
- 凸的NN,以前也有人做过。比如:Yoshua Bengio的Convex Neural Networks,还有 Convex Deep Learning via Normalized Kernels。
activation 是凸函数,多层之后好多凸函数的composition 也不一定是凸的。
- $f(x)=e^{-x}f(x)=e^{-x}$
多层神经网络,大部分局部极小值都在底部 ,已经非常接近全局最小值
deep learning是在一个非常高维的世界里做梯度下降。这时的 local minimum 很难形成,因为局部最小值要求函数在所有维度上都是局部最小。更实际得情况是,函数会落到一个saddle-point上
- img

- saddle-point上会有一大片很平坦的平原,让梯度几乎为0,导致无法继续下降。反倒是local/global minimum的问题,大家发现其实不同的local minimum其实差不多(反正都是over-fitting training data,lol)
作者:Filestorm
高维优化为什么难?
【2022-5-18】关于神经网络,一个学术界搞错了很多年的问题
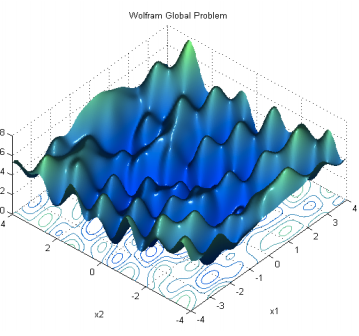
人们普遍认为较大的神经网络中包含很多局部极小值(local minima),使得算法容易陷入到其中某些点。这种看法持续二三十年,至少数万篇论文中持有这种说法。比如,如著名的Ackley函数 。对于基于梯度的算法,一旦陷入到其中某一个局部极值,就很难跳出来了。
2014年,一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》,指出高维优化问题中根本没有那么多局部极值。作者依据统计物理,随机矩阵理论和神经网络理论的分析,以及一些经验分析提出高维非凸优化问题之所以困难,是因为存在大量的鞍点(梯度为零并且Hessian矩阵特征值有正有负)而不是局部极值。
鞍点(saddle point)如下图(来自wiki)和局部极小值
- 相同点:在该点处的梯度都等于零
- 不同点:在鞍点附近Hessian矩阵有正的和负的特征值,即是不定的,而在局部极值附近的Hessian矩阵是正定的。 鞍点附近,基于梯度的优化算法(几乎目前所有的实际使用的优化算法都是基于梯度的)会遇到较为严重的问题,可能会长时间卡在该点附近。在鞍点数目极大的时候,这个问题会变得非常严重
- img
造成神经网络难以优化的一个重要(乃至主要)原因是存在大量鞍点。造成局部极值这种误解的原因在于,人们把低维的直观认识直接推到高维的情况。
鞍点
鞍点也是驻点,鞍点处的梯度为零,在一定范围内沿梯度下降会沿着鞍点附近走,这个区域很平坦,梯度很小。- 优化过程不是卡在鞍点不动了(像人们以为的局部极值那样),而是在鞍点附近梯度很小,于是变动的幅度越来越小,loss看起来就像是卡住了。但是和local minima的差别在于,如果运行时间足够长,SGD一类的算法是可以走出鞍点附近的区域的(看下面的两个链接)。由于这需要很长时间,在loss上看来就像是卡在local minima了。然而,从一个鞍点附近走出来,很可能会很快就进入另一个鞍点附近了。
- 直观来看增加一些扰动,从下降的路径上跳出去就能绕过鞍点。但在高维的情形,这个鞍点附近的平坦区域范围可能非常大。此外,即便从一个鞍点跳过,这个跳出来的部分很可能很快进入另一个鞍点的平坦区域—— 鞍点的数量(可能)是指数级的。
遗传算法和进化算法(EA)
先说优点,EA通常是不依赖于函数值的,而只依赖于点之间的大小关系,comparison-based,这样进行迭代的时候不会受到梯度太小的影响。看起来似乎是一个可行的路子?下面说一下缺点。
- 先说CMA-ES, 这是效果最好最成功的进化算法之一,尤其是在ill-conditioned 问题和non-separable 问题上。CMA-ES (Covariance Matrix Adaptation-Evolution Strategy)和EDA (Estimation of Distribution Algorithm)的特点是 model-based,他们从一个正态分布采样产生一组新解,使用较好的一部分(一半)新解更新分布的参数(mean, cov或对应的Cholesky factor,对CMA-ES来说还有一个独立步长)。CMA-ES和EDA这样基于分布的算法大体上都能从information geometric optimization (IGO) 用natural gradient 得到。IGO流的收敛性和算法本身在一类问题上的收敛性都不是问题,Evolution path更是动量的类似。然而这些方法最大的问题在于,由于依赖随机采样,当维度很高的时候采样的空间极大,需要极多的样本来逐渐估计cov ()量级),采样产生新解的时候的复杂度是(不低于))。EA的论文普遍只测试30,50-100维,500-1000维以上的极少,即便是各种large scale的变种也大多止步于1000。对于动辄 量级的神经网络优化,基本是不可行的。
- DE/PSO这类算法。特点是无模型,不实用概率分布采样的方法产生新解,使用多个点(称为一个种群,population)之间的相互(大小)关系来模拟一个下降方向。这种基于种群的方法对有较多局部极值的问题效果较好,但是对ill-conditioned 问题性能较差,在non-separable+ill-conditioned问题效果有限。更进一步的,这类算法为了维持种群多样性,通常只进行两两比较(两两比较的选择压力小于截断选择,即某些新解不比父本好,但是比种群中其他解好,这样的解被丢弃了),好的个体进入下一代。然而随着维度增加,新生个体比父代好的比例急剧下降,在ellipsoid函数上100维左右的时候就已经降低到5%以下。实验研究 Differential Evolution algorithms applied to Neural Network training suffer from stagnation 总体上,EA在连续优化问题上的主要问题就是搜索效率不高,相比基于梯度的算法要多倍的搜索。与此相似的实际上是坐标下降法(coordinate descent),同样不使用梯度,同样要求多倍的搜索。
最优化问题的两大类:连续优化与离散优化
- 关于约束条件,理想很美好,现实很骨感,在现实生活中,我们会遇到比如预算有限、时间有限、外部强制性条件等各种各样的问题,与目标函数一样,这些限制条件不是单一存在的,也可能同时存在同一个问题里,对于某一个优化问题来讲,限制条件越复杂,求解就越困难。
- 基于此,我们简单根据它的约束条件以及目标函数变量类型将最优化问题分成两大类,连续优化和离散优化。
- 相较而言,离散优化会更难解决,因为离散优化多了一条限制条件 – 不连续的集合。很多时候,我们要求我们的变量是一个整数,或者来自一个给定的区间,所以说离散优化会比连续优化更难解,而两种算法也会有非常大的不一样。
- 从学术角度而言,连续优化与离散优化对应的是两个比较独立的学科,离散优化可能更多的应用于统计、大数据相关的场景,连续优化则会跟计算机密码学相关,更多的与我们现实生活中的运筹优化应用相关。
全局优化与局部优化
- 从目标函数出发,它的最优值也分为两类,局部最优和全局最优。看图中黄色的点,在局部区域内是最低的,这个值叫做局部最优值,但是当看整个图时,红色的点才是最低的,所以这个点我们叫全局最优值。
- 通常来说,取局部最优值是相较容易的,因为基本上只需要看它临近一小部分的信息就可以准确判断是否局部最优,而在现实应用中,其实仅仅知道局部最优值就足以解决很多问题。而更难的问题在于全局最优值,因为前提是你需要看到整个画面。
- 所以,对于这一类问题,目前没有一个特别好的解决方法。现实生活中,会有比较多的方法去求局部最优值,而往往找到的几乎跟实际上的全局最优值不一样。
- 但有一个问题是例外,这类问题它具有比较好的性质,只要找到局部最优值,它就肯定是全局最优值,这类问题就叫凸优化。
凸优化问题中的最优值
凸优化的关键字在“凸”,要定义什么样的东西是凸的呢?看上图,蓝色区域代表优化问题里变量可以取值的空间,当取值空间是凸的时候,这是凸优化的一个必要条件。
那么什么样的集合是凸的集合?在集合里任意选两点X、Y,将这两点连成线,从X到Y的这条线上所有的点都必须在集合里,只有这样的集合才叫做凸的集合。
相反,如果有任意一个点在集合之外,那就不是凸的集合。而对于一个凸优化的问题而言,它所有的变量取值必须来自于凸的集合。
所以说,对于所有的离散优化而言,它都不是凸优化的,因为它的取值其实不是一个空间,而是一个洞一个洞的,它是很多洞的集合。
所以,通常求解这类问题时很困难,很多时候我们求解的都是一个局部最优值。在实际生活中,我们求解的都是局部优化的问题,而这类问题在所有问题中所占比例是非常非常低的。
如果把整个集合看作一个优化问题的集合,那么相对来讲,比较小的一部分是属于连续优化的问题,其他更大的区域属于离散优化的问题,而在连续优化的空间里只有很小的一部分属于凸优化的问题。所以说,在最优化的领域里,我们真正解决的只是实际问题中的冰山一角。
凸优化问题的经典算法
【2020-10-4】凸优化-笔记整理(1)——引入,优化实例分析,凸集举例与相关性质
- 1940年,Bellman发展了
动态规划算法 (Dynamic Programming,DP)。这个算法的关键在于,状态转移不再是从前往后,而是从后往前。这样的话可以避免很多重复计算。 - 提到
凸优化,一般会提单纯形法(Simplex Method),1947年由Dantzig完善。 - 说到
数值优化,都会提一下内点法(Interior Point Method)。内点法是1984年由Karmarkar完善。 - 而之后的很多优化的发展,都关注在了内点法的很多细节上。
凸优化算法总结
对于凸优化的问题,黄铂博士给大家介绍几个最经典的算法。
- (1)第一个算法,
最速下降法。- 首先,这是一个等高线,可以把它理解为高楼,每一个圈代表一层,最中心是最高的位置,最终目标是用最快的方式上到中心位置。
- 那么,最速下降法是怎么做的呢?比如从一楼上二楼可以有多种方法,很明显我们从垂直方向往上跳,在局部来看是最快的,然后以这样的方法上到最高层。
最速下降法有哪些特点呢?每一步都做到了最优化,但很遗憾的是,对于整个算法而言,它并不是非常好的算法。- 因为它的收敛速度是线性收敛,线性收敛对于最优化算法而言是一种比较慢的算法,但也是凸优化里最自然的一个算法,最早被应用。
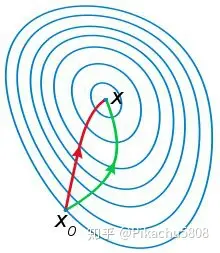
- (2)第二个算法,
共轭梯度法。与最速下降法相比较(看下图),绿色的线是最速下降法的迭代,从最外层到中心点可能需要五步迭代,但是共轭梯度法可能只需两步迭代(红色线)。共轭梯度法最大特点是汲取前面的经验再做下一步的动作,比如从四楼上五楼,会考虑方向是否最佳,汲取之前跳过的四步经验,再探索新的方向往上跳。从数学的角度来讲,每一步前进的方向和之前所有走过的路径都是垂直的,因为这样的性质,共轭梯度法的收敛速度远远高于最速下降法。
- (3)第三个算法,
牛顿法。前面两种算法,从数学的角度讲,他们只用到了一阶导数的信息,对于牛顿法而言,它不仅仅用到了局部一阶导的信息,还用到了二阶导的信息。- 相比前面两种算法,牛顿法的每一步,它在决定下一步怎么走时,不仅考虑当前的下降速度是否足够快,还会考虑走完这一步后,下一步坡度是否更陡,下一步是否更难走。可见,牛顿法所看到的区间会更远,收敛速度更快,属于二阶收敛速度。
- 如果最速下降法需要100步的话,牛顿法就只需要10步,但也正因为牛顿法使用了二阶导的信息,所以它需要更多的运算量。
- (4)第四个算法,
拟牛顿法。1970年,Broyden、Fletcher、Goldfarb、Shanno四人几乎同一时间发表了论文,对于传统的牛顿法进行了非常好的改进,这个算法叫拟牛顿法,它的收敛速度与牛顿法相似,但是它不再需要计算二阶导数,所以每一步的迭代速度大大增加。- 它是通过当前一阶导数的信息去近似二阶导数的信息,因此整个运算速度大幅度增加。由于这个算法是四个人几乎同一时间发现的,所以也叫
BFGS算法。下图中的照片是他们四个人聚在普林斯顿时拍的,很幸运的是,Goldfarb是我博士时期的导师。 - 实际生活中,被应用最广的两种算法,一个是BFGS,另一个就是共轭梯度法。这两种算法经常会出现在很多的程序包里或者开源代码里,如果使用在大规模的优化问题或者成千上万个变量的问题中,也会有非常好的效果。
- 它是通过当前一阶导数的信息去近似二阶导数的信息,因此整个运算速度大幅度增加。由于这个算法是四个人几乎同一时间发现的,所以也叫
牛顿法和梯度下降法都是求解无约束最优化问题的常用方法
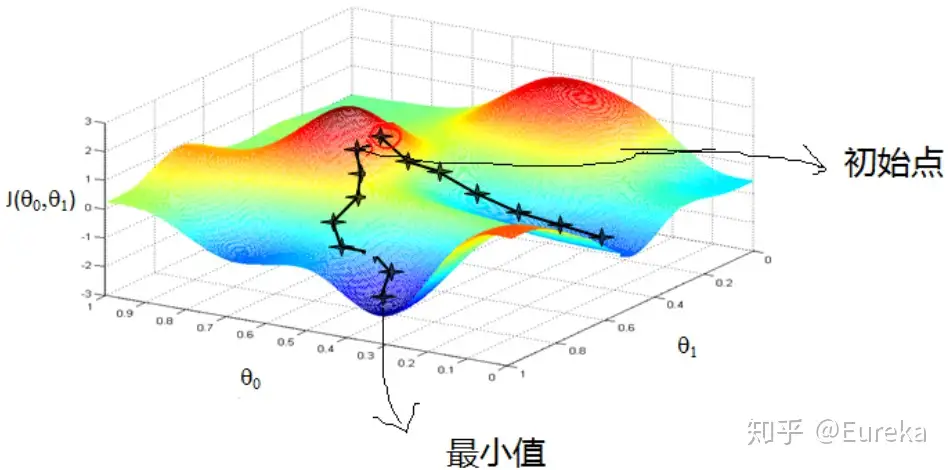
牛顿法是二阶收敛梯度下降法是一阶收敛
所以牛顿法更快,如图:红色路径代表牛顿法,绿色路径代表梯度下降法
然而,深度学习中,往往采用梯度下降法作为优化算子,而很少采用牛顿法,主要原因:
- 神经网络通常是非凸的,这种情况下,牛顿法的收敛性难以保证;
- 即使是凸优化,只有在迭代点离全局最优很近时,牛顿法才会体现出收敛快的优势;
- 可能被鞍点吸引。
牛顿法(Newton method)和拟牛顿法(quasi Newton method)是求解无约束最优化问题的常用方法,有收敛速度快的优点。
牛顿法是迭代算法,每一步都需求解目标函数的海塞矩阵(Hessian Matrix),计算比较复杂。拟牛顿法通过正定矩阵近似海塞矩阵的逆矩阵或海塞矩阵,简化了这一计算过程
梯度下降 —— 一阶导
梯度下降法(Gradient descent)或最速下降法(steepest descent)是求解无约束最优化问题的一种常用的、实现简单的方法。
假设 $f(x)$ 是 $R^n$ 上具有一阶连续偏导数的函数, 求解无约束最优化问题:$\min_{x \in R^{n}}f(x)$
- $f^*$ 表示目标函数 $f(x)$ 的极小点
梯度下降法是一种迭代算法。选取适当的初值 $x_0$ ,不断迭代,更新 $x$ 的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数下降最快的的方向,在迭代的每一步,以负梯度方向更新 $x$ 的值,从而达到减少函数值的目的
- 迭代公式:$x^{(k+1)} \leftarrow x^{(k)}+\lambda_{k} p_{k}$
使用梯度下降时,哪些地方需要调优呢?
- 算法的步长选择。步长取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。
- 步长太大,会导致迭代过快,甚至有可能错过最优解。
- 步长太小,迭代速度太慢,很长时间算法都不能结束。
- 所以算法的步长需要多次运行后才能得到一个较为优的值。
- 算法参数的初始值选择。
- 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;
- 当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
- 归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化。
梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
梯度下降法和最小二乘法相比
- 梯度下降法需要选择步长,而最小二乘法不需要。
- 梯度下降法是迭代求解,最小二乘法是计算解析解。
- 如果样本量不算很大,且存在
解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。 - 但是如果样本量很大,用最小二乘法由于需要求一个超级大的
逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法大家族(BGD,SGD,MBGD)
批量梯度下降法(Batch Gradient Descent)- 批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
随机梯度下降法(Stochastic Gradient Descent)- 随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的样本的数据,而是仅仅选取一个样本来求梯度。
- 随机梯度下降法,和批量梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
小批量梯度下降法(Mini-batch Gradient Descent)- 小批量梯度下降法是
批量梯度下降法和随机梯度下降法的折衷,也就是对于 $m$ 个样本,我们采用 $x$ 个样子来迭代, $1<x<m$ 。一般可以取 $x=16,32,64,…$ ,当然根据样本的数据,可以调整这个 $x$ 的值。
- 小批量梯度下降法是
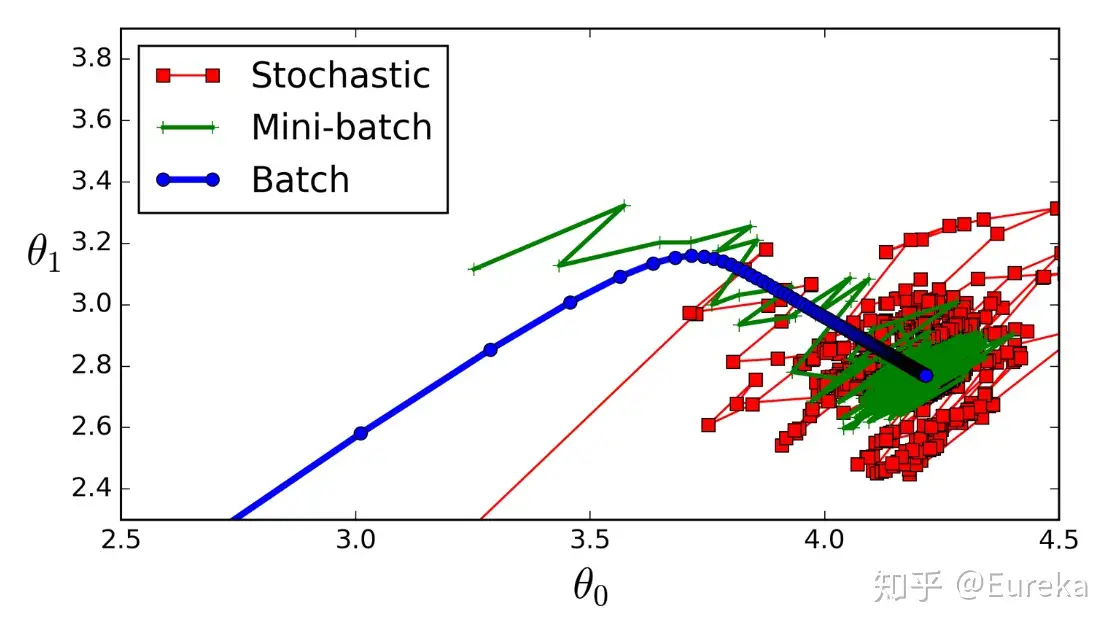
三种方法得到局部最优解的过程
代码
随机梯度下降
import random
import matplotlib.pyplot as plt
class Solutin():
def gradient_descent(self,n):
x = float(random.randint(1, 100)) # 随机初始化
lr = 0.00001 # 学习率
loss = [] # 记录损失
# 损失阈值
while (abs(x ** 2 - n) > 0.0000000001):
# x(n+1) = x(n) - lr * g(x(n))
x = x - lr * 4 * x * (x ** 2 - n)
loss.append((x ** 2 - n)**2) # 记录损失
return loss,x
if __name__ == '__main__':
n=100
loss,a = Solutin().gradient_descent(n)
print( a)
# 画损失图
x = range(len(loss))
plt.plot(x, loss, color='b')
plt.xlim(0,1000)
plt.show()
批量梯度下降法python实现
def train(X, y, W, B, alpha, max_iters):
'''
使用了所有的样本进行梯度下降
X: 训练集,
y: 标签,
W: 权重向量,
B: bias,
alpha: 学习率,
max_iters: 最大迭代次数.
'''
dW = 0 # 权重梯度收集器
dB = 0 # Bias梯度的收集器
m = X.shape[0] # 样本数
for i in range(max_iters):
dW = 0 # 每次迭代重置
dB = 0
for j in range(m):
# 1. 迭代所有的样本
# 2. 计算权重和bias的梯度保存在w_grad和b_grad,
# 3. 通过增加w_grad和b_grad来更新dW和dB
W = W - alpha * (dW / m) # 更新权重
B = B - alpha * (dB / m) # 更新bias
return W, B
共轭梯度(CG) —— 一阶导
- 共轭梯度方法也是一种迭代方法,不同于Jacobi,Gauss-Seidel和SOR方法,理论上只要n步就能找到真解,实际计算中,考虑到舍入误差,一般迭代3n到5n步,每步的运算量相当与矩阵乘向量的运算量,对稀疏矩阵特别有效。
- 共轭梯度方法对于求解大型稀疏矩阵是很棒的方法,但是这个方法看起来总不是太靠谱。这个方法也不是越迭代精度越高,有时候可能迭代多了,反而出错,对迭代终止条件的选择,要求还是很高的。
- 共轭梯度法收敛的快慢依赖于系数矩阵的谱分布情况,当特征值比较集中,系数矩阵的条件数很小,共轭梯度方法收敛得就快。“超线性收敛性”告诉我们,实际当中,我们往往需要更少的步数就能得到所需的精度的解。
共轭梯度法并不适用于任意线性方程,它要求系数矩阵对称且正定
资料
牛顿法 —— 二阶导
牛顿法的原理是使用函数 $f(x)$ 的泰勒级数的前面几项来寻找方程 $f(x)=0$ 的根。
泰勒级数: 参考牛顿法和拟牛顿法
- 函数 $f(x)$ 在 $x_0$ 出展开成泰勒级数,取其线性部分作为 $f(x)$ 的近似,$f(x_{0})+f^{\prime}(x_{0})(x-x_{0})=0$
- $f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}+\ldots$
- 得到: $x_{1}=x_{0}-\frac{f(x_{0})}{f^{\prime}(x_{0})}$
注意:
- 一阶泰勒展开只是对$f(x)$的近似,并非 $f(x)=0$ 的解,只能说是 $f(x_1)$ 比 $f(x_0)$ 跟接近0
- 迭代公式: $x_{n+1}=x_{n}-\frac{f(x_{n})}{f^{\prime}(x_{n})}$
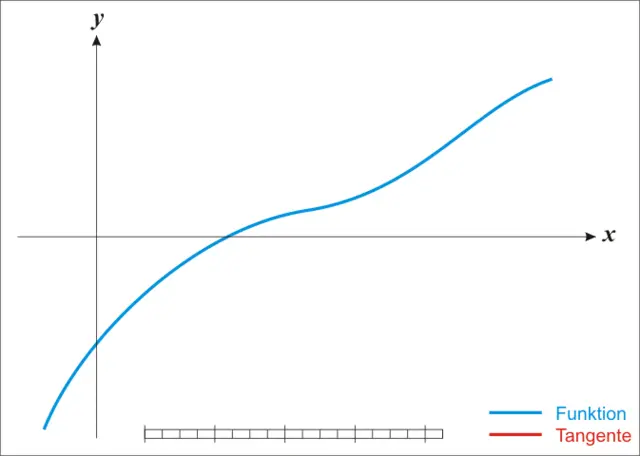
目标函数
- 是二次函数时,
海塞矩阵退化成一个常数矩阵,从任一初始点出发,牛顿法可一步到达,因此它是一种具有二次收敛性的算法。 - 对于非二次函数,若函数的二次性态较强,或迭代点已进入极小点的邻域,则其收敛速度也是很快的,这是牛顿法的主要优点。
牛顿法的迭代公式中由于没有步长因子,是定步长迭代,对于非二次型目标函数,有时会使函数值上升
牛顿法主要应用在两个方面
- 1:求方程的根;
- 梯度下降法常用语求解函数极小值的情况,而牛顿法常用于求解函数零点的情况,即 L = 0 时方程的根
- 2:最优化。
代码
牛顿法求解 $\sqrt{x}=0$
class sqrt(object):
def s(self,x):
a = x
while a * a > x:
a = (a + x / a) / 2
print(a)
if __name__ == '__main__':
x = 169
sqrt().s(x)
拟牛顿法 —— 改进
牛顿法虽然收敛速度快,但是需要计算海塞矩阵的逆矩阵 $H^{-1}$,而且有时目标函数的海塞矩阵无法保持正定,从而使得牛顿法失效。
为了克服这两个问题,人们提出了拟牛顿法。基本思想:不用二阶偏导数而构造出可以近似海塞矩阵(或海塞矩阵的逆)的正定对称阵。
不同的构造方法就产生了不同的拟牛顿法。
- DFP算法: DFP算法用 $G_k$ 作为 $H_k^{-1}$ 的近似
- BFGS算法: 用 $B_k$ 作为 $H_k$ 的近似,与DFP相比,BFGS性能更佳。
- L-BFGS算法:
- 在BFGS中,需要用到一个 $N$ 阶矩阵 $G_k$ ,当 $N$ 很大时,存储这个矩阵将消耗大量计算机资源。
- 为了解决这个问题,减少BFGS迭代过程中所需的内存开销,就有了L-BFGS(Limited-memory BFGS或Limited-storage BFGS)。
- 基本思想:不再存储完整的矩阵 $G_k$ ,而是存储计算过程中的向量序列, 来代替, 这样存储空间由 $O(N^2)$ 降至 $O(mN)$ 。
通常并不直接对 $H_k$ 进行求逆,而是将其转化为求解线性代数方程组 $H_kd_k=-g_k$,此时可根据系数矩阵$H_k$的性态来选择合适的迭代法,如预条件共轭梯度法(PCG)、代数多重网格法(AMG)等。
初始值
beale函数
- Beale函数是在二维中定义的多峰非凸连续函数。通常在(x,y)∈[-4.5,4.5]范围内进行评估。Beale函数是一个介于-4.5和4.5之间的双变量函数
- 该函数只有一个全局最小值(x,y)=(3,0.5
用beale函数分析初始化值对优化的影响,选择三个典型函数
- 随机梯度下降:随机梯度下降(SGD)算法每次执行一次更新,计算每一步的梯度。。
- momentum:通过考虑梯度在一段时间内的动量,解决了随机梯度下降更新缓慢的问题。
- Adam:被认为是最流行的优化算法。
可视化表示
更换初始值
参考:初始值对优化的影响
算法类型
各类算法在 TensorFlow/PyTorch 中的实践,详见站内专题:神经网络调参技巧
优化算法总结
【2022-1-12】
- An overview of gradient descent optimization algorithms
- How to Escape Saddle Points Efficiently
- SGD算法比较,代码
- 如下图,注意:v是动量部分,g是梯度部分
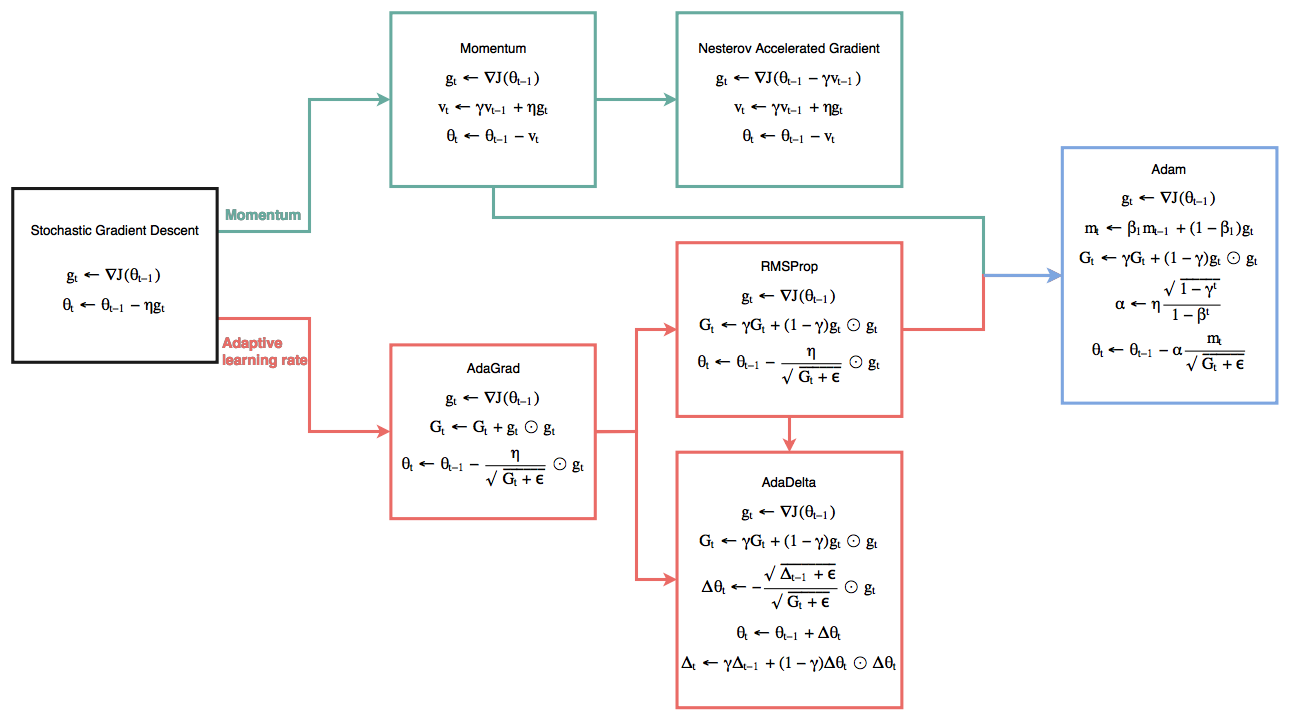
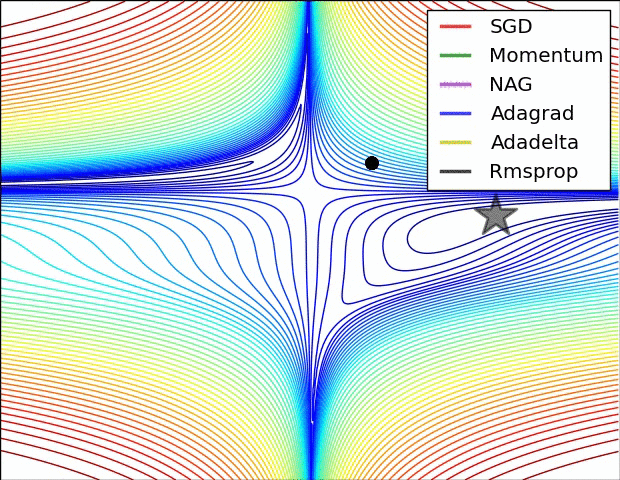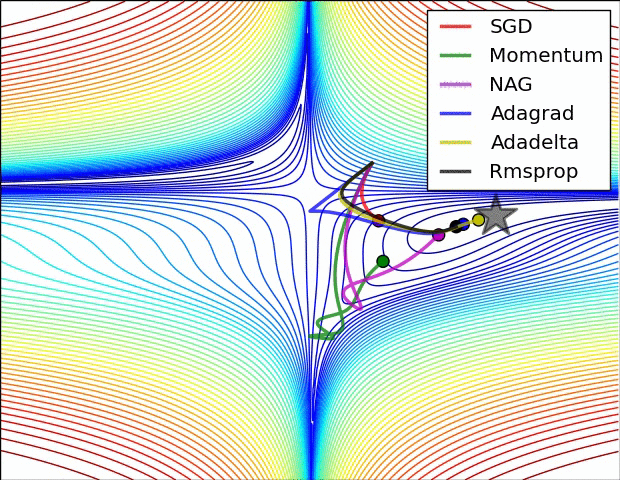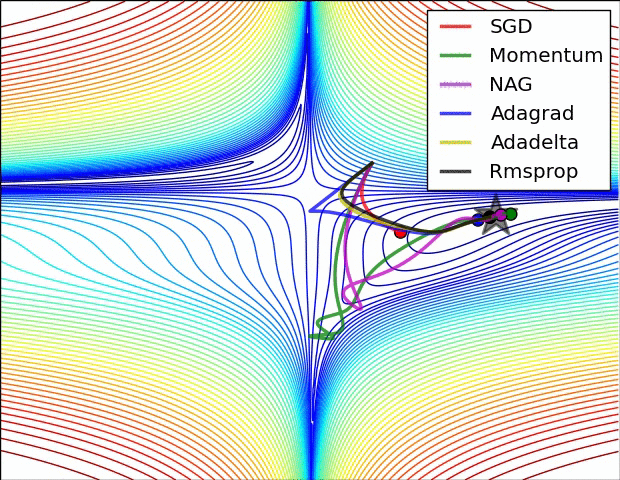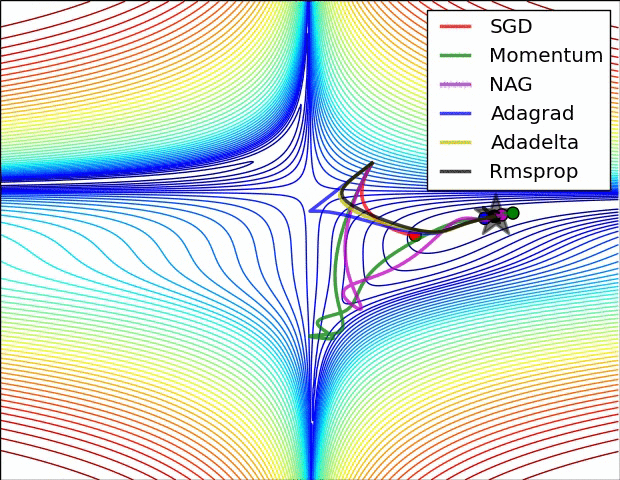
- Note Book 实践: Colab
梯度下降 GD
通过迭代地沿着梯度的负方向来寻找最优解
【2021-11-9】梯度下降方法的视觉解释(动量,AdaGrad,RMSProp,Adam),原文:A Visual Explanation of Gradient Descent Methods (Momentum, AdaGrad, RMSProp, Adam
机器学习中,梯度下降的目标是损失函数最小化。好的算法可以快速/可靠地找到最小值,即不会陷入局部最小值,鞍点或平稳区域,而会求出全局最小值。
基本的梯度下降算法遵循这样的思想,即梯度的相反方向指向下部区域的位置。 因此,它会沿梯度的相反方向迭代地采取步骤。
对于每个参数theta,它执行以下操作:
- 增量delta =- 学习率 * 梯度
- θ += 增量
Delta是算法每次迭代后theta的变化量; 希望随着每个这样的变化,θ逐渐接近最佳值。
Vanilla SGD
随机梯度下降法(Stochastic Gradient Descent, SGD)
- 随机梯度下降在算法效率上做了优化,不使用全量样本计算当前的梯度,而是使用小批量(mini-batch)样本来估计梯度,大大提高了效率
原因
- 使用更多样本来估计梯度方法的收益低于线性
- 对于大多数优化算法基于梯度下降,如果每一步中计算梯度的时间大大缩短,则它们会更快收敛。
- 且训练集通常存在冗余,大量样本都对梯度做出了非常相似的贡献。
- 此时基于小批量样本估计梯度的策略也能够计算正确的梯度,但是节省了大量时间。
SGD的缺点是容易陷入局部最优解,可结合其他优化算法如动量法或Adam等来提高收敛效果。
Vannilla梯度下降法是普通的,因为仅对梯度起作用
- 朴素 SGD (Stochastic Gradient Descent) 最为简单,没有动量的概念
优点
- SGD具有快速收敛的特点
- 适用于处理大规模数据集和分布式计算环境。
缺点
- 收敛速度慢,可能在鞍点处震荡。
- 如何合理的选择学习率是 SGD 的一大难点。
代码实现
import numpy as np
# 定义损失函数
def loss_function(w, X, y):
return np.sum(np.square(X.dot(w) - y)) / len(y)
# 定义梯度函数
def gradient(w, X, y):
return X.T.dot((X.dot(w) - y)) / len(y)
# 定义SGD优化器
def sgd(X, y, learning_rate=0.01, epochs=100):
n_features = X.shape[1]
w = np.zeros(n_features)
for epoch in range(epochs):
for i in range(len(X)):
grad = gradient(w, X[i], y[i])
w -= learning_rate * grad
print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))
return w
动量 Momentum
SGD 在遇到沟壑时容易陷入震荡。为此,引入动量 Momentum,加速 SGD 在正确方向的下降并抑制震荡。
- 动量算法(或简称为动量)的梯度下降借鉴了物理学的思想。 想象一下,将球滚动到无摩擦碗内。 累积的动量并没有停止在底部,而是将其向前推动,并且球不断来回滚动。
- 公式
- 增量 =- 学习率 * 梯度 + 上一个增量衰变率
- θ += 增量
- Momentum descent with decay_rate = 1.0 (no decay).
- 引入动量有效的加速了梯度下降收敛过程。
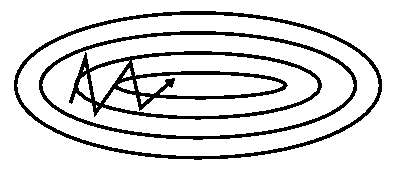
优点:
- 动量只是移动得更快(因为它累积了所有动量)
- 动量有逃避局部最小值的作用(因为动量可能将其推离局部最小值),或更好地通过高原地区。
动量法(Momentum)
动量法(Momentum)和 Nesterov 动量法
- 动量法通过引入一个动量项来加速梯度下降法的收敛速度。
- Nesterov 动量法是对动量法的改进,在每一步迭代中考虑了未来的信息,从而更好地指导参数的更新方向。
动量法和Nesterov 动量法适用于非凸优化问题,能够跳出局部最优解并加速收敛。
Nesterov Accelerated Gradient
- 人们希望下降的过程更加智能:算法能够在目标函数有增高趋势之前,减缓更新速率。
- NAG 即是为此而设计的,其在 SGD-M 的基础上进一步改进了步骤 1 中的梯度计算公式
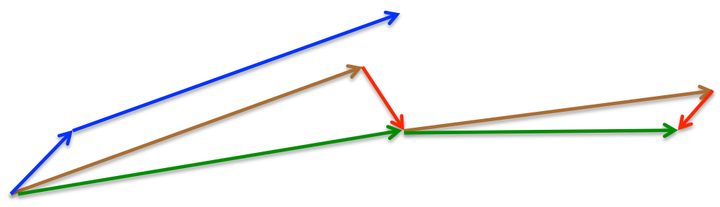
学习率优化
机器学习中,稀疏特征的平均梯度通常很小,因此这些特征的训练速度慢。
解决方法之一: 为每个特征设置不同的学习率,但这会很快变得混乱。
AdaGrad
AdaGrad解决思路:
- 当前更新的特征越多,将来更新的特征就越少,从而为其他特征(例如稀疏功能)提供了赶超的机会。
- AdaGrad(以及其他类似的基于梯度平方的方法,如RMSProp和Adam)可以更好地逃避鞍点。
- AdaGrad将走一条直线,而梯度下降(或相关的动量)则采取 “让我先滑下陡坡,然后再担心慢速方向” 的方法。 有时,原生梯度下降可能会在两个方向的梯度均为0且在此处完全满足的鞍点处停止。
自适应梯度算法(或简称AdaGrad)是跟踪梯度平方的总和,并使用它来适应不同方向的梯度。
- SGD、SGD-M 和 NAG 均是以相同的学习率去更新各个分量。而深度学习模型中往往涉及大量的参数,不同参数的更新频率往往有所区别。对于更新不频繁的参数(典型例子:更新 word embedding 中的低频词),我们希望单次步长更大,多学习一些知识;对于更新频繁的参数,我们则希望步长较小,使得学习到的参数更稳定,不至于被单个样本影响太多。
- Adagrad算法即可达到此效果。其引入了二阶动量
总结
- AdaGrad 是一种自适应学习率的优化算法,能够根据参数的历史梯度来动态调整学习率。
- RMSprop则是对AdaGrad的改进,引入一个指数衰减的平均来平滑历史梯度的方差。
- AdaGrad和RMSprop适用于处理稀疏数据集和具有非平稳目标函数的优化问题。
RMSprop —— 给劲AdaGrad
AdaGrad的问题在于它的运行速度非常慢
- 在 Adagrad 中,Vt 单调递增,使得学习率逐渐递减至0,可能导致训练过程提前结束。
- Adagrad 梯度平方的总和只会增加而不会缩小(单调递增)。
- RMSProp(用于均方根传播)通过添加衰减因子来解决此问题。即:梯度平方的和实际上是梯度平方的衰减的和
- AdaGrad white(白色)最初与RMSProp(绿色)保持一致,这与调整后的学习速率和衰减速率一样。 但是AdaGrad的平方平方和累积起来如此之快,以至于很快就变得庞大起来(由动画中的平方大小证明)。 他们付出了沉重的代价,最终AdaGrad实际上停止了前进。 另一方面,由于衰减率的原因,RMSProp始终将正方形保持在可管理的大小范围内。 这使得RMSProp比AdaGrad更快。
在计算二阶动量时不累积全部历史梯度,而只关注最近某一时间窗口内的下降梯度。根据此思想有了 RMSprop
Adadelta
- 待补充
Adam
深度学习默认首选,融合动量+RMSProp
Adam 优化器之旅可以说是过山车(roller-coaster)式的。
- 2014 年推出,直觉的简单想法:既然明确地知道某些参数需要移动得更快、更远,那么为什么每个参数还要遵循相同的学习率?因为最近梯度的平方每一个权重可以得到多少信号,所以可以除以这个,以确保即使是最迟钝的权重也有机会发光。
- Adam 接受了这个想法,在过程中加入了标准方法,就这样产生了 Adam 优化器(稍加调整以避免早期批次出现偏差)!
Adam(Adaptive Moment Estimation) 是带有动量项的RMSprop,利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
- 优点: 经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
2014年
- Adam是 RMSprop 和 Momentum 的结合。
- 和 RMSprop 对二阶动量使用指数移动平均类似,Adam 中对一阶动量也是用指数移动平均计算。

Adam(自适应矩估计的缩写)兼具动量和RMSProp的优点,Adam从动量获得速度,并从RMSProp获得了在不同方向适应梯度的能力。 两者的结合使其功能强大。
Adam在经验上表现良好,因此近年来是深度学习问题的首选。
Pytorch Adam
Adam 算法
torch.optim 实现了多种优化算法包,大多数通用的方法都已支持,提供了丰富的接口调用
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr = 0.0001)
self.optimizer_D_B = torch.optim.Adam(self.netD_B.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
# params(iterable):可用于迭代优化的参数或者定义参数组的dicts。
# lr (float, optional) :学习率(默认: 1e-3)
# betas (Tuple[float, float], optional):用于计算梯度的平均和平方的系数(默认: (0.9, 0.999))
# eps (float, optional):为了提高数值稳定性而添加到分母的一个项(默认: 1e-8)
# weight_decay (float, optional):权重衰减(如L2惩罚)(默认: 0)
def step(closure=None)
# 函数:执行单一的优化步骤
pass
def closure (callable, optional):
# 用于重新评估模型并返回损失的一个闭包
pass
参数:
params(iterable) – 待优化参数的iterable或者是定义了参数组的dictlr(float, 可选) – 学习率(默认:1e-3), 或步长因子,控制权重的更新比率(如 0.001)。- 较大的值(如 0.3)在学习率更新前会有更快的初始学习
- 较小的值(如 1.0E-5)会令训练收敛到更好的性能。
betas(Tuple[float, float], 可选): 计算梯度以及梯度平方的运行平均值系数(默认:0.9,0.999)- betas = (beta1,beta2)
- beta1:一阶矩估计的指数衰减率(如 0.9)。
- beta2:二阶矩估计的指数衰减率(如 0.999)。该超参数在稀疏梯度(如在 NLP 或计算机视觉任务中)中应该设置为接近 1 的数。
eps(float, 可选): 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)- epsilon:非常小的数,其为了防止在实现中除以零(如 10E-8)。
weight_decay(float, 可选): 权重衰减(L2惩罚)(默认: 0)
完整示例
import torch
import torch.optim as optim
import numpy as np
# 定义损失函数和梯度函数(这里使用PyTorch的自动梯度计算)
loss_function = torch.nn.MSELoss() # 均方误差损失函数
gradient = torch.autograd.grad # 自动梯度计算函数
# 定义Adam优化器(这里使用了PyTorch的Adam类)
optimizer = optim.Adam([torch.Tensor([0.])], lr=0.01) # 学习率设置为0.01,初始权重为0向量(注意:PyTorch中优化器的权重参数需要是tensor对象)
optimizer.zero_grad() # 清除历史梯度信息(如果使用其他优化器,可能需要手动清除梯度)
output = loss_function(torch.Tensor([1]), torch.Tensor([[1, 2], [3, 4]]), torch.Tensor([[2], [4]])) # 计算损失函数值(这里使用了PyTorch的Tensor类,模拟了线性回归问题的数据和目标)
output.backward() # 反向传播计算梯度(这里使用了PyTorch的backward方法)
optimizer.step() # 更新权重(这里使用了PyTorch的step方法)
NAdam
- NAdam在 Adam 之上融合了 NAG 的思想。
AdamW
【2017】当前训练神经网络最快的方式:AdamW优化算法+超级收敛
2017 年末,Adam 又重获新生。Ilya Loshchilov 和 Frank Hutter 在论文《Fixing Weight Decay Regularization in Adam》中指出:每个库在 Adam 上实施的权重衰减似乎都是错误的,并提出了一种简单的方法(AdamW)来修复它。
- 只有深度学习框架:Sylvain 编码的 fastai再用AdamW。由于缺乏可用的广泛框架,日常实践者就只能固守又旧又不好用的 Adam。
AdanW:权重衰减与 L2 正则化
Sophia
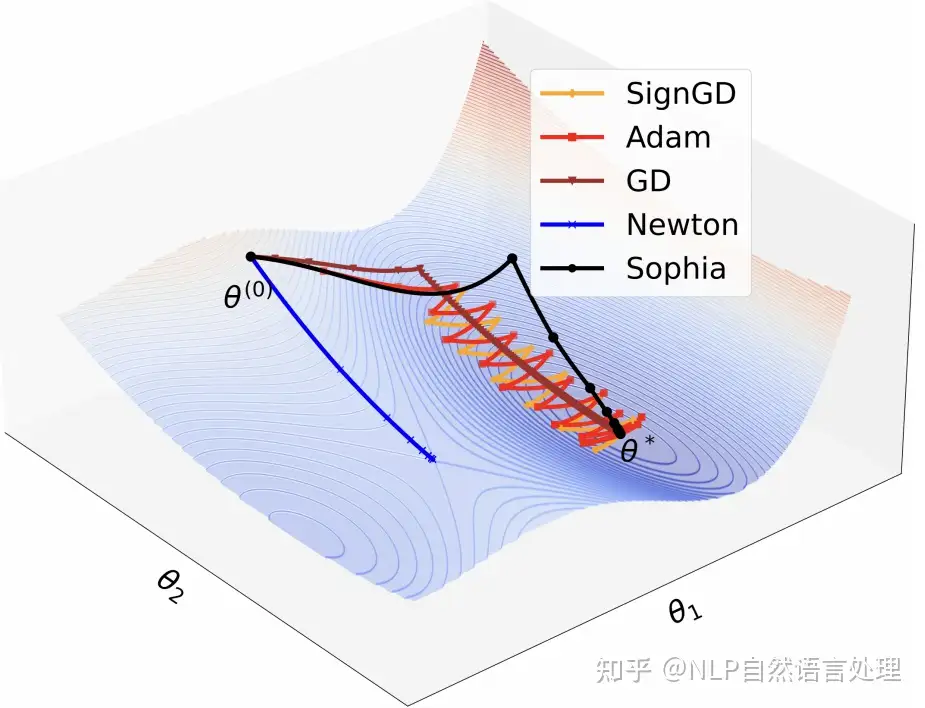
【2023-5-27】Adam该换了!斯坦福最新Sophia优化器,比Adam快2倍,几行代码即可实现
大模型预训练过程主要优化器就是Adam及其变体。例如 GPT、OPT、Gopher和LLAMA。「为LLM预训练设计更快的优化器具有挑战性」。
- 首先,对于Adam中一阶(基于梯度的)预调节器的好处当前并没有一个很好的解释。
- 其次,预调节器的选择受到限制,因为只能提供轻量级选项,其开销可以通过迭代次数的加速来抵消。例如K-FAC中的块对角线 Hessian 预调节器对于LLM来说过于昂贵。另一方面,在基于轻量级梯度的预调节器中自动搜索并识别Lion,在视觉Transformer和扩散模型上比Adam要快得多,但在LLM上的加速效果是有限的。
一种新的模型预训练优化器:Sophia(Second-order Clipped Stochastic Optimization)
- 轻量级二阶优化器,使用Hessian对角线的廉价随机估计作为预调节器,并通过限幅机制来控制最坏情况下的更新大小。
- GPT-2等预训练语言模型上,Sophia以比Adam少了50%的步骤,且实现了相同的预训练损失。由于Sophia几乎每步的内存和平均时间都保持在50%的Adam步骤,因此也就可以说其在总的时间上面也减少了50%
「得益于基于hessian的预调节器,Sophia比Adam更有效地适应了不同参数尺寸的非均匀曲率」,而这种非均匀曲率经常发生在LLS损失的情况下,并导致模型训练不稳定或减速。
- Sophia具有比Adam更激进的预调节器:相比平坦维度(Hessian较小),Sophia对尖锐维度(Hessian较大)的更新具有更强的惩罚力度,以确保所有参数维度的损失均匀减少。相比之下,Adam的更新在所有参数维度上基本一致,导致平面维度的损失减少较慢,这些使得Sophia可以在更少的迭代中收敛。
Muon
当大家习惯在 Adam 及变体中调参时,一个完全不同哲学思想的优化器——Muon Optimizer,进入视野。
【2025-3-17】Muon: 新一代神经网络优化器
Muon (Momentum Orthogonalized by Newton-Schulz) 近期引起广泛关注,一种利用牛顿–舒尔茨迭代对梯度动量进行正交化处理的优化算法。
Muon 优化器专门针对神经网络隐藏层的二维权重参数设计
核心思想: 每次参数更新前,对梯度更新矩阵进行近似正交化处理,从而改善优化动力学。
凭借这一独特机制,Muon 在实际训练中取得了惊人的加速效果:
- 例如,被用于 NanoGPT 和 CIFAR-10 等任务的训练,并刷新了这些任务的速度纪录
Muon 原理:
利用牛顿–舒尔茨迭代高效地逼近梯度矩阵的正交化形式,并将其用于更新神经网络中的二维权重参数,从而加速训练收敛

def newtonschulz5(G, steps=5, eps=1e-7):
assert G.ndim == 2
a, b, c = (3.4445, -4.7750, 2.0315)
X = G.bfloat16()
X /= (X.norm() + eps)
if G.size(0) > G.size(1):
X = X.T
for _ in range(steps):
A = X @ X.T
B = b * A + c * A @ A
X = a * X + B @ X
if G.size(0) > G.size(1):
X = X.T
return X
Muon 优化器的设计初衷: 针对神经网络中的线性变换层(即权重为矩阵的层,例如全连接层、卷积层等)提供一种专门优化方案。
- 传统优化器(如 SGD 或 Adam)对所有参数一视同仁地应用统一的更新规则
- 而 Muon 采取模块化的视角:根据层类型的不同采用不同的优化策略,以充分利用每类层结构的特性。
- 这种“为不同网络模块定制优化器”的理念正是深度学习优化最新趋势的一部分。
- Muon 优化器聚焦于二维权重矩阵参数(例如全连接层的权重矩阵或卷积核张量展平后的矩阵),通过对这些矩阵形式的梯度更新进行特殊处理,以提升优化效果
Muon 和 Adam 区别
- Muon 给出的更新量是经过 msign 运算,所有奇异值都相等,即有效秩是满秩的;
- 而一般矩阵,奇异值通常都是有大有小,并且以前面几个奇异值为主,从有效秩的角度看是低秩的,对Adam更新量的假设也是如此。
- 这个假设并不新鲜,比如高阶muP同样假设了Adam更新量的低秩性。
Muon 由 Keller Jordan 和 Jeremy Bernstein 首次提出,不再拘泥于参数空间 (parameter space),而是从功能空间 (function space) 出发,构建其更新规则。
- 这个思想在国内由 Kimi AI 在其 Kimi K2 等工作中发扬光大并得到了成功的实践,展示了其巨大的潜力。
- 然而,K2 模型的公开材料中也敏锐地指出棘手问题:如果将原版 Muon 优化器直接应用于 Transformer 的 Query (Q) 和 Key (K) 权重矩阵,训练过程会变得非常不稳定,甚至崩溃。
理论的优雅,在实践中遇到了壁垒。
好奇心:
- 现象背后的根本原因是什么?
- 能否沿着 Muon 的”第一性原理”,试提出一种适用于 QK 更新的修正思路?
为什么标准Muon不适用于QK?
Muon 约束(功能空间): Muon 的哲学则完全不同。不应该关心参数 W 本身移动了多远,而应该关心这次移动对模型”功能”的影响有多大。
苏剑林分析: 问题出在 Attention 机制的双线性(bilinear)本质上。
- 浅层的、直觉的解释是功能耦合
- 更深层的原因 与 Muon 优化器的满秩更新特性有关
作者:机智Ry
理论基础
优化算法
要点
- 梯度(一阶导数)
- Hesse 矩阵(二阶导数)
- Jacobi 矩阵
各类算法的优缺点:
- 梯度下降类的优化算法:优点是简单、快速,常用于深度神经网络模型;缺点是可能得到的是局部最优解。
- 牛顿法:优点是二阶收敛,收敛速度快;缺点是需要计算目标函数的Hessian矩阵,计算复杂度高。
- 模拟退火算法:优点是避免陷入局部最优解,能够找到全局最优解;缺点是收敛速度慢,需要大量时间。
- 遗传算法:优点是通过变异机制避免陷入局部最优解,搜索能力强;缺点是编程复杂,需要设置多个参数,实现较为复杂。
- 粒子群优化算法:优点是简单、收敛快、计算复杂度低;缺点是多样性丢失、容易陷入局部最优,实现较为复杂。
Hesse 矩阵
Hesse 矩阵常被应用于牛顿法解决的大规模优化问题
Jacobi 矩阵
Jacobi 矩阵是向量值函数的梯度矩阵,假设F:Rn→Rm 是一个从n维欧氏空间转换到m维欧氏空间的函数。
梯度
某点的梯度信息
- 梯度方向:该点坡度最陡的方向
- 梯度大小:坡度到底有多陡。
注意
- 梯度也提供了其他方向的变化速度(二维情况下,按照梯度方向倾斜的圆在平面上投影成一个椭圆)。
牛顿法(Newton’s Method)和拟牛顿法(Quasi-Newton Methods)
总结
- 牛顿法是一种基于目标函数的二阶导数信息的优化算法,通过构建二阶导数矩阵并对其进行求解来逼近最优解。
- 拟牛顿法是牛顿法的改进,构造一个对称正定矩阵来逼近目标函数的二阶导数矩阵的逆矩阵,从而避免了直接计算二阶导数矩阵的逆矩阵。
牛顿法和拟牛顿法适用于二阶可导的目标函数,具有较快的收敛速度,但在计算二阶导数矩阵时需要较大的存储空间。
import numpy as np
from scipy.linalg import inv
# 定义损失函数和Hessian矩阵
def loss_function(w, X, y):
return np.sum(np.square(X.dot(w) - y)) / len(y)
def hessian(w, X, y):
return X.T.dot(X) / len(y)
# 定义牛顿法优化器
def newton(X, y, learning_rate=0.01, epochs=100):
n_features = X.shape[1]
w = np.zeros(n_features)
for epoch in range(epochs):
H = hessian(w, X, y)
w -= inv(H).dot(gradient(w, X, y))
print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))
return w
共轭梯度法(Conjugate Gradient)
共轭梯度法是介于梯度下降法和牛顿法之间的一种方法,利用共轭方向进行搜索。
共轭梯度法的优点
- 每一步迭代中不需要计算完整的梯度向量,而是通过迭代的方式逐步逼近最优解。
该方法适用于大规模问题,尤其是稀疏矩阵和对称正定的问题。
LBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)
一种有限内存的Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法,主要用于解决大规模优化问题。
由于只需要有限数量的计算机内存,因此特别适合处理大规模问题。
LBFGS算法的目标是最小化一个给定的函数,通常用于机器学习中的参数估计。
import numpy as np
from scipy.optimize import minimize
# 目标函数
def objective_function(x):
return x**2 - 4*x + 4
# L-BFGS算法求解最小值
result = minimize(objective_function, x0=1, method='L-BFGS-B')
x_min = result.x
print(f"L-BFGS的最小值为:{objective_function(x_min)}")
SA(Simulated Annealing)
一种随机搜索算法,其灵感来源于物理退火过程。
该算法通过接受或拒绝解的移动来模拟退火过程,以避免陷入局部最优解并寻找全局最优解。
在模拟退火算法中,接受概率通常基于解的移动的优劣和温度的降低,允许在搜索过程中暂时接受较差的解,这有助于跳出局部最优,从而有可能找到全局最优解。
import numpy as np
from scipy.optimize import anneal
# 目标函数
def objective_function(x):
return (x - 2)**2
# SA算法求解最小值
result = anneal(objective_function, x0=0, lower=-10, upper=10, maxiter=1000)
x_min = result.x
print(f"SA的最小值为:{objective_function(x_min)}")
AC-SA(Adaptive Clustering-based Simulated Annealing)
一种基于自适应聚类的模拟退火算法。通过模拟物理退火过程,利用聚类技术来组织解空间并控制解的移动。该方法适用于处理大规模、高维度的优化问题,尤其适用于那些具有多个局部最优解的问题。
遗传算法是一种基于自然选择和遗传学机理的生物进化过程的模拟算法,适用于解决优化问题,特别是组合优化问题。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
PSO(Particle Swarm Optimization)
PSO是一种基于种群的随机优化技术,模拟了鸟群觅食的行为(吐槽下,智能优化算法的领域真是卷麻了!!!)。粒子群算法模仿昆虫、兽群、鸟群和鱼群等的群集行为,这些群体按照一种合作的方式寻找食物,群体中的每个成员通过学习它自身的经验和其他成员的经验来不断改变其搜索模式。PSO算法适用于处理多峰函数和离散优化问题,具有简单、灵活和容易实现的特点。
KKT 条件
KKT条件(Karush–Kuhn–Tucker conditions) 是最优化(特别是非线性规划)领域最重要的成果之一
- 判断某点是极值点的必要条件
- 适用于 不等式约束的优化问题

【2020-9-5】直观理解KKT条件
- KKT最优化条件是Karush[1939],以及Kuhn和Tucker 1951年先后独立发表出來的。这组最优化条件在Kuhn和Tucker发表之后才逐渐受到重视,因此许多情况下只记载成
库恩塔克条件(Kuhn-Tucker conditions) - 库恩塔克条件(Kuhn-Tucker conditions)是非线性规划领域里最重要的理论成果之一,是确定某点为极值点的必要条件。如果所讨论的规划是凸规划,那么库恩-塔克条件也是充分条件。
含有一个不等式约束的KKT条件

- 详见 KKT条件,原来如此简单
KKT条件:
- 原可行性:g(x*)≤0
- 对偶可行性: α≥0
- 互补松弛条件:αg(x*)=0
- 拉格朗日平稳性: ▽f(x)=α×▽g(x)
为了找到具有不等式约束的优化问题的极值,要搜索必须满足所有KKT条件的点(x*)
拉格朗日平稳性
- 下面是具有等式约束的优化问题的等高线图(它是通过绘制2D格式上的目标函数值的常量切片来表示3D表面的图)。
- 上述问题只发生了两种可行点:1、切点 2、交点。
- 切点是水平曲线(等高线)和约束线彼此相切的点。
- 交点是水平曲线和约束线相交的点。
- 结论:
-
- 约束优化问题的极值总是发生在切点上
-
- 函数的梯度和函数的水平曲线的相切是正交的
- 函数的梯度和函数的水平曲线的相切是正交的
-
- 约束梯度(▽g)始终指向约束控制的可行区域(g(x,y)≥0,g(x,y)≤0方向分别相反)
- 总结:约束的梯度(▽g)和目标函数的梯度(▽f)在极值处(切线点)方向是相同或者相反的。表达式:▽f(x)=α×▽g(x)
-
- 上述问题只发生了两种可行点:1、切点 2、交点。
多目标优化
【2021-7-29】多目标优化之帕累托最优
多目标优化问题的数学模型
以两个目标的最优化问题为例
| 指标 | 目标1 | 目标2 |
|---|---|---|
| 空间曲线 | 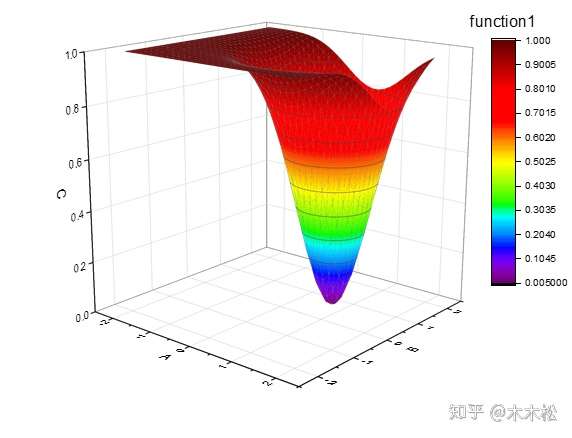 |
 |
在设计空间均匀的取点阵,然后计算所有点的真实目标值,便可以得到解空间和目标空间的分布情况
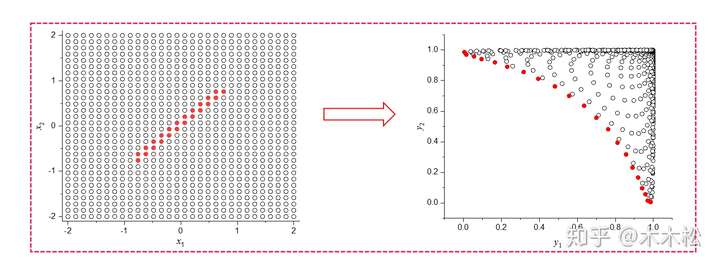
表示n个目标函数,目标是都使之达到最小,
是其变量的约束集合,可以理解为变量的取值范围
帕累托最优基本概念
介绍具体的解之间的支配,占优关系,不用公式,通俗易懂。
-
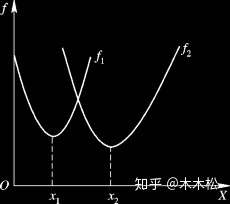
- 解A优于解B(解A强帕累托支配解B)
- 假设现在有两个目标函数,解A对应的目标函数值都比解B对应的目标函数值好,则称解A比解B优越,也可以叫做解A强帕累托支配解B
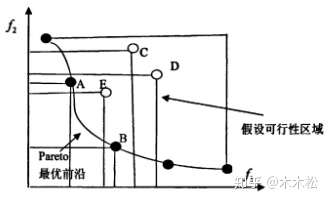
- 横纵坐标表示两个目标函数值,E点表示的解所对应的两个目标函数值都小于C,D两个点表示的解所对应的两个目标函数值,所以解E优于解C,D.
- 解A无差别于解B(解A能帕累托支配解B)
- 修改:此处的“能”应该是与前文的“强”对应,时间比较久了,A,B两点严格意义上是非支配关系
- 解A对应的一个目标函数值优于解B对应的一个目标函数值,但是解A对应的另一个目标函数值要差于解B对应的一个目标函数值,则称解A无差别于解B,也叫作解A能帕累托支配解B
- 点C和点D就是这种情况,C点在第一个目标函数的值比D小,在第二个函数的值比D大。
- 最优解
- 假设在设计空间中,解A对应的目标函数值优越其他任何解,则称解A为最优解
- 举个例子,下图的x1就是两个目标函数的最优解,使两个目标函数同时达到最小,但是前面也说过,实际生活中这种解是不可能存在的。真要存在就好了,由此提出了帕累托最优解
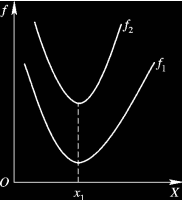
解释
- 左图是解空间的均匀点阵,右图是对应的目标空间两个目标的值
- 右图红色点不被任意其他点支配,所以是Pareto前沿点(如果解空间点阵足够密集,就是一条线了)
- 左图的设计空间的红色点,就是其对应的Pareto最优解集
- 所以现在的一些多目标优化算法主要就是求解问题的Pareto前沿或者近似前沿。从目标空间来看,就是他的边界了。
Pareto帕累托最优解
假设两个目标函数,对于解A而言,在 变量空间 中找不到其他的解能够优于解A(注意这里的优于一定要两个目标函数值都优于A对应的函数值),那么解A就是帕累托最优解 图
Pareto帕累托最优前沿
帕累托最优解,实心点表示的解都是帕累托最优解,所有的帕累托最优解构成帕累托最优解集,这些解经目标函数映射构成了该问题的Pareto最优前沿或Pareto前沿面,说人话,即帕累托最优解对应的目标函数值就是帕累托最优前沿。图
对于两个目标的问题,其Pareto最优前沿通常是条线。而对于多个目标,其Pareto最优前沿通常是一个超曲面。
帕累托最优经济学讲解
帕累托最优:
资源分配的一种理想状态,假定固有的一群人和可分配的资源,从一种分配状态到另一种状态的变化中,在没有使任何人境况变坏的前提下,使得至少一个人变得更好,这就是帕累托改进或帕累托最优化。
注意
纳什均衡是指博弈双方中单方利益最大化, 而不是集体利益最大化。
其实帕累托最优是一个错误描述,并没有指定帕累托的最优原则。
- 实际上一个系统达到帕累托最优后,还可以有任意多个帕累托最优。
- 但是多个帕累托最优之间的切换一定时间段内一定是以非帕累托最优的状况下切换的。
- 也就是说:$ 帕累托最优 -> 非帕累托最优 -> 帕累托最优 $。类似于一个高山多个峰。
- 所以帕累托最优并不是从今以后 除非剥夺他人 则无法增加自身利益。而是:
- $ 帕累托最优 -> 公平失衡 -> 非帕累托最优 -> 公平重平衡 -> 新的帕累托最优 $
根据经济学定义,帕累托最优需要同时满足以下3个条件:
- 交换最优;
- 生产最优;
- 产品混合最优。
什么是帕累托改进 (Pareto Improvements)
什么是帕累托改进?在没有人变坏的前提下让有些人更好。
- 假设A和B两人手上各有一只橘子,A只想用橘子皮泡水喝,B只想吃它的果肉,所以对于A来说,橘子皮是有用的,果肉没用,对于B来说,果肉是有用的,橘子皮没用。于是他们商量后决定把自己没用的那部分相互交换,这样A就能得到两份橘子皮,B能得到两份果肉,两人都比之前多了一倍。
- 这个例子像不像两个国家在利用各自优势进行贸易互换?没错,基于比较优势理论的全球分工合作模式就是一种
帕累托改进。
什么是帕累托最优 (Pareto Optimality)
理解了帕累托改进就不难理解帕累托最优。
帕累托最优就是指再也找不到任何帕累托改进的余地的状态。如上所述,A和B交换橘子皮和果肉的过程就是持续的帕累托改进,每交换一片果肉和一片橘子皮都是一次帕累托改进,直到交换完整只橘子为止,而这个完成的状态就叫帕累托最优,此时你不可能再得到更多的橘子皮和果肉了。
什么是卡尔多-希克斯改进
进化版:卡尔多-希克斯改进
- 帕累托改进描述的是一种理想状态,在帕累托改进中没有任何人的利益会受损,每个人至少要好于或等于当前状态,从而使整体的福利得到增加。
- 经济学里的福利指的是物质或精神的满足。
- 但在现实中这种情况过于理想化了,不妨设想一种更常见的场景,即对于集体来讲,部分受益、部分受损,但只要受益部分大于受损部分,那么集体的总福利也可以得到提升,此时受益者也可以给予受损者一定补偿以使其免遭损失。
- 这个过程就是
卡尔多-希克斯改进。
像国家宏观层面的改革基本都遵循卡尔多-希克斯改进的原则,即只要改革受益者所得足以补偿受损者的所失,那这个改革就值得一试。
- 比如改革开放之初,邓公一句“允许让一部分人先富起来”正是对卡尔多-希克斯改进的最好实践。
- 仔细分析一下这句话,首先如何让一部分人先富起来?就是要打破吃大锅饭的局面,但是在没有经济外生动力的情况下,蛋糕无法做大,那么要让一部分先富起来只能重新切分蛋糕。
- 假如我少吃一块蛋糕幸福感-1,而你多吃一块蛋糕幸福感+2,那么为了使我们整体的幸福感更高,是不是我要持续地给你喂蛋糕?
- 这其实就是改革开放后东部沿海城市率先发力的逻辑,当时中央举全国之力,人为压低中西部各类资源要素价格如农产品、矿产品等,用以支持东部沿海制造业发展,正是在这种“宏观调控”背景下,中国践行了卡尔多-希克斯改进,并使经济得到了飞速发展。
卡尔多-希克斯改进的问题
卡尔多-希克斯改进也有问题
场景:
- 甲乙两人能力相仿,同时入职同一家公司,但甲却率先得到了提拔。在这个极简场景中,乙没有受损,同时甲得到了好处,是典型的
帕累托改进。 - 理论上, 整体福利提升应该是个不错的结果,但实际并非如此。人性素来不患寡而患不均,凭什么我俩能力差不多,你得到提拔而我却没有?难道仅仅是运气差吗?会不会你背后在搞小动作?于是各种猜忌、嫉妒、甚至愤怒涌上心头,表现在工作积极性上会大打折扣,最终可能导致对公司而言,整体的福利反而是下降的。
- 同样的,
卡尔多-希克斯改进也存在着价值选择的问题,难道为了增加集体的利益牺牲掉一部分人的利益是理所当然的?那谁又愿意当那一部分人?这有点像哲学中“失控火车”的问题。- 一列失控的火车沿着铁轨疾驰,火车前方铁轨上有五名工人,如果火车撞上他们,这五个人都不可能存活。
- 但是你可以通过按下按钮改变火车路线并将其引向另一条铁轨,在那条铁轨上的不远处也有工人,但只有一名。你会按下这个按钮吗?
- 仅从数量上看,这样做确实可以使福利最大化,但是这么做真的是道德的吗?让这个无辜的人死去是正确的选择吗?
再引申一点,当前社会提倡共同富裕,讲的就是鼓励富人拿出一部分钱分给穷人,这也是卡尔多-希克斯改进的逻辑。
- “劫富济贫”能使社会的总福利更高,因为对富人来讲,100元九牛一毛,但是对穷人来讲就很重要,他可以饱餐一顿或者买些生活必需品,顺带还能促进一下消费。
- 但这里有个非常关键的隐含条件,就是假设经济蛋糕不会变小。然而如果富人因为财富的被动转移而降低造富的积极性,那么经济蛋糕就会不断萎缩,社会总福利可能不升反降。
此外,卡尔多-希克斯改进还存在一个度量难的问题,即受益和受损如何裁定和量化,能量化的只是物质部分
- 比如上文提到的分蛋糕的例子,我把蛋糕给你,我幸福感-1,你幸福感+2,我们作为整体幸福感是上升的,这里的幸福感泛指那些可以被量化的部分。但是如果我一直把蛋糕分给你,你的幸福感是提高了,但我的幸福感却越来越低,最终就会“冰火两重天”。
- 投射到社会层面上,就造成了贫富差距过大,而贫富差距过大是容易激化社会矛盾,影响社会安定的。而此等危害岂是可以度量的?
总结
总结
- 帕累托改进描述的就是在没有人变得不好的前提下让有些人更好的过程。
- 帕累托改进的终极形态是帕累托最优。改进是过程,最优是结果,帕累托最优就是指再没有改进余地的状态。
- 在达到帕累托最优后,如果还要进一步改进,就不得不牺牲一部分人利益来换取集体更大的利益,这个过程叫作卡尔多-希克斯改进。
- 任何改革都是帕累托改进和卡尔多-希克斯改进的践行,我国改革开放之初大力发展东部沿海城市就是遵循卡尔多-希克斯改进的思想进行的。
- 虽然“两个改进”看上去很美好,但在实践中会存在不少弊端,比如缺乏对人性的考量、对道德的判断,对福利的度量等。
知乎:小奥爱吃奥利奥
帕累托最优与卡尔多最优
讲到资源分配效率,帕累托效率和卡尔多希克斯效率表现的其实是人们寻求最优决策的过程,先来看一看这两种资源分配改进的定义。
卡尔多-希克斯效率是指第三者的总成本不超过交易的总收益,或者说从结果中获得的收益完全可以对所受到的损失进行补偿,这种非自愿的财富转移的具体结果就是卡尔多-希克斯效率,总而言之就是寻求群体利益的最大化。帕累托效率是指资源分配的一种理想状态,假定固有的一群人和可分配的资源,从一种分配状态到另一种状态的变化中,在没有使任何人境况变坏的前提下,使得至少一个人变得更好,这就是帕累托改进或帕累托最优化。
其实绝大多数经济决策面临的都是如何在效率和公平之间选择,这两者很难两全。
卡尔多希克斯效率体现的是一种绝对功利主义的思想,也就是将效率放在了公平之前,追求的是一个整体的最大福利;- 而
帕累托改进相对而言加强了对公平的重视,也就是对总体福利的改进不能建立在某一个个体的损失之上,寻求的是一种公平与效率的平衡。
由于卡尔多希克斯效率更加重视效率,也就是总体的福利,这就导致了一般情况下卡尔多希克斯最优的社会总福利会高于帕累托最优的社会总福利,但是当从某一个个体的角度来看这种绝对功利主义的改进未必是好事。
【2022-10-9】参考:帕累托效率与卡尔多-希克斯效率
工程实践
多目标
- 多个loss引入pareto优化理论
【2024-4-26】Pareto optimal solution
MGDA 作为基础后改进,MGDA是这篇文章:
- Multiple-gradient descent algorithm (MGDA) for multiobjective optimization.
LibMTL
代码
- 多任务学习 PyTorch 库 LibMTL
Features Unified: LibMTL provides a unified code base to implement and a consistent evaluation procedure including data processing, metric objectives, and hyper-parameters on several representative MTL benchmark datasets, which allows quantitative, fair, and consistent comparisons between different MTL algorithms. Comprehensive: LibMTL supports many state-of-the-art MTL methods including 8 architectures and 16 optimization strategies. Meanwhile, LibMTL provides a fair comparison of several benchmark datasets covering different fields. Extensible: LibMTL follows the modular design principles, which allows users to flexibly and conveniently add customized components or make personalized modifications. Therefore, users can easily and fast develop novel optimization strategies and architectures or apply the existing MTL algorithms to new application scenarios with the support of LibMTL.
组合优化
大模型优化
HeurAgenix
【2025-8-14】 HeurAgenix:大语言模型驱动的组合优化“全能教练”
在物流规划、生产排程、能源调度等行业应用场景中,组合优化问题往往规模庞大、约束复杂,长期依赖专家手工调参的启发式算法已难以应对动态多变的现实需求。
微软亚洲研究院最新提出的 HeurAgenix 框架,将大语言模型视作“全能教练”,为启发式算法带来了自进化与自适应的能力,并通过蒸馏压缩实现快速响应。
HeurAgenix 不仅全面超越了现有 LLMs 超启发式方法,在多数任务中甚至优于专业求解器,为组合优化的通用化、智能化和实际落地开辟了新路径。
许多关键的决策问题都可以抽象为组合优化(combinatorial optimization)。
- 物流公司需要在海量路线中选择最优的运输路径;
- 制造企业要在紧张的时间和资源约束下排定生产计划;
- 电网运营商则需在不断变化的供需中优化能源调度。
这类问题往往规模庞大、约束复杂,精确求解在计算上难以承受,因此产业界和学术界长期以来都依赖启发式算法来寻找近似最优解。
启发式方法以求解效率高见长,但也存在明显短板——需要依赖专家不断调参来适配不同问题,泛化性差,且性能表现不够稳定。
- 依赖专家经验:算法设计与调参往往依赖专家经验,耗费较多时间;
- 泛化性差:传统启发式算法往往“一场景一写法”,适配新问题时需要重新调整,开发和维护成本极高;
- 效果受限:由于组合优化问题的复杂性,单一启发式算法通常力不从心,难以稳定高效求解。
这些大大限制了动态、多变的实际场景中的应用潜力。
【2025-6-18】为突破这些瓶颈,微软亚洲研究院的研究员们提出 HeurAgenix
- 论文地址:HeurAgenix: Leveraging LLMs for Solving Complex Combinatorial Optimization Challenges
- 代码开源链接:https://github.com/microsoft/He
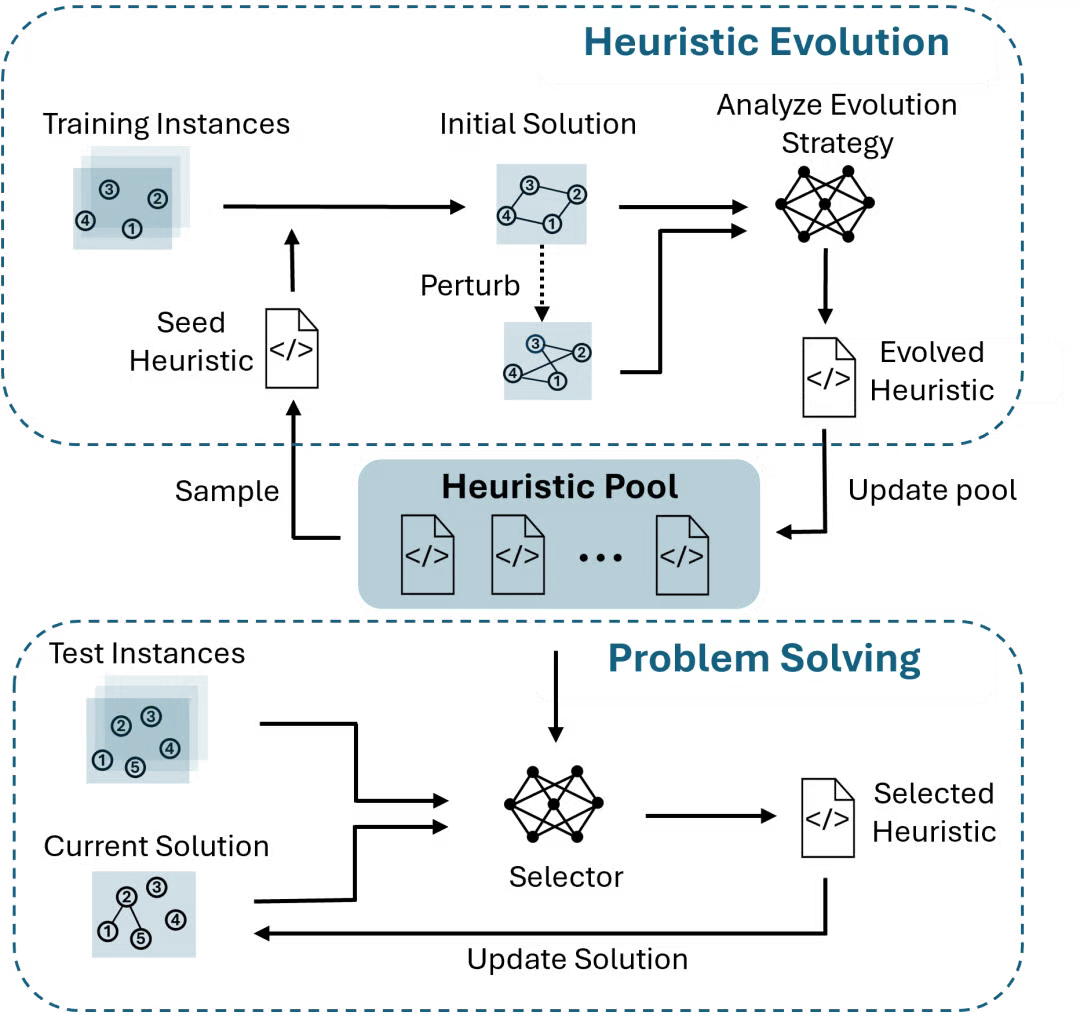
HeurAgenix 将大语言模型(LLMs)视作“总教练”
- 平时对启发式算法这群“球员”进行持续“训练”,让其自动发现弱点并自我进化,且过程中无需专家干预;
- 求解阶段实时“排兵布阵”,灵活切换最优策略,确保解的稳定性与高效性;
- 同时,研究员们将大模型的决策洞见蒸馏至轻量化模型,使得系统能够实现毫秒级响应,显著降低计算成本。
多个经典问题实验表明
- HeurAgenix 不仅能超越现有的、基于 LLMs 的超启发式方法,还在多数场景下超过了手工调参的专业求解器,展现出强大的通用性与实用价值。
HeurAgenix 的创新体现在三个方面:
- 自进化框架:提出数据驱动的启发式进化框架,无需先验知识和人工调参;
- 自适应调度:利用 LLMs 的状态感知能力,结合测试时缩放(TTS)技术,动态选出最优算法,在求解速度与解质量间取得较好的平衡;
- 轻量化蒸馏:提出“结果偏好+状态感知”双重奖励机制,高效地将高阶模型的选择能力蒸馏到轻量级模型,提高响应速度。
主要流程
资料
- 资料如下
- 从 SGD 到 Adam —— 深度学习优化算法概览(一)
- 最优化算法的前世今生
- 大岩资本黄铂博士结合生活实践中的案例,深入浅出阐释了最优化算法的前世今生。从实际生活中最基础的应用切入,黄铂将抽象的算法概念生动化,解释了什么叫最优化问题、凸优化及算法分类、机器学习与人工智能应用。
- 凸优化:算法和复杂性 by Sebastien Bubeck



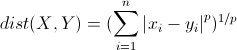

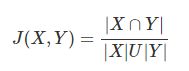

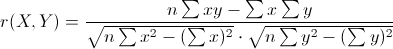
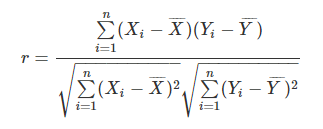
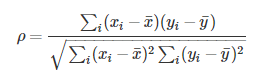
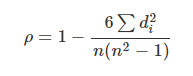


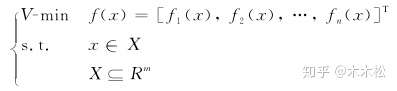
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
