- 总结
- 广告行业
- LTR 排序学习
- CTR 广告预估
- CTR预估
- 工程实现
- 结束
总结
- 【2021-6-22】阿里定向广告智能投放技术体系
- 第一部分先介绍广告业务的背景: 广告生态里,包括广告主,媒体(或者广告平台)和用户。广告的逻辑就是广告主在媒体上付费,通过媒体对目标用户进行营销信息传达,影响用户,让用户购买广告主的商品,形成信息和金钱的流动,也形成用户广告之间物质的流动。
- 第二部分会沿着如何帮助广告主更好地做好营销的历史脉络,讲解智能投放体系和技术的演进过程
- 最后会给出整个演进的总结,以及对未来的展望。
- 【2020-12-08】互联网广告的“冰”与“火”
- 网站分析基础知识
广告行业
广告目标
广告核心目标:最大化平台收入,提升广告价值,增加广告主预算
- 用户:通过媒体平台获取信息
- 广告主:通过投放系统进行广告创意投放,目标是ROI最大化
- 媒体:今日头条、抖音、Tiktok等平台
广告类型
广告类型:
- 品牌广告
- 效果广告
| 广告类型 | 效果 | 目的 |
|---|---|---|
| 品牌广告 | 长期效果 | 树立产品品牌形象,维持品牌知名度 |
| 效果广告 | 见效快 | 广告主只为可衡量的结果付费 |
广告类型
- 品牌广告:广告主追求广告曝光度,目标在提升品牌价值,核心指标为展示量。广告主为了自己的推广计划在平台上购买需要的流量,并且愿意付出溢价。一般买量较大,对展示量的要求较高,适合大广告主。
CPT:按时长计费,广告主选择广告位和投放时间 。GD:担保式保量投放,即保量广告,在广告投放前已经约定好广告的价格和投放量。
- 效果广告:广告主对 ROI 等指标有明确的要求,也更有意愿让平台进行效果优化。广告主更关心最后结果,例如消耗多少钱可以带来多少点击、APP下载、商品购买、表单填写、ROI等。平台可以利用数据 + 算法进行深度优化。效果广告需要控制计费比(平均转化成本 / 目标转化成本)= 1
接入形式
广告接入形式:
- 独立广告:
- 客户端直接请求商业化广告,独立展示,和用户侧内容不耦合
- 框架:手机 → pack api → Engine(广告投放引擎)+ Pack(广告素材)
- 示例:开屏广告、激励广告、link广告、下拉刷新广告等
- 开屏广告:用户注意力集中,价值大——位置优越、整平显示、针对性强、强制性曝光、流量巨大;难点:加载时间长(冷启动、热启动时给没有多少加载时间)会影响用户体验,所有需要预加载
- 嵌入式广告:
- 在用户侧生态内容中混排展示,样式尽可能与用户侧内容形式一致
- 框架:手机产品使用中 → APP服务器 → Engine(请求广告)+Pack(广告素材)→ 返回广告信息流
- 示例:信息流广告、搜索广告、视频相关推荐广告
- 信息流广告:用户在自然内容刷新中触达广告,广告混排在推荐流中出现。特点:流量大,借助预估流量可以做到精细化变现,广告展示触达样式多样化
用户在客户端刷新发起广告请求后
- 匹配:找个符合定向的广告候选集
- 预估:对所有广告执行ctr预估
- 排序:综合广告出价计算ecpm后排序
- 投放:最终展示在客户端样式
- 回传:客户端事件上报
- 数据处理:针对回传的时间计费、统计、模型训练等
出价类型
ECPM:每一千次展示预估可以获得的广告收入。
因此对平台核心目标来讲,每次流量,最终排序的目标是衡量ECPM.
| 出价类型 | ecpm | 计费点 | 说明 | 问题 | 适合广告主 |
|---|---|---|---|---|---|
CPM |
bid * 1000 | 展示 | 收入稳定,流量不分高低,难以控制转化效果,广告主承担主要风险 | 品牌广告主,只适合曝光 | |
CPC |
bid * pctr * 1000 | 点击 | 流量以ctr细分,pctr不准使平台受损,广告系统和广告主的能动性都得到一定发挥 | 决策周期长,线上转化率低的行业(如汽车、房产等) | |
CPA |
bid * pctr * pcvr * 1000 | 转化 | 按转化收费,下载、激活等 | 流量以cvr细分,pcvr不准使平台受损,更偏向广告主,平台风险大,存在广告主作弊风险,e.g. 广告主不回传真实转化量 | 适合线上转化率高,决策周期短(如电商、电影、外卖等) |
oCPM |
bid * pctr * pcvr * 1000 | 展示 | 广告主按转化出价,平台按send收钱 | pctr & pcvr风险转嫁,广告主有动力优化ctr和cvr,平台可能超成本 | 追求转化,没有能力优化投放策略,cvr和ctr均较高的广告主 |
计费方式
互联网广告竞价计费方法的目的是确保广告主在出价时有动力提出自己真实的最高价值,并消除广告主故意压价的因素。
| 计费方法 | 描述 | 优缺点 |
|---|---|---|
GFP(Generalized First Price) |
广告主出多少,就收多少钱 | 1. 广告主会频繁调价,对于频繁调价的广告主更有利 2. 广告主更关注和其他人的价格优势,而不是广告位真实的价值 |
GSP(Generalized Second Price) |
按排在该广告下一名的出价计费(二价计费,再加上一个最小单位) | 1. 广告主可直接给出自己能承受的最大价格广告主无频繁调价动机 |
VCG(Vickrey-Clarke-Groves) |
按该广告竞价成功给其他广告带来的损失计费 | 1. 广告主普遍存在理解门槛 2. “损失”定义&计算复杂,难解释,FB 部分场景使用。竞价广告扣费机制的博弈论原理 |
张维迎的《博弈论与社会》——一本博弈论的科普书,一边在介绍博弈论原理,一边借助博弈论来解释政治、经济和生活中的现象。在现在常见的竞价广告系统中,博弈论同样应用广泛
有2个前提:
- 媒体追求利益最大化:这很容易理解,因为媒体想要充分利用自己的流量,让每次广告曝光的收益都最大化,不浪费每一个挣钱的机会。
- 广告主追求利益最大化:广告主也是理性的,它需要从广告中获得收益,广告主的收益=广告引流产生的价值-广告成本。
广告投放环节
定向
广告定向是提供给广告主投放广告的产品,支持广告主投放符合条件的人群
- 地域定向
- 基础定向(性别,年龄,语言)
- 兴趣 & 行为定向 等。
定向实现的核心方式是建立倒排索引以及对应满足对应定向条件广告的bitmap
- ad -> tags => tag -> adids => tag -> bitmap
召回
召回的目标是从百/千万级广告,选出万级别Top广告,一般召回由多路组成,主要的召回建模方式有
- 使用双塔模型建模出User Embedding 和Ad Embedding (建模目标例如recall2send,LTR)
- ANN快速检索(FBT, HNSW)
- 暴力检索
- Deep Retrieval 幼儿园版
粗排
精排模型一般比较复杂,计算耗时较多,难以处理万级别的候选,因此需要粗排再进行一次筛选,粗排一般使用双塔模型,广告侧向量离线计算好并缓存到粗排inference的机器上(viking),在线只计算用户侧向量以及和广告候选的两两内积。因此粗排模型不能出现(用户-广告)match特征,也不能在NN中将用户特征和广告特征做交叉。
主要建模方式也有两种
- 建模ctr, cvr,计算ecpm
- 建模LTR
精排
精排主要针对 CTR/CVR/Deep CVR等进行建模,需要使用丰富多样的Feature,模型结构最大化模型预估效果。
混排
混排阶段将自然推荐的内容和商业广告进行merge,在平台利益和用户体验找到合适的平衡点,实现平台长期价值。目标是在满足用户体验、和一些业务约束的情况下(ad gap, 广告最高出现的位置,置顶新闻,cpt广告),将排好序的广告序列和自然内容序列合并,使得整体序列收益最大。
对于广告是ECPM,内容的排序分(CU)也rescale到ECPM量纲,主要的思路有:
- 按照根据ECPM大小排序。
- 我们认为广告/内容出现在不同的位置、以及认为context gid对target gid的价值会造成影响,因此需要穷举所有可能的序列,找到全局最优解 参考
出价
出价是提供给广告主的产品
广告主诉求
广告主的买量诉求很多样:
- 我要买平均xx元一个的激活
- 我要花500元买尽量多的转化
- 我希望你能给我xx激活的同时,优化付费成本
- 我要你给我1000000次至少点击率为1.5%的展示
出价产品
- Cost Cap产品:设计优化目标是在成本约束和预算约束下最大化转化量。对于这类成本约束的产品,传统的出价设计策略将优化目标拆分为成本控制和消耗控制。
- Lowest Cost (Nobid)产品:由广告主设置计划预算,无出价设置入口,在一天结束或广告计划(或广告组)排期结束时,尽可能在消耗完全部预算的前提下实现成本最低的出价产品。
- 深度转化出价:广告主考核更后端的转化效果,例如重度游戏广告的转化漏斗从浅到深是点击->下载安装->游戏付费->游戏付费ROI(付费金额/广告主消耗成本)
| 出价方案 | ecpm | 优点 | 缺点 |
|---|---|---|---|
| 自动出价(pacing出价) | ecpm = cpa_bid * pctr * pcvr (预估到安装) * deep_cvr * deep_cvr_coef |
||
| deep_cvr_coef 通过pacing算法拟合前端计费比为1 | 广告主操作简单 | 后续优化空间有限 | |
| 直接投深度转化事件 AEO | 正常ocpm出价,直投深度事件 ecpm = rankbid * pctr * pcvr |
保证广告主关键事件的成本 | 对冷启动、风控出价要求高 |
| ROI产品 | Ecpm = rankbid * pctr * pcvr(预估到付费) * p预估付费金额 * coef |
出价策略
- rank_bid:出价策略将广告主的诉求(cpa_bid、budget)等映射到单次请求的价值rank_bid, 进而达到优化流量分配的作用 (ECPM = rankbid * pctr * pcvr)
- 流控出价:消耗控制策略基于实时的消耗反馈通过pid或mpc等pacing算法实时动态调整出价,力求保证广告主预算进行的消耗平滑。
- 风控出价:成本控制策略基于实时的投放后验或预估数据,计算实时计费比,通过pid或mpc等pacing算法实时动态调整出价,力求保证计费比目标的达成。
- SPB出价:针对Cost Cap产品的一种新型出价策略,利用模型预估cost2convert,来实现每天根据目标成本,自动规划出广告的期望消耗,复用Lowest Cost调控消耗的能力进行实时出价。
经验
app广告转化
基本过程
- impression(展现) —(
CTR)–> ads click(广告点击) —(CVR)–> downlaods click(下载点击) —(1-drop ratio)—> true install(安装) - 最后一步是offsite singal,其余都是onsite signal
备注:
- 苹果iOS14发布了新的隐私政策SKAdNetwork,限制了跨不同App的用户行为追踪,媒体平台无法再获知一个用户看过广告后是否真实发生了转化,简单来说,转化率模型拿不到正样本。
LTR 排序学习
互联网的出现,意味着”信息大爆炸”。用户担心的,不再是信息太少,而是信息太多。如何从大量信息之中,快速有效地找出最重要的内容,成了互联网的一大核心问题。
各种各样的排名算法,是目前过滤信息的主要手段之一。对信息进行排名,意味着将信息按照重要性依次排列,并且及时进行更新。排列的依据,可以基于信息本身的特征,也可以基于用户的投票,即让用户决定,什么样的信息可以排在第一位。
下面整理和分析一些基于用户投票的排名算法。
- 参考资料
- 【2020-8-5】十张图带你领略知乎答案排序算法之美
- 基于用户投票的 6 个排名算法【转载+整理】
Learning to Ranking简介
Learning to Rank (LTR)是指一系列基于机器学习的排序算法,最初主要应用于信息检索(Information Retrieval,IR)领域,最典型的是解决搜索引擎对搜索结果的排序问题。除了信息检索以外,Learning to Rank 也被应用到许多其他排序问题上,如商品推荐、计算广告、生物信息学等。
Facebook用它来优化你的朋友圈文章,Airbnb用它来优化你的搜索结果排序,Quora用它来给各种答案进行排序。Bing常常标榜它有着最好的机器学习得到的搜索结果,但是Google从前常常标榜不怎么用Learning to rank。
排序学习的定义为:基于机器学习中用于解决分类与回归问题的思想,提出利用机器学习方法解决排序的问题。排序学习的目标在于自动地从训练数据中学习得到一个排序函数,使其在文本检索中能够针对文本的相关性、重要性等衡量标准对文本进行排序。机器学习的优势是:整合大量复杂特征并自动进行参数调整,自动学习最优参数,降低了单一考虑排序因素的风险;同时,能够通过众多有效手段规避过拟合问题。
机器学习的几个关键组成部分:
- 输入空间(input space),以特征向量来表示的样本,特征是以某种方式提取出来的。
- 输出空间(output space),对input处理后的展现形式,包括两种,一是task的最后形式,另一种是Machine Learning 中间便于处理的形式。
- 假设空间(hypothesis space),它定义了一系列从input space 到output space的映射函数。
- 损失函数(loss function),ML的目的就是在training set上定义一个loss function来学习一个optimal hypothesis。loss function在ML中扮演了一个非常关键的角色。
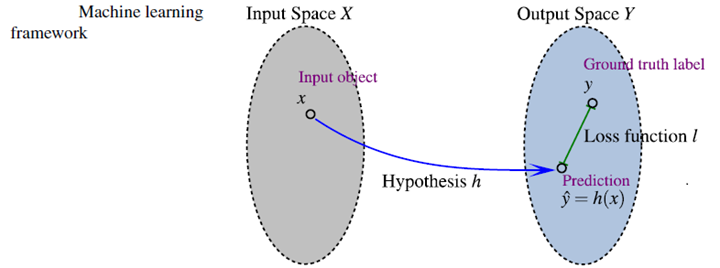
LTR的定义:
广义定义:使用机器学习技术来解决ranking问题的都称为LTR方法。 狭义定义:满足以下两点的ranking方法:
- Feature Based,样本以特征向量的形式体现。
- Discriminative Training,(有识别性的训练)a learning-to-rank method has its own input space, output space, hypothesis space, and loss function.Discriminative Training是一个基于训练集的自动学习过程。
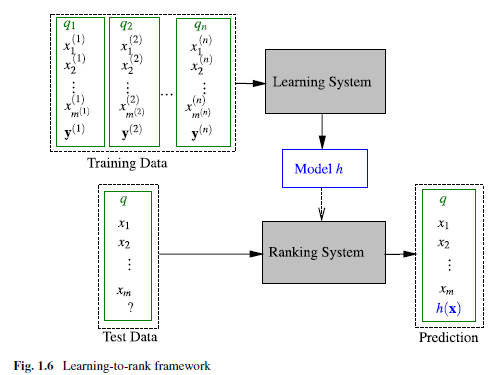
LTR框架
LTR是有监督学习,因此是需要有标注的training set。很多机器学习都可以套在上述流程图中。不同的方法主要体现在不同的input space,不同的的output space,不同的假设空间,不同的损失函数。经典Learning to Rank框架如下:
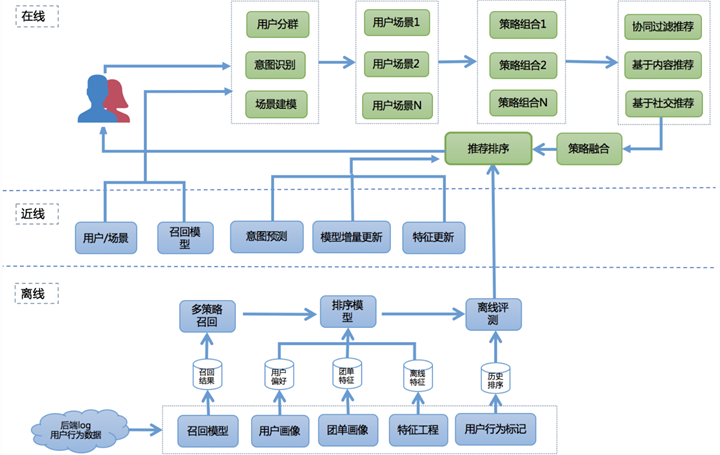
排序学习在现代推荐架构中处于非常关键的环节,它可以完成不同召回策略的统一排序,也可将离线、近线、在线的推荐结果根据用户所处的场景进行整合和实时调整,完成打分重排并推荐给用户。美团推荐框架:
LTR的优点
LTR 则是基于特征,通过机器学习算法训练来学习到最佳的拟合公式,相比传统的排序方法,优势有很多:
- 可以根据反馈自动学习并调整参数
- 可以融合多方面的排序影响因素
- 避免过拟合(通过正则项)
- 实现个性化需求(推荐)
- 多种召回策略的融合排序推荐(推荐)
- 多目标学习(推荐)
LTR的局限性
- 在一个机器学习的系统当中,人们很难理解为什么一个结果比另一个结果要好。机器学习系统像一个黑盒子,大部分时候告诉我们结果1比结果2更加相关的概率,但不会告诉我们是因为什么原因结果1比结果2要好。
- 很多information retrieval当中发现的特征很难在机器学习模型中产生效果。因为这些特征常常是针对某一类检索问题,然而对于那一类检索问题,常见的机器学习算法可能会为了模型的概括性以及防止overfitting,忽略特定的特征。这也是为什么当有了足够多的ranking engineer,大部分人都会专注改进rule-based scoring方法,去直接针对特定问题进行改进。
Learning to Rank 算法分类
排序学习的模型通常分为单点法(Pointwise Approach)、配对法(Pairwise Approach)和列表法(Listwise Approach)三大类,三种方法并不是特定的算法,而是排序学习模型的设计思路,主要区别体现在损失函数(Loss Function)、以及相应的标签标注方式和优化方法的不同。
单点法(Pointwise)
单点法排序学习模型的每一个训练样本都仅仅是某一个查询关键字和某一个文档的配对。它们之间是否相关,与其他文档和其他查询关键字都没有关系。很明显,单点法排序学习是对现实的一个极大简化,但是对于训练排序算法来说是一个不错的起点。单点法将文档转换为特征向量后,机器学习系统根据从训练数据中学习到的分类或者回归函数对文档打分,打分结果即是搜索结果。
单点排序学习可以按照标注和损失函数设计的不同,将排序问题转化成回归、分类、和有序分类问题(有些文献也称有序回归)问题,可参考下图:

分别看一下损失函数的设计思想:
- 分类(Classification):输出空间包含的是无序类别,对每个查询-文档对的样本判断是否相关,可以是二分类的,如相关认为是正例,不相关认为是负例;也可以是类似 NDCG 那样的五级标注的多分类问题。分类模型通常会输出一个概率值,可根据概率值的排序作为排序最终结果。
- 回归(Regression):输出空间包含的是真实值相关度得分,可通过回归来直接拟合相关度打分。
- 有序分类(Ordinal Classification):有序分类也称有序回归(Ordinal Regression),输出空间一般包含的是有序类别,通常的做法是找到一个打分函数,然后用一系列阈值对得分进行分割,得到有序类别。
单点法(Pointwise)的应用
推荐系统领域,最常用就是二元分类的 Pointwise,比如常见的点击率(CTR)预估问题,之所以用得多,是因为二元分类的 Pointwise 模型的复杂度通常比 Pairwise 和 Listwise 要低,而且可以借助用户的点击反馈自然地完成正负样例的标注,而其他 Pairwise 和 Listwise 的模型标注就没那么容易了。成功地将排序问题转化成分类问题,也就意味着我们机器学习中那些常用的分类方法都可以直接用来解决排序问题,如 LR、GBDT、SVM 等,甚至包括结合深度学习的很多推荐排序模型,都属于这种 Pointwise 的思想范畴。
代表算法有:
- 基于神经网络的排序算法 RankProp
- 基于感知机的在线排序算法 Prank(Perception Rank)/OAP-BPM
- 基于 SVM 的排序算法
- Subset Ranking
- McRank
- Prank
- OC SVM
推荐系统中使用较多的 Pointwise 方法是 LR、GBDT、SVM、FM 以及结合 DNN 的各种排序算法。
单点法(Pointwise)的缺点
Pointwise 方法通过优化损失函数求解最优的参数,可以看到 Pointwise 方法非常简单,工程上也易实现,但是 Pointwise 也存在很多问题:
- Pointwise 只考虑单个文档同 query 的相关性,没有考虑文档间的关系,然而排序追求的是排序结果,并不要求精确打分,只要有相对打分即可;
- 通过分类只是把不同的文档做了一个简单的区分,同一个类别里的文档则无法深入区别,虽然我们可以根据预测的概率来区别,但实际上,这个概率只是准确度概率,并不是真正的排序靠前的预测概率;
- Pointwise 方法并没有考虑同一个 query 对应的文档间的内部依赖性。一方面,导致输入空间内的样本不是 IID 的,违反了 ML 的基本假设,另一方面,没有充分利用这种样本间的结构性。其次,当不同 query 对应不同数量的文档时,整体 loss 将容易被对应文档数量大的 query 组所支配,应该每组 query 都是等价的才合理。
- 很多时候,排序结果的 Top N 条的顺序重要性远比剩下全部顺序重要性要高,因为损失函数没有相对排序位置信息,这样会使损失函数可能无意的过多强调那些不重要的 docs,即那些排序在后面对用户体验影响小的 doc,所以对于位置靠前但是排序错误的文档应该加大惩罚。
配对法(Pairwise)
配对法的基本思路是对样本进行两两比较,构建偏序文档对,从比较中学习排序,因为对于一个查询关键字来说,最重要的其实不是针对某一个文档的相关性是否估计得准确,而是要能够正确估计一组文档之间的 “相对关系”。因此,Pairwise 的训练集样本从每一个 “关键字文档对” 变成了 “关键字文档文档配对”。也就是说,每一个数据样本其实是一个比较关系,当前一个文档比后一个文档相关排序更靠前的话,就是正例,否则便是负例,如下图。试想,有三个文档:A、B 和 C。完美的排序是 “B>C>A”。我们希望通过学习两两关系 “B>C”、“B>A” 和 “C>A” 来重构 “B>C>A”。
这里面有3个非常关键的假设:
- 我们可以针对某一个关键字得到一个完美的排序关系。在实际操作中,这个关系可以通过相关标签来获得,也可以通过其他信息获得,比如点击率等信息。然而,这个完美的排序关系并不是永远都存在的。试想在电子商务网站中,对于查询关键字 “哈利波特”,有的用户希望购买书籍,有的用户则希望购买含有哈利波特图案的 T 恤,显然,这里面就不存在一个完美排序。
- 我们寄希望能够学习文档之间的两两配对关系从而 “重构” 这个完美排序。然而,这也不是一个有 “保证” 的思路。用刚才的例子,希望学习两两关系 “B>C”、“B>A” 和 “C>A” 来重构完美排序 “B>C>A”。然而,实际中,这三个两两关系之间是独立的。特别是在预测的时候,即使模型能够正确判断 “B>C” 和 “C>A”,也不代表模型就一定能得到 “B>A”。注意,这里的关键是 “一定”,也就是模型有可能得到也有可能得不到。两两配对关系不能 “一定” 得到完美排序,这个结论其实就揭示了这种方法的不一致性。也就是说,我们并不能真正保证可以得到最优的排序。
- 我们能够构建样本来描述这样的两两相对的比较关系。一个相对比较简单的情况,认为文档之间的两两关系来自于文档特征(Feature)之间的差异。也就是说,可以利用样本之间特征的差值当做新的特征,从而学习到差值到相关性差异这样的一组对应关系。
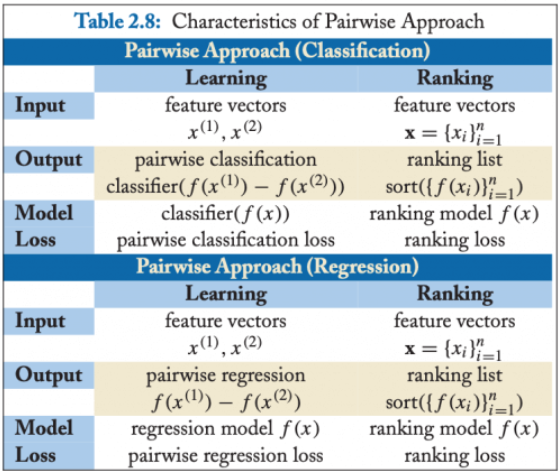
Pairwise 最终的算分,分类和回归都可以实现,不过最常用的还是二元分类,如下图:
配对法(Pairwise)的应用
代表算法:
- 基于 SVM 的 Ranking SVM 算法
- 基于神经网络的 RankNet 算法(2007)
- 基于 Boosting 的 RankBoost 算法(2003)
推荐系统中使用较多的 Pairwise 方法是贝叶斯个性化排序(Bayesian personalized ranking,BPR)。
配对法(Pairwise)的缺点
Pairwise 方法通过考虑两两文档之间的相关对顺序来进行排序,相比 Pointwise 方法有明显改善。但 Pairwise 方法仍有如下问题:
- 使用的是两文档之间相关度的损失函数,而它和真正衡量排序效果的指标之间存在很大不同,甚至可能是负相关的,如可能出现 Pairwise Loss 越来越低,但 NDCG 分数也越来越低的现象。
- 只考虑了两个文档的先后顺序,且没有考虑文档在搜索列表中出现的位置,导致最终排序效果并不理想。
- 不同的查询,其相关文档数量差异很大,转换为文档对之后,有的查询可能有几百对文档,有的可能只有几十个,这样不加均一化地在一起学习,模型会优先考虑文档对数量多的查询,减少这些查询的 loss,最终对机器学习的效果评价造成困难。
- Pairwise 方法的训练样例是偏序文档对,它将对文档的排序转化为对不同文档与查询相关性大小关系的预测;因此,如果因某个文档相关性被预测错误,或文档对的两个文档相关性均被预测错误,则会影响与之关联的其它文档,进而引起连锁反应并影响最终排序结果。
列表法(Listwise)
Listwise方法是直接优化排序列表,输入为单条样本为一个文档排列。相对于尝试学习每一个样本是否相关或者两个文档的相对比较关系,列表法排序学习的基本思路是尝试直接优化像 NDCG(Normalized Discounted Cumulative Gain)这样的指标,从而能够学习到最佳排序结果。列表法的相关研究有很大一部分来自于微软研究院。列表法排序学习有两种基本思路。第一种称为 Measure-specific,就是直接针对 NDCG 这样的指标进行优化。目的简单明了,用什么做衡量标准,就优化什么目标。第二种称为 Non-measure specific,则是根据一个已经知道的最优排序,尝试重建这个顺序,然后来衡量这中间的差异。
1)Measure-specific,直接针对 NDCG 类的排序指标进行优化
直接优化排序指标的难点在于,希望能够优化 NDCG 指标这样的 “理想” 很美好,但是现实却很残酷。NDCG、MAP 以及 AUC 这类排序标准,都是在数学的形式上的 “非连续”(Non-Continuous)和 “非可微分”(Non-Differentiable)。而绝大多数的优化算法都是基于 “连续”(Continuous)和 “可微分”(Differentiable)函数的。因此,直接优化难度比较大。
针对这种情况,主要有这么几种解决方法。
- 既然直接优化有难度,那就找一个近似 NDCG 的另外一种指标。而这种替代的指标是 “连续” 和 “可微分” 的 。只要我们建立这个替代指标和 NDCG 之间的近似关系,那么就能够通过优化这个替代指标达到逼近优化 NDCG 的目的。这类的代表性算法的有 SoftRank 和 AppRank。
- 尝试从数学的形式上写出一个 NDCG 等指标的 “边界”(Bound),然后优化这个边界。比如,如果推导出一个上界,那就可以通过最小化这个上界来优化 NDCG。这类的代表性算法有 SVM-MAP 和 SVM-NDCG。
- 希望从优化算法上下手,看是否能够设计出复杂的优化算法来达到优化 NDCG 等指标的目的。对于这类算法来说,算法要求的目标函数可以是 “非连续” 和 “非可微分” 的。这类的代表性算法有 AdaRank 和 RankGP。
2)Non-measure specific,尝试重建最优顺序,衡量其中差异
这种思路的主要假设是,已经知道了针对某个搜索关键字的完美排序,那么怎么通过学习算法来逼近这个完美排序。我们希望缩小预测排序和完美排序之间的差距。值得注意的是,在这种思路的讨论中,优化 NDCG 等排序的指标并不是主要目的。这里面的代表有 ListNet 和 ListMLE。
3)列表法和配对法的中间解法
第三种思路某种程度上说是第一种思路的一个分支,因为很特别,这里单独列出来。其特点是在纯列表法和配对法之间寻求一种中间解法。具体来说,这类思路的核心思想,是从 NDCG 等指标中受到启发,设计出一种替代的目标函数。这一步和刚才介绍的第一种思路中的第一个方向有异曲同工之妙,都是希望能够找到替代品。找到替代品以后,接下来就是把直接优化列表的想法退化成优化某种配对。这第二步就更进一步简化了问题。这个方向的代表方法就是微软发明的 LambdaRank 以及后来的 LambdaMART。微软发明的这个系列算法成了微软的搜索引擎 Bing 的核心算法之一,而且 LambdaMART 也是推荐领域中可能用到一类排序算法。
列表法(Listwise)的应用
代表算法:
- 基于 Measure-specific 的 SoftRank、SVM-MAP、SoftRank、LambdaRank、LambdaMART
- 基于 Non-measure specific 的 ListNet、ListMLE、BoltzRank。
推荐中使用较多的 Listwise 方法是 LambdaMART。
列表法(Listwise)的缺点
列表法相较单点法和配对法针对排序问题的模型设计更加自然,解决了排序应该基于 query 和 position 问题。但列表法也存在一些问题:
- 一些算法需要基于排列来计算 loss,从而使得训练复杂度较高,如 ListNet 和 BoltzRank。
- 位置信息并没有在 loss 中得到充分利用,可以考虑在 ListNet 和 ListMLE 的 loss 中引入位置折扣因子。
Learning to Ranking的评估指标
P@K
对于现在的大规模 IR 任务,每个 query 都有大量相关的 doc,因此很难再用查全率进行衡量召回质量,但是可以用 Precision at K 对召回质量进行评价。
Precision at K 通常表示为 P@K
MAP(Mean Average Precision)
DCG系列对比
累计增益(CG)- CG,cumulative gain,只考虑到了相关性的关联程度,没有考虑到位置因素。它是一个搜素结果相关性分数的总和。
折损累计增益(DCG)- DCG, Discounted 的CG,就是在每一个CG的结果上处以一个折损值,为什么要这么做呢?目的就是为了让排名越靠前的结果越能影响最后的结果。假设排序越往后,价值越低。
归一化折损累计增益(NDCG)- NDCG, Normalized 的DCG,由于搜索结果随着检索词的不同,返回数量是不一致的,而DCG是一个累加的值,没法针对两个不同的搜索结果进行比较,因此需要归一化处理,这里是处以IDCG。
【2022-9-13】Ranking算法评测指标之 CG、DCG、NDCG
举例,搜索到5个结果,其相关性分数分别是:3、2、3、0、1、2
- (0)Gain: 列表中每一个item的相关性分数
- 公式:$f(G)=r_i$
- (1)CG:Cumulative Gain, 对K个item的Gain进行累加;
- 只是对相关的分数进行了一个关联的打分,并没有召回的所在位置对排序结果评分对影响。
- 公式:$ f(CG@K)=\sum_{i=0}^{K}r_i $
- 得分:11
- (2)NCG:Discounted Cumulative Gain, 考虑了排序位置因素,排名越靠前,权重越大,反之,越低;权重通过log函数实现
- 公式:$ f(DCG@K)= \sum_{i=0}^{K}\frac{r_i}{log_2^{(i+1)}} $
- 当相关性分数r(i)只有(0,1)两种取值时,DCG@K有另一种表达。其实就是如果算法返回的排序列表中的item出现在真实交互列表中时,分子加1,否则跳过。
- $ f(DCG@K)= \sum_{i=0}^{K}\frac{2^{r_i}-1}{log_2^{(i+1)}} $
- 得分:6.86, img

- 公式:$ f(DCG@K)= \sum_{i=0}^{K}\frac{r_i}{log_2^{(i+1)}} $
- (3)NDCG:考虑了排序数量的影响,通过归一化消除排序数量对权重影响
- DCG能够对一个用户的推荐列表进行评价,如果用该指标评价某个推荐算法,需要对所有用户的推荐列表进行评价,由于用户真实列表长度不同,不同用户之间的DCG相比没有意义。所以要对不同用户的指标进行归一化,自然的想法就是计算每个用户真实列表的DCG分数,用IDCG表示,然后用每个用户的DCG与IDCG之比作为每个用户归一化后的分值,最后对每个用户取平均得到最终的分值,即NDCG。
-
公式:$ f(DCG@K)= \frac{DCG@K}{\left u \right }$, r是相关性分数,u表示用户 - 得分:8.37, IDCG@6
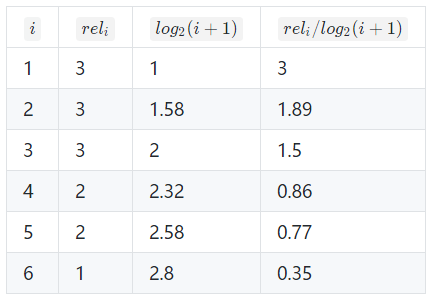
- $ NDCG=DCG/IDCG $
- NDCG值域是 $[0,1]$
NDCG(Normalized Discounted Cumulative Gain)
NDCG,Normalized Discounted cumulative gain 直接翻译为归一化折损累计增益。这个指标通常是用来衡量和评价搜索结果算法。DCG的两个思想:
- 高关联度的结果比一般关联度的结果更影响最终的指标得分
- 有高关联度的结果出现在更靠前的位置的时候,指标会越高
NDCG 优点
- NDCG 的主要优势是它考虑到了分等级的相关性值。当它们在数据集中可用时,NDCG 是一个很好的选择。
- 与 MAP 度量相比,它在评估排名项目的位置方面做得很好。它适用于二元的相关/非相关场景。
- 平滑的对数折现因子有一个很好的理论基础,该工作的作者表明,对于每一对显著不同的排名推荐系统,NDCG 度量始终能够确定更好的一个。 NDCG 缺点
- NDCG 在部分反馈方面有一些问题。当我们有不完整的评级时,就会发生这种情况。这是大多数推荐系统的情况。如果我们有完整的评级,就没有真正的任务去实现!在这种情况下,recsys 系统所有者需要决定如何归罪于缺失的评级。将缺少的值设置为 0 将把它们标记为不相关的项。其他计算值(如用户的平均/中值)也可以帮助解决这个缺点。
- 接下来,用户需要手动处理 IDCG 等于 0 的情况。当用户没有相关文档时,就会发生这种情况。这里的一个策略是也将 NDCG 设置为 0。
- 另一个问题是处理 NDCG@K。recsys 系统返回的排序列表的大小可以小于 k。为了处理这个问题,我们可以考虑固定大小的结果集,并用最小分数填充较小的集合。 正如我所说的,NDCG 的主要优势在于它考虑到了分级的相关性值。如果你的数据集有正确的形式,并且你正在处理分级相关性,那么 NDCG 度量就是你的首选指标。
import numpy as np
def getDCG(scores):
return np.sum(
np.divide(np.power(2, scores) - 1, np.log2(np.arange(scores.shape[0], dtype=np.float32) + 2)),
dtype=np.float32)
def getNDCG(rank_list, pos_items):
relevance = np.ones_like(pos_items)
it2rel = {it: r for it, r in zip(pos_items, relevance)}
rank_scores = np.asarray([it2rel.get(it, 0.0) for it in rank_list], dtype=np.float32)
idcg = getDCG(relevance)
dcg = getDCG(rank_scores)
if dcg == 0.0:
return 0.0
ndcg = dcg / idcg
return ndcg
l1 = [1, 4, 5]
l2 = [1, 2, 3]
a = getNDCG(l1, l2)
print(a)
# 0.4692787
MRR(Mean Reciprocal Rank)
平均倒数排名(Mean Reciprocal Rank, MRR)是一个国际上通用的对搜索算法进行评价的机制,其评估假设是基于唯一的一个相关结果,即第一个结果匹配,分数为 1 ,第二个匹配分数为 0.5,第 n 个匹配分数为 1/n,如果没有匹配的句子分数为0。最终的分数为所有得分之和。
MRR 的优点
- 该方法计算简单,解释简单。
- 这种方法高度关注列表的第一个相关元素。它最适合有针对性的搜索,比如用户询问“对我来说最好的东西”。
- 适用于已知项目搜索,如导航查询或寻找事实。 MRR 的缺点
- MRR 指标不评估推荐项目列表的其余部分。它只关注列表中的第一个项目。
- 它给出一个只有一个相关物品的列表。如果这是评估的目标,那找个度量指标是可以的。
- 对于想要浏览相关物品列表的用户来说,这可能不是一个好的评估指标。用户的目标可能是比较多个相关物品。
WTA(Winners Take All)
WTA,全称 Winners Take All,对于给定的查询 Query,如果模型返回的结果列表中,第一个文档是相关的,则 WTA =1, 否则为 0。
如对于一个 Query,本来有 5 个相关结果,查询结果中如果第一个结果是相关的,那么 WTA = 1,如果第一个结果是不相关的,则 WTA = 0。
ERR(Expected Reciprocal Rank)
ERR是受到cascade model的启发。点击模型中的cascade model,考虑到在同一个检索结果列表中各文档之间的位置依赖关系,假设用户从上至下查看,如果遇到某一检索结果项满意并进行点击,则操作结束;否则跳过该项继续往后查看。
NDCG和ERR指标的优势在于,它们对doc的相关性划分多个(>2)等级,而MRR和MAP只会对doc的相关性划分2个等级(相关和不相关)。并且,这些指标都包含了doc位置信息(给予靠前位置的doc以较高的权重),这很适合于web search。然而,这些指标的缺点是不平滑、不连续,无法求梯度,如果将这些指标直接作为模型评分的函数的话,是无法直接用梯度下降法进行求解的。
wilson 得分
【2022-8-15】威尔逊得分 Wilson Score 排序算法
如何选出最受欢迎的产品?
如何给出”某个时段”的排名,比如”过去24小时最热门的文章”。但是,很多场合需要的是”所有时段”的排名,比如”最受用户好评的产品”。
常见解法
- 得分 = 赞成票 - 反对票
- 得分 = 好评率 = 赞成票 / (赞成票 + 反对票)
当市场样本量过少,以上方法都不对!
场景:
- 假设平台售卖两款手机A和B。A手机有800人喜欢,200人不喜欢;B手机有9人喜欢,2人不喜欢。那么,用户更喜欢哪款手机?
那么,如何科学衡量喜好程度?
正确的算法是什么呢?
设定:
- (1)每个用户的投票都是独立事件。
- (2)用户只有两个选择,要么投赞成票,要么投反对票。
- (3)如果投票总人数为n,其中赞成票为k,那么赞成票的比例p就等于k/n。
以上是一种统计分布,叫做”二项分布“(binomial distribution)
- p越大,就代表这个项目的好评比例越高,越应该排在前面。
- 但是,p的可信度取决于有多少人投票,如果样本太小,p就不可信。
那么需要计算出p的置信区间。
- 所谓”置信区间”,就是说,以某个概率而言,p会落在的那个区间。
- 比如,某个产品的好评率是80%,但是这个值不一定可信。根据统计学,只能说有95%的把握可以断定,好评率在75%到85%之间,即置信区间是[75%, 85%]。
排名算法改进:
- 第一步,计算每个项目的”好评率”(即赞成票的比例)。
- 第二步,计算每个”好评率”的置信区间(以95%的概率)。
- 第三步,根据置信区间的下限值,进行排名。这个值越大,排名就越高。
原理是置信区间的宽窄与样本的数量有关。
- 比如,A有8张赞成票,2张反对票;B有80张赞成票,20张反对票。这两个项目的赞成票比例都是80%,但是B的置信区间(假定[75%, 85%])会比A的置信区间(假定[70%, 90%])窄得多,因此B的置信区间的下限值(75%)会比A(70%)大,所以B应该排在A前面。
置信区间的本质是进行可信度修正,弥补样本量过小的影响。
- 如果样本多,就说明比较可信,不需要很大的修正,所以置信区间会比较窄,下限值会比较大;
- 如果样本少,就说明不一定可信,必须进行较大的修正,所以置信区间会比较宽,下限值会比较小。
二项分布的置信区间有多种计算公式,最常见的是”正态区间“(Normal approximation interval),教科书里几乎都是这种方法。但是,它只适用于样本较多的情况(np > 5 且 n(1 − p) > 5),对于小样本,它的准确性很差。
1927年,美国数学家 Edwin Bidwell Wilson提出了一个修正公式,被称为”威尔逊区间“,很好地解决了小样本的准确性问题。
什么是wilson得分?
- 威尔逊得分排序算法,Wilson Score,用于质量排序,数据含有好评和差评,综合考虑评论数与好评率,得分越高,质量越高
- 公式
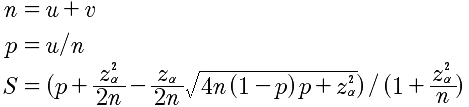
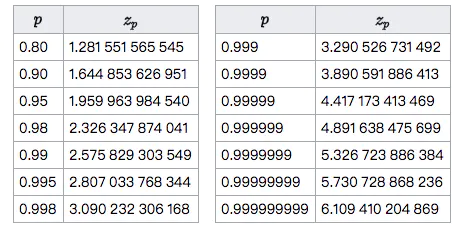
- u表示正例数(好评),v表示负例数(差评),n表示实例总数(评论总数),p表示好评率,z是正态分布的分位数(参数),S表示最终的威尔逊得分。z一般取值2即可,即95%的置信度
- 正态分布分位表
- 源码
算法性质:
- 得分S的范围是[0,1),效果:已经归一化,适合排序
- 当正例数u为0时,p为0,得分S为0;效果:没有好评,分数最低;
- 当负例数v为0时,p为1,退化为1/(1 + z^2 / n),得分S永远小于1;效果:分数具有永久可比性;
- 当p不变时,n越大,分子减少速度小于分母减少速度,得分S越多,反之亦然;效果:好评率p相同,实例总数n越多,得分S越多;
- 当n趋于无穷大时,退化为p,得分S由p决定;效果:当评论总数n越多时,好评率p带给得分S的提升越明显;
- 当分位数z越大时,总数n越重要,好评率p越不重要,反之亦然;效果:z越大,评论总数n越重要,区分度低;z越小,好评率p越重要;
实例:
- 假设医生A有100个评价,1个差评99个好评。医生B有2个评价,都是好评,那哪个应该排前面?
- 在z=2时,即95%的置信度,医生A的得分是0.9440,医生B的得分是0.3333,医生A排在前面。
PS:评分等级问题:如五星评价体系,或者百分评价体系,该怎么办呢?
- 将威尔逊得分的公式由
伯努利分布修改为正态分布即可。
威尔逊计算
Go 版
package main
import (
"fmt"
"math"
)
// 威尔逊得分(Wilson Score)排序算法
func main() {
// 计算结果:0.46844027984510983
wilsonScore(500, 1000, 2)
}
// 计算威尔逊得分
// u:好评数 zP:正态分布的分位数(一般取值2即可,即95%的置信度) s:威尔逊得分
func wilsonScore(u float64, n float64, zP float64) float64 {
p := u / n
println()
fmt.Println("好评率为:", p)
s := (p + (math.Pow(zP, 2) / (2. * n)) - ((zP / (2. * n)) * math.Sqrt(4.*n*(1.-p)*p+math.Pow(zP, 2)))) / (1. + math.Pow(zP, 2)/n)
fmt.Println("威尔逊得分为:", s)
return s
}
Python版
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Created by C.L.Wang
import numpy as np
def wilson_score(pos, total, p_z=2.):
"""
威尔逊得分计算函数
参考:https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
:param pos: 正例数
:param total: 总数
:param p_z: 正太分布的分位数
:return: 威尔逊得分
"""
pos_rat = pos * 1. / total * 1. # 正例比率
score = (pos_rat + (np.square(p_z) / (2. * total))
- ((p_z / (2. * total)) * np.sqrt(4. * total * (1. - pos_rat) * pos_rat + np.square(p_z)))) / \
(1. + np.square(p_z) / total)
return score
# 归一化后的威尔逊得分
def wilson_score_norm(mean, var, total, p_z=2.):
"""
威尔逊得分计算函数 正态分布版 支持如5星评价,或百分制评价
:param mean: 均值
:param var: 方差
:param total: 总数
:param p_z: 正太分布的分位数
:return:
"""
# 均值方差需要归一化,以符合正太分布的分位数
score = (mean + (np.square(p_z) / (2. * total))
- ((p_z / (2. * total)) * np.sqrt(4. * total * var + np.square(p_z)))) / \
(1 + np.square(p_z) / total)
return score
def test_of_values():
"""
五星评价的归一化实例,百分制类似
:return: 总数,均值,方差
"""
max = 5. # 五星评价的最大值
min = 1. # 五星评价的最小值
values = np.array([1., 2., 3., 4., 5.]) # 示例
norm_values = (values - min) / (max - min) # 归一化
total = norm_values.size # 总数
mean = np.mean(norm_values) # 归一化后的均值
var = np.var(norm_values) # 归一化后的方差
return total, mean, var
total, mean, var = test_of_values()
print "total: %s, mean: %s, var: %s" % (total, mean, var)
print 'score: %s' % wilson_score_norm(mean=mean, var=var, total=total)
print 'score: %s' % wilson_score(90, 90 + 10, p_z=2.)
print 'score: %s' % wilson_score(90, 90 + 10, p_z=6.)
print 'score: %s' % wilson_score(900, 900 + 100, p_z=6.)
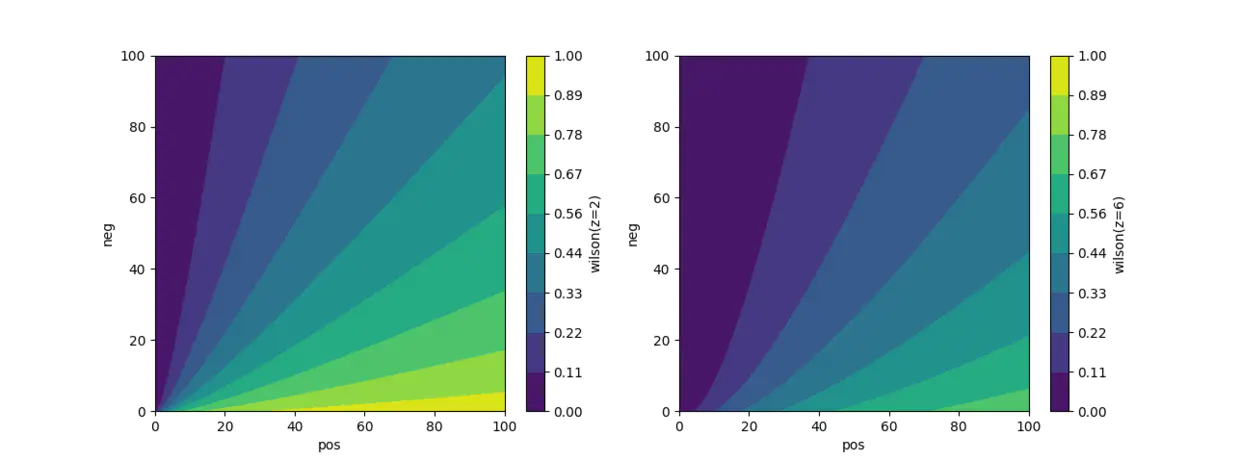
关于z参数,即正态分位数。正态分位数影响wilson得分的分布,z参数取值依据就是样本数量级。
- 举个例子:同样是100个样本,90个好评,z取值2或6,分数差别很大,体系所容纳(或区分)的样本数也相差较大(同样是0.82分和90%好评率,z=2需要100个样本,z=6需要1000个样本),一般而言,样本数的量级越大,z的取值大。
绘制威尔逊得分图
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Created by C.L.Wang
import matplotlib.pyplot as plt
import numpy as np
from wilson_score.wilson_score_model import wilson_score
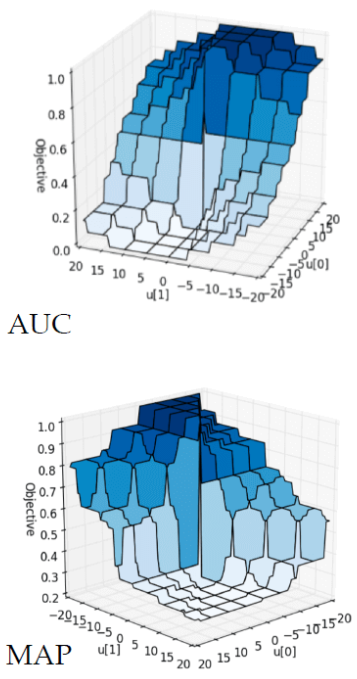
def show_wilson():
value = np.linspace(0.01, 100, 1000)
u, v = np.meshgrid(value, value)
fig, ax = plt.subplots(1, 2)
levels = np.linspace(0, 1, 10)
cs = ax[0].contourf(u, v, wilson_score(u, u + v), levels=levels)
cb1 = fig.colorbar(cs, ax=ax[0], format="%.2f")
cs = ax[1].contourf(u, v, wilson_score(u, u + v, 6.), levels=levels)
cb2 = fig.colorbar(cs, ax=ax[1], format="%.2f")
ax[0].set_xlabel(u'pos')
ax[0].set_ylabel(u'neg')
cb1.set_label(u'wilson(z=2)')
ax[1].set_xlabel(u'pos')
ax[1].set_ylabel(u'neg')
cb2.set_label(u'wilson(z=6)')
plt.show()
if __name__ == '__main__':
show_wilson()
抖音推荐应用
- 抖音的上热门的方法类似于威尔逊得分排序算法,但是远远又比威尔逊得分排序算法更复杂。
- 大概就是:机器审核 + 人工双重审核。
当一个视频初期上传
- 平台会给你一个初始流量,如果初始流量之后,根据点赞率,评论率,转发率,进行判断:该视频是否受欢迎,如果第一轮评判为受欢迎的,那么他会进行二次传播。
- 当第二次得到了最优反馈,那么就会给与推荐你更大的流量。
- 相反,在第一波或者第N波,反应不好,就不再推荐,没有了平台的推荐,你的视频想火的概率微乎其微,因为没有更多的流量能看见你。
- 你的视频火的第一步是被别人看见,第一步就把路给走死了,后续也只能依靠朋友星星点点的赞。
其实,不难看出这个抖音推荐机制算法背后思维逻辑:流量池,叠加推荐,热度加权及用户心理追求。
威尔逊得分(Wilson Score)排序算法:
- 对质量进行排序,评论中含有好评还有差评,综合考虑评论数与好评率,得分越高,质量越高。
Learning to Rank 常用算法
Pointwise常用算法:
- Classification
- Discriminative model for IR (SIGIR 2004)
- McRank (NIPS 2007)
- Regression
- Least Square Retrieval Function (TOIS 1989)
- Regression Tree for Ordinal Class Prediction (Fundamenta Informaticae, 2000)
- Subset Ranking using Regression (COLT 2006)
- Ordinal Classification
- Ranking with Large Margin Principles (NIPS 2002)
- Constraint Ordinal Regression (ICML 2005)
Pairwise常用算法:
- Learning to Retrieve Information (SCC 1995)
- Learning to Order Things (NIPS 1998)
- Ranking SVM (ICANN 1999)
- RankBoost (JMLR 2003)
- LDM (SIGIR 2005)
- RankNet (ICML 2005)
- Frank (SIGIR 2007)
- MHR(SIGIR 2007)
- GBRank (SIGIR 2007)
- QBRank (NIPS 2007)
- MPRank (ICML 2007)
- IRSVM (SIGIR 2006)
- LambdaRank (NIPS 2006)
- LambdaMART (inf.retr 2010)
Listwise常用算法:
- Measure-specific
- AdaRank (SIGIR 2007)
- SVM-MAP (SIGIR 2007)
- SoftRank (LR4IR 2007)
- RankGP (LR4IR 2007)
- LambdaMART (inf.retr 2010)(也可以做Listwise)
- Non-measure specific
- ListNet (ICML 2007)
- ListMLE (ICML 2008)
- BoltzRank (ICML 2009)
涉及的Learning to Rank的算法非常多。这楼里主要学习RankNet、LambdaRank、LambdaMART。
RankNet
RankNet是2005年微软提出的一种pairwise的Learning to Rank算法,它从概率的角度来解决排序问题。RankNet的核心是提出了一种概率损失函数来学习Ranking Function,并应用Ranking Function对文档进行排序。这里的Ranking Function可以是任意对参数可微的模型,也就是说,该概率损失函数并不依赖于特定的机器学习模型,在论文中,RankNet是基于神经网络实现的。除此之外,GDBT等模型也可以应用于该框架。
LambdaRank
上面介绍了以错误pair最少为优化目标的RankNet算法,然而许多时候仅以错误pair数来评价排序的好坏是不够的,像NDCG或者ERR等评价指标就只关注top k个结果的排序,当我们采用RankNet算法时,往往无法以这些指标为优化目标进行迭代,所以RankNet的优化目标和IR评价指标之间还是存在gap的。
LambdaMART
LambdaMART是LambdaRank的提升树版本,LambdaMART本质上也是属于pairwise排序算法,只不过引入Lambda梯度后,还显示的考察了列表级的排序指标,如NDCG等,因此,也可以算作是listwise的排序算法。LambdaMART由微软于2010年的论文Adapting Boosting for Information Retrieval Measures提出。
LambdaMART是基于 LambdaRank 算法和 MART (Multiple Additive Regression Tree) 算法,将排序问题转化为回归决策树问题。MART 实际就是梯度提升决策树(GBDT, Gradient Boosting Decision Tree)算法。GBDT 的核心思想是在不断的迭代中,新一轮迭代产生的回归决策树模型拟合损失函数的梯度,最终将所有的回归决策树叠加得到最终的模型。LambdaMART 使用一个特殊的 Lambda 值来代替上述梯度,也就是将 LambdaRank 算法与 MART 算法结合起来,是一种能够支持非平滑损失函数的学习排序算法。
MART又称作GBDT,是是一种 Boosting 思想下的算法框架。它通过加法模型,将每次迭代得到的子模型叠加起来;而每次迭代拟合的对象都是学习率与损失函数梯度的乘积。这两点保证了 MART 是一个正确而有效的算法。MART 中最重要的思想,就是每次拟合的对象是损失函数的梯度。值得注意的是,在这里,MART 并不对损失函数的形式做具体规定。实际上,损失函数几乎只需要满足可导这一条件就可以了。这一点非常重要,意味着我们可以把任何合理的可导函数安插在 MART 模型中。LambdaMART 就是用LambdaRank中提出的Lambda梯度代替了损失函数的梯度,将 Lambda和MART结合起来罢了。
LambdaMART具有很多优势:
- 适用于排序场景:不是传统的通过分类或者回归的方法求解排序问题,而是直接求解
- 损失函数可导:通过损失函数的转换,将类似于NDCG这种无法求导的IR评价指标转换成可以求导的函数,并且赋予了梯度的实际物理意义,数学解释非常漂亮
- 增量学习:由于每次训练可以在已有的模型上继续训练,因此适合于增量学习
- 组合特征:因为采用树模型,因此可以学到不同特征组合情况
- 特征选择:因为是基于MART模型,因此也具有MART的优势,可以学到每个特征的重要性,可以做特征选择
- 适用于正负样本比例失衡的数据:因为模型的训练对象具有不同label的文档pair,而不是预测每个文档的label,因此对正负样本比例失衡不敏感
CTR 广告预估
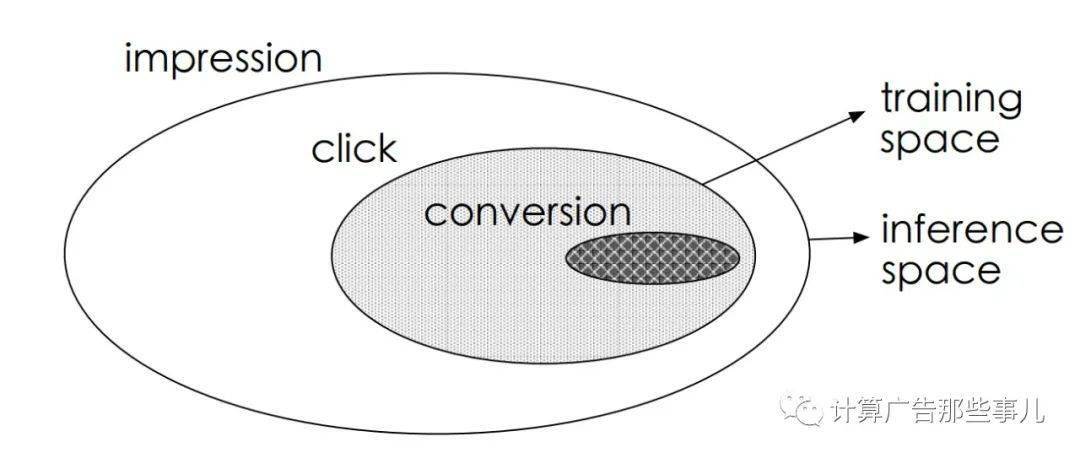
- 用户看到一条广告时,会选择点或者不点这条广告,点了这条广告之后,进入广告落地页,此时用户也有两个选择:买这个广告中的商品或者不买,如果买了,这就是转化(conversion)。
- 用户看到的这条广告,就叫做曝光(impression),点击率(click-through rate, CTR)就是点击次数除以总曝光数,转化率(conversion rate, CVR)是转化数除以点击次数。
这三者之间的关系就如图所示:
- impression → click → conversion
转化数据其实是非常少的,而且它是和点击数据存在前后的依赖关系,所以在转化率预估中就存在这样三个问题:
- (1)样本选择偏差(sample selection bias, SSB):影响泛化 传统的cvr模型在训练的时候用的是点击过的曝光数据(clicked impressions),但预测的时候却是对所有曝光,模型训练使用的数据只是预测数据的一部分。
- (2)训练数据过于稀疏( data sparsity, DS):拟合困难 和曝光数据比,转化样本太少,正负样本不均衡,模型训练困难。
- (3) 点击延迟 在点击后转化行为可能不会立刻发生,比如点进一个商品页面后,没有立刻去买,而是过了一段时间才想起来买,这也会对建模造成影响。但是这篇文章没有关注这个问题,原文是表示这个问题在他们的模型中是可被接受的。
参考:【2019-8-18】多任务学习在CVR预估中的应用:Entire Space Multi-Task Model(ESMM,阿里,SIGIR2018)
基本概念
- 【2021-3-14】多任务学习(MTL)在转化率预估上的应用
名词定义:
- CTR: 指曝光广告中,被点击的广告比例
- CVR: 指被点击的广告中,最终形成转化的广告比例
- CTCVR: 指曝光广告中,被点击且最终形成转化的广告比例
正如《oCPC中转化率模型与校准》中所讲,如果完全是按照CPC出价计费,那只需要建模CTR模型,而在oCPC场景下,需要对CTCVR进行建模,我们目前的业务恰好属于后者。前期分析表明,直接对CTCVR建模,会导致召回用户的CTR竞争力较低,影响最终曝光。所以建模需要同时考虑CTR和CTCVR两个指标。基于以上背景,我们在业务中引入多任务学习的建模方式。
- 样本选择偏差:用户在广告上的行为属于顺序行为模式impression -> click -> conversion,传统CVR建模训练时是在click的用户集合中选择正负样本,模型最终是对整个impression的用户空间进行CVR预估,由于click用户集合和impression用户集合存在差异(如下图),引起样本选择偏差。图
- 数据稀疏:推荐系统中有click行为的用户占比是很低的,相比曝光用户少1~3个数量级,在实际业务中,有click行为的用户占比不到4%,就会导致CVR模型训练数据稀疏,高度稀疏的训练数据使得模型的学习变的相当困难。由于用户行为遵循impression -> click -> conversion的顺序行为模式,预估结果遵循以下关系
广告界因果推断
【2021-3-30】
广告界有一句经久流传的话:
我知道我的广告费有一半浪费了,但遗憾的是,我不知道是哪一半被浪费了。
人们对这句话有着不同的解读,其中之一就是广告效果衡量的不足。正因为无法很精确地衡量广告的效果,所以没办法进行进一步的投放优化,只能白白浪费。
毫无疑问,每个广告主都想知道自己投出去的钱带来了多大收益。换言之,这个问题其实就是广告投放的因果效应。这里的 “因果” 限定为统计意义上的因果效应——如果我们把投放广告看作一种 “处理 (treatment)”,那么结果会有什么变化?在这个层面上,广告界对应的统计学问题“因果效应” 和其他领域并无二致。本文就沿用统计学因果推断的语言,来分享一下广告界的因果推断面临的困难和挑战。本文着重描述问题本身,对于解决方案仅作开放性的泛泛讨论,留给读者日后思考。
序言:没数据?
广告效果衡量之所以难,正是因为 “没数据”,即搜集数据的困难性。传统媒体广告,比如经常让人们津津乐道的在纽约时代广场投放的户外广告,其实是很难量化的。广告投放本身的花费是已知的,但其带来的曝光很难计算。比如,除了时代广场的人流量本身,还可能有媒体转载从而引发 “话题”。就算曝光可以被追踪到,消费者行为的变化则是更加难以追踪。而我们的终极问题,“到底有多少新增的产品销量是跟某一则广告的投放相关”,就变成了近似玄学。
好在随着这些年互联网的普及,从互联网上搜集数据变得格外容易(比如 “追踪像素” 等实现了跨站追踪),由此互联网广告的效果衡量便乘风而进。各大互联网公司其实多多少少都是广告公司。
- 美国市场上,谷歌 (Google) 80% 以上的收入来源于广告,脸书 (Facebook) 更是占到 98% 以上,连传统的电子商务公司亚马逊 (Amazon) 也开始受益于广告收入的快速增长。
- 中国市场上,阿里巴巴 40%多的营收来源于广告,腾讯有接近 20%,百度超过 70%,而新兴势力如拼多多、今日头条等等也很大程度上受益于广告收入。 庞大的广告收入背后对应的是人力资源。互联网企业中很多人力资源其实是投放在广告方面的,其中就包括很多专门从事广告效果分析的团队。那么在在线广告这个环境中,人们遇到了哪些挑战呢?
1. 随机对照实验的困难
在现实世界中,一个结果的产生往往会受到多重因素的影响。因此,对于单一因素效果衡量的本质就是要排除其他因素的影响,从而得到该因素本身的影响。统计学上因果推断的框架有不少,其中最直接的就是基于随机对照实验,因为在随机分配实验组和对照组的时候,“其他因素” 就被均匀分配了,唯一的区别就是处理本身,从而直接满足了统计学上所要求的 “外生性”,故而也被很多人认为是因果推断的黄金准则。直觉上可以理解为,假如我有一对一模一样的双胞胎,其中一个看到广告另一个没看到,我就可以得出广告投放的效果了。虽然现实中没有双胞胎,但我的实验对象足够多,且我其实只关心总体的效果,那么我便可以把他们一分为二从而大致相当。
随机对照实验作为一个因果推断的框架,本身也是有很多问题。
- (1)暂且不论哪些统计学上的挑战,单单在线广告投放这个领域,随机对照实验的实施便没有人们想象的那么简单。
- 医学上的随机对照实验可以使用 “安慰剂”,而在线广告领域并没有那么显然的安慰剂,因为简单的“安慰剂广告” 在经过广告投放算法优化之后,往往会带来实验组和对照组不可比的问题。我在 2017 年的时候曾经简单翻译过谷歌的 “幽灵广告” 一文,其中对此有比较详细的解释。脸书等公司也有类似的实验工具,来帮助实现随机对照实验。当然,广告界的随机对照实验也无法避免随机对照实验一般性的问题。我曾经在其他文章里面介绍过随机对照实验的若干问题,这里就不再重复了。
- (2)在线实验工具适用情况其实很有限,其中一个前提就是对于单一个体的广告投放是可以被控制的。这里其实依赖两个假设。
- 其一,广告投放平台知道谁是谁。这个问题其实并不显然,因为用户往往有多个设备,他们并不一定会登录同一个账号,而本地缓存的用户登录信息(即 cookie 文件)本身也有有效期和适用范围的问题。
- 其二,就算平台可以准确识别同一用户的不同身份,他们能不能控制针对这个用户的投放也不一定。很多时候,广告的买断是按时段和区域性,比如一群人一起在看重大体育赛事直播,从而他们看到的广告也是一样的。广告平台其实只能有效地控制一部分广告对于个体的投放,而不是全部。这一点虽然在线广告会比传统广告有着一些优势,但并不完美。 解决:
- 对于第一个问题,广告平台们往往采取统计预测模型来猜测用户身份,从而保证同一用户在不同设备上均可被识别。
- 对于第二个问题,随机分配的时候可能就没法在用户这个层面上进行了,而更可能是采取区域或者时段的随机,但这又会带来新的问题,比如如何划分区域才是干净的同时保证区域之间的可比性,用户的记忆效应如何去控制,不同用户之间的相互影响如何衡量等等。总之,虽然不完美,但是在随机对照实验可以被实施的时候,这依旧是好的办法。
2. 基于规则的归因(Attribution)
随机对照实验有种种的难处,那么大家就束手无策了吗?传统的因果推断教科书可能会开始介绍拟实验(Quasi-experimental)、各种模拟对照组的模型、工具变量,等等。其实换个思路,我们还可以利用更丰富的中间过程信息,找一个近似解,这就是广告归因模型(Attribution)。
严格地说,广告归因(Attribution)其实并不是一个数学模型,而是一系列基于假设的计算。比如,在用户的各种点击行为已知的情况下,我们可以设定一条规则:如果一个用户点击了广告,并且在 1 天之内完成了购买,那么这个购买就会被归因于点击的广告。这听起来很符合直觉啊,我看到广告有兴趣,然后点进去了,然后发现了我想买的东西,然后就买了,那最后的购买自然应该归功于我看到的那个广告。这种简单的情况可能符合某些购物的转化路径,但实际上人们的行为远远要比这个复杂。
- 反例 1:一个用户可能连续点了多个广告才最终实现了购买,那么显然把所有的功劳都归于最后一个点击的广告好像并不公平。
- 反例 2:另外一个用户点了广告看到了商品,然后当时没想买。结果过了几天,觉得还是想要,就回头去买了。这个时候已经过了 1 天的时限,所以购买并不会被归因于当时点击的广告。
- 反例 3:还有的用户在看直播的时候看到的广告,但是当时并不会点击,因为还想看直播。可能看完直播,用户回味起来有个广告里的商品很有意思,然后又去买了。这种情况下,点击也不能完全捕捉到最终的购买。
理论上,如果我们可以穷尽所有用户实现转化的路径,是不是就能得到一个完美的归因模型了呢?可现实的情况是,用户的行为五花八门, 而且他们自己可能都说不清楚哪些广告是真正有影响的,这使得基于因果链的推理变得格外困难,只能得到一个近似的效果。当我们的假设贴近用户实际的行为的时候,这个近似可能不算差。但是当真实的用户行为与我们假设的归因规则相去甚远的时候,归因模型给出的结果就变得没那么可信了。当然,归因模型也可以用在随机对照实验的实验组上,然后就可以拿归因模型跟随机对照实验的结果去对比,比如利用 Facebook 数据的这篇论文。
当然,因为归因模型用到了额外的数据(点击、浏览、时间点等),所以它其实承载了比简单的随机对照实验更丰富的信息。这些信息除了简单地用于基于规则的归因之外,亦可以用于更丰富的模型设定。在下一节,我们会探讨在多个广告媒介之间的效果衡量,归因模型也会因此得到拓展。
3. 多个广告媒介平台
对于广告主来说,投放广告的媒体会有很多,所以基本上不可能只在一家投放。如果一个广告主同时在谷歌搜索和脸书展现广告,那么他们关心的问题就不仅仅是总共的效果了, 而是更想知道每一个广告媒介的效果,从而知道如何调整每个渠道的广告预算。这个时候,因果推断问题就变得更有趣了,因为多个广告媒介之间很可能会有交互效应。
第一种情况是,这些广告平台都支持某种形式的随机对照实验,这样问题就转化为一个全因子实验设计(factorial design)的问题。最理想的情况自然是在每个平台上随机分配的对象是一致的,同时还可以把同一用户在不同平台上的身份联系起来,这样其实只需要进行方差分析就可以了。现实的情况是,就算不同的平台都支持随机对照实验,他们允许随机分配的对象可能是不同的,而且几乎不可能是完美的匹配同一用户在不同平台上的身份。因此,虽然每个平台上的实验依旧是有效的,把多个平台的数据放在一起分析就没有那么简单了。数据可能需要进行不同层面的加总,然后才可以在平台之间有可比性(比如把属于同一个地区的用户都加总起来)。
更常见的情况是,随机对照实验变得几乎不实施。这种时候,归因模型因为其实施的便利性,得到了极大的拓展。常见的有多触点归因模型 (Multi-Touch Attribution,缩写 MTA),其思想是考虑到用户在多个平台上的各种点击及浏览行为,然后把最终的用户转化分解开来,赋予每一个点击不同的权重百分比,然后加总计算每个平台的贡献。从这个思路来看,多触点归因模型依旧需要解决用户身份识别的问题,然后还需要把微观层面的所有行为数据汇总到一起,然后再假设或者基于经验赋予不同行为不同的权重,最终达成对于不同平台的归因。实践中,这显然不是一件容易的事情。
如果我们退而求其次,不要求保留用户的所有的行为数据,而直接利用汇总过的每个平台的归因数据,那么又会有什么样的思路呢?这时候就可以借鉴以前传统广告行业常用的市场组合模型 (Marketing Mix Model,缩写 MMM),即利用回归模型来分配不同广告渠道的贡献。MMM 虽然本身是一个简单的相关性分析 (correlation analysis),但是也可以引入随机对照实验的数据来进行改善。和简单的随机对照实验不同的是,MMM 加入了广告主企业本身的数据,比如企业销售渠道、产品特性、成本等等,可以更直接地对整体的企业利润进行分解而不仅仅是用户转化。
到这里,其实已经对因果推断做出了越来越多的妥协。有些妥协是受限于数据本身,所以引入模型和更多的假设来进行修正,带着对于离真相更进一步的美好期盼。有些妥协是对于因果推断严格性的需求降低,比如决策本身并不需要单一地依赖因果推断的结果,关联分析也可以给出一些有用的信息,加之其他方面的信息,亦可以指导下一步的决策。
4. 用户转化数据的不可追踪性
前面三节讨论的情况有一个不太明显但很必要的假设:用户的转化数据是可以跟踪的,比如通过序言一节中提到的追踪像素之类。然而这其实也是一个很强的假设。在现实生活中,我们很可能没法对用户转化数据实现完美的追踪。比如,用户很可能去家旁边的超市买洗发水而不是跑到广告主的线上网站上去购买。虽然有一些机制,例如会员卡、鼓励用户扫描购物小票等等,可以帮助部分商家打通线上线下的数据关联问题,但这些解决方案的适用范围往往颇为有限,亦有时效性的问题。此时,一种思路是类似前面的,把区域内的数据加总起来,比如厂商往往是知道自己在每个零售点的销售额的,然后在区域的层面进行对比。另一种思路则是,既然追踪不到用户最终的转化数据,那有没有办法间接的衡量转化呢?
这个时候,我们不得不对于严格的因果推断做进一步的妥协。虽然不能直接追踪到用户的最终转化,但有没有其他指标可以近似地反映用户的转化呢?这时候,一切可能被搜集到的数据就被动员了起来。比如用户的注意力数据(停留时长、心跳、眼球注视范围等生理指标),用户对于问卷调查的反馈,等等。当然,这些数据的获取也不是那么容易,比如生理数据需要用户安装相应的追踪设备,所以一般来说都是基于特定用户或者在实验室中进行的。问卷调查需要用户愿意回答才行,而且可能发放调查的成本。总之,人们发明了各种基于想象力的办法,来搜集一些直觉上可能相关的代理变量 (proxy variable),从而给出一个近似解。至于这个近似有多么近似,可能很大程度上就是基于大家的经验和信念了。
在这种只有代理变量的情况下,用户转化就变成了一个隐变量 (latent variable) 或者部分观测变量 (partially observed variable) 的问题。取决于有什么样的代理变量,和转化数据是不是可以在特定情况下被观测到,我们可以引入不同的统计模型来充分挖掘数据的价值。当然这些方法可以和随机对照实验或者归因模型进行结合,从而得到因果效应的近似解。
5. 优化–如何实现广告投放效果的最大化
前面所说的基本都是一个 “衡量” 问题,即给定一个处理,如何衡量它带来的效果。衡量的结果显然可以用来指导广告预算投放的优化,但是对于广告平台来说,最重要的是提高广告投放的效率,尤其是不单单通过宏观层面调整预算分配的手段。理想的情况下,如果我们知道一个用户需要看 10 则广告才会转化,而另一个用户只需要看 1 则广告就会转化了,那么在预算有限的情况下,我们肯定希望找到那些更容易转化的用户。如果我们知道每个人对于每个广告的个体处理效应(individual treatment effect),那么这个问题不就迎刃而解了吗?
个体处理效应或许是因果推断中更近乎玄学的一个概念。某种意义上,统计学之所以带有统计两个字,本身是一个群体的概念,而从群体推论到个体并不那么直接。Rubin 提出的潜在结果框架(potential outcome framework),某种意义上事先回答了一个哲学问题——当个体效应不可观测的时候,能不能观测到群体的平均效应呢?这里的 “能” 或者 “不能” 不是说计算的可行性,而是说这样做在哲学层面是不是有意义。随机对照实验显然是无法给出个体处理效应的结果的,那么匹配(matching)之类的方法会可行吗?通过时间序列或者其他模型来预测每个个体的潜在结果会可行吗?或者,我们用归因模型的近似解,是不是就可以绕过对于个体处理效应的依赖,直接去解决我们关心的广告投放的优化问题呢?
到这里,已经不单单是一个因果推断的问题了,而隐含了一场工程实现与哲学思考的较量。我有幸作为从业者,和我的小伙伴们在过去的十几年一路观察着业界和学界这些年不同的进展,细细品来其实颇为有趣。当然,还有一些其他的挑战,行业本身变化也很快,无法逐一叙述。这篇文章写下来,主要是想跟大家分享我的一些观察、思考和与朋友们的探讨。若是能引出更好的问题,也算是抛砖引玉了。
基于用户投票的排名算法应用
Delicious
- 最直接、最简单的算法,它按单位时间内用户的投票数进行排名。得票最多的 item 排在第一位。旧版 Delicious,有一个“热门书签排行榜”,就是这样统计出来的
-
每过 60 分钟,就统计一次。按照“60分钟内被收藏的次数”进行排名。
- 该算法
- 优点:简单、易部署、内容更新相当快
- 但缺点主要有两个:
- 1)排名变化不够平滑,前一个小时还排名靠前的item,第二个小时就一落千丈
- 2)缺乏自动淘汰旧 item 的机制,即某些热门内容可能会长期占据排行榜前列。
Hacker News
- Hacker News 是一个网络社区,可以张贴链接,或者讨论某个主题。
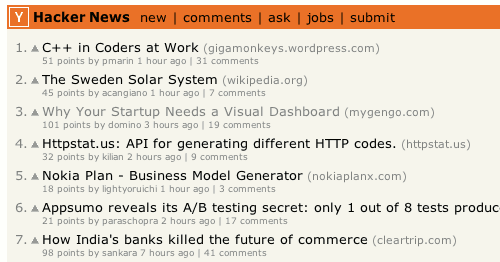
- 点击小三角,点赞
- 并非得票最多的文章就应该排在第一位,还要考虑时间因素,新文章应该比旧文章更容易得到好的排名。
- 算法数学公式
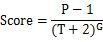
- P 表示帖子得票数,“减去1”表示忽略发帖人的投票。
- 在其他条件不变的情况下,得票越多,排名越高
- 如果不想让“高票帖子”与“低票帖子”的差距过大,可以在得票数上加一个小于 1 的指数
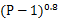
- T 表示距离发帖的时间(单位为小时),“加上 2”表示防止对于最新的帖子,导致分母过小(之所以选择 2,可能是因为从原始文章出现在其他网站,到转贴至 Hacker News,平均需要两个小时)。
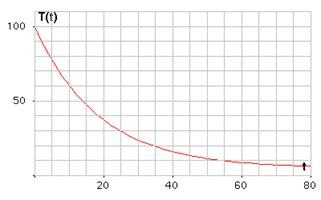
- 在其他条件不变的情况下,越是新发表的帖子,排名越高。或者说,一个帖子的排名,会随着时间而不断下降。因此,从图 4 看到,经过 24 小时后,所有帖子的得分基本上都小于 1,这意味着它们都将跌到排行榜的末尾,保证了排名前列的都将是较新的内容。
- G 表示“重力因子(gravityth power)”,即将帖子排名往下拉的力量,默认值为 1.8,后文会详细讨论这个值。
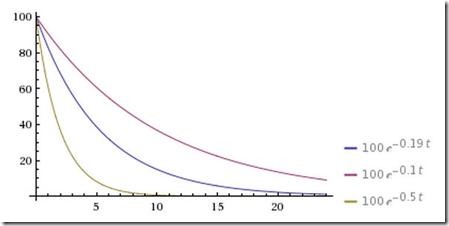
- 它的数值大小决定了排名随时间下降的速度。从图 4 右边看到,三个曲线的其他参数都一样,G 的值分别为 1.5、1.8 和 2.0。G 值越大,曲线越陡峭,排名下降得越快,意味着排行榜的更新速度越快。
- 上面 Hacker News 排名算法只能投赞成票,可用户当然也需要投反对票。或者说,除了好评以外,还可以给差评。
- Reddit 是美国最大的网上社区,每个帖子前面都有“向上”和“向下”箭头,分别表示“赞成”和“反对”。用户点击进行投票,Reddit根据投票结果,计算出最新的“热点文章排行榜”。
- 如何将赞成票和反对票结合起来,计算出一段时间内最受欢迎的文章?
-
如果文章 A 有 100 张赞成票、5 张反对票;文章 B 有 1000 张赞成票、950 张反对票,谁应该排在前面呢?
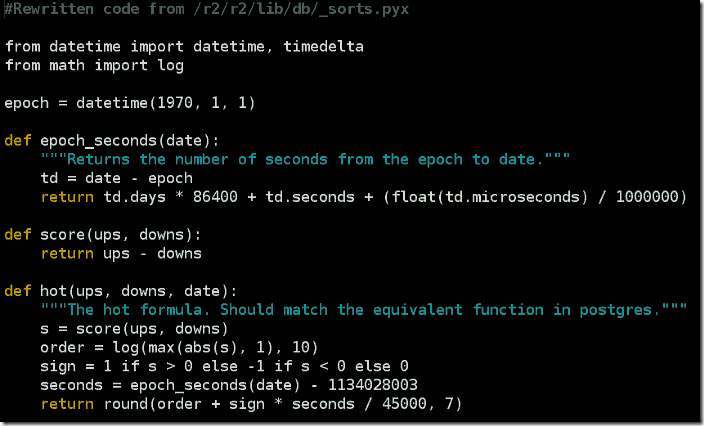
- Reddit 程序是开源的,使用 Python 语言编写。
- 算法公式
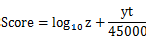
- 该算法考虑了 4 个因素,包括
- 帖子新旧程度
- 投票赞成与反对的差
- 投票倾向
- 帖子受肯定(否定)程度
- 问题是,对于那些有争议的文章(赞成票和反对票非常接近),它们不可能排到前列。假定同一时间有两个帖子发表,文章A有 1 张赞成票(发帖人投的)、0 张反对票;文章 B 有1000 张赞成票、1000 张反对票,那么 A 的排名会高于 B,这显然不合理。
- 因此,Reddit 排名,基本上由发帖时间决定,超级受欢迎的文章会排在最前面,一般性受欢迎的文章、有争议的文章都不会很靠前。这决定了 Reddit 是一个符合大众口味的社区,不是一个很激进、可以展示少数派想法的地方。
Stack Overflow
- Reddit 算法,用户可以投赞成票,也可以投反对票。即除了时间外,只需要考虑两个因素。
- 但是,对于一些特定的网站,必须考虑更多的因素。
- 如世界排名第一的程序员问答社区 Stack Overflow。
- 在上面提出各种关于编程的问题,然后等待别人回答。
- 访问者可以对你的问题进行投票(赞成或反对),以表示这个问题是否有价值。
- 一旦有人回答了你的问题,那么,其他人也可以对这个回答投票(赞成或反对),以表明对这个回答的态度。
- 排名算法的作用是,找出某段时间内的热点问题,即哪些问题最被关注、得到了最多的讨论。
- 在Stack Overflow 页面上,每个问题前面有三个数字,分别表示问题的得分、回答数,以及该问题的浏览次数。
- 创始人之一 Jeff Atwood,几年前,公开了该算法的计算公式
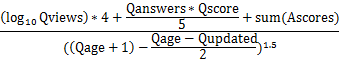
- 1)问题的浏览次数Qviews
- 2)问题得分Qanswers和回答的数量Qscore
- 3)回答得分 Ascores
- Stack Overflow 热点问题的排名,与参与度(Qviews 和 Qanswers)和质量(Qscore 和 Ascores)成正比,与时间(Qage 和 Qupdated)成反比。
牛顿冷却定律
- 一个通用的数学模型。
- 可以把”热文排名”想象成一个”自然冷却”的过程:
- 1)任一时刻,网站中所有的文章,都有一个“当前温度”,温度最高的文章就排在第一位。
- 2)如果一个用户对某篇文章投了赞成票,该文章的温度就上升一度。
- 3)随着时间流逝,所有文章的温度都逐渐“冷却”。
- 这样假设的意义在于,照搬物理学的冷却定律,使用现成的公式,建立“温度”与“时间”之间的函数关系,构建一个“指数式衰减(Exponential decay)”的过程。
- 牛顿早在 17 世纪就提出了温度冷却的数学公式,被后人称作“牛顿冷却定律(Newton’s Law of Cooling)”,用这个定律构建排名算法。
- 用一句话概括“牛顿冷却定律”:物体的冷却速度,跟其当前温度与室温之间的温差成正比。写成微分方程如下:
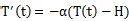
- T(t) 是温度T关于时间 t 的函数,则温度变化(冷却)的速率就是温度函数的导数 T’(t)。
- H 代表室温,T(t)-H 是当前温度与室温之间的温差。由于当前温度高于室温,所以这是一个正值。
- 常数 α(α>0) 表示室温与降温速率之间的比例关系。前面的负号表示降温。不同的物质有不同的 α 值。
- 方程求解
- 套用在“排名算法”,就相当于(假定本期没有增加净赞成票)
- “冷却系数”是一个你自己决定的值。如果假定一篇新文章的初始分数是100分,24小时之后”冷却”为1分,那么可以计算得到”冷却系数”约等于0.192。如果你想放慢”热文排名”的更新率,”冷却系数”就取一个较小的值,否则就取一个较大的值
迄今为止,这个系列都在讨论,如何给出”某个时段”的排名,比如”过去24小时最热门的文章”。但是,很多场合需要的是”所有时段”的排名,比如”最受用户好评的产品”。这时,时间因素就不需要考虑了。这个系列的最后两篇,就研究不考虑时间因素的情况下,如何给出排名。
威尔逊区间
- 一种常见的错误算法是:得分 = 赞成票 - 反对票
- 假定有两个项目,项目 A 是 60 张赞成票,40 张反对票,项目 B 是 550 张赞成票,450 张反对票。请问,谁应该排在前面?按照上面的公式,B 会排在前面,因为它的得分(550 - 450 = 100)高于A(60 - 40 = 20)。但是实际上,B的好评率只有 55%(550 / 1000),而A为 60%(60 / 100),所以正确的结果应该是 A 排在前面。Urban Dictionary 就是这种错误算法的实例
- 另一种常见的错误算法是:得分 = 赞成票 / 总票数
- 如果”总票数”很大,那么这种算法是有效的。否则,就会出错。假定 A 有 2 张赞成票、0 张反对票;B 有 100 张赞成票、1 张反对票。这种算法会使得 A 排在 B 前面。这显然是错误的。Amazon 就是这种错误算法的实例
那么,正确的算法是什么呢?
先做如下设定:
- 1)每个用户的投票都是独立事件。
- 2)用户只有两个选择,要么投赞成票,要么投反对票。
- 3)如果投票总人数为 n,其中赞成票为 k,那么赞成票的比例 p 就等于 k/n。
如果了解概率,这统计分布,叫“二项分布(binomial distribution)”
- 思路是,p 越大,就代表这个项目的好评比例越高,越应该排在前面。但 p 的可信性,取决于有多少人投票,如果样本太小,p 就不可信。好在我们已经知道,p 是二项分布中某个事件的发生概率,因此我们可以计算出p的置信区间。所谓“置信区间”,就是说,以某个概率而言,p 会落在的那个区间。比如,某个产品的好评率是 80%,但是这个值不一定可信。根据统计学,我们只能说,有 95% 的把握可以断定,好评率在 75%~85% 之间,即置信区间是 [75%, 85%]。
- 这样一来,排名算法就比较清晰了:
- 第一步,计算每个项目的“好评率”(即赞成票的比例)。
- 第二步,计算每个“好评率”的置信区间(以95%的概率)。
- 第三步,根据置信区间的下限值,进行排名。这个值越大,排名就越高。
- 这样做的原理是,置信区间的宽窄与样本的数量有关。比如,A 有 8 张赞成票,2 张反对票;B 有 80 张赞成票,20 张反对票。这两个项目的赞成票比例都是 80%,但是 B 的置信区间(假定 [75%, 85%])会比 A 的置信区间(假定 [70%, 90%])窄得多,因此,B 的置信区间的下限值(75%)会比 A(70%)大,所以 B 应该排在 A 前面。
- 置信区间的实质,就是进行可信度的修正,弥补样本量过小的影响。如果样本多,就说明比较可信,不需要很大的修正,所以置信区间会比较窄,下限值会比较大;如果样本少,就说明不一定可信,必须进行较大的修正,所以置信区间会比较宽,下限值会比较小。
- 二项分布的置信区间有多种计算公式,最常见的”正态区间(Normal approximation interval)”,但它只适用于样本较多的情况(np > 5 且 n(1 − p) > 5),对于小样本,它的准确性很差。
1927年,美国数学家 Edwin Bidwell Wilson 提出了一个修正公式,被称为”威尔逊区间(Wilson score interval)”,很好地解决了小样本的准确性问题。
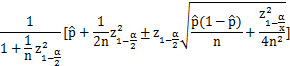
- 当 n 的值足够大时,这个下限值会趋向p^。如果 n 非常小(投票人很少),这个下限值会大大小于p^。实际上,起到了降低”赞成票比例”的作用,使得该项目的得分变小、排名下降。
- Reddit 的评论排名,目前就使用这个算法。
贝叶斯平均
- “威尔逊区间”解决了投票人数过少、导致结果不可信的问题。
- 举例来说,如果只有 2 个人投票,“威尔逊区间”的下限值会将赞成票的比例大幅拉低。这样做固然保证了排名的可信性,但也带来了另一个问题:排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会,排名可能会长期靠后。
- 以 IMDB 为例,它是世界最大的电影数据库,观众可以对每部电影投票,最低为 1 分,最高为 10 分。系统根据投票结果,计算出每部电影的平均得分。然后,再根据平均得分,排出最受欢迎的前250名的电影。
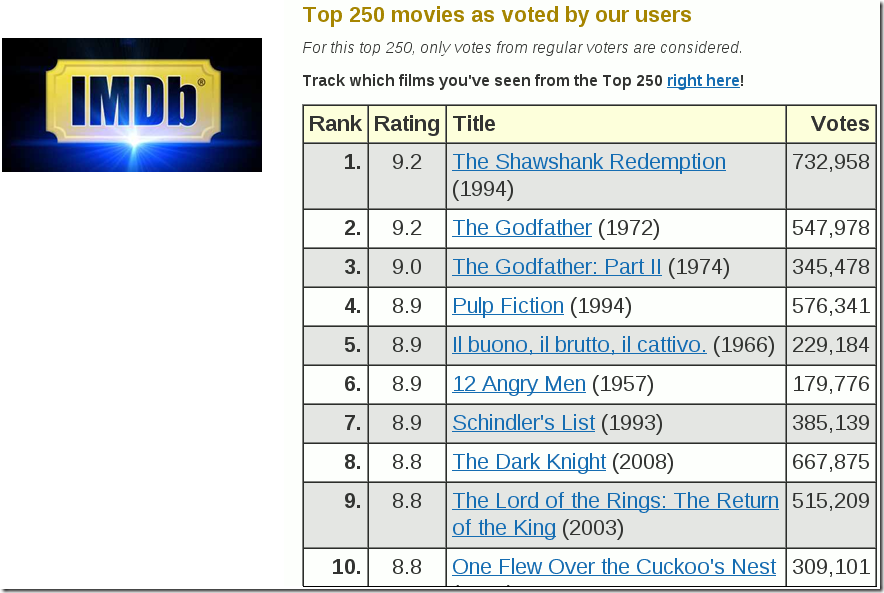
问题:热门电影与冷门电影的平均得分,是否真的可比?举例来说,一部好莱坞大片有 10000 个观众投票,一部小成本的文艺片只有 100 个观众投票。这两者的投票结果,怎么比较?如果使用“威尔逊区间”,后者的得分将被大幅拉低,这样处理是否公平,能不能反映它们真正的质量?
- 一个合理的思路是,如果要比较两部电影的好坏,至少应该请同样多的观众观看和评分。既然文艺片的观众人数偏少,那么应该设法为它增加一些观众。
- 在排名页面的底部,IMDB 给出了它的计算方法。
其中,
- WR,加权得分(weighted rating)。
- R,该电影的用户投票的平均得分(Rating)。
- v,该电影的投票人数(votes)。
- m,排名前250名的电影的最低投票数(现在为3000)。
- C, 所有电影的平均得分(现在为6.9)。
注:源自文章
仔细研究这个公式,你会发现,IMDB 为每部电影增加了 3000 张选票,并且这些选票的评分都为 6.9。这样做的原因是,假设所有电影都至少有 3000 张选票,那么就都具备了进入前250名的评选条件;然后假设这 3000 张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准);最后,用现有的观众投票进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。
把这个公式写成更一般的形式:
其中,
- C,投票人数扩展的规模,是一个自行设定的常数,与整个网站的总体用户人数有关,可以等于每个项目的平均投票数。
- n,该项目的现有投票人数。
- x,该项目的每张选票的值。
- m,总体平均分,即整个网站所有选票的算术平均值。
这种算法被称为“贝叶斯平均”(Bayesian average)。因为某种程度上,它借鉴了“贝叶斯推断”(Bayesian inference)的思想:既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
在这个公式中,m(总体平均分)是”先验概率”,每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的”贝叶斯平均”就越接近算术平均,对排名的影响就越小。
因此,这种方法可以给一些投票人数较少的项目,以相对公平的排名。
“贝叶斯平均”也有缺点,主要问题是它假设用户的投票是正态分布。比如,电影A有10个观众评分,5个为五星,5个为一星;电影B也有 10 个观众评分,都给了三星。这两部电影的平均得分(无论是算术平均,还是贝叶斯平均)都是三星,但是电影A可能比电影B更值得看。
解决这个问题的思路是,假定每个用户的投票都是独立事件,每次投票只有n个选项可以选择,那么这就服从“多项分布”(Multinomial distribution),就可以结合贝叶斯定理,估计该分布的期望值。由于这涉及复杂的统计学知识,这里就不深入了,感兴趣的朋友可以继续阅读William Morgan的 How to rank products based on user input。
CTR预估
背景
在推荐、搜索、广告等领域,CTR(click-through rate)预估是一项非常核心的技术,这里引用阿里妈妈资深算法专家朱小强大佬的一句话:“它(CTR预估)是镶嵌在互联网技术上的明珠”。
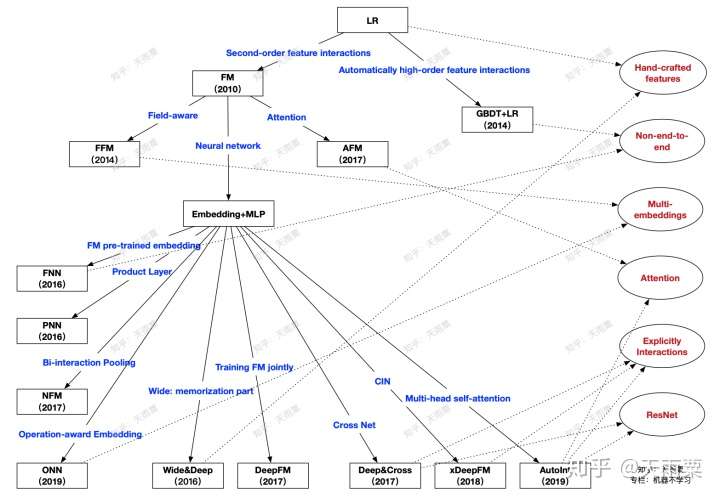
本篇文章主要是对CTR预估中的常见模型进行梳理与总结,并分成模块进行概述。每个模型都会从「模型结构」、「优势」、「不足」三个方面进行探讨,在最后对所有模型之间的关系进行比较与总结。本篇文章讨论的模型如下图所示(原创图),这个图中展示了本篇文章所要讲述的算法以及之间的关系,在文章的最后总结会对这张图进行详细地说明。
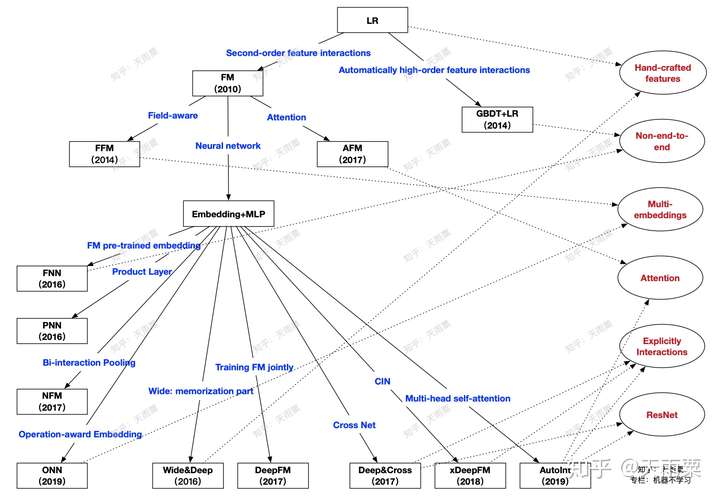
一. 分布式线性模型
Logistic Regression
Logistic Regression是每一位算法工程师再也熟悉不过的基本算法之一了,毫不夸张地说,LR作为最经典的统计学习算法几乎统治了早期工业机器学习时代。这是因为其具备简单、时间复杂度低、可大规模并行化等优良特性。在早期的CTR预估中,算法工程师们通过手动设计交叉特征以及特征离散化等方式,赋予LR这样的线性模型对数据集的非线性学习能力,高维离散特征+手动交叉特征构成了CTR预估的基础特征。LR在工程上易于大规模并行化训练恰恰适应了这个时代的要求。
模型结构:
优势:
- 模型简单,具备一定可解释性
- 计算时间复杂度低
- 工程上可大规模并行化
不足:
- 依赖于人工大量的特征工程,例如需要根据业务背知识通过特征工程融入模型
- 特征交叉难以穷尽
- 对于训练集中没有出现的交叉特征无法进行参数学习
二. 自动化特征工程
GBDT + LR(2014)—— 特征自动化时代的初探索
Facebook在2014年提出了GBDT+LR的组合模型来进行CTR预估,其本质上是通过Boosting Tree模型本身的特征组合能力来替代原先算法工程师们手动组合特征的过程。GBDT等这类Boosting Tree模型本身具备了特征筛选能力(每次分裂选取增益最大的分裂特征与分裂点)以及高阶特征组合能力(树模型天然优势),因此通过GBDT来自动生成特征向量就成了一个非常自然的思路。注意这里虽然是两个模型的组合,但实际并非是端到端的模型,而是两阶段的、解耦的,即先通过GBDT训练得到特征向量后,再作为下游LR的输入,LR的在训练过程中并不会对GBDT进行更新。
模型结构:
通过GBDT训练模型,得到组合的特征向量。例如训练了两棵树,每棵树有5个叶子结点,对于某个特定样本来说,落在了第一棵树的第3个结点,此时我们可以得到向量 ;落在第二棵树的第4个结点,此时的到向量
;那么最终通过concat所有树的向量,得到这个样本的最终向量
。将这个向量作为下游LR模型的inputs,进行训练。
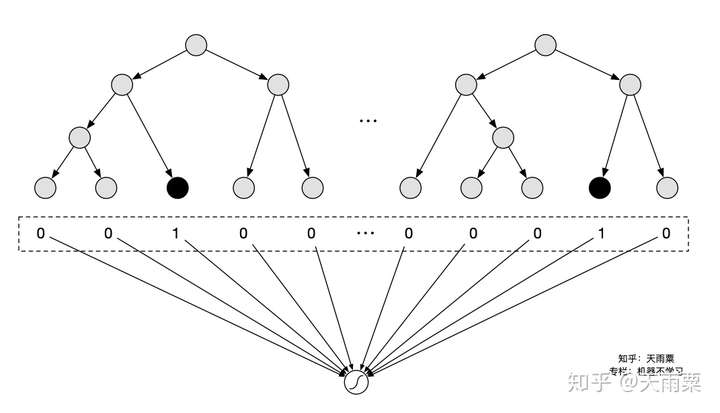
优势:
- 特征工程自动化,通过Boosting Tree模型的天然优势自动探索特征组合
不足:
- 两阶段的、非端到端的模型
- CTR预估场景涉及到大量高维稀疏特征,树模型并不适合处理(因此实际上会将dense特征或者低维的离散特征给GBDT,剩余高维稀疏特征在LR阶段进行训练)
- GBDT模型本身比较复杂,无法做到online learning,模型对数据的感知相对较滞后(必须提高离线模型的更新频率)
三. FM模型以及变体
(1)FM:Factorization Machines, 2010 —— 隐向量学习提升模型表达
FM是在2010年提出的一种可以学习二阶特征交叉的模型,通过在原先线性模型的基础上,枚举了所有特征的二阶交叉信息后融入模型,提高了模型的表达能力。但不同的是,模型在二阶交叉信息的权重学习上,采用了隐向量内积(也可看做embedding)的方式进行学习。
模型结构:
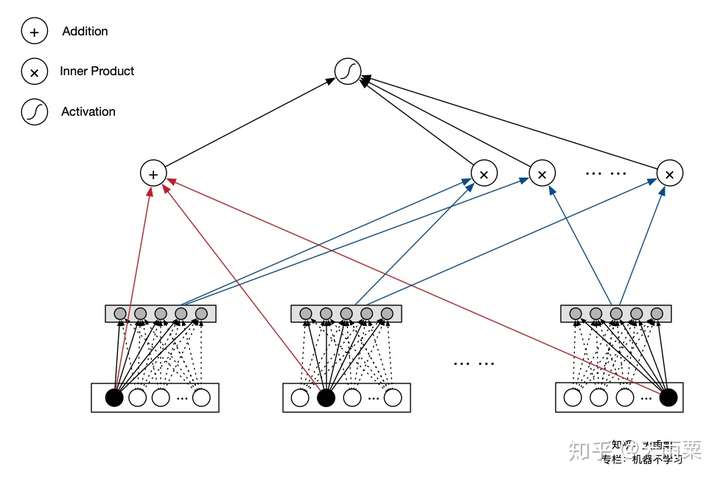
FM的公式包含了一阶线性部分与二阶特征交叉部分:
在LR中,一般是通过手动构造交叉特征后,喂给模型进行训练,例如我们构造性别与广告类别的交叉特征: (gender=’女’ & ad_category=’美妆’),此时我们会针对这个交叉特征学习一个参数
。但是在LR中,参数梯度更新公式与该特征取值
关系密切:
,当
取值为0时,参数
就无法得到更新,而
要非零就要求交叉特征的两项都要非零,但实际在数据高度稀疏,一旦两个特征只要有一个取0,参数
不能得到有效更新;除此之外,对于训练集中没有出现的交叉特征,也没办法学习这类权重,泛化性能不够好。
另外,在FM中通过将特征隐射到k维空间求内积的方式,打破了交叉特征权重间的隔离性(break the independence of the interaction parameters),增加模型在稀疏场景下学习交叉特征的能力。一个交叉特征参数的估计,可以帮助估计其他相关的交叉特征参数。例如,假设我们有交叉特征gender=male & movie_genre=war,我们需要估计这个交叉特征前的参数 ,FM通过将
分解为
的方式进行估计,那么对于每次更新male或者war的隐向量
时,都会影响其他与male或者war交叉的特征参数估计,使得特征权重的学习不再互相独立。这样做的好处是,对于traindata set中没有出现过的交叉特征,FM仍然可以给到一个较好的非零预估值。
优势:
- 可以有效处理稀疏场景下的特征学习
- 具有线性时间复杂度(化简思路:
)
- 对训练集中未出现的交叉特征信息也可进行泛化
不足:
- 2-way的FM仅枚举了所有特征的二阶交叉信息,没有考虑高阶特征的信息
FFM(Field-aware Factorization Machine)是Yuchin Juan等人在2015年的比赛中提出的一种对FM改进算法,主要是引入了field概念,即认为每个feature对于不同field的交叉都有不同的特征表达。FFM相比于FM的计算时间复杂度更高,但同时也提高了本身模型的表达能力。FM也可以看成只有一个field的FFM,这里不做过多赘述。
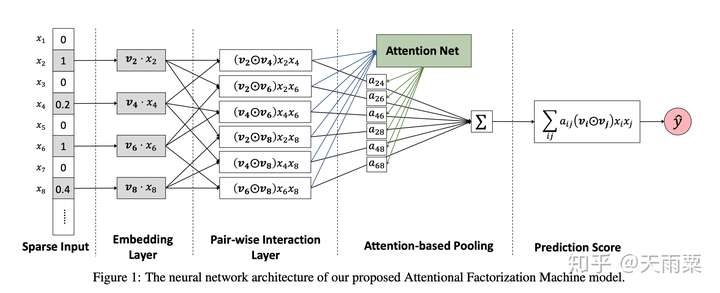
(2)AFM:Attentional Factorization Machines, 2017 —— 引入Attention机制的FM
AFM全称Attentional Factorization Machines,顾名思义就是引入Attention机制的FM模型。我们知道FM模型枚举了所有的二阶交叉特征(second-order interactions),即 ,实际上有一些交叉特征可能与我们的预估目标关联性不是很大;AFM就是通过Attention机制来学习不同二阶交叉特征的重要性(这个思路与FFM中不同field特征交叉使用不同的embedding实际上是一致的,都是通过引入额外信息来表达不同特征交叉的重要性)。
举例来说,在预估用户是否会点击广告时,我们假设有用户性别、广告版位尺寸大小、广告类型三个特征,分别对应三个embedding: ,
,
,对于用户“是否点击”这一目标
来说,显然性别与ad_size的交叉特征对于
的相关度不大,但性别与ad_category的交叉特征(如gender=女性&category=美妆)就会与
更加相关;换句话说,我们认为当性别与ad_category交叉时,重要性应该要高于性别与ad_size的交叉;FFM中通过引入Field-aware的概念来量化这种与不同特征交叉时的重要性,AFM则是通过加入Attention机制,赋予重要交叉特征更高的重要性。
模型结构:
AFM在FM的二阶交叉特征上引入Attention权重,公式如下:
其中
代表element-wise的向量相乘,下同。
其中, 是模型所学习到的
与
特征交叉的重要性,其公式如下:
我们可以看到这里的权重 实际是通过输入
和
训练了一个一层隐藏层的NN网络,让模型自行去学习这个权重。
对比AFM和FM的公式我们可以发现,AFM实际上是FM的更加泛化的一种形式。当我们令向量 ,权重
时,AFM就会退化成FM模型。
优势:
- 在FM的二阶交叉项上引入Attention机制,赋予不同交叉特征不同的重要度,增加了模型的表达能力
- Attention的引入,一定程度上增加了模型的可解释性
不足:
- 仍然是一种浅层模型,模型没有学习到高阶的交叉特征
四. Embedding+MLP结构下的浅层改造
本章所介绍的都是具备Embedding+MLP这样结构的模型,之所以称作浅层改造,主要原因在于这些模型都是在embedding层进行的一些改变,例如FNN的预训练Embedding、PNN的Product layer、NFM的Bi-Interaction Layer等等,这些改变背后的思路可以归纳为:使用复杂的操作让模型在浅层尽可能包含更多的信息,降低后续下游MLP的学习负担。
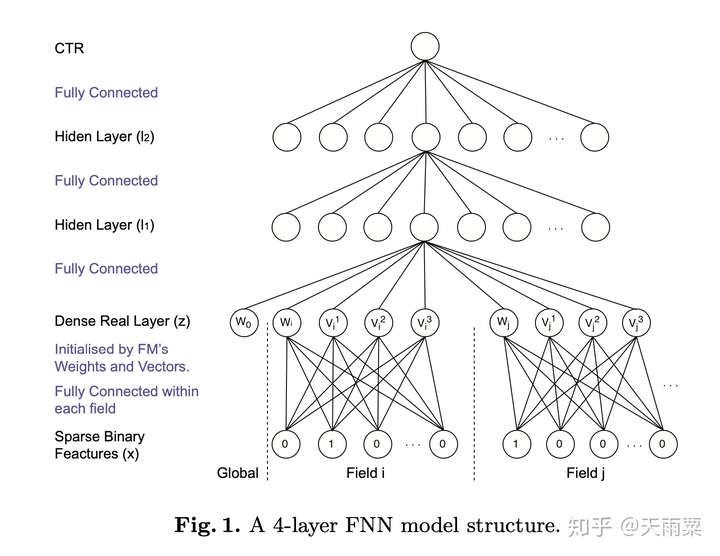
(1)FNN: Factorisation Machine supported Neural Network, 2016 —— 预训练Embedding的NN模型
FNN是2016年提出的一种基于FM预训练Embedding的NN模型,其思路也比较简单;FM本身具备学习特征Embedding的能力,DNN具备高阶特征交叉的能力,因此将两者结合是很直接的思路。FM预训练的Embedding可以看做是“先验专家知识”,直接将专家知识输入NN来进行学习。注意,FNN本质上也是两阶段的模型,与Facebook在2014年提出GBDT+LR模型在思想上一脉相承。
模型结构:
FNN本身在结构上并不复杂,如上图所示,就是将FM预训练好的Embedding向量直接喂给下游的DNN模型,让DNN来进行更高阶交叉信息的学习。
优势:
- 离线训练FM得到embedding,再输入NN,相当于引入先验专家经验
- 加速模型的训练和收敛
- NN模型省去了学习feature embedding的步骤,训练开销低
不足:
- 非端到端的两阶段模型,不利于online learning
- 预训练的Embedding受到FM模型的限制
- FNN中只考虑了特征的高阶交叉,并没有保留低阶特征信息
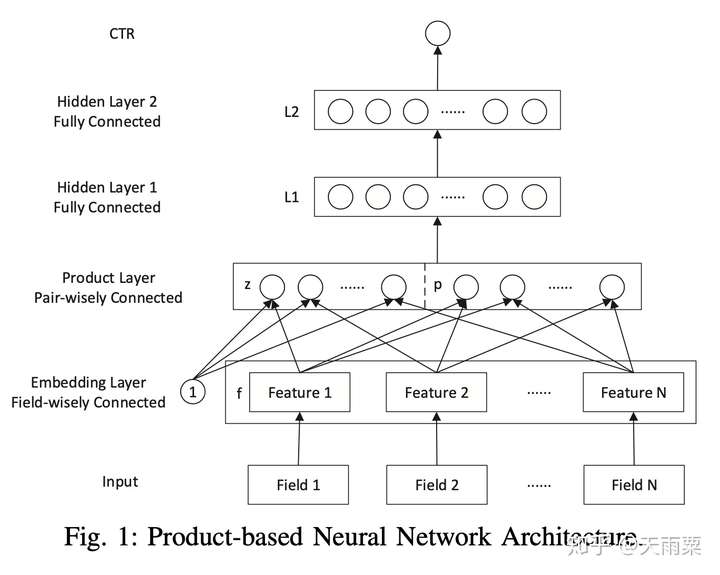
(2)PNN:Product-based Neural Network, 2016 —— 引入不同Product操作的Embedding层
PNN是2016年提出的一种在NN中引入Product Layer的模型,其本质上和FNN类似,都属于Embedding+MLP结构。作者认为,在DNN中特征Embedding通过简单的concat或者add都不足以学习到特征之间复杂的依赖信息,因此PNN通过引入Product Layer来进行更复杂和充分的特征交叉关系的学习。PNN主要包含了IPNN和OPNN两种结构,分别对应特征之间Inner Product的交叉计算和Outer Product的交叉计算方式。
模型结构:
PNN结构显示通过Embedding Lookup得到每个field的Embedding向量,接着将这些向量输入Product Layer,在Product Layer中包含了两部分,一部分是左边的 ,就是将特征原始的Embedding向量直接保留;另一部分是右侧的
,即对应特征之间的product操作;可以看到PNN相比于FNN一个优势就是保留了原始的低阶embedding特征。
在PNN中,由于引入Product操作,会使模型的时间和空间复杂度都进一步增加。这里以IPNN为例,其中 是pair-wise的特征交叉向量,假设我们共有N个特征,每个特征的embedding信息
;在Inner Product的情况下,通过交叉项公式
会得到
(其中
是对称矩阵),此时从Product层到
层(假设
层有
个结点),对于
层的每个结点我们有:
,因此这里从product layer到L1层参数空间复杂度为
;作者借鉴了FM的思想对参数
进行了矩阵分解:
,此时L1层每个结点的计算可以化简为:
,空间复杂度退化
。
优势:
- PNN通过
保留了低阶Embedding特征信息
- 通过Product Layer引入更复杂的特征交叉方式,
不足:
- 计算时间复杂度相对较高
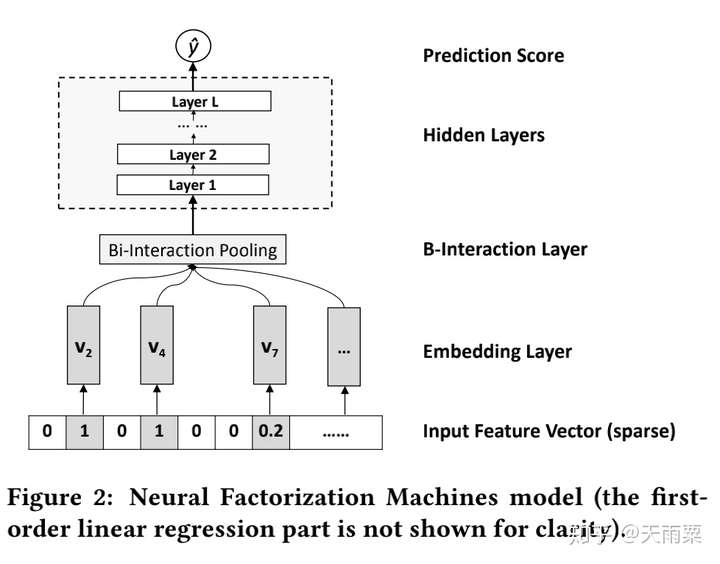
(3)NFM:Neural Factorization Machines, 2017 —— 引入Bi-Interaction Pooling结构的NN模型
NFM全程为Neural Factorization Machines,它与FNN一样,都属于将FM与NN进行结合的模型。但不同的是NFM相比于FNN是一种端到端的模型。NFM与PNN也有很多相似之出,本质上也属于Embedding+MLP结构,只是在浅层的特征交互上采用了不同的结构。NFM将PNN的Product Layer替换成了Bi-interaction Pooling结构来进行特征交叉的学习。
模型结构:
NFM的整个模型公式为:
其中 是Bi-Interaction Pooling+NN部分的输出结果。我们重点关注NFM中的Bi-Interaction Pooling层:
NFM的结构如上图所示,通过对特征Embedding之后,进入Bi-Interaction Pooling层。这里注意一个小细节,NFM的对Dense Feature,Embedding方式于AFM相同,将Dense Feature Embedding以后再用dense feature原始的数据进行了scale,即 。
NFM的Bi-Interaction Pooling层是对两两特征的embedding进行element-wise的乘法,公式如下:
假设我们每个特征Embedding向量的维度为 ,则
,Bi-Interaction Pooling的操作简单来说就是将所有二阶交叉的结果向量进行sum pooling后再送入NN进行训练。对比AFM的Attention层,Bi-Interaction Pooling层采用直接sum的方式,缺少了Attention机制;对比FM莫明星,NFM如果将后续DNN隐藏层删掉,就会退化为一个FM模型。
NFM在输入层以及Bi-Interaction Pooling层后都引入了BN层,也加速了模型了收敛。
优势:
- 相比于Embedding的concat操作,NFM在low level进行interaction可以提高模型的表达能力
- 具备一定高阶特征交叉的能力
- Bi-Interaction Pooling的交叉具备线性计算时间复杂度
不足:
- 直接进行sum pooling操作会损失一定的信息,可以参考AFM引入Attention
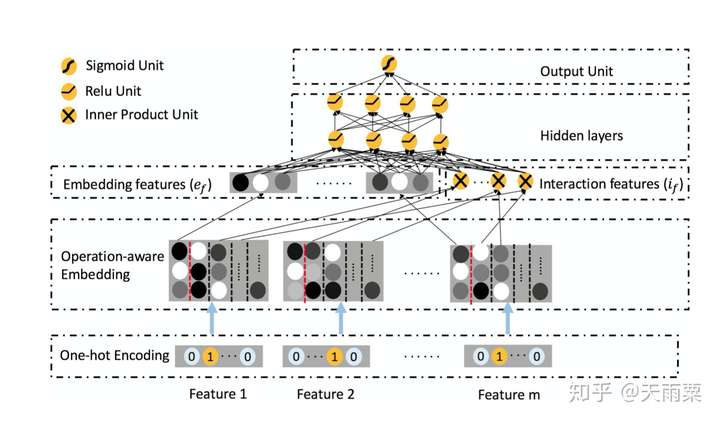
(4)ONN:Operation-aware Neural Network, 2019 —— FFM与NN的结合体
ONN是2019年发表的CTR预估,我们知道PNN通过引入不同的Product操作来进行特征交叉,ONN认为针对不同的特征交叉操作,应该用不同的Embedding,如果用同样的Embedding,那么各个不同操作之间就会互相影响而最终限制了模型的表达。
我们会发现ONN的思路在本质上其实和FFM、AFM都有异曲同工之妙,这三个模型都是通过引入了额外的信息来区分不同field之间的交叉应该具备不同的信息表达。总结下来:
- FFM:引入Field-aware,对于field a来说,与field b交叉和field c交叉应该用不同的embedding
- AFM:引入Attention机制,a与b的交叉特征重要度与a与c的交叉重要度不同
- ONN:引入Operation-aware,a与b进行内积所用的embedding,不同于a与b进行外积用的embedding
对比上面三个模型,本质上都是给模型增加更多的表达能力,个人觉得ONN就是FFM与NN的结合。
模型结构:
ONN沿袭了Embedding+MLP结构。在Embedding层采用Operation-aware Embedding,可以看到对于一个feature,会得到多个embedding结果;在图中以红色虚线为分割,第一列的embedding是feature本身的embedding信息,从第二列开始往后是当前特征与第n个特征交叉所使用的embedding。
在Embedding features层中,我们可以看到包含了两部分:
- 左侧部分为每个特征本身的embedding信息,其代表了一阶特征信息
- 右侧部分是与FFM相同的二阶交叉特征部分
这两部分concat之后接入MLP得到最后的预测结果。
优势:
- 引入Operation-aware,进一步增加了模型的表达能力
- 同时包含了特征一阶信息与高阶交叉信息
不足:
- 模型复杂度相对较高,每个feature对应多个embedding结果
五. 双路并行的模型组合
这一部分将介绍双路并行的模型结构,之所以称为双路并行,是因为在这一部分的模型中,以Wide&Deep和DeepFM为代表的模型架构都是采用了双路的结构。例如Wide&Deep的左路为Embedding+MLP,右路为Cross Feature LR;DeepFM的左路为FM,右路为Embedding+MLP。这类模型通过使用不同的模型进行联合训练,不同子模型之间互相弥补,增加整个模型信息表达和学习的多样性。
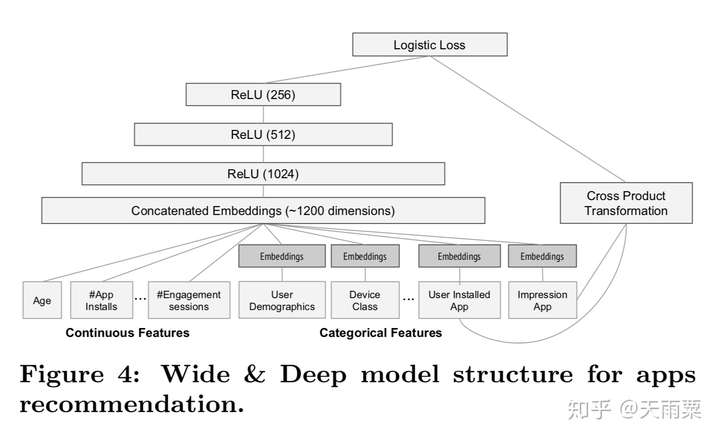
(1)WDL:Wide and Deep Learning, 2016 —— Memorization与Generalization的信息互补
Wide And Deep是2016年Google提出的用于Google Play app推荐业务的一种算法。其核心思想是通过结合Wide线性模型的记忆性(memorization)和Deep深度模型的泛化性(generalization)来对用户行为信息进行学习建模。
模型结构:
优势:
- Wide层与Deep层互补互利,Deep层弥补Memorization层泛化性不足的问题
- wide和deep的joint training可以减小wide部分的model size(即只需要少数的交叉特征)
- 可以同时学习低阶特征交叉(wide部分)和高阶特征交叉(deep部分)
不足:
- 仍需要手动设计交叉特征
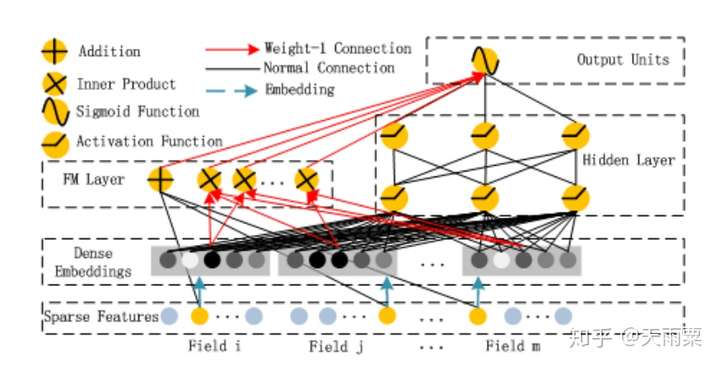
(2)DeepFM:Deep Factorization Machines, 2017 —— FM基础上引入NN隐式高阶交叉信息
我们知道FM只能够去显式地捕捉二阶交叉信息,而对于高阶的特征组合却无能为力。DeepFM就是在FM模型的基础上,增加DNN部分,进而提高模型对于高阶组合特征的信息提取。DeepFM能够做到端到端的、自动的进行高阶特征组合,并且不需要人工干预。
模型结构:
DeepFM包含了FM和NN两部分,这两部分共享了Embedding层:
左侧FM部分就是2-way的FM:包含了线性部分和二阶交叉部分右侧NN部分与FM共享Embedding,将所有特征的embedding进行concat之后作为NN部分的输入,最终通过NN得到。
优势:
- 模型具备同时学习低阶与高阶特征的能力
- 共享embedding层,共享了特征的信息表达
不足:
- DNN部分对于高阶特征的学习仍然是隐式的
六. 复杂的显式特征交叉网络
无论是以FNN、PNN、NFM、ONN为代表的Embedding+MLP,还是以Wide&Deep和DeepFM为代表的双路模型,基本都是通过DNN来学习高阶特征交叉信息。但DNN本身对于特征交叉是隐式的(Implicit)、bit-wise的,因此在这一阶段,以DCN、xDeepFM、AutoInt为代表的模型均把思路放在如何以Explicit的方式学习有限阶(bounded-degree)的特征交叉信息上。
Bit-wise:even the elements within the same field embedding vector will influence each other.
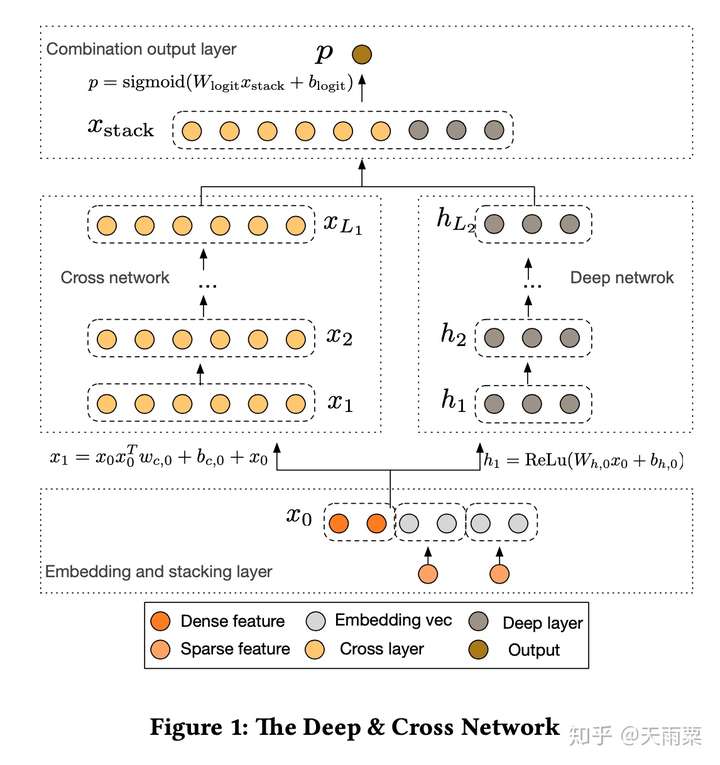
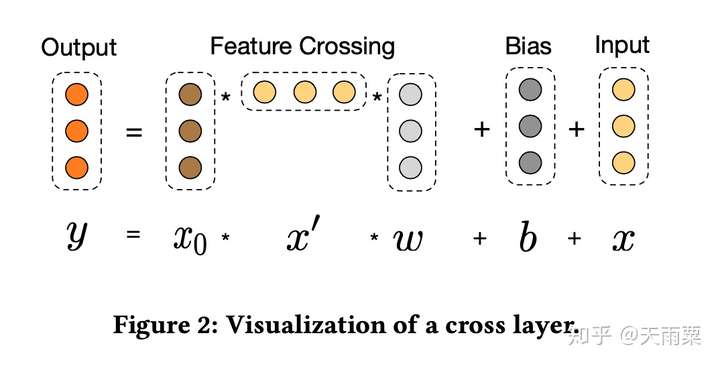
(1)Deep&Cross:Deep and Cross Network, 2017 —— 显式交叉网络Cross Net的诞生
Deep&Cross其实也属于双路并行的模型结构,只不过提出了一种新的模型叫做Cross Net来替代DeepFM中的FM部分。DNN本身虽然具备高阶交叉特征的学习能力,但其对于特征交叉的学习是隐式的、高度非线性的一种方式,因此作者提出了Cross Net,它可以显式地进行特征的高阶交叉,CrossNet相比于DNN的优势主要在于:
- 可以显式地(Explicitly)学习有限阶(bounded-degree)的特征交叉
- 计算时间复杂度相比于DNN更加低
模型结构:
DCN模型包含了两部分,左边一路是通过CrossNet来显式地学习有限阶特征交叉,右边一路是通过DNN来隐式学习交叉特征,进一步提高模型的多样性和表达能力。
CrossNet的主要思想是显式地计算内积来进行层与层之间的信息交叉;另外,CrossNet在设计上还借鉴了残差网络的思想,使得每一层的输出结果能够包含原始的输入信息。
对于CrossNet中的某一层,其计算方法如上图所示。分为三部分:
- Feature Crossing:对input embeddings与上一层的输出进行交叉
- Bias:偏置项
- Input:上一层的输出(也是本层的输入)
公式可以表达为:
其中 ,通过上式得到
,我们可以发现 mapping function
正好在拟合两层网络之间的残差。对于CrossNet中的第
层,其能够捕捉到的特征交叉的最高阶为
。
CrossNet本身在计算消耗上也不大,假设CrossNet共有 层,输入的input vector是一个
维向量,那么对于每一层来说有
两个参数,即
个参数,总共
层,共有
个参数,参数规模与输入的维度
呈线性相关。
优势:
- 具备显式高阶特征交叉的能力
- 结合ResNet的思想,可以将原始信息在CrossNet中进行传递
不足:
- CrossNet在进行交叉时是bit-wise方式
- CrossNet最终的输出有一定的局限性,CrossNet的每一层输出都是输入向量
的标量倍,这种形式在一定程度上限制了模型的表达能力
证明:
我们令CrossNet的输入为,忽略每一层中的bias项,对于第一次cross,有:
,其中
;
对于第二次cross,有:
,其中
基于上式进行推广可以得到,即证得CrossNet的输出是输入
的标量倍。
这里要注意的是,与
并不是线性关系,这是因为
也是关于
的函数。
(2)xDeepFM:eXtreme Deep Factorization Machine, 2018 —— Compressed Interaction Network的诞生
xDeepFM全称为eXtreme Deep Factorization Machine,可以看出其是在DeepFM基础上进行了改进。xDeepFM的贡献主要在于提出了压缩交互网络(Compressed Interaction Network),与DCN相同的是,都提出了要cross feature explicitly;但不同的是,DCN中的特征交叉是element-wise的,而CIN中的特征交叉是vector-wise的。
模型结构:
xDeepFM模型结构如下,整个模型分为三个部分:
- Linear Part:捕捉线性特征
- CIN Part:压缩交互网络,显式地、vector-wise地学习高阶交叉特征
-
DNN Part:隐式地、bit-wise地学习高阶交叉特征
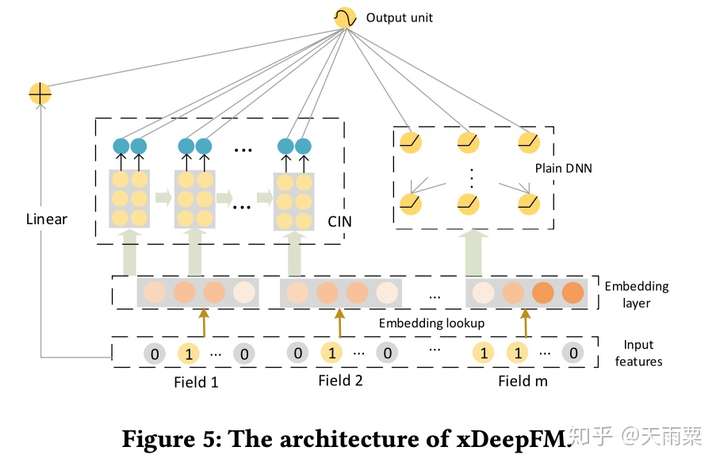
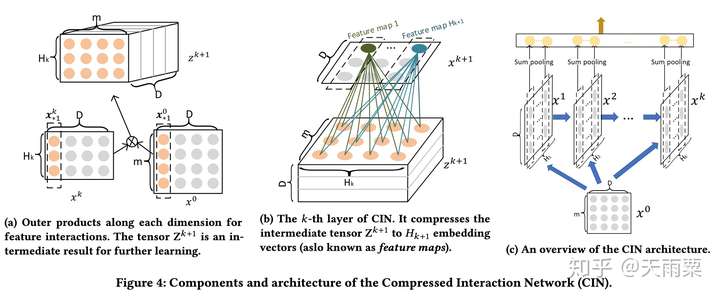
CIN网络的设计主要分为两步:交互(interaction)与压缩(compression)。
在交互部分,如下图(a)所示,将第 层的feature map与
(输入层,这里将输入层表示为一个
的tensor,其中m为特征个数,D为embedding的size)。在D的每一个维度上,进行外积计算,得到
。
在压缩部分,借鉴了CNN卷积+Pooling的思想,先通过 个filter将三维的
(可看做一张图片)进行压缩计算,得到
。紧接着在D维上进行sum pooling操作,得到最后输出向量(如c图中的黄色小圆圈)。
经过多个串行的压缩与交互步骤,可以得到多个输出向量,最终将这些向量concat起来,作为CIN的输出结果。
可以看出CIN在计算上相对比较复杂,但是由于CNN参数共享机制以及sum pooling层的存在,CIN部分的参数规模与特征的Embedding size大小 是无关的。假设输入field有
个,共有
层,每层有
个feature map,那么CIN部分的参数规模为
。
但是在时间复杂度上,CIN存在很大劣势,CIN的时间复杂度为 。
优势:
- xDeepFM可以同时学习到显式的高阶特征交叉(CIN)与隐式的高阶特征交叉(DNN)
- 在交叉特征的学习上,CIN采用了vector-wise的交叉(而不是DCN中的bit-wise交叉)
不足:
- CIN在实际计算中时间复杂度过高
- CIN的sum-pooling操作会损失一定的信息
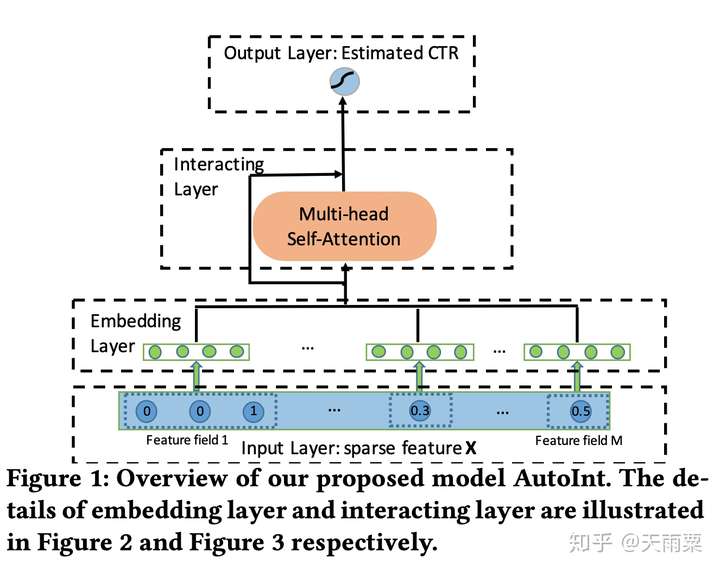
(3)AutoInt:Automatic Feature Interaction Learning, 2019 —— 跨领域NLP技术的引入:Multi-head Self-attention提升模型表达
AutoInt是2019年发表的比较新的论文,它的思路和DCN以及xDeepFM相似,都是提出了能够显式学习高阶特征交叉的网络。除此之外,AutoInt算法借鉴了NLP模型中Transformer的Multi-head self-attention机制,给模型的交叉特征引入了可解释性,可以让模型知道哪些特征交叉的重要性更大。
AutoInt的Attention机制采用了NLP中标准的Q,K,V形式,即给定Query词和候选的Key词,计算相关性 ,再用
对Value进行加权得到结果。
模型结构:
相比于DCN和xDeepFM采用交叉网络+DNN的双路结构,AutoInt直接采用了单路的模型结构,将原始特征Embedding之后,直接采用多层Interacting Layer进行学习(作者在论文的实验部分也列出了AutoInt+DNN的双路模型结构:AutoInt+)。
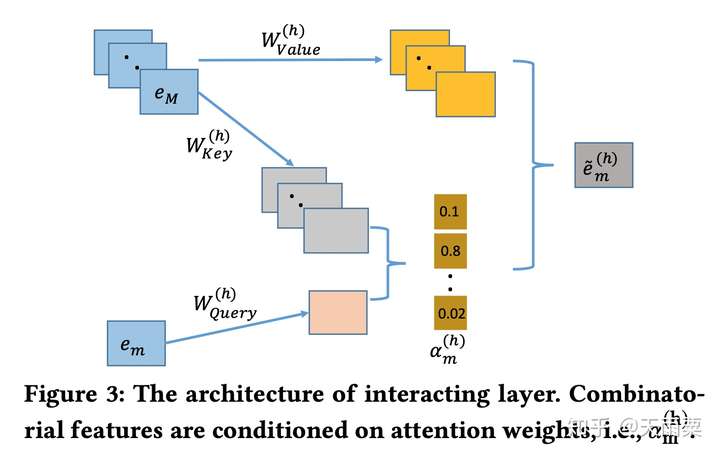
AutoInt中的Interacting Layer包含了两部分:Multi-head Self-Attention和ResNet部分。
在self-attention中,采用的是Q,K,V形式,具体来说:我们只考虑1个head self-attention的情况,假设我们共有 个特征,对于输入的第
个feature embedding来说,AutoInt认为它与
个特征交叉后的特征拥有不同的权重,对于我们第
个特征,它与第
个特征交叉的权重为:
其中 ,函数
是衡量两个向量距离的函数,在AutoInt中作者采用了简单高效的向量内积来计算距离。得到权重信息后,我们对M个特征的Value进行加权:
,得到向量m与其余特征的加权二阶交叉信息。
进一步地,作者使用了多个self-attention(multi-head self-attention)来计算不同subspaces中的特征交叉,其实就是进一步增加了模型的表达能力。采用h个multi-head之后,我们会得到h个 ,将这h个
concat起来,得到
。
为了保留上一步学到的交叉信息,AutoInt和CrossNet一样,都使用了ResNet的思想:
使用ResNet可以使得之前学习到的信息也被更新到新的层中,例如第一层原始的embedding也可以被融入到最终的输出中。
剩余的特征也以同样的方式进行multi-head attention计算,得到 ,将这M个向量concat之后连接输出层得到最终的预估值。
优势:
- AutoInt可以显示地、以vector-wise的方式地学习有限阶(bounded-degree)特征交叉信息
- 可以以low interacting layer学习到higher-order feature interaction
原文这里给出了一个例子,两层Interacting Layer就可以学习到4阶特征交叉。定义交叉函数为
, 假如我们有4个特征
,第一层Interacting Layer之后,我们可以得到
等二阶交叉信息,即两两特征的二阶交叉;将二阶交叉送入下一层Interacting Layer之后,由于输入第一层网络融入了二阶交叉信息,那么在本层中就可以得到四阶交叉,如
就可以通过
得到。
- Interacting Layer的参数规模与输入特征个数
无关。
七. CTR预估模型总结与比较
至此我们基本介绍完成了大多数常见的CTR预估模型,当然还有MLR、DIN、DIEN等其它的模型,由于篇幅限制暂时没有进行介绍。纵观整个CTR预估模型的发展过程,我们可以总结出一定的规律,这一部分主要是对上述模型的关系图谱以及特征进行总结。
(1)CTR预估模型关系图谱
现在我们再回头来看开篇的这张关系图:
从上往下,代表了整个CTR预估的发展趋势:
- LR的主要限制在于需要大量手动特征工程来间接提高模型表达,此时出现了两个发展方向:
- 以FM为代表的端到端的隐向量学习方式,通过embedding来学习二阶交叉特征
- 以GBDT+LR为代表的两阶段模型,第一阶段利用树模型优势自动化提取高阶特征交叉,第二阶段交由LR进行最终的学习
- 以FM为结点,出现了两个方向:
- 以FFM与AFM为代表的浅层模型改进。这两个模型本质上还是学习低阶交叉特征,只是在FM基础上为不同的交叉特征赋予的不同重要度
-
深度学习时代到来,依附于DNN高阶交叉特征能力的Embedding+MLP结构开始流行
- 以Embedding+MLP为结点:
- Embedding层的改造+DNN进行高阶隐式学习,出现了以PNN、NFM为代表的product layer、bi-interaction layer等浅层改进,这一类模型都是对embedding层进行改造来提高模型在浅层表达,减轻后续DNN的学习负担
- 以W&D和DeepFM为代表的双路模型结构,将各个子模块算法的优势进行互补,例如DeepFM结合了FM的低阶交叉信息和DNN的高阶交叉信息学习能力
- 显式高阶特征交叉网络的提出,这一阶段以更复杂的网络方式来进行显式交叉特征的学习,例如DCN的CrossNet、xDeepFM的CIN、AutoInt的Multi-head Self-attention结构
从整个宏观趋势来看,每一阶段新算法的提出都是在不断去提升模型的表达能力,从二阶交叉,到高阶隐式交叉,再到如今的高阶显示交叉,模型对于原始信息的学习方式越来越复杂的同时,也越来越准确。
图中右侧红色字体提取了部分模型之间的共性:
- Hand-crafted features:LR与W&D都需要进行手动的特征工程
- Non-end-to-end:GBDT+LR通过树模型提取特征+LR建模的两阶段,FNN则是FM预训练embedding+DNN建模的两阶段方式,这两者都是非端到端的模型
- Multi-embeddings:这里是指对于同一个特征,使用多个embedding来提升信息表达。包括FFM的Field-aware,ONN的Operation-aware
- Attention:Attention机制为CTR预估中的交叉特征赋予了不同的重要性,也增加了一定的可解释性。AFM中采用单个隐藏层的神经网络构建attention层,AutoInt在Interacting Layer中采用NLP中QKV形式学习multi-head self-attention
- Explicitly Interactions:DNN本身学习的是隐式特征交叉,DCN、xDeepFM、AutoInt则都提出了显式特征交叉的网络结构
- ResNet:ResNet的引入是为了保留历史的学习到的信息,CrossNet与AutoInt中都采用了ResNet结构
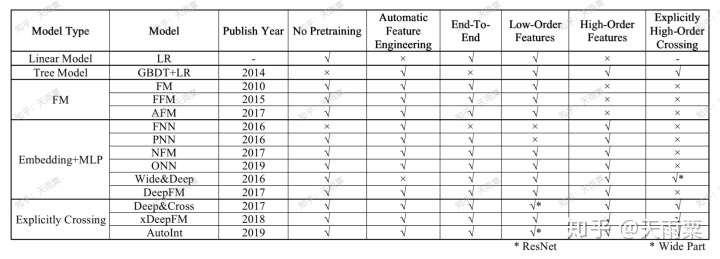
(2)CTR预估模型特性对比
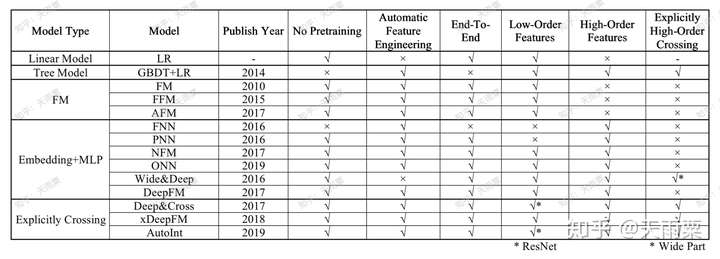
这里对比主要包含了一下几个方面:
- No Pretraining:是否需要预训练
- Automatic Feature Engineering:是否自动进行特征组合与特征工程
- End-To-End:是否是端到端的模型
- Low-Order Features:是否包含低阶特征信息
- High-Order Features:是否包含高阶特征信息
- Explicitly High-Order Crossing:是否包含显式特征交叉
结语
至此我们对于常见的CTR预估模型的演进过程与关系就讲解完毕,纵观整个过程,CTR预估模型从开始的LR,到利用树模型自动化组合特征,再发展到端到端的Embedding+MLP结构,再到如今越来越复杂的显式交叉网络等,每一次发展都是在不断提升模型对于用户行为的表达与学习能力。CTR预估不仅是一个数学优化问题,更是一个工程问题,因此如何能够以较低的计算成本,高效地提高模型表达能力将是未来需要努力的方向。
工程实现
TF-Ranking工具
TF-Ranking介绍
TF-Ranking,这是一个专为 Learning-to-Rank 打造的可扩展的 TensorFlow 库。它提供的统一框架包含一套最先进的 Learning-to-Rank 算法,并支持 Pairwise 或 Listwise 损失函数、多项目评分、排名指标优化以及无偏差 Learning-to-Rank。
TF-Ranking 运行速度快,易于使用,并可创建高质量的排名模型。统一的框架让机器学习研究人员、从业者和爱好者能够在单个库中评估并选择一组不同的排名模型。此外,作为一个实用的开源库,其核心不仅在于提供合理的默认值,还应当能让用户开发其自定义模型。因此,它提供了灵活的 API,用户可在此 API 中定义并插入自定义损失函数、评分函数和指标。
LTR 模型与标准的分类模型不同,标准的分类模型一次只对一个条目(item)进行分类,LTR 模型接收一个完整的条目列表作为输入,并学习一个排序算法,使整个列表的效用(utility)最大化。
虽然 LTR 模型最常用于搜索和推荐系统,但自其发布以来,我们已经看到 TF-Ranking 在除搜索以外的各领域,均有应用,其中包括电子商务、SAT 求解器和智能城市规划等。
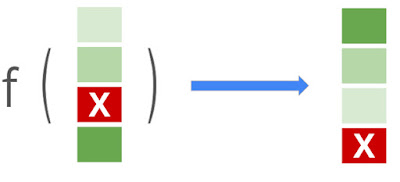
Learning-to-rank (LTR) 的目标是学习一个函数 f(),该函数会以项目列表(文件、产品、电影等)作为输入,并以最佳排序(相关性降序)输出项目列表。图解中,深浅不一的绿色表示项目的相关性水平,标有 “x” 的红色项目是不相关的
经验评估是所有机器学习或信息检索研究的重要一环。为确保兼容先前的研究,TF-Ranking 支持许多常用的排名指标,包括平均倒序排名 (MRR) 和标准化折扣累积收益 (NDCG)。训练期间,我们还可在 TensorBoard(一种开源的 TensorFlow 可视化信息中心)上轻松查看这些指标。
代码讲解
TF-Ranking 实现了 TensorFlow Estimator 接口,可通过封装训练、评估、预测和服务导出大幅度简化机器学习编程。TF-Ranking 与丰富的 TensorFlow 生态系统完美集成。如前文所述,您既可使用 Tensorboard 直观呈现 NDCG 和 MRR 等排名指标,也可以使用这些指标选出最佳模型检查点。待模型准备就绪,您便可使用 TensorFlow Serving 轻松将其部署至生产环境。
若有兴趣亲自试用 TF-Ranking,请查看GitHub 存储区,并浏览教程 示例。TF-Ranking 是一个活跃的研究项目,欢迎您为我们提供反馈和贡献。我们很高兴能见证 TF-Ranking 为信息检索和机器学习研究社区所带来的帮助。
TFR 框架主要这样实现的:
- 第一:tfr 通过 tfr.model.make_groupwise_ranking_fn 来对 Estimator 的 model_fn 进行了整体的封装。我们原有的基于 TensorFlow 的开发,在 Estimator 的 model_fn 这个参数内需要定义包括 Loss、Metrics 在内的完整的模型函数,但是在tfr这里就不需要了,make_groupwise_ranking_fn 会整体返回一个 Estimator 接收的 model_fn。
- 第二:tfr.model.make_groupwise_ranking_fn 函数的第一个参数 group_score_fn,这里是需要传入我们设计和开发的模型结构 (Scoring Function),但是这个模型是之前我们提到的,只需要计算出 logit 的模型。
- 第三:tfr.model.make_groupwise_ranking_fn 函数的第三个参数 transform_fn,对应调用 feature.py 中开发了兼容 TensorFlow 特征转换函数来对以 listwise 形式组织的数据(由 data.py 中的工具读取进来的 Dataset)进行转换,确保输入 Scoring Function 的数据格式正确。
- 第四:tfr.model.make_groupwise_ranking_fn 函数的第四个参数 ranking_head,对应调用了 tfr.head.create_ranking_head 函数,里面的三个参数分别定义了 loss、metrics 和 optimizer。loss 和 metrics 分别从 TFR 的 losses.py 和 metrics.py 中选择我们需要的,而 optimizer 还是使用 TensorFlow 中的 optimizer。
keras排序工作流
参考:
- TF-Ranking 中的 Keras API 让 LTR 模型构建更轻松
- TF-Ranking迎来大更新:兼容Keras更容易开发
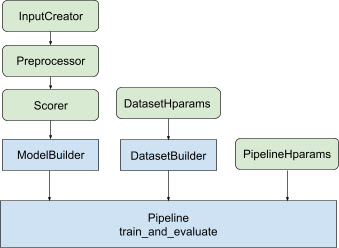
2021 年 5 月,谷歌发布了 TF-Ranking 的一个重要版本,实现了全面支持使用 Keras(TensorFlow 2 的一个高阶 API),以原生方式构建 LTR 模型。我们为原生 Keras 排序模型加入了全新的工作流设计,其中包括灵活的 ModelBuilder、用于设置训练数据的 DatasetBuilder, 以及利用给定数据集训练模型的 Pipeline。有了这些组件,构建自定义 LTR 模型会比以往更轻松,且有利于快速探索、生产和研究的新的模型结构。如果您选择的工具是 RaggedTensors,TF-Ranking 现在也可以和这些工具协作。
原生 Keras 的排序模型有一个全新的工作流设计,包括一个灵活的 ModelBuilder、一个用于设置训练数据的 DatasetBuilder 和一个用于使用所提供的数据集训练模型的 Pipeline。pipeline
利用 TFR-BERT 的 LTR
最近,BERT 之类的预训练语言模型在各种语言理解任务中性能表现突出。为利用这些模型,TF-Ranking 实现了一个新颖的 TFR-BERT 架构——通过结合 BERT 与 LTR 的优势,来优化列表输入的排序过程。举个例子,假设有一个查询和一个由 n 个文件组成的列表,而人们想要在对此查询响应中的文件进行排序。LTR 模型并不会为每个 <query, document> 学习独立的 BERT 表示,而是会应用一个排序损失来共同学习 BERT 表示,充分提升整个排序列表相对于参照标准标签的效用。图
具有可解释性的LTR
透明度和可解释性是在排序系统中部署 LTR 模型的重要因素,在贷款资格评估、广告定位或指导医疗决定等过程中,用户可以利用这些系统来确定结果。在这种情况下,每个单独的特征对最终排序的贡献应具有可检查性和可理解性,以此确保结果的透明度、问责制和公正性。
实现这一目标的可用方法之一是使用广义加性模型 (Generalized additive model,GAM),这是一种具有内在可解释性的机器学习模型,由唯一特征的平滑函数线性组合而成。然而,我们虽然已经在回归 (Regression analysis) 和分类任务方面对 GAM 进行了广泛的研究,但将其应用于排序设置的方法却并不明确。举个例子,虽然可以直接利用 GAM 对列表中的每个单独项目进行建模,然而对项目的相互作用和这些项目的排序环境进行建模,仍是一个更具挑战性的研究问题。为此,我们开发了神经排序 GAM,这是可为排序问题的广义加性模型所用的扩展程序。
与标准的 GAM 不同,神经排序 GAM 可以同时考虑到排序项目和背景特征(例如查询或用户资料),从而得出一个可解释的紧凑模型。这同时确保了各项目级别特征与背景特征的贡献具有可解释性。例如,在下图中,使用神经排序 GAM 可以看到在特定用户设备的背景下,距离、价格和相关性是如何对酒店最终排序作出贡献的。目前,神经排序 GAM 现已作为 TF-Ranking 的一部分发布。图
落地案例
爱奇艺
TensorFlow Ranking 框架在爱奇艺海外推荐业务中的实践与应用



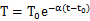

![clip_image002[19] clip_image002[19]](https://images0.cnblogs.com/blog/321721/201307/24001610-6cccd030f7364831af35c3b6ab95722d.gif)
![clip_image002[21] clip_image002[21]](https://images0.cnblogs.com/blog/321721/201307/24001610-5daecf7b9bec4dce9cb03f7b0d43ad21.gif)

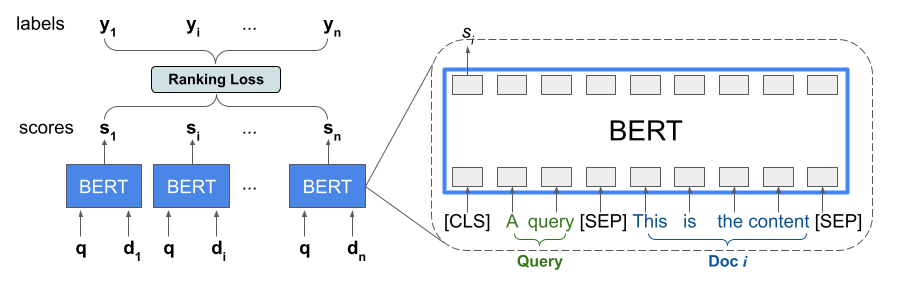 TFR-BERT 架构的说明,在这个架构中,通过使用单个 <query, document> 对的 BERT 表示,在包含 n 个文件的列表上构建了一个联合 LTR 模型
TFR-BERT 架构的说明,在这个架构中,通过使用单个 <query, document> 对的 BERT 表示,在包含 n 个文件的列表上构建了一个联合 LTR 模型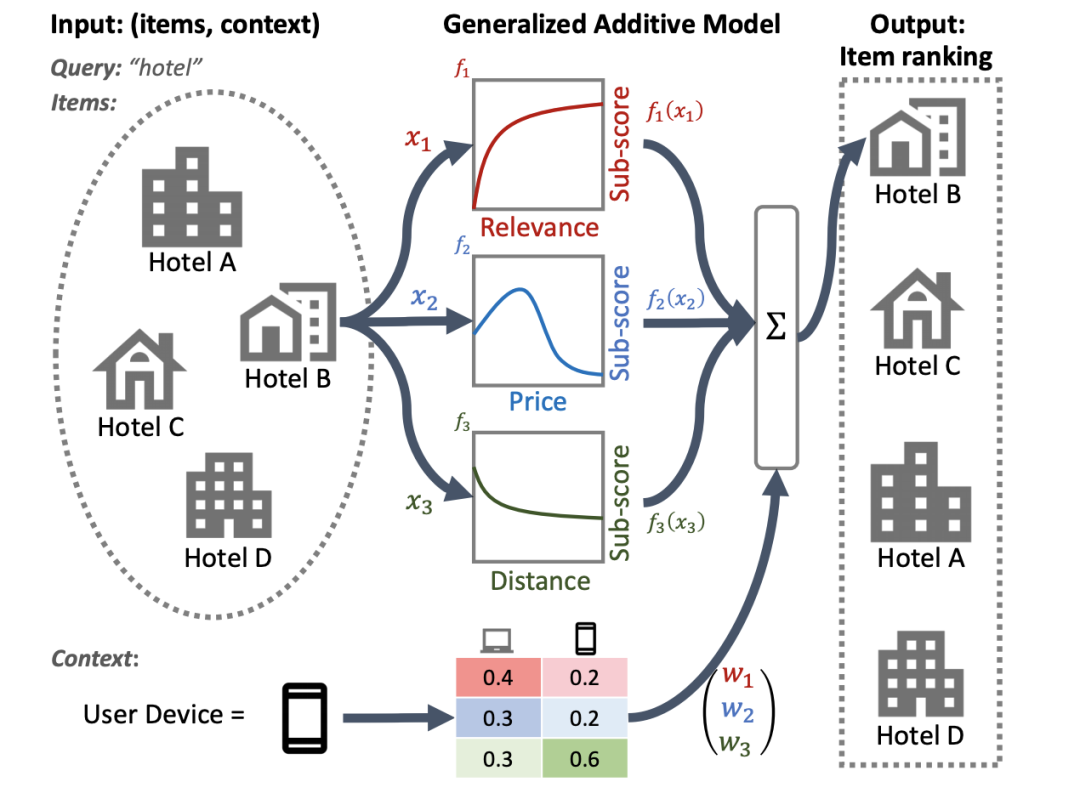
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
