- 总结
- 假设检验
- 在线实验
- interleaving
- 服务部署
- 结束
总结
- Innovating Faster on Personalization Algorithms at Netflix Using Interleaving,中文版本:Netflix推荐系统(Part Seven)-改善实验系统
假设检验
【2023-1-29】推论统计之——假设检验
假设检验(hypothesis testing),又称统计假设检验,是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。
显著性检验是假设检验中最常用的一种方法,也是一种最基本的统计推断形式,其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断。
什么是显著性检验
- “
显著性检验”的英文名称是“significance test”。在统计学中,显著性检验是“统计假设检验”(Statistical hypothesis tesing)的一种,显著性检验是检测科学实验中的实验组与对照组之间是否存在差异及差异是否显著的办法。 - “统计假设检验”指出了“显著性检验”的前提条件是“统计假设”,换言之“无假设,不检验”。任何人在使用显著性检验之前必须知道假设是什么。
- 一般而言,把要检验的假设称之为
原假设,记为H0,把与H0相对应的假设称之为备择假设,记为H1。- 第一类错误-弃真(α):如果原假设为真,而检验的结论却劝你放弃原假设,称为第一类错误,出现的概率记为α。
- 第二类错误-存伪(β):如果原假设不为真,而检验的结论却劝你接受原假设,称为第二类错误,出现的概率记为β。
- 通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。这样的假设检验称为
显著性检验,概率α称为显著性水平。 - 显著性水平是数学界约定俗成的,一般有α =0.05,0.025.0.01这三种情况。代表着显著性检验的结论错误率必须低于5%或2.5%或1%(统计学中,通常把在现实世界中发生几率小于5%的事件称之为“不可能事件”)(问:不是小概率事件吗?)。
假设检验基本理论
假设检验的基本思想:“小概率事件”原理,其统计推断方法是带有某种概率性质的反证法。
小概率思想是指小概率事件在一次试验中基本上不会发生。反证法思想是先提出检验假设,再用适当的统计方法,利用小概率原理,确定假设是否成立。-
即为了检验一个假设H0是否正确,首先假定该假设H0正确,然后根据样本对假设H0做出接受或拒绝的决策。如果样本观察值导致了“小概率事件”发生,就应拒绝假设H0,否则应接受假设H0。
- 参考:用Python如何实现“假设检验”

假设检验现实生活实例可参考 假设检验的逻辑是什么?
- 先确定原假设(零假设)和备则假设
- 原假设(H0):某个断言
- 备则假设(H1):原假设对立的断言
- 假设检验实际是对假设检验的断言进行试验,你对假设保持怀疑,随后如果有足够的拒绝证据,则拒绝;
- 假设检验无法给出绝对的证明,假定原假设为真的前提下,通过假设检验了解结果到底有多可靠。如果结果极不可能发生,就会成为证明原假设为假的证据
- 基本概念:
- 检验统计量:用于对假设进行检验的统计量
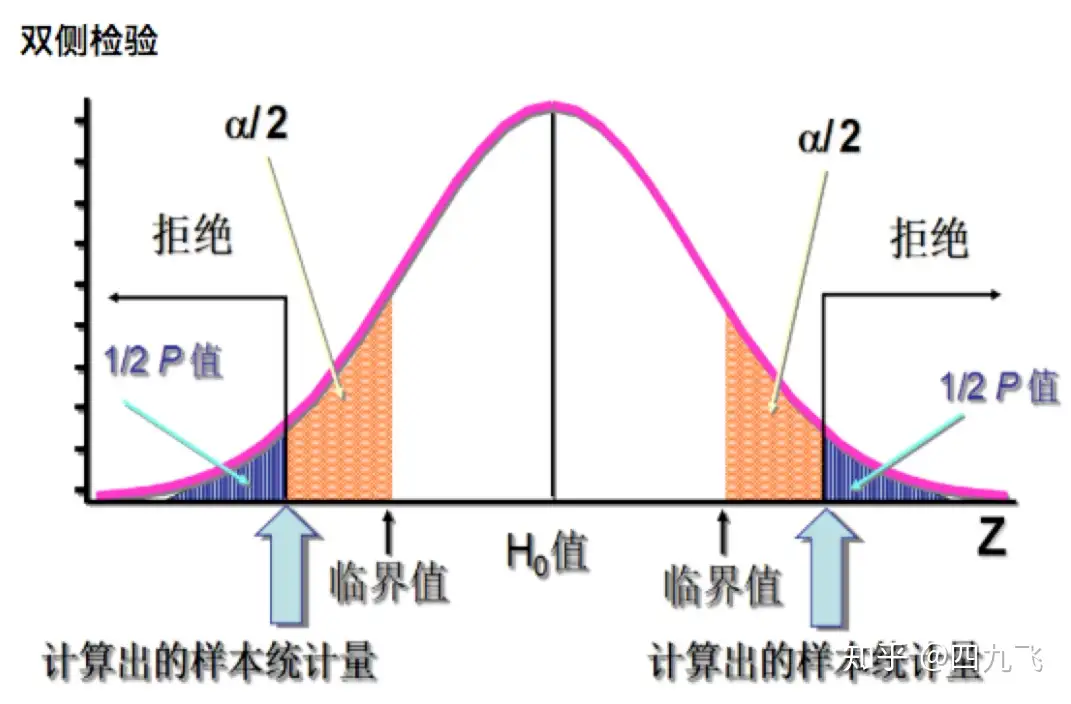
- 显著性水平:用 α 表示, 表明希望在观察结果的不可能程度达到多大时,拒绝H0;
P(X<c) < α 其中X为检验统计量,c为临界值,α为显著性水平。
如果α=5%,表示如果样本中的检验中的检验统计量落在概率分布的最低5%范围内,将否定断言(原假设H0)

-
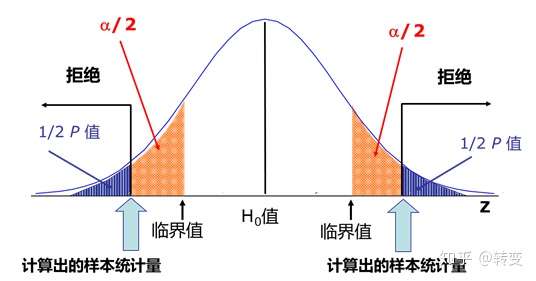
P值:某个小于或者等于拒绝域方向上的一个样本数值的概率;它是取得样本中的各种结果或者取得拒绝域方向上的某些更为极端的结果的概率;P值是在假定原假设为真时,得到与样本相同或者更极端的结果的概率。
- 如果P只位于拒绝域中,则拒绝H0;
- 如果P只位于拒绝域外,则没有充足证据,那么接受H0
- 假设检验分类:(主要通过备则假设判断)
- 单尾检验:拒绝域落在数据集一侧
- 如果H1是 ‘<’ 符号 左尾 此时拒绝域位于数据的低端
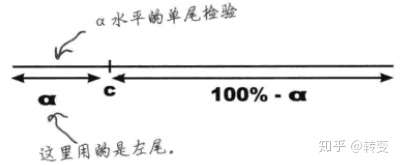
- 如果H1是 ‘>’ 符号 右尾

举例:某制药公司断言,某款药品针对某种病治愈率为90%患者,那么
- 原假设H0:P=0.9
- 备则假设H1: P<0.9
这就是左尾检验
无论是左尾检验还是右尾检验,P<α 即拒绝H0。
- 双尾检验:拒绝域一分为而于数据集两侧
如果H1是 ‘≠’ 符号 双尾

如果备则假设H1≠0.9, 则我们应使用双尾检验,我们应该查看检验统计量是否显著多于90%或者显著少于90%。
- 几个概念的区别
- 置信区间:代表“总体参数位于两个极限之间”这一结果的具有的可信程度
- 置信水平:总体参数位于置信区间的概率
- 显著性水平:反映数值位于某个极限以外的概率,一般为5%
显著性水平越小,则证据力度越大;为了拒绝H0,样本结果需要达到的不可能程度越高。
- 假设检验六个步骤:
- 确定进行检验的假设(H0, H1)
- 选择检验统计量
- 确定拒绝域
- 求出检验统计量的P值
- 查看样本结果是否位于拒绝域为
- 做出决策
置信区间
置信区间:
- 置信区间就是误差范围。 [a, b]
任何测量的数据都会存在误差,即使实验条件再精确也无法完全避免随机干扰的影响,所以科学实验往往要测量或实验多次,用取平均值之类的手段去取得结果。
- 多次测量是个排除偶然因素的好办法,但再好的统计手段也不能把所有的偶然因素全部排除。
- 所以,在科学实验中总是会在测量结果上加一个误差范围,这里的误差范围(区间)在统计概率中就叫做
置信区间。
置信水平
- 样本均值所构造的置信区间包含在总体均值中的概率,称为
置信水平。 - 置信水平 y%: $ P(a<均值<b)=y% $
假设检验方法
常用的假设检验方法: Z检验、t检验、卡方检验、F检验等。
Z检验
卡方检验
- 卡方检验(Chi-Square Test)在大数据技术场景中,通常用来检验某个变量或特征是不是和应变量有显著关系。
- 如:观察性别和在线买不买生鲜食品有没有关系。
t检验
适用范围
- 样本均值呈近似正态分布,且样本数量<30。
分为三种方法:
- a)单样本t检验(one-sample t test):比较一组样本均值与总体均值有无差异。可分为单侧检验和双侧检验。
单侧检验指按分布的一侧计算显著性水平概率的检验。用于检验大于、小于、高于、低于、优于、劣于等有确定性大小关系的假设检验问题。这类问题的确定是有一定的理论依据的。假设检验写作:μ1<μ2或μ1>μ2。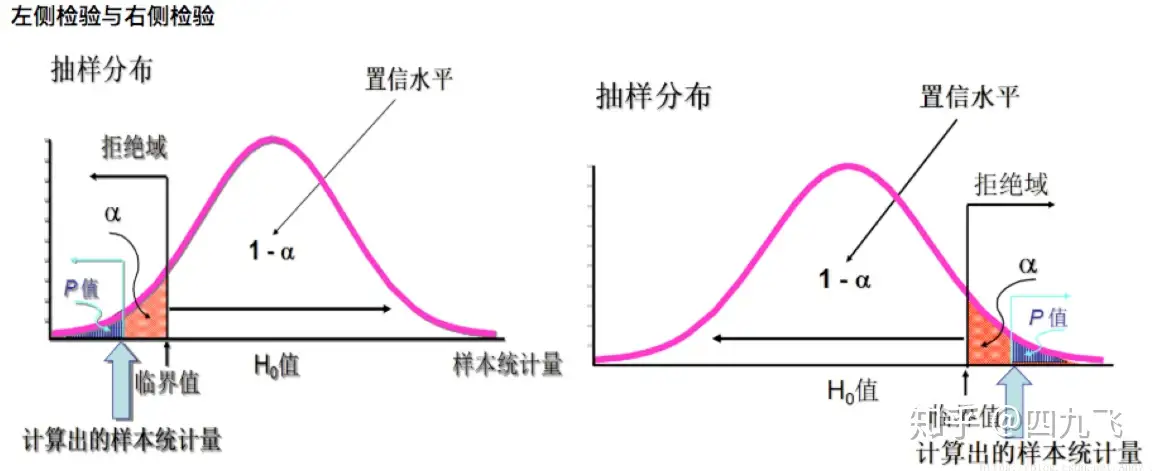
- 当关键词有不得少于/低于的时候用左侧,比如灯泡的使用寿命不得少于/低于700小时时。
- 当关键词有不得多于/高于的时候用右侧,比如次品率不得多于/高于5%时。
双侧检验指按分布两端计算显著性水平概率的检验, 应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作H1:μ1≠μ2。
- b)相关配对样本t检验(paired-sample t test):
- 比较一组样本在进行某种处理前后的均值有无差异。比如,你选取了5个人,分别在饭前和饭后测量了他们的体重,想检测吃饭对他们的体重有无影响,就需要用这个t检验。
- 注意,配对样本t检验要求严格配对,也就是说,每一个人的饭前体重和饭后体重构成一对。
- c)双独立样本t检验(independent t test):比较两组数据的平均值有无差异。
计算方法
- a)查看抽样分布类型
- 数据集近似正态分布,满足t分布使用条件 img
- b)计算统计数据量: t值的计算公式
- 样本均值:μ=data.mean()
- 样本标准差:s=data.std()
- 标准误差:se=sample_std/(np.sqrt(n)),n为样本大小
- 单样本检验与相关样本检验:使用scipy库的stats模块,用scipy计算出的p值是双尾检验。
# 用seaborn包绘制直方图和拟合曲线,查看是否符合t检验要求。
import seaborn as sns
sns.distplot(data)
plt.show()
# 单(1samp)样本t检验(ttest_1samp):
from scipy import stats
pop_mean = a #设置总体平均值
t,p_twoTail =stats.ttest_1samp(dataSer,pop_mean) #单样本检验的t值和p值
p_onetail = p_towTail/2
# 相关(related)样本t检验(ttest_rel):
from scipy import stats
t,p_twoTail = stats.ttest_rel(data['a'],data['b'])
p_onetail = p_towTail/2
# 双独立样本检验:使用statsmodels包计算t值、p值和df自由度:
import statsmodels.stats.weightstats as st
t,p_two,df=st.ttest_ind(data['A'],data['B'],usevar='unequal')
#usevar='unequal'两个总体方差不一样
F检验
在线实验
新模型上线,如何衡量模型效果?
总结
四种常见方法:twitter
- 1️⃣
A/B 测试- 将传入的请求在旧模型和候选模型之间非均匀分配。假设 10%的请求分配给候选模型,其余的仍然由旧模型提供服务
- 这限制候选模型的曝光,以避免任何潜在风险。
- 2️⃣
金丝雀测试Canary testing- A/B 测试通常影响所有用户,因为随机将“流量”分配给任一模型(无论用户是谁)。
- 金丝雀测试中,候选模型会暴露给生产环境中小部分用户,如果其指标显示成功,则会逐渐扩展到更多用户。
- 3️⃣
交错测试Interleaved testing- 混合多个模型的预测
- Netflix 推荐引擎中,一些电影推荐来自旧模型,而另一些则由候选模型生成。记录下游成功指标(点击率、观看时间、报告为无用推荐等),以便日后比较。
- 4️⃣
阴影测试Shadow testing- 以上所有技术都会影响某些(或所有)用户
- 影子测试(或暗度发布)在不影响用户体验时,在生产环境中测试新模型。
- 候选模型与现有的旧模型一起部署,并像旧模型一样处理请求。然而,输出不会发送回用户。相反,输出会被记录下来,以便日后将其性能与旧模型进行对比。
- 明确部署候选模型而不是进行离线测试,因为精确的生产环境难以在离线环境中复制。
- 影子测试可以在生产环境中对候选模型进行无风险的测试。
- 注意:影子测试中无法衡量面向用户的指标。由于候选模型的预测永远不会展示给用户,因此无法获得真实的互动数据,例如点击量、观看时长或转化率。Netflix、亚马逊和谷歌顶尖的机器学习团队安全推出新模型的方式,从不一次性全部切换,生产环境中进行测试、观察、比较,然后才会将模型推广到 100%的流量。
- 除此之外,还需要测量延迟、吞吐量、资源使用情况以及下游成功指标。一个准确率提高了 2%但速度慢 3 倍的模型从用户体验角度来看是不可取的
A/B实验
- 名言
- 不是每个想法都是好的,大部分想法都是不好的。
- Many times,we have to tell people that their new beautiful baby is actually…ugly。
- 在互联网背景下,快速试错已经成为产品持续迭代的必备能力。借鉴传统行业(医学等)成熟的实验理论(因果推断),互联网逐渐发展了以AB Test为核心的数据驱动决策之路。在以下场景中可以考虑使用A/B Test:
- 重大产品功能很难决策,不确定哪个方案效果最优。
- “后验”成本高,如果改版失败,业务风险较大。
- 通过 abtest 系统对迭代方案进行实验, 并结合数据进行分析,反向再验证和驱动方案,是一个发现问题、提出假设、印证猜想、不断优化的过程
因果推断
- 因果推断(Causal Inference)是指在一种现象已经发生的情况下推出因果关系结论的过程。比如说全球气候变暖,需要分析是什么因素导致的,各个因素对全球气候变暖影响有多大。
- 因果推断要做的是识别因果关系,量化因果作用。而这也是A/B测试要做的事情,即根据实验结果判断新版(B)相比原版(A)有无显著提升,如果有,提升了多少。
- 上面提到了因果关系,所谓因果关系(causality或causation),是一个事件(即”因”)和第二个事件(即”果”) 之间的作用关系,其中后一事件被认为是前一事件的结果。一般来说,一个事件是很多原因综合产生的结果,而且原因都发生在较早时间点,而该事件又可以成为其他事件的原因。
- 因果关系举例:
- 1). 睡得晚(因),长黑眼圈(果)。
- 2). 如果水温达到100度(因),水会沸腾(果)。
- 3). 长时间看电视(因),影响孩子视力(果)。
- 因果关系的结构可表示成顺序的因果逻辑:
- 因为事件A(前提:事件A已经发生),所以事件B(结论:事件B将要发生)
- 注意:相关 ≠ 因果
- 机器学习算法更加关注特征之间的相关性,而无法识别特征之间的因果性,而很多时候在做决策与判断的时候,我们需要的是因果性。分析因果关系的目的是通过改变”因”,从而对真实世界做出改变(“果”),这也是与相关关系最大不同。
- 传统的因果推断思想中,从因到果是一个封闭的系统。人们往往采用”控制”的方法,将影响结果的所有其他因素控制住,仅让关心的变量变化,这样结果的变化就是”关心的变量”造成的影响。随机化实验方法就是”控制”其他变量不变的常用手段,因此随机化试验是因果推断的黄金法则,而A/B Test恰好是随机化试验在互联网的应用。
- 机器学习大多数情况下仅作为一种可以拟合数据的特别函数f(x)[p(y|x)],近年来将机器学习方法应用到因果推理[p(y|do(x))]逐渐成为研究热点,图林获奖者获奖得者Judea Pearl(另一作者Dana Mackenzie)的新书,《The Book of Why: The New Science of Cause and Effect》,将因果推断带入大家视野。
什么是A/B测试
- A/B Test是一个系统工程,互联网实际应用中多参考Google的分层实验模型《Overlapping Experiment Infrastructure: More, Better, Faster Experimentation》
- 不同域之间共享100%流量,如上域1分流30%,域2分流70%。
- 同一个域的不同层之间,会重复使用这个域中的流量,且每次各层进入流量会重新打散,保证互相不影响。
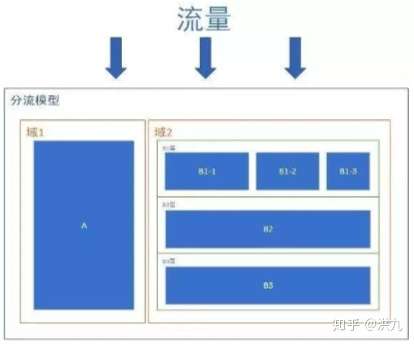
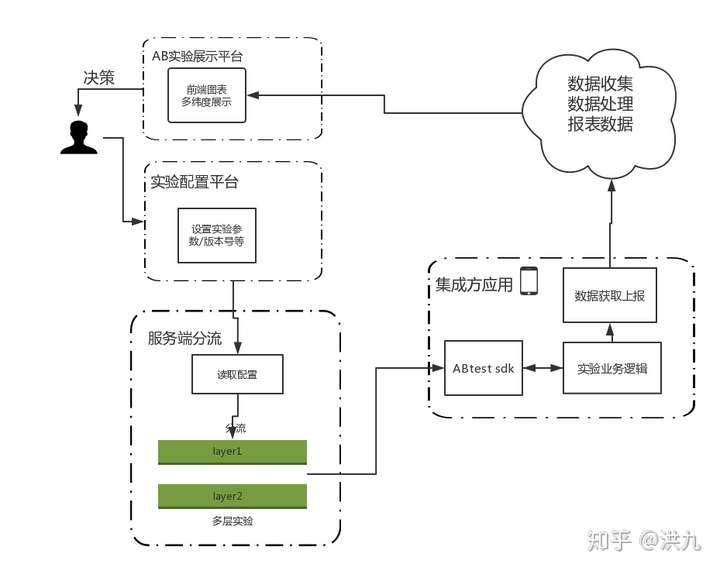
- 完整的A/B Test是一个衡量->发现->迭代->验证的持续循环过程,除去基本的分流和实验管理功能外,A/B Test还应该包括实验数据收集和实验数据分析功能,系统流程
- AB实验配置平台:产品经理/研发配置新实验。
- 分流服务:读取AB实验配置平台的配置数据,执行具体分流算法。
- 集成方应用:客户端上报实验分组和埋点(实验数据回收)。
- 数据分析:分析打点数据,生成报表数据。
- AB实验展示平台:实验数据可视化,用于辅助决策。
- A/B测试是一种用于提升App/H5/小程序产品转化率、优化获客成本的数据决策方法。
A/B 意义
- 基于A/B测试的灰度发布更重要的不是优化,而是保护性发布,先通过小流量的实际用户测试,有BUG或者新版本体验不好,可以立即回滚到老版本,简单有效。


分析用户行为时,常常会产生两个错误——“辛普森悖论”和“幸存者偏差”
灰度发布
A/B测试就是上两个方案,部署后看效果。根据效果和一些结果参数决定采用哪个方案。
- 灰度发布是切一部分业务使用新方案,看效果如何,是否有bug,会遇到什么问题。如果一切OK,就把全部业务切到新的方案上执行。发布后让部分用户使用新版本,其它用户使用旧版本,逐步扩大影响范围,最终达到全部更新的发布方式 。
- 灰度发布,又称金丝雀发布。
- 金丝雀发布这一术语源于煤矿工人把笼养的金丝雀带入矿井的传统。矿工通过金丝雀来了解矿井中一氧化碳的浓度,如果一氧化碳的浓度过高,金丝雀就会中毒,从而使矿工知道应该立刻撤离。 ——《DevOps实践指南》
- A/B测试系统的一个常用场景是App/小程序/后端服务精细化运营过程中的上线迭代管理,通常被称为灰度测试或者灰度上线。

知名概念
辛普森悖论 Simpson’s Pradox
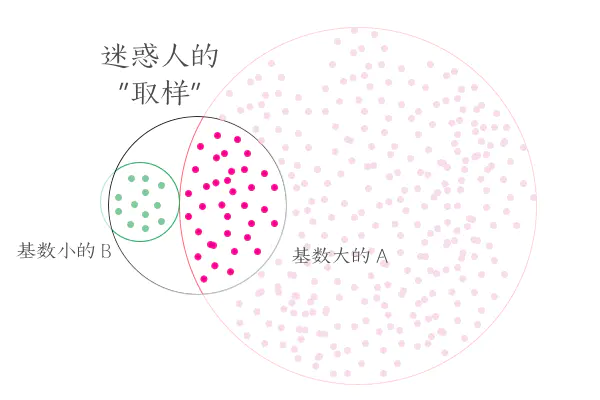
- 辛普森悖论(Simpson’s Paradox)亦有人译为辛普森诡论,为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的悖论,在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论。
- 正式定义:辛普森悖论是指数据集分组呈现的趋势与数据集聚合呈现的趋势相反的现象。
- 示例:Sophia和Carlo两家餐厅推荐指数,可以通过看男性和女性各组的评分,也可以看整体的评分

- 推断:Carlo’s 在男性和女性推荐率上都赢了,但却输在了总体推荐率上!
- 原因:只查看单独各组数据的百分比会忽略掉样本的大小,也就是评论者的人数。每个百分比都由推荐用户数与相对应的评论人数计算得到。Carlo’s 有更多的男性评论者,而Sophia’s 有更多的女性评论者,因此导致了矛盾的结果。
- 辛普森悖论的另一个现象:分组数据表现的相关性方向与整体数据表现的相关性方向截然相反。
如何避免?
- 不能简单的将分组数据汇总相加,而要仔细观察分组数据的特征。
- 为避免辛普森悖论出现,就需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必须了解该情境是否存在其他潜在因素而综合考虑。
辛普森悖论揭示了看到的数据并非全貌。我们不能满足于展示的数字或图表,要考虑整个数据生成过程,考虑因果模型。一旦理解了数据产生的机制,就能从图表之外的角度来考虑问题,找到其它影响因素。
幸存者偏差
幸存者偏差也称“生存者偏差”或“存活者偏差”,是一种常见的逻辑谬误。指的是当取得资讯的渠道仅来自于幸存者时,因为只能看到经过某种筛选而产生的结果,而没有意识到筛选的过程,因此忽略了被筛选掉的关键信息,此资讯可能会存在与实际情况不同的偏差。
- “幸存者偏差”:经过某种筛选而产生的结果,但没有意识到筛选的过程,因此忽略了被筛选掉的关键信息,进而得出错误的结论。
- 在“沉默的数据”、“死人不会说话”等等日常表达中,涉及幸存者偏差。此规律也适用于金融和商业领域,存活下来的企业往往被视为“传奇”,它们的做法被争相效仿,但其实有些也许只是因为偶然原因幸存下来了而已。
举例
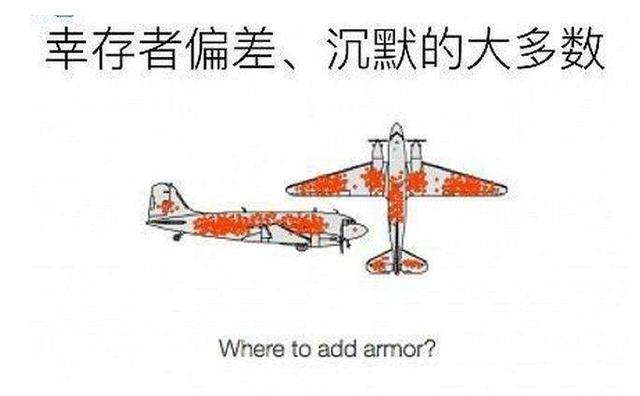
- 在二战期间,人们发现幸存的轰炸机中,机翼中弹的数量很多,而机身中弹的却很少。因此认为应该加固飞机机翼,其实不然,就是因为机翼中弹多还能飞回来,所以机翼中弹并没有影响飞机返航;而机身中弹的少则说明了子弹打中机身对飞机的影响更大,导致飞机不能返航,在这个飞机问题中,只统计到了幸存下来的飞机,以此下结论,是不正确的。
- 现实生活中也有很多幸存者偏差的案例,比如感觉周围都是本科以上的人,而实际上中国具备本科以上学历的人,只占总人口的3%。
- 为什么感觉知乎上应届生人人都是月薪过万,因为你看到的都是月薪过万的人在答题,月薪低于1万的都处于沉默状态。
- 再比如媒体调查“喝葡萄酒的人长寿”。一般是调查了那些长寿的老人,发现其中很多饮用葡萄酒。但还有更多经常饮用葡萄酒但不长寿的人已经死了,媒体根本不可能调查到他们。
- 回到投资领域,在投资理财类电视节目中,经常看到取得成功的投资者谈论其投资经验和方法,但观众往往会忽略了一个事实:采用同样经验和方法而投资失败的人是没有机会上电视的。
幸存者偏差现象可能导致以下的结果:
- (1) 投资成功者出书出名,失败者将默默无闻,导致电视上大量专家在传经布道、市面上充斥着太多投资成功学类的书籍,可能会让观众或读者高估了通过投资获得成功的概率;
- (2) 由于条件限制或者心理因素,投资成功者难以保证理性和客观,容易夸大自己能力、忽略运气因素、弱化当时所承担的风险等。
如何避免
- 应对幸存者偏差的办法是双盲实验设计和详细全面客观的数据纪录,即“兼听则明”,抛掉对个案的迷信,全面系统的了解才能克服这个偏差。
- 对于如何消除幸存者偏差的误区,没有好的办法,但如果能做到以下几点,应该有些好处:
- (1)在投资领域,我们改变不了生存者偏差现象的存在,但可以努力不盲从所谓的权威;
- (2)对于基金、私募以及个人投资者的能力评价,要看长期的、最好是跨越多个经济周期的业绩记录;
- (3)为了使样本更反映事实,更应该搜集介绍投资失败的案例和总结,不但要向成功的人学习如何成功,更要从失败的人那里总结为什么失败,因为投资很大程度上是个避免失败的过程。
基本比率谬误 Base Rate Fallacy
基本比率谬误(base rate fallacy)是指对统计学上的忽略基本比率而导致的推论谬误。
问题:买矿泉水的人多呢,还是买香奈儿香水的人多?
- 人群和需求概率明摆着,简直不是问题。但是人们往往会通过代表性来评估概率,忽视基本比率。代表性的意思是,通过比较 B 与 A 的相似程度来评估概率。例如,如果 A 能高度代表 B,人们就会认为 A 源自 B 的概率高。但如果 A 与 B 并不相似,人们就会认为 A 源自 B 的概率低。
经典问题:Jack 已经退休。那么他是图书馆员还是推销员?
- 需要考虑实际中推销员的比例远远大于图书馆员,而不能简单凭“退休”二字推测大概率为图书馆员。
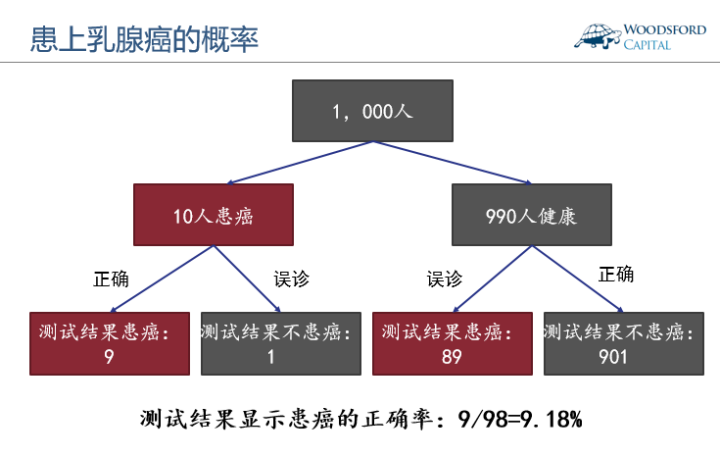
根据美国的统计数据,一个40岁左右的女性患乳腺癌的概率大约为1%。如果她通过乳房影像学检查来测试自己是否患乳腺癌,被误诊患上乳腺癌的概率约为9%。那么问题来了:如果一位40岁的女性去做了乳房影像学检查,结果显示她患上乳腺癌。她真正患上乳腺癌的概率是多少?是91%吗?
- 回答91%的朋友,恭喜你犯了基本比率谬误(base rate fallacy),即忽略了基本比率导致的推论谬误。我们假设对1000人进行检查,根据下图计算结果可知,正确答案约为9%。由于患上乳腺癌的女性的基本比率本来就很小,加上乳房影像检查自身带有的误诊率,其实只有9%左右的人真的患上了乳腺癌。
假设同性恋染上 G 病的概率是异性恋的 9 倍,张三染上了 G 病,而我们对他的性取向一无所知。试问张三是同性恋的概率是多少?
- 如果回答 90%,恭喜你又犯了基本比率谬误。事实上,如果我们不清楚同性恋和异性恋占整个群体的比率(即基本比率),就无法回答这个问题。
- 为方便起见,我们假定群体有 100 人,同性恋有 10 人(占 1/10 ),异性恋有 90 人(占 9/10 )。再假设异性恋染上 G 病的概率是 X,则同性恋染上 G 病的概率为 9X。我们可用下表表示各子群体的分布

- 张三是同性恋的概率是
- 来自直觉的概率判断(9/10),只有在同性恋与异性恋比例相等时才适用。假定群体有100人,同性恋、异性恋各50人,则可用下表表示各种子群体的分布
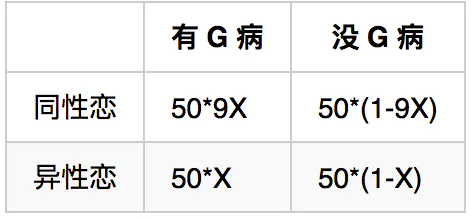
- 张三是同性恋的概率是 90%
如何避免?
- 做出任何判断前,首先需要对基本比率有个大致的认识,否则很容易不小心就陷入统计的陷阱
区群谬误
- 区群谬误(Ecological fallacy),又称生态谬误,层次谬误,是一种在分析统计资料时常犯的错误。和以偏概全相反,区群谬误是一种以全概偏,如果仅基于群体的统计数据就对其下属的个体性质作出推论,就是犯上区群谬误。这谬误假设了群体中的所有个体都有群体的性质(因此塑型(Sterotypes)也可能犯上区群谬误)。区群谬误的相反情况为化约主义(Reductionism)。
伯克森悖论 Berkson’s Paradox
- 定义:伯克森悖论指两个本来无关的变量之间体现出貌似强烈的相关关系
示例
- 为什么很多人会觉得帅哥都是混蛋?做个简化的假设,当你找男生约会的时候最看重两个条件:长得是不是帅,对你是不是好。两者至少满足其一你才会考虑跟他约会,长得不帅的渣男压根没有机会。因此对你所有的约会对象而言,两者有了负相关,于是你可能产生出渣男长得帅、暖男长得丑的印象。
- 同样的,演员的演技和长相成反比、学生文化课成绩和体育课成绩成反比也是伯克森悖论的例子
如何避免?
- 考虑变量本身之间是否存在关系或忽略了部分样本
罗杰斯现象 Will Rogers Phenomenon
- 罗杰斯现象,又称Will Rogers悖论,是指将某些事物从一个组移到另一个组,两组的平均值增大,虽然其中没有值变大。
- 因为当数据点从一个组重新归类到另一组的时候,如果这个点在原来组的平均线以下,但是在新组的平均线之上,那么这两个组的平均线都会提升。
- 这一悖论源于美国喜剧演员Will Rogers。他曾经开玩笑说,“当俄克流民离开俄克拉荷马州并且搬到加尼福尼亚州,他们同时提升了两个州的平均智力水平。”
举例说明
- 假设有6个人,分别为40、50、60、70、80、和90岁。现在将他们分为两组。第一组包括40岁和50岁的两人,因此组平均年龄为45岁。剩下的归入第二组,因此组平均年龄为75岁。
- 现在把第二组中的那位60岁的哥们,移去第一组。移过去以后,第一组的平均年龄变为50岁,而第二组的平均年龄变为80岁。两组的平均年龄都上升了。
罗杰斯现象,导致我们在医学领域产生一些容易让人混淆的,似是而非的结论。
- 前列腺特异抗原测试(PSA测试)可以帮助我们诊断前列腺癌。在没有发明这项测试前,很多人患了前列腺癌却不自知,因此他们被归入“健康”人群。而那些被确诊前列腺癌的患者,被归入“患者”人群。
- 有了PSA测试这项技术以后,很多人在年纪轻轻时也能通过该测试确诊自己是否患上前列腺癌。这部分人,就被移出“健康”人群,归入“患者”人群。
- 由于这个归类的变化,导致患上前列腺癌的“患者”人群,以及“健康”人群的平均寿命都得到了提高。因为“健康”人群中被移去一部分癌症患者,而这些癌症患者属于“轻度病患”(前列腺癌的致死率很低),因此“健康”和“患者”两个人群的寿命平均值均得到了提升,让人误以为PSA测试能够帮助我们延长寿命。
如何避免
- 需考虑平均值变大的根本原因,斟酌两次计算平均值前后分组之间的变化。
赌徒谬论 Gambler’s Fallacy
- 定义:赌徒谬误(Gambler’s Fallacy)亦称为蒙地卡罗谬误,是一种错误的信念,以为随机序列中一个事件发生的机会率与之前发生的事件有关,即事件发生的机会率会随着之前没有发生该事件的次数而上升。
- 如重复抛一个公平硬币,而连续多次抛出反面朝上,赌徒可能错误地认为,下一次抛出正面的机会会较大
赌徒谬误是生活中常见的一种不合逻辑的推理方式,认为一系列事件的结果都在某种程度上隐含了自相关的关系,即: 如果事件A的结果影响到事件B,那么就说B是“依赖”于A的。
- 例如,一晚上手气不好的赌徒总认为再过几把之后就会风水轮流转,幸运降临。
- 相反的例子,连续的好天气让人担心周末会下起大雨。
赌徒谬误亦指相信某一个特定的结果由于最近已发生了(“运气用尽了”)或最近没有发生(“交霉运”),再发生的机会会较低。
- 比如一个赌徒在打赌硬币是正面朝上或是背面朝上时的情景,前面5次的结果都是正面朝上,那么下一次他觉得反面朝上的概率会更大,这就是赌徒谬论。
- 为什么说是谬论呢?因为高中时就学过扔硬币这个问题的概率,每扔一次一枚硬币是一个独立的事件,正面朝上和反面朝上的概率相同都是0.5,不受前面扔了多少次的影响,也就是说虽然前面5次都是正常朝上,下一次仍是正面朝上的概率也还是0.5。
聊到这,可能有些人会不理解了,或者脑海里依稀记得好像老师讲过,扔一枚硬币扔个1000次,正面朝上和反面朝上的次数都是接近一半的呀,能想到这里的同学,恭喜你,已经入门了。确实如此,但请看清楚前提:扔1000次,这就是大数定理,当我们大量重复某一相同实验时,最后的结果会稳定在某一数值附近,但把大量重复事件的规律运用在少数的事情上就错了。
如何避免
- 赌徒谬误的产生是因为人们错误的诠释了“大数法则”的平均律。投资者倾向于认为大数法则适用于大样本的同时,也适用于小样本。Tversky and Kahneman把赌徒谬误戏称为“小数法则”(law of small numbers)。
- 一个独立的事件并不会受前一个独立事件结果的影响。
- 大数定理不能用于单个独立事件。
生日悖论 Birthday Paradox
假设你的班上一共有23位同学,其中任何两位同学生日撞期的概率为多少?
- 有人可能会这么想:一年有365天,把这23位同学分布在365天里,撞期的概率应该很小。大概不到10%吧。
- 事实上,23位同学中,生日撞期的概率为1/2。就是说,有一半的概率,这个班上至少有一对同学的生日相同。
- 算一下23位同学生日不撞期的概率。然后用1减去那个数字,就是这些同学生日撞期的概率。假设23位同学排队逐个进入教室。第一个进入教室的同学,其生日和其他同学不一样的概率为1。第二位同学,其生日和其他同学不一样的概率为364/365。第三位同学,其生日和前面两位同学生日不一样的概率为363/365。以此类推,所有同学生日不撞期的概率 = 1 * 364/365 * 363/365 … 然后用1减去上面的乘积,可以得出,p(n) = 1 - 365!/(365^n*(365-n)!)当教室里有23个同学时,其结果为0.5左右。
-

- 生日悖论(Birthday paradox)是指,如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。
- 计算与此相关的概率被称为生日问题,在这个问题之后的数学理论已被用于设计著名的密码攻击方法:生日攻击。
如何避免
- 以概率为依据做决策是不合逻辑的,然而逻辑和统计本身却是大不相同
- 在逻辑上,一个命题只有对和错两种划分
- 而在统计上,却可以说成对的概率有50%,错的概率为20%
- 就是这一点不确定性造就了以逻辑推理和统计为基础所得决策上的不一致,或者说矛盾,这就是统计关系不等于因果关系。
解决
- 很多的测试行为并不科学,特别是很多定向的用户测试经常会有这个弊端
- 要解决这个问题,对采样、聚类、流量分割等要求非常的高,这也是为什么A/B测试工具不能像很多统计工具一样,埋个点看数据,再根据数据反推业务逻辑,而是要充分与业务结合,从一开始就应该考虑业务策略,让用户去选择适合其口味的产品。
代理
正向/反向代理取决于代理的是出站请求,还是入站请求。
正向代理: 代理的出站请求, 客户端能感知到代理程序,架构上距离客户端更近。- 例子:vpn/梯子
反向代理: 代理的是入站请求,客户端认为代理程序就是服务器,客户端感知不到代理逻辑,架构上距离服务端更近。负载均衡(Load balancing): 反向代理可以提供负载均衡解决方案,将传入的流量均匀地分布在不同的服务器之间,以防止单个服务器过载。防止安全攻击: 由于真正的后端服务器永远不需要暴露公共 IP,所以 DDoS 等攻击只能针对反向代理进行, 这能确保在网络攻击中尽量多的保护你的资源,真正的后端服务器始终是安全的。缓存: 假设你的实际服务器与用户所在的地区距离比较远,那么你可以在当地部署反向代理,它可以缓存网站内容并为当地用户提供服务。SSL 加密: 由于与每个客户端的 SSL 通信会耗费大量的计算资源,因此可以使用反向代理处理所有与 SSL 相关的内容, 然后释放你真正服务器上的宝贵资源。
正向代理
正向代理类似一个跳板机,代理访问外部资源。从网站的角度,只在代理服务器来取内容的时候有一次记录,有时候并不知道是用户的请求,也隐藏了用户的资料,这取决于代理告不告诉网站。具体操作上,客户端必须设置正向代理服务器,当然前提是要知道正向代理服务器的IP地址,还有代理程序的端口。

总结:正向代理是一个位于客户端和原始服务器(origin server)之间的服务器,为了从原始服务器取得内容,客户端向代理发送一个请求并指定目标(原始服务器),然后代理向原始服务器转交请求并将获得的内容返回给客户端。客户端必须要进行一些特别的设置才能使用正向代理。
正向代理的用途:
- (1)访问原来无法访问的资源,如google
- (2)可以做缓存,加速访问资源
- (3)对客户端访问授权,上网进行认证
- (4)代理可以记录用户访问记录(上网行为管理),对外隐藏用户信息
参考:正向代理与反向代理总结
反向代理
反向代理(Reverse Proxy)是指以代理服务器来接受internet上的连接请求,然后将请求转发给内部网络上的服务器,并将从服务器上得到的结果返回给internet上请求连接的客户端,此时代理服务器对外就表现为一个服务器。
反向代理的作用:
- (1)保证内网的安全,可以使用反向代理提供WAF功能,阻止web攻击;大型网站,通常将反向代理作为公网访问地址,Web服务器是内网。
- (2)负载均衡,通过反向代理服务器来优化网站的负载
正向代理与反向代理的区别:
- 服务对象不同
- 正向代理,代理的是客户端,也就是例子中的A,服务端不知道实际发起请求的客户端;
 - 反向代理,代理的是服务端,也就是例子中的C,客户端不知道实际提供服务的服务端
- 反向代理,代理的是服务端,也就是例子中的C,客户端不知道实际提供服务的服务端
- 安全模型不同
- 正向代理允许客户端通过它访问任意网站并且隐藏客户端自身,因此必须采取安全措施以确保仅为授权的客户端提供服务
- 反向代理都对外都是透明的,访问者并不知道自己访问的是代理,访问者不知道服务节点的存在,认为处理请求的就是代理节点
总而言之,正向代理是从客户端的角度出发,服务于局域网用户,以访问非特定的服务,其中最典型的例子就是翻墙;反向代理正好与此相反,从服务端的角度出发,服务于所有用户,隐藏实际的服务节点,服务节点的架构对用户透明,以代理节点统一对外服务。

平滑发布
介绍
平滑发布就是发布的过程中不影响用户的使用,系统不会因发布而暂停对外服务,不会造成用户短暂性无法访问。
灰度发布与平滑发布其实是关联的。`
- 当服务器的数量只有一台的时候,不存在灰度发布,一旦发布了就是所有用户都更新了,所以这个时候只有平滑发布。
- 当服务器数量大于一台的时候,只要每台服务器都能达到平滑发布的方式,然后设定好需要发布的服务器占比数量,就可以实现灰度发布了。
实现方式
平滑分布一般通过Nginx负载均衡实现,示例见:平滑发布与灰度发布
vim /etc/nginx/nginx.conf # 编辑nginx配置文件
nginx -t
nginx -s reload # 重新加载

实施方案
- 1、跟nginx代理服务器约定了一个健康检查的接口
- 2、通过接口返回的http状态码来让ngx是否分流用户请求
- 3、根据提供的这个服务健康检查的接口:nginx判断只要某个实例的接口返回5xx的状态码,即把该实例下线(nginx不会把流量转发到该实例)
优化方案
平滑发布做完之后,确实给我带来很大的便利,不用每次发布都发公告,不重要的或者非功能性的内容发布了就是了。
但是用久了,客户量上去之后,又遇到一个问题,那就是每一次业务大变更,大型发布都是直接发布到生产,这样可能存在风险。设计师设计的功能,用户不一定完全接受,一旦上线新版本,收到一大堆的吐槽,都是用户呀,如果能在小范围人群内进行灰度试用,完成平稳的过度和使用反馈之后,优化后再上到生产会更好一点。
所以这边需要思考和设计一套统一的技术方案,未来无论云办公还是其他的业务系统,都能通过灰度发布在可指定的小范围内先进行体验和功能验证。基于上面的平滑,我们在Nginx反向代理服务器上动心思,让nginx来帮我们做ABTesting的方案。以下是我们尝试的几种方案:
Nginx反向代理:来路IP策略
步骤
- 1、进入云办公系统,进入Nginx反代服务器
- 2、Nginx读取来路IP的AB名单
- 3、根据IP AB名单进行流量转发(名单A走特定实例,名单B走云办公原有集群实例)

优缺点
- 1、配置简单,原资源平台的灰度升级就是根据IP名单来划分设计升级的
- 2、外部计算机很多都是非固定IP,这个适合在公司内网实现,比如只是配置公司内网的IP。
2、Nginx反向代理:$.Cookies策略
步骤
- 1、进入云办公系统,进入Nginx反代服务器
- 2、Nginx读取Http请求的Cokie的version信息(也可以是别的key)
- 3、根据Key的版本来进行流量转发(比如Version1.1走特定集群,Version1.0走通用集群实例)

优缺点
- 1、配置简单,根据Nginx的 $COOKIE_version 属性来判断
- 2、相对稳定,对需要开放名单的用户,在Cookie头部加入特定的版本即可,应用只要少许的开发量
- 3、首次访问静态页面可能不会产生cookie
备注:这是团队内认为最好的Nginx代理方案,同理,User-Agent和Header都可以做此种类型的判断,但是Header需要侵入底层HttpRequest去业务添加,不建议。
3、AB集群+业务代理方式

步骤
- 1、进入云办公系统,两种方式进入系统,一种是登录页登录:~/login ,一种是default页面带uckey登录:~/default?usertoken=#usertoken#
- 2、登录的时候和usertoken传入的时候进去 路由代理模块,进行用户信息校验,根据不同的人员和部门(人员和部门配置归属AB名单)分流到两个不同的AB集群
- 3、根据转发跳到具体的实例集群域名下(可以配置AB集群拥有不同域名,更容易区分)
优缺点
- 1、与Nginx剥离,不用依赖公司的通用平台和技术部的实现
- 2、需要申请AB集群,AB集群拥有不同的域名。
- 3、如果是前后端分离情况下,需要保证静态站点和服务站点均申请AB集群
- 4、所有入口需要统一做代理,有一定的开发量
抽样策略
- 在灰度测试的技术实现里,一个关键的部分是试用用户样本的选择策略。也就是说,新版本上线测试的首批(以及后续批次)灰度用户是怎么筛选出来,决定了灰度测试的技术选型和具体实现。每一个新功能分别由哪些测试用户来试用,谁扮演“小白鼠”的角色
- 广泛使用的样本选择策略
- 白名单
- 随机抽样
- 按照某种规则抽样
- A/B测试科学采样
实验组划分
- 实验分组的成功与否直接影响实验的数据,从而影响到实验的结果和结论。根据前文所述,随机化分组是控制实验无关变量(各组样本的条件尽量一致)的有效手段
2.1 完全随机化分组
- 随机抽样一般借助Hash函数依据实验对象ID(Hash因子)将实验对象映射到实验分桶。
BucketID=Hash(实验对象ID,策略ID,流量层ID)%100+1
- 这样每个实验对象会得到唯一的BucketID,同时会随机均匀散落在[1,100]范围内。在配置实验时,根据实际需求,为各个版本均匀切分流量。譬如A版本划分10%的流量,则BucketID从0~10的用户被划分到 A 版本,以此类推。
- 在实际应用中,假如实验对象为用户,实验对象ID可以取用户ID、用户手机号等。在大流量业务中(推荐、搜索等),完全随机化实验基本可以达到控制无关变量(消除无关变量影响)的目的。
2.2 分层随机抽样(Stratified sampling)

- 在试验对象数量较小的情况下,比如2000量级左右,完全随机抽样可能无法保证试验分组的无偏性。比如,在网约车业务中,司机的做单能力存在天然差异且方差较大,此时采用随机抽样存在试验各分组司机做单能力存在较大差异的风险,进而影响策略效果评估。此时,可以考虑分层随机抽样,即先根据司机的历史做单能力将司机分为不同的分组,然后在各分组内再随机抽样。
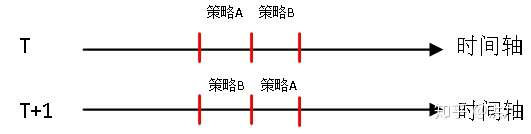
2.3 时间片分组
- 传统业务中,比如推荐、搜索等,流量因子是相互独立的、随机的,服从独立同分布。但是在O2O业务中,比如外卖、网约车等,实验对象(骑手、商家、司机等)面临着复杂的线下环境,由于存在一定程度的竞争关系,使得实验对象不再独立,此时传统的实验方式可能会存在问题。一种解决方法是采用时间片轮转分组方法。示意图如下:
2.4 分组合理性评估(A/A Test)
- 实验分组方案确定后,正式实验开始前,在有条件的情况下可以通过A/A Test确认分组间的无偏性,即是否控制住了无关变量。

- 所谓的A/A Test是指实验组与对照组采用相同的策略,用来验证试验分组是否存在天然的差异(比如点击率、平均阅读时长、留存、人均GMV、司机做单能力等)。
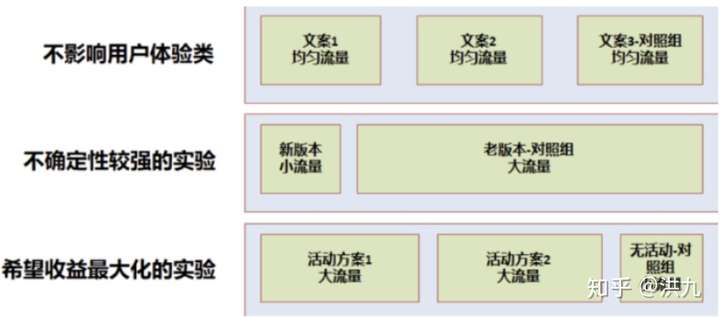
2.5 实验分组比例设计
- 根据不同 目的和实验风险,选择不同的实验划分方案,如下图:
A/B实验三大特性
- A/B测试具有三大特性:先验性、并行性和科学性。
- 先验性:互联网以往的方式是先发布版本,再通过数据验证效果,分析版本的好坏。而A/B 测试是通过采用代表性样本、用户流量划分以及小流量测试等方式,来获得具有代表性的试验结论。简单来说,就是先通过低代价,小流量的试验,再推广到全流量的用户。
- 并行性:将两个或两个以上的版本同时试验,确保每个版本所处环境的一致性,即其他条件都相同,同时发布同时生效,这样便于更加科学客观地进行对比。同时,可以节省验证的时间,无需在验证完一个版本之后再验证另一个。
- 科学性:即用户流量分配的科学性。将相似特征的用户均匀的分配到试验组中,确保每个组别的用户特征的相似性,从而避免出现数据偏差,使得试验的结果更有代表性。
A/B 测试的使用误区
- 误区一:轮流展现不同版本
- 先发布A版本一段时间后,再发布B版本,通过对比两个版本的数据情况来评定版本的好坏。这种做法并不能保证每个版本所处的环境相同,受众群体可能会有明显区别。以至于难以判断最终效果是否有差异,或导致效果不同的原因。
- 正确做法:不同版本并行(同时)上线试验,尽可能降低所有版本的测试环境差别。
- 误区二:选择不同应用市场投放/随机选取用户测试
- 将不同版本打包,分别投放到不同的应用市场,最终根据数据反馈最优的版本,将该版本全量上线。或随机选取一部分用户(甚至是公司内部人员)进行前期试用,根据数据反馈决定迭代版本。这种做法违背A/B测试的科学流量分配的原则。
- 正确做法:科学的进行流量分配,保证每个试验版本的用户特征类似。
- 误区三:让用户自主选择版本
- 同时发布多个版本,在产品界面提供版本入口,由用户自主选择使用哪一版本,再根据数据进行分析,从而评估出最好版本。这种做法无法预估每个版本的用户数、用户使用时长以及用户特征,最终导致了试验结果的不准确。正确做法:让用户展现对不同版本的真实使用体验,应实时关注各版本的数据表现,并根据数据反馈及时调整试验流量。
- 误区四:对试验结果的认知和分析过浅
- 这一误区又包括了两个不同的内容:
- 认为只有当试验版本结果优于原始版本时,试验才算成功。事实上,A/B 测试是用于选择最佳版本的工具。试验可能出现的结果分为三种:试验版本有提升(试验版本最佳)、无明显差异(试验版本和原始版本均可)、试验版本的表现比原始版本糟糕(原始版本最佳),但这三种结果均可说明试验的成功。
- 单从试验的整体数据结果,就推论所有场景的表现效果。例如:当A/B测试的数据表明试验版本差于原始版本时,就认定所有的地区或渠道的效果都是负面的。但如果细分每个版本中不同浏览器的数据,可能会发现:由于某一浏览器的明显劣势,导致整体试验数据不佳。
- 因此,不要只专注于试验数据的整体表现,而忽略了细分场景下可能导致的结果偏差。
- 正确做法:在分析试验整体数据的同时,需要从多个维度细分考量试验数据结果
- 这一误区又包括了两个不同的内容:
A/B方案
- AB实验的基本原理是“控制变量法”。
- 设指标数值=F({隐变量列}、{显变量列(含方案变量)})
A/B实现平台
业界的AB平台的设计都参考了谷歌重叠实验框架的论文:《Overlapping Experiment Infrastructure: More, Better, Faster Experimentation》,译文。
通常网站会利用分域、分层、分桶的机制保证流量高可用以及分流的灵活性和科学性。
实验分类
根据实验种类分类
- 水平实验:类似于Overlapping Layer中的实验,是属于同个“层”的实验,实验是互斥的,在同一“层”上实验可以理解为是同一种实验,例如:关键词“层”表示这一层的实验都是关键词相关的,该层上存在实验H1和H2,那么流量绝对不会同时命中H1和H2。
- 垂直实验:类似于Non-overlapping Layer中的实验,分布于不同“层”之间,实验是不互斥的,例如在关键词“层”和CTR“层”上在相同的分桶上配置了实验V1和V2,那么流量可以同时命中V1和V2。
- 条件实验:表示进入某“层”的实验需要满足某些条件,水平实验和垂直实验都可以是条件实验。
水平、垂直分流模型分为以下两个部分:
- 仅包含水平实验 : 最基础的实验需求,全部实验独占一个Layer,每个实验覆盖若干个桶,例如图4中的Layer_1,将流量分为10份,包含三个实验,这三个实验分别占用3、3、4份流量。
- 同时包含水平、垂直实验:一个Layer中同时包含垂直、水平两种类型的实验。例如图4中的Layer_2和Layer_3,将最后的4份流量用来做垂直实验,包含两个垂直实验,分别是Exp_6和Exp_7。

根据流量类别分类,主要了为了用户体验,使平台在操作上更加的简单、易用:
- 普通实验:最基本的实验,根据流量类别进行配置。
- 引用实验:流量分类是整个配置中心基础,但实际上存在一些实验是跨流量了,而引用实验则可以配置在不同的流量种类中。
- 全局实验:可以理解为特殊的引用实验,全局实验在所有流量上都生效。
分层实验模型
作为实验平台,支持同时运行大量AB实验是其基本要求。多实验并行的情况下,我们根据共享同一份流量情况下,两个实验效果是否会产生干扰,将实验之间的关系分为正交实验和互斥实验。
- 互斥实验:如果分层共享同一份流量就有可能出现实验效果之间相互干扰的问题,这样的实验叫互斥实验,也就是如果实验一和实验二是互斥关系,那么经过实验一的流量就不能进入到实验二。
- 正交实验:如果实验之间共享同一份流量实验效果之间不干扰,这样的实验我们叫正交实验,这种情况下,流经两个实验的流量是可以共享的,流经实验一的流量也可以流经实验二。
多实验并行过程中,既有正交实验,也有互斥实验并且要保证流量在实验过程中科学合理的分配。分层实验模型就提出了“层”的概念。层的原则是:同一层存在多个互斥实验,流量流经该层最多可以参与一个实验。层与层之间,流量是正交的,也就是说流量在穿越每一层实验时候,都会被再次随机打散,经过上层实验一的流量可能会经过下层的任何一个实 验,可能是实验一,也可能是实验二。

实验过程中,一般会从总体流量中按照一定维度划分流量区域来做实验,比如一部分实验做在PC端,一部分做在M端。如此,就引出了另外一个概念,“域”。这里划分出的流量池就是一个域,在这个域里还可以进行分层实验,不同域之间流量隔离,所有的流量域加起来共享100%流量。
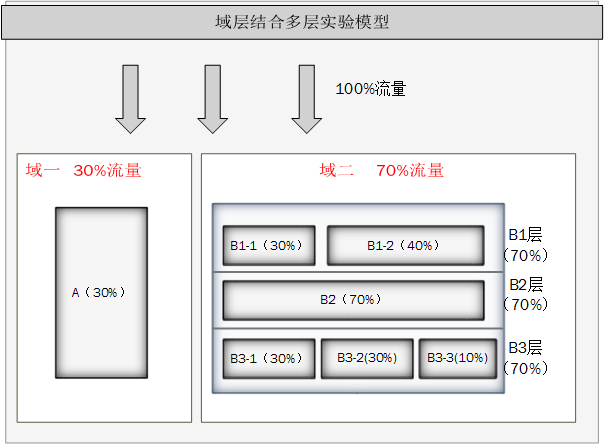
通过域、层、实验之间的嵌套关系组合,就可以满足我们很多场景的实验,划分想要的流量域,运行想要的各种不同的实验类型。
流量分桶
模型有了,怎么分流也很重要,那什么是分流呢?分流指根据分流算法策略为每层的每个实验分配相应的流量,从请求角度来说,是让每个请求都能在各层都能准确稳定的命中到相应实验。分流也叫流量分桶,为什么叫流量分桶呢?
每层的每个实验的实验组和对照组就是一个桶,每层的流量一共是100,假设这层有两个实验(实验一和实验二),流量配比各为50%,每个实验各有一实验组和对照组,实验组和对照组平分流量各得25%,那么每层实验就有4个桶。整体流量按桶划分,从0开始编号的话,可以认为,实验组一的桶装的是0-24的编号,实验组二的桶装的是25-49编号,类推,实验组二的桶装的是75~99的编号。一个流量请求在每一层中只能命中到一个实验组,也就是说只能被分到一个桶内。一般我们会选择用户id和实验层id哈希取模(mod=f(uid, layer)%100),得到的值在哪个桶内,该请求就命中哪个实验的那个组,这样 保证了用户在每层命中的实验是随机且是稳定的。
架构与实验
滴滴
【2021-5-11】滴滴:dtp服务请求apollo的时候会带一个唯一的id(如uid),apollo会根据这个uid来进行分组,一个uid会固定分到某个组,服务代码里植入Apollo的sdk,只区分控制组(对照组 group_id=0),另外开启一个监听接口,每隔几秒刷新Apollo上的配置文件,便于快速生成;实验开启后,Apollo平台上配置的关键指标及计算方法(SQL)开始展示,平台自动评估显著性,判定此次实验是否有效

- Apollo是适用于多种场景的线上A/B 实验与灰度发布平台,无论是想优化APP产品、后端算法还是运营策略,都可以通过实验来验证优化效果。与此同时,它支持复杂规则的定向投放、服务降级、配置同步、模型动态升级等应用场景。Apollo通过可视化的操作平台、科学的流量划分和一对一的实验设计,为产品经理、运营推广人员、数据分析师提供A/B 实验的指标计算及多维度的数据分析,为各种应用场景量身打造最优质的解决方案。
- A/B实验过程

- 第一步: 设计实验方案,包括确定实验对象,划分实验组,确定实验提升目标等。
- 第二步: 进行人群分组,一般是一个空白组加一个或多个实验组
- ① CR(Complete Randomization)完全随机分组 —— 由于完全随机的不确定性,分完组后,各个组的实验对象在某些指标特性上可能天然就分布不均。均值,标准差等差异较大。如果分组不均,则将会影响到第四步的实验效果分析的进行,可能遮盖或者夸大实验的效果。图
- ② 改进版:对CR进行简单的一步优化,即进行RR(Rerandomization),RR是在每次跑CR之后,验证CR的分组结果组间的差异是否小于实验设定的阈值。当各组的观察指标小于阈值或者重新分组次数大于最大允许分组次数后,停止分组。图
- RR通过牺牲计算时间,能在一定概率上得到符合要求的分组。重分组次数与输入的实验对象样本大小相关。样本量越大,需要进行重分的次数一般较少。但是RR分组能得到符合要求的分组有一定的概率,且需要花更多的时间。
- ③ 改进版:自适应分组,在一次分组过程中分出观察指标均匀的分组结果。
- Apollo实验平台实现了滴滴AI LAB团队设计的Adaptive(自适应)分组算法。Adaptive分组方法可以在只分组一次的情况下,让选定的观测指标在分组后每组分布基本一致,可以极大的缩小相对误差。相比于传统的CR分组,Adaptive分组的算法更加复杂,在遍历人群进行分组的同时,每个组都需要记录目前为止已经分配的样本数,以及已经分配的样本在选定的观测指标上的分布情况。从分流人群中拿到下一个要分的对象后。会对实验的各个组进行计算,计算该对象如果分配到本组。本组的观测指标分布得分情况。然后综合各个组的预分配得分情况,得到最终各个组对于该实验对象的分配概率。
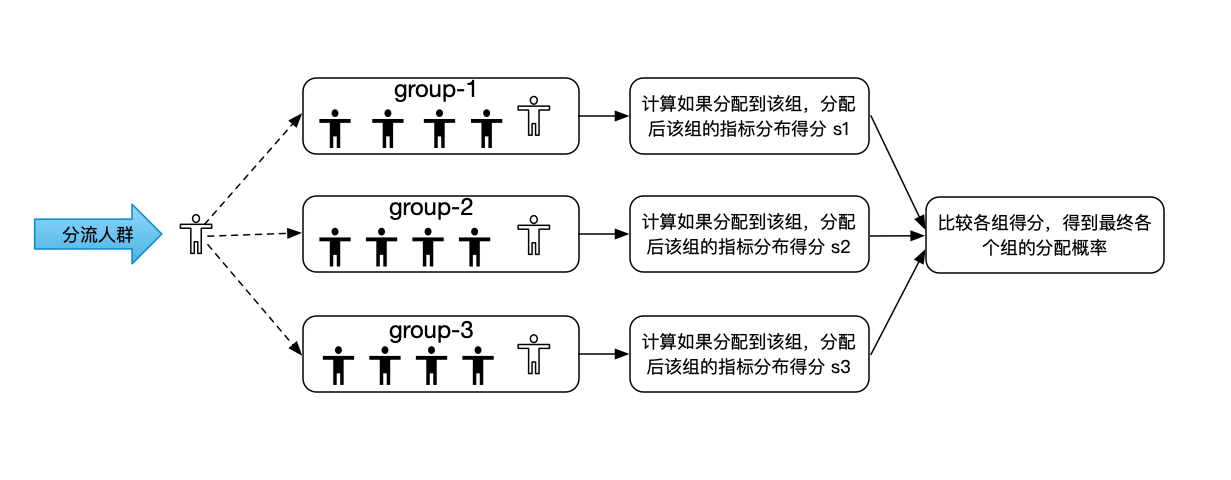
- ① CR(Complete Randomization)完全随机分组 —— 由于完全随机的不确定性,分完组后,各个组的实验对象在某些指标特性上可能天然就分布不均。均值,标准差等差异较大。如果分组不均,则将会影响到第四步的实验效果分析的进行,可能遮盖或者夸大实验的效果。图
- 第三步: 将需要实验的策略,方案或者功能施加到各个组,收集数据
- 第四步: 对实验关心的指标进行分析观察
- 心得
- 确认要实验的变量: 尽量保证每次实验只针对一个变量进行测试。
- 实验前明确关键指标: 基于假设,定义关键指标进行观测。不要订阅大量指标,或者,实验中后期再进行选择。
- 控制实验运行时间: 运行实验时不注意时间控制,随意结束实验的做法并不可取。
- 实验分组要保证受控: A/B 实验分组一定要保证在受控的情况下进行对比测试。受控是指除了要测试的变量外,所分组的组间差别尽量小,这样才能保证组间的差异对实验的影响是在可控范围内的。
- 实验结果分析要关注置信度: 不光要看指标本身的变化,还要看它的置信度。置信度是个统计学上的概念。我们抽取了一部分用户做实验,那么在这部分人身上
观察到的指标提升,是否在功能全量之后也能在全部用户中带来相同的指标提升呢?这就是置信度能告诉我们的。版本 B 带来了75%的转化率提升。于是,得出结论:版本 B 胜出。但这究竟对不对呢?结果并不一定,我们还要考虑以下两个情况:
- 样本特性:上面案例里,如果样本大小只有4个人,恰好其中3个喜欢按钮效果。那么这75%的提升置信度是极低的,因为真的放大到所有用户,喜欢按钮效果的人比例可能根本没有75%那么高。
- 提升幅度:如果样本量合理的情况下,例如在500人左右,转化率提升达到99%,那么这个结论的置信度是比较高的,很有可能放到全量之后,转化率也会提升到近似99%。但是如果观察到的提升率只有1%左右,那此时置信度就会比较低,很难说全量之后转化率就会提升1%。这1%的提升可能是抽样误差导致的,还需要更大的样本量来提高置信度。
参考:
- 【2017-5-22】是TA,让我们更懂用户!滴滴的神秘工具,Apollo!
- 【2020-5-29】滴滴数据驱动利器:AB实验之分组提效
美团
美团整体架构分为四层:
- Web层:提供平台UI,负责应用参数配置、实验配置、实验效果查看以及其他。
- 服务层:提供权限控制、实验管理、拉取实验效果等功能。
- 存储层:主要是数据存储功能。
- 业务层:业务层结合SDK完成获取实验参数和获取应用参数的功能。

贝壳

ab平台架构主要包括web层、api层、数据层、存储层,核心分流服务构成:
- web层:主要提供用户界面化的操作来配置实验,创建实验受众,创建白名单,查看实验实验效果等功能,其中用户配置实验过程中最重要的一部分就是实验受众。
- 实验受众:指的是用于实验的流量人群。目前受众分为两种,分别是基于维度标签组合形成的AB受众和基于用户画像标签圈定的人群包受众:
- AB受众:支持按照设备(ios、android)、城市、URL(比如区分贝壳pc和m站)等维度生成标签,再由标签之间组合形成各个维度的受众,比如北京安卓用户。这种受众通过解析请求的cookie信息,正则匹配标签内容判断是否应该进入对应受众。
- 人群包受众:因为人群包受众是通过DMP平台提供的用户画像标签(比如城市、最近的活跃度等)圈出来的人群id集合,所以也叫DMP受众,目前这部分受众的用户的id取值逻辑主要取自于设备id。通过判断用户请求信息的设备id是否包含在人群id集合中,来判断是否应该进入到该受众。
上面提到了白名单,那么白名单是什么呢?我们可以把白名单理解为一种特殊的受众,白名单中包含了人为添加的用户id。它一般应用于一个实验的某个实验组上,为这个实验组指定白名单,那么在对这个实验分流的时候,白名单的用户就忽略分流策略,直接命中配置了该白名单的实验组。白名单常用于测试情况下,指定测试人员命中实验组,方便测试。
配置实验受众、指定了实验起始和过期时间、配置实验组和对照组的流量之后,就可以开始实验了。

api层:提供业务方调用ab平台接口,用户请求ab平台的api时,解析请求header中的cookie信息判别受众以及获取用户id用于实验分流。根据实验场景不同,api分为客户端API和服务端API。
客户端api主要用于客户端实验比如UI等实验,API请求逻辑处理如图

服务端API主要用于后端逻辑优化、算法策略实验对比等,由于从前端到后端实验调用处,链路可能很长,对于请求信息的传递的保存和传递显得困难。因此,我们设计了uniqId,当用户请求线上域名的时候,负载均衡层会生成一个唯一的uniqId,将用户的请求信息保存到redis,之后的请求链路中,会将uniqid传递给后端,该参数也是请求ab服务时必不可少的参数。API逻辑如图所示

分流服务:主要提供流量划分的功能。
- 分流依据:ab平台利用用户id进行分流,这其中包括标记新用户或访客的lianjia_uuid、注册用户的lianjia_ucid、针对移动设备的lianjia_device_id。
- 分流实现:基于多层实验模型的流量分桶原理,ab平台对其做了适当的简化,以更加适合目前我们的业务需求。我们定义每层一个实验,各层之间流量正交。每个实验受众,可以理解为一个域。一个受众可以用于多个实验。
在程序设计中,我们取map集合,命名traffics,将运行中的实验加载到traffics中,traffics的key是每个实验的名字,比如exp1,traffics的值是traffic,每个traffic也是一个map结构,traffic的key是每个实验分组的名字,比如这里是group1,group2。traffic的值是每个实验组的桶内编号的集合,这里是一个set结构来存储。如图所示

分流过程

业务方通过解析得到的实验配置,控制该用户命中不同的逻辑。
数据层:将流量的实验分组信息与用户行为日志做关联,分析实验的指标数据。实验效果分析包括实时数据分析和离线数据分析,过程分别如下:
离线数据分析:流量分组日志实时写入到kafka,这部分分组数据作为离线数据一部分写入到hive表中,与存储在hive表中的用户行为数据,按照用户id做关联,关联得到的用户在各个实验方案下的行为数据写入到clickhouse中。
实时数据分析:流量分组日志实时写入到kafka,这部分分组数据作为实时数据写入到hbase中。同时,用户行为日志数据由dig埋点服务实时写入到行为日志的kafka中,spark-streaming实时任务仍然按照用户id整合kafka中的行为日志数据和存储在hbase中的流量分组数据。整合之后的数据实时写入到kafka,再由实时任务消费写入到clickhouse。
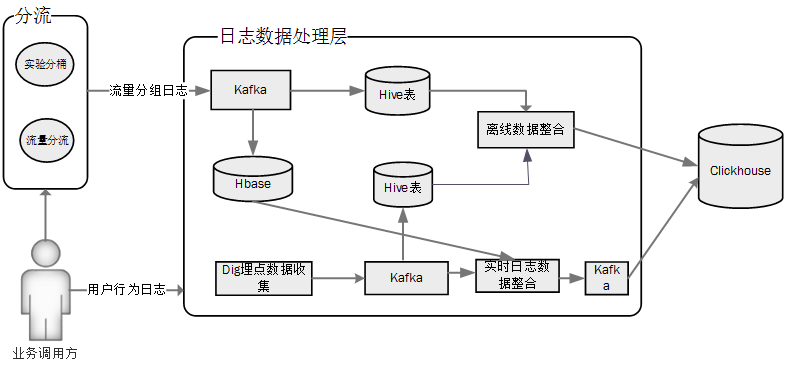
经过对存储在clickhouse中的数据通过复杂的SQL进行聚合分析,得到用户在相应实验方案下的pv、uv、转化等数据

存储层:ab平台的存储层主要包括:
- mysql:用于保存实验配置、白名单配置、实验受众信息。
- Hbase:存储用户命中AB实验分组信息,用于实时处理的分组日志数据整合。
- redis:借助其高性能的数据写入和读取特性,用于存储和用户请求分流直接相关的uniqId对应的cookie信息、白名单包含的用户id、人群包包含的用户id集合,保证请求分流能够1-2毫秒内快速高效完成。
- clickHouse:这是一款能够支持十亿级日志数据秒级自定义分析的查询引擎,其高效的存储性能以及丰富的数据聚合函数成为实验效果分析的不二选择。离线和实时整合后的用户命中的实验分组对应的行为日志数据最终都导入了clickhouse,用于计算用户对应实验的一些埋点指标数据(主要包括pv、uv)。

interleaving
问题
- 算法工程师们日益增长的AB Test需求和线上AB Test资源严重不足之间的矛盾 —— 需要一个快速的线上评估方法
- abtest的好处是能够对多个策略的效果差异给出定量的评估,但是也存在一些问题
- ① 如果两个策略的效果差异较小,abtest容易给出波动较大的结果;
- 即使AB两组之间重度可乐消费者的微小不平衡也可能对结论产生不成比例的影响
- 总的测试人群中,对于可乐的消费习惯肯定各不相同,从几乎不喝可乐到每天喝大量可乐的人都有。
- 可乐的重消费人群肯定只占总测试人群的一小部分,但他们可能占整体汽水消费的较大比例。
- Netflix场景下,非常活跃用户的数量是少数,但其贡献的观看时长却占较大的比例,因此,Netflix AB Test中活跃用户被分在A组的多还是被分在B组的多,将对结果产生较大影响,从而掩盖模型的真实效果。
- 如何解决这个问题呢?一个方法是不对测试人群进行分组,而是让所有测试者都可以自由选择,按比例平均,这个方案(interleaving)的优点
- 消除了AB组测试者自身属性分布不均的问题;
- 通过给予每个人相同的权重,降低了重度消费者对结果的过多影响。
- 即使AB两组之间重度可乐消费者的微小不平衡也可能对结论产生不成比例的影响
- ② 需要较长时间(一般是一周)才能判断结果,会导致效果迭代速度较慢。
- ① 如果两个策略的效果差异较小,abtest容易给出波动较大的结果;
interleaving
为了解决这个问题,采用interleaving效果评估方式作为补充。
- Interleaving方式的好处是所需流量较小,灵敏度较高,一般24小时之内可以给出结论,但是它只能给定性结论而不能给定量结论。
- Interleaving的基本思想是把两个策略的结果混合在一起,通过统计分析用户选择哪个策略的概率更大。具体列表混合的实现方式有多种。下面介绍比较简单使用的一种,叫Balanced方式。
Netflix设计了一个两阶段的线上测试过程(如图2)。参考:Netflix推荐系统模型的快速线上评估方法——Interleaving
- 第一阶段利用被称为Interleaving的测试方法进行候选算法的快速筛选,从大量初始想法中筛选出少量“优秀的”Ranking算法。
- 第二阶段是对缩小的算法集合进行传统的AB Test,以测量它们对用户行为的长期影响。
 使用Inter leaving进行快速线上测试。 用灯泡代表候选算法。 其中,最优的获胜算法用红色表示。Interleaving能够快速地将最初的候选算法集合进行缩减,相比传统的AB Test更快地确定最优算法。
使用Inter leaving进行快速线上测试。 用灯泡代表候选算法。 其中,最优的获胜算法用红色表示。Interleaving能够快速地将最初的候选算法集合进行缩减,相比传统的AB Test更快地确定最优算法。
AB Test和Interleaving之间的差异。
- 在传统的AB Test中,Netflix会选择两组订阅用户:一组接受Ranking算法A的推荐结果 ,另一组接受Ranking算法B的推荐结果。
-
在Interleaving测试中,只有一组订阅用户,这些订阅用户会接受到通过混合算法A和B的排名生成的交替排名。

- 传统AB Test和Interleaving 在传统AB Test中,测试用户分为两组,一组暴露于排名算法A ,另一组暴露于算法B,在两组之间进行比较观看时长等核心评估指标。另一方面,Interleaving将所有测试用户暴露于算法A和B的混合排名,再比较算法相对应的item的指标
这就使得用户同时可以在一行里同时看到算法A和B的推荐结果(用户无法区分一个item是由算法A推荐的还是算法B推荐的)。进而可以通过计算观看时长等指标来衡量到底是算法A好还是算法B好。
局限性
Interleaving方法也存在一定的局限性,主要是下面两点:
- 工程实现的框架较传统AB Test复杂。由于Interleaving实验的逻辑和业务逻辑纠缠在一起,因此业务逻辑可能会被干扰。而且为了实现Interleaving,需要将大量辅助性的数据标示添加到整个数据pipeline中,这都是工程实现的难点;
- Interleaving毕竟只是对用户对算法推荐结果偏好程度的相对测量,不能得出一个算法完整的表现。比如我们想知道算法A能够将用户整体的观看时长提高多少,使用Interleaving是无法得出这样的结论的。为此Netflix才设计了Interleaving+AB Test两级实验结构,完善整个线上测试的框架。
服务部署
- 蓝绿部署、A/B 测试以及灰度发布
- 蓝绿部署、 A/B 测试、灰度发布,这三者之间究竟有何不同?
蓝绿部署
- Martin Flower曾在文章中阐述了蓝绿部署的整体要点。
- 基本上,蓝绿部署是一种以可预测的方式发布应用的技术,目的是减少发布过程中服务停止的时间。简单来说,你需要准备两个相同的环境(基础架构),在蓝色环境运行当前生产环境中的应用,也就是旧版本应用,如图中App1 version1、App2 version1、App3 version3。

-
当你想要升级App2到version2,在蓝色环境中进行操作,即部署新版本应用,并进行测试。如果测试没问题,就可以把负载均衡器/反向代理/路由指向蓝色环境了。
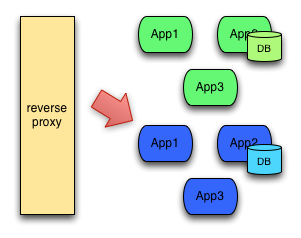
- 随后你需要监测新版本应用,也就是App2 version2是否有故障和异常。如果运行良好,就可以删除App2 version1使用的资源。如果运行出现了问题,你可以通过负载均衡器指向快速回滚到绿色环境。
- 理论上听起来很棒,但还是要注意一些细节:
- 当你切换到蓝色环境时,需要妥当处理未完成的业务和新的业务。如果你的数据库后端无法处理,会是一个比较麻烦的问题;
- 有可能会出现需要同时处理“微服务架构应用”和“传统架构应用”的情况,如果在蓝绿部署中协调不好这两者,还是有可能导致服务停止的;
- 需要提前考虑数据库与应用部署同步迁移/回滚的问题;
- 蓝绿部署需要有基础设施支持
- 在非隔离基础架构(VM、Docker等)上执行蓝绿部署,蓝色环境和绿色环境有被摧毁的风险
A/B Testing
- A/B测试跟蓝绿部署完全是两码事。A/B测试是用来测试应用功能表现的方法,例如可用性、受欢迎程度、可见性等等。A/B测试通常用在应用的前端上,不过当然需要后端来支持。
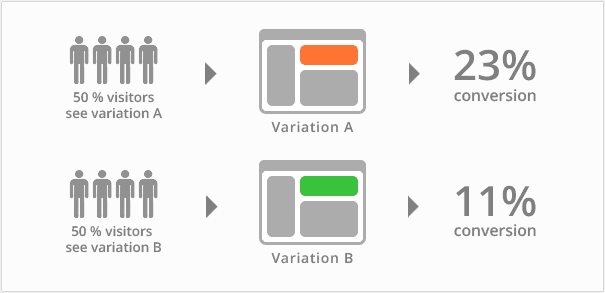
- A/B测试与蓝绿部署的区别在于,A/B测试目的在于通过科学的实验设计、采样样本代表性、流量分割与小流量测试等方式来获得具有代表性的实验结论,并确信该结论在推广到全部流量可信;蓝绿部署的目的是安全稳定地发布新版本应用,并在必要时回滚。A/B测试和蓝绿部署可以同时使用。
灰度发布/金丝雀发布
- 灰度发布是在原有版本可用的情况下,同时部署一个新版本应用作为“金丝雀”(金丝雀对瓦斯极敏感,矿井工人携带金丝雀,以便及时发发现危险),测试新版本的性能和表现,以保障整体系统稳定的情况下,尽早发现、调整问题。
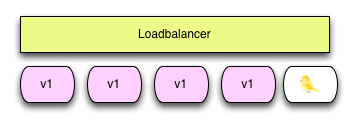
灰度发布/金丝雀发布由以下几个步骤组成:
- 准备好部署各个阶段的工件,包括:构建工件,测试脚本,配置文件和部署清单文件。
- 从负载均衡列表中移除掉“金丝雀”服务器。
- 升级“金丝雀”应用(排掉原有流量并进行部署)。
- 对应用进行自动化测试。
- 将“金丝雀”服务器重新添加到负载均衡列表中(连通性和健康检查)。
-
如果“金丝雀”在线使用测试成功,升级剩余的其他服务器。(否则就回滚)
- 灰度发布可以保证整体系统的稳定,在初始灰度的时候就可以发现、调整问题,以保证其影响度。
- 灰度发布/金丝雀部署适用的场景:
- 1、不停止老版本,额外搞一套新版本,不同版本应用共存。
- 2、灰度发布中,常常按照用户设置路由权重,例如90%的用户维持使用老版本,10%的用户尝鲜新版本。
- 3、经常与A/B测试一起使用,用于测试选择多种方案。AB test就是一种灰度发布方式,让一部分用户继续用A,一部分用户开始用B,如果用户对B没有什么反对意见,那么逐步扩大范围,把所有用户都迁移到B上面来。
滚动发布(rolling update)
- 滚动发布,一般是取出一个或者多个服务器停止服务,执行更新,并重新将其投入使用。周而复始,直到集群中所有的实例都更新成新版本。这种部署方式相对于蓝绿部署,更加节约资源——它不需要运行两个集群、两倍的实例数。我们可以部分部署,例如每次只取出集群的20%进行升级。
- 这种方式也有很多缺点,例如:
- (1) 没有一个确定OK的环境。使用蓝绿部署,能够清晰地知道老版本是OK的,而使用滚动发布,无法确定。
- (2) 修改了现有的环境。
- (3) 回滚很困难。举个例子,在某一次发布中,我们需要更新100个实例,每次更新10个实例,每次部署需要5分钟。当滚动发布到第80个实例时,发现了问题,需要回滚。此时,脾气不好的程序猿很可能想掀桌子,因为回滚是一个痛苦,并且漫长的过程。
- (4) 有的时候,我们还可能对系统进行动态伸缩,如果部署期间,系统自动扩容/缩容了,我们还需判断到底哪个节点使用的是哪个代码。尽管有一些自动化的运维工具,但是依然令人心惊胆战。
- 并不是说滚动发布不好,滚动发布也有它非常合适的场景。
红黑部署(Red-Black Deployment)
- 这是Netflix采用的部署手段,Netflix的主要基础设施是在AWS上,所以它利用AWS的特性,在部署新的版本时,通过AutoScaling Group用包含新版本应用的AMI的LaunchConfiguration创建新的服务器。测试不通过,找到问题原因后,直接干掉新生成的服务器以及Autoscaling Group就可以,测试通过,则将ELB指向新的服务器集群,然后销毁掉旧的服务器集群以及AutoScaling Group。
- 红黑部署的好处是服务始终在线,同时采用不可变部署的方式,也不像蓝绿部署一样得保持冗余的服务始终在线。
总结
- 对于云计算来说,以上三种策略都是可用的。不难想象,通过docker和kubernetes,我们可以很简单的实现蓝绿部署、A/B测试、灰度发布……比如好雨云,深度整合Docker和Kubernetes,提供给用户包括代码滚动上线、一键代码回滚等功能和特性在内的强大的CI/CD体验:)
应用
- 【2021-1-11】策略算法工程师之路-因果分析.科学实验评估
-
- A/B Test原理
-
- 实验分组划分
-
- 实验指标设计
-
- 实验效果评估
-
- 离线指标测算
-
- 实验结果分析
-
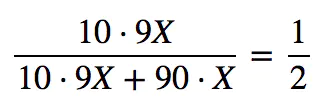
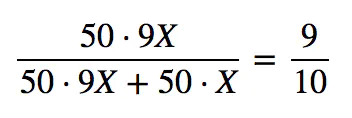





 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
