Scaling Law 缩放定律
Scaling Law 类型
(1) 世上没有永远持续的增长,只有S型曲线式增长
- 不存在无限增长的事情是个定则,即使把目光拉长放到宇宙级视野里,宇宙中最大速度也不可能超过光速,宇宙它再大也总有个边界
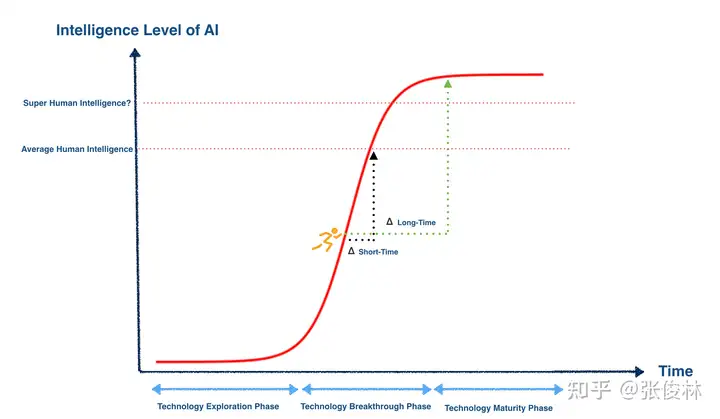
(2) S型智能曲线的叠加仍然是S型曲线
(3) 三种 Scaling Law: Pre-train、RL、Test Time
大模型训练有三个阶段:预训练、后训练和在线推理(inference)。
- 24年9月前,大模型领域只有一个Scaling Law,预训练阶段的Scaling Law,之前炒的比较热的“Scaling Law撞墙说”就是这个阶段。
- OpenAI o1推出后,另外两个阶段不再孤单,也各自拥有了姓名,产生了各自的Scaling Law,对应后训练阶段的强化学习Scaling Law(RL Scaling Law)和在线推理阶段的Inference Scaling Law(也叫Test Time Scaling Law)。
核心思想:本阶段,如果增加算力,则大模型效果会持续提升。
三阶段Scaling Law智能叠加
- 预训练阶段 Scaling Law 普遍认为已经走缓(绿色曲线,对应Sigmoid的K数值相对应该较低);
- 而O1/R1类模型开启了RL和Test Time阶段的新型Scaling Law。
- 很明显,这两个阶段Scaling Law对应Sigmoid函数K数值应该比较大,因为只需增加较少的算力,大模型的智力水平就得到了剧烈的增长,说明对应的走势是比较陡峭的(RL阶段比Test Time阶段应更陡峭些)。
- RL和Test Time Scaling law并不应和预训练阶段Scaling Law等效,它们增强的主要是逻辑推理能力
【2025-2-10】张俊林
Pretrain Scaling Law
中山大学 CMR Critical Mixture Ratio
- 【2024-7-25】CMR Scaling Law: Predicting Critical Mixture Ratios for Continual Pre-training of Language Models
持续预训练(CPT)在重放通用语料库的同时注入新领域特定或专有知识来增强LLM能力,以防止灾难性遗忘。
然而,通用语料库和特定领域语料库的数据混合比例通常是根据经验选择,导致实际中训练效率不佳。
尝试重新审视CPT下LLMs 缩放行为,并发现了损失、混合比例和训练令牌规模之间的幂律关系。形式化了通用和领域特定能力之间的权衡,导致了明确定义的通用和领域数据的关键混合比率(CMR)。
通过平衡CMR,保持模型的通用能力并实现所需的领域转移,确保充分利用可用资源。
因此,如果重视效率和效果之间的平衡,CMR可以被认为是最佳混合比率。通过广实验,确定CMR可预测性,并提出了CMR的缩放定律,并证实了其泛化性。这些发现为优化专业领域中LLM的训练提供了实用的指导,确保在高效管理训练资源的同时实现通用和领域特定的性能。
思考
Scaling Law 到头了
2024年2月末, 唐杰教授表示: Scaling Law 尽头不一定是AGI,从人脑的认知角度改进未来的AGI系统,使它变得更加智能,这是我们未来要思考的问题。
【2025-11-26】
Dwarkesh Patel 新一期播客采到了 Ilya
Ilya 最新采访:
- AI为什么总在泛化上输给人类?
- 如何保证安全与对齐?
- 预训练范式有什么问题?
目前主流「预训练 + Scaling」路线已经明显遇到瓶颈。与其盲目上大规模,不如把注意力放回到「研究范式本身」的重构上。
(1)时代转向
Ilya 给出非常清晰的时间线划分:
- 2012 - 2020 年是研究时代:大家都在尝试不同的 AI 想法。
- 2020 - 2025 年是 Scaling 时代: 自从 GPT-3 出现后,Scaling 成了共识,并吸走了所有的注意力和资源。
- 2025 开始,Pre-training 的 scaling law 已经失效了 (核心因为数据有限),所以,正在重新回到 “研究时代”。之后不会再比谁的 GPU 多,而是看谁能找到新的算法。
(2)SSI 规划
Ilya 创办的 SSI (Safe Superintelligence) 计划 Straight shot:即不发中间产品,直接憋大招做超级智能。
因为现在的 AI 公司为了市场份额,不得不陷入激烈竞争,不断妥协。所以,不发中间产品,不希望在中间过程受到市场干扰。
他对超级智能的定义是 “超级学习者”:发布的那一刻,更像是 “天才少年”,被投放到社会中,在各个岗位上快速实习、犯错、进步。
这种能像人类一样学习、进而变成超级智能的系统什么时候会出现?
- Ilya 很少给出具体的时间预测,但这次出乎意料地给了窗口期 —— 5-20 年。
外界质疑:SSI 只融 30 亿美金,可能比不过大厂
- Ilya 算账:大厂融钱虽多,但大部分要用来服务用户做推理、养庞大的工程和销售团队。
- SSI 的钱是实打实全部投入到纯粹的研究实验,这在 Research 层面上其实非常能打。
(3)如何高质量判断
Ilya 是公认的 Research Taste 最好的科学家
三个黄金标准:
- 生物学合理性:比如神经元概念,虽然大脑很复杂,但 “大量神经元连接”结构更为本质。
- 简洁美感:如果方案不够简洁、优雅,那大概率是错的。
- Top-down 信念:当实验数据和预期不符时,如果有基于第一性原理的信念感,会继续坚持坚持,相信只是代码有Bug。这是平庸研究者和顶级研究者的关键区别,因为这种信念支撑他度过了无数次失败。
(4)Value Function
Pre-training 红利吃完了,下一步重点:Value Function (价值函数)。
现在 RL 还很笨。比如做长推理题
- 模型要等到最后一步做完,才知道自己是对是错。
- 但人类下棋时丢了一个子,立刻就知道这局完了,而不需要等到整盘棋下完。
人类学习过程一向主要来自与环境互动和内心感觉,一种很高效的无监督学习形式。
未来的突破点:让模型也具备这种直觉性的中途判断能力。如果攻克了这个学习机制,AI 效率就会有质的飞跃。
质疑:“Value Function 可能很难学,因为推理的路径太复杂、太宽广”.
Ilya 回应: “你听起来像是对深度学习缺乏信仰”。
Ilya 非常笃信,只要信号存在,深度学习就能学到。虽然很难,但没有什么是深度学习做不到的 (echo 前面顶尖 researcher 的信念感)。
(5)RL认知
Ilya 反直觉的观点:RL 可能在糊弄模型。
预训练数据不仅仅是文字,还是“整个世界被人类投射到文本上的样子”。预训练之所以强,是因为试图捕捉这个庞大的 “人类思想投影”。而目前 RL 方法可能实际上是在 “Undoing the conceptual imprint of pre-training” (撤销预训练的概念印记)。
这是为什么经过重度 RL 对齐的模型,往往更笨或更缺乏创造力。RL 强行让 AI 去讨好人类的某个单一指标,却可能牺牲了原本宽广的通用智力。(像极了应试教育…)
RL 已经比 Pre-training 更烧钱
- RL 要做非常长的 Rollouts,不同推演,这极其消耗算力,而每做一次推演获得的有效学习信号却很少。
(6)情绪 = 终极的 Value Function
为什么人类能在信息不全的情况下做出正确的常识性决策,而 AI 经常一本正经地胡说八道?
Ilya 提到神经科学案例:一个因脑损伤失去 “情绪” 的人,虽然智商没变,但却连 “今天穿什么袜子” 都要纠结几个小时,完全无法做决策。
情绪就是人类进化出的最有效的 “压缩算法”,快速剪枝,知道什么是重要的,什么无关紧要。
而现在的 AI 就像那个失去情绪的病人,有逻辑,但缺乏那个指引 “什么是对的” 的内在罗盘。
这也许是通往 AGI 的最后一块拼图。
(7)同理心是理解世界的最佳捷径
Ilya 最关心的还是安全和对齐。
-
目前解法:找到一种编码机制,让 AI 真正关爱有感知力的生命 (sentient Life)。就像进化论在人类大脑中硬编码了同理心一样,我们要把这种对生命的关爱硬编码进超级智能里,这比通过各种规则约束,强行让 AI 听人类的话更靠谱
-
如果 AI 追求极致的预测效率和世界模型构建,可能会涌现出类似的 “移情” 机制。
这种机制能实现吗?可以,两点原因:
- 首先,这极其硬核,可以提升计算效率。人类之所以能理解别人的痛苦,是因为会用“模拟自己” 同一套神经回路去 “模拟别人”。这是大脑最高效的建模方式。同理心可能是智能提升过程中的一种涌现属性,因为它是理解世界的最佳捷径。
- 人类进化过程中非常神奇的特质,进化出一些高级奖励函数,比如 “社会地位”这种极其抽象的概念,大脑需要处理无数信息才能理解
如何连线神经元,才能让人类产生这种高级情感?
既然盲目的进化都能成功地把 “高级价值观” 对齐给人类,那么设计超级智能时,一定也存在某种方法,能把 “关爱生命” 这种高级目标硬编码进 AI 的底层——即使我们现在还不知道具体原理。
(8)语言对思维的影响
Ilya 提出有趣的现象:语言会反向塑造行业的研究方向。比如:
- 词汇 AGI 是为了反驳 Narrow AI(弱人工智能)而诞生,但这导致大家过度追求全能基础模型,而忽略了真正的智能其实是动态学习能力。
- 词汇 Scaling 出现后,所有人都觉得 “只要把模型做大就好”,而很大程度上停止探索了其他可能性
所以,警惕流行词!
(9)未来格局
未来是不是只有一家公司垄断 Superintelligence ?
- Ilya 给出基于生物进化的判断:不会,竞争喜欢专精(Competition loves specialization)。
- 即便 AI 再强,未来大概率也会出现分工。比如会有一家公司,不做别的,就专门做 “诉讼”。
LLM 为什么都是 6b/13b/52b…
需求:
- 训练10B模型,至少要多大数据?
- 1T数据能训练多大模型?
- 100张A100,应该用多少数据训一个多大模型,最终效果最好?
- 10B模型不满意,扩大到100B模型,效果能提升到多少?
以上这些问题都可以基于 Scaling Law 理论进行回答。
总结
scaling law 指导下,匹配当前的显卡资源和数据资源
最大尺寸版本确定的核心逻辑是: DeepMind 的 Chinchilla Scaling Law。
开发大模型时,清洗出来的开源数据数量是离散值。
- LLaMA-1 预训练时,从各种开源数据集凑够了 1.4T tokens,所以最大版本是70B,很接近
Chinchilla Scaling Law的计算结果。 - 用1024张A100,MFU=0.55情况下,训练时长大概是38天,这是一个比较可行的预训练方案。
- 至于更小版本选型比较随意,主要考虑调试时,计算量要控制在一个可控范围,比如一般会选择一个10^22 FLOPs计算量(差不多256卡两三天出结果)下的最优模型尺寸,因此最优尺寸肯定是在10B以内。由于一些矩阵维度的限制,一般都是6B,7B。
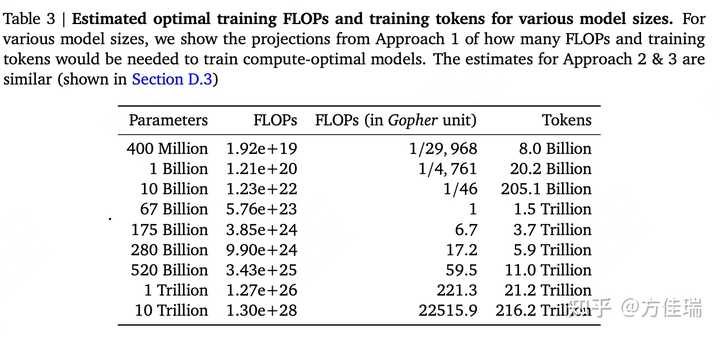
Chinchilla Scaling Law有些争议,正溯还是得看OpenAI文章Scaling laws for neural language models,过去一年内大家还是会follow这套理论。
LLM 一般都是基于Transormer结构,参数总和 = Embedding部分参数 + Transormer-Decoder部分参数
- Embedding 部分参数由词表大小和模型维度决定;
- Decoder 部分参数由模型层数和模型维度决定。
决定参数的几个因素有:词表大小、模型层数(深度)、模型维度(宽度)。
- 关于词表大小设置,越大的词表的压缩会更好,但可能导致模型训练不充分;越小的词表压缩会比较差,导致模型对长度需求较高。
- 关于层数设置问题,其实模型层数和维度具体设置成多少是最优的(但一般层数变大,维度也会变大),目前没有论文明确表明,但绝大多数感觉跟着GPT3的层数和维度来的。
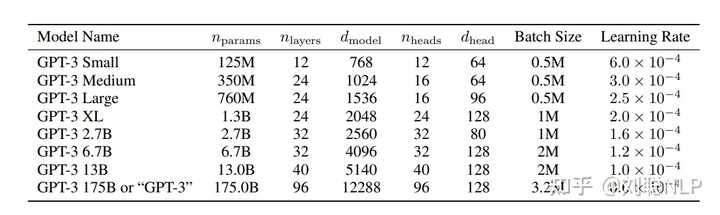
常见模型 6/7B 是32层、13B 是40层。
PS:由于GPT3模型先出,让OPT、Bloom等都是为了做开源的GPT3所提出的,因此参数规模是一致的。
- llama 为了对标GPT3,不过为了证明效果更好,也在中间多了
33B和65B规模。 130B只有GLM大模型是这个参数。
现在流传甚广的其实是6/7B(小)、13B(中),主要是由于更大的模型训练成本会更高,并且对于很多人来说13B的模型已经算顶配了(消费显卡跑得了)。
语言模型进化
【2024-8-10】大语言模型 Scaling Law:如何随着模型大小、训练数据和计算资源的增加而扩展
缩放定律
- 一个由三个关键部分组成的法则:
模型大小、训练数据和计算能力
过去几年,语言模型迅速发展壮大。
- 语言模型从 2018年的 BERT-base 的1.09亿参数规模,增长到 2022年的 PaLM 的5400亿参数。
- 每个模型不仅在模型规模上增加(即参数数量),还在训练令牌数量和训练计算量(以浮点运算或FLOPs计)上都有所增加。
| Time | Company | Model | Model Size #parameters |
Training data #tokens |
Training compute FLOPs |
Resources |
|---|---|---|---|---|---|---|
| 2018 | BERT-base |
109M | 250B | 1.6e20 | 64 TPU v2 for 4 days 16 v100 GPU for 33 hours |
|
| 2020 | OpenAI | GPT-3 |
175B | 300B | 3.1e23 | ~1000 x BERT-base |
| 2022 | PaLM |
540B | 780B | 2.5e24 | 64 TPU v4 for 2 months |
问题
- “这三个因素之间有什么关系?”
- 模型大小和训练数据对模型性能(即测试损失)的贡献是否相等?哪一个更重要?
- 如果将测试损失降低10%,我应该增加模型大小还是训练数据?需要增加多少?
幂律函数
幂律是两个量x和y之间的非线性关系,建模为:
- $ y = ax^k $
- $ logy = loga + klogx$
- 其中k和a是常数。
幂律曲线
import numpy as np
import matplotlib.pyplot as plt
def plot_power_law(k, x_range=(1, 100), num_points=100):
"""
Plot the power law function y = x^k for any non-zero k.
Parameters:
k (float): The exponent for the power law (can be positive or negative, but not zero).
x_range (tuple): The range of x values to plot (default is 0.1 to 10).
num_points (int): Number of points to calculate for a smooth curve.
"""
if k == 0:
raise ValueError("k cannot be zero")
# Generate x values
x = np.linspace(x_range[0], x_range[1], num_points)
# Calculate y values
y = x**k
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'ro', label=f'y = x^{k}')
#plt.barh(x, y)
plt.title(f'Power Law: y = x^{k}')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.legend()
plt.show()
plot_power_law(2) # y = x^2
plot_power_law(-0.5) # y = x^(-0.5)
三要素
大语言模型的预训练,通常伴随着模型容量、数据量、训练成本的三方权衡博弈。
这种三角形式的拔河关系存在一些三元悖论,比如
- 分布式计算领域中的公认定理:
CAP理论: 分布式系统不可能同时满足一致性、可用性和分区容错性,最多只能同时满足其中2个条件。 - 大语言模型训练同样存在类似这种三元关系的探索,这就是
缩放定律(Scaling Laws)。
大语言模型预训练过程中,交叉熵损失(cross-entropy loss)是一种常用的性能衡量标准,用于评估模型预测输出与真实情况之间的差异。较低的交叉熵损失意味着模型的预测更准确。训练的过程也是追求损失值的最小化的过程。
什么是 Scaling Laws
背景
源自浙大书籍《大语言模型》章节
- 模型规模和训练数据的增长带来巨大的计算、存储成本,大力出奇迹难以为继。
- 模型设计时,如何在资源消耗、性能提升之间找到平衡点?
大语言模型的扩展法则(Scaling Laws)诞生, 揭示模型能力岁模型规模和数据规模的变化关系,为 LLM 设计和优化提供指导建议。
Scaling Laws 意义:
- AI专业人士可通过 Scaling Laws 预测大模型在
参数量、数据量以及训练计算量这三个因素变动时,损失值的变化。 - 为LLM设计提供决策支持,比如在固定资源预算下,匹配模型的最佳大小和数据大小,而无需进行及其昂贵的试错。
规模化法则(缩放法则)(Scaling Law)指 模型性能与模型大小、数据集大小和计算资源等多种因素之间观察到的关系。
随着模型的扩展,这些关系遵循可预测模式。
扩展法则行为的关键因素如下:
- 模型大小:随着模型中参数数量的增加,性能通常会按照幂律改善。
- 数据集大小:更大的训练数据集通常带来更好的性能,也遵循幂律关系。
- 计算:用于训练的计算资源(浮点运算次数)与性能改善相关。
测试集损失与计算、数据集大小和模型参数之间遵循幂律关系(对数线性)
Training Compute= alpha *Model Size*Training Data- alpha ~ 6
每个参数和每个训练实例需要大约6次浮点运算(FLOPs)
- 前向传播中,需要恰好2次FLOPs将w与输入节点相乘,并将其添加到语言模型的计算图的输出节点中。(1次乘法和1次加法)
- 计算损失对w的梯度时,需要恰好2次FLOPs。
- 用损失的梯度更新参数w时,需要恰好2次FLOPs。
【2024-9-20】AI can’t cross this line and we don’t know why
Scaling Law 定义
主要有两个版本: OpenAI V.S DeepMind
- OpenAI 提出的
Kaplan-McCandlish扩展法则 - Google DeepMind 提出的
Chinchilla扩展法则
更多见【2024-1-5】OpenAI与DeepMind的Scaling Laws之争
2020 Kaplan-McCandlish Scaling Law
2020年, OpenAI 团队的 Jared Kaplan 和 Sam McCandlish 等人首次研究了神经网络性能与数据规模D、模型规模N之间的函数关系。 Kaplan-McCandlish
OpenAI
“Our mission is to ensure that artificial general intelligence—AI systems that are generally smarter than humans—benefits all of humanity.”
—— 2023年2月14日《Planning for AGI and beyond》
谷歌收购 DeepMind 后,为避免谷歌在AI领域形成垄断,埃隆·马斯克和其他科技行业人物于2015年决定创建OpenAI。
OpenAI 作为一个有声望的非营利组织,致力于开发能够推动社会进步的AI技术。不同于 DeepMind 像一个精于解决棋盘上复杂战术的大师,专注于解决那些有明确规则和目标的难题,OpenAI更像是一个擅长语言艺术的诗人,致力于让机器理解和生成自然的人类语言。
从坚持初期被外界难以理解的GPT路线信仰,直到拥有1750亿参数的GPT-3问世,OpenAI展示了其在生成式模型上无与伦比的能力,引领了另一个AI时代。类比Deepmind和谷歌的关联,OpenAI与科技巨头微软牵手,展开了深度的战略合作,进一步推进AI技术的发展。
OpenAI 发布
- 【2020-1-23】论文 Scaling Laws for Neural Language Models
- OpenAI 官方文章 Scaling laws for neural language models
- 解读
- 【2020-11-6】第二篇文章 OpenAI Scaling Paper: Scaling Laws for Autoregressive Generative Modeling, 解析大模型中的Scaling Law
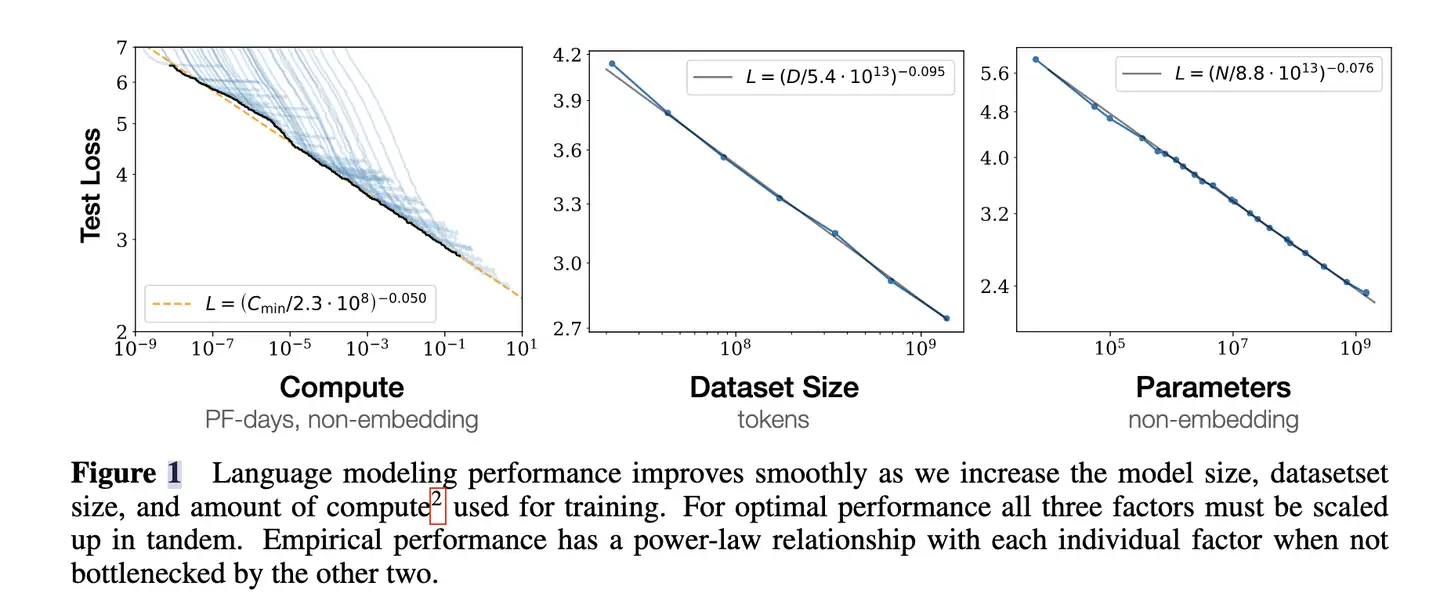
公式
$L(D)=\left(\frac{D}{D_{c}}\right)^{\alpha_{D}}, \alpha_{D} \sim-0.095, D_{c} \sim 5.4 \times 10^{13}$
$L(N)=\left(\frac{N}{N_{c}}\right)^{\alpha_{N}}, \alpha_{N} \sim-0.076, N_{c} \sim 8.8 \times 10^{13}$
说明
- L 值衡量模型拟合数据分布的准确性, 数值越小拟合越精确,对应学习能力就越强
- 模型最终性能主要与计算量
C,模型参数量N和数据大小D三者相关,而与模型结构(层数/深度/宽度)基本无关。 - 模型性能与模型规模以及数据规模这两个因素高度正相关,而规模相同时,模型架构对性能影响相对较小。
- 启发: 要提升模型性能,重点考虑扩大模型规模、丰富训练数据集
- L(N) 表示数据规模固定时, 不同模型规模下的交叉熵损失函数 —— 模型规模对拟合能力的影响
- L(D) 表示模型规模固定时, 不同数据规模下的交叉熵损失函数 —— 数据规模对模型学习能力的影响
核心结论
- 对于 Decoder-only 模型,计算量
C(Flops), 模型参数量N, 数据大小D(token数),三者满足:C ≈ 6ND- 如果计算预算
C增加, 模型要达到最优性能, 数据规模D、模型规模N, 应同步增加 - 但是, 模型规模增长速度应该略快于数据规模, 最优配置比例
Nopt ∝ C^0.73,Dopt ∝ C^0.27, 即 如果总计算预算增加10倍, 模型规模N应扩大 5.37 倍, 而数据规模应扩大 1.86 倍
- 如果计算预算
- 计算量
C,模型参数量N和数据大小D,当不受其他两个因素制约时,模型性能与每个因素都呈现幂律关系 - 为了提升模型性能,模型参数量
N和数据大小D需要同步放大,但模型和数据分别放大的比例还存在争议。 - Scaling Law 不仅适用于语言模型,还适用于其他模态以及跨模态的任务
论文首次提出模拟神经语言模型的模型性能(Loss)与模型大小、数据集大小和训练计算量的关系。
- 三者中任何一个因素受限时,Loss与其之间存在
幂律关系。 - 注:
幂律指一个变量与另一个变量的某个幂次成正比。体现在图表中,当两个轴都是对数时,图像呈现为直线
总结:
- 影响模型性能的三个要素之间,每个参数会受到另外两个参数的影响。
- 当没有其他两个瓶颈时,性能会急剧上升,影响程度为:
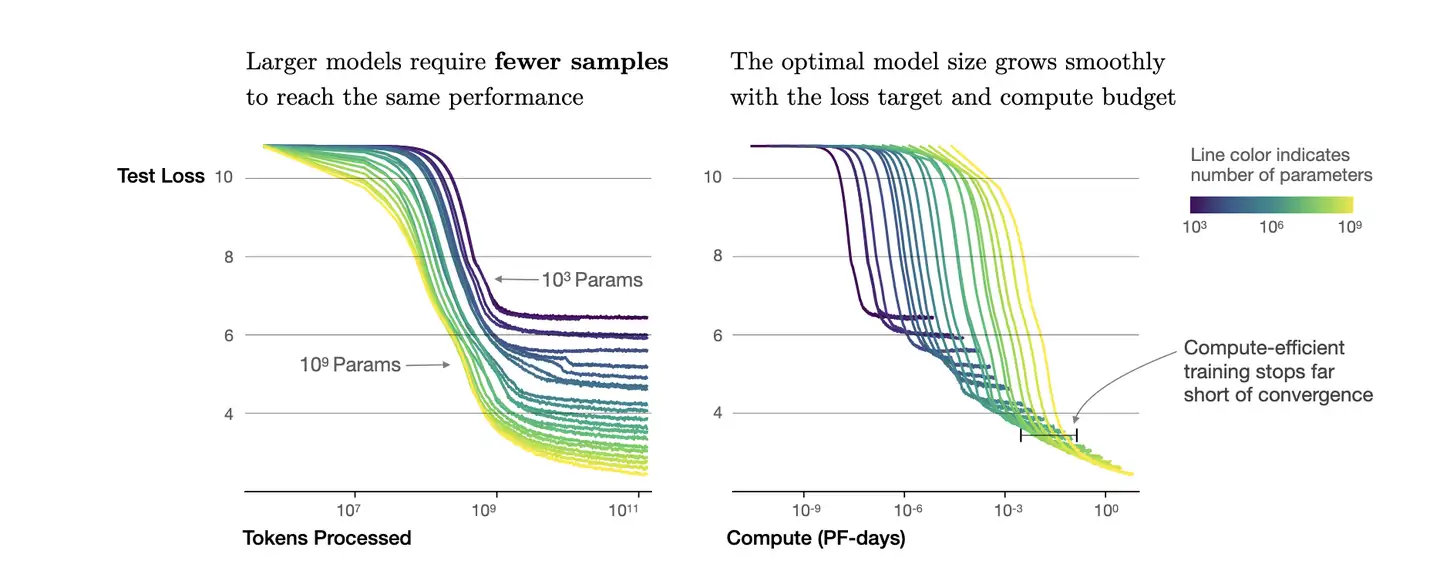
计算量>参数»数据集大小 - 固定计算预算训练时,最佳性能可通过训练参数量非常大的模型并在远离收敛前停止(Early Stopping)来实现。
- 更大的模型在样本效率方面表现更好,能以更少的优化步骤和使用更少的数据量达到相同的性能水平。
- 实际应用中,应该优先考虑训练较大的模型。
因为这项研究,OpenAI 有了在数据和参数规模上 Scaling-up 信心,在同年四月后,火爆全球的GPT3问世。
2022 Chinchilla Scaling Law 数据不变
DeepMind
We’re a team of scientists, engineers, ethicists and more, committed to solving intelligence, to advance science and benefit humanity.
—— DeepMind
DeepMind 成立于2010年, 并于2015年被谷歌收购,是 Alphabet Inc. 子公司。
- 该公司专注于开发能模仿人类学习和解决复杂问题能力的AI系统。
- 作为 Alphabet Inc.的一部分,DeepMind在保持高度独立的同时,也在利用谷歌的强大能力推动AI研究的发展。
DeepMind 在技术上取得了显著成就,包括
- 开发
AlphaGo,击败世界围棋冠军李世石的AI系统,展示了深度强化学习和神经网络的潜力,开启了一个AI时代。 AlphaFold,这是一个革命性的用于准确预测蛋白质折叠的工具,对生物信息学界产生了深远影响。DeepMind用AI进行蛋白质折叠预测的突破,将帮助我们更好地理解生命最根本的根基,并帮助研究人员应对新的和更难的难题,包括应对疾病和环境可持续发展。
OpenAI 说:
- 模型规模增长速度应该略快于数据规模 —— 真的吗?
【2022-3-29】 DeepMind 探索了更大范围的模型(7000w~160b)+数据规模(5b~500b个token),提出了 Chinchilla 扩展法则, 发表论文
- Training Compute-Optimal Large Language Models 根据
Scaling Law,给定计算量(FLOPS)训练出来的最优模型(达到最好模型效果)的训练数据集的token数和模型参数数目是确定的。
Chinchilla 扩展法则是 OpenAI 扩展法则的补充和优化。
- 强调 数据规模 对模型性能提升的重要性
- 模型规模+数据规模应该同等比例增加
开创了LLM发展新方向
- 不再单纯追求扩大模型规模,而是优化模型规模与数据规模比例 —— 别再“大力出奇迹”了!
公式
L(N,D) = E + A/Na + B/Db- E=1.69, A=406.4, B=410.7, a=0.34, b=0.28
- 指定计算量下的最优分配:数据集规模 D 与 模型规模 N
Nopt ∝ C^0.73–>Nopt ∝ C^0.46Dopt ∝ C^0.27–>Dopt ∝ C^0.54
- 数据集量 D 与模型规模同等重要
- 如果计算预算增加10倍,模型规模 和 数据规模 应该扩大约 3.16 倍
- 2023年5月,发布 PaLM2 技术报告,证实以上结论
另外, 理想数据集大小应当是模型规模的20倍
- 7b 模型最理想的训练数据为 140b 个token
- 而 OpenAI的
GPT-3模型最大版本175b, 但训练数据只有300b个token - 微软
MT-NLG模型 530b, 训练数据只有 270b - 于是,
DeepMind推出符合20倍原则的模型:Chinchilla, 70b, 1.4 万亿个token, 性能上取得突破
Gopher 模型计算量预算是 5.76 × 10^23 FLOPs,那么达到最优效果的参数量是 63B,数据集中Token数目为1.4T。
Deepmind 的 Hoffmann 等人团队提出与OpenAI截然不同的观点。
- OpenAI 建议在计算预算增加了10倍情况下,如果想保持效果,模型大小应增加5.5倍,而训练token数量仅需增加1.8倍。
- Deepmind 则认为模型大小和训练token数都应该按相等比例进行扩展,即都扩大3倍左右。
该团队还暗示许多像 GPT-3这样的千亿参数大语言模型实际上都过度参数化,超过了实现良好的语言理解所需,并训练不足。
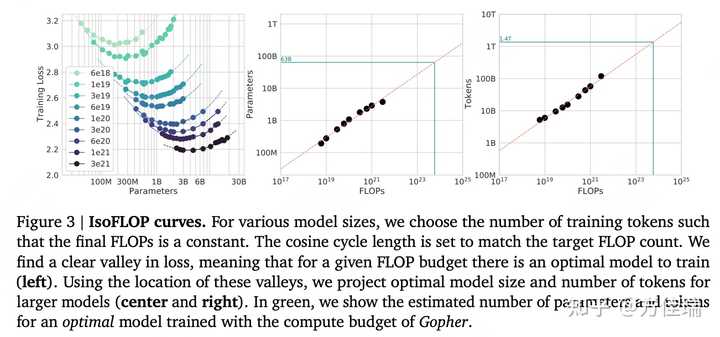
结论:
- 对于给定FLOP预算,损失函数有明显的谷底值:
- 模型太小时,在较少数据上训练较大模型将是一种改进;
- 模型太大时,在更多数据上训练的较小模型将是一种改进。
- 给定计算量下,数据量和模型参数量之间的选择平衡存在一个最优解。
- 计算成本达到最优情况下,模型大小和训练数据 (token) 数量应该等比例进行缩放,即:如果模型的大小加倍,那么训练数据的数量也应该加倍。
- 给定参数量模型,最佳训练数据集大小约为模型参数的20倍。
- 比如,对于一个7B模型,理想训练数据集大小应该约为 140B tokens。
大模型训练要更加关注数据集的扩展,但是只有数据是高质量的时候,更大数据集的益处才能体现出来。
大语言模型发展的一个新方向
- 从一味追求模型规模的增加,变成了优化模型规模和数据量的比例。
保持训练数据不变的情况下,扩大模型大小,当前的大型语言模型实际上训练不足
作者训练了从7000万到超过160亿参数的400多个语言模型,这些模型使用的训练令牌从50亿到5000亿不等,并得出结论:
- 对于计算优化的训练,模型大小和训练令牌数量应该同等规模化。
经验预测公式,将模型大小和训练数据与模型性能联系起来。
L(N,D) = A/N^α + B/D^β + E- N 是参数数量(即模型大小),D 是训练令牌。
- 符号 L(N,D) 指一个拥有 N 个参数并且在 D 个令牌上训练的模型的性能或测试损失。
- E 是一个常数,代表不可约减的损失,即模型在完美训练的情况下能够达到的最小损失。它考虑了模型所训练的任务的固有难度和数据中的噪声。
常数 A 和 B 以及指数 α 和 β 通过实验和数据拟合经验性地确定。
- α≈0.50 和 β≈0.50。
- 主要发现: 每翻倍增加模型大小时,训练令牌的数量也应该翻倍,以实现计算最优训练
边际效益递减
- 随着模型规模的增大,每增加相同数量的参数/计算资源,获得的性能提升逐渐减少的现象。
这是 Scaling Law 中非常关键的一个方面,它对于理解和决策模型设计及其部署策略有着重要的指导意义。
原因和表现
- 对数关系:很多研究中观察到,模型性能(如测试集上的准确率或其他指标)与模型大小(通常是参数数量或计算复杂度)呈对数关系。随着模型规模的扩大,要获得同样幅度的性能提升,需要的资源增加将更为显著。
- 资源效率的降低:当模型规模达到一定阶段后,继续增加模型的大小,其性能提升不再明显,而相对应的训练成本、时间和能源消耗却显著增加。这种现象表明,从成本效益角度出发,模型规模的无限扩大并不合理。
- 技术挑战:较大的模型更难训练,可能会面临梯度消失或爆炸、过拟合等问题,这些技术挑战也限制了模型性能的持续提升。
应对策略
- 模型和算法创新:通过改进模型架构、优化算法或引入新的训练技术(如稀疏化、量化等),可以在不显著增加参数的情况下提高模型的效率和效果。
多任务学习和迁移学习:利用多任务学习和迁移学习技术可以提高模型的泛化能力,使得模型在多个任务上具有更好的性能,这种方式可以在一定程度上克服单一任务上的边际效益递减问题。- 选择适当的规模:根据应用场景的实际需求和可用资源,选择合适的模型规模,避免资源的浪费,实现性能与成本的最优平衡。
缩放法则对AI研究者和工程师具有重大意义:
- 平衡规模化:Chinchilla 强调了同时对模型大小和训练数据进行等比例规模化以达到最佳性能的重要性。这挑战了之前仅增加模型大小的重点。
- 资源分配:理解这些关系可以更有效地分配计算资源,可能导致更具成本效益和环境可持续的人工智能发展。
- 性能预测:这些法则使研究人员能够根据可用资源做出有根据的模型性能预测,帮助设定现实的目标和期望。
Scaling Law 观点
Chomsky (乔姆斯基) 认为
- 尽管模型可以做到句法分析,但仍然无法理解语义
观点
- 句子可以有意义,但还不能让段落连贯起来。
最新质疑
- 数据马上就要耗尽了
- 数据质量不够高
- 模型不能进行推理等等
量化不管用
【2024-11-13】 Scaling Law终结,量化也不管用,AI大佬都在审视这篇论文
哈佛、斯坦福、MIT等团队的一项研究表明:训练的token越多,需要的精度就越高。
- 例如,Llama-3在不同数据量下(圆形8B、三角形70B、星星405B),随着数据集大小的增加,计算最优的精度也会增加。
- 对于大规模的训练任务,低精度的量化可能不再足够有效。
按照结论,对 Scaling Law 的遵循意味着需要保持更高精度,然而一直以来,人们通常会选择量化(将连续值或多精度值转换为较低精度)来节省计算资源。
一旦结论成立,GPU 设计和功能可能也需要相应调整,因为传统上,GPU 性能提升部分依赖于对低精度计算的优化。
结论:
- 如果量化是在后训练阶段进行,那么更多的预训练数据最终可能反而有害;
- 在高(BF16)和下一代(FP4)精度下进行预训练可能都是次优的设计选择;
这也引来OpenAI员工大赞特赞:
- 将非常酷地看到如何SOTA量化方案(mxfp,Pw≠Pkv≠Pa等)推动前沿;在我看来,将一半的计算预算用于一次大规模运行,以检查模型是否适用于大模型是值得的。
ttt 能继续挖掘
【2024-11-12】连OpenAI都推不动Scaling Law了?MIT把「测试时训练」系统研究了一遍,发现还有路
OpenAI 下一代旗舰模型的质量提升幅度不及前两款旗舰模型之间的质量提升,因为高质量文本和其他数据的供应量正在减少,原本的 Scaling Law(用更多的数据训练更大的模型)可能无以为继。此外,OpenAI 研究者 Noam Brown 指出,更先进的模型可能在经济上也不具有可行性,因为花费数千亿甚至数万亿美元训练出的模型会很难盈利。
从预训练来看,Scaling Law 可能会放缓;
但有关推理的 Scaling Law 还未被充分挖掘,OpenAI o1 的发布就证明了这一点。它从后训练阶段入手,借助强化学习、原生的思维链和更长的推理时间,把大模型能力又往前推了一步。
- 这种范式被称为「
测试时计算」,相关方法包括思维链提示、多数投票采样(self-consistency)、代码执行和搜索等。
扩展法则还没到上限
【2024-11-21】Dario Amodei:Scaling Law 还没遇到上限
Anthropic CEO Dario Amodei 在 “Machines of Loving Grace” 里, AGI 对世界的影响进行了预言:
- Powerful AI 预计会在 2026 年实现,足够强大的 AI 也能够将把一个世纪的科研进展压缩到 5-10 年实现(“Compressed 21st Century”)
和 Lex Fridman 的最新访谈中,Dario 解释了自己对于 Powerful AI 可能带来的机会的理解,以及 scaling law、RL、Compute Use 等模型训练和产品的细节进行了分享:
- • Scaling law 目前尚未见顶, 合成数据和 reasoning models 可能是解决数据限制的方案
- • 未来 post-training 环节的成本可能会超过 pre-training,只靠人类很难提高模型质量,需要更 scalable 的监督方法
- • Anthropic 的优势之一就是 RL,并且可能是做 RL 做得最好的,
- • Anthropic 内部工程师认为
Sonnet 3.5是第一个能节省时间的模型,但团队目前并不打算开发自己的 IDE, - • 出于安全性的考虑,Computer Use 目前不会直接面向 to C 开放,而是以 API 的形式发布 ,
- • “Compressed 21st Century” 的愿景下,AGI 可以在生物学和医学领域推动突破性进展,因为监管、伦理以及生物系统本身的复杂性,AI 建模生物系统的难度很高,但 AI 系统至少可以帮助改进临床试验系统,提高临床试验的效率和成功率
- • 今天科学家带领科研团队的模式在未来会变成科学家和 AI 系统一起工作,这些 AI 系统可以像研究助理一样被分配到具体研究任务中,
- • LLMs 领域还有很多问题值得研究,比如机制可解释性和 Long Horizon 是很值得关注的领域,
Ilya
【2024-9-5】Ilya 的公司 SSI 将以与OpenAI不同的方式, 继续 Scaling:
每个人都只是在说
Scaling Hypothesis,每个人都忽略了问:我们在Scaling什么?
- 有些人可以长时间工作,但他们只是以更快的速度走同样路径,这不是我们的风格。
- 但如果做些不同的事情,那么你就有可能做出一些特别的事情。
证伪
【2024-4-1】Scaling Law 被证伪,谷歌研究人员实锤研究力挺小模型更高效
Scaling Law 再次被 OpenAI带火,人们坚信:“模型越大,效果越好”
但谷歌研究院和约翰霍普金斯大学的研究人员对人工智能 (AI) 模型在图像生成任务中的效率有了新的认识:并非“越大越好”
实验设计 12 个文本到图像 LDM,其参数数量从 3900 万到惊人的 50 亿不等。
然后,这些模型在各种任务上进行了评估,包括文本到图像的生成、超分辨率和主题驱动的合成。
- 给定推理预算下(相同的采样成本)运行时,较小模型可胜过较大的模型。
- 当计算资源有限时,更紧凑的模型可能比较大、资源密集的模型能够生成更高质量的图像。
- 这为在模型规模上加速LDMs提供了一个有前景的方向。
- 采样效率在多个维度上是一致的
国内
国内讨论 Scaling Laws 论文不多。目前部分公开资料: 百川智能 Baichuan2 和 北京理工大学的明德大模型(MindLLM)论文中讲述了自己对scaling law的尝试。
两者在真正着手训练数十亿或者百亿参数的大语言模型之前,训练多个小型模型为训练更大的模型拟合拓展规律。
- 在同一套(足够大)的训练集上,采用一致的超参数设置,独立训练每个模型,收集训练的计算量和最终损失。
- 而后以OpenAI论文中结论的幂律关系拟合,预测出期望参数量模型的训练损失。
百川做法在开始训练7B和13B参数量模型前,设计大小从1000万到30亿不等的7个模型,采用一致的超参数,在高达1Ttoken的数据集上进行训练。
基于不同模型的损失,拟合出了训练浮点运算次数(flops)到训练损失的映射,并基于此预测了最终大参数模型的训练损失。
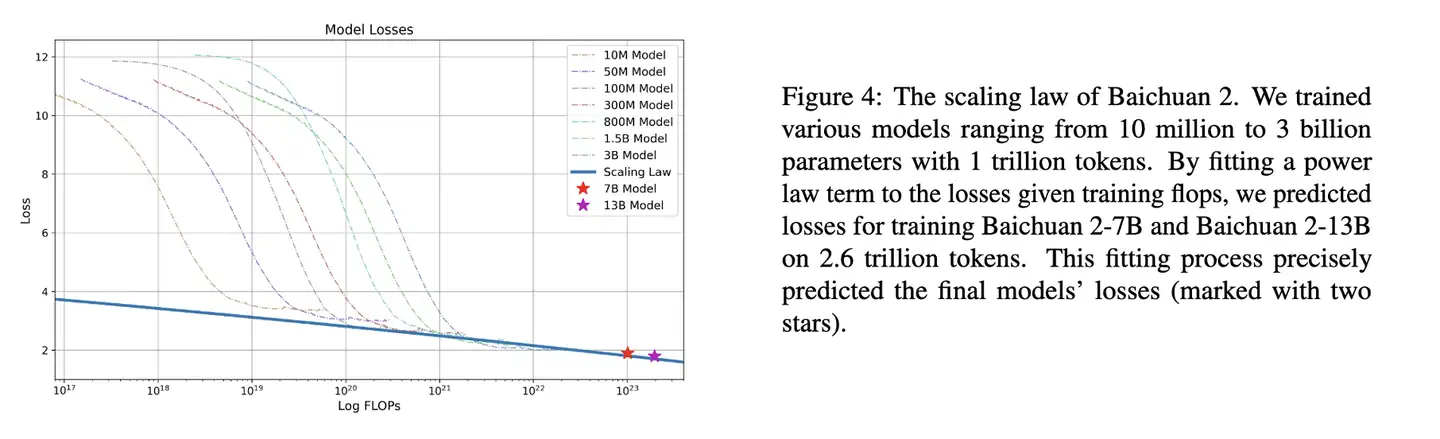
Baichuan2 缩放定律:
- 使用1万亿个token训练从1000万到30亿参数不等的7个模型,对给定训练浮点运算次数(flops)时的训练损失进行幂律拟合(蓝线),从而预测了在2.6万亿token上训练 Baichuan2-7B 和 Baichaun2-13B的损失。拟合过程精确预测了最终模型的损失(两颗星标记)
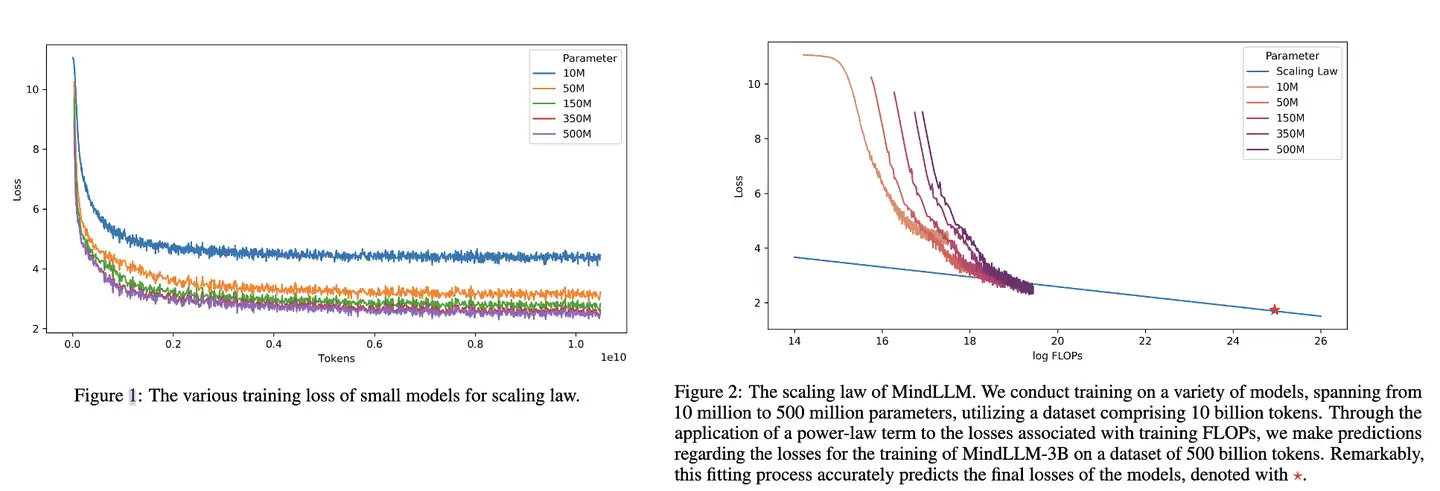
明德大模型团队的关注点与百川相似,在训练3B模型前,在10b Tokens 上训练了参数量从1000万到5亿的5个模型,通过分析各个模型的最终损失,同样基于幂律公式,建立从训练浮点运算次数(FLOPs)到目标损失的映射,以此预测最终大参数模型的训练损失。
MindLLM 缩放定律:
- 100亿token的数据集上训练参数从1000万到5亿参数的5个模型。通过对训练浮点运算次数(FLOPs)和损失幂律拟合,预测使用5000亿token的数据集训练MindLLM-3B的最终训练损失。该拟合过程准确预测了模型的最终损失,用星星标记。
李开复零一万物团队的黄文灏,在知乎上关于Yi大模型的回答也较有代表性:”Scaling Law is all you need:很多人都认为scaling law 就是用来算最优的数据和参数量的一个公式,但其实scaling law能做的事情远不止如此。
为了真正理解scaling law
- 第一件事就是忘记Chinchilla Scaling Law
- 然后打开 OpenAI 的 Scaling Law的paper,再把paper中OpenAI引用自己的更早的paper都详细的读几十遍”。
更多见【2024-1-5】OpenAI与DeepMind的Scaling Laws之争
【2025-12-9】谷歌 Agent Scaling Law
【2025-12-12】谷歌发布智能体Scaling Law:180组实验打破传统炼金术
尽管Agent已被广泛采用,但决定其性能的原则仍未被充分探索,导致从业者只能依赖启发式经验,而非有原理依托的设计选择
【2025-12-9】谷歌通过大量实验找到了智能体的 Scaling Law,称为 quantitative scaling principles,即定量扩展原则。
定义
- 智能体数量、协作结构、模型能力和任务属性之间的相互作用。
在四个不同的基准测试中对此进行了评估:Finance-Agent(金融推理)、BrowseComp-Plus(网络导航)、PlanCraft(游戏规划)和 Workbench(工作流执行)。
利用五种典型的智能体架构(单智能体系统以及四种多智能体系统:独立型、中心化、去中心化、混合型),并在三个 LLM 家族(OpenAI, Google, Anthropic)中进行实例化,谷歌这个团队对 180 种配置进行了受控评估,标准化了工具、提示结构和 token 预算,以将架构效应从实施混杂因素中隔离出来。
实验与结果:打破「人多力量大」的迷思
- 红榜(适合组团):
- 金融分析(Finance-Agent)任务中,多智能体协作是大杀器。中心化架构(有一个「指挥官」分派任务)能让性能暴涨 80.9%。为什么?因为这类任务可以拆分 —— 你查财报,我算汇率,他做总结,大家并行工作,效率极高。
- 黑榜(切忌组团):
- 游戏规划(PlanCraft)任务中,所有多智能体架构都翻车了,性能惨跌 39% 到 70%。原因在于这类任务环环相扣(必须先砍树,才能做木板),强行把流程拆给不同的人,光是沟通成本就把推理能力消耗殆尽了。
阻碍智能体扩展的三大核心因素:
- 第一,工具越多,协作越难(工具-协作权衡):
- 如果任务需要用到大量工具(比如 16 个以上的 API),再引入多智能体协作就是一场灾难。
- 实验数据显示,工具密集的任务会因巨大的沟通开销而不仅没变快,反而变慢、变笨。
- 第二,能力有天花板(能力饱和效应)
- 最反直觉:如果单个智能体已经够聪明了,就别再找帮手了。
- 数据表明,当单智能体的基线准确率超过 45% 时,再增加智能体进行协作,收益往往是负的。
- 所谓「帮倒忙」,在 AI 世界里是真实存在的。
- 第三,没有指挥官,错误会指数级放大
- 如果你让一群智能体各自为战(独立型架构),错误会被放大 17.2 倍, 因为没人检查,一个人的错会传给所有人。
- 但如果引入一个「指挥官」进行中心化管理,错误放大率能被控制在 4.4 倍。
- 这证明了在多智能体系统中,架构设计比单纯堆人数更重要。
应用
GPT-4
GPT4报告中 Scaling Law曲线,计算量C和模型性能满足幂律关系
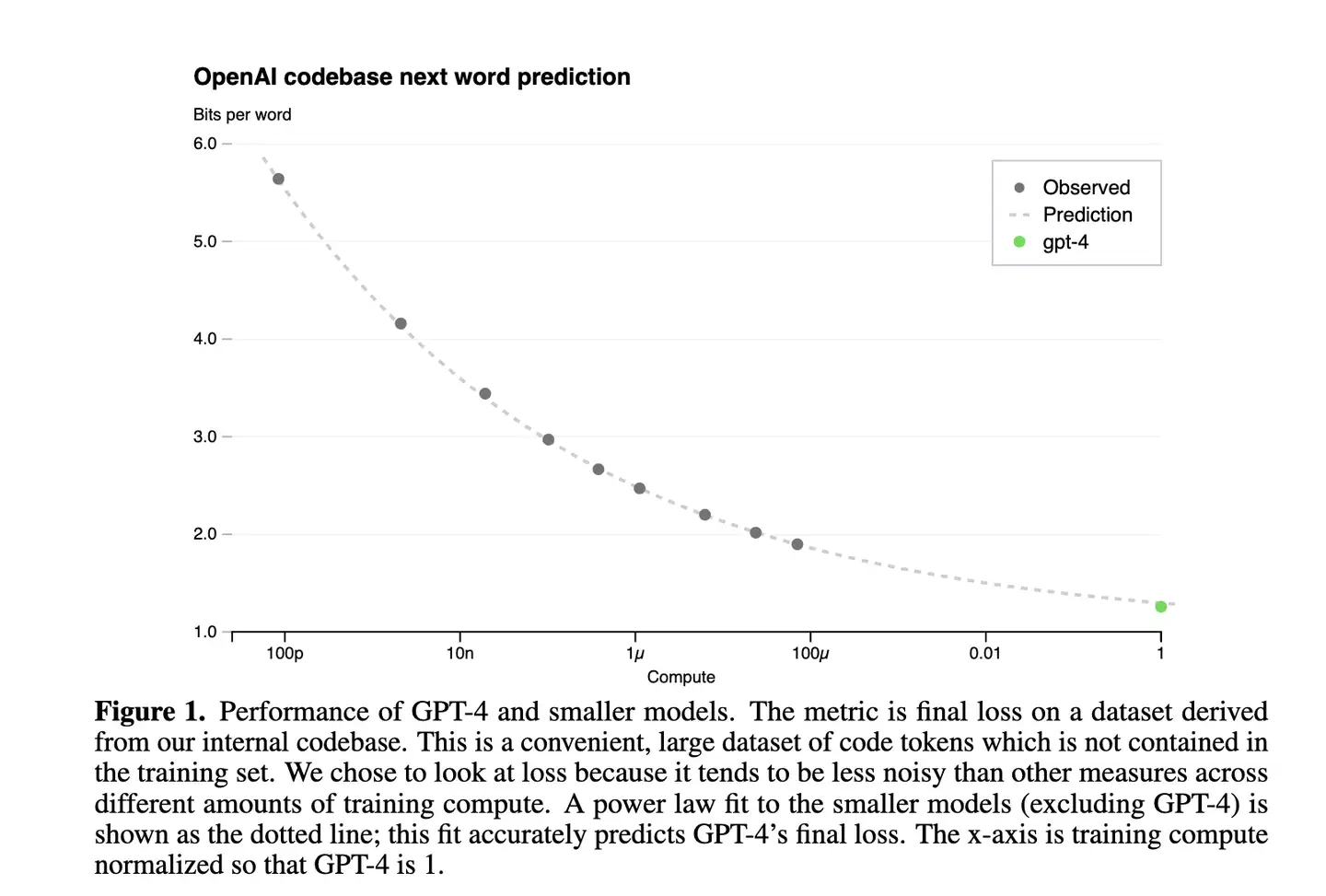
- 横轴是归一化之后的计算量,假设GPT4计算量为1。基于10,000倍小的计算规模,能预测最终GPT4的性能。
- 纵轴是”Bits for words”, 交叉熵单位。在计算交叉熵时,如果使用以 2 为底的对数,
交叉熵单位是 “bits per word”,与信息论中的比特(bit)概念相符。所以这个值越低,说明模型的性能越好。
Baichuan2
Baichuan2 技术报告中的 Scaling Law曲线。
基于10M~3B 模型在1T数据上训练的性能,可预测出最后7B模型和13B模型在2.6T数据上的性能
幂律定律
- 模型参数固定,无限堆数据并不能无限提升模型性能,模型最终性能会慢慢趋向一个固定值
实验数据
如何计算
如果模型参数量为 10^3(紫色线),数量达到10^9,模型基本收敛。继续增加数据,产生的计算量,没有同样计算量下提升模型参数量带来的收益大(计算效率更优)。
根据 C=6ND ,进一步转换成模型参数与计算量关系,即:
- 模型参数为 10^3,计算量为
6*10^12Flops,即7*10^(-8)PF-days时, 基本收敛。右图中紫色线拐点。
Baichuan 实验
- 中英场景下,7B 模型收敛时的算力是 10^23 FLOPS,对应数据量应该是 $ D=\frac{10^23}{6710^9}=2.3T $
计算效率最优时,模型参数与计算量幂次成线性关系,数据量大小也与计算量幂次成线性关系。
观点
- OpenAI 认为模型规模更重要,即 a=0.73, b=0.27
- 而 DeepMind 在 Chinchilla工作和Google在PaLM工作中都验证了 a=b=0.5 ,即模型和数据同等重要。
假定计算量整体放大10倍
- OpenAI 认为模型参数更重要,模型应放大 10^0.73=5.32 倍,数据放大 10^0.27=1.86 倍;
- DeepMind和Google认为模型参数量与数据同等重要,两者都应该分别放大 10^0.5=3.16 倍。
最好在自己的数据上做实验来获得你场景下的a,b
MindLLM
MindLLM 技术报告中 Scaling Law曲线。
基于10M~500M 模型在10B数据上训练的性能,预测出最后3B模型在500B数据上的性能。
LLaMA
LLaMA: 反Scaling Law 大模型
假设遵循计算效率最优来研发LLM,那么根据 Scaling Law,给定模型大小,可推算出最优计算量,进一步根据最优计算量就能推算出需要的token数量,然后训练就行。
但是计算效率最优是针对训练阶段而言,并不是推理阶段,实际应用中推理阶段效率更实用。
Meta 在 LLaMA 的观点是:
- 给定模型目标性能,并不需要用最优的计算效率在最快时间训练好模型,而应该在更大规模的数据上,训练一个相对更小模型,这样的模型在推理阶段的成本更低,尽管训练阶段的效率不是最优的(同样的算力其实能获得更优的模型,但是模型尺寸也会更大)。
- 根据 Scaling Law,10B模型只需200B数据,但是7B模型性能在1T数据后还能继续提升。
所以, LLaMA 重点是训练一系列语言模型,通过使用更多数据,让模型在有限推理资源下有最佳的性能。
- 确定模型尺寸后,Scaling Law 给到的只是最优数据量,一个至少的数据量,实际在训练中观察在各个指标上的性能表现,只要还在继续增长,就可以持续增加训练数据。
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
