编者按：平时收集了不少神经网络知识片段，过于零散，花了大半天时间将各种细节梳理，串联起来。

总结：

把之前收集的神经网络点点滴滴，梳理、串联起来，便于理解，如有不当，麻烦及时指出，邮箱：wqw547243068@163.com。

资料

深度学习资料

【2022-1-11】国外深度学习面试题书籍：DEEP LEARNING INTERVIEWS，github地址，电子书下载地址
【2020-6-18】【深度学习基础】《Deep Learning Fundamentals - YouTube》，B站地址
【2023-6-14】李沐领先出品，动手学深度学习，面向中文读者的能运行、可讨论的深度学习教科书，含 PyTorch、NumPy/MXNet、TensorFlow 和 PaddlePaddle 实现，包含 NLP 预训练章节

Challenges for Deep Learning towards Human-Level AI

【2018-11-8】蒙特利尔大学计算机科学与运筹学系教授Yoshua Bengio
让AI接近人类认知水平，深度学习所面临的挑战

人工智能发展到今天已经有很多进展，但AI的智力仍然远远不及人类，无法像人类一样拥有高度抽象的意识和能力。我们希望设计一种学习机制，让机器拥有更高层级的抽象层面的认知。

这要求我们抓住用于产生意识的信息之间的关系。我们将信息解构成变量来去了解它们之间的关系，近年研究热点之一是注意力机制，我认为机器的认知架构还可以分成两层表达：

高维度的潜意识
低维度的有意识

人的认知就可以分为两个系统，一个是直觉性的潜意识，另一个是意识。

以自然语言处理为例，为了能够真正理解语言，我们所做是两个系统的融合。
现在的自然语言处理通常需要通过大量的语料库进行训练，这是不够的，它们会出现很多错误。
仅仅通过文本无法真正解决自然语言理解的问题。除了对语言进行建模，还要对所处的环境进行建模。想一想人们在婴儿时期，会在理解环境后产生语言。因此给我们启发是，可以将语言学习和对世界运行方式的学习结合起来。
理解世界运行方式的一大关键是理解信息之间的因果联系（The book of why），我认为机器学习要花更多的时间做因果联系的研究，我们要研究一些新的学习理论。这是很难的，因为世界非常复杂，我们要做出更好的机器学习算法，充分利用机器学习去进行研究。

【总结】

人工智能发展至今，AI还远远比不上人类，因为缺乏高度抽象的意识和能力。那么机器如何具备这样的能力？近期流行的注意力机制开了个好头，但还不够，机器的认知结构应该包含两部分：高维的潜意识+低维的有意识。人类的语言就是这两个系统的结合。当前的NLP方法只是对语言进行建模，缺乏更重要的环境因素，接下来应该多研究因果，而不是关联（与Judea Pearl一致：The book of why），于是Yoshua Bengio做了个实验平台BabyAI，试图像婴儿一样跌跌撞撞的探索理解这个世界，好早点到达human level的AI
最近进行的一项工作是BabyAI平台。在这个平台中，我们为BabyAI提供一个场景或者一个游戏，像指导一个婴儿认知世界一样，人类通过与BabyAI的互动帮助它理解周围的环境，学习它应该学到的内容。我们设置了从容易到困难的不同关卡让BabyAI进行不同程度的学习，这一平台在提升训练中数据效率上取得了很大的进展。
【2021-4-2】国立台湾大学总结的深度学习发展史 History of Deep Learning
- ◉ 1960s: Perceptron (single layer neural network)
- ◉ 1969: Perceptron has limitation
- ◉ 1980s: Multi-layer perceptron
- ◉ 1986: Backpropagation
- ◉ 1989: 1 hidden layer is “good enough”, why deep?
- ◉ 2006: RBM initialization (breakthrough)
- ◉ 2009: GPU
- ◉ 2010: breakthrough in Speech Recognition (Dahl et al., 2010)
- ◉ 2012: breakthrough in ImageNet (Krizhevsky et al. 2012)
- ◉ 2015: “superhuman” results in Image and Speech Recognition
Why does deep learning show breakthrough in applications after 2010?
- 1. Data: big data
- 1. Hardware: GPU computing
- 1. Talent: design algorithms to allow networks to work for the specific problems
Why Deeper is Better?
- Universality Theorem 通用逼近定理
- Fat + Shallow（O(2d)） v.s. Thin + Deep（O(d^2)）：The deeper model uses less parameters to achieve the same performance，

Deep Learning模型若干年的重要进展

2018年，清华大学唐杰副教授及其学生丁铭结合其Aminer数据库整理出 Deep Learning 模型最近若干年的重要进展，共有4条脉络。

Track.1 CV/Tensor

1943 年出现雏形，1958 年研究认知的心理学家 Frank 发明了感知机，当时掀起一股热潮。后来 Marvin Minsky（人工智能大师）和 Seymour Papert 发现感知机的缺陷：不能处理异或回路、计算能力不足以处理大型神经网络。停滞！
1986 年 Hinton 正式地提出反向传播训练 MLP，尽管之前有人实际上这么做。
1979 年，Fukushima 提出 Neocognitron，有了卷积和池化的思想。
1998 年，以 Yann LeCun 为首的研究人员实现了一个七层的卷积神经网络 LeNet-5 以识别手写数字。

后来 SVM 兴起，这些方法没有很受重视。

2012 年，Hinton 组的 AlexNet 在 ImageNet 上以巨大优势夺冠，兴起深度学习的热潮。其实 Alexnet 是一个设计精巧的 CNN，加上 Relu、Dropout 等技巧，并且更大。这条思路被后人发展，出现了 VGG、GooLenet 等。
2016 年，青年计算机视觉科学家何恺明在层次之间加入跳跃连接，Resnet 极大增加了网络深度，效果有很大提升。一个将这个思路继续发展下去的是去年 CVPR Best Paper Densenet。CV 领域的特定任务出现了各种各样的模型（Mask-RCNN 等），这里不一一介绍。
2017 年，Hinton 认为反省传播和传统神经网络有缺陷，提出 Capsule Net。但是目前在 CIFAR 等数据集上效果一半，这个思路还需要继续验证和发展。

Track.2 生成模型

传统的生成模型是要预测联合概率分布 P(x,y)。
RBM 这个模型其实是一个基于能量的模型，1986 年的时候就有，他在 2006 年的时候重新拿出来作为一个生成模型，并且将其堆叠成为 Deep Belief Network，使用逐层贪婪或者 Wake-Sleep 的方法训练，不过这个模型效果也一般现在已经没什么人提了。但是从此开始 Hinton 等人开始使用深度学习重新包装神经网络。
Auto-Encoder 也是上个世纪 80 年代 Hinton 就提出的模型，此时由于计算能力的进步也重新登上舞台。Bengio 等人又搞了 Denoise Auto-Encoder。
Max Welling 等人使用神经网络训练一个有一层隐变量的图模型，由于使用了变分推断，并且最后长得跟 Auto-encoder 有点像，被称为 Variational Auto-encoder。此模型中可以通过隐变量的分布采样，经过后面的 decoder 网络直接生成样本。
GAN 是 2014 年提出的非常火的模型，他是一个隐的生成模型，通过一个判别器和生成器的对抗训练，直接使用神经网络 G 隐式建模样本整体的概率分布，每次运行相当于从分布中采样。
DCGAN 是一个相当好的卷积神经网络实现，WGAN 是通过维尔斯特拉斯距离替换原来的 JS 散度来度量分布之间的相似性的工作，使得训练稳定。PGGAN 逐层增大网络，生成机器逼真的人脸。

Track3 Sequence Learning

1982 年出现的 Hopfield Network 有了递归网络的思想。1997 年 Jürgen Schmidhuber 发明 LSTM，并做了一系列的工作。但是更有影响力的是 2013 年还是 Hinton 组使用 RNN 做的语音识别工作，比传统方法高出一大截。
文本方面 Bengio 在 SVM 最火的时期提出了一种基于神经网络的语言模型，后来 Google 提出的 Word2Vec 也有一些反向传播的思想。在机器翻译等任务上逐渐出现了以 RNN 为基础的 seq2seq 模型，通过一个 encoder 把一句话的语义信息压成向量再通过 decoder 输出，当然更多的要和 attention 的方法结合。
后来前几年大家发现使用以字符为单位的 CNN 模型在很多语言任务也有不俗的表现，而且时空消耗更少。self-attention 实际上就是采取一种结构去同时考虑同一序列局部和全局的信息，Google 有一篇耸人听闻的 Attention Is All You Need 的文章。

Track.4 Deep Reinforcement Learning

这个领域最出名的是 DeepMind，这里列出的 David Silver 是一直研究 RL 的高管。
Q-Learning 是很有名的传统 RL 算法，Deep Q-Learning 将原来的 Q 值表用神经网络代替，做了一个打砖块的任务很有名。后来有测试很多游戏，发在 Nature。这个思路有一些进展 Double Dueling，主要是 Q-learning 的权重更新时序上。
DeepMind 的其他工作 DDPG、A3C 也非常有名，他们是基于 policy gradient 和神经网络结合的变种（但是我实在是没时间去研究）
一个应用是 AlphaGo 大家都知道，里面其实用了 RL 的方法也有传统的蒙特卡洛搜索技巧。Alpha Zero 是他们搞了一个用 Alphago 框架打其他棋类游戏的游戏，吊打。

雷锋网注：

本文获唐杰副教授授权转自其微博。唐杰老师带领团队研发了研究者社会网络 ArnetMiner 系统，吸引了 220 个国家 277 万个独立 IP 的访问。AMiner 近期持续推出了 AI 与各领域结合的研究报告，可访问 AMiner 官网了解更多详情。

好玩儿的Python：从数据挖掘到深度学习

School-of-AI 入门教程

《Deep Learning》读书笔记

2017年8月在雷锋网上的读书分享，先后组织了五六次，面向400+初学者直播，并提供文字版材料
Ian Goodfellow的「Deep learning」这本书，久负盛名，号称是AI圣经，内容完整，层次鲜明，一共20章，600多页。初学者读起来压力山大，别着急，我这个读书分享系列轻松讲解各类知识，降低入门门槛，帮大家快速入门。
以下资料在文字版基础上稍作修改、矫正
目录: 「Deep Learning」读书全系列分享（已更新至第十章）
- 「Deep learning」读书分享第一章：前言
  - 这一部分主要是深度学习的一些基本介绍、一些发展历史。可以看一下这个封面，一幅漂亮的风景画，纽约中央公园遍地盛开的杜鹃花，仔细看有点不太正常，对了，这就计算机生成的，确切的说，是 Google deepmind 团队的杰作——梦幻公园。
- 「Deep Learning」读书系列分享第二章：线性代数
  - 今天分享的是第二章：线性代数。从 27 页到 42 页，内容不多，基本都是传统形式上的概念。同样，我只讲直观思路，尽可能的少用公式，毕竟好多人见着数学公式就头疼，更不用说在 PPT 上看了，效果不好，容易催眠，看着看着就身在朝野心在汉了。
- 「Deep Learning」读书系列分享第三章：概率和信息论
  - 这节课会讲到一些基本概念，常用的分布，频率学派和贝叶斯学派的差别，还有贝叶斯规则，概率图，最后是信息论。这里第四条可能很多人可能头一回见到，学了那么多概率，连这个都不知道，那你的概率真的白学了，真这样，不开玩笑。不过，老实说我也是前几年才知道这个学派的差别，因为浙大三版教材上就没提到这些，好像就提到一点，频率学派就是古典概率，没有什么其他的，这也是现行教材的缺陷。
- 「Deep Learning」读书系列分享第四章：数值计算
  - 其实我们大部分人在运用机器学习或者深度学习的时候是不需要考虑这一章的内容的，这章的内容更多是针对算法的数学分析，包括误差的增长以及系统的稳定性。
  - 第一，在机器学习、包括了深度学习中数值计算的应用。
  - 第二，数值误差的问题
  - 第三，简单的分析机器学习系统的稳定性问题
  - 最后，针对优化问题给出了两种不同的优化算法，一种是梯度下降法，一种是限制优化算法
- 「Deep Learning」读书系列分享第五章：机器学习基础
  - 5.1 学习算法
  - 5.2 Capacity, 过拟合和欠拟合
  - 5.3 超参数和验证集
  - 5.4 估计量，偏移值和方差
  - 5.5 最大似然估计
  - 5.6 贝叶斯统计
  - 5.7 监督学习算法
  - 5.8 无监督学习算法
  - 5.9 随机梯度下降
  - 5.10 构建机器学习算法
  - 5.11 挑战深度学习
- 「Deep Learning」读书系列分享第六章：前馈神经网络
  - 6.1 例子：学习异或
  - 6.2 基于梯度的学习
  - 6.3 隐藏层单元
  - 6.4 架构设计
  - 6.5 BP 算法和其他不同算法
  - 6.6 历史记录？
- 「Deep Learning」读书系列分享第七章：深度网络的正则化
  - 7.1 参数归一化惩罚
  - 7.2 归一化惩罚作为条件最优化
  - 7.3 正则化和欠约束问题
  - 7.4 数据集增大
  - 7.5 噪声鲁棒
  - 7.6 半监督学习
  - 7.7 多任务学习
  - 7.8 早期中止
  - 7.9 参数连接和参数共享
  - 7.10 稀疏表达
  - 7.11 Bagging and Other Ensemble Methods？
  - 7.12 Dropout
  - 7.13 对抗训练
  - 7.14 切线距离，Tangent Prop 和流行切分类器？
- 「Deep Learning」读书系列分享第八章：深度模型中的优化
  - 8.1学习和纯优化有什么不同
  - 8.2神经网络优化中的挑战
  - 8.3基本算法
  - 8.4参数初始化策略
  - 8.5自适应学习率算法
  - 8.6二阶近似方法
  - 8.7优化策略和元算法
- 「Deep Learning」读书系列分享第九章：卷积网络
  - 9.1 卷积运算
  - 9.2 动机
  - 9.3 池化
  - 9.4 卷积与池化作为一种无限强的先验
  - 9.5 基本卷积函数的变体
  - 9.6 结构化输出
  - 9.7 数据类型
  - 9.8 高效的卷积算法
  - 9.9 随机或无监督的特征
  - 9.10 卷积网络的神经科学基础
  - 9.11 卷积网络与深度学习的历史
- 「Deep Learning」读书系列分享第十章：序列建模：循环和递归网络
  - 10.1 展开计算图
  - 10.2 循环神经网络
  - 10.3 双向RNN
  - 10.4 基于编码 - 解码的序列到序列架构
  - 10.5 深度循环网络
  - 10.6 递归神经网络
  - 10.7 长期依赖的挑战
  - 10.8 回声状态网络
  - 10.9 渗透单元和其他多时间尺度的策略
  - 10.10 长短期记忆和其他门控 RNN
  - 10.11 优化长期依赖
  - 10.12 外显记忆
资料
- 麻省理工的书籍的英文原版。
- 北大张志华团队贡献的中文版Github，在线阅读。
备注
- 第一、二、三、六、七、九章分享人：王奇文，资深算法工程师，曾在百度和阿里工作，先后做过推荐系统、分布式、数据挖掘、用户建模、聊天机器人。“算法路上，砥砺前行”。
- 第四章分享人：陈安宁，Jakie，名古屋大学计算力学博士。
- 第五章分享人：吴楚，数学硕士，华大基因算法工程师。
- 第八、十章分享人：孙嘉睿，迅雷人工智能图像算法工程师，北京大学信息工程学院博士，京都大学情报学硕士。

第一章 Introduction

2017年8月在雷锋网上的分享记录：「Deep learning」读书分享 : 第一章前言 Introduction，重新组织下语言，更新下技术点，温故知新。

Ian Goodfellow的「Deep learning」这本书，久负盛名，号称是AI圣经，内容完整，层次鲜明，一共20章，600多页。初学者读起来压力山大，别着急，我这个读书分享系列轻松讲解各类知识，降低入门门槛，帮大家快速入门。

Ian Goodfellow的「Deep learning」这本书，久负盛名，号称是AI圣经，内容完整，层次鲜明，一共20章，600多页。初学者读起来压力山大，别着急，我这个读书分享系列轻松讲解各类知识，降低入门门槛，帮大家快速入门。

先讲第一章前言，主要是深度学习的一些基本介绍、发展历史。

这本书的封面是一幅漂亮的风景画，纽约中央公园，遍地盛开的杜鹃花，眼尖的人会发现有些异常：城堡、树枝怎么怪怪的？对了，这是计算机生成的假图，出自Google DeepMind团队的梦幻公园。

为什么要做这个分享？

第一，跟大家一起交流学习，深知自己的知识储备不够，脸皮厚，大胆分享，暴露不足，共同学习。
第二，借机给自己施加压力，因为人都是有些惰性的（砖头书啃不动）。
第三，内容挺多，有600多页，单凭我一个人的力量还不够，所以希望认识更多有识之士，团队协作。

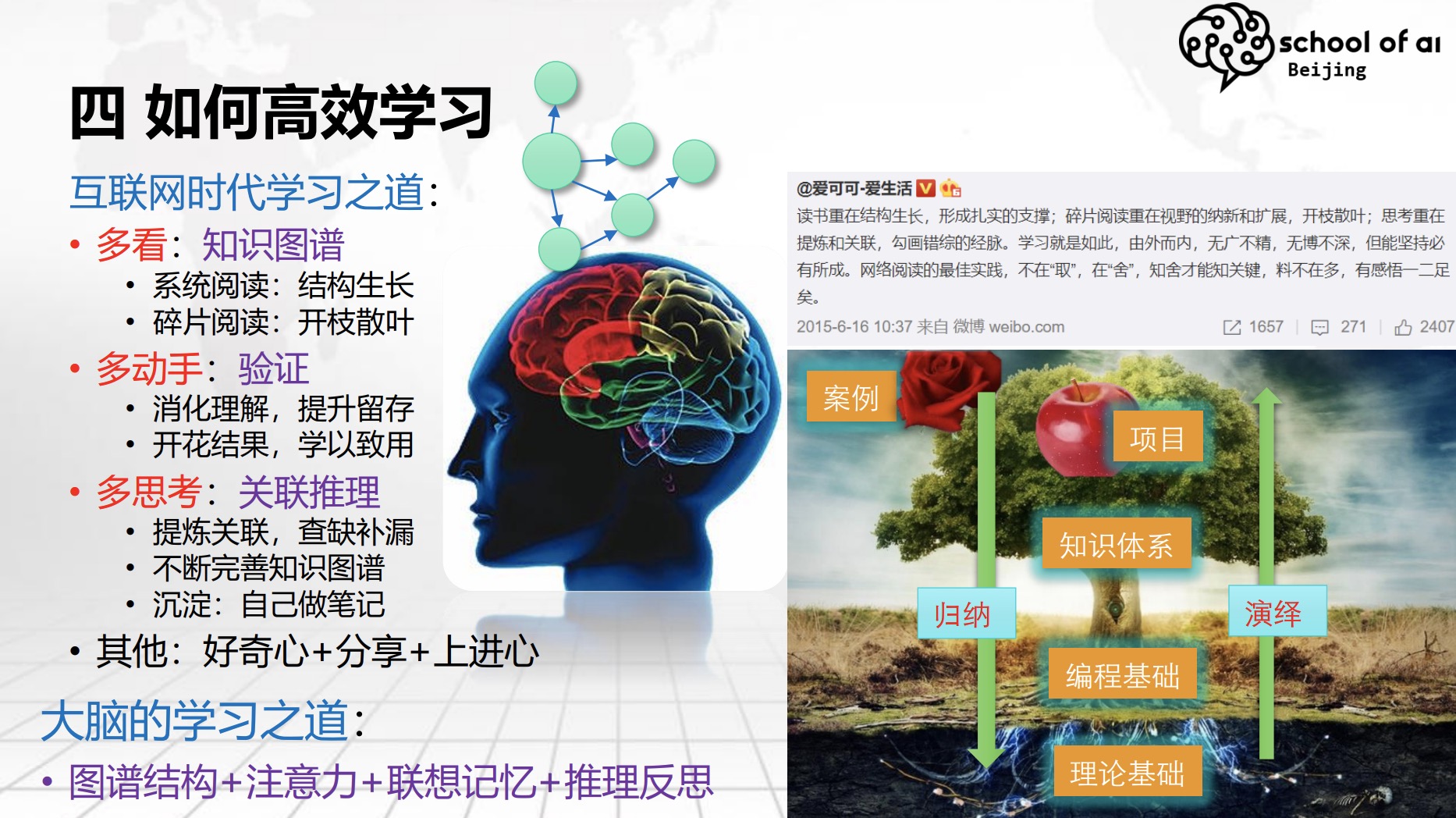
现在是互联网时代，信息泛滥，各种资讯浩如烟海，很容易碎片化，东一榔头西一棒子，不成体系，导致消化不良。

真想学好一门技术，还是要埋头啃砖头，这种方式看似最笨，但学到的知识体系最为扎实。
业界有个简单的方法判断一个人的技术实力：看多少书，啃的书越多，基础就越扎实，视野就越广。

这是一张珍藏已久的图，时刻提醒自己，注意学习方法

学习一门新技术，刚开始接触，大概一周后，不同的传递方式下，知识的留存率分别是多少。

听讲/阅读，也就是大家现在的状态，只听我讲（或看文章）。听完（看完）后一周，再回想下讲了什么，可能只记住5%，只是几个概念“深度学习”，或几张漂亮的图片、一个好玩的gif，说了一句比较有意思的话。注意：留存率才5%；
看书、其他的视频资料、别人演示，这时候，留存率能到30%，大幅提升；
主动学习，学完之后跟别人讨论，留存率反弹到50%；
动手写代码，那就接着涨到75%。
讲给别人听，留存率90%
- 这一步挺难，从读书、查资料、消化理解到做ppt，平均每个章节花费4-8小时，甚至更多，十分磨人。

如果真想学深度学习，建议尝试着给别人讲，组建学习小组，一起分享

子曰：赠人玫瑰，手留余香
子又曰：一个人走得快，一群人走得远

关于留存率的另一个经典概念：艾宾浩斯遗忘曲线 说：

接触新信息后，留存率20min、1h会急剧下降到58%
一周后，只剩可怜的25%

【2021-2-17】艾宾豪斯遗忘曲线记忆法
- 艾宾浩斯是德国著名心理学家，他根据人的短时记忆和长时记忆特征，发现了记忆遗忘规律，形成的坐标图曲线便是记忆遗忘曲线，也称为艾宾浩斯记忆遗忘曲线。我们可以按艾宾浩斯记忆遗忘曲线制定学习计划，这样记忆效果更好，学习效率更高。
- 艾宾浩斯记忆遗忘曲线是把各种记忆机制综合起来考虑，反映平均记忆力衰退的情况。人们把记忆类型粗分成短时记忆 (Short term memory) 和长时记忆 (Long term memory)。
- 在从短时记忆到长时记忆的转化中，一个重要的因素是训练间隔。实验表明，如果持续高强度的不停训练(massed training)，是不能直接形成长时记忆的。只有加上一定的间隔(spaced training)，才能有效将短时记忆转化成长时记忆。

这张图，总体描述了每个章节内容，章节之间的关系，有利于形成全局观。

图里面主要分成三部分：

第一部分：数学基础，涉及一些数学基础和概念，还有机器学习基础。其中，数学基础包含线性代数、概率论、信息论、数值分析，还有少量的最优化。
第二部分：深度学习基本算法。几种典型的神经网络，从DFFN(深度前馈网络)开始，演化到了怎么用正则、怎么优化，下面一部分的CNN是前馈网络的一种扩展，RNN也源自前馈网络，当然还有CNN，绝对正宗的前馈网络。最后是实践方法论，平时实践总结。
第三部分：进阶内容，涉及线性因子模型，编码器。这部分非常重要，提到了Hinton的RBF，鼎鼎有名的DBN。接下来 表示学习、蒙特卡洛方法、结构概率模型、深度生成模型，即大红大紫的GAN，生成对抗网络，很厉害的样子。

右上角是这个章节的目录，书上的实际内容不多，偏枯燥，为了方便大家理解，我会引入外部资料，结合自己的解释，把书的结构做一下调整。

新结构:

第一，什么是深度学习；
第二，跟机器学习什么关系；
第三，神经网络发展历史；
第四，深度学习为什么这么火；
第五，深度学习能做什么。

总体思路:

只提一些感性的认识
，而不讲具体的细节，更容易理解。人的记忆靠不住，不管多深刻，总会被时间磨灭，学习新知识的最高境界是深刻理解，融入到自己的知识体系里，这样才能做到事半功倍，信手拈来。
如果想深入了解，请踏实看书，学知识不要偷懒，不要偷懒，不要偷懒
- 今天偷的懒，明天会加倍偿还

这个时代在加速惩罚不学习的人（地铁里教育机构的广告语，紧张不？焦虑售卖完毕）

什么是深度学习？

书里面提到一句话：

AI系统必须具备从原始数据提取模式的能力
, 这种能力指机器学习。
- 什么是机器学习（ML）？从杂乱无章的数据中提取某种模式的能力
算法的性能高度依赖于数据表示，也就是“表示学习”, 机器学习里的一大方向。

传统的机器学习是怎么做的呢？

依赖于人工提取的特征，比如，图像里的SIFT、HoG、Harr小波等等人工经验。这几个特征很强大，霸占了图像处理几十年，但问题是扩展性有限。
深度学习跟传统机器学习相比，最大的区别就是把人工提取的过程自动化。

回过头来想想，什么是深度学习？

深度学习源于传统的神经网络，传统神经网络就是属于联结主义（机器学习中的一种方法），Geoffery Hinton在2006年首次提出
深度学习是传统神经网络方法的扩展、延伸，不同的是深层结构，通过多层神经元逐层抽象，从简单组件构建复杂概念，达到自动发现、提取分布式特征的能力。

深度学习的两个重要特点：

第一，特征自动提取，传统信息学习里面那一套复杂的特征工程基本不用了
- 注意：是基本不用了，不是全部不用了！总不能什么都不处理就扔给模型吧？
- 数据的适当加工能提升学习效率，只是跟传统机器学习相比，不用高度依赖人工特征工程了
第二，逐层抽象，主要通过深度结构来实现。

不同的表示方式对结果会有什么样的影响。

图中两个分类，圆圈和倒三角，分别对应两种类别的样本。
- 如果采用简单的线性模型，显然是分不开的。
- 但经过某种变换后，如从笛卡尔坐标系变到极坐标系，画一条垂直的直线就轻轻松松分开了。
所以说，数据集的表示方法不同，问题的难易程度也不同。你看，表示学习很重要吧？

深度学习是怎么通过深度结构解决问题？

底层对应的是整张图片，输入是像素点，一层一层由下往上，层级抽象。
第二层根据底层像素连接起来组成一些线段或复杂的边缘。
再到上面一层，形成局部轮廓，一个角或者一些轮廓线。
再往上层抽象变成了物体的一部分、或者整体。
最后，就能看到近似是一个物体（人）啦。

深度学习是通过一些深度结构进行逐层抽象，变相的把问题一步一步地简化。

既然是深度学习，那么首先就要问一句：到底什么是深度，怎么定义这个深度？

先看右边这张计算图，DAG图，描述一个计算任务的前后经过。实际上这是传统机器学习里面的逻辑回归
- 输入了一个样本，有两个特征X1、X2，分别乘以里面的权重W1、W2，乘起来，再累加求和，套一个sigmoid激励函数，本质上就是一个变换。
这个简单的计算过程，可以用左边的图描述出来，这只是一种描述方法；右边也是另一种描述方法。区别是，右边是逻辑概念意义上的概念，而左边是计算步骤上的描述。
- 左边的描述方式，网络的深度是3，注意，第一层不算。
- 右边这个描述方式，只有1层。这两种概念描述都是对的，就看喜欢哪一种。通常情况下，以右边这种为基准。按照逻辑概念划分时，又可以继续细分，标准就是要不要包含输入层。

看这张图，这个是input，就是传统网络，一提到神经网络，基本都会提到这样的结构，一个输入，再加上隐含层，再加上一个输出层。隐含层可以有多层。输入层，有的地方不算层级，有的算，通常情况下是输入是不算的，上图是一个两层的网络。

深度学习跟机器学习之间有什么关系

深度学习源于机器学习，但是高于机器学习

图里第二个是机器学习，DL是AI的一大分支，AI 还有其他的方法，这个只是其中的一个分支而已。

跟传统神经网络相比，深度学习的深度体现在复杂的网络结构上。那么怎样才叫复杂呢，一般在4到5层以上，因为传统的神经网络是在2到3层，比如BP网络，两到三层，超过的话就不好训练，也训练不出来，所以基本上只到4到5层左右，不会有太多。

这是一张韦恩图(Venn)，描述的各个概念之间的一些逻辑关系。这个就看的相对直观一些，最下面的红框里是机器学习，然后里面有一个流派叫表示学习，表示学习里面又有一个深度学习，层层嵌套的关系。

这张图描述的是不同的学习方法，区别体现在组成结构上。最左边是一个规则系统，希望通过一些逻辑推理去模拟学习的过程，这是最早的一版，人为设计的一个程序，输入数据，根据一定的规则，得到一个输出。它比较简单，中间实际上就两个过程。

传统的机器学习有什么区别，在上面它有一个特征映射。

表示学习的方法里面分成两部分，左边一个，还有右边一个。左边一个跟之前相比的话，在特征工程上会花了不少精力，特征工程非常复杂，依赖经验，人力投入大。深度学习是表示学习中的一种，在它的基础上做了一些优化，也算是一个变革，区别是在于多了这一部分：自动提取特征。

这是历史上几种不同的学习模型在基本流程上的差别。

神经网络的发展历史

一言以蔽之，神经网络命途多舛，先后经历了三次浪潮，也叫三起两落（邓爷爷三起两落）。这个第三落现在还不清楚，有人可能会问，深度学习这么火，怎么可能衰落？这个真不一定，前两次浪潮之巅上，大家也是这么想的。

第一次，1940年-1960年，控制论时代，主要是基于那些规则的方法来做。
- 控制论时代，诞生了第一个人工神经元。神经元看着挺像现在的样子，但就一个神经元，没有什么层级结构，就是多个输入得到一个输出，要求和、再sigmoid，产生一个输出，就是个神经元而已。注意，当时，神经元里面的权重是人工设置的。
- 后来Hebb学习法则指出权重是可以学习出来的。于是感知器降临，跟之前的神经元相比，除了有多层结构，还有权重从人工设置变成了自动化。感知器的网络结构一般2到3层，也就是传统的前馈网络。
- 不过，感知器诞生没多久，麻省理工的AI实验室创始人Marvin Minsky发现了这种结构的要害，专门写了一本书叫「Perceptrons」，直指感知器的两个核心问题：
  - 第一，连简单的非线性问题都解决不了
  - 第二，非线性问题理论上可以通过多层网络解决，但是难以训练（在当时基本不可能）。
- 非线性问题是数字逻辑里的异或门。他在书里提到，异或门是神经网络的命门。由于这两个问题打中了感知器的三寸，再加上Marvin Minsky的强大影响力，许多研究者纷纷弃城而逃，向神经网络这个方向说再见，直接导致了第一次寒冬，持续时间长达二三十年。
第二次，1986年左右，联结主义时代。
- 1974年，反向传播算法第一次被一个名不见经传的哈佛博士生提出，但由于正处寒冬，并未受人重视
- 直到1986年，hinton重新发明了BP算法，解决其中的问题，效果还不错，迎来了第二次兴起，大家又开始回归神经网络。
- 紧接着又出来一个新模型，也就是Vpnik的支持向量机 SVM（同时期PGM也诞生了。支持向量机这名字看起来怪怪的，为什么带个“机”字？因为当时带“机”的神经网络正在流行，加这个字是为了更好的发表）。跟近似黑盒的BP相比，SVM理论证明非常漂亮，更要命的是支持向量机是全局最优解，而神经网络是局部最优，于是，BP被SVM打趴了（SVM的复仇），神经网络进入第二次寒冬了。
第三次，2006年，深度学习时代
- Hinton卧薪尝胆，坐了十多年冷板凳，潜心研究神经网络，提出了自编码器和RBM，网络初始权重不再随机，有了更高的起点，再结合pre-training和fine-tune，解决了多层神经网络的训练问题，提出了深度学习概念，标记着深度学习的正式诞生（hinton是当之无愧的祖师爷）。
- 这股热潮一直持续至到现在，大火到现在已经烧了十几年，越来越旺，甚至要灭掉机器学习了。什么时候会熄灭？这个真说不清楚。

这段历史书里也有介绍，网上找的这张图解释得更加清晰，分成三个阶段。

底图是神经网络的一个电脑模拟图，不同网络连接起来，看起来就是很复杂很复杂。但是，再复杂也是由简单神经元组成。神经元是生物术语，核心部分在于神经元在突触之间传递信息，从一个神经元到另外一个神经元。两个神经元之间有电位差，超过一定阈值时，就释放化学信号，神经递质。信息传递的过程，从一个神经元到另外一个神经元。

能不能用数学模型去模拟这个过程？

下图是进一步的简化，就是三个神经元刺激传达到一个神经元，累加，电位差发生变化之后，然后出来两种结果，一种是兴奋，一种是抑制，对应两种状态。再往下是信息的接收与传递过程。

接下来是数学模型，模拟的就是神经元的结构。椭圆形的这一部分就是一个神经元，跟上一层有N个连接，每个连接的强度不同，对应于神经元的粗细；也就是W1j到Wij的权重，再累加求和，激励函数，卡一个阈值，决定是不是要输出。

注：阈值和偏置是一个东西吗？

答：阈值是早期的偏置，那时候用符号函数，结合偏置b，变相实现了阈值功能，后期不用符号函数了，就是真正的偏置。阈值只是个概念，对应于生物神经网络，借助于偏置来实现

这是数学模型对数据源的模拟，变过来就是这样一个公式。

历史回顾，三次热潮：

第一次，1958年，感知器诞生，这是第一次兴起；
第二次，BP网络诞生；
第三次，CNN和DBN的诞生，分别是Yann LeCun和Hinton两个人提出来，第三次兴起。

网络结构上的差别，第一个是单个神经元、到单层的神经网络，中间还有一个BP，BP过程加上了2到3层，会比这个更加复杂一些，最后到深度学习，层数很多，远不止前面的2到3层。

对应到具体每个时期是哪个人。

第一部分是基于一些逻辑推理的方法，最开始的一个神经元诞生是他们两个人提出来的，M-P模型（注意这不是multilayer perceptron，而是两个人名的简称，叫M-P更准确），可以解决与或非问题，控制论流行下的电子大脑时代。
再到1957年左右是感知器诞生，MLP，跟之前的区别是有多个神经元，W1和W2的权重是可以自动训练的（基于Hebb学习法则）。与或非问题不在话下，而异或难以用线性模型解决的。异或门成了神经网络的命门。图上面靠左的人就是Marvin Minsky，他写的书就直接导致了第一次寒冬。
- 【2021-10-18】为什么感知机不能解决异或(XOR),感知器的原型是–神经元模型。1943年，由McCulloch和Pitts提出，所以也被叫做“M-P神经元模型”。
- 在”异或”问题上找不到一条直线能把X和O分开，就是说这是一个不能用直线分类的问题，这类问题叫非线性问题。同理，”同或”问题一样不能解决。所谓感知机(单层神经网络)不能解决异或问题就是不能解决画一条线在平面实现所有分类的问题。
- 准确表述是：1943年发明的感知器（M-P神经元模型，线性累加）无法解决异或问题，而不是说所有的感知器、所有的单层神经网络都不能解决异或问题
- 感知器解决异或问题有两种方式：
  - ① 用多个线性函数对区域进行划分，然后再对每个神经元的输出做出逻辑运算。
  - ② 对神经元添加非线性项输入，使等效的输入维度变大：我们的输入还只是x1，x2，但是我们添加x1^2, x1*x2, x2^2项后，就由以前的两项可以生成后三项，而且这五项不再是线性的了
  - 原文链接，附单层感知器的代码

# -*- coding:utf-8 -*-
# -*- author：zzZ_CMing
# -*- 2018/01/11;10:05
# -*- python3.5

import numpy as np
import matplotlib.pyplot as plt

n = 0            #迭代次数
lr = 0.11        #学习速率

# 输入数据
X = np.array([[1,2,3],
              [1,4,5],
              [1,1,1],
              [1,5,3],
              [1,0,1]])
# 标签
Y = np.array([1,1,-1,1,-1])

# 权重初始化，取值范围-1到1
W = (np.random.random(X.shape[1])-0.5)*2
print('初始化权值：',W)

def get_show():
    # 所有样本的坐标
    all_x = X[:, 1]
    all_y = X[:, 2]
    # 额外注释标签为-1的负样本的坐标
    all_negative_x = [1, 0]
    all_negative_y = [1, 1]
    # 计算分界线斜率与截距
    k = -W[1] / W[2]
    b = -W[0]/ W[2]
    print('斜率 k=', k)
    print('截距 b=', b)
    print('分割线函数：y = ', k,'x +(', b, ')')
    xdata = np.linspace(0, 5)
    plt.figure()
    plt.plot(xdata,xdata*k+b,'r')
    plt.plot(all_x, all_y,'bo')
    plt.plot(all_negative_x, all_negative_y, 'yo')
    plt.show()

#更新权值函数
def get_update():
    global X,Y,W,lr,n
    n += 1
    #新输出：X与W的转置相乘，得到的结果再由阶跃函数处理，得到新输出
    new_output = np.sign(np.dot(X,W.T))
    #调整权重: 新权重 = 旧权重 + 改变权重
    new_W = W + lr*((Y-new_output.T).dot(X))/int(X.shape[0])
    W = new_W

def main():
    for _ in range(100):
        get_update()
        print('第',n,'次改变后的权重：',W)
        new_output = np.sign(np.dot(X, W.T))
        if (new_output == Y.T).all():
            print("迭代次数：", n)
            break
    get_show()

if __name__ == "__main__":
    main()

# -------------------------
'''
异或问题的解决方式有：增加非线性项:
     输入x1,x2；
     增加x1^2,x1*x2,x2^2
'''

import numpy as np
import matplotlib.pyplot as plt

n = 0            #迭代次数
lr = 0.11        #学习速率

#输入数据分别:偏置值,x1,x2,x1^2,x1*x2,x2^2
X = np.array([[1,0,0,0,0,0],
              [1,0,1,0,0,1],
              [1,1,0,1,0,0],
              [1,1,1,1,1,1]])

#标签
Y = np.array([-1,1,1,-1])

# 权重初始化，取值范围-1到1
W = (np.random.random(X.shape[1])-0.5)*2
print('初始化权值：',W)

def get_show():
    # 正样本
    x1 = [0, 1]
    y1 = [1, 0]
    # 负样本
    x2 = [0,1]
    y2 = [0,1]
    xdata = np.linspace(-1, 2)
    plt.figure()
    plt.plot(xdata, get_line(xdata,1), 'r')
    plt.plot(xdata, get_line(xdata,2), 'r')
    plt.plot(x1, y1, 'bo')
    plt.plot(x2, y2, 'yo')
    plt.show()

def get_line(x,root):
    a = W[5]
    b = W[2] + x*W[4]
    c = W[0] + x*W[1] + x*x*W[3]
    if root == 1:
        return (-b+np.sqrt(b*b-4*a*c))/(2*a)
    if root == 2:
        return (-b-np.sqrt(b*b-4*a*c))/(2*a)

#更新权值函数
def get_update():
    global X,Y,W,lr,n
    n += 1
    #新输出：X与W的转置相乘，得到的结果再由阶跃函数处理，得到新输出
    new_output = np.dot(X,W.T)
    #调整权重: 新权重 = 旧权重 + 改变权重
    new_W = W + lr*((Y-new_output.T).dot(X))/int(X.shape[0])
    W = new_W

def main():
    for _ in range(10000):
        get_update()
    get_show()
    last_output = np.dot(X,W.T)
    print('最后逼近值：',last_output)

if __name__ == "__main__":
    main()

多层的感知机，最开始的BP神经网络。1974年左右，就是BP神经网络诞生。那时美国和苏联撤走了神经网络相关研究经费，好多杂志都不接收神经网络的论文，所以BP网络诞生的时候是没有什么影响力。
接下来是Hinton，他把BP重新设计了下。支持向量机诞生，全局最优解，比BP看起来更加漂亮，所以第二次寒冬来了。

网络结构上可以分成几个阶段，第一个是单层网络，第二个两层，第三个多层。这三层网络在激活函数、异或问题和复杂问题上有所不同。

单层网络只有两种状态，一种激活或者抑制，所以是一个符号函数，函数值是1或者-1，异或函数解决不了，复杂问题也解决不了。
两层网络时，结构比之前复杂了，激活函数变了，不再是符号函数，中间是sigmoid。这个时候异或问题可以解决，但是复杂问题解决不了。
到了多层网络，也就是现在的深度学习，激活函数主要是ReLU，比之前的sigmoid要简单，异或问题可以解决，复杂问题也可以解决。
- 所以现在深度学习模型中的激活函数主要是ReLU，而不是之前sigmoid。
- 其实，八九十年代，ReLU就已经出现了，只是当时人们选神经网络激励函数时，有一种偏执的迷信，sigmoid这样的激励函数，处处可导、连续、数学模型也漂亮，而ReLU很显然在零这个点是一个突变，不可导，看起来不漂亮。
- 尽管出来比较早，但是不怎么用它，直到后来多次实验后发现效果比sigmoid要好得多，因为sigmoid存在一个大问题：饱和，正无穷或者负无穷这两个方向，函数值趋近于1或者-1，没什么反应了，就只对0附近的值敏感，对非常大的或者非常小的点，淡定的很，不予理睬（一条咸鱼）。这就是饱和问题。
- 实际上，代价函数的梯度必须足够大，且足够的预测性，指引学习方向，而饱和函数破坏了这一目标。sigmoid在小数据上表现较好，但是大数据集不佳，ReLU则由于提升系统识别性能和仿生的本质（神经元信号原理），在大数据集情形大显神威，重要性甚至超过隐含层权重。

除了网络结构的变化，还有计算能力、数据、算法等因素，促成深度学习的兴起。

单层神经网络是在晶体管时代的，数据量也比较少，学习算法就是基本的一些简单的推理；
两层神经网络，主要是用CPU来算，数据量大概是一千到一万，数据量指数增长，算法主要用的BP。
多层神经网络，主要通过集群或者GPU，甚至更高级的TPU，数据量继续急剧膨胀。训练方法跟BP不同，用Pre-training，还有drop-out，防止过拟合的。

这三种不同阶段，它的网络结构、它的计算能力、数据量算法都是不同的。

深度学习领域的大神

Hinton绝对是这个领域的祖师爷；
Yann LeCun（中文名：养乐村）在CNN上面贡献非常多；
Bengio是在RNN这一块。
还有Jordan，最近好像加入阿里了
右边研究概率图的（跟支持向量机兴起）
还有吴恩达（不是吴孟达）、LSTM之父Jürgen Schmidhuber（一袭白衣，处处树敌的大佬）
还有新生代的牛人：Ian Goodfellow（GAN发明人，84年的哟)
- 2016年, Ian Goodfellow被Schmidhuber告抄袭，不过业界没什么支持
中国人呢？有的有的，机器学习领域陈天奇、视觉领域何恺明、NLP领域李纪为、田渊栋等等，也是人才济济

这就是传说中的四王天王（叫起来顺口，不一定科学），前三位已获得2019年图灵奖，可见三位的功劳有目共睹。

随着深度学习的大红大紫，工业界一直在想办法争夺人才，把报的上名字的大神都找了个遍，一个一个拉下水，到工业界去研究了，只有Bengio还一直处于中立状态，不过最近的消息好像他也加入了工业界。本书的作者是 Ian Goodfellow，GAN的发明人，Bengio是他的老师。

还有大神们的众多门生，相继发明了word2vec和fasttext，李飞飞及高徒Andrej Karpathy（江湖人称AK47）。。。
关系错综复杂，但数来数去也就那么几个人，“近亲繁殖”现象严重。

什么是神经网络？

【2020-3-9】三综一蓝对神经网络的视频介绍
- 深度学习之神经网络的结构：part 1，part 2，part 3

简单介绍一下前馈网络的一些基本结构。

每一种网络实际上是模拟某一个复杂的函数，目标是要学习每一层连接里面那个权重。
权重达到了一个比较好的状态，就相当于这个函数已经逼近完毕。

书里面强调了一点：神经网络并不是目的，它不是为了完美的模拟大脑，而只是实现一种统计泛化，类似于一种函数近似机。因为人脑是非常复杂的，现在的网络结构远远达不到人脑的这种状态。

知名的网络结构主要两种

第一种是前馈，信息一层一层往下流动，一路向前不回头（不算误差反向传播）。以CNN为例；
第二种是反馈，把上一次训练状态留下来，作为本次的一个输入，前馈的一种扩展
- 特点是训练时把上一次训练结果拿过来用，再决定下一步的训练。
- 典型例子就是RNN，边走边看，回眸一笑百媚生。

深度学习之所以兴起有三个因素：海量的数据、计算能力、算法的突破。算法里面主要有几个RBM、BP，这是优化版的BP，还有一些训练方法pre-train，加上一些激活函数的变化。

数据因素

机器学习经常提到Iris数据集，量级很小；
MNIST数据集，量级在10的4次方左右；
ImageNet，越来越大

可见，深度学习面临的问题会比之前复杂的多，数据也复杂得多。

这个是MNIST的一个示例

Hinton说它是机器学习界的果蝇，生物实验里遗传实验，牺牲了无数的果蝇。
类似，CNN也会经常拿MNIST练手，算是深度学习里的Hello World（前馈神经网络的hello world是异或问题）。

随着硬件性能的提升，模型的复杂度越来越高。

模型复杂度就类似大脑的复杂度，果蝇的大脑其实相对于哺乳动物没有那么复杂。
大脑越复杂，它的连接的数目就越多。果蝇量级比较小，但哺乳动物高
人是最高的，可能有比人更高级的生物，只是我们不知道而已（比如普罗米修斯？）。

现在随着时间推移的话，神经网络也就会不断的升级，基本上是每隔2.4年就会翻一倍。

即便是现在最复杂的神经网络，复杂程度还比不上一只青蛙。
据说百度大脑达到2-3岁婴儿的水平

神经网络能做什么

现在的应用面已经非常广了，主要分为图像、语音、文字、游戏、无人驾驶等等。

图像领域的，给一张图像，让机器识别图像里面的内容，比如人、自行车、石头等等，每个结果都给出一定的置信度。

图像领域是深度学习擅长的领域，传统方法基本都败北。
语音其次，NLP最难，NLU不好解，尚在改变过程中。

好玩一点的，国民老公和“先定一个小目标一个亿” 王健林，能够根据图片识别出来是哪个人。还有明星的，经过整容以后脸都长的一个样，但是机器识别就能辨别出来，比如这是王珞丹和白百合，不知道你们能不能区分，反正我傻傻分不清。

图像领域的应用进展。深度学习用于猫狗识别的例子，多分类任务。

还有AlphaGo，和用CNN实现的玩游戏Flappy Bird。

图像识别的发展历史。沿着时间顺序从右往左

2010年以来识别错误率是逐步下降的
在2012年左右有非常大的下降。原因是谷歌首次使用了深度学习（CNN），直接导致了接近10个点的下降。
到了2014年也是谷歌的新一版的CNN，把错误率降到了6.7%。
再到2015年微软的残差网络，错误率降到了3.57%。
- 从数字上看好像没多大差别，但一方面越往上提升的空间越小，难度越大；
- 第二个，里面有一个标志性的里程碑，人的错误率是5.1%，而这个时候机器是3.57%，已经超过了，所以说这是里程碑式的事件。用的是李飞飞的开源数据集 ImageNet
在2016年的 ImageNet比赛里面中国团队就拿下了全部冠军，今年又拿下了一些冠军。在图像识别领域提升的空间不大了，今年这个比赛已经停止了，或许是已经没啥提升的空间了。

这是一些超级网络的图示，最早的是8层网络，到了19层，再到22层，已经眼花缭乱看不清了。这个PPT是来自台大的李宏毅，大家可以找一下。

第二章线性代数-Linear Algebra

引言

Ian Goodfellow的「Deep learning」这本书，久负盛名，号称是AI圣经，内容完整，层次鲜明，一共20章，600多页。初学者读起来压力山大，别着急，我这个读书分享系列轻松讲解各类知识，降低入门门槛，帮大家快速入门。

「Deep learning」读书分享 —— 第二章线性代数

上次讲的是「深度学习」第一章：简介，今天分享的是第二章：线性代数。

右上角是这一章的目录，从27页到42页，内容不多，基本都是传统形式上的概念介绍，堆满了催眠效果极佳的数学公式。
这次一样，只讲直观思路，少提枯燥的数学公式，手机上看数学公式，效果不好，头疼又容易催眠，身在曹营心在汉。

左侧是本章的基本框架

刚开始是数学概念的基本介绍，如标量、向量、矩阵、张量；
然后讲解向量、矩阵，矩阵分解。矩阵分解里面要特别强调：“特征值分解（MF）”和“奇异值分解”（SVD）；
接着向量和矩阵之间什么关系；（用过深度学习工具包tensorflow或pytorch的人，会联想到张量这个概念）
最后是应用案例。

这部分对机器学习/深度学习非常重要，算法从业者必备。AI新人入门时，常常畏惧庞大的数学基础，止步不前，别泄气，线性代数是所有数学基础里面最简单的，这篇文章会带领大家快速温习线性代数的核心概念，并深入理解其要义，尤其是肉眼可见的几何意义。

全文分成两部分来讲

第一部分，以传统方式讲解基本概念，向量、标量、逆、秩、行列式等等常规定义，帮大家快速温习久违的《线性代数》或《高等代数》（数学系教材），把还给老师的知识一点点拿回来！（学费不能白交是吧？）
- 有些枯燥，请大家集中注意力
第二部分，换一种方式重新理解线性代数的本质，这部分是精华，一般人都没见过，保证让你醍醐灌顶。
- 如果见过，也请勿骄勿躁，像托儿一样睁大眼睛读下去

第一部分：传统方法

几种数学类型：

（1）标量，简单来说就是一个数字，像X=3，它就是一个数值；而向量就是一列数或者一堆数，把它排成一行或者一列，然后就对应到线性空间里的一个点或者一个矢量（也就是带方向的线段）。这个线性空间可以是多维的，具体二维还是三维就看这里面堆了几个数。像x=(1,3,6)，对应的是三个坐标，就是三维空间里面的一个点；而三维空间的原点到这个点有向线段就是一个向量。
（2）矩阵，矩阵是把向量按照行方向或者是列方向排列起来，变成一个二维数组。像右侧矩阵A里面这样排列。
（3）张量，矩阵基础上更高维度的抽象，它的维度可能比前面还要高，主要对应于包含若干坐标轴的规则网格。

总结, 从刚才的那些讲解上可以发现：

标量相当于一维向量（暂时忽略方向，严格来说是向量单个维度的大小）
而向量是只有一维的矩阵
矩阵是张量的一个切片从上到下是维度的逐渐提升。反过来从下往上，张量、矩阵、向量、标量，是不断降维的过程。所以前面的类型只是后面的一个特殊形式，比如说任意一个向量，是张量的一种特殊形式。简而言之，张量囊括一切。

向量一般分成方向和长度两部分。像这个x是一个单位向量，它的特点是长度是1个单位。关于向量，有这两种理解：

①把它当做线性空间里面一个点
②把它当做带有方向一个线段这两种都可以。

跟向量有关的两种运算，一种是内积，第二种是外积。根据定义，内积会生成一个数，外积会生成一个向量；需要根据右手坐标系来定方向，保持手掌、四指与大拇指相互垂直，将手掌与四指分别对应两个向量，一比划，就得到大拇指的方向，大小就按照sin这个公式算出来。

有些特殊的向量，比如零向量就对应线性空间里面的原点；单位向量就是长度是一。还有概念叫正交，简单理解就是空间中两个向量相互垂直。垂直怎么判断？就是两个向量作内积，公式里有个cosθ，θ如果等于90度，结果就是零；这就是正交。

关于向量长度，有个度量方法：范数。向量长度按照范数来度量，分别对应不同的表达式。

L1范数，它会取每一个元素的绝对值，然后求和；
L2范数，L1的绝对值变成平方，外层开方；
还有P范数，这里面的P数值是自己指定的；
F范数一般只适用于矩阵，里面每一个元素取平方，然后再求和。可见，P范数是一般形式，p=1或2分别对应L1和L2（对应于机器学习里的L1、L2正则）

矩阵相关概念：

同型，两个矩阵A和B同型，是指A和B的维度是一样的，比如说A是M×N，B是X×Y，那么M等于X，N等于Y，这是关键；
方阵，对于一个M×N的矩阵，M等于N就是个方阵。
单位矩阵，对角线全部都是1，其余都是0；
对称，转置后矩阵不变；
秩和迹，秩对应的一个概念叫线性表出，也就是矩阵里面的每一行或者是每一列，选定一个方向（要么是行要么是列），取其中一列，跟其他的列做加减和数乘（只能是这两种操作），其中任意一列要不能由其他列的线性表出。现在听起来可能不太好理解，可以暂时放放。
行列式，是在矩阵外面，比如说这个3×3的矩阵，在外面取两边各加一条竖线，这就表示行列式；怎么算呢，每一行、每一列分别取一个数，相当于这里面三个元素全排列，之后再乘上一个逆序数（逆序数是指每组元素原始下标顺序，如果是逆序，就乘-1，把这所有的逆序数乘上去，最后就得到了一个方向，也就是行列式里面是正号还是负号）。
- 有正有负, 行列式是一个奇妙的数值，可以告诉我们很多秘密
逆矩阵，是矩阵A乘以某个矩阵后得到单位阵，这个矩阵就是逆矩阵；
伪逆矩阵是逆矩阵的一种扩展；
正交矩阵是每行每列都是单位向量，特性是AAt=I。

刚才的内容，可能不好理解，不过大家都学过线性代数的基本课程，还是能够回忆起来的。后面第二部分再给大家解释一下为什么会有这些东西。

矩阵运算，除了传统的矩阵乘法，还有一种特殊的乘积，这个就是对应元素乘积，它的表示方法是不一样，中间加个圆圈；两个矩阵（必须同型）对应元素相乘，得到一个新的矩阵，也是同型的。

看一下矩阵乘法。从右往左看，这个是作者（Ian Goodfellow）PPT里的一张图，老外的思维是从右往左看。这里是3×2的一个矩阵，和2×4的一个矩阵，两个矩阵相乘，就是两个矩阵中分别取一行和一列依次相乘，得到左边的矩阵。

范数的目标就是衡量矩阵的大小。有很多种类别，但不是什么函数都能当做范数的，有些基本的要求：比如必须要保证有一个零值，然后还要满足三角形不等式，也就是三角形两边之和大于第三边，还有数乘，对应的是等比例缩放。缩放就是一个函数乘以一个实数，这是一个线性空间里的基本运算。

这是P范数的表达式。其实P范数具有一种泛化的表达式，是一种通用的方式，可以包含L1、L2，还有无穷范式，这些都是由P的取值决定的，可以等于1、等于2、等于无穷。

行列式的计算方法比较复杂，公式我就不列了。直接给出直观理解：衡量一个向量在经过矩阵运算后会变成什么样子，即线性空间上进行了某种放缩，可能是放大或者缩小，缩放的倍率就是行列式值；行列式的符号（正或负），代表着矩阵变换之后坐标系的变化。

矩阵变换里面有这么几种，平移、缩放等等。这个后面再说，免得重复。

矩阵分解：

（1）特征值分解，是我们常规见到的。有一个定义，比如我们定义一个矩阵A，乘以一个向量得到的等于另外一个数字乘以同一个向量，Av=λv。满足这个表达式，就叫做矩阵的特征值分解，这是矩阵分解典型的形式。这个v就是一个特征向量，而这个λ就是特征值，它们是一一对应的（出生入死的一对好基友）。符合表达式可能还有其他取值，每一个矩阵A会对应多组特征向量和特征值；矩阵A的所有特征向量和特征值都是一一对应的。
- 如果矩阵是一个方阵（不只M等于N，还需要保证这个矩阵里面每一行、每一列线性无关），可以做这样的特征分解，把A分成了一个正交矩阵乘对角阵乘同一个正交矩阵的逆。对角阵是把每一个特征向量一个个排下来。
- 还有个概念叫正定，是对任意实数，满足xAxt>0，就叫正定；类似的还有半正定，大于等于0是半正定；负定就是小于零。
（2）奇异值分解，是矩阵特征分解的一种扩展，由于特征分解有个很强的约束——A必须是一个方阵。如果不是方阵怎么办呢，就没有办法了吗？有的，就是用SVD奇异值分解，这个在推荐系统用的比较多。

这是特征分解的示意图。从直观上理解，这个圆上面的两个向量V1、V2，经过矩阵变换之后在两个特征方向上进行缩放：在V1方向上面缩放λ1倍，变成了新的V1；V2在V2的方向做了λ2倍的缩放，变成新的V2。这两个特征，构成了完整的矩阵分解，也就是经过一个线性变换之后得到的效果——在特征向量方向上分别缩放特征值倍。

SVD分解就是一个扩展形式，表达方式就这样，不细说了。

向量和矩阵这两个组合起来就可以解决常见的线性方程组求解问题。

这里有几个概念，一个叫线性组合，就是一个矩阵，里面的一行或者一列，实际上就是多个向量，通过简单的加减还有数乘，组合出来一个新的向量，这叫线性组合。如果用基向量X1、X2执行加法和数乘操作，得到的是x3=k1x1+k2x2，一组向量组成的线性空间，即由X1、X2组合成的向量空间，就叫生成子空间。
如果对两个向量X和Y，可以按照α和1－α这两个数乘组合起来生成一个新的向量，这个叫线性表出，就是Z向量由X和Y进行线性表出，然后α和1－α都是一个数值，满足这个关系就叫线性相关。这就是说Z和X、Y是线性相关的，如果不满足，如果Z这个向量不能这样表出，就叫线性无关。

这是矩阵对应的一个线性方程组。这是一个矩阵，现在像右边这样把它展开，就是矩阵和线性方程组是对应的。这个挺常见的我不就不多说了。

矩阵方程组的求解是，把方程组每一个系数组成矩阵A，根据A这个矩阵本身的特性就可以直接判断这个方程组有没有解、有多少解，甚至无解。

这是矩阵方程组的一些求解，比较常规的，像AX=b这个线性方程组一般怎么解呢？常规方法：两边直接乘A的逆矩阵。它有个前提：A的逆必须存在，也就是说A里每一行、每一列不能线性相关。这种方法一般用于演示，比如算一些小型的矩阵，实际情况下，A的规模会非常大，按照这种方法算，代价非常大。

再看下什么矩阵不可逆。一个矩阵M×N，按照M、N的大小可以做这样的分类：如果行大于列，通常叫做长矩阵，反之叫宽矩阵；行大于列，而且线性无关，就是无解的情形。宽矩阵有无数个解，其中，每一列代表一个因变量，每一行代表一个方程式。

伪逆是逆的一种扩展，逆必须要求A这个矩阵式满秩，就是没有线性表出的部分。如果不满足，那么就得用伪逆来计算，这只是一种近似方法。SVD这种方法比较厉害，因为支持伪逆操作。

应用案例里，书里面只提到一个PCA，线性降维，也没有详细的展开。

其实书里很多章节都提到了PCA，所以我也给大家普及一下基本概念。

这个是PCA在图像上面的应用。这张图非常经典，凡是学过数字图像处理的都知道她——Lenna（提示：别去搜lena的全身图，不卖关子了，老实交代：这是图像处理专家喜欢的一个舞女，养眼，图案灰度也鲜明，于是歪打正着成了著名样本，参考cmu网站上的《The Lenna Story》）。原图像经过主成分分析降维之后就变成右边的图，可以看到大部分信息都都还在，只是有些模糊。这个过程叫降维，术语是图像压缩。

PCA的基本过程。PCA的思想是，原来一个矩阵有很多列，这些列里可能存在一些线性关系，如何把它降成更小的维度，比如说两三维，而且降维之后信息又能够得到很大程度的保留。怎么定义这个程度呢？一般是累计贡献率大概85%以上，这些主成份才有保留意义。这个累计贡献率是通过方差来体现的，样本分布带有一定的噪音或者随机分布，如果是在均值的左和右两个方向进行偏移的话，不会影响方差。方差等效于信息量。

这张图解释主成分分析的过程，用的是特征值分解，一个X的转置乘以X，然后对它做各种复杂的变换，大家看看就行了，想了解细节的话自己去找资料，具体过程一时半会儿讲不清楚。PCA最后有什么效果呢？看中间的坐标系给出示意图，原来的矩阵取了X1和X2两个维度，把样本点打出来能看到近似椭圆分布，而PCA的效果就是得到一组新的坐标系，分别在长轴和短轴方向，互相正交，一个方向对应一个主成分。实际上，数据特征多于两维，图里只是为了方便观察，这样就完成了一个降维的过程。

右上是一个示例，有一些动物样本，狗、小猫，还有个气垫船（非动物）。在特征空间里面显示成这样，理论上，动物会靠得比较近，非动物会远离。如果用PCA来做，可能得到的结果是这个样子，动物跟非动物区分的不是很明显。所以，PCA实际上只能解决一些线性问题，非线性情况下，解决的效果不太好。

怎么办呢？用非线性降维方法。典型的方法比如说t-SNE（t分布-随机近邻嵌入），流形学方法。

流形简单来说就是很多面片叠加形成的几何图形。基本假设是，同一个数据集中每个样本会近似服从一定的内在分布，比如说空间几何体里的圆形或球面，甚至正方形，都本身有一定内在结构。流形就是试图用非线性的方法找到内在结构，然后把它映射到低维的空间里面去。这个好像要讲深了，我先不做扩展（涉及拓扑几何）。后面好几个章节要提到流形，流形这个概念是需要了解的，后面自编码器章节还会提到。

这是一个复合、螺旋形的数据集，在空间里面显示出来是这个样子，用线性方法是不可能分开的。流形怎么办呢？近似于找到一种非线性的方法，假设这两个小人，把它拉伸，拉开之后，不同的类别就能够分开了。流行学习就相当于这两个小人把二维流形拉平了，从非线性的变成线性的。

这个图说的是PCA，2006年之前这种方法是非常实用的，一旦提到降维首选是PCA。基本思想就是在数据集里面方差变化最大的方向和垂直的方向选了两个主成分，就是V1和V2这两个主成分，然后对数据集做些变换，它是线性的。

非线性分布的情况，PCA是不行的，其他的线性方法也是不行的，必须用非线性。

这里要提到降维方法，降维其实用到的相关方案是非常多的，主要分成两类，一类是人工的方法，像信息论里面有一个霍夫曼编码，霍夫曼编码也算是一种降维，它是一种可逆的方法；然后还有其他的自动化方法，因为人工毕竟是代价比较大的，所以需要找自动化方案，比如PCA，非线性的t-SNE，还有后面的自编码器等等。下面这张图概括了常用的数据降维方法，线性方法有PCA、LDA，非线性的方法又分成保留局部特征和保留全局特征，再往下有很多很多，大家去自己去了解。

不过，图里没有提到t-SNE，因为t-SNE是新出来的，2012年左右开始流行起来的，它其实是Geoffery Hinton团队发明的，现在的用途主要在高维数据的可视化上。

像这样一个数据集，在三维空间里面，它是一个服从球面分布的一个数据集，然后用不同的非线性方法进行降维，总体上还是不错的。不同的颜色它分得比较清，没有大的混杂，基本上可以的。

再看一个，这是S型的结构，经过这几种非线性的方法进行降维之后，也分得比较清楚。

拿MNIST数据集来说明。MNIST是手写数字的一些图片，按照行方向拉伸成一维向量。因为这个图片是28×28的，所以拉伸成的一维向量是784维。由于维度比较高，人能直观看到的基本是二维或者三维的，所以这里面取两个像素点，比如图像里面第18行第15列这一个像素点，还有第7行、第12列这个像素点。然后一个X轴、一个Y轴可视化一下，看它的区分度怎么样。显然从这个结果上看不怎么样，不同的颜色都分的比较零散；所以直接取其中的几个像素来分，分不清。

那么看一下PCA是什么样的效果。它会把里面784维做一个降维，然后取了两个主成分，X轴Y轴是两个主成份。跟上面一张图相比，效果还是挺显著的，周围颜色已经比较靠近。但是中间一坨就不行了，这是它的局限性，部分的分割效果还行。

看着好一点的是t-SNE，明显跟上面不是一个量级的，不同的颜色聚合的比较紧，而且不同颜色之间还有一些分隔线，这些区域还非常清晰，这就是它厉害的地方。t-SNE在非线性降维里面绝对是排名第一的。

刚才讲的是第一部分，多而杂、浅显、不好懂，实际上这本书也是按照这个传统思路来讲的。数学本身就很抽象，但是，能不能变得更加形象一点呢？可以的。

第二部分：直观理解

恭喜你，已经趟过枯燥的雷区，进入了安全、新鲜的草地！

传统的教学方法，从初高中到大学，不少老师拿着书上的概念，堆公式、只灌输、不解释，也没说运算到底有什么几何意义，导致过目即忘记。这就是为什么很多人觉得以前都学过，甚至拿了高分，但是现在好像都还给老师了。没有从感性上去理解透的知识点，背的再多，随着时间推移，也都会忘记。

所以接下来换一种方式。进入第二个环节。

参考一些资料，比如说第一个是Essence of Linear Algebra，这是国外高手（3Blue1Brown，不盈利，接受捐助）制作的教学视频，可以去YouTube上看，bilibili上也有中文翻译版，优酷也有了。这个教程非常好，全部用视频可视化方法直观讲解线性代数。第二个是马同学高等数学，几篇公众号文章也很好，跟3Blue1Brown不谋而合。看完这两个教程后，会有一种相见恨晚、醍醐灌顶、重新做人的感觉。

线性代数的本质（几何意义）Essence of linear algebra

下面是视频里的几个观点：

事实上，国内外传统教学里一直把人当机器用，各种花式算行列式，不胜枚举，然而没有告诉你是什么，为什么？

很多人对数学有种与生俱来的恐惧感，不怪你，是某些老师把简单问题教复杂了，让你开始怀疑自己的智商，认定自己不是学数学的料，于是，见到数学就避而远之。对于初学者来说，良好的解释比象征性的证明重要得多。

下面切换我的有道笔记：《线性代数笔记》。

刚才说的有矩阵是吧？我们来看一下矩阵到底在干嘛。这个(x y z)这是一个向量，一个矩阵对它进行变换之后变成了(ax by cz)，对应的就是把原来的X、Y、Z三个方向分别作a、b、c放大。

在图上面怎么理解呢？看这个，这是一个矩阵，来看着坐标系的变化。这个是在X轴方向做1.5倍的放大，这是在Y轴的方向上做缩小到一半，效果就是这样子。X轴Y轴都做了一个缩放动作，对应的轴上面的坐标和点也要做这样的缩放，整个空间都被拉伸了，X轴方向被拉伸，Y轴方向被压缩。

假设取这些二维平面上的样本点，变化完之后就成这样的。X的范围从-1到1，变成了-1.2到+1.2，也就是在X方向做1.2倍的放缩，Y轴方向1.3倍的放缩（样本点之间距离拉开了）。

如果这里面有一个负值又是什么概念呢？就是轴方向的变化（术语：手性变化，比如左手变右手）。

比如这个Y轴的有一个负号，刚才是0.5，现在是-0.5，那就是把Y轴往下翻，负号就是反向，类似一个镜面反射。如果X也是负的话，就是相对于坐标原点的中心对称。

这里面放一个图形M，看起来会更加直观一些。M这个形状的数据集，经过这个变换之后成这样。对角线的第一个元素是作用在X轴上面的，X轴沿着Y轴作了一个对折，也就是镜面反射，原来M在这儿，翻过来到这，就是这个矩阵的作用；Y轴上没有任何变化，因为是1，不放大也不缩小。第二个里Y轴是负数，那么反过来就是沿着X轴翻一下。

如果两个都是负，那就是中心对称，从第一象限翻到了第三象限。

如果里面有这样情况，这就是矩阵不可逆的情况，它的行列式是0。0的话会有什么变化？原来这是一个坐标系，到这里变成一条线了，这就是做了一个降维操作，把两维的变成一位了。那一位能返回去吗？不可能的，所以这叫不可逆。

这个跟刚才相比的话，多了右上角一个元素0.3，这是一个上三角矩阵，是什么意思呢？看一下图的结果，沿着Y轴方向是不变的，X方向就做了一种错切，也叫推移（或错切、切变）。形象理解就是站在上面，然后把箱子往这边推，底部是不动的，那么就有一个推移的动作。为什么会这样？大家可以拿这个矩阵，随机取一个点去感受一下。

第一行始终作用在X轴方向上，它跟原来相比加了一项。说明X轴方向做了追加，把Y轴的信息拿过来追加延长X轴，而Y轴没有变化，所以Y是不变的，X是要做拉伸的。

红色的这个矩阵变到蓝色就有一种错切，有一股力从左边往右推。

这也是推移以后的效果。

刚才说的是上三角，然后变成下三角怎么样？那就是反过来，X轴不变，沿着Y轴方向推移，到这儿。

好，这一部分讲的是旋转。M通过这个矩阵就进行了旋转，这是个正交矩阵，正交就是矩阵行列式的值为1，意思是说是X和Y轴是不做任何缩放的，只做以原点为中心的旋转。这就是做一个旋转，按照π/4的角度做旋转。

刚才说了几种变化，第一个旋转，第二个错切，第三个平移，加上缩放。线性变换里不包含平移；线性变换加上平移的话，那就是仿射变化。那么到底什么是线性变换？线性空间的任意点在变化前后一直保持等距分布！

下面不是线性变换，因为距离不等。

矩阵分解是说，每一个矩阵都是由这几种基础变化组合而成的。这部分过了，有点难度。数值分析这门课讲到矩阵运算代价非常大，怎么让计算机跑起来更快呢，矩阵分解，把一个大矩阵分成几个小矩阵，算起来更快。矩阵分解的基本目的就是提高计算效率。

接下来讲矩阵的特征值和特征向量。先有直观概念，特征向量反映的是经过这次变换之后它的变化方向；特征值反映的是变换的幅度。为什么会这样？往下看。

这是一个坐标系X和Y，上面有一个向量，或者说二维平面上的一个点，乘以一个矩阵之后变成这样了。

再乘以另外一个矩阵可能变成这样。看看图像区别的话，v乘它之后仍然在这个方向上；变换前后的差别就是方向不变，只是大小做了拉伸。如果符合这样的情形的话，那么λ就是A的一个特征值，v就是A的一个特征向量。A矩阵可能还有其他的情形，可能还有其他一些特征值和特征向量。矩阵特征值分解的效果，就是对一个矩阵A，在平面上找到所有满足这种关系的向量集合。

这就是特征值表示的一些传统公式，A矩阵乘以一个向量，得到一个特征值乘一个向量，反映的就是在v的方向上面拉伸了多少倍。这就是通过特征值分解揭示矩阵本身的特性。

三棕一蓝的总结：

刚才提到一个特征向量和一个特征值，还有没有其他的？有的，这个也是，这个V就是它的一个特征向量，长度也对应一个特征值，这是A矩阵的两个特征值。

A矩阵对应的两个特征向量和两个特征值，如果对特征向量做数乘，比如拿这个V1乘以2、乘以3；每一个特征向量经过数乘操作组成的空间叫做特征空间。

这里有一种近似的、形象的表述，就是矩阵是一种运动。运动在物理里面运动就有两个概念，第一个往哪走，第二个走多少，对应的是速度加上方向。

运动是动态的，点表示瞬时的状态。站哪个位置是静态的，要观察到运动必须要借助一种实体，比如说要观察跑步现象，总得要找个实物，比如看人跑、还是看猪跑、看老虎跑，你总要找个物体附上去才能够看到它的变化过程。

对同一种运动，A代表这种运动，如果应用到一个向量上面多次，它会产生什么样的变化？像A这个矩阵是一种变换，作用到V这个特征向量上，一次得到的点是在这儿，两次到这，三次四次跑到这边来了。7次就沿着这个方向，然后如果8次、9次仍然这个方向。这里有种奇怪的现象，就是对一个向量做线性变换，N次以后它会趋近于一个方向走，就不会再继续变方向了。这个方向实际上是有一定的意义的，这个方向就是矩阵分解的最大特征值对应的方向。简单说就是反复利用矩阵乘法都会有一个最明显的特征，就是整个运动方向会朝着矩阵的最大的特征向量方向走，这是它的几何解释。在一般的代数里面，可能你根本想不到这一点。

补充：

一开始向量往这个方向走，变化特别大，这都反映的是矩阵本身的特征值，贫富悬殊非常大。两个不同方向上的特征值，一个是另一个的很多倍，它们的悬殊非常大。这种情况叫有一种术语叫病态，它的衡量是通过条件数，条件数的概念就是一个矩阵的最大特征值与最小的特征值之间的倍数。最大特征值除以最小特征值得到的倍率比如是3，还可以是10，肯定是10的时候病态更严重，已经病得无药可救了。

对这种矩阵做变换，要特别小心。在梯度下降里面如果碰到这种矩阵的话，很容易在整个优化空间里不停地震荡，很难收敛。

接下来看特征分解。这一个矩阵分解完之后，中间是个对角阵，对应的就是每一个特征值。像A这个矩阵，做一个特征分解之后，两个特征值是3和1，然后左边右边对应的就是一个特征向量。比如说左边矩阵的第一个列向量就是3这个特征值对应的特征向量，不信你可以试一下。

同理，左边矩阵的第二个列向量就是1对应的特征向量.这就是一一对应的特征向量。左右两个矩阵相比就是做了个转置而已。另外矩阵里是正交向量，左右的矩阵只会做旋转，不会做缩放；中间的对角矩阵有缩放。所以整个A矩阵的作用既有旋转又有缩放。

所以特征值一种拉伸，衡量沿着特征向量的方向拉伸多少；然后特征向量就是拉伸的方向。所以到现在应该比较好理解我们上来就说的那句话，叫特征值和特征向量就对应运动的速度和方向。

这个部分是讲矩阵的秩和线性方程组之间的关系。Ax=b这样一个线性方程组，它有唯一解的充要条件是矩阵的秩，等于它的增广矩阵的秩，等于N。这也就是说满秩，满秩的方程才有解；无解的条件就是它的矩阵的秩小于增广矩阵，简单说就是A不是满秩的，或者它是不可逆的；如果有多种解呢，像这样加上增广矩阵之后仍然小于N。这是数学上的表达，但还是不够形象。

那么现在形象理解一下，我把线性方程组做下简化，变成二元线性方程组。方程组画在空间里面就是两条直线，同时满足这两个方程组的解，就是两条直线的交叉。只有这一个点同时满足这两个方程，直观地看出来这是唯一解。所以这么理解的话，唯一解就是有且只有一个交点；无解的话，把一条直线变得和另一条平行，两条直线根本就没有交点，就是无解；有很多解呢，就把平行的直线往一起靠，叠加在一起，完全重合了，那么解就可以很多很多，因为直线可以包含任意无穷多的点。

看一下，矩阵解线性方程的几何意义。这个空间上面X轴Y轴，取了一组正交基i=(1,0)和j=(0,1)，然后空间里的点就可以ai+bi来表示，a、b是任意实数，这就是i和j张成的线性空间。

这个如果i和j共线，就是说i和j可以通过i=kj这个方式表达的话，就是共线。共线就相当于是一个降维操作，把原来的二维空间变成了一维的，这是不可逆的。

A是这个矩阵在对整个的方程的线性空间做变换，就是旋转。整个变换过程里，X点相对于变换后的这个坐标系是没有变化的，相对位置没有变化，但是相对于原来那个坐标系就发生了变化。

用形象的方法理解，好比我们去坐公交车，车在动，我们也在动；我们相对于车是静止的，但是我们相对地面是运动的。我们相对与地面运动的过程就是一个矩阵对一个向量做变化之后的效果，像这样。

地球坐标系就相当于地面，上车，再返回地球，就发生了位移。这个变换对空间里面每一个点都发生了变换。

回到线性方程组。Ax=b是线性方程的一种表示，它的形象解释就是找到这样一个向量，它在线性变换之后变到了B点，我们要找到x，就是b原来的样子，是一个可逆的操作。这就是线性方程组含义。

开脑洞时间：这一部分是我补充的。

比如刚才说从x到b，能不能从b回到x呢？如果可以，那就是可逆，对应的A这个变化是可逆的；如果不能，那就是不可逆。
这个不可逆，又是怎么理解？这就是一种降维打击，比如说把一个立方体拍成一个平面，像一张纸；然后把纸揉成一个团，然后再直接打到十八层地狱。这些就是降维打击，是不可恢复的。
不可逆的时候怎么办，想尽可能回去，有点偏差也行。伪逆就是这样的时光隧道（变成冤魂野鬼，回到当初的地点），对逆做一个扩展。一般的线性方程组里面有很多样本，点非常多；矩阵是不可逆的，那就求他的最小二乘解，让这条直线尽可能靠近所有点，这就是一种近似的方法，也就是不可逆，但是我们尽可能让他回去（中国人深入骨髓的思想：落叶归根）。
还有个概念，既然有降维，那就有升维。升维该怎么理解呢？假设从北京到西藏，要坐火车，时间很长，可能两天三夜，很累。但是有钱人，直接坐飞机嗖的一下就到了，这就是升维。飞机飞行的路线在垂直高度上是有差别的，火车的高度全程差别不大。（不同维度下的生活方式不同，有个笑话：“等我富了，天天吃包子！”，富豪的世界你不懂，乞丐的世界，你也不懂）
特征分解怎么理解呢？公交车沿着既定路线走，先往东两千米，再往西三千米，然后再往东北五千米，然后就到家了。这里的方向就是特征向量，走的幅度两千米、三千米、五千米就是特征值。行列式是什么意思？就是这个路线的长度。这样理解应该就直观得多了吧。
行列式大于零有放大的作用；行列式等于0是降维的作用，不可逆的；行列式小于零，是在坐标系上面做了一个反射。注：行列式和特征值与坐标系无关，反应的是矩阵本身的特质。

这是2×2的一个矩阵，我们看一下改变行列式的大小会有什么效果。当行列式是大于1的，就有一个放大作用；如果我调小行列式的值，就缩小，然后到1是不变的；在0到1这个范围内就缩小；注意看这一点，如果等于0的话就降维了，变成一个点了；再往右边，行列式是负数，A和B翻过来了，沿着Y轴把X轴往这边反射；然后缩放的情况跟正像方向是一样的。这个过程就好理解，这叫行列式的几何意义。

最后以一张图结束：

第三章概率论-Propability and Information Theory

「Deep learning」读书分享（三） —— 第三章概率和信息论

接着第二章之后分享的是「深度学习」这本书的第三章概率和信息论。

这节课会讲到一些基本概念，常用的分布，频率学派和贝叶斯学派的差别，还有贝叶斯规则，概率图，最后是信息论。这里第四条可能很多人可能头一回见到，学了那么多概率，连这个都不知道，那你的概率真的白学了，真这样，不开玩笑。不过，老实说我也是前几年才知道这个学派的差别，因为浙大三版教材上就没提到这些，好像就提到一点，频率学派就是古典概率，没有什么其他的，这也是现行教材的缺陷。

概率的概念就是描述一个事件发生的可能性，比如说今天下雨吗？我们平时的回答里面可能有一些口语化表达，比如可能、八成、好像会、天气预报说会。这是一种可能性或者一种可信度，怎么用数学方法去衡量它呢？就是通过概率。

为什么每一个事件有一些可能性？有时候可能发生、有时候可能不发生。它是由多种原因产生的，因为任何事情都存在一定的不确定性和随机性，它的来源第一个叫系统本身，也就是这个事件本身的随机性；第二个，即使你了解了系统的一些基本特性，在观测的时候也不一定都是准的，因为观测还会有随机误差，比如测量时设备因素；第三，比如你观测的变量上有一些事件是服从正态分布的，这个正态分布真的就是对的吗？也不一定，所以存在一个不完全建模的问题。这是不确定性和随机性的三种因素、三种原因。

概率就是对不确定性的事件进行表示和推理。书里面提到一点，就是往往简单而不确定的规则，比复杂而确定规则更实用，这个怎么理解呢？像第一句话，多数鸟儿会飞，这个好理解，但是其实第一条很不严谨，因为它有很多情况，有些鸟本身就不会飞（企鹅、鸵鸟），有些幼小、生病也不会飞；如果严谨一点，表述成下面“除了什么。。。什么。。。以外的鸟儿都会飞”，听着都累。这就是简单而不确定的规则比复杂而确定的规则更实用。

机器学习里面有一个类似的概念叫奥卡姆剃刀也是一样，简单的模型能满足差不多的效果就可以了，比那些复杂的模型、准确度高一些的要好得多。

事件有几种分类。必然事件，太阳从东边升起西边落下是必然的；不可能事件，1+1不可能不等于2（这个不要钻牛角尖，这方面的段子很多，千万别跟我说陈景润证明1+1=2，我跟你急）；买彩票中了五百万，这个概率是非常小的，即小概率事件。小概率怎么度量呢？就是正态分布里面三倍标准差以外，跟那个μ±3δ相关。

这是事件发生可能性的度量，三种类别：必然事件，随机事件，不可能事件。

前人做了一些实验——抛硬币，观察出现正面的可能性。可以看到2048次还是0.51，然后越来越多的时候，趋近于事务本身：抛硬币时，正面反面应该是1/2的概率。就是说实验次数越多，它越趋近于事件本身发生的概率，这个也叫大数定律。（注：皮尔逊真傻，扔了3.6w次，哈哈，科学家好像都挺“傻”的）

随机变量有两种分类，按照它的取值空间分为离散和连续，不同的分类有不同的概率密度函数。连续时是PDF概率密度函数，离散时是概率质量函数，对应不同的求解方法。这个在机器学习里面也会经常区分，如果是离散的，那么就是分类问题；如果连续的就是回归问题，这是一一对应的。

概率会满足一些性质，非负、可加、归一，归一就是和是1。

这是离散型的概率分布，X这个事件取得X1、X2等等情况的可能性。这是离散概率分布，如果是连续的话就变成积分的形式了。

这几个表达式我们见得多了，均值、方差、协方差。注意一点，方差前面的分母是N-1，因为这个地方用到的是期望，期望已经用掉了一个自由度，所以这个地方自由度要减一；这地方要注意，要不然的你算方差的时候这里是N就糗大了。

这个是时间序列，里面会检验一个序列的平稳性会做这样一个平稳性的检验，要知道它的期望是一个常数还是方差是一个常数。期望类似均值。图中绿色序列的期望是固定的，红色序列的期望是变化的。

方差是每一次的波动幅度要一样，图中绿色序列的方差是固定的，红色序列的方差是变化的。

还有一个叫协方差，自己跟自己比的话，每一次变化的周期要一致。像这个红色序列前面周期比较长，后面周期变短，然后又长了，它的周期就一直在变化，这个也是不稳定的。

方差的形象理解，就是期望对每一个值之间的差别，取平方、求和取近似均值（除N-1）。

协方差是衡量两个变量，两个随机事件X和Y之间的关系；这个关系指的是线性关系，不是任意的关系，如果X和Y成非线性关系，这个协方差解决不了，这是要注意的地方。

这个是相关系数，就是用的协方差，然后除以它的两个方差D(X)D(Y)；如果相关系数在不同的取值范围，表示有不同的相关度。0就是完全没有线性关系，-1是完全负相关，1是完全正相关；这都是指线性关系。

这是一个图形化的解释，线性就是这样，在二维空间里面的一条直线，有斜率；这种非线性的用协方差是度量不了的。

介绍几个概念。边缘概率是，如果联合分布涉及到x、y两个事件，那么固定x看它的平均分布，这叫边缘概率。条件概率是在一个事件发生的时候，另外一个事件的概率分布。

这个是全概率公式，是求B事件发生时候A的发生概率；B可能有多种取值，每种取值情况下都要算一下。

链式法则是，有可能有多种依赖。像这个联合分布里面，A、B、C三个事件，需要C发生且B发生，然后B和C同时发生的时候A发生，这就是链式法则。

这是概率里面的几个重要概率。条件概率和全概率刚才已经说了，贝叶斯概率是基于这两个基础上的。

【2020-3-9】贝叶斯定理的简洁证明

这是「生活大爆炸」里面Sheldon在验算这个。

常用的概率分布，均匀、伯努利；范畴分布里面就不再是一个值，而是多个值，实验一次有多种结果，相当于扔的是色子，而前面扔的是硬币，那么硬币只有两种取值；还有高斯分布，也叫正态分布。

这正态分布的钟形曲线。对于标准正态分布，均值是0，标准差为1；书里的图覆盖的是正负两个标准差的范围，有问题。正确的图应该画到正负三个标准差，这个范围内曲线下的面积是总的99.7%。

这是我单独整理的一张图，几种概率分布之间的关系；它们之间的变化是有规律的。

伯努利分布相当于是扔硬币，扔一次；
扔了很多次以后就变成二项分布；
扔多次直到成功就是几何分布，比如扔了三次，看第一次出现正面的概率；
负二项分布，是说实验n次，成功r次才停止；
超几何分布跟二项分布是不同的，最核心的不同在于它是不放回的抽样，而二项分布是放回的；
最重要的当然就是正态分布了。

这张图是碰到什么情况下该用哪种分布。先不细说了，大家等到以后要用时再说。

中心极限定律就是，多次随机变量的和，把它看成一个新的随机变量的话，它也是近似服从正态分布的，就这个意思。

书里有个高斯分布，就是说刚才提到的分布都比较简单，我们能不能把它们整合起来，设计我想要的分布。这就用到高斯混合模型，这个图里面他构造了三种概率分布：

第一种的表述是“各向同性”，其中x1、x2两个变量分布的方差，必须一样。那么从整个形成的几何形状看来，这些数据点就像一个球形或者是圆形。每一个方向的方差是一样的，是规则的形状。如果不满足就变成二和三的情形。
第二组是用一个对角阵，就是x1和x2在方阵的对角线上，其他位置是零，控制y这个维度上面的方差，把它放大了；相当于把第一种的变化做了一下拉伸。
第三种情况类似的，把X轴也做一下拉伸；当然在Y轴方向也有拉伸，这个是说x1、x2两个变量的方向可以做任意的控制，这就是高斯混合模型的作用，可以按照你想要的分布去设计。

这里提几个大人物，一个是数学王子高斯，他和阿基米德、牛顿并列为世界三大数学家。德国的货币叫马克，十马克上面印的头像就是高斯，头像左边就是正态分布；硬币上也有。好像只有德国把科学家印在纸币上面，其他的国家基本都是政治人物，这也体现日耳曼这个民族的可怕。（值得学习）

这是标准正态分布。一倍标准差、两倍、三倍的位置对应的面积不同，分别覆盖了68%、95%、99.7%。三倍标准差以外的事件就当作小概率事件，这也是它的定义方式。

右图是一些相关用法，比如假设检验里面会验证α，也叫分位数，比如就0.05以上的概率是什么，验证一下对点估计或者区间估计的可信度。

常用函数，这是一个sigmoid，它有饱和特性。

还有一个softplus，它是softmax的一种弱化；softmax从右往左下降会直接到0，在0的位置有一个突变，然后继续走；0这个点的左导数和右导数是不一样的，左导数是0，右导数是1，所以0这个点上的导数是不存在的。怎么办呢？为了数学上面好看，而且求导方便，那就把它变成softplus，在0这个点做变换之后就整个平滑起来，每个点的都是可导的。实际上在书里面也提到一点，平时其实深度网络DNN里面会经常用到ReLU，ReLU里就是softmax。softmax是ReLU的一种推广。ReLU里0点也是不可导的，就有一些规则的方法，就是如果到了这个点的话，他会给要么是0，要么是1，视具体情况而论。

这是一些概率函数的基本性质。sigmoid求导非常方便，还有其他一些特性。softplus也有一些很好的性质，(x)-(-x)起来就等于x，挺简单。

频率学派和贝叶斯学派。先讲讲贝叶斯这个人，他刚开始只是一个牧师，就是一个神职人员，滑稽的是，他做数学研究是为了研究神的存在；这个跟牛顿有点像，不过牛顿前期是不怎么研究，到老了研究上帝，最后没什么成果。贝叶斯是一个彻头彻尾的学术屌丝，在1742年就加入了皇家学会；当时也是有牛人给推荐了，他没有发表过任何论文，不知道怎么的就进去了；后来也挺凄惨，到1761年死了也没什么消息。1763年，他的遗作被人发现「论机会学说中一个问题的求解」，贝叶斯理论就从此诞生。

诞生时，还是波澜不惊，没有什么影响。直到20世纪，也就是过了几百年（对，等黄花菜都凉了，花儿都谢了），贝叶斯理论就开始越来越有用了，成为现在概率里面的第二大门派，一般提到概率就会提到频率学派和贝叶斯学派。这个人物跟梵高一样，生前一文不值，死后价值连城。贝爷（别想多了，不是荒野求生）非常非常的低调。

还有一个更加悲剧的数学天才——迦罗瓦，他是群论的创始人，法国人，也是非常厉害的一个天才。十几岁就提出五次多项式方程组的解不存在，论文先后给别人看，希望大神引荐、宣传一下，结果被柯西、傅里叶、泊松等人各种理由错失，有的遗失、有的拒绝，反正那些大师都不看好。然后到21岁的时候，年少气盛，一不开心就跟情敌决斗，这个情敌是个警探，居然用枪决斗，然后光荣的挂了。

当然，决斗前夜他知道自己会挂（明知要死，还有去送死，这是种什么精神？），所以连夜把自己的书稿整理一下，交代后事，这才有群论的诞生。后来人对他评判是“笨死的天才”，他的英年作死直接导致整个数学发展推迟了几十年。

上面图中是贝叶斯，不一定是他本人，因为这个人太低调，连张头像都找不到，没有人能够记清楚，所以这个不一定是。下面的就是迦罗瓦，中枪倒下ing。

这是贝叶斯规则，就是条件概率。x和y是两个随机变量，y发生的情况下x会发生的概率是 x单独发生的概率乘x发生的情况下y发生的概率，除以y单独发生概率。一般拿这个做一些判别分类。机器学习里面分两大类生成式和判别式，判别式的一个典型就是贝叶斯规则；生成式的方法跟判别式方法区别就是，生成式尽可能用模型去拟合它的联合分布，而判别式拟合的是一种条件分布。

贝叶斯学派和频率学派最大的不同、根儿上的不同，就是，假设模型 y=wx+b，其中的w和b两个参数，频率学派认为参数是固定的，只要通过不停的采样、不停的观测训练，就能够估算参数w和b，因为它们是固定不变的；而贝叶斯学派相反，他们认为这些参数是变量，它们是服从一定的分布的，这是它最根本的差别。在这个基础上演变的最大似然估计、或者MAP等等的都不一样。这完全是两个不同的流派，争争吵吵几十年。

由条件概率引申出来的贝叶斯规则。像这个a、b、c的联合分布可以表示成这样，然后它可以对应一个图，概率图。像这样。

a发生、b发生是有一定的依赖关系的。一般如果a、b、c完全是独立的就好说了，那p(a,b,c)就等于p(a)、p(b)、p(c)的乘积。这个图跟TensorFlow里面的图是一回事。

下面介绍一下信息论。信息论是香农这个人提出来的，在1948年他发表了一篇论文叫“通信的数学原理”，对信息通信行业的影响非常大，相当于计算机行业的冯诺依曼这个级别。不过他的功劳一直被低估（吴军《数学之美》）。

信息论主要解决什么问题呢？第一，概率是事件发生时的可能性，怎么度量信息量的大小？第二是对于某个随机事件，比如说今天下雨这句话，到底有多少什么信息量？如果是在南方的话，可能经常下雨，那信息量不大；如果在北方或者在北极，这个信息量就大了去了。还有今天是晴天还是可能下冰雹，实际上这是随机事件的概率分布，这个分布有多少信息量就用熵来衡量。上面就是自信息，有条件分布，对应的是条件熵；还有互信息等等。

总之，信息论是建立在概率论的基础上，概率论里面基本上每一种概率都能对应到信息论里面的解释。

这是香农和三种书里面提到的三种特性：

非常可能发生的事件，它的信息量比较少，因为它确定性比较高；
而不可能发生的，或者是很少发生的，它的信息量就比较大；
独立事件具有增量的信息，刚才说的下雨就是一个例子；另一个例子是太阳从东边升起和从西边升起，这两个事件是完全独立的，两个事件的信息量可以累加起来。

这是信息论的几个概念，自信息、互信息、条件熵。上面的公式是自信息的标准，直接就取一个对数而已，加上负号。熵就是把多种情况累加起来再取均值。

信息论现在是跟各个行业、各个领域都是密切相关的，像统计学、经济学、数学，影响非常大。

看左边的图是不同的熵之间的关系。左边整个圈是x事件的范围，中间交叉的部分是互信息。不同熵之间的关系用韦恩图来表示。

这里有一个交叉熵，也是重点提到的概念。这是衡量事件发生的概率，像左侧靠近零，说明这个事件发生的可能性很小，那么它对应的信息量较少；然后到中间0.5的地方，比如说扔硬币有两种结果，两种结果0.5基本上靠猜，完全随机了；对于这样分不清到底结果是什么样的，对应的信息量最大的；类似的到另外一个极端，就是这个事件确定是可以发生的，可能性很大的，那信息量也小。

这里还有一个KL散度，基本上是衡量两个概率分布的差异。这个公式也很复杂，你们自己去琢磨，必须要看，看一遍然后才有直观的理解。现在讲也讲不清楚。（注：信息论也可以形象起来，参考：colah’s blog,Visual Information Theory）

机器学习里面还有一个交叉熵，cross-entropy，跟熵是密切相关的，它的差别就是少了一项。

这是KL散度，它是不对称的，就是说概率p和概率q的顺序调一下是不同的概念，两个顺序不同要用于不同的场景。它的目标是要构造一个概率分布 q，去近似拟合、去模拟另外一个概率分布p。这个p分布是由两个正态分布组合起来的，两个叠加起来。怎么用q拟合它呢，如果用左边的散度去度量，算分布之间的误差，这个误差对应的就是KL散度，然后根据KL散度去有方向地去调整。这是它的过程，类似于机器学习里面的过程。

如果用左边的KL散度，p在前q在后，那我们会得到这样一个结果；绿色的是拟合的概率。它的效果是保证在高概率的地方，拟合的概率要高，而不考虑低概率的部分，所以结果就会做一个平滑。概率的总和还是1，要保证归一性嘛。右边反过来，q在前p在后，那么低概率要优先保证，高概率就忽略了，那么这个拟合的概率分布就尽量往一个峰靠，只能保证一个峰。这就解释了KL散度不对称性的应用，可以按照不同的应用场景取不同的方向。

刚才PPT里面讲的大致的内容，图都是来自于「大嘴巴漫谈数据挖掘」这本书，朱向军的，这本书全部用图的方式去解释，非常好；还有「数学之美」和一些概念。好，我这边讲完了。

概率统计思维如何避免偏见

概率思维如何避免偏见

3.1 样本偏差
- 最常见的样本偏差——根据一个人一次的表现就推断出这个人的整体情况。
- 如果所抽取的样本是随机的，根据这些样本数据所估计的各种参数（无偏的和一致的）能够准确反映总体的相关特性，而且随着抽取的样本越大,其对事件的总体特征分布的描述越是会准确。
- 但是当所抽取的样本不是随机的或者样本数量不够多时就会出现样本偏差。
- 为了避免样本偏差，应该：
  - 检查样本是否随机
  - 检查样本数量是否足够

3.2 幸存者偏差

当取得资讯的渠道，仅来自于幸存者时（因为死人不会说话），此资讯可能会存在与实际情况不同的偏差，即幸存者偏差。当只能看到经过某种筛选而产生的结果，而没有意识到筛选的过程，因此忽略了被筛选掉的关键信息。
预防性应对措施：
- （1）多角度分析
- （2）逆向思维
- （3）避免噪音

解决性措施：

（1）贝叶斯公式

例如用 Y = 1 代表得一种病，如肺癌。 X 代表该病的某种诱因，如吸烟。那么根据贝叶斯公式，只要在肺癌患者中统计一下吸烟者的比例 P(X

Y=1)，和普通人中的吸烟者比例 P(X) 比较一下，就能知道吸烟增加患肺癌风险的倍数。

（2）对照试验

同时考察 Y = 1 和 Y = 0 的数据，采用对照试验的方法，比较实验组分布 P(X

Y=1) 和对照组分布 P(X

Y=0) 之间有没有显著性差异。

3.3 概率偏差
- 直觉和客观概率常常是不相符的。行为经济学家把人类自以为的概率，称之为心理概率，心理概率和客观概率的不吻合，就叫做概率偏差。
- 三个原因导致：以偏概全；可得性偏差，也就是眼见为实；沉锚效应。也就是先入为主。
- 措施：
  - （1）学好概率和统计，不依靠主观判断。
  - （2）无验证办法时，不过于相信主观判断，多询问别人的建议。
3.4 信息茧房
- 是指人们的信息领域会习惯性地被自己的兴趣所引导，从而将自己的生活桎梏于像蚕茧一般的“茧房”中的现象。
- 假如每个人都只按照自己的心意选择自己喜欢看的消息，那么，每个人的世界阳景都只是他们所希望看到的，而不是世界本来应该拥有的样子。
- 生活在“信息茧房”里，公众就不可能考虑周全，因为他们自身的先人之见将逐渐根深蒂固。一些国家就由于这个原因走向灾难。对于生活在信息茧房的领导人和其他人而言，这是一个温暖、友好的地方。但是，重大的错误就是舒适的代价。对于私人和公共机构而言，茧房可能变成公众一种可怕的梦魔。
- 如何避免作茧自缚：
  - （1）主观刻意不去作茧
    - 海纳百川、博览群书、多听别人的意见、成长型思维学习等。
  - （2）培养发现美的眼睛
    - 主动去接触和聆听客观事物，培养发现美的眼睛，扩大自己的好奇面，这样就能充分调动自我的主观能动性，把“茧”变成“网”。

说人话的统计学

【2018-5-20】【精华】说人话的统计学-合集，【2019-08-30】统计之都

第四章数值计算

「Deep Learning」读书系列分享第四章：数值计算

大家好，我叫陈安宁，目前在名古屋大学攻读计算力学博士。今天我要和大家分享的是「Deep Learning」这本书的第四章节，Numerical Calculation，即“数值计算”。

其实大家如果翻过这本书的话，可以看出第四章是整本书所有章节里面篇幅最少的一章。为什么，是因为其实我们大部分人在运用机器学习或者深度学习的时候是不需要考虑这一章的内容的，这章的内容更多是针对算法的数学分析，包括误差的增长以及系统的稳定性。

今天分享的主要轮廓包括以下四个点，

第一，在机器学习、包括了深度学习中数值计算的应用。
第二，数值误差的问题
第三，简单的分析机器学习系统的稳定性问题
最后，针对优化问题给出了两种不同的优化算法，一种是梯度下降法，一种是限制优化算法。

我们首先来看一下机器学习中的数值计算问题。所谓的机器学习或者深度学习，其实最终的目标大部分都是极值优化问题，或者是求解线性方程组的问题。这两个问题无论哪个，我们现在的求解办法基本上都是基于计算机的反复迭代更新来求解。因为目前肯定是没有解析解的，大家都是通过离散数学来求解这两个问题。

既然这个过程有迭代或者大量的重复计算，那么肯定会牵扯到数据的累积。数据累积就极有可能会有误差的产生。误差如果过于大或者过于小，在某些特定的情况下都会对系统产生非常致命的影响。

数值误差的产生原因和避免方法

首先我们来看数值误差。所谓的数值误差是指由于计算机系统本身的一些特性产生的误差，比如说我们知道，无论你使用任何编程语言，它里面都有很多的数据类型，包括单精度、双精度、整形、长整型。那么每一种数据当你定义以后，它在计算机的内存里面都是有对应的数值范围和精度范围的。如果在反复的迭代计算过程中，你产生的数据超过了数据类型定义的范围，计算机会自动的进行取舍。

这时就会产生一个问题，因为取舍就导致了和真实值之间的变化，这个变化就极有可能产生很大的麻烦，如果一个很小的数出现在了分母上，那么计算机在计算过程中就会得到一个非常大的数，如果这个非常大的数超过了你所定义的数据类型的范围，计算机就会出现错误。

我们可以简单看一下PPT中这个函数，它叫softmax函数，softmax函数经常会在概率里面用到。它有很多特性，它的所有元素的softmax之和是等于1的；然后如果所有元素Xi也是相等的话，那么softmax的每一个元素也是相等的，等于所有n个元素合的1/n。

我们考虑一些比较特殊的情况，比如X是一个非常小的一个量，在指数函数中当这个X非常小的时候，这个指数函数也是非常小，无限趋于零的。无限趋于零的话，假如有限个值相加，比如n=10的话，十个数以后这个分母也是一个非常小的值；如果特别小，比如10-10，这个在计算机里面一算的话，softmax就会产生一个很大的数，经过多次累积的话，产生的这个大数极有可能超过你的所定义的数据范围，这个时候你的程序就会报错。所以我们在计算的时候要避免分母上出现一个极小的数的情况。

同理，分子 xi 如果是一个非常大的数字的话，它的指数也是趋向于无穷的，整个的softmax也是一个非常大的数。这也就是说，分子过大或者是分母过小，都是我们应该在计算过程中极力避免的事情。

举一个实际应用的例子，为什么会有这种过小或过大的情况产生。比如说有一条线，我们要计算某一个点到这个线的距离，这个距离d之后会出现在分母上。对于这样一个式子，如果这个点我们取得离线过于近的话，这个距离就非常之小，这在实际应用中是经常出现的。这种情况下softmax这个函数就极容易出现问题。

那么有人会问了，怎么样去避免这个问题呢？当然有很多方法，可以的最简单的办法就是定义一个max函数，里面带有一个常数比如10-4；如果这个距离D很小的话，我们就取这个10-4，限定了d的最小的值就是10-4。

当然这是一个朴素简单的想法，在实际应用当中，我们可以使用很多其他的方法，比如可以再取一个指数，那么如果这个值非常小的话，它的整个值就会是趋向于1的，实际上也是一个解决问题的办法。

这两个问题，一个叫做分母趋近于0，或者是分子趋近于无穷大，一个叫underflow，下溢，就是指分母过于小；一个是overflow，上溢，是指分子过于大，趋近于无穷。这两个问题都是由于计算机的数据有一个有限的范围而产生的，并不是我们的算法本身系统产生的。这是Numerical error其中的一种，我们可以把它理解为，数据类型的范围限定而导致的对于分子或者分母不能过大或过小而产生的限制。

还有一种极容易出现错误的方式，是我们所构造的系统产生的。比如我们在求解线性方程组Ax=B的时候，如果这个矩阵A的是一个病态矩阵，所谓的病态矩阵，最简单形象的理解就是其中的某些列向量，它们之间的相关性过于大，也就是说列向量非常的接近。

假设这是其中的两个列向量，取了其中一个列向量上的点。这两个列向量过于接近的话，对点进行一个微小的变化，它就有可能跑到了另外一个向量上，就是说它的解发生了发生了很大的变化；按理说这个点是属于向量1的，但仅仅是因为很小的一个扰动，它就跑到了向量2上，它的解就发生了很大的变化。

=====补充=====

摘自：《病态矩阵和条件数》

病态系统

现在有线性系统： Ax = b，解方程

很容易得到解为： x1 = -100, x2 = -200. 如果在样本采集时存在一个微小的误差，比如，将 A 矩阵的系数 400 改变成 401：

则得到一个截然不同的解： x1 = 40000, x2 = 79800. 当解集 x 对 A 和 b 的系数高度敏感，那么这样的方程组就是病态的 (ill-conditioned)

有一个一般的办法判断矩阵是否病态，就是把矩阵A所有的特征值λ求出来以后，然后把所有λ里的最大的值除以最小值，然后取它的模。我们根据这个值可以判断一个矩阵是否是病态矩阵。注：即无穷范数

线性系统 Ax = b 为什么会病态？归根到底是由于 A 矩阵列向量线性相关性过大，表示的特征太过于相似以至于容易混淆所产生的。举个例子, 现有一个两个十分相似的列向量组成的矩阵 A：

在二维空间上，这两个列向量夹角非常小。假设第一次检测得到数据 b = [1000, 0]^T, 这个点正好在第一个列向量所在的直线上，解集是 [1, 0]^T。现在再次检测，由于有轻微的误差，得到的检测数据是 b = [1000, 0.001]，这个点正好在第二个列向量所在的直线上，解集是 [0, 1]^T。两次求得到了差别迥异的的解集。

所以很多时候，在进行machine learning或者deep learning之前，我们会对数据进行一个筛选。筛选时候有时候很大的一个目的就是为了把其中的特征叫量过于接近的一些数据排除出去，让我们经过筛选后的矩阵，在它的每一个列向量上有明显的差异，尽量避免过于接近的列向量的产生。

优化算法的意义以及如何选择

下面我们来简单说一下优化算法。绝大部分的机器学习或者说深度学习，都是可以归结为一个求极值的最优化问题。最优化问题，我们想到的简单的办法当然可以有很多，比如说梯度下降，就是仅仅求一个导数就可以判断求极值点的方向。

最优化问题，所谓的最优化去找最小值或者是最大值，涉及到两个问题，一是我怎么找、往哪个方向走；第二个问题是，我知道了这个方案以后我应该怎么走，每一步走多少。这基本上是所有求最值的两个问题，一个是找方向，第二个是找步长。

这是Deep Learning书中关于一些基本函数的定义，包括objective funtion目标函数，或者也可以称为损失函数，或者也可以称为误差函数。这时候我们一般都是要求它的最小值，让误差或者损失尽量的小。

这里我们看一个非常简单的例子，怎么解释刚才说的两个问题，一个是找方向，一个是找步长。这是一个目标函数，一个非常简单的二次函数。我们看红色箭头指的这一点，先看刚才说的取方向、怎么走的问题。这里有无数种方法，每一条直线都可以代表它可以前进的一个方向。但是我们要从中找到一个，因为这个最低点是我们的目标点，我们要找到从这个点出发到目标点的最快的路径、一个方向。

这里面这条红线是书中原有的，我做了两条蓝色的线。我们从这三条线中可以比较出来，红线是这三条线里面朝目标点下降最快的一条线，因为红色线在这个点和目标函数的角度是最小的，所以它是过这个点的下降最快的一条线。

然后我们看第二个问题，就是知道了方向以后怎么去走。对于每一个步长，我们在这里面引入一个ε的权值，为了保持系统的稳定性，一般会取一个比较小的值，比如说0.001或者是10-4这样的一个小值，让这个点缓慢地沿着这个红色的这个方向，一小步一小步地，朝着目标函数前进。

但是这里面会有一些问题，比如说我们会遇到一些特殊的点。刚才的比较简单的二次函数是没有问题的，但是看一下后面一些复杂的函数。

这里是一些特殊的点，critical points，我们可以把它称为临界点。

所谓的临界点是指，它的一次导数为零，也就是说这个点往左或者往右都会都会变大或变小，这个点本身就是这个小的局部系统里面的一个极值点。如果你往两边走都是变大，那么它就是一个极小值点；如果你往两边走都是变小，那么它就是一个极大值点；如果一边减小、一边变大，这种情况是我们在计算里面最不想看到的情况，叫做驻点，虽然它的导数也是零，但是这个点并不是我们所期待的那个objective point，不是我们想要找的目标点。

我们看一个复杂一点的。像这个函数曲线，图中有三个点都满足我们刚才说的一阶导数为零，但是右侧这两个点就不是我们想要的，最左侧点的值更小。这个时候就有两个问题，就是局部极值和全局最值的问题。这三个点都可以称为局部的极值点，只要满足一阶导数为零，但是怎么判断你所求的局部极值点是否是全局的最值点？有一个简单的办法是把整个系统所有的极值点都找到，然后比从里面比较出最小值；但是在实际应用中是不会这么做的，一是浪费太多的计算资源，二是因为起点的不同，找这个局部极值点也会有很多的问题。

所以如果要是把每一个极值点都找的话，会非常的繁琐，会浪费大量的资源。那么，我们设计的系统怎么样保证找到的这个点是一个最优点、或者说是全局的最值点呢？

之前介绍的都是只有单个变量的系统，现在看一下有多个变量的系统。在单变量系统里面，我们只需要求一个输入的导数；但是在多变量的系统里面，有很多的输入，就有一个偏导数的概念，假定其它的变量固定、系统对其中的某一个变量求导的话，就称之为关于这个变量的偏导数。

把所有的变量的偏导数求出来，并用向量的形式表示出来，可以表示成这个形式。刚才我们分析过了，如果要找到局部极值点的话，我们最快的方向是求导数、沿着梯度的方向；那么多变量系统里面也一样，就是说我们要求一个系统的最小值的话，还是通过求导，但这次是多变量的系统，所以我们的求导要改成偏导数向量的方向来去寻找新的最值。

这种梯度下降算法在实现的时候会有一些不同，比如根据每次下降所采用的系统点数的不同，可以大致分为两大类，一种叫做Batch Gradient Desecent，就是批梯度下降。所谓的“批”就是批量，比如说我们现在有一个系统h(x)等于θi*xi的合集（右上角），这是一个非常简单的线性系统。按照我们之前所说的，首先要求出这个系统的目标函数，我们这里用了一个最小二乘法的目标函数，然后求这个目标函数的最小值问题。

首先我们要求它的偏导数，∂J(θ)/∂θj，它表示一个方向，然后沿着这个方向更新那个变量。在变量更新的时候，批梯度下降是指每一次的变量更新，都会用到所有的xj；然后从i=1到m，会用到所有的单独变量的偏导数。比如假设这个系统里面的每一个样本有五个特征的话，那么在更新任意一个权值的时候都要把这五个特征遍历一遍。

这样的话，如果是一个非常小的系统，比如说样本数量不是很多、每一个样本所包含的特征也不是很多的话，这个是完全可以的，因为它求解的是一个全局的最优，考虑了考虑到了每一个变量方向的梯度问题，所以求的是全局的最优下降的方向。但是所求的系统往往有大量的样本，同时每一个样本还包含了不少的特征，简单分析一下这个系统的计算量的话，假设它的样本数量是n，然后每一个的特征是m，那么其中一个样本的计算量是m×m；有n个样本的话，总的计算量是m×m×n。如果样本1万、2万、10万超级大的话，每一次迭代的计算量是非常大的。

这个时候大家就想到另外一种办法，我能不能在每一次更新权值的时候，不用到所有的特征，只用其中的所求变量的特征，这就是我们所谓的随机梯度下降Stochastic Gradient Descent。随机梯度就是说，每一次针对权值的更新，只随机取其中的一个i，就是随机取其中的一个特征来计算。这样它的计算量立马就下降了，同样是n个样本就变成了m×n。因为原来的公式里面有一个求和符号，需要求m个特征的值；这里面每次只求一个特征的。所以这个计算量就少了非常多。

这又引发了一个问题，通过刚才分析，我们知道BGD是全局自由梯度下降，SGD是随机梯度现象，随机梯度中只找了其中一个变量所在的方向进行搜索，向目标点前进，那么这种方法是否能保证最后到达目标呢？理论上是有证明的，是可以的，只是这个会收敛的非常慢。

这两个方法就有点矛盾，一个是计算量大，但是全局最优，收敛比较快；一个是计算量小，但是收敛比较慢，只能找到最优目标值的附近。所以又产生了一种调和的算法，叫做小批量梯度下降，Mini-Batch Gradient Descent。其实很简单，既不像批量用到所有的特征去更新权值，也不像随机梯度下降只用其中一个，我选取一部分，假设每个样本有100个特征，我只取其中的10个特征用于每一次的权值更新。那么首先它的计算量是下降的，其次它也并不是仅仅按照其中某一个、而是它是按照了10个特征向量所在的方向进行搜索，既保证了搜索速度，又保证了计算量，这是目前在梯度下降中用的比较多的一个方法，算是一个BGD和SGD两种方法的折中方法。

它们三者的优缺点分别就是，批量是计算量大，随机是计算量小，但是搜索精度有一定的问题；Mini-batch就是权衡了两者。

刚才所有的分析都是基于一阶导数，这也是在简单的线性系统优化中常用的。其实二阶导数对于系统的分析也是非常有用的。

看一下这几个简单的例子。我们知道一阶导数的意义表示的是f(x)的变化，二阶导数的意义就是一阶导数的变化情况。比如说第一幅图，它的一阶导数从正（上升）到0（水平）再到负的（下降），不停地减小，就可以知道它的二阶导数是小于0的。第二幅图一条直线的话，它的斜率也就是一阶导数是永远不变，那么它的二阶导数就永远是0；同理第三个图指的是二阶导数大于零的情况。

二阶导数的意义就是我们可以分析这个系统。下面先介绍一个雅克比矩阵（Jacobian Matrix），我们的系统是一个多输入、多输出的系统，它变量的范围是Rm 域的范围，输出是Rn 域的范围，那么f(x) 的雅克比矩阵就是，针对所有的输入啊求导，比如第一行是那个f1对所有的输入变量求导，第二行就是f2，f的第二个变量，对所有的变量求导；同理，最后一行就是fm对所有的变量求导。这就是雅克比矩阵的定义。雅克比矩阵是一阶的求导矩阵，还有二阶求导矩阵黑塞矩阵（Hessian Matrix）。

黑塞矩阵的定义其实也很简单，每一个f(x) 同时对两个方向的变量求二次导数。当然你也可以把它看成雅克比矩阵的变形，黑塞矩阵里的每一项相当于雅克比矩阵里面的每一项再求导，因为二阶导数可以看成一次求导再求导。这是黑塞矩阵的定义。

黑塞矩阵有一个特点，对于一个系统，如果它的偏导数不分方向的，就是说先对xi求导、或者先对xj求导，求导的先后顺序不影响二次导数值的话，那么黑塞矩阵就明显是一个对称矩阵，因为xi、xj可以互相交换。就是说对先对x2求导或者先对x1求导是没有关系的，那么∂x1∂x2和∂x2∂x1是相等的。

那么二阶矩阵有什么影响，它对先前的一阶矩阵梯度下降的不足有什么样的改进呢？简单分析一下，一个f(x) 可以做这样的泰勒展开，其中包含特定点的值，这个g 表示的是一阶导数，也就是梯度，然后H是一个二阶的梯度矩阵。

当我们更新x值的时候，比如说现在是x0，然后下一步更新到x0-εg的时候（这是刚才梯度下降的定义嘛），带入这个泰勒展开会得到图中下方的公式。

列出这个公式的主要目的是为了考察梯度下降的步长系数应该怎么取值比较好。刚才讲过了，刚开始我们可以随便给一个比较小的值，0.01、0.004或者更小的值。但是实际的情况下，我们不想随机给一个，而是通过数学的分析得到一个比较好的值，从而定义这个步长系数，可以走得既快又准确。

带入得到这个公式之后（当然这时候我们可以把约等号当作等号），我们可以把它当做一个关于ε的函数，其它的变量可以都当作常数。如果要得ε的一个比较优化的值的话，我们可以看作f(ε) 等于这个式子，然后对它关于ε求导，最后在所有可能的系数里面得到一个比较好的系数。有了这个系数就可以保证我们的步长取得又大又稳。

下面我介绍两个方法，一个是仅仅用了一阶导数的、我们前面提到的gradient descent；另一个是牛顿方法，这是用到二阶导数的方法。梯度下降仅仅用到了一阶导数，所以我们把它称为一阶优化算法；牛顿方法用到了二阶，我们就把牛顿方法称为二阶优化算法。

我们看一下牛顿迭代方法，这是刚才提到的泰勒展开，然后现在想要找到这个系统的极值点，当然，仅仅求导就行了。根据一阶导数为0，它的临界点就是图中下方这个公式。这样我们更新就按照这个公式。这个公式有什么意义呢？就是一次直接找到了这个critical point，过程中用到的是黑塞矩阵。因为在这里面用到了黑塞矩阵，所以我们把牛顿方法称为一个二阶方法。

这之前，我们遇到的所有求极值的问题都是就是无约束的，就是freestyle，x没有任何的约束。仅仅是求目标函数的最小值问题。但是实际情况里有大量的约束问题，这就牵扯到了另外的约束优化的问题。

这是维基百科上关于约束优化的定义。

首先f(x) 是目标函数，如果没有下面这一堆subject to的话，它就是我们之前讲到的最优化问题，你可以用梯度下降，也可以用牛顿法来求解。但是这个时候它有了很多的约束，比如x必须满足某一个函数，xi代进去要等于一个特定的值ci。这是一个等式，所以又把它称作等式约束；相反就是不等式约束问题。

遇到这样问题应该怎么做？很容易想到能不能把这两个约束的条件整合到目标函数里面，然后对这个整合的系统再求优化问题。其实我们做工程很多时候都是这样的，之前先有一个基本的、best的处理方法，再遇到一个问题以后，就想办法把新产生的问题去往已知的基本问题上靠拢。

这里介绍一个KKT的约束优化算法。KKT优化算法其实很简单，它就是构造了一个广义的拉格朗日函数，然后我们针对这个广义的拉格朗日函数，或者是这个系统来求它的极值。

我们可以从图片上来看这个约束问题。比如我们选了一个初始点，如果没有阴影部分的面积，那就从初始点随便怎么走去找这个最优的x。走的方法就是它的梯度方向。但是现在有约束问题的话，x的取值必须要在阴影范围之内走动，这是一个比较形象的约束问题的表征。

前面提到我们要构造拉格朗日函数。要构造拉格朗日函数也简单，我们现在有一个等式约束，还有一个不等式约束，只要在等式约束和不能约束之前加入一个系数，当然我们是把这些系数看作变量的。把这些系数加入到原来的函数之上，构成了一个新的函数系统，我们就可以把它叫做广义拉格朗日函数。

之前我们是仅仅是求f(x) 的最小值，现在加入了这两个，我们可以根据它的特征分析一下。

首先，h(x) 小于等于0的话，针对它的系数α，我们就要求它的最大值；然后看 λ，因为 λ 是一个常数，求最大或者最小是一样的；最后又归结到f(x)，还是求它的最小值。当然，我们也可以两个累加前面都变成负号，那么同理下面可以变成要求它的最小值。

其实也可以很好理解，就是说原来是一个f(x)，现在加入了一个东西，这个东西满足的条件是对于任意的x，h(x)都必须是小于等于0的。那么如果我的最大值都小于等于0的话，那肯定所有值都小于等于0了。所以我这边要求一个最小值。

当然我假设加入的这部分是正的，这边所有的α都是大于零的，那么L(x,λ,α) 里αjhj(x) 就始终是小于等于0的；小于等于0的话，我只要让它的最大值满足的小于等于0，那么它所有的其他值肯定也是满足这个条件的。这就是如何构建一个拉格朗日函数的方法。

有了这个构建的函数以后，它的极值问题就可以用梯度下降的方法来求解。

我们举一个简单的例子，最简单的，线性最小二乘法，这个是在求误差的时候最常用的损失函数或者目标函数了。那么我们可以用到前面讲到的梯度下降法，求它的导数，然后x更新的话就是用一个小的补偿系数乘以Δx，就是它的梯度。当然你也可以用牛顿方法，用求它的二阶导数来更新。

现在我们把这个系统稍微改一下，把它变成一个受限的系统。比如我们要求向量x满足这个条件，这样它就变成了一个带有限制的优化问题。这个时候我们可以构造拉格朗日函数，原函数不变，加上它的限制条件，前面加上一个λ变量，然后就可以写出它的目标函数。

首先f(x) 是不变的，然后因为xTx小于等于1，所以这边要求最大的（当然如果xTx大于等于1，你这边要求最小的）。然后怎么更新这个系统呢，x可以这样来表示

基本上就是求逆的操作。λ满足的一个梯度条件是，把它看作单变量，对它求导，它的导数需要满足

这样Deep Learning书的第四章书基本上就讲完了。

总结

最后简单总结一下，这一章主要讲的问题。第一，我们在做数值计算，包括深度学习或者机器学习的时候，我们要注意里面的变量，尤其是在分母上的变量，不要出于出现过小的值，比如距离，分母不要过桥，分子不要过大。现在是有软件是可以帮助我们检测的，但是因为我们平时用到的算法基本上是成熟的，或者是用了很多Library/库，其中已经对一些异常状况做过提前预防，所以我们的计算中是不存在这个问题的。一般是针对我们要自己动手设计出新的计算方法时才会考虑这个问题；平时的计算过程中一般不需要考虑系统的稳定性问题的。你如果设计一个新的系统，你就要分析一下这个系统的稳定性。

然后就是梯度下降的意义，就是我们找了一个什么样的方向去接近目标函数，有了方案以后我们应该怎么走，每一步应该走多少；有时候你走的过大的话，也会导致系统的发散。

其实在这本书的最后作者也说了，目前Deep Learning系统缺少严格的理论保障。为什么我们做机器学习的时候经常说调参数、调参数，就是因为很多东西可以说是试出来的，并没有严格的数学证明说某一个值应该怎么取。这一章节在最后也说了一个目前使用的深度学习算法的缺点，就是因为它的系统目前过于复杂，比如一层接一层的函数的叠加或者是相乘，它的系统分析就会很复杂，很难有一个明确的理论去分析这个系统的各种特征。如果仅仅是一个简单的f(x)=x2，这种系统无论怎么做都行，它已经被分析的太彻底了，无论怎么算都会有一个精确的算法在那里。所以前面讲的误差也仅仅是在一个常见的容易出错的地方给了一个比较好的指导，但实际的计算过程中还会遇到各种各样的问题。这个时候一是要靠经验，二是也希望会有越来越多的数学理论来支持深度学习的系统分析。

还有就是，我们在做计算的时候都知道有一个天然的矛盾，就是计算量和精度的问题。计算量大就会让精度提高，但是有时候过大的计算量又是我们承受不了的，所以这也是一个矛盾。现在的很多算法其实也就是在中和这个矛盾，既要降低计算量，要保持我们能够接受的精度。所以现在有很多前处理的方式，针对大量的数据要怎么样处理，让设计的系统最后既能够满足我们的要求，又尽量的减少计算量，同时也尽量避免一些不必要的误差。其实这是就是一个洗数据的过程，把数据洗得干净一点，把噪音和没有用的数据都淘汰掉的过程。

今天就和大家分享到这里，如果有什么问题的话，欢迎大家在群里面讨论。

机器学习的数学数学理论其实比较匮乏，所以有很多值得讨论的问题，包括其实有我刚才有好几个点想讲没有讲的，因为时间有限，比如说二阶的优化问题，怎么样去用二阶的优化问题去保证一阶优化找到那个全局的最小点，而不是局部的最小点。其实这个在多目标、多变量的系统里面，目前还没有特别好的方法，当然在单系统里面就不存在这个问题，有很多方法去解决。今天就先到这里，谢谢大家

变分编码器

【2021-10-26】变分自编码器(VAEs)在推荐系统中的应用,《Variational Autoencoders for Collaborative Filtering》,[论文源码】(https://github.com/dawenl/vae_cf)

AutoEncoder

AutoEncoder框架包含两大模块：编码过程和解码过程。通过将输入样本映射到特征空间，即编码过程；然后再通过将抽象特征映射回原始空间得到重构样本，即解码过程。优化目标则是通过最小化重构误差来同时优化encoder和decoder，从而学习得到针对输入样本的抽象特征表示。

AutoEncoder在优化过程中无需使用样本的label，本质上是把样本的输入同时作为神经网络的输入和输出，通过最小化重构误差希望学习到样本的抽象特征表示。这种无监督的优化方式大大提升了模型的通用性。

对于基于神经网络的AutoEncoder模型来说，则是Encoder部分通过逐层降低神经元个数来对数据进行压缩；Decoder部分基于数据的抽象表示逐层提升神经元数量，最终实现对输入样本的重构。

这里值得注意的是，由于AutoEncoder通过神经网络来学习每个样本的唯一抽象表示，这会带来一个问题：当神经网络的参数复杂到一定程度时AutoEncoder很容易存在过拟合的风险。

Denoising AutoEncoder(DAE)

为了缓解经典AutoEncoder容易过拟合的问题

一个办法是在输入中加入随机噪声，Vincent等人提出了Denoising AutoEncoder，即在传统AutoEncoder输入层加入随机噪声来增强模型的鲁棒性；
另一个办法就是结合正则化思想，Rifai等人提出了Contractive AutoEncoder，通过在AutoEncoder目标函数中加上Encoder的Jacobian矩阵范式来约束使得Encoder能够学到具有抗干扰的抽象特征。

下图是Denoising AutoEncoder的模型框架。目前添加噪声的方式大多分为两种：

添加服从特定分布的随机噪声；
随机将输入 xx 中特定比例的数值置为0；

DAE模型的优势：

通过与非破损数据训练的对比，破损数据训练出来的Weight噪声较小。因为擦除数据的时候不小心把输入噪声给擦掉了。
破损数据一定程度上减轻了训练数据与测试数据的代沟。由于数据的部分被擦掉了，因而这破损数据一定程度上比较接近测试数据。

Variational Autoencoders(VAEs)

变分自编码器是自动编码器的升级版本，其结构跟自动编码器是类似的，也由编码器和解码器构成。

回忆一下我们在自动编码器中所做的事，我们需要输入一张图片，然后将一张图片编码之后得到一个隐含向量，这比我们随机取一个随机噪声更好，因为这包含着原图片的信息，然后我们隐含向量解码得到与原图片对应的照片。

但是这样我们其实并不能任意生成图片，因为我们没有办法自己去构造隐藏向量，我们需要通过一张图片输入编码我们才知道得到的隐含向量是什么，这时我们就可以通过变分自动编码器来解决这个问题。

其实原理特别简单，只需要在编码过程给它增加一些限制，迫使其生成的隐含向量能够粗略的遵循一个标准正态分布，这就是其与一般的自动编码器最大的不同。

这样我们生成一张新图片就很简单了，我们只需要给它一个标准正态分布的随机隐含向量，这样通过解码器就能够生成我们想要的图片，而不需要给它一张原始图片先编码。

在实际情况中，我们需要在模型的准确率上与隐含向量服从标准正态分布之间做一个权衡，所谓模型的准确率就是指解码器生成的图片与原图片的相似程度。我们可以让网络自己来做这个决定，非常简单，我们只需要将这两者都做一个loss，然后在将他们求和作为总的loss，这样网络就能够自己选择如何才能够使得这个总的loss下降。另外我们要衡量两种分布的相似程度，有一个东西叫KL divergence来衡量两种分布的相似程度，这里我们就是用KL divergence来表示隐含向量与标准正态分布之间差异的loss，另外一个loss仍然使用生成图片与原图片的均方误差来表示。

我们可以给出KL divergence 的公式：

这里变分自编码器使用了一个技巧“重新参数化”来解决KL divergence的计算问题。

这时不再是每次产生一个隐含向量，而是生成两个向量，一个表示均值，一个表示标准差，然后通过这两个统计量来合成隐含向量，这也非常简单，用一个标准正态分布先乘上标准差再加上均值就行了，这里我们默认编码之后的隐含向量是服从一个正态分布的。这个时候我们是想让均值尽可能接近0，标准差尽可能接近1。
VAE通过Encoder学习出均值向量和方差向量（贝叶斯估计）。同时随机采样一个正态分布的向量。通过公式重采样得到（Sampled Latent Vector），它描述的是一个潜在多元正态分布（非高斯）的均值和标准差，这个正态分布就是用来生成VAE所训练的数据。最后通过Decoder进行重建。损失函数是Decoder后的输出与初始输入的差异，以及学习后的潜在分布和先验分布之间的KL散度作为正则化，的重参数技巧。

VAEs模型理论

MLE、MAP、Bayesian

几个概念

MLE是极大似然估计Maximum Likelihood Estimation。
MAP是最大后验概率Maximum A Posteriori Estimation

两者的区别就是在于求解最优参数时，有没有加入先验知识。也就是MAP融入了要估计量的先验分布在其中，因此MAP可以看做规则化的MLE。这也就解释了，为什么MLE比MAP更容易过拟合。因为MLE在求解最优时，没有对有先验的指导，因此中包括了一些 outlieroutlier 的数据样本时，就会很轻易让MLE去拟合 outlieoutlie 样本。而MAP加入了对的先验指导，例如L2正则化，那么就不易过拟合了。

同样的逻辑回归。

未正则化的逻辑回归就是MLE。
正则化的逻辑回归就是MAP。

MLE和MAP求解的都是一个最优的值，在预测时只有最优的参与预测过程。贝叶斯模型求解的是的后验分布，而不是最大化的后验分布。因此贝叶斯模型在某种程度上可以看作是一个集成模型，在预测时，让所有都参与预测，并将预测结果「以后验概率作为权重进行加和作为最终预测值」。

从 MLE 到变分推断

VAEs网络结构

VAEs的网络结构和 AutoEncoder(AE)一样，由两个网络构成，分别是 Encoder 和 Decoder 。非常自然地，对应上述 , 而对应上述。VAEs只是在 AE 的基础上用了变分推断，这也是其名字的由来。下图是一个简单的VAEs示意图，实际情况中网络结构可能更加复杂。蓝色分别为输入和输出，绿色为 Encoder / Decoder 的中间层，红色为 Encoder 的输出，一般是一个维度很低的向量 (仅限于早期简单的 VAE)，它有不同的名字，比如 code、latent representation、latent vector、embedding或者 bottleneck。

VAEs与AE的关系

最原始的 AE 的目标函数是:

其被称为 reconstruction error, 其目的便是希望近似于恒等变换，但是的输出维度非常小 (可以用矩阵分解 SVD 或者 NMF 来类比)。这看上去与 VAEs 的目标函数完全不同，但实际上有很强的联系。

Beta-VAE

Beta-VAE 是 VAEs 的简单推广，但十分有效。我们刚刚提到 VAEs 在 AE 的基础上增加了 regularization 从而得到更好的效果，那么我们可以直接增加一个 regularization factor 进一步提升效果

深度学习-Deep Learning

资料

深度学习资料

Challenges for Deep Learning towards Human-Level AI

Deep Learning模型若干年的重要进展

Track.1 CV/Tensor

Track.2 生成模型

Track3 Sequence Learning

Track.4 Deep Reinforcement Learning

好玩儿的Python：从数据挖掘到深度学习

School-of-AI 入门教程

《Deep Learning》读书笔记

第一章 Introduction

什么是深度学习？

深度学习跟机器学习之间有什么关系

神经网络的发展历史

第二章 线性代数-Linear Algebra

引言

第一部分：传统方法

第二部分：直观理解

第三章 概率论-Propability and Information Theory

概率统计思维如何避免偏见

说人话的统计学

第四章 数值计算

数值误差的产生原因和避免方法

优化算法的意义以及如何选择

总结

变分编码器

AutoEncoder

Denoising AutoEncoder(DAE)

Variational Autoencoders(VAEs)

VAEs模型理论

MLE、MAP、Bayesian

从 MLE 到变分推断

VAEs网络结构

VAEs与AE的关系

Beta-VAE

结束

Share

Related Posts

站内可视化导航

Comments

第二章线性代数-Linear Algebra

第三章概率论-Propability and Information Theory

第四章数值计算