- 遇事不决,量子力学;
- 解释不通,穿越时空;
- 脑洞不够,平行宇宙
总结
- 《道德经》:道生一、一生二、二生三、三生万物。
- 哲学和科学的最大区别:
科学是要能应用的,而哲学只需要想就行了。这是“写意”跟“写实”的区别,想和做是两码事。
量子计算
过去一百年,人类有两个伟大的文明突破,一个是计算机的发明,另一个是量子力学的发现。两者均促进人类世界发生跨越式的进步。大约二三十年前,这两个伟大的思想交叉碰撞,发展出量子信息科学。其中,量子计算机的构想,一方面提供了可以突破当前经典计算机物理局限的可能性,另一方面也成为科学工程上前所未有的一大挑战。
资料
- 一文读懂量子计算
- 量子计算机是怎样工作的、为什么它如此强大、它可能在哪些方面最具用途?
- Nielsen 的 Quantum Computing for the Very Curious
- 量子计算入门
- 量子计算:突破摩尔定律,开启算力新时代
量子力学
【2023-1-23】如果有一天,量子力学被证明是对的,人生将变得毫无意义
人之所以比动物高级,是因为人对万物保持好奇心和创造力,时至今日,我们已经掌握了无数高端的科技手段,也攻克了一个又一个的难题,甚至飞出地球,飞向银河系,向着神秘浩瀚的宇宙发起探索。
然而一直以来,有一个问题困扰许久:我们从哪里来,未来又将去向何处,如果有一天,量子力学被证明是对的,那么现实的人生还会有意义吗?
人生存在的意义
- 其实量子力学所带来的理论在某一程度上与中国古典的道家太极八卦思想是相契合的,物理学界与哲学界是可以相通的。我们不得不感慨几千年前老祖宗的智慧。
“种什么因,得什么果。” 人的意识不仅仅存在于精神世界中,更是有能量的,可以影响今后事情的发生,善恶就在一念之间,现在所做的选择是不可以被预测计算的,具有不确定性,现在的所有选择对今后的结果都会产生影响。
- 我们为了目标努力奋斗,意识就会对最后的结果产生正面影响
- 而消极怠工,得过且过,那意识就会对结果产生负面影响。
因此,即使有一天量子力学被证明是对的,每个人的存在依旧有意义,命运还是由自己掌握。
按照目前的观点,能量既不会凭空产生也不会凭空消失,我们无论是出生还是死亡都是存在的,活着是一种状态,人死亡之后,不过是换了一种存在的方式,还存在于这个空间中没有消逝。
- “道生一,一生二,二生三,三生万物”讲的就是这样一个道理。
我们生而为人,可以通过努力和意志主导自己的命运,而不是坐等着“拉普拉斯妖”的照拂,祈求神灵的帮助,每个人都是独一无二的不同存在,没有人可以被观测,也没有人可以被预测,每个人都面临着各种不同的分叉路口,此时的选择只能由你自己决定。
量子力学的建立
有一句打趣的话“遇事不决,量子力学。”
量子力学和相对论是20世纪物理学界的两大科学支柱,修正了牛顿的经典物理学只能使用了宏观低速物体的缺陷,深入物体的本质,解释了微观高速的原子以及原子核的理论,而20世纪以来,一直是哥本哈根学派所推崇的量子力学占据上风。
量子力学认为能量是解决一切反常现象的关键,整个宇宙就是一个能量的大合体,而难以解释的量子纠缠其实就是同一个粒子在不同宇宙的映射罢了,而不是一种简单的叠加状态,量子纠缠是分裂宇宙的证据。
微观粒子的运动具有波粒二象性和不确定性原理,应该利用波函数来解释粒子的存在和运动。
- 就像原子核外的电子云排布是随机有概率的,我们只能预测下一次原子在哪里出现的可能性大,却不能准确得出下一秒原子会去往哪里,每一个量子态的测量都有不同的结果。
量子不确定性原理使得你无法预知一个微观粒子未来的状态,正如爱因斯坦所说的:上帝不玩骰子,但是量子力学让我们不得不相信,上帝似乎是玩骰子的。
这些都暗示人类对量子的测量行为会破坏量子的叠加状态,但不能说物质是由于人类的意识而存在,而是因为不确定性原理,每一次的观测都存在偶然性,不能准确的预测出未来的发展状态,人类的意识是宇宙能量的一部分,每个人都与量子之间存在千丝万缕的联系,会影响今后的发展。
最有名的实验是人们常拿出来说的“薛定谔的猫”。
摩尔定律
超越摩尔定律的计算
- 1965年,英特尔联合创始人戈登·摩尔(Gordon Moore)观察到,微芯片上每平方英寸的晶体管数量每年会翻一番,同时成本却减少了一半(自1958年发明晶体管以来)。 这个观察结果被称为摩尔定律。
- 摩尔定律意义重大,因为它意味着随着时间的推移,计算机会变得越来越小、计算能力越来越强、计算速度越来越快。 然而,摩尔定律正在慢下来(有些人说停止了) ,传统计算机没有以过去那样的速度进步。
- 英特尔在过去50多年里一直依靠摩尔定律来推动芯片创新。现在,英特尔和其他计算机制造巨头已经暗示,基于晶体管的计算正在接近一堵墙。
- 2020年代的某个时候,如果我们想继续从计算能力的指数增长中获益,我们必须找到一种完全不同的信息处理方式——量子计算
什么是量子比特?
- 现在的计算机使用比特 (bit),它是一种表示1或0的电脉冲或光脉冲流。从微博、微信、iTunes歌曲到视频服务的所有内容都是这些二进制数字的长串。
- 量子计算机则使用了量子比特,其物理载体通常是亚原子粒子,例如电子或光子。就量子计算机而言,制备量子比特并对其进行控制是一项科学挑战。
- 一些如IBM、谷歌、Rigetti Computing、阿里巴巴、本源量子等公司,在量子计算机运行时,超导电路的冷却温度几乎接近宇宙最低温。而其它像IonQ 一样的公司,则在超高真空室中的硅芯片电磁场中去捕获单个原子。通过这两种方法,能够将量子比特隔离以达到控制的目的。
- 量子比特具有一些离奇的属性:它们的连接组可以提供比相同数量的二进制位更高的处理能力。
- 一个属性称为叠加(Superposition)
- 另一个则称为纠缠(Entanglement)。
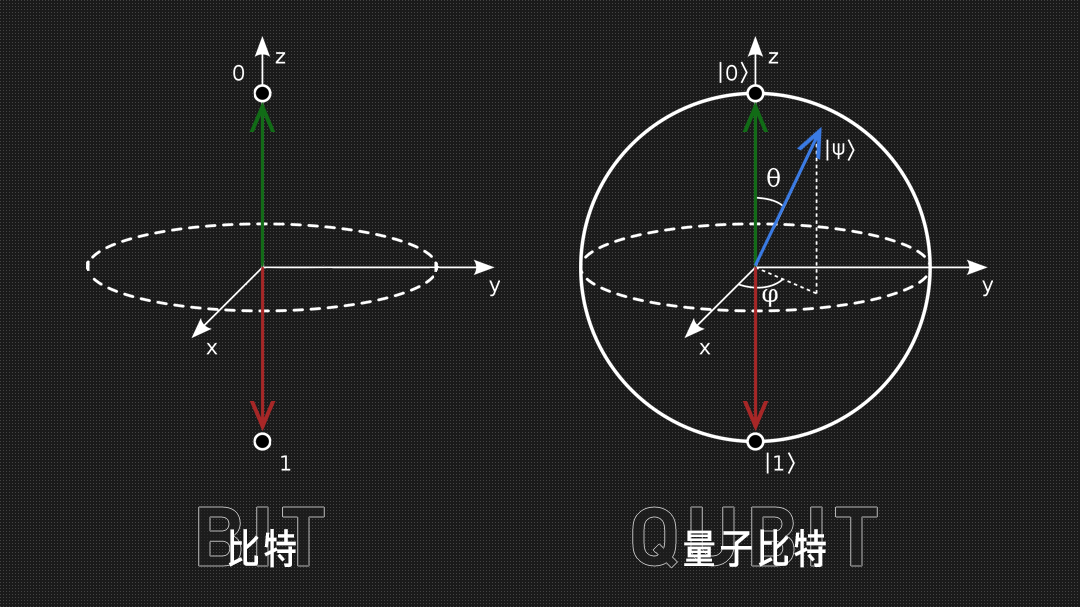
比特(Bit):数学上的 0 或者 1,物理上,一个比特可以被任何一种物理系统所表示,只要这种物理系统总是处在两个不同状态中的一个。常见的例子有:具有正反两面的银币,只有开和关的电子开关,只允许两个不同电压的电路。
计算机是由许多比特组成的,与之相似,量子计算机是由量子比特(Qubit)组成的。量子比特也被称为量子位。
- 像比特一样,
量子比特也有状态。比特的状态要么是 0,要么是 1。量子比特的状态却是一个矢量。更准确地说,量子比特的状态是一个存在于二维复矢量空间的矢量。这个矢量空间被叫做状态空间。比如,这是量子比特的一个可能状态:[ 0,1 ] - 用量子状态表示比特状态0:
- 量子状态表示比特状态1
物理上,量子比特可以是任何一种双态系统,它拥有两个不同的基态,对应于二维矢量空间中的基矢。
- 比如,电子的自旋,向上或向下。又或者是光子的极化,垂直极化和水平极化。在一个经典的系统中,一个比特必须处在两个状态中的一个,这时100%确定的。然而,量子力学允许量子比特处在一种两个基态的叠加态中,即一个任意二维矢量可以被两个基矢量表示。当您观察量子比特时,结果总是是随机的从两个基态种挑选一个,您永远无法预先确定的知道它的结果。叠加态是量子力学和量子计算的基本性质。
什么是量子叠加?
- 量子比特(Qubits)可以同时代表1和0的多种可能性组合,而这种同时处于多种状态的特性称之为叠加(Superposition)。研究人员使用精密激光或微波束操纵量子比特以使它们能处于叠加态。
- 具有多个量子比特叠加的量子计算机可以同时使得大量潜在的计算结果相互消融,导致其量子比特状态“坍塌(collapse)”为1或0,因此计算的最终结果,仅在测量量子比特时出现。
薛定谔的猫的故事,在打开盒子之前,猫处于一种既生又死的叠加态,而一旦打开盒子,猫就到达了一种确定的状态,要么生要么死,因为你的观测,导致猫死了,这就是所谓的好奇害死猫。观测动作会使量子从叠加态塌陷到确定态。观测导致态的塌陷,这对于薛定谔的猫是不好的,但对于量子计算机来说是必要的,这将有助于我们提取得到一次计算的结果。
注意:
- 结果状态有概率性,并不是每次的答案都是一样的,多次计算会给出多种可能的答案样本。 因此,量子计算机在设计时需要考虑多种答案的情况,结合统计学来计算多种答案中某一答案正确的可能性,可以通过调整该置信度来平衡速度和准确度。
基底:量子比特的任意状态
传统计算机中,0 和 1 构成比特取值空间中的基础取值。在量子态空间中也存在一组基,是量子比特的基础取值。对于一个量子比特的空间,这组基底是(使用狄拉克标记右括向量表示,也叫 ket),也就是量子比特的 0 和1
计算基础状态 和
只是一个量子比特可以处于的无穷多种状态中的两个。毕竟,一个量子状态是一个二维矢量。这是一个比特作为标量所不具备的特质。
有个图示,强调了量子态的矢量本质。
在这个例子中,态 0.6 + 0.8
代表了一种叠加态,它表示0.6倍的
基矢加上0.8倍的
基矢。也可以用常见的矩阵符号表示如下
叠加态
不同于传统计算机,一个比特的取值非0即1,在一个时间只存在一种状态。而量子比特则可以是1 同时也可以是 0,两种状态同时存在,可以表达成如下的形式,其中 alpha 和 beta 是两个复数。
当 和 其中一个为 0 时,处于基态,而都不为 0 时则处于叠加态。
纠缠态
对于两个及以上的量子比特,还存在一种特殊的叠加态,叫做纠缠态。当几个粒子在彼此相互作用后,由于各个粒子所拥有的特性已综合成为整体性质,无法单独描述各个粒子的性质,只能描述整体系统的性质,这种现象叫做量子纠缠。
其定义如下,两个量子比特的基如下:
 对于一个 2-qubit 的量子态
对于一个 2-qubit 的量子态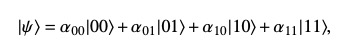
如果不能够表达成 product state 的形式,则称为纠缠态,例子如下:
在量子计算中,量子纠缠的意义很大,它可以使空间上分离的多个量子比特之间发生了联系,实现多个比特的联合计算,进而实现相比于传统计算机的指数级加速效果。
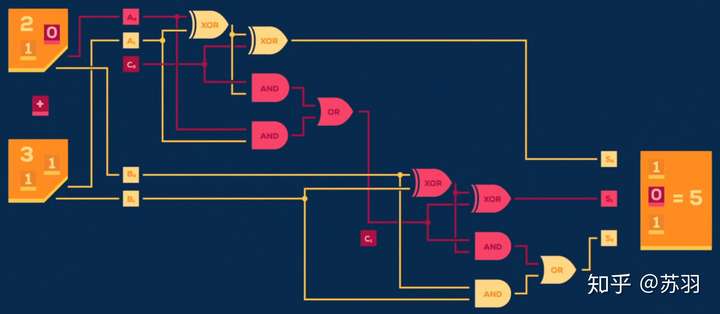
量子逻辑门
为了进行量子计算,仅仅了解量子态是不够的。我们还需要能够利用他们做一些有有意义的事!我们使用量子逻辑门 (Quantum Logic Gates)来做到这一点。
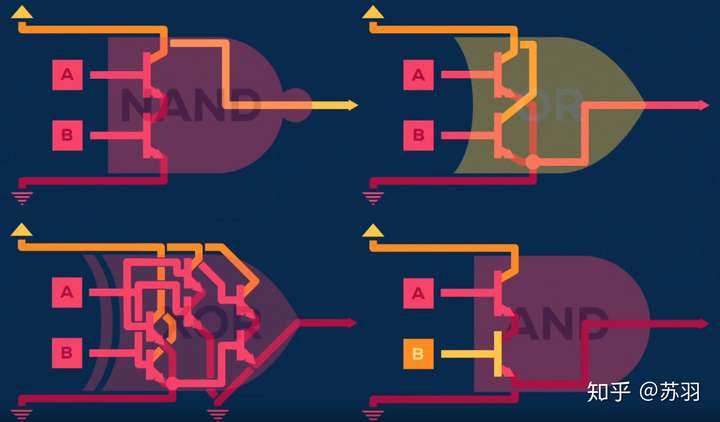
- 门其实就是量子力学中的算子。 量子逻辑门只是一种操纵量子信息的方式,量子信息被量子状态表示。它们类似于普通日常计算机中使用的经典逻辑门——诸如 AND、OR 和 NOT 之类的门。而且,就像经典门在传统计算机中的作用一样,量子门是量子计算的基本构建模块。它们也是描述许多其他量子信息处理任务的便捷方式(例如量子隐形传态)。
特别是,就像任何经典计算都可以使用 AND、OR 和 NOT 门构建一样,我们在接下来的几节中描述的量子门足以进行任何量子计算。
量子非门
量子非门(Quantum NOT Gate)是经典非门的推广。在计算基础状态上测量,量子非门完全符合您的预期,模仿经典非门。也就是说,它将 状态变为
,反之亦然:
将非门应用于一般叠加态,它是一个线性算符,
由于历史原因,从事量子计算的人们通常使用不同的符号,量子非门的符号是而不是NOT。
量子电路
量子电路(Quantum Circuit)是一种对量子计算可视化的表达,它对于我们理解量子计算至关重要。
以上表达 门工作的方式用的是的非常代数的方法。还有另一种表示,量子电路(Quantum Circuit)表示。在量子电路中,如果我们描绘一个
门,将如下所示:
从左到右的线就是所谓的量子线(Quantum Wire)。量子线代表单个量子位。术语“线”及其绘制方式看起来就像量子位在空间中移动。但是,将从左到右绘制的线视为代表时间的流逝才是正确的。所以最初的线段代表时间的流逝,量子位没有任何变化。然后 门被应用到量子位 ,量子位的状态改变。时间继续流逝,量子位的状态不再变化。
有时我们会将输入和输出的状态明确地画在量子电路中,比如:
量子计算的Hello World!
from qiskit import QuantumCircuit, BasicAer, execute
# create a quantum circuit with one qubit and one bit
qc = QuantumCircuit(1,1)
# apply not gate to the qubit with index 0
qc.x(0)
# measue the qubit with index 0 and store the result to bit with index 0
qc.measure(0,0)
# plot the circuit
qc.draw('mpl')
# simulation: run the quantum circuit 1000 times and print all results
backend = BasicAer.get_backend('qasm_simulator')
result = execute(qc, backend, shots=1000).result()
counts = result.get_counts(qc)
print(counts)
什么是量子纠缠?
- 研究人员可以制备“纠缠”的量子比特对,即是说一对量子比特对的两个量子比特存在于单个量子状态,当研究人员以可预测的方式改变其中一个量子比特的状态时,另一个量子比特的状态将瞬间改变。即使它们距离远隔宇宙之遥也会发生这种情况。
- 没有人真正知道量子纠缠是通过怎样的方式产生影响的,甚至让爱因斯坦也感到困惑,他曾将其描述为“鬼魅般的超距作用”。但量子纠缠是量子计算机凸显强大力量的关键因素。在传统的计算机中,将二进制位数加倍会使其处理能力加倍。但由于纠缠的特殊能力,在量子机器中添加额外的量子比特则会使其数字运算能力呈指数级增长。
- 量子计算机在量子daisy链中利用纠缠的量子比特来发挥它们的魔力,而其之所以有潜在的嗡嗡声是由于使用专门设计的量子算法以加速计算的缘故。
- 量子计算机能够加速计算是个好消息。但坏消息也随之而来:由于退相干的存在,量子计算机比传统计算机更容易出错。
诺贝尔物理学奖
【2022-10-4】纠缠,是一种强大的工具! 2022年诺贝尔物理学奖颁发,获得诺贝尔物理学奖的三位科学家——法国科学家阿兰·阿斯佩、美国科学家约翰·克劳泽、奥地利科学家安东·塞林格,他们通过开创性的实验展示了处于纠缠状态粒子的潜力,这三位获奖者对实验工具的开发,也为量子技术的新时代奠定了基础。
- “纠缠对”中,一个粒子发生的事情,会决定另一个粒子发生的事情(不管相距多远)。
- 量子力学的基础不仅仅是一个理论或哲学问题。其与全世界正密集研发的、以利用单个粒子系统的特殊属性来构建的量子计算机、改进测量、量子网络以及量子加密通信,都能息息相关。以上应用,均需依赖于量子力学如何允许两个或多个粒子以共享状态存在,甚至无论它们相隔千山万水,均能保持这一状态。这被称为纠缠。
自从该理论提出以来,它一直是量子力学中争论最多的元素之一。
- 两对纠缠粒子从不同的来源发射。每对粒子中的一个粒子以一种特殊的方式相互纠缠而聚集在一起。然后,其他两个粒子(图中的1和4)也被纠缠在一起。通过这种方式,两个从未接触过的粒子可以纠缠在一起。
- 阿尔伯特·爱因斯坦说这是“幽灵般的超距作用”,而埃尔温·薛定谔说这是量子力学最重要的特征
相关性究竟是不是因为纠缠对中的粒子包含隐藏变量。1960年代,约翰·斯图尔特·贝尔提出了以他的名字命名的数学不等式。这说明如果存在隐藏变量,则大量测量结果之间的相关性,永远不会超过某个值。然而,量子力学预测某种类型的实验将违反贝尔不等式,从而导致比其他方式产生了更强的相关性。
- 量子力学的纠缠对可与反方向抛出相反颜色球的机器相提并论。当鲍勃接住一个球,看到它是黑色的时,他立即知道爱丽丝抓住了一个白色的。在使用隐藏变量的理论中,球总是包含有关显示什么颜色的隐藏信息。然而,量子力学却说,这些球是灰色的,直到有人看着它们时,一个随机变成白色而另一个变成黑色。贝尔不等式关系表明,有实验可以区分这些情况。这样的实验证明了量子力学的描述是正确的
- 约翰·克劳泽发展了贝尔的想法,并通过一个实际的实验进行测量,测量结果通过明显违反贝尔不等式来支持量子力学。这意味着,量子力学不能被使用隐藏变量的理论所取代。
- 在约翰·克劳泽的实验之后,一些漏洞仍然存在。阿兰·阿斯佩开发了一种新设置,并以一种弥补重要漏洞的方式使用它。他能够在纠缠对离开其源后切换测量设置,因此在它们发射时既有设置就不会影响结果
- 使用改良工具和一系列长期实验,安东·塞林格的团队利用纠缠量子态证明了一种称为量子隐形传态的现象,它可以将量子态从一个粒子移动到远距离的另一个粒子
什么是退相干?
- 量子比特与环境之间的相互作用会导致量子行为衰减甚至最终消失,这被称为“退相干(Decoherence)”现象。量子比特的量子态非常脆弱,实验室中,“噪音”的最轻微振动或温度扰动的变化都可能导致它们在工作正常完成之前就发生量子行为的衰减。这就是为什么研究人员在那些超低温的制冷机和真空室中实验,以尽力保护量子比特不受外界影响的原因。
- 尽管研究人员已经足够努力,噪音依然会导致许多计算错误,而这将削弱量子计算机的大量计算能力。虽然一些量子算法可以纠正一部分错误,并且添加更多量子辅助比特也会有一定的帮助。但是,它可能需要数千个标准量子比特才能创建一个高度可靠的“逻辑”量子比特。
- 还有一个问题亟待解决:到目前为止,研究人员还无法构造超过128个标准量子比特的计算机。因此,我们距离量子计算机的广泛应用还有些时间。
- 但这并没有削弱开拓者希望成为第一个展示“量子霸权”团队的希望。
什么是量子霸权?
- 尽管研究人员已经足够努力,噪音依然会导致许多计算错误,而这将削弱量子计算机的大量计算能力。虽然一些量子算法可以纠正一部分错误,并且添加更多量子辅助比特也会有一定的帮助。但是,它可能需要数千个标准量子比特才能创建一个高度可靠的“逻辑”量子比特。
- 还有一个问题亟待解决:到目前为止,研究人员还无法构造超过128个标准量子比特的计算机。因此,我们距离量子计算机的广泛应用还有些时间。
- 但这并没有削弱开拓者希望成为第一个展示“量子霸权”团队的希望。
- 研究界对于实现这一里程碑的重要性有很多争论。但有些公司在“量子霸权”(Quantum Supremacy)的说法未被证实之前就已经开始试用由IBM、Rigetti 和加拿大D-Wave等公司制造的量子计算机。像阿里巴巴这样的中国公司也能够提供量子机器。一些企业购买量子计算机,而另一些企业则正在使用通过云计算服务提供的量子计算机。
量子计算机在哪些方面可能最有用?
- 量子计算机最有希望的应用前景之一是模拟物质在分子状态的行为。像大众汽车和戴姆勒这样的汽车制造商正在使用量子计算机模拟电动汽车电池的化学成分,希望可以帮助找到改善其性能的新方法,而制药公司利用它们来分析和比较可能创造出新药的化合物。
- 量子计算机也非常适合用于优化问题的解决方案
- 量子计算机可能还需要一些时间才能充分发挥其作用。目前从事该领域研究工作的大学和企业正面临着人才严重短缺的问题,而且缺乏一些关键部件的供应商。但是如果这些新构建的量子计算机能够发挥其性能,它们将颠覆整个行业的发展并推动全球新局面。
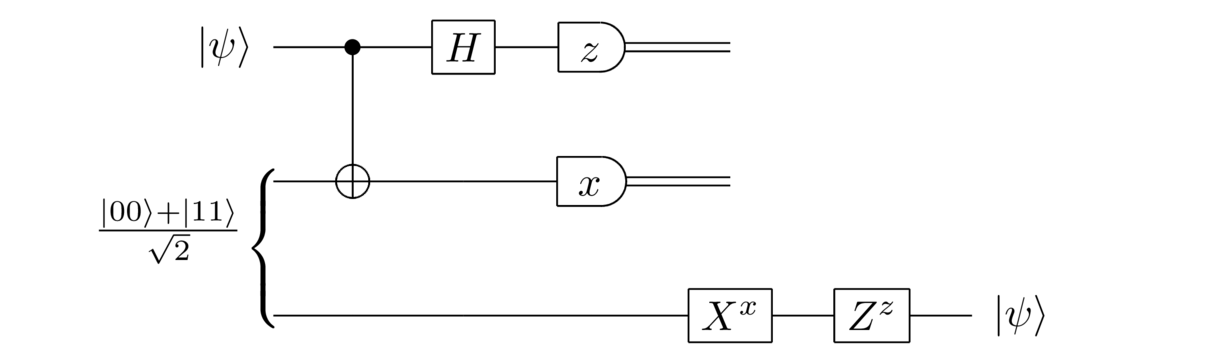
量子隐形传态——量子传输
【2022-4-24】量子隐形传态
量子隐形传态(Quantum Teleportaion)又被翻译成量子传送 。
根据一个古老的墨西哥民间故事,1593年10月24日,一个名叫吉尔-佩雷斯的西班牙士兵在马尼拉(即今天的菲律宾)守卫总督府。总督在前一天晚上被海盗刺杀,守卫宫殿的士兵们已经筋疲力尽。佩雷斯也不例外,他靠在墙上,睡了过去。
当他睁开眼睛时,他已经不在马尼拉了。不知何故,奇迹般地,他被瞬间传送到了太平洋彼岸。他在Zócalo,墨西哥城的大公共广场。他被卫兵发现,卫兵因他的制服而怀疑他是个逃兵,并把他扔进了监狱。为了自救,他告诉了卫兵总督在马尼拉死亡的消息,却不被相信。几个月后,当总督死亡的消息乘船抵达时,佩雷斯的故事得到了证实,他也被释放。
这是一个有趣的故事。几个世纪以来,传送尤其是传送人类, 一直是民间故事、魔术表演和科幻小说中的情节。但在1993年,一群物理学家发现了一种真正的量子传送,它能使量子状态被远距离传送,而不需要直接交换该量子状态的实例。
最初的量子传送论文是理论性的,使用量子力学的数学规则来预测传送现象。此后,这一预测被许多实验所证实,证明了这一效果。此外,事实证明,量子传送不仅仅是一个有趣的技巧。它是量子计算以及更广泛的量子信息科学中许多其他现象的基础。例如,它可以被用于减少噪音对量子计算机的影响,以及创造一种新的量子计算机。量子传送今天被看作是量子信息科学的一个核心原素。
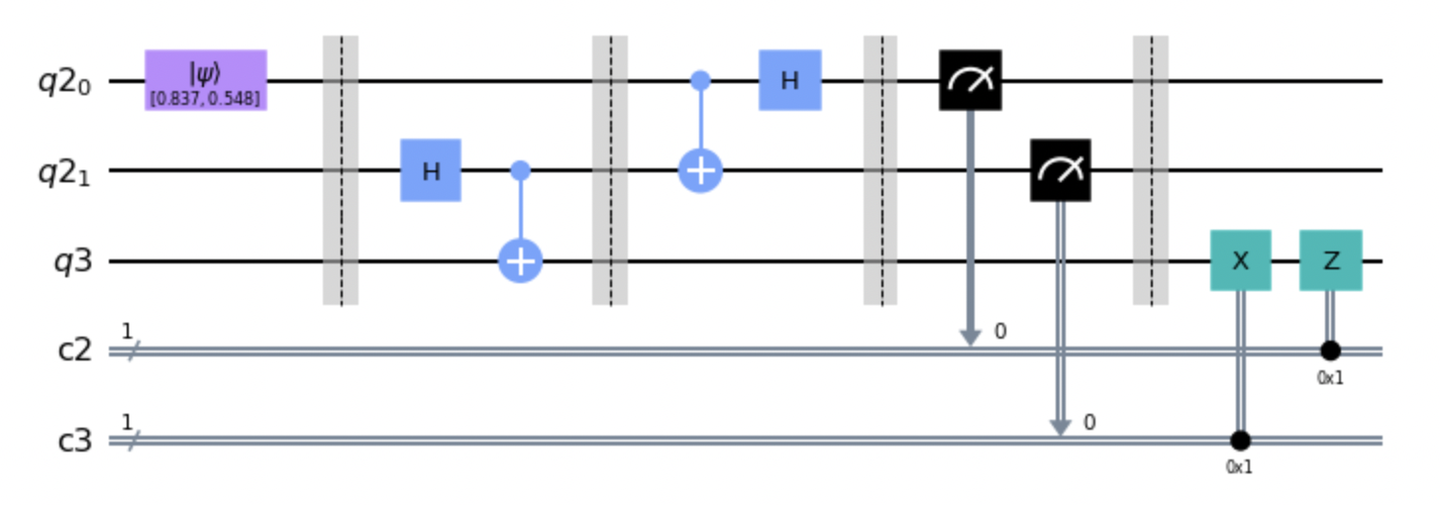
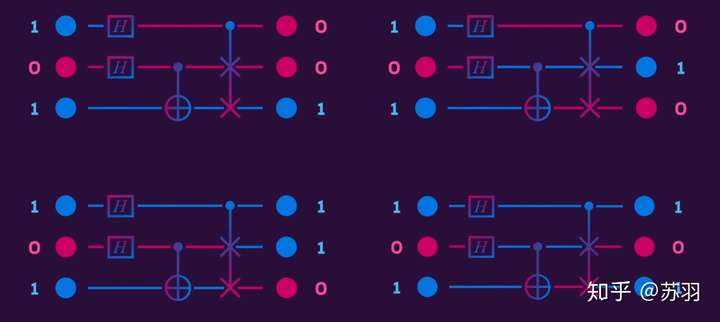
量子隐形传态的电路表示如下:
传送是通过四个步骤实现的:
- 初始状态: Alice 从单个量子位的量子状态
开始。 Alice 和 Bob 还共享两个量子位的量子态,
。
- 爱丽丝做了什么: 为了完成她的协议部分,爱丽丝在
和她的另一个量子位之间执行 CNOT 门,然后对第一个量子位应用哈达玛门。 然后 Alice 在计算基础状态上测量她的两个量子位,得到结果
或 1 和
或 1。四种测量结果中每一个出现的概率是 1/4。
- 经典通信: Alice 将经典位
和
发送给 Bob。
- Bob 恢复量子态
: Bob 将
应用于他的量子位,恢复原始状态
。
最后一点:在隐形传态协议结束时,Alice 不再拥有量子态 。 特别是,她的测量使她的两个量子位处于四种状态之一,
、
、
或
。 因此,您不应将传送视为复制状态
,而是将其视为接近光速移动状态的一种方式。
量子隐形传态(量子传送)在几个方面与人们通常认为的传送/瞬移不同,后者因星际迷航而闻名。
- 一方面,这与传送复杂物体(例如人类)无关。相反,它是关于传送基本量子系统的。尽管原则上可以传送更复杂的物体,但在可预见的未来似乎极不可能。
- 另一个区别是量子隐形传态不是物体在一个位置消失,然后在另一个位置立即重新出现。必须发送经典信息,并且 Bob 执行相应的操作。这让一些人感觉被骗了:“这不是真正的瞬移!”虽然“量子隐形传态”这个名字是伟大的营销,但它确实有点误导。
- 另一方面,量子隐形传态仍然令人震惊。测量量子态以确定其振幅是不可能的。直觉上,这应该使像量子隐形传态这样的事情变得不可能。然而,不知何故,仍然可以使用测量将状态从一个位置传输到另一个位置。
量子计算工具包
工具包汇总
- HiQ 由华为开发的经典-量子混合编程框架
- Paddle Quantum 百度用于量子机器学习的 Python 工具包
- QCompute 百度基于 Python 的量子软件开发工具包
- QPanda 本源量子基于C++的开源量子计算编程框架
GUI编程
量子计算图形化在线编程工具 本源量子云平台 提供图形化在线编程工具,通过拖拽操作构建量子线路,并在真实量子计算机或虚拟量子计算机上运行它们。
QPanda (C++)
量子计算编程框架 QPanda 是由本源量子开发的开源量子计算编程框架,它可以用于构建、运行和优化量子算法。QPanda作为本源量子计算系列软件的基础库,为OriginIR、Qurator、量子计算服务提供核心部件。
git clone https://github.com/OriginQ/QPanda-2.git
PyQPanda (Python)
PyQPanda python 版 QPanda, 为了兼容高效与便捷,通过pybind11工具,以一种直接和简明的方式,对QPanda中的函数、类进行封装,并且提供了几乎完美的映射功能。 封装部分的代码在QPanda2编译时会生成为动态库,从而可以作为python的包引入。
from pyqpanda import *
if __name__ == "__main__":
init(QMachineType.CPU)
qubits = qAlloc_many(3)
control_qubits = [qubits[0], qubits[1]]
prog = create_empty_qprog()
# 构建量子程序
prog << H(qubits) \
<< H(qubits[0]).dagger() \
<< X(qubits[2]).control(control_qubits)
# 对量子程序进行概率测量
result = prob_run_dict(prog, qubits, -1)
# 打印测量结果
print(result)
finalize()
hello world
代码示例:
- 在量子计算机中构建量子纠缠态 ( |00>+|11> ),对其进行测量,重复制备1000次。
- 预期的结果是约有50%的概率使测量结果分别在00或11上。
#include "QPanda.h"
USING_QPANDA
int main()
{
// 初始化量子虚拟机
init(QMachineType::CPU);
// 申请量子比特以及经典寄存器
auto q = qAllocMany(2);
auto c = cAllocMany(2);
// 构建量子程序
QProg prog;
prog << H(q[0])
<< CNOT(q[0],q[1])
<< MeasureAll(q, c);
// 量子程序运行1000次,并返回测量结果
auto results = runWithConfiguration(prog, c, 1000);
// 打印量子态在量子程序多次运行结果中出现的次数
for (auto &val: results)
{
std::cout << val.first << ", " << val.second << std::endl;
}
// 释放量子虚拟机
finalize();
return 0;
}
Qiskit
Qiskit实现
IBM的开源Python量子计算框架Qiskit,让我们可以足不出户,通过网络操作量子计算机。安装Python Qiskit Library。也可以直接在云端运行,IBM Quantum Lab
from math import sqrt, pi
from qiskit import QuantumCircuit, BasicAer, execute
from qiskit.visualization import plot_bloch_multivector
# change alpha beta as you want
alpha = 1/sqrt(2)
beta = 1j/sqrt(2)
# 2D complex vector representing the quantum state
vector = [alpha, beta]
# create a quantum circuit with only one qubit
qc = QuantumCircuit(1)
# initialzie the qubit as the vector we defined
# arg 0 is the index of the only qubit we created
qc.initialize(vector, 0)
# simulate the state
# note that statevector_simulator is used for calculating statevector (Quantum State)
backend = BasicAer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
state = result.get_statevector(qc)
# plot the state on a Bloch sphere
plot_bloch_multivector(state)

Example 7: 量子隐形传态
在这个练习中您将传送量子态
从 Alice 的量子位到 Bob 的量子位. 回顾传送算法包含的四个主要步骤:
- 初始化需要被传送的量子态。我们将在 Alice 的量子位
q0上做这件事。 - 创造相互纠缠的两个量子位。我们将使用
q1和q2做这件事。Alice 拥有q1,Bob拥有q2。 - 对 Alice 拥有的
q0和q1进行 Bell 测量。 - 对 Bob 拥有的
q2执行经典受控的操作,具体操作取决于第三步的测量结果。
# 1.)
def initialize_qubit(given_circuit, qubit_index):
import numpy as np
given_circuit.initialize([np.sqrt(0.70), np.sqrt(0.30)], qubit_index)
return given_circuit
# 2.)
def entangle_qubits(given_circuit, qubit_Alice, qubit_Bob):
given_circuit.h(qubit_Alice)
given_circuit.cx(qubit_Alice, qubit_Bob)
return given_circuit
# 3.)
def bell_meas_Alice_qubits(given_circuit, qubit1_Alice, qubit2_Alice, clbit1_Alice, clbit2_Alice):
given_circuit.cx(qubit1_Alice, qubit2_Alice)
given_circuit.h(qubit1_Alice)
given_circuit.barrier()
given_circuit.measure(qubit1_Alice, clbit1_Alice)
given_circuit.measure(qubit2_Alice, clbit2_Alice)
return given_circuit
# 4.)对 Bob 的量子位执行受控操作:
# 一个 X 门被施加在 Bob 的量子位上,如果对于 Alice 的第二个量子位的测量结果是1,即 clbit2_Alice=1。
# 一个 Z 门被施加在 Bob 的量子位上,如果对于 Alice 的第一个量子位的测量结果是1,即 clbit1_Alice=1。
def controlled_ops_Bob_qubit(given_circuit, qubit_Bob, clbit1_Alice, clbit2_Alice):
given_circuit.x(qubit_Bob).c_if(clbit2_Alice, 1)
given_circuit.z(qubit_Bob).c_if(clbit1_Alice, 1)
return given_circuit
# 汇总
### imports
from qiskit import QuantumCircuit
from qiskit import QuantumRegister, ClassicalRegister
### set up the qubits and classical bits
all_qubits_Alice = QuantumRegister(2)
all_qubits_Bob = QuantumRegister(1)
creg1_Alice = ClassicalRegister(1)
creg2_Alice = ClassicalRegister(1)
### quantum teleportation circuit here
# Initialize
mycircuit = QuantumCircuit(all_qubits_Alice, all_qubits_Bob, creg1_Alice, creg2_Alice)
initialize_qubit(mycircuit, 0)
mycircuit.barrier()
# Entangle
entangle_qubits(mycircuit, 1, 2)
mycircuit.barrier()
# Do a Bell measurement
bell_meas_Alice_qubits(mycircuit, all_qubits_Alice[0], all_qubits_Alice[1], creg1_Alice, creg2_Alice)
mycircuit.barrier()
# Apply classically controlled quantum gates
controlled_ops_Bob_qubit(mycircuit, all_qubits_Bob[0], creg1_Alice, creg2_Alice)
### Look at the complete circuit
mycircuit.draw()
# --------
from qiskit import BasicAer, execute
backend = BasicAer.get_backend('statevector_simulator')
result = execute(mycircuit, backend).result()
state = result.get_statevector(mycircuit)
import math
print(math.sqrt(0.7)) # 0.8366600265340756
print(math.sqrt(0.3)) # 0.5477225575051661
整个量子电路的最终状态一定属于下面四种情况的一种:
量子计算机
什么是量子计算机
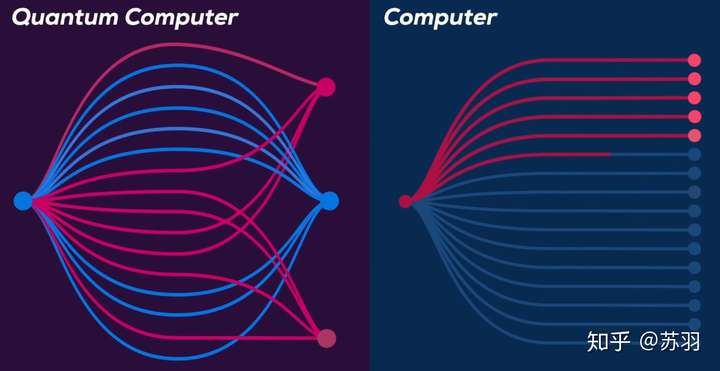
量子计算是一种使用量子逻辑进行通用计算的方法,被普遍认为是一种更新型的计算机技术。
在传统计算机中,信息量的基本单位是比特,它只能取 0 或 1 中的一个值。在量子计算机中,信息量的基本单位为量子比特或量子位。通过量子力学现象,这些量子位可以同步进行大量计算。理论上,利用量子力学现象,量子计算可以极大地改进信息存储和处理方式,算法比传统计算更高效,从而能更快地解决各种难题。
这会带来巨大的影响,比如说,今天使用的很多加密方法并不是理论上不可攻破的,而是由于目前计算机的物理限制,攻破的时间可能需要10000年,时间太长,我们也就认为这些加密是安全的了。但是,对于量子计算机而言,攻破可能就是分分钟的事情,你存在银行的钱都不安全了,影响之大不言而喻。
量子特性是叠加、“纠缠”。纠缠性可以让多个量子比特共享状态,创造出 “超级叠加” 的量子并行计算,计算能力随比特数增加呈指数级增长。
- 理论上, 拥有 300 个量子比特的量子计算机,瞬间所能执行的并行计算次数比宇宙中的原子总数还多。
- 对于量子计算的并行性,微软 CEO Satya Nadella 在 2017 年微软 Ignite 大会上,用找迷宫出口来比喻解释:
- 为了找到迷宫的出口,经典计算机先开启一条搜索路径,遇到障碍物后会沿原路返回。之后再次探寻新路,直到遇障返回或找到了正确出口。虽然最终能找到一个结果,但这种方法相当耗时。
- 对比之下,量子计算机解锁了神奇的并行性。它们同时探寻玉米迷宫中的每一条路。因此,量子计算机可能指数级减少解决问题的步骤。
- 中国科学院院士潘建伟也曾说:
- 如果传统计算机的速度是“自行车”,那么量子计算机的速度就是“飞机”。
量子机器学习(QML)
这种远远超过经典计算机的计算性能,正是机器学习所需要的。
众所周知,当下这次以机器学习方法为代表的人工智能浪潮,是算力、算法和数据相结合的结果。如果机器学习任务无法快速计算完成,那么经济价值就无法得到体现。当前,企业和学界普遍采用 GPU 和 FPGA 等适合并行计算的通用芯片来实现加速,但这些方法依然是基于经典计算机。速度远远超越经典计算机的量子计算机,自然而然和机器学习联系起来。
3类量子机器学习算法
目前已有的量子机器学习主要可以分为以下3类,分别是:
- 1) 第一类量子机器学习。该类算法将机器学习中复杂度较高的部分替换为量子版本进行计算,从而提高其整体运算效率。该类量子机器学习算法整体框架沿用原有机器学习的框架。其主体思想不变,不同点在于将复杂计算转换成量子版本运行在量子计算机上,从而得到提速。
- 2) 第二类量子机器学习。该类算法的特点是寻找量子系统的力学效应、动力学特性与传统机器学习处理步骤的相似点,将物理过程应用于传统机器学习问题的求解,产生出新的机器学习算法。该类算法与第一类不同,其全部过程均可在经典计算机上进行实现。在其他领域也有不少类似思路的研究,如退火算法、蚁群算法等。
- 3) 第三类量子机器学习。该类算法主要借助传统机器学习强大的数据分析能力,帮助物理学家更好的研究量子系统,更加有效的分析量子效应,作为物理学家对量子世界研究的有效辅助。该类算法的提出将促进我们对微观世界进一步的了解,并解释量子世界的奇特现象。
由于量子机器学习的大多数研究集中于第一类算法,第二类算法的研究还较少,第三类量子机器学习算法主要应用于物理领域 。
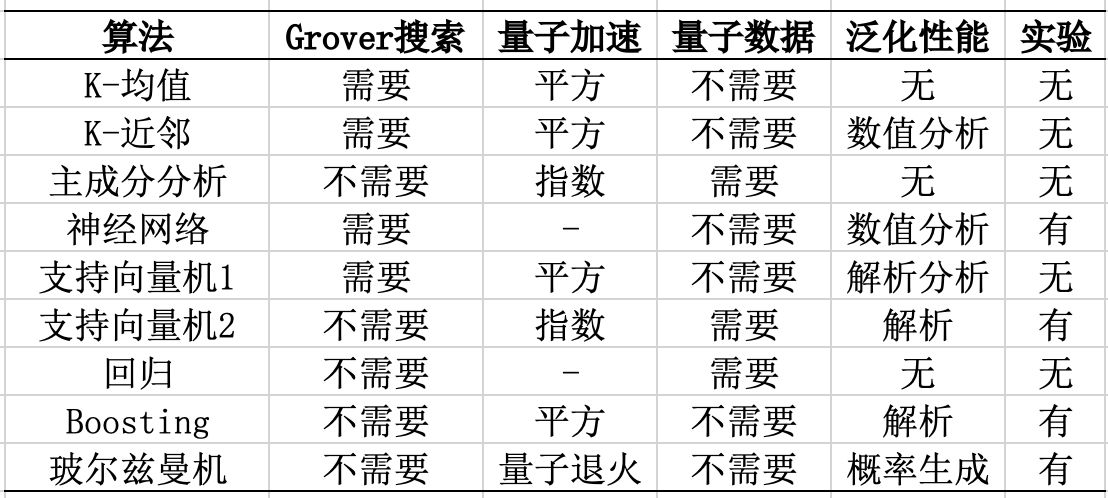
主要的量子机器学习算法汇总
主要的量子机器学习算法
量子机器学习的瓶颈及未来
(1)瓶颈
虽然量子技术领域取得了很大进展,但量子比特数量有限的通用误差纠正量子计算机还远未实现。
-
目前还不清楚量子计算机需要多少逻辑量子才能超越经典计算机。这为QML的实现增加了难度。
-
量子机器学习实现的难度现在看来是非常大的。
-
状态准备问题,任意状态准备在离散门集合的量子比特数上是指数级的,为所有算法的性能提供了界限,并对算法初始化时的状态有限制
(2)未来发展方向
现阶段量子机器学习属于蓬勃发展的时代,而量子计算是未来发展的主要方向之一,是一个可以帮助我们提升计算力的技术,成为对这些海量数据集进行有效和有意义的分析的下一步。美国麻省理工学院(MIT)塞斯·罗伊德(Seth Lloyd)教授提出理论预言,利用量子系统在处理高维向量上的并行计算优势,可以为机器学习带来指数量级的加速,将能远远超越现有经典计算机的运算速度。
视频
量子计算机竞赛
- 国际主流观点认为,量子计算机的发展将有三个阶段:
- 第一阶段,研制50个到100个量子比特的专用量子计算机,实现“量子优越性”里程碑式突破。
- 第二阶段,研制可操纵数百个量子比特的量子模拟机,解决一些超级计算机无法胜任、具有重大实用价值的问题,比如量子化学、新材料设计、优化算法等。
- 第三阶段,大幅提高量子比特的操纵精度、集成数量和容错能力,研制可编程的通用量子计算原型机。
- 目前,“九章”还处在第一阶段,但在图论、机器学习、量子化学等领域具有潜在应用价值。
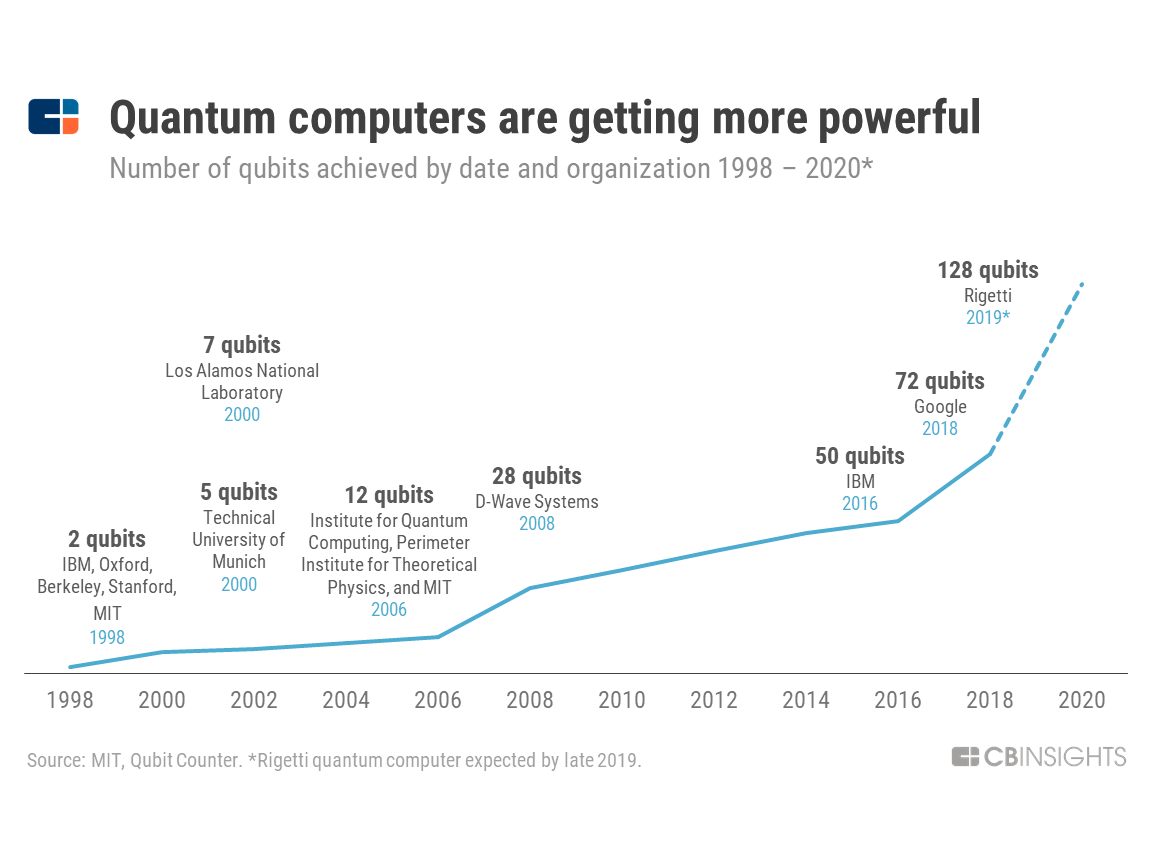
目前最先进的量子计算芯片,由总部位于伯克利的初创公司 Rigetti Computing 开发,可以使用多达19个量子比特,该公司宣布,到2019年底制造一个128个量子比特的芯片。但至少从20世纪90年代后期开始,建造功能最强大、量子比特最多的量子计算机的竞赛就已经开始了。
- 1998年,英国牛津大学的研究人员宣布,他们利用两个量子比特计算信息的能力取得了突破性进展。
- 快进到2017年,IBM证明了在50个量子比特上计算的能力。量子计算能力在20年内增长了25倍,与今天的发展速度相比,这似乎是一个缓慢的开始。
- 2018年,谷歌展示了用72个量子比特信息处理。8月,Rigetti Computing宣布了制作128量子比特量子芯片的计划。 投资公司Draper Fisher Jurvetson的常务董事史蒂夫·尤瑞森(Steve Jurvetson)是量子计算公司D-Wave Systems的投资者,他将量子计算机容量增加的现象称为“罗斯定律”(Rose’s Law)。量子计算中的罗斯定律与半导体处理器开发中的摩尔定律相似。简而言之,量子计算机的发展速度已经变得非常非常快。
- 【2019年9月】美国谷歌公司宣布研制出53个量子比特的计算机“悬铃木”,对一个数学问题的计算只需200秒,而当时世界最快的超级计算机“顶峰”需要2天,因此他们在全球首次实现了“量子优越性”(或“量子霸权”)。
- 科学术语解释:作为新生事物的量子计算机,一旦在某个问题上的计算能力超过了最强的传统计算机,就证明了量子计算机的优越性,跨过了未来多方面超越传统计算机的门槛。
九章
- 【2020-12-4】《科学》杂志公布了中国“九章”的重大突破。在一个特定赛道上,200秒的“量子算力”,相当于目前“最强超算”6亿年的计算能力!中国科学技术大学潘建伟、陆朝阳等学者研制的76个光子的量子计算原型机,推动全球量子计算的前沿研究达到一个新高度。尽管距离实际应用仍有漫漫长路,但成功实现了“量子计算优越性”的里程碑式突破。
- “九章”的突破,主要攻克了三大技术难关:高品质量子光源、高精度锁相技术、规模化干涉技术。
- 实验显示,“九章”对经典数学算法高斯玻色取样的计算速度,比目前世界最快的超算“富岳”快一百万亿倍,从而在全球第二个实现了“量子优越性”。
- 高斯玻色取样是一个计算概率分布的算法,可用于编码和求解多种问题。当求解5000万个样本的高斯玻色取样问题时,“九章”需200秒,而目前世界上最快的超级计算机“富岳”需6亿年;当求解100亿个样本时,“九章”需10小时,“富岳”需1200亿年。
- 潘建伟团队表示,相比“悬铃木”,“九章”有三大优势:
- 一是速度更快。虽然算的不是同一个数学问题,但与最快的超算等效比较,“九章”比“悬铃木”快100亿倍。
- 二是环境适应性。“悬铃木”需要零下273.12摄氏度的运行环境,而“九章”除了探测部分需要零下269.12摄氏度的环境外,其他部分可以在室温下运行。
- 三是弥补了技术漏洞。“悬铃木”只有在小样本的情况下快于超算,“九章”在小样本和大样本上均快于超算。
- 打个比方,就是谷歌的机器短跑可以跑赢超算,长跑跑不赢;我们的机器短跑和长跑都能跑赢。
- 九章问世!一文看懂什么是量子计算机
- 量子计算机的性能数据有点太过于“惊人”。
- “九章”量子计算机,在处理“高斯玻色采样”问题时,速度是目前最快的超级计算机的100万亿倍。也就是说九章量子计算机只要花200秒就能处理好的事情,目前世界上最快的超级计算机 要计算6亿年!这就是量子计算机相比经典计算机的性能“碾压”。
- 量子计算机之所以跟传统计算机不一样,是因为运算原理不一样
- 经典电子计算机是通过“逻辑门电路”来实现逻辑运算的。
- 而量子计算机的基本计算单元,叫做“量子比特”。
- 量子比特这个名词虽然看起来高大上,但实际上就是 “0或者1”。量子比特跟经典比特最大的区别在于,量子比特处理的0或者1,这两个数字是处于“量子叠加态”的。量子叠加态的0和1,有比较专业的符号来表示|0> 和|1>
- 在量子比特不超过50个的情况下,还不能取得对经典计算机的碾压优势。
- 比如说1个量子比特可以存储2个,2个量子比特可以存储4个,3个量子比特可以存储8个,4个量子比特可以存储16个。
- 但一旦超过50个量子比特,这个存储容量是远超过经典计算机结构的。
- 谷歌去年推出的量子计算机有53个,它的基本状态就是2的53次方个,也就是10的16次方个,也就是1亿亿个。
- 我们的九章量子计算机,有76个量子比特,也就是2的76次方,约等于10的30次方。
- 而目前全世界所有存储器加起来的存储容量,也只有10的22次方。
- 量子计算机还应用到量子纠缠这个神奇效应。意思是,两个量子叠加态粒子,会通过一些相互作用进入到“纠缠状态”。
- 如果我们对其中一个粒子进行测量,确认其处于|0>态,那么我们就可以瞬间知道另外一个粒子处于|1>态。而不管另外一个粒子距离有多远,哪怕距离几亿光年,我们也可以瞬间知道另外一个粒子会处于什么状态。这就是量子纠缠的超距效应。
本源司南
- 【2021-2-9】我国首个量子计算机操作系统“本源司南”正式发布,由合肥本源量子自主开发,实现了量子资源系统化管理、量子计算任务并行化执行、量子芯片自动化校准等全新功能,助力量子计算机高效稳定运行,标志着国产量子软件研发能力已达国际先进水平。本源司南提供的官方教程


- 目前,全球范围内可供使用的量子计算机约有50台,国内仅有本源量子等少数企业面向大众提供量子计算服务。量子计算资源仍然属于稀缺物种。
- 量子计算机操作系统将直接影响量子计算机的性能表现,但现有量子计算机操作系统(例如英国Deltaflow.OS量子计算机操作系统, 奥地利ParityOS量子计算机操作系统)在量子资源管理、多量子计算任务并行处理、量子芯片自动化校准功能方面,对有效利用当前稀缺的量子计算资源并没有做到极致优化。
- 量子客:司南,斯甚难!品观首款国产量子计算机操作系统发布
百度
【2022-3-10】量子计算国际顶会QIP2022召开 百度连续四年参会推动量子科技进步, 百度量子平台的三大主体项目,量桨、量易伏、量脉在2021年均迎来了全面升级:
量桨大幅提升多项核心技术指标,成为量子机器学习前沿研究的实用工具集,目前已在机器学习、量子化学、量子信息处理、基于测量的量子计算等多个重要方向上完成科研产出,多项工作在国际顶级学术会议和期刊上发表。量易伏迎来了重大突破,成为国内首个提供从应用到真机一站式量子计算服务的云原生量子计算平台,并拥有全球首个云原生量子集成开发环境YunIDE,提供企业级的“开箱即用”服务体验。量脉则升级至2.2版本,成为了同时支持超导电路、离子阱、核磁共振三类量子硬件的量子控制云平台,新增从脉冲优化到误差分析的全流程服务。
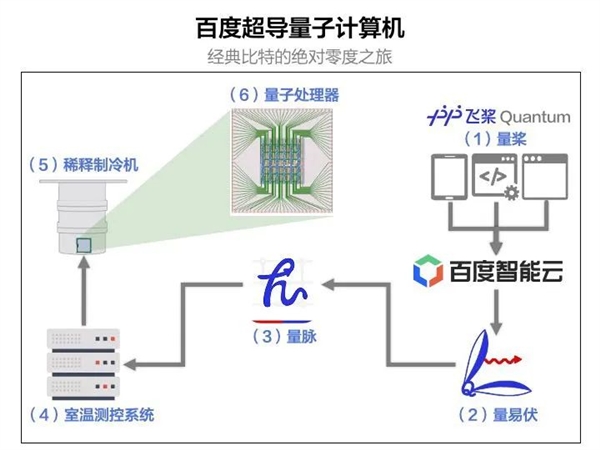
【2022-8-25】量子客:百度官宣,发布产业级超导量子计算机 以“量子计算产业化”为主题的量子开发者大会上,百度CTO王海峰重磅发布了集量子硬件、量子软件、量子应用于一体的产业级超导量子计算机——乾始。
- 乾始量子应用包含了人工智能、材料模拟、生物计算、金融科技等,以通过利用量子计算解决经典计算机无法处理的难题,加速数字经济量子化,提升数字经济生产力。
- 基于“乾始”产业级超导量子计算机的发布,百度由此形成了全球首个全平台量子软硬一体化解决方案的“量羲”,包含了量子机器学习“量桨”、量子操作系统“量易伏”、量子软硬件接口“量脉”等。
- 该量子计算机拥有很好的性能,其平均 T1 时间长度为 31.0μs,平均 T2 时间长度为 8.7μs。单量子比特门保真度为99.8%,双量子比特门(CX)保真度为96.4%,双量子比特门(CZ)保真度为96.4%。
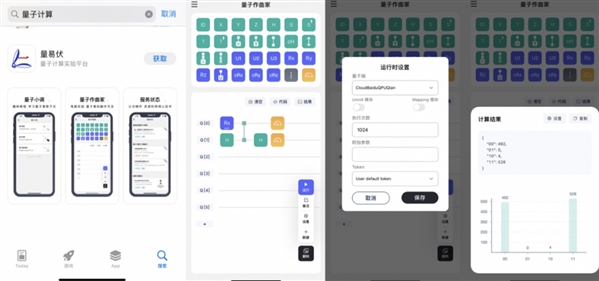
- 百度量子团队专门开发了“量易伏”APP,在手机端打开这个APP,开发者可以应用“量子作曲家”这个模块,轻松编写量子程序并运行,亲身感受量子计算的魅力。
社会比赛
【2022-4-7】CCF”司南杯”:量子计算编程挑战赛,比赛限定使用QPanda/pyQPanda编程框架
量子计算机历史
【2022-4-24】突破 0 和 1 的思维:量子计算介绍
- 1982年,理查德·费曼在一个著名的演讲中提出利用量子体系实现通用计算的想法,开启了量子计算的研究
- 1985年,大卫·杜斯提出了量子图灵机模型,证明了通用量子计算机的理论可行性
- 1994年,彼得·秀尔提出量子质因数分解算法后[9],证明量子计算机能做出离散对数运算[10],而且速度远胜传统计算机。这个算法对于量子计算的发展起到了很大的推动作用,因其对于现在通行于银行及网络等处的RSA加密算法可以破解而构成威胁之后,量子计算机变成了热门的话题,除了理论之外,也有不少学者着力于利用各种量子系统来实现量子计算机。
- 1996年,Lov Grover提出了可以用于数据库搜索和函数取反的 Grover 算法,进一步证明了量子计算相比于传统计算机的优势。
- 2011年,加拿大的D-Wave 系统公司发布了一款号称“全球第一款商用型量子计算机”的计算设备“D-Wave One”,含有128个量子位。
- 2019年,Google 在 nature 上发表文章,表明他们利用 54 量子比特的 Sycamore 量子计算机在 200 秒内完成了一个计算,而同样的计算用当今最强大的超级计算机 Summit 执行,需要约 10000 年。这也就是之前被广泛报道的 Google 实现了量子霸权(所谓量子霸权,指的就是量子计算机能够解决“经典(非量子)”计算机在合理时间范围之内无法解决的复杂难题这一关键性节点),这项成就被多方认为是量子计算领域的重大里程碑事件。
工作原理
量子计算机的工作原理:
- 量子比特(量子位)用于存储和表达信息,在计算前,量子计算机被预先定义在某一种状态。
- 量子门来处理信息和执行计算,在计算中,实现对量子比特状态的变换。
- 观测门用于提取信息来获得结果,在计算后,通过观测门得到量子比特的状态,并结合统计方法获取答案。 因此,算法的设计主要就是对量子门的排列组合实现特定的逻辑。
量子门
哈达玛门、非门、旋转
- X-Gate 实现量子位的反转,类似于传统计算机的非门,在量子计算机中则实现了基向量系数的交换。
- Hadamard 门:H门的作用可以将基态变换称为均匀的叠加态
- C-NOT 也就是受控非门,它有两部分组成:Control 和 Target。对于两个量子比特的受控非门,如果 control qubit 是,则没有变化;如果 control qubit 是 ,则 target qubit 会取非。这个门实现了 qubit 之间的联系,类似传统计算机中的条件判断,不同的控制值会导致不同的计算操作。C-NOT 门可以用于制造或者销毁量子纠缠。
总结
- X-Gate 是非门,也叫 NOT-Gate,实现对量子态的反转。
- Hadamard 门可以实现基态向叠加态的变换。
- C-NOT 门可以实现创建或销毁纠缠态。 通过这几个门,就可以实现对量子比特状态的改变。
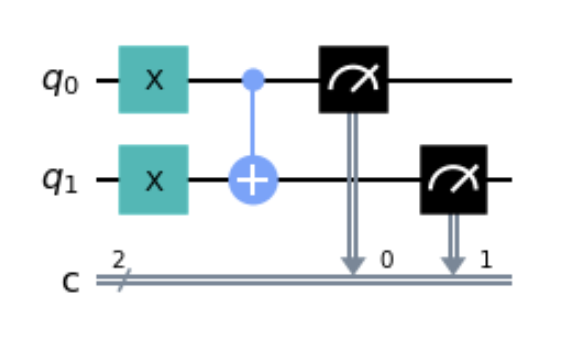
from qiskit import QuantumCircuit, BasicAer, execute
# create a quantum circuit with 2 qubits and 2 bits
qc = QuantumCircuit(2,2)
# apply x gate on qubit 0 and qubit 1
qc.x([0,1])
# apply cnot gate, qubit 0 is control, qubit 1 is target
qc.cx(0, 1)
# measure qubits [0, 1] to bits [0, 1]
qc.measure([0, 1], [0, 1])
# plot the circuit
qc.draw('mpl')
# simulation: run the quantum circuit 1000 times and print all results
backend = BasicAer.get_backend('qasm_simulator')
result = execute(qc, backend, shots=1000).result()
result.get_counts(qc)
酉矩阵
量子计算机使用量子门来对量子比特进行操作,而这些操作的算符都是幺正矩阵,将系统从一个状态变换到另一个状态,也叫幺正变换。
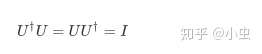 只通过幺正变换进行运算看似严格,但已经被证明 [Deutsch, 1985],这样的量子计算机可以实现图灵完备。
只通过幺正变换进行运算看似严格,但已经被证明 [Deutsch, 1985],这样的量子计算机可以实现图灵完备。
像普通(真实)空间中的旋转或反射,它们也不会改变长度。从某种意义上说,酉矩阵是真实旋转和反射的复杂推广。酉矩阵是唯一能保持矢量长度的矩阵。这就是代数条件 的几何解释(和直观意义)。
观测门
观测门用于信息提取
- 传统计算机,我们可以在任意时间来直接读取它的状态。而对于量子计算机,量子比特的状态不能够直接获得,必须通过观测门来收集得到。
薛定谔的猫
- 我们都听说过薛定谔的猫的故事,在打开盒子之前,猫处于一种既生又死的叠加态,而一旦打开盒子,猫就到达了一种确定的状态,要么生要么死,因为你的观测,导致猫死了,这就是所谓的好奇害死猫。
- 这里面说明了一点,就是观测动作会使量子从叠加态塌陷到确定态。观测导致态的塌陷,这对于薛定谔的猫是不好的,但对于量子计算机来说是必要的,这将有助于我们提取得到一次计算的结果。
结果概率性
- 对于一个量子状态,观测会使其以一定的概率塌陷到一个确定的状态,注意,这里的结果状态有概率性,并不是每次的答案都是一样的,多次计算会给出多种可能的答案样本。
因此,量子计算机在设计时需要考虑多种答案的情况,结合统计学来计算多种答案中某一答案正确的可能性,可以通过调整该置信度来平衡速度和准确度。
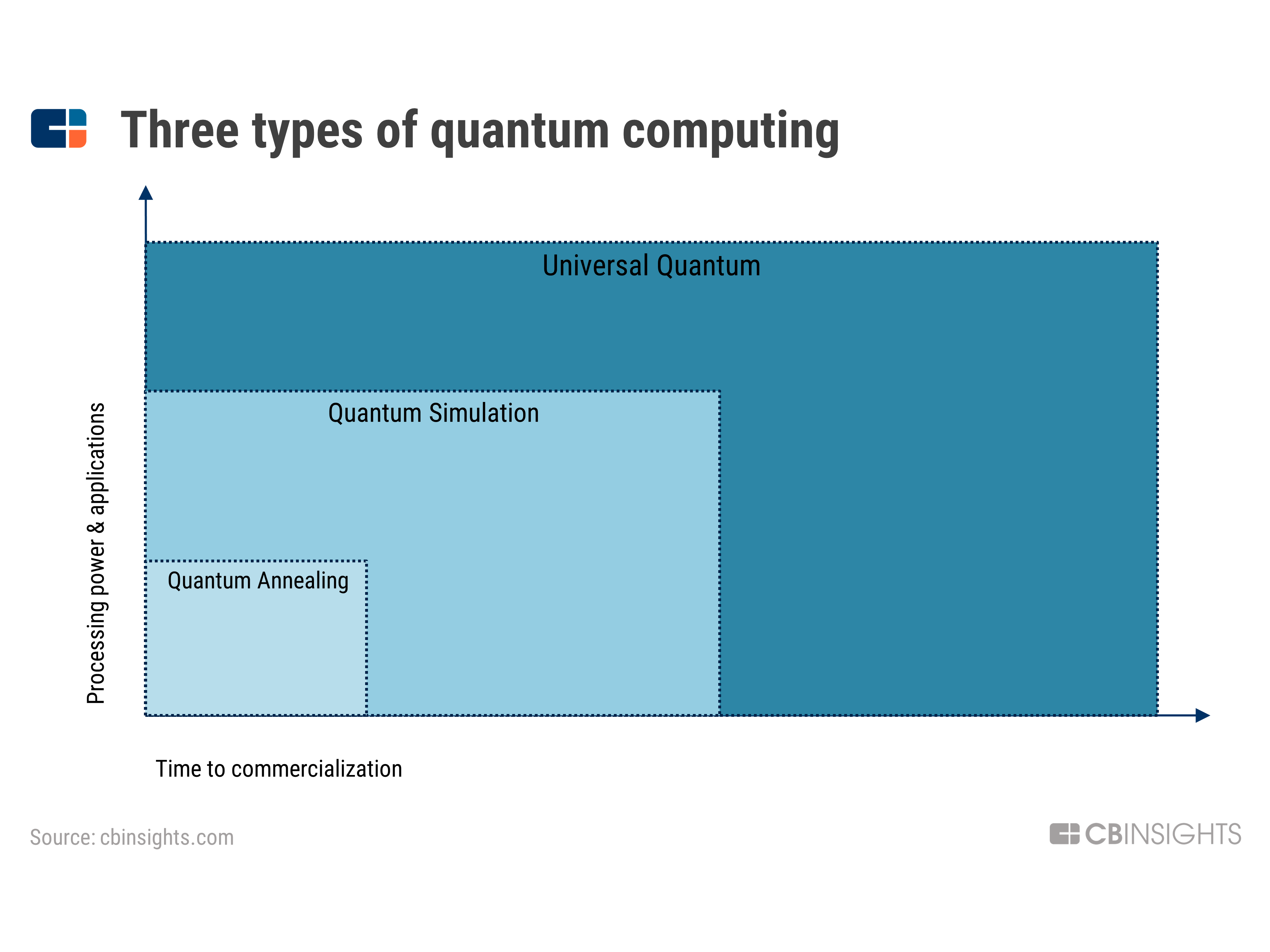
量子计算的类型
量子计算主要有三种类型。每种类型的不同之处在于所需的处理能力(量子比特)的数量,可能的应用数量,以及实现商业可行性所需的时间。
量子退火
量子退火是解决优化问题的最佳选择,在许多可能的变量组合中找到最佳(最有效)的可能配置; 量子退火是量子计算中功能最弱、应用范围最窄的一种形式。
量子模拟
量子模拟探索量子物理学中超出传统计算系统能力的特定问题。模拟复杂的量子现象可能是量子计算的重要应用之一。
一个特别有希望的领域,是模拟化学刺激对大量亚原子粒子的影响,称为量子化学。
量子模拟器可以用来模拟蛋白质折叠,这是生物化学中最棘手的问题之一。
- 错误折叠的蛋白质会导致像阿尔茨海默氏症和帕金森氏症这样的疾病,测试新疗法的研究人员必须通过使用随机计算机模型来了解哪些药物会引起每种蛋白质的反应。
- 据说,如果一种蛋白质要通过顺序取样所有可能的药物诱导效应而找到正确的折叠结构,它需要比宇宙年龄更长的时间才能找到其正确的自然状态。
- 绘制一个真实的蛋白质折叠序列,将是一个重大的科学和医疗保健突破,可以拯救生命。 量子计算机可以帮助计算大量可能的蛋白质折叠序列,以制造更有效的药物。 在未来,量子模拟将通过解释每一种可能的蛋白质-药物组合,使快速设计药物测试成为可能。
通用量子计算
通用量子计算机是最强大、最通用的,但也是最难制造的。一台真正通用的量子计算机可能会使用超过10万个量子比特,一些人估计会达到100万个量子比特。请记住,今天,我们能做到的最多的量子比特甚至不到128个。
通用量子计算机背后的基本思想是,你可以指导机器进行任何复杂的计算,并快速得到解决方案。这包括求解上述的退火方程,模拟量子现象,等等。
多年来,研究人员一直在设计只能在通用量子计算机上使用的算法。最著名的算法是Shor的分解数字算法(用于高级代码破解) ,以及Grover的快速搜索非结构化和海量数据集的算法(用于高级互联网搜索等)。
至少有50种其他独特的算法已经开发出来,可以在通用量子计算机上运行。在遥远的未来,通用量子计算机可以彻底改变人工智能领域。量子人工智能可以实现比传统计算机更快的机器学习。
最近的研究已经产生了可以作为量子机器学习基石的算法,但是对于我们来说,完全实现量子人工智能的硬件和软件仍然像一般的量子计算机本身一样难以捉摸。
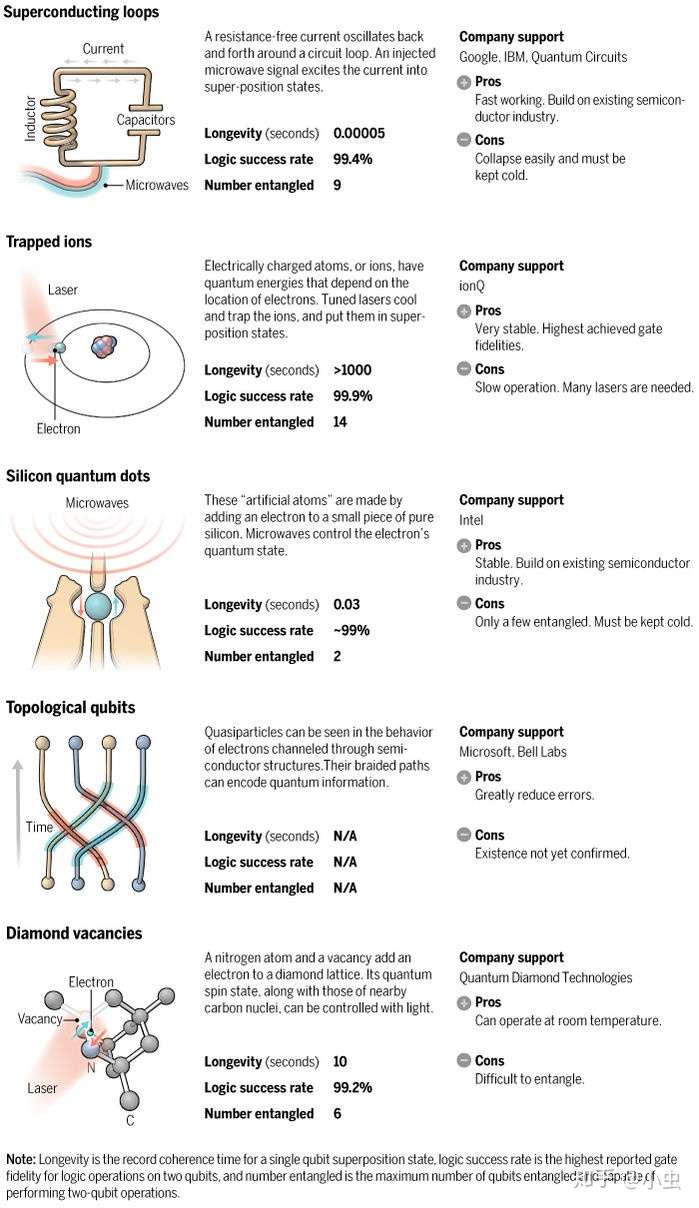
硬件实现
目前有几种方法可以构建量子计算机,如下图所示,给出了一些方法及其优缺点的对比,其中最受商业青睐的类型是绝热量子计算机和门模型量子计算机。
构建完全可扩展的量子计算机,量子技术还需要克服一些障碍。
- 例如,噪声会导致量子系统退相干并失去其量子特性。量子系统对噪声(即该系统定期调整的因素)的敏感度 远高于传统计算机。在设计量子纠错方案(也被称为“容错量子计算”),以及推动工程技术发展以抑制噪声影响方面,仍有很大提升空间。
适用场景
量子计算机不是万能的,要使用量子计算机解决“正确”的问题。
优化问题
- 虽然量子计算机具有强大的并行计算能力,不过没有人认为量子计算机会对文字处理或者邮件系统带来巨大的革命。但是在一些优化和搜索问题上,量子特性却能发挥重大的作用,比如:
- 在众多路经中寻找最优化的路径
- 在大数据集上进行特性数据的搜索和查找
- 发现新的化学催化剂
- 利用因数分解来解密数据
- 抽样问题
- 绝热量子计算机可以执行的另一功能。抽样可以顺利随机生成某些现象的 随机样例,而经典计算机却很难有效做到。 然而,如果可以控制复杂的量子状态(本 身具有概率性),便可更为有效地从这些状态抽样。
- 其他
- 对于其他一些可以转化为优化问题和抽样问题的问题,比如机器学习的基础是抽样和优化方法,所以完善这些技术就可以提高机器学习的能力。
文字
自上世纪电脑出现以来,半导体产业经历了数次飞跃,计算机性能指数级增长,且更小更强
但时至今日,传统计算机已接近现代物理的极限——元器件接近原子尺寸
- 来自英国卫报的消息,德国PDI固体电子学研究所、日本NTT基础研究实验室、美国海军等单位研制出了目前最小的晶体管,直径是167皮米(0.167nm)。0.167nm,是已知最强的IBM 7nm的1/42、头发的60万分之1、DNA链的1/15。
- 据悉,科学家是在一个砷化铟晶体上制备了12个带正电的铟原子环绕着一个酞菁染料分子。《自然·物理》称,在这样的原子尺度上,电子流通常很难得到可靠地控制,电子会跳到晶体管外,导致晶体管无效。
为了后面更好的说明,先来回顾下基本电路知识(基础好的同学可直接看后面):
首先,我们知道计算机是由基本元器件组成的,即电路的逻辑门,而每个逻辑单元则是由晶体管组成,仅能完成一些简单的操作(诸如加减乘除)
晶体管组成了各种逻辑门,与或非门等
多个逻辑门相组合在一起,方可完成相对更复杂的计算
晶体管是能让计算机处理数据的最基本单元,从功能上来说它像个开关,可阻挡或允许电流通过,高低电信号组成了数据,即比特——对一个比特来说,有0和1两种。比特位数越多,能表示的数也就越大。如今一个晶体管,已经可以做到几纳米的大小
由于已经小到仅有数个原子大小,电子有时会无视其中阻碍而直接通过一个已关闭的三极管开关,这种神奇的超自然现象被称为:量子隧道效应
在量子领域上,传统物理学不再适用,很多物理现象无法解释,所以传统计算机无法工作
目前人类遇到了真正的物理屏障,摩尔定律也失效了
接下来科学家要做的就是,利用量子特性,去研究量子计算机
-

- 传统计算机中,比特是最小的信息单位,分为0和1
- 量子计算机中,量子比特可被设为0和1中任意一个,或者模糊态(薛定谔的猫)

一个量子比特可以由任意二阶量子系统组成
例如:一个同时具有磁场和自旋的系统,或单一光子
- 该系统可存在0和1两种状态,就如光子可水平或垂直极化(电磁波在传播时的方向和电磁场相互垂直,我们把电波的电场方向叫电波的极化)
在量子世界里,量子比特可同时处于多种态,是几种不同量子态当中的任意几种归一化线性组合,这种状态即我们常听的:量子叠加态
不过,一旦你通过光子探测器去确定它的值时,它就会调皮的变为水平或垂直极化状态中的一种。
- 就是说,只要不被探测器观察,量子比特就处于叠加态(同时等于0和1)无法预测其值。
- 在被观察的那一刻,它就会坍缩为两种状态中的一种(参考薛定谔的猫)
量子叠加态的特性带来了极大的变革可能性
首先我们知道,传统比特在表示16种可能的组合时候,你只能选择其中一种
而在处于叠加态的量子比特中,你可认为它同时处于这16种中的所有状态
啥意思?简单点,举个例子:
- 一个内存仅有4位比特的简单计算机模型,它有2^4种状态,即16种
- 对于传统计算机,在任意一个时刻,它只能处于其中的一种状态
- 而在量子计算机中,4个量子比特都可处于叠加态,也就是说能同时工作在上述16种状态中!
即上述中1台量子计算机=16台传统计算机并行工作,综上可得:
- 1台n位的量子计算机= 2^n 台n位的传统计算机并行工作
由此可见,每多一位,量子计算机的优势呈指数级增长
更有趣的是,量子比特有个难以置信的特性就是:它可以处于量子纠缠态
顾名思义,也就是量子间有着无形的关系,像丝一样纠缠在一起,紧密的联系使得一个量子比特发生变化会立刻反应在另一个相关的量子比特上,无论多远。
这意味着我们只需要通过观测知道其中的一个状态,另一个的状态也就不言而喻了
但是,操纵量子比特也相当令人困惑。我们知道,普通逻辑门由一组输入即可得到一个确定的输出状态
而量子门,则用于操纵处于叠加态的量子比特,改变它被观测时可能出现的状态,并最终输出一个叠加态与之前不同的量子
因此,量子计算机会设置些量子比特,利用量子门让它们处于纠缠态,并操纵它们各个状态出现的可能性(可以想象为上帝之门)。再通过观测它们,使叠加态坍缩,可能的输出序列中的一种就会出现。这意味着,你可以同时进行多组不同的运算
最终,它们的结果便是期望中的一种
恰当的利用量子纠缠和叠加态,在某些时候它的效率将大大超过传统计算机
因此,尽管量子计算机在一些方面表现平平,比如你拿它来上网、看电影, 但诸如一些并行计算场景,便是它用武之地,在这些场景中它有着得天独厚的优势
例如,我们在数据库进行海量数据检索的时候,传统计算机需要遍历其中所有可能的匹配才能找到最终结果,但利用量子计算机中的匹配算法去寻找结果则可节省一个数量级以上的时间!
还有在计算机安全领域中,量子计算机也有着非凡意义和重要应用
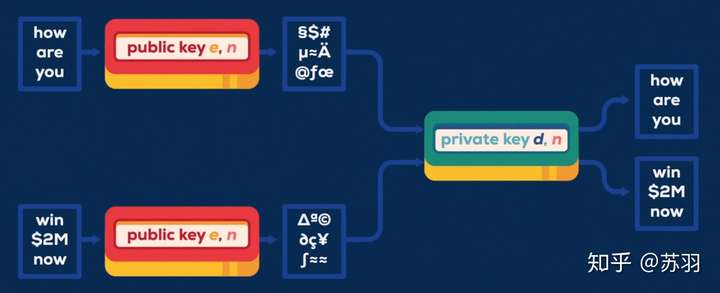
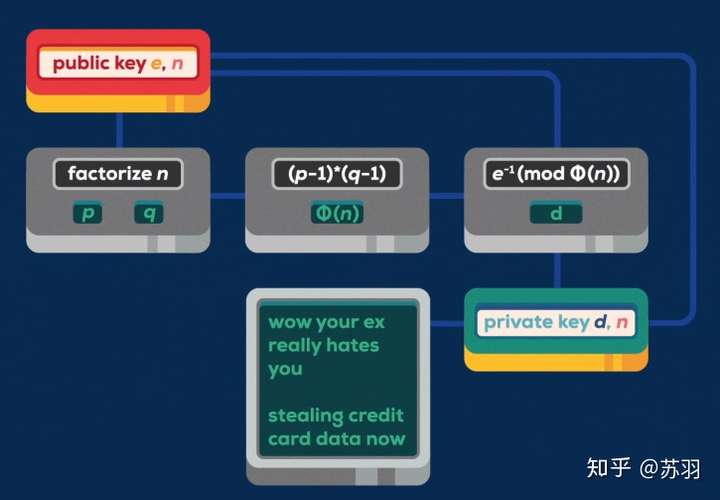
目前普遍的加密系统,通过公开分发的公钥加密数据,只能由对应私钥持有者才能解密
但关键就在于,获取公钥后其实是可通过数学方法去计算私钥的
那么问题来了,传统计算机去计算私钥,可能要花费数年甚至更久的时间,显然不太现实, 量子计算机的实现,可以指数倍的缩短、加快这个计算过程, 是的,一旦量子计算机取得突破性进展,那么现有的众多所谓安全加密的系统全部要被颠覆
此外,量子计算机还有模拟量子现象等等用途,模拟量子现象一般需要耗费海量资源(论大型超级计算机重要性)即便是模拟分子,精度也无法差强人意
通过这些模拟,能帮助我们了解各种蛋白质的特性,从而带来医学变革的可能,拯救人类
如今,众多顶尖科学家正前赴后继地研究这项前沿技术,让我们致以最崇高的敬意!他们是时代的先驱,是未来的开拓者,肩负着未来变革的重任!
我们在目前也还不知道这项科技能走多远,显然,只有交给时间,就让我们共同期待未来
应用
- 潘建伟:量子计算机在原理上具有超快的并行计算能力,可望通过特定算法在密码破译、大数据优化、天气预报、材料设计、药物分析等领域,提供比传统计算机更强的算力支持
量子力学的忽悠局
量子波动速读
- 「量子波动速读」是否存在?是不是骗局?
- 1分钟10万字大法:量子波动速读、蒙眼翻书穿针,这是席卷15省的最新智商税
- “量子波动速读”可能是个舶来品,创始人很可能是一位名叫飞谷由美子的日本阿姨











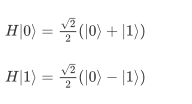














 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
