概率统计

科普

【2023-9-6】概率的尽头，是命运吗？

机器学习中的概率模型

注意

回归问题假设数据服从正态分布
分类问题假设数据服从多项式分布

【2024-3-9】机器学习中的概率模型

概率模型是机器学习算法中的大家族，从最简单的贝叶斯分类器，到让很多人觉得晦涩难懂的变分推断，到处都有它的影子。

为什么需要概率论？与支持向量机、决策树、Boosting、k均值算法这些非概率模型相比，概率模型好处：

对不确定性进行建模。假如根据一个人的生理指标预测他是否患有某种疾病。与直接给出简单的是与否的答案相比，如果算法输出结果是：他患有这种疾病的概率是0.9，显然后者更为精确和科学。再如强化学习中的马尔可夫决策过程，状态转移具有随机性，需要用条件概率进行建模。
分析变量之间的依赖关系。对于某些任务，我们要分析各个指标之间的依赖关系。例如，学历对一个人的收入的影响程度有多大？此时需要使用条件概率和互信息之类的方法进行计算。
实现因果推理。对于某些应用，我们需要机器学习算法实现因果之间的推理，这种模型具有非常好的可解释性，与神经网络之类的黑盒模型相比，更符合人类的思维习惯。
能够生产随机样本数据。有些应用要求机器学习算法生成符合某一概率分布的样本，如图像，声音，文本。深度生成模型如生成对抗网络是其典型代表。

有监督学习

(1) 有监督学习

贝叶斯分类器: 使用概率解决分类问题的典型代表, 假设每个类的样本都服从正态分布，就是正态贝叶斯分类器。
logistic回归: 二分类，没借助贝叶斯概率，直接根据特征向量x估计出正样本概率
- 伯努利分布 + 最大似然估计 = softmax回归
- logistic 回归拟合的是伯努利分布。
- logistic 回归虽然是一种概率模型，但不是生成模型，而是判别模型，因为没有假设样本的特征向量服从何种概率分布。
softmax回归: 多分类
- 多项分布 + 最大似然估计 = softmax回归
- softmax回归是 logistic回归的多分类版本，直接预测样本x属于每个类的概率，将其判定为概率最大的那个类
- 假设：样本类别标签值服从多项分布，因此它拟合的是多项分布。
- 最大化对数似然函数等价于最小化交叉熵损失函数。softmax回归训练时的目标是使得模型预测出的概率分布与真实标签的概率分布的交叉熵最小化。
变分推断
- 贝叶斯公式 + KL散度 = 变分推断
- 贝叶斯分类器是贝叶斯推断的简单特例，目标是计算出已知观测变量x时隐变量z的后验概率p(z|x)，从而完成因果推断
高斯过程回归
- 一组随机变量，假设服从多维正态分布，那么构成了高斯过程，任意增加一个变量之后，还是服从正态分布。
- 高斯过程回归是贝叶斯优化的核心模块之一。

无监督学习

(2) 无监督学习

SNE 降维算法
- 正态分布 + KL散度 = SNE
- 随机近邻嵌入（SNE）是一种基于概率的流形降维算法，将向量组变换到低维空间，得到向量组
- 思想: 高维空间中距离很近的点投影到低维空间中之后也要保持这种近邻关系，在这里距离通过概率体现。
t-SNE 降维算法
- t分布 + KL散度 = t-SNE
- t-SNE 是 SNE 的改进版本。核心改进: 将正态分布替换为t分布，t分布具有长尾特性，在远离概率密度函数中点处依然有较大的概率密度函数值，因此更易于产生远离中心的样本，从而能够更好的处理离群样本点。
高斯混合模型
- 多项分布 + 正态分布 = 高斯混合模型
- 正态分布具有很多良好的性质，应用问题中通常假设随机变量服从正态分布。不幸的是，单个高斯分布的建模能力有限，无法拟合多峰分布（概率密度函数有多个极值），如果将多个高斯分布组合起来使用则表示能力大为提升，这就是高斯混合模型。
Mean shift 算法
- 核密度估计 + 梯度下降法 = Mean shift算法
- 很多时候无法给出概率密度函数的显式表达式，此时用核密度估计。
- 核密度估计（KDE）也称为 Parzen窗技术，是一种非参数方法，无需求解概率密度函数的参数，而是用一组标准函数的叠加表示概率密度函数。
概率图模型
- 概率论 + 图论 = 概率图模型
- 概率图模型是概率论与图论相结合的产物。用图表示随机变量之间的概率关系，对联合概率或条件概率建模。
- 这种图中，顶点是随机变量，边为变量之间的依赖关系。如果是有向图，则称为概率有向图模型；如果是无向图，则称为概率无向图模型。
- 概率有向图模型的典型代表是贝叶斯网络，概率无向图模型的典型代表是马尔可夫随机场。
- 使用贝叶斯网络可以实现因果推理。
隐马尔可夫模型
- 马尔可夫链 + 观测变量 = 隐马尔可夫模型
- 马尔可夫过程是随机过程的典型代表。这种随机过程为随着时间进行演化的一组随机变量进行建模，假设系统在当前时刻的状态值只与上一个时刻有关，与更早的时刻无关，称为“无记忆性”。
受限玻尔兹曼机
- 玻尔兹曼分布 + 二部图 = 受限玻尔兹曼机
- 受限玻尔兹曼机（RBM）是一种特殊的神经网络，其网络结构为二部图。这是一种随机神经网络。在这种模型中，神经元的输出值是以随机的方式确定的，而不像其他的神经网络那样是确定性的。
- 受限玻尔兹曼机的变量（神经元）分为可见变量和隐藏变量两种类型，并定义了它们服从的概率分布。可见变量是神经网络的输入数据，如图像；隐藏变量可以看作是从输入数据中提取的特征。在受限玻尔兹曼机中，可见变量和隐藏变量都是二元变量，其取值只能为0或1，整个神经网络是一个二部图。

数据生成

(3) 数据生成问题

生成对抗网络
- 概率分布变换（生成器） + 二分类器（判别器） = 生成对抗网络
变分自动编码器
- 变分推断 + 神经网络 = 变分自动编码器

强化学习

(4) 强化学习

马尔可夫决策过程
- 马尔可夫过程 + 动作 + 奖励 = 马尔可夫决策过程
- 马尔可夫决策过程（MDP）是强化学模型的抽象，是对马尔可夫过程的扩充，在它的基础上加入了动作和奖励，动作可以影响系统的状态，奖励用于指导智能体学习正确的行为，是对动作的反馈。

统计学核心

【2021-11-5】统计学的核心到底是什么？，作者朱宏图

有幸重新拜读Breiman教授的访谈录，跟几年前相比，我在字里行间中体会了许多新东西。这个可能是因为我最近6年的不同于学术生活的经历了，用四个字来形容“人生如梦！”。我从UNC一个高校，到MD Anderson一个顶级癌症医院，到滴滴出行一个创业公司，再回UNC，转了一个大圈子。由此认识了各种背景的人，特别是学界和工业界（含医院和科技公司），在跟这些同仁的交往之中感受了他们对这个世界的看法和探索的方式是如此的不同。我从一个做数理统计开始，到做生物统计，到神经病研究，到近年做双边市场，再到神经科学，这个过程当中接触了不同层面的问题，使得在认知水平上的经历了一个巨大的变化。

Breiman教授的几句话：

统计就是”一门收集、分类、处理并且分析事实和数据的科学。 Fisher相信统计的存在是为了预测、解释和处理数据的。就统计应用的角度而言，我知道工业机构和政府在发生些什么，但是目前进行的学术研究却似乎离我们无比遥远，好像只是抽象数学的某一分支一样。

统计精髓之处是在收集和利用数据，来解决现实世界中有趣而又重要的问题

Breiman 是美国国家科学院院士（应用数学学部），不仅在概率论、统计、机器学习，做出了许多有巨大影响力的工作，特别是CART和bagging这些东西已经是科技公司每天都在用的工具；而且在咨询各个行业躬身力行，笃行不怠。可以说他是既懂数学，又懂统计，也懂应用的全才。

跟 Breiman 教授的观点几乎一样：“统计学一开始就从实践中来，通过数据来认识这个世界，最终去解决大的实践问题。” 一言而概之：统计学的核心是应用和数据，就是通过分析数据来深刻地探索这个世界。

统计学跟数学不一样
- 虽然统计学要用到数学的许多工具来把整个体系完备化，但是统计学中根本性的0-1大突破一定是从为了解决重大应用问题而产生的。比如，随机梯度算法就是Robbins和Monro (1951，统计年刊)为了做一个实验设计的问题提出来并解决的, 而它现在是深度学习和强化学习最重要的优化工具。那些高深的数学工具大概率不能给统计学的带来革命性的变革。
统计不是从工具到应用
- 许多统计学家主要是在做各种统计工具，讨论许多理论性质特别强调数学的美；有的会去找各种数据来试，看看能不能用的起来，只关心能不能发顶刊，根本不关心实际应用中的价值。这也是为什么Breiman说 “统计中吸引人的东西与目前的学术研究已经相去甚远，分道扬镳了”。其实最近20年，统计学在某种程度上是偏离了这个应用的本质。另外一方面，越来越多的智能型数据产品的出现，比如说最近Deepmind在Nature连续发了两篇文章，这些产品对蛋白质结构的预测，用到了好几个最新的分析方法，比如embedding，预训练，知识蒸馏，变换器，和图模型的表示。这些工具就是Breiman教授说 “我与机器学习和神经网络区域的人走得很近，因为他们正在为一些复杂的、困难的预测问题做一些非常重要的应用工作。他们以数据为方向，所做的也与Webster对统计的定义相一致，然而，他们几乎全都不是受过训练的统计学家！”。这些工具已经不能算是传统的统计方法，你可以说在最底层，它们跟统计非常有关系，但是其中有核心的创新是非统计的，是革命性的。这些突破带来不仅仅是学界的认可，它同时会影响政府机构（含各个funding机构）和金融投资机构。比如，美国NSF最近就成立了数十个AI相关的研究中心，但这些和统计社区关系不大，最终可能会进入一个恶性循环的生态环境。
数据问题的重要性
- 因为物联网的发展直接引导了新型产业的发展，像社交平台、搜索引擎和交易平台等等。由此在时空维度上, 对数据收集、存储和分析都发生了根本的革命。相关公司业务的发展极大地推动计算机软硬件的进步，数据的规模无论从复杂度和多样性都对未来时空数据分析方式提出了许多新的要求。有了数据，原来许多不可能的事情变得可能啦。最近人工智能的落地已经上升到国家层面，是新一代工业革命的核心技术，随着这些落地的进行，我们会看到更多、更大、更复杂的数据。
统计一定是从应用中来，到应用中去
- 第一个例子是关于ImageNet数据集。最近10年AI的发展，其根源就是数据上的突破，无论从数据的质量、问题的复杂度、还是标注方法的创新, ImageNet都是本世纪数据科学,特别是计算机视觉最重要的一个突破。它给了我们一个公正地评估和训练各种分类和预测方法的平台。一个好的数据是有影响力的统计研究的重要基础。
- 第二个例子是关于深度学习。现在大家公认深度学习是数据分析方法最近十几年的最大成果，影响深远。它无论对计算机视觉、自然语言处理、非参数模型、反问题、图像处理、偏微分方程数值解等领域都是根本性的革命，可以说现在许多领域里面都替代了传统方法，包含许多应用数学方法，虽然深度学习的理论研究严重落后于它的应用和算法创新。
- 第三个例子是关于AlphaGo。AlphaGo的成功反映了一个数据产品要成功，从顶层设计，到数据建设，到硬件，到高超的算法水平，都是缺一不可的。因为深度学习的发展，特别跟软硬件和其它方法的融合，极大地推动了智能数据产品的落地，比如说，AlphaZero和AlphaGo的开发，把现代数据科学可解决问题的深度和广度都推到了历史新高度，并在各个领域里面发挥了越来越重大的影响，特别在学术界和政府，现在已经上升到国家层面的核心生产力，成为新一代工业革命的核心技术。国家层面对AI的投入可以说是一个巨大的蛋糕。这也反映了我们未来要重视智能数据产品的开发和落地，不能只做整个问题中很小的一步，特别要培养统计专业学生的工程能力是非常关键的。
- 第四个例子是强化学习。AlphaGo和物联网的成功也带动了强化学习的复兴，强化学习已经从一个小众的分支，变成机器学习的头号分支。今年ICRL和neurIPS的顶会里面最多的文章都跟强化学习相关，现在强化学习已经从游戏，到机器人，到精准医疗，到各个市场的落地。我们在滴滴的团队一直用强化学习来优化平台的策略，都取得了很多成果。由于时空平台会越来越大而多，强化学习一定会成为主流数据分析工具。
- 第五个例子是因果推断。比如今年诺贝尔经济学奖就给了两个做因果推断的人，他们推广了Donald Rubin的因果模型，我认为Don能够做出这样漂亮的统计框架大部分归于他多年咨询工作中积攒的数据和应用相关分析的工作经验、收集数据能力的极大提升和最近因果模型的相关应用和研究的深入。并且随着收集数据能力特别是时空数据的极大提升，因果模型的相关应用和研究会越来越多和越来越深入，由此相关落地会产生出更大的影响力。
未来一段时间应用的核心
- 最近机器学习大佬Michael Jordan强调了机器学习与市场的融合。这一代人工智能的发展主要是落地在衣，食，住，行，教育，医疗，人力，和养老等相关的市场，系统地将消费者和商品紧密连接，把人、数据和现实中的问题和需求进行整合，成为一个可以创建经济新业态的平台。统计学必须从收集和提炼信息的阶段来思考如何搭建有效的数据平台，在推动业务发展的过程中逐渐从分析方法上抽象出一套完整的统计学基础理论，来推动人工智能在产业的落地，并产生巨大的社会价值。

因此，统计同仁们重视数据和应用，多思考应用的大问题，通过收集和清洗数据，来解决实际问题，进而发展出几个牛掰的统计工具，再证明几个深刻的数学公式，这样统计学就有着辉煌的未来。

概念

概率 vs 统计

概率论和统计学的区别

概率论和统计学解决的问题互逆。假设有一个具有不确定性过程（process），然后这个过程可以随机的产生不同的结果（outcomes）。则概率论和统计学的区别可以描述为：

概率论（probability theory）中，已知该过程的概率模型，该模型的不确定性由相应的概率分布来描述；概率论要回答的问题是该过程产生某个结果的可能性有多大这类问题。
统计学（statistics）中，该过程的概率模型是未知的，但是有一系列该过程产生的结果的观测值；希望通过这些观测值来推断出这个过程中的不确定性是什么样的。

总结：（类似归纳与演绎）

通过已知概率模型来精确的计算各种结果的可能性就是概率论；——演绎
根据观测结果来推断模型的不确定性就是统计学。——归纳

flowchart LR %%颜色定义 classDef red fill:#f02; classDef green fill:#5CF77B; classDef blue fill:#6BE0F7; classDef orange fill:#F7CF6B; classDef grass fill:#C8D64B; %%节点关系定义 A(过程):::blue A -->|概率论,演绎| B(结果) A -.-|描述不确定性| C(概率模型):::orange B -->|统计学,归纳| A B -.-> result subgraph result [观测结果] direction LR B1(结果1) B2(结果2) B3(结果3) end

概率学派

统计学领域中有两大学派：古典统计学（classical）和贝叶斯统计学（Bayesian，以英国数学家托马斯•贝叶斯命名）。古典统计学又称为频率论（frequentist）。

频率学派（Frequentist School）与贝叶斯学派（Bayesian School）：频率学派强调通过大量数据揭示客观规律
而贝叶斯学派则注重结合先验知识与新数据来更新信念。

总结

马同学高等数学

维度	频率派	古典派	主观派
理论基础	过往事实的归纳总结	不充分理由原则	知识和直觉
概率定义	频率稳定性	等概率	信念强度

维度	频率学派	贝叶斯学派
基本观点	世界是客观的，概率是事件在长时间内发生的频率。必须通过大量独立采样来获得统计均值。不主张先给出一个主观先验概率或假设。	概率是一种信念度，可以有主观的先验概率。通过观察新数据来不断更新先验概率，使之逼近客观事实。
优势	简单、可重复的实验场景下非常有效。	能够结合先验知识和新数据进行概率推断，更加灵活和实用。
局限	对于无法进行大量重复实验或实验成本高昂的现实场景，频率学派方法可能不适用。	先验概率的选择可能带有主观性，需要谨慎选择。
应用场景	适用于通过大量重复实验来获得统计规律的场景，如:抛硬币、掷骰子等	适用于需要估算概率但无法进行大量重复实验的现实场景，如赶: 飞机时间的估算、《狼来了》故事中村民对小孩诚实度的判断等。

频率 vs 贝叶斯

古典统计学和贝叶斯统计学

频率学派与贝叶斯学派之争：知乎网友解释

频率学派最先出现，疯狂打压新生的贝叶斯学派，贝叶斯很凄惨，就跟艺术圈的梵高一样，死后的论文才被自己的学生发表，经过拉普拉斯之手发扬光大，目前二派就像华山派的剑宗和气宗。
频率学派挺煞笔的，非得做大量实验才能给出结论，比如今年高考考上北大的概率是多少啊？频率学派就让考100次，然后用考上的次数除以100。
而贝叶斯学派会找几个高考特级教师对你进行一下考前测验和评估，然后让这几个教师给出一个主观的可能性，比如说：你有9成的把握考上北大。这个区别说大也大，说小也小。
（1）往大了说，世界观就不同
- 频率派认为参数客观存在，不会改变，虽然未知，但却是固定值；
- 贝叶斯派则认为参数是随机值，因为没有观察到，和随机数也没区别，因此参数也可以有分布，个人认为这个和量子力学某些观点不谋而合。
（2）往小处说，频率派最常关心的是似然函数，而贝叶斯派最常关心的是后验分布。
- 后验分布其实就是似然函数乘以先验分布再normalize一下使其积分到1。因此两者的很多方法都是相通的。
- 贝叶斯派因为所有的参数都是随机变量，都有分布，因此可以使用一些基于采样的方法（如MCMC）使得我们更容易构建复杂模型。
- 频率派的优点则是没有假设一个先验分布，因此更加客观，也更加无偏，在一些保守的领域（比如制药业、法律）比贝叶斯方法更受到信任。
- 频率 vs 贝叶斯 = P(X;w) vs P(X|w) 或 P(X,w)
- 频率学派认为参数固定，通过无数次实验估计出参数值——客观；
- 贝叶斯学派认为参数和数据都是随机的，参数也服从一定分布，需要借助经验——主观

关于这俩大学派孰优孰劣已有一个世纪的争论。本质区别在于对待未知模型或者参数的方法是不同的：

古典统计学认为，未知的模型或者参数是确定的，只不过我们不知道它确切的形式或者取值。
- 古典统计学通过进行大量重复实验并统计某个特定结果出现的频率作为对未知参数的估计。
- 大数定律
贝叶斯统计学认为，未知的模型或者参数变量是不确定的，但是这种不确定性可以由一个概率分布来描述。
- 贝叶斯统计学“使用概率的方法来解决统计学问题”——贝叶斯公式+主观概率
  - 先验分布（prior distribution）：根据主观判断或者过去的经验，猜测概率分布
  - 后验分布（posterior distribution）：根据越来越多的观测值（new data 或者 new evidence）来修正猜测得到的概率分布
- 贝叶斯统计学中的“概率”的概念可以被解释为对未知变量不同取值的信心程度的测度（measure of confidence）
- 贝叶斯统计学派被古典统计学派诟病的核心问题是对于未知变量的先验分布是非常主观的。
- 适合场景：选举、疾病诊断
  - 无法大量重复试验
  - 合理的先验分布对未知量的估计是非常有益的
- 关于贝叶斯统计的一个笑话，代表着很多吃瓜群众对贝叶斯统计的看法，以及贝叶斯统计学派的自嘲：
  - A Bayesian is one who, vaguely expecting a horse, and catching a glimpse of a donkey, strongly believes he has seen a mule.
  - 一个贝叶斯学派的学者是这样的：模糊的期待着一匹马（先验），却看到了一头驴（证据），于是便自信的认为那是一头骡子（后验）。

频率学派

频率学派（Frequentist School）

基本观点：世界是客观的，概率是事件在长时间内发生的频率。必须通过大量独立采样来获得统计均值。不主张先给出一个主观先验概率或假设。
应用场景：适用于通过大量重复实验来获得统计规律的场景，如:抛硬币、掷骰子等。
优势：简单、可重复的实验场景下非常有效。
局限：对于无法进行大量重复实验或实验成本高昂的现实场景，频率学派方法可能不适用。

根据大数定律, 大量实验来获取统计均值

不充分理由原则

雅各布·伯努利（1654－1705）提出，如果因为无知而没办法判断哪一个结果更容易出现，那么应该给予相同概率

以不充分理由原则为基础，经由皮埃尔-西蒙·拉普拉斯侯爵（1749－1827）之手，确立了 古典概率 定义，即：

未知的概率都为等概率

整个19世纪的人们都广泛接受这个定义，并发展出了一系列的定义和定理。
贝特朗悖论：法国数学家贝特朗（也翻译为“伯特兰”）于1888年在他的著作《Calcul des probabilités》中提到了这个悖论，锯木厂的木头，人们开始反思古典概率中的不合理之处：“等概率”的描述实在是太模糊了，存在歧义。
- 边长的分布是未知的，所以是等概率的
- 面积的分布是未知的，所以是等概率的
现代概率论通过分布来描述边长的随机性后，这种模糊性消失了，贝特朗悖论解决

贝叶斯学派

贝叶斯学派（Bayesian School）

基本观点：概率是一种信念度，可以有主观的先验概率。通过观察新数据来不断更新先验概率，使之逼近客观事实。
应用场景：适用于需要估算概率但无法进行大量重复实验的现实场景，如赶: 飞机时间的估算、《狼来了》故事中村民对小孩诚实度的判断等。
优势：能够结合先验知识和新数据进行概率推断，更加灵活和实用。
局限：先验概率的选择可能带有主观性，需要谨慎选择。

什么是贝叶斯统计（Bayesian Statistics）？

贝叶斯统计（Bayesian Statistics）是一种基于贝叶斯定理的统计推断方法，它利用先验信息和样本数据来更新我们对未知参数或事件概率的信念。

先验分布：统计推断前，对未知参数的初步判断，基于历史、专家经验或主观信念，不必客观。
后验分布：结合先验和样本信息，通过贝叶斯定理计算得到的未知参数新分布，综合了两者信息，是贝叶斯推断的基础。

贝叶斯网络（Bayesian Network），也称贝叶斯有向无环图（Bayesian Directed Acyclic Graph, BDAG）或概率依赖网络（Probabilistic Dependence Network），是一种强大的概率图模型，用于描述随机变量之间的概率依赖关系。

详见站内专题: 贝叶斯概率

参数估计

【2020-8-1】三种参数估计方法

两大流派：

频率学派：参数未知但固定。极大似然估计 MLE（点估计）
贝叶斯学派：参数未知且变化。最大后验估计 MAP（点估计）、贝叶斯估计（分布估计）
注：频率是贝叶斯的一个特例，隐含了先验知识

方法

极大似然估计：用样本数据进行点估计
最大后验估计：用样本数据+先验知识进行点估计
贝叶斯估计：用样本数据+先验知识进行分布估计

概率统计量

可能性描述

impossible（不可能，p=0） → unlikely（不太可能，p=1/6） → even chance（等概率） → likely（很有可能，p=4/5） → certain（确定，p=1）

p值

p=0 : impossible（不可能）
p=1/6: unlikely（不太可能）
p=1/N: even chance（等概率）
p=4/5: likely（很有可能）
p=1 : certain（确定）

how often do you exercise

100% Always
90% Usually
80% Nomally
70% Often
50% Sometimes
30% Occasionaly
10% Seldom
5% Hardly ever
0% Never

【2020-5-29】用4个数来概括一个分布

均值 mean: 第一矩, 表位置
方差 variance: 第二矩, 表胖瘦
偏度 skewness: 第三矩, 表歪斜
峰度 kurtosis: 第四矩, 表尾巴胖瘦

概率中常见的统计度量，首先是均值和方差，其定义与前面在统计学中看到的定义没有区别。

1．偏度（Skewness）
- 它表示了一个概率分布的横向偏差，即偏离中心的程度或对称性（非对称性）。一般来说，如果偏度为负，则表示向右偏离；如果为正，则表示向左偏离。下图描绘了偏度的统计分布。
- 分布形状对偏度的影响
2．峰度（Kurtosis）
- 峰度显示了分布的中心聚集程度。它定义了中心区域的锐度，也可以反过来理解，就是函数尾部的分布方式。
- 峰度的表达式如下。
- 直观地理解这些新的度量。分布形状对峰度的影响

摘自：机器学习需要哪些数学基础？

力学上的矩，质量（mass）：

0 阶矩：是总质量；
1 阶矩除以总质量是质心（质量中心）；
2 阶矩是惯性矩（moment of inertia）

统计学上的矩

0 阶矩：总概率，也就是 1；
1 阶矩：均值，
2 阶中心矩：方差；如果是多元，对应协方差
3 阶中心矩：偏度（skewness）
4 阶中心矩（归一化和平移）：峰态（kurtosis）

图解概率统计量

【2022-10-10】概率统计量演进

flowchart LR %%根节点 A(矩):::light %%颜色定义 classDef red fill:#f02; classDef green fill:#5CF77B; classDef blue fill:#6BE0F7; classDef orange fill:#F7CF6B; classDef start fill:#C8D64B; %%节点关系定义 A -->|0阶| B(总概率):::blue A -->|1阶| C(均值/mean):::green C -.-|位置| O[[描述特性]] A -->|2阶| D(方差/variance):::green %%C -.->|依赖| D D -.-|波动| O D -->|多元变量| E(协方差):::green E -.-|波动| O A -->|3阶| F(偏度/skewness):::orange F -.-|歪斜| O A -->|4阶| G(峰度/kurtosis):::orange G -.-|尾巴胖瘦| O %%注释 %%subgraph 图例 direction TB %%x(当前sota):::red %%y(次sota):::orange %%z(重要模型):::green %%z -.->y -.->x %%end

样本量多少才有统计意义？

【2022-11-11】知乎：样本数据达到多少统计指标才有意义？, 文章：样本量与置信区间

问题：如何从海量数据中选择合适样本集调研反馈，从而反映总体情况

在千万人口的城市进行某项调研，如何选择样本；
在某些国家的大选活动中，该发放多少问卷才能够反映整体情况；
在机器学习模型的精确率抽检过程中，究竟应该选择多少样本进行抽检，才能够反馈其模型的精确率；

常见的情况：

通过置信度（confidence level），置信区间（confidence interval），总体数量（population），来计算样本数（sample size）；
通过置信度（confidence level），总体数量（population），样本数量（sample size），比例（percentage），来计算置信区间（confidence interval）；

随机抽样

当一个调研是随机抽样时，通过统计方法确定最小样本数。

样本数计算

样本数选取规则：

最小样本数是 100：对于一份抽样数据而言，至少要抽取 100 个样本来进行评估；
- 全体总数小于 100 时，全部抽取；
最大样本数（maximum sample size）计算公式： $M=\min(1000,0.1*N)$
- 其中 N 表示总量；
- 当 N=5000 时，最大样本数可以选择 500；
- 当 N=20000 时，最大样本数只需要选择 1000 即可；

调研和抽样时，在最小样本数和最大样本数之间选择一个合适的值；

（1）选择靠近最小样本数的值：
- 有限的资金和时间；
- 只需要一个粗糙的估计；
- 不需要对总体做类别分析且只需要一个整体的结论即可；
- 大家对这个结论并不会有过多的质疑；
- 这个分析结果并不会过多影响下游的分析决策。
（2）选择靠近最大样本数的值：
- 充足的资金和时间；
- 想要得到发一个精确的估计；
- 有可能会对总体进行分组分析；
- 大家会对这个结论有质疑；
- 这个分析结果会导致下游的很多重要决策。

样本数选择参考：置信度 95% 的前提下

误差范围（置信区间）	总量>5000	总量=5000	总量>2500	总量>1000	总量>500	总量>200
正负 10%	96	94	93	88	81	65
正负 7.5%	171	165	160	146	127	92
正负 5%	384	357	333	278	217	132
正负 3%	1067	880	748	516	341	169

如果只需要保证置信度在 95%，当总量很大的时候，其实只需要抽取 1067 个样本进行分析即可。

在线计算样本量的网站有两个

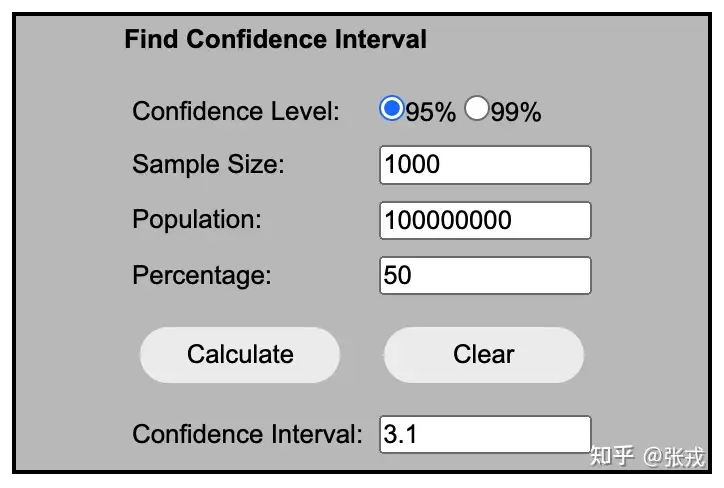
设置置信度（Confidence Level），置信区间（Confidence Interval），总量（Population）之后，就可以得到一个样本数量（Sample Size Needed）。其中，置信区间也就是误差范围（Margin of Error）。

例如，如果置信度是 95%，置信区间（confidence interval）= 4，在样本中有 47% 的比例选择了某个选项，那么就表示 95% 的置信度，在所有数据中有(47%-4%, 47%+4%)=(43%,51%) 的比例选择了某个选项。
95% 置信度表示这句话正确的概率是 95%，99% 置信度表示这句话正确的概率是 99%。

置信区间的计算

置信区间的计算是由三个因素决定的，分别是：置信度（Confidence Level），样本数量（Sample Size），总量（Population）。一般来说，

置信度：置信度越大，表示置信区间将会越大。相对 99% 的置信度而言，95% 的置信度所产生的置信区间会小；
样本大小：样本越多，越能够反映总体情况，置信区间将会越小；
占比（Percentage）：样本中选择某个结果的比例；由于选择 Percentage(p) 和 1-p 所得到的置信区间（Confidence Interval）是一样的，因此：
- （1）Percentage(p) 越接近 0 或者 1，则置信区间越小；
- （2）Percentage(p) 越接近 50%，则置信区间越大，因为此时的不确定性最高；

定律

大数定律

弱大数定理（辛钦大数定理）: 样本均值收敛到总体均值（期望）
- 独立同分布且具有均值μ的随机变量X1,…,Xn, 当n很大时, 算术平均 $ \frac{1}{n}\sum_{k=1}^n x_k $ 很可能接近于μ。
伯努利大数定理: 辛钦大数定理的一个重要推论, f/n -> p

中心极限定理

什么是中心极限定理呢？

中心极限定理：

样本平均值约等于总体平均值。
不管总体是什么分布，任意一个总体样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

中心极限定理其实包含了大数定理

概率分布

六大分布：伯努利分布、二项分布、多项式分布、Beta分布、Dirichlet分布、高斯分布

概率分布概览

六大概率分布
【2018-11-15】数说工作室：概率论-上帝的赌术，协和八：说人话的统计学，做统计，多少数据才算够，【2018-5-20】【精华】说人话的统计学-合集，【2019-08-30】统计之都，【2020-3-11】概率统计思维的建立

概率分布总结

一维随机变量的概率分布：

概率分布	数据类型	特点	举例
伯努利分布	离散	抛硬币，二选一	扔1次硬币
二项分布	离散	n重伯努利，出现k次“是”	扔n次硬币🪙
多项分布	离散	n重伯努利，出现k次“是”	扔n次骰子🎲
泊松分布	离散	二项分布的极限	每天供应多少馒头某地出现交通事故次数
几何分布	离散	n重伯努利，第k次首次出现“是”	n次实验才成功的概率
负二项分布	离散	几何分布的和	巴拿赫火柴盒
超几何分布	离散	不放回抽样的二项分布	n件产品中m件不合格的概率
均匀分布	连续	古典派中的几何概型	等公交车时间
正态分布	连续	二项分布的另外一种极限	身高分布考试分数
指数分布	连续	泊松分布的间隔，连续的几何分布	灯泡寿命第一位客人上门，店主等待时间

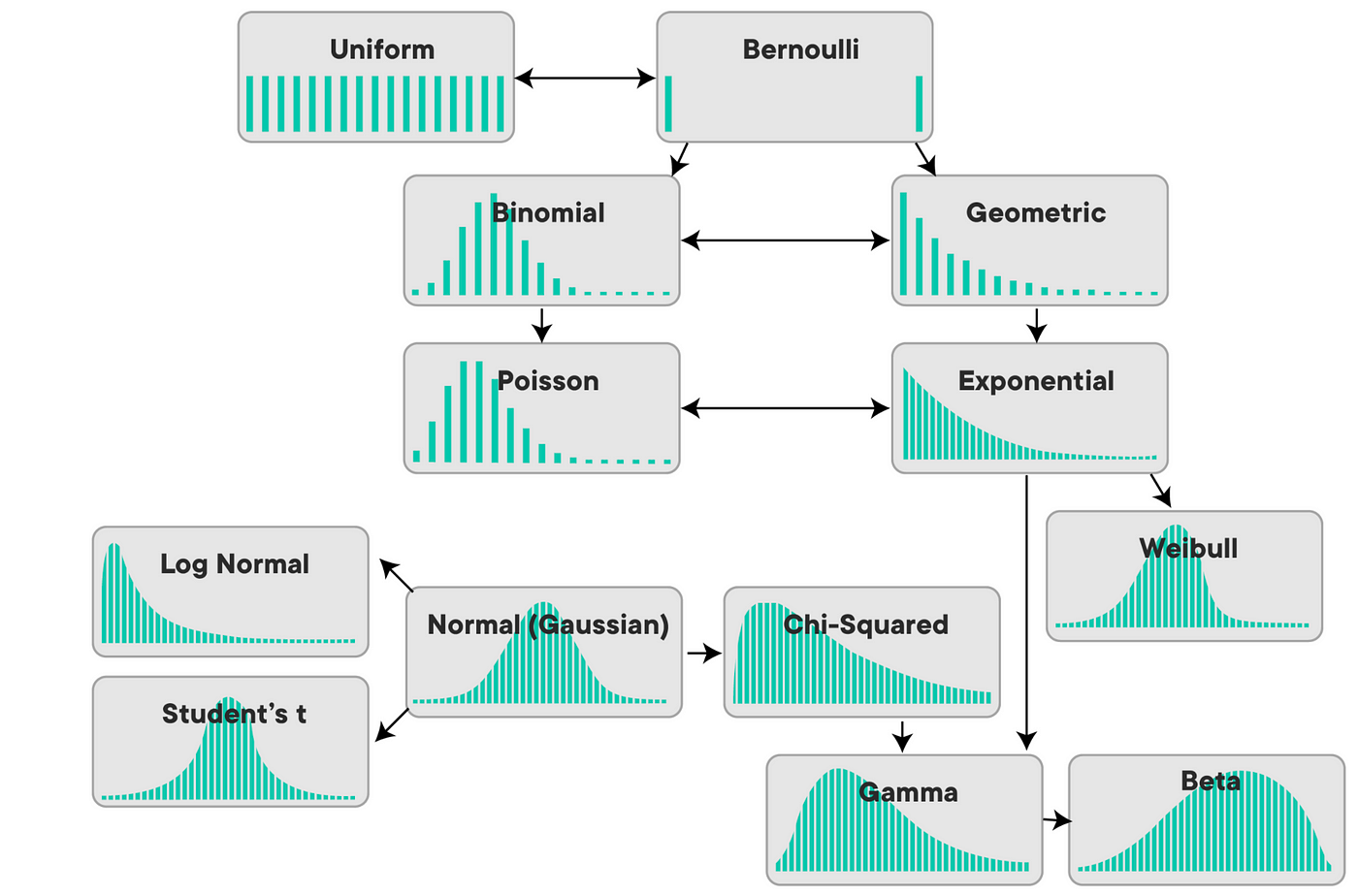
图解概率分布演进

【2022-10-10】概率统计量演进

【2022-10-10】Relationship between probability distributions

均匀分布

问题背景: 古典派中的几何概型

设车每10分钟来一班，且随机到来，问等车时间。

概率密度函数: X = U(a,b)

$X=U(a,b)$
$ p(x)=\left {\begin{array}{ll} \frac{1}{b-a} & a \leq x \leq b \ 0 & \text { else } \end{array} \right. $
期望和方差：$\frac{a+b}{2} , \frac{(b-a)^2}{12} $

伯努利分布

问题背景: 概率不同的是非题。

抛一枚硬币，是正面还是反面?
进来的顾客买还是不买东西?
人的眼睛是不是绿色?

概率质量函数

$p(x)=p^{x}(1-p)^{1-x} , x=1,0$
期望:p
方差:p(1−p)

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包

# 生成pmf
# --------分布参数---------
p = 0.5 # 得到"是"的概率
# ------------------------

X = np.arange(0,2,1) # [0,1]
p_list = stats.bernoulli.pmf(X,p) # [0.5,0.5] 

# 制图
plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X,0,p_list)
plt.xlabel("Random variable X ,X(Pos)=1,X(Neg)=0")
plt.ylabel('Probability')
plt.title("Bernuulli: p={}".format(p))

二项分布（n重伯努利出现k次）

问题背景: n重伯努利实验，出现k次是。

抛一枚硬币n次，出现k次正面。
随机抽n个人，有k个人眼睛是绿色。

概率质量函数

$X \sim b(n, p) , p(k)=P(X=k)=\left(\begin{array}{l} n \ k \end{array}\right) p^{k}(1-p)^{n-k}, \quad k=0,1, \cdots, n$
期望: np
方差: np(1-p)

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包

# --------分布参数---------
p = 0.5 # 得到"是"的概率
n = 50 # 实验次数
# ------------------------

X = np.arange(0, n+1, 1)
p_list = stats.binom.pmf(X,n,p)

plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X, 0, p_list)
plt.xlabel('Random Variable: X, X(Experimental Result) = the num of Pos')
plt.ylabel('Probability')
plt.title('binom n:{};p:{}'.format(n,p))

泊松分布（二项分布的极限）

问题背景: 二项分布 n → + ∞ 的极限。

每天应该供应多少馒头。
每天一个路口出现事故的次数。
一定时间内，某放射性物质放射出的α粒子数目。

总之，满足泊松分布的事件有着三个特性。

平稳性: 在一段时间T内，事件发生的概率相同。
独立性: 事件的发生彼此独立，没有关联或关联很弱。
普通性: 将T划分为无限个小的 $\Delta T$ , 在每个ΔT内，事件发生多次的概率几乎为0.

概率质量函数: X∼P(λ)

$X \sim P(\lambda)$
$ p(X=k)=\frac{\lambda^{k}}{k!} e^{-\lambda}$
期望: λ
方差: λ

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包

# --------分布参数---------
lam = 5 # 每天卖的馒头均值
# -----------------------------
X = np.arange(0, 21, 1)
p_list = stats.poisson.pmf(X,lam)

plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X, 0, p_list)
plt.xticks(np.arange(0, 21, 1))
plt.xlabel('Random Variable: X, X(Experimental Result) = the num of things happen in time interval T')
plt.ylabel('Probability')
plt.title('poisson, lambda:{}'.format(lam))

几何分布（n重伯努利第k次首次出现）

问题背景: n重伯努利实验，第k次首次出现是。

每次表白成功概率p, 表白k次才成功概率。

概率质量函数

$p(k)=P(X=k)=(1-p)^{k-1} p, k=1,2, \cdots$
期望、方差：$E(X)=\frac{1}{p}, \operatorname{Var}(X)=\frac{1-p}{p^{2}}$

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
p = 0.5  # 每次得到"是"的概率
# -----------------------------
X = np.arange(0, 21, 1)
p_list = stats.geom.pmf(X,p)

plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X, 0, p_list)
plt.xticks(np.arange(0, 21, 1))
plt.xlabel('Random Variable: X, X(Experimental Result) = First happen in k')
plt.ylabel('Probability')
plt.title('geom, p:{}'.format(p))

超几何分布（二项分布+不放回）

问题背景: 不放回抽样的二次分布.

有N件产品，其中有M件不合格品，随机抽取n件产品，则其中含有m件不合格产品的概率为多少

概率质量函数:X∼h(n,N,M)

$X \sim h(n, N, M)$
$P(X=m)=\frac{\left(\begin{array}{l} M \ m \end{array}\right)\left(\begin{array}{l} N-M \ n-m \end{array}\right)}{\left(\begin{array}{l} N \n \end{array}\right)}, m=0,1, \cdots, r $
期望和方差：$E(X)=n \frac{M}{N}, \operatorname{Var}(X)=n \frac{M}{N}\left(1-\frac{M}{N}\right)\left(1-\frac{n-1}{N-1}\right)$

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
n = 10 # 抽n次
N = 50 # 总共N个产品
M = 20 # 有M个次品
# -----------------------------
X = np.arange(0, n+1, 1)
p_list = stats.hypergeom.pmf(X,N,M,n)
plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X, 0, p_list)
plt.xticks(np.arange(0, n+1, 1))
plt.xlabel('Random Variable: X, X(Experimental Result) = # of inferior product')
plt.ylabel('Probability')
plt.title('hypergeom, n:{};N:{};M:{}'.format(n,N,M))

负二项分布（n重伯努利成功k次）

问题背景: 几何分布的和

巴拿赫火柴盒问题

概率质量函数:

$X \sim N b(r, p) \ p(k)=P(X=k)=\left(\begin{array}{l} k-1 \ r-1 \end{array}\right) p^{r}(1-p)^{k-r}, k=r, r+1, \cdots$
期望、方差：$E(X)=\frac{r}{p}, \operatorname{Var}(X)=\frac{r(1-p)}{p^{2}}$

指数分布（泊松过程时间间隔）

指数分布是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程

问题背景: 泊松分布的间隔，连续的几何分布

灯泡的寿命
等待小卖部第一位客人上门的等待时间。

概率密度函数：X∼Exp(λ)

$X \sim Exp(\lambda)$
$p(x)=\left{\begin{array}{ll}\lambda e^{-\lambda x} & \lambda \geq 0 \ 0 & \text { else } \end{array}\right.$
期望和方差：$E(X)=\frac{1}{\lambda},Var(X)=\frac{1}{\lambda^2} $

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
lam = 5 # 每天来5个人
offset = 0 # 偏移量，从offset开始
# -----------------------------
X = np.arange(0, 20, 0.01)
p_list = stats.expon.pdf(X,0,1/lam)  # 内置函数是使用1/lam作为参数，即间隔(每天来的人之间的间隔时间)。
plt.plot(X, p_list, linestyle='None', marker='.')
plt.xlabel('Random Variable: X, X(Experimental Result) = the interval between two happen things')
plt.ylabel('Probability')
plt.title('norm, lam:{}'.format(lam))

贝塔分布

贝塔分布(Beta distribution)需要先明确一下先验概率、后验概率、似然函数以及共轭分布的概念。

先验概率就是事情尚未发生前，我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率，称为客观先验概率；当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。例如抛一枚硬币头向上的概率为0.5，这就是主观先验概率。
后验概率是指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。
先验概率和后验概率的区别：
- 先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；
- 后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料。
- 另外一种表述：先验概率是在缺乏某个事实的情况下描述一个变量；而后验概率（Probability of outcomes of an experiment after it has been performed and a certain event has occured.）是在考虑了一个事实之后的条件概率。
似然函数
共轭分布(conjugacy)：后验概率分布函数与先验概率分布函数具有相同形式;共轭先验就是先验分布是beta分布，而后验分布同样是beta分布

在试验数据比较少的情况下，直接用最大似然法估计二项分布的参数可能会出现过拟合的现象

比如，扔硬币三次都是正面，那么最大似然法预测以后的所有抛硬币结果都是正面

为了避免这种情况的发生，可以考虑引入先验概率分布来控制参数，防止出现过拟合现象。

贝塔分布作为先验概率

Beta分布描述的是定义在区间[0,1]上随机变量的概率分布，由两个参数和决定

Beta分布通俗讲解

beta分布可以看作一个概率的概率分布，当不知道事件的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。
现在有一个棒球运动员，希望能够预测他在这一赛季中的棒球击球率是多少。可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题，可以用一个二项分布表示（一系列成功或失败），一个最好的方法来表示这些经验（在统计中称为先验信息）就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。
将这些先验信息转换为beta分布的参数，一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，可以取α=81,β=219

之所以取这两个参数是因为：

beta分布的均值是α/α+β=81/(81+219)=0.27
$\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27$
从图中可以看到这个分布主要落在了(0.2,0.35)间，这是从经验中得出的合理的范围

有了先验信息后，现在考虑一个运动员只打一次球，那么他现在的数据就是”1中;1击”。这时候就可以更新分布了，让这个曲线做一些移动去适应新信息。

beta分布在数学上就提供了这一性质，他与二项分布是共轭先验的（Conjugate_prior）。
Beta(α0+hits,β0+misses)
$\mbox{Beta}(\alpha_0+\mbox{hits}, \beta_0+\mbox{misses}) $ 其中α0和β0是一开始的参数，在这里是81和219。
所以在这一例子里，α增加了1(击中了一次)。β没有增加(没有漏球)。分布其实没多大变化，这是因为只打了1次球并不能说明什么问题。但是如果得到了更多的数据，假设一共打了300次，其中击中了100次，200次没击中，那么这一新分布就是： beta(81+100,219+200)
$\mbox{beta}(81+100, 219+200)$
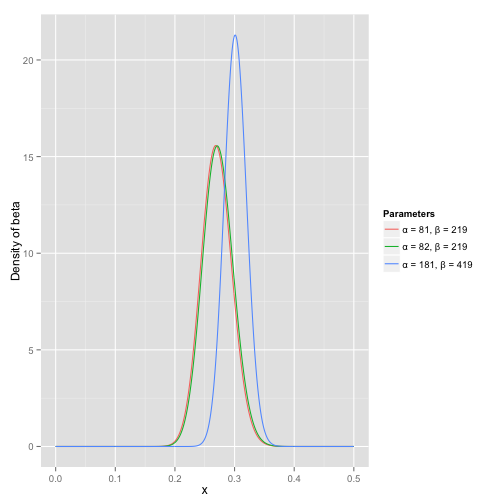
这个曲线变得更加尖，并且平移到了一个右边的位置，表示比平均水平要高

对于一个不知道概率是什么，而又有一些合理猜测时，beta分布能很好的作为一个表示概率的概率分布。

作者：链接

狄利克雷分布（多项分布共轭）

狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布，也就是它与多项分布具有相同形式的分布函数。

Dirichlet分布是关于定义在区间[0,1]上的多个随机变量的联合概率分布

Beta分布与Dirichlet分布的定义域均为[0,1]，在实际使用中，通常将两者作为概率的分布

Beta分布描述的是单变量分布
Dirichlet分布描述的是多变量分布

因此

Beta分布可作为二项分布的先验概率
Dirichlet分布可作为多项分布的先验概率

伽马分布（Gamma分布）

Gamma 函数是对阶乘在实数领域的扩展

据PRML第71页(2.14)式，Gamma函数在Beta分布和Dirichlet分布中起到了归一化的作用

伽马分布与卡方分布关系

一方面，自由度为n的卡方分布=自由度为n/2与1/2的伽马分布，即gamma(n/2,1/2)
另一方面，卡方分布只有一个参量，伽马分布有两个，从而卡方分布是伽马分布的一个特例

正态分布（二项分布另一种极限）

问题背景: 二项分布的另一种极限

人群中的身高分布。
考试中的分数分布。

总之，如果一个时间受很多因素影响。比如考试分数：受到智商、考试状态、任课老师水平等等因素影响，这些因素本身各有分布，由中心极限定理，这些分布加起来的分布就是正态分布。

概率密度函数: X∼N(u,σ^2)

$X \sim N(u, \sigma^2)$
$p(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-u)^{2}}{2 \sigma^{2}}}$
期望和方差：$E(X)=u, \operatorname{Var}(X)=\sigma^{2}$

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
mu = 160  # 均值
sigma = 5  # 方差
# -----------------------------
X = np.arange(150, 170, 0.1)
p_list = stats.norm.pdf(X,mu, sigma)
plt.plot(X, p_list, linestyle='None', marker='.')
plt.xlabel('Random Variable: X, X(Experimental Result) = The height of human')
plt.ylabel('Probability')
plt.title('norm, mu:{}; sigma:{}'.format(mu, sigma))

【2021-5-2】高中就开始学的正态分布，原来如此重要

机器学习的世界是以概率分布为中心的，而概率分布的核心是正态分布。正态分布也被称为高斯分布, 以天才卡尔·弗里德里希·高斯（Carl Friedrich Gauss）的名字命名的。简单的预测模型一般都是最常用的模型，因为易于解释，也易于理解。现在补充一点：正态分布因为简单而流行。

正态分布是一条倒钟形曲线，样本的平均值、众数以及中位数是相等

概率密度函数

示例，非常接近正态分布：人群的身高、成年人的血压、扩散后的粒子的位置、测量误差、人群的鞋码、员工回家所需时间。周围的大部分变量都呈置信度为 x% 的正态分布（x<100）

两个参数分别是：样本的平均值和标准差。

平均值——样本中所有点的平均值。
标准差——表示数据集与样本均值的偏离程度。分布的这一特性让统计人员省事不少，因此预测任何呈正态分布的变量准确率通常都很高。

为什么这么多变量近似正态分布？

大量随机变量上多次重复一个实验时，它们的分布总和将非常接近正态性（normality）—— 中心极限定理
把大量分布不同的随机变量加在一起，新变量最终也服从正态分布

分布转换

如果样本满足某个未知的分布，那么通过一系列操作，总是能变成正态分布。
相反，标准正态分布的叠加与转换，也一定能变化为任意未知分布。从标准正态转换到未知分布，就是很多机器学习模型希望做到的，不论是视觉中的 VAE 或 GAN，还是其它领域的模型。

但对于传统统计学，更希望将特征的分布转换成正态分布，因为正态分布简单又好算呀

转换为标准正态

线性变换
- x 可能服从某个未知分布，但是归一化后的 Z 是服从正态分布
Box-cox 变换: 用 Python 的 SciPy 包将数据转换成正态分布
- scipy.stats.boxcox(x, lmbda=None, alpha=None)
YEO-JOHBSON 变换
- Python 的 sci-kit learn 提供了合适的函数：
- sklearn.preprocessing.PowerTransformer(method=’yeo-johnson’, standardize=True, copy=True)

注意：

没有做任何分析的情况下不能轻易假设变量服从正态分布，以泊松分布（Poisson distribution）、t 分布（student-t 分布）或二项分布（Binomial distribution）的样本为例，如果错误地假设变量服从正态分布可能会得到错误的结果。

【2021-6-14】正态分布：核心的概率分布

常见的概率分布有泊松分布，二项分布，伯努利分布，正态分布，均匀分布。其中正态分布是最为核心的概率分布。

一、认识正态分布

正态分布，也称“常态分布”，又名高斯分布，正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

正态分布函数公式如下：

其中μ为均数，σ为标准差。μ决定了正态分布的位置，与μ越近，被取到的概率就越大，反之越小。σ描述的是正态分布的离散程度。σ越大，数据分布越分散曲线越扁平；σ越小，数据分布越集中曲线越陡峭。在一个标准正态分布中，约有 68.2% 的点落在 ±1 个标准差的范围内。约有 95.5% 的点落在 ±2 个标准差的范围内。约有 99.7% 的点落在 ±3 个标准差的范围内。

正态分布概念是由法国数学家棣莫弗于1733年首次提出的，后由德国数学家高斯率先将其应用于天文学研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，所以有了“高斯分布”的美称。

在我们的自然界，大多数物种的高度和重量都满足正态分布，它们围绕着均值对称分布，而且不会包含特别大或特别小的事件.

例如：我们从来没有遇到过1米长的蚂蚁，也没有看到过1千克重的大象。世界似乎被代表正态分布的“钟形”包围着，很多事物都是服从正态分布的：人的高度、胖瘦、寿命、雪花的尺寸、测量误差、灯泡的寿命、IQ分数、面包的分量、学生的考试分数，员工上班所需时间等等。

正态分布有以下几个特征：

集中性：曲线的最高峰位于正中央，且位置为均数所在的位置。
对称性：正态分布曲线以均数所在的位置为中心左右对称且曲线两端无线趋近于横轴。
均匀变动性：正态分布曲线以均数所在的位置为中心均匀向左右两侧下降。
面积恒等：曲线与横轴间的面积总等于1。

正态分布有两个非常重要的参数，它们分别是：样本的均值和标准差。均值是样本中所有点的平均值。均值定义了正态分布的峰值位置，大多数值都集中在均值周围。标准差是表示数据集与样本均值的偏离程度。标准差定义了正态分布的宽度，决定了观察值与均值的偏离程度。标准差越小，正态分布曲线越窄。标准差越大，正态分布曲线越宽。当分布较窄时，值落在均值附近的概率会更高。

正态分布的解释力非常强，因为分布的均值、众数和中位数是相等的；我们只要用平均值和标准差就可以解释整个分布。

就数学理论而言，正态分布有其优越性：

①两个正态分布的乘积仍然是正态分布；
②两个正态分布的和是正态分布；
③正态分布的傅里叶变换仍然是正态分布。

二、正态分布产生的原因

钟形分布曲线无处不在，这是为什么呢？其奥秘来自于中心极限定理。

中心极限定理：只要各随机变量是相互独立的，每个随机变量的方差都是有限的，且没有任何一小部分随机变量贡献了大部分变差，那N≥20个随机变量的和就近似一个正态分布。

中心极限定理告诉我们：

任何一个样本的平均值将会约等于其所在总体的平均值。

不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的平均值周围，并且呈正态分布。

案例1：在一个500人的小城镇中，人们的购买行为数据显示，每个人平均每个星期花费100美元。在这些人中，可能有些人这个星期只花50美元、下个星期则花150美元，另一部分人可能每3个星期花费300美元。而其他人则可能每个星期的花费在20至180美元之间。只要每个人的支出都只有有限的变差并且没有任何一小部分人贡献了大部分变差，那么分布的总和必定是一个正态分布，其均值为50000美元。每个星期的总支出也将是对称的：可能高于55000美元，也可能低于45000美元。
案例2：中心极限定理来解释人类身高的正态分布。一个人的身高取决于基因、环境以及两者之间的相互作用。基因的贡献率可能高达80%，因此不妨假设身高只取决于基因。研究表明，至少180个基因有助于人体长高。

例如，一个基因可能有助于长出较长的颈部或头部，另一个基因可能有助于长出更长的胫骨。虽然基因之间存在相互作用，但我们可以假设在“长高”这件事情上，每个基因都是相互独立的。如果身高等于180个基因贡献的总和，那么身高将呈现正态分布。

高尔顿钉板试验更加形象地证明了正态分布。弗朗西斯•高尔顿是英国著名的统计学家、心理学家和遗传学家。他设计了一个钉板实验，希望从统计的观点来解释遗传现象。

如下图所示，木板上钉了数排（n排）等距排列的钉子，下一排的每个钉子恰好在上一排两个相邻钉子之间；从入口处放入若干直径略小于钉子间距的小球，小球在下落的过程中碰到任何钉子后，都将以1/2的概率滚向左边，以1/2的概率滚向右边，碰到下一排钉子时又是这样。如此继续下去，直到滚到地板的格子里为止。试验表明，只要小球足够多，它们在底板堆成的形状将近似于正态分布。因此，高尔顿钉板实验直观地验证了中心极限定理。

中心定理并不是万能的，他拥有三个很重要的前提：随机、独立和相加。

首先，第一个前提就是取样需要随机。如果我们抽取人的时候，只抽取长的高的或者只抽取长得矮的人，那么结果自然不符合正态分布。
第二，影响结果的因素是相互独立或者是相互影响比较小的。以身高为例，影响一个人长高的因素有很多，例如：父母长得高还是矮、营养是否跟得上、是否热爱运动……等等。父母长得高还是矮，对营养的补充没有很大的关系，跟是否热爱运动也没有关系，所以可以看成是相互独立的因素，所以身高的人群分布曲线自然就符合正态分布。
第三是相加，如果一个事物受到多种因素的影响，不管每个因素本身是什么分布，它们加总后，结果的平均值就是正态分布。正态分布只适合各种因素累加的情况，如果这些因素不是彼此独立的，会互相加强影响，那么就不是正态分布了。如果各种因素对结果的影响不是相加，而是相乘，那么最终结果就变成了对数正态分布。

在一定条件下，各种随意形状概率分布生成的随机变量，它们加在一起的总效应，是符合正态分布的。中心极限定理告诉我们：无论引起过程的各种效应的基本分布是什么样的，当实验次数n充分大时，所有这些随机分量之和近似是一个正态分布的随机变量。

中心极限定理从理论上证明了，在一定的条件下，对于大量独立随机变量来说，只要每个随机变量在总和中所占比重很小，那么不论其中各个随机变量的分布函数是什么形状，也不论它们是已知还是未知，当独立随机变量的个数充分大时，它们的和的分布函数都可以用正态分布来近似。这就是为什么实际中遇到的随机变量，很多都服从正态分布的原因，这使得正态分布既成为统计理论的重要基础，又是实际应用的强大工具。中心极限定理和正态分布在概率论、数理统计、误差分析中占有极其重要的地位。

三、正态分布的应用场景

1、检验显著性

我们可以利用正态分布的规律来检验各种平均值的显著性差异。显著性检验就是事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设（备择假设）是否合理，即判断总体的真实情况与原假设是否有显著性差异。其原理就是“小概率事件实际不可能性原理”来接受或否定假设。如果经验均值与假设均值之间的偏差了超过两个标准差，那么社会科学家就会拒绝这两种均值相同的假设。

例如：现在提出这样一个假设，即旧金山的通勤时间与洛杉矶的通勤时间相同。假设数据表明，旧金山的通勤时间平均为33分钟，而洛杉矶为34分钟。如果这两个数据集的均值标准差都是1分钟，那么我们就不能拒绝旧金山和洛杉矶两地通勤时间相同的假设。虽然二者的均值不同，但只存在1个标准差。如果洛杉矶的平均通勤时间为37分钟，那么我们就会拒绝这个假设，因为均值之间相差4个标准偏差。

2、六西格玛方法

六西格玛方法是摩托罗拉公司于20世纪80年代中期提出的，目的是减少误差，该方法根据正态分布对产品属性进行建模。试想这个例子：一家企业专业生产制造门把手所用的螺栓。它生产的螺栓必须天衣无缝地与其他制造商生产的旋钮组装在一起。规格要求是螺栓直径为14毫米，但是任何直径介于13毫米与15毫米之间的螺栓也可以接受。如果螺栓的直径呈正态分布，均值为14毫米，标准差为0.5毫米，那么任何超过两个标准差的螺栓都是不合格的。

两个标准差事件发生的概率为5%，这个概率对于一家制造企业来说太高了。六个西格玛要求每一百万个机会中有3.4个出错的机会，即合格率是99.99966％。企业可以根据中心极限定理，从整体中抽样几百个，并根据这样一个样本来估计均值和标准差。然后推断出正态分布。这样一来，这家螺栓制造企业就可以得出一个基准标准差，然后花大力气去降低它。

3、对数正态分布

中心极限定理要求我们对随机变量求和或求平均值，以获得正态分布。如果随机变量是不可相加而是以某种方式相互作用的，或者如果它们不是相互独立的，那么产生的分布就不一定是正态分布。例如，独立随机变量之间的乘积就不是正态分布，而是对数正态分布。对数正态分布缺乏对称性，因为大于1的数字乘积的增长速度比它们的和的增长速度快，比如，4+4+4+4=16，但4×4×4×4=256；而小于1的数字的乘积则比它们的和小，比如，1/4+1/4+1/4+1/4=1，但1/4*1/4*1/4*1/4=1/256。如果将20个不均匀地分布在0到10之间的随机变量相乘，那么多次相乘后所得到的乘积将会包括一些很接近于零的结果与一些相当大的结果，从而生成如下图所示的对数正态分布。

对数正态分布

一个对数正态分布的尾部长度取决于随机变量相乘的方差。如果它们的方差很小，尾巴就会很短，如果方差很大，尾巴就可能会很长。如前所述，将一组很大的数相乘会产生一个非常大的数字。在各种各样的情况下都会出现对数正态分布，包括新冠肺炎的传染人数、大多数国家的收入分布也近似于对数正态分布。

一个简单的模型可以解释为什么收入分布更接近于对数正态分布而不是正态分布。这个模型将与工资增长有关的政策与这些政策所隐含的分布联系起来。大多数企业和机构都按某种百分比来分配加薪，表现高于平均水平的人能够得到更高百分比的加薪，表现低于平均水平的人则只能得到更低百分比的加薪。与这种加薪方法相反，企业和机构也可以按绝对金额来分配加薪。例如普通员工可以获得1000美元的加薪，表现更好的人可以获得更多，而表现更差的人则只能获得更少。

百分比加薪方法与绝对金额加薪方法两者之间的区别乍一看似乎只是语义上的区别，但其实不然。如果每一年的绩效都是相互独立且随机的，那么根据员工绩效按百分比加薪，就会产生一个对数正态分布。即使后来的表现相同，未来几年的收入差距也会加剧。

假设一名员工因过去几年表现良好，收入水平达到了80000美元，而另一名员工则只达到了60000美元。在这种情况下，当这两名员工的表现同样出色并都可以获得5%的加薪时，前者能够获得4000美元的加薪，后者却只能得到3000美元的加薪。这就是说，尽管绩效完全相同，不平等也会导致更大的不平等。如果企业按绝对数额分配加薪，那么两名绩效相同的员工将获得相同的加薪，由此产生的收入分布将接近正态分布。

总结

正态分布启示我们，要用整体的观点来看事物。用整体来看事物才能看清楚事物的本来面貌，才能得出事物的根本特性。不能只见树木不见森林，也不能以偏概全。同时正态分布曲线及面积分布图告诉我们一定要抓住重点，因为重点就是事物的主要矛盾，它对事物的发展起主要的、支配性的作用。正态分布是科学的世界观，也是科学的方法论，是我们认识和改造世界的最重要和最根本的工具之一，对我们的理论和实践有重要的指导意义。

正态分布如此重要，不仅因为它在自然界普遍存在，还因为它是被证明的、其他复杂概率分布的演化结果，可以说是所有概率分布的最终宿命。根据“熵增”原理，一个孤立系统的熵总是在不断增大。而对一个已知均值和方差的分布，正态分布的熵值最大，即这个孤立系统中的所有结果持续演化，最终一定是呈正态分布的稳定状态。对于宇宙熵增的最终稳定态，是宇宙各部分能量达到平衡，失去活力，陷入热寂。

对数正态分布

对数正态分布：Log-normal distribution

在自然界有很多事物有增长速度很慢，甚至可以忽略不计（small percentage changes），但是其效果是对整个事物的影响，即每次增长都是对前面增长的乘积运算，但如果把他放入对数域，则可以放大他们的增长效果。

学生氏分布

司徒顿t分布（Student’s t-distribution），简称 t分布，在概率论及统计学中用于根据小样本来估计总体呈正态分布且标准差未知的期望值。

若总体标准差已知，或是样本数足够大时（依据中心极限定理渐进正态分布），则应使用正态分布来进行估计。其为对两个样本期望值差异进行显著性测试的学生t检验之基础。

学生t 检验改进了Z检验（Z-test），因为在小样本中，Z检验以总体标准差已知为前提，Z检验用在小样本会产生很大的误差，因此必须改用学生t 检验以求准确。但若在样本数足够大（普遍认为超过30个即足够）时，可依据中心极限定理近似正态分布，以Z检验来求得近似值，

在总体标准差数未知的情况下，不论样本数量大或小皆可应用t检验。在待比较的数据有三组以上时，因为误差无法被压低，此时可以用方差分析（ANOVA）代替t检验

韦布尔分布

即韦伯分布（Weibull distribution），又称韦氏分布或威布尔分布，是可靠性分析和寿命检验的理论基础。

威布尔分布在可靠性工程中被广泛应用，尤其适用于机电类产品的磨损累计失效的分布形式。由于它可以利用概率值很容易地推断出它的分布参数，被广泛应用于各种寿命试验的数据处理。

Weibull Distribution是连续性的概率分布

$f(x ; \lambda, k)=\left{\begin{array}{ll} \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1} e^{-(x / \lambda)^{k}} & x \geq 0 \ 0 & x<0 \end{array}\right.$
x是随机变量，λ>0是比例参数（scale parameter），k>0是形状参数（shape parameter）
韦布尔分布的累积分布函数是扩展的指数分布函数
Weibull distribution与很多分布都有关系。
- k=1，它是指数分布；
- k=2，是Rayleigh distribution（瑞利分布）。

幂律分布

【2021-6-13】幂律分布一强者恒强、弱者愈弱

为什么在经济系统中会出现强者恒强，弱者愈弱的现象？社会中会出现了富者越富，穷者越穷的现象呢？按照马克思的理论解释，可能是因为资本主义的缺陷造成的。其实背后隐藏着一个巨大的数学定律“幂次法则”。

Peter Thiel《从0到1》一书中写到：“幂次法则是宇宙的力量，是宇宙最强大的力量。它完整定义了我们周围的环境，而我们几乎毫无察觉。”
《新约.马太福音》一书中提到：“凡是少的，就连他所有的，也要夺过来。凡是多的，还要给他，叫他多多益善。” 这就是著名的马太效应。
概率论给我们的启示是：“凡是相信大数定律的，凡是相信热力学第一定律的，就不要去赌博，不要去炒股，不要去买彩票，不要去进行任何投机，而应该去开赌场。”

什么是幂律分布？

在统计学中，幂律power law表示的是两个量之间的函数关系，其中一个量的相对变化会导致另一个量的相应幂次比例的变化，且与初值无关：表现为一个量是另一个量的幂次方。例如，正方形面积与边长的关系，如果长度扩大到两倍，那么面积扩大到四倍。

幂函数：y=x^a（a为有理数）
指数函数：y=a^x（a为常数且以a>0，a≠1）
幂律分布：是一种概率分布，假设变量x服从参数为α的幂律分布，则其概率密度函数可以表示为：概率密度函数为f(x)=cx^-a-1(x→∞）

有哪些幂律分布

常见的幂律分布有齐普夫定律、二八法则、长尾效应、马太效应等

齐普夫定律

1932年哈佛大学的语言学专家齐夫（Zipf）在研究英文单词出现的频率时，发现如果把单词出现的频率按由大到小的顺序排列，则每个单词出现的频率与它的名次的常数次幂存在简单的反比关系，这种分布就称为齐夫定律，即对于指数为2的幂律分布（a=2），事件的等级排列序号乘以它的大小等于常数，也就是事件等级×事件大小=常数。

各种语言中，只有极少数的词被经常使用，而绝大多数词很少被使用。2016年，江南大学的研究者以诺贝尔文学奖得主莫言的《红高粱》《蛙》和《透明的红萝卜》为主要研究对象，采用字频统计软件和汉语词频统计软件，统计莫言作品中字频、词频，发现都能满足齐普夫定律。所得结果与包括英语、西班牙语、法语等在内的多种语言研究结果一致。

二八法则

19世纪意大利经济学家帕雷托（VilfredoPareto）研究了个人收入的统计分布，发现少数人的收入要远多于大多数人的收入，提出了著名的80/20法则，即20%的人口占据了80%的社会财富。

长尾理论

克里斯·安德森（Chris Aderson）的“长尾理论”即是幂律的口语化表达。安德森系统研究了亚马逊、狂想曲公司、Blog、Google、eBay、Netflix等互联网零售商的销售数据，并与沃尔玛等传统零售商的销售数据进行了对比，观察到一种符合统计规律（大数定律）的现象。这种现象恰如以数量、品种二维坐标上的一条需求曲线，拖着长长的尾巴，向代表“品种”的横轴尽头延伸，长尾由此得名。

马太效应

马太效应是社会学家和经济学家们常用的术语，它反映着富者更富、穷者更穷，一种两极分化的社会现象。1968年，美国科学史研究者罗伯特·莫顿（Robert K. Merton）提出这个术语用以概括一种社会心理现象：“相对于那些不知名的研究者，声名显赫的科学家通常得到更多的声望；也就是任何个体、群体或地区，在某一个方面（如金钱、名誉、地位等）获得成功和进步，就会产生一种积累优势，就会有更多的机会取得更大的成功和进步。”此术语后为经济学界所借用，反映赢家通吃的经济学中收入分配不公的现象。

统计物理学家习惯把服从幂律分布的现象称为无标度现象，即系统中个体的尺度相差悬殊，缺乏一个优选的规模。凡有生命、有进化、有竞争的地方都会出现不同程度的无标度现象。

假设检验

详见另一篇文章：在线实验里的假设检验部分

说人话的统计学合辑

优质文章：说人话的统计学合辑

第1章高屋建瓴看统计

第2章算术平均数与正态分布

第3章 t检验：两组平均数的比较

第4章方差分析(ANOVA)：多组平均数的比较

第5章线性回归：统计建模初步

第6章广义线性模型：统计建模进阶

应用

三门问题

【2024-1-25】三门问题：专家都答错的三门问题

蒙提霍尔问题/三门问题（Monty Hall problem）, 知乎问答

某个电视节目比赛环节中，参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。参赛者选定了一扇门，但未开启它，随后节目主持人蒙提霍尔（Monty Hall）开启了剩下的两扇门中的一扇并且发现后面是一只山羊，此时主持人会给予选手重新选择的机会。问题是：此时参赛者换另一扇门会否增加赢得汽车的机率？

第一次选中的概率只有1/3，选错的概率是2/3，只要第一次选错了，换了就必中，只有第一次选对了，换才会不中，所以换会提高中奖几率

赌博

【2023-7-3】为什么逢赌必输？

赌王何鸿燊接手葡京赌场时，业务蒸蒸日上，但理性的赌王仍然忐忑，请教「赌圣」叶汉 ：

「如果这些赌客总是输，长此以往，他们不来了怎么办？」

叶汉笑道：「一次赌徒，一世赌徒，他们担心的是赌场不在怎么办。」

叶汉说的只是心理层面，现代赌场程序方面的设计，比叶汉当年要缜密得多，赌场集中了概率学、统计学的数学知识。

一个痴迷于发财梦的赌徒永远不明白

与自己对赌的不是运气，也不是庄家，而是狄利克雷、伯努利、高斯、纳什、凯利这样的数学大师。

一个普通赌徒，只要一直赌下去，一定血本无归…

不是逢赌必输，而是久赌必输。

赌场所有游戏项目都是基于反复论证的数学定理和巧妙设计的数学模型。赌客参与的任何游戏项目的获利期望值一定为负数。这个期望值也被称为“庄家优势”（house edge）。

庄家优势就是赌场能从每局游戏中1元赌资赚取的利润的期望值。

正因为这个庄家优势的存在，正规的赌场获利并不需要靠坑蒙拐骗，只靠规则和量化风险控制，和源源不断的赌客，以及人性的缺点就可以站在不败之地，不断盈利。

而相应的，对赌客来说则是久赌必输。

赌博看得到的是概率，看不到的是陷阱

数学家伯努利提出大数定律：

假设 n 是 N 次独立重复试验中事件 A 发生的次数，p 是每一次试验中 A 发生的概率，那么，当 N 趋于无穷时，$\lim_{N \rightarrow \infty} \frac{n}{N}=p$

大量重复的随机现象里其实藏着某种必然规律。

以掷硬币为例，当投掷次数足够大时，出现正（反）面的频率将逐渐接近于 1/2，且随着投掷次数的增加，偏差会越来越小

你以为的公平：

一枚硬币，一正一反，各50％概率，根据大数定律（大量重复随机现象隐藏的规律），50％是必然规律…

然而，这种想法误解了大数定律，陷入了赌徒谬论：大数定律要求的”大量”是多少？无穷大，现实案例中，往往远远未达到“足够多”的标准，就已经输得精光…

误解大数定律：

① 大数定律当”小数定律”，觉得游戏是无条件公平. 输赢50％本身有误导性：
- 抛硬币前代表可能性
- 抛硬币后，代表统计结果的平均值，而不是实际分布…
② 赌徒谬论，随机并不意味着均匀
- 如果过去不均匀，人们心理上会觉得以后会补回来，即：输了一把下一把赢的概率更大，这种赢回来的强烈错觉就是赌徒谬论…
- 实际上，上一把和下一把没有任何关联，错把独立事件变相关事件，大数定律不是为了平衡对抗

只要进了赌场，你就成了穷鬼…

赌徒破产困境，公平赌博中，任何一个拥有有限成本的赌徒，只要一直赌下去，一定会输个精光，庄家抽成2％
小小的2％，最后却让你输得倾家荡产、家破人亡。

这2个点赢的概率貌似不起眼，但配上“大数法则”，就成为了赌场赚钱的利器！

庄家赚的钱最终只跟玩家下注大小有关, 即“流水”，只要玩家不停地玩，庄家就会不停地赚。而不管玩家是输是赢，庄家始终是赢的。
为什么赌场有“最小投注额”，因为扩大“流水”才能将利润最大化，所以别以为自己有多聪明，你要庆幸自己玩得不够久而已，十赌九输正源于此。

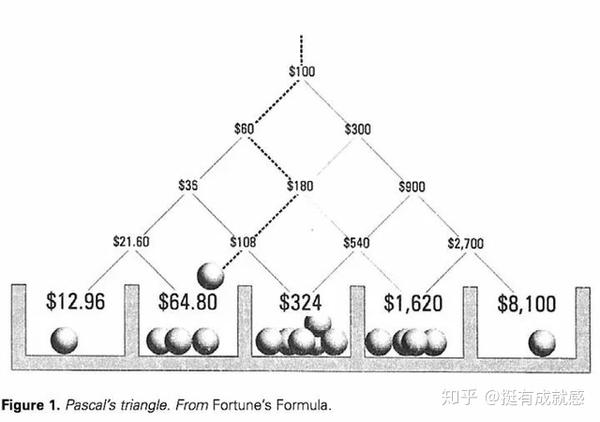
“无限财富”和“赌徒输光定律”

这个定理有许多应用，如：“姓氏消亡”、“线粒体夏娃假说”
在概率均等的情况下，谁的资本大，谁的赢率高。

分析：你和我对赌

你我各有5块钱，输光为止。那么你赢的概率是50%，输的概率也是50%。
你有5块钱，我有10块钱，输光为止，那么你赢的概率就只有33.3%，而输的概率有66.7%
- 这里涉及到高斯的概率论和泰勒的级数论，后面隐藏的就是赌场大BOSS凯利公式

对于小散户，赌场一般可以认为财富是无限多的，你赢不垮它，它却能吃了你。在赌场老板的眼里，世界只有两种人：一种现在是穷鬼，一种未来是穷鬼。

“无限财富定律”也解释了赌场设置最大投注额原因。

不是老板好心保护赌徒免遭破产，只是老板为了保护自己设置的安全屏障，想象下万一哪天比尔盖茨去赌场找乐子，一次性砸个几百亿进去，那赌场老板真的要哭了，虽然这种事情不太可能发生，但也不能不防，所以赌场根据自己的财富能力设计最高投注额，也就是为了抵抗“无限财富定理”！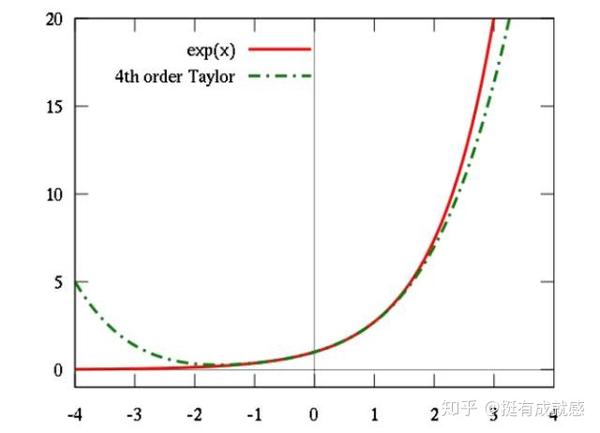

2赔1的赌局

扔硬币下注，硬币为正面则得2元，如果为反面则输掉1元
总资产为100元，每一次的押注都可投入任意金额。

决策

冒险主义者：要玩就玩票大的，一次性把100元全压上，幸运的话，一次正面就可以获得200元，又是一段值得炫耀的赌史；可是，如果输了得把100元资产拱手献给对方，你就一无所有，好不容易来趟拉斯维加斯，这肯定不是明策。
保守主义者：谨慎点，百分之一慢慢来。每次只下注1元，正面赢2元，反面输1元。玩了20把突然觉得，对方下注10元一次就赢得20元，自己一次才赢2元、10次才能赢得20元，后悔已经错过几个亿！

100太多1块太少，该投入多少比例下注？普通赌徒看似无解，但凯利公式告诉你答案是25%！

凯利公式：f* =（bp-q）/ b

各参数意义为：

f* = 应投注的资本比值
p = 获胜的概率（也就是抛硬币正面的概率）
q = 失败的概率，即1 - p（也就是硬币反面的概率）
ｂ = 赔率，等于期望盈利 ÷可能亏损（也就是盈亏比）
分子 bp-q 代表“赢面”，数学中叫“期望值”。

什么才是不多不少的合适赌注呢？凯利告诉我们要通过选择最佳投注比例，才能长期获得最高盈利。

回到前面提到的例子中，硬币抛出正反面的概率都是50%，所以p、q获胜失败的概率都为0.5，而赔率＝期望盈利÷可能亏损=2元盈利÷1元亏损，赔率就是2，要求的答案是f， (bp - q) ÷ b = (2 * 50% - 50%) ÷ 2 = 25%。

拿出资金的25%来进行下注，才能使赌局收益最大化

凯利公式不是凭空设想出来的，这个数学模型已经在华尔街得到验证，除了在赌场被奉为正神，也被称为“资金管理神器”，是比尔格罗斯等投资大佬的心头之爱，巴菲特依靠这个公式也赚了不少银子。

3条准则。

1、期望值（bp-q）为0时，赌局为公平游戏，这时不应下任何赌注。
2、期望值（bp-q）为负时，赌徒不具备任何优势，也不应下任何赌注。
3、期望值（bp-q）为正时，这时按照凯利公式投注赚钱最快，风险最小。

最终结论只有一个：除了100%赢，任何时候都不应下全部赌注，即使赢的概率高达99.9%。

除了100%赢，任何时候都不应下注

所有的赌场游戏，几乎都是对赌徒不公平的游戏。
这种不公平并非是庄家出老千，现代赌场光明正大地依靠数学规则赚取利润，从某种意义上来讲，赌场是最透明公开的场所，如果不是这样，进出赌场不知有多少狂命之徒，何鸿燊早怕九条命都不够。
凯利公式期望值(bp-q)为负时，赌徒不具备任何优势，也不应下任何赌注。这种赌博游戏，要下负赌注，也就是不如自己开个赌场当庄家。

世界上有为数不多的“赌神”，当中有信息论的发明者香农，数学家爱德华·索普，路径理论的创始人蒙特卡罗等，他们通过一系列复杂的计算和艰深的数学理论，把某些赌戏的赢率扳回到50％以上，例如21点靠强大的心算能力可以把概率拉上去。

赢得胜利的唯一法则：不赌

没有谁能说服一个堕落的赌徒，因为这是人格的缺陷。

你怎么可能赢得了庄家？

论理性，没有人能比赌场老板更理性。
论数学，没有人能比赌场老板请的专家更精通数学。
论赌本，没有人能比赌场老板的本钱更多。

如果你想真正赢得这场赌局，法则只有一个：不赌。

作者：挺有成就感

数学基础：概率统计 - Probability and statistics

概率统计

科普

机器学习中的概率模型

有监督学习

无监督学习

数据生成

强化学习

统计学核心

概念

概率 vs 统计

概率学派

总结

频率 vs 贝叶斯

频率学派

贝叶斯学派

参数估计

概率统计量

图解概率统计量

样本量多少才有统计意义？

随机抽样

样本数计算

置信区间的计算

定律

大数定律

中心极限定理

概率分布

概率分布概览

概率分布总结

图解概率分布演进

均匀分布

伯努利分布

二项分布（n重伯努利出现k次）

泊松分布（二项分布的极限）

几何分布（n重伯努利第k次首次出现）

超几何分布（二项分布+不放回）

负二项分布（n重伯努利成功k次）

指数分布（泊松过程时间间隔）

贝塔分布

Beta分布通俗讲解

狄利克雷分布（多项分布共轭）

伽马分布（Gamma分布）

正态分布（二项分布另一种极限）

一、认识正态分布

二、正态分布产生的原因

三、正态分布的应用场景

总结

对数正态分布

学生氏分布

韦布尔分布

幂律分布

什么是幂律分布？

有哪些幂律分布

齐普夫定律

二八法则

长尾理论

马太效应

假设检验

说人话的统计学合辑

第1章 高屋建瓴看统计

第2章 算术平均数与正态分布

第3章 t检验：两组平均数的比较

第4章 方差分析(ANOVA)：多组平均数的比较

第5章 线性回归：统计建模初步

第6章 广义线性模型：统计建模进阶

应用

三门问题

赌博

结束

Share

Related Posts

站内可视化导航

Comments

第1章高屋建瓴看统计

第2章算术平均数与正态分布

第4章方差分析(ANOVA)：多组平均数的比较

第5章线性回归：统计建模初步

第6章广义线性模型：统计建模进阶