信息论
介绍
克劳德·艾尔伍德·香农(英语:Claude Elwood Shannon,1916年4月30日-2001年2月26日),美国数学家、电子工程师和密码学家,被誉为信息论的创始人。香农是密歇根大学学士,麻省理工学院博士。1948年,香农发表了划时代的论文——通信的数学原理,奠定了现代信息论的基础。
基本知识
摘自:信息论基础
基本思想:
- 一件不太可能的事情发生, 要比一件非常可能的事情发生提供更多信息
性质:
- 非常可能发生的事情信息量较少
- 极端情况下,一定能够发生的事件应该没有信息量
- 比较不可能发生的事件具有更大的信息量
- 独立事件应具有增量信息。
- 例如,投掷的硬币两次正面朝上传递的信息量,应该是投掷一次硬币正面朝上的信息量的两倍。
熵
概率
信息量:概率分布能带来的信息,对应神经网络的一个神经元。香农熵:概率系统的混乱程度,对应神经网络。KL散度/交叉熵:两个概率系统的相对混乱程度,对应人脑和人工神经网络(深度学习网络)。
使用香农信息论的交叉熵,可以完美度量人脑和人工神经网络的混乱/相似程度,从而构造一个完美的损失函数。
熵变与焓变
【2022-8-25】熵、熵变、焓、焓变
化学反应的进行有两种:一种是自发进行的,一种是需要外加条件帮助它,(比如说加热,电解等)给他提供能量他才能进行. 但是无论哪种反应,在他反应的历程中,都存在着两个我们肉眼看不到的线索,就是焓变和熵变。
什么是熵、熵变?
- 熵是一个用来衡量系统混乱程度的物理学概念。
- 一个系统越混乱,熵越大;反之,一个系统越有序,熵越小。
- 熵是指物质内部的混乱度。
- 根据熵增定律,在一个封闭的系统中,熵只会增加(或不变),但不会减少。
- 在没人帮你打扫房间的情况下,房间只会越来越乱,不会自动变得整洁有序。
- 如果想要系统变得有序,就必须有能量从外部输入进来。否则,系统必将变得混乱无序,直至消亡。
- 在自然界中,发生的自发过程,一般都是朝着混乱度增大的方向进行。
- 混乱度越大,熵越大。
- 同种物质下,固态的熵值<液态<气态。
- 温度越高,熵值越大。绝对零度时,完整晶体的纯物质,熵值为零。
什么是熵变?
- 熵变是生成物蕴含的混乱度与反应物蕴含的混乱度之差。
- 化学反应的熵变,只取决于反应系统的始态和终态,与系统状态变化的途径无关。
什么是焓、焓变?
- 焓,在热力学中,表征物质系统能量的一个重要状态参量。
- 焓,指的是物质内部蕴含的能量。
- 焓变指的就是生成物的蕴含的能量与反应物蕴含的焓能量之差。
- 物质总是趋向于放出能量,变成更加稳定的结构
- 焓变,系统所吸收或释放的热量。
- 熵增焓减,反应自发;
- 熵减焓增,反应逆向自发;
- 熵增焓增,高温反应自发;
- 熵减焓减,低温反应自发。
熵的起源
【2022-8-26】熵是对系统中混沌状态的一种度量。 因为它比准确性/均方误差之类度量标准更具动态性,所以使用熵来优化从决策树到深度神经网络的算法已显示出可以提高速度和性能。
熵源于物理学-它是系统中无序或不可预测性的量度。
- 一个盒子里两种气体:一开始,系统的熵很低,因为这两种气体是完全可分离的。 但是,一段时间后,气体混合在一起,系统的熵增加。 有人说,在一个孤立的系统中,熵永远不会减小,没有外力,混沌就不会减弱。
熵的性质
- Shannon提出了熵的概念。熵是一个随机变量不确定性的度量
信息论之父克劳德·香农给出的信息熵的三个性质:
- 单调性,发生概率越高的事件,其携带的信息量越低;
- 非负性,信息熵可以看作为一种广度量,非负性是一种合理的必然;
- 累加性,即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和,这也是广度量的一种体现。
机器学习中的熵
【2022-8-25】理解熵:机器学习的黄金标准
适用于数据科学的大多数情况都介于天文学的高熵和极低熵之间。
- 高熵意味着低信息增益,而低熵意味着高信息增益。
- 可以将信息获取视为系统中的纯净性:系统中可用的纯净知识量。
决策树使用熵:为了尽可能有效地将一系列条件下的输入定向到正确的结果,将熵较低(信息增益较高)的特征拆分(条件)放在树上较高位置。
决策树计算特征的熵并对其进行排列,以使模型的总熵最小(并使信息增益最大)。 从数学上讲,这意味着将最低熵条件放在顶部,以便它可以帮助降低其下方的拆分节点的熵。
决策树训练中使用的信息增益和相对熵定义为两个概率质量分布p(x)和q(x)之间的”距离”,也称为 Kullback-Leibler(KL)散度或Earth Mover距离,用于训练对抗性网络以评估生成的图像与原始数据集中的图像相比的性能。img
像Kullback-Lieber发散(KLD)一样,交叉熵也处理两个分布p和q之间的关系,分别表示真实分布p和近似分布q。 但是,KLD衡量两个分布之间的相对熵,而交叉熵衡量两个分布之间的”总熵“。
度量定义为使用模型分布q对来自分布p的源的数据进行编码所需的平均位数。
- 如果考虑目标分布p和近似值q,希望减少使用q而不是p表示事件所需的位数。
- 另一方面,
相对熵(KLD)衡量从分布q中的p表示事件所需的额外位数。
交叉熵似乎是衡量模型性能的一种回旋方式,但是有几个优点:
- 基于准确性/错误的指标存在多个问题,包括对训练数据顺序的极端敏感性,不考虑置信度,并且对可能导致错误结果的各种数据属性缺乏鲁棒性。 它们是非常粗略的绩效指标(至少在培训期间)。
- 交叉熵可以衡量信息内容,因此比简单强调所有复选框的度量标准更具动态性和可靠性。 预测和目标被视为分布,而不是等待回答的问题列表。
- 它与概率的性质密切相关,并且特别适用于S型和SoftMax激活(即使它们仅用于最后一个神经元),有助于减少消失的梯度问题。 逻辑回归可以视为二进制交叉熵的一种形式。
尽管熵并不总是最佳的损失函数(尤其是在目标函数p尚未明确定义的情况下),但熵通常表现为性能增强,这说明了熵在任何地方都存在。
1. 自信息 ,信息熵,互信息
概念
- 信息量:度量概率分布带来的信息
- 自信息(self-information)计算信息量
- 熵(entropy),混乱度。熵越大,混乱度越高,系统的不确定性越强,系统的概率分布越混乱。
- 香农熵(Shannon Entropy):度量概率分布系统的混乱度
- 定义:系统中每一个事件的信息量的由概率赋权的信息量之和
- 相对熵(KL散度):从混乱度角度,度量两个概率分布系统的相似度
- 相对熵,又名KL散度(Killback-Leibler Divergence),是两个(不是一个,也不是多个)概率系统的相对混乱程度。
- 交叉熵:信息论和深度学习的桥梁
- 交叉熵越小,损失就越小,两个模型越接近。
自信息 - self-information
如果说概率P是对确定性的度量,信息是对不确定性的度量,这两者是相对的
事件发生的概率越大,那么事件的信息量就越小, 事件的概率与事件的信息量之间成反比。
举例来说:如果事件A发生的概率比事件B发生的概率要大,那么我们就说事件B的信息量要比事件A的信息量要大。
信息量能够量化以上性质,定义一个事件x的自信息为:
\(I(x) = -log(p(x))\)
- 当该对数的底数为自然对数 e 时,单位为
奈特(nats); - 当以 2 为底数时,单位为
比特(bit)或香农(shannons).
信息熵 – information-entropy
信息熵是对平均不确定性的度量,本质上是所有事件的信息量的期望, 对整个概率分布中的不确定性总量进行量化:
信息论中,记 0log0 = 0
- 当且仅当某个 $P(X_i)=1$,其余的都等于0时, H(X)= 0。
- 当且仅当某个$P(X_i)=\frac{1}{n},i=1, 2,……, n$时,$H(X)$ 有极大值 log n。
熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。
互信息
在概率论和信息论中,两个随机变量的互信息(mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。 不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布p(X,Y) 和分解的边缘分布的乘积p(X)p(Y) 的相似程度。
\[I(X,Y) = \sum_{y \in Y} \sum_{x \in X} p(x,y) log( \frac{p(x,y)}{p(x)p(y)})\]互信息 $I(X,Y)$ 取值为非负。当X、Y相互独立时,$I(X,Y)$ 最小为0。
2. 相对熵(KL散度) 与 交叉熵
1. 相对熵 – KL散度 : Kullback-Leibler divergence
如果对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL散度来衡量这两个分布的差异。
- 定义: P 对 Q 的
KL散度为:
含义:
- 在离散型变量的情况下,
KL散度衡量的是:当我们使用一种被设计成能够使得概率分布 Q 产生的消息的长度最小的编码,发送包含由概率分布 P 产生的符号的消息时,所需要的额外信息量。
性质:
- 非负: KL散度为 0,当且仅当P 和 Q 在离散型变量的情况下是相同的分布,或者在连续型变量的情况下是“几乎处处”相同的.
- 不对称:$D_p(q) != D_q(p)$
2. 交叉熵 - cross entropy
- 设 $p(x), q(x)$ 为 $X$ 中取值的两个概率分布,则 $p$ 对 $q$ 的
交叉熵为:
在一定程度上,相对熵可以度量两个随机变量的“距离”。
3. 交叉熵与KL散度的关系
- 针对 Q 最小化交叉熵等价于最小化 P 对 Q 的 KL散度,因为 Q 并不参与被省略的那一项。
最大似然估计中,最小化KL散度其实就是在最小化分布之间的交叉熵。
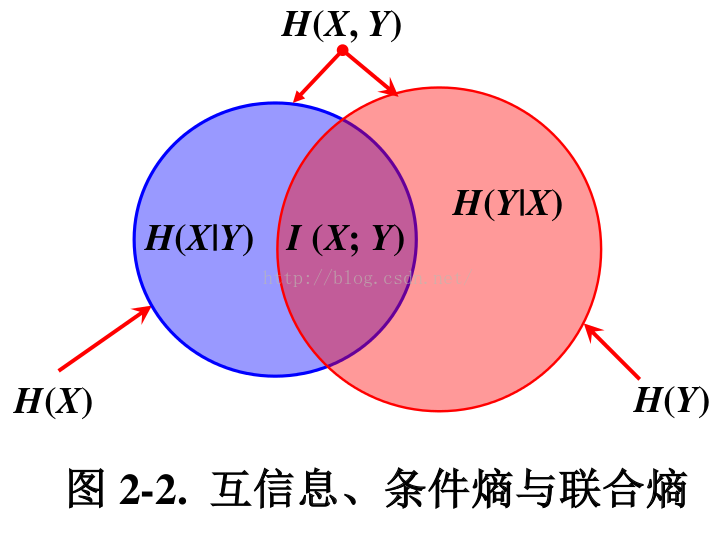
3. 联合熵与条件熵
联合熵$H(X,Y)$:两个随机变量X,Y的联合分布。条件熵$H(Y|X)$:在随机变量X发生的前提下,随机变量Y发生所新带来的熵定义为Y的条件熵,用来衡量在已知随机变量X的条件下随机变量Y的不确定性。
联合熵与条件熵的推导过程如下:
\[\begin{align} H(X, Y) - H(X) &= -\sum_{x,y} p(x,y) log \, p(x,y) + \sum_x p(x) log \, p(x) \\ &= -\sum_{x,y} p(x,y) log \, p(x,y) + \sum_x (\sum_y p(x,y)) \, log \, p(x) \qquad \text{边缘分布 p(x) 等于联合分布 p(x,y) 的和} \\ &= -\sum_{x,y} p(x,y) log \, p(x,y) + \sum_{x,y} p(x,y) \, log \, p(x) \\ &= -\sum_{x,y} p(x,y) log \frac{p(x,y)}{p(x)} \\ &= -\sum_{x,y} p(x,y) log p(y|x) \end{align}\]4. 互信息
- $I(X, Y)$ :两个随机变量X,Y的
互信息为X,Y的联合分布和各自独立分布乘积的相对熵。
- 推导过程:
可视化信息论
原文链接:Visual Information Theory
我喜欢用新的方式去思考世界,尤其是将一些模糊的想法形式化成具体的概念。比如,信息论。
信息论提供一种描述事务确定性的语言,比如某人多么善变?知道问题A对于知道问题B有什么帮助?一些想法和另一些想法有多么相似?小孩时,我就有一些粗略想法,但是信息论把这些问题抽象成具体而强大的概念。不管是从数据压缩,量子物理还是机器学习,以及其他很多和这三者有关的领域,信息论的概念都有着大量应用。
不幸的是很多人认为信息论挺难,其实并不是,可能是有些书写的太糟糕了,实际上完全可以用可视化的方法说清楚。
可视化概率分布
深入研究信息论之前,思考下如何可视化简单的概率分布。
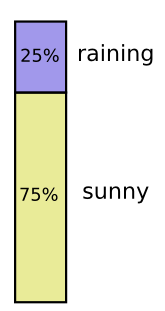
比如加利福尼亚有时下雨,但大多都是晴天,也就是说晴天的概率是75%。
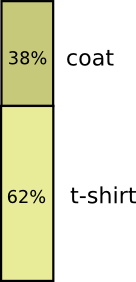
大多数时候,我都穿着T恤,但有时候会穿外套。假设穿外套的概率是38%。
怎么同时可视化这两个事件?如果不相关,很容易,独立即可。例如,今天我穿T恤或雨衣是不是真的与下周的天气相互作用。可以用轴代表不同因素:
注意垂直线和水平线一直通过。这就是独立的样子! 1
穿外套的概率不会随着一周内会下雨这一事实而改变。换句话说,我穿着外套并且下周会下雨的概率只是我穿着外套的概率,是下雨的概率。他们互不相关。
当变量相互作用时,特定变量的概率和其他变量的概率都会丢失。我穿着外套并且下雨的可能性很大,因为变量是相关的,它们使对方更有可能。更有可能的是,我在下雨的那天穿着外套,而不是我在一天穿外套的可能性,而在其他一些随机的日子下雨。
在视觉上,这看起来像一些方块以更大的概率膨胀,而其他方块缩小,因为这对事件不太可能在一起:
虽然这可能看起来很酷,但它对于理解正在发生的事情并不是很有用。
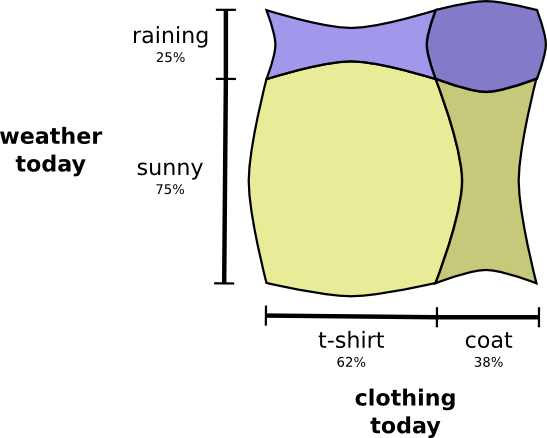
相反,让我们关注一个像天气一样的变量。我们知道它是晴天还是下雨的可能性。对于这两种情况,我们可以查看条件概率。如果天气晴朗,我穿T恤的可能性有多大?如果下雨,我穿外套的可能性有多大?
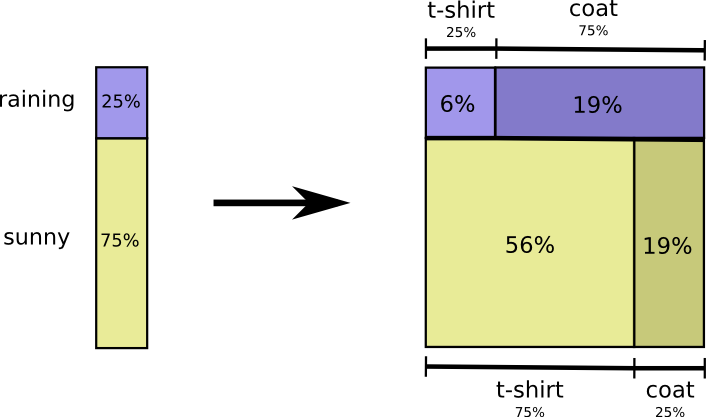
下雨的几率是25%。如果下雨,我有75%的机会穿上外套。因此,下雨和我穿着外套的概率是25%的75%,大约是19%。下雨的概率乘以我穿着外套下雨的概率,是下雨时我穿外套的概率。写这个:$ p(rain,coat) = p(rain)*p(coat|rain) $
这是概率论最基本身份之一:$p(x,y) = p(x) * p(y|x)$
将分配考虑在内,将其分解为两件产品。首先,我们看一个变量(如天气)将采取某个值的概率。然后我们看一下另一个变量(如我的衣服)在第一个变量上采用某个值的概率。
选择哪个变量是任意的。我们可以轻松地开始专注于我的衣服,然后看看它的天气条件。这可能感觉有点不那么直观,因为我们知道天气的因果关系会影响我穿什么而不是反过来…但它仍然有效!
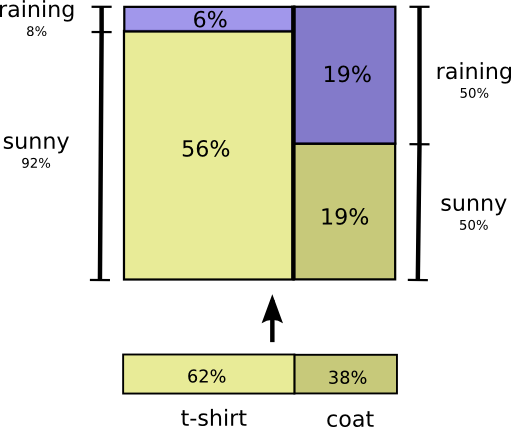
我们来看一个例子吧。如果我们选择一个随机的日子,那么我有38%的机会穿着外套。如果我们知道我穿着外套,下雨的可能性有多大?嗯,我更有可能在雨中穿一件外套而不是在阳光下,但在加利福尼亚州下雨很少见,所以它有50%的可能性在下雨。因此,下雨和我穿外套的可能性是我穿着外套的概率(38%),如果我穿着外套(50%)是下雨的可能性的概率是约19%。
$ p(rain,coat)=p(coat)*p(rain|coat) $
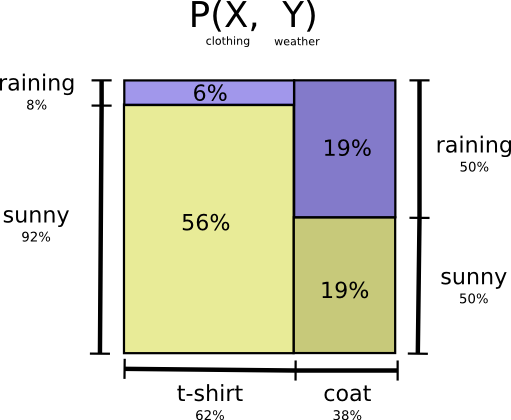
这提供了一种完全相同概率分布的可视化方法。
请注意,标签的含义与上图相比略有不同:T恤和外套现在是边缘概率,即我在不考虑天气的情况下衣服的可能性。另一方面,现在有两个下雨和晴天标签,因为他们的概率是以T恤和外套为条件的。
(您可能听说过贝叶斯定理。如果您愿意,您可以将其视为在这两种显示概率分布的不同方式之间进行转换的方式!)
旁白:辛普森悖论
用于可视化概率分布的这些技巧是否真的有用?我认为有用!将它们用于可视化信息论之前还需要一段时间,所以我想继续研究它并用它们来探索辛普森悖论。辛普森悖论是一个非常不直观的统计情况。在直观的层面上真的很难理解。迈克尔·尼尔森写了一篇可爱的文章重塑诠释,探讨了不同的解释方法。我想尝试自己解释它,使用我们在上一节中创造的技巧。
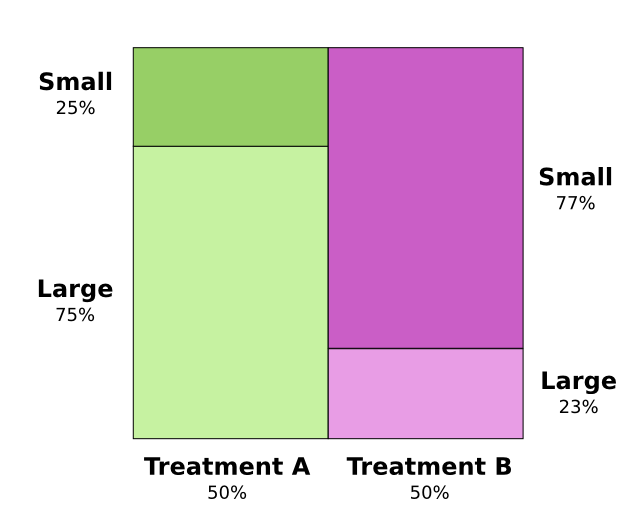
测试了两种肾结石治疗方法。一半患者接受治疗A而另一半接受治疗B。接受治疗B的患者比接受治疗A的患者更有可能存活。
然而,如果他们接受治疗,患有小肾结石的患者更有可能存活。如果他们接受治疗A,患有大肾结石的患者也更有可能存活!怎么会这样?
问题的核心是该研究没有适当随机化。接受治疗A的患者可能患有大量肾结石,而接受治疗B的患者更可能患有小结石。
事实证明,小肾结石患者更容易存活。
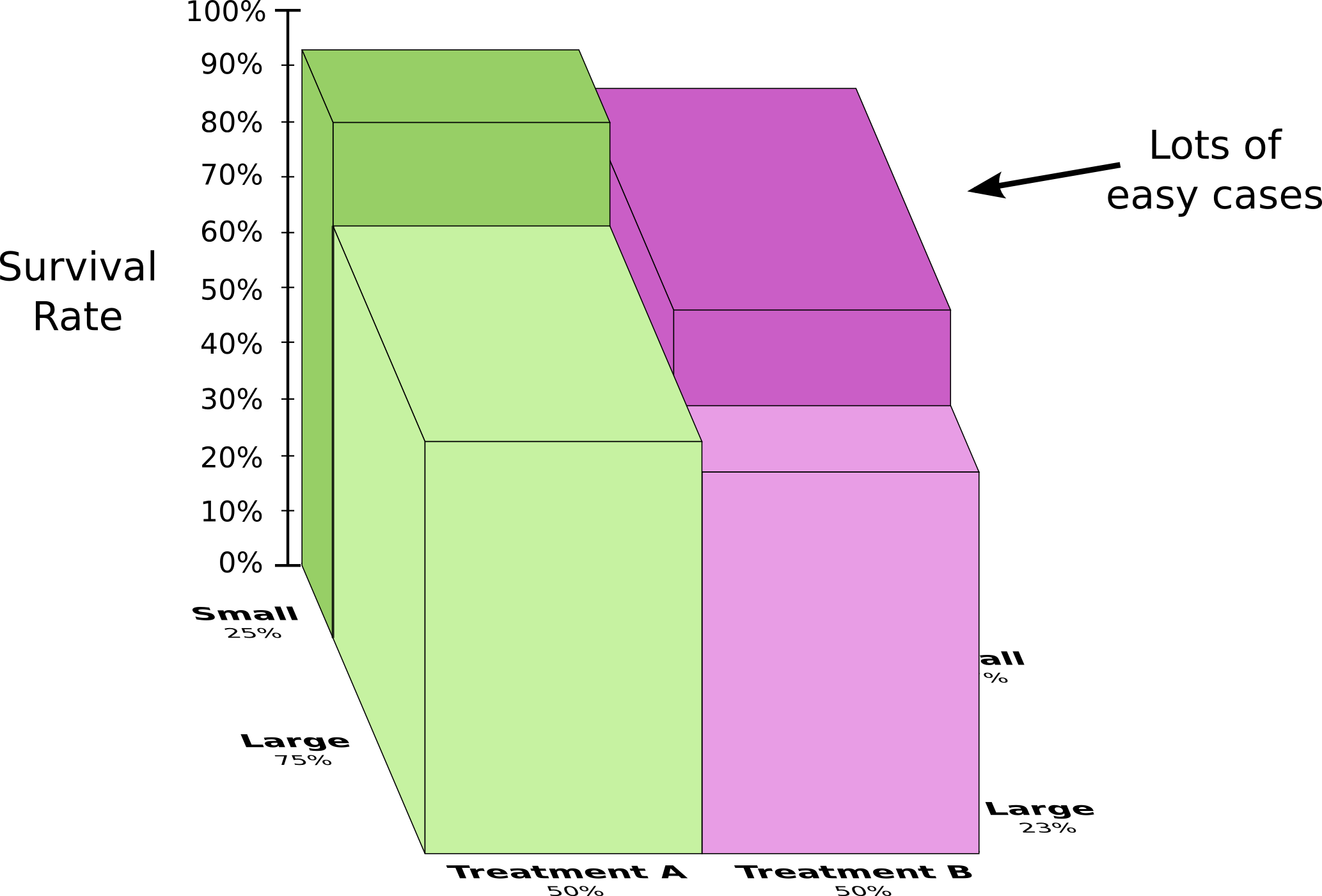
为了更好地理解这一点,我们可以结合前两个图表。结果是一个三维图表,存活率分为小型和大型肾结石。
我们现在可以看到,在小病例和大病例中,方案A与方案B比较,方案B似乎更好,因为它应用的患者更有可能在第一时间存活!
编码
现在我们有了可视化概率的方法,我们可以深入研究信息论。
让我告诉你我想象中的朋友鲍勃。鲍勃真的很喜欢动物。他经常把动物挂在嘴边。事实上,他只说了四个字:“狗”,“猫”,“鱼”和“鸟”。
几个星期前,出乎意料,鲍勃搬到了澳大利亚。促进了他,他只想以二进制方式进行交流。来自Bob的所有(虚构的)消息都是这样的:
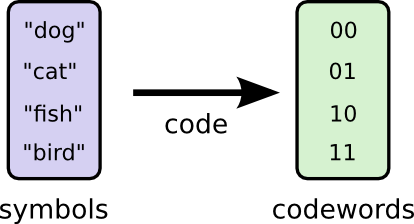
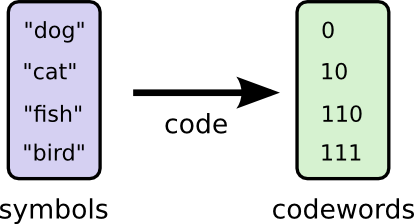
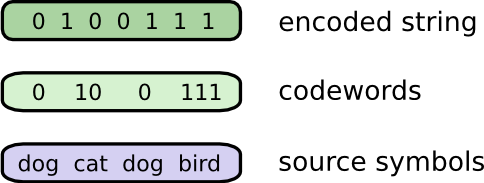
为了进行交流,Bob和我必须建立一种编码,一种将字映射到位序列的方法。
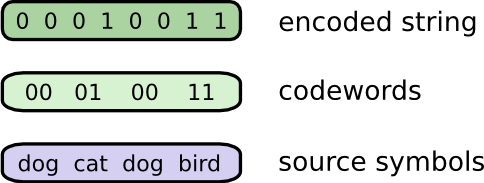
为了发送消息,Bob用相应的码字替换每个符号(字),然后将它们连接在一起以形成编码的字符串。
可变长度代码
不幸的是,想象中的澳大利亚的通信服务很昂贵。我每次必须从Bob收到的每条消息支付5美元。我是否曾提到鲍勃很喜欢说话?为了避免我破产,Bob和我决定我们应该研究是否有某种方法可以缩短我们的平均消息长度。
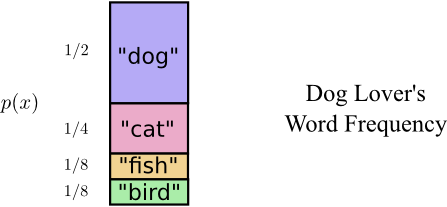
事实证明,鲍勃经常没有说出所有的话。鲍勃真的很喜欢狗。他一直在说狗。有时,他会说其他动物 - 特别是他的狗喜欢追逐的猫 - 但大多数时候他都在谈论狗。这是他的词频图:
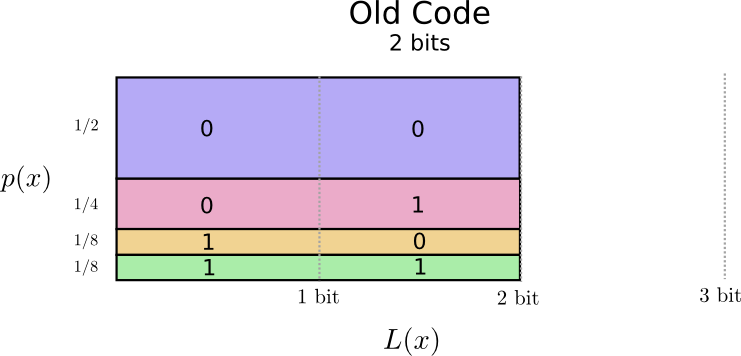
这似乎很有希望。我们的旧代码使用2位长的代码字,无论它们有多常见。
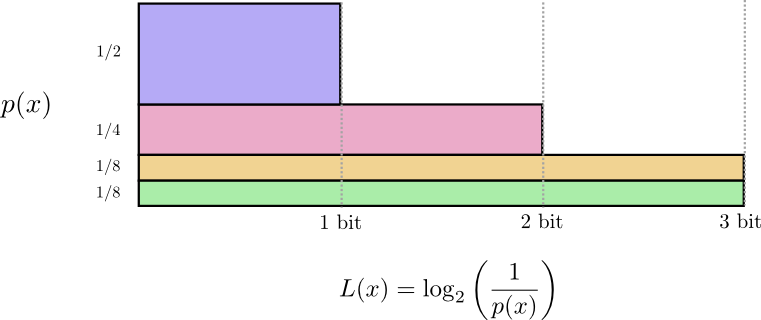
有一种可视化的方法。在下图中,我们使用垂直轴来显示每个单词的概率p(x),并使用水平轴可视化相应代码字的长度L(x)。请注意,该区域是我们发送的代码字的平均长度 - 在本例中为2位。
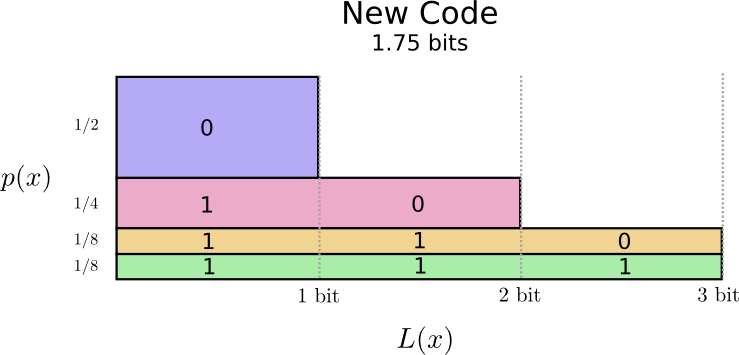
也许我们可以非常聪明地制作一个可变长度的代码,其中常见字的代码字特别短。问题在于代码字之间存在竞争 - 使得一些短的迫使我们使其他代码更长。为了最小化消息长度,我们将所有代码字都理想化缩短,但我们特别希望使用常用代码字。因此,生成的代码对于常见单词(如“dog”)具有较短的代码字,对于较不常见的单词(如“bird”)具有较长的代码字。
让我们再次想象一下。请注意,最常见的代码字变得更短,即使不常见的代码字变得更长。结果是,在网上,面积较小。这对应于较小的预期码字长度。平均来说,代码字的长度现在是1.75位!
(您可能想知道:为什么不将1本身用作代码字?悲伤的是,当我们解码编码的字符串时,这会导致歧义。我们将在稍后讨论这个问题。)
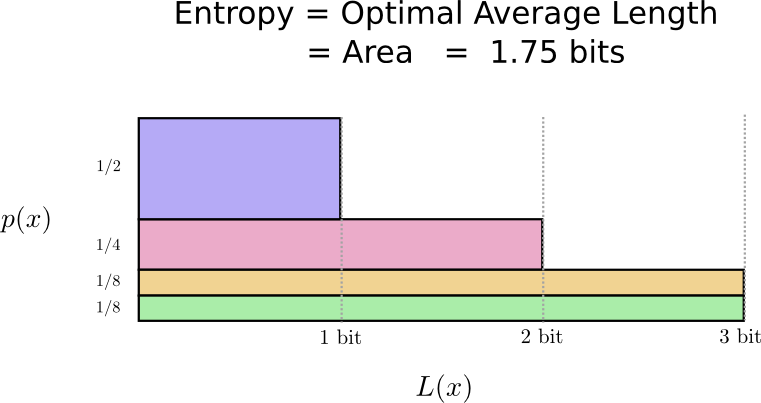
事实证明,这段代码是最好的代码。对于这种分布,没有代码可以为我们提供小于1.75位的平均代码字长度。
只有一个基本限制。传达所说的是什么,发生了这种分布的事件,要求我们平均至少传播1.75位。无论我们的代码多么聪明,都不可能让平均消息长度更短。我们将此基本限制称为熵分布 - 我们将在稍后更详细地讨论它。
如果想要理解这个限制,那么问题的关键在于理解在使一些代码字缩短和其他代码字长之间的权衡。一旦我们理解了这一点,就能够理解最好的代码是什么样的。
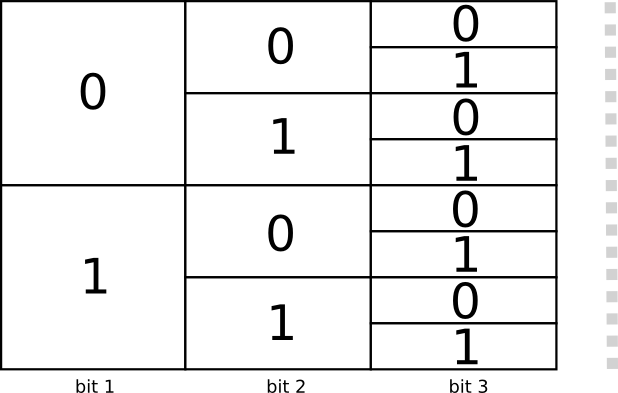
代码字的空间
有两个长度为1位的代码:0和1,有四个长度为2位的代码:00,01,10和11。添加的每个位都可能会使代码的数量翻倍。
我们对可变长度代码感兴趣,其中一些代码字比其他代码字长。我们可能有一些简单的情况,我们有8个3位长的代码字。也可能有更复杂的混合,比如长度为2的两个代码字和长度为3的四个代码字。是什么决定了我们可以有多少不同长度的代码字?
回想一下,Bob通过将每个单词替换为其代码字并将它们连接起来,将其消息转换为代码字符串。
在制作可变长度代码时,需要注意一个比较微妙的问题。我们如何将编码后的字符串拆分回代码字?当所有代码字长度相同时,很容易 - 只需每隔几步拆分字符串即可。但由于存在不同长度的代码字,我们需要关注实际内容。
我们十分希望代码是唯一可解码的,只有一种方法可以解码编码的字符串。我们从不希望它是模糊的,哪些代码字构成编码的字符串。如果我们有一些特殊的“代码字结尾”符号,这将很容易。2但我们没有 - 我们只发送0和1。我们需要能够查看一系列连接的代码字并告诉每个代码字停止的位置。
制作不可唯一解码的代码是非常可能的。例如,假设0和01都是代码字。然后不清楚代码字符串0100111的第一个代码字是什么 - 它可能是!我们想要的属性是,如果我们看到一个特定的代码字,就不应该有一个更长的版本也是一个代码字。另一种说法是,没有代码字应该是另一个代码字的前缀。这称为前缀属性,遵守它的代码称为前缀代码。
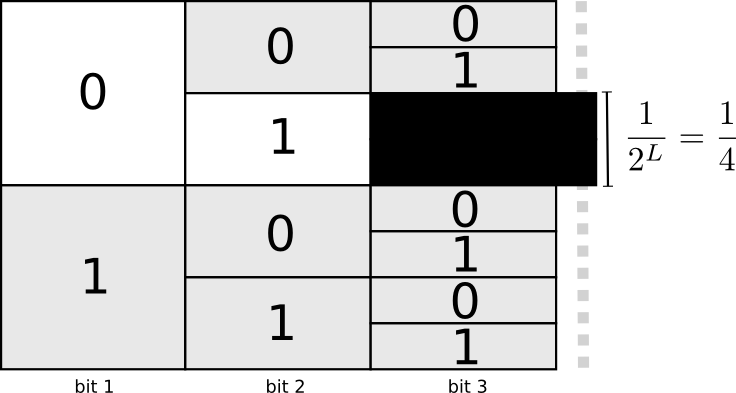
考虑这一点的一个有用方法是每个代码字都需要从可能的代码字空间中牺牲。如果我们使用代码字01,我们将无法使用任何代码字,它是前缀。由于含糊不清,我们不能再使用010或011010110 - 我们失去了它们。
由于所有代码字的四分之一都以01开头,因此我们牺牲了所有可能字的四分之一。这就是我们付出的代价,以换取一个只有2位长的代码字!反过来,这种牺牲意味着所有其他代码字需要更长一些。在不同代码字的长度之间总是存在这种权衡。短代码字要求您牺牲更多可能的代码字空间,以防止其他代码字变短。我们需要弄清楚正确的权衡取舍是什么!
最佳编码
可以将此视为使用有限的预算来获取短代码字。通过牺牲一小部分可能的代码字来得到一个代码字。
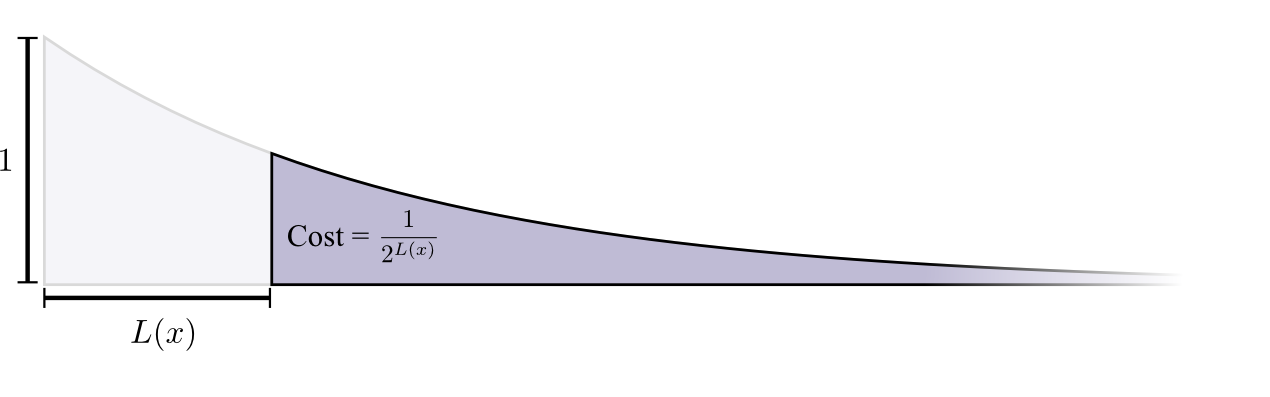
购买长度为0的代码字的成本是1,所有可能的代码字 - 如果你想要一个长度为0的代码字,你就不能拥有任何其他代码字。长度为1的代码字的成本,如“0”,是1/2,因为一半可能的代码字以“0”开头。长度为2的代码字的成本,如“01”,是1/4,因为所有可能的代码字中有四分之一以“01”开头。通常,代码字的成本随着代码字的长度呈指数下降。
请注意,如果成本以(自然)指数衰减,则它既是高度又是面积!3
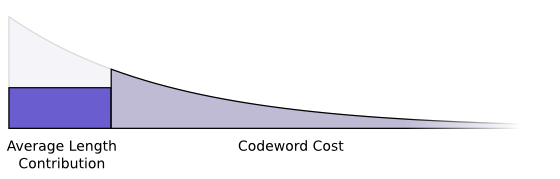
我们想要短代码字,因为我们想要短的平均消息长度。每个码字使得平均消息长度的概率乘以代码字的长度。例如,如果我们需要在50%的时间内发送4位长的代码字,那么我们的平均消息长度比不发送代该码字时的长2位。我们可以把它描绘成一个矩形。
这两个值与代码字的长度有关。我们支付的总数决定了代码字的长度。代码字的长度控制它增加平均消息长度的程度。我们可以将这两者结合在一起,就像这样。
短代码字减少了平均消息长度但是很昂贵,而长代码字增加了平均消息长度但是便宜。
使用有限预算的最佳方式是什么?应该在每个事件的代码字上花多少钱?
就像人们想要更多地投入经常使用的工具一样,我们希望在常用的代码字上花费更多。有一种特别自然的方法可以做到这一点:按照事件的常见程度分配我们的预算。因此,如果一个事件有50%的概率发生,我们将50%的预算用于购买短代码字。但如果事件只有1%的概率发生,我们只花费预算的1%,因为如果代码字很长,我们并不在意。
这是很自然的,但这是最好的方法吗?它是的,我会证明它!
以下证据是直观的,应该是可读的,但是需要工作才能完成,这绝对是本文中最难的部分。读者可以随意跳过接受这个并转到下一部分。
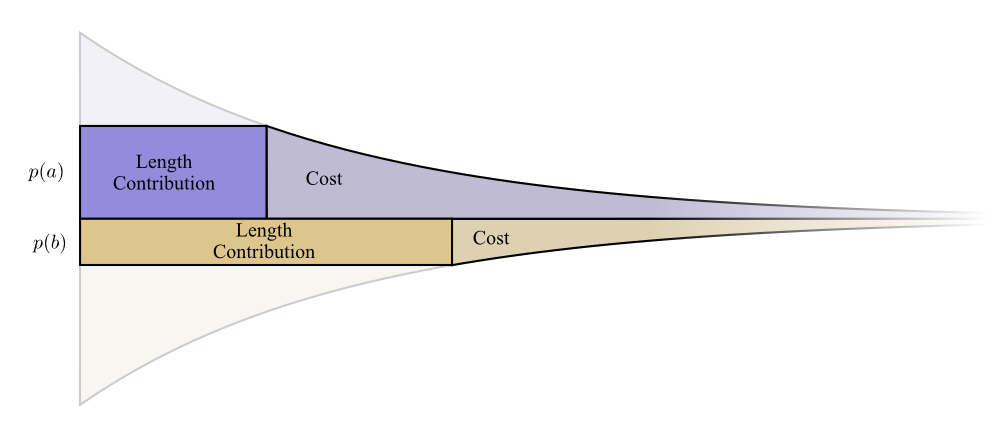
让我们描绘一个具体的例子,我们需要传达两个可能发生的事件中的某一个。事件a发生时间p(a) 和事件b发生时间p(b) 。我们以上述自然方式分配我们的预算,花费p(a) 用于获得a一个短代码字,以及p(b) 获得b一个短代码字。
成本和长度贡献边界排列地很好。这有什么意义吗?
好吧,如果我们略微改变代码字的长度,请考虑成本和长度贡献会发生什么。如果我们略微增加代码字的长度,则消息长度贡献将与其在边界处的高度成比例地增加,而成本将与其在边界处的高度成比例地减小。
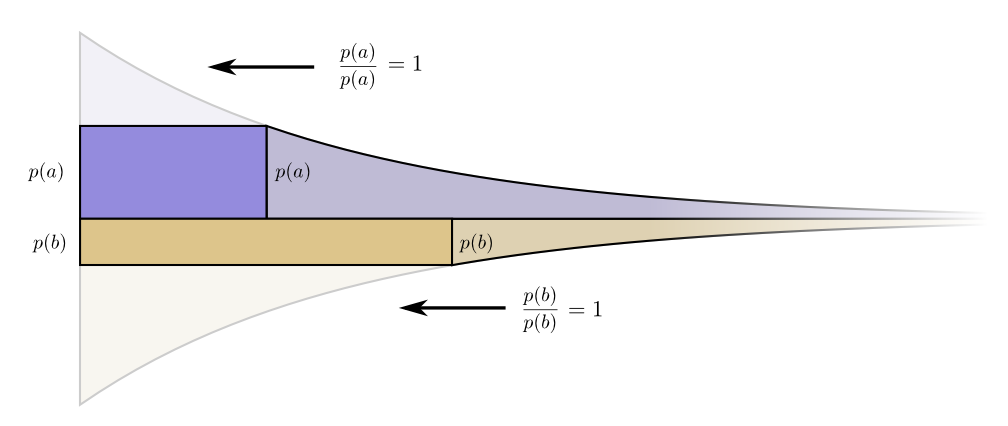
因此,使a的代码字更短的成本是p(a)。与此同时,我们并不关心每个代码字的长度,我们关心它们与我们使用它们的程度成正比。在a的情况下,即p(a)。使a的代码字缩短的好处是p(a)。
有趣的是,两种衍生物都是相同的。这意味着我们的初始预算具有有趣的属性,如果您有更多的花费,那么投资使任何代码字更短也同样好。最后,我们真正关心的是利益/成本比率 - 这就决定了我们应该投入更多资金。在这种情况下,比率为p(a)/p(a),等于一。这与p(a)的值无关它总是一。我们可以将相同的参数应用于其他事件。利益/成本总是一,所以在任何一个方面投入更多都是同等重要的。
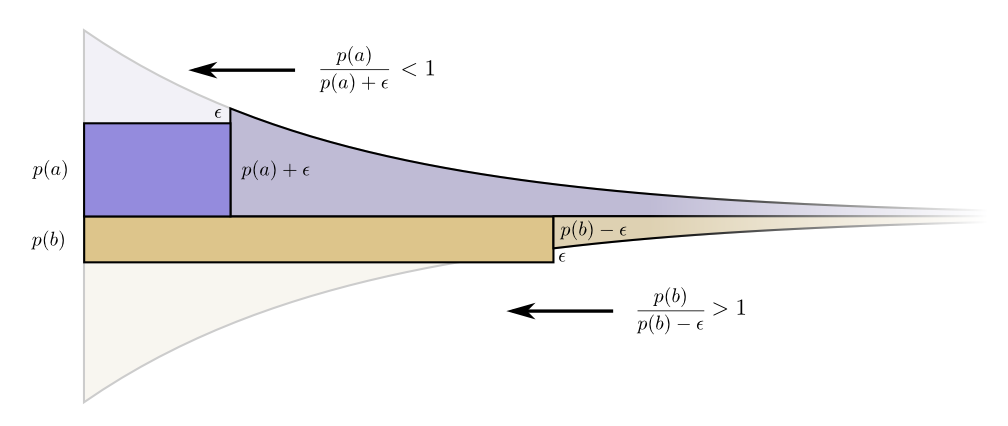
无限小,改变预算没有意义。但这并不能证明它是最好的预算。为了证明这一点,我们将考虑一个不同的预算,我们在一个代码字上花费一些额外费用而牺牲另一个代码字。我们会将ϵ少投资于b,并将其投资于a。这使得a的代码字更短,而b的代码字更长一些。
现在购买a的较短代码字的成本是 p(a)+ϵ,购买b的较短代码字的成本是p(b)-ϵ。但利益仍然是一样的。这导致购买的利益成本比 p(a)/(p(a)+ϵ) 小于一。另一方面,购买b的利益成本比是 p(b)/(p(b)−ϵ),它大于1。
价格不再平衡。 baba。
投资者尖叫:“购买b!出售a!“。我们这样做,之后就会结束回到原来的预算计划。所有的预算都会提高,从而转向我们的原计划。
原始预算 - 按照我们使用它的频率按比例投资每个代码字 - 不光是自然而然的事情,而是因为它是最佳选择。(虽然此证明仅适用于两个代码字,但它很容易被推广到适用于更多代码字。)
(细心的读者可能已经注意到,我们的最佳预算可能会建议代码字具有小数长度的代码。这似乎有什么关系?这是什么意思?当然,实际上,如果你想通过发送单个代码字,你必须四舍五入(round)。但正如我们稍后会看到的,有一个非常真实的意义,当我们一次发送多个代码字时可以发送小数代码字!请你耐心等待!)
计算熵
回想一下,长度为L的消息的成本是1/2^L。 我们给定量的消息的长度,可以将其反向处理获得花费成本:$log_2\frac{1}{cost}$。 由于我们在x的代码字上花费p(x),因此长度为 $ log_2\frac{1}{p(x)} $。这些是长度的最佳选择。
早些时候,我们讨论了如何从一个特定的概率分布中获得平均消息来传递事件的短暂性的基本限制,p。 这个限制,即使用最佳代码的平均消息长度,称为p的熵,H(p)。 现在知道了代码字的最佳长度,可以计算: $ H(p)=\sum {p(x)log_2\frac{1}{p(x)}}$
- 人们经用标识 $H(p)=−∑p(x)log_2(p(x))$ 改写成 $ log(1/a)=−log(a)$.我认为前者更直观,并将继续在本文中使用它。
无论我做什么,平均而言,如果我想要传达哪个事件,我需要发送至少这个位数。
通信所需的平均信息量对压缩有明显的影响。 但还有其他理由让我们应该关注它吗? 有!它描述了不确定性并给出了量化信息的方法。
如果我确切知道会发生什么,我根本不需要发送消息! 如果有两件事可能以50%的概率发生,我只需要发送1比特。但如果有64种不同的事情可能以相同的概率发生,我必须发送6比特。 概率越集中,我就越能用短平均消息写出聪明的代码。 概率越分散,我的消息就越长。
结果越不确定,平均来说,当我发现发生了什么时,我知道的越多。
交叉熵
在他搬到澳大利亚之前不久,鲍勃娶了爱丽丝,这是我想象中的另一个虚构。 为了让我自己以及我头脑中的其他人物感到惊讶,爱丽丝不是一个爱狗的人。 她是一个猫爱好者。 尽管如此,他们两人能够在他们对动物的共同喜好和词汇量非常有限的情况下找到共同点。
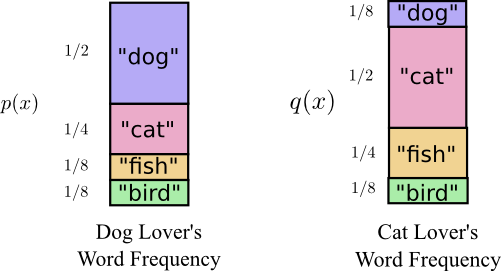
他们俩说不同频率的同一个词。 鲍勃一直在说狗,爱丽丝一直在说猫。
最初,Alice使用Bob的代码向我发送消息。不幸的是,她的消息比我和Bob需要的时间更长。 鲍勃的代码是针对他的概率分布进行了优化。 Alice具有不同的概率分布,并且代码对于它来说是次优的。 虽然Bob使用自己的代码时代码字的平均长度是1.75位,但当Alice使用他的代码时它是2.25。 如果两者越不相似,那么会更糟糕!
这个长度 - 从一个分布传递事件与另一个分布的最佳代码的平均长度 - 称为交叉熵。 形式上,我们可以将交叉熵定义为:4 Hp(q)=Σq(x)log2(1/p(x))
在这种情况下,爱丽丝的交叉熵是猫爱好者的单词频率相对于鲍勃爱好者的单词频率。
为了降低通信成本,我让Alice使用自己的代码。令我宽慰的是,这降低了她的平均消息长度。但它引入了一个新问题:有时Bob会不小心使用Alice的代码。令人惊讶的是,鲍勃不小心使用Alice的代码而Alice使用了Bob的代码,这样会更糟糕!
那么,现在我们有四种可能性:
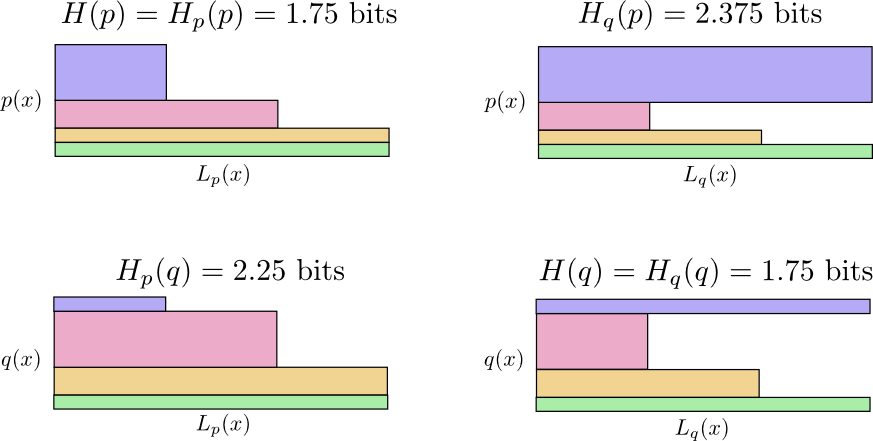
- Bob使用他自己的代码 H(p)=1.75 bits
- Alice使用Bob的代码 Hp(q)=2.25 bits
- Alice使用自己的代码 H(q)=1.75 bits
- Bob使用Alice的代码 Hq(p)=2.375 bits
这不一定像人们想象的那样直观。例如,我们可以看到Hp(q)≠Hq(p)。有什么方法可以看出这四个值如何相互关联?
在下图中,每个子图表示这4种可能性中的一种。每个子图可视化了平均消息长度,与我们之前的图表一样。它们被放在了一个正方形中,因此如果消息来自相同的分布,则图形彼此相邻,并且如果它们使用了相同的代码,则它们相互叠加。这允许您在视觉上将分布和代码一起滑动。
你能明白为什么Hp(q) ≠ Hq(p)吗? Hq(p)很大,因为在p下有一个非常常见的事件(蓝色)但得到一个长代码,因为它在q下非常罕见。 另一方面,q下的常见事件在p下较不常见,但差别不那么大,因此Hp(q) 不那么高。
交叉熵不是对称的。
那么,为什么要关心交叉熵呢? 好吧,交叉熵为我们提供了一种表达不同的两种概率分布的方法。 分布p和q越不同,p相对于q的交叉熵就越大于p的熵。
同样,p与q越不一样,q相对p的交叉熵就越大于q的熵。
真正有趣的是熵和交叉熵之间的差异。这种差异是我们的消息需要多长时间,因为我们使用了针对不同分布而优化的代码。如果分布相同,则此差异将为零。随着差异的增大,它会变得更大。
这种差异称为 Kullback-Leibler分歧,或 KL分歧。p相对于q,Dq(p),5 的KL偏差定义为:6
$ Dq(p) = Hq(p)−H(p) $
关于KL分歧的真正好处在于它就像两个分布之间的距离。它可以量化分布间的不同! (如果你认真对待这个想法,最终会得到信息几何。)
交叉熵和KL分歧在机器学习中非常有用。通常,我们希望一个分布与另一个分布接近。例如,我们可能希望预测的分布接近基本事实。 KL分歧为我们提供了一种自然的方式来实现这一目标,因此它无处不在。
熵和多变量
让我们回到之前的天气和衣服示例:
像许多父母一样,我的母亲有时会担心我不能适应天气。(她有合理的怀疑理由 - 我经常在冬天不穿外套。)所以,她经常想知道天气和我穿的衣服。 我要发送多少比特才能传达这个消息给她?
好吧,简单的方法是把概率分布拉平:
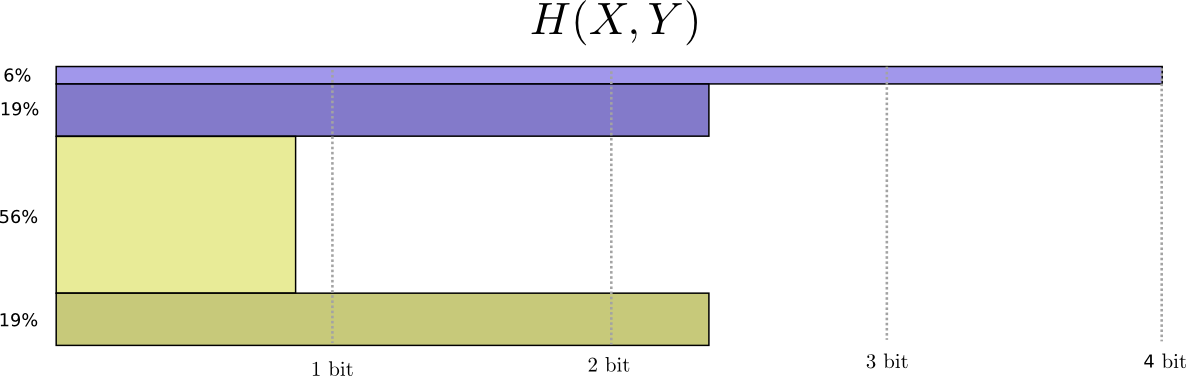
现在我们可以计算出这些概率事件的最优代码字,并计算平均消息长度:
我们称之为X和Y的联合熵 $ H(X,Y)=\sum_{x,y}p(x,y)log_2\frac{1}{p(x,y)}$
这与正常定义完全相同,除了是两个变量而不是一个变量之外。
考虑这个问题的一种稍好一点的方法是避免使分布变平,只需将代码长度看作第三维。 现在熵就是体积!
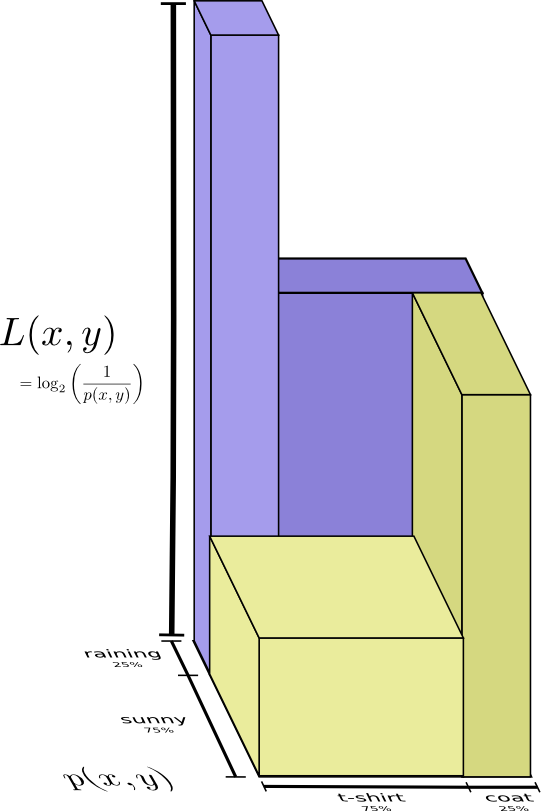
但是假设我妈妈已经知道天气了。 她可以在新闻上查看。 现在我需要提供多少信息?
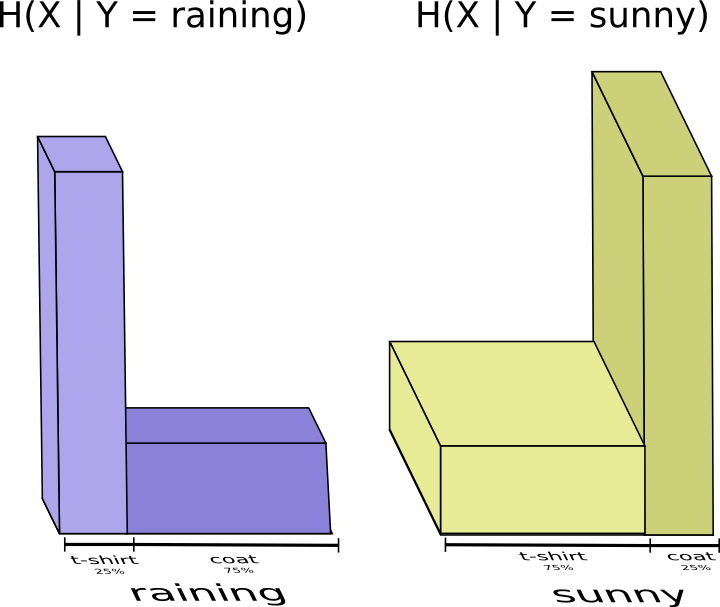
似乎我需要发送更多的信息来传达我穿的衣服。但实际上我发送的更少了,因为天气强烈暗示我会穿什么衣服! 让我们分别考虑下雨和晴天的情况。
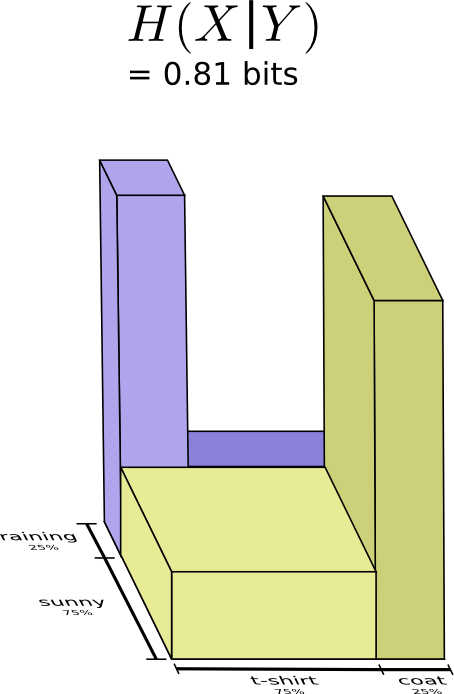
在这两种情况下,我不需要平均发送大量信息,因为天气让我很好地猜测了正确答案。 当天气晴朗时,我可以使用一个特殊的晴天优化代码,当下雨时我可以使用下雨优化的代码。 在这两种情况下,我发送的信息少于我使用通用代码的情况。为了获得我需要发送给我妈妈的平均信息量,我只是将这两个案例放在一起……
| 条件熵。如果你把它形式化成一个方程,会得到:$ H(X | Y)=\sum{y}p(y)=∑_xp(x | y)log_2\frac{1}{p(x | y)}=∑_{x,y}p(x,y)log_2\frac{1}{p(x | y)} $ |
互信息
在上一节中,观察到知道一个变量可能意味着传递另一个变量需要更少的信息。
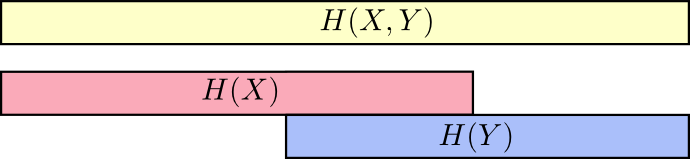
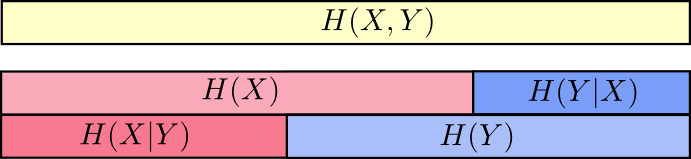
考虑这个问题的一个好方法是将大量信息想象成条形。 如果它们之间存在共享信息,则这些条重叠。 例如,X和Y中的一些信息在它们之间共享,因此H(X) 和H(Y) 是重叠条。 并且由于H(X,Y) 是两者中的信息,它是条形H(X) 和H(Y) 的并集。7
一旦我们以这种方式思考问题,会更容易看到很多事情。
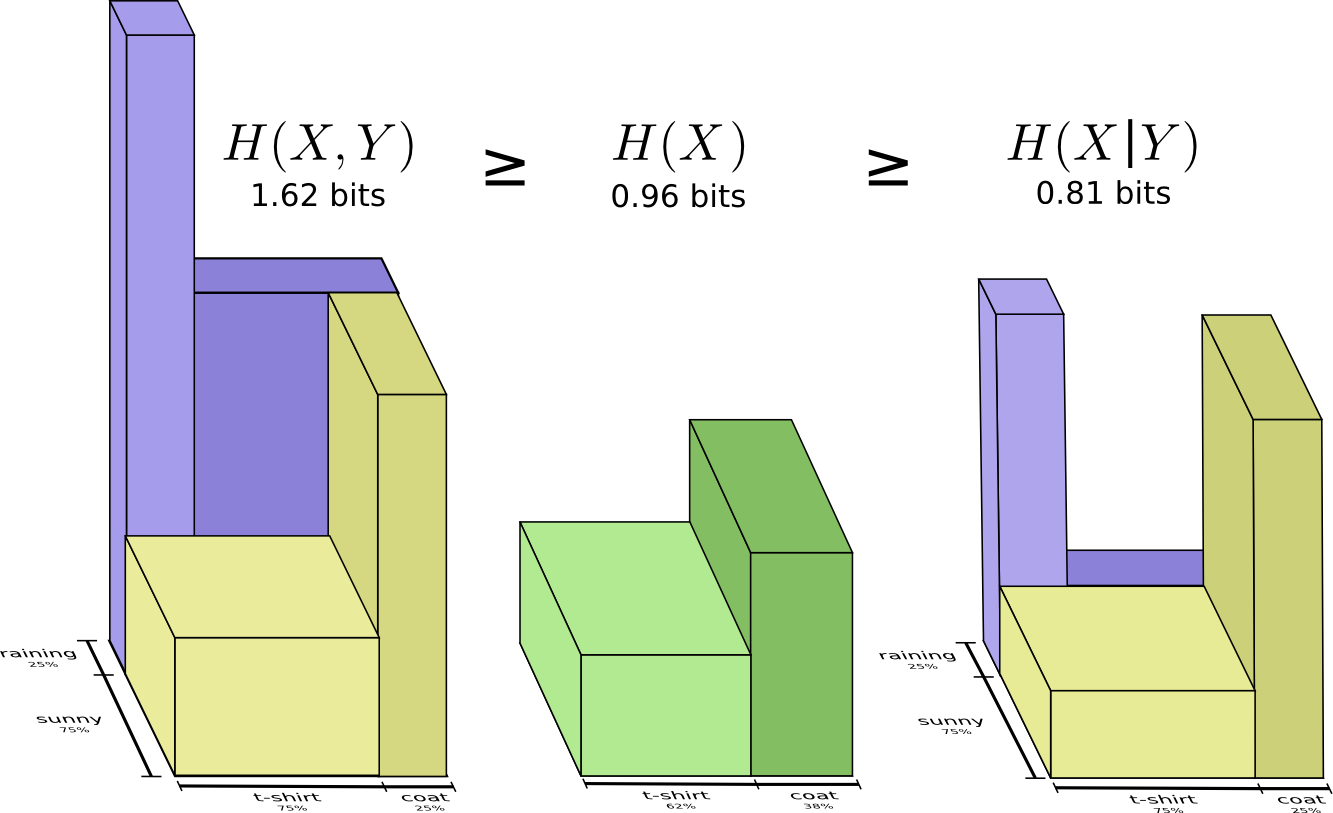
例如,我们之前注意到它需要更多信息来传达X和Y(“联合熵”,H(X,Y) 而不是仅仅需要 通信X(“边际熵”,H(X))。但是,如果你已经知道Y,那么传递X(“条件熵”,H(X|Y))所需的信息比你没有做的要少!
| 这听起来有点复杂,但是当我们从条形图的角度来考虑时,它非常简单。$ H(X | Y)$ 是我们需要发送以将X发送给已经知道Y的人的信息,X中的信息不在Y中。从可视化来看,这意味着 $ H(X | Y)$ 是H(X)条的一部分,它与H(Y)不重叠。 |
现在可以从下图中读取不等式 $ H(X,Y)≥H(X)≥H(X|Y) $。
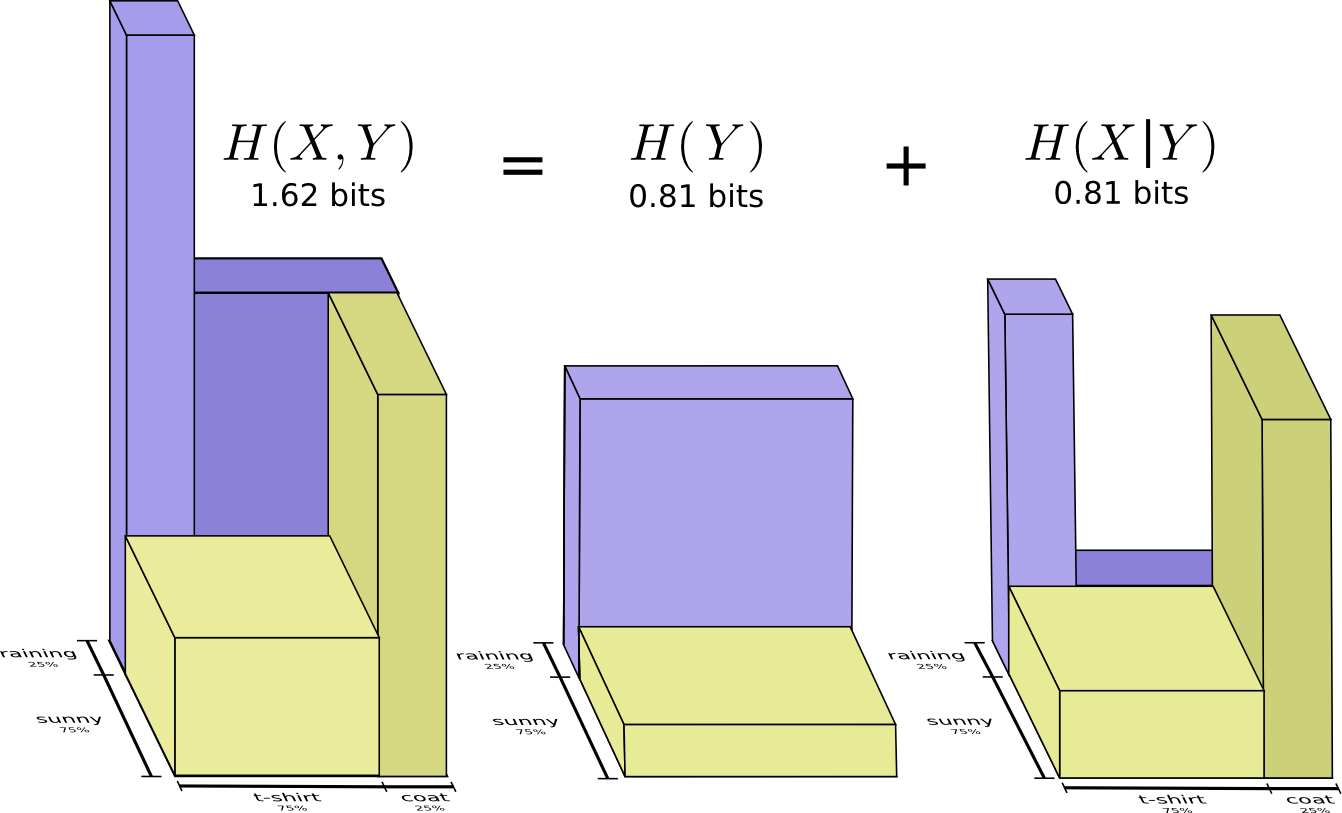
另一个标识是 $ H(X,Y)=H(Y)+H(X|Y) $。 也就是说,X和Y中的信息是 Y中的信息加上X不在Y中的信息。
同样,在方程中很难看到这些,但是如果你正在考虑这些重叠的信息条,那么很容易就可以看出来。
此时,我们已经通过多种方式破坏了X和Y中的信息。我们在每个变量中都有信息,H(X)和H(Y)。我们在H(X,Y)中都有信息的并集。我们有一个而不是另一个的信息,H(X|Y)和H(Y|X)。其中很多似乎都围绕着变量间共享的信息,即信息的交集。我们称之为“互信息”,I(X,Y),定义为:8 I(X,Y)=H(X)+H(Y)−H(X,Y)这个定义有效,因为H(X)+H(Y) 有两个互信息副本,因为它在X和Y中,而H(X,Y) 只有一个。(考虑前面的条形图。)
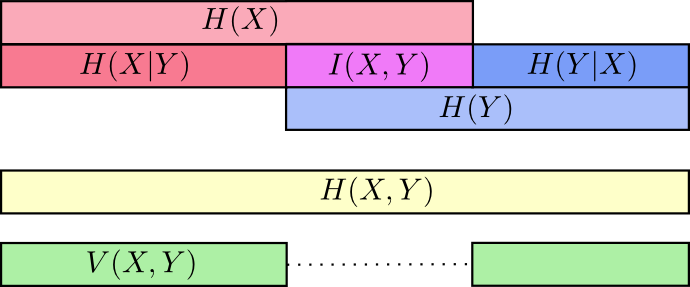
与互信息密切相关的是信息的变化。信息的变化是变量之间不共享的信息。我们可以像这样定义:V(X,Y)=H(X,Y)−I(X,Y),信息的变化很有意思,因为它给出了一个度量,不同的变量间距离的概念。如果知道一个变量的值就能知道另一个,则两个变量之间的信息变化为零,随着它们变得更加独立而增加距离值。
这与KL分歧有什么关系?这也给了我们一个距离概念?好吧,KL分歧给出了两个分布在同一个变量或一组变量上的距离。相反,信息的变化给出了两个联合分布变量之间的距离。 KL分歧在分布之间,分布内的信息变化。
可以将所有这些结合在一张图表,将所有这些不同的信息联系起来:
分数位
关于信息论的一个非常不直观的事情是我们可以得到小数位。这很奇怪。 一半是什么意思?
这是一个简单的答案:通常,我们对消息的平均长度而不是任何特定的消息长度感兴趣。 如果一半时间发送一个比特,一半时间发送两个比特,平均一个发送一个半比特。 平均值是分数的并不奇怪。
但这个答案实际上是在回避这个问题。 通常,代码字的最佳长度是分数。 那是什么意思?
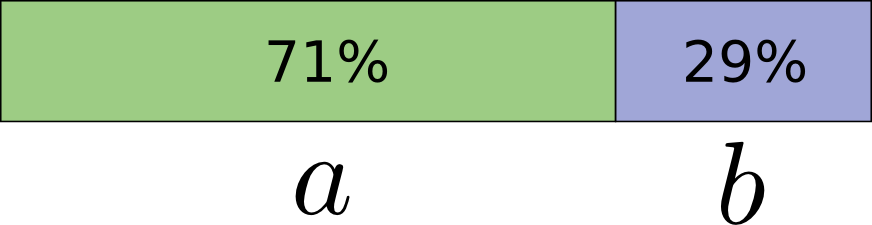
具体来说,让我们考虑概率分布,其中一个事件a发生概率为71%,另一个事件b发生概率为29%。
最佳代码将使用0.5位来表示a,使用1.7位来表示b。 好吧,如果我们想发送这些代码字中的一个,这是不可能了。 我们被迫四舍五入到整数位,平均发送1位。
…但如果我们一次发送多条消息,事实证明我们可以做得更好。 让我们考虑从这个分发版中发送两个事件。 如果我们独立发送它们,我们需要发送两位。 我们可以做得更好吗?
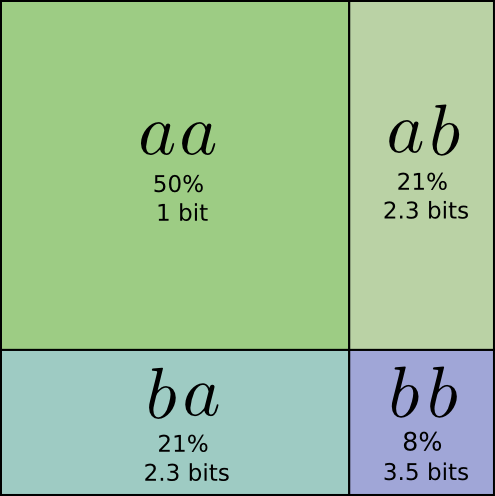
有一半的时间,我们需要发送aa,21%的时间我们需要发送ab或ba和花费8%的通信时间bb。 同样,理想的代码涉及小数位。
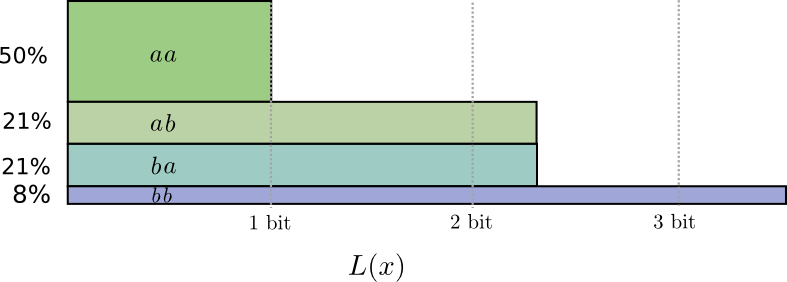
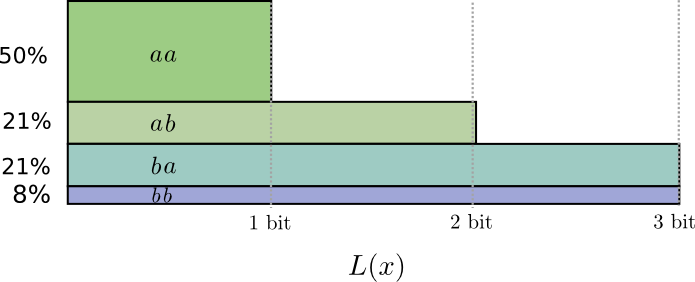
如果我们四舍五入代码字的长度,我们会得到这样的结果:
此代码为我们提供了1.8位的平均消息长度。当我们独立发送它们时,它小于2位。另一种思考方式是我们平均每个事件发送0.9位。如果我们要一次发送更多事件,它会变得更小。由于n趋于无穷大,由于四舍五入我们的代码而导致的开销将消失,并且每个代码字的位数将接近熵。
此外,注意a的理想代码字长度是0.5位,aa的理想代码字长度是1位。理想的代码字长度会增加,即使它们是分数!因此,如果我们一次发送很多事件,则会增加长度。
即使实际代码只能使用整数,也有一种非常真实的意义,即人们可以拥有小数部分的信息位。
(在实践中,人们使用特定的编码方案,这些编码方案在不同程度上是有效的。霍夫曼编码,基本上就是我们在这里描述的那种代码,不能非常优雅地处理小数位 - 你必须像我们上面做的那样对符号进行分组,或者使用更复杂的技巧来接近熵极限。算术编码有点不同,但优雅地处理小数位是渐近最优的。)
结论
如果我们关心以最小数量的比特进行通信,那么这些想法显然是基本的。如果我们关心数据压缩,信息论可以解决核心问题并为我们提供基本正确的抽象。但是如果我们不在乎呢?除了好奇心之外,还有什么?
信息论的想法出现在许多背景中:机器学习,量子物理学,遗传学,热力学,甚至赌博。这些领域的从业者通常不关心信息论,因为他们想要压缩信息。他们之所以在意,是因为信息论与他们的领域有着紧密的联系。量子纠缠可以用熵来描述.9统计力学和热力学的结果可以通过假设你不知道的事物的最大熵得出。10赌徒的胜负与KL分歧直接相关,特别是迭代设置。11
信息论之所以出现在这些地方,是因为它为我们需要表达的许多事情提供了具体的、有原则的形式化表述。它为我们提供了测量和表达不确定性的方法,两组信念的不同,以及一个问题的答案告诉了我们多少关于其他问题的信息:扩散概率是多少,概率分布之间的距离,以及两个变量的相关程度。有其他类似的想法吗?当然。但是,信息论的思想是清晰的,它们具有非常好的特性和原则性的起源。在某些情况下,它们正是你所关心的,而在其他情况下,它们是混乱世界中的一个方便代理。
机器学习是我最了解的,所以让我们谈谈这一点。机器学习中一种很常见的任务是分类。假设我们想看一张照片并预测它是狗还是猫的照片。我们的模型可能会说“这个图像是狗的概率为80%,而且有20%的可能性是猫。”假设正确的答案是狗 - 我们只说有80%的几率是一只狗,这到底是好还是坏?“85%会更好吗?
这是一个重要的问题,因为我们需要一些关于我们的模型是好是坏的概念,以便优化它做得更好。我们应该优化什么?正确答案实际上取决于我们使用该模型的原因:我们只关心上面的猜测是否正确,还是关心我们对正确答案的信心?自信错误有多糟糕?没有一个正确的答案。通常不可能知道正确的答案,因为我们不知道如何以足够精确的方式使用模型来形式化我们最终关心的内容。结果是,有些情况下交叉熵确实正是我们关心的,但情况并非总是如此。更常见的是,我们并不确切知道我们关心的是什么,交叉熵是一个非常好的代替工具。12
信息为我们提供了一个思考世界的强大新框架。有时它完全符合手头的问题;其他时候它并不完全合适,但仍然非常有用。这篇文章只涉及信息论的表面 - 有一些主要的主题,比如纠错码,我们根本没有涉及到 - 但我希望我已经展示了信息论是一个的美丽主题,不需要令人生畏。
为了帮助我成为一个更好的作家,请考虑填写这份反馈表格。
延伸阅读
克劳德·香农关于信息论的原始论文,通信的数学理论,非常易懂。(这似乎是早期信息论论文中反复出现的一种模式。是那个时代吗?缺少页面限制?来自贝尔实验室的文化?)
Cover & Thomas的信息论元素似乎是标准参考。我发现这很有用。
致谢
我非常感谢 Dan Mané, David Andersen, Emma Pierson和Dario Amodei花时间对这篇文章给出了非常详尽和广泛的评论。 我也很感谢Michael Nielsen, Greg Corrado, Yoshua Bengio, Aaron Courville, Nick Beckstead, Jon Shlens, Andrew Dai, Christian Howard, 和Martin Wattenberg的评论。
还要感谢我的前两个神经网络研讨会系列,作为这些想法的实验对象。
最后,感谢那些发现错误和遗漏的读者。 特别感谢Connor Zwick,Kai Arulkumaran,Jonathan Heusser,Otavio Good和一位匿名评论者。
-
- 用这个来可视化朴素的贝叶斯分类器很有趣,它们假设独立……↩
-
- 但非常低效! 如果我们在代码中使用了额外的符号,那么只在代码字的末尾使用它就会是一种可怕的浪费。↩
-
- 我在这里作弊。 我一直在使用底数为2的指数,这不是真的,我将切换到自然指数。 这节省了我们在证明中有很多log(2)s,并阅读体验更好。↩
-
- 注意,这种交叉熵的表示法是非标准的。 通常的表示法是H(p,q)。 由于两个原因,这种表示法很糟糕。 首先,联合熵也用完全相同的符号。 其次,它使得交叉熵看起来像是对称的。 这太荒谬了,我将用Hq(p)来代替。↩
-
- 也是非标准的表示法。↩
-
- 如果扩展KL分歧的定义,你得到:Dq(p)=∑p(x)log2(p(x)/q(x)) 这可能看起来有点奇怪。 我们该怎么解释呢? 那么,log2(p(x)/q(x))就是为q优化的代码和为p优化的代码将使用多少位之间的差异 表示x。 表达式作为整体是两个代码将使用多少位的预期差异。↩
-
- 这构建了Raymond W. Yeung论文中对信息理论的集合解释 A New Outlook on Shannon’s Information Measures.↩
-
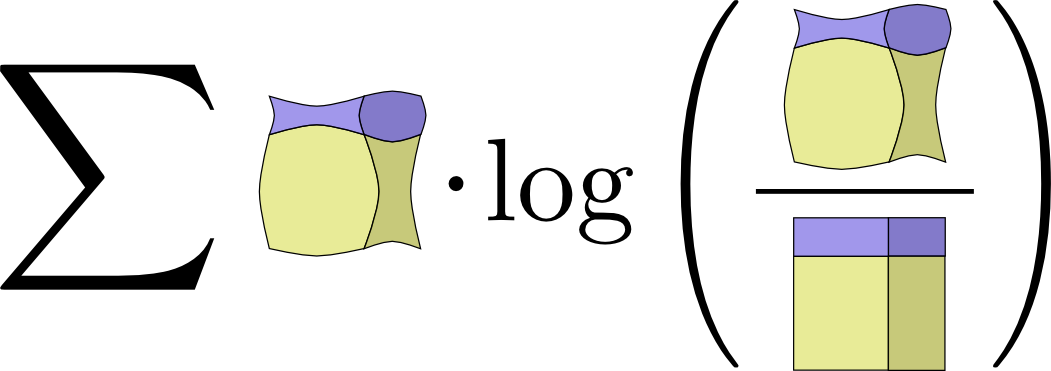
- 如果扩展互信息的定义,您会得到:$ I(X,Y)=∑p(x,y)log_2 \frac{p(x,y)}{p(x)p(y)} $
这看起来像 KL 分歧!这是怎么回事?
- 嗯,这是 KL 分歧。 它是 P(X,Y) 的KL分歧和它的朴素近似P(X)P(Y)。 也就是说,如果知道它们之间的关系而不是假设它们是独立的,那么您保存的位数代表X和Y.
一种很有趣的方法是把一个分布和它的朴素近似之间的比例画出来:
-
-
- 有一整个量子信息论领域。 我对这个问题一无所知,但我敢打赌,基于Michael的其他工作,Michael Nielsen和Issac Chuang的Quantum Computation和Quantum Information是一个很好的介绍。↩
-
- 作为一个对统计物理一无所知的人,我会非常紧张地试图勾勒出与我所理解的信息论的联系。
在Shannon发现信息论之后,许多人注意到热力学方程和信息论方程之间存在可疑的相似性。E.T. Jaynes 发现了一个非常深刻和有原则的联系。 假设您有一些系统,并进行一些测量,如压力和温度。 您认为系统的特定状态是多大概率? Jaynes建议我们应该假设概率分布,在我们测量条件的约束下,它最大化熵。 (请注意,这个“最大熵原理”比物理学更为普遍!)也就是说,我们应该假设具有最未知信息的可能性。 从这个角度可以得出许多结果。
- (阅读杰恩斯论文的前几节(part 1, part 2) 他们十分易读切让我印象深刻)
-
如果您对这种联系感兴趣但又不想完成论文的原始工作,那么Cover&Thomas中有一个部分可以从马尔可夫链中获得热力学第二定律的统计版本!↩
-
- 信息理论与赌博之间的联系最初是由约翰凯利在他的论文“信息率的新解释”中提出的。 这是一篇非常容易阅读的论文,虽然它需要我们在本文中没有提出的一些想法。
凯利对他的工作有一个有趣的动机。 他注意到熵正在许多成本函数中使用,这些函数与编码信息无关,并且需要一些原则性的原因。 在写这篇文章的时候,我也被同样的事情所困扰,并且非常感谢凯利的工作作为一个额外的视角。 也就是说,我并不觉得它完全令人信服:凯利只是因为他考虑了迭代投注,每次投注重新投入所有资金。 不同的设置不会导致熵。
关于凯利在博彩和信息理论之间联系的一个很好的讨论可以在信息理论的标准参考资料中找到,即Cover&Thomas的“信息理论要素”。↩
-
- 它并没有解决这个问题,但我无法抗拒为KL分歧提供进一步的防御。
有一个结果,盖斯和托马斯称斯坦因的引理,虽然它似乎与通常称为斯坦因引理的结果无关。从高层次来看,它是这样的:
假设您知道某些数据来自两个概率分布中的一个。你有信心确定它来自哪两个分发版?通常,随着获得更多数据点,信心应该呈指数级增长。例如,平均而言,对于看到的每个数据点,你可能会对哪个分布的真实性有1.5倍的信心。
信心增加多少取决于分布的差异。如果它们非常不同,您可能会很快变得自信。但如果它们只是略有不同,那么在你有一个肯定自信的答案之前,你可能需要看到大量的数据。
Stein的Lemma简单地说,乘以的数量是由KL分歧控制的。 (关于假阳性和假阴性之间的权衡有一些微妙之处。)这似乎是关心KL分歧的一个非常好的理由!↩








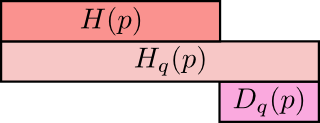
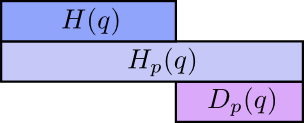
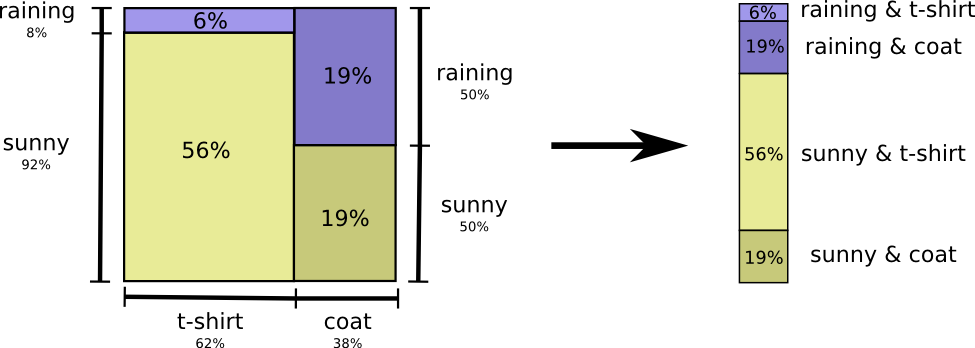
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
