总结
- 【2022-8-26】清华顾险峰数学与AI:AI的拓补几何基础
- 【2020-9-9】流形学习t-SNE,LLE,Isomap
- 【2020-9-19】流形学习前沿方向:隐图学习,Latent graph neural networks: Manifold learning 2.0?

- 【2014-3】NN-Manifolds-Topology
- 【2021-4-25】比如,三维空间的球体是一个二维流形嵌入在三维空间(2D manifold embedded in 3D space)。之所以是二维流形,是因为球上的任意一个点只需要用一个二维的经纬度来表达就可以了。
- 又如一个二维空间的旋转矩阵是2x2的矩阵,其实只需要一个角度就能表达了,这就是一个一维流形嵌入在2x2的矩阵空间。
深度学习里的Embedding?
- Embedding这个概念在深度学习领域最原初的切入点是所谓的Manifold Hypothesis(流形假设)。
- 流形假设是指“自然的原始数据是低维的流形嵌入于(embedded in)原始数据所在的高维空间”。
- 那么,深度学习的任务就是把高维原始数据(图像,句子)映射到低维流形,使得高维的原始数据被映射到低维流形之后变得可分,而这个映射就叫嵌入(Embedding)。比如Word Embedding,就是把单词组成的句子映射到一个表征向量。但后来不知咋回事,开始把低维流形的表征向量叫做Embedding,其实是一种误用
表示学习
- 机器学习的一个分支,复杂非线性问题经过特殊变换后变成简单的线性可分。
流形学习
Embedding(嵌入)
什么是 Embedding
Embedding(嵌入)是拓扑学里面的词,在深度学习领域经常和Manifold(流形)搭配使用。
- 三维空间的球体是一个二维流形嵌入在三维空间(2D manifold embedded in 3D space)。球上的任意一个点只需要用一个二维的经纬度来表达就可以了。
- 一个二维空间的旋转矩阵是2x2的矩阵,其实只需要一个角度就能表达了,这是一维流形嵌入在2x2的矩阵空间。
作者:刘斯坦
Embedding 就是把一个东西映射到一个向量 x。如果两个东西很像,那么得到的向量x1和x2的欧式距离很小。
- 例一:Word Embedding,把单词 w 映射到向量 x。如果两个词的原意接近,比如coronavirus和covid,那么它们映射后得到的两个词向量 x1 和 x2 的欧式距离很小。
- 例二:User Embedding,把用户 ID 映射到向量 x。推荐系统中需要用一个向量表示一个用户。如果两个用户的行为习惯接近,那么他们对应的向量 x1 和 x2 的欧式距离很小。
- 例三:Graph Embedding,把图中的每个节点映射成一个向量 x。如果图中两个节点接近,比如它们的最短路很小,那么它们embed得到的向量 x1 和 x2 的欧式距离很小。
Embedding 作用
Embedding 是一个将离散变量转为连续向量表示的一个方式。在神经网络中,embedding是非常有用的,因为它不光可以减少离散变量的空间维数,同时还可以有意义的表示该变量。
Embedding 有以下 3 个主要目的:
- 在 embedding 空间中查找最近邻,这可以很好的用于根据用户的兴趣来进行推荐。
- 作为监督学习任务的输入。
- 用于可视化不同离散变量之间的关系。
Embedding这个概念在深度学习领域最原初的切入点是所谓的Manifold Hypothesis(流形假设)。
- 流形假设:自然的原始数据是低维的流形嵌入(embedded in)原始数据所在的高维空间”。
- 深度学习的任务就是把高维原始数据(图像,句子)映射到低维流形,使得高维的原始数据被映射到低维流形之后变得可分,而这个映射就叫
嵌入(Embedding)。 - 比如Word Embedding是把单词组成的句子映射到一个表征向量。但后来不知咋回事,开始把低维流形的表征向量叫做Embedding,其实是一种误用。。。如果按照现在深度学习界通用的理解(其实是偏离了原意的),Embedding就是从原始数据提取出来的Feature,也就是那个通过神经网络映射之后的低维向量。
2014年的经典文章:Neural Networks, Manifolds, and Topology
Embedding 可视化
Embedding 最酷的一个地方在于可以用来可视化出表示的数据的相关性,为了便于观察,需要通过降维技术来达到 2 维或 3 维。最流行的降维技术是:t-Distributed Stochastic Neighbor Embedding (TSNE)。
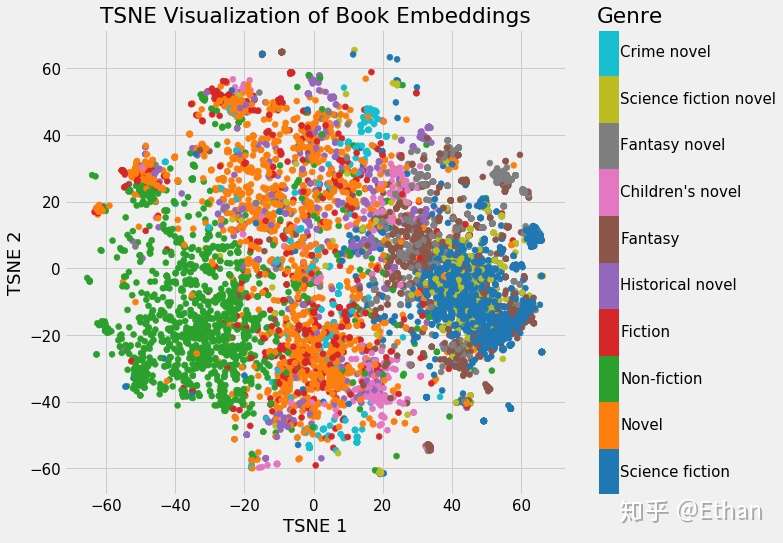
2016年12月,谷歌开源Embedding Projector,可将高维数据可视化
- 一款用于交互式可视化和高维数据分析的网页工具 Embedding Projector,通过PCA,T-SNE等方法将高维向量投影到三维坐标系。
- PCA 通常可以有效地探索嵌入的内在结构,揭示出数据中最具影响力的维度。
- t-SNE 可用于探索局部近邻值(local neighborhoods)和寻找聚类(cluster),可以让开发者确保一个嵌入保留了数据中的所有含义(比如在 MNIST 数据集中,可以看到同样的数字聚类在一起)。
- 自定义线性投影可以帮助发现数据集中有意义的「方向(direction)」,比如一个语言生成模型中一种正式的语调和随意的语调之间的区别——这让我们可以设计出更具适应性的机器学习系统。
- 其作为 TensorFlow 的一部分,能带来类似 A.I. Experiment 的效果。同时,谷歌也在 projector.tensorflow.org 放出了一个可以单独使用的版本,让用户无需安装和运行 TensorFlow 即可进行高维数据的可视化
- 论文, A.I. Experiment, Embedding Projector体验地址,使用介绍
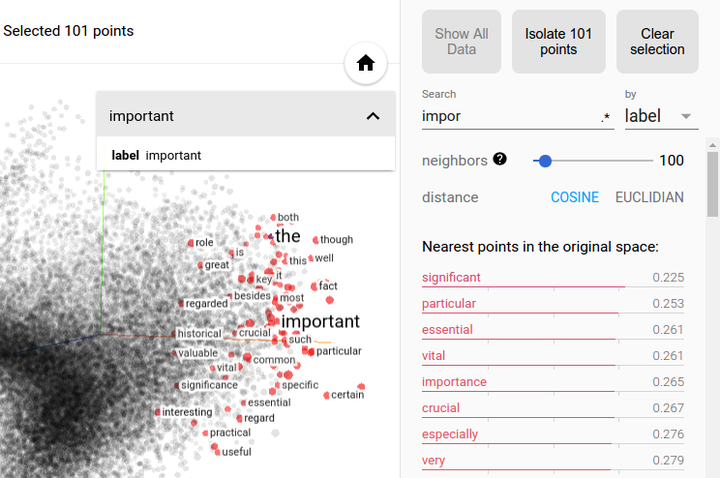
- Label by:可以选择Label和Index,将鼠标放到相应的点上,可以显示该点的Label或者Index
- Color by:可选Label和No color map,前者会根据不同的label给点赋予不同的颜色,后者不涂色,一律为黑白,如图所示。
- 可以根据Label查找某个类,如图,我们可以找到Label为4的点。
- 将projector用于代码:TensorBoard-PROJECTOR-高维向量可视化
import tensorflow as tf
import mnist_inference
import os
from tensorflow.contrib.tensorboard.plugins import projector
from tensorflow.examples.tutorials.mnist import input_data
batch_size = 128
learning_rate_base = 0.8
learning_rate_decay = 0.99
training_steps = 10000
moving_average_decay = 0.99
log_dir = 'log'
sprite_file = 'mnist_sprite.jpg'
meta_file = 'mnist_meta.tsv'
tensor_name = 'final_logits'
#获取瓶颈层数据,即最后一层全连接层的输出
def train(mnist):
with tf.variable_scope('input'):
x = tf.placeholder(tf.float32,[None,784],name='x-input')
y_ = tf.placeholder(tf.float32,[None,10],name='y-input')
y = mnist_inference.build_net(x)
global_step = tf.Variable(0,trainable=False)
with tf.variable_scope('moving_average'):
ema = tf.train.ExponentialMovingAverage(moving_average_decay,global_step)
ema_op = ema.apply(tf.trainable_variables())
with tf.variable_scope('loss_function'):
loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y,labels=tf.argmax(y_,1)))
with tf.variable_scope('train_step'):
learning_rate = tf.train.exponential_decay(
learning_rate_base,
global_step,
mnist.train.num_examples/batch_size,
learning_rate_decay,
staircase=True
)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)
train_op = tf.group(train_step,ema_op)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(training_steps):
xs,ys = mnist.train.next_batch(batch_size)
_,loss_value,step = sess.run([train_op,loss,global_step],feed_dict={x:xs,y_:ys})
if step % 100 == 0 :
print('step:{},loss:{}'.format(step,loss_value))
final_result = sess.run(y,feed_dict={x:mnist.test.images})
return final_result
def visualisation(final_result):
#定义一个新向量保存输出层向量的取值
y = tf.Variable(final_result,name=tensor_name)
#定义日志文件writer
summary_writer = tf.summary.FileWriter(log_dir)
#ProjectorConfig帮助生成日志文件
config = projector.ProjectorConfig()
#添加需要可视化的embedding
embedding = config.embeddings.add()
#将需要可视化的变量与embedding绑定
embedding.tensor_name = y.name
#指定embedding每个点对应的标签信息,
#这个是可选的,没有指定就没有标签信息
embedding.metadata_path = meta_file
#指定embedding每个点对应的图像,
#这个文件也是可选的,没有指定就显示一个圆点
embedding.sprite.image_path = sprite_file
#指定sprite图中单张图片的大小
embedding.sprite.single_image_dim.extend([28,28])
#将projector的内容写入日志文件
projector.visualize_embeddings(summary_writer,config)
#初始化向量y,并将其保存到checkpoints文件中,以便于TensorBoard读取
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
saver.save(sess,os.path.join(log_dir,'model'),training_steps)
summary_writer.close()
def main(_):
mnist = input_data.read_data_sets('MNIST_data',one_hot=True)
final_result = train(mnist)
visualisation(final_result)
if __name__ == '__main__':
tf.app.run()
生成sprite图和meta文件, 便于直接在动态图上看到数据标签
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import os
from tensorflow.examples.tutorials.mnist import input_data
log_dir = './log'
sprite_file = 'mnist_sprite.jpg'
meta_file = 'mnist_meta.tsv'
def create_sprite_image(images):
if isinstance(images,list):
images = np.array(images)
#获取图像的高和宽
img_h = images.shape[1]
img_w = images.shape[2]
#对图像数目开方,并向上取整,得到sprite图每边的图像数目
num = int(np.ceil(np.sqrt(images.shape[0])))
#初始化sprite图
sprite_image = np.zeros([img_h*num,img_w*num])
#为每个小图像赋值
for i in range(num):
for j in range(num):
cur = i * num + j
if cur < images.shape[0]:
sprite_image[i*img_h:(i+1)*img_h,j*img_w:(j+1)*img_w] = images[cur]
return sprite_image
if __name__ == '__main__':
mnist = input_data.read_data_sets('MNIST_data',one_hot=False)
#黑底白字变成白底黑字
to_visualise = 1 - np.reshape(mnist.test.images,[-1,28,28])
sprite_image = create_sprite_image(to_visualise)
#存储展示图像
path_mnist_sprite = os.path.join(log_dir,sprite_file)
plt.imsave(path_mnist_sprite,sprite_image,cmap='gray')
plt.imshow(sprite_image,cmap='gray')
#存储每个下标对应的标签
path_mnist_metadata = os.path.join(log_dir,meta_file)
with open(path_mnist_metadata,'w') as f:
f.write('Index\tLabel\n')
for index,label in enumerate(mnist.test.labels):
f.write('{}\t{}\n'.format(index,label))
执行tensorboard –logdir=log后,浏览器打开localhost:6006,即可观察到相应结果。每个高维向量都被投影到一个三维坐标系中,同一个类别的向量彼此靠近,形成一个一个的簇,且界限明显,可见分类效果较好
t-sne效果较好
摘自:Embedding的理解,英文原文
TensorFlow版本的Embedding实现:(参考:TensorFlow embedding小记)
- embedding_lookup 虽然是随机化地映射成向量,看起来信息量相同,但其实却更加超平面可分
- embedding_lookup 不是简单的查表,id对应的向量是可以训练的,训练参数个数应该是 category num*embedding size,也就是说lookup是一种全连接层。
- word embedding 其实有一个距离定义,即出现在同一上下文的词的词向量距离应该小,这样生成向量比较容易理解。autoencode、pca等做一组基变换,也是假设原始特征值越接近越相似。但id值的embedding应该是没有距离可以定义,没有物理意义,只是一种特殊的全连接层。
- 用embedding_lookup做id类特征embedding由google的deep&wide提出,但隐藏了具体实现细节
- 分类模型中用这种id类特征,主要是希望模型把这个商品记住。但id类特征维度太高,同一个商品的数据量也不大,因此也常常用i2i算法产出的item embedding来替代id特征。
import tensorflow as tf
# embedding矩阵
embeddings = tf.Variable( tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
# 将train_inputs(目标索引/编号)映射为向量
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# 执行
print(sess.run(input_embedding, feed_dict={input_ids:[[1, 2], [2, 1], [3, 3]]}))
pyecharts 可视化
将高维向量通过 t-sne降维,再用pyecharts(1.*以上版本)可视化出来
- t-sne降维
# 原始数据文件格式:[query, 0.23, 0.43, ..., 1.23], 将query嵌入到768的高维空间里
data_file = 'newhouse/all_data_embedding.txt'
#query_vec = pd.read_csv(data_file)
#query_vec
num = 0
n = 769
query_dict = {}
for line in open(data_file):
num += 1
#if num > 50:
# break
arr = line.strip().split(',')
query= arr[0]
vec = arr[1:]
if len(arr) != 769 or not query:
logging.error('格式异常: query={}, len={}, line={}'.format(query,len(arr),arr[:3]))
continue
query_dict[query] = vec
query_list = list(query_dict.values())
query_label = list(query_dict.keys())
print(len(query_dict.keys()))
# ----- t-SNE 降维 -----
import numpy as np
from sklearn.manifold import TSNE
X = np.array(query_list)
#X = np.array([[0,0,0],[0,1,1],[1,0,1],[1,1,1]])
tsne = TSNE(n_components = 3)
tsne.fit_transform(X)
X_new = tsne.embedding_ # 降维后的3维矩阵
print(query_label[10],X_new[10]) # 输出label、降维后的向量
# ----- pca ------
from sklearn.decomposition import PCA
pca=PCA(n_components=3)
- 数据加载、可视化
import random
from pyecharts import options as opts
from pyecharts.charts import Scatter3D
from pyecharts.faker import Faker
# --------- 加载数据 ---------
vec_tsne = np.load('/home/wangqiwen004/work/nlu_data/newhouse/vec_tsne.npy')
vec_label = np.load('/home/wangqiwen004/work/nlu_data/newhouse/vec_label.npy')
vec_label = vec_label.reshape((-1,1)) # label是1维时,需要转换成矩阵,才能拼接
print(vec_label.shape,vec_tsne.shape)
vec_tsne[:3].tolist()
np.hstack((vec_tsne[:3], vec_label[:3]))
# --------- 数据格式化 ---------
#Scatter_data = [(random.randint(0,50),random.randint(0,50),random.randint(0,50)) for i in range(50)]
#Scatter_data = vec_tsne[:10].tolist()
N = 50000
Scatter_data = np.hstack((vec_tsne, vec_label))[:N].tolist()
# --------- 绘图 ---------
c = (
Scatter3D(init_opts = opts.InitOpts(width='1500px',height='900px')) #初始化
.add("句子向量(t-sne)",Scatter_data,
grid3d_opts=opts.Grid3DOpts(
width=100, depth=100, rotate_speed=20, is_rotate=False
))
#设置全局配置项
.set_global_opts(
title_opts=opts.TitleOpts(title="新房驻场客服query分布(部分N={})".format(min(N,vec_label.shape[0]))), #添加标题
visualmap_opts=opts.VisualMapOpts(
max_=50, #最大值
pos_top=50, # visualMap 组件离容器上侧的距离
range_color=Faker.visual_color #颜色映射
)
)
)
c.render("新房驻场客服-query空间关系.html")
#c.render_notebook() # 渲染到jupyter notebook页面
什么是流形学习
流形是拓扑和微分几何中最为基本的概念,本质上就是很多欧氏空间粘贴在一起构成的空间。
-
一个流形(manifold)是一个拓扑空间
- 什么是
流形学习?传统的机器学习方法中,数据点之间的距离和映射函数f都是定义在欧式空间中的,然而在实际情况中,这些数据点可能不是分布在欧式空间中的,因此传统欧式空间的度量难以用于真实世界的非线性数据,从而需要对数据的分布引入新的假设。流形(Manifold)是局部具有欧式空间性质的空间,包括各种纬度的曲线曲面,例如球体、弯曲的平面等。流形是线性子空间的一种非线性推广。参考流形学习的简单介绍 流形学习:本质上,流形学习就是给数据降维的过程。这里假设数据是一个随机样本,采样自一个高维欧氏空间中的流形(manifold),流形学习的任务就是把这个高维流形映射到一个低维(例如2维)的空间里。流形学习可以分为线性算法和非线性算法,前者包括主成分分析(PCA)和线性判别分析(LDA),后者包括等距映射(Isomap),拉普拉斯特征映射(LE)等。流形学习可以用于特征的降维和提取,为后续的基于特征的分析,如聚类和分类,做铺垫,也可以直接应用于数据可视化等。注:摘自集智百科流形学习(优质,包含代码及案例)。- 拟合线性的流形学习模型:LLE, LTSA, Hessian LLE, 和Modified LLE
- 拟合非线性的流形学习模型:Isomap,MDS和Spectral Embedding
- 效果示意如下:

- 浙大何晓飞的流形学习ppt,讲的很清楚,全面,最佳资料
流形学习与深度学习
Neural Networks, Manifolds, and Topology,中文翻译版:神经网络、流形和拓扑
- 一个双曲正切层tanh(Wx+b)由以下组成:
- 1、由“权重”矩阵W的线性变换;
- 2、由矢量b的转换;
- 3、双曲正切函数的逐点应用。
- 连续变换如下图:
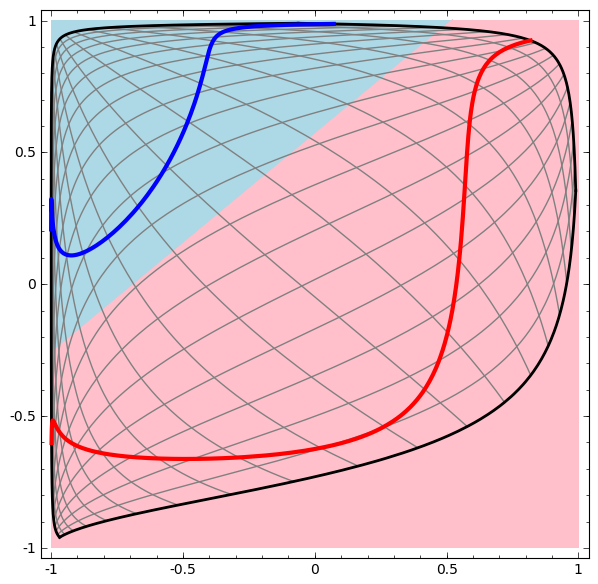
- 更复杂的网络,4个隐含层网络,“原始”表示转移到更高层次为了对数据进行分类。而螺旋最初是纠结的,最终他们是线性可分的。
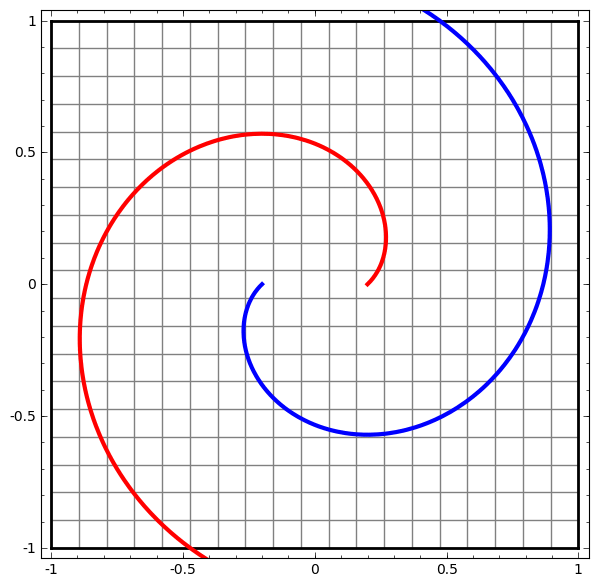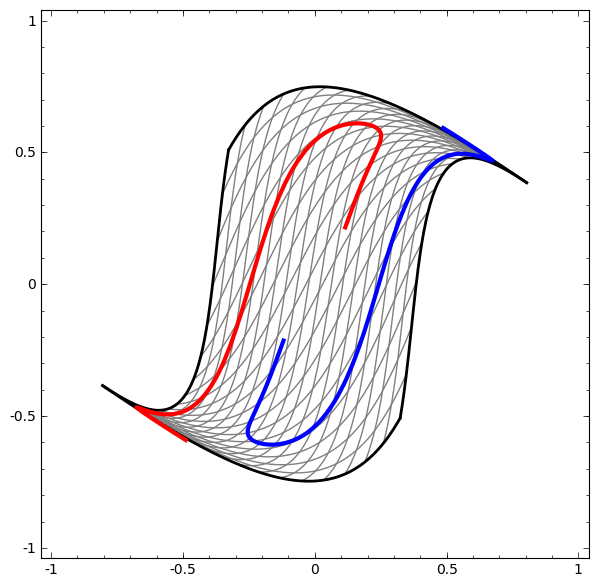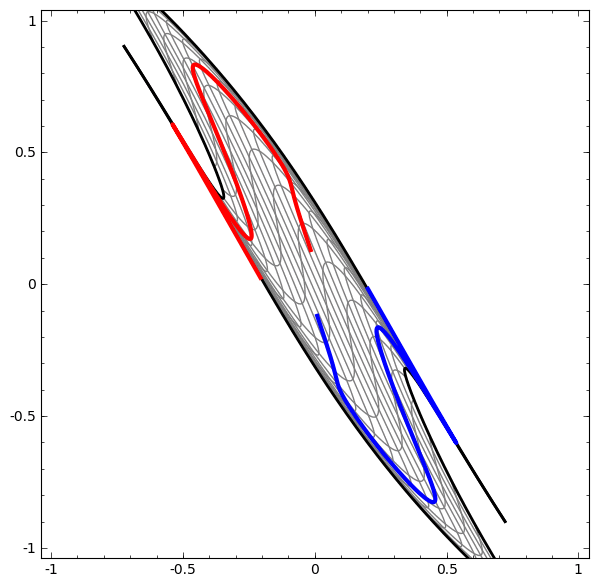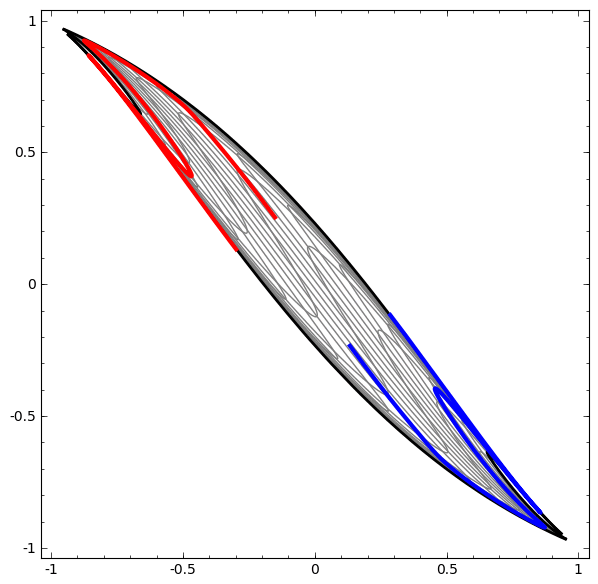
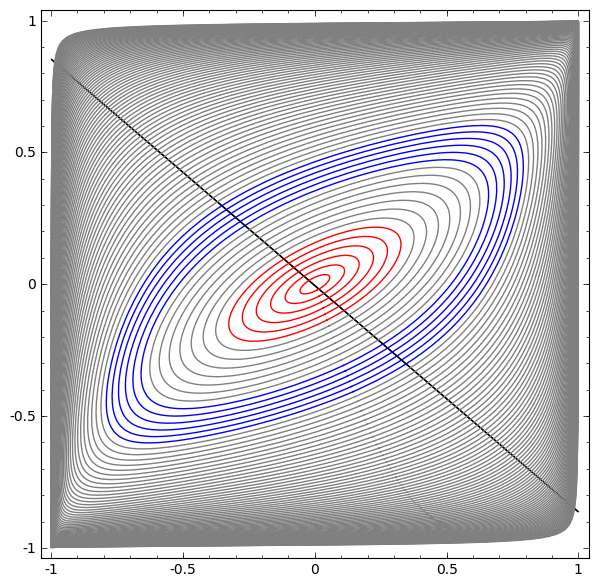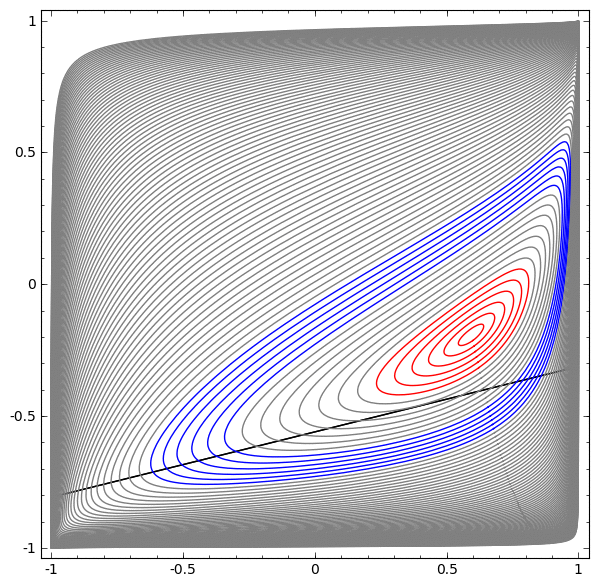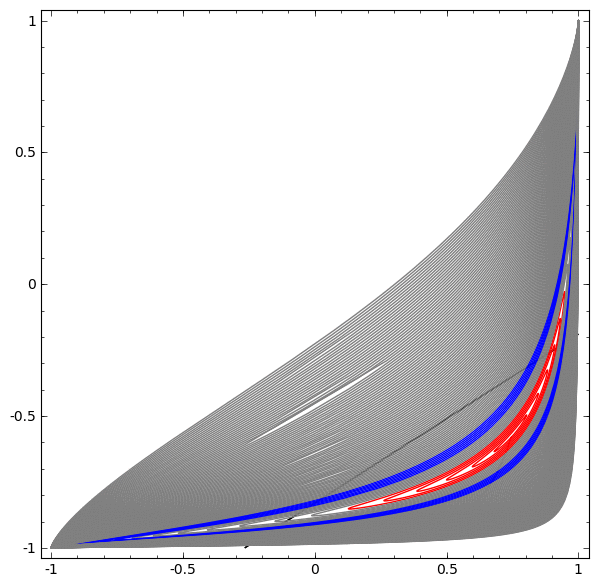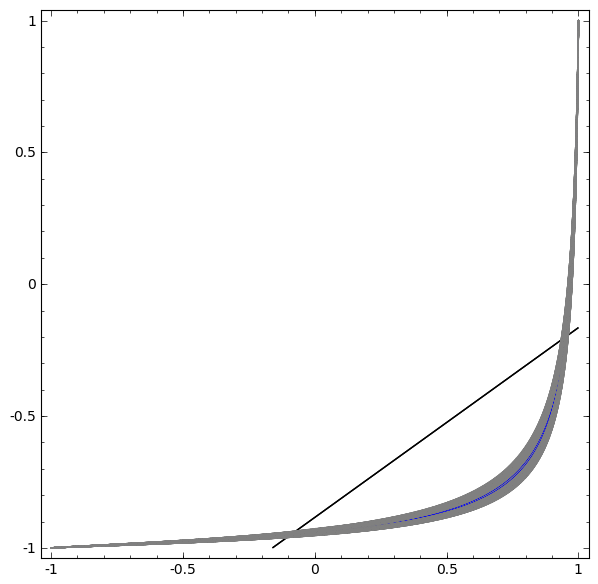
- 更多动图可视化见:Andrej Karpathy有很好的演示基于ConvnetJS,让您可以交互式地浏览网络
- 双曲正切层的拓扑
- 每一层都会拉伸和挤压空间,但永远不会切割、断裂和褶皱它。直观地说,tanh保留了拓扑性质。例如,一组数据将在转化后依然保持连接状态。
- 定理:具有N个输入和N个输出的层是同胚,如果权重矩阵W是非奇异的
这样的转换,不影响拓扑结构,被称为同胚。在形式上,他们是连续函数的双向映射。
作者:树石
【2022-8-26】数学与AI:AI的拓补几何基础
- 从几何角度而言,深度学习本质上是在学习高维背景空间中低维数据流形上的概率分布。
- 流形结构的学习基于
Whitney流形嵌入理论,由编码解码器来万有逼近; - 概率分布的学习依赖于
最优传输理论,在Wasserstein空间中做变分优化;
深度学习的成功是基于两条:
- 数据本身的内在规律
- 深度学习技术能够揭示并利用这些规律。
数据科学(或者信息科学)中的基本定律(或者更为保守的,基本假设)可以归结为:
流形分布定律:自然界中同一类别的高维数据,往往集中在某个低维流形附近。聚类分布定律:这一类别中不同的子类对应着流形上的不同概率分布,这些分布之间的距离大到足够将这些子类区分。
目前深度学习模型设计有内在缺陷,基本问题不可避免,例如模式坍塌。我们基于最优传输理论的几何观点,揭示模式坍塌的根本原因,提出基于几何变分的学习模型,提高计算准确性、稳定性和效率。
Manifold Distribution Principle(流形分布定则)
- Helmholtz Hypothesis (亥姆霍兹假设)
- 深度学习究竟在学什么?在脑神经科学中,有许多研究成果,其中一个叫做Helmholtz假设。这是说人类视觉中枢通过观看自然界的各种景象会产生相应的概念,这些概念都被记录在特定的神经元之中,从而形成某种表示。
- 数学语言:人脑视觉中的每个概念都可以归结于物理世界中的一个数据集,不同的概念实际上对应着不同的概率分布。
- 深度学习的第一步就是将这个曲面打到二维平面上,把每一个图像变成一个特征向量,从而实现了降维。深度学习所学习的概念最终是由概率统计的语言来描述的,某种特定的概率分布,这个概率分布是定义在高维背景空间中的某个低维数据流形上面的。
- Low Dimensional Example (低维算例)
- 假设二维弥勒佛曲面嵌入在三维欧氏空间之中,曲面上存在一个均匀分布。对于深度学习而言,第一步就要实现降维,计算由三维曲面到二维平面的映射。
- 降维的过程被称为编码,逆过程被称为解码。两种编码映射都将弥勒佛曲面映到平面单位圆盘上。第一种是基于黎曼映照的保角变换,第二种是基于最优传输的保面元映射。
- 深度学习的终极目的:第一是学会模型的拓扑结构,实现降维并将其映射到特征空间上;第二要保留数据流形上本来的概率分布,在特征空间上的概率分布保持原来流形上的真实分布。
- Central Tasks for DL (深度学习的中心任务)深度学习究竟想学什么?主要是有两个中心任务:
- (1)数据流形的拓扑结构
- (2)数据流形上的概率分布
- Generative Model Framework (生成模型的框架)
- 上行中,
编码映射将手写体数字流形映射到特征空间,将流形上的概率分布映射到隐空间上的概率分布;解码映射将隐空间映回数据流形。 - 下行中,
最优传输映射将长方形内的均匀分布映射到隐空间中的数据分布,这里最优传输映射是某一凸函数的梯度映射,此凸函数被称为是Brenier势能。
- Whitney Manifold Embedding(Whitney流形嵌入)
- Whitney流形定理是说任意给一个m维拓扑流形,我们可以将其嵌入在欧式空间中,欧氏空间的维数大约是流形维数的两倍。现在很多深度学习的算法本质上就是Whitney定理的实现。Whitney定理的证明需要先用一族开集覆盖流形,将每个开集嵌入到欧氏空间,然后用所谓的单位分解把局部嵌入整体粘起来得到一个全局嵌入。这时嵌入空间的维数等于流形的维数乘以开集的个数,我们在将嵌入的流形依次向低维线性子空间投影,直至无法进一步投影,这时子空间的维数等于流形维数的两倍。
- Universal Approximation(万有逼近)
- 深度神经网络具有万有逼近的性质,即只要给定一个连续映射,给定任意的逼近精度,都存在某个深度神经网络来进行逼近。这个性质的理论基础实际上是来自Hilbert 第13问题:任意一个多变元的连续函数,都可以由两个单变元函的有限复合以任意精度来逼近。我们可以看到深度学习的逼近理论大多是基于这个定理。
流形假设
- Manifold Hypothesis(
流形假设)- 流形假设:“自然的原始数据是低维的流形嵌入于(embedded in)原始数据所在的高维空间”
- 深度学习就是把高维原始数据(图像,句子)映射到低维流形,使得高维的原始数据被映射到低维流形之后变得可分,而这个映射就叫嵌入(Embedding)。如Word Embedding把单词组成的句子映射到一个表征向量。但后来把低维流形的表征向量叫做Embedding,其实是一种误用。
- Embedding就是从原始数据提取出来的Feature,也就是那个通过神经网络映射之后的低维向量。
-
流形学习假设所有处于高维空间的数据点都分布在一个低维的流形上。流形学习的目的就在于寻找一种映射,从高维空间中恢复出低维流形来,从而利用流形的低维坐标表示高位空间的数据点,实现数据降维的目的。常用的算法有
Isomap,LLE(Locally Linear Embedding),LE(Laplacian Eigenmaps),LLP(Locality Preserving Projection)等 - 虽然有一些维度缩减的变体是有监督的(例如线性/二次判别分析),流形学习通常指的是无监督的降维,其中类别没有提供给算法(虽然可能存在)
-
-
降维的目的在于寻找数据的“内在变量”,如图,丢弃掉数据之间你的公共信息(“A”的形状),发掘数据之间的变化信息(缩放尺度及旋转角度)。由于缩放尺度与旋转角度并非是线性分布的,因此更适合采用非线性降维方法。

- 什么是流形?manifold
- 瑞士卷一个是二维流形的例子.简而言之,二维流形是一种二维形状,它可以在更高维空间中弯曲或扭曲。
VC维
- VC维与模型复杂度、样本复杂度
- 物理意义:将假设集合的数量|H|比作假设集合的自由度,那么VC维就是假设集合在做二元分类的有效的自由度,即这个假设空间能够产生多少Dichotomies的能力(VC维说的是,到什么时候,假设集合还能shatter,还能产生最多的Dichotomies)
- 假设空间的容量越大,VC维越大,那么模型就越难学习
- VC维来龙去脉
- 如何通俗的理解机器学习中的VC维、shatter和break point?
学习VC维要先知道的概念有:增长函数(growth function)、对分(dichotomy)、打散(shattering)和断点(break point)
-
- 增长函数
- 增长函数表示假设空间H对m个示例所能赋予标记的最大可能结果数。
- 比如说现在数据集有两个数据点,考虑一种二分类的情况,可以将其分类成A或者B,则可能的值有:AA、AB、BA和BB,所以这里增长函数的值为4.
- 增长函数值越大则假设空间H的表示能力越强,复杂度也越高,学习任务的适应能力越强。不过尽管H中可以有无穷多的假设h,但是增长函数却不是无穷大的:对于m个示例的数据集,最多只能有2^m个标记结果,而且很多情况下也达不到2^m的情况。
- 增长函数
-
- 对分
- 对于二分类问题来说,H中的假设对D中m个示例赋予标记的每种可能结果称为对D的一种对分(dichotomy)。对分也是增长函数的一种上限。
- 对分
-
- 打散
- 打散指的是假设空间H能实现数据集D上全部示例的对分,即增长函数=2^m。但是认识到不打散是什么则更加重要
- 打散
-
- 断点
- 假设空间H的VC维数就是最大的非break point值,也就是break point-1
- 断点
- Vapink-Chervonenkis Dimension
- 引出VC维的定义了:假设空间H的VC维是能被H打散的最大的示例集(数据集)的大小
- 或:
- 对于一个假设空间H,如果存在m个数据样本能够被假设空间H中的函数按所有可能的2^h种形式分开 ,则称假设空间H能够把m个数据样本打散(shatter)。假设空间H的VC维就是能打散的最大数据样本数目m。若对任意数目的数据样本都有函数能将它们shatter,则假设空间H的VC维为无穷大
为什么要降维
目的:
- 加快后续训练算法(在某些情况下甚至可能去除噪声和冗余功能,使训练算法执行更好)。
- 可视化数据。
- 节省空间(压缩)
带来的问题
- 丢失了一些信息,可能会降低后续性能训练算法。
- 可能是计算密集型的
- 为机器学习流程增加了一些复杂性。
- 转换的过程通常难以解释。
降维可逆吗?
- 一些算法(如PCA)具有简单的逆向变换过程可以重建与原始数据相对类似的数据集
- 某些降维算法则没有逆变换的方法(如T-SNE)。
主要方法
降低维度的两种主要方法:投影和流形学习。
投影
- 适合所有训练实例实际上位于(或接近)高维空间的低维子空间内,这样就可以采用投影的降维方法。
- 如分布接近于2D子空间的3D数据集一个分布接近于2D子空间的3D数据集
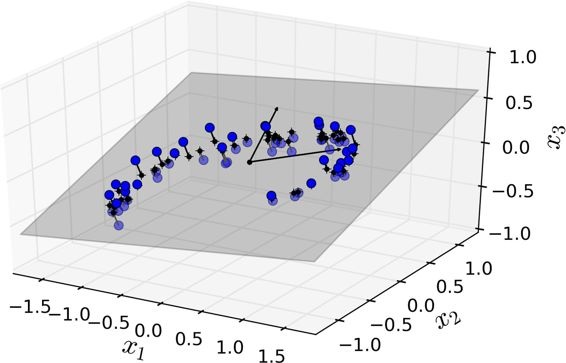
- 但是,投影并不总是降维的最佳方法。在很多情况下,子空间可能会扭曲和转动,如瑞士卷型数据集,S形分布
PCA
- 代表示例:PCA系列(SVD分解),如:增量 PCA,随机 PCA,核PCA(非线性投影,如RBF核的kPCA)
选哪种pca?
- 常规PCA是首选,仅当数据集适合内存时才有效。
- 增量PCA对于不适合内存的大型数据集很有用,但速度较慢比普通PCA,所以如果数据集适合内存,应该选择常规PCA。当需要时,增量PCA对在线任务也很有用。每当新实例到达时,PCA即时运行。
- 随机PCA:当想要大大降低维度并且数据集适合内存时,它比普通PCA快得多。
-
最后,核PCA是对非线性数据集很有用。
- PCA可以显著降低大多数数据集的维数,甚至是高度非线性的数据集,因为它可以消除无用特征(维度)的干扰。但是,如果没有无用的特征(维度),例如瑞士数据集卷,那么使用PCA降低维度会丢失太多信息。你想要展开瑞士卷,而不是挤压它
代码
from sklearn.decomposition import PCA
pca=PCA(n_components=2) # 指定主成分数目
#pca=PCA(n_components=0.95) # 指定累计贡献率
X2D=pca.fit_transform(X)
# 访问主成分
pca.components_.T[:,0]
# 方差解释率
print(pca.explained_variance_ratio_) # array([0.84248607, 0.14631839])
# 应用到新数据
X_reduced=pca.fit_transform(X)
#------ 核pca ------
from sklearn.decomposition import KernelPCA
rbf_pca=KernelPCA(n_components=2,kernel='rbf',gamma=0.04)
X_reduced=rbf_pca.fit_transform(X)
无监督学习的核pca如何调参?
- 使用 kPCA 将维度降至低维维,然后应用 Logistic 回归进行分类。然后使用 Grid SearchCV 为 kPCA 找到最佳的核和 gamma 值,以便在最后获得最佳的分类准确性.(引入模型,以最优化模型表现调参)
参考:机器学习算法(降维)总结及sklearn实践——主成分分析(PCA)、核PCA、LLE、流形学习
LLE
LLE:局部线性嵌入(Locally Linear Embedding)是一种非常有效的非线性降维(NLDR)方法。测量每个训练实例与其最近邻(c.n.)之间的线性关系,然后寻找能最好地保留这些局部关系的训练集的低维表示,擅长展开扭曲的流形。
代码:
from sklearn.manifold import LocallyLinearEmbedding
lle=LocallyLinearEmbedding(n_components=2,n_neighbors=10)
X_reduced=lle.fit_transform(X)
t-SNE
t-SNE是最广泛使用的可视化技术之一,但其性能在大型数据集中会受到影响。
- t-SNE映射是可逆的连续双射,即拓扑同胚。
UMAP
【2022-1-15】
PCA和tSNE,但是这二者都存在一些问题,
- PCA的速度相对很快,但代价是数据缩减后会丢很多底层的结构信息;
- tSNE可以保留数据的底层结构,但速度非常慢;
UMAP是McInnes等人的一项新技术。与t-SNE相比,它具有许多优势,最显著的是提高了速度并更好地保存了数据的全局结构。
- 例如,UMAP可以在3min之内处理完784维,70000点的MNIST数据集,但是t-SNE则需要45min。
- 此外,UMAP倾向于更好地保留数据的全局结构,这可以归因于UMAP强大的理论基础。
- 相对于t-SNE,其主要特点:降维快准狠
UMAP和t-SNE对一套784维Fashion MNIST高维数据集降维到3维的效果的比较。高清3D图

- 虽然这两种算法都表现出强大的局部聚类并将相似的类别分组在一起,但UMAP害将这些相似类别的分组彼此分开。另外,UMAP降维用了4分钟,而多核t-SNE用了27分钟。
UMAP是2018年被提出的降维和可视化算法,它使用Uniform流形近似和投影(UMAP),既可以获得PCA的速度优势,同时还可以保留尽可能多的数据信息,而且其可视化效果也非常美观。UMAP在很多竞赛中也得到了广泛应用,比如在高维数据集中更快更准确的进行异常值检测。
Uniform Manifold Approximation and Projection (UMAP,统一流形近似和投影) 是一种降维技术,它不仅可以进行降维,而且可用于可视化,类似于t-SNE,也可用于一般非线性降维。UMAP基于对数据的三个假设
- 数据均匀分布在黎曼流形上(Riemannian manifold);
- 黎曼度量是局部const(或可以近似为局部const);
- 流形是局部连接的 根据这些假设,可以用模糊拓扑结构对流形进行建模。UMAP的优点包括:
- 速度很快,相较于tSNE等快了非常多;
- 因为保留了尽可能多的数据信息,其可视化效果更好;
- 还可以用于异常检测等; 但UMAP的问题在于RAM消耗可能有些大。尤其是在装配和创建连接图等图表时,UMAP会消耗大量内存。
常用参数
umap包继承了sklearn类,因此与其他具有相同调用API的sklearn转换器紧密地放在一起。UMAP主要参数
- n_neighbors:这决定了流形结构局部逼近中相邻点的个数。更大的值将导致更多的全局结构被保留,而失去了详细的局部结构。一般来说,这个参数应该在5到50之间,10到15是一个合理的默认值。
- min_dist: 这控制了嵌入的紧密程度,允许压缩点在一起。数值越大,嵌入点分布越均匀;数值越小,算法对局部结构的优化越精确。合理的值在001到0.5之间,0.1是合理的默认值。
- n_components:作为许多scikit学习降维算法的标准,UMAP提供了一个n_components参数选项,允许用户确定将数据嵌入的降维空间的维数。与其他一些可视化算法(如t-SNE)不同,UMAP在嵌入维度上具有很好的伸缩性,因此您可以使用它进行二维或三维的可视化。
- metric: 这决定了在输入空间中用来测量距离的度量的选择。已经编写了各种各样的度量标准,用户定义的函数只要经过numba的JITd处理就可以传递。
UMAP中两个最常用的参数:n_neighbors 和min_dist,它们可有效地用于控制最终结果中局部结构和全局结构之间的平衡。
- n_neighbors 近似最近邻居数。它有效地控制了UMAP局部结构与全局结构的平衡,数据较小时,UMAP会更加关注局部结构,数据较大时,UMAP会趋向于代表大图结构,丢掉一些细节。
- min_dist 点之间的最小距离。此参数控制UMAP聚集在一起的紧密程度,数据较小时,会更紧密。较大的值会更松散,而将重点放在保留广泛的拓扑结构上。

代码实践
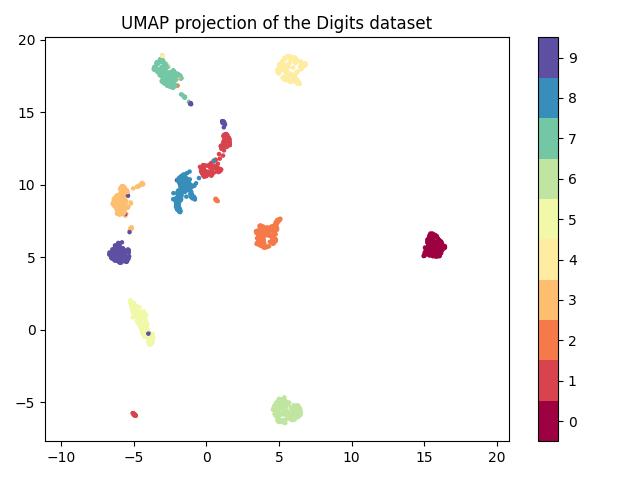
- 以sklearn内置的Digits Data这个数字手写识别数据库为例
# 安装:pip install umap-learn
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
digits = load_digits()
fig, ax_array = plt.subplots(20, 20)
axes = ax_array.flatten()
for i, ax in enumerate(axes):
ax.imshow(digits.images[i], cmap='gray_r')
plt.setp(axes, xticks=[], yticks=[], frame_on=False)
plt.tight_layout(h_pad=0.5, w_pad=0.01)
plt.show()
- 用umap降至2维并绘制散点图
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import umap
import numpy as np
digits = load_digits()
reducer = umap.UMAP(random_state=42)
embedding = reducer.fit_transform(digits.data)
print(embedding.shape)
plt.scatter(embedding[:, 0], embedding[:, 1], c=digits.target, cmap='Spectral', s=5)
plt.gca().set_aspect('equal', 'datalim')
plt.colorbar(boundaries=np.arange(11) - 0.5).set_ticks(np.arange(10))
plt.title('UMAP projection of the Digits dataset')
plt.show()
import umap
import umap.plot
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import QuantileTransformer
# 可视化
pipe = make_pipeline(SimpleImputer(), QuantileTransformer())
X_processed = pipe.fit_transform(X)
manifold = umap.UMAP().fit(X_processed, y)
umap.plot.points(manifold, labels=y, theme="fire")
# 和IsolationForest一起做异常检测
from sklearn.ensemble import IsolationForest
pipe = make_pipeline(SimpleImputer(), QuantileTransformer(), umap.UMAP(n_components=5))
X_processed = pipe.fit_transform(X)
# Fit IsolationForest and predict labels
iso = IsolationForest(n_estimators=500, n_jobs=9)
labels = iso.fit_predict(X_processed)
UMAP不足:
- 宽而稀疏的cluster中有密集的cluster。UMAP无法分离两个嵌套的群集,尤其是在维数较高时。

- UMAP在初始图形构造中局部距离的使用可以解释该算法无法处理情况的原因。由于高维点之间的距离趋于非常相似(维数的诅咒),所以可能会因此将其混合在一起。
维度诅咒
介绍
介绍所谓的“维度诅咒”,并解释在设计分类器时的重要性。为了直观理解这个概念,从一个维数诅咒导致过度拟合的例子开始。
一组图像,每个图像描绘一只猫或一只狗。创建一个能够自动区分狗和猫的分类器。
- 首先考虑可以用数字表示的每个对象类的描述符,使用这些数字来识别对象。
- 例如,猫和狗的颜色通常不同。区分这两个类的可能描述符可以由三个数组成; 图像的平均红色,平均绿色和平均蓝色。
一个简单的线性分类器可以线性组合这些特征,决定类标签:
- If 0.5red + 0.3green + 0.2*blue > 0.6 :
- return cat;
- else return dog;
然而,这三种颜色描述数字(特征)显然不足以获得完美的分类。因此,添加图像纹理特征,例如通过计算X和Y方向的平均边缘或梯度强度。
现在有5个特征组合在一起,可以通过分类算法来区分猫和狗。
为了分类更准确,根据颜色或纹理直方图,统计矩等添加更多功能。也许通过定义几百个这些功能来获得完美分类?听起来有点违反直觉:不,不能!。
事实上,某点之后,通过添加新特征增加问题的维度,实际上会降低分类器的性能,通常称为“维度诅咒”。
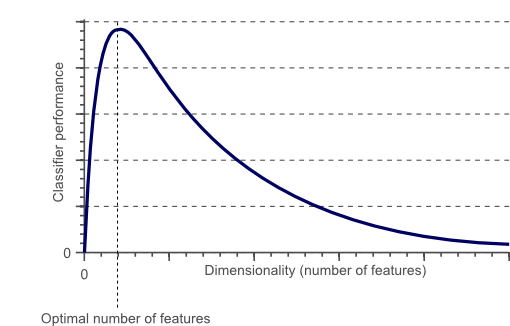
- 特征维度与分类器性能
- 随着维度的增加,分类器的性能先提高,直到达到最佳,接着增加维度,不增加训练样本的数量,反而导致分类器性能降低。
维度和过度拟合的诅咒
在早先介绍的猫和狗的例子中,假设有无数的猫和狗生活在星球上。然而,由于有限的时间和处理能力,我们只能获得10张猫狗照片。然后,分类的最终目标是基于这10个训练实例训练分类器,该分类器能够正确地分类不了解的无限数量的狗和猫实例。
现在用一个简单的线性分类器,并尝试获得一个完美的分类。从一个特征开始,例如图像中的平均“红色”颜色:

- 一维分类问题,单个功能不会导致我们的训练数据完美区分。
如果仅使用单个特征,则无法获得完美的分类结果。因此,可能决定添加另一个特征,例如图像中的平均“绿色”颜色:

- 二维分类问题
- 添加第二个特征仍然不会导致线性可分的分类问题:在此示例中,没有一条线可以将所有猫与所有狗分开。
最后,添加第三个特征,例如图像中的平均“蓝色”颜色,从而产生三维特征空间:

- 3D分类问题
- 示例中,添加第三个特征会导致线性可分的分类问题。存在一种将狗与猫完美分开的平面。
在三维特征空间中,我们现在可以找到一个完美地将狗与猫分开的平面。这意味着可以使用这三个特征的线性组合来获得10幅图像的训练数据的完美分类结果:
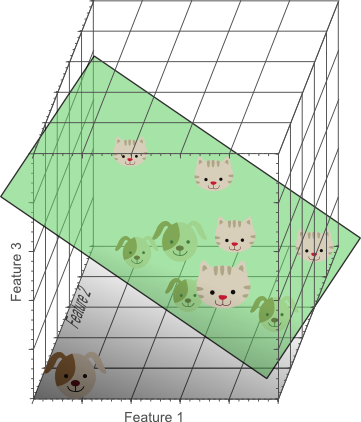
- 线性可分的分类问题
- 我们使用的特征越多,我们成功区分类的可能性就越高。
上面的插图似乎表明,在获得完美的分类结果之前增加特征的数量是训练分类器的最佳方式,而在引言中,如图1所示,我们认为情况并非如此。但是,请注意当我们增加问题的维数时,训练样本的密度如何呈指数下降。
在1D情况下(图2),10个训练实例覆盖了完整的1D特征空间,其宽度为5个单位间隔。因此,在1D情况下,样品密度为10/5 = 2个样品/间隔。然而,在二维情况下(图3),我们仍然有10个训练实例,现在覆盖了一个面积为5×5 = 25个单位正方形的2D特征空间。因此,在2D情况下,样品密度为10/25 = 0.4个样品/间隔。最后,在3D情况下,10个样本必须覆盖5x5x5 = 125个单位立方体的特征空间体积。因此,在3D情况下,样品密度为10/125 = 0.08个样品/间隔。
如果继续添加特征,则特征空间的维度会增长,并变得更稀疏和稀疏。由于这种稀疏性,找到可分离的超平面变得更加容易,因为当特征的数量变得无限大时,训练样本位于最佳超平面的错误侧的可能性变得无限小。但是,如果我们将高维分类结果投影回较低维空间,则与此方法相关的严重问题变得明显:

- 过度拟合
- 使用太多特征会导致过度拟合。分类器开始学习特定于训练数据的异常,并且在遇到新数据时不能很好地概括。
显示了投影到2D特征空间的3D分类结果。尽管数据在3D空间中是线性可分的,但在较低维度的特征空间中却不是这种情况。实际上,添加第三维以获得完美的分类结果,简单地对应于在较低维特征空间中使用复杂的非线性分类器。因此,分类器学习我们的训练数据集的特例和异常。因此,生成的分类器将在真实世界数据上失败,包括通常不遵守这些异常的无限量的看不见的猫和狗。
这个概念被称为过度拟合,是维度诅咒的直接结果。图7显示了仅使用2个特征而不是3个特征训练的线性分类器的结果:

- 线性分类器,图7.尽管训练数据未被完美分类,但该分类器在看不见的数据上比图5中的数据获得更好的结果。
具有决策边界的简单线性分类器似乎比图5中的非线性分类器表现更差,但是这个简单的分类器更好地概括了看不见的数据,因为它没有学习仅在我们的训练数据中的特定异常。巧合。换句话说,通过使用较少的特征,避免了维数的诅咒,使得分类器不会过度拟合训练数据。
下面的解释非常经典
图8以不同的方式说明了上述内容。假设我们想要仅使用一个值为0到1的单个特征来训练分类器。让我们假设这个特征对于每只猫和狗都是唯一的。如果我们希望我们的训练数据覆盖此范围的20%,那么所需的训练数据量将占整个猫狗数量的20%。现在,如果我们添加另一个特征,生成2D特征空间,事情会发生变化; 为了覆盖20%的2D特征范围,我们现在需要在每个维度中获得猫和狗总数的45%(0.45 ^ 2 = 0.2)。在3D情况下,这变得更糟:要覆盖20%的3D特征范围,我们需要在每个维度中获得总数的58%(0.58 ^ 3 = 0.2)。
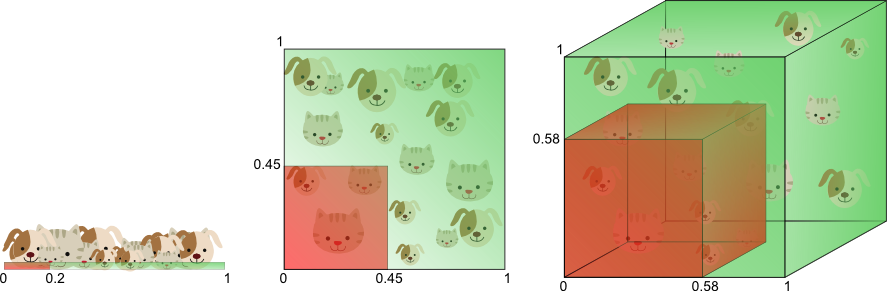
- 训练数据量随着维度的数量呈指数增长
- 覆盖20%特征范围所需的训练数据量随着维度的数量呈指数增长。
换句话说,如果可用的训练数据量是固定的,那么如果我们继续添加维度就会发生过度拟合。另一方面,如果我们不断增加维度,训练数据量需要以指数级增长,以保持相同的覆盖范围并避免过度拟合。
在上面的例子中,我们展示了维度的诅咒引入了训练数据的稀疏性。我们使用的特征越多,数据就越稀疏,因此准确估计分类器的参数(即其决策边界)变得更加困难。维度诅咒的另一个影响是,这种稀疏性不是均匀分布在搜索空间上。实际上,原点周围的数据(在超立方体的中心)比搜索空间的角落中的数据要稀疏得多。这可以理解如下:
想象一个代表2D特征空间的单位正方形。特征空间的平均值是该单位正方形的中心,距离该中心单位距离内的所有点都在一个单位圆内,该单位圆内接单位正方形。不属于该单位圆的训练样本更靠近搜索空间的角落而不是其中心。这些样本难以分类,因为它们的特征值差异很大(例如,单位正方形的相对角上的样本)。因此,如果大多数样本落在内接单位圆内,则分类更容易,如图9所示:

- 单位距离平均单位圆内的特征
- 位于单位圆外的训练样本位于特征空间的角落,并且比特征空间中心附近的样本更难分类。
现在一个有趣的问题是,当我们增加特征空间的维数时,圆(超球面)的体积如何相对于正方形(超立方体)的体积发生变化。尺寸d的单位超立方体的体积总是1 ^ d = 1. 尺寸d和半径0.5 的内切超球体的体积可以计算为:
$V(d)=\frac{\pi^{d / 2}}{\Gamma\left(\frac{d}{2}+1\right)} 0.5^{d}$
图10显示了当维度增加时,这个超球体的体积如何变化:
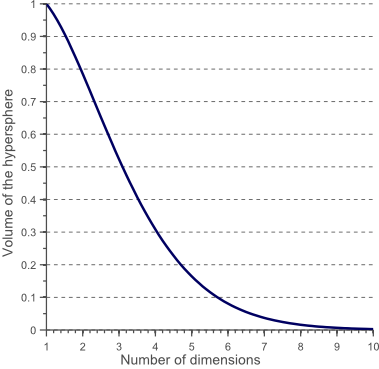
- 随着维度的增加,超球体的体积趋向于零
- 随着维数的增加,超球面的体积趋向于零。
则
这表明,当维数趋于无穷大时,超球体的体积倾向于零,而周围超立方体的体积保持不变。这种令人惊讶且相当反直觉的观察部分地解释了与分类中的维度诅咒相关的问题:在高维空间中,大多数训练数据驻留在定义特征空间的超立方体的角落中。如前所述,特征空间角落中的实例比超球面质心周围的实例更难分类。这由图11示出,其示出了2D单位正方形,3D单位立方体以及具有2 ^ 8 = 256个角的8D超立方体的创造性可视化:
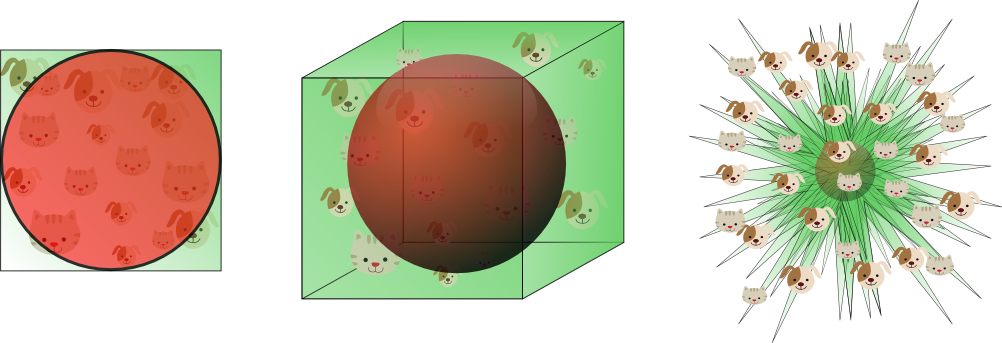
- 高维特征空间在其原点周围稀疏
- 随着维度的增加,更大比例的训练数据驻留在要素空间的角落中。
对于8维超立方体,大约98%的数据集中在其256个角上。因此,当特征空间的维数变为无穷大时,从样本点到质心的最小和最大欧几里得距离的差值与最小距离本身的比率趋向于零:
$\lim_{d \rightarrow \infty} \frac{\text { dist }{\max}-\text { dist }{\min }}{\text { dist }_{\min }} \rightarrow 0$
因此,距离测量开始失去其在高维空间中测量不相似性的有效性。由于分类器依赖于这些距离测量(例如欧几里德距离,马哈拉诺比斯距离,曼哈顿距离),因此在较低维空间中分类通常更容易,其中较少特征用于描述感兴趣对象。类似地,高斯似然性在高维空间中变为平坦且重尾的分布,使得最小和最大似然之间的差异与最小似然本身的比率趋于零。
如何避免维数的诅咒?
图1显示,当问题的维数变得太大时,分类器的性能会降低。那么问题是“太大”意味着什么,以及如何避免过度拟合。遗憾的是,没有固定的规则来定义在分类问题中应该使用多少特征。实际上,这取决于可用的训练数据量(特征的数量和样本数量有关),决策边界的复杂性以及所使用的分类器的类型。
如果理论无限数量的训练样本可用,则维度的诅咒不适用,我们可以简单地使用无数个特征来获得完美的分类。训练数据的大小越小,应使用的特征越少。如果N个训练样本足以覆盖单位区间大小的1D特征空间,则需要N ^ 2个样本来覆盖具有相同密度的2D特征空间,并且在3D特征空间中需要N ^ 3个样本。换句话说,所需的训练实例数量随着使用的维度数量呈指数增长。
此外,倾向于非常准确地模拟非线性决策边界的分类器(例如,神经网络,KNN分类器,决策树)不能很好地推广并且易于过度拟合。因此,当使用这些分类器时,维度应该保持相对较低。如果使用易于推广的分类器(例如朴素贝叶斯线性分类器),那么所使用的特征的数量可以更高,因为分类器本身不那么具有表现力(less expressive)。图6显示在高维空间中使用简单分类器模型对应于在较低维空间中使用复杂分类器模型。
因此,当在高维空间中估计相对较少的参数时,以及在较低维空间中估计大量参数时,都会发生过度拟合。例如,考虑高斯密度函数,由其均值和协方差矩阵参数化。假设我们在3D空间中操作,使得协方差矩阵是由3个独特元素组成的3×3对称矩阵(对角线上的3个方差和非对角线上的3个协方差)。与分布的三维均值一起,这意味着我们需要根据训练数据估计9个参数,以获得表示数据可能性的高斯密度。在1D情况下,仅需要估计2个参数(均值和方差),而在2D情况下需要5个参数(2D均值,两个方差和协方差)。我们再次可以看到,要估计的参数数量随着维度的数量而增长。
在前面的文章中,我们表明,如果要估计的参数数量增加(并且如果估计的偏差和训练数据的数量保持不变),参数估计的方差会增加。这意味着,由于方差的增加,如果维数上升,我们的参数估计的质量会降低。分类器方差的增加对应于过度拟合。
另一个有趣的问题是应该使用哪些特征。给定一组N个特征; 我们如何选择M个特征的最佳子集,使得M < N?一种方法是在图1所示的曲线中搜索最优值。由于为所有特征的所有可能组合训练和测试分类器通常是难以处理的,因此存在几种尝试以不同方式找到该最佳值的方法。这些方法称为特征选择算法,并且通常采用启发式(贪婪方法,最佳优先方法等)来定位最佳数量和特征组合。
另一种方法是用一组M个特征替换N个特征的集合,每个特征是原始特征值的组合。试图找到原始特征的最佳线性或非线性组合以减少最终问题的维度的算法称为特征提取方法。一种众所周知的降维技术是主成分分析(PCA),它产生原始N特征的不相关的线性组合。PCA试图找到较低维度的线性子空间,以便保持原始数据的最大方差。但是,请注意,数据的最大差异不一定代表最具辨别力的信息。
最后,在分类器训练期间用于检测和避免过度拟合的宝贵技术是交叉验证。交叉验证方法将原始训练数据分成一个或多个训练子集。在分类器训练期间,一个子集用于测试所得分类器的准确度和精度,而其他子集用于参数估计。如果用于训练的子集的分类结果与用于测试的子集的结果大不相同,则过度拟合正在发挥作用。如果只有有限数量的训练数据可用,则可以使用几种类型的交叉验证,例如k折交叉验证和留一交叉验证。
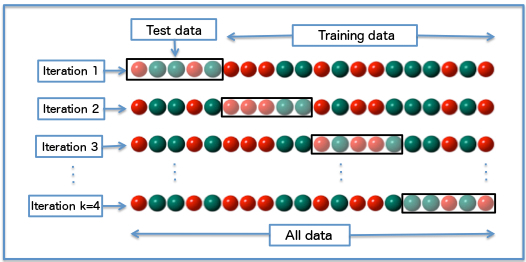
- Diagram of k-fold cross-validation with k=4
结论
在本文中,讨论了特征选择,特征提取和交叉验证的重要性,以避免由于维度的诅咒而过度拟合。通过一个简单的例子,我们回顾了维度诅咒在分类器训练中的重要影响,即过度拟合。
讲座
AI的拓补几何基础
清华顾险峰数学与AI:AI的拓补几何基础
- word文档见微云
2022年7月14日,由智谱AI支持,北京市科委、中关村管委会科普专项经费资助的系列栏目“科普大佬说”第三期于AI TIME 开讲,本次讲座邀请了纽约州立大学石溪分校计算机系帝国创新教授顾险峰老师。
顾险峰介绍
顾险峰介绍
- 1994年于清华大学获得计算机科学学士学位
- 2002年于哈佛大学获得计算机科学博士学位,师从国际著名微分几何大师丘成桐先生。
- 顾博士目前为纽约州立大学石溪分校计算机系帝国创新教授,与丘先生创立了计算共形几何跨领域学科,将现代拓扑与几何理论与计算机科学相结合,广泛应用于计算机图形学、视觉、网络、CAD/CAE、医学图像、计算力学等工程和医疗等领域。
- 近期,顾博士与合作者们将
微分几何、蒙日-安培方程与最优传输理论相结合,开发了最优传输映射的几何变分算法,应用于可解释深度学习等领域。 - 顾博士发表了300多篇学术论文,7部学术专著,其发明的调和映照、Abel微分、曲面Ricci流、几何最优传输映射等算法被广泛应用于很多工业医疗等领域。顾博士曾经获得美国国家自然科学基金CAREER奖,中国国家自然科学基金海外杰青,晨兴应用数学金奖等。
概要
深度学习方法在很多领域取得很大成功,但是深度学习的理论基础依然薄弱。
从几何拓扑的观点出发,分析深度学习的理论基础,力图回答这一领域的基本问题:
- 深度学习究竟在学习什么?深度学习如何进行学习?学习效果如何?
从几何角度而言,深度学习本质上是在学习高维背景空间中低维数据流形上的概率分布。
- 流形结构的学习基于
Whitney流形嵌入理论,由编码解码器来万有逼近; - 概率分布的学习依赖于
最优传输理论,在Wasserstein空间中做变分优化;
目前深度学习模型设计有内在缺陷,基本问题不可避免,例如模式坍塌。
- 基于最优传输理论的几何观点,揭示模式坍塌的根本原因,提出基于几何变分的学习模型,提高计算准确性、稳定性和效率。
深度学习如何学习
问题:深度学习究竟在学什么?深度学习是如何学习的?深度学习是否真正学会?
Manifold Distribution Principle
(流形分布定则)
Helmholtz Hypothesis (亥姆霍兹假设)
深度学习究竟在学什么?在脑神经科学中,有许多研究成果,其中一个叫做Helmholtz假设。这是说人类视觉中枢通过观看自然界的各种景象会产生相应的概念,这些概念都被记录在特定的神经元之中,从而形成某种表示。
用数学语言来讲的话,我们人脑视觉中的每个概念都可以归结于物理世界中的一个数据集,不同的概念实际上对应着不同的概率分布。
例如上图,左帧显示了Yann Lecunn收集的手写体数字图片,这里的概念是手写体数字,其对应的数据集就是所有的手写体数字图片。LeCunn把收集的这些数据集图片缩放成统一的比例,例如图像解析率为28*28,每个像素灰度取值为0或1。我们可以将每张图片看成是28*28维空间中的一个点,由此我们得到一个784维的背景空间,背景空间中的每个点代表一个图像。大量的图像是没有物理意义的,绝大多数有意义的图像也并不代表手写体数字,只是非常独特的一些图像才代表手写体数字。所有手写体图像在这784维的图像空间中构成一个点云,这个点云的维数是非常低的,我们称之为手写体数字对应的数据流形。
我们需要区分一下概念,我们有一个784维的背景空间,其中有一个特殊的点云,上面的每个点代表一个手写体数字,这个点云是数据流形。数据流形的维数是多少呢?Hinton发明了t-SNE算法将点云映射到二维平面上,即隐空间或者特征空间上。这个映射是可逆的连续双射,即拓扑同胚。这也就是说如果我们在隐空间中任取一点,它可以返回到数据流形上的原像,即生成一张图片。这意味着手写体数字的点云只有两维,即数据流形是两维的曲面,这张曲面嵌入在784维的背景空间之中。
深度学习的第一步就是将这个曲面打到二维平面上,把每一个图像变成一个特征向量,从而实现了降维。手写体数字从0到9共有10个数字,所以其在二维隐空间或者特征空间中有10个团簇。如上图中的右帧,每个团簇用不同的颜色来表示,各自代表一个手写体数字。每个手写体数字代表不同的概率分布,实际上在二维曲面上的分布是不均匀的。
由此我们可以看出,深度学习所学习的概念最终是由概率统计的语言来描述的,某种特定的概率分布,这个概率分布是定义在高维背景空间中的某个低维数据流形上面的。
Encoding (编码)
我们知道深度学习中的生成模型,模拟的是人类的想象力。我们在特征空间随便找一个采样点并映射回数据流形上,流形上每个点就是一幅图像,由此我们得到了想象出来的一幅图像。采样点需要精确选取。如上图所示,我们在特征空间设置一个10*10的采样矩阵,每个采样点对应右侧的一幅图像。我们可以看到如果采样点落在概率分布的支集(support)之内,生成的数字图像非常清晰;如果采样点落在支集之外,生成的数字图像比较模糊,并且并介于两个数字之间,难以辨认。因此在我们想象的时候,采样点需要落在有意义的区域之内,即落在支集之内;采样点落在支集之外,所造成的模糊现象被称为模式混淆。
General Model (通用模型)
我们可以用数学语言来描述,背景空间是一个图像空间,图像空间的维数就等于每张图像上像素的个数。某一自然概念对应的数据集就是图像空间中的一个点云,这个点云构成一个低维的流形,被称之为数据流形。我们在数据流形上选取一个开集,并通过编码映射到特征空间(隐空间)之中。
反之,从特征空间回到数据流形的映射被称为解码映射。所以编解码的过程相当于为流形建立了一个局部坐标。由此,我们可以把深度学习的语言翻译成拓扑语言。
Low Dimensional Example (低维算例)
如图所示,假设二维弥勒佛曲面嵌入在三维欧氏空间之中,曲面上存在一个均匀分布。对于深度学习而言,第一步就要实现降维,计算由三维曲面到二维平面的映射。
降维的过程被称为编码,逆过程被称为解码。这里我们显示了两种编码映射,它们都将弥勒佛曲面映到平面单位圆盘上。第一种是基于黎曼映照的保角变换,第二种是基于最优传输的保面元映射。
我们在黎曼映射的平面像上均匀采样,在将采样点拉回到三维曲面上。我们看到曲面上采样点分布不再均匀,这意味着这种编码映射破坏了数据流形上本来的概率分布。
我们在最优传输映射的平面像上均匀采样,在将采样点拉回到三维曲面上。我们看到曲面上采样点分布依然均匀,这意味着这种编码映射保持了数据流形上本来的概率分布。
这也显示了深度学习的终极目的:第一是学会模型的拓扑结构,实现降维并将其映射到特征空间上;第二要保留数据流形上本来的概率分布,在特征空间上的概率分布保持原来流形上的真实分布。
Central Tasks for DL (深度学习的中心任务)
深度学习究竟想学什么?主要是有两个中心任务:
(1)数据流形的拓扑结构
(2)数据流形上的概率分布
Generative Model Framework (生成模型的框架)
我们知道有很多的生成模型,这些模型的框架如图所示,上面一行显示了学习流形结构的过程,下面一行是学习概率分布的过程。在上行中,编码映射将手写体数字流形映射到特征空间,将流形上的概率分布映射到隐空间上的概率分布;解码映射将隐空间映回数据流形。在下行中,最优传输映射将长方形内的均匀分布映射到隐空间中的数据分布,这里最优传输映射是某一凸函数的梯度映射,此凸函数被称为是Brenier势能。
Human Facial Image Manifold (人脸图像流形)
在工程实践中,我们经常要生成许多人脸图像。这里对应的概念就是人脸图像,每张图像包含上百万像素,因此图像空间维数很高。在图像空间中的每个点代表一幅图片,所有人脸图像构成点云,即弯曲的数据流形。经过大幅度的降维,我们将人脸图像数据流形映射到隐空间上,不同类型的人脸表示成流形上不同的概率分布,深度生成模型的核心就是学习人脸图像的概率分布。
Manifold view of Generative Model
(流形观点下的生成模型)
我们在特征空间生成一个白噪声,均匀分布或者高斯分布,然后将其变换成特征空间中的数据分布。这样我们可以在特征空间产生随机采样点,其分布符合数据分布,在将隐空间的随机采样带映射回数据流形上,得到数据流形上的一个采样点,即为随机生成的人脸图像。
Manifold view of Denoising
(流形观点下的去噪)
假如我们想对图像进行去噪处理。如果用经典方法,第一步我们需要进行傅里叶分解将图像变换到频域,然后进行低通频滤波,滤除高频噪声,最后进行傅里叶逆变换。这种方法是普适的,而深度学习则是另一种思路。我们先用干净的图像训练出数据流形。带有噪音的图像被视为数据流形附近的点。我们将其投影到流形上,则流形上的垂足就是去除噪音的图像。如此我们就实现了图像的去噪处理,下面是相关的实验结果。
Manifold view of Denoising
(流形观点下的图像去噪)
我们给人脸图像加上白噪声并用上述提到的方法进行投影。我们发现这种方法相比传统方法仍旧存在缺点,即我们需要事先知道所处理图像的类别。另一方面,深度学习方法可以将大量的先验知识包含在数据流形之中,所以所实现的去噪效果要优于传统方法。
2 Manifold Learning
(流形学习)
Topological Theoretic Foundations
(拓扑理论基础)
深度学习如何学习流形的结构呢?这涉及一些拓补学上的定理。
我们进行模式识别的时候,每一类数据样本其实都是高维空间中的点云,不同类样本是不同的团簇,两个团簇可以用两个闭集覆盖。上述Urysohn定理表明了所需识别映射的存在性:即在一般的拓扑空间里肯定能找到一个连续映射,把第一个闭集映射成0,把第二个闭集映射成1。对于分类判别器而言,算法的核心就是求解这个映射。
一般而言,数据流形的拓扑结构可能非常复杂,彼此有嵌套、链接和扭曲。
考虑流形在欧氏空间中的嵌入,一般位置定理断言如果欧氏空间的维数足够高,那么流形的嵌入可以将扭结打开使其不再自我嵌套。因此,在深度网络模型中,前面几层的宽度逐步增加,从而提高嵌入空间的维数。
Whitney Manifold Embedding
(Whitney流形嵌入)
Whitney流形定理是说任意给一个m维拓扑流形,我们可以将其嵌入在欧式空间中,欧氏空间的维数大约是流形维数的两倍。现在很多深度学习的算法本质上就是Whitney定理的实现。Whitney定理的证明需要先用一族开集覆盖流形,将每个开集嵌入到欧氏空间,然后用所谓的单位分解把局部嵌入整体粘起来得到一个全局嵌入。这时嵌入空间的维数等于流形的维数乘以开集的个数,我们在将嵌入的流形依次向低维线性子空间投影,直至无法进一步投影,这时子空间的维数等于流形维数的两倍。
Universal Approximation
(万有逼近)
深度神经网络具有万有逼近的性质,即只要给定一个连续映射,给定任意的逼近精度,都存在某个深度神经网络来进行逼近。这个性质的理论基础实际上是来自Hilbert 第13问题:任意一个多变元的连续函数,都可以由两个单变元函的有限复合以任意精度来逼近。我们可以看到深度学习的逼近理论大多是基于这个定理。
目前基于流的深度学习模型日益普遍,这是基于变换群的逼近原理。我们希望逼近二阶光滑的可微变换群,其中有个无穷光滑的微分同胚子群,子群中的有限元素的乘积可以逼近原来大群中的任意元素。
类似的,无穷光滑的微分同胚群中存在一个基于流的子群,即由流速场诱导的变换子群;这个流变换子群存在更小的子群,即靠近恒同变换的子群。如此我们得到一系列嵌套的子群用子群中的有限复合来逼近原来大群中的任何一个元素。而最终的子群足够简单,可以用深度神经网络来精确表达。
Autoencoder
(自动编码器)
这里我们考察最简单的编码解码网络:自动编码器。以刚刚我们提到的手写体数字识别为例,编码器的输入样本是28*28的手写体图像,输出是复制的相同图像,损失函数是使生成图像与输入图像的距离。我们设计两个对称的网络,前面网络是编码器,后面网络是解码器,中间的瓶颈层代表了隐空间,瓶颈层节点的个数是隐空间的维数。前面网络将输入图像从784维降维两维,实际上相当于一个编码映射,后面网络从两维变回784维,相当于解码映射。训练的目的是得到恒同变换,即编码映射和解码映射彼此互逆,由此编码和解码映射是从数据流形到特征空间的拓扑同胚。
Encoding/Decoding (编码/解码)
我们这里举一个简单的例子,我们用自动编码器学习弥勒佛曲面的拓扑结构。我们在曲面上均匀采样,将3000个采样点作为自动编码器的输入。编码映射将曲面展平到二维平面上,解码映射将平面像映回到三维空间。我们看到重建的曲面和初始曲面非常接近,所有精细的几何细节都被完美保持。这证明了编码解码映射实现了拓扑同胚。
ReLU DNN (ReLU深度神经网络)
我们可以用ReLU DNN实现这个映射,ReLU DNN是线性变换与ReLU变换的多级复合,整体是一个分片线性映射。
Activated Path (激活路径)
如果给定一个训练样本,它会激活神经网络中的特定神经元,被激活的神经元构成网络中的通路,被称为是激活路径。
Cell Decomposition (胞腔分解)
如果有两个训练样本,它们的激活路径是相同的,那么我们认为它们彼此等价。这样,我们将空间按照等价分类,得到输入空间的胞腔分解。
Piecewise Linear Mapping (分片线性映射)
这里我们显示输入、输出空间和隐空间的胞腔分解,编码映射和解码映射在相应的胞腔间是线性映射,因而整体是分片线性映射。
Learning Capability (学习能力)
给定一个神经网络,该如何定量地衡量其学习能力?我们可以如下定义深度神经网络的学习能力:神经网络将输入空间进行胞腔分解,胞腔的个数越多,则网络能够表达的映射越非线性。由此,我们可以考察网络可能产生的所有胞腔分解,用胞腔个数的上限来表达网络的其学习能力。
RL Complexity Upper Bound (复杂度上限)
我们通过计算几何方法,可以估算其胞腔个数的上限。
RL Complexity of Manifold (流形复杂度)
如何表示学习一个流形的难度呢?观测上图左侧曲线,我们可以将其向平面进行投影,映射到一条直线段上,并且这个投影是同胚;而右侧曲线无论向任何方向投影都无法同胚映射到直线段上,我们必须将曲线分成几段,每段分别双射投影到直线段上。一般情形下,我们需要对流形分片,每片同胚投影到线性空间,所有分解方法中片数的下限定义了流形的复杂度。
Encodable Condition (能够编码的必要条件)
如果我们能用一个深度神经网络学会一个流形,那么神经网络的学习能力一定要大于等于流形的复杂程度。
Representation Limitation Theorem
如上图,我们可以递归定义的Peano曲线,每递归一层,其空间复杂度就会乘以4。通过Peano曲线,我们可以构造具有任意复杂度的流形。我们可以用这种流形来检测当前深度神经网络的学习能力。
3 Probability Measure Learning
(概率测度学习)
Generative Model (生成模型)
我们用深度神经网络的万有逼近能力来数据流形的拓扑结构,接下来学习概率分布,从而把白噪声转换成数据的概率分布。
GAN model (对抗生成模型)
GAN模型通过编码映射将数据流形打到特征空间,并得到隐空间的数据分布;然后在特征空间中生成白噪声,将白噪声变换到隐空间中的采样点;再通过解码将隐空间的采样点映射回到数据流形,得到生成样本。这个过程相当于一个生成器,所有生成图像在数据流形上得到了一个概率分布,即生成分布。判别器计算真实分布与生成分布之间的距离,从而区分这两种分布。
由此GAN模型拥有两套网络——生成器与判别器,并得到以下图解。
GAN Overview (GAN模型概览)
生成器Generator生成虚假的数据分布,判别器Discriminator要识别分布是真是假。那么用数学语言就是说,我们在特征空间有个白噪声分布,生成器将特征空间的白噪声分布变换成数据流形上的生成分布。图中数据流形上的生成分布是绿色曲线,数据流形上的真实分布是虚线。判别器判别两个分布的相异程度,生成器优化生成分布,使之尽量接近真实分布。两者相互竞争,最终系统达到平衡。
Wasserstein GAN Model
(Wasserstein GAN 模型)
如上图所示,生成器将特征空间的白噪声映射到数据流形上的生成分布,判别器计算从生成分布到真实分布的映射,从而判断其距离。在优化过程中的任意一步,这两个映射的复合直接给出了隐空间上白噪声到数据流形上真实分布的映射,即GAN模型的目标映射。这意味着GAN模型中生成器和判别器的竞争应该被合作而取代,从而提高效率。这里的两个映射都是计算两个概率分布之间的变换,因此都需要用到最优传输理论。
4 Optimal Transport Framework
(最优传输理论框架)
Overview (概览)
最优传输理论框架如图所示:我们考察一个黎曼流形上所有可能的概率分布,所有可能的概率分布构成一个无穷维的空间,即Wasserstein空间。深度学习的本质是在Wasserstein空间中优化,挑选出最佳的概率分布,使其满足某些观察(例如期望)并且优化某些能量(例如最大熵值)。
最优传输理论为Wasserstein空间定义了黎曼度量,从而定义了平行移动和协变微分,这使得变分优化得以在Wasserstein空间中施行。这也解释了为什么最优传输理论是深度学习的理论基础。
给定两个概率分布,它们之间的最优传输映射由蒙日-安培方程所控制,两个分布之间的测地线有McCann平移给出,Wasserstein空间某点处的切向量是底流形上的梯度场,其梯度场内积的加权积分定义了Wasserstein空间的黎曼度量。
Brenier’s Approach (Brenier的途径)
最优传输映射是在所有供需平衡的映射中是的总传输代价最小者。Brenier定理断言:如果传输代价是由从供给方到需求方的欧氏距离平方来界定,那么这个最优方案就会由一个凸函数的梯度给出,这个函数就被称为Brenier势能函数,且满足知名的Monge-Ampere方程。
那么我们如何高效而精确地求解蒙日-安培方程呢?
5 Convex Geometry
(凸几何)
Minkowski problem - General Case
(Minkowski问题)
如果在三维空间中给定一个凸多面体,我们知道每个面的面积和法向量(有向面积),并且有向面积总和为0,我们可否将这个凸多面体的形状确定下来?这个问题被称为是Minkowski问题。Minkowski证明了解的存在唯一性。
Alexandrov Theorem (Alexandrov 定理)
Alexandrov推广了Minkowski定理:考察开放凸多面体,平面上有一个凸集。凸多面体向平面上平行投影,多面体每个面的投影面积给定,每个面的法向量给定,那么这个凸多面体的形状被唯一确定下来。Alexandrov给出了基于代数拓扑的存在性证明,而我们需要一个构造性证明。
Variational Proof (变分证明)
2013年,在丘成桐先生的代领下,我们用几何变分法给出Alexandrov定理的一个构造性证明。Alexandrov定理和Brenier定理是等价的,这给出了最优传输与微分几何的桥梁。
由此,我们看到深度学习最终可以归结为概率统计,而概率统计中常用的最优传输理论可以用几何方法加以解决。
Computational Algorithm (计算方法)
基于我们的定理,我们可以设计算法求解最优传输映射。黎曼映射将弥勒佛曲面映射到平面单位圆盘上,从而将曲面的面元前推到圆盘上,得到黎曼映射诱导的测度。我们计算从圆盘上的勒贝格测度到黎曼映射诱导的测度之间的最优传输映射,左帧显示了相应的Brenier势能函数;其逆映射也是最优传输映射,其Brenier势能函数显示在右帧,两个势能函数互为勒让德变换。
由上图,我们可以看到最优传输变换保持曲面的面积元。
Wasserstein GAN Model (Wasserstein GAN模型)
我们再来回顾Wasserstein GAN模型,生成器其实可以求解一个最优传输映射,即求解蒙日-安培方程。判别器需要计算两个概率分布之间的Wasserstein距离,这等价于两个概率分布之间最优传输变换对应的总传输代价,因此也归结为求解蒙日-安培方程。
Power Diagram vs Optimal Transport
Map (Power图与最优传输映射)
我们用经典的计算几何算法来求解蒙日-安培方程。在实际深度学习应用中,给定的目标概率分布都是离散的,可以表示成狄拉克概率分布之和。
Semi-discrete Optimal Transportation
(半离散最优传输)
假设源概率分布为单位圆盘内的勒贝格测度,目标概率分布为离散的分布。求解最优传输映射等价于对单位圆盘进行胞腔分解,每个胞腔映射到一个目标采样点,使得胞腔的面积等于这个采样点对应的权重。我们在所有这样的胞腔分解之寻找总传输代价最少者。根据Brenier定理,这个半离散最优传输映射应该等于某个凸函数的梯度映射。
Power Diagram vs Optimal Transport
Map (Power图和最优传输映射)
深度学习算法本质上就是学习Brenier势能凸函数。这个势能函数可以表示成很多支撑平面构成的上包络。每个支撑平面将欧氏空间分成上下两半,所有上半空间的交集被称为上包络,其边界就是Brenier势能函数。
Learning Problem (学习问题)
由此我们看到深度学习算法学习的Brenier势能函数的表达式包含两部分,一部分是所有样本,所有深度学习神经网络记住了所有样本;一部分是每个支撑平面的截距,这是算法提炼出来的内在知识。由此我们看到所以深度神经网络的确确实记住了所有的训练样本,而且学会了一些新的知识。
6 Complexity of Geometric Optimal Transport
(几何最优传输的复杂度)
那么深度学习的效果如何呢?目前的算法具有不可避免的内在缺陷,体现为所谓的模式坍塌Mode Collapse现象。
Mode Collapse (模式坍塌)
(1)GAN训练非常困难,对于超参数非常敏感;
(2)GANs 具有模式坍塌现象,生成的分布无法覆盖所有模式;
(3)GANs 会产生失真的样本。
例如我们用传统的GAN生成了很多人脸图像,但是很多图像看上去根本不像人脸,这种情况就被称为模式坍塌。
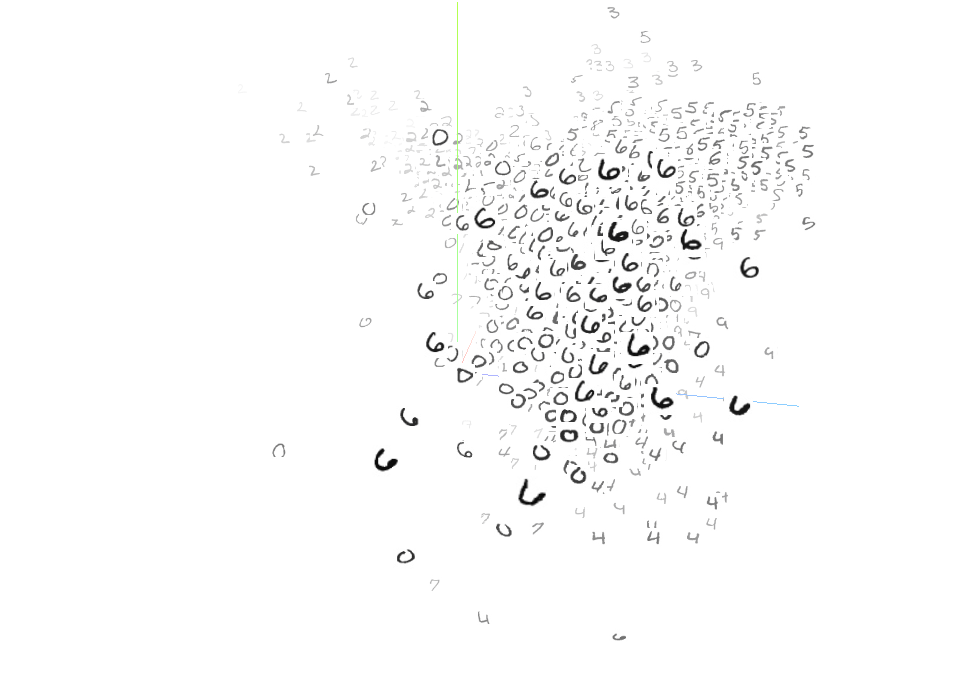
Experiments – mnist (Mnist实验结果)
我们用同样的传统算法生成了许多手写体数字图像,它会生成很多乱七八糟的乱码。模式坍塌是目前深度学习领域最大的问题之一。这个问题是由什么引起的呢?我们下面用最优传输理论加以解释。
Experiments - Mode Collapse (实验-模式坍塌)
如(a)帧所示,我们设计了平面上的一个概率分布,分布的支撑集显示为橘黄色的点,每一个点代表一个模式(mode)。GAN模型生成的样本用绿色的点来表示。在(b)帧中,GAN模型生成的绿色样本覆盖了一些橘黄色的点,但是依然有一些橘黄色的点没有被覆盖,这就是模式坍塌现象。在(c)帧中,所有橘黄色的点都被pacgan生成的绿色样本覆盖,即pacgan没有出现模式坍塌,但是它也生成了很多绿色样本介于橘黄色的点之间,这就是模式混淆现象。
模式坍塌现象的本质原因来自于最优传输映射的正则性理论。在经典的蒙日-安培方程理论中,人们研究最优传输映射大多是比较规则的情形,假设密度函数上下有界,支集是边界光滑的凸集,由此我们能够证明解的光滑性。但是如果目标区域非凸,则解可能非光滑,存在奇异集合。例如上届菲尔兹奖得主Figalli给出下面的例子:
在平面上有两个概率分布,左侧是单位圆盘上的均匀分布,右侧是海马形状区域中的均匀分布。我们计算最优传输映射,在圆盘内部有黑色的曲线,映射在这些曲线处间断。这意味着如果目标区域是非凸的,最优传输映射就有可能是非连续的。
在深度学习中,一切变换都用深度神经网络来表示。但是深度神经网络只能表达连续变换,而最优传输变换是非连续的。其非连续性使得深度神经网络无法学会,只会收敛到错误结果上。那么我们又该如何避免模式坍塌的问题呢?
Optimal Transportation Map
(最优传输映射)
我们针对上述问题提出了解决方案。最优传输映射由Brenier势能函数的梯度给出来,它可能是非连续的。但是Brenier势能函数本身确是整体连续的,但可能是非光滑的。因此我们可以用深度神经网络表达Brenier势能函数,而非最优传输映射。
Singularity Set Detection (奇异集合检测)
我们设计了一个物理实验来验证我们的想法。如图所示,我们用人脸图像集训练了一个数据流形,并用自动编码器将其映射到隐空间,降维到100维;然后在隐空间中求出白噪声分布到数据分布之间的最优传输映射。我们在白噪声支集内画了很多直线段,每条线段映成了特征空间上的一条曲线,后又映成数据流形上的一条曲线。流形上的每个点代表一个图像,一条连续曲线代表了人脸图像的连续变化过程。
如果最优传输变换存在奇异集合,那么某条线段可能会和奇异集合产生交点,这些交点被映射成人脸图像流形的边界。我们会在边界处看到这样的人脸图像,它们即在生理学上是合理的,但是在现实中碰到的概率为零。
如图右帧所示,我们从左上角棕发黑睛的男孩人脸开始,到右下角金发碧眼的女性结束,中间有一些图像是一只眼睛为黑色而另外一只眼睛为蓝色。这些人脸图像生理学上是合理的,但在现实生活中遇到的概率为零。
我们发现这个过程穿越了流形的边界。其中生成的一些图片虽然合理,但是现实中碰到的概率为0。这也在一定程度上说明我们的想象是合理的,人脸流形存在边界,产生的映射是连续的。
如何来避免模式坍塌呢?我们建立了如下模型。
Auntoencoder-OMT (自编码器-最优传输模型)
我们知道深度学习主要有两个核心任务:一是学习流形的拓扑结构,一是学习概率分布。我们将这两个任务解耦,流形拓扑结构用自动编码器来实现,概率分布通过最优传输理论利用几何方法来学习。模式坍塌主要由第二部分引起,用几何方法可以避免模式坍塌。从实验结果与传统方法的结果对比来看,这种方法完美避免了模式坍塌,提高了系统的可解释性。
Conclusion (结论)
我们通过几何和拓扑的观点,为深度学习建立了一个可解释的框架。
(1)每个自然(视觉)概念都对应物理世界中的一个数据集,其数学描述是嵌入在高维背景空间中的低维数据流形上的某种特定概率分布。
(2)深度学习的核心任务被解耦成两部分,一是学习数据流形的拓扑结构,一是学习流形上的概率分布
(3)数据流形拓扑结构的学习主要是用万有逼近定理,将流形映射到特征空间(隐空间);概率分布的学习实际是应用最优传输理论。最优传输理论为Wasserstein空间赋予了黎曼度量和协变微分,为在所有概率测度构成的空间中优化提供了理论框架。
(4)概率论中的Brenier理论和微分几何中的Minkowski-Alexandroff理论等价,从而可以从几何角度来解释概率统计,用几何变分法来求解最优传输映射。
(5)根据Brenier定理,我们看到GAN模型中的生成器和判别器应该合作而不是竞争,从而提高计算效率。
(6)根据Monge-Ampere方程的正则性理论,我们可以解释深度学习最核心的问题——模式坍塌。
(7)我们提出了一种新的几何框架,来设计新的深度学习模型以避免模式坍塌。


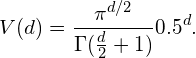

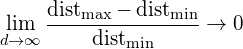
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
