鹤啸九天 自律更自由，平凡不平庸 Less is More

机器学习模型评估方法-The-Evaluation-of-Machine Learning

2020-08-05
鹤啸九天
机器学习
                               
阅读量次

Notes（温馨提示）:

  1. ★ 首次阅读建议浏览：导航指南, 或划到本页末尾, 或直接点击跳转, 查看全站导航图
  2. ★ 右上角工具条搜索文章，右下角二维码关注微信公众号（鹤啸九天），底栏分享、赞赏、评论。
  3. ★ 转载请注明文章来源，知识点积累起来不容易，水滴石穿，绳锯木断，谢谢理解
  4. ★ 如有疑问，邮件讨论，欢迎贡献优质资料

总结

sklearn 提供大量评估函数 机器学习方法选择

  • 也可以用 sklearn.metrics.make_scorer 打包供scoring参数调用。

机器学习问题类型

常见几类机器学习问题

  • 分类
  • 聚类
  • 回归

损失函数

损失函数见站内专题: 机器学习: 损失函数

回归MSE/分类CE？

回归、分类损失函数：

  • 回归问题常用mse作为损失函数，隐含的预设是数据误差符合高斯分布。
  • 分类问题常用交叉熵则是以数据分布服从多项式分布为前提。离散数据

回归问题能用交叉熵吗

  • 可以，虽然交叉熵用在回归问题看起来有些越俎代庖，「狗拿耗子多管闲事」，但「黑猫白猫能捉老鼠就是好猫」，搞清楚数据特点、使用场景，loss选择就能更贴合实际，最终的效果才是硬道理。

本质上回归应该用什么样的损失函数取决于数据分布。损失函数的选择本身也是一种先验偏好，选择mse意味着认为数据误差符合高斯分布，选择交叉熵则表示你倾向于认为数据接近多项式分布。如果你的先验直觉比较准确，符合实际情况，那模型效果应该会更好一些。 多项式分布一般和离散数据相关，但如果连续数据分桶后接近多项式分布，那选用mse可能就不合时宜了。

本质上，损失函数的选择是取决于对数据分布假设，不同的loss形式隐式地有对数据分布的要求，需要仔细分析数据特点进行判断。至于为什么A分布对应甲损失函数，B分布却对应乙损失函数，这也是一个值得展开的话题，简单来说这是最大熵原理约束下的选择。如对于高斯噪音分布，选择mse是满足最大熵要求的，它没有在高斯分布的假设之外增加额外的先验偏好。

知乎

【2022-8-20】为什么回归问题用 MSE？

  • 解答1：回归时，数据的残差有正有负，取平方求和后可以很简单的衡量模型的好坏。同时因为平方后容易求导数，比取绝对值还要分情况讨论好用 —— 经验主导，没有指出本质
  • 解答2：MSE对于偏差比较大的数据惩罚得比较多，但是会被outlier影响，同时MSE的优化目标是平均值，而MAE的优化目标是中位数。即如果我们的数据集足够大，对于同一个x会有多个y，MSE的目标是尽可能让预测值接近这些y的平均值。同时在做gradient descent的时候，MSE的梯度可以在越接近最小值的地方越平缓，这样不容易步子扯大了。而MAE的梯度一直不变，得手动调整learning rate。
  • 解答3：根据中心极限定理，误差服从正态分布，此时使得样本似然函数最大等价于使得MSE最小——Ian的《Deep Learning》

聚类指标

聚类算法评估指标

ScoringFunctionComment
‘adjusted_mutual_info_score’metrics.adjusted_mutual_info_score
‘adjusted_rand_score’metrics.adjusted_rand_score
‘completeness_score’metrics.completeness_score
‘fowlkes_mallows_score’metrics.fowlkes_mallows_score
‘homogeneity_score’metrics.homogeneity_score
‘mutual_info_score’metrics.mutual_info_score
‘normalized_mutual_info_score’metrics.normalized_mutual_info_score
‘rand_score’metrics.rand_score
‘v_measure_score’metrics.v_measure_score

回归指标

常见指标

  • 回归方差(反应自变量与因变量之间的相关程度)
  • 平均绝对误差

整理的回归模型评估指标。

ScoringFunctionComment
‘explained_variance’metrics.explained_variance_score可解释方差
‘max_error’metrics.max_error最大误差值
‘neg_mean_absolute_error’metrics.mean_absolute_error
‘neg_mean_squared_error’metrics.mean_squared_error
‘neg_root_mean_squared_error’metrics.mean_squared_error
‘neg_mean_squared_log_error’metrics.mean_squared_log_error
‘neg_median_absolute_error’metrics.median_absolute_error
‘r2’metrics.r2_score决定系数
‘neg_mean_poisson_deviance’metrics.mean_poisson_deviance
‘neg_mean_gamma_deviance’metrics.mean_gamma_deviance
‘neg_mean_absolute_percentage_error’metrics.mean_absolute_percentage_error
‘d2_absolute_error_score’metrics.d2_absolute_error_score
‘d2_pinball_score’metrics.d2_pinball_score
‘d2_tweedie_score’metrics.d2_tweedie_score

回归方差(反应自变量与因变量之间的相关程度)

explained_variance_score(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

平均绝对误差

mean_absolute_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

均方差

mean_squared_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

中值绝对误差

median_absolute_error(y_true, y_pred)

分类指标

  • 参考：深入理解AUC
  • 在机器学习的评估指标中，AUC是一个最常见也是最常用的指标之一。
  • AUC 基于几何，但是其意义十分重要，应用十分广泛。

总结

准确率accuracy、精确率precision，召回率recall等指标

分类算法评估指标

  • Confusion Matrix 混淆矩阵
  • Classification Report
  • 精确度 precision ＆召回率 Recall
  • F1值: 平衡 precision 和 Recall 效果
  • ROC曲线 和 AUC值: 仅适用于二分类
ScoringFunctionComment
‘accuracy’metrics.accuracy_score准确率
‘balanced_accuracy’metrics.balanced_accuracy_score平衡准确率
‘top_k_accuracy’metrics.top_k_accuracy_scoreTop_K准确率
‘average_precision’metrics.average_precision_score平均精确率
‘neg_brier_score’metrics.brier_score_loss
‘f1’metrics.f1_score
‘f1_micro’metrics.f1_scoremicro-averaged
‘f1_macro’metrics.f1_scoremacro-averaged
‘f1_weighted’metrics.f1_scoreweighted average
‘f1_samples’metrics.f1_scoreby multilabel sample
‘neg_log_loss’metrics.log_lossrequires predict_proba support
‘precision’ etc.metrics.precision_score精确率
‘recall’ etc.metrics.recall_score召回率
‘jaccard’ etc.metrics.jaccard_scoresuffixes apply as with ‘f1’
‘roc_auc’metrics.roc_auc_score
‘roc_auc_ovr’metrics.roc_auc_score
‘roc_auc_ovo’metrics.roc_auc_score
‘roc_auc_ovr_weighted’metrics.roc_auc_score
‘roc_auc_ovo_weighted’metrics.roc_auc_score

二分类

  • auc 只能用于 二分类 评价
  • 分类器只需要计算出预测概率分数，不需要自己设置threshold。 一个threshold会算出一个点，一般会自动尝试所有threshold，最后形成一个曲线。以下就不考虑threshold。
  • Auc 变化其实等价于左上角的面积（绿色部分）变化。 这个面积和两类数据的概率分布的重叠面积成正比 （容易分错类的部分）。 根各数据分布的重叠部分成正比。（这个数据不一定是原始数据，而是通过特征工程和模型高纬投影后的，各类数据分布）好的分类器，把两类分的很开，概率分布重叠小，左上面积小，auc大。最坏的情况是随机，概率分布完全重叠，auc是直线。
  • 转自：知乎xixihaha912

可用指标

多分类

分类报告

分类评估指标报告 包含: precision, recall, f1-score, support 四个指标，基本包括了分类需要看到的指标。

classification_report

classification_report 显示主要分类指标的文本报告

对应函数：

sklearn.metrics.classification_report(y_true, y_pred, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False)

参数

  • y_true: 1维数组，或标签指示器数组/稀疏矩阵，标签值。
  • y_pred: 1维数组，或标签指示器数组/稀疏矩阵，分类器预测值。
  • labels: array，shape = [n_labels]，报表中包含的标签索引的可选列表。
  • target_names: 字符串列表，与标签匹配的可选显示名称（相同顺序）。
  • sample_weight: 类似于shape = [n_samples] 数组，可选项，样本权重。
  • digits: int，输出浮点值的位数。

实现

# -*- coding: utf-8 -*-

from sklearn.metrics import classification_report

y_true = ['北京', '上海', '成都', '成都', '上海', '北京', '上海', '成都', '北京', '上海']
y_pred = ['北京', '上海', '成都', '上海', '成都', '成都', '上海', '成都', '北京', '上海']

res = classification_report(y_true, y_pred, target_names=['北京', '上海', '成都']) # 字符串形式
print('字符串形式: ', res)
res = classification_report(y_true, y_pred, target_names=['北京', '上海', '成都'], output_dict=True)
print('字典形式: ', res)

输出结果

字符串形式:
               precision    recall  f1-score   support

          北京       0.75      0.75      0.75         4
          上海       1.00      0.67      0.80         3
          成都       0.50      0.67      0.57         3

    accuracy                           0.70        10
   macro avg       0.75      0.69      0.71        10
weighted avg       0.75      0.70      0.71        10

字典形式:
 {'北京': {'precision': 0.75, 'recall': 0.75, 'f1-score': 0.75, 'support': 4.0}, '上海': {'precision': 1.0, 'recall': 0.6666666666666666, 'f1-score': 0.8, 'support': 3.0}, '成都': {'precision': 0.5, 'recall': 0.6666666666666666, 'f1-score': 0.5714285714285715, 'support': 3.0}, 'accuracy': 0.7, 'macro avg': {'precision': 0.75, 'recall': 0.6944444444444443, 'f1-score': 0.7071428571428572, 'support': 10.0}, 'weighted avg': {'precision': 0.75, 'recall': 0.7, 'f1-score': 0.7114285714285715, 'support': 10.0}}

confusion_matrix 方法可输出该多分类问题的混淆矩阵

混淆矩阵

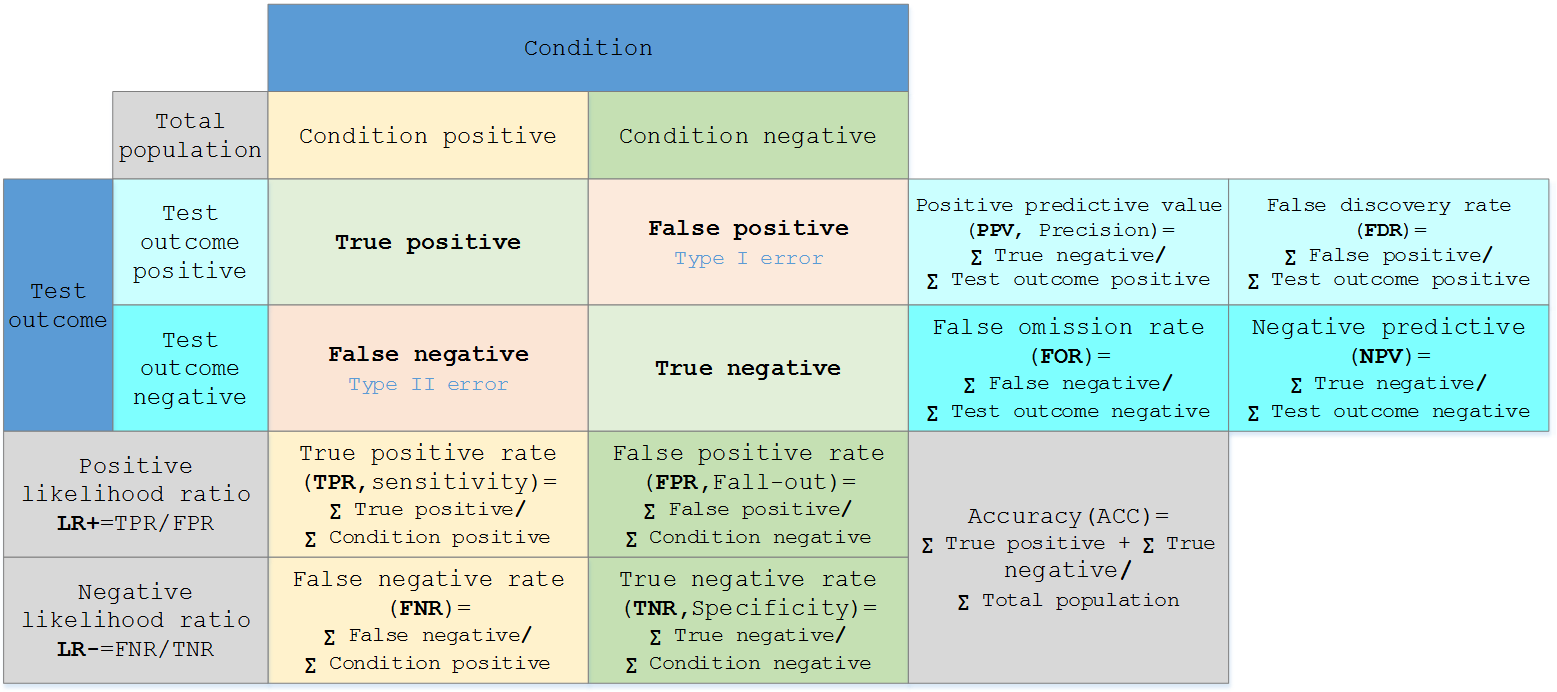
混淆矩阵（confusion matrix），又称为可能性表格或是错误矩阵

将预测结果和真实结果用混淆矩阵展示，可以用于二分类与多分类。

Confusion Matrix

混淆矩阵（Confusion Matrix），又称为可能性矩阵或错误矩阵。

混淆矩阵是可视化工具，特别用于监督学习，在无监督学习一般叫做匹配矩阵。

  • 图像精度评价中，主要用于比较分类结果和实际测得值，可以把分类结果的精度显示在一个混淆矩阵里面。

混淆矩阵要表达的含义：

  • 混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；
  • 每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目；每一列中的数值表示真实数据被预测为该类的数目。

混淆矩阵：

pred_label/true_label Positive Negative
Positive TP FP
Negtive FN TN

如上表所示，行表示预测的label值，列表示真实label值。

TP，FP，FN，TN分别表示如下意思：

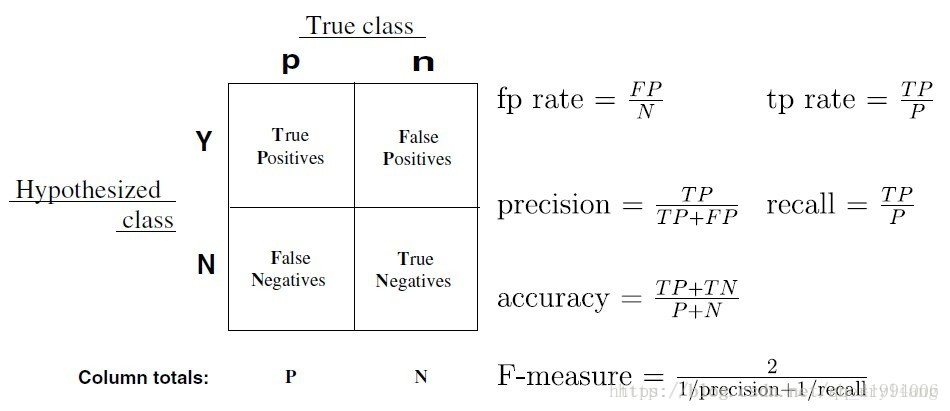
  • TP（true positive）：表示样本的真实类别为正，最后预测得到的结果也为正；
  • FP（false positive）：表示样本的真实类别为负，最后预测得到的结果却为正；
  • FN（false negative）：表示样本的真实类别为正，最后预测得到的结果却为负；
  • TN（true negative）：表示样本的真实类别为负，最后预测得到的结果也为负. 根据以上几个指标，可以分别计算出Accuracy、Precision、Recall（Sensitivity，SN），Specificity（SP）, img
  • Accuracy：表示预测结果的精确度，预测正确的样本数除以总样本数。
    • $Accuracy＝(TP+TN)/(TP+FP+FN+TN)$
  • Precision，准确率，表示预测结果中，预测为正样本的样本中，正确预测为正样本的概率；
    • $Precision=TP/(TP+FP)$
  • Recall，召回率，表示在原始样本的正样本中，最后被正确预测为正样本的概率；
    • $Recall＝TP/(TP+FN)$
  • Specificity，常常称作特异性，它研究的样本集是原始样本中的负样本，表示的是在这些负样本中最后被正确预测为负样本的概率。

实际中，往往希望得到的 precision和recall都比较高，比如当FN和FP等于0的时候，他们的值都等于1。但是，它们往往在某种情况下是互斥的，比如这种情况，50个正样本，50个负样本，结果全部预测为正，那么它的precision为1而recall却为0.5.所以需要一种折衷的方式，因此就有了F1-score。

  • F1-score表示的是precision和recall的调和平均评估指标
  • 类似的还有MCC

一张图总结：img

img

图解

sklearn 实现

confusion_matrix 方法可输出该多分类问题的混淆矩阵

对应函数：

sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)

参数

  • y_true: 1维数组，或标签指示器数组/稀疏矩阵，目标值。
  • y_pred: 1维数组，或标签指示器数组/稀疏矩阵，分类器返回的估计值。
  • labels: array，shape = [n_labels]，报表中包含的标签索引的可选列表。
  • sample_weight: 样本权重。

样本不均衡时，如 0占80%，1和-1各占10%，每个类数量差距很大，可选择加入 sample_weight 调整样本。

from sklearn.metrics import confusion_matrix

y_true = ['北京', '上海', '成都', '成都', '上海', '北京', '上海', '成都', '北京', '上海']
y_pred = ['北京', '上海', '成都', '上海', '成都', '成都', '上海', '成都', '北京', '上海']
res = confusion_matrix(y_true, y_pred, labels = ['北京', '上海', '成都']) # 输出字符串形式
print('混淆矩阵(默认): \n', res)
#  [[2 0 1]
#  [0 3 1]
#  [0 1 2]]

# sklearn compute_sample_weight 函数计算 sample_weight：
from sklearn.utils.class_weight import compute_sample_weight
sw = compute_sample_weight(class_weight='balanced',y=y_true)
print('不均衡权重:\n', sw)
#  [1.11111111 0.83333333 1.11111111 1.11111111 0.83333333 1.11111111
#  0.83333333 1.11111111 1.11111111 0.83333333]

# sw 和 ytrue 同 shape，每个数代表该样本所在的sample_weight。
# 具体计算方法是总样本数/（类数*每个类的个数），比如一个值为-1的样本，它的sample_weight就是300 / (3 * 30)。
cm =confusion_matrix(y_true, y_pred, sample_weight=sw)
print('混淆矩阵(不均衡)\n', cm)
#  [[2.5        0.         0.83333333]
#  [0.         2.22222222 1.11111111]
#  [1.11111111 0.         2.22222222]]

进一步把混淆矩阵变成图片

# -*- coding: utf-8 -*-
# author: Jclian91
# place: Daxing Beijing
# time: 2019-11-14 21:52

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import matplotlib as mpl

# 支持中文字体显示, 使用于Mac系统
zhfont=mpl.font_manager.FontProperties(fname="/System/Library/Fonts/STHeiti Light.ttc")

y_true = ['北京', '上海', '成都', '成都', '上海', '北京', '上海', '成都', '北京', '上海']
y_pred = ['北京', '上海', '成都', '上海', '成都', '成都', '上海', '成都', '北京', '上海']

classes = ['北京', '上海', '成都']
confusion = confusion_matrix(y_true, y_pred)

# 绘制热度图
plt.imshow(confusion, cmap=plt.cm.Greens)
indices = range(len(confusion))
plt.xticks(indices, classes, fontproperties=zhfont)
plt.yticks(indices, classes, fontproperties=zhfont)
plt.colorbar()
plt.xlabel('y_pred')
plt.ylabel('y_true')

# 显示数据
for first_index in range(len(confusion)):
  for second_index in range(len(confusion[first_index])):
    plt.text(first_index, second_index, confusion[first_index][second_index])
# 显示图片
plt.show()

更多总结

from sklearn.metrics import confusion_matrix
import numpy as np

# 输入示例1: list
y_true=[1,1,0,1,1,0]
y_pred=[0,0,0,0,0,0]
# 输入示例2: np.array
y_true=np.array([1,1,0,1,1,0])
y_pred=np.array([0,0,0,0,0,0])
# 统计数值
print(min(y_pred), max(y_pred), y_pred.min()) # 0 0 0
print(np.unique(y_true)) # [0 1]
print(np.unique(y_pred)) # [0]
print(np.unique(y_pred).size) # 1

print('count: ', np.bincount(y_true)) # count:  [2 4]

C = confusion_matrix(y_true, y_pred)
# 返回 np.array 结构
print(type(C),'\n', C)
# <class 'numpy.ndarray'> 
#  [[2 0]
#  [4 0]]

#------- 另一种导入方式 ---------
from sklearn import metrics

labels1_all_valid = [1,0,0,1]
predict1_all_valid = [1,0,1,1]
confusion_matrix = metrics.confusion_matrix(labels1_all_valid, predict1_all_valid)
print('python list: ', confusion_matrix)

# 字符串类型的标签, 默认按照字母顺序依次编号0~n-1
y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
print(set(y_true))
# 设置顺序
C = confusion_matrix(y_true, y_pred, labels=["bird", "cat", "ant"])
print('string + 调整label顺序: ', C)

precision 准确率

precision_score, recall_score, f1_score 有共同参数，以precision为例：

precision_score

对应函数：

sklearn.metrics.precision_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)
  • y_true：1维数组，或标签指示器数组/稀疏矩阵，目标值。
  • y_pred：1维数组，或标签指示器数组/稀疏矩阵，分类器返回的估计值。
  • labels：array，shape = [n_labels]，报表中包含的标签索引的可选列表。
  • pos_label：对二分类有用，一般不用管。
  • average：可选 None, ‘binary’ (default), ‘micro’, ‘macro’, ‘samples’, ‘weighted’。
    • ‘binary’ 为二分类；
    • ‘micro’, ‘macro’, ‘weighted’ 可用于多分类
    • micro: 所有的类放在一起算，具体到precision，就是把所有类的TP加和，再除以所有类的TP和FN的加和
      • micro 下, precision 和 recall 都等于accuracy
    • macro: 先分别求出每个类的precision再算术平均。
    • weighted: macro 改良版，不再是取算术平均、乘以固定weight（1/3）了，而是乘以该类占比。

代码实现

from sklearn.metrics import precision_score,recall_score,f1_score

y_true=['a','b','c','a','b']
y_pre=['b','b','c','a','b']

target_names=['class_a','class_b','class_c']

from sklearn.metrics import precision_score
precision_score(y_true, y_pred, average="micro") # 0.6333333333333333
precision_score(y_true, y_pred, average="macro") # 0.46060606060606063
precision_score(y_true, y_pred, average="weighted") # 0.7781818181818182

print(precision_score(y_true,y_pre))
print(recall_score(y_true,y_pre))
print(f1_score(y_true,y_pre))

'''
结果：
[[1 1 0]
 [0 2 0]
 [0 0 1]]
'''

recall 召回率

PR曲线

P-R曲线中，P为图中precision，即精准度，R为图中recall，即召回率。

AP的计算，此处参考的是PASCAL  VOC  CHALLENGE的2010年之前计算方法。首先设定一组阈值，[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值（比如recall>0.3），我们都会得到一个对应的最大precision。这样，我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。​

AP/mAP

原文链接

【2023-4-11】目标检测中的“神奇指南”——平均精度（mAP）

AP值的计算需要一系列指标做铺垫，涉及的名词：

  • （1）IOU：IOU是一个比值，是预测框与实际框的相交部分与两者全部面积的比值；
  • （2）TP：被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数；
  • （3）FP：被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
  • （4）FN：被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
  • （5）TN：被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。

IOU是预测边界框和参考边界框的交集和并集之间的比率，利用这个比值，可以知晓每个检测结果的正确性。

  • 将IOU与阈值进行比较，最常用的阈值是0.5，如果 IoU > 0.5，那么认为这是一个正确检测，否则认为这是一错误的检测。

mAP作为预测目标位置及类别类算法的性能度量指标，对评估目标定位模型、目标检测模型以及实例分割模型非常有用。

  • 计算出所有检测框的IOU值，求解其P与R，最终得出mAP值，利用这些平均精度值，便可以轻松地判断模型对任何给定类别的性能。

F 指标

Fbeta-measure 是一种可配置的单分指标，用于根据对正类的预测来评估二元分类模型

F1

P和R同等重要

F-Measure = ((1 + 1^2) * Precision * Recall) / (1^2 * Precision + Recall)
F-Measure = (2 * Precision * Recall) / (Precision + Recall)

代码计算方式

from sklearn.metrics import fbeta_score
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

# perfect precision, 50% recall
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
p = precision_score(y_true, y_pred)
r = recall_score(y_true, y_pred)
f = fbeta_score(y_true, y_pred, beta=0.5)
print('Result: p=%.3f, r=%.3f, f=%.3f' % (p, r, f))

F_beta

Fbeta 是 F 的抽象，调和均值计算中的精度和召回率的平衡, 由beta系数控制。

Fbeta = ((1 + beta^2) * Precision * Recall) / (beta^2 * Precision + Recall)

beta 参数用于 Fbeta-measure。

  • beta=2, 称为 F2-measure 或 F2-score。
  • beta=1, 称为 F1-measure 或 F1-score

beta 参数的三个常见值：

  • F0.5-Measure (beta=0.5)：精度上的权重更大，召回的权重更小。
  • F1-Measure (beta=1.0)：平衡准确率和召回率的权重。
  • F2-Measure (beta=2.0)：精度权重较小，召回权重较大
from sklearn.metrics import fbeta_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

# perfect precision, 50% recall
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
p = precision_score(y_true, y_pred)
r = recall_score(y_true, y_pred)
f = fbeta_score(y_true, y_pred, beta=1.0) # beta=1
f = fbeta_score(y_true, y_pred, beta=2.0) # beta=2
print('Result: p=%.3f, r=%.3f, f=%.3f' % (p, r, f))

ROC

弄懂 AUC 和 ROC 曲线之前，一定要彻底理解混淆矩阵的定义

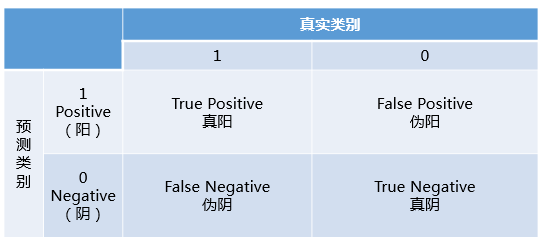
  • 混淆矩阵中有着Positive、Negative、True、False的概念，其意义如下：
    • 称预测类别为1的为Positive（阳性），预测类别为0的为Negative（阴性）。
    • 预测正确的为True（真），预测错误的为False（伪）。
  • 对上述概念进行组合，就产生了如下的混淆矩阵：
  • 由此引出True Positive Rate（真阳率）、False Positive（伪阳率）两个概念
  • 其实TPRate就是TP除以TP所在的列，FPRate就是FP除以FP所在的列，二者意义如下：
    • TPRate的意义是所有真实类别为1的样本中，预测类别为1的比例。
    • FPRate的意义是所有真实类别为0的样本中，预测类别为1的比例。
  • AUC, 即ROC曲线下的面积，而ROC曲线的横轴是FPRate，纵轴是TPRate，当二者相等时，即y=x，如下图:
    • 分类器对于正例和负例毫无区分能力，和抛硬币没什么区别——最差情况
    • 认为AUC的最小值为0.5（当然也存在预测相反这种极端的情况，AUC小于0.5，这种情况相当于分类器总是把对的说成错的，错的认为是对的，那么只要把预测类别取反，便得到了一个AUC大于0.5的分类器）
  • 希望得到的效果
    • 对于真实类别为1的样本，分类器预测为1的概率（即TPRate），要大于真实类别为0而预测类别为1的概率（即FPRate），即y＞x
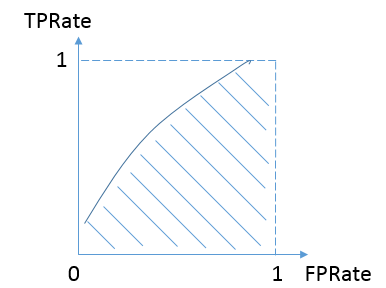
  • 最理想：既没有真实类别为1而错分为0的样本——TPRate一直为1，也没有真实类别为0而错分为1的样本——FP rate一直为0，AUC为1，这便是AUC的极大值。

【2021-9-17】你真的理解ROC与AUC吗？ 含AUC图解

  • 一个优秀模型的AUC接近于1，这意味着它具有良好区分性能。理想的分类结果，两条曲线完全分离，ROC曲线完全与边界重叠
  • AUC ∈ [0 , 1], 两个曲线重叠时，模型会引入假正和假负的错误。根据阈值可以最大化和最小化他们。当AUC是0.7是意味着模型有70%的机会能够区分正负类。
  • 而当 AUC 为 0.5 时，意味着该模型没有任何类别分离能力，等于随机猜测。
  • 一个坏的模型的AUC接近0，这意味着它具有最差的可分性（可能并不非常正确）。
  • AUC=0时，模型把类别预测反了（实际没有多少意义）

AUC

在统计和机器学习中，常用 AUC 评估二分类模型的性能。

AUC 定义

AUC 全称: area under the curve，即曲线下的面积。

ROC曲线早在第二次世界大战期间就被使用在电子工程和雷达工程当中，被用于军事目标检测。 后来，ROC曲线也被应用到心理学、医学、机器学习和数据挖掘等领域的模型性能评估。

对于二分类问题，预测模型会对每一个样本预测一个得分s或者一个概率p。 然后，可以选取一个阈值t，让得分s>t的样本预测为正，而得分s<t的样本预测为负。 这样一来，根据预测的结果和实际的标签可以把样本分为4类：

  正样本 负样本
预测为正 TP(真正例) FP(假正例)
预测为负 FN(假负例) TN(真负例)

随着阈值t选取的不同，这四类样本的比例各不相同。定义真正例率TPR和假正例率FPR为：

\[\text{TPR} = \frac{\text{TP}}{\text{TP} + \text{FN}} \\ \text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}\]

对于真正例率TPR，分子是得分>t里面正样本的数目，分母是总的正样本数目。 而对于假正例率FPR，分子是得分>t里面负样本的数目，分母是总的负样本数目。 因此，如果定义$N_+(t), N_-(t)$分别为得分大于t的样本中正负样本数目，$N_+, N_-$为总的正负样本数目， 那么TPR和FPR可以表达为阈值t的函数

\[\text{TPR}(t) = \frac{N_+(t)}{N_+} \\ \text{FPR}(t) = \frac{N_-(t)}{N_-}\]

随着阈值t的变化，TPR和FPR在坐标图上形成一条曲线，这条曲线就是ROC曲线。TPR又被成为sensitivity(灵敏度)，(1-FPR)又被成为specificity(特异度)

显然，如果模型是随机的，模型得分对正负样本没有区分性，那么得分大于t的样本中，正负样本比例和总体的正负样本比例应该基本一致。 也就是说

\[\frac{N_+(t)}{N_-(t)} = \frac{N_+}{N_-}\]

结合上面式子可知TPR和FPR相等，对应的ROC曲线是一条直线！

反之，如果模型的区分性非常理想，也就是说正负样本的得分可以完全分开，所有的正样本都比负样本得分高，此时ROC曲线表现为「 字形。 因为正例得分都比负例搞，所以要么TPR=0要么FPR=0！

ROC曲线

实际的模型的ROC曲线则是一条上凸的曲线，介于随机和理想的ROC曲线之间。而ROC曲线下的面积，即为AUC！

\[\text{AUC} = \int_{t=\infty}^{-\infty} y(t) d x(t)\]

这里的x和y分别对应TPR和FPR，也是ROC曲线的横纵坐标。

  • AUC的优化目标：TPR和(1-FPR)
  • F1的优化目标：Recall和Precision

AUC 概率解释

概率解释证明

AUC常常被用来作为模型排序好坏的指标

  • 原因: AUC可以看做随机从正负样本中选取一对正负样本，其中正样本的得分大于负样本的概率

考虑随机取得这对正负样本中，负样本得分在 [t, t + △t]之间的概率为

\[\begin{align*} & P(t \le s_- < t+\Delta t) \\ = &P( s_- \gt t) - P(s_- > t+\Delta t) \\ = & \frac{N_-(t) - N_-(t+\Delta t)}{N_-} \\ = & x(t) - x(t +\Delta t) = - \Delta x(t) \end{align*}\]

如果 $\Delta t$ 很小，那么该正样本得分大于该负样本的概率为

\[P(s_+ > s_- | t \le s_- < t+\Delta t) \\ \approx P(s_+ > t) = \frac{N_+(t)}{N_+} = y(t)\]

所以，

\[\begin{align*} & P(s_+ > s_- ) \\ = & \sum P(t \le s_- < t+\Delta t) P(s_+ > s_- | t \le s_- < t+\Delta t) \\ = & -\sum y(t) \Delta x(t) \\ = & -\int_{t=-\infty}^{\infty} y(t) d x(t) \\ = & \int_{t=\infty}^{-\infty} y(t) d x(t) \end{align*}\]

注意积分区间，$ t=-\infty $ 对应ROC图像最右上角的点，而 $t=\infty$ 对应ROC图像最左下角的点。所以，计算面积是 $\int_{t=\infty}^{-\infty}$

积分项里面实际上是这样一个事件的概率：随机取一对正负样本，负样本得分为t且正样本大于t！

因此，对这个概率微元积分就可以到正样本得分大于负样本的概率！

AUC 排序特性

根据上述概率解释，AUC实际上在说一个模型把正样本排在负样本前面的概率！ 所以，AUC常用在排序场景的模型评估，比如搜索和推荐等场景！ 这个解释还表明，如果将所有的样本的得分都加上一个额外的常数，并不改变这个概率，因此AUC不变！ 因此，在广告等需要绝对的点击率场景下，AUC并不适合作为评估指标，而是用logloss等指标。

AUC 对正负样本比例不敏感

利用概率解释，还可得到AUC另外一个性质: 对正负样本比例不敏感。

  • 训练模型时，如果正负比例差异比较大，例如正负比例为1:1000，训练模型要对负样本进行下采样。
  • 当一个模型训练完了之后，用负样本下采样后的测试集计算出来的AUC和未采样的测试集计算的AUC基本一致，或者说前者是后者的无偏估计！
  • 如果采样是随机的，对于给定的正样本，假定得分为 $s_+$ ，那么得分小于 $s_+$ 的负样本比例不会因为采样而改变！

假设采样前负样本里面得分小于 $s_+$ 的样本占比为70%，如果采样是均匀的，即 $>s_+$ 的负样本和 $<s_+$ 的负样本留下的概率是相同的，那么显然采样后这个比例仍然是70%！

该正样本得分大于选取的负样本的概率不会因为采样而改变，也就是$y(t)dx(t)$是不变的，因此，AUC也不变！

相比于其他评估指标，例如准确率、召回率和F1值，负样本下采样相当于只将一部分真实的负例排除掉了，然而模型并不能准确地识别出这些负例，所以用下采样后的样本来评估会高估准确率；因为采样只对负样本采样，正样本都在，所以采样对召回率并没什么影响。这两者结合起来，最终导致高估F1值！

AUC 计算

AUC 可以直接根据 ROC曲线，利用梯形积分进行计算。

此外，还有一个比较有意思的是，可以利用AUC与Wilcoxon-Mann-Whitney测试的U统计量的关系，来计算AUC。这可以从AUC的概率意义推导而来。

假设将测试集的正负样本按照模型预测得分 从小到大 排序，对于第$j$个正样本，假设它的排序为 $r_j$，

那么说明排在这个正样本前面的总样本有 $r_j - 1$个，其中正样本有 $j-1$个（因为这个正样本在所有的正样本里面排第j），

所以排在第j个正样本前面(得分比它小)的负样本个数为 $r_j - j$个。也就是说，对于第j个正样本来说，其得分比随机取的一个负样本大(排序比它靠后)的概率是 $(r_j - j) / N_-$,其中$N_-$是总的负样本数目。

所以，平均下来，随机取的正样本得分比负样本大的概率为

\[\frac{1}{N_+} \sum_{j=1}^{N_+}(r_j - j)/N_- = \frac{\sum_{j=1}^{N_+}r_j - N_+(N_+ + 1)/2}{N_+N_-}\]

所以

\[AUC = \frac{\sum_{j =1}^{N_+} r_j - N_+(N_+ + 1)/2}{N_+ N_-}\]

因此，很容易写出计算AUC的SQL代码

select
	(ry - 0.5*n1*(n1+1))/n0/n1 as auc
from(
	select
		sum(if(y=0, 1, 0)) as n0,
		sum(if(y=1, 1, 0)) as n1,
		sum(if(y=1, r, 0)) as ry
	from(
		select y, row_number() over(order by score asc) as r
		from(
			select y, score
			from some.table
		)A
	)B
)C

AUC 优化

采用极大似然估计对应的损失函数是 logloss，因此极大似然估计的优化目标并不是AUC。

  • 一些排序场景下，AUC比logloss更贴近目标，因此直接优化AUC可以达到比极大似然估计更好的效果。
  • pairwise 目标函数就可以看做一种对AUC的近似。因为损失函数都是作用与正负样本得分差之上！
类型 公式
rank-SVM $\max(0, - s_+ + s_- + \Delta)$
rank-net $\log (1 + \exp(- (s_+ - s_-)))$
指数损失 $\exp(- (s_+ - s_-))$
TOP 损失 $\sum_s \max(0, - s_c + s + \Delta)$

显然，这些损失函数都是对 $s_+<s_-$ 正负样本对进行惩罚！

此外，也有一些其它对AUC近似度更好的损失函数，例如

\[\mathbf{E} \left[ (1-w^T(s_+ - s_-))^2 \right] = \frac{1}{n_+n_-} \sum_{i=1}^{n_+} \sum_{j=1}^{n_-} (1-w^T(s_{i}^+ - s_{j}^-))^2\]

$s_i^+, s_j^-$ 分别表示正例和负例的得分。

这解释了为什么某些问题中，利用排序损失函数比logloss效果更好，因为在这些问题中排序比概率更重要！

AUC 多少才算好

AUC越大表示模型区分正例和负例的能力越强，那么AUC要达到多少才表示模型拟合的比较好呢？

实际建模中发现，预测点击的模型比预测下单的模型AUC要低很多，在月活用户里面预测下单和日活用户里面预测下单的AUC差异也很明显，预测用户未来1小时下单和预测未来1天的下单模型AUC差异也很大。这表明，AUC非常依赖于具体任务。

以预测点击和预测下单为例，下单通常决策成本比点击高很多，这使得点击行为比下单显得更加随意，也更加难以预测，所以导致点击率模型的AUC通常比下单率模型低很多。

那么月活用户和日活用户那个更容易区分下单与不下单用户呢？显然月活用户要容易一些，因为里面包含很多最近不活跃的用户，所以前者的AUC通常要高一些。

对于预测1小时和预测1天的模型，哪一个更加困难？因为时间越长，用户可能发生的意料之外的事情越多，也越难预测。举个极端的例子，预测用户下一秒中内会干啥，直接预测他会做正在干的事情即可，这个模型的准确率就会很高，但是预测长期会干啥就很困难了。所以对于这两个模型，后者更加困难，所以AUC也越低。

多分类

【2021-8-6】多分类模型Accuracy, Precision, Recall和F1-score的超级无敌深入探讨

  • 具体场景（如不均衡多分类）中到底应该以哪种指标为主要参考呢？
  • 多分类模型和二分类模型的评价指标有啥区别？
  • 多分类问题中
    • 为什么 Accuracy = micro precision = micro recall = micro F1-score?
    • 什么时候用 macro, weighted, micro precision/ recall/ F1-score?

Accuracy 是分类问题中最常用指标，它计算了分类正确的预测数与总预测数的比值。但是，对于不平衡数据集而言，Accuracy并不是一个好指标。如100张图片中91张图片是「狗」，5张是「猫」，4张是「猪」，训练一个三分类器，能正确识别图片里动物的类别。其中，狗这个类别就是大多数类 (majority class)。当大多数类中样本（狗）的数量远超过其他类别（猫、猪）时，如果采用Accuracy来评估分类器的好坏，即便模型性能很差 (如无论输入什么图片，都预测为「狗」)，也可以得到较高的Accuracy Score（如91%）。此时，虽然Accuracy Score很高，但是意义不大。当数据异常不平衡时，Accuracy评估方法的缺陷尤为显著。因此需要引入Precision （精准度），Recall （召回率）和F1-score评估指标。考虑到二分类和多分类模型中，评估指标的计算方法略有不同

在多分类（大于两个类）问题中，假设我们要开发一个动物识别系统，来区分输入图片是猫，狗还是猪。给定分类器一堆动物图片，产生了如下结果混淆矩阵。

  • 混淆矩阵中，正确的分类样本（Actual label = Predicted label）分布在左上到右下的对角线上。其中，Accuracy的定义为分类正确（对角线上）的样本数与总样本数的比值。Accuracy度量的是全局样本预测情况。而对于Precision和Recall而言，每个类都需要单独计算其Precision和Recall。

如果想评估该识别系统的总体功能，必须考虑猫、狗、猪三个类别的综合预测性能。那么，到底要怎么综合这三个类别的Precision呢？是简单加起来做平均吗？通常来说， 我们有如下几种解决方案（也可参考scikit-learn官网）

总结

How to avoid machine learning pitfalls: a guide for academic researchers

  • 不要对不平衡的数据集使用准确度（accuracy）指标。这个指标常用于分类模型，不平衡数据集应采用kappa系数或马修斯相关系数（MCC）指标。

kappa系数

【2021-9-13】kappa系数简介

Kappa系数是一个用于一致性检验的指标，也可以用于衡量分类的效果。因为对于分类问题，所谓一致性就是模型预测结果和实际分类结果是否一致。kappa系数的计算是基于混淆矩阵的，取值为-1到1之间,通常大于0。可分为五组来表示不同级别的一致性：

  • 0.0~0.20 极低的一致性(slight)
  • 0.21~0.40 一般的一致性(fair)
  • 0.41~0.60 中等的一致性(moderate)
  • 0.61~0.80 高度的一致性(substantial)
  • 0.81~1 几乎完全一致(almost perfect)

基于混淆矩阵的kappa系数计算公式如下：

  • 其中，p0=对角线元素之和/矩阵所有元素之和，及acc，pe是所有类别分别对应的“实际与预测数量的乘积”之总和，除以“样本总数的平方”

对于不均衡数据集，acc失灵，所以用kappa系数，惩罚模型“偏向性”的指标来代替acc。而根据kappa的计算公式，越不平衡的混淆矩阵，pe越高，kappa值就越低，正好能够给“偏向性”强的模型打低分。

代码：

import numpy as np
 
# 计算混淆矩阵的kappa
def kappa(confusion_matrix):
    pe_rows = np.sum(confusion_matrix, axis=0)
    pe_cols = np.sum(confusion_matrix, axis=1)
    sum_total = sum(pe_cols)
    pe = np.dot(pe_rows, pe_cols) / float(sum_total ** 2)
    po = np.trace(confusion_matrix) / float(sum_total)
    return (po - pe) / (1 - pe)
# 无偏向的混淆矩阵
balance_matrix = np.array(
    [
        [2,  1,  1],
        [1,  2,  1],
        [1,  1,  2]
    ]
)
# 有偏向的混淆矩阵
unbalance_matrix = np.array(
    [
        [0,  0,  3],
        [0,  0,  3],
        [0,  0,  6]
    ]
)
kappa_balance = kappa(balance_matrix)
print("kappa for balance matrix: %s" % kappa_balance)

kappa_unbalance = kappa(unbalance_matrix)
print("kappa for unbalance matrix: %s" % kappa_unbalance)
kappa for balance matrix: 0.25
kappa for unbalance matrix: 0.0

# --------- sklearn ----------
#sklearn计算kappa
from sklearn.metrics import cohen_kappa_score
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
kappa_value = cohen_kappa_score(y_true, y_pred)
print("kappa值为 %f" % kappa_value)
# kappa值为 0.428571
# --------- tensorflow ------------
# tensorflow计算kappa
import tensorflow as tf

y_t = tf.constant(y_true)
y_p = tf.constant(y_pred)
kappa, update = tf.contrib.metrics.cohen_kappa(y_t, y_p, 3)
with tf.Session() as sess:
    sess.run(tf.local_variables_initializer())
    print(kappa.eval(), update.eval())
    print(kappa.eval(), update.eval())

MCC系数

马修斯相关系数（MCC）是机器学习中衡量二分类的分类性能的指标。该指标考虑了真阳性、真阴性和假阳性和假阴性，通常认为该指标是一个比较均衡的指标，即使是在两类别的样本失衡时，也可以应用它。MCC本质上是一个描述实际分类与预测分类之间的相关系数，它的取值范围为

  • 1时表示对受试对象的完美预测
  • 0时表示预测的结果还不如随机预测的结果
  • -1是指预测分类和实际分类完全不一致

MCC介绍

代码：

import pandas as pd
from math import sqrt

def get_data():
    df = pd.read_csv('data.csv')
    TP = df.iloc[0]["zero"]
    FP = df.iloc[1]["zero"]
    FN = df.iloc[0]["one"]
    TN = df.iloc[1]["one"]
    return TP,FP,FN,TN

def calculate_data(TP,FP,FN,TN):
    numerator = (TP * TN) - (FP * FN) #马修斯相关系数公式分子部分
    denominator = sqrt((TP + FP) * (TP + FN) * (TN + FP) * (TN + FN)) #马修斯相关系数公式分母部分
    result = numerator/denominator
    return result

if __name__ == '__main__':
  # ----- 自定义 -------
  TP,FP,FN,TN = get_data()
  result = calculate_data(TP,FP,FN,TN)
  print(result) #打印出结果
  # ------- sklearn --------
  from sklearn.metrics import matthews_corrcoef
  y_true = [+1, +1, +1, -1]
  y_pred = [+1, -1, +1, +1]
  matthews_corrcoef(y_true, y_pred)

Macro-average方法

该方法最简单，直接将不同类别的评估指标（Precision/ Recall/ F1-score）加起来求平均，给所有类别相同权重。该方法能够平等看待每个类别，但是它的值会受稀有类别影响。

  • [公式]
  • [公式]

Weighted-average方法

该方法给不同类别不同权重（权重根据该类别的真实分布比例确定），每个类别乘权重后再进行相加。该方法考虑了类别不平衡情况，它的值更容易受到常见类（majority class）的影响。

  • [公式] (W代表权重，N代表样本在该类别下的真实数目)
  • [公式]
  • [公式]

Micro-average方法

该方法把每个类别的TP, FP, FN先相加之后，在根据二分类的公式进行计算。

  • [公式]
  • [公式]

其中，特别有意思的是，Micro-precision和Micro-recall竟然始终相同！这是为啥呢？

这是因为在某一类中的False Positive样本，一定是其他某类别的False Negative样本。听起来有点抽象？举个例子，比如说系统错把「狗」预测成「猫」，那么对于狗而言，其错误类型就是False Negative，对于猫而言，其错误类型就是False Positive。于此同时，Micro-precision和Micro-recall的数值都等于Accuracy，因为它们计算了对角线样本数和总样本数的比值，总结就是：

  • [公式]

代码

import numpy as np
import seaborn as sns
from sklearn.metrics import confusion_matrix
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, average_precision_score,precision_score,f1_score,recall_score

# create confusion matrix
y_true = np.array([-1]*70 + [0]*160 + [1]*30)
y_pred = np.array([-1]*40 + [0]*20 + [1]*20 + 
                  [-1]*30 + [0]*80 + [1]*30 + 
                  [-1]*5 + [0]*15 + [1]*20)
cm = confusion_matrix(y_true, y_pred)
conf_matrix = pd.DataFrame(cm, index=['Cat','Dog','Pig'], columns=['Cat','Dog','Pig'])

# plot size setting
fig, ax = plt.subplots(figsize = (4.5,3.5))
sns.heatmap(conf_matrix, annot=True, annot_kws={"size": 19}, cmap="Blues")
plt.ylabel('True label', fontsize=18)
plt.xlabel('Predicted label', fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.savefig('confusion.pdf', bbox_inches='tight')
plt.show()

问题

sklearn.metrics

variables with inconsistent numbers

【2024-7-18】报错

  • 维度不一致导致错误
C = confusion_matrix([1,1], [1,1,0])

ValueError: Found input variables with inconsistent numbers of samples: [6, 7]

Precision is ill-defined

代码

sklearn.metrics.f1_score(y_true, y_pred, average='weighted')
# sklearn.metrics.f1_score(y_true, y_pred, average='weighted',zero_division=0)

错误信息

/mnt/bn/flow-algo-cn/wangqiwen/bin/miniconda3/lib/python3.12/site-packages/sklearn/metrics/_classification.py:1509: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, f"{metric.capitalize()} is", len(result))

原因

  • 部分类目总数为0, 导致计算时出现分母为0

解决

  • 加参数 zero_division=0
sklearn.metrics.f1_score(y_true, y_pred, average='weighted', zero_division=0)
metrics.classification_report(labels_all, predict_all, zero_division=0)
# 以下两个函数没有 zero_division 这个参数!
# metrics.accuracy_score(labels_all, predict_all)
# metrics.confusion_matrix(labels_all, predict_all)

评分方法

业务指标

渗透率与覆盖率

拿QQ音乐举例覆盖率：

  • 覆盖率：使用QQ音乐的用户/线上音乐户规模
    • 这里用户包括了vip用户和普通用户，也就是说覆盖率和用户是否消费无关，和使用该产品的用户数量多少相关
  • 渗透率：qq音乐的销售额/用户在音乐领域消费的总规模
    • 通俗来说就是，你赚到的钱占这个行业的赚到的钱的多少

作者：西瓜真甜啊

【2022-2-11】滴滴渗透率指什么？

滴滴订单数3800万，是美国的五倍，但是渗透率只有1%，怎么算渗透率？

  • 我们今天还只看城镇人口，中国城镇人口有8亿人口，每个人一天出门一次到两次，所以8亿人每天出行大概是13亿次左右，大概是11-13亿次左右这么一个数量，我们今天提供1400万次的出行除以13亿次，这个渗透率是1%，这个是我们目前看到的市场空间。而旧金山这个数据是多少呢？是15%，也就是说我们的市场空间是巨大的。

柳青在这一情景下说的渗透率是指“市场渗透率”，表示的是一种产品或服务在市场上的覆盖程度。

用百分数表示的，公式如下：

  • 市场渗透率 = 商品的现有需求量 / 商品的潜在需求量

而滴滴得出1%的算法是：中国城镇人口有8亿人口，每个人一天出门一次到两次，所以8亿人每天出行大概是13亿次左右，大概是在11-13亿次左右，用滴滴现在提供的1400万次出行除以13亿次，这个渗透率是1%，也是滴滴目前看到的市场空间。

Elo机制

【2023-5-26】什么才是真正的Elo机制

什么是Elo？

Elo Rating System 是由匈牙利裔美国物理学家 Arpad Elo 创建的一个衡量各类对弈活动水平的评价方法，是当今对弈水平评估的公认的权威方法。

  • 被广泛用于博弈类比赛，国际象棋、围棋、足球、篮球等运动。网络游戏英雄联盟、魔兽世界内的竞技对战系统也采用此分级制度。
  • 电影 《社交网络》中 , 创办了 Facebook 的 Mark Zuckerberg 和 Eduardo Saverin 在 Harvard 读大二时， 一夜间搭建了网站 Facemash。这个网站每次会展示两张不同女生的照片，用户选择自己认为更好看的一张。每次选择后，便进入下一组女生照片的评选。最终， Facemash 将计算出全校女生的长相排名。这其中所用的算法，就是 Elo Rating System。

Elo不是游戏首创，在体育竞技中十分常见。篮球、乒乓球、围棋、国际象棋等等，都会使用Elo来衡量运动员的水平。

  • 系统基于统计学, 只是一种参考，并不能绝对衡量出运动员实力。
    • 体育竞技本身就是一种十分复杂的游戏，一场比赛的输赢受到许多因素的影响，运动员的状态、运气、心理素质、场地氛围等等，都可能左右一场比赛。
  • 设计之初，Elo Rating System 仅是一个国际象棋选手的排名系统。
    • Elo 成为公认最权威的方法，是因为比之前所有评分系统都先进，更容易准确反应一个选手的真实水平。
    • 1970年，国际棋联正式开始使用这个评分系统。
    • Elo遭1V1对抗时用的最多，预测多人对抗游戏并不是它的强项

Elo 原理

Elo评级系统是如何运行的呢？

Elo 用一个数字来衡量运动员的水平，每场比赛结束后，赢家会从输家那里获得积分。两名运动员之间的积分差异决定一场比赛后，获得或者失去的积分。

  • 如果评分高的运动员获胜，那么只会从评分低的运动员那里，获得一点点积分。
  • 相反 如果评分低的运动员爆冷，就会抢走评分高的运动员大量积分。
  • 如果平局，评分低的运动员，同样会抢走评分低的运动员一定的积分。

注意

  • 只要运动员的场次足够多，Elo就会真实地反应出运动员的真实水平。

如何实现对象的评价和排名

  • Elo假设每个玩家在每盘游戏中的表现是一个正态分布的随机变量
  • 尽管选手在不同的游戏中发挥可能差异很大，但每位选手在一段时间内表现的平均值变化很小。
  • Elo用随机变量的平均值来代表选手的真正水平。
  • 简单的说：每个选手在每盘游戏中的发挥都是不稳定的，80的实力可能发挥出85，或者发挥出75， 但是随着比赛的不断进行，可以越来越多的趋近80这个真实水准。而ELO是用这个平均值来作为真实水准

假设: ELO算法的原理及应用

一名选手当前实力受各种因素的影响, 在一定范围内波动，某个时刻用来描述其实力的函数应当符合正态分布

两名选手进行对战时的预期胜率

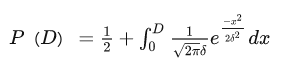
  • D为两者的分差。

利用了最小二乘法，得到与它的函数图向相近的另外的一个函数

当玩家A与玩家B的分差为D时，玩家A对玩家B的期望胜率为P(D)

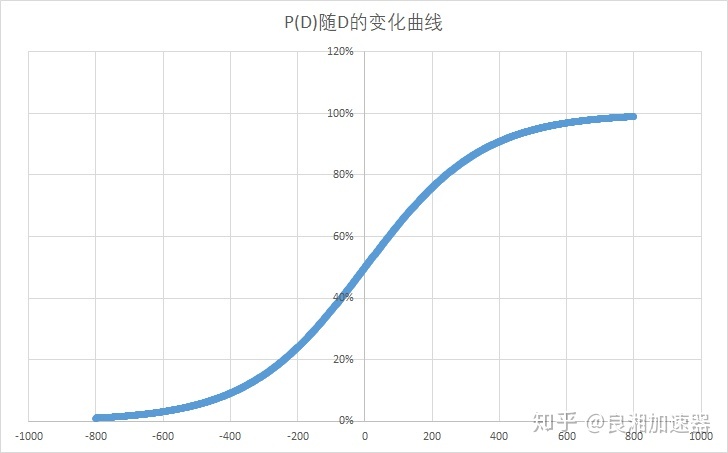
  • 玩家分数相同时，对战预期胜率为50%，分差越大，玩家之间的胜率差距也就越大，当分差大于400时，低分玩家的预期胜率将不足10%。
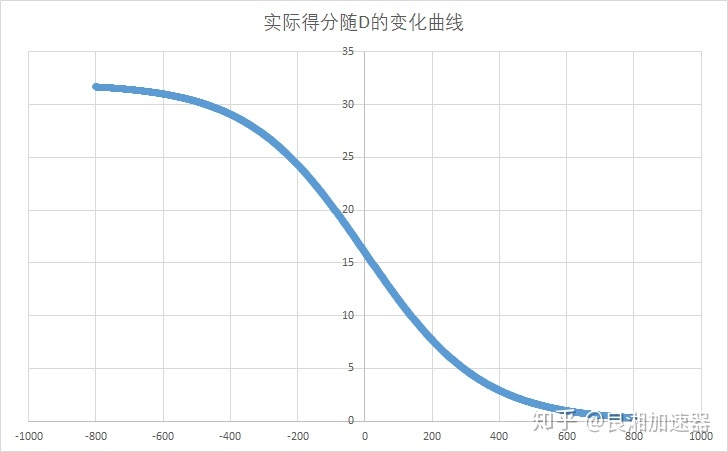
  • 取K=32时，玩家结束一场比赛后的实际得分数如图所示。可以看到玩家战胜比自己低800分的选手后（有近100%的胜率）基本不得分。

Elo 用一个数字衡量运动员水平，每场比赛结束后，赢家会从输家那里获得积分。

  • 两名运动员之间的积分差异，决定一场比赛后，获得或者失去的积分。
  • 如果评分高的运动员获胜，那么只会从评分低的运动员那里，获得一点点积分。
  • 相反，如果评分低的运动员爆冷，就会抢走评分高的运动员大量积分。
  • 如果平局，评分低的运动员，同样会抢走评分低的运动员一定的积分。

只要运动员的场次足够多，Elo就会真实地反应出运动员的真实水平。

Ra: A选手当前分数
Rb: B选手当前分数

# Ea: 预期A选手的胜负值
Ea = 1/(1+10^[(Rb-Ra)/400])

# Eb: 预期B选手的胜负值
Eb = 1/(1+10^[(Ra-Rb)/400])

E值也是预估的双方胜率，所以 Ea + Eb = 1

Sa: 实际胜负值，胜 = 1， 平 = 0.5， 负 = 0
K： 每场比赛能得到的最大分数，魔兽里 k=32 

R'a: A选手一场比赛之后的积分
R'a = Ra + K(Sa-Ea)

R'b: B选手一场比赛之后的积分
R'b = Rb + K(Sa-Eb)

举例

A队1500分，B队1600分，则
预估A队的胜负值 Ea = 1/(1+10^[(1600-1500)/400]) = 0.36
预估B队的胜负值 Eb = 1/(1+10^[(1500-1600)/400]) = 0.64

假设A队赢了，
A队最终得分为 R'a = 1500 + 32*(1-0.36) = 1500+20.5 = 1520, 赢20分，B队输20分。
假设B队赢了，
B队最终得分为 R'b = 1600 + 32*(1-0.64) = 1600 + 11.52 = 1612, 赢12分，A队输12分。

这就是为什么你赢高分队分数多，输给低分的输的也多，赢低分的分数很少。
其实K值就是这个方程的极限，所以理论上你最多可以赢一个队伍32分，实际上29-30已经差不多了，赢了不得分也是有可能的。

但是，Elo评分系统基于统计学，只是一种参考，并不能绝对衡量出运动员的实力。

  • 体育竞技本身就是一种十分复杂的游戏，一场比赛的输赢受到许多因素的影响，运动员的状态、运气、心理素质、场地氛围等等，都可能左右一场比赛。
  • 电竞是Elo应用最广泛的领域. CSGO、守望先锋、魔兽世界都采用Elo机制，或者Elo机制的升级版-Glicko-2

Elo之所以能成为公认最权威的方法，是因为它比之前所有的评分系统都先进，更容易更准确反应一个选手的真实水平。

  • 1970年，国际棋联正式开始使用这个评分系统。

Elo遭1V1对抗时用的最多，预测多人对抗游戏并不是强项。

Elo 会赋予每位玩家一个相同的初始积分，并进行以下计算：

  1. 根据积分差计算双方获胜概率；
  2. 每位玩家根据对方积分和游戏结果所表现出的水平分；
  3. 得出游戏后的积分变化。

Elo 工作模式总结：

  1. Elo 会给出玩家一场对局的获胜概率。Elo 积分相差越大，积分高的一方获胜概率就越大；
  2. 每场对局后，对阵双方都会进行一部分积分交换，胜者得分，败者失分；
  3. 如果两名玩家的积分相差很大，代表高分方获胜的概率极大，因此 即便赢了也涨不了多少分，败方也掉不了多少分。但倘若被低分方爆出冷门，那高分 方将失去大量分数。

Elo缺点

Elo Rating System 的缺点

任何算法系统都有优缺点，Elo 也不例外。

  • 初期的盲目性
    • Elo 积分在达到合理（趋近真实）水平之前需要一个过程。比如一个 2000 分的玩家玩小号，遇到的对手大概都是 1400 分水平，这时候 Elo 积分是不能准 确反映他的实力的。经过几局对战，这名玩家的积分会逐渐达到合理水平。这个 过程就是 Elo 积分的收敛过程。
  • 对时间不敏感
    • Elo 积分不会随着时间变化，当一位玩家很长时间没有游戏的时候，他的水 平可能会上下浮动，但他的 Elo 积分并不会随之改变。尤其对于顶尖玩家而言， 这时候的积分排名未必能反映玩家间真实的实力排名。

Elo 改进

Elo本来是一个好东西，但是游戏厂家一般都会对Elo进行魔改，这也是不同游戏，玩家对elo感知不同的原因。改得不好，简直就是一场灾难。

Elo 初次进入玩家视野，是王者荣耀策划 Donny 2018年在微博上发的一条关于匹配机制的解释。

关键点：

  1. 段位和Elo值共同决定匹配对手和队友；
  2. 如果等待时间过长，则放大Elo的寻找范围；
  3. 利用勇者积分机制，让玩家快速达到真实实力所在段位；

这些都是体育竞技中的Elo所没有的。因为这些特别的规则，玩家一些现象很容易解释，比如：

  • 王者荣耀中，为什么王者局，可以匹配到星耀2（星耀晋级后是王者段位）的玩家，这时因为这名星耀2玩家的Elo太高，已经达到了最强王者段位的水平。反之，最强王者匹配到星耀局，说明 Elo太低了。
  • 如此一来，又会出现一些问题。星耀2玩家因为Elo分数高去打王者局，在其他玩家实力大致相当的前提下，如果这名玩家实力是荣耀王者（最强王者50星），那么对手很容易被碾压。如果这名玩家是靠运气连胜导致Elo分数太高，又会成为队伍的累赘。

事实证明，双方实力大致相当的对局非常少。因为这名玩家需要足够多的场次，Elo值才能真实反应他的水平，而且即便如此，也不能排除他心情好，练一把英雄的情况……

再比如强行将匹配时长加入Elo机制中。

  • 玩家匹配等待时间过长，则放大Elo的寻找范围。

换句话说，假设9名最强王者玩家的Elo值都是1500分左右，但此时死活就是找不到一个1500分左右的最强王者玩家，那么系统就会扩大范围，强行匹配一个Elo 1600分，或者Elo 1400分的玩家。毫无疑问，出现这种情况，对局本身就不是公平的，更没有50%的胜率可言。

电竞中的Elo算法最大的问题是: 不能保证双方玩家的水平相当。

  • 对方70%能赢，己方30%能赢，结果阵容怎么好，英雄理解怎么到位，操作怎么溜，就是有一个坑货，怎么都赢不了。

关于Elo的错误认识。

  • 强行50%胜率
  • 拿败方MVP下把容易输
  • 隐藏分很高，下局逆风局
  • 连胜后必定连跪

换一种算法，是否能避免这种现象的出现？

  • 答案是不能，但可能减少。不能避免，是因为你总有达到属于自己实力段位的时候，总有运气爆棚连胜的时候，也会有运气差的时候。只要有一种算法，能保证双方在选阵容前，胜率是50%，双方水平相当，这种现象就会减少。

让我来告诉你，什么才是真正的Elo机制

Elo 实践

【2023-8-4】Elo Python实践代码

def expected_score(r1, r2):
    return 1 / (1 + 10**((r2 - r1) / 400))

def update_elo(r1, r2, score1):
    e1 = expected_score(r1, r2)
    e2 = expected_score(r2, r1)
    return r1 + K * (score1 - e1), r2 + K * ((1 - score1) - e2)

# K is a constant factor that determines how much ratings change
K = 32
# Convert scores to numeric values
score1 = 1 if score1 == 'A' else 0 if score1 == 'B' else 0.5
score2 = 1 if score2 == 'B' else 0 if score2 == 'A' else 0.5

# Average the scores
score = (score1 + score2) / 2

# Update ELO ratings
r1, r2 = prompt_ratings[prompt1], prompt_ratings[prompt2]
r1, r2 = update_elo(r1, r2, score)

评分卡

  • KDD的2019年会上，俄罗斯联邦储蓄银行（Sberbank）发布的论文《E.T.-RNN: Applying Deep Learning to Credit Loan Applications》，这是一篇将深度学习应用于风控领域的一个不错的探索
    • 传统评分卡方法: 信用评分是银行业务基础指标，经典的信用评分方法基于用户的申请单信息，用户的信用历史和其他关联的金融信息。传统的评分卡多采用经典的机器学习算法比如逻辑回归，GBDT，LighgtGBM等算法预测用户的贷后表现。
    • 尽管经典机器学习算法广泛应用且效果不错，但有以下不足：
      • 需要大量的特征工程工作和行业领域知识
      • 对于白户（无信用历史）的用户，很难给定评分
      • 传统算法模型没有充分利用用户数据
    • 论文提出了一种基于深度学习的评分卡算法，该方法基于到户交易数据利用RNN模型预测申请贷款用户的信用分。算法名称ETRNN全称Embedding Transactional Recurrent Neural Network，主要是利用用户的借记卡和信用卡的交易数据，只要用户有信用卡或者借记卡，就可以利用该方法。与传统的信用评分方法相比，ETRNN算法有以下有点：
      • 首先该方法效果超过了传统的方法。
      • 该方法基于用户的交易数据，不需要大量的特征工程方法和领域知识。
      • 该方法并部需要申请人除交易数据之外的其他数据，这意味着可以快速授信，改善用户体验。
      • 用户交易数据很难仿造。
      • 即使白户也可以利用交易数据评分。
    • 传统的评分卡方法，往往是对用户的交易流水历史做一些聚合，得到一些特征；而深度学习方法直接利用用户的交易流水数据，更好的利用用户消费的时序信息。

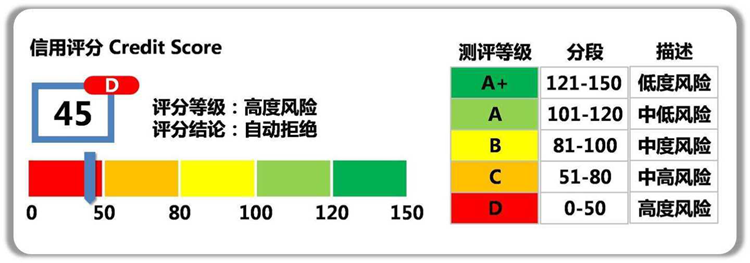
什么是信用评分卡模型？

评分卡模型又叫做信用评分卡模型，最早由美国信用评分巨头FICO公司于20世纪60年代推出，在信用风险评估以及金融风险控制领域中广泛使用。银行利用评分卡模型对客户的信用历史数据的多个特征进行打分，得到不同等级的信用评分，从而判断客户的优质程度，据此决定是否准予授信以及授信的额度和利率。相较资深从业人员依靠自身的经验设置的专家规则，评分卡模型的使用具有很明显的优点：

  • 判断快速：系统只需要按照评分卡逐项打分，最后通过相应的公式计算出总分，即可准确判断出是否为客户授信以及额度和利率。
  • 客观透明：评分卡模型的标准是统一的，无论是客户还是风险审核人员，都可以通过评分卡一眼看出评分结果和评判依据。
  • 应用范围广：由于评分卡的评分项是客观计算，其得出的分数具有广泛的参考性和适用性。例如，生活中常见的支付宝芝麻信用分，就是依据评分卡模型计算得出。

图

【2024-9-27】信用评分卡（A卡/B卡/C卡）的模型简介及开发流程

银行、消费金融公司等各种贷款业务机构，普遍使用信用评分，对客户实行打分制，以期对客户有一个优质与否的评判。

不是所有人都知道信用评分卡还分A,B,C卡三类

  • A卡（Application score card）申请评分卡
  • B卡（Behavior score card）行为评分卡
  • C卡（Collection score card）催收评分卡

评分机制区别：

  1. 使用时间不同。分别侧重贷前、贷中、贷后；
  2. 数据要求不同。A卡一般可做贷款0-1年的信用分析，B卡则是在申请人有了一定行为后，有了较大数据进行的分析，一般为3-5年，C卡则对数据要求更大，需加入催收后客户反应等属性数据。
  3. 每种评分卡的模型会不一样。在A卡中常用的有逻辑回归，AHP等，而在后面两种卡中，常使用多因素逻辑回归，精度等方面更好。

评分卡模型在银行不同的业务阶段体现的方式和功能也不一样。按照借贷用户的借贷时间，评分卡模型可以划分为以下三种：

  • 贷前：申请评分卡（Application score card），又称为A卡
    • 更准确地评估申请人的未来表现(违约率)，降低坏帐率
    • 加快(自动化)审批流程, 降低营运成本
    • 增加审批决策的客观性和一致性，提高客户满意度
  • 贷中：行为评分卡（Behavior score card），又称为B卡
    • 更好的客户管理策略, 提高赢利
    • 减少好客户的流失
    • 对可能拖欠的客户，提早预警
  • 贷后：催收评分卡（Collection score card），又称为C卡
    • 优化催收策略，提高欠帐的回收率
    • 减少不必要的催收行为，降低营运成本

评分卡模型示例： 图

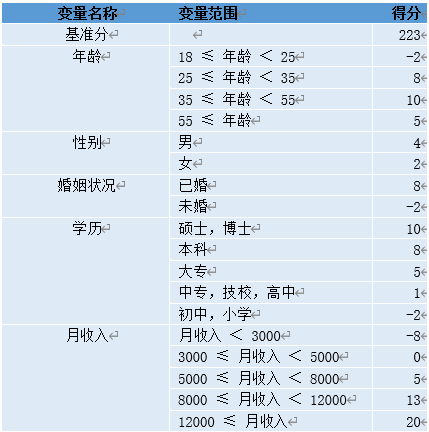
一个用户总的评分等于基准分加上对客户各个属性的评分。举个例子某客户年龄为27岁，性别为男，婚姻状况为已婚，学历为本科，月收入为10000，那么他的评分为：223+8+4+8+8+13=264

评分效果评估

专家训练场的评估分为三段：房源自述、小贝问答、推荐房源。最终的评分结果根据上述三个部分加权得到，现阶段没有完整数据可以标注，需要对各个阶段先进行评估，确保各阶段的评估合理。其中，推荐房源可以根据经纪人推荐的房源和系统候选房源进行对比，这个指标不需要评估，另外两个指标涉及意图识别及加权策略，需要进行评估。

评估使用基于pair-wise的方式，通过分析对比结果与评分之间的关系得出评估是否合理：

  • 如果相对好的数据评分相对高，则评价合理
  • 如果相对好的数据评分相对低，则评价不合理

文本为VR带看经纪人训练场中经纪人的文本，标注目标为标注文本A相对于文本B的好坏程度，数字的含义如下：

  • -2（很差），-1（较差），0（差不多），1（较好），2（很好）

标注的数据有两个部分：

  • （1）房源自述，对应的title为narrate，比较的时候参考以下标准：
    • 基础素质（讲解房源、小区、配套等）
  • （2）小贝问答，对应的title为show，比较的时候参考以下标准：
    • 服务态度（标注开场白、结束语等）
    • 需求理解与挖掘（理解客户需求，挖掘客户需求，比如购房意愿、金额等）

评分结果的验证分为以下几个方面：

  • （1）分数分布验证，检验是否为正态分布。如VR带看里，房源自述+小贝问答两种语料，检查概率分布
  • （2）一致性检验，即定性检验，检查标注的好坏是否与分差保持一致
    • 例如：文本A相对于文本B是1，文本A的分数是90，文本B是80，因为90 > 80，所以这条数据是通过一致性检验的。
    • 房源自述和小贝问答的一致率均大于 90%，说明一致率很高，简单理解评分的好坏准确率为90%以上。
  • （3）分值检验，即定量检验，检查标注的好坏程度是否与分差保持正比关系
    • 如果标注结果与分差正相关，那么打分的结果是比较合理的。
    • 例如：标注结果为文本A1相对于文本B1是1，实际分差为10分，标注结果为文本A2相对于文本B2是2，实际分差为20分，标注结果与分差是正相关的，说明评分的分数合理。
  • 参考

评分卡模型

如何搭信用评分卡模型？有了上面的评分卡示例，接下来需要考虑的是如何生成类似上面的表格：

  • 变量特征是如何选取的？
    • 剔除跟目标变量不太相关的特征, 涉及：变量两两相关性分析, 变量的多重共线性分析
    • 消除由于线性相关的变量，避免特征冗余
    • 减轻后期验证、部署、监控的负担
    • 保证变量的可解释性
  • 特征的变量范围是如何进行划分的？对变量进行分箱来实现变量的分段
    • 分箱的定义：①对连续变量进行分段离散化②将多状态的离散变量进行合并，减少离散变量的状态数
    • 常见的分箱类型：
      • ①无监督分箱。 无监督分箱仅仅考虑了各个变量自身的数据结构，并没有考虑自变量与目标变量之间的关系，因此无监督分箱不一定会带来模型性能的提升。
        • 等频分箱：把自变量按从小到大的顺序排列，根据自变量的个数等分为k部分，每部分作为一个分箱。
        • 等距分箱：把自变量按从小到大的顺序排列，将自变量的取值范围分为k个等距的区间，每个区间作为一个分箱。
        • 聚类分箱：用k-means聚类法将自变量聚为k类，但在聚类过程中需要保证分箱的有序性。
      • ②有监督分箱，包括 Split 分箱和 Merge 分箱
        • Split 分箱是一种自上而下(即基于分裂)的数据分段方法。Split 分箱和决策树比较相似，切分点的选择指标主要有 Entropy，Gini 指数和 IV 值等。
        • Merge 分箱，是一种自底向上(即基于合并)的数据离散化方法。Merge 分箱常见的类型为Chimerge分箱。
      • ③ChiMerge 分箱
        • ChiMerge 分箱是目前最流行的分箱方式之一，其基本思想是如果两个相邻的区间具有类似的类分布，则这两个区间合并；否则，它们应保持分开。Chimerge通常采用卡方值来衡量两相邻区间的类分布情况。
  • 每个字段的分值是如何设定的？

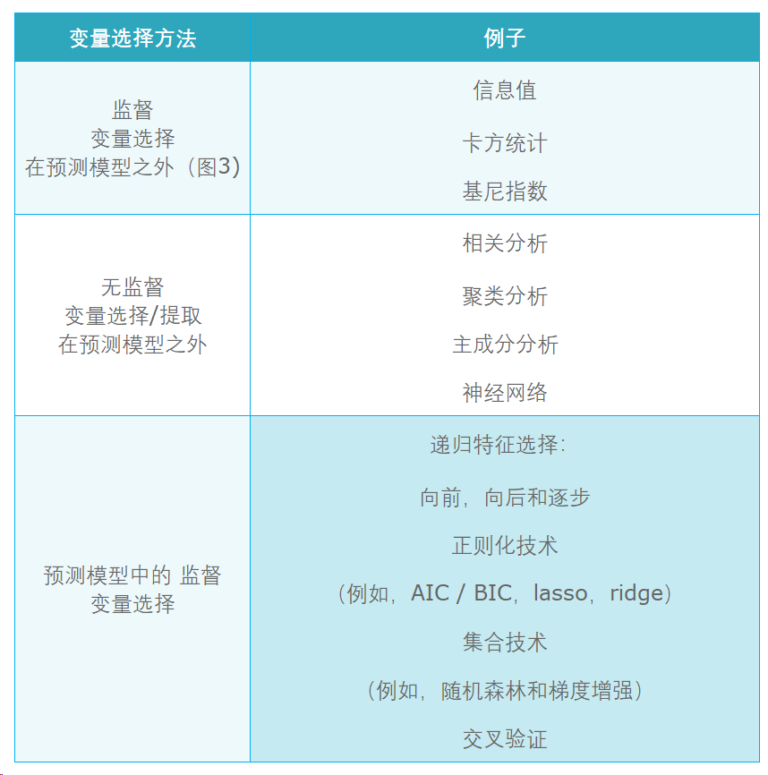
变量选择方法: 更多方法请参考：机器学习之特征选择方法 图

  • 【2021-7-27】风险控制：信用评分卡模型

  • 【2021-3-21】深入浅出评分卡的逻辑回归原理
  • 信贷评分卡的建模过程中，使用最多的算法就是逻辑回归（logistics regression）函数。下面，我们将围绕下面几点详细地讲述逻辑回归的数学来源和业务用途：
    • 什么是逻辑回归函数?
    • 为什么评分卡要使用逻辑回归函数？
    • 经济意义下逻辑回归函数的由来？（从金融角度揭示）
    • 怎么产生标准评分卡？（评分卡分数的线性转换）
      • 模型最终的产出还得是分数，上述的 s(x) 为对数比率分数，想要转化为千分制的分数还必须进行分数线性转化：
      • 以下2个假设用于定义分数刻度：
        • log 比率为 1:1的时候，分数为500分；
        • 好坏比（odds)每增加一倍，分数增加20分。
      • 解出，所以
      • 分数输出: 经过特征筛选、证据权重的计算、系数的回归，对每个特征分组都计算出一个分数，得出如下标准评分卡格式
    • 逻辑回归-标准评分卡的实操。
  • 银行决定是否给个人或企业贷款的关键因素是对未来违约概率的预测，逻辑回归函数能提供此技术支持。假设某银行挑选了 n 个特征进入评分卡给客户进行准入评分，且这 n 个特征包含了能判断客户是好还是坏的充分信息，若是想预测某个客户在将来违约的概率，那么只需要收集该客户的n个特征信息，代入公式，就得到一个介于(0,1)之间的值，称为好客户的概率。
  • 在逻辑回归函数的作用下，可以将客户的特征信息（如婚姻、年龄、历史以往信贷表现等）综合起来并转化为一个概率值，该值给银行预测客户好坏提供了一个直观依据。即 p(z) 值越大，证明该客户在将来违约的概率越小。

基本流程

  • （1）是否有label，如果有，需要先做特征分析，剔除无关特征
    • 正式建模之前，一般会对特征工程挖掘到的特征集进行筛选，以选择相关性高、稳定性强的特征，作为入模变量。
    • 常用特征筛选一般会考虑如下几方面：
      • 1）特征覆盖率(cover rate)，选取覆盖率达到一定阈值的特征；
      • 2）特征相关性：如根据特征本身的KS值、IV或卡方值，选择与建模label相关性高的特征；
      • 3）特征稳定性：比如通过衡量特征的PSI，选择随时间波动性尽可能小的特征。
      • 此外，还可以通过VIF、相关性系数等指标，排除特征之间的共线性。
  • （2）特征重要度数值+专家经验，制定组合方式，得到初步分数
  • （3）全局分布调整，转换到正太分布N（u，σ），u＜及格线，保证分数具备区分度
  • （4）打分反馈闭环，根据用户反馈，补充到label中，回到（1）

无监督评分卡也有些方法，如基于专家经验的层次分析法，熵权法等

评分卡建模

  • 机器学习在信用评分卡中的应用
  • 特征和样本标签准备好后，评分卡建模的过程则比较自然。虽然深度学习等技术在互联网领域已大行其道，在信用评分卡建模中，逻辑回归或GBDT等仍然是目前主流的建模算法。一方面是金融领域对特征的可解释性要求会更高，通过LR或GBDT建模，比较容易直观得到每个特征在模型结果中的权重，并根据业务经验解释权重系数的合理性。另一方面，实际评分卡建模中，一般入模特征维度并不高。在低维度建模中，LR和GBDT已经可以取得比较可观的效果。

模型评估

  • 模型建立后，需要对模型的预测能力、稳定性进行评估。信用评分模型常用的评估指标为KS、AUC等。 考虑到金融业务反馈周期长的特点，除了划分训练集、测试集外，通常会预留一段训练样本时间段之外的数据集，作为OOT（跨时间）集合，以测量模型在时间上的稳定性。
  • 评分分布图的区分度
    • 如果通过评分能将好坏用户完全区隔开来，那是理想中最好的评分卡模型，但实际情况中好坏用户的评分会有一定程度的重叠，我们要做的就是尽量减小重叠程度。
    • 好坏用户的得分分布最好都是正态分布，如果呈双峰或多峰分布，那么很有可能是某个变量的得分过高导致，这样对评分卡的稳定性会有影响。
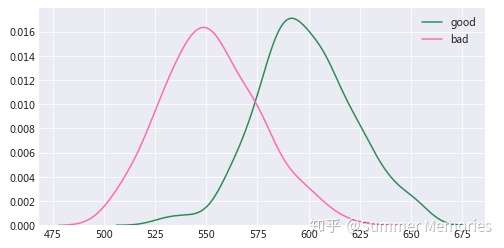
    • 摘自：评分卡模型的评估方法论, github 代码
  • 一文读懂评分卡的IV、KS、AUC、GINI指标
  • 当一张评分卡构建完成时，筛选出一组特征生成了分数，我们会想要知道这个分数是否靠谱，即是否可以依赖这个分数将好坏客户区分开来，这个时候就需要评判评分卡有效性的指标。
  • 测量评分卡好坏区分能力的指标有许多，本文就为大家介绍几个常用的定量指标：
    • ① 散度（分数为连续函数）与信息比率（IV);
    • ② KS值
    • ③ ROC曲线、AUROC值与GINI系数。

散度与信息比率

  • 散度为信息比率的连续版本。而评分卡分数是基于有限样本计算出的分数分布，并不一定是完全连续函数，所以就衍生出了离散版本的散度—-信息比率IV。
  • 在实际应用当中，IV值通常用来筛选变量，IV值越大，该变量的好坏区分能力越强。在评分卡建模的过程中，利用IV值筛选变量也是非常重要的一个环节。
  • 从IV值的公式中，易得变量的分组越多，IV值越大。但是分组分的太多，就会使得每个分组的数据量变少，导致细项分组的分布不稳定。所以，我们在使用IV值筛选变量的时候，不能为了提高IV值一味地将分箱的数目提高，也要兼顾变量的业务含义和分布的稳定性。

KS值

  • KS值是一个衡量好坏客户分数距离的上限值，具体做法为将对于各个分数区间对应的好坏客户累计占比进行相减，取最大值。
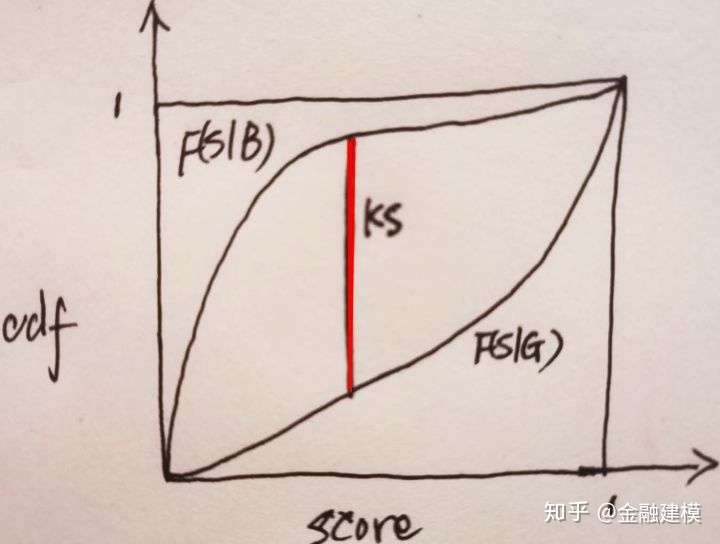
    • 为什么F(s|B)为凹函数、F(s|G)为凸函数？
    • 为什么F(s|B)-F(s|G)存在极大值（最大值）？
    • 为什么F(s|B)曲线在F(s|G)曲线之上？

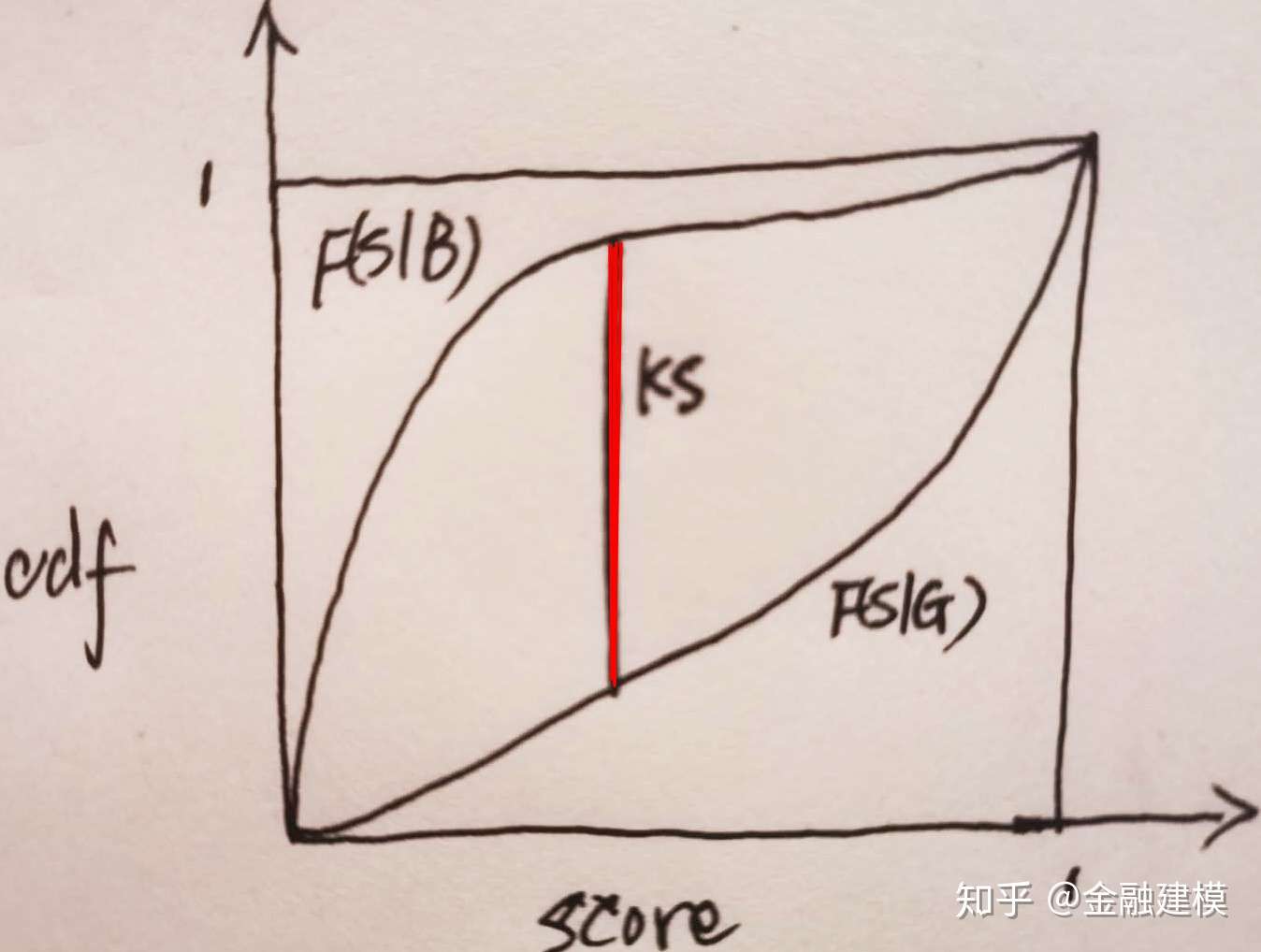
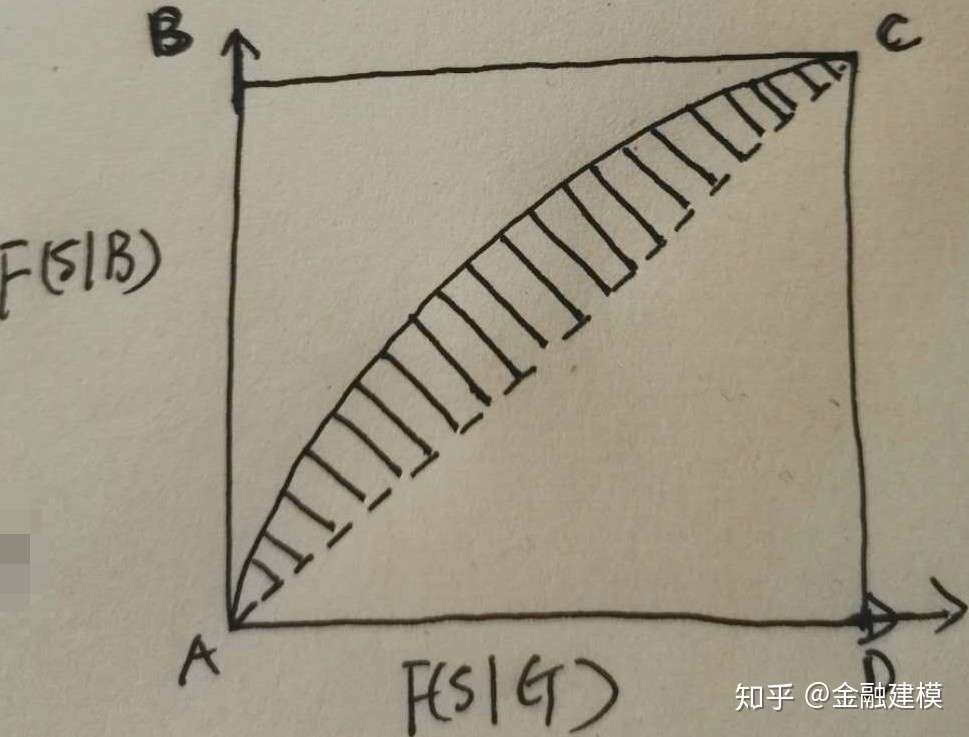
ROC曲线与AUROC值

  • ROC曲线也是评分卡度量指标中常用的指标工具，在介绍KS统计量的时候，其分布函数是由好客户和坏客户对应的累计概率密度函数F(s|B)与F(s|G)随着分数s变化的图形，而ROC曲线是好客户的累计概率密度相对于坏客户的累计概率密度函数的图形
  • 根据上文的分析，得出越接近B点的曲线，好坏客户的区分能力越强，这个时候，ROC曲线与X轴围成的面积就越大。由此，衍生出ROC曲线关于X轴面积的指标AUROC（Area under the ROC curve)。

GINI曲线

  • AUROC值是ROC曲线和X轴的面积，GINI系数定义为ROC曲线和对角线AC之间的面积占对角线AC曲线围成面积比，即 。
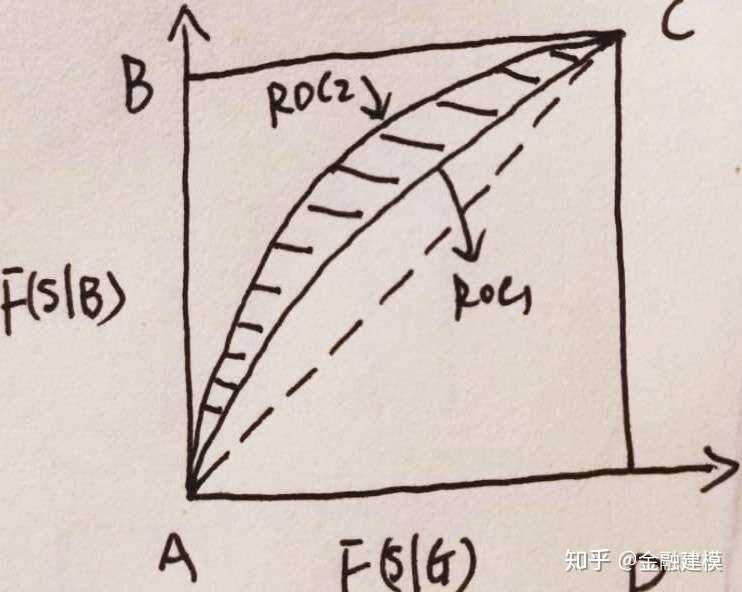    • 如果该评分系统异常完美，AUC曲线过点B(0,1)，这个时候GINI=1；
    • 如果评分卡毫无区分度，那么AUC曲线即为AC曲线，这时GINI=0;
  • 所以，GINI系数是一个介于(0,1)之间的函数，该值越大，模型的区分能力越强。

实战

  • Python实现的半自动评分，github地址，整个脚本的大概流程是：
    • PSI预筛选 –> 特征分箱 –> IV筛选特征 –> 相关性/多重共线性筛选 –> woe单调调整 – > 显著性筛选 –> 系数一致筛选 –> 建模 –> 模型评估 –> 标准评分转换

结束

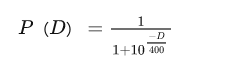
赏 支付宝打赏 微信打赏

~ 海内存知已，天涯若比邻 ~

Share

Similar Posts

Related Posts

上一篇 算法模型部署-Model Serving

下一篇 Docker学习笔记

标题：算法模型部署-Model Serving

摘要：如何将算法模型部署到线上？有哪些方法、工具及经验？

标题：Docker学习笔记

摘要：K8S，Docker 技术笔记

站内可视化导航

文章可视化导读：鼠标划过图形块时，如果出现蓝色光环, 点击即可跳转到对应主题

Comments

--disqus--

    Content
    My Moment ( 微信公众号 )
    欢迎关注鹤啸九天