- 损失函数
- 结束
损失函数
机器学习流程中重要一环: 损失函数
函数
数学定义
要素
- x 自变量
- y 因变量
- D 定义域
每一个x, 有且只有一个对应的y值与其对应
四种特性:
- 有界性
- 单调性
- 奇偶性
- 周期性
函数图像:
- 基本初等函数与初等函数
- 分段函数
类型
类型
- 函数 y=f(x)
- 反函数 $ y=f^{−1}(x) $
- 复合函数 y=f[g(x)]
- 隐函数
严格单调函数必有反函数
案例
- 常数函数
- 幂函数
- 指数函数
- 对数函数
- 三角函数
- 反三角函数
极限
求解
- 极限四则运算
- 洛必达法则
- 泰勒公式
损失函数定义
损失函数用来评价模型的预测值和真实值不一样的程度
- 损失函数越好,模型性能越好。
- 不同模型的损失函数一般也不一样。
【2023-1-18】损失函数权威指南
损失函数用于衡量预测输出与提供的目标值间的误差。通过将预测输出与预期输出进行比较, 来确定模型的性能
- 损失函数:算法模型离实现预期结果还有多远。
- “损失” 指模型因未能产生预期结果而受到的惩罚。
损失函数(称J)采用一对 <输出,目标> 输入,并计算一个值,该值估计输出与目标之间的距离。
- 预测输出 (y_pred)
- 目标值 (y)
- 损失:$ Loss=J(y_pred,y) $
损失函数是非负实值函数,通常使用L(Y, f(x))来表示
损失函数分为经验风险损失函数和结构风险损失函数。
经验风险损失函数: 预测结果和实际结果的差别结构风险损失函数: 经验风险损失函数+正则项。
【2021-10-13】机器学习初学者都应该知道的5类回归损失函数, 原文
- 最小化函数称为“
损失函数”,损失函数衡量模型预测预期结果的能力 - 最常用的最小化损失函数的方法是“
梯度下降法”,把损失函数想象成起伏的山脉,梯度下降法就像从山上滑下来到达最低点。 - 没有一个损失函数适用于所有类型数据,它取决于许多因素,包括异常值的存在,机器学习算法的选择,梯度下降法的时间效率和预测的置信度等。
损失函数总结
损失函数大致可分为:分类损失(预测数量)和回归损失(预测标签)
常用回归损失函数和分类损失函数
- (1)
回归:MAE/MSE/Huber loss(平滑MAE)/Log cosh loss/Quantile loss - (2)
分类:Log loss/Focal loss/KL Divergence(或相对熵)/Exponential loss/Hinge loss
激活函数
【2022-8-20】常见的激活函数, 一文概览深度学习中的激活函数

- 如果使用线性激活函数(恒等激励函数),那么,神经网络仅将输入线性组合再输出,在这种情况下,深层(多个隐藏层)神经网络与只有一个隐藏层的神经网络没有任何区别
- 两层使用线性激活函数的神经网络,可以简化成单层的神经网络,对于多个隐藏层的神经网络同样如此。因此,想要使神经网络的多个隐藏层有意义,需要使用非线性激活函数,也就是说想要神经网络学习到有意思的东西只能使用非线性激活函数。
- 需要一个非线性决策边界(non-linear decision boundary)来分离非线性数据集
总结
不是所有的函数都可以作为激活函数, 激活函数至少应该满足以下几点:
- 可微性:因为优化方法是基于梯度的,这个性质是必须的
- 单调性:当激活函数是单调的时候,能够保证单层网络是凸函数
- 输出值的范围:激活函数的输出值的范围可以有限也可以无限。当输出值是有限的时候,基于梯度的优化方法会更加稳定,因为特征的表示受有限权值的影响更加显著;当输出值是无限的时候,模型的训练会更加高效,不过在这种情况下,一般需要更小的learning rate
从目前来看,常见的激活函数多是分段线性和具有指数形状的非线性函数。
- 线性激活函数:这是一种简单的线性函数,公式为:f(x) = x。基本上,输入到输出过程中不经过修改
-
非线性激活函数:用于分离非线性可分的数据,是最常用的激活函数。非线性方程控制输入到输出的映射。非线性激活函数有 Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等。
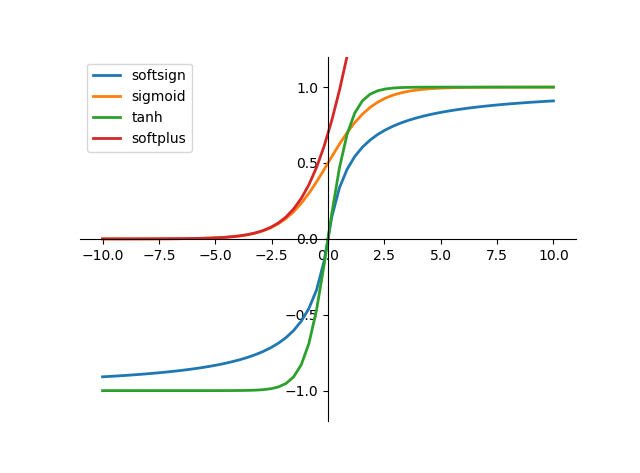
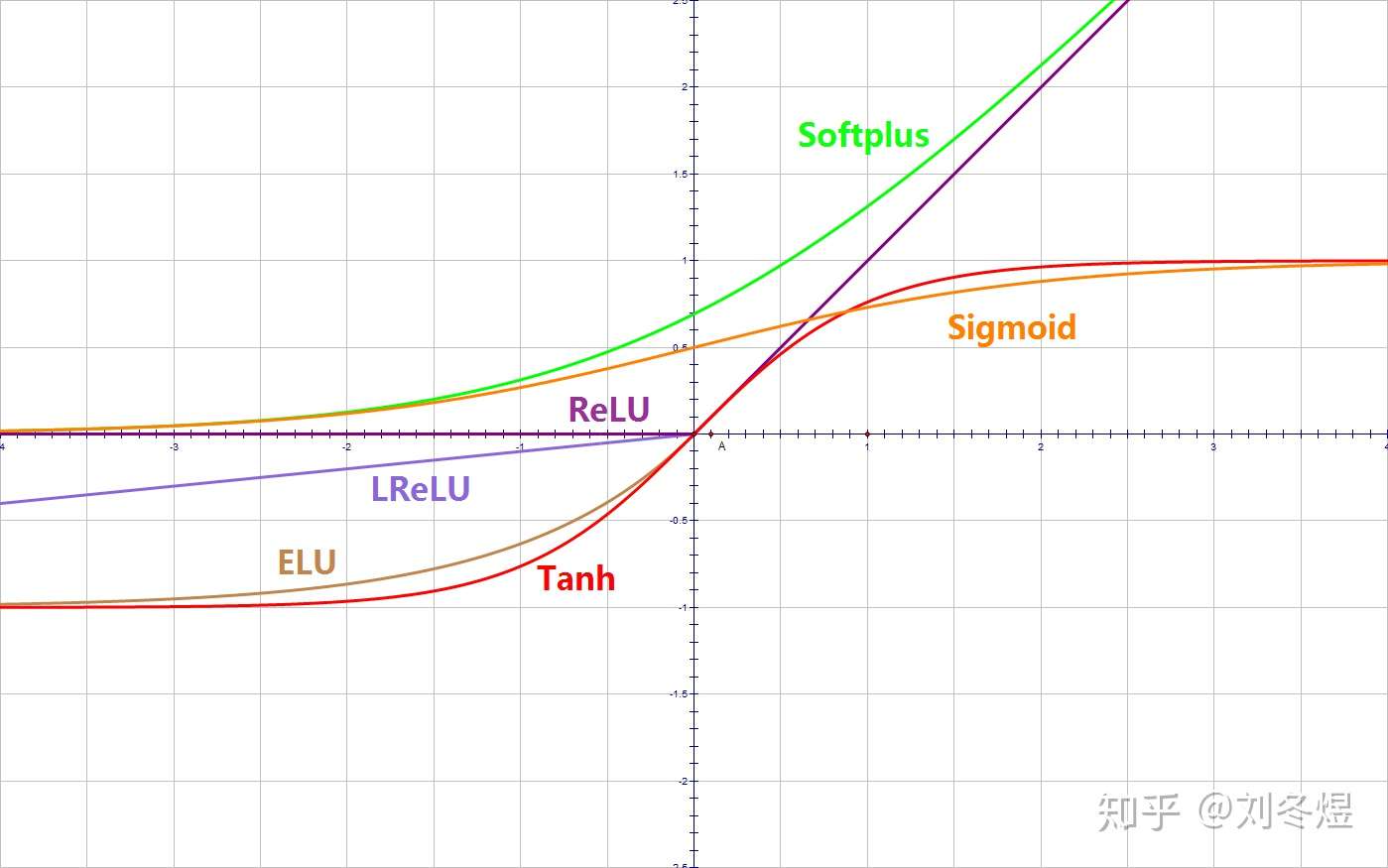
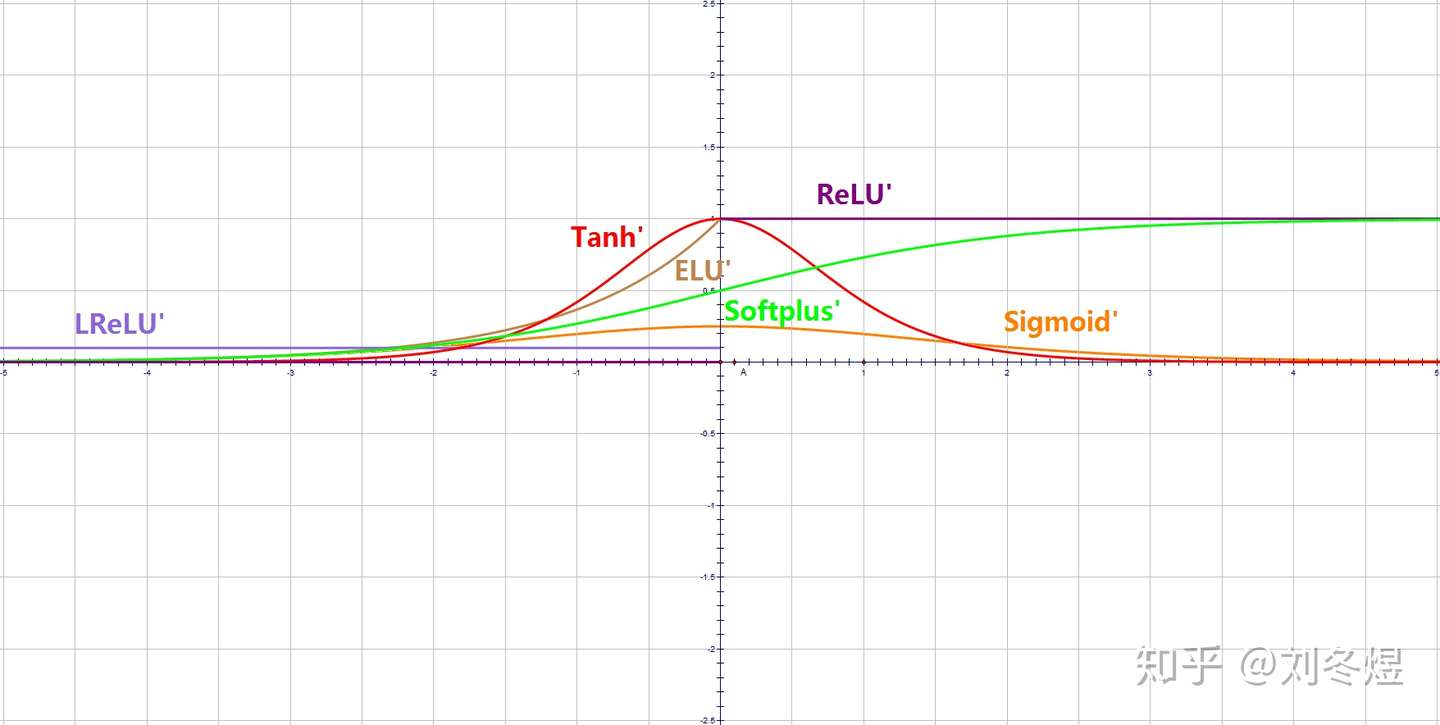
- 所有激活函数的导数值都是严格或不严格的大于零——这意味着输入值越大,输出值越大;反之,输入值越小,输出值越小。
- 参考:激活函数
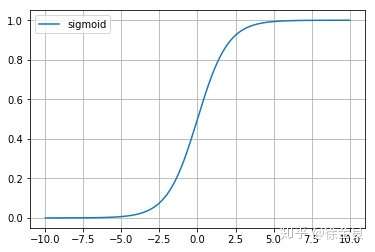
sigmoid(logistic回归)
公式
- $ y(x)=1/(1+exp^(1x)) $
sigmoid 函数值域为(0,1)
Sigmoid 三个主要缺陷:
- 梯度消失:注意:Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦,也就是说,Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时,输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此,这些神经元的权重不会更新。此外,与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此,想象一下,如果一个大型神经网络包含 Sigmoid 神经元,而其中很多个都处于饱和状态,那么该网络无法执行反向传播。
- 不以零为中心:Sigmoid 输出不以零为中心的。
- 计算成本高昂:exp() 函数与其他非线性激活函数相比,计算成本高昂。
#导入相关库
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:1/(1+np.exp(-x))
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='sigmoid')
plt.grid(True)#显示网格
plt.legend()#显示旁注#注意:不会显示后来再定义的旁注
plt.show(fig)
tanh
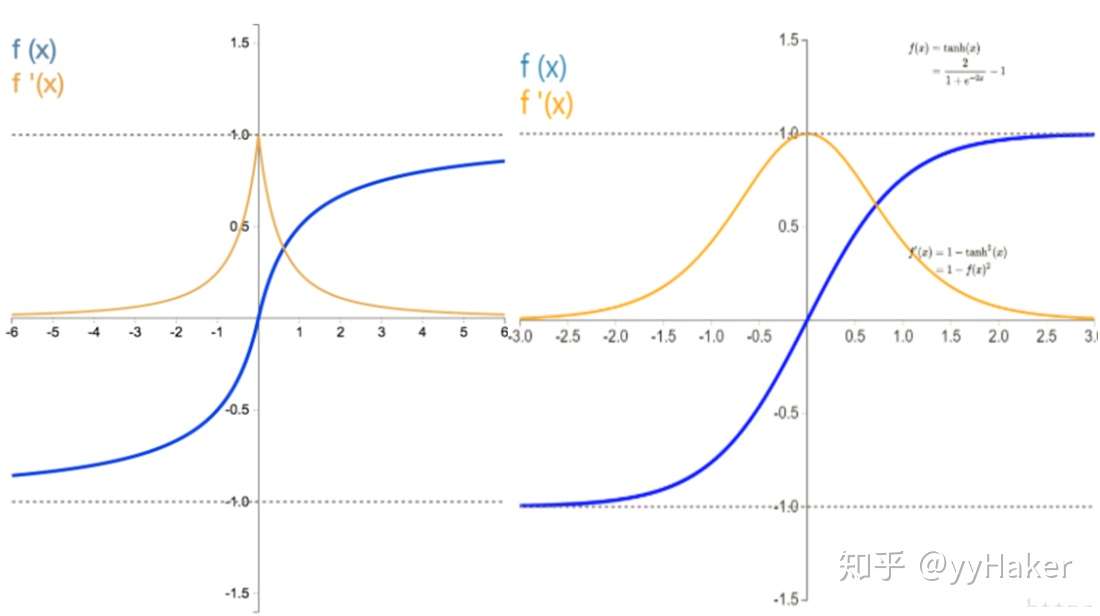
tanh函数是sigmoid函数向下平移和收缩后的结果
Tanh 激活函数又叫作双曲正切激活函数(hyperbolic tangent activation function)。
- 与 Sigmoid 函数类似,Tanh 函数也使用真值,但 Tanh 函数将其压缩至-1 到 1 的区间内。
- 与 Sigmoid 不同,Tanh 函数的输出以零为中心,因为区间在-1 到 1 之间。
- 可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值,零输入值的映射接近零,正数输入被当作正值。
唯一的缺点是:
- Tanh 函数也会有梯度消失的问题,因此在饱和时也会「杀死」梯度。
sigmoid和tanh激活函数有共同的缺点:
- 在z很大或很小时,梯度几乎为零,因此使用梯度下降优化算法更新网络很慢。
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:(np.exp(z)-np.exp(-z))/(np.exp(z)+np.exp(-z))
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='tanh')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
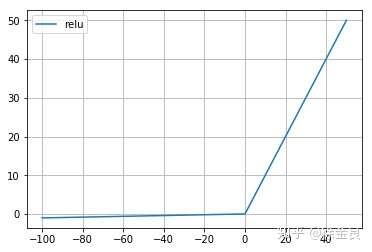
relu(修正线性单元)
为了解决梯度消失问题,另一个非线性激活函数——修正线性单元(rectified linear unit,ReLU),该函数明显优于前面两个函数,是现在使用最广泛的函数。
由于sigmoid和tanh的缺点,因此relu激活函数成为了大多数神经网络的默认选择。
当输入 x<0 时,输出为 0,当 x> 0 时,输出为 x。该激活函数使网络更快速地收敛。它不会饱和,即它可以对抗梯度消失问题,至少在正区域(x> 0 时)可以这样,因此神经元至少在一半区域中不会把所有零进行反向传播。由于使用了简单的阈值化(thresholding),ReLU 计算效率很高。
但是 ReLU 神经元也存在一些缺点:
- 不以零为中心:和 Sigmoid 激活函数类似,ReLU 函数的输出不以零为中心。
- 前向传导(forward pass)过程中,如果 x < 0,则神经元保持非激活状态,且在后向传导(backward pass)中「杀死」梯度。这样权重无法得到更新,网络无法学习。当 x = 0 时,该点的梯度未定义,但是这个问题在实现中得到了解决,通过采用左侧或右侧的梯度的方式。
但是relu也存在缺点:
- 在$z$小于0时,斜率即导数为0,因此引申出下面的 leaky relu 函数,但是实际上leaky relu使用的并不多。

import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:np.maximum(0,z)
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='relu')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
Leaky relu
为了解决 ReLU 激活函数中的梯度消失问题,当 x < 0 时,使用 Leaky ReLU——该函数试图修复 dead ReLU 问题。
该函数试图缓解 dead ReLU 问题。
Leaky ReLU 的概念是:
- 当 x < 0 时,它得到 0.1 的正梯度。
- 该函数一定程度上缓解了 dead ReLU 问题,但是使用该函数的结果并不连贯。
- 尽管它具备 ReLU 激活函数的所有特征,如计算高效、快速收敛、在正区域内不会饱和。
Leaky ReLU 可以得到更多扩展。不让 x 乘常数项,而是让 x 乘超参数,这看起来比 Leaky ReLU 效果要好。该扩展就是 Parametric ReLU。
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:np.maximum(0.01*z,z)
start=-100 #输入需要绘制的起始值(从左到右)
stop=50 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='relu')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
Parametric ReLU
引入了一个随机的超参数alpha,它可以被学习,因为可以对它进行反向传播。这使神经元能够选择负区域最好的梯度,有了这种能力,它们可以变成 ReLU 或 Leaky ReLU。
总之,最好使用 ReLU,但是可以使用 Leaky ReLU 或 Parametric ReLU 实验一下,看看它们是否更适合你的问题。
softmax
几种 max 方法
- hardmax: 直接取最大值, 粗暴, 不适合分类场景
- softmax: 综合考虑各种可能性, 增加置信度概念
将 Logits(逻辑值)输入 softmax 函数
- 目的: 将原始未经处理的分数转换为概率分布。
- Softmax 函数将 Logits 转化为归一化的概率值,使每个类别的分数都在 0~1之间,且所有类别的概率之和等于1。
- Softmax: 原始 Logits 较大值 被映射到更大概率,而较小值则对应较小概率。转换使得模型的输出更易于解释,用于多分类问题的决策和预测。
分类任务中,通常会选择最高概率的类别作为最终的预测结果。Softmax 有助于模型训练,因为它引入了梯度信息,使得模型更容易进行反向传播优化。
import numpy as np
a = np.array([1, 2, 3, 4, 5]) # 创建ndarray数组
a_max = np.max(a) # hard max
def softmax(x):
print(f'[debug] {x=}, {np.max(x)=}')
x -= np.max(x, axis= 0, keepdims=True)
f_x = np.exp(x) / np.sum(np.exp(x), axis=0, keepdims=True)
return f_x
logits = [0.1826171875, -0.98828125]
probs = softmax(logits)
probs
sigmoid vs softmax
【2025-2-21】Softmax函数与Sigmoid函数的区别与联系
- sigmoid 函数用于多标签分类问题,选取多个标签作为正确答案,它是将任意值归一化为
[0-1]之间,并不是不同概率之间的相互关联。 - 公式
Sigmoid(x) = 1 / (1 + e^(-x))
优点:
- Sigmoid 函数的输出在 (0,1) 之间,输出范围有限,优化稳定,用作输出层。
- 连续函数,便于求导。
缺点:
- 饱和性,从上图也不难看出其两侧导数逐渐趋近于0,容易造成梯度消失。
- 激活函数的偏移现象。Sigmoid函数的输出值均大于0,使得输出不是0的均值,这会导致后一层的神经元将得到上一层非0均值的信号作为输入,这会对梯度产生影响。
- 计算复杂度高,因为Sigmoid函数是指数形式。
Softmax 函数用于多分类问题,即从多个分类中选取一个正确答案。
- Softmax 综合了所有输出值的归一化,因此得到的是不同概率之间的相互关联。
Softmax 函数,又称归一化指数函数,函数表达式为:Softmax(x) = e^x / Σe^x
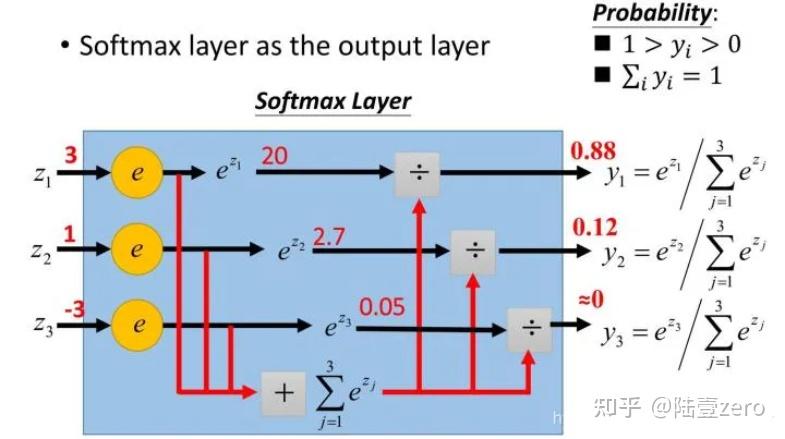
对于二分类而言,Sigmoid函数与Softmax函数理论上没有本质上的区别
| 函数 | 分类 | 公式 | 说明 |
|---|---|---|---|
| sigmoid | 二分类, 多标签分类 | Sigmoid(x) = 1 / (1 + e^(-x)) | R映射到 (0,1), 非概率意义 |
| Softmax | 二分类的推广:多分类 | Softmax(x) = e^x / Σe^x | 概率意义,不同结果之间相互关联 |
Softmax 函数是二分类函数 Sigmoid 在多分类上的推广,目的是将多分类的结果以概率形式展现出来。
Softmax 将原来输出是 3,1,-3 通过Softmax 函数映射成为 (0,1) 的值,而这些值的累和为1(满足概率的性质),理解成概率,在最后选取输出结点的时候,选取概率最大(也就是值对应最大的)结点,作为预测目标。
由于 Softmax 函数先拉大了输入向量元素之间的差异(通过指数函数),然后才归一化为一个概率分布,在应用到分类问题时,它使得各个类别的概率差异比较显著,最大值产生的概率更接近1,这样输出分布的形式更接近真实分布。
Softmax 可以由三个不同的角度来解释。从不同角度来看softmax函数,可以对其应用场景有更深刻的理解:
softmax可以当作arg max的一种平滑近似,与arg max操作中暴力地选出一个最大值(产生一个one-hot向量)不同,softmax将这种输出作了一定的平滑,即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。
softmax将输入向量归一化映射到一个类别概率分布,即 个类别上的概率分布(前文也有提到)。这也是为什么在深度学习中常常将softmax作为MLP的最后一层,并配合以交叉熵损失函数(对分布间差异的一种度量)。
从概率图模型的角度来看,softmax 概率无向图上的联合概率。因此 条件最大熵模型与softmax回归模型实际上是一致的,诸如这样的例子还有很多。由于概率图模型很大程度上借用了一些热力学系统的理论,因此也可以从物理系统的角度赋予softmax一定的内涵。
总结
- 如果模型输出为非互斥类别,且可同时选择多个类别,则采用 Sigmoid函数 计算该网络的原始输出值。
- 如果模型输出为互斥类别,且只能选择1个类别,则采用 Softmax函数 计算该网络的原始输出值。
- Sigmoid函数可以用来解决多标签问题,Softmax 函数用来解决单标签问题。
- 对于某个分类场景,当 Softmax 函数能用时,Sigmoid 函数 一定可以用。
Softsign
Softsign是tanh激活函数的另一个替代选择,从图中可以看到它和tanh的曲线极其相似,不过相比于tanh,Sotsign的曲线更平坦,导数下降的更慢一点,这个特性使得它可以缓解梯度消失问题,可以更高效的学习。
不过,Sofsign的导数相比tanh计算要更麻烦一点
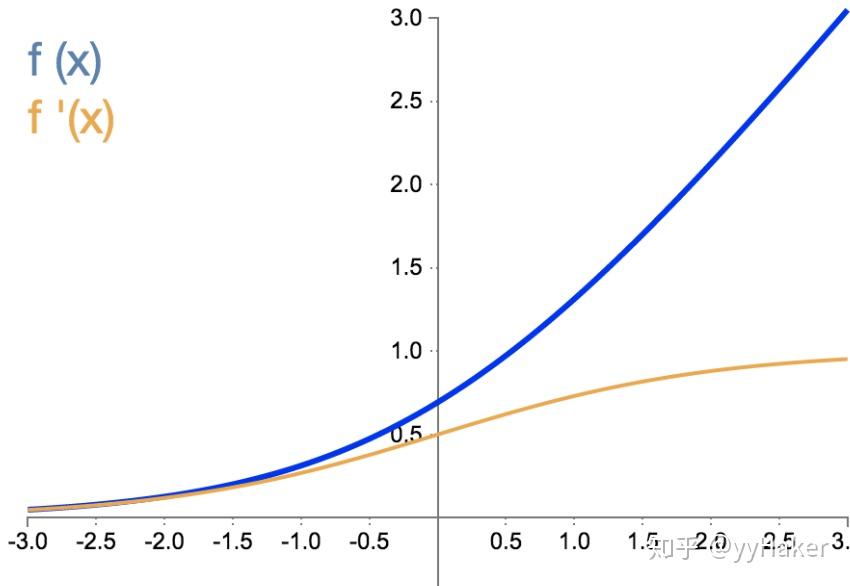
SoftPlus
SoftPlus可以作为ReLu的一个不错的替代选择,可以看到与ReLU不同的是,SoftPlus的导数是连续的、非零的、无处不在的,这一特性可以防止出现ReLU中的“神经元死亡”现象。
然而,SoftPlus是不对称的,不以0为中心,存在偏移现象;而且,由于其导数常常小于1,也可能会出现梯度消失的问题。
Maxout
Maxout出现在ICML2013上,作者Goodfellow将maxout和dropout结合后,号称在MNIST, CIFAR-10, CIFAR-100, SVHN这4个数据上都取得了start-of-art的识别率。
可以注意到,ReLU 和 Leaky-ReLU 都是它的一个变形。这个激活函数有点大一统的感觉,因为maxout网络能够近似任意连续函数,且当 为0时,退化为ReLU。Maxout能够缓解梯度消失,同时又规避了ReLU神经元死亡的缺点,但增加了参数和计算量。
Swish
该函数又叫作自门控激活函数,由谷歌的研究者发布. 根据论文,Swish 激活函数的性能优于 ReLU 函数。
在 x 轴的负区域曲线的形状与 ReLU 激活函数不同,因此,Swish 激活函数的输出可能下降,即使在输入值增大的情况下。大多数激活函数是单调的,即输入值增大的情况下,输出值不可能下降。而 Swish 函数为 0 时具备单侧有界(one-sided boundedness)的特性,它是平滑、非单调的。更改一行代码再来查看它的性能,似乎也挺有意思
函数拟合
多项式函数拟合
多项式拟合: np.polyfit
import numpy as np
import matplotlib.pyplot as plt
x = [10,20,30,40,50,60,70,80]
x = np.array(x)
print('x is :\n',x)
num = [174,236,305,334,349,351,342,323]
y = np.array(num)
print('y is :\n',y)
# f1 为各项的系数,3 表示想要拟合的最高次项是多少。
f1 = np.polyfit(x, y, 3)
# p1 为拟合的多项式表达式
p1 = np.poly1d(f1)
print('p1 is :\n',p1)
plt.plot(x, y, 's',label='original values')
yvals = p1(x) #拟合y值
plt.plot(x, yvals, 'r',label='polyfit values')
自定义函数拟合: curve_fit
对于自定义函数拟合,不仅可以用于直线、二次曲线、三次曲线的拟合,它可以适用于任意形式的曲线的拟合,只要定义好合适的曲线方程即可
from scipy.optimize import curve_fit
x = [20,30,40,50,60,70]
x = np.array(x)
num = [453,482,503,508,498,479]
y = np.array(num)
# 这里的函数可以自定义任意形式。
def func(x, a, b,c):
return a*np.sqrt(x)*(b*np.square(x)+c)
# popt返回的是给定模型的最优参数。我们可以使用pcov的值检测拟合的质量,其对角线元素值代表着每个参数的方差。
popt, pcov = curve_fit(func, x, y)
a = popt[0]
b = popt[1]
c = popt[2]
yvals = func(x,a,b,c) #拟合y值
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
损失函数总结
损失函数分类
PyTorch 损失函数分为两大类:回归损失和分类损失。(监督学习范畴)
- 当模型预测连续值(例如人的年龄)时,会使用回归损失函数。
- 当模型预测离散值时使用分类损失函数,例如电子邮件是否为垃圾邮件。
-
当模型预测输入之间的相对距离时使用排名损失函数,例如根据产品在电子商务搜索页面上的相关性对产品进行排名。
- 1、分类任务损失:
- 0-1 loss、熵与交叉熵loss、softmax loss及其变种、KL散度、Hinge loss、Exponential loss、Logistic loss、Focal Loss等待。
- 2、回归任务损失:
- L1 loss、L2 loss、perceptual loss、生成对抗网络损失、GAN的基本损失、-log D trick、Wasserstein GAN、LS-GAN、Loss-sensitive-GAN等等。
pytorch 实现
PyTorch 提供常见的 Loss Functions
nn.MSELoss(Mean Square Error)nn.NLLLoss(Negative Log Likelihood)nn.CrossEntropyLoss(交叉熵)
import torch
import torch.nn as nn
# ----- 数据准备 -------
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
# target = torch.tensor([1, 0, 4]) # 多分类,NLL
# target = torch.empty(3, dtype=torch.long).random_(5) # 交叉熵
# ----- 损失函数 -------
loss = nn.L1Loss() # MAE
loss = nn.MSELoss() # MSE
output = loss(input, target)
# NLL 负对数似然
m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss() # NLL
output = loss(m(input), target)
# 交叉熵
loss = nn.CrossEntropyLoss() # CE 交叉熵
# Hinge loss
loss = nn.HingeEmbeddingLoss() # Hinge loss
# 边际排名损失函数
input_one = torch.randn(3, requires_grad=True)
input_two = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()
ranking_loss = nn.MarginRankingLoss()
output = ranking_loss(input_one, input_two, target)
output.backward()
# 三元组边际损失
anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)
triplet_margin_loss = nn.TripletMarginLoss(margin=1.0, p=2)
output = triplet_margin_loss(anchor, positive, negative)
# KL散度
input = torch.randn(2, 3, requires_grad=True)
target = torch.randn(2, 3)
kl_loss = nn.KLDivLoss(reduction = 'batchmean')
output = kl_loss(input, target)
# ----- 反向传播 -------
output.backward()
# ----- 输出 -------
print('input: ', input)
print('target: ', target)
print('output: ', output)
自定义 Loss
如何创建自己的简单交叉熵损失函数?
- 方法一:创建自定义损失函数作为 python 函数
- 方法二:使用类定义创建自定义损失函数
# 方法一
def myCustomLoss(my_outputs, my_labels):
#specifying the batch size
my_batch_size = my_outputs.size()[0]
#calculating the log of softmax values
my_outputs = F.log_softmax(my_outputs, dim=1)
#selecting the values that correspond to labels
my_outputs = my_outputs[range(my_batch_size), my_labels]
#returning the results
return -torch.sum(my_outputs)/number_examples
# 方法二
class DiceLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(DiceLoss, self).__init__()
def forward(self, inputs, targets, smooth=1):
inputs = F.sigmoid(inputs)
inputs = inputs.view(-1)
targets = targets.view(-1)
intersection = (inputs * targets).sum()
dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)
return 1 - dice
损失函数监控
如何监控损失函数?
- 定义accuracy,结合Matplotlib 绘制
- notebook中监控PyTorch loss
- 使用 Neptune 监控 PyTorch 损失:网页形式监控
pytorch 损失函数
PyTorch torch.nn 模块有多个标准损失函数。
- 平均绝对误差损失(
MAE):又称L1损失,计算实际值和预测值之间的绝对差之和的平均值。- $\operatorname{loss}(x, y)=|x-y|$
- 均方误差损失(
MSE):又称L2损失,计算实际值和预测值之间的平方差的平均值。惩罚大误差。- $\operatorname{loss}(x, y)=(x-y)^{2}$
- 负对数似然损失(
NLL):负对数似然损失函数 (NLL) 仅适用于以 softmax 函数作为输出激活层的模型。- Softmax 是指计算层中每个单元的归一化指数函数的激活函数。
- NLL 使用否定含义,因为概率(或可能性)在0和1之间变化,并且此范围内值的对数为负。 最后,损失值变为正值。
- 模型因做出正确预测的概率较小而受到惩罚,并因预测概率较高而受到鼓励。 对数执行惩罚。NLL 不仅关心预测是否正确,还关心模型对高分预测的确定性。
- 适用场景:多分类问题
- 交叉熵损失(
CE):衡量两个概率分布之间的差异- 用于计算一个分数,体现预测值和实际值之间的平均差异
- 与负对数似然损失(NLL)不同,交叉熵惩罚不正确但置信度高的预测,以及正确但置信度较低的预测。
- 交叉熵函数有多种变体,最常见的是二元交叉熵 (BCE)。 BCE Loss主要用于二元分类模型
- 适用场景:
- ① 二元分类任务,Pytorch 中的默认损失函数。
- ② 创建有信心的模型——预测将是准确的,而且概率更高。
- 铰链嵌入损失(
Hinge):Hinge Embedding Loss 用于计算输入张量 x 和标签张量 y 时的损失。- Hinge Loss 函数,只要实际类别值和预测类别值之间的符号存在差异,就可以给出更多错误。
- 适用场景:目标值介于 {1, -1} 之间,这使其适用于二元分类任务
- ① 分类问题,尤其是在确定两个输入是不同还是相似时。
- ② 学习非线性嵌入或半监督学习任务。
- 边际排名损失(
MRL):Margin Ranking Loss 计算一个标准来预测输入之间的相对距离。- 直接从一组给定的输入进行预测。
- $ \operatorname{loss}(x, y)=\max (0,-y *(x 1-x 2)+\operatorname{margin}) $
- 适用场景:排名问题
- 三元组边际损失(
TML):Triplet Margin Loss 计算衡量模型中三重态损失的标准。- 此损失函数可以计算损失,前提是输入张量 x1、x2、x3 以及值大于零的边距。
- 三元组由 a(锚点)、p(正例)和 n(负例)组成。
- $ \mathrm{L}(\mathrm{a}, \mathrm{p}, \mathrm{n})=\max \left{\mathrm{d}\left(\mathrm{a}{\mathrm{i}}, \mathrm{p}{\mathrm{i}}\right)-\mathrm{d}\left(\mathrm{a}{\mathrm{i}}, \mathrm{n}{\mathrm{i}}\right)+\operatorname{margin}, 0\right} $
- 适用场景
- ① 确定样本之间存在的相对相似性。
- ② 用于基于内容的检索问题
- Kullback-Leibler 散度(
KL):Kullback-Leibler 散度,缩写为 KL 散度,计算两个概率分布之间的差异。- 计算在预测概率分布用于估计预期目标概率分布的情况下丢失的信息量(以位表示)。
- 输出两个概率分布的接近程度。
- 如果预测的概率分布与真实的概率分布相差甚远,就会导致很大的损失。
- 如果 KL Divergence 的值为零,则意味着概率分布相同。
- KL 散度的行为就像交叉熵损失,它们在处理预测概率和实际概率的方式上存在关键差异。 Cross-Entropy 根据预测的置信度对模型进行惩罚,而 KL Divergence 则不会。 KL 散度仅评估概率分布预测与地面实况分布有何不同。
- $\operatorname{loss}(x, y)=y \cdot(\log y-x)$
- 适用场景
- 逼近复杂函数
- 多类分类任务
- 如果想确保预测的分布与训练数据的分布相似
回归
MAE (L1损失)
平均绝对误差(Mean Absolute Error,MAE), 绝对偏差平均值即平均偏差,指各次测量值的绝对偏差绝对值的平均值。
平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小。
解释:
- 范围
[0,+∞),和MSE、RMSE类似,当预测值和真实值的差距越小,则模型越好;相反则越差。
平均绝对误差(MAE)用于回归模型的另一个损失函数,MAE是目标值和预测值之间绝对差的总和的平均值
绝对值损失函数是计算预测值与目标值的差的绝对值:
MAPE 平均绝对百分比误差
平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),平均绝对百分比误差之所以可以描述准确度是因为平均绝对百分比误差本身常用于衡量预测准确性的统计指标,如时间序列的预测。参考
计算公式:
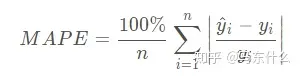
- MAPE就是mae 多了个分母。
解释:
- 和上面的MAE相比,在预测值和真实值的差值下面分母多了一项,除以真实值。
- 范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
Mape
- 好处:提供了一个便于比较的benchmark,即0值,当预测的y和真实的y完全相同的时候,Mape值最小为0,因此mape的结果约接近于0越好
- 然而比较致命的缺点:当真实值yi很小的时候,一点点的误差,mape的计算结果就很大;
注意
- 当真实值有数据等于0时,存在分母0除问题,该公式不可用!
# ------ 调用包 ----
from fbprophet.diagnostics import performance_metrics
df_p = performance_metrics(df_cv)
df_p.head()
# -------- 原生版 -----
def evalmape(preds, dtrain):
gaps = dtrain.get_label()
err = abs(gaps-preds)/gaps
err[(gaps==0)] = 0
err = np.mean(err)*100
return 'error',err
SMAPE 对称平均绝对百分比误差
对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error,SMAPE)
解释:
- 与MAPE相比,加了对称,其实就是将分母变为了真实值和预测值的中值。和MAPE的用法一样,范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
- smape是针对mape的问题的修正指标,可以较好的避免mape因为真实值yi小而计算结果太大的问题;
注意
- 当真实值有数据等于0,而预测值也等于0时,存在分母0除问题,该公式不可用!
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2021/12/21 15:05
# @Author : 府学路18号车神
# @Email :yurz_control@163.com
# @File : Evaluation_index.py
import numpy as np
from sklearn import metrics
# 将sklearn的也封装一下吧
# MSE
def mse(y_true, y_pred):
res_mse = metrics.mean_squared_error(y_true, y_pred)
return res_mse
# RMSE
def rmse(y_true, y_pred):
res_rmse = np.sqrt(metrics.mean_squared_error(y_true, y_pred))
return res_rmse
# MAE
def mae(y_true, y_pred):
res_mae = metrics.mean_absolute_error(y_true, y_pred)
return res_mae
# sklearn的库中没有MAPE和SMAPE,下面根据公式给出算法实现
# MAPE
def mape(y_true, y_pred):
res_mape = np.mean(np.abs((y_pred - y_true) / y_true)) * 100
return res_mape
# SMAPE
def smape(y_true, y_pred):
res_smape = 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100
return res_smape
# main
if __name__=='__main__':
# 由于没有用模型,这里就随机出几个值来测试下吧
y_true = np.random.random(10)
print(y_true)
y_pred = np.random.random(10)
print(y_pred)
# MSE
print(mse(y_true, y_pred))
# RMSE
print(rmse(y_true, y_pred))
# MAE
print(mae(y_true, y_pred))
# MAPE
print(mape(y_true, y_pred)) # 得到的值直接看成百分比即可
# SMAPE
print(smape(y_true, y_pred)) # 得到的值直接看成百分比即可
MSE (L2损失)
平均平方损失函数 (L2损失)
均方误差(MSE)是最常用的回归损失函数
MSE: 目标变量和预测值之间距离的平方和
平方损失函数标准形式:
特点:
- (1)经常应用与回归问题
MAE vs MSE
MSE与MAE的比较(L2损失与L1损失的比较)
- 使用平方误差更容易解决,但是使用绝对误差更有鲁棒性(MAE比MSE对异常值更稳健)
- 由于MSE平方了误差(y - y_predicted = e),若e大于1,误差(e)的将会增加很多。如果我们有一个离群值,e的值会大大增大,且MSE的值会远远大于e,这将会使MSE损失模型比MAE损失模型给与离散值更多的权重。若将RMSE作为损失的模型进行调整,损失模型将最小化异常点,而牺牲其他观测值,这回降低其整体性能
- MAE梯度始终使相同的,这意味着即使损失值很小,梯度也会很大
- 不均衡数据集下,两种损失函数都不好 → ①转换目标变量,②用别的损失函数,如Huber损失
# true: Array of true target variable
# pred: Array of predictions
def mse(true, pred):
return np.sum((true - pred)**2)
def mae(true, pred):
return np.sum(np.abs(true - pred))
# also available in sklearn
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
pytorch 实现
nn.MSELoss, 计算输入和目标之间的均方误差。
import torch
import torch.nn as nn
output = net(input)
target = torch.randn(10) # a dummy target, for example
target = target.view(1, -1) # make it the same shape as output
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)
net.zero_grad() # zeroes the gradient buffers of all parameters
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
Huber Loss (MAE+MSE结合)
平滑平均绝对误差(Smooth Mean Absolute Error)
为什么使用 Huber Loss?
MAE问题:梯度是一个比较大的常数,可能导致在使用梯度下降训练结束时,丢失了最小值。- 对于
MSE,梯度随着损失函数接近其最小值而减小,从而更容易找到最小值。 - Huber损失在在最小值附近减小了梯度,而且比
MSE更健壮。
因此,Huber损失结合了MSE和MAE优点
Huber损失的问题:
- 可能需要训练超参数δ,这是一个迭代的过程。
与平方误差损失相比,Huber损失对数据中的异常值不那么敏感,它在0处也是可微的。当误差很小的时候就变成了二次误差,误差有多小才能变成二次函数取决于超参数 δ (delta),这个超参数是可调的。取值选择很关键!
- 当超参数 δ ~ 0 时,Huber损失方法接近MAE;
- 当超参数 δ ~ ∞ 时,Huber损失方法接近MSE。
- 公式
- 曲线,不同颜色的曲线表示不同的超参数(真实值等于0)
# huber loss
def huber(true, pred, delta):
loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
return np.sum(loss)
Log-Cosh Loss
Log-Cosh 回归任务中使用的另一个函数,比L2更平滑,Log-cosh是预测误差的双曲线余弦的对数。
- Log-Cosh损失函数与预测值的曲线(真实值等于0):
- 优点:
- 当 x 较小时,log(cosh(x))近似等于(x**2)/2;
- x较大时,近似等于 abs(x) - log(2)。这意味这“logcosh”的工作原理与MSE非常相似,但不会受到偶尔出现异常值的影响。
- 它具有 Huber 损失的所有优点,且在任何情况下都是可微的。
为什么需要二阶导?
- 许多ML模型实现(如XGBoost)都使用牛顿方法来寻找最优值,这就是为什么使用二阶微分(Hessian)的原因。对于像XGBoost这样的ML框架,两次可微函数更受欢迎。
xgboost 目标函数:
其中 g_i 和 h_i 分别是损失函数l的一阶微分和二阶微分:
但是logcosh损失并不完美,当预测值与真实值偏差较大时,梯度和二阶微分是一个常数,不符合xgboost的分割条件 。
Huber 和 Log-cosh 损失函数 Python代码
# huber loss
def huber(true, pred, delta):
loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
return np.sum(loss)
# log cosh loss
def logcosh(true, pred):
loss = np.log(np.cosh(pred - true))
return np.sum(loss)
分位数损失 (MAE泛化)
大多数预测问题中,常常对预测中的不确定性感兴趣。
- 需要了解预测的范围(区间估计,而不是点估计),即想要预测一个区间而不是一个点时,分位数损失函数是有用的。
最小二乘回归的预测区间是基于残差(y-y_hat)在各自变量值之间具有恒定方差的假设。既不能相信违背这一假设的线性回归模型,也不能抛弃将线性回归模型作为基准来拟合的想法,因为使用非线性函数或基于树构建模型并非更好。
这就是分位数损失和分位数回归发挥作用的地方,基于分位数损失的回归为残差提供了合理的预测区间,即使残差的方差不是常数或非正态分布。
示例:最小二乘法
- 左图为同方差的数据,右图为异方差的数据,运用最小二乘法后的线性回归结果
- 分位数为0.05和0.95的分位数回归:虚线表示基于0.05和0.95的分位数损失的回归
分位数回归是在给定预测变量的条件下,估计响应变量的条件分位数。
- 分位数损失实际上是MAE的扩展,当分位数为0.5时,它就是MAE。
这个想法是根据想要给予正误差或负误差更多的值来选择分位数值,损失函数通过分位数来给高估的预测值或低估的预测值不同的惩罚权重,比如设置分位数 γ = 0.25时,分位数损失函数会给高估的预测值更多的惩罚,尽量保持预测值略低于中位数。
分位数损失函数
分位数 γ 的值在0和1之间,预测值和分位数回归损失函数的关系如下图(真实值等于0)
用这个损失函数来计算神经网络和基于树模型的预测区间,下面是一个用于梯度增强树回归的sklearn实现实例:
分类
0-1 Loss
0-1 损失函数(zero-one loss)
0-1损失: 预测值和目标值不相等为1, 否则为0:
特点:
- (1) 0-1损失函数直接对应分类判断错误的个数,但是它是一个非凸函数,不太适用.
- (2) 感知机就是用的这种损失函数。但是相等这个条件太过严格,因此可以放宽条件,即满足
时认为相等,
Hinge Loss
Hinge 损失函数标准形式如下:
特点:
- (1) hinge 损失函数表示如果被分类正确,损失为0,否则损失就为
。SVM就是使用这个损失函数。
- (2) 一般
是预测值,在-1到1之间,
是目标值(-1或1)。其含义是,
的值在-1和+1之间就可以了,并不鼓励
,即并不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差。
- (3) 健壮性相对较高,对异常点、噪声不敏感,但它没太好的概率解释。
Perceptron Loss (Hinge改进)
感知损失(perceptron loss)函数
感知损失函数的标准形式:
特点:
- (1) Hinge 损失函数的一个变种
- Hinge loss 对判定边界附近的点(正确端)惩罚力度很高。
- 而 perceptron loss只要样本的判定类别正确的话,它就满意,不管其判定边界的距离。
- 比 Hinge loss 简单,因为不是max-margin boundary,所以模型的泛化能力没 hinge loss强。
指数损失函数(exponential loss)
指数损失函数的标准形式:
特点:
- (1) 对离群点、噪声非常敏感。经常用在 AdaBoost算法中。
Log Loss 多分类
log 对数损失函数的标准形式:
特点:
- (1) log 对数损失函数非常好表征概率分布
- 在很多场景尤其是多分类,如果需要知道结果属于每个类别的置信度,非常适合。
- (2) 健壮性不强,相比于 hinge loss 对噪声更敏感。
- (3) 逻辑回归的损失函数就是log对数损失函数。
Cross-entropy Loss
适用于 二分类/多分类 问题, 与 sogmoid 激活函数搭配使用
CE 原理
nn.CrossEntropyLoss() 是一种交叉熵损失函数,用于多分类问题中。
该函数将输入值通过 softmax层 转换为概率分布,然后计算交叉熵损失。
- CE(p,y) = -log(p), if y=1
- CE(p,y) = -log(1-p), else
- log 指 ln, y=-ln(x)
Pytorch中,nn.CrossEntropyLoss() 可直接应用于神经网络输出的logits和标签之间的差异上
交叉熵损失函数的标准形式如下:
注意公式中 表示样本,
表示实际的标签,
表示预测的输出,
表示样本总数量。
特点:
- (1) 本质上也是一种对数似然函数,可用于二分类和多分类任务中。
- (2) 当使用 sigmoid 作为激活函数的时候,常用
交叉熵损失函数而不用均方误差损失函数,因为完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。
二分类问题中的loss函数(输入数据是softmax或者sigmoid函数的输出):
多分类问题中的loss函数(输入数据是softmax或者sigmoid函数的输出):
参数
默认参数: reduction, ignore_index, weight
size_average与reduce已被弃用,具体功能由参数reduction代替weight:赋予每个类的权重,指定权重必须是一维并且长度为C CC的数组,数据类型必须为tensor格式ignore_index:指定一个被忽略,并且不影响网络参数更新的目标类别,数据类型必须是整数,即只能指定一个类别-
reduction:指定损失输出的形式,有三种选择:nonemean sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数 - 注意:如果指定了ignore_index,则首先将ignore_index代表的类别损失删去,在剩下的损失数据里求均值,因此ignore_index所代表的的类别完全不会影响网络参数的更新
label_smoothing:指定计算损失时的平滑量,其中0.0表示不平滑,关于平滑量可参考论文《Rethinking the Inception Architecture for Computer Vision》
用法
交叉熵损失函数的实现代码:cross_entropy.
示例
import torch.nn as nn
import torch
x = torch.randn((2, 8))
# 在0-7范围内,随机生成两个数,当做标签
y = torch.randint(0, 8, [2])
ce = nn.CrossEntropyLoss()
out = ce(x, y)
print(x)
# tensor([[ 1.3712, 0.4903, -1.3202, 0.1297, -1.6004, -0.1809, -2.8812, -0.3088],
# [ 0.5855, -0.4926, 0.7647, -0.1717, -1.0418, -0.0381, -0.1307, -0.6390]])
print(y) # tensor([5, 0])
print(out) # tensor(1.9324) 得到的交叉熵损失,默认返回损失的平均值
class_weight 示例
解决样本不均衡问题
args.class_weight = '1,5'
class_weight = torch.tensor([float(x) for x in args.class_weight.split(",")]).to(device)
loss_function = nn.CrossEntropyLoss(weight=class_weight)
用 nn.CrossEntropyLoss() 的 weight 参数的示例:
(1)若有5个类别,第4个类别样本较少,将第4个类别的权重设置为2,其他类别的权重都为1。
class_weights = torch.tensor([1., 1., 1., 2., 1.])
loss_fn = nn.CrossEntropyLoss(weight=class_weights)
(2)若有10个类别,其中前3个类别的样本数量很少,将前3个类别的权重设置为10,其他类别的权重都为1。
class_weights = torch.ones(10)
class_weights[:3] = 10
loss_fn = nn.CrossEntropyLoss(weight=class_weights)
(3)若有7个类别,第5个类别的样本数量很多,将第5个类别的权重设置为0.5,其他类别的权重都为1。
class_weights = torch.ones(7)
class_weights[4] = 0.5
loss_fn = nn.CrossEntropyLoss(weight=class_weights)
注意
- 权重参数需要与标签数据的形状相同,即一维张量。
- 训练过程中,可根据实际情况调整权重参数的大小,以达到最佳的训练效果。
cross_entropy 源码
torch.nn vs torch.nn.functional
不同点
- 1: 调用方式
- nn.CrossEntropyLoss() 先实例化,再输入参数,以函数调用方式调用实例化的对象并传入输入数据:
- F.cross_entropy()直接可以传入参数和输入数据
- 2: nn.Sequential 便利性
- nn.xxx 继承于 nn.Module,能够很好的与nn.Sequential结合使用
- nn.functional.xxx 无法与nn.Sequential结合使用。
- 3: 是否维护 weight
- nn.xxx 不需要自己定义和管理 weight;
- 而 nn.functional.xxx 需要自己定义weight
import torch.nn as nn
loss = torch.nn.CrossEntropyLoss()
output = loss(x, y)
F.cross_entropy() 直接传入参数和输入数据
- 由于 F.cross_entropy() 得到的是一个向量, 对batch中每一个图像都会得到对应的交叉熵
- 所以计算出之后,会使用一个 mean() 函数,计算其总的交叉熵,再对其进行优化。
import torch.nn.functional as F
loss = F.cross_entropy(input, target).mean()
nn.xxx 继承于 nn.Module,能够很好的与nn.Sequential结合使用,而nn.functional.xxx 无法与nn.Sequential结合使用。
举个例子:
layer = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=3, padding=1),
nn.BatchNorm2d(num_features=64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2),
nn.Dropout(0.2)
)
不同点3:
- nn.xxx 不需要自己定义和管理 weight;
- 而 nn.functional.xxx 需要自己定义weight,每次调用时都要手动传入weight,不利于代码复用。
- 其实如果只保留了nn.functional下的函数,在训练或者使用时,就需要手动去维护weight, bias, stride 这些中间量的值;
- 如果只保留nn下的类,其实就牺牲了一部分灵活性,因为做一些简单的计算都需要创建一个类,这也与PyTorch的风格不符。
torch.nn
torch.nn 定义
- torch.nn下的 CrossEntropyLoss 类在forward时调用了nn.functional下的cross_entropy函数,当然最终的计算是通过C++编写的函数计算的。
class CrossEntropyLoss(_WeightedLoss):
__constants__ = ['ignore_index', 'reduction', 'label_smoothing']
ignore_index: int
label_smoothing: float
def __init__(self, weight: Optional[Tensor] = None, size_average=None, ignore_index: int = -100,
reduce=None, reduction: str = 'mean', label_smoothing: float = 0.0) -> None:
super(CrossEntropyLoss, self).__init__(weight, size_average, reduce, reduction)
self.ignore_index = ignore_index
self.label_smoothing = label_smoothing
def forward(self, input: Tensor, target: Tensor) -> Tensor:
return F.cross_entropy(input, target, weight=self.weight,
ignore_index=self.ignore_index, reduction=self.reduction,
label_smoothing=self.label_smoothing)
torch.nn.functional
def cross_entropy(
input: Tensor,
target: Tensor,
weight: Optional[Tensor] = None,
size_average: Optional[bool] = None,
ignore_index: int = -100,
reduce: Optional[bool] = None,
reduction: str = "mean",
label_smoothing: float = 0.0,
) -> Tensor:
if has_torch_function_variadic(input, target, weight):
return handle_torch_function(
cross_entropy,
(input, target, weight),
input,
target,
weight=weight,
size_average=size_average,
ignore_index=ignore_index,
reduce=reduce,
reduction=reduction,
label_smoothing=label_smoothing,
)
if size_average is not None or reduce is not None:
reduction = _Reduction.legacy_get_string(size_average, reduce)
return torch._C._nn.cross_entropy_loss(input, target, weight, _Reduction.get_enum(reduction), ignore_index, label_smoothing)
def cross_entropy(input, target, weight=None, size_average=None, ignore_index=-100,
reduce=None, reduction='mean'):
# type: (Tensor, Tensor, Optional[Tensor], Optional[bool], int, Optional[bool], str) -> Tensor
if size_average is not None or reduce is not None:
reduction = _Reduction.legacy_get_string(size_average, reduce)
return nll_loss(log_softmax(input, 1), target, weight, None, ignore_index, None, reduction)
分析
- input 和 target 是 Tensor格式
- 先计算 log_softmax,再计算 nll_loss。
- 实际上, softmax + log + nll_loss == CrossEntropyLoss
tf 和 pt 对softmax实现方式不同
- tf 先对类别进行 one-hot 编码, 再进行计算交叉熵
- 而 pt 不需要对标签one-hot编码,而是将通道维度压缩。即标签中的值为对应的类别数。
- 所有, 如果只有1个类别,需要单独处理
masks_pred = model(images)
if model.n_classes == 1:
# 通道压缩
loss = criterion(masks_pred.squeeze(1), true_masks.float())
loss += dice_loss(F.sigmoid(masks_pred.squeeze(1)), true_masks.float(), multiclass=False)
else:
loss = criterion(masks_pred, true_masks)
loss += dice_loss(
F.softmax(masks_pred, dim=1).float(),
F.one_hot(true_masks, model.n_classes).permute(0, 3, 1, 2).float(),
multiclass=True
)
class_weights 调权
【2024-7-25】 nn.CrossEntropyLoss() weight参数示例:
# (1)若有5个类别,其中第4个类别的样本数量较少,将第4个类别的权重设置为2,其他类别的权重都为1。
class_weights = torch.tensor([1., 1., 1., 2., 1.])
# (2)若有10个类别,其中前3个类别的样本数量很少,将前3个类别的权重设置为10,其他类别的权重都为1。
class_weights = torch.ones(10)
class_weights[:3] = 10
# (3)若有7个类别,其中第5个类别的样本数量很多,将第5个类别的权重设置为0.5,其他类别的权重都为1。
class_weights = torch.ones(7)
class_weights[4] = 0.5
# 传入 CE
loss_fn = nn.CrossEntropyLoss(weight=class_weights)
注意
- 权重参数需要与标签数据的形状相同,即一维张量。在训练过程中,根据实际情况调整权重参数的大小,以达到最佳的训练效果。
import torch.nn as nn
import torch
x = torch.randn((2, 2))
y = torch.tensor([0, 1])
# 不添加weight
ce = nn.CrossEntropyLoss(reduction='none')
# 添加weight
ce_w = nn.CrossEntropyLoss(weight=torch.tensor([0.5, 1.5]), reduction='none')
out = ce(x, y)
out_w = ce_w(x, y)
print(x) # tensor([0, 1])
print(y)
# tensor([[-1.1011, 0.6231],
# [ 0.2384, -0.3223]])
print(out)
# 不添加weight时的损失输出 tensor([1.8883, 1.0123])
print(out_w)
# weight定义为[0.5, 1.5]时的损失
# 第一个数据(batch中第一个元素)由于标签为0
# 因此对应的损失乘以weight中第一个权重
# 第二个数据类似
tensor([0.9441, 1.5184])
Balanced Cross Entropy (BCE)
改进 CE, 解决二分类不平衡问题
CE 问题
CE 假设所有类目同等重要, 数据集分布不均衡时, 模型会忽视少样本
BCE 介绍
Balanced Cross Entropy:
- 解决类不平衡方法。
引入了一个权重因子 α∈[0,1], 当为正样本时,权重因子就是 α,当为负样本时,权重因子为1-α
CE(pt) = -αlog(pt)- 当权重因子为0.75时,效果最好
BCELoss 是二元交叉熵损失函数(Binary Cross Entropy Loss)的简写。
- 输入经过 Sigmoid 函数激活后的预测概率和对应的真实标签(一般使用one-hot表示)。
- BCELoss 计算预测概率和真实标签之间的二元交叉熵损失,通过最小化该损失来优化模型。
BCE 实现
import torch
import torch.nn as nn
# 假设我们有一些预测值和目标值
predicted = torch.FloatTensor([2, -1, 0, 5])
target = torch.FloatTensor([1, 0, 1, 0])
criterion = nn.BCELoss()
# BCEWithLogitsLoss
# input:没有经过 Sigmoid 函数激活的预测概率 + 对应的真实标签(一般使用one-hot表示)
# 初始化BCEWithLogitsLoss
criterion = nn.BCEWithLogitsLoss()
# 计算loss
loss = criterion(predicted, target)
print(loss)
# 反向传播计算梯度
Focal loss 二分类
Focal loss 一般用于二分类, 也可以改造为多分类
- 二分类任务一般用
sigmoid作为最后的激活函数,输出只有一个代表样本为正的概率值p- CEL=−y∗log(p)−(1−y)∗log(1−p)
- 二分类非正即负,所以样本为负的概率值为1-p。
- 多分类一般以
softmax作为最后的激活函数的,输出有多个值,对应每个分类的概率值,和为1。- CEL=−∑_0^C−1 yi ∗ log(pi)=−log(pc)
- p的大小实际能反映出样本难易分类的程度
参考
- 【2023-3-28】Focal Loss的理解以及在多分类任务上的使用
BCE 问题
虽然 BCE 解决了正负样本不平衡问题,但并没有区分简单/难分样本。
当易区分负样本超级多时,整个训练过程将会围绕着易区分负样本进行,进而淹没正样本,造成大损失。
如 one-stage目标检测中, 正负样本数量极不平衡问题
- 目标类别与背景图类别之间的数量极不平衡。
Focal Loss 是 标准 Cross Entropy Loss 的一种改进。
Focal Loss 介绍
【2017.2.7】Facebook FAIR 何恺明 在目标检测任务中提出 Focal loss, 对简单样本进行decay的一种损失函数
Focal loss 基于二分类交叉熵CE, 一个动态缩放的交叉熵损失,通过一个动态缩放因子,可以动态降低训练过程中易区分样本的权重,从而将重心快速聚焦在那些难区分的样本(不再区分正样本/负样本)
演进:
Cross Entropy Loss(CE) ->Balanced Cross Entropy(BCE) ->Focal Loss(FL)
FL 对于简单样本(p比较大)回应较小的loss。 容易样本权重降低,而对难样本权重增加
- p=0.6 时, 标准的CE然后又较大的loss, 但是对于FL就有相对较小的loss回应。
对简单样本的一种decay。
- 其中 alpha 是对每个类别在训练数据中的频率有关
参考
- 非平衡数据集 focal loss 多类分类
- Focal Loss理解:降低了大量简单负样本在训练中所占的权重,也可理解为一种困难样本挖掘
- 普通的交叉熵对于正样本而言,输出概率越大损失越小。对于负样本而言,输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优
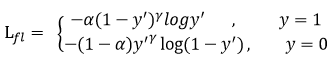

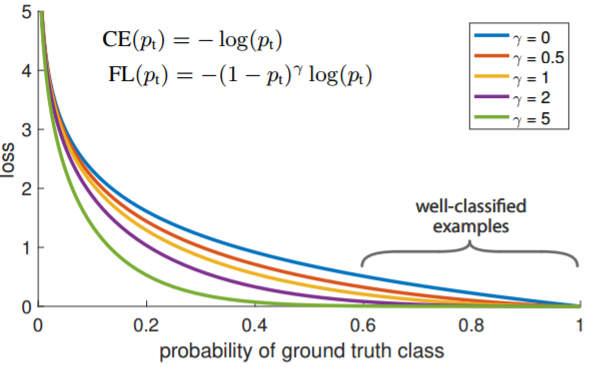
- 在原有的基础上加了一个因子,其中gamma>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。
- 只添加alpha虽然可以平衡正负样本的重要性,但是无法解决简单与困难样本的问题。
- gamma调节简单样本权重降低的速率,当gamma为0时即为交叉熵损失函数,当gamma增加时,调整因子的影响也在增加。实验发现gamma为2是最优。
Focal Loss 原理
公式
CE(pt) = -log(pt)- 数学定义: Focal loss 调变因子(modulating factor)乘以原来的交叉熵损失
FL(pt) = -αt(1-pt)^γ log(pt)
αt 抑制正负样本的数量失衡, γ 控制简单/难区分样本数量失衡
γ≥0,称为聚焦参数, 范围 [0,5]
- γ=0, 蜕变为 CE损失函数
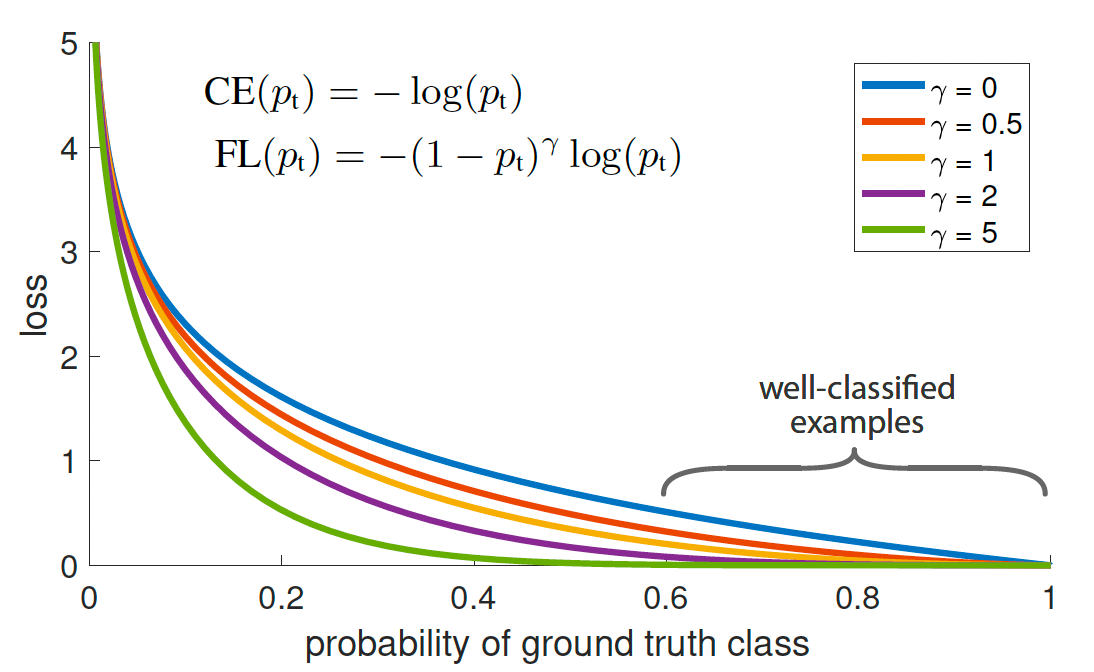
Focal loss 出自计算机视觉目标检测领域,作者是斩获多届顶会best paper的何凯明。
- 虽然出自目标检测,但是focal loss 思想在各个领域上都起到了很大的作用。
Focal Loss 是一个缓解分类问题中类别不平衡、难易样本不均衡的损失函数。
传统交叉熵损失函数形式:
其中,y为真值,p为预测概率,我们进一步可以将预测概率表示为:
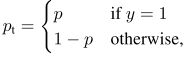
于是上述交叉熵的表达式可以简化为:
再来看一下Focal loss的具体形式:
对比可以看到,focal loss相较于交叉熵多了两项 与
. 这两项分别对应着前面提到的分类问题中类别不平衡、难易样本不均衡。
的作用与前面加权交叉熵中的权重一样,用于处理类别不平衡,而
则用于处理难易样本不均衡。其实很容易理解,当
较大的时候,说明样本比较容易被模型分类,此时
的值就会较小。反之
较小,样本难分,
就会加大。所以这也是一种加权。
Focal Loss 缺点
Focal Loss 缺点:
- 超参数选择:Focal Loss 引入额外超参数
gamma和alpha。- gamma 控制难易样本权重,并需要手动调整以适应不同的数据集。
- alpha 则用于平衡正负样本权重,同样需要根据具体情况进行选择。
- 超参数的选择可能会影响模型的性能,并需要较多的经验和试验来确定最佳值。
- 效果不稳定:Focal Loss 在某些情况下可能导致模型训练不稳定。
- 特别是当类别不平衡问题严重时,使用Focal Loss可能会导致梯度爆炸或消失问题,使得模型难以收敛或无法取得良好的结果。
- 这需要仔细调整超参数和优化策略,以避免不稳定性的影响。
- 仅适用于二分类问题:
- Focal Loss最初是为了解决二分类类别不平衡问题而设计的。
- 虽然可扩展到多分类问题,但在多分类问题中的应用效果可能不如在二分类问题中那么显著。在处理多分类问题时,可能需要考虑其他更适合的损失函数。
除了 Focal Loss,还有一些类似解决类别不平衡问题的损失函数,包括以下几种:
- 权重损失:使用权重损失,可以为不同类别的样本分配不同的权重。通过为少数类别分配较高的权重,可以平衡样本不平衡问题。在交叉熵损失函数中,可以通过设置权重来实现。
- 样本重采样:通过重新采样数据集,例如欠采样、过采样或生成合成样本等方法,使得类别之间的样本比例更加平衡。这可以在训练阶段减少类别不平衡带来的问题,但也可能引入一些其他问题,如过拟合等。
Focal Dice Loss:结合了Focal Loss和Dice Loss特点,用于解决医学图像分割等问题。- Dice Loss 处理类别不平衡时效果较好,而Focal Loss可以更好地处理难易样本。
- Focal Dice Loss 结合了两者的优势,并在图像分割任务中取得了较好的效果。
综上所述,虽然 Focal Loss 在解决类别不平衡问题上具有一定的优势,但也存在一些缺点。在实际应用中,根据具体问题和数据集的特点,选择合适的损失函数或组合多种方法来处理类别不平衡问题。
pytorch 实现
代码片段
class FocalLoss(nn.Module):
def __init__(self, gamma=2, weight=None):
super(FocalLoss, self).__init__()
self.gamma = gamma
self.weight = weight
def forward(self, inputs, targets):
ce_loss = nn.CrossEntropyLoss(weight=self.weight)(inputs, targets) # 使用交叉熵损失函数计算基础损失
pt = torch.exp(-ce_loss) # 计算预测的概率
focal_loss = (1 - pt) ** self.gamma * ce_loss # 根据Focal Loss公式计算Focal Loss
return focal_loss
二分类
完整示例
- (1) 使用 pytorch 实现
- (2) 自己实现 softmax 计算
(1) 使用 pytorch 实现
- 继承 torch.nn.Module 类来自定义一个 Focal Loss类
- 用 super() 函数调用父类的构造方法来初始化 alpha,gamma,weight 和 reduction 三个参数
- 参考
import torch
import torch.nn as nn
import torch.nn.functional as F
class FocalLoss(nn.Module):
"""
二分类 Focal loss
alpha: 正负样本权重,默认值为0.25
gamma: 难易样本权重,默认值为2
reduction: loss的计算方式,默认值为'mean'
当reduction='none'时,返回的是一个tensor,shape为[batch_size,]
"""
def __init__(self, alpha=0.25, gamma=2, reduction='mean'):
super(FocalLoss, self).__init__()
self.alpha = alpha
self.gamma = gamma
self.reduction = reduction
def forward(self, inputs, targets):
# softmax
ce_loss = F.cross_entropy(inputs, targets, reduction='none')
# 或 bce loss
# ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction='none')
pt = torch.exp(-ce_loss)
alpha = self.alpha * targets + (1 - self.alpha) * (1 - targets)
focal_loss = alpha * (1 - pt) ** self.gamma * ce_loss
if self.reduction == 'mean':
return focal_loss.mean()
elif self.reduction == 'sum':
return focal_loss.sum()
else:
return focal_loss
(2) 自己实现 softmax 计算
class Focal_Loss():
"""
二分类Focal Loss
"""
def __init__(self,alpha=0.25,gamma=2):
super(Focal_Loss,self).__init__()
self.alpha=alpha
self.gamma=gamma
def forward(self,preds,labels):
"""
preds:sigmoid的输出结果
labels:标签
"""
eps=1e-7
loss_1=-1*self.alpha*torch.pow((1-preds),self.gamma)*torch.log(preds+eps)*labels
loss_0=-1*(1-self.alpha)*torch.pow(preds,self.gamma)*torch.log(1-preds+eps)*(1-labels)
loss=loss_0+loss_1
return torch.mean(loss)
多分类
(1) pytorch 工具包实现
import torch
import torch.nn as nn
import torch.nn.functional as F
class FocalLoss(nn.Module):
"""
多分类 Focal loss
alpha: 正负样本权重,默认值为0.25
gamma: 难易样本权重,默认值为2
num_classes: 类目数
size_average: loss 累积方式
"""
def __init__(self, alpha=0.25, gamma=2, num_classes=3, size_average=True):
super(FocalLoss, self).__init__()
self.size_average = size_average
# 正负样本权重检查、矫正
if isinstance(alpha, list):
assert len(alpha) == num_classes
self.alpha = torch.Tensor(alpha)
else: # 自动设置list, 第一个类目为 alpha
assert alpha < 1
self.alpha = torch.zeros(num_classes)
self.alpha[0] += alpha
self.alpha[1:] += (1 - alpha) # α 最终为 [ α, 1-α, 1-α, 1-α, 1-α, ...] size:[num_classes]
# 难样本权重
self.gamma = gamma
def forward(self, preds, labels):
assert preds.dim() == 2 and labels.dim() == 1
self.alpha = self.alpha.to(preds.device)
log_soft = F.log_softmax(preds, dim=1)
soft = torch.exp(log_soft).gather(1, labels.view(-1, 1))
nulloss = F.nll_loss(log_soft, labels, weight=self.alpha, reduction="none").view(-1, 1)
# pt = torch.exp(-nn.CrossEntropyLoss(reduction="none")(preds, labels)).view(-1, 1)
# log_pt = nn.CrossEntropyLoss(weight=self.alpha, reduction="none")(preds, labels).view(-1, 1)
# loss = torch.mul((1 - pt) ** self.gamma, log_pt)
loss = torch.mul((1 - soft) ** self.gamma, nulloss)
if self.size_average:
loss = loss.mean()
else:
loss = loss.sum()
return loss
if __name__ == '__main__':
num = 3
inputs = torch.softmax(torch.rand(64 * 64, num), dim=-1)
target = torch.rand(64 * 64) > .5
func = FocalLoss(num_classes=num)
loss = func(inputs, target.long())
print(f'{inputs=}\n{target=}')
print(loss)
(2) 自定义
class Focal_Loss():
def __init__(self,weight,gamma=2):
super(Focal_Loss,self).__init__()
self.gamma=gamma
self.weight=weight
def forward(self,preds,labels):
"""
preds:softmax输出结果
labels:真实值
"""
eps=1e-7
y_pred =preds.view((preds.size()[0],preds.size()[1],-1)) #B*C*H*W->B*C*(H*W)
target=labels.view(y_pred.size()) #B*C*H*W->B*C*(H*W)
ce=-1*torch.log(y_pred+eps)*target
floss=torch.pow((1-y_pred),self.gamma)*ce
floss=torch.mul(floss,self.weight)
floss=torch.sum(floss,dim=1)
return torch.mean(floss)
tensorflow 实现
TensorFlow 对于 focal loss 同样没有封装,自定义:
def test_softmax_focal_ce_3(gamma, alpha, logits, label):
epsilon = 1.e-8
logits = tf.nn.sigmoid(logits)
logits = tf.clip_by_value(logits, epsilon, 1. - epsilon)
weight = tf.multiply(label, tf.pow(tf.subtract(1., logits), gamma))
if alpha is not None:
alpha_t = alpha
else:
alpha_t = tf.ones_like(label)
xent = tf.multiply(label, -tf.log(logits))
focal_xent = tf.multiply(alpha_t, tf.multiply(weight, xent))
reduced_fl = tf.reduce_sum(focal_xent, axis=1)
return tf.reduce_mean(reduced_fl)
yolo v8
YOLOv8 中的代码实现
- 参考 loss.py
import torch.nn as nn
import torch.nn.functional as F
class FocalLoss(nn.Module):
"""Wraps focal loss around existing loss_fcn(), i.e. criteria = FocalLoss(nn.BCEWithLogitsLoss(), gamma=1.5)."""
def __init__(self, ):
"""Initializer for FocalLoss class with no parameters."""
super().__init__()
@staticmethod
def forward(pred, label, gamma=1.5, alpha=0.25):
"""Calculates and updates confusion matrix for object detection/classification tasks."""
loss = F.binary_cross_entropy_with_logits(pred, label, reduction='none')
# p_t = torch.exp(-loss)
# loss *= self.alpha * (1.000001 - p_t) ** self.gamma # non-zero power for gradient stability
# TF implementation https://github.com/tensorflow/addons/blob/v0.7.1/tensorflow_addons/losses/focal_loss.py
pred_prob = pred.sigmoid() # prob from logits
p_t = label * pred_prob + (1 - label) * (1 - pred_prob)
modulating_factor = (1.0 - p_t) ** gamma
loss *= modulating_factor
if alpha > 0:
alpha_factor = label * alpha + (1 - label) * (1 - alpha)
loss *= alpha_factor
return loss.mean(1).sum()
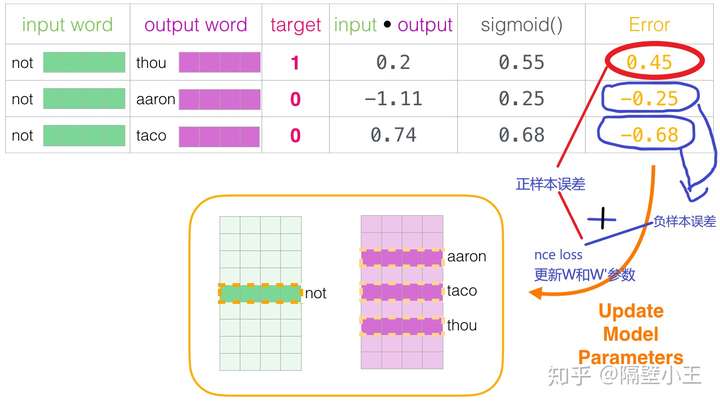
NCE Loss 类目多
当分类类别很多时,模型很难训练,速度很慢,nec_loss 可以解决这种问题
word2vec 模型训练过程中,不同词向量的个数可能有上百万个,直接采用 softmax 分类方式不太可行,nce_loss 可以采用随机负采样,相比hierarhical softmax 可以大幅度提高性能。
- 参考:知乎qiao
2016.6.15 Dice Loss
【2016-6-15】Dice Loss 在VNet 中提出,后来被广泛的应用在了医学影像语义分割之中。
- Dice loss 解决图像中前景与背景像素数目不平衡的问题。而正也正好对应到了分类问题中的正例与负例。
多标签文本分类的分类问题中,正例与负例的不平衡一直是一个很棘手问题。
- 1、训练与测试失配。
- 占据绝大多数的负例会支配模型的训练过程,导致模型倾向于负例,而测试时F1指标需要每个类都能准确预测;
- 2、简单负例过多。
- 负例占绝大多数也意味着其中包含了很多简单样本,简单样本对于模型学习困难样本几乎没有帮助,反而会在交叉熵的作用下推动模型遗忘对困难样本的知识。
分类问题一般都基于交叉熵作为损失函数,而交叉熵很明显特点:
- “平等”地看待每一个样本,无论正负,都尽力把它们推向1(正例)或0(负例)。
但实际上,对分类而言,将一个样本分类为负只需要它的概率<0.5 即可,完全没有必要将它推向0。
Dice Loss 原理
基于 Dice Loss 的自适应损失——DSC,训练时推动模型更加关注困难样本,降低简单负例的学习度,从而在整体上提高基于F1值的效果。
Dice Loss 怎么操作的,给定两个集合A和B,衡量两者之间的相似度:
如果把看作是模型预测的正例,
看作真实的正例。那么上式可以写成:
对于单个样本而言:
, 其中
为预测结果,
为真值。
表达了模型预测的正例与真正的正例之间的相似度,我们希望他们越相似越好,所以Dice Loss最基础的版本可以表达为:
对于二分类而言,如果为负例, 为0,这显然不太合理。所以加入了平滑系数
,即:
后来,Milletari et al. (2016)将分母改为平方和的形式以实现更好的收敛:
而在 ACL2020 提出的DSC中, 变为:
思想与 focal loss 一致,或者借鉴了focal loss的思想。
- 不过,Focal Loss 即使能对简单样本降低学习权重,但是它本质上仍然是在鼓励简单样本趋向0或1(本质上仍然是交叉熵),这就和DSC有了根本上的区别。
因此,DSC通过“平衡”简单样本和困难样本的学习过程,从而提高了最终的F1值。
同样,TensorFlow并没有dice loss和DSC的封装,还得自己写:
DiceLoss tensorflow
def dice_loss(y_true, y_pred, varepsilon):
epsilon = 1.e-8
y_true = tf.cast(y_true, tf.float32)
y_pred = tf.nn.sigmoid(y_pred)
y_pred = tf.clip_by_value(y_pred, epsilon, 1. - epsilon)
numerator = 2 * tf.reduce_sum(y_true * y_pred) + varepsilon
denominator = tf.reduce_sum(y_true + y_pred) + varepsilon
return 1 - numerator / denominator
DSC
def dsc_loss(y_true, y_pred, varepsilon):
epsilon = 1.e-8
y_true = tf.cast(y_true, tf.float32)
y_pred = tf.nn.sigmoid(y_pred)
y_pred = tf.clip_by_value(y_pred, epsilon, 1. - epsilon)
numerator = 2 * tf.reduce_sum(y_true * y_pred * (1-y_pred)) + varepsilon
denominator = tf.reduce_sum(y_true + y_pred * (1-y_pred)) + varepsilon
return 1 - numerator / denominator
2019 Class-Balanced Loss (改进Focal Loss)
谷歌对 CVPR 2019.1.16 上发表综述。
loss (softmax-cross-entropy、focal loss等)提出了一个针对每个类别重新加权方案,快速提高精度,特别是处理高度类不平衡的数据。
- 论文: Class-Balanced Loss Based on Effective Number of Samples
- [PyTorch实现源码]https://github.com/vandit15/Class-balanced-loss-pytorch)
效果
- 超过 Focal Loss
代码实现
[PyTorch实现源码]https://github.com/vandit15/Class-balanced-loss-pytorch)
import numpy as np
import torch
import torch.nn.functional as F
def focal_loss(labels, logits, alpha, gamma):
"""Compute the focal loss between `logits` and the ground truth `labels`.
Focal loss = -alpha_t * (1-pt)^gamma * log(pt)
where pt is the probability of being classified to the true class.
pt = p (if true class), otherwise pt = 1 - p. p = sigmoid(logit).
Args:
labels: A float tensor of size [batch, num_classes].
logits: A float tensor of size [batch, num_classes].
alpha: A float tensor of size [batch_size]
specifying per-example weight for balanced cross entropy.
gamma: A float scalar modulating loss from hard and easy examples.
Returns:
focal_loss: A float32 scalar representing normalized total loss.
"""
BCLoss = F.binary_cross_entropy_with_logits(input = logits, target = labels, reduction = "none")
if gamma == 0.0:
modulator = 1.0
else:
modulator = torch.exp(-gamma * labels * logits - gamma * torch.log(1 + torch.exp(-1.0 * logits)))
loss = modulator * BCLoss
weighted_loss = alpha * loss
focal_loss = torch.sum(weighted_loss)
focal_loss /= torch.sum(labels)
return focal_loss
def CB_loss(labels, logits, samples_per_cls, no_of_classes, loss_type, beta, gamma):
"""Compute the Class Balanced Loss between `logits` and the ground truth `labels`.
Class Balanced Loss: ((1-beta)/(1-beta^n))*Loss(labels, logits)
where Loss is one of the standard losses used for Neural Networks.
Args:
labels: A int tensor of size [batch].
logits: A float tensor of size [batch, no_of_classes].
samples_per_cls: A python list of size [no_of_classes].
no_of_classes: total number of classes. int
loss_type: string. One of "sigmoid", "focal", "softmax".
beta: float. Hyperparameter for Class balanced loss.
gamma: float. Hyperparameter for Focal loss.
Returns:
cb_loss: A float tensor representing class balanced loss
"""
effective_num = 1.0 - np.power(beta, samples_per_cls)
weights = (1.0 - beta) / np.array(effective_num)
weights = weights / np.sum(weights) * no_of_classes
labels_one_hot = F.one_hot(labels, no_of_classes).float()
weights = torch.tensor(weights).float()
weights = weights.unsqueeze(0)
weights = weights.repeat(labels_one_hot.shape[0],1) * labels_one_hot
weights = weights.sum(1)
weights = weights.unsqueeze(1)
weights = weights.repeat(1,no_of_classes)
if loss_type == "focal": # focal loss
cb_loss = focal_loss(labels_one_hot, logits, weights, gamma)
elif loss_type == "sigmoid": # bce loss
cb_loss = F.binary_cross_entropy_with_logits(input = logits,target = labels_one_hot, weights = weights)
elif loss_type == "softmax": # cb loss
pred = logits.softmax(dim = 1)
cb_loss = F.binary_cross_entropy(input = pred, target = labels_one_hot, weight = weights)
return cb_loss
if __name__ == '__main__':
no_of_classes = 5
logits = torch.rand(10,no_of_classes).float()
labels = torch.randint(0,no_of_classes, size = (10,))
beta = 0.9999
gamma = 2.0
samples_per_cls = [2,3,1,2,2]
loss_type = "focal"
cb_loss = CB_loss(labels, logits, samples_per_cls, no_of_classes,loss_type, beta, gamma)
print(cb_loss)
【2024-8-28】改进版: 去掉官方代码里冗余部分(focal loss), 更新参数名
- 函数版
- 面向对象版
def CB_loss1(labels, logits, num_per_cls, cls_num, beta):
"""
Class Balanced Loss 计算类目均衡损失
公式: ((1-beta)/(1-beta^n))*Loss(labels, logits)
参数:
labels: 标签列表 [batch].
logits: 预测矩阵 [batch, cls_num].
num_per_cls: 各类目样本频次 [cls_num].
cls_num: 总类目数 int
beta: Class balanced loss 超参, float.
返回:
cb_loss: class balanced loss
"""
effective_num = 1.0 - np.power(beta, num_per_cls)
weights = (1.0 - beta) / np.array(effective_num)
weights = weights / np.sum(weights) * cls_num
labels_one_hot = F.one_hot(labels, cls_num).float()
weights = torch.tensor(weights).float()
weights = weights.unsqueeze(0)
weights = weights.repeat(labels_one_hot.shape[0],1) * labels_one_hot
weights = weights.sum(1)
weights = weights.unsqueeze(1)
weights = weights.repeat(1,cls_num)
pred = logits.softmax(dim = 1)
cb_loss = F.binary_cross_entropy(input = pred, target = labels_one_hot, weight = weights)
return cb_loss
class CBLoss(nn.Module):
"""
Class Balanced Loss 计算类目均衡损失
公式: ((1-beta)/(1-beta^n))*Loss(labels, logits)
参数:
labels: 标签列表 [batch].
logits: 预测矩阵 [batch, cls_num].
num_per_cls: 各类目样本频次 [cls_num].
cls_num: 总类目数 int
beta: Class balanced loss 超参, float.
返回:
cb_loss: class balanced loss
"""
def __init__(self, cls_num, num_per_cls, beta=0.9999):
super(CBLoss, self).__init__()
self.beta = beta
# 正负样本权重检查、矫正
if isinstance(num_per_cls, list):
assert len(num_per_cls) == cls_num
self.cls_num = cls_num
self.num_per_cls = num_per_cls
def forward(self, preds, labels):
assert preds.dim() == 2 and labels.dim() == 1
effective_num = 1.0 - np.power(self.beta, self.num_per_cls)
weights = (1.0 - self.beta) / np.array(effective_num)
weights = weights / np.sum(weights) * self.cls_num
# labels_one_hot = F.one_hot(labels, self.cls_num).float()
# weights = torch.tensor(weights).float()
# gpu 上实测, 要将两个张量移动到相同设备, .to(preds.device), 否则报错
labels_one_hot = F.one_hot(labels, self.cls_num).float().to(preds.device)
weights = torch.tensor(weights).float().to(preds.device)
weights = weights.unsqueeze(0)
weights = weights.repeat(labels_one_hot.shape[0], 1) * labels_one_hot
weights = weights.sum(1)
weights = weights.unsqueeze(1)
weights = weights.repeat(1, self.cls_num)
pred = preds.softmax(dim = 1)
cb_loss = F.binary_cross_entropy(input = pred, target = labels_one_hot, weight = weights)
return cb_loss
if __name__ == '__main__':
cls_num = 5
logits = torch.rand(10,cls_num).float()
labels = torch.randint(0,cls_num, size = (10,))
print(f'类目数: {cls_num}\n{labels=}\n{logits=}')
beta = 0.9999
num_per_cls = [2,3,1,2,2]
cb_loss1 = CB_loss1(labels, logits, num_per_cls, cls_num, beta)
cb_loss_cls = CBLoss(cls_num, num_per_cls)
cb_loss2 = cb_loss_cls(preds=logits, labels=labels)
print(cb_loss, cb_loss1, cb_loss2)
2019 GHM loss (改进Focal Loss)
GHM loss:(focal loss改进)
Focal Loss 强制让模型关注难分类样本,但数据中可能也存在异常点,过度关注这些难分类样本,反而会让模型效果变差。
- Gradient Harmonized Single-stage Detector(AAAI 2019)提出了GHM Loss

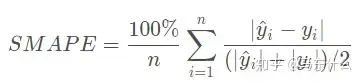
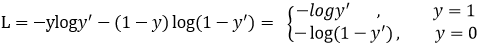
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
