- 因果科学
- 因果推理
- 引言
- 什么是因果科学
- 如何在观测数据下进行因果效应评估
- 因果科学实践
- 因果表示学习
- 资料
- 结束
因果科学
【2021-10-11】因果推断研究获2021诺贝尔经济学奖,北京时间10月11日下午,2021年诺贝尔经济学奖揭晓,颁发给三位学者。其中Joshua D. Angrist和Guido W. Imbens因“对因果关系分析的方法学贡献”而获奖。
- Causal Inference in Educational Systems: A Graphical Modeling Approach
- 标题:教育系统中的因果推理:一种图形化建模方法
快思考 vs 慢思考
【2021-7-8】对比《思考:快与慢》书籍中的人脑的快系统和慢系统,提出类似人脑慢系统的 System 2 Deep Learning,做为一个目标为人类水平智能的范式,将因果推理能力的内容作为其核心组件。Bengio指出人的认知系统包含两个子系统:
- System1是直觉系统,主要负责快速、无意识、非语言的认知,这是目前深度学习主要做的事情;
- System2是逻辑分析系统,是有意识的、带逻辑、规划、推理以及可以语言表达的系统,这是未来深度学习需要着重考虑的。
AI路线错了
当前AI方法论错了
- 自从AlphaGo一鸣惊人后,人工智能似乎一下子遍地开了花。智能音箱、智能导航、智能医疗——恍惚间,我们似乎已昂首阔步、意气风发走进了AI新时代。
然而有个人却说:

- 你们的方向都错了,现在的人工智能连“智能”的门还没摸到。
- 所有深度学习的成果,都只是曲线拟合。复杂而平庸。
- 目前的大数据和人工智能都只是停留在相关性的层面,其算法的核心都是基于过往的数据,来预测/产生新的东西
尤瓦尔·赫拉利在《人类简史》中说,想象和虚构的能力,让智人走上了食物链的顶端。同样,机器要想真的“智能”,也必须能想象和虚构。

- 也就是朱迪亚·珀尔强调的,真正的人工智能,光知道“相关”远远不够,而要懂得“因果”。
相关 vs 因果
相关≠因果
- 因果→相关
- 相关不一定是因果
相关性来源
相关性有三种来源:因果、混淆和样本选择。
- ① 因果关联例子就是天下雨地面会湿,这种关系是能够被人类所理解的、是可解释的、稳定的(无论在任何国家或城市,天下雨地都会湿)。
- ② 混淆关联是由混淆偏差(Confounding Bias)造成的。比如图中X是T和Y的共同原因(叉),但如果不对X进行观察,就会发现T和Y是具有相关性的,但T和Y之间是没有直接因果效应的,这就是产生了虚假相关。
- ③ 样本选择偏差(Selection Bias)也会产生相关性,比如之前的例子中,如果数据集中的狗都出现在沙滩上,而没有狗的图片都是草地,那么训练出的模型就会发现草地与狗之间是负相关的,这也产生了虚假相关。
虚假相关与因果关联相比,缺乏可解释性,且容易随着环境变化。在工业界和学术界中,都希望能判断两个变量之间的相关究竟是因果关联还是虚假相关。如果是虚假相关的话,可能会给实际的系统带来风险。
所以恢复因果可以提高可解释性,帮助决策,并在未来的数据集中做出稳定而鲁棒的预测,防止算法产生的偏差。无论数据集中有什么样的偏差,我们都希望能挖掘出没有偏差的因果关系,来指导算法。
【2020-10-22】如何在观测数据下进行因果效应评估:
- 相关性相比因果,更缺乏 可解释性(Explainability)、稳定性(Stability)(漂移)
- 可行动性(Actionability):这些虚假相关是由混淆变量产生的混杂偏倚(Confounding Bias),这种决策问题实际上是反事实问题,而不是预测问题。
- 公平性(Fairness):通过因果评估的框架,可以用Do-演算(Do-Calculus)等工具,干预收入的多少,来计算肤色与犯罪率之间真正的因果效应大小。
机器学习理论缺陷
2019年图灵奖得主Yoshua Bengio认为:“深度学习已经走到了瓶颈期,将因果关系整合到AI当中已经成为目前的头等大事“。
2011年图灵奖得主的Judea Pearl则提到:
“目前有太多深度学习项目都单纯关注缺少因果关系的粗糙关联性,这常常导致深度学习系统在真实条件下(明显不同于训练场景的条件下)进行测试时,往往拿不出良好的实际表现。”
- 图灵奖得主Judea Pearl:机器学习的理论局限性与因果推理的七大特性
- 【2018-5-10】近日,有越来越多的学者正在探讨机器学习(和深度学习)的局限性,并试图为人工智能的未来探路
- 纽约大学教授 Gary Marcus 就对深度学习展开了系统性的批判
- 图灵奖获得者,UCLA 教授 Judea Pearl 题为《Theoretical Impediments to Machine Learning with Seven Sparks from the Causal Revolution》的论文中,作者就已探讨了当前机器学习存在的理论局限性,并给出了面向解决这些问题,来自因果推理的七个启发。
- 当前的机器学习几乎完全是统计学或黑箱的形式,从而为其性能带来了严重的理论局限性。这样的系统不能推断干预和反思,因此不能作为强人工智能的基础。
因果推理
为了达到人类级别的智能,学习机器需要现实模型(类似于因果推理的模型)的引导。为了展示此类模型的关键性,总结 7 种当前机器学习系统无法完成的任务,并使用因果推理的工具完成。

| Level (Symbol) | Typical Activity | Typical Questions | Examples |
|---|---|---|---|
| 1. 关联 Association P(y|x) | Seeing | ①What is? ②How would seeing X change my belief inY ? |
①What does a symptom tell me about a disease? ②What does a survey tell us about the election results? |
| 2. 干预 Intervention P(y|do(x), z) | Doing Intervening | ①What if? ②What if I do X? |
① What if I take aspirin, will my headache be cured? ②What if we ban cigarettes? |
| 3. 反事实 Counterfactuals P(yx|x’, y’) | Imagining, Retrospection | ① Why? ②Was it X that caused Y ? ③What if I had acted differently? |
①Was it the aspirin that stopped my headache? ②Would Kennedy be alive had Oswald not shot him? ③What if I had not been smoking the past 2 years? |
- 【2021-3-31】厘清因果逻辑后的机器学习可以脱胎换骨吗?
- 人类与机器学习的一大不同即人类理解因果逻辑容易,机器学习理解因果却难如登天。机器学习算法,尤其是深度神经网络,擅长从大量数据中找出微妙的模式,但它们很难做出简单的因果推论,主要涉及的难题是独立和恒等分布数据(i.i.d)。
- (1)为什么机器学习模型不能超越其狭窄的领域和训练数据?
- “机器学习经常忽略动物大量使用的信息:自然环境中的干预、域的转化、时间结构——总的来说,这些因素是讨厌的并试图把它们处理掉,与此相一致的是,目前机器学习的大多数成功都归结为对独立和恒等分布数据(i.i.d)进行的大规模模式识别。”
- i.i.d.假设问题是空间中的随机观测不相互依赖,且有恒定的发生概率。最简单的例子就是抛硬币或掷骰子。每一次新的投掷结果都是独立于之前的,并且每个结果的概率保持不变。
- 计算机视觉等更复杂领域中,机器学习工程师试图通过在大样本集上训练模型,将问题转变为i.i.d.领域问题。假设有足够多的例子,机器学习模型将问题的一般分布编码到它的参数中。但在现实世界中,由于训练数据中无法考虑和控制的因素,分布往往会发生变化。例如,当物体的光照条件、角度或背景改变时,在数百万张图像上训练后的卷积神经网络仍然可能会失败。
- 随着外界变得越来越复杂,通过增加更多的训练示例来覆盖整个分布变得不再可能。在人工智能必须与外界互动的领域,如机器人和自动驾驶汽车领域情况尤其如此。缺乏对因果关系的理解使我们很难做出预测,也很难处理新情况。这就是为什么自动驾驶汽车在经过数百万英里的训练后仍然会犯一些奇怪和危险的错误。“要在i.i.d.环境之外很好地进行概括不仅需要学习变量之间的统计关联,还需要学习一个潜在的因果模型。”因果模型还允许人们将获得的知识用于新的领域
- (2)为什么尽管i.i.d.有明显的弱点,它仍然是机器学习的主导形式呢?
- 纯粹基于观察的方法容易扩展。可以通过添加更多的训练数据来继续实现精度的提高,还可以通过提高计算能力来加速训练过程。事实上,最近深度学习取得成功的关键因素就是更多可用数据和更强大的处理器。
- 基于i.i.d.的模型易于评估,将一个大型数据集拆分为训练集和测试集,在训练集上调整模型,并通过测量其在测试集上的预测精度来验证其性能。这个过程可以不断反复直到达到所需的精度。已经有很多公共数据集提供了这样的基准测试,比如ImageNet、CIFAR-10和MNIST,还有特定任务的数据集如用于COVID-19诊断的COVIDx数据集和威斯康星州乳腺癌诊断数据集。
- 精确的预测往往不足以为决策提供准确信息。例如在疫情期间,许多机器学习系统失灵了,因为它们训练的是统计规律而不是因果关系。随着生活模式的改变,模型的准确性逐渐下降。
- 统计分布改变时,因果模型仍然是稳健
- 因果模型还允许我们对我们之前没见过的情况做出反应,并思考反向事实,如我们不需要把车开下悬崖才知道会发生什么。反向事实在减少机器学习模型所需的训练实例数量方面发挥重要作用。
- 因果关系在处理对抗性攻击时也有关键作用。“这些攻击显然违反了作为统计机器学习基础的i.i.d.假设,”论文作者写道,并补充说,对抗性漏洞证明了人类智能和机器学习算法的鲁棒性机制存在差异。研究人员还指出,因果关系可能是对抗对抗性攻击的一种可能防御。对抗性攻击的目标是机器学习对i.id的敏感性。给这张熊猫图片添加了一层难以察觉的噪点,导致卷积神经网络误以为它是长臂猿。
- 从广义上讲,因果关系可以解决机器学习缺乏泛化的问题。研究人员写道:“公平地说,大多数当前的实践(解决i.i.d.基准问题)和大多数理论结果(关于在i.i.d.设置中的泛化)都未能解决跨问题泛化的严峻挑战。”
- 因果关系添加到机器学习:两个概念是“
结构因果模型”和“独立因果机制”。总的来说该原则表明,AI系统应该能够识别因果变量,并分离它们对环境的影响,而不是寻找表面的统计相关性。- 因果人工智能模型不需要庞大的训练数据集。
- 因果推理允许它对干预、反事实和潜在结果的效果得出结论
- 因果结构可以优化强化学习的训练
- 结合结构因果建模和表达学习,我们应该努力将SCM嵌入更大的机器学习模型,其输入和输出可以高维非结构化,但其内部运作至少部分由SCM(也可以用神经网络参数化)控制。其结果可能是一个模块化的架构,不同的模块可以单独调整并用于新的任务
- 实现这些概念需要面对以下几个挑战:
- (a)在许多情况下,我们需要从可用的低级输入特征中推断出抽象的因果变量;
- (b)对于数据的哪些方面显示了因果关系没有达成共识;
- (c)普通的测试集、实验方案不足以根据现有数据集推断和评价因果关系,可能需要建立新的基准;
- (d)缺乏可扩展的、在数值上合理的算法。
- 参考:Towards Causal Representation Learning论文中,马克斯普朗克研究所、蒙特利尔研究所学习算法(米拉)和谷歌的研究人员认为对于机器学习因果推论的挑战源自于机器学习模型缺乏因果关系的表达,在论文中他们为可以学习因果表达的人工智能系统提示了方向。
反事实改进深度学习
【2021-3-30】ICLR 2020 反事实因果理论如何帮助深度学习?
- 一个巨大的问题是深度神经网络的黑箱问题和不稳定性问题。其中的一个根本原因,基于相关性的统计模型容易学习到数据中的“伪关系(spurious relation)”,而非因果关系,从而降低了泛化能力和对抗攻击的能力。
- 一个潜在方向是采用从90年代以来以Judea Pearl为代表的研究者们提出的因果推断理论来改进现有的表示学习技术。
- 然而因果分析框架和表示学习并非天生相容。
- 因果分析通常是基于抽象的、高层次的统计特征来构建结构因果图;
- 而表示学习则基于海量数据提取具体的、低层次的表示特征来辅助下游任务。
- 为了结合这两者,MILA的Yoshua Bengio提出了System 2框架,Max Planck Institute的Bernhard Schölkopf提出的因果表示学习框架。这两者实际上的思考是一致的。ICLR 2020上因果表示学习的2项有代表性的工作:如何利用因果理论中的反事实(counterfactual)框架来提高算法的稳定性和可解释性。
- Learning the Difference That Makes A Difference with Counterfactually-Augmented Data
- 深度学习容易学到语言数据集上伪关系(spurious relation)的问题一直没有得到解决。因果推断理论告诉我们,这是由于混杂因子(confounding)造成的。
- 然而,将因果推断方法应用到自然语言处理面临着巨大的困难:什么是自然语言当中的随机变量?如何从表示中找出混杂因子?如何让学习结果更加稳定,避免受训练集中的伪关系影响?其中最大的困难,在于如何定义自然语言中的因果关系。
- 作者设计巧妙方法,绕开了随机变量的定义问题,转而采用因果理论中的另一个重要概念——反事实——来进行human in the loop的数据增强以避免伪关系的干扰。
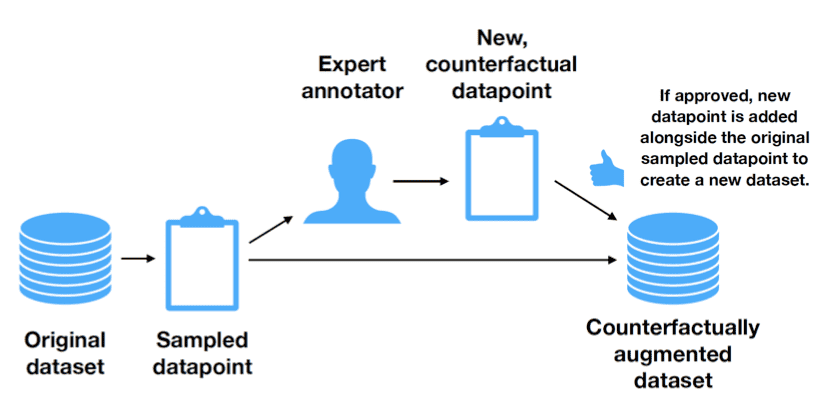
- 在情感分析的一个3分类数据集上,利用Amazon’s Mechanical Turk众包平台,要求人类对句子做轻微的修改。这些修改包括:
- 将事实变为希望:比如加入supposed to be表示虚拟语气
- 反讽语气:如加入引号修饰、改为反问句表示反讽
- 插入/替换修饰词:将interesting替换为boring
- 插入短语,修改评分等
- 使评论的情感分类发生变化(如从正面变为负面)来进行数据增强。实验证明,对于支持向量机,朴素贝叶斯,随机森林,Bi-LSTM和BERT:
- a) 在原有数据集上训练后,相比原测试集,反事实数据集上的测试结果要差许多。反之亦然。
- b) 在结合了反事实增强过的训练集上训练,模型性能相比原来有着巨大的提升。
- c) BERT不但在通常情况下表现最好,而且在反事实干扰的数据集上表现也降低得最少
- 台湾国立成功大学一篇论文把 BERT 拉下神坛!NLP 神话缺了数据集还不如随机,曾经狂扫 11 项记录的谷歌 NLP 模型BERT在一些基准测试中的成功仅仅是因为利用了数据集中的虚假统计线索(Spurious Statistical Cues),如若不然,还没有随机的结果好。
- 鉴于 R∧A→¬C,通过否定 claim 并反转每个数据点的标签来产生对抗性示例,将对抗性示例与原始数据进行组合,构建对抗测试集
- 实验表明:BERT准确率就从77%降到53%,几乎等同于随机猜。BERT 并不能做出正确 “理解”,只能利用虚假统计线索(Spurious Statistical Cues)
- Counterfactuals Uncover the Modular Structure of Deep Generative Models
- 有监督的视觉模型很容易会被伪关系干扰从而学出带有偏见的结果。比如,一个典型的例子是有监督CNN模型在识别狼和狗的图片时,实际上使用的统计特征是狼一般在雪中而狗在草地上。也就是说,模型认为“背景(草或雪)”与“目标(狗和狼)”之间存在某种关系。而实际上,这两种特征是解耦合的。我们希望能找到某些能学会解耦合的特征表示的模型。
- 检验模型能否推理反事实情况(比如狗在雪中,狼崽草上)。这样的反事实推理能力也是人类智能的一个重要标志,即推理未发生事件的结果的能力,属于因果学习的一个重要分支。反事实理论在计量经济学和公共卫生领域得到了广泛的应用,然而对于机器学习,这套理论的应用方法仍然是一片空白。将因果学习应用在表示学习上的一个重要改进的方向,就是来自Max Planck Institute的Scho ̈lkopf和MILA的Bengio目前倡议的causal representation learning. 本文即是Scho ̈lkopf在ICLR2020上的一篇尝试性的工作:通过验证模型推断反事实的能力,来验证生成式模型(BigGAN)可以学习到解耦合的模块化结构。提出了因果生成模型(Causal Generative Model)的分析框架来解耦合生成式模型的模块化结构
因果推理资料
因果推理简介
【2020-9-23】Introduction to Causal Inference
因果推理总结
【2021-1-1】文库资料:
- 因果推理
- 因果推理的分类:
- 由因推果:没有复习,所以考不好
- 由果推因:心情不好,所以一定发生了不好的事情
- 因果分析:一果多因、一因多果、同因异果、异因同果、互为因果
- 因果分析的关键:
- (1)分清主因和次因
- (2)结果形成的因果链
- (3)同因异果、异因同果、互为因果
- 异因同果表面上互不干涉,但用联系的眼光看问题,深入分析下去,背后有共同之处,排除表象的迷惑,接近本质
- 同因异果也是常见的相互关联,同样的原因在不同条件下可能产生不同的结果
- 因果推理的误区
- 因果倒置谬误
- 强加因果谬误:仅仅把时间上有先后顺序或伴随发生的事看成有因果关系
- 单一因果谬误:用一个简单、单一的原因解释事件的发生,这个事件可能只是促进作用的原因之一,不是根本原因
- 滑坡谬误:使用连串的因果推论,却夸大了每个环节的因果强度,即不合理的使用连串的因果关系,将“可能性”转化为“必然性”,而得到不合理的结论,以实现某种意图
- 臆测原因谬误:针对某个现象(而不是调查分析)得出结论,根据主观臆断推断原因,造成归因偏差
- 诉诸公众谬误:以多数人相信的命题为事实依据来证明该命题一定是真的
- 因果推理的运用
- 补充中间环节:挖掘背后的因果链,找到关键因素
- 积极归因:
- 因果推理的目的:清楚某一现象背后的真正原因,包含主因、次因;如果是好现象,引导人们去做,如果是坏现象,告诫人们不该做
- 因果推理的分类:
- 因果关系的推断 研究疾病里的因果
- 因果关联的几种方式:
- (1)单因单果 x → y
- (2)单因多果 x → y1,y2,y3
- (3)多因单果 x1,x2,x3 → y
- (4)多因多果 x1,x2,x3 → y1,y2,y3
- (5)直接/间接病因 x1 → x2 。。。 → xn → y
- 统计学关联的本质:原因、偏倚(系统误差)和机遇(随机误差)
- 统计学关联中,排除虚假关联、间接关联后,是直接关联,再剔除偏倚才是可能的因果关联
- 因果推断的标准
- 关联的时间顺序:从因到果,是必要和前提条件
- 关联的强度:与因果关联可能性成正比
- 关联的特异性:因果一一对应关系
- 关联的分布一致性
- 关联的一致性:多个研究结果的一致性/可重复性增强了因果关联的可能性
- 因果关联的几种方式:
观察性研究中的因果推断方法(三)30分钟.ppt, 百度文库
- 因果作用评价与因果网络学习及其结合
- 该报告介绍Pearl提出的因果推断的三个层级,综述因果推断的两个主要模型:潜在结果模型、因果网络。探讨因果作用和因果关系的可识别性,因果作用的可传递性,因果网络结构的学习算法,以及因果作用与因果网络结合的因果推断方法。
- 【2021-1-6】May 10, 2017, MIT Machine learning expert Jonas Peters of the University of Copenhagen presents “Four Lectures on Causality”.
- 从因果图模型开始,更广阔的定义了结构化的因果模型,以及如何从数据中识别因果关系。课程介绍了该领域当前(2017)比较前沿的研究,包括用传统机器学习方法进行因果推断的几篇论文。
- MIT 因果推断 Mini Lectures on Causality by Jonas Peters 2017 (无字幕)
- 【2021-1-28】将因果关系引入计算机视觉的”小学生”
- AI 仍是一个比人类更低维的生物,与人类之间存在很大差距,对事物的因果推理能力便是其中之一
- 张含望创立并带领的机器推理与学习实验室(Machine Reasoning and Learning Lab,简称“MReal”)是全球第一个将因果关系推理引入计算机视觉研究中的团队。
- 【因果推断】 A Brief Introduction to Causal Inference by Brady Neal
- 【2021-3-29】统计之都-因果推断专题
- Causal inference course written from a machine learning perspective,包含课程ppt列表
【2024-3-2】A-Survey-of-Deep-Causal-Models-and-Their-Industrial-Applications
【2021-3-3】yoshua bengio发表论文Towards Causal Representation Learning,
- 深度学习仍有许多问题亟待解决,例如将知识迁移到新问题上的能力。许多关键问题都可以归结为OOD(out-of-distribution)问题。因为统计学习模型需要满足独立同分布(i.i.d.)假设,而很多情形下,这个假设不成立,这时候就需要因果推断了:如何学习一个可以在不同分布下工作、蕴含因果机制的因果模型(Causal Model),并使用因果模型进行干预或反事实推断。
- 然而,因果模型往往处理的是结构化数据,并不能处理机器学习中常见的高维的低层次的原始数据,如图像。为此,回到最初的问题,因果表征即可理解为可以用于因果模型的表征,因果表征学习即为将图像这样的原始数据转化为可用于因果模型的结构化变量。因果表征学习就是连接因果科学与机器学习的桥梁,解决这一及相关问题,就可以很好的将因果推断与机器学习结合起来,构建下一代更强大AI。
【2020-9-2】Bengio讲授因果表示学习,Mila博士因果推理导论开课了,从机器学习的角度编写的《Introduction to Causal Inference》秋季课程,教材地址,YouTube地址,由 Yoshua Bengio 高徒 Brady Neal 主讲,主要讲述因果推理相关知识。此外,该课程整合了来自许多不同领域的见解,如流行病学、经济学、政治学和机器学习等,这些领域都利用到了因果推理。
内容:
- 图模型、后门调整和因果模型结构;
- 随机化实验、前门调整、do-calculus 和通用识别;
- 估值和条件平均处理效应(Conditional Average Treatment Effects);
- 未观察到的的混淆、边界以及敏感性分析;
- 工具变量、断点回归、双重差分和合成控制法;
- 有实验的因果关系发现;
- 无实验的因果关系发现;
- 可移植性和迁移学习;
- 反事实推理以及中介和特定路径效应(Mediation and Path-Specific Effects)。
乌鸦智能 > 鹦鹉智能
【2020-12-9】中科院计算所在读博士李奉治 因果阶梯与Do-演算:怎样完美地证明吸烟致癌?,视频地址有向图中的路径,只会有这三种基础结构,对应了“因果流”的三种模式:
- A→B→C :
链(Chain) 接合,其中B被称作“中介变量” (Mediator). 如果控制了中介变量B,A与C之间的因果关系传递就会被阻断。 - A←B→C :
叉(Fork) 接合,其中B被称作“混杂因子” (Confounder). 如果控制了混杂因子B,A与C之间就失去了相关性。 - A→B←C :
对撞(Collider) 接合,其中B被称作“对撞因子” (Collider). 原本A和C之间就是独立的,但如果控制了对撞因子B,根据辩解效应 (Pearl, 1988) 的存在,反而会打开A与C之间的因果关系传递通道。
上方三种接合模式都有对应的控制因果流的传递方法。对于更大的因果图,如何阻断某两个结点之间的因果信息流呢?这里就提供了一个判据,被称为d-分离。强制干预一个变量,就是do-演算框架中的 do算子。为了算出直接干预一个变量后其他变量变化的结果,2011年图灵奖得主 Judea Pearl 提出了一个do-演算的公理体系,包含三条公理,对观察项和干预项进行转换。
中科大统计学在读博士生龚鹤扬 因果科学:连接统计学、机器学习与自动推理的新兴交叉领域, 哲学中关于因果关系讨论中,其因果的分类方法非常有启发性,把因果分成了两类,一类是 Type causality(因推果) ,另一类是 Actual causality(果推因)。
- Type causality 关注的是某个原因会导致什么样的结果,例如吸烟是否导致肺癌,可理解成由因推果(Forward-looking),是一种干预思维,能帮助科学家进行预测;
- 而 Actual causality 关注某个事件发生的具体原因是什么,例如恐龙灭亡的原因是六千万年的小行星撞地球导致的吗,它是由果推因(Backward-looking),与反事实思维思维密切相关。
(1)The book of why
【2020-12-04】因果推理书籍索引,Which causal inference book you should read
《The book of Why》,豆瓣高达9.5分。其中文版《为什么:关于因果关系的新科学》由中信出版社推出
- 因果推理和贝叶斯网络的创始人,图灵奖得主
Judea Peral(朱迪亚·珀尔,贝叶斯网络之父)和科普作家 Mackenzie, Dana合作写的一本因果推理的入门书。- 朱迪亚•珀尓(Judea Pearl),加州大学洛杉矶分校计算机科学教授,“贝叶斯网络”之父。2011年,珀尔因“通过发展概率和因果推理对人工智能的奠基性贡献”获得了计算机科学的最高荣誉图灵奖;他的孩子,一名记者在巴以冲突的死亡,他为了纪念他的孩子还设立了一个基金。初读Judea Pearl的书,有什么感觉?

- 目录
- 导言:思维胜于数据
- 第一章:因果关系之梯
- 第二章:从海盗到豚鼠:因果推断的起源
- 第三章:从证据到因:当贝叶斯牧师(统计)遇见福尔摩斯先生(推理)
- 第四章:混杂和去混杂:或者,消灭潜伏变量
- 因果学习初探(2)——混杂和去混杂:随机试验是可以对付自然精灵的黄金法则。随机化带来的两个实际好处:
- (1)消除了混杂偏移;
- (2)能够量化不确定性(引出do算子)。
- 随机试验可以切断混杂因子,而非随机的试验很难做到。很多时候,因为一些伦理性的问题等,干预在事实上是不可行的。幸运的是,do算子提供了一种科学的方法,在非试验性研究中确定因果关系。借助do算子定义混杂:
- do算子和后门标准可以定义混杂、识别混杂,甚至是解决混杂因子带来的问题。除了三种结构外,我们引入另一条规则,控制一个变量的后代节点(替代物),如同部分的控制变量本身。为了去除X和Y之间的混杂,只需要阻断它们之间的非因果路径,而不去阻断或者干扰所有的因果路径就可以了。我们将后门路径定义为所有X和Y之间以指向X的箭头为开始的路径。对后门路径进行阻断,这些路径中有些需要进行约束,而有些不需要进行约束,来达到去混杂的目的。
- 因果学习初探(2)——混杂和去混杂:随机试验是可以对付自然精灵的黄金法则。随机化带来的两个实际好处:
- 第五章:烟雾缭绕的争论:消除迷雾,澄清事实
- 第六章:大量的悖论!
- 谁能直面矛盾,谁就能触摸现实。蒙提-霍尔悖论,伯克森悖论,辛普森悖论
- 第七章:超越调整:征服干预之峰
- 第八章:反事实:挖掘关于假如的世界
- 第九章:中介:寻找隐藏的作用机制
- 第十章:大数据,人工智能和大问题
【2021-3-29】《为什么:关于因果关系的新科学》思维导图
- 1、 文章结构
- 人类创造出了我们今天所享有的科技文明。所有这一切都源于我们的祖先提出了这样一个简单的问题:为什么?
- 因果推断正是关于这个问题的严肃思考。因果革命背后有数学工具上的发展作为支撑,这种数学工具最恰当的名称应该是“因果关系演算法”。其一为因果图(causal diagrams),用以表达我们已知的事物,其二为类似代数的符号语言,用以表达我们想知道的事物。
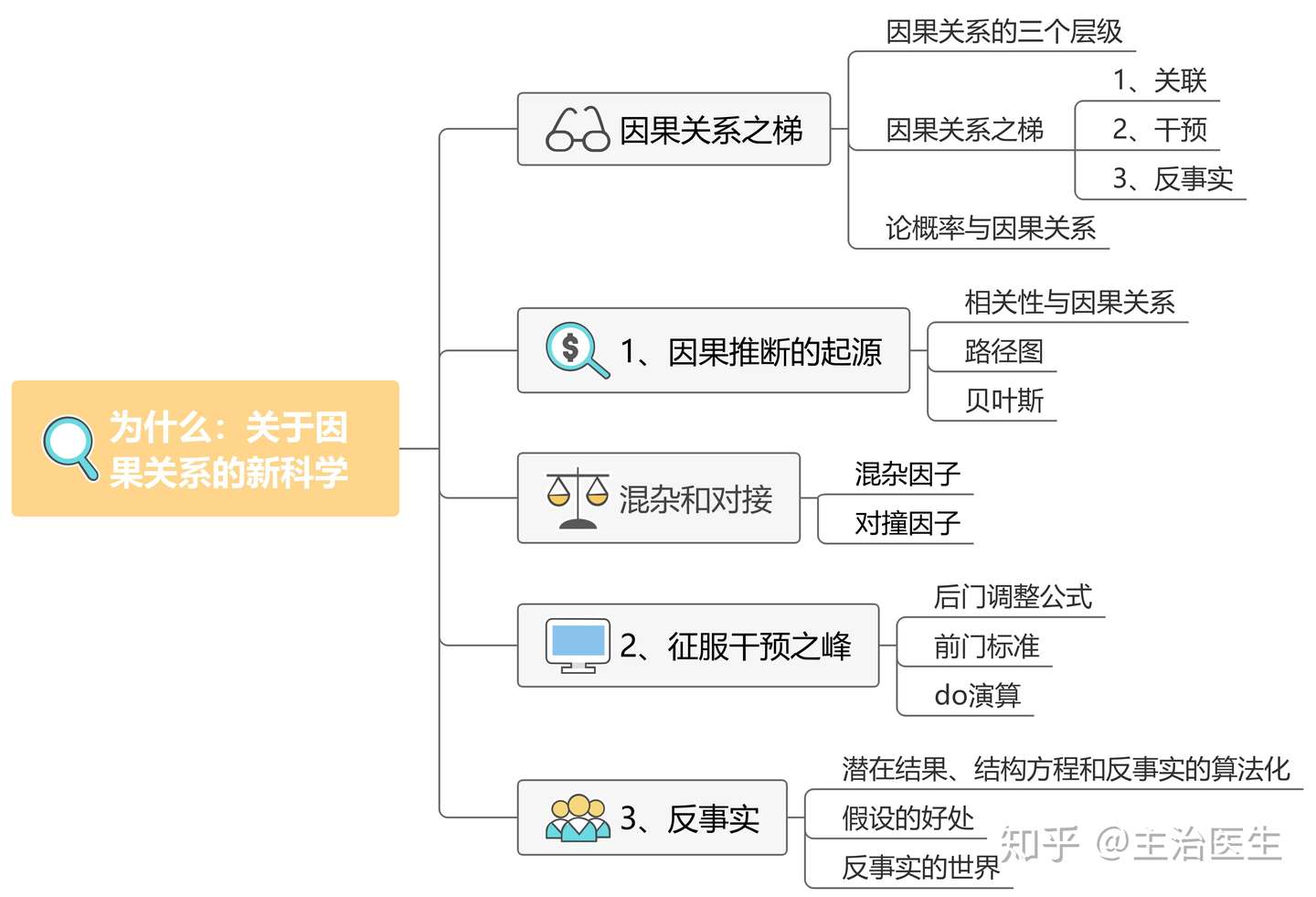
- 2、 因果关系之梯
- 如果第一层级对应的是观察到的世界,第二层级对应的是一个可被观察的美好新世界,那么第三层级对应的就是一个无法被观察的世界(因为它与我们观察到的世界截然相反)。
- 为了弥合第三层级与前两个层级之间的差距,我们需要掌握一种理解力,建立一种理论,据此预测在尚未经历甚至未曾设想过的情况下会发生什么——这显然是所有科学分支的圣杯。

- 3、 因果推断的起源
- 因果推断是用数学语言表达看似合理的因果知识,将其与经验数据相结合,回答具有实际价值的因果问题。将相关关系的知识与因果关系的知识相结合以获得某些结果的做法。而路径图在因果论和概率论之间建立的第一座桥梁,其跨越了因果关系之梯第二层级和第一层级之间的障碍。在建造了这座桥梁之后,就可以进行反向的实践,从根据数据测算出的相关性(第一层级)中发现隐藏在背后的因果量。

- 4、 混杂和对撞因子
- 我们在实际生活中似乎就是遵循着共因原则行事的,无论何时,只要观察到某种模式,我们就会去寻找一个因果解释。事实上,我们本能地渴望根据数据之外的某个稳定机制对观察结果做出解释。其中最令人满意的解释是直接因果关系:X导致Y。

- 5、 征服干预之峰
- 混杂因子是导致我们混淆“观察”与“干预”的主要障碍。在用“路径阻断”工具和后门标准消除这一障碍后,我们就能精确而系统地绘制出登上干预之峰的路线图。最安全的路线是后门调整和由此衍生的诸多同源路线,它们有些可以归于“前门调整”名下,有些则可以归于“工具变量”名下。一种通用的绘图工具,我们称之为“do演算”(do–calculus),它允许研究者探索并绘制出通往干预之峰的所有可能的路线,无论这些路线有多曲折。

- 6、 反事实
- “A导致B”解释为“假如没有A,则B就不会发生”。我们根本不需要争论这样的世界是否以物理或者形而上学的实体形式存在。如果我们的目的是解释人们所说的“A导致B”的含义,那么我们只需要假设人们有能力在头脑中想象出可能的世界,并能判断出哪个世界“更接近”我们的真实世界即可;最重要的是我们的想象和判断要前后一致,这有助于我们在群体中达成共识。
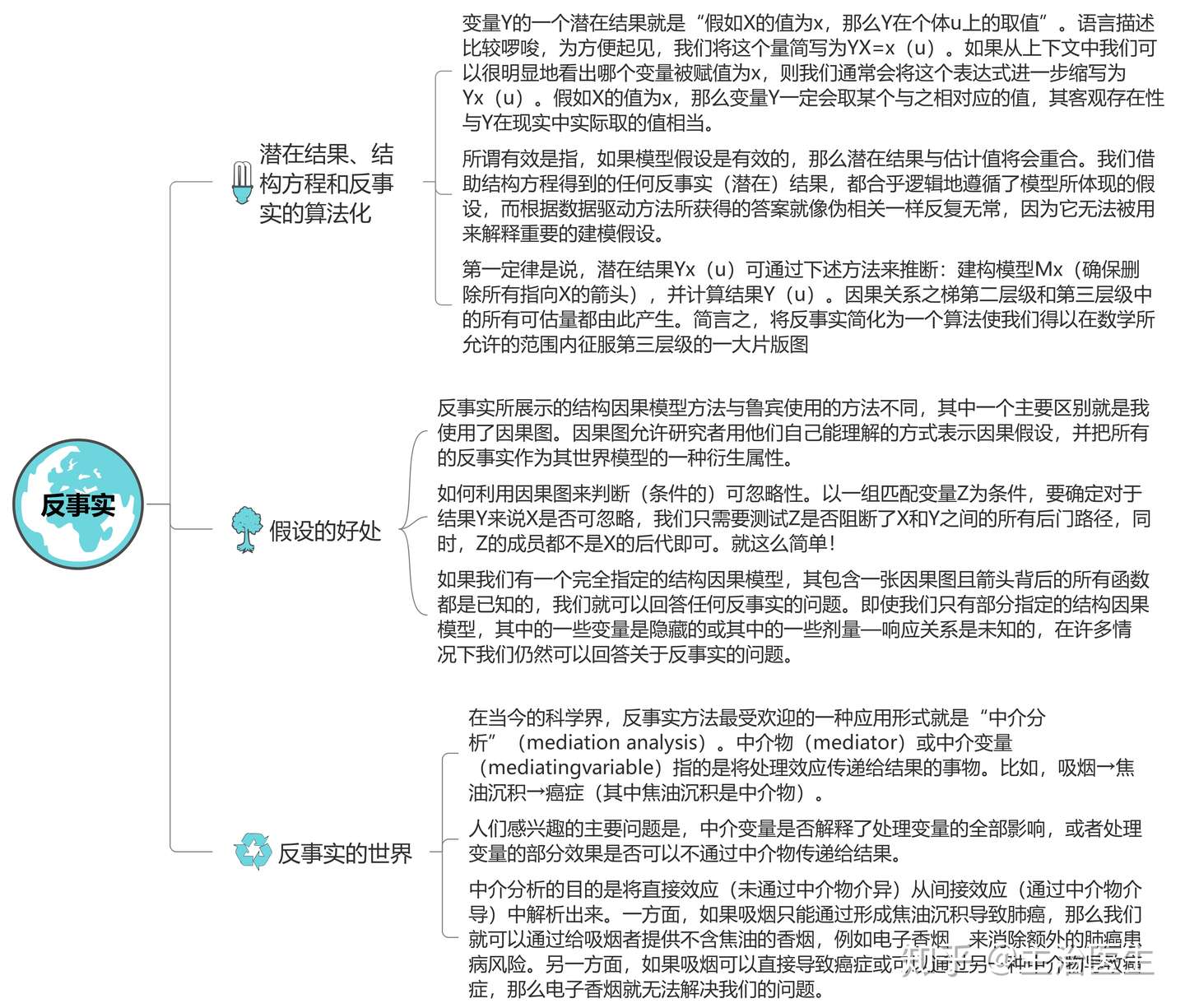
(2)因果关系:模型、论证与推断
2011 年图灵奖得主 Judea Pearl 的 《Causality : Models, Reasoning and Inference》(第二版)
- 作者:Judea Pearl
年度必读书,原因:
- 提出全新科学方法论——因果关系模型,其应用范围涉及众多领域。借助因果关系的视角,作者重新阐述了人类认知和科学文明的发展史。
- 因果推理将对人工智能产生革命性的跃迁,引领人工智能的未来发展,并赋予人工智能以真正的人类智慧甚至道德意识,让人工智能与人类能在彼此合作的基础上打造一个更好的未来世界。
目录
- 1 概率、图表和因果模型简介
- 2 推论因果关系理论
- 3 因果图和因果效应的识别
- 4 行动、计划和直接影响
- 5 社会科学和经济学中的因果关系和结构模型
- 6 辛普森悖论、混乱与崩溃
- 7 基于结构的反事实逻辑
- 8 个不完善实验:边界效应与反事实
- 9 因果关系的可能性:解释与识别
- 10 实际原因
-
11 与读者的思考、阐述和讨论
- Judea Pearl的《Causality》
主要内容:
- 第一章——前言:用通俗的语言介绍「什么是因果关系?」这一问题的讨论背景,并概括若干个传统的哲学观点,以及和下文的统计因果模型相比,这些传统定义存在的缺陷。
- 第二章——事件性因果
- 2.1. 随机对照试验
- 2.2. 介入主义的因果观
- 2.3. 虚拟事实模型(RCM)
- 2.4. 贝叶斯网络
- 2.5. 结构方程(SEM)+ 结构因果模型(SCM)
- 2.6. SCM的反事实推理
- 第三章——过程性因果:因果环路图(CLD)与微分方程
- 第四章——后记
除前言外,本文其他部分默认读者已经理解基础概率论(概率、条件概率、贝叶斯定理、随机变量、期望值、相互独立事件)、基础图论(节点、边、有向无环图)、概率图模型初步(贝叶斯网络、d分隔)、统计学基础(随机对照试验)等知识。
- 【2021-3-29】源自书籍总结:【综述长文】因果关系是什么?结构因果模型入门,高二学生的杰作!
因果推理
【2021-3-31】通俗解释因果推理 causal inference
- 推理(inference)是“使用离理智从某些前提产生结论”的行动。因果推理,也叫做反事实推理。反事实推理,就是解决 what if 之类的问题。举个例子,和家人的旅行之前,肯定会有一些疑问,这些疑问就叫做反事实疑问,获取反事实疑问的结果叫做因果推理。
什么是因果
什么是causality(因果)
- Formal Definition: Causality is a generic relationship between an effect and the cause that gives rise to it.
causality和statistical association的区别(因果性和相关性区别)
基本概念
常见概念
- unit: 单元,因果推理中原子研究对象,可以是实物,也可以是概念,可以是一个或者多个。在一些框架下,不同时刻的同一对象被认为是不同的units。
- treatment:干预/治疗,施加给unit的操作。也叫做干预、介入等。在二元Treatment的情况下(即𝑊=0 或 1 ),Treatment组包含接受Treatment为 𝑊=1 的unit,而对照组包含接受Treatment为 𝑊=0 的unit。
- variables: unit自带的一些属性,比如患者的年龄,性别,病史,血压等。在treatment过程中不受影响的variable叫做pre-treatment variables,比如患者的性别在多数情况下是不变的;对应的,收到影响的variable叫做post-treatment variables。多数情况下,variables指的是Pre-treatment variables。一些文献中也叫做context。
- Confounders: 会影响treatment选择和结果的一些变量。比如同一剂量的药剂在不同年龄的人群的结果可能不一样,或者说不同年龄的药剂选择会不同。有一些文献中也叫做协变量,covariate。
- causal effects: 对于个体(或者群体)施加了一个干预A,其结果不等于没有施加该操作的对象的结果,则称A构成了一个因果效应。施加对象是个体的话是个体因果效应,群体是群体因果效应。
- Treatment Effect —— 因果效应,对unit进行不同Treatment之后unit产生的Outcome的变化,这种效应可以定义在整体层面、treatment组层面、子组层面和个体层面
- 整体层面 —— Average Treatment Effect(
ATE),平均干预效果- 𝐴𝑇𝐸=𝐸[𝑌(𝑊=1)−𝑌(𝑊=0)]
- Treatment组层面 —— Average Treatment Effect on the Treated Group (
ATT),Treatment组中的平均干预效果- 𝐴𝑇𝐸=𝐸[𝑌(𝑊=1)∣𝑊=1]−𝐸[𝑌(𝑊=0)∣𝑊=1]
- 子组层面 —— Conditional Average Treatment Effect (
CATE)- 𝐶𝐴𝑇𝐸=𝐸[𝑌(𝑊=1)∣𝑋=𝑥]−𝐸[𝑌(𝑊=0)∣𝑋=𝑥]
- 个体层面 —— Individual Treatment Effect (
ITE)- 𝐼𝑇𝐸𝑖=𝑌𝑖(𝑊=1)−𝑌𝑖(𝑊=0)
- 整体层面 —— Average Treatment Effect(
- potential outcome: 潜在结果,施加给对象的操作所能产生的所有可能产生的结果。包含observed outcome和反事实结果。
- factual outcome/Observed Outcome: 观测结果,已经发生的事实, 施加给对象的操作最终观测到的结果,记做Y.
- 反事实结果counterfactual outcomes:某次操作没有产生的结果。从唯物主义的观点来看,事物是在时刻变化的,因此实验是不可逆的。而没有观测到的结果,是不可能看到的,即为反事实。
- Counterfactual Outcome —— 反事实结果, 已经发生事实的其他对立面,也即对某个unit未采用的其他treatment带来的潜在结果
- individualized treatment effect: Y(1)-Y(0).前者是事实结果,后者是反事实结果。或者说前者是treated,后者是control。如果是多个个体,则是期望。
- 反事实推理counterfactual inference:解决类似于“如果这个病人采用其他疗法,血压会降下来吗?”这样的问题的推理。
- 倾向分数propensity score:p(x) = P(Wi = 1|Xi = x),反映出样本x选择treatment的可能性。
- 选择偏倚selection bias:由于Confounders的存在,treatment组合对照组的分布有可能不一致,因此导致出现偏差,这也使得推理更加困难。
以下图为例,年龄对心脏病介入来说就是一个协变量,不同年龄会采取不同的措施:年轻的手术,年老的服药,手术和服药是两种不同的treatment;同时年龄又影响着结果,年轻人的生存时间是大于老年人的。
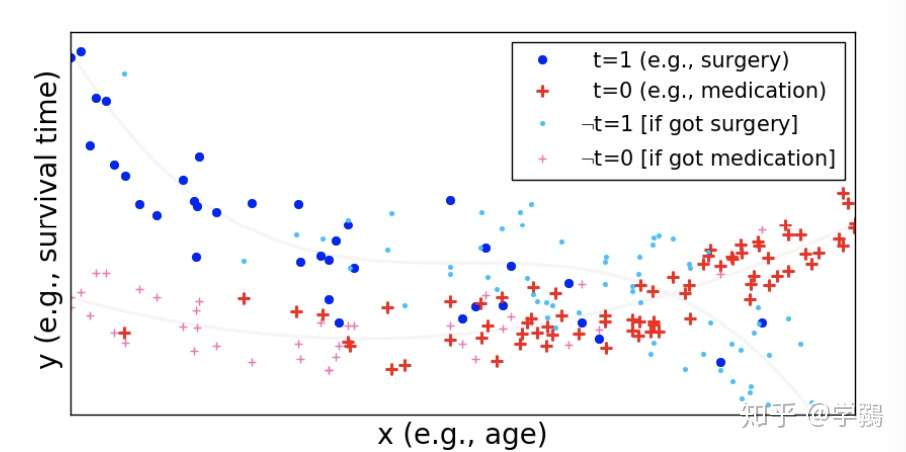
年龄作为协变量对手术的影响
因果分类
因果科学工作大致分
- 基础因果假设及框架(fundamental causal assumption and framework)
- 因果学习(causal learning): 因果学习又分因果结构学习和因果表示学习
- 因果结构学习(causal discovery/causal structure learning)
- 因果表示学习(causal representation learning)。
- 因果推断(causal reasoning/inference)
- 应用系统
Two main questions
- Causal discovery(因果关系挖掘): 比如研究温度升高是否是电费增加的原因?或者在商品价格,商品转化率,商品上市时间,商品成本等几个变量之间探究一个因果图,即变量两两之间是否有因果关系?如果有,谁是因谁是果?
- Causal effect Estimation(因果效应估计): 比如我们已经知道温度升高是电费增加的原因,我们想知道温度从20度升至30度,会对电费带来多少增加?
主要研究框架
- (1)Structural Causal Models(SCM) 结构因果模型
Judea Pearl: A causal model by SCMs consists of two components: the causal graph (causal diagram) and the structural equations. 即需要先得到一张因果图,然后对于因果图,使用Structural Equations来描述它。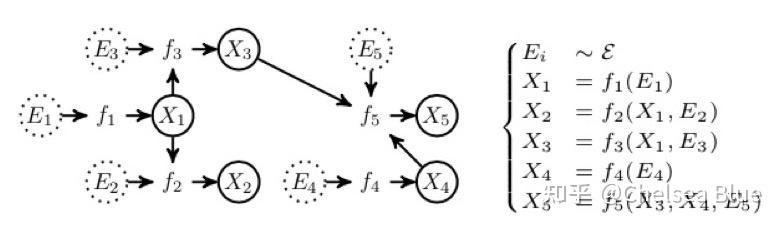
- 比如对于这一张因果图,箭头由因指向果,X和E都是变量。然后右边的一系列方程就是Structural Equations来描述这个图,每一个方程f都表示着由因到果的一个映射或者说一个表达式,这个方程可以是linear也可以是nonlinear的,取决于他们的因果关系是否线性。
- (2)Potential Outcome Framework 潜在结果框架
Donald Rubin: It is mainly applied to learning causal effect as it corresponds to a given treatment-outcome pair (D,Y). 简单来说,计算因果效应最直接的手段就是控制住所有的变量不变,只变化cause,比如把温度从20变到30度,然后直接看outcome变化,也就是直接用30度时的电费减去20度时的电费,既可以得到causal effect。HOWEVER,easier said than done!如果这个世界有两个平行时空,那么可以做这个实验,但是如果没有呢?温度不可能在同一个地方,同一个时间,即20度又30度,那么必然20度的时候,30度时的电费就叫potential outcome。而这个framework,就是相方设法从能观察到的数据中得到这个potential的结果,然后二者相减,就是我们想要的答案啦!
(一)Rubin 因果模型(潜在结果框架)
【2023-7-3】一文读懂潜在结果框架(Rubin因果模型)的三个假设
潜在结果模型
潜在结果模型是哈佛大学著名统计学家唐纳德·鲁宾(Donald B.Rubin)推出,因此又称鲁宾因果模型(Rubin Causal Model)。
核心
- 比较同一个研究对象(Unit)在接受干预(Treatment)和不接受干预(对照/控制组)时结果差异,认为这一结果差异就是接受干预相对于不接受干预的效果。
- 对于同一研究对象而言,通常不能同时观察干预/不干预的结果。
- 对于接受干预的研究对象而言,不接受干预时是“反事实”状态;
- 对于不接受干预的研究对象而言,接受干预时的状态也是一种“反事实”状态;
- 所以该模型又被某些研究者称之为反事实框架(Counter factual Framework)。
Rubin因果模型/潜在结果框架有三个基本构成要件:潜在结果、稳定性假设和分配机制
因果推断中,必须有干预,没有干预就没有因果。
(二)Pearl 结构因果模型(SCM)
研究 𝑋 和 𝑌 的因果关系
- 直接原因: 𝑌=𝑓(𝑥) 或 𝑌=𝑓(𝑥,𝑧,⋯),𝑋→𝑌 或 𝑋→𝑌←𝑍
- 间接原因: 𝑌=𝑓(𝑔(𝑥)),𝑋→𝑍→𝑌
结构化因果模型包含两类变量以及函数集合
- 外生变量 —— 对应DAG图的结点,没有祖先
- 内生变量 —— 对应DAG图的节点,至少是一个外生变量的后代
- 函数集合 —— 对应DAG图的边集合,每条边代表了一个变量之间的函数关系

上图的DAG图就对应一个结构因果模型:
- 集合 𝑈={𝑋,𝑊} 为外生变量集合,集合 𝑉={𝑍,𝑌} 为内生变量集合,集合 𝐹={𝑓,𝑔} 为函数集合
(1)因果发现 causal discovery
【2021-8-13】大白话谈因果系列文章(一):因果推断简介及论文介绍
贝叶斯网络是一个DAG(directed acyclic graph),即有向无环网络。然后可以把它当作一个概率图,也就是可以概率表达它。
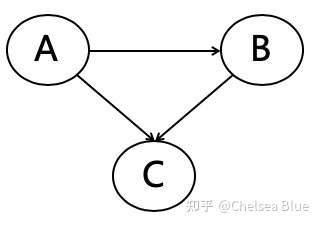
上图表达为 P(A,B,C) = P(C|A,B)*P(B|A)*P(A)。因为, C有AB两个变量指向他,而B同样只有A指向它。
因果发现总结
| 类型 | 图解 | 说明 | 其它 |
|---|---|---|---|
| head-to-head | 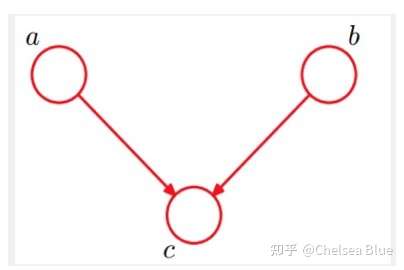 |
a与b独立 | |
| tail-to-tail |  |
a与b条件独立 | |
| head-to-tail |  |
a与b条件独立 |
对于head-to-head,我们有a与b独立,对于tail-to-tail,我们有given c,a与b条件独立,对于head-to-tail,我们有given c,a与b条件独立。换一个直观的例子:
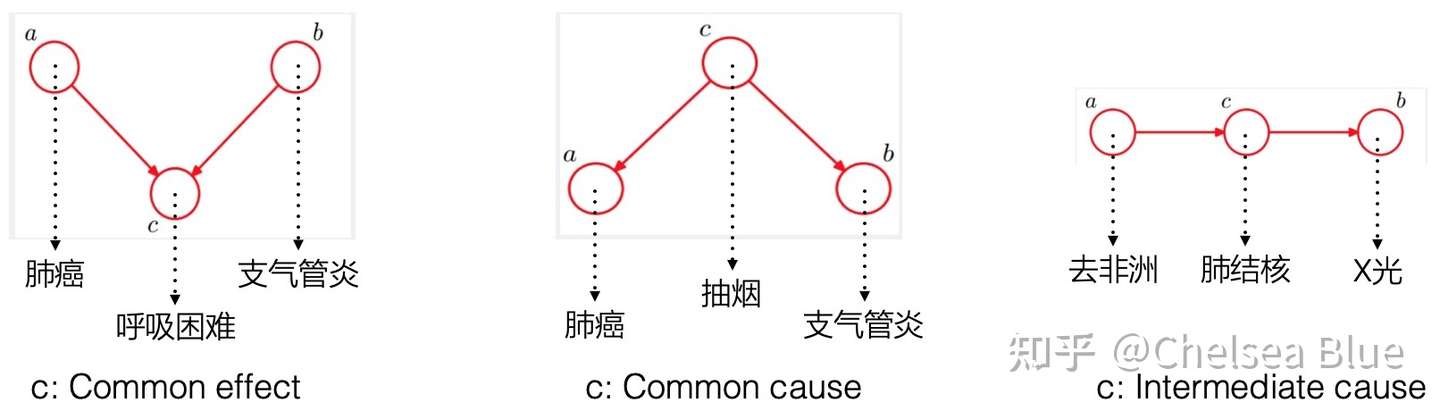
我们可以看到,因为c这个“搅屎棍”的存在,我们很可能在数据误以为a与b有因果关系,实际上他们只是有相关性,也可以说c d-separate/blocked a and b。但是对于a与b的关系,NONE of them are causality。而我们要做的就是找到这些关系,才能判断出真正的因果。我们定义一下,head-to-head叫做v-structure或者collider,tail-to-tail叫做confounder或者fork,head-to-tail叫做chain。以便于理解后面以及其他paper。
因果发现算法
Constraint-based Algorithms
这一类算法learn a set of causal graphs which satisfy the conditional independence embedded in the data。也就是通过找到上面三种结构来构建因果图,寻找方式就是通过条件独立的检验,一般的方式都是从一个无向的全链接图出发开始寻找,通过一系列规则最终生成一个图。
有两类重要假设:
- Faithfulness Assumption and Markov Assumption,即Conditional independence imply d-separate, vice versa。
- Sufficiency Assumption ,即 No unobserved confounder (common cause)。
缺点:
- 不能有unobserved confounder,这个条件即便在如今大数据的时代下,也很难满足。当然有类似IC*和FCI这种算法可以loose这个unobserved confounder的假设。所以这个缺点还好。
- 对于上面的chain和fork,由于他们都imply a和b基于c条件独立,故称为马尔可夫等价类,而这类算法无法从马尔可夫等价类中区分出不同的DAG,即对于这类算法,他认为chain和fork是一个东西,这也意味着对于上图,a有可能是c的因,也可能是果,这显然不make sense。
- 假设极其严格,需要非常多且高质量的数据,因为faithfulness假设使得我们只能通过conditional independence来测试,如果数据很少,有可能这些测试互相都会相斥,做起图非常困难
论文分享
- IC algorithm: 一个经典的constraint-based algorithm, 它是利用conditional independence 来确定v-structure, chain, confounder,然后由此来identify DAG。
- 方法见书:《Causality: models, reasoning, and inference》[ Judea_Pearl], p60
- IC* algorithm: IC算法的改良版,可以用在latent(unobserved) confounder存在的情况下。前两步与IC算法相同,第三步的判断规则基于存在latent confounder的假设下做了调整
- 方法见书:《Causality: models, reasoning, and inference》[ Judea_Pearl], p62
- PC algorithm: 也是一个经典的constraint-based algorithm, 和IC算法的思路很相近
- 方法见书 p136
Score-based Algorithms
这类算法是通过最优化一个给每个图打分的score function来找到最优的图。要想成为打分函数,其要有两个基本部分。
- structural equation from candidate G’
- other constraints of G’。
比如学过统计的朋友们都知道BIC就是一个打分函数:
他由两部分最成,Maximize likelihood(第一项)的同时regularize graph size(第二项),正好对应了上面的两个基本部分。
- 优点
- 由于使用goodness of fit替代了conditional independent,于是relax了上面的第一类假设
- 但缺点
- 仍然无法区分马尔可夫等价类
- 这类算法因为要找到最优的分数,就要搜索全部的图,这是一个NP-hard和NP-complete的问题,复杂度极高且容易陷入局部最优。
论文分享
- GES algorithm: 一个经典的scored-based algorithm, 使用下面BDeu这个打分函数来给每个图打分。但是这个方法只要求找到一个局部最优解即可。方法使用2阶段的贪婪搜索,第一阶段只insert edges,每轮insert operator只操作可以让这个打分函数最高分的三元组,直到达到local optimum。然后第二阶段只delete edges,同理delete operator只操作可以让这个打分函数最高分的三元组,直到达到local optimum。
- fGES algorithm: fast GES, 是快速版,复杂度低版的GES,有两处改变:parallelize and reorganize caching in the GES
FCMs-based Algorithms
这类算法的名字是我自己起的。什么是FCM (functional causal model)呢?不严谨的来说就是上面我提到的Structural Causal Models的图里右边那一堆function,假设我们能先得到这些function,我们就可以还原左边的图。大概就是这个思路。举个例子,对于s,d,y三个变量,如果我们通过某个算法得到了如下的等式关系,也就是一个下三角阵:

那可以通过它得到一个causal order,也就是一个序,比如对于s,d,y来说就是1,2,3。通过这个序,我们知道s一定在d和y前面,d一定在y前面,于是我们有下图的因果DAG

这类方法最大的优点就在于能够从马尔可夫等价类中区分出不同的DAG,从而保证有序的因果关系。
论文分享
- LiNGAM: 一个最经典的FCM-based algorithm, 用于continuous data。方法最常用的是用ICA(independent component analysis)作为求解的武器,核心逻辑就是估计一个类似上图的那种strictly lower triangle matrix (下三角阵),然后这个下三角阵就得到了一个unique的causal order。但是有严格的假设,分别是如下三个假设(a) the data generating process is linear, (b) there are no unobserved confounders, and (c) disturbance variables have non-Gaussian distributions of non-zero variances. 这个方法还有几个优化的变体,DirectLiNGAM,LvLiNGAM,SLIM,LiNGAM-GC-UK等
- BMLiNGAM: 和LiNGAM很像, 但是使用于两变量之间的,换句话说就是一个在确定两者有因果关系的变量之间找出谁是因谁是果。 他还有一个极其重要的优势就是可以用于unobserved confounders存在的情况下。类似的还有pairwise LiNGAM
- ANM: additive noise model: 也是一个处理两变量的方法。模型对LiNGAM第一个linear的假设做了放松(即variables和noise不需要再有linear relationship的假设了),然后对于noise,只要是additive的即可。还有一个ANM的优势是缩小了图的搜索空间。类似的可以处理多变量的模型还有一个叫CAM (causal additive model)的模型
DL/RL algorithm
这类方法有别于上述方法,更多使用深度学习或者强化学习等思路来挖掘因果图,里面的方法其实基本是也是上面的三类,只不过他们的实现路径不太好直接去归类到其中某一类,故我们就单列一类
论文分享
- CGNN: AWESOME! 一个极其强大的算法。可以在如下情况下使用,can be used for multi-variable, can be used in asymmetric distribution, can be used in unobserved confounder, non-linear cases.
- 回忆我们刚刚提到的FCM方程,里面有一个个f,这些f我们刚刚说可以是linear也可以是nonlinear的,这里是使用神经网络作为FCM 里的f,然后用他来生成拟合的一个FCM作为拟合出来的joint distribution来approximate the real joint distribution of data,用拟合的distribution和真正的distribution之间的差距作为损失函数,网络的目标即为最小化这个损失函数。损失函数表达如下:
,其中
是
的edge的个数。另外:
- 这里k就是某种核函数,衡量距离用的,MMD就是用来衡量两个分布的接近程度的,当两个分布完全一样时,MMD=0。所以大家其实可以看出来,这是一个score-based method,因为他的score function由两部分组成,一部分评估SCM的效果,一部分是对图的构造做了限制。不过这个方法理论上我理解是可以区分马尔可夫等价类的,所以也不算一般的score-based method
- 具体怎么实现呢?首先我们需要输入一个skeleton,就是一个先验的无向的因果图,这个图一般由专家知识得到。如果是score-based method,就会有一个搜索的策略,CGNN也是如此,他一共有3步搜索策略。
- 回忆我们刚刚提到的FCM方程,里面有一个个f,这些f我们刚刚说可以是linear也可以是nonlinear的,这里是使用神经网络作为FCM 里的f,然后用他来生成拟合的一个FCM作为拟合出来的joint distribution来approximate the real joint distribution of data,用拟合的distribution和真正的distribution之间的差距作为损失函数,网络的目标即为最小化这个损失函数。损失函数表达如下:
- 对于两两相邻的变量,通过这两个变量做一个pairwise CGNN,然后两个方向分别去训练一波,得到最优的损失,选比较小的损失作为选定的方向。于是我们就得到了两两的方向,即

- 顺着目前得到图的任意一个节点,找找有没有环,有环则把他reverse,这步就是保证不存在任意一个环,即

- 对于目前的图,不断的尝试reverse其中某个边,然后再去训练,看最后损失能不能减少,如果可以就reverse。这步一般使用hill-climbing算法。即

这样就得到了最后的图,所以NN其实是在每次需要计算score的时候都训练一遍,且参数并不保留,都是重新训练。还有就是,这个方法可以处理hidden confounder,方法就是把noise作为variables也放进图里。详细可以看原论文:https://arxiv.org/pdf/1711.08936.pdf
- SAM: recovering full causal models from continuous observational data along a multivariate non-parametric setting。也是可以处理有hidden confounder的情况。这篇文章比较骚的地方在于他提到自己不是上述任意一类的方法,他说他是一个集大成者,即用到了conditional independence如constraint-based,又做了regularization如score-based,同时又可以和CGNN,CAM等方法一样解决distributional asymmetries的问题。可见现在学术圈有多卷!
- 详细可以看原论文:https://arxiv.org/pdf/1803.04929.pdf
- CAUSAL DISCOVERY WITH REINFORCEMENT LEARNING: 这篇文章来自华为的诺亚实验室,他利用Reinforcement Learning (RL)来寻找得分最高的DAG. Its encoder-decoder model takes observable data as input and generates graph adjacency matrices that are used to compute rewards. It uses RL as a search strategy and its final output would be the graph, among all graphs generated during training, that achieves the best reward, is the best DAG. 使用RL作为因果挖掘的思想非常straightforward,因为在RL里的每个action可以看作是一个treatment的改变,而reward就可以是图的分数,这个思想非常好
- 详细可以看原论文:https://arxiv.org/pdf/1906.0447
(2)Causal Effect Estimation 因果效应估计
例子:发优惠券是因,购买转化率是果,想知道,发券时购买转化率会增加多少?这个问题就是一个典型的因果效应估计问题。
因果效应估计非常广,细分了很多领域,比如对ITE的估计,对ATE的估计,其中根据因果类型和数据特性,又有更多分类,比如对于连续性treatment的估计,对multi-cause的估计,对time-varying treatment的估计等等。这里我们主要focus在ATE和ITE的两种估计。
treatment是我们感兴趣的那个因,比如研究给用户发优惠券对购买转化率的影响,那么不发券(t=0),发券(t=1)。
假设treatment有两种 ,对于一个instance i,比如一个用户,他的转化率y是果,是否发券的t是因,
表示在treatment为t的情况下转化率y的值。我们就有ITE (Individual treatment effect)公式如下:
, 表示一个individual的treatment effect。那么如果我们想看一个大群体(一个普遍现象),就是ATE(average treatment effect)啦,ATE is the expectation of ITE over the whole population i=1,…,n:
那么介于两者中间呢,就有一个CATE(conditional average treatment effect),也就是一个subpopulation的average treatment effect。, 其实ITE就是CATE的变种,只不过这个subpopulation缩小到了一个人。
估计ATE
估计ATE的作用是做一些宏观的决策,或者对于整体population是否施加treatment做一些决策。举个例子,想要评估打疫苗对病变的效果,我们要评估一个overall的疫苗效应,这个时候我们去预估ATE就够了。
评估效果的时候,我们需要一个ground truth的ATE 以及我们infer出来的ATE
,我们评估的指标就是MAE:
估计ITE (CATE)
那么什么时候我们需要估计ITE呢?当整个population是heterogeneous的时候,即人群有异质性的时候,ATE可能会误导结论。举个例子,我们衡量大众点评评分对餐馆的销量影响的时候,ATE可能会误导,因为大城市的餐馆可能会更多被大众点评影响,小城市或农村可能影响更小。这时候其实我们要评估的每一个subpopulation的ATE,也即CATE(或者细粒度到每个individual的ITE)。那么我们怎么去定义各个subpopulation呢?就是靠除了treatment t之外的其他特征X,每一组X的取值就代表了一个subpopulation。
评估效果的时候,我们可能需要AB的环境,对于某个样本做treatment=0和1的两次实验得到结果 和
,然后我们算一个MSE:
重要假设
SCM这个结构中有一个重要假设叫sufficiency assumption,即我们没有unobserved confounder,confounder就是同时对t和y都有因果影响的变量,这里要求所有的confounder都在我们的数据特征X中。所以前期的很多方法都需要满足这个假设,不过大家也知道这个条件其实在现实生活中的假设是很难被满足的,这时候我们就会有一些方法可以relax这个假设。所以我们也可以把方法依据是否能在有unobserved confounder的情况下使用分成两类。
所以接下来的文章介绍其实就会根据用来估计ATE/ITE,是否要求no unobserved confounder这两方面去做分类。详见原文
- 要求no unobserved confounder的方法
- 不要求no unobserved confounder的方法
因果推理方法
在推理中的算法有很多,主要是克服选择偏倚,先介绍一些比较常见的做法,包括
- (1) Re-weighting methods; (重加权算法)
- (2) Stratification methods; (分层算法)
- (3) Matching methods; (匹配算法)
- (4) Tree-based methods; (基于树的方法)
- (5) Representation based methods; (表示学习)
- (6) Multi-task methods; (多任务学习)
- (7) Meta-learning methods。 (元学习)
摘自:因果推理综述——《A Survey on Causal Inference》一文的总结和梳理
Re-weighting methods
调整每个unit的权重,使得treatment组合和对照组的分布一致,解决选择偏差的问题。
干预组和对照组观测数据的分布不同,这就是选择偏倚带来的挑战。为了克服选择偏倚,可以考虑对样本进行重新加权。通过给观察数据集中的每个样本分配适当的权重,可以创建一个伪总体,使得干预组和对照组的分布相似。然后根据重加权后因果效应的评估。

上图展示了重加权的过程,当存在年龄Age这个混杂因子时,选择偏倚使得干预组和对照组的分布存在一定差异,对样本重新分配权重后(右图加粗部分,可以认为是增加了权重),使得干预组和对照组的分布相似,从而消除了混杂因子Age带来的选择偏倚。
倾向分数
它是给定观测协变量向量的特定干预分配的条件概率,反映出样本x选择treatment的可能性。
- e(x)=Pr(W=1∣X=x)
反向倾向加权(IPW)
给每个unit指定的权重为:
- 𝑟 = 𝑊/𝑒(𝑥) + (1−𝑊)/(1−𝑒(𝑥))
其中 𝑊 是treatment, e(x) 是倾向得分。重加权后在整体层面对平均干预效果进行估计:
理论结果表明,调整倾向得分足以消除由于所有观测到的协变量而产生的偏差。但是这种加权方法高度依赖倾向性得分的正确性。
双保险估计/增广IPW
它将基于倾向得分加权的重加权算法和结果回归相结合
当倾向性得分或者结果回归中只要有一个是正确的,就能做到无偏估计。
协变量平衡倾向得分(CBPS)
倾向性得分既可作为干预分配的概率,又可作为协变量平衡得分,CBPS利用了这一双重特征,通过解决下面这一问题来估计倾向性得分:
数据驱动变量分解(𝐷2𝑉𝐷D2VDD^{2}VD)
假设:观测变量可以分解为混杂变量、调整变量和无关变量
目的:区分混杂变量和调整变量,同时剔除无关变量。
重加权算法总结
Stratification Methods 分层算法
也叫subclassification或者blocking。直觉是把treatment组和对照组的样本分组,使得组内的treatment和对照组是同构的。最终的得分是所有小组的加权平均。
通过将整个组分成子组来调整选择偏差,在每个子组中,treatment组和对照组在某些测量值下是相似的,干预效果的估计结果是所有子组的加权平均。
利用分层算法估计的平均干预效果:
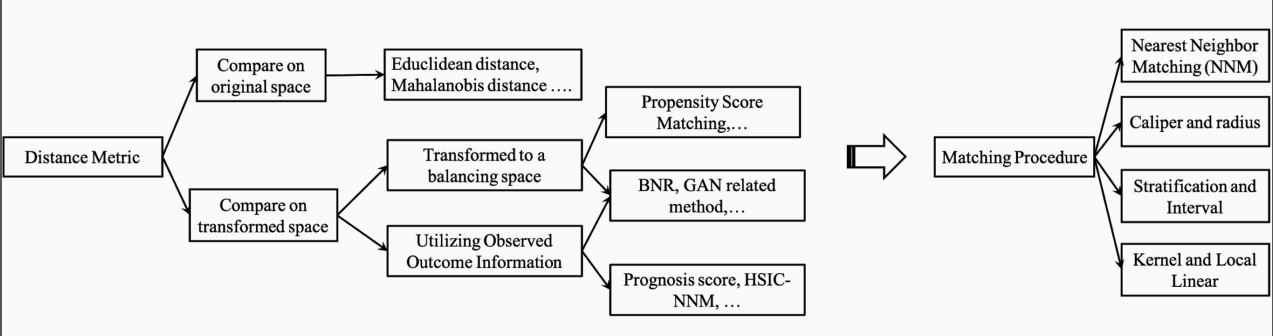
Matching Methods匹配算法
匹配算法使用下面的公式来估计后果:

Y(0)代表对照组,Y(1)表示实验组。J (i)代表在相反的组中和样本距离最近的样本。其中距离度量的方式很多,主要的有欧式距离和马氏距离。样本空间有原始空间,也包括转换后的空间。
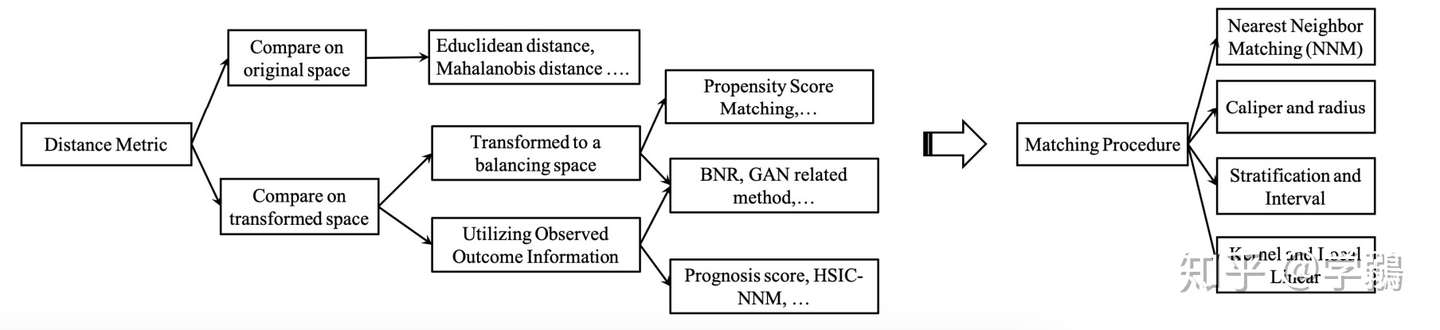
匹配算法归类
- 邻近算法
- Caliper算法
- 分层算法
- 核函数
Tree-based Methods
Tree-based Methods主要指的是决策树,包括CART树、BART树和RF。
深度学习方法
以上算法都是统计学习方法,一笔带过,现在主要介绍一些deep的方法。
Johansson, Learning Representations for Counterfactual Inference, ICML`16
介绍:基于表示学习。
做法:重新定义反事实问题为协变量转变的问题,进而定义成一个领域适应问题。因为事实分布和反事实结果分布式不一样的,因此可以使用领域适应来克服。主要有3点考虑:
- a. 最小化事实结果的错误率。
- b. 使用相关的事实结果来指导反事实结果,这是通过约束来完成的,使得类似的干预结果一样。
- c. 干预的分布是相似的。这个通过最小化所谓的discrepancy distance来克服。
这个discrepancy distance指的是在表示空间内,事实分布和反事实分布的差异,即

其中IPM指的是an Integral Probability Metrics,衡量的是两个分布之间的距离。损失函数由以上三项加起来即可,同时加上一个模型复杂度的正则项。后续,该作者继续提出一些改进,比如引入re-weight等。
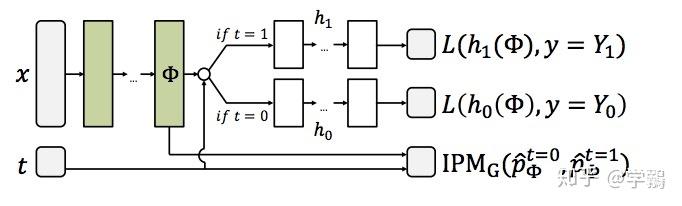
Shalit, Estimating individual treatment effect: generalization bounds and algorithms, ICML`17
主要内容:模型整体和前作很相似,改进了discrepancy distance,即IPM改进为联合分布的差异。
整体的loss如下,L是观测数据和预测数据的差异,wi是一个权重,这里模型的wi不是学习来的,后两项是模型的复杂度和discrepancy distance,确实和上一个论文很类似。
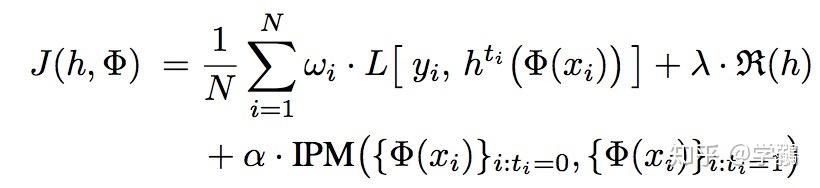
网络架构如图,其中的全连接分别对应表示层和回归层,即fi和h。
Sharma, MetaCI: Meta-Learning for Causal Inference in a Heterogeneous Population, NIPS`19
- 任务:借助于元学习开开展推理
- 做法:将meta learning中的reptile框架引入了推理中,元学习就是所谓的‘learn to learn’,旨在学习最适合任务的初始化参数等,通过少量的样本来调整参数,然后通过不同的任务来学习初始化的能力。文章引入了reptile这一个元学习策略并加以改进,提出了并行化的reptile。
元学习中的一个重要特点是多任务,少样本,因此和few-shot learning类似,而在因果推理框架中的多个任务则是由同样分布的子组(subgroup)组成。
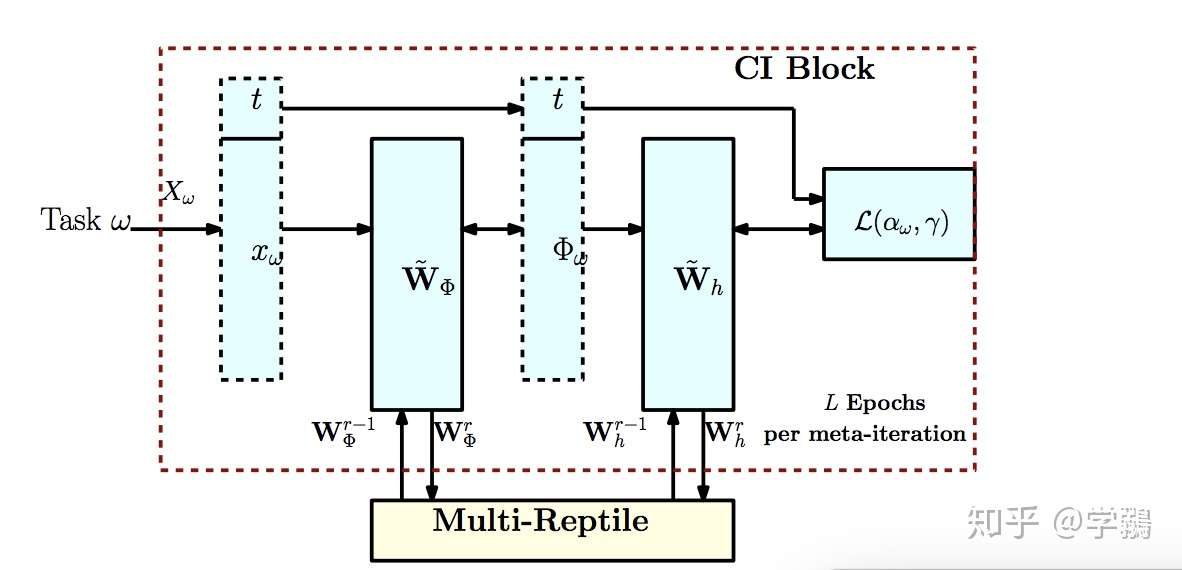
每次迭代的示意图如上,每个任务的support data并不同(元学习的每一个子任务的训练数据成为support data),获取表示之后进入全连接,然后获取loss,每个任务只进行几次迭代。
Hassanpour, CounterFactual Regression with Importance Sampling Weights, IJCAI`19
主要工作:把表示学习和re-weight结合起来,首先用表示学习使得选择偏倚尽可能缩小,同时保证事实结果尽可能正确。而re-weight可以调整样本的权重,使得观测数据和反事实数据的分布尽可能一致。
如下图所示,经过transform之后的特征空间和原始的x相比,不同treatment的样本分布逐渐接近,同时保证了Y是不变的。
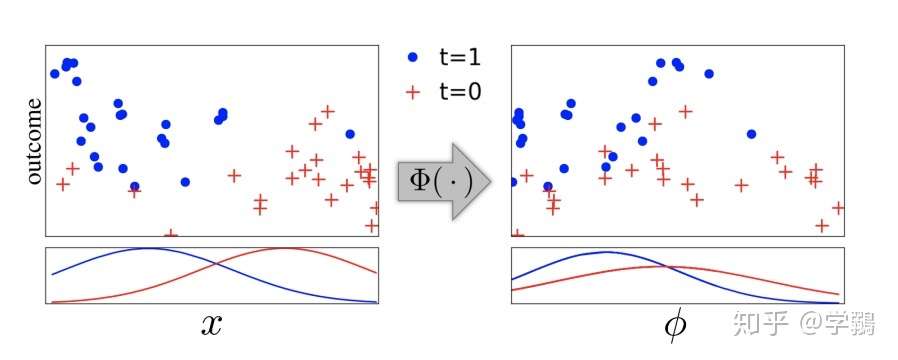
这篇文章是对之前其他工作的改进,主要是对第二篇文章的改进,上面知道第二个文章的loss中的wi是有概率直接得出,而该算法则是学习得到。如下图:
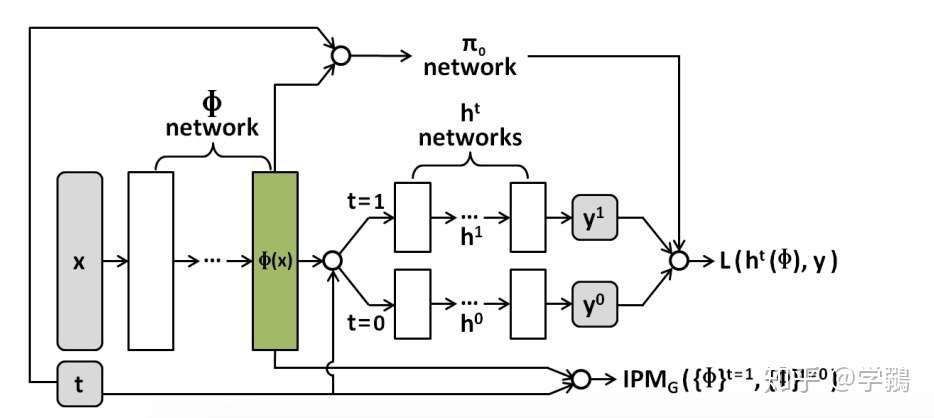
看出系数是通过表示向量学习出来的,即为重要性抽样:
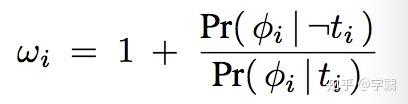
后半部分的分布计算起来比较麻烦,通过贝叶斯来变换:

其中的π就是图中的π网络,是一个简单的逻辑回归。其中的w和b依赖于t和表示向量。
Alaa, Deep Counterfactual Networks with Propensity-Dropout, ICML`17
主要做法:比起之前的领域适应的做法,该文章把反事实推理认为是一种多任务的框架,通过倾向分dropout来缓解选择偏倚:每一次迭代的时候有一定的dropout几率,而这个几率就依赖于倾向分。
| propensity score倾向分数:p(x) = P(Wi = 1 | Xi = x),反映出样本x选择treatment的可能性。 |
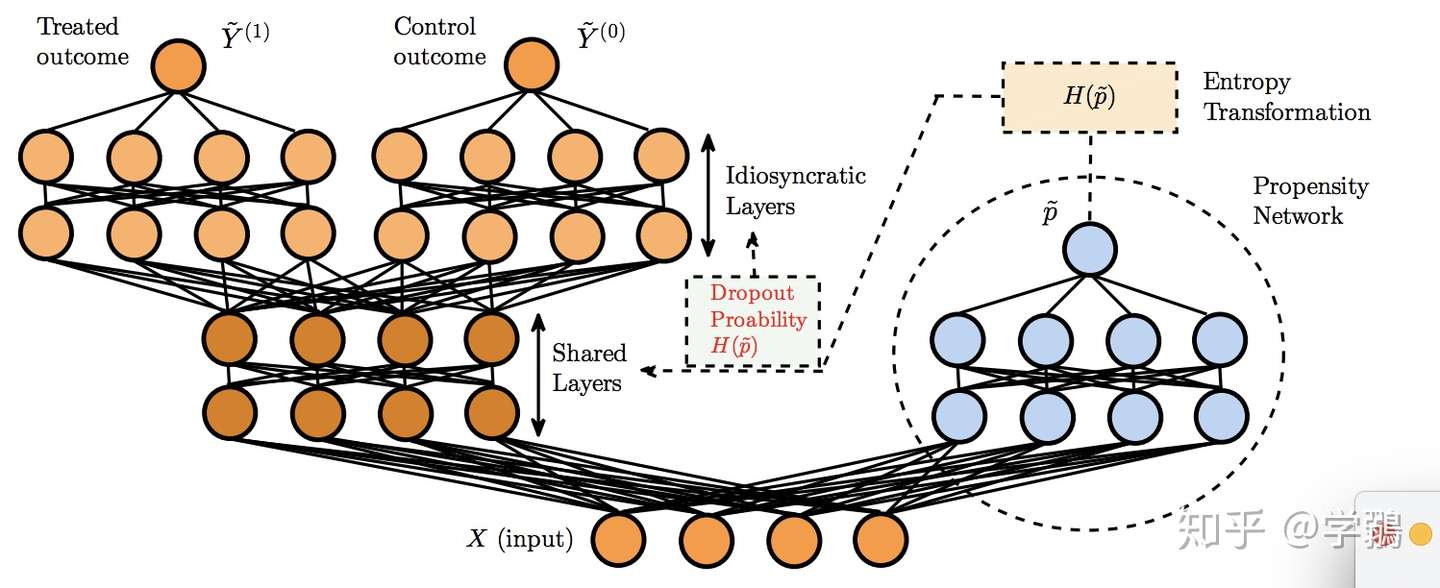
看图:
对于每一个输入,不同的treatment是首先共享前几层,然后再分化为不同的输出层,同时有一个倾向分网络来计算dropout概率。
这个倾向分的P,是对于简单的样本,取得极端值,比如0和1,对于复杂的样本,取得中间值,比如0.5.
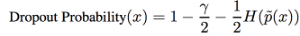
其中 0 ≤ γ ≤ 1,是一个超参数,文章设为1.
H(p) = −p log(p)−(1−p) log(1−p),香农熵。 您最近使用了:
因果推理模型的7种特性
- 【2021-1-9】和家人一起去一个未知的目的地度假。假期前后,你都在纠结一些与事实相悖的问题:
- 假期里我们应该做什么?
- 我们会开心吗?
- 我们为什么会觉得开心?
- 之后我们会有什么感觉?

- 考虑以下 5 个问题:
- 给定的疗法在治疗某种疾病上的有效性?
- 是新的税收优惠导致了销量上升吗?
- 每年的医疗费用上升是由于肥胖症人数的增多吗?
- 招聘记录可以证明雇主的性别歧视罪吗?
- 我应该放弃我的工作吗?
- 这些问题的一般特征是它们关心的都是原因和效应的关系,可以通过诸如「治疗」、「导致」、「由于」、「证明」和「我应该」等词识别出这类关系。这些词在日常语言中很常见,并且我们的社会一直都需要这些问题的答案。然而,直到最近也没有足够好的科学方法对这些问题进行表达,更不用说回答这些问题了。和几何学、机械学、光学或概率论的规律不同,原因和效应的规律曾被认为不适合应用数学方法进行分析。
- 这种误解有多严重呢?实际上仅几十年前科学家还不能为明显的事实「mud does not cause rain」写下一个数学方程。即使是今天,也只有顶尖的科学社区能写出这样的方程并形式地区分「mud causes rain」和「rain causes mud」。
- 过去三十年事情已发生巨大变化。一种强大而透明的数学语言已被开发用于处理因果关系,伴随着一套把因果分析转化为数学博弈的工具。这些工具允许我们表达因果问题,用图和代数形式正式编纂我们现有的知识,然后利用我们的数据来估计答案。进而,这警告我们当现有知识或可获得的数据不足以回答我们的问题时,暗示额外的知识或数据源以使问题变的可回答。
- 这种转化称为「因果革命」(Pearl and Mackenzie, 2018, forthcoming),而导致因果革命的数理框架我称之为「结构性因果模型」(SCM)。
- SCM 由三部分构成:
- 图模型
- 结构化方程
- 反事实和介入式逻辑
- 图模型作为表征知识的语言,反事实逻辑帮助表达问题,结构化方程以清晰的语义将前两者关联起来。
接下来介绍 SCM 框架的 7 项最重要的特性,并讨论每项特性对自动化推理做出的独特贡献。
- 编码因果假设—透明性和可试性
- 图模型可以用紧凑的格式编码因果假设,同时保留透明性和可试性。其透明性使我们可以了解编码的假设是否可信(科学意义上),以及是否有必要添加其它假设。可试性使我们(作为人类或机器)决定编码的假设是否与可用的数据相容,如果不相容,分辨出需要修改的假设。利用 d-分离(d-separate)的图形标准有助于以上过程的执行,d-分离构成了原因和概率之间的关联。通过 d-分离可以知道,对模型中任意给定的路径模式,哪些依赖关系的模式才是数据中应该存在的(Pearl,1988)。
- do-calculus 和混杂控制
- 混杂是从数据中提取因果推理的主要障碍,通过利用一种称为「back-door」的图形标准可以完全地「解混杂」。特别地,为混杂控制选择一个合适的协变量集合的任务已被简化为一种简单的「roadblocks」问题,并可用简单的算法求解。(Pearl,1993)
- 为了应对「back-door」标准不适用的情况,人们开发了一种符号引擎,称为 do-calculus,只要条件适宜,它可以预测策略干预的效应。每当预测不能由具体的假设确定的时候,会以失败退出(Pearl, 1995; Tian and Pearl, 2002; Shpitser and Pearl, 2008)。
- 反事实算法
- 反事实分析处理的是特定个体的行为,以确定清晰的特征集合。例如,假定 Joe 的薪水为 Y=y,他上过 X=x 年的大学,那么 Joe 接受多一年教育的话,他的薪水将会是多少?
- 在图形表示中使用反事实推理是将因果推理应用于编码科学知识的非常有代表性的研究。每一个结构化方程都决定了每一个反事实语句的真值。因此,我们可以解析地确定关于语句真实性的概率是不是可以从实验或观察研究(或实验加观察)中进行估计(Balke and Pearl, 1994; Pearl, 2000, Chapter 7)。
- 人们在因果论述中特别感兴趣的是关注「效应的原因」的反事实问题(和「原因的效应」相对)。(Pearl,2015)
- 调解分析和直接、间接效应的评估
- 调解分析关心的是将变化从原因传递到效应的机制。对中间机制的检测是生成解释的基础,且必须应用反事实逻辑帮助进行检测。反事实的图形表征使我们能定义直接和间接效应,并确定这些效应可从数据或实验中评估的条件(Robins and Greenland, 1992; Pearl, 2001; VanderWeele, 2015)
- 外部效度和样本选择偏差
- 每项实验研究的有效性都需要考虑实验和现实设置的差异。不能期待在某个环境中训练的模型可以在环境改变的时候保持高性能,除非变化是局域的、可识别的。上面讨论的 do-calculus 提供了完整的方法论用于克服这种偏差来源。它可以用于重新调整学习策略、规避环境变化,以及控制由非代表性样本带来的偏差(Bareinboim and Pearl, 2016)。
- 数据丢失
- 数据丢失的问题困扰着实验科学的所有领域。回答者不会在调查问卷上填写所有的条目,传感器无法捕捉环境中的所有变化,以及病人经常不知为何从临床研究中突然退出。对于这个问题,大量的文献致力于统计分析的黑箱模型范式。使用缺失过程的因果模型,我们可以形式化从不完整数据中恢复因果和概率的关系的条件,并且只要条件被满足,就可以生成对所需关系的一致性估计(Mohan and Pearl, 2017)。
- 挖掘因果关系
- 上述的 d-分离标准使我们能检测和列举给定因果模型的可测试推断。这为利用不精确的假设、和数据相容的模型集合进行推理提供了可能,并可以对模型集合进行紧凑的表征。人们已在特定的情景中做过系统化的研究,可以显著地精简紧凑模型的集合,从而可以直接从该集合中评估因果问询。
- NIPS 2017 研讨会 Q&A
- 我在一个关于机器学习与因果性的研讨会(长滩 NIPS 2017 会议之后)上发表了讲话。随后我就现场若干个问题作了回应。我希望从中你可以发现与博客主题相关的问题和回答。
- 一些人也想拷贝我的 PPT,下面的链接即是,并附上论文:
- NIPS 17 – What If? Workshop Slides PDF
- 问题 1:「因果革命」是什么意思?
- 回答:「革命」是诗意用法,以总结 Gary King 的奇迹般的发现:「在过去几十年里,对于因果推断的了解比以前所有历史记载的总和还要多」(参见 Morgan 和 Winship 合著的书的封面,2015)。三十年之前,我们还无法为「Mud does not cause Rain」编写一个公式;现在,我们可以公式化和评估每一个因果或反事实陈述。
- 问题 2:由图模型产生的评估与由潜在结果的方法产生的评估相同吗?
- 回答:是的,假设两种方法开始于相同的假设。图方法(graphical approach)中的假设在图中被展示,而潜在结果方法(potential outcome approach)中的假设则通过使用反事实词汇被审查者单独表达。
- 问题 3:把潜在的结果归因于表格个体单元的方法似乎完全不同于图方法中所使用的方法。它们的区别是什么?
- 回答:只在有可条件忽略的特定假设成立的情况下,归因才有效。表格本身并未向我们展示假设是什么,其意义是什么?为了搞明白其意义,我们需要一个图,因为没有人可在头脑中处理这些假设。流程上的明显差异反映了对假设可见的坚持(在图框架中),而不是使其隐藏。
- 问题 4:有人说经济学家并不使用图,因为其问题不同,并且也没能力建模整个经济。你同意这种解释吗?
- 回答:不同意!从数学上讲,经济问题与流行病学家(或其他科学家)面临的问题并无不同,对于后者来讲,图模型已经成为了第二语言。此外,流行病学家从未抱怨图迫使其建模整个人体解剖结构。(一些)经济学家中的图规避(graph-avoidance)是一种文化现象,让人联想到 17 世纪意大利教会天文学家避开望远镜。底线:流行病学家可以判断他们的假设的合理性——规避掉图的经济学家做不到(我提供给他们很多公开证明的机会,并且我不责怪他们保持沉默;没有外援,这个问题无法被处理)。
- 问题 5:深度学习不仅仅是盛赞曲线拟合?毕竟,曲线拟合的目标是最大化拟合,同时深度学习中很多努力也在最小化过拟合。
- 回答:在你的学习策略中不管你使用何种技巧来最小化过拟合或其他问题,你依然在优化已观察数据的一些属性,同时不涉及数据之外的世界。这使你立即回到因果关系阶梯的第一阶段,其中包含了第一阶段要求的所有限制。
实验示例
任务描述
- 任务:利用观察数据,如电子健康记录(EHR),评估几种不同药物对一种疾病的治疗效果
- 观测数据:
- 患者的人口统计信息
- 患者服用特定剂量的特定药物
- 医学测试结果
- 其他
- 研究对象:病人
- 干预:不同药物
- 结果:恢复/血样测试结果/其他
三个重要假设
- (1)稳定单位干预值假设(Stable Unit Treatment Value Assumption)
- 任何一个单元的潜在结果不会因分配给其他单元的treatment而有所不同,并且对于每个单元,每个treatment级别没有不同的形式或版本,不会导致不同的潜在结果。
- 这个假设强调以下几点:
- unit之间都是相互独立的,unit之间不会存在相互作用
- 同一treatment仅能存在一个版本。例如,在该假设下,不同剂量的同一种药物代表不同的治疗方法
- (2)可忽略性假设(Ignorability)
- 给定背景变量 𝑋 , 干预分配 𝑊 与潜在的结果无关
- 例如,由上文的药物治疗的例子来看,如果两个患者有相同的背景变量 𝑋 ,无论治疗任务是什么,他们的潜在结果应该是相同的
- 类似地,如果两个患者具有相同的背景变量值,那么他们的治疗分配机制应该是相同的,无论他们有什么潜在的结果
- (3)正值假设(Positivity)
- 对于X的任何一组值,处理分配不是确定的:
- 𝑃(𝑊=𝑤∣𝑋=𝑥)>0
- 如果某些X值的治疗分配是确定的,那么至少一种治疗的结果永远无法观察到。那么估计因果关系是不可能也没有意义的,这意味着干预组和对照组的“共同支持”或“重叠”。忽略性和积极性假设一起也被称为强可忽略性或强可忽略性治疗任务
- 对于X的任何一组值,处理分配不是确定的:
研究方法
一般研究方法
- 核心问题:如何估计特定人群的平均潜在治疗/控制结果?
- 想当然的解决方案: 计算平均治疗和对照结果之间的差异,即ATE
- 存在的问题:由于混杂因素(confounders)的存在,这种解决方案是不合理的
混杂因素
- 混杂因素(Condounders)是同时影响干预分配和最终结果的变量
举例说明, 在下图中,展示的是两种治疗方案对年轻/年老两种病人群体的治疗效果

抛开年龄从整体上来看,不难得出结论:A治疗方案更好;但是考虑年龄的话,无论在是年轻的病患群体中还是年老的病患群体中,B方案的治愈率明显更高,由此得到结论:B治疗方案更好。这两种结论显然是互相矛盾的,但是为什么考虑年龄之后,会得出截然相反的结论呢?
实际上,这是一种名为辛普森悖论的现象。辛普森悖论指的是同一组数据,整体的趋势和分组后的趋势完全不同。也就是说,整体数据和分组数据产生的结论截然相反。
辛普森悖论的解释:
- 在上面的例子中,数据分组的指标是年龄,而年龄同时影响着恢复率和治疗方案的选择。从恢复率数据来看,无论是哪种治疗方案下,年轻组的恢复率普遍比年老组高得多,而从治疗方案的选择来看,年轻组更倾向于选择A治疗方案,而年老组则更倾向于选择B治疗方案。正是这种共同影响的存在,使得整体结果和分组结果完全不同。
- 在这个例子中,干预分配显然就是治疗方案的选择,最终结果就是治愈率,显然可以得知,年龄在这里就是混杂因子。混杂因子的存在导致辛普森悖论现象的产生,因此,在混杂因素存在的情况下,我们不能针对观测数据轻易下结论。
选择偏倚
- 混杂因子的存在影响着干预分配的选择,treatment组和对照组的分布有可能不一致,因此导致出现偏差,这也使得反事实结果估计更加困难。
摘自:因果推理综述——《A Survey on Causal Inference》一文的总结和梳理
引言
- 2020年6月21日,图灵奖得主、贝叶斯网络之父 Judea Pearl 在第二届北京智源大会上做了《新因果科学与数据科学、人工智能的思考》的报告。
- Pearl说:
- 我们现在正处在第二次数学科学革命,这一革命是以科学为中心的因果革命,相对于第一次以数据为中心的革命,第二次显得有些沉默,但威力同样巨大。
- Pearl解释了因果科学为什么需要新的逻辑和新的推理机制,以及因果科学中新引擎的结构是什么。也对称之为“double-helix”两个因果推理的基本定理进行了交代;最后也给大家讲了基于因果智能的七种工具,以及这七种工具是如何给科学带来革命性变化。
什么是因果科学
-
- 因果科学就是回答因果问题的逻辑和工具,如上图一些因果问题的典型例子:
- 1、某项治疗对预防疾病的效果如何;
- 2、新的税收优惠政策和营销活动哪个是导致销售额上升的原因;
- 3、肥胖症每年造成的保健费用是多少;
- 4、雇用记录能否证明雇主有性别歧视行为;
- 5、我如果辞职了,会不会后悔?
- 上面这五个问题,显然无法用现在标准的科学语言(如数学公式)进行回答。为什么呢?因为这些问题都包含着不对称信息。毕竟“代数学科”从伽利略时代开始,就是专注于等式(完全对称的因果关系),即y=ax此类的表达式。
-
而现实中,大多数问题,如上标黄的单词,预防、导致、归因、歧视、后悔等等都是含有不对称属性的。相对于“等号=”表示对称信息,那么我们也可用箭头→表示非对称信息。在过去30年中,我和我的同事做了非常多的工作,就是为了找到非对称的表达工具,在后面我也会介绍一些工具。
- 因果推断
- 因果推断区分了人们可能想要估计的两种条件分布。机器学习中,通常只会估计一种分布,但在某些情况下,可能也需要估计第二种。
- 因果推断用的最多的模型是 Rubin Causal Model (RCM; Rubin 1978) 和 Causal Diagram (Pearl 1995)。Pearl (2000) 中介绍了这两个模型的等价性,但是就应用来看,RCM 更加精确,而 Causal Diagram 更加直观,后者深受计算机专家们的推崇。
- 观察给定一个x后,变量y会发生什么变化。这就引申出两种表述:
- (1)观察p(y|x):如果观察变量X取值于x,Y的相应分布是什么?这是我们常在监督学习中遇到问题,它是一个条件分布,可以从p(x,y,z,…)中计算出它的两个边缘概率:p(y|x) = p(x,y)/p(x)。相信所有人都不会对这个公式感到陌生,也都会计算。
- (2)介入p(y|do(x)):如果设X的值为x,那Y的相应分布是什么?这其实就是通过人为把X的值设为x来干预数据生成过程,但其余变量还是用原先的生成方式,以此观察Y的变化(请注意,数据生成过程与联合分布p(x,y,z,…)不同)。
- p(y|x)和p(y|do(x))不一样,p(y|do(x))实际上和x无关
- p(y|do(x))实际上就是一个普通的条件分布,但它不是基于 p(x,z,y,…)的,而是pdo(X=x)(x,z,y,…)。这里的pdo(X=x)是如果实际进行干预的话会观察到的数据的联合分布。所以p(y|do(x))是从随机对照试验或A/B测试收集到的数据中学习的条件分布,其中x由实验者控制。
- 即便不能从随机实验中直接估计p(y|do(x)),这个分布也是实际存在的。所以因果推断和do-calculus的主要观点是:
- 如果我不能在随机对照实验中直接测量p(y|do(x)),那我是否可以根据我在受控实验之外观察到的数据来估计它?
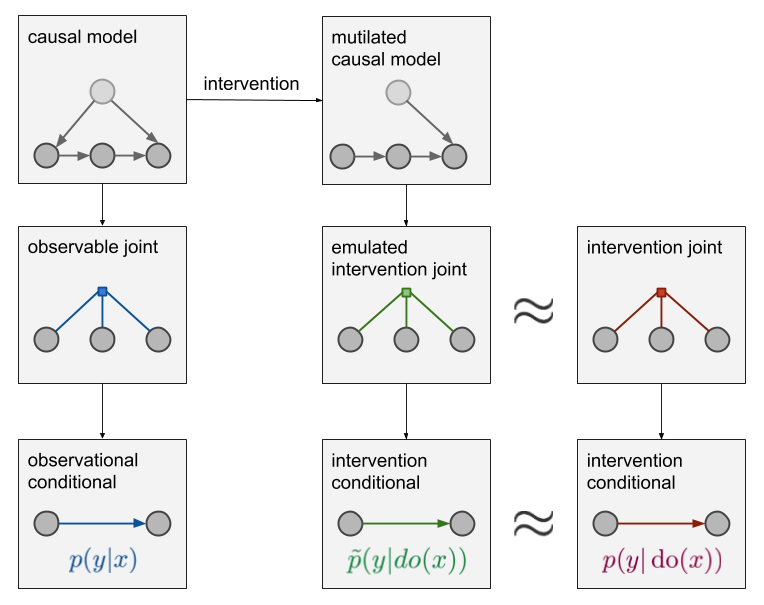
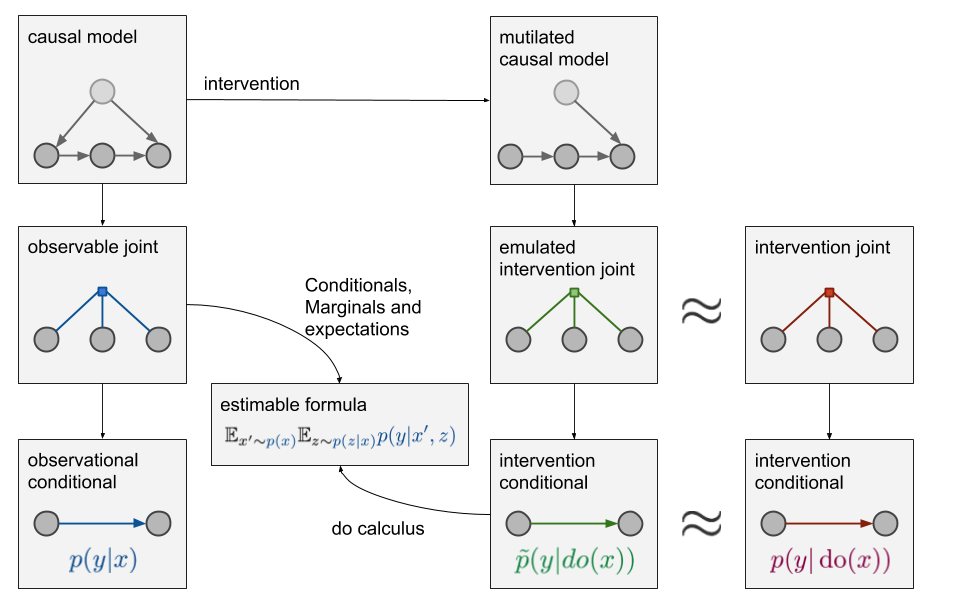
- 参考作者:骑驴看热闹,英文原文:ML beyond Curve Fitting: An Intro to Causal Inference and do-Calculus
推理引擎的结构
- 因果关系的学习者必须熟练掌握至少三种不同层级的认知能力:
观察能力(Seeing)、行动能力(Doing)和想象能力(Imagining)。”- 第一层级“
关联”表示观察能力,指发现环境中规律的能力- 一只猫头鹰观察到一只老鼠在活动,便开始推测老鼠下一刻可能出现的位置,这只猫头鹰所做的就是通过观察寻找规律;
- 第二层级“
干预”表示行动能力,指预测对环境刻意改变后的结果,并根据预测结果选择行为方案- 如果我做X这件事情,那么y会发生什么变化,一个具体的例子是如果我把香烟戒掉,那么得癌症的状况会发生什么变化;
- 第三层级“
反事实”表示想象能力,指想象并不存在的世界,并推测观察到的现象原因为何- 为什么是x导致了y,如果当时x没有发生,那么状况会是怎么样的,如果当时采取了其他措施,会发生什么?具体的例子是:我吃了阿司匹林能治好了我的头痛吗?假如奥斯沃德没有刺杀肯尼迪,肯尼迪会活着吗?假如在过去的两年里我没有吸烟会怎样?
| 层级 | 能力提现 | 数学表达 | 说明 |
|---|---|---|---|
| 反事实 | 想象 | P(y_x|x’, y’) | 因果推断的最高层 |
| 干预 | 行动 | P(y|do(x), z) | 执行某动作会带来的结果 |
| 关联 | 观察 | P(y|x) | 发现规律→机器学习 |
Judea Pearl 曾在他的书里《为什么》中提到:
- 第一层级“关联”和第二层级“干预”主要针对当前的弱人工智能,包括对现有贝叶斯网络在深度学习领域的拓展、前门标准实践、do-calculus 等核心算法;
- 而第三层级“反事实”是基于基于人的想象力和假设,是人类独有的思考能力,也是令人工智能达到人类智能的关键命门。
- 【2020-9-5】攀上因果关系的阶梯
- 珀尔描述了从仅仅观察相关性到检验因果性的转变,即从因果关系阶梯的第一级上升到第二级。
- 摘自:因果之箭指向何方?| 图灵奖得主珀尔的《为什么》
- 当前的机器学习无力回答反事实的问题,大多数机器学习模型甚至使用了不可能回答这一问题的表示。

- Pearl的因果推断理论共有7大支柱:
- 有意义而紧凑的因果假设表示(graphical表示)
- 混杂因子控制(back-door、front-door、do-calculus)
- 反事实算法(本文重点介绍的内容)
- 媒介分析(反事实的graphical表示)
- 学习迁移、外部验证、取样偏差(do-calculus、selection diagrams)
- 数据缺失(graphical标准)
- 因果发现(寻找和数据兼容的模型,并紧凑地表示它们)
- Pearl同时开发了结构化因果模型(Structural Causal Model, SCM),一个形式化地描述因果推断的框架
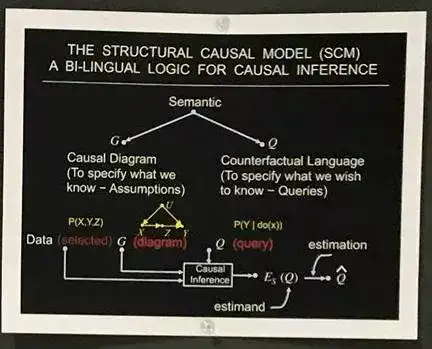
- 摘自:“无人问津”的贝叶斯网络之父Judea Pearl在NIPS 2017上到底报告了啥
因果前言
因果关系在生活中无处不在。经济、法律、医学、物理、统计、哲学、宗教等众多学科,都与因果的分析密不可分。然而,和其他概念,例如统计的相关性相比,因果(causality)非常难以定义。利用直觉,我们可以轻易判断日常生活中的因果关系;但是,用清晰、没有歧义的语言准确回答「因果关系是什么?」这个问题,往往超出了常人的能力范围。
(感兴趣的读者,不妨暂停阅读,然后试着给出一个「因果关系」的定义。)
不得不承认,回答这个问题是如此困难,以至于部分哲学家认为,因果关系是不可还原的、最基础的认知公理,无法被用其他方式描述。不过,本文即将描述的众多统计因果模型,将会是针对这一观点的有力反驳。
在知乎上,也有一些对于因果关系的探讨,例如哲学话题下的「因果关系是真实存在,还是我们认识世界的一种方法?」令人遗憾的是,这个问题下的大多数答案,都把重心放在了认知论上,即「如何回应休谟的归纳问题?」以及「我们怎么知道,我们认知的因果关系是可靠的?」大家似乎都默认,「什么是因果关系」是一个琐碎得不需要讨论的前提(但显然并非如此),陷入怀疑论和先验论,从而无法给出一个实用的因果模型。事实上,因果关系是一个本体论的话题:我们需要找到一个符合直觉、足够广泛,但也足够具体的定义来描述因果关系;在此基础之上,我们还需要一套可靠的判定因果的方法。
常用的统计因果模型都采用了介入主义(interventionism)的诠释:因果关系的定义依赖于「介入」的概念;外在的介入是因,产生现象的变化是果。
在此之前,我们先了解一下其他传统的对于「因果关系」的定义,以及为什么它们不符合直觉。

大卫·休谟(David Hume)
- 休谟:因果就是「经常性联结」(constant conjunction)。如果我们观察到,A总是在B之前发生,事件A与事件B始终联结在一起,那么A就导致了B,或者说A是B的原因。
- 反驳:令A表示公鸡打鸣,令B表示日出。自然条件下,日出之前总有公鸡打鸣,但不会有人认为公鸡打鸣导致了日出。假如我们进行介入,监禁了所有的公鸡,使它们无法打鸣,太阳仍然会照常升起。
在这里,有必要注意一个细节:
- 大卫·休谟(David Hume,1711年-1776年)。
- 卡尔·皮尔逊(Karl Pearson,1857年-1936年)。 提出「统计相关性」概念的皮尔逊,比休谟晚出生了一百多年。
我们现在的思维方式,并非是自古以来就存在的:我们眼里理所应当的常识,在古人脑中可能从未出现。
在统计学成为一门严谨的学科、皮尔逊清晰地分离相关性和因果性之前,大多数人都把相关性和因果性混为一谈。即便到了现在,认为相关就代表因果的人也不在少数。
我们没有必要因为休谟的历史地位,就把他下的定义奉为金科玉律。所以,休谟用的经常性联结只能定义相关性,不能定义因果性。

相关性未必意味着因果性
- 相关性不代表因果性。
- 相关性是对称的,而因果性是不对称的。如果A是B的原因,那么B是A的结果,但我们绝不会同时说「事件A是事件B的原因,事件A也是事件B的结果」。至于相关性,随机变量X与Y之间的相关性定义为
,所以必然有
。
因果关系的不对称性,曾被用于反驳亨佩尔用DN模型定义「科学解释」的做法,但这是属于科学哲学的题外话了。 以上两条直觉,可以反驳以下一系列不使用「介入」概念的因果定义。
- 充分因:
- 必然因:
- 朴素的反事实因果:
- 加入概率论,用相关性定义因果性。
一个典型的反例:用事件A表示「冰激凌销量增加」,用B表示「溺水死亡者数量增加」。A与B之间成正相关,但我们都知道,A与B之间不存在因果关系,它们都是由一个共同的因素「夏天」导致的。由此可见,仅仅使用概率统计的工具,并不足以让我们在现实中做出理性的因果推断。
- INUS条件:原因是Insufficient but Necessary parts of a condition which is itself Unnecessary but Sufficient。
是INUS条件,但不是原因的例子,并不难构造:闪电、干草堆、消防员玩忽职守、空气干燥都是一场火灾的INUS条件。但是,我们知道闪电和雷声永远符合「如果有闪电,那么必然有雷声」;因此,雷声也是火灾的INUS条件,却不是火灾的原因。
上述一系列模型/定义,都有一个共同的缺陷:给定一个因果关系,这些模型可以完美套用;然而,给定一个此类模型,我们却无法直接确定不同变量之间的因果关系,因为这样的单个模型可以同时描述多种不同的因果、甚至非因果的关系。
哲学家们看似没有对因果关系提出令人满意的诠释。但是,这至多只是一种流行于哲学爱好者之间的误解。普通哲学爱好者们在因果关系方面的了解,通常不会超过休谟与康德,能知道刘易斯、必然论、多元主义之类都极为难得。实际上,在统计、经济等领域,已经有大量成熟且投入使用的因果模型,它们准确反映了我们对因果的直觉认识,而且能被精确的数学语言描述。
事件性因果
当我们说「A是因,B是对应的果」的时候,A和B可以是什么「东西」?
一般而言,我们认为A和B是某种事件,而且A必须发生在B之前。因为「因」必须发生在「果」之前,所以如果A导致了B,那么不可能同时有B导致了A——两个事件无法互为因果。由此可见,因果关系存在一种不对称性。
针对「在时间上,因必须先于果」这一条件,哲学家们有过大量的讨论(Backward Causation),其中不少还涉及尖端的量子力学。不过,我们仍然没有理由放弃这一条件。因为,不同的模型有不同的适用范围,而因果模型的适用范围主要是宏观现象、经济、医疗、复杂动力/电路系统,不论微观物理的结论如何,它在已知领域的有效性都不受影响。
有人或许会质疑,为什么两个东西不能互为因果呢?例如,让A1表示草原上羊的数量,让B1表示草原上狼的数量;其他条件不变,狼的增加会导致羊的减少,羊的减少会导致狼的减少,狼的减少会反而导致羊的增加,羊的增加进而导致狼的增加;A1和B1互为因果。
值得注意,A1与B1表示了某种过程,而不是某些固定时间点上的事件,所以A1与B1之间完整的因果关系无法用事件性因果表示。所以,对于这种质疑,我有以下几条回应:
- 我们可以按照时间顺序,把每个时间点上的A和B拆分为单独的事件,即B1(狼增加)→A1(羊减少)→B2(狼减少)→A2(羊增加)。如此一来,事件性因果也能表达A与B之间的关系。
- 针对过程性的因果,我们有另一种模型——因果环路图(CLD),将在本文第三章介绍。
- 过程性因果比事件性因果复杂。在理解过程性因果模型之前,我们需要先理解更简单的事件性因果模型。
对于事件性因果,当前最成熟、最广泛的模型是结构因果模型(Structural Causal Model,以下简称SCM)。SCM结合了结构方程(SEM)、虚拟事实模型(RCM)、概率图模型(主要是贝叶斯网络),并将其应用于因果分析。各类常用因果模型,都可以看作SCM的子类。接下来,我将以RCM、贝叶斯网络、SEM的顺序,按照SCM的发展思路,对其进行详细的介绍。
2.1. 随机对照试验
任何一本初级统计学课本都会提到,基于观测的统计模型无法可靠地识别因果关系。要确定因果关系,必须通过随机对照试验(Randomized Controlled Trial)。
在一个简单随机对照试验中,试验对象(通常是参加研究的志愿者,下文每一个对象用u表示)会被随机分入两组:实验组(treatment group,下文用t表示)和对照组(control group,下文用c表示)。
我们有多种不同的随机分组方式,例如简单随机分组、随机区组设计、配对设计。使用随机区组设计时,研究者会先根据个体的特征(年龄、性别等)将其分入不同的区组,再在每个区组内实施简单随机分组。使用配对设计时,研究者会把在各方面都非常相似的个体(例如双胞胎、不同时间节点的同一个人)配成对,在每一对个体中随机选一个作为实验组,另一个作为对照组。
实验组的对象会接受干预,但对照组的对象不会受到任何干预/介入。在医学实验中,实验组的对象会接受真正的治疗,而对照组的对象只会收到安慰剂。实验结束后,研究者会比较实验组和对照组的结果。
如果我们用Y表示我们感兴趣的结果变量,那么我们可以用以下符号表示随机对照试验的结果:
是在对照组条件下,对象u展现出的结果变量Y。
是在实验组条件下,对象u展现出的结果变量Y。
在研究中,我们通常会探究 是否统计显著地不同于
。这一过程涉及较为具体的统计假设检验,与本文的主要内容无关。但是,我们至少可以意识到,t与c的区别是因果关系中的「因」,
与
的区别是因果关系中的「果」。
2.2. 介入主义的因果观
在随机对照实验的基础框架上,我们可以建立起一个介入主义(interventionism)因果观。
一个介入主义的因果模型包括三部分:
- 所有的系统
:一个包含所有系统
的集合。一个系统
我们讨论的对象,可以是人体、机械、星球、化学反应系统、经济实体等。
- 所有的介入方式
:一个包含所有可能的介入方式
的集合。例如,假设我们讨论的系统
是一个有两个按钮的黑箱,一个按钮是红色的,另一个按钮是绿色的,那么所有可能的介入方式为 {按红按钮,按绿按钮,两个按钮都按,两个按钮都不按} 。(在这个具体的例子里,根据黑箱的结构不同,可能的介入方式或许不止四种,所以这只是一个经过简化,以便直观理解的模型。)
- 状态函数
:输入一个系统
和一种介入方式
,输出系统的某个状态
,写作
。例如,在一个医疗实验中,
可以反映「u(病人甲)在受到干预t(服用降压药)之后的y(血压)」。注意,y不一定要完整描述u的状态的所有部分,只反映几个变量也是可以的。我们当然可以让y表示某个病人全身所有分子的运动状态,但这类过于复杂的状态函数,往往没有太大的实用价值。可是,在简单电路这样的系统中,完整表达电路每个节点的状态不仅可行,而且有利。因此,在建立因果模型时,我们需要具体问题具体分析,选择一个合适的状态函数。
值得注意的是,因为「果」的定义涉及到 与
的区别,而单次介入只说明了t却没有说明c,所以
必须包含一种表示「不介入」的介入方式
。也就是说,在一个因果模型中,任何一个系统都必须有一种不受干预的「自然状态」。如果现实情况过于复杂,很难找到不受干预的自然状态,我们可以把某种介入方式
默认为「不介入」。
因此:
- 任意一个介入主义的因果模型,都必须明确指出一种代表「不介入」的介入方式。
- 当我们在问「为什么发生了现象
」的时候,我们其实在问:「在我对世界建立的因果模型中,自然状态的现象是
,但是我观察到了现象
。于是,我认为实际发生的情况是
,其中
。
与
之间的区别是什么?」
- 或者,更简单地说,当我们问「为什么A」的时候,我们往往省略了后半句:「为什么A,而不是B?
以知乎搜索「为什么」前几个结果为例,我们可以发现,「默认状态」的思维方式的确无处不在。
默认状态:男生应当追女生。
默认状态:一般人不会花两百多块买一杯咖啡。
另一些情形中,两个对话者可能选择了不同的默认状态,便带来了以下的对话:
- 甲:「你为什么做了A这件事?」(默认「不做A」是自然状态,要求乙为「做A」提供理由)
- 乙:「为什么不呢?」(默认「做A」是自然状态,把论证的责任转移到甲身上) 在下一部分(2.3),我们将把这一系列直觉发展为正式的虚拟事实模型。
不过,我希望先对格兰杰因果(Granger causality)做出一些澄清。格兰杰因果的定义:如果得知事件A的发生有助于预测之后的事件B,那么我们说A是B的格兰杰因。然而,格兰杰因果只包含了观测,却没有包含介入,直接操纵A并不一定能影响B,这与我们日常对因果的直觉不符。所以,格兰杰因果虽然名叫「因果」,却只是一个统计相关性的概念,而非真正的因果概念。在下文中,我不会对格兰杰因果做更多讨论。
2.3. 虚拟事实模型
虚拟事实模型(Rubin Causal Model,简称RCM)由Donald Rubin提出。在RCM中,因果关系「果」的定义是 。
在实际生活中,我们考虑的系统往往不止一个——对于某个正在研发的药品,我们最感兴趣的无疑是它在所有目标人群上的效果,而不仅仅是某个病人甲。继续采用RCM对于因果的定义,那么一个介入「因」对群体内所有个体的「果」是 。(由期望值的线性可得)
在上帝视角下,上述定义并不复杂。即使变量 不是一个数值变量,我们也可以通过其他方式定义
。从更广泛的角度考虑,RCM定义中的减法未必是实数域的减法;针对更复杂的变量y(例如张量、概率分布),我们可以采用其他的减法,只要符合数学规范和具体研究需要即可。
可是在实际生活中,我们无法获得完美的信息:
- 无法同时知晓
与
。由于每个人都是独一无二的,每个时间节点也是独一无二的,所以在受到了一种介入,并表现出新状态之后,这个系统不可能完美恢复到原来的状态,重新接受另一种介入。这种情况被称为「因果推断的根本问题」(the Fundamental Problem of Causal Inference,以下简称FPCI)。
- 无法同时知晓每个个体的情况。正如在检测手机在极端条件下的质量时,我们不可能去砸坏每一个手机一样,我们只能随机从群体中抽取样本,再利用样本的统计数据推断群体参数。
「无法同时知晓每个个体」的问题,已经有常规的统计学手段解决。但为了避免FPCI,我们必须对群体参数的分布做出额外的假设,包括但不限于以下的一种或多种:
- 个体处理效应稳定假设(Stable unit treatment value assumption,简称SUTVA):对于任意个体
的干预不会影响到另一个任意个体
的状态。SUTVA使我们可以把样本中每个个体的反应看作独立事件,从而降低了我们需要的样本体积、模型体积和建模时间。
- 同效果假设(assumption of constant effect):对于所有的个体,某种介入方式造成的效果是相同的。例如,某个降压药对所有人的效果都是降低血压,不会产生增高血压的情况——即使有,也只不过是统计的噪声,可以用大样本、大数定理和中心极限定理消解。于是,我们可以得到
,用样本内的平均效果估算这一介入方法对所有个体的因果效果。
- 同质性假设(assumption of homogeneity):对于任意个体
和
,以及任意介入方式
,始终有
。同质性假设强于同效果假设。例如,一个简单的FizzBuzz电脑程序在不同时间点上的性质理应完全相同。虽然在同一时间点上,我们无法同时测试它在不同输入下的输出,但是它在不同时间点上的表现必然相同。如果我们把「不同时间点上的FizzBuzz程序」看作一个群体,那么其中个体「每个时间点上的FizzBuzz程序」均符合同质性假设。
2.3.1. 虚拟事实模型的不足
虽然RCM提供了一个可以用数学、统计定义的因果模型,但是它的缺点也很明显:在介入时,我们通常一次只能改变一个变量,观测的状态也只有一个变量。如果我们增加变量,模型的体积、需要的训练数据、训练时间都将以指数级增长。在下一部分,我们可以看到,贝叶斯网络先验的条件独立信息可以缓解这一困难。
此外,RCM从自变量的「因」到应变量的「果」的结构几乎完全是个黑箱,缺乏更清晰的可解释性。因此,单个RCM所能解决的问题也较为有限。相比之下,结构因果模型能为因果律、多变量之间的因果关系提供更详细的解释。
2.4. 贝叶斯网络
贝叶斯网络是一种基于有向无环图(directed acyclic graph,简称DAG)的概率图模型。虽然贝叶斯网络并不能直接表示因果,只能表示相关,但是它的图结构是SCM的基础。
贝叶斯网络示例
在一个贝叶斯网络中,每个节点是一个随机变量,代表一个事件。通常,这个随机变量服从某个离散或连续的分布。一个节点 中,储存了给定它的所有父节点
时
的分布,即
。
表示节点X的所有父节点,即所有「拥有直接指向X的有向边」的节点。以上图为例,
。
贝叶斯网络(以及其他所有的概率图模型)相比于原始的联合分布模型,最大的优势在于增加了变量之间条件独立的先验信息,从而减小了模型的体积,与模型进行推断、学习的时间。例如,上图共有5个变量,如果用朴素的联合分布模型建模,条件概率表格的体积将会是 ,而采用贝叶斯网络后,条件概率表格的总体积为
。在小型的网络中,这种简化的效果尚不明显,但在大型网络中,假设每个变量有a种取值,那么联合分布模型的体积将为
,而一个合适的贝叶斯网络或许能把体积复杂度降低到多项式级别。最极端的情况是朴素贝叶斯,即所有的随机变量均独立,此时模型的体积复杂度为
。
条件独立的信息是先验的,它们往往由任务相关的专家提供,而非从数据中学习得到。这种做法能保证网络结构的可靠。(此处讨论的是parameter learning而非structure learning,网络结构已知而参数未知;对于后者,我们有Chow-Liu算法,但此处不讨论。)之后,我们也会发现,类似的先验因果假设在SCM中有重要地位。
2.4.1. d分隔
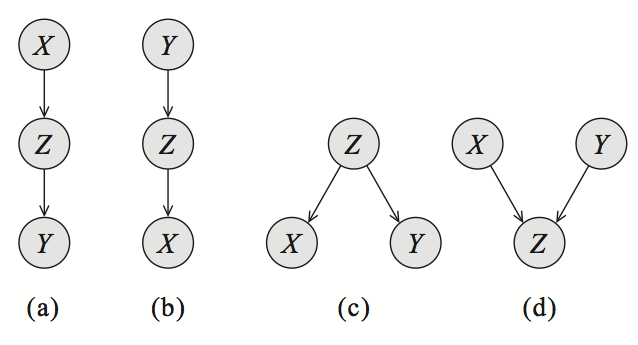
如图所示,对于一个贝叶斯网络中的三个节点/变量而言,一共有三种基本的结构。两种不同的条件独立假设。用 表示X与Y之间独立:
- cascade:
,则必有
以及
。
- common parent:
,同样有
以及
。
- V-structure:
,必有
与
,与前两种基本结构的条件独立情况不同。
为了回答「给定一个随机变量的集合Z,随机变量A与B之间是否条件独立」这个问题,我们需要引入d分隔的概念。d分隔(d-separation)的全名是「有向分隔」(directed separation)。
某个节点集合O能d分隔节点A与节点B,当且仅当:给定O时,A与B之间不存在有效路径(active path)。
对于A与B之间的无向无环路径P,如果P上的每三个连续节点,都符合以下四种情况中的一种,那么P就是一条有效路径:
- X←Y←Z且Y∉O
- X→Y→Z且Y∉O
- X←Y→Z且Y∉O
- X→Y←Z且Y∈O。这种情况被称为伯克森悖论(Berkson’s Paradox):当两个独立事件的共同结果被观察到时,这两个独立事件就不再相互独立了。例如,扔两个硬币,硬币A朝上的面和硬币B朝上的面之间,应该是相互独立的;然而,如果我们已知「有一个硬币正面朝上」,那么A与B朝上的面之间就不再相互独立了。
相应地,如果给定O之后,一条路径P不是一条有效路径,那么我们称O节点集合 d分隔 了路径P。d分隔的概念适用于两个节点,也适用于两个节点之间的路径,后者在「后门准则」的定义中非常有用。
如果两个变量没有被d分隔,那么它们之间的状态被称为d联结(d-connection)。
d分隔能极大简化贝叶斯网络中 等条件独立情况的判定。Pearl将其进一步泛化,提出了拟图(graphoid)的概念。一个graphoid是一组形如「已知变量Z,则变量X与变量Y相互独立」的陈述,服从以下五条拟图公理:
关于graphoid中文翻译的备注:graphoid尚无权威的中文翻译,而且在互联网上几乎没有任何相关的中文材料。我在选择译名时,参考了matroid的翻译。既然matrix是矩阵,而matroid是拟阵,那么graph是图,所以graphoid应该被称为拟图。
拟图的概念只出现在Pearl的著作中。不过,如果我们采用概率论对于「独立事件」的定义,那么我们可以把它们当做定理推导得出,可见概率论的「独立」符合拟图公理体系。当然,intersection的成立需要一个额外条件:针对所有的事件A,如果 ,那么
。
2.4.2. 为什么贝叶斯网络不适合做因果模型?
有了一个学习完毕的贝叶斯网络后,我们可以用它进行各类推断,主要是概率推断 :已知
等随机变量的值,求另一随机变量
的条件概率。贝叶斯网络的优越性体现于,即使有大量的缺失、未知变量值,它也能利用边缘化操作,毫无障碍地进行概率推断。在SCM中,这一功能仍然有相当重要的地位。
如果我们把箭头看作从因指向果,把A→B看作A导致了B,那么贝叶斯网络看起来似乎能表达因果关系。然而,贝叶斯网络本身无法区分出因果的方向。例如,A←B←C与A→B→C的因果方向完全相反,但在贝叶斯网络的模型描述下,它们表达的概率分布和条件独立假设完全相同。
此外,概率论「给定/已知随机变量Z」里的「给定/已知」只能用于表达观察,而非介入。例如,P(下雨|地面是湿的)与P(地面是湿的|下雨)的概率值都很高,其中「给定“地面是湿的”」与「给定“下雨”」都是观察而非介入的结果。用do(X)表示「介入,使得事件X发生」,现在考虑另一种情况:P(下雨|do(地面是湿的))。根据直觉,显然P(下雨|do(地面是湿的)) < P(下雨|地面是湿的),因为把地面弄湿并不能导致下雨。
综上所述,贝叶斯网络虽然十分强大,但无法准确描述因果关系。下文的SEM将主要解决这个问题。在学习贝叶斯网络的过程中,我们也应该尽量避免使用「因果」相关的词语——贝叶斯网络中,A→B未必等同于A导致B。
2.5. 结构方程+结构因果模型
为了表示因果关系,我们需要对贝叶斯网络进行改进。结构方程模型(Structural Equation Model,简称SEM)在经济与工程领域十分常用。在贝叶斯网络的基础上加入SEM的成分之后,我们就离完善的SCM(结构因果模型)更近了一步。
2.5.1. 打破对称性
在贝叶斯网络中,节点 的概率分布
由它的父节点
决定,记录在一个条件概率表格中。然而,条件概率表格和一些简单的连续概率分布都是可逆的。例如,对于随机变量
和
,如果
,那么我们可以操纵代数表达式,得到
。然而,这种对称性在因果关系里是不符合直觉的。对称的代数表达式表明,如果我们改变Y,X就会发生相应的改变;可是,修改温度计的读数并不会改变环境温度,调整闹钟的时针并不会改变真正时间的流动。
因此,在SEM中,我们用函数式的方程表示某个变量 :
。其中,
表示X的父节点中的内生变量(endogenous variable);
表示X的父节点中的外生变量(exogenous variable),只有一个。内生变量依赖于其他变量,在SCM中表示为「存在父节点的节点」,即至少有一条边指向该节点;外生变量独立于其他变量,在SCM中表示为「不存在父节点的节点」,即没有边指向该节点。
传统的路径分析研究中, 通常是一个线性函数,因果律的定义也局限与
中的
。但是,在数据越发复杂的现在,我们完全可以采用非线性函数、非参数模型。相对地,「因果」的定义也从路径参数
变成了更广义的「变化传递」,参见前文RCM的部分。作为一个广泛的模型框架,SCM可以产生各式各样的复杂模型。
在最广泛的条件下,函数 是不可逆的。我们需要把
理解为「(大自然/模型本身)对X的赋值」,而不仅仅是一个普通的代数等式。SCM要求所有的箭头
必须表示「A直接导致B」。所以,在因果推断的过程中,我们必须按照因果箭头的方向进行推理,不能颠倒顺序。
图1:结构因果模型示意图
如上图所示, 与
是外生变量, X与Y是内生变量,X可以导致Y。在图(a)中,
与
之间没有边相连,而在图(b)中,
与
之间有一条用虚线表示的双向箭头。在SCM里,我们用单向箭头表达直接的因果关系,用双向箭头表明两个外生变量之间可能存在未知的混杂因素(confounding variable)。
与
等外生变量可以表示「模型没有考虑到的环境噪音」,从而为看似非随机的结构方程模型加入随机的成分。因此,SEM并非完全确定,它也可以拥有概率、不确定性等特征;SCM比普通的贝叶斯网络更广泛。此外,一个SCM描述了数据的生成原理,而不仅是表面观测到的概率分布,所以SCM比贝叶斯网络更稳定。
2.5.2. 介入
如上文所言,SCM是对于贝叶斯网络的一种泛化。一般的贝叶斯网络可以解答两类问题:
- 条件概率:
,其中Y是我们感兴趣的一组未知变量,E是一组我们观察到的已知变量,e是我们观察到的E的值。E可以是空集,代表「我们没有观察到任何变量」。
- 最大后验概率(MAP):
,我们想要找到的是一组最有可能的Y值。
如果不考虑算法复杂度,一个能估计条件概率的模型必然能估计MAP,所以下文将只讨论条件概率的情况。
在「观察」的基础上,SCM还能做到「介入」: 。其中,我们对系统进行介入,迫使一组变量X拥有值x。在X是一个空集的情况下,SCM与普通的贝叶斯网络差别不大。
以下图为例,我将展示SCM实现介入的方法。
图2:一个SCM
在这个SCM中,变量X、Y、Z之间的关系可以用以下的结构方程表示:
在此模型中,我们假设 与
与
这三个外生变量独立。所以,图(a)与图(b)中的
与
与
之间均没有边相连。
如图(b)所示,当我们进行介入 时,我们切断了所有指向X的边,并将X赋值为
。于是,新的SCM包括了一套新的结构方程:
综上所述,一个SCM(写作 )估计
的方式为:完成对原有模型
的介入
之后,得到一个新的模型
。随后,在
上估计
。
有人可能会产生疑问:「观察和介入,有什么本质区别吗?」
一个日常例子式的回答如下:
- 用A代表「环境温度」,用B代表「温度计读数」,A与B之间的因果关系为
。在默认状态下,温度计不会受到外在干预。因此,观察到温度计读数升高,我们可以推断出环境温度升高。但是,当我们直接干预温度计时(例如用手握住温度计),我们进行了介入
,使温度计的读数变成了
;同时,因为是介入而非观察,从A到B的因果箭头被切断了,我们有
或
。
- 假设
是一个较高的温度,那么
代表「在自然状态下,观察到温度计的读数是
时,实际的环境温度为
的概率」;
代表「在外在干预使温度计读数成为
时,实际的环境温度为
的概率」。显然,
,可见观察与介入是两种完全不同的行为。观察不会影响模型的自然状态,但介入会。
2.5.3. 因果推断的数学原理
在这一部分,我将介绍SCM进行因果推断的数学基础。
我们说一个SCM具有马尔可夫性质,当且仅当这个SCM不包含任何的有向环,且所有外生变量均相互独立。因为外生变量通常被理解为某种「误差项」或「噪音项」,所以如果某些外生变量之间存在相关性,那么它们之间可能存在混淆变量。在一个马尔可夫式SCM中,我们可以得到以下的基本定理:
因果马尔可夫条件:
其中, 代表我们感兴趣的变量,
代表它的父节点中的所有内生变量。利用因果马尔可夫条件,我们可以把一个联合概率分布分解为多个条件概率分布的积。
一个符合因果马尔可夫条件的SCM经过介入之后,仍然符合因果马尔可夫条件,条件概率计算如下:
其中,X是一系列受到干预的变量,x是X中变量受干预之后的数值。 表示,
里同时也在X里(即在
中)的变量将被赋值为
的对应值。
以图2为例,在干预之前, ,而在干预
之后,
。注意,由于从Z到X的因果箭头已经被切断,
,因为直接改变X无法影响Z。
在《Causality》中,Pearl证明了一个更广泛的结论:
其中,每一个t都代表X所有父节点的一种可能取值。由于所有直接指向X的箭头已经被切断,所以自然有 。
2.5.4. 后门准则(back-door criterion)
考虑如下图3所示的SCM:
在SCM中,如果一条无向连接X与Y的路径有一条指向X的箭头,那么我们把这条路径称为从X到Y的后门路径。按照正常的因果链,「X导致Y」的结构应该是 ;然而,如果X与Y之间后门路径存在,那么实际结果中很可能出现虚假的统计相关性。
因此,当一个变量集合S符合以下两个条件时,我们称S符合后门准则:
- S中不包括X的后代。
- S能d分隔所有从X到Y的后门路径。
例如,在图3里, 等集合都满足后门准则,但
不满足后门准则。
后门准则的重要性在于,它进一步泛化了2.5.3.结尾的公式。如果S满足从X到Y的后门准则,那么,我们可以推导得到:
这极大简化了SCM推导时的运算。
2.6. SCM的反事实推理
反事实推理(counterfactual inference)的核心在于:虽然现实情况下 ,但是假如
的话,Y会怎么样呢?
有些人后悔,「如果我当年……,那么我现在就能……。」这一思维方式就是反事实推理。
反事实推理与FPCI(因果推断的根本问题)息息相关。对于一个已经接受了实验组介入的样本u,我们只能观察到u的 ,却永远无法观察到
,反之亦然。RCM(虚拟事实模型)对反事实推理有一定的描述,但RCM整体不如SCM清晰、明确、易解释。
下面,我将用SCM重新表达2.2部分中提到的介入主义因果观。
- RCM考虑的对象是一个种群
内的所有个体
。在很多情形下,同质性假设不成立,每个个体都不尽相同。在SCM中,个体的差异会被误差项
表示(外生变量
会相对应地影响内生变量
)。除了
之外,模型
本身所代表的「自然法则」保持不变。
- RCM的表达式
可以表示为
。即:我们对模型M进行干预,使得变量T赋值为t;同时,我们观察到所有外生变量U的值为u;在此情况下,我们向模型M查询我们感兴趣变量Y的条件概率。
- RCM要求模型拥有一个「不受介入」的默认状态。显然,SCM符合要求:
因此,SCM可以回答类似「假如 而非现实中的
,Y的值是什么?」的反事实问题。但是,在现实生活中,由于个体信息
通常未知,而复杂的非线性结构方程可能会随着U的分布变化而变化,所以反事实推理普遍比较困难。
总而言之,所有RCM均可以用SCM表达,而且SCM的白箱比RCM的黑箱更清晰、更稳定。
过程性因果
在第二章,我们使用的SCM(结构因果模型)建立在三条基本直觉上:
- 因和果都是单独时间点上的单独事件
- 因在前,果在后
- (由1和2可得)两个事件无法互为因果
不过,在其他一些情境中,例如掠食者的数量与猎物的数量,两个变量似乎「互为因果」。SCM与贝叶斯网络不允许环路的存在,故无法表示此类直觉上的因果关系。所以,我们需要一个更复杂的因果模型——因果环路图(Causal Loop Diagram,简称CLD)。
CLD中的变量基于以下的直觉:
- 因和果是某种过程,有一段持续的时间
- 因和果的持续时间段可以相互重叠
- 两个过程可以互为因果,甚至一个过程自身也可以形成因果环路
因果环路图:银行存款与利息
和SCM相比,CLD尚未有那么严谨、广泛的理论框架。我们可以把CLD理解为一个「从时间标量(实数)到一个SCM集」的函数映射。为了方便建模,所有的变量都是数值变量,而且多个过程变量之间的相互影响往往都是线性的,形如 。如果
,那么我们说从X到Y的链接是正链接;如果
,那么我们说从X到Y的链接是负链接。
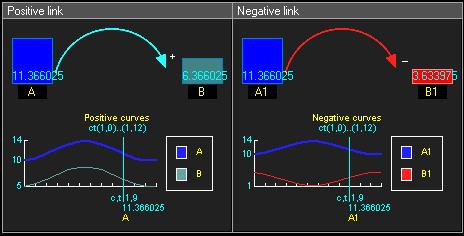
正链接(左)与负链接(右)
对于因果环路 :
- 如果A起初的一点增加(或减少)会通过因果环路,导致A进一步增加(或减少),那么我们称之为强化反馈回路。
- 如果A起初的一点增加(或减少)会通过因果环路,反而导致A减少(或增加),从而中和最初的增加(减少),那么我们称之为平衡反馈回路。
假设A>0且B>0,那么:
-
如果
与
的链接正负相同,那么我们通常可以得到一个强化反馈回路。
-
如果
与
的链接正负相反,那么我们通常可以得到一个平衡反馈回路。
更一般地,在一个因果环路图中:
- 如果有偶数个负链接,那么它是一个强化反馈回路。
- 如果有奇数个负链接,那么它是一个平衡反馈回路。
反馈回路的实际意义通常如下:
- 强化反馈回路通常意味着指数增加、指数衰减,例如「利滚利」的银行存款与利息、不受限制的人口增长。
- 平衡反馈回路通常意味着达到某个平衡状态,例如洛特卡-沃尔泰拉方程的解。
在未来,一个可能的研究方向是把SCM中较为成熟、广泛的因果推断框架推广到CLD上。研究的重点在于引入非线性、非参数的复杂因果链接。此类研究必然十分困难,但随着电脑计算能力的增强,我们将逐渐有能力构建更复杂的CLD。
四因论
在批判了柏拉图的“理型论”基础上,亚里士多德建立了自己的哲学思想体系,其核心就是“四因说”。“四因说”是亚里士多德对他之前古希腊哲学思想中对“本原”、“本体”问题的研究作了一个总结。“四因”分别指: 质料因、形式因、动力因、目的因。
亚里士多德的“四因说”,是为了说明事物运动的原因。
质料因:事物由不变的质料构成,以此解释事物为什么在运动中继续存在。形式因:不同的事物各有特定的形式,用来表述本质的定义,以此解释为什么事物会以某种特定的形式运动。动力因:事物受到推动者和作用者的推动和作用,因此事物会开始或停止运动。目的因:事物的运动是有朝向有目的的,所以可以解释事物为什么要运动。
亚里士多德强调,形式因、动力因和目的因通常是一致的,因为:
- 一、形式因是事物的本质,而一个事物在运动中朝向的目的就是它所缺乏的形式,所应该有的本质;
- 二,一个事物只能接受与它本质相同的东西的作用,比如人生人、元素推动元素” 因此,形式因、目的因和动力因都属于心事,或者说,统一于“形式”这一概念。
亚里士多德强调三者的一致性是为了把“四因”最终归结为质料与形式的区分。另一方面,运动的三本原也可以归结为质料与形式(缺乏也是一种形式)的区分,潜在与现实也分别表现为质料与形式。这样,运动的本原、原因和本质就都可以用质料与形式的关系加以说明了。三本原说、四因说和潜在与现实关系说都从不同角度和方面,对运动中事物的质料与形式关系进行分析,它们是将分析方法运用于运动现象所得到的产物。
详见知乎帖子
应用
因果推理的应用可以分为三个方向
- 决策评估 —— 这与Treatment效果评估的目标是一致的。
- 反事实估计 —— 反事实学习极大地帮助了与决策相关的领域,因为它可以提供不同决策选择(或策略)的潜在结果。
- 处理选择偏差 —— 在许多实际应用程序中,出现在收集的数据集中的记录并不代表感兴趣的整个群体。如果不恰当地处理选择偏差,将影响训练模型的泛化。
下面是这三个方向适用的应用场景:
广告
决策评估
正确衡量广告活动的效果是品牌方成功营销的关键,如新广告是否增加点击量,或新广告是否增加销售额等。
衡量方法
- 随机试验 —— 成本高且耗时,不应采纳
- 从观察数据中估计广告效果
- 随机最近邻匹配法 —— 估计数字营销活动的治疗效果
- 协变量平衡广义倾向得分(CBGPS)—— 用于分析政治广告的有效性
处理选择偏差
由于广告系统中现有的选择机制,显示和未显示的事件之间存在分布差异。忽视这种偏差会使广告点击预测不准确,从而造成收入损失。
电子邮件营销
决策评估
目的:瞄准潜在客户,增加收入。
使用决策评估帮助在不同的促销电子邮件设计中进行选择。
推荐系统
决策评估
在推荐系统中给用户推送商品的过程,相当于给原子研究对象施加干预,通过用户的点击、消费等行为评估干预(推荐)的效果。
系统的推荐建议与评估的干预效果高度相关。
处理选择偏差
推荐系统中使用的数据集通常由于用户的自我选择而产生偏差。
例如,在电影收视率数据集中,用户倾向于对自己喜欢的电影进行评分:恐怖电影的收视率大多由恐怖电影迷制作,而浪漫电影的影迷则较少。
对于广告推荐,推荐系统只会将广告推荐给系统认为对这些广告感兴趣的用户。
在上面的例子中,数据集中的记录并不代表整个群体,这就是选择偏差。这种选择偏差给推荐模型的训练和评价带来了挑战。基于倾向得分的样本再加权是解决选择偏差问题的有效方法。
药物治疗
反事实估计
当可以估计不同的可用药物的疗效时,医生可以据此开出更好的处方。
教育
反事实估计
通过比较不同教学方法对学生群体的影响,可以确定一种更好的教学方法。
因果工具
- 因果模型
- 当只有蓝色分布中的采样数据时,怎么凭空造出绿色分布中的数据。这时就要用到do-calculus。它允许慢慢探索绿色条件分布,直到可以根据蓝色分布下的各种边际分布、条件分布和期望来表
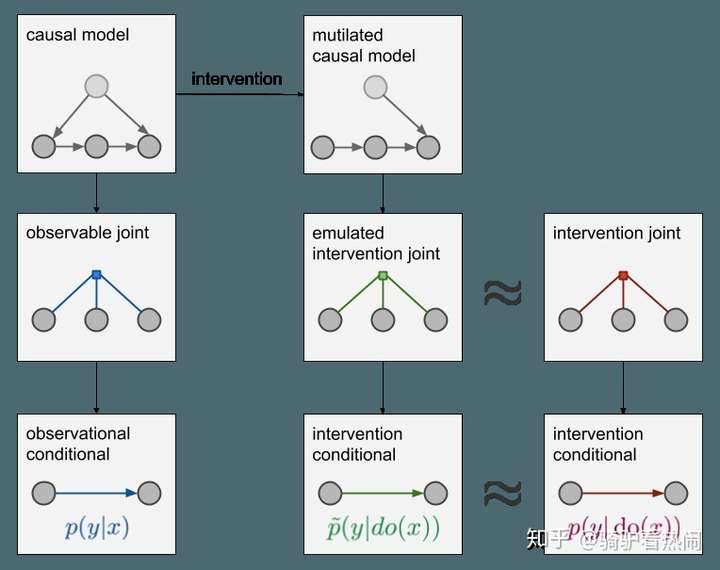
- Do-calculus(do算子)
- 最终如果能获得一个p̃(y|do(x))的等价公式,(不再有任何do操作符),则因果查询p̃(y|do(x))是可识别,否则不能识别

数据集、开源代码及研究框架。
【2021-7-26】因果科学算法、框架、数据集汇总, 因果科学的工作大致分为
- 基础因果假设及框架(fundamental causal assumption and framework)
- 因果学习(causal learning)
- 因果结构学习(causal discovery/causal structure learning)
- 因果表示学习(causal representation learning)
- 因果推断(causal reasoning/inference)
- 应用系统
概率编程框架
| 类型 | 框架名称 | 所属团队 | 特性 |
|---|---|---|---|
| 概率编程框架 | pyro | Uber | 基于pytorch |
| 概率编程框架 | pymc3 | ThePyMC DeveIopment Team | 基于theano |
| 概率编程框架 | pgmPY | AnkurAnkan | 概率图 |
| 概率编程框架 | pomegranate | JacobSchreiber | 面向图模型和概率模型,基于cpython |
数据集
由于反事实的结果永远无法被观察到,因此很难找到一个完全满足实验要求的数据集,即具有基本真实数据集 (ITE) 的观测数据集。
现在很多研究中使用到的数据集基本上都是半人工合成的数据集,合成的规则不尽相同,如IHDP数据集,是从随机数据集中按照一定的生成过程生成其观测结果,并去除一个有偏子集来模拟观测数据集中的选择偏差。一些数据集,如Jobs数据集,将随机数据集和观察控制数据集结合起来,产生选择偏差。
数据集
| 类型 | 工具包名称 | 维护团队 | 特性 |
|---|---|---|---|
| 因果推断数据集 | MIMIC II/III Data,1.4 | PhysioNet | ICU数据 |
| 因果推断数据集 | Advertisement Data | 谷歌 | 广告 |
| 因果推断数据集 | Geo experiment data | 谷歌 | 地理数据 |
| 因果推断数据集 | Economic data for Spanish regions | - | 没有Groundtruth |
| 因果推断数据集 | Californa’s Tobacco Control Program | - | - |
| 因果推断数据集 | Air Quality Data | - | - |
| 因果推断数据集 | Monetary POlicy Data | - | - |
| 因果发现数据集 | 见表下方介绍, 真实数据集,合成数据集等 | - | - |
| 因果推断基准 | JustCause | Maximilian Franz, Florian Wilhelm | 支持IHDP,IBM ACIC等数据集和STOA算法 |
| 因果发现基准 | Causeme | 巴伦西亚大学图像和信号处理组,德国宇航中心JAKOBRUNGE | 多为时间序列 |
目前可用基准数据集
- IHDP
- Jobs
- Twins
- ACIC dataset
- 2016
- 2018
- 2019
- IBM causal inference benchmark
- BlogCatalog
- Flickr
- News
- MVICU
- TCGA
- Saccharomyces cerevisiae (yeast) cell cycle gene expression dataset
- THE
- FERTIL2
工具包
-
- Uber开源Causal ML,支持树形的一些算法,地址
- causalml - Meta-Learner Example Notebook
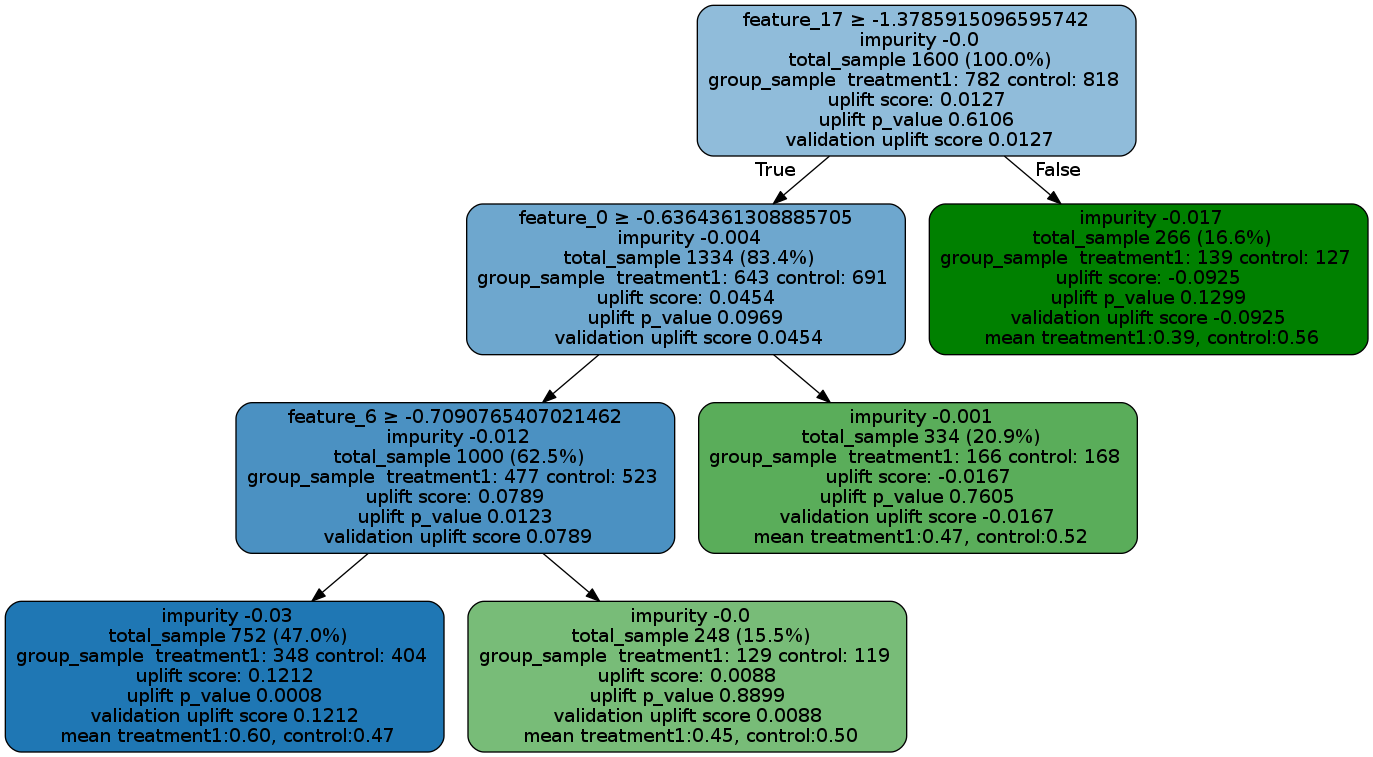
- 【2021-1-5】awesome-causality-algorithms
| 类型 | 工具包名称 | 维护团队 | 特性 |
|---|---|---|---|
| 因果结构学习 | TETRAD | 卡内基梅隆因果发现中心(CCD) | 生物医学 |
| 因果结构学习 | CausalDiscoveryToolbox | FenTechSolutions | DAG/Pair生成器、数据集接囗、独立性分析、因果结构学习、评价指标 |
| 因果结构学习 | gCastle | 华为诺亚 | 数据生成和处理、因果结构学习、评价指标 |
| 因果结构学习 | tigramite | JakobRunge | 从时间序列学习 |
| 因果推断 | Ananke | TheAnankeTeam | 集成了ID算法进行do演算 |
| 因果推断 | EconML | 微软 | 计量经济学 |
| 因果推断 | dOWhy | 微软 | 支持中介分析 |
| 因果推断 | causalml | Uber | 营销增益 |
| 因果推断 | WhyNot | JohnMiller | 提供了模拟器和环境 |
| 因果推断 | Causallmpact | 谷歌 | 时间序列因果效应估计,如广告宣传,对点击量的提升,R语言 |
| 因果推断 | Causal-Curve | Kobrosly,R、W. | 估计连续型干预变量,如价格、时间、收入 |
| 因果推断 | grf | 斯坦福grf-lab | R语言 |
| 因果推断 | dosearch | SanttuTikka | R语言 |
| 端到端 | causalnex | QuantumBlack | 集成因果结构学习、领域专家调整、因果推断,但版本是0.10.0 |
DoWhy(微软)
「因果推断」(causal inference)是基于观察数据进行反事实估计,分析干预与结果之间的因果关系的一门科学。虽然在因果推断领域已经有许多的框架与方法,但大部分方法缺乏稳定的实现。
DoWhy工具 An end-to-end library for causal inference
- 开始使用dowhy
- 微软的DoWhy是一个基于python的因果推理和分析库,它试图简化在机器学习应用程序中采用因果推理的过程。受到朱迪亚·珀尔的因果推理演算的启发,DoWhy在一个简单的编程模型下结合了几种因果推理方法,消除了传统方法的许多复杂性。
DoWhy 是微软发布的一个用于进行端到端因果推断的 Python 库,其特点在于:
- 提供了一种原则性的方法将给定的问题转化为一张因果图,保证所有假设的明确性
- 提供了一种面向多种常用因果推断方法的统一接口,并结合了两种主要的因果推断框架
- 自动化测试假设的正确性及估计的鲁棒性 如上所述,DoWhy 基于因果推断的两大框架构建:「图模型」与「潜在结果模型」。
- 具体来说,其使用 基于图的准则 与 do-积分 来对假设进行建模并识别出非参数化的因果效应;
- 而在估计阶段则主要基于潜在结果框架中的方法进行估计。
DoWhy 的整个因果推断过程可以划分为四大步骤:
- 「建模」(model):利用假设(先验知识)对因果推断问题建模
- 「识别」(identify):在假设(模型)下识别因果效应的表达式(因果估计量)
- 「估计」(estimate):使用统计方法对表达式进行估计
- 「反驳」(refute):使用各种鲁棒性检查来验证估计的正确性
DoWhy将工作流中的任何因果推理问题建模为四个基本步骤: 建模、识别、估计和反驳。
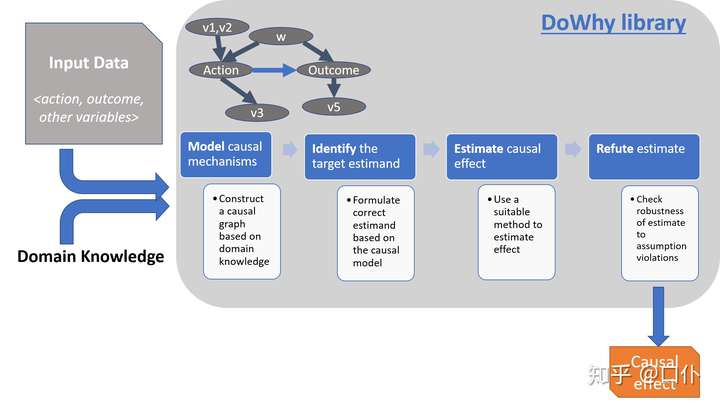
- (1) 建模: 从数据和给定的图创建一个因果模型。
- DoWhy使用因果关系图对每个问题建模。有助于使每个因果假设明确。该图不必是完整的,可以提供一个局部图,以表示有关某些变量的先验知识。 DoWhy会自动将其余变量视为潜在的混杂因素。
- DoWhy的当前版本支持两种图形输入格式:
gml(首选)和dot。图中可能包含了变量之间因果关系的先验知识,但DoWhy不做任何直接的假设。 - DoWhy 支持如下形式的因果假设:
- 「图」(Graph):提供 gml 或 dot 形式的因果图,具体可以是文件或字符串格式
- 「命名变量集合」(Named variable sets):直接提供变量的类型,包括
- 「混杂因子」(common causes / cofounders)
- 「工具变量」(instrumental variables)
- 「结果修改变量」(effect modifiers)
- 「前门变量」(front-door variables)等
- 函数:model =
CausalModel(data=data[“df”], treatment=data[“treatment_name”], outcome=data[“outcome_name”], graph=data[“gml_graph”])
- (2) 识别: 识别因果效应并返回目标的估计量(estimands)
- 基于因果图,DoWhy根据图形模型找到所有可能的方法来标识期望的因果关系。它使用基于 图的准则(graph-based criteria)和 do-演算(do-calculus)来找到可能的方式来找到可以识别因果关系的表达式。
- 支持的识别准则有:
- 「后门准则」(Back-door criterion)
- 「前门准则」(Front-door criterion)
- 「工具变量」(Instrumental Variables)
- 「中介-直接或间接结果识别」(Mediation-Direct and indirect effect identification)
- 函数:identified_estimand = model.
identify_effect()
- (3) 估计: 基于可识别的目标量,使用统计方法估计目标量(这里是计算因果效应)
- DoWhy使用匹配或工具变量等统计方法估计因果效应。DoWhy的当前版本支持基于倾向性分层或倾向性评分匹配的估计方法,这些方法侧重于估计处理任务,以及侧重于估计响应面的回归技术。
- DoWhy支持基于后门准则(back-door criterion)和工具变量( instrumental variables)的方法。它还提供了一个非参数置换检验(non-parametric permutation test)来检验估计到的估计量的统计显著性。
- 目前,其支持的后门准则的方法有
- (1)基于估计处理任务(the treatment assignment)的方法:
- Propensity-based Stratification
- Propensity Score Matching
- Inverse Propensity Weighting
- (2)基于响应层面(response surface)的方法:Regression, 其支持的基于工具变量的方法有
- Binary Instrument/Wald Estimator
- Regression discontinuity
- DoWhy 支持一系列基于上述识别准则的估计方法,此外还提供了非参数置信空间与排列测试来检验得到的估计的统计显著性。具体支持的估计方法列表如下:
- 「基于估计干预分配的方法」
- 基于倾向的分层(Propensity-based Stratification)
- 倾向得分匹配(Propensity Score Matching)
- 逆向倾向加权(Inverse Propensity Weighting)
- 「基于估计结果模型的方法」
- 线性回归(Linear Regression)
- 广义线性模型(Generalized Linear Models)
- 「基于工具变量等式的方法」
- 二元工具/Wald 估计器(Binary Instrument/Wald Estimator)
- 两阶段最小二乘法(Two-stage least squares)
- 非连续回归(Regression discontinuity)
- 「基于前门准则和一般中介的方法」
- 两层线性回归(Two-stage linear regression)
- 「基于估计干预分配的方法」
- 此外,DoWhy 还支持调用外部的估计方法,例如 EconML 与 CausalML。
- (1)基于估计处理任务(the treatment assignment)的方法:
- estimate = model.
estimate_effect(identified_estimand, method_name=”backdoor.propensity_score_matching”)
- (4) 反驳: 使用多个鲁棒性的检查方法来反驳得到的估计,验证估计到的因果效应的有效性。
- DoWhy提供的方法有:
- Placebo Treatment
- Irrelevant Additional Confounder
- Subset validation
- 函数:refute_results = model.
refute_estimate(identified_estimand, estimate, method_name=”random_common_cause”) - DoWhy强调其输出的可解释性。分析时,我们都可以检查未经检验的假设,已确定的估计值(如果有)和估计值(如果有)。
- DoWhy 支持多种反驳方法来验证估计的正确性,具体列表如下:
- 「添加随机混杂因子」:添加一个随机变量作为混杂因子后估计因果效应是否会改变(期望结果:不会)
- 「安慰剂干预」:将真实干预变量替换为独立随机变量后因果效应是否会改变(期望结果:因果效应归零)
- 「虚拟结果」:将真实结果变量替换为独立随机变量后因果效应是否会改变(期望结果:因果效应归零)
- 「模拟结果」:将数据集替换为基于接近给定数据集数据生成过程的方式模拟生成的数据集后因果效应是否会改变(期望结果:与数据生成过程的效应参数相匹配)
- 「添加未观测混杂因子」:添加一个额外的与干预和结果相关的混杂因子后因果效应的敏感性(期望结果:不过度敏感)
- 「数据子集验证」:将给定数据集替换为一个随机子集后因果效应是否会改变(期望结果:不会)
- 「自助验证」:将给定数据集替换为同一数据集的自助样本后因果效应是否会改变(期望结果:不会)
- DoWhy提供的方法有:
DoWhy是根据两个指导原则创建的:明确要求因果假设,并测试对违反这些假设的估计的稳健性。换句话说,DoWhy将因果效应的识别与其相关性的估计分开,这使得能够推断出非常复杂的因果关系。
DoWhy支持Python 3+,它需要以下包:
- numpy
- SciPy
- scikit-learn
- pandas
- networkx(用于分析因果图)
- matplotlib(用于一般情节绘图)
-
sympy(用于呈现符号表达式)
- Jupyter notebook示例
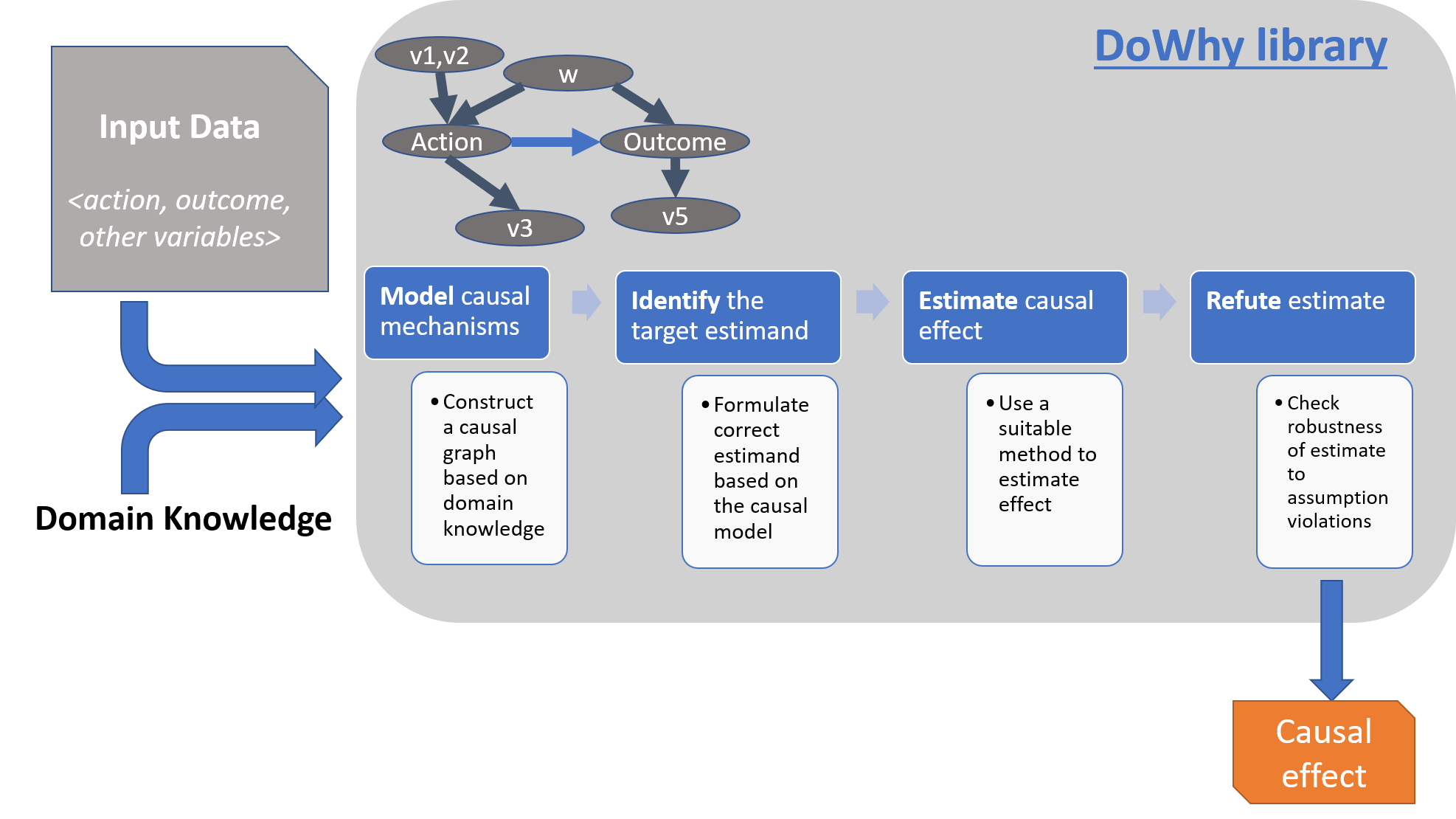
- 参考:精华-微软因果推理框架DoWhy入门
安装
pip install dowhy
# brew install graphviz
pip install pygraphviz # 图可视化
- 代码示例
- 因果图
import os, sys
sys.path.append(os.path.abspath("../../../")) # 添加一个读取路径
import numpy as np
import pandas as pd
import dowhy
from dowhy import CausalModel
import dowhy.datasets
# ------- 数据准备 ---------
# 模拟不同变量之间的「线性」关系
data = dowhy.datasets.linear_dataset(beta=10, # beta 表示真实的因果效应
num_common_causes=5, # 混杂因子,用 W 表示,作用于干预变量和结果变量
num_instruments=2, # 工具变量,用 Z 表示,作用于干预变量(间接影响结果)
num_effect_modifiers=1, # 效果修改变量,用 X 表示,作用于结果变量
num_samples=10000, # 样本数量
treatment_is_binary=True, # 干预为二元变量,用 v 表示
num_discrete_common_causes=1)
df = data["df"] # DoWhy 使用 pandas 的 dataframe 来载入数据
print(df.head())
print(data["dot_graph"]) # 还可以输出 gml_graph,内容一致只是表达形式不同
# ------- 建模 ---------
# 以 GML 图的形式构建因果图(「建模阶段」)
# With graph
model=CausalModel(
data = df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=data["gml_graph"]
)
# INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
# Without graph 或者不带图
model= CausalModel(
data=df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
instruments=data["instrument_names"], # 官网漏了这一行
common_causes=data["common_causes_names"],
effect_modifiers=data["effect_modifier_names"])
# ------- 识别 ---------
# 「识别阶段」可以脱离于数据,仅根据图进行识别,其给出的结果是一个用于计算的「表达式」。
identified_estimand = model.identify_effect()
print(identified_estimand)
# 可以通过 proceed_when_unidentifiable=True 参数来忽略观察性数据中未观测混杂因子的 warning。
# ------- 估计 ---------
# 识别阶段得到的表达式将在「估计阶段」基于实际数据进行计算,注意这两个阶段是独立开来的
estimate = model.estimate_effect(identified_estimand, method_name="backdoor.propensity_score_stratification")
print(estimate)
print("Causal Estimate is " + str(estimate.value))
# 可以通过 target_units 参数来选择因果效应分析的群体,如 ate(群体层面)、att(干预组)、ate(对照组)。也可以指定结果修改变量来分析不同变量对结果的影响。
# ------- 反驳 ---------
# 添加一个随机的混杂因子变量
res_random=model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause")
print(res_random)
# Refute: Add a Random Common Cause
# Estimated effect:9.124260741049653
# New effect:9.13487620983324
# 添加一个未观测的混杂因子变量
res_unobserved=model.refute_estimate(identified_estimand, estimate, method_name="add_unobserved_common_cause",
confounders_effect_on_treatment="binary_flip", confounders_effect_on_outcome="linear",
effect_strength_on_treatment=0.01, effect_strength_on_outcome=0.02)
print(res_unobserved)
# Refute: Add an Unobserved Common Cause
# Estimated effect:9.124260741049653
# New effect:8.129085846396725
# 用随机变量代替干预
res_placebo=model.refute_estimate(identified_estimand, estimate, method_name="placebo_treatment_refuter", placebo_type="permute")
print(res_placebo)
# Refute: Use a Placebo Treatment
# Estimated effect:9.124260741049653
# New effect:-0.010832019791737903
# p value:0.48
# 移除数据的一个随机子集
res_subset=model.refute_estimate(identified_estimand, estimate, method_name="data_subset_refuter", subset_fraction=0.9)
print(res_subset)
# Refute: Use a subset of data
# Estimated effect:9.124260741049653
# New effect:9.090515505813006
# p value:0.37
酒店预订案例
- 估计当消费者在预定酒店时,为其分配与之前预定过的房间不同的房间对消费者取消当前预定的影响。
- 分析此类问题的金标准是「随机对照试验」(Randomized Controlled Trials),即每位消费者被随机分配到两类干预中的一类:为其分配与之前预定过的房间相同或不同的房间。
- 然而,实际上酒店其不可能进行这样的试验,只能使用历史数据(观察性数据)来进行评估。
- 因果图
- 代码
import dowhy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import logging
logging.getLogger("dowhy").setLevel(logging.INFO)
dataset = pd.read_csv('https://raw.githubusercontent.com/Sid-darthvader/DoWhy-The-Causal-Story-Behind-Hotel-Booking-Cancellations/master/hotel_bookings.csv')
dataset.columns # 参数说明
# Index(['hotel', 'is_canceled', 'lead_time', 'arrival_date_year',
# 'arrival_date_month', 'arrival_date_week_number',
# 'arrival_date_day_of_month', 'stays_in_weekend_nights',
# 'stays_in_week_nights', 'adults', 'children', 'babies', 'meal',
# 'country', 'market_segment', 'distribution_channel',
# 'is_repeated_guest', 'previous_cancellations',
# 'previous_bookings_not_canceled', 'reserved_room_type',
# 'assigned_room_type', 'booking_changes', 'deposit_type', 'agent',
# 'company', 'days_in_waiting_list', 'customer_type', 'adr',
# 'required_car_parking_spaces', 'total_of_special_requests',
# 'reservation_status', 'reservation_status_date'],
# dtype='object')
# 数据预处理,减少原始数据的维度。具体来说,我们将创建如下三个特征:
# 「Total Stay」 = stays_in_weekend_nights + stays_in_week_nights
# 「Guests」 = adults + children + babies
# 「Different_room_assigned」 = 1 if reserved_room_type & assigned_room_type are different, 0 otherwise
# Total stay in nights
dataset['total_stay'] = dataset['stays_in_week_nights']+dataset['stays_in_weekend_nights']
# Total number of guests
dataset['guests'] = dataset['adults']+dataset['children'] +dataset['babies']
# Creating the different_room_assigned feature
dataset['different_room_assigned']=0
slice_indices =dataset['reserved_room_type']!=dataset['assigned_room_type']
dataset.loc[slice_indices,'different_room_assigned']=1
# Deleting older features
dataset = dataset.drop(['stays_in_week_nights','stays_in_weekend_nights','adults','children','babies'
,'reserved_room_type','assigned_room_type'],axis=1)
# 对缺失值与布尔值进行预处理,并去除部分特征
dataset.isnull().sum() # Country,Agent,Company contain 488,16340,112593 missing entries
dataset = dataset.drop(['agent','company'],axis=1)
# Replacing missing countries with most freqently occuring countries
dataset['country']= dataset['country'].fillna(dataset['country'].mode()[0])
dataset = dataset.drop(['reservation_status','reservation_status_date','arrival_date_day_of_month'],axis=1)
dataset = dataset.drop(['arrival_date_year'],axis=1)
# Replacing 1 by True and 0 by False for the experiment and outcome variables
dataset['different_room_assigned']= dataset['different_room_assigned'].replace(1,True)
dataset['different_room_assigned']= dataset['different_room_assigned'].replace(0,False)
dataset['is_canceled']= dataset['is_canceled'].replace(1,True)
dataset['is_canceled']= dataset['is_canceled'].replace(0,False)
dataset.dropna(inplace=True) # 新增对NA值的处理
dataset.columns
# Index(['hotel', 'is_canceled', 'lead_time', 'arrival_date_month',
# 'arrival_date_week_number', 'meal', 'country', 'market_segment',
# 'distribution_channel', 'is_repeated_guest', 'previous_cancellations',
# 'previous_bookings_not_canceled', 'booking_changes', 'deposit_type',
# 'days_in_waiting_list', 'customer_type', 'adr',
# 'required_car_parking_spaces', 'total_of_special_requests',
# 'total_stay', 'guests', 'different_room_assigned'],
# dtype='object')
# -------- 提取假设 -------
# 针对目标变量 is_cancelled 与 different_room_assigned ,随机选取 1000 次观测查看有多少次上述两个变量的值相同(即可能存在因果关系),重复上述过程 10000 次取平均
counts_sum=0
for i in range(1,10000):
counts_i = 0
# (1)期望频数是 「518」,即两个变量有约 50% 的时间是不同的,目前还无法判断其中的因果关系。
rdf = dataset.sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
# (2)分析预约过程中没有发生调整时(即变量booking_changes=0)两个变量相等的期望频数,结果为 「492」
rdf = dataset[dataset["booking_changes"]==0].sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
# (3)再分析预约过程中发生调整时的期望频数,结果变成了 「663」,与之前产生了明显的差异,663 ≠ 492
rdf = dataset[dataset["booking_changes"]>0].sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
counts_sum+= counts_i
counts_sum/10000
# 可以不严谨地认为预约调整这一变量是一个「混杂因子」。类似地,我们对其他变量进行分析,并作出一些假设,作为因果推断的先验知识。DoWhy 并不需要完整的先验知识,未指明的变量将作为潜在的混杂因子进行推断。在本例中,我们将给出如下的假设:
# - market_segment 参数有两种取值:TA 指旅行者,TO 指旅游公司,该参数会影响 lead_time(即预约和到达之间的时间间隔)
# - country 参数会决定一个人是否会提早预订(即影响 lead_time )以及其喜爱的食物(即影响 meal )
# - lead_time 会影响预订的等待时间( days_in_waiting_list )
# - 预订的等待时间 days_in_waiting_list、总停留时间 total_stay 以及客人数量 guests 会影响预订是否被取消
# - 之前预订的取消情况 previous_bookings_not_canceled 会影响该顾客是否为 is_repeated_guest;这两个变量也会影响预订是否被取消
# - booking_changes 会影响顾客是否被分配到不同的房间,也会影响预订取消情况
# - 除了 booking_changes 这一混杂因子外,一定还存在着其他混杂因子,同时影响干预和结果
# -------- 创建因果图 -----------
import pygraphviz
causal_graph = """digraph {
different_room_assigned[label="Different Room Assigned"];
is_canceled[label="Booking Cancelled"];
booking_changes[label="Booking Changes"];
previous_bookings_not_canceled[label="Previous Booking Retentions"];
days_in_waiting_list[label="Days in Waitlist"];
lead_time[label="Lead Time"];
market_segment[label="Market Segment"];
country[label="Country"];
U[label="Unobserved Confounders"];
is_repeated_guest;
total_stay;
guests;
meal;
market_segment -> lead_time;
lead_time->is_canceled; country -> lead_time;
different_room_assigned -> is_canceled;
U -> different_room_assigned; U -> lead_time; U -> is_canceled;
country->meal;
lead_time -> days_in_waiting_list;
days_in_waiting_list ->is_canceled;
previous_bookings_not_canceled -> is_canceled;
previous_bookings_not_canceled -> is_repeated_guest;
is_repeated_guest -> is_canceled;
total_stay -> is_canceled;
guests -> is_canceled;
booking_changes -> different_room_assigned; booking_changes -> is_canceled;
}"""
# 构建因果模型
model= dowhy.CausalModel(
data = dataset,
graph=causal_graph.replace("\n", " "),
treatment='different_room_assigned',
outcome='is_canceled')
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
# ------- 识别因果效应 -------
# 称「干预」(Treatment)导致了「结果」(Outcome)当且仅当在其他所有状况不变的情况下,干预的改变引起了结果的改变。因果效应即干预发生一个单位的改变时,结果变化的程度。
#Identify the causal effect
identified_estimand = model.identify_effect()
print(identified_estimand)
# -------- 估计因果效应 ---------
# 因果效应即干预进行单位改变时结果的变化程度。DoWhy 支持采用各种各样的方法计算因果效应估计量,并最终返回单个平均值。
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_stratification",target_units="ate")
# ATE = Average Treatment Effect
# ATT = Average Treatment Effect on Treated (i.e. those who were assigned a different room)
# ATC = Average Treatment Effect on Control (i.e. those who were not assigned a different room)
# 选择估计平均干预效应(ATE),也可以选择估计干预组(ATT)或对照组(ATC)的因果效应。估计方法选择的是「倾向得分匹配」
print(estimate)
# ---------- 反驳结果 ---------
# 上述因果并不是基于数据,而是基于所做的假设(即提供的因果图),数据只是用于进行统计学的估计。因此,需要验证假设的正确性。
# DoWhy 支持通过各种各样的鲁棒性检查方法来测试假设的正确性。
「添加随机混杂因子」。如果假设正确,则添加随机的混杂因子后,因果效应不会变化太多。
refute1_results=model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause")
print(refute1_results)
# Refute: Add a Random Common Cause
# Estimated effect:-0.3359905635051836
# New effect:-0.3365742386420179 # 基本保持稳定
# 「安慰剂干预」。将干预替换为随机变量,如果假设正确,因果效应应该接近 0。
refute2_results=model.refute_estimate(identified_estimand, estimate, method_name="placebo_treatment_refuter")
print(refute2_results)
# Refute: Use a Placebo Treatment
# Estimated effect:-0.3359905635051836
# New effect:-0.00028277666065981027 # 因果效应归零
# p value:0.43999999999999995
# p value 对比的是新的估计量与 0 之间的显著性差异(如果假设正确,则预期为无差异)
#「数据子集验证」。在数据子集上估计因果效应,如果假设正确,因果效应应该变化不大。
refute3_results=model.refute_estimate(identified_estimand, estimate, method_name="data_subset_refuter")
print(refute3_results)
# Refute: Use a subset of data
# Estimated effect:-0.3359905635051836
# New effect:-0.33647521997465524
# p value:0.35
# 因果模型基本可以通过上述几个测试(即取得预期的结果)。因此,根据估计阶段的结果,我们得出结论:当消费者在预定房间时,为其分配之前预定过的房间( different_room_assigned = 0 )所导致的平均预定取消概率( is_canceled )要比为其分配不同的房间( different_room_assigned = 1 )低 「33%」。
根据估计阶段的结果,我们得出结论:
- 当消费者在预定房间时,为其分配之前预定过的房间( different_room_assigned = 0 )所导致的平均预定取消概率( is_canceled )要比为其分配不同的房间( different_room_assigned = 1 )低 「33%」
- 用一个预测模型对数据进行训练,并分析不同特征的特征重要性。这里选择 XGBoost 作为预测模型
# plot feature importance using built-in function
from xgboost import XGBClassifier
from xgboost import plot_importance
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
from matplotlib import pyplot
# split data into X and y
X = dataset_copy # 这里使用的是copy,请自行复制(处理完后的数据)
y = dataset_copy['is_canceled']
X = X.drop(['is_canceled'],axis=1)
# One-Hot Encode the dataset
X = pd.get_dummies(X)
# split data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=26)
# fit model no training data
model = XGBClassifier()
model.fit(X_train, y_train)
# make predictions for test data and evaluate
y_pred = model.predict(X_test)
predictions = [int(value) for value in y_pred] # 注意这里之前用的是round,会报错
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
print(classification_report(y_test, predictions))
# Accuracy: 86.40%
# precision recall f1-score support
#
# False 0.88 0.92 0.90 15001
# True 0.85 0.79 0.82 8877
#
# accuracy 0.87 23878
# macro avg 0.86 0.85 0.86 23878
# weighted avg 0.867 0.87 0.87 23878
# plot feature importance
# 特征重要性排行(这里权重值为特征在树中出现的次数)
plot_importance(model,max_num_features=20)
pyplot.show()
different_room_assigned 变量的特征权重并不是非常高,这与我们的因果推断结果有一定的差异性,这也体现了因果推断模型和传统机器学习模型在原理上的差异性,
import numpy as np
from dowhy import CausalModel
import dowhy.datasets
# 加载数据,DoWhy依赖于panda dataframes来捕获输入数据
rvar = 1 if np.random.uniform() >0.5 else 0
data_dict = dowhy.datasets.xy_dataset(10000, effect=rvar, sd_error=0.2)
df = data_dict['df']
print(df[["Treatment", "Outcome", "w0"]].head())
# 因果推理
model= CausalModel(
data=df,
treatment=data_dict["treatment_name"],
outcome=data_dict["outcome_name"],
common_causes=data_dict["common_causes_names"],
instruments=data_dict["instrument_names"])
model.view_model(layout="dot")
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
# 确定图标中的因果关系
identified_estimand = model.identify_effect()
# 估计因果关系
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression")
# Plot Slope of line between treamtent and outcome =causal effect
dowhy.plotter.plot_causal_effect(estimate, df[data_dict["treatment_name"]], df[data_dict["outcome_name"]])
# 反驳因果估计
res_random=model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause")
- 结果
- justcause
代码
开源的研究框架(工具箱)
- Dowhy —— 微软研发,基于Python
- Causal ML —— Uber研发,基于Python
- EconML —— 微软研发,基于Python
- causalToolbox —— 基于R语言
开源因果推理方法
基于Python语言
- PSM1/PSM2
- Perfect Match
- CMGP
- BART
- GANITE
- BNN/CFR
- CEVAE
- SITE
- dragonet
- DRNets
- Network Decondounder
- Network Embeddings
- LCVA
基于R语言
- IPW
- DR
- Principal Stratification
- Stratification
- Matching based
- optimal matching
- CEM
- TMLE1/TMLE2
- BART
- grf
- R-learning
- Residual Balancing
- CBPS
- Entropy Balancing
如何在观测数据下进行因果效应评估
- 【2020-10-22】如何在观测数据下进行因果效应评估
导语
- 什么是因果?因果性与相关性的区别是什么?相关性有哪几种来源?如何评估因果效应?在2020年集智-凯风研读营中,浙江大学计算机学院助理教授况琨就上述问题做了系统梳理,本篇是文字整理版。
- 自9月20日(周日)开始,集智俱乐部联合北京智源人工智能研究院还将举行一系列有关因果推理的读书会,欢迎更多的有兴趣的同学和相关研究者参加,一起迎接因果科学的新时代。
1. 因果性与相关性
1.1 什么是因果

什么是因果呢?“因”其实就是引起某种现象发生的原因,而“果”就是某种现象发生后产生的结果。因果问题在我们日常生活中十分常见。
- 首先在医疗方面。比如在这次新冠疫情中,各个国家都在争先恐后地研发疫苗,但在疫苗上市之前还需要做很多次单盲实验、双盲实验,其背后就是基于随机对照实验的一些因果推理和因果效应评估,确定药物于病人康复之间的因果效应。
- 其次在社会科学方面。比如在国家出台新的政策前,就要利用因果推理手段来估计这个政策会给民众、经济效应和社会效应带来多大影响。
- 最后在市场营销方面。比如在推广告之前,就需要使用随机对照试验或者A/B测试,选择广告推送的策略以实现效益最大化。
1.2 因果性与相关性的区别
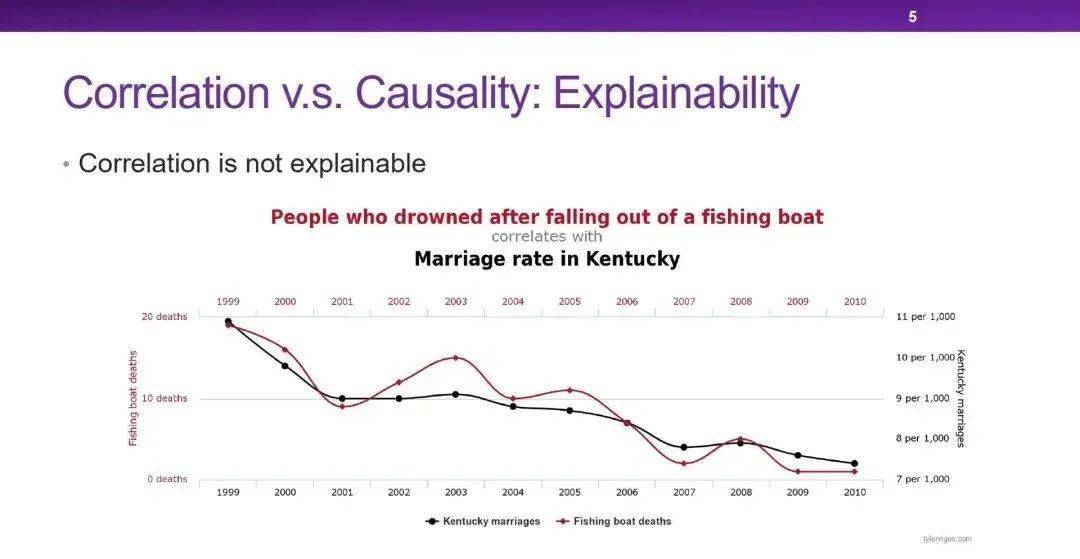
- (1)相关性比因果性更缺乏 可解释性(Explainability)。这张图中,黑线是肯塔基州的结婚率,而红线是渔船事故死亡人数,两者具有很高的相关性,但两者之间却没有任何因果关系。我们在使用数据的时候就需要知道,这里的相关性是不可靠的、不可解释的。
 另外一个例子是太阳镜与冰淇淋的销售量之间的关系,两者之间呈现着明显的正相关性。但如果我们直接关闭太阳镜商店,进行干预,会影响冰淇淋的销量吗?并不会。因为两者之间的虚假相关性是由天气引发的,在太阳炎热时两者的消费量都会提升,强制干预其中一个的销量并不会直接影响另一个。
另外一个例子是太阳镜与冰淇淋的销售量之间的关系,两者之间呈现着明显的正相关性。但如果我们直接关闭太阳镜商店,进行干预,会影响冰淇淋的销量吗?并不会。因为两者之间的虚假相关性是由天气引发的,在太阳炎热时两者的消费量都会提升,强制干预其中一个的销量并不会直接影响另一个。
- (2)相关性比因果性更缺乏 稳定性(Stability)。比如我们训练模型去识别图片中的狗,但数据集中90%的狗都是在草地上的,那么在这个数据集中草地与狗就十分相关。那么如果我们利用传统机器学习的方法,无论是逻辑斯蒂回归还是深度模型,大概率会把草地识别为重要的特征。但如果测试数据集中的狗是在沙滩上或者水中,模型就有很大概率会失败。
传统机器学习使基于关联驱动的,对于未知的测试数据集很难达到稳定预测。传统机器学习在关联挖掘中会发现一些非因果特征,比如草地背景与标签的关系,并利用这种强的虚假相关(Spurious Correlation)进行预测。如果我们能够发现特征与标签之间的因果关系,比如我们人类在识别狗的时候就会去关注够的鼻子、眼睛和耳朵这些因果特征,那么无论狗是在什么背景下,我们都可以正确识别。

- (3)第三个区别是 可行动性(Actionability)。比如某个电商在推广某个商品时,需要从两个广告推荐算法中进行选择,看哪个算法能带来的收益更大。 如图所示,前期的试验发现,新算法B比旧算法 A 的总体成功率更高。但如果将用户按收入分为两层,却会发现算法A在低收入人群和高收入人群中的效果反而都优于 B 。两个算法的试验对象中,收入分布的差别很大,如果不进行控制,就会产生错误的结果。而除了收入之外,可能还需要考虑地域、年龄等多个变量,否则就会产生算法与成功率之间的虚假相关。 这些虚假相关是由混淆变量产生的混杂偏倚(Confounding Bias)。这种决策问题实际上是反事实问题,而不是预测问题。

- (4)第四个区别是 公平性(Fairness)。Google曾开发了根据人像判断犯罪率的软件,输入为黑人时犯罪率就会比白人更高。而肤色与犯罪率之间不应该存在因果关系,这就出现了公平性的问题。实际上如图所示,真正起决定性作用的变量是“收入”,黑人的收入普遍偏低,而低收入人群的犯罪率较高,因此肤色和犯罪率之间出现了虚假相关。 而通过因果评估的框架,我们可以利用Do-演算(Do-Calculus)等工具,干预收入的多少,来计算肤色与犯罪率之间真正的因果效应大小。实际上,收入和犯罪率才是强因果相关的,而肤色和犯罪率之间因果效应可以弱到忽略不计。
1.3 相关性的三种来源

相关性有三种来源:因果、混淆和样本选择。
- 因果关联例子就是天下雨地面会湿,这种关系是能够被人类所理解的、是可解释的、稳定的(无论在任何国家或城市,天下雨地都会湿)。
- 混淆关联是由混淆偏差(Confounding Bias)造成的。比如图中X是T和Y的共同原因,但如果不对X进行观察,就会发现T和Y是具有相关性的,但T和Y之间是没有直接因果效应的,这就是产生了虚假相关。
- 样本选择偏差(Selection Bias)也会产生相关性,比如之前的例子中,如果数据集中的狗都出现在沙滩上,而没有狗的图片都是草地,那么训练处的模型就会发现草地与狗之间是负相关的,这也产生了虚假相关。
虚假相关与因果关联相比,缺乏可解释性,且容易随着环境变化。在工业界和学术界中,我们都希望能判断两个变量之间的相关究竟是因果关联还是虚假相关。如果是虚假相关的话,可能会给实际的系统带来风险。
所以说,恢复因果可以提高可解释性,帮助我们做出决策,并在未来的数据集中做出稳定而鲁棒的预测,防止算法产生的偏差。无论数据集中有什么样的偏差,我们都希望能挖掘出没有偏差的因果关系,来指导算法。
1.4 符号定义
这里给出关于因果的一个比较实际的定义:变量 T 的变量 Y 的原因,变量 Y 是变量 T 的结果,当且仅当在控制其他所有变量不变时,改变 T 会引发 Y 的变化。而因果效应(Causal Effect)就是改变变量 T 一个单位时,变量 Y 发生改变的大小。这里的两个重点是:一、只修改 T 的值,二、保持其他变量不变。
这里给出因果效应评估(Causal Effect Estimation)的数学形式。以评估药物的因果效应为例,干预变量(Treatment Variable)T 的值为1时代表吃了药,0代表没吃药,而这对应了两者不同的潜在结果。平均因果效应(Average Causal Effect, ATE)就是吃药的潜在结果与不吃药的潜在结果在所有病人上的差值平均值。个体因果效应(Individual Causal Effect, ICE)就是吃药的潜在结果与不吃药的潜在结果在某个病人上的差值。
这里还涉及反事实的问题:对于某个病人,我们只能观测到他吃药或不吃药其中一种情况的结果,想要探究未发生的另一种情况的结果,就需要假象存在一个平行世界,这个世界里病人做出了与之前不同的选择,除此之外都保持完全一致,对比两个世界的结果进行求解。
在实际应用中,随机化实验(Randomized Experiments)是因果效应评估的金标准。比如在疫苗研发中,就需要做双盲实验和单盲实验以评估因果效应。在足够大的实验人群中,通过完全随机的方法使其中一半人接种疫苗,这样就排除了其他变量的影响,求得平均因果效应。这种方法在政策评估、健康医疗和市场营销等多个领域都有重要应用,但这种方法的花销巨大,且可能涉及伦理道德问题。那么我们可否在巨量的历史观测数据中进行挖掘,评估出因果效应呢?
比如在一个数据集中,有吃药和未吃药的两群人。如果在数据收集时是使用单盲或双盲实验,那么就可以直接去计算平均因果效应。但如果没有保证分配药物的随机性,就可能会有体质、性别、年龄等混杂因子 X 使结果产生偏倚。因果推理的本质就是去控制吃药和不吃药的两群人之间其他特征的分布。
2. 因果效应评估的方法
现在我们考虑干预变量为二值的情况,要去平衡其他变量的分布,再做因果效应评估。在这里介绍三种方法:Matching、Propensity Score Based Methods 和 Directly Confounder Balancing。
- 首先给出在观测数据下做因果推理的三个假设:
- 一、Stable Unit Treatment Value(SUTV) 变量之间是独立的:我是否吃药的结果不受别人是否吃药的影响。
- 二、Unconfounderness 所有混淆变量都被观测到了。
- 三、Overlap 各种干预变量的取值概率都应该在0到1之间。
2.1 Matching
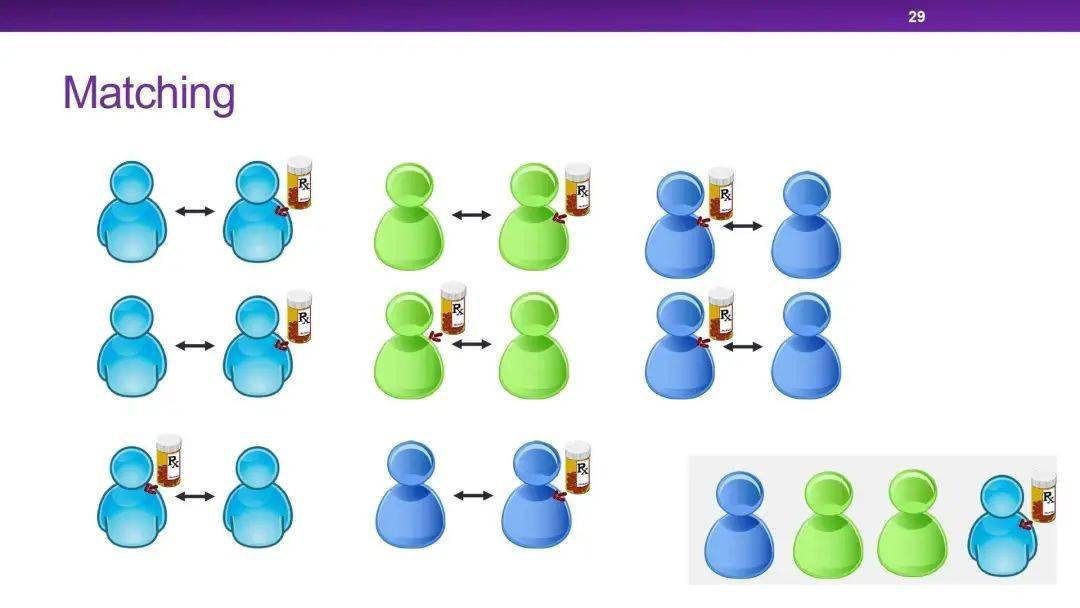
第一种方法叫 Mathching。在两个不同的处理群体之间,逐一寻找并匹配其他特征变量都相同的个体,如果找不到就舍弃此个体,这样就可以保证有匹配的那些样本中其他特征的分布在一定范围内是相似的,进而初步去评估因果效应。
Matching 的问题就是如何去评估两个个体的相似度,并需要设定可以接受的差异阈值,在舍弃样本数和相似度之间进行平衡。其次对于高维数据,很难找到相似样本:比如有10个二值变量,就需要至少1025个样本才能保证找到相同个体。
2.2 Propensity Score Based Methods

第二类方法是基于倾向指数/倾向得分(Propensity Score)的。倾向指数的定义就是在干预变量之外的其他特征变量为一定值的条件下,个体被处理的概率。Rubin 证明了在给定倾向指数的情况下,Unconfounderness 假设就可以满足。倾向指数其实概括了群体的特征变量,如果两个群体的倾向指数相同,那他们的干预变量就是与其他特征变量相独立的。
比如说,如果能保证两群人的他吃药的概率完全一样,那么可以说这两群人其他特征分布也是一样。

倾向指数在实际应用中是观测不到的,但可以使用有监督学习的方法进行估计。根据估计到的倾向指数,第一种方法就是去做 Matching,这样能解决在高维数据中难以找到相似样本的问题。
第二种是使用 Inverse of Propensity Weighting 方法,对于干预变量为1的样本使用倾向指数的倒数进行加权,而对于为0的样本使用(1-倾向指数)的倒数进行加权,两类样本的加权平均值之差就是平均因果效应的大小。这里有一个假设,就是估计出的倾向指数与真实的倾向指数是相等的。
因此这个方法有两个弱点,一是需要对倾向指数的估计足够精确;二是如果倾向指数过于趋近0或1,就会导致某些权重的值过高,使估计出的平均因果效应的方差过大。
第三种方法叫 Doubly Robust。这个方法需要根据已有数据,再学习一个预测的模型,反事实评估某个个体在干预变量变化后,结果变量的期望值。只要倾向指数的估计模型和反事实预测模型中有一个是对的,计算出的平均因果效应就是无偏的;但如果两个模型估计都是错误的,那产生的误差可能会非常大。
以上的这三种基于倾向指数的方法比较粗暴,把干预变量和结果变量之外的所有变量都当作混淆变量。而在高维数据中,我们需要精准地找出那些真正需要控制的混淆变量。我们提出了一种数据驱动的变量分解算法(D²VD),将干预变量和结果变量之外的其他变量分为了三类:
- 混淆变量(Confounders):既会影响到干预变量,还会影响到结果变量
- 调整变量(Adjustment Variables):与干预变量独立,但会影响到结果变量
- 无关变量:不会直接影响到干预变量与结果变量
进行分类之后,就可以只用混淆变量集去估计倾向指数。而调整变量集会被视为对结果变量的噪声,进行消减。最后使用经过调整的结果,去估计平均因果效应。我们从理论上证明了,使用这种方法可以得到无偏的平均因果效应估计,而且估计结果的方差不会大于 Inverse of Propensity Weighting 方法。
我的学生又拓展了我的工作,与表征学习相结合,提出了 Decomposed Representation。其中增加了一类变量:
- 工具变量:与结果变量独立,但会影响到干预变量
通过实验发现,与传统方法相比,此方法可以很准确地把变量分离出来,提高平均因果效应的准确性。
2.3 Directly Confounder Balancing
总的来说,基于倾向指数的方法还是需要估计倾向指数的模型是准确的。既然倾向指数就是用于计算权重的,我们可不可以直接去估计权重呢?
第三类方法就是 Directly Confounder Balancing,直接对样本权重进行学习。这类方法的动机就是去控制在干预变量下其他特征变量的分布。而一个变量的所有阶的矩(moment)可以唯一确定它的分布,所以只需要去控制它所有阶的矩(比如一阶矩就是均值,二阶矩就是方差)就可了。在实验中我们发现,只考虑一阶矩就可以达到很好的效果,因此这里先不考虑二阶及以上的矩。通过这个手段就可以直接学习样本权重,进行平均因果效应估计了。
这个概念首先出现于 Entrophy Balancing 方法之中,通过学习样本权重,使特征变量的分布在一阶矩上一致,同时还约束了权重的熵(Entropy)。但这个方法的问题也是将所有变量都同等对待了,把过多变量考虑为混杂变量。
第二种方法叫 Approximate Residual Balancing。第一步也是通过计算样本权重使得一阶矩一致,第二步与 Doubly Robust 的思想一致,加入了回归模型,并在第三步结合了前两步的结果估计平均因果效应。只要样本权重的估计和反事实预测模型中有一个是对的,计算出的平均因果效应就是无偏的。但这里也是将所有变量都同等对待了。
我们提出的方法叫做混淆变量区分性平衡(Differentiated Confounder Balancing, DCB),考虑到的就是不同的特征变量对于平均因果效应的影响是不同的。我们在传统方法上加入了混淆变量权重(Confounder Weights)β:当β为0时,代表所对应的变量不是混淆变量,对因果效应不会带来影响;当β较大时,说明此变量对因果效应的影响较大。其中的β正好是从干预变量的增广到结果变量的回归系数。通过一系列实验发现,我们的方法在高维数据下对平均因果效应的估计偏差几乎为0,优于其他方法。
2.4 Generative Adversial De-confounding
上述的所有方法中,干预变量都是二值的,那如何去处理多值的或者连续的干预变量呢?我们今年的一个工作 Generative Adversial De-confounding 就尝试估计这类复杂情况下干预变量与结果变量之间的因果效应。这里的核心思想就是如何保证干预变量与其他特征变量的分布相独立。我们利用了 GAN 的思想,去凭空构造出另一个干预变量与其他特征变量相独立的分布。
我们使用了随机打乱(Random Shuffle)的方法,只打乱干预变量,这样就可以使干预变量与其他特征变量相独,并保留了两者的分布。我们再使用样本权重估计的方法,使原来数据集的加权分布结果与构造出的分布相一致。在实验中,可以发现我们的方法成功降低了干预变量与其他特征变量的相关性,并有效提高了因果效应评估的准确性。
因果科学实践
阿里飞猪广告预算分配里的因果推断技术
- 【2021-3-14】datafun 2020 资料
- 基本思想:控制其他因子,只留一个因子
- ①切断X→T:随机试验,若T的分配随机,则与任何变量独立
- ②切断X→T和X→Y:特征工程,若X包含所有confounder(同时影响T和Y的变量),给定X,不同treatment group下影响Y的协变量分布一样
快手因果推断
滴滴因果推理森林
- Whitney:
- 在某个条件下的 群体的平均ite,w=1表示这个病人采用了这个治疗手段(treatment 组),w=0表示这个病人没采用治疗手段(control 组),Y表示在w干预情况下的outcome。也就是说,假设这个病人在治疗组的outcome 减去 假设这个病人在对照组的outcome。一般只能知道 这个病人在治疗组的outcome 或者 这个病人在对照组的outcome。已知的那个叫事实,另外一个不知道的就叫反事实,要知道这个治疗方案到底有没有效果,就要算ite。所以需要推理反事实
增益模型 Uplift
详见站内专题:大模型因果推理
Uplift+因果森林
【2021-5-12】滴滴连续因果森林模型的构造与实践:
目前大多数增益模型仅讨论二元处理变量情况下的处理效应估计,然而在网约车市场中存在大量多维、连续的处理变量。针对这一困境,构造了连续因果森林模型,并成功地应用在了网约车交易市场策略上,量化价格对网约车供需关系的影响,这对于精细化定价补贴策略的制定和优化有着重要的意义。
因此这类问题通常被放在因果推断(Causal Inference)框架下进行讨论。大多数流行的增益模型框架(如CausalML, pylift, grf),都很好地支持了二元处理变量(如发券或不发券,吃药或不吃药)的效应估计。
但在多元/连续处理变量方面,尚无很好的支持。而在广大应用场景中,多元或连续处理变量更为普遍。
- 例如,价格就是一个连续变量,存在理论上无限多的可能值。
那是否可以在因果推断框架下实现对多元或连续处理变量的效应估计?经过一段时间的开发和测试,在二元因果森林的基础上,扩展研发了连续因果森林,初步解决了部分场景下连续变量处理效应的估计问题。
- 因果森林(Causal Forest)是由Susan Athey、Stefan Wager等人开发,专门估计异质处理效应的机器学习模型,是当前增益模型领域最为流行的算法之一。
- 目前,官方有基于C++/R语言的算法实现。与其他增益树模型(Tree-based Uplift Model)类似,因果森林以随机森林为基础,通过对特征空间进行重复划分(Recursive Partitioning),以达到局部特征空间的数据同质/无混淆。在一定的假设下,可以得到各个维度上异质处理效应(Heterogeneous Treatment Effect)的无偏估计

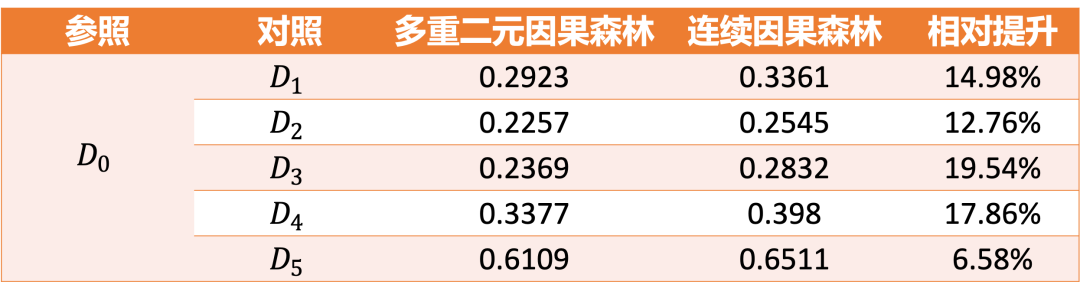
- 目前连续因果森林仍处于早期的开发阶段,存在大量的优化空间。例如:
- 可否使用非线性假设
- 如何处理无单调关系的处理变量(如不同套餐)
- 如何估计多维处理效应(如多个产品线价格间的相互影响)
因果表示学习
【2021-3-3】yoshua bengio发表的论文Towards Causal Representation Learning, 解读:因果表征学习最新综述:连接因果科学和机器学习的桥梁
- 深度学习仍有许多问题亟待解决,例如将知识迁移到新问题上的能力。许多关键问题都可以归结为
OOD(out-of-distribution)问题。因为统计学习模型需要满足独立同分布(i.i.d.)假设,而很多情形下,这个假设不成立,测试数据与训练数据来自不同的分布,统计模型往往出错,这时候就需要因果推断了:- 如何学习一个可以在不同分布下工作、蕴含因果机制的因果模型(Causal Model),并使用因果模型进行干预或反事实推断。
- 然而,因果模型往往处理的是结构化数据,并不能处理机器学习中常见的高维低层次的原始数据,如图像。为此,回到最初的问题,因果表征即可理解为可以用于因果模型的表征,因果表征学习即为将图像这样的原始数据转化为可用于因果模型的结构化变量。因果表征学习就是连接因果科学与机器学习的桥梁,解决这一及相关问题,就可以很好的将因果推断与机器学习结合起来,构建下一代更强大的AI。
内容:
- 物理世界的不同模型的层次,统计模型与因果模型的区别包括模型的能力相关的假设及挑战,学习因果模型所必需的独立因果机制原则,学习因果模型的方法,如何学习因果表征,以及从因果的角度重新审视了诸多机器学习的挑战并指出了因果带来的启示。
一 因果模型层级
微分方程组根据时间的演变建模物理机制,可以让我们预测物理系统未来的行为,推断干预的效果以及预测变量间的统计相关性;还可以提供物理本质,让我们可以解读因果结构。
如果说微分方程是对物理系统全面详尽的表述,那么统计模型(Statistical Model)可被看作表面的粗糙的描述。它无法预测干预的效果,但是的优点在于通常可以从观察数据中学习,而前者通常需要专家来提出。因果建模则存在于这两个极端之间,它期望能够像物理模型一样预测干预的效果,但同时可以在一些假设下,通过数据驱动的方法找到这样的模型,来取代专家知识。

模型的分类与层级,分级的依据——越高层的模型拥有更多更强的能力,这些能力从低到高分别是:
- 在i.i.d.条件下预测的能力 → 在分布偏移/干预下预测的能力 → 回答反事实问题的能力 → 是否蕴含物理本质
接下来首先讨论这些能力,并在下一个章节具体解析统计模型与因果模型的区别。
- 基于统计模型的机器学习模型只能建模相关关系,而相关关系往往会随着数据分布的变化而变化;
- 而因果模型所建模的因果关系则是更本质的,反应数据生成机制的关系,这样的关系是更鲁棒的,具有OOD泛化的能力。
在独立同分布条件下预测的能力
统计模型只是对现实的粗浅描述,因为它们只关注关联关系。对于样本 和标签 ,我们可以通过估计 来回答这样的问题:“这张特定照片中中有狗的概率是多少?”,“给定一些症状,心力衰竭的概率是多少?”。这样的问题是可以通过观察足够多的 )产生的i.i.d.数据来回答的。尽管机器学习算法可以把这些事做的很好,但是准确的预测对于我们的决策是不够,而因果科学提供了一个尚未完全探索的补充。举例来说,鹳出现的频率是和欧洲的人口出生率正相关的,我们的确可以训练一个统计学习模型来通过鹳的频率预测出生率,但显然这两者并没有什么直接的因果关系。统计模型只有在i.i.d.的情况下才是准确的,如果我们做任何的干预来改变数据分布,就会导致统计学习模型出错。
在分布偏移/干预条件下预测的能力
我们进一步讨论干预问题,它是更具挑战性的,因为干预会使我们跳出统计学习中i.i.d.的假设。继续用鹳的例子
- “在一个国家中增加鹳的数量会增加该国的出生率吗?”就是一个干预问题。显然,人为的干预会使得数据分布发生变化,统计学习依赖的条件就会被打破,所以它会失效;另一方面,如果我们可以在干预的情况下学习一个预测模型,那么这有可能让我们得到一个对现实环境中的分布变化鲁棒的模型。实际上这里所谓的干预并不是什么新鲜事,很多事情本身就是随时间变化的,例如人的兴趣偏好,或者模型的训练集与测试集本身就有分布的不匹配。对神经网络的鲁棒性,已经有越来越多的关注,成为了一个与因果推断紧密连接的研究话题。作者认为对于在分布偏移下预测的研究不能只局限于在测试集上取得高准确率,如果我们希望在实际决策中使用学习算法,那么我们必须相信在实验条件改变的情况下,模型的预测也是有效的。笔者认为,作者在此处的意思是,实际应用中的分布偏移是任意多样的,仅仅在某些测试集上取得好效果不能代表我们可以在任何情况下都信任该模型,它可能只是恰好符合这些测试集的偏置。
为了使我们可以在尽可能多的情况下信任预测模型,就要采用具有回答干预问题能力的模型,至少统计学习模型是不行的。
回答反事实问题的能力
反事实问题涉及到推理事情为什么会发生,想象不同行为的后果,并由此可以决定采取何种行为来达到期望的结果。回答反事实问题更加困难的,但也是对于AI非常关键的挑战。
- 如果一个干预问题是“如果我们说服一个病人规律的锻炼,那么它心力衰竭的概率会如何变化?”,那么对应的反事实问题就是“如果这个已经心力衰竭的病人一年前就开始锻炼,那他还会心力衰竭吗?”。
- 显然回答这样的反事实问题对于强化学习中的智能体是很重要的,它们可以通过反思自己的决策,制定假说,再通过实践验证,就像我们的科学研究一样。
数据的特点:观察的—干预的,结构化的-非结构化的
数据的形式往往决定了我们可以推断什么样的关系。作者将数据分为两个维度:
- 观察的与因果的
- 人工总结的(结构化的)与原始的(非结构化的)。
观察的与干预的数据
一个极端情况是,常假设的从同一个分布中i.i.d.采样的观察数据,但这样的条件很少能被严格的满足;另一个极端是在已知的不同的干预下的产生的数据。在这两者之间,是偏移或者干预未知的数据。
结构化的与非结构化的数据
在传统的AI中,数据常被假设为高层有语义的结构化变量,它们有些可能对应着潜在图中的因果变量。而非结构化原始数据是指那些无法直接提供因果信息的数据,例如图像。
尽管统计模型比因果模型要弱,但是它们可以同时有效地在结构化或者非结构化学习。另一方面,尽管只从观察数据中学习因果关系的方法是存在的,但常常还是需要从多个环境中收集数据,或者需要能够做干预。至此,我们已经可以一窥问题的核心:
- 因果模型具有回答干预问题和反事实问题的能力,然而只能用于结构化的数据
- ML模型虽然可以从raw data中有效的学习,但却逃不出i.i.d.设定的桎梏 那么如何将两者结合,使机器学习突破当前的瓶颈呢?答案即如本文题目所言Towards Causal Representation Learning!因果表征学习,即从非结构化的数据中提取出可以用于因果推断的结构化变量。一言以蔽之,如果解决了因果表征学习的问题,就克服了因果推断领域和机器学习领域间的最关键障碍,就可构建下一代更强大的AI。
愿景虽好,脚踏实地才可为其提供保证,在接下来的章节中,作者一步一个脚印地介绍了因果模型和相关假设及挑战、估计因果关系的必要机制、传统的和与神经网络结合的因果发现方法、学习因果变量(表征)的关键问题,最后用因果的语言讨论了对机器学习领域诸多问题的启示。
二、因果模型和推断
独立同分布数据驱动的方法
从传统机器学习模型谈起,机器学习的成功有4个重要的因素:
- (1) 大量基于模拟器或人工标注的数据
- (2) 强大的机器学习系统,如神经网络
- (3) 高性能计算系统,这对因果推断也至关重要
- (4) 问题是i.i.d.的。
对于i.i.d.的数据,统计学习理论对模型提供了强大的保证,因此取得超越人类的表现也不足为奇。但是却在对人类很简单的不满足i.i.d.的情景下表现很差,即在不同问题间迁移的能力。
为了进一步理解,i.i.d.带来的问题,考虑下面的例子。
- Alice在想在网上买一个笔记本电脑包,网上商店的推荐系统于是向Alice推荐了笔记本电脑。这个推荐看起来很不合理,因为很可能Alice是已经买了电脑才去买包。假设该网站推荐系统使用统计模型仅仅基于统计相关性来推荐,那么我们已知事件“Alice买了包”对于事件“Alice是否会买电脑”的不确定性减少,和已知事件“Alice买了电脑”对于事件“Alice是否会买包”的不确定性减少是相等的,都为两个随机事件的互信息。这就导致我们丢失了重要的方向信息,即买电脑往往导致买包。
The Reichenbach Principle:从统计到因果
如何实现从统计相关到因果的跨越呢?Reichenbach清晰的阐述了二者的联系:
- Common Cause Principle:如果两个可观察量 X 和 Y 是统计相关的,那么一定存在一个变量 Z 因果的影响 X 和 Y,并且可以解释它们之间全部的相关性,即给定 Z, X和 Y是条件独立的。
注意:上述原理包含Z与X或Y重合的特殊情况。
- 沿用前文鹳的例子,鹳的频率为X,出生率为Y,二者统计相关。如果鹳能带来孩子则是 X->Y,孩子会吸引鹳则是 X<-Y,有其他因素导致两者则为X<-Z->Y 。没有额外的假设,我们不能从观察数据中根据统计相关性区分这三种情况,所以因果模型比统计模型包含更多信息。
尽管只有两个变量情况下的因果发现很困难,但是在有更多变量的情况下则会简单很多,因为多变量情况下,因果图会蕴含更多条件独立性质。这会将Reichenbach Principle推广到接下来介绍的因果图模型或结构因果模型。
结构因果模型
结构因果模型(Structural causal models, SCM),是考虑一系列变量 X1,X2,…,Xn 作为有向无环图(DAG)的顶点,每个变量值都由如下结构方程赋予
- 因果图模型:上述的DAG(被称为因果图,Causal Graph),以及噪声的独立性蕴含了联合分布的规范分解,称之为因果(解耦)分解,(causal(disentangled) factorization)
- 隐变量和混淆因子:上述的图模型其实需要一个因果充分性假设,即不存在未观察到的共同原因变量。若该假设不满足,则会让因果推断变得很困难。因为它可能会让两个因果无关的可观测变量产生统计相关性,或者它们之间的因果关系被混淆因子的所污染
- 干预:修改SCM(1)中结构方程的一部分
统计模型,因果图模型,结构因果模型的区别
- 统计模型也可以被定义成一个图(例如贝叶斯网络),图中变量的概率分布与因果图模型一样可以根据因果马尔可夫性进行分解,但这样的模型中的边并不一定是因果的。
- 结构因果模型则包含因果变量和带有独立噪声的结构方程,也可以计算干预分布,因为他可以表达成因果图模型的概率分解的形式;也可以进行反事实推理。在进行反事实推理的时候,我们需要噪声变量的值固定。
总结
- 统计学习的概念基础是联合分布P(Y,X1,X2,…,Xn),期望通过特定模型在i.i.d.情况下学习E[ Y|X ]。
- 因果学习(发现)需要考虑更多的假设,希望把联合分布进行因果分解,当得到因果模型后,就可以进行干预或反事实推理。
三、独立因果机制
独立因果机制原则(Independent Causal Mechanisms Principle, ICM Principle):
- 一个系统的变量的因果生成过程使由一系列自主模块构成,它们不会影响彼此,也无法提供彼此的信息
四、因果发现与机器学习
五、学习因果变量
因果表征学习的三个机器学习问题。
- 问题一 :学习解耦的表征
- 问题二:学习可迁移的机制
- 问题三:学习可被干预世界模型与推理
- 因果表示学习应该要比传统的只关注统计相关性的表示学习更进一步,去学习支持干预、规划、推理的模型,实现康拉德·洛伦兹的“思考即为在想象中行动”的概念。这最终需要反思行为,想象可能的情况的能力,甚至可能需要自由意志(的幻觉)。这对社会和文化学习是至关重要的,是一个尚未登上机器学习领域舞台,但却是人类智能的核心。
六、对机器学习研究的启示
上述的所有关于学习范式的讨论,都不基于常用的i.i.d.假设。因此,我们需要一个更弱的假设:模型将要被应用的数据是来自不同的分布,但设计几乎相同的因果机制。这会带来几个严肃的挑战:
- 我们需要从给定的低层次输入特征中抽象因果变量
- 哪方面的数据可以揭示因果关系尚无共识
- 传统的实验方案不足以推断和评估因果模型,我们需要新的基准测试
- 即使是在我们了解的有限案例中,仍然缺乏可大规模使用的算法 尽管如此,这样的努力对于机器学习有很多具体的影响。
更多见原文
资料
大模型
Causal AI 长时间在商业领域裹足不前的主因: Causal Modeling 过程非常依赖于人类专家的知识和干预,难以完全自动化。 但利用大模型替代或辅助人类专家进行 Causal Modeling 研究有了不错的进展。
微软
- 【2023-4-28】微软论文《Causal Reasoning and Large Language Models》展示了大模型在“点对点”和“整图”级别的因果关系识别都超越了传统算法
- 解读
基于大语言模型的方法在多个因果基准测试任务上表现出最高的准确性。
大语言模型引入一种基于文本和元数据(变量名)新推理方式来实现这一目标,基于知识的因果推理(knowledge-based causal reasoning),
基于GPT-3.5/4的算法在多项因果推理任务中胜过现有算法,包括成对因果发现任务(97%,提高13个百分点),反事实推理任务(92%,提高20个百分点),和实际因果关系(在确定事件的必要和充分原因方面具有86%的准确性)。





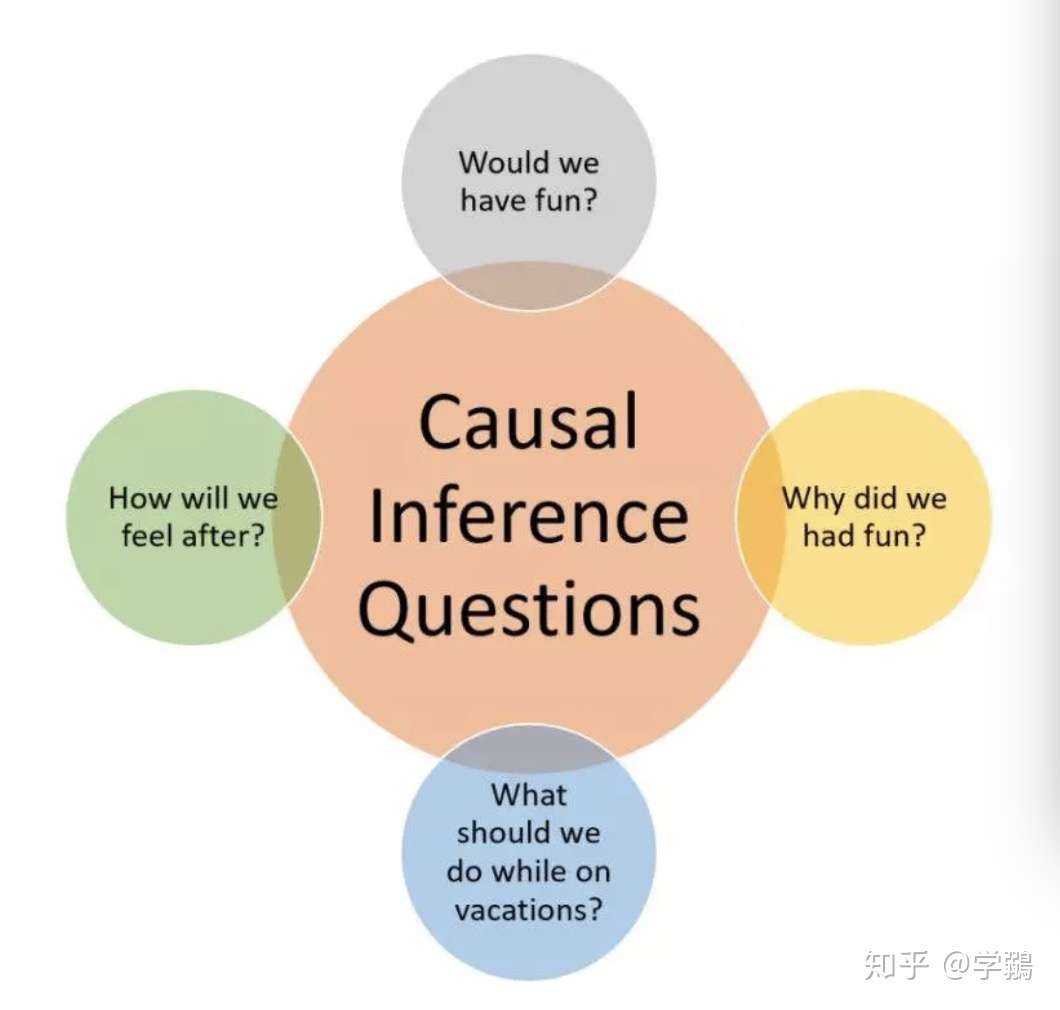
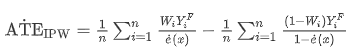
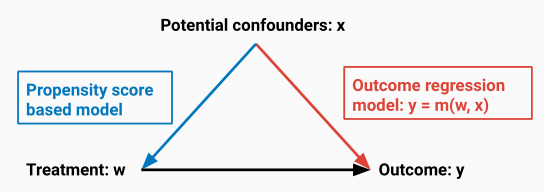
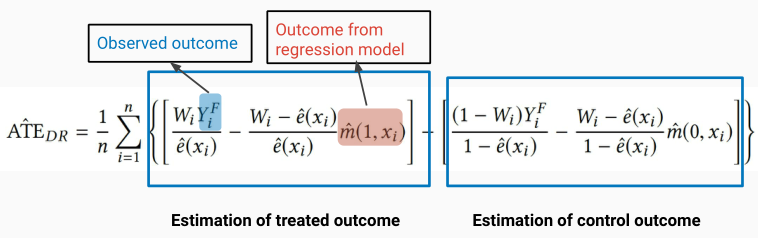





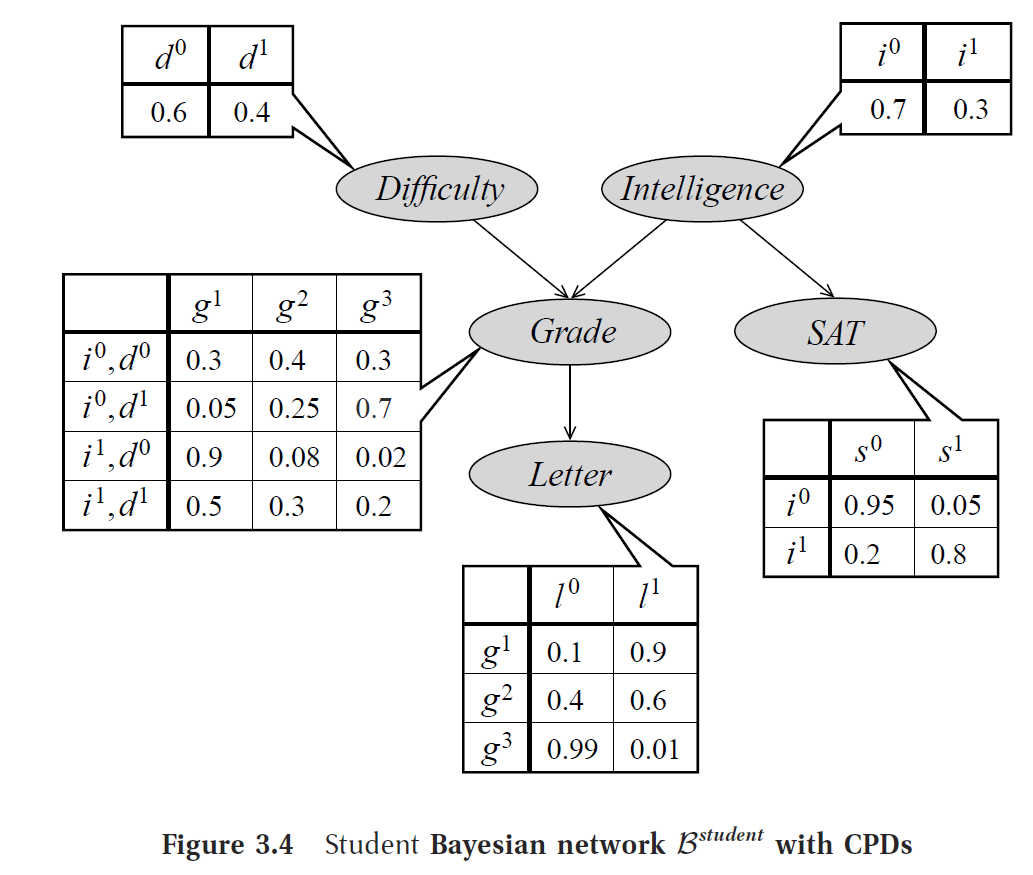

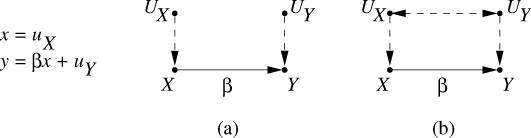
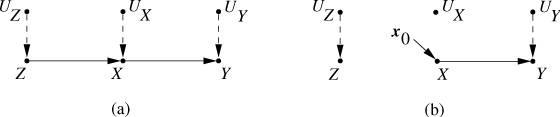
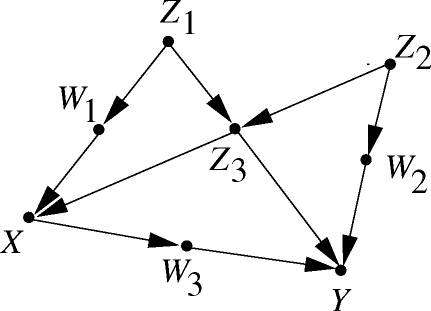
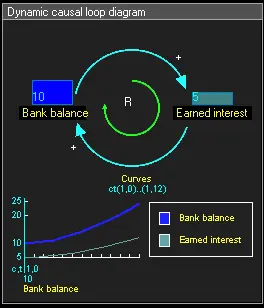




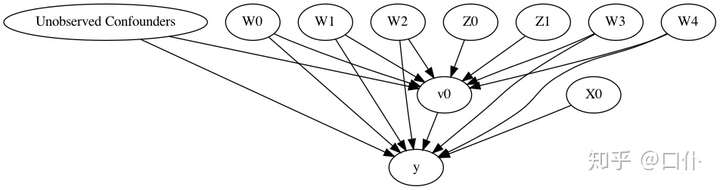
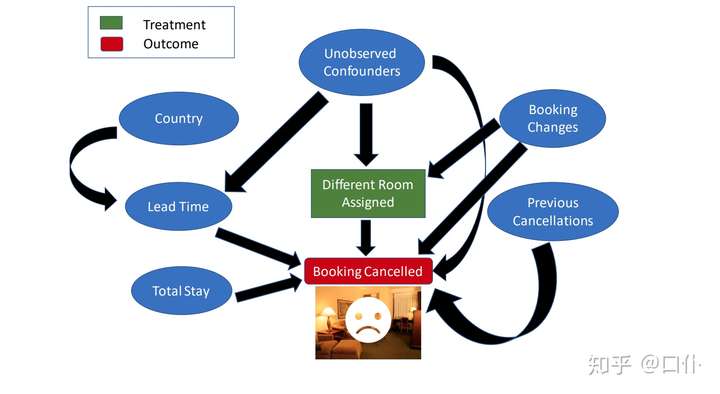
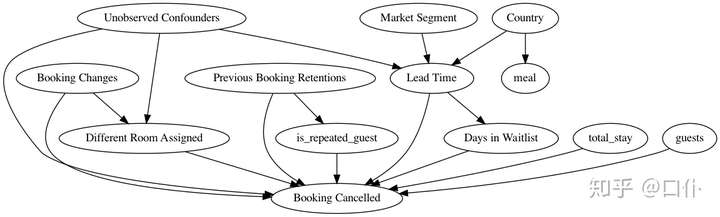


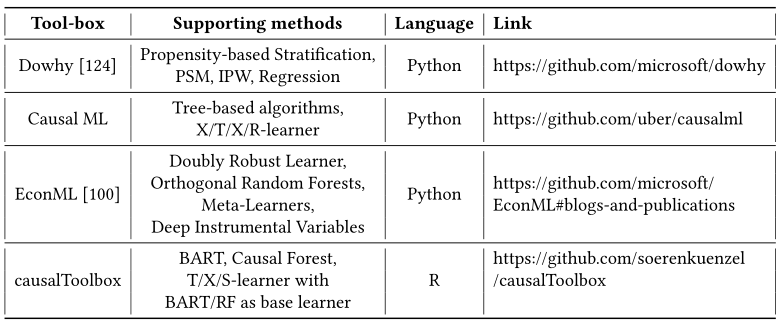


















 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
