- 调参经验
- 超参优化
- 初始化
- Normalization
- 调参实践
- 案例
- 结束
调参经验
- 【2022-6-22】深度学习调参技巧
- 李飞飞高徒、特斯拉AI总结发布机器学习33条秘技,原文链接
- 详解深度学习中的Normalization,BN/LN/WN
- The Black Magic of Deep Learning - Tips and Tricks for the practitioner
- 【2020-3-2】如何优雅地训练大型模型?
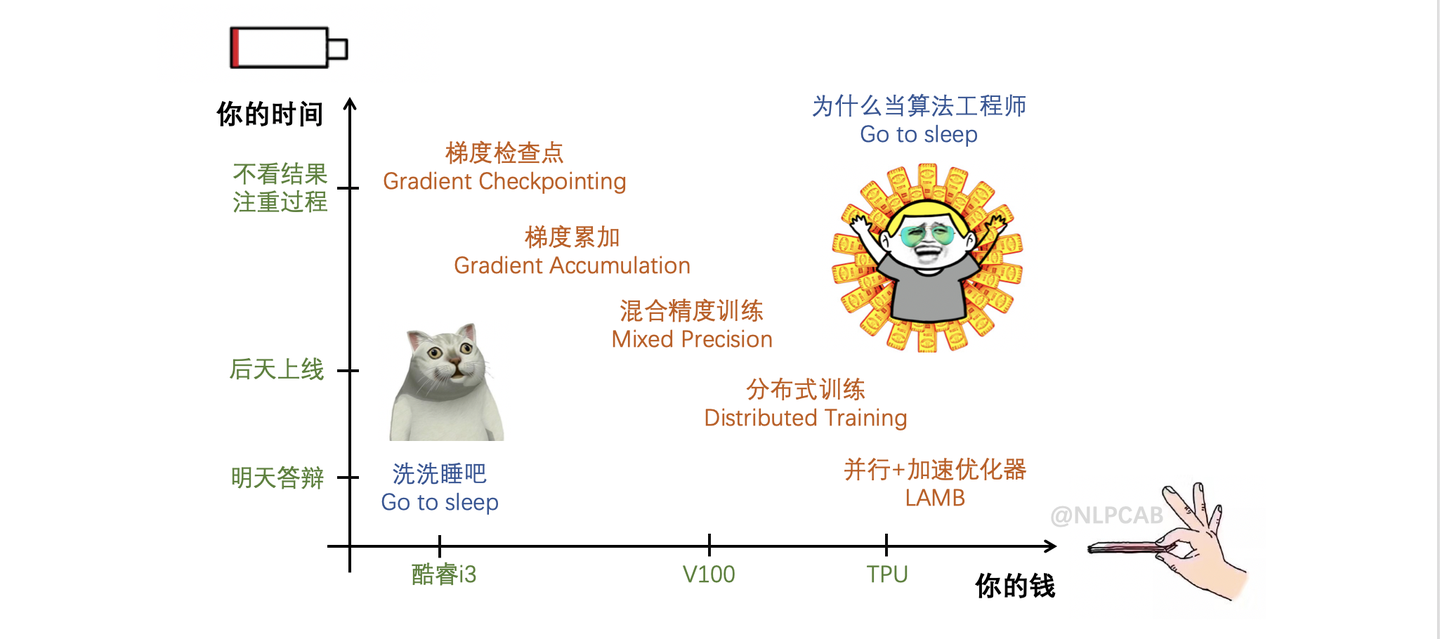
- 现实总是残酷的,其实限制大模型训练只有两个因素:时间和空间(=GPU=钱),根据不同情况可以使用的方案大致如下:
- 【2024-8-29】 谷歌、哈佛出品: 深度学习调优指南中文版
【2025-7-16】一句话加速模型训练,适用于 pytorch 动量优化器
# Caution an Optimizer (OPT) in PyTorch
# param p, update u from OP T, grad g
m = (u * g > 0).to(g.dtype)
p.add (u * m/(m.mean()+eps), alpha=-lr)
训练流程
pin_memory 是 锁页内存, GPU 存储
计算机运行进程, 先将进程和数据读到内存里。
计算机内存一般比较小,很难存的下太多的数据。但是,某个进程在某个时间段所需的进程和数据往往是比较少的,某个时间点不需要将一个进程所需要的所有资源都放在内存里。
将这些暂时用不到的数据或进程存放在硬盘一个被称为虚拟内存的地方。进程运行时,不断交换内存和虚拟内存的数据, 减少内存所需存储的数据。而且这些交换往往是通过某些规律预测下个时刻进程会用到的数据和代码并提前交换至内存的,这些规律的使用以及预测的准确性将会影响到进程的速度。
锁页内存:
- 不允许系统将某些内存里的数据交换至
虚拟内存,这将会提升进程的运行速度。但是也会是内存的存储占用消耗很多。
pin_memory 为 true 的时候速度的提升会有多大
参数调优价值
scaling law: 模型越大,高质量数据越多,效果越好。
但随着预训练样本的质量不断提升,训练手段的优化, 新模型效果往往能轻松反超参数量两倍模型。
例如,最新出 minicpm,微信内部评测效果也是非常棒。
- 跟规模相对接近的2b、7b模型比,得分比qwen2b高,和qwen7b比有的高有的低。
参数初始化
参数初始化方法
- 用高斯分布初始化
- 用xavier
- word embedding:xavier训练慢结果差,改为uniform,训练速度飙升,结果也飙升。
- 良好的初始化,可以让参数更接近最优解,这可以大大提高收敛速度,也可以防止落入局部极小。
- relu激活函数:初始化推荐使用He normal
- tanh激活函数:推荐使用xavier(Glorot normal)
一些参数的经验值,避免大家调参的时候,毫无头绪。
- learning rate: 1 0.1 0.01 0.001, 一般从1开始尝试。很少见learning rate大于10的。学习率一般要随着训练进行衰减。
- 衰减系数一般是0.5。
- 衰减时机:验证集准确率不再上升时,或固定训练多少个周期以后。
- 建议使用自适应梯度的办法,例如adam, adadelta, rmsprop等,这些一般使用相关论文提供的默认值即可,可以避免再费劲调节学习率。对RNN来说,有个经验,如果RNN要处理的序列比较长,或者RNN层数比较多,那么learning rate一般小一些比较好,否则有可能出现结果不收敛,甚至Nan等问题。
- 网络层数: 先从1层开始。
- 每层结点数: 16 32 128,超过1000的情况比较少见。超过1W的从来没有见过。
- batch size: 128上下开始。batch size值增加,的确能提高训练速度。但是有可能收敛结果变差。如果显存大小允许,可以考虑从一个比较大的值开始尝试。因为batch size太大,一般不会对结果有太大的影响,而batch size太小的话,结果有可能很差。
- clip c(梯度裁剪): 限制最大梯度,其实是value = sqrt(w1^2+w2^2….),如果value超过了阈值,就算一个衰减系系数,让value的值等于阈值: 5,10,15
- dropout: 0.5
- L2正则:1.0,超过10的很少见。
- 词向量embedding大小:128,256
- 正负样本比例: 这个是非常忽视,但是在很多分类问题上,又非常重要的参数。很多人往往习惯使用训练数据中默认的正负类别比例,当训练数据非常不平衡的时候,模型很有可能会偏向数目较大的类别,从而影响最终训练结果。除了尝试训练数据默认的正负类别比例之外,建议对数目较小的样本做过采样,例如进行复制。提高他们的比例,看看效果如何,这个对多分类问题同样适用。
- 在使用mini-batch方法进行训练的时候,尽量让一个batch内,各类别的比例平衡,这个在图像识别等多分类任务上非常重要。
超参
【2022-6-22】深度学习调参技巧
批量随机梯度下降算法
关键参数
学习率直接影响模型收敛状态,batchsize则影响模型的泛化性能
- 两者又是分子、分母直接关系,相互影响
Batch Size 和 学习率 之间存在密切关系。
- Batch Size 大小与学习率大小成正比。
- Batch Size 越大,每次权重更新时使用的样本信息越多,模型对训练数据的拟合程度就越高,因此可以选择较大的学习率来加快收敛速度。
策略
- batchsize 增大N倍时,要保证经过同样的样本后更新的权重相等,按照线性缩放规则,学习率应该增加为原来的N倍。
- 但是,如果要保证权重的方差不变,则学习率应该增加为原来的 sqrt(N) 倍
参考
【2024-5-27】 model size 与 学习率有什么关系?知乎,没有什么关系。Loss is all u need.
- 美团 Unraveling the Mystery of Scaling Laws:Part I: 只要超参(如 batch size、learning rate和learning rate scheduler)的设置处于合理的范围内,它们主要影响的是模型的收敛速度,而对最终的收敛【oSS影响不大。这意味着在估计L(N)时,无需对超参数进行细致调整,仅需采用一组固定的超参数设置即可。
- 质谱+清华 Understanding Emergent Abilities of Language Models from the Loss Perspective
filter
filter
- 用3x3大小
- 数量:2^n
- 第一层的filter数量不要太少,否则根本学不出来(底层特征很重要)
批大小 batch_size
batch_size 大小
- 每一次训练神经网络送入模型的样本数
- 可直接设置为 16 或 64。
- 通常取值:
[16, 32, 64, 128]
- 通常取值:
batch size 取值
- 选择 2次方(即64、128、256、512、1024等), 更加直接和易于管理
- batchsize <= 数据集样本数 * 0.1
为什么是2的指数倍?
- CPU讨厌 16,32,64……这样的数值
- GPU不会,GPU推荐取32的倍数,和 wrap 一致。
cpu有预取, gpu有合并访问, 不仅仅要求2的次方, 内存地址也是有要求。
经验:
- batch_size 大:收敛得快,需要训练的次数少,准确率上升得稳定,GPU利用更充分,但是精度不高,泛化能力差。
- batch_size 小:收敛得慢,准确率可能来回震荡,所以把基础学习速率降低些;但是最终精度较高,泛化能力强。有效避免样本中的冗余信息
batchsize越大越好
- 震荡明显减少
- 收敛速度加快
- 同样学习率下大batch可以收敛到更好的水平。
batch_size与2的倍数
batch_size = 2^n
观点
batch的大小并没有固定模式,不需要非要2^n的size。
一般根据GPU显存,设置为最大,而且是8的倍数(比如32,128),GPU内部并行运算效率最高。
- 方法一: 8的倍数,然后是稍微大一点(一般而言)。
- 方法二: 选择一部分数据,跑几个batch, 看loss是否变小,选择一个合适的。
Batch_Size
- Batch_Size = 1, 每次只训练一个样本, 在线学习(Online Learning)
- 在线学习,每次修正方向以各自样本的梯度方向修正,横冲直撞各自为政,难
- Batch_Size = N, full batch是特殊的mini batch, Full Batch Learning 并不适用大数据集,
batch size 分析
不同batch size的特点:
| 维度 | 小batch size | 大 batch size |
|---|---|---|
| 每次update的速度(不含平行计算) | 快 | 慢 |
| 每次update的速度(含平行计算) | 一样 | 几乎一样 |
| 训练一个epoch的时间 | 慢 | 快 |
| Gradient | Noisy | Stable |
| Optimization | 更好 | 不好 |
| 泛化能力 | 更好 | 不好 |
Flat minima vs Sharp minima

图解
- 黑色实线为 Training loss 曲线,存在不同类型的minima。
- 其中相对平坦的minima 叫
Flat minima,而相对峡谷 minima 叫Sharp minima。 - 而
Flat minima好于Sharp minima,因为- Testing Loss 曲线可能在 Training Loss 附近。而如果参数优化到了Sharp minima,那很可能得到非常大的Testing loss,进而影响性能
- 所以Flat minima是要好于Sharp minima的。
- 而小batch 更有利于收敛到Flat minima,因为
- 计算gradient 时会有很多的Noisy,这些Noisy的gradient使得曲线很有可能跳出Sharp minima,而优化到Flat minima的位置。
梯度累积
梯度累积 - gradient accumulation
- 变量名示例: gradient_accumulation_steps
batch_size 大小对模型效果(准确性和收敛速度)有很大影响。
- 一定条件下,batch_size 越大,模型就越稳定。
- batch_size 值通常设置在 8-32 之间
然而, batch_size 大小 受到GPU内存限制
GPU内存不变时,模型越大,batch_size只能越小, 怎么办?
- 梯度累积(Gradient Accumulation)可解决这个问题。
梯度累积(Gradient Accumulation)不需要额外硬件资源, 就可以增加批量样本数量(Batch Size)的训练技巧。
- 时间换空间: 将多个Batch训练数据的梯度进行累积,达到指定累积次数后,使用累积梯度统一更新一次模型参数,以达到一个较大Batch Size 模型训练效果。
- 累积梯度=多个Batch训练数据梯度的平均值。
梯度累积过程,梯度下降所用的梯度,实际上是多个样本算出来的梯度的平均值
以 batch_size=128 为例
- ① 一次性算出128个样本的梯度然后平均
- ② 每次算6个样本的平均梯度,然后缓存累加起来,算够了8次之后,然后把总梯度除以8,然后才执行参数更新。
一定条件下,batch_size 越大, 训练效果越好
- 梯度累加则实现了 batch_size 变相扩大
- 如果 accumulation_steps 为8,则 batch_size 变相 扩大了8倍,解决显存受限的trick
注意:
- 学习率也要适当放大。
常规深度学习训练流程:
optimizer.zero_grad()将前一个batch计算之后的网络梯度清零- 正向传播将数据和标签传入网络,过infer计算得到预测结果
- 根据预测结果与label,计算损失值
loss.backward(),利用损失进行反向传播,计算参数梯度optimizer.step(),利用计算的参数梯度更新网络参数
for i, (inputs, labels) in enumerate(trainloader):
optimizer.zero_grad() # 梯度清零
outputs = net(inputs) # 正向传播
loss = criterion(outputs, labels) # 计算损失
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新参数
if (i+1) % evaluation_steps == 0:
evaluate_model()
一个batch的数据,计算一次梯度,更新一次网络。
梯度累积
- 正向传播,将数据传入网络,得到预测结果
- 根据预测结果与label,计算损失值
- 利用损失进行反向传播,计算参数梯度
- 重复1-3,不清空梯度,而是将梯度累加
- 梯度累加达到固定次数之后,更新参数,然后将梯度清零
梯度累积时,每个batch 仍然正常前向传播以及反向传播,但是反向传播后并不进行梯度清零
- 因为 PyTorch
backward()执行梯度累加操作,所以当调用N次loss.backward()后,这N个batch 的梯度都会累加起来。但是,我们要的是一个平均梯度,或者说平均损失,所以将每次计算得到的 loss 除以 accum_steps。
for i, (inputs, labels) in enumerate(trainloader):
optimizer.zero_grad() # 梯度清零
outputs = net(inputs) # 正向传播
loss = criterion(outputs, labels) # 计算损失
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新参数
if (i+1) % evaluation_steps == 0:
evaluate_model()
# 梯度累积
for i, (inputs, labels) in enumerate(trainloader):
# optimizer.zero_grad()
outputs = net(inputs) # 正向传播
loss = criterion(outputs, labels) # 计算损失函数
# 新增计算梯度均值
loss = loss / accumulation_steps # 梯度均值,损失标准化
loss.backward() # 梯度均值累加,反向传播,计算梯度
# optimizer.step()
# 累加到指定的 steps 后再更新参数
if (i+1) % accumulation_steps == 0:
optimizer.step() # 更新参数
optimizer.zero_grad() # 梯度清零
if (i+1) % evaluation_steps == 0:
evaluate_model()
【2024-7-25】 Deepspeed 框架已实现梯度累积功能,所以使用ds时,不用手动求平均
激活函数
激活函数的选取
- 给神经网络加入一些非线性因素,使得网络可以解决较为复杂的问题
- 输出层:
- 多分类任务:softmax输出
- 二分类任务:sigmoid输出
- 回归任务:线性输出
- 中间层:优先选择 relu,有效的解决sigmoid和tanh出现的梯度弥散问题
- CNN:先用ReLU
- RNN:优先选用tanh激活函数
dropout
dropout
- 可防止过拟合,人力成本最低的Ensemble
- 加dropout,加BN,加Data argumentation
- dropout可以随机的失活一些神经元,从而不参与训练
示例 【Dropout 缓解过拟合】:
- 任务:拟合数据点(根据x值预测y值)
- 构建过拟合网络,比如这里使用了2层,每层节点数=200的网络
- 使用dropout和不使用dropout,看拟合的效果
- 对于过拟合(模型对训练集拟合得很好)的情况下,使用dropout,能够降低在测试集上的loss,和真实值预测的更贴近。

动量
momentum大小
- 使用默认的0.9
迭代次数
迭代次数
- 整个训练集输入到神经网络进行训练的次数
- 当训练集错误率和测试错误率想相差较小时:迭代次数合适
- 当测试错误率先变小后变大:迭代次数过大,需要减小,否则容易过拟合
优化器
优化器
- 自适应:Adagrad, Adadelta, RMSprop, Adam
- 整体来讲,Adam是最好的选择
- SGD:虽然能达到极大值,运行时间长,可能被困在鞍点
- Adam: 学习速率3e-4。能快速收敛。
残差
残差块和BN
- 残差块:可以让你的网络训练的更深
- BN:加速训练速度,有效防止梯度消失与梯度爆炸,具有防止过拟合的效果
- 构建网络时最好加上这两个组件
学习率 learning_rate
学习速率
- 优化算法中更新网络权重的幅度大小
- 可以恒定、逐渐下降的、基于动量的或者是自适应的
- 优先调这个LR:会很大程度上影响模型的表现
- 如果太大,会很震荡,类似于二次抛物线寻找最小值
- 一般学习率从0.1或0.01开始尝试
- 通常取值 [0.01, 0.001, 0.0001]
- 学习率一般要随着训练进行衰减。衰减系数设0.1,0.3,0.5均可,衰减时机,可以是验证集准确率不再上升时,或固定训练多少个周期以后自动进行衰减。
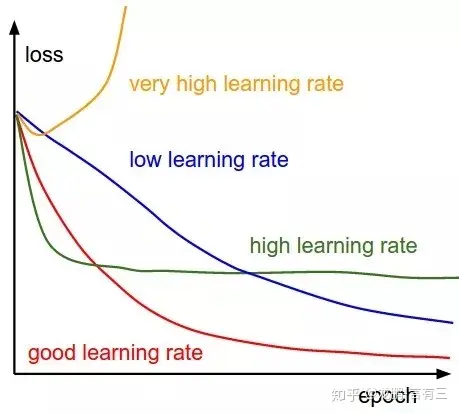
学习率与loss趋势分析
学习率与loss趋势分析
有人设计学习率的原则是监测一个比例:每次更新梯度的norm除以当前weight的norm,如果这个值在10e-3附近,且小于这个值,学习会很慢,如果大于这个值,那么学习很不稳定。

- 红线:初始学习率太大,导致振荡,应减小学习率,并从头开始训练
- 紫线:后期学习率过大导致无法拟合,应减小学习率,并重新训练后几轮
- 黄线:初始学习率过小,导致收敛慢,应增大学习率,并从头开始训练
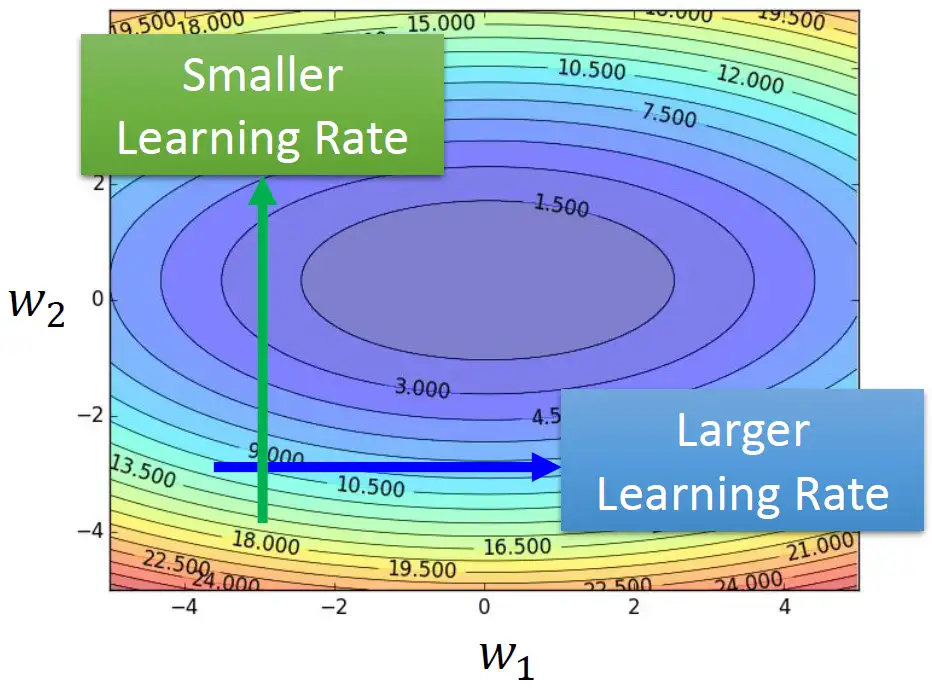
说明
- 梯度比较大的纵轴设置小的learning rate
- 梯度比较平坦的横轴设置大的learning rate

不同学习率对loss收敛的影响
优化算法
- Adagrad:对梯度平方根, 坡度大,学习率较小, 坡度小时学习率较大
- RMSprop的另一个改进版:Adam, 既考虑方向,又考虑大小
- RMSprop解决陡峭程度不同的问题
- AdamW就是Adam优化器加上L2正则,来限制参数值不可太大
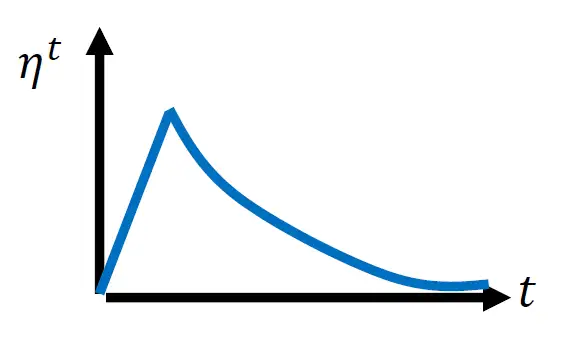
warm up 学习率调整策略
计算统计结果,某个方向有多陡/平滑。所以看了足够多的数据才精准。
- 一开始的统计不精准,计算是不准确的。
- 所以希望参数不离初始的地方太远。
- 这也是一开始learning rate小的原因,先去探索,收集统计数据,再让learning rate慢慢拉升。
学习率 与 batch size
学习率和batchsize的关系
- batchsize 变大 k 倍,学习率也要相应变大 $\sqrt{k}$ 倍,本质是梯度方差保持不变;
为什么要不变?
- 解决陷入局部最优和一个sharp 最小值(类似于V底)问题,增强泛化能力;增加了学习率,就增大了步长。
学习率直接影响模型的收敛状态,batchsize 影响模型的泛化性能。
- 学习率决定了权重迭代的步长,因此非常敏感
- 学习率对模型性能的影响体现在两个方面
- 初始学习率的大小
- 学习率的变换方案
策略
- 通常增加batchsize为原来的 N 倍时,要保证经过同样的样本后更新的权重相等,按照线性缩放规则,学习率应该增加为原来的 N 倍。
- 但是如果保证权重的方差不变,则学习率应该增加为原来的 $\sqrt{N}$ 倍
目前这两种策略都被研究过,使用前者的明显居多。
学习率和batchsize都是同时增加的。
- 学习率是一个非常敏感的因子,不可能太大,否则模型会不收敛。
- 同样batchsize也会影响模型性能
如何调整这两个参数?
衰减学习率可以通过增加batchsize来实现类似的效果,这实际上从SGD的权重更新式子就可以看出来两者确实是等价的,文中通过充分的实验验证了这一点。
对于一个固定的学习率,存在一个最优的batchsize能够最大化测试精度,这个batchsize和学习率以及训练集的大小正相关。
两个建议:
- 如果增加了学习率,那么batch size最好也跟着增加,这样收敛更稳定。
- 尽量使用大学习率,因为更大的学习率有利于提高泛化能力。如果真的要衰减,可以尝试其他办法,比如增加batch size,学习率对模型的收敛影响真的很大,慎重调整。
【2024-3-21】如何选择模型训练的batch size和learning rate
调参过程指南
- 【1】刚开始,先上小规模数据,模型往大了放(能用256个filter就别用128个),直接奔着
过拟合去(此时都可不用测试集验证集)- 验证训练脚本的流程。小数据量,速度快,便于测试。
- 如果小数据、大网络,还不能过拟合,需要检查输入输出、代码是否错误、模型定义是否恰当、应用场景是否正确理解。比较神经网络没法拟合的问题,这种概率太小了。
- 【2】loss设计要合理
- 分类问题:softmax
- 回归:L2 loss。
- 输出也要做归一化。如果label为10000,输出为0,loss会巨大。
- 多任务情况时,各个loss限制在同一个量级上。
- 【3】观察loss胜于观察准确率
- 优化目标是loss
- 准确率是突变的,可能原来一直未0,保持上千代迭代,突变为1
- loss不会突变,可能之前没有下降太多,之后才稳定学习
- 【4】确认分类网络学习充分
- 分类 =》类别之间的界限
- 网络从类别模糊到清晰,可以看softmax输出的概率分布。
- 刚开始,可能预测值都在0.5左右(模糊),学习之后才慢慢移动到0、1的极值
- 【5】学习速率是否设置合理
- 太大:loss爆炸或者nan
- 太小:loss下降太慢
- 当loss在当前LR下一路下降,但是不再下降了 =》可进一步降低LR
- 【6】对比训练集和验证集的loss
- 可判断是否过拟合
- 训练是否足够
- 是否需要early stop
- 【7】清楚receptive field大小
- CV中context window很重要
- 对模型的receptive field要有数
- 【8】在验证集上调参
【2022-10-16】知乎分享
- 先overfit 再trade off,首先保证你的模型capacity能够过拟合,再尝试减小模型,各种正则化方法;
- lr ,最重要的参数,一般nlp bert类模型在1e-5级别附近,warmup,衰减;cv类模型在1e-3级别附近,衰减;具体需要多尝试一下。
- batch size 在表示学习,对比学习领域一般越大越好,显存不够上累计梯度,否则模型可能不收敛… 其他领域看情况;
- dropout,现在大部分任务都需要使用预训练模型,要注意模型内部dropout ratio是一个很重要的参数,使用默认值不一定最优,有时候dropout reset到0有奇效
- 初始化方法,linear / cnn一般选用kaiming uniform 或者normalize,embedding 一般选择截断 normalize,论文很多,可以去看看。
- 序列输入上LN,非序列上BN
- 基于banckbone 构建层次化的neck 一般都比直接使用最后一层输出要好,reduce function 一般attention 优于简单pooling,多任务需要构建不同的qkv
- 数据增强要结合任务本身来设计
- 随机数种子设定好,否则很多对比实验结论不一定准确
- cross validation方式要结合任务设计,数据标签设计,其中时序数据要避免未来信息泄漏
- 优化器,nlp,抽象层次较高或目标函数非常不平滑的问题adam优先,其他可以尝试下sgd(一般需要的迭代次数高于sgd)
- 不要过早的early stopping,有时候收敛平台在后段,你会错过,参考1. ,先过拟合train set
调参秘方
- 摘自:训练模型的“处方”
- 总的来说,Andrej Karpathy的技巧就是:不要心急 (文章结尾会道出原因) ,从简单到复杂逐步完善你的神经网络。
- 1、先别着急写代码
- 训练神经网络前,别管代码,先从预处理数据集开始。我们先花几个小时的时间,了解数据的分布并找出其中的规律。
- Andrej有一次在整理数据时发现了重复的样本,还有一次发现了图像和标签中的错误。所以先看一眼数据能避免我们走很多弯路。
- 由于神经网络实际上是数据集的压缩版本,因此您将能够查看网络(错误)预测并了解它们的来源。如果你的网络给你的预测看起来与你在数据中看到的内容不一致,那么就会有所收获。
- 一旦从数据中发现规律,可以编写一些代码对他们进行搜索、过滤、排序。把数据可视化能帮助我们发现异常值,而异常值总能揭示数据的质量或预处理中的一些错误。
- 2、设置端到端的训练评估框架
- 处理完数据集,接下来就能开始训练模型了吗?并不能!下一步是建立一个完整的训练+评估框架。
- 在这个阶段,我们选择一个简单又不至于搞砸的模型,比如线性分类器、CNN,可视化损失。获得准确度等衡量模型的标准,用模型进行预测。
- 这个阶段的技巧有:
- 固定随机种子: 使用固定的随机种子,来保证运行代码两次都获得相同的结果,消除差异因素。
- 简单化: 在此阶段不要有任何幻想,不要扩增数据。扩增数据后面会用到,但是在这里不要使用,现在引入只会导致错误。
- 在评估中添加有效数字: 在绘制测试集损失时,对整个测试集进行评估,不要只绘制批次测试损失图像,然后用Tensorboard对它们进行平滑处理。
- 在初始阶段验证损失函数: 验证函数是否从正确的损失值开始。例如,如果正确初始化最后一层,则应在softmax初始化时测量-log(1/n_classes)。
- 初始化: 正确初始化最后一层的权重。如果回归一些平均值为50的值,则将最终偏差初始化为50。如果有一个比例为1:10的不平衡数据集,请设置对数的偏差,使网络预测概率在初始化时为0.1。正确设置这些可以加速模型的收敛。
- 人类基线: 监控除人为可解释和可检查的损失之外的指标。尽可能评估人的准确性并与之进行比较。或者对测试数据进行两次注释,并且对于每个示例,将一个注释视为预测,将第二个注释视为事实。
- 设置一个独立于输入的基线: 最简单的方法是将所有输入设置为零,看看模型是否学会从输入中提取任何信息。
- 过拟合一个batch: 增加了模型的容量并验证我们可以达到的最低损失。
- 验证减少训练损失: 尝试稍微增加数据容量。
- 在训练模型前进行数据可视化: 将原始张量的数据和标签可视化,可以节省了调试次数,并揭示了数据预处理和数据扩增中的问题。
- 可视化预测动态: 在训练过程中对固定测试批次上的模型预测进行可视化。
- 使用反向传播来获得依赖关系:一个方法是将第i个样本的损失设置为1.0,运行反向传播一直到输入,并确保仅在第i个样本上有非零的梯度。
- 概括一个特例:对正在做的事情编写一个非常具体的函数,让它运行,然后在以后过程中确保能得到相同的结果。
- 3、过拟合
- 首先我们得有一个足够大的模型,它可以过拟合,减少训练集上的损失,然后适当地调整它,放弃一些训练集损失,改善在验证集上的损失)。
- 这一阶段的技巧有:
- 挑选模型: 为了获得较好的训练损失,我们需要为数据选择合适的架构。不要总想着一步到位。如果要做图像分类,只需复制粘贴ResNet-50,我们可以在稍后的过程中做一些自定义的事。
- Adam方法是安全的: 在设定基线的早期阶段,使用学习率为3e-4的Adam 。根据经验,亚当对超参数更加宽容,包括不良的学习率。
- 一次只复杂化一个: 如果多个信号输入分类器,建议逐个输入,然后增加复杂性,确保预期的性能逐步提升,而不要一股脑儿全放进去。比如,尝试先插入较小的图像,然后再将它们放大。
- 不要相信学习率衰减默认值: 如果不小心,代码可能会过早地将学习率减少到零,导致模型无法收敛。我们完全禁用学习率衰减避免这种状况的发生。
- 4、正则化
- 理想的话,我们现在有一个大模型,在训练集上拟合好了。现在,该正则化了。舍弃一点训练集上的准确率,可以换取验证集上的准确率。
- 这里有一些技巧:
- 获取更多数据: 至今大家最偏爱的正则化方法,就是添加一些真实训练数据。不要在一个小数据集花太大功夫,试图搞出大事情来。有精力去多收集点数据,这是唯一一个确保性能单调提升的方法。
- 数据扩增: 把数据集做大,除了继续收集数据之外,就是扩增了。旋转,翻转,拉伸,做扩增的时候可以野性一点。
- 有创意的扩增: 还有什么办法扩增数据集?比如域随机化 (Domain Randomization) ,模拟 (Simulation) ,巧妙的混合 (Hybrids) ,比如把数据插进场景里去。甚至可以用上GAN。
- 预训练: 当然,就算你手握充足的数据,直接用预训练模型也没坏处。
- 跟监督学习死磕: 不要对无监督预训练太过兴奋了。至少在视觉领域,无监督到现在也没有非常强大的成果。虽然,NLP领域有了BERT,有了会讲故事的GPT-2,但我们看到的效果很大程度上还是经过了人工挑选。
- 输入低维一点: 把那些可能包含虚假信号的特征去掉,因为这些东西很可能造成过拟合,尤其是数据集不大的时候。同理,如果低层细节不是那么重要的话,就输入小一点的图片,捕捉高层信息就好了。
- 模型小一点: 许多情况下,都可以给网络加上领域知识限制 (Domain Knowledge Constraints) ,来把模型变小。比如,以前很流行在ImageNet的骨架上放全连接层,但现在这种操作已经被平均池化取代了,大大减少了参数。
- 减小批尺寸: 对批量归一化 (Batch Normalization) 这项操作来说,小批量可能带来更好的正则化效果 (Regularization) 。
- Dropout: 给卷积网络用dropout2d。不过使用需谨慎,因为这种操作似乎跟批量归一化不太合得来。
- 权重衰减: 增加权重衰减 (Weight Decay) 的惩罚力度。
- 早停法: 不用一直一直训练,可以观察验证集的损失,在快要过拟合的时候,及时喊停。
- 也试试大点的模型: 注意,这条紧接上条 (且仅接上条) 。我发现,大模型很容易过拟合,几乎是必然,但早停的话,模型可以表现很好。
- 最后的最后,如果想要更加确信,自己训练出的网络,是个不错的分类器,就把第一层的权重可视化一下,看看边缘 (Edges) 美不美。
- 如果第一层的过滤器看起来像噪音,就需要再搞一搞了。同理,激活 (Activations) 有时候也会看出瑕疵来,那样就要研究一下哪里出了问题。
- 5、调参
- 读到这里,你的AI应该已经开始探索广阔天地了。这里,有几件事需要注意。
- 随机网格搜索: 在同时调整多个超参数的情况下,网格搜索听起来是很诱人,可以把各种设定都包含进来。但是要记住,随机搜索才是最好的。直觉上说,这是因为网络通常对其中一些参数比较敏感,对其他参数不那么敏感。如果参数a是有用的,参数b起不了什么作用,就应该对a取样更彻底一些,不要只在几个固定点上多次取样。
- 超参数优化: 世界上,有许多许多靓丽的贝叶斯超参数优化工具箱,很多小伙伴也给了这些工具好评。但我个人的经验是,State-of-the-Art都是用实习生做出来的 (误) 。
- 读到这里,你的AI应该已经开始探索广阔天地了。这里,有几件事需要注意。
- 6、还能怎么压榨**
- 当你已经找到了好用的架构和好用的超参数,还是有一些技巧,可以在帮你现有模型上获得更好的结果,榨干最后一丝潜能:
- 模型合体: 把几个模型结合在一起,至少可以保证提升2%的准确度,不管是什么任务。如果,你买不起太多的算力,就用蒸馏 (Distill) 把模型们集合成一个神经网络。
- 放那让它训练吧: 通常,人类一看到损失趋于平稳,就停止训练了。但我感觉,还是训练得昏天黑地,不知道多久了,比较好。有一次,我意外把一个模型留在那训练了一整个寒假。我回来的时候,它就成了State-of-the-Art。
- 当你已经找到了好用的架构和好用的超参数,还是有一些技巧,可以在帮你现有模型上获得更好的结果,榨干最后一丝潜能:
超参优化
【2020-4-23】机器学习中模型性能的好坏往往与超参数(如batch size,filter size等)有密切的关系。
超参数优化存在着一些比较复杂的问题:
- 1、非线性,比如不能单独的固定xgboost的所有参数,单独优化n_estimators,因为参数和最终的评价指标之间并不一定是线性关系;
- 2、非凸,比如逻辑回归的正则化系数,直接写入损失函数中作为一个变量你会发现无法使用梯度下降法来求解,
- 3、组合优化:不同超参数的组合非常多,比如神经网络的层数,每层的神经元个数,每层使用的激活函数,使用的最优化算法等,这些参数随便组合起来就上百万了。
- 4、混合优化:参数中既有连续变量(比如lr的正则项系数),又有类别变量(比如选择l1或者l2)。
- 5、成本高,每一次训练都消耗一定的时间,如果数据量大模型复杂更是消耗时间,所以不可能穷举。
- 最开始为了找到一个好的超参数,通常都是靠人工试错的方式找到”最优”超参数。但是这种方式效率太慢,所以相继提出了
网格搜索(Grid Search, GS) 和随机搜索(Random Search,RS)。 - 但是GS和RS这两种方法总归是盲目地搜索,所以
贝叶斯优化(Bayesian Optimization,BO) 算法闪亮登场。BO算法能很好地吸取之前的超参数的经验,更快更高效地最下一次超参数的组合进行选择。 - 调参算法的输入是用户指定的参数及其范围,比如设定学习率范围为[0.0001, 0.01]。比较常见的算法为
网格搜索,随机搜索和贝叶斯优化等。
一般也是先用Gird Search的方法,得到所有候选参数,然后每次从中随机选择进行训练。
【2024-4-23】一文汇总超参自动优化方法
- 超参自动优化方法,像网格搜索、随机搜索、贝叶斯优化和 Hyperband,并附有相关的样例代码
网格搜索 Grid search —— 组合爆炸
Grid search 遍历所有可能的参数组合。
网格搜索是暴力搜索,在给定超参搜索空间内,尝试所有超参组合,最后搜索出最优的超参组合
原理
网格搜索很容易理解和实现
- 超参数A有2种选择,超参数B有3种选择,超参数C有5种选择,那么所有超参数组合就有2 * 3 * 5=30种
- 遍历这30种组合并且找到最优方案
- 对于连续值还需要等间距采样。
- 实际上这30种组合不一定取得全局最优解,而且计算量很大,很容易组合爆炸,并不是一种高效的参数调优方法。
- 注:为什么不一定全局最优?
sklearn.model_selection.GridSearchCV 重要参数说明:
estimator: scikit-learn模型。param_grid: 超参搜索空间,即超参数字典。scoring: 在交叉验证中使用的评估策略。n_jobs: 并行任务数,-1为使用所有CPU。cv: 决定采用几折交叉验证。
工程实现
官方源码: sklearn.model_selection.GridSearchCV
from sklearn import svm, datasets
from sklearn.model_selection import GridSearchCV
import pandas as pd
# 导入数据
iris = datasets.load_iris()
# 定义超参搜索空间
parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]}
# 初始化模型
svc = svm.SVC()
# 网格搜索
clf = GridSearchCV(estimator = svc,
param_grid = parameters,
scoring = 'accuracy',
n_jobs = -1,
cv = 5)
clf.fit(iris.data, iris.target)
返回:GridSearchCV(cv=5, estimator=SVC(), n_jobs=-1,
param_grid={'C': [1, 10], 'kernel': ('linear', 'rbf')},
scoring='accuracy')
# 打印结果
print('详细结果:\n', pd.DataFrame.from_dict(clf.cv_results_))
print('最佳分类器:\n', clf.best_estimator_)
print('最佳分数:\n', clf.best_score_)
print('最佳参数:\n', clf.best_params_).
# 返回:
# 详细结果:
# mean_fit_time std_fit_time mean_score_time std_score_time param_C ... split3_test_score split4_test_score mean_test_score std_test_score rank_test_score
# 0 0.000788 0.000394 0.000194 0.000389 1 ... 0.966667 1.0 0.980000 0.016330 1
# 1 0.000804 0.000402 0.000199 0.000399 1 ... 0.933333 1.0 0.966667 0.021082 4
# 2 0.000593 0.000484 0.000593 0.000484 10 ... 0.966667 1.0 0.973333 0.038873 3
# 3 0.000593 0.000484 0.000399 0.000489 10 ... 0.966667 1.0 0.980000 0.016330 1
# [4 rows x 15 columns]
# 最佳分类器:
# SVC(C=1, kernel='linear')
# 最佳分数:
# 0.9800000000000001
# 最佳参数:
# {'C': 1, 'kernel': 'linear'}
随机搜索 Random search —— 改进:减少次数
Random search 限定搜索次数,随机选择参数进行实验。
原理
随机搜索是在搜索空间中采样出超参组合,选出采样组合中最优的超参组合
如搜索两个参数,但参数A重要,而参数B并没有想象中重要,网格搜索9个参数组合(A, B),而由于模型更依赖于重要参数A,所以只有3个参数值是真正参与到最优参数的搜索工作中。
- 反观随机搜索,随机采样9种超参组合,在重要参数A上会有9个参数值参与到搜索工作中
所以,某些参数对模型影响较小时,使用随机搜索有更多的探索空间。
- 适用于 参数重要性不同 的情形
业界公认 Random search效果会比Grid search好,Random search其实就是随机搜索
- 例如前面的场景A有2种选择、B有3种、C有5种、连续值随机采样,那么每次分别在A、B、C中随机取值组合成新的超参数组合来训练。
- 虽然有随机因素,但随机搜索可能出现效果特别差、也可能出现效果特别好,在尝试次数和Grid search相同的情况下一般最值会更大
Bengio在Random Search for Hyper-Parameter Optimization中指出,Random Search比Gird Search更有效。
工程实现
相比于网格搜索,sklearn 随机搜索中主要改变的参数是 param_distributions,负责提供超参值分布范围
from sklearn import svm, datasets
from sklearn.model_selection import RandomizedSearchCV
import pandas as pd
from scipy.stats import uniform
# 导入数据
iris = datasets.load_iris()
# 定义超参搜索空间
distributions = {'kernel':['linear', 'rbf'], 'C':uniform(loc=1, scale=9)}
# 初始化模型
svc = svm.SVC()
# 网格搜索
clf = RandomizedSearchCV(estimator = svc,
param_distributions = distributions,
n_iter = 4,
scoring = 'accuracy',
cv = 5,
n_jobs = -1,
random_state = 2021)
clf.fit(iris.data, iris.target)
返回:RandomizedSearchCV(cv=5, estimator=SVC(), n_iter=4, n_jobs=-1,
param_distributions={'C': <scipy.stats._distn_infrastructure.rv_frozen object at 0x000001F372F9A190>,
'kernel': ['linear', 'rbf']},
random_state=2021, scoring='accuracy')
# 打印结果
print('详细结果:\n', pd.DataFrame.from_dict(clf.cv_results_))
print('最佳分类器:\n', clf.best_estimator_)
print('最佳分数:\n', clf.best_score_)
print('最佳参数:\n', clf.best_params_)
# 返回:
# 详细结果:
# mean_fit_time std_fit_time mean_score_time std_score_time param_C ... split3_test_score split4_test_score mean_test_score std_test_score rank_test_score
# 0 0.000598 0.000489 0.000200 0.000400 6.4538 ... 0.966667 1.0 0.986667 0.016330 1
# 1 0.000997 0.000002 0.000000 0.000000 4.99782 ... 0.966667 1.0 0.980000 0.026667 3
# 2 0.000798 0.000399 0.000399 0.000488 3.81406 ... 0.966667 1.0 0.980000 0.016330 3
# 3 0.000598 0.000488 0.000200 0.000399 5.36286 ... 0.966667 1.0 0.986667 0.016330 1
# [4 rows x 15 columns]
# 最佳分类器:
# SVC(C=6.453804509266643)
# 最佳分数:
# 0.9866666666666667
# 最佳参数:
# {'C': 6.453804509266643, 'kernel': 'rbf'}
贝叶斯搜索 Bayesian Optimization
目标函数 f 常是被称作 expensive blackbox function,计算开销大且不一定为凸函数。
为此,贝叶斯优化出现了,特别适合针对 expensive blackbox function 找到全局最优。
Bayesian Optimization 原理:
- Practical Bayesian Optimization of Machine Learning Algorithms
- Duane Rich《How does Bayesian optimization work?》
- 目标
- 找到一组最优的超参组合,能使目标函数f达到全局最小值。
原理
每次尝试一种超参值 x,计算 f(x) 代价昂贵,为了减轻开销,贝叶斯优化采用了代理模型(surrogate model)
- 一个简单模型去拟合原本复杂且不好理解的模型
- f(x) 计算太昂贵了,就用代理模型去代替它。
贝叶斯优化使用高斯过程(gasussian processes, GP) 构建代理模型,基于给定的输入和输出,GP会推断出一个模型(代理模型)。假设从昂贵的 f(x) 采样了4个点,然后把这4个点交给GP,它会返回一个代理模型
问题: “如何找到下一个合适的点?”,本质是在问:“哪里有全局最小的点?”,为了解决这个问题,关注两个地方:
- (1) 已开发区域: 在绿色实线上最低的超参点。因为很可能它附近存在全局最优点。
- (2) 未探索区域: 绿色实线上还未被探索的区域。比如图4,相比于0.15-0.25区间,0.65-0.75区间更具有探索价值(即该区间Uncertainty更大)。探索该区域有利于减少猜测的方差。
为了实现以上探索和开发的平衡(exploration-exploitation trade-off) ,贝叶斯优化使用了采集函数(acquisition function) ,平衡好全局最小值的探索和开发。
采集函数有很多选择,其中最常见的是expectated of improvement(EI)
SMBO是简洁版的贝叶斯优化
业界的很多参数调优系统都是基于贝叶斯优化的,如 Google Vizier, SigOpt
- 该算法要求已经存在几个样本点(一开始可以采用随机搜索来确定几个初始点),并且通过高斯过程回归(假设超参数间符合联合高斯分布)计算前面n个点的后验概率分布,得到每一个超参数在每一个取值点的期望均值和方差,其中均值代表这个点最终的期望效果,均值越大表示模型最终指标越大,方差表示这个点的效果不确定性,方差越大表示这个点不确定是否可能取得最大值非常值得去探索。
- 但是BO算法也有它的缺点:
- 对于那些具有未知平滑度和有噪声的高维、非凸函数,BO算法往往很难对其进行拟合和优化,而且通常BO算法都有很强的假设条件,而这些条件一般又很难满足。
- 为了解决上面的缺点,有的BO算法结合了
启发式算法(heuristics),但是这些方法很难做到并行化
贝叶斯优化好像在实践中用的不多, 原因是贝叶斯的开销太大
- 每次循环选超参值的时候,贝叶斯优化都需要将 带入昂贵的目标函数 中,去得到输出值y,当目标函数特别复杂时,这种情况的评估开销是很大的,更何况随着搜索空间和搜索次数的变大,计算会越发昂贵。
工程实现
贝叶斯调参的Python库,可以上手即用:
- jaberg/hyperopt, 比较简单。
- fmfn/BayesianOptimization,比较复杂,支持并行调参。
Hyperopt 开源代码库已实现基于TPE(Tree-structured Parzen Estimator Approach) 的贝叶斯优化
- Hyperopt: Distributed Hyperparameter Optimization, 代码: hyperopt
from sklearn import svm, datasets
from sklearn.model_selection import cross_val_score
from hyperopt import hp, fmin, tpe, space_eval
import pandas as pd
# 导入数据
iris = datasets.load_iris()
# step1: 定义目标函数
def objective(params):
# 初始化模型并交叉验证
svc = svm.SVC(**params)
cv_scores = cross_val_score(svc, iris.data, iris.target, cv=5)
# 返回loss = 1 - accuracy (loss必须被最小化)
loss = 1 - cv_scores.mean()
return loss
# step2: 定义超参搜索空间
space = {'kernel':hp.choice('kernel', ['linear', 'rbf']),
'C':hp.uniform('C', 1, 10)}
# step3: 在给定超参搜索空间下,最小化目标函数
best = fmin(objective, space, algo=tpe.suggest, max_evals=100)
返回: best_loss: 0.013333333333333308(即accuracy为0.9866666666666667)
# step4: 打印结果
print(best)
返回:{'C': 6.136181888987526, 'kernel': 1}(PS:kernel为0-based index,这里1指rbf)
Hyperband – 随机搜索变种
除了格子搜索、随机搜索和贝叶斯优化,还有其它自动调参方式。例如 Hyperband optimization
Hyperband 本质是随机搜索的一种变种,用早停策略和Sccessive Halving算法去分配资源,结果是Hyperband能评估更多的超参组合,同时在给定的资源预算下,比贝叶斯方法收敛更快
- 代码: HpBandSte
Hyperband之后,还出现了BOHB,它混合了贝叶斯优化和Hyperband。Hyperband和BOHB的开源代码可参考HpBandSter库
初始化
Normalization
- 详解深度学习中的Normalization,BN/LN/WN
- 深度神经网络模型训练之难众所周知,其中一个重要的现象就是
Internal Covariate Shift. Batch Norm 大法自 2015 年由 Google 提出之后,就成为深度学习必备之神器。自 BN 之后, Layer Norm / Weight Norm / Cosine Norm 等也横空出世。本文从 Normalization 的背景讲起,用一个公式概括 Normalization 的基本思想与通用框架,将各大主流方法一一对号入座进行深入的对比分析,并从参数和数据的伸缩不变性的角度探讨 Normalization 有效的深层原因。
1 为什么需要 Normalization
深度学习中的 Internal Covariate Shift 问题及其影响
1.1 独立同分布与白化
- 机器学习界的炼丹师们最喜欢的数据有什么特点?窃以为莫过于 “独立同分布” 了,即 independent and identically distributed,简称为
i.i.d. 独立同分布并非所有机器学习模型的必然要求- 比如 Naive Bayes 模型就建立在特征彼此独立的基础之上
- 而 Logistic Regression 和 神经网络 则在非独立的特征数据上依然可以训练出很好的模型)
- 但独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力,已经是一个共识。
- 因此,在把数据喂给机器学习模型之前,“白化(whitening)” 是一个重要的数据预处理步骤。白化一般包含两个目的:
- (1)去除特征之间的相关性 —> 独立;
- (2)使得所有特征具有相同的均值和方差 —> 同分布。
- 白化最典型的方法就是 PCA,可以参考阅读 PCA Whitening(http://t.cn/R9xZyMG )。
1.2 深度学习中的 Internal Covariate Shift
- 深度神经网络模型的训练为什么会很困难?
- 其中一个重要的原因是,深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。
- 为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
- Google 将这一现象总结为 Internal Covariate Shift,简称 ICS. (Covariate协变量)什么是 ICS 呢?@魏秀参在一个回答中做出了一个很好的解释:
- 大家都知道在统计机器学习中的一个经典假设是 “源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。
- 如果不一致,那么就出现了新的机器学习问题,如 transfer learning / domain adaptation 等。
- 而 covariate shift 就是分布不一致假设之下的一个分支问题,它是指源空间和目标空间的条件概率是一致的,但是其边缘概率不同
- 神经网络的各层输出经过了层内操作作用,其分布显然与各层对应的输入信号分布不同,而且差异会随着网络深度增大而增大,但它们 “指示” 的样本标记(label)仍然是不变的,这便符合了 covariate shift 的定义。由于是对层间信号的分析,也即是 “internal” 的来由。
1.3 ICS 会导致什么问题?
简而言之,每个神经元的输入数据不再是 “独立同分布”。
- 其一,上层参数需要不断适应新的输入数据分布,降低学习速度。
- 其二,下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。
- 其三,每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
2 Normalization 的通用框架与基本思想
从主流 Normalization 方法中提炼出的抽象框架
- 由于 ICS 问题的存在,x 的分布可能相差很大。要解决独立同分布的问题,“理论正确” 的方法就是对每一层的数据都进行白化操作。然而标准的白化操作代价高昂,特别是我们还希望白化操作是可微的,保证白化操作可以通过反向传播来更新梯度。
- 因此,以 BN 为代表的 Normalization 方法退而求其次,进行了简化的白化操作。
- 基本思想是:在将 x 送给神经元之前,先对其做平移和伸缩变换, 将 x 的分布规范化成在固定区间范围的标准分布。
- 通用变化框架

- 这个公式中的各个参数。
- (1)μ 是平移参数(shift parameter),σ 是缩放参数(scale parameter)。通过这两个参数进行 shift 和 scale 变换:x1 = (x-μ)/σ, 得到的数据符合均值为 0、方差为 1 的标准分布。
- (2)b 是再平移参数(re-shift parameter),g 是再缩放参数(re-scale parameter)。将 上一步得到的x1, 进一步变换为 y = g*x1+b
最终得到的数据符合均值为 b、方差为g^2的分布
- 第一步的变换将输入数据限制到了一个全局统一的确定范围(均值为 0、方差为 1)。下层神经元可能很努力地在学习,但不论其如何变化,其输出的结果在交给上层神经元进行处理之前,将被粗暴地重新调整到这一固定范围。
- (1)说好的处理 ICS,第一步都已经得到了标准分布,第二步怎么又给变走了?
- 答案是——为了保证模型的表达能力不因为规范化而下降。
- (2)难道我们底层神经元人民就在做无用功吗?
- 为了尊重底层神经网络的学习结果,将规范化后的数据进行再平移和再缩放,使得每个神经元对应的输入范围是针对该神经元量身定制的一个确定范围(均值为 b、方差为g^2)。
- ①rescale 和 reshift 的参数都是可学习的,这就使得Normalization 层可以学习如何去尊重底层的学习结果。
- ②保证获得非线性的表达能力. Sigmoid 等激活函数在神经网络中有着重要作用,通过区分饱和区和非饱和区,使得神经网络的数据变换具有了非线性计算能力。而第一步的规范化会将几乎所有数据映射到激活函数的非饱和区(线性区),仅利用到了线性变化能力,从而降低了神经网络的表达能力。而进行再变换,则可以将数据从线性区变换到非线性区,恢复模型的表达能力。
- (3)变回来再变过去,会不会跟没变一样?
- 不会。因为,再变换引入的两个新参数 g 和 b,可以表示旧参数作为输入的同一族函数,但是新参数有不同的学习动态。在旧参数中,x 的均值取决于下层神经网络的复杂关联;但在新参数中,y=g*x1+b,仅由 b 来确定,去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习,简化了神经网络的训练。
- (4)这样的 Normalization 离标准的白化还有多远?
- 标准白化操作的目的是 “独立同分布”。独立就不说了,暂不考虑。变换为均值为 b、方差为g^2的分布,也并不是严格的同分布,只是映射到了一个确定的区间范围而已。
3 主流 Normalization 方法梳理
结合上述框架,将 BatchNorm / LayerNorm / WeightNorm / CosineNorm 对号入座,各种方法之间的异同水落石出。BN, LN, WN 和 CN 之间的来龙去脉
- Normalization 的通用公式
- 对照于这一公式,我们来梳理主流的四种规范化方法。
3.1 Batch Normalization —— 纵向规范化
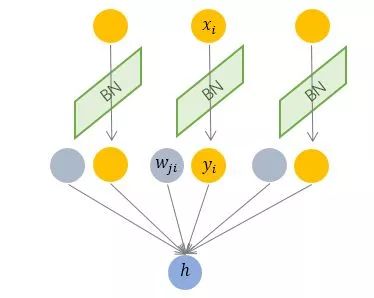
- Batch Normalization 于 2015 年由 Google 提出,开 Normalization 之先河。其规范化针对单个神经元进行,利用网络训练时一个 mini-batch 的数据来计算该神经元的均值和方差, 因而称为 Batch Normalization。
- 其中 M 是 mini-batch 的大小。按上图所示,相对于一层神经元的水平排列,BN 可以看做一种纵向的规范化。由于 BN 是针对单个维度定义的,因此标准公式中的计算均为 element-wise 的。BN 独立地规范化每一个输入维度xi,但规范化的参数是一个 mini-batch 的一阶统计量和二阶统计量。这就要求 每一个 mini-batch 的统计量是整体统计量的近似估计,或者说每一个 mini-batch 彼此之间,以及和整体数据,都应该是近似同分布的。分布差距较小的 mini-batch 可以看做是为规范化操作和模型训练引入了噪声,可以增加模型的鲁棒性;但如果每个 mini-batch 的原始分布差别很大,那么不同 mini-batch 的数据将会进行不一样的数据变换,这就增加了模型训练的难度。
- 因此,BN 比较适用的场景是:每个 mini-batch 比较大,数据分布比较接近。在进行训练之前,要做好充分的 shuffle. 否则效果会差很多。
- 另外,由于 BN 需要在运行过程中统计每个 mini-batch 的一阶统计量和二阶统计量,因此不适用于动态的网络结构 和 RNN 网络。不过,也有研究者专门提出了适用于 RNN 的 BN 使用方法
3.2 Layer Normalization —— 横向规范化
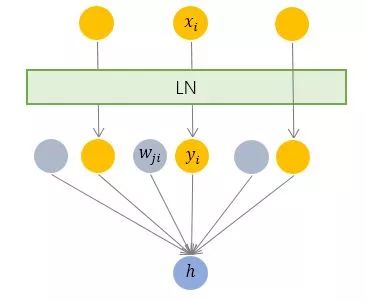
- 层规范化就是针对 BN 的上述不足而提出的。与 BN 不同,LN 是一种横向的规范化,如图所示。它综合考虑一层所有维度的输入,计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
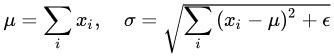
- 其中 i 枚举了该层所有的输入神经元。对应到标准公式中,四大参数 μ,σ,g,b 均为标量(BN 中是向量),所有输入共享一个规范化变换。
- LN 针对单个训练样本进行,不依赖于其他数据,因此可以避免 BN 中受 mini-batch 数据分布影响的问题,可以用于 小 mini-batch 场景、动态网络场景和 RNN,特别是自然语言处理领域。此外,LN 不需要保存 mini-batch 的均值和方差,节省了额外的存储空间。
- 但是,BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。
3.3 Weight Normalization —— 参数规范化
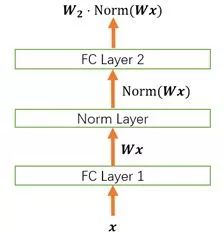
- 前面我们讲的模型框架
中,经过规范化之后的 y 作为输入送到下一个神经元,应用以 w 为参数的fw(-), 函数定义的变换。最普遍的变换是线性变换fw(x)=w*x
- BN 和 LN 均将规范化应用于输入的特征数据 x,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 w,这就是 WN 名称的来源。
- WN 提出的方案是,将权重向量 w 分解为向量方向 v 和向量模 g 两部分
- BN 和 LN 是用输入的特征数据的方差对输入数据进行 scale,而 WN 则是用 神经元的权重的欧氏范式对输入数据进行 scale。虽然在原始方法中分别进行的是特征数据规范化和参数的规范化,但本质上都实现了对数据的规范化,只是用于 scale 的参数来源不同。
- 另外,我们看到这里的规范化只是对数据进行了 scale,而没有进行 shift,因为我们简单地令μ=0。但事实上,这里留下了与 BN 或者 LN 相结合的余地——那就是利用 BN 或者 LN 的方法来计算输入数据的均值 μ。
- WN 的规范化不直接使用输入数据的统计量,因此避免了 BN 过于依赖 mini-batch 的不足,以及 LN 每层唯一转换器的限制,同时也可以用于动态网络结构。
3.4 Cosine Normalization —— 余弦规范化
- Normalization 还能怎么做?
- 我们再来看看神经元的经典变换fw(x)=w*x
- 对输入数据 x 的变换已经做过了,横着来是 LN,纵着来是 BN。
- 对模型参数 w 的变换也已经做过了,就是 WN。
- 好像没啥可做的了。
- 然而天才的研究员们盯上了中间的那个点, 对数据进行规范化的原因,是数据经过神经网络的计算之后可能会变得很大,导致数据分布的方差爆炸,而这一问题的根源就是我们的计算方式——点积,权重向量 w 和 x 特征数据向量 的点积。向量点积是无界(unbounded)的啊!
- 有没有其他的相似度衡量方法呢?有,夹角余弦就是其中之一啊!而且关键的是,夹角余弦是有确定界的啊,[-1, 1] 的取值范围,多么的美好
- 于是,Cosine Normalization 就出世了。他们不处理权重向量 w,也不处理特征数据向量 x ,就改了一下线性变换的函数
- 总结,CN 与 WN 还是很相似的。我们看到上式中,分子还是 w 和 x 的内积,而分母则可以看做用 w 和 x 二者的模之积进行规范化。一定程度上可以理解为,WN 用 权重的模对输入向量进行 scale,而 CN 在此基础上用输入向量的模对输入向量进行了进一步的 scale.
- CN 通过用余弦计算代替内积计算实现了规范化,但成也萧何败萧何。原始的内积计算,其几何意义是 输入向量在权重向量上的投影,既包含 二者的夹角信息,也包含 两个向量的 scale 信息。去掉 scale 信息,可能导致表达能力的下降,因此也引起了一些争议和讨论。具体效果如何,可能需要在特定的场景下深入实验。
其它
- 超越BN和GN!谷歌提出新的归一化层:FRN
- 目前主流的深度学习模型都会采用BN层(Batch Normalization)来加速模型训练以及提升模型效果,对于CNN模型,BN层已经上成为了标配。
- 但是BN层在训练过程中需要在batch上计算中间统计量,这使得BN层严重依赖batch,造成训练和测试的不一致性,当训练batch size较小,往往会恶化性能。
- GN(Group Normalization)通过将特征在channel维度分组来解决这一问题,GN在batch size不同时性能是一致的,但对于大batch size,GN仍然难以匹敌BN。这里介绍谷歌提出的一种新的归一化方法FRN,和GN一样不依赖batch,但是性能却优于BN和GN。
- 以CNN模型为例,中间特征的维度为[B, H, W, C],BN首先在计算在(N H, W)维度上的均值[公式]和方差[公式],然后各个通道上(C维度)进行标准归一化。最后对归一化的特征进行放缩和平移(scale and shift),这里[公式]和[公式]是可学习的参数(参数大小为C)。
- BN的一个问题是训练时batch size一般较大,但是测试时batch size一般为1,而均值和方差的计算依赖batch,这将导致训练和测试不一致。
- BN的解决方案
- (1)在训练时估计一个均值和方差量来作为测试时的归一化参数,一般对每次mini-batch的均值和方差进行指数加权平均(滑动平均)来得到这个量。
- 虽然解决了训练和测试的不一致性,但是BN对于batch size比较敏感,当batch size较小时,模型性能会明显恶化。对于一个比较大的模型,由于显存限制,batch size难以很大,比如目标检测模型,这时候BN层可能会成为一种限制。
- 当训练集和测试集分布差异大时,训练集上预计算好的数据并不能代表测试数据,这就导致在训练,验证,测试这三个阶段存在inconsistency
- (2)另外一个方向是避免在batch维度进行归一化,这样当然就不会带来训练和测试的不一致性问题。这些方法包括Layer Normalization (LN), Instance Normalization (IN)以及最新的Group Normalization(GN),这些方法与BN的区别可以从图1中看出来:
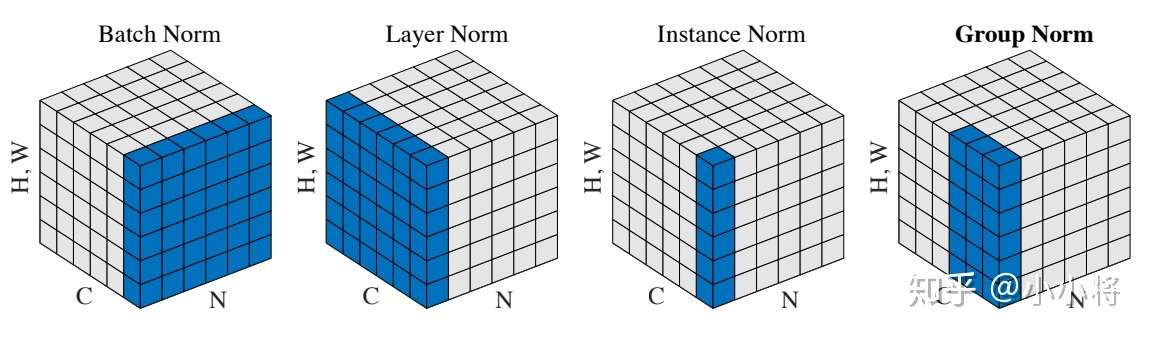
- 这些方法处理方式和BN类似,但是归一化的维度不一样,BN是在(N, H, W)维度上,LN是在(H,W,C)维度上,IN是在(H,W)维度上,GN更巧妙,其通过对C分组,此时特征可以从[N, H, W, C]变成[N, H, W, G, C/G],GN的计算是在[H, W, G]维度上。LN,IN以及GN都没有在B维度上进行归一化,所以不会有BN的问题.GN基本不受batch size的影响,而BN在batch size较小时性能大幅度恶化,但是在较大batch size,BN的效果是稍好于GN的。
- (3)解决BN在小batch性能较差的另外一个方向是直接降低训练和测试之间不一致性
- 比较常用的方法是Batch Renormalization (BR),它主要的思路是限制训练过程中batch统计量的值范围。
- 另外的一个解决办法是采用多卡BN方法训练,相当于增大batch size。
- (1)在训练时估计一个均值和方差量来作为测试时的归一化参数,一般对每次mini-batch的均值和方差进行指数加权平均(滑动平均)来得到这个量。
- FRN
- 谷歌的提出的FRN层包括归一化层FRN(Filter Response Normalization)和激活层TLU(Thresholded Linear Unit),如图3所示。FRN层不仅消除了模型训练过程中对batch的依赖,而且当batch size较大时性能优于BN。

4 Normalization 为什么会有效?
从参数和数据的伸缩不变性探讨 Normalization 有效的深层原因。
- 以这个简化的神经网络为例
4.1 Normalization 的权重伸缩不变性
- 权重伸缩不变性(weight scale invariance)指的是,当权重 W 按照常量 λ 进行伸缩时,得到的规范化后的值保持不变
- 作用
- 权重伸缩不变性可以有效地提高反向传播的效率
- 权重伸缩不变性还具有参数正则化的效果,可以使用更高的学习率
4.2 Normalization 的数据伸缩不变性
- 数据伸缩不变性(data scale invariance)指的是,当数据 x 按照常量 λ 进行伸缩时,得到的规范化后的值保持不变
- 数据伸缩不变性仅对 BN、LN 和 CN 成立。因为这三者对输入数据进行规范化,因此当数据进行常量伸缩时,其均值和方差都会相应变化,分子分母互相抵消。而 WN 不具有这一性质。
- 数据伸缩不变性可以有效地减少梯度弥散,简化对学习率的选择。
调参实践
epoch
过拟合
【2025-7-23】多少Epoch不会过拟合
大模型训练多少 Epoch 不会过拟合?
首先:
- 没有固定的“多少 Epoch 不会过拟合”的标准答案
- 因为 Epoch 的合理范围取决于数据质量、模型复杂度、任务特性三者的匹配关系。
基础原理层面
过拟合本质是模型“学到了训练数据中的噪声而非通用规律”,而 Epoch 是训练数据被完整遍历的次数。
- 当模型复杂度(如参数规模)远大于数据所能提供的“有效信息密度”时,即使较少的 Epoch(如 3 - 5 轮)也可能过拟合;
- 反之,若数据规模大、多样性高,且模型复杂度适中,即使 100 轮以上也可能保持泛化能力。
应用场景上:
- 小样本任务(如几千样本微调大模型):通常 1 - 3 轮足够,多了容易记住样本细节;
- 大规模预训练(万亿级文本):可能需要 100 轮以上,因为数据多样性高,模型需要反复学习不同模式;
- 数据质量差(含大量重复 / 噪声):即使百万级样本,5 - 10 轮也可能过拟合,因为模型会优先“记住”重复信息。
实际中更有效的思路是动态监控 + 自适应调整:
- 通过验证集损失、泛化指标(如测试集准确率)实时判断,而非预设固定值。
- 核心是让 Epoch 数量与“数据能支撑的有效学习轮次”匹配——数据越优质、多样,模型可训练的 Epoch 越多。
GPU 相关
GPU OOM
错误
RuntimeError: CUDA Out of memory
解法,按代码更改的顺序递增:
- 减少“batch_size”
- 模型微调: 二分法,不断调小 batch size
- batchsize = 1 还有问题,继续往下找
- max_seq_len
- 调小序列长度, 减少内存开销
- 【2024-3-29】A100 80G 跑 InternLM,报错 OOM, 差 1G 空间,将 max_seq_len 降低后成功
- 降低精度
- Pytorch-Lightning: 将精度更改为“float16”
- 风险: 可能引起 Double 和 Float 张量间不匹配
- 按照错误提示操作
- 更改 GPU 配置
- 清除缓存
- 终端:
- ipython:
x.detach()和x.cpu()
- 修改模型/训练
- 不要保存整个tensor,当你在epoch结束需要汇总损失的时候,使用
loss.item() preds.detach().cpu()从 GPU 中删除预测和目标
- 不要保存整个tensor,当你在epoch结束需要汇总损失的时候,使用
CUDA error: device-side assert triggered
【2024-824】将 bert 模型的分类数从两个升级为多个时
错误信息
File "/mnt/bn/flow-algo-cn/wangqiwen/bin/miniconda3/lib/python3.12/site-packages/torch/autograd/__init__.py", line 142, in _make_grads
torch.ones_like(out, memory_format=torch.preserve_format)
RuntimeError: CUDA error: device-side assert triggered
CUDA kernel errors might be asynchronously reported at some other API call, so the stacktrace below might be incorrect.
For debugging consider passing CUDA_LAUNCH_BLOCKING=1.
Compile with `TORCH_USE_CUDA_DSA` to enable device-side assertions.
重点: Assertion t >= 0 && t < n_classes failed.
错误原因:
- 模型输出的类别与标签的类别个数不一致
- 例如模型输出3类,但标签里有4类
loss 曲线分析
第2个epoch陡降
loss 陡降的原因
- 大模型强大的特征学习能力和记忆效应
- 第1个epoch已经初步适应数据分布, loss 显著下降
- 学习率的调整策略
- sft 阶段学习率较小
- 训练初期,warmup 机制防止不稳定
多个 epoch 的问题与讨论
- 过拟合风险: loss 陡降是过拟合信号,降低泛化能力
- 需要根据任务难度来控制采样次数
应对策略
- 加入验证集监控 val loss,平衡记忆能力和泛化能力
- Dropout与其他正则化手段
- 合理设置数据采样次数: 简单规律的数据少采样,难度大(数学/代码),OOD(垂类)任务多采样
- 进行数据集增广和扩充,混合更多通用数据,确保模型更加通用、全局
第二个epoch后,loss为何突然下降?
- ✅✅学习率调整: 在SFT中,学习率通常会在初期进行Warm-up,第二个epoch时,学习率达到预设值,优化器开始更有效地更新参数,导致loss快速下降。
- ✅✅迁移学习效应: 大模型在预训练时已经学到了大量通用特征,进入SFT后,模型能迅速将这些特征迁移到目标任务,第一epoch后,模型参数得到有效优化,第二个epoch时性能显著提升。
- ✅✅数据分布与样本难易度: 第一epoch中,模型可能遇到一些较难的样本,第二个epoch时,模型已对较简单样本有较好表现,进而导致loss下降。
- ✅✅梯度稳定: 在训练初期,梯度可能存在不稳定(如梯度爆炸或消失),随着训练的进行,梯度变得更加稳定,优化过程变得更加平滑,loss下降加速。
- ✅✅正则化效果: 正则化策略(如Dropout)在第二个epoch时可能更有效,帮助模型更好地泛化,从而使loss下降。
loss 迟迟不降
什么是 logloss
参考
问题
- logloss 大于1吗?
- 可以,但二元分类中,p>1, 说明模型比较糟糕, p=0.8 也很糟糕。
- logloss 的正常范围应该是多少?
- 一般多小的logloss,是好的分类器?
二分类的 log loss 数学表达式
logloss = -plog(p) -(1-p)log(1-p)
logloss 取值范围是 [0,+∞)
- 如果 p=0,预测概率为0,−log0 是正无穷,logloss 正无穷大。
LogLoss是越小越好,至于多小是好,并没有统一标准。
- LogLoss 做标准的比赛,一个第一名是0.01左右,另外一个是0.4左右。
logloss 取值表
| p | logloss |
|---|---|
| 0.1 | 0.325 |
| 0.2 | 0.500 |
| 0.3 | 0.611 |
| 0.4 | 0.673 |
| 0.5 | 0.693 |
| 0.6 | 0.673 |
| 0.7 | 0.611 |
| 0.8 | 0.500 |
| 0.9 | 0.325 |
最差的情况: 样本正好是一半阳性一半阴性
此时 logloss=0.693, 模型已经混乱了
logloss 不降?
【2024-7-25】二分类logloss不降的原因及分析
问题
- 现象: 当二分类loss 0.693, 并且一直不降
分析
- 模型出问题,模型结构,或参数设置不合适。
- 数据分布问题
- 训练数据集本身
- 网络权重参数等
解决方案
解决方案三个方面:
- 全连接层权重添加 weight_decay,一般设为
1e-3 - 改变模型参数初始化时的方差大小
- 增加Batch Normalization
1. 全连接层权重添加 weight_decay
weight_decay 可在定义optimizer的时候添加,如:
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, weight_decay=1e-3)
注意,以上代码对所有参数都加了weight_decay。
也可以指定对指定参数进行权重衰减,比如:
trainer = torch.optim.SGD([{ "params": model.weight, 'weight_decay': wd},
{ "params": model.bias}], lr=lr)
# 或者
optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 对权重参数衰减
optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr) # 不对偏差参数衰减
...
# 更新时
optimizer_w.step()
optimizer_b.step()
2. 改变模型参数初始化方差大小
初始化 model.weigh:
self.weight = nn.Parameter(torch.FloatTensor(num_class, embed_dim))
torch.init.xavier_uniform_(self.weight)
初始化出来的参数方差可能非常小,接近于0的值太多了,会导致经过 softmax/sigmoid 后都是0。
于是,增大方差:
self.weight = nn.Parameter(torch.FloatTensor(num_class, embed_dim))
torch.init.xavier_uniform_(self.weight, gain=math.sqrt(2.0))
# 对于激活函数ReLU,推荐gain值为sqrt(2.0),这个可以在pytorch官方文档查到
# 或改变初始化参数的分布情况,如从均匀uniform改为正太分布normal:
self.weight = nn.Parameter(torch.FloatTensor(num_class, embed_dim))
torch.init.xavier_uniform_(self.weight) ->torch.init.xavier_normal_(self.weight)
3. 增加 Batch Normalization
bn用于防止过拟合,可是模型才刚刚训练,怎么会过拟合呢?
猜测:
bn可以将控制输入数据分布。
一般都是在全连接层和激活函数之间添加bn
Wx_plus_b = self.weight.mm(combined.t())
# batch_normalization
if self.norm:
bn = nn.BatchNorm1d(Wx_plus_b.shape[1], affine=True)
Wx_plus_b = bn(Wx_plus_b)
模型是:input layer -> enc1 -> enc2 -> output layer,在enc1后enc2前加入了BN层。
目前只尝试了第二和第三种方式,结果是loss正常下降。
- 尤其是加入了bn后,loss从一开始就为0.692,后续还在下降。
- 而且,同等条件下,添加了bn后的模型比没有添加bn的模型loss下降得更快,训练了150个epoch,roc_auc、precision、acc、micro-F1、macro-F1、recall指标均超过了0.8,而这些指标在没有bn层的模型里,运行了200个epoch后只有roc_auc超过了上述含bn层的模型。
loss 尖刺
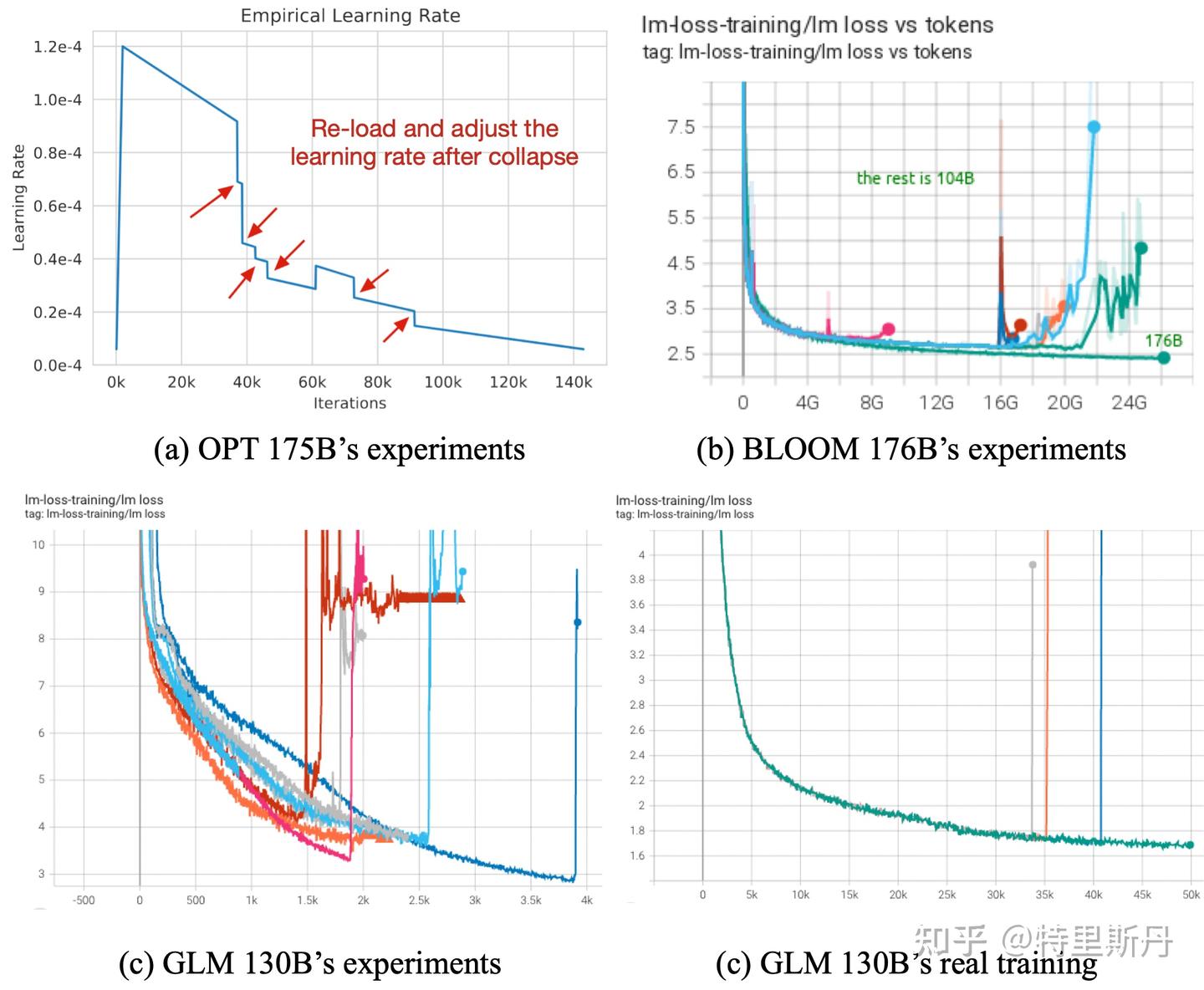
【2024-9-13】大模型训练loss突刺问题(loss spike)
loss spike 是什么?
loss spike 指预训练过程中(尤其大模型,100B以上)出现的loss突然暴涨现象。
- 【2023-4-26】META 论文 A Theory on Adam Instability in Large-Scale Machine Learning
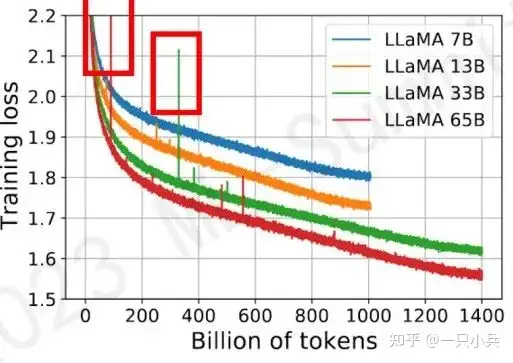
影响:
- 导致一系列的问题发生,如模型需要很长时间才能回到spike之前的状态,或者loss再也无法 drop back down,即模型再也无法收敛。
loss spike会导致一系列问题发生,譬如模型需要很长时间才能再次回到spike之前的状态(论文中称为pre-explosion),或者更严重的就是loss再也无法drop back down,即模型再也无法收敛。
原因
更新参数的变化过程想象成为一个从两端(非稳态)向中间(稳态)收拢的过程。
中心极限定理:
- 随机事件的叠加进入单峰
正态分布的必要条件之一: 各个随机事件事件之间应该是相互独立,但是梯度变化以及更新参数变化并不满足独立性条件,而这恰恰是导致更新参数振荡,loss spike 出现以及loss 不收敛的重要原因之一
所有模型都面临训练不稳定,它可能发生在预训练的开始、中间或结束阶段(图(a)和(b)分别取自OPT和BLOOM)
loss spike的出现与以下三个条件密切相关:
- 梯度更新幅度
- 虽然浅层(embedding层)参数长时间不更新,但是深层的参数依然一直在更新。长时间这样的状态之后,batch之间的样本分布变化可能就会直接导致浅层(embedding层)再次出现较大的梯度变化(可以想象成一个水坝蓄水太久终于被冲开了。
- 至于小模型为什么不会出现这种情况,推测是小模型函数空间小,无法捕获样本的分布变化,越大规模的模型对样本之间不同维度的特征分布变化越敏感)。
- 浅层网络参数突然进入到了之前长时间不在的状态与模型深层参数当前的状态形成了连锁反应造成了模型进入非稳态。——这也对应了更换样本重新训练有可能会减少loss spike的出现频率,实际上就是选择分布变化较小的样本,减小浅层梯度变换幅度。
防止 loss spike
一些方法:
- PaLM和GLM130B提到的出现 loss spike后, 更换batch样本的方法(常规方法,但是成本比较高)
- 减小learning rate,治标不治本,对更新参数的非稳态没有做改进
- 减小 e 大小。或者直接把 e设为0,重新定义 u 在v等于0时候的值(值得尝试的办法)
- 减少max_grad_norm的大小,如0.1
- 把浅层梯度直接乘以缩放系数 \(\alpha\) 来减小浅层梯度更新值
- 使用FP32 计算注意力的 softmax
- Meta,变色龙,z-loss正则化
训练末期 loss 上升
待定
模型坍缩
自监督研究社区认为一个好的自监督学习模型真正起作用的原因:
- (1). 模型学习到了由数据增强带来的显式不变性 (invariance);
- (2). 模型避免学习到的嵌入存在维度/特征坍塌。
基于负样本的方法通过将编码器生成的嵌入投影到超球体中,将各个实例对应的表征相互拉开,使超球体上均匀分布,避免模型的坍塌。
因此要避开负样本时,会产生一个问题:
- 假设只有正例,模型推动正例在表示空间内相互靠齐,这种情况下模型会很快找到一个trival solution,即将所有实例映射到一个点上,模型收敛到常数解,模型便坍塌了。
什么是模式坍缩 (Modal Collapse)
模式坍缩 (Modal Collapse, Mode Collapse) 现象
- 无论输入数据分布如何,模型输出结果单一,丧失多样性,不可逆
2014年提出GAN,随后发现生成图片的清晰度和真实性单一,缺乏多样性,即坍缩
2017年,模式坍缩的研究增多,ICLR和NIPS多篇高引文章关于模式坍缩。
示例
- 二维空间的8个高斯分布的数据,gan 最终只生成了其中1个分布。
- 虽然看上去生成结果还不错,但是多样性无法保证。
- MINST数字生成,原始的gan倾向于生成一个数字。
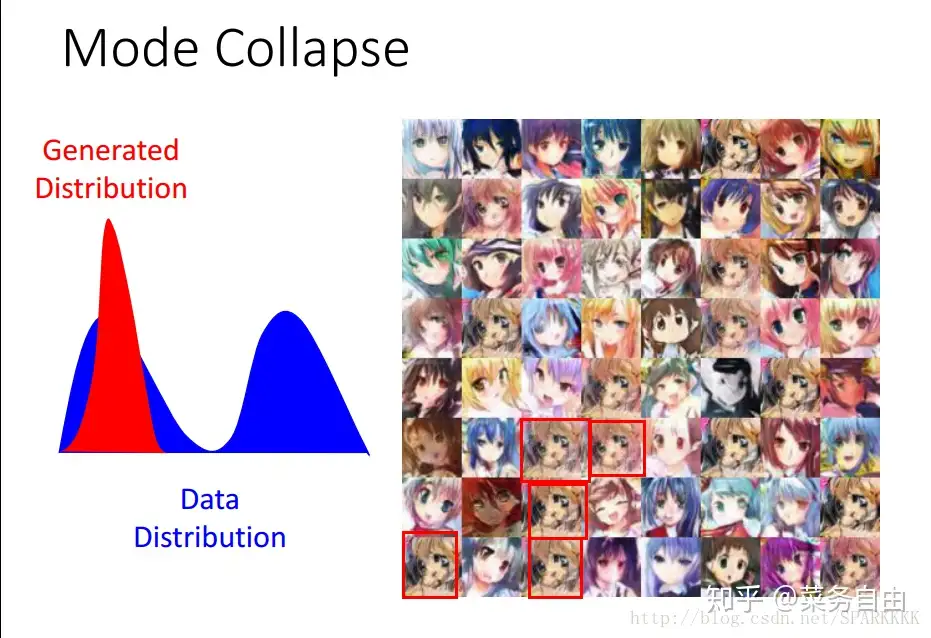
什么是模型坍缩 (Model Collapse)
「模型坍缩」(Model Collapse)指训练生成模型时,模型生成的输出变得重复、无意义和缺乏多样性。
- 【2023-5-31】牛津、剑桥发表论文 The Curse of Recursion: Training on Generated Data Makes Models Forget
- 主要作者: 伊利亚·舒迈洛夫(Ilia Shumailov)
模型坍缩是一种退化过程,影响生成模型的生成结果,输出数据最终会污染下一代模型的训练集;用被污染的数据训练
Model Collapseis a degenerative process affecting generations of learned generative models, where generated data end up polluting the training set of the next generation of models; being trained on polluted data, they then misperceive reality- The name is inspired by the
Generative Adversarial Networks(GAN) literature onmode collapse, where GANs start producing a limited set of outputs that all trick the discriminator.Model Collapseis a process whereby models eventually converge to a state similar to that of a GAN Mode Collapse. The original version of this paper referred to this effect as ‘model dementia’, but we decided to change this following feedback that it trivialised the medical notion of ‘dementia’ and could cause offence.
模型坍缩
- 定义:模型学习中的退化过程
- 观点
- 合成数据会稀释人工数据,损害模型性能
- 模型坍缩存在于各种生成式模型、数据集中
- 解法:使用真实的人工生成数据
模式坍缩 vs 模型坍缩
模式坍缩 vs 模型坍缩
模型坍缩受 GAN里的模型坍缩启发,概念相似- 区别
模式坍缩特指GAN系列神经网络里的丧失多样性现象模型坍缩是模式坍缩的泛化,推广到生成式模型里的退化现象,如 LLMs, VAEs and GMMs
Model collapse explained: How synthetic training data breaks AI
Model collapse vs Modal collapse
- The term
model collapseis inspired by literature onmodal collapsein generative adversarial networks (GANs).
The terms are similar, but have some key differences:
Modal collapseis specific to GANs, which are a type of machine learning model. It occurs when the generator in a GAN begins producing a very limited variety of samples regardless of the input. It is called modal collapse because it fails to capture the multiple modes in a diverse data distribution.Model collapseis a general term for a model failing to learn properly. It applies to many types of machine learning models and generative AI systems, including LLMs, VAEs and GMMs. It is inherent in all machine learning models and is a result of using synthetic training data.
如何识别模式坍缩
怎么识别模式坍缩
模式坍缩识别难度大。
- 一种办法是在二维混合高斯分布上以及MINST等标签已知的toy数据集上验证
- 由于数据分布和真实数据分布差异过大,结果仅能作为参考。
学术界由深度学习三巨头之一的Bengio大神在17年在MODE中提出两种指标:
- (1)有标签数据,简单方法可以采用生成数据和真实数据的分类直方图相关系数,或者使用改进后的KL散度
- (2)无标签数据,比如 celebaA,在训练过程中额外训练一个辅助判别器D。然后是测试,假设真实样本有10个mode,从每个mode中抽取一个真实数据,当D(x)=0.5时,证明生成器在这个mode上是均衡的;反之,如果D(x)接近1,证明p(real)很强而p(G(z))很弱,这个mode是collapse的
工业界,谷歌在Unrolling GAN提出2种基于距离的评价指标:
- (1)inference via optimization。从测试集采样样本,然后从生成图像中选择L2距离最接近的样本,计算平均L2距离。如果生成器发生模式坍缩,总的L2距离会比没有模式坍缩的生成图像要大。
- (2)Pairwise Distance,随机选择两个生成样本,计算两张图像每个像素的L2距离,然后取均值。沿着这个思路,[6] 提出将随机的100对生成样本之间的LPIPS分数差距作为多样性指标。因为L2距离在高维下不能很好地反映出样本之间的距离。
怎么解决模式坍缩
实践
【2024-5-10】在 v100s 单机8卡,训练 bigbird 模型时, 实现序列标注(session切分),出现 坍缩现象
- bigbird-roberta-large: 更改窗口、数据集再均衡,依然坍缩
- bigbird-roberta-base: 刚开始正常,训练轮数上升时,开始坍缩
解法
- 调大 batch_size 即可跳出坍缩
- v100 OOM 内存超限, 改用 a100 训练
总结
【如何逃脱递归训练的陷阱】
- AI模型在自己生成的数据上递归训练,可能导致模型坍缩,模型质量下降。但14名学者认为模型坍缩并非不可避免。
- 另一组学者去年提出了“递归诅咒”理论,合成数据会稀释真实数据,削弱模型性能。
- 但新论文认为如果累积真实数据和合成数据进行训练,不会出现模型坍缩。
- 前人研究都基于每代AI只在前代生成的数据上训练的假设,而实际上不同世代的数据可以累积而不会被丢弃。
- 但另一篇论文,合成数据不会像真实数据那样随数量增长而使性能提升,反而会降低性能。她们反对新论文的结论。
- 要保持性能,最好始终使用原始数据集,不要完全依赖合成数据。递归退化仍然存在。
- 先前的“递归诅咒”论文作者认为,大公司更容易避免模型坍缩,小公司将更艰难。新论文并没有推翻这个结论。
参考 《Experts divided over training AI with more data from AI • The Register》
GANs
用 Wassernstein距离代替JS散度:wgan
在梯度上加惩罚项:wgan-gp
- 引入pixel级别loss,特别是在训练早期,如L1, L2等
- 引入Encoder,将图像域逆向映射到z域。比如,MODE Regularization[1]和VEEGAN[2]
- 对基于GAN的风格迁移模型,任务是从A域映射到B域,同样可以增加一个encoder将B逆向映射到A。参考U-GAT-IT[3]中的 A2B B2A A2A loss.
- 引入unrolling loss[4],在二维高斯分布上的效果也不错,下面第一行是Unrolled GAN,第二行是原始GAN
相关学者便通过精巧的构造与设计,试图在不使用负样本的情况下,模型依旧不会坍塌
- 3.1 基于不对称结构进行优化
- 2 基于冗余降低进行优化
掺入真实数据
论文
- 【2024-4-29】斯坦福 Is Model Collapse Inevitable? Breaking the Curse of Recursion by Accumulating Real and Synthetic Data
方法
- 通过积累真实和合成数据来打破递归的诅咒, 即 每个阶段都掺入真实数据
反方观点
- 【2024-4-30】Elvis Dohmatob 发论文,通过回归案例证明:合成数据添加到模型训练不会产生任何后果 —— 不对
误差分解
机器学习中, 误差可以分解为:偏差,方差与噪声之和。即:
误差=偏差^2 +方差+噪声
$ error(x) = {bias}^2(x) + var(x) + \varepsilon^2$
解释
偏差:学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。方差:同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。噪声:当前任务上学习任何算法所能达到的期望泛化误差的下界。

详见站内 机器学习笔记
训练曲线
训练时,合理情形:loss 曲线稳定下降,趋于平缓,先快后慢
注意
- loss 下降合理,不代表模型参数最佳,只表示训练正常
问题定位
模型训练环节,损失函数(loss曲线)出现不同情形,如何快速定位?
- 知识点
- 学习率:学习率越大,波动越剧烈,学习率越小,波动越平缓。
- 过拟合
- batch size:batchsize越小,波动越剧烈,batchsize越大,波动越平缓。
- 梯度下降算法:梯度就是曲线的斜率,如果要最小化目标函数,反向传播过程中,每个参数在梯度方向上减小一定幅度,最终网络收敛到一个局部最优值,减小的幅度大小由学习率决定。
【2025-6-23】llama-factory 中只有个简单的曲线图,无法获取更详细信息
- 详见 小红书视频
解法
- 使用 wandb 或 swanlab
| loss曲线症状 | 分析 | 解法 | 其他 |
|---|---|---|---|
| 始终高位徘徊 | ① 学习率太小,参数更新不够 ②数据本身没有任何规律,大量异常值和缺失值 |
①增大学习率 |
少见 |
| 下降速度太慢 | 训练不够充分 | 增加训练轮数(10轮以内) | |
| 起伏不定(sin曲线) | ①学习率过大,导致震荡 ②batch_size太小 |
||
| 下降到某个轮数后,稳定不降 | ①学习率衰减到某个值 ②陷入局部最优 ③过拟合 |
①调大学习率②调大 bs | |
| 下降到某个值后,反弹 | ①数据集有问题,噪声、异常值 ②学习率太大或增然增大,冲过最优解 |
train & eval loss
理想状态
- train loss 和 eval loss 同步下降
症状
- train loss 持续下降,而 eval loss 在某个点反弹 → 过拟合
- train loss 和 eval loss 都处于高位 → 欠拟合
- train loss 持续处于高位,而 eval loss 持续下降 → 数据分布问题,eval 集合比train 集合更简单
- train loss 下降速度显著慢于 eval loss → 数据分布问题,eval 更简单, 或 train 存在困难样本
详见 小红书视频
loss 曲线不降
训练时,loss曲线 不下降
- 模型结构问题。当模型结构不好、规模小时,模型对数据的拟合能力不足。
- 训练时间问题。不同的模型有不同的计算量,当需要的计算量很大时,耗时也会很大
- 权重初始化问题。常用的初始化方案有全零初始化、正态分布初始化和均匀分布初始化等,合适的初始化方案很重要,之前提到过神经网络初始化为0可能会带来的影响
- 正则化问题。L1、L2以及Dropout是为了防止过拟合的,当训练集loss下不来时,就要考虑一下是不是正则化过度,导致模型欠拟合了。正则化相关可参考正则化之L1 & L2
- 激活函数问题。全连接层多用ReLu,神经网络的输出层会使用sigmoid 或者 softmax。激活函数可参考常用的几个激活函数。在使用Relu激活函数时,当每一个神经元的输入为负时,会使得该神经元输出恒为0,导致失活,由于此时梯度为0,无法恢复。
- 优化器问题。优化器一般选取Adam,但是当Adam难以训练时,需要使用如SGD之类的其他优化器。常用优化器可参考机器学习中常用的优化器有哪些?
- 学习率问题。学习率决定了网络的训练速度,但学习率不是越大越好,当网络趋近于收敛时应该选择较小的学习率来保证找到更好的最优点。所以,我们需要手动调整学习率,首先选择一个合适的初始学习率,当训练不动之后,稍微降低学习率。
- 梯度消失和爆炸。这时需要考虑激活函数是否合理,网络深度是否合理,可以通过调节sigmoid -> relu,假如残差网络等,相关可参考为什么神经网络会有梯度消失和梯度爆炸问题?如何解决?
- batch size问题。过小,会导致模型损失波动大,难以收敛,过大时,模型前期由于梯度的平均,导致收敛速度过慢。
- 数据集问题。
- (1)数据集未打乱,可能会导致网络在学习过程中产生一定的偏见
- (2)噪声过多、标注有大量错误时,会导致神经网络难以学到有用的信息,从而出现摇摆不定的情况,噪声、缺失值、异常值
- (3)数据类别不均衡使得少数类别由于信息量不足,难以学到本质特征,样本不均衡相关可以看样本不均衡及其解决办法。
- 特征问题。特征选择不合理,会使网络学习难度增加。之前有提到过特征选择的文章,如何找到有意义的组合特征,特征选择方法
测试时 loss 不下降
- 训练的时候过拟合导致效果不好
- 交叉检验,通过交叉检验得到较优的模型参数;
- 特征选择,减少特征数或使用较少的特征组合,对于按区间离散化的特征,增大划分的区间;
- 正则化,常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;
- 如果有正则项则可以考虑增大正则项参数;
- 增加训练数据可以有限的避免过拟合;
- Bagging ,将多个弱学习器Bagging 一下效果会好很多,比如随机森林等.
- 早停策略。本质上是交叉验证策略,选择合适的训练次数,避免训练的网络过度拟合训练数据。
- DropOut策略。
- 应用场景不同导致。本来训练任务是分类猫和狗,测试用的皮卡丘和葫芦娃。
- 噪声问题。训练数据大概率都是经过去噪处理的,而真实测试时也应该去除噪声。
权重衰减
正则化方式有 L1 和 L2 正则项两种。其中 L2 正则项又被称为权值衰减(weight decay)
学习率
学习率衰减策略
学习率衰减策略:固定策略的学习率衰减和自适应学习率衰减
- 固定学习率衰减:分段衰减、逆时衰减、指数衰减等
- piecewise decay 分段常数衰减: 训练过程中不同阶段设置不同的学习率,便于更精细的调参。
- 在目标检测任务如Faster RCNN 和 SSD 的训练中都采用分段常数衰减策略,调整学习率。
- exponential decay 指数衰减:学习率以指数的形式进行衰减,其中指数函数的底为decay_rate, 指数为 global_step / decay_steps
- natural exponential decay 自然指数衰减: 学习率以自然指数进行衰减,其中指数函数底为自然常数e, 指数为 -decay_rate * global_step / decay_step, 相比指数衰减具有更快的衰减速度。
- polynomial decay 多项式衰减:调整学习率的衰减轨迹以多项式对应的轨迹进行。
- 其中(1 - global_step / decay_steps) 为幂函数的底; power为指数,控制衰减的轨迹。
- cosine decay 余弦衰减:学习率以cosine 函数曲线进行进行衰减
- linear cosine decay 线性余弦衰减:动机式在开始的几个周期,执行warm up 操作,线性余弦衰减比余弦衰减更具aggressive,通常可以使用更大的初始学习速率。
- 循环学习率衰减
- 参考Stochastic Gradient Descent with warm Restart (SGDR),学习率以循环周期进行衰减。
- piecewise decay 分段常数衰减: 训练过程中不同阶段设置不同的学习率,便于更精细的调参。
- 自适应学习率衰减:AdaGrad、 RMSprop、 AdaDelta等。
一般情况,两种策略会结合使用。
| 衰减策略 | 说明 | 图解 |
|---|---|---|
| 分段衰减 | 不同阶段设置不同的学习率 |  |
| 指数衰减 | 以指数的形式进行衰减 |  |
| 自然指数衰减 | 自然指数进行衰减 |  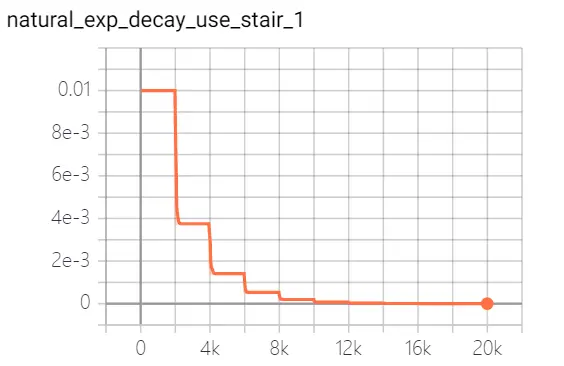 |
| 多项式衰减 | 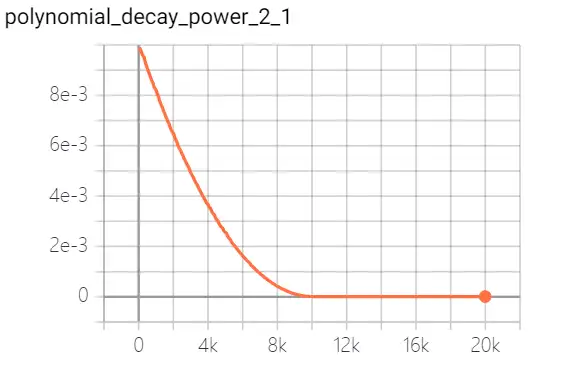 |
|
| 余弦衰减 |  |
|
| 线性余弦衰减 | 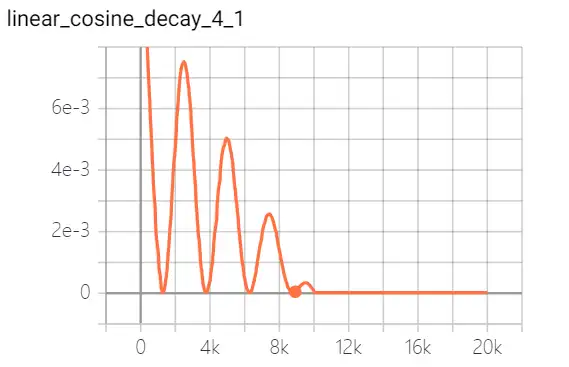 |
|
| 循环学习率衰减 |  |
学习率衰减策略很大程度上是依赖于经验与具体问题
PyTorch 学习率衰减
torch.optim 中实现了多种优化算法
Pytorch optim
创建optimizer时,提供需优化的模型参数
- 模型参数必须是iterable类型且顺序不变。
- Optimizer 还可以指定一些优化参数,如:learning rate和weight decay等,不同优化算法的优化参数不同,默认情况下优化参数作用于所有模型参数,也可以为不同的模型参数提供不同的优化参数。
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr=0.0001)
# 最外层的优化参数作为default选项用于没设置该优化参数的模型参数组。
optim.SGD([
{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}
], lr=1e-2, momentum=0.9)
# 在梯度计算之后来用梯度更新参数
for input, target in dataset:
optimizer.zero_grad() # 清理梯度值
output = model(input)
loss = loss_fn(output, target)
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新参数
# 传入closure
for input, target in dataset:
def closure():
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
return loss
optimizer.step(closure) # 允许重新计算模型
更新模型参数的三种方式:forloop, foreach和fused
- 性能排序为
forloop<foreach<fused - Forloop 方式遍历每个param来对其进行更新;
- Foreach 方式将同一param group的所有param组合成一个multi-tensor来一次性更新所有参数,内存使用多但减少kernel calls;
- Fused 方式在一个kernel中执行所有计算。
- Foreach和Fused要求所有的模型参数在CUDA上,而Fused进一步要求所有模型的参数类型为float。
PyTorch中实现的所有优化算法默认使用实现方式为foreach(SparseAdam,LBFGS除外,只有forloop方式),只有Adam和AdamW支持fused实现方式。
torch.optim.Optimizer 是所有优化算法的父类。
变量:
param_groups:存放需要优化的模型参数,Tensor或dict组成的iterable;defaults:存放指定的优化参数,不同优化算法的优化参数不同;state:存放优化器的当前状态,不同优化算法的内容不同;
函数:
state_dict():返回优化器的状态,包括packed_state和param_groups;load_state_dict():从参数中加载state_dict;zero_grad():将每个参数的梯度设置为None或0;step():为空函数,实现单步优化;add_param_group():向Optimizer的param_groups中添加需要优化的模型参数组;
class Optimizer(object):
def __init__(self, params, defaults):
self.defaults = defaults
self.state = defaultdict(dict)
self.param_groups = [] #dict的列表,[{'params':[Tensor|Dict]}]
param_groups = list(params) #Tensor或dict的列表
if not isinstance(param_groups[0], dict):
param_groups = [{'params': param_groups}]
for param_group in param_groups:
self.add_param_group(param_group)
def __getstate__(self):
return {
'defaults': self.defaults,
'state': self.state,
'param_groups': self.param_groups,
}
def state_dict(self):
...
return {
'state': packed_state,
'param_groups': param_groups,
}
def load_state_dict(self, state_dict):
...
def zero_grad(self, set_to_none: bool = False):
for group in self.param_groups:
for p in group['params']:
if p.grad is not None:
if set_to_none:
p.grad = None
else:
p.grad.zero_() #简化写法
def step(self, closure):
raise NotImplementedError
def add_param_group(self, param_group):
...
pytorch 中4种常用衰减类型:指数衰减、固定步长的衰减、多步长衰、余弦退火衰减。
Learning Rate
PyTorch的 torch.optim.lr_scheduler 中提供多种方法来根据epoch数量调整学习率。学习率的调整应该在参数更新之后,在每个epoch最后执行。而且大多数learning rate scheduler可以叠加使用。
from torch.optim.lr_scheduler import ExponentialLR, MultiStepLR
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
scheduler = ExponentialLR(optimizer, gamma=0.9)
scheduler2 = MultiStepLR(optimizer, milestones=[30,80], gamma=0.1)
for epoch in range(20):
for input, target in dataset:
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
scheduler.step()
scheduler2.step()
PyTorch中提供的lr scheduler。
- StepLR
- MultiStepLR
- ExponentialLR
- MultiplicativeLR
- CosineAnnealingLR
- CosineAnnealingWarmRestarts
- CyclicLR
- OneCycleLR
- ReduceLROnPlateau
__all__ = ['LambdaLR', 'MultiplicativeLR', 'StepLR', 'MultiStepLR', 'ConstantLR', 'LinearLR',
'ExponentialLR', 'SequentialLR', 'CosineAnnealingLR', 'ChainedScheduler', 'ReduceLROnPlateau',
'CyclicLR', 'CosineAnnealingWarmRestarts', 'OneCycleLR', 'PolynomialLR', 'LRScheduler']
1. 固定学习率
设置固定学习率的方法有两种,第一种是直接设置一些学习率,网络从头到尾都使用这个学习率
optimizer = torch.optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
第二种方法是,可以针对不同的参数设置不同的学习率,设置方法如下:这里给subnet2子结构设置的学习率为0.01 ,如果对某个参数不指定学习率,就使用最外层的默认学习率,这里其他结构默认使用0.03
optimizer =optim.SGD([
{'params': net.subnet1.parameters()}, # lr=0.03
{'params': net.subnet2.parameters(), 'lr': 0.01}
], lr=0.03)
2. 固定步长衰减
每隔多少步就去乘以一个系数,这里的step_size表示运行这么多次的step()才会更新一次。
optimizer_StepLR = torch.optim.SGD(net.parameters(), lr=0.1)
StepLR = torch.optim.lr_scheduler.StepLR(optimizer_StepLR, step_size=step_size, gamma=0.65)
gamma参数表示衰减的程度,step_size参数表示每隔多少个step进行一次学习率调整
3. 多步长衰减
固定步长的衰减的虽然能够按照固定的区间长度进行学习率更新,但是有时我们希望不同的区间采用不同的更新频率,或者是有的区间更新学习率,有的区间不更新学习率,这就需要使用MultiStepLR来实现动态区间长度控制:
optimizer_MultiStepLR = torch.optim.SGD(net.parameters(), lr=0.1)
torch.optim.lr_scheduler.MultiStepLR(optimizer_MultiStepLR,
milestones=[200, 300, 320, 340, 200], gamma=0.8)
其中milestones参数为表示学习率更新的起止区间,在区间[0. 200]内学习率不更新,而在[200, 300]、[300, 320]…..[340, 400]的右侧值都进行一次更新;gamma参数表示学习率衰减为上次的gamma分之一。milestones以外的区间学习率始终保持不变。
4. 指数衰减
学习率指数衰减是比较常用的策略,首先确定需要针对哪个优化器执行学习率动态调整策略,定义好优化器以后,就可以给这个优化器绑定一个指数衰减学习率控制器
optimizer_ExpLR = torch.optim.SGD(net.parameters(), lr=0.1)
ExpLR = torch.optim.lr_scheduler.ExponentialLR(optimizer_ExpLR, gamma=0.98)
gamma表示衰减的底数,选择不同的gamma值可以获得幅度不同的衰减曲线
5. 余弦退火
余弦退火策略不应该算是学习率衰减策略,因为它使得学习率按照周期变化,其定义方式如下:
optimizer_CosineLR = torch.optim.SGD(net.parameters(), lr=0.1)
CosineLR = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer_CosineLR, T_max=150, eta_min=0)
6. ReduceLRonPlateau
这个方法是对梯度进行监控,其中mode是模式设置,具有两种模式,min 和max指的是如果梯度不下降,或者不上升,就进行调整;factor是调整因子;patience指的是连续多少次不变化就调整;threshold表示只有超过阈值之后,才关注学习率的变化;threshold_mode有两种模式,rel模式:max模式下如果超过best(1+threshold)为显著,min模式下如果低于best(1-threshold)为显著,abs模式:max模式下如果超过best+threshold为显著,min模式下如果低于best-threshold为显著;cooldown是指调整后,有一段冷却时间,多少次不对学习率进行监控;verbose表示是否打印日志;min_lr表示学习率下限;eps 表示学习率衰减最小值;
lr_scheduler.ReduceLROnPlateau(
optimizer,
mode='min',
factor=0.1,
patience=10,
verbose=False,
threshold = 0.0001,
threshold_mode = 'rel',
cooldown=0,
min_lr = 0,
eps = 1e-08
)
7. 自定义学习率LambdaLR
通过一个lambda来自定义学习率计算方式
lr_scheduler.LambdaLR(
optimizer,
lr_lambda,
last_epoch=-1
)
其中lr_lambda 表示自定义的函数,一个例子如下
scheduler = LambdaLR(optimizer, lr_lambda = lambda epoch: 0.1 ** ( eopch // 10 ))
TensorFlow 学习率衰减
# 分段衰减
tf.train.piecewise_constant_decay()
piecewise_with_warmup() # 分段常数衰减
# 指数衰减
tf.train.exponential_decay()
# learning_rate: 基学习率;
# decay_rate: 衰减率;
# decay_steps: 衰减步数(周期)
# staircase: 是否以离散的时间间隔衰减学习率
# 自然指数衰减
tf.train.natural_exp_decay()
# learning_rate: 基学习率;
# decay_rate: 衰减率;
# decay_steps: 衰减步数/周期;
# staircase: 是否以离散的时间间隔衰减学习率
# 多项式衰减
tf.train.polynomial_decay()
# learning_rate: 基学习率;decay_steps: 衰减率衰减步数;power: 多项式的幂;end_learning_rate:最小学习率
# 余弦衰减
tf.train.cosine_decay()
# learning_rate: 基学习率;decay_steps: 衰减率衰减步数;alpha: 最小学习率
tf.train.linear_cosine_decay() # 线性余弦衰减
cosine_decay_with_warmup() # 带预热的余弦衰减
# 循环学习率衰减
tf.train.cosine_decay_restarts()
# learning_rate: 基学习率;first_decay_steps: 第一个衰减周期迭代次数; t_mul: 迭代次数因子,用于推导第i个周期的迭代次数;m_mul: 学习率衰减因子,用于推导第i个周期的初始学习率;alpha:最小学习率
exponential_decay_with_burnin() # 单循环学习率衰减
Warmup
参考
什么是 Warmup
Warmup 是ResNet论文中的一种学习率预热方法
- 训练开始用一个较小的学习率,训一些epoches或steps(比如4个epoches,10000steps),再修改为预先设置的学习率训练。
为什么要 Warmup
为什么使用Warmup
- 刚开始训练时, 模型权重(weights)随机初始化,此时若选择较大学习率,可能模型不稳定(振荡)
- Warmup预热学习率方式,开始训练的几个epoches或者一些steps内学习率较小, 在预热的小学习率下,模型可以慢慢趋于稳定,等模型相对稳定后,再选择预先设置的学习率进行训练,使得模型收敛速度变得更快,模型效果更佳。
Warmup 策略
1 constant warmup
Resnet论文用一个110层的ResNet在cifar10上训练
- 先用0.01的学习率训练直到训练误差低于80%(大概训练了400个steps)
- 然后使用0.1的学习率进行训练。
2 gradual warmup
constant warmup 不足之处:
- 从一个很小的学习率一下变为比较大的学习率可能会导致训练误差突然增大。
- 2018年Facebook提出了
gradual warmup,从最初的小学习率开始,每个step增大一点点,直到达到最初设置的比较大的学习率时,采用最初设置的学习率进行训练。
gradual warmup 实现代码如下:
"""
Implements gradual warmup, if train_steps < warmup_steps, the
learning rate will be `train_steps/warmup_steps * init_lr`.
Args:
warmup_steps:warmup步长阈值,即train_steps<warmup_steps,使用预热学习率,否则使用预设值学习率
train_steps:训练了的步长数
init_lr:预设置学习率
"""
import numpy as np
warmup_steps = 2500
init_lr = 0.1
# 模拟训练15000步
max_steps = 15000
for train_steps in range(max_steps):
if warmup_steps and train_steps < warmup_steps:
warmup_percent_done = train_steps / warmup_steps
warmup_learning_rate = init_lr * warmup_percent_done #gradual warmup_lr
learning_rate = warmup_learning_rate
else:
#learning_rate = np.sin(learning_rate) #预热学习率结束后,学习率呈sin衰减
learning_rate = learning_rate**1.0001 #预热学习率结束后,学习率呈指数衰减(近似模拟指数衰减)
if (train_steps+1) % 100 == 0:
print("train_steps:%.3f--warmup_steps:%.3f--learning_rate:%.3f" % (
train_steps+1,warmup_steps,learning_rate))
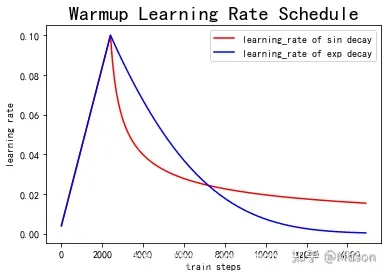
Warmup预热学习率以及学习率预热完成后衰减(sin or exp decay)的曲线图如下:
3 WarmupMultiStepLR
1 build_lr_scheduler
# ->箭头表示函数输出返回值类型
# LR_SCHEDULER_NAME有两种WarmupMultiSetpLR, WarmupCosineLR
def build_lr_scheduler(cfg: CfgNode, optimizer: torch.optim.Optimizer) -> torch.optim.lr_scheduler._LRScheduler:
"""
Build a LR scheduler from config.
"""
name = cfg.SOLVER.LR_SCHEDULER_NAME
if name == "WarmupMultiStepLR":
return WarmupMultiStepLR(
optimizer,
cfg.SOLVER.STEPS, # tuple (300, 400)
cfg.SOLVER.GAMMA, #[0.1]
warmup_factor=cfg.SOLVER.WARMUP_FACTOR, # 0.001
warmup_iters=cfg.SOLVER.WARMUP_ITERS, # 1000
warmup_method=cfg.SOLVER.WARMUP_METHOD, # 'linear'
)
elif name == "WarmupCosineLR":
return WarmupCosineLR(
optimizer,
cfg.SOLVER.MAX_ITER,
warmup_factor=cfg.SOLVER.WARMUP_FACTOR,
warmup_iters=cfg.SOLVER.WARMUP_ITERS,
warmup_method=cfg.SOLVER.WARMUP_METHOD,
)
else:
raise ValueError("Unknown LR scheduler: {}".format(name))
2 WarmupMultiSetpLR
class WarmupMultiStepLR(torch.optim.lr_scheduler._LRScheduler):
def __init__(
self,
optimizer: torch.optim.Optimizer,
milestones: List[int],
gamma: float = 0.1,
warmup_factor: float = 0.001,
warmup_iters: int = 1000,
warmup_method: str = "linear",
last_epoch: int = -1,
):
if not list(milestones) == sorted(milestones):
raise ValueError(
"Milestones should be a list of" " increasing integers. Got {}", milestones
)
self.milestones = milestones
self.gamma = gamma
self.warmup_factor = warmup_factor
self.warmup_iters = warmup_iters
self.warmup_method = warmup_method
super().__init__(optimizer, last_epoch)
def get_lr(self) -> List[float]:
warmup_factor = _get_warmup_factor_at_iter(
self.warmup_method, self.last_epoch, self.warmup_iters, self.warmup_factor
)
return [
base_lr * warmup_factor * self.gamma ** bisect_right(self.milestones, self.last_epoch)
for base_lr in self.base_lrs
##################################################
## self.base_lrs 【0.001,.... 0.001】 len = 84
#################################################
]
def _compute_values(self) -> List[float]:
# The new interface
return self.get_lr()
def _get_warmup_factor_at_iter(method: str, iter: int, warmup_iters: int, warmup_factor: float) -> float:
"""
Return the learning rate warmup factor at a specific iteration.
See https://arxiv.org/abs/1706.02677 for more details.
Args:
method (str): warmup method; either "constant" or "linear".
iter (int): iteration at which to calculate the warmup factor.
warmup_iters (int): the number of warmup iterations.
warmup_factor (float): the base warmup factor (the meaning changes according
to the method used).
Returns:
float: the effective warmup factor at the given iteration.
"""
if iter >= warmup_iters:
return 1.0
if method == "constant":
return warmup_factor
elif method == "linear":
alpha = iter / warmup_iters
return warmup_factor * (1 - alpha) + alpha
else:
raise ValueError("Unknown warmup method: {}".format(method))
3 仿真
import bisect
from bisect import bisect_right
import matplotlib.pyplot as plt
warmup_factor = 0.001
Steps = (300,400)
gamma = 0.1
warmup_iters = 1000
base_lr = 0.001
import numpy as np
lr = []
iters=[]
for iter in range(500):
alpha = iter/warmup_iters
warmup_factor = warmup_factor*(1-alpha)+alpha
lr.append( base_lr * warmup_factor * gamma ** bisect_right(Steps, iter))
iters.append(iter)
plt.plot(iters,lr)
plt.show()
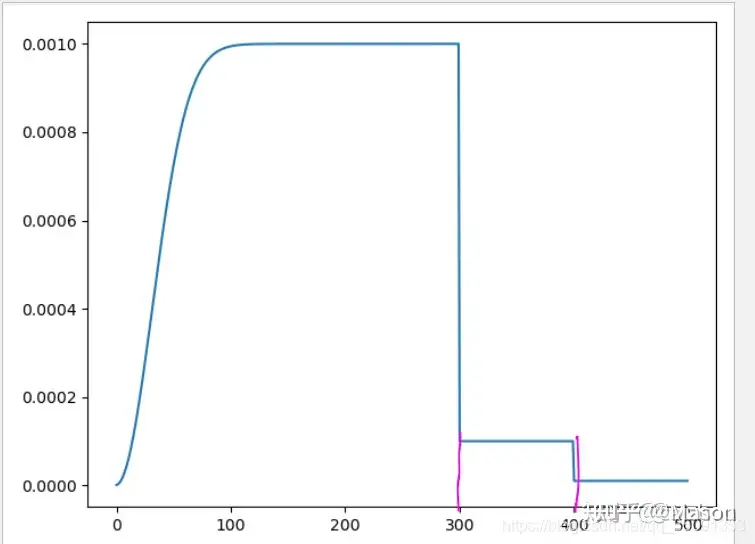
Warmup 实现
PyTorch学习率调整策略通过torch.optim.lr_scheduler接口实现。
PyTorch 提供的学习率调整策略分为三大类
- 有序调整:等间隔调整(Step),按需调整学习率(MultiStep),指数衰减调整(Exponential)和余弦退火CosineAnnealing。
- 自适应调整:自适应调整学习率 ReduceLROnPlateau。
- 自定义调整:自定义调整学习率 LambdaLR。
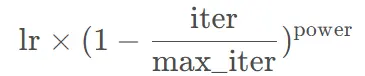
def create_lr_scheduler(optimizer,
num_step: int, # every epoch has how much step
epochs: int,
warmup=True,
warmup_epochs=1, # warmup进行多少个epoch
warmup_factor=1e-3):
"""
:param optimizer: 优化器
:param num_step: 每个epoch迭代多少次,len(data_loader)
:param epochs: 总共训练多少个epoch
:param warmup: 是否采用warmup
:param warmup_epochs: warmup进行多少个epoch
:param warmup_factor: warmup的一个倍数因子
:return:
"""
assert num_step > 0 and epochs > 0
if warmup is False:
warmup_epochs = 0
def f(x):
"""
:x epoch或者iteration
:return 根据step数返回一个学习率倍率因子
注意在训练开始之前,pytorch似乎会提前调用一次lr_scheduler.step()方法
"""
if warmup is True and x <= (warmup_epochs * num_step):
alpha = float(x) / (warmup_epochs * num_step)
# warmup过程中lr倍率因子大小从warmup_factor -> 1
return warmup_factor * (1 - alpha) + alpha # 对于alpha的一个线性变换,alpha是关于x的一个反比例函数变化
else:
# warmup后lr的倍率因子从1 -> 0
# 参考deeplab_v2: Learning rate policy
return (1 - (x - warmup_epochs * num_step) / ((epochs - warmup_epochs) * num_step)) ** 0.9
# (1-a/b)^0.9 b是当前这个epoch结束训练总共了多少次了(除去warmup),这个关系是指一个epcoch中
return torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=f)
# lr_lambda是lr变化的规则,是一个函数
使用
model = net()
loss_function = L1loss()
optimizer = tc.optim.Adam(net.parameters(), lr=para['lr'])
train_loader, eval_loader, test_loader = data_loader()
lr_scheduler = create_lr_scheduler(optimizer, len(train_loader), para['epoch'], warmup=True,warmup_epochs=1)
for epoch in para['epoch']:
for img,lab in train_loader:
optimizer.zero_grad()
pred = net(img)
loss_function = loss(lab,pred)
loss.backward()
optimizer.step()
lr_scheduler.step()
if __name__ == '__main__':
lr_scheduler = create_lr_scheduler(optimizer, 10, 20, warmup=True)
for i in range(20):
print('-------')
for j in range(10):
print(lr_scheduler.get_lr()[0])#获得当前学习率
lr_scheduler.step()
实践
【2024-3-20】 每隔 4 步更新梯度,而每步都执行 学习率更新,导致报错:
lr_scheduler.step()出现在optimizer.step()前面
UserWarning: Detected call of `lr_scheduler.step()` before `optimizer.step()`. In PyTorch 1.1.0 and later, you should call them in the opposite order: `optimizer.step()` before `lr_scheduler.step()`. Failure to do this will result in PyTorch skipping the first value of the learning rate schedule. See more details at https://pytorch.org/docs/stable/optim.html#how-to-adjust-learning-rate
warnings.warn("Detected call of `lr_scheduler.step()` before `optimizer.step()`. "
解决方式:
- 将 学习率更新 语句放到 optimizer 更新后,同步进行
for epoch in range(args.num_epochs):
logging.info('Epoch [{}/{}]'.format(epoch + 1, args.num_epochs))
for i, (x, seq_len, mask, labels, _) in enumerate(train_iter):
trains = (x.to(device), seq_len, mask.to(device))
labels = labels.to(device)
outputs = model(trains) # trains[0].shape [batch_size, dim], trains[1].shape [batch_size], trains[2].shape [64, 512]
loss = loss_functioin(outputs[:, :2], labels[:, 0]) # 判断损失
loss = loss / accumulate_step
loss.backward()
# accumulate_step = 4
if ((i + 1) % accumulate_step == 0) or (i + 1 == len(train_iter)):
optimizer.step()
optimizer.zero_grad()
scheduler.step() # 更新学习率: warmup 策略
# scheduler.step() # 更新学习率: warmup 策略 --- 此处出错!
更多示例解释为什么
import torch
import torch.nn as nn
import torch.optim as optim
model = nn.Conv2d(3, 64, 3)
optimizer = optim.SGD(model.parameters(), lr=0.5)
lr_scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=2)
for i in range(5):
optimizer.zero_grad()
x = model(torch.randn(3, 3, 64, 64))
loss = x.sum()
loss.backward()
optimizer.step()
lr_scheduler.step()
optimizer_state = optimizer.state_dict()
scheduler_state = lr_scheduler.state_dict()
# resume
optimizer = optim.SGD(model.parameters(), lr=0.5)
lr_scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=2)
optimizer.load_state_dict(optimizer_state)
lr_scheduler.load_state_dict(scheduler_state) # 加上这句即可矫正
for i in range(5):
optimizer.zero_grad()
x = model(torch.randn(3, 3, 64, 64))
loss = x.sum()
loss.backward()
print('{} optim: {}'.format(i, optimizer.param_groups[0]['lr']))
optimizer.step()
print('{} scheduler: {}'.format(i, lr_scheduler.get_lr()[0]))
lr_scheduler.step()
为什么scheduler.step() 需要在optimizer.step()的后面调用
- scheduler.step() 一个作用是调整学习率,如果调用 scheduler.step(), 则会改变 optimizer 学习率
import torch
import torch.nn as nn
import torch.optim as optim
model = nn.Conv2d(3, 64, 3)
optimizer = optim.SGD(model.parameters(), lr=0.5)
lr_scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=2)
for i in range(5):
optimizer.zero_grad()
x = model(torch.randn(3, 3, 64, 64))
loss = x.sum()
loss.backward()
# 错误位置
# print('{} scheduler: {}'.format(i, lr_scheduler.get_lr()[0]))
# lr_scheduler.step()
print('{} optim: {}'.format(i, optimizer.param_groups[0]['lr']))
optimizer.step()
# 正确位置
print('{} scheduler: {}'.format(i, lr_scheduler.get_lr()[0]))
lr_scheduler.step()
异常值
NaN
NaN(Not a Number)是神经网络训练过程中最不愿意碰到却又不可避免的问题。
【2024-8-19】PyTorch训练过程中出现NaN的排查笔记
loss 变 NaN
训练深度模型过程中,数值突然变成了NaN。
- 如训到一定轮次(30+)后,损失值就变成了NaN
原因
理论: NaN 本质原因出现了 下溢 和 上溢 现象。
上溢出:- 模型中指数运算,因为模型中的数值过大,做
exp(x)操作出现上溢出 x/0,不是参数的值过大,而是具体操作的原因。
- 模型中指数运算,因为模型中的数值过大,做
下溢出:一般是log(0)或exp(x)操作出现问题。- 可能是学习率设定过大,需要降低学习率。
损失变 NaN 可能原因:
- 数据错误
- 模型训练前,通常会对数据进行预处理,例如归一化、标准化等操作。
- 如果在这个过程中出现了错误,可能会导致测试数据的值超出了模型能够处理的范围,从而导致测试损失变为NaN。
- 因此,仔细检查数据预处理的代码,并确保没有问题。
- 学习率过大
- 学习率是控制模型参数更新的重要超参数。
- 如果学习率设置得过大,模型参数更新的幅度可能会过大,从而导致损失值发散。测试损失的值可能会变为NaN。
- 尝试减小学习率,以确保模型稳定地收敛。
- 模型设计问题
- 测试损失变为NaN还可能是模型设计存在问题。
- 模型架构可能导致数值不稳定,从而出现NaN值。这可能是由于某些操作(例如relu、softmax等)在特定情况下产生了数值溢出或欠溢出。
- 尝试改变模型的架构,例如,使用不同的激活函数或正则化操作,来处理这个问题。
- 尺度不平衡的初始化
- “尺度不平衡的初始化”: 权重初始化得过大或过小,造成了梯度更新时的不稳定性。
- 使用适合激活函数的初始化方法(如He或Xavier初始化)可以有效地解决这一问题。
如何排查
定位到底是哪一层,哪一个模块出了问题?
def train(model,train_x,train_y,optimizer,criterion):
model.train()
model.zero_grad()
probs = model(train_x)
# 1. 先看probs是不是nan
assert torch.isnan(probs).sum() == 0, print(probs)
loss = criterion(probs, train_y)
# 2. 再检查看loss是不是nan
assert torch.isnan(loss).sum() == 0, print(loss)
_, pred = torch.max(probs, dim=1)
loss.backward()
optimizer.step()
return pred, loss
模型内张量检查
- 进入model内部, 一轮 forward后, 判断输出张量是否为NaN
self.net = nn.Sequential(self.conv1, self.chomp1, self.bn1, self.relu1,
self.conv2, self.chomp2, self.bn2, self.relu2)
# 逐层提那家 异常值判断
out = self.conv1(x)
assert torch.isnan(out).sum() == 0, print(out)
out = self.chomp1(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.relu1(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.dropout1(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.conv2(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.chomp2(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.relu2(out)
assert torch.isnan(out).sum() == 0, print(out)
out = self.dropout2(out)
训练求梯度过程中,增加异常检测。
with torch.autograd.detect_anomaly():
loss.backward()
#loss.backward()
案例
案例:人脸特征点检测
这篇文章(Using convolutional neural nets to detect facial keypoints tutorial)是14年获得kaggle人脸特征点检测第二名的post,详细的描述了如何构建模型并一步步的优化,里面的一些思路其实很直接干脆
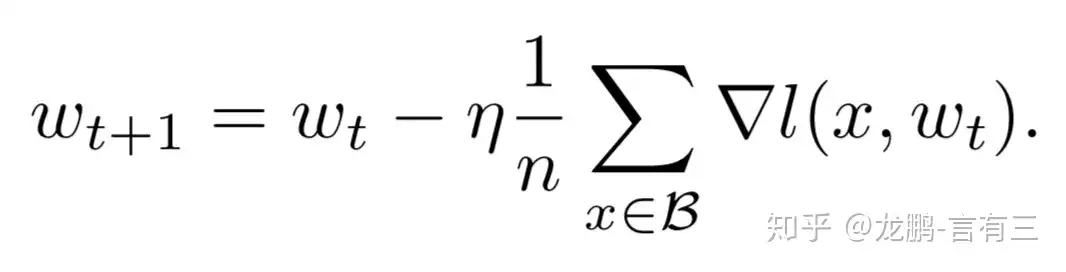

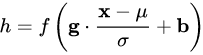
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
