鹤啸九天 自律更自由，平凡不平庸 Less is More

基础算法总结-Classical Algorithm

2018-10-30
风之筝
计算机基础
                           
阅读量次

Notes（温馨提示）:

  1. ★ 首次阅读建议浏览：导航指南, 或划到本页末尾, 或直接点击跳转, 查看全站导航图
  2. ★ 右上角工具条搜索文章，右下角二维码关注微信公众号（鹤啸九天），底栏分享、赞赏、评论。
  3. ★ 转载请注明文章来源，知识点积累起来不容易，水滴石穿，绳锯木断，谢谢理解
  4. ★ 如有疑问，邮件讨论，欢迎贡献优质资料

  • 本栏目汇总各类经典的基础算法

总结

  • 【2022-5-24】脉脉帖子: 近期面试了100多人，大部分人能力都比较差。
    • 凸包算法，经提示能写出来的2个。
    • 二叉树的 morris 遍历，能写出来的5个。
    • 孤岛问题，10来个人。
    • 接雨水，能想到双指针法的10个不到，动规或单调栈的10来个，哪怕最起码暴力解也不到一半人。
    • 最简单的二分，依然有30％以上做不出来。
    • 是我收到简历的质量太差了吗？看脉脉，几乎人均秒 medium , hard 也不是什么难事；
    • 有趣的是，我向大家透露了社招真实环境里这些题目的能写出来的比例，这可比 lc 上的 ac 率真实多了，被一顿狂喷。那些喷我的人，他们下次当面试官时，照样去 Ic 上找几道 medium 甚至 hard ，稍微改改考面试者。
  • 【2022-2-28】labuladong 的算法小抄，fucking-algorithm，GitHub Pages，总共 60 多篇原创文章，都是基于 LeetCode 的题目，涵盖了所有题型和技巧，而且一定要做到举一反三，通俗易懂，绝不是简单的代码堆砌，后面有目录。刷题刷题，刷的是题，培养的是思维，本仓库的目的就是传递这种算法思维。
  • 【2021-11-7】The Algorithms，项目地址, 分别提供了用 Python、Java、C、C++ 等数十种编程语言实现的算法，每种语言都有自己的 GitHub 算法代码库。如下领域的算法：
    • 排序（Sorts）算法
    • 搜索（Searches）算法
    • 动态规划（Dynamic Programming）算法: 编辑距离（Edit Distance）、子集和问题（Sum of Sunset）、最小分区（Minimum Partition）等子算法。
    • 加密（Ciphers）算法
    • 数据结构（Data Structures）算法
    • 数学（Math）算法
    • 数字图像处理（Digital Image Processing）算法
  • 【2022-5-24】计算机基础笔记，有道云

观点

【2012-8-22】陈皓：为什么我反对纯算法面试题

  • 问难的算法题并没有错，错的很多面试官只是在肤浅甚至错误地理解着面试算法题的目的。
  • 能解算法题并不意味着这个人就有能力就能在工作中解决问题，你可以想想，小学奥数题可能比这些题更难，但并不意味着那些奥数能手就能解决实际问题。
  • 纯算法题根本不能反映一个程序员的综合能力
  • 要考量程序员的那些综合素质呢？
    • 会不会做需求分析？怎么理解问题的？
    • 解决问题的思路是什么？想法如何？
    • 会不会对基础的算法和数据结构灵活运用？
  • 工程上，难是的是这些挑战：
    • 软件的维护成本远远大于软件的开发成本。
    • 软件的质量变得越来越重要，所以，测试工作也变得越来越重要。
    • 软件的需求总是在变的，软件的需求总是一点一点往上加的。
    • 程序中大量的代码都是在处理一些错误的或是不正常的流程。
  • 对于编程能力上，应该主要考量程序员如下能力：
    • 设计是否满足对需求的理解，并可以应对可能出现的需求变化。
    • 程序是否易读，易维护？
    • 重构代码的能力如何？
    • 会不会测试自己写好的程序？

代码实战

C++ 面试题

【2022-5-20】wqw547243068/DS_Algorithm

  • crack the coding interview： C++ 编写
  • 剑指offer

在线调试

在线代码调试

  • bejson, 支持各种语言的调试

解题技巧

【有道云笔记】基础算法总结（面试）

常见解题思路

【2022-6-19】Question List Tips Acknowledgements

条件 首选思路 其他
数组已排序 input array is sorted 二分查找（Binary search）、双指针（Two pointers）  
全排列/子集 asked for all permutations/subsets 回溯 Backtracking  
树 given a tree DFS，BFS  
图 graph DFS，BFS  
链表 given a linked lis 双指针（Two pointers）  
禁止递归 recursion is banned 栈 stack  
空间限制 must solve in-place 交换数值 Swap corresponding values，指针存放多个值 Store one or more different values in the same pointer  
最大/最小 序列/子集/选项 asked for maximum/minimum subarray/subset/options 动态规划 Dynamic programming  
最大最小k个 asked for top/least k items 堆 Heap  
公共子串 asked for common strings Map，Trie；Map/Set for 0(1) time & 0( n ) space；Sort input for 0(nlogn) time and 0(1) space  
     
  • （1）If input array is sorted then
    • Binary search
    • Two pointers
  • （2）If asked for all permutations / subsets then
    • Backtracking
  • （3）If given a treethen
    • DFS
    • BFS
  • （4）If given a graph then
    • DFS
    • BFS
  • （4）If given a linked list then
    • Two pointerS
  • （5）If recursion is banned then
    • Stack
  • （6）If must solve in-place then
    • Swap corresponding values
    • Store one or more different values in the same pointer
  • （7） If asked for maximum / minimum subarray / subset / options then
    • Dynamic programming
  • （8）If asked for top / least k items then
    • Heap
  • （9）If asked for common strings then
    • Map
    • Trie
  • ELse
    • Map / Set for 0(1) time & 0( n ) space - Sort input for 0( nlogn ) time and 0(1) space

【2024-8-29】 含各种模式解题思路及代码

LeetCode 刷题时，很多题目看似复杂，但实际上，许多问题可以归纳为几种常见算法模式。

掌握这些模式，就能高效地解决大量问题。

动态规划

动态规划：运筹学中一种最优化方法，典型案例 最长递子序列，最小编辑距离

特点

  • 1️⃣ 最优子结构，子问题相互独立
  • 2️⃣ 重叠子问题

dp问题的核心: 穷举，暴力穷举效率太低，所以需要备忘录/dp table来优化穷举过程，避免不必要的计算

  • dp自底向上，从最简单底层子问题开始
  • 而备忘录自顶向下，从大问题逐步拆解到子问题

列出状态转移方程才能正确穷举，怎么写？

  • 1️⃣ 极端情况是什么，如最简单最难情形
  • 2️⃣ 问题有什么状态
  • 3️⃣ 每个状态做出什么选择让状态变化？
  • 4️⃣ 如何定义dp数组来表示选择和状态

窗口类

滑动窗口：优化子数组和子字符串问题

滑动窗口是常用技巧，特别适合解决子数组和子字符串相关问题。

  • 问题输入是线性数据结构，如: 链表、数组或字符串
  • 题目要求查找最长/最短的子字符串、子数组或所需值

核心思想

  • 在一个可变大小的窗口中维护一些信息，并通过窗口移动来缩小问题范围。

滑动窗口模式对给定数组或链表的特定窗口大小, 执行所需操作

  • 例如：查找包含所有1的最长子序列。

滑动窗口从第一个元素开始，每次向右移动一个元素并根据要解决的问题调整窗口的长度。

在某些情况下，窗口的大小保持不变，而在其他情况下，大小会增大或缩小。

三问三答的形式进行思考：

  • 1、对于每一个右指针 right 所指的元素 ch ，做什么操作？
  • 2、什么时候要令左指针 left 右移？left对应的元素做什么操作？【循环不变量】
  • 3、什么时候进行 ans 更新？

这三个问题，本质上对应滑窗问题要考虑的三个基本要素：

  • 1、right 指针以及所对应的元素 ch
  • 2、left 指针以及所对应的元素 left_ch
  • 3、ans 答案变量

题目

  • LeetCode 3. 无重复字符的最长子串
  • LeetCode 76. 最小覆盖子串
    • 给定两个字符串 s 和 t ，找到 s 中包含 t 所有字母的最小子串。
  • LeetCode 567. 字符串的排列
    • 给定两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。
  • LeetCode 438. 找到字符串中所有字母异位词
    • 给定一个字符串 s 和一个非空字符串 p ，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。
  • LeetCode 30. 串联所有单词的子串
    • 给定一个字符串 s 和一个字符串数组 words，返回所有串联形成的子串在 s 中的起始位置。
  • 滑动窗口的最大值（剑指offer）
  • 滑动窗口中位数（LEETCODE）
  • K 个不同整数的子数组（LEETCODE）

双指针：高效遍历与查找

双指针技巧适用于数组和字符串的遍历与查找问题，尤其是在需要高效处理对称性或前后关系时。

双指针技巧：

  • 1️⃣ 左右指针，适用于链表
    • 案例：链表是否有环，返回环起点，寻找无环链表中点，链表中第k个元素
  • 2️⃣ 快慢指针，适用于数组
    • 案例：二分搜索，两数和，反转数组，滑动窗口

双指针基本思想

  • 用两个指针串联迭代数据结构，知道1-2个指针达到某个条件停止。在排序数组或链表中搜索元素对时，两个指针通常很有用， 例如将数组的每个元素与其他元素进行比较时。
  • 通常需要两个指针是因为如果只采用单个指针，必须不断循环数组才能找到答案。

这种解决方案虽然确实可行，但是对时间和空间复杂度来说明显是低效的 O(N^2)。

在许多情况下，使用双指针可以找到具有更好空间或时间复杂度的解决方案。

三问三答形式进行思考：

  • 如何初始化两个指针？
  • 如何移动指针以满足条件？
  • 如何更新结果或停止移动？

本质上对应了双指针问题需要考虑的三个基本要素：

  • 指针的初始化
  • 指针的移动逻辑
  • 结果的更新或停止条件

应用场景

  • 问题为排序数组或链表，并且需要满足某些约束的一组元素问题

  • 数组中元素集是一对，三元组，甚至是子数组

  • N-sum 问题（LEETCODE）
    • 两数和思路
      • 最简单：两重循环，逐个遍历——O(n^2)、O(1)
      • 优化版：O(nlogn)、O(n)
        • 选定a, b=targe-a，即在数组中寻找是否存在b
          • 方法一：排序，再二分查找——排序费时间 nlogn
          • 方法二：hash，建字典，用O(n)空间来降时间（O(nlogn)→O(1)）
          • 注意：哈希无法存储相同元素，因为相同元素有相同的哈希值——用反向遍历，hash记录已遍历过的元素
    • 变种：找和为k的两个元素（可能为负数），若没有，则返回最接近的；
    • 三数和（题目地址）、最接近的三数和（题目）
  • 无重复字符的最长子串（LEETCODE）
  • 接雨水（LEETCODE）
  • 长度最小的子数组（LEETCODE）

题目

  • LeetCode 167. 两数之和 II - 输入有序数组
  • LeetCode 344. 反转字符串
    • 给定一个字符串数组，使用双指针将其反转。
  • LeetCode 125. 验证回文串
    • 判断一个字符串是否是回文串，忽略大小写和非字母数字字符。
  • LeetCode 524. 通过删除字母匹配到字典里最长单词
    • 从给定的字符串和字典中找出最长的单词，这个单词可以通过删除原字符串中的某些字符得到。
  • LeetCode 283. 移动零
    • 将数组中的所有零移动到数组末尾，同时保持非零元素的相对顺序。

快慢指针

快慢指针也称“龟兔算法”，基本思想

  • 用两个指针以不同速度在数组或链表中移动。
  • 在处理循环链接列表或数组时，此方法非常有用。

通过以不同的速度移动（例如，在循环链表中），算法证明两个指针必然会相遇。一旦两个指针都处于循环中，快速指针就应该捕获慢速指针。

应用场景

  • 链表或数组循环
  • 用于找中间元素
  • 需要知道某个元素的位置或链表的总长度

举个栗子

  • 环形链表（LEETCODE）– 6
  • 相交链表（LEETCODE）– Y
  • 环形链表入口节点（LEETCODE）

合并区间

合并间隔模式是处理重叠间隔的有效技术。

涉及间隔的许多问题中，可以需要找到重叠间隔或合并间隔（如果它们重叠）。

给定两个间隔 a和b，可能存在6种不同的间隔交互情况

  • ab不重叠
    • a前b后
    • b前a后
  • ab重叠
    • a前b后
    • a包含b
    • b前a后
    • b包含a

应用场景

  • 要求生成仅具有互斥间隔的列表
  • 出现“overlapping intervals”一词

举个栗子

  • 合并区间（LEETCODE）
  • 会议室（LEETCODE）
  • Range模块（LEETCODE）
  • 区间列表的交集（LEETCODE）

区间合并思路

先将所有区间按照开头进行排序，然后开始遍历，用目前已确定的区间的尾部 和 即将要判断的区间的头部 比较大小，

  • 1）尾部>=头部，证明有交集，就去看这两个区间谁的尾部更大，取更大的尾部；
  • 2）尾部<头部，证明没有交集，那么直接把这个已确定的区间放入返回结果中，然后继续判断。

首先按输入 intervals 分别生成 starts 和 ends, 然后将 starts 和 ends 排序.

示例：

  • 情况1，有“交集”
  • 情况2，无“交集”
情况1，有“交集”
starts: ●    ●       ●
  ends:    ●      ●     ●
情况2，无“交集”
starts: ●    ●       ●
  ends:                 ●      ●     ●

重叠的部分其实就是: starts[i+1] > ends[i]

class Solution(object):
    def merge(self, intervals):
        """
        :type intervals: List[Interval]
        :rtype: List[Interval]
        """
        if len(intervals) == 0: return []
        intervals = sorted(intervals, key = lambda x: x.start)  # 根据每个小list的第一个值进行递增排序
        res = [intervals[0]]
        for n in intervals[1:]:
            if n.start <= res[-1].end: res[-1].end = max(n.end, res[-1].end)  # 第二个的开始小于res中最大区间的尾部（用-1找到）（证明两者有交集，然后尾部取这两个交集尾部的较大值）
            else: res.append(n)  # 如果第二个区间的小值比res中最大区间的尾部还大（证明没有交集）
        return res

排序

循环排序

循环排序模式描述一种处理涉及包含给定范围内数字数组问题的有趣方法。

拓扑排序用于查找彼此依赖的元素的线性排序。

  • 例如，如果事件“B”依赖于事件“A”，则“A”在拓扑排序中位于“B”之前

其一次遍历数组一个数字，如果正在迭代的当前数字不是正确的索引，则将其与正确索引处的数字交换。

应用场景

  • 涉及给定范围内数字的排序数组
  • 要求在已排序/旋转的数组中找到缺失/重复/最小的数字
  • 需要处理没有定向循环的图
  • 按排序顺序更新所有对象
  • 如果有一组遵循特定顺序的对象

举个栗子

  • 课程表系列（LEETCODE）
  • 矩阵中的最长递增路径（LEETCODE）
  • 序列重建（LEETCODE）
  • 缺失数字（LEETCODE）
  • 寻找重复数（LEETCODE）——类似问题：找不重复的元素（位操作，连续异或运算）
  • 缺失的第一个正数（LEETCODE）

拓扑排序：任务调度与依赖

拓扑排序用于解决具有依赖关系的任务排序问题，通常在有向无环图（DAG）中应用。

三问三答的形式进行思考：

  • 如何构建图和入度数组？
  • 如何处理入度为 0 的节点？
  • 如何更新其他节点的入度？

本质上对应了拓扑排序问题需要考虑的三个基本要素：

  • 图的构建
  • 入度为 0 的节点处理
  • 入度更新

题目

  • LeetCode 207. 课程表
  • LeetCode 210. 课程表 II
    • 这题是在课程表问题的基础上，要求返回完成所有课程的顺序。
  • LeetCode 329. 矩阵中的最长递增路径
    • 在一个整数矩阵中，找到从任意单元格出发的最长递增路径。
  • LeetCode 444. 序列重建
    • 根据子序列判断是否能够唯一地重建原始序列。
  • LeetCode 802. 找到最终的安全状态
    • 在一个有向图中，找到所有能够到达终点的安全节点。

K-way Merge （多路归并）

K-way Merge 用于解决涉及一组排序数组的问题。

  • 给出’K’排序数组，可以使用Heap有效地执行所有数组的所有元素的排序遍历。
  • 在Min Heap中push每个数组的最小元素以获得最小值。
  • 获得总体最小值后，将下一个元素从同一个数组推送到堆中。
  • 然后，重复此过程以对所有元素进行排序遍历。

应用场景

  • 适用于排序的数组，列表或矩阵
  • 问题要求合并排序列表，在排序列表中查找最小元素等

举个栗子

  • 合并两个有序链表（LEETCODE）
  • 合并K个排序链表（LEETCODE）
  • 丑数系列（LEETCODE）

查找

二分查找：寻找分割点

二分查找是一种高效查找方法，特别适合用于有序数组或具有一定规律的数据结构中。

二分查找核心思想

  • 每次将搜索区间缩小一半，以此快速逼近答案。

三问三答的形式进行思考：

  • 对于每个中间点 mid，应该如何处理？
  • 如何调整左右指针 left 和 right 以缩小搜索范围？
  • 什么条件下可以直接返回答案？

这三个问题，本质上对应了二分查找问题需要考虑的三个基本要素：

  • mid 指针以及所对应的元素 mid_val
  • 左右指针 left 和 right 及其变化
  • 返回答案的条件

举个栗子

  • 搜索旋转排序数组（LEETCODE）
    • 【2020-6-9】多次命中，旋转数组里的二分查找
  • 寻找两个有序数组的中位数（LEETCODE）
  • 寻找旋转排序数组中的最小值（LEETCODE）

题目

  • LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置
  • LeetCode 33. 搜索旋转排序数组
    • 在一个升序排列的数组中，数组中的元素进行了部分旋转，找到指定的目标值的位置，如果不存在则返回 -1。
  • LeetCode 74. 搜索二维矩阵
    • 在一个矩阵中，每行元素从左到右排序，每列元素从上到下排序，判断是否存在一个目标值。
  • LeetCode 81. 搜索旋转排序数组 II
    • 包含重复元素的旋转排序数组，要求找到目标值的位置，如果不存在则返回 -1。
  • LeetCode 153. 寻找旋转排序数组中的最小值
    • 在一个旋转排序数组中找到最小值，数组中不存在重复元素。

堆：寻找 top-k 元素

堆是一种适合解决 top-k 问题的数据结构。

  • 给定集合中找到 最大/最小/频繁 “K”元素

通过维护一个 k 大小的堆，可以高效地找到数组中的前 k 个最大或最小元素。

  • 根据问题将’K’个元素插入到最小堆或最大堆中；
  • 迭代剩余的数字，如果找到一个比堆中的数字大的数字，则删除该数字并插入较大的数字

三问三答的形式进行思考：

  • 如何初始化堆？
  • 如何处理新的元素以维护堆的性质？
  • 如何从堆中提取最终答案？

这三个问题，本质上对应了堆问题需要考虑的三个基本要素：

  • 堆的初始化
  • 堆的维护操作
  • 结果的提取

应用场景

  • 找到给定集合的最大/最小/频繁“K”元素；
  • 对数组进行排序以找到确切的元素

举个栗子

  • 前K个高频元素（LEETCODE）
  • 前K个高频单词（LEETCODE）
  • 第k个排列（LEETCODE）

题目

  • LeetCode 215. 数组中的第 K 个最大元素
  • LeetCode 347. 前 K 个高频元素
    • 找到一个数组中出现频率最高的 k 个元素。
  • LeetCode 973. 最接近原点的 K 个点
    • 给定一个平面上的点列表，找到离原点最近的 k 个点。
  • LeetCode 658. 找到 K 个最接近的元素
    • 找到一个数组中最接近目标值的 k 个元素。
  • LeetCode 295. 数据流的中位数
    • 维护一个数据流，随时能够找到当前数据流的中位数。

双堆 Two heaps

许多问题中，给出了一系列元素，将其分成两部分。

为了解决这个问题，知道一个部分中的最小元素和另一个部分中的最大元素。

这种模式使用两个堆：找到最大元素的Min Heap和找到最小元素的Max Heap。

工作原理

  • 将前半部分的数字存储在Max Heap中，这是因为希望在上半部分找到最大的数字。
  • 然后将数字的后半部分存储在Min Heap中，因为希望在后半部分找到最小的数字。
  • 在任何时候，可以从两个堆的顶部元素计算当前数字列表的中值。

应用场景

  • 优先队列，调度等情况
  • 找到集合中的最小/最大/中值元素
  • 有时，在以二叉树数据结构为特征的问题中很有用

举个栗子

  • 数据流的中位数（LEETCODE）
  • 滑动窗口的最大值（剑指offer）

树图遍历

BFS vs DFS

树遍历算法：bfs 广度优先搜索，dfs 深度优先搜索

  • dfs是回溯算法 …
  • bfs 核心思想: 用队列存储周围节点，bfs 找到的路径一定最短，但代价空间复杂度比dfs大很多

案例：

  • 二叉树最小高度，打开密码锁最小步数

改进：

  • 双向bfs，起点终点同时开始扩散，两边有交集时终止，遵循bfs框架，但不用队列，而是hashset，更容易判断集合是否交集…

局限: 必须知道终点…

bfs空间复杂度都一样

回溯也是穷举，但不用找状态转移方程，是一个决策树遍历过程，多叉树遍历问题…

几个要点：

  • 1️⃣ 路径
  • 2️⃣ 选择条件
  • 3️⃣ 结束条件

案例：全排列，n皇后问题

深度优先搜索（DFS）：遍历图和树的基础

深度优先搜索（DFS）是一种遍历或搜索图、树结构的算法，常用于解决全路径、连通性等问题。

树DFS基于深度优先搜索（DFS）技术来遍历树。

Tree DFS的基本思想: 用递归（或迭代方法的堆栈）遍历时跟踪所有先前（父）节点。

从树的根开始，如果节点不是叶子，则需要做三件事：

  • 决定是立即处理当前节点（先序遍历），还是在之间处理两个子节点（中序遍历）或处理两个子节点之后（后序遍历）。
  • 为当前节点的两个子节点进行两次递归调用来处理它们。

三问三答的形式进行思考：

  • 如何处理当前节点？
  • 如何递归到子节点？
  • 如何处理递归返回后的结果？

本质上对应了 DFS 问题需要考虑的三个基本要素：

  • 当前节点的处理
  • 递归调用的处理
  • 递归返回后的结果处理

应用场景

  • 涉及树的先序、中序或者后续遍历问题
  • 如果问题涉及搜索节点离叶子更近的目标

举个栗子

  • 求根到叶子节点数字之和（LEETCODE）
  • 二叉树的最大深度（LEETCODE）
  • 从中序与后序遍历序列构造二叉树（LEETCODE）
  • 路径总和系列（LEETCODE）

题目

  • LeetCode 104. 二叉树的最大深度
  • LeetCode 543. 二叉树的直径
    • 计算二叉树的直径，即任意两节点路径中，边的最大数目。
  • LeetCode 130. 被围绕的区域
    • 在二维矩阵中，如果被 ‘X’ 包围的 ‘O’ 被替换为 ‘X’。
  • LeetCode 200. 岛屿数量
    • 计算二维矩阵中岛屿的数量，岛屿由相邻的陆地‘1’组成，水域为‘0’。
  • LeetCode 39. 组合总和
    • 找到所有和为目标值的组合，元素可重复使用。

广度优先搜索（BFS）：层级遍历与最短路径

广度优先搜索（BFS）是一种层级遍历算法，特别适合用于搜索最短路径或进行层级遍历的问题。

基于广度优先搜索（BFS）技术来遍历树，并使用队列在跳到下一层之前记录下该层的所有节点

三问三答的形式进行思考：

  • 如何处理当前层的节点？
  • 如何扩展到下一层的节点？
  • 如何确定搜索是否完成？

本质上对应了 BFS 问题需要考虑的三个基本要素：

  • 当前层节点的处理
  • 扩展到下一层的处理
  • 搜索完成的条件

应用场景

  • 涉及到层序遍历树

举个栗子

  • N叉树的层序遍历（LEETCODE）
  • 二叉树的层序遍历（LEETCODE）
  • 二叉树的锯齿形层次遍历

题目

  • LeetCode 102. 二叉树的层序遍历
  • LeetCode 111. 二叉树的最小深度
    • 找出二叉树的最小深度，即从根节点到最近的叶子节点的最短路径。
  • LeetCode 752. 打开转盘锁
    • 给定一个只包含 0 到 9 的四位密码锁，找到解锁的最小步数。
  • LeetCode 127. 单词接龙
    • 给定两个单词，找到从第一个单词到第二个单词的最短转换序列，每次只能改变一个字母，且每一步必须是一个有效单词。
  • LeetCode 200. 岛屿数量
    • 计算二维矩阵中岛屿的数量，岛屿由相邻的陆地‘1’组成，水域为‘0’。这个题目既可以用DFS解决，也可以用BFS。

子集与组合：子集生成与组合求解

子集与组合问题涉及生成所有子集、组合或排列，通常使用回溯法进行求解。

一组给定元素的排列和组合。

Subsets模式描述了一种有效的广度优先搜索（BFS）方法来处理所有这些问题。（全部组合）

  • 例如给定一个数组 [1, 5, 3]
  • 首先初始化一个空数组：[[ ]]
  • 将第一个数字(1)添加到所有现有子集，以创建新的子集: [[], [1]]
  • 继续添加[[], [1], [5], [1, 5]]
  • [[], [1], [5], [1, 5], [3], [1, 3], [5, 3], [1, 5, 3]]

三问三答的形式进行思考：

  • 如何选择当前元素加入子集？
  • 如何递归生成子集或组合？
  • 如何处理递归返回后的结果？

本质上对应了子集与组合问题需要考虑的三个基本要素：

  • 当前元素的选择
  • 递归生成的处理
  • 递归返回的结果处理

题目

  • LeetCode 78. 子集
  • LeetCode 39. 组合总和
    • 找到所有和为目标值的组合，元素可重复使用。
  • LeetCode 90. 子集 II
    • 与子集不同，这道题允许数组中有重复元素，要求生成所有可能的子集，且子集不能重复。
  • LeetCode 40. 组合总和 II
    • 与组合总和不同，这道题的候选数组有重复元素，每个元素只能使用一次。
  • LeetCode 46. 全排列
    • 找到给定数组的所有排列组合。

趣味问题

6个人最多能建多少个群

【2022-11-9】都说3个女人一台戏，那么，一个女寝有6个人，最多可以建多少微信群？

（1）组合问题

  • 两个人的群：6*5/2=15
  • 三个人的群：654/3/2=20
  • 四个人的群：654*3/4/3/2=15
  • 五个人的群：6
  • 六个人的群：1

所以

  • $N=\sum_{i=2}^{6} = C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=15+20+15+6+1=57$
  • 15+20+15+6+1=57

如果两个人的不算，那就是42个。

  • $N=\sum_{i=3}^{6} = C_6^3+C_6^4+C_6^5+C_6^6=20+15+6+1=42$

（2）另一种思路

  • 任何一个群，对于每个人来说，有“在群里”和“不在群里”两种状态，总共是2^6=64种
  • 然而两个人无法建群，6个人里选两个总共有 6*5/2=15 种，再去除1个人的6种和0个人的1种
  • 总共为：64-15-6-1=42种。

推广一下，如果有n个人，总共建群的方式有：

  • $ 2^n-n*(n-1)/2-n-1$种建群的方式。

作者：沙尘

数据结构与算法

  • 【2020-6-18】快速刷题：算法模板，最科学的刷题方式，最快速的刷题路径，你值得拥有~ Gitbook
  • 【2021-1-23】可视化解释A、Dijkstra、BFS寻路算法，在线体验地址，完整代码Interactive pathfinding - Visual explanation of pathfinding algorithms and how a, Dijkstra and BFS can be seen as the same algorithm with different parameter/data structures used under the hood’ by Nicolò Pretto
  • 【2021-4-14】算法经验总结，labuladong, gitee地址，各种类型题目解题思路，如动态规划，pdf文件

【2024-9-6】各类树图算法总结

算法 时间复杂度 优点 缺点
Dijkstra 朴素算法 O(n^2) 算法稳定，易实现 边权不能为负
Dijkstra + Heap O((n+m)logn) 算法稳定，效率高 边权不能为负
Bellman - Ford O(nm) 可以处理负权边 稠密图效率低
SPFA O(nm) 稀疏图效率高 特殊情况会退化
Floyd - warshall O(n^3) 多源最短路，代码简单 时间复杂度高
       

目录概览

总结

数据结构与算法是程序设计的两大基础，大型的IT企业面试时也会出数据结构和算法的题目，它可以说明你是否有良好的逻辑思维，用来测试潜力，即使技术存在某些缺陷，面试公司也会认为你很有培养价值，至少在一段时间之后，技术可以很快得到提高

程序设计

数据结构 vs 算法

算法与数据结构区别

  • 数据结构只是静态描述了数据元素之间的关系。
  • 高效的程序要在数据结构基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：

  • 算法为解决实际问题而设计
  • 数据结构是算法需要处理的问题载体

算法特性

算法的五大特性

  • 输入: 算法具有0个或多个输入
  • 输出: 算法至少有1个或多个输出
  • 有穷性: 算法在有限的步骤之后会自动结束而不会无限循环，并且每一个步骤可以在可接受的时间内完成
  • 确定性：算法中的每一步都有确定的含义，不会出现二义性
  • 可行性：算法的每一步都是可行的，也就是说每一步都能够执行有限的次数完成

算法复杂度

计算复杂度: 一个特定算法在运行时所消耗的计算资源(时间和空间)的度量。

计算复杂度又分为两类:

  • 1、时间复杂度
    • 时间复杂度不是测量一个算法或一段代码在某个机器或者条件下运行所花费的时间。时间复杂度一般指时间复杂性，时间复杂度是一个函数，它定性描述该算法的运行时间，允许我们在不运行它们的情况下比较不同的算法。例如，带有O(n)的算法总是比O(n²)表现得更好，因为它的增长率小于O(n²)。
  • 2、空间复杂度
    • 就像时间复杂度是一个函数一样，空间复杂度也是如此。 从概念上讲，它与时间复杂度相同，只需将时间替换为空间即可。 维基百科将空间复杂度定义为：

算法时间效率可用“大O记法”来表示。

  • “大O记法”：对于单调整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有 f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为 f(n)=O(g(n))。在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。
  • 时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为 T(n)=O(g(n))，则称 O(g(n)) 为算法A的渐近时间复杂度，简称时间复杂度，记为 T(n)

算法或计算机程序的空间复杂度是解决计算问题实例所需的存储空间量，以特征数量作为输入的函数。

时间复杂度基本计算规则

  • 基本操作，即只有常数项，认为其时间复杂度为 O(1)
  • 顺序结构，时间复杂度按加法进行计算 —— 先执行a，然后执行b，再执行c
  • 循环结构，时间复杂度按乘法进行计算 —— for(){while()…}
  • 分支结构，时间复杂度取最大值 —— if{}else{}

判断一个算法的效率时，只需关注操作数量的最高次项，其它次要项和常数项可以忽略

  • 在没有特殊说明时，所分析的算法时间复杂度都是指最坏时间复杂度

常见时间复杂度

执行次数函数举例 阶 非正式术语
12 O(1) 常数阶
2n + 3 O(n) 线性阶
3n² +2n + 1O(n²) 平方阶  
5log2n+20 O(logn) 对数阶
2n+3nlog2n+19 O(nlogn) nlogn阶
6n³ +2n² +3n + 1 O(n³) 立方阶
2^n O(2^n) 指数阶

注意，经常将log2n（以2为底的对数）简写成logn

所消耗的时间从小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

【2022-8-23】常用数据结构操作与算法复杂度总结

各种复杂度的总结对比

不同时间复杂度的增长速度对比如下，图片来自Big-O Cheat Sheet Poster

渐进复杂度分析输入规模较大时的情况，输入规模较小时呢？

  • 在输入规模较小时，就不能轻易地忽略掉常数𝑐的作用，如下图所示，图片来自Growth Rates Review。复杂度增长快的在输入规模较小时可能会小于复杂度增长慢的。
  • 选择算法时，不能无脑上看起来更快的高级数据结构和算法，还得具体问题具体分析，因为高级数据结构和算法在实现时往往附带额外的计算开销，如果其带来的增益无法抵消掉隐含的代价，可能就会得不偿失。

这同时也给了我们在代码优化方向上的启示，

  • 一是从𝑓(𝑛)上进行优化，比如使用更高级的算法和数据结构；
  • 还有是对常数𝑐进行优化，比如移除循环体中不必要的索引计算、重复计算等。

除了大𝑂记号，还有大Ω记号和Θ记号，分别表示下界和确界，

  • Ω(𝑓(𝑛)): 𝑐⋅𝑓(𝑛)≤𝑇(𝑛)
  • Θ(𝑓(𝑛)): 𝑐1⋅𝑓(𝑛)≤𝑇(𝑛)≤𝑐2⋅𝑓(𝑛)

关系如下图所示，图片截自邓俊辉-数据结构C++描述第三版

常用数据结构操作与算法的复杂度

（1）数据结构

  • 逻辑结构
    • 集合：无逻辑关系
    • 线性结构
      • 一般：线性表，元素顺序排列；
      • 顺序表：
        • 基本思想：元素的存储空间是连续的。在内存中是以顺序存储，内存划分的区域是连续的。
      • 链式表：
        • 基本思想：元素的存储空间是离散的，单独的（物理），它们可以通过在逻辑上指针的联系使得它成为了整体的链表。
        • 链表每个节点分成数据域 data + 指针域 next，图
          • 单链表：head指向头节点，尾节点next指针为空（null）
          • 双链表：除了next，新增pre指针，指向上一个节点，尾结点的next指针仍然为空，图
          • 循环链表：尾结点指向头结点，形成环状，图
      • 特殊：队列、栈
        • 队列: FIFO(先进后出), 循环队列, LRU(最近最少用), LFU(历史最少用)
        • 栈: 后进先出、先进后出
      • 推广：数组、广义表
    • 非线性结构：树、图、多维数组
  • 存储结构：涉及多种存储结构
    • 顺序、链式、索引、散列

特殊数据结构：

  • 1️⃣ 单调栈，栈内元素有序，求解下一个最大元素问题，循环数组
  • 2️⃣ 单调队列，元素有序，求解滑动窗口最大值

（2）算法

  • 排序：
  • 内部排序：只用内存
    • 插入排序：直接插入排序、希尔排序
    • 选择排序：简单选择排序、堆排序
    • 交换排序：冒泡排序、快速排序
    • 归并排序：
    • 基数排序：
  • 外部排序：内存和外存结合使用
  • 查找：
    • 静态查找表
      • 二分查找
      • 顺序查找
      • 分块查找
    • 动态查找表
      • 二叉排序树
      • 平衡二叉树
      • B-树

基础算法

栈和队列是特殊的线性表，既然特殊就有不同点。

顺序 vs 链式

顺序存储结构

  • 优点
    • 实现比较简单
    • 查找指定位置的元素效率很快，时间复杂度为常数阶O(1)　
    • 无需额外存储元素之间的逻辑关系（链式存储由于存储空间随机分配，需要存储元素之间的逻辑关系）
  • 缺点
    • 需要预先分配存储空间，如果数据元素数量变化较大，很难确定存储容量，并导致空间浪费
    • 若频繁进行插入删除操作，则可能需要频繁移动大量数据元素
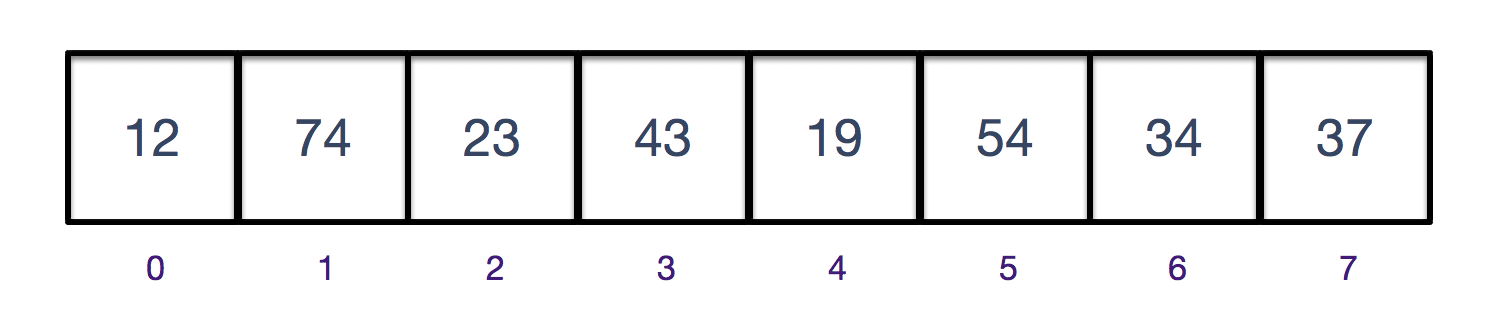
  • 顺序存储结构，是用一段地址连续的存储单元依次存储线性表的数据元素

链式存储结构

  • 优点
    • 不需要提前分配存储空间，元素个数不受限制
    • 对于插入删除操作，在已找到目标位置前提下，效率很高，仅需处理元素之间的引用关系，时间复杂度为O(1)
  • 缺点
    • 实现相对复杂
    • 查找效率较低，最坏情况下需要遍历整张表
    • 由于物理存储位置不固定，需要额外存储数据元素之间的逻辑关系
  • 链式存储结构，用一组任意的存储单元来存储数据元素，不要求物理存储单元的连续性，由一系列结点组成，每个结点除了要存储数据外，还需存储指向后继结点或前驱结点的存储地址。

栈

顺序栈（Sequence Stack）

  • 基本思想：后进先出（先进后出）即栈中元素被处理时，按后进先出的顺序进行，栈又叫后进先出表（LIFO）。

（1）数组实现栈

#include <stdio.h>
#include <stdlib.h>
// 完整版
struct Stack{
	int capability;
	int sp;
	int *data;
};
typedef struct Stack *slink;

// 精简版
typedef struct {
    ElemType *elem; // 元素类型
    int top; // 栈顶元素位置
    int size; // 栈空间
    int increment;
} SqSrack;

（2）链表实现栈

#include <stdio.h>
#include <stdlib.h>

struct Stack{
	int size;
	struct List{ // 链表节点
		int item;
		struct List *next;
	} *head; // 定义链表
};
typedef struct Stack *slink;

队列

队列（Sequence Queue）

  • 基本思想：先进先出即先被接收的元素将先被处理，又叫先进先出表（FIFO）。

分类

  • 顺序队列
    • 判断队满和队空的标志，总结：
      1. 队空：head = tail
      2. 队满：tail = m
  • 循环队列
    • 判断队满和队空
      1. 队空：head = tail
      2. 队满：tail + 1 = head(在队列中会留一个空着的空间，所以要加1)

队列数据结构

（1）使用数组实现队列

#include <stdio.h>
#include <stdlib.h>
// 完整格式
struct Queue{
	int capibility; // 容量
	int *data; // 数组内容指针
	int head; // 头元素位置
	int rear; // 尾元素位置
};
typedef struct Queue *qlink;
// 精简格式
typedef struct {
    ElemType * elem;
    int front;
    int rear;
    int maxSize;
}SqQueue;

完整代码：

（2）使用链表list实现队列

#include <stdio.h>
#include <stdlib.h>
// 定义链表
struct List{
	int item;
	struct List *next;
};
// 定义队列
struct Queue{
	int size; // 队列大小
	struct List *head; // 头指针
	struct List *rear; // 尾指针
};
typedef struct Queue *qlink; // 定义队列

完整代码

循环队列

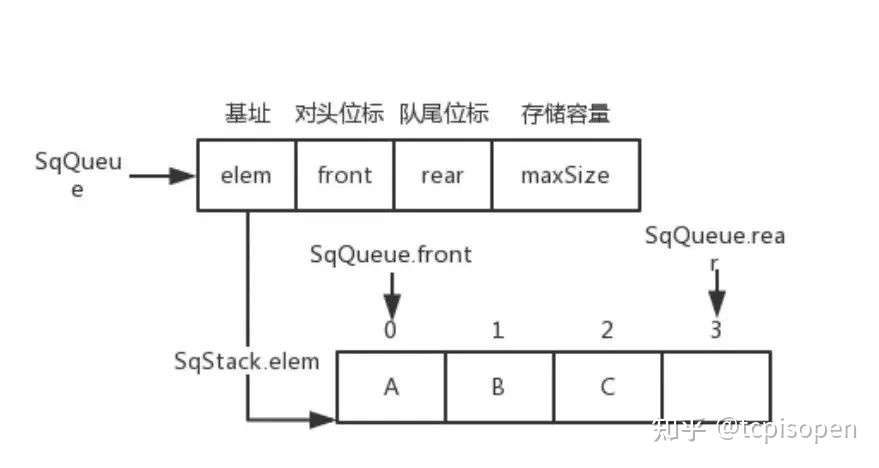
  • SqQueue.rear++

非循环队列

  • SqQueue.rear = (SqQueue.rear + 1) % SqQueue.maxSize

其它队列

  • LRU : Least recently used 最近最少使用
    • 新数据插入链表头部
    • 缓存数据访问时，将数据移到链表头部
    • 链表满时，淘汰尾部数据
  • Two queues：两个缓存队列，一个FIFO队列，一个LRU队列
    • 新数据插入FIFO队列
    • 若FIFO里的数据没有被访问，则按照FIFO规则淘汰
    • FIFO队列里的数据再次被访问，则移到LRU队列头部
    • LRU队列里的数据再次被访问，则移到头部
    • LRU队列淘汰尾部的数据
  • Multi Queue（MQ）
  • LFU: Least Frequently Used 历史最少使用
    • 每个数据都需要维护引用计数
    • 新数据插入队列尾部 (因为引用计数为1)
    • 队列数据被访问后，引用计数增加，队列重新排序
    • 淘汰数据时，从尾部淘汰 (淘汰引用计数最小的数据)

顺序表

顺序表数据结构

typedef struct {
    ElemType *elem;
    int length;
    int size;
    int increment;
} SqList;

链表

三者的区别（从上面三个图我们可以总结出来）：

  • 1、它们都有数据域（data(p)）和指针域(next(p))，但是从图中可以看出双链表有两个指针域，一个指向它的前节点，一个指向它的后节点。
  • 2、单链表最后一个节点的指针域为空，没有后继节点；循环链表和双链表最后一个节点的指针域指向头节点，下一个结点为头节点，构成循环；
  • 3、单链表和循环链表只可向一个方向遍历；双链表和循环链表，首节点和尾节点被连接在一起，可视为“无头无尾”；双链表可以向两个方向移动，灵活度更大。

代码

// 定义链表节点
struct LinkNode
{
	int data; // 数据域
	struct LinkNode *next; // 指针域
	//struct LinkNode *pre; // 双链表
};
// 定义链表，一个指向节点的指针即可
typedef struct LinkNode *llink; 

// 精简版：链表结构
typedef struct LNode {
    ElemType data;
    struct LNode *next;
} LNode, *LinkList;

完整函数实现：

C++类来表示节点的结构如下：参考

struct Node{
   int m_data;//存储数据部分
   Node* m_next;//存储下一个节点的地址
};
// 或者
struct ListNode
{
    double value;
    ListNode *next;
};
// 定义链表：定义一个空的head指针即可
ListNode *head = nullptr;
// 创建链表
head = new ListNode; //分配新结点
head->value = 12.5; //存储值
head->next = nullptr; //表示链表的结尾


List a;//创建一个链表对象a
a.push_back(1);//将整数1放入链表a

void push_back(Node*& b, int i)
{
    b = new Node;
    b->m_data = i;
    b->m_next = nullptr;
}

Node* a = nullptr;
push_back(a, 1);
push_back(a, 2); // 错误，指针没有移动
// 改正
push_back(a, 1);
push_back(a->m_next, 2);
push_back(a->m_next->m_next, 3);
push_back(a->m_next->m_next->m_next, 4);
// 改进，增加尾指针
Node* a = nullptr; 
Node* tail = nullptr;
push_back(a, 1); 
tail = a;
push_back(tail->m_next, 2); 
tail = tail->m_next;
push_back(tail->m_next, 3); 
tail = tail->m_next;

C++ 方式

  • 给它提供一个或多个构造函数，那将会带来很大的方便，因为这样将使得结点在创建时即可初始化。前文还曾经提到过，构造函数可以像常规函数一样，使用默认形参来定义，而为结点的后继指针提供一个默认的 nullptr 形参是很常见的。
struct ListNode
{
    double value;
    ListNode *next;
    //构造函数
    ListNode(double valuel, ListNode *nextl = nullptr)
    {
        value = value1;
        next = next1;
    }
};
// 创建链表
ListNode *secondPtr = new ListNode(13.5);
ListNode *head = new ListNode(12.5, secondPtr);
// 循环创建链表
double number;
while (numberFile >> number)
{
    //创建一个结点以保存该数字
    numberList = new ListNode(number, numberList);
}
// 遍历链表
ListNode *ptr = numberList;
while (ptr != nullptr)
{
    cout << ptr->value << " "; //处理结点（显示结点内容）
    ptr = ptr->next; //移动到下一个结点
}

完整示例

// This program illustrates the building
// and traversal of a linked list.
#include <iostream>
#include <fstream>
using namespace std;
struct ListNode
{
    double value;
    ListNode *next;
    // Constructor
    ListNode(double value1, ListNode *next1 = nullptr)
    {
        value = value1; next = next1;
    }
};

int main()
{
    double number; // Used to read the file
    ListNode *numberList = nullptr; // List of numbers
    // Open the file
    ifstream numberFile("numberFile•dat");
    if (!numberFile)
    {
        cout << "Error in opening the file of numbers.";
        exit (1);
    }
    //Read the file into a linked list
    cout << "The contents of the file are: " << endl;
    while (numberFile >> number)
    {
        cout << number << " ";
        // Create a node to hold this number
        numberList = new ListNode(number, numberList);
    }
    // Traverse the list while printing
    cout << endl << "The contents of the list are: " << endl;
    ListNode *ptr = numberList;
    while (ptr != nullptr)
    {
        cout << ptr->value << " "; // Process node
        ptr = ptr->next; // Move to next node
    }
    return 0;
}

链表翻转

就地反转链表

许多问题中，可能要求反转链表的一组节点之间的链接。

  • 约束就是需要就地执行此操作，即使用现有节点对象而不使用额外内存。

此模式一次反转一个节点，从一个指向链表头部的变量（当前）开始，一个变量（上一个）将指向已处理的上一个节点。以锁步方式，将通过将当前节点指向前一个节点，然后再转到下一个节点来反转当前节点。此外，更新变量“previous”以始终指向你已处理的上一个节点。

hash哈希

哈希函数：

  • H(key): K -> D , key ∈ K 构造方法
  • 直接定址法
  • 除留余数法
  • 数字分析法
  • 折叠法
  • 平方取中法 冲突处理方法
  • 链地址法：key 相同的用单链表链接
  • 开放定址法
    • 线性探测法：key 相同 -> 放到 key 的下一个位置，Hi = (H(key) + i) % m
    • 二次探测法：key 相同 -> 放到 Di = 1^2, -1^2, …, ±（k)^2,(k<=m/2）
    • 随机探测法：H = (H(key) + 伪随机数) % m

作者：tcpisopen

typedef char KeyType;

typedef struct {
    KeyType key;
}RcdType;

typedef struct {
    RcdType *rcd;
    int size;
    int count;
    bool *tag;
}HashTable;

排序算法

总结

口诀：快希堆归并

  • 快希堆：nlog(n)
  • 堆选归并：不稳定
排序算法 平均时间复杂度 最差时间复杂度 空间复杂度 数据对象稳定性
冒泡排序 O(n2) O(n2) O(1) 稳定
选择排序 O(n2) O(n2) O(1) 数组不稳定、链表稳定
插入排序 O(n2) O(n2) O(1) 稳定
快速排序 O(n*log2n) O(n2) O(log2n) 不稳定
堆排序 O(n*log2n) O(n*log2n) O(1) 不稳定
归并排序 O(n*log2n) O(n*log2n) O(n) 稳定
希尔排序 O(n*log2n) O(n2) O(1) 不稳定
计数排序 O(n+m) O(n+m) O(n+m) 稳定
桶排序 O(n) O(n) O(m) 稳定
基数排序 O(k*n) O(n2) 稳定  

均按从小到大排列

  • k：代表数值中的 “数位” 个数
  • n：代表数据规模
  • m：代表数据的最大值减最小值

img img

插入排序

  • （1）简介：直接插入排序，从字面意思可以看出，直接插入数据完成排序
  • （2）基本思想：在插入第i个数时，假设前i-1数已经排好序了，只需要将第i个数插入到i-1中，使得这i个数也是顺序的
    • 注意：插入时，片段整体后移
void insertSort(vector<int>& nums){
  int len=nums.size();
  for(int i=1;i<len;i++){
    int key=nums[i];
    int j=i-1;
    while(j>=0 and nums[j]>key){
      nums[j+1]=nums[j];
      j--;
    }
    nums[j+1]=key;
  }
}

希尔排序（Shell）—— 改进插入排序

  • （1）简介： 希尔排序又称为缩小增量排序，是对直接插入排序方法的改进。（挪动次数太多）
  • （2）基本思想：从局部有序到整体有序
    • 将整个序列分成多个子序列，然后分别进行直接插入排序，直到整个序列中的所有数基本有序时，再对整体进行一次直接插入排序。
  • 案例：假设有10个数
    1. d1 = n/2 = 5, 每隔5个元素相互比较，执行直接插入排序
    2. d2 = d1/2 = 3, 取奇数
    3. d3 = d2/2 = 1, 取奇数

简单选择排序

  • （1）简介：简单选择排序也叫直接选择排序，其实说白了跟直接插入排序的道理特别简单，效率低。
  • （2）基本思想：前半部分全局有序
    • 首先在 n个数中选择一个最小的数，并将它从中删除，作为新的一组数的第一个；
    • 再在剩下的数中选择最小的数，将它从中删除，作为新的一组数的第二个。。。。
    • 如此反复，直到排序完成，最后得到一组从小到大排序的数。
  • img

冒泡排序

  • （1）简介：冒泡排序，就跟水里的物体一样，小的往上浮，大的往下沉。
  • （2）基本思想：将数组垂直排列，取出最后一个元素逐个向上交换，得到大数（小数），继续步骤一的操作，直到排序完成。
  • img img

快排 —— 内排中速度最快

  • （1）简介：快速排序是目前内部排序中速度最快的一种排序算法。
  • （2）基本思想：
    • 选取一个数据（通常是数组的第一个数）作为关键数据，然后将所有比它小的数都放在它前面，所有比它大的数都放在它后面，这个过程称为一趟快速排序
    • 再从分开的部分选取基准数，进行分组划分，重复执行，直到完成。
  • img

快排存在的问题，如何优化

  • 3 种快排基准选择方法：随机（rand函数）、固定（队首、队尾）、三数取中（队首、队中和队尾的中间数）

  • 4种优化方式：
  • 优化1：当待排序序列的长度分割到一定大小后，使用插入排序
  • 优化2：在一次分割结束后，可以把与Key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割
  • 优化3：优化递归操作
  • 优化4：使用并行或多线程处理子序列
void swap(vector<int>& vec,int a,int b){
    vec[a]=vec[a]^vec[b];
    vec[b]=vec[a]^vec[b];
    vec[a]=vec[a]^vec[b];
}
int partition(vector<int>& vec,int start,int end){
    int pivot=vec[start+(end-start)/2];
    while(start<end){
        while(start<end and vec[start]<pivot) start++;
        while(start<end and vec[end]>pivot) end--;
        if(start<end) swap(vec,start,end);
    }
    return start;
}
void quickSort(vector<int>& vec,int start,int end){
    if(start>end) return;
    int pivot=partition(vec,start,end);
    quickSort(vec,start,pivot-1);
    quickSort(vec,pivot+1,end);
}

归并排序

  • （1）简介：归并排序又称为二路合并操作，使用合并操作完成排序的算法。
  • （2）基本思想：将两个或两个以上的有序表合并成一个新的有序表，最后将所有的有序表合成一个整体有序表。
  • img img

基数排序

  • （1）简介：前面介绍的排序方法都是对元素进行的，基数排序是对元组进行的。
  • （2）基本思想：从低位到高位依次对待排序的数进行分配和收集，经过d趟分配和收集，就可以得到一个有序序列。
  • img img

堆排序——简单选择排序改进

  • （1）简介：堆排序是一个相当有用的排序技术，特别适用于对大量的记录进行排序。同时，堆排序也是对简单选择排序的改进。
    • 堆的定义：n个元素的序列｛K1，K2，…，Kn｝当满足下列关系时，称为堆：Ki≤K2i且Ki≤K2i+1或者Ki≥K2i且Ki≥K2i+1。注意：堆树必须是一颗完全二叉树。
  • （2）基本思想：利用堆积树这种数据结构所设计的一种排序，可以利用数组的特点快速的定位指定索引的元素。

种类

  • 最大堆：父结点大于或等于儿子结点
  • img
  • 最小堆：父结点小于或等于儿子结点
  • img

堆排序的基本过程：

  • 将n个元素的序列构建一个大顶堆或小顶堆
  • 将堆顶的元素放到序列末尾
  • 将前n-1个元素重新构建大顶堆或小顶堆，重复这个过程，直到所有元素都已经排序

将序列｛20,60,26,30,36,10｝调整为递增序列。

  • 1、首先将数据建立完全二叉树，填充规则是按层次遍历将数据一一填入，最后构建最小堆；
  • 2、提取堆顶并调整删除队顶后的元素为新堆；
  • 3、重复第2步，直到堆空；
  • 4、每次提取的堆顶依次排序即为递增序列。

整体时间复杂度为nlogn

#include<iostream>
#include<vector>
using namespace std;
void swap(vector<int>& arr, int a,int b){
    arr[a]=arr[a]^arr[b];
    arr[b]=arr[a]^arr[b];
    arr[a]=arr[a]^arr[b];
}
void adjust(vector<int>& arr,int len,int index){
    int maxid=index;
    // 计算左右子节点的下标   left=2*i+1  right=2*i+2  parent=(i-1)/2
    int left=2*index+1,right=2*index+2;

    // 寻找当前以index为根的子树中最大/最小的元素的下标
    if(left<len and arr[left]<arr[maxid]) maxid=left;
    if(right<len and arr[right]<arr[maxid]) maxid=right;

    // 进行交换，记得要递归进行adjust,传入的index是maxid
    if(maxid!=index){
        swap(arr,maxid,index);
        adjust(arr,len,maxid);
    }
}
void heapsort(vector<int>&arr,int len){
    // 初次构建堆，i要从最后一个非叶子节点开始，所以是(len-1-1)/2，0这个位置要加等号
    for(int i=(len-1-1)/2;i>=0;i--){
        adjust(arr,len,i);
    }

    // 从最后一个元素的下标开始往前遍历，每次将堆顶元素交换至当前位置，并且缩小长度（i为长度），从0处开始adjust
    for(int i=len-1;i>0;i--){
        swap(arr,0,i);
        adjust(arr,i,0);// 注意每次adjust是从根往下调整，所以这里index是0！
    }
}
int main(){
    vector<int> arr={3,4,2,1,5,8,7,6};

    cout<<"before: "<<endl;
    for(int item:arr) cout<<item<<" ";
    cout<<endl;

    heapsort(arr,arr.size());

    cout<<"after: "<<endl;
    for(int item:arr)cout<<item<<" ";
    cout<<endl;

    return 0;
}

外部排序

外排序（External sorting）是指能够处理极大量数据的排序算法。通常来说，外排序处理的数据不能一次装入内存，只能放在读写较慢的外存储器（通常是硬盘）上。外排序通常采用的是一种“排序-归并”的策略。在排序阶段，先读入能放在内存中的数据量，将其排序输出到一个临时文件，依此进行，将待排序数据组织为多个有序的临时文件。尔后在归并段阶将这些临时文件组合为一个大的有序文件，也即排序结果。

查找

  • 查找：
    • 静态查找表
      • 二分查找
      • 顺序查找
      • 分块查找
    • 动态查找表
      • 二叉排序树
      • 平衡二叉树
      • B-树

总结

查找算法 平均时间复杂度 空间复杂度 查找条件  
顺序查找 O(n) O(1) 无序或有序  
二分查找（折半查找） O(log2n) O(1) 有序  
插值查找 O(log2(log2n)) O(1) 有序  
斐波那契查找 O(log2n) O(1) 有序  
哈希查找 O(1) O(n) 无序或有序  
二叉查找树（二叉搜索树查找） O(log2n)      
红黑树 O(log2n)      
2-3树 O(log2n - log3n)  
B树/B+树 O(log2n)      

静态查找

静态查找

  • 若查找目的是为了查询某个特定的数据是否在表中或检索某个特定数据的各种属性，则此类查找表为静态查找表。

性能分析

顺序查找

基本原理：

  • 从表一端开始逐个和关键字进行比较，若找到一个记录和给定值相等，则查找成功，反之失败。
  • 再简单点就是，一个一个的比大小，看看是否相等。

顺序查找更适合于顺序存储结构和链式存储结构的查找表。顺序查找需要一个个的去比较，效率很低。

折半查找（二分查找）

基本原理：

  1. 把序列分成左中右三部分，左部分小于中间值，右部分大于中间值；
  2. 把给定值与中间值比较，确定下次查找是在左部分还是右部分
  3. 继续上面两步操作，直到成功或失败。

注意：折半查找需要注意给定的序列必须是一个有序序列。

二分查找的前提

  • 目标函数的单调性（单调递增或者递减）
  • 存在上下界（bounded）
  • 能够通过索引访问（index accessible）

示例：求 $\sqrt{x}$ 的值, leetcode 题目

# 二分查找方式解决
class Solution:
    def mySqrt(self, x: int) -> int:
        l, r, ans = 0, x, -1
        while l <= r:
            mid = (l + r) // 2
            if mid * mid <= x:
                ans = mid
                l = mid + 1
            else:
                r = mid - 1
        return ans

C语言版本

int sqrt(int x)
{
    if (x < 2)	// 处理特殊情况
        return x;
    
    int left = 1, right = x / 2;
    while (left <= right) {
        # 避免溢出，相当于 mid = (left + right) / 2
        int mid = left + ((right - left) >> 1);
        if (mid == x / mid)
            return mid;
        else if (mid > x / mid)
            right = mid - 1;
        else
            left = mid + 1;
    }
    return right;
}

分块查找（折中）

基本原理：

  • 顺序查找和二分法查找的折中，先分块，在块中顺序查找。

注意：

  • 分成的各块内部数据可能无序；
  • 各块之间有序（第二个块中的元素都比第一个块中元素都大）；
  • 建立了索引表，索引表按关键字有序。

img img

牛顿查找（查找加速）

牛顿—拉弗森迭代法（简称牛顿法）使用以直代曲的思想，是一种求解函数的方法，不仅仅适用于求解开方计算。当然使用牛顿法求解函数也存在很多坑，但对于求解开方而言，牛顿法是安全的。

牛顿迭代法：

  • 在迭代过程中，以直线代替曲线，用一阶泰勒展开式（即在当前点的切线）代替原曲线，求直线与x轴的交点，重复这个过程直到收敛。img

$\begin{aligned} & y-f\left(x_{i}\right)=f\left(x_{i}\right)^{\prime}\left(x-x_{i}\right)
\Longrightarrow & y-\left(x_{i}^{2}-n\right)=2 x_{i}\left(x-x_{i}\right)
\Longrightarrow & y+x_{i}^{2}+n=2 x_{i} x \end{aligned}$

# 牛顿迭代法解决（python）
class Solution(object):
    def mySqrt(self, x):
        r = x
        while r*r > x:
            r = (r + x/r) / 2
        return r

C语言版本

// 牛顿迭代法解决（C语言）
float InvSqrt(float x){
    float xhalf = 0.5f*x;
    int i = *(int*)&x;
    i = 0x5f3759df   // Magic Number
    x = *(float*)&i;
    x = x*(1.5f - xhalf*x*x);
    return x;
}

动态查找（修改表）

若再查找的过程中同时插入查找表中不存在的数据，或从查找表中删除已存在的某个数据，则称此类查找表为动态查找表。

二叉排序树

定义：

  1. 若它的左子树非空，则左子树上所有的结点的值均小于根结点的值；
  2. 若它的右子树非空，则右子树上所有的结点的值均大于根结点的值；
  3. 左右子树本身就是两棵二叉排序树。

img

定义看上去不是特别好理解，其实特别简单，我们再以例子简单的说一下。左子树的所有节点：3，1，6，4，7，都小于父节点8，右子树所有节点：10，14，13，都大于父节点。什么时候都是父节点大于左孩子，小于右孩子例如：8>3，8<10；3>1，3<6。

平衡二叉树

定义：

  1. 它或者是一棵空树
  2. 或者树中任一结点的左右子树深度相差不超过1。

注意：

  • 从定义我们可得到：想要一颗树平衡，有三种情况，节点的平衡度要么为了0，要么为1，要么为-1。（平衡度：节点左子树的高度减去其右子树的高度。）
  • img 每个节点上标出了平衡度，所有的节点的平衡度的绝对值都小于等于0或1，所以它是一棵平衡二叉树。

案例

找到首次出现的元素

【2024-8-12】腾讯

  • (1) 线性遍历: 从左到右逐个查找,遇到就返回, 否则返回 length — 时间复杂度 O(n)
  • (2) 二分法:找到相同值, 然后向左滑动找边界 — 时间复杂度: log(n)

极端情况怎么办? array 全部都是目标值

  • 二分法改造: 除了比较 array[mid] == target, 还比较 array[start],array[mid],array[end], 只要其中有相同值, 就更新 start,end,mid
//#include <iostream>
//#include <vector>
#include<stdio.h>

//using namespace std;

// 该函数负责返回数组中target第一次出现的下标位置，数组有序，存在有重复数字
int find(int * array, int length, int target){
	/* 
        (1) 线性遍历: 从左到右逐个查找,遇到就返回, 否则返回 length --- 时间复杂度 O(n)
        (2) 二分法:找到相同值, 然后向左滑动找边界 --- 时间复杂度: log(n)
        {2,4,5,5,5,7,8,12,15}
    */
    // 空数组识别
	if(length<=0){
	    return -1;
	}
	if(length==1){
	    if(length==target) {return 0;}
	    else return -2;
	}
	// 判断增序还是降序
// 	int order = 0; // 1 增序, -1 降序
// 	if(array[0]<=array[1]) order = 1;
// 	else order = -1;
	
    // 初始化
	int start = 0;
	int end = length -1;
	int mid = 0;
	while(start<end){
		mid = (int)((end+start)/2);
		printf("[%d,%d] mid=%d -> mid_val=%d, target=%d\n", start, end, mid, array[mid], target);
		if(array[mid] == target){
			// 找到元素
			break;
			printf("找到目标数值: [%d, %d] mid=%d -> %d\n", start, end, mid, target);
		}else if(array[mid] <= target){
			// 往左移动
			start = mid+1;
		}else{// 往右移动
			end = mid-1;
		}
	}
	printf("跳出循环:[%d,%d] mid=%d -> %d\n", start, end, mid, target);
	// 跟mid值判断结果
	if(mid>end || mid<start){
		// 越界
		return -2;
	} 
	// 找到目标数值, 向左寻找等值边界
	int left = mid-1;
	while(left>=0 && array[left]==array[mid]){
		left--;
	}
	return left+1;
}

int main(){
	int array[] = {2,4,5,5,5,7,8,12,15};
    // 测试值: [1,5,8, 13, 16]
    int target_list[5] = {1,5,8, 13, 16};
    // 计算数组长度
	int len = sizeof(array) / sizeof(array[0]);
	printf("长度: %d\n", len);
    
    for(int i=0;i<5;i++)
    {
	   int idx = find(array, len, target_list[i]);
	   //int idx = 0;
       printf("【测试】第%d个: %d -> %d\n", i+1, target_list[i], idx); 
       if(i>5){break;}
    }
	return 0;
}

递归

递归概念

  • 函数直接或间接地调用自身

递归与分治

分治法

  • 问题的分解

  • 问题规模的分解

  • 折半查找（递归）
  • 归并查找（递归）
  • 快速排序（递归）

递归与迭代

  • 迭代：反复利用变量旧值推出新值
  • 折半查找（迭代）
  • 归并查找（迭代）

阿克曼函数

阿克曼(Ackermann)函数是一种增长”极快”的函数.

  • img
  • 比如如果输入为4,2,这个数字大于全世界的原子数量总和.

阿克曼(Ackmann)函数A(m，n)中，m，n定义域是非负整数(m<=3,n<=10)，函数值定义为：

  • akm(m,n) = n+1; (m=0时)
  • akm(m,n) = akm(m-1,1); (m>0,n=0时)
  • akm(m,n) = akm(m-1,akm(m, n-1)); （m,n>0时)
#include <iostream>

using namespace std;
long int answer = 0;
 
int Ackermann(int m,int n){// 递归函数
	if (m == 0){
		answer = n + 1;
		return answer;
	}
	if (m != 0 && n == 0){
		answer = Ackermann(m - 1,1);
		return answer;
	}
	if (m != 0 && n != 0){
		answer = Ackermann(m - 1,Ackermann(m,n-1));
		return answer;
	}
}
 
int main(){
	cout<<"阿克曼函数测试, 请输入m和n"<<endl;
	int m,n;
	cin >> m >> n;
	cout << Ackermann(m,n);
	return 0;
}

树

基本概念

图

  • 1、结点的度
    • 结点的度是子结点的个数。例如：结点1有三个字结点2，3，4，所以结点1的度为3。
  • 2、树的度
    • 树的度等于所有结点度中度最高的值。例如：上图中结点度最高为3，所以树的度为3。
  • 3、叶子结点
    • 叶子结点是度为0的结点即没有子结点的结点。例如：上图中3，5，6，7，9，10。
  • 4、分支结点
    • 分支结点是除了叶子结点，树中的其他所有结点。例如：上面树的分支结点为1，2，4，8。
  • 5、内部结点
    • 内部结点是除了根结点以及叶子结点或在分支结点的基础之上在去掉根结点。例如：上面树的内部结点为2，4，8。
  • 6、父结点、子结点、兄弟结点
    • 父节点、子结点和兄弟结点是相对而言的。例如：结点1是结点2，3，4的父节点，结点2，3，4也是结点1的子结点，结点2，3，4又是兄弟结点。
  • 7、层次
    • 图中我们已经表出来了，根为第一层，根的孩子为第二层，依此类推，若某结点在第i层，则其孩子结点在第i+1层。

树与二叉树区别

  • 1、树可以有多个子结点，二叉树最多只能两个结点。
  • 2、树中的子结点是无序的，二叉树是分左子结点和右子结点。
  • 3、二叉树不是特殊树，而是独立的数据结构。

代码定义

C 完整代码

struct BTree{
	int vertex;
	struct BTree *left;
	struct BTree *right;
};
typedef struct BTree *btlink;

二叉树

数据结构(二)之二叉树

二叉树类型

  • 满二叉树: 叶节点个数比分支节点的个数多1
  • 完全二叉树
  • 非完全二叉树

二叉树性质

  • 非空二叉树第 i 层最多 2(i-1) 个结点 （i >= 1）
  • 深度为 k 的二叉树最多 2k - 1 个结点 （k >= 1）
  • 度为 0 的结点数为 n0，度为 2 的结点数为 n2，则 n0 = n2 + 1
  • 有 n 个结点的完全二叉树深度 k = ⌊ log2(n) ⌋ + 1
  • 对于含 n 个结点的完全二叉树中编号为 i （1 <= i <= n） 的结点
    • 若 i = 1，为根，否则双亲为 ⌊ i / 2 ⌋
    • 若 2i > n，则 i 结点没有左孩子，否则孩子编号为 2i
    • 若 2i + 1 > n，则 i 结点没有右孩子，否则孩子编号为 2i + 1存储结构二叉树数据结构typedef struct BiTNode
{
    TElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

树的存储结构

  • 双亲表示法
  • 双亲孩子表示法
  • 孩子兄弟表示法

遍历方式

遍历方式

  • 先序遍历
  • 中序遍历
  • 后续遍历

  • 层次遍历

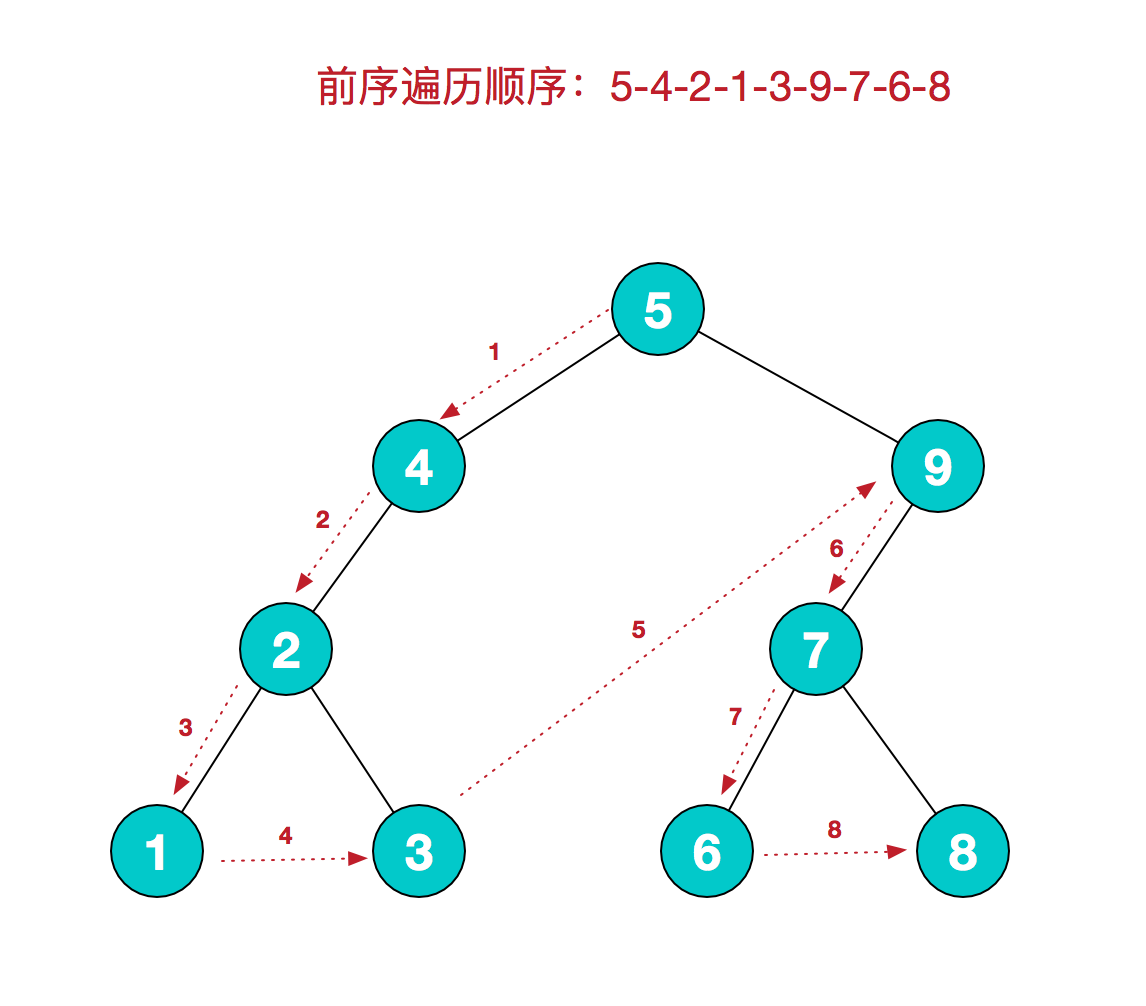
  • 1、前序遍历：前序遍历就是先访问根结点，再访问叶子结点。(根左右)
    • 图中树的前序遍历为：1，2，5，6，7，3，4，8，9，10。
  • 2、中序遍历：限二叉树, (左根右)
    • 基本思想：先中序遍历左子树，然后再访问根结点，最后再中序遍历右子树, 即左—根—右。
    • 图中中序遍历结果是：4，2，7，8，5，1，3，6。
  • 3、后序遍历：后序遍历就是先访问子结点，再访问根结点。(左右根)
    • 图中树的后序遍历为：5，6，7，2，3，9，10，8，4，1。
  • 4、层次遍历：从第一层开始，依此遍历每层，直到结束。(根左右)
    • 图中树的层次遍历为：1，2，3，4，5，6，7，8，9，10。

先序遍历

略

中序遍历

【2024-10-17】 微软考题

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.data = val
        self.left = left
        self.right = right

# 1 2 3 4 5 6 7 8

# 树构建
#          4
#     2        6
# 1     3    5     7

t = TreeNode(4)
t.left = TreeNode(2)
t.right = TreeNode(6)
t.left.left = TreeNode(1)
t.left.right = TreeNode(3)
t.right.left = TreeNode(5)
t.right.right = TreeNode(7)

def traverseMiddle(t):
    """
        中序遍历()
    """
    # 左根右
    if not t.data:
        return ''
    if t.left:
        traverseMiddle(t.left)
    print(f'{t.data}', end=',')
    if t.right:
        traverseMiddle(t.right)

traverseMiddle(t) # 1,2,3,4,5,6,7

节点删除

对于二叉排序树的其他操作，比如插入，遍历等，比较容易理解；而删除操作相对复杂些。对于要删除的结点，有以下三种情况：

  1. 叶子结点；
  2. 仅有左子树或右子树的结点；
  3. 左右子树都有结点；

对于1（要删除结点为叶子结点）直接删除，即直接解除父节点的引用即可，对于第2种情况（要删除的结点仅有一个儿子），只需用子结点替换掉父节点即可；而对于要删除的结点有两个儿子的情况，比较常用处理逻辑为，在其子树中找寻一个结点来替换，而这个结点我们成为中序后继结点。

特殊二叉树

图

一般二叉树性质：

  • 在非空二叉树的k层上，至多有2^k个节点(k>=0)
  • 高度为k的二叉树中,最多有2^(k+1)-1个节点(k>=0)
  • 对于任何一棵非空的二叉树,如果叶节点个数为n0，度数为2的节点个数为n2，则有: n0 = n2 + 1

完全二叉树性质:

  • 具有n个节点的完全二叉树的高度k为[log2n]
  • 对于具有n个节点的完全二叉树,如果按照从上(根节点)到下(叶节点)和从左到右的顺序对二叉树中的所有节点从0开始到n-1进行编号,则对于任意的下标为k的节点，有：
    • 如果k=0,则它是根节点，它没有父节点；如果k>0,则它的父节点的下标为[(i-1)/2];
    • 如果2k+1 <= n-1,则下标为k的节点的左子结点的下标为2k+1;否则,下标为k的节点没有左子结点.
    • 如果2k+2 <= n-1,则下标为k的节点的右子节点的下标为2k+2;否则,下标为k的节点没有右子节点

满二叉树性质:

  • 在满二叉树中，叶节点的个数比分支节点的个数多1

分类

  • 满二叉树
  • 完全二叉树（堆）
    • 大顶堆：根 >= 左 && 根 >= 右
    • 小顶堆：根 <= 左 && 根 <= 右
  • 二叉查找树（二叉排序树）：左 < 根 < 右
  • 平衡二叉树（AVL树）：| 左子树树高 - 右子树树高 | <= 1
  • 最小失衡树：平衡二叉树插入新结点导致失衡的子树：调整：
    • LL型：根的左孩子右旋
    • RR型：根的右孩子左旋
    • LR型：根的左孩子左旋，再右旋
    • RL型：右孩子的左子树，先右旋，再左旋

b树和应用场景

B树也叫做B-树，或者平衡多路树，它是每个节点最多有m个子树的平衡树。一个m阶的B树具有如下几个特征：

  1. 根结点至少有两个子女。
  2. 每个中间节点都包含至多m个子树 ， 每个节点包含的元素个数是其子树个数-1（其中 m/2 <= k <= m）
  3. 所有的叶子结点都位于同一层。
  4. 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个子树包含的元素的值域分划。

b树主要应用于文件系统中，在数据库中（mongoDB）也有应用，与B+树相比好处应该是有时不需要访问到叶节点就可以获取数据。查询时间复杂度是logN

B+树

B+树是一种特殊的B树，它把数据都存储在叶子节点，并且叶节点间有指针连接。内部只存关键字（其中叶子节点的最小值作为索引）和孩子指针，简化了内部节点。应用场景主要是数据库的索引，查询时间复杂度也是logN

B/B+树区别

这都是由于B+树和B具有不同的存储结构所造成的区别，以一个m阶树为例。

  1. 关键字的数量不同；B+树中分支结点有m个关键字，其叶子结点也有m个，其关键字只是起到了一个索引的作用，但是B树虽然也有m个子结点，但是其只拥有m-1个关键字。
  2. 存储的位置不同；B+树中的数据都存储在叶子结点上，也就是其所有叶子结点的数据组合起来就是完整的数据，但是B树的数据存储在每一个结点中，并不仅仅存储在叶子结点上。
  3. 分支结点的构造不同；B+树的分支结点仅仅存储着关键字信息和儿子的指针（这里的指针指的是磁盘块的偏移量），也就是说内部结点仅仅包含着索引信息。
  4. 查询不同；B树在找到具体的数值以后，则结束，而B+树则需要通过索引找到叶子结点中的数据才结束，也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。

B+树优点：由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引，而B树则常用于文件索引。

红黑树

红黑树是一种特殊的二叉查找树，它在每一个节点上都使用红色或黑色进行标记，通过一些性质确保它是始终平衡的。 它的性质是这样的：

  1. 每个节点不是红色就是黑色。
  2. 根节点是黑色的。
  3. 叶节点的空节点是黑色的。
  4. 如果一个节点是红色的，那么它的两个子节点是黑色的。
  5. 对于任意节点，从它到叶节点的每条路径上都有相同数目的黑色节点。

红黑树的插入，查询，删除在一般情况和最坏情况下的时间复杂度都是O(log(n))

应用场景主要是STL中map，set的实现，优点在于支持频繁的修改，因为查询删除插入时间复杂度都是logN

图

总结

图搜索算法 数据结构 遍历时间复杂度 空间复杂度              
BFS广度优先搜索 邻接矩阵 邻接链表 O( v 2) O( v + E )
DFS深度优先搜索 邻接矩阵 邻接链表 O( v 2) O( v + E )

其他算法

算法 思想 应用
分治法 把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并 循环赛日程安排问题、排序算法（快速排序、归并排序）
动态规划 通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法，适用于有重叠子问题和最优子结构性质的问题 背包问题、斐波那契数列
贪心法 一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法 旅行推销员问题（最短路径问题）、最小生成树、哈夫曼编码

简介

树具有层次关系，上层元素可以与下一个多个元素连接，但是只能和上层的一个元素连接。在图结构中，节点间的连接是任意的，任何一个元素都可以与其他元素连接。

图遍历

从图中某一个顶点出发，访问图中的每一个结点，并要求只能访问一次，不能重复访问

  • img 总结，图的广度优先遍历和深度优先遍历的结果并不唯一。

（1）广度优先遍历

  • 基本思想：首先访问顶点，再访问顶点的全部未访问的邻结点，再访问邻结点的所有结点即可（类似树的层次遍历）。
  • 广度优先遍历：V1，V2，V3，V4，V5，V6 或 V1，V4，V3，V2，V6，V5

（2）深度优先遍历

  • 基本思想：首先访问顶点，再访问顶点的每个邻结点，从该点继续深度优先遍历（类似于树的前序遍历）
  • 深度优先遍历：V1，V2，V5，V3，V6，V4 或 V1，V4，V6，V3，V5，V2

最小生成树

（1）普里姆（Prim）算法

  • 基本思想：选一个顶点开始，查找与顶点相邻且代价（边值）最小的边的另一个顶点，直到最后。
  • 例如：V1作为顶点，V1->V3->V6->V4，V3->V2->V5，连接图中所有的结点即可。

（2）克鲁斯卡尔（Kruskal）算法

  • 基本思想：选择图中最小的边，直到所有结点都连通。
  • 例如：第一小边：V1->V3，第二小边：V4->V6，第三小边：V2-V5，第四小边：V3->V6，第五小边：V3->V2，此时所有的结点都连到了一起。

（3）算法对比

  • 普里姆算法更加注重的是结点，点与点之间距离最短的优先；
  • 克鲁斯卡尔算法更加注重的是边，将边排序，最小边排在前面，最大边排在后面。

图匹配

【2022-8-25】二分图的最大匹配、完美匹配和匈牙利算法

无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。

  • 二分图：如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。
    • 把一个图的顶点划分为两个不相交集 U 和 V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。
    • 二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。
  • 匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。
  1 2 3 4
  Bipartite Graph(1) Bipartite Graph(2) Matching Maximum Matching

定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

  • 最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。
  • 完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

  • 0

匈牙利算法

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

  • 5

  • 交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
  • 增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：
  • 6

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。

匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：

1 2 3
7 8 9

这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

下面给出匈牙利算法的 DFS 和 BFS 版本的代码：

匈牙利算法的要点如下

  • 从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。
    • 如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数 +1，停止搜索。
    • 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。
  • 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈，而 BFS 版本使用 prev 数组。

性能比较

两个版本的时间复杂度均为 O(V⋅E)。DFS 的优点是思路清晰、代码量少，但是性能不如 BFS。我测试了两种算法的性能。对于稀疏图，BFS 版本明显快于 DFS 版本；而对于稠密图两者则不相上下。在完全随机数据 9000 个顶点 4,0000 条边时前者领先后者大约 97.6%，9000 个顶点 100,0000 条边时前者领先后者 8.6%, 而达到 500,0000 条边时 BFS 仅领先 0.85%。

补充定义和定理：

  • 最大匹配数：最大匹配的匹配边的数目
  • 最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择
  • 最大独立数：选取最多的点，使任意所选两点均不相连
  • 最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。
  • 定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）
  • 定理2：最大匹配数 = 最大独立数
  • 定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

串匹配算法

串匹配在实际使用中有着广泛的需求，从计算机领域简单的文本搜索，到生物科学领域复杂的氨基酸序列匹配，都离不开高效的串匹配方法。

KMP算法是经典的串匹配算法，由Knuth和Pratt师徒发明，同一时间Morris也发明了这一算法。因此按照姓氏首字母，这一算法得名“KMP”算法。简单而言，KMP算法主要通过根据对成功匹配段的复用以及对失败匹配段的学习来加快字符串匹配的速度，其时间复杂度为O(n)。

为方便下文的表述，我们作如下的约定：

  • 文本串 T（Text String）：需要查询的全量字符串，其长度为n
  • 模式串 P（Pattern String）：查询的片段字符串，其长度为m
  • 匹配算法的结果为模式串在文本串中首次出现的位置（序号从0开始），不存在时应返回-1。

例如文本串T = "helloworldhello"，模式串P = "ello"，则匹配算法应返回1。

字符串匹配问题是在给定符号序列（文本）中按照一定的匹配条件，搜索给定符号序列或给定符号序列集合中元素（模式）出现位置的搜索问题。

  • 搜索给定符号序列 → 只有一个模式 → 单模式匹配
  • 搜索给定符号序列“集合”→ 要同时搜索多个模式 → 多模式匹配
  • 按一定搜索条件 → 允许一定匹配误差, 不要求模式一定完全出现，搜索最像模式的局部 → 模糊匹配

单模式匹配

  • BF（Brute Force）算法 - 暴力算法
    • 复杂度：最好的情况下只需进行 p次比较，最坏情况下要进行p(s-p+1)次比较，时间复杂度为O(sp)。
    • 没有从前一次的失败匹配中学习到任何信息
  • KMP 算法(Knuth-Morris-Pratt)
    • 参考：如何更好地理解和掌握 KMP 算法?
    • 思想
      • 1、而每一次失败都换来一些信息：已匹配部分（在已匹配部分，主串和模式串是完全相同的）。
      • 2、根据已匹配部分的最大的 一致“前缀和后缀“，增大模式串移动的步长。（前缀后缀重叠的部分肯定匹配不上，可以跳过）
      • 3、对于模式串，使用next 数组（动态规划），记录失配字符位置应移动的步长
    • 示例图
    • 复杂度：时间复杂度 O(s+p)
    • 特点：充分利用了已匹配部分和模式串自身的信息
    • 为什么说 KMP 算法和状态机有关？KMP实际上是AC自动机的退化版本，即模式串个数为1的情况
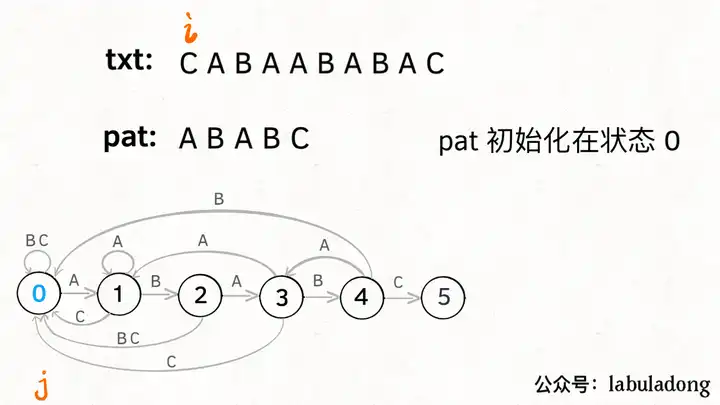
      • 模式匹配就是状态转移，KMP 算法最关键的步骤就是构造这个状态转移图。要确定状态转移的行为，得明确两个变量，一个是当前的匹配状态，另一个是遇到的字符；确定了这两个变量后，就可以知道这个情况下应该转移到哪个状态。
  • BM算法

多模式匹配

  • KMP实际上是AC自动机的退化版本，即模式串个数为1的情况。

  • 同时执行多个模式匹配，怎么办？

  • （1）笨方法：拆成多个单模匹配问题
    • 但是在文本串较大、目标字符串众多的时候效率比较低。
  • （2）ac自动机
    • 内容参考自：多模字符串匹配算法之AC自动机—原理与实现
    • AC自动机的基础是Trie树。和Trie树不同的是，树中的每个结点除了有指向孩子的指针，还有一个fail指针，它表示输入的字符与当前结点的所有孩子结点都不匹配时，自动机的状态应转移到的状态。fail指针的功能可以类比于KMP算法中next数组的功能。每个结点的fail指针表示由根结点到该结点所组成的字符序列的所有后缀　和　整个Trie树中的所有前缀 两者中最长公共的部分。
    • AC自动机匹配过程
      • 1）表示当前结点的指针指向AC自动机的根结点，即curr = root
      • 2）从文本串中读取（下）一个字符
      • 3）从当前结点的所有孩子结点中寻找与该字符匹配的结点，
        • 若成功：判断当前结点以及当前结点fail指向的结点是否表示一个字符串的结束，若是，则将文本串中索引起点记录在对应字符串保存结果集合中（索引起点= 当前索引-字符串长度+1）。curr指向该孩子结点，继续执行第2步
        • 若失败：执行第4步。
      • 4）若fail == null（说明目标字符串中没有任何字符串是输入字符串的前缀，相当于重启状态机）curr = root, 执行步骤2，
        • 否则，将当前结点的指针指向fail结点，执行步骤3)
    • 特点
      • 本质是前缀树加上KMP算法
      • 前缀树能加速的本质是因为采用了哈希算法；但与哈希表也稍有不同。采用了树形结构，树形结构能让其采用更少的储存空间，避免了哈希冲突。
      • KMP算法的本质是因为能够复用已经比较过计算，从而提升匹配的效率。
    • 工程实现
      • Ahocorasick：使用Aho-Corasick自动机的方式，根据一组关键词进行匹配，返回关键词出现的位置。用C实现，python包装
      • Acora：多关键字搜索引擎，使用Aho-Corasick以及NFA-to-DFA自动机的方式
      • Esmre：也是使用的AhoCorasick自动机的方式，做了一些细微的修改。也是用C实现，python包装
  • （3）WM（Wu-Manber）算法
    • WM算法是对BM算法的延伸继承，用BM算法的核心框架，用字符块来计算shift表（取代坏字符表）进行跳转，在进行匹配时，用hash和prefix计算前后缀的hash值来从众多可选的模式串中快速筛选出正确匹配的模式串。

模糊匹配

  • 不要求精确匹配，允许部分损失

  • A：笨方法，一点点移动算编辑距离
    • 类似BF算法，移动一次算一次编辑距离，最后取最大的编辑距离得分。
    • 时间复杂度：移动 S（长字符串） 次，每次计算编辑距离 P^2, 所以总体复杂度= S * P * P
  • B: fuzzywuzzy, 先找出相似片段，在片段附近计算最大编辑距离得分
    • 1、找出所有相似片段（所有的最长公共字串）
      • 基本复杂度：<= S*P
      • difflab.SequenceMatcher (python 官方库，可以比较任何类型的序列对，只要序列元素为 hashable 对象)
        • api文档
        • 自动垃圾启发式计算: SequenceMatcher 支持使用启发式计算来自动将特定序列项视为垃圾。
      • SequenceMatcher 在最坏情况下为平方时间而在一般情况下的行为受到序列中有多少相同元素这一因素的微妙影响；在最佳情况下则为线性时间。
      • python-Levenshtein.SequenceMatcher（针对字符串匹配做了优化，可以做到4-10倍的加速）
    • 2、对每个相似片段（共K个），在长文本S的位置，向前后扩充到 模式 P 的长度，进行编辑距离得分计算。
      • 计算编辑距离复杂度 K*P^2
    • 3、找出最大的编辑距离相似度，作为模式的最终得分
      • 复杂度 ：K

深度语义匹配

  • 如DSSM等系列

蛮力算法

字符串匹配的蛮力算法，可以将模式串逐一与文本串中长度为m的子串进行匹配。例如在文本串”abcabdab”中查找子串”abd”：

序号 0 1 2 3 4 5 6 7 8
文本串 a b c a b d a b d
匹配1 a b d            
匹配2   a b d          
匹配3     a b d        
匹配4       a b d      

其对应的暴力算法代码为（Java）：

public int match(String P, String T) {
	int n = T.length(); // 文本串长度
	int m = P.length(); // 模式串长度
	for (int i = 0; i < n - m + 1; i ++) { // 文本串中的起始查找位置
		if (T.substring(i, i + m).equals(P)) return i; // 匹配子串
	}
	return -1;
}

为了披露更多的算法细节，这里我们不使用Java内置函数实现，以为接下来的KMP算法的理解做准备：

public int match(String P, String T) {
	int n = T.length(), i = 0; // 文本串长度及当前比对字符
	int m = P.length(), j = 0; // 模式串长度及当前比对字符
	while ((i < n) && (j < m)) {
		if (T.charAt(i) == P.charAt(j)) {
			i ++; j ++; // 匹配，转到下一字符
		} else {
			i -= j - 1; j = 0; // 文本串回退，模式串复位
		}
	}
	return (i - j > n - m) ? -1 : i - j; // 若匹配成功，则i-j表示匹配初始位置
}

很显然，蛮力算法由于需要对于每个子串进行比较，其时间复杂度在最差情况下为O(mn)。

蛮力算法的思考

再次回顾蛮力算法过程的例子：

序号 0 1 2 3 4 5 6 7 8
文本串 a b c(i=2) a b d a b d
匹配1 a b d(j=2)            

第一次匹配在i=2及j=2处失败后，文本串回退，模式串复位：

序号 0 1 2 3 4 5 6 7 8
文本串 a b(i=1) c a b d a b d
匹配2   a(j=0) b d          

很显然第二次匹配的时候同样失败了。那这个失败是偶然的吗？并不是。可以发现由于第一次匹配时已经成功匹配了字符串"ab"，因此文本串一定是"abxxxxxx"。因此在i=1的位置，模式串一定不能和文本串进行匹配，因此这次失败是注定的。

KMP算法

为了使得已经成功的信息得到充分的利用，KMP算法对于“注定的失败”采取了聪明的避让措施，该算法的核心是next数组。

next数组

为了尽可能地利用已经匹配的信息，我们可以在安全的前提下，对模式串进行快速移动，而不是像暴力算法一样一次仅前进一格。很显然，模式串向右移动的距离之和自身有关，即无论何时，只要匹配到"abd"中的'd'失败后，就需要将模式串的j移动到next[j]的位置，称之为模式串P的next数组。

例如在上述的例子中，匹配到"abd"中的'd'失败后，我们知道当前位置的前两个字符一定为"ab"，因此我们可以直接向右将模式串移动两位，即next[2] = 0，表示将j=2对应的’d’字符直接移动到’a’字符进行比对。这一比对过程为：

序号 0 1 2 3 4 5 6 7 8 备注
文本串 a b c a b d a b d  
匹配1 a b d(j=2)             j=2匹配失败，移动j=next[j]=0
移动模式串     a(j=0) b d          

当文本串与模式串的第一个字符都不匹配时，模式串应当右移一位，继续和下一和文本串字符进行对比。为了统一起见，我们可以令next[0] = -1，表示当第0号字符不匹配时，需要将其移动到-1的位置，也即向右移动一位模式串。

通过上述例子，我们可以写出任意模式串的next数组，例如对于P = "chinchilla"，其next表为：

j 0 1 2 3 4 5 6 7 8 9
T[j] c h i n c h i l l a
next[j] -1 0 0 0 0 1 2 3 0 0
  • j = 0时，匹配失败说明该位置的文本串与模式串的第一位不相等，此时应右移一位，即next[0] = -1;
  • j = 1时，文本串中"c"匹配成功，说明文本串格式为"cxxxx"，应向右移动一位，即next[1] = 0;
  • j = 2时，文本串中"ch"匹配成功，说明文本串格式为"chxxxx"，应向右移动两位（因为如果只移动一位，文本串变为"hxxxx"，模式串为"chin..."，必然匹配失败），即next[2] = 0;
  • j = 3时，文本串中"chi"匹配成功，说明文本串格式为"chixxxx"，应向右移动三位，即next[3] = 0;
  • j = 4时，文本串中"chin"匹配成功，说明文本串格式为"chinxxxx"，应向右移动四位，即next[4] = 0;
  • j = 5时，文本串中"chinc"匹配成功，说明文本串格式为"chincxxxx"，此时我们发现如果将模式串右移四位，则文本串变为"cxxxx"，与模式串"chin..."有可能匹配成功，因此next[5] = 1，即使得字符'h'移动到前面的'h'处;
  • …
  • j = 8时，文本串中"chinchil"匹配成功，说明文本串格式为"chinchilxxxx"，此时我们必须将模式串右移8位，否则无论如何均不能与模式串"chinchilla"匹配成功，因此next[8] = 0；
  • …

通过上述方法，我们即可得到任意字符串的next数组。

KMP算法匹配

根据next数组的定义，我们可以很快写出KMP算法进行匹配计算的代码：

public int KMP(String P, String T) {
	int n = T.length(), i = 0; // 文本串指针
	int m = P.length(), j = 0; // 模式串指针
	int[] next = buildNext(P); // 构建模式串P的next表
	while ((j < m) && (i < n)) {
		if ((j < 0) || (P.charAt(j) == T.charAt(i))) { // 匹配时，移动到下一字符
			j ++; i ++;
		} else { // 不匹配时，加速移动模式串
			j = next[j];
		}
	}
	return (i - j > n - m) ? -1 : i - j;
}

由于文本串指针永远不会后退，模式串指针只可能进行加1操作或者next操作（相等于做减法），因此该方法最多只可能进行2*n次操作，因此KMP算法中除next表构建外，其时间复杂度为O(n)。根据后续的分析，我们得到next表的构建最多需要O(m)时间，因此KMP算法的时间复杂度不超过O(m+n)。同时对于构建好的next表，只要模式串不发生变化，就可以连续不断使用，这也使得渐进复杂度接近于O(n)。

next数组的改进

当模式串P = "chinchilla"时，我们构造以下文本串T = "chincy..."，其比对过程如下：

序号 0 1 2 3 4 5 6 7 8 9 备注
文本串 c h i n c y(i=5) x x x x  
匹配1 c h i n c h(j=5) i l l a j=5匹配失败，j=next[j]=1
移动模式串         c h(j=1) i n c h  

显然这次匹配也会失败，而这次失败也是必然的。我们发现，当模式串匹配到"chinch"而失败时，不仅说明此时文本串为"chincxxxx"，同时还说明文本串中下一个字符必不为'h'。掌握这个细节，我们可以对next数组进行改进：

j 0 1 2 3 4 5 6 7 8 9
T[j] c h i n c h i l l a
next[j] -1 0 0 0 -1 0 0 3 0 0
  • j = 4时，文本串中"chin"匹配成功，'c'匹配失败，说明文本串格式为"chin[非c]xxxx"，此时我们现如果将模式串右移4位，则文本串变为"[非c]xxxx"，与模式串"chin..."仍然匹配失败，因此必须将模式串移动5位，即next[4] = -1（注意和改进前的区别）;
  • j = 5时，文本串中"chinc"匹配成功，'h'匹配失败，说明文本串格式为"chinc[非h]xxx"，此时我们发现如果将模式串右移4位，则文本串变为"c[非h]xxx"，与模式串"chin..."仍然匹配失败，因此必须将模式串移动5位，即next[5] = 0（注意和改进前的区别）;
  • j = 7时，文本串中"chinchi"匹配成功，'l'匹配失败，说明文本串格式为"chinchi[非l]xxxx"，此时我们将模式串右移4位，文本串变为"chi[非l]xxxx"，与模式串有概率匹配。因此next[7] = 3；

利用这种方式创建的next表，不仅可以从“成功”中获取经验，还可以从“失败”中获取教训，使得模式串可以尽可能快地移动。

next表构建分析

通过上述分析，我们已经对next表的计算方法有了一定的认知。总结来看，next表中next[j]的计算方法为：

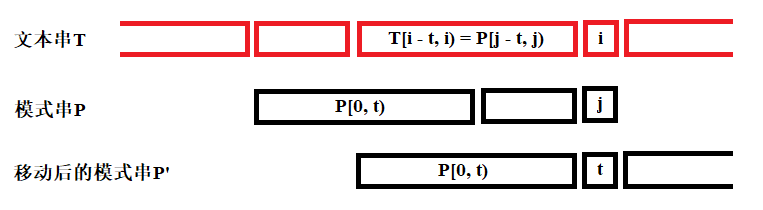
  1. 由于模式串匹配到j位时失败，因此对于模式串的前j-1位必然与文本串匹配，即P[0, j) = T[i - j, i)。同时由于匹配失败，还可以得到P[j] ≠T[i]。
  2. 若我们下一轮匹配时，令T[i]和P[t]对齐，说明我们将模式串向右移动了j-t位。若此时能有与已知的文本串匹配，应有P[0, t) = T[i - t, i]，同时在P[t] ≠P[j]的情况下才有可能与T[i]进行匹配。
  3. 若存在很多组t，保险起见我们应当使得移动距离最小，因此需要使得next[j] = max(t)。

归纳为数学语言如下：

next[j] = max({ t | P[0, t) = P[j - t, j) 且 P[t] ≠P[j] })

因此实质上，next表的构建是一个自我匹配的过程，仿照匹配代码，我们可以写出next表的构建代码：

public int[] buildNext(String P) {
	int m = P.length();
	int[] next = new int[m];
	next[0] = -1; // 初始化next表
	int t = -1, j = 0; // j为“主”串指针，t为移动串指针
	while (j < m - 1) {
		if ((t < 0) || (P.charAt(j) == P.charAt(t))) {
			// 匹配的情况下，若后一元素不相等时才能移动到t，否则要直接移动到next[t]
			j ++; t ++;
			next[j] = (P.charAt(j) != P.charAt(t) ? t : next[t]);
		} else { // 不匹配时，加速移动模式串
			t = next[t];
		}
	}
	return next;
}

这里可以看出来，当模式串进行移动的时候，只有next[t]才能成为候选者，因此利用已构建的部分next表，可以避免无用的移动。

手动计算next表

使用代码计算next表的过程很快，但是却不够直观。根据next表的数学定义，我们可以采用稍微繁琐，但是却非常直观地方式进行手动计算：

  1. 在第一行写上完整的模式串P，并标明其序号；
  2. 依次向右移动模式串，若可以匹配，则继续向后写，否则停止，并在后面标明首次失配位置indexT(首次失配位置在原串中的位置)和indexP（首次失配时在移动串中的位置）。需要注意的是，全匹配时，失配位置不存在；
  3. 查找next[j]时，由上向下查找indexT列，首次出现j值的行对应的indexP值即为next[j]。若不存在j值，则应填-1。

以"chinchillach"为例，手动计算其next表如下：

0 1 2 3 4 5 6 7 8 9 10 11 indexT indexP
c h i n c h i l l a c h    
  c                     1 0
    c                   2 0
      c                 3 0
        c h i n         7 3
          c             5 0
            c           6 0
              c         7 0
                c       8 0
                  c     9 0
                    c h - -
                      c 11 0

根据上述表格，我们可以轻易得到next表的结果为：

j 0 1 2 3 4 5 6 7 8 9 10 11
P[j] c h i n c h i l l a c h
next[j] -1 0 0 0 -1 0 0 3 0 0 -1 0

再以字符串"abababb"为例，其计算过程为：

0 1 2 3 4 5 6 indexT indexP
a b a b a b b    
  a           1 0
    a b a b a 6 4
      a       3 0
        a b a 6 2
          a   5 0
            a 6 0

因此其next表为：

j 0 1 2 3 4 5 6
P[j] a b a b a b b
next[j] -1 0 -1 0 -1 0 4

通过这两个例子，想必对于next表的手动计算也不会再害怕了。

二叉树是一种常用的数据结构，一般意义上对树的遍历均需要O(n)的时间复杂度和O(logn)的空间复杂度。本文将介绍一种O(1)空间复杂度的算法，这就是Morris树遍历算法。

二叉树遍历

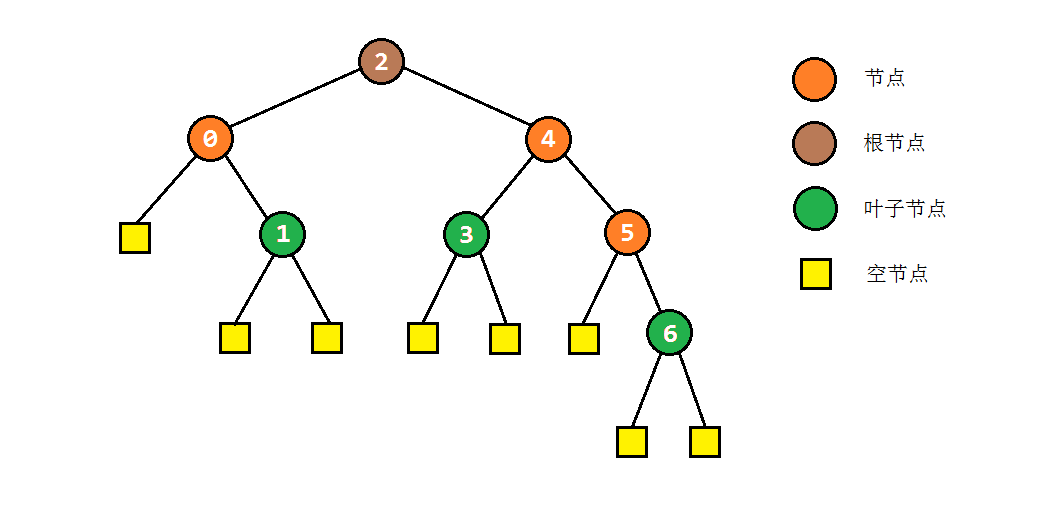
一般意义上来说，二叉树由很多个树节点构成的，非线性的数据结构。每个节点都拥有两个“子节点”，这个节点也被称之为子节点的“父节点”。通常地，我们称没有父节点的节点为“根节点”，两个子节点均为null的节点为“叶子节点”，如下图所示。

为统一起见，本文定义树节点的格式为：

class TreeNode {
	public Value val;       // 节点的值
	public TreeNode left;   // 左孩子
	public TreeNode right;  // 右孩子
}

而为了将这种非线性结构转化为线性结构使用，各种遍历顺序应运而生，一般包括：

  1. 先序遍历：按照 父节点 -> 左孩子 -> 右孩子 的顺序遍历，与DFS（深度优先搜索）有一定联系；
  2. 中序遍历：按照 左孩子 -> 父节点 -> 右孩子 的顺序遍历。当二叉树为二叉搜索树时，中序遍历返回结果为有序序列，因此也叫顺序遍历；
  3. 后序遍历：按照 左孩子 -> 右孩子 -> 父节点 的顺序遍历。
  4. 层次遍历：从左到右，一层一层遍历整个树，与BFS（广度优先搜索）有一定联系。

递归遍历方法

利用递归处理二叉树的遍历问题非常方便，以先序遍历为例，其遍历方法如下：

public void preOrderTraversal(TreeNode root) {
	if (root == null) return;
	visit(root);                    // 访问节点
	preOrderTraversal(root.left);   // 访问左子树
	preOrderTraversal(root.right);  // 访问右子树
}

中序遍历、后序遍历与先序遍历类似，仅仅需要调整访问顺序即可。可以看出，递归方法的时间复杂度为O(n)，空间复杂度与递归深度有关，最优情况与一般情况下为O(logn)，最差情况下甚至需要O(n)的空间。

层次遍历利用递归则稍显复杂，在此不赘述。

非递归遍历方法

为使用非递归遍历方法遍历整个二叉树，往往需要借助栈/队列等数据结构辅助实现。

先序遍历

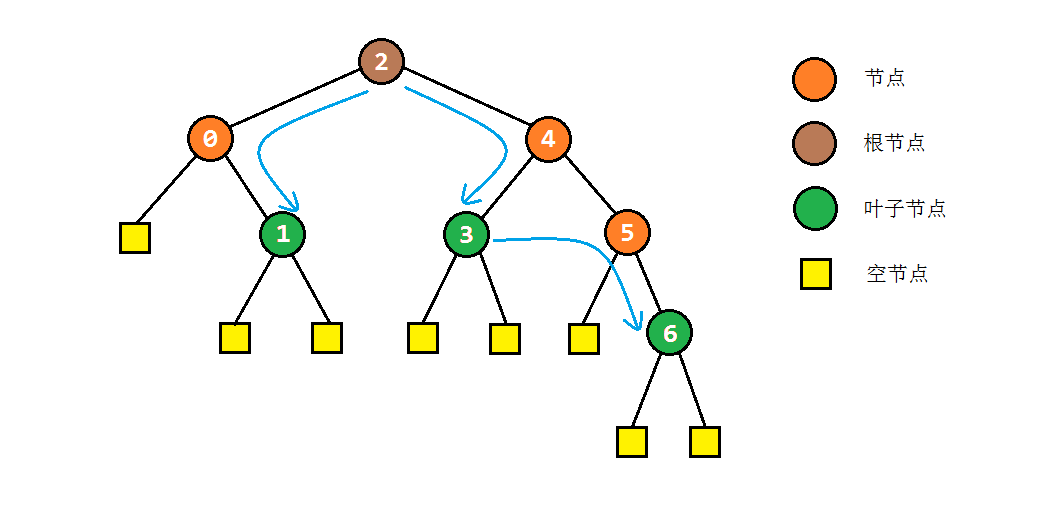
先序遍历的概念非常清晰，利用栈的辅助，在访问完该节点之后将子树入栈即可：

public void preOrderTraversal(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	stack.push(root);

	while (!stack.isEmpty()) {
		TreeNode node = stack.pop(); // 取出一个节点，表示开始访问以该节点为根的子树
		visit(node); // 首先访问该节点（先序），之后顺序入栈右子树、左子树
		if (node.right != null) stack.push(node.right);
		if (node.left != null) stack.push(node.left);
	}
}

或者使用如下方法，在节点到达null层时进行判断：

public void preOrderTraversal2(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	TreeNode node = root;
	
	while (!stack.isEmpty() || node != null) { // stack为空且node为null时，说明已经遍历结束
		if (node != null) { // 可以深入左孩子时，先访问，再深入
			visit(node);
			stack.push(node);
			node = node.left;
		} else { // 否则深入栈中节点的右孩子
			node = stack.pop().right;
		}
	}
}

以之前的树为例，其先序遍历结果应为：2 -> 0 -> 1 -> 4 -> 3 -> 5 -> 6

中序遍历

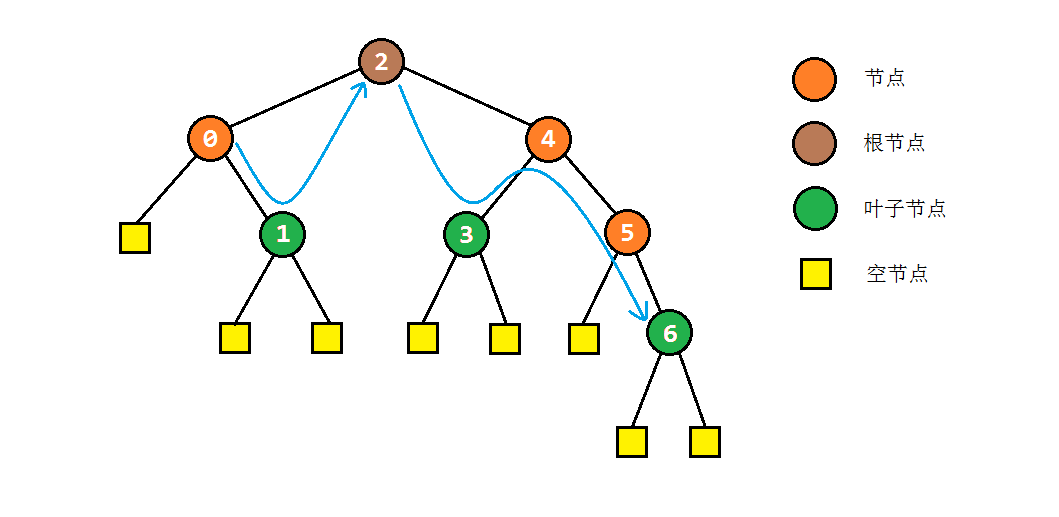
中序遍历的思想是：

  1. 若节点还有左子树，就要先把左子树访问完
  2. 没有左子树可访问时，访问该节点，并尝试访问右子树

按照这种思路，我们可以写出一种直接的方法：

public void inOrderTraversal(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	TreeNode node = root;
	
	while (node != null) { // 当node为null时，说明已经遍历结束
		if (node.left != null) { // 存在左子树时，入栈并深入左子树
			stack.push(node);
			node = node.left;
		} else { // 否则就寻找可以深入右子树的节点
			while (!stack.isEmpty() && node.right == null) {
				// 对于不能深入右子树的节点：直接访问，此时子树访问结束
				visit(node);
				node = stack.pop();
			}
			visit(node); // 如果可以深入右子树，访问该节点后，深入右子树
			node = node.right;
		}
	}
}

或者根据先序遍历方法2进行修改，在节点出栈时访问节点：

public void inOrderTraversal2(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	TreeNode node = root;
	
	while (!stack.isEmpty() || node != null) { // stack为空且node为null时，说明已经遍历结束
		if (node != null) { // 可以深入左孩子
			stack.push(node);
			node = node.left;
		} else { // 否则访问栈中节点，并深入右孩子
			node = stack.pop();
			visit(node);
			node = node.right;
		}
	}
}

以之前的树为例，其中序遍历结果应为：0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6

后序遍历

后序遍历从想法上是最难实现的，其主要思想是：

  1. 尝试按顺序访问该节点的左右子树
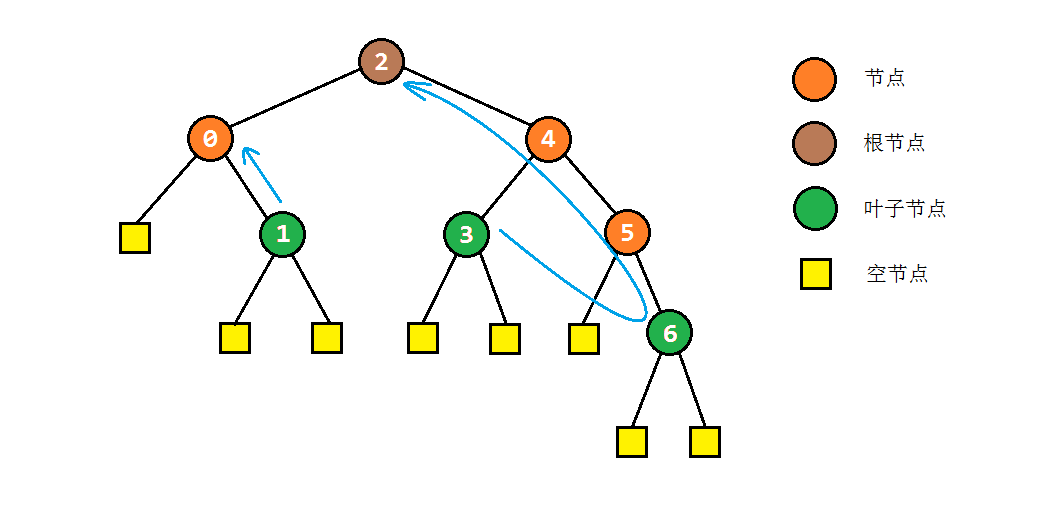
  2. 当左右子树都访问完毕时，才可以访问该节点

因此可以考虑采用栈的方式，依次将根节点、右孩子、左孩子入栈，以保证访问次序。由于后续遍历的回溯过程只可能上升一层，因此可以添加临时变量lastNode记录刚刚访问的节点，如果当前节点是上次访问节点的父节点，则说明子树访问完成，可以访问当前节点了。

public void postOrderTraversal(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	stack.push(root);
	TreeNode lastNode = root; // 为了判断父子节点关系
	
	while (!stack.isEmpty()) {
		TreeNode node = stack.pop(); // 取出一个节点，表示开始访问以该节点为根的子树
		if ((node.left == null && node.right == null) || // 如果该节点为叶子节点
			(node.left == lastNode || node.right == lastNode)) { // 或者已经访问过该节点的子节点
			visit(node); // 直接访问
			lastNode = node;
		} else { // 否则就按顺序把当前节点、右孩子、左孩子入栈
			stack.push(node); 
			if (node.right != null) stack.push(node.right);
			if (node.left != null) stack.push(node.left);
		}
	}
}

当然，对上述方法的一个修改是添加“哨兵”节点，用于判断回溯位置。不过显然这种方式还需要对一些方法进行添加，并不是特别“优雅”：

public void postOrderTraversal2(TreeNode root) {
	if (root == null) return;
	Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
	stack.push(root);
	
	while (!stack.isEmpty()) {
		TreeNode node = stack.pop(); // 取出一个节点，表示开始访问以该节点为根的子树
		if (!node.isValid()) { // 判断是“哨兵”节点，说明之后的节点为父节点，可以直接访问
			node = stack.pop();
			visit(node);
		} else if ((node.left == null && node.right == null)) { // 如果该节点为叶子节点，也可直接访问
			visit(node);
		} else { // 否则就按顺序把当前节点、“哨兵”节点、右孩子、左孩子入栈
			stack.push(node); 
			stack.push(new TreeNode(new Value(Value.INVALID_VALUE)));
			if (node.right != null) stack.push(node.right);
			if (node.left != null) stack.push(node.left);
		}
	}
}

以之前的树为例，其后序遍历结果应为：1 -> 0 -> 3 -> 6 -> 5 -> 4 -> 2

层次遍历

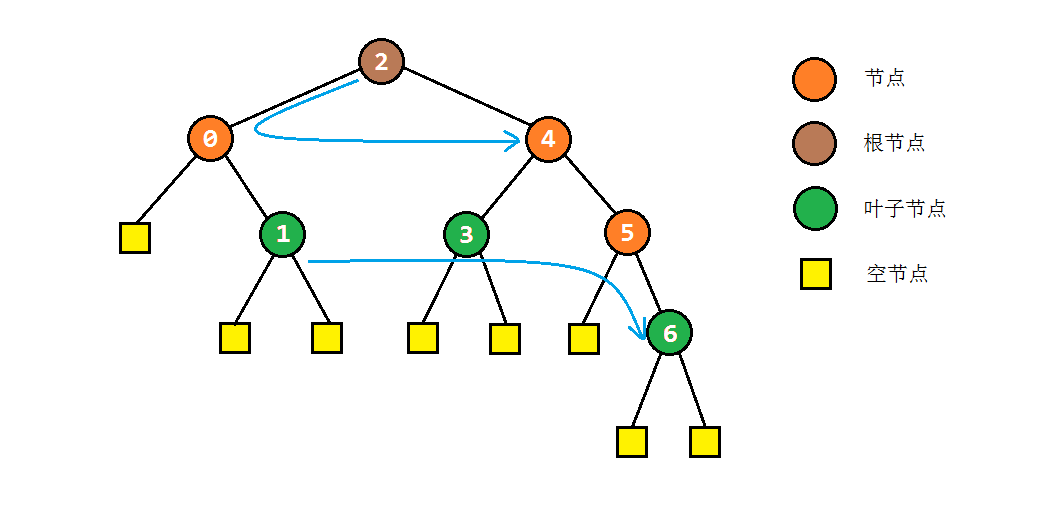
相较于前面几种遍历方式，层次遍历是最直观的遍历方式，可以利用队列来辅助实现：

public void levelTraversal(TreeNode root) {
	if (root == null) return;
	Queue<TreeNode> queue = new LinkedList<TreeNode>(); // 利用队列进行临时存储
	queue.offer(root);
	
	while(!queue.isEmpty()) { // 取出一个节点，并将其左右节点入列
		TreeNode node = queue.poll();
		visit(node);
		if (node.left != null) queue.offer(node.left);
		if (node.right != null) queue.offer(node.right);
	}
}

可以看到，层次遍历和先序遍历相比，只是将栈换成了队列，其余处理方式完全相同。以之前的树为例，其层次遍历结果应为：2 -> 0 -> 4 -> 1 -> 3 -> 5 -> 6

复杂度分析

很显然，无论哪种遍历方式，一个节点最多只可能被访问两次，因此其时间复杂度均为O(n)。而由于借助了栈和队列这样的辅助数据结构，其空间复杂度与树高有直接关系，因此其空间复杂度为最好和平均O(logn)，最差O(n)，与递归方式的实现相同。

Morris遍历

主要思想

Morris遍历方法打破了一般遍历思想上的“禁锢”，通过临时对子节点引用的修改来实现“后继”节点的保存，之后再次遍历到时可以恢复树的结构，以此仅仅通过O(1)的空间实现树的遍历。没错，这又是KMP算法里面的Morris发明的（为什么别人可以这么聪明……）

先以中序遍历为例，介绍Morris算法的核心思想。

回顾一下中序遍历的内容：

  1. 若节点还有左子树，就要先把左子树访问完
  2. 没有左子树可访问时，访问该节点，并尝试访问右子树

之前提到过，如果这棵树是一棵二叉搜索树，那么中序遍历的结果应当是一个有序数组。为了方便起见，我们可以按照中序遍历的结果，将整个树组成一个链表，每一个节点都有“前驱”节点和“后继”节点。例如在之前示例的二叉树上，0是1的前驱节点，而2是1的后继节点。

显然，中序遍历可以转化为对后继节点的计算过程。后继节点的计算方法为：

  1. 对于存在右子树的节点A，其后继节点是其右子树中最左侧的节点；
  2. 对于没有右子树的节点B，其后继节点是其自下而上的父节点中第一个将其作为左子树的节点。

节点A的后继计算非常简单。然而由于二叉树的信息中不包括父节点的信息，因此第2条操作起来非常困难，这也是为何之前采用了栈/队列的方式存储父节点的信息。

但是我们注意到，虽然对于这样的节点B，求取其后继节点非常困难；但是其后继节点来说，由于节点B是其子树中的一个节点，因此求前驱节点就很容易了！为了使得访问到节点B时能够直接得到后继信息，我们可以暂时使用B节点右子树的链接，存储后继节点，以实现对后继节点的直接获取，同时不占用额外的空间。这就是Morris遍历算法的主要思想。

Morris中序遍历算法

根据上述分析，我们可以写出程序的主要计算过程：

  1. 从根节点开始访问。
  2. 如果当前节点C不存在左子树，按中序遍历的规则，应当访问节点C，并进入其右子树进行遍历。
  3. 如果当前节点C存在左子树，就找到C的前驱节点B，并将B的右孩子指向C（存储后继），同时当前节点转入左子树进行遍历。
  4. 步骤2中访问右子树时，如果节点本身没有右子树，则会直接转入其后继节点C。根据中序遍历的规则，说明此时C的左子树遍历完成。为了还原树结构，我们需要重新找到C的前驱节点，并将其右孩子设置为null。之后我们访问节点C，并进入其右子树进行遍历。

以之前的示例树为例，图解一下morris遍历的部分过程：

因此，我们写出Morris中序遍历算法的程序如下：

public void morrisInOrderTraversal(TreeNode root) {
	TreeNode node = root, prev = null; // 仅存放两个临时变量，O(1)空间复杂度
	while (node != null) { // 当前节点为空时，说明访问完成
		if (node.left == null) { // 左子树不存在时，访问+进入右节点
			visit(node);
			node = node.right;
		} else { // 左子树存在，寻找前驱节点。注意寻找前驱节点时，会不断深入右子树。不加判断时，若前驱节点的右子树已指向自己，会引起死循环
			prev = node.left;
			while (prev.right != null && prev.right != node) prev = prev.right;
			if (prev.right == null) { // 前驱节点未访问过，存放后继节点
				prev.right = node;
				node = node.left;
			} else { // 前驱节点已访问过，恢复树结构
				visit(node); // 确定访问过左子树后，访问当前节点
				prev.right = null;
				node = node.right;
			}
		}
	}
}

其中最关键的一步是判断前驱节点是否访问过。注意到如果前驱节点访问过，则其右孩子必然为当前节点，否则必然为空。据此可以判断应当深入左子树还是右子树。

复杂度分析

O(1)的空间复杂度是毋庸置疑的，但是该算法是否与普通的遍历算法具有相同的时间效率？我们对时间复杂度进行简要的分析。

整个计算过程中，我们可以看到，主要的复杂度为计算前驱的循环，这里的复杂度与树高有直接关系，一般为O(logn)。但这是否说明Morris遍历的复杂度为O(nlogn)呢？仔细分析后发现，对于每一个有左子树的节点，其寻找前驱的过程只会执行两次，一次是建立前驱-后继关系的时候，一次是恢复树结构的时候。因此事实上，二叉树的每条路最多只可能被循环访问两次，其时间复杂度必然为O(n)。

当然，我们也可以逐层计算循环总计算次数。例如对于一棵满二叉树，其倒数第二层的节点树为n/4，寻找前驱的长度为2，以此类推，我们可以得到：

\[C = \sum_{i=1}^{\log_2(n/2)} \frac{n}{2^{i+1}} \times i = \frac{n}{4} \times 1 + \frac{n}{8} \times 2 + \frac{n}{16} \times 3 + \cdots + 1 \times \log_2(\frac{n}{2}) = n - 1 - \log_2(n) \sim O(n)\]

Morris先序遍历与后序遍历算法

介绍完了Morris中序遍历，其先序遍历和后序遍历都是在中序遍历的基础之上加以改动得到的。例如先序遍历时，需要先访问节点，再决定深入左子树或右子树：

public void morrisPreOrderTraversal(TreeNode root) {
	TreeNode node = root, prev = null; // 仅存放两个临时变量，O(1)空间复杂度
	while (node != null) { // 当前节点为空时，说明访问完成
		if (node.left == null) { // 左子树不存在时，访问+进入右节点
			visit(node);
			node = node.right;
		} else { // 左子树存在，寻找前驱节点。注意寻找前驱节点时，会不断深入右子树。不加判断时，若前驱节点的右子树已指向自己，会引起死循环
			prev = node.left;
			while (prev.right != null && prev.right != node) prev = prev.right;
			if (prev.right == null) { // 前驱节点未访问过，存放后继节点
				visit(node); // 在确定前驱节点未访问过时，访问当前节点（注意与中序遍历的区别）
				prev.right = node;
				node = node.left;
			} else { // 前驱节点已访问过，恢复树结构
				prev.right = null;
				node = node.right;
			}
		}
	}
}

后序遍历相比中序遍历稍微复杂一些，但是后序遍历也有其特性：若一个节点是右孩子，或该节点是左孩子但是没有兄弟节点，则访问完该节点后立刻会访问该节点的父节点。

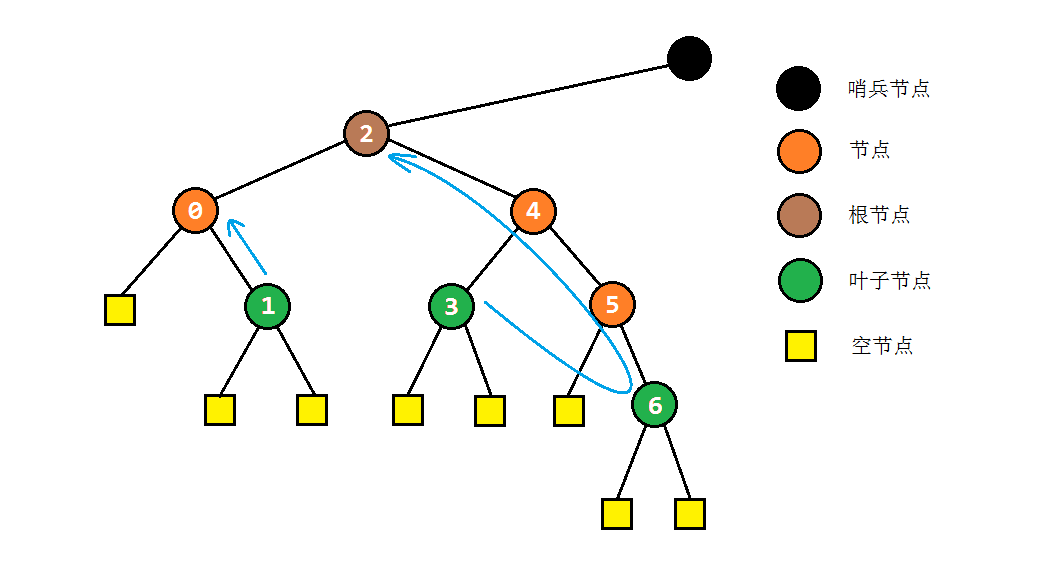
推广到Morris遍历里，可以得到：

  • 当访问到任何节点C的前驱节点B时，由B到C的路径（不包括节点C）即为之后的访问顺序。

因此所有的访问过程可以化为由B到C的访问。得到的Morris后序遍历程序如下，注意为了保证程序能够顺利访问右子树，为根节点添加了一个哨兵节点：

public void morrisPostOrderTraversal(TreeNode root) {
	TreeNode temp = new TreeNode(new Value(Value.INVALID_VALUE)), node = temp, prev = null; // 仅存放一个“哨兵”节点和两个临时变量，O(1)空间复杂度
	temp.left = root;
	while (node != null) { // 当前节点为空时，说明访问完成
		if (node.left == null) { // 左子树不存在时，进入右节点
			node = node.right;
		} else { // 左子树存在，寻找前驱节点。注意寻找前驱节点时，会不断深入右子树。不加判断时，若前驱节点的右子树已指向自己，会引起死循环
			prev = node.left;
			while (prev.right != null && prev.right != node) prev = prev.right;
			if (prev.right == null) { // 前驱节点未访问过，存放后继节点
				prev.right = node;
				node = node.left;
			} else { // 前驱节点已访问过，恢复树结构
				visitReverse(node.left, prev); // 确定访问过左子树后，逆序访问沿路节点（注意与中序遍历的区别）
				prev.right = null;
				node = node.right;
			}
		}
	}
}

对于逆序访问函数visitReverse()，我们可以采用链表翻转的方式实现，一个参考实现如下：

public void visitReverse(TreeNode node1, TreeNode node2) {
	reverse(node1, node2); // 首先进行翻转
	TreeNode node = node2; // 之后进行顺序访问
	while (node != node1) {
		visit(node);
		node = node.right;
	}
	visit(node1);
	reverse(node2, node1); // 恢复结构
}

public void reverse(TreeNode node1, TreeNode node2) {
	// 实现链表翻转
	TreeNode prev = node1;
	TreeNode current = prev.right;
	TreeNode next = current.right;
	while (prev != node2) {
		current.right = prev;
		prev = current;
		current = next;
		next = next.right;
	}
}

以此实现后序遍历结果。由于相比较其他两种遍历，后序遍历多了逆序访问的过程，其时间复杂度与链表长度成正比。因此后序遍历的时间复杂度仍然为O(n)。

编程实践

代码示例

C++ 示例

【2022-6-1】LeetCode C++代码

两数和的实现代码：add-two-numbers.cpp

  • (1) 定义数据结构
  • (2) 定义solution类，写public方法
// Time:  O(n) 时间复杂度
// Space: O(1) 空间复杂度

// Definition for singly-linked list.
// 定义数据结构——单链表
struct ListNode {
    int val; // 元素取值
    ListNode *next;	 // 指节点针
	// 构造函数，同类
    ListNode(int x) : val(x), next(NULL) {}
};
// 定义求解类
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode dummy{0}; // 初始化只有一个元素0的单链表
        auto curr = &dummy;

        auto carry = 0;
        while (l1 || l2 || carry) {
            auto a = l1? l1->val : 0, b = l2? l2->val : 0;
            auto val = carry + a + b;
            curr->next = new ListNode(val % 10);
            carry = val / 10;
			// 链表往下遍历一位
            l1 = l1 ? l1->next : nullptr;
            l2 = l2 ? l2->next : nullptr;
            curr = curr->next;
        }

        return dummy.next;
    }
};

二叉树复制

// Time:  O(n)
// Space: O(h)

// Definition for a binary tree node.
// 定义二叉树结构
struct TreeNode {
    int val; // data取值
    TreeNode *left; // 左孩子
    TreeNode *right; // 右孩子
	// 构造函数
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int v, int d) {
        if (d == 0 || d == 1) {
            auto node = new TreeNode(v);
            (d == 1 ? node->left : node->right) = root;
            return node;
        }
        if (root && d >= 2) {
            root->left  = addOneRow(root->left,  v, d > 2 ? d - 1 : 1);
            root->right = addOneRow(root->right, v, d > 2 ? d - 1 : 0);
        }
        return root;
    }
};

常见问题

top k 问题

拜托，面试别再问我TopK了

TopK 是问得比较多的几个问题之一，到底有几种方法，优化思路究竟是怎么样的

  • 问题描述：从 arr[1, n] 这n个数中，找出最大的k个数，这就是经典的TopK问题。
  • 栗子：从 arr[1, 12] = {5,3,7,1,8,2,9,4,7,2,6,6} 这 n=12 个数中，找出最大的 k=5 个。

TopK，不难；其思路优化过程，不简单：

  1. 全局排序，O(n*lg(n))
    • 最简单：将n个数排序之后，取出最大的k个
    • 分析：明明只需要TopK，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢？
  2. 局部排序，只排序TopK个数，O(n*k)
    • 不再全局排序，只对最大的k个排序；冒泡是一个很常见的排序方法，每冒一个泡，找出最大值，冒k个泡，就得到TopK。
    • 分析：冒泡，将全局排序优化为了局部排序，非TopK的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopK，是不是这最大的k个元素也不需要排序呢？这就引出了第三个优化方法。
  3. 堆，TopK个数也不排序了，O(n*lg(k))
    • 思路：只找到TopK，不排序TopK，将冒泡的TopK排序优化为了TopK不排序，节省了计算资源
    • 先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素
    • 接着从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。
    • 直到，扫描完所有n-k个元素，最终堆中的k个元素，就是猥琐求的Top
  4. TopK 另一个解法：随机选择+partition
    • 随机选择是《算法导论》中经典算法，其时间复杂度为O(n)，是一个线性复杂度方法。核心算法思想是分治法。
    • 分治法（ Divide & Conquer）把一个大的问题，转化为若干个子问题（Divide），每个子问题“都”解决，大的问题便随之解决（Conquer）。
    • 关键词是“都”。从伪代码里可以看到，快速排序递归时，先通过 partition 把数组分隔为两个部分，两个部分“都”要再次递归。 - 减治法（ Reduce & Conquer），分治法特例,把大问题转化为若干个子问题（Reduce），这些子问题中“只”解决一个，大的问题便随之解决（Conquer）。
    • 关键词是“只”。二分查找 binary_search，BS，是一个典型的运用减治法思想的算法 - 分治法：每个分支“都要”递归
    • 例如：快速排序，O(n*lg(n)) - 减治法：分治法特例叫减治法。“只要”递归一个分支
    • 例如：二分查找O(lg(n))，随机选择O(n); 二分查找，大问题可以用一个mid元素，分成左半区，右半区两个子问题。而左右两个子问题，只需要解决其中一个，递归一次，就能够解决二分查找全局的问题。 - 通过分治法与减治法的描述，可以发现，分治法的复杂度一般来说是大于减治法的： - TopK是希望求出 arr[1,n] 中最大的k个数，那如果找到了第k大的数，做一次partition，不就一次性找到最大的k个数了么？问题变成了arr[1, n]中找到第k大的数 - 随机选择（randomized_select），找到arr[1, n]中第k大的数，再进行一次partition，就能得到TopK的结果 知其然，知其所以然。思路比结论重要。

分治和减治

  • 分治法，大问题分解为小问题，小问题都要递归各个分支，例如：快速排序 O(n*lg(n))
  • 减治法，大问题分解为小问题，小问题只要递归一个分支，例如：二分查找 O(lg(n))，随机选择
// 快排伪代码 —— 分治算法
void quick_sort(int[]arr, int low, inthigh){
    if(low == high) return;
    int i = partition(arr, low, high); // 快排核心，比i小的放左边，否则右边，保持整体大致有序
    quick_sort(arr, low, i-1);
    quick_sort(arr, i+1, high);
}
// 二分法伪代码 —— 减治算法
int BS(int[]arr, int low, inthigh, int target){
    if(low> high) return -1;
    mid= (low+high)/2;
    if(arr[mid]== target) return mid;
    if(arr[mid]> target)
        return BS(arr, low, mid-1, target);
    else
        return BS(arr, mid+1, high, target);
}
// 随机选择算法randomized_select，RS —— 减治算法
int RS(arr, low, high, k){
  if(low== high) return arr[low];
  i= partition(arr, low, high);
  temp= i-low; //数组前半部分元素个数
  if(temp>=k)
      return RS(arr, low, i-1, k); //求前半部分第k大
  else
      return RS(arr, i+1, high, k-i); //求后半部分第k-i大
}

【2023-6-3】快速排序简洁代码，由大模型claude提供

def quick_sort(arr): 
    if len(arr) <= 1: 
        return arr
    pivot = arr[len(arr)//2]  
    left = [x for x in arr if x < pivot]  
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

arr = [5,3,8,6,7,2]
print(quick_sort(arr))
# [2, 3, 5, 6, 7, 8]

最长公共子串

【2022-5-17】最长公共子序列和最长公共子串

问题描述：

  • 给定两个序列：X[ 1...m ] 和 Y[ 1...n ]，求在两个序列中同时出现的最长子序列的长度。
  • 假设 X 和 Y 的序列如下：
    • X[ 1...m] = {A, B, C, B, D, A, B}
    • Y[ 1...n] = {B, D, C, A, B, A}

最长公共子串（Longest Common Substring）与最长公共子序列（Longest Common Subsequence）的区别：

  • 子串要求在原字符串中是连续的，而子序列则只需保持相对顺序，并不要求连续。
  • 例如 X = {a, Q, 1, 1}; Y = {a, 1, 1, d, f}，那么，{a, 1, 1}是X和Y的最长公共子序列，但不是它们的最长公共字串。

最长公共子串

X 和 Y 的最长公共子串有：BD, AB

最大公共子串要求的字串是连续的

求子串的方法和求子序列方法类似：

  • 当str1[i] == str2[j]时，子序列长度 veca[i][j] = veca[i - 1][j - 1] + 1；
  • 当str1[i] != str2[j]时，veca[i][j] 长度要为0，而不是 max{ veca[i - 1][j], veca[i][j - 1] }。

下面是求解时的动态规划表，可以看出 X 和 Y 的最长公共子串的长度为2：

// 动态规划求解LCS问题
#include <iostream>
#include <string>
#include <vector>
using namespace std;
 
int max(int a, int b) 
{
	return (a>b)? a:b;
}
 
/**
 * 返回X[0...m-1]和Y[0...n-1]的LCS的长度 
 */
int lcs(string &X, string &Y, int m, int n)
{
	int biggest = 0;
	// 动态规划表，大小(m+1)*(n+1)
	vector<vector<int>> table(m+1,vector<int>(n+1));  
 
	for(int i=0; i<m+1; ++i)
	{
		for(int j=0; j<n+1; ++j)
		{
			// 第一行和第一列置0
			if (i == 0 || j == 0)
				table[i][j] = 0;
			else if(X[i-1] == Y[j-1])
			{
				table[i][j] = table[i-1][j-1] + 1;
				if(table[i][j] > biggest)  // 增加了一个最大值
                                        biggest = table[i][j];
			}
			else
				table[i][j] = 0;  // 此处变化
		}
	}
 
	return biggest;
}
 
int main()
{
	string X = "ABCBDAB";
	string Y = "BDCABA";
 
	cout << "The length of LCS is " << lcs(X, Y, X.length(), Y.length());
	cout << endl;
 
	getchar();
	return 0;
}

求解时的动态规划表，可以看出 X 和 Y 的最长公共子串的长度为2：

输出最长公共子串很简单，只需要判断table[i][j]是否等于最长公共子串的长度即可，然后沿着对角线往左上角找大于等于1的数字即可；

  • 如果 table[i][j] == lcs_len（lcs_len指最长公共子串长度），则把这个字符放入LCS中，并跳入table[i-1][j-1]中继续进行判断；
  • 直到 table[i][j] < 1 为止；倒序输出LCS放入set中。 从上图的红色路径显示，X 和 Y 的最长公共子串有 3 个，分别为 “BD”、“AB”、“AB”。因“AB”与“AB”重复，故只输出“BD”、“AB”即可。
// 动态规划求解并输出所有LCS
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;

string x = "ABCBDAB";
string y = "BDCABA";
vector<vector<int>> table; // 动态规划表
set<string> setOflcs;      // set保存所有的LCS

/**
 * 构造表，并返回X和Y的LCS的长度
 */
int lcs(int m, int n)
{
    int biggest = 0;
    // 表的大小为(m+1)*(n+1)
    table = vector<vector<int>>(m+1, vector<int>(n+1));
    for(int i = 0; i < m+1; i++)
    {
        for(int j = 0; j < n+1; j++)
        {
            // 第一行和第一列置0
            if(i == 0 || j == 0)
                table[i][j] = 0;
            else if(x[i-1] == y[j-1])
            {
		table[i][j] = table[i-1][j-1] + 1;
		if(table[i][j] > biggest)
                    biggest = table[i][j]; // 存放LCS的长度
	    }
	    else
		table[i][j] = 0;
        }
    }
    return biggest;
}

/**
 * 求出所有的最长公共子串，并放入set中
 */
void traceBack(int m, int n, int lcs_len)
{
    string strOflcs;
    for(int i = 1; i < m+1; i++)
    {
        for(int j = 1; j < n+1; j++)
        {
            // 查到等于lcs_len的值，取字符
            if(table[i][j] == lcs_len)
            {
                int ii = i, jj = j;
                while(table[ii][jj] >= 1)
                {
                    strOflcs.push_back(x[ii-1]);
                    ii--;
                    jj--;
                }
                string str(strOflcs.rbegin(), strOflcs.rend()); // strOflcs逆序
                if((int)str.size() == lcs_len)                       // 判断str的长度是否等于lcs_len
                {
                    setOflcs.insert(str);
                    strOflcs.clear();                           // 清空strOflcs
                }
            }
        }
    }
}

// 输出set
void print()
{
    set<string>::iterator iter = setOflcs.begin();
    for(; iter != setOflcs.end(); iter++)
        cout << *iter << endl;
}

int main()
{
    int m = x.length();
    int n = y.length();
    int res = lcs(m, n);
    cout << "res = " << res << endl;

    traceBack(m, n, res);
    print();

    getchar();
    return 0;
}

最长公共子序列

X 和 Y 的最长公共子序列有 “BDAB”、“BCAB”、“BCBA”，即长度为4。

（1）穷举法

用穷举法来解决这个问题，即求出 X 中所有子序列，看 Y 中是否存在该子序列。

  • X 有多少子序列 —— 2m 个
  • 检查一个子序列是否在 Y 中 —— θ(n) 穷举法在最坏情况下的时间复杂度是 θ(n * 2m)，也就是说花费的时间是指数级的

（2）动态规划

LCS 问题是否具有动态规划问题的两个特性。

  • ① 最优子结构
    • 设 C[ i,j] = | LCS(x[ 1...i], y[ 1...j]) |，即 C[ i,j] 表示序列 X[ 1…i] 和 Y[ 1…j] 的最长公共子序列的长度，则 C[ m,n] = |LCS(x,y)| 就是问题的解。
    • 递归推导式：
    • 从这个递归公式可以看出，问题具有最优子结构性质！
  • ② 重叠子问题
    • 求LCS长度的递归伪代码：
LCS(x,y,i,j)
if x[i] = y[j]
	then C[i,j] ← LCS(x,y,i-1,j-1)+1
else C[i,j] ← max{LCS(x,y,i-1,j),LCS(x,y,i,j-1)}
	return C[i,j]

【2022-5-17】小冰命中一次，写成半成品

# x = "ace"
# y = "bcedf"
# dp: lcs -> f(n) = max{ f(n-1)+1, f(n-1) }
max_seq = []

def lcs(x, y, max_seq):
	""" 最长公共子串 """
	# (0 ) 边界条件
	if not ( len(x) and len(y)):
		return 0
	# (1) 最后一位相同
	if x[0] == y[0]:
		max_seq.append(x[0])
		return lcs(x[1:], y[1:], max_seq)
	else: # (2) 最后一位不同，取大
		tmp = [lcs(x[1:], y, max_seq), lcs(x, y[1:], max_seq), lcs(x[1:], y[1:], max_seq)]
		# 字符串不连续时清空
		if tmp[0] == tmp[2]:
			max_seq = []
		return max(tmp)

print(''.join(max_seq))
# 效率：O(mn)
# 优化：备忘录、DP Table

c++简单递归求解

// 简单的递归求解LCS问题
#include <iostream>
#include <string>
using namespace std;
 
int max(int a, int b) 
{
	return (a>b)? a:b;
}
 
// Return the length of LCS for X[0...m-1] and Y[0...n-1]
int lcs(string &X, string &Y, int m, int n)
{
	if (m == 0 || n == 0)
		return 0;
	if (X[m-1] == Y[n-1])
		return lcs(X, Y, m-1, n-1) + 1;
	else
		return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}

int main()
{
	string X = "ABCBDAB";
	string Y = "BDCABA";
	// 输出最长公共子序列长度
	cout << "The length of LCS is " << lcs(X, Y, X.length(), Y.length());
	cout << endl;
	getchar();
	return 0;
}

简单递归，在最坏情况下（X 和 Y 的所有字符都不匹配，即LCS的长度为0）的时间复杂度为 θ(2n)。这和穷举法一样还是指数级的，太慢了。

根据程序中 X 和 Y 的初始值，画出部分递归树：

  • 递归树中红框标记的部分被调用了两次。画出完整的递归树后，可以发现有很多重复调用，这个问题具有重叠子问题的特性。

递归之所以和穷举法一样慢，因为在递归过程中进行了大量的重复调用。而动态规划就是解这个问题的，通过用一个表来保存子问题的结果，避免重复的计算，以空间换时间。前面已经证明，最长公共子序列问题具有动态规划所要求的两个特性，所以 LCS 问题可以用动态规划来求解。

改进版：DP Table存储，防止重复计算数值

// 动态规划求解LCS问题 
#include <iostream>
#include <string>
#include <vector>
using namespace std;
 
int max(int a, int b) 
{
	return (a>b)? a:b;
}
 
/**
 * 返回X[0...m-1]和Y[0...n-1]的LCS的长度 
 */
int lcs(string &X, string &Y, int m, int n)
{
	// 动态规划表，大小(m+1)*(n+1)
	vector<vector<int>> table(m+1,vector<int>(n+1));  
 
	for(int i=0; i<m+1; ++i)
	{
		for(int j=0; j<n+1; ++j)
		{
			// 第一行和第一列置0
			if (i == 0 || j == 0)
				table[i][j] = 0;
			else if(X[i-1] == Y[j-1])
				table[i][j] = table[i-1][j-1] + 1;
			else
				table[i][j] = max(table[i-1][j], table[i][j-1]);
		}
	}
	return table[m][n];
}
 
int main()
{
	string X = "ABCBDAB";
	string Y = "BDCABA";
 
	cout << "The length of LCS is " << lcs(X, Y, X.length(), Y.length());
	cout << endl;
 
	getchar();
	return 0;
}

动态规划解决LCS问题的时间复杂度为θ(mn)，这比简单递归实现要快多了。

  • 空间复杂度是θ(mn)，因为使用了一个动态规划表。
  • 当然，空间复杂度还可以进行优化，即根据递推式可以只保存填下一个位置所用到的几个位置就行了。

总结：

  • 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。
  • 其中的关键在于解决冗余（重复计算），这是动态规划算法的根本目的。
  • 动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其它的算法。

动态规划解决最优化问题的一般步骤：

  1. 分析最优解的性质，并刻划其结构特征。
  2. 递归地定义最优值。
  3. 以自底向上的方式或自顶向下的记忆化方法计算出最优值。
  4. 根据计算最优值时得到的信息，构造一个最优解。

步骤(1)—(3)是动态规划算法的基本步骤。在只需要求出最优值的情形，步骤(4)可以省略，若需要求出问题的一个最优解，则必须执行步骤(4)。此时，在步骤(3)中计算最优值时，通常需记录更多的信息，以便在步骤(4)中，根据所记录的信息，快速地构造出一个最优解。

输出一个最长公共子序列并不难（网上很多相关代码），难点在于输出所有的最长公共子序列，因为 LCS 通常不唯一。

总之，需要在动态规划表上进行回溯 —— 从table[m][n]，即右下角的格子，开始进行判断：

  • 如果格子table[i][j]对应的X[i-1] == Y[j-1]，则把这个字符放入 LCS 中，并跳入table[i-1][j-1]中继续进行判断；
  • 如果格子table[i][j]对应的 X[i-1] ≠ Y[j-1]，则比较table[i-1][j]和table[i][j-1]的值，跳入值较大的格子继续进行判断；
  • 直到 i 或 j 小于等于零为止，倒序输出 LCS 。 如果出现table[i-1][j]等于table[i][j-1]的情况，说明最长公共子序列有多个，故两边都要进行回溯（这里用到递归）
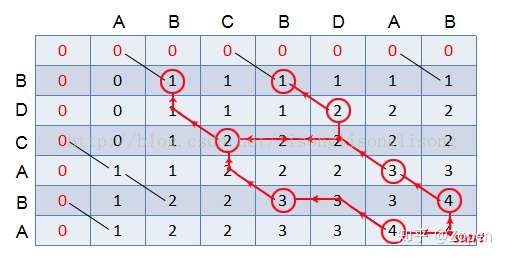
  • 从上图的红色路径显示，X 和 Y 的最长公共子序列有 3 个，分别为 “BDAB”、“BCAB”、“BCBA”。
// 动态规划求解并输出所有LCS
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;

string X = "ABCBDAB";
string Y = "BDCABA";
vector<vector<int>> table; // 动态规划表
set<string> setOfLCS;      // set保存所有的LCS

int max(int a, int b)
{
	return (a>b)? a:b;
}

/**
 * 构造表，并返回X和Y的LCS的长度
 */
int lcs(int m, int n)
{
	// 表的大小为(m+1)*(n+1)
	table = vector<vector<int>>(m+1,vector<int>(n+1));

	for(int i=0; i<m+1; ++i)
	{
		for(int j=0; j<n+1; ++j)
		{
			// 第一行和第一列置0
			if (i == 0 || j == 0)
				table[i][j] = 0;
			else if(X[i-1] == Y[j-1])
				table[i][j] = table[i-1][j-1] + 1;
			else
				table[i][j] = max(table[i-1][j], table[i][j-1]);
		}
	}

	return table[m][n];
}

/**
 * 求出所有的最长公共子序列，并放入set中
 */
void traceBack(int i, int j, string lcs_str, int lcs_len)
{
	while (i>0 && j>0)
	{
		if (X[i-1] == Y[j-1])
		{
			lcs_str.push_back(X[i-1]);
			--i;
			--j;
		}
		else
		{
			if (table[i-1][j] > table[i][j-1])
				--i;
			else if (table[i-1][j] < table[i][j-1])
				--j;
			else   // 相等的情况
			{
				traceBack(i-1, j, lcs_str, lcs_len);
				traceBack(i, j-1, lcs_str, lcs_len);
				return;
			}
		}
	}

	string str(lcs_str.rbegin(), lcs_str.rend()); // lcs_str逆序
        if((int)str.size() == lcs_len)                // 判断str的长度是否等于lcs_len
            setOfLCS.insert(str);
}

void print()
{
    set<string>::iterator beg = setOfLCS.begin();
	for( ; beg!=setOfLCS.end(); ++beg)
		cout << *beg << endl;
}
int main()
{
	int m = X.length();
	int n = Y.length();
	int length = lcs(m, n);
	cout << "The length of LCS is " << length << endl;

	string str;
	traceBack(m, n, str, length);
	print();

	getchar();
	return 0;
}

反转一个链表（招银网络二面）

ListNode* reverse(ListNode* root){
  ListNode* pre=nullptr,cur=root,nxt;
  while(cur!=nullptr){
    nxt=cur->next;
    cur->next=pre;
    pre=cur;cur=nxt;
  }
  return pre;
}

Top K问题（重点）

Top K 问题的常见形式：

给定10000个整数，找第K大（第K小）的数
给定10000个整数，找出最大（最小）的前K个数
给定100000个单词，求前K词频的单词

解决Top K问题若干种方法

  • 使用最大最小堆。求最大的数用最小堆，求最小的数用最大堆。
  • Quick Select算法。使用类似快排的思路，根据pivot划分数组。
  • 使用排序方法，排序后再寻找top K元素。
  • 使用选择排序的思想，对前K个元素部分排序。
  • 将1000…..个数分成m组，每组寻找top K个数，得到m×K个数，在这m×k个数里面找top K个数。
  1. 使用最大最小堆的思路 （以top K 最大元素为例）

按顺序扫描这10000个数，先取出K个元素构建一个大小为K的最小堆。每扫描到一个元素，如果这个元素大于堆顶的元素（这个堆最小的一个数），就放入堆中，并删除堆顶的元素，同时整理堆。如果这个元素小于堆顶的元素，就直接pass。最后堆中剩下的元素就是最大的前Top K个元素，最右的叶节点就是Top 第K大的元素。

note：最小堆的插入时间复杂度为log(n)，n为堆中元素个数，在这里是K。最小堆的初始化时间复杂度是nlog(n)

C++中的最大最小堆要用标准库的priority_queue来实现。

struct Node {
    int value;
    int idx;
    Node (int v, int i): value(v), idx(i) {}
    friend bool operator < (const struct Node &n1, const struct Node &n2) ; 
};

inline bool operator < (const struct Node &n1, const struct Node &n2) {
    return n1.value < n2.value;
}

priority_queue<Node> pq; // 此时pq为最大堆
  1. 使用Quick Select的思路（以寻找第K大的元素为例）

Quick Select脱胎于快速排序，提出这两个算法的都是同一个人。算法的过程是这样的：

  • 首先选取一个枢轴，然后将数组中小于该枢轴的数放到左边，大于该枢轴的数放到右边。
  • 此时，如果左边的数组中的元素个数大于等于K，则第K大的数肯定在左边数组中，继续对左边数组执行相同操作；
  • 如果左边的数组元素个数等于K-1，则第K大的数就是pivot；
  • 如果左边的数组元素个数小于K，则第K大的数肯定在右边数组中，对右边数组执行相同操作。

这个算法与快排最大的区别是，每次划分后只处理左半边或者右半边，而快排在划分后对左右半边都继续排序。

//此为Java实现
public int findKthLargest(int[] nums, int k) {
  return quickSelect(nums, k, 0, nums.length - 1);
}

// quick select to find the kth-largest element
public int quickSelect(int[] arr, int k, int left, int right) {
  if (left == right) return arr[right];
  int index = partition(arr, left, right);
  if (index - left + 1 > k)
    return quickSelect(arr, k, left, index - 1);
  else if (index - left + 1 == k)
    return arr[index];
  else
    return quickSelect(arr, k - (index - left + 1), index + 1, right);

}
  1. 使用选择排序的思想对前K个元素排序 （ 以寻找前K大个元素为例）

扫描一遍数组，选出最大的一个元素，然后再扫描一遍数组，找出第二大的元素，再扫描一遍数组，找出第三大的元素。。。。。以此类推，找K个元素，时间复杂度为O(N*K)

8G的int型数据，计算机的内存只有2G，怎么对它进行排序？（外部排序）（百度一面）

可以使用外部排序来对它进行处理。首先将整个文件分成许多份，比如说m份，划分的依据就是使得每一份的大小都能放到内存里。然后我们用快速排序或者堆排序等方法对每一份数据进行一个内部排序，变成有序子串。接着对这m份有序子串进行m路归并排序。取这m份数据的最小元素，进行排序，输出排序后最小的元素到结果中，同时从该元素所在子串中读入一个元素，直到所有数据都被输出到结果中为止。

布隆过滤器原理与优点

布隆过滤器是一个比特向量或者比特数组，它本质上是一种概率型数据结构，用来查找一个元素是否在集合中，支持高效插入和查询某条记录。常作为针对超大数据量下高效查找数据的一种方法。

它的具体工作过程是这样子的：

假设布隆过滤器的大小为m（比特向量的长度为m），有k个哈希函数，它对每个数据用这k个哈希函数计算哈希，得到k个哈希值，然后将向量中相应的位设为1。在查询某个数据是否存在的时候，对这个数据用k个哈希函数得到k个哈希值，再在比特向量中相应的位查找是否为1，如果某一个相应的位不为1，那这个数据就肯定不存在。但是如果全找到了，则这个数据有可能存在。

为什么说有可能存在呢？

因为不同的数据经过哈希后可能有相同的哈希值，在比特向量上某个位置查找到1也可能是由于某个另外的数据映射得到的。

支持删除操作吗

目前布隆过滤器只支持插入和查找操作，不支持删除操作，如果要支持删除，就要另外使用一个计数变量，每次将相应的位置为1则计数加一，删除则减一。

布隆过滤器中哈希函数的个数需要选择。如果太多则很快所有位都置为1，如果太少会容易误报。

布隆过滤器的大小以及哈希函数的个数怎么选择？

k 为哈希函数个数，m 为布隆过滤器长度，n 为插入的元素个数，p 为误报率

智力题

（1） 扔鸡蛋

100层楼，只有2个鸡蛋，想要判断出那一层刚好让鸡蛋碎掉，给出策略（滴滴笔试中两个铁球跟这个是一类题）

  • （给定了楼层数和鸡蛋数的情况）二分法+线性查找 从100/2=50楼扔起，如果破了就用另一个从0扔起直到破。如果没破就从50/2=25楼扔起，重复。

  • 动态规划

（2） 毒药问题

1000瓶水，其中有一瓶可以无限稀释的毒药，要快速找出哪一瓶有毒，需要几只小白鼠

用二进制的思路解决问题。2的十次方是1024，使用十只小鼠喝一次即可。方法是先将每瓶水编号，同时10个小鼠分别表示二进制中的一个位。将每瓶水混合到水瓶编号中二进制为1的小鼠对应的水中。喝完后统计，将死亡小鼠对应的位置为1，没死的置为0，根据死亡小鼠的编号确定有毒的是哪瓶水，如0000001010表示10号水有毒。

（4） 先手必胜策略问题

100本书，每次能够拿1-5本，怎么拿能保证最后一次是你拿

寻找每个回合固定的拿取模式。最后一次是我拿，那么上个回合最少剩下6本。那么只要保持每个回合结束后都剩下6的倍数，并且在这个回合中我拿的和对方拿的加起来为6（这样这个回合结束后剩下的还是6的倍数），就必胜。关键是第一次我必须先手拿（100%6=4）本（这不算在第一回合里面）。

（5） 蚂蚁🐜

放n只蚂蚁在一条树枝上，蚂蚁与蚂蚁之间碰到就各自往反方向走，问总距离或者时间。

碰到就当没发生，继续走，相当于碰到的两个蚂蚁交换了一下身体。其实就是每个蚂蚁从当前位置一直走直到停止的总距离或者时间。

（6） 瓶子换饮料问题

1000瓶饮料，3个空瓶子能够换1瓶饮料，问最多能喝几瓶

拿走3瓶，换回1瓶，相当于减少2瓶。但是最后剩下4瓶的时候例外，这时只能换1瓶。所以我们计算1000减2能减多少次，直到剩下4.（1000-4=996，996/2=498）所以1000减2能减498次直到剩下4瓶，最后剩下的4瓶还可以换一瓶，所以总共是1000+498+1=1499瓶。

（7）时针分针重合

在24小时里面时针分针秒针可以重合几次

24小时中时针走2圈，而分针走24圈，时针和分针重合24-2=22次，而只要时针和分针重合，秒针一定有机会重合，所以总共重合22次

（8） 天平问题

有一个天平，九个砝码，一个轻一些，用天平至少几次能找到轻的？

  • 至少2次：第一次，一边3个，哪边轻就在哪边，一样重就是剩余的3个；
  • 第二次，一边1个，哪边轻就是哪个，一样重就是剩余的那个；

（9） 找轻砝码

有十组砝码每组十个，每个砝码重10g，其中一组每个只有9g，有能显示克数的秤最少几次能找到轻的那一组砝码？

砝码分组1~10，第一组拿一个，第二组拿两个以此类推。第十组拿十个放到秤上称出克数x，则y = 550 - x，第y组就是轻的那组

（10）生成随机数问题

给定生成1到5的随机数Rand5()，如何得到生成1到7的随机数函数Rand7()？

思路：

  • 由大的生成小的容易，比如由Rand7()生成Rand5()，所以我们先构造一个大于7的随机数生成函数。

记住下面这个式子：

  • RandNN= N( RandN()-1 ) + RandN() ; // 生成1到N^2之间的随机数

可以看作是在数轴上撒豆子。N是跨度/步长，是RandN()生成的数的范围长度，RandN()-1的目的是生成0到N-1的数，是跳数。后面+RandN()的目的是填满中间的空隙

比如 Rand25= 5( Rand5()-1 ) + Rand5()可以生成1到25之间的随机数。我们可以只要1到21（3*7）之间的数字，所以可以这么写

int rand7(){
  int x=INT_MAX;
  while(x>21){
    x=5*(rand5()-1)+rand5();
  }
  return x%7+1;
}

赛马

有25匹马，每场比赛只能赛5匹，至少要赛多少场才能找到最快的3匹马？

  • 第一次，分成5个赛道ABCDE，每个赛道5匹马，每个赛道比赛一场，每个赛道的第12345名记为 A1,A2,A3,A4,A5 B1,B2,B3,B4,B5等等，这一步要赛5场。
  • 第二次，我们将每个赛道的前三名，共15匹。分成三组，然后每组进行比赛。这一步要赛3场。
  • 第三次，我们取每组的前三名。共9匹，第一名赛道的马编号为1a,1b,1c，第二名赛道的马编号为2a,2b,2c，第三名赛道的马编号为3a,3b,3c。这时进行分析，1a表示第一名里面的第一名，绝对是所有马中的第一，所以不用再比了。2c表示第二名的三匹里头的最后一匹，3b和3c表示第三名里面的倒数两匹，不可能是所有马里面的前三名，所以也直接排除，剩下1b,1c,2a,2b,,3a，共5匹，再赛跑一次取第一第二名，加上刚筛选出来的1a就是所有马里面的最快3匹了。这一步要赛1场。
  • 所以一共是5+3+1=9场。

烧 香/绳子/其他

确定时间问题：有两根不均匀的香，燃烧完都需要一个小时，问怎么确定15分钟的时长？

（说了求15分钟，没说开始的15分钟还是结束的15分钟，这里是可以求最后的15分钟）点燃一根A，同时点燃另一根B的两端，当另一根B烧完的时候就是半小时，这是再将A的另一端也点燃，从这时到A燃烧完就正好15分钟。

掰巧克力问题

掰巧克力问题

NM块巧克力，每次掰一块的一行或一列，掰成11的巧克力需要多少次？（1000个人参加辩论赛，1V1，输了就退出，需要安排多少场比赛）

每次拿起一块巧克力，掰一下（无论横着还是竖着）都会变成两块，因为所有的巧克力共有N*M块，所以要掰N*M-1次，-1是因为最开始的一块是不用算进去的。

每一场辩论赛参加两个人，消失一个人，所以可以看作是每一场辩论赛减少一个人，直到最后剩下1个人，所以是1000-1=999场。

大厂高频题

字节高频题目

【2022-10-27】字节高频算法题，整体分布

最长子串

3. 无重复字符的最长子串

思路：滑动窗口

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        i,j = 0,0
        maxlen = 0
 
        while j<len(s):
            
            while True:
                if s[j] not in s[i:j]:
                    break
                i+=1
            
            maxlen = max(maxlen,j-i+1)
            j+=1
            
        return maxlen

最小栈

155. 最小栈

思路：辅助栈

class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = [math.inf]
 
    def push(self, x: int) -> None:
        self.stack.append(x)
        self.min_stack.append(min(x, self.min_stack[-1]))
 
    def pop(self) -> None:
        self.stack.pop()
        self.min_stack.pop()
 
    def top(self) -> int:
        return self.stack[-1]
 
    def getMin(self) -> int:
        return self.min_stack[-1]

接雨水

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例

  • 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
  • 输出：6

解释：

  • 上面由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

解法汇总

思路：单调栈

class Solution:
    def trap(self, height: List[int]) -> int:
        ans = 0
        current = 0
        stack = []
        while current<len(height):
            while len(stack)>0 and height[current]>height[stack[-1]] :
                top = stack.pop()
                if len(stack)==0:
                    break
                distance = current-stack[-1]-1
                bounded_height = min(height[stack[-1]],height[current])-height[top]
                ans+=distance*bounded_height
            
            stack.append(current)
            current+=1
        return ans

买卖股票时机

121. 买卖股票最佳时机

思路：动态规划

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
 
        dp = [0]*len(prices)
        min_prices = prices[0]
 
        for i in range(1,len(prices)):
            dp[i] = max(dp[i-1],prices[i]-min_prices)
            min_prices = min(min_prices,prices[i])
 
        return dp[-1]

二叉树右视图

199. 二叉树的右视图

思路：层序遍历

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
     # deque来自collections模块，不在力扣平台时，需要手动写入
     # 'from collections import deque' 导入
     # deque相比list的好处是，list的pop(0)是O(n)复杂度，deque的popleft()是O(1)复杂度
     
        if not root:
            return []
        
        queue = deque([root])
        right_list = []
 
        while queue:
            node = queue[-1]
            right_list.append(node.val)
 
            for _ in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        
        return right_list

栈实现队列

232. 用栈实现队列

思路：两个栈互相倒酒

class MyQueue:
 
    def __init__(self):
        self.stack_in = []
        self.stack_out = []
 
    def empty(self) -> bool:
        return not (self.stack_in or self.stack_out)
 
    def push(self, x: int) -> None:
        self.stack_in.append(x)
 
    def pop(self) -> int:
        if self.empty():
            return None
        if self.stack_out:
            return self.stack_out.pop()
        else:
            for i in range(len(self.stack_in)):
                self.stack_out.append(self.stack_in.pop())
            return self.stack_out.pop()
 
 
    def peek(self) -> int:
        """
        Get the front element.
        """
        ans = self.pop()
        self.stack_out.append(ans) #取出来 还要放回去
        return ans
 
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()

前序、中序构建二叉树

105. 从前序与中序遍历序列构造二叉树

思路：递归

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        # 实际上inorder 和 postorder一定是同时为空的，因此你无论判断哪个都行
        if not preorder:
            return None
        root = TreeNode(preorder[0])
 
        i = inorder.index(root.val)
        root.left = self.buildTree(preorder[1:i + 1], inorder[:i])
        root.right = self.buildTree(preorder[i + 1:], inorder[i+1:])
 
        return root

最长回文子串

5. 最长回文子串

思路：递归

class Solution:
    def expandAroundCenter(self, s, left, right):
        while left >= 0 and right < len(s) and s[left] == s[right]:
            left -= 1
            right += 1
        return left + 1, right - 1
        # 注意这里是left+1 和 right-1
 
    def longestPalindrome(self, s: str) -> str:
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = self.expandAroundCenter(s, i, i)
            left2, right2 = self.expandAroundCenter(s, i, i + 1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start: end + 1]

对称二叉树

101. 对称二叉树

思路：递归 出口写好来

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
 
        def compare(p, q):
            if p==None and q!=None:
                return False
            if p!=None and q==None:
                return False
            if p==None and q==None:
                return True
 
            if p!=None and q!=None:
 
                if p.val != q.val:
                    return False
                else:
                    return compare(p.left, q.right) and compare(p.right, q.left)
        
        if not root:
            return True
        
        return compare(root.left, root.right)

打家劫舍

198. 打家劫舍

思路：动态规划

class Solution:
    def rob(self, nums: List[int]) -> int:
        dp = [0]*len(nums)
        dp[0] = nums[0]
        for i in range(1,len(nums)):
            if(i<2):
                dp[i]= max(dp[i-1],nums[i])
            else:
                dp[i] = max(dp[i-1],dp[i-2]+nums[i])
 
        return dp[-1]

【精】x平方根

69. x 的平方根

解法

  • 解析解：数学公式表达
  • 数值解：一步步迭代，得到指定误差的数值
    • 通过一个公式多次迭代来无限接近于这个解。

几种方法：

  • 牛顿迭代法 – O(log(n)) ?
  • 二分查找法 – O(log(n))
  • 魔术数 – O(1)

二分法
class Solution(object):
    def mySqrt(self, x):
        if x == 0 or x == 1:
            return x
 
        low, high, res = 1, x, -1
 
        while low <= high:
            mid = (low + high) // 2
            if mid * mid <= x:
                res = mid
                low = mid + 1
            else:
                high = mid - 1
 
        return res
牛顿迭代法

求函数 f(x)=x^2−t=0 的解

int mySqrt(int x) 
{
    if(x==0||x==1)
        return x;
    double x0=x;
    double t=x;
    x0=x0/2+t/(2*x0);
    while(fabs(x0*x0-t)>0.00001)
    {
        x0=x0/2+t/(2*x0);
    }
    cout<<x0<<endl;
    return int(x0);
}
位运算：魔术数

Quake-III Arena (雷神之锤3)是90年代的经典游戏之中的一个。该系列的游戏不但画面和内容不错，并且即使计算机配置低，也能极其流畅地执行。这要归功于它3D引擎的开发人员约翰-卡马克（John Carmack）。

  • 早在90年代初DOS时代，仅仅要能在PC上搞个小动画都能让人惊叹一番的时候。John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励，doom, doomII, Quake… 每次都把3-D技术推到极致。他的3D引擎代码资极度高效，差点儿是在压榨PC机的每条运算指令。当初MS的 Direct3D 也得听取他的意见，改动了不少API。
  • 早期，QUAKE的开发商ID SOFTWARE 遵守GPL协议，公开了QUAKE-III的原代码，让世人有幸目睹Carmack传奇的3D引擎的原码。这是QUAKE-III原代码的下载地址
  • 官方的下载网址，搜索 “quake3-1.32b-source.zip” 能够找到一大堆中文网页

越底层的函数, 调用越频繁。3D引擎归根究竟还是数学运算。那么找到最底层的数学运算函数（在game/code/q_math.c）必定是精心编写的。

  • 里面有非常多有趣的函数，非常多都令人惊奇。预计几年时间都学不完。在game/code/q_math.c里发现了这样一段代码。
  • 作用是将一个数开*方并取倒，经測试这段代码比 (float)(1.0/sqrt(x)) 快4倍：

算法原理不复杂, 牛顿迭代法,用 x-f(x)/f’(x) 来不断的逼近 f(x)=a 根。

  • 一般的求平方根都是循环迭代
  • 可卡马克(quake3作者)选择了一个神奇的常数 0x5f3759df 来计算推測值，那一行算出的值很接近 1/sqrt(n)。这样仅须2次牛顿迭代就能够达到精度。

更多见：

float Q_rsqrt( float number )
{
        long i;
        float x2, y;
        const float threehalfs = 1.5F;
        x2= number * 0.5F;
        y   = number;
        // 两句话就完毕了开方运算。核心是定点移位运算。速度极快！特别在非常多没有乘法指令的RISC结构CPU上，这样做是极其高效的。
        i   = * ( long * ) &y;   // evil floating point bit level hacking
        i   = 0x5f3759df - ( i >> 1 ); // what thefuck?
        y   = * ( float * ) &i;
        y   = y * ( threehalfs - ( x2 * y * y ) ); //1st iteration
        //y   = y * ( threehalfs - ( x2 * y * y )); // 2nd iteration, this can be removed
        return y;
}

一个版本

float InvSqrt(float x)
{
	float xhalf = 0.5f*x;
	int i = *(int*)&x; // get bits for floating VALUE 
	i = 0x5f375a86- (i>>1); // gives initial guess y0
	x = *(float*)&i; // convert bits BACK to float
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

	return 1/x;
}
位运算的极致——快速平方根倒数算法

【2023-6-27】位运算的极致——快速平方根倒数算法

快速平方根倒数算法最早见于1999年的3D游戏Quake III Arena的源代码中。该算法一经公布，立刻因它的巧妙而被广为流传

  • 当时，计算机的算力和算法还没有现在这样厉害，浮点数乘除法的计算代价都很高，更不要说平方根了。
  • 另一方面，3D物理引擎几乎要求你每时每刻都要计算各种平方根。比如，计算力矢量在某个方向上的分量，需要计算 $\hat v=\dfrac{\vec v}{\mid\vec v\mid}$，就会用到平方根倒数

一般人写出来的：

float rsqrt(float x) {
    return 1 / sqrt(x);
}

看起来人畜无害

  • 当时，sqrt函数使用的算法本身就很慢，导致使用上面的函数计算平方根倒数效率极低

Quake使用的快速平方根倒数算法：

float q_rsqrt(float x) {
    long i;
    float x2, y;
    const float threehalves = 1.5F;
    x2 = x * 0.5F;
    y = x;
    i = *(long*) &y;
    i = 0x5f3759df - (i >> 1);
    y = *(float*) &i;
    y = y * (threehalves - (x2 * y * y));
    // y = y * (threehalves - (x2 * y * y));
    return y;
}

浮点数的计算机表示

  • $(101101.01101)_2$
# 假设一个二进制小数，01组成的二进制串
_ _ _ _ _ _ _ _   _ _ _ _ _ _ _ _   _ _ _ _ _ _ _ _   _ _ _ _ _ _ _ _

# 只要在这个二进制串的某一个地方点一个小数点，小数点左边的作为**整数位**，右边的作为**小数位**
_ _ _ _ _ _ _ _   _ _ _ _ _ _ _ _  .  _ _ _ _ _ _ _ _   _ _ _ _ _ _ _ _
# 比如，二进制小数 101101.01101，可以写成：
0 0 0 0 0 0 0 0   0 0 1 0 1 1 0 1  .  0 1 1 0 1 0 0 0   0 0 0 0 0 0 0 0

小数的加减法简单，因为小数点永远固定，只需要忽略掉小数点，全都当作二进制整数整数进行加减即可

  • 定点数，假设小数点在某一个固定位置不会移动
  • 浮点数，字面意思是：小数点能够移动

科学计数法：一个数可以被分解成一个 $1$ 到 $10$ 之间的小数和某个 $10$ 的次幂之积。比如：

  • \[34567.89=3.456789\times 10^{4}\]

只要写下 $1$ 到 $10$ 之间的有效数字，以及数的次幂（或者说是小数点的位置），即可唯一确定这个数

  • 有效数字一定在$1$到$10$之间，小数点左边必须有且只有一位数字

对于二进制数，也可以进行类比，只不过底数不再是10，而是2：

  • \[(101101.01101)_2=(1.0110101101)_2\times 2^{(101)_2}\]

那么：可直接存储有效数字和小数点位置。这就是浮点数的基本思路

当然，有效数字的开头一定不能是 $0$，否则一定可以写成另一个数字乘上$2$的负数次方。 例如：

  • \[(0.01011)_2=(1.011)_2\times 2^{(-10)_2}\]

而二进制中，除了$0$，那么必然是$1$。二进制有效数字的第一位必须是1。所以可不用存储有效数字的首位，只存储小数点后的数字，计算的时候在开头补上$1$即可。

最后，为了能够表示负数，需要单独拿出来一位二进制作为符号位（0为正，1为负）。我们得到了浮点数的IEEE754规则：

S   E E E E E E E E   M M M M M M M M M M M M M M M M M M M M M
  • 第1位是符号位 $S$ ，0表示正数，1表示负数。
  • 第2到9位是指数位$E$，$E$的范围是$0$到$255$，会自动减去$127$，否则无法表示负数指数，也就是说它的实际值应该是$-127$到$128$
  • 第10到32位是有效数字位$M$，共23位，运算时需要在在前面脑补一位$1$和小数点

这一串二进制所表示的浮点数实际值等于：

  • \[(-1)^S\times 2^{E-127}\times (1+\frac{M}{2^{23}})\]

算法的第一部分

平方根倒数的求解过程

  • 显然负数不可能有平方根，因此可默认输入的$x$必须是正数，也就是符号位$S$为0

如果平方根不好求的话，不妨先算一下$x$的对数

难道对数不应该更难计算吗？没关系，请看下面：

\[\begin{align*} x & = 2^{E-127}\times (1+\frac{M}{2^{23}}) \\ \log_2 x & = \log_2(1+\frac{M}{2^{23}}) + \log_2\left(2^{E-127}\right) \\ & = \log_2(1 + \frac{M}{2^{23}}) + E - 127 \end{align*}\]

现在式子还是有点复杂，不妨取一个近似：当$a\in[0,1]$ 时，$\log(1+a)$可以近似成aa加上某个常数$\sigma$

\[\log(1+a)\approx a+\sigma\]

q-rsqrt-0

绿色曲线为$\log_2(1+x)$，黄色直线为$x+\sigma$。如果想让误差最小，那么$\sigma$应该取大约$0.043$，通过微积分可以算出准确值，这里就不写了

有了这个知识，原式可以近似成：

  • \[\log_2 x \approx \frac{M}{2^{23}}+\sigma+E-127\]
  • \[\log_2 x=\frac 1{2^{23}}(M+E\cdot 2^{23}) - (127 - \sigma)\]

为什么要这样整理呢？不妨考虑另一件事：如果我们强行将这个浮点数的二进制表达解读成整数，会得到什么呢？

0   E E E E E E E E M M M M M M M M M M M M M M M M M M M M M

第一位是符号位，而后面31位是数字位，最终我们得到了一个整数：

\[\bar x=\overline{EM}=E\cdot 2^{23}+M\]

暂且将这个数称为浮点数的整数值。不难看出刚刚推导$\log_2 x$时就推出了一模一样的表达式！接着将$\bar x$代回原式，得到：

\[\log_2x\approx\frac{\bar x}{2^{23}}-(127-\sigma)\]

现在知道了：浮点数的对数，约等于它的整数值减去某一个常数

这样就能理解之前代码中的这个步骤了：

i = *(long*) &y;

这其实就是在计算浮点数的整数值！ 注意，直接写i = (long) y;是错的，因为这样会算出来浮点数下取整，而不是刚刚提到的整数值

那么有了这个结论，求出平方根倒数就很简单了：

  • \(\log_2 y=\log_2(\frac1{\sqrt{x}})=-\frac12\log_2(x)\approx\frac 12(127-\sigma)-\frac 12\frac{\bar x}{2^{23}}\)​

那么$y=1/\sqrt{x}$的整数值为：

\[\begin{align*} \bar y &\approx 2^{23}\log_2 y + 2^{23}(127-\sigma) \\ & = (2^{22} + 2^{23})(127 - \sigma) - \frac{\bar x}{2} \\ & \approx \text{0x5F3759DF} - \frac{\bar x}{2} \end{align*}\]

其中0x5F3759DF就是大名鼎鼎的“魔法值”。最后只需要将$\bar y$再强行转换成浮点数即可

以上就是算法的第一部分

当然，这里还有另一个技巧：i >> 1表示将整数$i$整个向右移动1个二进制位，也就是将$i$除以$2$

i    = 00011011 01101100      >>> right shift 1 digit
i>>1 = 00001101 10110110

综上所述，代码：

i = *(long*) &y;
i = 0x5F3759DF - (i >> 1);
y = *(float*) &i;

你能试试求出64位浮点数的“魔法值”吗？

代码的第二部分

上面所有推导用的几乎全都是约等于号，而不是等于号，因此计算出来的这个数字仍然有一定的误差。后续接着使用牛顿迭代法求出精确解。

那牛顿迭代法又是什么？

假设现在一个函数$f$，目标是求出它的根（即所有$x_0$使得$f(x_0)=0$），而只知道一个函数上的点$A=(x, f(x))$，怎么办？

  • q-rsqrt-1

现在，作一条$A$点上的切线，切线与横轴的交点作为第一轮迭代的结果

  • q-rsqrt-2

迭代后的点离函数的根已经近了很多

  • q-rsqrt-3

还可以将一轮迭代的结果作为新的起点，进行第二轮迭代，接着第三轮、第四轮、……，最终就可以无限接近函数的根，并且迭代的收敛速度非常快

那么对于“求解平方根倒数”的这个例子，可以构造一个函数：

  • \[f(y)=\frac 1{y^2}-x\]

令$x$为一个常数，而$y$为变量，不难发现这个函数的根就是$y=1/\sqrt{x}$，那么我们的任务就是求解这个函数的根

那么，从$y_0$开始，采用上面的方法迭代，即

  • \[y_{n+1}=y_n-\dfrac{f(y_n)}{f'(y_n)}\]

代入$f(y)=\dfrac1{y^2}-x$，得到：

  • \[y_{n+1}=\dfrac{y_n(3-xy_n^2)}{2}=y_n\left(\dfrac32-\dfrac12xy_n^2\right)\]

这也就是代码最下方那个奇怪的表达式的含义：

y = y * (threehalves - (x2 * y * y));

经过一轮迭代，已经差不多能将误差控制在小数点后4位左右了，如果想要更加精确，也可以接着进行2、3、4轮迭代

以上就是算法的全过程，最后再贴一遍完整代码：

float q_rsqrt(float x) {
    long i;
    float x2, y;
    const float threehalves = 1.5F;

    x2 = x * 0.5F;
    y = x;
    i = *(long*) &y;
    i = 0x5f3759df - (i >> 1);
    y = *(float*) &i;
    y = y * (threehalves - (x2 * y * y));
    // y = y * (threehalves - (x2 * y * y));

    return y;
}

这个算法有什么意义？

如果认真看完了上面的全过程，遗憾的告诉你：你可能永远也用不上它

  • 现在早已不是1999年了，硬件的更新和算法的改进让任何编程语言的内置函数都无法轻易被超越
  • 如果用C语言或者C++进行测试的话，会发现库函数sqrt(x)的速度要远远超过上面的算法。但是，把这个算法当作一个精致的艺术品反复观赏，也是一件挺有意思的事情，你也可以从里面学到不少

链表倒数第k个节点

剑指 Offer 22. 链表中倒数第k个节点

思路：双指针

# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
 
class Solution:
    def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
 
        fast, slow = head, head
        for i in range(k):
            fast = fast.next
        
        while fast:
            slow = slow.next
            fast = fast.next
        return slow

环形链表

142. 环形链表 II

思路：双指针

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        slow, fast = head, head
 
        while fast!=None and fast.next!=None:
            slow = slow.next
            fast = fast.next.next
 
            if slow==fast:
                p = head
                q = slow
                while p!=q:
                    p = p.next
                    q = q.next
 
                return p
 
        return None

寻找重复数

287. 寻找重复数

思路：双指针

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
 
        slow, fast = 0, 0
        while True:
            slow = nums[slow]           # 类比链表slow=slow.next
            fast = nums[nums[fast]]     # 类比链表fast=fast.next.next
            if fast == slow:    # 首次相遇点
                break
        
        fast = 0                # fast回到起点
        while slow != fast:     # 再次相遇点即为重复数字
            slow = nums[slow]
            fast = nums[fast]
        
        return fast

滑动窗口最大值

239. 滑动窗口最大值

思路：双向队列

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
 
        # 如果数组为空或 k = 0，直接返回空
        if not nums or not k:
            return []
        # 如果数组只有1个元素，直接返回该元素
        if len(nums) == 1:
            return [nums[0]]
 
        # 初始化队列和结果，队列存储数组的下标
        queue = []
        res = []
 
        for i in range(len(nums)):
            # 如果当前队列最左侧存储的下标等于 i-k 的值，代表目前队列已满。
            # 但是新元素需要进来，所以列表最左侧的下标出队列
            if queue and queue[0] == i - k:
                queue.pop(0)
 
            # 对于新进入的元素，如果队列前面的数比它小，那么前面的都出队列
            while queue and nums[queue[-1]] < nums[i]:
                queue.pop()
            # 新元素入队列
            queue.append(i)
 
            # 当前的大值加入到结果数组中
            if i >= k-1:
                res.append(nums[queue[0]])
 
        return res

反转链表

剑指 Offer II 024. 反转链表

思路：双指针迭代

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        cur, pre = head, None
        while cur:
            tmp = cur.next # 暂存后继节点 cur.next
            cur.next = pre # 修改 next 引用指向
            pre = cur      # pre 暂存 cur
            cur = tmp      # cur 访问下一节点
        return pre

k个数组翻转链表

25. K 个一组翻转链表

思路：多指针

力扣

class Solution:
    # 翻转一个子链表，并且返回新的头与尾
    def reverse(self, head: ListNode, tail: ListNode):
        prev = tail.next
        p = head
        while prev != tail:
            nex = p.next
            p.next = prev
            prev = p
            p = nex
        return tail, head
 
    def reverseKGroup(self, head: ListNode, k: int) -> ListNode:
        hair = ListNode(0)
        hair.next = head
        pre = hair
 
        while head:
            tail = pre
            # 查看剩余部分长度是否大于等于 k
            for i in range(k):
                tail = tail.next
                if not tail:
                    return hair.next
            nex = tail.next
            head, tail = self.reverse(head, tail)
            # 把子链表重新接回原链表
            pre.next = head
            tail.next = nex
            pre = tail
            head = tail.next
        
        return hair.next

字符串相加

415. 字符串相加

思路：双指针

class Solution:
    def addStrings(self, num1: str, num2: str) -> str:
        res = ""
        i, j, carry = len(num1) - 1, len(num2) - 1, 0
        while i >= 0 or j >= 0:
            n1 = int(num1[i]) if i >= 0 else 0
            n2 = int(num2[j]) if j >= 0 else 0
            tmp = n1 + n2 + carry
            carry = tmp // 10
            res = str(tmp % 10) + res
            i, j = i - 1, j - 1
        return "1" + res if carry else res

相交链表

160. 相交链表

思路：双指针

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        A, B = headA, headB
        while A != B:
            A = A.next if A else headB
            B = B.next if B else headA
        return A

有效的括号

20. 有效的括号

思路：用栈匹配

class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        
        for item in s:
            if item == '(':
                stack.append(')')
            elif item == '[':
                stack.append(']')
            elif item == '{':
                stack.append('}')
            elif not stack or stack[-1] != item:
                return False
            else:
                stack.pop()
        
        return True if not stack else False

最长递增子序列

300. 最长递增子序列

思路：动态规划

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        dp = [1] * len(nums)
        for i in range(len(nums)):
            for j in range(i):
                if nums[j] < nums[i]: # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

二分法：

class Solution:
    def lengthOfLIS(self, nums: [int]) -> int:
        tails, res = [0] * len(nums), 0
        for num in nums:
            i, j = 0, res
            while i < j:
                m = (i + j) // 2
                if tails[m] < num: i = m + 1 # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                else: j = m
            tails[i] = num
            if j == res: res += 1
        return res

二叉树最近公共祖先

236. 二叉树的最近公共祖先

思路：递归

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 当前节点为空，直接返回空
        if root == None:
            return None
        # 如果 root 等于 p 或者 q，那最近公共祖先一定是 p 或者 q
        if root == p or root == q:
            return root
        # 递归左右子树，保存递归结果
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        # 如果 left 和 right 都非空，那证明 p 和 q 一边一个，那么最近公共祖先就是 root
        if left and right:
            return root
        # 如果 right 为空，只需要看 left
        if left and right == None:
            return left
        # 如果 left 为空，只需要看 right 
        if left == None and right:
            return right
        # 如果都为空，返回空
        if left == None and right == None:
            return None

岛屿数量

200. 岛屿数量

思路：dfs 或 bfs

class Solution:
    def numIslands(self, grid: [[str]]) -> int:
        def dfs(grid, i, j):
            if not 0 <= i < len(grid) or not 0 <= j < len(grid[0]) or grid[i][j] == '0': return
            grid[i][j] = '0'
            dfs(grid, i + 1, j)
            dfs(grid, i, j + 1)
            dfs(grid, i - 1, j)
            dfs(grid, i, j - 1)
        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == '1':
                    dfs(grid, i, j)
                    count += 1
        return count

class Solution:
    def numIslands(self, grid: [[str]]) -> int:
        def bfs(grid, i, j):
            queue = [[i, j]]
            while queue:
                [i, j] = queue.pop(0)
                if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == '1':
                    grid[i][j] = '0'
                    queue += [[i + 1, j], [i - 1, j], [i, j - 1], [i, j + 1]]
        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == '0': continue
                bfs(grid, i, j)
                count += 1
        return count

螺旋矩阵

54. 螺旋矩阵

思路：找规律 按规律来

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        m = len(matrix)
        n = len(matrix[0])
        res = []
        l, r, t, b = 0, n - 1, 0, m - 1
        num, tar = 1, m * n
        while num <= tar:
            if t<=b:
                for i in range(l, r + 1): # left to right
                    res.append(matrix[t][i])
                    num+=1
            t += 1
            if l<=r:
                for i in range(t, b + 1): # top to bottom
                    res.append(matrix[i][r])
                    num+=1
            r -= 1
            if t<=b:
                for i in range(r, l - 1, -1): # right to left
                    res.append(matrix[b][i])
                    num+=1
            b -= 1
            if l<=r:
                for i in range(b, t - 1, -1): # bottom to top
                    res.append(matrix[i][l])
                    num+=1
            l += 1
        return res
 
function= Solution()
matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
print(function.spiralOrder(matrix))

合并有序数组

88. 合并两个有序数组

思路：双指针

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        sorted = []
        p1, p2 = 0, 0
        while p1 < m or p2 < n:
            if p1 == m:
                sorted.append(nums2[p2])
                p2 += 1
            elif p2 == n:
                sorted.append(nums1[p1])
                p1 += 1
            elif nums1[p1] < nums2[p2]:
                sorted.append(nums1[p1])
                p1 += 1
            else:
                sorted.append(nums2[p2])
                p2 += 1
        nums1[:] = sorted

也可以把list2加到list1后 快排 或者 归并排序

多数元素

169. 多数元素

思路：动脑筋

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        nums.sort()
        return nums[len(nums) // 2]

路径总和

113. 路径总和 II

思路：dfs+回溯

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
 
        def addpath(root, presum):
            
            if not root.left and not root.right:
                if presum == 0:
                    result.append(path[:])
                    return 
 
            if root.left:
                path.append(root.left.val)
                addpath(root.left, presum-root.left.val)
                path.pop()
            if root.right:
                path.append(root.right.val)
                addpath(root.right, presum-root.right.val)
                path.pop()
 
 
        result = []
        
        if not root:
            return []
        path = [root.val]
        addpath(root,targetSum-root.val)
        return result

反转链表

92. 反转链表 II

思路：双指针

class Solution:
    def reverseBetween(self, head: ListNode, left: int, right: int) -> ListNode:
        def reverse_linked_list(head: ListNode):
            # 也可以使用递归反转一个链表
            pre = None
            cur = head
            while cur:
                next = cur.next
                cur.next = pre
                pre = cur
                cur = next
 
        # 因为头节点有可能发生变化，使用虚拟头节点可以避免复杂的分类讨论
        dummy_node = ListNode(-1)
        dummy_node.next = head
        pre = dummy_node
        # 第 1 步：从虚拟头节点走 left - 1 步，来到 left 节点的前一个节点
        # 建议写在 for 循环里，语义清晰
        for _ in range(left - 1):
            pre = pre.next
 
        # 第 2 步：从 pre 再走 right - left + 1 步，来到 right 节点
        right_node = pre
        for _ in range(right - left + 1):
            right_node = right_node.next
        # 第 3 步：切断出一个子链表（截取链表）
        left_node = pre.next
        curr = right_node.next
 
        # 注意：切断链接
        pre.next = None
        right_node.next = None
 
        # 第 4 步：同第 206 题，反转链表的子区间
        reverse_linked_list(left_node)
        # 第 5 步：接回到原来的链表中
        pre.next = right_node
        left_node.next = curr
        return dummy_node.next

rand7实现rand10

470. 用 Rand7() 实现 Rand10()

思路：玩脑袋

class Solution:
    def rand10(self) -> int:
        while True:
            row = rand7()
            col = rand7()
            idx = (row - 1) * 7 + col
            if idx <= 40:
                return 1 + (idx - 1) % 10

逆时针输出矩阵

【腾讯】

题目

  • 输入 [[1,2,3],[4,5,6], [7,8,9]]
  • 输出 [1,2,3,5,9,8,7,4,5]
#include<stdio.h> 

int main(){
	int n;
	scanf("%d",&n);
	int a[100][100];
	if(n%2!=0){
		a[n/2][n/2]=n*n;
	}
	int i,j;
	int num=1;
	for(i=0;i<n/2;i++){
		for(j=i;j<n-i-1;j++){   //down
			a[j][i]=num++;
		}
		for(j=i;j<n-i-1;j++){  	//right
			a[n-i-1][j]=num++;
		}
		for(j=n-i-1;j>=i+1;j--){	//up
			a[j][n-i-1]=num++;
		}
		for(j=n-i-1;j>=i+1;j--){  //left
			a[i][j]=num++;
		}
	}
	for (i = 0; i < n; i++)
		{
			for (j = 0; j < n; j++)
			{
				printf("%02d ", a[i][j]);
			}          
		printf("\n");  
		}
	return 0;
}

搜索二维矩阵

74. 搜索二维矩阵

思路：二分法

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        '''两次二分法'''
        """
        思路：
            第一次二分法确定目标位于哪一行
            第二次二分法，判断是否在这一行
        """
        # 第一次二分法确定目标位于哪一行
        m = len(matrix)
        n = len(matrix[0])
        l = 0
        r = m - 1
        while l < r:
            mid = (l + r + 1) // 2
            if matrix[mid][0] < target:
                l = mid 
            elif matrix[mid][0] > target:
                r = mid - 1
            else:
                return True
        row = l  # 记录在哪一行
 
        # 第二次二分法，判断是否在这一行
        l = 0
        r = n - 1
        while l <= r:
            mid = (l + r) // 2
            if matrix[row][mid] < target:
                l = mid + 1
            elif matrix[row][mid] > target:
                r = mid - 1
            else:
                return True
        return False

单词搜索

79. 单词搜索

思路：dfs+回溯

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
 
        m = len(board)
        n = len(board[0])
        if(len(word)>m*n):
            return False
        track = []
        res = []
 
 
        def dfs(board, i,j, step):
 
            if(len(track)==len(word)):
                res.append(track)
 
            if (not 0<=i<=m-1 or not 0<=j<=n-1 or len(track)>len(word) or step>len(word)-1 or board[i][j]!=word[step] or board[i][j] == '#'):
                return
            
            track.append(board[i][j])
            
            tmp = board[i][j]
            board[i][j] = '#'
 
            dfs(board, i-1, j, step+1)
            dfs(board,i,j-1,step+1) 
            dfs(board,i+1,j,step+1) 
            dfs(board, i,j+1,step+1)
 
            board[i][j] = tmp
            track.pop()
 
 
        for i in range(m):
            for j in range(n):
                step = 0
 
                if(board[i][j]==word[0]):
                    dfs(board,i,j,step)
                    
        if(len(res)!=0):
            return True
 
        else:
            return False

有序数组查找

【腾讯】 返回数组中target第一次出现的下标位置，数组有序，存在有重复数字

//#include <iostream>
//#include <vector>
#include<stdio.h>

//using namespace std;

// 该函数负责返回数组中target第一次出现的下标位置，数组有序，存在有重复数字
int find(int * array, int length, int target){
 /* 
        (1) 线性遍历: 从左到右逐个查找,遇到就返回, 否则返回 length --- 时间复杂度 O(n)
        (2) 二分法:找到相同值, 然后向左滑动找边界 --- 时间复杂度: log(n)
        {2,4,5,5,5,7,8,12,15}
    */
    // 空数组识别
 if(length<=0){
     return -1;
 }
 if(length==1){
     if(length==target) {return 0;}
     else return -2;
 }
 // 判断增序还是降序
//  int order = 0; // 1 增序, -1 降序
//  if(array[0]<=array[1]) order = 1;
//  else order = -1;
 
    // 初始化
 int start = 0;
 int end = length -1;
 int mid = 0;
 while(start<end){
  mid = (int)((end+start)/2);
  printf("[%d,%d] mid=%d -> mid_val=%d, target=%d\n", start, end, mid, array[mid], target);
  if(array[mid] == target){
   // 找到元素
   break;
   printf("找到目标数值: [%d, %d] mid=%d -> %d\n", start, end, mid, target);
  }else if(array[mid] <= target){
   // 往左移动
   start = mid+1;
  }else{// 往右移动
   end = mid-1;
  }
 }
 printf("跳出循环:[%d,%d] mid=%d -> %d\n", start, end, mid, target);
 // 跟mid值判断结果
 if(mid>end || mid<start){
  // 越界
  return -2;
 } 
 // 找到目标数值, 向左寻找等值边界
 int left = mid-1;
 while(left>=0 && array[left]==array[mid]){
  left--;
 }
 return left+1;
}

int main(){
 int array[] = {2,4,5,5,5,7,8,12,15};
    // 测试值: [1,5,8, 13, 16]
    int target_list[5] = {1,5,8, 13, 16};
    // 计算数组长度
 int len = sizeof(array) / sizeof(array[0]);
 printf("长度: %d\n", len);
    
    for(int i=0;i<5;i++)
    {
    int idx = find(array, len, target_list[i]);
    //int idx = 0;
       printf("【测试】第%d个: %d -> %d\n", i+1, target_list[i], idx); 
       if(i>5){break;}
    }
 return 0;
}

有序数组中找头尾位置

34. 在排序数组中查找元素的第一个和最后一个位置

思路：二分法 注意范围

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        result = []
        left, right = 0, len(nums)-1
        while left<right:
            mid = (left+right)//2
            if(target>nums[mid]):
                left = mid+1
            elif(target<nums[mid]):
                right = mid-1
            else:
                right = mid
        if(len(nums)>left>-1 and nums[left]==target):
            result.append(left)
        else:
            result.append(-1)
        #print(result)
        left, right = 0, len(nums)-1
        while left<right:
            mid = ceil((left+right)/2)
            if(target>nums[mid]):
                left = mid+1
            elif(target<nums[mid]):
                right = mid-1
            else:
                left = mid
        if(len(nums)>right>-1 and nums[right]==target):
            result.append(right)
        else:
            result.append(-1)
        
        return result

三数之和

15. 三数之和

思路：双指针

class Solution:
    def threeSum(self, nums):
        ans = []
        n = len(nums)
        nums.sort()
        for i in range(n):
            left = i + 1
            right = n - 1
            if nums[i] > 0:
                break
            if i >= 1 and nums[i] == nums[i - 1]:
                continue
            while left < right:
                total = nums[i] + nums[left] + nums[right]
                if total > 0:
                    right -= 1
                elif total < 0:
                    left += 1
                else:
                    ans.append([nums[i], nums[left], nums[right]])
                    while left != right and nums[left] == nums[left + 1]: left += 1
                    while left != right and nums[right] == nums[right - 1]: right -= 1
                    left += 1
                    right -= 1
        return ans

两数之和

1. 两数之和

思路：哈希表匹配

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hashtable = dict()
        for i, num in enumerate(nums):
            if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i
        return []

二叉树的锯齿形层序遍历

103. 二叉树的锯齿形层序遍历

思路：层序遍历

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        sum_ = float('-inf')
        result = float('-inf')
        for i in range(len(nums)):
            if sum_>0:
                sum_ = sum_ + nums[i]
            else:
                sum_ = nums[i]
            
            result = max(sum_, result)
        return result

环形链表

141. 环形链表

思路：双指针

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        slow, fast = head, head
 
        while fast!=None and fast.next!=None:
            slow = slow.next
            fast = fast.next.next
 
            if slow==fast:
                return True
 
        return False

合并两个有序链表

21. 合并两个有序链表

思路：双指针

class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        result = ListNode(0)
        real = result
        p1 = list1
        p2 = list2
        while p1!=None and p2!=None:
            if(p1.val<=p2.val):
                tmp = ListNode(p1.val)
                result.next = tmp
                result = tmp
                p1 = p1.next
            else:
                tmp = ListNode(p2.val)
                result.next = tmp
                result = tmp
                p2 = p2.next
        
        if(p1!=None):
            result.next = p1
        if(p2!=None):
            result.next = p2
        
        return real.next

颠倒字符串单词

151. 颠倒字符串中的单词

思路：双指针

class Solution:
    #1.去除多余的空格
        def trim_spaces(self,s):     
            n=len(s)
            left=0
            right=n-1
        
            while left<=right and s[left]==' ':       #去除开头的空格
                left+=1
            while left<=right and s[right]==' ':        #去除结尾的空格
                right-=1
            tmp=[]
            while left<=right:                                    #去除单词中间多余的空格
                if s[left]!=' ':
                    tmp.append(s[left])
                elif tmp[-1]!=' ':                                  
                    #当前位置是空格，但是相邻的上一个位置不是空格，则该空格是合理的
                    tmp.append(s[left])
                left+=1
            return tmp
    #2.翻转字符数组
        def reverse_string(self,nums,left,right):
            while left<right:
                nums[left], nums[right]=nums[right],nums[left]
                left+=1
                right-=1
            return None
    #3.翻转每个单词
        def reverse_each_word(self, nums):
            start=0
            end=0
            n=len(nums)
            while start<n:
                while end<n and nums[end]!=' ':
                    end+=1
                self.reverse_string(nums,start,end-1)
                start=end+1
                end+=1
            return None
 
    #4.翻转字符串里的单词
        def reverseWords(self, s): #测试用例："the sky is blue"
            l = self.trim_spaces(s)                     
            #输出：['t', 'h', 'e', ' ', 's', 'k', 'y', ' ', 'i', 's', ' ', 'b', 'l', 'u', 'e'
            self.reverse_string( l,  0, len(l) - 1)   
            #输出：['e', 'u', 'l', 'b', ' ', 's', 'i', ' ', 'y', 'k', 's', ' ', 'e', 'h', 't']
            self.reverse_each_word(l)               
            #输出：['b', 'l', 'u', 'e', ' ', 'i', 's', ' ', 's', 'k', 'y', ' ', 't', 'h', 'e']
            return ''.join(l)

全排列

46. 全排列

思路：dfs 回溯

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
 
        track = []
        tracklist = []
 
        def dfs(nums,track,tracklist):
            
             
            if(len(track)==len(nums)):
                tracklist.append(track.copy())
                return 
            
            
            for i in range(len(nums)):
                if(nums[i] in track):
                    continue
                track.append(nums[i])
                dfs(nums,track,tracklist)
                track.pop()
 
        dfs(nums,track,tracklist)
        return tracklist

验证二叉搜索树

98. 验证二叉搜索树

思路：中序遍历 看是否升序

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        candidate_list = []
        # 中序遍历
 
        def traverse(root):
 
            if not root:
                return 
            traverse(root.left)
            candidate_list.append(root.val)
            traverse(root.right)
 
        def issorted(nums):
            for i in range(1, len(nums)):
                if nums[i]<=nums[i-1]:
                    return False
 
            return True
 
        traverse(root)
        return issorted(candidate_list)

回文链表

234. 回文链表

思路：双指针

快指针走到末尾，慢指针刚好到中间。其中慢指针将前半部分反转。然后比较。

class Solution:
    def isPalindrome(self, head: ListNode) -> bool:
        slow = head
        fast = head
        pre = head
        prepre = None
        while fast and fast.next:
            #pre记录反转的前半个列表，slow一直是原表一步步走
            pre = slow
            slow = slow.next
            fast = fast.next.next
 
            pre.next = prepre
            prepre = pre
 
        if fast:#长度是奇数还是偶数对应不同情况 进入后是奇数
            slow = slow.next  
        
        while slow and pre:
            if slow.val != pre.val:
                return False
            slow = slow.next
            pre = pre.next
        return True

739. 每日温度

思路：单调栈 存下标（好处：能记住位置 也能对应到值）

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
 
        res = [0]*len(temperatures)
        stack = []
 
        for i in range(len(temperatures)):
            while stack and temperatures[i]>temperatures[stack[-1]]:
                small = stack.pop()
                res[small] = i-small
 
            stack.append(i)
 
        return res

二叉树展开为链表

114. 二叉树展开为链表

思路：多指针移动

class Solution:
    def flatten(self, root: TreeNode) -> None:
        curr = root
        while curr:
            if curr.left:
                predecessor = nxt = curr.left
                while predecessor.right:
                    predecessor = predecessor.right
                predecessor.right = curr.right
                curr.left = None
                curr.right = nxt
            curr = curr.right

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if not lists:
            return None
        n = len(lists)
        return self.merge_sort(lists, 0, n - 1)
    
 
    def merge_sort(self, lists: List[ListNode], l: int, r: int) -> ListNode:
        if l == r:
            return lists[l]
        mid = (l + r) // 2
        L = self.merge_sort(lists, l, mid)
        R = self.merge_sort(lists, mid + 1, r)
        return self.merge(L, R)
    
    def merge(self, a: ListNode, b: ListNode) -> ListNode:
        dummy = ListNode(-1)
        x = dummy
        while a and b:
            if a.val < b.val:
                x.next = a
                a = a.next
            else:
                x.next = b
                b = b.next
            x = x.next
        if a:
            x.next = a
        if b:
            x.next = b
        return dummy.next

Done

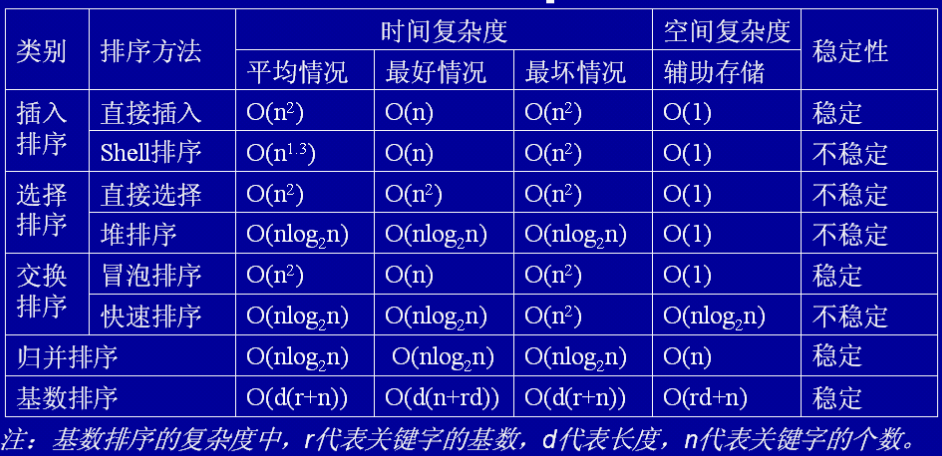
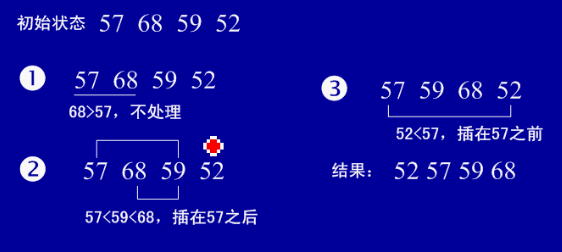
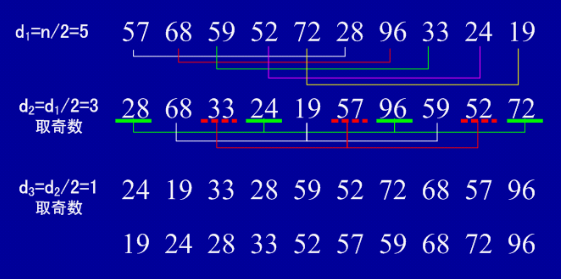
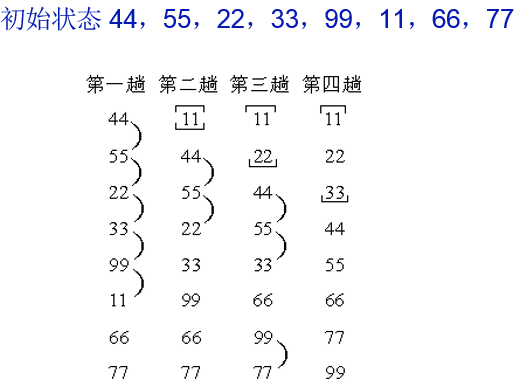
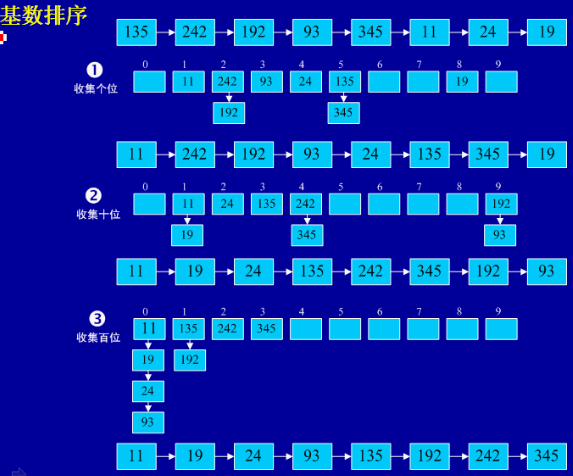
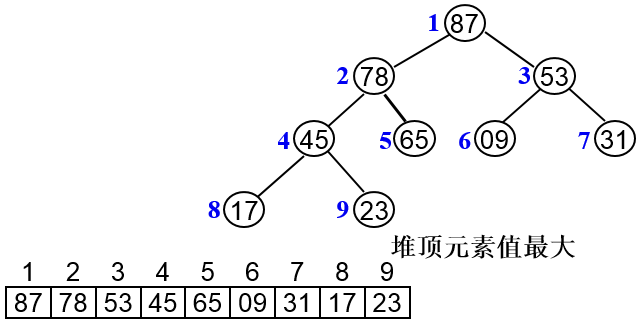
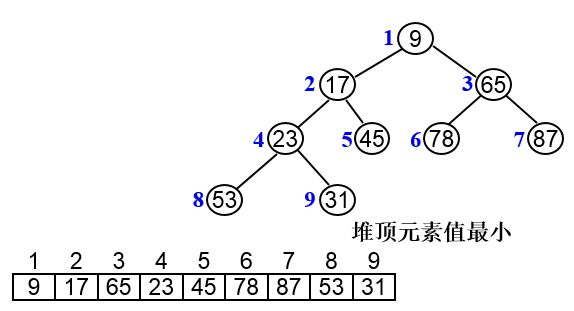
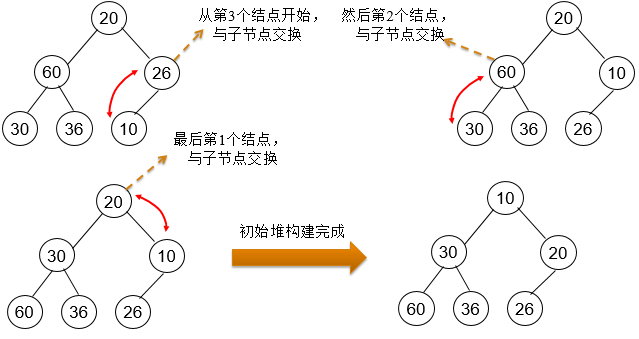
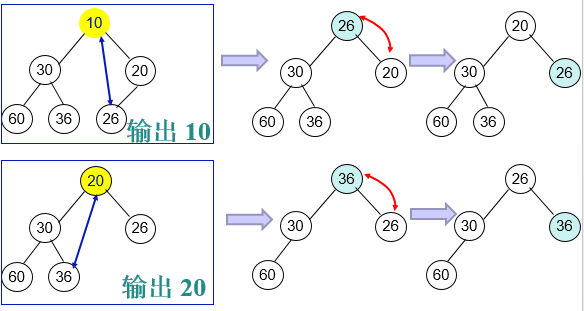
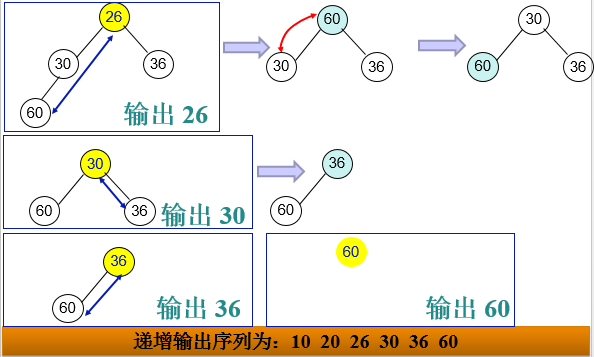
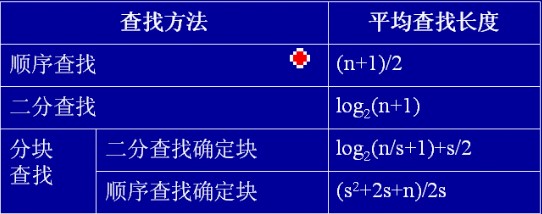
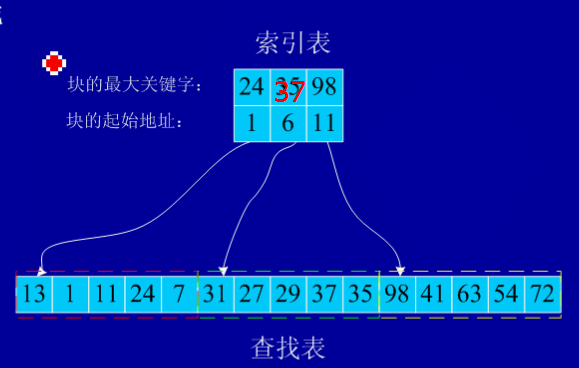
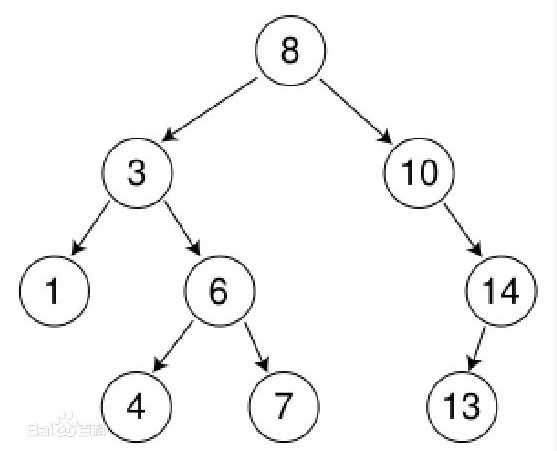
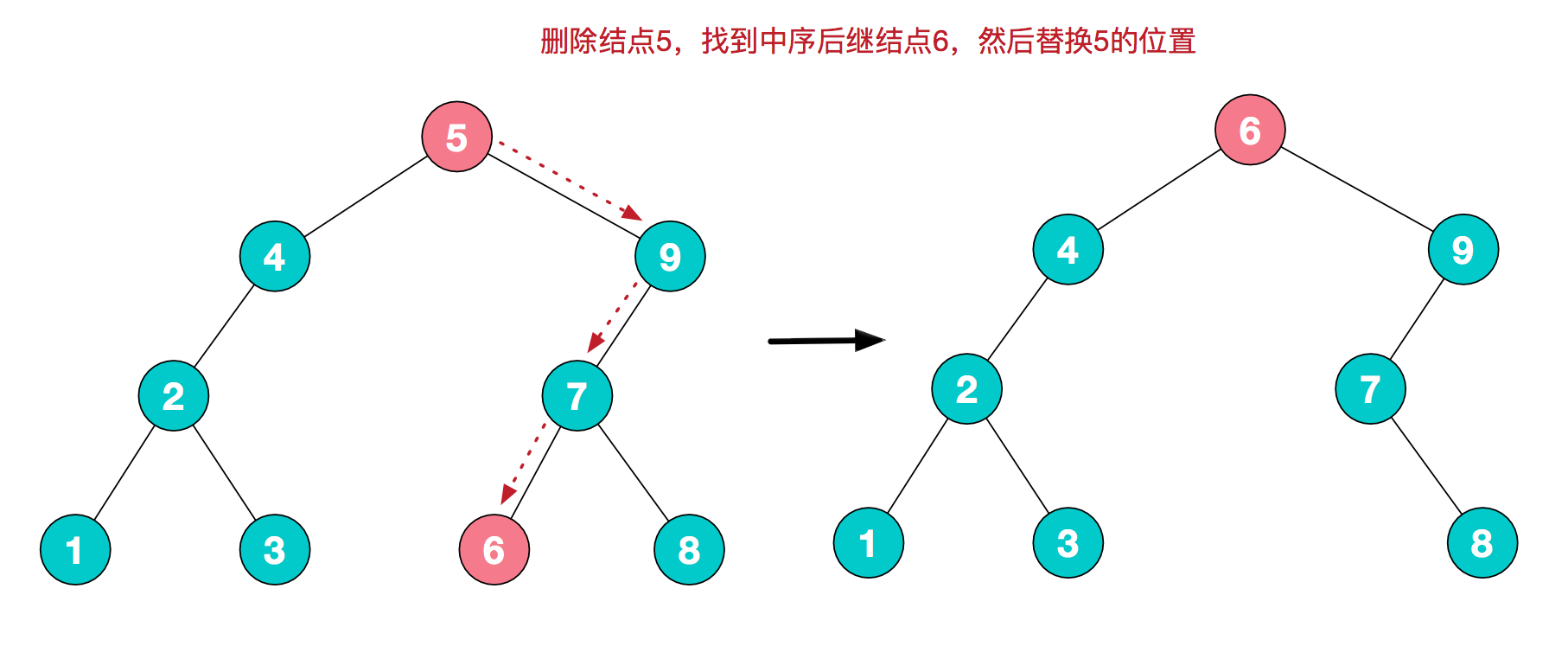
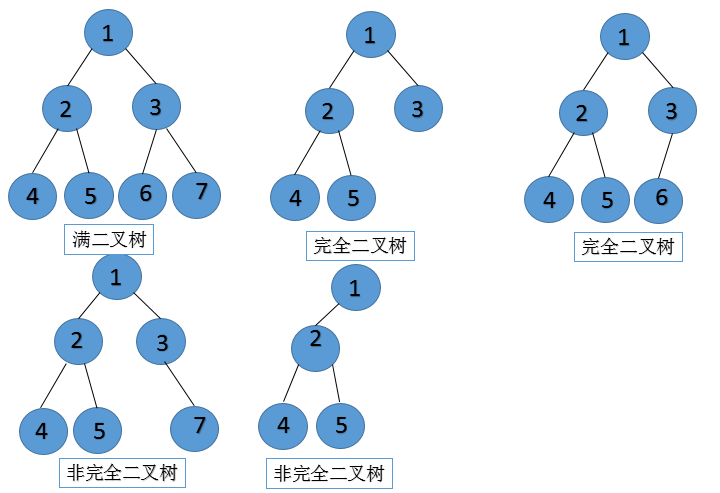
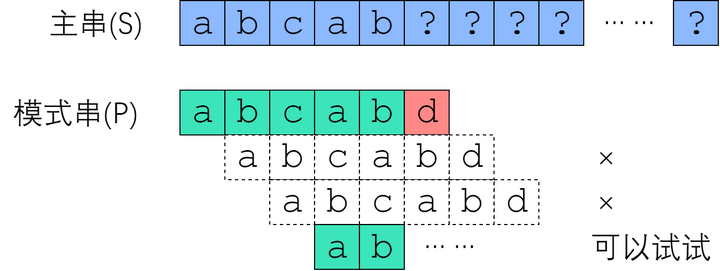
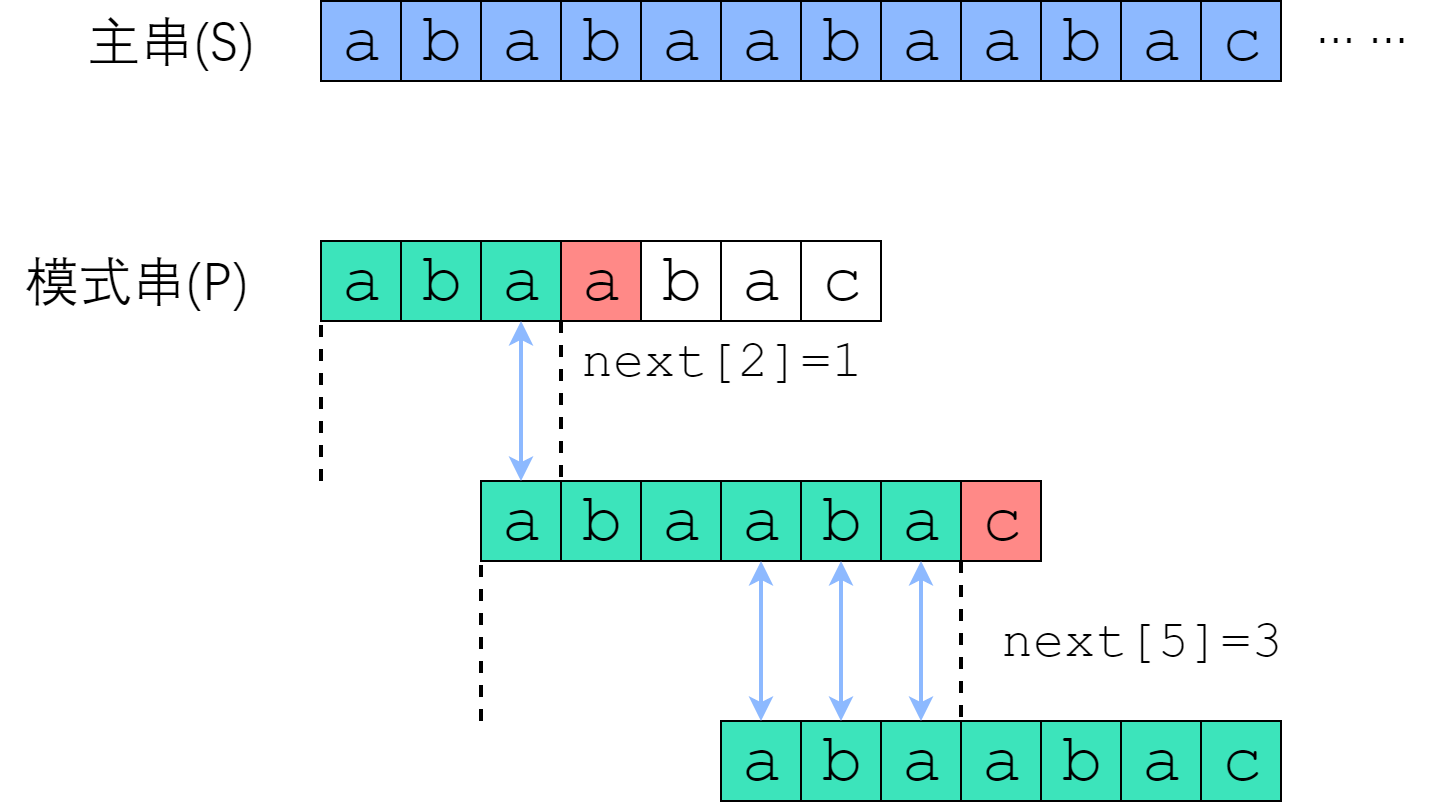
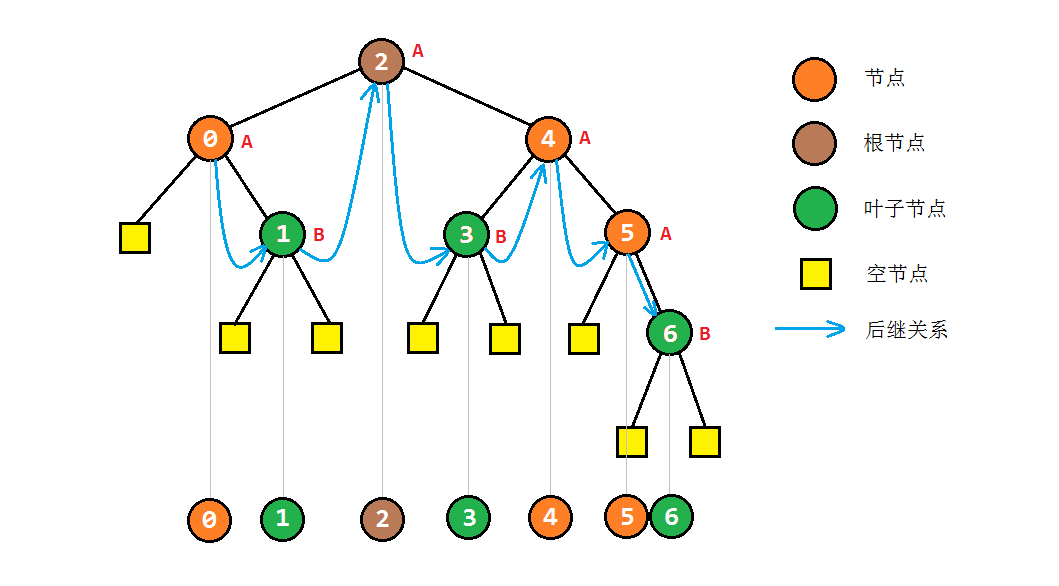
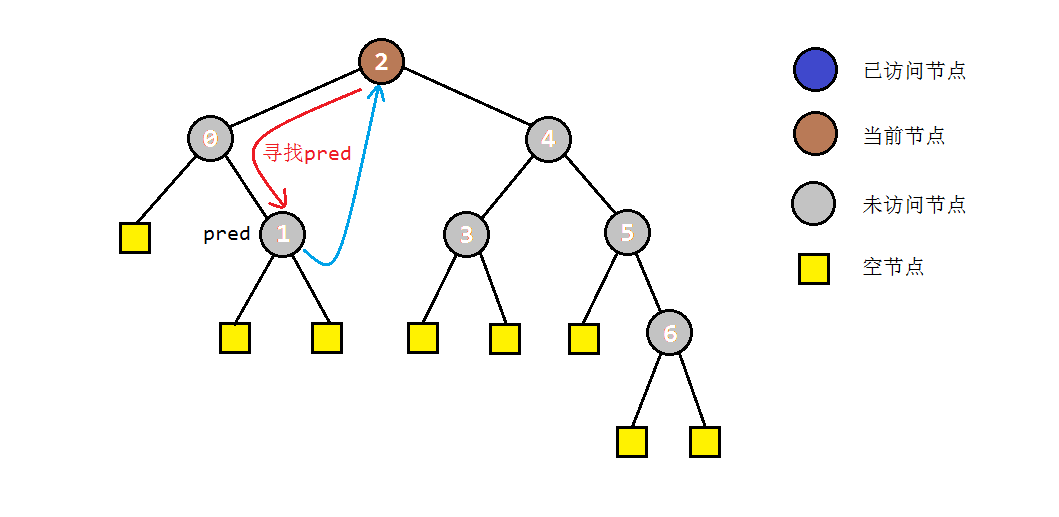
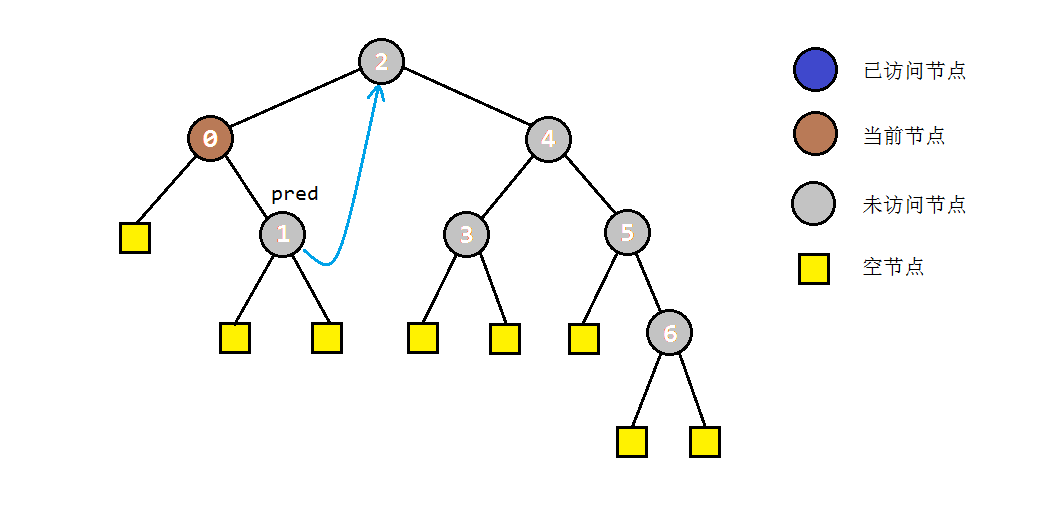
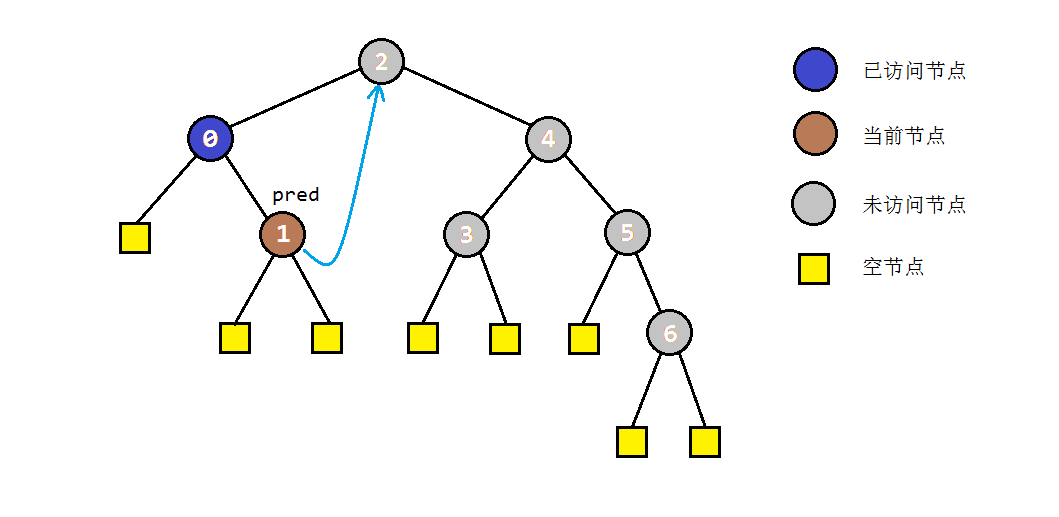
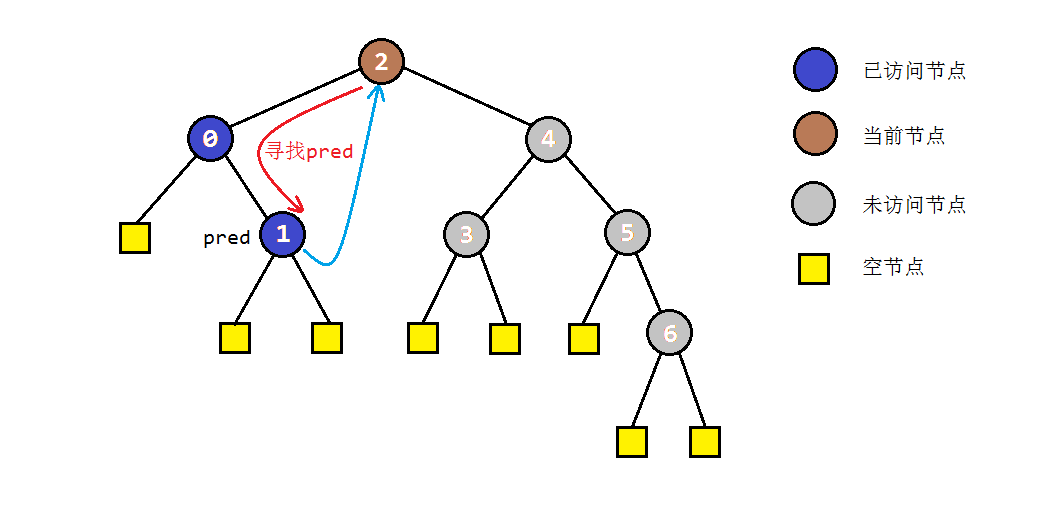
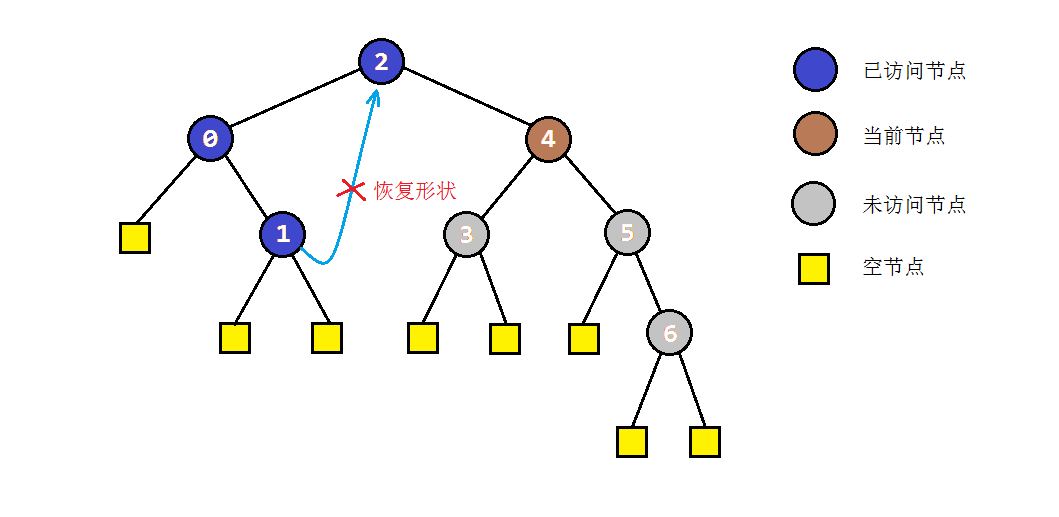
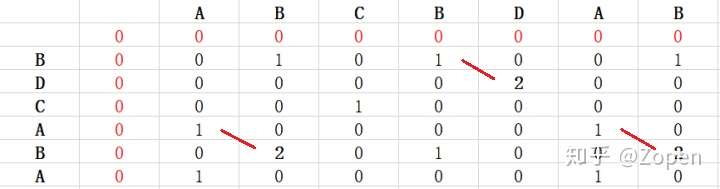
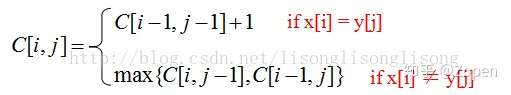
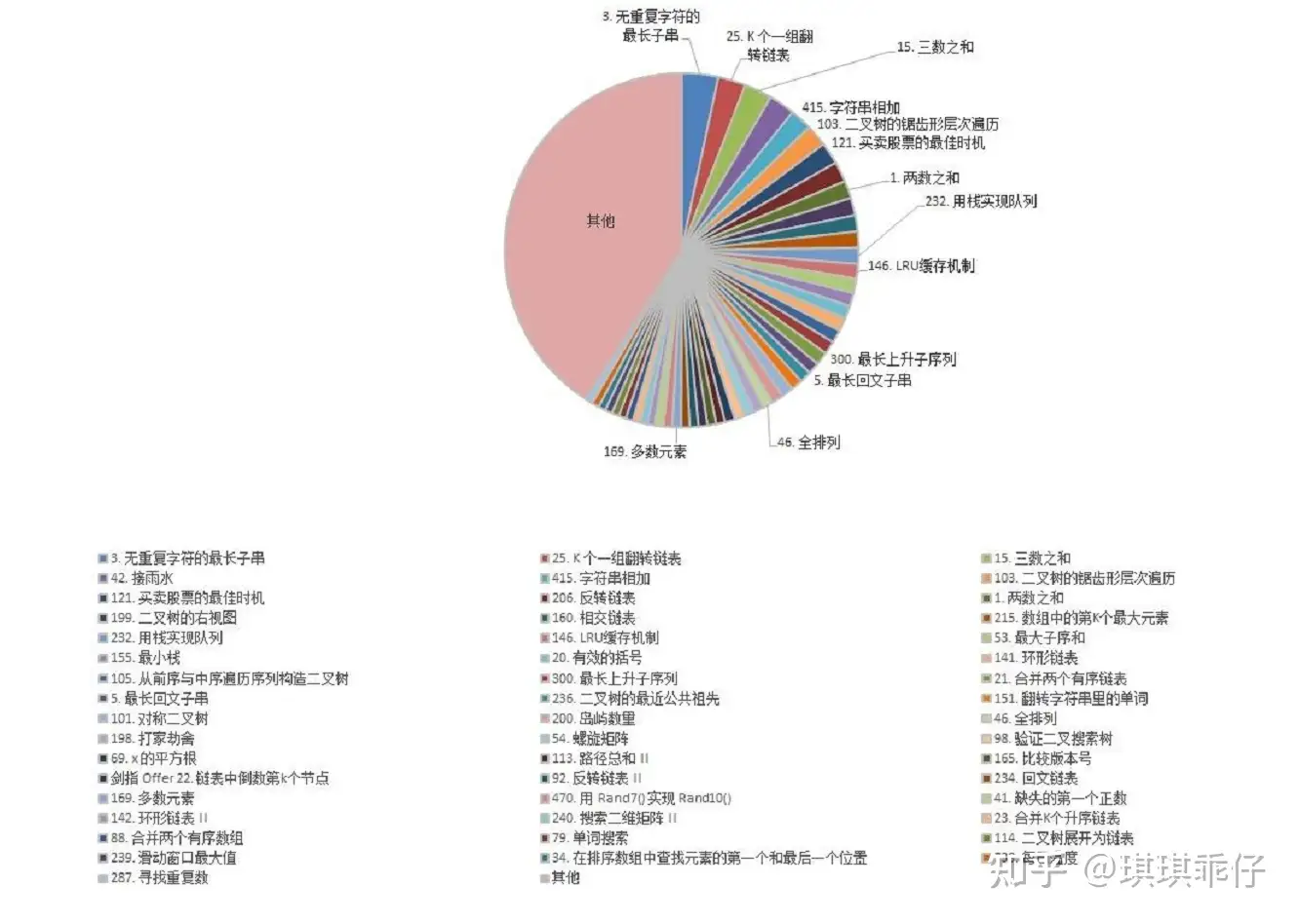
赏 支付宝打赏 微信打赏

~ 海内存知已，天涯若比邻 ~

Share

Related Posts

上一篇 学术界名人经验总结-Experience from Doctor's life

下一篇 面试指南及算法工程师成长-The Guide for Interview

标题：学术界名人经验总结-Experience from Doctor's life

摘要：值得深思的好文章，现任Facebook人工智能研究院（FAIR LAB）研究员/研究经理，前Google无人驾驶部门软件工程师。本科和硕士毕业于上海交通大学，并在卡内基梅隆大学获得机器人方向博士学位。

标题：面试指南及算法工程师成长-The Guide for Interview

摘要：AI初学者不要过于迷信企业项目，忽略基本功的学习，不要mnist都没研究透彻就嫌简单，直奔难度更大的resnet，好高骛远，得不偿失，学东西请务必戒骄戒躁，一步一个脚印，才能越走越远。企业项目的事实跟你想象的大不一样

站内可视化导航

文章可视化导读：鼠标划过图形块时，如果出现蓝色光环, 点击即可跳转到对应主题

Comments

--disqus--

    Content
    My Moment ( 微信公众号 )
    欢迎关注鹤啸九天