资料
- 【2022-2-9】人类社会与概率分布关系:天道正态分布,人道幂率分布,参考
-
- 人会努力: 人的努力,带来的就是内卷,内卷带来的就是幂律分布。
-
- 天不会努力: 天地不仁,以万物为刍狗。所以万物才会正态分布
-
- 六大概率分布
-
【2018-11-15】数说工作室:概率论-上帝的赌术,协和八:说人话的统计学,做统计,多少数据才算够,【2018-5-20】【精华】说人话的统计学-合集,【2019-08-30】统计之都,【2020-3-11】概率统计思维的建立
- 【2018-8-13】贝叶斯概率模型一览,贝叶斯概率-精简讲解
- 统计学习根据任务类型可以分为监督学习、半监督学习、无监督学习、增强学习等
- 每类任务中,又可以将各类模型归结为概率模型和非概率模型,以监督学习为例
概率模型(生成模型)通过函数 F 来描述 X 和 Y 的联合概率或者条件概率分布,如 P(X|Y);非概率模型(判别模型)通过函数 F 来直接描述 X 到 Y 的映射,如 Y = f(X)。
- 【2018-8-16】可视化讲解贝叶斯推断
- 【2018-9-7】深度学习与贝叶斯暑期培训教程DeepBayes,含ppt、视频,github地址:Seminars DeepBayes Summer School 2018,video视频,slides资料
- 【2018-11-30】透彻理解马尔科夫蒙特卡洛,马尔科夫链可视化讲解Markov Chains
- 【2018-11-29】透彻理解最大似然估计
- 统计学基础知识【脑图笔记】
HMM
基本概念
1.1 定义、假设和应用
一个例子了解隐马尔科夫模型HMM。假设:
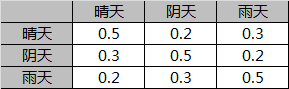
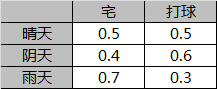
- (1)小明所在城市的天气有{晴天,阴天,雨天}三种情况,小明每天的活动有{宅,打球}两种选项。
- (2)我们只知道他每天参与了什么活动,而不知道他所在城市的天气是什么样的。
- (3)这个城市每天的天气情况,会和前一天的天气情况有点关系。譬如说,如果前一天是晴天,那么后一天是晴天的概率,就大于后一天是雨天的概率。
- (4)小明所在的城市,一年四季的天气情况都差不多。
- (5)小明每天会根据当天天气情况决定今天进行什么样的活动。
- (6)我们想通过小明的活动,猜测他所在城市的天气情况。
那么,城市天气情况和小明的活动选择,就构成了一个隐马尔科夫模型 HMM,我们下面用学术语言描述下:
- (1)HMM的基本定义:
HMM是用于描述由隐藏的状态序列和显性的观测序列组合而成的双重随机过程。
在前面的例子中,城市天气就是隐藏的状态序列,这个序列是观测不到的。小明的活动就是观测序列,这个序列是能够观测到的。这两个序列都是随机序列。
- (2)HMM的假设一:马尔科夫性假设
当前时刻的状态值,仅依赖于前一时刻的状态值,而不依赖于更早时刻的状态值。 每天的天气情况,会和前一天的天气情况有点关系。
马尔科夫性:随机过程中某事件的发生只取决于它的上一事件,是“无记忆”过程。
- (3)HMM的假设二:齐次性假设。
状态转移概率矩阵与时间无关。即所有时刻共享同一个状态转移矩阵。 小明所在的城市,一年四季的天气情况都差不多。
- (4)HMM的假设三:观测独立性假设。
当前时刻的观察值,仅依赖于当前时刻的状态值。 小明每天会根据当天的天气情况,决定今天进行什么样的活动。
-
(5)HMM的应用目的:通过可观测到的数据,预测不可观测的数据。想通过小明的活动,猜测他所在城市的天气情况。
- HMM被广泛应用于标注任务。在标注任务中,状态值对应着标记,任务会给定观测序列,以预测其对应的标记序列。
- HMM属于生成模型,是有向图。
1.2 三个基本问题
在学习HMM的三个问题:
- (1)概率计算问题:给定模型参数和观测序列,计算该观测序列的概率。是后面两个问题的基础。
- (2)学习训练问题:给定观测序列,估计模型参数。
- (3)解码预测问题:给定模型参数和观测序列,求概率最大的状态序列。 这三个问题会贯穿我们学习HMM的整个过程
2.概率计算问题
2.1 标记符号和参数
先约定一下HMM的标记符号,并通过套用上文的例子来理解:
(1)状态值集合(一共有N种状态值):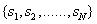
天气的状态值集合为{晴天,阴天,雨天}。
(2)观测值集合(一共有M种观测值):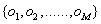
小明活动的观测值集合为{宅,打球}。
(3)状态值序列: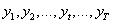
每一天的城市天气状态值构成的序列。
(4)观测值序列: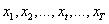
每一天的小明活动的观测值构成的序列。
(5)序列状态值、观测值下标:idx(t),表示t时刻的状态值或观测值,取的是状态值、观测值集合中的第idx(t)个。
再给出HMM模型的三个参数:A,B,π。
- A:状态转移概率矩阵。表征转移概率,维度为N*N。
- B:观测概率矩阵。表征发射概率,维度为N*M。
- π:初始状态概率向量。维度为N*1。
- λ=(A,B,π),表示模型的所有参数。
同样通过上文的例子来理解这三个参数。
状态转移概率矩阵A:
观测概率矩阵B:
初始概率状态向量π:

2.2 前向后向算法
我们通过前向后向算法,来计算特定观测序列出现的概率。
(2.2节和2.3节涉及大量的公式推导,没有兴趣的童鞋可以跳过不看,不影响文章其它部分的理解)
2.2.1前向算法模型
定义: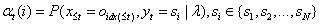
表示在模型参数已知的条件下,预测1~t时刻观测值为特定序列以及t时刻状态值为特定值的概率。
前向算法模型的思路是:利用t时刻的α值,去预测t+1时刻的α值。使用的是迭代的思路。
(1)模型初值: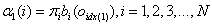
(2)迭代公式:
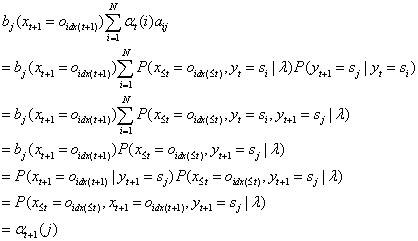
(3)模型终值:
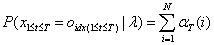
2.2.2后向算法模型
定义: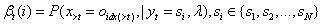
。表示在模型参数和t时刻状态值已知的条件下,预测t+1之后所有时刻观测值为特定序列的概率。
后算法模型的思路是:利用t+1时刻的β值,去预测t时刻的β值。使用的是递归的思路。
(1)模型初值:人为地定义,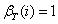
(2)递归公式:
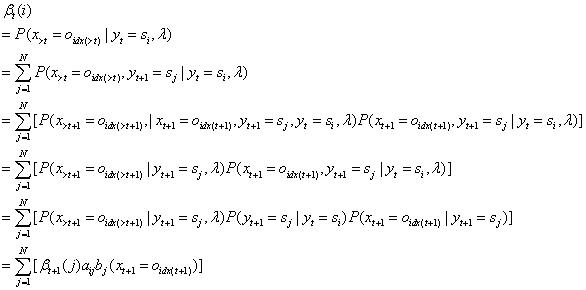
(3)模型终值:
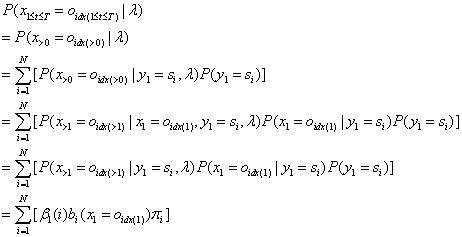
2.2.3前向后向算法模型公式
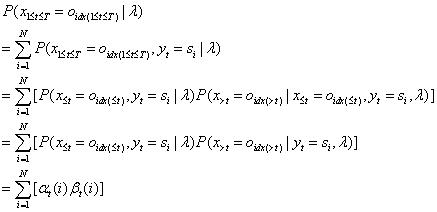
这个公式比李航教授书里的公式更容易理解些,《统计学习方法》书里的公式是:
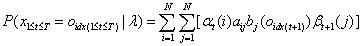
这两个公式都是正确的,这两个公式在推导过程中获取的以下两个公式,在2.3节有不同的应用:

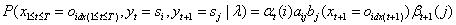
2.3 一些概率和期望的计算
2.3.1两个常用的概率公式
(1)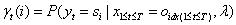
给定模型λ和观测序列,求时刻t处于指定状态的概率。
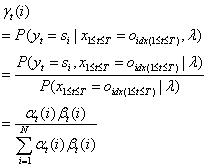
(2)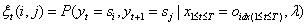
给定模型λ和观测序列,求时刻t和t+1处于指定状态的概率。
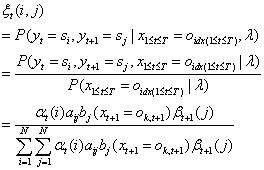
2.3.2 三个常用的期望公式
在观测序列O的条件下,状态i出现的期望值: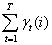
在观测序列O的条件下,由状态i转移的期望值: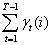
在观测序列O的条件下,由状态i转移到状态j的期望值: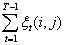
3.学习训练问题
模型参数的学习,可以根据有无标注数据,分为有监督和无监督两类。
在HMM里,如果训练数据包含观测序列和状态序列,即为有监督学习。如果训练数据只包含观测序列,即为无监督学习。
在有监督学习中,可以直接通过统计方法,求得模型的状态转移概率矩阵A、观测概率矩阵B、初始状态概率向量π。
在无监督学习中,模型使用Baum-Welch算法来求得模型参数。Baum-Welch算法是HMM模型中最难的部分,由于本文是“入门”文章,这里就不展开推导了。
注一:其实Baum-Welch算法和EM算法是一样的,只是Baum-Welch算法提出得比较早,当时EM算法还没有被归纳出来。
4 解码预测问题
4.1 贪心算法
贪心算法使用了条件独立性假设,认为不同时刻出现的状态是互相孤立的,是没有相关性的。所以,可以分别求取序列每个时刻最有可能出现的状态,再将各个时刻的状态按顺序组合成状态序列,作为预测结果。
贪心算法使用的公式,是2.3.1节推导出的
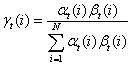
贪心算法的优点是计算简单。缺点是不同时刻的状态之间,实际上是概率相关的,这种算法可能导致陷入局部最优点,无法取到全局整体序列的最优值。
实际上,业界极少用贪心算法来解码预测HMM模型的状态序列。
4.2 维特比算法
维特比Viterbi算法使用了动态规划DP的思路,在这一节,我们不列举公式,而是通过一个例子,来呈现维特比算法是怎么工作的。
依旧使用前文的天气和活动的例子,模型参数和2.1节一样:
状态转移概率矩阵A:

观测概率矩阵B:

初始概率状态向量π:

现在已知小明在3天里的活动序列为:[宅,打球,宅],求最有可能的天气序列情况。
维特比算法预测过程:
步骤1:根据模型参数π和B,求得第1天天气的概率分布。
- P(D1,晴天,宅)=0.2*0.5=0.1
- P(D1,阴天,宅)=0.4*0.4=0.16
- P(D1,雨天,宅)=0.4*0.7=0.28
此时我们保存3个序列:
- 序列最后时刻为晴天的最大概率序列:[晴天:0.1]
- 序列最后时刻为阴天的最大概率序列:[阴天:0.16]
- 序列最后时刻为雨天的最大概率序列:[雨天:0.28]
步骤2:根据步骤1的3个序列,模型参数A和B,求得第2天天气的概率分布。
P(D2,晴天,打球) = max(P(D1,晴天) * P(D2,晴天|D1,晴天) * P(打球|D2,晴天),P(D1,阴天) * P(D2,晴天|D1,阴天) * P(打球|D2,晴天),P(D1,雨天) * P(D2,晴天|D1,雨天) * P(打球|D2,晴天)) = max(0.1 * 0.5 * 0.5, 0.16 * 0.3 * 0.5, 0.28 * 0.2 * 0.5) (前一时刻为雨天时,序列概率最大)= 0.028
序列最后时刻为晴天的最大概率序列:[雨天,晴天:0.028]
P(D2,阴天,打球) = max(0.1 * 0.2 * 0.6, 0.16 * 0.5 * 0.6, 0.28 * 0.3 * 0.6) (前一时刻为雨天时,序列概率最大)= 0.0504
序列最后时刻为阴天的最大概率序列:[雨天,阴天:0.0504]
P(D2,雨天,打球) = max(0.1 * 0.3 * 0.3, 0.16 * 0.2 * 0.3, 0.28 * 0.5 * 0.3) (前一时刻为雨天时,序列概率最大)= 0.042
序列最后时刻为雨天的最大概率序列:[雨天,雨天:0.042]
步骤3:根据步骤2的3个序列,模型参数A和B,求得第3天天气的概率分布。
P(D3,晴天,宅) = max(0.028 * 0.5 * 0.5, 0.0504 * 0.3 * 0.5, 0.042 * 0.2 * 0.5) (前一时刻为阴天时,序列概率最大)= 0.00756
序列最后时刻为晴天的最大概率序列:[雨天,阴天,晴天:0.00756]
P(D3,阴天,宅) = max(0.028 * 0.2 * 0.4, 0.0504 * 0.5 * 0.4, 0.042 * 0.3 * 0.4) (前一时刻为阴天时,序列概率最大)= 0.01008
序列最后时刻为阴天的最大概率序列:[雨天,阴天,阴天:0.01008]
P(D3,雨天,宅) = max(0.028 * 0.3 * 0.7, 0.0504 * 0.2 * 0.7, 0.042 * 0.5 * 0.7) (前一时刻为雨天时,序列概率最大)= 0.0147
序列最后时刻为雨天的最大概率序列:[雨天,雨天,雨天:0.0147]
步骤4:对比步骤3的3个序列,选出其中概率最大的那个状态序列。
[雨天,阴天,晴天:0.00756],[雨天,阴天,阴天:0.01008],[雨天,雨天,雨天:0.0147]中,概率最大的序列为[雨天,雨天,雨天],概率值为0.0147。
所以最优可能的天气序列情况为:[雨天,雨天,雨天]
最后,简单地描述下维特比算法的思路:
- (1)若状态值集合有N个取值,则需维护N个状态序列,以及N个状态序列对应的概率。每个状态序列存储的是:序列最后一个时刻取值为特定状态(共N个状态)时,概率最大的状态序列。本节案例中,就维护晴天、阴天、雨天三个状态序列,及其概率。
- (2)自第1个时刻开始,根据状态子序列和模型参数,计算和更新N个状态序列及其概率值。本节的案例中,对于当前时刻的晴天、阴天、雨天3个状态值,分别拼接上一时刻的状态序列和当前时刻的状态。例如D3晴天分别拼接D2状态序列得到:[雨天,晴天]+[晴天],[雨天,阴天]+[晴天],[雨天,雨天]+[晴天]3个新序列。通过计算求得其中概率最大的序列为[雨天,阴天,晴天],最后更新晴天状态序列为[雨天,阴天,晴天],丢弃另外两个序列,并保存概率值0.00756。D3状态为阴天和雨天的状态序列更新流程与此相同。
- (3)一直迭代到最后一个时刻,对比所有状态序列的概率值,概率值最大的状态序列即为最大状态概率序列。
注:4.2小节的例子数据,引用自李航《统计学习方法》。
5 HMM的局限性
- 马尔科夫性(有限历史性):实际上在NLP领域的文本数据,很多词语都是长依赖的。
- 齐次性:序列不同位置的状态转移矩阵可能会有所变化,即位置信息会影响预测结果。
- 观测独立性:观测值和观测值(字与字)之间是有相关性的。
- 单向图:只与前序状态有关,和后续状态无关。在NLP任务中,上下文的信息都是必须的。
- 标记偏置LabelBias:若状态A能够向N种状态转移,状态B能够向M种状态转移。若N«M,则预测序列更有可能选择状态A,因为A的转移概率较大。
6 工程实现
在具体实现过程中,为避免多个很小的数相乘导致浮点数下溢,所以可以取对数,使相乘变为相加。
由于HMM的EM算法中存在求和操作(Viterbi算法只有乘积操作),所以不能简单地使用取对数来避免浮点数下溢,采用的方式是设置一个比例系数,将概率值乘以它来放大;当每次迭代结束后,再把比例系数取消掉,继续下一次迭代。
7 jieba分词源码解读
分词任务是NLP的几个基础任务之一,jieba分词是一个应用得很广泛的开源项目。jieba分词使用了好几个不同的分词算法,我们在这一节对其中的HMM分词代码进行解读。
7.1 HMM分词基本概念
利用HMM算法进行分词,实际上就是执行一个序列标注任务。
我们看到的词语是观测序列,我们要预测一个状态序列,最后通过状态序列,来执行分词操作。
状态序列包括B、M、E、S四种状态。单个字构成的词,被标注为S。多个字构成的词,词语的第一个字被标注为B,最后一个字被标注为E,中间的若干个子被标注为M。
7.2 模型参数
jieba分词通过有监督的方式,获取模型参数A,B,π。
状态转移概率矩阵A被保存在文件prob_trans中:

观测概率矩阵B被保存在文件prob_emit中:

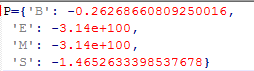
初始状态概率向量π被保存在文件prob_start中:
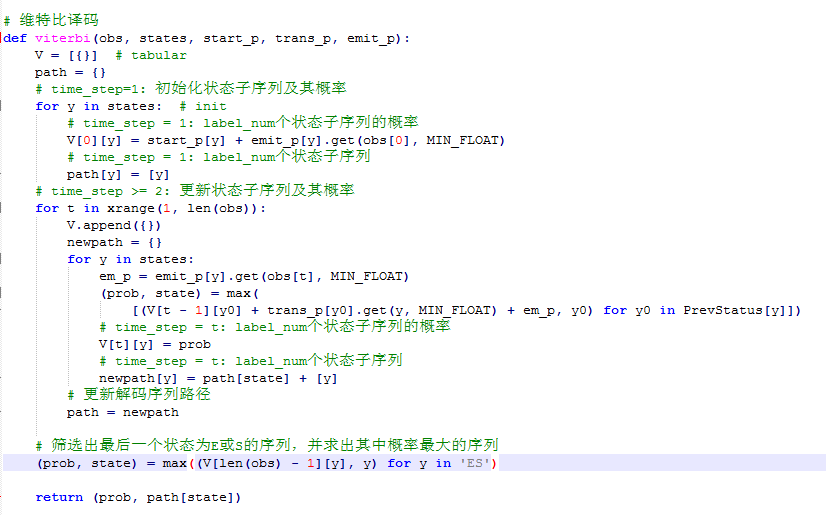
7.3 维特比算法
如截图所示,维特比解码流程同4.2节的描述完全一致,关键的部分我已经添加了注释。
唯一需要注意的是,HMM的工程实践中,大部分概率值都被取了对数,所以乘法操作在代码里体现为加法操作。
7.4 分词
根据维特比算法输出的标注状态序列,输出分词结果。

CRF
【2020-8-14】条件随机场(CRF)与隐马尔可夫模型(HMM)的区别是显而易见的。虽然这两种方法都用于对顺序数据建模,但它们是不同的算法。
- 隐马尔可夫模型具有生成性,通过对联合概率分布建模给出了输出。
- 条件随机场具有判别性,并对条件概率分布进行了建模。CRFs不依赖于独立假设(即标签彼此独立),并且避免了标签偏差。
- 隐马尔可夫模型是条件随机场的特例,转移概率使用了常数。
- HMMs基于朴素贝叶斯,从逻辑回归得到,CRFs就是从逻辑回归得到的。
1. CRF概述
1.1 随机场的定义
在这一小节,我们将会由泛化到特例,依次介绍随机场、马尔科夫随机场、条件随机场、线性链条件随机场的概念。
(1)随机场是一个图模型,是由若干个结点(随机变量)和边(依赖关系)组成的图模型,当给每一个结点按照某种分布随机赋予一个值之后,其全体就叫做随机场。 (2)马尔科夫随机场是随机场的特例,它假设随机场中任意一个结点的赋值,仅仅和它的邻结点的取值有关,和不相邻的结点的取值无关。用学术语言表示是:满足成对、局部或全局马尔科夫性。 (3)条件随机场CRF是马尔科夫随机场的特例,它假设模型中只有X(输入变量,观测值)和Y(输出变量,状态值)两种变量。输出变量Y构成马尔可夫随机场,输入变量X不具有马尔科夫性。 (4)线性链条件随机场,是状态序列是线性链的条件随机场。
注1:马尔科夫性:随机过程中某事件的发生只取决于它的上一事件,是“无记忆”过程。
我们的应用领域是NLP,所以本文只针对线性链条件随机场进行讨论。
线性链条件随机场有以下性质: (1)对于状态序列y,y的值只与相邻的y有关系,体现马尔科夫性。 (2)任意位置的y与所有位置的x都有关系。 (3)我们研究的线性链条件随机场,假设状态序列Y和观测序列X有相同的结构,但是实际上后文公式的推导,对于状态序列Y和观测序列X结构不同的条件随机场也适用。 (4)观测序列X是作为一个整体,去影响状态序列Y的值,而不是只影响相同或邻近位置(时刻)的Y。 (5)线性链条件随机场的示意图如下:
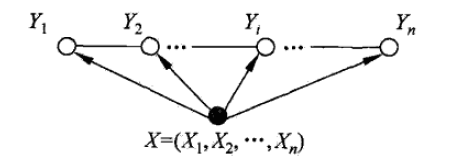
注二:李航老师的《统计学习方法》里,使用了两种示意图来描述线性链条件随机场,一种是上文所呈现的,这张图更能够体现性质(4),另一种如下图,关注点是X和Y同结构:
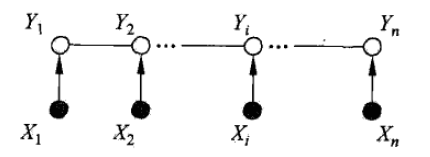
1.2 CRF的应用
线性链条件随机场CRF是在给定一组随机变量X(观测值)的条件下,获取另一组随机变量Y(状态值)的条件概率分布模型。在NLP领域,线性链条件随机场被广泛用于标注任务(NER、分词等)。
1.3 构建CRF的思路(重要)
我们先给出构建CRF模型的核心思路,现在暂不需要读懂这些思路的本质思想,但是我们要带着这些思路去阅读后续的内容。 (1)CRF是判别模型,是黑箱模型,不关心概率分布情况,只关心输出结果。 (2)CRF最重要的工作,是提取特征,构建特征函数。 (3)CRF使用特征函数给不同的标注网络打分,根据分数选出可能性最高的标注网络。 (4)CRF模型的计算过程,使用的是以e为底的指数。这个建模思路和深度学习输出层的softmax是一致的。先计算各个可能情况的分数,再进行softmax归一化操作。
2.CRF模型的概率计算
(对数学公式推导没兴趣的童鞋,只需要看2.1和2.2)
2.1标记符号和参数
先约定一下CRF的标记符号:
观测值序列:
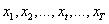
状态值序列:
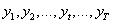
转移(共现)特征函数及其权重:
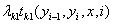
状态(发射)特征函数及其权重:
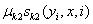
简化后的特征函数及其权重:
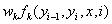
特征函数t的下标:k1
特征函数s的下标:k2
简化后的特征函数f的下标:k
2.2 一个栗子
在进行公式推导前,我们先通过一个直观的例子,初步了解下CRF。
例:输入观测序列为X=(x1,x2,x3),输出状态序列为Y=(y1,y2,y3),状态值集合为{1,2}。在已知观测序列后,得到的特征函数如下。求状态序列为Y=(y1,y2,y3)=(1,2,2)的非规范化条件概率。
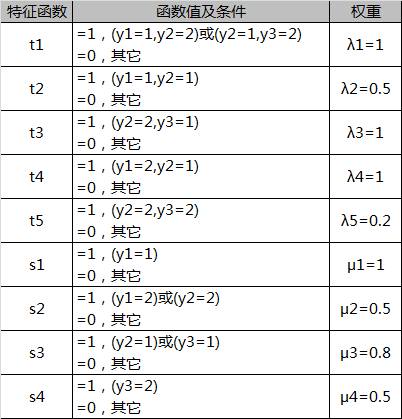
解:参照状态序列取值和特征函数定义,可得特征函数t1,t5,s1,s2,s4取值为1,其余特征函数取值为0。乘上权重后,可得状态序列(1,2,2)的非规范化条件概率为:1+0.2+1+0.5+0.5=3.2
2.3 特征函数
在这一小节,我们描述下特征函数,以及它的简化形式和矩阵形式。
(1)线性链条件随机场的原始参数化形式
分数:
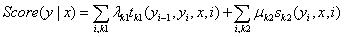
归一化概率:

其中,归一项为:
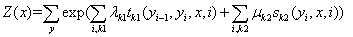
_t_为定义在边上的特征函数,通常取值0或1,依赖于两个相邻结点的状态,_λ_为其权重。_t_有时被称为转移特征,其实称为共现特征更合适些。因为图模型更强调位置关系而不是时序关系。
_s_为定义在节点上的特征函数,通常取值0或1,依赖于单个结点的状态,_μ_为其权重。_s_有时被称为状态特征。
需要强调的是:CRF模型中涉及的条件概率,不是真实的概率,而是通过分值softmax归一化成的概率。
(2)线性链条件随机场的简化形式
特征函数:
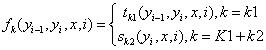
权重:
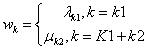
对特征函数在各个位置求和,将局部特征函数转化为全局特征函数:
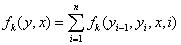
归一化概率:
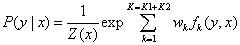
向量化:
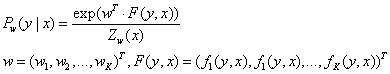
(3)线性链条件随机场的矩阵形式
构建矩阵_Mi(x)_。位置_i_和观测值序列_x_是矩阵的自变量。
矩阵的维度是m*m,m为状态值y的集合的元素个数,矩阵的行表示的是位置i-1的状态,矩阵的列表示的是位置i的状态,矩阵各个位置的值表示位置i-1状态和位置i状态的共现分数,并以e为底取指数。
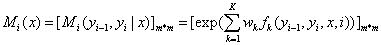
2.4 前向后向算法
(1)前向算法模型
| (a)_αi(yi=s | x)_表示状态序列y在位置i取值s,在位置1~i取值为任意值的可能性分数的非规范化概率。 |
定义:
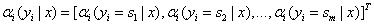
(b)递归公式:
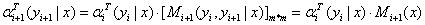
(c)人为定义:
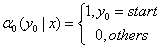
(d)归一项:
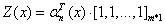
(2)后向算法模型
| (a)_βi(yi=s | x)_表示状态序列y在位置i取值s,在位置i+1~n取值为任意值的可能性分数的非规范化概率。 |
定义:
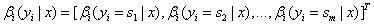
(b)递归公式:
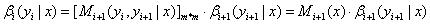
(c)人为定义:
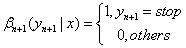
(d)归一化项:
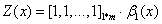
注:在前向算法和后向算法中,人为地定义了α(0)和β(n+1),采用的是李航老师书里的定义方法。但是,我认为采用先验概率(类似HMM中的初始概率分布)或者全部定义成1更合适。因为这里的概率模型应该表现得更通用一点,而不要引入实际预测序列的第一项和最后一项的信息。
2.5 一些概率和期望的计算
(1)两个常用的概率公式
状态序列y,位置i的取值为特定值,其余位置为任意值的可能性分数的归一化条件概率:
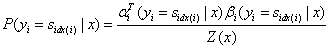
状态序列y,位置i-1,i的取值为特定值,其余位置为任意值的可能性分数的归一化条件概率:
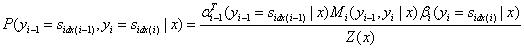
(1)两个常用的期望公式
| 特征函数_f_关于条件分布P(Y | X)的数学期望: |
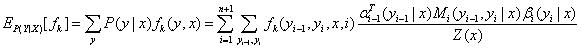
特征函数_f_关于联合分布P(X,Y)的数学期望:
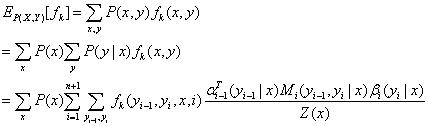
3. CRF模型的训练和预测
3.1 学习训练问题
CRF模型采用正则化的极大似然估计最大化概率。
采用的最优化算法可以是:迭代尺度法IIS,梯度下降法,拟牛顿法。
相应的知识可以通过最优化方法的资料进行学习,本文篇幅有限,就不作展开了。
3.2 预测解码问题
和HMM完全一样,采用维特比算法进行预测解码,这里不作展开。
4.CRF的优缺点(重要)
4.1 CRF相对于HMM的优点
(1)规避了马尔科夫性(有限历史性),能够获取长文本的远距离依赖的信息。 (2)规避了齐次性,模型能够获取序列的位置信息,并且序列的位置信息会影响预测出的状态序列。 (3)规避了观测独立性,观测值之间的相关性信息能够被提取。 (4)不是单向图,而是无向图,能够充分提取上下文信息作为特征。 (5)改善了标记偏置LabelBias问题,因为CRF相对于HMM能够更多地获取序列的全局概率信息。 (6)CRF的思路是利用多个特征,对状态序列进行预测。HMM的表现形式使他无法使用多个复杂特征。
4.2 条件随机场CRF的缺点
(1)CRF训练代价大、复杂度高。 (2)每个特征的权重固定,特征函数只有0和1两个取值。 (3)模型过于复杂,在海量数据的情况下,业界多用神经网络。 (4)需要人为构造特征函数,特征工程对CRF模型的影响很大。 (5)转移特征函数的自变量只涉及两个相邻位置,而CRF定义中的马尔科夫性,应该涉及三个相邻位置。
4.3 标记偏置LabelBias
在HMM中的体现:对于某一时刻的任一状态,当它向后一时进行状态刻转移时,会对转移到的所有状态的概率做归一化,这是一种局部的归一化。即使某个转移概率特别高,其转移概率也不超过1。即使某个转移概率特别低,如果其它几个转移概率同样低,那么归一化后的转移概率也不会接近0。
在CRF被规避的原因:CRF使用了全局的归一化。在进行归一化之前,使用分数来标记状态路径的可能性大小。待所有路径所有位置的分数都计算完成后,再进行归一化。某些某个状态转移的子路径有很高的分数,会对整条路径的概率产生很大的影响。
5. 基于TensorFlow的BiLSTM-CRF
BiLSTM-CRF是当前用得比较广泛的序列标注模型。
BiLSTM-CRF模型由BiLSTM和CRF两个部分组成。
BiLSTM使用的是分类任务的配置,最终输出一个标注好的序列。也就是说,即使没有CRF,BiLSTM也能独立完成标注任务。
CRF接收BiLSTM输出的标注序列,进行计算,最后输出修正后的标注序列。
TensorFlow提供了CRF的开发包,路径为:tf.contrib.crf。需要强调的是,TensorFlow的CRF,提供的是一个严重简化后的CRF,和原始CRF差异较大。虽然减小了模型复杂度,但是在准确率上也一定会有所损失。
下面简要介绍下TensorFlow中CRF模块的几个关键函数。
(1)crf_log_likelihood
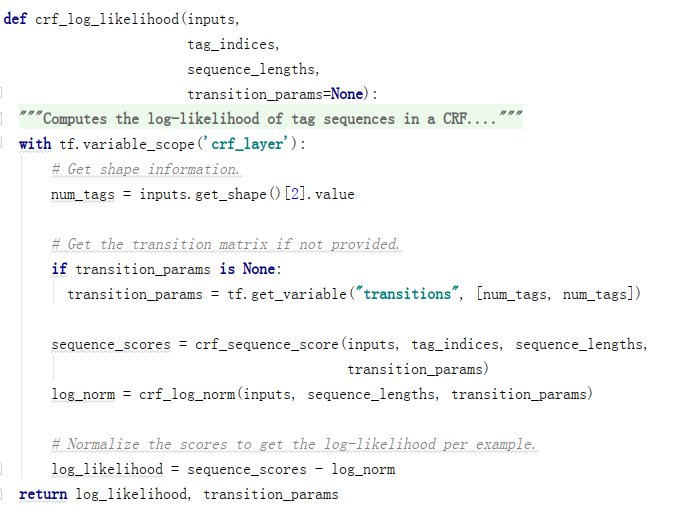
BiLSTM模块输出的序列,通过参数inputs输入CRF模块。
CRF模块通过crf_sequence_score计算状态序列可能性分数,通过crf_log_norm计算归一化项。
最后返回log_likelihood对数似然。
(2)crf_sequence_score
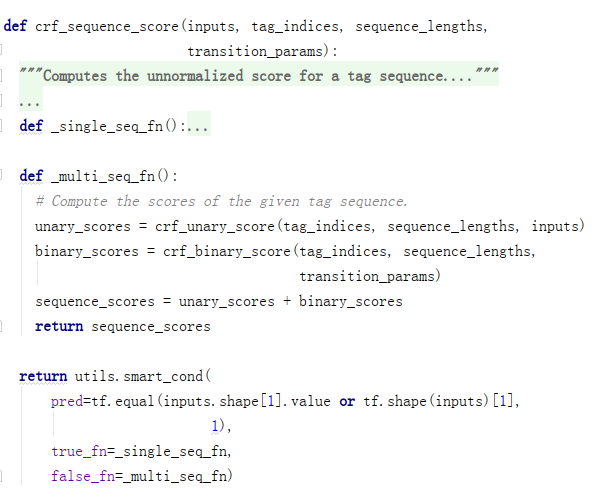
crf_sequence_score通过crf_unary_score计算状态特征分数,通过crf_binary_score计算共现特征分数。
(3)crf_unary_score
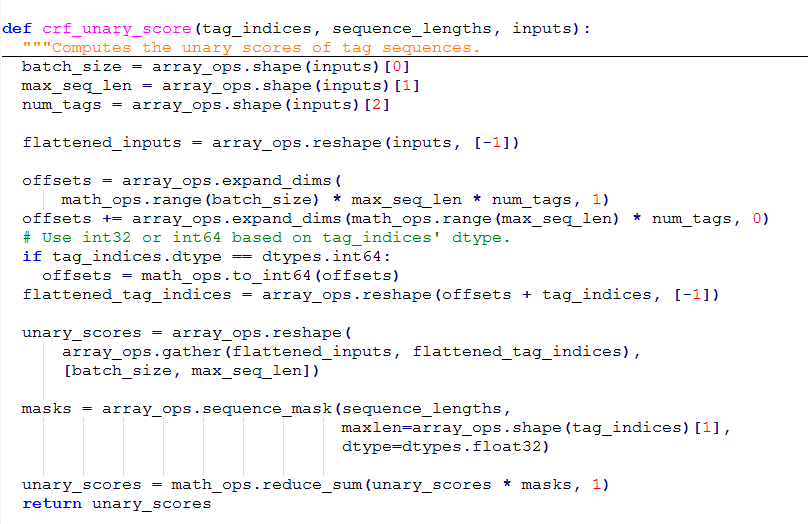
crf_unary_score利用掩码的方式,计算得出一个类似交叉熵的值。
(4)crf_binary_score

crf_binary_score构造了一个共现矩阵transition_params,表示不同状态共现的概率,这个矩阵是可训练的。最后通过共现矩阵返回共现特征分数。
(5)crf_log_norm
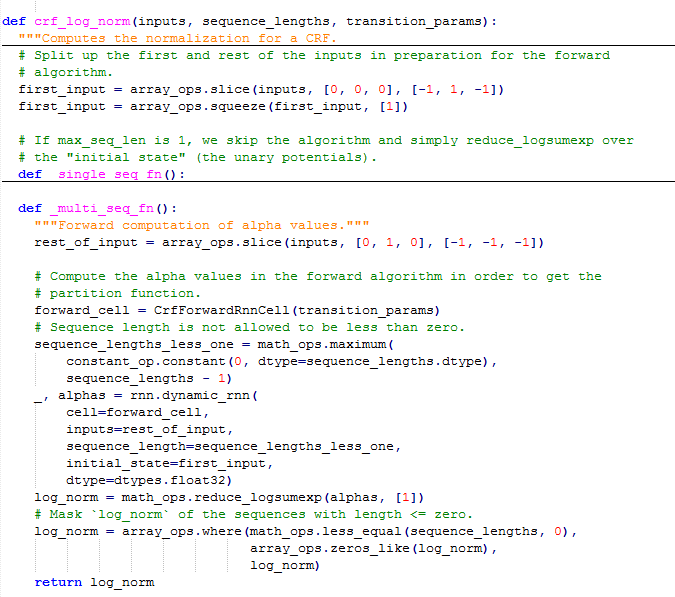
归一化项。
深入讲解贝叶斯背后的哲学与数学思想
- 2019-01-14 12:13:57
数理统计中有频率学派和贝叶斯学派之分。关于两者的差异,众说纷纭,网上博客、知乎有专门的讨论。
然而,从更高的哲学上看待这个问题,就会发觉,贝叶斯论和频率论的真正区别在于人们如何解释概率之间的哲学差异。
本文将透彻分析贝叶斯背后的哲学与数学思想。让大家从一个更高的视角来把应用贝叶斯思想及推理,不光是应用于机器学习算法,还能指导工作生活。
贝叶斯定理的证据思想
将A视为关于世界的一些命题,将B视为一些数据或证据。例如,A代表今天下雨的命题,B代表外面人行道潮湿的证据,那么分析一下这个贝叶斯推理过程的思想。
p(雨|湿) 问道,”外面潮湿,下雨的几率是多少?” 为了评估这个问题,让我们来看看方程式的右侧。在看地面之前,下雨的概率是多少, p(下雨)?将此视为对世界的假设的合理性。然后我们问在这个假设下,外面潮湿的观察有多少可能性, 即p(潮湿|下雨)?根据证据,这个过程有效地更新了我们对一个命题的初步信念,在一些观察的支持下最终衡量了降雨的合理性。
我们的初始信念由先验分布p(下雨)表示,我们的最终信念由后验分布p(雨|湿)表示。分母只是问:”证据的总合理性是多少?”,我们必须考虑所有假设,以确保后验是一个合适的概率分布。
这种思维方式可以帮助你摆脱对世界的黑白解释,而不是通过概率镜头来观察事物和解释。
从一个基于证据的世界观开始,如果引入新证据,你的初始世界观的概率会发生变化。
贝叶斯哲学本质:动态的看待世界
贝叶斯定理本质:
贝叶斯定理是一种基于最佳可用证据(观察,数据,信息)计算信念(假设,主张,命题)的有效性的方法。最本真的描述:最初的信念加上新的证据=新的和改进的信念。
所以你对自己信仰的确定性并不是固定的,而是流动的、可塑的。您应该能够根据新证据修改您的意见。
辩证法强调不要静止的看问题,要动态的看问题。所以为突出强调动态看问题的哲学思想,进一步的描述为:
我们用客观信息修改我们的观点:初始信念+最近的客观数据=新的和改进的信念。每次重新计算系统时,后验都成为新迭代的先验。这是一个不断发展的系统,每一点新信息都越来越接近于确定性。
这种思维方式可以帮助人们减少确认偏差的影响,从而开启对新可能性的看法。
贝叶斯推理过程,是一个不断修正的趋近于真理的过程。
贝叶斯定理的另一个用法是判断一个假设发生在另一个假设上的可能性。
中心前提是第一原则,即这个世界上大多数事物都是不确定的。很多时候你没有完美的信息,你不知道一切,你需要做出推论。
贝叶斯定理,在一个充满不确定性的世界中,为我们的决策提供信息。随着新信息的出现,需要反思这些新证据如何改变对事物的看法,然后根据它进行修正。
贝叶斯哲学精神:科学的客观性和精确性
伯茨麦格雷恩有一个对贝叶斯的经典陈述:
贝叶斯坚信,现代科学需要客观性和精确性。贝叶斯是信仰的衡量标准。它说我们甚至可以从缺失和不充分的数据,近似和无知中学到东西。
随着人们开始认识到人类思考和决策方式的固有不完善性,贝叶斯思想的应用正在不断增长。
很长一段时间,经典的经济学模型将人视为理性行为者,在开明的自我利益的基础上做出决策是完美的。现在我们开始意识到这种观点是有缺陷的,相反,人类行为经济学作为认知偏见的牺牲品的观点正变得越来越普遍。
贝叶斯思维也是我们学习方法的一个很好的近似。纳特•西尔弗在《信号与噪音》中说:
- 相反,它(贝叶斯定理)是一种在数学和哲学上表达我们如何了解宇宙的声明:我们通过近似来了解它,在我们收集更多证据时越来越接近真相。
贝叶斯数学思想:用数据调整先验
贝叶斯推理是非常强大的工具,可用于对任何随机变量进行建模,例如回归参数的值、人口统计数据、业务KPI或单词的词性。对于在机器学习建模中当数据有限、担心过拟合等情况下更有非常有用。
接下来通过高斯分布估计来讲解贝叶斯在应用于参数估计中的数学思想与方法。
在分布参数前提下的数据的概率:条件概率分布
假设我们给出了高斯随机变量X的样本数据集,D = {x1,…,xN},并且给出数据的方差是σ2
对μ的最佳猜测是什么?这里假设数据是独立的并且分布相同。
把高斯分布写成似然函数的形式如下,就是在当前参数下数据发生的概率密度函数:
我们希望选择最大化此表达式的μ。
贝叶斯概率
对于上边高斯分布参数估计,我们用贝叶斯定理的思想解决,我们的目的是求得参数,换作概率的表达就是,求在参数d的概率条件下的θ的概率,即p(θ|d):
| p(d | θ)是似然函数,概率的形式,实质上就是上文中写成条件概率形式的概率密度函数。p(θ) |
是先验概率(先前的信念)。
| 归一化常数,也就是证据的总合理性量度,必须考虑所有假设。p(θ | d)是后验分布,在面对数据时重新调整我们先前的信念(先验概率)。 |
这样,我们就把一个求取参数的过程转化为贝叶斯定理的求解过程。
最大后验概率估计MAP
在高斯分布估计中,假设我们事先认为某个随机变量X的平均值是μ0,我们的信念的方差是σ02,然后我们给出X的样本数据集,d = {x1,…,xN},如下图所示,并且以某种方式知道数据的方差是σ2,本文只给出求取一个参数的情况。
现在求后验分布参数μ?
上面的假设,已知知道高斯分布两个参数如下,即先验。
根据贝叶斯概率,我们所求即为:
p(d|u)是似然函数,如下图所示:
p(u)是μ的先验概率:
后验概率可写为:
根据两个高斯分布的乘积也是高斯分布,后验概率也是高斯:
通过变换形式,最后得到:

 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
