线性代数与矩阵

为什么会有矩阵，矩阵的乘法运算为什么是这个样子，矩阵的意义到底是什么？

历史

九章算术

汉代《九章算术》中“方程章”的第一题就利用算筹排成的矩形数阵来表示一个线性方程组，在其中的“方程术”的消元过程中，使用了把某行乘以某一非零实数、从某行中减去另一行等运算技巧，相当于矩阵的初等变换。

凯莱

19世纪末，矩阵的概念由英国数学家凯莱(A. Cayley, 1821–1895)首先提出。

一般被公认为是矩阵论的创立者, 因为首先把矩阵作为一个独立的数学概念提出来, 并首先发表了关于这个题目的一系列文章.
1858年, 凯莱发表第一篇论文《矩阵论的研究报告》, 系统地阐述了关于矩阵的理论. 文中他定义了矩阵的相等、矩阵的运算法则、矩阵的转置以及矩阵的逆等一系列基本概念, 指出了矩阵加法的可交换性与可结合性。

概念

优化函数时的决策目标总是： min 或 max。不少高质量的论文中总是写成：inf 或 sup。

inf 是 infimum 的简称，一个集合最大的下界
sup 是 supremum 的简称，一个集合最小的上界

什么是矩阵

参考：YourMath

元素

矩阵中元素为单位，将矩阵理解为许多数字排成的矩形数阵。

案例

电子黑白照片(灰度图像), 是由一个0255之间的整数构成的矩阵储存的, 其中0代表纯黑色, 255代表纯白色, 中间的整数从小到大, 表示由黑到白的过渡色
矩阵表示的网络图
马尔科夫转移矩阵

行

矩阵的行为单位，将矩阵理解为若干长度相等的行排成的矩形数阵

案例

矩阵理解为一个齐次或者非齐次的线性方程组。
矩阵的每一行看作向量空间中的向量，那么可以将矩阵理解为一个行向量组
矩阵的每一行与一个线性微分方程对应，那么可以将一个矩阵理解为一个 线性微分方程组。

列

以矩阵的列为单位，将矩阵理解为若干长度相等的列排成的矩形数阵。

案例

矩阵的每一列看作向量空间中的向量，那么可以将矩阵理解为一个列向量组。
每一列看作线性空间中向量的坐标，那么可以将矩阵理解为一个线性空间中的向量组

矩阵

整个矩阵为单位，将矩阵理解为一个映射

案例

方阵可以理解线性空间的线性变换
一般矩阵可以理解不同线性空间之间的线性映射

特殊矩阵

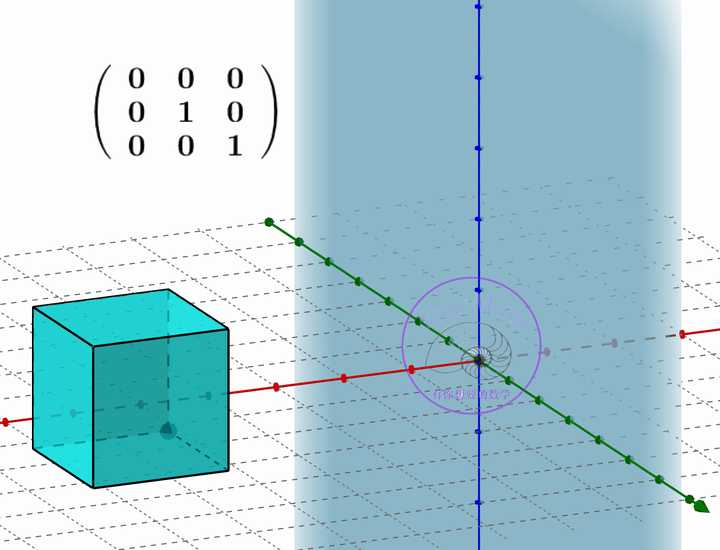
一些特殊矩阵还可以理解为二次曲面、二次曲线、坐标系、一组基等等

案例

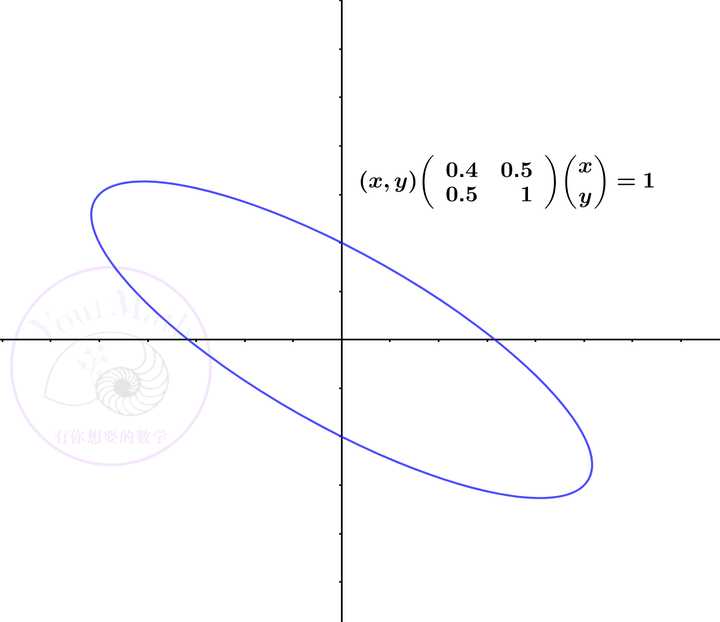
一个实对称矩阵与一个实二次型一一对应。一般的，如果令一个二元或者三元的二次型为一个常数，这个代数表达式可以表示一个二次曲线或者二次曲面。
对于一个可逆矩阵而言，如果将行或者列理解为向量空间中的向量，那么可以将矩阵理解为向量空间中的一个坐标系。
- 例如正交矩阵就可以理解为一个单位直角坐标系

各种变换关系

关系总结

线性变换：
- 几种基础类型：旋转、缩放、剪切、反射
- 会导致形变
仿射变换：
- 线性变换 + 平移变换
- 其中包含形变。
刚体变换
- 仿射变换的一种，要求大小形状不变

【2023-4-6】刚体变换、仿射变换、线性变换的概念

刚体变换是指在三维空间中，把一个物体做旋转、平移，是一种保持物体大小和形状不变的仿射变换，刚体变换又称为欧式变换、齐次变换。
仿射变换是指物体从一个向量空间进行一次线性变换并接上一个平移，变换到另一个向量空间。
- 平移、旋转、缩放、剪切、反射以及它们任意次序的组合都是仿射变换

线性变换具有以下几个性质

变换前是直线的，变换后依然是直线，且比例保持不变
变换前是原点的，变换后依然是原点

旋转、推移都是线性变换

旋转变换

旋转变换有两种：

向量旋转：物体在固定坐标系下的旋转，旋转后坐标发生改变
坐标系旋转：旋转后物体坐标不变

图解见原文

【2023-4-6】理解刚体运动与矩阵变换

数学空间

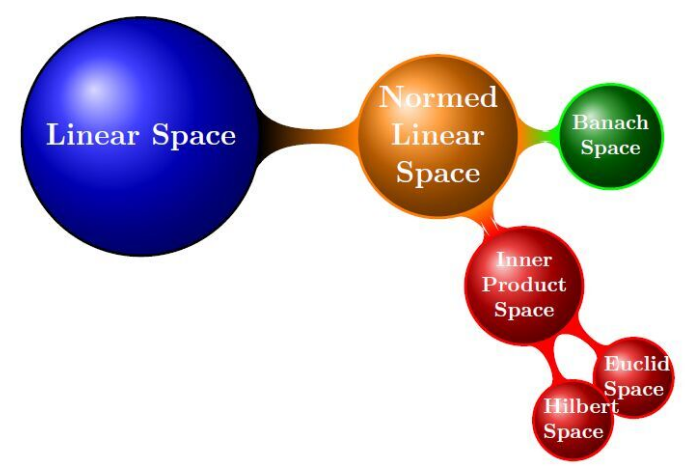
理解数学空间，从距离到希尔伯特空间
演变关系
- 线性空间（向量空间，对数乘和向量加法封闭所组成的空间）–（定义范数）–>赋范线性空间（向量具有的长度）–（定义内积）–>内积空间（向量之间具有了角度）–（完备化）–>希尔伯特空间→欧式空间（有限维）。

总结
- 距离 ⟶ 范数 ⟶ 内积
- 向量空间+范数 ⟶ 赋范空间+线性结构 ⟶ +线性结构 ⟶ 线性赋范空间+内积运算 ⟶ 内积空间+完备性 ⟶希尔伯特空间
- 内积空间+有限维 ⟶ 欧几里德空间
- 赋范空间+完备性 ⟶ +完备性 ⟶ 巴拿赫空间
知乎：如何理解希尔伯特空间

巴拿赫空间是以波兰数学家斯特凡·巴拿赫的名字来命名，他和汉斯·哈恩及爱德华·赫利于1920-1922年提出此空间

泛函分析之中，巴拿赫空间（英语：Banach space）是一个完备赋范向量空间。

巴拿赫空间是一个具有范数并对此范数完备的向量空间。其完备性体现在，空间内任意向量的柯西序列总是收敛到一个良定义的位于空间内部的极限。

巴拿赫空间有两种常见的类型：“实巴拿赫空间”及“复巴拿赫空间”，分别是指将巴拿赫空间的向量空间定义于由实数或复数组成的域之上。

许多在数学分析中学到的无限维函数空间都是巴拿赫空间，包括由连续函数（紧致赫斯多夫空间上的连续函数）组成的空间、由勒贝格可积函数组成的Lp空间及由全纯函数组成的哈代空间。
上述空间是拓扑向量空间中最常见的类型，这些空间的拓扑都自来其范数。
希尔伯特空间是完备的内积空间；巴拿赫空间的一种，其标准诱导内积遵循平行四边形原则

什么是完备？

完备空间，或完备度量空间（英语：Complete metric space）是具有下述性质的一种度量空间：

空间中的任何柯西序列都收敛在该空间之内

欧氏空间

约在公元前300年，古希腊数学家欧几里德建立了角和空间中距离之间联系的法则，现称为欧几里德几何。欧几里德首先开创了处理平面上二维物体的平面几何，接着分析三维物体的立体几何，所有欧几里德的公理已被编排到叫做二维或三维欧几里德空间的抽象数学空间中。
这些数学空间可以被扩展而应用于任何有限维度，这种空间叫做n维欧几里德空间（简称n维空间）或有限维实内积空间。
简单来说，欧式空间就是二维空间、三维空间以及继承三维空间定理的N维空间。
欧式空间的定义：
- 设V是实数域R上的线性空间(或称为向量空间)，若V上定义着正定对称双线性型g(g称为内积)，则V称为(对于g的)内积空间或欧几里得空间(有时仅当V是有限维时，才称为欧几里得空间)。
- 具体来说，g是V上的二元实值函数，满足如下关系：（对称+加法+数乘+距离有效）
  - (1) g(x,y) = g(y,x)
  - (2) g(x+y,z) = g(x,z) + g(y, z)
  - (3) g(kx,y) = kg(x,y)
  - (4) g(x,y) >= 0,而且g(x,y)=0当且仅当x=0时成立。
- 这里x,y,z是V中任意向量,k是任意实数。
标准欧几里得空间
- 四维空间被称为标准欧几里得空间，可以拓展到n维；四维时空指的是闵可夫斯基空间概念的一种误解。人类作为三维物体可以理解四维时空(三个空间维度和一个时间维度)但无法认识以及存在于四维空间，因为人类属于第三个空间维度生物。通常说时间是第四维即四维时空下的时间维度。四维空间的第四维指与x,y,z同一性质的空间维度。然而四维时空并不是标准欧几里得空间，时间的本质是描述运动的快慢。
通过一维，二维，三维空间的演变，人们提出了关于四维空间的一些猜想。尽管这些猜想现在并不能证明是正确的，但科学理论有很多是猜想开始的。现今科学理论一般是基于现象总结规律，而关于四维空间的现象没有足够准确清晰的认识，或者看到了这种现象却并没有想到是四维空间引起的。

非欧氏空间

摘自：欧式空间与非欧式空间
爱因斯坦曾经形象地比喻过非欧几何：
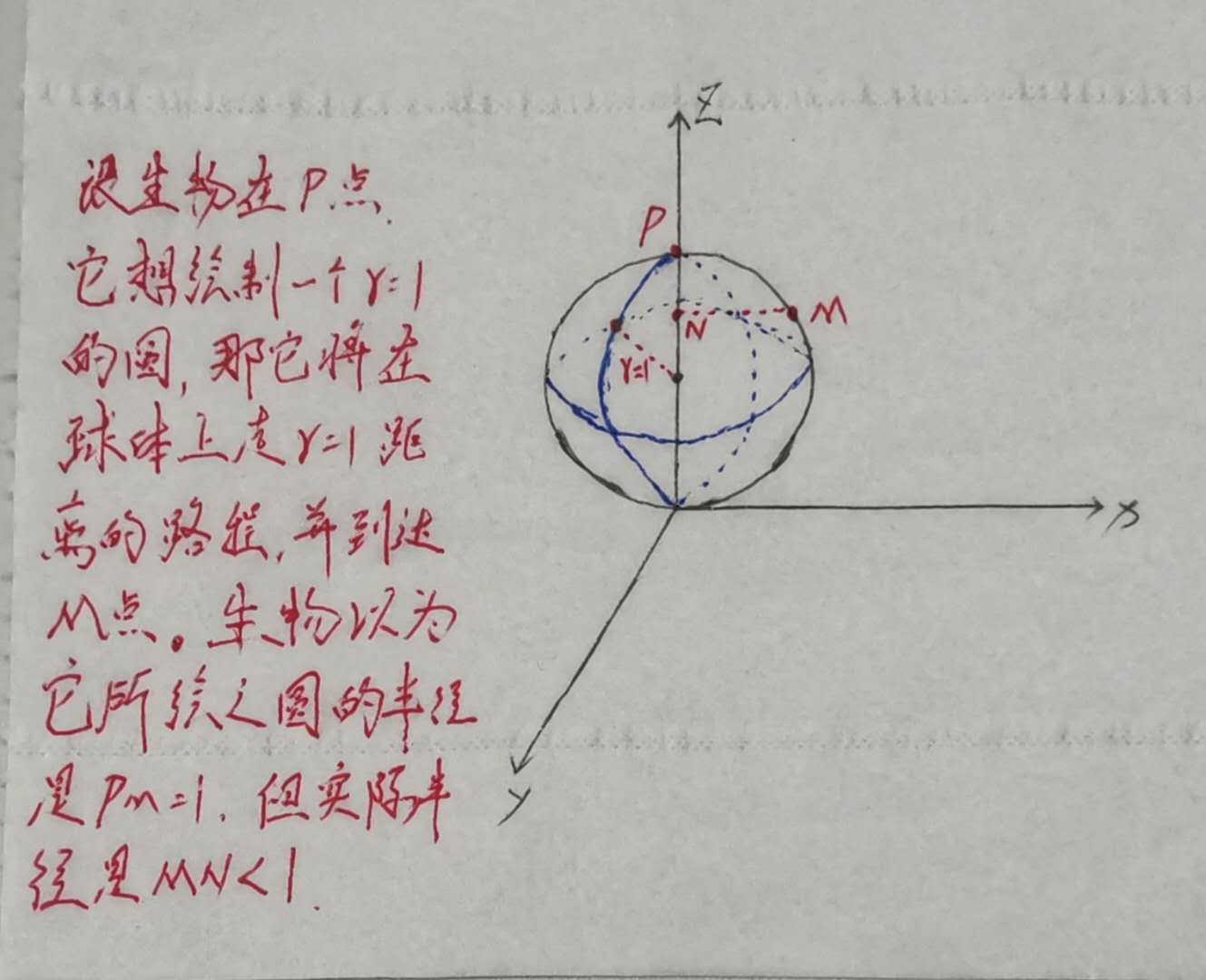
- 假设有一种生活在二维平面的生物，但它们不是生活在绝对的平面上，而是生活在一个球面上，那么，当它们在小范围内研究圆周率的时候，会像我们一样发现圆周率是3.1415926……
- 但是，如果它们画一个很大的圆，去测量圆的周长和半径，就会发现周长小于2πr，圆越大，周长比2πr小得越多。为了能够适用于大范围的研究，它们就必须修正它们的几何方法。
如果空间有四维，而我们生活的三维空间在空间的第四个维度中发生了弯曲，那我们的几何就必须进行修正，这就是非欧几何。在非欧几何中，平行的直线只在局部平行，就像地球的经线只在赤道上平行一样。
二维生物画圆的解释如下：

希尔伯特空间

摘自：

欧式空间与希尔伯特空间
Hilbert Space
希尔伯特空间：
- 在数学中，希尔伯特空间是欧几里得空间的一个推广，其不再局限于有限维的情形。与欧几里得空间相仿，希尔伯特空间也是一个内积空间，其上有距离和角的概念(及由此引申而来的正交性与垂直性的概念)。此外，希尔伯特空间还是一个完备的空间，骑上所有的柯西序列等价于收敛序列，从而微积分中的大部分概念都可以无障碍的推广到希尔伯特空间中。希尔伯特空间为基于任意正交系上的多项式表示的傅里叶级数和傅里叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。希尔伯特精简是公式化数学和量子力学的关键性概念之一。
希尔伯特空间是欧几里德空间的直接推广。对希尔伯特空间及作用在希尔伯特空间上的算子的研究是泛函分析的重要组成部分。
设H是一个实的线性空间，如果对H中的任何两个向量x和y，都对应着一个实数，记为(x，y)、满足下列条件：
- ① 共轭对称性：对H中的任何两个向量x，y，有(x，y)=(y，x);
- ② 线性：对H中的任何三个向量x、y、z及实数α、β，有(αx+βy，z)=α(x，z)+β(y，z);
- ③ 正定性：对H中的一切向量x，均有(x，x)≥0，且(x，x)=0的充分必要条件是x=0。
则(x，y)称为是H上的一个内积，而H称为内积空间。
完备的内积空间称为希尔伯特空间，希尔伯特空间的概念还可以推广到复线性空间上。

再生希尔伯特空间

【2023-4-11】A Story of Basis and Kernel - Part II: Reproducing Kernel Hilbert Space

再生希尔伯特空间：reproducing kernel Hilbert space (RKHS)

矩阵的本质

矩阵理解

如何通俗讲解放射变换？ _ 在线几何作图GeoGebra（源自马同学高等数学）
3Blue1Brown出品（接受捐助）：线性代数的本质-Essence of Linear Algebra-视频教程，Bilibili上《线性代数本质》双语视频教程.文字版,类似视频还有微积分本质,笔记.制作教学视频的代码
【2021-2-20】国外通俗易懂讲解数学betterexplained
【2019-10-24】马同学高等数学-线性代数学习笔记，【2019-12-31】交互式线性代数-Interactive Linear Algebra -【2018-9-4】Google出品：动图解释反向传播
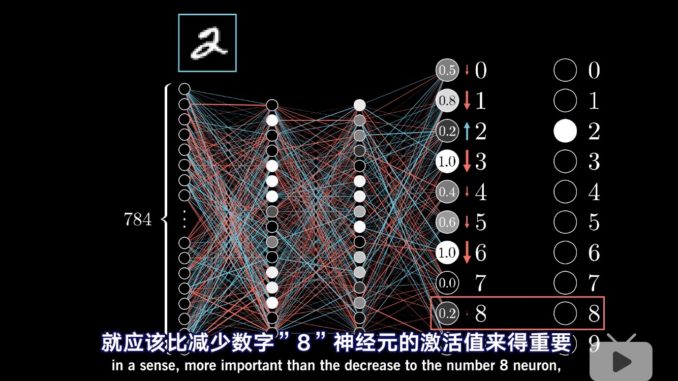
行列式的本质（马同学高等数学）.《数学拾遗》英文版百度云地址.
矩阵分解(加法偏),矩阵分解(乘法篇)，很不错
如何通俗的解释放射变换,生动讲解矩阵的空间变换：平移、缩放、旋转、对称（xy或原点）、错切、组合。行列式的本质是什么？—万门大学童哲的解释:行列式就是线性变换的放大率！理解了行列式的物理意义，很多性质你根本就瞬间理解到忘不了！
【2018-8-17】广义线性模型是什么鬼？
行列式：行列式，记作 det(A)，是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是 0，那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是 1，那么这个转换保持空间体积不变
【2017-11-24】遇见数学：图解线性代数

矩阵的线性变换视角

相信很多读者第一次了解矩阵都是从解线性方程开始的，我们将从一个很接近的角度来得到矩阵，认为矩阵的本质就是 有限维线性空间中的线性变换.

我们还是从一维的情况开始吧，也就是标量的线性变换 $y = ax$。所谓一个变换$y = f(x)$是线性的，是指这个变换遵循两个线性运算的规律：

对于数乘可以交换，$f(\lambda x) = \lambda f(x)$
对于元素加法可交换， $f(x_1 + x_2) = f(x_1) + f(x_2)$

对于第一条规律，标量线性变换显然是满足的，因为$a \cdot(\lambda x) = \lambda (a x)$，这是由乘法结合律带来的。对于第二条规律，利用乘法对加法的分配率也容易验证，$a(x_1+x_2) = a x_1 + a x_2$。简单地理解，线性变换就是没有常数项的一次函数！显然，一维情况的线性变换可以只用一个常数a来描述就可以了，不需要其他参数！

那么，对于高维情况呢？我们考虑最简单的二维情况，一般情况下，二维的线性变换可以表达为没有常数项的二元一次函数

\[y_1 = a_{11} x_1 + a_{12} x_2 \\ y_2 = a_{21} x_1 + a_{22} x_2\]

相比一维情况只要1个参数就可以描述，二维则需要4个参数！依次类推下去，n维线性变换自然需要$n^2$个参数才能描述！把这些参数排列成方正就是我们的矩阵了！

\[A = \left[ \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right]\]

因此，每一个矩阵都是有限维线性空间中的一个线性变换。线性方程组只不过是已知线性变换和像求原像的问题。反过来，是否有限维线性空间中的任意线性变换都一定可以用一个矩阵表示出来呢？答案是肯定的！这就是说，矩阵和有限维线性空间中的线性变换是一一对应！考虑线性变换$y = f(x), x\in R^n, y\in R^m$，令$\{e_i,i=1,..n\}$是$R^n$中的一组标准正交基，$\{g_i,i=1,..m\}$是$R^m$中的一组标准正交基，线性代数的知识告诉我们一定可以找到这样两组组标准正交基！那么，利用线性变量的两组性质可得

\[f(x) = f(\sum_i x_i e_i) = \sum_i x_i f(e_i)\]

这里$x_i$是向量$x$在标准正交基下的坐标！又因为$f(e_i) \in R^m$，根据线性代数的知识可知，一定可以把它表示成标准正交基的线性组合

\[f(e_i) = \sum_j a_{ji} g_j, i=1,...,n\]

代入上式可得

\[y = f(x) = \sum_j \left( \sum_i a_{ji} x_i \right) g_j\]

因为$g_j$是标准正交基，所以前面的数就是y在这组基下的坐标

\[y_i = \sum_j a_{ij} x_j\]

这表明线性变换$f$可以用矩阵$A=[a_{ij}]$表示出来！

对于有限维线性空间，矩阵和线性变换一一对应，那么对于无限维线性空间呢？泛函分析就是研究无限维线性空间的理论，在无限维线性空间中，线性算子有很多和矩阵相似的性质，但是一般很难用矩阵表示出来。

矩阵的坐标框架视角

矩阵另外一个图像是坐标框架转换，前面我们把坐标框架——也就是基向量固定，让向量进行变换，我们也可以反过来，让向量不变，重新选取一组坐标基。运动是相对的，所以这两种图像实际上是等价的！假设在坐标框架$\{e_i, i=1,..,n\}$下，向量$v = \sum_i x_i e_i$，$x_i$是在这组基下的坐标。现在我们重新选取一组基$\{g_i, i=1,...,n\}$，向量$v = \sum_i y_i g_i$，$y_i$是在这组基下的坐标。那么这两组坐标之间有什么关系呢？因为$g_i$也是向量，所以它应该也可以用$e_i$表示，不妨设$g_j = \sum_i a_{ij} e_i$，那么

\[v = \sum_j y_j g_j \\ = \sum_i (\sum_j y_j a_{ij}) e_i\]

利用向量空间唯一表示定理，即向量v在$e_i$框架下的坐标是唯一的！所以有 $x_i = \sum_j a_{ij} y_j$！可以看到，坐标的变换系数矩阵实际上就是坐标框架基向量的变换矩阵。这种图像，在描述某些场景时更方便，例如傅里叶变换就可以看做同一个函数在时域基$\{\delta(t - s); s \in R\}$表示到频域基$\{e^{-i wt}; w\in R\}$表示的变换，详情可以参考深入理解傅里叶变换这篇文章！

矩阵的张量积视角

如果我们把矩阵也看做线性空间中的向量，那么它也应该有基向量，或者叫做基矩阵更合适。张量积可以用来从低阶张量构造高阶张量，向量是一阶张量，矩阵是二阶张量，可以利用张量积从向量构造出矩阵！

\[A = \sum_i \sum_j a_{ij} g_i \otimes e_j\]

这里假设都是正交基，$g_i \otimes e_j$是两个基向量的张量积，也可以看做矩阵的基矩阵！矩阵对向量的变换可以看做内积运算

\[Ax = \sum_i \sum_j a_{ij} x_j (g_i \otimes e_j, e_j) \\ =\sum_i a_{ij} x_j g_i\]

这表明矩阵对向量x的内积相当于完成了向量x从一组基到另外一组基的重新表示！

量子力学中，常用狄拉克括号表示向量及运算，张量积视角就更加自然了

\[A = \sum_i \sum_j a_{ij} |i\rangle \langle j| \\ x = \sum_i x_i |i\rangle \\ Ax = \sum_i\sum_j\sum_k a_{ij} x_k |i\rangle \langle j| k \rangle =\sum_i\sum_j a_{ij} x_j |i\rangle\]

矩阵的乘法

我在第一次学习矩阵的乘法的时候，十分好奇为什么矩阵乘法是那样的定义。这里，我们通过线性变换的角度比较容易说明。

我们还是从一维的情况说起吧，现在我有两个线性变换 $y = a x, z = b y$，我想用一个变换$z = c x$来代替，那么，显然有$c= b\cdot a$！也就是说，在一维情况，两个数的乘法实际上可以看做是用一个线性变换$c$来代替两个变换$a, b$的依次变换的结果，即

\[z = c \cdot x = b \cdot (a \cdot x)\]

我们把这个思想运用到高维不就可以得到矩阵乘法了吗？假设两个矩阵为A和B，对应的变换是$y = A x, z = B y$，我们想用一个矩阵C来代替这两个变换的依次作用的效果，即

\[z = C x = B(A x)\]

我们把上式右边展开可得

\[\begin{align*} z_{11} =& b_{11}(a_{11}x_1 + ... a_{1n} x_n) + ... + b_{1n}(a_{n1}x_1 + ... a_{nn} x_n) \\ = &\left(b_{11} a_{11} + ... + b_{1n} a_{n1}\right) x_1 + \\ &\left(b_{11} a_{12} + ... + b_{1n} a_{n2}\right) x_2 + \\ & ...\\ &\left(b_{11} a_{1n} + ... + b_{1n} a_{nn}\right) x_n \end{align*}\]

因此可知

\[c_{11} = b_{11} a_{11} + ... + b_{1n} a_{n1} \\ ...\\ c_{1n} = b_{11} a_{1n} + ... + b_{1n} a_{nn}\]

把上述代入过程用求和符号改写可以简化为

\[z_{i} = \sum_j c_{ij} x_j \\ = \sum_k b_{ik} \left(\sum_j a_{kj} x_j\right) \\ = \sum_j \left(\sum_k b_{ik} a_{kj} \right) x_j\]

最后一个等式利用了求和符号的交换，这表明

\[c_{ij} = \sum_k b_{ik} a_{kj}\]

这就是矩阵乘法的运算法则，把B矩阵第i行与A矩阵第j列的内积作为C矩阵的第(i, j)个元素的值！这表明，矩阵乘法运算法则是一种必然的结果，而不是某种人为规定的奇怪的运算法则！矩阵的乘法，实际上就是两个线性变换的乘法，变换的乘法运算就是定义为依次映射，

\[(B \cdot A) x = B \cdot (A x)\]

这种定义是为了让乘法满足结合律很自然的结果！

特征值和特征向量

在学习特征值和特征向量的时候，很多人都会很迷惑，这搞得是啥玩意儿！？但是，只要把来龙去脉搞清楚，就不难理解了。特征值和特征向量是最重要的概念之一！

我们还是从一维开始说起，一维的线性变换就是简单的把x放大a倍！但是，这个直观的图像在高维情况就不那么直观了！我们还是从二维说起。这种不直观的根本原因在于交叉项$a_{12}, a_{21}$的存在，如果这两项为0，那么矩阵就是对角阵

\[A = \left[ \begin{matrix} a_{11} & 0 \\ 0 & a_{22} \end{matrix} \right]\]

这个对角矩阵有个直观的图像，经过它变换的向量，在$x, y$两个方向上分别放大$a_{11}, a_{22}$倍！这种情况，我们也说在这种变换下，不同坐标间没有耦合，各坐标是独立伸缩变换的！

对于一般的方阵，是否也有类似的图像？显然对于一般的方阵A，肯定不是在$x, y$两个方向上的独立伸缩变换。那是不是可以找到两个独立的方向呢？如果能够找到，那么方阵A可以看做一个旋转变换加上两个独立方向上的伸缩变换，最后再旋转回来这三个变换构成！写成公式就是

\[A = T^{-1} \Lambda T\]

其中$T$是一个旋转变换，$\Lambda$是对角方阵代表两个方向上的独立伸缩变换。没错，这就是矩阵的相似对角化！

线性代数的知识告诉我们，对于一般的方阵，并不都是可以相似对角化的，只能相似到一个若尔当标准型。但是如果A是对称阵（对于复数则是厄米对称），那么答案就是肯定的！

特征值方程

假设对于对称矩阵A，两个独立的方向单位向量是$v_1, v_2$，那么有

\[Av_1 = \lambda_1 v_1, \\ Av_2 = \lambda_2 v_2\]

$\lambda_1, \lambda_2$是两个实数，代表这两个独立方向上的伸缩变换比例！并且这两个方向向量构成一组标准正交基！因此，对于一般的向量x，可以选取这两个向量作为基向量，重新表达

\[x = x_1 v_1 + x_2 v_2\]

那么，矩阵A对向量x的变换为

\[A x = (x_1 \lambda_1) v_1 + (x_2 \lambda_2) v_2\]

特征值的含义

也就是向量x在$v_1,v_2$两个独立的正交方向上分别放大了 $\lambda_1, \lambda_2$倍！

因此，特征向量可以看做矩阵的多个主方向，在这些方向上，矩阵对应的变换将向量在这些方向上的分量分别伸缩$\lambda_i$倍！

利用上述图像，我们很容易得到矩阵的谱范数为最大特征值的绝对值！

\[\rho(A) = \sup_{||x||_ 2 = 1} ||Ax||_ 2 = \max_i |\lambda_i|\]

因为谱范数实际上就是矩阵A能把一个单位向量最大放大多少倍！显然在绝对值最大的特征值对应的特征向量方向上具有最大放大倍数！

利用特征值和特征向量的图像，还可以得到幂方法求矩阵特征值的方法。想象有一个普通的向量v，它是如此的普通，以至于不与A的任何特征向量垂直，虽然我们一开始不知道特征向量方向，但是要让v不和它们垂直还是很容易的，随机初始化即可。如果对于这个向量v，不断地应用矩阵A进行变换，那么随着应用次数不断增加，向量$A^k v$的方向将无限趋近于绝对值最大特征值对应的特征向量方向！如果该特征值对应的特征向量有多个，那么$A^k v$将无限趋近于这个特征子空间！

特征值和特征向量是两个非常普适的概念，在无限维线性空间中也同样重要。

在不同场景下，这些主方向和特征值都是有特定意义的。

例如，在描述曲面上的曲率的时候，会用一个曲率张量（就是一个二阶对称方阵）来描述，该张量的两个特征向量就是两个曲率最大和最小的方向，而两个特征值就是这两个方向的曲率！

平面上的二次曲线都是用一个二次型表示，二次型对应的对称方阵的两个特征向量就是长短轴的方向，而两个特征值就是长短轴的大小（相差一个常数）！

在量子力学中，物理量都是用算符表示，在有限维空间就是矩阵，其对应的特征向量就是本征态，特征值就是物理量的测量值！

特征函数

与矩阵特征值和特征向量类似，存在特征值 $\lambda$ 和特征函数 $\phi(x)$

每个函数都可以看做一个无限维的向量，那么二元函数 $K(x,y)$ 就可以看做是一个无限维的矩阵。
如果二元函数满足正定性+对称性，那么就是一个核函数
特征向量：将函数看做无限维向量

Mercer定理

任何半正定函数都可以作为核函数。

将 $\sqrt{\lambda_i}\phi_i$ 作为一组正交基构建一个希尔伯特空间。这个空间中的任何一个函数（向量）都可以表示为这组基的线性组合。

核的可再生性(reproducing)，H 也被叫做可再生核希尔伯特空间(RKHS, reproducing kernel Hilbert space)。

【2023-4-11】再生核希尔伯特空间与核方法

行列式

初学行列式的时候，对这样一个概念和计算规则非常难理解。可能很多人都了解过一种解释，行列式就是列向量张成平行多面体体积（有向体积）！这个结论当然是没什么问题的，但是结论不够直观，而且跟矩阵本身的意义缺乏关联。

平行多面体

我们可以从线性变换的角度考虑另外一个意义，考虑欧式空间中的一个平行多面体，这个多面体的边长为1，且都是矩阵A的特征向量。那么这个多面体通过矩阵A变换之后，会变成怎么样呢？我们知道矩阵A在特征向量方向就是做简单的伸缩变换，伸缩系数就是特征值！因此，这个多面体经过A变换之后，每个方向上分别放大了$\lambda_i, i=1,...,n$倍！那么它的体积自然就放大了$\Pi_i \lambda_i$倍，这正是矩阵A的行列式！

\[\text{det}(A) = \Pi_i \lambda_i\]

由此可见，矩阵A的行列式就是该线性变换的体积放大倍数！如果，我们这个平行多面体是由单位基向量构成，经过A变换后就变成了A的列向量对应的平行多面体了，所以 这个放大倍数自然就是列向量对应的平行多面体有向体积 了！

综上，我们从线性变换图像的角度，直观解释了行列式的两个意义！他们是一致且直观的！

矩阵的逆

有了前面的图像，矩阵的逆就很好解释了，就是逆映射嘛。但是在矩阵这个特殊场景下，还有一些其他更有意思的图像理解。

对于可逆方阵A，$y = A x$表示将向量x通过矩阵A变换到y。如果已知y求x，那么就是求逆$x = A^{-1} y$。这个求逆过程可以看做将向量y按照A的列向量展开求对应的系数，也就是用A的列向量作为基向量求对应的坐标！

对于一般矩阵，会有所谓的伪逆。上述线性方程可能无解，可以通过求解最优化问题

\[\min ||Ax - y||^2\]

得到最佳x。上述优化问题可以看做用A的列向量来表达y，但是y不在A的列向量所张成的空间中，所以无法精确表达。所以可以先将y投影到A的列向量所张成的空间中，然后求解

\[Ax = P_A y\]

$P_A$ 是到A列空间投影操作，上述方程可以看做向量y投影到A的列空间中，然后以A的列向量为基得到的坐标为x！

泛函分析

泛函分析（Functional Analysis）是现代数学的一个分支，隶属于分析学，其研究的主要对象是函数构成的空间。

泛函分析是由对函数的变换（如傅立叶变换等）性质的研究和对微分方程以及积分方程的研究发展而来的。
使用泛函作为表述源自变分法，代表作用于函数的函数。

巴拿赫（Stefan Banach）是泛函分析理论的主要奠基人之一，而数学家兼物理学家维多·沃尔泰拉（Vito Volterra）对泛函分析的广泛应用有重要贡献。

泛函分析与SVM

线性不可分的情况下，SVM通过某种事先选择的非线性映射（核函数）将输入变量映到一个高维特征空间，将其变成在高维空间线性可分，在这个高维空间中构造最优分类超平面。其中，核函数的理论根基是mercer定理，映射后，希尔伯特空间转到再生希尔伯特空间，直接基于后者运算就线性可分了，这些是泛函分析里的概念

线性代数与矩阵论-Linear Algebra and Matrix

线性代数与矩阵

历史

九章算术

凯莱