分形几何
分形几何学的基本思想:
- 客观事物具有自相似性的层次结构,局部和整体在形态,功能,信息,时间,空间等方面具有统计意义上的相似性,称为自相似性,自相似性是指局部是整体成比例缩小的性质。
分形理论
自然界的很多事物,例如树木、云彩、山脉、闪电、雪花以及海岸线等等都呈现出传统的几何学不能描述的形状。这些形状都有如下的特性:
- 有着十分精细的不规则的结构
- 整体与局部相似,例如一根树杈的形状和一棵树很像 分形几何学就是用来研究这样一类的几何形状的科学,借助计算机的高速计算和图像显示,使得我们可以更加深入地直观地观察分形几何。
视频
- 【PBS纪录片】寻找隐藏的维度
- 维度-数学漫步系列视频:二维
- 【官方双语】分形并不一定自相似
分形维
维度缺乏正式的定义是个问题
康托尔认为线段、正方形和立方体中的点集必须具有不同的势,就像一条10个点的线、一个10×10的点网格和一个10×10×10的点立方体有不同数量的点。然而,在1877年,他发现线段中的点与正方形(以及所有维度的立方体)中的点之间存在一一对应关系,这表明它们具有相同的势。凭借直觉,他证明了尽管维度不同,线、正方形和立方体都具有相同数量的无穷小的点。
康托尔意识到这一发现威胁到n维空间需要n个坐标来描述的直觉观念,因为n维立方体中的每个点都可以由一段区间中的一个数字唯一标识。因此,从某种意义上说,这些高维立方体相当于一维线段。然而,正如戴德金指出的那样,康托尔的函数是极不连续的——它本质上是将一条线段分成无限多个部分,然后将它们重新组合成一个立方体。
1890年,朱塞佩·皮亚诺 (Giuseppe Peano) 发现,可以将一维曲线缠绕得如此紧密且连续,以至于可以填充二维正方形中的每个点。这是第一条空间填充曲线(space-filling curve)。
数学家需要证明维度是一个真实的概念。例如,当n≠ m时,n维和m维欧几里得空间的某些基本性质是不同的。这个目标被称为“维度不变性”(invariance of dimension)问题。
终于,1912年,在康托尔的发现之后将近半个世纪,多次证明维数不变性的尝试失败之后,布劳威尔(L.E.J. Brouwer)使用自己创造方法取得了成功。从本质上讲,他证明了不可能将一个更高维的物体放入较低维度的空间中,以及在不将物体分成许多部分(如康托尔所做的那样)、不允许物体与自身相交(如皮亚诺所做的那样)的情况下,使用较低维度的物体填满较高维度的空间。此外,大约在这个时候,布劳威尔等人给出了各种严格的定义,例如,可以根据球在n维空间中的边界是n-1维这一事实,帮助归纳地确定维数。
尽管布劳威尔的工作将维度概念置于强大的数学基础上,但它无助于增强我们对高维空间的直觉:对3维空间的熟悉太容易使我们误入歧途。正如托马斯·班乔夫 (Thomas Banchoff) 所写,“我们所有人都是对自己所在维度存有偏爱的奴隶。”
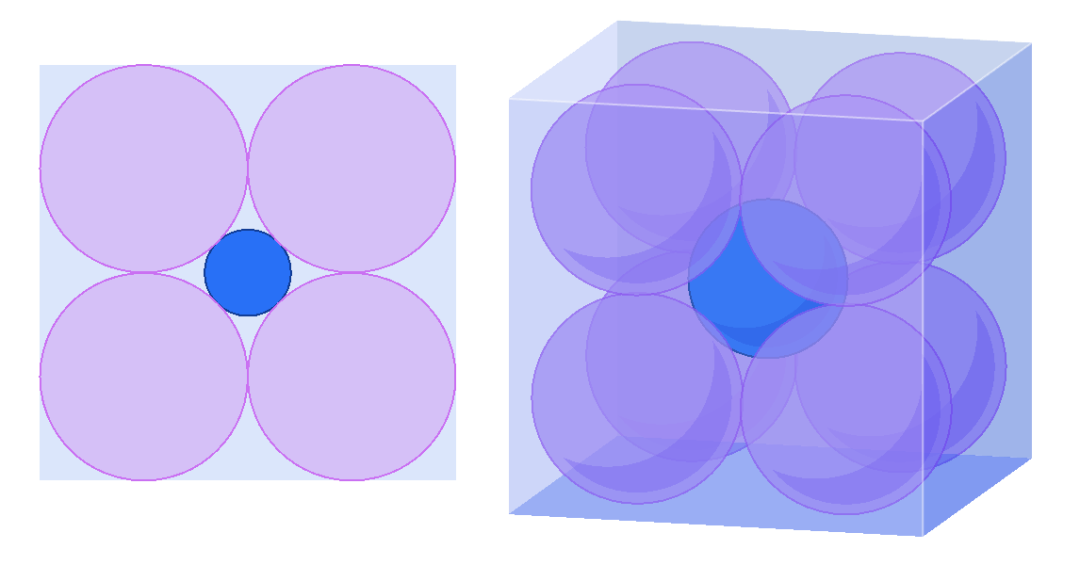
例如,假设我们将2n个半径为1的球体放置在边长为4的n维立方体中,然后将另一个球体放置在与它们中心相切的位置。随着n增加,中心球体的大小随之增加——它的半径为√n -1。但是,令人震惊的是,当n≥10时,这个球体会伸出立方体的边。中心球体随着维度的增加而变大,最终会突出到立方体外面。
高维空间中令人惊讶的现实导致统计和数据分析出现问题,统称为“维数灾难”(curse of dimensionality)。许多统计方法所需的样本点数量随维度增加呈指数增长。此外,随着维度增加,点形成聚类的概率会降低。因此,找到为高维数据降维的方法十分重要。
维度的故事并没有因为布劳威尔而终结。仅仅几年之后,费利克斯·豪斯多夫(Felix Hausdorff)提出了一个新的维度定义,之后的数学发展证明该定义对现代数学至关重要。
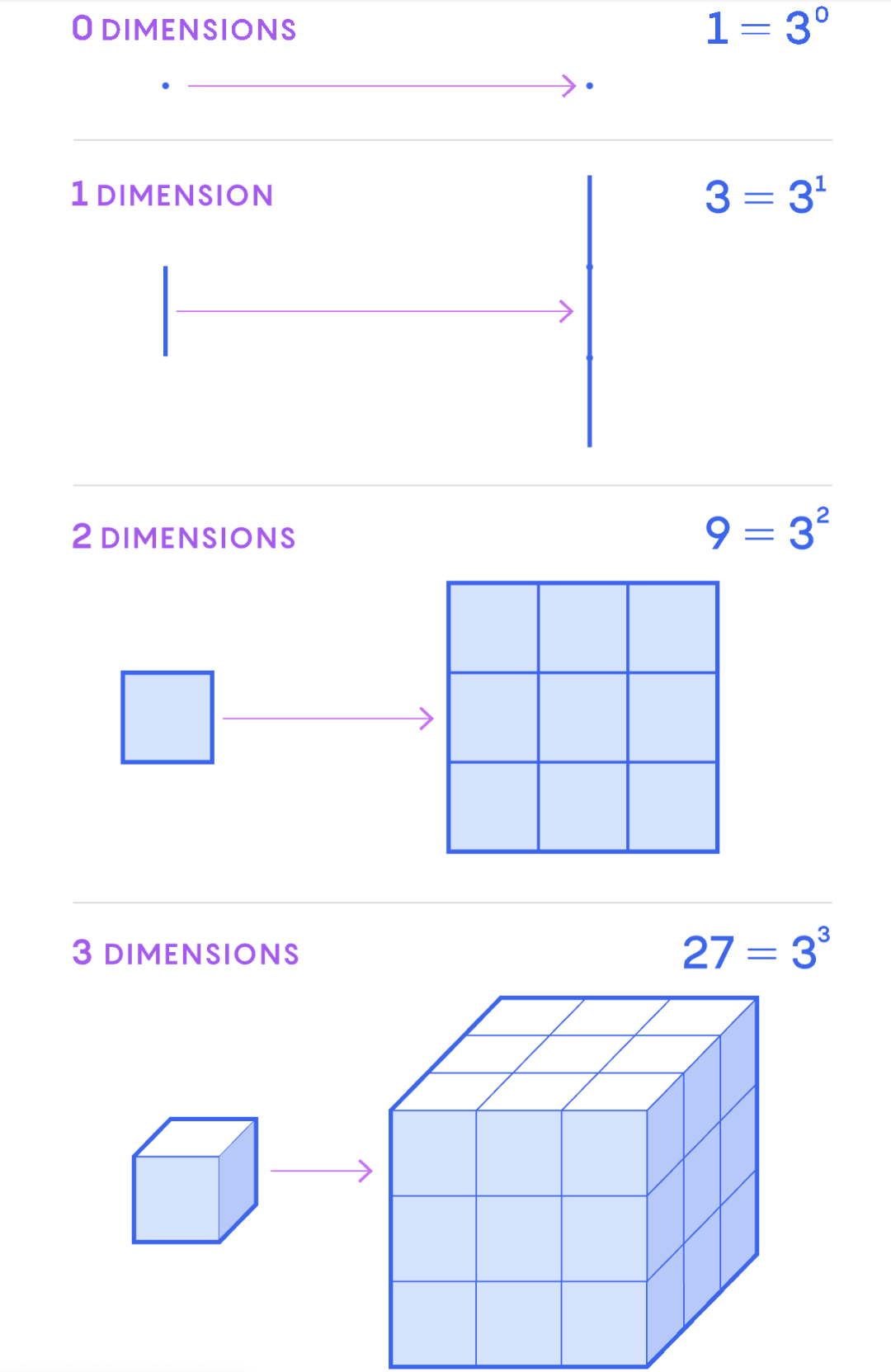
考虑维度的一种直观方式是,如果我们将d维物体均匀地缩放或放大k倍,它的大小会增加到kd倍。假设我们将一个点、一条线段、一个正方形和一个立方体放大3倍,点的尺寸不变(3^0=1),线段变成3倍(3^1=3),正方形变成9倍 (3^2=9),立方体变成27倍 (3^3=27)。
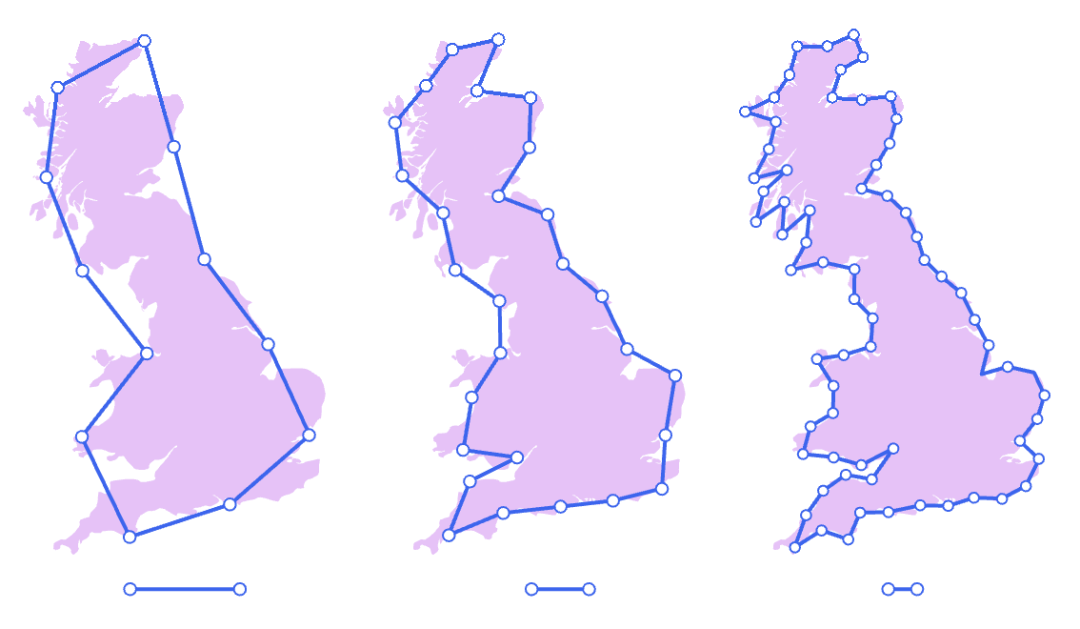
豪斯多夫定义的一个令人惊讶的结果是,物体可能具有非整数维度。几十年后,当伯努瓦·曼德尔布罗特(Benoit B. Mandelbrot)问道:“不列颠的海岸有多长?”时,结果证明非整数维度正是他所需要的。海岸线如此参差不齐,以至于无法用任何尺子精确测量——尺子越短,测量结果越大越精确。曼德尔布罗特认为,豪斯多夫维数提供了一种量化这种锯齿状海岸线的方法,并在 1975 年提出了术语“分形”来描述这种无限复杂的形状。
以迭代方式生成的科赫曲线(Koch curve)。我们从线段开始。在每个阶段,我们删除每个线段的中间三分之一,并用与删除的线段长度相等的两个线段替换它,无限次地重复此过程以获得科赫曲线。仔细研究它,你会发现它包含4个与整个曲线相同但大小只有三分之一的部分。因此,如果我们将这条曲线缩放3倍,我们将获得原始曲线的4个副本。这意味着其豪斯多夫维数d满足 3d=4,因此,d=log3(4)≈1.26。科赫曲线并不像皮亚诺曲线那样完全充满空间,所以它不是二维的,但它也不是一条一维线,而是1.26 维。
参考:集智俱乐部 几何、分形与时空:跨越百年的维度定义之旅
分形的重要概念
无边的奇迹源自简单规则的无限重复。
—— 分形之父 Benoit B. Mandelbrot
自相似性(Self-similarity)
自相似是指局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性,比如树干和枝桠的自相似,大的旋涡和小旋涡的自相似等等。
无标度性(Scale-free)
所谓无标度性,是指当我们变换不同的尺度,都会发现系统还是那样,它没有变化(即自相似性),也就是标度不变性。比如我们所说的大漩涡套着小旋涡,它们发生在不同的尺度,但是却表现出相似性,这就称为无标度特性。
非线性(Nonlinear)
非线性就是和线性相对,线性是指成比例,而非线性则指输入和输出不成比例,比如抛物线就是非线性的。在复杂系统中,非线性是最重要的特性之一。
分形案例
【2021-9-1】分形几何图形绘制,参考:
【2022-8-30】计算机中要显示颜色,一般都是用R、G、B三个0-255范围内的整数来描述。
康托尔集(Cantor set)
分形的起源是康托尔集(Cantor set)。我们取一个线段,把它中间的1/3去掉得到两个分开的线段,再对剩下的两段进行相同的操作,得到4个线段,这样重复进行下去直到无穷,最后得到的图形集合就是康托尔集。
曼德勃罗集
曼德布洛特集合(Mandelbrot set),这是一种在复平面上组成分形的点的集合,以数学家伯努·瓦曼德布洛特(Benoît B. Mandelbrot)的名字命名。Mandelbrot集合与Julia集合有些相似的地方,例如他们都使用相同的复二次多项式来进行迭代。曼德布洛特集合可以用复二次多项式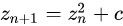 ,曼德布洛特集主要是通过固定z0=0,不断迭代c得到的,产生一组发散数列
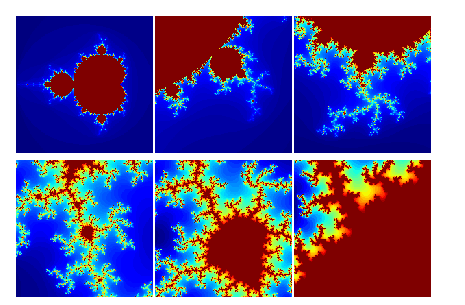
,曼德布洛特集主要是通过固定z0=0,不断迭代c得到的,产生一组发散数列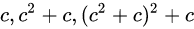 ,如果数列发散,则在二维平面内,将所有不属于集合内的点标记为黑色,属于集合内的点按照发散速度赋予不同的颜色,就可以得到经典的曼德布洛特集图像。
,如果数列发散,则在二维平面内,将所有不属于集合内的点标记为黑色,属于集合内的点按照发散速度赋予不同的颜色,就可以得到经典的曼德布洛特集图像。
Python实现
import numpy as np
import pylab as pl
import time
from matplotlib import cm
def iter_point(c):
z = c
for i in xrange(1, 100): # 最多迭代100次
if abs(z)>2: break # 半径大于2则认为逃逸
z = z*z+c
return i # 返回迭代次数
def draw_mandelbrot(cx, cy, d):
"""
绘制点(cx, cy)附近正负d的范围的Mandelbrot
"""
x0, x1, y0, y1 = cx-d, cx+d, cy-d, cy+d
y, x = np.ogrid[y0:y1:200j, x0:x1:200j]
c = x + y*1j
start = time.clock()
mandelbrot = np.frompyfunc(iter_point,1,1)(c).astype(np.float)
print "time=",time.clock() - start
pl.imshow(mandelbrot, cmap=cm.jet, extent=[x0,x1,y0,y1])
pl.gca().set_axis_off()
x,y = 0.27322626, 0.595153338
pl.subplot(231)
draw_mandelbrot(-0.5,0,1.5)
for i in range(2,7):
pl.subplot(230+i)
draw_mandelbrot(x, y, 0.2**(i-1))
pl.subplots_adjust(0.02, 0, 0.98, 1, 0.02, 0)
pl.show()
C语言实现
- 计算机中要显示颜色,一般都是用R、G、B三个0-255范围内的整数来描述。
- 用三段 140 字符以内的代码生成一张 1024×1024 的图片
- 更多效果图及代码:Tweetable Mathematical Art
- 知乎专题:有没有一段代码,让你为人类的智慧击节叫好?
// NOTE: compile with g++
// g++ create_image.cpp -o generate --std=c++11
#include <iostream>
#include <cmath>
#include <cstdlib>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // square
#define _cb(x) abs((x)*(x)*(x)) // absolute value of cube
#define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // cube root
unsigned char GR(int,int);
unsigned char BL(int,int);
// 曼德勃罗集合
unsigned char RD(int i,int j){
// Red 红色
float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}
return log(k)*47;
}
unsigned char GR(int i,int j){
// Green 绿色
float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}
return log(k)*47;
}
unsigned char BL(int i,int j){
// Blue 蓝色
float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}
return 128-log(k)*23;
}
// 波纹生成
unsigned char RD(int i,int j){
#define P 6.03
float s=3./(j+250),y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127;}
unsigned char GR(int i,int j){
float s=3./(j+250);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;
return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127;}
unsigned char BL(int i,int j){
float s=3./(j+250);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;
return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127;}
void pixel_write(int,int);
FILE *fp;
int main(){ // 图片生成主函数
//fp = fopen("test.png","wb");
char file_name[] = "new.png";
fp = fopen(file_name, "wb");
//fp = fopen("MathPic.ppm","wb"); // PPM 图片可以使用 ps 打开
printf("创建图片文件:%s\n", file_name);
fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM);
for(int j=0;j<DIM;j++)
for(int i=0;i<DIM;i++)
pixel_write(i,j);
fclose(fp);
printf("图片生成完毕...请打开文件%s查看\n", file_name);
return 0;
}
void pixel_write(int i, int j){
static unsigned char color[3];
color[0] = RD(i,j)&255;
color[1] = GR(i,j)&255;
color[2] = BL(i,j)&255;
fwrite(color, 1, 3, fp);
}
Julia 集合
Julia集 和 Mandelbrot 集具有相同的数学表示形式,唯一的不同是,Julia集是通过固定c,不断迭代,计算z的值得到的,产生一组发散序列 
同理,将所有不属于集合内的点标记为黑色,属于 集合内的点按照发散速度赋予不同的颜色,会得到不同的Julia集图像。
C语言实现
- 计算机中要显示颜色,一般都是用R、G、B三个0-255范围内的整数来描述。
- 用三段 140 字符以内的代码生成一张 1024×1024 的图片
// NOTE: compile with g++
// g++ create_image.cpp -o generate --std=c++11
#include <iostream>
#include <cmath>
#include <cstdlib>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // square
#define _cb(x) abs((x)*(x)*(x)) // absolute value of cube
#define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // cube root
unsigned char GR(int,int);
unsigned char BL(int,int);
// julia 集合
unsigned short red_fn(int i, int j){
#define D(x) (x-DIM/2.)/(DIM/2.)
float x=D(i),y=D(j),X,Y,n=0;while(n++<200&&(X=x*x)+(Y=y*y)<4){x=X-Y+.36237;y=2*x*y+.32;}return log(n)*256;}
unsigned short green_fn(int i, int j){
float x=D(i),y=D(j),X,Y,n=0;while(n++<200&&(x*x+y*y)<4){X=x;Y=y;x=X*X-Y*Y+-.7;y=2*X*Y+.27015;}return log(n)*128;}
unsigned short blue_fn(int i, int j){
float x=D(i),y=D(j),X,Y,n=0;while(n++<600&&(x*x+y*y)<4){X=x;Y=y;x=X*X-Y*Y+.36237;y=2*X*Y+.32;}return log(n)*128;}
void pixel_write(int,int);
FILE *fp;
int main(){ // 图片生成主函数
//fp = fopen("test.png","wb");
char file_name[] = "new.png";
fp = fopen(file_name, "wb");
//fp = fopen("MathPic.ppm","wb");
printf("创建图片文件:%s\n", file_name);
fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM);
for(int j=0;j<DIM;j++)
for(int i=0;i<DIM;i++)
pixel_write(i,j);
fclose(fp);
printf("图片生成完毕...请打开文件%s查看\n", file_name);
return 0;
}
void pixel_write(int i, int j){
static unsigned char color[3];
color[0] = RD(i,j)&255;
color[1] = GR(i,j)&255;
color[2] = BL(i,j)&255;
fwrite(color, 1, 3, fp);
}
科赫曲线 Koch curve
科赫曲线(Koch curve)是一种神奇的曲线,因为形态跟雪花很像,所以也称为科赫雪花,最早出现在海里格·冯·科赫(Helge von Koch)的论文中,通过下面这个动图,你知道科赫雪花是如何形成的吗?
- 第一步:画一个等边三角形,并把每一边三等分;
- 第二步:取三等分后的一边中间一段为边向外作正三角形,并把这“与主三角形靠近的一边”擦掉;
- 第三步:重复上述步骤,画出更小的三角形;
- 第四步:一直重复。
由上述步骤所画出的曲线叫做科赫曲线(Koch curve)。
谢尔宾斯基三角形 Sierpinski triangle
一个平面三角形的维度是二维的,但是在分形几何中,三角形有不同的维度计算方法。谢尔宾斯基三角形(Sierpinski triangle)也是一种分形典型示例,由波兰数学家谢尔宾斯基于1915年提出。它是自相似集的例子。它的豪斯多夫维数是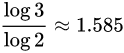
可以通过多种方法得到这个三角形,这里介绍其中的一种方法:
- 第一步:取一个实心的三角形。(多数情况下使用等边三角形);
- 第二步:沿三边中点的连线,将它分成四个小三角形;
- 第三步:去掉中间的那一个小三角形;
- 第四步:对其余三个小三角形重复步骤一。

分形树
用turtle动态绘制分形树
## 绘制分型树,末梢的树枝的颜色不同
import turtle
def draw_brach(brach_length):
if brach_length > 5:
if brach_length < 40:
turtle.color('green')
else:
turtle.color('red')
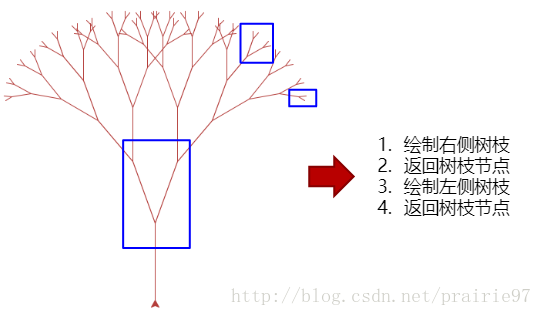
# 绘制右侧的树枝
turtle.forward(brach_length)
print('向前',brach_length)
turtle.right(25)
print('右转20')
draw_brach(brach_length-15)
# 绘制左侧的树枝
turtle.left(50)
print('左转40')
draw_brach(brach_length-15)
if brach_length < 40:
turtle.color('green')
else:
turtle.color('red')
# 返回之前的树枝上
turtle.right(25)
print('右转20')
turtle.backward(brach_length)
print('返回',brach_length)
def main():
turtle.left(90)
turtle.penup()
turtle.backward(150)
turtle.pendown()
turtle.color('red')
draw_brach(100)
turtle.exitonclick()
if __name__ == '__main__':
main()
樱花树
from turtle import *
from random import *
from math import *
def tree(n, l):
pd() # 下笔
# 阴影效果
t = cos(radians(heading() + 45)) / 8 + 0.25
pencolor(t, t, t)
pensize(n / 3)
forward(l) # 画树枝
if n > 0:
b = random() * 15 + 10 # 右分支偏转角度
c = random() * 15 + 10 # 左分支偏转角度
d = l * (random() * 0.25 + 0.7) # 下一个分支的长度
# 右转一定角度,画右分支
right(b)
tree(n - 1, d)
# 左转一定角度,画左分支
left(b + c)
tree(n - 1, d)
# 转回来
right(c)
else:
# 画叶子
right(90)
n = cos(radians(heading() - 45)) / 4 + 0.5
pencolor(n, n*0.8, n*0.8)
circle(3)
left(90)
# 添加0.3倍的飘落叶子
if(random() > 0.7):
pu()
# 飘落
t = heading()
an = -40 + random()*40
setheading(an)
dis = int(800*random()*0.5 + 400*random()*0.3 + 200*random()*0.2)
forward(dis)
setheading(t)
# 画叶子
pd()
right(90)
n = cos(radians(heading() - 45)) / 4 + 0.5
pencolor(n*0.5+0.5, 0.4+n*0.4, 0.4+n*0.4)
circle(2)
left(90)
pu()
#返回
t = heading()
setheading(an)
backward(dis)
setheading(t)
pu()
backward(l)# 退回
bgcolor(0.5, 0.5, 0.5) # 背景色
ht() # 隐藏turtle
speed(0) # 速度,1-10渐进,0最快
tracer(0, 0)
pu() # 抬笔
backward(100)
left(90) # 左转90度
pu() # 抬笔
backward(300) # 后退300
tree(12, 100) # 递归7层
done()
分形树叶

import numpy as np
import matplotlib.pyplot as pl
import time
# 蕨类植物叶子的迭代函数和其概率值
eq1 = np.array([[0,0,0],[0,0.16,0]])
p1 = 0.01
eq2 = np.array([[0.2,-0.26,0],[0.23,0.22,1.6]])
p2 = 0.07
eq3 = np.array([[-0.15, 0.28, 0],[0.26,0.24,0.44]])
p3 = 0.07
eq4 = np.array([[0.85, 0.04, 0],[-0.04, 0.85, 1.6]])
p4 = 0.85
def ifs(p, eq, init, n):
"""
进行函数迭代
p: 每个函数的选择概率列表
eq: 迭代函数列表
init: 迭代初始点
n: 迭代次数
返回值: 每次迭代所得的X坐标数组, Y坐标数组, 计算所用的函数下标
"""
# 迭代向量的初始化
pos = np.ones(3, dtype=np.float)
pos[:2] = init
# 通过函数概率,计算函数的选择序列
p = np.add.accumulate(p)
rands = np.random.rand(n)
select = np.ones(n, dtype=np.int)*(n-1)
for i, x in enumerate(p[::-1]):
select[rands<x] = len(p)-i-1
# 结果的初始化
result = np.zeros((n,2), dtype=np.float)
c = np.zeros(n, dtype=np.float)
for i in range(n):
eqidx = select[i] # 所选的函数下标
tmp = np.dot(eq[eqidx], pos) # 进行迭代
pos[:2] = tmp # 更新迭代向量
# 保存结果
result[i] = tmp
c[i] = eqidx
return result[:,0], result[:, 1], c
start = time.clock()
x, y, c = ifs([p1,p2,p3,p4],[eq1,eq2,eq3,eq4], [0,0], 100000)
time.clock() - start
pl.figure(figsize=(6,6))
pl.subplot(121)
pl.scatter(x, y, s=1, c="g", marker="s", linewidths=0)
pl.axis("equal")
pl.axis("off")
pl.subplot(122)
pl.scatter(x, y, s=1,c = c, marker="s", linewidths=0)
pl.axis("equal")
pl.axis("off")
pl.subplots_adjust(left=0,right=1,bottom=0,top=1,wspace=0,hspace=0)
pl.gcf().patch.set_facecolor("#D3D3D3")
pl.show()
Logistic Hills
效果:
unsigned char RD(int i,int j){
#define A float a=0,b,k,r,x
#define B int e,o
#define C(x) x>255?255:x
#define R return
#define D DIM
R BL(i,j)*(D-i)/D;
}
unsigned char GR(int i,int j){
#define E DM1
#define F static float
#define G for(
#define H r=a*1.6/D+2.4;x=1.0001*b/D
R BL(i,j)*(D-j/2)/D;
}
unsigned char BL(int i,int j){
F c[D][D];if(i+j<1){A;B;G;a<D;a+=0.1){G b=0;b<D;b++){H;G k=0;k<D;k++){x=r*x*(1-x);if(k>D/2){e=a;o=(E*x);c[e][o]+=0.01;}}}}}R C(c[j][i])*i/D;
}
其它分形图(分形龙、谢尔宾斯基三角等)

from math import sin, cos, pi
import matplotlib.pyplot as pl
from matplotlib import collections
class L_System(object):
def __init__(self, rule):
info = rule['S']
for i in range(rule['iter']):
ninfo = []
for c in info:
if c in rule:
ninfo.append(rule[c])
else:
ninfo.append(c)
info = "".join(ninfo)
self.rule = rule
self.info = info
def get_lines(self):
d = self.rule['direct']
a = self.rule['angle']
p = (0.0, 0.0)
l = 1.0
lines = []
stack = []
for c in self.info:
if c in "Ff":
r = d * pi / 180
t = p[0] + l*cos(r), p[1] + l*sin(r)
lines.append(((p[0], p[1]), (t[0], t[1])))
p = t
elif c == "+":
d += a
elif c == "-":
d -= a
elif c == "[":
stack.append((p,d))
elif c == "]":
p, d = stack[-1]
del stack[-1]
return lines
rules = [
{
"F":"F+F--F+F", "S":"F",
"direct":180,
"angle":60,
"iter":5,
"title":"Koch"
},
{
"X":"X+YF+", "Y":"-FX-Y", "S":"FX",
"direct":0,
"angle":90,
"iter":13,
"title":"Dragon"
},
{
"f":"F-f-F", "F":"f+F+f", "S":"f",
"direct":0,
"angle":60,
"iter":7,
"title":"Triangle"
},
{
"X":"F-[[X]+X]+F[+FX]-X", "F":"FF", "S":"X",
"direct":-45,
"angle":25,
"iter":6,
"title":"Plant"
},
{
"S":"X", "X":"-YF+XFX+", "Y":"+XF-YFY-FX+",
"direct":0,
"angle":90,
"iter":6,
"title":"Hilbert"
},
{
"S":"L--F--L--F", "L":"+R-F-R+", "R":"-L+F+",
"direct":0,
"angle":45,
"iter":10,
"title":"Sierpinski"
},
]
def draw(ax, rule, iter=None):
if iter!=None:
rule["iter"] = iter
lines = L_System(rule).get_lines()
linecollections = collections.LineCollection(lines)
ax.add_collection(linecollections, autolim=True)
ax.axis("equal")
ax.set_axis_off()
ax.set_xlim(ax.dataLim.xmin, ax.dataLim.xmax)
ax.invert_yaxis()
fig = pl.figure(figsize=(7,4.5))
fig.patch.set_facecolor("papayawhip")
for i in xrange(6):
ax = fig.add_subplot(231+i)
draw(ax, rules[i])
fig.subplots_adjust(left=0,right=1,bottom=0,top=1,wspace=0,hspace=0)
pl.show()
混沌
什么是混沌
什么是混沌分形理论?详见混沌分形理论
- 首先,混沌是指现实世界中存在的一种貌似混乱无序的复杂运动形态。但混沌不表示混乱,它是“一种更高层次的次序”。混沌的背后拥有精细的结构,这种精细的结构具有自相似性,称为分形。
- 其次,复杂的事物都有简单的开始,一颗大树分解后就是一个个树杈,股市分解后就是一涨一跌,大道至简,复杂的事物由基本的分形迭代演化而成,部分和整体自相似,这就是分形,一颗大树是由无数的树杈叠加构成,从微观上看,这颗大树就是一大堆基本粒子,处于混沌态,但在树杈的基本分形规则之下构成大树。更微观上说,树杈的结构是遗传密码决定的,基因组排序不同,构成的生物也不同。为何会有这样的基因排序,因为这是生物长期自然选择进化的结果,植物生长靠吸收阳光获取能量,树杈的结构能以最小的阻力最快的速度接近阳光,吸收更多的光能,利于生存竞争和基因传承,吸收的能量大于耗散的能量,能量差为正,就是不断长大的过程,能量差为负,吸收小于耗散,就是不断衰老过程,直至能量差消失,回归平衡。
- 最后,分形理论与混沌理论同属非线性理论,是从不同的角度同时表达的对动态复杂系统的研究。
混沌分形理论具有三项主要原则
- 第一项,宇宙中的每个事物遵循最小阻力途径;
- 第二项,最小阻力途径由潜在并通常不可见的结构所决定;
- 第三项,这种潜在并通常不可见的结构能够被发现并能够改变。
【2022-11-5】混沌理论还有一个是发展特征,其有三个原则:
- 1、能量永远会遵循阻力最小的途径。
- 2、始终存在着通常不可见的根本结构,这个结构决定阻力最小的途径。
- 3、这种始终存在而通常不可见的根本结构,不仅可以被发现,而且可以被改变。
混沌案例
洛伦兹混沌吸引子

logistic映射
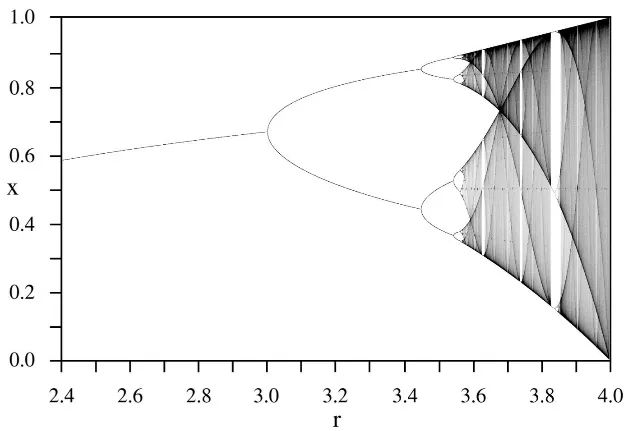
双摆
元胞自动机
介绍
元胞自动机(cellular automata) 是离散而抽象的计算系统。元胞自动机在时间和空间上是离散的,最小单位是简单元胞(单元格)。每个元胞会产生有限数量的状态集,后续元胞由其邻域元胞的状态确定。这里所说的领域元胞,是指当前元胞的前一个元胞(记作元胞A)以及元胞A左右两个元胞。也就是说,邻域元胞总共包含三个元胞。给定初始层的状态,基于一定规则,我们可以不断更新下一层元胞的状态。通俗的讲,元胞自动机就是基于一定规则的“繁衍机器”。
示例
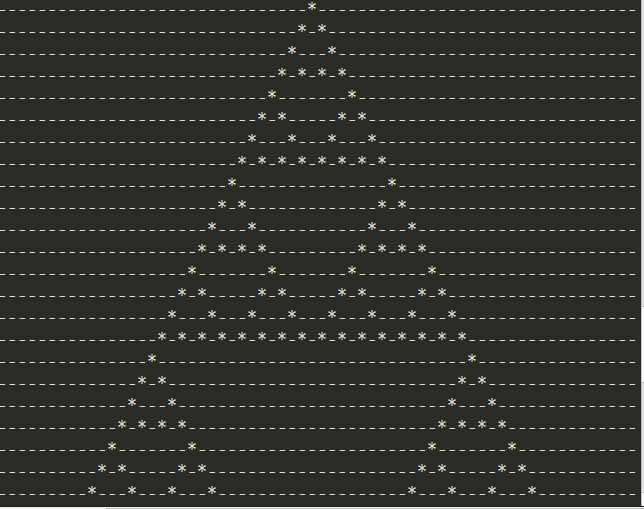
import time
def print_seq(seq, speed=0.5):
for item in seq:
if item:
print('*', end='')
else:
print('-', end='')
print('')
time.sleep(speed)
class Cell:
def __init__(self, deepth=31):
self.ca = [0 if i != 31 else 1 for i in range(64)]
self.ca_new = []
self.deepth = deepth
def process(self):
print_seq(self.ca)
for i in range(self.deepth):
self._rule()
print_seq(self.ca_new)
self.ca = self.ca_new
self.ca_new = []
def _rule(self):
for i in range(64):
if 0 < i < 63:
if self.ca[i - 1] == self.ca[i + 1]:
self.ca_new.append(0)
else:
self.ca_new.append(1)
elif i == 0:
if self.ca[1]:
self.ca_new.append(1)
else:
self.ca_new.append(0)
else:
if self.ca[62]:
self.ca_new.append(1)
else:
self.ca_new.append(0)
def main():
cell = Cell()
cell.process()
if __name__ == '__main__':
main()
图灵斑图
【2021-9-24】图灵YYDS!60年前不被看好的理论再次被证,这次是原子层面的
你以为,斑马的黑白条纹,贝壳的复杂花纹,都只是随便长长?并不!
这些自然界的重复图案,有相当一部分能用一组方程式描述。听上去有些离谱,但确实是图灵本人搞出来的——60年前,他对大自然进行一番研究后,给出了这组方程式。

- 公式认为,任何重复的自然图案,都是通过两种具有特定特征的事物(如分子、细胞)进行相互作用而产生的。
- 两种事物的特定特征为:速度不同、能在空间内传播、其中一种是催化剂。这种催化剂,能自动激活、并随后产生抑制剂,使得它比催化剂的传播速度更快,导致催化剂中途停止,最终生成相应的图案。
- 只需要对反应扩散方程的不同条件进行约束,这两种事物,就能自发地组成斑纹、条纹、环纹、螺旋或斑点等图案。 这组方程式适用于不少自然界的图案,包括斑马、贝壳、鱼类、豹的条纹等。他们给这类图案统一起了个名字,叫图灵斑图 (turing pattern).但无论是斑马、豹、贝壳还是鱼类,基本都属于宏观尺度的图案,微观尺度上的图灵斑图研究少之又少。现在,来自斯坦福等高校的科学家终于发现,一种晶体生长的微观纹路,也可以用图灵斑图来描述,这种晶体名叫铋,它在特殊条件下的原子生长模式,与图灵方程式预测的形态非常相似,目前研究成果已经刊登到Nature Physics上。仅凭一组公式预测图案的图灵,60年后再次跨越了微观和宏观的界限。





 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
