- 聚类算法
- 聚类效果评估
- sklearn聚类算法
- 案例
- 结束
聚类算法
聚类 vs 分类
机器学习三大最常见任务:
- 回归方法
- 分类方法
- 聚类方法
分类与聚类的比较
分类:有训练数据,且训练数据包含输入和输出(有监督学习),已知分类的类别(即训练数据的输出)。学习出一个模型,用该模型对未分好类(预测数据)的数据进行预测分类(已知的类别中)。聚类:训练数据只有输入(无监督学习)。- 训练过程即预测过程(聚类过程),且不知道类别,甚至不知道有多少个类别,类别的数量需要指定(K-means),也可以直接通过算法学习出来(DBSCAN)。只能通过特征的相似性对样本分类。该过程即聚类。
聚类分析是研究如何在没有训练的条件下把样本划分为若干类。
在分类中,对于目标数据库中存在哪些类是知道的,将每一条记录分别属于哪一类标记出来。
聚类需要解决的问题是将已给定的若干无标记的模式聚集起来使之成为有意义聚类
- 聚类是在预先不知道目标数据库到底有多少类的情况下,希望将所有的记录组成不同的类或者说聚类,并且使得在这种分类情况下,以某种度量(例如:距离)为标准的相似性,在同一聚类之间最小化,而在不同聚类之间最大化。
- 与分类不同,
无监督学习不依赖预先定义的类或带类标记的训练实例,需要由聚类学习算法自动确定标记,而分类学习的实例或数据样本有类别标记。
p(y|x)与p(z|x)的区别,z是latent variable,y是label
聚类介绍
【2021-11-12】聚类分析(超全超详细版)
聚类分析是一种典型的无监督学习(分类是有监督学习), 用于对未知类别的样本进行划分,将它们按照一定的规则划分成若干个类族,把相似(距高相近)的样本聚在同一个类簇中, 把不相似的样本分为不同类簇,从而揭示样本之间内在的性质以及相互之间的联系规律
聚类分析是根据在数据中发现的描述对象及其关系的信息,将数据对象分组。目的是组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。组内相似性越大,组间差距越大,说明聚类效果越好。也就是说,聚类的目标是得到较高的簇内相似度和较低的簇间相似度,使得簇间的距离尽可能大,簇内样本与簇中心的距离尽可能小
- 简而言之,同类相近,异类相远
聚类得到的簇可以用聚类中心、簇大小、簇密度和簇描述等来表示
- 聚类中心是一个簇中所有样本点的均值(质心)
- 簇大小表示簇中所含样本的数量
- 簇密度表示簇中样本点的紧密程度
- 簇描述是簇中样本的业务特征
聚类过程
聚类的过程
- 数据准备:包括特征标准化和降维;
- 特征选择:从最初的特征中选择最有效的特征,并将其存储于向量中;
- 特征提取:通过对所选择的特征进行转换形成新的突出特征;
- 聚类(或分组):首先选择合适特征类型的某种距离函数(或构造新的距离函数)进行接近程度的度量,而后执行聚类或分组;
- 聚类结果评估:是指对聚类结果进行评估,评估主要有3种:外部有效性评估、内部有效性评估和相关性测试评估
良好聚类算法的特征
- 良好的可伸缩性
- 处理不同类型数据的能力
- 处理噪声数据的能力
- 对样本顺序的不敏感性
- 约束条件下的表现
- 易解释性和易用性
聚类算法
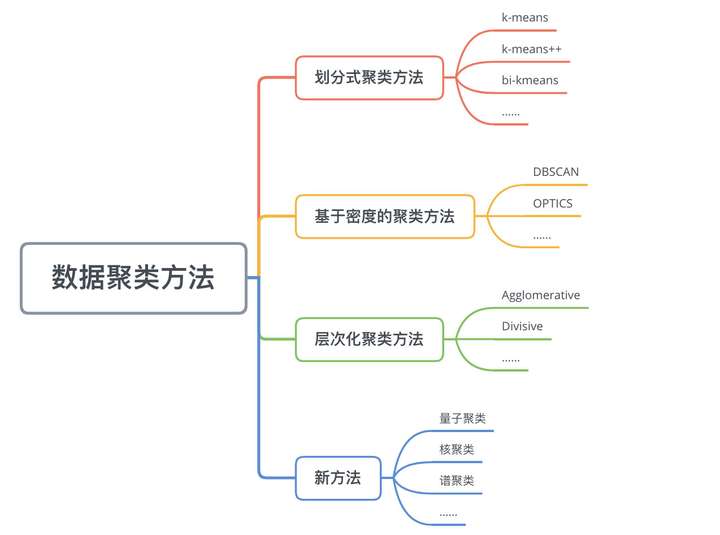
数据聚类方法主要可以分为:划分式聚类方法(Partition-based Methods)、基于密度的聚类方法(Density-based methods)、层次化聚类方法(Hierarchical Methods)等。
聚类的分类
- 基于划分的聚类(
k‐均值算法、k‐medoids算法、k‐prototype算法) - 基于层次的聚类
- 基于密度的聚类(
DBSCAN算法、OPTICS算法、DENCLUE算法) - 基于网格的聚类
-
基于模型的聚类(模糊聚类、Kohonen神经网络聚类)
总结
聚类算法对比总结, sklearn Overview of clustering methods,知乎
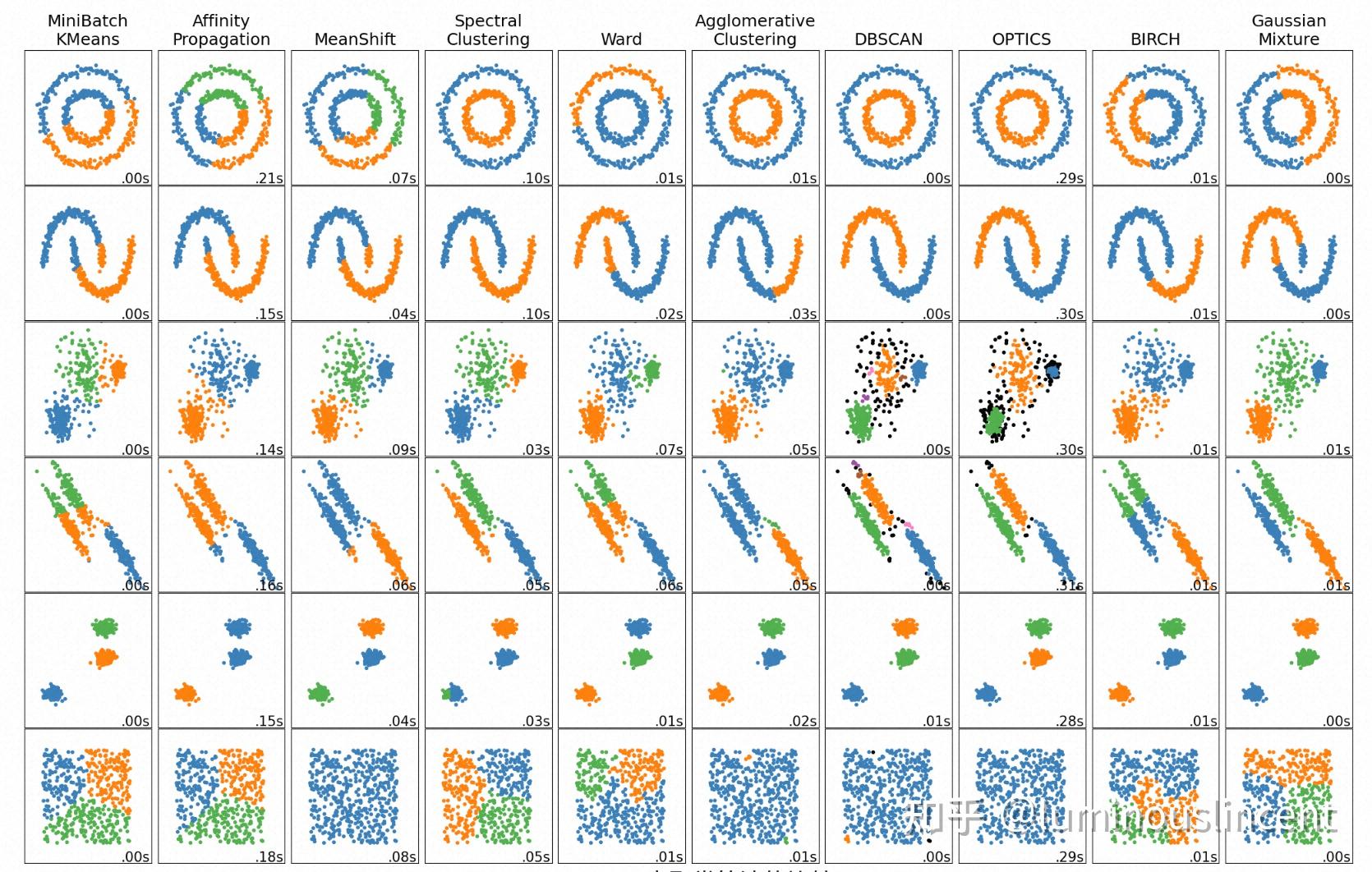

- 任意形状聚类: 谱聚类(
Spectral Clustering)、密度聚类(DBSCAN/HDBSCAN/OPTICS)- 谱聚类: 不适合密集平面集, 不会识别噪声点, 需要指定聚类数目
- 密度聚类: 整体效果最好,
HDBSCAN/OPTICS, 需要指定最小成员数/近邻数
- 凸集聚类
| 聚类算法 | 类别 | 是否提前指定类簇 | 使用数据 | |
|---|---|---|---|---|
| kmeans | 质心聚类 | 需要 | 大样本、计算快 | |
| even cluster size | 非球形簇、初始簇心影响大 | |||
| meanshift | 质心聚类 | 不需要 | uneven cluster size | 初始参数敏感 |
| Agglomerative clustering | 层次聚类 | 不需要 | 可提供连接约束 | 初始值敏感 |
| Affinity Propagation | 图论 | 不需要 | 能处理非凸形状簇 | |
| uneven cluster size | 计算复杂度高、对于噪声点和离群点的处理能力弱 | |||
| DBSCAN | 密度聚类 | 不需要 | uneven cluster sizes | |
| OPTICS | 密度聚类 | 不需要 | uneven cluster sizes,相比dbscan可以识别可变的cluster density | |
| Spectral clustering | 谱聚类 | 需要 | even cluster size | |
| Gaussian mixtures | 模型聚类 | |||
算法选择要点
- 类簇数量
- 已知类簇数量较少:适用kmeans、谱聚类
- 样本数量
- 基于密度的聚类、kmeans均需要较大的样本量(k),谱聚类需要较中等的样本量(0.1k)
- 类簇平衡度
- kmeans、谱聚类 需要聚类size均衡
- 基于密度的聚类、meanshift可以处理不均衡的聚类,但是对需要对初始参数做详细调节
- 数据分布几何
- 上图可以看到kmeans,Affinity propagation,层次聚类、meanshift对非凸数据处理不佳
【2023-12-15】总结知名聚类算法
基于划分的聚类
划分式聚类方法需要事先指定簇类的数目或者聚类中心,通过反复迭代,直至最后达到”簇内的点足够近,簇间的点足够远”的目标。经典的划分式聚类方法有k-means及其变体k-means++、bi-kmeans、kernel k-means等。
K-means聚类- K-means:基于质心
- 聚类效果示意:

- K-means++聚类:k-modes 用简单匹配来度量相似度
- 拓展:KNN和K-means的不同
- K-means算法把一个数据集分割成簇,使得形成的簇是同构的,每个簇里的点相互靠近。该算法试图维持这些簇之间有足够的可分离性。由于无监督的性质,这些簇没有任何标签。
- KNN算法尝试基于其k(可以是任何数目)个周围邻居来对未标记的观察进行分类。它也被称为懒惰学习法,因为它涉及最小的模型训练。因此,它不用训练数据对未看见的数据集进行泛化
- K-means:基于质心
k‐medoids算法- K-means对噪声敏感,k‐medoids 算法将质心替换成中心点解决了噪声问题
- PAM算法:
- k‐medoids聚类的一种典型实现是围绕中心点划分(Partitioning Around Mediods, PAM)算法 。PAM 算法中簇的中心点是一个真实的样本点而不是通过距离计算出来的中心。PAM算法与k均值一样,使用贪心策略来处理聚类过程
- CLARA算法:大数据
- CLARA(Clustering LARge Applications)是应用于大规模数据的聚类,它弥补了k-mediod / PAM算法只能应用于小规模数据的缺陷。
- CLARANS算法:综合PAM和CLARA优点
- CLARANS算法是在CLARA的基础上发展而来的,在CLARA确定中心之后,按照PAM中的方法,在子集上选取一个与当前中心x(Medoid)不一样的对象y(New Medoid),计算用y(New Medoid)替换x(Medoid)后绝对误差是否下降,下降则替换否则不变,重复一定的次数后,我们可以认为此时的中心点为局部中心最优解;整体数据集所有子集均重复m次后,得出的中心点为全局局部最优解。CLARANS算法融合了PAM和CLARA两者的优点,是第一个用于空间数据库的聚类算法。除了这个算法,还有CLARANS+算法
k‐prototype算法- K-prototype是处理混合属性聚类的典型算法。它继承K-means算法和K-modes算法的思想,适用于数值类型与字符类型集合的数据。
总结基于划分的几种算法
k-means:是一种典型的划分聚类算法,它用一个聚类的中心来代表一个簇,即在迭代过程中选择的聚点不一定是聚类中的一个点,该算法只能处理数值型数据k-modes:K-Means算法的扩展,采用简单匹配方法来度量分类型数据的相似度k-prototypes:结合了K-Means和K-Modes两种算法,能够处理混合型数据k-medoids:在迭代过程中选择簇中的某点作为聚点,PAM是典型的k-medoids算法CLARA:CLARA算法在PAM的基础上采用了抽样技术,能够处理大规模数据CLARANS:CLARANS算法融合了PAM和CLARA两者的优点,是第一个用于空间数据库的聚类算法PCM:模糊集合理论引入聚类分析中并提出了PCM模糊聚类算法
基于层次的聚类
- 自底向上的聚合聚类
- AGNES
- BIRCH(平衡迭代削减聚类法)
- CURE算法(使用代表点的聚类法)
- ROCK(A Hierarchical ClusteringAlgorithm for Categorical Attributes)——离散数据
总结基于划分的几种算法
CURE:采用抽样技术先对数据集D随机抽取样本,再采用分区技术对样本进行分区,然后对每个分区局部聚类,最后对局部聚类进行全局聚类ROCK:也采用了随机抽样技术,该算法在计算两个对象的相似度时,同时考虑了周围对象的影响CHEMALOEN(变色龙算法):首先由数据集构造成一个K-最近邻图Gk ,再通过一个图的划分算法将图Gk 划分成大量的子图,每个子图代表一个初始子簇,最后一个凝聚的层次聚类算法反复合并子簇,找到真正的结果簇SBAC:SBAC算法则在计算对象间相似度时,考虑了属性特征对于体现对象本质的重要程度,对于更能体现对象本质的属性赋予较高的权值BIRCH:BIRCH算法利用树结构对数据集进行处理,叶结点存储一个聚类,用中心和半径表示,顺序处理每一个对象,并把它划分到距离最近的结点,该算法也以作为其他聚类算法的预处理过程BUBBLE:BUBBLE算法则把BIRCH算法的中心和半径概念推广到普通的距离空间BUBBLE-FM:BUBBLE-FM算法通过减少距离的计算次数,提高了BUBBLE算法的效率
基于密度的聚类
DBSCAN算法WS-DBSCAN算法:提高DBSCAN的算法效率,同时保证聚类精度MDCA算法(密度最大值聚类算法)- MDCA(Maximum Density Clustering Application)算法基于密度的思想引入划分聚类中,使用密度而不是初始点作为考察簇归属情况的依据,能够自动确定簇数量并发现任意形状的簇。另外MDCA一般不保留噪声,因此也避免了阈值选择不当情况下造成的对象丢弃情况。
- MDCA算法的基本思路是寻找最高密度的对象和它所在的稠密区域
总结基于密度的几种算法
DBSCAN:DBSCAN算法是一种典型的基于密度的聚类算法,该算法采用空间索引技术来搜索对象的邻域,引入了“核心对象”和“密度可达”等概念,从核心对象出发,把所有密度可达的对象组成一个簇GDBSCAN:算法通过泛化DBSCAN算法中邻域的概念,以适应空间对象的特点OPTICS:OPTICS算法结合了聚类的自动性和交互性,先生成聚类的次序,可以对不同的聚类设置不同的参数,来得到用户满意的结果FDC:FDC算法通过构造k-d tree把整个数据空间划分成若干个矩形空间,当空间维数较少时可以大大提高DBSCAN的效率
基于网格的聚类(gird-based methods)
基于划分和层次聚类方法都无法发现非凸面形状的簇,真正能有效发现任意形状簇的算法是基于密度的算法,但基于密度的算法一般时间复杂度较高,1996年到2000年间,研究数据挖掘的学者们提出了大量基于网格的聚类算法,网格方法可以有效减少算法的计算复杂度,且同样对密度参数敏感。
基于网格的聚类通常将数据空间划分成有限个单元的网格结构,所有的处理都是以单个的单元为对象。这样做起来处理速度很快,因为这与数据点的个数无关,而只与单元个数有关。代表算法有:STING,CLIQUE,WaveCluster。
- STING:基于网格多分辨率,将空间划分为方形单元,对应不同分辨率
- CLIQUE:结合网格和密度聚类的思想,子空间聚类处理大规模高维度数据
- WaveCluster:用小波分析使簇的边界变得更加清晰
这些算法用不同的网格划分方法,将数据空间划分成为有限个单元(cell)的网格结构,并对网格数据结构进行了不同的处理,但核心步骤是相同的:
- 1、 划分网格
- 2、 使用网格单元内数据的统计信息对数据进行压缩表达
- 3、 基于这些统计信息判断高密度网格单元
- 4、 最后将相连的高密度网格单元识别为簇
网格聚类算法对比
更多资料
总结基于网格的几种算法
- STING:利用网格单元保存数据统计信息,从而实现多分辨率的聚类
- WaveCluster:在聚类分析中引入了小波变换的原理,主要应用于信号处理领域。(备注:小波算法在信号处理,图形图像,加密解密等领域有重要应用,是一种比较高深和牛逼的东西)
- CLIQUE:是一种结合了网格和密度的聚类算法
- OPTIGRID
基于模型的聚类
基于模型的方法(Model-based methods)主要是指基于概率模型的方法和基于神经网络模型的方法,尤其以基于概率模型的方法居多。这里的概率模型主要指概率生成模型(generative Model),同一”类“的数据属于同一种概率分布。这中方法的优点就是对”类“的划分不那么”坚硬“,而是以概率形式表现,每一类的特征也可以用参数来表达;但缺点就是执行效率不高,特别是分布数量很多并且数据量很少的时候。其中最典型、也最常用的方法就是高斯混合模型(GMM,Gaussian Mixture Models)。基于神经网络模型的方法主要就是指SOM(Self Organized Maps),唯一一个非监督学习的神经网络了。
- 基于神经网络模型的聚类
- 自组织神经网络SOM(Self Organized Maps):该算法假设在输入对象中存在一些拓扑结构或顺序,可以实现从输入空间(n维)到输出平面(2维)的降维映射,其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。 SOM网络包含输入层和输出层。输入层对应一个高维的输入向量,输出层由一系列组织在2维网格上的有序节点构成,输入节点与输出节点通过权重向量连接。学习过程中,找到与之距离最短的输出层单元,即获胜单元,对其更新。同时,将邻近区域的权值更新,使输出节点保持输入向量的拓扑特征。
- 基于概率模型的聚类
- 基于概率模型的聚类技术已被广泛使用,并且已经在许多应用中显示出有希望的结果,从图像分割,手写识别,文档聚类,主题建模到信息检索。基于模型的聚类方法尝试使用概率方法优化观察数据与某些数学模型之间的拟合。
- 高斯混合模型(GMMs,Gaussian Mixture Models ):K-means只考虑更新质心的均值,而GMMs则考虑更新数据的均值和方差。高斯混合模型假设存在一定数量的高斯分布,并且每个分布代表一个簇。高斯混合模型倾向于将属于同一分布的数据点分组在一起。”它是一种概率模型,采用软聚类方法将数据点归入不同的簇中,或者说,高斯混合模型使用软分类技术将数据点分配至对应的高斯分布(正态分布)中
总结基于模型的聚类
- SOM:该方法的基本思想是–由外界输入不同的样本到人工的自组织映射网络中,一开始时,输入样本引起输出兴奋细胞的位置各不相同,但自组织后会形成一些细胞群,它们分别代表了输入样本,反映了输入样本的特征
- COBWeb:COBWeb是一个通用的概念聚类方法,它用分类树的形式表现层次聚类
- CLASSIT
- AutoClass:是以概率混合模型为基础,利用属性的概率分布来描述聚类,该方法能够处理混合型的数据,但要求各属性相互独立
算法对比分析
scikit-learn 中聚类算法的比较, 详见官方中文文档
| Method name(方法名称) | Parameters(参数) | Scalability(可扩展性) | Usecase(使用场景) | Geometry (metric used)(几何图形(公制)) |
|---|---|---|---|---|
| K-Means(K-均值) | number of clusters(聚类形成的簇的个数) | 非常大的 n_samples, 中等的 n_clusters 使用 MiniBatch 代码) | 通用, 均匀的 cluster size(簇大小), flat geometry(平面几何), 不是太多的 clusters(簇) | Distances between points(点之间的距离) |
| Affinity propagation | damping(阻尼), sample preference(样本偏好) | Not scalable with n_samples(n_samples 不可扩展) | Many clusters, uneven cluster size, non-flat geometry(许多簇,不均匀的簇大小,非平面几何) | Graph distance (e.g. nearest-neighbor graph)(图距离(例如,最近邻图)) |
| Mean-shift | bandwidth(带宽) | Not scalable with n_samples (n_samples不可扩展) | Many clusters, uneven cluster size, non-flat geometry(许多簇,不均匀的簇大小,非平面几何) | Distances between points(点之间的距离) |
| Spectral clustering | number of clusters(簇的个数) | 中等的 n_samples, 小的 n_clusters | Few clusters, even cluster size, non-flat geometry(几个簇,均匀的簇大小,非平面几何) | Graph distance (e.g. nearest-neighbor graph)(图距离(例如最近邻图)) |
| Ward hierarchical clustering | number of clusters(簇的个数) | 大的 n_samples 和 n_clusters | Many clusters, possibly connectivity constraints(很多的簇,可能连接限制) | Distances between points(点之间的距离) |
| Agglomerative clustering | number of clusters(簇的个数), linkage type(链接类型), distance(距离) | 大的 n_samples 和 n_clusters | Many clusters, possibly connectivity constraints, non Euclidean distances(很多簇,可能连接限制,非欧氏距离) | Any pairwise distance(任意成对距离) |
| DBSCAN | neighborhood size(neighborhood 的大小) | 非常大的 n_samples, 中等的 n_clusters | Non-flat geometry, uneven cluster sizes(非平面几何,不均匀的簇大小) | Distances between nearest points(最近点之间的距离) |
| Gaussian mixtures(高斯混合) | many(很多) | Not scalable(不可扩展) | Flat geometry, good for density estimation(平面几何,适用于密度估计) | Mahalanobis distances to centers( 与中心的马氏距离) |
| Birch | branching factor(分支因子), threshold(阈值), optional global clusterer(可选全局簇). | 大的 n_clusters 和 n_samples | Large dataset, outlier removal, data reduction.(大型数据集,异常值去除,数据简化) |
【2021-11-12】不同的聚类算法有不同的应用背景,有的适合于大数据集,可以发现任意形状的聚簇;有的算法思想简单,适用于小数据集。总的来说,数据挖掘中针对聚类的典型要求包括:
- (1)可伸缩性:当数据量从几百上升到几百万时,聚类结果的准确度能一致。
- (2)处理不同类型属性的能力:许多算法针对的数值类型的数据。但是,实际应用场景中,会遇到二元类型数据,分类/标称类型数据,序数型数据。
- (3)发现任意形状的类簇:许多聚类算法基于距离(欧式距离或曼哈顿距离)来量化对象之间的相似度。这种方式往往只能发现相似尺寸和密度的球状类簇或者凸型类簇。但是,实际中类簇的形状可能是任意的。
- (4)初始化参数的需求最小化:很多算法需要用户提供一定个数的初始参数,比如期望的类簇个数,类簇初始中心点的设定。聚类的结果对这些参数十分敏感,调参数需要大量的人力负担,也非常影响聚类结果的准确性。
- (5)处理噪声数据的能力:噪声数据通常可以理解为影响聚类结果的干扰数据,包含孤立点,错误数据等,一些算法对这些噪声数据非常敏感,会导致低质量的聚- 类。
- (6)增量聚类和对输入次序的不敏感:一些算法不能将新加入的数据快速插入到已有的聚类结果中,还有一些算法针对不同次序的数据输入,产生的聚类结果差异很大。
- (7)高维性:有些算法只能处理2到3维的低纬度数据,而处理高维数据的能力很弱,高维空间中的数据分布十分稀疏,且高度倾斜。
- (8)可解释性和可用性:我们希望得到的聚类结果都能用特定的语义、知识进行解释,和实际的应用场景相联系。
几种常用的聚类算法从可伸缩性、适合的数据类型、高维性(处理高维数据的能力)、异常数据的抗干扰度、聚类形状和算法效率6个方面进行了综合性能评价
| 算法名称 | 算法类型 | 可伸缩性 | 适合的数据类型 | 高维性 | 异常数据的抗干扰性 | 聚类形状 | 算法效率 |
|---|---|---|---|---|---|---|---|
| ROCK | 层次聚类 | 很高 | 混合型 | 很高 | 很高 | 任意形状 | 一般 |
| BIRCH | 层次聚类 | 较高 | 数值型 | 较低 | 较低 | 球形 | 很高 |
| CURE | 层次聚类 | 较高 | 数值型 | 一般 | 很高 | 任意形状 | 较高 |
| CLARANS | 划分聚类 | 较低 | 数值型 | 较低 | 较高 | 球形 | 较低 |
| DENCLUE | 密度聚类 | 较低 | 数值型 | 较高 | 一般 | 任意形状 | 较高 |
| DBSCAN | 密度聚类 | 一般 | 数值型 | 较低 | 较高 | 任意形状 | 一般 |
| WaveCluster | 网格聚类 | 很高 | 数值型 | 很高 | 较高 | 任意形状 | 很高 |
| OptiGrid | 网格聚类 | 一般 | 数值型 | 较高 | 一般 | 任意形状 | 一般 |
| CLIQUE | 网格聚类 | 较高 | 数值型 | 较高 | 较高 | 任意形状 | 较低 |
新技术
Boids
Boids 算法,模拟鸟群、鱼群等的运动
群体运动模型Boids模型
鸟群作为一个整体运动,不断的变化形状,绕过障碍物;受到惊吓会破坏队伍但是又能重新集结。
- 1986年,Craig Reynolds 创造了模拟鸟类集体行为的仿真模拟,成为”类鸟群模型“。这种模型只用了3个简单的规则,控制个体间的相互作用,就产生了类似鸟群的行为,后来也被广泛用在计算机动画中。
- 1995年,在Boids模型的基础上,Vicsek等人对其进行简化,从统计力学的角度来研究集群集群运动,提出了Vicsek模型。这个模型中粒子能够将自己的速度与周围的几个粒子平行,但是又会受到噪声的影响,Vicsek等人通过调节噪声与密度,发现整体能够呈现出随机运动与整体一致运动之间的转变。
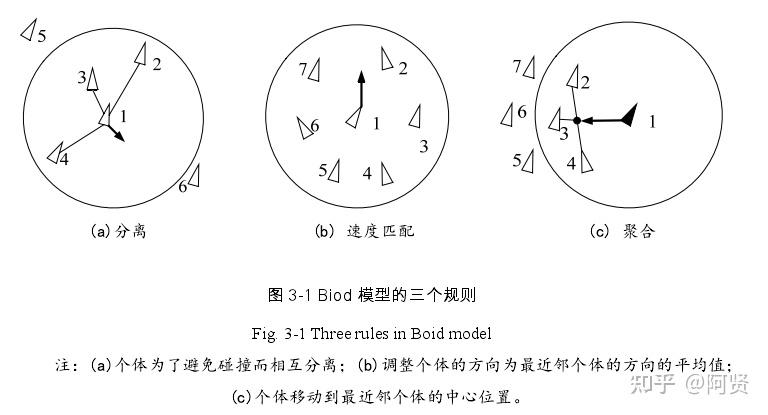
模拟鸟类运动的三大规则如下:
- 分离:类鸟检测某个范围内的所有类鸟的位置,计算出质心,然后产生一个远离质心的速度
- 平行:类鸟检测某个范围内的所有类鸟的速度,计算出平均速度,然后产生一个与平均速度方向一致的速度
- 内聚:类鸟检测某个范围内(与分离规则的范围不同)的所有类鸟的位置,计算出质心,然后产生一个指向质心的速度
扭矩聚类
【2025-2-17】AI扭矩聚类算法:自主学习、无需标注,准确率高达97.7%的颠覆性突破
悉尼科技大学研究人员开发了一种名为“扭矩聚类”(Torque Clustering)的全新 AI 算法,不需要人工干预,可以极大提升 AI 系统自主学习和识别数据模式的能力。
该算法模拟自然智能,在测试中准确率高达 97.7%,超越现有方法,有望引领 AI 学习的范式转变。
悉尼科技大学的杰出教授CT Lin表示:
- “在自然界中,动物通过观察、探索和与周围环境互动来学习,而不需要明确的指示。
- 几乎所有AI技术都依赖于‘
监督学习’,需要人类使用预定义的类别或标签来标记大量数据,以便AI能够进行预测和发现关系。 - 然而,监督学习存在许多局限性:标记数据不仅成本高、耗时长,而且在处理复杂或大规模任务时往往不切实际。相比之下,无监督学习不需要标记数据,能够直接揭示数据集中的固有结构和模式。”
- 下一代人工智能——‘
无监督学习’,正是试图模仿这种自然的学习方式。”
Torque Clustering 方法的论文,刚发表在人工智能领域的顶级期刊《IEEE模式分析与机器智能学报》上。
- Jie Yang, Sheng-Ku Lin, “Shedding New Light on Traditional Image Clustering: A Non-Deep Approach With Competitive Performance and Interpretability”, 2024 IEEE
- 非深度学习模型 MaxFeature Torque Clustering (MFTC) 在图像聚类任务中达到sota
- 【2025-2-11】悉尼科技大学官网 Truly autonomous AI is on the horizon
- 代码实现 TorqueClustering
该算法通过快速查找质量和距离峰值来实现自主聚类,表现优于传统的无监督学习方法,具有潜在的范式转变意义。它完全自主、无需参数调整,并且能够以极高的计算效率处理大型数据集。
扭矩聚类的独特之处:
- 基于物理学中扭矩概念,自主识别聚类,并无缝适应不同形状、密度和噪声程度的数据类型。
- 高效地处理大型数据集。与传统监督学习相比,扭矩聚类无需人工标注数据即可识别模式,使其更具扩展性和效率。对于复杂或大规模的任务,监督学习需要大量人工标注的数据,成本高、耗时长,且不切实际。而扭矩聚类算法的诞生,无疑为这些问题提供了完美的解决方案。
灵感源于星系合并过程中引力相互作用的扭矩平衡,基于质量和距离宇宙的两个基本属性,通过模拟自然界中的学习方式,让 AI 像动物一样通过观察、探索和与环境互动来学习。
扭矩聚类算法在 1000 个不同的数据集上进行了严格测试,平均调整互信息(AMI)得分高达 97.7%,而其他最先进的方法得分仅在 80% 左右。
应用范围极其广泛。
- 不仅适用于生物学、化学、天文学、心理学,还适用于金融和医学等领域。
- 通过发现疾病趋势、识别欺诈活动和理解人类行为等,扭矩聚类算法的应用场景不胜枚举。
然而,AI扭矩聚类算法并非无所不能。
- 尽管它在某些领域表现出色,但在处理某些特定类型的数据时可能效果不佳。
- 算法的准确率受到数据集质量的影响,如果数据集存在较大噪声或误报,算法的表现可能会受到影响。
因此,在使用该算法时,要根据具体情况进行适当的调整和优化。
总的来说,AI扭矩聚类算法以其独特的优势和广泛的应用领域,无疑为AI领域带来了新的突破。它以自主学习、无需标注的特点,以及对数据的高效处理能力,为我们打开了新的视野。随着该算法的不断完善和优化,我们有理由相信,它将为更多的领域带来革命性的改变。作为科研人员,我们期待着扭矩聚类算法在未来的发展,同时也期待着AI技术为人类社会带来的更多可能性。
聚类效果评估
【2021-8-18】聚类算法评估指标
聚类算法属于非监督学习,并不像分类算法那样可以使用训练集或测试集中得数据计算准确率、召回率等。那如何评估聚类算法得好坏呢?好的聚类算法,一般要求类簇具有:(即高内聚、低耦合)
- 高类内 (intra-cluster) 相似度: 通过一个单一的量化得分来评估算法好坏
- 低类间 (inter-cluster) 相似度: 通过将聚类结果与已经有“ground truth”分类进行对比。要么通过人类进行手动评估,要么通过一些指标在特定的应用场景中进行聚类用法的评估。不过该方法是有问题, 实际应用中往往都没label, 而且这些label只反映了数据集的一个可能的划分方法,它并不能告诉你存在一个不同的更好的聚类算法。
内部评价指标
如果聚类结果是类间相似性低,类内相似性高,那么内部评估方法会给予较高的分数评价。
不过内部评价方法的缺点是:
- 那些高分的算法不一定可以适用于高效的信息检索应用场景;
- 这些评估方法对某些算法有倾向性,如k-means聚类都是基于点之间的距离进行优化的,而那些基于距离的内部评估方法就会过度的赞誉这些生成的聚类结果。
内部评估方法可以基于特定场景判定一个算法要优于另一个,不过这并不表示前一个算法得到的结果比后一个结果更有意义。假设这种结构事实上存在于数据集中的,如果一个数据集包含了完全不同的数据结构,或者采用的评价方法完全和算法不搭
- 如k-means只能用于凸集数据集上,许多评估指标也是预先假设凸集数据集。在非凸数据集上不论是使用k-means还是使用假设凸集的评价方法,都是徒劳的。
相似度度量方法
样本间相似度
相似度度量方法
- 明可夫斯基(Minkowski)距离就是Lp范数(p≥1),而 曼哈顿(Manhattan)距离、欧式(Euclidean)距离、切比雪夫距离(Chebyshev)距离分别对应 p=1,2,∞ 时的情形。

簇间相似度
除了需要衡量对象之间的距离之外,有些聚类算法(如层次聚类)还需要衡量cluster之间的距离 ,假设Ci和Cj为两个 cluster,则前四种方法定义的Ci和Cj之间的距离如下表所示

- 单链 Single-link:定义两个cluster之间的距离为两个cluster之间距离最近的两个点之间的距离,这种方法会在聚类的过程中产生链式效应,即有可能会出现非常大的cluster
- Complete-link:定义的是两个cluster之间的距离为两个cluster之间距离最远的两个点之间的距离,这种方法可以避免链式效应,对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类
- UPGMA:是Single-link和Complete-link方法的折中,他定义两个cluster之间的距离为两个cluster之间所有点距离的平均值
- WPGMA:计算的是两个 cluster 之间两个对象之间的距离的加权平均值,加权的目的是为了使两个 cluster 对距离的计算的影响在同一层次上,而不受 cluster 大小的影响,具体公式和采用的权重方案有关。
SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式:SSE=∑(Yi-yi)^2,SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。
- $\sum_{i=1}^{n} (y_i-\hat{y_i})^{2}$
示例:
#断崖图选取最优K值
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# '利用SSE选择k'
SSE = [] # 存放每次结果的误差平方和
for k in range(1,9):
estimator = KMeans(n_clusters=k) # 构造聚类器
estimator.fit(df[['calories','sodium','alcohol','cost']])
SSE.append(estimator.inertia_)
N = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(N,SSE,'o-')
plt.show()
轮廓系数 Silhouette Coefficient
轮廓系数适用于实际类别信息未知的情况。对于单个样本,设a是与它同类别中其他样本的平均距离,b是与它距离最近不同类别中样本的平均距离,其轮廓系数为:
-
$s=\frac{b-a}{max(a,b)}$
- 对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1],同类别样本距离越相近不同类别样本距离越远,分数越高。
- 缺点:不适合基高密度的聚类算法DBSCAN。
from sklearn import metrics
from sklearn.metrics import pairwise_distances
from sklearn import datasets
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
import numpy as np
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.silhouette_score(X, labels, metric='euclidean')
Calinski-Harabaz Index
在真实的分群label不知道的情况下,Calinski-Harabasz可以作为评估模型的一个指标。Calinski-Harabasz指标通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。从而,CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
- $s(k)=\frac{tr(B_k)}{tr(W_k)} \frac{m-k}{k-1} $
-
其中m为训练样本数,k是类别个数,$B_k$是类别之间协方差矩阵,$W_k$是类别内部数据协方差矩阵,tr为矩阵的迹。也就是说,类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。同时,数值越小可以理解为:组间协方差很小,组与组之间界限不明显。
- 优点
- 当 cluster (簇)密集且分离较好时,分数更高,这与一个标准的 cluster(簇)有关。
- 得分计算很快与轮廓系数的对比,最大的优势:快!相差几百倍!毫秒级。
- 缺点
- 凸的簇的 Calinski-Harabaz index(Calinski-Harabaz 指数)通常高于其他类型的 cluster(簇),例如通过 DBSCAN 获得的基于密度的 cluster(簇)。所以不适合基于密度的聚类算法,DBSCAN。
import numpy as np
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
print(metrics.calinski_harabaz_score(X, labels))
Compactness(紧密性)(CP)
CP计算每一个类各点到聚类中心的平均距离CP越低意味着类内聚类距离越近。著名的 K-Means 聚类算法就是基于此思想提出的。
- 缺点:没有考虑类间效果。
$\overline{C P}{i}=\frac{1}{n{i}} \sum_{x \in C_{i}}\left|x_{i}-\mu_{i}\right|$
$\overline{C P}=\frac{1}{k} \sum_{k=1}^{k} \overline{C P}_{k}$
Separation(间隔性)(SP)
SP计算各聚类中心两两之间平均距离,SP越高意味类间聚类距离越远。缺点:没有考虑类内效果。
$\overline{S P}=\frac{2}{k_{2}-k} \sum_{i=1}^{k} \sum_{j=i+1}^{k}\left|\mu_{i}-\mu_{j}\right|$
Davies-Bouldin Index(戴维森堡丁指数)(分类适确性指标)(DB)(DBI)
DB计算任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离求最大值。DB越小意味着类内距离越小同时类间距离越大。该指标的计算公式:
$\mathrm{DB}=\frac{1}{n} \sum_{i=1}^{n} \max {j \neq i}\left(\frac{\sigma{i}+\sigma_{j}}{d\left(c_{i}, c_{j}\right)}\right)$
其中n是类别个数,ci是第i个类别的中心,σi是类别i中所有的点到中心的平均距离;d(ci,cj)中心点ci和cj之间的距离。算法生成的聚类结果越是朝着类内距离最小(类内相似性最大)和类间距离最大(类间相似性最小)变化,那么Davies-Bouldin指数就会越小。
- 缺点:因使用欧式距离所以对于环状分布聚类评测很差。
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.metrics import davies_bouldin_score
from sklearn.datasets.samples_generator import make_blobs
# loading the dataset
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.50, random_state=0)
# K-Means
kmeans = KMeans(n_clusters=4, random_state=1).fit(X)
# we store the cluster labels
labels = kmeans.labels_
print(davies_bouldin_score(X, labels))
Dunn Validity Index (邓恩指数)(DVI)
DVI计算任意两个簇元素的最短距离(类间)除以任意簇中的最大距离(类内)。DVI越大意味着类间距离越大同时类内距离越小。
- $D=\frac{\min _{1 \leq i<j \leq n} d(i, j)}{\max _{1 \leq k \leq n} d^{\prime}(k)}$
其中d(i,j)表示类别i,j之间的距离;d′(k)表示类别k内部的类内距离:
- 类间距离d(i,j)可以是任意的距离测度,例如两个类别的中心点的距离;
- 类内距离d′(k)可以以不同的方法去测量,例如类别kk中任意两点之间距离的最大值。 因为内部评估方法是搜寻类内相似最大,类间相似最小,所以算法生成的聚类结果的Dunn指数越高,那么该算法就越好。缺点:对离散点的聚类测评很高、对环状分布测评效果差。
import pandas as pd
from sklearn import datasets
from jqmcvi import base
# loading the dataset
X = datasets.load_iris()
df = pd.DataFrame(X.data)
# K-Means
from sklearn import cluster
k_means = cluster.KMeans(n_clusters=3)
k_means.fit(df) #K-means training
y_pred = k_means.predict(df)
# We store the K-means results in a dataframe
pred = pd.DataFrame(y_pred)
pred.columns = ['Type']
# we merge this dataframe with df
prediction = pd.concat([df, pred], axis = 1)
# We store the clusters
clus0 = prediction.loc[prediction.Species == 0]
clus1 = prediction.loc[prediction.Species == 1]
clus2 = prediction.loc[prediction.Species == 2]
cluster_list = [clus0.values, clus1.values, clus2.values]
print(base.dunn(cluster_list))
外部评价指标
外部评估方法中,聚类结果是通过使用没被用来做训练集的数据进行评估。例如已知样本点的类别信息和一些外部的基准。这些基准包含了一些预先分类好的数据,比如由人基于某些场景先生成一些带label的数据,因此这些基准可以看成是金标准。这些评估方法是为了测量聚类结果与提供的基准数据之间的相似性。然而这种方法也被质疑不适用真实数据。
纯度(Purity)
纯度(Purity)是一种简单而透明的评估手段,为了计算纯度(Purity),我们把每个簇中最多的类作为这个簇所代表的类,然后计算正确分配的类的数量,然后除以N。形式化表达如下:
$\text { purity }(\Omega, \mathbb{C})=\frac{1}{N} \sum_{k} \max {j}\left|\omega{k} \cap c_{j}\right|$
其中:
- Ω={w1,w2,…,wk}是聚类的集合,wk表示第k个聚类的集合。
- ℂ={c1,c2,…,cj}是文档集合,cj表示第J个文档。
- N表示文档总数。 上述过程即给每个聚类簇分配一个类别,且这个类别的样本在该簇中出现的次数最多,然后计算所有 K 个聚类簇的这个次数之和再归一化即为最终值。Purity值在0~1之间 ,越接近1表示聚类结果越好。
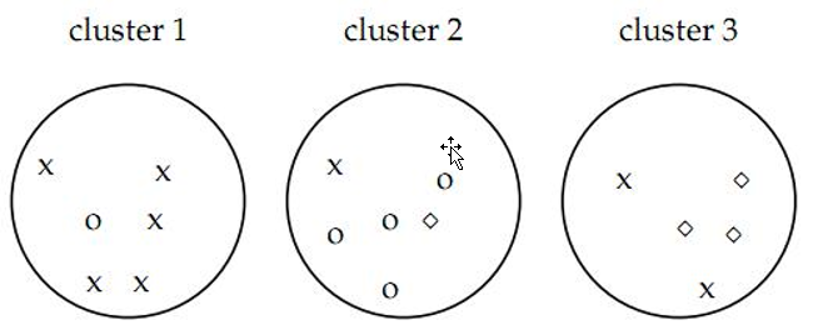
- 如图认为x代表一类文档,o代表一类文档,方框代表一类文档。如上图的 purity = ( 3+ 4 + 5) / 17 = 0.71,其中第一类正确的有5个,第二个4个,第三个3个,总文档数17。
当簇的数量很多的时候,容易达到较高的纯度——特别是,如果每个文档都被分到独立的一个簇中,那么计算得到的纯度就会是1。因此,不能简单用纯度来衡量聚类质量与聚类数量之间的关系。另外Purity无法用于权衡聚类质量与簇个数之间的关系。
def purity(result, label):
# 计算纯度
total_num = len(label)
cluster_counter = collections.Counter(result)
original_counter = collections.Counter(label)
t = []
for k in cluster_counter:
p_k = []
for j in original_counter:
count = 0
for i in range(len(result)):
if result[i] == k and label[i] == j: # 求交集
count += 1
p_k.append(count)
temp_t = max(p_k)
t.append(temp_t)
return sum(t)/total_num
标准化互信息(NMI)
互信息(Normalized Mutual Information)是用来衡量两个数据分布的吻合程度。也是一有用的信息度量,它是指两个事件集合之间的相关性。互信息越大,词条和类别的相关程度也越大。NMI (Normalized Mutual Information) 即归一化互信息
- $\mathrm{NMI}(\Omega, C)=\frac{I(\Omega ; C)}{(H(\Omega)+H(C) / 2)}$
- 其中,I表示互信息(Mutual Information), H为熵,当 log 取 2 为底时,单位为 bit,取 e 为底时单位为 nat。
互信息I(Ω;C)表示给定类簇信息C的前提条件下,类别信息Ω的增加量,或者说其不确定度的减少量。互信息还可以写出如下形式:H(Ω;C)=H(Ω)−H(Ω|C)
- $H(\Omega ; C)=H(\Omega)-H(\Omega \mid C)$
- 互信息的最小值为 0, 当类簇相对于类别只是随机的, 也就是说两者独立的情况下, Ω对于C未带来任何有用的信息.如果得到的Ω与C关系越密切, 那么I(Ω;C)值越大。如果Ω完整重现了C, 此时互信息最大
- 当K=N时,即类簇数和样本个数相等,MI 也能达到最大值。所以 MI 也存在和纯度类似的问题,即它并不对簇数目较大的聚类结果进行惩罚,因此也不能在其他条件一样的情况下,对簇数目越小越好的这种期望进行形式化。NMI 则可以解决上述问题,因为熵会随着簇的数目的增长而增大。当K=N时,H(Ω)会达到其最大值logN , 此时就能保证 NMI 的值较低。之所以采用(H(Ω)+H(C)/2作为分母是因为它是 I(Ω,C)的紧上界, 因此可以保证NMI∈[0 , 1]。计算方法见原文
# sklearn
from sklearn.metrics.cluster import normalized_mutual_info_score
print(normalized_mutual_info_score([0, 0, 1, 1], [0, 0, 1, 1]))
# 不用sklearn
def NMI(result, label):
# 标准化互信息
total_num = len(label)
cluster_counter = collections.Counter(result)
original_counter = collections.Counter(label)
# 计算互信息量
MI = 0
eps = 1.4e-45 # 取一个很小的值来避免log 0
for k in cluster_counter:
for j in original_counter:
count = 0
for i in range(len(result)):
if result[i] == k and label[i] == j:
count += 1
p_k = 1.0*cluster_counter[k] / total_num
p_j = 1.0*original_counter[j] / total_num
p_kj = 1.0*count / total_num
MI += p_kj * math.log(p_kj /(p_k * p_j) + eps, 2)
# 标准化互信息量
H_k = 0
for k in cluster_counter:
H_k -= (1.0*cluster_counter[k] / total_num) * math.log(1.0*cluster_counter[k] / total_num+eps, 2)
H_j = 0
for j in original_counter:
H_j -= (1.0*original_counter[j] / total_num) * math.log(1.0*original_counter[j] / total_num+eps, 2)
return 2.0 * MI / (H_k + H_j)
调整互信息AMI( Adjusted mutual information)
已知聚类标签与真实标签,互信息(mutual information)能够测度两种标签排列之间的相关性,同时忽略标签中的排列。有两种不同版本的互信息以供选择,一种是Normalized Mutual Information(NMI),一种是Adjusted Mutual Information(AMI)
优点
- 随机(统一)标签分配的AMI评分接近0)
- 有界范围 [0, 1]: 接近 0 的值表示两个主要独立的标签分配,而接近 1 的值表示重要的一致性。此外,正好 0 的值表示 purely(纯粹) 独立标签分配,正好为 1 的 AMI 表示两个标签分配相等(有或者没有 permutation)。
- 对簇的结构没有作出任何假设: 可以用于比较聚类算法
缺点:
- 与 inertia 相反, MI-based measures 需要了解 ground truth classes,而在实践中几乎不可用,或者需要人工标注或手动分配(如在监督学习环境中)。然而,基于 MI-based measures (基于 MI 的测量方式)也可用于纯无人监控的设置,作为可用于聚类模型选择的 Consensus Index (共识索引)的构建块。
- NMI 和 MI 没有调整机会。
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.adjusted_mutual_info_score(labels_true, labels_pred))
Rand index兰德指数
兰德指数 (Rand index, RI), 将聚类看成是一系列的决策过程,即对文档集上所有N(N-1)/2个文档 (documents) 对进行决策。当且仅当两篇文档相似时,我们将它们归入同一簇中。
Positive:
- TP 将两篇相似文档归入一个簇 (同 – 同)
- TN 将两篇不相似的文档归入不同的簇 (不同 – 不同) Negative:
- FP 将两篇不相似的文档归入同一簇 (不同 – 同)
- FN 将两篇相似的文档归入不同簇 (同- 不同) (worse) RI 则是计算「正确决策」的比率(精确率, accuracy):
- $R I=\frac{T P+T N}{T P+F P+T F+F N}=\frac{T P+T N}{C_{N}^{2}}$
RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合。
def contingency_table(result, label):
total_num = len(label)
TP = TN = FP = FN = 0
for i in range(total_num):
for j in range(i + 1, total_num):
if label[i] == label[j] and result[i] == result[j]:
TP += 1
elif label[i] != label[j] and result[i] != result[j]:
TN += 1
elif label[i] != label[j] and result[i] == result[j]:
FP += 1
elif label[i] == label[j] and result[i] != result[j]:
FN += 1
return (TP, TN, FP, FN)
def rand_index(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*(TP + TN)/(TP + FP + FN + TN)
调整兰德系数 (Adjusted Rand index)
对于随机结果,RI并不能保证分数接近零。为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德系数(Adjusted rand index)被提出,它具有更高的区分度:
- $\mathrm{ARI}=\frac{\mathrm{RI}-E[\mathrm{RI}]}{\max (\mathrm{RI})-E[\mathrm{RI}]}$ ARI取值范围为[-1,1],值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲,ARI衡量的是两个数据分布的吻合程度。
优点:
- 对任意数量的聚类中心和样本数,随机聚类的ARI都非常接近于0
- 取值在[-1,1]之间,负数代表结果不好,越接近于1越好
- 对簇的结构不需作出任何假设:可以用于比较聚类算法。 缺点:
- 与 inertia 相反,ARI 需要 ground truth classes 的相关知识,ARI需要真实标签,而在实践中几乎不可用,或者需要人工标注者手动分配(如在监督学习环境中)。然而,ARI 还可以在 purely unsupervised setting (纯粹无监督的设置中)作为可用于 聚类模型选择(TODO)的共识索引的构建块。
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.adjusted_rand_score(labels_true, labels_pred))
F值方法
这是基于上述RI方法衍生出的一个方法,我们可以 FN 罚更多,通过取Fβ中的β大于 1, 此时实际上也相当于赋予召回率更大的权重:
\[\begin{array}{c} \text { Precision }=P=\frac{T P}{T P+F P} \\ \text { Recall }=R=\frac{T P}{T P+F N} \\ F_{\beta}=\frac{\left(1+\beta^{2}\right) P \times R}{\beta^{2} P+R} \end{array}\]RI方法有个特点就是把准确率和召回率看得同等重要,事实上有时候我们可能需要某一特性更多一点,这时候就适合F值方法。
def precision(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*TP/(TP + FP)
def recall(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*TP/(TP + FN)
def F_measure(result, label, beta=1):
prec = precision(result, label)
r = recall(result, label)
return (beta*beta + 1) * prec * r/(beta*beta * prec + r)
Fowlkes-Mallows scores FM指数
Fowlkes-Mallows Scores(FMI) FMI是成对的precision(精度)和recall(召回)的几何平均数。取值范围为 [0,1],越接近1越好。定义为:
- $\mathrm{FMI}=\frac{T P}{\sqrt{(T P+F P)(T P+F N)}}$
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.fowlkes_mallows_score(labels_true, labels_pred))
调和平均V-measure
说V-measure之前要先介绍两个指标:
- 同质性(homogeneity):每个群集只包含单个类的成员。
- 完整性(completeness):给定类的所有成员都分配给同一个群集。 同质性和完整性分数基于以下公式得出(见原文)
V-measure是同质性homogeneity和完整性completeness的调和平均数,V-measure取值范围为 [0,1],越大越好,但当样本量较小或聚类数据较多的情况,推荐使用AMI和ARI。公式:$v=2 \cdot \frac{h \cdot c}{h+c}$
优点:
- 分数明确:从0到1反应出最差到最优的表现;
- 解释直观:差的调和平均数可以在同质性和完整性方面做定性的分析;
- 对簇结构不作假设:可以比较两种聚类算法如k均值算法和谱聚类算法的结果。 缺点:
- 以前引入的度量在随机标记方面没有规范化,这意味着,根据样本数,集群和先验知识,完全随机标签并不总是产生相同的完整性和均匀性的值,所得调和平均值V-measure也不相同。特别是,随机标记不会产生零分,特别是当簇的数量很大时。
- 当样本数大于一千,聚类数小于10时,可以安全地忽略该问题。对于较小的样本量或更大数量的集群,使用经过调整的指数(如调整兰德指数)更为安全。
- 这些指标要求的先验知识,在实践中几乎不可用或需要手动分配的人作注解者(如在监督学习环境中)。
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.homogeneity_score(labels_true, labels_pred))
print(metrics.completeness_score(labels_true, labels_pred))
print(metrics.v_measure_score(labels_true, labels_pred))
Jaccard 指数
该指数用于量化两个数据集之间的相似性,该值得范围为0-1.其中越大表明两个数据集越相似:
- $J(A, B)=\frac{|A \cap B|}{|A \cup B|}=\frac{T P}{T P+F P+F N}$ 该指数和近年来的IOU计算方法一致
Dice 指数
该指数是基于jaccard指数上将TP的权重置为2倍。
-
$J(A, B)=\frac{ A \cap B }{ A \cup B }=\frac{2 T P}{2 T P+F P+F N}$
sklearn聚类算法
参考:
- sklearn聚类算法详解
- scikit-learn中的无监督聚类算法
- scikit-learn主要由分类、回归、聚类和降维四大部分组成,其中分类和回归属于有监督学习范畴,聚类属于无监督学习范畴,降维适用于有监督学习和无监督学习。scikit-learn的结构示意图如下所示:
-
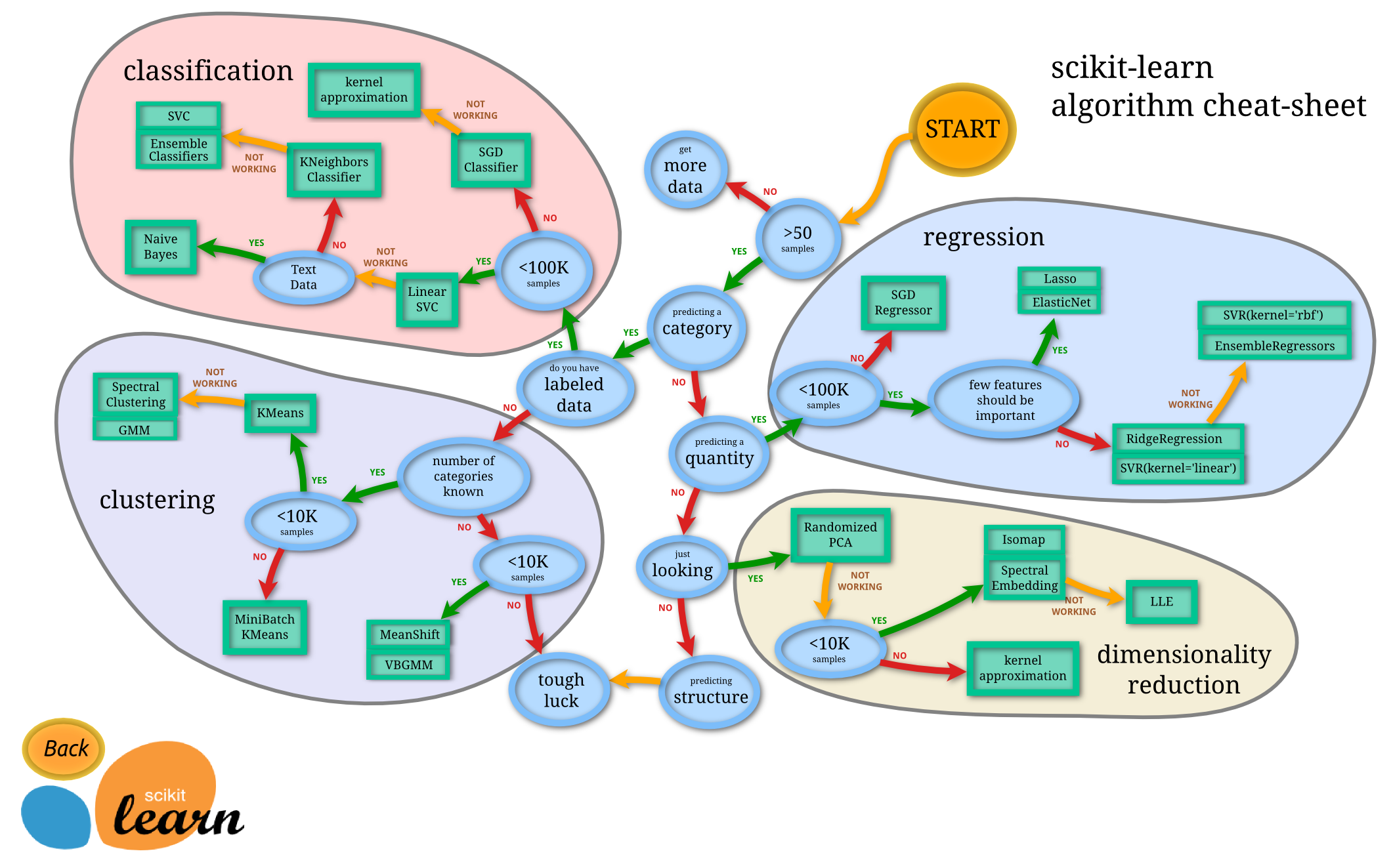
- scikit-learn中的聚类算法主要有:
- K-Means(cluster.KMeans)
- AP聚类(cluster.AffinityPropagation)
- 均值漂移(cluster.MeanShift)
- 层次聚类(cluster.AgglomerativeClustering)
- DBSCAN(cluster.DBSCAN)
- BRICH(cluster.Brich)
- 谱聚类(cluster.Spectral.Clustering)
- 高斯混合模型(GMM)∈期望最大化(EM)算法(mixture.GaussianMixture)
企业应用
腾讯信息流聚类
【2021-11-11】腾讯张露丹:腾讯信息流聚类方法探索及实践,面对聚类瓶颈,如何判断策略生效的关键节点? 常用聚类方法各自的优点和缺点:
| 聚类方法 | 类型 | 优点 | 缺点 |
|---|---|---|---|
| K-means | 基于距离 | 实现简单快速、聚出的类别相对均匀 | 受初始点选择影响较大、无法自定义距离、无法识别离群点 |
| DBSCAN | 基于密度 | 可以识别离群点、对特殊分部效果好 | 聚出的类别欠均匀、受密度定义影响较大、不擅长处理密度不均的数据 |
| AP | 层次聚类 | 对特殊分布效果好、类的层次关系具有一定价值 | 有时聚出的类别欠均匀、内存不友好 |
- 基于距离——K-means。优点是实现简单快速、聚出的类别相对均匀;缺点是受初始点选择影响较大、无法自定义距离、无法识别离群点;
- 基于密度——DBSCAN。优点是可以识别离群点、对特殊分部效果好。缺点是聚出的类别欠均匀、受密度定义影响较大、不擅长处理密度不均的数据;
- 层次聚类。优点是对特殊分布效果好、类的层次关系具有一定价值。缺点是有时聚出的类别欠均匀、内存不友好。
常用用户聚类的方法都会遇到局限,常见的局限有以下三个:
- 聚出来的类不均匀。举例:在做一个PMF分析的时候,我们发现有50%以上的用户都是视频和图文的综合偏好。但是,这样的类别不能支持我们更精细地知道我们需要给这样的人群提供什么样的内容。所以需要细化。
- 聚类不灵敏。举例:我们知道近期的指标波动是因为近期喜欢看图文的用户活跃度上升。但是,因为无法精确地定位子人群,我们也无法有效地加强运营去保证活跃度持续上涨的趋势。
- 聚类方法难应用。举例:发现喜欢看视频的用户活跃度高但是并不能有效分析出帮助运营的策略方法。主要也是因为聚类粒度比较粗,无法有目标性地去帮助运营。
总体概括,所遇到的局限都可以概括为人群粒度粗,无法形成有效策略;更本质上,则是因为聚类所使用的统计特征无法反应用户的行为细节。因此,我们也就需要比统计特征更具有区分客户特性的特征。
基于用户使用路径的聚类方法
主要讲两个方法:
- N-gram
- action2vec
n-gram
- 以用户使用路径为例,这个用户今天来了两次,所以他有两个session,在第一个session中,他是先使用app,然后在小说首页翻看,再进入某小说看简介,阅读小说后退出app。过了几分钟,他又启动了app,回到上次看的小说,推出小说进入信息流,然后点击查看图文,最后退出app。
- 如果我们选择N-gram的 N=3,则该用户的路径可以生成例如下面的3-gram:启动app——在小说首页翻看——进入某小说简介;在小说首页翻看——进入某小说看简介——阅读小说;等等。
- 如何选择N-gram需要结合场景和需要解决问题的特点。举例:session之间如何连接N-gram,是将行为session间直接连接,还是删除一些不重要的行为再将消费行为进行连接都与场景和需要解决问题的特点有关。
聚类步骤:
- 首先可以得到similaritymatrix 相似度矩阵 或者distancematrix 距离矩阵
- 用NormalizedPolarDistance计算两个用户的相似性
- 基于这些matrix,用各种各样的算法来对其做聚类

action2vec
action2vec是借鉴word2vec的思想,将用户的行为embedding到低维空间,利用embedding的结果进行聚类。action2vec有两种模型,CBOW和Skip-gram,此次我们主要讲解Skip-gram的思想。主要看用户的当前行为对他未来n个行为的预测作用。在有了action2vec之后,我们有了每个用户的行为所对应的矢量。
1 KMeans
1.1 算法描述
- 随机选择k个中心
- 遍历所有样本,把样本划分到距离最近的一个中心
- 划分之后就有K个簇,计算每个簇的平均值作为新的质心
- 重复步骤2,直到达到停止条件
- 停止条件:
- 聚类中心不再发生变化;所有的距离最小;迭代次数达到设定值,
- 代价函数:误差平方和(SSE)
1.2 算法优缺点
优点:
- 算法容易理解,聚类效果不错
- 具有出色的速度
- 当簇近似高斯分布时,效果比较好
缺点:
- 需要提前确定K值,k值的选定是比较难确定
- 对初始中心点敏感
- 不适合发现非凸形状的簇或者大小差别较大的簇
- 特殊值/离群值对模型的影响比较大
从数据先验的角度来说,在 Kmeans 中,我们假设各个 cluster 的先验概率是一样的,但是各个 cluster 的数据量可能是不均匀的。举个例子,cluster A 中包含了10000个样本,cluster B 中只包含了100个。那么对于一个新的样本,在不考虑其与A cluster、 B cluster 相似度的情况,其属于 cluster A 的概率肯定是要大于 cluster B的。
1.3 效果评价
- 从簇内的稠密程度和簇间的离散程度来评估聚类的效果。
- 常见的方法有轮廓系数
Silhouette Coefficient和Calinski-Harabasz Index
1.3.1 轮廓系数
- 轮廓系数(Silhouette Coefficient)结合了聚类的凝聚度(Cohesion)和分离度(Separation),用于评估聚类的效果。该值处于-1~1之间,值越大,表示聚类效果越好。具体计算方法如下:
- 对于第i个元素$x_i$,计算$x_i$与其同一个簇内的所有其他元素距离的平均值,记作$a_i$,用于量化簇内的凝聚度。
- 选取$x_i$外的一个簇b,计算$x_i$与b中所有点的平均距离,遍历所有其他簇,找到最近的这个平均距离,记作$b_i$,用于量化簇之间分离度。
- 对于元素$x_i$,轮廓系数$s_i = (b_i – a_i)/max(a_i,b_i)$
- 计算所有x的轮廓系数,求出平均值即为当前聚类的整体轮廓系数
先是计算每一个样本的轮廓系数,然后计算所有样本的轮廓系数,求平均值作为整体轮廓系数
从上面的公式,不难发现若s_i小于0,a_i > b_i, 说明x_i与其簇内元素的平均距离大于最近的其他簇,表示聚类效果不好。如果a_i趋于0,或者b_i足够大,那么s_i趋近与1,说明聚类效果比较好。
sklearn.metric库的silhouette_score函数,silhouette_score的参数有:X、labels、metric,X为距离矩阵,labels为聚类结果,metric为度量方法。由于我们输入的是距离矩阵,因此选择”precomputed”。
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
silhouettteScore = []
for i in range(2,15):
# 构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = silhouette_score(iris_data,kmeans.labels_)
silhouettteScore.append(score)
plt.figure(figsize=(10,6))
plt.plot(range(2,15),silhouettteScore,linewidth=1.5, linestyle="-")
plt.show()
1.3.2 Calinski-Harabasz Index
聚成几个类别合适?
类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。
在scikit-learn中, Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score。
from sklearn.metrics import calinski_harabaz_score
for i in range(2,7):
# 构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = calinski_harabaz_score(iris_data,kmeans.labels_)
print('iris数据聚%d类calinski_harabaz指数为:%f'%(i,score))
CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果
示例
import numpy as np
from sklearn.cluster import KMeans
# 用kmeans自带的
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_metrics.calinski_harabaz_score(X, labels)
# 货使用Calinski-Harabasz Index评估的聚类分数: 分数越高,表示聚类的效果越好
from sklearn.metrics import calinski_harabaz_score
print(calinski_harabaz_score(X, y_pre)) # 3088.084577541466
参考博客:KMeans
1.3.3 FMI
FMI:需要真实值
from sklearn.metrics import fowlkes_mallows_score
for i in range(2,7):
##构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = fowlkes_mallows_score(iris_target,kmeans.labels_)
print('iris数据聚%d类FMI评价分值为:%f' %(i,score))
1.4 K值确定
- 结合业务分析,确定需要分类的个数,这种情况往往有业务上聚类的个数范围
- 手肘原则,选定不同的K值,计算每个k值时的代价函数。Kmeans聚类的效果评估方法是SSE,是计算所有点到相应簇中心的距离均值,当然,k值越大 SSE越小,我们就是要求出随着k值的变化SSE的变化规律,找到SSE减幅最小的k值,这时k应该是相对比较合理的值。
如图,在k=3之后,代价函数变化缓慢,选择聚类的个数为3
- 算法特点
- Distances between points(点之间的距离)
- 优点:
- 算法容易理解,聚类效果不错
- 具有出色的速度:O(NKt)
- 当簇近似高斯分布时,效果比较好
- 缺点:
- 需要人工预先确定初试K值,且该值和真是的数据分布未必吻合
- 对初始中心点敏感
- 不适合发现非凸形状的簇或者大小差别较大的簇
- 特殊值/离散值(噪点)对模型的影响比较大
- 算法只能收敛到局部最优,效果受初始值影响很大
- 从数据先验的角度来说,在 Kmeans 中,我们假设各个 cluster 的先验概率是一样的,但是各个 cluster 的数据量可能是不均匀的。举个例子,cluster A 中包含了10000个样本,cluster B 中只包含了100个。那么对于一个新的样本,在不考虑其与A cluster、 B cluster 相似度的情况,其属于 cluster A 的概率肯定是要大于 cluster B的。
- 适用场景
- 通用, 均匀的 cluster size(簇大小), flat geometry(平面几何), 不是太多的 clusters(簇)
- 非常大的 n_samples、中等的 n_clusters 使用 MiniBatch code
- 样本量<10K时使用k-means,>=10K时用MiniBatchKMeans
- 不太适用于离散分类
- 代码
print(__doc__)
# Author: Phil Roth <mr.phil.roth@gmail.com>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
plt.figure(figsize=(12, 12))
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Incorrect Number of Blobs")
# Anisotropicly distributed data
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
# Different variance
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3,
random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show()
改进:k-means++
k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似,改变的地方只有初始质心的选取:用轮盘法选下一个聚类中心
改进:bi-kmeans算法
一种度量聚类效果的指标是SSE(Sum of Squared Error),他表示聚类后的簇离该簇的聚类中心的平方和,SSE越小,表示聚类效果越好。
bi-kmeans是针对kmeans算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理,首先将所有的数据点视为一个簇,然后将该簇一分为二,之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否能最大程度的降低SSE的值。
对比
- k-means每次计算出来的SSE都较大且不太稳定
- k-means++计算出来的SSE较稳定并且数值较小
- bi-kmeans 4次计算出来的SSE都一样,并且计算的SSE都较小,说明聚类的效果也最好。
2 DBSCAN——密度聚类
- DBSCAN(Density-Based Spatial Clustering of Application with Noise)基于密度的空间聚类算法。
- 两个参数:
-
- Eps邻域半径(epsilon,小量,小的值)
-
- MinPts(minimum number of points required to form a cluster)定义核心点时的阈值。
-
3个点
- 核心点:对应稠密区域内部的点
- 边界点:对应稠密区域边缘的点
- 噪音点:对应稀疏区域中的点
上图红色为核心点,黄色为边界点,蓝色为噪音点
minPts=4时,A为核心点,B、C是边界点,而N是噪声点
4种点的关系
几个概念:
- Ε邻域:给定对象半径为Ε内的区域称为该对象的Ε邻域;
- 核心对象:对于任一样本点,如果其Eps邻域内至少包含MinPts个样本点,那么这个样本点就是核心对象。(一个点)
- 密度可达:对于样本集合D,给定一串样本点p1,p2….pn,p= p1,q= pn,假如对象pi从pi-1直接密度可达,那么对象q从对象p密度可达。
- 密度相连:存在样本集合D中的一点o,如果对象o到对象p和对象q都是密度可达的,那么p和q密度相联。
- 直接密度可达:对于样本集合D,如果样本点q在p的Ε邻域内,并且p为核心对象,那么对象q从对象p直接密度可达。
可以发现,密度可达是直接密度可达的传递闭包,并且这种关系是非对称的。密度相连是对称关系。DBSCAN目的是找到密度相连对象的最大集合。
- Eg: 假设半径Ε=3,MinPts=3,点p的E邻域中有点{m,p,p1,p2,o}, 点m的E邻域中有点{m,q,p,m1,m2},点q的E邻域中有点{q,m},点o的E邻域中有点{o,p,s},点s的E邻域中有点{o,s,s1}.
- 那么核心对象有p,m,o,s(q不是核心对象,因为它对应的E邻域中点数量等于2,小于MinPts=3);
- 点m从点p直接密度可达,因为m在p的E邻域内,并且p为核心对象;
- 点q从点p密度可达,因为点q从点m直接密度可达,并且点m从点p直接密度可达;
- 点q到点s密度相连,因为点q从点p密度可达,并且s从点p密度可达。
算法流程:

- 构建ε邻域的过程可以使用kd-tree进行优化,循环过程可以使用Numba、Cython、C进行优化
- 聚类过程示意图
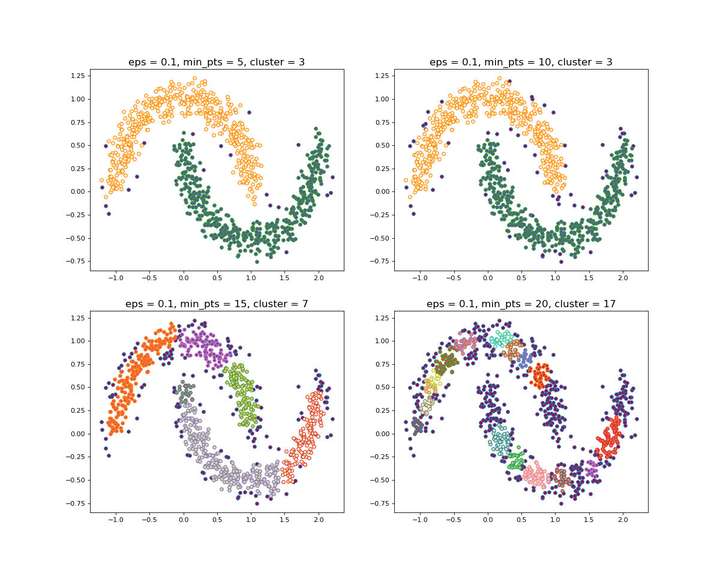
DBSCAN的聚类是一个不断生长的过程。先找到一个核心对象,从整个核心对象出发,找出它的直接密度可达的对象,再从这些对象出发,寻找它们直接密度可达的对象,一直重复这个过程,直至最后没有可寻找的对象了,那么一个簇的更新就完成了。也可以认为,簇是所有密度可达的点的集合。
- DBSCAN核心思想:从某个选定的核心点出发,不断向密度可达的区域扩张,从而得到一个包含核心点和边界点的最大化区域,区域中任意两点密度相连。
bdscan vs kmeans
- DBSCAN 可对任意形状的稠密数据集进行聚类,而 k-means 之类的聚类算法一般只适用于凸数据集
- 聚类同时发现异常点,对数据集中的异常点不敏感。
- 聚类结果没有偏倚,而 k-means 之类算法的初始值对聚类结果有很大影响。
结论:聚类效果好于K-means

优缺点
优点
优点:
- 不需要指定cluster的数目,如K-means方法需要提前指定k(或多次运行,通过肘部法则获取k)
- 聚类的形状可以是任意的
- 能找出数据中的噪音,对噪音不敏感
- 算法应用参数少,只需要两个:Ε 和 MinPts
- 聚类结果几乎不依赖于节点的遍历顺序,即对样本顺序不敏感,对于处于簇类之间边界样本,可能会根据哪个簇类优先被探测到而其归属有所摆动。
缺点
- 当样本集密度不均匀、聚类间距差相差很大时,DBSCAN 算法聚类效果不好
- 这种情形,参数Eps,MinPts不好选择
- 如果密度大,选一个小的邻域半径就可以把这些数据点聚类,但对于那些密度小的数据点,设置的小的邻域半径,并不能把密度小的这些点给全部聚类。
- 调试参数比较复杂时,主要需要对半径r和阈值 MinPts 进行联合调参,不同参数组合对最后的聚类效果有较大影响。
- 数据量过大时, 容易报错内存溢出,聚类收敛时间较长,故可能需要数据削减策略
- 改进:对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
- 聚类效果依赖于距离公式的选取,实际中常用的距离是欧几里得距离,由于‘
维数灾难’,距离的度量标准已变得不再重要。- 分类器性能随着特征数量的增加而不断提升,但过了某一值后,性能不升反而下降,这种现象称为维数灾难。对于维度灾难的理解:维度灾难的理解
聚类形状可以是任意的,来个图直观感觉一下:
代码
在sklearn中的应用
from sklearn.cluster import DBSCAN
DBSCAN(eps=0.5, # 邻域半径
min_samples=5, # 最小样本点数,MinPts
metric='euclidean', # 可以自定义函数
metric_params=None,
algorithm='auto', # 'auto','ball_tree','kd_tree','brute',4个可选的参数 寻找最近邻点的算法,例如直接密度可达的点
leaf_size=30, # balltree,cdtree的参数
p=None, #
n_jobs=1)
- 完整版代码
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle ##python自带的迭代器模块
from sklearn.preprocessing import StandardScaler
##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=750
##生产数据:此实验结果受cluster_std的影响,或者说受eps 和cluster_std差值影响
X, lables_true = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.4,
random_state =0)
##设置分层聚类函数
db = DBSCAN(eps=0.3, min_samples=10)
# 自定义函数
#DB = skc.DBSCAN(eps=400,min_samples=min_samples_num, metric=lambda a, b: haversine(a,b)).fit(X)
##训练数据
db.fit(X)
##初始化一个全是False的bool类型的数组
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
'''
这里是关键点(针对这行代码:xy = X[class_member_mask & ~core_samples_mask]):
db.core_sample_indices_ 表示的是某个点在寻找核心点集合的过程中暂时被标为噪声点的点(即周围点
小于min_samples),并不是最终的噪声点。在对核心点进行联通的过程中,这部分点会被进行重新归类(即标签
并不会是表示噪声点的-1),也可也这样理解,这些点不适合做核心点,但是会被包含在某个核心点的范围之内
'''
core_samples_mask[db.core_sample_indices_] = True
##每个数据的分类
lables = db.labels_
##分类个数:lables中包含-1,表示噪声点
n_clusters_ =len(np.unique(lables)) - (1 if -1 in lables else 0)
##绘图
unique_labels = set(lables)
'''
1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
2)plt.cm 一个颜色映射模块
3)生成的每个colors包含4个值,分别是rgba
4)其实这行代码的意思就是生成4个可以和光谱对应的颜色值
'''
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
plt.figure(1)
plt.clf()
for k, col in zip(unique_labels, colors):
##-1表示噪声点,这里的k表示黑色
if k == -1:
col = 'k'
##生成一个True、False数组,lables == k 的设置成True
class_member_mask = (lables == k)
##两个数组做&运算,找出即是核心点又等于分类k的值 markeredgecolor='k',
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=14)
'''
1)~优先级最高,按位对core_samples_mask 求反,求出的是噪音点的位置
2)& 于运算之后,求出虽然刚开始是噪音点的位置,但是重新归类却属于k的点
3)对核心分类之后进行的扩展
'''
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
3 OPTICS——密度聚类,改进DBSCAN
DBSCAN算法中,使用了统一的ε值,当数据密度不均匀的时候,如果设置了较小的ε值,则较稀疏的cluster中的节点密度会小于minPts,会被认为是边界点而不被用于进一步的扩展;如果设置了较大的ε值,则密度较大且离的比较近的cluster容易被划分为同一个cluster
对于密度不均的数据选取一个合适的ε是很困难的,对于高维数据,由于维度灾难(Curse of dimensionality),ε的选取将变得更加困难。
怎样解决DBSCAN遗留下的问题呢?
The basic idea to overcome these problems is to run an algorithm which produces a special order of the database with respect to its density-based clustering structure containing the information about every clustering level of the data set (up to a “generating distance” [公式]), and is very easy to analyze. 即能够提出一种算法,使得基于密度的聚类结构能够呈现出一种特殊的顺序,该顺序所对应的聚类结构包含了每个层级的聚类的信息,并且便于分析。
OPTICS(Ordering Points To Identify the Clustering Structure, OPTICS)是DBSCAN算法的一种有效扩展,主要解决对输入参数敏感的问题。即选取有限个邻域参数εi (0 <= εi <= ε)进行聚类,这样就能得到不同邻域参数下的聚类结果。
- OPTICS不显式地生成数据聚类,只是对数据对象集合中的对象进行排序,得到一个有序的对象列表。 概念
- 核心距离(core-distance)
- 给定参数eps,MinPts,使得某个样本点成为核心对象(核心点)的最小邻域半径,这个最小邻域半径为该样本点的核心距离。
- 在DBSCAN中,给定领域半径eps和MinPts可以确定一个核心对象,如果eps比较大,在核心对象的邻域半径eps内的点的总数就会大于你所设定的MinPts,所以核心距离就是一个核心点在满足MinPts时的一个最小邻域半径。
- 可达距离(reachability-distance)
- rd(y,x)表示使得‘x为核心点’且‘y从x直接密度可达’同时成立的最小邻域半径。

- rd(y,x)表示使得‘x为核心点’且‘y从x直接密度可达’同时成立的最小邻域半径。
OPTICS算法过程演示
最终获取知识是一个输出序列,该序列按照密度不同将相近密度的点聚合在一起,而不是输出该点所属的具体类别,如果要获取该点所属的类型,需要再设置一个参数提取出具体的类别。
效果对比 DBSCAN与OPTICS
DBSCAN
 OPTICS
OPTICS
OPTICS第一步生成的输出序列较好的保留了各个不同密度的簇的特征,根据输出序列的可达距离图,再设定一个合理的ε,便可以获得较好的聚类效果。
4 Spectral Clustering 谱聚类(任意形状,全局最优)
1)概述
- Spectral Clustering(SC,即谱聚类),是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最有解,其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类.它与样本特征无关而只与样本个数有关。
- 基本思路:将样本看作顶点,样本间的相似度看作带权的边,从而将聚类问题转为图分割问题:找到一种图分割的方法使得连接不同组的边的权重尽可能低(这意味着组间相似度要尽可能低),组内的边的权重尽可能高(这意味着组内相似度要尽可能高).
2)图解过程
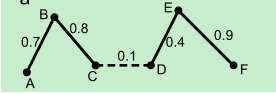
如上图所示,断开虚线,六个数据被聚成两类。
3)Spectral Clustering算法函数
a)核心函数:sklearn.cluster.SpectralClustering
因为是基于图论的算法,所以输入必须是对称矩阵。
b)主要参数(参数较多,详细参数)
- n_clusters:聚类的个数。(官方的解释:投影子空间的维度)
- affinity:核函数,默认是’rbf’,可选:”nearest_neighbors”,”precomputed”,”rbf”或sklearn.metrics.pairwise_kernels支持的其中一个 - 内核之一。
- gamma :affinity指定的核函数的内核系数,默认1.0
c)主要属性
-
labels_ :每个数据的分类标签
- 算法特点
- Graph distance (e.g. nearest-neighbor graph)(图形距离(例如最近邻图))
- 适用场景
- 几个簇,均匀的簇大小,非平面几何
- 中等的 n_samples, 小的 n_clusters
- 代码
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import spectral_clustering
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from itertools import cycle ##python自带的迭代器模块
##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=3000
##生产数据
X, lables_true = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.6,
random_state =0)
##变换成矩阵,输入必须是对称矩阵
metrics_metrix = (-1 * metrics.pairwise.pairwise_distances(X)).astype(np.int32)
metrics_metrix += -1 * metrics_metrix.min()
##设置谱聚类函数
n_clusters_= 4
lables = spectral_clustering(metrics_metrix,n_clusters=n_clusters_)
##绘图
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
##根据lables中的值是否等于k,重新组成一个True、False的数组
my_members = lables == k
##X[my_members, 0] 取出my_members对应位置为True的值的横坐标
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
5 Hierarchical Clustering——层次聚类
密度聚类几种算法在较小的复杂度内获取较好的结果,但是这几种算法却存在一个链式效应的现象,比如:A与B相似,B与C相似,那么在聚类的时候便会将A、B、C聚合到一起,但是如果A与C不相似,就会造成聚类误差,严重的时候这个误差可以一直传递下去。为了降低链式效应,这时候层次聚类就该发挥作用了。
层次聚类算法 (hierarchical clustering) 在不同层次上对数据集进行划分,形成树状的聚类结构。先将数据集划分为一层一层的 clusters,后面一层生成的 clusters 基于前面一层的结果,直到满足条件为止。
层次聚类算法一般分为两类:
- 凝聚
Agglomerative层次聚类:又称自底向上(bottom-up)的层次聚类,每一个对象最开始都是一个 cluster,每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster,如此往复,直至最终所有的对象都属于一个 cluster。这里主要关注此类算法。 - 分裂
Divisive层次聚类: 又称自顶向下(top-down)的层次聚类,最开始所有的对象均属于一个 cluster,每次按一定的准则将某个 cluster 划分为多个 cluster,如此往复,直至每个对象均是一个 cluster。(较少用)
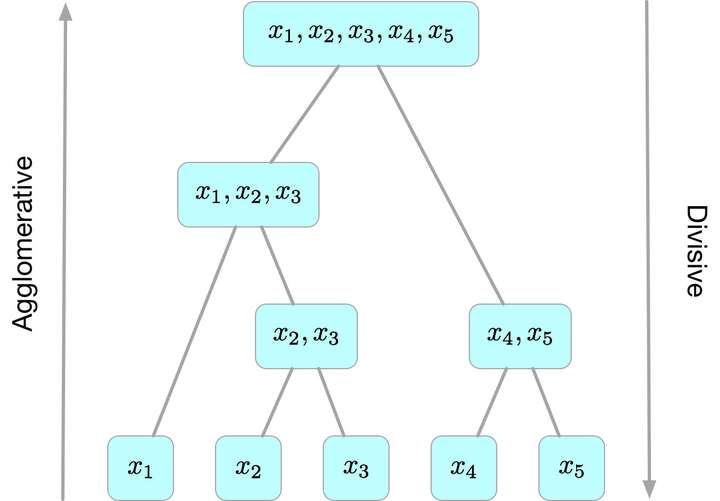
比较新的算法:
BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies利用层次方法的平衡迭代规约和聚类)主要是在数据量很大的时候使用,而且数据类型是numerical连续型。首先利用树的结构对对象集进行划分,然后再利用其它聚类方法对这些聚类进行优化;- sklearn.cluster.Birch
ROCK(A Hierarchical Clustering Algorithm for Categorical Attributes)主要用在categorical离散型的数据类型上;Chameleon(A Hierarchical Clustering AlgorithmUsing Dynamic Modeling)里用到的linkage是kNN(k-nearest-neighbor)算法,并以此构建一个graph,Chameleon的聚类效果被认为非常强大,比BIRCH好用,但运算复杂度很高,O(n^2)。
注意:
- 绝大多数层次聚类属于凝聚型层次聚类,它们只是在簇间相似度的定义上有所不同
- 层次聚类算法是一种贪心算法(greedy algorithm),因其每一次合并或划分都是基于某种局部最优的选择。
3)图解过程
优缺点
优点:
- 1,距离和规则的相似度容易定义,限制少;
- 2,不需要预先制定聚类数;
- 3,可以发现类的层次关系;
- 4,可以聚类成其它形状
缺点:
- 1,计算复杂度太高;
- 2,奇异值也能产生很大影响;
- 3,算法很可能聚类成链状
簇距离度量
- 这里的关键在于:如何计算聚类簇之间的距离?
- ①最小距离:单链接single-linkage算法,两个簇的样本对之间距离的最小值
- ②最大距离:单链接complete-linkage算法,两个簇的样本对之间距离的最大值
- ③平均距离:单链接average-linkage算法,两个簇的样本对之间距离的平均值
- 一是非加权组平均(UPGMA)
- 二是加权组平均(WPGMA)
- 注:非加权更为可靠,除非由于重采样等原因,导致需要考虑样本权值时,才会使用加权。
- 一是非加权组平均(UPGMA)
- ④ 质心距离:质心距离指的是簇质心与簇质心之间的距离。这里简单描述两种质心距离。
- 一种是UPGMC
- 另一种是WPGMC,即新簇质心取合并的两个簇的质心均值(取质心的方法不同)。
- 注:使用质心距离计算簇间相似度的方法,与其他方法有一个明显的区别,就是用于计算距离的数据,可能是不存在于样本的数据
- ⑤ 方差最小化(ward)距离:
Agglomerative聚类(凝聚)
Agglomerative原理是:最初将每个对象看成一个簇,然后将这些簇根据某种规则被一步步合并,就这样不断合并直到达到预设的簇类个数。
算法步骤(凝聚)
- a)将每个对象归为一类, 共得到N类, 每类仅包含一个对象. 类与类之间的距离就是它们所包含的对象之间的距离.
- b)找到最接近的两个类并合并成一类, 于是总的类数少了一个.
- c)重新计算新的类与所有旧类之间的距离.
- d)重复第2步和第3步, 直到最后合并成一个类为止(此类包含了N个对象).
层次聚类可视化
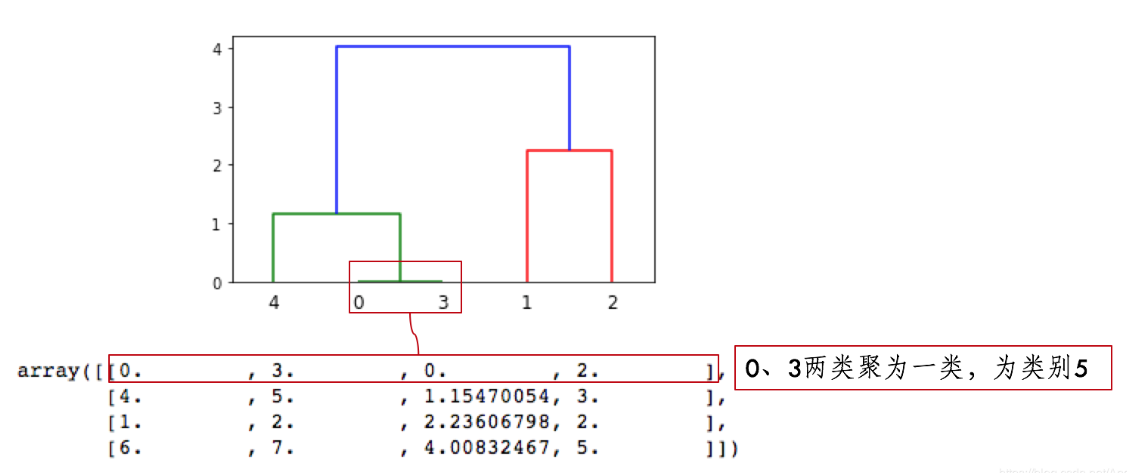
X一共有5个样本,那么在进行层次聚类
- 5个样本各自一类,类别名称是0、1、2、3、4
- 第一行:[0, 3]意思是类别0和类别3距离最近,首先聚成一类,并自动定义类别为5(=len(X)-1+1)
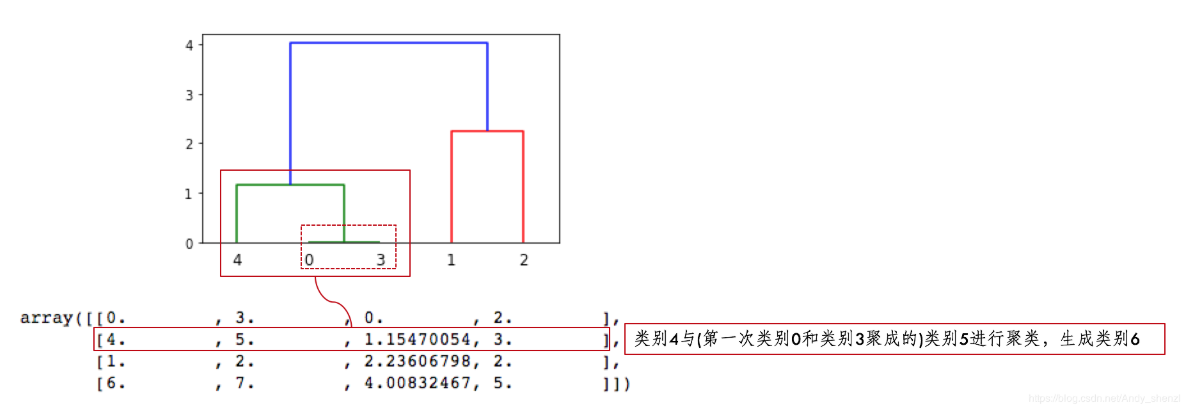
- 第二行:[4, 5]意思是类别4和上面聚类的新类别5距离为第二近,4、5聚成一类,类别为6(=len(X)-1+2)
- 第三行:[1, 2]意思是类别1、类别2距离为第三近,聚成一类,类别为7(=len(X)-1+3)
- 第四行:[6, 7]意思是类别6、7距离为第四近,聚成一类,类别为8(=len(X)-1+4)
- 因为类别5有两个样本,加上类别4形成类别6,有3个样本;
- 类别7是类别1、2聚类形成,有两个样本;
- 类别6、7聚成一类后,类别8有5个样本,这样X全部样本参与聚类,聚类完成。
sklearn里的层次聚类
sklearn中没有可视化效果
import numpy as np
#import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
data = np.random.randint(0,10,size=[10,2])
# 层次聚类
clustering = AgglomerativeClustering().fit(X) # 训练模型
# 输出聚类结果
clustering.labels_ # array([1, 0, 0, 1, 1])
# 输出层次结构
clustering.children_
# array([[0, 3],
# [4, 5],
# [1, 2],
# [6, 7]])
AgglomerativeClustering类的构造函数的参数有簇的个数n_clusters,连接方法linkage,连接度量选项affinity三个重要参数。下面就这三个参数进行描述。
- 簇的个数
n_clusters:需要用户指定的,按照常理来说,凝聚层次聚类是不需要指定簇的个数的,但是sklearn的这个类需要指定簇的个数。算法会根据簇的个数判断最终的合并依据,这个参数会影响聚类质量。 - 连接方法
linkage:指的是衡量簇与簇之间的远近程度的方法。具体说来包括最小距离,最大距离和平均距离三种方式。对应于簇融合的方法,即簇间观测点之间的最小距离作为簇的距离,簇间观测点之间的最大距离作为簇的距离,以及簇间观测点之间的平均距离作为簇的距离。一般说来,平均距离是一种折中的方法。 -
连接度量
affinity:是一个簇间距离的计算方法,包括各种欧式空间的距离计算方法以及非欧式空间的距离计算方法。此外,该参数还可以设置为‘precomputed’,即用户输入计算好的距离矩阵。距离矩阵的生成方法:假设用户有n个观测点,那么先依次构造这n个点两两间的距离列表,即长度为n*(n-1)/2的距离列表,然后通过scipy.spatial.distance的dist库的squareform函数就可以构造距离矩阵了。这种方式的好处是用户可以使用自己定义的方法计算任意两个观测点的距离,然后再进行聚类。 聚类结束以后,需要对聚类质量进行评估。 - a)sklearn.cluster.AgglomerativeClustering
- b)主要参数(详细参数)
- n_clusters:一个整数,指定分类簇的数量, None时表示不限类目,此时需要threshlod > 0
- connectivity:一个数组或者可调用对象或者None,用于指定连接矩阵
- affinity:一个字符串或者可调用对象,用于计算距离。可以为:’euclidean’,’l1’,’l2’,’mantattan’,’cosine’,’precomputed’,如果 linkage=’ward’,则affinity必须为’euclidean’
- memory:用于缓存输出的结果,默认为不缓存
- n_components:在 v-0.18中移除
- compute_full_tree:通常当训练了n_clusters后,训练过程就会停止,但是如果compute_full_tree=True,则会继续训练从而生成一颗完整的树
- linkage:一个字符串,用于指定链接算法, 指定层次聚类判断相似度的方法,有三种:
- ‘ward’:方差最小化ward, 单链接 single-linkage,采用dmin
- ‘single’:组间距离等于两类对象之间的最小距离
- ‘complete’:组间距离等于两组对象之间的最大距离, 全链接 complete-linkage算法,采用dmax
- ‘average’:组间距离等于两组对象之间的平均距离, 均连接 average-linkage算法,采用davg
- pooling_func:一个可调用对象,它的输入是一组特征的值,输出是一个数
- c)主要属性
- labels_: 每个数据的分类标签
- n_leaves_:分层树的叶节点数量
- n_components:连接图中连通分量的估计值
- children:一个数组,给出了每个非节点数量
参考资料 聚类算法
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
"""
产生数据
"""
def create_data(centers,num=100,std=0.7):
X,labels_true = make_blobs(n_samples=num,centers=centers, cluster_std=std)
return X,labels_true
"""
数据作图
"""
def plot_data(*data):
X,labels_true=data
labels=np.unique(labels_true)
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
colors='rgbycm'
for i,label in enumerate(labels):
position=labels_true==label
ax.scatter(X[position,0],X[position,1],label="cluster %d"%label),
color=colors[i%len(colors)]
ax.legend(loc="best",framealpha=0.5)
ax.set_xlabel("X[0]")
ax.set_ylabel("Y[1]")
ax.set_title("data")
plt.show()
"""
测试函数
"""
def test_AgglomerativeClustering(*data):
X,labels_true=data
clst=cluster.AgglomerativeClustering()
predicted_labels=clst.fit_predict(X)
print("ARI:%s"% adjusted_rand_score(labels_true, predicted_labels))
"""
考察簇的数量对于聚类效果的影响
"""
def test_AgglomerativeClustering_nclusters(*data):
X,labels_true=data
nums=range(1,50)
ARIS=[]
for num in nums:
clst=cluster.AgglomerativeClustering(n_clusters=num)
predicted_lables=clst.fit_predict(X)
ARIS.append(adjusted_rand_score(labels_true, predicted_lables))
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.plot(nums,ARIS,marker="+")
ax.set_xlabel("n_clusters")
ax.set_ylabel("ARI")
fig.suptitle("AgglomerativeClustering")
plt.show()
"""
考察链接方式对聚类结果的影响
"""
def test_agglomerativeClustering_linkage(*data):
X,labels_true=data
nums=range(1,50)
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
linkages=['ward','complete','average']
markers="+o*"
for i,linkage in enumerate(linkages):
ARIs=[]
for num in nums:
clst=cluster.AgglomerativeClustering(n_clusters=num,linkage=linkage)
predicted_labels=clst.fit_predict(X)
ARIs.append(adjusted_rand_score(labels_true, predicted_labels))
ax.plot(nums,ARIs,marker=markers[i],label="linkage:%s"%linkage)
ax.set_xlabel("n_clusters")
ax.set_ylabel("ARI")
ax.legend(loc="best")
fig.suptitle("AgglomerativeClustering")
plt.show()
centers=[[1,1],[2,2],[1,2],[10,20]]
X,labels_true=create_data(centers, 1000, 0.5)
test_AgglomerativeClustering(X,labels_true)
plot_data(X,labels_true)
test_AgglomerativeClustering_nclusters(X,labels_true)
test_agglomerativeClustering_linkage(X,labels_true)
当n_clusters=4时,ARI指数最大,因为确实是从四个中心点产生的四个簇。三种链接方式随分类簇的数量的总体趋势相差无几。但是单链接方式ward的峰值最大,且峰值最大的分类簇的数量刚好等于实际生成的簇的数量。
-
- 算法特点
- Distances between points(点之间的距离)
- 适用场景
- 很多的簇,可能连接限制
- 大的 n_samples 和 n_clusters
代码
# Authors: Gael Varoquaux
# License: BSD 3 clause (C) INRIA 2014
print(__doc__)
from time import time
import numpy as np
from scipy import ndimage
from matplotlib import pyplot as plt
from sklearn import manifold, datasets
digits = datasets.load_digits(n_class=10)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
np.random.seed(0)
def nudge_images(X, y):
# Having a larger dataset shows more clearly the behavior of the
# methods, but we multiply the size of the dataset only by 2, as the
# cost of the hierarchical clustering methods are strongly
# super-linear in n_samples
shift = lambda x: ndimage.shift(x.reshape((8, 8)),
.3 * np.random.normal(size=2),
mode='constant',
).ravel()
X = np.concatenate([X, np.apply_along_axis(shift, 1, X)])
Y = np.concatenate([y, y], axis=0)
return X, Y
X, y = nudge_images(X, y)
#----------------------------------------------------------------------
# Visualize the clustering
def plot_clustering(X_red, labels, title=None):
x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
X_red = (X_red - x_min) / (x_max - x_min)
plt.figure(figsize=(6, 4))
for i in range(X_red.shape[0]):
plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
color=plt.cm.nipy_spectral(labels[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
plt.xticks([])
plt.yticks([])
if title is not None:
plt.title(title, size=17)
plt.axis('off')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
#----------------------------------------------------------------------
# 2D embedding of the digits dataset
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")
from sklearn.cluster import AgglomerativeClustering
for linkage in ('ward', 'average', 'complete', 'single'):
clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
t0 = time()
clustering.fit(X_red)
print("%s :\t%.2fs" % (linkage, time() - t0))
plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)
plt.show()
scipy里的层次聚类
scipy工具包附加树状可视化效果
(1)linkage(y, method=’single’, metric=’euclidean’)
- 共包含3个参数: y是距离矩阵,可以是1维压缩向量(距离向量),也可以是2维观测向量(坐标矩阵)。若y是1维压缩向量,则y必须是n个初始观测值的组合,n是坐标矩阵中成对的观测值。返回值:(n-1)*4的矩阵Z(后面会仔细的讲解返回值各个字段的含义)
-
linkage方法用于计算两个聚类簇s和t之间的距离d(s,t),这个方法的使用在层次聚类之前。当s和t形成一个新的聚类簇u时,s和t被从森林(已经形成的聚类簇群)中移除,而用新的聚类簇u来代替。当森林中只有一个聚类簇时算法停止。而这个聚类簇就成了聚类树的根。 距离矩阵在每次迭代中都将被保存,d[i,j]对应于第i个聚类簇与第j个聚类簇之间的距离。每次迭代必须更新新形成的聚类簇之间的距离矩阵。 假定现在有 u 个初始观测值u[0],…,u[ u -1]在聚类簇u中,有 v 个初始对象v[0],…,v[ v -1]在聚类簇v中。回忆s和t合并成u。让v成为森林中的聚类簇,而不是u。 - method是指计算类间距离的方法,比较常用的有3种:
- ① single:最近邻,把类与类间距离最近的作为类间距
- ② complete:最远邻,把类与类间距离最远的作为类间距
- ③ average:平均距离,类与类间所有pairs距离的平均
- 其他的method还有如weighted,centroid等等,具体可以参考
(2)fcluster(Z, t, criterion=’inconsistent’, depth=2, R=None, monocrit=None)
- 第一个参数Z是linkage得到的矩阵,记录了层次聚类的层次信息;
- t是一个聚类的阈值-“The threshold to apply when forming flat clusters”,在实际中,这个阈值的选取还是蛮重要的. 其他的参数是默认的,具体可以参考
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from matplotlib import pyplot as plt
X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
# 层次聚类编码为一个linkage矩阵。
# Z共有四列组成,第一字段与第二字段分别为聚类簇的编号,在初始距离前每个初始值被从0~n-1进行标识,每生成一个新的聚类簇就在此基础上增加一对新的聚类簇进行标识,第三个字段表示前两个聚类簇之间的距离,第四个字段表示新生成聚类簇所包含的元素的个数。
Z = linkage(X, 'ward') # 计算各个簇之间的距离
#method =
# ’single’:一范数距离
# ’complete’:无穷范数距离
# ’average’:平均距离
# ’centroid’:二范数距离
# ’ward’:离差平方和距离
#array([[0. , 3. , 0. , 2. ],
# [4. , 5. , 1.15470054, 3. ],
# [1. , 2. , 2.23606798, 2. ],
# [6. , 7. , 4.00832467, 5. ]])
# 开始聚类, fcluster 从给定链接矩阵定义的层次聚类中形成平面聚类
# 参数Z表示上面的linkage矩阵
# 参数scalar:形成扁平簇的阈值。
# 参数criterion:
# ’inconsistent’:预设的,如果一个集群节点及其所有后代的不一致值小于或等于 t,那么它的所有叶子后代都属于同一个平面集群。当没有非单例集群满足此条件时,每个节点都被分配到自己的集群中。
# ’distance’:每个簇的距离不超过t
f = fcluster(Z,4,'distance') # 输出是每一个特征的类别
fig = plt.figure(figsize=(5, 3))
# 绘制层次聚类图
dn = dendrogram(Z)
plt.show()
# -------- 补充 --------
def llf(id):
if id < n:
return str(id)
else:
return '[%d %d %1.2f]' % (id, count, R[n-id,3])
# 定制label
# The text for the leaf nodes is going to be big so force a rotation of 90 degrees.
dendrogram(Z, leaf_label_func=llf, leaf_rotation=90)
# 定制label颜色
dendrogram(Z, link_color_func=lambda k: colors[k])
更多dendrogram参数配置
# modified from https://www.machinelearningplus.com/plots/top-50-matplotlib-visualizations-the-master-plots-python/
import matplotlib.pyplot as plt
import pandas as pd
import scipy.cluster.hierarchy as shc
# import data
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/USArrests.csv')
print(df)
# Plot
plt.figure(figsize=(16, 10), dpi= 80)
plt.title("USArrests Dendograms", fontsize=22)
dend = shc.dendrogram(shc.linkage(df[['Murder', 'Assault', 'UrbanPop', 'Rape']],
method='ward'), labels=df.State.values, color_threshold=100)
plt.xticks(fontsize=12)
#plt.savefig('USArrests_Dendograms.png')
plt.show()
AP聚类(近邻传播)
2.1 简介
- AP(Affinity Propagation)通常被翻译为近邻传播算法或者亲和力传播算法,是在2007年的Science杂志上提出的一种新的聚类算法。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar),然后数据点两两之间连线构成一个网络(相似度矩阵),再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心。
2.2 算法原理
概念:
- 吸引度(responsibility)矩阵R:其中r(i,k)描述了数据对象k适合作为数据对象i的聚类中心的程度,表示的是从i到k的消息。
- 归属度(availability)矩阵A:其中a(i,k)描述了数据对象i选择数据对象k作为其据聚类中心的适合程度,表示从k到i的消息。
- 相似度(similarity)矩阵S:通常S(i,j)取i,j的欧氏距离的负值,当i=j时,通常取整个矩阵的最小值或者中位数(Scikit-learn中默认为中位数),取得值越大则最终产生的类数量越多。
算法步骤
- 算法初始,吸引度矩阵和归属度矩阵均初始化为0矩阵。
- 更新吸引度矩阵
- 更新归属度矩阵
- 根据衰减系数λ对两个公式进行衰减
- 重复步骤2/3/4直至矩阵稳定或者达到最大迭代次数,算法结束。最终取a+r最大的k作为聚类中心。
2.3 算法特点
-
Graph distance (e.g. nearest-neighbor graph)(图形距离(例如,最近邻图))
- 优点:
- 与其他聚类算法不同,AP聚类不需要指定K(经典的K-Means)或者是其他描述聚类个数的参数
- 一个聚类中最具代表性的点在AP算法中叫做Examplar,与其他算法中的聚类中心不同,examplar是原始数据中确切存在的一个数据点,而不是由多个 数据点求平均而得到的聚类中心
- 多次执行AP聚类算法,得到的结果完全一样的,即不需要进行随机选取初值步骤.
- AP算法相对于Kmeans优势是不需要指定聚类数量,对初始值不敏感
- 模型对数据的初始值不敏感。
- 对初始相似度矩阵数据的对称性没有要求。
- 相比与k-centers聚类方法,其结果的平方差误差较小。
- 缺点:
- AP算法需要事先计算每对数据对象之间的相似度,如果数据对象太多的话,内存放不下,若存在数据库,频繁访问数据库也需要时间。
- AP算法的时间复杂度较高,一次迭代大概O(N3)
- 聚类的好坏受到参考度和阻尼系数的影响
2.4 适用场景
- 许多簇,不均匀的簇大小,非平面几何
- 不可扩展的 n_samples
- 特别适合高维、多类数据快速聚类
- 图像、文本、生物信息学、人脸识别、基因发现、搜索最优航线、 码书设计以及实物图像识别等领域
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import AffinityPropagation
from sklearn.metrics import euclidean_distances
#聚类算法之AP算法:
#1--与其他聚类算法不同,AP聚类不需要指定K(金典的K-Means)或者是其他描述聚类个数的参数
#2--一个聚类中最具代表性的点在AP算法中叫做Examplar,与其他算法中的聚类中心不同,examplar
#是原始数据中确切存在的一个数据点,而不是由多个数据点求平均而得到的聚类中心
#3--多次执行AP聚类算法,得到的结果完全一样的,即不需要进行随机选取初值步骤.
#算法复杂度较高,为O(N*N*logN),而K-Means只是O(N*K)的复杂度,当N》3000时,需要算很久
#AP算法相对于Kmeans优势是不需要指定聚类数量,对初始值不敏感
#AP算法应用场景:图像、文本、生物信息学、人脸识别、基因发现、搜索最优航线、 码书设计以及实物图像识别等领域
#算法详解: http://blog.csdn.net/helloeveryon/article/details/51259459
if __name__=='__main__':
#scikit中的make_blobs方法常被用来生成聚类算法的测试数据,直观地说,make_blobs会根据用户指定的特征数量、
# 中心点数量、范围等来生成几类数据,这些数据可用于测试聚类算法的效果。
#函数原型:sklearn.datasets.make_blobs(n_samples=100, n_features=2,
# centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]
#参数解析:
# n_samples是待生成的样本的总数。
#
# n_features是每个样本的特征数。
#
# centers表示类别数。
#
# cluster_std表示每个类别的方差,例如我们希望生成2类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0, 3.0]。
N=400
centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
#生成聚类算法的测试数据
data,y=ds.make_blobs(N,n_features=2,centers=centers,cluster_std=[0.5, 0.25, 0.7, 0.5],random_state=0)
#计算向量之间的距离
m=euclidean_distances(data,squared=True)
#求中位数
preference=-np.median(m)
print 'Preference:',preference
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12,9),facecolor='w')
for i,mul in enumerate(np.linspace(1,4,9)):#遍历等差数列
print 'mul=',mul
p=mul*preference
model=AffinityPropagation(affinity='euclidean',preference=p)
af=model.fit(data)
center_indices=af.cluster_centers_indices_
n_clusters=len(center_indices)
print ('p=%.1f'%mul),p,'聚类簇的个数为:',n_clusters
y_hat=af.labels_
plt.subplot(3,3,i+1)
plt.title(u'Preference:%.2f,簇个数:%d' % (p, n_clusters))
clrs=[]
for c in np.linspace(16711680, 255, n_clusters):
clrs.append('#%06x' % c)
for k, clr in enumerate(clrs):
cur = (y_hat == k)
plt.scatter(data[cur, 0], data[cur, 1], c=clr, edgecolors='none')
center = data[center_indices[k]]
for x in data[cur]:
plt.plot([x[0], center[0]], [x[1], center[1]], color=clr, zorder=1)
plt.scatter(data[center_indices, 0], data[center_indices, 1], s=100, c=clrs, marker='*', edgecolors='k',
zorder=2)
plt.grid(True)
plt.tight_layout()
plt.suptitle(u'AP聚类', fontsize=20)
plt.subplots_adjust(top=0.92)
plt.show()
ROCK——层次聚类
ROCK(A Hierarchical Clustering Algorithm for Categorical Attributes)主要用在categorical离散型的数据类型上;
Chameleon——层次聚类
Chameleon(A Hierarchical Clustering AlgorithmUsing Dynamic Modeling)里用到的linkage是kNN(k-nearest-neighbor)算法,并以此构建一个graph,Chameleon的聚类效果被认为非常强大,比BIRCH好用,但运算复杂度很高,O(n^2)。
6 Mean-shift 均值迁移
1)概述
- Mean-shift(即:均值迁移)的基本思想:在数据集中选定一个点,然后以这个点为圆心,r为半径,画一个圆(二维下是圆),求出这个点到所有点的向量的平均值,而圆心与向量均值的和为新的圆心,然后迭代此过程,直到满足一点的条件结束。(Fukunage在1975年提出)
- 后来Yizong Cheng 在此基础上加入了 核函数 和 权重系数 ,使得Mean-shift 算法开始流行起来。目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。
2)图解过程
为了方便大家理解,借用下几张图来说明Mean-shift的基本过程。
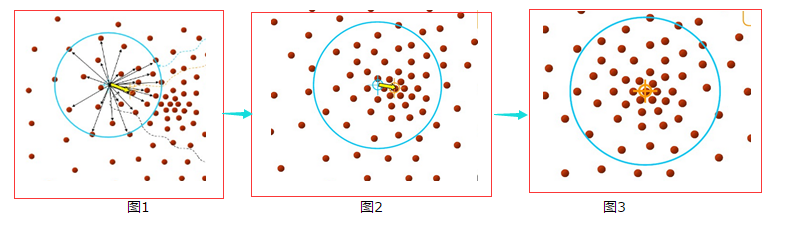
由上图可以很容易看到,Mean-shift 算法的核心思想就是不断的寻找新的圆心坐标,直到密度最大的区域。
3)Mean-shift 算法函数
a)核心函数:sklearn.cluster.MeanShift(核函数:RBF核函数) 由上图可知,圆心(或种子)的确定和半径(或带宽)的选择,是影响算法效率的两个主要因素。所以在sklearn.cluster.MeanShift中重点说明了这两个参数的设定问题。
b)主要参数
- bandwidth :半径(或带宽),float型。如果没有给出,则使用sklearn.cluster.estimate_bandwidth计算出半径(带宽).(可选)
- seeds :圆心(或种子),数组类型,即初始化的圆心。(可选)
- bin_seeding :布尔值。如果为真,初始内核位置不是所有点的位置,而是点的离散版本的位置,其中点被分类到其粗糙度对应于带宽的网格上。将此选项设置为True将加速算法,因为较少的种子将被初始化。默认值:False.如果种子参数(seeds)不为None则忽略。
c)主要属性
- cluster_centers_ : 数组类型。计算出的聚类中心的坐标。
-
labels_ :数组类型。每个数据点的分类标签。、
- 算法特点
- Distances between points(点之间的距离)
- 圆心(或种子)的确定和半径(或带宽)的选择,是影响算法效率的两个主要因素。
- 该算法不是高度可扩展的,因为在执行算法期间需要执行多个最近邻搜索。
- 该算法保证收敛,但是当质心的变化较小时,算法将停止迭代。
- 通过找到给定样本的最近质心来给新样本打上标签。
- 适用场景
- 许多簇,不均匀的簇大小,非平面几何
- 不可扩展的 n_samples
- 适用于类别数量未知,且样本数量<10K
- 目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。
代码
print(__doc__)
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs
# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
# #############################################################################
# Compute clustering with MeanShift
# The following bandwidth can be automatically detected using
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters_)
# #############################################################################
# Plot result
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
7 BIRCH——层次聚类
简介
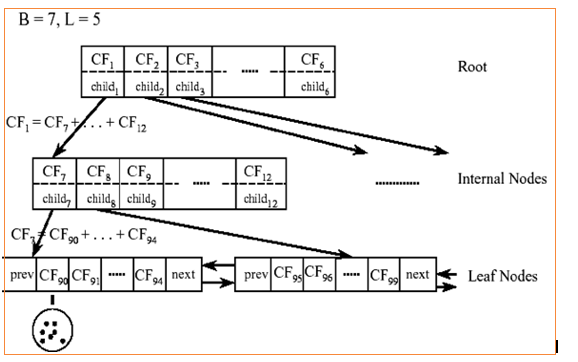
- Birch(利用层次方法的平衡迭代规约和聚类):就是通过聚类特征(CF)形成一个聚类特征树,root层的CF个数就是聚类个数。
算法原理
- 相关概念
- 聚类特征(CF):每一个CF是一个三元组,可以用(N,LS,SS)表示.其中N代表了这个CF中拥有的样本点的数量;LS代表了这个CF中拥有的样本点各特征维度的和向量,SS代表了这个CF中拥有的样本点各特征维度的平方和。
- 如上图所示:N = 5
- LS=(3+2+4+4+3,4+6+5+7+8)=(16,30)
- SS =(32+22+42+42+32,42+62+52+72+82)=(54,190)
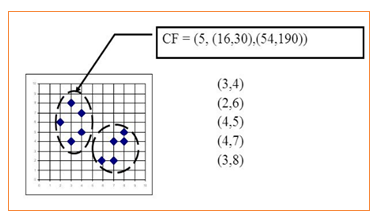
- 聚类过程
- 对于上图中的CF Tree,限定了B=7,L=5, 也就是说内部节点最多有7个CF(CF90下的圆),而叶子节点最多有5个CF(CF90到CF94)。叶子节点是通过双向链表连通的。
- 特点
- Euclidean distance between points(点之间的欧式距离)
- 适用场景
- 大数据集,异常值去除,数据简化
- 大的 n_clusters 和 n_samples
class sklearn.cluster.Birch(threshold=0.5, branching_factor=50, n_clusters=3, compute_labels=True, copy=True)
- threshold:一个浮点数,指定空间阈值 五、BIRCH - 图1 。
- branching_facto:一个整数,指定枝平衡因子 五、BIRCH - 图2 。叶平衡因子 五、BIRCH - 图3 也等于该数值。
- n_clusters:一个整数或者None 或者sklearn.cluster 模型,指定最终聚类的数量。
- 如果为None,则由算法自动给出。
- 如果为一个整数,则使用AgglomerativeClustering 算法来对CF 本身执行聚类,并将聚类结果返回。这使得最终的聚类数量就是n_clusters 。
- 如果为一个sklearn.cluster 模型,则该模型对CF 本身执行聚类,并将聚类结果返回。
- compute_labels:一个布尔值,指定是否需要计算簇标记。
- copy:一个布尔值,指定是否拷贝原始数据。
属性:
- root_:一个_CFNode对象,表示CF树的根节点。
- subcluster_centers_:一个数组,表示所有子簇的中心点。它直接从所有叶结点中读取。
- subcluster_labels_:一个数组,表示所有子簇的簇标记。可能多个子簇会有同样的簇标记,因为子簇可能会被执行进一步的聚类。
- labels_:一个形状为[ n_samples,] 的数组,给出了每个样本的簇标记。如果执行分批训练,则它给出的是最近一批样本的簇标记。 方法:
- fit(X[, y]):训练模型。
- partial_fit(X[, y]):分批训练模型(在线学习)。
- fit_predict(X[, y]):训练模型并执行聚类,返回每个样本所属的簇标记。
- predict(X):对每个样本预测其簇标记。根据每个子簇的中心点来预测样本的簇标记。
- transform(X):将样本转换成子簇中心点的坐标:维度五、BIRCH - 图4 代表样本距离第 五、BIRCH - 图5 个子簇中心的距离。
- fit_transform(X[, y]):训练模型并将样本转换成子簇中心点的坐标。
完整版代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import Birch
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本2个特征,共4个簇,簇中心在[-1,-1], [0,0],[1,1], [2,2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.3, 0.4, 0.3],random_state =9)
##设置birch函数
# n_cluster为None表示算法自动给出合适的簇数目
birch = Birch(n_clusters = None)
##训练数据
y_pred = birch.fit_predict(X)
##绘图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
GaussianMixtureModel(混合高斯模型,GMM)
- 正太分布也叫高斯分布,正太分布的概率密度曲线也叫高斯分布概率曲线
1)介绍
- 聚类算法大多数通过相似度来判断,而相似度又大多采用欧式距离长短作为衡量依据。
- 而GMM采用了新的判断依据:概率,即通过属于某一类的概率大小来判断最终的归属类别。
- GMM的基本思想就是:任意形状的概率分布都可以用多个高斯分布函数去近似,也就是说GMM就是有多个单高斯密度分布(Gaussian)组成的,每个Gaussian叫一个”Component”,这些”Component”线性加成在一起就组成了 GMM 的概率密度函数,也就是下面的函数。
2)原理
- 高斯混合模型是由K个高斯分布(正态分布)函数组成,而该算法的目的就是找出各个高斯分布最佳的均值、方差、权重。
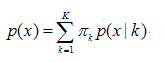
- 指定K的值,并初始随机选择各参数的值
- E步骤。根据当前的参数,计算每个点由某个分模型生成的概率
- M步骤。根据E步骤估计出的概率,来改进每个分模型的均值、方差和权重
- 重复步骤2、3,直至收敛。
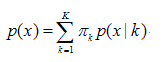
列出来公式只是方便理解下面的函数中为什么需要那些参数。
K:模型的个数,即Component的个数(聚类的个数)
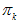 为第k个高斯的权重
为第k个高斯的权重
p(x |k) 则为第k个高斯概率密度,其均值为μk,方差为σk 上述参数,除了K是直接给定之外,其他参数都是通过EM算法估算出来的。(有个参数是指定EM算法参数的)
3)GaussianMixtureModel 算法函数
a)from sklearn.mixture.GaussianMixture b)主要参数(详细参数)
- n_components :高斯模型的个数,即聚类的目标个数
- covariance_type : 通过EM算法估算参数时使用的协方差类型,默认是”full”
- full:每个模型使用自己的一般协方差矩阵
- tied:所用模型共享一个一般协方差矩阵
- diag:每个模型使用自己的对角线协方差矩阵
-
spherical:每个模型使用自己的单一方差
- 算法特点
- Mahalanobis distances to centers(Mahalanobis 与中心的距离)
- 优点
- 可以给出一个样本属于某类的概率是多少
- 不仅用于聚类,还可用于概率密度的估计
- 可以用于生成新的样本点
- 缺点
- 需要指定K值
- 使用EM算法来求解
- 往往只能收敛于局部最优
- 适用场景
- 平面几何,适用于密度估计
- Not scalable(不可扩展)
- 代码
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold
print(__doc__)
colors = ['navy', 'turquoise', 'darkorange']
def make_ellipses(gmm, ax):
for n, color in enumerate(colors):
if gmm.covariance_type == 'full':
covariances = gmm.covariances_[n][:2, :2]
elif gmm.covariance_type == 'tied':
covariances = gmm.covariances_[:2, :2]
elif gmm.covariance_type == 'diag':
covariances = np.diag(gmm.covariances_[n][:2])
elif gmm.covariance_type == 'spherical':
covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
v, w = np.linalg.eigh(covariances)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan2(u[1], u[0])
angle = 180 * angle / np.pi # convert to degrees
v = 2. * np.sqrt(2.) * np.sqrt(v)
ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
180 + angle, color=color)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.5)
ax.add_artist(ell)
ax.set_aspect('equal', 'datalim')
iris = datasets.load_iris()
# Break up the dataset into non-overlapping training (75%) and testing
# (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))
X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]
n_classes = len(np.unique(y_train))
# Try GMMs using different types of covariances.
estimators = {cov_type: GaussianMixture(n_components=n_classes,
covariance_type=cov_type, max_iter=20, random_state=0)
for cov_type in ['spherical', 'diag', 'tied', 'full']}
n_estimators = len(estimators)
plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(bottom=.01, top=0.95, hspace=.15, wspace=.05,
left=.01, right=.99)
for index, (name, estimator) in enumerate(estimators.items()):
# Since we have class labels for the training data, we can
# initialize the GMM parameters in a supervised manner.
estimator.means_init = np.array([X_train[y_train == i].mean(axis=0)
for i in range(n_classes)])
# Train the other parameters using the EM algorithm.
estimator.fit(X_train)
h = plt.subplot(2, n_estimators // 2, index + 1)
make_ellipses(estimator, h)
for n, color in enumerate(colors):
data = iris.data[iris.target == n]
plt.scatter(data[:, 0], data[:, 1], s=0.8, color=color,
label=iris.target_names[n])
# Plot the test data with crosses
for n, color in enumerate(colors):
data = X_test[y_test == n]
plt.scatter(data[:, 0], data[:, 1], marker='x', color=color)
y_train_pred = estimator.predict(X_train)
train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
plt.text(0.05, 0.9, 'Train accuracy: %.1f' % train_accuracy,
transform=h.transAxes)
y_test_pred = estimator.predict(X_test)
test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
plt.text(0.05, 0.8, 'Test accuracy: %.1f' % test_accuracy,
transform=h.transAxes)
plt.xticks(())
plt.yticks(())
plt.title(name)
plt.legend(scatterpoints=1, loc='lower right', prop=dict(size=12))
plt.show()
最近邻
ANN(Approximate nearest neighbor)是一系列用于解决最近邻查找问题的近似算法,通过牺牲精度来换取时间和空间的方式从大量样本中获取最近邻。
ANN 方法常见分类有:
- 树方法,如 KD-tree
- 哈希方法,如 Local Sensitive Hashing (LSH)
- 图方法,如 Hierarchical Navigable Small World (HNSW)
【2024-7-17】HNSW算法原理
KD-Tree
LSM
HNSW
【2024-7-17】HNSW算法原理
HNSW 算法受跳表思想的启发,利用分层结构快速找到查询向量的近邻,时间复杂度为logN。
Delaunay Triangulation
在数学和计算几何中,三角剖分指将平面离散点集细分为三角网格,要求满足下面条件:
- 每个网格都是曲边三角形;
- 任何两个这样的曲边三角形,要么不相交,要么恰好相交于一条公共边(不能同时交两条或两条以上的边)
Delaunay三角剖分:给出一种“好的”三角网格定义方式,即满足:
- 空圆性:DT(Delaunay Triangulation)是唯一的(任意四点不能共圆),DT中任意三角形的外接圆范围内不会有其它点存在
- 最大化最小角:在点集可能形成的三角剖分中,DT所形成的三角形的最小角最大。从这个意义上讲,DT是最接近于规则化的三角剖分。具体的说是在两个相邻的三角形构成凸四边形的对角线,在相互交换后,两个内角的最小角不再增大。
Delonay图中,最接近的三点形成三角形且各线段(三角形的边)皆不相交,因为可以利用Delonay三角剖分解决近邻点查找问题。
NSW
NSW 算法思想
可导航小世界(Navigable Small World,NSW)将候选集合 C 构建成可导航小世界图 G(V,E),利用基于贪婪搜索的kNN算法从图中查找与查询点 q 距离最近的k个顶点。
如图所示,向图中逐个插入点,对于每个新插入点,使用近似kNN搜索(approximate kNN search)算法从图中找到与其最近f个点集合,该集合中所有点与插入点连接。
通过上述方式构建的是近似Delonay图,与标准Delonay图相比,随着越来越多的点被插入到图中,初期构建的短距离边会慢慢变成长距离边,形成可导航的小世界,从而在查找时减少跳数加快查找速度。
搜索算法
- 朴素贪婪搜索算法: 贪婪搜索算法查找的最近点是局部最优点,而不是全局最优点。
- 近似kNN搜索: 执行m次贪婪搜索,在每次搜索过程中随机选择一个进入点遍历,最后从m次搜索选出距离查询点最近的k个结果。
- 随着搜索次数的增加,找不到最近点的概率指数衰减,因此在不改变图结构的情况下能提高搜索准确性。
跳表
在n个节点有序链表查找第t(0<t<n)个节点 需要跳转 t-1 次。跳表通过构建多个有序链表和分层指针能够提高查询效率。
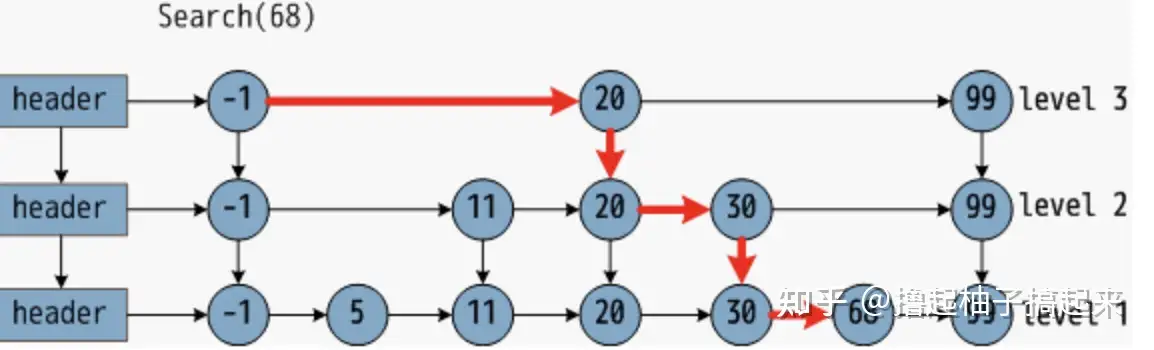
HNSW
分层可导航小世界(Hierarchical Navigable Small World,HNSW)是基于图的数据结构
- 将节点划分成不同层级,贪婪地遍历来自上层的元素,直到达到局部最小值
- 然后切换到下一层,以上一层中的局部最小值作为新元素重新开始遍历,直到遍历完最低一层。
与NSW相比,HNSW的改进方法:
- 使用分层的结构
- 使用了一种启发式方法选择某节点的邻居。
建图流程
搜索流程
实现
- C++ 版本: hnswlib
案例
文本聚类
字符串相似度
字符串的相似性比较应用场合很多,像拼写纠错、文本去重、上下文相似性等。
评价字符串相似度最常见的办法就是:把一个字符串通过插入、删除或替换这样的编辑操作,变成另外一个字符串,所需要的最少编辑次数,这种就是编辑距离(edit distance)度量方法,也称为Levenshtein距离。海明距离是编辑距离的一种特殊情况,只计算等长情况下替换操作的编辑次数,只能应用于两个等长字符串间的距离度量。
其他常用的度量方法还有:Jaccard distance、J-W距离(Jaro–Winkler distance)、余弦相似性(cosine similarity)、欧氏距离(Euclidean distance)等。
代码
【2021-11-8】Python Levenshtein 计算文本之间的距离
- pip install difflib
- pip install python-Levenshtein
import difflib
query_str = '市公安局'
s1 = '广州市邮政局'
s2 = '广州市公安局'
s3 = '广州市检查院'
seq = difflib.SequenceMatcher(None, s1, s2)
ratio = seq.ratio()
print 'difflib similarity1: ', ratio
# difflib 去掉列表中不需要比较的字符
seq = difflib.SequenceMatcher(lambda x: x in ' 我的雪', str1,str2)
ratio = seq.ratio()
print 'difflib similarity2: ', ratio
print(difflib.SequenceMatcher(None, query_str, s1).quick_ratio())
print(difflib.SequenceMatcher(None, query_str, s2).quick_ratio())
print(difflib.SequenceMatcher(None, query_str, s3).quick_ratio())
# 0.4
# 0.8 --> 某一种相似度评判标准下的最相似的文本……
# 0.08695652173913043
import Levenshtein
# (1) 汉明距离,str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数
Levenshtein.hamming('hello', 'world') # 4
Levenshtein.hamming('abc', 'abd') # 1
# (2) 编辑距离(也成Levenshtein距离)。是描述由一个字串转化成另一个字串最少的操作次数,在其中的操作包括插入、删除、替换
Levenshtein.distance('hello', 'world') # 4
Levenshtein.distance('abc', 'abd') # 1
Levenshtein.distance('abc', 'aecfaf') # 4
# (3) 莱文斯坦比。计算公式 r = (sum - ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和,ldist是类编辑距离
# 注意:这里的类编辑距离不是2中所说的编辑距离,2中三种操作中每个操作+1,而在此处,删除、插入依然+1,但是替换+2
# 这样设计的目的:ratio('a', 'c'),sum=2,按2中计算为(2-1)/2 = 0.5,’a’,'c’没有重合,显然不合算,但是替换操作+2,就可以解决这个问题。
Levenshtein.ratio('hello', 'world') # 0.2
Levenshtein.ratio('abc', 'abd') # 0.6666666666666666
Levenshtein.ratio('abc', 'aecfaf') # 0.4444444444444444
# (4) jaro距离
Levenshtein.jaro('hello', 'world') # 0.43333333333333335
Levenshtein.jaro('abc', 'abd') # 0.7777777777777777
Levenshtein.jaro('abc', 'aecfaf') # 0.6666666666666666
# (5) Jaro–Winkler距离
Levenshtein.jaro_winkler('hello', 'world') # 0.43333333333333335
Levenshtein.jaro_winkler('abc', 'abd') # 0.8222222222222222
Levenshtein.jaro_winkler('abc', 'aecfaf') # 0.7
pyecharts可视化
将高维向量通过 t-sne降维,再用pyecharts(1.*以上版本)可视化出来
- t-sne降维
# 原始数据文件格式:[query, 0.23, 0.43, ..., 1.23], 将query嵌入到768的高维空间里
data_file = 'newhouse/all_data_embedding.txt'
#query_vec = pd.read_csv(data_file)
#query_vec
num = 0
n = 769
query_dict = {}
for line in open(data_file):
num += 1
#if num > 50:
# break
arr = line.strip().split(',')
query= arr[0]
vec = arr[1:]
if len(arr) != 769 or not query:
logging.error('格式异常: query={}, len={}, line={}'.format(query,len(arr),arr[:3]))
continue
query_dict[query] = vec
query_list = list(query_dict.values())
query_label = list(query_dict.keys())
print(len(query_dict.keys()))
# ----- t-SNE 降维 -----
import numpy as np
from sklearn.manifold import TSNE
X = np.array(query_list)
#X = np.array([[0,0,0],[0,1,1],[1,0,1],[1,1,1]])
tsne = TSNE(n_components = 3)
tsne.fit_transform(X)
X_new = tsne.embedding_ # 降维后的3维矩阵
print(query_label[10],X_new[10]) # 输出label、降维后的向量
# ----- pca ------
from sklearn.decomposition import PCA
pca=PCA(n_components=3)
- 数据加载、可视化
import random
from pyecharts import options as opts
from pyecharts.charts import Scatter3D
from pyecharts.faker import Faker
# --------- 加载数据 ---------
vec_tsne = np.load('/home/wangqiwen004/work/nlu_data/newhouse/vec_tsne.npy')
vec_label = np.load('/home/wangqiwen004/work/nlu_data/newhouse/vec_label.npy')
vec_label = vec_label.reshape((-1,1)) # label是1维时,需要转换成矩阵,才能拼接
print(vec_label.shape,vec_tsne.shape)
vec_tsne[:3].tolist()
np.hstack((vec_tsne[:3], vec_label[:3]))
# --------- 数据格式化 ---------
#Scatter_data = [(random.randint(0,50),random.randint(0,50),random.randint(0,50)) for i in range(50)]
#Scatter_data = vec_tsne[:10].tolist()
N = 50000
Scatter_data = np.hstack((vec_tsne, vec_label))[:N].tolist()
# --------- 绘图 ---------
c = (
Scatter3D(init_opts = opts.InitOpts(width='1500px',height='900px')) #初始化
.add("句子向量(t-sne)",Scatter_data,
grid3d_opts=opts.Grid3DOpts(
width=100, depth=100, rotate_speed=20, is_rotate=False
))
#设置全局配置项
.set_global_opts(
title_opts=opts.TitleOpts(title="新房驻场客服query分布(部分N={})".format(min(N,vec_label.shape[0]))), #添加标题
visualmap_opts=opts.VisualMapOpts(
max_=50, #最大值
pos_top=50, # visualMap 组件离容器上侧的距离
range_color=Faker.visual_color #颜色映射
)
)
)
c.render("新房驻场客服-query空间关系.html")
#c.render_notebook() # 渲染到jupyter notebook页面







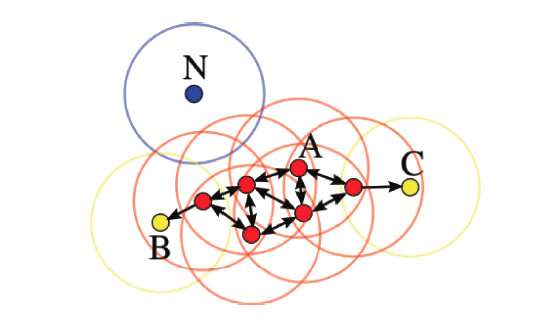


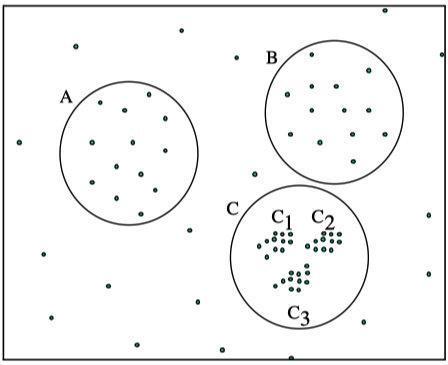
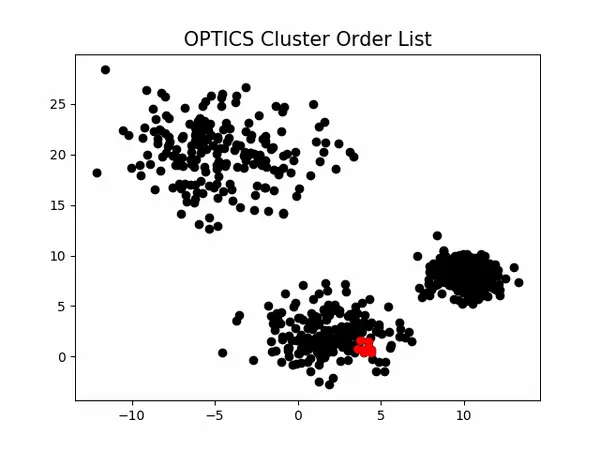
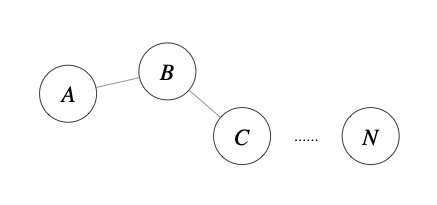
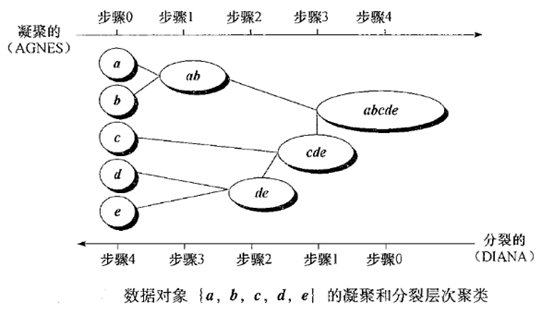
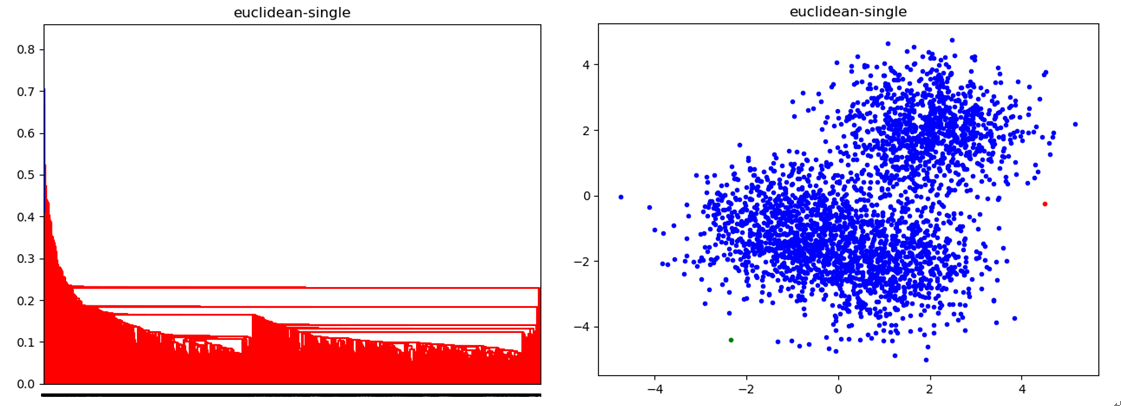
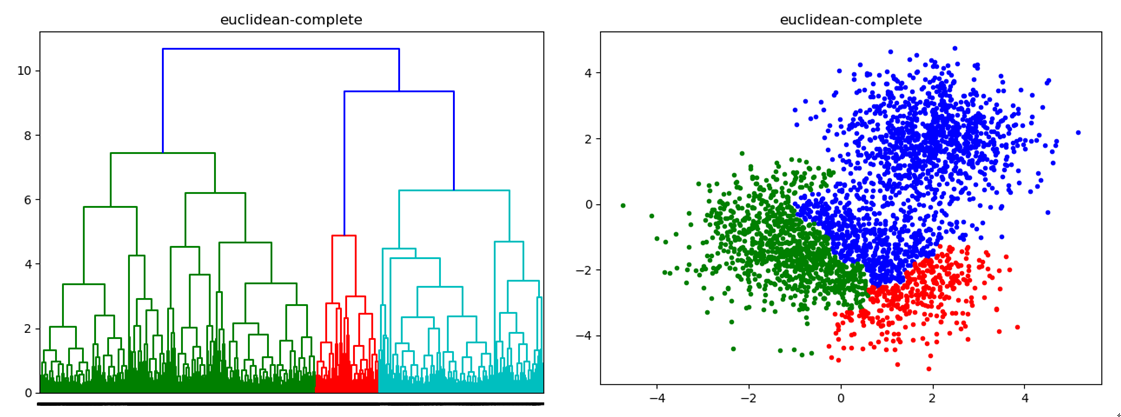
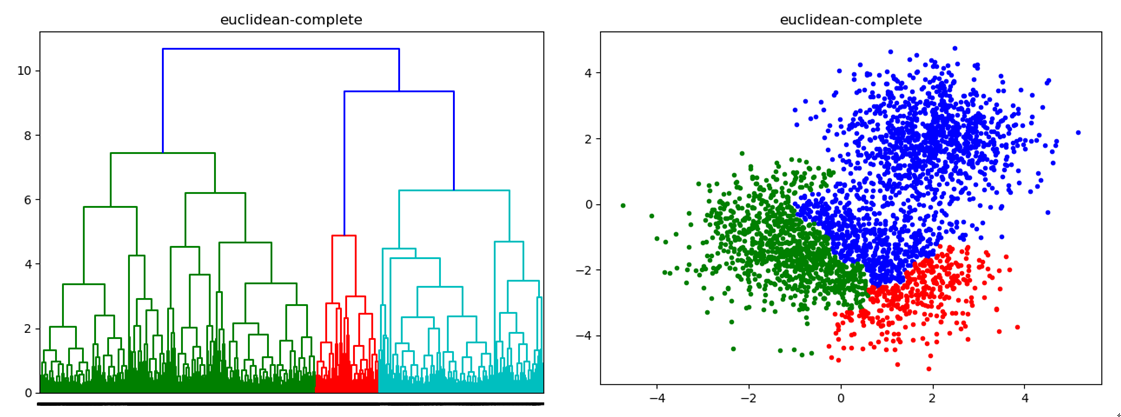
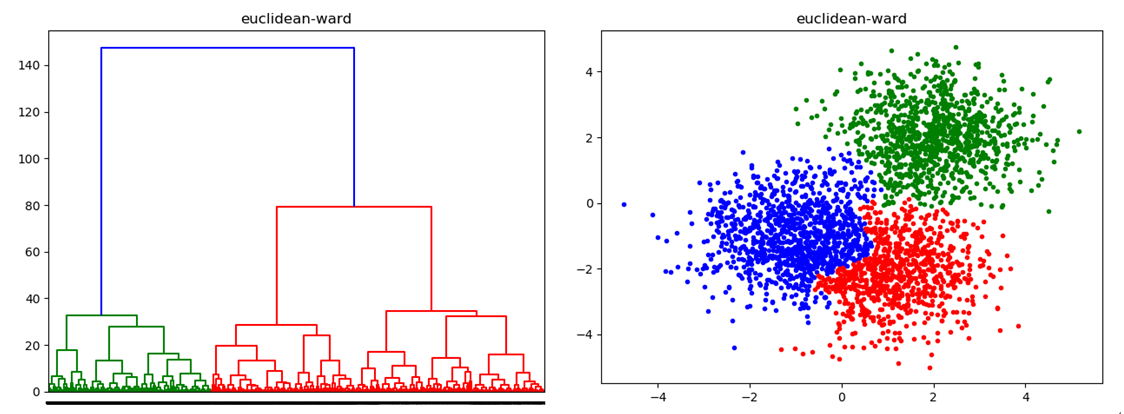
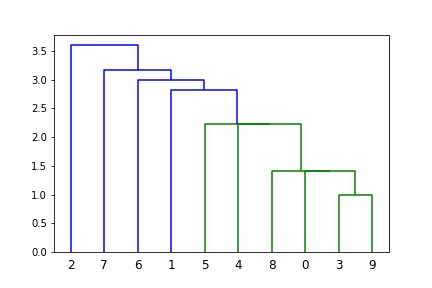
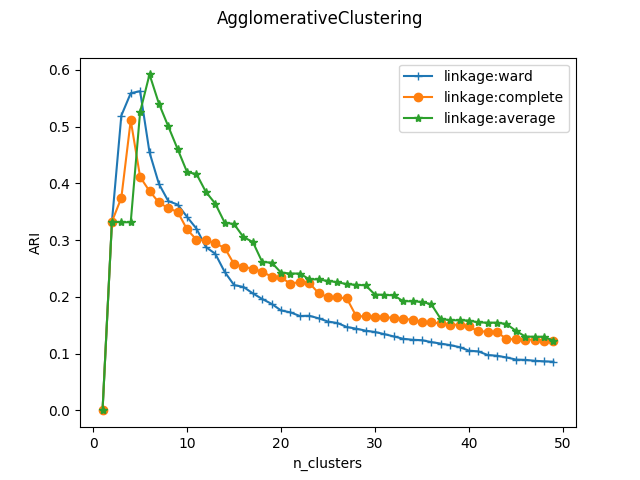
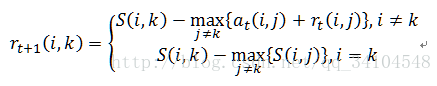
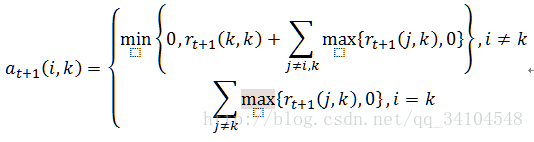
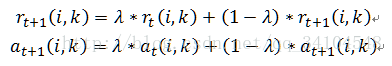
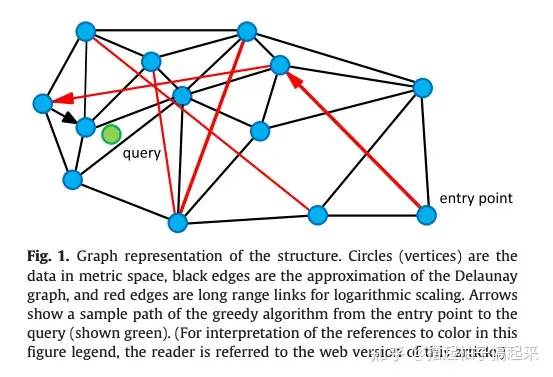
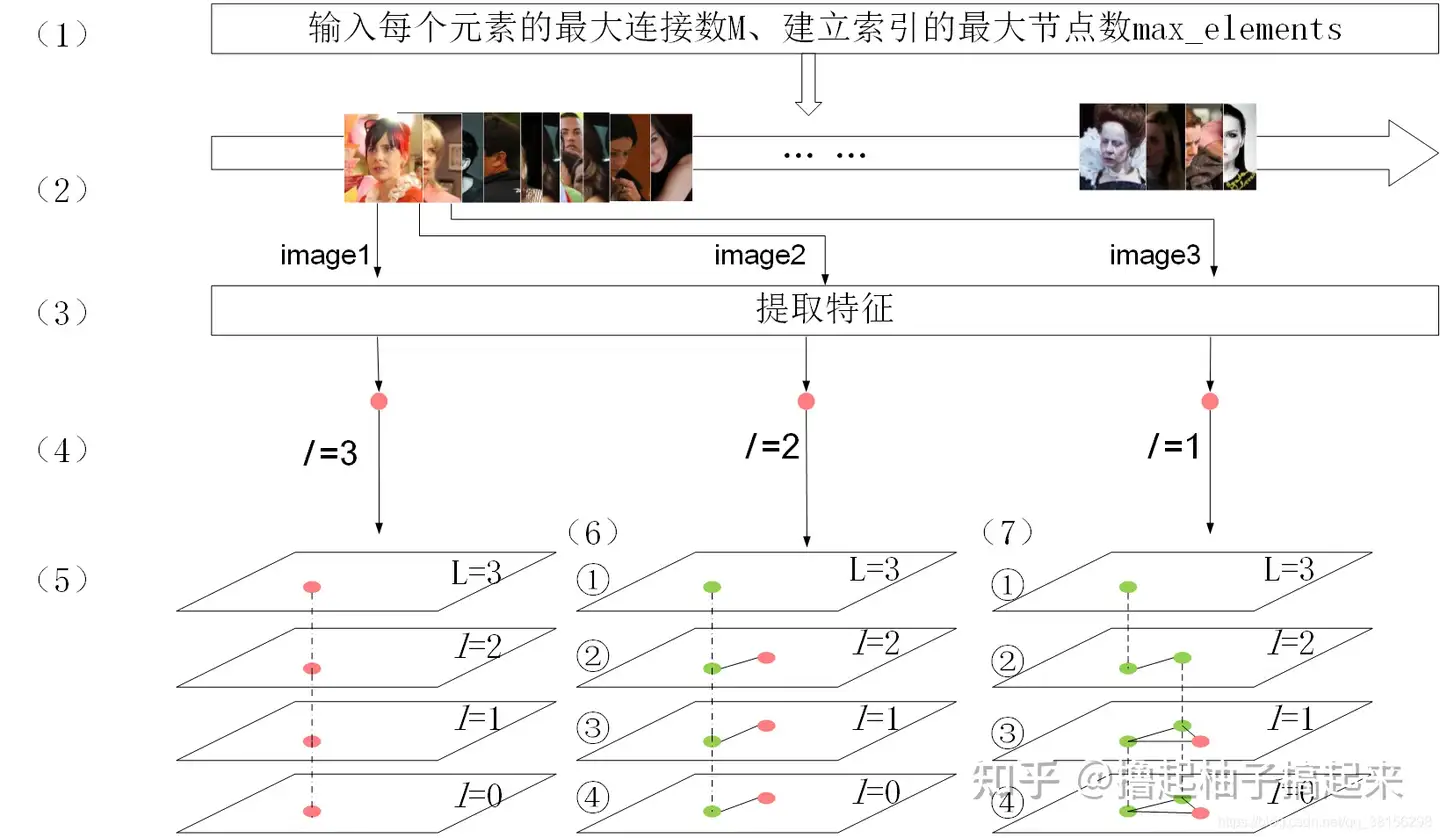
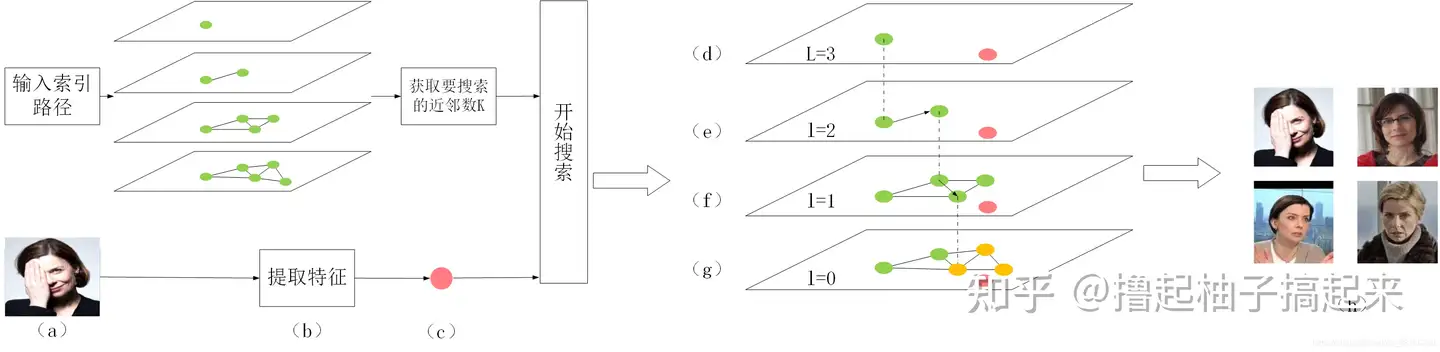
 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
