资料

• 【2020-7-28】The Next Generation of Neural Networks, Geoffrey Hinton，对下一代神经网络，比学习的来龙去脉，以及现在的SOTA模型 SimCLR

• 【2021-3-15】伯克利CS 182《深度学习：深度神经网络设计、可视化与理解》课程 2021，课程主页地址,Designing, Visualizing and Understanding Deep Neural Networks

神经网络结构

Hopfield 网络

【2024-10-10】很多朋友都熟悉 Hinton，但对 Hopfield 不太了解，主要在于 Hopfield 网络今天已鲜有人用。但它作为人工神经网络的前身，在思想和方法上都起到奠基作用。

趁着诺奖热度，仔细读了 Hopfield 在1982年发表的论文

• 《Neural networks and physical systems with emergent collective computational abilities》

作者在认知、模型、算法上都有着深刻的洞察，体现了这位跨界学者在学科之间游刃有余的深刻功力：

• 认知行为是一种涌现行为。可以从神经元的微观机制解释学习与记忆。
• 智能是一种普世现象，在人与人之间差异不太大，意味着这种涌现行为不敏感地依赖于模型细节（例如：声音可以在空气和水里传播）。
• Hebbian 学习理论（1940s提出）可以在神经元层面提供微观机制。
• 物理学里的伊辛模型（1920s提出）提供一种基于能量和统计力学的解决方案——把电子自旋替换成神经元突触的激发态即可。
• 神经元突触的交互关系等价于求解伊辛系统的能量最低态。这个求解过程就是“学习”，解就是“记忆”。
• 涌现的稳定性来自一定程度的随机性，涌现现象（记忆）表现为稳定平衡态（local minima）。
• 记忆就是这种稳定平衡态。持续学习导致一个平衡态跃迁至另一个平衡态。
• 以上特征使得异步并行算法可行。

后来的故事大家都熟悉了：

• Hinton 将 Hopfield network 推广到带有隐藏单元的 Boltzman machine 玻尔兹曼机
• 随后又提出更便于梯度衰减算法的 Restricted Boltzmann machine 受限玻尔兹曼机
• 在 backpropagation 加持下发展出了前馈神经网络，从此开启了机器学习算法的全新篇章。

周志华：深度学习为什么深？

• 【2018-4-16】周志华最新演讲：深度学习为什么深？有多好的人才，才可能有多好的人工智能

2018京东人工智能创新峰会举行，京东集团副总裁、AI 平台与研究部负责人周伯文揭开了京东技术布局下的 AI 战略全景图。这个全景图概括起来说就是“三大主体、七大应用场景和五个人工智能产业化的布局方向”，即：以 AI 开放平台 、AI 基础研究、AI 商业创新三个主体，通过产学研相结合，高端人才培养，以及核心人才引进打造科技能力，将 AI 用于金融科技、智慧物流、智能消费、智能供应、对外赋能。在峰会上，京东AI开放平台NeuHub正式发布，“JD Dialog Challenge” 全球首届任务导向型多轮对话系统大奖赛正式启动。

会上，南京大学计算机系主任、人工智能学院院长周志华教授进行了题为《关于深度学习的思考》的主题演讲。周志华教授从深度学习的理论基础说起，从模型复杂度的角度探讨了“深度神经网络为什么深”的问题，提出深度学习在有很多成功应用的同时，也存在调参困难、可重复性差等问题，在很多任务上并不是最好的选择。因此，探索深度神经网络之外的模型是很重要的挑战。

周志华教授最后提到人工智能产业发展的看法，他说，“人工智能时代最缺的就是人才。因为对这个行业来说，你有多好的人才，才可能有多好的人工智能。”近日，新智元报道周志华教授出任京东集团人工智能研究院学术委员会委员，同时京东集团已启动在南京建立京东人工智能研究院南京分院，周志华教授将担任该分院学术总顾问。南京大学将在AI人才培养等方面和京东展开密切合作。

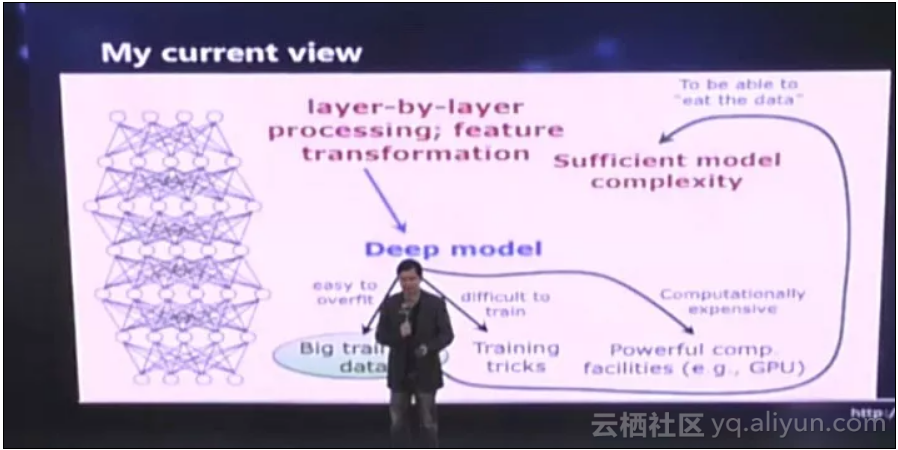
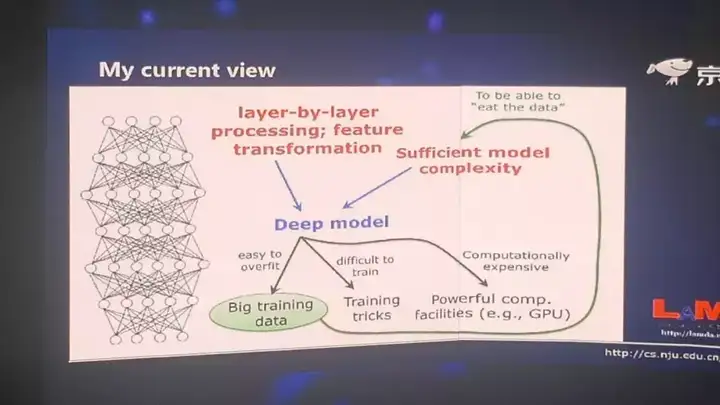
为什么会产生这样的结果？周志华从深度神经网络的深层含义说起，条分缕析地总结出神经网络取得成功的三大原因：

• 有逐层的处理
• 有特征的内部变化
• 有足够的模型复杂度 并得出结论：如果满足这三大条件，则并不一定只能用深度神经网络。

以下是周志华教授的演讲内容：

• 

周志华：

首先很高兴今天来参加京东的活动，各位可能最近都听说我们南京大学成立了人工智能学院，这是中国的 C9 高校的第一个人工智能学院。我们和京东会在科学研究和人才培养等方面开展非常深入的合作，具体的合作内容可能过一段时间会陆续地告诉大家。

感谢周伯文博士的邀请。来之前我问他今天说点什么好，他告诉我在座的有不少技术人士，建议我谈谈关于一些前沿学术问题的思考，所以今天我就跟大家谈一谈我们关于深度学习的一点点非常粗浅的看法，仅供大家来批评，一起来讨论。我们都知道直接掀起人工智能热潮的最重要的技术之一，就是深度学习技术。今天，其实深度学习已经有各种各样的应用，到处都是它，不管图像也好，视频也好，声音自然语言处理等等。那么我们问一个问题，什么是深度学习？

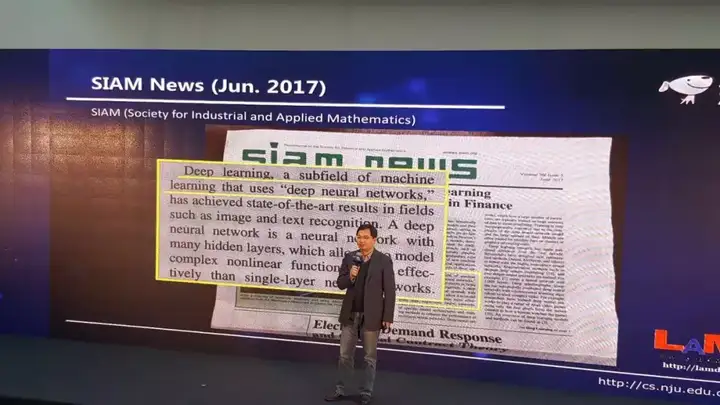
深度学习的理论基础尚不清楚

我想大多数人的答案，就是深度学习差不多就等于深度神经网络。有一个非常著名的学会叫SIAM，是国际工业与应用数学学会，他们有一个旗舰的报纸叫SIAM news。在去年的 6 月份，这个报纸的头版上就有这么一篇文章，直接就说了这么一句话，说深度学习是机器学习中使用深度神经网络的的子域（subfield）。

• 

所以谈深度学习的话是绕不开深度神经网络的。首先我们必须从神经网络说起。神经网络其实并不是一个新生事物，神经网络可以说在人工智能领域已经研究了超过半个世纪。但是以往的话，一般会用这样的神经网络，就是中间有一个隐层，或者有两个隐层。在这样的神经网络里面，它的每一个单元是个非常简单的计算模型。我们收到一些输入，这些输入通过一些连接放大，它就是这么一个非常简单的公式。所谓的神经网络，是很多这样的公式经过嵌套迭代得到的一个系统。那么今天当我们说用深度神经网络的时候，其实我们指的是什么？简单来说，就是用的层数会很深很深，很多层。在 2012 年深度学习刚刚开始受到大家重视的时候，那时候 ImageNet竞赛的冠军是用了8层的神经网络。那么到了 2015 年是用了 152 层，到了 2016 年是 1207层。这是个非常庞大非常巨大的系统，把这么一个系统训练出来，难度是非常大的。

• 

有一点非常好的消息。神经网络里面的计算单元，最重要的激活函数是连续的、可微的。比如说我们在以往常用这样的sigmoid函数，它是连续可微的，现在大家常用的ReLu函数或者它的变体，也是这样。这使得我们可以容易地进行梯度计算，这样就可以很容易用著名的BP算法来训练。通过这样的算法，我们的神经网络已经取得了非常多的胜利。

但是实际上在学术界大家一直没有想清楚一件事情，就是我们为什么要用这么深的模型？今天深度学习已经取得了很多的成功，但是有一个很大的问题，就是理论基础不清楚。我们理论上还说不清楚它到底是怎么做，为什么会成功，里面的关键是什么？如果我们要做理论分析的话，我们先要有一点直觉，知道它到底为什么有用？这样才好着手去分析。 但现在其实我们根本就不知道该从什么角度去看它。

深度学习为什么深？模型复杂度的角度

关于深度神经网络为什么能深呢？到今天为止，学术界都还没有统一的看法。有很多的论述。我在这里面跟大家讲一个我们前段时间给出的一个论述。这个论述其实主要是从模型的复杂度的角度来讨论。

一个机器学习模型，它的复杂度实际上和容量有关，而容量又跟它的学习能力有关。所以就是说学习能力和复杂度是有关的。机器学习界早就知道，如果我们能够增强一个学习模型的复杂度，那么它的学习能力能够提升。

那怎么样去提高复杂度，对神经网络这样的模型来说，有两条很明显的途径。

• 一条是我们把模型变深
• 一条是把它变宽。 如果从提升复杂度的角度，那么变深是会更有效。当你变宽的时候，你只不过是增加了一些计算单元，增加了函数的个数，在变深的时候不仅增加了个数，其实还增加了它的嵌入的程度。

所以从这个角度来说，我们应该尝试去把它变深。

• 

那大家可能就会问了，那既然要变深，那你们早就不知道这件事了吗？那么现在才开始做？这就涉及到另外一个问题，我们把机器学习的学习能力变强了，这其实未必是一件好事。因为机器学习一直在斗争的一个问题，就是经常会碰到过拟合（overfit）。这是一种什么样的现象？你给我一个数据集，我做机器学习要把数据集里面的东西学出来，学出来之后，我希望学到的是一般规律，能够用来预测未来的事情。但是有时候呢我可能把这个数据本身的一些特性学出来了，而不是一般规律。错误地把它当成一般规律来用的时候，会犯巨大的错误。这种现象就是所谓的过拟合。

那为什么会把这个数据本身的一些特性学出来呢？其实大家都很清楚，就是因为模型学习能力太强。当能力非常强的时候，可能就把一些特性学出来，当成一般规律。所以以往通常不太愿意用太复杂的模型。

那现在我们为什么可以用这样的模型？有很多因素。

• 第一个因素是现在有很大的数据。比如说我手上如果只有 3000 个数据，那我学出来的特性一般不太可能是一般规律。但是如果有 3000 万，3000 万万的数据，那这个数据里面的特性可能本身就已经是一般规律。所以使用大的数据是缓解过拟合的一个关键的途径。
• 第二，今天我们有了很多很强大的计算设备，这使得我们能够训练出这样的模型。
• 第三，通过我们这个领域很多学者的努力，有了大量的训练这样复杂模型的技巧、算法，用复杂模型成为可能。 总结一下就是：第一我们有了更大的数据；第二我们有强力的计算设备；第三我们有很多有效的训练技巧。这导致我们可以用高复杂度的模型，而深度神经网络恰恰就是一种很便于实现的高复杂度模型。

所以用这么一套理论，好像是能够解释我们现在为什么能够用深度神经网络，为什么深度神经网络能成功？就是因为复杂度大。

• 

在一年多之前，我们把这个解释说出来的时候，其实国内外很多同行也还很赞同，觉得还蛮有道理的。但是其实我自己一直对这个解释不是特别的满意，因为一个潜在的问题我们一直没有回答。

神经网络最重要的是表示学习的能力

如果从复杂度这个角度去解释的话，我们就没法说清楚为什么扁平的（flat），或者宽的网络做不到深度神经网络的性能？实际上我们把网络变宽，虽然它的效率不是那么高，但是它同样也能起到增加复杂度的能力。

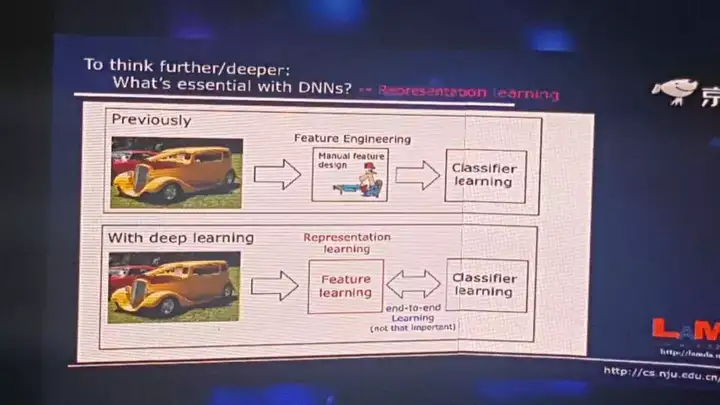
实际上只要有一个隐层，加无限多的神经元进去，它的复杂度也会变得很大。但是这样的模型在应用里面怎么试，我们都发现它不如深度神经网络好。所以从复杂度的角度可能很难回答这个问题，我们需要一点更深入的思考。所以我们要问这么一个问题：深度神经网络里面最本质的东西到底是什么？

• 

今天我们的回答是，表示学习的能力。以往用机器学习解决一个问题的时候，首先我们拿到一个数据，比如说这个数据对象是个图像，然后我们就用很多特征把它描述出来，比如说颜色、纹理等等。这些特征都是我们人类专家通过手工来设计的，表达出来之后我们再去进行学习。而今天我们有了深度学习之后，现在不再需要手工去设计特征了。你把数据从一端扔进去，模型从另外一端就出来了，中间所有的特征完全可以通过学习自己来解决。所以这就是我们所谓的特征学习，或者说表示学习。这和以往的机器学习技术相比可以说是一个很大的进步。我们不再需要依赖人类专家去设计特征了。

有些朋友经常说的一个东西是端到端学习。对这个其实我们要从两方面看，一方面，当我们把特征学习和分类器的学习联合起来考虑的时候，可以达到一个联合优化的作用，这是好的方面。但是另外一方面，如果这里面发生什么我们不清楚，这样的端到端学习就不一定真的是好的。因为里面很可能第一个部分在往东，第二个部分在往西，合起来看，好像它往东走的更多一点，其实内部已经有些东西在抵消了。所以实际上机器学习里面早就有端到端学习，比如说我们做特征选择，可能大家知道有一类基于wrapper的方法，它就是端到端的学习，但这类方法是不是比别的特征选择方法一定强呢？不一定。所以这不是最重要的。

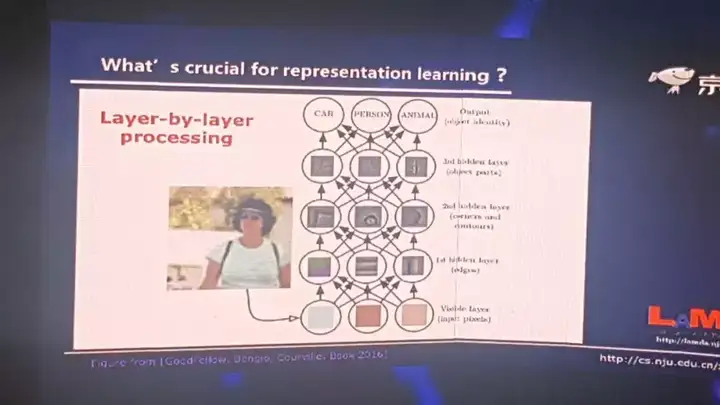
真正重要的还是特征学习，或者表示学习。那如果我们再问下一个问题，表示学习最关键的又是什么呢？我们现在有这么一个答案，就是逐层的处理。我引述最近非常流行的一本书，《深度学习》这本书里面的一个图，当我们拿到一个图像的时候，我们如果把神经网络看作很多层，首先它在最底层，好像我们看到的是一些像素这样的东西。当我们一层一层往上的时候，慢慢的可能有边缘，再网上可能有轮廓，甚至对象的部件等等。当然这实际上只是个示意图，在真正的神经网络模型里面不见得会有这么清楚的分层。但是总体上当我们逐渐往上的时候，它确实是不断在对对象进行抽象。我们现在认为这好像是深度学习为什么成功的关键因素之一。因为扁平神经网络能做很多深层神经网络能做的事，但是有一点它是做不到的。当它是扁平的时候，它就没有进行这样的一个深度的加工。 所以深度的逐层抽象这件事情，可能是很关键的。

• 

大家可能就会问，“逐层地处理”在机器学习里面也不是新东西。比如说决策树就是一种逐层处理，这是非常典型的。决策树模型已经有五六十年的历史了，但是它为什么做不到深度神经网络这么好呢？我想答案是这样。首先它的复杂度不够，决策数的深度，如果我们只考虑离散特征的话，它最深的深度不会超过特征的个数，所以它的模型复杂度是有限的。第二，整个决策树的学习过程中，它内部没有进行特征的变换，始终是在一个特征空间里面进行的。这可能也是它的一个问题。大家如果对高级点的机器学习模型了解，你可能会问，那boosting呢？比如说现在很多获胜的模型，xgboost 等等都属于这个boosting的一类，它也是一层一层的往下走。你说他为什么没有取得像深度神经网络这样的成功呢？我想其实问题是差不多的，首先它的复杂度还不够。第二可能是更关键的一点，它始终是在原始空间里面做事情，所有的这些学习器都是在原始特征空间，中间没有进行任何的特征变化。所以现在我们的看法是，深度神经网络到底为什么成功？或者成功的关键原因是什么？我想第一是逐层地处理，第二我们要有一个内部的特征变换。

深度学习成功的三个因素

而当我们考虑到这两件事情的时候，我们就会发现，其实深度模型是一个非常自然的选择。有了这样的模型，我们很容易就可以做上面两件事。但是当我们选择用这么一个深度模型的时候，我们就会有很多问题，它容易overfit，所以我们要用大数据；它很难训练，我们要有很多训练的trick；这个系统的计算开销非常大，所以我们要有非常强有力的计算的设备，比如 GPU 等等。

• 

实际上所有这些东西是因为我们选用了深度模型之后产生的一个结果，它们不是我们用深度学习的原因。所以这和以往的思考不太一样，以往我们认为有了这些东西，导致我们用深度模型。其实现在我们觉得这个因果关系恰恰是反过来，因为我们要用它，所以我们才会考虑上面这些东西。另外还有一点我们要注意的，当我们有很大的训练数据的时候，这就要求我们必须要有很复杂的模型。否则假设我们用一个线性模型的话，给你 2000 万样本还是 2 亿的样本，其实对它没有太大区别。它已经学不进去了。而我们有了充分的复杂度，恰恰它又给我们使用深度模型加了一分。所以正是因为这几个原因，我们才觉得这是深度模型里面最关键的事情。

这是我们现在的一个认识：

• 第一，我们要有逐层的处理；
• 第二，我们要有特征的内部变换；
• 第三，我们要有足够的模型复杂度。 这三件事情是我们认为深度神经网络为什么能够成功的比较关键的原因。或者说，这是我们给出的一个猜测。如果满足这几个条件，我其实可以马上想到，不一定真的要用神经网络，神经网络是选择的几个方案之一，我只要同时做到这三件事，别的模型也可以，并不一定只能用深度神经网络。
• 

深度学习存在的问题

那如果满足这几个条件，我们其实马上就可以想到，那我不一定要用神经网络。神经网络可能只是我可以选择的很多方案之一，我只要能够同时做到这三件事，那我可能用别的模型做也可以，并不是一定只能是用深度神经网络。

• 第一，凡是用过深度神经网络的人都会知道，你要花大量的精力来调它的参数，因为这是个巨大的系统。那这会带来很多问题。首先我们调参数的经验其实是很难共享的。有的朋友可能说，你看我在第一个图像数据集上调参数的经验，当我用第二个图像数据集的时候，这个经验肯定是可以重用一部分。但是我们有没有想过，比如说我们在图像上面做了一个很大的深度神经网络，这时候如果要去做语音的时候，其实在图像上面调参数的经验，在语音问题上基本上不太有借鉴作用。所以当我们跨任务的时候，这些经验可能就很难共享。
• 第二个问题，今天大家都非常关注我们做出来的结果的可重复性，不管是科学研究也好，技术发展也好，都希望这个结果可重复。 而在整个机器学习领域，可以说深度学习的可重复性是最弱的。我们经常会碰到这样的情况，有一组研究人员发文章说报告了一个结果，而这个结果其他的研究人员很难重复。因为哪怕你用同样的数据，同样的方法，只要超参数的设置不一样，你的结果就不一样。

还有很多问题，比如说我们在用深度神经网络的时候，模型复杂度必须是事先指定的。因为我们在训练这个模型之前，我们这个神经网络是什么样就必须定了，然后我们才能用 BP算法等等去训练它。其实这会带来很大的问题，因为我们在没有解决这个任务之前，我们怎么知道这个复杂度应该有多大呢？所以实际上大家做的通常都是设更大的复杂度。

如果大家关注过去 3、4 年深度学习这个领域的进展，你可以看到很多最前沿的工作在做的都是在有效的缩减网络的复杂度。比如说 RestNet 这个网络通过加了shortcuts，有效地使得复杂度变小。还有最近大家经常用的一些模型压缩，甚至权重的二值化，其实都是在把复杂度变小。实际上它是先用了一个过大的复杂度，然后我们再把它降下来。那么我们有没有可能在一开始就让这个模型的复杂度随着数据而变化，这点对神经网络可能很困难，但是对别的模型是有可能的。

还有很多别的问题，比如说理论分析很困难，需要非常大的数据，黑箱模型等等。那么从另外一个方面，有人可能说你是做学术研究，你们要考虑这些事，我是做应用的，什么模型我都不管，你只要能给我解决问题就好了。其实就算从这个角度来想，我们研究神经网络之外的模型也是很需要的。

• 

虽然在今天深度神经网络已经这么的流行，这么的成功，但是其实我们可以看到在很多的任务上，性能最好的不见得完全是深度神经网络。比如说如果大家经常关心Kaggle上面的很多竞赛，它有各种各样的真实问题，有买机票的，有订旅馆的，有做各种的商品推荐等等。我们去看上面获胜的模型，在很多任务上的胜利者并不是神经网络，它往往是像随机森林，像xgboost等等这样的模型。深度神经网络获胜的任务，往往就是在图像、视频、声音这几类典型任务上。而在别的凡是涉及到混合建模、离散建模、符号建模这样的任务上，其实它的性能可能比其他模型还要差一些。那么，有没有可能做出合适的深度模型，在这些任务上得到更好的性能呢？

我们从学术的观点来总结一下，今天我们谈到的深度模型基本上都是深度神经网络。如果用术语来说的话，它是多层、可参数化的、可微分的非线性模块所组成的模型，而这个模型可以用 BP算法来训练。

那么这里面有两个问题：

• 第一，我们现实世界遇到的各种各样的问题的性质，并不是绝对都是可微的，或者能够用可微的模型做最佳建模；
• 第二，过去几十年里面，我们的机器学习界做了很多很多模型出来，这些都可以作为我们构建一个系统的基石，而中间有相当一部分模块是不可微的。
• 

那么这样的东西能不能用来构建深度模型？能不能通过构建深度模型之后得到更好的性能，能不能通过把它们变深之后，使得深度模型在今天还比不上随机森林等等这些模型的任务上，能够得到更好的结果呢？现在有这么一个很大的挑战，这不光是学术上的，也是技术上的一个挑战，就是我们能不能用不可微的模块来构建深度模型？

所以我们现在有一个很大的挑战，这不光是学术上也是技术上的挑战，就是我们能不能用不可微的模块来构建深度模型。

• 

其实这个问题一旦得到回答，我们同时就可以得到好多其他问题的回答。比如说深度模型是不是就是深度神经网络？我们能不能用不可微的模型把它做深，这个时候我们不能用 BP 算法来训练，同时我们能不能让深度模型在更多的任务上获胜。这个问题其实我们提出来之后在国际上也有一些学者提出了一些相似看法。比如大家都知道深度学习非常著名的领军人物 Geoffrey Hinton 教授，他也提出来希望深度学习以后能不能摆脱 BP 算法来做，他提出这个想法比我们要更晚一些。所以我想这一些问题是站在很前沿的角度上做的探索。

我想这样的问题是应该是站在一个很前沿的角度上探索。刚才跟大家分析所得到的三个结论

• 第一我们要做逐层处理
• 第二我们要做特征的内部变换
• 第三，我们希望得到一个充分的模型复杂度。

探索深度学习之外的方法：深度森林

我自己领导的研究组最近在这方面做了一些工作。我们最近提出了一个叫做Deep Forest（深度森林）的方法。这个方法是一个基于树模型的方法，它主要是借用了集成学习里面的很多的想法。第二，在很多不同的任务上，它的模型得到的结果可以说和深度神经网络是高度接近的。除了一些大规模的图像任务，这基本上是深度神经网络的杀手锏应用，它在很多的其它任务上，特别是跨任务的表现非常好。我们可以用同样一套参数，用不同的任务，性能都还不错，就不再需要逐任务的慢慢去调参数，同时它要调的超参数少很多，容易调的多。还有一个很重要的特性，它有自适应的模型复杂度，可以根据数据的大小，自动的来判定模型该长到什么程度。

另外一方面，我们要看到，这实际上是在深度学习这个学科领域发展思路上一个全新的探索。所以今天虽然它已经能够解决一部分问题了，但是我们应该可以看到它再往下发展下去，它的前景可能是今天我们还不太能够完全预见到的。

• 

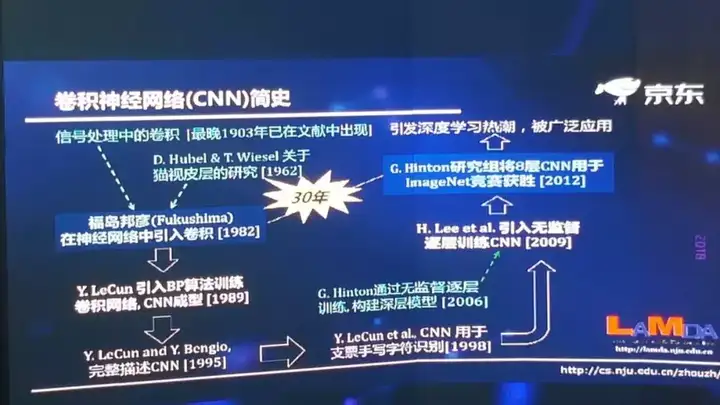
我经常说我们其实没有什么真正的颠覆性的技术，所有的技术都是一步一步发展起来的。比方说现在深度神经网络里面最著名的CNN，从首次提出到ImageNet上获胜是经过了30年，从算法完全成形算起，到具备在工业界广泛使用的能力也是经过了20年，无数人的探索改进。所以，今天的一些新探索，虽然已经能够解决一些问题，但更重要的是再长远看，经过很多进一步努力之后，可能今天的一些探索能为未来的技术打下重要的基础。

以前我们说深度学习是一个黑屋子，这个黑屋子里面有什么东西呢？大家都知道，有深度神经网络。现在我们把这个屋子打开了一扇门，把深度森林放进来了，那我想以后可能还有很多更多的东西。可能这是从学科意义来看，这个工作更重要的价值。

AI时代最重要的是人才

最后我想谈一谈关于人工智能产业发展的一些看法，因为大家都知道我们南京大学人工智能学院马上要跟京东开展深入的在科学研究和人才培养方面的合作。关于人工智能产业的发展，我们要问一个问题，我们到底需要什么？大家说需要设备吗？做人工智能的研究，不需要特殊机密的设备，你只要花钱，这些设备都能买得到。那么缺数据吗？现在我们的数据收集、存储、传输、处理的能力大幅度提升，到处都是数据。

真正缺的是什么？人工智能时代最缺的就是人才。因为对这个行业来说，你有多好的人才，才可能有多好的人工智能。所以我们现在可以看到，全球是在争抢人工智能人才。不光是中国，美国也是这样。所以我们要成立人工智能学院，其实就有这样的考虑。

• 

信息化之后，人类社会必然进入智能化，可以说这是个不可逆转、不可改变的一个趋势。我们基于数据信息，为人提供智能辅助，让人做事的时候更容易，那是我们所有人的愿望。蒸汽机的革命是把我们从体力劳动里面解放出来。人工智能革命应该是把我们从一些繁复性强的、简单智力劳动中解放出来。

人工智能这个学科，它和其他的一些短期的投资风口和短期的热点不太一样。它经过 60 多年的发展，已经有一个庞大的、真正的知识体系。而高水平的人工智能人才稀缺，这是一个世界性的问题。我们的很多企业现在都在重金挖人，但实际上挖人不能带来增量。所以我觉得我们要从源头做起，为国家、社会、产业的发展培养高水平的人工智能人才，所以在这个方面，我们感谢京东作为一个有社会责任感的企业，愿意在我这个学院旁边专门建一个研究院，一起对源头性的人工智能高水平人才培养合作开展新型探索。最后欢迎各界朋友以各种方式支持我们南京大学人工智能学院，谢谢！

深度学习核心

深度学习的核心

说明

该文档为“3Blue1Brown - 深度学习系列视频”的整理，主要包括三个视频

• 神经网络的结构
• 梯度下降法
• 反向传播算法

跟着3Blue1Brown从偏数学的角度来理解神经网络（原视频假设观众对神经网络没有任何背景知识）

【2020-3-9】三综一蓝对神经网络的视频介绍

• 深度学习之神经网络的结构：part 1，part 2，part 3

目录

• 资料
  • 神经网络结构
    • Hopfield 网络
  • 周志华：深度学习为什么深？
    • 深度学习的理论基础尚不清楚
    • 深度学习为什么深？模型复杂度的角度
    • 神经网络最重要的是表示学习的能力
    • 深度学习成功的三个因素
    • 深度学习存在的问题
    • 探索深度学习之外的方法：深度森林
    • AI时代最重要的是人才
  • 深度学习核心
• 神经网络结构
  • 神经网络可视化
    • 视频
    • 2D 可视化
    • 3D 可视化
  • 神经网络如何记忆
  • 神经元（隐藏单元）与隐藏层
  • 神经网络的运作机制
    • 权重和偏置
  • 神经网络泛化能力
    • Nature 神经网络泛化能力超过人
  • 非线性激活函数
    • ReLU
  • 神经网络理论
    • 叠加定理
    • KAN
    • UAT 万能逼近定理
  • 梯度下降法
    • 损失函数（Loss Function）
    • 梯度下降法（Gradient Descent）
      • 理解梯度下降法的另一种思路
      • 随机梯度下降（Stochastic Gradient Descent）
  • 神经网络的优化难题
  • 再谈神经网络的运作机制
  • 推荐阅读
  • 反向传播算法（Backpropagation Algorithm, BP）
    • Jacobian 矩阵
    • 反向传播的直观理解
    • BP 算法小结
    • 相关代码
    • 反向传播的微积分原理
      • 示例：每层只有一个神经元的网络
      • 更复杂的示例
      • 反向传播的 4 个基本公式
• 闲话神经网络
  • 神经网络发展历史
  • 神经网络基础回顾
  • 隐含层有什么用？
    • 对隐含层的感性认知
    • 隐含层的理性认知
  • 光说不练假把式
    • 案例一: 动图显示神经网络各层之间的效果
    • 案例二： Playground
  • 到底应该多少个隐含层
    • 一 隐层数
    • 二 隐层节点数
    • 到底多少神经元？
  • 隐含层越胖越好？
  • 更宽还是更胖？Wider or deeper？
  • 神经网络可解释性
• 结束

总结

【2018-6-9】@毅马当闲

• 最近越来越多的证据表明，通过拟合数据得到的深度神经网络模型（在classification，detection，segmentation等）对输入很小的数值扰动和很小的变换deformation（甚至平移）都不稳定（unstable)，更谈不上鲁棒。
• 不要再相信别人show的成功例子 – 我过去就是被别人show的一些例子迷糊，有些相信这样的模型（通过在augmented数据上训练）会是稳定的，而自己没有去做严格的验证 – 肠子都有些悔青了。但应该不会再被忽悠了。
• 所以目前基于深度学习的“人工智能”，用在不痛不痒的应用上，也就罢了。把这样的模型用在严肃的问题上（例如需要有安全、隐私、可靠性保障的），应该是十分危险的。虽然这并不是说，通过系统严格的改进，深度模型和算法就不能没有性能上保障。
• 但那需要建立一套完整的理论体系，正确的模型需要推导出来（而不是试错出来），而其性能保证也必须要有严格的证明。其实不少顶尖的研究人员都已经意识到这一点，今后几年，大家应该会看到系统的理论研究的强势回归。不会让深度学习把传统工程理论已经得到的常识和教训再从新发明一遍

神经网络结构

内容：

• 神经网络是什么？
• 神经网络的结构
• 神经网络的工作机制
• 深度学习中的“学习”指的是什么？
• 神经网络的不足

示例：一个用于数字手写识别的神经网络

这个示例相当于深度学习领域中的 “Hello World”.

神经网络可视化

视频

【2020-12-18】回形针 交互视频《一个人工智能的诞生》宣传片

2D 可视化

TensorFlow 官网提供的神经网络可视化 playground, 浏览器交互体验 MLP 神经网络效果

【2021-5】CNN Explainer， 中国博士可视化了卷积神经网络，将每一层的变化都展示得非常清楚，只需要点击对应的神经元，就能看见“操作”。

• TensorFlow.js 加载的一个10层预训练模型，相当于在浏览器上就能跑CNN模型，也可以实时交互，显示神经元的变化。
• video

3D 可视化

神经网络算法的3D模拟

• 在MNIST训练集上对感知机、多层感知机、卷积神经网络再到最近的脉冲神经网络的视觉模拟
• b站， Youtube

【2023-10-13】Neural Network Visualization

• 

实时交互可视化

• 【2018】Unity Realtime Interactive Visualization of Convolutional Neural Networks in Unity ， 知乎文章讲解：神经网络的3D可视化
• 

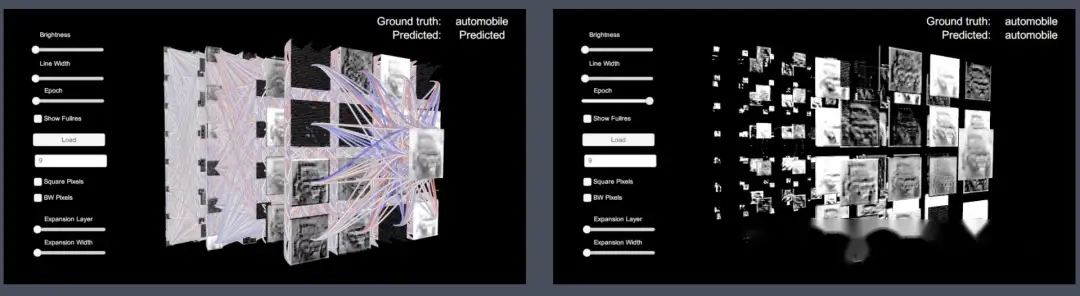
TensorSpace 是一款 3D 模型可视化框架。

• TensorSpace Playground
• 

【2023-12-4】 GPT 3D可视化及动态演示: bbycroft, 支持 Nano-GPT，GPT-2和GPT-3，可交互

神经网络如何记忆

【2023-9-21】神经网络是如何存储记忆的？, 英文视频讲解

神经元（隐藏单元）与隐藏层

神经元（隐藏单元）

• 简单来说，神经元可以理解为一个用来装数字的容器，而这个数称为激活值
  • 图源自：3Blue1Brown深度学习笔记 深度学习之神经网络的结构 Part 1 ver 2.0

• 需要强调的是，激活值的值域取决于使用的激活函数，大多数激活函数的值域都是正值

  

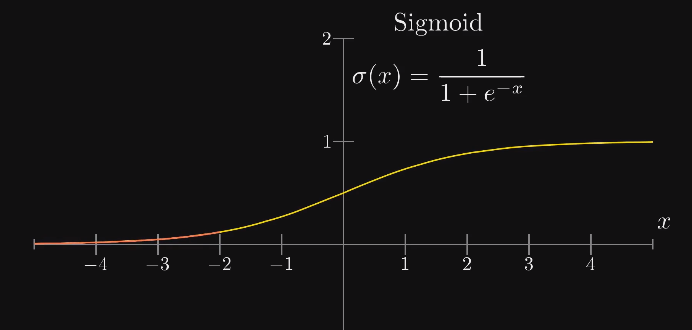
  如果使用 sigmoid 激活函数，那么这个数字就在 0 到 1 之间；但通常来说，无论你使用哪种激活函数，这个数字都比较小

• 输入层也可以看做是一组神经元，它的激活值就是输入本身

  

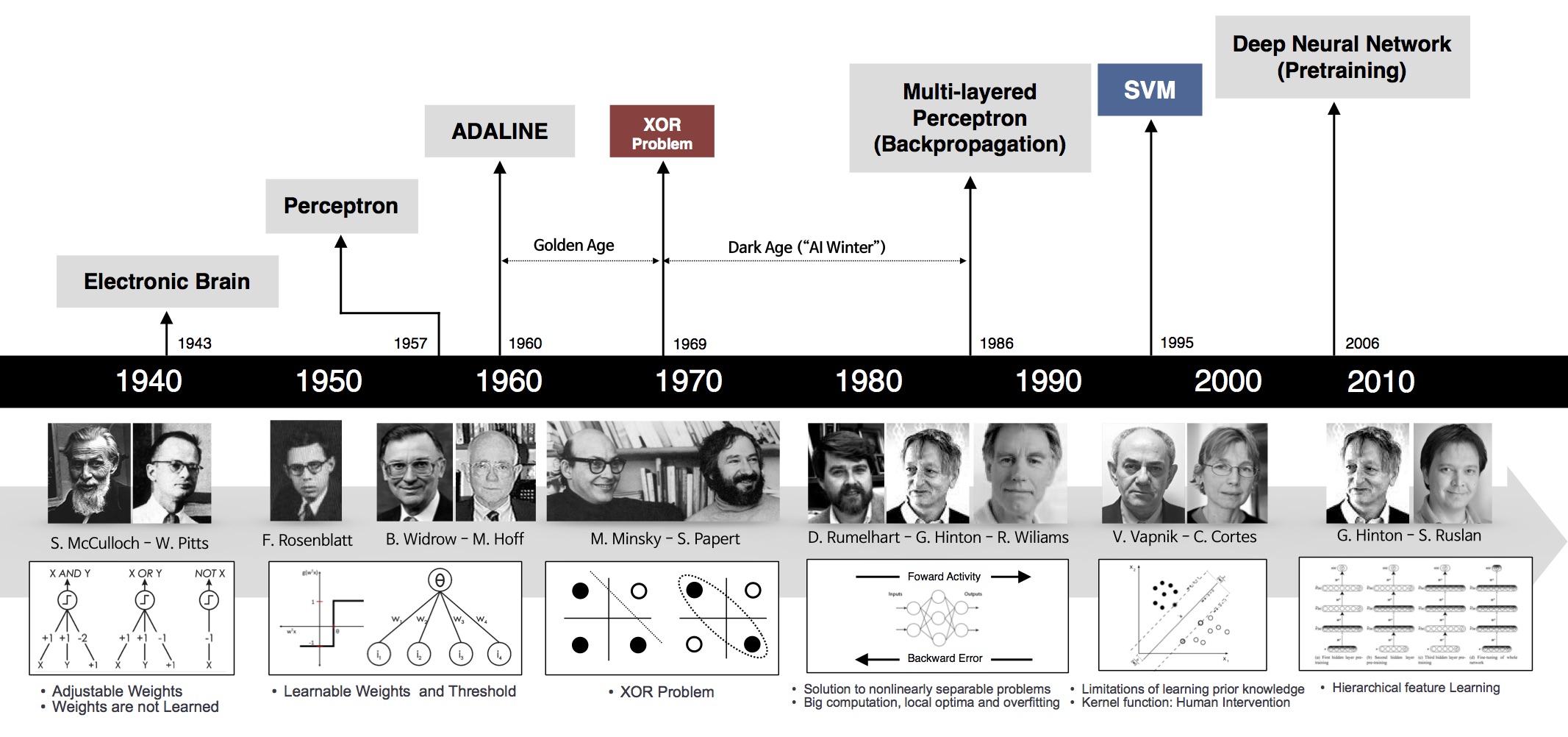
  基本的神经网络只能处理向量型的输入，所以需要将这个 28*28 的像素图（矩阵），重排成长为 784 的向量

  如果使用卷积神经网络，则可以直接处理矩阵型的输入

• 对于分类问题，输出层中的激活值代表这个类别正确的可能性

  如果使用了 softmax 函数，那么整个输出层可以看作每个类别的概率分布

• 所谓的“神经元被激活”实际上就是它获得了一个较大的激活值

  

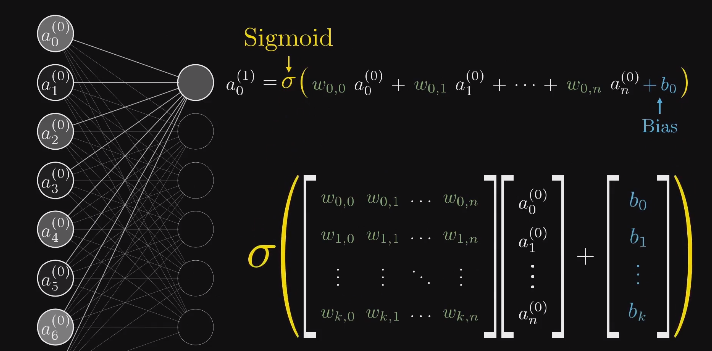
隐藏层

• 包含于输入层与输出层之间的网络层统称为“隐藏层”

  

  在这个简单的网络中，有两个隐藏层，每层有 16 个神经元

  为什么是两层和 16 个？——层数的大小与问题的复杂度有关，而神经元的数量目前来看是随机的——网络的结构在实验时有很大的调整余地

神经网络的运作机制

• 神经网络在运作的时候，隐藏层可以视为一个“黑箱”
• 每一层的激活值将通过某种方式计算出下一层的激活值——神经网络处理信息的核心机制
• 

每一层被激活的神经元不同，（可能）会导致下一层被激活的神经元也不同

为什么神经网络的分层结构能起作用？

• 人在初识数字时是如何区分的？——组合数字的各个部分

• 

• 在理想情况下，我们希望神经网络倒数第二层中的各隐藏单元能对应上每个基本笔画（pattern）

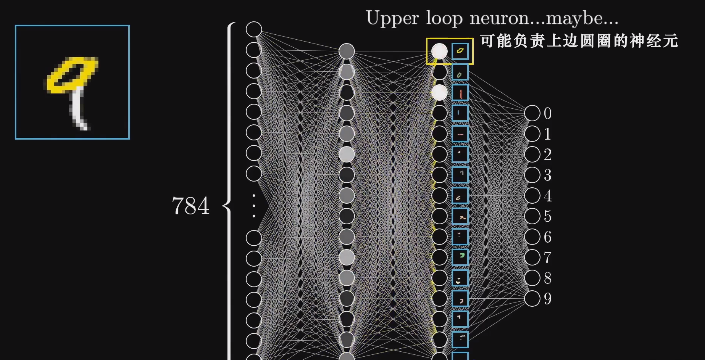
• 当输入是 9 或 8 这种顶部带有圆圈的数字时，某个神经元将被激活（激活值接近 1）
• 不光是 9 和 8，所有顶部带有圆圈的图案都能激活这个隐藏单元

• 这样从倒数第二层到输出层，我们的问题就简化成了“学习哪些部件能组合哪些数字”

• 类似的，基本笔画也可以由更基础的部件构成

• 

• 理想情况下，神经网络的处理过程
• 

  从输入层到输出层，网络的抽象程度越来越高

深度学习的本质：通过组合简单的概念来表达复杂的事物

• 神经网络是不是这么做的，不得而知（所以是一个“黑箱”），但大量实验表明：神经网络确实在做类似的工作——通过组合简单的概念来表达复杂的事物
• 

  语音识别：原始音频 → 音素 → 音节 → 单词

隐藏单元是如何被激活的？

• 我们需要设计一个机制，这个机制能够把像素拼成边，把边拼成基本图像，把基本图像拼成数字
• 这个机制的基本处理方式是：通过上一层的单元激活下一层的单元

示例：如何使第二层的单个神经元识别出图像中的某块区域是否存在一条边

• 根据激活的含义，当激活值接近 1 时，表示该区域存在一条边，反之不存在

• 怎样的数学公式能够表达出这个含义？

• 
• 
• 考虑对所有输入单元加权求和
• 图中每条连线关联一个权值：绿色表示正值，红色表示负值，颜色越暗表示越接近 0
• 此时，只需将需要关注的像素区域对应的权值设为正，其余为 0
• 这样对所有像素的加权求和就只会累计我们关注区域的像素值
• 为了使隐藏单元真正被“激活”，加权和还需要经过某个非线性函数，也就是“激活函数”
• 早期最常用的激活函数是 sigmoid 函数（又称 logistic/逻辑斯蒂曲线）

从 sigmoid 的角度看，它实际上在对加权和到底有多“正”进行打分

• 但有时，可能加权和大于 10 时激活才有意义；
• 此时，需要加上“偏置”，保证不能随便激发，比如 -10。然后再传入激活函数

权重和偏置

• 每个隐藏单元都会和上一层的所有单元相连，每条连线上都关联着一个权重；
• 每个隐藏单元又会各自带有一个偏置

偏置和权重统称为网络参数

每一层都带有自己的权重与偏置，这样一个小小的网络，就有 13002 个参数

权重与偏置的实际意义

• 宏观来看，权重在告诉你当前神经元应该更关注来自上一层的哪些单元；或者说权重指示了连接的强弱

• 偏置则告诉你加权和应该多大才能使神经元的激发变得有意义；或者说当前神经元是否更容易被激活

矢量化编程

• 把一层中所有的激活值作为一列向量 a
• 层与层之间的权重放在一个矩阵 W 中：第 n 行就是上层所有神经元与下层第 n 个神经元的权重
• 类似的，所有偏置也作为一列向量 b
• 最后，将 Wa + b 一起传入激活函数

sigmoid会对结果向量中的每个值都取一次sigmoid

• 所谓“矢量化编程”，实际上就是将向量作为基本处理单元，避免使用 for 循环处理标量
• 通过定制处理单元（GPU运算），可以大幅加快计算速度

机器“学习”的实质

当讨论机器如何“学习”时，实际上指的是机器如何正确设置这些参数

• 

神经网络泛化能力

Nature 神经网络泛化能力超过人

【2023-10-26】Nature：神经网络“举一反三”能力甚至超人类

• Nature：人工智能“突破”:神经网络具有类似人类的泛化语言能力。
• 基于神经网络的人工智能在快速将新单词折叠到其词典中方面优于ChatGPT，这是人类智能的一个关键方面。

“举一反三”、系统概括的能力更专业点叫做系统性泛化能力。像小孩子一样，一旦学会了如何“跳”，他们就可以理解如何“向后跳”、“绕锥体跳过两次”。

早在1988年，认知科学家Fodor、Pylyshyn就提出了系统性挑战，认为人工神经网络缺乏这种能力。

• 人类语言和思维的精髓在于系统性组合，而神经网络只能表示特定的事物，缺乏这种系统性组合能力。

反驳观点

• 一是尽管人类的组合技能很重要，但它们可能并不具有Fodor、Pylyshyn所说的那样的系统性和规则性。
• 二是虽然神经网络在基本形式上受到了限制，但使用复杂的架构可以增强系统性。

虽然最近几年，神经网络在自然语言处理等方面有了很大进展和突破，相关辩论也随之升级。但时至今日，系统性的问题仍没有一个定论。

纽约大学心理与数据科学助理教授 Brenden M. Lake、西班牙加泰罗尼亚研究所（ICREA）研究教授Marco Baroni提出了一种叫做MLC的元学习神经网络模型。

• 一种通过特殊指导和人类示例来指定模型行为的方法，然后要求神经网络通过元学习获得正确的学习技巧。
• MLC使用的是标准的Seq2Seq架构，常见的神经网络并没有添加符号机制，也没有手动设计内部表示或归纳偏见。

举例说明训练过程。

• 给神经网络模型一个“连续跳跃两次”（skip twice）的指令。并用箭头和小人来展示学习示例，告诉机器jump（跳）、skip（跳过）、jump twice是怎样的。
• 然后将输出的skip twice和行为目标比较：
• 

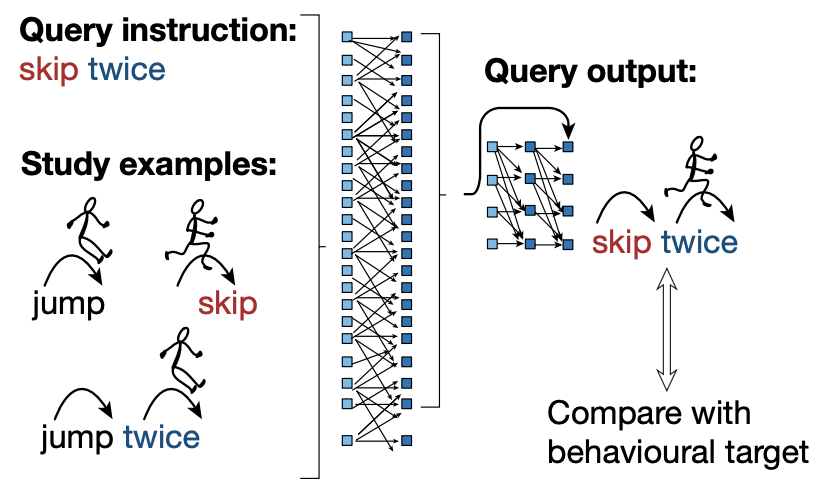
类似情境，引入下一个词“向后踮脚尖绕过一个锥体”，要求神经网络组合向后走（walk backwards）、踮脚尖（tiptoe）、绕锥体行走（walk around a cone）的动作，推出如何“向后踮脚尖绕过一个锥体”。

• 

Nature的这篇文章 Human-like systematic generalization through a meta-learning neural network 中表示，研究人员用一种叫做 MLC（meta-learning for compositionality）的方法，通过在动态变化的组合任务流中训练，神经网络可以获得人类般的组合推理能力。

他们还将MLC和人类在相同的系统性泛化测试中进行了比较。结果 机器学习的系统性泛化基准测试表明，MLC错误率不到1%，并且还可以模拟人类的认知偏见导致的错误。

相比之下，GPT-4 在相同的任务中平均失败率在42%到86%之间，具体取决于研究人员如何提出任务。

非线性激活函数

神经网络本质上是一个函数

• 每个神经元可以看作是一个函数，其输入是上一层所有单元的输出，然后输出一个激活值
• 宏观来看，神经网络也是一个函数

一个输入 784 个值，输出 10 个值的函数；其中有 13000 个参数

• 早期最常用的激活函数是 sigmoid 函数，它是一个非线性函数

• 暂不考虑它其他优秀的性质（使其长期作为激活函数的首选）以及缺点（使其逐渐被弃用）；

  而只考虑其非线性

为什么要使用非线性激活函数？——神经网络的万能近似定理

视频中没有提到为什么使用非线性激活函数，但这确实是神经网络能够具有如此强大表示能力的关键

• 使用非线性激活函数的目的是为了向网络中加入非线性因素，从而加强网络的表示能力

为什么加入非线性因素能够加强网络的表示能力？

• 首先要有这样一个认识，非线性函数具有比线性函数更强的表示能力。
• 如果不使用非线性激活函数，那么每一层输出都是上层输入的线性组合；

容易验证，此时无论有多少层，神经网络都只是一个线性函数。

ReLU

新时代的激活函数——线性整流单元 ReLU

这里简单说下 sigmoid 的问题：

• sigmoid 函数在输入取绝对值非常大的正值或负值时会出现饱和现象，此时函数会对输入的微小改变会变得不敏感

饱和现象：在图像上表现为函数值随自变量的变化区域平缓（斜率接近 0）

• 饱和现象会导致基于梯度的学习变得困难，并在传播过程中丢失信息（梯度消失）

线性整流单元 ReLU

• 

• ReLU 取代 sigmoid 的主要原因就是：使神经网络更容易训练（减缓梯度消失）
• 此外，一种玄学的说法是，早期引入 sigmoid 的原因之一就是为了模仿生物学上神经元的激发

而 ReLU 比 sigmoid 更接近这一过程。

神经网络理论

【2024-7-28】综述, 2024，通用逼近定理（UAT），函数逼近，Kolmogorov–Arnold定理（KAT），任意深度/宽度的网络逼近

• 论文 ​A Survey on Universal Approximation Theorems
• 代码 nn-python

要点

• 神经网络（NN）
• 通用逼近定理（UATs）
• UAT：前身
• UAT：任意宽度的情况
• UAT：任意深度情况

叠加定理

哈密顿一元七次方程

无心插柳：苏联数学家柯尔莫哥洛夫与神经网络的新生

神经网络复兴的数学保障是通用逼近定理（universal approximation theorem），源头是柯尔莫哥洛夫-阿诺德叠加。

1900年, 大卫·希尔伯特在第二届国际数学家大会提出了23个待解数学问题，这些问题指引了后续的数学发展。

5次以上方程没有求根公式。

但一元5次和6次方程可分别变换为：

• x^5 + ax + 1 = 0
• x^6 + ax^2 + bx +1 = 0

1836年爱尔兰数学家哈密尔顿证明了 7次方程可以通过变换简化为：

• x^7+ax^3+bx^2+cx+1=0

解表示为系数a，b，c的函数，即 x=f(a, b, c)。

希尔伯特第13问题: 这个三元函数是否可以表示为二元函数的组合?

希尔伯特第13问题：

• 7次方程的解能否用两个变量的函数的组合表示？
• Impossibility of the solution of the general equation of the 7-th degree by means of functions of only two arguments

希尔伯特猜测: 不能。

希尔伯特提出的第13个问题，相较于其他问题，并不出名。

1956年, 柯尔莫哥洛夫首先证明:

• 任意多元函数可用有限个三元函数叠加构成。

19岁的前苏联数学家阿诺德在此基础上证明两元足矣。复杂函数可以表示为简单函数的组合

他们的成果被称为柯尔莫哥洛夫-阿诺德表示定理，或柯尔莫哥洛夫叠加定理，有时也被称为阿诺德-柯尔莫哥洛夫叠加（AK叠加），因为是阿诺德完成了最后的临门一脚。

这一成果刚发布就引起了轰动。

柯尔莫哥洛夫的本意不完全是为了解决希尔伯特第13问题，但叠加定理事实上构成了对希尔伯特对第13问题原来猜测的（基本）否定。

KA叠加定理：img

• 任意多元连续函数都可表示为若干一元函数和加法的叠加。
• 加法是唯一的二元函数。简单函数都可以通过加法和一元函数叠加而成
• 

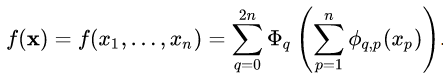
所有初等运算都可以通过一元运算和加法完成。加法是通用的（universal），用加法叠加做其他运算时并不需增加额外的维度。

赫克-尼尔森指出，KA叠加定理可以通过两层网络实现，每层实现叠加中的一个加号。这个实现网络称为“柯尔莫哥洛夫网络”。

法国数学家卡汉（Jean-Pierre Kahane，1926-2017），在1975年改进了KA叠加定理

1988年, 数学出身的工学教授赛本科（George Cybenko），证明了有两个隐层且具sigmoid激活函数的神经网络可以逼近任意连续函数。

赛本科的文章更具细节和证明。虽然没有引用Hecht-Nielsen-1986，但引用了Kolmogorov-1957

这些相关的结论及各种变体和推广被统称为“通用逼近定理”（Universal Approximation Theorem）。

• 除了连续函数，也有人力图证明非连续函数也可以用三层神经网络逼近(Ismailov,2022)。

叠加定理为后续神经网络研究奠定了理论基础, 明斯基导致的神经网络危机翻篇了

1974年，哈佛大学的一篇统计学博士论文证明了神经网络的层数增加到三层，并且利用“反向传播”（back-propagation）学习方法，就可以解决XOR问题。这篇论文的作者沃波斯（Paul Werbos），后来得了IEEE神经网络学会的先驱奖

文章刚发表时，并没有在神经网络圈子里引起多少重视，主要原因是沃波斯的导师是社会学和政治学领域的，他想解决的问题也是统计学和社会科学的。把“反向传播”放到多层神经网络上就成了“深度学习”。

KAN

2024年5月，KA叠加定理又重新得到重视。麻省理工学院的物理学家和科普作家 Max Tegmark 力图复活KA叠加定理。

• 原始的柯尔莫哥洛夫网络只有两层，如果把层数加深，把宽度拓广，也许可以克服平滑性的问题。他们把推广的网络称为KAN（Kolmogorov-Arnold Network），而事实上，赫克-尼尔森早就把实现KA叠加定理的网络称为Kolmogorov Network

KAN最关键的创新点

• (1) 把计算放在网络的边（edge）上而不是点（node）上，点上只执行加法运算，这样可以缩小网络的规模。KAN和多层感知器 (MLP) 没有本质区别
• (2) 学习激活函数而不是学习权重。但学习函数比学习权重要困难得多。KAN中，激活函数是用B-spline来拟合的，B-spline的所有劣势自然也会被带进KAN中。如果学习激活函数的成本很高，网络就丧失了通用性（universality）。

样条（spline）是一种特殊函数，由多项式分段定义。

• spline function是一类分段（片）光滑、并且在各段交接处也有一定光滑性的函数
• 样条的英语单词spline来源于可变形的样条工具，那是一种在造船和工程制图时用来画出光滑形状的工具。
• 中国大陆，早期曾经被称做齿函数。后来因为工程学术语中放样一词而得名
• 

样条插值

• 厄尔密样条（Hermite spline）
  • 三次厄尔密样条
  • 基数样条（cardinal spline）
  • Catmull-Rom样条
  • Kochanek-Bartels样条
• B样条
• 非均匀有理B样条（non-uniform rational B-spline，NURBS）
• de Boor算法，计算B样条的一个有效方法
• 贝塞尔样条

UAT 万能逼近定理

万能近似定理 通用逼近定理

• 神经网络如果具有至少一个非线性输出层，那么只要给予网络足够数量的隐藏单元，它就可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的函数。
• 这极大的扩展了神经网络的表示空间

《深度学习》 6.4.1 万能近似性质和深度

通用逼近定理（UATs）是与 NN 逼近能力相关的理论结果。

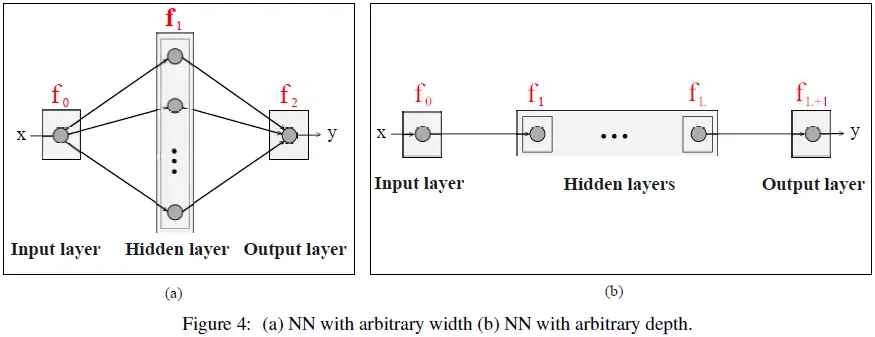
UAT 在以下方向进行探讨：

• 任意宽度：研究具有任意数量神经元（但隐藏层数量有限）的 NN 的逼近能力。
  • 例如，图 4(a)显示了一个具有一个隐藏层并且具有任意数量神经元的 NN。
• 任意深度：研究具有任意数量隐藏层（但每层神经元数量有限）的 NN 的逼近能力。
  • 例如，图 4(b) 显示了一个具有任意数量隐藏层且每层有一个神经元的 NN。

梯度下降法

内容：

• 梯度下降的思想
• 网络的能力分析
• 隐层神经元的真实目的

网络示例依然是那个手写识别的例子：

神经网络是怎样学习的？

• 我们需要一种算法：通过喂给这个网络大量的训练数据——不同的手写数字图像以及对应的数字标签

  算法会调整所有网络参数（权重和偏置）来提高网络对训练数据的表现

  此外，我们还希望这种分层结构能够举一反三，识别训练数据之外的图像——泛化能力

• 虽然使用了“学习”的说法，但实际上训练的过程更像在解一道微积分问题

  训练的过程实际上在寻找某个函数的（局部）最小值

• 在训练开始前，这些参数是随机初始化的

  确实存在一些随机初始化的策略，但目前来看，都只是“锦上添花”

损失函数（Loss Function）

显然，随机初始化不会有多好的表现

• 此时需要定义一个“损失函数”来告诉计算机：正确的输出应该只有标签对应的那个神经元是被激活的

• 比如这样定义单个样本的损失：

• 
• 
• 当网络分类正确时，这个值就越小

• 这里使用的损失函数为“均方误差”（mean-square error, MSE）

• 现在可以用所有训练样本的平均损失来评价整个网络在这个任务上的“糟糕程度”

  在实践中，并不会每次都使用所有训练样本的平均损失来调整梯度，这样计算量太大了 随机梯度下降

实际上，神经网络学习的过程，就是最小化损失函数的过程

神经网络与损失函数的关系

• 神经网络本身相当于一个函数
• 

  输入是一个向量，输出是一个向量，参数是所有权重和偏置

• 损失函数在神经网络的基础上，还要再抽象一层：

所有权重和偏置作为它的输入，输出是单个数值，表示当前网络的性能；参数是所有训练样例（？）

• 

• 从这个角度看，损失函数并不是神经网络的一部分，而是训练神经网络时需要用到的工具

梯度下降法（Gradient Descent）

如何优化这些网络参数？

• 能够判断网络的“糟糕程度”并不重要，关键是如何利用它来优化网络参数

示例 1：考虑只有一个参数的情况

• 如果函数只有一个极值点，那么直接利用微积分即可

如果函数很复杂的话，问题就不那么直接了，更遑论上万个参数的情况

• 

• 

• 一个启发式的思路是：先随机选择一个值，然后考虑向左还是向右，函数值会减小；

  准确的说，如果你找到了函数在该点的斜率，斜率为正就向左移动一小步，反之向右；

  然后每新到一个点就重复上述过程——计算新的斜率，根据斜率更新位置；

  最后，就可能逼近函数的某个局部极小值点

  

• 这个想法最明显的问题是：由于无法预知最开始的值在什么位置，导致最终会到达不同的局部极小值；

  关键是无法保证落入的局部极小值就是损失函数可能达到的全局最小值；

  这也是神经网络最大的问题：

  

示例 2：考虑两个参数的情况

• 输入空间是一个 XY 平面，代价函数是平面上方的曲面

  此时的问题是：在输入空间沿哪个方向移动，能使输出结果下降得最快

  

• 如果你熟悉多元微积分，那么应该已经有了答案：

  函数的梯度指出了函数的“最陡”增长方向，即沿着梯度的方向走，函数增长最快；

  换言之，沿梯度的负方向走，函数值也就下降得最快；

  此外，梯度向量的长度还代表了斜坡的“陡”的程度。

• 处理更多的参数也是同样的办法，

  这种按照负梯度的倍数，不断调整函数输入值的过程，就叫作梯度下降法

• 直观来看，梯度下降法能够让函数值收敛到损失函数图像中的某一个“坑”中

  

理解梯度下降法的另一种思路

• 梯度下降法的一般处理方式：
  • 将所有网络参数放在一个列向量中，那么损失函数的负梯度也是一个向量

• 负梯度中的每一项实际传达了两个信息

  1. 正负号在告诉输入向量应该调大还是调小——因为是负梯度，所以正好对应调大，负号调小

  2. 每一项的相对大小表明每个输入值对函数值的影响程度；换言之，也就是调整各权重对于网络的影响

     

• 宏观来看，可以把梯度向量中的每个值理解为各参数（权重和偏置）的相对重要度，

  同时指出了改变其中哪些参数的性价比最高

• 这个理解思路同样可以反馈到图像中

  

  • 一种思路是在点 (1,1) 处沿着 [3,1] 方向移动，函数值增长最快

  • 另一种解读就是变量 x 的重要性是 y 的三倍；

    也就是说，至少在这个点附近，改变 x 会造成更大的影响

梯度下降法描述：

1. 计算损失函数对所有参数的（负）梯度
2. 按梯度的负方向下降一定步长（直接加上负梯度）
3. 重复以上步骤，直到满足精度要求

• 其中计算梯度的算法——反向传播算法——是整个神经网络的核心

梯度下降法与反向传播算法

• 梯度下降法是寻找局部最小值的一种策略

  其中最核心的部分利用损失函数 L(θ) 的梯度来更新所有参数 θ

• 反向传播算法是求解函数梯度的一种方法；

  其本质上是利用链式法则对每个参数求偏导

损失函数的平滑性

• 为了能达到函数的局部最小值，损失函数有必要是平滑的

  只有如此，损失函数才能基于梯度下降的方法，找到一个局部最小值

• 这也解释了为什么要求神经元的激活值是连续的

  生物学中的神经元是二元式的

随机梯度下降（Stochastic Gradient Descent）

• 基本的梯度下降法要求每次使用所有训练样本的平均损失来更新参数，也称为“批量梯度下降”

原则上是这样，但是为了计算效率，实践中并不会这么做

• 一种常用的方法是每次只随机选取单个样本的损失来计算梯度，该方法称为“随机梯度下降”（Stochastic Gradient Descent, SGD），它比批量梯度下降法要快得多

• 但更常用的方法是小批量梯度下降，它每次随机选取一批样本，然后基于它们的平均损失来更新参数

• SGD 与 小批量梯度下降的优势在于：它们的计算复杂度与训练样本的数量无关

  很多情况下，并不区分 SGD 和小批量梯度下降；有时默认 SGD 就是小批量梯度下降，比如本视频

批大小的影响：

• 较大的批能得到更精确的梯度估计，但回报是小于线性的。
• 较小的批能带来更好的泛化误差，泛化误差通常在批大小为 1 时最好。但是，因为梯度估计的高方差，小批量训练需要较小的学习率以保持稳定性，这意味着更长的训练时间。

  原因可能是由于小批量在学习过程中加入了噪声，它们会有一些正则化效果 (Wilson and Martinez, 2003)

• 内存消耗和批的大小成正比，当批量处理中的所有样本可以并行处理时。

• 在某些硬件上使用特定大小可以减少运行时间。尤其是在使用 GPU 时，通常使用 2 的幂数作为批量大小可以获得更少的运行时间。一般，2 的幂数的取值范围是 32 到 256，16 有时在尝试大模型时使用。

  《深度学习》 8.1.3 批量算法和小批量算法

神经网络的优化难题

• 有一个策略可以保证最终解至少能到达一个局部极小值点：使每次移动的步幅和斜率成正比；

  因为在最小值附近的斜率会趋于平缓，这将导致每次移动步幅越来越小，防止跳出极值点

  但是，这对于现代各种巨大的神经网络而言，是一个负优化策略——它反而会限制网络的学习，导致其陷入某个局部极小值点

• 当参数数量非常庞大时，可能存在无数个极值点，而其中某些极值点的结果可能非常差。

  优化问题是深度学习最核心的两个问题之一，另一个是正则化

• 也不要太过担心因为局部最小值点太多而无法优化；

  事实上，只要你使用的数据不是完全随机，或者说有一定结构，那么最终网络倾向收敛到的各个局部最小值点，实际上都差不多

  你可以认为如果数据集已经结构化了，那么你可以更轻松的找到局部最小值点

  [1412.0233] The Loss Surfaces of Multilayer Networks https://arxiv.org/abs/1412.0233

再谈神经网络的运作机制

• 在第一章介绍神经网络的运作机制时，我们对神经网络的期望是：

  第一个隐藏层能够识别短边，第二个隐藏层能够将短边拼成圆圈等基本笔画，最后将这些部件拼成数字

  

• 利用权重与所有输入像素对应相乘的方法，可以还原每个神经元对应的图案

  

  期望（左）与现实（右）

• 事实上，与其说它们能识别各种散落的短边，它们不过都是一些松散的图案

  就像“在如深海般的 13000 维参数空间中，找到了一个不错的局部最小值位置住了下来”

  尽管它们能成功识别大部分手写数字，但它不像我们期望的能识别各种图案的基本部件

• 一个明显的例子：传入一张随机的图案

  如果神经网络真的很“智能”，它应该对这个输入感到困惑——10个输出单元都没有明确的激活值

  但实际上，它总会会给出一个确切的答案

  

  它能将一张真正的 “5” 识别成 5，也能把一张随机的噪声识别成 5

• 或者说，这个神经网络知道怎么识别数字，但它不知道怎么写数字

  原因可能是，很大程度上它的训练被限制在了一个很窄的框架内；

  “从神经网络的视角来看，整个世界都是由网络内清晰定义的静止数字组成的，它的损失函数只会促使它对最后的判断有绝对的自信。”

• 有一些观点认为，神经网络/深度学习并没有那么智能，它只是记住了所有正确分类的数据，然后尽量把那些跟训练数据类似的数据分类正确

• 但是，有些观点认为神经网络确实学到了某些更智能的东西：

  如果训练时使用的是随机的数据，那么损失函数的下降会很慢，而且是接近线性的过程；也就是说网络很难找到可能存在的局部最小值点；

  但如果你使用了结构化的数据，虽然一开始的损失会上下浮动，但接下来会快速下降；也就是很容易就找到了某个局部最小值——这表明神经网络能更快学习结构化的数据。

  

推荐阅读

• Neural Networks and Deep Learning: http://neuralnetworksanddeeplearning.com/
• Chris Olah’s blog: http://colah.github.io/
  • Neural Networks, Manifolds, and Topology
  • Understanding LSTM Networks
• Distill — Latest articles about machine learning https://distill.pub/
• Videos on machine learning:
  • Learning To See [Part 1: Introduction] - YouTube https://www.youtube.com/watch?v=i8D90DkCLhI
  • Neural Networks Demystified [Part 1: Data and Architecture] - YouTube https://www.youtube.com/watch?v=bxe2T-V8XRs

反向传播算法（Backpropagation Algorithm, BP）

Jacobian 矩阵

【2023-7-11】Jacobian 矩阵：从手推反向传播梯度开始

• 
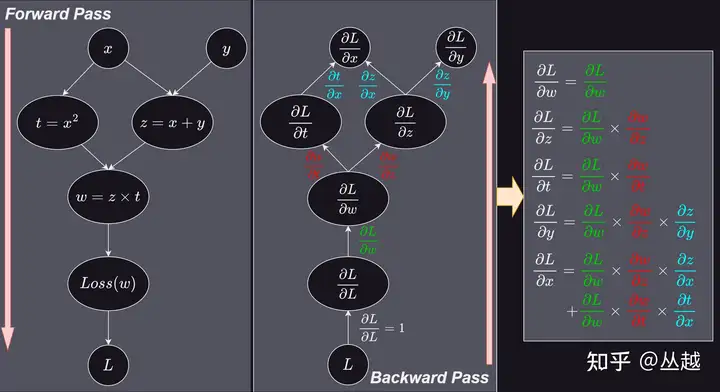
• 变量的梯度 = 上游变量的梯度 * 当前变量的J矩阵
• 如果把整个J矩阵看成一个偏导数，那么这个模式就是微分中的链式法则, 手动推导时只需将列出计算图，构建好每个变量的J矩阵，就可以简单的按照链式法则去计算每个变量的梯度，模式统一，简单明了，非常直观。

下面是使用J矩阵和梯度表示的计算图，圆圈中为 Loss 函数对当前变量的梯度，箭头上代表的是上游变量对当前变量的 J 矩阵：

• 

J 矩阵是否解决了本文开头提出的几个问题：

• 梯度路径的复杂度。
  • 通过上面的分析可知，网络中任意变量都可通过梯度向量与 矩阵来计算，模式统一，无需单独分析每条梯度路径。
• 参数维度的复杂度。
  • 矩阵可以表达任意维度，高维变量只需展开即可，后文会详细讨论。
• 梯度计算的复杂度。
  • 使用矩阵乘法计算梯度，无需单独分析合并简化。
• 没有统一的计算模式，无法充分利用现代计算机硬件的并行处理能力。
  • 矩阵是 GPU\CPU 友好的数据结构，可以充分发挥现代硬件的并行能力。

这个 J 矩阵，就是 Jacobian 矩阵。

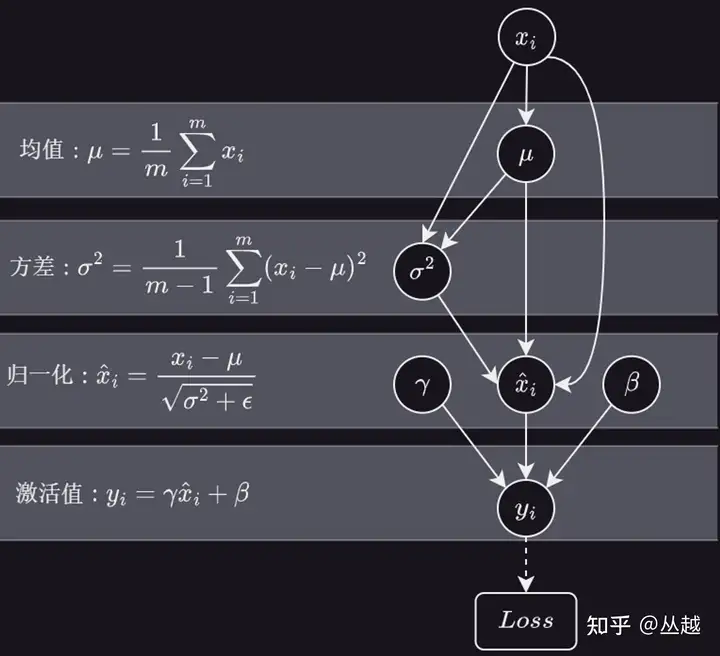
BN 算法流程

• 

反向传播的直观理解

• 梯度下降法中需要用到损失函数的梯度来决定下降的方向，

  其中 BP 算法正是用于求解这个复杂梯度的一种方法

• 在阐述 BP 算法之前，记住梯度的另一种理解方式——

  梯度向量中的每一项不光告诉我们每个参数应该增大还是减小，还指示了调整每个参数的“性价比”

  

示例：单个训练样本对参数调整的影响

• 假设现在的网络还没有训练好，那么输出层的激活值看起来会很随机

  而我们希望的输出应该是正确类别对应的输出值最大，其他尽可能接近 0

  因此，我们希望正确类别对应的激活值应该增大，而其他都减小

  需要注意的是，激活值是由输入值和权重及偏置决定的；网络不会调整激活值本身，只能改变权重和偏置

• 一个简单的直觉是：激活值变动的幅度应该与当前值和目标值之间的误差成正比

  

  我们希望第三个输出值增大，其他减小

  显然，这里增加 “2” 的激活值比减少 “8” 的激活值更重要；因为后者已经接近它的目标了

• 激活值的计算公式指明了调整的方向

  

• 以 “2” 对应的神经元为例，如果需要增大当前激活值，可以：

  1. 增大偏置
  2. 增大权重
  3. 调整上一层的激活值

     如果使用的是 sigmoid 或 ReLU 作为激活函数，那么激活值都 ≥ 0；但无论激活值正负，都是类似的调整方法

如何调整权重和偏置？

• 偏置只关注当前神经元，因此，可以正比于当前值和目标值之间的差来调整偏置

• 权重指示了连接的强弱；换言之，与之相连的上层激活值越大，那么该权重对当前神经元的影响也越大。显然，着重调整这个参数的性价比更高

  因此，可以正比于与之关联的上层激活值来调整权重

• 这种学习的偏好将导致这样一个结果——一同激活的神经元被关联在一起；生物学中，称之为“赫布理论”（Hebbian theory）

  这在深度学习中，并不是一个广泛的结论，只是一个粗略的对照；事实上，早期的神经网络确实在模仿生物学上大脑的工作；但深度学习兴起之后，其指导思想已经发生了重要转变——组合表示

如何改变上层激活值？

• 因为权重带有正负，所以如果希望增大当前激活值，应该使所有通过正权连接的上层激活值增大，所有通过负权连接的上层激活值减小

• 类似的，与修改权重时类似，如果想造成更大的影响，应该对应权重的大小来对激活值做出成比例的改变；

  但需要注意的是，上层激活值的大小也是由上层的权重和偏置决定的，

• 所以更准确的说法是，每层的权重和偏置会根据下一层的权重和偏置来做出成比例的改变，而最后一层的权重个偏置会根据当前值和目标值之间的误差来成比例调整

反向传播

• 除了需要增大正确的激活值，同时还要减小错误的。而这些神经元对于如何改变上一层的激活值都有各自的想法；

  因此，需要将这些神经元的期待全部相加，作为改变上层神经元的指示；

  这些期待变化，不仅对应权重的倍数，也是每个神经元激活值改变量的倍数。

  

• 这其实就是在实现“反向传播”的理念了——

  将所有期待的改变相加，就得到了希望对上层改动的变化量；然后就可以重复这个过程，直到第一层

• 上面只是讨论了单个样本对所有参数的影响，实践时，需要同时考虑每个样本对权重与偏置的修改，然后将它们期望的平均作为每个参数的变化量；

  不严格的来说，这就是梯度下降中的需要的“负梯度”

  

  η 表示倍数

BP 算法小结

• 反向传播算法计算的是单个训练样本对所有权重和偏置的调整——包括每个参数的正负变化以及变化的比例——使其能最快的降低损失。

• 真正的梯度下降需要对训练集中的每个样本都做一次反向传播，然后计算平均变化值，继而更新参数。

  但这么操作会导致算法的复杂度与训练样本的数量相关。

• 实践时，会采用“随机梯度下降”的策略：
  1. 首先打乱所有样本；
  2. 然后将所有样本分发到各个 mini-batch 中；
  3. 计算每个 mini-batch 的梯度，调整参数
  4. 循环至 Loss 值基本不再变化

  最终神经网络将会收敛到某个局部最小值上

相关代码

• mnielsen/neural-networks-and-deep-learning/network.py

反向传播的微积分原理

从数学的角度看，反向传播本质上就是利用链式法则求导的过程；

本节的目标是展示机器学习领域是如何理解链式法则的。

示例：每层只有一个神经元的网络

• 从最后两个神经元开始：

  记最后一个神经元的激活值为 a^(L) 表示在第 L 层，上层的激活值为 a^(L-1)；

  给定一个训练样本，其目标值记为 y；

  则该网络对于单个训练样本的损失，可以表示为：

  

  其中

  

  为了方便，记加权和为 z，于是有

  

• 整个流程可以概括为：

  

  • 先使用前一个激活值和权重 w 以及偏置 b 计算出 z
  • 再将 z 传入激活函数计算出 a
  • 最后利用 a 和目标值 y 计算出损失

• 我们的目标是理解代价函数对于参数的变化有多敏感；

  从微积分的角度来看，这实际上就是在求损失函数对参数的导数。

• 以 w^(L) 为例，求 C 对 w^(L)的（偏）导数，记作：

  

  把 ∂w^(L) 看作对 w 的微小扰动，比如 0.001；把 ∂C 看作“改变 w 对 C 造成的变化”

  这实际上就是在计算 C 对 w^(L) 的微小变化有多敏感；

  3B1B - 微积分系列视频

• 根据链式法则，有

  

• 进一步分解到每个比值，有

  

• 类似的，对偏置的偏导：

  

  对上层激活值的偏导：

  

• 更上层的权重与偏置也是类似的方法，只是链的长度会更长而已

  

• 一个直观的理解，考虑将它们分别对应到一个数轴上；

  

  • w^(L) 的微小变化会导致 z^(L) 的微小变化
  • z^(L) 的微小变化会导致 a^(L) 的微小变化
  • a^(L) 的微小变化最终会影响到损失值 C
  • 反向传播的过程就是将 C 的微小变化传回去

• 以上只是单个训练的损失对 w^(L) 的导数，实践中需要求出一个 mini-batch 中所有样本的平均损失

• 进一步的，∂C/∂w^(L) 只是梯度向量 ▽C 的一个分量；
• 而梯度向量本身有损失函数对每个参数的偏导构成：
• 

本系列视频称损失函数为“代价函数”，所以使用 C 表示代价（Cost）；更多会用 L 表示损失（Loss）；二者没有区别，但这里已经使用 L 表示网络的层数，所以使用 C 表示损失函数

更复杂的示例

• 更复杂的神经网络在公式上并没有复杂很多，只有少量符号的变化
• 首先，利用下标来区分同一层不同的神经元和权重
• 

以下的推导过程几乎只是符号的改变：

• 

然后求偏导：

• 

唯一改变的是，对 (L-1) 层的偏导：

• 

此时激活值可以通过不同的途径影响损失函数

只要计算出倒数第二层损失函数对激活值的敏感度，就可以重复以上过程，计算喂给倒数第二层的权重和偏置。

• 事实上，如果都使用矢量表示，那么整个推导公式跟单神经元的网络几乎是完全一样的
• 链式法则给出了决定梯度每个分量的偏导，使我们能不断下探，最小化神经网络的损失。

反向传播的 4 个基本公式

• 问题描述：

  反向传播算法的目标是求出损失函数对所有参数的梯度，具体可分解为对每个权重和偏置的偏导

  可以用 4 个公式总结反向传播的过程

• 标量形式：

• 
• 
• 
• 

  其中，上标 (l) 表示网络的层次，(L) 表示输出层（最后一层）；下标 j 和 k 指示神经元的位置；

  w_jk 表示 l 层的第 j 个神经元与(l-1)层第 k 个神经元连线上的权重

  以 均方误差（MSE） 损失函数为例，有

• 

根据以上公式，就可以反向求出所有损失函数对所有参数的偏导了

• 矢量形式：

  在标量形式的基础上，修改下标即可

• 
• 
• 
• 

注意：其中向量相乘都是以按元素相乘的形式，一般用 ⊙ 符号表示。

• 以上是纯微积分形式的表达，一些机器学习相关书籍上总结了更简洁的形式，比如：
• 

The four fundamental equations behind backpropagation

注意：前两个公式为矢量形式，后两个具体到单个参数的是标量形式。

其中，符号 ⊙ 按元素相乘：

• 

闲话神经网络

• 资料
  • 神经网络结构
    • Hopfield 网络
  • 周志华：深度学习为什么深？
    • 深度学习的理论基础尚不清楚
    • 深度学习为什么深？模型复杂度的角度
    • 神经网络最重要的是表示学习的能力
    • 深度学习成功的三个因素
    • 深度学习存在的问题
    • 探索深度学习之外的方法：深度森林
    • AI时代最重要的是人才
  • 深度学习核心
• 神经网络结构
  • 神经网络可视化
    • 视频
    • 2D 可视化
    • 3D 可视化
  • 神经网络如何记忆
  • 神经元（隐藏单元）与隐藏层
  • 神经网络的运作机制
    • 权重和偏置
  • 神经网络泛化能力
    • Nature 神经网络泛化能力超过人
  • 非线性激活函数
    • ReLU
  • 神经网络理论
    • 叠加定理
    • KAN
    • UAT 万能逼近定理
  • 梯度下降法
    • 损失函数（Loss Function）
    • 梯度下降法（Gradient Descent）
      • 理解梯度下降法的另一种思路
      • 随机梯度下降（Stochastic Gradient Descent）
  • 神经网络的优化难题
  • 再谈神经网络的运作机制
  • 推荐阅读
  • 反向传播算法（Backpropagation Algorithm, BP）
    • Jacobian 矩阵
    • 反向传播的直观理解
    • BP 算法小结
    • 相关代码
    • 反向传播的微积分原理
      • 示例：每层只有一个神经元的网络
      • 更复杂的示例
      • 反向传播的 4 个基本公式
• 闲话神经网络
  • 神经网络发展历史
  • 神经网络基础回顾
  • 隐含层有什么用？
    • 对隐含层的感性认知
    • 隐含层的理性认知
  • 光说不练假把式
    • 案例一: 动图显示神经网络各层之间的效果
    • 案例二： Playground
  • 到底应该多少个隐含层
    • 一 隐层数
    • 二 隐层节点数
    • 到底多少神经元？
  • 隐含层越胖越好？
  • 更宽还是更胖？Wider or deeper？
  • 神经网络可解释性
• 结束

编者按： 平时收集了不少神经网络知识片段，过于零散，花了大半天时间将各种细节梳理，串联起来。

总结：

这一篇杂文，把之前收集的神经网络点点滴滴，梳理、串联起来，便于理解，如有不当，麻烦及时指出，邮箱：wqw547243068@163.com。

神经网络发展历史

先看看这几张图：

• 
• 

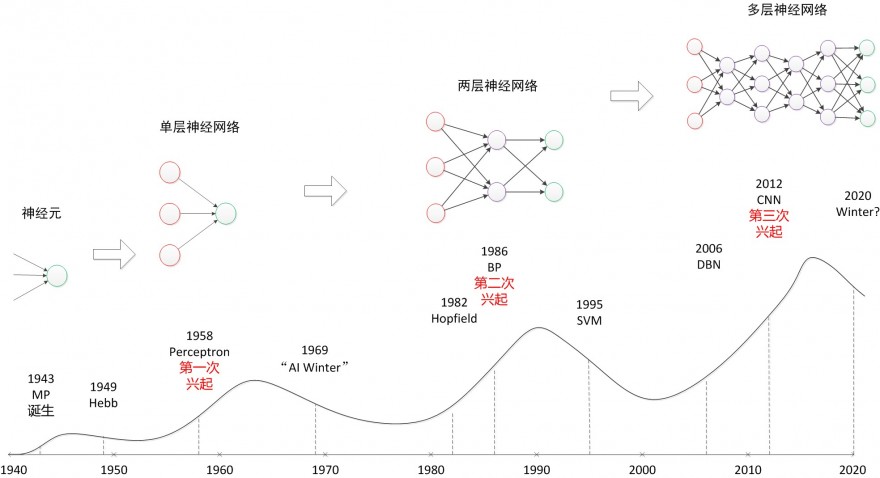
神经网络三次兴起：

• 第一次，控制论时代，1958年，感知器诞生，能分类，但解决不了异或问题；
• 第二次，联结主义时代，BP网络诞生，加非线性激活函数，解决了异或，但受限于理论不完善（局部最优，黑盒）+数据少+训练方法+计算能力，败于SVM与概率图；
• 第三次，2006年，祖师爷Goeffrey Hinton坐了几十年冷板凳，琢磨出pre-training，DBN等，接着一发不可收拾。Yann LeCun将CNN发扬光大（将BP与CNN结合，推出第一个可用的Le-Net，深度学习入门者的hello world），Jürgen Schmidhuber 90年代发明的LSTM，沉寂多年后复活了，Yoshua Bengio开创了神经网络语言模型。加上大数据时代，GPU的发展等，诸多因素导致深度学习“大爆炸”。

  注：这里不做过多介绍，详情参考，「Deep Learning」读书系列分享（一）

神经网络基础回顾

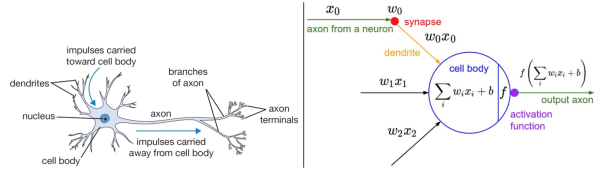
左边是一个生物学的神经元，右边是一个常用的数学模型。人工神经网络中的神经元设计受到生物神经元的启发。

要点：

• 生物神经元（左图）中，树突将信号传递到细胞体，信号在细胞体中相加。如果和高于某个阈值，那么神经元将会激活，向其轴突输出一个峰值信号，注意这里是脉冲信号。
• 数学计算模型（右图）中，将输入进行加权求和加上偏置，输入到激活函数（模拟生物中神经元）中，继续往后传递。
• 生物中神经元复杂得多，其中一种多输入单输出，这里的输出是一个脉冲信号，而不是一个值，现在也有脉冲人工神经网络（号称第三代神经网络）。
• 

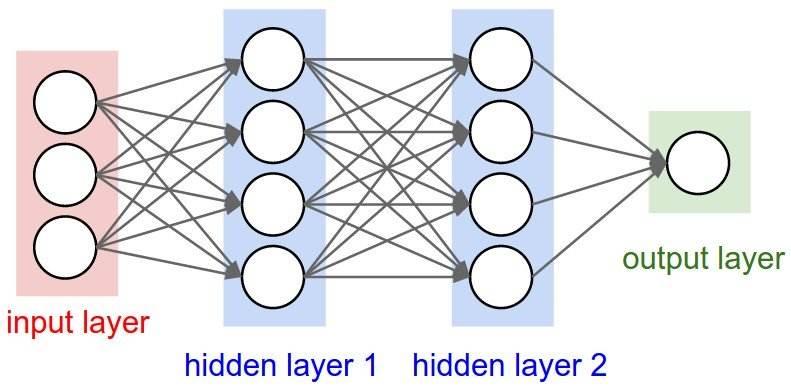
经典的网络结构由多个神经元组合起来，按照输入层，隐含层和输出层的顺序，组成神经网络。常见的是前馈神经网络（FFN，feedforward neural network），代表例子是多层感知器（MLP：multi-layer perception），变种是循环神经网络（RNN: 时间上共享）和卷积神经网络（CNN: 空间上共享）等。

• 当然，80-90年代，还有诞生过其他结构的网络，如
  • 反馈神经网络（输出与输入直接关联，如Elman网络和Hopfield网络）
  • 自组织神经网络（无监督，每次竞争，只更新一个神经元，参数和网络结构自适应）
  • 模糊神经网络（结合模糊数学理论）
  • 径向基神经网络（跟早期的BP网络同步，RBF）
• 等等，只是这些网络应用效果欠佳，逐渐淹没在时代潮流里，几十年不曾提及。

参考：神经网络用作分类器

十万个为什么

神经网络从名不见经传到现在大红大紫，成了AI浪潮的主力。只要跟AI相关，基本都要扯上神经网络，从多层感知器MLP，到卷积神经网络CNN，循环神经网络RNN，再到自编码器AE，变分自编码VAE，生成对抗网络GAN，一个又一个，让人应接不暇。

身处信息爆炸时代的初学者，如果人云亦云，没有自己的思考，很容易陷入懵逼状态：

• 神经网络到底是什么“神经”物种？神经元？人类大脑？
  • 外行一听，觉得高端大气上档次，却又遥不可及，只得双手合十，顶礼膜拜，不可理解推敲焉，只好找个佛龛供起来，一方面自己有了信仰，心里不慌，另一方面又能“吓唬”别人，^_^。
• 神经网络怎么工作的？为什么具备这么强的拟合能力？
  • 以第二代神经网络MLP（含BP机制，第一代是感知器，第二代是BP网络，第三代是脉冲神经网络）为例，结构并不复杂：输入层，隐含层和输出层，训练期间，根据预设的目标通过BP反向传播机制学习出一组隐含层参数。
  • 万能近似定理

    提供了坚实的神经网络理论保障。

万能近似定理（universal approximation theorem）(Hornik et al., Cybenko, 1989) 表明

一个前馈神经网络（FFN）如果具有线性输出层和至少1层有任何“挤压”性质的激活函数（例如logistic sigmoid激活函数）的隐藏层，只要给予网络足够数量的隐藏单元，就能以任意精度来近似任何从有限维空间到另一个有限维空间的`Borel`可测函数（定义在紧集上的连续函数）。（《Deep learning》英文版P194，中文版P171）

带着这些问题，接着往下走

注：如果对神经网络工作原理缺乏了解，但想在30min内有个基本轮廓，建议看完以下视频：

• 3Blue1Brown科普:什么是神经网络？
• 相关视频：《线性代数本质》、《微积分》等
• 三棕一蓝很优秀，很无私
• 

隐含层有什么用？

对隐含层的感性认知

神经网络给大家留下了深刻的印象，但是总让人琢磨不透。权重和偏置量能自动地学习得到，但是这并不意味着能解释神经网络是怎么样得出的这些参数。现在仍然没人说清楚为什么某某节点的权重参数为什么取值为某个值。

所以，第二次寒潮被人批评的槽点至今还在：

• 神经网络模型是个黑盒子

  ，凭什么让我信任？o(╯□╰)o。

这个“黑盒子”，主要是指隐含层，光看名字就有种神秘感，隐形人，神秘人

作为好奇心爆棚的人类，有想过，隐含层到底在做什么吗？

从一个问题开始，如何区分以下三张图哪个是人？

• 

这个人脸识别任务中，神经网络模型该怎么建立？简单起见，图像里所有像素作为输入，输出是是或否的标签。

那么隐含层怎么分析呢？ 如果是人，我们会试着将这个问题分解为一些列的子问题

比如：

• 在上方有头发吗？
• 在左上、右上各有一个眼睛吗？
• 在中间有鼻子吗？
• 在下方中间位置有嘴巴吗？
• 在左、右两侧有耳朵吗？
• …

识别眼睛这个子任务，可能对应一个子网络：

• 

这个子网络还可以进一步分解，一层又一层地分解，直到能由一个神经元给出结果。

• 

这么说，隐含层承担的角色是子任务的识别、组合，从一系列简单、具体得问题开始，建立更复杂、抽象的概念。

隐含层的理性认知

刚才是从人的感性角度来理解，这次换成无感情的物理角度。(神经网络隐含层的物理含义)

多层神经网络，将原始输入数据在隐含层上做了多个二分类，隐含层有多少个神经元，就有多少个分类。

• 

注：源自Youtube上的一个优秀的教学视频：A Friendly Introduction to Machine Learning

假设在平板上玩改版的水果忍者，同时飞过来一堆圣女果和葡萄，怎么分开？

• 如果刚好线性可分，那么轻松划一刀就好了。
• 如果葡萄都聚集在中间三角区的呢？这时就以迅雷不及掩耳之势，连砍三刀，K.O.

等等，这游戏跟神经网络什么关系？

水果在平板上的坐标就是输入数据，维度是2，即x1和x2，线性可分，一个分类器就行；线性不可分的三角形区域，就得综合3个二分类器的结果，即y1、y2和y3围成的区域。其实，这就是有3个神经元的隐含层。细心的话，会发现，你砍的每一刀（每个神经元）就是一个LR回归（自行脑补LR数学表达式）

对于高维数据，不清楚分类面长啥样，隐含层的层数以及每层中神经元的个数，只能通过多次训练调整。

这就是为什么多层神经网络有多个隐含层。

AI圣经《Deep Learning》中有一部分解释的很清楚，隐含层的意义就是让线性不可分的数据变得线性可分：

• 

• 高维空间上的数据就像一张白纸上的两类点，分类面奇奇怪怪。对折足够多次后，总能找到近似平行的线段
• 每个线段附近的分类任务对应一个神经元
• 每次折叠对应一个隐含层
• 要点：深层网络的表示能力具备指数级优势
  • 注：《deep learning》中文版第6章P124，以上是个人理解，不一定正确

既然隐含层这么重要，是不是越多越好呢？

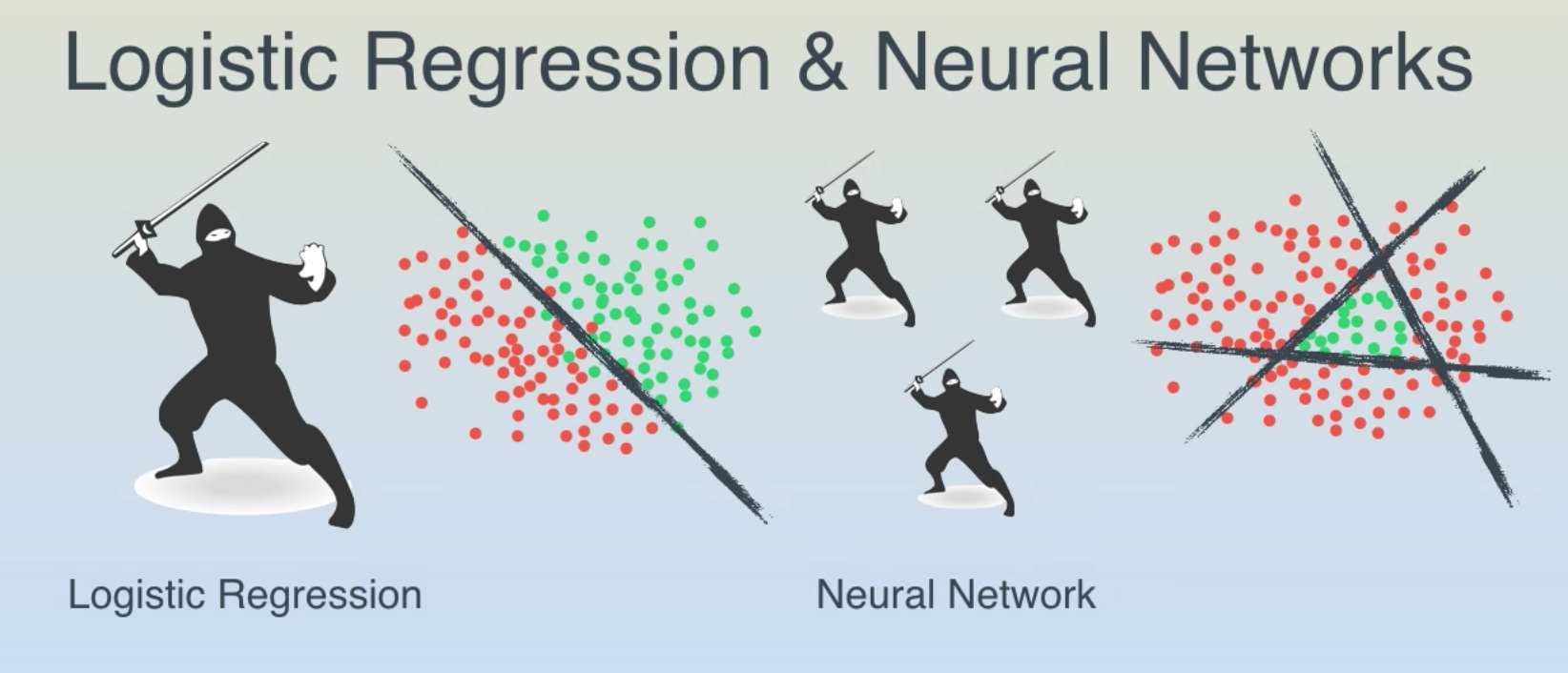
有更多神经元的神经网络可以表达更复杂的函数。然而这既是优势也是不足，优势是可以分类更复杂的数据，不足是可能造成对训练数据的过拟合。

• 

注：过拟合（Overfitting）是网络对数据中的噪声有很强的拟合能力，而没有重视数据间（假设）的潜在基本关系。举例来说，有20个神经元隐层的网络拟合了所有的训练数据，但代价是把决策边界变成了许多不相连的红绿区域。而有3个神经元的模型表达能力只能用比较宽泛的方式去分类。它将数据看做是两个大块，并把个别在绿色区域内的红色点看做噪声。实际上，在测试数据中会获得更好的泛化（generalization）能力。

反过来，如果数据不是足够复杂，似乎小一点的网络更好，可以防止过拟合。然而并非如此，防止神经网络的过拟合有很多方法（L2正则化，dropout和输入噪音等），后面会详细讨论。在实践中，使用这些方法来控制过拟合比减少网络神经元数目要好得多。

原因是小网络更难使用梯度下降等局部方法来进行训练：虽然小型网络的损失函数的局部极小值更少，也比较容易收敛到这些局部极小值，但是这些最小值一般都很差，损失值很高。相反，大网络拥有更多的局部极小值，但就实际损失值来看，这些局部极小值表现更好，损失更小。因为神经网络是非凸的，就很难从数学上研究这些特性。即便如此，还是有一些文章尝试对这些目标函数进行理解，例如The Loss Surfaces of Multilayer Networks 这篇论文。在实际中，你将发现如果训练的是一个小网络，那么最终的损失值将展现出多变性：某些情况下运气好会收敛到一个好的地方，某些情况下就收敛到一个不好的极值。从另一方面来说，如果训练一个大的网络，你将发现许多不同的解决方法，但是最终损失值的差异将会小很多。所有的解决办法都差不多，而且对于随机初始化参数好坏的依赖也会小很多。

正则化强度是控制神经网络过拟合的好方法。看下图结果：

• 

（不同正则化强度的效果：每个神经网络都有20个隐层神经元，但是随着正则化强度增加，它的决策边界变得更加平滑。）

需要记住的是：

• 不应该因为害怕出现过拟合而使用小网络

  。相反，应该进尽可能使用大网络，然后使用正则化技巧来控制过拟合。

参考：神经网络七：神经网络设置层的数量和尺寸

光说不练假把式

学习金字塔有云：阅读演示的留存率不到30%，实践的留存是75%。

• 

看完这篇文章一段时间后大部分都会忘记，为了加深印象，我们来“实践”吧！建议大家消化理解后做笔记，用费曼技巧（参考：号称终极快速学习法的费曼技巧，究竟是什么样的学习方法？）讲给别人听，这不是浪费时间，看好了，留存率90%！

案例一: 动图显示神经网络各层之间的效果

Andrej karparthy的ConvNetJS web页面上有很多很好的交互demo，如mnist、CFAIR-10的降维可视化、自编码器

• ConvnetJS demo: toy 2d classification with 2-layer neural network
• 直接构建3层的神经网络：
  • fc(6) → tanh(6) → fc(4) → tanh(4) → fc(2) → tanh(2) → softmax(2)
• 仔细看以下动图：
  • 左侧的数据集样例，这里默认选用球形数据集，分成两类：绿色和红色，支持人工编辑
  • 右侧是神经网络各层学习到的分类面
• 分析：越往后，分类面越简洁、清晰（低维线性不可分映射到高维空间，使其线性可分）

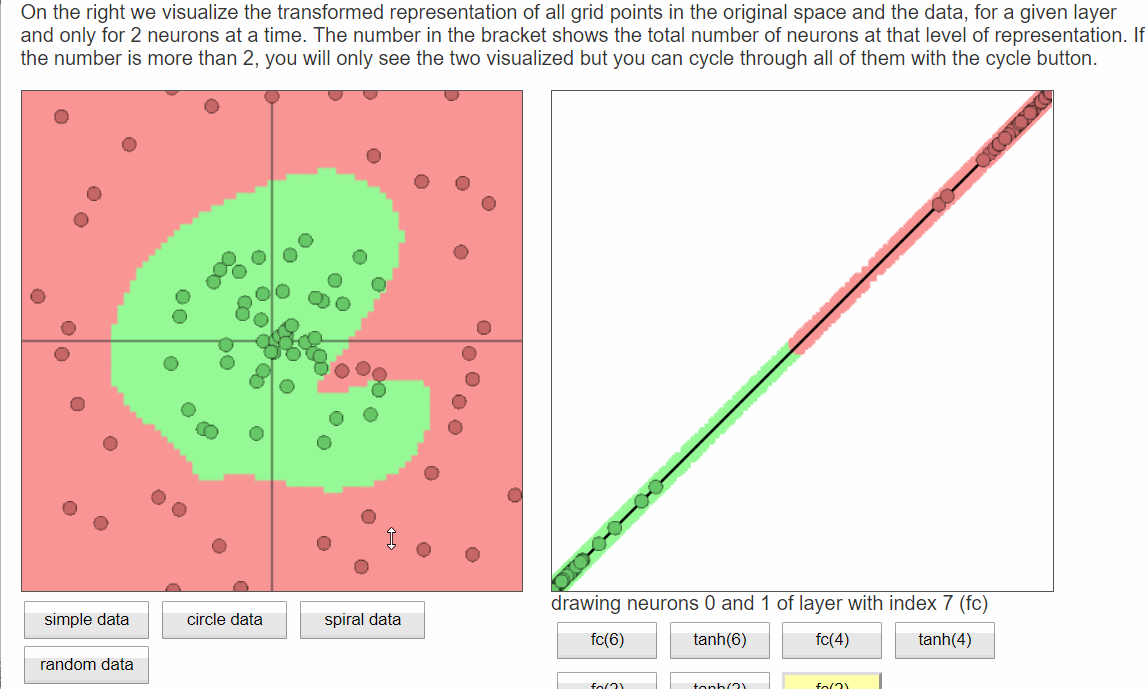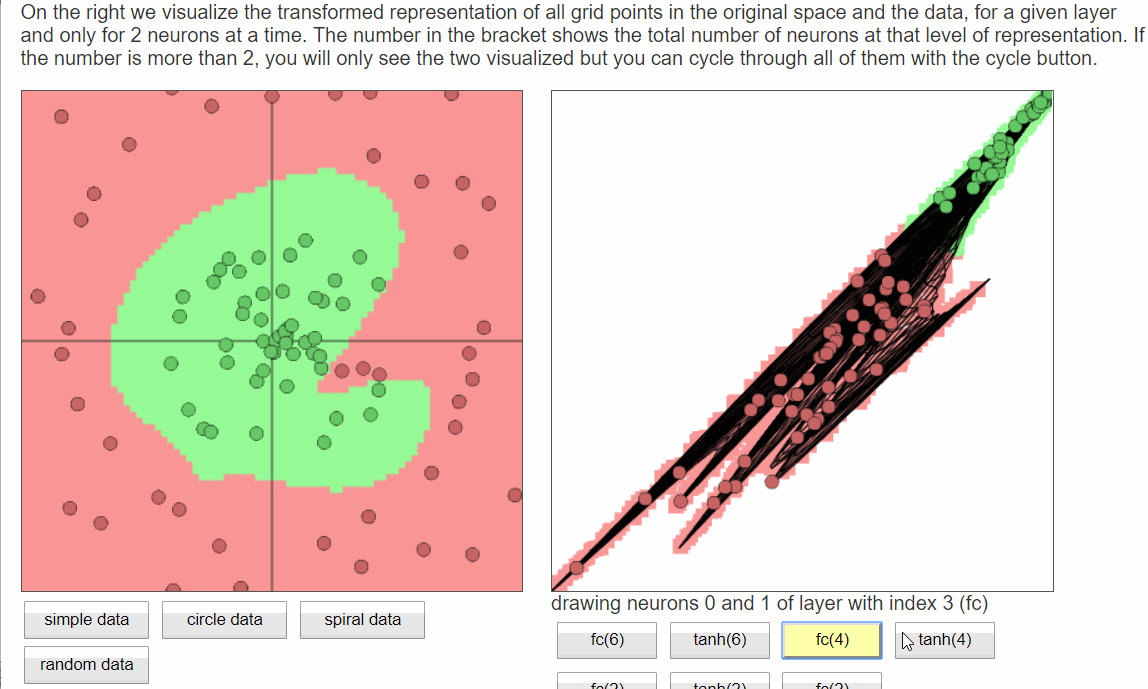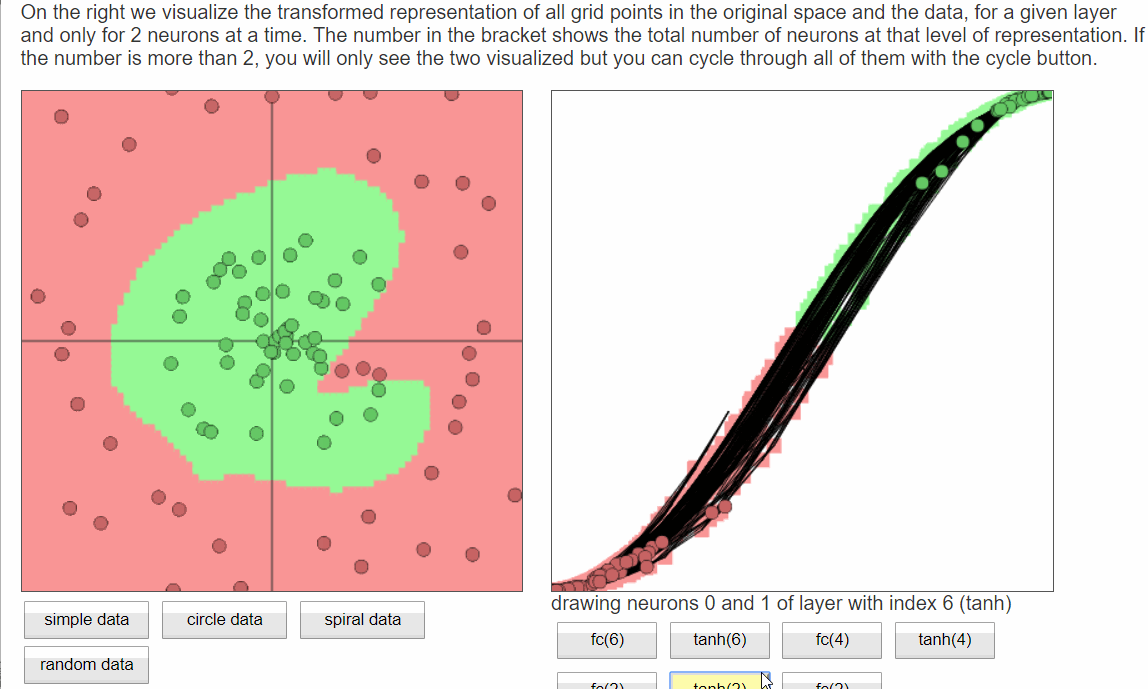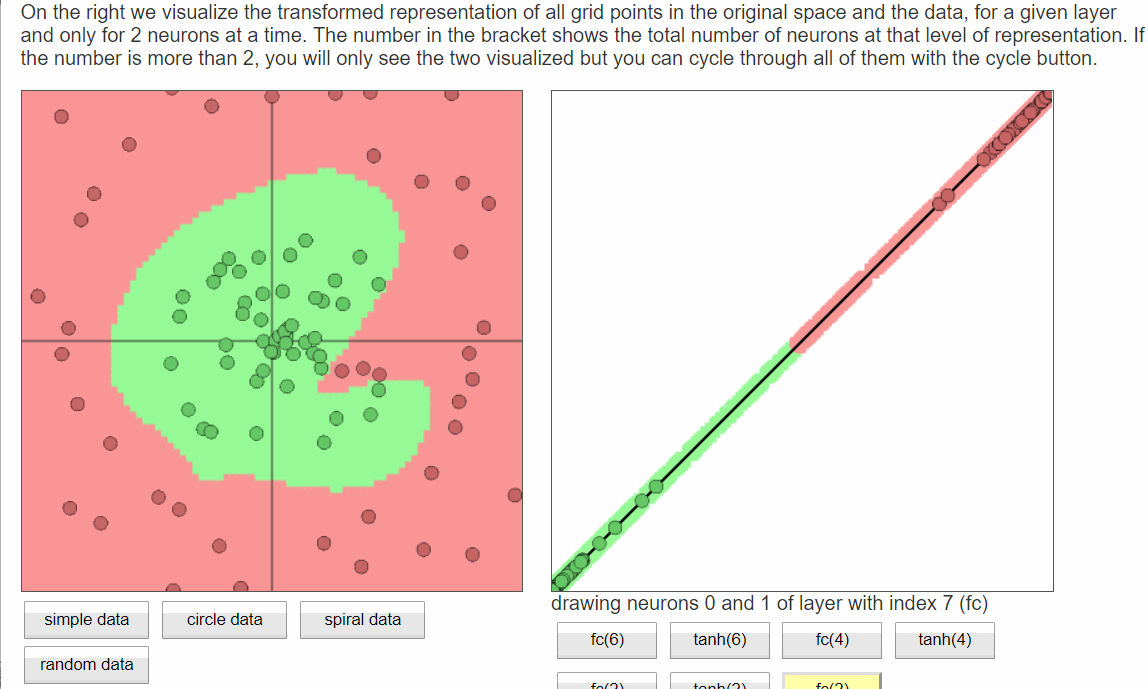
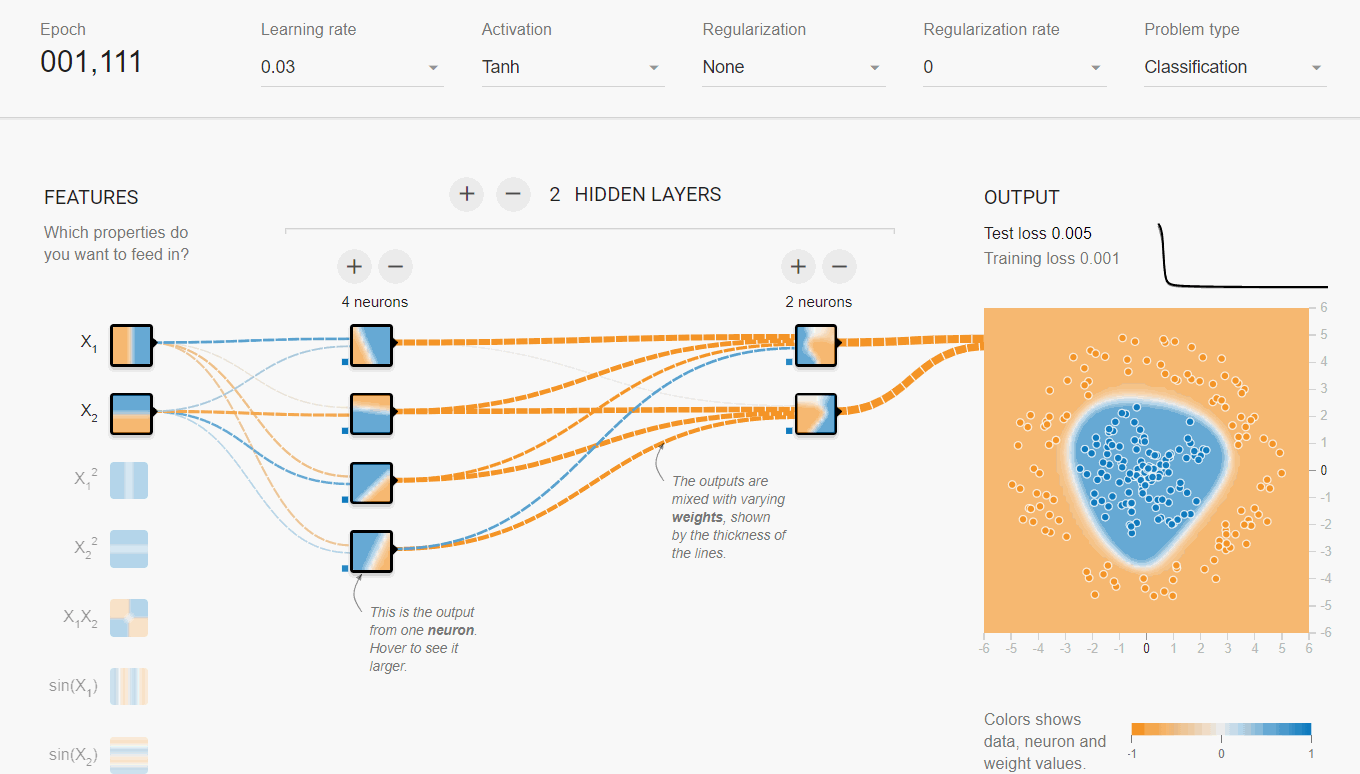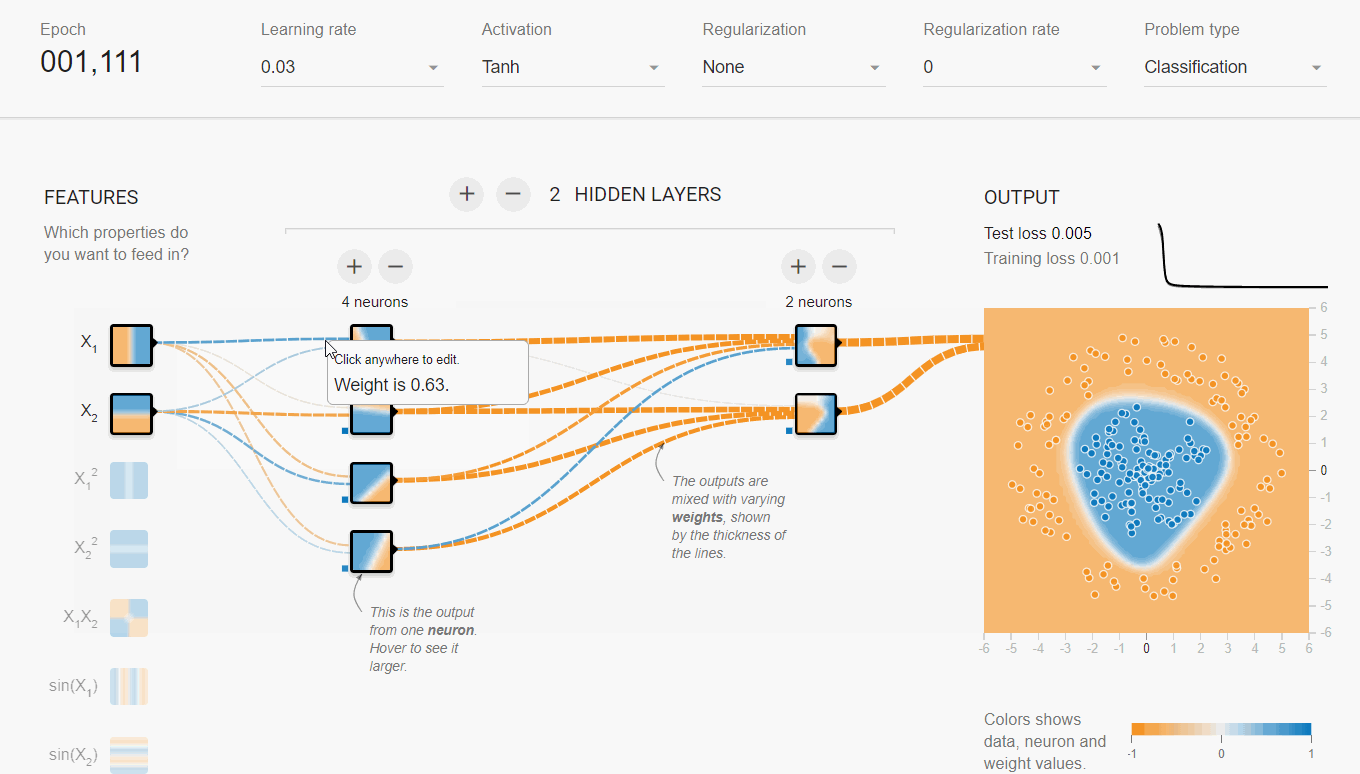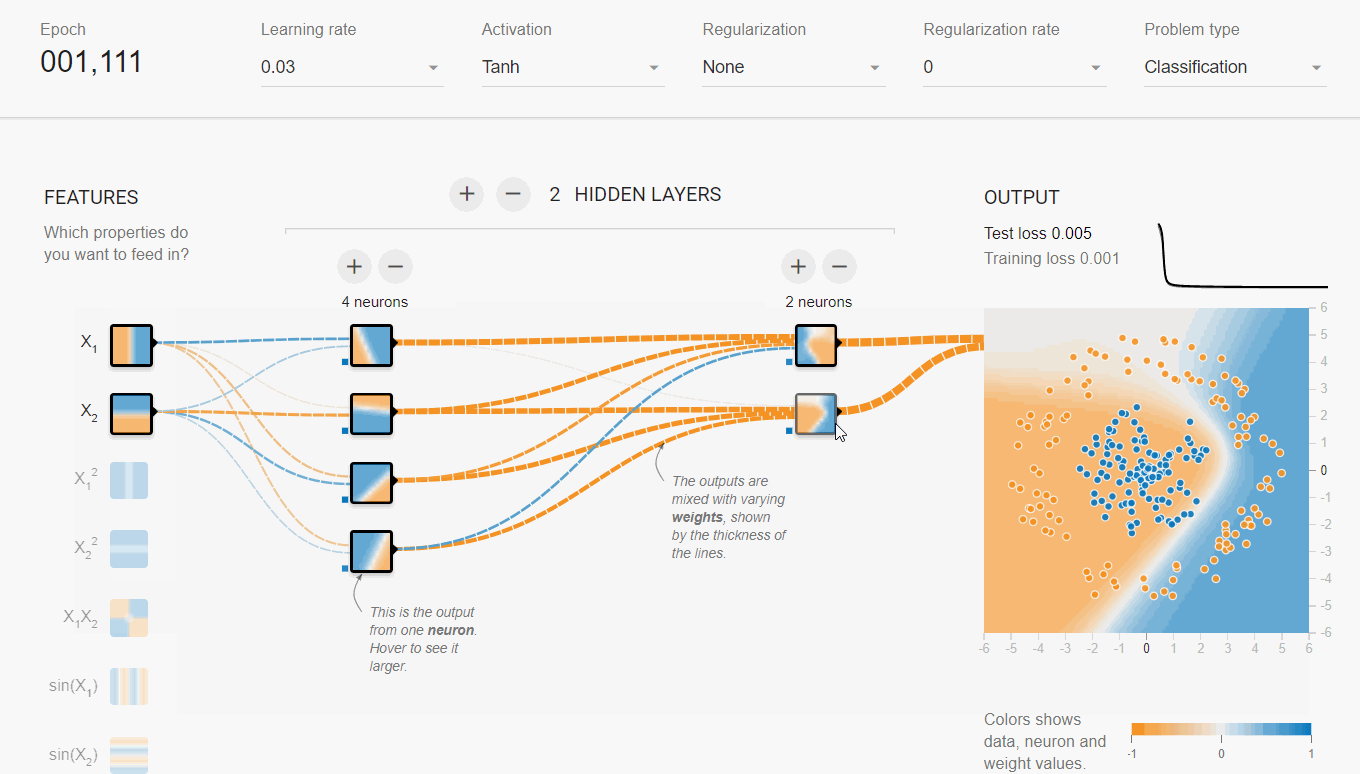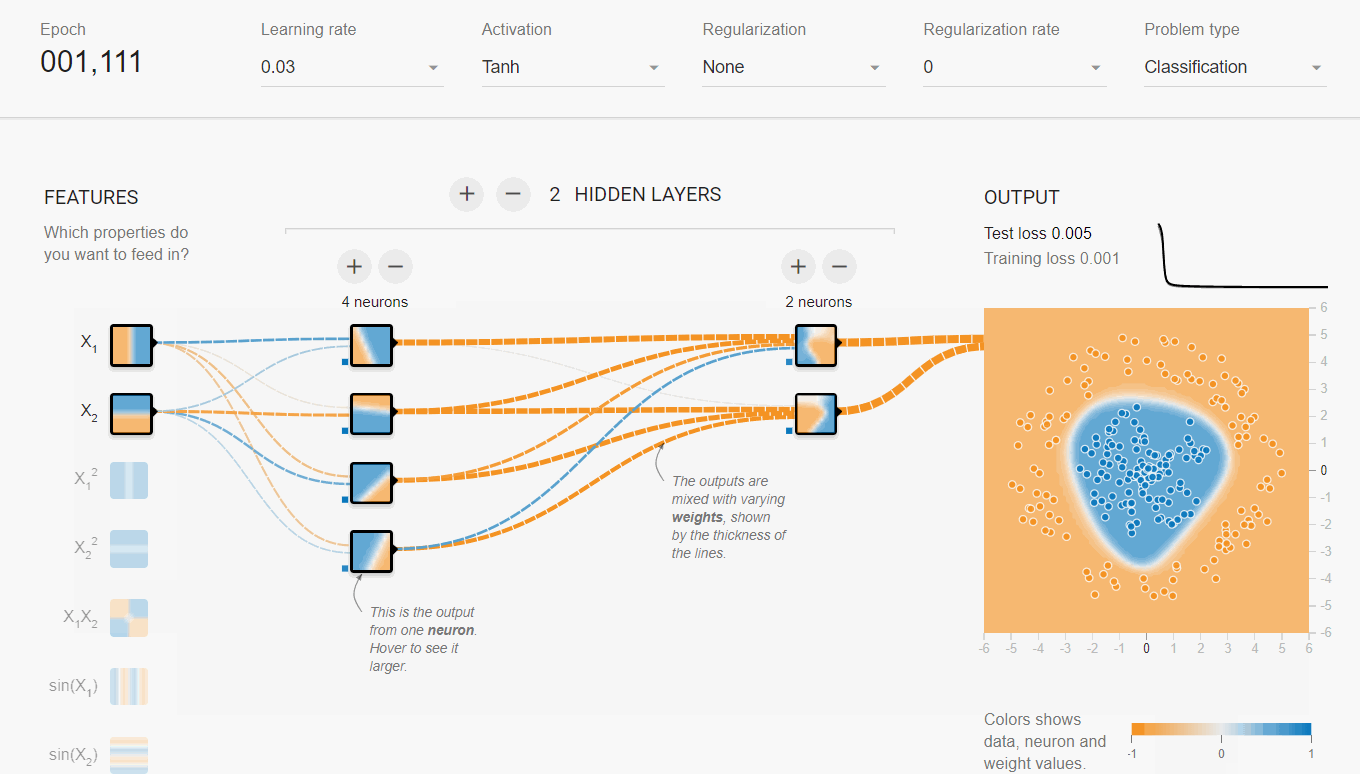
案例二： Playground

Playground这个网页提供了更详细的神经网络交互体验功能，用户可以更灵活的控制神经网络结构，还能看到训练过程中各层分类面的样子。

• 同样选取球形数据集，蓝色和橙色两类，不可编辑；可设置噪声比例，测试集比例，以及batch size大小
• MLP网络结构：可随意指定输入特征、网络深度、宽度，以及激活函数类型

动图：

• 

分析：

• 第一个隐含层只是完成简单的二分类，第二个隐含层将前面的分类面组合起来，形成复杂的分类面，最终在输出层将两类数据完美的分开。
• 隐含层越宽、越深，学习能力（网络容量）越强，收敛速度越快
• 其他问题，建议自行体验：
  • 不同激活函数会影响收敛速度吗？
  • 加入交叉特征，收敛会更快吗？
  • 网络越深/宽越好吗？
  • 深度和宽度，哪个更重要？

到底应该多少个隐含层

神经网络中隐层数和隐层节点数问题的讨论

一 隐层数

一般认为，增加隐层数可以降低网络误差（也有文献认为不一定能有效降低），提高精度，但也使网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向。一般神经网络应优先考虑3层网络（即有1个隐层）。靠增加隐层节点数来获得较低的误差，代价要比增加隐层数更小。对于没有隐层的神经网络模型，实际上就是一个线性或非线性（取决于输出层采用线性或非线性转换函数型式）回归模型。

二 隐层节点数

在BP 网络中，隐层节点数的选择非常重要，不仅对建立的神经网络模型的性能影响很大，还是“过拟合”的直接原因，但目前理论上还没有一种科学的和普遍的确定方法。 多数文献中提出的确定隐层节点数的计算公式都是针对训练样本任意多的情况，而且多数是针对最不利的情况，一般工程实践中很难满足，不宜采用。事实上，各种计算公式得到的隐层节点数有时相差几倍甚至上百倍。为了尽可能避免训练时出现“过拟合”现象，保证足够高的网络性能和泛化能力，确定隐层节点数的最基本原则是：在满足精度要求的前提下取尽可能紧凑的结构，即取尽可能少的隐层节点数。

研究表明，隐层节点数不仅与输入/输出层的节点数有关，更与需解决的问题复杂程度和转换函数的型式以及样本数据的特性等因素有关。

在确定隐层节点数时必须满足下列条件：

• （1）隐层节点数必须小于N-1（其中N为训练样本数，不是特征数！），否则，网络模型的系统误差与训练样本的特性无关而趋于零，即建立的网络模型没有泛化能力，也没有任何实用价值。同理可推得：输入层的节点数（变量数）必须小于N-1。
• (2) 训练样本数必须多于网络模型的连接权数，一般为2~10倍，否则，样本必须分成几部分并采用“轮流训练”的方法才可能得到可靠的神经网络模型。

总之，若隐层节点数太少，网络可能根本不能训练或网络性能很差；若隐层节点数太多，虽然可使网络的系统误差减小，但一方面使网络训练时间延长，另一方面，训练容易陷入局部极小点而得不到最优点，也是训练时出现“过拟合”的内在原因。因此，合理隐层节点数应在综合考虑网络结构复杂程度和误差大小的情况下用节点删除法和扩张法确定。

到底多少神经元？

当训练集确定之后，输入层结点数和输出层结点数随之而确定，首先遇到的一个十分重要而又困难的问题是如何优化隐层结点数和隐层数。实验表明，如果隐层结点数过少，网络不能具有必要的学习能力和信息处理能力。反之，若过多，不仅会大大增加网络结构的复杂性（这一点对硬件实现的网络尤其重要），网络在学习过程中更易陷入局部极小点，而且会使网络的学习速度变得很慢。隐层结点数的选择问题一直受到高度重视。

• 方法1： fangfaGorman指出隐层结点数s与模式数N的关系是：s＝log2N；
• 方法2： Kolmogorov定理表明，隐层结点数s＝2n＋1（n为输入层结点数）；
• 方法3： s＝sqrt（0.43mn＋0.12nn＋2.54m＋0.77n＋0.35）＋0.51
• （m是输入层的个数，n是输出层的个数）。

隐含层越胖越好？

保证准确率的前提下隐藏层节点数最少可以是多少个？

《神经网络隐藏层节点数最少可以是多少个？》搭建了一个81n2的神经网络，通过改变n的值测量这个网络隐藏层节点数量的极小值。

实验：

• 训练集和测试集是mnist的0和1，经过1/3的池化变成9*9的图片，每个n值进行200批，每10批测量一次准确率。
• 每批的batchsize是20个用放回取样，每批迭代1000次。
• 学习率是0.1，没有偏置，激活函数用sigmoid，并同时统计每批次的运行时间。
• 

对于这个81n2的网络的隐藏层节点数最小值可以是2，还是挺令人震惊的的，也就是8122的网络就可以运行准确率可以达到93%，和81502的网络的性能差不多，但是时间只有81502的0.076，也就是说用8122的网络比81502的网络可以省下92%的时间。

一个非常明显的规律：当隐藏层节点数大于20个以后，平均每节点耗时大约都是16.44ms左右的定值，也就是说当节点数大于20个以后网络的耗时基本上可以按照 耗时=nX16.44 的公式算出来。但是网络的性能确没有增加。

• 
• 

按照耗时曲线找到拐点附近的点，就是用时最少同时性能也有保证的隐藏层节点数量。比如这道题就是20个节点左右耗时曲线的第5个点。

更宽还是更胖？Wider or deeper？

有两个以上隐含层的神经网络，称为深度神经网络，deep neural networks，简称为 DNN。

对很多现实问题，深层网络比浅层网络效果更好，原因是深度神经网络建立了更加复杂的体系结构，结果更理想。

那么，传统机器学习方法中就没有这种意识吗？就没有层次结构吗？

当然有，如决策树，不断的加深层次，分裂特征区间，但为什么效果没有DNN好呢？

原因是：

• 决策树方法的仅限于特征间的筛选，模型本身也不复杂，表示能力不如DNN

综上，深度学习算法跟传统机器学习算法相比，要点在于：

• 第一，逐层处理
• 第二，特征内部变化
• 第三，足够的模型复杂度
  • 注：摘自周志华2018年4月16日的演讲，深度学习为什么深？

回到正题，对神经网络这样的模型来说有两条很明显的途径，一条是我们把模型变深，一条是我们把它变宽，但是如果从提升复杂度的角度，变深会更有效。变宽时只不过增加了一些计算单元、增加了函数的个数，而在变深时不仅增加了个数，其实还增加了嵌入的层次，所以泛函的表达能力会更强。有点类似乘法（层间）与加法（层内）的区别。

但是，刚才不是说两层前馈网络能拟合任意精度的函数吗？我就不信胖子就不行！

怀疑的好，来看下李宏毅的提供的实验：

• 同样的隐含层神经元数目，一种矮胖，一种瘦高
• 
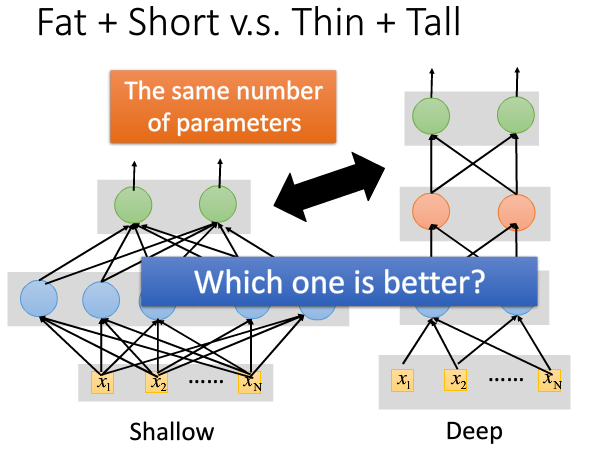
• 语音识别任务下的对比，采用字错误率。
• 

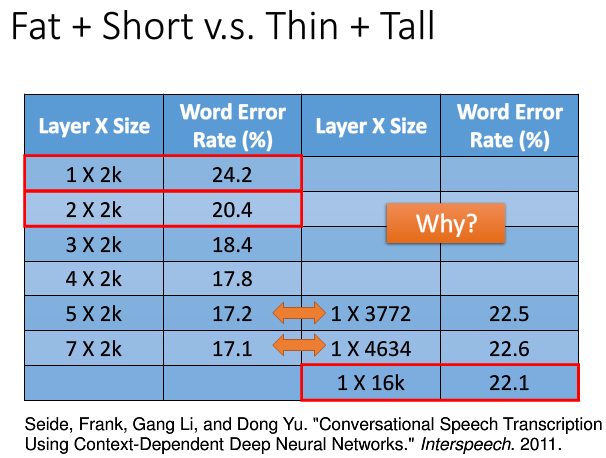
虽然有研究表明，浅而肥的网络也可以拟合任何的函数，但需要非常的“肥胖”，可能一层就要成千上万个神经元，直接导致参数的数量增加到很多很多。当准确率差不多的时候，参数的数量却相差数倍。这也说明用深层神经网络而不是浅层“肥胖”网络。

附：2018年2月，Google tensorflow dev submmit上Google工程师的解答：

• Why deeper models？
  • One explanation：multi-level feature abstraction
  • Each layer is a relatively simple model
  • Each layer generally loses some information due to the use of nonlinear functions——so it needs to remember something good

神经网络可解释性

上面只是简答的示例，有更复杂的案例吗？

• The Building Blocks of Interpretability（交互地址）
• 2分钟论文：用 谷歌「AI可解释性」 看懂机器学习

神经网络可解释性仍然是一个模糊地带，没有达成共识。

结束