{
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "Scikit-learn学习笔记.ipynb",
"version": "0.3.2",
"provenance": [],
"collapsed_sections": [],
"toc_visible": true,
"include_colab_link": true
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
},
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "view-in-github",
"colab_type": "text"
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "nokThLBHbFoF",
"colab_type": "text"
},
"source": [
"# Scikit-learn学习笔记\n",
"- 机器学习工具包\n",
"- 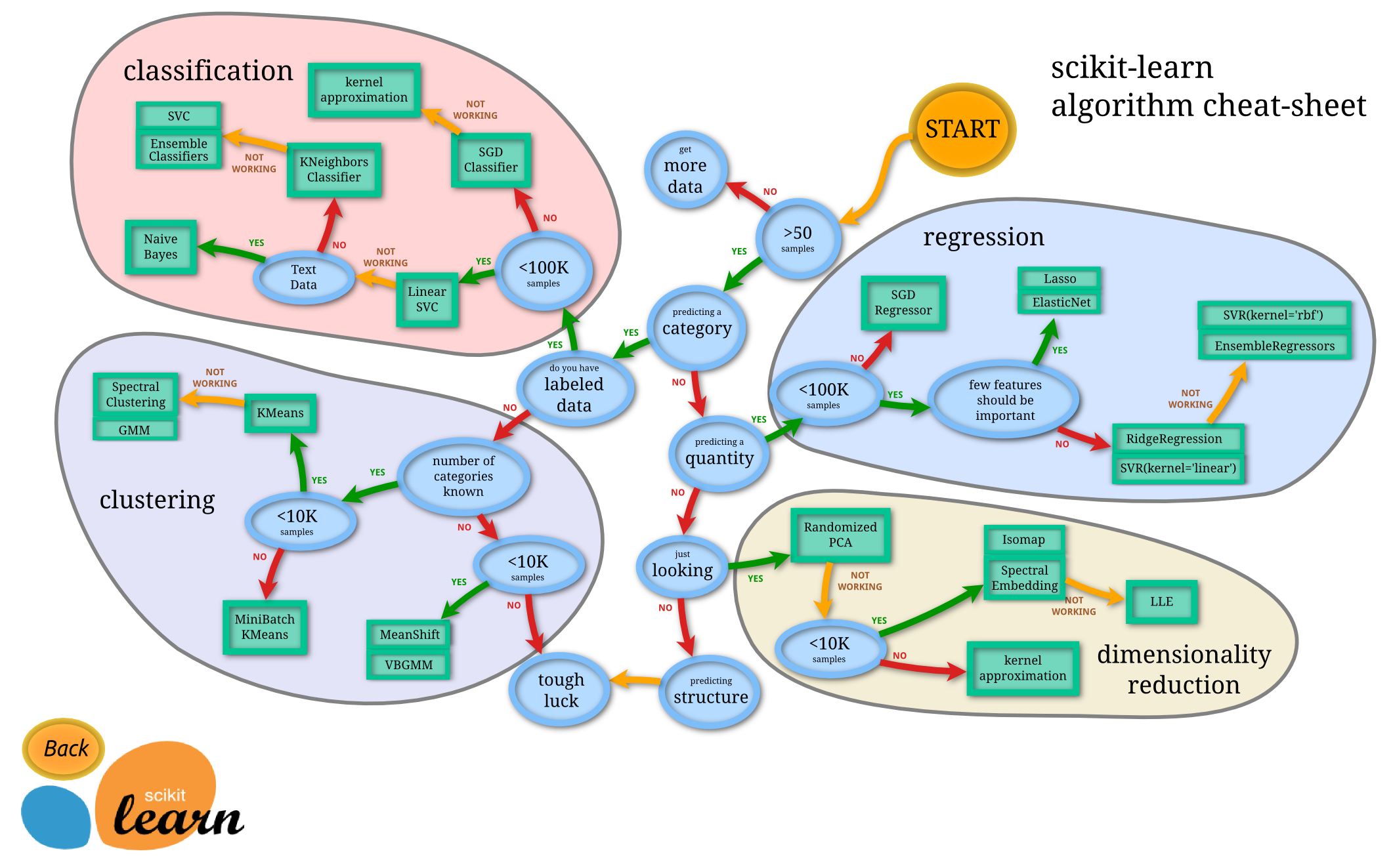\n",
" - [机器学习算法交互体验](https://codepen.io/collection/DPWwaj/2/)\n",
"- 江湖名言\n",
" - 数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已\n",
"## 简介\n",
"- 机器学习流程(参考:[机器学习之 sklearn中的pipeline](http://frankchen.xyz/2018/04/08/pipeline-in-machine-learning/))\n",
"\n",
"- sklearn流程(参考:[机器学习该如何入门](https://blog.csdn.net/u013709270/article/details/76058123))\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NMpsxZs4bkoG",
"colab_type": "text"
},
"source": [
"## datasets包\n",
"- sklearn中自带了各种数据集来满足不同的任务需求,例如使用iris数据进行分类任务。\n",
"- (1)直接导入已有数据集——load_*\n",
"- (2)单独创建数据集——make_*\n",
"- (3)下载数据集——fetch_*"
]
},
{
"cell_type": "code",
"metadata": {
"id": "xSe-D83yRdf1",
"colab_type": "code",
"outputId": "ac717fb4-fee8-49a5-ed60-b8db1981c770",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"from sklearn import datasets as d\n",
"import numpy as np\n",
"\n",
"#datasets.*? #查看datasets下的方法,同dir(datasets)\n",
"#dir(datasets)\n",
"#datasets.load_*? #直接加载数据集\n",
"#datasets.fetch_*? #下载某些数据集\n",
"#datasets.*?\n",
"#datasets.make_*? #创建样本数据集\n",
"#创建回归数据集\n",
"reg_data = d.make_regression() \n",
"reg_data[0].shape,reg_data[1].shape #获取矩阵大小\n",
"#自定义更复杂的数据集\n",
"complex_reg_data = d.make_regression(1000, 10, 5, 2, 1.0)\n",
"complex_reg_data[0].shape,complex_reg_data[1].shape\n",
"#创建一个非均衡数据集\n",
"classification_set = d.make_classification(weights=[0.1])\n",
"np.bincount(classification_set[1])\n",
"#reg_data[0][1:4,1:7] #截取\n",
"#reg_data[0].shape"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"array([10, 90])"
]
},
"metadata": {
"tags": []
},
"execution_count": 5
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "AcFGGG4Xo3Ai",
"colab_type": "text"
},
"source": [
"# 回归"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "A3kfPyL8fhB6",
"colab_type": "text"
},
"source": [
"## boston数据集"
]
},
{
"cell_type": "code",
"metadata": {
"id": "aBTKblJ1RdgB",
"colab_type": "code",
"outputId": "4c5ebb08-b4b4-4009-de4f-8995cb7f9c92",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 316
}
},
"source": [
"#加载boston数据集——数据并非numpy类型,而是bunch类型(含data自变量和target隐变量,继承自dict的设计模式)\n",
"boston = d.load_boston()\n",
"#print(boston.DESCR)\n",
"X, y = boston.data, boston.target\n",
"print len(X),len(y)\n",
"#下载加州房价数据\n",
"#housing = datasets.fetch_california_housing()\n",
"#print(housing.DESCR)\n",
"#创建聚类数据集\n",
"import sklearn.datasets as d\n",
"from matplotlib import pyplot as plt\n",
"import numpy as np\n",
"\n",
"blobs = d.make_blobs(200)\n",
"f = plt.figure(figsize=(8, 4))\n",
"ax = f.add_subplot(111)\n",
"ax.set_title(\"A blob with 3 centers\")\n",
"colors = np.array(['r', 'g', 'b'])\n",
"ax.scatter(blobs[0][:, 0], blobs[0][:, 1], color=colors[blobs[1].astype(int)], alpha=0.75)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"506 506\n"
],
"name": "stdout"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
]
},
"metadata": {
"tags": []
},
"execution_count": 6
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfUAAAEICAYAAABGRG3WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzsnXl8lNX1/99nZpJMVrKQhDUggrsC\nioiCWvflZ6u2Lqi1LnWpVqmt2lZta23dWmvdvyp1q3bR1g2XatW6UhQFBIsoIELYErKRPZnMcn9/\nnDzMJCTsEyA579freeWZ57nPfe4Mvvzcc+6554hzDsMwDMMwdn5823sAhmEYhmFsG0zUDcMwDKOX\nYKJuGIZhGL0EE3XDMAzD6CWYqBuGYRhGL8FE3TAMwzB6CSbqhpFkRORdEbmom3vDRcSJSGAT+vm1\niPxlG4+tREQaRcS/gTZOREZuy/cahpEcTNQNYwtpF+u1IpK2vceypTjnljvnspxzUdjwBGRTEJHJ\nIrJQROpEpEJE/iwiOdtuxJs0hm0++TGMnQUTdcPYAkRkOHAo4IBvbdfB7Fj8F5jonOsHjAACwM3b\nd0ibx6Z4TQxjR8VE3TC2jO8BHwFPAOdtQvtdReRjEakXkWkikt9VIxEZJCIviUiNiHwlIhd3ahIU\nkWdEpEFE5ojI6G76uUlE7ms/TxGRJhG5o/1zuoi0ikh+ovtfRG5BJyr3t7vk70/o8mgRWSwitSLy\ngIhIV+91zq1wzlUlXIoC3bruRWRvEXmz/fuuEZHr26/7ROTnIrJERKpF5B/eb5Yw5vNEZLmIVInI\nDe33jgeuB85s/w7z2q/3E5FHRaRMRFaJyM3ekoOInC8i/xWRu0SkGvi1iIwUkffaPQ5VIvJMd9/B\nMHYkTNQNY8v4HvDX9uM4ESnehPYXAgOBCHBvN+2eBlYCg4DTgFtF5MiE+ycD/wTygb8BL4pIShf9\nvAd8o/38QKAcOKz988HAQudcTeIDzrkbgA+AK9pd8lck3D6pvZ/9gDOA47r7oiIySUTqgAbgO8Dd\n3bTLBt4CXm//viOB/7TfvhI4BTi8/d5a4IFOXUwCdgeOAn4lIns6514HbgWeaf8O3qTnCfR3HwmM\nBY4FEpcZDgK+BoqBW4DfAm8AecAQ4L7uvq9h7EiYqBvGZiIik4BhwD+cc7OBJcDZG3nsKefcfOdc\nE/BL4IzOwWkiMhSYCPzMOdfqnJsLPIJOCDxmO+eedc6FgT8CQWBCF+/7EBglIgWomD8KDBaRLFQo\n39u8b83tzrla59xy4B1gTHcNnXPT293vQ4A7gGXdND0JKHfO3dn+fRucczPb7/0AuME5t9I5FwJ+\nDZzWyTV+k3OuxTk3D5gHdOe1KAZOBK5yzjU55yqAu4DJCc1WO+fuc85FnHMtQBj9Nx7UPrbp3f80\nhrHjYKJuGJvPecAbCW7mv7FxF/yKhPNSIAXo36nNIKDGOdfQqe3grvpxzsWIW/UdaBemWaiAH4aK\n+Ax00rAlol6ecN4MZG3sAefcKtQKf7qbJkPRCVFXDANeaHf31wJfoK78RI/Ipo5pGPp7lyX09zBQ\nlNBmRadnfgoI8LGIfC4iF3bTt2HsUFhAiGFsBiKSjrqf/SLiiUoakCsio9utxq4YmnBeglqCVZ2u\nrwbyRSQ7QdhLgFVd9SMiPtQaXt3NO98DjkTdzZ+0fz4OGA+8380z27psYwDYtZt7K+hoLXe+d6Fz\n7r+db7QHKW6Izt9hBRAC+jvnIpvyjHOuHLi4/X2TgLdE5H3n3FcbebdhbFfMUjeMzeMU1GLcC3VB\njwH2RNeiv7eB574rInuJSAbwG+BZbxuZh3NuBWpN3yYiQRHZD/g+kLg96wAR+Xa7G/oqVKw+6uad\n77WPaYFzrg14F11HXuqcq+zmmTVo1PoWISLniEhJ+/kwdH36P900fwUYKCJXiUiaiGSLyEHt9x4C\nbmnvAxEpFJGTN3EYa4Dh7ZMenHNl6Pr4nSKS0x6Et6uIHL6B73G6iAxp/7gWFf3YJr7fMLYbJuqG\nsXmcBzzevr+73DuA+4FzNrAd6ik0WKscXQef0k27s4DhqPX9AnCjc+6thPvTgDNRoTkX+Hb7+npX\nzADSiVvlC4BWurfSAe5B167Xikh3wXwbYi9ghog0odvbFtJu8Xam3RtxDPBN9HdZDByRMI6XgDdE\npAGduBzUVT9d8M/2v9UiMqf9/HtAKvobrAWeRYMWu+NAYKaINLaP40fOua838f2Gsd0Q57a1t80w\nDMMwjO2BWeqGYRiG0UswUTcMwzCMXoKJumEYhmH0EkzUDcMwDKOXsFPuU+/fv78bPnz49h6GYRiG\nYfQIs2fPrnLOFW6s3U4p6sOHD2fWrFnbexiGYRiG0SOISOmmtDP3u2EYhmH0EkzUDcMwDKOXYKJu\nGIZhGL2EpIq6iOwuInMTjnoRuapTm2+ISF1Cm18lc0yGYRiG0VtJaqCcc24h7XWX22tHr0LzWXfm\nA+fcSckci2EYhpFc2tqguRn69QOR7T2avklPut+PApY45zYpgs8wDMPYOWhrgzvugAkT4NBD4YQT\n4IMPtveo+iY9KeqTgb93c+9gEZknIq+JyN5dNRCRS0RklojMqqzsrmqkYRiG0dPcdhs8/jhkZEBB\nAVRVwRVXwPz523tkfY8eEXURSQW+RbwkYiJzgGHOudHAfcCLXfXhnJvqnBvnnBtXWLjR/feGYRhG\nD1BXB88/D/37Q0qKut2zsyEWgyee2N6j63v0lKV+AjDHObem8w3nXL1zrrH9/F9Aioj076FxGYZh\nGFtBVZUKud/f8Xp6OnxtFeh7nJ4S9bPoxvUuIgNENKRCRMa3j6m6h8ZlGIZhbAWDB0MgoOvqiTQ3\nwwEHbJ8x9WWSniZWRDKBY4BLE679AMA59xBwGnCZiESAFmCyc84le1yGYRjGpjNnDkybBqEQHH88\nHHYY+HwQDOr6+R136Hlamrrks7PhvPO296g3nVAIZs7Uv+PGQV7e9h7RliE7o36OGzfOWe53wzCM\nnuHhh+G++9TNLgLRKJx4Ivz+9/rZOfj3v+HRR2HNGjj4YLj8chg2bHuPfNP49FP44Q+hqUk/i8Av\nfwnf+c72HVciIjLbOTduo+1M1A3DMIzuKCuDY4+F3Fx1s4MGwVVXw2OPwfjxPT+mxYthwQKNtJ8w\nIT6uLaG1FY44AsJh9S6ALiU0NGgA4MiR22bMW8umivpOWaXNMAzD2DZ88AH89a9QUwNHHQWTJ2vy\nGI85c9RyTRROnw8iEXjkEaitVcvcE8RkEo3CDTfAq6+qd8Dng4ED1UMwZMiW9Tlzpq7/5+fHr6Wm\n6rtef12XFnYmTNQNwzD6GFVV8Oyz8M9/qsWbn697zO+9V9fNn3kmLtKZmetnh6uuhmXLoLERPvpI\nRfDOO+Hww5M77mnT4KWXoLBQBR1g9Wr4+c/hL3/Zsj5DIZ0gdIXnjt+ZsIIuhmEYfYjSUjj5ZBXw\nGTOgvh5WrFCRLCrS+y8mZAs5+GDIytLgN1AR/Oor3cI2dKi6wP1++MlP1GpPJv/4h26V8yUoV0EB\nzJsHFRVb1ueBB2p/idH7sZhOZI44YuvGuz0wUTcMw+hD3HWXCnRGhrrUU1NVxErbE3inpsJ//xtv\nn5YGU6eq5V5TAytXqmU7cqRGu4P21dYG06cnd+xtbR0F3UNElwO2hLw8uP56XUOvqNCjuhpOPVUF\nf2fD3O+GYRh9iPffVyGLRFScnVNxb2jQ83AYBg3q+Mzee8N//gOffaZu++ef77gGDfps573qGyMW\n04lCdrZOHjbGN7+pW+cSlwTq6jTKfuDAzXt3ImecAWPHwmuvQUsLfOMbGgC4MxalMVE3DMPoQ+Tk\naMS3369i3tKi6V19Pg0Y8/vhzDPXfy4QgP33V1f8yy/rpMALnguH9fmDD970cbz1Ftx6K1RW6jsn\nT1YXfmpq989Mngxvvw1z52ogm8+n47n99q0X4FGj9NjZMVE3DMPoQ3z3u3DTTbB2rVrXsVi8XGpa\nmgrk7rt3//xuu8HFF8Of/qTCCirK116r5489ptb3hAlwyCFdu8s//RR+/GNdH+/fXycFTz6pf3/5\ny+7fnZ6uhWOmT1dhHzgQjjtOt9sZiu1TNwzD6EOsWqUWd0ODirFzau3266fW89Chm9bP55/DO++o\nhTxhggbP3XabCjPo9cMPh3vuWX8f+RVX6DJAQUH8WiSiQXvTp/fM9ridjU3dp26BcoZhGH2IGTPU\nOh47Vq3u/faDPfdU4Z0xY9P72XtvtdjLyuCCC+DCCzUpjHMaRd+/P7z7LrzxxvrPlpaq1Q3avrZW\nt6bV1MCXX26Tr9lnMVE3DMPoQ8RiKqSpqbq+nhigFottXl833qjbzAKBeIKa0lJ17YvoWv0rr6z/\n3Lhxugc8FoNFi/QoK9P98xdfvHmTC6MjJuqGYRh9iIkT16+qFg6rK37SpE3rY/lyDVq75x515y9b\nFt/b7fOpQINe8yzyRC68UF3+S5fG97ZHIjrRKC+Hyy7b8i1qfR0TdcMwjD7EkCHw05/q+vWaNXrU\n12ug26asp4dC6m7/7DMV8JQUnSCEw/Eo+LY2FeVYDL797fX7GDpUs9YVFOhEwHsuFtMsdQsX6t54\nY/Ox6HfDMIw+xne/C4ceqmveoPuyN7Wi2vTpmqCluFgT0TQ3x136kYhGxPfrpxb4RRdpBHxXDBum\nAXtffRXP4+7zqcjHYhpdf8klW1espS9iP5dhGEYfZNiwLat3XlWlotvSoiIeicTLr0YiKva33QZH\nHw2DB3ffz5w5WkzGy68ei6mFn5amLvtoVNPX7rLLln2/voq53w3DMIxNZs894+vmIro27u1FDwZ1\nXfzb396woDune+UzM/V5j1hMxXzECJ0g5OQk97v0RkzUDcMwjE1m33210ElNjX4OheLZ3UAD3X70\nI5g1C845J75lbq+94KCDVMxLS9Xt3q+f5pBPS9MjGFTB/9//1MU/eXJ8icDYNCz5jGEYhrFZhMNq\njb/7rrrhU1P1cE4FvrhYRT4jQ0W+vl6fKynRKPvhwzVqPidH18wrKtTV3tKizw8YALvuqulsQyGN\nsn/7bU2Ok5UFZ58N557bt9bbLfmMYRiGscWEQlqC9ayz4Hvfg3//O153PCVFC6v076/nnqBHIirI\nNTW6Vp6Son/T0vS8vFwT06xYAaNHa7tYTK/tuae680eO1DS1gYAKeDSq73/+eZ0o1Nfru3/1q+37\n++yoJF3URWSZiPxPROaKyHrmtSj3ishXIvKZiOyf7DEZhmEY3dPaCqefru7zF17Q7Wcnn6zVzLz9\n43vsoVvjUlPjqWGHDNEjFNL18tZWFXsRtdCj0fgxZgwce6wKe22tVlsrLFx/Lb6lRe8VFem7MjK0\n3csva/S90ZGecl4c4Zyr6ubeCcCo9uMg4MH2v4ZhGMZ2YNo0zeseiaiFHQioEL/yCjz3nLrXr7lG\n95OHQlrKdY891JJuatLo9dRUtdC9yHjnVNi96nC77aZV2crK1IIfOBBOOkn7S8xyV1+vE4REfD7t\n5+uvdRJhxNkR3O8nA0865SMgV0S2ojKuYRiGsaU4B7//vYpzJKKWcmNj/P5dd6n4zp+vn30+LZ86\nb56mhw0E9HmfT/tKT1ehDofVNb9mjd5LS9PrAwdqHvoBA2DKFLXK16zRHPAff6zvbmhQAffG4a3d\nbyjCvq/SE5a6A94QEQc87JzrnCdoMLAi4fPK9mtliY1E5BLgEoCSkpLkjdYwDKMP4ZyK5yefqMXt\nnFZg86xrT5y9uutffqkC7a2jp6XFs8HddBOccILe2203XftubNSodhEV57Y2dZ9fc41WY3v4YS0O\nAxr8Fg7rvbY27dMrDRsK6R75YcO0r0mTNJjO6EhPiPok59wqESkC3hSRL51z729uJ+2Tgamg0e/b\nepCGYRh9hUgEPvpILewHH1RRD4dVfL1IdQ8vp7sn8J7V7eWOF1ERb2tTN3lqql4/9FA9olF1lc+e\nrclucnN1cgBqlf/whxrV7hWFmT1b08i2tcWruUUi+s5oVPPM//jHcP31HcfpHLz3nq61i8A3vwmH\nHabnfYmki7pzblX73woReQEYDySK+iogMePwkPZrhmEYxjamtBS+/33dRrZ6NVRXq8impamgRyIq\n3sGgBrpBPNht7Fj48MN4FLx3LxRSMS8p6fjZW/uGeLU2T9BB96nX1Kjr/oAD9Nqnn+rzX3+tE4pQ\nKP7+nBz1Jpx5Zsd1due0Ytxzz8Xf9/rr2u6Xv0zO77ijktQ1dRHJFJFs7xw4FpjfqdlLwPfao+An\nAHXOuTIMwzCMbYpz6tquqFBxrK9XsYxG4/nbQc8DAbWSvXzsBQUaDLehvhct0vX2Aw6Agw+Ghx7S\nvkHFu7lZ35k4KRDpWDEuPV0nHp7bP7FtJKKBdZ9/3vHdCxbolrf+/XWcBQWQn69lYRct2rrfbGcj\n2ZZ6MfCCqP8jAPzNOfe6iPwAwDn3EPAv4ETgK6AZuCDJYzIMw+iTrFqlEev5+bpGDnH3dHNzx7Ze\nTnaPlBT429+6r7melgY/+IEGvBUWqlDfe6++p7BQLfXVqzUILiVF96J7NdhHj47346WN7Vwe1hP4\njAx49lndP+8xe3bHrHYQ30I3a5au7/cUzmnAYGZmxyj+niKpou6c+xoY3cX1hxLOHfDDZI7DMAyj\nr+OcCqonyqmpKnyRSNwa9oTQa++5yjMydP3bmwh0JrGgS3a2XktL08nD1KkqtsXFKtI1NerWnz9f\nA93uvFOv/+lP8MYbWtI1L2/9SQaoFT9ypFryiWRnx93uifj9PZs//p134JZb4hOXyZN1/T9xySHZ\n9KEke4ZhGH2Tzz+HG27QfOvLlqno7L67JnRZuTIu6p6gB4O6lg1qZdfWdi2aHiJ65Od3vJ6SolZr\nv34q8rvuqu+srdX+b7sNJk6E007TcXkTgpoaGDRI+/QmHT4f7LOPPrvffh3fc8QRKviNjXFLv6FB\nrx1++Nb8cpvO3Lm6JS8Y1GWAcBieeEK/Z0+u6+8I+9QNwzCMJFFZCRdcoNZt//4q5o2NahEHgx3z\np4voteJiteT794+vqXtHV/nWMzK0slrnSPNQSJ/3LFUv2K2kRNe98/LULb98ub4zI0O3rGVk6Np5\nfr6Keiymz9TW6vmPftTxPbm5GsUfDOokYu1a7ePhh+MThWTz+OPxqnWg37mgQJcKGhp6Zgxglrph\nGEav5pVX1JVdWKifc3Jg//1VSPfZR4V37Vq10lNSVDSrqzsmiAG9HwjEt7hBPJgtOxv+7//UUq2q\nUsu8tVXd9eeeC6++Gl/zFtF73lr6iy929AKkpOi+9WXLYNQomDBBLfe1azU//JQpOv7OjBun7u/5\n8/Ude+/dswVfli5Vz0Ai3vtranpucmGibhiG0QtwTq1ykbiAg4p3Zws6NTWeaKZfP22/cGE8MC0a\nhRNP1L8zZ6orOTtbreiFC7WNiIr+oEHa3xdfwF//qhXVZs/W65deCkcdpYltPvpI+0tPVw/AxRdr\nidWBA+Nuf49AQK30e+7ZcMR9ZwIBzSm/PTjgAPjnP9VD4OGlvB0woOfGYaJuGIaxk7NkCfzsZyq4\nzqkFfOutKsL7769ik4i3fa2kBBYvVpfx6NFqDXtJXkR0r3j//mpZ+/0aER8IqMU9aJCKVUqKWvZL\nl8JFF6kbPJFbblFX+ogR6vZvbNQo/Cee0Gj6lBR9X329ThycU2t/zBhdKthZuPBC+Ne/dGKVkxMv\nG/uLX/RsFLytqRuGYezENDXB+eerOBcUqAj/73+6jh4KwTHHaIDamjUqvosWqYt6n320ChuohR4I\nqMWenq7C+sUX2l9hIey7r14fPVot6P3206xv3lp5LNZxW5pHba3uFS8s1GPQIBU7zwXvBdZ5766u\nVlf1kUfC/ffvXNnghg7V73rSSfE0uffe23HrXU9glrphGMZOzDvvqHj27x+/VlCg1u706er+fuop\nrYj2zDMqlHl5msXtwQfh6qvh7rvVgnZOxbW1VfvzRNUTXdAJxIsvqpD7/WphDxkC/+//rT+21as1\n0K2iQv96kex+f3zLWna2Tip+8hOdLKSn65LAzsiwYXD77dt3DCbqhmEYOzEVFfF65olEIuoKBnWX\nz5mjFrfnCnZO18tPPx3efVdFPisLhg/XbWC+Tn7cQECjuH/zG9hrL3WdNzXB2WfDccdpoFxFhRZa\nOf54fc8XX6gL34uc9yLZU1PXT/Pa0tKza8+9FRN1wzCMnZi99lI3eFubiqzPF0/Gstde2mb+fBXT\nxLVdb3vaW29pZTVvP7dzmuBl+fKOFnN9vVrjgQB897t6ALz9tuaSj0T03muvqeDfd5+u63tudb9f\n39nUpOMtLtYxrVqlSwN33aWW/fnnrx9Fbmw6JuqGYRg7MePH69r0zJnxLWYicPLJapmDWsVecFzi\nOnU0qq74RETg179Woa6sVKGORFSEL7mkY9twWJPaBIPxqG/ndBLxwAP63IgReq+8XMcQDOrR0KCJ\nb1padK29pUUnAh99pHu+O3sKjE3DRN0wDGMnZsECXT8vKdEgMxEV8ZUr43vL99lH171XrVIRF9Eg\nOhE49dT1+xwzBqZN06j5pUt1D/jJJ6+/1v3VV7o2nphJzktgM2tW/PPAgXqAWuWHHaaC//LL6hXw\n9nCnp+sywSefwEEHbfvfqi9gom4YhrET89JL+nfwYD08amq0jOmBB6qwPvig1jNfuFDFPiNDXeh3\n3qlb2Q4+WCcGmZlwyCE6CTj+eH3uscfUzX7ZZSq2K1fqGnxLi/bV2QPgWeh1dWqRe6IdDqsFfvnl\n+vyMGR2Tsnjr7gsXmqhvKSbqhmEYOzHeOnpXeNngQC1uL32qz6die999GhjX2qpr4SkpujUrNVXd\n7489Fi/SMneuXps4UcXYE/HKShXrgQP1mrfP/ayzNMHMD36gEwwvv/zVV2uU+5o1XWd8CwQsYG5r\nMFE3DMPYiTnmGHWVx2JxcffSsHrZ1SKReBKU/HwV3rIyfaalRc/T0uJbzjIydF29qCgusGlpGsj2\n179qQhsvtWs0qoFwXtU357Qy2SGH6P2334YPP9T3jBunfYK64AsLNWLec9/X1Oj9nirC0hsxUTcM\nw9iJOewwOPZYLVuaWEL1llvixUWWLNF96F5QnFdC1e9XUY3F4pni6upUyJub16+d3tiowp9IYaH2\n87vfqUW/994dg++CQa2i1pm0NPjzn3XyMHOmjn38eN0ytz3qkPcWTNQNwzB2Ynw++MMfNGr83Xc1\nRemJJ+qatkdmZse175QUPU+smQ4dt72lpHR034MKut/fsQCLtwd92LD4FrpNZcgQeOSReBWznip6\n0psxUTcMw9jJ8fnU3e25vDszZIiuY3/2mWabS09Xoa+v17Xw0lJ1yYuo+zsc1naBgFr16em6Dz41\nVSPgEwPjGht1IrHbbls+fhPzbYftBDQMw+gD3Hmnbh/zypgWFWmEuc+na9rOqZA3NKgL/he/UJd6\nIKBb5tra4LTTVNg//FC3nS1Zoh6AO+7o2TKnRvfYP4NhGEYfYMAAeP553ddeU6Nr3/n5GuTW2Kii\n/f77Ku7f+IZOAED3p9fW6jazSy7RZ3Jz9blIRKPbJ0zYrl/NSECcF1mxEzFu3Dg3y8tsYBiGYSSd\n731Pq7/l5savtbTo2vt771kGuGQjIrOdc+M21i5p/wwiMlRE3hGRBSLyuYj8qIs23xCROhGZ2378\nKlnjMQzDMLacRYs6FmEBXWtfu1b3yhs7Bsl0v0eAq51zc0QkG5gtIm865xZ0aveBc+6kJI7DMAzD\n2Ep2312zwCVuV2tpUXd8Z7E3th9Js9Sdc2XOuTnt5w3AF8DgDT9lGIZh7IhceaUGxdXV6da3piaN\nnp8yxVzvOxI98k8hIsOBscDMLm4fLCLzROQ1Edl7A31cIiKzRGRWpVck2DAMw+gRxo2DqVNh1101\n0C4/X6Pjv/Od7T0yI5GkB8qJSBbwHnCLc+75TvdygJhzrlFETgTucc6N2lifFihnGIax4xKLxZPS\nGNuG7R4o1z6IFOA54K+dBR3AOVfvnGtsP/8XkCIi/ZM5JsMwDCM5lJfDVVfB6NGad/4Xv9DtcEbP\nkbRAORER4FHgC+fcH7tpMwBY45xzIjIenWRUJ2tMhmEYRnJobYVzz9XiMF4ymxde0P3tzzxj6+49\nRTKj3ycC5wL/E5G57deuB0oAnHMPAacBl4lIBGgBJrudceO8YRhGH+ftt9VSLyyMXyssVFH/5BOr\nj95TJE3UnXPTgQ2uqDjn7gfuT9YYDMMwjJ7h6681Oj4REbXYV6wwUe8pzCFiGIZhbDW77daxehvE\nS8EmVowzkouJumEYhrHVHH64ll+tqNAqb6GQno8ZA2PHbu/R9R1M1A3DMIytJi0N/vxnOP10LQ7j\nHJx/Pjz0kG1t60msoIthGIZh7ODsEPvUDcMwDMPoOUzUDcMwDKOXYKJuGIZhGL0EE3XDMAzD6CWY\nqBuGYRhGL8FE3TAMwzB6CSbqhmEYhtFLMFE3DMMwjF6CibphGIZh9BJM1A3DMAyjl2CibhiGYRi9\nBBN1wzAMw+glmKgbhmEYRi/BRN0wDMMwegkm6oZhGIbRS0i6qIvI8SKyUES+EpGfd3E/TUSeab8/\nU0SGJ3tMhmEYhtEbSaqoi4gfeAA4AdgLOEtE9urU7PvAWufcSOAu4HfJHJNhGIZh9FaSbamPB75y\nzn3tnGsDngZO7tTmZODP7efPAkeJiCR5XIZhGIbR60i2qA8GViR8Xtl+rcs2zrkIUAcUJHlchmEY\nhtHr2GkC5UTkEhGZJSKzKisrt/dwDMMwDGOHI9mivgoYmvB5SPu1LtuISADoB1R37sg5N9U5N845\nN66wsDBJwzUMwzCMnZdki/onwCgR2UVEUoHJwEud2rwEnNd+fhrwtnPOJXlchmEYhtHrCCSzc+dc\nRESuAP4N+IHHnHOfi8hvgFnOuZeAR4GnROQroAYVfsMwDMMwNpOkijqAc+5fwL86XftVwnkrcHqy\nx2EYhmEYvZ2dJlDOMAzDMIwNY6JuGIZhGL0EE3XDMAzD6CWYqBuGYRhGL8FE3TAMwzB6CSbqhmEY\nhtFLMFE3DMMwjF6CibphGIZ4RqqqAAAgAElEQVRh9BJM1A3DMAyjl2CibhiGYRi9BBN1wzAMw+gl\nmKgbhmEYRi/BRN0wDMMwegkm6oZhGIbRSzBRNwzDMIxegom6YRiGYfQSTNSNnqehAaqqwLntPRLD\nMIxehYm60XPU1cGPfwyHHAJHHAHf/CZ8+un2HpVhGEavwUTd6BmcgylT4I03IC8PCgpg9Wq46CJY\nuXJ7j84wDKNXYKJu9AxffQVz5kBhIfj9IAL9+kEoBC+8oG0qKmDqVLj+enjuOWhu3r5jNgzD2MkI\nJKNTEbkD+CbQBiwBLnDO1XbRbhnQAESBiHNuXDLGY2xjnIOyMvD5YMCADbf94gu4/354/321yAMB\nyM2N3w8EYNkymD8fLrhAhdzvh5degkcfhb/+VS17wzAMY6Mky1J/E9jHObcfsAi4bgNtj3DOjTFB\n30n48ks49VQ47jg45hg480woLe2+7TnnwAcfQDAIra2wcKEGyXlEInDggfCrX+l5UZG65gsLVewf\nfbRHvpZhGEZvICmi7px7wzkXaf/4ETAkGe8xepiGBrjwQhXbggI9vvhCLexQaP32//d/EA5ru6ws\nGDhQrfxly6ClBdasgSFDYOJEWLRI3fGJ5OTA66/3xDczDMPoFfTEmvqFwGvd3HPAGyIyW0Qu2VAn\nInKJiMwSkVmVlZXbfJB9mmhUj43xn/9Afb26w0X0KChQy/u//12//bx5kJ0d/1xSArvuqm77jAyd\nIPztb5Cfr9disfXHlZkZ/1xRAT//OYwdC+PHw+9+B01NW/adDcMweiFbvKYuIm8BXS2o3uCcm9be\n5gYgAvy1m24mOedWiUgR8KaIfOmce7+rhs65qcBUgHHjxtkG521BdbUK42uvqQV9zDFw3XXqAu+K\nioquxT8a1b46M3w4fPYZpKXpZy84Lj0d/v1vSEmJtz3qKI2MLyzUdrGYCvY55+j95mY9X71aJwGx\nGPz5z+opePxxfcYwDKOPs8Wi7pw7ekP3ReR84CTgKOe6zjLinFvV/rdCRF4AxgNdirqxBTgHH32k\nkeQNDXDCCXDiiZCaquvXF1wAX3+tIgkqqgsWaJCaJ8SJ7LuvBrY5FxfRWEyt7L32Wr/9pZfCJZeo\nOGdmqou+thauvLKjoAPceKO64+fP1/6iUTj9dPjOd/T+W29BeXnHCUdREcyeDf/7H+y339b/XoZh\nGDs5yYp+Px74KXC4c67LfUkikgn4nHMN7efHAr9Jxnj6LA8/rJHnPp9GlE+froI9dSp8+KGubRcW\nxtsXFWlU+3vvwbHHrt/fQQfpMWOGus+d07Xx44/vWtQPOUTF+rrrdLKQkqIifdFF67fNzdVI9wUL\nVNx3203X2z0WLVrfPe8tASxbZqJuGIZBkkQduB9IQ13qAB85534gIoOAR5xzJwLFwAvt9wPA35xz\nFhW1raisVEF3Ti3kjAzo3x8+/hjefVfvd+VKb2vrPhmMzwcPPADPPgsvvqhW+2mnwcknq7hGIuoR\nyM7We83N6hpPSYE999SxzJgBN90EN9+8fv8isPfeenRm5Eh9fyLO6VFSstk/j2EYRm8kKaLunBvZ\nzfXVwInt518Do5PxfgMNalu2TM89d3lGhlrm06erde3zdXSlO6cCPGJE9/2mpenatrfW7T33t7/B\nffdBY6NGul9xhbZdvrzjXvbMTJg2Td3yiWIcDsOSJTqWUaPWF/Bjj9X+16yJr6mvXatBc6PtPyPD\nMAywjHK9l6efVss5JUXX0AMBXduuqdGI9fHjYZ99NPgtFFILvaJCBXXSpM1714svwi236Hn//vr3\n1lt1DJ3F2efTY/Fi/fz555oDPjcX9t8fjjxSBfzzzzs+l5EBf/mL3lu7Vr0AZ50FDz1kQXKGYRjt\nSDcxbDs048aNc7Nmzdrew9hxaW7WhC6rV6sFHAio8IXDev/zz2HYMHWVP/iginIspuJ6xRXr7xff\nGMceqwFwidvPmprUavf5Oq7bO6eR8k8/rW76k0/W9XIRXfePRPT6LrvAm2+q1d8Z779ZE3PDMPoI\nIjJ7U5K0JWtN3dieeAFku+2mLu3W1vi9UaNU0EHF86c/1WNrWLUqbqF7pKdrVbbsbLWsc3N14lBd\nrWOYPl2j8letigfARaMq7A0N+uy778JJJ+m9hgaYNUsnCePHa/+GYRhGB8z93htJT4fDD1dreZ99\nNPBsjz00mvySDeT48YLkNreQyt57q+gm0tCgEemPP64iXlWl1vx+++lE47bbVNirqnTS0damR3Oz\nRtSXlmoUvnO6p/0b34CrrtJKb4cfrtH7hmEYRgdM1HsrN96ogWg1NeoGb2nRgLLvfrdju2hUc7Nf\neKGK8/HHa9rWP/xBXeEeTU1w111w6KG65v6732l2OYCrr9a2NTW6Pl9To5/POw+eeAKWLlWX/kUX\n6b74FStUzMPhuCsd4tHszunzzz+vkfI/+5nGBeTnx/fUX3ll/P2GYRgGYGvqvZtIRKujPfqouq7T\n0tQdfu21cMopaiFfeqlaxGVl6vpOSdHtYy0tcNllKp7OwbnnaunUfv3UtV9bq9vUnnlG1+w//VTX\n5xcuVLf/uefCL3+p7vbcXJ08VFRoAhlQkfYs867IzlarvrRUg+QGDep4v6oKbr8d/t//S+5vaBiG\nsQNga+qGiu2cOSq4hYUq2M3N8JOfaA3z6mrN4NbYGI+QD4d1G9puu8GTT6qwz5mjedyLiuLBaUVF\nGuA2fbq6xseO1aQ2Hk8+qf17QXIpKRp1v3SpijTEI+ETk8oEAjq56N8/nnWuq2Ix3v57wzAMYx0m\n6skiFFLL9e9/VyE97DANSPOC1HpqDF7BFE8gq6o0Kn7aNBVTzwWemBa2tlbFPi0NvvpKXeZeopqy\nMrW2IxEV4BkzVNQ7M3++PlNbq/2kp2t0vJekJiVFxdsL6vP74xOLaFRFvbZWvQk+n/6G3mQgHNZn\nxo9P6s9nGIaxs2Ginix+/nMN8MrN1apm778Pc+dqmtaCguS+e/lyuPdeePtttaZLSqC4WF3q5eUq\nniIqts6pcIbDcfEE/RyL6br40Udr0pdVq3Si4Ilva6u69gcMUJf9hAl6r7UVPvlErfJA+39iubma\n1CYvT9fnve11KSkq4jk5er2tTSc+q1frBCQ1VWuxf/aZfofMTB3nlCkd08gahmEYJupJobRUC5AU\nFsaTr/Tvr6lZX3wRvv/95L27okKTstTWqpCKqKXd0hK3dKNRFdfMTB2r368C7rmzPbd4SYkWS5k9\nW+978RfOxa3sVavghhv0uxYUqMg//7xeT03V5/z+ePDcKafo2ObOVWHPyFBX/3e+A6+8omlsa2t1\nG1z//rpfPRDQSUVdncYAfOtbXaeSNQzD6OOYqCeD5ctVyDpnUwsEtFRod1RUaFKW2bPV8j3nnA2n\nbO2Kf/xDxa+oSK3etDS1gEtLNcgtEtFrgwap6NbXq0Wck6PC6/OpmA4apGlmW1tVvL31dtB+c3L0\nr2eJFxSoEF91lbroCwvV7V9aqu8QUav83nvV8v74Y+2/pEQnGVOmaH/p6fo7eOvsDQ36ub5er730\nkkboG4ZhGOthop4MPKHyypJ6RCJdVzMD3R8+ebIKYzCowWnPPw9/+hOMG6d7u//wB/jvf1Wczz1X\nt6EFOv0TzpsXt5C/+CJezKW1Va11Ea1zHgxq+4EDNdJ8yhS48051caem6kSgqSlunScWfxHR4Drn\n9Pvl5ur13FwV6lAo3s8ee+hYYjGdbHjeggkT9IhE4IgjVPAzMjTbXTis76uqUgvd71exD4fV23HG\nGXD33XDccet/f8MwjD6M7VNPBsOG6Tp0ZaUKXDSq57m5mha1Kx54QAW9qEit4P79VTx/+1u1fM85\nRwU9N1eF8O679V5nRo1Si7e2tuP6dzCoudWHDFExrqnRw++HRx6Ji2x5uYpnJBIXcs8dn1j4xTu8\nwiqhUDzo7cADtW8Pn0/bHHmkfp4xQ4V5zBit715WpksB3ru9CYc3MYpG40JfVqb73C+9VLezdVdR\nzjAMow9iZk6yuP12XQ/++99V0I44Aq65pvsguenT18+5npOj0edPPaVu6KIive7tJ3/+efjhD+PX\nQdfT//EPFUhPdCMRfW9amh7XXafiH4vpGKdM0TrmzqkF/sUX2mfnHAYiHdfVPVpb49XY8vO1rOq5\n5+pExtuylp+v3/+DD9Qj4ZV+9SYKmZk6EfH7498vEtH73nq+58L3lgPKyrTPp5/e8n8nwzCMXoSJ\nerJIS1OxnDJl09rn5alIJW4ti0TU0l64sON1UOELBNRqTRT1oUM1NeuUKWoR+/0qtp6F7vPpev2B\nB2r7667TYLjCQhXLggIdx4EHaiT8qlXxyUEiWVnqEYhE9H55ubrc//AHde+//LKuf3/5pbrgv/Wt\nuKeirCxu1XuC/eWX+u5QSMcYCGg/y5Zpu6wsXT5wTicDXrDe/PkaKd85OY1hGEYfxER9R+GCCzSK\nPBhUQYvF1IX93e/qevJHH3Vs71ngQ4eu39e+++p2ulNP1W1l+fnadu1aTRXrCXokAq++qvc9i9nL\n/Pbcc/HofefUks7OVpH3RNfv1/ahkIruAw/AAQdov0uW6A6Azz9XL0B9vUa5/+9/+h4v1sCrzNbW\npmvqNTX63QYN0snK2rXx/fTRqAo76Hp7dbX2U15uom4YhoGtqe84nHIK/OAH6mZfu1bF7aSTNK/6\n5MkqmtXV8a1nlZVq9SZa6Ymkpqrb/owztH0kAt/7nmZ98wTcW69ODOYrK9P2fr+65ktK9BzUm5CT\nExdzz4LPyNCAuzVr4NvfVtf+YYdplTW/X/fLX3ONFpPpnO8d4u9/+GFNYbv77jqJqKvTYMCHHtKU\ntN5YMzPje+1jMa2zbhiGYVju9x2OujrdBjZgQEfBXrQIfv97rU6Wk6MW/CWXxDPFbSkXX6xeAK90\n6ty5ukZeXKyiDiryq1fDn/+sonz++WoxR6PqUk9PV49Bebla8KtXx6u2eZa+F2zX0BDfFZA4uQgG\n1ZoPBPR9q1apB8GLrG9t1QDE+vqOVv7IkTphmTVLhd4wDKMXYrnfd1b69dNCJp3ZbTeNUvcCxrYV\nv/iFBrVVVcWro6WldczWFgio6/3AA1XAr71Wx+KJ6+DBOgkpL9fxL1kSX0JobtZnReLZ4pYu7bjd\nz+fT5Qdve1pa2vr784NBFXAvdaxXtS0QUA/GTjg5NQzD2NaYqO9sbCtBb22Fd95Rr8C118YT1JSX\nw2uvxV3u3va3o4+O7zH/0Y90SWD+fLWkx46FE06I3w8GVcw7b4ELBNSib2mJb6dLTdUlgptv3viE\n5VvfUm/B0KHxdlVVWg62cyChYRhGHyRpoi4ivwYuBirbL13vnPtXF+2OB+4B/MAjzrnbkzWmPkVV\nlQr10KHrZ7YrK9P19cTCLCNGqGBmZWn7N96IC+cee2gZ1USKi/Xw2GcffSY9XS33hQvjz3t12UtK\n9Fpeni4lHHSQlm594QWt0T58uL5nwoSuv9Nll8HMmbB4cXzchYXqbTAMwzCSbqnf5Zz7Q3c3RcQP\nPAAcA6wEPhGRl5xzC5I8rs2isqmSZbXLGJg9kCE5O3gRkepquP56TVTjpXy9+WY45JB4m1tvjady\n9Vi8WKPXb7hBM8stXqx75AcM0CQx3VnQzul69rBh6l6vqlIrPRLR9ffUVG2Tn6/jqarSDHlnnKHj\n+Oc/9V5Ojk4yLr1UhX6PPdZ/V06O7sF//30d35AhmtAmPX3b/oaGYRg7KUkLlGu31Bs3IuoHA792\nzh3X/vk6AOfcbRvqu6cC5WIuxu3Tb+fp+U/jFz8RF+HIXY7k9qNuJz1lBxQS5zTz3Gef6Z5vn0+T\nyUQiag0PH67nY8aokHoudlBBjsU0EG9Tqa/XYL3PP9d3t7XpdriWFhXagQN1MhAMwtln6/UJEzQR\nT2OjRsh7RWdCIbW86+o06v+2Df4nYBiG0afYUQLlrhCR7wGzgKudc2s73R8MrEj4vBI4qKuOROQS\n4BKAkpKSJAx1fZ6e/zR/+ewv9M/oj9/nJ+ZivLnkTYoyirjhsBt6ZAybxeLFus7tpZgFdadXVqpF\nfO21eq2zOx7iyVw2hz/+sWPiGi+z3KBBOoHwqKzUYLlrrolfq6iIV29bvjye3CYrS133m0Nzs26b\nW7VKt8NNmmQ54Q3D6JNs1T51EXlLROZ3cZwMPAjsCowByoA7t+ZdzrmpzrlxzrlxhYlu4yTy5Lwn\nyUrNwu9TsfOJj/z0fJ774jkisUiPjCGR5nAzzy14juv/cz1/mv0nKpoqOjaoqoqXRE0kEFDB886P\nP17d9B7OaVT5qadu+mCc0zKyeXnr3hdqbaQhTWirqezYNhDQBDSJDBmiYvz11/H0r4GAjqOqatPH\nsWKF5oC/7jrNh3/lleoV8LbUGYZh9CG2ypxxzh29Ke1E5E/AK13cWgUkpkQb0n5th6A+VE+Kv+M+\n8IAvQCgaoi3aRsDXc9bg2pa1nP382ayoW4FPfMRcjKlzpvLEyU+wd1F7bfHdd48XPamqUld7Xp5G\nhh98cLyzn/1M971//XU8ocsBB2gg2oaortYMdKWluu0uEgGfj5hzLK1dSnVTJYGsEMEIPDFiCTcv\nGkLq2noV6ry8jtHtGRlq0ZeWxq30SETFvbJSE/Dk5W38h/n1r/W7evvsnVNvxaOPahlYwzCMPkQy\no98HOufK2j+eCszvotknwCgR2QUV88nA2cka0+Zy2LDDeGXRKxRmxj0Dta217FO4DxkpGT06lkfm\nPEJpbSnFWfGI87Uta/nVO7/i2TOeRby87cOGaRS6V8999Wp1aR96aLyzggJNAztzplY5GzFCRX1D\n28kWLYLzzlMLWESD2ZqbIRqlLDNKVXMVqYFUctvCTC+BV/qtYSjlXLlYdBzPPKOW+A03xN+Tl6cR\n8WvX6np8QYFGzjc3b5qoNzfrd0gskiOiAXUvvWSibhhGnyOZpubvRWQM4IBlwKUAIjII3bp2onMu\nIiJXAP9Gt7Q95pz7PIlj2iyuHH8lM1bMoLKpkhR/CuFomGAgyC8O6/ktVP9e8m9y0nI6XMsN5rKw\neiFljWV8XvE5zdVljCtfzODddotXQRs0SAX+9dc15aqH398xIn5j3Hijimji0seqVRCN0lq2kkIH\n+MJUDMjm2WP7kVu1nL/u6bhy6SDdVpeSotXUjjwy/t6JE3X9fJ994n22tqoVP2QTdhlsKCJ/c+MD\nDMMwegFJE3Xn3LndXF8NnJjw+V/AevvXe4JILMK88nmEoiFGF48mMzWzw/3BOYN54cwXeHbBs8xb\nM4+R+SM5Y+8ztsu2toyUDOpCdR2uxVyMUCTEyX8/mVA0hGtuQg5dzWXlQ7msbM94w9pa+PTTLX95\nfb0GxHkubo+CAkhN5c592hhV66d8QCaf7plHuKWRlIYKqtPBjRqJ0C6+IprYxhP1c89Vi7qiQvO5\nh0Lqir/55k1L+ZqeDocfDu+9F59sOKcTmgkT1AuxKZMDwzCMXkKfDRH+supLLn/1cqpbqhEEv/i5\n6YibOGm3kzq0K8go4NJxl26nUcY5Z99zuOm9m8hIycAnPpxzVDdX0xxupl+wHwUZBeDLJNJWzgOD\nVzGhIYexjdn6cDi8ftrVrmhuVss5L69j9HogEK+LnmgBR6MqxieeyGOlH9A/s90N3gJrU6JMqsuP\nCzrEc8B7FBXBs8/Ck0/qvvpBg9TF71WR2xRuvFFz0a9cqS78srJ4EZm334bTT9fkNF1F/BuGYfQy\n+qSoh6NhLn3lUupD9eSn5wPQGmnlhv/cwF6FezEibxMEsIc5ba/TWFC5gOe/eB6f+KgL1amlHg3h\naM81EAwS6JcLzVW8nFfJ2IYs3fcdDKq4bYinnyZ2x++JRcL4YyBjx8Jdd6k1npGhlu+bb2oymmBQ\nBb6xEa68kmsOmcin5Z/Glyl8bWSRwrULC+L7K6JR/Xtiu5OmvFy34BUXa+33q6/esh+mqEit/Q8/\nhN/8RicwQ4aoiEej6vLfbz+tgmcYhtHL6ZPmyyerP6G2pZbcYO66a8FAkIiL8MqiroL0t55wNExl\nU+UWb4Xz+9ST8PLZLzM4ZzABX4BUXyqNbY18WfUlq+tXa8NdRyL9+tEWblU39C67wGOPbdANHft4\nJtU3/ITPahcxp2Upn4aXU//huyq0kYhautOnx9348+drxPlJJ8FZZzEibwTTJk/jhwf+kIlDJ/LD\n8Vfw0neeZdemNG1XUaGBb+edp9nkfvtbOOooOPNMre9eWKhJcxYv3qLfhkBA1+XLy+OCDmqxp6er\nsBuGYfQB+qSl3hxu7vK6INSH6rfpu5xzPDLnEabOmUooEiIzNZMp46cweZ/JGrG+mSypWcLyuuUM\nyRmCc46K5gqcc6xqWEX/zP4EfAFcURHHffceKB7P8mgNf5//NAun3c2YAWOYvM9kijI71mD//J5f\nkNJaQzQ7jRTxEXNRvqSKvT58n6w774Tnn1fhLSrS6PfKSi2ukpD1rSiziMsO7LQl7u2DtaZ6c7O6\n1HfdVdO8PvaYinxLi66dh8Masb9kiVrd3dWI3xChkP7t/Jv6/ZoD3zAMow/QJy31sQPGgqj17BFz\nulf68GGHb9N3/eWzv3DXR3eR4kvRdW/g5vdv5tXFr25Rfx8s/wARQUTw+XwMzx1OOBamOdzM3LK5\nlNaW8q3dv8WkXY/kf83LOPUf3+apz55i3pp5TJ09lVOePoXS2tJ1/UVjUVZ8/SkuEMAn+p+DT/z4\nfH6qQjWaiS4nJ17/PCdHo9nffHPj5U5zclT8J09WQW9rg5/+VNe96+vVC9DSon23tOi1557bot+F\n4uJ4vXUP53SJ4IQTtqxPwzCMnYw+KeoFGQVcc/A11LXWUdFUQXVzNdXN1Ry1y1FMLJm4zd7jnOPh\n2Q/TL9iPtICWBg0GgmSkZvDQrIe2bOzpBesmILFYjNUNq/GJj4AvQFZqFj7xkRfMQ0S45YNbiMai\nFGYWkpOWQ2FmIfWheu6Zec+6/prDzcwYmUYw0lGggxFo8kXjCWESqEuD20uWM/GxiUx6bBJ3fXhX\nt96PDrzwglr5Pl/8AN3G5gXhbW6KWA8RuOUW7aOyUt3+VVVah/7cLjdiGIZh9Dr6pPsd4NzR5zJm\nwBimLZxGU7iJY0Ycw+HDDl9nrW4Loi5KdUs1xZnFHa4HA0FWN6zeoj6/tfu3ePTTR2kJt9DU1kRz\nuBmf+MhMzWTPwj2JuRhPfvYkZ+17Fp+t+Ww9V3tuMJcPln+w7nNWahbzJo1ixWfzKKlqoy3gIxCN\nEXFR3rjoSPau2w3eemvdlrGIxLhg5Hy+LBRygZiLMnXOVOaUzeHJU5/c8JLCtGkaWV9T09HKj8Xi\nwXf77rtFvwug6/OvvKIu/BUr1OV/zDHat2EYRh+gz4o6wL7F+7Jv8VaIyEYI+AKMyh/FqoZVHRLH\nNIQadAlgCxiWO4w7j72T69++njVNa4i5GOkp6YzKH0UkFiHmYvjwsbh6MRkpGYRjYVL98T3f4ViY\nvGA8U5uIMOXoG7i6aQrHzm/moK9aKct0vHlgPjf98A5ozdbSqpWVkJLCB7m1LM4OUzR4X6Td+1Cc\nWczcNXOZXTabcYM2UETI59Noeq80ayQhaDAnRyvHbU7++a4oLoaLL966PgzDMHZS+rSo9wQ/m/gz\nfvDKD1gVWoWIEI1FyUzJ5KoJW57C9KgRR/F+yfv88p1f8vwXz1OYUcjS2qU0tGkRE7/4aQg1MHmf\nyTz26WMUZhbinCMUDVHfWs+U8VM69HfMrseQdfpjPDTiIaavXcZ+xfvx2wMvZ8/C9gQ206bpWvf8\n+SweVkUk8AmSGU+TKyI451hSs2TDov6d72j0/F57qbVeXq5BbMGg3vvxj1XYDcMwjC3CRD3JjB4w\nmpJ+JXy48kPaom2kBdLYrWC3rd4LnxZIY8pBU3hzyZssqFxAxEUISIBwLIzP5+PW6bfy4pkvUt5Y\nzpPznlTBdzAwe2CHXPYr61fy0cqPSPOncc/x93TY5reOggKtmw4MXfwagbf+t14Tn/g2nmnvm9+E\nGTM0Za2Ibj/Ly4PHH9+05DiGYRjGBjFRTxLOOUSE+z++n6W1S9mveL91Fu2y2mX88cM/cuM3btzs\nPj8t/5RF1YsozixmYslErhh/BT96/UcIQtRFyQ3mMiJvBLWttby97G1S/ankpecxJHsImamZhKIh\nrnnjGp469Sk+Wf0J9868l6iL4hMfqb5U7j7+bg4ddmi3YzhilyMozixmTdMa8tPzcc5R01LDiLwR\nHDTkoA1/gUAAfv97uOACTTtbUKCFZtLSNut3MAzDMLpG3Ma2Je2AjBs3zs2aNWt7D6NLXl30Kvd+\nfC/L65aza96uLKpeRGFmYcd17WiYpnATcy6Zs8l71UOREFf86wo+WvkRURcl4AswIGsAZ+97Nn/8\n8I/rIt9T/Ck451hcvZg0fxrlTeUUpBcwtN/QdRH41c3VjCkew6drPqVfWr915WWbw83EYjHeu+C9\nDVahK2so49YPbuWdZe8gIhy363FcN+m6dVv2DMMwjG2LiMx2zm1gfVMxS30b8vLCl/n5Wz8nMzWT\n4sxiyhvLWV63nFR/ageXt098m51Z7i+f/YX/rvgvRZlF6yYCZQ1lvLroVWIuRoo/ZV3k/tK1S6lq\nqWJw9mBEhJrWGhraGti3eF8CvgDBQJC5a+YSjUU71IvPSMmgqqmK+z++n/4Z/RmRN4JJJZPWqxs/\nMHsg9514H+FoGBHp0bryhmEYRvfY/423IffMvIfM1Mx11d6y07LJDeayvG55B1GvbqnmhJEnbNBK\nD0VCPPrpo/x9/t+JxCJUNVWRnZbd4Zn89HzmrpnL2AFjmVc+j+y0bCKxCGua1tAvrR9DcoZQ1VyF\niBCOhalqqmJA9gCaw80Mzx3O0rVLO7yzLdrGstplPDTrIVL9qaT4UxiVP4rHTn6sy7X2xAmBYRiG\nsf0xUd9GRGNRVtWvojQdWjwAAByLSURBVDir4570XXJ3YX7lfKqaq4jGovh9fgZlDeLaQ67tti/n\nHKc8fQrvlb6HwxHwBQhHw6QF0hhdPBq/z084GmZR1SLq2+pJ9aXSEmkhGAhqkpmMQnbJ2wW/z8+Q\nnCGU1pUSi8Woba3F5/ORG8zlxxN+zFWvX7VuTABf13xNJBZZl1veOcfC6oU88PED3HDYDd2O9+u1\nX/PgJw/yyepPGJQ9iIv3v5gjdjli2/ywhmEYxiZjor6N8Pv8lPQrYW3r2g512dtibRwz4hgu2v8i\nFlcvZmT+SI7c5UjSU9LX62Pmypk8OOtBZiyfwZLaJQT9QdICacRcDIejua2ZmuYaCrMKWbp2KfVt\n9fQL9qMoq4jcaC7L1i5DRKhtraWssYyBWQMpziom1Z/Kstpl5KXnccZeZ3DxARczMGsgF4y9gMfn\nPk4kFkEQ1rauZWT+yHXudBEhN5jLK4tf6VbUl9UuY/Kzk2kON5OTlsOXVV9yxWtXcOPhN3LG3mck\n58c2DMMwusQC5bYhry1+jWveuIb0lHQyUzNpbGskFAnx0EkPMalk0gaffWvJW/z43z/G7/PzVfVX\nNEc0U1xGSgZ+n59oLEpzuJmC9AJygjmsqFtBMBBkz8I9SfOnsbhmMdXN1WSlZuH3+altrSUnNYc9\nC/ekLlRHMBDkpckvredJWFi1kA9XfkiKL4Xfvv9bctJyaAo30RpuJS2QRiQWoaGtgRNHnshhww4j\n4AtQ2VzJmAFjmFQyiRvfvZFpX07rsLzQGmkFB+9f8L656A3DMLYBFii3HThh1AkEfAHu+/g+ltYu\nZVT+KK466KqNCrpzjtv/e/u6yUCUKCKyrl56hi8Dn/jw+/xcfuDlZKZmcv/H9zM0ZygBf4DGtkZq\nW2tJ8amA7lGwB8vrllPepIF6hw07jOsPvX49QQfYvf/u7N5/d5xz3P3R3cxePZsYsQ5tslOzmbFy\nBn+b/zeC/iBFmUWEIiGG5g7FxRxZqVkd2gcDQWqaa6hsrmRQ9qCt/FUNwzCMTcVEfRtzzK7HcMyu\nx2zWM7WttSxdu5R+wX7EYjGyUrKojdUSI0YkGsEFNBtcVmoWF+1/EemBdN5Y8gY1LTVk+7PXFVOJ\nESM/PV+rt+UNJxgIcvmBl3PlQVdudAx3f3Q3n1V8tp6gg27BK2sow4eP1mgrK+pXICKUNZYR8AfI\nSc1h9/67rwvi86Liu0xkYxiGYSSNpIi6iDwD7N7+MReodc6N6aLdMqABiAKRTXEt7KjUtdbx9Pyn\neXfZuxRkFHDOvudw8NCDN/rcgsoFXP7q5ZQ1lqlItu8/bw43E4qGQNSdnRZI44ABB3D8X47H4da1\naY200hppJRKLEAwE6Rfst67vgD9ASb+S9d4ZiUVYXL2YFH8Ku+btisNxx4w7EASf+BBk3To+oOv5\n4WbSA+k0tjUS8AXISM3AL/51a/FrGtcwIHsA4WiYmpYazh9z/gb3uhuGYRjbnqSIunPuTO9cRO4E\n6jbQ/AjnXFUyxtFTNIQaOOu5syitLSU9JZ0FVQt4d9m7XH/o9Zy979ndPheKhLjk5UtoDjczJGcI\nqxpWEXMxVjWsIis1i0hrhLz0PCYOmUhlSyWrG1dTkFGAIFQ2V5IeSOf0vU7ntcWvsbp+NaFIiAUV\nC8hOy6Z/Rn/y0/M5esTRHd45c+VMrn3zWupa63A4huUO46eH/JSWSMu6fe4igg8fURfVz6gF7gm9\nFy3vcAQDQQoyCmgON1PVVEVqIJWL9r+IKQd1zC9vGIZhJJ+kut9F/bFnAEcm8z3bktLaUu6deS/T\nV0wnL5jH+WPO54y9z9hgSdYXvnyB0rpSirLiZU7bom38YcYfOHn3kztEw4NmdHt76dvMKZtDZVMl\nA7MHrqvitrphNS3hFsLRMIOzB5OZmsmimkWEY2EGZg9c10d+ej6VTZWsaVpDVUsVoweMprSulPpQ\nPbWtteQF83jilCfITM0kEovgFz8VTRVc9upl+H1+8jM0xeuKuhVc/5/ryUrNIhQOIWgq285kp2XT\n1NYEsC5rXczFKMoswic+jhlxDDccdgNZqVkdsucZhmEYPUey19QPBdY45xZ3c98Bb4iIAx52zk3t\nriMRuQS4BKCkZH2X8ragvLGcyc9NpiHUQG4wl5qWGn7z3m9YWb+Saw65ptvn3it9jzR/x/zlqf5U\nmtuaWVyzmDED4isPH5R+wI9e/xFt0TbqQ/VUNFXQFmtjWL9hDM4ZTGOoUQU9ZzDDcocBug+8sa2x\ng6h7vLnkTdJT0klPSWeP/nsQiUWIxqI0tjXyZeWXXP7q5SyuWUxxZjH7Fe1Ha6R1XcCciJCXnkdN\ncw37D9ift5e+jYu6DuvqqZJKv2A/CtILWBVdBeiExSc+CtILyE/Pp6alhpN2O4n8dKuwZhiGsT3p\n3vzcCCLylojM7+I4OaHZWcDfN9DNJOfc/sAJwA9F5LDuGjrnpjrnxjnnxhUWFnbXbKt4ev7T1Ifq\nKcwsJMWfQmZqJgUZBTz12VPUttZ2+9ygrEG0Rds6j5dILNJB6FojrVz9xtWk+FMozCxkaL+h+MXP\nmsY11IfqAagL1RHwB8hLj9c8L8oooqmtiZiLdehfEFIDqR3StAZ8AVL9qTS2NXLRyxfxQekHlDeU\nM7d8Lv+/vXsPj6o+Ezj+fWcmM0yuhNwgF24CAQKIgkFgFRFR9FERgYKiomK9tHS1+qyLVVepVbv4\nrFi329W6VbTVIrYoVrmIF7zQikCFEiTILVxCbiQhIZlkcmbmt39MMk0kXJIwCSbv53nyZHLmnDlv\nzpnknd85v9/7+/225n8Pg2Fsxtgm99EBHOIgMSqR4cnDue/C+yj8t0Kev/J5UmNSSY1JJSoiivKa\ncq7NvJYJfSe04EgrpZQKh1a31I0xl53seRFxANcDo07yGvn134tF5G0gG/istTG11ZbCLXRzdGuy\nzGFzYMPGgYoDJ+zNPXvYbFbsXEGNVYM7wk3ABDjiOUJ2WnaTjmpfF3yN1+8NJXqn3Ul6XDp5R/M4\nWHkQX8CHwdDd1Z0YZwwQTN5VdVUAbMzfSIwzhl4xvajz1zE4cTCjeo3i9W2vNylmU+mt5Jj3GJXe\nSrpFdMMmNowx1Fg1lHhKGBgYiM0W/DznD/gxxrAsZxlWwAqNiTcYfMbHEc8RCo4V8NyG50iOSubO\nUXcyfch0Pt73MRXeCrLTshmePPy0J6ZRSikVPq1uqZ+Gy4BcY8yh5p4UkSgRiWl4DFwO5IQxnlMa\nlDAIr8/bZFnABPAZHz2je55wu6zkLBZNXhScPKWmjLKaMsZnjOfZy59tsp6IhDqdNUiNSSUjNoOs\nxCyuHHAld5x/B3GuuFCLubCqkL1H95IUmUR6bDo1vhr2lu9l5tCZvHrdq9w9+m7SY9MpqS6hvKac\nkuoSRASf8YUmeTHG4DfByVv8AT8FVQUcrT1KWU0ZpTWlzMyaSW5pLlbACn2waFAXqGPf0X1gYPGX\nizHGkBCZwMysmdxx/h2hKWWVUkp1vHDeU5/Ndy69i0gq8H/GmKuAFODt+oTgAN4wxqwOYzyndOPw\nG/nzN3/maO1R4lxxWAErdHk5OSr5pNtOGTCFSf0mkXc0jxhXTLMfAs7reR7uiOCwsIaCLQ1D0Z65\n/BkuSLsAy2/x6CePsnLXSgThQMUBEt2JnNPjHESEtNg0SqpL8AV8xLhisPwWk/tP5sVNL1JWW0Zm\nQiaLJi9i9p9mU+4rx/Jb1Ppqg4m6PldPGzyN0ppS3A4304dOB2DhuoUn/N2E4Jh0EaHaqj6u2Myp\nlHpKqfBW0Duut87oppRSYaRlYr9ja+FWnvz8SXKKc3A73Nww/AZ+kv2T0FzkbfVV/lf86P0f4fV7\nCZgANmzcdt5t/PTCnzZp8RYcK2DT4U0s+HBBk171ADVWDQmRCbx/4/s89NFDrMhdQfdu3bECFoVV\nhbgdbkb1GsXyHctDU7yKBHu1Ox1OhiQO4cNbPgzdBljw4QIWrV/UpIXeWIwzOPvbsORhfHnHlycd\nCdBYpbeShz9+mHX71mGz2Yh2RvPoxY8yZcCU1hw6pZTqsrRMbCud2/Ncls1chtfnxWFzhMZkt5XH\n8vDBng/4tvRb7rvwPlz24EQt2WnZ9Ivvd9z6vWJ6Man/JJx2J5bfalJD3WN5GN19NIVVhbz37Xsk\nRiZysPIgxdXFoaFm1XXVxLvjKfGUhLaLsEeQmZCJ5bf4NO9Tpg2ZBsDfDv2NGFdMqLPedxmCr3nX\n6LtOO6EDPLj2QT4/8DmJkYnYxIbH8vDg2gdJi0ljeMrw034dpZRSp0eT+gmcqZY5QFFVETctv4nC\nqkIMBhEhKTKJ169/vdlharW+2mDVtohI5oyYw8tfv0y8O54IW0So09wd59/BwYqDOCRY+724uhi7\n2KkL1GEFLIqqi4hxxhDvikdsQjd7N3rG9CTaGU1xVXFw0pV6sc5Y+nbvy84jO6nz1zVpsdvFTsAE\nmNR/ErePvP20f+eCYwWsP7g+lNABIiMi8dR5eCPnDZ5Oebq1h1MppdQJhLOjnKq3+MvFHK46TGJU\nIklRSSRGJlJcXcwzf32myXrbirYx661ZjHpxFNkvZfP0509z9+i7uWf0PdT56yjxlJAUmcSvr/w1\nI3uOpHdc71APdQzU+GqwAhYQbJV7fMEysoMTBjMgYUCwSl3Ah01sjEkfE9rvTSNuwvJbDEseRkpU\nCg5xIAgxETFkJmRyw7AbWDp9aYs6xJXVlGEX+3Ete6fDSX5lfhuOplJKqRPRlnor1Pnr+LrgawBG\n9hx5ylb96t2rjyvM0sPdg7V71wbHm4twqPIQt624DV/AR1JUEr6Aj9//4/eUeEp49opnueeCe6j1\n1RIVEYWIUFhVyNs73iY6Ipq88jx8AV9oHLsgOO1O/AE/3ezdKKgqCMZogvfW7xx1J/3j+4dimZk1\nk91lu1mas5SU6BSSopI4v9f53H7e7fSJ6xMqgtMcj+Vh1a5VbMjfQEZsBtOGTCM9Np1+8f1w2Bx4\nfd4mx6fWV8v4jPEtPuZKKaVOTZN6C23M38i9q++luq4aEcHlcLH4isWMyxh3wm2cdmeTwjEQHCrX\nMFUqwB+3/ZFaXy2JkYlUeivxWB4i7BGs2bOGw8cOkxqTGup1nlOcw20rbqPGCtZrdzlcVFvVGAxO\nuxOX3YUxBrvYSY5K5taRt4aqxF1xzhVNKtwB2MTGwxc/zA9H/ZA9ZXvoGd2z2fv831XpreSm5Tex\nt3xvaHz7K1te4cWrX+SCtAu4f+z9PPX5UzgsR/DKgeUhNTqVWcNmnfK1lVJKtZwm9Rao9FZyz/v3\nICL0iAy2vKvrqpm/cj5rb15LQmRCs9vNGDqDJVuWkByVHOqFXlZTxpzhc0KXtHeX7abWV8uXh77E\nCljYxEaELQK72NlSuCU0L7kxhsc+eQzLb5EUFays18Pdgy2FW4IzqIkDv/FjExsDegzAClhM7DeR\nC9IuOOXvlxyVfMqhe4394R9/YE/Znia98495j/Hwxw+z5qY13Dj8Rvp278trW1+jpLqES/pewpwR\nc3RKVqWUChNN6i3wad6neP1eEiMTQ8uinFGUVJfwSd4nzBg6o9nt5mfPZ8eRHWw+vDnUCW106mju\nvfDe0DpWwGJf+b5gRzqEAAHq/HXYbXbezHmTqwZeBQTLyO4s3dkkBhEhMzGTnSU7iXZFE+uKJdYV\nS6W3khEpIxidGp4ZbT/Y88Fxk9VEO6MprCok/1g+6bHpjMsYd9KrGEoppc4cTeotUG1VH3cZHcBv\n/KEZzJoTGRHJy9e+TE5xDvsr9tM7rneT0qq1vlr+XvD3UCu+YXnABIh1xLK5YDMey0NkRCQuuwub\n2AiYAHb553C7gAmQnZ7N+b3OZ/Xu1dT6ahnZcyRXD7yaEk9Jkxa4MYb1B9fz1va3qPRWMmXgFKZm\nTj2uRO6pNHS8a8xgMMbgdrhPsJVSSqlw0d7vLZCdlh2cZzzgDy3zB/w4xNGkN3lzRIThKcO5etDV\nx5VWPVhxEAi2+hvuszfcr28YJ99QXtYd4WbKgCmU1pSGpkj1B4IfKuadN49fXvZLfnHpL4Bgb/qn\nvniKya9NZvmO5aH9vbD5Be5+727W7V/H1qKtLFy3kHkr5h03Kc2pzBk+B6/PGzoexhhKPaWM7z3+\nhLcilFJKhY+21Fugf3x/5o6cy5ItS4B/VmmbPWw2mQmZrX7dhMgEAiZAojuRwkAhbpsbEcHyWxgM\nF/W+qMmELY9c/AjF1cVsLtiMXez4jZ9ZWbOYmTWTkuoSHvn4EdwR7lDL2+vz8vi6xxmTNgaXw8UL\nG18g3h0fKtkaa2LZWrSVj/Z+xJUDrzztuKcMmMI3Jd+wZOuSUI35YcnDePLSJ1t9LJRSSrWeJvUW\nemDsA1zU+yJW7lpJwASY0HcC24q2Mem1SdhtdqYPmc6tI29t0aXsHu4eXDXwKt7JfYeoiCg8lge/\nCc6eNihhEI9d8liT9WNdsbwy9RV2le2isKqQgT0GhorYfH7g81A9+QYuh4sKbwWf7f8suJ7QpAa7\niGATG18c+KJFSV1EeGDcA9x87s3sPBK8zz84cbBO8KKUUh1Ek3oLiQhj0scwJn0MvoCPG/58A9uL\ntxPrisVgeH7D82w6vImXrnmpRcntsQmPEWGPYMWOFXh8weFs80bO494L721SIrZxHIMSBjEoYVCT\n5QEToLl6/pbfYkP+BtJi04JV4xrdu2/YrqE3fUu1tNe8Ukqp8NCk3gZfHPiC3JLc0FA1ALfDzYb8\nDWwt2nrcePCTcUe4eWLiEywYv4BKbyXJUcmtqjs/PmM8dpudOn8dTrsTgOKqYg5WHGTVrlXYbXby\nK/Op8laFZn7zWB4cNgfXDb6uxfs7HRW1FfiN/7gCPEoppc4s7SjXBrlHcvEZX5MWr4gQMAF2le5q\n1WtGOaPoFdOr1RPJ9Irpxc8u+hnHvMcoqiricOVh9pbvJS02jdTYVFKiU8hMyKSyrpLCqkLKa8px\niIPnrniOvt37tmqfJ1JcXcxd793F+JfHc/ErFzPrrVmtPi5KKaVOTVvqbZAem45Djj+EdrE3O1FL\ne5k9bDbjMsaxLm8dXxd8zardq5rEE+2KJjU6lbkj53Jt5rUMShh0xuc59wf83L7idvKO5pEQmYAg\n5JbmMveduayas4q4bnFndH9KKaW0pd4ml/a7lITIBI5UHyFgAgRMgOLqYjJiM7gw/cIOja13XG9u\nOfcWJvWfdMJ78j3cPRiaNPSMJ3SAjYc3cqDiAElRSdjEFtrfMe8x1uxZc8b3p5RSSpN6m0RGRPLa\ntNfITsum1FNKqaeUiX0n8sp1r4QlUbbG2PSx2MWO1+cNLfMFfNjFzsS+E8O236KqomaXBwhwqPJQ\n2ParlFJd2dmReb7Hesf15ndTf4fH8iBIk/HkZ4OEyAQWXrKQ//jkP6jwVgQnerHZmZ89n4EJA8O2\n38zETIwxBEwgNP2qMQYbNkakjAjbfpVSqivTpH6GREZEntHXK68p59m/Pctfvv0LAFcPupr7x97f\nqh7kUwdPJTstm3V566jz13FRn4uaTL0aDoMTBzP5nMms3r2aKGcUNrFxzHuMrOQsJvSZENZ9K6VU\nVyXNjWk+240ePdps2rSpo8MIG1/Ax/Rl09lVuiuUxMtryjmnxzksn7X8pJf2PZaHd3a8w0d5H5Hg\nTmBW1ixGpY5qr9Cb8AV8vJnzJm9ufxPLb3FN5jXccu4toSlklVJKnR4R2WyMOeXsXG1qqYvITOBx\nYAiQbYzZ1Oi5h4B5gB/4V2PMcb2jRKQfsBRIADYDNxtjWlaAvBP668G/srd8LynRKaFlydHJ7Du6\nj/UH1jOhb/MtXY/l4eblN5NbmovL7sIKWKzctZJHLn6E2cNmt1f4IQ6bgzkj5jBnxJx237dSSnVF\nbe0olwNcD3zWeKGIDAVmA1nAFOA3ItLcwOv/BBYbYwYA5QQ/BHR5+4/uP272Mwi2fPdX7D/hdu99\n+x65pbkkRSYR1y2OxMhE4rrFsWj9IqrqqsIZslJKqbNAm5K6MWaHMWZnM09NBZYaY7zGmH3AbiC7\n8QoSrNhyKfCn+kWvAuEpafY906d7n2YvsUfYIugT1+eE263LW4fT7mxSDMdpd2KMIfdIblhiVUop\ndfYI15C2NOBgo58P1S9rLAE4aozxnWSdEBG5U0Q2icimkpKSMxrs2WZcxjj6x/enuLoYy29h+S2K\nqoroF9+P8b3Hn3C7pMgkLL/VZJkxBr/xE+fSYi9KKdXZnTKpi8iHIpLTzNfU9giwgTHmt8aY0caY\n0UlJrZt45PvCYXOwZOoSZgyZgcfyUG1VM2PoDJZMXXLSTnI/yPoBNrFR66sF6uc3ryllSOIQBvQY\n0F7hK6WU6iCn7ChnjLmsFa+bD2Q0+jm9flljpUB3EXHUt9abW6fLinfHs3DiQhZOXHja22QlZ/Hk\npU/y889+TnlNOX7jZ1jyMH415Vc6HapSSnUB4Rqn/i7whog8C6QCA4GvGq9gjDEi8gkwg2AP+LnA\nijDF02Vck3kNl59zOTtLdxLrij3jk7QopZQ6e7XpnrqITBORQ8BY4H0RWQNgjNkOLAO+AVYDPzbG\n+Ou3WSkiqfUv8e/A/SKym+A99t+1JR4V5HK4GJEyQhO6Ukp1MVp8RimllDrLnW7xGZ3QRSmllOok\nNKkrpZRSnYQmdaWUUqqT0KSulFJKdRLfy45yIlICnLgIesdJBI50dBBdnJ6DjqfnoOPpOTg7nMnz\n0McYc8rKa9/LpH62EpFNp9M7UYWPnoOOp+eg4+k5ODt0xHnQy+9KKaVUJ6FJXSmllOokNKmfWb/t\n6ACUnoOzgJ6Djqfn4OzQ7udB76krpZRSnYS21JVSSqlOQpO6Ukop1UloUm8jEZkpIttFJCAio7/z\n3EMisltEdorIFR0VY1cjIo+LSL6IbKn/uqqjY+oqRGRK/ft9t4gs6Oh4uiIRyRORbfXvfZ35qp2I\nyMsiUiwiOY2W9RCRtSKyq/57fLjj0KTedjnA9cBnjReKyFBgNpAFTAF+IyL29g+vy1psjBlZ/7Wy\no4PpCurf3/8DXAkMBW6o/ztQ7W9i/Xtfx6q3nyUE/9c3tgD4yBgzEPio/uew0qTeRsaYHcaYnc08\nNRVYaozxGmP2AbuB7PaNTql2lQ3sNsbsNcbUAUsJ/h0o1ekZYz4Dyr6zeCrwav3jV4Hrwh2HJvXw\nSQMONvr5UP0y1T7mi8g/6i+Jhf2SlwL0PX+2MMAHIrJZRO7s6GC6uBRjTEH940IgJdw7dIR7B52B\niHwI9GzmqYeNMSvaOx518nMC/C/wBMF/bk8A/wXc3n7RKdWh/sUYky8iycBaEcmtb0WqDmSMMSIS\n9jHkmtRPgzHmslZslg9kNPo5vX6ZOgNO95yIyEvAe2EORwXpe/4sYIzJr/9eLCJvE7wtokm9YxSJ\nSC9jTIGI9AKKw71DvfwePu8Cs0XEJSL9gIHAVx0cU5dQ/8fTYBrBzowq/DYCA0Wkn4g4CXYUfbeD\nY+pSRCRKRGIaHgOXo+//jvQuMLf+8Vwg7Fd2taXeRiIyDfhvIAl4X0S2GGOuMMZsF5FlwDeAD/ix\nMcbfkbF2IYtEZCTBy+95wF0dG07XYIzxich8YA1gB142xmzv4LC6mhTgbRGB4P/3N4wxqzs2pK5B\nRP4IXAIkisgh4DHgl8AyEZlHcLrwH4Q9Di0Tq5RSSnUOevldKaWU6iQ0qSullFKdhCZ1pZRSqpPQ\npK6UUkp1EprUlVJKqU5Ck7pSSinVSWhSV0oppTqJ/wdoIucYMQ+uRwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "WeuwbMoBfrh4",
"colab_type": "text"
},
"source": [
"## 数据预处理"
]
},
{
"cell_type": "code",
"metadata": {
"id": "RB6x5g1fRdgF",
"colab_type": "code",
"outputId": "4b89d534-db9a-4b79-aaf0-ef41c0f5446f",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"#数据预处理\n",
"from sklearn import preprocessing\n",
"import numpy as np\n",
"from sklearn import datasets as d\n",
"#加载波士顿数据集\n",
"boston = d.load_boston()\n",
"X, y = boston.data, boston.target\n",
"X[:, :3].mean(axis=0) #前三个特征的均值\n",
"#array([ 3.59376071, 11.36363636, 11.13677866])\n",
"X[:, :3].std(axis=0) #前三个特征的标准差\n",
"X_2 = preprocessing.scale(X[:, :3]) #标准\n",
"X_2.mean(axis=0)\n",
"#array([ 6.34099712e-17, -6.34319123e-16, -2.68291099e-15])\n",
"X_2.std(axis=0)\n",
"#array([ 1., 1., 1.])"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"array([1., 1., 1.])"
]
},
"metadata": {
"tags": []
},
"execution_count": 7
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "nyRuxo7-RdgK",
"colab_type": "code",
"outputId": "57aac38a-6304-460c-8399-be09f1a33722",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 286
}
},
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"#%matplotlib inline\n",
"#随机生成一个实数,范围在(0.5,1.5)之间\n",
"cluster1 = np.random.uniform(0.5,1.5,(2,10))\n",
"cluster2 = np.random.uniform(3.5,4.5,(2,10))\n",
"#hstack拼接操作\n",
"X = np.hstack((cluster1, cluster2)).T\n",
"plt.figure()\n",
"plt.axis([0,5,0,5])\n",
"plt.grid(True)\n",
"plt.plot(X[:,0],X[:,1],'k.')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"[]"
]
},
"metadata": {
"tags": []
},
"execution_count": 8
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAD8CAYAAABXe05zAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAADipJREFUeJzt3VGIpeV9x/Hfz9k97OK45CLTIK6y\nhdaBrNBNXSyDpZxxSbBG0l5GSK4K40UaLBXT5qrkou6VIRdNoUvUuiRNGDBCsTStTPZUZE9qXDOm\njpuRkApVAou0YZ0Lc5zdfy/mTM46O7PnHee853n/c74fOOyMvnPO30f9zcPz/p/ndUQIAJDHTaUL\nAADsDsENAMkQ3ACQDMENAMkQ3ACQDMENAMkcqHKR7bckvSfpiqT1iDhZZ1EAgJ1VCu6++Yh4t7ZK\nAACVsFQCAMm4ys5J2/8t6f8khaR/iIgz21yzIGlBkg4dOnT3HXfcMeJSc7p69apuuonfj4zDAGMx\nwFgMvPnmm+9GxEyVa6sG920R8Y7t35L0gqQvR8SLO10/Ozsbq6urlQvezzqdjtrtdukyimMcBhiL\nAcZiwPaFqvcPK/2qi4h3+n9ekvScpHs+enkAgL0YGty2b7Z9y+bXkj4j6fW6CwMAbK9KV8knJD1n\ne/P6f4qIH9RaFQBgR0ODOyJ+Ien3xlALAKACbucCQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3AD\nQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADaIRut6vTp0+r2+2W\nLqXxqjy6DABq1e12derUKfV6PbVaLS0tLWlubq50WY3FjBtAcZ1OR71eT1euXFGv11On0yldUqMR\n3ACKa7fbarVampqaUqvVUrvdLl1So7FUAqC4ubk5LS0tqdPpqN1us0wyBMENoBHm5uYI7IpYKgGA\nZAhuAEiG4AaAZAhuAEiG4AaAZAhuAEiG4AaQzqSfa0IfN4AP6Xa7jd4Iw7kmBDeAa2QIxe3ONWla\njXVjqQTAb2Q47IlzTZhxA7jGZihuzribGIqca0JwA7hGllCc9HNNCG4AHzLpoZhB5TVu21O2f2L7\n+ToLAtBsk96K1wS7mXE/IumipCM11QKg4TJ0nUyCSjNu20clfVbSt+otB0CTZeg6mQRVZ9zfkPQV\nSbfsdIHtBUkLkjQzM8O/0L61tTXGQozDtTKPxZEjR3TgwAFFhA4cOKAjR47s6Z9l61isrKxoeXlZ\nJ06c0PHjx/de8H4VETd8SXpQ0t/3v25Len7Yz9x5552BDefOnStdQiMwDgPZx+L8+fPx+OOPx/nz\n5/f8XteOxfnz5+Pw4cMxNTUVhw8fHsn7ZyLplRiSrZuvKjPueyV9zvYDkg5JOmL72xHxhXp+lQBo\nsrq6TtgRWd3QNe6I+GpEHI2IY5I+L+mHhDaAUWNHZHX0cQNohCybf5pgV8EdER1JnVoqATDx2PxT\nDYdMAUAyBDcAJENwA0AyBDcAJENwA0AyBDcw4UZ92h+nB9aPPm5ggo36tD9ODxwPZtzABBv1aX+c\nHjgeBDcwwUa9zZxt6+PBUgkwwUa9zZxt6+NBcAMTbtTbzJu6bb3b7e6bXygEN4BGqCtYu92uzp49\nq6efflrr6+v74qYpwQ2guLq6UTbf9/333998MMy+OOubm5MAiqurG2XzfTdD2/a+uGlKcAMorq5u\nlK3v+/DDD6dfJpFYKgHQAHV1o+zXLheCG0Aj1NWN0tQul71gqQQAkiG4ASAZghsAkiG4ASAZghsA\nkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkhka\n3LYP2X7Z9mu2V2x/bRyFAQC2V+XRZb+WdF9ErNk+KOkl2/8aET+quTYAwDaGBndsPNd+rf/twf4r\n6iwKALAzb+TykIvsKUkXJP2OpG9GxF9tc82CpAVJmpmZuXtxcXHEpea0tram6enp0mUUxzgMMBYD\njMXA/Pz8hYg4WeXaSsH9m4vtj0l6TtKXI+L1na6bnZ2N1dXVyu+7n3U6HbXb7dJlFMc4DDAWA4zF\ngO3Kwb2rrpKI+JWkc5Lu/yiFAQD2rkpXyUx/pi3bhyV9WtLP6i4MALC9Kl0lt0p6pr/OfZOkxYh4\nvt6yAAA7qdJV8lNJnxpDLQCACtg5CQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzB\nDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJ\nENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwA\nkAzBDQDJDA1u27fbPmf7Ddsrth8ZR2EAgO0dqHDNuqRHI+JV27dIumD7hYh4o+baAADbGDrjjohf\nRsSr/a/fk3RR0m11FwYA2J4jovrF9jFJL0q6KyIub/l7C5IWJGlmZubuxcXF0VWZ2Nramqanp0uX\nURzjMMBYDDAWA/Pz8xci4mSVaysHt+1pSf8h6W8j4vs3unZ2djZWV1crve9+1+l01G63S5dRHOMw\nwFgMMBYDtisHd6WuEtsHJT0r6TvDQhsAUK8qXSWW9KSkixHx9fpLAgDcSJUZ972SvijpPtvL/dcD\nNdcFANjB0HbAiHhJksdQCwCgAnZOAkAyBDcAJENwA0AyBDcAJENwA0AyBDcAJENwA0AyBDcAJENw\nA0AyBDcAJENwA0AyBDcAJENwA0AyBDcAJENwA0AyBHch3W5Xp0+fVrfbLV0KgGSGPkgBo9ftdnXq\n1Cn1ej21Wi0tLS1pbm6udFkAkmDGXUCn01Gv19OVK1fU6/XU6XRKlwQgEYK7gHa7rVarpampKbVa\nLbXb7dIlAUiEpZIC5ubmtLS0pE6no3a7zTIJgF0huAuZm5sjsAF8JCyVNARdJgCqYsbdAHSZANgN\nZtwNQJcJgN0guBuALhMAu8FSSQPQZQJgNwjuhqDLBEBVLJUAQDIENwAkQ3A3CL3cAKpgjbsh6OUG\nUBUz7m2UmPnSyw2gKmbcW5Sa+W72cm9+Lr3cAHZCcG+x3cx3HMFNLzeAqoYGt+2nJD0o6VJE3FV/\nSWWVnPnSyw2giioz7n+U9HeSztZbSjMw8wXQdEODOyJetH2s/lKaI/PMt9vt8ksH2OccEcMv2gju\n52+0VGJ7QdKCJM3MzNy9uLg4ohJzW1tb0/T09Fg+a2VlRY8++qg++OADHTx4UE888YSOHz8+ls8e\nZpzj0HSMxQBjMTA/P38hIk5WuXZkNycj4oykM5I0OzsbdEVs2Jz9jkO329X6+rquXr2q9fV1Xb58\nuTHdKeMch6ZjLAYYi4+GPu59hONhgclAO2DD7GWNmhurwGSo0g74XUltSR+3/bakv4mIJ+subBJt\nt/lH0q6COPONVQDVVOkqeWgcheD6zT9nz57VM888w/klAD6ENe4G2bpGLYnzSwBchzXuBtm6Ri3p\nQzNubjYCkAjuxtm6Rs3NRgBbEdwNx81GAFuxxg0AyRDcAJAMwQ0AyRDcAJAMwQ0AyUx0cI/rocAl\nHj4MYP+a2HbAcT0UeGVlRY899hjb1gGMzMTOuLd7KHAdlpeX2bYOYKQmNrjHdXb1iRMnrvsclk4A\n7MXELpWM6+zq48ePX3f+yDiWaADsXxMb3NL4tpNf+zmnT5++bumE4AawGxO7VFIKjxcDsFcTPeMu\ngceLAdgrgrsATvwDsBcslQBAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3\nACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMpWC2/b9tldt/9z2X9ddFABgZ0OD2/aU\npG9K+mNJn5T0kO1P1l0YAGB7VWbc90j6eUT8IiJ6kr4n6U/qLQsAsJMqDwu+TdL/XPP925L+YOtF\nthckLfS//bXt1/de3r7wcUnvli6iARiHAcZigLEYmK164cie8h4RZySdkSTbr0TEyVG9d2aMxQbG\nYYCxGGAsBmy/UvXaKksl70i6/Zrvj/b/GgCggCrB/WNJv2v7t223JH1e0j/XWxYAYCdDl0oiYt32\nn0v6N0lTkp6KiJUhP3ZmFMXtE4zFBsZhgLEYYCwGKo+FI6LOQgAAI8bOSQBIhuAGgGRGGtxsjd9g\n+ynbl+hll2zfbvuc7Tdsr9h+pHRNpdg+ZPtl26/1x+JrpWsqzfaU7Z/Yfr50LSXZfsv2f9lertIW\nOLI17v7W+DclfVobm3R+LOmhiHhjJB+QiO0/krQm6WxE3FW6npJs3yrp1oh41fYtki5I+tMJ/e/C\nkm6OiDXbByW9JOmRiPhR4dKKsf2Xkk5KOhIRD5aupxTbb0k6GRGVNiONcsbN1vi+iHhR0v+WrqMJ\nIuKXEfFq/+v3JF3Uxm7ciRMb1vrfHuy/JrY7wPZRSZ+V9K3StWQzyuDebmv8RP4Piu3ZPibpU5L+\ns2wl5fSXBpYlXZL0QkRM7FhI+oakr0i6WrqQBghJ/277Qv/4kBvi5iTGwva0pGcl/UVEXC5dTykR\ncSUiTmhjB/I9tidyKc32g5IuRcSF0rU0xB9GxO9r4xTWL/WXW3c0yuBmazy21V/PfVbSdyLi+6Xr\naYKI+JWkc5LuL11LIfdK+lx/bfd7ku6z/e2yJZUTEe/0/7wk6TltLD3vaJTBzdZ4XKd/Q+5JSRcj\n4uul6ynJ9oztj/W/PqyNG/k/K1tVGRHx1Yg4GhHHtJEVP4yILxQuqwjbN/dv3Mv2zZI+I+mGHWkj\nC+6IWJe0uTX+oqTFClvj9yXb35XUlTRr+23bf1a6poLulfRFbcyolvuvB0oXVcitks7Z/qk2Jjov\nRMREt8FBkvQJSS/Zfk3Sy5L+JSJ+cKMfYMs7ACTDzUkASIbgBoBkCG4ASIbgBoBkCG4ASIbgBoBk\nCG4ASOb/AdBN/i/qd/jaAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "mQCn6aRIous1",
"colab_type": "text"
},
"source": [
"# 分类\n",
"- 分类的核心目的是给定一个样本的数据观测,根据一个数据模型得出预测该样本属于哪个类别"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "q-KM9kSegKvH",
"colab_type": "text"
},
"source": [
"## 二分类-LR回归\n",
"- [logistics回归详解](http://blog.csdn.net/xlinsist/article/details/51289825)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ItwnqlGoRdgU",
"colab_type": "code",
"outputId": "22a1d237-bb0d-4d3a-ccf4-37955f6b2a35",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 90
}
},
"source": [
"#logistics回归详解:http://blog.csdn.net/xlinsist/article/details/51289825\n",
"from sklearn import datasets\n",
"import numpy as np\n",
"from sklearn.model_selection import train_test_split\n",
"from sklearn.metrics import accuracy_score\n",
"\n",
"iris = datasets.load_iris() # 由于Iris是很有名的数据集,scikit-learn已经原生自带了。\n",
"X = iris.data[:, [2, 3]]\n",
"y = iris.target # 标签已经转换成0,1,2了\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) # 为了看模型在没有见过数据集上的表现,随机拿出数据集中30%的部分做测试\n",
"\n",
"# 为了追求机器学习和最优化算法的最佳性能,我们将特征缩放\n",
"from sklearn.preprocessing import StandardScaler\n",
"sc = StandardScaler()\n",
"sc.fit(X_train) # 估算每个特征的平均值和标准差\n",
"sc.mean_ # 查看特征的平均值,由于Iris我们只用了两个特征,所以结果是array([ 3.82857143, 1.22666667])\n",
"sc.scale_ # 查看特征的标准差,这个结果是array([ 1.79595918, 0.77769705])\n",
"X_train_std = sc.transform(X_train)\n",
"# 注意:这里我们要用同样的参数来标准化测试集,使得测试集和训练集之间有可比性\n",
"X_test_std = sc.transform(X_test)\n",
"\n",
"# 训练感知机模型\n",
"from sklearn.linear_model import Perceptron\n",
"# n_iter:可以理解成梯度下降中迭代的次数\n",
"# eta0:可以理解成梯度下降中的学习率\n",
"# random_state:设置随机种子的,为了每次迭代都有相同的训练集顺序\n",
"ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)\n",
"ppn.fit(X_train_std, y_train)\n",
"\n",
"# 分类测试集,这将返回一个测试结果的数组\n",
"y_pred = ppn.predict(X_test_std)\n",
"# 计算模型在测试集上的准确性,我的结果为0.9,还不错\n",
"accuracy_score(y_test, y_pred)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/stochastic_gradient.py:152: DeprecationWarning: n_iter parameter is deprecated in 0.19 and will be removed in 0.21. Use max_iter and tol instead.\n",
" DeprecationWarning)\n"
],
"name": "stderr"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
"0.8"
]
},
"metadata": {
"tags": []
},
"execution_count": 14
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "ae6u5xVsRdgY",
"colab_type": "code",
"outputId": "70ab2f30-ae24-4e34-f920-3ec329ea9013",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
}
},
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"def sigmoid(h):\n",
" return 1.0 / (1.0 + np.exp(-h))\n",
"\n",
"h = np.arange(-10, 10, 0.1) # 定义x的范围,像素为0.1\n",
"s_h = sigmoid(h) # sigmoid为上面定义的函数\n",
"plt.plot(h, s_h)\n",
"plt.axvline(0.0, color='k') # 在坐标轴上加一条竖直的线,0.0为竖直线在坐标轴上的位置\n",
"plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted') # 加水平间距通过坐标轴\n",
"plt.axhline(y=0.5, ls='dotted', color='k') # 加水线通过坐标轴\n",
"plt.yticks([0.0, 0.5, 1.0]) # 加y轴刻度\n",
"plt.ylim(-0.1, 1.1) # 加y轴范围\n",
"plt.xlabel('h')\n",
"plt.ylabel('$S(h)$')\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEKCAYAAAAIO8L1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XmYVPWd7/H3t6s3aKDZ931XURQR\n15hS0YBRiCELSZgoZgYTNYmZ8eaG8YYkmueOTsxNTCbG0WjQaAKJEgWC4hbJRCOrrLK1rL2wQ3dD\nb9Vdv/tHFU3RVkN101Wnls/refqps/yq6tunTtenz/mdxZxziIiINJXldQEiIpKcFBAiIhKVAkJE\nRKJSQIiISFQKCBERiUoBISIiUSkgREQkKgWEiIhEpYAQEZGosr0u4Fx0797dDR482OsyRD5m69at\nAIwaNcrjSkQ+bvXq1Yeccz3O1i6lA2Lw4MGsWrXK6zJEPsbv9wPwzjvveFqHSDRmtjuWdtrFJCIi\nUSkgREQkKgWEiIhEpYAQEZGoFBAiIhKVAkJERKJSQIiISFQKCBERiUoBISIiUSkgREQkKgWEiIhE\npYAQEZGoFBAiIhJVQgLCzJ4xswNmtrGZ+WZmvzCzIjNbb2bjElGXiIg0L1FbEHOBSWeYPxkYEf6Z\nBfw6ATWJiMgZJOR+EM65v5nZ4DM0mQo855xzwPtm1tnM+jjnyhJRn4hkhmDQUR901AeDoceG0HBD\n0BF04JzDOUI/nJoWdAChecGT84Khx5Ptg87hOL19MDzvJBcxEjH59DanzTm9YeScoT0K6FPY7lwX\nyRklyw2D+gF7I8aLw9M+FhBmNovQVgYDBw5MSHEiEn/VdQ0cq66jorqeipoAFdWB8GM9lTUBKmvq\nqQ40UBNooCYQpCbQQHWggdpAkJr6U9PrG4IEgo6GoCPQEPryPxkEQXf2OlLFjz8zhhlXDIrreyRL\nQMTMOfck8CTA+PHj0+jjFklfFTUB9hyuYs+RKvYeqWJ/RS0HKms4UFnLwfDP8dr6M75GXnYW7XJ9\n5Gf7aJfrIy87i/wcH/k5WXQtyCU/OzSc7csix2dkZ2XhyzJyfIYvKyv8aOT4QtOzT/6Ex7MMDMMM\nzMLjBllmQMQ0Ts0zM4xQG2tuWvg1T7LIX+q06adG7LRGpz/HwjMHd2sf8/JvrWQJiBJgQMR4//A0\nEUkhx2vr2bqvks1lFWzZV8GWsko+Onico1WB09oV5Pro2SmfHh3zOL9vJ3p2zKNHxzy6tM+lU34O\nndplhx9z6JSfTcf8HHKzddBloiVLQCwE7jWzecDlQLn6H0SS38HKWlbuOsKKnUdYvvMIW/ZVNO5P\n75iXzeg+HZk0pg+DurVnUNf2DOzWnoFd29MxP8fbwiUmCQkIM/sD4Ae6m1kx8AMgB8A59wSwBLgZ\nKAKqgJmJqEtEWiYYdKwtPsYbH+7nrc372bb/OADtcnxcOqgL375hBBf0LeS8Ph3p17ld4+4QSU2J\nOorpS2eZ74B7ElGLiLTctv2VvLS6mJfXlrC/opbsLOPyoV357Lj+XD6kK2P6FZLj0y6gdJMsu5hE\nJMnU1QdZsqGMZ97dyfricrKzDP+onvz7zX3wj+xJYXvtJkp3CggROU1VXT3P/WM3c9/dxb6KGob1\nKGDOLecz5eK+dO+Q53V5kkAKCBEBINAQZN7Kvfzire0crKzl6uHd+I9pF/LJET3IylJfQiZSQIgI\nf99+iO+/spGdh04wYXBXnpgxjksHdfW6LPGYAkIkgx2rquPHf9nMi6uLGdK9gGfuGM91o3rq6CMB\nFBAiGetv2w7yr39cy7GqAPdcN4xvXj+C/Byf12VJElFAiGSYhqDjsbe288u3tzOyZ0eeu/Nyzu/b\nyeuyJAkpIEQyyLGqOu79/Qf8vegQ08b158efGUO7XG01SHQKCJEMUXqsmq8+s4I9h6t4ZNqFfGH8\nAPU1yBkpIEQywLb9lXz16RWcqK3nua9N4Iqh3bwuSVKAAkIkza3be4x/eno5+Tk+5t91pfobJGYK\nCJE0tm1/Jbf/dgWF7XP4/T9fwYCu8b+HgKQPXV1LJE3tOVzFjN8sJ9eXxQtfUzhIy2kLQiQNHaio\n4StPv09dQ5A/3nUlAxNw9zFJP9qCEEkztfUNzPrdag4fr+PZmRMY2auj1yVJitIWhEgacc7x/Zc3\nsnbvMZ6YMY6xAzp7XZKkMG1BiKSR59/fzR9XFfPN64czaUwfr8uRFKeAEEkTq3Yd4UeLPuSG0T35\nzsSRXpcjaUABIZIGKmsCfHveWvp1acfPpl+s+zdIm1AfhEgaeHDRh5SVV/Onr19Fp3zdClTahrYg\nRFLc0k37+NPqYu72D+fSQV28LkfSiAJCJIUdrKxl9oINXNC3E9+6YYTX5UiaUUCIpLAfLdrE8dp6\nfv7Fi8nN1p+ztC2tUSIp6t2iQyxeX8Y9/uGM0MlwEgcKCJEUVFvfwPdf2cigbu2565NDvS5H0pSO\nYhJJQU//fSc7Dp7gtzMv032kJW60BSGSYkqOVfPLt4q46fxeXDeqp9flSBpTQIikmIdf3YLDMefW\n870uRdKcAkIkhWwsKWfRulK+ds0Q+nfRJbwlvhQQIinkJ0u3Utguh1nXDvO6FMkACgiRFPGPjw6z\nbNtB7rluGIXtdDkNiT8FhEgKcM7xn0u30LtTPl+9crDX5UiGUECIpIA3PtzPB3uOcd/EETqsVRJG\nASGS5Jxz/OzN7QzpXsDnLu3vdTmSQRQQIknunW0H2VxWwd3+YWT79CcriaO1TSTJPf7XIvoW5jP1\n4n5elyIZRgEhksRW7DzCyl1HmXXtUF2tVRJOa5xIEnv8nSK6FeTyxcsGel2KZCAFhEiS2lRazjtb\nD3LnNUNol6sjlyTxFBAiSeqJZTvokJfNjCsGeV2KZCgFhEgS2ldew5INZUy/bIDOmhbPKCBEktAL\ny3cTdI7brxrsdSmSwRQQIkmmJtDA75fv4YbRvRjQVVdsFe8oIESSzOL1ZRw+UcfMqwd7XYpkOAWE\nSBJxzvHbd3cyomcHrhrWzetyJMMpIESSyOrdR9lUWsEdVw/GzLwuRzKcAkIkicx9bxed8rO57RJd\nVkO8p4AQSRKHj9eydNM+PnfpANrnZntdjogCQiRZvLSmmECD40sTBnhdigiggBBJCs455q3cy6WD\nujCiV0evyxEBFBAiSWHFziPsOHiC6Zdp60GShwJCJAnMW7mXjnnZfPqiPl6XItJIASHisfKqAEs2\nlDH1kr7qnJakooAQ8difPyimtj7IdN3zQZKMAkLEY/NW7uXCfoWM6VfodSkip1FAiHhoU2k5W/ZV\n8oXx/b0uReRjFBAiHlqwpoQcn3HLRX29LkXkYxQQIh4JNAR5ZW0JN4zuRZeCXK/LEfkYBYSIR/5n\n+0EOHa/js+N03SVJTgoIEY+8tLqErgW5+Ef19LoUkagUECIeKK8K8Mbm/UwZ25fcbP0ZSnLSmini\ngcUbSqmrDzJtnI5ekuSlgBDxwII1JYzs1YEx/Tp5XYpIsxQQIgm290gVq3cfZerF/XTXOElqCgiR\nBPvLhjIApozVuQ+S3BQQIgm2aF0pYwd0ZkDX9l6XInJGCgiRBNpx8DibSiu4VZf1lhSggBBJoMXr\nyzBDl9aQlKCAEEkQ5xwL15Vy2eCu9C7M97ockbNSQIgkyNb9lRQdOM6t6pyWFKGAEEmQRetKyTKY\nPKa316WIxEQBIZIAzjkWry/j6uHd6d4hz+tyRGKigBBJgA0l5ew+XMWt6pyWFKKAEEmARetKyfEZ\nn7pAu5ckdSggROIsGAztXvrkyB4Uts/xuhyRmCkgROJs9Z6jlJXX6NwHSTktDggzKzAzXzyKEUlH\ni9eVkpedxcTze3ldikiLnDUgzCzLzL5sZn8xswPAFqDMzD40s5+Y2fD4lymSmuobgvxlQxk3nNeT\nDnnZXpcj0iKxbEH8FRgGzAZ6O+cGOOd6AtcA7wOPmNmMONYokrKW7zzCoeN1OnpJUlIs/9JMdM4F\nmk50zh0BXgJeMjP1vIlEsWhdKQW5Pq4brftOS+o5a0CcDAczux74CnAM2AisBzY652qjBYhIpnMO\nXtu0jxvP70V+jrrtJPW0pJP6GWARod1KQ4E5wKZYn2xmk8xsq5kVmdn3osy/w8wOmtna8M8/t6A2\nkaRTXh3gWFVA116SlNWSXrPdzrmXw8N/asmbhI96+hVwI1AMrDSzhc65D5s0ne+cu7clry2SrA4f\nr6VLfjafGNHD61JEWiWWo5ieM7P7gPfN7F9b+T4TgCLn3A7nXB0wD5jaytcSSXpB5zhSVcfkMX3I\nzdbpRpKaYllz5wIG9AL+ycx2m9lCM3vIzD4f4/v0A/ZGjBeHpzU1zczWm9mLZjbgbC+6detW5s6d\nC0AgEMDv9/P8888DUFVVhd/vZ/78+QCUl5fj9/tZsGABAIcOHcLv97No0SIA9u3bh9/v57XXXgNg\n7969+P1+3nzzTQB27NiB3+9n2bJlje/t9/t57733ANi4cSN+v5+VK1cCsHbtWvx+P2vXrgVg5cqV\n+P1+Nm7cCMB7772H3+9n69atACxbtgy/38+OHTsAePPNN/H7/ezdG1psr732Gn6/n3379gGwaNEi\n/H4/hw4dAmDBggX4/X7Ky8sBmD9/Pn6/n6qqKgCef/55/H4/gUCou2ju3Ln4/f7GZfnUU08xceLE\nxvHHH3+cyZMnN44/9thjTJkypXH80UcfZdq0aY3jDz/8MNOnT28cf+ihh5gx49TBbXPmzGHmzJmN\n47Nnz2bWrFmN4/fffz/33HNP4/h9993Hfffd1zh+zz33cP/99zeOz5o1i9mzZzeOz5w5kzlz5jSO\nz5gxg4ceeqhxfPr06Tz88MON49OmTePRRx9tHJ8yZQqPPfZY4/jkyZN5/PHHG8cnTpzIU0891Tju\n9/vPuO6tWbOWuuPHuGVsH617WvcSuu7F8r0Xq1g6qd8G3j45bmbZwHnAWEJbBi3a3XQGi4A/OOdq\nzewu4Fng+qaNzGwWMAsgL09XxZTkFAgG8WUZVw7txonjlV6XI9Iq5pw7cwMzc2dpdLY2ZnYl8EPn\n3KfC47MBnHP/0Ux7H3DEOVd4pvcdP368W7Vq1RnrF0m0E7X19Bg5jh4d89i9caXX5Yh8jJmtds6N\nP1u7mE6UM7NvmtnAJm+Qa2bXm9mzwO1neY2VwAgzG2JmucB0YGGT14u8i/sUYHMMtYkknTc37yfo\nnO77ICkvlqOYJgF3An8wsyGEzoNoRyhcXgd+7pz74Ewv4JyrN7N7gaWAD3jGObfJzB4EVjnnFgLf\nMrMpQD1wBLijlb+TiKcWrSsjNzuLjvm6tIaktlj6IGqAx4HHw2dMdweqnXPHWvJGzrklwJIm0+ZE\nDM8mdDkPkZRVXh1g2bYDdCvQ1oOkvlgOc33LzC6AxrOqLwPuNbMJ8S5OJNW8vmkfgQZHtw65Xpci\ncs5i6YPo75zbBGBmVwG/AwYCc83stngWJ5JqFq0vY0DXdrpyq6SFWAKiImL4q8ATzrlZgB/43/Eo\nSiQVHT5ey7tFh3TlVkkbsQREkZl9zsx6Ap8BXgFwzh0AtKNVJOzVjftoCDrdOU7SRiwB8R3gLqAE\nWOOcew8g3GHdIY61iaSUhetKGdajgPP6dPS6FJE2EctRTPuAG80syzkXjJh1HaGbCYlkvLLyalbu\nOsJ9N4zEzLwuR6RNxNyT1iQccM69Tug8CJGMt3hdGc7BlIu1e0nShy4zKdIGFq4r5aL+hQzpXuB1\nKSJtRgEhco52HDzOhpJypujGQJJmFBAi52jhulLM0NFLknYUECLnwDnHwnWlXD6kK70L870uR6RN\nKSBEzsGm0gp2HDzBlLHR7n8lktoUECLnYOG6UnJ8xuQxvb0uRaTNKSBEWikYdCxaV8q1I3rQpUAX\n55P0o4AQaaVVu49SVl6jcx8kbSkgRFrplbUl5OdkMfG8Xl6XIhIXCgiRVgg0BFmyoYwbz+9NgS7t\nLWlKASHSCn/bdpCjVQGdHCdpTQEh0goL1pTQtSAX/6geXpciEjcKCJEWKq8K8MaH+5kyti85Pv0J\nSfrS2i3SQos3lFLXEGTauP5elyISVwoIkRZ6aXUxI3t1YEy/Tl6XIhJXCgiRFth56ARr9hzjs+P6\n68ZAkvYUECItsGBNMVkGt12iay9J+lNAiMQoGHQsWFPC1cO706uTrtwq6U8BIRKj93cepuRYtTqn\nJWMoIERiNG/FXjrlZzNJV26VDKGAEInB0RN1vLZxH7dd0o/8HJ/X5YgkhAJCJAYLPiihriHIly4f\n6HUpIgmjgBA5C+cc81bs4eIBnRndW+c+SOZQQIicxZo9R9l+4DhfmjDA61JEEkoBIXIWf1ixl4Jc\nH7dcpCu3SmZRQIicQUVNgMXrS5lycT/d90EyjgJC5AwWrC6mJhDkyxPUOS2ZRwEh0oxg0PHsP3Yz\nbmBnLuxf6HU5IgmngBBpxrLtB9l56AR3XD3E61JEPKGAEGnG3Hd30atTHpN15rRkKAWESBRFB46z\nbNtBZlw+SHeNk4ylNV8kiuf+sYtcX5bOnJaMpoAQaaKiJsCLq4u5dWxfunfI87ocEc8oIESamLdi\nD1V1Ddxx1WCvSxHxlAJCJEJNoIGn/mcnVw/vpkNbJeMpIEQivLSmmIOVtdztH+51KSKeU0CIhNU3\nBPnvZTsYO6AzVw3r5nU5Ip5TQIiE/WVDGXuOVHG3fxhm5nU5Ip5TQIgQuqzG43/9iBE9O3Djeb28\nLkckKSggRIC3thxg6/5KvuEfRlaWth5EQAEhQkPQ8ejSrQzu1p5bx+qeDyInKSAk4y1cV8LW/ZX8\n202jdFkNkQj6a5CMVlcf5Kevb+OCvp349IV9vC5HJKkoICSj/X75boqPVvPdSaPV9yDShAJCMtbx\n2np++XYRVw7txrUjuntdjkjSUUBIxnpy2UccPlHHdyeN0nkPIlEoICQj7Tp0gieW7WDqxX25ZGAX\nr8sRSUoKCMk4zjl+sHATudlZPHDzeV6XI5K0FBCScZZu2s+ybQf5zo0j6dkp3+tyRJKWAkIySlVd\nPQ8u2sTo3h25/cpBXpcjktQUEJJRfvbGNkrLa3joM2PI1klxImekvxDJGO/vOMxv/r6Tr1w+kMsG\nd/W6HJGkp4CQjFBRE+Df/riOQV3b88Cn1TEtEotsrwsQSYQfLfyQsvJqXvzGVbTP1WovEgttQUja\ne3VDGS+tKeae64YzTuc8iMRMASFprehAJf/rxfWM7V/It24Y4XU5IilFASFpq7w6wL88t5r8nCx+\nPeNSXcpbpIW0M1bSUjDo+M78tew9UsXv/+UK+nZu53VJIilH/1JJWnpk6Rbe3nKAH0y5gAlDdEir\nSGsoICTt/Pqdj/jvZTuYccVAZlw+0OtyRFKWAkLSyvPv7+aR17Yw9eK+/GjKGF3GW+QcKCAkbSxY\nU8z3X9nIDaN78ujnx+LTHeJEzok6qSUtPP33nTy0+EOuGtaNX31lnI5YEmkDCghJac45HnltK08s\n+4hJF/Tm59MvJj/H53VZImlBASEpq6qunn9fsIGX15bylcsH8uDUMdqtJNKGFBCSkooOHOfuF1az\n/cBx7r9pJPdcN1wd0iJtTAEhKcU5xytrS3ngzxvIy/Hx7MwJXDuyh9dliaQlBYSkjNJj1Xz/5Y28\nteUAlw7qwn99+RL6FOoMaZF4UUBI0qurD/LC8t08unQrQQf/59PnMfPqIepvEIkzBYQkrWDQsWh9\nKT99fRt7jlTxiRHd+b+3XciAru29Lk0kIyggJOnU1QdZvL6UJ/+2gy37KhnduyO/veMy/KN6qCNa\nJIEUEJI0ysqreWl1Mb97fzf7K2oZ0bMDP/viWKaO7UeWdieJJJwCQjxVXhXgzc37+fMHJbz70SGc\ng2uGd+eRaRfxyZHaYhDxkgJCEqoh6Niyr4J/fHSYtzYfYMWuIzQEHf27tOOb149g2rh+DOpW4HWZ\nIoICQuKsvDrAlrIK1u49xvKdR1i56wiVNfUAjOjZgbuuHcqN5/dibP/O2o0kkmQSFhBmNgl4DPAB\nv3HOPdxkfh7wHHApcBj4onNuV6Lqk9YLBh0Hj9ey+3AVuw+fYNfhE2wpq2TLvkpKjlU3thvao4Bb\nLurL5UO6ctmQrvTTXd5EklpCAsLMfMCvgBuBYmClmS10zn0Y0exrwFHn3HAzmw48AnwxEfXJx9XV\nB6moCVBRHaCypp7y6gCHT9RyoKKWA5W1HKys5UBlDQcqayk9Vk1NINj4XF+WMaxHAZcO6sKMKwYx\nuk9HxvQtpEfHPA9/IxFpqURtQUwAipxzOwDMbB4wFYgMiKnAD8PDLwL/ZWbmnHNtXUxNoIETtaHd\nHA5wDhwuNNJ0WuNw6DIPkdU02yZiPpx6TuTrNk5rMh5tWtA5GoKO+uCpx2DjePDU9IbQY4MLz2sI\nzasJNFATCFITaKC2PvRYc/Ix0EBtIEhNfQNVdQ1UVAeoqAmc9oXfVLscHz075dGzYx6je3fk+lE9\nGdStPQO7FTCwa3v6dW5HbrYuty2S6hIVEP2AvRHjxcDlzbVxztWbWTnQDTjU1sXMfW8XD7+6pa1f\nNqmZQX62j/ycLPJzfOTn+MjLzmp87NI+l36dfRS2y6FTuxw65WfTqV0OHfOz6ZQfmtatIJeenfIp\nyPXp6CKRDJByndRmNguYBTBwYOvuN3zN8O78aMoFnPyOs9ALY6GH8DTDLDwvPN0ITTg1rclz7NTz\naK5NxOueahc5zRprMjv1mtk+w5dl+OzkcBbZWaFpJx99jeNZp6b7jPxsHzk+05e6iLRIogKiBBgQ\nMd4/PC1am2IzywYKCXVWn8Y59yTwJMD48eNbtftpTL9CxvQrbM1TRUQyRqJ2FK8ERpjZEDPLBaYD\nC5u0WQjcHh7+HPB2PPofREQkNgnZggj3KdwLLCV0mOszzrlNZvYgsMo5txB4GvidmRUBRwiFiIiI\neCRhfRDOuSXAkibT5kQM1wCfT1Q9IiJyZjoWUUREolJAiIhIVAoIERGJSgEhIiJRKSBERCQqBYSI\niESlgBARkagUECIiEpUCQkREolJAiIhIVAoIERGJSgEhIiJRKSBERCQqS+VbLpjZQWB3K5/enTjc\nzrSNJGttqqtlVFfLJWtt6VbXIOdcj7M1SumAOBdmtso5N97rOqJJ1tpUV8uorpZL1toytS7tYhIR\nkagUECIiElUmB8STXhdwBslam+pqGdXVcslaW0bWlbF9ECIicmaZvAUhIiJnkNYBYWafN7NNZhY0\ns/FN5s02syIz22pmn2rm+UPMbHm43Xwzy41DjfPNbG34Z5eZrW2m3S4z2xBut6qt62jmPX9oZiUR\n9d3cTLtJ4eVYZGbfS0BdPzGzLWa23sz+bGadm2mXkGV2tt/fzPLCn3NReH0aHK9aIt5zgJn91cw+\nDP8NfDtKG7+ZlUd8vnPiXVfEe5/xs7GQX4SX2XozG5eAmkZFLIu1ZlZhZvc1aZOQZWZmz5jZATPb\nGDGtq5m9YWbbw49dmnnu7eE2283s9nMqxDmXtj/AecAo4B1gfMT084F1QB4wBPgI8EV5/h+B6eHh\nJ4BvxLnenwJzmpm3C+ie4OX3Q+D+s7TxhZffUCA3vFzPj3NdNwHZ4eFHgEe8Wmax/P7A3cAT4eHp\nwPwEfHZ9gHHh4Y7Atih1+YHFiVynYv1sgJuBVwEDrgCWJ7g+H7CP0PkCCV9mwLXAOGBjxLT/BL4X\nHv5etPUe6ArsCD92CQ93aW0dab0F4Zzb7JzbGmXWVGCec67WObcTKAImRDYwMwOuB14MT3oW+Ey8\nag2/3xeAP8TrPeJkAlDknNvhnKsD5hFavnHjnHvdOVcfHn0f6B/P9zuLWH7/qYTWHwitTzeEP++4\ncc6VOefWhIcrgc1Av3i+ZxubCjznQt4HOptZnwS+/w3AR8651p6Ie06cc38DjjSZHLkeNfd99Cng\nDefcEefcUeANYFJr60jrgDiDfsDeiPFiPv7H0w04FvFFFK1NW/oEsN85t72Z+Q543cxWm9msONbR\n1L3hTfxnmtmkjWVZxtOdhP7TjCYRyyyW37+xTXh9Kie0fiVEeJfWJcDyKLOvNLN1ZvaqmV2QqJo4\n+2fj9Xo1neb/WfNqmfVyzpWFh/cBvaK0adPllt3aJyYLM3sT6B1l1gPOuVcSXU80Mdb4Jc689XCN\nc67EzHoCb5jZlvB/GXGrDfg18BChP+aHCO0Cu/Nc3/Nc6zq5zMzsAaAeeKGZl4nLMkslZtYBeAm4\nzzlX0WT2GkK7UI6H+5deBkYkqLSk/WzCfY1TgNlRZnu5zBo555yZxf0Q1JQPCOfcxFY8rQQYEDHe\nPzwt0mFCm7XZ4f/6orVpkxrNLBv4LHDpGV6jJPx4wMz+TGjXxjn/QcW6/MzsKWBxlFmxLMs2r8vM\n7gBuAW5w4Z2vUV4jLsusiVh+/5NtisOfdSGh9SuuzCyHUDi84Jxb0HR+ZGA455aY2eNm1t05F/dr\nDsXw2cRlvYrRZGCNc25/0xleLjNgv5n1cc6VhXe3HYjSpoRQP8lJ/Qn1wbZKpu5iWghMDx9dMoTQ\nfwArIhuEv3T+CnwuPOl2IF5bJBOBLc654mgzzazAzDqeHCbUSbsxWtu21GSf723NvOdKYISFjvjK\nJbRpvjDOdU0CvgtMcc5VNdMmUcsslt9/IaH1B0Lr09vNhVpbCfdxPA1sds79v2ba9D7ZF2JmEwh9\nHyQiuGL5bBYCXw0fzXQFUB6xeyXemt2a92qZhUWuR819Hy0FbjKzLuFdwjeFp7VOvHvjvfwh9KVW\nDNQC+4GlEfMeIHT0yVZgcsT0JUDf8PBQQsFRBPwJyItTnXOBrzeZ1hdYElHHuvDPJkK7WRKx/H4H\nbADWh1fOPk1rC4/fTOgomY8SUVv489gLrA3/PNG0rkQus2i/P/AgoQADyA+vP0Xh9WloApbRNYR2\nDa6PWE43A18/ua4B94aXzTpCnf1XJWi9ivrZNKnNgF+Fl+kGIo5CjHNtBYS+8AsjpiV8mREKqDIg\nEP4O+xqhfqu3gO3Am0DXcNvxwG8inntneF0rAmaeSx06k1pERKLK1F1MIiJyFgoIERGJSgEhIiJR\nKSBERCQqBYSIiESlgBBpQ2Z77I1iAAAAnUlEQVQ2OPIKnCKpTAEhIiJRKSBE2p7PzJ6y0H0YXjez\ndl4XJNIaCgiRtjcC+JVz7gLgGDDN43pEWkUBIdL2djrnTt4ZcDUw2MNaRFpNASHS9mojhhtIg6sm\nS2ZSQIiISFQKCBERiUpXcxURkai0BSEiIlEpIEREJCoFhIiIRKWAEBGRqBQQIiISlQJCRESiUkCI\niEhUCggREYnq/wNXSVXIOwzDJAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "S5Jpj5cqgWE0",
"colab_type": "text"
},
"source": [
"## 多分类-iris数据集"
]
},
{
"cell_type": "code",
"metadata": {
"id": "jF0bTnwIRdgd",
"colab_type": "code",
"outputId": "6e9655f1-2f4a-4498-a074-478c35b36abf",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
}
},
"source": [
"#iris数据集散点图\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None) # 加载Iris数据集作为DataFrame对象\n",
"X = df.iloc[:, [0, 2]].values # 取出2个特征,并把它们用Numpy数组表示\n",
"\n",
"plt.scatter(X[:50, 0], X[:50, 1],color='red', marker='o', label='setosa') # 前50个样本的散点图\n",
"plt.scatter(X[50:100, 0], X[50:100, 1],color='blue', marker='x', label='versicolor') # 中间50个样本的散点图\n",
"plt.scatter(X[100:, 0], X[100:, 1],color='green', marker='+', label='Virginica') # 后50个样本的散点图\n",
"plt.xlabel('petal length')\n",
"plt.ylabel('sepal length')\n",
"plt.legend(loc=2) # 把说明放在左上角,具体请参考官方文档\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEKCAYAAAARnO4WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XucVXW9//HXZxgIRkzw0skgwI6J\nIXfQUDsOgpeTetCOkhle0PyR2g8Qfl0oK6aLv+rYI0RLDVOx5IQeyk73MnW8/ToqEHjBMDNQ8AKi\njKCiwHx+f6y9mT3DzKy1915r39b7+Xisx7DWXpfPXtlnf/dnf7/fZe6OiIjUvrpyByAiIqWhhC8i\nkhJK+CIiKaGELyKSEkr4IiIpoYQvIpISSvgiIimhhC8ikhJK+CIiKVFf7gByHXjggT5kyJByhyEi\nUjVWrFjxirsfFGXfikr4Q4YMYfny5eUOQ0SkapjZ+qj7qqQjIpISSvgiIimhhC8ikhKJ1fDNbChw\ne86mDwBfdfer8znPzp072bBhAzt27Ig1vjTq3bs3AwcOpGfPnuUORUTKILGE7+5rgdEAZtYD2Ajc\nme95NmzYwL777suQIUMws5ijTA93Z8uWLWzYsIFDDjmk3OGISBmUqqQzGfi7u0f+NTlrx44dHHDA\nAUr2RTIzDjjgAH1TEkmxUiX8TwA/LfRgJft46D6KpFviCd/MegFTgP/q4vUZZrbczJZv3rw56XBE\nRIo2cfFEJi6eWO4w8laKFv5HgZXu/nJnL7r7Incf7+7jDzoo0mCxirV48WJeeOGFcochItKpUoy0\nPYciyjnVZPHixQwfPpz3ve995Q5FRBKQbdXft/6+duvN05vLE1CeEm3hm9k+wInAz5O8TjtLlsCQ\nIVBXF/xdsqSo073xxhuceuqpjBo1iuHDh3P77bezYsUKGhsbGTduHCeffDIvvvgiy5YtY/ny5Uyb\nNo3Ro0fz1ltvcffddzNmzBhGjBjBRRddxNtvvw3AvHnzGDZsGCNHjuSzn/0sAL/61a/48Ic/zJgx\nYzjhhBN4+eVOvxCJiBTO3StmGTdunHe0Zs2avbZ16bbb3Bsa3KFtaWgIthdo2bJlfvHFF+9Z37p1\nqx999NG+adMmd3dfunSpX3jhhe7u3tjY6I8++qi7u7/11ls+cOBAX7t2rbu7n3feeb5gwQJ/5ZVX\n/LDDDvPW1lZ3d3/ttdfc3f3VV1/ds+3GG2/0uXPnFhxzd/K6nyLSqcZbGr3xlsZyh+Hu7sByj5hj\na2uk7RVXwJtvtt/25pvB9gKNGDGCu+66iy984Qs88MADPP/88zzxxBOceOKJjB49mm9+85ts2LBh\nr+PWrl3LIYccwmGHHQbABRdcwP33389+++1H7969+dSnPsXPf/5zGhoagGC8wcknn8yIESO46qqr\nePLJJwuOWUSkMxU1W2bRnnsuv+0RHHbYYaxcuZLf/va3fPnLX2bSpEkcccQR/PnPfy7ofPX19Tzy\nyCPcfffdLFu2jO9///vcc889zJw5k7lz5zJlyhSam5tpamoqOGYRSVa11Ow7qq0W/qBB+W2P4IUX\nXqChoYFzzz2Xz33uczz88MNs3rx5T8LfuXPnntb4vvvuy7Zt2wAYOnQo69at45lnngHgJz/5CY2N\njWzfvp2WlhZOOeUUFixYwOrVqwFoaWlhwIABANx6660Fxysiyev37X70+3a/coeRt9pq4V95JcyY\n0b6s09AQbC/Q448/zuc+9znq6uro2bMn119/PfX19cyaNYuWlhZ27drF5ZdfzhFHHMH06dO55JJL\n6NOnD3/+85+55ZZbmDp1Krt27eLII4/kkksu4dVXX+X0009nx44duDvf+973AGhqamLq1Kn079+f\nSZMm8Y9//KPYuyEi0o4FNf/KMH78eO/4AJSnnnqKD33oQ9FPsmRJULN/7rmgZX/llTBtWsyRVq+8\n76eI7JFt1be83QLAfu/aD4Ct87aWLSYzW+Hu46PsW1stfAiSuxK8iBSh2vrXR1V7CV9EJCHZlny2\npV/Oln0hlPBFRDKqfSRtGCV8EZE8VVvLPksJX0QkI9uSr7WWfVZt9cMXEZEuKeGXwVe/+lX+9Kc/\n5X1cc3Mzp512WgIRiUiu5unNNde6hxos6bhD7oOdOq6XLo7MZEV1e3+mfv3rXy9JDLt27aK+vub+\nJxapCeUoG9VUC7+pCebMCZI8BH/nzAm2F2revHn84Ac/yLlGE9/97ne56qqrOPLIIxk5ciTz588H\nYN26dQwdOpTzzz+f4cOH8/zzzzN9+nSGDx/OiBEjWLBgAQDTp09n2bJlADz66KMcc8wxjBo1iqOO\nOopt27axY8cOLrzwQkaMGMGYMWO4995794rr1Vdf5YwzzmDkyJFMmDCBxx57bE985513Hsceeyzn\nnXde4W9cRGpOzTT/3GHrVli4MFhfsCBI9gsXwuzZhbf0zz77bC6//HI+85nPAHDHHXfwhS98gYce\neohHHnkEd2fKlCncf//9DBo0iL/97W/ceuutTJgwgRUrVrBx40aeeOIJALZubf/L/jvvvMPZZ5/N\n7bffzpFHHsnrr79Onz59WLhwIWbG448/zl//+ldOOukknn766XbHzp8/nzFjxvCLX/yCe+65h/PP\nP59Vq1YBsGbNGh588EH69OmT/xsWkUSVs+tnzSR8syDJQ5Dks4l/9uxge6FlnTFjxrBp0yZeeOEF\nNm/eTP/+/Xn88cf54x//yJgxYwDYvn07f/vb3xg0aBCDBw9mwoQJAHzgAx/g2WefZebMmZx66qmc\ndNJJ7c69du1aDj74YI488kgA3v3udwPw4IMPMnPmTAAOP/xwBg8evFfCf/DBB/nZz34GwKRJk9iy\nZQuvv/46AFOmTFGyl5pVqz1oSqFmEj60Jf1ssofikn3W1KlTWbZsGS+99BJnn30269ev54tf/CKf\n/vSn2+23bt069tlnnz3r/fv3Z/Xq1fzhD3/ghhtu4I477uDmm28uLpgIcmMQkcpSzq6fNVXDz9bs\nc+XW9At19tlns3TpUpYtW8bUqVM5+eSTufnmm9m+fTsAGzduZNOmTXsd98orr9Da2sqZZ57JN7/5\nTVauXNnu9aFDh/Liiy/y6KOPArBt2zZ27drFv/zLv7Ak82jGp59+mueee46hQ4e2OzZ3n+bmZg48\n8MA93xBEatHExROZuHgi962/j/vW37dnXaKrmRZ+Ntlna/a5NXworqV/xBFHsG3bNgYMGMDBBx/M\nwQcfzFNPPcXRRx8NQN++fbntttvo0aNHu+M2btzIhRdeSGtrKwDf+ta32r3eq1cvbr/9dmbOnMlb\nb71Fnz59+NOf/sRll13GpZdeyogRI6ivr2fx4sW8613vandsU1MTF110ESNHjqShoUFz6ItUmXKU\npGpqeuSmpuCH22xyz34I9OtXXE+dWqLpkaXaqYbfXmqnR25qat8bJ1vTL0c/fBGRSlNTCR/2Tu5K\n9iK1RS37wtXUj7YiUt3i+CG2FD/mVusPxkr4IiIpkWhJx8z6AT8ChgMOXOTuf07ymiJSfeIYfVqK\nEazV/oCUpGv4C4Hfu/tZZtYLaEj4eiIVp9qSgtSuxBK+me0HHAdMB3D3d4B3krpeUo4//njmzZvH\nySefvGfb1VdfzerVq9m2bdueSdCiuvjii5k7dy7Dhg3rcp8bbriBhoYGzj///ILjFqkm2Q/D7LNi\nC/lwLMUI1mp/QEqSLfxDgM3ALWY2ClgBzHb3NxK8ZuzOOeccli5d2i7hL126lP/4j//guOOO22v/\nsCmJf/SjH4Ve85JLLiksWKko1f71v5Sy96bl7ZZ267pX8UryR9t6YCxwvbuPAd4A5nXcycxmmNly\nM1u+efPmWC4c5y/oZ511Fr/5zW94553gy8m6det44YUXeP/738/w4cMBWLx4MVOmTGHSpElMnjyZ\n1tZWLrvsMg4//HBOPPFETjnllD3fBCZOnEh2cFnfvn254oorGDVqFBMmTODll18G2qZgBnjmmWc4\n4YQTGDVqFGPHjuXvf/8727dvZ/LkyYwdO5YRI0bw3//937G8V0m3WundUoqHl1TrA1KSbOFvADa4\n+8OZ9WV0kvDdfRGwCIKRtgnGU5D999+fo446it/97necfvrpLF26lI9//ONYhw7+K1eu5LHHHmP/\n/fdn2bJlrFu3jjVr1rBp0yY+9KEPcdFFF+117jfeeIMJEyZw5ZVX8vnPf54bb7yRL3/5y+32mTZt\nGvPmzeNjH/sYO3bsoLW1lV69enHnnXfy7ne/m1deeYUJEyYwZcqUvWKS8qr2r/+lpHtVGoklfHd/\nycyeN7Oh7r4WmAysSep6kNxX6GxZJ5vwb7rppr32OfHEE9l///2BYOriqVOnUldXx3vf+16OP/74\nTs/bq1evPY8sHDduHHfddVe717dt28bGjRv52Mc+BkDv3r0B2LlzJ1/60pe4//77qaurY+PGjbz8\n8su8973vLep9Sjqpd0t6JN1LZyawJNND51ngwoSvl4jTTz+dOXPmsHLlSt58803GjRvHunXr2u1T\nyJTEPXv23NMq79GjB7t27Yp03JIlS9i8eTMrVqygZ8+eDBkyhB07duR9fSkNJbXodK+SlWjCd/dV\nQKRJfeKQ1NfCvn37cvzxx3PRRRdxzjnnhO5/7LHHcuutt3LBBRewefNmmpub+eQnP5n3dffdd18G\nDhzIL37xC8444wzefvttdu/eTUtLC+95z3vo2bMn9957L+vXry/kbUkVKfa/6e6Or6TeLWr5J0sj\nbSM655xzWL16daSEf+aZZzJw4ECGDRvGueeey9ixY9lvv/0Kuu5PfvITrrnmGkaOHMkxxxzDSy+9\nxLRp01i+fDkjRozgxz/+MYcffnhB5xaRdKmp6ZEryfbt2+nbty9btmzhqKOO4qGHHqqIGnu13s+0\n6lj7bhzcCERvARd7fKlUS5yVKLXTI1eS0047ja1bt/LOO+/wla98pSKSvUgxVG6pfkr4CWlubi53\nCFIDiq2vZ/ev/3p9QceXirpllkZVJHx3Vx/zGFRS+U5KIztVwW7f3W5967ytkc+hLpW1o+ITfu/e\nvdmyZQsHHHCAkn4R3J0tW7bs6csv0cSR3MKSbJQknJbkmpb3WS4Vn/AHDhzIhg0biGvahTTr3bs3\nAwcOLHcYUkLZD5FsSSefln2Wyi21o+ITfs+ePTnkkEPKHYakTBxljGzLPTshWMeWfNjrccjGnS3p\nKGmnW8UnfBGpDPqQqH4V3w9fpJxKUcPPllt2fbXrqTWSHGkb1zWkPPLph6+RtiIiKaEWvkiZRBld\nWooRqBrlWt3UwhcpoVI81KMSpOV91jL9aCtSJlG6O1bSTJZS/ZTwRQqUlhGoaXmfaaCEL1Jmq15a\nFbpPKZKrEnjtU8IXKVBaSiFpeZ9poIQvUialGGkrkksJX6RIaWnxpuV91jIlfJEy6TinTnct+1KM\ntJXap374IiIpoRa+pJY75D5ioeN6qURp2RfaJVJdKiWXWvhSteq/Xr9n4rHOdDcytKkJ5swJkjwE\nf+fMCbbHrVZGqNbK+0gztfAlddxh61ZYuDBYX7AgSPYLF8Ls2eVr6Xcm2xLP1vkLfaatWvYCCSd8\nM1sHbAN2A7uiTvAj0p1sqz77UI+O0wuHlTHMgiQPQZLPJv7Zs4PtcSX7OMop2WOyXTcLOUfH+RHz\n/UBTWah2lKKFf7y7v1KC60iNSTKxZJP+wpbgGixujjXZV4qmpuDbzL0LmjFrK13165dM+Uoqm0o6\nUnWyLfmuHhwSpYyRTXy55syJt4VfbDkm95hCW/ZxlK5UFqodSSd8B/5oZg780N0XJXw9qQFJlxDc\n4f1fmcjGFmBIcI0BV0xk4UZgTnwt/TjKMcWIs3RVbFlIKkPSCf8j7r7RzN4D3GVmf3X3+3N3MLMZ\nwAyAQYMGJRyOVIo4kl93jwTs7txmUF8PAwbAxsy2Qw8N/varb5/Iiolz3TrYtQvo2bbtmWeCUkq+\n5ZRC79Oe0tXCtm35JnuVhWpHognf3Tdm/m4yszuBo4D7O+yzCFgEwROvkoxHqkMpSgjrmppxh+Nv\nbbtGnK1WdzhjazMLF0Kvr/ajTx8YvaqZ+xbC1hL2BCq2dFVNPZokXGIJ38z2AercfVvm3ycBX0/q\nelIdKqnHR8dE1VnLvtA4zWDV6IkMuAI21rXwztvBD8QDroAF32guabLPJufcZA3Rkn6pejRJaSTZ\nwv8n4E4L/ouoB/7T3X+f4PWkxhTzIRB1FG3SHzSHHgob17dfL1WSNAvKLrnJOZu8+/Xr/v7krsdR\nFpLKoIeYS1kk2bLP1pyzSam7mnNYHFHi7GqfPS3snK6f5WgZh334hd2v3G8KWWrhV45YH2JuZsea\n2V1m9rSZPWtm/zCzZ4sPUyR+uTXn7NQJ2WS1devevU2SjCN73QEDoLExSJK5cZVKd6WrsPvV2tq+\nLNTaWr73IcWLUtK5CZgDrCAYMStStKRKKVFrzlFq9K2te6/X5TSRujtHtpwyaxZc/Y223i3ue5dT\nkhalXANd3684ykJSGaJMntbi7r9z903uviW7JB6ZSIFyk1JWvuWHiRNh3LggyUPwd9y4YHs1iTJJ\nXNj9ampqv57dP/ccpZyMTorg7p0uwNjM8m3gKuDonG1juzqumGXcuHEuUqzWVvfZs7Pt6WCZPTvY\n3lHjLY3eeEtju227d7uPHh0cN3p05+th58iNIXvtjutJixpDPvermOtIMoDlHjHHdpfw7+1muSfq\nBfJZlPClWPkmn86StXuQ1EeNap8ER43aO9l3d45iE2nueQpdD4shrmQd13uV/OWT8EN76ZjZB9z9\n2bBtcVAvHYlDPr10ujvHa6/BNde0bZs1C/r3z69M4d6+7t/aWtgo167eS5T3GhZDHPcrjvcqhcmn\nl074VwBY2cm2FVE/UfJZ1MKXuIS1gsOOnTWrfWs1u8yaVbpWb1jre/fu8NZ51BiKuV9xvFcpHDGV\ndA4HzgT+Dvx7zjIdeDLqBfJZlPClEnRWzgkr63RUqlJJd6+XqrauGn555ZPwu+uWORQ4DegH/FvO\n9m3A/4r8fUNqjhfZ/S7K8cVeI4qO3Syz63V1QTlj1ChYvbrt9VGjgu25x3QVZ9TujGHvM2yUa9jr\nUbtUFiOfrptSZmGfCMDRUT89il3Uwu/6B8BKMX9+5y3M+fPjO77Ya0TR2Ni+x022J05jY9s1O5Z1\nOpZzosTZXakk6vGFtvCjxBCnUl1H2iOPFn6UfvifNLNrOizfMLPTk/0okkrjIaMyPWTUZZTji71G\nFK2t0NICq1a19bUfNy5Yb2mB3buDa15zTfvRpddc0xZT1Di7GuUa9V50N8o16ijY7kbaxqlU15Ei\nhH0iEExdfD8wM7M0A7cAvwSujvrJEmVJcws/27KnCaeJim3pF9uijHp80j8A5vatzy65Lf44Wt9x\n3IuwOObPb//NI/vNJOq3DKl+xNwt83+AY92DJ0abWT3wAPAR4HF3HxbXh0+au2V2HKbfOLgRqMzH\nyXk33e/i6CYYdZ9itbZCjx5t67t3R6vPR40zznvRVRzZ7qNXX912jcsvb+s+GleXS6lcsU6eBvQH\n+uas7wPsn/kAeLuA+KQTzdObaZ7eTOPgRhoHN+5ZrzTZhJErnzJHd8dHuUZcsmWcXLlTKUB4iaIU\n96K7OLLXyC01ZUtR2YnPKmEiOakgYV8BgE8B/yAo4ywGngUuJkj8V0X9KhFlSXNJJ6tSSznu0brf\nFdtNsBRd/PKdOqFc9yKKOH7UlepGnCUdADM7mODxhACPuvsL8X/0pLukUy2KLVNEOb4UZYiJE4Mf\naFesCGLNtvj32w+am+M7R3f3Io4Ywq4R5XWpbrGOtM18IAwAjgGOyy5RP1HyWdTCrw5x/Cjb3fmi\n7lOsji35KC37LLXwpVIQx0jbPTvAd4B1wG+AX2WWX0a9QD6LEn51S9uIyzjLV4Uk4zimXpDql0/C\nj/IAlDOAoe6uH2ilW3GNLoWuR8FGFeUaxYpjlGsxz4oNu9/ZEcMaASt7hH0iAL8D+kb9BClmUQu/\nNhQ7ujRsFGyYUozUzT1vkv3wo8ZRzLpUN2IeafsmsMrMfpg72jbJDyGpbsWMLg0bBZvbbbIzUa4R\nh9zzFjLKNerxUYR1H9UIWMmKUtL5ZWYRKUq2pODe/vmps2a1lRzMgl4rY8cGST47MGrUqLbeLNB1\nySbqM23jeC/FlEs04ZiUQ9RumX2AQe6+Nslg1C2z9kV5sEjYPnGNYI1Dsb8VlOK3BqltsY60NbN/\nA1YBv8+sjzYztfglb+57J3II1l97ra2S3d0+UUaPZrflinukblax5RKVW6SUotTwmwgGXW0FcPdV\nwAcSjEmqXMc6e1jdPZc73Hdf569lty9YELT4Fy4MWvELF7aVhSB6bbzjB0C+6yLVJkrC3+nuLR22\nRf6/sJn1MLO/mNmv8wtNqtHEie3npMn+6DpxYtB67d8/SM65suUas/YPH8mV+/CRr32t82t/7Wtd\n18Znz25fG29qav8BkP1WkFtW6u51kWoUJeE/aWafBHqY2QfN7Frg/+VxjdnAUwVFJ1UlSg+b+fM7\nPzZ3+733QmNj+9cbG4PtUcpCTU2dPxUqt77fXVlIk45JzQrrtwk0AFcCjwLLM//uHaXPJzAQuBuY\nBPw6bH/1w69+3c0zH8fkabt3l+YB45qSQKoFcU+eVigzWwZ8C9gX+Ky7n9bJPjOAGQCDBg0at379\n+sTikdL0Culunvmw+duz+3TXC6epCV59Fa69tu0aM2fC/vvnV3IJ68lTqp4+IsXIp5dOl/3wzexX\nQJefBu4+JSSI04BN7r7CzCZ2c55FBE/VYvz48fqynKBSzELZ1TzzuX3oo8SZ+0GULcnkDlp64IH2\nxzzwAEzp9r/I9rrqydPx3nT1ukhV6qrpDzR2t4R9dSBo2W8gmHjtJYIRu7d1d4xKOsmphHnmd+0q\nPoZSzGWvScekmhDH5Gnu3kXnuMgfJF8EvgiQaeF/1t3PLeacUrhSjECtqwvmch89uq1Fv2JF2xzv\nPXoUH0NdXVtLPnck7ujRwfYo3yI06ZikVaI1/D0XaUv4e9Xwc2mkbfKSrktn6+sLF7aVRmbPbl9f\njyOGsOfRRhH2e0Ypfu8QKVbcz7Qtmrs3hyV7SV5Xdem4PvOz3R2vvbZ9d8Zrr413FKw7zJ3bftvc\nufm/D006JqkTtfZTikU1/OSU6uEkra17d5vMdpeMI4a0PWRFJAxx1PCL7aUjlaVUszN2Nwq2qan4\nGDTLpEjhuqzhm1ljpy9keJE/6nZGNfzkJVmXzvap7zgKFoLpE3L73hcbg+rrIoFY+uEnkdCl/Gql\nLl0r70OklKJMj/xBM1tmZmvM7NnsUorgpLpEmRxNk5KJlE+UXjq3ANcDu4DjgR8DtyUZlFSv7iZH\ny/bi0aRkIuURJeH3cfe7Cer96929CTg12bCkGmUT+DXXtJ+L/ppr2rpiZqcqzp3LPu7HD4pI56I8\n0/ZtM6sD/mZm/xvYCPRNNizpTKX/UBm1B82CBW2jbLPrHd9Hpb9XkWoUJeHPJpgieRbwDYKpji9I\nMijZWykmPotDlInPwiYlq5b3KlJtQks67v6ou28HXgdmufu/u/v/JB+aZFVb7burHjS5cXf1+MFq\ne68i1SS0hW9m4wl+uN03s94CXOTuKxKOTTJKMfFZKeRT8oHqfq8ilSh08jQzewz4jLs/kFn/CHCd\nu4+MOxgNvOpe0hOflUqU+nytvFeRpMU9edrubLIHcPcHCbpoSgklPfFZKYUNmqql9ypSSaIk/PvM\n7IdmNtHMGs3sOqDZzMaa2dikA0yTjgmt4+Ck7mrftSJN71Wk1KL00hmV+dtxSM0YgsnVJsUaUUqF\n9UxZtSp4yMf3vhe8/r3vwX33BdtrqdShydFEkhOa8N39+FIEkma5PVMgSHAdW7mjRwfrc+cGr8+d\nGyT72bNrr496WNdOESlMlB9t/wn4v8D73P2jZjYMONrdb4o7mDT/aJtbysjKbeWGvS4i6ZTPj7ZR\nEv7vCLplXuHuo8ysHviLu48oPtT20pzwIbxninquiEhHcffSOdDd7wBaAdx9F7C7iPikE2E9U9Rz\nRUSKFSXhv2FmB5B5+pWZTQBaEo0qZcJ6prS2queKiBQvSi+ducAvgX82s4eAg4CzEo0qZcJ6ptTV\nqeeKiBQvtIYPkKnbDwUMWOvuO5MIRjX87kegagZJEeko1hq+mU0lmBP/SeAM4HYNuEpG2AhUPdZP\nRIoRpYb/FXfflplDZzJwE8ETsKQCdTVaV0Qk0lw6mb+nAje6+2+AXmEHmVlvM3vEzFab2ZNm9rVi\nApVwel6siHQnSsLfaGY/BM4Gfmtm74p43NvAJHcfBYwG/jXTw0cSoHnkRSRMlF46Hwf+Ffiuu281\ns4OBz4Ud5MGvwdszqz0zi9JOQmplznwRSU6kXjoFn9ysB7ACOBT4gbt/oZN9ZgAzAAYNGjRu/fr1\nicWTBhqNK5IucY+0LZi773b30cBA4CgzG97JPovcfby7jz/ooIOSDKfmaTSuiHQn0YSf5e5bgXsJ\nSkOSAM0jLyJhotTwC2JmBwE7M3X/PsCJwHeSul7aaR55EQmTWMIHDgZuzdTx64A73P3XCV4v9TSP\nvIh0J7GE7+6PETwVS0pIo3FFpCslqeGLiEj5KeGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikhBK+\niEhKKOGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikhBK+iEhKKOGLiKSEEr6ISEoo4YuIpIQSvohI\nSijhi4ikhBK+iEhKKOGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikRGIJ38zeb2b3mtkaM3vSzGYn\ndS0REQlXn+C5dwH/x91Xmtm+wAozu8vd1yR4TRER6UJiLXx3f9HdV2b+vQ14ChiQ1PVERKR7Janh\nm9kQYAzwcCevzTCz5Wa2fPPmzaUIR0QklRJP+GbWF/gZcLm7v97xdXdf5O7j3X38QQcdlHQ45bNk\nCQwZAnV1wd8lS6r7OiJSdZKs4WNmPQmS/RJ3/3mS16poS5bAjBnw5pvB+vr1wTrAtGnVdx0RqUrm\n7smc2MyAW4FX3f3yKMeMHz+OTP/wAAAMA0lEQVTely9fnkg8ZTVkSJB8Oxo8GNatq77riEjFMLMV\n7j4+yr5JlnSOBc4DJpnZqsxySoLXq1zPPZff9kq/johUpcRKOu7+IGBJnb+qDBrUect70KDqvI6I\nVCWNtC2FK6+Ehob22xoagu3VeB0RqUpK+KUwbRosWhTU0s2Cv4sWxf9D6rRpcMEF0KNHsN6jR7Ae\n93Uuuwzq64P3Ul8frMdNvY1E4ufuFbOMGzfOpQi33ebe0OAObUtDQ7A9Lpde2v782eXSS+O7Rine\nh0iNAJZ7xBybWC+dQtRsL51SKUUvnfp62L177+09esCuXfFcQ72NRCKrlF46Umql6KXTWbLvbnsh\n1NtIJBFK+HEJqznHUfc+4YTg+OxywgntX++qN06cvXSyvw9E3V6IUrwPkRRSwo9DdoTr+vVBxTk7\nwjWb9C+7DK6/vq0VvHt3sJ5P0j/hBLj77vbb7r67fdI/pYthDl1tL0R25G7U7YVQbyORRKiGH4ew\nmnMcdW/rZkhD9n/DUtW+L7ss6GW0e3fwHmbMgOuui+/8EHxYXnFFUMYZNChI9poeQmQvquEnobuS\nTVjNOWrdO6xkEyZK7TustKTukCK1K2p3nlIsFdstM6yb4ODBnXdVHDw4eL1Hj85f79Gj7RqTJ3e+\nz+TJweudvZZdsnr37vz13r2D18O6VEbpDqlumSIVhTy6ZZY9yecuFZvwwxJ6WIKKkiTDEnqvXp2/\n1qtX9HOEffCEvc8o5yjF/RaRPfJJ+Oko6RRbpggrlYSNpL3uOhg2rP2xw4blV/feuTO/7Z0JKy1F\nKQlFKU8lfb9FpDBRPxlKsSTSwo+jPLDPPp23OPfZJ9rxcbTwo8QQdo66us5fq6sLXo+jhR/H/VYL\nXyQy1MLPccUVbQ8EyXrzzWB7VG+9ld/2jhYtCt/eq1fn+2S3FxsDQJ8+3W+P0h0yrFtmHPdb3TJF\nkhH1k6EUSyItfLPOW4tm0c8R1nKO4/iwOKOcI2yfKPfittuClrRZ8Lezlvmll7a19Hv0aP9NJY77\nHTUOEVELv50oozbDas5RRpd2d44ox4fFGeUcYftEuRfTpgV99ltbg7+d9X0/9lgYODD4vWLgwGC9\ns3N1dY0oosQhInmp/YR/6KHdbw8bJQvhZYywc0QZnRpWxpg4sfNz5G4Pu04cpZKw91qK0b4iUpio\nXwVKsSRS0omjK6J792WMKOfo7vis7soYccQZdo0owuLQD64iJYWmR84RNiVBXV3wt7PjWlujXSOO\nc1TCNeKIo1RxauoFEUBTK7QXR107TClmd9x///y2JyXsvZbiXkQpw4nIXmo/4Zeirp2mboRh77UU\n9yKOrp8iaRS19lOKpeAaflhdOum6dlzn6E5c3R3jEPZe03QvRMqMVNXws1/vc1t8DQ3JPCS8nPTY\nvza6FyJ7pKuGn5av92kqG4XRvRApSGIJ38xuNrNNZvZEUtcASjfRVrnniQ+boC1NdC9ECpJYScfM\njgO2Az929+FRjimopFOKr/dpKRuJSNWpiJKOu98PvJrU+fdQrxARkUjKXsM3sxlmttzMlm/evDn/\nE5Ti673mZxeRGpBoLx0zGwL8OtGSTimoV4iIVKiKKOnUFPUKEZEaoIQfhXqFiEgNqE/qxGb2U2Ai\ncKCZbQDmu/tNSV0vcdOmKcGLSFVLLOG7+zlJnVtERPKnko6ISEoo4YuIpIQSvohISijhi4ikhBK+\niEhKVNR8+Ga2GehkSGvJHAi8UsbrR6U446U441UNcVZDjBAtzsHuflCUk1VUwi83M1sedYhyOSnO\neCnOeFVDnNUQI8Qfp0o6IiIpoYQvIpISSvjtLSp3ABEpzngpznhVQ5zVECPEHKdq+CIiKaEWvohI\nSqQ24ZtZDzP7i5n9upPXppvZZjNblVkuLlOM68zs8UwMez0ZxgLXmNkzZvaYmY2t0DgnmllLzv38\napni7Gdmy8zsr2b2lJkd3eH1st/PCDGW/V6a2dCc668ys9fN7PIO+1TCvYwSZ9nvZyaOOWb2pJk9\nYWY/NbPeHV5/l5ndnrmfD2ceLpW3xGbLrAKzgaeAd3fx+u3u/r9LGE9Xjnf3rvrhfhT4YGb5MHB9\n5m85dBcnwAPuflrJouncQuD37n6WmfUCOjzVpiLuZ1iMUOZ76e5rgdEQNJyAjcCdHXYr+72MGCeU\n+X6a2QBgFjDM3d8yszuATwCLc3b7FPCaux9qZp8AvgOcne+1UtnCN7OBwKnAj8odS5FOB37sgf8B\n+pnZweUOqhKZ2X7AccBNAO7+jrtv7bBbWe9nxBgrzWTg7+7eccBkpf232VWclaIe6GNm9QQf8i90\neP104NbMv5cBk83M8r1IKhM+cDXweaC1m33OzHwVXWZm7y9RXB058EczW2FmMzp5fQDwfM76hsy2\nUguLE+BoM1ttZr8zsyNKGVzGIcBm4JZMKe9HZrZPh33KfT+jxAjlv5e5PgH8tJPt5b6XHXUVJ5T5\nfrr7RuC7wHPAi0CLu/+xw2577qe77wJagAPyvVbqEr6ZnQZscvcV3ez2K2CIu48E7qLtk7XUPuLu\nYwm+Hn/GzI4rUxxhwuJcSTD8exRwLfCLUgdI0IIaC1zv7mOAN4B5ZYijO1FirIR7CUCm5DQF+K9y\nxRBFSJxlv59m1p+gBX8I8D5gHzM7N4lrpS7hA8cCU8xsHbAUmGRmt+Xu4O5b3P3tzOqPgHGlDXFP\nHBszfzcR1B6P6rDLRiD328fAzLaSCovT3V939+2Zf/8W6GlmB5Y4zA3ABnd/OLO+jCC55ir3/QyN\nsULuZdZHgZXu/nInr5X7XubqMs4KuZ8nAP9w983uvhP4OXBMh3323M9M2Wc/YEu+F0pdwnf3L7r7\nQHcfQvA17x53b/dp2qHWOIXgx92SMrN9zGzf7L+Bk4AnOuz2S+D8TI+ICQRfBV+stDjN7L3ZeqOZ\nHUXw313e/7EWw91fAp43s6GZTZOBNR12K+v9jBJjJdzLHOfQdZmk7P9t5ugyzgq5n88BE8ysIRPL\nZPbOOb8ELsj8+yyCvJX3IKo099Jpx8y+Dix3918Cs8xsCrALeBWYXoaQ/gm4M/PfYj3wn+7+ezO7\nBMDdbwB+C5wCPAO8CVxYoXGeBVxqZruAt4BPFPIfawxmAksyX/GfBS6swPsZFmNF3MvMh/uJwKdz\ntlXavYwSZ9nvp7s/bGbLCMpLu4C/AIs65KSbgJ+Y2TMEOekThVxLI21FRFIidSUdEZG0UsIXEUkJ\nJXwRkZRQwhcRSQklfBGRlFDCl5pnweyn74uw32IzOyvq9hji+lLOv4eYWcdxFiKxUsKXNJhOMGS9\n0nwpfBeR+CjhS1XJtIT/amZLLJgvfpmZNWReG2dm92UmcfuDmR2caZmPJxjMtMrM+pjZV83sUQvm\nHl+Uz6yDnV0js73ZzL5jZo+Y2dNm9i+Z7Q1mdoeZrTGzOy2Yy3y8mX2bYHbEVWa2JHP6HmZ2owXz\nov/RzPrEe/ck7ZTwpRoNBa5z9w8BrwOXmVlPgsmvznL3ccDNwJXuvgxYDkxz99Hu/hbwfXc/0t2H\nA32ASHOhd3WNnF3q3f0o4HJgfmbbZQTzmA8DvkJmXiZ3nwe8lYlpWmbfDwI/cPcjgK3AmfnfGpGu\naWoFqUbPu/tDmX/fRvDwiN8Dw4G7Mg32HgRTzXbmeDP7PMG84/sDTxLMkBpmaMg1fp75uwIYkvn3\nRwgeaoK7P2Fmj3Vz/n+4+6pOziESCyV8qUYd5wNxwIAn3f3oTvbfw4JHx10HjHf3582sCejd3TG5\nh4dcIzvD6m4K+//W2zn/3k3w7UMkNirpSDUaZG3Pev0k8CCwFjgou93Melrbwyy2Aftm/p1N7q+Y\nWV+CybOi6u4aXXkI+Hhm/2HAiJzXdmbKRCIloYQv1WgtwYNWngL6Ezww5B2C5P0dM1sNrKJtTvHF\nwA1mtoqgFX0jwRTOfwAejXrRkGt05TqCD4k1wDcJykctmdcWAY/l/GgrkijNlilVxcyGAL/O/OBa\n8Sx4eHZPd99hZv8M/AkYmvnwECkp1fBFktUA3Jsp3RhwmZK9lIta+CIiKaEavohISijhi4ikhBK+\niEhKKOGLiKSEEr6ISEoo4YuIpMT/B+DytdzsoSEwAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "MYCIhC3nRdgl",
"colab_type": "code",
"colab": {}
},
"source": [
"#!/usr/bin/env python\n",
"# coding=utf-8\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from matplotlib.colors import ListedColormap\n",
"\n",
"\n",
"def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):\n",
" # setup marker generator and color map\n",
" markers = ('s', 'x', 'o', '^', 'v')\n",
" colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')\n",
" cmap = ListedColormap(colors[:len(np.unique(y))])\n",
" # plot the decision surface\n",
" x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1\n",
" x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1\n",
" xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))\n",
" Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)\n",
" Z = Z.reshape(xx1.shape)\n",
" plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)\n",
" plt.xlim(xx1.min(), xx1.max())\n",
" plt.ylim(xx2.min(), xx2.max())\n",
" # plot class samples\n",
" for idx, cl in enumerate(np.unique(y)):\n",
" plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],alpha=0.8, c=cmap(idx),marker=markers[idx], label=cl)\n",
" # highlight test samples\n",
" if test_idx:\n",
" X_test, y_test = X[test_idx, :], y[test_idx]\n",
" plt.scatter(X_test[:, 0], X_test[:, 1], c='', alpha=1.0, linewidth=1, marker='o', s=55, label='test set')"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "eM7B0TASRdgp",
"colab_type": "code",
"outputId": "d6fb956f-9b3f-4861-b366-a1e15f7edc02",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 514
}
},
"source": [
"#logistics回归\n",
"#依赖以上自定义function: plot_decision_regions\n",
"from sklearn import datasets\n",
"import numpy as np\n",
"from sklearn.model_selection import train_test_split\n",
"\n",
"iris = datasets.load_iris()\n",
"X = iris.data[:, [2, 3]]\n",
"y = iris.target\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)\n",
"\n",
"from sklearn.preprocessing import StandardScaler\n",
"sc = StandardScaler()\n",
"sc.fit(X_train)\n",
"X_train_std = sc.transform(X_train)\n",
"X_test_std = sc.transform(X_test)\n",
"\n",
"X_combined_std = np.vstack((X_train_std, X_test_std))\n",
"y_combined = np.hstack((y_train, y_test))\n",
"\n",
"from sklearn.linear_model import LogisticRegression\n",
"lr = LogisticRegression(C=1000.0, random_state=0)\n",
"lr.fit(X_train_std, y_train)\n",
"lr.predict_proba(X_test_std[0,:]) # 查看第一个测试样本属于各个类别的概率\n",
"plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))\n",
"plt.xlabel('petal length [standardized]')\n",
"plt.ylabel('petal width [standardized]')\n",
"plt.legend(loc='upper left')\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.\n",
" FutureWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.py:460: FutureWarning: Default multi_class will be changed to 'auto' in 0.22. Specify the multi_class option to silence this warning.\n",
" \"this warning.\", FutureWarning)\n"
],
"name": "stderr"
},
{
"output_type": "error",
"ename": "ValueError",
"evalue": "ignored",
"traceback": [
"\u001b[0;31m\u001b[0m",
"\u001b[0;31mValueError\u001b[0mTraceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 20\u001b[0m \u001b[0mlr\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mLogisticRegression\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mC\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m1000.0\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mrandom_state\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 21\u001b[0m \u001b[0mlr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfit\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_train_std\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 22\u001b[0;31m \u001b[0mlr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpredict_proba\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_test_std\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;31m# 查看第一个测试样本属于各个类别的概率\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 23\u001b[0m \u001b[0mplot_decision_regions\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_combined_std\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my_combined\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mclassifier\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mlr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtest_idx\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mrange\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m105\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m150\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 24\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mxlabel\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'petal length [standardized]'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.pyc\u001b[0m in \u001b[0;36mpredict_proba\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 1409\u001b[0m self.solver == 'liblinear')))\n\u001b[1;32m 1410\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0movr\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1411\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0msuper\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mLogisticRegression\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_predict_proba_lr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1412\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1413\u001b[0m \u001b[0mdecision\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdecision_function\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/base.pyc\u001b[0m in \u001b[0;36m_predict_proba_lr\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 293\u001b[0m \u001b[0mmulticlass\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0mhandled\u001b[0m \u001b[0mby\u001b[0m \u001b[0mnormalizing\u001b[0m \u001b[0mthat\u001b[0m \u001b[0mover\u001b[0m \u001b[0mall\u001b[0m \u001b[0mclasses\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 294\u001b[0m \"\"\"\n\u001b[0;32m--> 295\u001b[0;31m \u001b[0mprob\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdecision_function\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 296\u001b[0m \u001b[0mprob\u001b[0m \u001b[0;34m*=\u001b[0m \u001b[0;34m-\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 297\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mexp\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mprob\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprob\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/base.pyc\u001b[0m in \u001b[0;36mdecision_function\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 255\u001b[0m \"yet\" % {'name': type(self).__name__})\n\u001b[1;32m 256\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 257\u001b[0;31m \u001b[0mX\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcheck_array\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0maccept_sparse\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'csr'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 258\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 259\u001b[0m \u001b[0mn_features\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcoef_\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mshape\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/utils/validation.pyc\u001b[0m in \u001b[0;36mcheck_array\u001b[0;34m(array, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, ensure_min_samples, ensure_min_features, warn_on_dtype, estimator)\u001b[0m\n\u001b[1;32m 550\u001b[0m \u001b[0;34m\"Reshape your data either using array.reshape(-1, 1) if \"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 551\u001b[0m \u001b[0;34m\"your data has a single feature or array.reshape(1, -1) \"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 552\u001b[0;31m \"if it contains a single sample.\".format(array))\n\u001b[0m\u001b[1;32m 553\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 554\u001b[0m \u001b[0;31m# in the future np.flexible dtypes will be handled like object dtypes\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mValueError\u001b[0m: Expected 2D array, got 1D array instead:\narray=[0.70793846 1.51006688].\nReshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample."
]
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "JROXtJtsv9MB",
"colab_type": "code",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 364
},
"outputId": "1ab37906-370c-432b-a966-bbe70c07b01d"
},
"source": [
"import numpy as np \n",
"from sklearn import datasets \n",
"from sklearn.cross_validation import train_test_split\n",
"from sklearn.preprocessing import StandardScaler \n",
"from sklearn.linear_model import Perceptron \n",
"from sklearn.metrics import accuracy_score \n",
"\n",
"iris = datasets.load_iris() \n",
"X = iris.data[:,[2,3]] \n",
"y = iris.target \n",
"\n",
"# 处理数据集,得到训练集和测试集。 \n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) \n",
"\n",
"# 对特征数据进行标准化处理 \n",
"sc = StandardScaler() \n",
"sc.fit(X_train) \n",
"X_train_std = sc.transform(X_train) \n",
"X_test_std = sc.transform(X_test) \n",
"\n",
"# 训练分类器 \n",
"ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0) \n",
"ppn.fit(X_train_std, y_train) \n",
"\n",
"# 预测并评估分类器性能\n",
"y_pred = ppn.predict(X_test_std) \n",
"acc_score = accuracy_score(y_test, y_pred)"
],
"execution_count": 1,
"outputs": [
{
"output_type": "error",
"ename": "ImportError",
"evalue": "ignored",
"traceback": [
"\u001b[0;31m\u001b[0m",
"\u001b[0;31mImportError\u001b[0mTraceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mnumpy\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mdatasets\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcross_validation\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mtrain_test_split\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 4\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpreprocessing\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mStandardScaler\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlinear_model\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mPerceptron\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mImportError\u001b[0m: No module named cross_validation",
"",
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0;32m\nNOTE: If your import is failing due to a missing package, you can\nmanually install dependencies using either !pip or !apt.\n\nTo view examples of installing some common dependencies, click the\n\"Open Examples\" button below.\n\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n"
]
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "KunfzGFHRdgs",
"colab_type": "code",
"outputId": "f2c609c7-e58b-450e-d374-a5ee87d6263a",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 286
}
},
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy import optimize\n",
"\n",
"x=np.arange(1,13,1)\n",
"y=np.array([17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18 ])\n",
"plt.plot(x,y)\n",
"plt.grid()\n",
"plt.show()\n",
"print 's'"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3Xl41NW9x/H3yb6ShOwrgYQdEkhQ\nQFxIREUFVGjr0qqtWrVXqVat2l4XrNbbahdrta29tlatFRdQISiKGEQRUNZAEiAhJGQjC5CQfZtz\n/yDeBy02gczMmfnN9/U88xgmk8znGPLhl19+c75Ka40QQgj352U6gBBCCPuQQhdCCIuQQhdCCIuQ\nQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIvwceaTRUVF6dTUVGc+5Wlra2sjODjY\ndAyHsPLawNrrk7W5r6Gsb+vWrY1a6+iBHufUQk9NTWXLli3OfMrTtm7dOmbPnm06hkNYeW1g7fXJ\n2tzXUNanlKoYzOPklIsQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLqw\njM6ePl7YcID9TX3IaEXhiZz6wiIhHOnZ/FL++FEpAC/szefSjHjmZyQwMWEYSinD6YRwPCl0YQkH\nD7fz3PoyLpkcRwJHKOkK4W+fHOC5j8tIjQxiXkYC8zLjGRsbKuUuLEsKXVjCo6uK8PFSPDRvInu2\nb+KB2WdytK2b1YWHyCuo4U/rSnkmv5T0mBDmZcQzLyOB9JgQ07GFsCspdOH2Pt7XwJqiOu6dO5a4\nsAD29N8fEezH1WemcPWZKTS0dLF6dy0rC2r5w9oSnvqwhPHxw5jXf1omJTLI6BqEsAcpdOHWuntt\nPLKykNTIIG48e+Q3Pi461J9rZ6Zy7cxUDjV38u6uWvIKanjy/b08+f5eMpLCmJcRz6UZCSSGBzpx\nBULYjxS6cGsvflZOWUMbf//+NPx9vAf1MXFhAdxw9khuOHskVUfbWVVQS15BLY+/u4fH391DVko4\n8zISuDQjnthhAQ5egRD2I4Uu3Fb9sU7+sLaEnLHR5I6LPa3PkRQRxC3npXHLeWmUN7axalctK3fW\n8Iu8Ih5dVcQZqcOZnxHPxZPjiQrxt/MKhLAvKXThtn69ei9dvX08NH+iXT5falQwt+Wkc1tOOqX1\nreQV1JBXUMuD7xTy8IpCzkqLYl5GPHMnxREe5GeX5xTCnqTQhVvadvAoy7ZVcet5aYyMsv+Um/SY\nEO6cM4Y7zh/N3roW8nYeP+d+//JdPPD2bs4eHcW8jATOSovEx9t5l0Ha5AVT4j+QQhdux2bTLFlR\nSOwwfxbnpjv0uZRSjIsbxri4Ydx94RgKa46xsqCGvJ213PPGToc+98nkJPuQm+P0pxVuQgpduJ03\ntlZSUNXMU1dOIdjfeX+FlVJMSgxjUmIY988dx/bKJopqjjnt+T/e18BHxXVUHmknebhcZin+nRS6\ncCvNHT08sXov00ZEcNmUBGM5lFJkpUSQlRLhtOc8f3wM+cV1/OXj/fzyislOe17hPmRzLuFWnvpw\nH0fau1myYKLHvYQ/PiyQc5J8eGNLFbXNHabjCBckhS7cxt5DLby0sYJrzkxhUmKY6ThGXDrKF5vW\nPPdxmekowgVJoQu3oLXmkZWFhPj7cM+FY03HMSYq0ItFWUm8+vlB6o91mo4jXIwUunAL7+0+xGf7\nD3PPhWOICPbsa8D/KyeNXpvmr+vlKF18lRS6cHkd3X38clUx4+JCufrMFNNxjBsRGcxlmQm8svkg\nja1dpuMIFyKFLlzenz/eT3VTB48smIiPt/yVBbgtN53O3j6e/+SA6SjChch3h3BplUfa+cvH+5mf\nmcD0UZGm47iMtOgQ5mUk8PLGco62dZuOI1yEFLpwaY+tKsJbKX5+yTjTUVzO4tx02rqPz1EVAqTQ\nhQv7pKSB9wvruD03nfgw2aP868bEhnLxpDhe2FBOc0eP6TjCBUihC5fU02fjkZVFjBhgcIWnuz03\nnZauXl78rNx0FOECpNCFS3rxs3JK61t58NIJBPgObnCFJ5qYEMac8bH87dMDtHTKUbqnk0IXLqeh\npYs/fFjC7LHRnD8+xnQcl/fj89Np7ujh5U0VpqMIw6TQhct5YvUeOnv7eGjeBI/br+V0ZCSFM3ts\nNM9/coD27l7TcYRBAxa6UipAKfW5UmqnUqpQKfVI//3/UEodUErt6L9NcXxcYXXbDx7lja1V3HD2\nSEZFh5iO4zYW547mSFs3r2w6aDqKMGgwR+hdQK7WOhOYAsxVSs3of99PtdZT+m87HJZSeIQvB1fE\nhPqzOHe06ThuJXtEBGenR/Hc+jI6e/pMxxGGDFjo+rjW/j/69t9kDpawuze3VrGzqpmfXTKOECcO\nrrCKxbnpNLZ28erncpTuqZQexIxCpZQ3sBVIB57VWt+nlPoHMJPjR/Brgfu11v+2sYRS6mbgZoDY\n2NjspUuX2i+9A7W2thISYs0f+V1xbW09mvs/aSc2yIv/nh4wpHPnrrg+exlobf+zuYO6ds0T5wbi\n58RZp/Zg5a8bDG19OTk5W7XW0wZ8oNZ60DcgHMgHJgHxgAL8gReBhwb6+OzsbO0u8vPzTUdwGFdc\n2yMrCnXq/Xl6V1XTkD+XK67PXgZa26clDXrEfXn6pY3lzglkR1b+umk9tPUBW/QgOvqUrnLRWjf1\nF/pcrXVt/3N1AS8AZ57K5xLiSyV1Lby4sZyrzvDcwRX2clZaJFkp4fxl3X66e22m4wgnG8xVLtFK\nqfD+twOBC4A9Sqn4/vsUcDmw25FBhTVprVmyspBgP29+epHnDq6wF6UUPz5/NNVNHby1vcp0HOFk\ngzlCjwfylVIFwBfAGq11HvCKUmoXsAuIAh5zXExhVe8XHmJD6WHuvnAswz18cIW9nDcmmoykMJ7N\n309vnxyle5IBLyXQWhcAU09yf65DEgmP0dHdx6N5xwdXfHe6DK6wF6UUi3NH88OXtvDOjhoWZSeZ\njiScRF4pKox5bv3xwRVLZHCF3c0ZH8P4+GE8m19Kn02uMvYU8l0kjKg80s6f1+1nXkY8M2Rwhd0p\npfhxbjpljW3kFdSYjiOcRApdGPH4u8V4KcXPLxlvOoplXTQxjjGxITzzUSk2OUr3CFLowuk2lDby\n3u5D3JaTRkK4DK5wFC8vxe25oympb2V14SHTcYQTSKELp+rps7FkRSEpw4O46ZxRpuNY3qWT4xkV\nHczTa0vkKN0DSKELp3ppYwUl9a08OE8GVziDt5fi9px09hxq4cPiOtNxhINJoQunaWzt4qk1+zh3\nTDRzZHCF0yzITGBEZBB//Kj0yy08hEVJoQuneWL1Hjp6+nh4vgyucCYfby9um53Orupm1u1tMB1H\nOJAUunCKHZVNvL7l+OCKNBlc4XRXZCWSGB7I0x+VyFG6hUmhC4ez2TQPrygkOtSfxbnppuN4JF9v\nL/4rJ43tB5vYUHrYdBzhIFLowuGWbatiZ2UT988dR2iAr+k4Hutb2UnEhwXw9NoS01GEg0ihC4c6\n1tnDr1fvISslnCumJpqO49H8fby55dxRfF5+hE1lcpRuRVLowqGe/rCEw23dPLJgEl5e8otQ0646\nM4XoUH85SrcoKXThMKX1Lfzjs3KuOiOZyUkyuMIVBPgeP0r/bP9htpQfMR1H2JkUunAIrTVLVhQR\n5OfNPRfK4ApXcs30FCKD/Xj6o1LTUYSdSaELh3i/sI5PSxu564IxRIb4m44jThDk58NN54xi/b4G\ndlQ2mY4j7EgKXdhdZ08fj60qYmxsKN+bMcJ0HHES184cQXiQL898JOfSrUQKXdjdcx+XUXVUBle4\nshB/H26cNZIPi+vZXd1sOo6wE/luE3ZVdbSdP60r5dKMeGamyeAKV3b9rFRCA3x4Rs6lW4YUurCr\nx98tRilkcIUbGBbgyw9mjWR14SH2HDpmOo6wAyl0YTeflTby7q5D3DY7nUQZXOEWbpiVSrCftxyl\nW4QUurCLnj4bS1YWkjw8kB+eK4Mr3EV4kB/XnZXKql21lNa3mo4jhkgKXdjFPzdVsK+ulQcvlcEV\n7uams0cS4OPNs/lylO7upNDFkDW2dvG7Nfs4Z3QUF0yINR1HnKLIEH++NyOFd3ZUU97YZjqOGAIp\ndDFkv3l/Lx3dfTw8f6IMrnBTPzx3FL7eXnKU7uak0MWQFFQ18dqWSn4wK5X0GBlc4a5iQgO4+swU\n3tpeTeWRdtNxxGmSQhen7cvBFZHB/vz4/NGm44ghuvW8NLyU4k/r9puOIk6TFLo4bcu3V7P9YBP3\nXyyDK6wgLiyA75yRxJtbK6lp6jAdR5wGKXRxWlo6e/jVe3uYmhLOQhlcYRm3npeG1vDcx3KU7o6k\n0MVpeXptCYfbunhkwUQZXGEhSRFBfCs7iVe/qKT+WKfpOOIUSaGLU1Za38oLG8q5cloyGUnhpuMI\nO/uv2en02TTPrS8zHUWcIil0cUq01jyyspBAP2/uuUgGV1hRSmQQl09J5JXNFTS2dpmOI06BFLo4\nJWuK6vik5PjgiigZXGFZP5qdRmePjeXbqkxHEadACl0MWmdPH4+uKmJMbIgMrrC49JgQpqaEs2xr\nNVpr03HEIEmhi0H73/VlVB7pYMn8ifjK4ArLW5iVxN66FopqZWtddyHflWJQqps6eHZdKZdMjuOs\n9CjTcYQTzM+Ix9dbsWxrtekoYpCk0MWgPP5uMSCDKzxJeJAf54+LZcXOanr6bKbjiEGQQhcD+mx/\nI6sKavnReekkRQSZjiOcaGFWIo2t3XxS0mA6ihiEAQtdKRWglPpcKbVTKVWolHqk//6RSqnNSqlS\npdRrSik/x8cVztbbZ+ORFUUkRQRyy3kyuMLTzB4bQ0SQL8u2yWkXdzCYI/QuIFdrnQlMAeYqpWYA\nvwZ+r7VOB44CNzoupjDln5sq2FvXwgMyuMIj+fl4cdmURNYU1dHc0WM6jhjAgIWuj/tyNpVv/00D\nucCb/fe/CFzukITCmMMnDK64aKIMrvBUC7MS6e618e6uWtNRxAAGdQ5dKeWtlNoB1ANrgP1Ak9a6\nt/8hVYDs0GQxv/lgL+3dfTw8f4IMrvBgkxPDSI8JkRcZuQF1Ki8aUEqFA28BDwL/6D/dglIqGXhP\naz3pJB9zM3AzQGxsbPbSpUvtkdvhWltbCQmx5sCGwaytvLmPRzZ2cmGqD1ePc69XhHr6184R8sq6\neXNfD0+cG0hMkGOupbDy1w2Gtr6cnJytWutpAz5Qa31KN+Ah4KdAI+DTf99M4P2BPjY7O1u7i/z8\nfNMRHGagtfX12fQVz36qsx9do5s7up0Tyo48+WvnKNVH23Xq/Xn692v2Ouw5rPx103po6wO26EH0\n82CuconuPzJHKRUIXAAUA/nAt/ofdj3wzqn+qyNc09s7qtl2sIn75o5lmAyuEEBCeCBnpUWyfJts\nBeDKBvOzUzyQr5QqAL4A1mit84D7gLuUUqVAJPA3x8UUztLS2cP/vLeHKcnhLMpKMh1HuJCFU5M4\neKSdrRVHTUcR38BnoAdorQuAqSe5vww40xGhhDnPfFRKQ0sXz183TQZXiK+YOymOB97ezbJt1UxL\nHW46jjgJeaWo+H/7G1r5+4YDfGdaEpnJMrhCfFWwvw8XT4ojr6CGzp4+03HESUihC+DLwRVFBPh4\nc+/ccabjCBe1MCuJls5e1hbXm44iTkIKXQDwYXE96/c1cKcMrhD/wcy0SOKGBcg16S5KCl0cH1yR\nV8TomBCumymDK8Q38/ZSXD41kXX7GmQ8nQuSQhc8/0kZB4+0s2SBDK4QA1uYlUifTfPOjhrTUcTX\nyHevh6tp6uDZ/P1cPCmOWTK4QgzCmNhQJieGyWkXFySF7uEef7cYm9YyuEKckoVZiRTWHGPPIRlP\n50qk0D3YprLD5BXU8qPZaSQPl8EVYvAWZCbg46V4S/ZJdylS6B6qt8/GkhWFJIYHcut5aabjCDcT\nGeLP7LExvLW9mj6bbAXgKqTQPdS/Pj/InkMtPDhvvAyuEKdlUVYi9S1dbChtNB1F9JNC90At3Zrf\nfrCPWemRXDQxznQc4aZyx8cwLMBHfjnqQqTQPdCykm5au3pZMn+iDK4Qp83fx5v5mQmsLjxEa1fv\nwB8gHE4K3cPsrm7m48perp+ZyujYUNNxhJtbmJVEZ4+N92Q8nUuQQvcwT324jxBfuGPOaNNRhAVk\npYSTGhnEcrnaxSVIoXuQyiPtrN1Tz+xkX8ICZXCFGDqlFAuzkthYdpiqo+2m43g8KXQP8s/NFXgp\nxezkAbfBF2LQrph6fD68bAVgnhS6h+js6eP1Lyq5YHwskYHyZRf2kzw8iDNHDmfZtioZT2eYfGd7\niJU7azja3sN1Z8luisL+FmUlUtbQxs6qZtNRPJoUugfQWvPSxgpGx4Qwc1Sk6TjCgi6eHI+/j5dc\nk26YFLoH2FHZxK7qZq6bOUKuOxcOMSzAlwsnxrFiZw1dvTKezhQpdA/w8sYKQvx9uCIryXQUYWEL\nsxJpau8hf0+D6SgeSwrd4hpbu8grqGVRViIh/nJ1i3Ccc9KjiA71l9MuBkmhW9xrX1TS3WfjWhkt\nJxzMx9uLy6ckkL+3niNt3abjeCQpdAvr7bPxyqYKZqVHkh4jL/MXjrcwK4mePk1egVyTboIUuoWt\n3VNPTXMn185INR1FeIjx8cMYHz+MZbIVgBFS6Bb20sZyEsICmDM+xnQU4UEWZSWys7KJ0vpW01E8\njhS6RZXWt7Ch9DDfnTECH2/5MgvnWTAlAS8Fb22XX446m3ynW9TLGyvw8/biyjOSTUcRHiYmNIBz\nx0Tz1rZqbDKezqmk0C2otauXZduquTQjnqgQf9NxhAdamJVETXMnmw4cNh3Fo0ihW9Bb26po7erl\nOrlUURhy4YRYQv19ZJ90J5NCt5gv922ZnBjGlORw03GEhwrw9eaSyfG8t6uW9m4ZT+csUugWs7Hs\nMCX1rbJvizBuYVYibd19fFBYZzqKx5BCt5iXN1YQHuTL/MwE01GEhzsjdThJEYEsk60AnEYK3UJq\nmzv4oKiOK89IJsDX23Qc4eG8vBQLpyayobSRQ82dpuN4BCl0C/nX5oPYtOZ70+WXocI1XJGVhE3D\n2zvkl6POIIVuEV29fbz6+UHOHxdD8vAg03GEAGBkVDBZKeEs2yrj6ZxBCt0iVu8+RGNrN9fOTDUd\nRYivWJiVREl9K4U1x0xHsTwpdIt48bNyUiODOCc9ynQUIb5ifkYCft5e8stRJxiw0JVSyUqpfKVU\nkVKqUCl1R//9S5RS1UqpHf23SxwfV5zM7upmth1s4tqZqXh5yaWKwrWEBfkyZ0IMK3bU0NNnMx3H\n0gZzhN4L3K21ngDMAG5TSk3of9/vtdZT+m/vOiyl+I9e2lhOoK8338qWEXPCNS2cmsThtm7W75Px\ndI40YKFrrWu11tv6324BioFERwcTg9PU3s07O2q4fGoiYYG+puMIcVLnjY1meLCfbAXgYKd0Dl0p\nlQpMBTb333W7UqpAKfV3pVSEnbOJQXh9SyVdvTbZt0W4NF9vLxZkJrCmuI7m9h7TcSxLDfZSIqVU\nCPAx8Eut9XKlVCzQCGjgUSBea33DST7uZuBmgNjY2OylS5faK7tDtba2EhISYjrGf2TTmvvWdxAR\noPj59MBBf5w7rG0orLw+d15beXMfSzZ28v2JfsxO/vefJt15bYMxlPXl5ORs1VpPG/CBWusBb4Av\n8D5w1ze8PxXYPdDnyc7O1u4iPz/fdIQBfVRcp0fcl6dX7Kg+pY9zh7UNhZXX585rs9lses5v1+lF\nf9pw0ve789oGYyjrA7boQXT1YK5yUcDfgGKt9e9OuD/+hIddAewe/L83wh5e3FhOTKg/F02MMx1F\niAEppViYlcSWiqNUHG4zHceSBnMOfRZwLZD7tUsUn1BK7VJKFQA5wE8cGVR8VXljGx/va+DqM1Pw\n85GXEwj3cPnUBJRCfjnqID4DPUBr/Slwsoub5TJFg/65qQJvpbhmeorpKEIMWnxYILPSoli+vYo7\n54yWLZ7tTA7t3FBHdx+vb6nkoklxxA4LMB1HiFOyMCuRyiMdbKk4ajqK5Uihu6F3dlRzrLOX62Xf\nFuGGLpoYR5CfN8tlKwC7k0J3M7p/xNy4uFDOSJVL/4X7Cfb3Ye6kOPIKauns6TMdx1Kk0N3M1oqj\nFNUe47qZqXL+UbitRVlJtHT2sqZIxtPZkxS6m3lpYwWhAT5cPlVGzAn3NWNUJPFhAXLaxc6k0N1I\nfUsn7+2u5dvZyQT5DXiBkhAuy9tLccXURNaXNFLfIuPp7EUK3Y0s/bySnj7NtbJvi7CAhVmJ9Nk0\nK3bUmI5iGVLobqKnz8Yrmys4d0w0I6OCTccRYsjSY0LJTAqTFxnZkRS6m1hTVEfdsS6umyFH58I6\nFmYlUVR7jOJaGU9nD1LobuLFz8pJiggkZ1yM6ShC2M38zAR8vBRvbZejdHuQQncDew+1sPnAEb43\nYwTeMmJOWMjwYD9yxsXw1vZq+myD28pbfDMpdDfw0sZy/H28uHJasukoQtjdoqxEGlq6KDosLzIa\nKil0F3ess4e3tlczPzOBiGA/03GEsLuccTGEBfqyoabXdBS3J4Xu4pZtraK9u0/2bRGW5e/jzWVT\nEvjiUB+7qppNx3FrUuguzGbTvLyxginJ4UxOCjMdRwiH+cmcMYT5Kxa/uo3WLjlSP11S6C5sw/5G\nyhrbuP4suVRRWFtEsB+3ZPhz8Eg7D7y168vRluIUSaG7sJc2VhAZ7Mclk+MHfrAQbm7scG/unDOG\nt3fUsExebHRapNBdVNXRdtYW13HVmcn4+3ibjiOEU9yWk86MUcN58O3d7G9oNR3H7Uihu6hXNh8E\n4JrpcrpFeA5vL8UfrppKoJ83t72yTfZLP0VS6C6os6ePpZ8f5IIJsSSGB5qOI4RTxQ4L4DffzmDP\noRYef7fYdBy3IoXuglYV1HK0vYfr5FJF4aFyx8Vy09kjeWljBat3HzIdx21IobuglzaWkxYdzFlp\nkaajCGHMvXPHMTkxjHvf3EnV0XbTcdyCFLqL2VHZxM6qZhkxJzyen48Xz1wzFZuGO5buoLfPZjqS\ny5NCdzEvbSwn2M+bhVmJpqMIYdyIyGAeXziZrRVHeerDEtNxXJ4Uugs53NpFXkEtC7OSCA3wNR1H\nCJewIDOBK6cl8+y6UjaUNpqO49Kk0F3Ia1sq6e61cZ2MmBPiKx5eMIG06BDufG0Hja1dpuO4LCl0\nF9Fn07yy6SAzR0UyOjbUdBwhXEqQnw/PXDOV5o4e7np9JzbZO/2kpNBdxNriOqqbOmTfFiG+wbi4\nYTw0bwLr9zXwv5+UmY7jkqTQXcTLmyqIDwtgzvhY01GEcFnfnZ7CxZPiePL9vWw/eNR0HJcjhe4C\n9je08klJI9+dnoKPt3xJhPgmSil+tTCD2GEBLH51O80dPaYjuRRpDxfw8sYKfL0VV56RYjqKEC4v\nLMiXp6+eSm1zJz9fLlvtnkgK3bCjbd0s21rFpZPjiQ71Nx1HCLeQPSKCey4cy6pdtSz9otJ0HJch\nhW5Q/t565v5hPR09fdx49ijTcYRwK7ecO4pzRkexZEUh++paTMdxCVLoBrR29fKz5QX84IUvCAv0\n5e3bZsmIOSFOkZeX4nffmUJogC+3/2sbHd2y1a4UupNtKjvM3KfWs/SLSm45bxQrF5/NpEQpcyFO\nR3SoP7+/MpN9da38Iq/QdBzjfEwH8BSdPX08sXovf99wgNTIIN68dSbZI4abjiWE2ztndDQ/mp3G\nn9ft56y0KOZnJpiOZIwUuhNsP3iUu9/YSVlDG9fPHMF9F48jyE/+1wthL3ddMIZNZYf5+fJdZCaF\nkxIZZDqSEXLKxYG6e208+f4eFv35Mzq7+3jlpuk8ctkkKXMh7MzX24unr5oKChYv3U53r2dutTtg\noSulkpVS+UqpIqVUoVLqjv77hyul1iilSvr/G+H4uO6jqOYYC575lGfz97MoK4nVPzmXWelRpmMJ\nYVnJw4P49aIMdlY28dsP9pqOY8RgjtB7gbu11hOAGcBtSqkJwP3AWq31aGBt/589Xm+fjWc+KuGy\nZz+lsbWb56+bxpPfzmSYbIcrhMNdMjme705P4bn1ZazbW286jtMNWOha61qt9bb+t1uAYiARuAx4\nsf9hLwKXOyqkuyitb2XRXzbymw/2cdHEONb85FzmTJC9WYRwpgfnTWBcXCh3v76T+mOdpuM41Smd\nQ1dKpQJTgc1ArNa6tv9dhwCPbS6bTfO3Tw9w6dOfUHG4jT9ePZVnrskiItjPdDQhPE6ArzfPXDOV\n9u4+7nxtB30etNWuGuw+CEqpEOBj4Jda6+VKqSatdfgJ7z+qtf638+hKqZuBmwFiY2Ozly5dap/k\nDtba2kpISMiAj2tot/H8ri72HrWRGe3NDyb5Ee7v2r9rHuza3JWV1ydrG7z1VT38fXc3C0f7siDN\n/MHVUNaXk5OzVWs9bcAHaq0HvAG+wPvAXSfctxeI7387Htg70OfJzs7W7iI/P/8/vt9ms+l/ba7Q\nEx58T098aLV+7YuD2mazOSfcEA20Nndn5fXJ2gbPZrPpxf/apkf9bJX+/MBhu37u0zGU9QFb9CC6\nejBXuSjgb0Cx1vp3J7xrBXB9/9vXA+8M9l8bd3eouZPvv/AFP1u+i8zkcFbfeQ7fmZbM8f9VQghX\noJTil1dMIjE8kDte3U5Te7fpSA43mHMDs4BrgVyl1I7+2yXAr4ALlFIlwJz+P1ua1pq3t1dz4e8/\nZvOBw/zison888bpJEV45osYhHB1oQG+PHPNVBpau7j3zQLLb7U74CtctNafAt906Hm+feO4rsOt\nXfz3W7tZXXiIrJRwfvudKYyMCjYdSwgxgIykcO6bO47HVhXz8qYKrpuZajqSw8hLFgfh/cJD/Hz5\nLlo6e7n/4nH88JxReHvJ6RUh3MUNs0ayobSRx/KKyR4RwcQEa26I59qXYxjW3N7DXa/t4JaXtxIX\nFsDKxWdz63lpUuZCuBkvL8Vvvp1JRLAvi1/dTltXr+lIDiGF/g12NfRy0VPreWdnDXecP5q3b5vF\n2LhQ07GEEKcpMsSfp66cyoGCIThUAAAIAklEQVTGNh56x5pb7copl69p6+rll+8W86+tXaTHhPDX\n67LJSAof+AOFEC5vZloki3NH8/TaEiJD/LjqjGRGRVvnun4p9BNsLjvMPW/upOpoB3NTfXjqxrMJ\n8PU2HUsIYUc/zk1nf30rf11fxl/XlzEhfhjzMuOZn5FA8nD3vmJNCp3jwyeefP/48InkiCBev2Um\nbeUFUuZCWJCPtxfPfjeLB5o7WFVQS15BLU+s3ssTq/eSmRzO/Ix4LpkcT0J4oOmop8zjC31nZRN3\nvb6D/Q1tXDtjBPdfPI5gfx/WlZtOJoRwpPiwQG46ZxQ3nTOKyiPtrNpVS15BDY+tKuaxVcVMGxHB\nvP5yjxkWYDruoHhsoXf32vjjRyX8ad1+YkL9eemGMzl3TLTpWEIIA5KHB3HreWncel4aBxrbWFVQ\nQ15BLUtWFvFIXhHTRw5nXkYCF0+KIzLE33Tcb+SRhb7n0DHuem0nRbXHWJSVxEPzJxAWKPuVCyFg\nZFQwt+eO5vbc0ZTUtZBXUMvKghoeeHs3D68o5Ky0SOZlxHPRxDjCg8xv+nUijyr03j4bf/2kjN+v\n2UdYoC9/vTabCyfGmY4lhHBRo2ND+ckFodw5ZzTFtS3k9R+537dsFw+8vZtzRkczLyOeCybEEuoC\nQ2w8ptDLGlq5+42dbD/YxCWT43js8skMl/3KhRCDoJRiQsIwJiQM46cXjWVXdTN5BbWsKqjloz31\n+Pl4MXtMNPMyE5gzPsbY3GDLF7rNpnlxYzm/Xr0Hfx9v/nDVFBZkJsjOiEKI06KUIiMpnIykcO6f\nO47tlU3kFdTw7q5aPiiqI8DXi/PHxTIvI56ccTFOvVrO0oVedbSdn75RwMayw+SMjeZXizKIdZPf\nVgshXJ+XlyJ7RATZIyJ48NIJfFF+hLyCWt7bXcuqXbUE+3kzZ0Is8zMS0E6YnGTJQtda8/qWSh7N\nK0Zrza8XTZb9yoUQDuXlpZg+KpLpoyJ5eP4ENh84Ql5BDe/tPsQ7O2q4bYo/Fzg4g+UKve5YJ/cv\nKyB/bwMzRg3nyW9luv2rv4QQ7sXH24tZ6VHMSo/iF5dN4tPSRnqqHL9/jGUKXWvNyoJaHnx7N509\nfTw8fwLXz0zFS3ZGFEIY5OvtRc7YGNbVFjn8uSxR6Efaunnw7d2s2lXL1JRwfvPtTNIstOGOEEIM\nhtsX+pqiOn62vIDmjh7unTuWm88ZhY+37AoshPA8blvoxzp7+MXKIt7cWsX4+GG8fON0xscPMx1L\nCCGMcctC/7SkkXvf3EldSxeLc9NZnDsaPx85KhdCeDa3KvT27l7+5909vLypgrToYJb96CymJMvw\nCSGEADcq9C3lR7j7jZ0cPNLOTWeP5J6Lxsp+5UIIcQK3KPQ/ri3hdx/uIykikFd/OIMZoyJNRxJC\nCJfjFoU+IiqYq89M4eeXjCfE3y0iCyGE07lFOy7ITGBBZoLpGEII4dLk0hAhhLAIKXQhhLAIKXQh\nhLAIKXQhhLAIKXQhhLAIKXQhhLAIKXQhhLAIKXQhhLAIpbXjB5f+/5Mp1QBUOO0JhyYKaDQdwkGs\nvDaw9vpkbe5rKOsbobWOHuhBTi10d6KU2qK1nmY6hyNYeW1g7fXJ2tyXM9Ynp1yEEMIipNCFEMIi\npNC/2V9NB3AgK68NrL0+WZv7cvj65By6EEJYhByhCyGERUihn0AplayUyldKFSmlCpVSd5jOZG9K\nKW+l1HalVJ7pLPamlApXSr2plNqjlCpWSs00nclelFI/6f87uVsp9apSKsB0pqFQSv1dKVWvlNp9\nwn3DlVJrlFIl/f+NMJnxdH3D2p7s/3tZoJR6SynlkGHIUuhf1QvcrbWeAMwAblNKTTCcyd7uAIpN\nh3CQPwCrtdbjgEwssk6lVCLwY2Ca1noS4A1cZTbVkP0DmPu1++4H1mqtRwNr+//sjv7Bv69tDTBJ\na50B7AN+5ognlkI/gda6Vmu9rf/tFo4XQqLZVPajlEoCLgWeN53F3pRSYcC5wN8AtNbdWusms6ns\nygcIVEr5AEFAjeE8Q6K1Xg8c+drdlwEv9r/9InC5U0PZycnWprX+QGvd2//HTUCSI55bCv0bKKVS\nganAZrNJ7Oop4F7AZjqIA4wEGoAX+k8pPa+UCjYdyh601tXAb4CDQC3QrLX+wGwqh4jVWtf2v30I\niDUZxoFuAN5zxCeWQj8JpVQIsAy4U2t9zHQee1BKzQPqtdZbTWdxEB8gC/iz1noq0Ib7/sj+Ff3n\nki/j+D9aCUCwUup7ZlM5lj5++Z3lLsFTSv03x0/tvuKIzy+F/jVKKV+Ol/krWuvlpvPY0SxggVKq\nHFgK5Cql/mk2kl1VAVVa6y9/onqT4wVvBXOAA1rrBq11D7AcOMtwJkeoU0rFA/T/t95wHrtSSn0f\nmAd8VzvoenEp9BMopRTHz8EWa61/ZzqPPWmtf6a1TtJap3L8F2ofaa0tc5SntT4EVCqlxvbfdT5Q\nZDCSPR0EZiilgvr/jp6PRX7h+zUrgOv7374eeMdgFrtSSs3l+OnOBVrrdkc9jxT6V80CruX40euO\n/tslpkOJQVsMvKKUKgCmAI8bzmMX/T91vAlsA3Zx/PvWrV9VqZR6FdgIjFVKVSmlbgR+BVyglCrh\n+E8lvzKZ8XR9w9qeAUKBNf298heHPLe8UlQIIaxBjtCFEMIipNCFEMIipNCFEMIipNCFEMIipNCF\nEMIipNCFEMIipNCFEMIipNCFEMIi/g8k0m79y/YQ8gAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
},
{
"output_type": "stream",
"text": [
"s\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "n4nAqdkZghRh",
"colab_type": "text"
},
"source": [
"## 多分类-文本分类"
]
},
{
"cell_type": "code",
"metadata": {
"id": "FywO1N_GRdgw",
"colab_type": "code",
"outputId": "9762840a-ee9c-4af5-eb75-3abe5e8959af",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"#[2017-7-25]sklearn文本分类\n",
"from sklearn import datasets as d\n",
"from sklearn.datasets import fetch_20newsgroups\n",
"\n",
"data_all = d.load_iris()\n",
"data_x = data_all['data']\n",
"data_y = data_all['target_names']\n",
"#print data_y\n",
"#print data_x\n",
"print len(data_x)\n",
"#dir(d)\n",
"\n",
"# print d.fetch_mldata(subset='train')\n",
"# newsgroup_train = fetch_20newsgroups(subset='train')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"150\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "F1UB3FpPRdgz",
"colab_type": "code",
"outputId": "67aba6ce-bb0e-4d17-b473-e60658f6b71d",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 70
}
},
"source": [
"#[2017-7-25]应用sklearn做文本分类:http://blog.csdn.net/abcjennifer/article/details/23615947\n",
"from sklearn.datasets import fetch_20newsgroups \n",
"#下载指定的数据集\n",
"#newsgroup_train = fetch_20newsgroups(subset='train') \n",
"categories = ['comp.graphics', \n",
" 'comp.os.ms-windows.misc', \n",
" 'comp.sys.ibm.pc.hardware', \n",
" 'comp.sys.mac.hardware', \n",
" 'comp.windows.x']\n",
"newsgroup_train = fetch_20newsgroups(subset = 'train', categories = categories); #训练数据\n",
"newsgroup_test = fetch_20newsgroups(subset = 'test', categories = categories);#测试数据\n",
"dir(newsgroup_train)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"Downloading 20news dataset. This may take a few minutes.\n",
"Downloading dataset from https://ndownloader.figshare.com/files/5975967 (14 MB)\n"
],
"name": "stderr"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
"['DESCR', 'data', 'filenames', 'target', 'target_names']"
]
},
"metadata": {
"tags": []
},
"execution_count": 26
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "ezHVcpFoRdg3",
"colab_type": "code",
"outputId": "d995d19a-e28f-4e61-d549-01c28eec73ee",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 105
}
},
"source": [
"from pprint import pprint \n",
"pprint(list(newsgroup_train.target_names)) "
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"['comp.graphics',\n",
" 'comp.os.ms-windows.misc',\n",
" 'comp.sys.ibm.pc.hardware',\n",
" 'comp.sys.mac.hardware',\n",
" 'comp.windows.x']\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "-bAr2yVFRdg6",
"colab_type": "code",
"outputId": "d81c2a2c-5a49-4108-f3e2-d50c53a08c9a",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 230
}
},
"source": [
"#从文本中提取特征\n",
"from sklearn.feature_extraction.text import HashingVectorizer \n",
"#只取了10000个词,即10000维feature,稀疏度还不算低,实际上用TfidfVectorizer统计可得到上万维的feature\n",
"vectorizer = HashingVectorizer(stop_words = 'english',non_negative = True, n_features = 10000) \n",
"fea_train = vectorizer.fit_transform(newsgroup_train.data) \n",
"fea_test = vectorizer.fit_transform(newsgroup_test.data); \n",
"#return feature vector 'fea_train' [n_samples,n_features] \n",
"print 'Size of fea_train:' + repr(fea_train.shape) \n",
"print 'Size of fea_train:' + repr(fea_test.shape) \n",
"#11314 documents, 130107 vectors for all categories \n",
"print 'The average feature sparsity is {0:.3f}%'.format(fea_train.nnz/float(fea_train.shape[0]*fea_train.shape[1])*100); "
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n"
],
"name": "stderr"
},
{
"output_type": "stream",
"text": [
"Size of fea_train:(2936, 10000)\n",
"Size of fea_train:(1955, 10000)\n",
"The average feature sparsity is 1.002%\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "riSm3jlxRdg_",
"colab_type": "code",
"colab": {}
},
"source": [
""
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "1VmhpeyCpEnq",
"colab_type": "text"
},
"source": [
"# 聚类"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6xSAT3IZf9gQ",
"colab_type": "text"
},
"source": [
"## k-means聚类\n",
"- [k-means聚类分析](http://www.cnblogs.com/wuchuanying/p/6264025.html)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "Ub2XaI6BRdgR",
"colab_type": "code",
"outputId": "12087184-0518-4857-8d6e-e0f9bc3596a3",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 313
}
},
"source": [
"#coding:utf-8\n",
"#k-mean聚类分析:http://www.cnblogs.com/wuchuanying/p/6264025.html\n",
"#我们计算K值从1到10对应的平均畸变程度:\n",
"from sklearn.cluster import KMeans\n",
"#用scipy求解距离\n",
"from scipy.spatial.distance import cdist\n",
"K=range(1,10)\n",
"meandistortions=[]\n",
"for k in K:\n",
" kmeans=KMeans(n_clusters=k)\n",
" kmeans.fit(X)\n",
" meandistortions.append(sum(np.min(\n",
" cdist(X,kmeans.cluster_centers_,\n",
" 'euclidean'),axis=1))/X.shape[0])\n",
"plt.plot(K, meandistortions, 'bx-')\n",
"plt.xlabel('k')\n",
"plt.ylabel(u'平均畸变程度')\n",
"#plt.ylabel(u'平均畸变程度',fontproperties=font)\n",
"#plt.title(u'用肘部法则来确定最佳的K值',fontproperties=font)\n",
"plt.title(u'用肘部法则来确定最佳的K值')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"Text(0.5,1,u'\\u7528\\u8098\\u90e8\\u6cd5\\u5219\\u6765\\u786e\\u5b9a\\u6700\\u4f73\\u7684K\\u503c')"
]
},
"metadata": {
"tags": []
},
"execution_count": 12
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEWCAYAAAB1xKBvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XmUnHWd7/H3J50EskASkibGLAQk\n7MjWSaquKAQlBi4C6sjiMsgdJ8qBuThzz3jQq6A4jl5m0eugIAciOiIMsmhU1nsN4lxZkmAghAAJ\ne2IwTUICIUDo5nv/eJ6yK52qTnW6n36quj6vc55T9SxV9YWj/eG3PY8iAjMzs50ZkncBZmbWGBwY\nZmZWEweGmZnVxIFhZmY1cWCYmVlNHBhmZlYTB4aZmdVkaN4FmNVK0mnA31c4dRcwt8LxdRHxMUm/\nAMZXOP8XwOeAD1Q49w1geJXfuw34CfDTBvrN3YFngGER0SFJwHeBE4H3A9+v9tmIeLHCcWtCDgxr\nJJOAr0bE/ykdkDQauBq4JyK+XH6xpJvSt29FxLHdzv0zyR/Rg4DjI6Kj7NwpwMT0fKXfuxwY2WC/\nWX5sCHAlUASOi4g/Sarps9bcHBhmzaUFuAY4nCS0NuRcjzUQB4ZZc7kOmAKcEBGb8i7GGosHvc2a\ny1zgZw4L2xVuYZg1l1OAX0l6OSIW5F2MNRYHhllz+T3wIZLQeCMiKs26MqvIgWHWZCLit5I+Atwq\n6c2IuDnvmqwxODDMmlBE3C3pTOA/JG3Lux5rDB70NmsCEfFsRKh87UdE/DoiRkfEL/OszRqHWxjW\naP5F0stl+y3AWuBTko7tdm1p5fLhku7pdu5dJIvhAP6vpPJHT44H/qWH33sqfd9ov9mTvnzWmoT8\niFYzM6uFu6TMzKwmDgwzM6vJoBrDmDBhQkyfPj3vMszMGsbSpUtfiojWWq4dVIExffp0lixZkncZ\nZmYNQ9JztV7rLikzM6uJA8PMzGriwDAzs5o4MMzMrCYODDMzq0lTB8Zll8GiRdsfW7QoOW5mZttr\n6sCYORPOOKMrNBYtSvZnzsy3LjOzejSo1mH01pw5cN118KEPwemnw513wo03JsfNzGx7Td3CADjx\nRHj77SQ4zjvPYWFmVk3TB8Y990BnJ4wfD1dcseOYhpmZJZo6MEpjFp/8JGzYANdcs/2YhpmZdWnq\nwFi8OBmz+MQnkv3hw5P9xYvzrcvMrB419aD3F76QvL76KgwZAvfdB1/7mscxzMwqyayFIWmqpEWS\nHpO0QtKFFa6RpO9KWi3pEUlHl507R9KqdDsnqzoB9tgDDjsM7r8/y18xM2tsWXZJdQD/IyIOAQrA\n+ZIO6XbNScCMdJsPXAEgaS/gEmA2MAu4RNK4DGulWIQHHkhmTJmZ2Y4yC4yIWBcRD6XvXwVWApO7\nXXYa8ONI3A+MlTQJ+CBwd0RsjIiXgbuBeVnVCklgbN4MK1dm+StmZo1rQAa9JU0HjgIe6HZqMvBC\n2f6a9Fi145W+e76kJZKWtLe373KNhULy6m4pM7PKMg8MSaOBm4HPR8Qr/f39EXFVRLRFRFtra01P\nGazogANgr72SgW8zM9tRpoEhaRhJWFwXEbdUuGQtMLVsf0p6rNrxzEhJK8OBYWZWWZazpARcA6yM\niH+tctlC4C/T2VIFYHNErAPuBOZKGpcOds9Nj2WqUIDHHoNNm7L+JTOzxpPlOoz3AJ8Clktalh77\nEjANICKuBG4DTgZWA1uBc9NzGyV9HSgtobs0IjZmWCuQDHwDPPggzJ2b9a+ZmTWWzAIjIv4T0E6u\nCeD8KucWAAsyKK2qWbOSrqn77nNgmJl119S3Buluzz3h0EM9U8rMrBIHRjfFYhIYXsBnZrY9B0Y3\nhUIy6P3EE3lXYmZWXxwY3ZQGvt0tZWa2PQdGNwceCGPHej2GmVl3DoxuhgyB2bMdGGZm3TkwKigW\nYcUKeKXfb2RiZta4HBgVFIsQkSzgMzOzhAOjglmzklcPfJuZdXFgVDB2LBxyiMcxzMzKOTCqKC3g\ni8i7EjOz+uDAqKJQgI0bYdWqvCsxM6sPDowqSgv43C1lZpZwYFRx8MHJzQgdGGZmCQdGFaUFfJ4p\nZWaWcGD0oFiE5cvh1VfzrsTMLH9ZPqJ1gaT1kh6tcv7vJS1Lt0cldUraKz33rKTl6bklWdW4M8Vi\ncpvzxYt3fq2Z2WCXZQvjWmBetZMR8U8RcWREHAl8Efhtt8ewzknPt2VYY49mz05e3S1lZpZhYETE\nvUCtz+E+G7g+q1p21bhxcNBBHvg2M4M6GMOQNJKkJXJz2eEA7pK0VNL8nXx+vqQlkpa0t7f3e31e\nwGdmlsg9MIAPAf+vW3fUsRFxNHAScL6k91X7cERcFRFtEdHW2tra78UVCvDSS/DUU/3+1WZmDaUe\nAuMsunVHRcTa9HU9cCswK4e6AC/gMzMryTUwJI0BjgN+UXZslKQ9Su+BuUDFmVYD4ZBDYI89HBhm\nZkOz+mJJ1wPHAxMkrQEuAYYBRMSV6WUfBu6KiNfKPjoRuFVSqb6fRsQdWdW5My0tye3OPVPKzJpd\nZoEREWfXcM21JNNvy489DRyRTVW7pliEb34TXnsNRo3Kuxozs3zUwxhG3SsUoLPTC/jMrLk5MGpQ\nKCSv7pYys2bmwKjB+PFwwAEe+Daz5ubAqFGhkASGF/CZWbNyYNSoWIT2dnjmmbwrMTPLhwOjRl7A\nZ2bNzoFRo0MPTabUOjDMrFk5MGo0dKgX8JlZc3Ng9EKxCA8/DFu35l2JmdnAc2D0QqEAHR2wdGne\nlZiZDTwHRi+UFvB5HMPMmpEDoxdaW2H//R0YZtacHBi9VCj4CXxm1pwcGL1ULMKLL8Jzz+VdiZnZ\nwHJg9JIX8JlZs3Jg9NLhh8PIkV6PYWbNJ7PAkLRA0npJFR+vKul4SZslLUu3i8vOzZP0hKTVki7K\nqsZdMXQozJzpFoaZNZ8sWxjXAvN2cs3vIuLIdLsUQFIL8D3gJOAQ4GxJh2RYZ68VCvCHP8Drr+dd\niZnZwMksMCLiXmDjLnx0FrA6Ip6OiG3ADcBp/VpcHxWLyQK+hx7KuxIzs4GT9xhGUdLDkm6XdGh6\nbDLwQtk1a9JjdcML+MysGQ3N8bcfAvaJiC2STgZ+Dszo7ZdImg/MB5g2bVr/VljFxImw774ODDNr\nLrm1MCLilYjYkr6/DRgmaQKwFphadumU9Fi177kqItoioq21tTXTmssVi34Cn5k1l9wCQ9I7JCl9\nPyutZQOwGJghaV9Jw4GzgIV51VlNsQjr1sELL+z8WjOzwSCzLilJ1wPHAxMkrQEuAYYBRMSVwF8A\n50nqAF4HzoqIADokXQDcCbQACyJiRVZ17qrycYwB6gkzM8tVZoEREWfv5PzlwOVVzt0G3JZFXf3l\niCNgxIhkAd+ZZ+ZdjZlZ9vKeJdWwhg2DtjYPfJtZ83Bg9EGhkKzFeOONvCsxM8ueA6MPikV4661k\n1beZ2WDnwOgDL+Azs2biwOiDSZNgn30cGGbWHBwYfVQs+lbnZtYcHBh9VCzCmjXJZmY2mDkw+qg0\njuFWhpkNdg6MPjrySNh9d49jmNng58Doo+HD4ZhjHBhmNvg5MPpBaQHfm2/mXYmZWXYcGP2gWEzC\nYtmyvCsxM8uOA6MfeAGfmTUDB0Y/mDwZpk71TCkzG9wcGP2k9AQ+M7PByoHRTwoFeP55+OMf867E\nzCwbmQWGpAWS1kt6tMr5T0h6RNJySb+XdETZuWfT48skLcmqxv5ULCav7pYys8EqyxbGtcC8Hs4/\nAxwXEYcDXweu6nZ+TkQcGRFtGdXXr446KlmT4W4pMxussnxE672Spvdw/vdlu/cDU7KqZSDsthsc\nfbQDw8wGr3oZw/gr4Pay/QDukrRU0vycauq1YhGWLoVt2/KuxMys/9XUwpB08U4uWR8RV+5KAZLm\nkATGsWWHj42ItZL2Bu6W9HhE3Fvl8/OB+QDTpk3blRL6TbEI3/42PPwwzJyZaylmZv2u1i6pAnAW\noCrnfwT0OjAkvRu4GjgpIjaUjkfE2vR1vaRbgVlAxcCIiKtIxz/a2tqitzX0p/IFfA4MMxtsau2S\n6oyIVyJic6WNpAupVyRNA24BPhURT5YdHyVpj9J7YC5QcaZVvZk6NVnE55lSZjYY1drC2Fkg7HBe\n0vXA8cAESWuAS4BhAGn31cXAeOD7kgA60hlRE4Fb02NDgZ9GxB011pk7L+Azs8Gq1sAYJmnPKucE\ntHQ/GBFn9/SFEfEZ4DMVjj8NHLHjJxpDoQA33QQvvgjveEfe1ZiZ9Z9aA+N+4PM9nL+9h3NNpXwB\n3+mn51uLmVl/6s20WvWwWeroo2HYMHdLmdngU2sLYzYZzJIajHbfPVn17cAws8Emt1lSg1mxCEuW\nwFtv5V2JmVn/qTUwej1LqpkVi/D66/DII3lXYmbWf2oNjGGS9qyyjaHCLKlm5ifwmdlg5FlSGZg2\nDSZNSmZKXXBB3tWYmfWP3tyt1rOhaiR5AZ+ZDT6eJZWRQgFuuQXWr4e99867GjOzvvMsqYz4CXxm\nNth4llRGjjkGhg51t5SZDR6Z3Uuq2Y0YAUce6RaGmQ0eniWVoWIRrrkGOjqS1oaZWSPzvaQyVCjA\n1q2wfHnelZiZ9Z1nSWWofOD7qKPyrcXMrK88SypD06fDxIke+DazwcGzpDIkJd1SDgwzGwwyvZeU\npAWS1kuq+ExuJb4rabWkRyQdXXbuHEmr0u2c3v+j1YdiEVavhpdeyrsSM7O+yXqW1LXA5cCPq5w/\nCZiRbrOBK4DZkvYieQZ4G0nrZamkhRHxco311o3ycYxTTsm3FjOzvsh0llRE3Ats7OE7TwN+HIn7\ngbGSJgEfBO6OiI1pSNwNzOtFrXXjmGOgpcXdUmbW+PKeJTUZeKFsf016rNrxHUiaD8wHmDZt2i6U\nkK1Ro+CII7yAz8waX8PPkoqIqyKiLSLaWltb8yqjR8UiPPggdHbmXYmZ2a7Le5bUWmBq2f6U9Fi1\n4w2pUIAtW+DRikP/ZmaNIe8n7i0E/jKdLVUANkfEOuBOYK6kcZLGAXPTYw3Jd641s8GgP2ZJiSqz\npCRdDxwPTJC0hmTm0zCAiLgSuA04GVgNbAXOTc9tlPR1YHH6VZdGRE+D53Vtv/2gtTUZ+P7sZ/Ou\nxsxs12Q66B0RZ/f0pRERwPlVzi0AFtRYX13zAj4zGwwaftC7URSL8OSTsGFD3pWYme2avAe9m0Zp\nHOOBB/Ktw8xsV+U96N002tpgyBB3S5lZ4+rtoHe1MYw7+qecwWv0aHj3uz1TyswaV02BERFfy7qQ\nZlAowHXXJQv4WtwmM7MG05t7SVkfFYvw6qvw2GN5V2Jm1nsOjAHkBXxm1sgcGANo//1h/HgPfJtZ\nY3JgDKDSAj63MMysETkwBlixCCtXwssN9ygoM2t2DowBVigkr17AZ2aNxoExwGbNShbwuVvKzBqN\nA2OA7bEHHHaYB77NrPE4MHJQKCRdUm+/nXclZma1c2DkoFiEzZvh8cfzrsTMrHYOjByUFvC5W8rM\nGkmmgSFpnqQnJK2WdFGF89+WtCzdnpS0qexcZ9m5hVnWOdBmzIBx4xwYZtZYar1bba9JagG+B5wI\nrAEWS1oYEX++k1JE/G3Z9X8DHFX2Fa9HxJFZ1ZenIUO8gM/MGk+WLYxZwOqIeDoitgE3AKf1cP3Z\nwPUZ1lNXisXkJoSbN+ddiZlZbbIMjMnAC2X7a9JjO5C0D7Av8Juyw7tLWiLpfkmnV/sRSfPT65a0\nt7f3R90DolCACC/gM7PGUS+D3mcBN0VEZ9mxfSKiDfg48B1J76r0wYi4KiLaIqKttbV1IGrtF7Nn\nJ/eWcreUmTWKLANjLTC1bH9KeqySs+jWHRURa9PXp4F72H58o+HtuScceqgHvs2scWQZGIuBGZL2\nlTScJBR2mO0k6SBgHHBf2bFxknZL308A3gMMuscOlQa+vYDPzBpBZoERER3ABcCdwErgxohYIelS\nSaeWXXoWcENERNmxg4Elkh4GFgHfKp9dNVgUi7BpEzz5ZN6VmJntXGbTagEi4jbgtm7HLu62/9UK\nn/s9cHiWtdWD0p1r77sPDjoo31rMzHamXga9m9JBB8HYsR7HMLPG4MDI0ZAhyWwpz5Qys0bgwMhZ\noQCPPgqvvJJ3JWZmPXNg5KxYTBbwPfhg3pWYmfXMgZGz2bOTV3dLmVm9c2DkbOxYOPhgD3ybWf1z\nYNSBYjFpYWy3EsXMrM44MOpAsQgbN8KqVXlXYmZWnQOjDpQv4DMzq1cOjDpwyCHJzQg98G1m9cyB\nUQdKC/jcwjCzeubAqBOFAixfDq++mnclZmaVOTDqRLGY3OZ8yZK8KzEzq8yBUSdKC/jcLWVm9cqB\nUSf22gsOPNCBYWb1y4FRR7yAz8zqWaaBIWmepCckrZZ0UYXzn5bULmlZun2m7Nw5klal2zlZ1lkv\nikV46SV46qm8KzEz21FmT9yT1AJ8DzgRWAMslrSwwqNW/yMiLuj22b2AS4A2IICl6WdfzqreelC+\ngG///fOtxcysuyxbGLOA1RHxdERsA24ATqvxsx8E7o6IjWlI3A3My6jOunHooTB6tBfwmVl9yjIw\nJgMvlO2vSY9191FJj0i6SdLUXn4WSfMlLZG0pL29vT/qzk1LC8ya5YFvM6tPeQ96/xKYHhHvJmlF\n/Ki3XxARV0VEW0S0tba29nuBA61YhEcegddey7sSM7PtZRkYa4GpZftT0mN/FhEbIuLNdPdq4Jha\nPztYFYvQ2ekFfGZWf7IMjMXADEn7ShoOnAUsLL9A0qSy3VOBlen7O4G5ksZJGgfMTY8Nel7AZ2b1\nKrNZUhHRIekCkj/0LcCCiFgh6VJgSUQsBP67pFOBDmAj8On0sxslfZ0kdAAujYiNWdVaTyZMgBkz\nHBhmVn8Ug2iVWFtbWywZBH0555wDd9wBL74IUt7VmNlgJmlpRLTVcm3eg95WQaEA69fDM8/kXYmZ\nWRcHRh0qFpNXd0uZWT1xYNShww6DUaO8gM/M6osDow4NHQozZ7qFYWb1xYFRhy67DN75Tnj4Ydi6\nNTm2aFFy3MwsLw6MOjRzJvzqV9DRAUuXJmFxxhnJcTOzvDgw6tCcOfDDHybv//qv4bTT4B/+Adpq\nmvhmZpYNr8OoYzNmwOrV2x975zvhgAOSp/MdeGDX++nTk7EPM7Pe6M06DP+JqVOLFsGmTXDRRfCD\nH8CFF8Lw4fDEE/Dkk/Czn8HGsrXvw4bBu97VFSDlr3vv7QWAZtZ3Dow6VBqzuPHGpHtq7tyu/S9+\nseu6DRu6AqT89Y47YNu2ruvGjKkcJDNmJNN3zcxq4S6pOnTZZckA95w5XccWLYLFi+ELX9j55zs7\n4fnnK4fJCy9sf+2UKTt2bx1wAOyzT/J8jv6sy8zqT2+6pBwYTWbrVli1ascgeeIJ2Ly567rhw5PH\nxJYHyZYt8LWvJS2dE07YsSVkZo3HYxhW1ciRcMQRyVYuAtrbdwySlSuTKb5vvdV17Qc+kAy+v/QS\nnHkmrF2brErff38YP97jJWaDlVsYtlMdHfDss10h8pOfwEMPJWMjr7yShE3JmDFJcMyYkbyWbx58\nN6s/bmFYvxo6tOuP/ogR8I//CF/5ClxxBdx+ezLesXr19tvixclMrs7Oru8ZPXrHECltkybBEK8K\nMqtrDgyrWfcxizlzuvZPOWXH67dtg+ee2zFMHnkEfv7zpOVSMmJE9TCZMqXnMPFgvNnAyDQwJM0D\n/jfJE/eujohvdTv/d8BnSJ641w78t4h4Lj3XCSxPL30+Ik7NslbbucWLtx/gnjMn2V+8uPKg9/Dh\nSdfUjBk7nuvoSGZslUJk1ark9fHH4de/3n5a8G67wX77bR8ipS6vqVOTsCgPsvJgM7P+k9kYhqQW\n4EngRGANyeNWz46Ix8qumQM8EBFbJZ0HHB8RZ6bntkTE6N78pscwBofOzmQgvXvLpLS9/nrXtcOG\nwb77wrhxyc0ajz0WHngAvvzlZP3KxInQ2upV8GbV1MW0WklF4KsR8cF0/4sAEfHNKtcfBVweEe9J\n9x0YtoO334Z16yoHyYoV28/mKpGS2VsTJyYD7xMndm2V9nfffeD/uczyUi+D3pOB8mVia4DZPVz/\nV8DtZfu7S1pC0l31rYj4eaUPSZoPzAeYNm1anwq2+jdkCEyenGzHHdd1vNQNde65cPXV8NWvJtf8\n6U/Jtn591/vFi5P9V1+t/Bt77tlzqJQfGz26+swvj63YYFMXDXVJnwTagLI/AewTEWsl7Qf8RtLy\niHiq+2cj4irgKkhaGANSsNWV7oPxJ53Utf/Rj1b/3NatXUFSHijl+489lnx/+X27yo0YUb2lsmUL\nfPjD8J3vwKmnwrJlyboVj61Yo8oyMNYCU8v2p6THtiPpA8D/BI6LiDdLxyNibfr6tKR7gKOAHQLD\nrLeD8SUjRyZ3+Z0+fee/8dZbycLGSi2W0v7zzye/2d6+/XTic8/tej9xInzpS8k04mpba+uOt2Ux\nqwdZjmEMJRn0fj9JUCwGPh4RK8quOQq4CZgXEavKjo8DtkbEm5ImAPcBp5UPmFfiMQyrB2+/nbRI\nSmFy+eVw661QLCZ3FF63rmt7+eUdP9/SkrRQegqVd7wj2Xbbrff1uavMytXFGEZEdEi6ALiTZFrt\ngohYIelSYElELAT+CRgN/ExJR3Bp+uzBwA8kvU3ykKdv7SwszOrFkCEwYUKyrV8Pv/td10LHb3xj\n+z/Ub7wBL77YFSDl79etgz/+MXnq4vr1SRB1t9dePQdLaRtdNn3E05BtV/nWIGYZ6T620pebNXZ0\nJF1d5WFSaXvxxe3XsJSMHr19gHR0JLfBP+EE+O1v4eKL4fjjYezY5PYuY8YkU5Zt8KuLabV5cGBY\nPcmj6yci6Q7bWbCsWwevvdbzd40c2RUgtbx2PzZqVO/uHeausnw4MMysR4sWwcc+Bh//OPz7v8Ml\nlyQLIDdvTp70uLPXTZsqr3kp19JSe9iMGQPPPJM8u/7f/i2Z6bZsGZx1lm+fnzUHhplV1R9dZRHJ\n+EutAVPp9ZVXdv47e+yRdKGNH1/71t8LLwd7y6cuBr3NrD7t6jTkclKyBmXEiGS21q7o7EwWT3YP\nkgUL4Be/gPe+Fw4/PHkU8YYNsGZNcvuXDRuSNTTVjBxZOUgmTKgeMmPGVO8+8ySBLm5hmFndKP0x\nPu+8ZFZZtVbPG290BUmt28aN2z+7pVxLSzLjrFqgtLcndxA4/XT45S/h+9+Hk09OWkCN/owXd0mZ\nWcPpz1lllXR2Jq2Y3gbNG29U/84hQ7oG/MeOTW6CWf5a7X3ptS/dZ/3VVeYuKTNrOP3RVdaTlpau\nFkNvbN2atCo+97nkuS8LF8L8+UlX3KZNyeLL0kSAl1/uWpC5adP2d1auZLfdag+X7u+PPnrgu8rc\nwjAz60FfWj5vvtkVJuXh0j1kqr0vv8VMJSNGJL8xeXISTrvSGnMLw8ysn/Sl5bPbbl03pOytiGSt\nzM7C5Te/SZ5i+ZWvZD/92C0MM7MGVeskgZ70poXRw5OSzcysXpV3jV16afJ6xhnJ8aw4MMzMGlBP\nXWVZcZeUmVkTc5eUmZn1OweGmZnVxIFhZmY1cWCYmVlNHBhmZlaTQTVLSlI78NwufnwC8FI/ltNf\nXFfvuK7ecV29Mxjr2iciWmu5cFAFRl9IWlLr1LKB5Lp6x3X1juvqnWavy11SZmZWEweGmZnVxIHR\n5aq8C6jCdfWO6+od19U7TV2XxzDMzKwmbmGYmVlNHBhmZlaTpg8MSQskrZf0aN61lEiaKmmRpMck\nrZB0Yd41AUjaXdKDkh5O6/pa3jWVk9Qi6Q+SfpV3LeUkPStpuaRlkurmdsqSxkq6SdLjklZKKtZB\nTQem/55K2yuSPp93XQCS/jb93/2jkq6XtHveNQFIujCtaUXW/66afgxD0vuALcCPI+KwvOsBkDQJ\nmBQRD0naA1gKnB4Rj+Vcl4BREbFF0jDgP4ELI+L+POsqkfR3QBuwZ0Scknc9JZKeBdoioq4WfEn6\nEfC7iLha0nBgZERsyruuEkktwFpgdkTs6oLc/qplMsn/3g+JiNcl3QjcFhHX5lzXYcANwCxgG3AH\n8LmIWJ3F7zV9CyMi7gU25l1HuYhYFxEPpe9fBVYCk/OtCiKxJd0dlm518V8ckqYA/xW4Ou9aGoGk\nMcD7gGsAImJbPYVF6v3AU3mHRZmhwAhJQ4GRwB9zrgfgYOCBiNgaER3Ab4GPZPVjTR8Y9U7SdOAo\n4IF8K0mk3T7LgPXA3RFRF3UB3wG+ALyddyEVBHCXpKWS5uddTGpfoB34YdqNd7WkUXkX1c1ZwPV5\nFwEQEWuBfwaeB9YBmyPirnyrAuBR4L2SxksaCZwMTM3qxxwYdUzSaOBm4PMR8Ure9QBERGdEHAlM\nAWalTeJcSToFWB8RS/OupYpjI+Jo4CTg/LQbNG9DgaOBKyLiKOA14KJ8S+qSdpGdCvws71oAJI0D\nTiMJ2ncCoyR9Mt+qICJWAv8LuIukO2oZ0JnV7zkw6lQ6RnAzcF1E3JJ3Pd2l3ReLgHl51wK8Bzg1\nHSu4AThB0k/yLalL+l+nRMR64FaS/ua8rQHWlLUQbyIJkHpxEvBQRPwp70JSHwCeiYj2iHgLuAX4\nLznXBEBEXBMRx0TE+4CXgSez+i0HRh1KB5evAVZGxL/mXU+JpFZJY9P3I4ATgcfzrQoi4osRMSUi\nppN0Y/wmInL/rz8ASaPSiQukXT5zSboRchURLwIvSDowPfR+INdJFd2cTZ10R6WeBwqSRqb//3w/\nydhi7iTtnb5OIxm/+GlWvzU0qy9uFJKuB44HJkhaA1wSEdfkWxXvAT4FLE/HCwC+FBG35VgTwCTg\nR+nslSHAjRFRV1NY69BE4NbkbwxDgZ9GxB35lvRnfwNcl3b/PA2cm3M9wJ+D9UTgs3nXUhIRD0i6\nCXgI6AD+QP3cJuRmSeOBt4Dzs5y80PTTas3MrDbukjIzs5o4MMzMrCYODDMzq4kDw8zMauLAMDOz\nmjgwzDIkaXo93QnZrC8cGGZmVhMHhtkAkbRfeqO/mXnXYrYrmn6lt9lASG/BcQPw6Yh4OO96zHaF\nA8Mse63AL4CP5P0QLLO+cJcbSg0fAAAAa0lEQVSUWfY2k9y87ti8CzHrC7cwzLK3DfgwcKekLRGR\n2d1EzbLkwDAbABHxWvqgp7vT0FiYd01mveW71ZqZWU08hmFmZjVxYJiZWU0cGGZmVhMHhpmZ1cSB\nYWZmNXFgmJlZTRwYZmZWk/8PcscVqX8ktL8AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "cquHlN5hpHZQ",
"colab_type": "text"
},
"source": [
"# 降维"
]
},
{
"cell_type": "code",
"metadata": {
"id": "X_MxEsO_wrFH",
"colab_type": "code",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
},
"outputId": "60b4923e-5828-4ba8-ab93-d6b1ff89ae76"
},
"source": [
"from sklearn.decomposition import PCA\n",
"from sklearn.datasets import load_iris\n",
"\n",
"iris = load_iris()\n",
"X = iris.data\n",
"pca = PCA(n_components=2)\n",
"reduced_X = pca.fit_transform(X)\n",
"\n",
"X.shape \t\t\t# (150, 4)\n",
"reduced_X.shape \t# (150, 2)"
],
"execution_count": 2,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"(150, 2)"
]
},
"metadata": {
"tags": []
},
"execution_count": 2
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "J7ZEc7v0pJGe",
"colab_type": "text"
},
"source": [
"# 其它"
]
}
]
}
"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "nokThLBHbFoF",
"colab_type": "text"
},
"source": [
"# Scikit-learn学习笔记\n",
"- 机器学习工具包\n",
"- \n",
" - [机器学习算法交互体验](https://codepen.io/collection/DPWwaj/2/)\n",
"- 江湖名言\n",
" - 数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已\n",
"## 简介\n",
"- 机器学习流程(参考:[机器学习之 sklearn中的pipeline](http://frankchen.xyz/2018/04/08/pipeline-in-machine-learning/))\n",
"\n",
"- sklearn流程(参考:[机器学习该如何入门](https://blog.csdn.net/u013709270/article/details/76058123))\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NMpsxZs4bkoG",
"colab_type": "text"
},
"source": [
"## datasets包\n",
"- sklearn中自带了各种数据集来满足不同的任务需求,例如使用iris数据进行分类任务。\n",
"- (1)直接导入已有数据集——load_*\n",
"- (2)单独创建数据集——make_*\n",
"- (3)下载数据集——fetch_*"
]
},
{
"cell_type": "code",
"metadata": {
"id": "xSe-D83yRdf1",
"colab_type": "code",
"outputId": "ac717fb4-fee8-49a5-ed60-b8db1981c770",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"from sklearn import datasets as d\n",
"import numpy as np\n",
"\n",
"#datasets.*? #查看datasets下的方法,同dir(datasets)\n",
"#dir(datasets)\n",
"#datasets.load_*? #直接加载数据集\n",
"#datasets.fetch_*? #下载某些数据集\n",
"#datasets.*?\n",
"#datasets.make_*? #创建样本数据集\n",
"#创建回归数据集\n",
"reg_data = d.make_regression() \n",
"reg_data[0].shape,reg_data[1].shape #获取矩阵大小\n",
"#自定义更复杂的数据集\n",
"complex_reg_data = d.make_regression(1000, 10, 5, 2, 1.0)\n",
"complex_reg_data[0].shape,complex_reg_data[1].shape\n",
"#创建一个非均衡数据集\n",
"classification_set = d.make_classification(weights=[0.1])\n",
"np.bincount(classification_set[1])\n",
"#reg_data[0][1:4,1:7] #截取\n",
"#reg_data[0].shape"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"array([10, 90])"
]
},
"metadata": {
"tags": []
},
"execution_count": 5
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "AcFGGG4Xo3Ai",
"colab_type": "text"
},
"source": [
"# 回归"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "A3kfPyL8fhB6",
"colab_type": "text"
},
"source": [
"## boston数据集"
]
},
{
"cell_type": "code",
"metadata": {
"id": "aBTKblJ1RdgB",
"colab_type": "code",
"outputId": "4c5ebb08-b4b4-4009-de4f-8995cb7f9c92",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 316
}
},
"source": [
"#加载boston数据集——数据并非numpy类型,而是bunch类型(含data自变量和target隐变量,继承自dict的设计模式)\n",
"boston = d.load_boston()\n",
"#print(boston.DESCR)\n",
"X, y = boston.data, boston.target\n",
"print len(X),len(y)\n",
"#下载加州房价数据\n",
"#housing = datasets.fetch_california_housing()\n",
"#print(housing.DESCR)\n",
"#创建聚类数据集\n",
"import sklearn.datasets as d\n",
"from matplotlib import pyplot as plt\n",
"import numpy as np\n",
"\n",
"blobs = d.make_blobs(200)\n",
"f = plt.figure(figsize=(8, 4))\n",
"ax = f.add_subplot(111)\n",
"ax.set_title(\"A blob with 3 centers\")\n",
"colors = np.array(['r', 'g', 'b'])\n",
"ax.scatter(blobs[0][:, 0], blobs[0][:, 1], color=colors[blobs[1].astype(int)], alpha=0.75)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"506 506\n"
],
"name": "stdout"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
]
},
"metadata": {
"tags": []
},
"execution_count": 6
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfUAAAEICAYAAABGRG3WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzsnXl8lNX1/99nZpJMVrKQhDUggrsC\nioiCWvflZ6u2Lqi1LnWpVqmt2lZta23dWmvdvyp1q3bR1g2XatW6UhQFBIsoIELYErKRPZnMcn9/\nnDzMJCTsEyA579freeWZ57nPfe4Mvvzcc+6554hzDsMwDMMwdn5823sAhmEYhmFsG0zUDcMwDKOX\nYKJuGIZhGL0EE3XDMAzD6CWYqBuGYRhGL8FE3TAMwzB6CSbqhpFkRORdEbmom3vDRcSJSGAT+vm1\niPxlG4+tREQaRcS/gTZOREZuy/cahpEcTNQNYwtpF+u1IpK2vceypTjnljvnspxzUdjwBGRTEJHJ\nIrJQROpEpEJE/iwiOdtuxJs0hm0++TGMnQUTdcPYAkRkOHAo4IBvbdfB7Fj8F5jonOsHjAACwM3b\nd0ibx6Z4TQxjR8VE3TC2jO8BHwFPAOdtQvtdReRjEakXkWkikt9VIxEZJCIviUiNiHwlIhd3ahIU\nkWdEpEFE5ojI6G76uUlE7ms/TxGRJhG5o/1zuoi0ikh+ovtfRG5BJyr3t7vk70/o8mgRWSwitSLy\ngIhIV+91zq1wzlUlXIoC3bruRWRvEXmz/fuuEZHr26/7ROTnIrJERKpF5B/eb5Yw5vNEZLmIVInI\nDe33jgeuB85s/w7z2q/3E5FHRaRMRFaJyM3ekoOInC8i/xWRu0SkGvi1iIwUkffaPQ5VIvJMd9/B\nMHYkTNQNY8v4HvDX9uM4ESnehPYXAgOBCHBvN+2eBlYCg4DTgFtF5MiE+ycD/wTygb8BL4pIShf9\nvAd8o/38QKAcOKz988HAQudcTeIDzrkbgA+AK9pd8lck3D6pvZ/9gDOA47r7oiIySUTqgAbgO8Dd\n3bTLBt4CXm//viOB/7TfvhI4BTi8/d5a4IFOXUwCdgeOAn4lIns6514HbgWeaf8O3qTnCfR3HwmM\nBY4FEpcZDgK+BoqBW4DfAm8AecAQ4L7uvq9h7EiYqBvGZiIik4BhwD+cc7OBJcDZG3nsKefcfOdc\nE/BL4IzOwWkiMhSYCPzMOdfqnJsLPIJOCDxmO+eedc6FgT8CQWBCF+/7EBglIgWomD8KDBaRLFQo\n39u8b83tzrla59xy4B1gTHcNnXPT293vQ4A7gGXdND0JKHfO3dn+fRucczPb7/0AuME5t9I5FwJ+\nDZzWyTV+k3OuxTk3D5gHdOe1KAZOBK5yzjU55yqAu4DJCc1WO+fuc85FnHMtQBj9Nx7UPrbp3f80\nhrHjYKJuGJvPecAbCW7mv7FxF/yKhPNSIAXo36nNIKDGOdfQqe3grvpxzsWIW/UdaBemWaiAH4aK\n+Ax00rAlol6ecN4MZG3sAefcKtQKf7qbJkPRCVFXDANeaHf31wJfoK78RI/Ipo5pGPp7lyX09zBQ\nlNBmRadnfgoI8LGIfC4iF3bTt2HsUFhAiGFsBiKSjrqf/SLiiUoakCsio9utxq4YmnBeglqCVZ2u\nrwbyRSQ7QdhLgFVd9SMiPtQaXt3NO98DjkTdzZ+0fz4OGA+8380z27psYwDYtZt7K+hoLXe+d6Fz\n7r+db7QHKW6Izt9hBRAC+jvnIpvyjHOuHLi4/X2TgLdE5H3n3FcbebdhbFfMUjeMzeMU1GLcC3VB\njwH2RNeiv7eB574rInuJSAbwG+BZbxuZh3NuBWpN3yYiQRHZD/g+kLg96wAR+Xa7G/oqVKw+6uad\n77WPaYFzrg14F11HXuqcq+zmmTVo1PoWISLniEhJ+/kwdH36P900fwUYKCJXiUiaiGSLyEHt9x4C\nbmnvAxEpFJGTN3EYa4Dh7ZMenHNl6Pr4nSKS0x6Et6uIHL6B73G6iAxp/7gWFf3YJr7fMLYbJuqG\nsXmcBzzevr+73DuA+4FzNrAd6ik0WKscXQef0k27s4DhqPX9AnCjc+6thPvTgDNRoTkX+Hb7+npX\nzADSiVvlC4BWurfSAe5B167Xikh3wXwbYi9ghog0odvbFtJu8Xam3RtxDPBN9HdZDByRMI6XgDdE\npAGduBzUVT9d8M/2v9UiMqf9/HtAKvobrAWeRYMWu+NAYKaINLaP40fOua838f2Gsd0Q57a1t80w\nDMMwjO2BWeqGYRiG0UswUTcMwzCMXoKJumEYhmH0EkzUDcMwDKOXsFPuU+/fv78bPnz49h6GYRiG\nYfQIs2fPrnLOFW6s3U4p6sOHD2fWrFnbexiGYRiG0SOISOmmtDP3u2EYhmH0EkzUDcMwDKOXYKJu\nGIZhGL2EpIq6iOwuInMTjnoRuapTm2+ISF1Cm18lc0yGYRiG0VtJaqCcc24h7XWX22tHr0LzWXfm\nA+fcSckci2EYhpFc2tqguRn69QOR7T2avklPut+PApY45zYpgs8wDMPYOWhrgzvugAkT4NBD4YQT\n4IMPtveo+iY9KeqTgb93c+9gEZknIq+JyN5dNRCRS0RklojMqqzsrmqkYRiG0dPcdhs8/jhkZEBB\nAVRVwRVXwPz523tkfY8eEXURSQW+RbwkYiJzgGHOudHAfcCLXfXhnJvqnBvnnBtXWLjR/feGYRhG\nD1BXB88/D/37Q0qKut2zsyEWgyee2N6j63v0lKV+AjDHObem8w3nXL1zrrH9/F9Aioj076FxGYZh\nGFtBVZUKud/f8Xp6OnxtFeh7nJ4S9bPoxvUuIgNENKRCRMa3j6m6h8ZlGIZhbAWDB0MgoOvqiTQ3\nwwEHbJ8x9WWSniZWRDKBY4BLE679AMA59xBwGnCZiESAFmCyc84le1yGYRjGpjNnDkybBqEQHH88\nHHYY+HwQDOr6+R136Hlamrrks7PhvPO296g3nVAIZs7Uv+PGQV7e9h7RliE7o36OGzfOWe53wzCM\nnuHhh+G++9TNLgLRKJx4Ivz+9/rZOfj3v+HRR2HNGjj4YLj8chg2bHuPfNP49FP44Q+hqUk/i8Av\nfwnf+c72HVciIjLbOTduo+1M1A3DMIzuKCuDY4+F3Fx1s4MGwVVXw2OPwfjxPT+mxYthwQKNtJ8w\nIT6uLaG1FY44AsJh9S6ALiU0NGgA4MiR22bMW8umivpOWaXNMAzD2DZ88AH89a9QUwNHHQWTJ2vy\nGI85c9RyTRROnw8iEXjkEaitVcvcE8RkEo3CDTfAq6+qd8Dng4ED1UMwZMiW9Tlzpq7/5+fHr6Wm\n6rtef12XFnYmTNQNwzD6GFVV8Oyz8M9/qsWbn697zO+9V9fNn3kmLtKZmetnh6uuhmXLoLERPvpI\nRfDOO+Hww5M77mnT4KWXoLBQBR1g9Wr4+c/hL3/Zsj5DIZ0gdIXnjt+ZsIIuhmEYfYjSUjj5ZBXw\nGTOgvh5WrFCRLCrS+y8mZAs5+GDIytLgN1AR/Oor3cI2dKi6wP1++MlP1GpPJv/4h26V8yUoV0EB\nzJsHFRVb1ueBB2p/idH7sZhOZI44YuvGuz0wUTcMw+hD3HWXCnRGhrrUU1NVxErbE3inpsJ//xtv\nn5YGU6eq5V5TAytXqmU7cqRGu4P21dYG06cnd+xtbR0F3UNElwO2hLw8uP56XUOvqNCjuhpOPVUF\nf2fD3O+GYRh9iPffVyGLRFScnVNxb2jQ83AYBg3q+Mzee8N//gOffaZu++ef77gGDfps573qGyMW\n04lCdrZOHjbGN7+pW+cSlwTq6jTKfuDAzXt3ImecAWPHwmuvQUsLfOMbGgC4MxalMVE3DMPoQ+Tk\naMS3369i3tKi6V19Pg0Y8/vhzDPXfy4QgP33V1f8yy/rpMALnguH9fmDD970cbz1Ftx6K1RW6jsn\nT1YXfmpq989Mngxvvw1z52ogm8+n47n99q0X4FGj9NjZMVE3DMPoQ3z3u3DTTbB2rVrXsVi8XGpa\nmgrk7rt3//xuu8HFF8Of/qTCCirK116r5489ptb3hAlwyCFdu8s//RR+/GNdH+/fXycFTz6pf3/5\ny+7fnZ6uhWOmT1dhHzgQjjtOt9sZiu1TNwzD6EOsWqUWd0ODirFzau3266fW89Chm9bP55/DO++o\nhTxhggbP3XabCjPo9cMPh3vuWX8f+RVX6DJAQUH8WiSiQXvTp/fM9ridjU3dp26BcoZhGH2IGTPU\nOh47Vq3u/faDPfdU4Z0xY9P72XtvtdjLyuCCC+DCCzUpjHMaRd+/P7z7LrzxxvrPlpaq1Q3avrZW\nt6bV1MCXX26Tr9lnMVE3DMPoQ8RiKqSpqbq+nhigFottXl833qjbzAKBeIKa0lJ17YvoWv0rr6z/\n3Lhxugc8FoNFi/QoK9P98xdfvHmTC6MjJuqGYRh9iIkT16+qFg6rK37SpE3rY/lyDVq75x515y9b\nFt/b7fOpQINe8yzyRC68UF3+S5fG97ZHIjrRKC+Hyy7b8i1qfR0TdcMwjD7EkCHw05/q+vWaNXrU\n12ug26asp4dC6m7/7DMV8JQUnSCEw/Eo+LY2FeVYDL797fX7GDpUs9YVFOhEwHsuFtMsdQsX6t54\nY/Ox6HfDMIw+xne/C4ceqmveoPuyN7Wi2vTpmqCluFgT0TQ3x136kYhGxPfrpxb4RRdpBHxXDBum\nAXtffRXP4+7zqcjHYhpdf8klW1espS9iP5dhGEYfZNiwLat3XlWlotvSoiIeicTLr0YiKva33QZH\nHw2DB3ffz5w5WkzGy68ei6mFn5amLvtoVNPX7rLLln2/voq53w3DMIxNZs894+vmIro27u1FDwZ1\nXfzb396woDune+UzM/V5j1hMxXzECJ0g5OQk97v0RkzUDcMwjE1m33210ElNjX4OheLZ3UAD3X70\nI5g1C845J75lbq+94KCDVMxLS9Xt3q+f5pBPS9MjGFTB/9//1MU/eXJ8icDYNCz5jGEYhrFZhMNq\njb/7rrrhU1P1cE4FvrhYRT4jQ0W+vl6fKynRKPvhwzVqPidH18wrKtTV3tKizw8YALvuqulsQyGN\nsn/7bU2Ok5UFZ58N557bt9bbLfmMYRiGscWEQlqC9ayz4Hvfg3//O153PCVFC6v076/nnqBHIirI\nNTW6Vp6Son/T0vS8vFwT06xYAaNHa7tYTK/tuae680eO1DS1gYAKeDSq73/+eZ0o1Nfru3/1q+37\n++yoJF3URWSZiPxPROaKyHrmtSj3ishXIvKZiOyf7DEZhmEY3dPaCqefru7zF17Q7Wcnn6zVzLz9\n43vsoVvjUlPjqWGHDNEjFNL18tZWFXsRtdCj0fgxZgwce6wKe22tVlsrLFx/Lb6lRe8VFem7MjK0\n3csva/S90ZGecl4c4Zyr6ubeCcCo9uMg4MH2v4ZhGMZ2YNo0zeseiaiFHQioEL/yCjz3nLrXr7lG\n95OHQlrKdY891JJuatLo9dRUtdC9yHjnVNi96nC77aZV2crK1IIfOBBOOkn7S8xyV1+vE4REfD7t\n5+uvdRJhxNkR3O8nA0865SMgV0S2ojKuYRiGsaU4B7//vYpzJKKWcmNj/P5dd6n4zp+vn30+LZ86\nb56mhw0E9HmfT/tKT1ehDofVNb9mjd5LS9PrAwdqHvoBA2DKFLXK16zRHPAff6zvbmhQAffG4a3d\nbyjCvq/SE5a6A94QEQc87JzrnCdoMLAi4fPK9mtliY1E5BLgEoCSkpLkjdYwDKMP4ZyK5yefqMXt\nnFZg86xrT5y9uutffqkC7a2jp6XFs8HddBOccILe2203XftubNSodhEV57Y2dZ9fc41WY3v4YS0O\nAxr8Fg7rvbY27dMrDRsK6R75YcO0r0mTNJjO6EhPiPok59wqESkC3hSRL51z729uJ+2Tgamg0e/b\nepCGYRh9hUgEPvpILewHH1RRD4dVfL1IdQ8vp7sn8J7V7eWOF1ERb2tTN3lqql4/9FA9olF1lc+e\nrclucnN1cgBqlf/whxrV7hWFmT1b08i2tcWruUUi+s5oVPPM//jHcP31HcfpHLz3nq61i8A3vwmH\nHabnfYmki7pzblX73woReQEYDySK+iogMePwkPZrhmEYxjamtBS+/33dRrZ6NVRXq8impamgRyIq\n3sGgBrpBPNht7Fj48MN4FLx3LxRSMS8p6fjZW/uGeLU2T9BB96nX1Kjr/oAD9Nqnn+rzX3+tE4pQ\nKP7+nBz1Jpx5Zsd1due0Ytxzz8Xf9/rr2u6Xv0zO77ijktQ1dRHJFJFs7xw4FpjfqdlLwPfao+An\nAHXOuTIMwzCMbYpz6tquqFBxrK9XsYxG4/nbQc8DAbWSvXzsBQUaDLehvhct0vX2Aw6Agw+Ghx7S\nvkHFu7lZ35k4KRDpWDEuPV0nHp7bP7FtJKKBdZ9/3vHdCxbolrf+/XWcBQWQn69lYRct2rrfbGcj\n2ZZ6MfCCqP8jAPzNOfe6iPwAwDn3EPAv4ETgK6AZuCDJYzIMw+iTrFqlEev5+bpGDnH3dHNzx7Ze\nTnaPlBT429+6r7melgY/+IEGvBUWqlDfe6++p7BQLfXVqzUILiVF96J7NdhHj47346WN7Vwe1hP4\njAx49lndP+8xe3bHrHYQ30I3a5au7/cUzmnAYGZmxyj+niKpou6c+xoY3cX1hxLOHfDDZI7DMAyj\nr+OcCqonyqmpKnyRSNwa9oTQa++5yjMydP3bmwh0JrGgS3a2XktL08nD1KkqtsXFKtI1NerWnz9f\nA93uvFOv/+lP8MYbWtI1L2/9SQaoFT9ypFryiWRnx93uifj9PZs//p134JZb4hOXyZN1/T9xySHZ\n9KEke4ZhGH2Tzz+HG27QfOvLlqno7L67JnRZuTIu6p6gB4O6lg1qZdfWdi2aHiJ65Od3vJ6SolZr\nv34q8rvuqu+srdX+b7sNJk6E007TcXkTgpoaGDRI+/QmHT4f7LOPPrvffh3fc8QRKviNjXFLv6FB\nrx1++Nb8cpvO3Lm6JS8Y1GWAcBieeEK/Z0+u6+8I+9QNwzCMJFFZCRdcoNZt//4q5o2NahEHgx3z\np4voteJiteT794+vqXtHV/nWMzK0slrnSPNQSJ/3LFUv2K2kRNe98/LULb98ub4zI0O3rGVk6Np5\nfr6Keiymz9TW6vmPftTxPbm5GsUfDOokYu1a7ePhh+MThWTz+OPxqnWg37mgQJcKGhp6Zgxglrph\nGEav5pVX1JVdWKifc3Jg//1VSPfZR4V37Vq10lNSVDSrqzsmiAG9HwjEt7hBPJgtOxv+7//UUq2q\nUsu8tVXd9eeeC6++Gl/zFtF73lr6iy929AKkpOi+9WXLYNQomDBBLfe1azU//JQpOv7OjBun7u/5\n8/Ude+/dswVfli5Vz0Ai3vtranpucmGibhiG0QtwTq1ykbiAg4p3Zws6NTWeaKZfP22/cGE8MC0a\nhRNP1L8zZ6orOTtbreiFC7WNiIr+oEHa3xdfwF//qhXVZs/W65deCkcdpYltPvpI+0tPVw/AxRdr\nidWBA+Nuf49AQK30e+7ZcMR9ZwIBzSm/PTjgAPjnP9VD4OGlvB0woOfGYaJuGIaxk7NkCfzsZyq4\nzqkFfOutKsL7769ik4i3fa2kBBYvVpfx6NFqDXtJXkR0r3j//mpZ+/0aER8IqMU9aJCKVUqKWvZL\nl8JFF6kbPJFbblFX+ogR6vZvbNQo/Cee0Gj6lBR9X329ThycU2t/zBhdKthZuPBC+Ne/dGKVkxMv\nG/uLX/RsFLytqRuGYezENDXB+eerOBcUqAj/73+6jh4KwTHHaIDamjUqvosWqYt6n320ChuohR4I\nqMWenq7C+sUX2l9hIey7r14fPVot6P3206xv3lp5LNZxW5pHba3uFS8s1GPQIBU7zwXvBdZ5766u\nVlf1kUfC/ffvXNnghg7V73rSSfE0uffe23HrXU9glrphGMZOzDvvqHj27x+/VlCg1u706er+fuop\nrYj2zDMqlHl5msXtwQfh6qvh7rvVgnZOxbW1VfvzRNUTXdAJxIsvqpD7/WphDxkC/+//rT+21as1\n0K2iQv96kex+f3zLWna2Tip+8hOdLKSn65LAzsiwYXD77dt3DCbqhmEYOzEVFfF65olEIuoKBnWX\nz5mjFrfnCnZO18tPPx3efVdFPisLhg/XbWC+Tn7cQECjuH/zG9hrL3WdNzXB2WfDccdpoFxFhRZa\nOf54fc8XX6gL34uc9yLZU1PXT/Pa0tKza8+9FRN1wzCMnZi99lI3eFubiqzPF0/Gstde2mb+fBXT\nxLVdb3vaW29pZTVvP7dzmuBl+fKOFnN9vVrjgQB897t6ALz9tuaSj0T03muvqeDfd5+u63tudb9f\n39nUpOMtLtYxrVqlSwN33aWW/fnnrx9Fbmw6JuqGYRg7MePH69r0zJnxLWYicPLJapmDWsVecFzi\nOnU0qq74RETg179Woa6sVKGORFSEL7mkY9twWJPaBIPxqG/ndBLxwAP63IgReq+8XMcQDOrR0KCJ\nb1padK29pUUnAh99pHu+O3sKjE3DRN0wDGMnZsECXT8vKdEgMxEV8ZUr43vL99lH171XrVIRF9Eg\nOhE49dT1+xwzBqZN06j5pUt1D/jJJ6+/1v3VV7o2nphJzktgM2tW/PPAgXqAWuWHHaaC//LL6hXw\n9nCnp+sywSefwEEHbfvfqi9gom4YhrET89JL+nfwYD08amq0jOmBB6qwPvig1jNfuFDFPiNDXeh3\n3qlb2Q4+WCcGmZlwyCE6CTj+eH3uscfUzX7ZZSq2K1fqGnxLi/bV2QPgWeh1dWqRe6IdDqsFfvnl\n+vyMGR2Tsnjr7gsXmqhvKSbqhmEYOzHeOnpXeNngQC1uL32qz6die999GhjX2qpr4SkpujUrNVXd\n7489Fi/SMneuXps4UcXYE/HKShXrgQP1mrfP/ayzNMHMD36gEwwvv/zVV2uU+5o1XWd8CwQsYG5r\nMFE3DMPYiTnmGHWVx2JxcffSsHrZ1SKReBKU/HwV3rIyfaalRc/T0uJbzjIydF29qCgusGlpGsj2\n179qQhsvtWs0qoFwXtU357Qy2SGH6P2334YPP9T3jBunfYK64AsLNWLec9/X1Oj9nirC0hsxUTcM\nw9iJOewwOPZYLVuaWEL1llvixUWWLNF96F5QnFdC1e9XUY3F4pni6upUyJub16+d3tiowp9IYaH2\n87vfqUW/994dg++CQa2i1pm0NPjzn3XyMHOmjn38eN0ytz3qkPcWTNQNwzB2Ynw++MMfNGr83Xc1\nRemJJ+qatkdmZse175QUPU+smQ4dt72lpHR034MKut/fsQCLtwd92LD4FrpNZcgQeOSReBWznip6\n0psxUTcMw9jJ8fnU3e25vDszZIiuY3/2mWabS09Xoa+v17Xw0lJ1yYuo+zsc1naBgFr16em6Dz41\nVSPgEwPjGht1IrHbbls+fhPzbYftBDQMw+gD3Hmnbh/zypgWFWmEuc+na9rOqZA3NKgL/he/UJd6\nIKBb5tra4LTTVNg//FC3nS1Zoh6AO+7o2TKnRvfYP4NhGEYfYMAAeP553ddeU6Nr3/n5GuTW2Kii\n/f77Ku7f+IZOAED3p9fW6jazSy7RZ3Jz9blIRKPbJ0zYrl/NSECcF1mxEzFu3Dg3y8tsYBiGYSSd\n731Pq7/l5savtbTo2vt771kGuGQjIrOdc+M21i5p/wwiMlRE3hGRBSLyuYj8qIs23xCROhGZ2378\nKlnjMQzDMLacRYs6FmEBXWtfu1b3yhs7Bsl0v0eAq51zc0QkG5gtIm865xZ0aveBc+6kJI7DMAzD\n2Ep2312zwCVuV2tpUXd8Z7E3th9Js9Sdc2XOuTnt5w3AF8DgDT9lGIZh7IhceaUGxdXV6da3piaN\nnp8yxVzvOxI98k8hIsOBscDMLm4fLCLzROQ1Edl7A31cIiKzRGRWpVck2DAMw+gRxo2DqVNh1101\n0C4/X6Pjv/Od7T0yI5GkB8qJSBbwHnCLc+75TvdygJhzrlFETgTucc6N2lifFihnGIax4xKLxZPS\nGNuG7R4o1z6IFOA54K+dBR3AOVfvnGtsP/8XkCIi/ZM5JsMwDCM5lJfDVVfB6NGad/4Xv9DtcEbP\nkbRAORER4FHgC+fcH7tpMwBY45xzIjIenWRUJ2tMhmEYRnJobYVzz9XiMF4ymxde0P3tzzxj6+49\nRTKj3ycC5wL/E5G57deuB0oAnHMPAacBl4lIBGgBJrudceO8YRhGH+ftt9VSLyyMXyssVFH/5BOr\nj95TJE3UnXPTgQ2uqDjn7gfuT9YYDMMwjJ7h6681Oj4REbXYV6wwUe8pzCFiGIZhbDW77daxehvE\nS8EmVowzkouJumEYhrHVHH64ll+tqNAqb6GQno8ZA2PHbu/R9R1M1A3DMIytJi0N/vxnOP10LQ7j\nHJx/Pjz0kG1t60msoIthGIZh7ODsEPvUDcMwDMPoOUzUDcMwDKOXYKJuGIZhGL0EE3XDMAzD6CWY\nqBuGYRhGL8FE3TAMwzB6CSbqhmEYhtFLMFE3DMMwjF6CibphGIZh9BJM1A3DMAyjl2CibhiGYRi9\nBBN1wzAMw+glmKgbhmEYRi/BRN0wDMMwegkm6oZhGIbRS0i6qIvI8SKyUES+EpGfd3E/TUSeab8/\nU0SGJ3tMhmEYhtEbSaqoi4gfeAA4AdgLOEtE9urU7PvAWufcSOAu4HfJHJNhGIZh9FaSbamPB75y\nzn3tnGsDngZO7tTmZODP7efPAkeJiCR5XIZhGIbR60i2qA8GViR8Xtl+rcs2zrkIUAcUJHlchmEY\nhtHr2GkC5UTkEhGZJSKzKisrt/dwDMMwDGOHI9mivgoYmvB5SPu1LtuISADoB1R37sg5N9U5N845\nN66wsDBJwzUMwzCMnZdki/onwCgR2UVEUoHJwEud2rwEnNd+fhrwtnPOJXlchmEYhtHrCCSzc+dc\nRESuAP4N+IHHnHOfi8hvgFnOuZeAR4GnROQroAYVfsMwDMMwNpOkijqAc+5fwL86XftVwnkrcHqy\nx2EYhmEYvZ2dJlDOMAzDMIwNY6JuGIZhGL0EE3XDMAzD6CWYqBuGYRhGL8FE3TAMwzB6CSbqhmEY\nhtFLMFE3DMMwjF6CibphGIZ4RqqqAAAgAElEQVRh9BJM1A3DMAyjl2CibhiGYRi9BBN1wzAMw+gl\nmKgbhmEYRi/BRN0wDMMwegkm6oZhGIbRSzBRNwzDMIxegom6YRiGYfQSTNSNnqehAaqqwLntPRLD\nMIxehYm60XPU1cGPfwyHHAJHHAHf/CZ8+un2HpVhGEavwUTd6BmcgylT4I03IC8PCgpg9Wq46CJY\nuXJ7j84wDKNXYKJu9AxffQVz5kBhIfj9IAL9+kEoBC+8oG0qKmDqVLj+enjuOWhu3r5jNgzD2MkI\nJKNTEbkD+CbQBiwBLnDO1XbRbhnQAESBiHNuXDLGY2xjnIOyMvD5YMCADbf94gu4/354/321yAMB\nyM2N3w8EYNkymD8fLrhAhdzvh5degkcfhb/+VS17wzAMY6Mky1J/E9jHObcfsAi4bgNtj3DOjTFB\n30n48ks49VQ47jg45hg480woLe2+7TnnwAcfQDAIra2wcKEGyXlEInDggfCrX+l5UZG65gsLVewf\nfbRHvpZhGEZvICmi7px7wzkXaf/4ETAkGe8xepiGBrjwQhXbggI9vvhCLexQaP32//d/EA5ru6ws\nGDhQrfxly6ClBdasgSFDYOJEWLRI3fGJ5OTA66/3xDczDMPoFfTEmvqFwGvd3HPAGyIyW0Qu2VAn\nInKJiMwSkVmVlZXbfJB9mmhUj43xn/9Afb26w0X0KChQy/u//12//bx5kJ0d/1xSArvuqm77jAyd\nIPztb5Cfr9disfXHlZkZ/1xRAT//OYwdC+PHw+9+B01NW/adDcMweiFbvKYuIm8BXS2o3uCcm9be\n5gYgAvy1m24mOedWiUgR8KaIfOmce7+rhs65qcBUgHHjxtkG521BdbUK42uvqQV9zDFw3XXqAu+K\nioquxT8a1b46M3w4fPYZpKXpZy84Lj0d/v1vSEmJtz3qKI2MLyzUdrGYCvY55+j95mY9X71aJwGx\nGPz5z+opePxxfcYwDKOPs8Wi7pw7ekP3ReR84CTgKOe6zjLinFvV/rdCRF4AxgNdirqxBTgHH32k\nkeQNDXDCCXDiiZCaquvXF1wAX3+tIgkqqgsWaJCaJ8SJ7LuvBrY5FxfRWEyt7L32Wr/9pZfCJZeo\nOGdmqou+thauvLKjoAPceKO64+fP1/6iUTj9dPjOd/T+W29BeXnHCUdREcyeDf/7H+y339b/XoZh\nGDs5yYp+Px74KXC4c67LfUkikgn4nHMN7efHAr9Jxnj6LA8/rJHnPp9GlE+froI9dSp8+KGubRcW\nxtsXFWlU+3vvwbHHrt/fQQfpMWOGus+d07Xx44/vWtQPOUTF+rrrdLKQkqIifdFF67fNzdVI9wUL\nVNx3203X2z0WLVrfPe8tASxbZqJuGIZBkkQduB9IQ13qAB85534gIoOAR5xzJwLFwAvt9wPA35xz\nFhW1raisVEF3Ti3kjAzo3x8+/hjefVfvd+VKb2vrPhmMzwcPPADPPgsvvqhW+2mnwcknq7hGIuoR\nyM7We83N6hpPSYE999SxzJgBN90EN9+8fv8isPfeenRm5Eh9fyLO6VFSstk/j2EYRm8kKaLunBvZ\nzfXVwInt518Do5PxfgMNalu2TM89d3lGhlrm06erde3zdXSlO6cCPGJE9/2mpenatrfW7T33t7/B\nffdBY6NGul9xhbZdvrzjXvbMTJg2Td3yiWIcDsOSJTqWUaPWF/Bjj9X+16yJr6mvXatBc6PtPyPD\nMAywjHK9l6efVss5JUXX0AMBXduuqdGI9fHjYZ99NPgtFFILvaJCBXXSpM1714svwi236Hn//vr3\n1lt1DJ3F2efTY/Fi/fz555oDPjcX9t8fjjxSBfzzzzs+l5EBf/mL3lu7Vr0AZ50FDz1kQXKGYRjt\nSDcxbDs048aNc7Nmzdrew9hxaW7WhC6rV6sFHAio8IXDev/zz2HYMHWVP/iginIspuJ6xRXr7xff\nGMceqwFwidvPmprUavf5Oq7bO6eR8k8/rW76k0/W9XIRXfePRPT6LrvAm2+q1d8Z779ZE3PDMPoI\nIjJ7U5K0JWtN3dieeAFku+2mLu3W1vi9UaNU0EHF86c/1WNrWLUqbqF7pKdrVbbsbLWsc3N14lBd\nrWOYPl2j8letigfARaMq7A0N+uy778JJJ+m9hgaYNUsnCePHa/+GYRhGB8z93htJT4fDD1dreZ99\nNPBsjz00mvySDeT48YLkNreQyt57q+gm0tCgEemPP64iXlWl1vx+++lE47bbVNirqnTS0damR3Oz\nRtSXlmoUvnO6p/0b34CrrtJKb4cfrtH7hmEYRgdM1HsrN96ogWg1NeoGb2nRgLLvfrdju2hUc7Nf\neKGK8/HHa9rWP/xBXeEeTU1w111w6KG65v6732l2OYCrr9a2NTW6Pl9To5/POw+eeAKWLlWX/kUX\n6b74FStUzMPhuCsd4tHszunzzz+vkfI/+5nGBeTnx/fUX3ll/P2GYRgGYGvqvZtIRKujPfqouq7T\n0tQdfu21cMopaiFfeqlaxGVl6vpOSdHtYy0tcNllKp7OwbnnaunUfv3UtV9bq9vUnnlG1+w//VTX\n5xcuVLf/uefCL3+p7vbcXJ08VFRoAhlQkfYs867IzlarvrRUg+QGDep4v6oKbr8d/t//S+5vaBiG\nsQNga+qGiu2cOSq4hYUq2M3N8JOfaA3z6mrN4NbYGI+QD4d1G9puu8GTT6qwz5mjedyLiuLBaUVF\nGuA2fbq6xseO1aQ2Hk8+qf17QXIpKRp1v3SpijTEI+ETk8oEAjq56N8/nnWuq2Ix3v57wzAMYx0m\n6skiFFLL9e9/VyE97DANSPOC1HpqDF7BFE8gq6o0Kn7aNBVTzwWemBa2tlbFPi0NvvpKXeZeopqy\nMrW2IxEV4BkzVNQ7M3++PlNbq/2kp2t0vJekJiVFxdsL6vP74xOLaFRFvbZWvQk+n/6G3mQgHNZn\nxo9P6s9nGIaxs2Ginix+/nMN8MrN1apm778Pc+dqmtaCguS+e/lyuPdeePtttaZLSqC4WF3q5eUq\nniIqts6pcIbDcfEE/RyL6br40Udr0pdVq3Si4Ilva6u69gcMUJf9hAl6r7UVPvlErfJA+39iubma\n1CYvT9fnve11KSkq4jk5er2tTSc+q1frBCQ1VWuxf/aZfofMTB3nlCkd08gahmEYJupJobRUC5AU\nFsaTr/Tvr6lZX3wRvv/95L27okKTstTWqpCKqKXd0hK3dKNRFdfMTB2r368C7rmzPbd4SYkWS5k9\nW+978RfOxa3sVavghhv0uxYUqMg//7xeT03V5/z+ePDcKafo2ObOVWHPyFBX/3e+A6+8omlsa2t1\nG1z//rpfPRDQSUVdncYAfOtbXaeSNQzD6OOYqCeD5ctVyDpnUwsEtFRod1RUaFKW2bPV8j3nnA2n\nbO2Kf/xDxa+oSK3etDS1gEtLNcgtEtFrgwap6NbXq0Wck6PC6/OpmA4apGlmW1tVvL31dtB+c3L0\nr2eJFxSoEF91lbroCwvV7V9aqu8QUav83nvV8v74Y+2/pEQnGVOmaH/p6fo7eOvsDQ36ub5er730\nkkboG4ZhGOthop4MPKHyypJ6RCJdVzMD3R8+ebIKYzCowWnPPw9/+hOMG6d7u//wB/jvf1Wczz1X\nt6EFOv0TzpsXt5C/+CJezKW1Va11Ea1zHgxq+4EDNdJ8yhS48051caem6kSgqSlunScWfxHR4Drn\n9Pvl5ur13FwV6lAo3s8ee+hYYjGdbHjeggkT9IhE4IgjVPAzMjTbXTis76uqUgvd71exD4fV23HG\nGXD33XDccet/f8MwjD6M7VNPBsOG6Tp0ZaUKXDSq57m5mha1Kx54QAW9qEit4P79VTx/+1u1fM85\nRwU9N1eF8O679V5nRo1Si7e2tuP6dzCoudWHDFExrqnRw++HRx6Ji2x5uYpnJBIXcs8dn1j4xTu8\nwiqhUDzo7cADtW8Pn0/bHHmkfp4xQ4V5zBit715WpksB3ru9CYc3MYpG40JfVqb73C+9VLezdVdR\nzjAMow9iZk6yuP12XQ/++99V0I44Aq65pvsguenT18+5npOj0edPPaVu6KIive7tJ3/+efjhD+PX\nQdfT//EPFUhPdCMRfW9amh7XXafiH4vpGKdM0TrmzqkF/sUX2mfnHAYiHdfVPVpb49XY8vO1rOq5\n5+pExtuylp+v3/+DD9Qj4ZV+9SYKmZk6EfH7498vEtH73nq+58L3lgPKyrTPp5/e8n8nwzCMXoSJ\nerJIS1OxnDJl09rn5alIJW4ti0TU0l64sON1UOELBNRqTRT1oUM1NeuUKWoR+/0qtp6F7vPpev2B\nB2r7667TYLjCQhXLggIdx4EHaiT8qlXxyUEiWVnqEYhE9H55ubrc//AHde+//LKuf3/5pbrgv/Wt\nuKeirCxu1XuC/eWX+u5QSMcYCGg/y5Zpu6wsXT5wTicDXrDe/PkaKd85OY1hGEYfxER9R+GCCzSK\nPBhUQYvF1IX93e/qevJHH3Vs71ngQ4eu39e+++p2ulNP1W1l+fnadu1aTRXrCXokAq++qvc9i9nL\n/Pbcc/HofefUks7OVpH3RNfv1/ahkIruAw/AAQdov0uW6A6Azz9XL0B9vUa5/+9/+h4v1sCrzNbW\npmvqNTX63QYN0snK2rXx/fTRqAo76Hp7dbX2U15uom4YhoGtqe84nHIK/OAH6mZfu1bF7aSTNK/6\n5MkqmtXV8a1nlZVq9SZa6Ymkpqrb/owztH0kAt/7nmZ98wTcW69ODOYrK9P2fr+65ktK9BzUm5CT\nExdzz4LPyNCAuzVr4NvfVtf+YYdplTW/X/fLX3ONFpPpnO8d4u9/+GFNYbv77jqJqKvTYMCHHtKU\ntN5YMzPje+1jMa2zbhiGYVju9x2OujrdBjZgQEfBXrQIfv97rU6Wk6MW/CWXxDPFbSkXX6xeAK90\n6ty5ukZeXKyiDiryq1fDn/+sonz++WoxR6PqUk9PV49Bebla8KtXx6u2eZa+F2zX0BDfFZA4uQgG\n1ZoPBPR9q1apB8GLrG9t1QDE+vqOVv7IkTphmTVLhd4wDKMXYrnfd1b69dNCJp3ZbTeNUvcCxrYV\nv/iFBrVVVcWro6WldczWFgio6/3AA1XAr71Wx+KJ6+DBOgkpL9fxL1kSX0JobtZnReLZ4pYu7bjd\nz+fT5Qdve1pa2vr784NBFXAvdaxXtS0QUA/GTjg5NQzD2NaYqO9sbCtBb22Fd95Rr8C118YT1JSX\nw2uvxV3u3va3o4+O7zH/0Y90SWD+fLWkx46FE06I3w8GVcw7b4ELBNSib2mJb6dLTdUlgptv3viE\n5VvfUm/B0KHxdlVVWg62cyChYRhGHyRpoi4ivwYuBirbL13vnPtXF+2OB+4B/MAjzrnbkzWmPkVV\nlQr10KHrZ7YrK9P19cTCLCNGqGBmZWn7N96IC+cee2gZ1USKi/Xw2GcffSY9XS33hQvjz3t12UtK\n9Fpeni4lHHSQlm594QWt0T58uL5nwoSuv9Nll8HMmbB4cXzchYXqbTAMwzCSbqnf5Zz7Q3c3RcQP\nPAAcA6wEPhGRl5xzC5I8rs2isqmSZbXLGJg9kCE5O3gRkepquP56TVTjpXy9+WY45JB4m1tvjady\n9Vi8WKPXb7hBM8stXqx75AcM0CQx3VnQzul69rBh6l6vqlIrPRLR9ffUVG2Tn6/jqarSDHlnnKHj\n+Oc/9V5Ojk4yLr1UhX6PPdZ/V06O7sF//30d35AhmtAmPX3b/oaGYRg7KUkLlGu31Bs3IuoHA792\nzh3X/vk6AOfcbRvqu6cC5WIuxu3Tb+fp+U/jFz8RF+HIXY7k9qNuJz1lBxQS5zTz3Gef6Z5vn0+T\nyUQiag0PH67nY8aokHoudlBBjsU0EG9Tqa/XYL3PP9d3t7XpdriWFhXagQN1MhAMwtln6/UJEzQR\nT2OjRsh7RWdCIbW86+o06v+2Df4nYBiG0afYUQLlrhCR7wGzgKudc2s73R8MrEj4vBI4qKuOROQS\n4BKAkpKSJAx1fZ6e/zR/+ewv9M/oj9/nJ+ZivLnkTYoyirjhsBt6ZAybxeLFus7tpZgFdadXVqpF\nfO21eq2zOx7iyVw2hz/+sWPiGi+z3KBBOoHwqKzUYLlrrolfq6iIV29bvjye3CYrS133m0Nzs26b\nW7VKt8NNmmQ54Q3D6JNs1T51EXlLROZ3cZwMPAjsCowByoA7t+ZdzrmpzrlxzrlxhYlu4yTy5Lwn\nyUrNwu9TsfOJj/z0fJ774jkisUiPjCGR5nAzzy14juv/cz1/mv0nKpoqOjaoqoqXRE0kEFDB886P\nP17d9B7OaVT5qadu+mCc0zKyeXnr3hdqbaQhTWirqezYNhDQBDSJDBmiYvz11/H0r4GAjqOqatPH\nsWKF5oC/7jrNh3/lleoV8LbUGYZh9CG2ypxxzh29Ke1E5E/AK13cWgUkpkQb0n5th6A+VE+Kv+M+\n8IAvQCgaoi3aRsDXc9bg2pa1nP382ayoW4FPfMRcjKlzpvLEyU+wd1F7bfHdd48XPamqUld7Xp5G\nhh98cLyzn/1M971//XU8ocsBB2gg2oaortYMdKWluu0uEgGfj5hzLK1dSnVTJYGsEMEIPDFiCTcv\nGkLq2noV6ry8jtHtGRlq0ZeWxq30SETFvbJSE/Dk5W38h/n1r/W7evvsnVNvxaOPahlYwzCMPkQy\no98HOufK2j+eCszvotknwCgR2QUV88nA2cka0+Zy2LDDeGXRKxRmxj0Dta217FO4DxkpGT06lkfm\nPEJpbSnFWfGI87Uta/nVO7/i2TOeRby87cOGaRS6V8999Wp1aR96aLyzggJNAztzplY5GzFCRX1D\n28kWLYLzzlMLWESD2ZqbIRqlLDNKVXMVqYFUctvCTC+BV/qtYSjlXLlYdBzPPKOW+A03xN+Tl6cR\n8WvX6np8QYFGzjc3b5qoNzfrd0gskiOiAXUvvWSibhhGnyOZpubvRWQM4IBlwKUAIjII3bp2onMu\nIiJXAP9Gt7Q95pz7PIlj2iyuHH8lM1bMoLKpkhR/CuFomGAgyC8O6/ktVP9e8m9y0nI6XMsN5rKw\neiFljWV8XvE5zdVljCtfzODddotXQRs0SAX+9dc15aqH398xIn5j3Hijimji0seqVRCN0lq2kkIH\n+MJUDMjm2WP7kVu1nL/u6bhy6SDdVpeSotXUjjwy/t6JE3X9fJ994n22tqoVP2QTdhlsKCJ/c+MD\nDMMwegFJE3Xn3LndXF8NnJjw+V/AevvXe4JILMK88nmEoiFGF48mMzWzw/3BOYN54cwXeHbBs8xb\nM4+R+SM5Y+8ztsu2toyUDOpCdR2uxVyMUCTEyX8/mVA0hGtuQg5dzWXlQ7msbM94w9pa+PTTLX95\nfb0GxHkubo+CAkhN5c592hhV66d8QCaf7plHuKWRlIYKqtPBjRqJ0C6+IprYxhP1c89Vi7qiQvO5\nh0Lqir/55k1L+ZqeDocfDu+9F59sOKcTmgkT1AuxKZMDwzCMXkKfDRH+supLLn/1cqpbqhEEv/i5\n6YibOGm3kzq0K8go4NJxl26nUcY5Z99zuOm9m8hIycAnPpxzVDdX0xxupl+wHwUZBeDLJNJWzgOD\nVzGhIYexjdn6cDi8ftrVrmhuVss5L69j9HogEK+LnmgBR6MqxieeyGOlH9A/s90N3gJrU6JMqsuP\nCzrEc8B7FBXBs8/Ck0/qvvpBg9TF71WR2xRuvFFz0a9cqS78srJ4EZm334bTT9fkNF1F/BuGYfQy\n+qSoh6NhLn3lUupD9eSn5wPQGmnlhv/cwF6FezEibxMEsIc5ba/TWFC5gOe/eB6f+KgL1amlHg3h\naM81EAwS6JcLzVW8nFfJ2IYs3fcdDKq4bYinnyZ2x++JRcL4YyBjx8Jdd6k1npGhlu+bb2oymmBQ\nBb6xEa68kmsOmcin5Z/Glyl8bWSRwrULC+L7K6JR/Xtiu5OmvFy34BUXa+33q6/esh+mqEit/Q8/\nhN/8RicwQ4aoiEej6vLfbz+tgmcYhtHL6ZPmyyerP6G2pZbcYO66a8FAkIiL8MqiroL0t55wNExl\nU+UWb4Xz+9ST8PLZLzM4ZzABX4BUXyqNbY18WfUlq+tXa8NdRyL9+tEWblU39C67wGOPbdANHft4\nJtU3/ITPahcxp2Upn4aXU//huyq0kYhautOnx9348+drxPlJJ8FZZzEibwTTJk/jhwf+kIlDJ/LD\n8Vfw0neeZdemNG1XUaGBb+edp9nkfvtbOOooOPNMre9eWKhJcxYv3qLfhkBA1+XLy+OCDmqxp6er\nsBuGYfQB+qSl3hxu7vK6INSH6rfpu5xzPDLnEabOmUooEiIzNZMp46cweZ/JGrG+mSypWcLyuuUM\nyRmCc46K5gqcc6xqWEX/zP4EfAFcURHHffceKB7P8mgNf5//NAun3c2YAWOYvM9kijI71mD//J5f\nkNJaQzQ7jRTxEXNRvqSKvT58n6w774Tnn1fhLSrS6PfKSi2ukpD1rSiziMsO7LQl7u2DtaZ6c7O6\n1HfdVdO8PvaYinxLi66dh8Masb9kiVrd3dWI3xChkP7t/Jv6/ZoD3zAMow/QJy31sQPGgqj17BFz\nulf68GGHb9N3/eWzv3DXR3eR4kvRdW/g5vdv5tXFr25Rfx8s/wARQUTw+XwMzx1OOBamOdzM3LK5\nlNaW8q3dv8WkXY/kf83LOPUf3+apz55i3pp5TJ09lVOePoXS2tJ1/UVjUVZ8/SkuEMAn+p+DT/z4\nfH6qQjWaiS4nJ17/PCdHo9nffHPj5U5zclT8J09WQW9rg5/+VNe96+vVC9DSon23tOi1557bot+F\n4uJ4vXUP53SJ4IQTtqxPwzCMnYw+KeoFGQVcc/A11LXWUdFUQXVzNdXN1Ry1y1FMLJm4zd7jnOPh\n2Q/TL9iPtICWBg0GgmSkZvDQrIe2bOzpBesmILFYjNUNq/GJj4AvQFZqFj7xkRfMQ0S45YNbiMai\nFGYWkpOWQ2FmIfWheu6Zec+6/prDzcwYmUYw0lGggxFo8kXjCWESqEuD20uWM/GxiUx6bBJ3fXhX\nt96PDrzwglr5Pl/8AN3G5gXhbW6KWA8RuOUW7aOyUt3+VVVah/7cLjdiGIZh9Dr6pPsd4NzR5zJm\nwBimLZxGU7iJY0Ycw+HDDl9nrW4Loi5KdUs1xZnFHa4HA0FWN6zeoj6/tfu3ePTTR2kJt9DU1kRz\nuBmf+MhMzWTPwj2JuRhPfvYkZ+17Fp+t+Ww9V3tuMJcPln+w7nNWahbzJo1ixWfzKKlqoy3gIxCN\nEXFR3rjoSPau2w3eemvdlrGIxLhg5Hy+LBRygZiLMnXOVOaUzeHJU5/c8JLCtGkaWV9T09HKj8Xi\nwXf77rtFvwug6/OvvKIu/BUr1OV/zDHat2EYRh+gz4o6wL7F+7Jv8VaIyEYI+AKMyh/FqoZVHRLH\nNIQadAlgCxiWO4w7j72T69++njVNa4i5GOkp6YzKH0UkFiHmYvjwsbh6MRkpGYRjYVL98T3f4ViY\nvGA8U5uIMOXoG7i6aQrHzm/moK9aKct0vHlgPjf98A5ozdbSqpWVkJLCB7m1LM4OUzR4X6Td+1Cc\nWczcNXOZXTabcYM2UETI59Noeq80ayQhaDAnRyvHbU7++a4oLoaLL966PgzDMHZS+rSo9wQ/m/gz\nfvDKD1gVWoWIEI1FyUzJ5KoJW57C9KgRR/F+yfv88p1f8vwXz1OYUcjS2qU0tGkRE7/4aQg1MHmf\nyTz26WMUZhbinCMUDVHfWs+U8VM69HfMrseQdfpjPDTiIaavXcZ+xfvx2wMvZ8/C9gQ206bpWvf8\n+SweVkUk8AmSGU+TKyI451hSs2TDov6d72j0/F57qbVeXq5BbMGg3vvxj1XYDcMwjC3CRD3JjB4w\nmpJ+JXy48kPaom2kBdLYrWC3rd4LnxZIY8pBU3hzyZssqFxAxEUISIBwLIzP5+PW6bfy4pkvUt5Y\nzpPznlTBdzAwe2CHXPYr61fy0cqPSPOncc/x93TY5reOggKtmw4MXfwagbf+t14Tn/g2nmnvm9+E\nGTM0Za2Ibj/Ly4PHH9+05DiGYRjGBjFRTxLOOUSE+z++n6W1S9mveL91Fu2y2mX88cM/cuM3btzs\nPj8t/5RF1YsozixmYslErhh/BT96/UcIQtRFyQ3mMiJvBLWttby97G1S/ankpecxJHsImamZhKIh\nrnnjGp469Sk+Wf0J9868l6iL4hMfqb5U7j7+bg4ddmi3YzhilyMozixmTdMa8tPzcc5R01LDiLwR\nHDTkoA1/gUAAfv97uOACTTtbUKCFZtLSNut3MAzDMLpG3Ma2Je2AjBs3zs2aNWt7D6NLXl30Kvd+\nfC/L65aza96uLKpeRGFmYcd17WiYpnATcy6Zs8l71UOREFf86wo+WvkRURcl4AswIGsAZ+97Nn/8\n8I/rIt9T/Ck451hcvZg0fxrlTeUUpBcwtN/QdRH41c3VjCkew6drPqVfWr915WWbw83EYjHeu+C9\nDVahK2so49YPbuWdZe8gIhy363FcN+m6dVv2DMMwjG2LiMx2zm1gfVMxS30b8vLCl/n5Wz8nMzWT\n4sxiyhvLWV63nFR/ageXt098m51Z7i+f/YX/rvgvRZlF6yYCZQ1lvLroVWIuRoo/ZV3k/tK1S6lq\nqWJw9mBEhJrWGhraGti3eF8CvgDBQJC5a+YSjUU71IvPSMmgqqmK+z++n/4Z/RmRN4JJJZPWqxs/\nMHsg9514H+FoGBHp0bryhmEYRvfY/423IffMvIfM1Mx11d6y07LJDeayvG55B1GvbqnmhJEnbNBK\nD0VCPPrpo/x9/t+JxCJUNVWRnZbd4Zn89HzmrpnL2AFjmVc+j+y0bCKxCGua1tAvrR9DcoZQ1VyF\niBCOhalqqmJA9gCaw80Mzx3O0rVLO7yzLdrGstplPDTrIVL9qaT4UxiVP4rHTn6sy7X2xAmBYRiG\nsf0xUd9GRGNRVtWvojQdWjwAAByLSURBVDir4570XXJ3YX7lfKqaq4jGovh9fgZlDeLaQ67tti/n\nHKc8fQrvlb6HwxHwBQhHw6QF0hhdPBq/z084GmZR1SLq2+pJ9aXSEmkhGAhqkpmMQnbJ2wW/z8+Q\nnCGU1pUSi8Woba3F5/ORG8zlxxN+zFWvX7VuTABf13xNJBZZl1veOcfC6oU88PED3HDYDd2O9+u1\nX/PgJw/yyepPGJQ9iIv3v5gjdjli2/ywhmEYxiZjor6N8Pv8lPQrYW3r2g512dtibRwz4hgu2v8i\nFlcvZmT+SI7c5UjSU9LX62Pmypk8OOtBZiyfwZLaJQT9QdICacRcDIejua2ZmuYaCrMKWbp2KfVt\n9fQL9qMoq4jcaC7L1i5DRKhtraWssYyBWQMpziom1Z/Kstpl5KXnccZeZ3DxARczMGsgF4y9gMfn\nPk4kFkEQ1rauZWT+yHXudBEhN5jLK4tf6VbUl9UuY/Kzk2kON5OTlsOXVV9yxWtXcOPhN3LG3mck\n58c2DMMwusQC5bYhry1+jWveuIb0lHQyUzNpbGskFAnx0EkPMalk0gaffWvJW/z43z/G7/PzVfVX\nNEc0U1xGSgZ+n59oLEpzuJmC9AJygjmsqFtBMBBkz8I9SfOnsbhmMdXN1WSlZuH3+altrSUnNYc9\nC/ekLlRHMBDkpckvredJWFi1kA9XfkiKL4Xfvv9bctJyaAo30RpuJS2QRiQWoaGtgRNHnshhww4j\n4AtQ2VzJmAFjmFQyiRvfvZFpX07rsLzQGmkFB+9f8L656A3DMLYBFii3HThh1AkEfAHu+/g+ltYu\nZVT+KK466KqNCrpzjtv/e/u6yUCUKCKyrl56hi8Dn/jw+/xcfuDlZKZmcv/H9zM0ZygBf4DGtkZq\nW2tJ8amA7lGwB8vrllPepIF6hw07jOsPvX49QQfYvf/u7N5/d5xz3P3R3cxePZsYsQ5tslOzmbFy\nBn+b/zeC/iBFmUWEIiGG5g7FxRxZqVkd2gcDQWqaa6hsrmRQ9qCt/FUNwzCMTcVEfRtzzK7HcMyu\nx2zWM7WttSxdu5R+wX7EYjGyUrKojdUSI0YkGsEFNBtcVmoWF+1/EemBdN5Y8gY1LTVk+7PXFVOJ\nESM/PV+rt+UNJxgIcvmBl3PlQVdudAx3f3Q3n1V8tp6gg27BK2sow4eP1mgrK+pXICKUNZYR8AfI\nSc1h9/67rwvi86Liu0xkYxiGYSSNpIi6iDwD7N7+MReodc6N6aLdMqABiAKRTXEt7KjUtdbx9Pyn\neXfZuxRkFHDOvudw8NCDN/rcgsoFXP7q5ZQ1lqlItu8/bw43E4qGQNSdnRZI44ABB3D8X47H4da1\naY200hppJRKLEAwE6Rfst67vgD9ASb+S9d4ZiUVYXL2YFH8Ku+btisNxx4w7EASf+BBk3To+oOv5\n4WbSA+k0tjUS8AXISM3AL/51a/FrGtcwIHsA4WiYmpYazh9z/gb3uhuGYRjbnqSIunPuTO9cRO4E\n6jbQ/AjnXFUyxtFTNIQaOOu5syitLSU9JZ0FVQt4d9m7XH/o9Zy979ndPheKhLjk5UtoDjczJGcI\nqxpWEXMxVjWsIis1i0hrhLz0PCYOmUhlSyWrG1dTkFGAIFQ2V5IeSOf0vU7ntcWvsbp+NaFIiAUV\nC8hOy6Z/Rn/y0/M5esTRHd45c+VMrn3zWupa63A4huUO46eH/JSWSMu6fe4igg8fURfVz6gF7gm9\nFy3vcAQDQQoyCmgON1PVVEVqIJWL9r+IKQd1zC9vGIZhJJ+kut9F/bFnAEcm8z3bktLaUu6deS/T\nV0wnL5jH+WPO54y9z9hgSdYXvnyB0rpSirLiZU7bom38YcYfOHn3kztEw4NmdHt76dvMKZtDZVMl\nA7MHrqvitrphNS3hFsLRMIOzB5OZmsmimkWEY2EGZg9c10d+ej6VTZWsaVpDVUsVoweMprSulPpQ\nPbWtteQF83jilCfITM0kEovgFz8VTRVc9upl+H1+8jM0xeuKuhVc/5/ryUrNIhQOIWgq285kp2XT\n1NYEsC5rXczFKMoswic+jhlxDDccdgNZqVkdsucZhmEYPUey19QPBdY45xZ3c98Bb4iIAx52zk3t\nriMRuQS4BKCkZH2X8ragvLGcyc9NpiHUQG4wl5qWGn7z3m9YWb+Saw65ptvn3it9jzR/x/zlqf5U\nmtuaWVyzmDED4isPH5R+wI9e/xFt0TbqQ/VUNFXQFmtjWL9hDM4ZTGOoUQU9ZzDDcocBug+8sa2x\ng6h7vLnkTdJT0klPSWeP/nsQiUWIxqI0tjXyZeWXXP7q5SyuWUxxZjH7Fe1Ha6R1XcCciJCXnkdN\ncw37D9ift5e+jYu6DuvqqZJKv2A/CtILWBVdBeiExSc+CtILyE/Pp6alhpN2O4n8dKuwZhiGsT3p\n3vzcCCLylojM7+I4OaHZWcDfN9DNJOfc/sAJwA9F5LDuGjrnpjrnxjnnxhUWFnbXbKt4ev7T1Ifq\nKcwsJMWfQmZqJgUZBTz12VPUttZ2+9ygrEG0Rds6j5dILNJB6FojrVz9xtWk+FMozCxkaL+h+MXP\nmsY11IfqAagL1RHwB8hLj9c8L8oooqmtiZiLdehfEFIDqR3StAZ8AVL9qTS2NXLRyxfxQekHlDeU\nM7d8Lv+/vXsPj6o+Ezj+fWcmM0yuhNwgF24CAQKIgkFgFRFR9FERgYKiomK9tHS1+qyLVVepVbv4\nrFi329W6VbTVIrYoVrmIF7zQikCFEiTILVxCbiQhIZlkcmbmt39MMk0kXJIwCSbv53nyZHLmnDlv\nzpnknd85v9/7+/225n8Pg2Fsxtgm99EBHOIgMSqR4cnDue/C+yj8t0Kev/J5UmNSSY1JJSoiivKa\ncq7NvJYJfSe04EgrpZQKh1a31I0xl53seRFxANcDo07yGvn134tF5G0gG/istTG11ZbCLXRzdGuy\nzGFzYMPGgYoDJ+zNPXvYbFbsXEGNVYM7wk3ABDjiOUJ2WnaTjmpfF3yN1+8NJXqn3Ul6XDp5R/M4\nWHkQX8CHwdDd1Z0YZwwQTN5VdVUAbMzfSIwzhl4xvajz1zE4cTCjeo3i9W2vNylmU+mt5Jj3GJXe\nSrpFdMMmNowx1Fg1lHhKGBgYiM0W/DznD/gxxrAsZxlWwAqNiTcYfMbHEc8RCo4V8NyG50iOSubO\nUXcyfch0Pt73MRXeCrLTshmePPy0J6ZRSikVPq1uqZ+Gy4BcY8yh5p4UkSgRiWl4DFwO5IQxnlMa\nlDAIr8/bZFnABPAZHz2je55wu6zkLBZNXhScPKWmjLKaMsZnjOfZy59tsp6IhDqdNUiNSSUjNoOs\nxCyuHHAld5x/B3GuuFCLubCqkL1H95IUmUR6bDo1vhr2lu9l5tCZvHrdq9w9+m7SY9MpqS6hvKac\nkuoSRASf8YUmeTHG4DfByVv8AT8FVQUcrT1KWU0ZpTWlzMyaSW5pLlbACn2waFAXqGPf0X1gYPGX\nizHGkBCZwMysmdxx/h2hKWWVUkp1vHDeU5/Ndy69i0gq8H/GmKuAFODt+oTgAN4wxqwOYzyndOPw\nG/nzN3/maO1R4lxxWAErdHk5OSr5pNtOGTCFSf0mkXc0jxhXTLMfAs7reR7uiOCwsIaCLQ1D0Z65\n/BkuSLsAy2/x6CePsnLXSgThQMUBEt2JnNPjHESEtNg0SqpL8AV8xLhisPwWk/tP5sVNL1JWW0Zm\nQiaLJi9i9p9mU+4rx/Jb1Ppqg4m6PldPGzyN0ppS3A4304dOB2DhuoUn/N2E4Jh0EaHaqj6u2Myp\nlHpKqfBW0Duut87oppRSYaRlYr9ja+FWnvz8SXKKc3A73Nww/AZ+kv2T0FzkbfVV/lf86P0f4fV7\nCZgANmzcdt5t/PTCnzZp8RYcK2DT4U0s+HBBk171ADVWDQmRCbx/4/s89NFDrMhdQfdu3bECFoVV\nhbgdbkb1GsXyHctDU7yKBHu1Ox1OhiQO4cNbPgzdBljw4QIWrV/UpIXeWIwzOPvbsORhfHnHlycd\nCdBYpbeShz9+mHX71mGz2Yh2RvPoxY8yZcCU1hw6pZTqsrRMbCud2/Ncls1chtfnxWFzhMZkt5XH\n8vDBng/4tvRb7rvwPlz24EQt2WnZ9Ivvd9z6vWJ6Man/JJx2J5bfalJD3WN5GN19NIVVhbz37Xsk\nRiZysPIgxdXFoaFm1XXVxLvjKfGUhLaLsEeQmZCJ5bf4NO9Tpg2ZBsDfDv2NGFdMqLPedxmCr3nX\n6LtOO6EDPLj2QT4/8DmJkYnYxIbH8vDg2gdJi0ljeMrw034dpZRSp0eT+gmcqZY5QFFVETctv4nC\nqkIMBhEhKTKJ169/vdlharW+2mDVtohI5oyYw8tfv0y8O54IW0So09wd59/BwYqDOCRY+724uhi7\n2KkL1GEFLIqqi4hxxhDvikdsQjd7N3rG9CTaGU1xVXFw0pV6sc5Y+nbvy84jO6nz1zVpsdvFTsAE\nmNR/ErePvP20f+eCYwWsP7g+lNABIiMi8dR5eCPnDZ5Oebq1h1MppdQJhLOjnKq3+MvFHK46TGJU\nIklRSSRGJlJcXcwzf32myXrbirYx661ZjHpxFNkvZfP0509z9+i7uWf0PdT56yjxlJAUmcSvr/w1\nI3uOpHdc71APdQzU+GqwAhYQbJV7fMEysoMTBjMgYUCwSl3Ah01sjEkfE9rvTSNuwvJbDEseRkpU\nCg5xIAgxETFkJmRyw7AbWDp9aYs6xJXVlGEX+3Ete6fDSX5lfhuOplJKqRPRlnor1Pnr+LrgawBG\n9hx5ylb96t2rjyvM0sPdg7V71wbHm4twqPIQt624DV/AR1JUEr6Aj9//4/eUeEp49opnueeCe6j1\n1RIVEYWIUFhVyNs73iY6Ipq88jx8AV9oHLsgOO1O/AE/3ezdKKgqCMZogvfW7xx1J/3j+4dimZk1\nk91lu1mas5SU6BSSopI4v9f53H7e7fSJ6xMqgtMcj+Vh1a5VbMjfQEZsBtOGTCM9Np1+8f1w2Bx4\nfd4mx6fWV8v4jPEtPuZKKaVOTZN6C23M38i9q++luq4aEcHlcLH4isWMyxh3wm2cdmeTwjEQHCrX\nMFUqwB+3/ZFaXy2JkYlUeivxWB4i7BGs2bOGw8cOkxqTGup1nlOcw20rbqPGCtZrdzlcVFvVGAxO\nuxOX3YUxBrvYSY5K5taRt4aqxF1xzhVNKtwB2MTGwxc/zA9H/ZA9ZXvoGd2z2fv831XpreSm5Tex\nt3xvaHz7K1te4cWrX+SCtAu4f+z9PPX5UzgsR/DKgeUhNTqVWcNmnfK1lVJKtZwm9Rao9FZyz/v3\nICL0iAy2vKvrqpm/cj5rb15LQmRCs9vNGDqDJVuWkByVHOqFXlZTxpzhc0KXtHeX7abWV8uXh77E\nCljYxEaELQK72NlSuCU0L7kxhsc+eQzLb5EUFays18Pdgy2FW4IzqIkDv/FjExsDegzAClhM7DeR\nC9IuOOXvlxyVfMqhe4394R9/YE/Znia98495j/Hwxw+z5qY13Dj8Rvp278trW1+jpLqES/pewpwR\nc3RKVqWUChNN6i3wad6neP1eEiMTQ8uinFGUVJfwSd4nzBg6o9nt5mfPZ8eRHWw+vDnUCW106mju\nvfDe0DpWwGJf+b5gRzqEAAHq/HXYbXbezHmTqwZeBQTLyO4s3dkkBhEhMzGTnSU7iXZFE+uKJdYV\nS6W3khEpIxidGp4ZbT/Y88Fxk9VEO6MprCok/1g+6bHpjMsYd9KrGEoppc4cTeotUG1VH3cZHcBv\n/KEZzJoTGRHJy9e+TE5xDvsr9tM7rneT0qq1vlr+XvD3UCu+YXnABIh1xLK5YDMey0NkRCQuuwub\n2AiYAHb553C7gAmQnZ7N+b3OZ/Xu1dT6ahnZcyRXD7yaEk9Jkxa4MYb1B9fz1va3qPRWMmXgFKZm\nTj2uRO6pNHS8a8xgMMbgdrhPsJVSSqlw0d7vLZCdlh2cZzzgDy3zB/w4xNGkN3lzRIThKcO5etDV\nx5VWPVhxEAi2+hvuszfcr28YJ99QXtYd4WbKgCmU1pSGpkj1B4IfKuadN49fXvZLfnHpL4Bgb/qn\nvniKya9NZvmO5aH9vbD5Be5+727W7V/H1qKtLFy3kHkr5h03Kc2pzBk+B6/PGzoexhhKPaWM7z3+\nhLcilFJKhY+21Fugf3x/5o6cy5ItS4B/VmmbPWw2mQmZrX7dhMgEAiZAojuRwkAhbpsbEcHyWxgM\nF/W+qMmELY9c/AjF1cVsLtiMXez4jZ9ZWbOYmTWTkuoSHvn4EdwR7lDL2+vz8vi6xxmTNgaXw8UL\nG18g3h0fKtkaa2LZWrSVj/Z+xJUDrzztuKcMmMI3Jd+wZOuSUI35YcnDePLSJ1t9LJRSSrWeJvUW\nemDsA1zU+yJW7lpJwASY0HcC24q2Mem1SdhtdqYPmc6tI29t0aXsHu4eXDXwKt7JfYeoiCg8lge/\nCc6eNihhEI9d8liT9WNdsbwy9RV2le2isKqQgT0GhorYfH7g81A9+QYuh4sKbwWf7f8suJ7QpAa7\niGATG18c+KJFSV1EeGDcA9x87s3sPBK8zz84cbBO8KKUUh1Ek3oLiQhj0scwJn0MvoCPG/58A9uL\ntxPrisVgeH7D82w6vImXrnmpRcntsQmPEWGPYMWOFXh8weFs80bO494L721SIrZxHIMSBjEoYVCT\n5QEToLl6/pbfYkP+BtJi04JV4xrdu2/YrqE3fUu1tNe8Ukqp8NCk3gZfHPiC3JLc0FA1ALfDzYb8\nDWwt2nrcePCTcUe4eWLiEywYv4BKbyXJUcmtqjs/PmM8dpudOn8dTrsTgOKqYg5WHGTVrlXYbXby\nK/Op8laFZn7zWB4cNgfXDb6uxfs7HRW1FfiN/7gCPEoppc4s7SjXBrlHcvEZX5MWr4gQMAF2le5q\n1WtGOaPoFdOr1RPJ9Irpxc8u+hnHvMcoqiricOVh9pbvJS02jdTYVFKiU8hMyKSyrpLCqkLKa8px\niIPnrniOvt37tmqfJ1JcXcxd793F+JfHc/ErFzPrrVmtPi5KKaVOTVvqbZAem45Djj+EdrE3O1FL\ne5k9bDbjMsaxLm8dXxd8zardq5rEE+2KJjU6lbkj53Jt5rUMShh0xuc59wf83L7idvKO5pEQmYAg\n5JbmMveduayas4q4bnFndH9KKaW0pd4ml/a7lITIBI5UHyFgAgRMgOLqYjJiM7gw/cIOja13XG9u\nOfcWJvWfdMJ78j3cPRiaNPSMJ3SAjYc3cqDiAElRSdjEFtrfMe8x1uxZc8b3p5RSSpN6m0RGRPLa\ntNfITsum1FNKqaeUiX0n8sp1r4QlUbbG2PSx2MWO1+cNLfMFfNjFzsS+E8O236KqomaXBwhwqPJQ\n2ParlFJd2dmReb7Hesf15ndTf4fH8iBIk/HkZ4OEyAQWXrKQ//jkP6jwVgQnerHZmZ89n4EJA8O2\n38zETIwxBEwgNP2qMQYbNkakjAjbfpVSqivTpH6GREZEntHXK68p59m/Pctfvv0LAFcPupr7x97f\nqh7kUwdPJTstm3V566jz13FRn4uaTL0aDoMTBzP5nMms3r2aKGcUNrFxzHuMrOQsJvSZENZ9K6VU\nVyXNjWk+240ePdps2rSpo8MIG1/Ax/Rl09lVuiuUxMtryjmnxzksn7X8pJf2PZaHd3a8w0d5H5Hg\nTmBW1ixGpY5qr9Cb8AV8vJnzJm9ufxPLb3FN5jXccu4toSlklVJKnR4R2WyMOeXsXG1qqYvITOBx\nYAiQbYzZ1Oi5h4B5gB/4V2PMcb2jRKQfsBRIADYDNxtjWlaAvBP668G/srd8LynRKaFlydHJ7Du6\nj/UH1jOhb/MtXY/l4eblN5NbmovL7sIKWKzctZJHLn6E2cNmt1f4IQ6bgzkj5jBnxJx237dSSnVF\nbe0olwNcD3zWeKGIDAVmA1nAFOA3ItLcwOv/BBYbYwYA5QQ/BHR5+4/uP272Mwi2fPdX7D/hdu99\n+x65pbkkRSYR1y2OxMhE4rrFsWj9IqrqqsIZslJKqbNAm5K6MWaHMWZnM09NBZYaY7zGmH3AbiC7\n8QoSrNhyKfCn+kWvAuEpafY906d7n2YvsUfYIugT1+eE263LW4fT7mxSDMdpd2KMIfdIblhiVUop\ndfYI15C2NOBgo58P1S9rLAE4aozxnWSdEBG5U0Q2icimkpKSMxrs2WZcxjj6x/enuLoYy29h+S2K\nqoroF9+P8b3Hn3C7pMgkLL/VZJkxBr/xE+fSYi9KKdXZnTKpi8iHIpLTzNfU9giwgTHmt8aY0caY\n0UlJrZt45PvCYXOwZOoSZgyZgcfyUG1VM2PoDJZMXXLSTnI/yPoBNrFR66sF6uc3ryllSOIQBvQY\n0F7hK6WU6iCn7ChnjLmsFa+bD2Q0+jm9flljpUB3EXHUt9abW6fLinfHs3DiQhZOXHja22QlZ/Hk\npU/y889+TnlNOX7jZ1jyMH415Vc6HapSSnUB4Rqn/i7whog8C6QCA4GvGq9gjDEi8gkwg2AP+LnA\nijDF02Vck3kNl59zOTtLdxLrij3jk7QopZQ6e7XpnrqITBORQ8BY4H0RWQNgjNkOLAO+AVYDPzbG\n+Ou3WSkiqfUv8e/A/SKym+A99t+1JR4V5HK4GJEyQhO6Ukp1MVp8RimllDrLnW7xGZ3QRSmllOok\nNKkrpZRSnYQmdaWUUqqT0KSulFJKdRLfy45yIlICnLgIesdJBI50dBBdnJ6DjqfnoOPpOTg7nMnz\n0McYc8rKa9/LpH62EpFNp9M7UYWPnoOOp+eg4+k5ODt0xHnQy+9KKaVUJ6FJXSmllOokNKmfWb/t\n6ACUnoOzgJ6Djqfn4OzQ7udB76krpZRSnYS21JVSSqlOQpO6Ukop1UloUm8jEZkpIttFJCAio7/z\n3EMisltEdorIFR0VY1cjIo+LSL6IbKn/uqqjY+oqRGRK/ft9t4gs6Oh4uiIRyRORbfXvfZ35qp2I\nyMsiUiwiOY2W9RCRtSKyq/57fLjj0KTedjnA9cBnjReKyFBgNpAFTAF+IyL29g+vy1psjBlZ/7Wy\no4PpCurf3/8DXAkMBW6o/ztQ7W9i/Xtfx6q3nyUE/9c3tgD4yBgzEPio/uew0qTeRsaYHcaYnc08\nNRVYaozxGmP2AbuB7PaNTql2lQ3sNsbsNcbUAUsJ/h0o1ekZYz4Dyr6zeCrwav3jV4Hrwh2HJvXw\nSQMONvr5UP0y1T7mi8g/6i+Jhf2SlwL0PX+2MMAHIrJZRO7s6GC6uBRjTEH940IgJdw7dIR7B52B\niHwI9GzmqYeNMSvaOx518nMC/C/wBMF/bk8A/wXc3n7RKdWh/sUYky8iycBaEcmtb0WqDmSMMSIS\n9jHkmtRPgzHmslZslg9kNPo5vX6ZOgNO95yIyEvAe2EORwXpe/4sYIzJr/9eLCJvE7wtokm9YxSJ\nSC9jTIGI9AKKw71DvfwePu8Cs0XEJSL9gIHAVx0cU5dQ/8fTYBrBzowq/DYCA0Wkn4g4CXYUfbeD\nY+pSRCRKRGIaHgOXo+//jvQuMLf+8Vwg7Fd2taXeRiIyDfhvIAl4X0S2GGOuMMZsF5FlwDeAD/ix\nMcbfkbF2IYtEZCTBy+95wF0dG07XYIzxich8YA1gB142xmzv4LC6mhTgbRGB4P/3N4wxqzs2pK5B\nRP4IXAIkisgh4DHgl8AyEZlHcLrwH4Q9Di0Tq5RSSnUOevldKaWU6iQ0qSullFKdhCZ1pZRSqpPQ\npK6UUkp1EprUlVJKqU5Ck7pSSinVSWhSV0oppTqJ/wdoIucYMQ+uRwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "WeuwbMoBfrh4",
"colab_type": "text"
},
"source": [
"## 数据预处理"
]
},
{
"cell_type": "code",
"metadata": {
"id": "RB6x5g1fRdgF",
"colab_type": "code",
"outputId": "4b89d534-db9a-4b79-aaf0-ef41c0f5446f",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"#数据预处理\n",
"from sklearn import preprocessing\n",
"import numpy as np\n",
"from sklearn import datasets as d\n",
"#加载波士顿数据集\n",
"boston = d.load_boston()\n",
"X, y = boston.data, boston.target\n",
"X[:, :3].mean(axis=0) #前三个特征的均值\n",
"#array([ 3.59376071, 11.36363636, 11.13677866])\n",
"X[:, :3].std(axis=0) #前三个特征的标准差\n",
"X_2 = preprocessing.scale(X[:, :3]) #标准\n",
"X_2.mean(axis=0)\n",
"#array([ 6.34099712e-17, -6.34319123e-16, -2.68291099e-15])\n",
"X_2.std(axis=0)\n",
"#array([ 1., 1., 1.])"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"array([1., 1., 1.])"
]
},
"metadata": {
"tags": []
},
"execution_count": 7
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "nyRuxo7-RdgK",
"colab_type": "code",
"outputId": "57aac38a-6304-460c-8399-be09f1a33722",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 286
}
},
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"#%matplotlib inline\n",
"#随机生成一个实数,范围在(0.5,1.5)之间\n",
"cluster1 = np.random.uniform(0.5,1.5,(2,10))\n",
"cluster2 = np.random.uniform(3.5,4.5,(2,10))\n",
"#hstack拼接操作\n",
"X = np.hstack((cluster1, cluster2)).T\n",
"plt.figure()\n",
"plt.axis([0,5,0,5])\n",
"plt.grid(True)\n",
"plt.plot(X[:,0],X[:,1],'k.')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"[]"
]
},
"metadata": {
"tags": []
},
"execution_count": 8
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAD8CAYAAABXe05zAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAADipJREFUeJzt3VGIpeV9x/Hfz9k97OK45CLTIK6y\nhdaBrNBNXSyDpZxxSbBG0l5GSK4K40UaLBXT5qrkou6VIRdNoUvUuiRNGDBCsTStTPZUZE9qXDOm\njpuRkApVAou0YZ0Lc5zdfy/mTM46O7PnHee853n/c74fOOyMvnPO30f9zcPz/p/ndUQIAJDHTaUL\nAADsDsENAMkQ3ACQDMENAMkQ3ACQDMENAMkcqHKR7bckvSfpiqT1iDhZZ1EAgJ1VCu6++Yh4t7ZK\nAACVsFQCAMm4ys5J2/8t6f8khaR/iIgz21yzIGlBkg4dOnT3HXfcMeJSc7p69apuuonfj4zDAGMx\nwFgMvPnmm+9GxEyVa6sG920R8Y7t35L0gqQvR8SLO10/Ozsbq6urlQvezzqdjtrtdukyimMcBhiL\nAcZiwPaFqvcPK/2qi4h3+n9ekvScpHs+enkAgL0YGty2b7Z9y+bXkj4j6fW6CwMAbK9KV8knJD1n\ne/P6f4qIH9RaFQBgR0ODOyJ+Ien3xlALAKACbucCQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3AD\nQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADQDIENwAkQ3ADaIRut6vTp0+r2+2W\nLqXxqjy6DABq1e12derUKfV6PbVaLS0tLWlubq50WY3FjBtAcZ1OR71eT1euXFGv11On0yldUqMR\n3ACKa7fbarVampqaUqvVUrvdLl1So7FUAqC4ubk5LS0tqdPpqN1us0wyBMENoBHm5uYI7IpYKgGA\nZAhuAEiG4AaAZAhuAEiG4AaAZAhuAEiG4AaQzqSfa0IfN4AP6Xa7jd4Iw7kmBDeAa2QIxe3ONWla\njXVjqQTAb2Q47IlzTZhxA7jGZihuzribGIqca0JwA7hGllCc9HNNCG4AHzLpoZhB5TVu21O2f2L7\n+ToLAtBsk96K1wS7mXE/IumipCM11QKg4TJ0nUyCSjNu20clfVbSt+otB0CTZeg6mQRVZ9zfkPQV\nSbfsdIHtBUkLkjQzM8O/0L61tTXGQozDtTKPxZEjR3TgwAFFhA4cOKAjR47s6Z9l61isrKxoeXlZ\nJ06c0PHjx/de8H4VETd8SXpQ0t/3v25Len7Yz9x5552BDefOnStdQiMwDgPZx+L8+fPx+OOPx/nz\n5/f8XteOxfnz5+Pw4cMxNTUVhw8fHsn7ZyLplRiSrZuvKjPueyV9zvYDkg5JOmL72xHxhXp+lQBo\nsrq6TtgRWd3QNe6I+GpEHI2IY5I+L+mHhDaAUWNHZHX0cQNohCybf5pgV8EdER1JnVoqATDx2PxT\nDYdMAUAyBDcAJENwA0AyBDcAJENwA0AyBDcw4UZ92h+nB9aPPm5ggo36tD9ODxwPZtzABBv1aX+c\nHjgeBDcwwUa9zZxt6+PBUgkwwUa9zZxt6+NBcAMTbtTbzJu6bb3b7e6bXygEN4BGqCtYu92uzp49\nq6efflrr6+v74qYpwQ2guLq6UTbf9/333998MMy+OOubm5MAiqurG2XzfTdD2/a+uGlKcAMorq5u\nlK3v+/DDD6dfJpFYKgHQAHV1o+zXLheCG0Aj1NWN0tQul71gqQQAkiG4ASAZghsAkiG4ASAZghsA\nkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkiG4ASAZghsAkhka\n3LYP2X7Z9mu2V2x/bRyFAQC2V+XRZb+WdF9ErNk+KOkl2/8aET+quTYAwDaGBndsPNd+rf/twf4r\n6iwKALAzb+TykIvsKUkXJP2OpG9GxF9tc82CpAVJmpmZuXtxcXHEpea0tram6enp0mUUxzgMMBYD\njMXA/Pz8hYg4WeXaSsH9m4vtj0l6TtKXI+L1na6bnZ2N1dXVyu+7n3U6HbXb7dJlFMc4DDAWA4zF\ngO3Kwb2rrpKI+JWkc5Lu/yiFAQD2rkpXyUx/pi3bhyV9WtLP6i4MALC9Kl0lt0p6pr/OfZOkxYh4\nvt6yAAA7qdJV8lNJnxpDLQCACtg5CQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzB\nDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJ\nENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwAkAzBDQDJENwA\nkAzBDQDJDA1u27fbPmf7Ddsrth8ZR2EAgO0dqHDNuqRHI+JV27dIumD7hYh4o+baAADbGDrjjohf\nRsSr/a/fk3RR0m11FwYA2J4jovrF9jFJL0q6KyIub/l7C5IWJGlmZubuxcXF0VWZ2Nramqanp0uX\nURzjMMBYDDAWA/Pz8xci4mSVaysHt+1pSf8h6W8j4vs3unZ2djZWV1crve9+1+l01G63S5dRHOMw\nwFgMMBYDtisHd6WuEtsHJT0r6TvDQhsAUK8qXSWW9KSkixHx9fpLAgDcSJUZ972SvijpPtvL/dcD\nNdcFANjB0HbAiHhJksdQCwCgAnZOAkAyBDcAJENwA0AyBDcAJENwA0AyBDcAJENwA0AyBDcAJENw\nA0AyBDcAJENwA0AyBDcAJENwA0AyBDcAJENwA0AyBHch3W5Xp0+fVrfbLV0KgGSGPkgBo9ftdnXq\n1Cn1ej21Wi0tLS1pbm6udFkAkmDGXUCn01Gv19OVK1fU6/XU6XRKlwQgEYK7gHa7rVarpampKbVa\nLbXb7dIlAUiEpZIC5ubmtLS0pE6no3a7zTIJgF0huAuZm5sjsAF8JCyVNARdJgCqYsbdAHSZANgN\nZtwNQJcJgN0guBuALhMAu8FSSQPQZQJgNwjuhqDLBEBVLJUAQDIENwAkQ3A3CL3cAKpgjbsh6OUG\nUBUz7m2UmPnSyw2gKmbcW5Sa+W72cm9+Lr3cAHZCcG+x3cx3HMFNLzeAqoYGt+2nJD0o6VJE3FV/\nSWWVnPnSyw2giioz7n+U9HeSztZbSjMw8wXQdEODOyJetH2s/lKaI/PMt9vt8ksH2OccEcMv2gju\n52+0VGJ7QdKCJM3MzNy9uLg4ohJzW1tb0/T09Fg+a2VlRY8++qg++OADHTx4UE888YSOHz8+ls8e\nZpzj0HSMxQBjMTA/P38hIk5WuXZkNycj4oykM5I0OzsbdEVs2Jz9jkO329X6+rquXr2q9fV1Xb58\nuTHdKeMch6ZjLAYYi4+GPu59hONhgclAO2DD7GWNmhurwGSo0g74XUltSR+3/bakv4mIJ+subBJt\nt/lH0q6COPONVQDVVOkqeWgcheD6zT9nz57VM888w/klAD6ENe4G2bpGLYnzSwBchzXuBtm6Ri3p\nQzNubjYCkAjuxtm6Rs3NRgBbEdwNx81GAFuxxg0AyRDcAJAMwQ0AyRDcAJAMwQ0AyUx0cI/rocAl\nHj4MYP+a2HbAcT0UeGVlRY899hjb1gGMzMTOuLd7KHAdlpeX2bYOYKQmNrjHdXb1iRMnrvsclk4A\n7MXELpWM6+zq48ePX3f+yDiWaADsXxMb3NL4tpNf+zmnT5++bumE4AawGxO7VFIKjxcDsFcTPeMu\ngceLAdgrgrsATvwDsBcslQBAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3\nACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMgQ3ACRDcANAMpWC2/b9tldt/9z2X9ddFABgZ0OD2/aU\npG9K+mNJn5T0kO1P1l0YAGB7VWbc90j6eUT8IiJ6kr4n6U/qLQsAsJMqDwu+TdL/XPP925L+YOtF\nthckLfS//bXt1/de3r7wcUnvli6iARiHAcZigLEYmK164cie8h4RZySdkSTbr0TEyVG9d2aMxQbG\nYYCxGGAsBmy/UvXaKksl70i6/Zrvj/b/GgCggCrB/WNJv2v7t223JH1e0j/XWxYAYCdDl0oiYt32\nn0v6N0lTkp6KiJUhP3ZmFMXtE4zFBsZhgLEYYCwGKo+FI6LOQgAAI8bOSQBIhuAGgGRGGtxsjd9g\n+ynbl+hll2zfbvuc7Tdsr9h+pHRNpdg+ZPtl26/1x+JrpWsqzfaU7Z/Yfr50LSXZfsv2f9lertIW\nOLI17v7W+DclfVobm3R+LOmhiHhjJB+QiO0/krQm6WxE3FW6npJs3yrp1oh41fYtki5I+tMJ/e/C\nkm6OiDXbByW9JOmRiPhR4dKKsf2Xkk5KOhIRD5aupxTbb0k6GRGVNiONcsbN1vi+iHhR0v+WrqMJ\nIuKXEfFq/+v3JF3Uxm7ciRMb1vrfHuy/JrY7wPZRSZ+V9K3StWQzyuDebmv8RP4Piu3ZPibpU5L+\ns2wl5fSXBpYlXZL0QkRM7FhI+oakr0i6WrqQBghJ/277Qv/4kBvi5iTGwva0pGcl/UVEXC5dTykR\ncSUiTmhjB/I9tidyKc32g5IuRcSF0rU0xB9GxO9r4xTWL/WXW3c0yuBmazy21V/PfVbSdyLi+6Xr\naYKI+JWkc5LuL11LIfdK+lx/bfd7ku6z/e2yJZUTEe/0/7wk6TltLD3vaJTBzdZ4XKd/Q+5JSRcj\n4uul6ynJ9oztj/W/PqyNG/k/K1tVGRHx1Yg4GhHHtJEVP4yILxQuqwjbN/dv3Mv2zZI+I+mGHWkj\nC+6IWJe0uTX+oqTFClvj9yXb35XUlTRr+23bf1a6poLulfRFbcyolvuvB0oXVcitks7Z/qk2Jjov\nRMREt8FBkvQJSS/Zfk3Sy5L+JSJ+cKMfYMs7ACTDzUkASIbgBoBkCG4ASIbgBoBkCG4ASIbgBoBk\nCG4ASOb/AdBN/i/qd/jaAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "mQCn6aRIous1",
"colab_type": "text"
},
"source": [
"# 分类\n",
"- 分类的核心目的是给定一个样本的数据观测,根据一个数据模型得出预测该样本属于哪个类别"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "q-KM9kSegKvH",
"colab_type": "text"
},
"source": [
"## 二分类-LR回归\n",
"- [logistics回归详解](http://blog.csdn.net/xlinsist/article/details/51289825)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ItwnqlGoRdgU",
"colab_type": "code",
"outputId": "22a1d237-bb0d-4d3a-ccf4-37955f6b2a35",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 90
}
},
"source": [
"#logistics回归详解:http://blog.csdn.net/xlinsist/article/details/51289825\n",
"from sklearn import datasets\n",
"import numpy as np\n",
"from sklearn.model_selection import train_test_split\n",
"from sklearn.metrics import accuracy_score\n",
"\n",
"iris = datasets.load_iris() # 由于Iris是很有名的数据集,scikit-learn已经原生自带了。\n",
"X = iris.data[:, [2, 3]]\n",
"y = iris.target # 标签已经转换成0,1,2了\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) # 为了看模型在没有见过数据集上的表现,随机拿出数据集中30%的部分做测试\n",
"\n",
"# 为了追求机器学习和最优化算法的最佳性能,我们将特征缩放\n",
"from sklearn.preprocessing import StandardScaler\n",
"sc = StandardScaler()\n",
"sc.fit(X_train) # 估算每个特征的平均值和标准差\n",
"sc.mean_ # 查看特征的平均值,由于Iris我们只用了两个特征,所以结果是array([ 3.82857143, 1.22666667])\n",
"sc.scale_ # 查看特征的标准差,这个结果是array([ 1.79595918, 0.77769705])\n",
"X_train_std = sc.transform(X_train)\n",
"# 注意:这里我们要用同样的参数来标准化测试集,使得测试集和训练集之间有可比性\n",
"X_test_std = sc.transform(X_test)\n",
"\n",
"# 训练感知机模型\n",
"from sklearn.linear_model import Perceptron\n",
"# n_iter:可以理解成梯度下降中迭代的次数\n",
"# eta0:可以理解成梯度下降中的学习率\n",
"# random_state:设置随机种子的,为了每次迭代都有相同的训练集顺序\n",
"ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)\n",
"ppn.fit(X_train_std, y_train)\n",
"\n",
"# 分类测试集,这将返回一个测试结果的数组\n",
"y_pred = ppn.predict(X_test_std)\n",
"# 计算模型在测试集上的准确性,我的结果为0.9,还不错\n",
"accuracy_score(y_test, y_pred)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/stochastic_gradient.py:152: DeprecationWarning: n_iter parameter is deprecated in 0.19 and will be removed in 0.21. Use max_iter and tol instead.\n",
" DeprecationWarning)\n"
],
"name": "stderr"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
"0.8"
]
},
"metadata": {
"tags": []
},
"execution_count": 14
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "ae6u5xVsRdgY",
"colab_type": "code",
"outputId": "70ab2f30-ae24-4e34-f920-3ec329ea9013",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
}
},
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"def sigmoid(h):\n",
" return 1.0 / (1.0 + np.exp(-h))\n",
"\n",
"h = np.arange(-10, 10, 0.1) # 定义x的范围,像素为0.1\n",
"s_h = sigmoid(h) # sigmoid为上面定义的函数\n",
"plt.plot(h, s_h)\n",
"plt.axvline(0.0, color='k') # 在坐标轴上加一条竖直的线,0.0为竖直线在坐标轴上的位置\n",
"plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted') # 加水平间距通过坐标轴\n",
"plt.axhline(y=0.5, ls='dotted', color='k') # 加水线通过坐标轴\n",
"plt.yticks([0.0, 0.5, 1.0]) # 加y轴刻度\n",
"plt.ylim(-0.1, 1.1) # 加y轴范围\n",
"plt.xlabel('h')\n",
"plt.ylabel('$S(h)$')\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEKCAYAAAAIO8L1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XmYVPWd7/H3t6s3aKDZ931XURQR\n15hS0YBRiCELSZgoZgYTNYmZ8eaG8YYkmueOTsxNTCbG0WjQaAKJEgWC4hbJRCOrrLK1rL2wQ3dD\nb9Vdv/tHFU3RVkN101Wnls/refqps/yq6tunTtenz/mdxZxziIiINJXldQEiIpKcFBAiIhKVAkJE\nRKJSQIiISFQKCBERiUoBISIiUSkgREQkKgWEiIhEpYAQEZGosr0u4Fx0797dDR482OsyRD5m69at\nAIwaNcrjSkQ+bvXq1Yeccz3O1i6lA2Lw4MGsWrXK6zJEPsbv9wPwzjvveFqHSDRmtjuWdtrFJCIi\nUSkgREQkKgWEiIhEpYAQEZGoFBAiIhKVAkJERKJSQIiISFQKCBERiUoBISIiUSkgREQkKgWEiIhE\npYAQEZGoFBAiIhJVQgLCzJ4xswNmtrGZ+WZmvzCzIjNbb2bjElGXiIg0L1FbEHOBSWeYPxkYEf6Z\nBfw6ATWJiMgZJOR+EM65v5nZ4DM0mQo855xzwPtm1tnM+jjnyhJRn4hkhmDQUR901AeDoceG0HBD\n0BF04JzDOUI/nJoWdAChecGT84Khx5Ptg87hOL19MDzvJBcxEjH59DanzTm9YeScoT0K6FPY7lwX\nyRklyw2D+gF7I8aLw9M+FhBmNovQVgYDBw5MSHEiEn/VdQ0cq66jorqeipoAFdWB8GM9lTUBKmvq\nqQ40UBNooCYQpCbQQHWggdpAkJr6U9PrG4IEgo6GoCPQEPryPxkEQXf2OlLFjz8zhhlXDIrreyRL\nQMTMOfck8CTA+PHj0+jjFklfFTUB9hyuYs+RKvYeqWJ/RS0HKms4UFnLwfDP8dr6M75GXnYW7XJ9\n5Gf7aJfrIy87i/wcH/k5WXQtyCU/OzSc7csix2dkZ2XhyzJyfIYvKyv8aOT4QtOzT/6Ex7MMDMMM\nzMLjBllmQMQ0Ts0zM4xQG2tuWvg1T7LIX+q06adG7LRGpz/HwjMHd2sf8/JvrWQJiBJgQMR4//A0\nEUkhx2vr2bqvks1lFWzZV8GWsko+Onico1WB09oV5Pro2SmfHh3zOL9vJ3p2zKNHxzy6tM+lU34O\nndplhx9z6JSfTcf8HHKzddBloiVLQCwE7jWzecDlQLn6H0SS38HKWlbuOsKKnUdYvvMIW/ZVNO5P\n75iXzeg+HZk0pg+DurVnUNf2DOzWnoFd29MxP8fbwiUmCQkIM/sD4Ae6m1kx8AMgB8A59wSwBLgZ\nKAKqgJmJqEtEWiYYdKwtPsYbH+7nrc372bb/OADtcnxcOqgL375hBBf0LeS8Ph3p17ld4+4QSU2J\nOorpS2eZ74B7ElGLiLTctv2VvLS6mJfXlrC/opbsLOPyoV357Lj+XD6kK2P6FZLj0y6gdJMsu5hE\nJMnU1QdZsqGMZ97dyfricrKzDP+onvz7zX3wj+xJYXvtJkp3CggROU1VXT3P/WM3c9/dxb6KGob1\nKGDOLecz5eK+dO+Q53V5kkAKCBEBINAQZN7Kvfzire0crKzl6uHd+I9pF/LJET3IylJfQiZSQIgI\nf99+iO+/spGdh04wYXBXnpgxjksHdfW6LPGYAkIkgx2rquPHf9nMi6uLGdK9gGfuGM91o3rq6CMB\nFBAiGetv2w7yr39cy7GqAPdcN4xvXj+C/Byf12VJElFAiGSYhqDjsbe288u3tzOyZ0eeu/Nyzu/b\nyeuyJAkpIEQyyLGqOu79/Qf8vegQ08b158efGUO7XG01SHQKCJEMUXqsmq8+s4I9h6t4ZNqFfGH8\nAPU1yBkpIEQywLb9lXz16RWcqK3nua9N4Iqh3bwuSVKAAkIkza3be4x/eno5+Tk+5t91pfobJGYK\nCJE0tm1/Jbf/dgWF7XP4/T9fwYCu8b+HgKQPXV1LJE3tOVzFjN8sJ9eXxQtfUzhIy2kLQiQNHaio\n4StPv09dQ5A/3nUlAxNw9zFJP9qCEEkztfUNzPrdag4fr+PZmRMY2auj1yVJitIWhEgacc7x/Zc3\nsnbvMZ6YMY6xAzp7XZKkMG1BiKSR59/fzR9XFfPN64czaUwfr8uRFKeAEEkTq3Yd4UeLPuSG0T35\nzsSRXpcjaUABIZIGKmsCfHveWvp1acfPpl+s+zdIm1AfhEgaeHDRh5SVV/Onr19Fp3zdClTahrYg\nRFLc0k37+NPqYu72D+fSQV28LkfSiAJCJIUdrKxl9oINXNC3E9+6YYTX5UiaUUCIpLAfLdrE8dp6\nfv7Fi8nN1p+ztC2tUSIp6t2iQyxeX8Y9/uGM0MlwEgcKCJEUVFvfwPdf2cigbu2565NDvS5H0pSO\nYhJJQU//fSc7Dp7gtzMv032kJW60BSGSYkqOVfPLt4q46fxeXDeqp9flSBpTQIikmIdf3YLDMefW\n870uRdKcAkIkhWwsKWfRulK+ds0Q+nfRJbwlvhQQIinkJ0u3Utguh1nXDvO6FMkACgiRFPGPjw6z\nbNtB7rluGIXtdDkNiT8FhEgKcM7xn0u30LtTPl+9crDX5UiGUECIpIA3PtzPB3uOcd/EETqsVRJG\nASGS5Jxz/OzN7QzpXsDnLu3vdTmSQRQQIknunW0H2VxWwd3+YWT79CcriaO1TSTJPf7XIvoW5jP1\n4n5elyIZRgEhksRW7DzCyl1HmXXtUF2tVRJOa5xIEnv8nSK6FeTyxcsGel2KZCAFhEiS2lRazjtb\nD3LnNUNol6sjlyTxFBAiSeqJZTvokJfNjCsGeV2KZCgFhEgS2ldew5INZUy/bIDOmhbPKCBEktAL\ny3cTdI7brxrsdSmSwRQQIkmmJtDA75fv4YbRvRjQVVdsFe8oIESSzOL1ZRw+UcfMqwd7XYpkOAWE\nSBJxzvHbd3cyomcHrhrWzetyJMMpIESSyOrdR9lUWsEdVw/GzLwuRzKcAkIkicx9bxed8rO57RJd\nVkO8p4AQSRKHj9eydNM+PnfpANrnZntdjogCQiRZvLSmmECD40sTBnhdigiggBBJCs455q3cy6WD\nujCiV0evyxEBFBAiSWHFziPsOHiC6Zdp60GShwJCJAnMW7mXjnnZfPqiPl6XItJIASHisfKqAEs2\nlDH1kr7qnJakooAQ8difPyimtj7IdN3zQZKMAkLEY/NW7uXCfoWM6VfodSkip1FAiHhoU2k5W/ZV\n8oXx/b0uReRjFBAiHlqwpoQcn3HLRX29LkXkYxQQIh4JNAR5ZW0JN4zuRZeCXK/LEfkYBYSIR/5n\n+0EOHa/js+N03SVJTgoIEY+8tLqErgW5+Ef19LoUkagUECIeKK8K8Mbm/UwZ25fcbP0ZSnLSmini\ngcUbSqmrDzJtnI5ekuSlgBDxwII1JYzs1YEx/Tp5XYpIsxQQIgm290gVq3cfZerF/XTXOElqCgiR\nBPvLhjIApozVuQ+S3BQQIgm2aF0pYwd0ZkDX9l6XInJGCgiRBNpx8DibSiu4VZf1lhSggBBJoMXr\nyzBDl9aQlKCAEEkQ5xwL15Vy2eCu9C7M97ockbNSQIgkyNb9lRQdOM6t6pyWFKGAEEmQRetKyTKY\nPKa316WIxEQBIZIAzjkWry/j6uHd6d4hz+tyRGKigBBJgA0l5ew+XMWt6pyWFKKAEEmARetKyfEZ\nn7pAu5ckdSggROIsGAztXvrkyB4Uts/xuhyRmCkgROJs9Z6jlJXX6NwHSTktDggzKzAzXzyKEUlH\ni9eVkpedxcTze3ldikiLnDUgzCzLzL5sZn8xswPAFqDMzD40s5+Y2fD4lymSmuobgvxlQxk3nNeT\nDnnZXpcj0iKxbEH8FRgGzAZ6O+cGOOd6AtcA7wOPmNmMONYokrKW7zzCoeN1OnpJUlIs/9JMdM4F\nmk50zh0BXgJeMjP1vIlEsWhdKQW5Pq4brftOS+o5a0CcDAczux74CnAM2AisBzY652qjBYhIpnMO\nXtu0jxvP70V+jrrtJPW0pJP6GWARod1KQ4E5wKZYn2xmk8xsq5kVmdn3osy/w8wOmtna8M8/t6A2\nkaRTXh3gWFVA116SlNWSXrPdzrmXw8N/asmbhI96+hVwI1AMrDSzhc65D5s0ne+cu7clry2SrA4f\nr6VLfjafGNHD61JEWiWWo5ieM7P7gPfN7F9b+T4TgCLn3A7nXB0wD5jaytcSSXpB5zhSVcfkMX3I\nzdbpRpKaYllz5wIG9AL+ycx2m9lCM3vIzD4f4/v0A/ZGjBeHpzU1zczWm9mLZjbgbC+6detW5s6d\nC0AgEMDv9/P8888DUFVVhd/vZ/78+QCUl5fj9/tZsGABAIcOHcLv97No0SIA9u3bh9/v57XXXgNg\n7969+P1+3nzzTQB27NiB3+9n2bJlje/t9/t57733ANi4cSN+v5+VK1cCsHbtWvx+P2vXrgVg5cqV\n+P1+Nm7cCMB7772H3+9n69atACxbtgy/38+OHTsAePPNN/H7/ezdG1psr732Gn6/n3379gGwaNEi\n/H4/hw4dAmDBggX4/X7Ky8sBmD9/Pn6/n6qqKgCef/55/H4/gUCou2ju3Ln4/f7GZfnUU08xceLE\nxvHHH3+cyZMnN44/9thjTJkypXH80UcfZdq0aY3jDz/8MNOnT28cf+ihh5gx49TBbXPmzGHmzJmN\n47Nnz2bWrFmN4/fffz/33HNP4/h9993Hfffd1zh+zz33cP/99zeOz5o1i9mzZzeOz5w5kzlz5jSO\nz5gxg4ceeqhxfPr06Tz88MON49OmTePRRx9tHJ8yZQqPPfZY4/jkyZN5/PHHG8cnTpzIU0891Tju\n9/vPuO6tWbOWuuPHuGVsH617WvcSuu7F8r0Xq1g6qd8G3j45bmbZwHnAWEJbBi3a3XQGi4A/OOdq\nzewu4Fng+qaNzGwWMAsgL09XxZTkFAgG8WUZVw7txonjlV6XI9Iq5pw7cwMzc2dpdLY2ZnYl8EPn\n3KfC47MBnHP/0Ux7H3DEOVd4pvcdP368W7Vq1RnrF0m0E7X19Bg5jh4d89i9caXX5Yh8jJmtds6N\nP1u7mE6UM7NvmtnAJm+Qa2bXm9mzwO1neY2VwAgzG2JmucB0YGGT14u8i/sUYHMMtYkknTc37yfo\nnO77ICkvlqOYJgF3An8wsyGEzoNoRyhcXgd+7pz74Ewv4JyrN7N7gaWAD3jGObfJzB4EVjnnFgLf\nMrMpQD1wBLijlb+TiKcWrSsjNzuLjvm6tIaktlj6IGqAx4HHw2dMdweqnXPHWvJGzrklwJIm0+ZE\nDM8mdDkPkZRVXh1g2bYDdCvQ1oOkvlgOc33LzC6AxrOqLwPuNbMJ8S5OJNW8vmkfgQZHtw65Xpci\ncs5i6YPo75zbBGBmVwG/AwYCc83stngWJ5JqFq0vY0DXdrpyq6SFWAKiImL4q8ATzrlZgB/43/Eo\nSiQVHT5ey7tFh3TlVkkbsQREkZl9zsx6Ap8BXgFwzh0AtKNVJOzVjftoCDrdOU7SRiwB8R3gLqAE\nWOOcew8g3GHdIY61iaSUhetKGdajgPP6dPS6FJE2EctRTPuAG80syzkXjJh1HaGbCYlkvLLyalbu\nOsJ9N4zEzLwuR6RNxNyT1iQccM69Tug8CJGMt3hdGc7BlIu1e0nShy4zKdIGFq4r5aL+hQzpXuB1\nKSJtRgEhco52HDzOhpJypujGQJJmFBAi52jhulLM0NFLknYUECLnwDnHwnWlXD6kK70L870uR6RN\nKSBEzsGm0gp2HDzBlLHR7n8lktoUECLnYOG6UnJ8xuQxvb0uRaTNKSBEWikYdCxaV8q1I3rQpUAX\n55P0o4AQaaVVu49SVl6jcx8kbSkgRFrplbUl5OdkMfG8Xl6XIhIXCgiRVgg0BFmyoYwbz+9NgS7t\nLWlKASHSCn/bdpCjVQGdHCdpTQEh0goL1pTQtSAX/6geXpciEjcKCJEWKq8K8MaH+5kyti85Pv0J\nSfrS2i3SQos3lFLXEGTauP5elyISVwoIkRZ6aXUxI3t1YEy/Tl6XIhJXCgiRFth56ARr9hzjs+P6\n68ZAkvYUECItsGBNMVkGt12iay9J+lNAiMQoGHQsWFPC1cO706uTrtwq6U8BIRKj93cepuRYtTqn\nJWMoIERiNG/FXjrlZzNJV26VDKGAEInB0RN1vLZxH7dd0o/8HJ/X5YgkhAJCJAYLPiihriHIly4f\n6HUpIgmjgBA5C+cc81bs4eIBnRndW+c+SOZQQIicxZo9R9l+4DhfmjDA61JEEkoBIXIWf1ixl4Jc\nH7dcpCu3SmZRQIicQUVNgMXrS5lycT/d90EyjgJC5AwWrC6mJhDkyxPUOS2ZRwEh0oxg0PHsP3Yz\nbmBnLuxf6HU5IgmngBBpxrLtB9l56AR3XD3E61JEPKGAEGnG3Hd30atTHpN15rRkKAWESBRFB46z\nbNtBZlw+SHeNk4ylNV8kiuf+sYtcX5bOnJaMpoAQaaKiJsCLq4u5dWxfunfI87ocEc8oIESamLdi\nD1V1Ddxx1WCvSxHxlAJCJEJNoIGn/mcnVw/vpkNbJeMpIEQivLSmmIOVtdztH+51KSKeU0CIhNU3\nBPnvZTsYO6AzVw3r5nU5Ip5TQIiE/WVDGXuOVHG3fxhm5nU5Ip5TQIgQuqzG43/9iBE9O3Djeb28\nLkckKSggRIC3thxg6/5KvuEfRlaWth5EQAEhQkPQ8ejSrQzu1p5bx+qeDyInKSAk4y1cV8LW/ZX8\n202jdFkNkQj6a5CMVlcf5Kevb+OCvp349IV9vC5HJKkoICSj/X75boqPVvPdSaPV9yDShAJCMtbx\n2np++XYRVw7txrUjuntdjkjSUUBIxnpy2UccPlHHdyeN0nkPIlEoICQj7Tp0gieW7WDqxX25ZGAX\nr8sRSUoKCMk4zjl+sHATudlZPHDzeV6XI5K0FBCScZZu2s+ybQf5zo0j6dkp3+tyRJKWAkIySlVd\nPQ8u2sTo3h25/cpBXpcjktQUEJJRfvbGNkrLa3joM2PI1klxImekvxDJGO/vOMxv/r6Tr1w+kMsG\nd/W6HJGkp4CQjFBRE+Df/riOQV3b88Cn1TEtEotsrwsQSYQfLfyQsvJqXvzGVbTP1WovEgttQUja\ne3VDGS+tKeae64YzTuc8iMRMASFprehAJf/rxfWM7V/It24Y4XU5IilFASFpq7w6wL88t5r8nCx+\nPeNSXcpbpIW0M1bSUjDo+M78tew9UsXv/+UK+nZu53VJIilH/1JJWnpk6Rbe3nKAH0y5gAlDdEir\nSGsoICTt/Pqdj/jvZTuYccVAZlw+0OtyRFKWAkLSyvPv7+aR17Yw9eK+/GjKGF3GW+QcKCAkbSxY\nU8z3X9nIDaN78ujnx+LTHeJEzok6qSUtPP33nTy0+EOuGtaNX31lnI5YEmkDCghJac45HnltK08s\n+4hJF/Tm59MvJj/H53VZImlBASEpq6qunn9fsIGX15bylcsH8uDUMdqtJNKGFBCSkooOHOfuF1az\n/cBx7r9pJPdcN1wd0iJtTAEhKcU5xytrS3ngzxvIy/Hx7MwJXDuyh9dliaQlBYSkjNJj1Xz/5Y28\nteUAlw7qwn99+RL6FOoMaZF4UUBI0qurD/LC8t08unQrQQf/59PnMfPqIepvEIkzBYQkrWDQsWh9\nKT99fRt7jlTxiRHd+b+3XciAru29Lk0kIyggJOnU1QdZvL6UJ/+2gy37KhnduyO/veMy/KN6qCNa\nJIEUEJI0ysqreWl1Mb97fzf7K2oZ0bMDP/viWKaO7UeWdieJJJwCQjxVXhXgzc37+fMHJbz70SGc\ng2uGd+eRaRfxyZHaYhDxkgJCEqoh6Niyr4J/fHSYtzYfYMWuIzQEHf27tOOb149g2rh+DOpW4HWZ\nIoICQuKsvDrAlrIK1u49xvKdR1i56wiVNfUAjOjZgbuuHcqN5/dibP/O2o0kkmQSFhBmNgl4DPAB\nv3HOPdxkfh7wHHApcBj4onNuV6Lqk9YLBh0Hj9ey+3AVuw+fYNfhE2wpq2TLvkpKjlU3thvao4Bb\nLurL5UO6ctmQrvTTXd5EklpCAsLMfMCvgBuBYmClmS10zn0Y0exrwFHn3HAzmw48AnwxEfXJx9XV\nB6moCVBRHaCypp7y6gCHT9RyoKKWA5W1HKys5UBlDQcqayk9Vk1NINj4XF+WMaxHAZcO6sKMKwYx\nuk9HxvQtpEfHPA9/IxFpqURtQUwAipxzOwDMbB4wFYgMiKnAD8PDLwL/ZWbmnHNtXUxNoIETtaHd\nHA5wDhwuNNJ0WuNw6DIPkdU02yZiPpx6TuTrNk5rMh5tWtA5GoKO+uCpx2DjePDU9IbQY4MLz2sI\nzasJNFATCFITaKC2PvRYc/Ix0EBtIEhNfQNVdQ1UVAeoqAmc9oXfVLscHz075dGzYx6je3fk+lE9\nGdStPQO7FTCwa3v6dW5HbrYuty2S6hIVEP2AvRHjxcDlzbVxztWbWTnQDTjU1sXMfW8XD7+6pa1f\nNqmZQX62j/ycLPJzfOTn+MjLzmp87NI+l36dfRS2y6FTuxw65WfTqV0OHfOz6ZQfmtatIJeenfIp\nyPXp6CKRDJByndRmNguYBTBwYOvuN3zN8O78aMoFnPyOs9ALY6GH8DTDLDwvPN0ITTg1rclz7NTz\naK5NxOueahc5zRprMjv1mtk+w5dl+OzkcBbZWaFpJx99jeNZp6b7jPxsHzk+05e6iLRIogKiBBgQ\nMd4/PC1am2IzywYKCXVWn8Y59yTwJMD48eNbtftpTL9CxvQrbM1TRUQyRqJ2FK8ERpjZEDPLBaYD\nC5u0WQjcHh7+HPB2PPofREQkNgnZggj3KdwLLCV0mOszzrlNZvYgsMo5txB4GvidmRUBRwiFiIiI\neCRhfRDOuSXAkibT5kQM1wCfT1Q9IiJyZjoWUUREolJAiIhIVAoIERGJSgEhIiJRKSBERCQqBYSI\niESlgBARkagUECIiEpUCQkREolJAiIhIVAoIERGJSgEhIiJRKSBERCQqS+VbLpjZQWB3K5/enTjc\nzrSNJGttqqtlVFfLJWtt6VbXIOdcj7M1SumAOBdmtso5N97rOqJJ1tpUV8uorpZL1toytS7tYhIR\nkagUECIiElUmB8STXhdwBslam+pqGdXVcslaW0bWlbF9ECIicmaZvAUhIiJnkNYBYWafN7NNZhY0\ns/FN5s02syIz22pmn2rm+UPMbHm43Xwzy41DjfPNbG34Z5eZrW2m3S4z2xBut6qt62jmPX9oZiUR\n9d3cTLtJ4eVYZGbfS0BdPzGzLWa23sz+bGadm2mXkGV2tt/fzPLCn3NReH0aHK9aIt5zgJn91cw+\nDP8NfDtKG7+ZlUd8vnPiXVfEe5/xs7GQX4SX2XozG5eAmkZFLIu1ZlZhZvc1aZOQZWZmz5jZATPb\nGDGtq5m9YWbbw49dmnnu7eE2283s9nMqxDmXtj/AecAo4B1gfMT084F1QB4wBPgI8EV5/h+B6eHh\nJ4BvxLnenwJzmpm3C+ie4OX3Q+D+s7TxhZffUCA3vFzPj3NdNwHZ4eFHgEe8Wmax/P7A3cAT4eHp\nwPwEfHZ9gHHh4Y7Atih1+YHFiVynYv1sgJuBVwEDrgCWJ7g+H7CP0PkCCV9mwLXAOGBjxLT/BL4X\nHv5etPUe6ArsCD92CQ93aW0dab0F4Zzb7JzbGmXWVGCec67WObcTKAImRDYwMwOuB14MT3oW+Ey8\nag2/3xeAP8TrPeJkAlDknNvhnKsD5hFavnHjnHvdOVcfHn0f6B/P9zuLWH7/qYTWHwitTzeEP++4\ncc6VOefWhIcrgc1Av3i+ZxubCjznQt4HOptZnwS+/w3AR8651p6Ie06cc38DjjSZHLkeNfd99Cng\nDefcEefcUeANYFJr60jrgDiDfsDeiPFiPv7H0w04FvFFFK1NW/oEsN85t72Z+Q543cxWm9msONbR\n1L3hTfxnmtmkjWVZxtOdhP7TjCYRyyyW37+xTXh9Kie0fiVEeJfWJcDyKLOvNLN1ZvaqmV2QqJo4\n+2fj9Xo1neb/WfNqmfVyzpWFh/cBvaK0adPllt3aJyYLM3sT6B1l1gPOuVcSXU80Mdb4Jc689XCN\nc67EzHoCb5jZlvB/GXGrDfg18BChP+aHCO0Cu/Nc3/Nc6zq5zMzsAaAeeKGZl4nLMkslZtYBeAm4\nzzlX0WT2GkK7UI6H+5deBkYkqLSk/WzCfY1TgNlRZnu5zBo555yZxf0Q1JQPCOfcxFY8rQQYEDHe\nPzwt0mFCm7XZ4f/6orVpkxrNLBv4LHDpGV6jJPx4wMz+TGjXxjn/QcW6/MzsKWBxlFmxLMs2r8vM\n7gBuAW5w4Z2vUV4jLsusiVh+/5NtisOfdSGh9SuuzCyHUDi84Jxb0HR+ZGA455aY2eNm1t05F/dr\nDsXw2cRlvYrRZGCNc25/0xleLjNgv5n1cc6VhXe3HYjSpoRQP8lJ/Qn1wbZKpu5iWghMDx9dMoTQ\nfwArIhuEv3T+CnwuPOl2IF5bJBOBLc654mgzzazAzDqeHCbUSbsxWtu21GSf723NvOdKYISFjvjK\nJbRpvjDOdU0CvgtMcc5VNdMmUcsslt9/IaH1B0Lr09vNhVpbCfdxPA1sds79v2ba9D7ZF2JmEwh9\nHyQiuGL5bBYCXw0fzXQFUB6xeyXemt2a92qZhUWuR819Hy0FbjKzLuFdwjeFp7VOvHvjvfwh9KVW\nDNQC+4GlEfMeIHT0yVZgcsT0JUDf8PBQQsFRBPwJyItTnXOBrzeZ1hdYElHHuvDPJkK7WRKx/H4H\nbADWh1fOPk1rC4/fTOgomY8SUVv489gLrA3/PNG0rkQus2i/P/AgoQADyA+vP0Xh9WloApbRNYR2\nDa6PWE43A18/ua4B94aXzTpCnf1XJWi9ivrZNKnNgF+Fl+kGIo5CjHNtBYS+8AsjpiV8mREKqDIg\nEP4O+xqhfqu3gO3Am0DXcNvxwG8inntneF0rAmaeSx06k1pERKLK1F1MIiJyFgoIERGJSgEhIiJR\nKSBERCQqBYSIiESlgBBpQ2Z77I1iAAAAnUlEQVQ2OPIKnCKpTAEhIiJRKSBE2p7PzJ6y0H0YXjez\ndl4XJNIaCgiRtjcC+JVz7gLgGDDN43pEWkUBIdL2djrnTt4ZcDUw2MNaRFpNASHS9mojhhtIg6sm\nS2ZSQIiISFQKCBERiUpXcxURkai0BSEiIlEpIEREJCoFhIiIRKWAEBGRqBQQIiISlQJCRESiUkCI\niEhUCggREYnq/wNXSVXIOwzDJAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "S5Jpj5cqgWE0",
"colab_type": "text"
},
"source": [
"## 多分类-iris数据集"
]
},
{
"cell_type": "code",
"metadata": {
"id": "jF0bTnwIRdgd",
"colab_type": "code",
"outputId": "6e9655f1-2f4a-4498-a074-478c35b36abf",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
}
},
"source": [
"#iris数据集散点图\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None) # 加载Iris数据集作为DataFrame对象\n",
"X = df.iloc[:, [0, 2]].values # 取出2个特征,并把它们用Numpy数组表示\n",
"\n",
"plt.scatter(X[:50, 0], X[:50, 1],color='red', marker='o', label='setosa') # 前50个样本的散点图\n",
"plt.scatter(X[50:100, 0], X[50:100, 1],color='blue', marker='x', label='versicolor') # 中间50个样本的散点图\n",
"plt.scatter(X[100:, 0], X[100:, 1],color='green', marker='+', label='Virginica') # 后50个样本的散点图\n",
"plt.xlabel('petal length')\n",
"plt.ylabel('sepal length')\n",
"plt.legend(loc=2) # 把说明放在左上角,具体请参考官方文档\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEKCAYAAAARnO4WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XucVXW9//HXZxgIRkzw0skgwI6J\nIXfQUDsOgpeTetCOkhle0PyR2g8Qfl0oK6aLv+rYI0RLDVOx5IQeyk73MnW8/ToqEHjBMDNQ8AKi\njKCiwHx+f6y9mT3DzKy1915r39b7+Xisx7DWXpfPXtlnf/dnf7/fZe6OiIjUvrpyByAiIqWhhC8i\nkhJK+CIiKaGELyKSEkr4IiIpoYQvIpISSvgiIimhhC8ikhJK+CIiKVFf7gByHXjggT5kyJByhyEi\nUjVWrFjxirsfFGXfikr4Q4YMYfny5eUOQ0SkapjZ+qj7qqQjIpISSvgiIimhhC8ikhKJ1fDNbChw\ne86mDwBfdfer8znPzp072bBhAzt27Ig1vjTq3bs3AwcOpGfPnuUORUTKILGE7+5rgdEAZtYD2Ajc\nme95NmzYwL777suQIUMws5ijTA93Z8uWLWzYsIFDDjmk3OGISBmUqqQzGfi7u0f+NTlrx44dHHDA\nAUr2RTIzDjjgAH1TEkmxUiX8TwA/LfRgJft46D6KpFviCd/MegFTgP/q4vUZZrbczJZv3rw56XBE\nRIo2cfFEJi6eWO4w8laKFv5HgZXu/nJnL7r7Incf7+7jDzoo0mCxirV48WJeeOGFcochItKpUoy0\nPYciyjnVZPHixQwfPpz3ve995Q5FRBKQbdXft/6+duvN05vLE1CeEm3hm9k+wInAz5O8TjtLlsCQ\nIVBXF/xdsqSo073xxhuceuqpjBo1iuHDh3P77bezYsUKGhsbGTduHCeffDIvvvgiy5YtY/ny5Uyb\nNo3Ro0fz1ltvcffddzNmzBhGjBjBRRddxNtvvw3AvHnzGDZsGCNHjuSzn/0sAL/61a/48Ic/zJgx\nYzjhhBN4+eVOvxCJiBTO3StmGTdunHe0Zs2avbZ16bbb3Bsa3KFtaWgIthdo2bJlfvHFF+9Z37p1\nqx999NG+adMmd3dfunSpX3jhhe7u3tjY6I8++qi7u7/11ls+cOBAX7t2rbu7n3feeb5gwQJ/5ZVX\n/LDDDvPW1lZ3d3/ttdfc3f3VV1/ds+3GG2/0uXPnFhxzd/K6nyLSqcZbGr3xlsZyh+Hu7sByj5hj\na2uk7RVXwJtvtt/25pvB9gKNGDGCu+66iy984Qs88MADPP/88zzxxBOceOKJjB49mm9+85ts2LBh\nr+PWrl3LIYccwmGHHQbABRdcwP33389+++1H7969+dSnPsXPf/5zGhoagGC8wcknn8yIESO46qqr\nePLJJwuOWUSkMxU1W2bRnnsuv+0RHHbYYaxcuZLf/va3fPnLX2bSpEkcccQR/PnPfy7ofPX19Tzy\nyCPcfffdLFu2jO9///vcc889zJw5k7lz5zJlyhSam5tpamoqOGYRSVa11Ow7qq0W/qBB+W2P4IUX\nXqChoYFzzz2Xz33uczz88MNs3rx5T8LfuXPnntb4vvvuy7Zt2wAYOnQo69at45lnngHgJz/5CY2N\njWzfvp2WlhZOOeUUFixYwOrVqwFoaWlhwIABANx6660Fxysiyev37X70+3a/coeRt9pq4V95JcyY\n0b6s09AQbC/Q448/zuc+9znq6uro2bMn119/PfX19cyaNYuWlhZ27drF5ZdfzhFHHMH06dO55JJL\n6NOnD3/+85+55ZZbmDp1Krt27eLII4/kkksu4dVXX+X0009nx44duDvf+973AGhqamLq1Kn079+f\nSZMm8Y9//KPYuyEi0o4FNf/KMH78eO/4AJSnnnqKD33oQ9FPsmRJULN/7rmgZX/llTBtWsyRVq+8\n76eI7JFt1be83QLAfu/aD4Ct87aWLSYzW+Hu46PsW1stfAiSuxK8iBSh2vrXR1V7CV9EJCHZlny2\npV/Oln0hlPBFRDKqfSRtGCV8EZE8VVvLPksJX0QkI9uSr7WWfVZt9cMXEZEuKeGXwVe/+lX+9Kc/\n5X1cc3Mzp512WgIRiUiu5unNNde6hxos6bhD7oOdOq6XLo7MZEV1e3+mfv3rXy9JDLt27aK+vub+\nJxapCeUoG9VUC7+pCebMCZI8BH/nzAm2F2revHn84Ac/yLlGE9/97ne56qqrOPLIIxk5ciTz588H\nYN26dQwdOpTzzz+f4cOH8/zzzzN9+nSGDx/OiBEjWLBgAQDTp09n2bJlADz66KMcc8wxjBo1iqOO\nOopt27axY8cOLrzwQkaMGMGYMWO4995794rr1Vdf5YwzzmDkyJFMmDCBxx57bE985513Hsceeyzn\nnXde4W9cRGpOzTT/3GHrVli4MFhfsCBI9gsXwuzZhbf0zz77bC6//HI+85nPAHDHHXfwhS98gYce\neohHHnkEd2fKlCncf//9DBo0iL/97W/ceuutTJgwgRUrVrBx40aeeOIJALZubf/L/jvvvMPZZ5/N\n7bffzpFHHsnrr79Onz59WLhwIWbG448/zl//+ldOOukknn766XbHzp8/nzFjxvCLX/yCe+65h/PP\nP59Vq1YBsGbNGh588EH69OmT/xsWkUSVs+tnzSR8syDJQ5Dks4l/9uxge6FlnTFjxrBp0yZeeOEF\nNm/eTP/+/Xn88cf54x//yJgxYwDYvn07f/vb3xg0aBCDBw9mwoQJAHzgAx/g2WefZebMmZx66qmc\ndNJJ7c69du1aDj74YI488kgA3v3udwPw4IMPMnPmTAAOP/xwBg8evFfCf/DBB/nZz34GwKRJk9iy\nZQuvv/46AFOmTFGyl5pVqz1oSqFmEj60Jf1ssofikn3W1KlTWbZsGS+99BJnn30269ev54tf/CKf\n/vSn2+23bt069tlnnz3r/fv3Z/Xq1fzhD3/ghhtu4I477uDmm28uLpgIcmMQkcpSzq6fNVXDz9bs\nc+XW9At19tlns3TpUpYtW8bUqVM5+eSTufnmm9m+fTsAGzduZNOmTXsd98orr9Da2sqZZ57JN7/5\nTVauXNnu9aFDh/Liiy/y6KOPArBt2zZ27drFv/zLv7Ak82jGp59+mueee46hQ4e2OzZ3n+bmZg48\n8MA93xBEatHExROZuHgi962/j/vW37dnXaKrmRZ+Ntlna/a5NXworqV/xBFHsG3bNgYMGMDBBx/M\nwQcfzFNPPcXRRx8NQN++fbntttvo0aNHu+M2btzIhRdeSGtrKwDf+ta32r3eq1cvbr/9dmbOnMlb\nb71Fnz59+NOf/sRll13GpZdeyogRI6ivr2fx4sW8613vandsU1MTF110ESNHjqShoUFz6ItUmXKU\npGpqeuSmpuCH22xyz34I9OtXXE+dWqLpkaXaqYbfXmqnR25qat8bJ1vTL0c/fBGRSlNTCR/2Tu5K\n9iK1RS37wtXUj7YiUt3i+CG2FD/mVusPxkr4IiIpkWhJx8z6AT8ChgMOXOTuf07ymiJSfeIYfVqK\nEazV/oCUpGv4C4Hfu/tZZtYLaEj4eiIVp9qSgtSuxBK+me0HHAdMB3D3d4B3krpeUo4//njmzZvH\nySefvGfb1VdfzerVq9m2bdueSdCiuvjii5k7dy7Dhg3rcp8bbriBhoYGzj///ILjFqkm2Q/D7LNi\nC/lwLMUI1mp/QEqSLfxDgM3ALWY2ClgBzHb3NxK8ZuzOOeccli5d2i7hL126lP/4j//guOOO22v/\nsCmJf/SjH4Ve85JLLiksWKko1f71v5Sy96bl7ZZ267pX8UryR9t6YCxwvbuPAd4A5nXcycxmmNly\nM1u+efPmWC4c5y/oZ511Fr/5zW94553gy8m6det44YUXeP/738/w4cMBWLx4MVOmTGHSpElMnjyZ\n1tZWLrvsMg4//HBOPPFETjnllD3fBCZOnEh2cFnfvn254oorGDVqFBMmTODll18G2qZgBnjmmWc4\n4YQTGDVqFGPHjuXvf/8727dvZ/LkyYwdO5YRI0bw3//937G8V0m3WundUoqHl1TrA1KSbOFvADa4\n+8OZ9WV0kvDdfRGwCIKRtgnGU5D999+fo446it/97necfvrpLF26lI9//ONYhw7+K1eu5LHHHmP/\n/fdn2bJlrFu3jjVr1rBp0yY+9KEPcdFFF+117jfeeIMJEyZw5ZVX8vnPf54bb7yRL3/5y+32mTZt\nGvPmzeNjH/sYO3bsoLW1lV69enHnnXfy7ne/m1deeYUJEyYwZcqUvWKS8qr2r/+lpHtVGoklfHd/\nycyeN7Oh7r4WmAysSep6kNxX6GxZJ5vwb7rppr32OfHEE9l///2BYOriqVOnUldXx3vf+16OP/74\nTs/bq1evPY8sHDduHHfddVe717dt28bGjRv52Mc+BkDv3r0B2LlzJ1/60pe4//77qaurY+PGjbz8\n8su8973vLep9Sjqpd0t6JN1LZyawJNND51ngwoSvl4jTTz+dOXPmsHLlSt58803GjRvHunXr2u1T\nyJTEPXv23NMq79GjB7t27Yp03JIlS9i8eTMrVqygZ8+eDBkyhB07duR9fSkNJbXodK+SlWjCd/dV\nQKRJfeKQ1NfCvn37cvzxx3PRRRdxzjnnhO5/7LHHcuutt3LBBRewefNmmpub+eQnP5n3dffdd18G\nDhzIL37xC8444wzefvttdu/eTUtLC+95z3vo2bMn9957L+vXry/kbUkVKfa/6e6Or6TeLWr5J0sj\nbSM655xzWL16daSEf+aZZzJw4ECGDRvGueeey9ixY9lvv/0Kuu5PfvITrrnmGkaOHMkxxxzDSy+9\nxLRp01i+fDkjRozgxz/+MYcffnhB5xaRdKmp6ZEryfbt2+nbty9btmzhqKOO4qGHHqqIGnu13s+0\n6lj7bhzcCERvARd7fKlUS5yVKLXTI1eS0047ja1bt/LOO+/wla98pSKSvUgxVG6pfkr4CWlubi53\nCFIDiq2vZ/ev/3p9QceXirpllkZVJHx3Vx/zGFRS+U5KIztVwW7f3W5967ytkc+hLpW1o+ITfu/e\nvdmyZQsHHHCAkn4R3J0tW7bs6csv0cSR3MKSbJQknJbkmpb3WS4Vn/AHDhzIhg0biGvahTTr3bs3\nAwcOLHcYUkLZD5FsSSefln2Wyi21o+ITfs+ePTnkkEPKHYakTBxljGzLPTshWMeWfNjrccjGnS3p\nKGmnW8UnfBGpDPqQqH4V3w9fpJxKUcPPllt2fbXrqTWSHGkb1zWkPPLph6+RtiIiKaEWvkiZRBld\nWooRqBrlWt3UwhcpoVI81KMSpOV91jL9aCtSJlG6O1bSTJZS/ZTwRQqUlhGoaXmfaaCEL1Jmq15a\nFbpPKZKrEnjtU8IXKVBaSiFpeZ9poIQvUialGGkrkksJX6RIaWnxpuV91jIlfJEy6TinTnct+1KM\ntJXap374IiIpoRa+pJY75D5ioeN6qURp2RfaJVJdKiWXWvhSteq/Xr9n4rHOdDcytKkJ5swJkjwE\nf+fMCbbHrVZGqNbK+0gztfAlddxh61ZYuDBYX7AgSPYLF8Ls2eVr6Xcm2xLP1vkLfaatWvYCCSd8\nM1sHbAN2A7uiTvAj0p1sqz77UI+O0wuHlTHMgiQPQZLPJv7Zs4PtcSX7OMop2WOyXTcLOUfH+RHz\n/UBTWah2lKKFf7y7v1KC60iNSTKxZJP+wpbgGixujjXZV4qmpuDbzL0LmjFrK13165dM+Uoqm0o6\nUnWyLfmuHhwSpYyRTXy55syJt4VfbDkm95hCW/ZxlK5UFqodSSd8B/5oZg780N0XJXw9qQFJlxDc\n4f1fmcjGFmBIcI0BV0xk4UZgTnwt/TjKMcWIs3RVbFlIKkPSCf8j7r7RzN4D3GVmf3X3+3N3MLMZ\nwAyAQYMGJRyOVIo4kl93jwTs7txmUF8PAwbAxsy2Qw8N/varb5/Iiolz3TrYtQvo2bbtmWeCUkq+\n5ZRC79Oe0tXCtm35JnuVhWpHognf3Tdm/m4yszuBo4D7O+yzCFgEwROvkoxHqkMpSgjrmppxh+Nv\nbbtGnK1WdzhjazMLF0Kvr/ajTx8YvaqZ+xbC1hL2BCq2dFVNPZokXGIJ38z2AercfVvm3ycBX0/q\nelIdKqnHR8dE1VnLvtA4zWDV6IkMuAI21rXwztvBD8QDroAF32guabLPJufcZA3Rkn6pejRJaSTZ\nwv8n4E4L/ouoB/7T3X+f4PWkxhTzIRB1FG3SHzSHHgob17dfL1WSNAvKLrnJOZu8+/Xr/v7krsdR\nFpLKoIeYS1kk2bLP1pyzSam7mnNYHFHi7GqfPS3snK6f5WgZh334hd2v3G8KWWrhV45YH2JuZsea\n2V1m9rSZPWtm/zCzZ4sPUyR+uTXn7NQJ2WS1devevU2SjCN73QEDoLExSJK5cZVKd6WrsPvV2tq+\nLNTaWr73IcWLUtK5CZgDrCAYMStStKRKKVFrzlFq9K2te6/X5TSRujtHtpwyaxZc/Y223i3ue5dT\nkhalXANd3684ykJSGaJMntbi7r9z903uviW7JB6ZSIFyk1JWvuWHiRNh3LggyUPwd9y4YHs1iTJJ\nXNj9ampqv57dP/ccpZyMTorg7p0uwNjM8m3gKuDonG1juzqumGXcuHEuUqzWVvfZs7Pt6WCZPTvY\n3lHjLY3eeEtju227d7uPHh0cN3p05+th58iNIXvtjutJixpDPvermOtIMoDlHjHHdpfw7+1muSfq\nBfJZlPClWPkmn86StXuQ1EeNap8ER43aO9l3d45iE2nueQpdD4shrmQd13uV/OWT8EN76ZjZB9z9\n2bBtcVAvHYlDPr10ujvHa6/BNde0bZs1C/r3z69M4d6+7t/aWtgo167eS5T3GhZDHPcrjvcqhcmn\nl074VwBY2cm2FVE/UfJZ1MKXuIS1gsOOnTWrfWs1u8yaVbpWb1jre/fu8NZ51BiKuV9xvFcpHDGV\ndA4HzgT+Dvx7zjIdeDLqBfJZlPClEnRWzgkr63RUqlJJd6+XqrauGn555ZPwu+uWORQ4DegH/FvO\n9m3A/4r8fUNqjhfZ/S7K8cVeI4qO3Syz63V1QTlj1ChYvbrt9VGjgu25x3QVZ9TujGHvM2yUa9jr\nUbtUFiOfrptSZmGfCMDRUT89il3Uwu/6B8BKMX9+5y3M+fPjO77Ya0TR2Ni+x022J05jY9s1O5Z1\nOpZzosTZXakk6vGFtvCjxBCnUl1H2iOPFn6UfvifNLNrOizfMLPTk/0okkrjIaMyPWTUZZTji71G\nFK2t0NICq1a19bUfNy5Yb2mB3buDa15zTfvRpddc0xZT1Di7GuUa9V50N8o16ijY7kbaxqlU15Ei\nhH0iEExdfD8wM7M0A7cAvwSujvrJEmVJcws/27KnCaeJim3pF9uijHp80j8A5vatzy65Lf44Wt9x\n3IuwOObPb//NI/vNJOq3DKl+xNwt83+AY92DJ0abWT3wAPAR4HF3HxbXh0+au2V2HKbfOLgRqMzH\nyXk33e/i6CYYdZ9itbZCjx5t67t3R6vPR40zznvRVRzZ7qNXX912jcsvb+s+GleXS6lcsU6eBvQH\n+uas7wPsn/kAeLuA+KQTzdObaZ7eTOPgRhoHN+5ZrzTZhJErnzJHd8dHuUZcsmWcXLlTKUB4iaIU\n96K7OLLXyC01ZUtR2YnPKmEiOakgYV8BgE8B/yAo4ywGngUuJkj8V0X9KhFlSXNJJ6tSSznu0brf\nFdtNsBRd/PKdOqFc9yKKOH7UlepGnCUdADM7mODxhACPuvsL8X/0pLukUy2KLVNEOb4UZYiJE4Mf\naFesCGLNtvj32w+am+M7R3f3Io4Ywq4R5XWpbrGOtM18IAwAjgGOyy5RP1HyWdTCrw5x/Cjb3fmi\n7lOsji35KC37LLXwpVIQx0jbPTvAd4B1wG+AX2WWX0a9QD6LEn51S9uIyzjLV4Uk4zimXpDql0/C\nj/IAlDOAoe6uH2ilW3GNLoWuR8FGFeUaxYpjlGsxz4oNu9/ZEcMaASt7hH0iAL8D+kb9BClmUQu/\nNhQ7ujRsFGyYUozUzT1vkv3wo8ZRzLpUN2IeafsmsMrMfpg72jbJDyGpbsWMLg0bBZvbbbIzUa4R\nh9zzFjLKNerxUYR1H9UIWMmKUtL5ZWYRKUq2pODe/vmps2a1lRzMgl4rY8cGST47MGrUqLbeLNB1\nySbqM23jeC/FlEs04ZiUQ9RumX2AQe6+Nslg1C2z9kV5sEjYPnGNYI1Dsb8VlOK3BqltsY60NbN/\nA1YBv8+sjzYztfglb+57J3II1l97ra2S3d0+UUaPZrflinukblax5RKVW6SUotTwmwgGXW0FcPdV\nwAcSjEmqXMc6e1jdPZc73Hdf569lty9YELT4Fy4MWvELF7aVhSB6bbzjB0C+6yLVJkrC3+nuLR22\nRf6/sJn1MLO/mNmv8wtNqtHEie3npMn+6DpxYtB67d8/SM65suUas/YPH8mV+/CRr32t82t/7Wtd\n18Znz25fG29qav8BkP1WkFtW6u51kWoUJeE/aWafBHqY2QfN7Frg/+VxjdnAUwVFJ1UlSg+b+fM7\nPzZ3+733QmNj+9cbG4PtUcpCTU2dPxUqt77fXVlIk45JzQrrtwk0AFcCjwLLM//uHaXPJzAQuBuY\nBPw6bH/1w69+3c0zH8fkabt3l+YB45qSQKoFcU+eVigzWwZ8C9gX+Ky7n9bJPjOAGQCDBg0at379\n+sTikdL0Culunvmw+duz+3TXC6epCV59Fa69tu0aM2fC/vvnV3IJ68lTqp4+IsXIp5dOl/3wzexX\nQJefBu4+JSSI04BN7r7CzCZ2c55FBE/VYvz48fqynKBSzELZ1TzzuX3oo8SZ+0GULcnkDlp64IH2\nxzzwAEzp9r/I9rrqydPx3nT1ukhV6qrpDzR2t4R9dSBo2W8gmHjtJYIRu7d1d4xKOsmphHnmd+0q\nPoZSzGWvScekmhDH5Gnu3kXnuMgfJF8EvgiQaeF/1t3PLeacUrhSjECtqwvmch89uq1Fv2JF2xzv\nPXoUH0NdXVtLPnck7ujRwfYo3yI06ZikVaI1/D0XaUv4e9Xwc2mkbfKSrktn6+sLF7aVRmbPbl9f\njyOGsOfRRhH2e0Ypfu8QKVbcz7Qtmrs3hyV7SV5Xdem4PvOz3R2vvbZ9d8Zrr413FKw7zJ3bftvc\nufm/D006JqkTtfZTikU1/OSU6uEkra17d5vMdpeMI4a0PWRFJAxx1PCL7aUjlaVUszN2Nwq2qan4\nGDTLpEjhuqzhm1ljpy9keJE/6nZGNfzkJVmXzvap7zgKFoLpE3L73hcbg+rrIoFY+uEnkdCl/Gql\nLl0r70OklKJMj/xBM1tmZmvM7NnsUorgpLpEmRxNk5KJlE+UXjq3ANcDu4DjgR8DtyUZlFSv7iZH\ny/bi0aRkIuURJeH3cfe7Cer96929CTg12bCkGmUT+DXXtJ+L/ppr2rpiZqcqzp3LPu7HD4pI56I8\n0/ZtM6sD/mZm/xvYCPRNNizpTKX/UBm1B82CBW2jbLPrHd9Hpb9XkWoUJeHPJpgieRbwDYKpji9I\nMijZWykmPotDlInPwiYlq5b3KlJtQks67v6ou28HXgdmufu/u/v/JB+aZFVb7burHjS5cXf1+MFq\ne68i1SS0hW9m4wl+uN03s94CXOTuKxKOTTJKMfFZKeRT8oHqfq8ilSh08jQzewz4jLs/kFn/CHCd\nu4+MOxgNvOpe0hOflUqU+nytvFeRpMU9edrubLIHcPcHCbpoSgklPfFZKYUNmqql9ypSSaIk/PvM\n7IdmNtHMGs3sOqDZzMaa2dikA0yTjgmt4+Ck7mrftSJN71Wk1KL00hmV+dtxSM0YgsnVJsUaUUqF\n9UxZtSp4yMf3vhe8/r3vwX33BdtrqdShydFEkhOa8N39+FIEkma5PVMgSHAdW7mjRwfrc+cGr8+d\nGyT72bNrr496WNdOESlMlB9t/wn4v8D73P2jZjYMONrdb4o7mDT/aJtbysjKbeWGvS4i6ZTPj7ZR\nEv7vCLplXuHuo8ysHviLu48oPtT20pzwIbxninquiEhHcffSOdDd7wBaAdx9F7C7iPikE2E9U9Rz\nRUSKFSXhv2FmB5B5+pWZTQBaEo0qZcJ6prS2queKiBQvSi+ducAvgX82s4eAg4CzEo0qZcJ6ptTV\nqeeKiBQvtIYPkKnbDwUMWOvuO5MIRjX87kegagZJEeko1hq+mU0lmBP/SeAM4HYNuEpG2AhUPdZP\nRIoRpYb/FXfflplDZzJwE8ETsKQCdTVaV0Qk0lw6mb+nAje6+2+AXmEHmVlvM3vEzFab2ZNm9rVi\nApVwel6siHQnSsLfaGY/BM4Gfmtm74p43NvAJHcfBYwG/jXTw0cSoHnkRSRMlF46Hwf+Ffiuu281\ns4OBz4Ud5MGvwdszqz0zi9JOQmplznwRSU6kXjoFn9ysB7ACOBT4gbt/oZN9ZgAzAAYNGjRu/fr1\nicWTBhqNK5IucY+0LZi773b30cBA4CgzG97JPovcfby7jz/ooIOSDKfmaTSuiHQn0YSf5e5bgXsJ\nSkOSAM0jLyJhotTwC2JmBwE7M3X/PsCJwHeSul7aaR55EQmTWMIHDgZuzdTx64A73P3XCV4v9TSP\nvIh0J7GE7+6PETwVS0pIo3FFpCslqeGLiEj5KeGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikhBK+\niEhKKOGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikhBK+iEhKKOGLiKSEEr6ISEoo4YuIpIQSvohI\nSijhi4ikhBK+iEhKKOGLiKSEEr6ISEoo4YuIpIQSvohISijhi4ikRGIJ38zeb2b3mtkaM3vSzGYn\ndS0REQlXn+C5dwH/x91Xmtm+wAozu8vd1yR4TRER6UJiLXx3f9HdV2b+vQ14ChiQ1PVERKR7Janh\nm9kQYAzwcCevzTCz5Wa2fPPmzaUIR0QklRJP+GbWF/gZcLm7v97xdXdf5O7j3X38QQcdlHQ45bNk\nCQwZAnV1wd8lS6r7OiJSdZKs4WNmPQmS/RJ3/3mS16poS5bAjBnw5pvB+vr1wTrAtGnVdx0RqUrm\n7smc2MyAW4FX3f3yKMeMHz+OTP/wAAAMA0lEQVTely9fnkg8ZTVkSJB8Oxo8GNatq77riEjFMLMV\n7j4+yr5JlnSOBc4DJpnZqsxySoLXq1zPPZff9kq/johUpcRKOu7+IGBJnb+qDBrUect70KDqvI6I\nVCWNtC2FK6+Ehob22xoagu3VeB0RqUpK+KUwbRosWhTU0s2Cv4sWxf9D6rRpcMEF0KNHsN6jR7Ae\n93Uuuwzq64P3Ul8frMdNvY1E4ufuFbOMGzfOpQi33ebe0OAObUtDQ7A9Lpde2v782eXSS+O7Rine\nh0iNAJZ7xBybWC+dQtRsL51SKUUvnfp62L177+09esCuXfFcQ72NRCKrlF46Umql6KXTWbLvbnsh\n1NtIJBFK+HEJqznHUfc+4YTg+OxywgntX++qN06cvXSyvw9E3V6IUrwPkRRSwo9DdoTr+vVBxTk7\nwjWb9C+7DK6/vq0VvHt3sJ5P0j/hBLj77vbb7r67fdI/pYthDl1tL0R25G7U7YVQbyORRKiGH4ew\nmnMcdW/rZkhD9n/DUtW+L7ss6GW0e3fwHmbMgOuui+/8EHxYXnFFUMYZNChI9poeQmQvquEnobuS\nTVjNOWrdO6xkEyZK7TustKTukCK1K2p3nlIsFdstM6yb4ODBnXdVHDw4eL1Hj85f79Gj7RqTJ3e+\nz+TJweudvZZdsnr37vz13r2D18O6VEbpDqlumSIVhTy6ZZY9yecuFZvwwxJ6WIKKkiTDEnqvXp2/\n1qtX9HOEffCEvc8o5yjF/RaRPfJJ+Oko6RRbpggrlYSNpL3uOhg2rP2xw4blV/feuTO/7Z0JKy1F\nKQlFKU8lfb9FpDBRPxlKsSTSwo+jPLDPPp23OPfZJ9rxcbTwo8QQdo66us5fq6sLXo+jhR/H/VYL\nXyQy1MLPccUVbQ8EyXrzzWB7VG+9ld/2jhYtCt/eq1fn+2S3FxsDQJ8+3W+P0h0yrFtmHPdb3TJF\nkhH1k6EUSyItfLPOW4tm0c8R1nKO4/iwOKOcI2yfKPfittuClrRZ8Lezlvmll7a19Hv0aP9NJY77\nHTUOEVELv50oozbDas5RRpd2d44ox4fFGeUcYftEuRfTpgV99ltbg7+d9X0/9lgYODD4vWLgwGC9\ns3N1dY0oosQhInmp/YR/6KHdbw8bJQvhZYywc0QZnRpWxpg4sfNz5G4Pu04cpZKw91qK0b4iUpio\nXwVKsSRS0omjK6J792WMKOfo7vis7soYccQZdo0owuLQD64iJYWmR84RNiVBXV3wt7PjWlujXSOO\nc1TCNeKIo1RxauoFEUBTK7QXR107TClmd9x///y2JyXsvZbiXkQpw4nIXmo/4Zeirp2mboRh77UU\n9yKOrp8iaRS19lOKpeAaflhdOum6dlzn6E5c3R3jEPZe03QvRMqMVNXws1/vc1t8DQ3JPCS8nPTY\nvza6FyJ7pKuGn5av92kqG4XRvRApSGIJ38xuNrNNZvZEUtcASjfRVrnniQ+boC1NdC9ECpJYScfM\njgO2Az929+FRjimopFOKr/dpKRuJSNWpiJKOu98PvJrU+fdQrxARkUjKXsM3sxlmttzMlm/evDn/\nE5Ti673mZxeRGpBoLx0zGwL8OtGSTimoV4iIVKiKKOnUFPUKEZEaoIQfhXqFiEgNqE/qxGb2U2Ai\ncKCZbQDmu/tNSV0vcdOmKcGLSFVLLOG7+zlJnVtERPKnko6ISEoo4YuIpIQSvohISijhi4ikhBK+\niEhKVNR8+Ga2GehkSGvJHAi8UsbrR6U446U441UNcVZDjBAtzsHuflCUk1VUwi83M1sedYhyOSnO\neCnOeFVDnNUQI8Qfp0o6IiIpoYQvIpISSvjtLSp3ABEpzngpznhVQ5zVECPEHKdq+CIiKaEWvohI\nSqQ24ZtZDzP7i5n9upPXppvZZjNblVkuLlOM68zs8UwMez0ZxgLXmNkzZvaYmY2t0DgnmllLzv38\napni7Gdmy8zsr2b2lJkd3eH1st/PCDGW/V6a2dCc668ys9fN7PIO+1TCvYwSZ9nvZyaOOWb2pJk9\nYWY/NbPeHV5/l5ndnrmfD2ceLpW3xGbLrAKzgaeAd3fx+u3u/r9LGE9Xjnf3rvrhfhT4YGb5MHB9\n5m85dBcnwAPuflrJouncQuD37n6WmfUCOjzVpiLuZ1iMUOZ76e5rgdEQNJyAjcCdHXYr+72MGCeU\n+X6a2QBgFjDM3d8yszuATwCLc3b7FPCaux9qZp8AvgOcne+1UtnCN7OBwKnAj8odS5FOB37sgf8B\n+pnZweUOqhKZ2X7AccBNAO7+jrtv7bBbWe9nxBgrzWTg7+7eccBkpf232VWclaIe6GNm9QQf8i90\neP104NbMv5cBk83M8r1IKhM+cDXweaC1m33OzHwVXWZm7y9RXB058EczW2FmMzp5fQDwfM76hsy2\nUguLE+BoM1ttZr8zsyNKGVzGIcBm4JZMKe9HZrZPh33KfT+jxAjlv5e5PgH8tJPt5b6XHXUVJ5T5\nfrr7RuC7wHPAi0CLu/+xw2577qe77wJagAPyvVbqEr6ZnQZscvcV3ez2K2CIu48E7qLtk7XUPuLu\nYwm+Hn/GzI4rUxxhwuJcSTD8exRwLfCLUgdI0IIaC1zv7mOAN4B5ZYijO1FirIR7CUCm5DQF+K9y\nxRBFSJxlv59m1p+gBX8I8D5gHzM7N4lrpS7hA8cCU8xsHbAUmGRmt+Xu4O5b3P3tzOqPgHGlDXFP\nHBszfzcR1B6P6rDLRiD328fAzLaSCovT3V939+2Zf/8W6GlmB5Y4zA3ABnd/OLO+jCC55ir3/QyN\nsULuZdZHgZXu/nInr5X7XubqMs4KuZ8nAP9w983uvhP4OXBMh3323M9M2Wc/YEu+F0pdwnf3L7r7\nQHcfQvA17x53b/dp2qHWOIXgx92SMrN9zGzf7L+Bk4AnOuz2S+D8TI+ICQRfBV+stDjN7L3ZeqOZ\nHUXw313e/7EWw91fAp43s6GZTZOBNR12K+v9jBJjJdzLHOfQdZmk7P9t5ugyzgq5n88BE8ysIRPL\nZPbOOb8ELsj8+yyCvJX3IKo099Jpx8y+Dix3918Cs8xsCrALeBWYXoaQ/gm4M/PfYj3wn+7+ezO7\nBMDdbwB+C5wCPAO8CVxYoXGeBVxqZruAt4BPFPIfawxmAksyX/GfBS6swPsZFmNF3MvMh/uJwKdz\ntlXavYwSZ9nvp7s/bGbLCMpLu4C/AIs65KSbgJ+Y2TMEOekThVxLI21FRFIidSUdEZG0UsIXEUkJ\nJXwRkZRQwhcRSQklfBGRlFDCl5pnweyn74uw32IzOyvq9hji+lLOv4eYWcdxFiKxUsKXNJhOMGS9\n0nwpfBeR+CjhS1XJtIT/amZLLJgvfpmZNWReG2dm92UmcfuDmR2caZmPJxjMtMrM+pjZV83sUQvm\nHl+Uz6yDnV0js73ZzL5jZo+Y2dNm9i+Z7Q1mdoeZrTGzOy2Yy3y8mX2bYHbEVWa2JHP6HmZ2owXz\nov/RzPrEe/ck7ZTwpRoNBa5z9w8BrwOXmVlPgsmvznL3ccDNwJXuvgxYDkxz99Hu/hbwfXc/0t2H\nA32ASHOhd3WNnF3q3f0o4HJgfmbbZQTzmA8DvkJmXiZ3nwe8lYlpWmbfDwI/cPcjgK3AmfnfGpGu\naWoFqUbPu/tDmX/fRvDwiN8Dw4G7Mg32HgRTzXbmeDP7PMG84/sDTxLMkBpmaMg1fp75uwIYkvn3\nRwgeaoK7P2Fmj3Vz/n+4+6pOziESCyV8qUYd5wNxwIAn3f3oTvbfw4JHx10HjHf3582sCejd3TG5\nh4dcIzvD6m4K+//W2zn/3k3w7UMkNirpSDUaZG3Pev0k8CCwFjgou93Melrbwyy2Aftm/p1N7q+Y\nWV+CybOi6u4aXXkI+Hhm/2HAiJzXdmbKRCIloYQv1WgtwYNWngL6Ezww5B2C5P0dM1sNrKJtTvHF\nwA1mtoqgFX0jwRTOfwAejXrRkGt05TqCD4k1wDcJykctmdcWAY/l/GgrkijNlilVxcyGAL/O/OBa\n8Sx4eHZPd99hZv8M/AkYmvnwECkp1fBFktUA3Jsp3RhwmZK9lIta+CIiKaEavohISijhi4ikhBK+\niEhKKOGLiKSEEr6ISEoo4YuIpMT/B+DytdzsoSEwAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "MYCIhC3nRdgl",
"colab_type": "code",
"colab": {}
},
"source": [
"#!/usr/bin/env python\n",
"# coding=utf-8\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from matplotlib.colors import ListedColormap\n",
"\n",
"\n",
"def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):\n",
" # setup marker generator and color map\n",
" markers = ('s', 'x', 'o', '^', 'v')\n",
" colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')\n",
" cmap = ListedColormap(colors[:len(np.unique(y))])\n",
" # plot the decision surface\n",
" x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1\n",
" x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1\n",
" xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))\n",
" Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)\n",
" Z = Z.reshape(xx1.shape)\n",
" plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)\n",
" plt.xlim(xx1.min(), xx1.max())\n",
" plt.ylim(xx2.min(), xx2.max())\n",
" # plot class samples\n",
" for idx, cl in enumerate(np.unique(y)):\n",
" plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],alpha=0.8, c=cmap(idx),marker=markers[idx], label=cl)\n",
" # highlight test samples\n",
" if test_idx:\n",
" X_test, y_test = X[test_idx, :], y[test_idx]\n",
" plt.scatter(X_test[:, 0], X_test[:, 1], c='', alpha=1.0, linewidth=1, marker='o', s=55, label='test set')"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "eM7B0TASRdgp",
"colab_type": "code",
"outputId": "d6fb956f-9b3f-4861-b366-a1e15f7edc02",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 514
}
},
"source": [
"#logistics回归\n",
"#依赖以上自定义function: plot_decision_regions\n",
"from sklearn import datasets\n",
"import numpy as np\n",
"from sklearn.model_selection import train_test_split\n",
"\n",
"iris = datasets.load_iris()\n",
"X = iris.data[:, [2, 3]]\n",
"y = iris.target\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)\n",
"\n",
"from sklearn.preprocessing import StandardScaler\n",
"sc = StandardScaler()\n",
"sc.fit(X_train)\n",
"X_train_std = sc.transform(X_train)\n",
"X_test_std = sc.transform(X_test)\n",
"\n",
"X_combined_std = np.vstack((X_train_std, X_test_std))\n",
"y_combined = np.hstack((y_train, y_test))\n",
"\n",
"from sklearn.linear_model import LogisticRegression\n",
"lr = LogisticRegression(C=1000.0, random_state=0)\n",
"lr.fit(X_train_std, y_train)\n",
"lr.predict_proba(X_test_std[0,:]) # 查看第一个测试样本属于各个类别的概率\n",
"plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))\n",
"plt.xlabel('petal length [standardized]')\n",
"plt.ylabel('petal width [standardized]')\n",
"plt.legend(loc='upper left')\n",
"plt.show()"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.\n",
" FutureWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.py:460: FutureWarning: Default multi_class will be changed to 'auto' in 0.22. Specify the multi_class option to silence this warning.\n",
" \"this warning.\", FutureWarning)\n"
],
"name": "stderr"
},
{
"output_type": "error",
"ename": "ValueError",
"evalue": "ignored",
"traceback": [
"\u001b[0;31m\u001b[0m",
"\u001b[0;31mValueError\u001b[0mTraceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 20\u001b[0m \u001b[0mlr\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mLogisticRegression\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mC\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m1000.0\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mrandom_state\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 21\u001b[0m \u001b[0mlr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfit\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_train_std\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 22\u001b[0;31m \u001b[0mlr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpredict_proba\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_test_std\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;31m# 查看第一个测试样本属于各个类别的概率\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 23\u001b[0m \u001b[0mplot_decision_regions\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX_combined_std\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my_combined\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mclassifier\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mlr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtest_idx\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mrange\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m105\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m150\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 24\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mxlabel\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'petal length [standardized]'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/logistic.pyc\u001b[0m in \u001b[0;36mpredict_proba\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 1409\u001b[0m self.solver == 'liblinear')))\n\u001b[1;32m 1410\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0movr\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1411\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0msuper\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mLogisticRegression\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_predict_proba_lr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1412\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1413\u001b[0m \u001b[0mdecision\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdecision_function\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/base.pyc\u001b[0m in \u001b[0;36m_predict_proba_lr\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 293\u001b[0m \u001b[0mmulticlass\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0mhandled\u001b[0m \u001b[0mby\u001b[0m \u001b[0mnormalizing\u001b[0m \u001b[0mthat\u001b[0m \u001b[0mover\u001b[0m \u001b[0mall\u001b[0m \u001b[0mclasses\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 294\u001b[0m \"\"\"\n\u001b[0;32m--> 295\u001b[0;31m \u001b[0mprob\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdecision_function\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 296\u001b[0m \u001b[0mprob\u001b[0m \u001b[0;34m*=\u001b[0m \u001b[0;34m-\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 297\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mexp\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mprob\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprob\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/linear_model/base.pyc\u001b[0m in \u001b[0;36mdecision_function\u001b[0;34m(self, X)\u001b[0m\n\u001b[1;32m 255\u001b[0m \"yet\" % {'name': type(self).__name__})\n\u001b[1;32m 256\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 257\u001b[0;31m \u001b[0mX\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcheck_array\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0maccept_sparse\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'csr'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 258\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 259\u001b[0m \u001b[0mn_features\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcoef_\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mshape\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python2.7/dist-packages/sklearn/utils/validation.pyc\u001b[0m in \u001b[0;36mcheck_array\u001b[0;34m(array, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, ensure_min_samples, ensure_min_features, warn_on_dtype, estimator)\u001b[0m\n\u001b[1;32m 550\u001b[0m \u001b[0;34m\"Reshape your data either using array.reshape(-1, 1) if \"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 551\u001b[0m \u001b[0;34m\"your data has a single feature or array.reshape(1, -1) \"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 552\u001b[0;31m \"if it contains a single sample.\".format(array))\n\u001b[0m\u001b[1;32m 553\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 554\u001b[0m \u001b[0;31m# in the future np.flexible dtypes will be handled like object dtypes\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mValueError\u001b[0m: Expected 2D array, got 1D array instead:\narray=[0.70793846 1.51006688].\nReshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample."
]
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "JROXtJtsv9MB",
"colab_type": "code",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 364
},
"outputId": "1ab37906-370c-432b-a966-bbe70c07b01d"
},
"source": [
"import numpy as np \n",
"from sklearn import datasets \n",
"from sklearn.cross_validation import train_test_split\n",
"from sklearn.preprocessing import StandardScaler \n",
"from sklearn.linear_model import Perceptron \n",
"from sklearn.metrics import accuracy_score \n",
"\n",
"iris = datasets.load_iris() \n",
"X = iris.data[:,[2,3]] \n",
"y = iris.target \n",
"\n",
"# 处理数据集,得到训练集和测试集。 \n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) \n",
"\n",
"# 对特征数据进行标准化处理 \n",
"sc = StandardScaler() \n",
"sc.fit(X_train) \n",
"X_train_std = sc.transform(X_train) \n",
"X_test_std = sc.transform(X_test) \n",
"\n",
"# 训练分类器 \n",
"ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0) \n",
"ppn.fit(X_train_std, y_train) \n",
"\n",
"# 预测并评估分类器性能\n",
"y_pred = ppn.predict(X_test_std) \n",
"acc_score = accuracy_score(y_test, y_pred)"
],
"execution_count": 1,
"outputs": [
{
"output_type": "error",
"ename": "ImportError",
"evalue": "ignored",
"traceback": [
"\u001b[0;31m\u001b[0m",
"\u001b[0;31mImportError\u001b[0mTraceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mnumpy\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mdatasets\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcross_validation\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mtrain_test_split\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 4\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpreprocessing\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mStandardScaler\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0msklearn\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlinear_model\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mPerceptron\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mImportError\u001b[0m: No module named cross_validation",
"",
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0;32m\nNOTE: If your import is failing due to a missing package, you can\nmanually install dependencies using either !pip or !apt.\n\nTo view examples of installing some common dependencies, click the\n\"Open Examples\" button below.\n\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n"
]
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "KunfzGFHRdgs",
"colab_type": "code",
"outputId": "f2c609c7-e58b-450e-d374-a5ee87d6263a",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 286
}
},
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy import optimize\n",
"\n",
"x=np.arange(1,13,1)\n",
"y=np.array([17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18 ])\n",
"plt.plot(x,y)\n",
"plt.grid()\n",
"plt.show()\n",
"print 's'"
],
"execution_count": 0,
"outputs": [
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3Xl41NW9x/H3yb6ShOwrgYQdEkhQ\nQFxIREUFVGjr0qqtWrVXqVat2l4XrNbbahdrta29tlatFRdQISiKGEQRUNZAEiAhJGQjC5CQfZtz\n/yDeBy02gczMmfnN9/U88xgmk8znGPLhl19+c75Ka40QQgj352U6gBBCCPuQQhdCCIuQQhdCCIuQ\nQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIuQQhdCCIvwceaTRUVF6dTUVGc+5Wlra2sjODjY\ndAyHsPLawNrrk7W5r6Gsb+vWrY1a6+iBHufUQk9NTWXLli3OfMrTtm7dOmbPnm06hkNYeW1g7fXJ\n2tzXUNanlKoYzOPklIsQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLoQQliEFLqw\njM6ePl7YcID9TX3IaEXhiZz6wiIhHOnZ/FL++FEpAC/szefSjHjmZyQwMWEYSinD6YRwPCl0YQkH\nD7fz3PoyLpkcRwJHKOkK4W+fHOC5j8tIjQxiXkYC8zLjGRsbKuUuLEsKXVjCo6uK8PFSPDRvInu2\nb+KB2WdytK2b1YWHyCuo4U/rSnkmv5T0mBDmZcQzLyOB9JgQ07GFsCspdOH2Pt7XwJqiOu6dO5a4\nsAD29N8fEezH1WemcPWZKTS0dLF6dy0rC2r5w9oSnvqwhPHxw5jXf1omJTLI6BqEsAcpdOHWuntt\nPLKykNTIIG48e+Q3Pi461J9rZ6Zy7cxUDjV38u6uWvIKanjy/b08+f5eMpLCmJcRz6UZCSSGBzpx\nBULYjxS6cGsvflZOWUMbf//+NPx9vAf1MXFhAdxw9khuOHskVUfbWVVQS15BLY+/u4fH391DVko4\n8zISuDQjnthhAQ5egRD2I4Uu3Fb9sU7+sLaEnLHR5I6LPa3PkRQRxC3npXHLeWmUN7axalctK3fW\n8Iu8Ih5dVcQZqcOZnxHPxZPjiQrxt/MKhLAvKXThtn69ei9dvX08NH+iXT5falQwt+Wkc1tOOqX1\nreQV1JBXUMuD7xTy8IpCzkqLYl5GPHMnxREe5GeX5xTCnqTQhVvadvAoy7ZVcet5aYyMsv+Um/SY\nEO6cM4Y7zh/N3roW8nYeP+d+//JdPPD2bs4eHcW8jATOSovEx9t5l0Ha5AVT4j+QQhdux2bTLFlR\nSOwwfxbnpjv0uZRSjIsbxri4Ydx94RgKa46xsqCGvJ213PPGToc+98nkJPuQm+P0pxVuQgpduJ03\ntlZSUNXMU1dOIdjfeX+FlVJMSgxjUmIY988dx/bKJopqjjnt+T/e18BHxXVUHmknebhcZin+nRS6\ncCvNHT08sXov00ZEcNmUBGM5lFJkpUSQlRLhtOc8f3wM+cV1/OXj/fzyislOe17hPmRzLuFWnvpw\nH0fau1myYKLHvYQ/PiyQc5J8eGNLFbXNHabjCBckhS7cxt5DLby0sYJrzkxhUmKY6ThGXDrKF5vW\nPPdxmekowgVJoQu3oLXmkZWFhPj7cM+FY03HMSYq0ItFWUm8+vlB6o91mo4jXIwUunAL7+0+xGf7\nD3PPhWOICPbsa8D/KyeNXpvmr+vlKF18lRS6cHkd3X38clUx4+JCufrMFNNxjBsRGcxlmQm8svkg\nja1dpuMIFyKFLlzenz/eT3VTB48smIiPt/yVBbgtN53O3j6e/+SA6SjChch3h3BplUfa+cvH+5mf\nmcD0UZGm47iMtOgQ5mUk8PLGco62dZuOI1yEFLpwaY+tKsJbKX5+yTjTUVzO4tx02rqPz1EVAqTQ\nhQv7pKSB9wvruD03nfgw2aP868bEhnLxpDhe2FBOc0eP6TjCBUihC5fU02fjkZVFjBhgcIWnuz03\nnZauXl78rNx0FOECpNCFS3rxs3JK61t58NIJBPgObnCFJ5qYEMac8bH87dMDtHTKUbqnk0IXLqeh\npYs/fFjC7LHRnD8+xnQcl/fj89Np7ujh5U0VpqMIw6TQhct5YvUeOnv7eGjeBI/br+V0ZCSFM3ts\nNM9/coD27l7TcYRBAxa6UipAKfW5UmqnUqpQKfVI//3/UEodUErt6L9NcXxcYXXbDx7lja1V3HD2\nSEZFh5iO4zYW547mSFs3r2w6aDqKMGgwR+hdQK7WOhOYAsxVSs3of99PtdZT+m87HJZSeIQvB1fE\nhPqzOHe06ThuJXtEBGenR/Hc+jI6e/pMxxGGDFjo+rjW/j/69t9kDpawuze3VrGzqpmfXTKOECcO\nrrCKxbnpNLZ28erncpTuqZQexIxCpZQ3sBVIB57VWt+nlPoHMJPjR/Brgfu11v+2sYRS6mbgZoDY\n2NjspUuX2i+9A7W2thISYs0f+V1xbW09mvs/aSc2yIv/nh4wpHPnrrg+exlobf+zuYO6ds0T5wbi\n58RZp/Zg5a8bDG19OTk5W7XW0wZ8oNZ60DcgHMgHJgHxgAL8gReBhwb6+OzsbO0u8vPzTUdwGFdc\n2yMrCnXq/Xl6V1XTkD+XK67PXgZa26clDXrEfXn6pY3lzglkR1b+umk9tPUBW/QgOvqUrnLRWjf1\nF/pcrXVt/3N1AS8AZ57K5xLiSyV1Lby4sZyrzvDcwRX2clZaJFkp4fxl3X66e22m4wgnG8xVLtFK\nqfD+twOBC4A9Sqn4/vsUcDmw25FBhTVprVmyspBgP29+epHnDq6wF6UUPz5/NNVNHby1vcp0HOFk\ngzlCjwfylVIFwBfAGq11HvCKUmoXsAuIAh5zXExhVe8XHmJD6WHuvnAswz18cIW9nDcmmoykMJ7N\n309vnxyle5IBLyXQWhcAU09yf65DEgmP0dHdx6N5xwdXfHe6DK6wF6UUi3NH88OXtvDOjhoWZSeZ\njiScRF4pKox5bv3xwRVLZHCF3c0ZH8P4+GE8m19Kn02uMvYU8l0kjKg80s6f1+1nXkY8M2Rwhd0p\npfhxbjpljW3kFdSYjiOcRApdGPH4u8V4KcXPLxlvOoplXTQxjjGxITzzUSk2OUr3CFLowuk2lDby\n3u5D3JaTRkK4DK5wFC8vxe25oympb2V14SHTcYQTSKELp+rps7FkRSEpw4O46ZxRpuNY3qWT4xkV\nHczTa0vkKN0DSKELp3ppYwUl9a08OE8GVziDt5fi9px09hxq4cPiOtNxhINJoQunaWzt4qk1+zh3\nTDRzZHCF0yzITGBEZBB//Kj0yy08hEVJoQuneWL1Hjp6+nh4vgyucCYfby9um53Orupm1u1tMB1H\nOJAUunCKHZVNvL7l+OCKNBlc4XRXZCWSGB7I0x+VyFG6hUmhC4ez2TQPrygkOtSfxbnppuN4JF9v\nL/4rJ43tB5vYUHrYdBzhIFLowuGWbatiZ2UT988dR2iAr+k4Hutb2UnEhwXw9NoS01GEg0ihC4c6\n1tnDr1fvISslnCumJpqO49H8fby55dxRfF5+hE1lcpRuRVLowqGe/rCEw23dPLJgEl5e8otQ0646\nM4XoUH85SrcoKXThMKX1Lfzjs3KuOiOZyUkyuMIVBPgeP0r/bP9htpQfMR1H2JkUunAIrTVLVhQR\n5OfNPRfK4ApXcs30FCKD/Xj6o1LTUYSdSaELh3i/sI5PSxu564IxRIb4m44jThDk58NN54xi/b4G\ndlQ2mY4j7EgKXdhdZ08fj60qYmxsKN+bMcJ0HHES184cQXiQL898JOfSrUQKXdjdcx+XUXVUBle4\nshB/H26cNZIPi+vZXd1sOo6wE/luE3ZVdbSdP60r5dKMeGamyeAKV3b9rFRCA3x4Rs6lW4YUurCr\nx98tRilkcIUbGBbgyw9mjWR14SH2HDpmOo6wAyl0YTeflTby7q5D3DY7nUQZXOEWbpiVSrCftxyl\nW4QUurCLnj4bS1YWkjw8kB+eK4Mr3EV4kB/XnZXKql21lNa3mo4jhkgKXdjFPzdVsK+ulQcvlcEV\n7uams0cS4OPNs/lylO7upNDFkDW2dvG7Nfs4Z3QUF0yINR1HnKLIEH++NyOFd3ZUU97YZjqOGAIp\ndDFkv3l/Lx3dfTw8f6IMrnBTPzx3FL7eXnKU7uak0MWQFFQ18dqWSn4wK5X0GBlc4a5iQgO4+swU\n3tpeTeWRdtNxxGmSQhen7cvBFZHB/vz4/NGm44ghuvW8NLyU4k/r9puOIk6TFLo4bcu3V7P9YBP3\nXyyDK6wgLiyA75yRxJtbK6lp6jAdR5wGKXRxWlo6e/jVe3uYmhLOQhlcYRm3npeG1vDcx3KU7o6k\n0MVpeXptCYfbunhkwUQZXGEhSRFBfCs7iVe/qKT+WKfpOOIUSaGLU1Za38oLG8q5cloyGUnhpuMI\nO/uv2en02TTPrS8zHUWcIil0cUq01jyyspBAP2/uuUgGV1hRSmQQl09J5JXNFTS2dpmOI06BFLo4\nJWuK6vik5PjgiigZXGFZP5qdRmePjeXbqkxHEadACl0MWmdPH4+uKmJMbIgMrrC49JgQpqaEs2xr\nNVpr03HEIEmhi0H73/VlVB7pYMn8ifjK4ArLW5iVxN66FopqZWtddyHflWJQqps6eHZdKZdMjuOs\n9CjTcYQTzM+Ix9dbsWxrtekoYpCk0MWgPP5uMSCDKzxJeJAf54+LZcXOanr6bKbjiEGQQhcD+mx/\nI6sKavnReekkRQSZjiOcaGFWIo2t3XxS0mA6ihiEAQtdKRWglPpcKbVTKVWolHqk//6RSqnNSqlS\npdRrSik/x8cVztbbZ+ORFUUkRQRyy3kyuMLTzB4bQ0SQL8u2yWkXdzCYI/QuIFdrnQlMAeYqpWYA\nvwZ+r7VOB44CNzoupjDln5sq2FvXwgMyuMIj+fl4cdmURNYU1dHc0WM6jhjAgIWuj/tyNpVv/00D\nucCb/fe/CFzukITCmMMnDK64aKIMrvBUC7MS6e618e6uWtNRxAAGdQ5dKeWtlNoB1ANrgP1Ak9a6\nt/8hVYDs0GQxv/lgL+3dfTw8f4IMrvBgkxPDSI8JkRcZuQF1Ki8aUEqFA28BDwL/6D/dglIqGXhP\naz3pJB9zM3AzQGxsbPbSpUvtkdvhWltbCQmx5sCGwaytvLmPRzZ2cmGqD1ePc69XhHr6184R8sq6\neXNfD0+cG0hMkGOupbDy1w2Gtr6cnJytWutpAz5Qa31KN+Ah4KdAI+DTf99M4P2BPjY7O1u7i/z8\nfNMRHGagtfX12fQVz36qsx9do5s7up0Tyo48+WvnKNVH23Xq/Xn692v2Ouw5rPx103po6wO26EH0\n82CuconuPzJHKRUIXAAUA/nAt/ofdj3wzqn+qyNc09s7qtl2sIn75o5lmAyuEEBCeCBnpUWyfJts\nBeDKBvOzUzyQr5QqAL4A1mit84D7gLuUUqVAJPA3x8UUztLS2cP/vLeHKcnhLMpKMh1HuJCFU5M4\neKSdrRVHTUcR38BnoAdorQuAqSe5vww40xGhhDnPfFRKQ0sXz183TQZXiK+YOymOB97ezbJt1UxL\nHW46jjgJeaWo+H/7G1r5+4YDfGdaEpnJMrhCfFWwvw8XT4ojr6CGzp4+03HESUihC+DLwRVFBPh4\nc+/ccabjCBe1MCuJls5e1hbXm44iTkIKXQDwYXE96/c1cKcMrhD/wcy0SOKGBcg16S5KCl0cH1yR\nV8TomBCumymDK8Q38/ZSXD41kXX7GmQ8nQuSQhc8/0kZB4+0s2SBDK4QA1uYlUifTfPOjhrTUcTX\nyHevh6tp6uDZ/P1cPCmOWTK4QgzCmNhQJieGyWkXFySF7uEef7cYm9YyuEKckoVZiRTWHGPPIRlP\n50qk0D3YprLD5BXU8qPZaSQPl8EVYvAWZCbg46V4S/ZJdylS6B6qt8/GkhWFJIYHcut5aabjCDcT\nGeLP7LExvLW9mj6bbAXgKqTQPdS/Pj/InkMtPDhvvAyuEKdlUVYi9S1dbChtNB1F9JNC90At3Zrf\nfrCPWemRXDQxznQc4aZyx8cwLMBHfjnqQqTQPdCykm5au3pZMn+iDK4Qp83fx5v5mQmsLjxEa1fv\nwB8gHE4K3cPsrm7m48perp+ZyujYUNNxhJtbmJVEZ4+N92Q8nUuQQvcwT324jxBfuGPOaNNRhAVk\npYSTGhnEcrnaxSVIoXuQyiPtrN1Tz+xkX8ICZXCFGDqlFAuzkthYdpiqo+2m43g8KXQP8s/NFXgp\nxezkAbfBF2LQrph6fD68bAVgnhS6h+js6eP1Lyq5YHwskYHyZRf2kzw8iDNHDmfZtioZT2eYfGd7\niJU7azja3sN1Z8luisL+FmUlUtbQxs6qZtNRPJoUugfQWvPSxgpGx4Qwc1Sk6TjCgi6eHI+/j5dc\nk26YFLoH2FHZxK7qZq6bOUKuOxcOMSzAlwsnxrFiZw1dvTKezhQpdA/w8sYKQvx9uCIryXQUYWEL\nsxJpau8hf0+D6SgeSwrd4hpbu8grqGVRViIh/nJ1i3Ccc9KjiA71l9MuBkmhW9xrX1TS3WfjWhkt\nJxzMx9uLy6ckkL+3niNt3abjeCQpdAvr7bPxyqYKZqVHkh4jL/MXjrcwK4mePk1egVyTboIUuoWt\n3VNPTXMn185INR1FeIjx8cMYHz+MZbIVgBFS6Bb20sZyEsICmDM+xnQU4UEWZSWys7KJ0vpW01E8\njhS6RZXWt7Ch9DDfnTECH2/5MgvnWTAlAS8Fb22XX446m3ynW9TLGyvw8/biyjOSTUcRHiYmNIBz\nx0Tz1rZqbDKezqmk0C2otauXZduquTQjnqgQf9NxhAdamJVETXMnmw4cNh3Fo0ihW9Bb26po7erl\nOrlUURhy4YRYQv19ZJ90J5NCt5gv922ZnBjGlORw03GEhwrw9eaSyfG8t6uW9m4ZT+csUugWs7Hs\nMCX1rbJvizBuYVYibd19fFBYZzqKx5BCt5iXN1YQHuTL/MwE01GEhzsjdThJEYEsk60AnEYK3UJq\nmzv4oKiOK89IJsDX23Qc4eG8vBQLpyayobSRQ82dpuN4BCl0C/nX5oPYtOZ70+WXocI1XJGVhE3D\n2zvkl6POIIVuEV29fbz6+UHOHxdD8vAg03GEAGBkVDBZKeEs2yrj6ZxBCt0iVu8+RGNrN9fOTDUd\nRYivWJiVREl9K4U1x0xHsTwpdIt48bNyUiODOCc9ynQUIb5ifkYCft5e8stRJxiw0JVSyUqpfKVU\nkVKqUCl1R//9S5RS1UqpHf23SxwfV5zM7upmth1s4tqZqXh5yaWKwrWEBfkyZ0IMK3bU0NNnMx3H\n0gZzhN4L3K21ngDMAG5TSk3of9/vtdZT+m/vOiyl+I9e2lhOoK8338qWEXPCNS2cmsThtm7W75Px\ndI40YKFrrWu11tv6324BioFERwcTg9PU3s07O2q4fGoiYYG+puMIcVLnjY1meLCfbAXgYKd0Dl0p\nlQpMBTb333W7UqpAKfV3pVSEnbOJQXh9SyVdvTbZt0W4NF9vLxZkJrCmuI7m9h7TcSxLDfZSIqVU\nCPAx8Eut9XKlVCzQCGjgUSBea33DST7uZuBmgNjY2OylS5faK7tDtba2EhISYjrGf2TTmvvWdxAR\noPj59MBBf5w7rG0orLw+d15beXMfSzZ28v2JfsxO/vefJt15bYMxlPXl5ORs1VpPG/CBWusBb4Av\n8D5w1ze8PxXYPdDnyc7O1u4iPz/fdIQBfVRcp0fcl6dX7Kg+pY9zh7UNhZXX585rs9lses5v1+lF\nf9pw0ve789oGYyjrA7boQXT1YK5yUcDfgGKt9e9OuD/+hIddAewe/L83wh5e3FhOTKg/F02MMx1F\niAEppViYlcSWiqNUHG4zHceSBnMOfRZwLZD7tUsUn1BK7VJKFQA5wE8cGVR8VXljGx/va+DqM1Pw\n85GXEwj3cPnUBJRCfjnqID4DPUBr/Slwsoub5TJFg/65qQJvpbhmeorpKEIMWnxYILPSoli+vYo7\n54yWLZ7tTA7t3FBHdx+vb6nkoklxxA4LMB1HiFOyMCuRyiMdbKk4ajqK5Uihu6F3dlRzrLOX62Xf\nFuGGLpoYR5CfN8tlKwC7k0J3M7p/xNy4uFDOSJVL/4X7Cfb3Ye6kOPIKauns6TMdx1Kk0N3M1oqj\nFNUe47qZqXL+UbitRVlJtHT2sqZIxtPZkxS6m3lpYwWhAT5cPlVGzAn3NWNUJPFhAXLaxc6k0N1I\nfUsn7+2u5dvZyQT5DXiBkhAuy9tLccXURNaXNFLfIuPp7EUK3Y0s/bySnj7NtbJvi7CAhVmJ9Nk0\nK3bUmI5iGVLobqKnz8Yrmys4d0w0I6OCTccRYsjSY0LJTAqTFxnZkRS6m1hTVEfdsS6umyFH58I6\nFmYlUVR7jOJaGU9nD1LobuLFz8pJiggkZ1yM6ShC2M38zAR8vBRvbZejdHuQQncDew+1sPnAEb43\nYwTeMmJOWMjwYD9yxsXw1vZq+myD28pbfDMpdDfw0sZy/H28uHJasukoQtjdoqxEGlq6KDosLzIa\nKil0F3ess4e3tlczPzOBiGA/03GEsLuccTGEBfqyoabXdBS3J4Xu4pZtraK9u0/2bRGW5e/jzWVT\nEvjiUB+7qppNx3FrUuguzGbTvLyxginJ4UxOCjMdRwiH+cmcMYT5Kxa/uo3WLjlSP11S6C5sw/5G\nyhrbuP4suVRRWFtEsB+3ZPhz8Eg7D7y168vRluIUSaG7sJc2VhAZ7Mclk+MHfrAQbm7scG/unDOG\nt3fUsExebHRapNBdVNXRdtYW13HVmcn4+3ibjiOEU9yWk86MUcN58O3d7G9oNR3H7Uihu6hXNh8E\n4JrpcrpFeA5vL8UfrppKoJ83t72yTfZLP0VS6C6os6ePpZ8f5IIJsSSGB5qOI4RTxQ4L4DffzmDP\noRYef7fYdBy3IoXuglYV1HK0vYfr5FJF4aFyx8Vy09kjeWljBat3HzIdx21IobuglzaWkxYdzFlp\nkaajCGHMvXPHMTkxjHvf3EnV0XbTcdyCFLqL2VHZxM6qZhkxJzyen48Xz1wzFZuGO5buoLfPZjqS\ny5NCdzEvbSwn2M+bhVmJpqMIYdyIyGAeXziZrRVHeerDEtNxXJ4Uugs53NpFXkEtC7OSCA3wNR1H\nCJewIDOBK6cl8+y6UjaUNpqO49Kk0F3Ia1sq6e61cZ2MmBPiKx5eMIG06BDufG0Hja1dpuO4LCl0\nF9Fn07yy6SAzR0UyOjbUdBwhXEqQnw/PXDOV5o4e7np9JzbZO/2kpNBdxNriOqqbOmTfFiG+wbi4\nYTw0bwLr9zXwv5+UmY7jkqTQXcTLmyqIDwtgzvhY01GEcFnfnZ7CxZPiePL9vWw/eNR0HJcjhe4C\n9je08klJI9+dnoKPt3xJhPgmSil+tTCD2GEBLH51O80dPaYjuRRpDxfw8sYKfL0VV56RYjqKEC4v\nLMiXp6+eSm1zJz9fLlvtnkgK3bCjbd0s21rFpZPjiQ71Nx1HCLeQPSKCey4cy6pdtSz9otJ0HJch\nhW5Q/t565v5hPR09fdx49ijTcYRwK7ecO4pzRkexZEUh++paTMdxCVLoBrR29fKz5QX84IUvCAv0\n5e3bZsmIOSFOkZeX4nffmUJogC+3/2sbHd2y1a4UupNtKjvM3KfWs/SLSm45bxQrF5/NpEQpcyFO\nR3SoP7+/MpN9da38Iq/QdBzjfEwH8BSdPX08sXovf99wgNTIIN68dSbZI4abjiWE2ztndDQ/mp3G\nn9ft56y0KOZnJpiOZIwUuhNsP3iUu9/YSVlDG9fPHMF9F48jyE/+1wthL3ddMIZNZYf5+fJdZCaF\nkxIZZDqSEXLKxYG6e208+f4eFv35Mzq7+3jlpuk8ctkkKXMh7MzX24unr5oKChYv3U53r2dutTtg\noSulkpVS+UqpIqVUoVLqjv77hyul1iilSvr/G+H4uO6jqOYYC575lGfz97MoK4nVPzmXWelRpmMJ\nYVnJw4P49aIMdlY28dsP9pqOY8RgjtB7gbu11hOAGcBtSqkJwP3AWq31aGBt/589Xm+fjWc+KuGy\nZz+lsbWb56+bxpPfzmSYbIcrhMNdMjme705P4bn1ZazbW286jtMNWOha61qt9bb+t1uAYiARuAx4\nsf9hLwKXOyqkuyitb2XRXzbymw/2cdHEONb85FzmTJC9WYRwpgfnTWBcXCh3v76T+mOdpuM41Smd\nQ1dKpQJTgc1ArNa6tv9dhwCPbS6bTfO3Tw9w6dOfUHG4jT9ePZVnrskiItjPdDQhPE6ArzfPXDOV\n9u4+7nxtB30etNWuGuw+CEqpEOBj4Jda6+VKqSatdfgJ7z+qtf638+hKqZuBmwFiY2Ozly5dap/k\nDtba2kpISMiAj2tot/H8ri72HrWRGe3NDyb5Ee7v2r9rHuza3JWV1ydrG7z1VT38fXc3C0f7siDN\n/MHVUNaXk5OzVWs9bcAHaq0HvAG+wPvAXSfctxeI7387Htg70OfJzs7W7iI/P/8/vt9ms+l/ba7Q\nEx58T098aLV+7YuD2mazOSfcEA20Nndn5fXJ2gbPZrPpxf/apkf9bJX+/MBhu37u0zGU9QFb9CC6\nejBXuSjgb0Cx1vp3J7xrBXB9/9vXA+8M9l8bd3eouZPvv/AFP1u+i8zkcFbfeQ7fmZbM8f9VQghX\noJTil1dMIjE8kDte3U5Te7fpSA43mHMDs4BrgVyl1I7+2yXAr4ALlFIlwJz+P1ua1pq3t1dz4e8/\nZvOBw/zison888bpJEV45osYhHB1oQG+PHPNVBpau7j3zQLLb7U74CtctNafAt906Hm+feO4rsOt\nXfz3W7tZXXiIrJRwfvudKYyMCjYdSwgxgIykcO6bO47HVhXz8qYKrpuZajqSw8hLFgfh/cJD/Hz5\nLlo6e7n/4nH88JxReHvJ6RUh3MUNs0ayobSRx/KKyR4RwcQEa26I59qXYxjW3N7DXa/t4JaXtxIX\nFsDKxWdz63lpUuZCuBkvL8Vvvp1JRLAvi1/dTltXr+lIDiGF/g12NfRy0VPreWdnDXecP5q3b5vF\n2LhQ07GEEKcpMsSfp66cyoGCIThUAAAIAklEQVTGNh56x5pb7copl69p6+rll+8W86+tXaTHhPDX\n67LJSAof+AOFEC5vZloki3NH8/TaEiJD/LjqjGRGRVvnun4p9BNsLjvMPW/upOpoB3NTfXjqxrMJ\n8PU2HUsIYUc/zk1nf30rf11fxl/XlzEhfhjzMuOZn5FA8nD3vmJNCp3jwyeefP/48InkiCBev2Um\nbeUFUuZCWJCPtxfPfjeLB5o7WFVQS15BLU+s3ssTq/eSmRzO/Ix4LpkcT0J4oOmop8zjC31nZRN3\nvb6D/Q1tXDtjBPdfPI5gfx/WlZtOJoRwpPiwQG46ZxQ3nTOKyiPtrNpVS15BDY+tKuaxVcVMGxHB\nvP5yjxkWYDruoHhsoXf32vjjRyX8ad1+YkL9eemGMzl3TLTpWEIIA5KHB3HreWncel4aBxrbWFVQ\nQ15BLUtWFvFIXhHTRw5nXkYCF0+KIzLE33Tcb+SRhb7n0DHuem0nRbXHWJSVxEPzJxAWKPuVCyFg\nZFQwt+eO5vbc0ZTUtZBXUMvKghoeeHs3D68o5Ky0SOZlxHPRxDjCg8xv+nUijyr03j4bf/2kjN+v\n2UdYoC9/vTabCyfGmY4lhHBRo2ND+ckFodw5ZzTFtS3k9R+537dsFw+8vZtzRkczLyOeCybEEuoC\nQ2w8ptDLGlq5+42dbD/YxCWT43js8skMl/3KhRCDoJRiQsIwJiQM46cXjWVXdTN5BbWsKqjloz31\n+Pl4MXtMNPMyE5gzPsbY3GDLF7rNpnlxYzm/Xr0Hfx9v/nDVFBZkJsjOiEKI06KUIiMpnIykcO6f\nO47tlU3kFdTw7q5aPiiqI8DXi/PHxTIvI56ccTFOvVrO0oVedbSdn75RwMayw+SMjeZXizKIdZPf\nVgshXJ+XlyJ7RATZIyJ48NIJfFF+hLyCWt7bXcuqXbUE+3kzZ0Is8zMS0E6YnGTJQtda8/qWSh7N\nK0Zrza8XTZb9yoUQDuXlpZg+KpLpoyJ5eP4ENh84Ql5BDe/tPsQ7O2q4bYo/Fzg4g+UKve5YJ/cv\nKyB/bwMzRg3nyW9luv2rv4QQ7sXH24tZ6VHMSo/iF5dN4tPSRnqqHL9/jGUKXWvNyoJaHnx7N509\nfTw8fwLXz0zFS3ZGFEIY5OvtRc7YGNbVFjn8uSxR6Efaunnw7d2s2lXL1JRwfvPtTNIstOGOEEIM\nhtsX+pqiOn62vIDmjh7unTuWm88ZhY+37AoshPA8blvoxzp7+MXKIt7cWsX4+GG8fON0xscPMx1L\nCCGMcctC/7SkkXvf3EldSxeLc9NZnDsaPx85KhdCeDa3KvT27l7+5909vLypgrToYJb96CymJMvw\nCSGEADcq9C3lR7j7jZ0cPNLOTWeP5J6Lxsp+5UIIcQK3KPQ/ri3hdx/uIykikFd/OIMZoyJNRxJC\nCJfjFoU+IiqYq89M4eeXjCfE3y0iCyGE07lFOy7ITGBBZoLpGEII4dLk0hAhhLAIKXQhhLAIKXQh\nhLAIKXQhhLAIKXQhhLAIKXQhhLAIKXQhhLAIKXQhhLAIpbXjB5f+/5Mp1QBUOO0JhyYKaDQdwkGs\nvDaw9vpkbe5rKOsbobWOHuhBTi10d6KU2qK1nmY6hyNYeW1g7fXJ2tyXM9Ynp1yEEMIipNCFEMIi\npNC/2V9NB3AgK68NrL0+WZv7cvj65By6EEJYhByhCyGERUihn0AplayUyldKFSmlCpVSd5jOZG9K\nKW+l1HalVJ7pLPamlApXSr2plNqjlCpWSs00nclelFI/6f87uVsp9apSKsB0pqFQSv1dKVWvlNp9\nwn3DlVJrlFIl/f+NMJnxdH3D2p7s/3tZoJR6SynlkGHIUuhf1QvcrbWeAMwAblNKTTCcyd7uAIpN\nh3CQPwCrtdbjgEwssk6lVCLwY2Ca1noS4A1cZTbVkP0DmPu1++4H1mqtRwNr+//sjv7Bv69tDTBJ\na50B7AN+5ognlkI/gda6Vmu9rf/tFo4XQqLZVPajlEoCLgWeN53F3pRSYcC5wN8AtNbdWusms6ns\nygcIVEr5AEFAjeE8Q6K1Xg8c+drdlwEv9r/9InC5U0PZycnWprX+QGvd2//HTUCSI55bCv0bKKVS\nganAZrNJ7Oop4F7AZjqIA4wEGoAX+k8pPa+UCjYdyh601tXAb4CDQC3QrLX+wGwqh4jVWtf2v30I\niDUZxoFuAN5zxCeWQj8JpVQIsAy4U2t9zHQee1BKzQPqtdZbTWdxEB8gC/iz1noq0Ib7/sj+Ff3n\nki/j+D9aCUCwUup7ZlM5lj5++Z3lLsFTSv03x0/tvuKIzy+F/jVKKV+Ol/krWuvlpvPY0SxggVKq\nHFgK5Cql/mk2kl1VAVVa6y9/onqT4wVvBXOAA1rrBq11D7AcOMtwJkeoU0rFA/T/t95wHrtSSn0f\nmAd8VzvoenEp9BMopRTHz8EWa61/ZzqPPWmtf6a1TtJap3L8F2ofaa0tc5SntT4EVCqlxvbfdT5Q\nZDCSPR0EZiilgvr/jp6PRX7h+zUrgOv7374eeMdgFrtSSs3l+OnOBVrrdkc9jxT6V80CruX40euO\n/tslpkOJQVsMvKKUKgCmAI8bzmMX/T91vAlsA3Zx/PvWrV9VqZR6FdgIjFVKVSmlbgR+BVyglCrh\n+E8lvzKZ8XR9w9qeAUKBNf298heHPLe8UlQIIaxBjtCFEMIipNCFEMIipNCFEMIipNCFEMIipNCF\nEMIipNCFEMIipNCFEMIipNCFEMIi/g8k0m79y/YQ8gAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
},
{
"output_type": "stream",
"text": [
"s\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "n4nAqdkZghRh",
"colab_type": "text"
},
"source": [
"## 多分类-文本分类"
]
},
{
"cell_type": "code",
"metadata": {
"id": "FywO1N_GRdgw",
"colab_type": "code",
"outputId": "9762840a-ee9c-4af5-eb75-3abe5e8959af",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
}
},
"source": [
"#[2017-7-25]sklearn文本分类\n",
"from sklearn import datasets as d\n",
"from sklearn.datasets import fetch_20newsgroups\n",
"\n",
"data_all = d.load_iris()\n",
"data_x = data_all['data']\n",
"data_y = data_all['target_names']\n",
"#print data_y\n",
"#print data_x\n",
"print len(data_x)\n",
"#dir(d)\n",
"\n",
"# print d.fetch_mldata(subset='train')\n",
"# newsgroup_train = fetch_20newsgroups(subset='train')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"150\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "F1UB3FpPRdgz",
"colab_type": "code",
"outputId": "67aba6ce-bb0e-4d17-b473-e60658f6b71d",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 70
}
},
"source": [
"#[2017-7-25]应用sklearn做文本分类:http://blog.csdn.net/abcjennifer/article/details/23615947\n",
"from sklearn.datasets import fetch_20newsgroups \n",
"#下载指定的数据集\n",
"#newsgroup_train = fetch_20newsgroups(subset='train') \n",
"categories = ['comp.graphics', \n",
" 'comp.os.ms-windows.misc', \n",
" 'comp.sys.ibm.pc.hardware', \n",
" 'comp.sys.mac.hardware', \n",
" 'comp.windows.x']\n",
"newsgroup_train = fetch_20newsgroups(subset = 'train', categories = categories); #训练数据\n",
"newsgroup_test = fetch_20newsgroups(subset = 'test', categories = categories);#测试数据\n",
"dir(newsgroup_train)"
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"Downloading 20news dataset. This may take a few minutes.\n",
"Downloading dataset from https://ndownloader.figshare.com/files/5975967 (14 MB)\n"
],
"name": "stderr"
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
"['DESCR', 'data', 'filenames', 'target', 'target_names']"
]
},
"metadata": {
"tags": []
},
"execution_count": 26
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "ezHVcpFoRdg3",
"colab_type": "code",
"outputId": "d995d19a-e28f-4e61-d549-01c28eec73ee",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 105
}
},
"source": [
"from pprint import pprint \n",
"pprint(list(newsgroup_train.target_names)) "
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"['comp.graphics',\n",
" 'comp.os.ms-windows.misc',\n",
" 'comp.sys.ibm.pc.hardware',\n",
" 'comp.sys.mac.hardware',\n",
" 'comp.windows.x']\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "-bAr2yVFRdg6",
"colab_type": "code",
"outputId": "d81c2a2c-5a49-4108-f3e2-d50c53a08c9a",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 230
}
},
"source": [
"#从文本中提取特征\n",
"from sklearn.feature_extraction.text import HashingVectorizer \n",
"#只取了10000个词,即10000维feature,稀疏度还不算低,实际上用TfidfVectorizer统计可得到上万维的feature\n",
"vectorizer = HashingVectorizer(stop_words = 'english',non_negative = True, n_features = 10000) \n",
"fea_train = vectorizer.fit_transform(newsgroup_train.data) \n",
"fea_test = vectorizer.fit_transform(newsgroup_test.data); \n",
"#return feature vector 'fea_train' [n_samples,n_features] \n",
"print 'Size of fea_train:' + repr(fea_train.shape) \n",
"print 'Size of fea_train:' + repr(fea_test.shape) \n",
"#11314 documents, 130107 vectors for all categories \n",
"print 'The average feature sparsity is {0:.3f}%'.format(fea_train.nnz/float(fea_train.shape[0]*fea_train.shape[1])*100); "
],
"execution_count": 0,
"outputs": [
{
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n",
"/usr/local/lib/python2.7/dist-packages/sklearn/feature_extraction/hashing.py:102: DeprecationWarning: the option non_negative=True has been deprecated in 0.19 and will be removed in version 0.21.\n",
" \" in version 0.21.\", DeprecationWarning)\n"
],
"name": "stderr"
},
{
"output_type": "stream",
"text": [
"Size of fea_train:(2936, 10000)\n",
"Size of fea_train:(1955, 10000)\n",
"The average feature sparsity is 1.002%\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "riSm3jlxRdg_",
"colab_type": "code",
"colab": {}
},
"source": [
""
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "1VmhpeyCpEnq",
"colab_type": "text"
},
"source": [
"# 聚类"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6xSAT3IZf9gQ",
"colab_type": "text"
},
"source": [
"## k-means聚类\n",
"- [k-means聚类分析](http://www.cnblogs.com/wuchuanying/p/6264025.html)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "Ub2XaI6BRdgR",
"colab_type": "code",
"outputId": "12087184-0518-4857-8d6e-e0f9bc3596a3",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 313
}
},
"source": [
"#coding:utf-8\n",
"#k-mean聚类分析:http://www.cnblogs.com/wuchuanying/p/6264025.html\n",
"#我们计算K值从1到10对应的平均畸变程度:\n",
"from sklearn.cluster import KMeans\n",
"#用scipy求解距离\n",
"from scipy.spatial.distance import cdist\n",
"K=range(1,10)\n",
"meandistortions=[]\n",
"for k in K:\n",
" kmeans=KMeans(n_clusters=k)\n",
" kmeans.fit(X)\n",
" meandistortions.append(sum(np.min(\n",
" cdist(X,kmeans.cluster_centers_,\n",
" 'euclidean'),axis=1))/X.shape[0])\n",
"plt.plot(K, meandistortions, 'bx-')\n",
"plt.xlabel('k')\n",
"plt.ylabel(u'平均畸变程度')\n",
"#plt.ylabel(u'平均畸变程度',fontproperties=font)\n",
"#plt.title(u'用肘部法则来确定最佳的K值',fontproperties=font)\n",
"plt.title(u'用肘部法则来确定最佳的K值')"
],
"execution_count": 0,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"Text(0.5,1,u'\\u7528\\u8098\\u90e8\\u6cd5\\u5219\\u6765\\u786e\\u5b9a\\u6700\\u4f73\\u7684K\\u503c')"
]
},
"metadata": {
"tags": []
},
"execution_count": 12
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEWCAYAAAB1xKBvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi40LCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcv7US4rQAAIABJREFUeJzt3XmUnHWd7/H3J50EskASkibGLAQk\n7MjWSaquKAQlBi4C6sjiMsgdJ8qBuThzz3jQq6A4jl5m0eugIAciOiIMsmhU1nsN4lxZkmAghAAJ\ne2IwTUICIUDo5nv/eJ6yK52qTnW6n36quj6vc55T9SxV9YWj/eG3PY8iAjMzs50ZkncBZmbWGBwY\nZmZWEweGmZnVxIFhZmY1cWCYmVlNHBhmZlYTB4aZmdVkaN4FmNVK0mnA31c4dRcwt8LxdRHxMUm/\nAMZXOP8XwOeAD1Q49w1geJXfuw34CfDTBvrN3YFngGER0SFJwHeBE4H3A9+v9tmIeLHCcWtCDgxr\nJJOAr0bE/ykdkDQauBq4JyK+XH6xpJvSt29FxLHdzv0zyR/Rg4DjI6Kj7NwpwMT0fKXfuxwY2WC/\nWX5sCHAlUASOi4g/Sarps9bcHBhmzaUFuAY4nCS0NuRcjzUQB4ZZc7kOmAKcEBGb8i7GGosHvc2a\ny1zgZw4L2xVuYZg1l1OAX0l6OSIW5F2MNRYHhllz+T3wIZLQeCMiKs26MqvIgWHWZCLit5I+Atwq\n6c2IuDnvmqwxODDMmlBE3C3pTOA/JG3Lux5rDB70NmsCEfFsRKh87UdE/DoiRkfEL/OszRqHWxjW\naP5F0stl+y3AWuBTko7tdm1p5fLhku7pdu5dJIvhAP6vpPJHT44H/qWH33sqfd9ov9mTvnzWmoT8\niFYzM6uFu6TMzKwmDgwzM6vJoBrDmDBhQkyfPj3vMszMGsbSpUtfiojWWq4dVIExffp0lixZkncZ\nZmYNQ9JztV7rLikzM6uJA8PMzGriwDAzs5o4MMzMrCYODDMzq0lTB8Zll8GiRdsfW7QoOW5mZttr\n6sCYORPOOKMrNBYtSvZnzsy3LjOzejSo1mH01pw5cN118KEPwemnw513wo03JsfNzGx7Td3CADjx\nRHj77SQ4zjvPYWFmVk3TB8Y990BnJ4wfD1dcseOYhpmZJZo6MEpjFp/8JGzYANdcs/2YhpmZdWnq\nwFi8OBmz+MQnkv3hw5P9xYvzrcvMrB419aD3F76QvL76KgwZAvfdB1/7mscxzMwqyayFIWmqpEWS\nHpO0QtKFFa6RpO9KWi3pEUlHl507R9KqdDsnqzoB9tgDDjsM7r8/y18xM2tsWXZJdQD/IyIOAQrA\n+ZIO6XbNScCMdJsPXAEgaS/gEmA2MAu4RNK4DGulWIQHHkhmTJmZ2Y4yC4yIWBcRD6XvXwVWApO7\nXXYa8ONI3A+MlTQJ+CBwd0RsjIiXgbuBeVnVCklgbN4MK1dm+StmZo1rQAa9JU0HjgIe6HZqMvBC\n2f6a9Fi145W+e76kJZKWtLe373KNhULy6m4pM7PKMg8MSaOBm4HPR8Qr/f39EXFVRLRFRFtra01P\nGazogANgr72SgW8zM9tRpoEhaRhJWFwXEbdUuGQtMLVsf0p6rNrxzEhJK8OBYWZWWZazpARcA6yM\niH+tctlC4C/T2VIFYHNErAPuBOZKGpcOds9Nj2WqUIDHHoNNm7L+JTOzxpPlOoz3AJ8Clktalh77\nEjANICKuBG4DTgZWA1uBc9NzGyV9HSgtobs0IjZmWCuQDHwDPPggzJ2b9a+ZmTWWzAIjIv4T0E6u\nCeD8KucWAAsyKK2qWbOSrqn77nNgmJl119S3Buluzz3h0EM9U8rMrBIHRjfFYhIYXsBnZrY9B0Y3\nhUIy6P3EE3lXYmZWXxwY3ZQGvt0tZWa2PQdGNwceCGPHej2GmVl3DoxuhgyB2bMdGGZm3TkwKigW\nYcUKeKXfb2RiZta4HBgVFIsQkSzgMzOzhAOjglmzklcPfJuZdXFgVDB2LBxyiMcxzMzKOTCqKC3g\ni8i7EjOz+uDAqKJQgI0bYdWqvCsxM6sPDowqSgv43C1lZpZwYFRx8MHJzQgdGGZmCQdGFaUFfJ4p\nZWaWcGD0oFiE5cvh1VfzrsTMLH9ZPqJ1gaT1kh6tcv7vJS1Lt0cldUraKz33rKTl6bklWdW4M8Vi\ncpvzxYt3fq2Z2WCXZQvjWmBetZMR8U8RcWREHAl8Efhtt8ewzknPt2VYY49mz05e3S1lZpZhYETE\nvUCtz+E+G7g+q1p21bhxcNBBHvg2M4M6GMOQNJKkJXJz2eEA7pK0VNL8nXx+vqQlkpa0t7f3e31e\nwGdmlsg9MIAPAf+vW3fUsRFxNHAScL6k91X7cERcFRFtEdHW2tra78UVCvDSS/DUU/3+1WZmDaUe\nAuMsunVHRcTa9HU9cCswK4e6AC/gMzMryTUwJI0BjgN+UXZslKQ9Su+BuUDFmVYD4ZBDYI89HBhm\nZkOz+mJJ1wPHAxMkrQEuAYYBRMSV6WUfBu6KiNfKPjoRuFVSqb6fRsQdWdW5My0tye3OPVPKzJpd\nZoEREWfXcM21JNNvy489DRyRTVW7pliEb34TXnsNRo3Kuxozs3zUwxhG3SsUoLPTC/jMrLk5MGpQ\nKCSv7pYys2bmwKjB+PFwwAEe+Daz5ubAqFGhkASGF/CZWbNyYNSoWIT2dnjmmbwrMTPLhwOjRl7A\nZ2bNzoFRo0MPTabUOjDMrFk5MGo0dKgX8JlZc3Ng9EKxCA8/DFu35l2JmdnAc2D0QqEAHR2wdGne\nlZiZDTwHRi+UFvB5HMPMmpEDoxdaW2H//R0YZtacHBi9VCj4CXxm1pwcGL1ULMKLL8Jzz+VdiZnZ\nwHJg9JIX8JlZs3Jg9NLhh8PIkV6PYWbNJ7PAkLRA0npJFR+vKul4SZslLUu3i8vOzZP0hKTVki7K\nqsZdMXQozJzpFoaZNZ8sWxjXAvN2cs3vIuLIdLsUQFIL8D3gJOAQ4GxJh2RYZ68VCvCHP8Drr+dd\niZnZwMksMCLiXmDjLnx0FrA6Ip6OiG3ADcBp/VpcHxWLyQK+hx7KuxIzs4GT9xhGUdLDkm6XdGh6\nbDLwQtk1a9JjdcML+MysGQ3N8bcfAvaJiC2STgZ+Dszo7ZdImg/MB5g2bVr/VljFxImw774ODDNr\nLrm1MCLilYjYkr6/DRgmaQKwFphadumU9Fi177kqItoioq21tTXTmssVi34Cn5k1l9wCQ9I7JCl9\nPyutZQOwGJghaV9Jw4GzgIV51VlNsQjr1sELL+z8WjOzwSCzLilJ1wPHAxMkrQEuAYYBRMSVwF8A\n50nqAF4HzoqIADokXQDcCbQACyJiRVZ17qrycYwB6gkzM8tVZoEREWfv5PzlwOVVzt0G3JZFXf3l\niCNgxIhkAd+ZZ+ZdjZlZ9vKeJdWwhg2DtjYPfJtZ83Bg9EGhkKzFeOONvCsxM8ueA6MPikV4661k\n1beZ2WDnwOgDL+Azs2biwOiDSZNgn30cGGbWHBwYfVQs+lbnZtYcHBh9VCzCmjXJZmY2mDkw+qg0\njuFWhpkNdg6MPjrySNh9d49jmNng58Doo+HD4ZhjHBhmNvg5MPpBaQHfm2/mXYmZWXYcGP2gWEzC\nYtmyvCsxM8uOA6MfeAGfmTUDB0Y/mDwZpk71TCkzG9wcGP2k9AQ+M7PByoHRTwoFeP55+OMf867E\nzCwbmQWGpAWS1kt6tMr5T0h6RNJySb+XdETZuWfT48skLcmqxv5ULCav7pYys8EqyxbGtcC8Hs4/\nAxwXEYcDXweu6nZ+TkQcGRFtGdXXr446KlmT4W4pMxussnxE672Spvdw/vdlu/cDU7KqZSDsthsc\nfbQDw8wGr3oZw/gr4Pay/QDukrRU0vycauq1YhGWLoVt2/KuxMys/9XUwpB08U4uWR8RV+5KAZLm\nkATGsWWHj42ItZL2Bu6W9HhE3Fvl8/OB+QDTpk3blRL6TbEI3/42PPwwzJyZaylmZv2u1i6pAnAW\noCrnfwT0OjAkvRu4GjgpIjaUjkfE2vR1vaRbgVlAxcCIiKtIxz/a2tqitzX0p/IFfA4MMxtsau2S\n6oyIVyJic6WNpAupVyRNA24BPhURT5YdHyVpj9J7YC5QcaZVvZk6NVnE55lSZjYY1drC2Fkg7HBe\n0vXA8cAESWuAS4BhAGn31cXAeOD7kgA60hlRE4Fb02NDgZ9GxB011pk7L+Azs8Gq1sAYJmnPKucE\ntHQ/GBFn9/SFEfEZ4DMVjj8NHLHjJxpDoQA33QQvvgjveEfe1ZiZ9Z9aA+N+4PM9nL+9h3NNpXwB\n3+mn51uLmVl/6s20WvWwWeroo2HYMHdLmdngU2sLYzYZzJIajHbfPVn17cAws8Emt1lSg1mxCEuW\nwFtv5V2JmVn/qTUwej1LqpkVi/D66/DII3lXYmbWf2oNjGGS9qyyjaHCLKlm5ifwmdlg5FlSGZg2\nDSZNSmZKXXBB3tWYmfWP3tyt1rOhaiR5AZ+ZDT6eJZWRQgFuuQXWr4e99867GjOzvvMsqYz4CXxm\nNth4llRGjjkGhg51t5SZDR6Z3Uuq2Y0YAUce6RaGmQ0eniWVoWIRrrkGOjqS1oaZWSPzvaQyVCjA\n1q2wfHnelZiZ9Z1nSWWofOD7qKPyrcXMrK88SypD06fDxIke+DazwcGzpDIkJd1SDgwzGwwyvZeU\npAWS1kuq+ExuJb4rabWkRyQdXXbuHEmr0u2c3v+j1YdiEVavhpdeyrsSM7O+yXqW1LXA5cCPq5w/\nCZiRbrOBK4DZkvYieQZ4G0nrZamkhRHxco311o3ycYxTTsm3FjOzvsh0llRE3Ats7OE7TwN+HIn7\ngbGSJgEfBO6OiI1pSNwNzOtFrXXjmGOgpcXdUmbW+PKeJTUZeKFsf016rNrxHUiaD8wHmDZt2i6U\nkK1Ro+CII7yAz8waX8PPkoqIqyKiLSLaWltb8yqjR8UiPPggdHbmXYmZ2a7Le5bUWmBq2f6U9Fi1\n4w2pUIAtW+DRikP/ZmaNIe8n7i0E/jKdLVUANkfEOuBOYK6kcZLGAXPTYw3Jd641s8GgP2ZJiSqz\npCRdDxwPTJC0hmTm0zCAiLgSuA04GVgNbAXOTc9tlPR1YHH6VZdGRE+D53Vtv/2gtTUZ+P7sZ/Ou\nxsxs12Q66B0RZ/f0pRERwPlVzi0AFtRYX13zAj4zGwwaftC7URSL8OSTsGFD3pWYme2avAe9m0Zp\nHOOBB/Ktw8xsV+U96N002tpgyBB3S5lZ4+rtoHe1MYw7+qecwWv0aHj3uz1TyswaV02BERFfy7qQ\nZlAowHXXJQv4WtwmM7MG05t7SVkfFYvw6qvw2GN5V2Jm1nsOjAHkBXxm1sgcGANo//1h/HgPfJtZ\nY3JgDKDSAj63MMysETkwBlixCCtXwssN9ygoM2t2DowBVigkr17AZ2aNxoExwGbNShbwuVvKzBqN\nA2OA7bEHHHaYB77NrPE4MHJQKCRdUm+/nXclZma1c2DkoFiEzZvh8cfzrsTMrHYOjByUFvC5W8rM\nGkmmgSFpnqQnJK2WdFGF89+WtCzdnpS0qexcZ9m5hVnWOdBmzIBx4xwYZtZYar1bba9JagG+B5wI\nrAEWS1oYEX++k1JE/G3Z9X8DHFX2Fa9HxJFZ1ZenIUO8gM/MGk+WLYxZwOqIeDoitgE3AKf1cP3Z\nwPUZ1lNXisXkJoSbN+ddiZlZbbIMjMnAC2X7a9JjO5C0D7Av8Juyw7tLWiLpfkmnV/sRSfPT65a0\nt7f3R90DolCACC/gM7PGUS+D3mcBN0VEZ9mxfSKiDfg48B1J76r0wYi4KiLaIqKttbV1IGrtF7Nn\nJ/eWcreUmTWKLANjLTC1bH9KeqySs+jWHRURa9PXp4F72H58o+HtuScceqgHvs2scWQZGIuBGZL2\nlTScJBR2mO0k6SBgHHBf2bFxknZL308A3gMMuscOlQa+vYDPzBpBZoERER3ABcCdwErgxohYIelS\nSaeWXXoWcENERNmxg4Elkh4GFgHfKp9dNVgUi7BpEzz5ZN6VmJntXGbTagEi4jbgtm7HLu62/9UK\nn/s9cHiWtdWD0p1r77sPDjoo31rMzHamXga9m9JBB8HYsR7HMLPG4MDI0ZAhyWwpz5Qys0bgwMhZ\noQCPPgqvvJJ3JWZmPXNg5KxYTBbwPfhg3pWYmfXMgZGz2bOTV3dLmVm9c2DkbOxYOPhgD3ybWf1z\nYNSBYjFpYWy3EsXMrM44MOpAsQgbN8KqVXlXYmZWnQOjDpQv4DMzq1cOjDpwyCHJzQg98G1m9cyB\nUQdKC/jcwjCzeubAqBOFAixfDq++mnclZmaVOTDqRLGY3OZ8yZK8KzEzq8yBUSdKC/jcLWVm9cqB\nUSf22gsOPNCBYWb1y4FRR7yAz8zqWaaBIWmepCckrZZ0UYXzn5bULmlZun2m7Nw5klal2zlZ1lkv\nikV46SV46qm8KzEz21FmT9yT1AJ8DzgRWAMslrSwwqNW/yMiLuj22b2AS4A2IICl6WdfzqreelC+\ngG///fOtxcysuyxbGLOA1RHxdERsA24ATqvxsx8E7o6IjWlI3A3My6jOunHooTB6tBfwmVl9yjIw\nJgMvlO2vSY9191FJj0i6SdLUXn4WSfMlLZG0pL29vT/qzk1LC8ya5YFvM6tPeQ96/xKYHhHvJmlF\n/Ki3XxARV0VEW0S0tba29nuBA61YhEcegddey7sSM7PtZRkYa4GpZftT0mN/FhEbIuLNdPdq4Jha\nPztYFYvQ2ekFfGZWf7IMjMXADEn7ShoOnAUsLL9A0qSy3VOBlen7O4G5ksZJGgfMTY8Nel7AZ2b1\nKrNZUhHRIekCkj/0LcCCiFgh6VJgSUQsBP67pFOBDmAj8On0sxslfZ0kdAAujYiNWdVaTyZMgBkz\nHBhmVn8Ug2iVWFtbWywZBH0555wDd9wBL74IUt7VmNlgJmlpRLTVcm3eg95WQaEA69fDM8/kXYmZ\nWRcHRh0qFpNXd0uZWT1xYNShww6DUaO8gM/M6osDow4NHQozZ7qFYWb1xYFRhy67DN75Tnj4Ydi6\nNTm2aFFy3MwsLw6MOjRzJvzqV9DRAUuXJmFxxhnJcTOzvDgw6tCcOfDDHybv//qv4bTT4B/+Adpq\nmvhmZpYNr8OoYzNmwOrV2x975zvhgAOSp/MdeGDX++nTk7EPM7Pe6M06DP+JqVOLFsGmTXDRRfCD\nH8CFF8Lw4fDEE/Dkk/Czn8HGsrXvw4bBu97VFSDlr3vv7QWAZtZ3Dow6VBqzuPHGpHtq7tyu/S9+\nseu6DRu6AqT89Y47YNu2ruvGjKkcJDNmJNN3zcxq4S6pOnTZZckA95w5XccWLYLFi+ELX9j55zs7\n4fnnK4fJCy9sf+2UKTt2bx1wAOyzT/J8jv6sy8zqT2+6pBwYTWbrVli1ascgeeIJ2Ly567rhw5PH\nxJYHyZYt8LWvJS2dE07YsSVkZo3HYxhW1ciRcMQRyVYuAtrbdwySlSuTKb5vvdV17Qc+kAy+v/QS\nnHkmrF2brErff38YP97jJWaDlVsYtlMdHfDss10h8pOfwEMPJWMjr7yShE3JmDFJcMyYkbyWbx58\nN6s/bmFYvxo6tOuP/ogR8I//CF/5ClxxBdx+ezLesXr19tvixclMrs7Oru8ZPXrHECltkybBEK8K\nMqtrDgyrWfcxizlzuvZPOWXH67dtg+ee2zFMHnkEfv7zpOVSMmJE9TCZMqXnMPFgvNnAyDQwJM0D\n/jfJE/eujohvdTv/d8BnSJ641w78t4h4Lj3XCSxPL30+Ik7NslbbucWLtx/gnjMn2V+8uPKg9/Dh\nSdfUjBk7nuvoSGZslUJk1ark9fHH4de/3n5a8G67wX77bR8ipS6vqVOTsCgPsvJgM7P+k9kYhqQW\n4EngRGANyeNWz46Ix8qumQM8EBFbJZ0HHB8RZ6bntkTE6N78pscwBofOzmQgvXvLpLS9/nrXtcOG\nwb77wrhxyc0ajz0WHngAvvzlZP3KxInQ2upV8GbV1MW0WklF4KsR8cF0/4sAEfHNKtcfBVweEe9J\n9x0YtoO334Z16yoHyYoV28/mKpGS2VsTJyYD7xMndm2V9nfffeD/uczyUi+D3pOB8mVia4DZPVz/\nV8DtZfu7S1pC0l31rYj4eaUPSZoPzAeYNm1anwq2+jdkCEyenGzHHdd1vNQNde65cPXV8NWvJtf8\n6U/Jtn591/vFi5P9V1+t/Bt77tlzqJQfGz26+swvj63YYFMXDXVJnwTagLI/AewTEWsl7Qf8RtLy\niHiq+2cj4irgKkhaGANSsNWV7oPxJ53Utf/Rj1b/3NatXUFSHijl+489lnx/+X27yo0YUb2lsmUL\nfPjD8J3vwKmnwrJlyboVj61Yo8oyMNYCU8v2p6THtiPpA8D/BI6LiDdLxyNibfr6tKR7gKOAHQLD\nrLeD8SUjRyZ3+Z0+fee/8dZbycLGSi2W0v7zzye/2d6+/XTic8/tej9xInzpS8k04mpba+uOt2Ux\nqwdZjmEMJRn0fj9JUCwGPh4RK8quOQq4CZgXEavKjo8DtkbEm5ImAPcBp5UPmFfiMQyrB2+/nbRI\nSmFy+eVw661QLCZ3FF63rmt7+eUdP9/SkrRQegqVd7wj2Xbbrff1uavMytXFGEZEdEi6ALiTZFrt\ngohYIelSYElELAT+CRgN/ExJR3Bp+uzBwA8kvU3ykKdv7SwszOrFkCEwYUKyrV8Pv/td10LHb3xj\n+z/Ub7wBL77YFSDl79etgz/+MXnq4vr1SRB1t9dePQdLaRtdNn3E05BtV/nWIGYZ6T620pebNXZ0\nJF1d5WFSaXvxxe3XsJSMHr19gHR0JLfBP+EE+O1v4eKL4fjjYezY5PYuY8YkU5Zt8KuLabV5cGBY\nPcmj6yci6Q7bWbCsWwevvdbzd40c2RUgtbx2PzZqVO/uHeausnw4MMysR4sWwcc+Bh//OPz7v8Ml\nlyQLIDdvTp70uLPXTZsqr3kp19JSe9iMGQPPPJM8u/7f/i2Z6bZsGZx1lm+fnzUHhplV1R9dZRHJ\n+EutAVPp9ZVXdv47e+yRdKGNH1/71t8LLwd7y6cuBr3NrD7t6jTkclKyBmXEiGS21q7o7EwWT3YP\nkgUL4Be/gPe+Fw4/PHkU8YYNsGZNcvuXDRuSNTTVjBxZOUgmTKgeMmPGVO8+8ySBLm5hmFndKP0x\nPu+8ZFZZtVbPG290BUmt28aN2z+7pVxLSzLjrFqgtLcndxA4/XT45S/h+9+Hk09OWkCN/owXd0mZ\nWcPpz1lllXR2Jq2Y3gbNG29U/84hQ7oG/MeOTW6CWf5a7X3ptS/dZ/3VVeYuKTNrOP3RVdaTlpau\nFkNvbN2atCo+97nkuS8LF8L8+UlX3KZNyeLL0kSAl1/uWpC5adP2d1auZLfdag+X7u+PPnrgu8rc\nwjAz60FfWj5vvtkVJuXh0j1kqr0vv8VMJSNGJL8xeXISTrvSGnMLw8ysn/Sl5bPbbl03pOytiGSt\nzM7C5Te/SZ5i+ZWvZD/92C0MM7MGVeskgZ70poXRw5OSzcysXpV3jV16afJ6xhnJ8aw4MMzMGlBP\nXWVZcZeUmVkTc5eUmZn1OweGmZnVxIFhZmY1cWCYmVlNHBhmZlaTQTVLSlI78NwufnwC8FI/ltNf\nXFfvuK7ecV29Mxjr2iciWmu5cFAFRl9IWlLr1LKB5Lp6x3X1juvqnWavy11SZmZWEweGmZnVxIHR\n5aq8C6jCdfWO6+od19U7TV2XxzDMzKwmbmGYmVlNHBhmZlaTpg8MSQskrZf0aN61lEiaKmmRpMck\nrZB0Yd41AUjaXdKDkh5O6/pa3jWVk9Qi6Q+SfpV3LeUkPStpuaRlkurmdsqSxkq6SdLjklZKKtZB\nTQem/55K2yuSPp93XQCS/jb93/2jkq6XtHveNQFIujCtaUXW/66afgxD0vuALcCPI+KwvOsBkDQJ\nmBQRD0naA1gKnB4Rj+Vcl4BREbFF0jDgP4ELI+L+POsqkfR3QBuwZ0Scknc9JZKeBdoioq4WfEn6\nEfC7iLha0nBgZERsyruuEkktwFpgdkTs6oLc/qplMsn/3g+JiNcl3QjcFhHX5lzXYcANwCxgG3AH\n8LmIWJ3F7zV9CyMi7gU25l1HuYhYFxEPpe9fBVYCk/OtCiKxJd0dlm518V8ckqYA/xW4Ou9aGoGk\nMcD7gGsAImJbPYVF6v3AU3mHRZmhwAhJQ4GRwB9zrgfgYOCBiNgaER3Ab4GPZPVjTR8Y9U7SdOAo\n4IF8K0mk3T7LgPXA3RFRF3UB3wG+ALyddyEVBHCXpKWS5uddTGpfoB34YdqNd7WkUXkX1c1ZwPV5\nFwEQEWuBfwaeB9YBmyPirnyrAuBR4L2SxksaCZwMTM3qxxwYdUzSaOBm4PMR8Ure9QBERGdEHAlM\nAWalTeJcSToFWB8RS/OupYpjI+Jo4CTg/LQbNG9DgaOBKyLiKOA14KJ8S+qSdpGdCvws71oAJI0D\nTiMJ2ncCoyR9Mt+qICJWAv8LuIukO2oZ0JnV7zkw6lQ6RnAzcF1E3JJ3Pd2l3ReLgHl51wK8Bzg1\nHSu4AThB0k/yLalL+l+nRMR64FaS/ua8rQHWlLUQbyIJkHpxEvBQRPwp70JSHwCeiYj2iHgLuAX4\nLznXBEBEXBMRx0TE+4CXgSez+i0HRh1KB5evAVZGxL/mXU+JpFZJY9P3I4ATgcfzrQoi4osRMSUi\nppN0Y/wmInL/rz8ASaPSiQukXT5zSboRchURLwIvSDowPfR+INdJFd2cTZ10R6WeBwqSRqb//3w/\nydhi7iTtnb5OIxm/+GlWvzU0qy9uFJKuB44HJkhaA1wSEdfkWxXvAT4FLE/HCwC+FBG35VgTwCTg\nR+nslSHAjRFRV1NY69BE4NbkbwxDgZ9GxB35lvRnfwNcl3b/PA2cm3M9wJ+D9UTgs3nXUhIRD0i6\nCXgI6AD+QP3cJuRmSeOBt4Dzs5y80PTTas3MrDbukjIzs5o4MMzMrCYODDMzq4kDw8zMauLAMDOz\nmjgwzDIkaXo93QnZrC8cGGZmVhMHhtkAkbRfeqO/mXnXYrYrmn6lt9lASG/BcQPw6Yh4OO96zHaF\nA8Mse63AL4CP5P0QLLO+cJcbSg0fAAAAa0lEQVSUWfY2k9y87ti8CzHrC7cwzLK3DfgwcKekLRGR\n2d1EzbLkwDAbABHxWvqgp7vT0FiYd01mveW71ZqZWU08hmFmZjVxYJiZWU0cGGZmVhMHhpmZ1cSB\nYWZmNXFgmJlZTRwYZmZWk/8PcscVqX8ktL8AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"tags": []
}
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "cquHlN5hpHZQ",
"colab_type": "text"
},
"source": [
"# 降维"
]
},
{
"cell_type": "code",
"metadata": {
"id": "X_MxEsO_wrFH",
"colab_type": "code",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
},
"outputId": "60b4923e-5828-4ba8-ab93-d6b1ff89ae76"
},
"source": [
"from sklearn.decomposition import PCA\n",
"from sklearn.datasets import load_iris\n",
"\n",
"iris = load_iris()\n",
"X = iris.data\n",
"pca = PCA(n_components=2)\n",
"reduced_X = pca.fit_transform(X)\n",
"\n",
"X.shape \t\t\t# (150, 4)\n",
"reduced_X.shape \t# (150, 2)"
],
"execution_count": 2,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"(150, 2)"
]
},
"metadata": {
"tags": []
},
"execution_count": 2
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "J7ZEc7v0pJGe",
"colab_type": "text"
},
"source": [
"# 其它"
]
}
]
}