- 总结
- 知识追踪
- 神经认知诊断
- 落地案例
- 结束
总结
- 【2022-8-5】可解释深度知识追踪模型
- 当前知识追踪方法多针对知识点建模,忽略了习题信息建模与用户个性化表征,并且对于预测结果缺乏可解释性.
- 针对以上问题,提出了一个可解释的深度知识追踪框架.首先引入习题的上下文信息挖掘习题与知识点间的隐含关系,得到更有表征能力的习题与知识点表示,缓解数据稀疏问题.接着建模用户答题序列获得其当前知识状态,并以此学习个性化注意力,进而得到当前习题基于用户知识状态的个性化表示.最后,对于预测结果,依据个性化注意力选择一条推理路径作为其解释.相较于现有方法,所提模型不仅取得了更好的预测结果,还能为预测结果提供推理路径层面的解释,体现了其优越性.
- knowledge-tracing最新进展
- 深度知识追踪(Deep Knowledge Tracing)论文学习
知识追踪
什么是知识追踪
Knowledge Tracing
Def: Knowledge tracing is the task of modelling student knowledge over time so that we can accurately predict how students will perform on future interactions. Usually by observing the correctness of doing exercises.
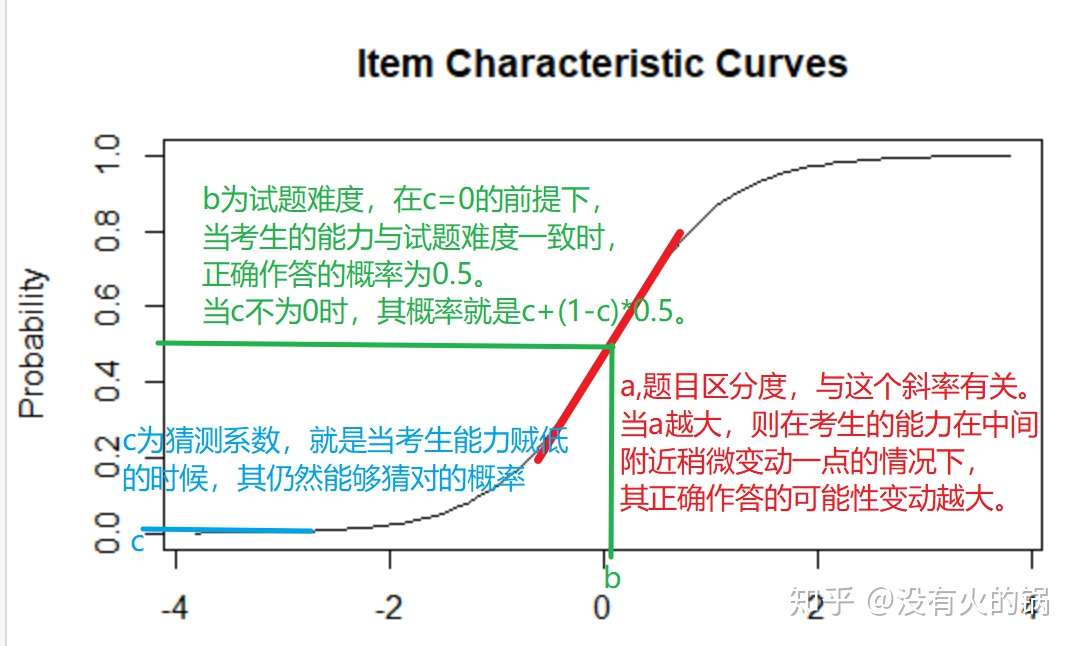
- 认知诊断在在线智能教育领域是一个非常经典的问题。根据学生的答题历史记录,分析学生对于各个知识点的掌握情况。如图1所示,总共有4道习题,学生对四道习题进行作答,认知诊断模型将根据学生的作答记录分析出学生对于题目中包含知识点的掌握情况。

认知诊断问题需要从以下三个方面去考虑:学生模型,试题模型,学生试题交互模型。
- 学生模型:将学生对于各个知识点的掌握程度向量
作为学生建模结果。
- 试题建模:试题建模分为两个部分
- 其一是试题中包含哪些知识点,这些都是通过人工标注的Q矩阵得到的;
- 其二就是试题本身的特征,比如试题难度,试题的区分度等等。
- 学生-试题交互建模:通过神经网络模拟学生与试题之间的交互建模。向网络中输入学生模型与试题模型,最终输出学生做出各个习题的概率。
- 知识追踪是基于学生行为序列进行建模,预测学生对知识的掌握程度。知识追踪是构建自适应教育系统的核心和关键。在自适应的教育系统中,无论是做精准推送,学生学习路径规划或知识图谱构建,第一步都是能够精准预测学生对知识的掌握程度。

- 这个学生一共做了50道题(横轴),在深度知识追踪中,每道题关联一个知识点,在上面这50道题中,共考察了6个知识点,如左边显示
- 深蓝色表示“Line graph intuition”这个知识点
- 橘黄色表示“Slope of a line”这个知识点等等
- 学生的实际答题情况由图上方的圆圈表示
- 圆圈的颜色表示了这道题考察的是哪个知识点
- 实心圆表示答对
- 空心圆表示答错。
- 图中间的蓝绿色网格表示模型的预测结果,由深蓝色到浅绿色表示答对概率越来越高。
- 具体解释一下,这个学生开始答对了两道红棕色的题(考察知识点“Square roots”),那么网格前两列,对于知识点“Square roots”模型预测其作答准确率就很绿(答对概率高),而对于其它没考察的知识点就很蓝(答对概率低),第三道题做错一道浅蓝色的题,第四到第九道题都是做错了紫色的题,那么对浅蓝色知识点和紫色知识点会预测其答对概率降低。
知识追踪问题可以描述为:
- 给定一学生的观测序列 $ x_0 ,……, x_t $ 预测下次表现 $x_{(t+1)}$ ,通常 $ x_t = { qt , at }$, $x_t={q_t,a_t}$ ,其中
- $q_t$代表回答的问题成分(如对应的知识点)
- $a_t$ 代表对应的回答是否正确,通常 $a_t={0,1}$ 。
- 上图描述了一个学生在八年级数学中的知识追踪结果可视化展示。
- KT被制定为监督序列学习问题:给定学生过去的练习情况,预测学生正确回答新练习的概率。
知识追踪的任务是根据学生与智能教学系统之间的交互,自动跟踪学生的知识状态随时间的变化过程
- 知识追踪具有自动化和个性化的特点。
知识追踪简单的说就是“边学边测”问题,连续追踪学生在学习过程中的能力变化(即tracing)。
- 这个概念区别于专注于测试学生能力水平的模型,如
项目反应理论(IRT)模型,测试场景的目标是快速、准确的测量出学生的水平。
常见题型包括:选择题、填空题、判断题、简答题、论述题、计算题、案例分析
Q&A
概念对比
- 狭义的KT是专指正确率预估模型,本质是一个二分类深度学习模型,给出的结果是正确率:$ P(人,题)$。
- IRT是用来建模题目和人的能力的数学模型,简单的说:$ 正确率 = S曲线(人的能力 - 题目的难度) $,但大家常说的IRT和Bi-Factor是用贝叶斯概率模型来求解人的能力和题目的难度。
- IRT是只考虑全局能力
- Bi-Factor增加了人在知识点上的能力
- KLearning是一个推题策略,对标的是原有的“按照75%正确率推荐题目”的推题策略,Klearning想要对学生做题的提升度进行估计,按照单步提升度最大来推题。
KT在什么时候是可信的?什么时候不准?
- 按照目前的经验,一个题目被做了5~10次之后KT是准的。题目<5次的情况下,准确率会下降比较多。
- 做题次数过少的情况下,模型其实是按照题目的泛化属性,比如“同知识点”的题目来估计的。如果知识点也是新的,没有任何可以参考的信息,模型就只能参考所有人的全局准确率、该用户的全局准确率来估计。
KT能能估计考试吗?
- 题目维度的预估一定要有作答数据,否则效果跟使用学生知识点掌握度预估成绩类似。考题有其他学生的作答数据也可以。
英语/语文可以使用KT模型吗?
- 英语有很多公司是使用KT来预测的,这块公开的研究也比较多。但是其主要作用是提升了产品的留存率,即是在体验方面的提升。语文可能也是类似的,模型可能非常依赖做题数据来估计人的能力和题目的难度。
知识追踪发展
- 目前,教育领域通过引入人工智能的技术,使得在线的教学系统成为了智能教学系统(ITS),ITS不同与以往的MOOC形式的课程。ITS能够个性化的为学生制定有效的学习路径,通过根据学生的答题情况追踪学生当前的一个知识点掌握状况,从而可以做到因材施教。
知识追踪演化图
知识追踪发展历程
DKT:只建模问题SKT:只建模知识点DIKT:同时建模问题、知识点
知识追踪方法总结
对学生的知识点掌握状况进行一个追踪判断:
CTT经典测验模型- 根据学生做题分数衡量学生能力
- 问题:不够客观,精确
IRT(Item response theory)项目反应理论- IRT理论即
项目反应理论(Item Response Theory, IRT)。F. Lord 在 1951年 从普林斯顿大学毕业时的博士论文《A Theory of Test Scores》被认为是IRT理论的开端之作。IRT最早使用在心理学领域,目的是做能力评估。现在已广泛应用于教育行业,用于校准评估测试、潜在特征的评分等。 - 使用结构化的因子(人的能力、题的难度、题的区分度)。可以给出题目难度、区分度,学生能力值等数据。
- 如:单参数IRT模型(Rasch模型)
- IRT理论即
BKT(Bayesin knowledge tracing) 基于贝叶斯网络的学生知识点追踪模型- 1995年,Corbett, A. T. 和 Anderson, J. R. 提出 贝叶斯知识追踪(Bayesian Knowledge Tracing,BKT)
- 早期的知识追踪模型都是依赖于一阶马尔科夫模型,例如贝叶斯知识追踪(Bayesian Knowledge Tracing)
- 虽然BKT模型在很多场景下效果良好,但还是存在一些不足。如,BKT是对”知识点“进行建模的,没有包含”学生个体”和”题目”的差异信息。
- 缺点:
- 需要标记数据
- 对每个知识点分别进行表达
- 缺乏提取未定义概念和模拟复杂概念状态转换的能力;
- BKT不能捕捉不同概念之间的相关性,不能有效地表示复杂的概念状态转化。
DKT(Deep konwledge traing) 基于深度神经网络的学生知识点追踪模型- 利用LSTM来解决BKT的问题,DKT总结了学生在一个隐藏状态下所有概念的知识状态,这使其很难追踪学生掌握了某个概念的多少,而且很难指出学生擅长或不熟悉的概念。
- 将深度学习的方法引入知识追踪最早出现于发表在NeurIPS 2015上的一篇论文《Deep Knowledge Tracing》,作者来自斯坦福大学。在这篇论文中,作者提出了使用深度知识追踪(Deep Knowledge Tracing)的概念,利用RNN对学生的学习情况进行建模,之后引出了一系列工作
- 优点:
- 比BKT模型有更好的预测能力,同时不需要专家对习题的知识点进行标注。
- 缺点:
- 表示能力受限:LSTM将所有的记忆存储在一个隐藏的向量中,很难准确地记住超过数百个时间步长的序列
MANN:记忆增强神经网络—— 解决DKT问题- 2019年已经有使用Transformer代替RNN和LSTM并且达到了SOTA的论文。
DKVMN(动态键值记忆网络)- DKVMN模型可以自动学习输入练习和基础概念之间的相关性,并为每个概念维护概念状态。在每个时间步,只有相关的状态会更新。
- 优点
- 借鉴了MANN的思想,同时又结合的BKT和DKT的优点,所以总体来说,它的预测性能是比较好的。与LSTM相比,它能避免过拟合、参数少,以及通过潜在概念自动发现相似练习。
- 缺点
- 计算知识增长的局限性
- 过于依赖模型本身的遗忘机制
- 预测过程中没有考虑遗忘机制
LPKT(基于学习过程的知识追踪)- LPKT旨在通过模拟学生的学习和记忆过程来完成知识追踪。
- LPKT过程:
- 注意力机制:计算一个问题涉及的知识点数和每个知识点所占的比例
- 读过程:观察一段时间内学生在学习系统中的学习序列数据
- 写过程:给定一个学生问答活动,代表学生的知识状态矩阵V由t-1时刻状态到t时刻状态
- 在读过程中,模型根据当前知识状态计算知识遗忘量,再参考LSTM的遗忘机制,计算下一个时刻的知识状态。这个知识状态就比较符合学生的学习规律。
- 而写过程则是根据MANN模型机制,在知识追踪的过程中跟新学生的动态知识状态。在更新状态时,会同时考虑遗忘机制,在DKVMN中被称作erase。遗忘过程中,不应该只考虑知识增量,同时还应该考虑学生学习持续时间。
- LPKT相较于传统的BKT和DKT,都有较大的优势。同时它又结合了DKVMN的思想与优点,改进了遗忘机制上的不足,使得知识追踪的效率得到提高。
由于深度学习并不需要人类教会模型不同题目的难易、考核内容等特定的知识,避免了大量的手工标注特征工作量,而且在互联网在线教育行业兴起后,拥有了海量的学生答题记录,这些答题记录就能教会模型将题库中成千上万条题目encode为一个向量,并且能类似于word2vec那样找出题目之间的关联。
数据集
数据集汇总
Knowledge Tracing任务有一些开源的数据集:Synthetic、Assistments、Junyi和Ednet等
EdNet 论文中对比数据集的数据情况
数据组织方式
一个学生做了8道题,考察了5个知识点,如果:
- 每道题考察1个知识点:one-hot
- 每道题考察多个知识点:one-hot 换成 muti-hot
one-hot编码:
- 数据共考察了M个知识点,所有题目都属于这M个知识点
- 将输入$x_t$设置为学生交互元组$h_t={q_t,a_t}$的一次one-hot编码,$q_t$表示题目标签,$a_t$表示是否答对(0/1)
- 对于某道考察了第i个知识点的题
- 做对时, 向量的第M+i个位置为1,其余位置为0;
- 做错时, 第i个位置为1,其余位置为0,向量总长度为2M,因此 $x_t\in{0,1}^{2M}$
- 为什么将题目标签和是否答对连接起来呢?
- 因为单独表示会降低性能。
- one-hot表示比较方便,但是一旦知识点的数量非常大之后,向量就会变得高维、稀疏。
- 解法:压缩感知机,一个针对信号采样的技术,在采样过程中完成了数据的压缩。通过压缩感知算法将高维稀疏的输入数据进行压缩到低维空间($log_2^M$)中
| 题目id | 知识点id | 作答结果 | 编码向量(前错后对) |
|---|---|---|---|
| 1 | 2 | 0 | [0,1,0,0,0,0,0,0,0,0] |
| 2 | 4 | 1 | [0,0,0,0,0,0,0,0,1,0] |
| 3 | 1 | 1 | [0,0,0,0,0,1,0,0,0,0] |
| 4 | 1 | 1 | [0,0,0,0,0,1,0,0,0,0] |
| 5 | 2 | 0 | [0,1,0,0,0,0,0,0,0,0] |
| 6 | 5 | 0 | [0,0,0,0,0,0,0,0,0,1] |
| 7 | 5 | 1 | [0,0,0,0,0,0,0,0,0,1] |
| 8 | 3 | 0 | [0,0,1,0,0,0,0,0,0,0] |
| 8 | 3,5 | 0 | [0,0,1,0,0,0,0,0,0,1] |
Assistments
- 数据集
- 格式说明,处理后的数据集
- Each line contains two fields separated by
\t. - The first field is the question id sequence answered by the user.
- The second filed is the corresponding answer sequence. 1 means correct, 0 means wrong.
| 编号 | 题目编号序列 | 答题结果序列(0/1) |
|---|---|---|
| 1 | 45,45,45,47,47,47,28,28,28,28,28,17,17,17,28,28,28 | 1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1 |
| 2 | 19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19 | 0,0,0,0,0,0,0,1,0,0,1,1,0,1,1,1 |
| 3 | 49,49,49,49,49,49,49,92,92,92,92,92,26,26,26,26,26,26 | 0,1,0,0,1,1,1,0,0,1,1,1,1,0,0,1,1,1 |
专题比赛
同时,EdNet在Kaggle上的RIID比赛:Riiid Answer Correctness Prediction
- kaggle上公开的方案主要是采用的ML方法,复现SAKT算法,并开放了提交的完整代码,开放的Baseline模型AUC为0.751,是目前开源KT类模型中效果最好的。
- 可以根据我开放的baseline做进一步的工作,复现SAINT+等基于Transformer的模型,单模型的AUC可以轻松达到0.77+
- 代码:
知识追踪SOTA
【2022-9-8】Knowledge Tracing on EdNet
- 当前各种算法效果排名
- $ SAINT+ > SAINT > PEBG+DKT > PEBG+DKVMN > DKVMN > SAKT > DKT > GIKT $
传统方法
- 传统的认知诊断模型,比如
IRT,MIRT,DINA都是基于概率模型,相比于神经网络模型,具有有限的拟合能力。同时传统的认知诊断模型往往需要较多的人工标注工作,因此会耗费大量的人力。
CTT 经典测验模型
最初,教育测评还没有依赖智能教育时,对学生进行测评主要是通过经典测验模型(Classical Test Theory, CTT)
- 给学生们统一出了一份卷子,固定好每道题的分值,然后通过学生对这一份卷子的答题结果进行评价,学生得多少分就代表他的能力。
- 同样,卷子难度的评价也是通过学生对这道题的答题情况分布来进行的。
但是,这样不够客观,如何能够更快更精确的评价学生的能力呢?
IRT 项目反应理论
项目反应理论(Item Response Theory, IRT)】应运而生
- 核心思想:综合考虑学生能力与试卷的题目情况(难度、区分度、猜测性等),而不是两个单独的计算过程。
- IRT建立了一个学生能力和作答正确率的模型函数,其中包括了题目的难度、区分度、猜测性参数
IRT理论即项目反应理论(Item Response Theory, IRT)。
- F. Lord在1951年从普林斯顿大学毕业时的博士论文《A Theory of Test Scores》被认为是IRT理论的开端之作。
- IRT最早使用在心理学领域,目的是做能力评估。现在已广泛应用于教育行业,用于校准评估测试、潜在特征的评分等。
IRT模型是用于评估被试对某一项目或某一类项目的潜在特质。
IRT模型是建立在一定的假设之下:
- 单维性假设,即假设某个测验只测量被试的某一种能力。
- 独立性假设,即假设被试在每一个项目上的作答反应是相互独立,互不影响的,作答反应只与被试自身的能力水平有关,与其他元素无关。
- 模型假设,即被试在项目上的正确反应概率与被试的能力水平有一定的函数关系。
IRT有一参数、两参数、三参数模型,三参数模型的数学公式
- $p_{i}(\theta)=c_{i}+\frac{1-c_{i}}{1+e^{\left.-d a_{i}\left(\theta-b_{i}\right)\right)}}$
相关参数的定义如下:
| 参数 | 定义 | 解释 |
|---|---|---|
| d | 常数 | 1.702 |
| ai | 项目区分度系数 | 表示项目或题目的区分度,在曲线中影响曲线中部的斜率,当斜率越小,那么就很难将被试的测试分数结果区分开 |
| bi | 项目难度系数 | 表示项目或题目的难度,在曲线中代表曲线横轴方向的位移,难度系数越大,则被试想要获得比较高的分数就需要比较高的能力 |
| ci | 项目猜测系数 | 表示即使被试对测试的项目一点先验知识都没有,靠蒙也能蒙对的概率,比如选择题有0.25的概率才对 |
| theta | 被试的能力值 | 表示被试在项目或题目所要考核的知识点或能力方面的掌握程度 |
| pi(theta) | 被试做对该项目的概率 |
IRT简化的一参数模型 Rasch模型:
- $ p_{i}(\theta)=\frac{1}{1+e^{\left.-d\left(\theta-b_{i}\right)\right)}} $
在Rasch模型中,所有的曲线,其形状都是一样的。实际上,这是不合理的。比如,有两道难度相同(比如难度等于2)的题目,一道是判断题,一道是选择题(4个选项)。对于判断题,即使学渣完全不知道怎么做,也有大约有50%概率能答对,而学霸也是50%左右的概率能答对。对于选择题,学渣大约有25%概率能答对,而学霸仍然是50%左右。因此,选择题比判断题能够更好的区分学霸和学渣,我们称它的区分度(discrimination)更高。
IRT模型的参数估计方法有很多,包括极大似然估计,EM算法,贝叶斯算法等
详见:知识追踪系列之IRT
- 传统的测试理论:正确率就是知识点掌握程度。
- $ 正确率 = 知识掌握程度 $
IRT(项目反应理论):- 通过正确率来推测知识点掌握程度。
- $ 正确率 → 知识掌握程度 $
- 正确率是知识点掌握程度有什么问题?
- 假如一个老师出了一套卷子很难,小明学习很好,只考了60分。
- 老师又出了一套卷子很简单,小红学习很差,考了90分。
- 这个90分和60分是无法比较的。
- 测评的本质是什么?把不同人在同一个度量空间里区分开来。
- 运用IRT自适应的算法,每个人虽然做的题目不一样(由前一道题的答题情况决定下一道题测什么),但是测出来的知识点掌握程度是可以比较的。
IRT理论的奠基人是被称为美国测试之父的罗德(Lord)和丹麦数学/统计学家赖氏(Rasch)。
罗德因为参与筹建美国测试中心(ETS,也就是负责托福考试的美国考试教育研究机构,类似公司),后来成为部门高级统计学家。所以,这个理论成了现代考试制度的理论基础,比如多项选择题的编制。这也是中国高考制度恢复之后不久,借鉴了托福考试而开始引入的标准化考试题型。Rasch模型: 从Rasch的角度出发,他推出的Rasch Theory是更为简洁的表达方式,主要是测试儿童阅读,认知能力时候,后来推广到体能,kinetics 等领域的测试。也是美国主导的PISA研究的测试理论基础之一。- 但是实际上早在二人之前,Thurstone, Guttman 等人就已经发展了丰富的测试理论基础。之后IRT理论变得越来越庞大和细分,陆续出现了Samejima等人提出的更为复杂的测试理论模型。主要的理论期刊是psychometrika ,美国心理学会负责。
简单说
- 大多数考试的场景是,根据原始分数打分,即答对了几道题,答错了几道题,按照100分,给考生给出一定分数;
- 而通过IRT则引入了对试题难度,考生实际能力的参数估计。用模型、概率估计的方式来估计考生的分数和能力。
- 好处是考试题变得更加客观,可以动态的针对不同能力的人来出题,以此来考察考生的答题情况,继而描述其真实能力。但是,考试题库必须绝对安全。即使是答过题的人,也不可以分享题目内容,否则题目的测试质量就下降了。这是托福考试等要求考生在考试之前申明保密协议的原因。
IRT模型起源于上世纪60年代,是机器学习算法的一种。大部分机器学习算法,都是通过现象来推测本质规律。IRT是通过学生答题情况来推测潜在特质(知识点掌握程度),通过建立数学模型,根据答题情况的目标函数来求出知识点掌握程度(或者叫能力值)。仔细看IRT数学模型,实际是变形了的逻辑斯蒂克回归模型。求解可用极大似然估计和牛顿迭代法来求
假设
- 学生的能力值,与该学生某道题做对的概率,之间呈一个s型曲线的关系。这个也是
项目特征曲线(Item characteristic curve),也称ICC曲线 
- 1916年,推孟(Terman)对智力测验的发明者比奈—西蒙(Binet——Simon)的智力量表进行分析,便发现了一条神奇的曲线,这条曲线的x轴是智力水平,y轴是试题正确率,而这是项目反应理论的最初雏形。
- 上世界五六十年代,ETS的统计学家Lord经过一系列的工作,正式开创了IRT理论。
- 整个理论的核心就是受测者的心理品质是正态分布的,年龄越高智力也就越高,答对的比率也搞,也就是说受测者的能力越高,答对某道题的概率相对于能力低的来说较高。由此逐渐演化出了ICC(项目特征曲线)。
- 以前的ICC曲线还经历过小于某个值恒为0,大于某个值恒为1的,意思是如果考生能力大于某个值,就肯定做对,小于某个值,就肯定做错。也经历过一条斜向上的直线的,就是考生能力对答对可能性的影响的边际效用是恒定的。
- 但经过不断的发展,现在认为
s型曲线更符合实际情况。- 学生能力太差,那么做对某题目的概率可能就很低。考生能力高,做对的概率就高。
最基本的 IRT模型—Rasch模型 就描述了考生能力、题目难度与考生是否答对之间的关系:
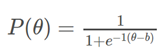

- $\theta$代表考生能力,$b$代表题目难度,$P(\theta)$代表能力为θ的考生在该题目上作答正确的概率
- 横轴代表考生能力;纵轴代表正确作答概率。蓝色曲线的含义是,能力越高的考生作答正确的概率越高。
- 当考生能力θ等于题目难度b时,P值为0.5。IRT中难度的定义就是考生答对概率为0.5时,对应的能力值。在这里可以看出这道题的难度基本是0
- a可以代表题目区分度,b可以代表试题难度,c可以代表猜测系数。
IRT 进化
在不断的研究中,对IRT的扩展也越来越多,比如
- 希望不只考虑学生单一能力,想要将能力值体现在更多维度,于是出现了
多维项目反应理论(Muti Item Response Theory,MIRT)。 - 0/1计分模型已经无法满足我们的测评需求,比如一道题可能会有多个得分,或者是分部计分的,然后就出现了
等级反应模型GRM、广义分部评分模型GPCM、评定量表模型RSM等。
还有其他很多更复杂的模型适用于更精确的测量不同的题型,SAT, TOFEL, GRE等考试都是以项目反应理论为基础构建的测验,通过考生答对的题目的难度来确定考生的能力。
- 如rasch模型,GRM模型,甚至是4PL模型等
上面的这些模型理论只能给出一个学生的能力值啊,不能表示出学生具体的知识掌握状态,因此认知诊断理论发展了起来。
- 认知诊断理论,加入了认知属性(
知识点),常用的有【规则空间模型】、【DINA模型】、【NIDA模型】。- DINA模型适用于对二值计分项目测验进行认知诊断)
以上就是认知诊断模型的一个大概的思路,但是也存在一定的限制,比如
- 知识掌握状态只有0/1两种
- 当知识点数过多计算会相当困难,适合小样本。
新版测验理论
后面就进入了新一代的测验理论,主要也是基于上述思想的改进。
【2022-10-9】知识追踪/认知诊断常用模型总结
1、静态认知诊断
目标是对学习者某一给定段时间的学习数据进行整体研究, 综合分析这些数据得到且仅得到学生当前的知识掌握度水平。
- (1)矩阵分解:【PMF】以及【NMF】;
- (2)用户画像:【LDA (Latent Dirichlet Allocation)】;
- (3)机器学习优化:
- ① 【FuzzyCDM (Fuzzy Cognitive Diagnosis Model)】是针对DINA模型的改进,引入模糊逻辑控制,实现了知识掌握状态为连续值,而不是0/1;
- ② 【KPGRM (Knowledge Plus Gaming Response Model) 】;
- ③ 【NeuralCD (Neural Cognitive Diagnose)】:脱离IRT和DINA模型中由人工定义的交互函数,使用隐藏层实现交互函数进行训练,认知状态为连续值,实现了“掌握程度”,适合应用于大样本数据。
2、动态认知诊断(知识追踪)
前面介绍的大多是有了一段时间的学生的测评数据,然后通过数据分析得到对学生的评价。
- 但是针对:学生不断的做题,需要不断的更新学生的状态,也就是这个过程是动态的,学生的认知水平也在随着学习过程在动态变化。
(1)传统知识追踪
- ① 【贝叶斯知识追踪(Bayesian knowledge tracing, BKT)】;
- ② 【表现因子分析(Performance Factors Analysis, PFA)】;
- ③ 【学习因子分析(Learning Factors Analysis, LFA)】;
- ④ 【(Knowledge Proficiency Tracing, KPT)模型】;
(2)深度知识追踪
深度知识追踪就是把学生的做题记录当成一个序列,目前主要基于RNN模型进行训练。
- ① 【深度知识追踪(Deep Knowledge Tracing,
DKT)】模型:一种seq2seq的循环神经网络模型, 每一个时刻的输出是对下一个时刻学习者表现情况的预测; - ② 【DKT-Tree】通过决策树加入了更多的题目属性;
- ③ 【DKT+forgetting】向DKT中引入了三种遗忘特征;
- ④ 【PDKT-C 】融合了知识点先后序关系;
- ⑤ 【DKVMN(Dynamic Key-Value Memory Networks)】将学习者的学习过程建模为读和写两个过程;
- ⑥ 【EERNN(Exercise-Enhanced Recurrent Neural Network)】提出用试题文本来增强深度知识追踪;
- ⑦ 【EKT(Exercise-aware Knowledge Tracing) 】添加了题目的知识点属性,使用了内存网络衡量学习者在学习每一个练习题时,对其多维知识掌握的影响程度,其精确性和可解释性都很大程度优于以往的模型。
参考
BKT 贝叶斯知识追踪
BKT介绍
贝叶斯知识追踪(Bayesian Knowledge Tracking,BKT)是建立学生学习时间模型最常用的方法。BKT将学习者的潜在知识状态建模为一组二元变量,每个变量代表对单个概念的理解或不理解。当学习者正确或错误地回答给定概念的练习时,隐马尔可夫模型(HMM)被用来更新这些二进制变量中的每一个的概率。
BKT是最常用的一个模型,BKT是含有隐变量的马尔可夫模型(HMM)。可以用EM算法 或者 bruteForce 算法求解参数。
学生对知识点的掌握有两个状态 {掌握, 未掌握},每经过一次学习动作(阅读、做题、学习课程),学生就有一定的概率从 未掌握 -> 掌握,对整个序列求解。
问题的难点在于:
- 一些学习动作没有反馈(比如阅读材料)
- 有反馈的动作(比如做题)也有很多噪音,$ P(做对) 不完全= P(掌握) $,比如学生是猜对的,学生掌握了但不小做错了,学生“生搬硬套”做对了。
一个不恰当的比方:把学生学习过程类比抽奖过程
- 学生面前有N个抽奖盒,每个盒子的中奖概率是不一样的,学生连续的去从每个盒子里面抽一次,最后离开了。可以观察到这个人抽奖完之后是否开心,越开心推测他已经中奖的概率越高。
- 观察到学生的表现: 没笑,笑了,没笑,大笑, …
- 问题:学生最后有没有中奖?学生是在第几个盒子中的奖?
贝叶斯知识追踪模型在观测到一系列的行为和结果后,可以通过建模来指示学生在每一个环节上的能力值水平。能力水平的变化值可以给教学人员提供决策信息。
BKT是对学生知识点的一个变化进行追踪,可以知道学生知识点的一个掌握情况变化。
- 一般有个stop_policy准则,用于判断学生是否经过多轮的做题掌握了相应的知识点。
- Once that probability reaches 0.95, the student can be assumed to have learned the skill. The Cognitive Tutors use this threshold to determine when a student should no longer be asked to answer questions of a particular skill
BKT模型原理
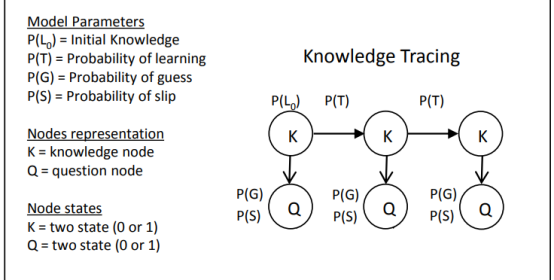
(1)首先我们来看一下BKT的模型是如何的:
- 如下图,是BKT的一个模型,以及对应的4个主要参数,L0,T,G,S。模型需要根据学生以往的历史答题系列情况学习出这4个对应的参数。
- BKT是对不同的的知识点进行建模的,理论上来说,训练数据有多少个知识点,就有多少组对应的$(L_0,T,G,S)$参数。
- $L_0$:表示学生的未开始做这道题目时,或者为开始连续这项知识点的时候,他的一个掌握程度如何(即掌握这个知识点的概率是多少),这个一般我们可以从 - 训练数据里面求平均值获得,也可以使用经验,比如一般来说掌握的程度是对半概率,那么L0=0.5
- $T$ :表示学生经过做题练习后,知识点从不会到学会的概率
- $G$:表示学生没掌握这项知识点,但是还是蒙对的概率
- $S$:表示学生实际上掌握了这项知识点,但是还是给做错了的概率 通过这4个参数,可以构造一个HMM的模型,剩下的事就是训练这个模型
(2)有什么改进的吗?
- 其实可以发现,这样构造模型,还是非常简单的,模型只是简单的针对知识点进行训练,所有的学生都是用的同一个模型。但是学生有好有坏,因此可以加个节点,不同的学生使用不同的L0。
- 另外题目的难度也是可以应用到模型的,比如难度系数大的 G S参数就可以不一样。根据难度系数训练多组G S
参考论文:
- From Predictive Models to Instructional Policies
BKT缺点
最初的模型公式假设,一旦学习了一项技能,它就永远不会被忘记。该模型最近的扩展包括猜测和滑动估计的情境化,估计单个学习者的先验知识,以及估计问题难度。
无论有没有这样的扩展,知识追踪都会遇到几个困难。
- 首先,学生理解的二进制表示可能是不切实际。
- 其次,隐藏变量的含义及其在练习中的映射可能是模糊的,很少能满足模型对每个练习只有一个概念的期望。已经开发了几种技术来创建和改进概念类别和概念练习映射。当前的黄金标准,认知任务分析是一个艰难而迭代的过程,领域专家要求学习者在解决问题的同时讨论他们的思维过程。
- 最后,用于建模转换的二元响应数据限制了可以建模的练习类型。
【2015】DKT(明显优于BKT)
人类的学习受到许多不同属性的支配(材料、上下文、呈现的时间进程和涉及的个人),其中许多属性很难量化,只依靠第一原则为练习分配属性或构建图形模型。
深度学习的好处(非深度学习方法也可以做,深度学习更灵活):
- 多目标建模:可以对学生的正确率、做题用时同时建模,如果C端产品需要留存,也可以对中断进行建模
- 行为数据建模:可以高效的使用各种行为数据,比如做题用时,看解答时间
- 跨场景建模:可以对学习、练习、考试等场景进行综合建模
- 多模态建模:可以利用行为数据、语音、图像等数据建模
DKT模型
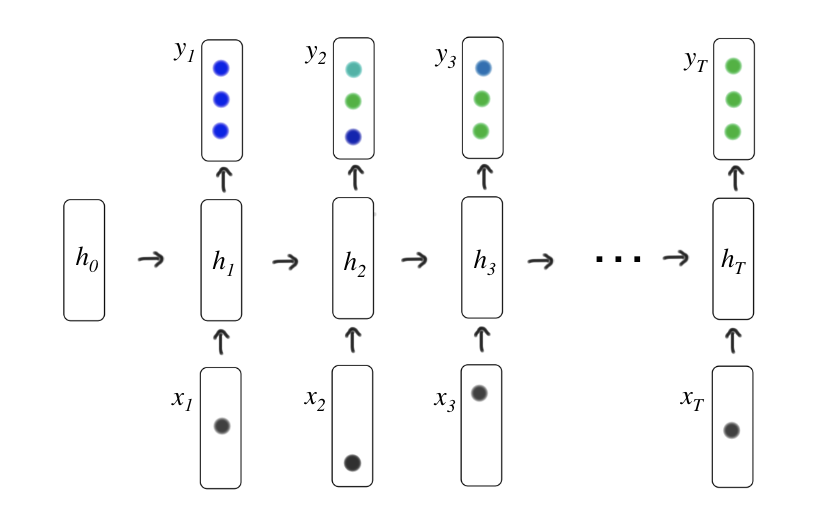
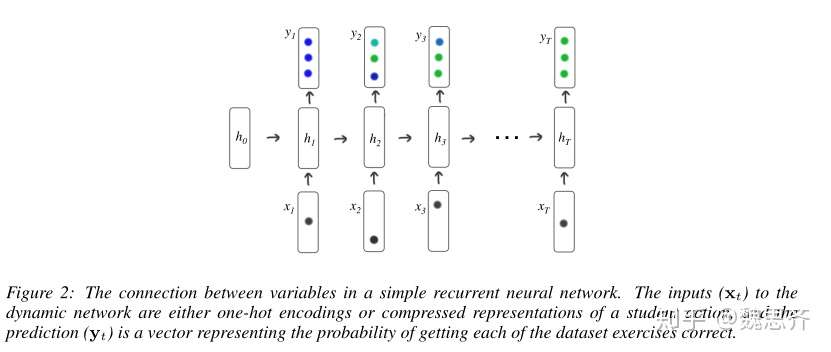
DKT的内容:img
其中向量 表示的是用户答题记录的独热编码,由于独热编码太长,太稀疏,所以我们将其降维成小一些的向量
,之后将向量
输入到循环神经网络中。其中循环神经网络中隐向量
表示的是用户的知识建模,循环神经网络输出向量
表示的是用户接下来做对题目的概率。
DKT算法明显优于BKT算法。
介绍完深度知识追踪模型之后,如何将遗忘机制加入到DKT模型当中。首先要介绍的是与遗忘相关的信息。
<object type="application/pdf" data="http://stanford.edu/~cpiech/bio/papers/deepKnowledgeTracing.pdf"
id="review" style="width:100%; height:800px; margin-top:0px; margin-left:0px" >
</object>
改进
遗忘机制
- 论文阅读笔记【13,参考遗忘的深度知识追踪模型】
- WWW’19的一篇论文《Augmenting Knowledge Tracing by Considering Forgetting Behavior》。本论文其实是对原有知识追踪模型DKT(Deep Knowledge Tracing)的一种优化。DKT默认用户学到知识以后,是不会忘记的,但是实际上,学生学完知识以后如果很久都没有复习的话,依然是会产生遗忘的。
知识追踪要解决的问题有两个:
- (1)通过学生与学习系统内容的交互来对学生的知识进行建模
- (2)预测学生在未来做题中的表现。
用户行为
- 论文阅读笔记【14,考虑用户行为的知识追踪】
- 西北大学团队发表在TURC19的一篇文章《Muti-behavior Features based Knowledge Tracking using Decision Tree improved DKVMN》。
- 该论文所要解决的问题仍然是知识追踪问题,其目的有二,其一:追踪学生对于各个知识点的掌握情况;其二:根据学生当前对知识点的掌握情况,预测学生答对下一道题目的概率。
- 该论文是对于2017年论文《Dynamic Key-Value Memory Networks for Knowledge Tracing》的改进。其具体改进点在于:DKVMN模型没有在意用户在答题过程中的具体行为,仅仅在意用户最终是否答对习题。在e-learning环境下,这显然是有缺陷的。因为在线环境下,用户不仅仅可以在教学系统进行习题解答,还可以在教学系统查看答案,查看答案之后再对习题解答。试想,如果用户查看答案后,直接将答案复制下来,粘贴到作答区,这样学生知识水平或许完全没有变化,但是根据DKVMN模型,用户对于该知识点的理解一定会有提高,所以与事实不符合。
- 该论文正是关注到了用户行为对于答题情况,对于用户知识水平具有很大的影响,所以在这方面加以改进,提出了论文中所提到的模型Dynamic Key-Value Memory Networks with Decision Tree (DKVMN-DT)。
知识点先验
- 论文阅读笔记【16,考虑知识点先验关系的知识追踪】
- 北师大团队投稿在IEEE的论文。该论文同样是介绍知识追踪知识。论文的创新点在于,考虑了知识点之间的先验关系。
- 深度知识追踪DKT模型仅仅关注了学生的做题历史,将各个知识点视为是独立的毫无关联的个体,根据学生的做题历史去更新学生知识水平上的变化。但是现实生活中,知识点之间是存在先验关系得,比如java和spring就存在先验关系,没有学习过java语法得人,很难学会spring的知识。
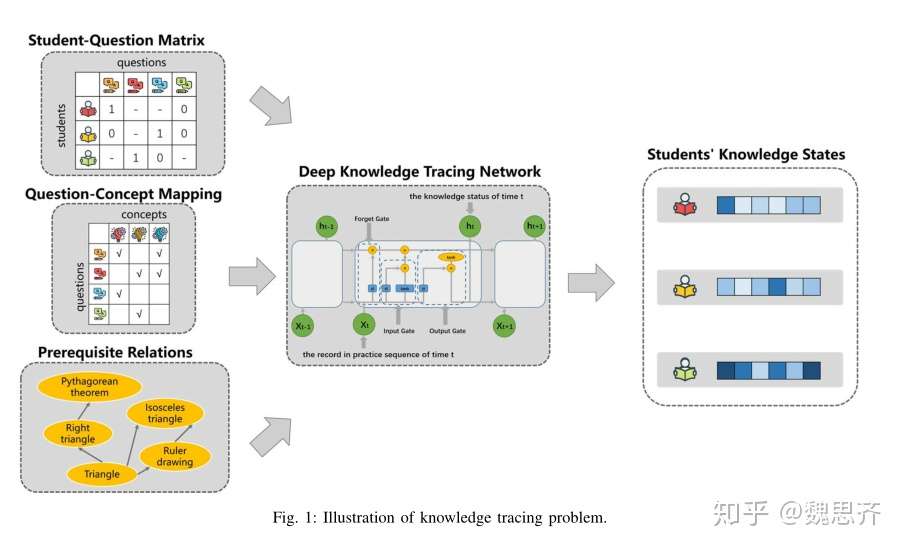
- 其中模型的输入有三个矩阵,最上面是学生的做题矩阵,描述的是每个学生的做题历史。中间的是试题-知识点矩阵,描述的是每道题目都包含了哪些知识点。最下面的是知识点之间的先验关系图,描述的是知识点之间的先验关系。
- 其实本文所使用的知识追踪方法和传统的DKT方法其实异曲同工,所选用的循环神经网络模型是GRU。
- 只是在描述知识点先验关系对知识追踪影响这个部分加入了一个先验条件。如果k1是k2的先验知识,那么如果学习者会k2,那么他学会k1的概率就会很大;相反如果学习者k1没有掌握,那么他学会k2的概率就会很低。举个例子就是,如果一个学生掌握了Spring,那么他很大概率就会掌握Java;相反如果一个学生没有掌握java,那么他很大程度没有掌握Spring。作者在原有DKT模型,加入了这个约束,从而可以根据知识点之间的先验关系去做知识追踪。
题目相关性
- 论文阅读笔记【17,考虑问题之间关系得知识追踪】
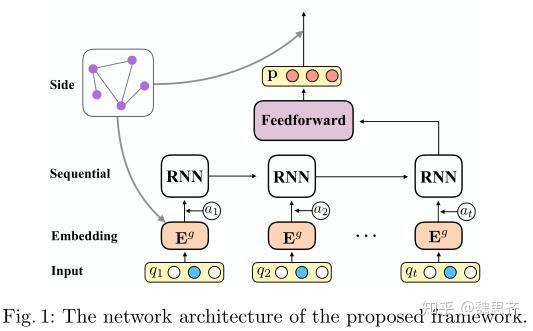
- 密歇根州立大学与TAL AI lab的一篇论文Deep Knowledge Tracing with Side Information,论文的目的依旧是知识追踪。该论文的创新点在于考虑了习题与习题之间的相关性。该论文基于传统模型DKT加以改进,提出了全新的模型DKTS,新模型考虑了问题之间的相关性。
- 众所周知,众多的习题并不是单独的个体,而是具有相关性的。不同的习题可能考察了相同的知识点,从而具有相关性。可能是考察相似的技能,从而具有相关性。但是传统模型DKT仅仅关注到学生对于习题的练习历史,但是并没有考虑到习题之间的相关性。
代码实现
DKT模型实现,github
import torch
import torch.nn as nn
class DKT(nn.Module):
def __init__(self, embed_dim, input_dim, hidden_dim, layer_num, output_dim, dropout, device="cpu", cell_type="lstm", ):
"""
第一个DKT模型
The first deep knowledge tracing network architecture.
embed_dim: int, the embedding dim for each skill.
input_dim: int, the number of skill(question) * 2.
hidden_dim: int, the number of hidden state dim.
layer_num: int, the layer number of the sequence number.
output_dim: int, the number of skill(question).
device: str, 'cpu' or 'cuda:0', the default value is 'cpu'.
cell_type: str, the sequence model type, it should be 'lstm', 'rnn' or 'gru'.
"""
super(DKT, self).__init__()
self.embed_dim = embed_dim # 嵌入维度
self.input_dim = input_dim # 字典大小,知识点数*2
self.hidden_dim = hidden_dim # 隐含层维度
self.layer_num = layer_num # 层数
self.output_dim = output_dim + 1 # 输出维度,知识点数
self.dropout = dropout
self.device = device # 默认cpu,'cpu' or 'cuda:0'
self.cell_type = cell_type # 基本单元:RNN,LSTM,GRU
self.rnn = None # 基本单元组件
# 知识点嵌入矩阵,向量化,最后一个编号作为填充值
self.skill_embedding = nn.Embedding(
self.input_dim, self.embed_dim, padding_idx=self.input_dim - 1
)
# 基本单元适配
if cell_type.lower() == "lstm":
self.rnn = nn.LSTM(
self.embed_dim,
self.hidden_dim,
self.layer_num,
batch_first=True,
dropout=self.dropout,
)
elif cell_type.lower() == "rnn":
self.rnn = nn.RNN(
self.embed_dim,
self.hidden_dim,
self.layer_num,
batch_first=True,
dropout=self.dropout,
)
elif cell_type.lower() == "gru":
self.rnn = nn.GRU(
self.embed_dim,
self.hidden_dim,
self.layer_num,
batch_first=True,
dropout=self.dropout,
)
# 全连接层
self.fc = nn.Linear(self.hidden_dim, self.output_dim)
# 异常参数,非lstm、rnn和gru
if self.rnn is None:
raise ValueError("cell type only support lstm, rnn or gru type.")
def forward(self, q, qa, state_in=None):
""" 定义网络结构
:param x: The input is a tensor(int64) with 2 dimension, like [H, k]. H is the batch size,
k is the length of user's skill/question id sequence.
:param state_in: optional. The state tensor for sequence model.
:return:
"""
# 问题编号映射
qa = self.skill_embedding(qa)
h0 = torch.zeros((self.layer_num, qa.size(0), self.hidden_dim), device=self.device)
c0 = torch.zeros((self.layer_num, qa.size(0), self.hidden_dim), device=self.device)
# 使用默认权重
if state_in is None:
state_in = (h0, c0)
# 使用自定义权重
state, state_out = self.rnn(qa, state_in)
logits = self.fc(state) # 全连接层
return logits, state_out
简版实现:参考地址
class DKT(nn.Module):
def __init__(self, input_dim, hidden_dim, layer_dim, output_dim):
super(DKT, self).__init__()
self.hidden_dim = hidden_dim
self.layer_dim = layer_dim
self.output_dim = output_dim
# 直接使用RNN单元
self.rnn = nn.RNN(input_dim, hidden_dim, layer_dim, batch_first=True, nonlinearity='tanh')
self.fc = nn.Linear(self.hidden_dim, self.output_dim)
# 二分类:sigmoid函数转化成概率
self.sig = nn.Sigmoid()
def forward(self, x):
h0 = Variable(torch.zeros(self.layer_dim, x.size(0), self.hidden_dim))
out,hn = self.rnn(x, h0)
res = self.sig(self.fc(out))
return res
MANN 记忆增强神经网络(one-shot learning)
2016年Google deepmind的论文:Meta-Learning with Memory-Augmented Neural Networks
- Despite recent breakthroughs in the applications of deep neural networks, one setting that presents a persistent challenge is that of “one-shot learning.” Traditional gradient-based networks require a lot of data to learn, often through extensive iterative training. When new data is encountered, the models must inefficiently relearn their parameters to adequately incorporate the new information without catastrophic interference. Architectures with augmented memory capacities, such as Neural Turing Machines (NTMs), offer the ability to quickly encode and retrieve new information, and hence can potentially obviate the downsides of conventional models. Here, we demonstrate the ability of a memory-augmented neural network to rapidly assimilate new data, and leverage this data to make accurate predictions after only a few samples. We also introduce a new method for accessing an external memory that focuses on memory content, unlike previous methods that additionally use memory locationbased focusing mechanisms.
DKVMN模型
- 香港中文大学学者所写的《Dynamic Key-Value Memory Networks for Knowledge Tracing》,该论文发表在2017年的IW3C2上
- 知识追踪场景下的动态key-value记忆网络
- KT的一个重要目的是个性化练习序列,以帮助学生有效地学习知识概念。KT被制定为监督序列学习问题:给定学生过去的练习情况,预测学生正确回答新练习的概率。
知识追踪(KT)的目标是根据学生过去的练习表现来追踪学生的知识状态。KT是在线学习平台的重要任务。导师可以根据学生的个人优势和弱点,提供适当的提示并定制练习练习的顺序。学生可以了解他们的学习进度,并可以将更多精力投入到不太熟悉的概念上,以便更有效地学习。- 贝叶斯知识追踪和深度知识追踪等现有方法要么单独为每个预定义概念建立知识状态,要么无法精确确定学生擅长或不熟悉的概念。
- 虽然
贝叶斯知识追踪(BKT)可以输出学生对某些预定义概念的掌握程度,但它缺乏提取未定义概念和模拟复杂概念状态转换的能力。深度知识追踪(DKT)利用LSTM来解决BKT的问题,DKT总结了学生在一个隐藏状态下所有概念的知识状态,这使其很难追踪学生掌握了某个概念的多少,而且很难指出学生擅长或不熟悉的概念。 - 本文提出了DKVMN,具有利用概念之间的关系以及跟踪每个概念状态的能力。 DKVMN模型可以自动学习输入练习和基础概念之间的相关性,并为每个概念维护概念状态。在每个时间步,只有相关的状态会更新。
- 为解决上述问题,本文提出了
动态键值记忆网络(DKVMN),可以利用基础概念之间的关系,直接输出学生对每个概念的掌握程度。与利用单个记忆矩阵或多个静态记忆矩阵的记忆增强神经网络不同,我们的模型有一个静态矩阵(键)用来存储知识概念,还有一个动态矩阵(值)用来存储和更新对应概念的掌握程度。DKVMN模型可以自动发现通常由人类注释执行的练习的基本概念,并描绘学生不断变化的知识状态。 
LPKT 学习过程一致的知识追踪
2021年,中科大,基于深度学习的知识追踪
- Knowledge Tracking Model Based on Learning Process一文中,介绍了一种知识追踪模型
LPKT。这是一种基于现存深度学习的知识追踪模型的改进,该模型采用了记忆增强神经网络(MANN)的思想。
现存模型的缺陷
- 对于计算知识增长的局限性
- 模型遗忘机制不完善
现有的 KT 方法大多追求学生成绩预测的高精度,而忽略了学生不断变化的知识状态与学习过程的一致性。这存在一个默认的假设,即未来更高精度的预测近似于知识状态的更好估计。
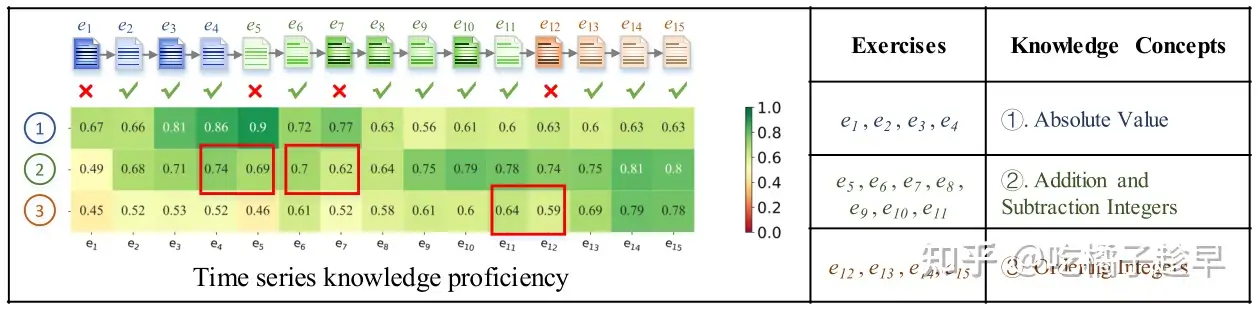
- 当学生回答关于3个不同知识点的15个练习时,DKT不断跟踪学生关于这3个知识点的知识状态。红框表示DKT认为学生回答错误后知识状态会下降。尽管学生在犯错后知识状态的这种下降趋势可能会带来未来成绩预测的高准确性,但这并不符合认知理论,因为错误也能学得知识。
2021年,KDD论文:
【2019】SAKT——DKVMN改进:处理稀疏数据
- 2015年,Deep Knowledge Tracing这篇论文首次将知识追踪任务转换为Seq-to-Seq任务,并用RNN实现,取得的跨越式的进展。但是,由于DKT用的是RNN,局限性还比较大。
- 2019年,A Self-Attentive model for Knowledge Tracing这篇论文用Self-Attention模型取代了RNN,取得了更好的性能。同时,后期基于Transformer类的一些论文,可以说都是在SAKT的基础上进行改进的,因此本篇文章主要是根据论文用pytorch实现模型。
【2022-9-5】A Self-Attentive model for Knowledge Tracing
- Knowledge tracing is the task of modeling each student’s mastery of knowledge concepts (KCs) as (s)he engages with a sequence of learning activities. Each student’s knowledge is modeled by estimating the performance of the student on the learning activities. It is an important research area for providing a personalized learning platform to students.
- In recent years, methods based on Recurrent Neural Networks (RNN) such as Deep Knowledge Tracing (DKT) and Dynamic Key-Value Memory Network (DKVMN) outperformed all the traditional methods because of their ability to capture complex representation of human learning.
- However, these methods face the issue of not generalizing well while dealing with sparse data which is the case with real-world data as students interact with few KCs.
- DKT模型的解释性差。
- DKVMN具有更好的解释性:key:知识概念矩阵,value:知识状态表达矩阵。
- 但这两个模型都不能很好的泛化处理稀疏数据。
- In order to address this issue, we develop an approach that identifies the KCs from the student’s past activities that are $ \textit{relevant}$ to the given KC and predicts his/her mastery based on the relatively few KCs that it picked. Since predictions are made based on relatively few past activities, it handles the data sparsity problem better than the methods based on RNN. For identifying the relevance between the KCs, we propose a self-attention based approach, Self Attentive Knowledge Tracing (SAKT). Extensive experimentation on a variety of real-world dataset shows that our model outperforms the state-of-the-art models for knowledge tracing, improving AUC by 4.43% on average.
-
SAKT首先识别学生过去所有交互的相关性,然后预测学生的表现。比如学习方程前,学生要先掌握加减乘除
- 【2019年】代码实现
【2020】SAINT——改进SAKT,引入transfomer
一个基于transformer的知识跟踪模型
论文:解说
- SAINT:Towards an Appropriate Query, Key, and Value Computation for Knowledge Tracing
- SAINT: Separated Self-AttentIve Neural Knowledge Tracing
- The empirical evaluations on a large-scale knowledge tracing dataset show that SAINT achieves the state-of-the-art performance in knowledge tracing with the improvement of AUC by 1.8% compared to the current state-of-the-art models.
<object type="application/pdf" data="https://arxiv.org/pdf/2010.12042.pdf"
id="review" style="width:100%; height:800px; margin-top:0px; margin-left:0px" >
</object>
SAINT模型
论文模型本质就是 transformer,和 SAKT 不同,这里使用了 encoder 和 decoder 两部分
SAKT两个缺点
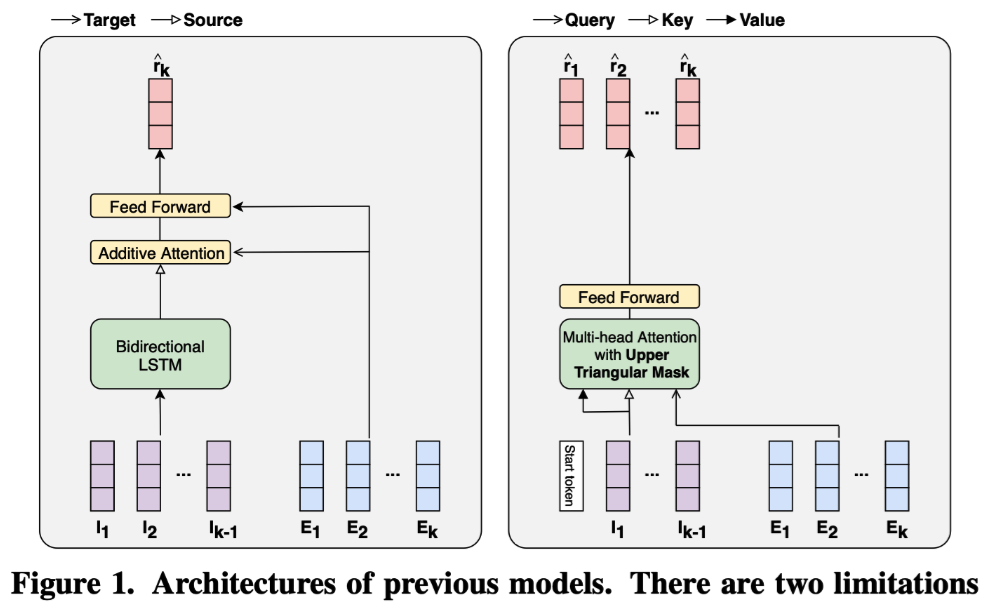
- 注意力层浅,特征捕获能力弱。First, the models have attention layers too shallow to capture the complex relationships among different exercises and responses.
- 依赖做题练习。Second, the models rely on the same recipe: exercises for queries and interactions for keys and values.
模型结构改进
SAINT贡献:
- 1)SAINT中,exercise embedding sequence 和the response embedding sequence分别独立的进入encoder 和decoder。
- 2)SAINT使用深度自注意力有效的捕捉了练习题和答案之间复杂的关系。
- 3)SAINT比目前优秀的模型完成了AUC的1.8%的提升。
基于transformer的变种
Transformer based Variants
SAINT with three different architectures based on multiple stacked attention layers:
- Lower Triangular Masked Transformer withInteraction sequence (LTMTI)
- Upper Triangular Masked Transformer with Interaction sequence (UTMTI)
- Stacked variant of SAKT (SSAKT)
【2021】改进版:SAINT+
- SAINT+: Integrating Temporal Features for EdNet Correctness Prediction
- 引入 temporal feature embeddings,Experimental results show that SAINT+ achieves state-of-the-art performance in knowledge tracing with an improvement of 1.25% in area under receiver operating characteristic curve compared to SAINT, the current state-of-the-art model in EdNet dataset.
代码实践
代码:
【2019】GKT——知识点图谱化
2019 ACM,Graph-based Knowledge Tracing: Modeling Student Proficiency Using Graph Neural Network
- 论文题目:《基于图的知识追踪:基于图神经网络的学生能力建模》
- 代码地址:代码
论文:解说
- Graph-based Knowledge Tracing: Modeling Student Proficiency Using Graph Neural Network
- 基于图的知识追踪:利用图神经网络建模学生熟练度
受图神经网络的启发,本文提出了一种基于图神经网络的知识跟踪方法,即基于图的知识跟踪。将知识结构转化为一个图,使得我们能够将知识跟踪任务重新表述为GNN中的时间序列节点级分类问题。
本文基于以下三个假设:
- 1)课程知识被分解成一定数量的知识概念。
- 2) 学生有自己的时间知识状态,代表他们对课程概念的熟练程度。
- 3) 课程知识的结构是一个图形,它影响着学生知识状态的更新:如果学生正确或错误地回答了一个概念,那么他/她的知识状态不仅会受到所回答概念的影响,还会受到其他相关概念的影响,这些概念在图形中表示为相邻节点。
缘由
从数据结构的角度来看,课程作业可以潜在地结构化为图。而将图结构的性质这种先验知识合并到知识追踪模型中可以提高模型的性能。
- 而以往的基于深度学习的方法,如DKT,并没有考虑这种性质。以往基于深度学习的方法的体系架构,如RNN,虽然在序列数据上通常表现良好,但不能有效地处理图结构数据。
GNN
GNN对图形结构数据建模具有相当强的表达能力
- Battaglia等人[^2]从关系型归纳偏差的角度解释了GNN的表达能力,关系型归纳偏差通过结合人类对数据性质的先验知识提高了机器学习模型的样本效率。
然而,在一些知识追踪设置的情况下,图结构本身即关联的知识点和这种关联的强度,并没有明确提供。
- 尽管研究人员可以启发式地和手动地注释知识点关联,但这个工作需要深厚的领域知识和大量的时间,因此很难预先定义一个在线学习平台中所有知识点的图结构。作者称这个问题为隐式图结构问题。
- 一个解决方案:使用简单的统计数据来定义图结构,这些统计数据可以自动从数据中导出,比如知识点回答的转移概率。
- 另一种解决方案:在学习图结构本身的同时并行优化主要任务。
GKT诞生
基于GNN的知识跟踪方法,即基于图的知识跟踪(GKT)。这种模型将知识跟踪重新表述为GNN中的一个时间序列节点级分类问题,能够在考虑潜在知识结构的同时预测作业熟练程度的过程。
这种表述基于三个假设:
- 课程知识能够被分解成一定数量的知识点。
- 学生有自己的时序的知识状态,这代表了学生对课程知识点的掌握程度。
- 课程知识被构造成一个图,它能够影响学生知识状态的更新:如果学生回答了一个概念,无论正确与否,他/她的知识状态不仅会受到所回答的知识点的影响,还会受到其他相关知识点的影响,这些相关知识点在图中以邻居节点的形式表示。
模型结构

深度学习方法
- 迫切希望构造出可以自动识别且具有较大拟合能力的认知诊断模型。
NeuralCDM模型
- 【2021-3-30】论文阅读笔记【12,神经认知诊断】,中科大陈恩红,刘淇团队发表在AAAI 2019 Interpretable Cognitive Diagnosis with Neural Network for Intelligent Educational Systems
示例
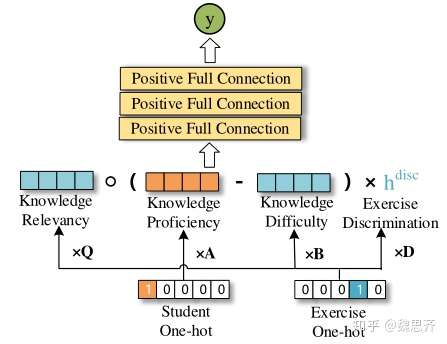
- 解释
- Student One-hot向量是表示学生向量,是一个one-hot向量,将其与A矩阵相乘,得到的是反应该学生知识水平的向量。
- Exersice One-hot向量是表示练习向量
- 将其与Q矩阵相乘,得到的是表示试题包含知识点的向量
(与
维度相同);
- 将其与B矩阵相乘,得到的是表示试题难度的向量;
- 将其与D向量相乘,得到的是表示试题区分度的标量。
- 将其与Q矩阵相乘,得到的是表示试题包含知识点的向量
通过计算式1,得到全连接层的输入x。
将x输入到全连接层以后,得到的是认知诊断模型对于学生作对题目的预测。
我们通过学生答对题目的预测概率值与真实值的交叉熵损失函数,更新各个参数。从而进行模型的训练。
以上就是NeuralCDM模型的分析。作者发现之前的认知诊断模型都是考虑学生做题日志,很少有考虑到习题内容本身的,但是习题内容本身又是十分重要的因素,很多时候,通过阅读习题内容,便可以了解到习题考察了什么知识点。因此,作者通过CNN技术,对习题内容进行学习,通过习题的文本内容,对习题所包含哪些知识点进行分类。由于Q矩阵是由权威专家标注的,因此具有更高的权威性,因此,通过CNN网络学习的内容往往只是达到补强枪效果。
比如图三所示。Q矩阵显示该题目包含知识点3和知识点4。但是CNN模型显示包含知识点1和知识点3。这时,我们会综合考量Q矩阵和CNN,但是Q矩阵的权重更大,而CNN的权重较小。所以知识点1的考察度仅仅为0.3,知识点三由于既被Q矩阵标注又被CNN所识别,所以知识点3的权重最大。
下面我们介绍一下NeuralCDM和传统模型IRT以及MIRT的兼容性。
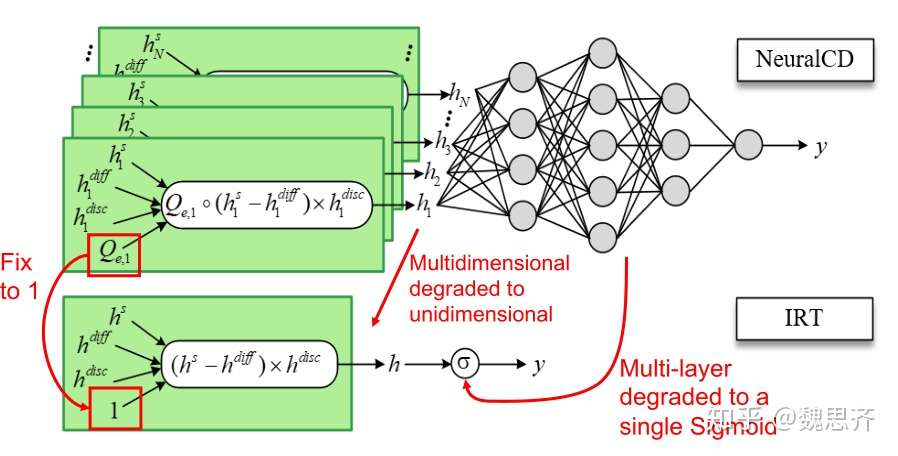
图4所示,NeuralCDM模型相较于IRT模型,可以考察更多的试题-学生交互历史,而IRT仅仅可以考虑一个交互历史;同时NeuralCDM具有多层神经网络,而IRT仅仅有单一算式,因此NeuralCDM相较于IRT具有更高的拟合性。
图5所示,是NeuralCDM相较于MIRT的区别,两者都可以考察多交互历史,但是NeuralCDM相较于MIRT具有更高的拟合能力。
神经认知诊断
- 认知诊断就是“诊断”被试内部的“认知加工过程”
- 以前只知道学生学习后的结果–分数,以此判定学生的水平、level、等级—-标准评价;却不知道学生到底好在哪儿、差在哪儿(不是一般意义上知识好在哪儿差在哪儿);学生在同一个水平时,为啥同样的教学方法下,学生的提高程度却不同。
- 认知诊断可以把学生认知加工过程/心理过程展现给评价者。
- 学生认知加工过程/心理过程是指学生学习时,到底学到了什么知识点,怎么学到的这个知识,会不会用,为啥能学会这个却学不会另一个知识点,学生为啥会用这个而不会用那个……同样的,不同学生为啥有人能学会有人学不会,有人知识点全记住了却答不对题,有人没记住书上原理却能解决题目……
- 例子:十以内的加法。有的孩子是背下来的,毕竟十以内就这么几个数,靠记忆是完全可以的;有的学生是需要靠着实物帮助点数数出来 ;有的学生可以用接着数的方法算出来的;有的学生可能还会以5个一组来速算。表面上我们看到这些孩子是都会了十以内加法,是一样的,但其实他们的思考过程与方法都不一样。
- 以前只能靠老师和家长去发现孩子心理认知过程。有了认知诊断,就可以让评价者、教师更轻松了解学生内在心理的不同。当然,认知诊断理论需要有科学、有效的认知诊断模型、测量模型,才能达到精准“诊断”“认知加工过程”的目的。
- 知乎atticess
传统教育
考试这档子事,目前的问题在于反馈不准 & 反馈太慢:
- 反馈不准:一张卷子考了辣么多知识点,你丫就给我一个分数?我怎么知道哪些知识点掌握了,哪些还懵着?
- 反馈太慢:一个月,甚至一个学期才考一次。等到考的时候,都忘得差不多了。那难不成你要一天一考、一课一考?
认知诊断主要解决「反馈不准」的问题,至于改进反馈的即时性,可以用游戏化的手法解决
答题进阶 —— IRT演进过程
先看一张成绩单:
| 学生 | 题1 | 题2 | 题3 | 题4 | 题5 | 做对题数 |
|---|---|---|---|---|---|---|
| 丁一 | ✓ | ✓ | ✓ | ✓ | ✓ | 5 |
| 陈二 | ✗ | ✓ | ✓ | ✓ | ✓ | 4 |
| 张三 | ✗ | ✗ | ✓ | ✓ | ✓ | 3 |
| 李四 | ✗ | ✗ | ✗ | ✓ | ✓ | 2 |
| 王五 | ✗ | ✗ | ✗ | ✗ | ✓ | 1 |
| 赵六 | ✓ | ✗ | ✗ | ✗ | ✗ | 1 |
| 做错的人数 | 4 | 4 | 3 | 2 | 1 |
思考
- 王五和赵六都只得了 1 分,他俩学得一样好吗?
- 赵六做出来的那道题,全班只有他和丁一做出来了
- 而王五做出来的那题,全班除了赵六都能做出来。
- 每道题的难度是不一样的,是不是该区分一下啊?
于是,把「做错的人数」近似地看作「题目的难度」,重新给每道题赋分。
- 注:如果要细究「难度的定义」,应该从「涉及的知识点」去考虑。
| 学生 | 题1 | 题2 | 题3 | 题4 | 题5 | 得分 |
|---|---|---|---|---|---|---|
| 丁一 | 4 | 4 | 3 | 2 | 1 | 14 |
| 陈二 | 0 | 4 | 3 | 2 | 1 | 10 |
| 张三 | 0 | 0 | 3 | 2 | 1 | 6 |
| 李四 | 0 | 0 | 0 | 2 | 1 | 3 |
| 王五 | 0 | 0 | 0 | 0 | 1 | 1 |
| 赵六 | 4 | 0 | 0 | 0 | 0 | 4 |
这时,李四该跳起来了:
我做对了 2 道题,赵六才做对了 1 道,凭什么他的分比我还高?也许那一题是他蒙对的呢?
有道理啊,但我怎么知道他是不是蒙的呢?李四愤愤不平:
你看赵六那人就不是能做出题 1 的人,他其他题一道都没做出来,肯定是蒙的!
有点道理。那就用「总共做对了几道题」近似地去评估「一个人的总体实力」。实力越强,蒙的可能性越低;实力越弱,越可能是蒙的。
用「实力 - 难度」试试:
| 学生 | 题1 | 题2 | 题3 | 题4 | 题5 | 得分 |
|---|---|---|---|---|---|---|
| 丁一 | 5-4 | 5-3 | 5-2 | 5-1 | 5-0 | 15 |
| 陈二 | 0 | 4-3 | 4-2 | 4-1 | 4-0 | 10 |
| 张三 | 0 | 0 | 3-2 | 3-1 | 3-0 | 6 |
| 李四 | 0 | 0 | 0 | 2-1 | 2-0 | 3 |
| 王五 | 0 | 0 | 0 | 0 | 1-0 | 1 |
| 赵六 | 1-4 | 0 | 0 | 0 | 0 | -3 |
「实力-难度」这个指标不光是一个算分的中间值,它还是一个用来衡量「某人做出这道题的可能性大小」的工具。比如,哪怕让丁一去做题 1 ,也会很费劲 5 - 4 = 1;但让他去做题 5 ,则很轻松 5 - 0 = 5 。
那如果这几道题,不是考题,而是知识点呢?能不能用这个工具去评估学生对各个知识点的掌握程度呢?我们只需要对它做一个 logistic 变换,就可以把它变成一个 0 到 1 之间的小数,能否用这个小数作为「某人做出某道题的概率」?某人做出某道题的概率P
\[P = \frac{1}{1 + \exp^{-(实力-难度)}}\]| 学生 | 知识点1 | 知识点2 | 知识点3 | 知识点4 | 知识点5 |
|---|---|---|---|---|---|
| 丁一 | 0.73 | 0.88 | 0.95 | 0.98 | 0.99 |
| 陈二 | 0.50 | 0.73 | 0.88 | 0.95 | 0.98 |
| 张三 | 0.50 | 0.50 | 0.73 | 0.88 | 0.95 |
| 李四 | 0.50 | 0.50 | 0.50 | 0.73 | 0.88 |
| 王五 | 0.50 | 0.50 | 0.50 | 0.50 | 0.73 |
| 赵六 | 0.05 | 0.50 | 0.50 | 0.50 | 0.50 |
奇怪,为什么好些个没拿分的题显示的是 0.5 呢?其实,0.5 在 logistic 的语境中,就是「不确定」的意思。概率很大,接近于 1 ,就是「掌握了」;概率很小,接近于 0 ,就是「没掌握」。
如果横向不是学生,而是一道道题呢?如果这不是一张成绩单,而是一张「知识点涵盖矩阵」呢?
| 题号 | 知识点1 | 知识点2 | 知识点3 | 知识点4 | 知识点5 | 做对与否 |
|---|---|---|---|---|---|---|
| 一 | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| 二 | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ |
| 三 | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| 四 | ✗ | ✗ | ✗ | ✔ | ✔ | ✓ |
| 五 | ✗ | ✗ | ✗ | ✗ | ✔ | ✓ |
| 六 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| 做对该知识点的数目 | 0 | 0 | 0 | 1 | 2 | |
| 知识点的难度 | 4 | 4 | 3 | 2 | 1 |
题一涵盖了全部知识点,而题六只涵盖了知识点 1 。那不就能用这种方式做到「评估知识点的掌握情况」了?需要注意的,实力那的值就不是这道题涵盖的知识点的个数了,而是学生做对某个知识点上的个数。
假设学生甲只做对了题四、题五
| 知识点 | 知识点1 | 知识点2 | 知识点3 | 知识点4 | 知识点5 |
|---|---|---|---|---|---|
| 掌握程度 | 1 / (1 + exp(-(0 - 4))) | 1 / (1 + exp(-(0 - 4))) | 1 / (1 + exp(-(0 - 3))) | 1 / (1 + exp(-(1 - 2))) | 1 / (1 + exp(-(2 - 1))) |
| 值 | 2% | 2% | 5% | 27% | 73% |
可以看到,甲对知识点 5 掌握得最好。简单来说,思路其实相当相当简单:
- 做对该知识点越多,掌握得越好;
- 该知识点在整套题中出现得越罕见,难度越大,越不容易掌握;
但上面这套算法没有解决一个很关键的问题:知识点之间是存在依赖关系的。
- 比如:要想掌握分数的通分,至少得先学会整数的加减、求公分母……吧。但以上算法并没有考虑这个。
解决的思路其实也很简单:挨个考察这个知识点「所有的先修知识点」的掌握情况。
首先,我们得先细致地考察一番知识点的内在结构。我们用一个矩阵来做这事。其实这完全是为了数学上处理方便,用 if-else 同样解决问题。

- 画反了!!!知识点内在结构:1 表示行号节点是列号节点的「直接」先修知识点;0 表示没有联系。
但我们正在想要的是,能够回答「节点 i 是不是节点 j 的先修知识点,直接或者间接都行」的矩阵。其实我们只要对上面这个矩阵加上一个单位矩阵,再反复自相乘直到收敛就行了。注意是布尔相乘哦。
画反了!!!直达矩阵
现在,你问「知识点 2 是不是知识点 5 的先修知识点?」,只要查第 2 行第 5 列是否为 1 就行了。我们先给个记号:q(5 → 2) = 1 。「q」就是 required 的意思啦。
好,搞定第一个工具。
下面要讲的,数学形式可能和上面那个「实力 - 难度」公式不同,但本质是一个意思。
下面我们构造一个矩阵,如果甲同学在题 i 中掌握了知识点 j 所需的所有知识点,记作 1;反之,为 0 :
| 题号 | 知识点1 | 知识点2 | 知识点3 | 知识点4 | 知识点5 | 做对与否 |
|---|---|---|---|---|---|---|
| 一 | 0 | 0 | 0 | 0 | 0 | ✗ |
| 二 | 0 | 0 | 0 | 0 | 0 | ✗ |
| 三 | 0 | 0 | 0 | 0 | 0 | ✗ |
| 四 | 0 | 0 | 0 | 1 | 1 | ✓ |
| 五 | 0 | 0 | 0 | 0 | 1 | ✓ |
| 六 | 0 | 0 | 0 | 0 | 0 | ✗ |
落地案例
在线教育
- 【2021-3-31】宝宝巴士与HarmonyOS携手打造更具交互性的早教体验,宝宝巴士开发团队与华为HarmonyOS合作,设法利用智能手机、平板、智能电视和音箱等现有智能设备,构建一个沉浸式、交互式的早教场景体验
- 【2020-12-30】AI在扇贝的应用:基于TensorFlow的DKT(深度知识追踪)系统实现
- 深度知识追踪系统可以实时地预测用户对词表上每个词回答正确的概率。介绍扇贝是如何实现深度追踪模型并运用到英语学习者词汇水平评估中去。
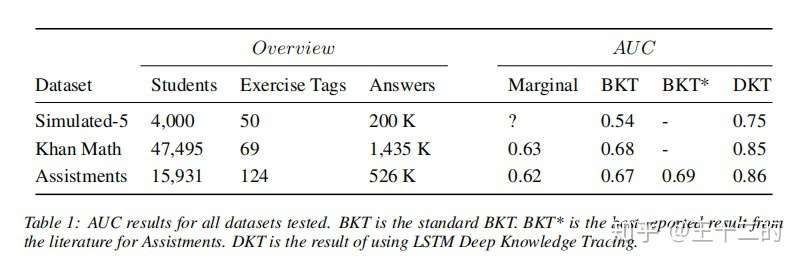
- 总序列数量已经累积到千万级别,这为使用深度学习模型提供了坚实的基础。模型方面,我们选用了斯坦福大学 Piech Chris 等人在 NIPS 2015 发表的 Deep Knowledge Tracing (DKT) 模型 [1],该模型在 Khan Academy Data 上进行了验证,有着比传统 BKT 模型更好的效果。

- 【2018-11-22】67岁AI教父跳槽中国,放弃千亿美金巨头加盟初创公司, 11月16日,全球机器学习教父、人工智能领域顶尖科学家Tom Mitchell教授,正式宣布加入了中国一家教育创业公司——松鼠AI,出任首席人工智能科学家,引起圈里一阵惊叹。Mitchell长期从事机器学习、认知神经学科等研究,全世界最经典应用最广的机器学习教材,就出自他之手。在全球机器学习领域,Mitchell教授是公认的行业“教父”,Machine Learning第一人。
- “我对教育领域一直很感兴趣,我编写过教材,始终认为教育是我职业生涯中的重要一环,我最近开始深度关注AI对教育的应用,因为现在时机比较成熟了。”在最近一场关于AI+教育的主题大会上,Mitchell如是说。
- AI在教育领域应用时机的成熟,很可能意味着这个自古以来的传统行业,也要真正进入到数字化的快车道了。
- 全球范围内,教育行业的核心痛点只有一个,没有之一:缺乏优质的教师资源。
- 据今年8月教育部发布《2017年全国教育事业发展统计公报》显示,全国共有义务教育阶段学校21.89万所,招生3313.78万人,在校生1.45亿人,专任教师949.36万人。而特级教师不到千分之一,这个巨大的差距,使得保证基本教学质量就已经成为一个艰巨的任务,更遑论能够让孩子学习效率得到最大提升的个性化问题了。
- 过去互联网和移动互联网,只是解决了教育行业的“太花钱”的问题,包括录刻式的教育或者是手机APP的教育。所谓录刻,只是把线下的教育搬移到了线上,降低了成本,但也暴露出新的问题:
- 一是完课率非常低
- 二是交互性差,学生学习过程中碰到问题没有人解决和帮助,对学生自主性要求非常高,学习时间无法保证,所以学习效能没有显著提高。
- 而之前流行的在线“一对一”教育的形式,虽然带来个性化学习,但是,这种模式对老师的依赖性非常强,好老师的资源始终有限,他们的精力也有限,当学生数量迅速增加时,优质的老师的比例就会被严重稀释,整体教学质量很难维持,而且也需要巨大的成本支出来维持、甚至争夺优质教师的资源。
- 而事实上,一个特级教师出来授课的课时费,是每小时4000元,收费每小时150到300元的无论线上线下一对一,是不可能找到最优质的师资的,这也是为什么几百万上千万的学区房仍旧被趋之若鹜。
- 正是存在着优质教师资源这个核心的限制条件,这也是为什么教育行业没有出现垄断性的巨头的原因,即使强大如新东方和好未来,发展近20年,市场占有率也仍然不高,无法体现出规模效应。而且,好的老师主要集中一、二线城市,下面的三、四、五线城市就难以找到一个好老师,扩张起来就更加困难。
- 以AI为基础的自适应教育,理论上能够从根本上解决这个问题
- 智适应学习的概念,源于“自适应学习”(adaptive learning),诞生于人工智能时代,自上个世纪七十年代起流行。智适应学习模式,融合了计算机科学、人工智能、心理测量学、教育学、心理学和脑科学等专业领域。简单说来,它主要是使用计算机算法来调节与学习者的互动,并提供定制化的资源和学习活动,以满足每个学习者的独特需求。
- 近两年来,国内几乎所有具备实力的教育机构,已经有50多家都提出了“AI+”的发展目标。“AI+教育”到底可以做什么,场景也逐一清晰,目前已经被几亿家长们体验到的就包括——智能测评、拍照搜题、智能排课、表情识别、语音识别等等。
- 而上述这些方法在整个K12产业的落地还十分有限。来自艾瑞的数据显示,总规模达3万亿的中国教育市场,K12课外辅导总市场规模6000亿,新东方和好未来在其中只占到了2%的份额。如此来看,K12课外辅导行业空间巨大,急需新的、革命性的教学方法。
- 传统的非自适应方法学习模式中,由于学生的学习路径、认知过程、成绩反馈等数据无法得到大规模地追踪,存储和分析,难以实现量身定制个性化的学习模式。
- AI智适应系统也一改过去所有线上线下教育以老师为中心的教学模式,而成为根据学生的用户画像实施千人千面的因材施教,几千年来,学生第一次真正成为主角!
- “人类教师在教学过程中会制定许多决策。我们的研发任务就是模拟老师可能会制定的所有决策,并且通过计算机搜集的学生数据来最终制定决策。”Mitchell告诉钛媒体,教师经常需要选择最佳方式来提高教学质量,他需要快速地明白,不同水平的学生应该学习不同的知识,不同性格的学生目前最需要什么不同的帮助,以及下一步该采取什么行动。
- 智适应在学习中的应用之一:学生在学习过程中如何制定动态的学习目标?90分和60分的孩子的学习目标应该是完全不同的,同样都是60分的孩子,学习能力不同目标也不相同,所以学习路径就应该被不断调整达到精准有效。
- 概念
- 知识地图的概念,这个概念是由ALEKS创造的,这也是个性化教育的一个重要基础。通过知识地图,可以用1/10的题目测出每个孩子哪个知识点会,哪个知识点不会。因为我们传统的中考高考只能测出孩子是八十分或者是六十分的孩子,但是5个80分的孩子,他们每个知识点会和不会的地方其实是完全不一样的。
- 松鼠AI在知识地图的基础上,又提出了错因重构知识地图的理念,“错因”的概念是这样的:如果这个孩子某个知识点没掌握,不一定是知识点的问题,可能是其他的错因,比如说题干的语义理解有问题,也可能是单纯的马虎遗漏,他其实是掌握这个知识点的,所以,如果我们没有把所有的错因抓出来,或者只给孩子训练知识点,其实他已经掌握了,等于又浪费了时间,同时他自己真正错的原因还没有解决,以后遇到类似题目仍旧会做错。
- 栗浩洋举例说,关于一元二次方程,ALEKS拆解为了13个知识点,而松鼠AI团队拆解为了107个;初中英语听力知识点拆分为了8000多个。
解题
【2022-8-8】PNAS最新研究:81%解题率,神经网络 Codex 推开高等数学世界大门
- 论文, 原文链接: 研究团队证明了 OpenAI 的 Codex 模型可以进行程序合成从而解决大规模的数学问题,并通过小样本学习自动解决数据集中 81%的数学课程问题,并且 Codex 在这些任务的表现上达到了人类水平。
这项研究颠覆了人们普遍认为神经网络无法解决高等数学问题的共识。Codex 之所以能做到实现这样的能力,正是因为团队进行了一大创新,过去那些不成功的研究只使用了基于文本的预训练,而此次现身的 Codex 神经网络不仅要基于文本进行预训练,并且还对代码进行了微调。
- 问题数据集选用来自 MIT 的六门数学课程和哥伦比亚大学的一门数学课程,从七门课程中随机抽取 25 个问题:MIT的单变量微积分、多变量微积分、微分方程、概率与统计概论、线性代数和 计算机科学数学和哥伦比亚大学的 COMS3251 计算线性代数。
- 同时,研究团队使用了一个用于评估数学推理的最新高级数学问题基准 MATH,用 MATH 来检测OpenAI Codex 的能力,MATH 从6大数学板块:初级代数,代数,计数和概率,中级代数,数论,和初级微积分中各抽取15个问题。
- Codex 解决了问题数据集和 MATH 数据集中的 265 个问题,其中有 213 个是自动解决的
Transformer 发布后,基于 Transformer 的语言模型在各种自然语言处理 (NLP) 任务,包括在零样本和少样本语言任务中取得了巨大成功。但是因为 Transformer 仅在文本上进行了预训练,所以这些模型基本上不能解决数学问题,GPT-3就是一个典型例子
后来,通过小样本学习(few-shot learning)和思维链 (Chain-of-thought, CoT) 提示,GPT-3 的数学推理能力得到了提高;然而,在没有代码的情况下,即便有小样本学习和 CoT 提示, GPT-3 在大学水平数学问题和 MATH 基准测试中仍然无能为力。
过去关于解数学题的研究,可能在相对简单的数学水平上有一定成绩。举个例子,基于协同训练输出来验证或预测表达式树的技术,比如 MAWPS 和 Math23k,能够以超过 81% 的准确率解决小学级别的数学问题,但是其不能解决高中、奥林匹克数学或大学难度的课程。协同训练与图神经网络 (GNN) 相结合以预测算术表达式树,能够以高达 95% 的准确率解决机器学习中的大学水平问题。但是这项工作也仅限于数字答案,并且产生了过拟合,不能推广到其他课程。
而这项工作的最大创新点之一就是,不仅对Codex 这种Transformer 模型进行了文本上的预训练,还在代码上进行了微调,使得其可以生成大规模解决数学问题的程序。
- 仅对文本进行预训练的语言模型 (GPT-3 text-davinci-002) 仅自动解决了课程问题中的18%和 MATH基准测试问题中的25.5%。
- 使用
零样本学习和对文本进行预训练并在代码上进行微调的神经网络(OpenAI Codex code-davinci-002)合成的程序可以自动解决课程问题中的 71%和 MATH 基准测试问题中的72.2%。 - 使用相同的神经网络 Codex 再加上少样本学习,便可自动解决课程中 81% 的问题和 MATH 基准测试中 81.1% 的问题。
- 而其余模型无法自动解决的 19% 的课程问题和 18.9% 的MATH基准问题,最后通过手动提示解决。
代码实现
【2022-8-30】paperwithcode 里的Deep Knowledge Tracing sota榜单








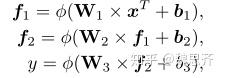
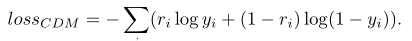


 支付宝打赏
支付宝打赏  微信打赏
微信打赏 
